
New Monetarist Economics*
Abstract:
1 Introduction
The purpose of this essay is to articulate the principles and practice of a school of thought we call New Monetarist Economics. Although there is by now a large body of work in the area, our label is novel, and we feel we should say why we use it. First, New Monetarists find much that is appealing in Old Monetarist economics epitomized by the writings of Milton Friedman, and some of his followers, although we also disagree with their ideas in several important ways. Second, New Monetarism has little in common with New Keynesianism, although this may have as much to do with the way New Keynesians approach monetary economics and the microfoundations of macroeconomics than with their assumptions about sticky prices. Moreover, we think it was a healthy state of affairs when, even in the halcyon days of Old Keynesianism, there was a dissenting view presented by Old Monetarists, at the very least as voice of caution to those who thought macro and monetary economics were "solved" problems.1 We think it would be similarly healthy today if more people recognized that there is an alternative to New Keynesianism. We dub this alternative New Monetarism.
An impression has emerged recently that there is a consensus that New Keynesianism is the most useful approach to analyzing macroeconomic phenomena and guiding monetary policy. The view that there is consensus is surprising to us, as we encounter much sympathy for the position that there are fundamental flaws in the New Keynesian approach. It must then be the case that those of us who do not think New Keynesianism is the only game in town, or who think that approach has issues that need to be discussed, are not speaking with enough force and clarity. In part, this essay is an attempt to rectify this state of affairs and foster more healthy debate. The interaction we envision between New Monetarists and Keynesians is in some ways similar to the debates in the 1960s and 1970s, and in other ways different, of course, since much of the method and language has changed in economics since then. To bring the dialogue to the 21st century, we first need to describe what New Monetarists are doing.
New Monetarism encompasses a body of research on monetary theory and policy, and on banking, financial intermediation, and payments, that has taken place over the last few decades. In monetary economics, this includes the seminal work using overlapping generations models by Lucas (1972) and some of the contributors to the Models of Monetary Economies volume edited by Kareken and Wallace (1980), although antecendents exist, including Samuelson (1956), of course. More recently, much monetary theory has adopted the search and matching approach, an early example of which is Kiyotaki and Wright (1989), although there are also antecendents for this, including Jones (1976). In the economics of banking, intermediation, and payments, which builds on advances in information theory that occurred mainly in the 1970s, examples of what we have in mind include Diamond and Dybvig (1983), Diamond (1984), Williamson (1986,1987), Bernanke and Gertler (1989), and Freeman (1995). Much of this research is abstract and theoretical in nature, but the literature has turned more recently to empirical and policy issues.
In Section 2 we first explain what New Monetarism is not, by describing Keynesianism and Old Monetarism. Then we lay out a set of New Monetarist principles. As a preview, we think New Monetarists agree more or less with the following: 1. Microfoundations matter: productive analysis of macro and monetary economics, including policy discussions, requires adherence to sound and internally consistent economic theory. 2. In the quest to understand monetary phenomena and monetary policy, it is decidedly better to use models that are explicit about the frictions that give rise to a role for money in the first place. 3. In modeling frictions, one has to have an eye for the appropriate level of abstraction and tractability - e.g. the fact that in some overlapping generations models people live two periods, or that in some search models people meet purely at random, may make them unrealistic but does not make them uninteresting. 4. No single model should be an all-purpose vehicle in monetary economics, and the right approach may depend on the question, but at the same time it is desirable to have a class of models, making use of consistent assumptions and similar technical devices, that can be applied to a variety of issues. 5. Financial intermediation is important: while bank liabilities and currency sometimes perform similar roles as media of exchange, for many issues treating them as identical leads one astray.
In Section 3 we review developments in monetary theory over the past two decades that are consistent with these basic principles. We try to say why the models are interesting, and why they were constructed as they were - what lies behind particular assumptions, abstractions and simplifications. In Section 4 we move to more recent models, that are better suited to address certain empirical and policy issues, while at the same time are tractable enough to deliver sharp analytic results. We lay out a benchmark New Monetarist model, based on Lagos and Wright (2005), and show how it can be used to address a range of issues. Again, we try to explain what lies behind the assumptions, and we give some of its basic properties - e.g. money is neutral but not superneutral, the Friedman rule is optimal but may not give the first best, etc. We also show how this benchmark can be extended to address classic issues pertaining to money and capital accumulation and to inflation and unemployment. As one example, we generate a negatively-sloped Phillips curve that is stable in the long run. In our example, anticipated policy can exploit this trade-off, but it turns out it ought not (the Friedman rule is still optimal), illustrating the value of being explicit about micro details.
Much of Sections 3 and 4 is already in the literature; Section 5 presents novel applications. First, we show how the benchmark can be used to formalize Friedman's (1968) views about the short-run Phillips curve, using a signal extraction problem, as in Lucas (1972). This yields some conclusions that are similar to those of Friedman and Lucas, but also some that are different, again showing the importance of micro details. Having shown how the model can be used to think about Old Monetarist ideas, we then use it to illustrate New Keynesian ideas, by introducing sticky prices. This generates policy conclusions similar to those in Clarida et al. (1999) or Woodford (2003), but there are also differences, again illustrating how details matter. Although the examples in this Section rederive known results, in a different context, they also serve to make it clear that other approaches are not inconsistent with our formal model. One should not shy away from New Monetarism even if one believes sticky prices, imperfect information, and related ingredients are critical, as these are easily incorporated into micro-based theories of the exchange process.2
In Section 6, discuss applications related to banking and payments. These extensions contain more novel modeling choices and results, although the substantive issues we address have of course been raised in earlier work. One example incorporates ideas from payments economics similar in spirit to Freeman (1995), but the analysis looks different through the lens of the New Monetarist model. Another example incorporates existing ideas in the theory of banking emulating from Diamond and Dybvig (1983), but again some details look different. In particular, we have genuinely monetary versions of these models, which seems relevant or at least realistic since money has a big role in actual banking and payments systems.3 In Section 7, we present another application, exploring a New Monetarist approach to asset pricing. This approach emphasizes liquidity. and focuses on markets where assets trade can be complicated by various frictions, including private information.
These examples and applications illustrate the power and flexibility of the New Monetarist approach. As we hope the reader will appreciate, although the various models differ with respect to details, they share many features, and build upon consistent principles. This is true for the simplest models of monetary exchange, and the extensions to integrate banking, credit arrangements, payments mechanisms, and asset markets. We think that this is not only interesting in terms of theory, but that there are also lessons to be learned for understanding the current economic situation and shaping future policy. To the extent that the recent crisis has at its roots problems related to banking, to mortgage and other credit arrangements, or to information problems in asset markets, one cannot hope to address the issues without theories that take seriously the exchange process. Although New Keynesians have had some admirable success, not all economic problems are caused by sticky prices. Despite the suggestions of Krugmaniacs, not every answer is hanging on the Old Keynesian cross. Given this, we present our brand of Monetarism as a relevant and viable alternative for both academics and policy makers. What follows is our attempt to elaborate this position.
2 Old and New Perspectives
To understand the basic principles behind our approach, we first need to summarize some popular alternative schools of thought. This will allow us to highlight what is different about New Monetarism, and how it is useful for understanding monetary phenomena and guiding monetary policy.
2.1 Keynesianism
Keynesian economics of course originated with the General Theory in 1936. Keynes's ideas were popularized in Hicks's (1937) IS-LM model, which became enshrined in the undergraduate curriculum, and was integrated into the so-called Neoclassical Synthesis of the 1960s. New Keynesian economics, as surveyed in Clarida et al. (1999) or Woodford (2003), makes use of more sophisticated tools than Old Keynesian economists had at their disposal, but much of the language and many of ideas are essentially the same. New Keynesianism is typically marketed as a synthesis that can be boiled down to an IS relationship, a Phillips curve, and a policy rule determining the nominal interest rate, the output gap, and the inflation rate. It is possible to derive a model featuring these equations from slightly more primitive ingredients, including preferences, but often practitioners do not bother with these details. As a matter of principle, we find this problematic, since reduced-form relations from one model need not hold once one changes the environment, but we don't want to dwell here on such an obvious point.
All New Keynesian models have weak foundations for the assumption at the heart of the theory: prices must be set in nominal terms, and are sticky in the sense that they cannot be changed except at times specified rather arbitrarily, or at a cost. If nominal prices can be indexed to observables -
if e.g. a seller can say "my price ![]() increases one-for-one with aggregate
increases one-for-one with aggregate ![]() ," which
does not seem especially complicated or costly - the main implications of the theory would be overturned. An implication that we find unattractive is this: agents in the model are often not doing as well as they could, in the sense that gains from trade are left on the table when exchanges are
forced at the wrong prices. This is in sharp contrast to some theory, the purest of which is mechanism design, where by construction agents do as well they can subject to constraints imposed by the environment, including technology and also incentives. There can be frictions including private
information, limited commitment, etc. that make doing as well as we can fairly bad, of course. It is silly to regard the outcome as a Panglossian "best of all possible worlds," since the world could be better with fewer constraints, but at least in those theories we are not acting suboptimally
given the environment.4
," which
does not seem especially complicated or costly - the main implications of the theory would be overturned. An implication that we find unattractive is this: agents in the model are often not doing as well as they could, in the sense that gains from trade are left on the table when exchanges are
forced at the wrong prices. This is in sharp contrast to some theory, the purest of which is mechanism design, where by construction agents do as well they can subject to constraints imposed by the environment, including technology and also incentives. There can be frictions including private
information, limited commitment, etc. that make doing as well as we can fairly bad, of course. It is silly to regard the outcome as a Panglossian "best of all possible worlds," since the world could be better with fewer constraints, but at least in those theories we are not acting suboptimally
given the environment.4
Despite these issues, it is commonly argued that the New Keynesian paradigm is consistent with the major revolutionary ideas developed in macroeconomics over the past few decades, such as the Lucas Critique and Real Business Cycle Theory. If we take Woodford (2003) as representing the state of the art, the main tenets of the approach are the following:
- The key friction that gives rise to short-run nonneutralities of money, and the primary concern of monetary policy, is sticky prices. Because some prices are not fully flexible, inflation or deflation induces relative price distortions, and this has consequences for welfare.
- The frictions that we encounter in relatively deep monetary economics, or even not-so-deep monetary economics, like cash-in-advance models, are at best of second-order importance. In monetary theory these frictions include explicit descriptions of specialization that make direct exchange difficult, and information problems that make credit difficult, giving rise to a fundamental role for media of exchange and to different implications for policy.
- There is a short-run Phillips curve trade-off between inflation and output (if not inflation and unemployment, since these theories typically do not have detailed descriptions of the labor market, with a few exceptions, like Gertler and Trigari 2008). Monetary policy can induce a short-run increase in aggregate output with an increase in inflation.
- The central bank is viewed as being able to set a short-term nominal interest rate, and the policy problem is presented as the choice over alternative rules for how this should be done in response to economic conditions.
We also think it is fair to say that New Keynesians tend to be supportive of current practice by central banks. Elements of the modeling approach in Woodford (2003) are specifically designed to match standard operating procedures, and he appears to find little in the behavior of central banks that he does not like. And the feeling seems to be mutual, which may be what people have in mind when they suggest that there is a consensus. Interest in New Keynesianism has become intense recently, especially in policy circles, and some economists (e.g. Goodfriend 2007) profess that New Keynesianism is the default approach to analyzing and evaluating monetary policy.
2.2 Monetarism
Old Monetarist ideas are represented in the writing of Friedman (1960,1968,1969) and Friedman and Schwartz (1963). In the 1960s and 1970s, the approach was viewed as an alternative to Keynesianism with different implications for how policy should be conducted. Friedman put much weight on empirical analysis and the approach was often grounded only informally in theory - even if some of his work, such as the theory of the consumption function in Friedman (1957), is about microfoundations. Although there are few professed monetarists in the profession these days, the school has had a lasting impression in macroeconomics and the practice of central banking.5
The central canons of Old Monetarism include the following:
- Sticky prices, while possibly important in generating short-run nonneutralities, are unimportant for monetary policy.
- Inflation, and inflation uncertainty, generate significant welfare losses.
- The quantity theory of money is an essential building block. There exists a demand function for money which is an empirically stable function of a few variables.
- There may exist a short-run Phillips curve trade-off, but the central bank should not attempt to exploit it. There is no long-run Phillips curve trade-off (although Friedman tempered this position between 1968 and 1977 when he discussed the possibility of an upward-sloping long-run Phillips curve).
- Monetary policy is viewed as a process of determining the supply of money in circulation, and an optimal monetary policy involves minimizing the variability in the growth rate of some monetary aggregate.
- Money is any object that is used as a medium of exchange, and whether these objects are private or government liabilities is irrelevant for the analysis of monetary theory and policy.
Friedman and his followers tended to be critical of contemporary central banking practice, and this tradition was carried on through such institutions as the Federal Reserve Bank of St. Louis and the Shadow Open Market Committee. A lasting influence of monetarism is the notion that low inflation should be a primary goal of policy, which is also a principle stressed by New Keynesian economists. However, Friedman's monetary policy prescription that central banks should adhere to strict targets for the growth of monetary aggregates is typically regarded as a practical failure. Old Monetarism tended to emphasize the long run over the short run: money can be nonneutral in the short run, but exploitation of this by the central bank only makes matters worse (in part due to Friedman's infamous "long and variable lags), and policy should focus on long-run inflation. Monetarists also tended to favor relatively simple models, as compared to the Keynesian econometric tradition. Some but definitely not all of these ideas carry over to New Monetarism.
2.3 New Monetarism
The foundations for New Monetarism can be traced to a conference at the Federal Reserve Bank of Minneapolis in the late 1970s, with the proceedings and some post-conference contributions published in Kareken and Wallace (1980). Important antecedents are Samuelson (1956), which is a legitimate model of money in general equilibrium, and Lucas (1972), which sparked the rational expectations revolution and with it a move toward incorporating serious theory in macroeconomics. Kareken and Wallace (1980) contains a diverse body of work with a common goal of moving the profession toward a deeper understanding of the role of money and the proper conduct of monetary policy. This volume spurred much research using the overlapping generations model of money, much of which was conducted by Wallace and his collaborators during the 1980s. Some findings from that research are the following:
- Because traditional monetarists neglect key elements of economic theory, their prescriptions for policy can go dramatically wrong (Sargent and Wallace 1982).
- The fiscal policy regime is critical for the effects of monetary policy (Sargent and Wallace 1981, Wallace 1981).
- Monetary economics can make good use of received theory in other fields, like finance and public economics (Bryant and Wallace 1979,1984).
A key principle, laid out first in the introduction to Kareken and Wallace (1980), and elaborated in Wallace (1998), is that progress can be made in monetary theory and policy analysis only by modeling monetary arrangements explicitly. In line with the arguments of Lucas (1976), to conduct a policy experiment in an economic model, the model must be invariant to the experiment under consideration. One interpretation is the following: if we are considering experiments involving the operating characteristics of the economy under different monetary policy rules, we need a model in which economic agents hold money not because it enters utility or production functions, in a reduced-form fashion, but because money ameliorates some fundamental frictions. Of course the view that monetary theory should " look frictions in the face" goes back to Hicks (1934). Notice that here we are talking about explicit descriptions of frictions in the exchange process, as opposed to frictions in the price setting process, like the nominal rigidities in Keynesian theory, where money does not help, and indeed is really the cause of the problem.
We now know that there are various ways to explicitly model frictions. Just as Old Monetarists tended to favor models that are simple, so do New Monetarists. One reason is they still like to focus more on long-run issues, such as the cost of steady state inflation, instead of business cycles. This is mainly because they tend to think the long run is more important, from a welfare perspective, but as a by-product it allows them to adopt simpler models (at least compared to many New Keynesian models, e.g. Altig et al. 2007). Overlapping generations models can be simple, although one can also complicate them as one likes. Much research in monetary theory in the last 20 years has been conducted using matching models, rather than overlapping generations models, however. These build more on ideas in search and game theory rather than general equilibrium theory. Early work includes Kiyotaki and Wright (1989,1993), which build on ideas and tools in Jones (1976) and Diamond (1982,1984).6
Matching models prove to be very tractable for many questions in monetary economics, though a key insight that eventually arose from this literature is that spatial separation per se is not the critical friction making money essential. As emphasized by Kocherlakota (1998), with credit due to earlier work by Ostroy (19xx) and Townsend (1987,1989), money is essential because it overcomes a double coincidence of wants problem in the context of limited commitment and imperfect record-keeping. As is well known, by now, perfect record keeping would imply that efficient allocations could be supported through insurance and credit markets, or various other institutions, without monetary exchange. Random bilateral matching among a large number of agents is a convenient way to generate a double coincidence problem, and also to motivate incomplete record keeping, but it is not the only way to proceed, as we discuss below.
New Monetarism is not just about the role of currency in exchange; it attempts to study a host of related institutions. An important departure from Old Monetarism is to take seriously the role of financial intermediaries and their interactions with the central bank. Developments in intermediation and payment theories over the last 25 years are critical to our understanding of credit and banking arrangements. A difference between Old and New Monetarists regarding the role of intermediation is reflected in their respective evaluations of Friedman's (1960) proposal for 100% reserve requirements on transactions deposits. His argument was based on the premise that tight control of the money supply by the central bank was key to controlling the price level. However, since transactions deposits at banks are part of what he means by money, and the money multiplier is subject to randomness, even if we could perfectly control the stock of outside money, inside money would move around unless we impose 100% reserves. Old Monetarists thus viewed 100% reserves as desirable. What this ignores, however, is that banks perform a socially beneficial function in transforming illiquid assets into liquid liabilities (transactions deposits), and 100% reserve requirements inefficiently preclude this activity.
The 1980s saw important developments in the theory of banking and financial intermediation, spurred by earlier developments in information theory. One influential contribution was the model of Diamond and Dybvig (1983), which we now understand to be a useful approach to studying banking as liquidity transformation and insurance (it does however require some auxiliary assumptions to produce anything resembling a banking panic or run; see Ennis and Keister 2008). Other work involved well-diversified intermediaries economizing on monitoring costs, including Diamond (1984) and Williamson (1986). In these models, financial intermediation is an endogenous phenomenon. The resulting intermediaries are well-diversified, process information in some manner, and transform assets in terms of liquidity, maturity or other characteristics. The theory of financial intermediation has also been useful in helping us understand the potential for instability in banking and the financial system (again see Ennis and Keister 2008), and how the structure of intermediation and financial contracting can affect aggregate shocks (Williamson 1987, Bernanke and Gertler 1989).
A relatively new sub-branch of this theory studies the economics of payments. This involves the study of payments systems, particularly among financial institutions, such as Fedwire in the US, where central banks can play an important role. See Freeman (1995) for an early contribution, and Nosal and Rocheteau (2009) for a recent survey. The key insights from this literature are related to the role played by outside money and central bank credit in the clearing and settlement of debt, and the potential for systemic risk as a result of intraday credit. Even while payment systems are working well, this area is important, since the cost of failure is potentially so great given the amount of money processed through such systems each day. New Monetarist economics not only has something to say about these issues, it is almost by definition the only approach that does. How can one hope to understand payments and settlement without modeling the exchange process?
To reiterate some of what was said earlier, New Monetarists more or less agree to and try to abide by the following principles:
- Useful analysis in macro and monetary economics, including policy analysis, requires sound micro economic theory, which involves using what we know from general equilibrium, as well as game theory, search theory, etc.
- Especially important is a clear and internally consistent description of the exchange process, and the means by which money and related institutions facilitate that process, which means the theory must be built on environments with explicit frictions.
- While perhaps no one model can answer all questions, in monetary economics, there are important characteristics that good models share, including internal consistency, tractability, and the right amount of abstraction.
- Relatively simple models are preferred, in part due to relative emphasis of the longer run.
- Rigorous models of financial intermediation are important for monetary theory and policy: credit, banking, and payment systems matter.
We now develop a series of models leading to a useful benchmark framework, after which we present several variations and put them work in different applications.
3 Recent Monetary Theory
The simplest model in the spirit of the principles laid out above is a version of first-generation monetary search theory, long the lines of Kiyotaki and Wright (1993), which is a stripped-down version of Kiyotaki and Wright (1989), and uses methods in early search equilibrium models, especially Diamond (1982). Such a model makes strong assumptions, which will be relaxed later, but even with these assumptions in place the approach captures something of the essence of money as an institution that facilitates exchange. What makes exchange difficult in the first place is the presence of frictions, including a double coincidence problem generated by specialization and random matching, combined with limited commitment and imperfect memory. Frictions like this, or at least informal descriptions thereof, have been discussed in monetary economics since Smith, Jevons, Menger, Hicks, etc. The goal of recent theory is to formalize the ideas, to see which are valid under what assumptions, and to develop new insights.7
3.1 The Simplest Model
Time is discrete and continues forever. There is a ![]() continuum of infinite-lived agents. To make the exchange process interesting, these agents specialize in production and consumption
of differentiated commodities and trade bilaterally. It is a venerable idea that specialization is intimately related to monetary exchange, so we want this in the environment. Although there are many ways to set this up, we simply assume the following: There is a set of goods, that for now are
indivisible and nonstorable. Each agent produces at cost
continuum of infinite-lived agents. To make the exchange process interesting, these agents specialize in production and consumption
of differentiated commodities and trade bilaterally. It is a venerable idea that specialization is intimately related to monetary exchange, so we want this in the environment. Although there are many ways to set this up, we simply assume the following: There is a set of goods, that for now are
indivisible and nonstorable. Each agent produces at cost ![]() goods in some subset, and derives utility
goods in some subset, and derives utility ![]() from consuming goods in a different subset. It is formally equivalent, but for some applications it helps the discussion, to consider a pure exchange scenario. Thus, if each agent is endowed with a good each period that he can consume for utility
from consuming goods in a different subset. It is formally equivalent, but for some applications it helps the discussion, to consider a pure exchange scenario. Thus, if each agent is endowed with a good each period that he can consume for utility ![]() , but he may meet someone with another good that gives him utility
, but he may meet someone with another good that gives him utility ![]() , the analysis is basically
the same, but
, the analysis is basically
the same, but ![]() is interpreted as an opportunity rather than a production cost.
is interpreted as an opportunity rather than a production cost.
Let ![]() be the probability of meeting someone each period. There are different types of potential trade meetings. Let
be the probability of meeting someone each period. There are different types of potential trade meetings. Let ![]() be the probability that you like what your partner can produce but not vice versa - a single coincidence meeting - and
be the probability that you like what your partner can produce but not vice versa - a single coincidence meeting - and ![]() the
probability that you like what he can produce and vice versa - a double coincidence meeting.8 The environment is symmetric, and for the representative agent,
the efficient allocation clearly involves producing whenever someone in a meeting likes what his partner can produce. Let
the
probability that you like what he can produce and vice versa - a double coincidence meeting.8 The environment is symmetric, and for the representative agent,
the efficient allocation clearly involves producing whenever someone in a meeting likes what his partner can produce. Let ![]() be the payoff from this cooperative allocation, described
recursively by
be the payoff from this cooperative allocation, described
recursively by
If agents could commit, ex ante, they would all agree to execute the efficient allocation. If they cannot commit, we have to worry about ex post incentive conditions.
The binding condition is that to get agents to produce in single-coincidence meetings, as opposed to simply walking away, we require
![]() , where
, where ![]() is the deviation payoff, depending on what
punishments we have at our disposal. Suppose we can punish a deviator by allowing him in the future to only trade in double-coincidence meetings. It is interesting to consider other assumptions about feasible punishments, but this one has a nice interpretation in terms of what a mechanism designer
can see and do. We might like e.g. to trigger to autarky - no trade at all - after a deviation, but it is not so obvious we can enforce this in double-coincidence meetings. Having trade only in double-coincidence meetings - a pure barter system - is self enforcing (it is an equilibrium), with
payoff
is the deviation payoff, depending on what
punishments we have at our disposal. Suppose we can punish a deviator by allowing him in the future to only trade in double-coincidence meetings. It is interesting to consider other assumptions about feasible punishments, but this one has a nice interpretation in terms of what a mechanism designer
can see and do. We might like e.g. to trigger to autarky - no trade at all - after a deviation, but it is not so obvious we can enforce this in double-coincidence meetings. Having trade only in double-coincidence meetings - a pure barter system - is self enforcing (it is an equilibrium), with
payoff
![]() . If we take
. If we take
![]() , algebra reduces the relevant incentive condition to
, algebra reduces the relevant incentive condition to
If every potential trade meeting involves a double-coincidence, i.e. if ![]() , then pure barter suffices to achieve efficiency and there is no incentive problem. But with
, then pure barter suffices to achieve efficiency and there is no incentive problem. But with ![]() , given imperfect commitment, (1) tells us that we can achieve efficiency iff production is not too expensive (
, given imperfect commitment, (1) tells us that we can achieve efficiency iff production is not too expensive (![]() is small), search and specialization frictions are not too severe (
is small), search and specialization frictions are not too severe (![]() and
and ![]() are big), etc. If (1) holds, one can interpret exchange as a credit system, as discussed in Williamson and Sanchez (2009), but there is no role for money. A fundamental result in Kocherlakota (1998) is that money is not
essential - i.e. it does nothing to expand the set of incentive-feasible allocations - when we can use trigger strategies as described above. Obviously this requires that deviations can be observed and recalled. Lack of perfect monitoring or record keeping, often referred to as incomplete memory,
is necessary for money to be essential. There are several way to formalize this. Given a large number of agents that match randomly, suppose that they observe only what happens in their own meetings, not other meetings. Then, if an agent deviates, the probability someone he meets later will know it
is 0.9 Hence, no one ever produces in single-coincidence meetings.
are big), etc. If (1) holds, one can interpret exchange as a credit system, as discussed in Williamson and Sanchez (2009), but there is no role for money. A fundamental result in Kocherlakota (1998) is that money is not
essential - i.e. it does nothing to expand the set of incentive-feasible allocations - when we can use trigger strategies as described above. Obviously this requires that deviations can be observed and recalled. Lack of perfect monitoring or record keeping, often referred to as incomplete memory,
is necessary for money to be essential. There are several way to formalize this. Given a large number of agents that match randomly, suppose that they observe only what happens in their own meetings, not other meetings. Then, if an agent deviates, the probability someone he meets later will know it
is 0.9 Hence, no one ever produces in single-coincidence meetings.
In this case, we are left with only direct barter, unless we introduce money. Although we soon generalize this, for now, to make the point starkly, assume that are ![]() units of some
object that agents can store in units
units of some
object that agents can store in units
![]() . This object is worthless in consumption and does not aid in production; so if it is used as a medium of exchange, it is by definition fiat money (Wallace 1980). Let
. This object is worthless in consumption and does not aid in production; so if it is used as a medium of exchange, it is by definition fiat money (Wallace 1980). Let ![]() be the payoff to an agent with
be the payoff to an agent with
![]() . Then
. Then
since someone without money can still barter in double-coincidence meetings, and now has another option: if he meets someone with money who likes his good but cannot produce anything he likes, he could trade for cash, and
since an agent with money can still barter, and now he can also make a cash offer in single-coincidence meetings, which is accepted with probability
The best response condition gives the maximizing choice of ![]() , taking
, taking ![]() as
given, and Nash equilibrium is a fixed point. More completely, equilibrium is a list
as
given, and Nash equilibrium is a fixed point. More completely, equilibrium is a list
![]() satisfying (2)-(3) and the best response condition. Obviously
satisfying (2)-(3) and the best response condition. Obviously ![]() is always an equilibrium, and
is always an equilibrium, and ![]() is an equilibrium iff
is an equilibrium iff
The model is obviously rudimentary, but it captures the idea that money can be a socially beneficial institution that helps facilitate exchange. This contrasts with cash-in-advance models, where money is a hindrance to trade - or worse, sticky-price models, where money plays no role except that
we are forced to quote prices in dollars and not allowed to change them easily. Contrary to standard asset-pricing theory, there are natural equilibria where an intrinsically worthless object can be valued as a medium of exchange, or for its liquidity. Such equilibria
have good welfare properties, relative to pure barter, even if they may not achieve the first best. The fact that ![]() is always an equilibrium points to the tenuousness of fiat money (Wallace 1980). Yet it is also robust, in that equilibrium with
is always an equilibrium points to the tenuousness of fiat money (Wallace 1980). Yet it is also robust, in that equilibrium with ![]() survives even if we endow the fiat object with some
bad characteristics, like a transaction or storage cost, or if we tax it. Many of these and other predictions of the model ring true.11
survives even if we endow the fiat object with some
bad characteristics, like a transaction or storage cost, or if we tax it. Many of these and other predictions of the model ring true.11
3.2 Prices
Prices were fixed up to now, since every trade was a one-for-one swap. Beginning the next generation of papers in this literature, Shi (1995) and Trejos-Wright (1995) endogenize prices by allowing divisible goods while maintaining the assumption
![]() . Let
. Let ![]() denote the output given by the producer to the consumer in
exchange for currency. Preferences are given by
denote the output given by the producer to the consumer in
exchange for currency. Preferences are given by ![]() and
and ![]() , where
, where
![]() ,
,
![]() ,
,
![]() ,
,
![]() , and
, and
![]() . For future reference, let
. For future reference, let ![]() solve
solve
![]() . It is easy to show the efficient outcome involves an agent producing
. It is easy to show the efficient outcome involves an agent producing ![]() in every meeting where his partner likes his good. To facilitate the presentation, for now we set
in every meeting where his partner likes his good. To facilitate the presentation, for now we set ![]() , so that all trade meetings are
single-coincidence meetings and there is no direct barter; we return to
, so that all trade meetings are
single-coincidence meetings and there is no direct barter; we return to ![]() below. Also, we focus on equilibria where money is accepted with probability
below. Also, we focus on equilibria where money is accepted with probability ![]() .
.
To determine ![]() , consider the generalized Nash bargaining solution, with the bargaining power of the consumer given by
, consider the generalized Nash bargaining solution, with the bargaining power of the consumer given by ![]() and threat points given by continuation values.12 Thus,
and threat points given by continuation values.12 Thus, ![]() solves:
solves:
A stationary equilibrium is a list
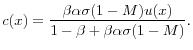
In the symmetric case
![]() and
and ![]() , one can show that in any equilibrium
, one can show that in any equilibrium
![]() , so that monetary exchange cannot achieve the efficient allocation. However,
, so that monetary exchange cannot achieve the efficient allocation. However,
![]() as
as
![]() . To understand this, consider an Arrow-Debreu version of the environment, which means the same preferences and technology but no frictions. In that economy, given agents can
turn their production into instantaneous consumption through the market, it can easily be seen that they choose
. To understand this, consider an Arrow-Debreu version of the environment, which means the same preferences and technology but no frictions. In that economy, given agents can
turn their production into instantaneous consumption through the market, it can easily be seen that they choose
![]() . But in our economy, with frictions, they must turn production into cash, which can only be used in future single-coincidence meetings with someone in need of money. Thus, as long
as
. But in our economy, with frictions, they must turn production into cash, which can only be used in future single-coincidence meetings with someone in need of money. Thus, as long
as ![]() , our agents are willing to produce less than they would in a frictionless model. Now, one can get
, our agents are willing to produce less than they would in a frictionless model. Now, one can get ![]() to increase, by raising
to increase, by raising ![]() e.g., and for big enough
e.g., and for big enough ![]() we sometimes have
we sometimes have
![]() . Still, the model illustrates clearly how frictions and discounting drive a wedge between the return on currency and the marginal rate of substitution, affecting the price
level and allocation, as will come up again below.13
. Still, the model illustrates clearly how frictions and discounting drive a wedge between the return on currency and the marginal rate of substitution, affecting the price
level and allocation, as will come up again below.13
3.3 Distributions
We now relax the restriction
![]() . There are various approaches, but here we use the one in Molico (2006), which allows
. There are various approaches, but here we use the one in Molico (2006), which allows
![]() . This means that we have to deal with the endogenous distribution of money across agents,
. This means that we have to deal with the endogenous distribution of money across agents, ![]() , while previously this was trivial, since
, while previously this was trivial, since ![]() agents had
agents had ![]() and
and ![]() had
had ![]() . Now, in a single-coincidence meeting where the
consumer has
. Now, in a single-coincidence meeting where the
consumer has ![]() and the producer has
and the producer has ![]() , let
, let
![]() be the amount of output and
be the amount of output and
![]() money traded. Again setting
money traded. Again setting ![]() , for expositional purposes, the
generalization of (2)-(3) is
, for expositional purposes, the
generalization of (2)-(3) is
The first term is the expected value of buying from a producer with
In this model, we can easily add injections of new currency, say by lump sum or proportional transfers, which was not so easy with
![]() . With lump sum transfers, e.g. we simply change
. With lump sum transfers, e.g. we simply change ![]() on the RHS to
on the RHS to
![]() , where
, where ![]() is the aggregate money supply, governed by
is the aggregate money supply, governed by
![]() . This greatly extends the class of policies that can be analyzed, but for now we keep
. This greatly extends the class of policies that can be analyzed, but for now we keep
![]() fixed. Then a stationary equilibrium is a list of functions
fixed. Then a stationary equilibrium is a list of functions
![]() such that: given
such that: given
![]() ,
,
![]() and
and ![]() ,
, ![]() solves (5); given
solves (5); given ![]() ,
,
![]() and
and
![]() are determined by some bargaining solution, such as
are determined by some bargaining solution, such as
where the maximization is s.t.
This model is unfortunately hard to handle. Not much can be said about equilibrium analytically, and it is even hard to solve numerically. Rather than go into computational details, we offer the following intuition. Typical heterogeneous-agent, incomplete-market, macro models of the sort
analyzed by Hugget (1993) or Krusell and Smith (1998) also have an endogenous distribution as a state variable, but the agents in those models do not care about this distribution per se. They only care about market prices. Of course prices depend on the distribution, but one can typically
characterize accurately prices as functions of a small number of moments. In a search model, agents care about ![]() directly, since they are trading with each other and not just against their
budget equations. Still, Molico computes the model, and uses it to discuss several interesting issues, including a welfare-enhancing effect of inflation achieved through lump sum transfers that serve as partial insurance, but we do not have space to get into these results.15
directly, since they are trading with each other and not just against their
budget equations. Still, Molico computes the model, and uses it to discuss several interesting issues, including a welfare-enhancing effect of inflation achieved through lump sum transfers that serve as partial insurance, but we do not have space to get into these results.15
4 More Recent Monetary Theory
Some models use devices that allow one to avoid having to track the distribution of money. There are two main approaches. The first, dating back to Shi (1997), uses the assumption of large households to render the money distribution degenerate. Thus, each decision making unit consists of many
members who search randomly, as in the above models, but at the end of each trading round they return to the homestead where they share the money they bring back (and sometimes also consumption). Loosely speaking, by the large of large numbers, each household starts the next trading round with the
same ![]() . The large household is a natural extension for random-matching models of the "worker-shopper pair" discussed in the cash-in-advance literature (Lucas 1980). Several useful papers
use this environment, many of which are cited in Shi (2006). We will, however, instead focus on the model in Lagos and Wright (2005), which uses markets instead of large families.
. The large household is a natural extension for random-matching models of the "worker-shopper pair" discussed in the cash-in-advance literature (Lucas 1980). Several useful papers
use this environment, many of which are cited in Shi (2006). We will, however, instead focus on the model in Lagos and Wright (2005), which uses markets instead of large families.
One reason to use the Lagos-Wright model is that it allows us to address a variety of issues, in addition to rendering the distribution of money tractable without extreme assumptions like
![]() . In particular, it also serves to reduce the gap between monetary theory with some claim to microfoundations and standard macro. As Azariadis (1993) put it, "Capturing the
transactions motive for holding money balances in a compact and logically appealing manner has turned out to be an enormously complicated task. Logically coherent models such as those proposed by Diamond (1982) and Kiyotaki and Wright (1989) tend to be so removed from neoclassical growth theory as
to seriously hinder the job of integrating rigorous monetary theory with the rest of macroeconomics." And as Kiyotaki and Moore (2001) put it, "The matching models are without doubt ingenious and beautiful. But it is quite hard to integrate them with the rest of macroeconomic theory - not least
because they jettison the basic tool of our trade, competitive markets."
. In particular, it also serves to reduce the gap between monetary theory with some claim to microfoundations and standard macro. As Azariadis (1993) put it, "Capturing the
transactions motive for holding money balances in a compact and logically appealing manner has turned out to be an enormously complicated task. Logically coherent models such as those proposed by Diamond (1982) and Kiyotaki and Wright (1989) tend to be so removed from neoclassical growth theory as
to seriously hinder the job of integrating rigorous monetary theory with the rest of macroeconomics." And as Kiyotaki and Moore (2001) put it, "The matching models are without doubt ingenious and beautiful. But it is quite hard to integrate them with the rest of macroeconomic theory - not least
because they jettison the basic tool of our trade, competitive markets."
The idea in Lagos and Wright (2005) is to bring the jettisoned markets back on board in a way that maintains an essential role for money and makes the model closer to mainstream macro. At the same time, rather than complicating matters, integrating some competitive markets with some search markets actually makes the analysis much easier. We also believe that this is a realistic way to think about economic activity. Clearly, in reality, there is some activity in our economic lives that is relatively centralized - it is fairly easy to trade, credit is available, we take prices as given, etc. - which can be well captured by the notion of a competitive market. But there is also much activity that is relatively decentralized - it is not easy to find trading partners, it can be hard to get credit, etc. - as captured by search theory. Of course, one might imagine that there are various ways to integrate search and competitive markets. Here we present one.
4.1 A Benchmark Model
Each period, suppose agents spend one subperiod in a frictionless centralized market CM, as in standard general equilibrium theory, and one in a decentralized market DM with frictions as in the search models discussed above. Sometimes the setup is described by saying the CM convenes during the
day and the DM at night; this story is not important for the theory, and we only use it when it helps keep the timing straight, e.g. in modeling payments systems.16 There is one consumption good ![]() in the CM and another
in the CM and another ![]() in the DM, but it is easy to have
in the DM, but it is easy to have ![]() come in many varieties, or to interpret
come in many varieties, or to interpret ![]() as a vector as in standard GE theory (Rocheteau et al. 2008). For now
as a vector as in standard GE theory (Rocheteau et al. 2008). For now ![]() and
and ![]() are produced one-for-one using labor
are produced one-for-one using labor ![]() and
and ![]() , so the real wage
is
, so the real wage
is ![]() . Preferences are separable over time, and across a period encompassing one CM and DM, described by
. Preferences are separable over time, and across a period encompassing one CM and DM, described by
![]() . What is important for tractability, although not for the theory, in general, is quasi-linearity:
. What is important for tractability, although not for the theory, in general, is quasi-linearity:
![]() should be linear in either
should be linear in either ![]() or
or ![]() . With general preferences, the model requires numerical methods, as in Chiu and Molico (2007); with quasi-linearity, we can derive interesting results analytically.17
. With general preferences, the model requires numerical methods, as in Chiu and Molico (2007); with quasi-linearity, we can derive interesting results analytically.17
For now we actually assume
In the DM, the value function ![]() would be described exactly by (5) in the last section, except for one thing: wherever
would be described exactly by (5) in the last section, except for one thing: wherever
![]() appears on the RHS, replace it with
appears on the RHS, replace it with ![]() , since before going
to the next DM agents now get to visit the CM, where
, since before going
to the next DM agents now get to visit the CM, where ![]() denotes the payoff. In particular,
denotes the payoff. In particular,
| st |
where
Based on this last result, we should expect, and we would be right, a degenerate
![]() - i.e. everyone takes the same
- i.e. everyone takes the same ![]() out of the CM, regardless of
the
out of the CM, regardless of
the ![]() they brought in.19 Using this plus
they brought in.19 Using this plus
![]() , and replacing
, and replacing
![]() with
with ![]() , (5) simplifies rather
dramatically to
, (5) simplifies rather
dramatically to
Effectively, with quasi-linearity, the CM is a settlement subperiod where agents reset their liquidity positions. Without this feature, the analysis is interesting but a lot more difficult, and we think it is nice to have a benchmark model that is tractable. By analogy, while models with heterogeneous agents and incomplete markets are obviously interesting, it is nice to have the basic neoclassical growth theory with complete markets and homogeneous agents as a benchmark. Since serious monetary theory with complete markets and homogeneous agents is a non-starter, we need to find another benchmark. The DM-CM model with quasi-linearity is a candidate.
But this is not all we get in terms of tractability. Replacing
![]() with
with ![]() and using
and using
![]() , the bargaining solution (6) reduces to20
, the bargaining solution (6) reduces to20
This expression may look complicated but it is very easy to use, and simplifies a lot in some special cases - e.g.
We have established
![]() and
and
![]() depends on
depends on ![]() but not
but not ![]() . Differentiating (7), we now get
. Differentiating (7), we now get
The marginal benefit of DM money is the value of carrying it into the next CM with probability
An equilibrium can be defined as a list including ![]() ,
, ![]() ,
,
![]() , and so on, satisfying the obvious conditions (see Lagos-Wright), but (10) reduces all this to a simple difference equation determining paths for
, and so on, satisfying the obvious conditions (see Lagos-Wright), but (10) reduces all this to a simple difference equation determining paths for ![]() , given a path for
, given a path for ![]() . Here we focus on steady states, where
. Here we focus on steady states, where ![]() and
and ![]() are constant.21 For this to make sense, we impose
are constant.21 For this to make sense, we impose
![]() with
with ![]() constant. Of course, one has to also consider the
consolidated monetary-fiscal budget constraint
constant. Of course, one has to also consider the
consolidated monetary-fiscal budget constraint
![]() , where
, where ![]() is government consumption (in the CM). But notice that it
does not matter for (10) whether changes in
is government consumption (in the CM). But notice that it
does not matter for (10) whether changes in ![]() are offset by changing
are offset by changing ![]() or
or ![]() . Individuals would of course prefer lower taxes, given
. Individuals would of course prefer lower taxes, given ![]() does not enter utility, but this does not affect their decisions about real balances or consumption in our quasi-linear model. We actually do not have to specify how money transfers are accomplished for the purpose of describing equilibrium
does not enter utility, but this does not affect their decisions about real balances or consumption in our quasi-linear model. We actually do not have to specify how money transfers are accomplished for the purpose of describing equilibrium ![]() and
and ![]() .
.
In steady state, (10) simplifies to
![]() , which yields
, which yields ![]() as a function of the money
growth (equals inflation) rate
as a function of the money
growth (equals inflation) rate ![]() . Or, if we price real and nominal bonds between two meetings of the CM, assuming these bonds cannot be traded in the DM, maybe because they are merely book
entries that cannot be transfered, we can get the nominal and real interest rates
. Or, if we price real and nominal bonds between two meetings of the CM, assuming these bonds cannot be traded in the DM, maybe because they are merely book
entries that cannot be transfered, we can get the nominal and real interest rates
![]() and
and
![]() and rewrite the steady state condition as
and rewrite the steady state condition as
This equates the marginal benefit of liquidity to its cost, the nominal rate. It is equivalent for policy makers here to set either money growth, inflation, or the nominal rate. Obviously the initial stock
In what follows we assume ![]() , although we do consider the limit as
, although we do consider the limit as
![]() (it is not possible to have
(it is not possible to have ![]() in equilibrium). Existence of a
a monetary steady state, i.e. an
in equilibrium). Existence of a
a monetary steady state, i.e. an ![]() such that
such that ![]() , is straightforward
given standard assumptions like
, is straightforward
given standard assumptions like
![]() . Uniqueness is more complicated because
. Uniqueness is more complicated because ![]() is not
generally monotone, except under strong assumptions, like
is not
generally monotone, except under strong assumptions, like
![]() , or decreasing absolute risk aversion. But Wright (2009) establishes that there is a unique monetary steady state even if
, or decreasing absolute risk aversion. But Wright (2009) establishes that there is a unique monetary steady state even if ![]() is not monotone. Given this, DM output
is not monotone. Given this, DM output ![]() is unambiguously decreasing in
is unambiguously decreasing in ![]() , as is total output, since CM
, as is total output, since CM
![]() is independent of
is independent of ![]() .22 For a given policy, one can also show
.22 For a given policy, one can also show ![]() is increasing in consumer bargaining power
is increasing in consumer bargaining power
![]() , the single-coincidence probability
, the single-coincidence probability
![]() , etc. One can also show
, etc. One can also show
![]() for all
for all ![]() , for any
, for any ![]() . In fact,
. In fact,
![]() only in the limit when
only in the limit when ![]() and we set
and we set ![]() . The former condition,
. The former condition, ![]() , is the Friedman rule, and is standard. The latter,
, is the Friedman rule, and is standard. The latter, ![]() , is a version of the Hosios (1990) condition describing how to efficiently split the surplus, and this does not appear in theories that do not have bargaining.
, is a version of the Hosios (1990) condition describing how to efficiently split the surplus, and this does not appear in theories that do not have bargaining.
To understand this, note that in general there is a holdup problem in money demand, analogous to the usual problem with ex ante investments and ex post negotiations. Agents make an investment here when they acquire cash, which pays off in single-coincidence meetings since it allows trade to
occur. But if ![]() producers capture some of the gains from trade, leading agents to under invest. The Hosios condition tells us that investment is efficient when the bargaining
solution delivers a payoff to the investor commensurate with his contribution to the total surplus, which in this case means
producers capture some of the gains from trade, leading agents to under invest. The Hosios condition tells us that investment is efficient when the bargaining
solution delivers a payoff to the investor commensurate with his contribution to the total surplus, which in this case means ![]() . This is not merely a theoretical detail. In calibrated
versions of the model, the welfare cost of inflation is an order of magnitude bigger than found in the reduced-form models (e.g. Cooley and Hansen 1989 or Lucas 2000), leading New Monetarists to rethink some traditional some policy conclusions. As there is not space to present these results in
detail, we refer readers to Craig and Rocheteau (2008) for a survey.
. This is not merely a theoretical detail. In calibrated
versions of the model, the welfare cost of inflation is an order of magnitude bigger than found in the reduced-form models (e.g. Cooley and Hansen 1989 or Lucas 2000), leading New Monetarists to rethink some traditional some policy conclusions. As there is not space to present these results in
detail, we refer readers to Craig and Rocheteau (2008) for a survey.
4.2 Money and Capital
Because of worries mentioned above about this kind of theory being "so removed" from mainstream macro, we sketch an extension to include capital as in Aruoba et al. (2009). In this version, capital ![]() is used as a factor of production in both markets, but is does not compete with
is used as a factor of production in both markets, but is does not compete with ![]() as media of exchange in the DM. To motivate this, it is easy enough to assume
as media of exchange in the DM. To motivate this, it is easy enough to assume ![]() is not portable, making it hard to trade directly in the DM, but of course this does not explain why claims to capital cannot circulate. On the one hand, this is no different from the result that
agents cannot pay in the DM using claims to future endowment or labor income: this can be precluded by imperfect commitment and monitoring. On the other hand, if there is trade in capital in the CM, one can imagine agents exchanging certified claims on it that might also circulate in the DM. One
approach is to introduce informational frictions, so that claims to
is not portable, making it hard to trade directly in the DM, but of course this does not explain why claims to capital cannot circulate. On the one hand, this is no different from the result that
agents cannot pay in the DM using claims to future endowment or labor income: this can be precluded by imperfect commitment and monitoring. On the other hand, if there is trade in capital in the CM, one can imagine agents exchanging certified claims on it that might also circulate in the DM. One
approach is to introduce informational frictions, so that claims to ![]() are difficult to recognize (perhaps they can be counterfeited) in the DM even if they can be verified in the CM; we
defer a detailed analysis of this idea until later.23
are difficult to recognize (perhaps they can be counterfeited) in the DM even if they can be verified in the CM; we
defer a detailed analysis of this idea until later.23
The CM technology produces output ![]() that can be allocated to consumption
that can be allocated to consumption ![]() or investment; the DM technology is represented by a cost function
or investment; the DM technology is represented by a cost function ![]() that gives an agent's disutility of producing
that gives an agent's disutility of producing ![]() when he has
when he has ![]() , where lower (upper) case denotes individual (aggregate) capital. The CM problem is
, where lower (upper) case denotes individual (aggregate) capital. The CM problem is
| (12) | ||
| st |
where
Generalizing what we found in the baseline model,
In the DM, instead of assuming that agents may be consumers or producers depending on who they meet, Aruoba et al. proceed as follows. After the CM closes, agents draw preference and technology shocks determining whether they can consume or produce, with ![]() denoting the probability of being a consumer and of being a producer. Then the DM opens and consumers and producers are matched bilaterally. This story helps motivate why capital cannot be used for DM payments: one can
say that it is fixed in place physically, and consumers have to travel without their capital to producers' locations to trade. Thus, producers can use their capital as an input in the DM but consumers cannot use their capital as payment. In any case, with preference and technology shocks, the
equations actually look exactly the the same as what we had with random matching and specialization, except
denoting the probability of being a consumer and of being a producer. Then the DM opens and consumers and producers are matched bilaterally. This story helps motivate why capital cannot be used for DM payments: one can
say that it is fixed in place physically, and consumers have to travel without their capital to producers' locations to trade. Thus, producers can use their capital as an input in the DM but consumers cannot use their capital as payment. In any case, with preference and technology shocks, the
equations actually look exactly the the same as what we had with random matching and specialization, except ![]() replaces
replaces
![]() .
.
One can again show ![]() , so the Nash bargaining outcome depends on the consumer's
, so the Nash bargaining outcome depends on the consumer's ![]() but not the producer's
but not the producer's ![]() , and on the producer's
, and on the producer's ![]() but not the
consumer's
but not the
consumer's ![]() . Abusing notation slightly,
. Abusing notation slightly, ![]() solves
solves
![]() , where
, where
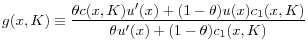
![\displaystyle =W(m,k)+\gamma\left\{ u\left[ x(m,K)\right] -\frac{\phi m}{w\left( 1-t_{h}\right) }\right\}](img192.gif) |
||
![\displaystyle +\gamma\left\{ \frac{\phi M}{w\left( 1-t_{h}\right) }-c\left[ x(M,k),k\right] \right\} .](img193.gif) |
Inserting
Finally, we have the resource constraint
Equilibrium is defined as (positive, bounded) paths for
![]() satisfying (14)-(17), given monetary and fiscal policy, plus an initial condition
satisfying (14)-(17), given monetary and fiscal policy, plus an initial condition ![]() . As a special case, in nonmonetary equilibrium we have
. As a special case, in nonmonetary equilibrium we have ![]() while
while ![]() solves the system ignoring (15) and setting the last term in (16) to 0. These are exactly the equilibrium conditions for
solves the system ignoring (15) and setting the last term in (16) to 0. These are exactly the equilibrium conditions for ![]() in the standard (nonmonetary) growth model described in e.g. Hansen (1986).24 In monetary
equilibria, we get sometime even more interesting. The last term in (16) generally captures the idea that if a producer buys an extra unit of capital in the CM, his marginal cost is lower in the DM for a given
in the standard (nonmonetary) growth model described in e.g. Hansen (1986).24 In monetary
equilibria, we get sometime even more interesting. The last term in (16) generally captures the idea that if a producer buys an extra unit of capital in the CM, his marginal cost is lower in the DM for a given ![]() , but
, but ![]() increases as an outcome of bargaining. This is a holdup problem on investment, parallel to the one on money demand discussed above. With
a double holdup problem there is no value of
increases as an outcome of bargaining. This is a holdup problem on investment, parallel to the one on money demand discussed above. With
a double holdup problem there is no value of ![]() that delivers efficiency, which has implications for the model's empirical performance and welfare predictions.25
that delivers efficiency, which has implications for the model's empirical performance and welfare predictions.25
Aruoba et al. (2009) compare calibrated versions of the model with versions that assume price taking instead of bargaining. Interestingly, the price-taking version generates a much bigger effect of monetary policy on investment, basically because in the bargaining version ![]() is relatively low and unresponsive to what happens in the DM due to the holdup problems. In some versions, the effect of inflation on investment is quite sizable compared to what has been found in
earlier work using short cuts like cash-in-advance specifications (e.g. Cooley and Hansen 1989). One can also study the interaction between fiscal and monetary policy. We cannot get into the quantitative results in detail here, but we do want to emphasize that it is not so hard to integrate modern
monetary theory, with explicit references to search, bargaining, information, commitment, etc., and mainstream macro, with capital, neoclassical production functions, fiscal policy, etc.
is relatively low and unresponsive to what happens in the DM due to the holdup problems. In some versions, the effect of inflation on investment is quite sizable compared to what has been found in
earlier work using short cuts like cash-in-advance specifications (e.g. Cooley and Hansen 1989). One can also study the interaction between fiscal and monetary policy. We cannot get into the quantitative results in detail here, but we do want to emphasize that it is not so hard to integrate modern
monetary theory, with explicit references to search, bargaining, information, commitment, etc., and mainstream macro, with capital, neoclassical production functions, fiscal policy, etc.
4.3 The Long-Run Phillips Curve
In the baseline model, we saw that DM output ![]() is decreasing in
is decreasing in ![]() , and CM output
, and CM output
![]() is independent of
is independent of ![]() . Hence total output and therefore total employment
goes down with inflation. This seems to be a reasonable prediction for long-run (steady state) effects, whatever may be the case in the short-run. If we think of the Phillips curve broadly as the relation between inflation and output/employment, this theory predicts it is not vertical, and in fact
inflation reduces output. But here we want to take the Phillips curve more literally and model more carefully the relation between inflation and unemployment. We do several things to make this rigorous. First, we explicitly introduce another friction to generate unemployment in the CM. Second, we
re-cast the DM as a pure exchange market, so that employment and unemployment are determined exclusively in the CM. Third, we allow nonseparable utility, so that CM output and employment are not independent of monetary policy.
. Hence total output and therefore total employment
goes down with inflation. This seems to be a reasonable prediction for long-run (steady state) effects, whatever may be the case in the short-run. If we think of the Phillips curve broadly as the relation between inflation and output/employment, this theory predicts it is not vertical, and in fact
inflation reduces output. But here we want to take the Phillips curve more literally and model more carefully the relation between inflation and unemployment. We do several things to make this rigorous. First, we explicitly introduce another friction to generate unemployment in the CM. Second, we
re-cast the DM as a pure exchange market, so that employment and unemployment are determined exclusively in the CM. Third, we allow nonseparable utility, so that CM output and employment are not independent of monetary policy.
A principle explicated in Friedman (1968) is that, while there may exist a Phillips curve trade-off between inflation and unemployment in the short run, there is no trade-off in the long run. The natural rate of unemployment is defined as "the level that would be ground out by the Walrasian system of general equilibrium equations, provided there is embedded in them the actual structural characteristics of the labor and product markets" (although, as Lucas 1980 notes, Friedman was "not able to put such a system down on paper"). Friedman (1968) said monetary policy cannot engineer deviations from the natural rate in the long run. However, he tempered this view in Friedman (1977) where he said "There is a natural rate of unemployment at any time determined by real factors. This natural rate will tend to be attained when expectations are on average realized. The same real situation is consistent with any absolute level of prices or of price change, provided allowance is made for the effect of price change on the real cost of holding money balances." Here we take this real balance effect seriously.
Of the various ways to model unemployment, in this presentation we adopt the indivisible labor model of Rogerson (1988).26 This has a nice bonus feature:
we do not need quasi-linearity, because in indivisible-labor models agents act as if utility were quasi-linear. For simplicity, we revert to the case where ![]() is
produced one-for-one with
is
produced one-for-one with ![]() , but now
, but now
![]() for each individual. Also, as we said, to derive cleaner results we use a version where there is no production in the DM. Instead, agents have an endowment
for each individual. Also, as we said, to derive cleaner results we use a version where there is no production in the DM. Instead, agents have an endowment ![]() , and gains from trade arise due to preference shocks. Thus, DM
, and gains from trade arise due to preference shocks. Thus, DM![]() utility is
utility is
![]() where
where ![]() is a shock realized after
is a shock realized after ![]() is chosen in the CM. Suppose
is chosen in the CM. Suppose ![]() or
or ![]() with equal probability, where
with equal probability, where
![]() , and then in the DM everyone that draws
, and then in the DM everyone that draws ![]() is matched with someone that draws
is matched with someone that draws ![]() . The indices
. The indices ![]() and
and ![]() indicate which agents will be buyers and sellers in matches, for obvious reasons. We also assume that there is discounting between one DM and the next CM, but not
between the CM and DM, but this is not important. What is interesting will be nonseparability in
indicate which agents will be buyers and sellers in matches, for obvious reasons. We also assume that there is discounting between one DM and the next CM, but not
between the CM and DM, but this is not important. What is interesting will be nonseparability in
![]() .
.
As in any indivisible labor model, agents choose a lottery
![]() in the CM where
in the CM where ![]() is
the probability of employment - i.e. the probability of working
is
the probability of employment - i.e. the probability of working ![]() - while
- while ![]() and
and
![]() are CM purchases of goods and cash conditional on
are CM purchases of goods and cash conditional on ![]() . There is no
direct utility generated in the CM; utility is generated by combining
. There is no
direct utility generated in the CM; utility is generated by combining ![]() with
with ![]() in the DM. Hence, the CM problem is27
in the DM. Hence, the CM problem is27
| (18) | ||
| st 0 |
As is well known,
Letting ![]() be the Lagrangian multiplier for the budget constraint, FOC for an interior solution are
be the Lagrangian multiplier for the budget constraint, FOC for an interior solution are
Rocheteau et al. (2007) provide assumptions to guarantee
In DM meetings, for simplicity we assume take-it-or-leave-it offers by the buyer. Also, although it is important to allow buyers' preferences to be nonseparable, let sellers' preferences be separable. Then the DM terms of trade do not depend on anything in a meeting except the buyer's
![]() : in equilibrium, he pays
: in equilibrium, he pays ![]() , and chooses the
, and chooses the ![]() that makes the seller just willing to accept, independent of the seller's
that makes the seller just willing to accept, independent of the seller's ![]() . In general, buyers in the DM who
were employed or unemployed in the CM get a different
. In general, buyers in the DM who
were employed or unemployed in the CM get a different ![]() since they have different
since they have different ![]() . In any case, we can use the methods discussed above to describe
. In any case, we can use the methods discussed above to describe ![]() , differentiate it, and insert the results into (19)-(21) to get
conditions determining
, differentiate it, and insert the results into (19)-(21) to get
conditions determining
![]() . From this we can compute aggregate employment
. From this we can compute aggregate employment
![]() . It is then routine to see how endogenous variables depend on policy.
. It is then routine to see how endogenous variables depend on policy.
It is easy to check
![]() , since as in any such model the first-order effect of inflation is to reduce DM trade. The effect on unemployment depends on the cross derivatives of buyer
preferences utility function as follows:
, since as in any such model the first-order effect of inflation is to reduce DM trade. The effect on unemployment depends on the cross derivatives of buyer
preferences utility function as follows:
-
 is separable between
is separable between  and
and
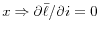
-
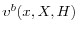 is separable between
is separable between  and
and
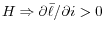 iff
iff
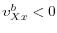
-
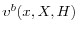 is separable between
is separable between  and
and
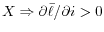 iff
iff
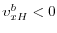
The economics here is simple and intuitive. Consider case 2. Since inflation decreases ![]() , if
, if ![]() and
and ![]() are complements then it also reduces
are complements then it also reduces ![]() , and hence the
, and hence the
![]() used to produce
used to produce ![]() ; but if
; but if ![]() and
and ![]() are substitutes then inflation increases
are substitutes then inflation increases ![]() and
and
![]() . In other words, when
. In other words, when ![]() and
and ![]() are substitutes, inflation causes agents to move from DM to CM goods, increasing CM production and reducing unemployment. A similar intuition applies in Case 3, depending on whether
are substitutes, inflation causes agents to move from DM to CM goods, increasing CM production and reducing unemployment. A similar intuition applies in Case 3, depending on whether ![]() is a complement or substitute for leisure.
is a complement or substitute for leisure.
In either case, we can get a downward-sloping Phillips curve under simple and natural conditions, without any complications like imperfect information or nominal rigidities. And this relation is exploitable by policy makers in the long run: given the right cross derivatives, it is feasible to
achieve permanently lower unemployment by running a higher anticipated inflation, as Keynesians used to think. But this is never optimal: it is easy to check that the efficient policy here is still Friedman's prescription, ![]() .
.
4.4 Benchmark Summary
We think this benchmark model, with alternating CM and DM trade, delivers interesting economic insights. A model with only CM trade could not capture as well the fundamental role of money, which is why one has to resort to short cuts like cash-in-advance or money-in-the-utility-function assumptions. The earlier work on microfoundations with only DM trade does capture the role of money, but requires harsh restrictions on money holdings, and hence cannot easily be used to discuss many policy and empirical issues, or becomes intractable in terms of analytic results. There are devices different from our alternating markets that achieve a similar generality plus tractability, including Shi (1977) and Menzio et al. (2009), which are also very useful. One reason to like alternating markets is that, in addition to imparting tractability, it integrates some search and some competitive trade, and thus reduces the gap between the literature on the microfoundations of money and mainstream macro. Alternating markets themselves do not yield tractability; we also need something like quasi-linerity or indivisibilities. This does not seem a huge price to pay for tractability, but one could also dispense with such assumptions, and rely on numerical methods, as much of macro does anyway.
Many other applications in the literature could be mentioned, but we want to get to new results.28 Before we do, however, we mention one variation of the
baseline by Rocheteau and Wright (2005), since this is something we use below. This is usually presented as an environment with two permanently distinct types, called buyers and sellers, where the former are always consumers in the DM and the latter are always producers in the DM. This does not
work in models with only DM trades, since no one would produce in one DM if he cannot spend the proceeds in a subsequent DM. Here sellers may want to produce in every DM, since they can spend the money in the CM; and buyers may want to work in every CM, since they need the money for the DM.
Monetary equilibrium no longer entails a degenerate distribution, but all sellers choose ![]() , while all buyers choose the same
, while all buyers choose the same ![]() . This raises a point that should be emphasized: the monetary equilibrium distribution is degenerate only conditional on agents' type, as we previously saw in the indivisible-labor model. This is all we need for tractability, however. Indeed, the
key property of the model is that the choice of
. This raises a point that should be emphasized: the monetary equilibrium distribution is degenerate only conditional on agents' type, as we previously saw in the indivisible-labor model. This is all we need for tractability, however. Indeed, the
key property of the model is that the choice of ![]() is history independent, not that it is the same for all agents.
is history independent, not that it is the same for all agents.
Having two types is interesting for several reasons, including the fact that one can introduce a generalized matching technology taking as inputs the measures of buyers and sellers, and one can incorporate a free entry or participation decision for either sellers or buyers in the DM.29 But notice for this we do not really need permanently distinct types: it would be equivalent to have types determined each period, in a deterministic or a random
way. As long as the realization occurs before the CM closes, agents can still choose ![]() conditional on type, and in any case we could still incorporate a generalized matching technology
and a participation decision. This is another way in which the framework proves convenient: although the horizon is infinite, which is obviously good for thinking about money and many other applications, in a sense the analysis can be reduced to something almost like a sequence of two-period
economies. The demographics in simple overlapping generations models perform a related function, of course. The point is not that the alternating-market structure is the only way to achieve tractability, but that it is one way that works in a variety of applications.
conditional on type, and in any case we could still incorporate a generalized matching technology
and a participation decision. This is another way in which the framework proves convenient: although the horizon is infinite, which is obviously good for thinking about money and many other applications, in a sense the analysis can be reduced to something almost like a sequence of two-period
economies. The demographics in simple overlapping generations models perform a related function, of course. The point is not that the alternating-market structure is the only way to achieve tractability, but that it is one way that works in a variety of applications.
5 New Monetary Theory
In the previous sections we presented results already in the literature. Although we think it is useful to survey what has been done, we also want to present new material. Here we analyze in a novel way some ideas in the Old Monetarist tradition and in the New Keynesian tradition, showing how similar results can be derived in our framework, although sometimes with interesting differences. We first introduce additional informational frictions to show how a signal extraction problem can lead to a short-run Phillips curve, as in Old Monetarist theory, discussed by Friedman (1968), and later formalized by Lucas (1972). Then we analyze what happens when prices are sticky, for some exogenous reason, as in the standard New Keynesian model in Woodford (2003) or Clarida et al. (1999).30
5.1 The Short-Run Phillips Curve
Here we discuss some ideas about the correlations defining the short-run Phillips curve, and the justification for predictable monetary policy, in Old Monetarist economics. For simplicity, we take the Phillips curve to mean a positive relation between money growth or inflation on the one hand,
and output or employment the other hand, rather than a negative relation between inflation and unemployment since we do not want to go into details on the labor market or the source of unemployment here (although we saw in the previous section that this is not so hard). Also, although it is not
critical, we use the model where agents do not become consumers or producers in the DM based on who they meet, nor based on preference and technology shocks, but instead there are two distinct types called buyers and sellers. Also, we sometimes describe the CM and DM subperiods as the day and night
markets when this helps keep track of the timing, and to yield clean results we use
![]() .31
.31
We modify the benchmark model by including both real and monetary shocks. First, some fraction of the population is inactive each period. In particular, suppose that a fraction
![]() of buyers participates in (both) markets in period
of buyers participates in (both) markets in period ![]() - the rest rest.
As well, a fraction
- the rest rest.
As well, a fraction
![]() of sellers does not participate in period
of sellers does not participate in period ![]() Assume that
Assume that
![]() is a random variable, and realizations are not publicly observable. Second, money growth
is a random variable, and realizations are not publicly observable. Second, money growth ![]() is now random, and realizations are not publicly observable. So that agents have no direct information on the current money injection by the central bank, only indirect information coming from price signals, we add some new actors to the story that we call government
agents. During the day in period
is now random, and realizations are not publicly observable. So that agents have no direct information on the current money injection by the central bank, only indirect information coming from price signals, we add some new actors to the story that we call government
agents. During the day in period ![]() , a new set of government agents appears. Each of them has linear utility
, a new set of government agents appears. Each of them has linear utility ![]() , and can produce one unit of
, and can produce one unit of ![]() for each unit of
for each unit of ![]() . If
. If ![]() , then government gives money to these extra agents, and they collectively consume
, then government gives money to these extra agents, and they collectively consume
![]() ; if
; if ![]() , these agents collectively produce
, these agents collectively produce
![]() . We will assume
. We will assume ![]() is always above
is always above ![]() here, so government agents never actually produce. In any case, their role is purely a technical one, designed to make signal extraction non-trivial.
here, so government agents never actually produce. In any case, their role is purely a technical one, designed to make signal extraction non-trivial.
During the day, agents learn last period's money stock ![]() and observe the price
and observe the price ![]() , but not the current aggregate shocks
, but not the current aggregate shocks
![]() and
and ![]() . For an individual buyer acquiring money in the CM, the
current value of money may be high (low), either because the demand for money is high (low), or because money growth is low (high). For simplicity, assume active buyers make take-it-or-leave-it offers to sellers in the DM, which implies
. For an individual buyer acquiring money in the CM, the
current value of money may be high (low), either because the demand for money is high (low), or because money growth is low (high). For simplicity, assume active buyers make take-it-or-leave-it offers to sellers in the DM, which implies
Then an active buyer's FOC from the CM reduces by the usual manipulations to
Assume the measure of active buyers is
If ![]() were a continuous random variable, in principle we could solve for equilibrium as in Lucas (1972). For illustrative purposes, however, we adopt the approach in Wallace (1992),
using a finite state space (see also Wallace 1980). To make the point, it suffices to consider an example. Thus,
were a continuous random variable, in principle we could solve for equilibrium as in Lucas (1972). For illustrative purposes, however, we adopt the approach in Wallace (1992),
using a finite state space (see also Wallace 1980). To make the point, it suffices to consider an example. Thus, ![]() and
and
![]() are independent i.i.d. processes, where
are independent i.i.d. processes, where ![]() is
is ![]() or
or
![]() each with probability
each with probability ![]() ; and
; and
![]() is
is
![]() or
or
![]() each with probability
each with probability ![]() . We assume that
. We assume that
so that agents cannot distinguish between high money demand and high money growth, on the one hand, and low money demand and low money growth on the other hand.
Using (23)-(25) we can obtained closed-form solutions for prices and quantities. Let ![]() and
and ![]() denote the CM price and the DM quantity when
denote the CM price and the DM quantity when
![]() . Then straightforward algebra yields
. Then straightforward algebra yields
Let total output in the day and night be
for
Total output in real terms is
The scatter plot of aggregate output ![]() against money growth
against money growth ![]() , using time
series observations generated by the model, is displayed Figure 1 where the four dots represent money and output in each of the four states. There is a positive correlation between money growth and aggregate output. This results from agents' confusion, since if there were full information about
aggregate shocks, we would have
, using time
series observations generated by the model, is displayed Figure 1 where the four dots represent money and output in each of the four states. There is a positive correlation between money growth and aggregate output. This results from agents' confusion, since if there were full information about
aggregate shocks, we would have
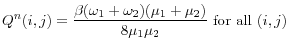
A standard narrative associated with the ideas of Friedman (1968) and Lucas (1972,1976) is that 1960s and 1970s macroeconomic policy erred because policy makers treated the dots in (their empirical version of) Figure 1 as capturing a structural relationship between money growth and output.
Policy makers took for granted that more output is good and more inflation is bad, and they took the observed correlation as evidence that if the central bank permanently increased money growth this would achieve permanently higher output. Although we saw above that permanent trade-offs are not
impossible, the important point emphasized by Friedman, Lucas, Wallace and others is that observed empirical relations may lead one far astray. What happens in this example if we permanently set money growth to ![]() ? It is straightforward to show that the data points we would generate would be the two squares in Figure 1, with high (low) output when money demand is high (low). Rather than increasing output, higher inflation lowers output in all states of the world.
? It is straightforward to show that the data points we would generate would be the two squares in Figure 1, with high (low) output when money demand is high (low). Rather than increasing output, higher inflation lowers output in all states of the world.
What is an optimal policy? Efficient exchange in DM meetings requires
![]() . If we can find a monetary policy rule that achieves
. If we can find a monetary policy rule that achieves
![]() in equilibrium, this rule is optimal. From (24), an efficient equilibrium has the property that
in equilibrium, this rule is optimal. From (24), an efficient equilibrium has the property that
Then, from (23) and (34),
Substituting and rearranging, we obtain
This is the Friedman rule, dictating that the money supply decrease on average at the rate of time preference, with a higher (lower) money growth rate when money demand is high (low) relative to the previous period.
It might appear that the monetary authority cannot implement such a rule, because it seems to require the observability of the aggregate shock
![]() . However, (35) and (36) imply
. However, (35) and (36) imply
![]() , so that prices decrease at a constant rate in the efficient equilibrium. Therefore, the monetary authority need not observe the underlying aggregate shock, and
can attain efficiency, simply by a constant rate of deflation. In equilibrium, the price level is predictable, and carries no information about the aggregate state. It is not necessary for the price level to reveal aggregate information, since efficiency requires that buyers acquire the same
quantity of real balances in the CM and receive the same quantity in the DM independent of the aggregate shock.
, so that prices decrease at a constant rate in the efficient equilibrium. Therefore, the monetary authority need not observe the underlying aggregate shock, and
can attain efficiency, simply by a constant rate of deflation. In equilibrium, the price level is predictable, and carries no information about the aggregate state. It is not necessary for the price level to reveal aggregate information, since efficiency requires that buyers acquire the same
quantity of real balances in the CM and receive the same quantity in the DM independent of the aggregate shock.
In one sense, these results are consistent with the thrust of Friedman (1968) and Lucas (1972). Monetary policy can confuse price signals, and this can result in nonneutrality that generate a positive Phillips curve, provided that real shocks do not dominate. However, the policy prescription derived from the model is in line with Friedman (1969) rather than Friedman (1968): the optimal money growth rate is not constant, and should respond to aggregate real disturbances, to correct intertemporal distortions. This feature of the model appears consistent with some of the reasons that money growth targeting by central banks failed in practice in the 1970s and 1980s. Of course we do not intend the model in this section to be taken literally - it is meant as an example to illustrate once again, but here in the context of our benchmark framework, the pitfalls of naive policy making based on empirical correlations that are incorrectly assumed to be structural.
5.2 Sticky Prices
We now modify our benchmark model to incorporate sticky prices, capturing ideas in New Keynesian economics along the lines of e.g. Woodford (2003) and Clarida et al. (1999). We will first construct a cashless version, as does Woodford (2003), then modify it to include currency transactions. In our cashless version, all transactions are carried out using credit. New Keynesian models typically use monopolistic competition, where individual firms set prices, usually according to a Calvo (1983) mechanism. Here, to fit into our benchmark model, we assume that some prices are sticky in the DM in bilateral random matching between buyers and sellers. We use the version with permanently distinct buyer and seller types.
In the cashless model, in spite of the fact that money is not held or exchanged, prices are denominated in units of money. As in the benchmark model, the price of money in the CM ![]() is flexible. In the DM, each buyer-seller pair conducts a credit transaction where goods are received by the buyer in exchange for a promise to pay in the next CM. To support these credit transactions we assume that there is perfect memory or record keeping. That is, if a buyer defaults during the
day, this is observable to everyone, and there is an exogenous legal system that can impose severe punishment on a defaulter. Thus, in equilibrium all borrowers pay off their debts.
is flexible. In the DM, each buyer-seller pair conducts a credit transaction where goods are received by the buyer in exchange for a promise to pay in the next CM. To support these credit transactions we assume that there is perfect memory or record keeping. That is, if a buyer defaults during the
day, this is observable to everyone, and there is an exogenous legal system that can impose severe punishment on a defaulter. Thus, in equilibrium all borrowers pay off their debts.
During the day, suppose that in an individual match the terms of trade between a buyer and seller is either flexible with probability
1/2, or fixed with probability
1/2. In a flexible match, as in the benchmark model, the buyer makes a take-it-or-leave-it offer to the seller. Letting
![]() denote the number of units of money the buyer offers to pay in the following day for each unit of goods produced by the flexible-price seller during the night, and
denote the number of units of money the buyer offers to pay in the following day for each unit of goods produced by the flexible-price seller during the night, and
![]() the quantity of goods produced by the seller, the take-it-or-leave it offer satisfies
the quantity of goods produced by the seller, the take-it-or-leave it offer satisfies
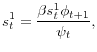
Then, in a flexible price contract, the buyer chooses ![]() to satisfy
to satisfy
so that
![\displaystyle \max_{s_{t}^{2}}\left[ u(s_{t}^{2})-\frac{s_{t}^{2}\phi_{t+1}}{\phi_{t}% }\right] ,](img317.gif)
Now, thus far there is nothing to determine the sequence
![]() In Woodford (2003), one solution approach is to first determine the price of a nominal bond. In our model, during the day in period
In Woodford (2003), one solution approach is to first determine the price of a nominal bond. In our model, during the day in period ![]() the price
the price ![]() in units of money of a promise to pay one unit of money in the daytime
during period
in units of money of a promise to pay one unit of money in the daytime
during period ![]() is given by
is given by
Then, following Woodford's approach, we could argue that
Given the model, it seems consistent with New Keynesian logic to consider
![]() as an exogenous sequence of prices that can be set by the government. In terms of what matters for agents' decisions, suppose it is equivalent to say that the
government sets the path for the inflation rate (in the daytime Walrasian market), where the gross inflation rate is defined by
as an exogenous sequence of prices that can be set by the government. In terms of what matters for agents' decisions, suppose it is equivalent to say that the
government sets the path for the inflation rate (in the daytime Walrasian market), where the gross inflation rate is defined by
![]() Then, from (37) the path for the inflation rate is irrelevant for
Then, from (37) the path for the inflation rate is irrelevant for
![]() but from (38)
but from (38) ![]() is increasing in
is increasing in
![]() In fixed-price transactions, buyers write a credit contract under which the nominal payment they make during the day to settle the previous night's credit transaction is
determined by the flexible-price contract from the previous period. When inflation increases, therefore, the implicit real interest rate on a credit transaction in a fixed-price contract falls, and the buyer then purchases more goods during the night. Note that, when the buyer in a fixed-price
meeting in the night of period
In fixed-price transactions, buyers write a credit contract under which the nominal payment they make during the day to settle the previous night's credit transaction is
determined by the flexible-price contract from the previous period. When inflation increases, therefore, the implicit real interest rate on a credit transaction in a fixed-price contract falls, and the buyer then purchases more goods during the night. Note that, when the buyer in a fixed-price
meeting in the night of period ![]() repays the loan in period
repays the loan in period ![]() that the buyer
produces
that the buyer
produces
![]() so the effect of inflation on night production is determined by the elasticity of
so the effect of inflation on night production is determined by the elasticity of ![]() with respect to the inflation rate
with respect to the inflation rate
![]() which in turn depends on the curvature of
which in turn depends on the curvature of ![]()
We again assume
![]() which implies that daytime production is invariant to the path for the inflation rate. Then, the only component of aggregate output affected by inflation is output produced in
fixed-price meetings during the night, and from (38) we have
which implies that daytime production is invariant to the path for the inflation rate. Then, the only component of aggregate output affected by inflation is output produced in
fixed-price meetings during the night, and from (38) we have
![]() , so that there is a short-run and long-run Phillips curve relationship. A temporarily higher rate of anticipated inflation increases output temporarily, and a
permanently higher rate of inflation permanently increases output. The model predicts that the Phillips curve will exist in the data, and that it is exploitable by the central bank.
, so that there is a short-run and long-run Phillips curve relationship. A temporarily higher rate of anticipated inflation increases output temporarily, and a
permanently higher rate of inflation permanently increases output. The model predicts that the Phillips curve will exist in the data, and that it is exploitable by the central bank.
Should the central bank exploit the Phillips curve? The answer is no. The equilibrium is in general inefficient due the sticky price friction, and the inefficiency is manifested in a suboptimal quantity of output exchanged in fixed-price contracts. For efficiency, we require that
![]() which implies from (38) that
which implies from (38) that
![]() a constant, for all
a constant, for all ![]() so that the optimal inflation rate is zero.
Further, from (39), the optimal nominal bond price consistent with price stability, is
so that the optimal inflation rate is zero.
Further, from (39), the optimal nominal bond price consistent with price stability, is
![]() That is, the optimal nominal interest rate is Woodford's " Wicksellian natural rate."
That is, the optimal nominal interest rate is Woodford's " Wicksellian natural rate."
Now, suppose an environment where memory is imperfect, so that money plays a role. In a fraction ![]() of non-monitored meetings between buyers and sellers during the night, the seller
does not have access to the buyer's previous history of transactions, and anything that happens during the meeting remains private information to the individual buyer and seller. Further, assume that it is the same set of sellers that engage in these non-monitored meetings for all
of non-monitored meetings between buyers and sellers during the night, the seller
does not have access to the buyer's previous history of transactions, and anything that happens during the meeting remains private information to the individual buyer and seller. Further, assume that it is the same set of sellers that engage in these non-monitored meetings for all ![]() A fraction
A fraction ![]() of matches during the night are monitored, just as in the cashless
economy. In a monitored trade, the seller observes the buyer's entire history, and the interaction between the buyer and the seller is public information. The buyer and seller continue to be matched into the beginning of the next day, so that default is publicly observable. As before, we assume an
exogenous legal system that can impose infinite punishment for default. The Walrasian market on which money and goods are traded opens in the latter part of the day, and on this market only the market price (and not individual actions) is observable.
of matches during the night are monitored, just as in the cashless
economy. In a monitored trade, the seller observes the buyer's entire history, and the interaction between the buyer and the seller is public information. The buyer and seller continue to be matched into the beginning of the next day, so that default is publicly observable. As before, we assume an
exogenous legal system that can impose infinite punishment for default. The Walrasian market on which money and goods are traded opens in the latter part of the day, and on this market only the market price (and not individual actions) is observable.
Just as with monitored transactions involving credit, half of the nonmonitored transactions using money are flexible-price transactions, and half are fixed-price transactions. The type of meeting that a buyer and seller are engaged in (monitored or nonmonitored, flexible-price or fixed-price) is determined at random, but the buyer knows during the day what the type of transaction will be during the following night.
As in the cashless model, the quantities of goods traded in flexible-price and fixed-price credit transactions, respectively, are ![]() and
and
![]() with
with
![]() and
and ![]() determined by (38). For
flexible-price transactions where there is no monitoring, and money is exchanged for goods, the buyer will carry
determined by (38). For
flexible-price transactions where there is no monitoring, and money is exchanged for goods, the buyer will carry ![]() units of money from the day into the night and make a
take-it-or-leave-it offer to the seller which involves an exchange of all this money for goods. The quantity of goods
units of money from the day into the night and make a
take-it-or-leave-it offer to the seller which involves an exchange of all this money for goods. The quantity of goods ![]() received by the buyer is then
received by the buyer is then
so that the implicit flexible price of goods in terms of money is
As buyers choose money balances optimally in the daytime, we then obtain the following first-order conditions for buyers in monetary flexible-price and fixed-price transactions, respectively.
Assume that money is injected by the government by way of lump-sum transfers to sellers during the day, and suppose that the aggregate money stock grows at the gross rate ![]() In
equilibrium, the entire money stock must be held by buyers at the end of the day who will be engaged in monetary transactions at night. Thus, we have the equilibrium condition
In
equilibrium, the entire money stock must be held by buyers at the end of the day who will be engaged in monetary transactions at night. Thus, we have the equilibrium condition
Now, consider the equilibrium where
![]() grows at the gross rate
grows at the gross rate ![]() and all real quantities are
constant for all
and all real quantities are
constant for all ![]() Then, from (38), and (40)-(44), equilibrium quantities
Then, from (38), and (40)-(44), equilibrium quantities
![]()
![]() for
for ![]() are the solution to
are the solution to
From a policy perspective, it is impossible to support an efficient allocation in equilibrium where
![]() for
for ![]() However, we can find the money growth
rate that maximizes welfare
However, we can find the money growth
rate that maximizes welfare ![]() defined here as the weighted average of total surplus across nighttime transactions, or
defined here as the weighted average of total surplus across nighttime transactions, or
![\displaystyle W(\mu)=\frac{\alpha}{2}\left[ u(q_{t}^{1})-q_{t}^{1}+u(q_{t}^{2})-q_{t}% ^{2}\right] +\frac{\left( 1-\alpha\right) }{2}\left[ u(s_{t}^{1}% )-s_{t}^{1}+u(s_{t}^{2})-s_{t}^{2}\right]](img363.gif)
Now, for an equilibrium we require that
What do we learn form this version of the New Keynesian model? One principle of New Monetarism is that it is important to be explicit about the frictions underlying the role for money in the economy, as well as other financial frictions,. What do the explicit frictions in this model tell us that typical New Keynesian models do not? A line of argument in Woodford (2003) is that it is sufficient to use a cashless model, like the one constructed above, to analyze monetary policy. Woodford views typical intertemporal monetary distortions that can be corrected by a Friedman rule as secondary to sticky price distortions. Further, he argues that one can construct monetary economies that behave essentially identically to the cashless economy, so that it is sufficient to analyze the economy that we get with the cashless limit.
The cashless limit would be achieved in our cash/credit model if we let
![]() In the cash/credit model, quantities traded in different types of transactions are independent of
In the cash/credit model, quantities traded in different types of transactions are independent of ![]() The only effects of changing
The only effects of changing ![]() are on the price level and the fraction of exchange that is supported by credit. As well, the optimal money
growth rate will tend to rise as
are on the price level and the fraction of exchange that is supported by credit. As well, the optimal money
growth rate will tend to rise as ![]() decreases, with
decreases, with
![]() in the limit as
in the limit as
![]() . The key feature of the equilibrium we study in the cash/credit model that is different from the cashless economy is that the behavior of prices is tied to the behavior
of the aggregate money stock, in line with the quantity theory of money.
. The key feature of the equilibrium we study in the cash/credit model that is different from the cashless economy is that the behavior of prices is tied to the behavior
of the aggregate money stock, in line with the quantity theory of money.
Confining analysis to the cashless economy is not innocuous. First, it is important that we not assume at the outset which frictions are important for monetary policy. It is crucial that all potentially important frictions, including intertemporal distortions, play a role, and then quantitative work can sort out which ones are most important. In contrast to Woodford's assertion that intertemporal distortions are irrelevant, as we discussed above, some New Monetarist models find that quantitatively the welfare losses from intertemporal distortions are much larger than in found in traditional monetary models.
Also, the cash/credit model gives the monetary authority control over a monetary quantity, not direct control over a market interest rate, the price level, or the inflation rate. In reality, the central bank intervenes mainly through exchanges of central bank liabilities for other assets and through lending to financial institutions. Though central banks may conduct this intervention so as to target some market interest rate, it is important to model the means by which this is done. How else could we evaluate whether, for example, it is preferable in the short run for the central bank to target a short-term nominal interest rate or the growth rate in the aggregate money stock?
Our cash/credit model is not intended to be taken seriously as a vehicle for monetary policy analysis. New Monetarists are generally uncomfortable with sticky-price models even when, as in Golosov and Lucas (2005) e.g., there are explicit costs to changing prices. The source of these menu costs is typically unexplained, and once they are introduced it seems that one should consider many other types of costs in a firm's profit maximization problem if we take menu costs seriously. The idea here, again, is simply to show that if one thinks it is critical to have nominal rigidities in a model, this is not inconsistent with theories that try to be explicit about the exchange process and the role of money or related institutions in that process.
6 More New Monetary Theory
In this section we analyze extensions of the benchmark New Monetarist model that incorporates payments arrangements, along the lines of Freeman (1995), and banks, along the lines of Diamond and Dybvig (1983). We construct environments where outside money is important not only for accomplishing the exchange of goods but for supporting credit arrangements.
6.1 A Payments Model
We modify the benchmark model by including two types of buyers and two types of sellers. A fraction ![]() of buyers and a fraction
of buyers and a fraction ![]() of sellers are type 1 buyers and sellers, respectively, and these buyers and sellers meet in the DM in non-monitored matches. Thus, when a type 1 buyer meets a type 1 seller, they can trade only if the former has money. As well, there
are
of sellers are type 1 buyers and sellers, respectively, and these buyers and sellers meet in the DM in non-monitored matches. Thus, when a type 1 buyer meets a type 1 seller, they can trade only if the former has money. As well, there
are ![]() type 2 buyers and
type 2 buyers and ![]() type 2 sellers, who are monitored at
night, and hence can trade using credit, which we again assume are perfectly enforced.
type 2 sellers, who are monitored at
night, and hence can trade using credit, which we again assume are perfectly enforced.
In the day, type 1 sellers, and all buyers, participate. Then, at night, bilateral meetings occur between the type 2 buyers and type 2 sellers who were matched during the previous night. Finally, type 1 buyers meet in the second Walrasian market with type 2 sellers, with the price of money
denoted by
![]() During the day, buyers can only produce in the Walrasian markets where they are present. The government intervenes by making lump-sum money transfers in Walrasian markets
during the day, so that there are two opportunities to intervene during any period. Lump-sum transfers are made in equal quantities to the sellers in the Walrasian market.
During the day, buyers can only produce in the Walrasian markets where they are present. The government intervenes by making lump-sum money transfers in Walrasian markets
during the day, so that there are two opportunities to intervene during any period. Lump-sum transfers are made in equal quantities to the sellers in the Walrasian market.
Our interest is in studying an equilibrium where trade occurs as follows. First, in order to purchase goods during the night, type 1 buyers need money, which they can acquire either in the first Walrasian market or the second Walrasian market during the day. Arbitrage guarantees that
![]() and we will be interested in the case where
and we will be interested in the case where
![]() Then, in the first Walrasian market during the day, type 2 buyers produce in exchange for the money held by type 1 sellers. Then, type 2 buyers meet type 2
sellers and repay the debts acquired in the previous night with money. Next, in the second Walrasian market during the day, type 2 sellers exchange money for the goods produced by type 1 buyers. Then, in the night, meetings between type 1 buyers and sellers involve the exchange of money for goods,
while meetings between type 2 buyers and sellers are exchanges of IOU's for goods. The equilibrium interactions among sets of economics agents in the model are summarized in Figure 3.
Then, in the first Walrasian market during the day, type 2 buyers produce in exchange for the money held by type 1 sellers. Then, type 2 buyers meet type 2
sellers and repay the debts acquired in the previous night with money. Next, in the second Walrasian market during the day, type 2 sellers exchange money for the goods produced by type 1 buyers. Then, in the night, meetings between type 1 buyers and sellers involve the exchange of money for goods,
while meetings between type 2 buyers and sellers are exchanges of IOU's for goods. The equilibrium interactions among sets of economics agents in the model are summarized in Figure 3.
All bilateral meetings in the night involve exchange subject to a take-it-or-leave-it offer by the buyer. In an equilibrium where
![]() , letting
, letting ![]() denote the quantity of goods
received by a type 1 buyer in exchange for goods during the night, optimal choice of money balances by the type 1 buyer yields the first-order condition
denote the quantity of goods
received by a type 1 buyer in exchange for goods during the night, optimal choice of money balances by the type 1 buyer yields the first-order condition
To repay his or her debt that supported the purchase of
Now, let
To solve for equilibrium quantities and prices, substitute for prices in (46) and (47) using (48) and (49) to obtain
Then, given
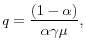
What is efficient? To maximize total surplus in the two types of trades, we need
![]() for all
for all ![]() So from (50) and (51), this gives
So from (50) and (51), this gives ![]() and
and
![]() . At the optimum, in line with the Friedman rule, money should shrink over time at the rate of time preference, but we also need the central bank
to make a money injection in the first market that increases with the fraction of credit transactions relative to cash transactions, so as to support the optimal clearing and settlement of credit.
. At the optimum, in line with the Friedman rule, money should shrink over time at the rate of time preference, but we also need the central bank
to make a money injection in the first market that increases with the fraction of credit transactions relative to cash transactions, so as to support the optimal clearing and settlement of credit.
6.2 Banking
This example extends the benchmark model by including banking in the spirit of Diamond and Dybvig (1983). Currency and credit are both used in transactions, and a diversified bank essentially allows agents to avoid waste. While the role for banking is closely related to the role Diamond-Dybvig
banking models, this has nothing to do with risk-sharing here because of quasi-linear utility. As in the payments model, there are ![]() type 1 sellers who engage in non-monitored DM
exchange using currency and
type 1 sellers who engage in non-monitored DM
exchange using currency and ![]() type 2 sellers who engage in monitored exchange. During the night there will be
type 2 sellers who engage in monitored exchange. During the night there will be ![]() type 1 buyers (each one matched with a type 1 seller) and
type 1 buyers (each one matched with a type 1 seller) and ![]() type 2 buyers (each one matched with a type 2 seller), but a buyer's type is
random, and learned at the end of the previous day, after production and portfolio decisions are made. There exists an intertemporal storage technology, which takes as input the output produced by buyers during the afternoon of the day, and yields
type 2 buyers (each one matched with a type 2 seller), but a buyer's type is
random, and learned at the end of the previous day, after production and portfolio decisions are made. There exists an intertemporal storage technology, which takes as input the output produced by buyers during the afternoon of the day, and yields ![]() units of the consumption good per unit input during the morning of the next day. Assume that
units of the consumption good per unit input during the morning of the next day. Assume that ![]() . All buyers and type
1 sellers are together in the Walrasian market that opens during the afternoon of the day, while only type 2 buyers are present during the morning of the day.
. All buyers and type
1 sellers are together in the Walrasian market that opens during the afternoon of the day, while only type 2 buyers are present during the morning of the day.
First suppose that banking is prohibited. To trade with a type 2 seller, a buyer needs to store goods during the day before meeting the seller at night. Since the trade is monitored, the seller is able to verify that the claim to storage offered in exchange for goods by the buyer is valid. To
trade with a type 1 seller, a buyer needs to have cash on hand. Thus, during the afternoon of the day, the buyer acquires nominal money balances ![]() and stores
and stores ![]() units of output and given take-it-or-leave-it offers at night, solves
units of output and given take-it-or-leave-it offers at night, solves
Assume that the monetary authority makes lump sum transfers during the afternoon of the day to buyers. Then, a Friedman rule is optimal: the money supply grows at gross rate
There is an insurance role for banks here, but it differs from their role in Diamond-Dybvig (1983). In that model, there is a risk-sharing role for a diversified bank, which insures against the need for liquid assets. In our model, the role of a diversified bank is to prevent the wasteful
storage. A diversified bank can be formed in the afternoon of the day, which takes as deposits the output of buyers, and issues Diamond-Dybvig deposit claims. For each unit deposited with the bank in period ![]() , the depositor can either withdraw
, the depositor can either withdraw
![]() units of cash at the end of the day, or trade claims to
units of cash at the end of the day, or trade claims to
![]() units of storage during the ensuing night. We assume a buyer's type is publicly observable at the end of the day.
units of storage during the ensuing night. We assume a buyer's type is publicly observable at the end of the day.
Suppose the bank acquires ![]() from a depositor at the beginning of period
from a depositor at the beginning of period ![]() The bank then chooses a portfolio of
The bank then chooses a portfolio of ![]() units of money and
units of money and ![]() units of
storage satisfying the constraint
units of
storage satisfying the constraint
The bank then maximizes the expected utility of the depositor given
subject to (54). Letting
From (55) and the envelope theorem, the optimal choice of ![]() gives
gives
which determines
which determines
A policy that we can analyze in this model is Friedman's 100% reserve requirement. This effectively shuts down financial intermediation and constrains buyers to holding outside money and storing independently, rather than holding deposits backed by money and storage. We then revert to our
solution where banking is prohibited, and we know that the resulting equilibrium is inefficient. It would also be straightforward to consider random fluctuations in ![]() or
or ![]() which would produce endogenous fluctuations in the quantity of inside money. Optimal monetary policy would involve a response to these shocks, but at the optimum the monetary authority should not
want to smooth fluctuations in a monetary aggregate.
which would produce endogenous fluctuations in the quantity of inside money. Optimal monetary policy would involve a response to these shocks, but at the optimum the monetary authority should not
want to smooth fluctuations in a monetary aggregate.
7 Asset Markets
The class of models we have been studying has recently been used to study trading in asset markets. This area of research is potentially very productive, as it permits the examination of how frictions and policy affect the liquidity of assets, and also how it affects asset prices, and the volume of trade on asset markets.32
Modify our benchmark new monetarist model as follows. The population consists, as before, of buyers and sellers, with equal masses of each. For a buyer,
![]() where
where ![]() is strictly increasing and strictly concave, with
is strictly increasing and strictly concave, with
![]()
![]() and
and ![]() defined to be the solution to
defined to be the solution to
![]() For a seller,
For a seller,
![]() During the day, each buyer and seller have access to a technology that produces one unit of consumption good for each unit of labor input. Neither buyer nor seller can produce
during the night.
During the day, each buyer and seller have access to a technology that produces one unit of consumption good for each unit of labor input. Neither buyer nor seller can produce
during the night.
In the day market, output can be produced from labor, but agents also possess another technology that can produce labor using capital. In particular, at the beginning of the day, before the Walrasian market opens, a buyer with ![]() units of capital can produce
units of capital can produce
![]() units of the consumption good. Similarly, a seller with
units of the consumption good. Similarly, a seller with ![]() units of capital can produce
units of capital can produce
![]() Assume that
Assume that ![]() is strictly concave and twice continuously
differentiable with
is strictly concave and twice continuously
differentiable with
![]()
![]()
![]() and
and ![]() Each seller has a technology to convert
consumption goods into capital, one-for-one, at the end of the day after the Walrasian market closes. Capital produced in the daytime of period
Each seller has a technology to convert
consumption goods into capital, one-for-one, at the end of the day after the Walrasian market closes. Capital produced in the daytime of period ![]() becomes productive at the beginning of the
day in period
becomes productive at the beginning of the
day in period ![]() and it then immediately depreciates by 100%.
and it then immediately depreciates by 100%.
In addition to capital, there is a second asset, which we will call a share. To normalize, let there be 1/2 shares in existence, with each share being a claim to ![]() units of consumption goods during each day. Assume that each seller is endowed with one share at the beginning of period 0. A share trades in the daytime Walrasian market at the price
units of consumption goods during each day. Assume that each seller is endowed with one share at the beginning of period 0. A share trades in the daytime Walrasian market at the price ![]() It is straightforward to reinterpret this second asset as money, if
It is straightforward to reinterpret this second asset as money, if ![]() and the quantity of "shares" in existence can be augmented or diminished by the government
through lump-sum transfers and taxes. During the night, each buyer is matched with a seller with probability
and the quantity of "shares" in existence can be augmented or diminished by the government
through lump-sum transfers and taxes. During the night, each buyer is matched with a seller with probability ![]() so that there are
so that there are ![]() buyers who are matched and
buyers who are matched and ![]() who are not, and similarly for sellers.
who are not, and similarly for sellers.
Recall that buyers and sellers do not produce or consume during the night, so that a random match between a buyer and seller during the night represents only an opportunity for asset trade. The available technology prohibits buyers from holding capital at the end of the day. Thus, a match during the night is an opportunity for a buyer to exchange shares for capital.
For now, confine attention to equilibria where a buyer will trade away all of his or her shares during the night, given the opportunity. Then, a buyer's problem during the day is
That is,
Optimization implies that the following must hold:
Now, consider a match between a buyer and seller during the night, where the buyer has ![]() shares and the seller has
shares and the seller has ![]() units of capital. With the exchange constrained by
units of capital. With the exchange constrained by ![]() and
and ![]() the buyer exchanges
the buyer exchanges ![]() shares for
shares for ![]() units of capital. The
buyer's surplus, in units of period
units of capital. The
buyer's surplus, in units of period ![]() consumption goods, is
consumption goods, is
![]() and the seller's surplus is
and the seller's surplus is
![]() With generalized Nash bargaining between the buyer and seller, it is straightforward to show that the quantity of capital held by the seller will not
constrain trading. However, due to a holdup problem, in equilibrium
With generalized Nash bargaining between the buyer and seller, it is straightforward to show that the quantity of capital held by the seller will not
constrain trading. However, due to a holdup problem, in equilibrium ![]() will always constrain the Nash bargaining solution, as long as the seller has some bargaining power. Then, Nash
bargaining allows us to solve for
will always constrain the Nash bargaining solution, as long as the seller has some bargaining power. Then, Nash
bargaining allows us to solve for ![]() according to
according to
where
Then, the first-order conditions from the buyer's and seller's optimization problems give us, respectively,
Suppose first that ![]() which implies that there is no asset trading at night. Then, from (64) and (65), the solution is
which implies that there is no asset trading at night. Then, from (64) and (65), the solution is
In the case where ![]() so that there are some meetings between buyers and sellers at night, there may exist an equilibrium where shares trade at their fundamental price, and
shares are held at the end of the day by both buyers and sellers. Restrict attention to steady states, where
so that there are some meetings between buyers and sellers at night, there may exist an equilibrium where shares trade at their fundamental price, and
shares are held at the end of the day by both buyers and sellers. Restrict attention to steady states, where
![]() ,
, ![]() and
and
![]() for all
for all ![]() where
where ![]()
![]() and
and ![]() are positive constants. To construct this equilibrium, first note from (64) that
are positive constants. To construct this equilibrium, first note from (64) that
![]() for all
for all ![]() implies that
implies that
and (65) gives
Then equations (66) and (67) solve for
Thus, in this equilibrium, the dividend on shares is high enough so that the price of shares is sufficiently large in equilibrium that the total value of shares is more than buyers wish to hold to trade with sellers. As a result, given the holdup problem in trade between buyers and sellers at night, sellers will hold some of the stock of shares at the end of the day, and buyers will hold the rest. Shares trade at their fundamental price, and it is easy to show that there is inefficient trade between buyers and sellers (due to the holdup problem) with
In this equilibrium, only buyers will hold shares, so that
![]() and, from (64)
and, from (64)
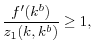
which then solve for
7.1 Example 1: 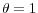
If ![]() so that the take-it-or-leave-it offer is made by the buyer in a nighttime random match, then our problem is somewhat different from the general case, due to the absence of a
holdup problem for the buyer. Here, if in a random match between a buyer and seller the buyer is holding a quantity of shares
so that the take-it-or-leave-it offer is made by the buyer in a nighttime random match, then our problem is somewhat different from the general case, due to the absence of a
holdup problem for the buyer. Here, if in a random match between a buyer and seller the buyer is holding a quantity of shares ![]() satisfying
satisfying
then the buyer will trade the quantity
![\displaystyle m-\left[ \frac{f(k)-f\left( \frac{k}{2}\right) }{\phi_{t+1}+y}\right]](img492.gif)
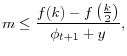
In a steady state fundamentals equilibrium we have
![]() and it will be the case that sellers hold some of the stock of shares at the end of the day, or buyers hold some shares from one day until the next day. Trading in random
matches will be unconstrained by the quantity of shares held by the buyer, so (71) holds, or
and it will be the case that sellers hold some of the stock of shares at the end of the day, or buyers hold some shares from one day until the next day. Trading in random
matches will be unconstrained by the quantity of shares held by the buyer, so (71) holds, or
![\displaystyle y\geq(1-\beta)\left[ f(k^{\ast})-f\left( \frac{k^{\ast}}{2}\right) \right] ,](img500.gif)
In the case where
![\displaystyle y\leq(1-\beta)\left[ f(k^{\ast})-f\left( \frac{k^{\ast}}{2}\right) \right] ,](img502.gif)
In this constrained equilibrium, the rate of return on shares is lower than the rate of time preference and
7.2 Example 2: 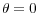
Now, consider the case where ![]() so that the seller makes a take-it-or-leave-it offer. As the buyer receives no surplus, in this case shares must trade at their fundamental value,
with
so that the seller makes a take-it-or-leave-it offer. As the buyer receives no surplus, in this case shares must trade at their fundamental value,
with
![]() From the seller's problem, there then exists a continuum of equilibria with
From the seller's problem, there then exists a continuum of equilibria with
![]() with
with ![]() satisfying
satisfying
7.3 Monetary Equilibrium
It is easy to modify the model to reinterpret shares as money. That is, let ![]() and allow the quantity of shares in existence to be augmented by the government through lump-sum transfers
during the day. The fundamentals equilibrium is then the non-monetary equilibrium where
and allow the quantity of shares in existence to be augmented by the government through lump-sum transfers
during the day. The fundamentals equilibrium is then the non-monetary equilibrium where
![]() for all
for all ![]() and this equilibrium always exists. There is also a steady
state monetary equilibrium where
and this equilibrium always exists. There is also a steady
state monetary equilibrium where
![]() for all
for all ![]() and
and
![]() for all
for all ![]() Then, letting
Then, letting ![]() denote the gross money growth rate, we obtain two equations, analogous to (69) and (70),
denote the gross money growth rate, we obtain two equations, analogous to (69) and (70),
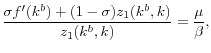
This is a simple model that captures exchange on asset markets where asset returns can include liquidity premia. Such liquidity premia seem potentially important in practice, since it is clear that money is not the only asset in existence whose value depends on its use in facilitating transactions. For example, U.S. Treasury bills play an important role in facilitating overnight lending in financial markets, as T bills are commonly used as collateral in overnight lending. Potentially, models such as this one, which allow us to examine the determinants of liquidity premia, can help to explain the apparently anomalous behavior of relative asset returns and asset prices.
8 Conclusion
New Monetarists are committed to modeling approaches that are explicit about the frictions that make monetary exchange socially useful, and that capture the relationship among credit arrangements, banking, and currency transactions. Ideally, economic models that are designed for analyzing and evaluating monetary policy should be able to answer basic questions concerning the necessity and role of central banking, the superiority of one type of central bank operating procedure over another, and the differences in the effects of central bank lending and open market operations.
New Monetarist economists have made progress in advancing the understanding of the key frictions that make monetary exchange socially useful, and in the basic mechanisms by which monetary policy can correct intertemporal distortions. However, much remains to be learned about the sources of short-run nonneutralities of money and their quantitative significance, and the role of central banking. This paper takes stock of how a new monetarist approach can build on advances in monetary theory and the theory of financial intermediation and payments, constructing a basis for progress in the theory and practice of monetary policy.
We conclude by borrowing from Hahn (1973), one of the editors of the previous Handbook of Monetary Economics. He begins his analysis by suggesting "The natural place to start is by taking the claim that money has something to do with the activity of exchange, seriously." He concludes as follows: " I should like to end on a defensive note. To many who would call themselves monetary economists the problems which I have been discussing must seem excessively abstract and unnecessary. ... Will this preoccupation with foundations, they may argue, help one iota in formulating monetary policy or in predicting the consequences of parameter changes? Are not IS and LM sufficient unto the day? ... It may well be that the approaches here utilized will not in the event improve our advise to the Bank of England; I am rather convinced that it will make a fundamental difference to the way in which we view a decentralized economy."
9 References - Incomplete
- Berentsen, A., Menzio, G., and Wright, R. 2008.
- " Inflation and Unemployment in the Long Run," working paper, University of Pennsylvania.
- Bernanke, B. and Gertler, M. 1989.
- "Agency Costs, New Worth, and Business Fluctuations," American Economic Review 79, 14-31.
- Bryant, J. and Wallace, N. 1979.
- "The Inefficiency of Interest-Bearing Government Debt," Journal of Political Economy 86, 365-381.
- Bryant, J. and Wallace, N. 1984.
- "A Price Discrimination Analysis of Monetary Policy," Review of Economic Studies 51, 279-288.
- Calvo, G. 1983.
- "Staggered Prices in a Utility Maximizing Framework," Journal of Monetary Economics 12, 383-398.
- Clarida, R., Gali, J., and Gertler, M. 1999.
- "The Science of Monetary Policy: A New Keynesian Perspective," Journal of Economic Literature 37, 1661-1707.
- Cooley, T. and Hansen, G., 1989.
- The inflation tax in a real business cycle model. American Economic Review 79, 733-748.
- Diamond, D. 1984.
- "Financial Intermediation and Delegated Monitoring," Review of Economic Studies 51, 393-414.
- Diamond, D., and Dybvig, P. 1983.
- "Bank Runs, Deposit Insurance, and Liquidity," Journal of Political Economy 91, 401-419.
- Ennis, H. and Keister, T. 2008.
- "Run Equilibria in a Model of Financial Intermediation," working paper, Federal Reserve Bank of New York, Richmond Federal Reserve Bank.
- Friedman, M. 1960.
- A Program for Monetary Stability, Fordham University Press, New York.
- Friedman, M. 1968.
- "The Role of Monetary Policy," American Economic Review 58, 1-17.
- Friedman, M. 1969.
- The Optimum Quantity of Money and Other Essays, Aldine Publishing Company, New York.
- Friedman, M. and Schwartz, A. 1963.
- A Monetary History of the United States, 1867-1960, National Bureau of Economic Research, Cambridge, MA.
- Golosov, M. and Lucas, R. 2005.
- "Menu Costs and Phillips Curves," Journal of Political Economy 115, 171-199.
- Goodfriend, M. 2007.
- "How the World Achieved Consensus on Monetary Policy," Journal of Economic Perspectives 21, 47-68.
- Hahn, F.H. (1973)
- "On the Foundations of Monetary Theory," in Essays in Modern Economics, ed. Michael Parkin with A. R. Nobay, New York, Barnes & Noble.
- Hansen, G. 1985.
- "Indivisible Labor and the Business Cycle," Journal of Monetary Economics 16, 309-337.
- Hicks, J.R. 1937.
- "Mr. Keynes and the `Classics:' A Suggested Interpretation," Econometrica 5, 147-159.
- Jones, R. 1976.
- "The Origin and Development of Media of Exchange," Journal of Political Economy 84, 757-775.
- Kareken, J. and Wallace, N. 1980.
- Models of Monetary Economies, Federal Reserve Bank of Minneapolis, Minneapolis, MN.
- Kiyotaki, N. and Wright, R. 1989.
- "On Money as a Medium of Exchange," Journal of Political Economy 97, 927-954.
- Kocherlakota, N. 1998.
- "Money is Memory," Journal of Economic Theory 81, 232-251.
- Lagos, R. 2008.
- "Asset Prices and Liquidity in an Exchange Economy," working paper, New York University.
- Lagos, R. and Wright, R. 2005.
- "A Unified Framework for Monetary Theory and Policy Analysis," Journal of Political Economy 113, 463-484.
- Lester, B., Postlewaite, A., and Wright, R. 2009.
- " Information and Liquidity," working paper, University of Pennsylvania.
- Lucas, R. 1972.
- "Expectations and the Neutrality of Money," Journal of Economic Theory 4, 103-124.
- Lucas, R. 1976.
- "Econometric Policy Evaluation: A Critique," Carnegie-Rochester Conference Series on Public Policy 1, 19-46.
- Lucas, R. and Stokey, N. 1987.
- "Money and Interest in a Cash-in-Advance Economy," Econometrica 55, 491-515.
- Mankiw, N. 1985.
- "Small Menu Costs and Large Business Cycles: A Macroeconomic Model of Monopoly," Quarterly Journal of Economics 100, 529-537.
- Mayer, Duesenberry and Aliber. 1981.
- Money, Banking, and the Economy.
- Mortensen, D. and Pissarides, C. 1994.
- "Job Creation and Job Destruction in the Theory of Unemployment," Review of Economic Studies 61, 397-416.
- Nosal, E. and Rocheteau, G. 2006.
- "The Economics of Payments," working paper, Federal Reserve Bank of Cleveland.
- Ravikumar, B. and Shao, E. 2006.
- "Search Frictions and Asset Price Volatility," working paper, University of Iowa.
- Rocheteau, G. 2009.
- "A Monetary Approach to Asset Liquidity," working paper, University of California-Irvine.
- Rocheteau, G. and Wright, R. 2005.
- "Money in Search Equilibrium, in Competitive Equilibrium, and in Competitive Search Equilibrium," Econometrica 73, 175-202.
- Rogerson, R. 1988.
- "Indivisible Labor, Lotteries, and Equilibrium," Journal of Monetary Economics 21, 3-16.
- Samuelson, P. 1958.
- "An Exact Consumption-Loan Model with or without the Social Contrivance of Money," Journal of Political Economy 66, 467-482.
- Sargent, T. and Wallace, N. 1981.
- "Some Unpleasant Monetarist Arithmetic," Minneapolis Federal Reserve Bank Quarterly Review, Fall.
- Sargent, T. and Wallace, N. 1982.
- "The Real Bills Doctrine versus the Quantity Theory: A Reconsideration," Journal of Political Economy 90, 1212-1236.
- Shi, S. 1995.
- "Money and Prices: A Model of Search and Bargaining," Journal of Economic Theory 67, 467-496.
- Townsend, R. 1987.
- "Economic Organization with Limited Communication," American Economic Review 77, 954-970.
- Townsend, R. 1989.
- "Currency and Credit in a Private Information Economy," Journal of Political Economy 97, 1323-1345.
- Trejos, R. and Wright, R. 1995.
- "Search, Bargaining, Money, and Prices," Journal of Political Economy 103, 118-141.
- Wallace, N. 1981.
- "A Modigliani-Miller Theorem for Open Market Operations," American Economic Review 71, 267-274.
- Wallace, N. 1992.
- "Lucas's Signal Extraction Model: A Finite-State Exposition with Aggregate Real Shocks, Journal of Monetary Economics 30, 433-447.
- Wallace, N. 1998.
- "A Dictum for Monetary Theory," Federal Reserve Bank of Minneapolis Quarterly Review, Winter, 20-26.
- Williamson, S. 1986.
- "Costly Monitoring, Financial Intermediation and Equilibrium Credit Rationing," Journal of Monetary Economics 18, 159-179.
- Williamson, S. 1987.
- "Financial Intermediation, Business Failures, and Real Business Cycles," Journal of Political Economy 95, 1196-1216.
- Woodford, M. 2003.
- Interest and Prices, Princeton University Press, Princeton NJ.
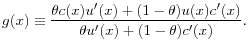
![\displaystyle \frac{g(x_{t})}{M_{t}}=\beta\frac{g(x_{t+1})}{M_{t+1}}\left[ 1+\ell (x_{t+1})\right] .%](img145.gif)
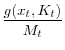
![\displaystyle =\frac{\beta g(x_{t+1},K_{t+1})}{M_{t+1}% }\left[ 1-\gamma+\gamma\frac{u^{\prime}(x_{t+1})}{g_{1}(x_{+1},K_{+1}% )}\right]](img202.gif)
![\displaystyle -\beta\gamma\left[ c_{2}(x,K)-c_{1}\left( x,K\right) \frac{g_{2}% (x,K)}{g_{1}(x,K)}\right] .](img204.gif)
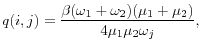 for
for 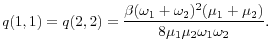
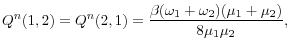
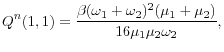
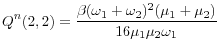
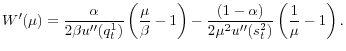
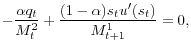
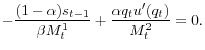
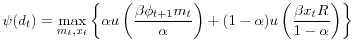
![\displaystyle \max_{k_{t+1}^{b}}\left\{ -\frac{\phi_{t}z(k_{t+1}^{b},k_{t+1})}{\phi _{t+1}+y}+\beta\left[ \sigma f(k_{t+1}^{b})+(1-\sigma)z(k_{t+1}^{b}% ,k_{t+1})\right] \right\}%](img449.gif)
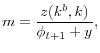
![\displaystyle z(k^{b},k)=\frac{\theta f^{\prime}(k^{b})[f(k)-f(k-k^{b})]+(1-\theta )f^{\prime}(k-k^{b})f(k^{b})}{\theta f^{\prime}(k^{b})+(1-\theta)f^{\prime }(k-k^{b})}%](img461.gif)
![\displaystyle \left[ \frac{\phi_{t+1}+y}{\phi_{t}}\right] \left[ \frac{\sigma f^{\prime }(k_{t+1}^{b})+(1-\sigma)z_{1}(k_{t+1}^{b},k_{t+1})}{z_{1}(k_{t+1}^{b}% ,k_{t+1})}\right] =\frac{1}{\beta}%](img462.gif)
![\displaystyle \left[ \frac{z(k^{b},k)}{z(k^{b},k)-y}\right] \left[ \frac{\sigma f^{\prime}(k^{b})+(1-\sigma)z_{1}(k^{b},k)}{z_{1}(k^{b},k)}\right] =\frac {1}{\beta},%](img487.gif)
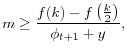
![\displaystyle \left[ \frac{f(k^{\ast})-f(k^{\ast}-k^{b})}{f(k^{\ast})-f(k^{\ast}-k^{b}% )-y}\right] \left[ \frac{\sigma f^{\prime}(k^{b})+(1-\sigma)f^{\prime }(k^{\ast}-k^{b})}{f^{\prime}(k^{\ast}-k^{b})}\right] =\frac{1}{\beta} %](img506.gif)