Abstract: The last decade has seen a burst of micro price studies. Many analyze data underlying national CPIs and PPIs. Others focus on more granular sub-national grocery store data. We review these studies with an eye toward the role of price setting in business cycles. We summarize with ten stylized facts: Prices change at least once a year, with temporary price discounts and product turnover often playing a nontrivial role. After excluding many short-lived prices, prices change closer to once a year. The frequency of price changes differs widely across goods, however, with more cyclical goods exhibiting greater price flexibility. The timing of price changes is little synchronized across sellers, with the hazard if anything falling with the age of a price. The cross-sectional distribution of price changes is thick-tailed but contains many small price changes too.
Prepared for the Handbook of Monetary Economics (Benjamin Friedman and Michael Woodford, editors). This research was conducted with restricted access to U.S. Bureau of Labor Statistics (BLS) data. Rob McClelland provided us invaluable assistance and guidance in using BLS data. We thank Margaret Lay and Krishna Rao for excellent research assistance and Mark Bils for helpful suggestions. The views expressed here are those of the authors and do not necessarily reflect the views of the BLS or the Federal Reserve System.
1. Introduction
Recent years have seen a wealth of rich micro price data become available. Many studies have examined data underlying nationally-representative consumer and producer price indices from national statistical agencies. A smaller set of studies have focused on finer scanner data for a subset of stores or products. The U.S. and Western European countries have received the most attention, but evidence on emerging markets has grown rapidly.
Such micro data offer many insights on the importance of price stickiness for business cycles. We review the literature by stating a series of ten facts modelers may want to know about price setting.
First, individual prices change at least once a year. The frequency is more like twice a year in the U.S. versus once a year in the Euro Area. Thus we need a "contract multiplier" to explain why real effects of nominal shocks appear to last several years.
Second, temporary price discounts ("sales") and product turnover are important to micro price flexibility. This is particularly true in the U.S., which plays a role in its greater price flexibility than in the Euro Area. We provide evidence that such sale prices partially cancel out with cross-sectional and time aggregation, but appear to contain macro content.
Third, if one drops a broad set of short-lived prices (more than just temporary price discounts), a stickier "reference" price emerges that changes about once a year in the U.S. This filtering conceals considerable novelty in non-reference prices, and these deviations could be responding to aggregate shocks as they do not seem to wash out with aggregation. Still, reference price inflation is considerably more persistent than overall inflation, perhaps suggesting sticky plans and/or sticky information.
Fourth, goods differ greatly in how frequently their prices change. At one extreme are goods that change prices at least once a month (fresh food, energy, airfares), and at the other extreme are services that change prices much less often than once a year. Such heterogeneity makes mean price durations much longer than median durations, and could help explain a big contract multiplier if combined with strategic complementarities.
Fifth, goods with more cyclical quantities (e.g., cars and apparel) exhibit greater micro price flexibility than goods with little business cycle (e.g., medical care). Durables, as a whole, change prices more frequently than nondurables and services. Including temporary price changes, nondurables change price more frequently than services. Such non-random heterogeneity in price stickiness may hold down the contract multiplier.
Sixth, micro price changes are much bigger on average than needed to keep up with aggregate inflation, suggesting the dominance of idiosyncratic forces (intertemporal price discrimination, inventory clearance, etc.). In state-dependent pricing models, price changers can be selected on their idiosyncratic shocks, thereby speeding price adjustment and depressing the contract multiplier.
Seventh, many small price changes occur. Thus, although micro evidence exists for selection, it does not seem as strong as predicted by models with a single menu cost. Small price changes are suggestive of weakened selection, as in time-dependent or information-constrained pricing models.
Eighth, relative price changes are transitory. Idiosyncratic shocks evidently do not persist as long as aggregate shocks do. Sellers may be implementing price changes for temporary, idiosyncratic reasons while failing to incorporate macro shocks (e.g., as in rational inattention models).
Ninth, the timing of price changes is little synchronized across products. Most movements in inflation (from month to month or quarter to quarter) are due to changes in the size rather than the frequency of price changes. This may be a byproduct of the stable inflation rates in the past few decades in the U.S. and Euro Area. In countries with more volatile inflation, such as Mexico, the frequency of price changes has shown more meaningful variation. This lack of synchronization is consistent with the importance of idiosyncratic pricing considerations over macro ones. When combined with strategic complementarities, price staggering paves the way for coordination failure and a high contract multiplier. It is also consistent with rational inattention toward macro shocks. Perhaps related, consumer price changes (both increases and decreases) have increased noticeably in the recent U.S. recession.
Tenth and finally, the hazard rate of price changes falls with the age of a price for the first few months (mostly due to sales and returning to regular prices), and is largely flat thereafter (other than a spike at one year for services). This finding holds in the U.S. and Euro Area, and for both consumer and producer prices. Such a pattern is consistent with a mix of Calvo and Taylor time-dependent pricing, but can also be generated under state-dependent pricing. Meanwhile, at least for U.S. consumer prices, the size of price changes is largely unrelated to the time between price changes. This fact seems more discriminating, and favors state-dependent over time-dependent pricing. If price spell length is exogenous, more shocks should accumulate and make for bigger price changes after longer price spells. Under state-dependent pricing, longer price spells reflect stable desired prices rather than pent-up demand for price changes.
We organize the rest of this chapter as follows. Section 2 briefly outlines the micro data sources commonly used in the recent literature. Section 3 discusses evidence on the frequency of price changes. Section 4 describes what we know about the size of price changes. Section 5 delves into price setting dynamics - for example, synchronization and what types of price changes cancel out with aggregation across products and time. Section 6 reviews, at greater length, the ten stylized facts we just discussed. Section 7 offers conclusions.
2. Data Sources
The recent literature includes studies of the data underlying consumer (CPI) and producer (PPI) price indices, of scanner and online data collected from retailers, and of information gleaned from surveys of price setters. In this section we briefly describe these datasets.
Until recently, empirical evidence on price-setting at the microeconomic level was somewhat limited, consisting mostly of studies that focused on relatively narrow sets of products (e.g., Carlton 1986, Cecchetti 1986, and Kashyap 1995). This changed as datasets underlying official CPIs and PPIs became available to researchers. These datasets, compiled by national statistical agencies, contain a large number of monthly price quotes tracking individual items over several years or more. The samples aim to be broadly representative - in terms of products, outlets, and cities covered - of national consumer expenditure (or industrial production). For example, the CPI Research Database (CPI-RDB), maintained by the U.S. Bureau of Labor Statistics (BLS), contains prices for all categories of goods and services other than shelter, or about 70% of consumer expenditure. It begins in January 1988 and includes about 85,000 prices per month (Klenow and Kryvtsov, 2008 and Nakamura and Steinsson, 2008a).
Nakamura and Steinsson (2008a) point out that interpreting the PPI data is somewhat more complicated than interpreting evidence on consumer prices.1 First, the BLS collects PPI data through a survey of firms rather than a sample of "on-the-shelf" prices. Second, the definition of a PPI good is meant to capture all "price-determining variables", which often include the buyer of the good. Intermediate prices may be part of (explicit or implicit) long-term contracts, and thus observed prices might not reflect the true shadow prices faced by the buyer (Barro, 1977). Related, in wholesale markets, the seller may choose to vary quality margins, such as delivery lags, rather than varying the price (Carlton, 1986). Mackowiak and Smets (2008) point out that repeated interactions (say, for legal services) and varying quality margins (say, waiting in order to purchase a good at the published price) are also present in some consumer retail markets.
A critical open question for macroeconomists in interpreting prices is whether they conform to the Keynesian sticky price paradigm of "call options with unlimited quantities."2 On-the-shelf consumer prices may have this feature so long as they are available in inventory (see Bils, 2004, on stockouts in the CPI). Gopinath and Rigobon (2008) argue that import prices usually do appear to be call options for buyers. Still, unlike for consumer prices, it is not clear whether new buyers of producer goods have the option to buy at prices prevailing for existing buyers.
Tables 1 and 2 list several studies that have made use of CPI and PPI data, respectively. These include studies for the United States, for countries in the Euro Area (Austria, Belgium, Finland, France, Germany, Italy, Luxembourg, the Netherlands, Portugal, and Spain), and for a handful of other developed (Canada, Denmark, Israel, Japan, Norway, South Africa) and developing economies (Brazil, Colombia, Chile, Hungary, Mexico, Sierra Leone, Slovakia). Although differences in methodology and coverage make cross-country comparisons challenging, the Inflation Persistence Network (IPN) has coordinated efforts of the many researchers in the Euro Area to allow for such comparisons (Dhyne et al. 2006 and Vermeulen et al. 2007).
A related set of studies has made use of micro data that the BLS collects to construct import and export price indices for the United States. These include Gopinath and Rigobon (2008), Gopinath, Itskhoki, and Rigobon (forthcoming), Gopinath and Itskhoki (forthcoming), and Nakamura and Steinsson (2009). The prices are collected "at-the-dock" and thus represent wholesale markets. One benefit to using international data is the ability to analyze price-setting behavior in response to large, identified shocks (i.e., nominal exchange rate shocks).
Another source of microeconomic evidence on pricing comes from scanner (i.e., barcode) data collected from supermarkets, drugstores, and mass merchandisers. These data cover a narrower set of goods than the data underlying price indices, but they provide deeper information. Scanner data usually cover many more items per outlet, and often contain information on quantities sold (and sometimes wholesale cost). Data are usually collected at a weekly frequency and may come from one particular retailer (e.g., Eichenbaum, Jaimovich and Rebelo 2009 or studies using Dominick's data) or from multiple retailers (e.g., through AC Nielsen). A number of these studies are listed in Table 3.
Other researchers have begun collecting price information from retailers by "scraping" prices from websites. The ongoing "Billion Prices Project" of Cavallo and Rigobon (e.g., Cavallo, 2009) collects daily prices from numerous retailers in over 50 countries. Useful aspects of this dataset include the daily frequency, comparability across many countries, and detailed information on each product including sales and price control indicators.
A final source of microeconomic information comes from surveying firms about their price-setting practices, as opposed to collecting longitudinal information about individual prices. These surveys allow researchers to ask about aspects of pricing that cannot be captured from datasets of observed prices, such as the frequency with which price setters review prices and the importance of particular theories of price stickiness for explaining their pricing decisions. Blinder et al. (1998) was a pioneering study for the United States, and subsequent surveys have been conducted in many countries, as shown in Table 4. The surveys typically ask firms to focus on their main product (or most important products).
3. Frequency of Price Changes
We begin our review of the substantive findings of the literature by looking at the frequency with which prices change. A theme that will arise throughout the paper is the presence of a great deal of heterogeneity in price-setting behavior, and we therefore report results along a number of different dimensions. These include measures of the "average" time between price changes, the variation of these measures across different samples and types of goods, the importance of temporary sales and product turnover, and some discussion of the determinants of the frequency of price change.
3.1 Average Frequency
Table 1, drawn primarily from a survey by Álvarez (2008), presents estimates of the mean frequency of price changes obtained from the datasets underlying national CPIs.3 Prices clearly exhibit nominal stickiness, as the (unweighted) median across these studies for the estimated mean frequency of price change is 19%. The degree of stickiness varies considerably across countries, with prices in the Euro area appearing to change less frequently than those in the U.S., which in turn change less frequently than those in high-inflation developing countries (Brazil, Chile, Mexico, Sierra Leone, Slovakia). We will return to the question of what can explain these cross-country differences after we take a closer look at individual country studies.
We will give particular attention to the multiple U.S. CPI studies (Bils and Klenow 2004, Klenow and Kryvtsov 2008, and Nakamura and Steinsson 2008a) in order to shed light on a number of features of the data and provide understanding on how different methodologies impact results. Moreover, since we have access to the micro data from the BLS, we will be able to construct some new results as we proceed. We begin by describing the structure of the micro data. The BLS divides goods and services into 300 or so categories of consumption known as Entry Level Items (ELIs). Within these categories are prices for particular products sold at particular outlets (which we will refer to as "quote-lines"). The BLS collects prices monthly for all products in the three largest metropolitan areas (New York, Los Angeles, and Chicago) and for food and fuel products in all areas, and bimonthly for all other prices. The statistics we report from Klenow and Kryvtsov (2008) and Nakamura and Steinsson (2008a) are for prices collected monthly from the top three cities.4
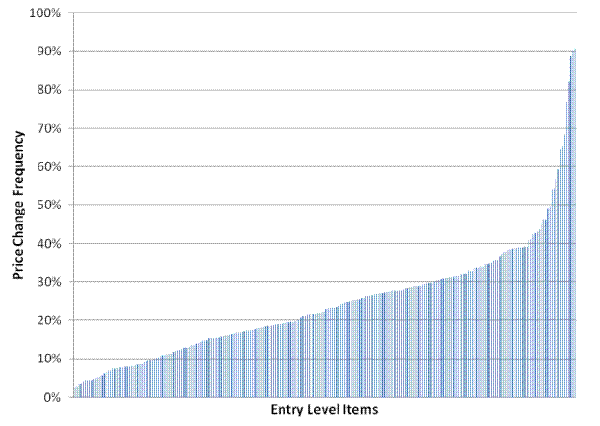
To construct their average monthly frequency that we report in Table 1, Klenow and Kryvtsov (2008) first estimate frequencies for each ELI category and then take the weighted mean across categories to arrive at a figure of 36.2% (for posted prices) between 1988 and 2004. Of course, this is not the only possible measure of the "average" frequency of price change. They report a weighted median frequency of price changes of 27.3%. The mean is higher than the median because the distribution of the frequency of price changes across ELIs, shown in Figure 1 for 1998-2009 data, is convex (Jensen's inequality). Related, the mean implied duration (from the mean of the inverse frequencies across ELIs) of 6.8 months is higher than the median (the inverse of the median frequency) of 3.7 months.
Turning to producer prices, the median country in Table 2 has a mean frequency of price change of 21%. Nakamura and Stiensson (2008a) compare price flexibility with consumer goods by matching 153 ELI categories from the CPI with product codes from the PPI. In general, they find the frequency of price change for producer prices to be similar to that of consumer prices excluding sales, but lower than consumer prices including sales. Vermeulen et al. (2007) document producer price setting in six European countries. Not controlling for the composition of the CPI and PPI baskets, they find producer prices change somewhat more frequently than what Dhyne et al. (2006) reported for consumer prices. This pattern persists when they focus on similar products in the `processed food' and `non-food non-energy consumer goods' sectors.
Gopinath and Rigobon (2007) find that U.S. export and import (wholesale) prices are sticky in the currency in which they are reported. The median implied duration in the currency of pricing is 10.6 (12.8) months for imports (exports) during their 1994-2005 sample.5 They go on to compare the duration of their cross-border transactions to domestic transactions by using product category descriptions to match international price (IPP) categories with PPI categories. Restricting their sample to these matched categories (69 of them), they find a mean duration of 10.3 months for the IPP and 10.6 months for the PPI.
Table 3 provides frequencies from a number of scanner data studies. Although the underlying data is weekly, the numbers in the table are monthly frequencies of price change (with the exception of Eichenbaum et al., 2009, who report a weekly frequency). Frequencies vary, even across studies using the same dataset, because of different sample choices and reported measures. For example, for Dominick's, Midrigan (2009) reports a mean frequency for one store, while Burstein and Hellwig (2007) consider many stores and report the frequency of the median product category. Despite these differences, the studies have very similar results: average posted (non-sale) prices change at least every three (five) months.
Table 4 presents information on price flexibility that comes from asking firms how frequently they changed their prices in the past year (or the average in recent years). The firms surveyed tend to sell their main product to other firms, and thus, the survey data pertains primarily to producer prices. The median frequency of price change, about once a year in most countries, exhibits more stickiness than the PPI micro data, although the results are not directly comparable due to different time periods, samples of firms, etc.
To recap, prices do not change continuously but do change "on average" at least once a year. We use "on average" in a loose sense, as we have already seen that the complexity of the micro data make it difficult to summarize with one statistic (such as the mean or median). We now explore this complexity in more detail, first investigating heterogeneity in the frequency with which prices change across different types of goods and then discussing the treatment of sales and product substitution.
3.2 Heterogeneity
Figure 1 shows a tremendous amount of heterogeneity across ELI categories, as the price change frequency ranges from 2.7% for "Intracity Mass Transit" to 91% for "Regular Unleaded Gasoline". Indeed, while half of all prices have an implied duration less than 3.4 months, almost a fifth last longer than a year. This heterogeneity also helps to explain the finding that "average" consumer prices adjust more frequently than in the narrower investigations predating the latest generation of micro studies. For example, Cecchetti (1986) found the length of time between changes in the newsstand prices of US magazines ranged from 1.8 to 14 years, but Nakamura and Steinsson (2008a) find that "Single-Copy Newspapers and Magazines", with a duration of 17.2 months in their sample, change prices less frequently than 84% of non-housing consumption.
Table 5 illustrates the heterogeneity in the frequency of price changes in additional ways. It reports the weighted median and mean implied price durations in the U.S. CPI from January 1988 through July 2009 separately for posted and regulars covering: (a) All Items; (b) Durables, Nondurables, and Services; (c) Processed and Raw goods; and (d) eight Major Groups. For conciseness, consider the mean durations of posted prices. For Durables the mean price duration is 3.0 months, whereas for Nondurables it is 5.5 months and for Services it is 9.2 months. For raw goods (energy and food commodities) prices last about 1.1 months, whereas for processed goods and services it is 6.7 months. Among Major Groups, price durations range from 2.9 months in Apparel to 14.4 months in Other Goods and Services.
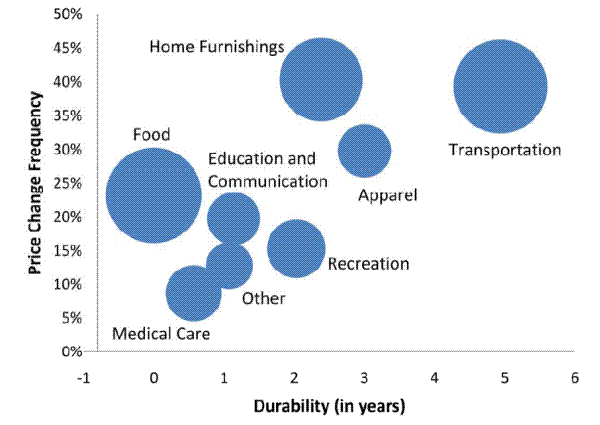
We further explore the connection between durability and price change frequency at a more disaggregated level in U.S. consumer prices. For each of 64 Expenditure Classes of the CPI (more disaggregated than the 300+ ELIs, less aggregated than the Major Groups), we estimated durability from the data in Bils and Klenow (1998). For interpretability, in Figure 2 we aggregate back up to the Major Groups. The figure plots the average frequency of posted price changes against average durability in years, with each dot proportional to the group's average expenditure weight. Transportation stands out as durable, flexible, and important. For example, Motor Vehicles have a high weight (16% of the non-shelter sample weight), high durability (9 years), and high frequency (38% per month). Food, on the other hand, is nondurable, flexible and important. As a result, Table 6 reports no significant relationship between frequency and durability across the 64 Expenditure Classes: the weighted least squares estimate is 0.57% (standard error 0.69). Excluding the five Expenditure Classes with raw goods (fresh food and energy) - which are nondurable, flexibly-priced and often dropped from the data for business cycle analysis - the relationship becomes significantly positive. For processed goods, each year of durability goes along with 1.44% higher frequency (standard error 0.41), so that a good lasting 10 years tends to have 14% point higher price change frequency than a nondurable. The connection is similar for regular price changes among processed goods.
The positive correlation between durability and price flexibility (at least for processed goods and services) could have important implications for business cycles. The more durable the good, the more cyclical expenditures and production tend to be. This is true in both theory and practice (see Bils and Klenow 1998 for one example). Barsky, House and Kimball (2007) present a model in which monetary non-neutrality is closely connected to price stickiness for durables, with the stickiness of nondurables of no importance. That said, we hasten to reiterate that the relationship in the data is not significant if raw good categories are included.
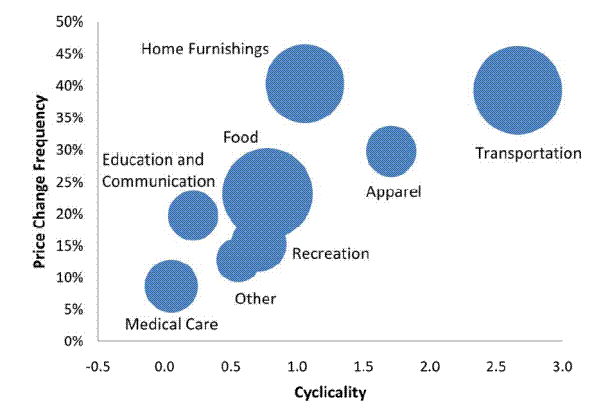
Durability and cyclicality are not synonymous, of course. We therefore gauged cyclicality directly for each of the 64 BLS Expenditure Classes based on the coefficient from regressing its NIPA real consumption expenditure growth on NIPA aggregate real consumption growth. For each Expenditure Class we ran a single OLS regression (with a constant) for the available NIPA sample from February 1990 through March 2009, which is close to our CPI-RDB 1988-2009 monthly sample. Figure 3 shows a clear positive association between price change frequencies and cyclicality across the Major Groups. Inside Transportation, for example, Motor Vehicles stands out in terms of its combination of price flexibility (38% frequency), cyclicality (5.7% higher expenditure growth for every 1% higher aggregate consumption growth), and sampling weight (16% of the non-shelter sample). Apparel is also fairly flexible (30% frequency if one includes sale prices) and fairly cyclical (cyclicality coefficient 1.75). In Table 6, the WLS regression coefficient of price frequency on cyclicality across the 64 Expenditure Classes is 3.16 (standard error 1.07). If we look only at the 58 Expenditure Classes for processed goods, the WLS coefficient is similar at 3.23 (but more precisely estimated, with a standard error of 0.59). The relationship is strong still for regular price changes across processed goods at 3.75 (s.e. 0.49).
The frequency-cyclicality nexus could arise because cyclicality induces price changes, the other way around, or because they share driving forces. If price flexibility is responding to cyclical shocks, however, then the pattern may suggest more price flexibility than in models with exogenous variation in price change frequency across goods, such as Carvalho (2006) and Nakamura and Steinsson (2008b). Causality running from frequency to cyclicality would presumably work for "supply" shocks (for which price flexibility should amplify the response of real expenditure growth) but not for "demand" shocks (for which price flexibility would dampen the response of real expenditure growth) - see Bils, Klenow and Kryvtsov (2003).6
Another dimension of heterogeneity that apparently affects the frequency of price changes is the type of retail establishment at which goods are sold. In Europe, prices are more flexible in large outlets, such as supermarkets and department stores, than in smaller retail outlets (e.g., Jonker et al 2004, Veronese et al 2005, and Dias et al 2004).
Heterogeneity is also evident for producer prices. Nakamura and Steinsson (2008a) report a median implied duration of 8.7 months for finished producer goods, 7.0 months for intermediate goods, and 0.2 months for crude materials from 1998 to 2005. Within finished producer goods, the median frequency of price change ranges from 1.3% for "Lumber and Wood Products" to 87.5% for "Food Products". Vermeulen et al. (2007) also document
significant heterogeneity across sectors and investigate the causes. Firms with a higher labor share in total costs tend to change price less frequently, whereas firms with higher shares of energy and non-energy intermediate goods change price more frequently. Moreover, they find that the higher the degree of competition, the higher is the frequency of price changes, particularly decreases.
3.3 Sales, Product Turnover, and Reference Prices
One lesson from the theoretical price-setting literature is that different types of price adjustments (e.g., transitory or permanent, selected or random) can have substantially different macroeconomic implications. Researchers have thus investigated how measures of the frequency of price change are altered when the data is filtered in different ways, such as excluding temporary sales and product turnover. It turns out that the answer can vary considerably depending on how exactly this is done.
In the U.S. CPI data, a "sale" price is (a) temporarily lower than the "regular" price, (b) available to all consumers, and (c) usually identified by a sign or statement on the price tag. Klenow and Kryvtsov (2008) report that roughly 11% of the prices in their sample are identified as sale prices by BLS price collectors. Another approach is to use a "sales filter" to identify "V-shaped" patterns in the data as sales. Nakamura and Steinsson (2008a) report results for a variety of sales filters, allowing for asymmetric and multi-period V's. Concerning product turnover, "forced item substitutions" occur when an item in the sample has been discontinued from its outlet and the price collector identifies a similar replacement item in the outlet to price going forward, often taking the form of a product upgrade or model changeover. The monthly rate of force item substitutions is about 3% in the BLS sample.7
Table 7 demonstrates the impact on the implied duration of prices of applying various filters to the data. We follow Klenow and Kryvtsov (2008) but with a U.S. CPI sample that extends through July 2009 (rather than January 2005). Depending on the treatment of sales, the median duration of prices ranges from 3.3 months (all prices included) to 6.9 months (excluding BLS-flagged sales). The one-period V-shape filter - in which every time a middle price is lower than its identical neighbors it is replaced by its neighbors - produces an intermediate duration of 5.0 months, reflecting that many sales, such as clearance sales, are not V-shaped.8 "Like" prices compare a regular price only to the previous regular price and a sale price only to the previous sale price, thus allowing for the possibility that sale prices are sticky even if they do not return to the previous regular price. This raises the implied median duration to 5.9 months. The fact that "like" prices change more frequently than regular prices (every 5.9 months vs. every 6.9 months) indicates a sale price is more likely to differ from a previous sale price than a regular price is to differ from a previous regular price.
Table 7 also shows that removing all forced item substitutions from the data increases the median implied duration to 8.1 months from 6.9 months. Klenow and Kryvtsov (2008) report that item substitutions display price changes about 80% of the time, much more frequently than the average over a product's life cycle. Purging substitution-related price changes can imply prices have a longer duration than the products themselves: for apparel,
regular prices excluding substitutions change about every 27 months, whereas the average item lasts only 10 months. Finally, comparing only consecutive regular monthly prices between substitutions pushes the duration up from 8.1 months to 8.9 months. Price changes are more frequent after items return to stock, come back into season, or return from sales.
Nakamura and Steinsson (2008a) underscore that sales and forced item substitutions are much more important in some categories than others in the U.S. CPI. For example, 87% of price changes in Apparel and 67% in Home Furnishings are sale-related price changes, while Utilities, Vehicle Fuel, and Services have virtually no sale-related changes. The monthly rate of forced item substitutions is about 10% in Apparel and in Transportation, compared to 3% for all goods. This uneven distribution of sales and substitutions is important for explaining why excluding them has a sizable impact on the implied median duration of U.S. consumer prices: the sectors in which sales and substitutions are concentrated are those with a frequency of price change that is relatively close to the median.
Sales have become more important over time for U.S. consumer prices but continue to play a small role in other countries. Nakamura and Steinsson (2008a) document a strong increase in the frequency of U.S. sales from 1988 to 2005, especially in processed food and apparel where the frequency of sales doubled. Available evidence from European countries suggests that sales are a less important source of price flexibility. Wulfsberg (2009) reports that sale prices account for only 3% of price observations in Norwegian CPI data, and removing these observations increases the mean duration by only 0.3 months. Dhyne et al. (2006) similarly report that sales have small effects on the estimated frequency of price change in France and Austria.
As emphasized by Mankiw and Reis (2002), Burstein (2006), Woodford (2009) and others, price changes may be part of a sticky plan and hence fail to incorporate current macro information. This can be true of regular price changes, not just movements between regular and sale prices. One sign of such a plan might be the existence of only a few prices over the life of an item. In the top three cities of the U.S. CPI, the weighted median (mean) length of a quote-line is 50 (53) monthly prices. In Table 8 we report the cumulative share of price quotes represented by the "top" (i.e., most common) 1, 2, 3 and 4 prices over the quote-line. The median (mean) share of the most common price is 32% (38%). The top four prices over the typical 4.3 year quote-line together represent a median (mean) of 70% (66%) of all prices. Table 8 reports the figures for Major Groups as well. There is a natural tendency for higher shares where there are shorter quote-lines (apparel) or less frequent nominal price changes (medical care, recreation). Relative to its moderate frequency of price changes, Food stands out in having a 42% median for the top price and 86% median for the top 4 prices. Even Transportation - which is highly cyclical and exhibits frequent price changes - has a 16% median share of the top price and 46% median share of the top 4 prices.
Given that nominal prices change every four months or so, there are on average around 13 prices per quote-line. A Taylor model (and perhaps Calvo model as well) would therefore imply a median top 2 price share of less than 20%, whereas the actual share in the data is over 50%.9 The disproportionate importance of a few prices appears supportive of downward-sloping hazards and/or sticky nominal plans.10 In favor of the former, two-thirds of top price spells are uninterrupted by other prices. Before discarding less common prices, however, research could explore how aggregate quantities produced and sold relate to changes in common vs. rare prices. It is conceivable that cyclical quantities are sensitive to the rare prices (e.g., clearance sales in apparel).
Eichenbaum, Jaimovich and Rebelo (2009) usefully propose a way of measuring sticky "reference" prices amidst shorter-lived new prices. Using weekly price data covering 2004-2006 from a large U.S. supermarket chain, they define the reference price for each UPC as the modal price in each quarter. They find such reference prices are responsible for 62% of all weekly prices and 50% of quantities sold. Importantly, they report that reference prices only change every 11.1 months. This is considerably stickier than regular (non-sale) prices in the same supermarket, which change about once per quarter. They go on to present a simple model in which the frequency of reference price changes is the key to monetary non-neutrality, as deviations from reference prices largely reflect idiosyncratic considerations.
Do sticky reference prices exist in the U.S. CPI more broadly? The CPI data is monthly, so it is not possible to implement the exact Eichenbaum et al. methodology on the CPI. We instead defined the reference price in each month (for an item) as the most common price in the 13-month window centered on the current month. We broke ties in favor of the current price. An advantage of a rolling window is that it allows the reference price to change every month, whereas the calendar definition imposes at most one reference price change per quarter. Using this 13-month window, we find that the posted price equals the reference price 79% of the time on average (84% median) when looking across weighted quote-lines. Table 9 provides reference price statistics for all items and Major Groups. The share of reference prices is modestly higher in Food (88.1% median). The only Major Group with a reference price share below 70% is Transportation (62.5% median); albeit an important exception given its cyclicality. We find that the weighted median duration of reference prices is 10.6 months across ELI's in the CPI. Note that reference prices change less frequently than regular prices (median duration 6.9 months), so that some regular price changes must be temporary deviations from reference prices. The median duration is higher for Food at 13.6 months, and lower for Transportation at 6.1 months. We conclude that the Eichenbaum et al. reference price phenomenon extends not only to most food items, but to most items in the non-shelter CPI more generally.
We add several caveats to our reference price results for the U.S. CPI. First, our definition of reference prices is not strictly comparable to that of Eichenbaum et al. With our definition, a combination of a high share and high duration of references - which we do observe - suggests more stickiness than either of these without the other. Second, there is considerable variation in the share of reference prices across quote-lines (weighted standard deviation 41%), even within product categories (see Table 9). Third, it is possible that cyclical quantities are sensitive to non-reference prices along with reference prices.
A related statistic is the fraction of prices which are "novel", which we define as prices that do not appear in any of the previous 12 months for the same item (quote-line). For the top three cities of the U.S. CPI, we find the weighted median (mean) share of prices that are novel to be 16.0% (24.8%). These fractions are consistent with genuinely new prices every four to seven months. We take this to mean that deviations from the most common prices exhibit considerably novelty. Table 10 also breaks the statistic down by Major Group. Novelty is naturally correlated with the frequency of price changes. Food exhibits less than average novelty (10.4% median vs. the overall item median of 16.0%, 13.9% average vs. the overall average of 24.8%) despite having average frequency of price changes. Thus caution may be warranted in drawing lessons from grocery store scanner datasets. Prices appear more novel in more cyclical categories (Transportation, Apparel). If cyclical quantities are linked to these novel prices, they could well contribute to macro price flexibility.
3.4 Determinants of Frequency
Researchers have also investigated factors affecting the frequency of price change. Some studies have made use of the substantial variation in frequencies along different dimensions to identify important determinants, while others have directly asked price-setters to assess the importance of various theories of price stickiness. A (non-exhaustive) list of determinants include (a) the level and variability of inflation, (b) the frequency and magnitude of cost and demand shocks (broadly construed to include price discrimination), (c) the structure and degree of market competition (including regulation of discounts), and d) the price collecting methods of statistical agencies (e.g., do they report temporary sales?).
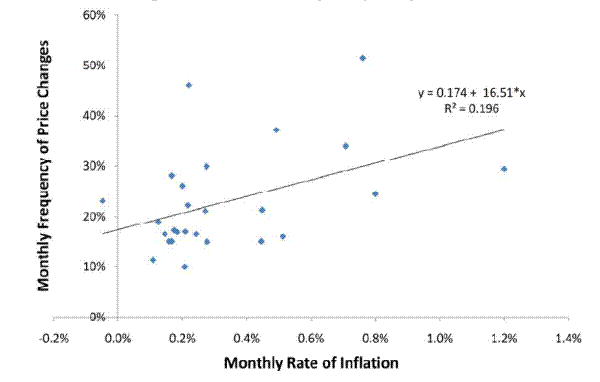
We begin by looking at the cross-country evidence reported in Table 1. Following Golosov and Lucas (2007) and Mackowiak and Smets (2008), Figure 4 simply plots the mean frequency of price change against the average inflation rate for these studies. The OLS regression coefficient of price frequency on inflation is 16.5 (standard error 6.8). Of course, this exercise comes with a few well-known caveats. First, the studies differ in many details, such as sample composition and different price-collecting methodologies. Second, periods of high inflation are often periods of volatile inflation, so it is unclear whether the relationship in Figure 4 reflects the importance of the level or the variability of inflation (probably both). Still, the relationship is provocative.
Dhyne et al. (2006) investigate the impact of inflation (and other factors) on the frequency of price change by running regressions on European data. They regress the frequency of price change across 50 product categories in 9 countries on dummy variables for product type (unprocessed and processed food, energy, non-energy industrial goods, and services), country dummies, the mean and standard deviation of inflation at the product category level, an indicator for whether sale prices occur and are reported, the share of prices set at attractive levels ("price points"), and an indicator for whether the price is typically regulated. They find that mean inflation is not significantly correlated with the overall frequency, but is correlated with the frequency of increases and decreases separately. The overall frequency (and increases and decreases, respectively) are significantly higher in sectors in which the variability of inflation is higher. A higher frequency of price change is also found when sales and temporary price cuts are included, when the share of attractive prices is lower, and when prices are not subject to regulatory control.
For U.S. consumer prices, Bils and Klenow (2004) consider regressions relating the frequency of price change in different product categories to measures of market structure: the concentration ratio, wholesale markup, and rate of non-comparable substitutions in those categories. After controlling for whether a good is raw or processed, they find that the first two measures do not have statistically significant effects, while the rate of product turnover remains a robust predictor of the frequency of price changes. They interpret the role of product turnover and raw materials in explaining the frequency of price changes as reflecting the importance of the volatility of shocks to the supply of and demand for goods.
Boivin, Giannoni, and Mihov (2009) find a relationship between the volatility of sectoral shocks and the frequency of price change. Using disaggregated PCE inflation series, they disentangle inflation fluctuations due to sector-specific conditions from those due to macroeconomic factors. They find that sectors with more volatile sector-specific shocks have a higher frequency of price change.
Other studies provide evidence consistent with the importance of cost shocks, as goods with more sticky input prices tend to change price less frequently. For example, looking at Euro Area producer prices, Vermeulen et al. (2007) find that goods with a higher labor share in total costs tend to change price less frequently, whereas firms with a higher share of intermediate goods change prices more frequently. For consumer prices, Nakamura and Steinsson (2008a) report a high correlation between the frequency of price changes upstream (PPI) and downstream (CPI). Eichenbaum et al. (2009) find a similar pattern using detailed cost and price data for one large U.S. retailer.
Survey data also provides useful insights on the determinants of price change. Fabiani et al. (2005) report the top four reasons Euro area firms refrain from changing prices include: (1-2) implicit and explicit contracts with customers; (3) cost-based pricing (i.e., input costs are slow to change); and (4) coordination failure (not wanting to raise one's price out of fear of losing market share to competitors who do not follow suit). These reasons were also ranked in the top five by firms in the United States (Blinder et al. 1998), United Kingdom (Hall et al. 2000), Sweden (Apel et al. 2005) and Canada (Amirault et al. 2006). On the other hand, physical costs (menu costs) and costly information are among the reasons least favored by firms. The main impediments to more frequent price adjustment appear to be associated with price changes rather than price reviews.
Dhyne et al. (2006) try to account for the higher frequency of price changes in the U.S. than in the Euro Area. The U.S. had somewhat higher level and volatility of inflation, but to arguably little effect. Differences in consumption patterns do not help at all, as the expenditure share of more flexible components of the CPI is actually larger in the Euro Area. Heterogeneity of outlets may play a role: smaller shops, which change prices less frequently, have a higher market share in Euro area. Differences in occurrence and treatment of temporary sales are important. For example, 1 in 5 price changes is related to sales in U.S., compared to less than 1 in 8 in France. Many other Euro Area countries do not record sale prices. Finally, a higher variability of wages (and other input prices) and less anti-competitive regulation may help explain the higher frequency of price changes in the U.S.
4. Size of Price Changes
We now move from the extensive margin - how often prices change - to the intensive margin - how large are the price changes. Again, there is substantial heterogeneity in the micro data, and it is thus useful to characterize the distribution of the size of price changes.
4.1 Average magnitude
A common finding across studies is that price changes are large on average. For example, in the U.S. CPI Klenow and Kryvtsov (2008) report a mean (median) absolute change in posted prices of 14% (11.5%), while regular price changes are smaller but still large with a mean (median) of 11% (10%). The average consumer price decrease (increase) is 10% (8%) in the Euro area (Dhyne et al. 2006), and emerging markets also display large changes (e.g., Barros et al. 2009, Konieczny and Skrzypacz 2005). For U.S. finished goods producer prices, Nakamura and Steinsson (2008a) report a median magnitude of 7.7%.
Given the low level and volatility of aggregate inflation in the U.S. and Europe, most price changes are not simply keeping up with overall inflation (i.e., indexed). But perhaps many micro price changes incorporate idiosyncratic or sectoral considerations, but not aggregate shocks. See Mackowiak and Smets (2008) for a further discussion of this rational inattention hypothesis in the context of large micro price changes.
4.2 Increases vs. Decreases
A second feature of the size distribution is that price declines are very common. Nakamura and Steinsson (2008a) report that around 40% of both CPI and PPI monthly price changes in the U.S. are decreases, and Dhyne et al. (2006) report similar numbers for the Euro area. These facts help reconcile the finding of large average absolute price changes with small average price changes (14% vs. 0.8% according to Klenow and Kryvtsov 2008) and suggest an important role for idiosyncratic shocks (or price discrimination) in driving price changes. The prevalence of price declines also varies across sectors; in particular, they are relatively uncommon in the services sector (Dhyne et al. 2006 and Nakamura and Steinsson 2008a).
4.3 Higher Moments of the Size Distribution
Using scanner data, Midrigan (2009) emphasizes that the distribution of non-zero price changes has more weight in the vicinity of zero than predicted by a normal distribution, while the tails are somewhat fatter. Formally, the distribution of price changes in leptokurtic (i.e., has positive excess kurtosis). We have confirmed this pattern in the U.S. CPI data, where the kurtosis of the price change distribution is 10.0 for posted prices and 17.4 for regular prices (vs. 3 for a normal distribution). As maintained by Midrgian, fat tails suggest weaker selection, with more price changes large and therefore infra-marginal. For this reason, the fraction of price increases vs. decreases can be less sensitive to macro shocks (see also Gertler and Leahy, 2008).
Other studies have documented the prevalence of small price change more directly. In the U.S. CPI, around 44% of regular price changes are smaller than 5% in absolute value, 25% are smaller than 2.5%, and 12% are smaller than 1% (Klenow and Kryvtsov 2008). Note that this is not just due to frequent shopper cards (as in scanner data that report average weekly prices inclusive of coupons and frequent shopper discounts). Wulfsberg (2009) reports that 45% of price changes are smaller than 5% in Norway, while in Brazil, where the mean absolute size is 13%, over a third of price changes are smaller than 5% (Barros et al. 2009). For producer prices, Vermeulen et al. (2007) find that a quarter of both increases and decreases are smaller than 1%, compared to a mean price change of 4% in the Euro area.
5. Dynamic Features of Price Changes
In addition to the unconditional statistics that we have highlighted so far, researchers have documented a number of features concerning how prices change over time. These include the synchronization of price changes, how the frequency and size of price changes correlate with the duration of the existing price, and the response of prices to shocks that would be expected to alter a firm's desired price. These features are of interest because in the presence of nominal stickiness (like we see in the data), price setters have dynamic decision problems, and thus, dynamic features of the data are particularly helpful in distinguishing between the various theories of price setting.
5.1 Synchronization
Since at least Taylor (1980), staggered price-setting has played an important role in modeling persistent real effects of monetary shocks. The staggering of price adjustments is readily apparent from the observation that not all prices change in any given period. Moreover, when price setters do change their price, they often take the prevailing price of their competition into consideration (Levy et al. 1998), which only makes sense if (at least some) competitors' prices are expected to remain active for a period of time. Recent studies have looked at time variation in the frequency of price changes as a measure of the extent of synchronization (or, conversely, uniform staggering) in price setting. Time variation also provides relevant evidence for distinguishing between some time-dependent vs. state-dependent pricing models.
Klenow and Kryvtsov (2008) decompose monthly inflation (![]() into the fraction (
into the fraction (![]() of items with price changes and the average size (
of items with price changes and the average size (![]() of those price changes:
of those price changes:
![]() . In their sample (U.S., 1988-2004), they found the fraction to be relatively stable and not so correlated with inflation (correlation 0.25), while the average size was
more volatile and had commoved almost perfectly with inflation (correlation 0.99). In addition, they decompose the variance of inflation over time into an "intensive margin" (IM) and "extensive margin" (EM) as follows:
. In their sample (U.S., 1988-2004), they found the fraction to be relatively stable and not so correlated with inflation (correlation 0.25), while the average size was
more volatile and had commoved almost perfectly with inflation (correlation 0.99). In addition, they decompose the variance of inflation over time into an "intensive margin" (IM) and "extensive margin" (EM) as follows:
This decomposition is interesting because different models of price-setting have distinct implications for this decomposition. For example, in staggered TDP models, the intensive margin will account for all of inflation's variance, whereas the fraction of items changing price plays a substantial role in some SDP models, such as Dotsey, King and Wolman (1999). Klenow and Kryvtsov (2008) find that the IM term accounts for between 86% and 113% of the variance of inflation, implying that the fraction of items changing price are a relatively unimportant source of fluctuations in inflation, at least for their sample period. Note that other SDP models (such as Golosov and Lucas, 2007), can fit this decomposition; the key is to include (realistically) large idiosyncratic price changes so that aggregate shocks have offsetting effects on the frequency of increases vs. decreases.
Gagnon (2009) first emphasized the usefulness of further decomposing inflation into terms due to price increases and decreases. Note that ![]() and
and
![]() , where
, where ![]() and
and ![]() (
(![]() and
and ![]() denote the frequency (absolute size) of price increases and decreases, respectively. So, even if the average size of price increases and decreases remain constant over time, significant variation in the average size of price changes could result due to offsetting movements in the frequency of price
increases and decreases, which would also imply little variation in the overall frequency of price changes. This is the type of pattern we see in the U.S.: Klenow and Kryvtsov (2008) report that a 1 percentage point increase in inflation is associated with a 5.5 (-3.1) percentage point change in
the fraction of price increases (decreases), and a 0.6 (-1) percentage point change in the size of price increases (decreases). When they additively decompose the variance of inflation (splitting the covariance term), they find fluctuations in increases and decreases equally important to inflation
volatility.11
denote the frequency (absolute size) of price increases and decreases, respectively. So, even if the average size of price increases and decreases remain constant over time, significant variation in the average size of price changes could result due to offsetting movements in the frequency of price
increases and decreases, which would also imply little variation in the overall frequency of price changes. This is the type of pattern we see in the U.S.: Klenow and Kryvtsov (2008) report that a 1 percentage point increase in inflation is associated with a 5.5 (-3.1) percentage point change in
the fraction of price increases (decreases), and a 0.6 (-1) percentage point change in the size of price increases (decreases). When they additively decompose the variance of inflation (splitting the covariance term), they find fluctuations in increases and decreases equally important to inflation
volatility.11
While inflation was relatively low and stable in the United States during the sample period considered by Klenow and Kryvtsov (2008), Gagnon (2009) notes that Mexico experienced episodes of both high and low inflation from 1994 to 2002. He finds that when the annual rate of inflation was below 10-15%, the average frequency (size) of price changes co-moves weakly (strongly) with inflation due to offsetting movements in the frequency of price increases and decreases. When inflation rises beyond 10-15%, however, few price decreases are observed and both the frequency and average size are important determinants of inflation. Thus, over the entire sample period, the extensive margin accounts for more than half of the variance of inflation.
Wulfsberg (2009) studies Norwegian consumer price data over a 30-year period in which inflation was at first high and volatile (1975-1989) and then low and stable (1990-2004). He uses a different metric to assess the importance of the extensive and intensive margins. Specifically, he constructs
the average monthly inflation in year ![]() as the weighed product-sum of item-specific average frequencies and magnitudes of price changes,
as the weighed product-sum of item-specific average frequencies and magnitudes of price changes,
![]() , where
, where ![]() is the average frequency of price increases, and so on. To assess the importance of the extensive (intensive) margin, he computes the conditional inflation rate where the size (frequency) of price changes are kept constant at their
means while allowing the frequency (size) of price changes to vary. He finds that the
is the average frequency of price increases, and so on. To assess the importance of the extensive (intensive) margin, he computes the conditional inflation rate where the size (frequency) of price changes are kept constant at their
means while allowing the frequency (size) of price changes to vary. He finds that the
extensive margin is strongly correlated with CPI inflation (0.91), while the intensive margin is negatively correlated with CPI inflation (-0.12) and interprets this as evidence of strong state dependence in price setting. Restricting his sample to the low and stable inflation period of 1990-2004, he finds the intensive margin has a higher correlation with CPI inflation: 0.51 vs. 0.36.
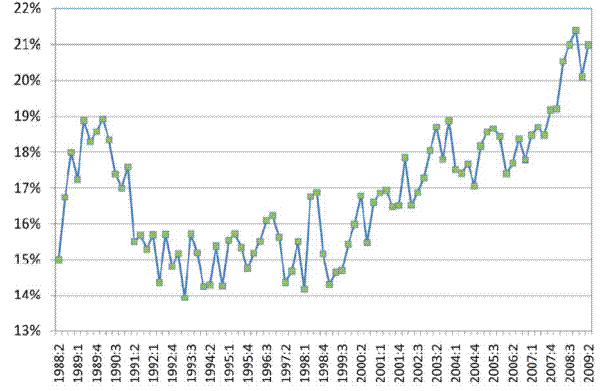
We next consider evidence of price-change synchronization in the U.S. during the recent recession. Figure 5 plots the average frequency of price changes in the top three cities, based on regular prices for processed items. We first calculated the monthly frequency of price changes (the weighted mean across ELIs) from July 1988 through June 2009. We then took out seasonal (monthly) dummies, and calculated deviations from them. Finally, we averaged the monthly deviations in each quarter, and added back the mean across all quarters to produce quarterly data from 1988:2 through 2009:2. The monthly frequency of price changes increased a couple of percentage points from the end of 2007 onward, from about 18.5% to about 20.5%. We do not have a good metric for whether this is an economically large shift, but the issue deserves deeper investigation. For example, did the frequency increase more rapidly for cyclical goods? Did the increase reflect endogenously more attention given the magnitude of the recession? We do know that the increase holds for non-raw posted prices as well as all posted prices. Also, the size of increases and decreases for regular processed items were little changed (if we include raw items, there were some unusually large energy price declines near the end of the sample).
Another form of synchronization is seasonality. Nakamura and Steinsson (2008a) find that the weighted median frequency of (regular) consumer price changes declines monotonically over the four quarters of the year, with local spikes in the first month of each quarter. The quarterly seasonal pattern in producer prices mirrors the seasonal pattern in consumer prices qualitatively, but is substantially larger, with the frequency of price change in January more than twice the average for the rest of the year. For the Euro area, Dhyne et al. (2006) emphasize that various goods are more likely to exhibit seasonal patterns: unprocessed foods due to seasonality in agricultural producer prices, certain industrial goods due to "end-of-season" sales, and services because they show an inclination to change prices at the beginning of the year and refrain from changing price at the end of the year.
The Euro area consumer price studies (Dhyne et al 2006) also investigated synchronization at the product level using the Fisher - Koniezcny (2000) measure, which takes a value of 1 in case of perfect synchronization and a value of 0 in the case of uniform staggering of price changes. They calculated the measure for each of the 50 product categories in their common sample. The degree of synchronization was, in general, rather low except for energy prices, with the median synchronization ratio across products ranging between 0.13 in Germany and 0.48 in Luxembourg. The higher ratio observed in Luxembourg compared to Germany likely reflects the difference in the size of the market upon which the ratio is computed and the relatively small number of outlets in Luxembourg.
Other studies have focused on the synchronization of prices at the outlet level. Using scanner data for a number of retailers in the United States, Nakamura (2008) decomposes price variation for individual products into variation that is common across all stores (16%), variation that is common only to stores within the same retail chain (65%), and variation that is completely idiosyncratic to particular stores (17%). These findings suggest that retail-level shocks, rather than manufacturer-level shocks, may be quite important for understanding fluctuations in retail prices. Midrigan (2009) finds the probability a particular product experiences a price change depends on the fraction of other prices within its store that change, especially those in its own product category. He also finds some evidence, albeit weaker, of synchronization across stores in a particular city. Related, Lach and Tsiddon (1992, 1996) analyze prices of different meat products and wines at retail stores in Israel. They find that, when stores change price, they seem to change price for most of their products at the same time, but these adjustments occur at different times for different stores.
5.2 Sales, Reference Prices, and Aggregate Inflation
A key question for macroeconomists when thinking about sale-related price changes is whether they respond to macro shocks or instead reflect entirely idiosyncratic forces. Midrigan (2009) and Nakamura and Steinsson (2008a) implicitly take the latter view when they replace sale prices with previous regular prices in their empirical analysis. Guimaraes and Sheedy (2008) rationalize the latter in a specific model, generating oscillation between sticky regular and sale prices as an optimal form of price discrimination. Similarly, Eichenbaum, Jaimovich and Rebelo (2009) describe a model with menu costs to changing a "sticky pair" of prices that sellers can freely oscillate between. Kehoe and Midrigan (2008) take an intermediate position, modeling sale-related price changes as subject to (smaller) menu costs and responding to macro as well as idiosyncratic shocks. Because sale prices tend to revert to previous regular prices (both in their theory and in the data), their theoretical sale prices contribute notably less to macro price flexibility than do regular price changes (which can be arbitrarily persistent).
The answer to whether sale-related price changes contribute to macro price flexibility is ultimately empirical, of course. According to Klenow and Kryvtsov (2008), more than 40% of sale price episodes do not return to the previous regular price, opening the door to more macro price flexibility. Klenow and Willis (2007), using bi-monthly data for all cities in the CPI, find that the magnitude of price discounts indeed correlates with cumulative inflation since the item last changed price. Another possibility, which has not yet been investigated, is that clearance sales (more common for apparel and appliances, less common for food) react to unwanted inventory build-up at the macro level.
To provide some evidence on the macro content of sale prices, we calculated inflation for posted prices and regular prices separately in the U.S. CPI from February 1988 through July 2009 for the top three cities. We took out separate monthly dummies for each to remove seasonal effects. Table 11 summarizes some of the resulting moments for posted vs. regular price inflation in the U.S. CPI. For the residuals, the variance of regular price inflation equaled 87% of the variance of posted price inflation, so that sale prices "accounted for" 13% of the aggregate variance. By comparison, sale prices represent about 19% of all price changes (see Klenow and Kryvtsov, 2008). When we aggregated up to the quarterly level, however, sale prices contributed only 8% of the variance of quarterly posted price inflation. Thus sale-related price changes do not fully wash out with cross-sectional aggregation, but do significantly cancel out with time aggregation.
The serial correlation of posted price inflation in the U.S. CPI is modestly lower (0.395, standard error 0.053) than the serial correlation for regular price inflation (0.418, s.e. 0.052) - see also Bils, Klenow and Malin (2009). The same is true of quarterly inflation rates 0.165 serial
correlation for posted price inflation, 0.134 for regular price inflation). To get at whether price changes build or fade, we regressed cumulative inflation from month ![]() to
to ![]() on inflation from month
on inflation from month ![]() to
to ![]() . As given in Table 11, following a 1% price increase in the first month, regular prices are 1.38% (s.e. 0.29) higher after 12 months. The aggregate component of sale-related price changes is surprisingly persistent: the difference between posted and
regular prices is 1.09% (s.e. 0.17) higher after 12 months (following a 1% increase in the first month in the difference between posted and regular price inflation).
. As given in Table 11, following a 1% price increase in the first month, regular prices are 1.38% (s.e. 0.29) higher after 12 months. The aggregate component of sale-related price changes is surprisingly persistent: the difference between posted and
regular prices is 1.09% (s.e. 0.17) higher after 12 months (following a 1% increase in the first month in the difference between posted and regular price inflation).
Table 12 provides statistics on aggregate reference price inflation, again obtained as residuals from separate monthly dummies for the top three cities in the U.S CPI. Recall that, in the spirit of Eichenbaum et al. (2009), we defined the reference price as the most common price in the 13-month window centered on the current month for each item. As discussed, reference prices represent about 80% of all prices in the CPI by this definition, and change every 11 months. By comparison, regular prices represent about 90% of all prices and change roughly every 7 months.12 Thus, in practice, reference prices more aggressively filter out short-lived prices (though this need not be the case in principle, as our definition allows the reference price to conceivably change every month). The variance of aggregate monthly reference price inflation is only 45% of the variance of posted price inflation in the U.S. CPI. The monthly posted price inflation rate is similarly correlated with reference price inflation (0.69) and with the deviations from reference price inflation (0.74). Monthly reference price inflation is more serially correlated (0.45, standard error 0.05), however, than are the deviations from reference price inflation (0.13, s.e. 0.06). This is not by construction, as the deviations from reference prices could have exhibited more persistent changes. Reference price changes build to 3.50% (s.e. 0.38) after one year, whereas deviations from reference prices do not build but do not fade either (coefficient 0.93%, s.e. 0.16).
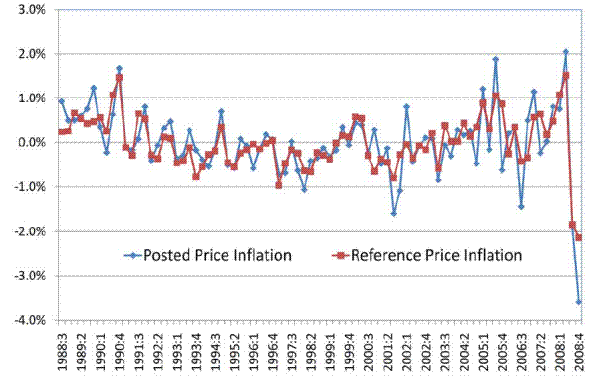
As Table 12 shows, reference price inflation becomes more volatile and persistent relative to posted price inflation when we aggregate up to the quarterly level. The variance of reference price inflation rises to about 57% of overall quarterly inflation (from about 45% at the monthly frequency). At the quarterly level, posted price inflation is more correlated with reference price inflation (0.81) than with deviations from it (0.66). The serial correlation of quarterly reference price inflation is 0.45 (standard error 0.09), vs. -0.23 (0.11) for deviations from quarterly reference price inflation. Figure 6 plots these quarterly series. [Both rates plunge at the end of 2008 due to energy price declines, but these two quarters do not drive any of the statistics.] We conclude that reference price inflation picks up responses to more persistent shocks to inflation, whereas deviations from reference price inflation reflect more fleeting disturbances.
5.3 Hazard Rates
Another "dynamic" feature that has been documented in many studies is the shape of the hazard function of price change, i.e., how the probability of changing price varies depending upon the age of the price. One reason for this is that price-setting models often have fairly stark predictions for the shape of the hazard function. The Calvo (1983) model assumes a flat hazard function, while the deterministic timing of price adjustment in the Taylor (1980) model predicts a zero hazard except at a single age, where the hazard is one. Menu-cost models can generate a variety of shapes, depending on, among other things, the relative importance of transitory and permanent shocks to marginal costs. Permanent shocks, which accumulate over time, tend to yield an upward sloping hazard function, while transitory shocks tend to flatten or even produce a downward-sloping hazard (e.g., sellers may be more attentive to getting prices right when revenue is temporarily high for a product due to idiosyncratic supply or demand considerations).
The general finding in the literature is that hazard rates for individual products are not upward-sloping. Klenow and Kryvtsov (2008) find the frequency of (regular) price changes conditional on reaching a given age is downward sloping if all goods are considered together, but note that this could simply reflect a mix of heterogeneous flat hazards and survivor bias. Once they take out decile fixed effects (i.e., average frequencies of price change in each decile of price change frequency), they characterize the hazard rate as flat (other than a spike at 12 months). Álvarez (2008) reports a similar pattern in Euro area consumer price data. Nakamura and Steinsson (2008a) estimate separate hazard functions for each Major Group, however, and find hazards are downward sloping for the first few months and generally flat after that. They find similar patterns for producer prices.
5.4 Size vs. Age
Klenow and Kryvtsov (2008) undertake an analogous exercise for the (absolute) size of price changes. They find that the size of price changes rises with age, but once they control for heterogeneity across goods, the size of price changes is unrelated to the age of the price for a given item. In contrast, many models predict a positive relationship between size and age. For example, models in which shocks accumulate over time and the timing of price changes are exogenous (Calvo 1983) or driven primarily by having a low menu-cost draw (Dotsey et al. 1999) fall into this category.
5.5 Transitory Relative Price Changes
The persistence of relative price changes can shed light on the relative importance of idiosyncratic versus aggregate shocks and also help to distinguish between different price-setting models. Indirect evidence on this aspect of the data comes from investigating the behavior of sales. Nakamura and Steinsson (2008a) report that (a) sales spells are short - the average length is just 1.8-2.3 months; (b) sales price changes are twice as large as other price changes on average; and (c) many prices return to their original price following a sale. Taking these facts together suggests highly transient relative price changes for both sales prices and all posted prices, as sales are quite common in the U.S. CPI data (representing about 20% of price changes according to Klenow and Kryvtsov, 2008). Scanner data studies uncover similar patterns. For example, Kehoe and Midrigan (2008) find that price changes are large and dispersed and most are of a "temporary" nature, again suggesting transitory relative price changes.
The transitory nature of relative price changes is not just a sales-related phenomenon, however, as it has been found after filtering out sales as well. Campbell and Eden (2005) document that grocers choose, and then quickly abandon, extreme relative prices (rather than arriving at those prices through the gradual erosion of their fixed nominal price by other sellers' price adjustments). Midrigan (2009) reports that the probability a firm's next price change will have the same sign as the current one is fairly low (between 32% and 41%). Klenow and Willis (2006) construct relative prices as the ratio of individual prices to the weighted average of prices in a sector, and report an across-sector weighted mean serial correlation of new relative prices (i.e., across months with price changes) of 0.32.
To provide a metric for how transitory these relative price changes are, it is useful to consider what they imply for the persistence of shocks in structural models. The general finding is that transitory, idiosyncratic shocks are an important input that enables structural models to replicate pricing patterns in the data. Klenow and Willis (2006) estimate a monthly persistence of 0.7 for the idiosyncratic technology shock in their model in order to match the serial correlation of new relative prices. The shocks that trigger price changes in Midrigan (2009) are similarly transitory and tend to be reversed. Nakamura and Steinsson (2008a) calibrate the size of the menu cost and the idiosyncratic-shock persistence and volatility to match the frequency of (regular) price changes, the fraction of changes that are increases, and the size of changes. The idiosyncratic shock is large and has a serial correlation of 0.66. Other models that produce transitory relative price changes include Burstein and Hellwig (2006) who incorporate transitory demand shocks in addition to marginal cost shocks, Kehoe and Midrigan (2008) who give firms the option of a "one-period markdown" at a lower menu cost than a permanent price change, and Eichenbaum et al. (2008) whose sticky-plan firms can switch between a small number of prices at no cost.
5.6 Response to Shocks
Evidence on the response of prices to identified shocks is particularly useful for shedding light on the nature of firms' price-setting decisions because most (if not all) theories of price-setting posit a tight link between (desired) prices and the underlying cost and demand conditions facing the firm. Of course, precisely identifying shocks in the data is not an easy task, but recent studies have made use of novel datasets to do just this. These include studies of the response of import/export prices or of prices on either side of a border to exchange rate shocks, evidence of price-setting around the time of a significant event like the Euro changeover or an increase in VAT rates, and studies of scanner data which contain both wholesale costs and retail prices.
Researchers have made use of well-identified and sizable movements in exchange rates to evaluate how prices respond to shocks. Gopinath and Rigobon (2008) measure medium-run exchange rate pass-through as the change in a price in response to the cumulative change in the exchange rate since the price was last changed and find that the trade weighted exchange rate pass-through into U.S. import prices is low, at 22%. Gopinath, Itskhoki and Rigobon (2009) document that non-dollar priced goods display much higher medium-run pass-through than do dollar priced goods. They present a sticky-price model in which firms choose their currency based on their average desired pass-through over the period of price non-adjustment. Incomplete desired pass-through - whether it is driven by variable mark-ups, imported inputs or decreasing returns to scale in production - is thus seen as the reason that the majority of U.S. import goods are priced in dollars. Gopinath and Itskhoki (2009) find further evidence consistent with variable mark-ups or variable marginal costs in the form of a positive correlation between the frequency of price adjustment and long-run pass-through, the life-long change in the price of a good (relative to U.S. inflation) on the (real) exchange rate over the same period. Fitzgerald and Haller (2008) use micro data on domestic and export prices set by Irish producers. Because they have matched price quotes for the same product produced in the same plant but sold in multiple markets, they are able to control for changes in marginal costs in addition to exchange rate movements. They find strong evidence of pricing-to-market for products whose export prices are invoiced in the destination currency: conditioning on price changes in both markets, relative prices move one-for-one with exchange rate changes (i.e., zero pass-through of exchange rate changes).
Burstein and Jaimovich (2008) and Gopinath et al. (2009) evaluate scanner data from a major retailer that has multiple locations in Canada and the US to investigate the effect of the border on pricing decisions. They both find evidence that the border effectively segments markets. Gopinath et al. (2009) find large discontinuities of retail prices and wholesale costs between adjacent stores on either side of the border, and note that these border gaps co-move almost one to one with changes in the nominal exchange rate. Burstein and Jaimovich (2008) document substantial pricing-to-market for traded goods and build a model in which the border segments competitors across countries, nominal exchange rate movements affect relative labor costs, and exporters' prices vary with the costs of their closest competitor.
Other identifiable aggregate shocks include changes in tax rates or in the nation's currency. A number of European studies, summarized in Álvarez et al. (2005), have consistently found that changes in the value-added tax rate lead to temporary increases in the frequency of CPI price changes. The frequency of price change also increased noticeably after countries converted to the euro in January 2002 (Álvarez et al. 2005). Although the response of aggregate inflation to the introduction of the euro was not particularly large, Hobijn et al. (2006) emphasize the dramatic increase in euro area restaurant prices and explain this increase with a menu-cost model in which firms decide when to adopt the new currency.
Eichenbaum et al. (2009) are able to provide information on the price response to (potentially disaggregated) shocks. They investigate the relationship of prices to costs using scanner data for one large US retailer. Prices typically do not change in the absence of a change in cost, but a cost change is not sufficient to induce a change in price. This allows markups (both actual and reference) to display substantial variation. When the retailer does decide to change its reference price, it almost always re-establishes the unconditional markup over the reference cost. That is, the retailer passes through 100% of the cumulative change in reference cost that occurred since the last reference price change.
Bils, Klenow, and Malin (2009) do not condition upon identified shocks but instead document how "reset prices" evolve over time in response to reduced-form impulses. A reset price for an individual firm is the price it would choose if it implemented a price change in the current period. Models with sizeable strategic complementarities predict that the impact of a shock to reset prices will build over time, as price setters wait for the average price to respond. In the U.S. CPI data, however, the reset price actually overshoots - it changes more on impact than it does in the long-run.
5.7 Higher Moments of Price Changes and Aggregate Inflation
Various authors have investigated the relationship between higher moments of the distribution of price changes and inflation (i.e., the first moment). Relative price variability is generally found to be positively correlated with inflation, as predicted by menu cost or incomplete information models. Lach and Tsiddon (1992) point out that menu cost models imply that the variability is affected by expected inflation, while incomplete information models imply a relationship with unexpected inflation. They find that expected inflation had a stronger effect on variability than unexpected inflation for a sample of foodstuffs in Israel between 1978 and 2004. Koneiczny and Skrzypacz (2005) reach similar conclusions using data on 52 goods in Poland from 1990 to 1996.
Ball and Mankiw (1995) focus on the third moment and find that innovations in inflation are positively associated with the skewness in relative-price changes for four-digit U.S. PPI data from 1949 to 1989. Indeed, the inflation-skewness relationship is stronger than the inflation-variance relationship. They show these findings are consistent with a menu-cost model: when price adjustment is costly, firms adjust to large shocks but not to small shocks, and therefore large shocks have disproportionate effects on the price level. They also explore the idea that asymmetric relative-price changes represent aggregate supply shocks.
Domberger and Fiebig (1993) look at individual price changes in 80 disaggregated industry groups in the UK. They also find that an increasing (decreasing) average price is associated with a rightward (leftward) skew, but note that when the absolute magnitude of inflation (deflation) increases, the distribution of individual price changes becomes less skewed. They suggest that the higher the skewness of the price-change distribution, the more staggered (less synchronized) are changes.
We complement these studies by calculating monthly measures of higher moments of the distribution of price changes for the top three cities in the U.S. CPI from 1988 to 2009. We then construct the correlation of the variance, skewness, and kurtosis of (non-zero) price changes with inflation. We find few robust significant relationships. The variance is negatively correlated with inflation, both for posted prices (-0.16, s.e. 0.06) and for regular prices (-0.29, s.e. 0.06). These results are fragile, however, being highly influenced by deflation during the last few months of 2008. Omitting the last year of the sample (August 2008 - July 2009), the inflation-variance correlation is still statistically significant for regular prices (-0.15, s.e. 0.06) but not for posted prices (-0.07, s.e. 0.06). Moreover, the correlation between skewness and inflation becomes significant: correlation of 0.15 (s.e. 0.06) for regular prices and 0.17 (s.e. 0.06) for posted prices. That is, the late-2008 plunge in inflation was accompanied by a spike in the variance of price changes, but no fall in skewness. We find that skewness is more robustly (if modestly) related to absolute inflation (0.15, s.e. 0.06 for both posted prices and regular prices).
More study of the relationship between inflation and higher moments thus seems warranted. For example, Ball and Mankiw's interpretation of skewness as representing an aggregate supply shock suggests a more nuanced inflation-skewness relationship than might be picked up by a simple correlation. Indeed, they argue that the absence of asymmetry when inflation fell in the 1975 and 1982 recessions can be viewed as evidence in favor of their hypothesis, as it suggests that causation does not run from inflation to skewness.
6. Ten Facts and Implications for Macro Models
We now summarize the findings from the empirical literature on individual price data with ten stylized facts and their potential lessons for models. These touch on two broad themes. The first is the frequency and nature (e.g., state-dependent vs. time-dependent pricing) of micro price changes. The second is the potential magnitude and source of the "contract multiplier", i.e., how long it takes for the macro effects of price stickiness to fade after a permanent shock relative to the duration of individual prices.
Fact 1: Prices change at least once a year.
In the U.S. CPI, prices change every 4 months or so. Prices appear stickier in the U.S. PPI (around 8 months for the median), and stickier still in the Euro Area (around once a year for the median). But median price durations in emerging markets (tilted toward food, as actual household budgets are) are typically closer to the U.S. than the Euro Area.
In contrast, a large literature has estimated that permanent monetary shocks have real effects lasting several years.13 Real effects of nominal shocks therefore last three to five times longer than individual prices. Nominal stickiness appears insufficient to explain why aggregate prices respond so sluggishly to monetary policy shocks. For this reason, nominal price stickiness is usually combined with a "contract multiplier" (in Taylor's 1980 phrase). Ball and Romer (1990) and Kimball (1995) are early examples, and Christiano, Eichenbaum and Evans (2005) a more recent one. Possible sources of big contract multipliers include strategic complementarities, countercyclical markups, sticky plans, and sticky information (e.g., rational inattention).
Of course, prices do not change continuously either. Nominal stickiness is a pervasive feature of the data in all country-years with moderate inflation rates. Models that generate persistence in aggregate prices without any nominal stickiness, for example via indexation (Christiano et al., 2005) or convex costs of price adjustment (Rotemberg 1982), are at odds with this fact.
Fact 2: Sales and product turnover are often important for micro price flexibility.
Large price discounts and product turnover account for about one-third of consumer price changes in the United States. Sales are much more frequent for some types of goods (food and apparel), and usually revert to the previous regular price afterward (more so for food, less so for apparel). Sales are much less frequent in the Euro Area than in the U.S. Within the U.S., sales are less prevalent for producer prices than consumer prices. Product turnover ushers in nominal price changes, and is much more common for durables (and apparel) than food or services. Both sales and product turnover exhibit clear seasonal patterns, suggesting a time-dependent component.
Given their temporary and seasonal nature, sale-related price changes may contribute more to micro than macro price flexibility. Put differently, the contract multiplier may be larger for price changes related to sales and product turnover. That said, sale- and turnover-related price changes do not wash out with aggregation in the U.S., consistent with macro content. It remains an open question whether such prices respond to aggregate shocks.
In addition to interesting empirical questions concerning the macroeconomic important of sales and substitutions, more theoretical research is necessary for us to better understand how these types of price changes affect the monetary transmission mechanism. It is awkward to simply apply menu cost models to data in which some price changes have been filtered out. Alternative approaches have been pursued in the literature. Kehoe and Midrigan (2008) model one-period price discounts as incurring a lower menu cost. They find sales-related price changes can contribute to macro price flexibility, but not as much as regular price changes. Guimaraes and Sheedy (2008) build a model in which firms face consumers with different price sensitivities and therefore choose a pricing strategy with a high price at some moments and a low price at other moments. Even though "sales" decisions are completely flexible at the micro level, this does not translate into flexibility at the macro level because sales are strategic substitutes: a firm gains little from a sale if its competitors are having sales. Thus, different models of sales have different implications for aggregate flexibility. Empirical work could help distinguish between and refine this theorizing.
Fact 3: Reference prices are stickier and more persistent than regular prices.
Eichenbaum, Jaimovich and Rebelo (2009) document many temporary regular price changes in a major U.S. grocery store chain. We find a similar pattern of sticky "reference" prices in most U.S. CPI items. Whereas posted prices change every 4 months and regular prices every 7 months, reference prices change every 10-11 months.
Deviations from reference prices do not cancel out across items, so that they affect aggregate inflation. Perhaps not surprising, reference price inflation is considerably more persistent than either posted or regular price inflation. Changes in reference prices build over time, whereas other price changes tend to be much more transitory. Reference pricing behavior is suggestive of sticky plans and/or sticky information, rather than menu costs per price change, and hence could explain the sizable contract multiplier. That said, temporary prices exhibit considerable novelty relative to prices appearing in the previous year, so that more than two new prices appear per year.
A related fact is that U.S. CPI quote-lines, which typically span over four years, are dominated by a few prices. The top price alone captures one-third of prices, and the top two prices more than one-half of prices. This fact may reflect downward-sloping hazards rather than sticky information or plans, though, given that two-thirds of top prices occur without interruption by other prices.
Future research could explore whether the reference price phenomenon extends to U.S. producer prices and to prices in other countries. There might be more frequent reference price changes in countries and timeframes with more persistent inflation than in recent U.S. decades. Moreover, a vital question remains: how do reference vs. non-reference prices respond to aggregate shocks?
Fact 4: There is substantial heterogeneity in the frequency of price change across goods.
Every micro dataset to date has displayed large, persistent heterogeneity in the frequency of price changes across types of goods. Universally, service prices are stickier than those of goods. Among goods, "raw" goods (energy, fresh produce) are more flexible than "processed" goods (goods with low intermediate shares and high labor shares).
As stressed by Carvalho (2006) and Nakamura and Steinsson (2008b), such heterogeneity can combine powerfully with strategic complementarities to boost the contract multiplier. But evidence for strategic complementarities in micro price data is mixed. In the supportive column, Gopinath and collaborators have consistently found that exchange rate changes gradually pass-through into import prices. In the skeptical column, Klenow and Willis (2006) stress that sellers routinely change prices relative to close substitutes (e.g., temporary sales are not synchronized among competing brands of a narrow product) and argue that large relative price movements are inconsistent with strong "micro" real rigidities. Using evidence on product-level prices and market shares, Burstein and Hellwig (2006) also conclude that "micro" pricing complementarities are too weak to generate large aggregate real effects. Kryvtsov and Midrigan (2009) note that strong "macro" complementarities imply stable markups, and hence are hard to reconcile with countercyclical inventory-sales ratios. And Bils, Klenow and Malin (2009) find that consumer price changers tend to overshoot, rather than undershoot as predicted by slow pass-through.
Fact 5: More cyclical goods change prices more frequently.
In the U.S. CPI, prices change more frequently in categories with more procyclical real consumption growth - in particular transportation (cars, airfares) and apparel. This fact probably extends to U.S. producer prices, given the high correlation between upstream and downstream price change frequency (Nakamura and Steinsson, 2008a). In other countries, we also note the strong tendency for durables to change prices more frequently than services.
This form of price change heterogeneity could do the opposite of what idiosyncratic sources of heterogeneity (say different-sized menu costs or idiosyncratic shocks) do, namely reduce the contract multiplier. See, in particular, Barsky, House and Kimball (2007). Natural topics for further investigation include the source of this connection (does cyclicality cause flexibility or the other way around?) and its quantitative importance for the contract multiplier in various models.
Fact 6: Price changes are big on average.
Micro price changes are an order of magnitude larger than needed to keep up with aggregate inflation in the U.S. and Euro Area. Thus idiosyncratic forces dominate macro shocks. Golosov and Lucas (2007) show that the former can limit the contract multiplier. In their SDP model, a positive aggregate monetary shock results in more idiosyncratic price increases (and fewer idiosyncratic price decreases), thereby speeding the response of the aggregate price level. Bils, Klenow and Malin (2009) find that "reset price inflation" behaves as if it strongly affected by such selection.
Fact 7: Many small price changes occur.
Many price changes are small, too, so that there is a "missing middle" in the distribution of price changes emerging from SDP models with a single, large menu cost. This need not be true if menu costs are variable (as in Dotsey, King and Wolman, 1998) or are small but shocks arrive infrequently (as in Gertler and Leahy, 2008).
Meanwhile, Midrigan (2009) makes the point that TDP models can easily fit the whole size distribution. He argues the missing middle in SDP models is a byproduct of overstated selection. Alternatively, the small price changes generated by his SDP model with multiproduct firms reflect weakened selection and hence greater departures from monetary neutrality, akin to TDP models. Woodford (2009) lays out a model in which information constraints can lead to small price changes as well (costly information updating results in little change ex post sometimes, though not on average). As in TDP, the result of information constraints can be a bigger contract multiplier than under SDP.
Fact 8: Relative price changes are transitory.
A corollary to large idiosyncratic price changes is big relative price movements. Even within narrower categories of the CPI (Expenditure Classes, ELIs) and U.S. grocery scanner data, these relative price changes are large. Such relative price movements tend to fade over time - they are far less persistent than a random walk. This is true across stores of different chains, but also across competing brands within chains. It is also true even for regular prices, i.e., excluding the (often temporary) sale price discounts from regular prices. This fact is a corollary to many regular price changes being temporary in nominal terms.
The persistence of relative prices can matter for macroeconomic questions. First, in menu cost models the Ss band for non-adjustment is narrower when firms are selling more and wider when firms are selling less. Thus the selection effect of macro shocks can change with the persistence of idiosyncratic shocks. Second, big transitory movements in relative prices require either that micro complementarities be weak, or that idiosyncratic shocks be large. Weaker complementarities imply a smaller contract multiplier in response to monetary shocks. Third, transitory movements may reflect micro flexibility amidst a sticky macro plan/information (i.e., frequently respond to big, temporary idiosyncratic shocks within the plan, less frequently change the macro plan/information given that persistent macro shocks are smaller).
Fact 9: Price changes are typically not synchronized over the business cycle.
The contract multiplier can be lower if sellers accelerate price increases in response to positive monetary shocks and postpone them in response to negative monetary shocks. For moderate inflation episodes such as the last two decades in the U.S., sellers do not seem to synchronize their timing in this way. This is consistent with time-dependent pricing, but need not nullify the selection effect of state-dependent pricing completely. As predicted by state-dependent models and time-dependent models alike, the composition of price increases vs. decreases correlates positively with inflation movements. But lack of synchronization may mean weaker selection, or even a preoccupation with idiosyncratic over aggregate shocks (e.g., rational inattention).
Staggered nominal price stickiness is also critical for how strategic complementarities can help produce a big contract multiplier. Synchronized price changes are not subject to coordination failure in magnitude. The less price changes are synchronized, the more sellers may slow their adjustment as they wait for other prices (of competitors and input suppliers) to adjust. That said, the evidence for strategic complementarities appears mixed. The lack of synchronization even among closely competing brands, itself, is hard to understand if micro real rigidities are strong.
Periods of greater macro volatility may exhibit more synchronization. In Mexico in recent decades, the frequency of price changes moved up and down with aggregate inflation movements. In the recent U.S. recession, the frequency of consumer price changes appears to have surged. Intriguingly, both price increases and decreases became more common, perhaps because of more frequent updating of sticky plans or sticky information.
Fact 10: Neither frequency nor size is increasing in the age of a price.
In both the U.S. and Euro Area, and for both consumer and producer prices, the hazard rate of price changes is falling over the first few months and largely flat afterward. The exception is a spike in price change frequency for services, suggestive of annual updating for the stickiest category of products. The downward slope is much less pronounced if one looks at regular prices (i.e., excludes sale-related price changes), and may be flat if one fully controls for survivor bias.
For a state-dependent pricing model, standard intuition would have the hazard of price changes increasing in the time since a price change as shocks accumulate and the desired price drifts farther away from the current price. This force can be weakened by thicker-tailed or Poisson shocks, and by periods with wider vs. narrower Ss bands (which create an intertemporal form of survivor bias). Scanner studies find clear evidence of state-dependence in rising hazards in distance from the average markup. Again, state-dependence can imply a smaller contract multiplier than time-dependent pricing.
For a time-dependent model, analogous intuition would imply that the size of price changes is increasing in the duration of stickiness, as more shocks accumulate the longer the spell between price changes. Evidence on this question is far more limited (to U.S. consumer prices), but there seems to be little connection between the size of price changes and the duration of price spells. This pattern is consistent with state-dependent pricing, under which spell length is endogenous to the shocks accumulated. A long spell without a price change may signal that the desired price did not move much, so that it need not change unduly when the spell ends. This question could use more study in the U.S. and elsewhere.
7. Conclusion
We review the recent empirical literature on individual price data and distill ten salient facts for macro models. Prices change quite frequently, although much of this flexibility is associated with price movements that are temporary in nature. Even if all short-lived prices are excluded, however, the resulting nominal stickiness, by itself, appears insufficient to account for the sluggish movement of aggregate prices. These findings point to the need for a large contract multiplier to bridge the gap between micro flexibility and macro inertia.
Other micro price facts provide evidence on the plausibility of various mechanisms for generating a large contract multiplier. The lack of synchronization in the timing of price changes provides scope for strategic complementarities to amplify the real effects of nominal stickiness. The presence of substantial heterogeneity across goods in the average frequency of price change can bolster this channel, although the fact that more cyclical goods exhibit greater price flexibility may work in the opposite direction. The presence of many large, transitory price changes raises concerns about the relevance of real rigidities at the individual-item level, but is consistent with macro rigidities or with rationally inattentive sellers who respond to sizeable idiosyncratic shocks but not to smaller aggregate impulses. Finally, the fact that the size of price changes does not increase with the age of a price provides evidence for state-dependent pricing and thus selection. The stronger the selection effect, the smaller the contract multiplier, although the presence of many small price changes suggests the selection effect may be muted.
A number of open empirical (and related theoretical) questions remain. How do temporary price changes (related to sales, product turnover, or a movement to a non-reference price) respond to aggregate shocks? How should these temporary movements be modeled, and what impact do they have on the contract multiplier? What drives the relationship between the cyclicality of goods and the frequency with which prices change? Related, what aspects of micro heterogeneity in price-setting are important to consider in macro models? Finally, what evidence can be used to distinguish between different sources of the contract multiplier, such as rational inattention, sticky plans, or strategic complementarities?
Álvarez, Luis J. (2008), "What Do Micro Price Data Tell Us on the Validity of the New Keynesian Phillips Curve?" Economics - The Open-Access, Open-Assessment E-Journal 2(19).
Álvarez, Luis J. and I. Hernando (2006), "Price Setting Behaviour in Spain. Evidence from Consumer Price Micro-data," Economic Modelling 23:699-716.
Álvarez, Luis J. and I. Hernando (2007), "The Price Setting Behaviour of Spanish Firms: Evidence from Survey Data," Pricing Decisions in the Euro Area: How Firms Set Prices and Why, Oxford University Press, S. Fabiani, C. Loupias, F. Martins, and R. Sabbatini, eds.
Álvarez, Luis J. et al. (2005), "Price Setting in the Euro Area: Some Stylized Facts from Individual Consumer Price Data," ECB Working Paper 524.
Álvarez, Luis, et al. (2006), "Sticky Prices in the Euro Area: A Summary of New Micro-Evidence," Journal of the European Economic Association 4 (April-May): 575-584.
Álvarez, L.J., P. Burriel and I. Hernando (2008), "Price Setting Behaviour in Spain: Evidence From Micro PPI Data," forthcoming in Managerial and Decision Economics.
Amirault, D., C. Kwan, and G. Wilkinson (2006), "Survey of Price-Setting Behaviour of Canadian Companies," Bank of Canada Working Paper 2006-35.
Apel, Mikael, Richard Friberg, and Kerstin Hallsten (2005), "Microfoundations of Macroeconomic Price Adjustment: Survey Evidence from Swedish Firms," Journal of Money, Credit and Banking, 37 (April): 313-338.
Aucremanne, Luc and Emmanuel Dhyne (2004), "How Frequently Do Prices Change? Evidence Based on the Micro Data Underlying the Belgian CPI," ECB Working Paper 331.
Aucremanne, Luc and M. Druant (2005), "Price-Setting Behaviour in Belgium: What Can be Learned from an Ad Hoc Survey," ECB Working Paper 448.
Baharad, Eyal and Benjamin Eden (2004), "Price Rigidity and Price Dispersion: Evidence from Micro Data," Review of Economic Dynamics 7 (July): 613-641.
Ball, Laurence and N. Gregory Mankiw (1995), "Relative-Price Changes as Aggregate Supply Shocks," Quarterly Journal of Economics 110 (February): 161-193.
Ball, Laurence and David Romer (1990), "Real Rigidities and the Non-neutrality of Money," Review of Economic Studies 57 (April): 183-203.
Barro, Robert J. (1977), "Long-term Contracting, Sticky Prices and Monetary Policy," Journal of Monetary Economics 3 (July): 305-316.
Barros, Rebecca, Marco Bonomo, Carlos Carvalho, and Silvia Matos (2009), "Price Setting in a Variable Macroeconomic Environment: Evidence from Brazilian CPI," unpublished paper, Getulio Vargas Foundation and Federal Reserve Bank of New York.
Barsky, Robert, Christopher L. House, and Miles Kimball (2007), "Sticky-Price Models and Durable Goods," American Economic Review 97 (June): 984-998.
Baudry, L., H. Le Bihan, P. Sevestre and S. Tarrieu (2007), "What Do Thirteen Million Price Records Have to Say about Consumer Price Rigidity?" Oxford Bulletin of Economics and Statistics 69 (2): 139-183.
Baumgartner, J., E. Glatzer, R. Rumler, and A. Stiglbauer (2005), "How Frequently Do Consumer Prices Change in Austria? Evidence from Micro CPI Data," ECB Working Paper 523.
Bernanke, Ben S., Jean Boivin, and Piotr Eliasz (2005), "Measuring the Effects of Monetary Policy: A Factor-Augmented Vector Autoregressive (FAVAR) Approach," Quarterly Journal of Economics 120 (February): 387-422.
Bils, Mark (2004), "Studying Price Markups from Stockout Behavior," unpublished paper, University of Rochester (December).
Bils, Mark and Peter J. Klenow (1998), "Using Consumer Theory to Test Competing Business Cycle Models," Journal of Political Economy 103 (April): 233-261.
Bils, Mark and Peter J. Klenow (2004), "Some Evidence on the Importance of Sticky Prices," Journal of Political Economy 112 (October): 947-985.
Bils, Mark, Peter J. Klenow, and Oleksiy Kryvtsov (2003), "Sticky Prices and Monetary Policy Shocks," Federal Reserve Bank of Minneapolis Quarterly Review (Winter): 2-9.
Bils, Mark, Peter J. Klenow, and Benjamin A. Malin (2009), "Reset Price Inflation and the Impact of Monetary Policy Shocks," NBER Working Paper 14787.
Blinder, Alan S., Elie Canetti, David Lebow, and Jeremy Rudd (1998), Asking About Prices: A New Approach to Understanding Price Stickiness. New York: Russell Sage Foundation.
Boivin, Jean, Marc Giannoni and Ilian Mihov (2009), "Sticky Prices and Monetary Policy: Evidence from Disaggregated U.S. Data," American Economic Review 99 (March): 350-384.
Broda, Christian and David Weinstein (2007), "Product Creation and Destruction: Evidence and Price Implications," NBER Working Paper 13041.
Burstein, Ariel (2006), "Inflation and Output Dynamics with State Dependent Pricing Decisions," Journal of Monetary Economics 53 (7/October): 1235-1257.
Burstein, Ariel and Christian Hellwig (2007), "Prices and Market Shares in a Menu Cost Model," unpublished paper, UCLA.
Burstein, Ariel and Nir Jaimovich (2009), "Understanding Movements in Aggregate and Product-Level Real-Exchange Rates," unpublished paper, UCLA and Stanford University.
Calvo, Guillermo A. (1983), "Staggered Prices in a Utility-Maximizing Framework," Journal of Monetary Economics 12 (September): 383-398.
Campbell, Jeffrey R. and Benjamin Eden (2005), "Rigid Prices: Evidence from U.S. Scanner Data," unpublished paper, Federal Reserve Bank of Chicago and Vanderbilt University.
Carlton, Dennis W. (1986), "The Rigidity of Prices," American Economic Review 76 (September): 637-658.
Carvalho, Carlos (2006), "Heterogeneity in Price Stickiness and the Real Effects of Monetary Shocks," Frontiers of Macroeconomics 2(1), Article 1.
Castanon, V., J.A. Murillo, and J. Salas (2008), "Formacion de precios en la industria manufacturer de Mexico," El Trimestre Economico, 75(1): 143-181.
Cavallo, Alberto (2009), "Scraped Online Data and Sticky Prices: Frequency, Hazards and Synchronization," unpublished paper, Harvard University.
Cecchetti, Stephen G. (1986), "The Frequency of Price Adjustment: a Study of Newsstand Prices of Magazines," Journal of Econometrics 31 (April): 255-274.
Christiano, Lawrence J., Martin Eichenbaum, and Charles Evans (1999), "Monetary Policy Shocks: What Have We Learned and to What End?," Handbook of Macroeconomics, volume 1A, Elsevier: New York, John B. Taylor and Michael Woodford, eds.
Christiano, Lawrence J., Martin Eichenbaum, and Charles Evans (2005), "Nominal Rigidities and the Dynamic Effects of Shocks to Monetary Policy," Journal of Political Economy 113 (February): 1-45.
Copaciu, M., R. Neagu and H. Braun-Erdei (2007), "Survey Evidence on Price Setting Patterns of Romanian Firms," unpublished paper, National Bank of Romania.
Coricelli, F. and R. Horváth (2006), "Price Setting Behaviour: Micro Evidence on Slovakia," CEPR Discussion Papers 5445.
Cornille, David and Maarten Dossche (2008), "Some Evidence on the Adjustment of Producer Prices," Scandinavian Journal of Economics 110 (September): 489-518.
Creamer, K. (2008), "Price Setting Behaviour in South Africa - Stylised Facts using Producer Price Microdata," unpublished paper, University of the Witwatersrand.
Creamer, Kenneth and Neil A. Rankin (2008), "Price Setting in South Africa 2001-2007 - stylised facts using consumer price micro data," Journal of Development Perspectives, 1(4): 93-118.
Dabusinskas, A. and M. Randveer (2006), "Comparison of Pricing Behaviour of Firms in the Euro Area and Estonia," Bank of Estonia Working Paper 2006-08.
Dhyne, Emmanuel et al. (2006), "Price Setting in the Euro Area and the United States: Some Facts from Individual Consumer Price Data," Journal of Economic Perspectives 20 (Spring): 171-192.
Dias, D.A., C. Robalo Marques, P.D. Neves, and J.M.C. Santos Silva (2005), "On the Fisher-Konieczny Index of Price Changes Synchronization," Economics Letters 87: 279-283.
Dias, M., D. Dias and P. Neves (2004), "Stylised Features of Price Setting Behaviour in Portugal: 1992-2001," ECB Working Paper 332.
Domberger, Simon and Denzil G. Fiebig (1993), "The Distribution of Price Changes in Oligopoly," The Journal of Industrial Economics 41 (September): 295-313.
Dotsey, Michael, Robert King and Alexander Wolman (1999), "State-Dependent Pricing and the General Equilibrium Dynamics of Money and Output," Quarterly Journal of Economics 114 (May): 655-690.
Eichenbaum, Martin, Nir Jaimovich, and Sergio Rebelo (2008), "Reference Prices and Nominal Rigidities," unpublished paper, Northwestern Univserity and Stanford University.
Fabiani, Silvia et al. (2005), "The Pricing Behavior of Firms in the Euro Area: New Survey Evidence," ECB Working Paper 535.
Fabiani, Silvia, A. Gatulli, and R. Sabbatini (2007), "The Pricing Behavior of Italian Firms. New Survey Evidence on Price Stickiness," Pricing Decisions in the Euro Area: How Firms Set Prices and Why, Oxford University Press, S. Fabiani, C. Loupias, F. Martins, and R. Sabbatini, eds.
Fisher, Timothy C.G. and Jerzy D. Konieczny (2000), "Synchronization of Price Changes by Multiproduct Firms: Evidence from Canadian Newspaper Prices," Economics Letters, 68: 271-277.
Gabriel, P. and A. Reiff (2008), "Price setting in Hungary - a Store-level Analysis," unpublished paper, Magyar Nemzeti Bank.
Gagnon, Etienne (2009), "Price Setting during Low and High Inflation: Evidence from Mexico," Quarterly Journal of Economics 124 (August): 1221 - 1263.
Gautier, Erwan (2008), "The Behaviour of Producer Prices: Some Evidence from the French PPI Micro Data," Empirical Economics, 35 (September): 301-332.
Gertler, Mark and John Leahy (2008), "A Phillips Curve with an Ss Foundation," Journal of Political Economy 116 (June): 533-572.
Golosov, Mikhail and Robert E. Lucas, Jr. (2007), "Menu Costs and Phillips Curves," Journal of Political Economy 115 (April): 171-199.
Gopinath, Gita, Pierre-Olivier Gourinchas, Chang-Tai Hsieh, and Nicholas Li (2009), "Estimating the Border Effect: Some New Evidence," unpublished paper, Harvard University, University of California at Berkeley and University of Chicago.
Gopinath, Gita and Oleg Itskhoki (forthcoming), "Frequency of Price-Adjustment and Pass-through," Quarterly Journal of Economics.
Gopinath, Gita, Oleg Itskhoki, and Roberto Rigobon (forthcoming), "Currency Choice and Exchange Rate Pass-through," American Economic Review.
Gopinath, Gita and Roberto Rigobon (2008), "Sticky Borders," Quarterly Journal of Economics 123 (May): 531-575.
Gouvea, Solange (2007), "Price Rigidity in Brazil: Evidence from CPI Micro Data," Central Bank of Brazil Working Paper 143.
Guimaraes, Bernardo and Kevin D. Sheedy (2008), "Sales and Monetary Policy," CEPR Discussion Paper 6940.
Hansen, B.W. and N.L. Hansen (2006), "Price Setting Behavior in Denmark: A Study of CPI Micro Data 1997-2005," Danmarks Nationalbank Working Paper 39.
Harchaoui, Tarek M., C. Michaud and J. Moreau (2008), "Consumer Price Changes in Canada, 1995-2006," Yearbook on Productivity 2007. Statistics Sweden.
Hobijn, Bart, Federico Ravenna, and Andrea Tambalotti (2006), "Menu Costs at Work: Restaurant Prices and the Introduction of the Euro," Quarterly Journal of Economics 121 (August): 1103 - 1131.
Hoeberichts, M. and A. Stokman (2006), "Pricing Behaviour of Dutch Companies: Results of a Survey," ECP Working Paper 607.
Hoffmann, Johannes and Jeong-Ryeol Kurz-Kim (2006), "Consumer Price Adjustment under the Microscope: Germany in a Period of Low Inflation," ECB Working Paper 652.
Jonker, N., H. Blijenberg and C. Folkertsma (2004), "Empirical Analysis of Price Setting Behaviour in the Netherlands in the Period 1998-2003 using Micro Data," ECB Working Paper 413.
Julio, J.M. and H.M. Zárate (2008), "The Price Setting Behaviour in Colombia: Evidence from PPI Micro Data," Borradores de Economía. Banco de la República. Colombia.
Kashyap, Anil K. (1995), "Sticky Prices: New Evidence from Retail Catalogues," Quarterly Journal of Economics 110 (February): 245-274.
Kimball, Miles S. (1995), "The Quantitative Analytics of the Basic Neomonetarist Model," Journal of Money, Credit, and Banking 27 (November): 1241-1277.
Klenow, Peter J. and Kryvtsov, Oleksiy (2008), "State-Dependent or Time-Dependent Pricing: Does It Matter For Recent U.S. Inflation?" Quarterly Journal of Economics 123 (August): 863-904.
Klenow, Peter J. and Jonathan L. Willis (2006), "Real Rigidities and Nominal Price Changes," unpublished paper, Stanford University and Federal Reserve Bank of Kansas City.
Klenow, Peter J. and Jonathan L. Willis (2007), "Sticky Information and Sticky Prices," Journal of Monetary Economics 54 (September): 79-99.
Konieczny, Jerzy D. and Andrzej Skrzypacz (2005), "Inflation and Price Setting in a Natural Experiment," Journal of Monetary Economics 52 (April): 621-632.
Kovanen, A. (2006), "Why Do Prices in Sierra Leone Change so Often? A Case Study using Micro-level Price Data," International Monetary Fund Working Paper 06/53.
Kryvtsov, Oleksiy and Virgiliu Midrigan (2009), "Inventories, Markups, and Real Rigidities in Menu Cost Models," unpublished paper, Bank of Canada.
Kwapil, C., J. Baumgartner and J. Scharler (2005), "The Price-setting Behaviour of Austrian Firms: Some Survey Evidence," ECB Working Paper 464.
Lach, Saul and Daniel Tsiddon (1992), "The Behavior of Prices and Inflation: An Empirical Analysis of Disaggregated Price Data," Journal of Political Economy 100 (April): 349 - 389.
Lach, Saul and Daniel Tsiddon (1996), "Staggering and Synchronization in Price-Setting: Evidence from Multiproduct Firms," American Economic Review 86 (December): 1175 - 1196.
Levy, Daniel, Shantanu Dutta, Mark Bergen, and Robert Venable (1998), "Price Adjustment and Multiproduct Retailers," Managerial and Decision Economics 19: 81-120.
Levy, Daniel, Dongwon Lee, Haipeng (Allan) Chen, Robert J. Kauffman, and Mark Bergen (2007), "Price Points and Price Rigidity," Working Paper 04-07, The Rimini Center for Economic Analysis.
Loupias, C. and R. Ricart (2004), "Price Setting in France: New Evidence from Survey Data," ECB Working Paper 423.
Lünnemann, P. and T. Mathä (2005), "Consumer Price Behaviour in Luxembourg: Evidence from Micro CPI Data," ECB Working Paper 541.
Lünnemann, P. and T. Mathä (2006), "New Survey Evidence on the Pricing Behavior of Luxenbourg Firms," ECB Working Paper 617.
Mackowiak, Bartosz and Frank Smets (2008), "Implications of Micro Price Data for Macroeconomic Models," CEPR Discussion Paper 6961.
Mackowiak, Bartosz and Mirko Wiederholt (2008), "Business Cycle Dynamics Under Rational Inattention," unpublished paper, European Central Bank and Northwestern University.
Mankiw, N. Gregory, and Ricardo Reis (2002), "Sticky Information versus Sticky Prices: A Proposal to Replace the New Keynesian Phillips Curve," Quarterly Journal of Economics 117 (November), 1295-1328.
Martins, F. (2005), "The Price Setting Behavior of Portuguese Firms: Evidence from Survey Data," ECP Working Paper 562.
Medina, J. P., D. Rappoport, and C. Soto (2007), "Dynamics of Price Adjustment: Evidence from Micro Level Data for Chile," Central Bank of Chile Working Paper 432.
Midrigan, Virgiliu (2009), "Menu Costs, Multiproduct Firms, and Aggregate Fluctuations," unpublished paper, New York University.
Nakagawa, S., R. Hattori, and I. Takagawa (2000), "Price Setting Behavior of Japanese Companies," research paper, Bank of Japan.
Nakamura, Emi (2008), "Pass-Through in Retail and Wholesale," American Economic Review 98 (May): 430-437.
Nakamura, Emi and Jon Steinsson (2008a), "Five Facts About Prices: A Reevaluation of Menu Cost Models," Quarterly Journal of Economics 123 (November): 1415-1464.
Nakamura, Emi and Jon Steinsson (2008b), "Monetary Non-Neutrality in a Multi-Sector Menu Cost Model," NBER Working Paper 14001 (May).
Nakamura, Emi and Jon Steinsson (2009), "Lost in Transit: Product Replacement Bias and Pricing to Market," unpublished paper, Columbia University.
Peersman, Gert and Frank Smets (2003), "The Monetary Transmission Mechanism in the Euro Area: More Evidence from VAR Analysis," Monetary Policy Transmission in the Euro Area, Cambridge University Press: Cambridge, I. Angeloni, A. Kashyap, and B. Mojon, eds.
Romer, David H. and Christina D. Romer (2004), "A New Measure of Monetary Shocks: Derivation and Implications," American Economic Review 94 (September): 1055-1084.
Rotemberg, Julio J. (1982), "Monopolistic Price Adjustment and Aggregate Output," Review of Economic Studies, 49 (October): 517-531.
Sabbatini, R., S. Fabiani, A. Gatulli, and G. Veronese (2006), "Producer Price Behaviour in Italy: Evidence From Micro PPI Data," unpublished paper, Banca d'Italia.
Sahinoz, S. and B. Saracoglu (2008), "Price Setting Behaviour in Turkish Industries: Evidence from Survey Data," Turkish Economic Association Discussion Paper 2008/3.
Saita, Y., I. Takagawa, K. Nishizaki, and M. Higo (2006), "Price Setting in Japan: Evidence from Individual Retail Price Data," Bank of Japan Working Paper Series, No. 06-J-02, (in Japanese).
Stahl, H. (2005), "Price Setting in German Manufacturing: New Evidence from New Survey Data", Discussion Paper 43/2005, Deutsche Bundesbank.
Stahl, H. (2006), "Producer Price Adjustment at the Micro Level: Evidence from Individual Price Records Underlying the German PPI", unpublished paper, Deutsche Bundesbank.
Taylor, John B. (1980), "Aggregated Dynamics and Staggered Contracts," Journal of Political Economy 88 (February): 1-24.
Vermeulen, Philip, et al. (2007), "Price Setting in the Euro Area: Some Stylized Facts from Individual Producer Price Data," ECB Working Paper 727.
Veronese, G., S. Fabiani, , A. Gattulli, and R. Sabbatini (2006), "Consumer Price Setting in Italy," Giornale degli Economisti e Annali di Economia 65 (1).
Vilmunen, Juouko and H. Laakkonen (2005), "How Often Do Prices Change in Finland? Micro-level Evidence from the CPI," unpublished paper, Bank of Finland.
Wulfsberg, Fredrik (2009), "Price Adjustments and Inflation: Evidence from Consumer Price Data in Norway 1975-2004," Norges Bank WP 2009/11.
Woodford, Michael (2009), "Information-Constrained State-Dependent Pricing," unpublished paper, Columbia University (June).
| Country | Paper | Sample Period | Frequency ( in %) |
|---|---|---|---|
| Austria | Baumgartner et al. (2005) | 1996:01 − 2003:12 | 15.1 |
| Belgium | Aucremanne and Dhyne (2004) | 1989:01 − 2001:01 | 16.9 |
| Brazil | Barros et al. (2009) | 1996:03 − 2008:12 | 37.2 |
| Brazil | Gouvea (2007) | 1996:01 − 2006:12 | 37 |
| Canada | Harchaoui et al. (2008) | 1995:01 − 2006:12 | 28.1 |
| Chile | Medina et al. (2007) | 1999:01 − 2005:07 | 46.1 |
| Denmark | Hansen and Hansen (2006) | 1997:01 − 2005:12 | 17.3 |
| Euro Area | Dhyne et al. (2006) | 1996:01 − 2001:01 | 15.1 |
| Finland | Vilmunen and Laakkonen (2005) | 1997:01 − 2003:12 | 16.5 |
| France | Baudry et al. (2007) | 1994:07 − 2003:02 | 18.9 |
| Germany | Hoffmann and Kurz-Kim (2006) | 1998:02 − 2004:01 | 11.3 |
| Hungary | Gabriel and Reiff (2008) | 2001:12 − 2007:06 | 15.1 |
| Israel | Baharad and Eden (2004) | 1991:01 − 1992:12 | 24.5 |
| Italy | Veronese et al. (2006) | 1996:01 − 2003:12 | 10 |
| Japan | Saita et al. (2006) | 1999:01 − 2003:12 | 23.1 |
| Luxembourg | Lunnemann and Matha (2005) | 1999:01 − 2004:12 | 17 |
| Mexico | Gagnon (2009) | 1994:01 − 2004:12 | 29.4 |
| Netherlands | Jonker et al. (2004) | 1998:11 − 2003:04 | 16.5 |
| Norway | Wulfsberg (2009) | 1975:01 − 2004:12 | 21.3 (21.9) |
| Portugal | Dias et al. (2004) | 1992:01 − 2001:01 | 22.2 |
| Sierra Leone | Kovanen (2006) | 1999:01 − 2003:04 | 51.5 |
| Slovakia | Coricelli and Horvath (2006) | 1997:01 − 2001:12 | 34 |
| South Africa | Creamer and Rankin (2008) | 2001:12 − 2006:02 | 16 |
| Spain | Álvarez and Hernando (2006) | 1993:01 − 2001:12 | 15 |
| United States | Bils and Klenow (2004) | 1995:01 − 1997:12 | 26.1 |
| United States | Klenow and Kryvtsov (2008) | 1988:02 − 2005:01 | 29.9 (36.2) |
| United States | Nakamura and Steinsson (2008a) | 1988:01 − 2005:12 | 21.1 (26.5) |
| Country | Paper | Sample Period | Frequency (in %) |
|---|---|---|---|
| Belgium | Cornille and Dossche (2008) | 2001:01 − 2005:01 | 24 |
| Colombia | Julio and Zarate (2008) | 1999:06 − 2006:10 | 20.2 |
| Euro Area | Vermuelen et al. (2007) | Various | 21 |
| France | Gautier (2008) | 1994:01 − 2005:06 | 25 |
| Germany | Stahl (2006) | 1997:01 − 2003:09 | 22 |
| Italy | Sabbatini et al. (2006) | 1997:01 − 2002:12 | 15 |
| Portugal | Dias et al. (2004) | 1995:01 − 2001:01 | 23 |
| South Africa | Creamer (2008) | 2001:12 − 2006:02 | 19.5 |
| Spain | Álvarez et al. (2008) | 1991:01 − 1999:02 | 21 |
| United States | Nakamura-Steinsson (2008a) | 1988:01 − 2005:12 | 24.7 |
| Data Source | Paper | Sample Period | Frequency |
|---|---|---|---|
| Dominick's | Midrigan (2009) | 1989 − 1997 | 45 (23) |
| Dominick's | Burstein and Hellwig (2007) | 1989 − 1997 | 41 (26) |
| Large U.S. Retailer | Eichenbaum et al. (2009) | 2004 − 2006 | 43 |
| AC Nielsen ERIM Database | Campbell and Eden (2005) | 1985 − 1987 | 47 |
| AC Nielsen ERIM Database | Midrigan (2009) | 1985 − 1987 | 36 (25) |
| AC Nielsen ScanTrak | Nakamura (2008) | 2004 | 44 (19) |
| AC Nielsen Homescan | Broda and Weinstein (2007) | 1994 − 2003 | NA |
| Country | Paper | <1 | 1 | 2-3 | ≥4 | Median | Mean (in months) |
|---|---|---|---|---|---|---|---|
| Austria | Kwapil et al. (2005) | 24 | 51 | 15 | 11 | 1 | 12.7 |
| Belgium | Aucremanne and Druant (2005) | 18 | 55 | 18 | 8 | 1 | 11.9 |
| Canada | Amirault et al. (2006) | 8 | 27 | 23 | 44 | 2-3 | 6.8 |
| Estonia | Dabusinskas and Randveer (2006) | 14 | 43 | 25 | 18 | 1 | 10 |
| Euro Area | Fabiani et al. (2005) | 27 | 39 | 20 | 14 | 1 | 12.3 |
| France | Loupias and Ricart (2004) | 21 | 46 | 24 | 9 | 1 | 11.8 |
| Germany | Stahl (2005) | 44 | 14 | 21 | 21 | 1 | 13.5 |
| Italy | Fabiani et al. (2007) | 20 | 50 | 19 | 11 | 1 | 11.9 |
| Japan | Nakagawa et al. (2000) | 23 | 52 | 11 | 14 | 1 | 12.5 |
| Luxembourg | Lunnemann and Matha (2006) | 15 | 31 | 27 | 27 | 2-3 | 9 |
| Mexico | Castanon et al. (2008) | - | - | - | - | - | 5.7 |
| Netherlands | Hoeberichts and Stokman (2006) | 10 | 60 | 19 | 11 | 1 | 10.7 |
| Portugal | Martins (2005) | 24 | 51 | 14 | 12 | 1 | 12.7 |
| Romania | Copaciu et al. (2007) | - | - | - | - | - | 4.1 |
| Spain | Álvarez and Hernando (2007) | 14 | 57 | 15 | 14 | 1 | 11.1 |
| Sweden | Apel et al. (2005) | 29 | 43 | 6 | 20 | 1 | 12.7 |
| Turkey | Sahinoz and Saracoglu (2008) | - | - | - | - | - | 3 |
| United Kingdom | Hall et al. (2000) | 6 | 37 | 44 | 14 | 2-3 | 8.2 |
| United States | Blinder et al. (1998) | 10 | 39 | 29 | 22 | 1 | 8.8 |
| Posted Median | Posted Mean | Regular Median | Regular Mean | % of CPI | |
|---|---|---|---|---|---|
| All Items | 3.3 | 6.1 | 6.9 | 7.8 | 100.00% |
| Durable Goods | 1.8 | 3 | 1.8 | 5 | 22 |
| Nondurable Goods | 3.3 | 5.5 | 7.2 | 8 | 48.3 |
| Services | 7.5 | 9.2 | 7.5 | 9.5 | 29.7 |
| Raw Goods | 1 | 1.1 | 1 | 1.2 | 12.1 |
| Processed Goods | 4.3 | 6.7 | 7.6 | 8.7 | 87.9 |
| Apparel | 2.8 | 2.9 | 9.3 | 10.1 | 7.1 |
| Education and Communication | 5.5 | 5.6 | 5.5 | 5.7 | 7 |
| Food | 3.4 | 6.9 | 8.4 | 9.3 | 22.6 |
| Home Furnishings | 1.9 | 3.5 | 2 | 5.4 | 17.2 |
| Medical Care | 10 | 14.1 | 12.5 | 14.6 | 7.9 |
| Recreation | 6.3 | 7.5 | 9.4 | 9.8 | 8.6 |
| Transportation | 1.8 | 3 | 1.8 | 3.1 | 24 |
| Other Goods and Services | 8.6 | 14.8 | 12.1 | 16.7 | 5.5 |
| Durability | Cyclicality | |
|---|---|---|
| WLS of Frequency on the Posted Prices of All Items | 0.57 | 3.16 |
| WLS of Frequency on the Posted Prices of All Items Standard Errors | (0.69) | (1.07) |
| WLS of Frequency on the Regular Prices of All Items | 0.47 | 3.72 |
| WLS of Frequency on the Regular Prices of All Items Standard Errors | (0.72) | (1.09) |
| WLS of Frequency on the Posted Prices of Processed Items | 1.44 | 3.23 |
| WLS of Frequency on the Posted Prices of Processed Items Standard Errors | (0.41) | (0.59) |
| WLS of Frequency on the Regular Prices of Processed Items | 1.4 | 3.75 |
| WLS of Frequency on the Regular Prices of Processed Items Standard Errors | (0.39) | (0.49) |
Table 7
U.S. CPI Price Durations under Various Exclusions
| Case | Implied Median Duration | Implied Mean Duration |
|---|---|---|
| Posted Prices | 3.3 months | 6.1 months |
| No V Shapes | 5 | 6.9 |
| Like Prices | 5.9 | 7.1 |
| Regular Prices | 6.9 | 7.8 |
| No Substitutions | 8.1 | 9.9 |
| Adjacent Prices | 8.9 | 11 |
| 1988-1997 Posted | 3.6 | 6.1 |
| 1998-2009 Posted | 3.3 | 6.4 |
No V shapes: lower middle prices are replaced with identical neighbors.
Like prices: regular (sale) price is compared only to the previous regular (sale) price.
Regular prices: posted prices excluding sale prices.
No substitutions: only regular prices in between item substitutions are compared.
Adjacent prices: only consecutive monthly regular prices in between substitutions.
1988−1997 only: sample is confined to 1988−1997 (posted prices).
1998−2009 only: sample is confined to 1998−2009 (posted prices).
| Top Price | Top 2 Price | Top 3 Price | Top 4 Price | # of Quotes | |
|---|---|---|---|---|---|
| Median for All Items | 31.5 | 51.0 | 62.9 | 70.2 | 50 |
| Mean for All Items | (37.6) | (53.3) | (61.4) | (66.2) | (53.0) |
| Median for Apparel | 36.7 | 58.3 | 71.4 | 79.0 | 38 |
| Mean for Apparel | (41.3) | (59.9) | (70.5) | (77.1) | (41.3) |
| Median for Education and Communication | 29.4 | 47.5 | 61.3 | 72.7 | 42 |
| Mean for Education and Communication | (33.3) | (50.2) | (61.6) | (69.2) | (52.4) |
| Median for Food | 42.4 | 66.7 | 79.3 | 85.5 | 52 |
| Mean for Food | (47.0) | (66.6) | (76.3) | (81.3) | (51.8) |
| Median for Home Furnishings | 24.1 | 40.5 | 50.0 | 56.9 | 56 |
| Mean for Home Furnishings | (30.6) | (43.6) | (50.6) | (54.8) | (63.0) |
| Median for Medical Care | 48.9 | 72.3 | 82.6 | 88.0 | 50 |
| Mean for Medical Care | (53.3) | (71.2) | (79.0) | (84.1) | (49.6) |
| Median for Recreation | 40.5 | 64.9 | 77.7 | 85.2 | 49 |
| Mean for Recreation | (46.3) | (65.5) | (75.5) | (81.2) | (49.0) |
| Median for Transportation | 16.3 | 28.6 | 38.0 | 46.2 | 49 |
| Mean for Transportation | (22.7) | (34.9) | (43.2) | (50.0) | (53.1) |
| Median for Other Goods and Services | 50.0 | 70.7 | 79.3 | 84.0 | 51 |
| Mean for Other Goods and Services | (54.1) | (68.6) | (74.7) | (78.3) | (52.6) |
| Median % | Mean % | S.D. % | Median Duration (Months) | |
|---|---|---|---|---|
| All Items | 84.2 | 78.5 | 41.0 | 10.6 |
| Apparel | 78.0 | 77.1 | 35.2 | 11.0 |
| Education and Communication | 92.9 | 83.1 | 57.4 | 7.9 |
| Food | 88.1 | 82.1 | 27.2 | 13.6 |
| Home Furnishings | 81.8 | 77.9 | 47.0 | 6.9 |
| Medical Care | 100.0 | 93.7 | 27.1 | 18.8 |
| Recreation | 92.6 | 87.5 | 36.3 | 15.0 |
| Transportation | 62.5 | 64.2 | 70.6 | 6.1 |
| Other Goods and Services | 96.3 | 89.4 | 36.9 | 17.6 |
Table 10
Share of Prices that are "Novel" in Each U.S. CPI Quote-Line by Major Group
| Median | Mean | |
|---|---|---|
| All Items | 16.0 | 24.8 |
| Apparel | 21.2 | 26.2 |
| Education and Communication | 23.1 | 28.1 |
| Food | 10.4 | 13.9 |
| Home Furnishings | 23.5 | 35.7 |
| Medical Care | 6.7 | 8.2 |
| Recreation | 9.8 | 12.9 |
| Transportation | 34.7 | 38.1 |
| Other Goods and Services | 7.1 | 10.7 |
| Posted Price p | Regular Price p | Difference | |
|---|---|---|---|
| Variance relative to that of Posted Price p | 1 | 0.872 | 0.128 |
| Correlation with Posted Price p | 1 | 0.963 | 0.371 |
| Correlation with Posted Price p Standard Errors | (0.005) | (0.054) | |
| Serial Correlation | 0.395 | 0.418 | -0.074 |
| Serial Correlation Standard Errors | (0.053) | (0.052) | (0.062) |
| Cumulative Price Increase After 1 Year | 1.417 | 1.381 | 1.087 |
| Cumulative Price Increase After 1 Year Standard Errors | (0.294) | (0.291) | (0.170) |
| Posted Price p | Regular Price p | Difference | |
|---|---|---|---|
| Variance relative to that of Posted Price p | 1 | 0.917 | 0.083 |
| Correlation with Posted Price p | 1 | 0.979 | 0.304 |
| Correlation with Posted Price p Standard Errors | (0.005) | (0.100) | |
| Serial Correlation | 0.165 | 0.134 | -0.016 |
| Serial Correlation Standard Errors | (0.107) | (0.108) | (0.110) |
| Posted Price p | Reference Price p | Difference | |
|---|---|---|---|
| Variance relative to that of Posted Price p | 1 | 0.448 | 0.552 |
| Correlation with Posted Price p | 1 | 0.685 | 0.743 |
| Correlation with Posted Price p Standard Errors | (0.034) | (0.029) | |
| Serial Correlation | 0.4 | 0.454 | 0.133 |
| Serial Correlation Standard Errors | (0.054) | (0.051) | (0.063) |
| Cumulative Price Increase After 1 Year | 1.856 | 3.497 | 0.929 |
| Cumulative Price Increase After 1 Year Standard Errors | (0.272) | (0.383) | (0.163) |
| Posted Price p | Reference Price p | Difference | |
|---|---|---|---|
| Variance relative to that of Posted Price p | 1 | 0.573 | 0.427 |
| Correlation with Posted Price p | 1 | 0.813 | 0.658 |
| Correlation with Posted Price p Standard Errors | (0.038) | (0.064) | |
| Serial Correlation | 0.175 | 0.451 | -0.227 |
| Serial Correlation Standard Errors | (0.110) | (0.090) | (0.107) |