
A Comparison of Forecast Performance Between Federal Reserve Staff Forecasts, Simple Reduced-Form Models, and a DSGE Model
Keywords: Real time data, macroeconomic forecasting, Bayesian estimation, large-scale DSGE models
Abstract:
1 Introduction
This paper compares the forecasts of an estimated dynamic stochastic general equilibrium (DSGE) model with that of the Federal Reserve staff and reduced-form time-series models. The paper has three goals. First, much of the related literature has compared forecasts from DSGE models with simple reduced-form forecasting techniques: Our comparison with Federal Reserve staff forecasts provides a potentially more stringent test, given that previous research has shown the Federal Reserve staff forecast to be of high-quality relative to alternative methods.1 In addition, some of the research regarding DSGE models has found strong support for DSGE specifications using Bayesian measures of fit (such as posterior odds or marginal likelihoods); however, these measures can be dependent on the analyst's prior views and, as emphasized by Sims [2003], often appear too decisive. Given this concern, we focus on out-of-sample forecast performance.2 Finally, we examine forecast performance for both top-line macroeconomic variables--that is, the state of the labor market, growth of Gross Domestic Product, inflation, and the federal funds rate--and for detailed subcategories of aggregate expenditure--that is, consumption of nondurables and services and investment in consumer durables, residential capital, and business capital. This detailed focus is not common in DSGE models, which typically lump several of these categories into one broad category; however, policymakers have expressed interest in such details (see, for example, Kohn [2003]), and large macroeconometric models like the Federal Reserve's FRB/US model often produce forecasts at similar, or even more disaggregated levels.
Our DSGE model is the result of the Federal Reserve Board's project on Estimated, Dynamic, Optimization-based models; that is, the Edo model. This model contains a rich description of production, expenditure, labor supply, and pricing decisions for the economy of the United States. We have presented detailed descriptions of the model's structure, our estimation strategy, and results in previous papers (see Edge et al. [2008] and Edge et al. [2007a]) and so we present only a brief summary of the model's structure in section 2. For now, we simply highlight that the model has been designed to address a broad range of policy questions, as emphasized in Edge et al. [2008]. For example, Gali and Gertler [2007] discuss two important contributions of DSGE models to monetary policy analysis: microeconomic foundations for economic dynamics merged with rational expectations for economic agents, and the role of fluctuations in natural rates of output and interest in policy determination. The Edo model has been used to analyze these issues, especially the latter, in Edge et al. [2008]. We have also investigated the fluctuations in the U.S. housing market, which have been considerable over the past decade, using the Edo model (see Edge et al. [2007b]). Importantly, we use the same model in this other research as in the forecasting analysis herein. While many academic investigations will consider specific models that are designed to address individual questions, the large number and broad range of questions that arise under significant time pressures within a policy institution require that the core models used for policy work be capable of spanning multiple questions. Indeed, Meyer [1997] emphasizes the multiple roles of macroeconomic models in policymaking and private-sector consulting work, of which forecasting is but one example.
Our period of analysis spans macroeconomic developments in the United States from mid-1996 to late-2004 (where the end-point is determined by the public availability of data for forecast evaluation at the time of this study). This period was chosen for two reasons. First, the Federal Reserve's FRB/US model--a macroeconometric model specified with a neoclassical steady state and dynamic behavior designed to address the Lucas critique through consideration of the influence of expectations and other sources of dynamics--entered operation in mid-1996. As we aim to compare a cutting-edge DSGE model with existing practices at the Federal Reserve (and, to some extent, at other central banks), we focus on the period over which current practices have been employed. Second, the structure of our DSGE model--which, as discussed below, has two production sectors that experience "slow" and "fast" productivity growth--requires detailed data for estimation, and we have available the relevant "real-time" data since about mid-1996.
Of course, the period we examine is also interesting for several economic reasons. Between 1996 and 2004, the U.S. economy experienced substantial swings in activity. From 1996 to early 2000, economic growth was rapid and inflation was low--the "Goldilocks" economy as dubbed by Gordon [1998]. A recession followed in 2001 and, while the recession was brief, the labor market was slow to recover (see Langdon et al. [2004]). Our analysis over this period allows an examination of the success of our model and other techniques at capturing this business cycle. Inflation developments were also significant during this period. For example, the Federal Open Market Committee highlighted the risk of an unwelcome fall in inflation in the spring of 2003, as the rate of change in the consumer price index excluding food and energy prices dropped to around 1 percent that year when measured on a real-time basis. Price inflation stepped up after 2003.
Our analysis yields support to the notion that a richly-specified DSGE model can contribute to the forecasting efforts at policy institutions. We find that the forecast accuracy of the Edo model is as good as, and in many cases better than, that of the forecasts of the Federal Reserve staff and the FRB/US model or projections from time-series methods.
We should emphasize one important caveat to these conclusions. While we base our forecasts on data available in "real-time" to place these forecasts on equal footing with the Greenbook and FRB/US model forecasts, the forecasts from the vector autoregressions and Edo are not truly real time since we have carried out the analysis retrospectively. As a result, we have been able, for example, to check that all of our codes are correct and that our data is correct. Moreover, we have also benefited, at least indirectly, from our previous research and that of others on what types of models are likely to explain the data. It is impossible to purge our analysis of these influences. In fact, some of this potential "advantage" to our ex-post real-time exercise is apparent in our discussion of the amendments to our original DSGE model that we intend to implement in response to this analysis; as detailed in the analysis that follows, we can identify periods when our DSGE model performed poorly and we have identified changes to our model's specification that would result in better ex-post fits to the data. For these reasons, we are cautious in our final verdict.
Before turning to our analysis, we would like to highlight several pieces of related research. Smets and Wouters [2007] demonstrated that a richly-specified DSGE model could fit the U.S. macroeconomic data well and provide out-of-sample forecasts that are competitive or superior to reduced-form vector-autoregressions. We build on their work in several ways. First, our model contains a more detailed description of sectoral production and household/business expenditure decisions--which, as noted earlier, appears to be a prerequisite for a policy-relevant model. Second, we measure all economic variables in a manner more consistent with the official statistics published by the U.S. Bureau of Economic Analysis (the statistics that form the basis of policy deliberations and public discussion of economic fluctuations), whereas in contrast, Smets and Wouters [2007] make adjustments to published figures on consumption and investment in order to match the relative price restrictions implied by their one-sector model. Finally, and most importantly, we examine out-of-sample forecast performance using real-time data and compare our DSGE model's forecast performance with Federal Reserve staff forecasts and models, thereby pushing further on the question of whether DSGE models can give policy-relevant forecast information.
Research by Adolfson et al. [2007] is closely related to our analysis. These authors compare the forecast performance of the DSGE model of the Riksbank to Bayesian vector autoregression (BVAR) models and, like our analysis, central bank forecasts. However, these authors do not use real-time data, and they do not compare their DSGE model to another "structural" model as we do to the pre-existing FRB/US model. Finally, our focus on U.S. data and Federal Reserve forecasts is of independent interest given previous analyses of the quality of the Federal Reserve's forecasts (see Romer and Romer [2000] and Sims [2002]).
Other relevant research includes Lees et al. [2007], who compare the forecast performance of the Reserve Bank of New Zealand's official forecasts with those from a vector-autoregressive model informed by priors from a DSGE model as suggested in Del Negro and Schorfheide [2004]. Our analysis shares the idea of comparing forecasts to staff forecasts at a central bank; such a comparison seems especially likely to illuminate the relevance of such techniques for policy work. However, we focus on forecasts from a DSGE model rather than those informed by a DSGE prior. The latter approach is something of a "black-box", as the connection of the DSGE structure to the resulting forecast is tenuous (and asymptotically completely absent, as the data dominate the prior). Moreover, our reliance on a DSGE model directly allows us to make economically interesting inferences regarding the aspects of the model that contribute to its successes and failures. Finally, Lees et al. [2007] examine a very small set of variables--specifically, output, inflation, and the policy interest rate. Our experience with larger models like FRB/US at the Federal Reserve suggests that such small systems are simply not up to the challenge of addressing the types of questions demanded of models at large central banks (as we discuss in Edge et al. [2008]).
Adolfson et al. [2006] and Christoffel et al. [2007] examine out-of-sample forecast performance for DSGE models of the Euro area. Their investigations are very similar to ours in directly considering a fairly large DSGE model. However, the focus of each of these pieces of research is on technical aspects of model evaluation. We eschew this approach and instead attempt to identify the economic sources of the successes and failures of our model. Also, neither of these studies uses real-time data, nor do they compare forecast performance to an alternative model employed at a central bank or official staff forecasts. As discussed, we focus on real-time data and compare forecast performance to the FRB/US model and Federal Reserve Greenbook forecasts. Overall, we view both Adolfson et al. [2006] and Christoffel et al. [2007] as complementary to our analysis, but feel that the explicit comparison to "real-world" central bank practices is especially valuable.
The paper is organized as follows. Section 2 provides an overview of the Edo model. Section 3 discusses the estimation and evaluation of both the Edo model as well as the alternative forecasting models used in the paper's analysis. Section 4 introduces the alternative forecasts that the paper considers: We focus on our DSGE model (Edo) forecasts, the Federal Reserve Board's staff projections, including those from the FRB/US model, and the forecasts from autoregressions and vector autoregessions. We also discuss our real-time data in the fourth section. Section 5 presents the comparison between Edo and time-series models. Section 6 examines the Federal Reserve forecasts and subsample results that illustrate important economic successes and failures of our model. We discuss amendments to our DSGE model that address some of these failures and hence provide an example of the type of lesson for structural modelers that can be gleaned from forecast exercises. Section 7 concludes and points to directions for future research.
2 A Two-Sector DSGE Model for Forecasting
Research on policy applications of dynamic, stochastic, general-equilibrium (DSGE) models has exploded in the last five years. On the policy front, the GEM project at the International Monetary Fund (see Bayoumi et al. [2004]) and the SIGMA project at the Federal Reserve (see Erceg et al. [2006]) have provided examples of richly-specified models with firm microeconomic foundations that can be applied to policy questions. However, even these rich models have not had the detail on domestic economic developments, such as specifications of highly disaggregated expenditure decisions, to address the range of questions typically analyzed by large models like the Federal Reserve's FRB/US model.3 The Estimated, Dynamic, Optimization-based (Edo) model project at the Federal Reserve has been designed to build on earlier work at policy institutions, as well as academic research such as Smets and Wouters [2007] and Altig et al. [2004], by expanding the modeling of domestic economic decisions while investigating the ability of such DSGE models to examine a range of policy questions. For a detailed description and discussion of previous applications, the reader is referred to Edge et al. [2008], Edge et al. [2007a], and Edge et al. [2007b].
Figure 1 provides a graphical overview of the economy described by the Edo model. The model possesses two final goods (good "CBI" and good "KB", described more fully below), which are produced in two stages by intermediate- and then final-goods producing firms (shown in the center of the figure). On the model's demand-side, there are four components of private spending (each shown in a box surrounding the producers in the figure): consumer nondurable goods and services (sold to households), consumer durable goods, residential capital goods, and non-residential capital goods. Consumer nondurable goods and services and residential capital goods are purchased (by households and residential capital goods owners, respectively) from the first of economy's two final goods producing sectors (good "CBI" producers), while consumer durable goods and non-residential capital goods are purchased (by consumer durable and residential capital goods owners, respectively) from the second sector (good "KB" producers). We "decentralize" the economy by assuming that residential capital and consumer durables capital are rented to households while non-residential capital is rented to firms. In addition to consuming the nondurable goods and services that they purchase, households also supply labor to the intermediate goods-producing firms in both sectors of the economy.
Our assumption of a two-sector production structure is motivated by the trends in certain relative prices and categories of real expenditure apparent in the data. Relative prices for investment goods, especially high-tech investment goods, have fallen and real expenditure on (and production of)
such goods has grown more rapidly than that for other goods and services. A one-sector model is unable to deliver long-term growth and relative price movements that are consistent with these stylized facts. As a result, we adopt a two-sector structure, with differential rates of technical progress
across sectors. These different rates of technological progress induce secular relative price differentials, which in turn lead to different trend rates of growth across the economy's expenditure and production aggregates. We assume that the output of the slower growing sector (denoted
![]() ) is used for consumer nondurable goods and services and residential capital goods and the output of a faster growing sector (denoted
) is used for consumer nondurable goods and services and residential capital goods and the output of a faster growing sector (denoted
![]() ) is used for consumer durable goods and non-residential capital goods, roughly capturing the long-run properties of the data.
) is used for consumer durable goods and non-residential capital goods, roughly capturing the long-run properties of the data.
While differential trend growth rates are the primary motivation for our disaggregation of production, our specification of expenditure decisions is related to the well-known fact that the expenditure categories that we consider have different cyclical properties (see Edge et al. [2008] for more details). Beyond the statistical motivation, our disaggregation of aggregate demand is motivated by the concerns of policymakers. A recent example relates to the divergent movements in household and business investment in the early stages of the U.S. expansion following the 2001 recession, a topic discussed in Kohn [2003]. We believe that providing a model that may explain the shifting pattern of spending through differential effects of monetary policy, technology, and preference shocks is a potentially important operational role for our disaggregated framework.
The remainder of this section provides an overview of the decisions made by each of the agents in our economy. Given some of the broad similarities between our model and others, our presentation is selective.
2.1 The Intermediate Goods Producer's Problem
We begin our description in the center of figure 1. Intermediate goods producers in both sectors (specifically, sector "![]() " and sector "
" and sector "![]() ") produce output using a production technology that yields output (denoted
") produce output using a production technology that yields output (denoted
![]() ) from labor input,
) from labor input,
![]() , capital input,
, capital input,
![]() where the superscript "
where the superscript "![]() " denotes utilized capital and the
superscript "
" denotes utilized capital and the
superscript "![]() " indicates nonresidential capital, and economy-wide and sector-specific productivity,
" indicates nonresidential capital, and economy-wide and sector-specific productivity, ![]() , and
, and ![]() .4 Specifically,
.4 Specifically,
Note that labor input is a Dixit-Stiglitz aggregate of differentiated labor inputs; this assumption will be an input in the wage Phillips curve discussed below.
The exogenous productivity terms contain a unit root, that is, they exhibit permanent movements in their levels. We assume that the stochastic processes ![]() and
and
![]() evolve according to
evolve according to
where
where
Each intermediate-good producers' output enters a final-goods production technology for its sector that takes the form of the Dixit-Stiglitz aggregator. As a result, intermediate goods producers are monopolistic competitors. We further assume that the intermediate goods producers face a
quadratic cost of adjusting the nominal price they charge. Consequently, an intermediate goods producing firm chooses the optimal nominal price (and the quantity it will supply consistent with that price), taking as given the marginal cost,
![]() , of producing a unit of output,
, of producing a unit of output,
![]() , the aggregate price level for its sector,
, the aggregate price level for its sector, ![]() , and households'
valuation of a unit of nominal rental income in each period,
, and households'
valuation of a unit of nominal rental income in each period,
![]() , to solve:
, to solve:
The profit function reflects price-setting adjustment costs (the size which depend on the parameter
The constraint against which the firm maximizes its profits is the demand curve it faces for its differentiated good, which derives from the final goods producing firm's cost-minimization problem. Of particular importance for our estimation strategy and forecasting analysis is the parameter
![]() , the stochastic elasticity of substitution between the differentiated intermediate goods inputs used in the production of the consumption or capital goods sectors. We assume
that
, the stochastic elasticity of substitution between the differentiated intermediate goods inputs used in the production of the consumption or capital goods sectors. We assume
that
where
A lengthier treatment of the structure of our model is provided in Edge et al. [2007a], which further details the cost-minimization problem facing intermediate goods producers in choosing the optimal mix of factors of production. This problem determines the factors influencing marginal cost and hence pricing. At this point, we emphasize that the production and pricing decisions of the intermediate goods firms in our model economy are influenced by four "aggregate supply" shocks: two productivity shocks, corresponding to economy-wide and capital-specific technology shocks, and two markup shocks that induce transitory fluctuations in the nominal prices in each sector.
2.2 The Capital Owner's Problem
We now shift from producers' decisions to spending decisions (that is, those by agents encircling our producers in figure 1). Non-residential capital owners choose investment in non-residential capital,
![]() , the stock of non-residential capital,
, the stock of non-residential capital,
![]() (which is linked to the investment decision via the capital accumulation identity), and the amount and utilization of non-residential capital in each production sector,
(which is linked to the investment decision via the capital accumulation identity), and the amount and utilization of non-residential capital in each production sector,
![]() ,
,
![]() ,
,
![]() , and
, and
![]() .5 (Recall, that production in
equation 1 depends on utilized capital
.5 (Recall, that production in
equation 1 depends on utilized capital
![]() .) This decision is described by the following maximization problem (in which the rental rate on non-residential capital,
.) This decision is described by the following maximization problem (in which the rental rate on non-residential capital,
![]() , the price of non-residential capital goods,
, the price of non-residential capital goods,
![]() , and households' valuation of nominal capital income in each period,
, and households' valuation of nominal capital income in each period,
![]() are taken as given):
are taken as given):
The parameter
The variable
The problems solved by the consumer durables and residential capital owners are slightly simpler than the nonresidential capital owner's problems. Because utilization rates are not variable for these types of capital, their owners make only investment and capital accumulation decisions. Taking
as given the rental rate on consumer durables capital,
![]() , and the price of consumer-durable goods,
, and the price of consumer-durable goods,
![]() , and households' valuation of nominal capital income,
, and households' valuation of nominal capital income,
![]() , the capital owner chooses investment in consumer durables,
, the capital owner chooses investment in consumer durables,
![]() , and its implied capital stock,
, and its implied capital stock,
![]() , to solve:
, to solve:
The residential capital owner's decision is analogous:
The notation for the consumer durables and residential capital stock problems parallels that of non-residential capital. In particular, the capital-efficiency shocks,
We emphasize two points related to capital accumulation. First, capital accumulation is subject to adjustment costs, and hence investment responds slowly to many shocks. In addition, the "capital accumulation technologies" are themselves subject to efficiency shocks. These three shocks to the efficiency of investment--business investment, residential investment, and investment in consumer durables--enter the optimality conditions driving investment decisions as shocks to the "intertemporal IS curves."
2.3 The Household's Problem
The final private agent in the model that we will discuss is the representative household, which makes both expenditures and labor-supply decisions. The household derives utility from four sources: its purchases of the consumer non-durable goods and non-housing services, the flow of services from its rental of consumer-durable capital, the flow of services from its rental of residential capital, and its leisure time, which is equal to what remains of its time endowment after labor is supplied to the market. Preferences are separable over all arguments of the utility function.
The utility that the household derives from the three components of goods and services consumption is influenced by its habit stock for each of these consumption components, a feature that has been shown to be important for consumption dynamics in similar models. A household's habit stock for
its consumption of non-durable goods and non-housing services is equal to a factor ![]() multiplied by its consumption last period
multiplied by its consumption last period
![]() . Its habit stock for the other components of consumption is defined similarly.
. Its habit stock for the other components of consumption is defined similarly.
The household chooses its purchases of consumer nondurable goods and services,
![]() , the quantities of residential and consumer durable capital it wishes to rent,
, the quantities of residential and consumer durable capital it wishes to rent, ![]() and
and
![]() , its holdings of bonds,
, its holdings of bonds, ![]() , its wage for each sector,
, its wage for each sector,
![]() and
and
![]() , and supply of labor consistent with each wage,
, and supply of labor consistent with each wage,
![]() and
and
![]() . This decision is made subject to the household's budget constraint, which reflects the costs of adjusting wages and the mix of labor supplied to each sector, as well as the demand
curve it faces for its differentiated labor. Specifically, the household solves:
. This decision is made subject to the household's budget constraint, which reflects the costs of adjusting wages and the mix of labor supplied to each sector, as well as the demand
curve it faces for its differentiated labor. Specifically, the household solves:
In the utility function the parameter ![]() is the household's discount factor,
is the household's discount factor, ![]() denotes its inverse labor supply elasticity, while
denotes its inverse labor supply elasticity, while
![]() ,
,
![]() ,
,
![]() , and
, and
![]() are scale parameter that tie down the ratios between the household's consumption components. The stationary, unit-mean, stochastic variables
are scale parameter that tie down the ratios between the household's consumption components. The stationary, unit-mean, stochastic variables
![]() ,
,
![]() ,
,
![]() , and
, and
![]() represent aggregate shocks to the household's utility of its consumption components and its disutility of labor.
represent aggregate shocks to the household's utility of its consumption components and its disutility of labor.
Letting
![]() denote the log-deviation of
denote the log-deviation of
![]() from its steady-state value of unity, we assume that
from its steady-state value of unity, we assume that
The variable
The household's budget constraint reflects wage setting adjustment costs, which depend on the parameter ![]() and the lagged and steady-state wage inflation rate. These costs, and the
monopoly power enjoyed by household's in the supply of differentiated labor input to intermediate goods producers as discussed above, yield a wage Phillips curve much like the price Phillips curve discussed previously. In addition, there are costs in changing the mix of labor supplied to each
sector, which depend on the parameter
and the lagged and steady-state wage inflation rate. These costs, and the
monopoly power enjoyed by household's in the supply of differentiated labor input to intermediate goods producers as discussed above, yield a wage Phillips curve much like the price Phillips curve discussed previously. In addition, there are costs in changing the mix of labor supplied to each
sector, which depend on the parameter ![]() . These costs incurred by the household when the mix of labor input across sectors changes may be important for sectoral comovements.
. These costs incurred by the household when the mix of labor input across sectors changes may be important for sectoral comovements.
In summary, the household's optimal decisions are influenced by four structural shocks: shocks to the utility associated with nondurable and services consumption, durables consumption, housing services, and labor supply. The first three affect "intertemporal IS curves" associated with consumption choices, while the last enters the intratemporal optimality condition influencing labor supply.
2.4 Monetary Authority
We now turn to the last important agent in our model, the monetary authority. It sets monetary policy in accordance with an Taylor-type interest-rate feedback rule. Policymakers smoothly adjust the actual interest rate ![]() to its target level
to its target level
![]()
where the parameter
In equation (13),
2.5 Measuring Aggregate Output
We have focused on sectoral production decisions so far and have not yet discussed Gross Domestic Product (GDP). The growth rate of real GDP is defined as the Divisia (share-weighted) aggregate of final spending in the economy, as given by the identity:
In equation (14),
Stationary unmodeled output is exogenous and is assumed to follow the process:
The inflation rate of the GDP deflator, represented by
![]() , is defined implicitly by:
, is defined implicitly by:
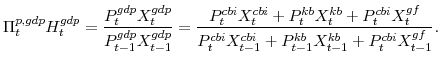
2.6 Summary
Our presentation of the model has been brief. However, it has highlighted that our model, although it considers production and expenditure decisions in a bit more detail, shares many features with other DSGE models in the literature, including imperfect competition, nominal price and wage rigidities, and real frictions like adjustment costs and habit persistence. The rich specification of structural shocks (to productivity, preferences, capital efficiency, and mark-ups) and adjustment costs allows our model to be brought to the data with some chance of finding empirical validation.
While the fluctuations in economic variables within Edo reflect complex interactions between the large set of decisions made within the economy, we would also highlight a couple of structural features that may play an important role in its forecast performance. First, the model assumes a stochastic structure for productivity shocks in each sector that allows for important business-cycle frequency fluctuations in technology. This view contrasts significantly with the view in early versions of the FRB/US model, where technology was modeled as a linear time trend with breaks. More recent versions of the FRB/US model have allowed for more variation in "trend" total factor productivity, but the structure of the FRB/US model is not embedded in the tradition started by Kydland and Prescott [1982] and, as a result, the role of technology in fluctuations--and forecasts--of economic activity may be quite different between Edo and models or forecasting techniques similar to those embedded in the FRB/US model.
In addition, the Edo model summarizes the state of the "labor market" through the behavior of hours per capita. Policy discussions will often highlight distinctions between employment and hours per worker and between employment and unemployment. We view extensions of the Edo model along these dimensions as interesting topics for future research. For now, we simply note that, over the period from the mid-1980s through 2004, the correlation between hours per capita and the unemployment rate (using currently published data) exceeded 0.85, suggesting that our focus on hours per capita provides a reasonable first step in examining the ability of the model to capture the state of the labor market, broadly interpreted. That said, we acknowledge that the ability of the model to adequately address the welfare implications of changes in unemployment is more open to question.
Finally, we would emphasize that the behavior of prices and wages in the Edo model is governed by versions of "New-Keynesian" price and wage Phillips curves. There has been a spirited debate over the empirical performance of such specifications (see Kiley [2007], Laforte [2007], and Rudd and Whelan [2007]).
3 Estimation and Evaluation of the DSGE and other models
Before turning to our "real-time" forecast exercise, it is instructive to consider an evaluation of the DSGE model that focuses on within sample fit because such metrics have dominated recent research (see Smets and Wouters [2007]). We focus on the marginal likelihood for the DSGE model and some time-series alternatives.
The DSGE model is estimated using (twelve) economic time series for the United States:
- Real gross domestic product;
- Real consumption expenditure on nondurables and services;
- Real consumption expenditure on durables;
- Real residential investment expenditure;
- Real business investment expenditure, which equals real gross private domestic investment minus real residential investment;6
- GDP price inflation;
- Inflation for consumer nondurables and services;
- Inflation for consumer durables;
- Hours, which equals hours of all persons in the non-farm business sector;7
- Real wage inflation, which equals the percent change in compensation per hour in the non-farm business sector deflated by the price level for consumer nondurables and services;
- The federal funds rate;
- The yield on the ten-year U.S. Treasury Note.
As is the standard practice, we estimate a log-linearized approximation to our model, which we cast in its state space representation for the set of (in our case 12) observable variables listed above. We then use the Kalman filter to evaluate the likelihood of the observed variables, and form
the posterior distribution of the parameters of interest by combining the likelihood function with a joint density characterizing some prior beliefs over parameters. Since we do not have a closed-form solution of the posterior, we rely on Markov-Chain Monte Carlo (MCMC) methods. We also add
measurement errors processes, denoted ![]() , for all of the observed series used in estimation except the nominal interest rate and the aggregate hours series.
, for all of the observed series used in estimation except the nominal interest rate and the aggregate hours series.
Our estimation results depend upon our specification of priors and calibration of certain parameters. We use the same priors and calibration strategy for our full-sample estimation and for the out-of-sample forecast exercises we present below. A number of parameters are calibrated and held fixed
throughout. As reported in table 1, we fix the household's discount factor (![]() ), the Cobb-Douglas share of capital input (
), the Cobb-Douglas share of capital input (![]() ), the curvature parameter associated with costs of varying capital utilization (
), the curvature parameter associated with costs of varying capital utilization (![]() ), the depreciation rates
(
), the depreciation rates
(
![]() ,
,
![]() ,
,
![]() ), and the elasticities of substitution between differentiated intermediate goods and labor input (
), and the elasticities of substitution between differentiated intermediate goods and labor input (
![]() ,
,
![]() ,
,
![]() ). Forecast performance is not very sensitive to reasonable (small) variation in these parameters. To some extent, our specifications of priors and (to a lesser degree) our
calibrations of certain parameters are yet another reason why, as discussed in section 1, our analysis is not strictly real time. Specifically, it is likely that some of our priors and calibrations are informed by research undertaken previous to this study but after the reference date of our
real-time DSGE model forecast (and therefore may be based on subsequently available data). This contamination of the pure real-time forecasting exercise will likely allow the DSGE model forecast to perform better than it would had it actually been undertaken at the forecast reference date.
Consequently, as discussed previously, some caution in interpreting our final results is warranted.
). Forecast performance is not very sensitive to reasonable (small) variation in these parameters. To some extent, our specifications of priors and (to a lesser degree) our
calibrations of certain parameters are yet another reason why, as discussed in section 1, our analysis is not strictly real time. Specifically, it is likely that some of our priors and calibrations are informed by research undertaken previous to this study but after the reference date of our
real-time DSGE model forecast (and therefore may be based on subsequently available data). This contamination of the pure real-time forecasting exercise will likely allow the DSGE model forecast to perform better than it would had it actually been undertaken at the forecast reference date.
Consequently, as discussed previously, some caution in interpreting our final results is warranted.
We also "calibrate", in real time, a number of parameters important for steady-state growth and inflation. Specifically, we set the steady-state rate of inflation for nondurable and services consumption equal to the average realized over the five years prior to the start of the forecast
period, and we estimate the steady-state rate of productivity growth in each sector to match the rate of growth of real GDP and real wages implied by the model to the corresponding values in the data from the fourth quarter of 1984 to the start of the forecast period. These choices determine the
parameters
![]() ,
,
![]() , and
, and
![]() . Therefore, these parameters vary as we move our forecast window foreword, but are not based on information from the relevant forecast period.
. Therefore, these parameters vary as we move our forecast window foreword, but are not based on information from the relevant forecast period.
The remainder of the model parameters are estimated in real-time.8 The priors placed over the model parameters are reported in table 2 and table 3. We highlight the following: the parameters governing habit persistence (![]() ,
, ![]() ,
, ![]() ) have prior distributions spanning the interval 0 to 1 that are centered on 0.5 and relatively uninformative; the
parameters determining the indexation or price and wage inflation to lagged inflation are centered on 0, consistent with the "theory" of the New-Keynesian Phillips curve that often implies no indexation (that is, indexation is typically added as an ad hoc adjustment to
fit the data); and, the parameters governing the autocorrelation in the structural shocks have prior distributions that span 0 to 1 and typically are centered on moderate to high degrees of persistence.9
) have prior distributions spanning the interval 0 to 1 that are centered on 0.5 and relatively uninformative; the
parameters determining the indexation or price and wage inflation to lagged inflation are centered on 0, consistent with the "theory" of the New-Keynesian Phillips curve that often implies no indexation (that is, indexation is typically added as an ad hoc adjustment to
fit the data); and, the parameters governing the autocorrelation in the structural shocks have prior distributions that span 0 to 1 and typically are centered on moderate to high degrees of persistence.9
In addition to the DSGE model, we consider a number of other reduced form models in our forecasting exercises below. Before turning to those exercises, the remainder of this section reports different measures of fit for our DSGE model and different specifications of (Bayesian) vector autoregressions (BVAR) in the twelve variables we consider. Given the relatively large size of our system, our BVAR follows the approach of Banbura et al. [2008] for the specification of the prior distribution over parameters.10 However, their prior distribution of the covariance matrix of the errors is improper, thereby making it impossible for us to compute the marginal likelihood. As an alternative for the model comparison exercise, we compute the marginal data density of a Bayesian VAR model using a Normal-Wishart prior distribution (as in Kadiyala and Karlsson [1997] and Fernandez-Villaverde and Rubio-Ramirez [2004]). The key difference between the two prior distributions is the characterization of the covariance matrix.
Table 4 reports the marginal likelihood of the DSGE model and Bayesian VAR models as well as the Akaike (AIC) and Schwarz (SIC) information criteria for different lag orders of the VAR model (all for the sample period 1984Q4 to 2004Q4). The Bayesian model comparison exercise indicates the DSGE model outperforms the BVAR models. The good performance of the structural model can be explained by the presence of measurement errors--in addition to structural shocks--in its state-space form representation. Despite some differences in the characterization of the prior distributions, we rely on these results to motivate our pick of a lag order of two for our subsequent out-of-sample forecasting analysis of BVAR models. For the VAR model the statistical criteria present a different take on the optimal lag order. The AIC prefers a more complex specification of the model while the SIC criterion favors a more parsimonious parametrization. These results are consistent with previous findings based on simulated and historical data (see Koehler and Murphree [1988]). Because the literature commonly suggests that the SIC is preferable, we have opted for a lag order of one in the case of the VAR model. This decision was also reinforced by the practical issue that the frequency of estimating a non-stationary system from OLS regressions increases with the lag length of the VAR specification. We turn now to an evaluation of out-of-sample forecast accuracy that focuses on the success in forecasting individual series may provide more information to help improve the model.
4 Alternative Forecasts
We compare the forecasts from our DSGE model with four alternatives: The Federal Reserve Board's staff's judgemental projection for FOMC meetings, commonly called the Greenbook projection, the FRB/US model projection, and two reduced form vector-autoregressive models.
4.1 The Greenbook Forecast
The first set of forecasts that we compare with our DSGE model projection are those produced by the staff at the Federal Reserve Board. The Federal Open Market Committee (FOMC) meets eight times a year at slightly irregularly spaced intervals. In the lead up to each of these meetings, the staff at the Board of Governors put together a detailed forecast of the economic outlook that is published (usually a bit less than a week before the FOMC meeting) in a document unofficially known as the Greenbook. The Greenbook forecast, which are most readily available on the web-site of the Federal Reserve Bank of Philadelphia, reflect the views of the staff and not the Committee members.
The maximum projection horizon for the Greenbook forecast vintages that we analyze in this paper vary from six to ten quarters. In September of each year, the staff extend the forecast to include the year following the next in the projection period. Since the third quarter is not yet finished at the time of the September forecast, that quarter is included in the Greenbook projection horizon, generating a maximum horizon of ten quarters. The end point of the projection horizon remains fixed for subsequent forecasts as the starting point moves forward. As a result, by the July/August forecast round of the following year the projection period extends out only six quarters. In our analysis, we consider a maximum forecast horizon of eight quarters because the number of observations for nine and ten quarters is very small. Note also that the nature of the Greenbook forecast horizon implies that the number of observations for a forecast horizon of eight quarters will be smaller than the number of observations for horizons of six quarters and less. Specifically, of the eight Greenbook projections prepared each year, only five--that is, those prepared for the September, November, December, January, and March FOMC meeting--include forecasts that extend for eight quarters. In contrast, all eight projections prepared each year include forecasts that extend six quarters or less. In the exercises that we undertake in section 5 (and present in tables 5 to 9), when comparing eight-quarter ahead projections, we only consider forecasts (and forecast errors) generated by the alternative models that correspond to the September, November, December, January, and March Greenbook. We also report the number of forecast observations that we are using in each case.
We use the forecasts produced for the FOMC meetings starting in September 1996 and ending in December 2002; this period includes the beginning of the period over which the FRB/US model (discussed below) has been employed. We choose December 2002 as the end point because Greenbook forecasts are made public only with a five-year lag, so forecasts through 2002 are the most recent vintage that is publicly available. An appendix provides detailed information on the dates of Greenbook forecasts we use and the horizons covered in each forecast. One important aspect of our analysis is that we link our forecast timing to the timing of FOMC meetings. As a result, we will compare eight forecasts a calendar year, and the "real-time" jumping off point for these forecasts is somewhat irregular. All of our model and forecast comparisons will use the databases employed by the Federal Reserve staff in "real-time;" this includes our comparison to time-series methods, which we can extend through forecasts generated with data available as of November 2004.
4.2 The FRB/US Model Forecast
The Greenbook projection is a judgmental projection that is derived from quantitative data, qualitative information, different economic models, and various forecasting techniques; it is not the output of any one model. The second set of forecasts that we compare with our DSGE model projection are those produced by the Federal Reserve's FRB/US model, which is one of the tools that is used as an input into the deliberations that lead to the Greenbook projection. These model forecasts are prepared at the same time as each Greenbook forecast is prepared and also have the same projection horizon as each Greenbook forecast. The FRB/US model forecast conditions on the same path for the federal funds rate used in the Greenbook projection, so all statistics related to the federal funds rate in our comparisons are identical between the Greenbook and FRB/US forecasts.
With regard to model structure, the FRB/US model differs significantly from Edo and similar DSGE models. First, while the FRB/US model's equations for most economic decisions are related to those based on explicit optimization like in Edo, ad hoc elements are introduced to the model to improve model fit in many cases. In addition, the specification of FRB/US has largely proceeded along an "equation-by-equation" route, with only a small role in estimation for full-model dynamics--a feature that has been criticized for an insufficient attention to system properties and econometric rigor (see Sims [2002] and Sims [2008]). Finally, expectations in forecasting exercises using FRB/US are not "rational" or "model-consistent," but instead are based upon least-squares projection rules estimated using data realizations over the last several decades.
4.3 Forecasts Generated by Reduced-form Models
We consider the forecasts generated by two variants of reduced-form vector-autoregressive (VAR) models. The first model is a one-lag VAR system in the twelve variables used to estimate Edo. The second model is a two-lag BVAR that introduces onto the coefficients a modified version of the dummy-observation prior outlined earlier. The key features of their specifications were motivated in section 3. We re-estimate these models each forecast.
Readers will likely recognize that the data in our model is released with different delays. For example, interest rate data are available daily and immediately while GDP--or more specifically, NIPA--data in the United States are first released about a month after a quarter ends. We do not account for these differences and we ignore any data pertaining to later periods that are available at the time of the the latest release of the quarterly GDP data.11 As a result, our information set in the estimation of the reduced-form models is, in this regard, sparser than the true real-time data actually used in the Federal Reserve staff forecasts.12
4.4 Generating Real Time Forecasts
An accurate comparison of the performance of different forecasts requires the use of real-time data. The Federal Reserve Board's Greenbook and FRB/US model projections are real-time forecasts as they are archived when the Greenbook forecast is closed.
Since March 1996 the staff have stored the Greenbook projection from each FOMC forecasting round in readable electronic databases that contain the level of detail needed for a rich DSGE model like Edo. Importantly for the purposes of this research, these databases also include historical data for the data series the staff forecast that extend back to about 1975. Because these databases were archived at the time that each particular Greenbook forecast was closed, the historical data from these databases represent the real-time data available to the staff at the time that they were preparing their forecast. Consequently, we estimate our DSGE and time-series models with historical data from these historical Greenbook databases, on the assumption that the Greenbook forecasts were generated using the same information set. Constructing real-time datasets on which to estimate our DSGE and atheoretic models simply involves pulling the relevant series, reported earlier in our description of the series used to estimate our DSGE model, from the Greenbook database. As with the reduced form models, we do not account for differences in model-data availability schedules such that the information set for estimating the DSGE model is sparser than the "real-time" data used in the Federal Reserve staff forecasts.
In principle, the construction of real-time forecasts from the DSGE model presents no additional difficulties. In practice, however, some issues arise. The DSGE model involves modeling the joint stochastic process followed by a large number of variables, which may improve the estimates of underlying structural parameters and hence forecast accuracy. In addition, the solution and estimation of the DSGE model is somewhat more involved than that associated with simple time series regressions (which can be estimated almost instantly in virtually any software package, including even simple spreadsheets). As a result, estimation in the DSGE model is performed using the real-time datasets once per year, specifically in the July/August round in which an annual rebenchmarking of the NIPA data takes place. This contrasts with the approach followed for the VAR forecasts, where re-estimation is performed for each forecast. Parameter estimates for Edo are then held constant for the forecasts generated in subsequent rounds until the following July/August, at which point the model is re-estimated using the four additional quarters of data.13 Note, however, that it is only the data used to estimate the model that remains constant across the forecasts for the year. The "jumping-off" period that is used for each forecast generated by the DSGE model is the staff's estimate of the last quarter of history taken from the corresponding Greenbook database.
We compute statistics on forecast accuracy by comparing the forecasts based on real-time data to the realizations of these series contained in the data's "first final" release.14
5 Comparison to Reduced-form Model Forecasts
We focus on two distinct sets of variables. The first are the "top-line" macroeconomic aggregates--specifically, the percent change in real GDP per capita, GDP price inflation, detrended hours per capita, and the federal funds rate. The second are the disaggregated categories of expenditure--the percent changes in real personal consumption expenditures on nondurables and services, real personal consumption expenditures on durables, real business investment, and real residential investment. We evaluate forecast accuracy along two dimensions, the absolute size of errors and the bias in errors. We measure the absolute size of errors using the root-mean-squared error (RMSE), while bias is measured by the mean average error. We use forecasts generated by an AR(2) model as the benchmark against which we compare our model forecasts; this serves as a challenging point of comparison given that univariate models have been documented by several authors to have more accurate forecasting ability than multivariate models (see D'Agostino et al. [2006], Marcellino et al. [2006], and Atkenson and Ohanian [2001]).
5.1 The Main Macroeconomic Aggregates
The main macroeconomic aggregates examined are real GDP growth, GDP price inflation, detrended hours per capita, and the federal funds rate. This set captures aggregate activity and is the focus of many small modeling efforts. In addition, the focus on this set of variables will link directly to some of the main macroeconomic developments over the 1996 to 2005 period.
5.1.1 Real GDP Growth
The first set of results presented in table 5 focus on the forecasts for real GDP growth. The line labeled AR(2) reports the RMSE at various forecast horizons (specifically, one through four quarters out and eight quarters out), in percentage points, for the forecast of the percent change in GDP per capita generated by the AR(2) model. The RMSEs equal about 1/2 percentage point (not an an annual rate). The remainder of the reported figures for GDP growth report the relative RMSEs for the other forecast methods; values below 1 indicate that the model performs better than AR(2) model. The relative RMSE for the DSGE/Edo model is below 1 at each reported horizon, although the only significant difference (at the 5 percent level) according to the Diebold and Mariano [1995] statistic is associated with the two-quarter ahead forecasts. (Note that at the one- to four-quarter ahead horizons there are 66 forecasts, despite the fact that our sample spans less than 10 years, because we produce forecasts on an FOMC meeting basis and there are eight FOMC meetings a year). The VAR(1) and BVAR(2) models tend to perform worse than the AR(2) at the reported horizons, with relative RMSEs exceeding 1; for both models, the difference at the initial horizon is statistically significant.
The results on bias for GDP growth are shown in the upper part of table 6 (where a positive value shown in the table, implies that a variable's forecast is over-predicting its realized value). The biases associated with each method are small, typically well below 0.1 percentage point (in absolute value), and are negative, indicating a general tendency by all forecast methods to under-predict real GDP growth.
5.1.2 GDP price inflation
The next set of results reported in table 5 focus on the forecasts for GDP prices. The line for the AR(2) indicates that the RMSE for GDP price inflation is about 0.25 percentage point at each horizon. The comparison across forecast methods indicates that the DSGE/Edo model, the VAR(1), and the BVAR(2) all tend to forecast worse than the AR(2) model, and these differences are statistically significant at horizons of three quarters or less. The DSGE/Edo model has slightly better relative RMSEs than the VAR methods.
The average biases for GDP price inflation, in table 6, are quite small and are mostly positive, indicating a tendency to over-predict inflation of the sample.
5.1.3 Hours per capita
As noted earlier, the state of the labor market in Edo is summarized by detrended hours worked per capita. And the state of the labor market is one side of the Federal Reserve's dual mandate of full employment and price stability, so the ability of the Edo model to forecast hours per capita, relative to the ability of other models, is an important metric for model evaluation. We focus on detrended hours per capita as it is the closest analogue in our model to a notion of slack, such as the deviation of the unemployment rate from its natural rate. As will be apparent, errors in forecasts of detrended hours per capita can stem from errors in estimates of the trend or in the forecast going forward.
The third set of lines in table 5 report the RMSE statistics related to detrended hours per capita. These errors are large, between 3 and 6 percentage points at the reported horizons. The large size of these errors reflects the real-time nature of the exercise: Historical data on hours per capita can be revised substantially, making forecasting difficult.
The remaining lines in the panel referring to hours per capita report the RMSE for the VAR(1), BVAR(2) and Edo models relative to the RMSE for the AR(2) model. Several results are apparent. First, the Edo model seems to perform better than the AR(2) almost uniformly, while the BVAR(2) has RMSEs essentially identical to the AR(2). The VAR(1) model performs a bit worse than the AR(2) beyond the two-quarter horizon. However, according to Diebold and Mariano [1995] test, none of the reported poorer performance of the alternative forecasts reported for hours per capita in table 5 are significant in the statistical sense.
Table 6 presents the bias of the each forecast of hours per capita. In all cases, the bias is positive and large--about 2 percentage points at the one-quarter horizon. The bias in the model forecasts over this period suggests that each of the forecasts tended to systematically overstate the "tightness" in the labor market over this period. In order to gauge whether the size of the bias and revisions in detrended hours per capita from revisions to trend are reasonable, it is useful to look at related statistics for estimates of the natural rate of unemployment (which has been studied more than hours). For example, the CBO's revision to its 1997Q1 estimate of the natural rate of unemployment (NAIRU) from the January 1997 estimate to the estimate of January 2008 is -0.7 percentage point from 5.8 to 5.1 percent (see Congressional Budget Office [1997] and Congressional Budget Office [2008]). An ordinary-least-squares regression of the unemployment rate on hours per capita yields a coefficient of 0.3; using this 0.3 coefficient to translate the revision in the CBO's natural rate into a revision for the trend in hours yields a figure around 2 percentage points (that is, 0.7/0.3), suggesting that the revision noted above (1.9 percentage points) and the bias statistics (2 percentage points at the one-quarter horizon) are reasonable. These results on detrended hours per capita highlight again the difficulty that detrending creates for gauging the state of the economy in monetary policy applications, a point forcefully emphasized by Orphanides and van Norden [2003].
5.1.4 The Federal Funds Rate
The final set of results reported in table 5 focus on the forecasts for the federal funds rate. The line for the AR(2) indicates that the RMSE for the federal funds rate is about 0.2 percentage point at the one-quarter horizon and rises to 0.6 percentage point at the eight-quarter horizon. The DSGE/Edo model performs worse than the AR(2) for horizons out to four quarters but only to a statistically significant degree, for the first two quarters. The VAR(1) model outperforms the AR(2) at short horizons, but its performance deteriorates at long horizons--where the VAR(1) RMSE exceeds that of the DSGE model.
5.2 Disaggregated Measures of Expenditure
Looking underneath aggregate GDP growth provides further insight into forecast performance. Policymakers are often interested in developments within individual sectors, such as the strength of business investment, the state of the housing market, or diverging trends in consumer and business spending (see Kohn [2003]).
We consider the forecast performance of the various methods under consideration for the percent changes in real personal consumption expenditures on nondurables and services, real personal consumption expenditures on durables, real business investment, and real residential investment in table 7. The structure of the reported statistics is the same as in table 5. We take away two summary points. First, the forecasts of the Edo DSGE model, as summarized by the RMSE, are more accurate than those of the AR(2), VAR(1) and BVAR(2) for the components of durables consumption and business investment at nearly all horizons and in some cases (especially for business investment) more accurate by large and statistically significant margins. Second, Edo has more difficulty forecasting residential investment than the other models over this period; we return to this finding in the next section.
5.3 Summary of Empirical Results
Overall, we have found that our DSGE model provides forecasts for activity and inflation that are competitive with those from univariate and multivariate time-series models for a broad range of variables. Nonetheless, the forecasts from our DSGE model, and from the multivariate VAR models, are most often not superior to forecasts from a univariate autoregression by a statistically significant margin even in those cases when the RMSEs are somewhat lower from these multivariate alternatives. As a result, it is not clear from these exercises whether our DSGE model provides information that would prove useful in a policy context. To address this question, the next section examines the policy-relevance question by comparing the accuracy of forecasts from our DSGE model relative to the accuracy of Federal Reserve staff forecasts.
6 Comparison to Federal Reserve Staff Forecasts
We now present the forecast performance of the Edo/DSGE model along with that of Federal Reserve staff forecasts and forecasts from the Federal Reserve's FRB/US model. We have two goals. First, a comparison to existing methods at the Federal Reserve is more policy relevant than a comparison to AR and (B)VAR forecasts, in part because Federal Reserve forecasts have not placed much weight on projections from these types of models. Second, we attempt to identify what features of our model or the data contribute to the successes and failures recorded by the Edo model along the forecast dimension from 1996 to 2004, with an eye toward future changes in specification or research projects that attempt to incorporate additional features into our DSGE framework in order to improve its forecast performance and its utility as a policy tool more generally. The public availability of Federal Reserve staff forecasts have led us to focus on comparisons of forecasts using data for FOMC meetings from September 1996 to December 2002.
6.1 Forecast Performance
Table 8 and 9 present statistics on forecast accuracy for the projections generated using the data from the September 1996 FOMC meeting to the December 2002 FOMC meeting.
With regard to the labor market, it is apparent that the staff projections in the Greenbook and from the FRB/US model for detrended hours per capita share the dominant feature reported earlier: The errors are very large, exceeding 3 percentage points even at the one-quarter horizon. As we emphasized earlier, this reflects the difficulty of detrending in "real-time."15 While the errors are uniformly large across methods, the forecast performance of the Edo model dominates that of the Greenbook and FRB/US model at all horizons.
The results for other measures of economic activity are also revealing. The forecast accuracy (in a RMSE sense) of Edo is better than the Greenbook projections for GDP growth (table 8), the growth of the components of consumption expenditures, and growth of business investment for nearly all horizons (table 9). However, few of these forecasts are better than the AR(2) forecast in the statistical sense (or, for that matter, from each other).16
The result that Edo (or AR(2) models) have similar or lower "real-time" out-of-sample RMSEs for many real activity measures may be surprising, especially at short horizons, where the Federal Reserve staff devote significant resources to assessing near-term developments (see Romer and Romer [2000] and Sims [2002]). We think this is a significant finding. As we have emphasized in previous work (for example, Edge et al. [2008]), the ability of a structural model like our DSGE model to tell economically meaningful stories can make such models more attractive in a policy context than time-series alternatives, and the additional result that forecast performance may be acceptable as well adds further support to the consideration of such tools.
It is also interesting to note that the Edo model and the Greenbook made large errors in their forecasts of residential investment, with the Edo model doing poorly relative to the Greenbook at the 8 quarter horizon. This performance will be one of the topics discussed in the next subsection.
Returning to table 8, the results for GDP price inflation continue to suggest that the Edo model is competitive with best practices. In particular, the Edo model has RMSEs for inflation that are lower than those of the Greenbook at some (that is, the one- and eight-quarter) horizons and greater than those of the Greenbook at other. Sims [2002] reported that the near-term inflation forecasts in the Greenbook were very good, so the competitive performance of the DSGE model even at such short horizons provides a signal that this type of model may provide valuable additional information in the inflation forecasts at the Federal Reserve. And such forecasts may be quite important: the dual mandate has price stability as one objective, and many discussions of monetary policy emphasize the importance of inflation forecasts in the setting of monetary policy.
Finally, the results for the federal funds rate show that the staff Greenbook projection is better than the Edo or AR(2) projections by a a large and statistically significant margin (with relative RMSEs around 0.7) for the period spanning the September 1996 to December 2002 Greenbooks. We will discuss this finding in the next subsection.
6.2 Implications
We interpret the entire set of results in three ways. First, the performance of Edo in explaining labor market developments seems competitive with other approaches. Nonetheless, the forecast errors for hours per capita are large and the bias has been significant over the 1996 to 2004 period. As a result, we view as a high priority efforts to model the labor market in a more nuanced way. Such efforts include an allowance for factors that may improve detrending--such as factors that allow for permanent shocks to households supply of hours that would be estimable via the Kalman filter and may reflect economic factors like demographics--as well as including in Edo model features (such as those considered by Gertler et al. [2008]) that allow for the adjustment of hours along both the intensive and extensive margins.
It is also interesting that the Edo model forecasts poorly the nominal federal funds rate, especially relative to the staff projections from the Federal Reserve. The performance relative to the Federal Reserve staff projection may reflect an information advantage; that is, that the staff has insight into the likely course of policy from interactions with policymakers. However, Edo also had a somewhat worse forecast performance for the federal funds rate than the VAR methods, and perusal of full-sample VAR parameter estimates suggests a possible reason: Lags of (log) hours per capita have sizable and statistically significant coefficients in a reduced-form (VAR-model) federal funds rate regression over our sample period, and this relationship appears tighter than that to real GDP growth. Such a relationship seems reasonable, since, as we emphasized earlier, the dual mandate of the Federal Reserve includes full employment, and hours per capita are the closest analogue in the first-generation of the Edo model to the deviation of unemployment from its natural rate. As a result of these findings, we have explored different policy-rule specifications and, in particular, we have emphasized the role for hours per capita in subsequent research (see Edge et al. [2007b]).
The most notable other aspect of the results for economic activity is the poor forecast performance for residential investment. The pace of growth in residential investment over 2001 to 2004 was extraordinary (although, of course, residential investment weakened substantially after this period). Indeed, even around the recession of 2001 residential investment was not as weak as is typical during economic downturns. Factors such as greater availability of mortgage finance may have been one factor influencing residential investment over this period as may also have been behavioral factors, such as speculative investment. We view structural investigations of these issues in general equilibrium models as an interesting topic for research.
In addition, the relatively poor performance in forecasting residential investment, compared to the very good performance forecasting business investment, may reflect the attention to modelling of business investment in the Edo model. As we emphasized in the introduction, we adopted a two-sector growth model with fast technological progress in the sector producing business investment (and consumer durable) goods in order to match the steady-state growth facts across different expenditure categories. In doing so, we built on a literature developed in the second half of the 1990s (see Greenwood et al. [2000] and Whelan [2003]). It is certainly possible, as we emphasized in the introduction, that our use of "real-time" data has insufficiently controlled for the influence of developments leading up to the Edo model and that our forecast performance is aided by the fact that we have specified our model after the data has been realized. While it is impossible to remove the effect of such influences from our analysis, the fact that residential investment if forecasted less well and business investment is forecasted well may reflect the focus on business investment in our model development.
7 Conclusions
Our goal has been to provide a comparison between forecasts from a richly-specified DSGE model with those from time-series alternatives and the staff forecasts of the Federal Reserve. Our analysis has demonstrated that DSGE models with rich detail on domestic production and spending decisions can provide forecasts of macroeconomic aggregates that are competitive with the approaches used in central banks.
We take several lessons from these findings both for policy-related analyses and future research. Most importantly, the finding that a complex DSGE model is competitive with reasonable forecast alternatives provides support for the use of such models in forecasting and other policy-relevant work. We also suspect that our findings provide interesting clues regarding the structure of the economy that may help inform monetary policy. For example, DSGE models like Edo have a structure that implies a very important role for fluctuations in technology, or productivity, in the business cycle, whereas more traditional models at central banks like the FRB/US model give fluctuations in technology a smaller role. Another example may relate to inflation, where the Edo model provides good forecasts. Some research has been very critical of New-Keynesian models of the Phillips curve (notably, Rudd and Whelan [2007]), but the forecast success reported herein suggests a dimension of empirical validation for such models that has not been previously emphasized.
Our discussion also highlighted two areas where results suggest that further research and perhaps amendments to the structure of models like Edo are warranted. The first was the structure of the labor market, including modeling of the intensive and extensive margin and, perhaps, an explicit role for search or other frictions. The second was the role of financial innovation in the rise, and subsequent fall, of residential investment after 2001.
Finally, we would like to emphasize again a caveat to our "real-time" evaluation. We took great care to base our forecasts using Edo and vector autoregressions on data and information available in "real-time" to place these forecasts on equal footing with the Greenbook and FRB/US model forecasts. However, the forecasts from the vector autoregressions and Edo are not truly real time. We have benefited, at least indirectly, from our previous research and that of others on what types of models are likely to explain the data. It is impossible to purge our analysis of these influences. As a result, we are cautious in our final verdict. Specifically, we view our analysis as clearly indicating that DSGE models like Edo are valuable forecasting tools and are likely to prove competitive with best practices at institutions like the Federal Reserve. We have some confidence in this view because our findings are fairly systematic and do not result from excessive search (as, for example, we employ the same model previously employed in Edge et al. [2008], Edge et al. [2007a], and Edge et al. [2007b]). However, we think it is reasonable to expect that the relative forecast performance of models like Edo in true real-time will be less successful than reported herein. We have been generating and archiving such true real-time forecasts since the May 2007 FOMC meeting and so a true real-time evaluation of Edo is some years away.
International Journal of Central Banking, 3(4):111-144.
Sveriges Riksbank Working Paper Series, No. 190.
Manuscript.
Econometric Reviews, 26(2-4):205-210.
Federal Reserve Bank of Minneapolis, Quarterly Review, pages 2-11.
ECB Working Paper Series, No. 966.
IMF occasional paper, No. 239.
Carnegie-Rochester Conference Series on Public Policy, 47(1):43-81.
Manuscript, European Central Bank.
A CBO Report.
A CBO Report.
ECB Working Paper Series, No. 605.
International Economic Review, 45(2):643-673.
Journal of Business and Economic Statistics, 13(3):253-263.
Federal Reserve Board FEDS Working Paper Series, No., 2007-53.
Manuscript.
Journal of Economic Dynamics and Control, 32(8):2512-2535.
International Journal of Central Banking, 2(1):1-50.
NBER Working Paper Series, No. W13397.
Journal of Econometrics, 123(1):153-187.
Journal of Economic Perspectives, 21(4):25-45.
Journal of Money, Credit and Banking, forthcoming.
Econometric Reviews, 18:1-126.
Brookings Papers on Economic Activity, No. 2, pages 297-333.
European Economic Review, 44(1):91-115.
Journal of Applied Econometrics, 12(2):99-132.
Journal of Money, Credit, and Banking, 39(1):101-125.
Applied Statistics, 37(2):187-195.
Remarks at the Conference on Finance and Macroeconomics sponsored by the Federal Reserve Bank of San Francisco and Stanford Institute for Economic Policy Research, San Francisco, California, February 28.
Econometrica, 50(6):1345 - 1370.
Journal of Money, Credit, and Banking, 39(1):127-154.
Monthly Labor Review, pages 49-56.
Reserve Bank of New Zealand Discussion Paper Series, No. 2007-01.
Journal of Econometrics, 135(1-2):499-526.
Remarks at the American Economic Association panel on monetary and fiscal policy, New Orleans.
Review of Economics and Statistics, 84(4):569-583.
Carnegie-Rochester Conference Series on Public Policy, 47(1):1-37.
Federal Reserve Board FEDS Working Paper Series, No. 2007-60.
American Economic Review, 90(3):429-457.
Journal of Money, Credit, and Banking, 39(1):155-170.
Brookings Papers on Economic Activity, No. 2, 2:1-63.
Manuscript.
Journal of Economic Dynamics and Control, 32(8):2460-2475.
American Economic Review, 97(3):586-606.
Federal Reserve Board FEDS Working Paper Series, No. 2005-31.
Journal of Money, Credit, and Banking, 35(4):627-656.
|
|---|
|
|---|
|
|---|
Table 5 (part B)RSMEs of Models: Sep. 1996-Nov. 2004
| GDP Price Inflation | 1Q | 2Q | 3Q | 4Q | 8Q |
|---|---|---|---|---|---|
| AR(2) | 0.276 | 0.258 | 0.243 | 0.281 | 0.288 |
| Relative RMSE DSGE B | 1.064 | 1.065 | 1.061 | 1.038 | 0.925 |
| Relative RMSE VAR(1) | 1.139 | 1.175 | 1.222 | 1.231 | 1.258 |
| Relative RMSE BVAR(2) | 1.088 | 1.137 | 1.150 | 1.192 | 1.177 |
Table 5 (part C)RSMEs of Models: Sep. 1996-Nov. 2004
| Hours Per Capita | 1Q | 2Q | 3Q | 4Q | 8Q |
|---|---|---|---|---|---|
| AR(2) | 3.128 | 3.599 | 4.099 | 4.442 | 5.974 |
| Relative RMSE DSGE/Edo | 1.007 | 0.997 | 0.985 | 0.957 | 0.846 |
| Relative RMSE VAR(1) | 0.994 | 1.019 | 1.036 | 1.055 | 1.033 |
| Relative RMSE BVAR(2) | 1.012 | 1.029 | 1.035 | 1.038 | 1.004 |
Table 5 (part D)RSMEs of Models: Sep. 1996-Nov. 2004
| Nominal Funds Rate | 1Q | 2Q | 3Q | 4Q | 8Q |
|---|---|---|---|---|---|
| AR(2) | 0.170 | 0.260 | 0.339 | 0.426 | 0.618 |
| Relative RMSE DSGE/Edo | 1.224 | 1.208 | 1.153 | 1.092 | 0.941 |
| Relative RMSE VAR(1) | 0.986 | 1.068 | 1.116 | 1.144 | 1.248 |
| Relative RMSE BVAR(2) | 1.006 | 1.054 | 1.084 | 1.104 | 1.058 |
| Number of Obs. | 66.000 | 66.000 | 66.000 | 66.000 | 43.000 |
|
|---|
Table 6 (part B)Mean Bias of Models: Sep. 1996-Nov. 2004
| GDP Price Inflation | 1Q | 2Q | 3Q | 4Q | 8Q |
|---|---|---|---|---|---|
| AR(2) | 0.075 | 0.087 | 0.104 | 0.126 | 0.092 |
| DSGE/Edo | 0.072 | 0.094 | 0.108 | 0.125 | 0.079 |
| VAR(1) | 0.044 | 0.023 | 0.024 | 0.026 | -0.038 |
| BVAR(2) | 0.032 | 0.020 | 0.016 | 0.021 | -0.052 |
Table 6 (part C)Mean Bias of Models: Sep. 1996-Nov. 2004
| Hours Per Capita | 1Q | 2Q | 3Q | 4Q | 8Q |
|---|---|---|---|---|---|
| AR(2) | 2.593 | 2.806 | 3.100 | 3.143 | 3.348 |
| DSGE/Edo | 2.592 | 2.834 | 3.146 | 3.193 | 3.558 |
| VAR(1) | 2.639 | 2.923 | 3.327 | 3.479 | 4.096 |
| BVAR(2) | 2.669 | 2.971 | 3.361 | 3.501 | 4.106 |
Table 6 (part D)Mean Bias of Models: Sep. 1996-Nov. 2004
| Nominal Funds Rate | 1Q | 2Q | 3Q | 4Q | 8Q |
|---|---|---|---|---|---|
| AR(2) | 0.050 | 0.089 | 0.129 | 0.178 | 0.309 |
| DSGE/Edo | 0.086 | 0.152 | 0.202 | 0.251 | 0.336 |
| VAR(1) | 0.048 | 0.087 | 0.127 | 0.177 | 0.282 |
| BVAR(2) | 0.057 | 0.099 | 0.138 | 0.185 | 0.255 |
| Number of Obs. | 66.000 | 66.000 | 66.000 | 66.000 | 43.000 |
Notes: A positive value in the table indicates that a variable's forecast is on average over-predicting its realized value.
|
|---|
Table 7 (part B)RSMEs of Models, Disaggregated Variables: Sep. 1996-Nov. 2004
| Real Cons. Growth, Durables | 1Q | 2Q | 3Q | 4Q | 8Q |
|---|---|---|---|---|---|
| AR(2) | 2.773 | 2.642 | 2.379 | 2.897 | 3.076 |
| Relative RMSE DSGE B | 0.975 | 0.988 | 0.981 | 0.979 | 0.989 |
| Relative RMSE VAR(1) | 1.018 | 1.040 | 1.128 | 1.033 | 1.026 |
| Relative RMSE BVAR(2) | 0.999 | 1.043 | 1.057 | 1.012 | 1.021 |
Table 7 (part C)RSMEs of Models, Disaggregated Variables: Sep. 1996-Nov. 2004
| Real Inv. Growth, Business | 1Q | 2Q | 3Q | 4Q | 8Q |
|---|---|---|---|---|---|
| AR(2) | 3.976 | 3.805 | 3.586 | 3.804 | 3.534 |
| Relative RMSE DSGE/Edo | 0.904 | 0.898 | 0.892 | 0.902 | 0.952 |
| Relative RMSE VAR(1) | 1.050 | 1.043 | 1.010 | 1.019 | 1.047 |
| Relative RMSE BVAR(2) | 0.984 | 1.059 | 1.008 | 1.006 | 1.039 |
table 7 (part D)RSMEs of Models, Disaggregated Variables: Sep. 1996-Nov. 2004
| Real Inv. Growth, Residential | 1Q | 2Q | 3Q | 4Q | 8Q |
|---|---|---|---|---|---|
| AR(2) | 2.080 | 1.932 | 1.967 | 2.057 | 2.380 |
| Relative RMSE DSGE/Edo | 1.149 | 1.471 | 1.705 | 1.772 | 1.650 |
| Relative RMSE VAR(1) | 0.996 | 1.224 | 1.496 | 1.463 | 1.405 |
| Relative RMSE BVAR(2) | 0.914 | 1.123 | 1.379 | 1.336 | 1.212 |
| Number of Obs. | 66.000 | 66.000 | 66.000 | 66.000 | 43.000 |
|
|---|
Table 8 (part B)RSMEs of Models: Sep. 1996-Dec. 2002
| GDP Price Inflation | 1Q | 2Q | 3Q | 4Q | 8Q |
|---|---|---|---|---|---|
| AR(2) | 0.289 | 0.280 | 0.256 | 0.301 | 0.303 |
| Relative RMSE DSGE/Edo | 1.028 | 1.041 | 1.043 | 1.052 | 0.916 |
| Relative RMSE VAR(1) | 1.114 | 1.110 | 1.122 | 1.109 | 1.024 |
| Relative RMSE BVAR(2) | 1.066 | 1.097 | 1.059 | 1.093 | 0.981 |
| Relative RMSE Greenbook | 1.063 | 0.835 | 0.752 | 0.701 | 0.934 |
| Relative RMSE FRB/US model | 0.941 | 1.023 | 0.947 | 0.918 | 0.865 |
Table 8 (part C)RSMEs of Models: Sep. 1996-Dec. 2002
| Hours Per Capita | 1Q | 2Q | 3Q | 4Q | 8Q |
|---|---|---|---|---|---|
| AR(2) | 3.039 | 3.744 | 4.386 | 4.847 | 6.843 |
| Relative RMSE DSGE/Edo | 0.991 | 0.981 | 0.967 | 0.947 | 0.850 |
| Relative RMSE VAR(1) | 0.995 | 1.010 | 1.030 | 1.047 | 1.038 |
| Relative RMSE BVAR(2) | 1.005 | 1.015 | 1.018 | 1.026 | 1.007 |
| Relative RMSE Greenbook | 1.004 | 1.018 | 1.020 | 1.024 | 0.983 |
| Relative RMSE FRB/US model | 0.992 | 0.998 | 1.001 | 1.009 | 0.929 |
Table 8 (part D)RSMEs of Models: Sep. 1996-Dec. 2002
| Nominal Funds Rate | 1Q | 2Q | 3Q | 4Q | 8Q |
|---|---|---|---|---|---|
| AR(2) | 0.186 | 0.283 | 0.368 | 0.464 | 0.687 |
| Relative RMSE DSGE/Edo | 1.204 | 1.173 | 1.124 | 1.073 | 0.963 |
| Relative RMSE VAR(1) | 0.961 | 1.049 | 1.100 | 1.120 | 1.167 |
| Relative RMSE BVAR(3) | 1.015 | 1.063 | 1.100 | 1.114 | 1.023 |
| Relative RMSE Greenbook | 0.743 | 0.721 | 0.812 | 0.888 | 0.983 |
| Relative RMSE FRB/US model | 0.743 | 0.721 | 0.812 | 0.888 | 0.983 |
| Number of Obs. | 51.000 | 51.000 | 51.000 | 51.000 | 32.000 |
|
|---|
Table 9 (part B)RSMEs of Models, Disaggregated Variables: Sep. 1996-Dec. 2002
| Real Cons. Growth, Durables | 1Q | 2Q | 3Q | 4Q | 8Q |
|---|---|---|---|---|---|
| AR(2) | 2.936 | 2.686 | 2.635 | 3.099 | 3.260 |
| Relative RMSE DSGE/Edo | 0.921 | 0.960 | 0.980 | 0.973 | 0.970 |
| Relative RMSE VAR(1) | 1.001 | 1.062 | 1.099 | 1.020 | 1.024 |
| Relative RMSE BVAR(2) | 0.951 | 1.094 | 1.036 | 0.997 | 1.016 |
| Relative RMSE Greenbook | 1.367 | 1.187 | 1.107 | 1.052 | 1.029 |
| Relative RMSE FRB/US model | 1.341 | 1.105 | 0.978 | 0.959 | 1.044 |
Table 9 (part C)RSMEs of Models, Disaggregated Variables: Sep. 1996-Dec. 2002
| Real Inv. Growth, Business | 1Q | 2Q | 3Q | 4Q | 8Q |
|---|---|---|---|---|---|
| AR(2) | 4.191 | 4.065 | 3.610 | 4.094 | 3.792 |
| Relative RMSE DSGE/Edo | 0.879 | 0.881 | 0.902 | 0.909 | 0.980 |
| Relative RMSE VAR(1) | 1.083 | 1.070 | 1.067 | 1.047 | 1.092 |
| Relative RMSE BVAR(2) | 1.022 | 1.082 | 1.066 | 1.029 | 1.082 |
| Relative RMSE Greenbook | 1.075 | 1.135 | 1.218 | 1.157 | 1.024 |
| Relative RMSE FRB/US model | 1.040 | 1.234 | 1.093 | 0.982 | 1.056 |
Table 9 (part D)RSMEs of Models, Disaggregated Variables: Sep. 1996-Dec. 2002
| Real Inv. Growth, Residential | 1Q | 2Q | 3Q | 4Q | 8Q |
|---|---|---|---|---|---|
| AR(2) | 2.098 | 1.941 | 1.874 | 2.227 | 2.178 |
| Relative RMSE DSGE/Edo | 1.046 | 1.241 | 1.445 | 1.446 | 1.605 |
| Relative RMSE VAR(1) | 1.044 | 1.278 | 1.736 | 1.493 | 1.509 |
| Relative RMSE BVAR(2) | 0.921 | 1.197 | 1.603 | 1.370 | 1.266 |
| Relative RMSE Greenbook | 1.027 | 1.388 | 1.295 | 1.191 | 1.077 |
| Relative RMSE FRB/US model | 0.916 | 1.141 | 1.073 | 0.953 | 1.146 |
| Number of Obs. | 51.000 | 51.000 | 51.000 | 51.000 | 32.000 |
Appendix: Greenbook Forecasts and Real-time Data
|
|---|
|
|---|
|
|---|
|
|---|
|
|---|
|
|---|
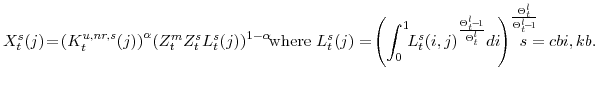
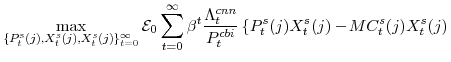
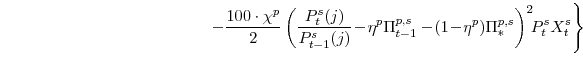
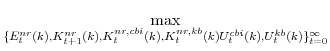
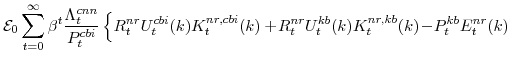
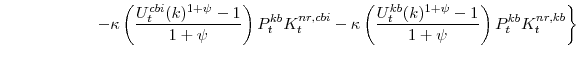
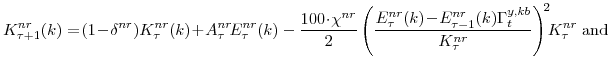
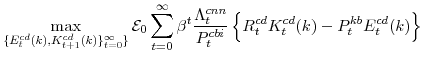
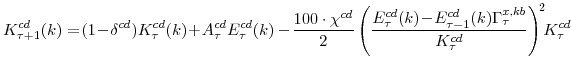
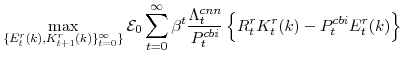
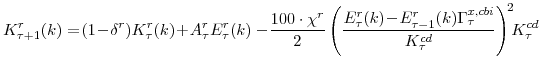
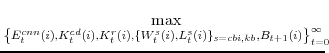
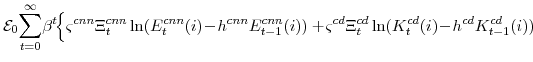
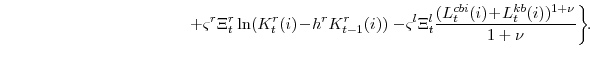
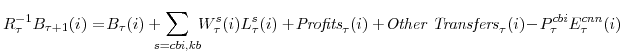
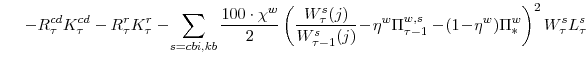
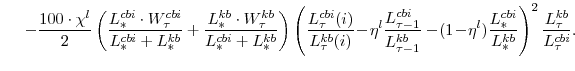
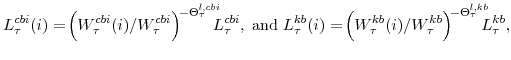
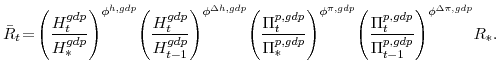
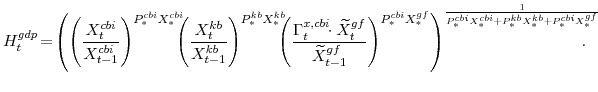
![\includegraphics[width=6.5in]{figure_for_smets.eps}](img180.gif)