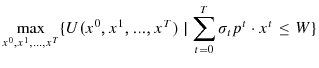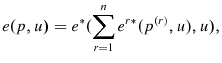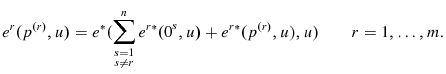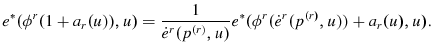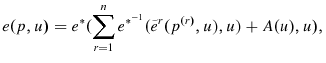Rational Seasonality
November 28, 2006
Keywords: Seasonality, index, numbers, separability, aggregation, duality theory
Abstract:
JEL Classification: C43; D11; E31
1 Introduction
Economic indexes are often treated as given; the complicated aggregation theory underlying the construction of the index is ignored in empirical research. But aggregation and statistical index number theory has returned the favor and largely ignored the consensus that seasonal fluctuations, due to by phenomena such as seasonal patterns in the growing cycle, Christmas shopping, etc., are endemic to economic time series including economic indexes. Relatively little work has attempted to incorporate seasonal fluctuations into the theory, even though seasonality can invalidate the separability assumptions that justify the construction of aggregate economic indexes.
Seasonality has usually been addressed econometrically. Standard econometric approaches view seasonality as an undesirable characteristic of the data. Consequently, the bulk of the research on seasonality has treated seasonal fluctuations as noise that is corrupting the underlying signal. Econometric research has focused on how to smooth or remove seasonal fluctuations. Econometric seasonal-adjustment techniques--ranging from the inclusion of seasonal dummies in regression analysis to the complicated procedures, such as the X-12 procedure, implemented by statistical agencies to produce seasonally adjusted data--rely on statistical models of seasonality. No matter how statistically sophisticated, these models share a fundamental weakness in that they have little or no connection to economic theory. Diewert(1996b), page 39 describes such models as "more or less arbitrary."
With few exceptions (Miron & Zeldes(1988),Ghysels(1988),Osborn(1988),Miron(1996)), research on seasonal-adjustment explicitly or implicitly assumes that seasonality is not the result of economic behavior. Grether & Nerlove(1970) acknowledge that seasonal phenomena in economic data is generated by customs and institutions, and should be expected to be more complex than meteorological phenomena. Nevertheless, the main approaches to econometric seasonal adjustment are based on unobserved component models historically developed to model astronomical phenomena. In a series of papers Diewert(1980,1996b,1998,1999),Diewert(1983) argues that much of the seasonality in economic time series is produced by the behavior of economic agents, and that such behavior should consequently be modeled with economics rather than econometrics.
Diewert focuses on the fact that many economic time series are constructed as statistical index numbers. The construction of statistical index numbers is justified, in the economic approach to index number theory, by their connection to specific economic models. Diewert stresses that these models do not account for behavior that varies across seasons, and, consequently, the economic indexes are not valid in the presence of seasonality. He examines two different ways that seasonal behavior of economic agents can be rationalized in a neoclassical framework, and concludes that only one of these possibilities is consistent with the economic approach to constructing index numbers.
Seasonal behavior can be rational if the agent is optimizing a time varying objective function. However, a time varying objective function generally cannot be tracked by an economic index,2Alternatively, the agent's objective function is not separable at the observed seasonal frequency. The implications of this lack of separability on the functional structure of the agent's decision is more amenable to analysis than general time variability. Diewert(1980) concludes that research into seasonal behavior should focus on decision problems that are not time separable at seasonal frequencies; in his subsequent papers he adapts a standard utility maximization problem to account for seasonality. His seasonal decision problem can be used to construct economic indexes from data that contains seasonality; Diewert(1998), page 457 describes his research as filling a gap:
"The problem of index number construction when there are seasonal commodities has a long history. However, what has been missing is an exposition of the assumptions on the consumer's utility function that are required to justify a particular formula. We systematically list separability assumptions on intertemporal preferences that can be used to justify various seasonal index number formulas from the viewpoint of the economic approach to index number theory."
Diewert's approach deseasonalizes statistical index numbers by their construction. Diewert's models and the resulting indexes have an obvious advantage over econometric models; their connection to economic theory obviates the development of econometric criteria for evaluating different adjustment methods. Economic theory directly justifies the index number approach to seasonal adjustment.
In this paper, I further extend the aggregation theory approach to seasonal adjustment. While this paper extends Diewert's line of research, the focus is slightly different. I focus more on defining seasonal aggregates, rather on the resulting index formulae, as defining aggregates is logically prior to defining the indexes that track them. In addition, although I am weakening the conditions necessary to rationalize seasonal aggregates the resulting indexes are the same as in Diewert(1999) so focusing on the index formulae would be redundant. Using duality theory, I extend Diewert's results to a larger class of decision problems. I also relax Diewert's assumption of homotheticity. The most novel result is a justification of Diewert's moving year index, which is his preferred seasonal index, using only separability assumptions. The derivation, which follows from a theorem of Gorman(1968), is not only sufficient, it is also shown to be necessary.
The remainder of this paper is organized as follows. Section 2 briefly discusses econometric seasonal adjustment methods. Section 3 reviews the index number approach to seasonal adjustment developed by Diewert. Section 4 presents different types of separability for the expenditure and distance functions. Section 5 provides the necessary conditions supporting the construction of seasonal indexes. In particular, Diewert's moving year index is derived from a separability assumption. An argument for why these particular separability assumptions are reasonable is also advanced. Although no empirical analysis of the index number approach to seasonality is provided, Section 6 comments on some empirical implications of the theory. The last section concludes.
2 Econometric Adjustment
This section briefly discusses econometric adjustment techniques; see Hylleberg(1992),Nerlove et al.(1979),Bell & Hillmer(1984) and Miron(1996) for more extensive reviews. The discussion focuses on how difficult it is to establish criteria for determining how to econometrically adjust series for seasonality. The lack of criteria makes the choice of which method to use subjective. The situation is similar to the difficulties in choosing a statistical index number formula solely on the basis of their axiomatic properties.
The majority of seasonal adjustment techniques are based on decomposing a series, or multiple series, into unobserved components. Grether & Nerlove(1970), page 686, in discussing the " desiderata" of seasonal adjustment, note that the unobserved components methods originated in astronomy, and state,
"It is of course, quite debatable whether the idea of unobserved components, appropriate as it may be in the analysis of astronomical observations, is usefully applied to economic data or even to meteorological data. Nonetheless, we believe that this idea lies behind both present methods of seasonal adjustment and the desire for seasonally adjusted time series."
Grether & Nerlove(1970) and Nerlove et al.(1979) show that `optimal' econometric seasonal adjustment depends on both the model of seasonality and the model in which the data are to be used. Nerlove et al.(1979), page 171 conclude, "...it is clear that (a) no single method of adjustment will be best for all potential users of the data and (b) it is essential to provide economic time series data in unadjusted form." They additionally conclude that despite the increase in sophistication of the econometric techniques, "...in terms of modeling explicitly what is going on, there seems to have been remarkably little progress." This conclusion remains valid.
The lack of an empirical standard leads Bell & Hillmer(1984) to conclude that seasonal adjustment methods should be judged on whether the model of seasonality implicit in the method is consistent with the observed seasonality in the data. This would suggest that different adjustment methods should be applied to different data series, so there is no unique `optimal' method. Seasonal adjustment has also been characterized as a signal extraction problem in the frequency domain. Grether & Nerlove(1970) argue against evaluating adjustment methods using empirical criteria based on the spectral properties of the adjustment, although they do not discount its usefulness for characterizing the effects of different methodologies. The lack of a consensus on how to seasonally adjust has led some authors to focus on the effects on the statistical properties of the data when the data is seasonally adjusted using the wrong statistical model (Wallis(1974), discusses this issue).
Several authors, notably Lovell(1963,1966) and Jorgenson(1964) try to derive a set of axioms that a seasonal adjustment method should satisfy. Jorgenson's approach is to specify that the adjustment method should satisfy the properties of the unique minimum invariance, linear, estimator. While this seems reasonable, it still provides an indeterminate solution, because other statistical models, for example a minimum distance estimator or weighted least squares, are just as sensible. In addition, Lovell(1966) showed that Jorgenson's method does not satisfy Lovell's orthogonality axiom, so the adjusted series is correlated with the seasonal adjustment component.
The approach in Lovell(1963) is perhaps the most intriguing relative to Diewert's approach, because it is reminiscent of the axiomatic approach to index number theory developed in Fisher(1922)'s Fisher(1922) seminal work.
Just like the axiomatic approach to index numbers,3 this axiomatic approach to seasonal adjustment is flawed by the fact that sensible sets of axioms are inconsistent with each
other. Lovell is up-front about the difficulty. Lovell(1963), page 994 shows in Theorem 2.1 that the only operators that preserve sums, in the sense that
![]() , and preserve products, in the sense that
, and preserve products, in the sense that
![]() are trivial in that either
are trivial in that either
![]() or
or
![]() . These two axioms are intuitive because the first one implies that accounting identities are unchanged by the adjustment, and the second one implies that the relationship between
prices, quantities, and expenditure are not altered by the adjustment. Consequently, this result shows that two of the most intuitive axioms for seasonal adjustment are inconsistent; Lovell(1963), page 994 characterizes this result as `disturbing' and concludes that
"it suggests that two quite simple criteria rule our the possibility of a generally acceptable `ideal' technique for adjusting economic time series."
. These two axioms are intuitive because the first one implies that accounting identities are unchanged by the adjustment, and the second one implies that the relationship between
prices, quantities, and expenditure are not altered by the adjustment. Consequently, this result shows that two of the most intuitive axioms for seasonal adjustment are inconsistent; Lovell(1963), page 994 characterizes this result as `disturbing' and concludes that
"it suggests that two quite simple criteria rule our the possibility of a generally acceptable `ideal' technique for adjusting economic time series."
The solution to the inconsistency of the axiomatic approach to index numbers is the economic approach. The economic approach allows evaluation of index formulae by appealing to theory. Indexes that have a stronger connection to economic theory under weaker assumptions are judged to be superior. The usefulness of such criteria can be seen in how superlative indexes (Diewert(1976)) are now accepted as the definitive approach to constructing index numbers, not only by theorists, but also by statistical agencies. Diewert's approach to constructing seasonal index numbers by defining seasonal economic aggregates can similarly answer how indexes should be seasonally adjusted by appealing to economic theory.
3 Review of Diewert's Approach
Diewert(1996b,1998,1999) treats the problem of seasonality as part of the economic approach to constructing bilateral index numbers and justifies different seasonal index number formulae on the basis of different separability assumptions.4The theoretical basis of this work allows it to be used as a standard for seasonal adjustment. This section reviews Diewert's approach. It focuses on three of his definitions of seasonal indexes: Annual, Year-over-year, and Moving Year. The notation largely follows Diewert's, but a different separability definition will be used.
For exposition, a number of simplifying assumptions are made. First, the consumption space will be assumed to be of constant dimension in each season. Diewert(1998) divides seasonal commodities into type-1 and type-2. Type-1 commodities are goods that are not available in every season. These are type of goods are particularly problematic for index number theory. The assumption that the dimension of the commodity space does not change in a season means that type-1 goods are not allowed to be randomly missing. Note that if a good is not consumed, it does not necessarily mean it was unavailable. It could be that the price of the good was above its reservation price. This case is observationally equivalent to the first, however, and in aggregate data it seems reasonable to assume that if a good is not consumed it is unavailable, so the focus is on type-2 goods.
Diewert(1998) also assumes that type-2 seasonal commodities can be further divided into type-2a and type-2b commodities. Type-2a commodities are commodities whose seasonal fluctuations correspond to rational optimizing behavior over a set of seasons where prices fluctuate but preferences for the commodity remain unchanged. Type-2b commodities are those where this does not apply. Type-2a commodities can be aggregated under normal assumptions. In the following, I do not differentiate between the type-2 sub-commodities; any group of commodities is assumed to contain at least one type-2b commodity so that aggregation of the group requires further assumptions to rationalize the seasonal behavior.
The effect of inflation is also ignored. Consequently, current period prices are used rather than spot prices. Thus, the cost indexes are futures price indexes rather than spot price indexes (Pollak(1975)). As noted by In a low inflation environment using the current period prices is not a major concern and it removes a level of complexity from the exposition.
The simplifying assumptions can be relaxed without much difficulty following Diewert(1998,1999).
Some notation is needed to define the seasonal decision problem:
The (representative) agent is assumed to have a transitive, reflexive, complete, and continuous preference ordering on ![]() Preferences are also assumed to be non-decreasing and convex.
Under these assumptions, preferences can be represented by a real-valued utility function
Preferences are also assumed to be non-decreasing and convex.
Under these assumptions, preferences can be represented by a real-valued utility function
![]() that satisfies:
that satisfies:
The following decision problem then represents a basic utility maximization problem adapted to the seasonal notation:
where
Diewert makes a series of structural assumptions on this general utility maximization problem to define annual, year-over-year, and Moving Year seasonal aggregates and economic indexes.
In order to define annual economic indexes, Diewert(1998,1999) assumes that the utility function in (1) takes the form
| (2) |
where
From Theorem 5.8 in Blackorby et al.(1978), pages 206-207, the annual aggregator functions satisfy additive price aggregation, and define annual economic quantity aggregates because of their homogeneity. The dual unit expenditure function is the annual economic price aggregate. Annual Konüs(1939) true cost-of-living indexes and Malmquist(1953) economic quantity indexes can be defined:
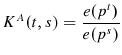 and
and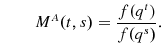
The deseasonalization of the annual index is a by-product of the time aggregation that takes place. The annual indexes also represents Diewert's (1980) preferred method for time aggregating economic data, as these assumptions place the fewest restrictions on intertemporal preferences. This method was implemented in constructing annual indexes from monthly data in Anderson et al.(1997); the annual indexes calculated from seasonally adjusted and non-seasonally adjusted data are indistinguishable.6
Year-over-year indexes, which were suggested by Mudgett(1955) and Stone(1956), give a measure for each season, but require further assumptions. Diewert(1999), page 50 assumes that the annual aggregator function, for
each
![]() takes the form
takes the form
| (3) |
where
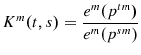 and
and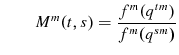
The separability assumptions imply that the solution achieved by solving the general problem in (1) will also be the solution to the following multistage decision problem: in the first stage, the consumer chooses the optimal amount of wealth to allocate to each
year to maximize the overall utility function
![]() ; in the second stage, for each year, the consumer chooses the optimal amount of the allocated wealth from the first stage to allocate to expenditure in each season to maximize
; in the second stage, for each year, the consumer chooses the optimal amount of the allocated wealth from the first stage to allocate to expenditure in each season to maximize
![]() ; and in the third stage, the consumer chooses the optimal quantities of the different seasonal goods subject to the allocated wealth to maximize
; and in the third stage, the consumer chooses the optimal quantities of the different seasonal goods subject to the allocated wealth to maximize
![]() .
.
The multi-stage decision justifies defining annualized year-over-year indexes, by first constructing year-over-year indexes, suitably normalized in the base period, and then constructing an annual index from the seasonal indexes.7 Clearly, the annual index calculated in stages generally requires stronger assumptions than the actual annual indexes. Superlative indexes constructed in such a two-stage algorithm will not generally equal a superlative annual index, because superlative indexes only approximately satisfy consistency in aggregation (Diewert(1978)).
Diewert's (1999) last type of index is the moving year index.8 Diewert makes the additional assumption that
![]() satisfies
satisfies
| (4) |
where
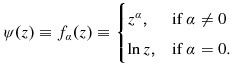 |
(5) |
This assumption implies that the intertemporal utility function
| (6) |
for
Under the CES assumptions,the change in the annual aggregates can be tracked through the same two-stage method discussed previously. The difference is that at the second stage the aggregator functions are assumed to have the restricted CES form. As Diewert(1996) notes,
the strong assumption that
![]() is CES might be puzzling. Its usefulness is that aggregation to be extended to non-calendar years; under the CES assumption there exists an annual aggregator function for any
sequential run of the
is CES might be puzzling. Its usefulness is that aggregation to be extended to non-calendar years; under the CES assumption there exists an annual aggregator function for any
sequential run of the ![]() seasons. Thus, for each season, an annual index can be calculated from the previous
seasons. Thus, for each season, an annual index can be calculated from the previous ![]() seasons (e.g. in July, an index could be calculated over the monthly data from the previous August through July). These moving year annual indices are already seasonally adjusted by construction.
seasons (e.g. in July, an index could be calculated over the monthly data from the previous August through July). These moving year annual indices are already seasonally adjusted by construction.
The notation will be simplified by the following lag function:
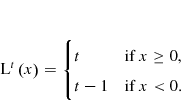
With this function the Moving year indexes can be written as follows:
![\displaystyle K(m,t,s)=\frac{\psi\{\sum_{i=1}^{M}{\beta_{i}\psi}^{-1}{[e}^{i}{(p^{L^{t}% (m-i)i})]\}}}{\psi\{\sum_{i=1}^{M}{\beta_{i}\psi}^{-1}{[e}^{i}{(p^{L^{s}% (m-i)i})]\}}}%](img55.gif) |
(7) |
and
![\displaystyle M(m,t,s)=\frac{\psi^{-1}\{\sum_{i=1}^{M}{\beta_{i}\psi\lbrack f}^{i}% {(q^{L^{t}(m-i)i})]\}}}{\psi^{-1}\{\sum_{i=1}^{M}{\beta_{i}\psi\lbrack f}% ^{i}{(q^{L^{s}(m-i)i})]\}}}%](img56.gif) |
(8) |
for
As a further sophistication, Diewert(1999) suggests centering the non-calendar years. The lag function is no longer sufficient; the following centering function will be used:
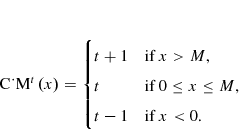
The following definition centers the moving year indexes assuming there are an even number of seasons as is the norm. Effectively, the index is calculated by taking the ![]() terms centered
around the season
terms centered
around the season ![]() and adding half of the value of two extra terms:
and adding half of the value of two extra terms: ![]() seasons
ahead and
seasons
ahead and ![]() seasons prior. Notationally, this accomplished by averaging two sequences of
seasons prior. Notationally, this accomplished by averaging two sequences of ![]() terms where the second sequence is lagged one season relative to the first.
terms where the second sequence is lagged one season relative to the first.
![\begin{displaymath}K^{C}(m,t,s)=\frac{% \begin{array}[c]{c}% \psi\{\frac{1}{2}\sum_{i=1}^{M}{\beta_{i}\psi}^{-1}{[e}^{i}{(p^{C_{M}% ^{t}(m+M/2-i)i})]}\\ {+\frac{1}{2}\sum_{i=1}^{M}{\beta_{i}\psi}^{-1}{[e}^{i}{(p^{C_{M}% ^{t}(m-1+M/2-i)i})]}\}}% \end{array} }{% \begin{array}[c]{c}% \psi\{\frac{1}{2}\sum_{i=1}^{M}{\beta_{i}\psi}^{-1}{[e}^{i}{(p^{C_{M}% ^{s}(m+M/2-i)i})]}\\ {+\frac{1}{2}\sum_{i=1}^{M}{\beta_{i}\psi}^{-1}{[e}^{i}{(p^{C_{M}% ^{s}(m-1+M/2-i)i})]}\}}% \end{array} }% \end{displaymath}](img60.gif)
|
(9) |
and
![\begin{displaymath}M^{C}(m,t,s)=\frac{% \begin{array}[c]{c}% \psi^{-1}\{\frac{1}{2}\sum_{i=1}^{M}{\beta_{i}\psi\lbrack f}^{i}{(q^{C_{M}% ^{t}(m+M/2-i)i})]}\\ {+\frac{1}{2}\sum_{i=1}^{M}{\beta_{i}\psi\lbrack f}^{i}{(q^{C_{M}% ^{t}(m-1+M/2-i)i})]}\}}% \end{array} }{% \begin{array}[c]{c}% \psi^{-1}\{\frac{1}{2}\sum_{i=1}^{M}{\beta_{i}\psi\lbrack f}^{i}{(q^{C_{M}% ^{s}(m+M/2-i)i})]}\\ {+\frac{1}{2}\sum_{i=1}^{M}{\beta_{i}\psi\lbrack f}^{i}{(q^{C_{M}% ^{s}(m-1+M/2-i)i})]}\}}% \end{array} }% \end{displaymath}](img61.gif)
|
(10) |
for
The seasonal indexes reviewed in this section are connected to economic theory by their derivation from the utility maximization problem. The various indexes were derived by assuming more and more about the structure of the utility function. The section followed Diewert's in that separability was only implicitly mentioned as the rationale for the functional structures. This seeming oversight is justified by the assumption that the nested utility functions are homothetic. Implicitly, Diewert is assuming that preferences are homothetically strictly separable at the annual and seasonal frequencies. Homotheticity, which Swamy(1965) called a `Santa Claus assumption,' allows the most elegant treatment of aggregation and statistical index number theory. But, homotheticity is a strong assumption and not necessary.
4 Duality and Separability
Diewert implicitly connected the seasonal structures and indexes defined in Section 3 to an agent's preferences through assuming homothetic strict separability. The seasonal indexes that Diewert derived can be supported under weaker conditions than he used; weakening Diewert's conditions provides broader theoretical support for the seasonal indexes and helps inoculate the theoretical approach to seasonality from criticism that claims the assumptions are unrealistic.
As telegraphed at the end of the previous section, the first step to weakening Diewert's conditions is to weaken the homotheticity assumption. Relaxing homotheticity leads naturally to focusing on the expenditure and distance function representation of preferences. The benefit of beginning with the expenditure and distance function is twofold. First, these two dual representations are always homogeneous in prices and quantities respectively. This property led Konüs(1939) to define the true cost of living index through the expenditure function. Similarly, Malmquist(1953) originally used the distance function to define economic quantity indexes. The weakest conditions that support the various seasonal structures are naturally specified on the functions that are used in the definition of the indexes. Clearly, this argues for using the expenditure function; the similar argument for the distance function is obscured by Diewert's assumption of homotheticity. Second, the duality between the expenditure and distance functions is stronger than between other representation of preferences. Imposing functional structure on the expenditure function implies that the distance function will have the same property and vice versa. This is not generally true for other representations of preferences. In particular, assuming the utility function has a separable structure does not generally imply that the expenditure function will have the same structure, unless homotheticity is also imposed. These statements are clarified in the first subsection, which presents the expenditure and distance function and discusses their duality.
The second step to weakening Diewert's conditions is to make the separability assumptions explicit. This will make clear what Diewert is implicitly assuming when deriving the different functional structures that account for seasonal decision-making. The second subsection presents a variety of definitions of separability. Using these definitions, the weakest conditions that rationalize the annual and seasonal indexes can be established. These definitions also set up the subsequent section which discusses the moving year indexes.
4.1 The Dual Expenditure and Distance Functions
The strong connection between the expenditure and distance function stems from the fact that they are both conic representation of preferences. The expenditure function, which is the negative of the support function, and the distance function are equivalent mathematical representations of a convex set. For a utility level, both functions are positive linearly homogeneous convex functions.11 Gorman(1970), page 105 refers to the pair as `perfect' duals as they always share the same properties. Section 2.3.3 in Blackorby et al.(1978), pages 26-33 provides some further intuition for the strong connection between the expenditure and distance function by showing that the functions switch roles with regard to the indirect utility function; the distance function can be viewed as an indirect expenditure function and the expenditure function can be viewed as an indirect distance function. The two functions can be defined in terms of the utility problem in (1) as follows:
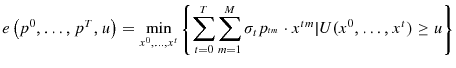 |
(11) |
| (12) |
Although the distance function has been used in economics since at least Debreu(1954), it is less familiar. For a given ![]() , the distance function measures the amount
that
, the distance function measures the amount
that
![]() must be scaled up or down such that
must be scaled up or down such that ![]() is in the boundary of the superior
set: i.e.
is in the boundary of the superior
set: i.e.
![]() . For more discussion, see Deaton & Muellbauer(1980).
. For more discussion, see Deaton & Muellbauer(1980).
Given the prior assumptions made on preferences in defining the utility function, the expenditure function will have the following properties: continuity in
![]() ; non-decreasing, and concave in
; non-decreasing, and concave in ![]() ; and increasing in
; and increasing in
![]() where
where
![]() and
and ![]() . The expenditure function has an additional property
that is extremely useful in aggregation and statistical index number theory, positive linear homogeneity (PLH) in
. The expenditure function has an additional property
that is extremely useful in aggregation and statistical index number theory, positive linear homogeneity (PLH) in ![]() which means that
which means that
As per our discussion, the distance function has the same properties except that it is strictly negatively monotonic in ![]() and
and ![]() takes the role of
takes the role of ![]() :
:
The duality of the expenditure and distance functions can be made clearer using the fact that away from points of global satiation,
![]() if and only if
if and only if
![]() . Consequently, the expenditure function can be defined as
. Consequently, the expenditure function can be defined as
As noted, the key properties of the expenditure and distance functions is their PLH and their functional equivalence. This first implies that separability assumptions can be applied to support the construction of seasonal indexes without assuming homotheticity. Without homotheticity, separability assumptions do not necessarily commute from one representation of preferences to another. The second property enables this to be avoided.
4.2 Separability
The basic definition of separability used here is originally due to Bliss(1975). This definition is more general than the familiar definition developed independently by Sono(1961) and Leontief(1947,1947b) as it does not require differentiability. In addition, strict separability (Stigum(1967)) is used; strict separability is equivalent to Gorman's (1968) definition of separability. Finally, complete (strict) separability is defined. Homothetic versions of the various forms of separability are also discussed. The definitions will be presented for the expenditure function. Equivalent definitions exist for the distance function with quantities replacing prices. Similar definitions also exist for the utility function, but let me reiterate that imposing separability on the utility function does not generally imply anything about the expenditure function and vice versa.
The definition of separability depends on the existence of a collection of subsets being nested. Let
![]() be a collection of subsets of some set. The collection is nested if
be a collection of subsets of some set. The collection is nested if
![]() either
either
![]() or
or
![]() . Some further notation is required:
. Some further notation is required:
![\displaystyle I^{[n]}=\left\{ {I^{(1)},I^{(2)},\ldots,I^{(r)},\ldots,I^{(n)}}\right\} =\bigcup\limits_{j=1}^{n}{I^{(j)}},](img95.gif) |
(13) |
where
For simplicity, only the case where a sector is separable from its complement in ![]() is presented. The generality lost by making this assumption is not a problem for the seasonal
structures. The assumption means that the partition used in definitions of separability assumes
is presented. The generality lost by making this assumption is not a problem for the seasonal
structures. The assumption means that the partition used in definitions of separability assumes ![]() rather than the fully general case where
rather than the fully general case where ![]() The general case can be found in Blackorby et al.(1978). The following function will be used:
The general case can be found in Blackorby et al.(1978). The following function will be used:
| (14) |
This function defines a collection of subsets
for a fixed scalar
Properties of the sets defined in (15) are used to define separability, strict separability, and complete (strict) separability:
Defining homothetic (strict) separability for the expenditure function is more complicated as the function is already PLH in ![]() . Note that both separability and strict separability define a
preference ordering on
. Note that both separability and strict separability define a
preference ordering on
![]() for every
for every
![]() ;
;
![]() is preferred to
is preferred to
![]() on
on
![]() conditionally on
conditionally on ![]() if
if
![]() for every
for every
![]() . If a consumer is indifferent between
. If a consumer is indifferent between
![]() and
and
![]() for this conditional preference ordering, they are always indifferent between
for this conditional preference ordering, they are always indifferent between
![]() and
and
![]() for every
for every ![]() . To see this, suppose it is not true. Then
there exists
. To see this, suppose it is not true. Then
there exists
![]() ,
,
![]() , and
, and ![]() such that the consumer conditionally
strictly prefers either
such that the consumer conditionally
strictly prefers either
![]() or
or
![]() although they are indifferent between
although they are indifferent between
![]() and
and
![]() . Without loss of generality, suppose
. Without loss of generality, suppose
![]() is strictly preferred to
is strictly preferred to
![]() . This implies that that there exists a
. This implies that that there exists a
![]() , such that
, such that
![]() . Multiply both sides by
. Multiply both sides by ![]() . Homogeneity of the expenditure function implies that
. Homogeneity of the expenditure function implies that
![]() . This violates the
assumption that the consumer is indifferent between
. This violates the
assumption that the consumer is indifferent between
![]() and
and
![]() . Consequently, indifference between
. Consequently, indifference between
![]() and
and
![]() implies that the consumer is indifferent between
implies that the consumer is indifferent between
![]() and
and
![]() for every
for every ![]() for all
for all
![]() and the conditional preference ordering on
and the conditional preference ordering on
![]() is always homothetic for a particular
is always homothetic for a particular
![]() .
.
There is however a sensible definition of homothetic (strict) separability for the expenditure function. Generally, the conditional preference ordering on the ![]() sector depends on
sector depends on
![]() . If it does not depend on
. If it does not depend on ![]() , the sector is defined to be homothetically
(strictly) separable. The definition will need the following:
, the sector is defined to be homothetically
(strictly) separable. The definition will need the following:
![\displaystyle {\ }_{0}I^{[n]}=\bigcup\limits_{j=0}^{n}{I^{(j)}}%](img143.gif)
The following definition uses this extended partition:
This condition implies that the conditional preference ordering is not dependent on ![]() The rationale for calling this condition homothetic (strict) separability is that it implies, and is
implied by, homothetic (strict) separability of the utility function. As noted previously, homothetic separability is an exception to the statement that, in general, (strict) separability of one of the representations of preferences has no implications for separability of the other dual
representations. It should be apparent that Diewert is implicitly assuming homothetic separability, so that he can use the dual unit expenditure function.
The rationale for calling this condition homothetic (strict) separability is that it implies, and is
implied by, homothetic (strict) separability of the utility function. As noted previously, homothetic separability is an exception to the statement that, in general, (strict) separability of one of the representations of preferences has no implications for separability of the other dual
representations. It should be apparent that Diewert is implicitly assuming homothetic separability, so that he can use the dual unit expenditure function.
5 Seasonal Decision-making
With the separability apparatus developed in the previous section, the seasonal indexes developed in Section 3 can be revisited.
First, note that a current year annual aggregate can be defined if the expenditure function is separable.
Furthermore if
-
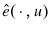 is increasing;
is increasing; - each
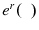 satisfy Condition 18;
satisfy Condition 18; -
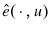 and each
and each
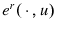 inherit (partial) differentiability in prices;14 and
inherit (partial) differentiability in prices;14 and - each
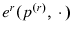 inherits (strict) convexity and positive linear homogeneity in
inherits (strict) convexity and positive linear homogeneity in 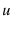 .
.
By the strong duality of the expenditure and distance functions, the equivalent theorem holds for the distance function. The following corollary is immediate:
Corollary 31.
and
An annual separability assumption on either the expenditure or distance function is sufficient to define annual economic indexes, albeit ones that depend on ![]() . This is significantly weaker
than assuming homothetic strict separability. Unfortunately, separability is not quite enough, because the annual economic indexes cannot be guaranteed to satisfy weak factor reversal under only separability even though strong factor reversal holds. Consequently, separability of the expenditure
function is sufficient to define economic aggregates, but strict separability is necessary (and sufficient) to define annual economic indexes. Not surprisingly, since the difference between separability and strict separability disappears under homotheticity, if homothetic separability is assumed
weak factor reversal holds--in fact homotheticity makes weak and strong factor reversal equivalent. Strict separability is still a much weaker assumption than homothetic separability.
. This is significantly weaker
than assuming homothetic strict separability. Unfortunately, separability is not quite enough, because the annual economic indexes cannot be guaranteed to satisfy weak factor reversal under only separability even though strong factor reversal holds. Consequently, separability of the expenditure
function is sufficient to define economic aggregates, but strict separability is necessary (and sufficient) to define annual economic indexes. Not surprisingly, since the difference between separability and strict separability disappears under homotheticity, if homothetic separability is assumed
weak factor reversal holds--in fact homotheticity makes weak and strong factor reversal equivalent. Strict separability is still a much weaker assumption than homothetic separability.
Similar assumptions rationalizes year-over-year aggregates. Define a partition
![]() where for every
where for every ![]() ,
,
![]() indexes
indexes ![]() for
for
![]() . Furthermore, define the partition
. Furthermore, define the partition
![]() where
where ![]() indexes the complement of
indexes the complement of ![]() .
.
Corollary 32.:
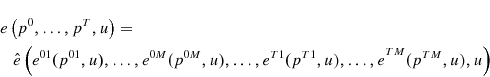
and the distance function is separable in
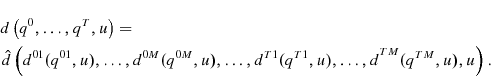
The discussion about annual aggregates and indexes is appropriate here as well. Consequently, year over year seasonal indexes can be rationalized by only the imposition of strict separability. Note that there is another generalization here. The seasonal indexes are not nested inside an annual index, so the assumptions on preferences are relaxed somewhat. Of course, the same result could be applied to Definition 7. In this case, the seasonal pattern of the decision problem does not imply that it is not separable at frequencies higher than a year. It simply implies that preferences are not stationary.15 This type of time variation can be handled by the index approach, at least to some extent. At least some of the time-varying utility functions that have been used to model seasonal behavior fit into this framework: for example, Osborn(1988).
The results so far demonstrate that homotheticity is not necessary to rationalize constructing seasonal index numbers. As discussed previously, separability in the utility and expenditure functions are not generally related to each other. Consequently, the developments in this section extend the class of preferences that can be used to justify seasonal aggregates and indexes. The most interesting extension addresses the Moving Year Seasonal Indexes, however.
In order to derive the Moving Year Index, Diewert was assumed that the utility function had a constant elasticity form. Diewert's modus operandi was to "systematically list separability assumptions on intertemporal preferences" to rationalize the index numbers. The CES assumption does not seem to follow from any separability condition, so the assumption seems out of place. This apparent problem can be rectified. Either one of the following conditions is sufficient:
The following theorem gives a representation for complete strict separability:
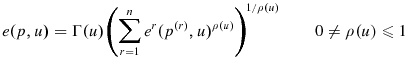
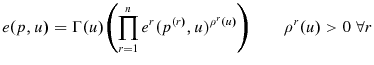
To prove this theorem, the following lemma is needed:
Moreover,
which contradicts the continuity of
where
By repeated application of Lemma 36, this representation can be extended to the boundary of
where
Let
 for
for
Since
Homotheticity of each
where each
Letting
Rearranging terms, this implies, for each
Call the right-hand side of (25)
Using (22), substitute (26) into (18) to get
where
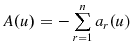 . The fact that
. The fact that
for each
| (28) |
This completes the proof by a theorem of Eichhorn(1974), page 24.
The immediate corollary provides a basis for the moving year seasonal indexes using complete strict separability:
Corollary 37.
Assume, in addition to satisfying Condition 18, the expenditure function satisfies either: Then it has a CES functional form in the seasonal aggregates if it is completely strictly separable in
These sufficient conditions may not be necessary. Nevertheless, they would seem to be the weakest separability conditions sufficient to rationalize the moving year indexes that can be expected to hold.
This result gives some insight into the discussion in Section 3. It is not surprising that an index can be defined for non-calendar years if its is completely separable in seasons. Remember that complete separability means that any subset of the partition is also completely strictly separable. Thus, complete strict separability allows us to define aggregates over arbitrary partitions of the seasons. Non-calendar years are just one of the possibilities. For example, econometric seasonal adjustment is often done using filters that contain more than just 12 leads or lags.
The CES or alternatively the complete strict separability assumption may seem overly strong, but there is a sensible argument for this condition. The calendar year is not necessarily intrinsically special. For example, the fiscal year may be more important economically. In the discussion at the start of Section 2, the consumer was normally assumed to re-optimize or re-plan at the beginning of the period. I adapted this to re-optimizing at the beginning of each year in order to finesse how strong the separability conditions needed to be. However, there is nothing intrinsic to seasonality to suggest that the consumer can not still be allowed to re-plan every period rather than sticking with his plan for an entire year.
The presumption that seasonality in the data implies that decision problem is not separable at periods shorter than a year still seems reasonable. So the model is that the consumer solves a problem in say the first month of the year, where his or her preferences are separable over the year but not for any shorter time-period. Then in the next period, the consumer resolves a problem, where his or her preferences are separable over the year but not for any shorter time-period. This is called `rolling plan optimization.' But, these are not the same years. The first year runs from January through December and the second run from February through January. If this is viewed as being embedded in a larger, possibly infinite horizon problem, then this implies the existence of overlapping separable sectors. If each sector is strictly separable and January in either the first or second years is strictly essential, then Gorman's (1968) overlapping theorem implies that January commodities in year 0, February through December commodities, and January year commodities in year 1 are all strictly separable. In fact, the theorem states that they are completely strictly separable. If this thought experiment is iterated, it implies that each month's commodities are completely strictly separable. To the extent that it seems sensible that consumer's plan over an annual horizon and re-plan throughout the year the CES assumption seems plausible.
6 Empirical Implications
This paper contains no empirical analysis, but there are some interesting implications of the index number approach to seasonality. First, Diewert(1999) brings up some practical reasons to favor the index number method. First, the method is perhaps less arcane than current econometric practices, and could be applied more easily. Second, the data indexes could be produced in a timely manner. Third, the data would be subject to fewer historical revisions, perhaps only those associated with switching to the centered version from a preliminary non-centered index after six months. These are cogent arguments for using index number method. However, most statistical agencies will require substantial empirical analysis before they would consider switching methods, so a few suggestions for future research seem warranted.
A natural way to analyze seasonal adjustment is in the frequency domain. Examining the index formula advanced he should make it apparent that these formula remove all power at frequencies higher than annual. Consequently, it might be interesting to view the index numbers as acting like a low pass filter. This is in contrast to some seasonal adjustment methods, which are more like a notch filter: see Nerlove(1964). One well-known problem in finite filtering theory is that the optimal low pass filter is not realizable. An interesting question is whether seasonal indexes approximate the ideal filter by effectively pooling data. This is almost a stochastic index number viewpoint. Given the perspective that the index number formula effectively clips all higher order power, the indexes should be relatively smooth. Consequently, the moving year indexes, which average these seasonal indexes should be expected to be exceptionally smooth. The moving year indexes should be expected to be isolating largely the long-run trend.
In addition, the econometric adjustment literature often takes linearity as a desirable property for seasonal adjustment, despite the fact that the X-12 procedure, its predecessors and related methods are not, generally, linear. A fair amount of work has been undertaken trying to demonstrate that these procedures are approximately linear. The index number method suggests that the linearity criterion is misguided. Clearly, the index number adjustment is non-linear. In fact, looking at Lovell's axioms, it preserves products by definition, so it cannot preserve sums in general. An interesting question is whether or not a linear method can approximate the index number methods. If not, an open question would be whether there are non-linear econometric methods that can approximate the index number approach.
Finally, the fact that the index number approach satisfies the product preserving axiom suggests that economic indexes, if not adjusted using the index number methods, should be adjusted by techniques that are also product preserving rather than sum preserving. Furthermore, many economic time series are not indexes, so the index number approach is not applicable. Consequently, the development of econometric techniques that approximate the output of index number methods as closely as possible would be useful to maintain consistency.
7 Conclusion
This paper has further developed the rational behind the index number approach. The class of preferences that can rationalize the seasonal indexes advocated by Diewert(1998,1999) were extended. In particular, sufficient conditions for the moving year index based on a separability assumption were pdeveloped. Additionally, a heuristic argument was proposed based on Gorman's (1968) overlapping theorem that supports this separability assumption if an agent reoptimizes over a new time horizon each period.
Judging among econometric seasonal adjustment methods is confounded by the lack of obvious criteria; different optimality criteria lead to alternative techniques. The index number approach to seasonality solves this indeterminacy problem. By referring to the economic theory as a arbiter, it provides a criterion for judging among different techniques. It does not obviate the need, or probably the desire to have econometric techniques for seasonal adjustment, series that are not economic indexes can not be adjusted this way. However, because it provides as standard, it could also be used to judge among econometric methods in situations, where it itself is not directly applicable. In order for the index number approach to serve as an arbiter, empirical characterizations of its properties are required.