Rounding and the Impact of News: A Simple Test of Market Rationality
Keywords: News Announcements, Rounding, Market Efficiency, Rational Inattention.
Abstract:
JEL Classification: E44, G14.
1. Introduction.
Market efficiency requires all available information to be reflected in asset prices. Although it is widely agreed that asset returns are somewhat predictable, it is not clear whether this reflects time-variation in discount rates or a failure of market efficiency, for which we have to look beyond standard rational asset pricing models. This debate is central to modern finance.
Occasionally, natural experiments arise that provide simple and direct tests of market efficiency (e.g. Lamont and Thaler, 2003). This note describes one such experiment. Scheduled macroeconomic news announcements represent the canonical mechanism by which public information is released. In the United States, these announcements are made under tightly controlled conditions. Many important releases come out at 8:30 am sharp. Reporters are given the text of the release and allowed to write their stories earlier, but are prevented from transmitting these stories until 8:30 am. The releases are extremely closely watched by the markets, and standard theory would predict that they should cause a jump in the prices of financial assets. And indeed, much empirical work on the reaction of asset prices to these news announcements finds a very sudden reaction.
Some important U.S. macroeconomic data releases include a rounded headline number that is reported on the first page of the release, and that is widely quoted in newswire stories, and then a more precise number in the text of the release. Importantly, the whole release comes out concurrently. If markets are efficient, they should react to the precise number. On the other hand, if they are not efficient, they may react to the headline number alone, ignoring the more complete information in the text of the release. In this paper, we propose a test of whether markets react to the rounded or unrounded numbers. We consider three releases for which the commonly reported rounded number is not the most precise information available--core CPI inflation, core PPI inflation, and the unemployment rate. For the core CPI, a prominent release for which the rounding in the headline number is large relative to the information content of the release, we find evidence that markets overlook some of the information in the unrounded numbers..
2. Rounded and Unrounded News Announcements
We first describe the rounding that applies to the release of the core CPI price index (and other Bureau of Labor Statistics (BLS) price indices). The price index is first rounded to one decimal point and this price index is reported in the text of the news announcement. More precise price index data are prepared by the BLS but not reported to the public, so for our purposes in studying market reactions, it is as though these data do not exist.1 The month-on-month percent change in the one-decimal precision published price index is computed, then rounded to the nearest tenth of a percentage point, and reported on the first page of the news announcement. This statistic is heavily reported by the press and newswire services.2
For example, the March 2006 CPI release showed the seasonally adjusted core CPI price index rising 0.3 percent from the prior month, and this headline number alone was reported in most press discussion of the release. A reader who reads on to page 12 of the same release can, however, see that the March core CPI was 204.2, up from 203.5 in February, representing core CPI inflation of 0.344 percent, which only just rounds down to three tenths.3 A simple test of market efficiency is therefore given by considering whether or not the market on average reacts to the rounding error, which is -0.044 percent in this example.
We assume that if markets are efficient, the change in yields in a short window around the news announcement, ![]() , will be a linear function of the unexpected component of the
unrounded news announcement. That is,
, will be a linear function of the unexpected component of the
unrounded news announcement. That is,
where
Under specification (1) (markets react to the most precise data available),
The data announcements that we consider are core CPI inflation, core PPI inflation (hereon denoted as core CPI and core PPI, respectively) and the unemployment rate, each important macroeconomic news announcements produced by the BLS and released monthly at 8:30 am on a scheduled date. These
data are never released on the same day. For each of these announcements ![]() , the ex-ante expectation of the release, is measured as the median expectation from the Money Market
Services (MMS) survey taken the previous Friday. The actual value of the release is taken as the real-time announced value. For core CPI and the unemployment rate, the sample period is July 1991 to September 2006, for a total of 180 observations per regression. For core PPI, the sample period is
April 1997 to September 2006. Prior to April 1997, the BLS published only the rounded number for seasonally adjusted core PPI inflation, not the corresponding price index, so we are unable to conduct our test before that date. Some summary statistics are reported in Table 1. The rounding
error is economically substantial, especially in the case of core CPI - the standard deviation of the rounding error is about one third the size of the standard deviation of the surprise component of the release itself, so that the rounding is substantial relative to the information content of the
release.
, the ex-ante expectation of the release, is measured as the median expectation from the Money Market
Services (MMS) survey taken the previous Friday. The actual value of the release is taken as the real-time announced value. For core CPI and the unemployment rate, the sample period is July 1991 to September 2006, for a total of 180 observations per regression. For core PPI, the sample period is
April 1997 to September 2006. Prior to April 1997, the BLS published only the rounded number for seasonally adjusted core PPI inflation, not the corresponding price index, so we are unable to conduct our test before that date. Some summary statistics are reported in Table 1. The rounding
error is economically substantial, especially in the case of core CPI - the standard deviation of the rounding error is about one third the size of the standard deviation of the surprise component of the release itself, so that the rounding is substantial relative to the information content of the
release.
For each of the three types of news announcements that we consider, we estimate regressions of the form of equation (3) where ![]() represents the change in the two-year Treasury
yield, the ten-year Treasury yield or a eurodollar futures rate4 from 8:25am to 8:40am on the days of announcements. Separate regressions are run for the core CPI, core
PPI, and unemployment rate announcements, as the three announcements are never simultaneous. Other important scheduled news announcements can, however, come out at the same time as core CPI, core PPI or unemployment rate announcements. In particular, the widely watched change in nonfarm payrolls is
always released at the same time as the unemployment rate. To control for this, we augment the regressions with the unexpected components of nonfarm payrolls, retail sales growth, and initial jobless claims announcements that come out concurrently.5
represents the change in the two-year Treasury
yield, the ten-year Treasury yield or a eurodollar futures rate4 from 8:25am to 8:40am on the days of announcements. Separate regressions are run for the core CPI, core
PPI, and unemployment rate announcements, as the three announcements are never simultaneous. Other important scheduled news announcements can, however, come out at the same time as core CPI, core PPI or unemployment rate announcements. In particular, the widely watched change in nonfarm payrolls is
always released at the same time as the unemployment rate. To control for this, we augment the regressions with the unexpected components of nonfarm payrolls, retail sales growth, and initial jobless claims announcements that come out concurrently.5
The results are shown in Table 2. The coefficients on the rounding error are significantly negative for core CPI for all three yield changes, meaning that investors react to the rounded headline number rather than to all the available information. Indeed, it is not possible to reject the null
hypothesis that
![]() , implying that markets focus exclusively on the rounded number.
, implying that markets focus exclusively on the rounded number.
The estimated coefficient on the rounding error for core PPI is not statistically significantly different from zero and the point estimate is positive (the `wrong' sign given that a positive core PPI surprise causes yields to rise). The standard error is large. Such imprecision is not wholly
unexpected as the rounding error is very small relative to the standard deviation of core PPI surprises. An alternative method is to estimate a common coefficient for surprises and rounding errors to core CPI and core PPI releases.6 To make the variables comparable and the common coefficient meaningful requires scaling the surprises and rounding errors by the standard deviation of surprises of the respective variable. In this way, the common surprise
coefficient measures the response of asset markets to a one-standard deviation surprise and the common rounding-error coefficient measures the response to a similarly standardized unit of rounding.7 Estimating over the sample from April 1997 (our start date for core PPI), the joint coefficient on the rounding errors is found to be negative and strongly significantly different from zero for two- and ten-year yields and
eurodollar futures rates, as shown in Table 3. In addition, one cannot reject the null hypothesis for the joint coefficients that
![]() at conventional levels of significance.
at conventional levels of significance.
In the unemployment regression, the estimated coefficient on the rounding error is not significant but the point estimate is positive, which is the expected sign if markets focus only on the rounded number, given that on average higher-than-expected unemployment causes yields to fall. The unemployment rate is always released concurrently with the employment report, which receives much more market attention. While we control for the unexpected component of the nonfarm payrolls release in the unemployment regression, it is possible that news about unemployment can be overshadowed by the employment report, especially on days when the payrolls surprise is big.8
Overall, the effect of rounding seems most important for the core CPI, this being the release for which the rounding error is largest relative to the size of the data surprise. The large standard deviation of core PPI surprises hinders estimation of that variable but when combined with core CPI rounding errors, the joint coefficient is significantly negative and we cannot reject the hypothesis that markets focus exclusively upon the rounded numbers.
3. Imprecision of Survey Expectations - a Monte Carlo approach
It is standard in the macroeconomic news announcement literature to use MMS surveys to measure agents' expectations for upcoming releases, and the available statistical evidence is quite strong that these surveys correctly measure conditional expectations (see, for example, Balduzzi, Elton and Green, 2001). Still, there is presumably some measurement error in these expectations, and the median survey expectations for core CPI, core PPI, and the unemployment rate respectively are rounded and recorded to the nearest tenth of a percentage point. We were concerned about biases and size distortions that could be induced in our test by this measurement error and rounding.
To investigate this, we did some Monte-Carlo simulations. The design of the experiment is as follows:
(i) We simulated random draws of artificial unrounded released data, ![]() , that are iid
, that are iid
![]() where
where ![]() , the simulated expectation of the data, is itself
drawn from an iid
, the simulated expectation of the data, is itself
drawn from an iid
![]() distribution.
distribution.
(ii) The simulated survey expectation of the data is given by
![]() , where
, where ![]() is iid
is iid
![]() and so is equal to the sum of the expectation
and so is equal to the sum of the expectation ![]() plus zero-mean
measurement error, and is then subject to rounding.
plus zero-mean
measurement error, and is then subject to rounding.
(iii) The simulated change in yields is
![]() where
where ![]() is iid
is iid
![]() and the population R-squared from this regression is
and the population R-squared from this regression is
![]() .
.
All of the errors in this model are mutually independent and the sample size is ![]() . We then ran the regression
. We then ran the regression
Table 4 reports the simulated rejection rates for a wide range of choices of these parameters. Our choices of ![]() and
and![]() comfortably span the corresponding sample variances for core CPI, core PPI, and the unemployment rate reported in Table 1. The population R2 ranges from 0 to 40 percent, which likewise easily brackets the degree of predictability of yield changes in the wake of these news announcements that we and others have found. The sample size is set to 100 or 200, again in line with our application. Finally, we include cases
where
comfortably span the corresponding sample variances for core CPI, core PPI, and the unemployment rate reported in Table 1. The population R2 ranges from 0 to 40 percent, which likewise easily brackets the degree of predictability of yield changes in the wake of these news announcements that we and others have found. The sample size is set to 100 or 200, again in line with our application. Finally, we include cases
where ![]() (no measurement error in the survey, just rounding) and in which
(no measurement error in the survey, just rounding) and in which ![]() is quite large (two tenths of a percentage point). In every case, the empirical size of the test is between 3.8 and 7.9 percent, meaning that any size distortions are very modest. This leads us to conclude that our finding that
is quite large (two tenths of a percentage point). In every case, the empirical size of the test is between 3.8 and 7.9 percent, meaning that any size distortions are very modest. This leads us to conclude that our finding that ![]() is significantly different from zero for the core CPI release is not simply the artifact of some size distortion caused by measurement error and/or rounding in the survey.
is significantly different from zero for the core CPI release is not simply the artifact of some size distortion caused by measurement error and/or rounding in the survey.
4. Conclusion
Our results suggest that market participants might be focusing irrationally on the headline number, as opposed to the most precise available data in a data release. And, while this does not necessarily imply that irrationality of market participants explains a large share of overall asset price movements, reading the text of the data release seems to be something that should be extraordinarily easy for the markets. To the extent that we find evidence that they may not do this, it motivates work outside of models of rational asset pricing. Some recent research in macroeconomics and finance has discussed the possibility of "rational inattention" in which agents optimally choose not to collect information because it is costly to do so (e.g. Sims, 2006). Looking up the unrounded number in an anticipated and closely-watched data release is surely not costly. Accordingly, if some investors are looking only at the headline number, this seems more like irrational inattention to us.
References
Balduzzi, Pierluigi, Edwin J. Elton and Clifton T. Green (2001): Economic News and Bond Prices: Evidence from the U.S. Treasury Market. Journal of Financial and Quantitative Analysis, 36, pp. 523-543.
Lamont, Owen A. and Richard H. Thaler (2003): Can the Market Add and Subtract? Mispricing in Tech Stock Carve-Outs, Journal of Political Economy, 111, pp. 227-268.
Sims, Christopher A. (2006): Rational Inattention: Beyond the Linear-Quadratic Case, American Economic Review, 96, pp. 158-163.
Veronesi, P. (1999): Stock Market Overreaction to Bad News in Good Times: A Rational Expectations Equilibrium Model, Review of Financial Studies, 12, pp. 975-1007.
| Announcement | Standard Deviation of MMS Expectations | Standard Deviation of Surprises |
Standard Deviation of Rounding Error |
|---|---|---|---|
| CPI (core)1 | 0.05 | 0.10 | 0.03 |
| PPI (core)2 | 0.08 | 0.27 | 0.03 |
| Unemployment Rate3 | 0.98 | 0.14 | 0.03 |
1. Percentage points, month-over-month. Sample July 1991 to September 2006. Return to Table
2. Percentage points, month-over-month. Sample April 1997 to September 2006 Return to Table
3. Percentage points. Sample July 1991 to September 2006. Return to Table
| Asset Return : Announcement | Surprise | Rounding Error |
|---|---|---|
| Change in
two-year yield : CPI (core) |
18.54
***
(2.71) |
-16.10**
(7.16) |
| Change in
two-year yield : PPI (core) |
3.56
***
(1.13) |
3.76
(7.45) |
| Change in
two-year yield : Unemployment Rate |
-11.67
***
(3.00) |
6.19
(16.05) |
| Change in
ten-year yield : CPI (core) |
19.68
***
(2.69) |
-23.11**
(9.66) |
| Change in
ten-year yield : PPI (core) |
4.22
***
(0.83) |
7.19
(7.04) |
| Change in
ten-year yield : Unemployment Rate |
-7.38
***
(2.39) |
-2.35
(13.61) |
| Change in eurodollar
futures rate : CPI (core) |
20.27
***
(3.04) |
-19.92**
(8.12) |
| Change in eurodollar
futures rate : PPI (core) |
5.29***
(1.21) |
2.91
(8.49) |
| Change in eurodollar
futures rate : Unemployment Rate |
-13.89***
(3.89) |
8.59
(18.85) |
Notes: Included regressors are those released at 8.30 am on any given day and are measured as the difference between unrounded released and expected values. Standard errors shown in parentheses are White heteroskedasticity robust standard errors. *** indicates significance at the 1-percent level (Return to Table), ** at the 5-percent level (Return to Table) and * at the 10-percent level. Constant term included but not shown and insignificantly different from zero. Regressions include coefficients on the surprise components of concurrently released non-farm payrolls, retail sales and initial jobless claims, which are all significantly different from zero but not shown.
| Asset Return | Announcements | Surprise | Rounding Error |
|---|---|---|---|
| Change in
two-year yield |
CPI (core) and
PPI (core) |
1.14
***
(0.21) |
-1.74
***
(0.67) |
| Change in
ten-year yield |
CPI (core) and
PPI (core) |
1.31
***
(0.20) |
-2.78
***
(1.02) |
| Change in eurodollar
futures rate |
CPI (core) and
PPI (core) |
1.50
***
(0.23) |
-2.44
***
(0.74) |
Notes: The surprise and rounding error regressors have been divided by the standard deviation of surprises of the respective announcement variable (see Table 1 for these values). A common coefficient is estimated for the response of asset markets to a one-standard deviation surprise to CPI (core) and PPI (core), and another common coefficient for the response to the rounding error proportional to a one-standard deviation surprise. *** indicates significance at the 1-percent level (Return to Table). All other details are as described in the notes to Table 1.
Table 4: Monte Carlo rejection rates from simulation experiment with different parameter values (effective size in percentage points for test with 5 percent nominal size).
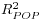 , , |
 =0 =0 |
 =0.05 =0.05 |
 =0.1 =0.1 |
 =0.2 =0.2 |
 =0 =0 |
 =0.05 =0.05 |
 =0.1 =0.1 |
 =0.2 =0.2 |
 =0 =0 |
 =0.05 =0.05 |
 =0.1 =0.1 |
 =0.2 =0.2 |
 =0 =0 |
 =0.05 =0.05 |
 =0.1 =0.1 |
 =0.2 =0.2 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.1, 0.05 | 6.5 | 6.2 | 6.2 | 6.3 | 6.9 | 7.3 | 7.3 | 7.5 | 5.0 | 5.4 | 5.4 | 5.8 | 6.2 | 6.1 | 6.1 | 6.4 |
| 0.1, 0.1 | 6.6 | 6.5 | 6.5 | 6.2 | 4.0 | 4.1 | 4.6 | 4.2 | 5.3 | 5.3 | 5.8 | 5.8 | 6.5 | 6.4 | 6.5 | 6.4 |
| 0.1, 0.2 | 6.1 | 5.5 | 5.8 | 5.8 | 6.3 | 6.0 | 6.7 | 6.7 | 6.1 | 6.2 | 5.8 | 5.9 | 6.5 | 6.7 | 6.5 | 6.3 |
| 0.1, 0.5 | 6.1 | 6.1 | 6.2 | 6.5 | 5.8 | 5.4 | 4.9 | 5.2 | 5.6 | 5.6 | 6.0 | 6.2 | 5.2 | 5.1 | 5.1 | 5.2 |
| 0.2, 0.05 | 6.9 | 6.0 | 5.9 | 5.9 | 7.1 | 7.5 | 7.8 | 7.7 | 5.0 | 5.2 | 5.2 | 5.9 | 6.2 | 6.1 | 6.2 | 6.2 |
| 0.2, 0.1 | 6.9 | 6.1 | 6.2 | 6.0 | 3.9 | 4.2 | 4.0 | 4.4 | 5.4 | 5.4 | 5.6 | 5.8 | 6.3 | 6.2 | 6.4 | 6.2 |
| 0.2, 0.2 | 5.5 | 6.1 | 5.9 | 5.7 | 6.5 | 6.3 | 6.3 | 6.5 | 6.1 | 6.0 | 5.5 | 5.9 | 6.4 | 6.7 | 6.8 | 6.1 |
| 0.2, 0.5 | 6.3 | 5.4 | 6.3 | 6.7 | 5.8 | 5.2 | 4.7 | 5.0 | 5.5 | 5.9 | 6.3 | 6.3 | 5.2 | 5.1 | 5.4 | 5.2 |
| 0.3, 0.05 | 7.0 | 5.8 | 5.6 | 5.9 | 7.1 | 7.8 | 7.7 | 7.8 | 5.3 | 5.3 | 5.5 | 5.9 | 6.2 | 6.1 | 6.2 | 6.4 |
| 0.3, 0.1 | 6.9 | 6.3 | 6.0 | 6.1 | 4.0 | 4.0 | 4.0 | 4.4 | 5.4 | 5.3 | 6.0 | 6.1 | 6.4 | 6.3 | 6.7 | 6.3 |
| 0.3, 0.2 | 6.1 | 5.7 | 5.7 | 6.4 | 6.7 | 6.4 | 6.4 | 6.9 | 6.4 | 6.0 | 5.6 | 5.8 | 6.4 | 6.8 | 6.7 | 5.9 |
| 0.3, 0.5 | 6.4 | 5.8 | 6.3 | 6.4 | 5.9 | 5.3 | 4.8 | 5.2 | 5.4 | 6.3 | 6.2 | 6.5 | 5.1 | 4.8 | 5.5 | 5.0 |
| 0.4, 0.05 | 6.7 | 5.5 | 5.2 | 5.8 | 7.5 | 7.6 | 7.9 | 7.6 | 5.3 | 5.0 | 5.5 | 6.1 | 6.1 | 6.1 | 6.1 | 6.0 |
| 0.4, 0.1 | 7.3 | 6.3 | 6.3 | 5.7 | 4.1 | 3.8 | 3.9 | 4.4 | 5.4 | 5.2 | 6.0 | 5.7 | 6.4 | 6.3 | 6.5 | 6.1 |
| 0.4, 0.2 | 6.1 | 5.4 | 6.0 | 6.2 | 7.1 | 6.3 | 6.7 | 6.5 | 6.2 | 6.3 | 5.5 | 5.8 | 6.3 | 6.8 | 6.6 | 5.4 |
| 0.4, 0.5 | 6.7 | 6.2 | 6.1 | 6.4 | 5.9 | 5.3 | 4.6 | 5.3 | 5.3 | 6.7 | 6.6 | 6.7 | 5.1 | 4.9 | 5.6 | 5.1 |
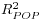 , , |
 =0 =0 |
 =0.05 =0.05 |
 =0.1 =0.1 |
 =0.2 =0.2 |
 =0 =0 |
 =0.05 =0.05 |
 =0.1 =0.1 |
 =0.2 =0.2 |
 =0 =0 |
 =0.05 =0.05 |
 =0.1 =0.1 |
 =0.2 =0.2 |
 =0 =0 |
 =0.05 =0.05 |
 =0.1 =0.1 |
 =0.2 =0.2 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.1, 0.05 | 4.7 | 4.9 | 4.4 | 4.1 | 7.6 | 7.2 | 7.3 | 6.5 | 6.2 | 6.5 | 6.3 | 6.1 | 5.7 | 5.9 | 5.9 | 6.0 |
| 0.1, 0.1 | 4.9 | 5.1 | 5.5 | 4.9 | 5.5 | 5.8 | 5.1 | 5.7 | 5.6 | 5.3 | 5.3 | 5.3 | 5.9 | 5.8 | 5.4 | 5.1 |
| 0.1, 0.2 | 5.5 | 6.1 | 5.6 | 5.6 | 4.4 | 4.3 | 4.4 | 4.1 | 5.8 | 5.7 | 5.9 | 6.0 | 4.5 | 4.6 | 4.7 | 4.1 |
| 0.1, 0.5 | 7.0 | 6.7 | 6.9 | 6.9 | 5.4 | 5.7 | 5.9 | 6.1 | 5.1 | 5.4 | 5.0 | 5.2 | 5.6 | 5.7 | 5.8 | 6.0 |
| 0.2, 0.05 | 4.6 | 4.8 | 4.4 | 4.2 | 7.6 | 6.6 | 6.5 | 6.5 | 6.4 | 6.2 | 6.0 | 6.2 | 5.7 | 5.8 | 5.9 | 6.1 |
| 0.2, 0.1 | 4.8 | 5.2 | 5.0 | 5.6 | 5.7 | 5.8 | 4.8 | 5.3 | 5.7 | 5.6 | 5.3 | 4.9 | 5.8 | 5.8 | 5.3 | 5.2 |
| 0.2, 0.2 | 5.4 | 5.8 | 5.7 | 5.6 | 4.4 | 4.3 | 4.7 | 4.4 | 5.9 | 6.0 | 6.1 | 6.5 | 4.5 | 4.4 | 4.3 | 4.0 |
| 0.2, 0.5 | 7.2 | 6.4 | 6.7 | 6.6 | 5.3 | 5.9 | 6.0 | 6.3 | 5.1 | 5.3 | 5.2 | 5.3 | 5.6 | 6.0 | 6.0 | 6.2 |
| 0.3, 0.05 | 4.4 | 4.8 | 4.4 | 4.3 | 7.4 | 6.3 | 6.3 | 6.1 | 6.3 | 6.3 | 6.0 | 6.0 | 5.8 | 5.8 | 6.1 | 6.1 |
| 0.3, 0.1 | 5.1 | 5.8 | 6.1 | 6.2 | 5.5 | 5.9 | 4.7 | 4.8 | 5.7 | 5.4 | 5.3 | 4.1 | 5.8 | 5.5 | 5.1 | 5.1 |
| 0.3, 0.2 | 4.9 | 5.6 | 5.4 | 5.5 | 4.4 | 4.7 | 4.9 | 4.4 | 6.0 | 6.0 | 6.5 | 6.4 | 4.6 | 4.4 | 4.2 | 4.3 |
| 0.3, 0.5 | 7.0 | 6.2 | 6.4 | 6.4 | 5.3 | 5.8 | 6.1 | 5.9 | 5.3 | 5.6 | 5.2 | 5.6 | 5.6 | 5.8 | 5.9 | 6.3 |
| 0.4, 0.05 | 4.7 | 5.0 | 4.8 | 4.5 | 7.3 | 6.4 | 6.3 | 5.7 | 6.1 | 6.3 | 5.9 | 6.3 | 5.7 | 5.8 | 6.3 | 5.8 |
| 0.4, 0.1 | 5.1 | 5.8 | 6.4 | 6.3 | 5.8 | 5.7 | 4.8 | 4.6 | 5.6 | 5.2 | 5.3 | 4.5 | 5.8 | 5.5 | 5.4 | 5.2 |
| 0.4, 0.2 | 5.2 | 5.5 | 5.3 | 5.2 | 4.2 | 4.9 | 4.6 | 4.3 | 6.0 | 6.1 | 6.5 | 6.5 | 4.5 | 4.3 | 4.0 | 5.0 |
| 0.4, 0.5 | 7.0 | 5.9 | 6.3 | 6.6 | 5.3 | 5.8 | 6.1 | 5.7 | 5.5 | 5.8 | 6.2 | 6.2 | 5.8 | 5.7 | 5.8 | 6.3 |
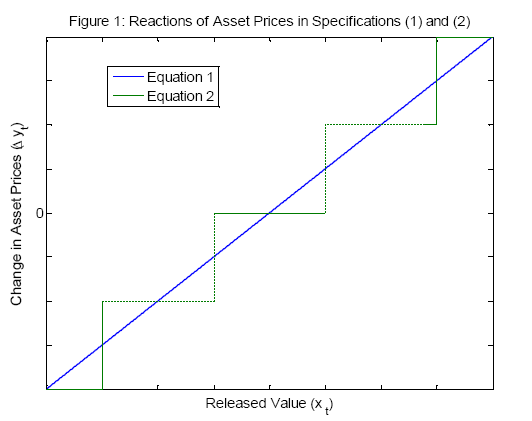
Notes: This graph plots the relationship between the released value, ![]() , and the expected change in asset prices,
, and the expected change in asset prices, ![]() , under specification (1) (the solid line), according to which asset prices react to the unrounded number, and under specification (2) (the dotted line), according to which asset prices react to the rounded number only.
, under specification (1) (the solid line), according to which asset prices react to the unrounded number, and under specification (2) (the dotted line), according to which asset prices react to the rounded number only.