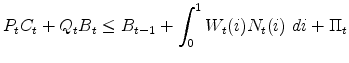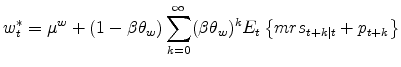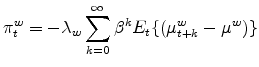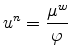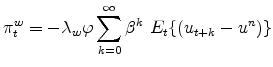Skip to: [Printable Version (PDF)] [Bibliography] [Footnotes]

International Research Forum on Monetary Policy: Screen Reader version ^♣

The Return of the Wage Phillips Curve *

Jordi Galí

CREI, Universitat Pompeu Fabra, and Barcelona GSE

February 2010 (first draft: May 2009)

Keywords: Staggered nominal wage setting, New Keynesian model, unemployment fluctuations.

Abstract:

The standard New Keynesian model with staggered wage setting is shown to imply a simple dynamic relation between wage inflation and unemployment. Under some assumptions, that relation takes a form similar to that found in empirical applications-starting with the original Phillips (1958) curve-and may thus be viewed as providing some theoretical foundations to the latter. The structural wage equation derived here is shown to account reasonably well for the comovement of wage inflation and the unemployment rate in the U.S. economy, even under the strong assumption of a constant natural rate of unemployment.

1 Introduction

The past decade has witnessed the emergence of a new popular framework for monetary policy analysis, the so called New Keynesian (NK) model. The new framework combines some of the ingredients of Real Business Cycle theory (e.g. dynamic optimization, general equilibrium) with others that have a distinctive Keynesian flavor (e.g. monopolistic competition, nominal rigidities).

Many important properties of the NK model hinge on the specification of its wage-setting block. While basic versions of that model, intended for classroom exposition, assume fully flexible wages and perfect competition in labor markets, the larger, more realistic versions (including those developed in-house at different central banks and policy institutions) typically assume staggered nominal wage setting which, following the lead of Erceg, Henderson and Levin (2000), are modeled in a way symmetric to price setting.¹ The degree of nominal wage rigidities and other features of wage setting play an important role in determining the response of the economy to monetary and other shocks. Furthermore, the coexistence of price and wage rigidities has important implications for the optimal design of monetary policy.² Yet, and despite the central role of the wage-setting block in the NK model, the amount of work aimed at assessing its empirical relevance has been surprisingly scant.³ This is in stark contrast with the recent but already large empirical literature on price inflation dynamics and firms' pricing patterns, which has been motivated to a large extent by the desire to evaluate the price-setting block of the NK model.⁴

The present paper seeks to fill part of that gap, by providing evidence on the NK model's ability to account for the observed patterns of wage inflation in the U.S. economy. In order to do so, I reformulate the standard version of the NK wage equation in terms of a (suitably defined) unemployment rate. The main advantage of that reformulation is the observability of the associated driving force (the unemployment rate), which contrasts with the inherent unobservability of the wage markup or the output gap, which are the driving forces in standard formulations of the NK wage inflation equation.

The staggered wage setting model à la Calvo (1983) embedded in standard versions of the New Keynesian framework is shown to imply a simple dynamic relation between wage inflation and the unemployment rate, which I refer to as the New Keynesian Wage Phillips Curve. Under certain assumptions, that relation takes the same form as the original equation of Phillips (1958). Furthermore, in the presence of wage indexation to past inflation -an assumption often made in extensions of the basic model- the resulting wage dynamics are consistent with a specification often used in applied work. The analysis developed here can thus be seen as providing some theoretical foundations for those specifications, as well as a structural interpretation to its coefficients.

In the second part of the paper I turn to the empirical evidence, and show how the New Keynesian Wage Phillips Curve accounts reasonably well for the behavior of wage inflation in the U.S. economy, even under the strong assumption of a constant natural rate of unemployment. In particular, the model can account for the strong negative correlation between wage inflation and the unemployment rate observed since the mid-1980s. On the other hand, the lack of a significant correlation between the same variables for the postwar period as a whole can be explained as a consequence of the large fluctuations in price inflation in and around the 1970s, in combination with wage indexation to past CPI inflation.

The remainder of the paper is organized as follows. Section 2 describes the basic model of staggered nominal wage setting. Section 3 introduces the measure of unemployment latent in that model, and reformulates the wage inflation equation in terms of that variable. Section 4 provides an empirical assessment of the model's implied relation between wage inflation and unemployment using postwar U.S. data. Section 5 concludes.

2 Staggered Wage Setting and Wage Inflation Dynamics

This section introduces a variant of the staggered wage setting model originally developed in Erceg, Henderson and Levin (2000; henceforth, EHL). That model (and extensions thereof) constitutes one of the key building blocks of the monetary DSGE frameworks that have become part of the toolkit for policy analysis in both academic and policy circles. The variant presented here assumes that labor is indivisible, with all variations in hired labor input taking place at the extensive margin (i.e. in the form of variations in employment). The assumption of indivisible labor leads to a definition of unemployment consistent with its empirical counterpart.

The model assumes a (large) representative household with a continuum of members represented by the unit square and indexed by a pair $(i,j)\in \lbrack 0,1]\times \lbrack 0,1]$ . The first dimension, indexed by $i\in \lbrack 0,1]$ , represents the type of labor service in which a given household member is specialized. The second dimension, indexed by $j\in \lbrack 0,1]$ , determines his disutility from work. The latter is given by $% \chi _{t}j^{\varphi }$ if he is employed and zero otherwise, where $\varphi \geq 0$ determines the elasticity of the marginal disutility of work, and $% \chi _{t}>0$ is an exogenous preference shifter. Furthermore, utility is logarithmic in consumption and there is full risk sharing among household members, as in Merz (1995).

The household period utility corresponds to the integral of its members' utilities, and is thus given by

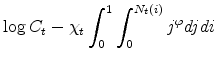$\displaystyle U(C_{t},\{N_{t}(i)\},\chi _{t})$	$\displaystyle \equiv$	$\displaystyle \log C_{t}-\chi _{t}\int_{0}^{1}\int_{0}^{N_{t}(i)}j^{\varphi }djdi$
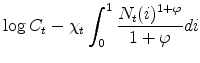	$\displaystyle =$	$\displaystyle \log C_{t}-\chi _{t}\int_{0}^{1}\frac{N_{t}(i)^{1+\varphi }}{1+\varphi }di$

where $C_{t}$ denotes household consumption, and $N_{t}(i)\in \lbrack 0,1]$ is the fraction of members specialized in type

labor who are employed in period

. Below I discuss the robustness of the main findings to a generalization of the previous utility function that is consistent with (empirically more plausible) smaller wealth effects on labor supply.

The relevant decision unit is the household. The latter seeks to maximize

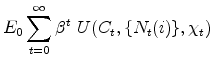$\displaystyle E_{0}\sum_{t=0}^{\infty }\beta ^{t}\ U(C_{t},\{N_{t}(i)\},\chi _{t})$

subject to a sequence of budget constraints

$\displaystyle P_{t}C_{t}+Q_{t}B_{t}\leq B_{t-1}+\int_{0}^{1}W_{t}(i)N_{t}(i)\ di+\Pi _{t}$

(1)

where $P_{t}$ is the price of the consumption bundle, $W_{t}(i)$ is the nominal wage for labor of type

, $B_{t}$ represents purchases of a nominally riskless one-period bond (at a price $Q_{t}$ ), and $\Pi _{t}$ is a lump-sum component of income (which may include, among other items, dividends from ownership of firms). The above sequence of period budget constraints is supplemented with a solvency condition which prevents the household from engaging in Ponzi schemes.

As in EHL, and following the formalism of Calvo (1983), workers supplying a labor service of a given type (or a union representing them) get to reset their (nominal) wage with probability $1-\theta _{w}$ each period. That probability is independent of the time elapsed since they last reset their wage, in addition to being independent across labor types. Thus, a fraction of workers $\theta _{w}$ keep their wage unchanged in any given period, making that parameter a natural index of nominal wage rigidities. Once the wage has been set, the quantity of workers employed is determined unilaterally by firms, with households willingly meeting that demand (to the extent that the wage remains above the disutility of work for the marginal worker), by sending its specialized workers with the lowest work disutility.

When reoptimizing their wage in period , workers choose a wage $% W_{t}^{\ast }$ in order to maximize household utility (as opposed to their individual utility), subject to a sequence of isoelastic demand schedules for their labor type, and the usual sequence of household flow budget constraints.⁵ The first order condition associated with that problem can be written as:

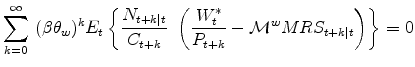$\displaystyle \sum_{k=0}^{\infty }\ (\beta \theta _{w})^{k}E_{t}\left\{ \frac{N_{t+k\vert t}}{% C_{t+k}}\ \left( \frac{W_{t}^{\ast }}{P_{t+k}}-\mathcal{M}% ^{w}MRS_{t+k\vert t}\right) \right\} =0$

where $N_{t+k\vert t}$ denotes the quantity demanded in period

of a labor type whose wage is being reset in period

, $MRS_{t+k\vert t}\equiv \chi _{t+k}C_{t+k}N_{t+k\vert t}^{\varphi }$ is the relevant marginal rate of substitution between consumption and employment in period

, and $% \mathcal{M}^{w}\equiv \frac{\epsilon _{w}}{\epsilon _{w}-1}$ is the desired (or flexible wage) markup, with $\epsilon _{w}$ denoting the (constant) wage elasticity of demand for the services of each labor type.

Log-linearizing the above optimality condition around a perfect foresight zero inflation steady state, and using lower case letters to denote the logs of the corresponding variable, we obtain the approximate wage setting rule

$\displaystyle w_{t}^{\ast }=\mu ^{w}+(1-\beta \theta _{w})\sum_{k=0}^{\infty }(\beta \theta _{w})^{k}E_{t}\left\{ mrs_{t+k\vert t}+p_{t+k}\right\}$

(2)

where $\mu ^{w}\equiv \log \mathcal{M}^{w}$ . Note that in the absence of nominal wage rigidities ( $\theta _{w}=0$ ) we have $w_{t}^{\ast }=w_{t}=\mu ^{w}+mrs_{t}+p_{t}$ , implying a constant markup $\mu ^{w}$ of the wage $w_{t}$ over the price-adjusted marginal rate of substitution, $mrs_{t}+p_{t}$ . When nominal wage rigidities are present, new wages are set instead as a constant markup $\mu ^{w}$ over a weighted average of current and expected future price-adjusted marginal rates of substitution.

Letting $mrs_{t}\equiv c_{t}+\varphi \ n_{t}+\xi _{t}$ denote the economy's average (log) marginal rate of substitution, where $\xi _{t}\equiv \log \chi _{t}$ , we can write

$\displaystyle mrs_{t+k\vert t}$	$\displaystyle =$	$\displaystyle mrs_{t+k}+\varphi (n_{t+k\vert t}-n_{t+k})$	(3)
	$\displaystyle =$	$\displaystyle mrs_{t+k}-\epsilon _{w}\varphi (w_{t}^{\ast }-w_{t+k}) \notag$

Furthermore, log-linearizing the expression for aggregate wage index around a zero inflation steady state we obtain

$\displaystyle w_{t}=\theta _{w}w_{t-1}+(1-\theta _{w})w_{t}^{\ast }$

(4)

As in EHL (2000), we can combine equations (2) through (4) and derive the baseline wage inflation equation

$\displaystyle \pi _{t}^{w}=\beta E_{t}\{\pi _{t+1}^{w}\}-\lambda _{w}(\mu _{t}^{w}-\mu ^{w})$

(5)

where $\pi _{t}^{w}\equiv w_{t}-w_{t-1}$ is wage inflation, $\mu _{t}^{w}\equiv w_{t}-p_{t}-mrs_{t}$ denotes the (average) wage markup, and $% \lambda _{w}\equiv \frac{(1-\theta _{w})(1-\beta \theta _{w})}{\theta _{w}(1+\epsilon _{w}\varphi )}>0$ . In words, wage inflation depends positively on expected one period ahead wage inflation and negatively on the deviation of the average wage markup from its desired value.⁶ Equivalently, and solving (5) forward, we have

$\displaystyle \pi _{t}^{w}=-\lambda _{w}\sum_{k=0}^{\infty }\beta ^{k}E_{t}\{(\mu _{t+k}^{w}-\mu ^{w})\}$

(6)

i.e. wage inflation is proportional to the discounted sum of expected deviations of current and future average wage markups from their desired levels. Intuitively, if average wage markups are below (above) their desired level, workers that have a chance to reset their wage will tend to adjust it upward (downward), thus generating positive (negative) wage inflation.

Estimated versions of the model above found in the literature generally allow for automatic indexation to price inflation of the wages that are not reoptimized in any given period. Here I assume the following indexation rule:

$\displaystyle w_{t+k\vert t}=w_{t+k-1\vert t}+\gamma \overline{\pi }_{t+k-1}^{p}+(1-\gamma )\pi ^{p}+g$

(7)

for

where $w_{t+k\vert t}$ is the period

(log) wage for workers who last re-optimized their wage in period

(with $w_{t\vert t}\equiv w_{t}^{\ast }$ ), $\overline{\pi }_{t}^{p}$ is the price inflation variable to which wages are indexed, $\pi ^{p}$ denotes steady state price inflation, and

is the rate of growth of productivity (and real wages) in the steady state. In that case the following wage inflation equation can be derived:

$\displaystyle \pi _{t}^{w}-\gamma \overline{\pi }_{t-1}^{p}=\alpha +\beta E_{t}\{\pi _{t+1}^{w}-\gamma \overline{\pi }_{t}^{p}\}-\lambda _{w}(\mu _{t}^{w}-\mu ^{w})$

(8)

where $\alpha \equiv (1-\beta )((1-\gamma )\pi ^{p}+g)$ .

While in existing applications it is often assumed $\overline{\pi }% _{t}^{p}\equiv \pi _{t}^{p}\equiv p_{t}-p_{t-1}$ (e.g. Smets and Wouters (2003, 2007)), it is important to note that the model allows for inflation measures other than the one-period lagged inflation as an indexing variable. In particular, some of the estimates below use the moving average $\overline{% \pi }_{t}^{p}\equiv (1/4)(\pi _{t}^{p}+\pi _{t-1}^{p}+\pi _{t-2}^{p}+\pi _{t-3}^{p})$ as a "smoother" alternative indexing variable.

3 Wage Inflation and Unemployment: A New Keynesian Wage Phillips Curve

Next I introduce unemployment explicitly in the model above.⁷ Consider household member , specialized in type labor and with disutility of work $\chi _{t}j^{\varphi }$ . Using household welfare as a criterion, and taking as given current labor market conditions (as summarized by the prevailing wage for his labor type), he will find it optimal to participate in the labor market in period if and only if

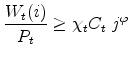$\displaystyle \frac{W_{t}(i)}{P_{t}}\geq \chi _{t}C_{t}\ j^{\varphi }$

i.e. whenever the real wage prevailing in his trade is above his disutility from working, expressed in terms of consumption using the household's marginal valuation of the latter.

Thus, the marginal supplier of type labor (employed or unemployed), which I denote by $L_{t}(i)$ , is implicitly given by

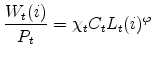$\displaystyle \frac{W_{t}(i)}{P_{t}}=\chi _{t}C_{t}L_{t}(i)^{\varphi }$

Taking logs and integrating over we obtain

$\displaystyle w_{t}-p_{t}=c_{t}+\varphi \ l_{t}+\xi _{t}$

(9)

where $l_{t}\equiv \int_{0}^{1}l_{t}(i)di$ can be interpreted as the model's implied aggregate participation rate, and $w_{t}\equiv \int_{0}^{1}w_{t}(i)di$ is the average wage, both expressed in logs.

I define the unemployment rate $u_{t}$ as

$\displaystyle u_{t}\equiv l_{t}-n_{t}$

(10)

which, for rates of unemployment of the magnitude observed in the postwar U.S. economy, is a close (and algebraically convenient) approximation to the more conventional measure $(L_{t}-N_{t})/L_{t}$ .

Combining (9) and (10) with the expression for the average wage markup $\mu _{t}^{w}\equiv (w_{t}-p_{t})-(c_{t}+\varphi n_{t}+\xi _{t})$ used above yields the following simple linear relation between the wage markup and the unemployment rate

$\displaystyle \mu _{t}^{w}=\varphi \ u_{t}$

(11)

Let us define the natural rate of unemployment, $u_{t}^{n}$ , as the rate of unemployment that would prevail in the absence of nominal wage rigidities. It follows from the assumption of a constant desired wage markup that $u_{t}^{n}$ is constant and given by

$\displaystyle u^{n}=\frac{\mu ^{w}}{\varphi }$

(12)

Finally, combining (5), (11), and (12) we obtain the following New Keynesian Wage Phillips curve (NKWPC, for short):

$\displaystyle \pi _{t}^{w}=\beta E_{t}\{\pi _{t+1}^{w}\}-\lambda _{w}\varphi \ (u_{t}-u^{n})$

(13)

Note that the simple linear relation between the wage markup and unemployment derived in this section holds irrespective of the details of the wage setting process. In particular, it also holds in the presence of wage indexation as described in equation (7). In that case we can derive the implied wage Phillips curve by combining equations (8) and (11) to obtain:

$\displaystyle \pi _{t}^{w}=\alpha +\gamma \overline{\pi }_{t-1}^{p}+\beta E_{t}\{\pi _{t+1}^{w}-\gamma \overline{\pi }_{t}^{p}\}-\lambda _{w}\varphi \ (u_{t}-u^{n})$

(14)

which I refer to henceforth as the augmented NKWPC.

3.1 Relation to the original wage Phillips curve

In his seminal paper, Phillips (1958) uncovered the existence of a strong inverse empirical relation between wage inflation and the unemployment rate in the U.K. over the period 1861-1957. His analysis was subsequently replicated using U.S. data by Samuelson and Solow (1960), who showed that a similar empirical relation had been prevalent in the U.S., with the exception of the New Deal period and the early years of the first World War. Much of subsequent empirical work turned its focus instead to the relation between price inflation and unemployment, usually in the context of a discussion of NAIRU and its changes (e.g. Gordon (1997) and Staiger, Stock and Watson (1997)).⁸

Note that, like the original Phillips (1958) curve, the NKWPC establishes a relationship between wage inflation and the unemployment rate. But two key differences with respect to Phillips' original curve (and some of its subsequent amendments) are worth emphasizing.

Firstly, (13) is a microfounded structural relation between wage inflation and unemployment, with coefficients that are functions of parameters that have a structural interpretation, and which are independent of the policy regime.⁹ In particular, the steepness of the slope of the implied wage inflation-unemployment curve (given expected wage inflation) is decreasing in the degree of wage rigidity $\theta _{w}$ (which is inversely related to $\lambda _{w}$ ). In the limit, as $\theta _{w}$ approaches zero (the case of full wage flexibility), the curve becomes vertical. Also, the slope of the $(\pi ^{w},u)$ relation is decreasing in the size of the Frisch labor supply elasticity (which corresponds to the inverse of $\varphi$ ). That structural nature of (13) stands in contrast with the purely empirical basis of Phillips (1958) original curve, whose only theoretical underpinning was the plausibility of the principle that "when demand for labour is high and there are very few unemployed we should expect employers to bid wage rates up quite rapidly...".¹⁰

Secondly, note that (13) implies that wage inflation is a forward looking variable, which is inversely related to current unemployment but also to its expected future path. This feature, which reflects the forward looking nature of wage setting, is immediately seen by solving (13) forward to obtain

$\displaystyle \pi _{t}^{w}=-\lambda _{w}\varphi \sum_{k=0}^{\infty }\beta ^{k}\ E_{t}\{(u_{t+k}-u^{n})\}$

(15)

which contrasts with the static, contemporaneous nature of the original Phillips curve, in which expectations play no role.

Next I briefly discuss two extensions of the previous framework. The first one allows for changes over time in desired markups, whereas the second introduces a specification of preferences that allows for limited short run wealth effects on labor supply.

3.2 An Extension with Time-Varying Desired Wage Markups

Estimated, medium-scale versions of the New Keynesian model often allow for a time-varying, exogenous desired wage markup, $\{\overline{\mu }_{t}^{w}\}$ (see, e.g. Smets and Wouters (2003, 2007)). In that case, the wage inflation equation (shown in its version without indexation, for simplicity) is given by

$\displaystyle \pi _{t}^{w}=\beta E_{t}\{\pi _{t+1}^{w}\}-\lambda _{w}(\mu _{t}^{w}-% \overline{\mu }_{t}^{w})$

(16)

while the corresponding NKWPC now takes the form

$\displaystyle \pi _{t}^{w}=\beta E_{t}\{\pi _{t+1}^{w}\}-\lambda _{w}\varphi (u_{t}-u_{t}^{n})$

where $u_{t}^{n}\equiv \frac{\overline{\mu }_{t}^{w}}{\varphi }$ denotes the (now time-varying) natural rate of unemployment. Variations in the latter variable, resulting from changes in desired wage markups, may thus potentially shift the relation between wage inflation and the unemployment rate.¹¹

Note that we can also write

$\displaystyle \pi _{t}^{w}=\beta \ E_{t}\{\pi _{t+1}^{w}\}-\lambda _{w}\varphi \ u_{t}+v_{t}$

(17)

$v_{t}\equiv \lambda _{w}\overline{\mu }_{t}^{w}$ The previous specification can be compared against one often used in the literature which relies on (16) combined with the definition of the average wage markup, and which takes the form

$\displaystyle \pi _{t}^{w}=\beta E_{t}\{\pi _{t+1}^{w}\}-\lambda _{w}(w_{t}-p_{t}-c_{t}-\varphi n_{t})+v_{t}^{\prime }$

where now the error term is given by $v_{t}^{\prime }\equiv \lambda _{w}% \overline{\mu }_{t}^{w}+\lambda _{w}\xi _{t}$ , i.e. it is influenced by both wage markup shocks and preference shocks. That property contrasts with (17), whose error term captures exclusively wage markup shocks, but not preference shocks (even though the latter have been allowed for in the model). This feature should in principle allow one to overcome the identification problem raised by Chari, Kehoe and McGrattan (2008) in their critique of current New Keynesian models. That potential advantage of the present formulation is discussed in detail in Galí, Smets and Wouters (2010), who re-estimate the Smets and Wouters (2007) model using an unemployment-based wage equation, and re-assess some of the findings therein in light of the new estimates.

3.3 Robustness to a Specification of Preferences with Limited Short-Run Wealth Effects

The assumptions on preferences made above, while analytically convenient, have implications on labor supply that are rather implausible from an empirical viewpoint. In particular, the strong wealth effects implied by the logarithmic specification, while seemingly needed in order to remain consistent with balanced growth, are likely to be counterfactual. This becomes clear by looking at the labor participation equation (9), which implies that the wage-consumption ratio $(w_{t}-p_{t}-c_{t})$ should be positively correlated to labor participation, at least conditional on shocks other than preference shocks being the source of fluctuations. In postwar U.S. data, and possibly due to the wage rigidities of the kind emphasized in the present paper, $w_{t}-p_{t}-c_{t}$ is clearly countercyclical, while participation is procyclical (albeit moderately so). Thus, and unless one is willing to attribute a dominant weight to preference shocks as a source of cyclical fluctuations in wages, consumption and participation, equation (9) provides an unsatisfactory account of fluctuations in the labor force.¹²

Here I consider a simple extension of the preferences assumed above that can in principle overcome that problem, by allowing for arbitrarily small short-run wealth effects while remaining consistent with a balanced growth path. Thus, individual utility from consumption is now assumed to be given by $\Theta _{t}\log C_{t}(i,j)$ , where $\Theta _{t}$ is a preference shifter taken as exogenously given by each household, but determined by the ratio of aggregate consumption $\overline{C}_{t}$ to a measure of its trend level. More precisely, I assume $\Theta _{t}=\overline{C}_{t}/Z_{t}$ where $% Z_{t}=Z_{t-1}^{\vartheta }\overline{C}_{t}^{1-\vartheta }$ , for all . Aggregation of individual utilities thus yields the following period utility for the household

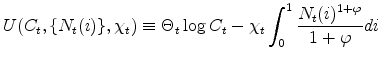$\displaystyle U(C_{t},\{N_{t}(i)\},\chi _{t})\equiv \Theta _{t}\log C_{t}-\chi _{t}\int_{0}^{1}\frac{N_{t}(i)^{1+\varphi }}{1+\varphi }di$

The derivation of the wage inflation equation (5) (or (8), in the presence of indexation) carries over to this case, with the relevant marginal rate of substitution in the optimal wage setting problem now being given by $MRS_{t+k\vert t}\equiv (\chi _{t+k}/\Theta _{t+k})C_{t+k}N_{t+k\vert t}^{\varphi }$ . Note, however, that in a symmetric equilibrium $C_{t}=\overline{C}_{t}$ for all , which allows us to write the equilibrium (log) marginal rate of substitution as $mrs_{t}=z_{t}+% \varphi n_{t}+\xi _{t}$ , where $z_{t}\equiv \log Z_{t}$ evolves over time according to $z_{t}=\vartheta z_{t-1}+(1-\vartheta )c_{t}$ . The equations for the average wage markup and participation are now respectively given by

$\displaystyle \mu _{t}^{w}\equiv (w_{t}-p_{t})-(z_{t}+\varphi n_{t}+\xi _{t})$

$\displaystyle w_{t}-p_{t}=z_{t}+\varphi \ l_{t}+\xi _{t}$

which can be combined to yield the same simple proportional relation between the wage markup and the unemployment rate as above, i.e. $\mu _{t}^{w}=\varphi u_{t}$ . Note that the previous specification is still consistent with a balanced growth path since, in the long run, $z_{t}$ will grow at the same rate as consumption. In the short run, however, the impact of changes in consumption on the marginal rate of substitution may be rendered arbitrarily small by increasing parameter $\vartheta$ , thus yielding a more plausible labor supply model. Yet, and most importantly for the purposes of the present paper, the specification of the NKWPC in (13) (or (14)) remains unaffected.¹³

3.4 A Reduced Form Representation for the NKWPC

Next I derive a simple reduced form representation of the NKWPC, thus setting the stage for the empirical analysis below. Consider the case of an exogenous, stationary process for the unemployment rate. As discussed below, this process turns out to provide a good approximation to the behavior of U.S. unemployment in the postwar period. Formally,

$\displaystyle \widehat{u}_{t}=\phi _{1}\widehat{u}_{t-1}+\phi _{2}\widehat{u}% _{t-2}+\varepsilon _{t}$

(18)

where $\widehat{u}_{t}\equiv u_{t}-u^{n}$ and $\{\varepsilon _{t}\}$ is white noise. Combining (18) with (14) yields the wage inflation equation

$\displaystyle \pi _{t}^{w}=\alpha +\gamma \overline{\pi }_{t-1}^{p}+\psi _{0}\widehat{u}% _{t}+\psi _{1}\widehat{u}_{t-1}$

(19)

where

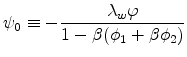$\displaystyle \psi _{0}\equiv -\frac{\lambda _{w}\varphi }{1-\beta (\phi _{1}+\beta \phi _{2})}$

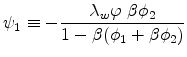$\displaystyle \psi _{1}\equiv -\frac{\lambda _{w}\varphi \ \beta \phi _{2}}{1-\beta (\phi _{1}+\beta \phi _{2})}$

or, equivalently,

$\displaystyle \pi _{t}^{w}=\alpha ^{\prime }+\gamma \overline{\pi }_{t-1}^{p}-\delta \widehat{u}_{t}-\psi _{1}\Delta \widehat{u}_{t}$

(20)

where $\delta \equiv -(\psi _{0}+\psi _{1})$ .

Estimates of the unemployment process (18) using postwar U.S. data unambiguously point to the following properties: $\phi _{1}>1$ , $-1<\phi _{2}<0$ and $0<\phi _{1}+\phi _{1}<1$ , the latter being a requirement for stationarity If those inequalities hold then we have $\psi _{0}<0$ , $\psi _{1}>0$ , and $\delta >0$ . Thus, under the previous assumptions and conditional on the relevant lagged price inflation measure used for indexation purposes, wage inflation should respond negatively to both the level and the first difference of the unemployment rate, with the size of that response being a well defined function of structural parameters, including those characterizing the process for the unemployment rate.

Interestingly, a specification like (20) has often been proposed and used in empirical applications, albeit without any strong theoretical justification (e.g. Blanchard and Katz (1999)), as well as in mainstream undergraduate textbooks (though the latter typically omit lagged unemployment). In fact, in his seminal paper Phillips (1958) himself argued that it was plausible that wage inflation would depend negatively on both the level and the change of the unemployment rate, since both captured important dimensions of the degree of tightness or excess demand in labor markets, and tried to uncover their joint influence on the unemployment rate.

The following section revisits and updates estimates of equations (19) and (20) and reinterprets them through the lens of the New Keynesian model developed above.

4 Empirical Evidence

The present section provides an empirical assessment of the NKWPC developed above. More specifically, I want to evaluate to what extent a version of the NKWPC with a constant natural rate can account for the joint behavior of unemployment and wage inflation in the U.S. economy.

First, I use simple statistics and graphical tools to seek evidence of a prima facie negative relationship between wage inflation and unemployment of the sort predicted by the theory. Secondly, I compare the observed behavior of wage inflation with that predicted by an estimated version of the model above, conditional on the unemployment rate.¹⁴

The empirical analysis relies on quarterly postwar U.S. data drawn from the Haver database. I use the civilian unemployment rate as my measure of unemployment. All measures of price inflation are constructed using the consumer price index. There are two main alternative sources for average wage data that one may use to construct measures of wage inflation: the earnings data for production and nonsupervisory workers from the Establishment Survey (starting in 1964Q1), and the compensation data from the "Productivity and Costs" publication of the Bureau of Labor Statistics (available from 1948Q1 onwards). Aside from their time span, the main difference between the two is that "compensation" is a more encompassing measure of the cost to the employer, and as such it includes employer contributions to employee-benefit plans or irregular bonuses, whereas "earnings" is restricted to wage income proper (including premium pay for overtime). Unfortunately, and as noted by several authors, the discrepancy between their implied inflation measures is far from negligible.¹⁵ This is made clear by Figure 1, which plots wage inflation based on both measures. Note that in this and subsequent figures -though not in the formal econometric work below-wage inflation is measured as the centered four-quarter difference of the log nominal wage expressed in percent terms (i.e., 100*( $w_{t+2}-w_{t-2}$ )), in order to smooth the high volatility associated with quarter-to-quarter log-differences.

Three features stand out in Figure 1. First, the two measures display very similar medium-run patterns, both picking up during the Great Inflation episode, dropping during the Volcker disinflation, and fluctuating around a low and stable mean during the Great Moderation years. This is reflected in their high contemporaneous correlation ( 0.82). Secondly, their mean values in the common sample period are noticeably different: 4.44 percent for the earnings-based measure, 5.36 percent for the compensation-based one. Finally, and perhaps more strikingly, the compensation-based measure appears far more volatile than the earnings-based measure, especially over the past two decades. A possible explanation for the difference in volatility lies in the inclusion of the payoffs from the exercise of employee stock options in the compensation measure. As argued by Mehran and Tracy (2001), the impact of changes in that (increasingly important) component of compensation on wage inflation is substantial, even if it only accounts for a small fraction of overall compensation.

Interestingly, and those differences notwithstanding, both sources are used in empirical macro applications, often with little or no discussion regarding the choice. While the compensation-based measure has an advantage in its longer span, its sizable high frequency variations render it somewhat suspicious, and suggest the presence of substantial measurement error. Thus, in the empirical analysis below I will use the earnings-based wage inflation as a baseline measure, but will check and discuss the robustness of the main findings to the use of the alternative, compensation-based, wage inflation measure. Perhaps surprisingly, given the seemingly large differences observed in Figure 1, none of the key qualitative findings in the empirical analysis below hinge on the choice of wage inflation measure.

4.1 A Quick Glance at the Data

The New Keynesian Wage Phillips curve derived in section 3 implies an inverse relation between wage inflation and the unemployment rate, albeit not a simple or contemporaneous one, especially in the presence of indexation. As a first pass in the empirical assessment of the model it seems natural to check whether the raw data hint at any such an inverse relation.

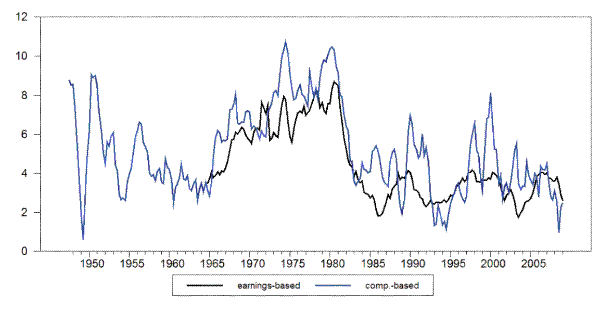
Figure 2 displays two scatterplots of wage inflation and the unemployment rate for the U.S. economy, using both measures of wage inflation. The scatterplots reveal the absence of a stable negative relation between the two variables. Similar graphs, though typically focusing on price inflation, have often been used to demonstrate "the empirical failure of the Phillips curve." That visual impression is confirmed by the correlation between the two series, which is as low as 0.02 and -0.01, respectively.

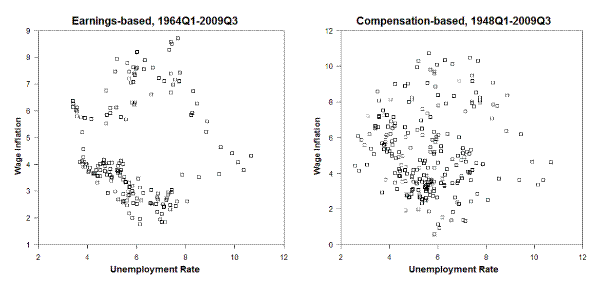
Figure 3 displays the evolution of unemployment and wage inflation over time, using the earnings-based measure of the latter. While no stable relation seems evident at a first glance, a more careful examination points to a strong inverse relation starting sometime around the mid-1980s and prevailing up to the end of the sample. That inverse relation is confirmed by the scatterplots of Figure 4, which are now restricted to the post-1984 period, i.e. the so-called Great Moderation era. For the restricted sample period the correlations are -0.76 and -0.27, respectively.

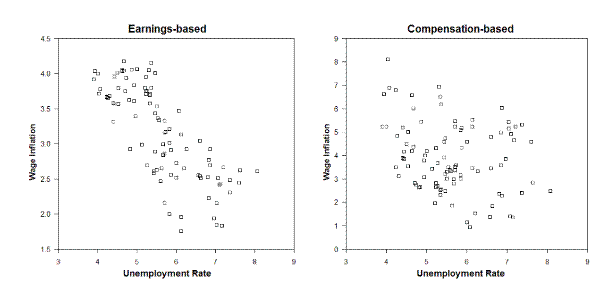
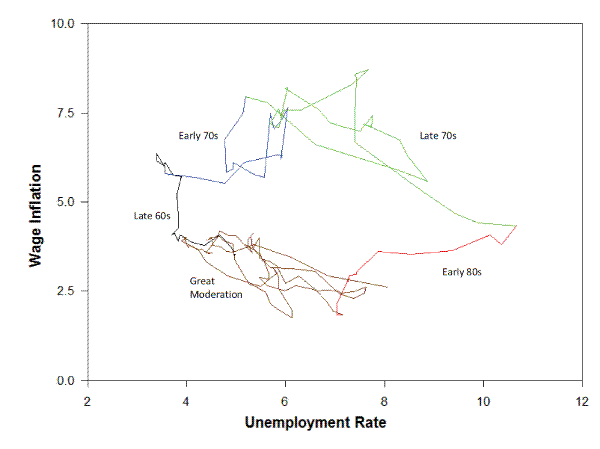
Figure 5 adds a temporal dimension to the Phillips curve scatterplots initially shown in Figure 2, now restricted to the earnings-based wage inflation It suggests that the paths of U.S. wage inflation and unemployment have completed a full circle, returning in recent years to the same downward locus that characterized the 1960s. The evidence thus points to the presence of a stable negative relation between wage inflation and unemployment during periods of relatively low and stable price inflation. That relation is broken during transitions from low to high inflation (early 70s), or from high to low inflation (the early 80s), leading to an overall lack of correlation, as suggested by Figure 2.

Thus, it seems clear from the previous quick glance at the data that any model that implies a simple inverse relation between wage inflation and unemployment will be at odds with the behavior of those two variables during the long 1970-1985 episode. Yet, one cannot rule out that extensions of such a model which allow for indexation to price inflation may be consistent with the evidence. I explore that hypothesis in the next subsection, using the augmented version of the New Keynesian Wage Phillips curve.

Why has the re-emergence of a stable negative relation between wage inflation and unemployment over the past two decades gone unnoticed among academic economists? A possible explanation lies in the focus on price inflation and away from wage inflation in much of the empirical research of recent years, combined with a lack of a significant empirical relation between price inflation and unemployment. The correlation between those two series over the post-1984 period is low and insignificant (-0.13), and its negative value is due exclusively to the most recent observations: if I end the sample period in 2007Q4 the correlation becomes even smaller and with the wrong sign ( 0.08). Of course, the theory developed above has nothing to say, by itself, about the relation between price inflation and the unemployment rate, since that relation is likely to be influenced by factors other than wage setting, including features of price setting and the evolution of labor productivity, among others.¹⁶

Next I turn to a more formal empirical assessment of the New Keynesian Wage Phillips curve.

4.2 Estimates of the Reduced Form New Keynesian Wage Phillips Curve

In the present subsection I report estimates of the reduced form wage equation (19). The focus on (19) is motivated by the good fit of an process for the unemployment rate. Using data starting in 1948Q1 I estimate the following model

$\displaystyle u_{t}=\ \underset{(0.08)}{0.22}^{\ast \ast }+\ \underset{(0.08)}{1.66}^{\ast \ast }\ u_{t-1}-\ \underset{(0.08)}{0.70}^{\ast \ast }\ u_{t-2}+\varepsilon _{t}$

with any further lags of the unemployment rate not being significant. Thus, and as discussed above, under that simple univariate process, the wage inflation equation should have a negative coefficient on the current unemployment rate and a positive one on its lag, in addition to a positive coefficient on lagged price inflation in the presence of indexation. Furthermore, the model (19) implies the cross-equation restriction $\psi _{1}=\psi _{0}\beta \phi _{2}$ , which can be easily tested conditional on a value for $\beta$ , which I set to 0.99.

Table 1 reports OLS estimates of several specifications of the wage inflation equation, each of which can be seen as a restricted version of (19). The wage inflation data is based on the earnings series, and the sample period starts in 1964Q1. The first three columns report estimates including only the current value of the unemployment rate, augmented in the case of columns (2) and (3) with lagged quarter-to-quarter price inflation (column (2)) and year-on-year price inflation (column (3)), with the latter expressed as a quarterly rate to facilitate comparison of coefficients. Note that when price inflation is not controlled for, the coefficient on unemployment is very close to zero and statistically insignificant. When lagged inflation is added as a regressor its coefficient is highly significant, while the coefficient on unemployment increases in absolute value and becomes significant (though only at the 10 percent level when quarter-to-quarter inflation is used as a regressor). Columns (5) and (6) include the lagged unemployment rate, and are thus consistent with the specification implied by the model. In both cases the coefficients on the unemployment rates have the sign predicted by the theory, though they are only significant when year-on-year price inflation is used as the indexing variable. Also, as shown in the row labeled , the cross-equation restriction specified above cannot be rejected when both equations are estimated jointly. The final two rows report the implied estimates of the Calvo wage rigidity parameter $\theta _{w}$ , conditional on calibrated values for $\varphi$ and $\epsilon _{w}$ , since the three parameters are not separately identified. Note that $\varphi$ is the inverse Frisch labor supply elasticity, a controversial parameter. I consider two alternative calibrations, $\varphi =1$ and $\varphi =5$ , which span the range of values often assumed in the literature. Given $\varphi$ , I use (12) to set $\epsilon _{w}$ to a value consistent with a natural rate of unemployment of 5 percent, which is roughly the average unemployment rate over the sample period considered.¹⁷ The point estimates range from 0.62 to 0.89, suggesting substantial wage rigidities, with those associated with the $% \varphi =5$ calibration implying average durations that may be viewed as implausibly long (though the non-negligible size of the standard errors allow for more plausible underlying degrees of wage rigidity).

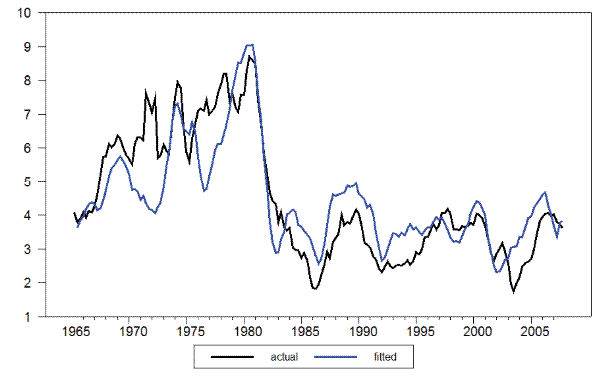
A more detailed analysis of the fit of the estimated wage equations reported in columns (5) and (6), suggests a poor fit during the recent recession. The reason is simple: the rapid increase in the unemployment rate and the very low levels of price inflation (which became deflation for some quarters), lead the fitted wage equation to predict substantial nominal wage deflation. While actual wage inflation was brought down by the recession, it has always remained positive. The presence of downward nominal wage rigidities, which are ignored in the standard wage setting model developed above, could in principle account for that poor fit. Motivated by that observation, columns (7) and (8) in Table 1 report estimates of the wage equation using data up to 2007Q4, thus avoiding any distortion resulting from the use of recent data. Note that for both specifications, the coefficients on current and lagged unemployment increase substantially and now become highly significant even when quarter-to-quarter price inflation is used as a regressor. Figure 6 displays actual and fitted wage inflation, using the estimates shown in column (8). While the estimated model misses much of the high frequency variations, it appears to capture well most movements at medium-term frequencies, with the exception of the spikes in 1971-72 and 1976-77. The correlation between the two series is 0.83.

Table 2 reports estimates of wage inflation equations using the measure based on compensation, and with the sample period starting in 1948Q1. Most of the findings in Table 1 appear to be robust to the use of the alternative wage inflation measure, which is indeed surprising given the large discrepancies between the two inflation measures. Note however that the exclusion of post-2007 data does not have much of an impact now, possibly because of its reduced weight in the longer sample period. In particular, the coefficients on unemployment and its lagged value in column (5) are now significant, in addition of having the right pattern of signs and relative magnitude.

4.3 A Measure of Fundamental Wage Inflation in the Spirit of Campbell-Shiller

The previous subsection reported estimates of a reduced form wage inflation equation implied by the NKWPC, under the assumption that the unemployment rate follows an exogenous process. While the previous assumption provides a fairly good approximation to the dynamics of unemployment in the postwar period and leads to a reduced form specification which makes contact with that used in Phillips (1958) and in subsequent applied work, one may legitimately wonder whether the favorable empirical assessment of the NKWPC hinges on that assumption. Relaxing that assumption has an additional justification: simple Granger-causality tests reject the null of no-Granger causality from wage and price inflation to unemployment. Thus, in particular, the four lags of (earnings-based) wage inflation and price inflation are significant at the one percent level in a regression of the unemployment rate on its own four lags and the lags of the two inflation measures over the 1964Q1-2009Q3 sample period. An analogous test using the compensation-based measure of wage inflation and extended over the sample period 1948Q1-2009Q3 only rejects the null of no-Granger causality at the 7 percent significance level.

Motivated by the previous observation, and in the spirit of Campbell and Shiller's (1987) proposed assessment of present value relations, I start by defining the following measure of "fundamental" or "model-based" wage inflation:

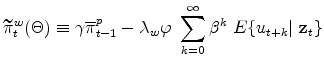$\displaystyle \widetilde{\pi }_{t}^{w}(\Theta )\equiv \gamma \overline{\pi }% _{t-1}^{p}-\lambda _{w}\varphi \ \sum_{k=0}^{\infty }\beta ^{k}\ E\{u_{t+k}\vert\ \mathbf{z}_{t}\}$

where vector $\Theta \equiv \lbrack \gamma ,\theta _{w},\beta ,\epsilon _{w},\varphi ]$ collects the exogenous parameters of the model and where $% \mathbf{z}_{t}=[u_{t},\pi _{t}^{w}-\gamma \overline{\pi }% _{t-1}^{p},...,u_{t-q},\pi _{t-q}^{w}-\gamma \overline{\pi }_{t-1-q}^{p}]$ for some finite

. Under the null hypothesis that model (19) is correct, it is easy to check that $\widetilde{\pi }_{t}^{w}(\Theta )=\pi _{t}^{w}$ , for all

. In other words, given the structure of the conditioning variable $\mathbf{z}_{t}$ the use of a limited information set is not restrictive under the null.

Next I estimate $\widetilde{\pi }_{t}^{w}(\Theta )$ and plot it against actual wage inflation, to evaluate the extent to which the simple model developed here can explain observed fluctuations in that variable. I assume that the joint dynamics of unemployment and wage inflation are well captured by the first order vector autoregressive model

$\displaystyle \mathbf{z}_{t}=\mathbf{A\ z}_{t-1}+\mathbf{\varepsilon }_{t}$

where $E\{\mathbf{\varepsilon }_{t}\vert\ \mathbf{z}_{t-1}\}=0$ for all

. Thus, and letting $\mathbf{e}_{i}$ denote the $i^{th}$ unit vector in $% \mathbb{R}^{2q}$ , we have $E\{u_{t+k}\vert\ \mathbf{z}_{t}\}=\mathbf{e}% _{1}^{\prime }\mathbf{A}^{k}\mathbf{z}_{t}$ , implying

$\displaystyle \widetilde{\pi }_{t}^{w}(\Theta )=\gamma \ \overline{\pi }_{t-1}^{p}-\lambda _{w}\varphi \ \mathbf{e}_{1}^{\prime }(\mathbf{I}-\beta \mathbf{A})^{-1}\ \mathbf{z}_{t}$

(21)

I exploit the previous result to construct a time series for fundamental inflation $\widetilde{\pi }_{t}^{w}(\Theta )$ using a minimum distance estimator. Since not all structural parameters in $\Theta$ are separately identified, I calibrate three of them ( $\beta ,\epsilon _{w},\varphi$ ) and estimate the remaining two ( $\gamma ,\theta _{w}$ ), which define the degree of rigidities and indexation. As above, I set $\beta =0.99$ and report results for both $\varphi =1$ and $\varphi =5$ , with $\epsilon _{w}$ set to imply a natural unemployment rate of 5 percent in each case. I estimate the two remaining parameters, $\theta _{w}$ and $\gamma$ , by minimizing $% \sum_{t=0}^{T}(\pi _{t}^{w}-\widetilde{\pi }_{t}^{w}(\Theta ))^{2}$ subject to (21), over all possible values $(\theta _{w},\gamma )\in \lbrack 0,1]\times \lbrack 0,1]$ , and given the calibrated values for ( $\beta ,\epsilon _{w},\varphi$ ) and the OLS estimate for matrix $\mathbf{A}$ (with ). As in the empirical analysis above I use lagged quarterly and annual inflation as an indexing variable, and both earnings-based and compensation-based measures of wage inflation.

Table 3 reports the main results for the exercise.¹⁸The estimates of $\gamma$ , the degree of indexation, are always highly significant and lie between 0.52 and 0.83, depending on the specification, values which are slightly higher than those obtained in the previous subsection. The point estimates for the Calvo parameter $\theta _{w}$ are also highly significant in all cases. Under the $\varphi =1$ assumption they lie between 0.52 and 0.65, implying an average duration between two and three quarters. When $\varphi =5$ is assumed, the estimates are substantially higher (between 0.75 and 0.82), but still within the range of plausibility, given the evidence uncovered by micro studies.¹⁹ Interestingly, my estimates for $\gamma$ and $% \theta _{w}$ are very close to those obtained by Smets and Wouters (2007) using a very different approach (and one that does not use information on the unemployment rate, among other differences): 0.58 and 0.7, respectively.

The "multivariate" model analyzed here implies some restrictions that can be subject to formal testing. In particular, note that if the model holds exactly, we must have

$\displaystyle \mathbf{e}_{2}^{\prime }+\lambda _{w}\varphi \ \mathbf{e}_{1}^{\prime }=\beta \mathbf{e}_{2}^{\prime }\mathbf{A}$

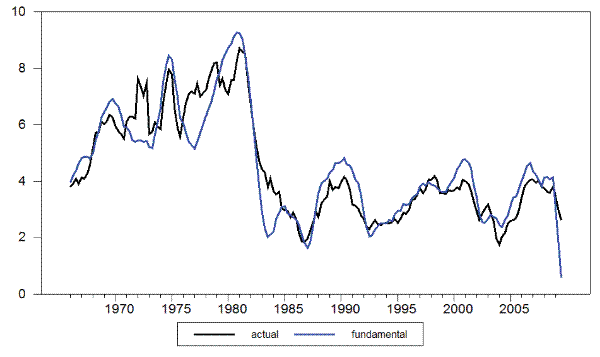
Unfortunately the previous set of restrictions is rejected at very low significance levels for our sample and baseline calibration. This may not be surprising, given the simplicity of the model. But, following Campbell and Shiller (1987), I seek a more informal evaluation of the model by comparing actual and fundamental wage inflation. The last row of Table 3 displays the correlation between the four-quarter centered moving averages of both variables: the correlations are positive and high (above 0.75) in all cases, suggesting a good fit of the model. This is also illustrated in Figure 7, which displays actual (earnings-based) wage inflation and fundamental wage inflation, where the latter is based on the estimates using annual price inflation as an indexing variable and $\varphi =1$ . While the fit is far from perfect, it is clear that the model-based series captures pretty well the bulk of the low and medium frequency fluctuations in actual wage inflation (with the exception of some episodes, including the 2008-09 recession). The fact that such a good fit is obtained using a model for wage inflation that assumes a constant natural rate of unemployment makes that finding perhaps even more surprising.

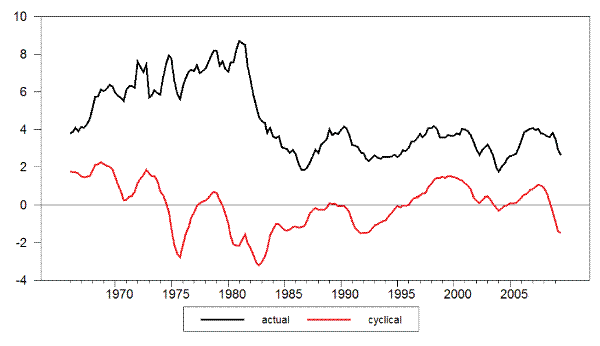
Given the large fluctuations in price inflation over the sample period considered and the well known positive correlation between price and wage inflation, one may wonder to what extent the high correlation between actual and fundamental inflation is largely a consequence of indexation to past price inflation. In order to address that question I construct a measure of the "cyclical" component of fundamental inflation, by subtracting from the latter the inflation indexation component, $\gamma \overline{\pi }_{t-1}^{p}$ . The cyclical component is thus driven exclusively by current and anticipated future unemployment rates. Figure 8 displays the cyclical component of fundamental inflation thus constructed, together with actual wage inflation. It is clear from that evidence that while the cyclical component did not have a dominant role in accounting for the fluctuations in wage inflation in the Great Inflation era, one can still detect several episodes in which it shapes the shorter-term fluctuations in observed wage inflation, including the 1968-69 hump and the 1974-75 trough. It is not until the advent of the Great Moderation period and the associated stability in price inflation that the cyclical component of fundamental wage inflation emerges as a central factor behind fluctuations in wage inflation, as Figure 8 makes clear.

5 Concluding comments

In his seminal 1958 paper, A.W. Phillips uncovered a tight inverse relation between unemployment and wage inflation in the U.K.. That relation was largely abandoned on both theoretical and empirical grounds. From a theoretical viewpoint, it was not clear why the rate of change of the nominal wage (as opposed to the level of the real wage) should be related to unemployment. From an empirical viewpoint, economists' attention shifted to the relation between price inflation and unemployment, but hopes of establishing a stable relationship between those variables faded with the stagflation of the 1970s.

The present paper has made two main contributions. First, it provides some theoretical foundations to a Phillips-like relation between wage inflation and unemployment. It does so not by developing a new model but, instead, by showing that such a relation underlies a standard New Keynesian framework with staggered wage setting, even though versions of the latter found in the literature do not explicitly incorporate or even discuss unemployment. Secondly, the implied wage equation is shown to account reasonably well for the comovement of wage inflation and the unemployment rate in the U.S. economy, even under the strong assumption of a constant natural rate of unemployment. In particular, that equation can explain the strong negative comovement between wage inflation and unemployment observed during the past two decades of price stability.

It is far from the objective of the present paper to claim that the staggered wage setting model of Erceg, Henderson and Levin (2000) provides an accurate description of U.S. labor markets. It is clear that some of its underlying assumptions,-most noticeably, the unilateral setting of the wage by a monopoly union-are at odds with arrangements prevailing in most sectors. Yet, as a matter of fact, the EHL structure underlies most of the medium-scale DSGE models that have been developed in recent years, by both academics and institutions. Identifying and testing further predictions coming out of those models would seem a worthy undertaking and a source of guidance in any effort to improve the frameworks available for policy analysis. This is, if nothing else, the spirit of the present paper.

References

Bils, Mark and Peter J. Klenow (2004): "Some Evidence on the Importance of Sticky Prices," Journal of Political Economy, vol 112 (5), 947-985.

Blanchard, Olivier and Lawrence Katz (1999): "Wage Dynamics: Reconciling Theory and Evidence," American Economic Review, Vol. 89, No. 2, pp. 69-74

Blanchard, Olivier J. and Jordi Galí (2007): "Real Wage Rigidities and the New Keynesian Model," Journal of Money, Credit, and Banking, supplement to volume 39, no. 1, 35-66.

Blanchard, Olivier J. and Jordi Galí (2010): "Labor Markets and Monetary Policy: A New Keynesian Model with Unemployment," American Economic Journal: Macroeconomics, forthcoming.

Calvo, Guillermo (1983): "Staggered Prices in a Utility Maximizing Framework," Journal of Monetary Economics, 12, 383-398.

Casares, Mikel (2009): "Unemployment as Excess Supply of Labor: Implications for Wage and Price Inflation," Universidad Pública de Navarra, mimeo.

Campbell, John Y., and Robert J. Shiller (1987): "Cointegration and Tests of Present Value Models," Journal of Political Economy 95 (5), 1062-1088.

Chari, V.V., Patrick J. Kehoe, and Ellen R. McGrattan (2009): "New Keynesian Models: Not Yet Useful for Policy Analysis," American Economic Journal: Macroeconomics 1 (1), 242-266.

Christoffel, Kai, Günter Coenen, and Anders Warne (2008): "The New Area-Wide Model of the Euro Area: A Micro-Founded Open-Economy Model for Forecasting and Policy Analysis,"

Edge, Rochelle M., Michael T. Kiley and Jean-Philippe Laforte (2007): "Documentation of the Research and Statistics Division's Estimated DSGE Model of the U.S. Economy: 2006 Version," Finance and Economics Discussion Series 2007-53, Federal Reserve Board, Washington D.C.

Eichenbaum, Martin, and Jonas D.M. Fisher (2007): "Estimating the frequency of re-optimization in Calvo-style models," Journal of Monetary Economics 54 (7), 2032-2047.

Erceg, Christopher J., Luca Guerrieri, Christopher Gust (2006): "SIGMA: A New Open Economy Model for Policy Analysis," International Journal of Central Banking, vol. 2 (1), 1-50.

Erceg, Christopher J., Dale W. Henderson, and Andrew T. Levin (2000): "Optimal Monetary Policy with Staggered Wage and Price Contracts," Journal of Monetary Economics vol. 46, no. 2, 281-314.

Galí, Jordi (1996): "Unemployment in Dynamic General Equilibrium Economies," European Economic Review 40, 839-845.

Galí, Jordi and Mark Gertler (1999): "Inflation Dynamics: A Structural Econometric Analysis," Journal of Monetary Economics, vol. 44, no. 2, 195-222.

Galí, Jordi, Mark Gertler, David López-Salido (2001): "European Inflation Dynamics," European Economic Review vol. 45, no. 7, 1237-1270.

Galí, Jordi (2008): Monetary Policy, Inflation and the Business Cycle: An Introduction to the New Keynesian Framework, Princeton University Press.

Galí, Jordi, Frank Smets, and Rafael Wouters (2010): "Unemployment in an Estimated New Keynesian Model," mimeo.

Gordon, Robert J. (1997): "The Time-Varying NAIRU and its Implications for Economic Policy," Journal of Economic Perspectives 11(1), 11-32.

Jaimovich, Nir and Segio Rebelo (2009): "Can News about the Future Drive the Business Cycle?," American Economics Review 99 (4), 1097-1118.

Mackowiak, Bartosz and Frank Smets (2008): "On the Implications of Micro Price Data for Macro Models," unpublished manuscript.

Mehran, Hamid and Joseph Tracy (2001): "The Effects of Employee Stock Options on the Evolution of Compensation in the 1990s," FRBNY Economic Policy Review, 17-33.

Merz, Monika (1995): "Search in the Labor Market and the Real Business Cycle", Journal of Monetary Economics, 36, 269-300.

Nakamura, Emi and Jón Steinsson (2008): "Five Facts about Prices: A Reevaluation of Menu Cost Models," Quarterly Journal of Economics, vol. CXXIII, issue 4, 1415-1464.

Phillips, A.W. (1958): "The Relation between Unemployment and the Rate of Change of Money Wage Rates in the United Kingdom, 1861-1957," Economica 25, 283-299.

Samuelson, Paul a. and Robert M. Solow (1960): "Analytical Aspects of Anti-Inflation Policy," American Economic Review 50 (2), 177-194.

Sbordone, Argia (2002): "Prices and Unit Labor Costs: Testing Models of Pricing Behavior," Journal of Monetary Economics, vol. 45, no. 2, 265-292.

Sbordone, Argia (2006): "U.S. Wage and Price Dynamics: A Limited Information Approach," International Journal of Central Banking vol. 2 (3), p. 155-191.

Smets, Frank, and Rafael Wouters (2003): "An Estimated Dynamic Stochastic General Equilibrium Model of the Euro Area," Journal of the European Economic Association, vol 1, no. 5, 1123-1175.

Smets, Frank, and Rafael Wouters (2007): "Shocks and Frictions in US Business Cycles: A Bayesian DSGE Approach," American Economic Review, vol 97, no. 3, 586-606.

Staiger, Douglas, James H. Stock, and Mark W. Watson (1997): "The NAIRU, Unemployment and Monetary Policy," Journal of Economic Perspectives 11 (1), 33-49.

Taylor, John B. (1999): "Staggered Price and Wage Setting in Macroeconomics," in J.B. Taylor and M. Woodford eds., Handbook of Macroeconomics, chapter 15, 1341-1397, Elsevier, New York.

Thomas, Carlos (2008a): "Search and Matching Frictions and Optimal Monetary Policy," Journal of Monetary Economics 55 (5), 936-956.

Woodford, Michael (2003): Interest and Prices. Foundations of a Theory of Monetary Policy, Princeton university Press (Princeton, NJ).

Table 1. Estimated Wage Inflation Equations: Earnings-based

	(1)	(2)	(3)	(5)	(6)	(7)	(8)
$\mu_{t}$	-0.001	-0.030*	-0.079**	-0.177	-0.377**	-0.334**	-0.552**
$\mu_{t}$ standard errors	(0.019)	(0.017)	(0.015)	(0.114)	(0.083)	(0.095)	(0.076)
$\mu_{t-1}$			0.153	0.304**	0.294**	0.453**
$\mu_{t-1}$ standard errors			(0.112)	(0.078)	(0.095)	(0.073)
$\pi_{t-1}$		0.415**		0.427**		0.503**
$\pi_{t-1}$ standard errors		(0.043)		(0.052)		(0.036)
$\pi_{t-1}^{(4)}$			0.565**		0.611**		0.687**
$\pi_{t-1}^{(4)}$ standard errors			(0.038)		(0.041)		(0.038)
$\rho$ - value				0.71	0.52	0.67	0.06
$\theta_{w}(\varphi$ = 1)				0.788**	0.629**	0.755**	0.607**
$\theta_{w}(\varphi$ = 1) standard errors				(0.083)	(0.059)	(0.061)	(0.063)
$\theta_{w}(\varphi$ = 5)				0.896**	0.805**	0.879**	0.792**
$\theta_{w}(\varphi$ = 5) standard errors				(0.044)	(0.036)	(0.033)	(0.039)

Table 2. Estimated Wage Inflation Equations: Compensation-based

	(1)	(2)	(3)	(5)	(6)	(7)	(8)
$\mu_{t}$	-0.015	-0.046*	-0.087**	-0.227**	-0.387**	-0.241**	-0.397**
$\mu_{t}$ standard errors	(0.028)	(0.024)	(0.028)	(0.099)	(0.125)	(0.091)	(0.101)
$\mu_{t-1}$			0.189**	0.310**	0.189**	0.301**
$\mu_{t-1}$ standard errors			(0.096)	(0.116)	(0.090)	(0.098)
$\pi_{t-1}$		0.500**		0.505**		0.522**
$\pi_{t-1}$ standard errors		(0.046)		(0.046)		(0.046)
$\pi_{t-1}^{(4)}$			0.578**		0.610**		0.642**
$\pi_{t-1}^{(4)}$ standard errors			(0.058)		(0.060)		(0.052)
$\rho$ - value				0.57	0.79	0.54	0.66
$\theta_{w}(\varphi$ = 1)				0.709**	0.637**	0.675**	0.569**
$\theta_{w}(\varphi$ = 1) standard errors				(0.086)	(0.059)	(0.069)	(0.057)
$\theta_{w}(\varphi$ = 5)				0.853**	0.780**	0.833**	0.767**
$\theta_{w}(\varphi$ = 5) standard errors				(0.049)	(0.043)	(0.040)	(0.037)

Table 3. Estimated Parameters using Minimum Distance Estimator

	Earnings: $\pi_{t-1}$ : $\varpi$ =1	Earnings: $\pi_{t-1}$ : $\varpi$ =5	Earnings: $\pi_{t-1}^{(4)}$ : $\varpi$ =1	Earnings: $\pi_{t-1}^{(4)}$ : $\varpi$ =5	Compensation: $\pi_{t-1}$ : $\varpi$ =1	Compensation: $\pi_{t-1}$ : $\varpi$ =5	Compensation: $\pi_{t-1}^{(4)}$ : $\varpi$ =1	Compensation: $\pi_{t-1}^{(4)}$ : $\varpi$ =5
$\gamma$	0.52	0.52	0.83	0.81	0.58	0.59	0.80	0.79
$\gamma$ standard errors	(0.013)	(0.017)	(0.130)	(0.110)	(0.020)	(0.030)	(0.170)	(0.107)
$\theta_{\omega}$	0.65	0.82	0.52	0.74	0.64	0.81	0.54	0.75
$\theta_{\omega}$ standard errors	(0.013)	(0.008)	(0.080)	(0.020)	(0.035)	(0.020)	(0.060)	(0.002)
$\rho(\widetilde{\pi}^{\omega}_{t},\pi^{\omega}_{t})$	0.82	0.82	0.91	0.91	0.77	0.78	0.77	0.76

Figure 1: Two Measures of Wage Inflation

Figure 2: Wage Inflation and Unemployment

Figure 3: Wage Inflation and Unemployment over Time

Figure 4: Wage Inflation and Unemployment during the Great Moderation

Figure 5: The Wage Phillips Curve over Time

Figure 6: Actual vs. Fitted Wage Inflation 1964Q1-2007Q4

Figure 7: Actual vs. Fundamental Wage Inflation

Figure 8: Wage Infaltion and its Cyclical Component

Footnotes

* Correspondence: CREI, Ramon Trias Fargas 25; 08005 Barcelona (Spain). E-mail: [email protected]. I have benefited from comments during presentations at the CREI Macro Lunch, the Reserve Bank of Australia, Reserve Bank of New Zealand, U. Rovira i Virgili, NBER Summer Institute, Kiel EES Workshop, New York Fed, Columbia, NYU and Oxford University. Tomaz Cajner and Lien Laureys provided excellent research assistance. I am grateful to the European Research Council, the Ministerio de Ciencia e Innovación, the Barcelona GSE Research Network and the Government of Catalonia for financial support. Return to Text

1. See, e.g., Smets and Wouters (2003,2008) and Christiano, Eichenbaum and Evans (2005). For a descriptions of versions of those models developed at policy institutions, see Christoffel, Coenen, and Warne (2008), Edge, Kiley and Laforte (2007), and Erceg, Guerrieri and Gust (2006), among others. Return to Text

2. See Erceg, Henderson and Levin (2000), Woodford (2003, chapter 6) or Galí (2008, chapter 6) for a detailed discussion of the policy implications of the coexistence of nominal wage and price stickiness. Return to Text

3. A recent exception is Sbordone (2006). Return to Text

4. See, e.g. Galí and Gertler (1999), Galí, Gertler and López-Salido (2001), Sbordone (2002) and Eichenbaum and Fisher (2007) for examples of papers using aggregate data. Micro evidence on price-setting patterns and its implications for aggregate models can be found in Bils and Klenow (2004), Nakamura and Steinsson (2008), and Mackowiak and Smets (2008), among others. Return to Text

5. Details of the derivation of the optimal wage setting condition can be found in EHL (2000). Return to Text

6. Note that the previous equation is the wage analog to the price inflation equation resulting from a model with staggered price setting à la Calvo. See Galí and Gertler (1999) and Sbordone (2002) for a derivation and empirical assessment. Return to Text

7. The general approach builds on Galí (1996). Other recent applications to the New Keynesian model can be found in Blanchard and Galí (2007) and, more closely related (although developed independently), Casares (2009). Return to Text

8. Gordon (1997) claims that the shift in focus towards price inflation has been "deliberate." In his words, "...[t]he earlier fixation on wages was a mistake. The relation of prices to wages has changed over time...The Fed's goal is to control inflation, not wage growth, and models with separate wage growth and price markup equations do not perform as well as the [price inflation] equation...in which wages are only implicit...." Return to Text

9. Needless to say this is only true to the extent that one is willing to take the assumptions of the Calvo formalism literally, including the exogeneity of parameter $\theta _{w}$ . Return to Text

10. Phillips (1958) also emphasized the likely existence of nonlinearities due to workers' reluctance "to offer their services at less than the prevailing rates when the demand for labour is low and unemployment is high, so that wage rates fall only very slowly." In the analysis of the present paper, as in standard versions of the New Keynesian model, the possible existence of such asymmetries is ignored. Return to Text

11. Equivalently, we can write

$\displaystyle \pi _{t}^{w}=\beta \ E_{t}\{\pi _{t+1}^{w}\}-\lambda _{w}\varphi \ u_{t}+v_{t}$

$v_{t}\equiv \lambda _{w}\overline{\mu }_{t}^{w}$ . In contrast with the representation of the wage equation found in Smets and Wouters (2003, 2007), the error term in the wage inflation formulation proposed here captures exclusively "wage markup shocks," and not preference shocks (even though the latter have been allowed for in the model above). This feature should in principle allow one to overcome the basic identification problem raised by Chari, Kehoe and McGrattan (2008) in their critique of current New Keynesian models. Return to Text

12. The previous observation is closely related to other implausible predictions of macro models that rely on similar preferences, including the negative impact on activity of higher anticipated productivity, as emphasized by the recent literature on "news shocks." Return to Text

13. An identical robustness result can be shown to obtain under a period utility function of the sort assumed by Jaimovich and Rebelo (2009) with a similar motivation, namely

$\displaystyle U(C_{t},\{N_{t}(i)\},Z_{t})=\frac{1}{1-\sigma }\left( C_{t}-\chi _{t}\ Z_{t}\int_{0}^{1}\frac{N_{t}(i)^{1+\varphi }}{1+\varphi }di\right) ^{1-\sigma }$

where $Z_{t}=Z_{t-1}^{\vartheta }\overline{C}_{t}^{1-\vartheta }$ . The non-separability of the previous specification for household utility, however, prevents one from interpreting it as the aggregation of the utilities of individual household members. Return to Text

14. The observability of the unemployment rate, may be viewed as an advantage of the present framework relative to Sbordone (2006), who focuses instead on a parameterized version of (5). Return to Text

15. See, e.g. Abraham, Spletzer and Stewart (1999). Return to Text

16. See, e.g. Blanchard and Galí (2009) and Thomas (2009) for an analysis of the relation between price inflation and unemployment in a model with labor market frictions. Return to Text

17. Note that $\epsilon _{w}=(1-\exp \{-\varphi u^{n}\})^{-1}$ . This implies setting $\epsilon _{w}=20.5$ when $\varphi =1$ , and $\epsilon _{w}=4.52$ when $\varphi =5$ . Return to Text

18. Standard errors are obtained by drawing from the empirical distribution of $% \mathbf{A}$ , and re-estimating $\theta _{w}$ and $\gamma$ for each draw. Return to Text

19. See, e.g., Taylor (1999). Return to Text

^♣ This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to Text