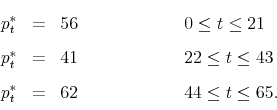The Heterogeneous Expectations Hypothesis:
Some Evidence from the Lab *
Roetersstraat 11, NL-1018 WB Amsterdam, Netherlands
Keywords: Heterogeneous Expectations, bounded rationality, learning, heuristics switching.
Abstract:
"Recent theoretical work is making it increasingly clear that the multiplicity of equilibria ... can arise in a wide variety of situations involving sequential trading, in competitive as well as finite-agent games. All but a few of these equilibria are, I believe, behaviorally uninteresting: They do not describe behavior that collections of adaptively behaving people would ever hit on. I think an appropriate stability theory can be useful in weeding out these uninteresting equilibria ... But to be useful, stability theory must be more than simply a fancy way of saying that one does not want to think about certain equilibria. I prefer to view it as an experimentally testable hypothesis, as a special instance of the adaptive laws that we believe govern all human behavior" (Lucas, 1986, pp. S424-425).
1 Introduction
Individual expectations about future aggregate outcomes is the key feature that distinguishes social sciences and economics from the natural sciences. Daily weather forecasts, either by the public or by experts, do not affect the probability of rain. In contrast, overly optimistic expectations about the economic outlook may have exaggerated the strong rise in world wide financial markets in the late 1990s and, more recently, the excessive growth in housing prices in 2000-2008, while an overly pessimistic outlook by the public and by economists may have amplified the recent financial crisis and deepened the current economic crisis.
Economic decisions today thus depend upon expectations about the future state of the economy. A theory of individual expectations or market beliefs is therefore a crucial part of economic theory. The market is an expectations feedback system and any dynamic economic model depends crucially upon its underlying expectations hypothesis. But how then should one model individuals who learn from the past and adapt their behavior as more and more market realizations become available over time?
Since the seminal works of Muth (1961) and Lucas (1972), the Rational Expectations Hypothesis (REH) has become the leading paradigm on expectation formation in economics, and rational expectations representative agent models have become the mainstream tool of analysis. In such a framework, all agents are the same and forecast rationally, using all available information. Rational expectations are by assumption model consistent and coincide on average with realizations, without systematic forecasting errors. The rational expectations (RE) approach has important advantages: it is simple, elegant and puts strong discipline on individual (forecasting) behavior minimizing the number of free parameters. But drawbacks of the rational agent paradigm are also well known: it is unrealistic in assuming perfect knowledge about the economy (typically it assumes knowledge of the law of motion of the economy) and, even if such knowledge were known, RE requires extremely strong computing abilities of the agents to compute the equilibrium. Most importantly, RE models are at odds with empirical observations and behavior in laboratory experiments wit human subjects and, for example, the decline of worldwide financial markets by almost 50% between October 2008 and March 2009 is hard to reconcile with rational behavior.
Economics, or at least a significant part of it, is currently witnessing a paradigm shift to an alternative, behavioral view, where agents are boundedly rational. This alternative view dates back to Simon (1957) and contains many elements from psychology, e.g. through the work of Tversky and Kahnemann (1974). The need for a new paradigm in economics has recently been forcefully advocated by Akerlof and Shiller (2009), Colander et al. (2009) and DeGrauwe (2009). Concerning expectations of boundedly rational agents, an alternative theory of adaptive learning has been developed, see e.g. Sargent (1993) for an early and Evans and Honkapohja (2001) for a more detailed overview. Boundedly rational agents do not know the law of motion of the economy, but instead use time series observations to form expectations and adapt their behavior trying to learn model parameters of their perceived law of motion as more observations become available. Adaptive learning sometimes enforces convergence to REE, but it may also lead to non-RE equilibria, such as the learning equilibria in Bullard (1994). Adaptive learning models are sometimes "cautious modifications of rational expectations theories" (Sargent, 2008, p26) and other times large deviations from rationality explaining excess volatility through expectations driven fluctuations (Grandmont, 1998). Bounded rationality however also has important drawbacks. In particular, the `wilderness" of bounded rationality (Sims, 1980) leads to (too) many degrees of freedom and too many free parameters. There are simply too many ways of modeling non-rational behavior. This "wilderness" of bounded rationality, seems particularly relevant when individuals have heterogeneous expectations.
A rough estimate indicates that in the past 20 years more than 1000 papers on bounded rationality and learning have appeared. Among these, in the last decade hundreds of (theoretical) papers on agent-based models populated with boundedly rational agents employing heterogeneous strategies/expectations have appeared, especially with applications in finance; see the comprehensive surveys of LeBaron (2006) and Hommes (2006) in the Handbook of Computational Economics Volume 2: Agent-Based Computational Economics (Tesfatsion and Judd, 2006 and very recent surveys by Hommes and Wagener (2009) and Chiarella et al. (2009) in the Handbook of Financial Markets: Dynamics and Evolution (Hens and Schenk-Hoppé, 2009) as well as papers and references in the Handbook of Economic Complexity (Rosser, 2009)1. Most of these papers present stylized, theoretical models or larger, agent-based simulation models, with the realistic feature that these models can mimic many stylized facts in financial time series (Lux, 2009) and in macro data (Delli-Gatti et al., 2008).
The empirical validation of heterogeneity is an important area of current research. For example, Baak (1999) and Chavas (2000) estimate heterogeneous agent models (HAMs) on hog and beef market data, and found empirical evidence for heterogeneity of expectations. For the beef market Chavas (2000) estimates that about 47% of the beef producers behave naively (using only the last price in their forecast), 18% of the beef producers behaves rationally, whereas 35% behaves quasi-rationally (i.e. use a univariate autoregressive time series model to forecast prices). A number of recent contributions have estimated heterogeneous agent models with fundamentalists and chartist strategies on stock prices (e.g. Boswijk et al. (2007), de Jong, Verschoor and Zwinkels (2009), exchange rates (e.g. Gilli and Winker (2003), Westerhoff and Reitz (2003) and several commodities (e.g. gold prices (Alfarano et al., 2005), and oil prices (ter Ellen and Zwinkels, 2009)). Most of these studies find significant time-variation in the fractions of agents using a mean-reverting fundamental versus a trend-following strategy. Empirical evidence for heterogeneous trading strategies in the Spanish Stock Market Exchange has been found in Vaglica et al. (2008); in particular, Lillo et al. (2008) show that the investors can be classified in different groups, including trend followers and contrarians, whose change of inventory of the stock is positively respectively negatively correlated with stock return.
A related, complementary branch of empirical literature uses survey data to measure individual expectations; see Pesaran and Weale (2006) for a stimulating overview. An advantage of survey data analysis is that it can focus exclusively on the expectations-generating process, avoiding the dilemma of testing joint hypotheses. There is quite some evidence on forecasting heterogeneity in survey data. For example, Frankel and Froot (1987, 1990), Allen and Taylor (1990) and Taylor and Allen (1992) already found that financial experts use different forecasting strategies to predict exchange rates. They tend to use trend extrapolating rules at short horizons (up to 3 months) and mean-reverting fundamentalists rules at longer horizons (6 months to 1 year) and, moreover, the weight given to different forecasting techniques changes over time. Vissing-Jorgensen (2003) presents evidence of heterogeneous beliefs of individual investors about the prospect of the stock market, while Shiller (2000) finds evidence that investor's sentiment changes over time, with both institutions and individual investors becoming more optimistic in response to recent significant increases of the stock market. Evidence concerning heterogeneity in survey data on exchange rate expectations can also be found in MacDonald and Marsh (1996), Elliott and Ito (1999), Prat and Uctum (2000) and Bénassy-Quéré et al. (2003). Dreger and Stadtmann (2008) show that for exchange rate forecasts at a 6 months horizon, different expectations about macroeconomic fundamentals is what drives heterogeneity. Mankiw et al. (2003) find evidence for heterogeneity in inflation expectations in the Michigan Survey of Consumers and show that the data are inconsistent with either rational or adaptive expectations, but may be consistent with a sticky information model. Capistrán and Timmermann (2009) show that heterogeneity of inflation expectations of professional forecasters varies systematically over time, and depends on the level and the variance of current inflation. Pfajfar and Santoro (2009) measure the degree of heterogeneity in private agents' inflation forecasts by exploring time series of percentiles from the empirical distribution of survey data. They show that heterogeneity in inflation expectations is pervasive and identify three regions of the distribution corresponding to different expectations formation mechanisms: a static or highly autoregressive region on the left hand side of the median, a nearly rational region around the median and a fraction of forecasts on the right hand side of the median consistent with adaptive learning and sticky information. Branch (2004, 2007) estimates a simple switching model with heterogeneous expectations, along the lines of Brock and Hommes (1997), and provides empirical evidence suggesting that models which allow the degree of heterogeneity to change over time provide a better fit on exchange rate survey data.
In this paper, we discuss laboratory experiments with human subjects that can be used to validate expectations hypotheses and learning models. Lucas (1986) already stressed the importance of laboratory experiments in studying adaptive learning and its stability (see the quote at the beginning). In particular, we are interested in the potential role of heterogeneity in expectations. We quote from Muth (1961, p.321, emphasis added) on expectations heterogeneity and its aggregate effect: "Allowing for cross-sectional differences in expectations is a simple matter, because their aggregate affect is negligible as long as the deviation from the rational forecast for an individual firm is not strongly correlated with those of the others. Modifications are necessary only if the correlation of the errors is large and depends systematically on other explanatory variables"
In this paper we discuss learning to forecast experiments (LtFEs) which provide a controlled laboratory environment to study individual expectations as well as aggregate outcomes, and investigate questions such as:
- How do individuals form expectations and how do they
bf learn and adapt their behaviour? - How do individual forecasting rules interact at the micro level and which aggregate outcome do they co-create at the macro level ?
- Will coordination occur, even when there is limited information, or will heterogeneity persist?
- When does learning enforce convergence to REE and when do "learning equilibria" arise?
The goals of this paper are twofold. Firstly, we summarize a number of LtFEs in different market environments. Secondly, we fit a theory of heterogeneous expectations to the experimental data and discuss how well the model explains the data across different market settings. This poses a particular challenge: is there a general, perhaps even a universal theory of heterogeneous expectations, that is, can one come up with one single expectations hypothesis explaining all LtFEs across different market settings?
The paper is organized as follows. Section 2 summarizes related literature on experiments on expectations. Section 3 discusses an experiment in a cobweb market modeling framework, while Section 4 describes an asset pricing experiment. Section 5 presents a simple forecasting heuristics switching model, where agents switch between different forecasting rules based upon their recent performance, and fits the model to the asset pricing experiments. In Section 6 the same switching model is fitted to experimental data in different market settings, where the only difference comes from the type of expectations feedback, positive versus negative. Section 7 briefly discusses some recent experiments in a New Keynesian macro setting and Section 8 concludes.
2 Learning-to-forecast experiments (LtFEs)
Laboratory experiments with human subjects, with full control over the market environment and economic fundamentals, form an ideal tool to study interactions at the micro-level and how individual behavior affects aggregate market outcomes. Duffy (2008ab) provides stimulating and up to date surveys of "experimental macroeconomics". Early work in this area focussed on market mechanisms, such as double auctions, and the availability of information and futures markets, ensuring that equilibrium will be reached (e.g. Smith (1962), Plott ad Sunder (1982), Sunder (1995) and Plott and Smith (20xx)). More recently, unstable market environments where equilibrium may not be reached, but instead bubbles and crashes may arise have also been designed (e.g. Smith et al. (1988) and Lei et al. (2001).
In experimental work expectations often plays an indirect or implicit role. However, in order to avoid joint hypothesis testing there is an expanding literature on exclusive experimental testing of the expectations hypothesis. An early example is Schmalensee (1976), who presents subjects with historical data on wheat prices and asks them to predict the mean wheat price for the next 5 periods. Williams (1987) considers expectation formation in an experimental double auction market, which varies from period to period by small shifts in the market clearing price. Participants predict the mean contract price for 4 or 5 consecutive periods and the participant with the lowest forecast error earns $1.00. In Dwyer et al. (1993) and Hey (1994) subjects have to predict a time series generated by an (exogenous) stochastic process such as a random walk or a simple linear first order autoregressive process. Kelley and Friedman (2002) consider learning in an Orange Juice Futures price forecasting experiment, where prices are driven by a linear stochastic process with two exogenous variables (weather and competing supply). But in these papers there is no expectations feedback, since market realizations are not affected by individual forecasts.
Here, we focus on so-called learning-to-forecast experiments (LtFEs), where subject's only task is to forecast the price of some commodity for a number, say 50-60, periods, with the realized market price in each period determined by (average) individual expectations. In LtFEs subjects' forecasting decisions are thus separated from market-trading decisions. The subjects in the experiments do not participate themselves directly in other market activities, such as trading or producing, but are forecasters (e.g. advisors to large producers or financial investors) whose earnings increase when forecasting errors decrease. At the beginning of each period, individual forecasts are collected, which feed directly into (unknown) demand and/or supply functions and computerized trading yields a market price, derived from equilibrium between aggregate demand and supply, that becomes available to the subjects at the end of the period. Demand and supply curves are derived from maximization of expected utility, profit or wealth and thus consistent with rational optimizing behavior.
These LtFEs were motivated by the bounded rationality literature, in order to distinguish between different theories of expectations and learning. Sargent (1993), for example, emphasizes two different requirements of rational expectations. The first requirement imposes that individuals maximize an objective function (utility, profit, wealth, etc.) subject to perceived constraints, while the second requirement imposes mutual consistency of these perceptions. Marimon and Sunder (1994) were the first to set up experiments testing individual rationality and mutual consistency either jointly or separately and used different experimental designs to distinguish between "learning-to-optimize" versus "learning-to-forecast" experiments (Marimon and Sunder, 1994, p.134). The LtFEs focus exclusively on the role of expectations, using computerized optimal individual demand and supply schedules once these individual forecasts have been made.
In LtFEs, subjects typically only have qualitative information about the market. They know that the price ![]() is an aggregation of individual forecasts, derived from equilibrium
between demand and supply and are able to infer the type of expectations feedback, positive or negative. Positive (negative) feedback means that an increase of (average) individual forecasts leads to a higher (lower) market equilibrium price. Positive feedback is important in
speculative asset markets, where higher market expectations lead to an increase of speculative demand and therefore an increase of the realized asset price. Negative feedback may be dominant in supply driven commodity markets, where an increase in expected prices leads to higher production and thus
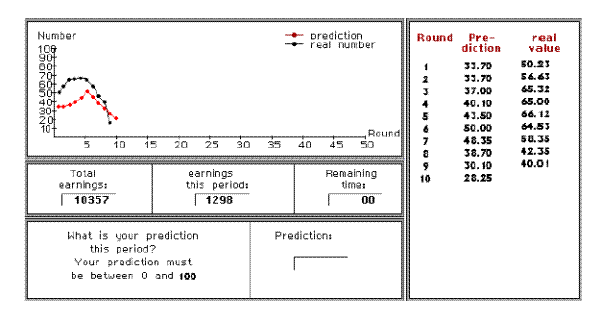
to a lower realized market price. Subjects in the LtFEs know past prices and their own past forecasts and earnings, typically in table as well as in graphic form, as illustrated by an example in Figure 1. They do however not know the forecasts of other
participants, the exact market equilibrium equation, the exact demand and supply schedules and the exact number of other demanders and/or suppliers in the market. The type of information in the experiment is thus very similar to models of bounded rationality and adaptive learning, were agents try
to learn a perceived law of motion, based upon time series observations without knowing the underlying actual law of motion of the market.
is an aggregation of individual forecasts, derived from equilibrium
between demand and supply and are able to infer the type of expectations feedback, positive or negative. Positive (negative) feedback means that an increase of (average) individual forecasts leads to a higher (lower) market equilibrium price. Positive feedback is important in
speculative asset markets, where higher market expectations lead to an increase of speculative demand and therefore an increase of the realized asset price. Negative feedback may be dominant in supply driven commodity markets, where an increase in expected prices leads to higher production and thus
to a lower realized market price. Subjects in the LtFEs know past prices and their own past forecasts and earnings, typically in table as well as in graphic form, as illustrated by an example in Figure 1. They do however not know the forecasts of other
participants, the exact market equilibrium equation, the exact demand and supply schedules and the exact number of other demanders and/or suppliers in the market. The type of information in the experiment is thus very similar to models of bounded rationality and adaptive learning, were agents try
to learn a perceived law of motion, based upon time series observations without knowing the underlying actual law of motion of the market.
Quite a number of LtFEs have appeared in the literature. In a series of papers, Marimon, Spear and Sunder studied expectation formation in inflationary overlapping generations economies. Marimon, Spear and Sunder (1993) find experimental evidence for expectationally driven cycles and coordination of beliefs on a sunspot 2-cycle equilibrium, but only after agents have been exposed to exogenous shocks of a similar kind. Marimon and Sunder (1995) present experimental evidence that a "simple" rule, such as a constant growth of the money supply, can help coordinate agents' beliefs and help stabilize the economy. More recently, a number of LtFEs within other macro economic frameworks have been performed. Adam (2007) uses a simple model of sticky prices and shows that a restricted perception equilibrium explains the experimental data better than the RE benchmark solution. Pfajfar and Santoro (2009) and Assenza et al. (2009) run LtFEs in a new Keynesian framework. Pfajfar and Santoro (2009) find evidence for heterogeneity of expectations in their experimental data and three different types of forecasting rules: simple heuristics (e.g. trend following rules), adaptive learning and rational expectations. The LtFEs of Assenza et al. (2009) will be briefly discussed in Section 7.
A learning to forecast experiment may be seen as a test bed for the expectations hypothesis in a benchmark model, assuming that all other assumptions such as rational, utility and profit maximizing behavior are satisfied. A learning to forecast experiment thus provides clean data on
individual expectations as well as aggregate price behavior. Here we will discuss learning to forecast experiments, based on three benchmark models: (1) the cobweb model, (2) a standard asset pricing model and (3) a New Keynesian macro model. The underlying laws of motion are of the
form
In the cobweb LtFE experiments in Hommes al. (2007), the realized market price
Finally, in the New Keynesian macro model expectations on two different variables interact and realized inflation ![]() and realized output gap
and realized output gap ![]() in (2.3) simultaneously depend (linearly) on all two-period ahead individual forecasts of both inflation and the output gap. In Section 7 we will briefly discuss the LtFE of
Assenza et al. (2009), where the dynamics of inflation and the output gap is driven simultaneously by individual expectations of both inflation and the output gap.
in (2.3) simultaneously depend (linearly) on all two-period ahead individual forecasts of both inflation and the output gap. In Section 7 we will briefly discuss the LtFE of
Assenza et al. (2009), where the dynamics of inflation and the output gap is driven simultaneously by individual expectations of both inflation and the output gap.
3 Cobweb Experiments
In this section we discuss LtFE in the classical cobweb framework. This is exactly the same framework employed in the seminal paper of Muth (1961) introducing rational expectations. These cobweb LtFEs may thus be seen as a direct test of the REH in the cobweb model, assuming all other modeling assumptions (e.g. producers' profit maximization and consumers utility maximization) are satisfied. Carlson (1967) already conducted hand-run experiments with subjects as cobweb suppliers. Holt and Villamil (1986) and Hommes et al. (2000) conducted individual cobweb experiments, where price fluctuations are induced by decisions of a single individual. Wellford (1989) conducted several computerized cobweb experiments, where market prices were determined by subjects’ quantity decisions.
Here we focus on the LtFEs in Hommes et al. (2007) with ![]() participants per session. The participants were asked to predict next period's price of a commodity under limited information on
the structural characteristics of the market. Participants were only informed about the basic principles of the cobweb-type market. They were advisors to producers, whose only job is to accurately forecast the price of the good for 50 subsequent periods. Pay-offs were defined as a quadratic
function of squared forecasting errors, truncated at 0:2
participants per session. The participants were asked to predict next period's price of a commodity under limited information on
the structural characteristics of the market. Participants were only informed about the basic principles of the cobweb-type market. They were advisors to producers, whose only job is to accurately forecast the price of the good for 50 subsequent periods. Pay-offs were defined as a quadratic
function of squared forecasting errors, truncated at 0:2
Participants were informed that the price would be determined by market clearing and that it would have to be within the range
The realized price ![]() in the experiments was determined by the (unknown) market equilibrium between demand and supply:
in the experiments was determined by the (unknown) market equilibrium between demand and supply:
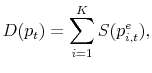 |
(3.2) |
with
| (3.3) |
with
| (3.4) |
This increasing, nonlinear supply schedule can be derived from producer's expected profit maximization with a convex cost function. Subjects in the experiment thus do not participate themselves in production decisions, but supply is computed as if each individual producer maximizes expected profit, given his/her individual price forecast. The parameter
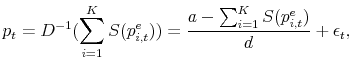 |
(3.5) |
where
Figure 2: Cobweb dynamics in the strongly unstable treatment in two benchmark simulations. Left Panel: convergence to a (noisy) 2-cycle under naive expectations. Right Panel: convergence to (noisy) RE equilibrium price under learning by average.
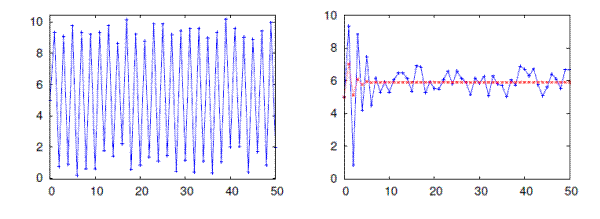
Figure 3: Cobweb Learning to Forecast Experiments Top Panels: stable: coordination on RE unstable: persistent heterogeneity Middle Panels: Bottom Panels: degree of heterogeneity measured by standard deviations of individual forecasts (6 individuals) averaged over the six groups in each treatment.

Under rational expectations, all individuals would predict the unique price ![]() , at which demand and supply intersect. Given that all individuals have rational expectations, realized
prices will be given by
, at which demand and supply intersect. Given that all individuals have rational expectations, realized
prices will be given by
that is, small random fluctuations around the RE steady state. Given the limited market information one can not expect that all individuals have rational expectations at the outset, but one can hope that in such a simple, stationary environment individuals would learn to have rational expectations. For example, if price expectations are given by the sample average of past prices, convergence to the RE-price is enforced, as illustrated in Fig. 2 (right panel). The LtFE has in fact been designed to test whether individuals are able to learn from their systematic mistakes under naive expectations and coordinate on a learning algorithm enforcing convergence to the RE steady state.
Figure 3 shows time series of realized market prices together with the individual forecasts (top panels) as well as the average forecast (middle panels) for two typical experimental groups, one stable treatment (left panels) and one strongly unstable treatment (right panels). An immediate observation is that in the stable treatment, after a short learning phase of about 10 periods, the price volatility is low and individual forecasts as well as average forecasts are very close to the RE benchmark, with price fluctuations entirely driven by the small random shocks in the experiments. Aggregate price behaviour and individual forecasts are very different in the strongly unstable treatment. Realized prices exhibit large fluctuations, while individual forecasts are very volatile, even towards the end of the experiment. The bottom panel of figure 3 shows the degree of heterogeneity, as measured by the standard deviations of individual forecasts (6 individuals) averaged over the six groups, in the stable respectively the strongly unstable treatments. In the stable treatment heterogeneity quickly decreases over time, showing that individuals coordinate on a forecast close to the RE-benchmark steady state. In the strongly unstable treatment heterogeneity decreases somewhat over time, but only slowly, and remains at least 3 times as high as in the stable treatment. Hence, in the classical cobweb framework used in Muth (1961) to introduce rational expectations, our LtFEs show that only in the stable cobweb case, the interaction of individual forecasting rules enforces convergence to the RE-benchmark. In the unstable treatment, heterogeneity in forecasting is persistent and leads to an aggregate effect upon prices characterized by excess volatility.
The behaviour in Figure 3 is typical for all cobweb experiments. Hommes et al. (2007) summarize the stylized facts of the cobweb LtFE experiments as follows: (1) the sample mean of realized prices is close to the RE benchmark
![]() in all treatments; (2) the sample variance of realized prices depends on the treatment: it is close to the RE benchmark in the stable treatment, but significantly higher in the unstable
treatment; (3) realized market prices are irregular and do not exhibit significant linear autocorrelations.
in all treatments; (2) the sample variance of realized prices depends on the treatment: it is close to the RE benchmark in the stable treatment, but significantly higher in the unstable
treatment; (3) realized market prices are irregular and do not exhibit significant linear autocorrelations.
These stylized facts across different treatments appear hard to explain by standard learning mechanisms offered by the theoretical literature. For example, naive expectations are inconsistent with the experiments, because in the unstable treatment it predicts too much regularity (convergence to a 2-cycle) in aggregate price behavior. Average price expectations, which is just the simplest form of adaptive learning obtained when regressing prices on a constant, also are inconsistent with the experiments, because for both treatment it predicts convergence to the RE-benchmark (see Fig. 2, right panel). Hommes (2009) discusses a number of other homogeneous learning algorithms and concludes that heterogeneity in forecasting rules is needed to explain the stylized facts of the cobweb experiments across different treatments. Apparently, the interaction of agents' individual forecasting rules washes out linear predictability in aggregate price behavior. In the stable treatment, this interaction leads to coordination on the "correct" RE benchmark steady state, but in the unstable treatment heterogeneity persists and prices are excessively volatile.
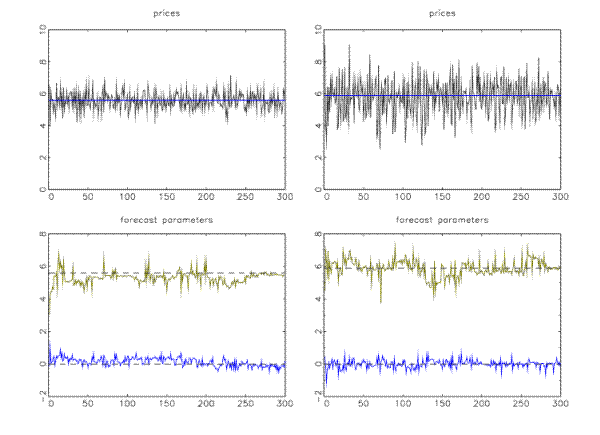
Hommes and Lux (2009) present a model of heterogenous individual learning via genetic algorithms (GAs) to explain the cobweb LtFEs3. Genetic algorithms
require a functional specification of the forecasting rule, whose fitness-maximizing parameter values are searched for via the evolutionary algorithm. Hommes and Lux (2009) use a simple first order autoregressive rule:
Such a first order autoregressive (AR1) rule seems a natural forecasting scheme as agents could implement it using the sample average as their estimate of
Hommes and Lux (2009) show that the interaction of individual GA-learning rules simultaneously reproduces all stylized facts in aggregate price behaviour observed in the experiments across the different treatments. Figure ![]() shows typical price time series under GA-learning as well as time series of the two parameters in the AR1 forecasting rule for the stable treatment (left panel) and the strongly unstable treatment (right panel). In the stable treatment the
parameters converge to a neighborhood of the RE benchmark, consistent with the observed coordination of individual forecasts in the experiments, while in the strongly unstable treatment parameters continue to fluctuate and prices keep moving away from the RE-benchmark, consistent with the
persistent heterogeneity in the strongly unstable treatment of the experiments (cf. Fig. 3).
shows typical price time series under GA-learning as well as time series of the two parameters in the AR1 forecasting rule for the stable treatment (left panel) and the strongly unstable treatment (right panel). In the stable treatment the
parameters converge to a neighborhood of the RE benchmark, consistent with the observed coordination of individual forecasts in the experiments, while in the strongly unstable treatment parameters continue to fluctuate and prices keep moving away from the RE-benchmark, consistent with the
persistent heterogeneity in the strongly unstable treatment of the experiments (cf. Fig. 3).
4 Asset Pricing Experiment
Before discussing the asset pricing Learning-to-forecast experiments (LtFEs) in Hommes et al. (2005), we briefly discuss the underlying benchmark model.
4.1 An asset pricing model with heterogeneous beliefs
This section discusses a standard one-period asset pricing model, extended to the case with heterogeneous beliefs, as in Campbell et al. (1997) and Brock and Hommes (1998). Agents can either invest in a risk free or in a risky asset. The risk free asset is in perfect elastic supply and pays a
fixed rate of return ![]() ; the risky asset pays an uncertain dividend. Let
; the risky asset pays an uncertain dividend. Let ![]() be the
price per share (ex-dividend) of the risky asset at time
be the
price per share (ex-dividend) of the risky asset at time ![]() , and let
, and let ![]() be the
stochastic dividend process of the risky asset. Next period's wealth is given by
be the
stochastic dividend process of the risky asset. Next period's wealth is given by
where
where
where the conditional variance
where
The quantity
4.2 Experimental Design
In the asset pricing LtFEs six subjects are forecast advisors to large pension funds. Subjects only task is to forecast the price of a risk asset for 50 periods and, based on this forecast, the pension fund ten decides how much to invest in the risky asset according to the mean-variance demand function (4.3). The realized asset price in the experiment is given as
where
The fraction of robot traders increases as the price moves further away from the fundamental benchmark. The fundamental trader thus acts as a "far from equilibrium" stabilizing force in the market, mimicking the feature that more traders in the market expect the price to return in the direction of the fundamental when the deviations becomes large8. Subjects' earnings depend on forecasting performance and are given by a quadratic scoring rule
so that forecasting errors exceeding 7 would result in no reward at a given period. At the end of the session the accumulated earnings of every participant were converted to euros ( 1 point computed as in (4.8) corresponded to 50 cents).
4.3 Benchmark Simulations
Figure 5: Simulation benchmarks: Top Panels RE (left) and naive (right); Bottom Panels: average expectations (left) ad AR2 trend following rule 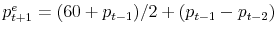 .
.
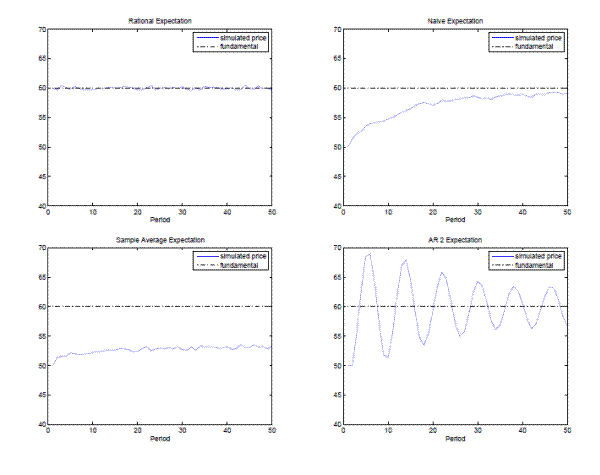
Fig. 5 shows the simulation of realized prices, which would occur for a number of homogeneous benchmark expectations rules. When all individuals use the rational, fundamental forecasting rule,
![]() , for all
, for all ![]() and
and ![]() , the realized price
, the realized price
![]() randomly fluctuates around the fundamental level
randomly fluctuates around the fundamental level ![]() with small amplitude, due to the small socks. In the experiment, one can not expect rational behavior at the outset, but aggregate prices might converge to their fundamental value through individual learning. Under naive expectations the price slowly converges towards its fundamental value. The
same is true under average expectations, the simplest form of adaptive learning obtained when regressing the price on a constant, but the convergence is extremely slow. If all subjects would use the simple AR2 rule
with small amplitude, due to the small socks. In the experiment, one can not expect rational behavior at the outset, but aggregate prices might converge to their fundamental value through individual learning. Under naive expectations the price slowly converges towards its fundamental value. The
same is true under average expectations, the simplest form of adaptive learning obtained when regressing the price on a constant, but the convergence is extremely slow. If all subjects would use the simple AR2 rule
price oscillations as illustrated in the bottom right panel of Fig. 5 arise. This is an example of an anchoring and adjustment rule, which plays an important role in psychology (Tversky ad Kahneman, 1974), because it extrapolates the last price change from a reference point or anchor
4.4 Experimental Results
Figure 6: Asset Pricing Experiments: realized market prices, six individual predictions (middle part of each panel) and individual errors (bottom part of each panel).
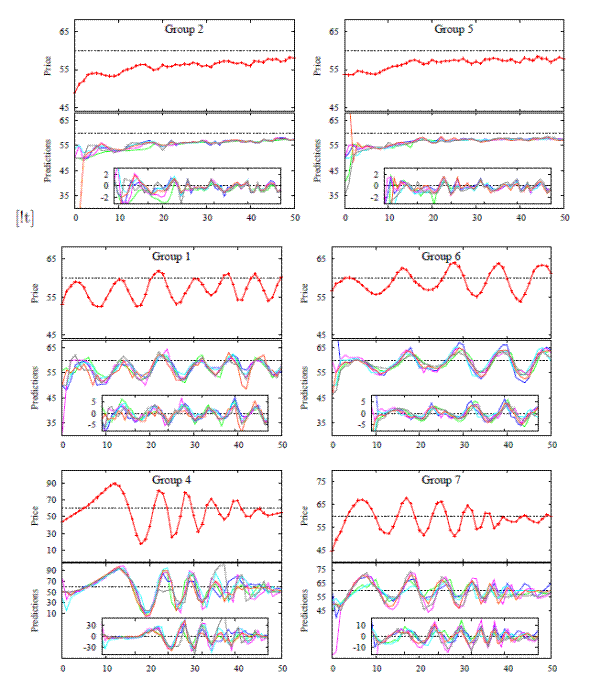
Fig. 6 shows time series of prices, individual predictions and forecasting errors in six different markets of the experiment. A striking feature of aggregate price behavior is that three different qualitative patterns emerge. The prices in groups ![]() and 5 converge slowly and almost monotonically to the fundamental price level. In groups
1 and 6 persistent oscillations are observed during the entire experiment. In
groups 4 and 7 prices are also fluctuating but their amplitude is
decreasing.10
and 5 converge slowly and almost monotonically to the fundamental price level. In groups
1 and 6 persistent oscillations are observed during the entire experiment. In
groups 4 and 7 prices are also fluctuating but their amplitude is
decreasing.10
A second striking result concerns individual predictions. In all groups participants were able to coordinate their forecasting activity. The forecasts, as shown in the lower parts of the panels in Fig. 7, are dispersed in the first periods but then become very close to each other in all groups. The coordination of individual forecasts has been achieved in the absence of any communication between subjects and knowledge of past and present predictions of other participants.
Figure 7: Left Panels: prices for laboratory experiments in three different groups. Lower parts of left panels show individual predictions and forecasting errors (inner frames). Right Panels: Evolution of the degree of heterogeneity as measured by the standard deviation of individual forecasts in corresponding groups.
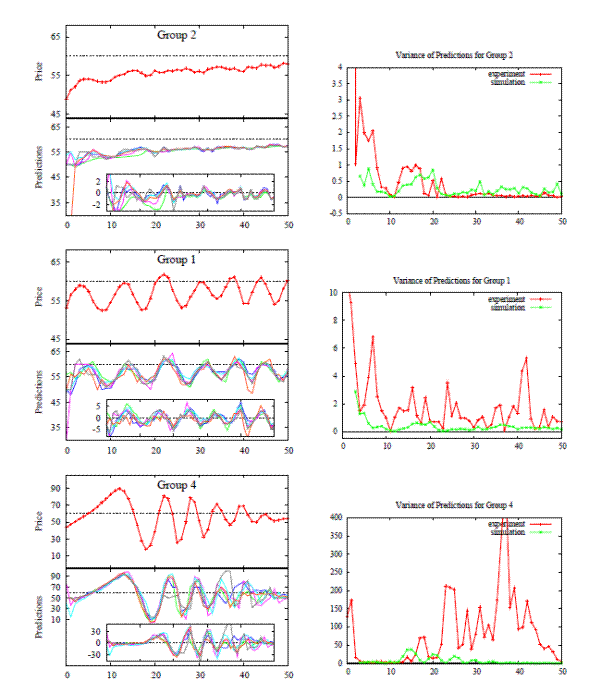
Figure 7 (right panel) illustrates the degree of heterogeneity, as measured by the standard deviation of individual forecasts, in three different groups. A first observation is that for each of the three groups, there is considerable time variation in the degree of heterogeneity. In the converging group 2 heterogeneity quickly decreases, to a level below 1 after period 15 and close to 0 after period 25. It should be noted that despite the fact that coordination is quick, prices are not close to the fundamental value. Hence, coordination on the "wrong", non-fundamental price occurs. In the oscillating group 1, heterogeneity fluctuates, with stronger coordination (i.e. a smaller degree of heterogeneity) during trends and weaker coordination during trend reversals. The same features, but in a more extreme form, arise in the dampened oscillation group 4. During the strong trend from periods 4-13 coordination is very strong, with the degree of heterogeneity falling from a initial level above 150 to values less than 5. Thereafter, coordination weakens and the degree of heterogeneity peaks at price trend reversals, becomes very high after period 23 (note the scale on the vertical axis) with an extremely high peak around period 36-37. Note that, as heterogeneity increases, the asset price stabilizes.
To summarize, in the asset pricing LtFEs we observe the following stylized facts:
- participants were unable to learn the rational, fundamental price; only in some cases individual predictions moved (slowly) in the direction of the fundamental price towards the end of the experiment;
- alltough the sessions were designed in exactly the same, three different price patterns were observed: (i) slow, (almost) monotonic convergence, (ii) persistent price oscillations with almost constant amplitude, and (iii) large initial oscillations dampening slowly towards the end of the experiment;
- already after a short transient, participants were able to coordinate their forecasting activity, submitting similar forecasts in every period.
One would like to have a model explaining all these stylized facts simultaneously. We have not bee able to come up wit a homogeneous expectations model fitting all these experiments. The fact that qualitatively different aggregate outcomes can arise suggests that path dependence and heterogeneous expectations play a key role.
5 A Heterogeneous Expectations Model
In the last 15 years a large literature on heterogenous agent models has developed, as surveyed e.g. by Hommes (2006) ad LeBaron(2006). In particular, Brock ad Hommes (1997) introduced a heterogeneous expectations model, where agents tend to switch towards forecasting strategies that have performed better in the recent past. Here we discuss a modified version, a heuristics switching model, which has recently been fitted to the asset pricing LtFEs by Anufriev and Hommes (2009)11.
Agents can choose from a number of simple forecasting heuristics. To discipline the wilderness of bounded rationality, the set of forecasting heuristics needs to be carefully chosen. We will choose forecasting heuristics that are similar to those obtained from estimations of linear models on individual forecasting data in the LtFEs in Hommes et al. (2005) and Heemeijer et al. (2009). To further discipline the wilderness of bounded rationality two forms of individual learning are introduced. First, for some heuristics adaptive learning takes place, tat is, some parameters of the heuristics are updated over time. Second, evolutionar selection or performance based reinforcement learning takes place, that is, agents evaluate the performances of all heuristics, and tend to switch to more successfully rules. Hence, the impact of each of the rules is evolving over time.
To keep the model as simple as possible, Anufriev and Hommes (2009) restricted attention to only four forecasting heuristics:
| ADA |
(5.1) | ||
| WTR |
(5.2) | ||
| STR |
(5.3) | ||
| LAA |
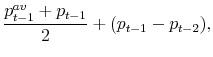 |
(5.4) |
were
Subjects switch between the different forecasting rules based upon quadratic forecasting errors, consistent with the earnings incentives in the experiments. The fitness or performance measure of forecasting heuristic ![]() is given by
is given by
| (5.5) |
where the parameter
In the special case
In all simulations below, we fix the parameters at the benchmark values
![]() 13 and the
initial fractions of the four strategies are equal, i.e.
13 and the
initial fractions of the four strategies are equal, i.e.
![]() . The simulations thus only differ in their initial prices, which have been chosen exactly the same as in the first two periods in the corresponding experimental group
. The simulations thus only differ in their initial prices, which have been chosen exactly the same as in the first two periods in the corresponding experimental group
Figure 8: Left Panels: prices for laboratory experiments in different groups (red) with corresponding one-step ahead predictions of the evolutionary model (blue). Lower parts of left panels show predictions and forecasting errors (inner frames) of four heuristics. Right Panels: Evolution of heuristic impacts during the one-step ahead predictions of the model. Fractions of four forecasting heuristics: adaptive expectations (ADA, purple), weak trend followers (WTR, black), strong trend followers (STR, blue) and anchoring adjustment heuristic (LAA, red).

Fig. 8 compares the experimental data with the one-step ahead predictions made by the heuristics switching model, for one converging group (group 5), one oscillating group (group 6) and one dampened oscillating group (group 7); the other
groups yield very similar results; see Anufriev and Hommes (2009). Fig. 8 suggests that the switching model with four heuristics fits the experimental data quite nicely. The one-step ahead predictions of the nonlinear switching model in
Fig. 8 use past experimental price data to determine the forecasts and the fractions of the strategies at each period ![]() , i.e., the model simulation uses exactly the same information that was available to participants in the experiments. An immediate observations by comparing these simulations is that the one-period ahead forecasts can easily follow the different patterns in aggregate price behavior,
slow monotonic convergence, sustained oscillations as well as dampened oscillations.
, i.e., the model simulation uses exactly the same information that was available to participants in the experiments. An immediate observations by comparing these simulations is that the one-period ahead forecasts can easily follow the different patterns in aggregate price behavior,
slow monotonic convergence, sustained oscillations as well as dampened oscillations.
The right panels in Fig. 8 show the corresponding fractions of the four strategies for each group. In different groups different heuristics are taking the lead after starting from a uniform distribution. In the monotonically converging
group, the impact of the different rules stays more or less equal, although the impact of adaptive expectations gradually increases and slightly dominates the other rules in the last 25
periods. The oscillatory group yields similar results as, with the LAA rule dominating the market early and its impact increasing to about ![]() towards the end of the experiment. Finally,
for the group with the dampened oscillations, one step ahead forecast produces a rich evolutionary selection dynamics (bottom panel), with three different phases where the STR, the LAA and the ADA heuristics subsequently dominate. The STR dominates during the initial phase of a strong trend in
prices, but starts declining after it misses the first turning point of the trend. The LAA does a better job in predicting the trend reversal and its impact starts increasing. The LAA takes the lead in the second phase of the experiment, with oscillating prices. But the oscillations slowly dampen
and therefore, after period 35, the impact of adaptive expectations, which has been the worst performing rule until that point, starts increasing and adaptive expectations dominates the groups in the last 9 periods.
towards the end of the experiment. Finally,
for the group with the dampened oscillations, one step ahead forecast produces a rich evolutionary selection dynamics (bottom panel), with three different phases where the STR, the LAA and the ADA heuristics subsequently dominate. The STR dominates during the initial phase of a strong trend in
prices, but starts declining after it misses the first turning point of the trend. The LAA does a better job in predicting the trend reversal and its impact starts increasing. The LAA takes the lead in the second phase of the experiment, with oscillating prices. But the oscillations slowly dampen
and therefore, after period 35, the impact of adaptive expectations, which has been the worst performing rule until that point, starts increasing and adaptive expectations dominates the groups in the last 9 periods.
6 Positive versus Negative Feedback Experiments
Aggregate price behavior in the cobweb and the asset pricing LtFEs are quite different. While in the cobweb framework the price fluctuates around its fundamental value, with a sample average of realized prices very close to the RE price, in the asset pricing experiments persistent deviations from the fundamental price with long lasting under- or over-valuations have been observed. A key difference between the cobweb and asset pricing experiments is the type of feedback: the asset pricing (cobweb) framework exhibits positive (negative) feedback, that is the realized price depends positively (negatively) on the average price forecast. In the case of positive (negative) feedback, when an individual forecast increases, the realized market price goes up (down). A natural question then is whether the type of feedback, positive versus negative, explains these differences in aggregate behavior.
In most markets both types of feedback may play a role. Positive feedback however, seems particularly relevant in speculative asset markets. If many agents expect the price of an asset to rise they will start buying the asset, aggregate demand will increase and so, by the law of supply and demand, will the asset price. High price expectations thus become self-confirming and lead to high realized asset prices. In markets where the role of speculative demand is less important, e.g. in markets for non-storable commodities, negative feedback may play a more prominent role. Consider e.g. a supply-driven commodity market. If many producers expect future prices to be high they will increase production which, according to the law of supply and demand, will lead to a low realized market price.
Heemeijer et al. (2009) investigate how the expectations feedback structure affects individual forecasting behaviour and aggregate market outcomes by considering market environments that only differ in the sign of the expectations feedback, but are equivalent along all other dimensions. In this section we discuss these experiments and apply the heterogeneous expectations model of Section 5 to see whether it can explain the different aggregate outcomes.
The distinction between positive and negative expectation feedback is related to the concepts of strategic complements versus strategic substitutes. Haltiwanger and Waldman (1985) argue that when actions are strategic complements, agents have an incentive to imitate other agents. This is the case in an asset market, where predicting a price close to the predictions of the other participants turns out to be most profitable. However, coordination of predictions enhances the impact of the irrational participants upon realized prices and convergence to the rational equilibrium price becomes unlikely. When actions are strategic substitutes, agents have an incentive to deviate from what other agents are doing. This is the case in negative feedback markets, where agents have an incentive to predict high (low) prices when the majority predicts prices below (above) the equilibrium price. The impact of irrational individuals will be limited and convergence to the equilibrium price is more likely. Coordination of predictions will only take place after convergence.
In recent experiments Fehr and Tyran (2001, 2005, 2007) study the impact of different strategic environments (strategic complementarity versus strategic substitutability) on individual rationality and aggregate outcomes. Strategic substitutability (complementarity) prevails if an increase in the action of individual i generates an incentive for j to decrease (increase) his action. Fehr and Tyran study the adjustment of nominal prices after an anticipated money shock in a price setting game with positively (complements) or negatively sloped (substitutes) reaction curves, and find much faster convergence in the case of substitutes. Sutan and Willinger (2009) investigate a new variant of beauty contest games (BCG) in which players actions are strategic substitutes versus strategic complements and find that chosen numbers are closer to rational play in the case of strategic substitutes.
In the LtFEs of Heemeijer et al. (2009), the (unknown) price generating rules in the negative and positive feedback systems were respectively:
where
A common feature of the positive and negative feedback systems (6.1) and (6.2) is that both have the same RE equilibrium steady state ![]() ,
with
,
with ![]() when the shocks
when the shocks
![]() have mean 0. The only difference between (6.1) and (6.2) is therefore the sign of the slope of the
linear map,
have mean 0. The only difference between (6.1) and (6.2) is therefore the sign of the slope of the
linear map,
![]() resp.
resp.
![]() 14.
14.
Figure 9: Negative (left panel) vs. positive (right panel) feedback experiments with small IID shocks; prices (top panels), individual predictions (bottom panels) and forecast errors (small panels).
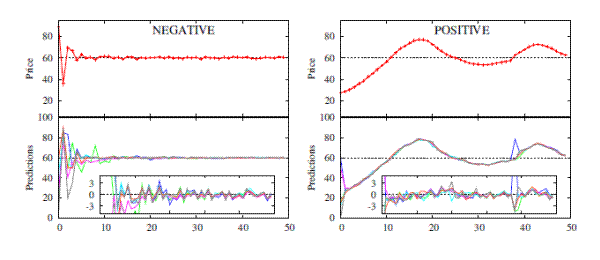
Figure 9 shows realized market prices as well as individual predictions in two typical groups. A striking feature is that aggregate price behavior is very different in the positive versus negative feedback cases. In the negative feedback case, the price relatively quickly settles down to the RE steady state price 60, while in the positive feedback case, the market price oscillates slowly around its fundamental value. Individual forecasting behavior is also different for the different feedback treatments: in the case of positive feedback, coordination of individual forecasts occurs extremely quickly, within 2-3 periods. The coordination however is on a "wrong" non-fundamental price. In contrast, in the negative feedback case coordination of individual forecasts is slower and takes about 10 periods. More persistence in heterogeneity of individual forecasts however ensures that, after 10 periods, the realized market price is very close to the RE benchmark of 60.
Figure 10: Positive feedback (bottom panels) and negative feedback (top panels) markets with small shocks. Realized and simulated prices (left panels) and corresponding evolution of fractions of 4 strategies in heuristics switching model.
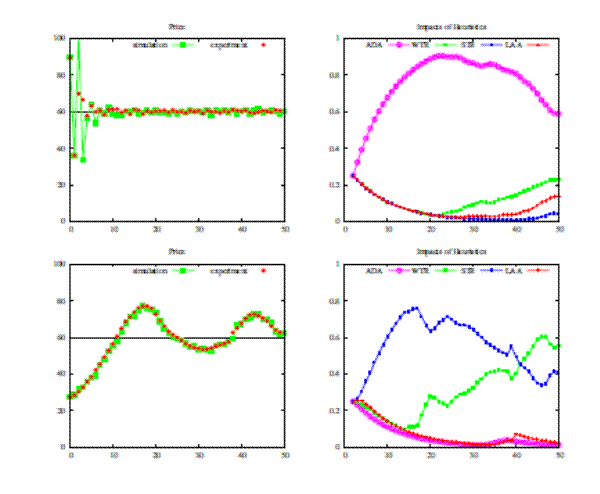
Can the heterogeneous expectations model of Section 5 explain these different outcomes in individual and aggregate behaviour? Figure 10 shows realized market prices together with the simulated prices (left panels),
and the corresponding evolution of the fractions of the four strategies (right panels) of the heuristics switching model with the same benchmark parameters as before, i.e.
![]() . The model matches aggregate price behaviour in both the negative and positive feedback treatment. Furthermore, the time series of the fractions of the
different forecasting heuristics (Figure 10, right panels) provide an intuitive explanation of why aggregate behavior is different. In the negative feedback treatment, the adaptive expectations strategy performs best and within 20 periods it captures more than
. The model matches aggregate price behaviour in both the negative and positive feedback treatment. Furthermore, the time series of the fractions of the
different forecasting heuristics (Figure 10, right panels) provide an intuitive explanation of why aggregate behavior is different. In the negative feedback treatment, the adaptive expectations strategy performs best and within 20 periods it captures more than
![]() of the market, thus enforcing convergence towards the fundamental equilibrium price. In contrast, in the positive feedback treatment the impact of the strong trend-following rule (STR)
quickly increases and it captures more than
of the market, thus enforcing convergence towards the fundamental equilibrium price. In contrast, in the positive feedback treatment the impact of the strong trend-following rule (STR)
quickly increases and it captures more than ![]() of the market after 15 periods. Thereafter, the impact of the STR rule gradually declines, while the fraction of weak trend-followers (WTR)
gradually increases due to the fact that the STR-rule makes (somewhat) larger mistakes (especially at the turning points) than the WTR-rule.
of the market after 15 periods. Thereafter, the impact of the STR rule gradually declines, while the fraction of weak trend-followers (WTR)
gradually increases due to the fact that the STR-rule makes (somewhat) larger mistakes (especially at the turning points) than the WTR-rule.
The difference in aggregate behavior is thus explained by the fact that trend following rules are successful in a positive feedback environment reinforcing price oscillations and persistent deviations from the fundamental equilibrium benchmark price, while the trend-following rules are driven out by adaptive expectations in the case of negative feedback.
Figure 11: Positive feedback (bottom panels) and negative feedback (top panels) markets with large permanent shocks to the equilibrium steady state level. Realized and simulated prices (left panels) and corresponding evolution of fractions of the 4 strategies in heuristics switching model.
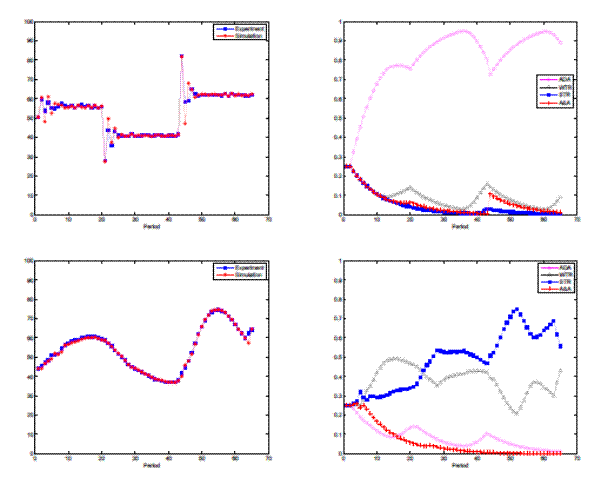
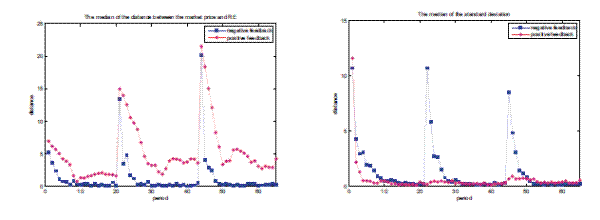
Figure 12: Positive/Negative Feedback; Large Shocks Coordination & Price Discovery; median absolute distance to RE fundamental price; median standard deviation of individual predictions
Bao et al. (2010) recently ran similar LtFEs with large permanent shocks
![]() to the price generating mechanisms (6.1) and (6.2). These shocks have been chosen such that, both in the negative and positive
feedback treatments, the fundamental equilibrium price
to the price generating mechanisms (6.1) and (6.2). These shocks have been chosen such that, both in the negative and positive
feedback treatments, the fundamental equilibrium price ![]() changes over time according to:
changes over time according to:
The purpose of these experiments was to investigate how the type of expectations feedback may affect the speed of learning of a new steady state equilibrium price. Figure 11 shows realized market prices together with the simulated market prices (left panels), together with the evolution of the fractions of the four strategies of the heuristics switching model (right panels) for a typical group of the negative feedback (top panels) and the positive feedback treatment (bottom panels). The heuristics switching model is exactly the same as in Anufriev and Hommes (2009), in the case of the asset pricing experiments (see Section 5), with the same benchmark parameters as before, i.e.
Figure 12 reveals some other striking features of aggregate price behavior and individual forecasts. The left panel shows the time variation of the median distance to the RE benchmark price over all groups in both treatments. For the negative feedback treatment, after each large shock the distance spikes but converges quickly back (within 5-6 periods) to 0, while for the positive feedback treatment after each shock the distance to the RE benchmark shows a similar spike but does not converge to 0 and only decreases slowly. The right panel shows how the degree of heterogeneity, that is, the median standard deviation of individual forecasts, changes over time. For the positive feedback treatment after each large shock heterogeneity decreases very quickly and converges to (almost) 0 within 3-4 periods, while in the negative treatment heterogeneity is more persistent for about 10 periods after each large shock. One may summarize these results in saying that in the positive feedback treatment individuals quickly coordinate on a common prediction, but that coordination on the "wrong" non-fundamental price occurs. On the other hand, in the negative feedback treatment coordination is slow, heterogeneity is more persistent but price convergence is quick. Stated differently, positive feedback markets are characterized by quick coordination and slow price discovery, while negative feedback markets are characterized by slow coordination, more persistent heterogeneity and quick price discovery. See Bao et al. (2009) for a more detailed discussion.
7 A New Keynesian Macro Model
As a final example, we briefly discuss the LtFEs experiments in a standard New Keynesian macro model of Assenza et al. (2009); see also Pfajfar and Santoro (2009) for closely related LtFEs. The New Keynesian model is described by the following equations:
where
In the LtFEs of Assenza et al. (2009), two different groups of 6 subjects have to provide two-period ahead forecasts of the inflation rate respectively the output gap for 50 periods. Realized inflation and realized output gap are determined by the (average) individual expectations of two different groups of 6 individuals. Subjects only obtain qualitative information about the macro-economy, but they do not know the underlying law of motion (7.1-7.3).
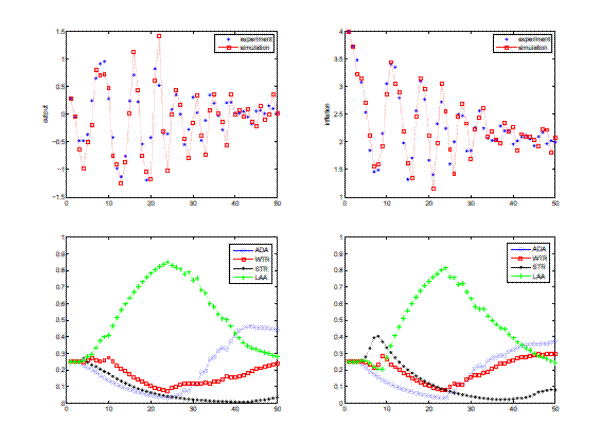
Figure 13: Learning to forecast experiment in New Keynesian Macro framework. Left panel: time series of realized inflation, individual inflation forecasts, interest rate and realized output gap. Right panel: time series of realized inflation, interest rate, realized output gap and individual forecasts of output gap. Parameter values: 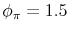 , ...
, ...
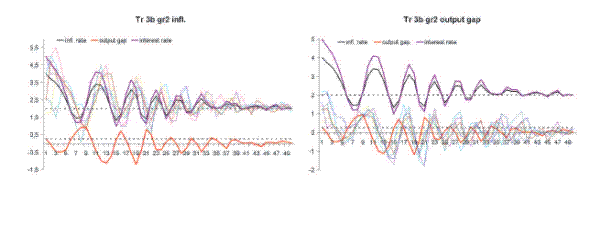
Figure 13 shows time series of realized inflation, output gap, interest rate together with individual forecasts of inflation and output gap. Both inflation and output gap exhibit dampened oscillations eventually converging to the RE benchmark steady state. An
interesting feature of these experiments is that an aggressive monetary policy described by a Taylor type interest rate rule that adjust the interest rate more than one point for one in response to inflation (with a coefficient
![]() ) is able to stabilize heterogeneous expectations.
) is able to stabilize heterogeneous expectations.
Figure 14 shows simulated time series of inflation and output gap, together with the fractions of the forecasting rules, of the benchmark heuristics switching model of Anufriev and Hommes (2009). The same heuristics switching model is used for both inflation and
output gap forecasts and the model fits the experimental data quite well. The patterns of the weight of the forecasting heuristics are quite similar for inflation and output, as one would expect since both time series are qualitatively similar. The Learning Anchor and Adjustment (LAA) rule
dominates most of the time, with a peak of about ![]() after 25 periods and the adaptive expectations rule dominating in the last 10 periods when the economy stabilizes. There is a slight
difference in the initial phase, with the strong trend rule STR dominating inflation forecasting in periods 5-10, picking up the stronger trend in inflation.
after 25 periods and the adaptive expectations rule dominating in the last 10 periods when the economy stabilizes. There is a slight
difference in the initial phase, with the strong trend rule STR dominating inflation forecasting in periods 5-10, picking up the stronger trend in inflation.
8 Concluding Remarks
LtFEs can be used to test theories of expectations and learning in benchmark model settings. LtFEs are Taylor made experiments to test exclusively the expectations hypothesis, computerizing all other model assumptions. Different outcomes in aggregate behavior have been observed in different market settings. To our best knowledge, no homogeneous expectations model fits all LtFEs across different settings. Quick convergence to the RE-benchmark only occurs in stable (i.e. stable under naive expectations) cobweb/negative feedback markets.
Lab experiments suggest that heterogeneity is a crucial aspect of a theory of expectations, because a heterogeneous expectations model can explain observed path dependence in the same market environment as well as different aggregate outcomes across different market settings.
A challenge to economic theory is to come up with a universal and plausible theory of heterogeneous expectations. The fact that a simple heuristics switching model fits different LtFEs gives some hope that a general heterogeneous expectations hypothesis may explain individual expectations and aggregate outcomes across different market settings.
![\displaystyle z_{ht} = \frac{E_{ht}[p_{t+1}+y_{t+1}-Rp_t]}{aV_{ht}[p_{t+1}+y_{t+1}-Rp_t]}= \frac{E_{ht}[p_{t+1}+y_{t+1}-Rp_t]}{a\sigma^2},](img64.gif)
![\displaystyle \sum_{h=1}^{H} n_{ht} \frac{E_{ht}[p_{t+1}+y_{t+1}-Rp_t]}{a\sigma^2} = z^s,](img68.gif)
![\displaystyle p_t = \frac{1}{1+r} \sum_{h=1}^{H} n_{ht}E_{ht}[p_{t+1} + y_{t+1}] - a\sigma^2 z^s.](img72.gif)
![\displaystyle p_t = \frac{1}{1+r} \sum_{h=1}^{H} n_{ht}E_{ht}[p_{t+1}] + \bar{y}.](img77.gif)
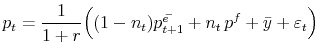
![\displaystyle e_{i,t} = \left\{ \begin{array}{cl} 1 - \left(\frac{p_t - p_{i,t}^e}{7}\right)^2 & \text{if} \quad \vert p_t - p_{i,t}^e \vert < 7\,,\\ [0.1cm] 0 & \text{otherwise}\,, \end{array} \right.](img87.gif)
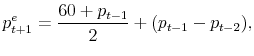
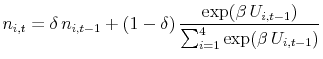
![\displaystyle p_t = 60 - \frac{20}{21}[\sum_{h=1}^6 \frac{1}{6} p_{ht}^e] - 60] + \epsilon_t, \hskip2cm](img135.gif) negative feedback
negative feedback![\displaystyle p_t = 60 + \frac{20}{21}[\sum_{h=1}^6 \frac{1}{6} p_{ht}^e - 60] + \epsilon_t, \hskip2cm](img136.gif) positive feedback
positive feedback