Fire Sales in a Model of Complexity
Keywords: Fire sales, complexity, financial network, cascades, markets freeze, crises, information cost, financial panic, credit crunch, pecuniary externality.
Abstract:
1 Introduction
Financial assets provide return and liquidity services to their holders. However, during severe financial crises many asset prices plummet, destroying their liquidity provision function at the worst possible time. These fire sales are at the core of the amplification mechanism observed in severe financial crises: Large amounts of distressed asset sales depress asset prices, which exacerbates financial distress, leading to further asset sales, and the downward spiral goes on.
There are many instances of these dramatic fire sales and the chaos they trigger in recent financial history. As explained by Treasury Secretary Paulson and Fed Chairman Bernanke to Congress in an emergency meeting soon after Lehman's collapse, the main goal of the TARP during the subprime crisis as initially proposed was, precisely, to put a floor on the price of the assets held by financial firms in order to contain the sharp contractionary feedback loop triggered by the confusion and panic caused by Lehman's demise. And a few years back, after the LTCM intervention, then Fed Chairman Greenspan wrote in his congressional testimony of October 1, 1998:
"Quickly unwinding a complicated portfolio that contains exposure to all manner of risks, such as that of LTCM, in such market conditions amounts to conducting a fire sale. The prices received in a time of stress do not reflect longer-run potential, adding to the losses incurred... ...a fire sale may be sufficiently intense and widespread that it seriously distorts markets and elevates uncertainty enough to impair the overall functioning of the economy. Sophisticated economic systems cannot thrive in such an atmosphere."
In this paper we propose a model of fire sales that builds on the idea that complexity, a feature strongly disliked by investors during downturns for the uncertainty it generates, rises endogenously during crises: As asset prices implode, more financial institutions (banks, for short) within the financial network may go under, which increases each bank's likelihood of being hit by an indirect shock from counterparty risk. This means that banks face an increasingly complex environment since they need to understand more and more interlinkages in making their financial decisions. Thus, perceived uncertainty rises with complexity and makes relatively healthy banks reluctant to buy since they now fear becoming embroiled in the cascade themselves, and no reasonable amount of research can rule out this option in the time available. The liquidity of the market quickly vanishes and a financial crisis ensues.
In Caballero and Simsek (2009) we show the basic interaction between the size of the equilibrium cascade in a financial network and the degree of complexity of the portfolio problem facing banks. In that model banks have bilateral linkages in order to insure each other against local liquidity shocks. The whole financial system is a complex network of linkages which functions smoothly in the environments for which it is designed, even though no bank knows with certainty all the many possible connections within the network (that is, each bank knows the identities of the other banks but not their exposures). However, these linkages may also be the source of contagion when an unexpected event of financial distress arises somewhere in the network. During normal times, banks only need to understand the financial health of their neighbors, which they can learn at low cost. In contrast, when a significant problem arises in parts of the network and the possibility of cascades arises, the number of nodes to be audited by each bank rises since it is possible that the shock may spread to the bank's counterparties. Eventually, the problem becomes too complex for them to fully figure out, which means that banks now face significant uncertainty and they react to it by retrenching into a liquidity-conservation mode.
This structure is the starting point of this paper. Our focus here is on secondary markets and on the feedback between that environment and the fire sales that arise in these markets. In particular, this paper introduces a secondary market in which banks in distress can sell their legacy assets to meet the surprise liquidity shock. The natural buyers of the legacy assets are other banks in the financial network, which may also receive an indirect hit. When the surprise shock is small, cascades are short and buyers can inspect their neighbors to rule out an indirect hit. In this case, buyers purchase the distressed banks' legacy assets at their " fair" prices (which reflect the fundamental value of the assets). In contrast, when the surprise shock is large, longer cascades become possible which increases the complexity of the environment, and buyers cannot rule out an indirect hit. As a precautionary measure, they hoard liquidity and disengage from trades in (now illiquid) legacy assets and may even turn into sellers. The price of legacy assets plummets to " fire-sale" levels.
A central aspect of our model is the dependence of the cascade size on the price of legacy assets, which leads to multiple equilibria for intermediate levels of the surprise shock. When legacy assets fetch a fair price in the secondary market, the banks in distress have access to more liquidity and thus the surprise shock is contained after fewer banks are bankrupt, leading to a relatively simple environment. When the environment is simple, the natural buyers rule out an indirect hit and demand legacy assets, which ensures that these assets trade at their fair prices. Set against this benign scenario is the possibility of a fire-sale equilibrium where the price of legacy assets collapses to fire-sale levels, which leads to a longer cascade and a greater level of complexity. As the level of complexity increases, natural buyers become worried about an indirect hit and they hoard liquidity and/or sell their own legacy assets, which reinforces the collapse of asset prices.
This amplification mechanism is exacerbated by a complexity-externality. As a potential asset buyer chooses to pull back, the size of the potential cascade grows and with it the degree of complexity of the environment (each bank needs to explore larger segments of the network to understand the risk it is exposed to). This rise in complexity induces other healthy banks to pull back as a precautionary measure, which further exacerbates the fire sale and cascade.1
Our framework has two additional (and more standard) externalities: A network-liquidity externality that stems from the interlinkages of the financial system; when a bank chooses to raise external liquidity rather than to generate it from its own resources, it spreads the distress to other banks. And a fire-sale externality that arises from the negative effects that a bank's distressed asset sales have on other banks' balance sheets. These two externalities are present in many network and liquidity models. They interact but are distinct from the complexity externality that we highlight, which stems from the feature that any decision that lengthens the potential cascade, increases the complexity of the environments that other banks need to consider.
This paper is related to several strands of literature. In the canonical model of fire sales, these happen because during financial crises the natural buyers of the assets (other banks) also experience financial distress (cf. Shleifer and Vishny (1992,1997)). More recently, Brunnermeier and Pedersen (2008) show that even if some potential buyers are not distressed or constrained, these may choose not to arbitrage the fire sale in the short run because they anticipate a better deal in the future. Our model lies somewhere in between these two views: Most potential buyers are unconstrained, as in Brunnermeier and Pedersen (2008), but they are confused and hence fearful of going about their normal arbitrage role (and in this sense they are distressed as in Shleifer and Vishny (1992)). It is the complexity of the environment that sidelines potential buyers.
There is an extensive literature that highlights the possibility of network failures and contagion in financial markets. An incomplete list includes Allen and Gale (2000), Lagunoff and Schreft (2000), Rochet and Tirole (1996), Freixas, Parigi and Rochet (2000), Leitner (2005), Eisenberg and Noe (2001), and Cifuentes, Ferucci and Shin (2005) (see Allen and Babus (2008) for a recent survey). These papers focus mainly on the mechanisms by which solvency and liquidity shocks may cascade through the financial network. In contrast, we take these phenomena as the reason for the rise in the complexity of the environment in which banks make their decisions, and focus on the effect of this complexity on banks' prudential actions. It is also worth pointing out that the complexity mechanism we emphasize in this paper is operational even for relatively small amounts of contagion. The contagion literature is sometimes criticized because it is hard to believe that many financial institutions would be caught up in a cascade of bankruptcies.2 That is, even if there is a cascade, it is reasonable to expect that it would eventually be contained (especially since banks take precautionary actions to fight the cascade). But as this paper illustrates, even partial cascades can have large aggregate effects, since they greatly increase the complexity of the environment.3
Our paper is also related to the literature on flight-to-quality and Knightian uncertainty in financial markets, as in Caballero and Krishnamurthy (2008), Routledge and Zin (2004), and Easley and O'Hara (2005); and to the related literature that investigates the effect of new events and innovations in financial markets, e.g., Liu, Pan, and Wang (2005), Brock and Manski (2008), and Simsek (2009). Our contribution relative to these literatures is in endogenizing the rise in uncertainty from the behavior of the financial network itself. More broadly, this paper belongs to an extensive literature on flight-to-quality and financial crises that highlights the connection between panics and a decline in the financial system's ability to channel resources to the real economy (see, e.g., Caballero and Kurlat (2008), for a survey).
The organization of this paper is as follows. In Section 2 we describe the financial network and the secondary market for assets, and we introduce a surprise shock (a rare event) in the network. We also discuss a benchmark case without complexity effects (because banks can understand the network at no cost). Section 3 contains our main results. There, banks have only local knowledge about the financial network, and a sufficiently large surprise shock increases the complexity of the environment and leads to a breakdown in secondary markets. This section also highlights the dependence of the level of complexity on asset prices and demonstrates the possibility of multiple equilibria. In Section 4 we describe the three externalities in our setup and analyze their role in our main results. The paper concludes with a final remarks section and several appendices.
2 Equilibrium without Complexity
In this section, we describe the basic environment and characterize the equilibrium for a benchmark case in which financial institutions (banks, for short) have full knowledge of the interlinkages between all the banks in the financial network. In this benchmark we show that if the network is deep (i.e., there is a large number of banks) secondary markets do not break down and the financial network is resilient to a perturbation. That is, the size of financial cascades is contained and aggregate loan contraction is limited. These relatively benign results contrast with those we obtain in the next section once we introduce complexity.
2.1 The Environment
We consider an economy with three dates
![]() in which a single good (one dollar) can be kept in liquid reserves or it can be loaned to production firms. If kept in liquid reserves, a unit of the good yields one
unit in the next date. Instead, if a unit is loaned to firms, it then yields
in which a single good (one dollar) can be kept in liquid reserves or it can be loaned to production firms. If kept in liquid reserves, a unit of the good yields one
unit in the next date. Instead, if a unit is loaned to firms, it then yields ![]() units at date 2. These new loans are completely illiquid.
units at date 2. These new loans are completely illiquid.
The economy has ![]() continuums of banks denoted by
continuums of banks denoted by
![]() . Each of these continuums is composed of identical banks and, for simplicity, we refer to each continuum
. Each of these continuums is composed of identical banks and, for simplicity, we refer to each continuum ![]() as bank
as bank ![]() , which is our unit of analysis.4 Each bank has initial assets which consist of
, which is our unit of analysis.4 Each bank has initial assets which consist of ![]() units of legacy loans,
units of legacy loans, ![]() units of demand deposits in one other bank, and
units of demand deposits in one other bank, and ![]() units of flexible reserves set aside
for making new loans at date 0. The bank's liabilities consist of a unit measure of demand deposits held by retail depositors and
units of flexible reserves set aside
for making new loans at date 0. The bank's liabilities consist of a unit measure of demand deposits held by retail depositors and ![]() units of demand deposits held by
one other bank. The demand deposit contracts in this economy pay 1 unit at date 1
(resp.
units of demand deposits held by
one other bank. The demand deposit contracts in this economy pay 1 unit at date 1
(resp. ![]() units at date 2) if the depositor arrives early (resp. late). There are no
liquidity driven depositors. I.e. as long as the bank is solvent, all retail depositors would rather arrive at date 2. Note that a bank that loans all of its flexible reserves has just enough
assets to pay its depositors at date 2. At date 0 (only) there is a secondary market for legacy loans and the (equilibrium) price for these loans is
units at date 2) if the depositor arrives early (resp. late). There are no
liquidity driven depositors. I.e. as long as the bank is solvent, all retail depositors would rather arrive at date 2. Note that a bank that loans all of its flexible reserves has just enough
assets to pay its depositors at date 2. At date 0 (only) there is a secondary market for legacy loans and the (equilibrium) price for these loans is ![]() (see below). The central trade-off in this economy will be whether the bank uses its flexible reserves to make new loans and to purchase legacy loans in the secondary market, or whether it hoards
some of this liquidity in response to a rare event (that we describe below).
(see below). The central trade-off in this economy will be whether the bank uses its flexible reserves to make new loans and to purchase legacy loans in the secondary market, or whether it hoards
some of this liquidity in response to a rare event (that we describe below).
The banks' cross demand deposit holdings form a financial network denoted by:
where
At date 0, the banks learn that a rare event has happened and one bank,
![]() , will become distressed. Similar to Allen and Gale (2000), in order to remain solvent this bank needs to make
, will become distressed. Similar to Allen and Gale (2000), in order to remain solvent this bank needs to make ![]() dollars of payment (to an outsider) at date 1.
dollars of payment (to an outsider) at date 1.
These losses might spill over to other banks via the financial network and may bring them into financial distress at date 1. To prepare for date 1, at date 0 the banks take one of the following actions
![]() , which are restricted to a discrete choice set for simplicity (see Caballero and Simsek (2009) for a related model with unrestricted action space). As the
most extreme precautionary measure, the bank may choose
, which are restricted to a discrete choice set for simplicity (see Caballero and Simsek (2009) for a related model with unrestricted action space). As the
most extreme precautionary measure, the bank may choose
![]() , to hoard all of its flexible reserves
, to hoard all of its flexible reserves ![]() as liquidity and sell all of its legacy loans
as liquidity and sell all of its legacy loans ![]() in the secondary market, keeping a completely liquid balance sheet. As a less extreme measure, the bank may
choose
in the secondary market, keeping a completely liquid balance sheet. As a less extreme measure, the bank may
choose
![]() , to hoard its flexible reserves as liquidity and to keep its legacy loans on its balance sheet. Alternatively, the bank may choose
, to hoard its flexible reserves as liquidity and to keep its legacy loans on its balance sheet. Alternatively, the bank may choose
![]() to keep its own legacy loans on its balance sheet and to be a potential buyer of loans. That is, this bank uses its flexible reserves either to make
new loans or to buy legacy loans in the secondary market (whichever is more profitable). At date 1, the bank chooses whether to keep or withdraw its deposits on the forward neighbor bank,
to keep its own legacy loans on its balance sheet and to be a potential buyer of loans. That is, this bank uses its flexible reserves either to make
new loans or to buy legacy loans in the secondary market (whichever is more profitable). At date 1, the bank chooses whether to keep or withdraw its deposits on the forward neighbor bank,
![]() .
.
Given the rare event, a bank may not be able to pay its depositors the contracted amount
![]() (despite the precautionary measures it takes), but instead it ends up paying some
(despite the precautionary measures it takes), but instead it ends up paying some
![]() to all depositors. Banks know that there are no liquidity driven retail depositors, thus a bank which is able to pay its depositors at least
to all depositors. Banks know that there are no liquidity driven retail depositors, thus a bank which is able to pay its depositors at least
![]() at date 2 can refuse to pay the retail depositors if they arrive
early. With this assumption, the continuation equilibrium for bank
at date 2 can refuse to pay the retail depositors if they arrive
early. With this assumption, the continuation equilibrium for bank ![]() at date 1
takes one of two forms. Either the bank is solvent, pays
at date 1
takes one of two forms. Either the bank is solvent, pays
![]() , and the retail depositors withdraw at date 2; or the
bank is insolvent, pays
, and the retail depositors withdraw at date 2; or the
bank is insolvent, pays
![]() , and all depositors draw their deposits at date 1.
, and all depositors draw their deposits at date 1.
The bank chooses actions
![]() to maximize
to maximize ![]() until it can meet its
liquidity obligations to depositors, that is, until
until it can meet its
liquidity obligations to depositors, that is, until
![]() . Increasing
. Increasing ![]() beyond 1 has no benefit for the bank, thus once it satisfies its liquidity obligations, it then tries to maximize the return to late depositors
beyond 1 has no benefit for the bank, thus once it satisfies its liquidity obligations, it then tries to maximize the return to late depositors ![]() . Note that the banks make their decisions while facing uncertainty about the network structure. For expositional simplicity we assume that banks are infinitely risk averse (rather than just risk averse) with respect to the financial network, i.e., they evaluate their
decisions according to the worst possible network realization which they find plausible.
. Note that the banks make their decisions while facing uncertainty about the network structure. For expositional simplicity we assume that banks are infinitely risk averse (rather than just risk averse) with respect to the financial network, i.e., they evaluate their
decisions according to the worst possible network realization which they find plausible.
Secondary Market for Legacy Loans
Legacy loans are traded in a centralized exchange that opens at date 0. Given the loan price ![]() , the banks that choose
, the banks that choose
![]() sell all of their legacy loans (
sell all of their legacy loans (![]() units for each bank) while the
banks that choose
units for each bank) while the
banks that choose
![]() are potential buyers of legacy loans and may spend up to
are potential buyers of legacy loans and may spend up to ![]() (their
flexible reserves). There is no demand or supply for legacy loans outside of the network.
(their
flexible reserves). There is no demand or supply for legacy loans outside of the network.
A legacy loan traded in the secondary market is held by a bank different than its originator, and it yields returns
![]() at date 2. We assume
at date 2. We assume ![]() which simplifies the subsequent analysis, but the economic results generalize also to the case
which simplifies the subsequent analysis, but the economic results generalize also to the case ![]() .6 Note that there is an upper bound on endogenous loan prices. In particular, potential buyers of legacy loans give up flexible reserves which they could also use to
make new loans, thus each loan has an opportunity cost of
.6 Note that there is an upper bound on endogenous loan prices. In particular, potential buyers of legacy loans give up flexible reserves which they could also use to
make new loans, thus each loan has an opportunity cost of ![]() units at date 2. Since
secondary loans return
units at date 2. Since
secondary loans return ![]() units at date 2, no potential buyer would demand
legacy loans at a price greater than
units at date 2, no potential buyer would demand
legacy loans at a price greater than
If
![]() , potential buyers spend all of their flexible reserves
, potential buyers spend all of their flexible reserves ![]() on legacy
loans, while if
on legacy
loans, while if
![]() , they are indifferent between buying legacy loans and making new loans. Thus, the market clearing condition for legacy loans can be written as
, they are indifferent between buying legacy loans and making new loans. Thus, the market clearing condition for legacy loans can be written as
The first term on the left hand side denotes the total supply of loans while the second term denotes the maximum potential demand. If the left hand side of Eq.
Equilibrium
Figure 1 recaps the timeline of events in this economy. We can now define equilibrium:
We next turn to the characterization of this equilibrium. Let
![]() denote the slot of the distressed bank
denote the slot of the distressed bank
![]() . Note that, for each financial network
. Note that, for each financial network
![]() and for each bank
and for each bank ![]() , there exists a unique
, there exists a unique
![]() such that
such that
2.2 The Benchmark without Complexity
We characterize the equilibrium in two steps: We start by describing the banks' actions and payoffs for a given price level of legacy loans, ![]() ; and then solve for the equilibrium price
using the legacy loan market clearing condition
; and then solve for the equilibrium price
using the legacy loan market clearing condition
![]() .
.
Suppose the loan prices are fixed at some
![]() and consider the banks' optimal actions and payments in this setting. Consider a distressed bank that needs to obtain liquidity at date
and consider the banks' optimal actions and payments in this setting. Consider a distressed bank that needs to obtain liquidity at date ![]() (e.g., the original distressed bank
(e.g., the original distressed bank
![]() ). This bank could try to obtain the required liquidity either by withdrawing its cross deposits at date 1 (i.e., by choosing
). This bank could try to obtain the required liquidity either by withdrawing its cross deposits at date 1 (i.e., by choosing
![]() ) and/or by taking a precautionary action at date 0 (i.e., by choosing
) and/or by taking a precautionary action at date 0 (i.e., by choosing
![]() ). It can be checked that the bank always weakly prefers ex-post liquidity withdrawal to the ex-ante precautionary actions, thus we fix banks' liquidity
pecking order as follows:
). It can be checked that the bank always weakly prefers ex-post liquidity withdrawal to the ex-ante precautionary actions, thus we fix banks' liquidity
pecking order as follows:
Assumption (LPO). The liquidity pecking order is such that a bank that will need at least ![]() units of liquidity at date 1 first chooses
units of liquidity at date 1 first chooses
![]() , and then (if there is need) resorts to ex-ante precautionary measures.
, and then (if there is need) resorts to ex-ante precautionary measures.
Under assumption (LPO) and the parametric condition
![]() , the original distressed bank
, the original distressed bank
![]() , which has to make a liquidity payment of
, which has to make a liquidity payment of ![]() at date 1, withdraws its deposits from the forward neighbor bank
at date 1, withdraws its deposits from the forward neighbor bank
![]() . This puts bank
. This puts bank
![]() also in need of
also in need of ![]() units of liquidity, which
also withdraws its deposits on the forward neighbor bank. As in Allen and Gale (2000), this triggers further withdrawals until, in equilibrium, all cross deposits are withdrawn, i.e.,
units of liquidity, which
also withdraws its deposits on the forward neighbor bank. As in Allen and Gale (2000), this triggers further withdrawals until, in equilibrium, all cross deposits are withdrawn, i.e.,
![]() for all
for all ![]() . In particular, a bank in need of liquidity (including the
original distressed bank
. In particular, a bank in need of liquidity (including the
original distressed bank
![]() ) tries, but cannot, obtain any net liquidity through cross withdrawals. Anticipating that it will not be able to obtain additional liquidity at date
1, the distressed banks try to obtain some liquidity by taking precautionary actions at date 0.
) tries, but cannot, obtain any net liquidity through cross withdrawals. Anticipating that it will not be able to obtain additional liquidity at date
1, the distressed banks try to obtain some liquidity by taking precautionary actions at date 0.
To simplify the characterization of the banks' date 0 actions, we assume
The left hand side of this condition is not new, as it follows from
We next conjecture that, under appropriate parametric conditions (including condition
![]() ), there exists a threshold
), there exists a threshold
![]() , which depends on loan prices, such that all banks with distance
, which depends on loan prices, such that all banks with distance
![]() are insolvent (there are
are insolvent (there are
![]() such banks) while the banks with distance
such banks) while the banks with distance
![]() remain solvent. That is, the crisis will partially cascade through the network but will be contained after
remain solvent. That is, the crisis will partially cascade through the network but will be contained after
![]() banks have failed. We refer to
banks have failed. We refer to
![]() as the cascade size.
as the cascade size.
The original distressed bank,
![]() , is insolvent as long as its required payment is greater than its buffer
, is insolvent as long as its required payment is greater than its buffer ![]() (and greater than
(and greater than ![]() so that assumption (LPO) applies), i.e., if and only if
so that assumption (LPO) applies), i.e., if and only if
Suppose this is the case so bank
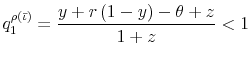
Consider next the bank
![]() with distance 1 from the distressed bank. To
remain solvent, this bank needs to pay 1 on its deposits to bank
with distance 1 from the distressed bank. To
remain solvent, this bank needs to pay 1 on its deposits to bank
![]() but it receives only
but it receives only
![]() on its deposits from the distressed bank
on its deposits from the distressed bank
![]() , so it loses
, so it loses
![]() in cross-deposits. Hence, bank
in cross-deposits. Hence, bank
![]() will also become insolvent if (and only if) its losses from cross-deposits are greater than its buffer,
will also become insolvent if (and only if) its losses from cross-deposits are greater than its buffer,
![]() , which can be rewritten as
, which can be rewritten as
From this point onwards, a pattern emerges. The payment by an insolvent bank
![]() (with
(with ![]() ) is given by
) is given by
then there exists a unique
| (7) | ||
| and |
If
then, Eq.
Note also that Eqs.
![]() and
and
![]() imply that
imply that
![]() is decreasing in
is decreasing in ![]() : with a higher loan price, the liquidation
value of each bank is greater, thus the crisis is contained after a smaller number of insolvencies. For future reference, we strengthen condition
: with a higher loan price, the liquidation
value of each bank is greater, thus the crisis is contained after a smaller number of insolvencies. For future reference, we strengthen condition
![]() to
to
so that there exists a partial cascade for any
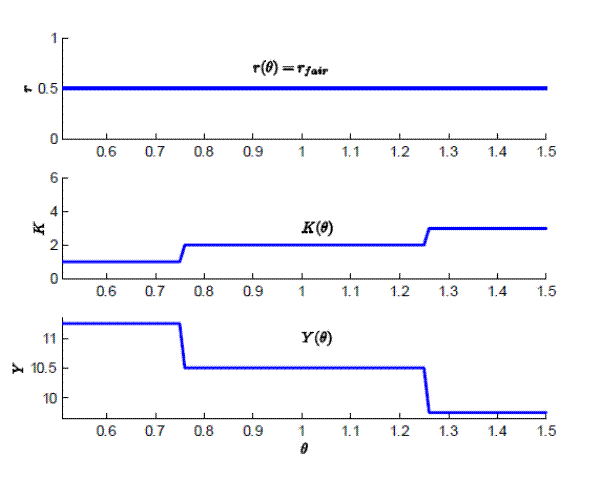
Figure 2 displays the equilibrium cascade size
![]() when the loan prices are exogenously fixed at some
when the loan prices are exogenously fixed at some
![]() for a particular parameterization of the model, illustrating that
for a particular parameterization of the model, illustrating that
![]() is decreasing in
is decreasing in ![]() . The negative dependence of the cascade size
on the price of loans will play an important role in the next section in which we consider the equilibrium with endogenous complexity
. The negative dependence of the cascade size
on the price of loans will play an important role in the next section in which we consider the equilibrium with endogenous complexity
We next consider the legacy loan market clearing condition and solve for the equilibrium level of prices in the free-information benchmark. We claim that if ![]() is sufficiently large, the
endogenous loan price in the free-information benchmark is given by
is sufficiently large, the
endogenous loan price in the free-information benchmark is given by
![]() .
.
To see this, note that the insolvent banks (there are
![]() of them) choose
of them) choose
![]() and sell all of their existing loans, hence the aggregate supply of loans is given by
and sell all of their existing loans, hence the aggregate supply of loans is given by
![]() . The transition bank
. The transition bank
![]() chooses to hoard liquidity, while the remaining solvent banks
chooses to hoard liquidity, while the remaining solvent banks
![]() (there are
(there are
![]() of them) choose
of them) choose
![]() , i.e., they are potential buyers of loans. Suppose
, i.e., they are potential buyers of loans. Suppose ![]() is sufficiently
large so that
is sufficiently
large so that
Under this condition, the demand from the potential buyers exceed the supply of loans for any price level
Intuitively, if the cascade is only partial and banks know the financial network, then there exist banks which will remain solvent and know that much. These banks do not hoard liquidity and are ready to use their flexible reserves to purchase loans from distressed banks. When there are
sufficiently many banks, the demand from these solvent banks is enough to absorb the supply from the distressed banks, ensuring that the secondary loans are traded at their fair price ![]() . We refer to condition
. We refer to condition
![]() as the deep secondary market assumption. The next proposition summarizes the above
discussion and characterizes the symmetric equilibrium for the free-information benchmark.
as the deep secondary market assumption. The next proposition summarizes the above
discussion and characterizes the symmetric equilibrium for the free-information benchmark.
(i) The unique equilibrium price is given by
![]() .
.
(ii) For the continuation equilibrium (at date 1): All banks choose
![]() . Banks with distance
. Banks with distance
![]() are insolvent while the banks with distance
are insolvent while the banks with distance
![]() are solvent.
are solvent.
(iii) For the ex-ante equilibrium (at date 0): The insolvent banks choose
![]() , the transition bank with distance
, the transition bank with distance
![]() chooses
chooses
![]() , and all other solvent banks (i.e., banks with distance
, and all other solvent banks (i.e., banks with distance
![]() ) choose
) choose
![]() .
.
(iv) For the loan market: The insolvent banks sell all of their loans in the secondary market, while the solvent banks with distance
![]() are indifferent between buying legacy loans and making new loans. These banks spend a portion of their flexible reserves to buy the legacy loans sold by the
insolvent banks and they make new loans with the rest of their reserves. The aggregate level of new loans made in this economy is given by:
are indifferent between buying legacy loans and making new loans. These banks spend a portion of their flexible reserves to buy the legacy loans sold by the
insolvent banks and they make new loans with the rest of their reserves. The aggregate level of new loans made in this economy is given by:
Discussion. Figure 3 displays the equilibrium in the benchmark economy for particular parameterization of the model. The figure demonstrates that the loan prices are fixed at ![]() , the cascade size is increasing in
, the cascade size is increasing in ![]() , and the aggregate level of new loans is decreasing in
, and the aggregate level of new loans is decreasing in ![]() . Intuitively, as
. Intuitively, as ![]() increases, there are more losses to be contained, which increases the spread of the insolvency. As the insolvency
spreads, more banks hoard their flexible reserves as liquidity instead of making new loans, which lowers
increases, there are more losses to be contained, which increases the spread of the insolvency. As the insolvency
spreads, more banks hoard their flexible reserves as liquidity instead of making new loans, which lowers
![]() . Note, however, that
. Note, however, that
![]() decreases "smoothly" with
decreases "smoothly" with ![]() . These results offer a benchmark
for the next section. There we show that once auditing becomes costly, both
. These results offer a benchmark
for the next section. There we show that once auditing becomes costly, both ![]() and
and
![]() may experience large changes with small increases in
may experience large changes with small increases in ![]() .
.
3 Endogenous Complexity and Fire Sales
Let us repeat the steps of the previous section but now with our key assumption: Banks only have local knowledge about the financial network
![]() .
.
Each bank observes its two forward neighbors but is otherwise uncertain about how the remaining banks are allocated to the remaining financial slots (cf. Eq.
![]() ). In particular, we assume this uncertainty takes a simple form: Banks with distance
). In particular, we assume this uncertainty takes a simple form: Banks with distance ![]() know their distances from the distressed bank, and banks with distance
know their distances from the distressed bank, and banks with distance ![]() are uncertain about their
distances and assign a positive probability to all distances
are uncertain about their
distances and assign a positive probability to all distances
![]() .
.
In this context, when the shock is small, the system behaves exactly as in the benchmark. But when the shock is large, banks need to understand distant (complex) linkages in order to assess the amount of counterparty risk they are facing. Their inability to figure out these complex linkages triggers a set of precautionary actions which overturns the relatively benign implications of the benchmark environment.
As in the benchmark, the original distressed bank
![]() withdraws its deposits from the forward neighbor bank, which triggers further withdrawals until, in equilibrium, all cross deposits are withdrawn, i.e.,
withdraws its deposits from the forward neighbor bank, which triggers further withdrawals until, in equilibrium, all cross deposits are withdrawn, i.e.,
![]() for all
for all ![]() . Since the distressed bank knows that it cannot obtain any
net liquidity at date 1, it tries to obtain liquidity at date 0. Under condition
. Since the distressed bank knows that it cannot obtain any
net liquidity at date 1, it tries to obtain liquidity at date 0. Under condition
![]() , it also knows that it cannot avoid insolvency, thus it chooses
, it also knows that it cannot avoid insolvency, thus it chooses
![]() .
.
Next consider a bank ![]() with distance
with distance ![]() , and note that a sufficient statistic for this bank to choose action
, and note that a sufficient statistic for this bank to choose action
![]() is the amount it will receive in equilibrium from its forward neighbor. In other words, to decide on the level of its
precautionary measure, this bank only needs to know whether (and how much) it will lose in cross-deposits. Formally, if the bank chooses
is the amount it will receive in equilibrium from its forward neighbor. In other words, to decide on the level of its
precautionary measure, this bank only needs to know whether (and how much) it will lose in cross-deposits. Formally, if the bank chooses
![]() at date 0 and its forward neighbor pays
at date 0 and its forward neighbor pays ![]() at date 1, then this bank's payment can be written as a function
at date 1, then this bank's payment can be written as a function
![]() . However, the bank chooses
. However, the bank chooses ![]() while facing uncertainty about the financial network, and consequently about
while facing uncertainty about the financial network, and consequently about ![]() . Note also that
. Note also that
![]() and
and
![]() are increasing in
are increasing in ![]() for any choice of action.
That is, the bank's payment is increasing in the amount it receives from its forward neighbor regardless of the ex-ante precautionary measure it takes. Thus, since the bank is infinitely risk averse, it will choose its precautionary action as if it will receive from its forward
neighbor the lowest possible payment
for any choice of action.
That is, the bank's payment is increasing in the amount it receives from its forward neighbor regardless of the ex-ante precautionary measure it takes. Thus, since the bank is infinitely risk averse, it will choose its precautionary action as if it will receive from its forward
neighbor the lowest possible payment ![]() .
.
To characterize the bank's optimal action further, we define a useful notion of equilibrium. We say that the equilibrium allocation is distance based and monotonic if the banks' equilibrium payments can be written as an increasing function of their distance from the
distressed bank. That is, there exists weakly increasing payment functions
![]() such that
such that
Under this conjecture, consider again a bank ![]() with distance
with distance ![]() , and
note that the payment of the bank's forward neighbor can be written as
, and
note that the payment of the bank's forward neighbor can be written as
![]() . Then, the bank's uncertainty about the forward neighbor's payment
. Then, the bank's uncertainty about the forward neighbor's payment
![]() reduces to its uncertainty about the forward neighbor's distance
reduces to its uncertainty about the forward neighbor's distance ![]() , which is equal to one less than its own distance
, which is equal to one less than its own distance ![]() . If the bank knows its distance to the distressed bank, i.e., if
. If the bank knows its distance to the distressed bank, i.e., if
![]() , then it chooses its optimal action
, then it chooses its optimal action
![]() knowing that it will receive
knowing that it will receive
![]() from its forward neighbor. On the other hand, if the bank is uncertain about its distance, i.e., if
from its forward neighbor. On the other hand, if the bank is uncertain about its distance, i.e., if ![]() , then it assigns a positive probability to all distances
, then it assigns a positive probability to all distances
![]() . Moreover, since
. Moreover, since
![]() is an increasing function, the payment
is an increasing function, the payment
![]() is minimal for the distance
is minimal for the distance
![]() . Hence a bank
. Hence a bank ![]() with distance
with distance ![]() chooses
chooses
![]() as if it will receive
as if it will receive
![]() from its forward neighbor. In words, the banks that are uncertain about their distances to the distressed bank choose their precautionary action as if they are closer to the distressed bank than they actually are.
from its forward neighbor. In words, the banks that are uncertain about their distances to the distressed bank choose their precautionary action as if they are closer to the distressed bank than they actually are.
Formally, our next lemma establishes that all banks with distance ![]() choose the action that the bank with distance
choose the action that the bank with distance
![]() would choose if the information was freely available (characterized in Lemma 1). If the free-information cascade size is given by
would choose if the information was freely available (characterized in Lemma 1). If the free-information cascade size is given by
![]() so that the bank with distance
so that the bank with distance
![]() would take the precautionary action
would take the precautionary action
![]() to avert insolvency, then all banks with
to avert insolvency, then all banks with ![]() also take the
precautionary action
also take the
precautionary action
![]() even though ex-post they end up not needing liquidity. If the free-information cascade size is even greater (i.e., if
even though ex-post they end up not needing liquidity. If the free-information cascade size is even greater (i.e., if
![]() ) so that the bank with distance
) so that the bank with distance
![]() would be insolvent and choose the most precautionary action
would be insolvent and choose the most precautionary action
![]() , then all banks with
, then all banks with ![]() fold by taking the most precautionary
action
fold by taking the most precautionary
action
![]() , which ensures that their insolvency (even though some of these banks would be solvent in the free-information economy). The proof of the following lemma is relegated to Appendix
A.1 since most of the intuition is provided by the above discussion.
, which ensures that their insolvency (even though some of these banks would be solvent in the free-information economy). The proof of the following lemma is relegated to Appendix
A.1 since most of the intuition is provided by the above discussion.
Then the equilibrium is distance based and monotonic. Each bank ![]() with distance
with distance
![]() chooses the same action that it would choose in the free-information economy (characterized in Lemma 1). Each bank
chooses the same action that it would choose in the free-information economy (characterized in Lemma 1). Each bank ![]() with distance
with distance
![]() chooses the same action that the bank with distance 3 would choose in the free-information economy. In particular, there are three cases to consider, depending on the cascade size:
chooses the same action that the bank with distance 3 would choose in the free-information economy. In particular, there are three cases to consider, depending on the cascade size:
If
![]() , then the crisis in the free-information economy would not cascade to bank with distance 3, which would choose
, then the crisis in the free-information economy would not cascade to bank with distance 3, which would choose
![]() . Thus, each bank
. Thus, each bank ![]() with distance
with distance
![]() chooses
chooses
![]() , and the equilibrium actions and payments are identical to the free-information economy described in Lemma 1. In particular, the cascade size is
given by
, and the equilibrium actions and payments are identical to the free-information economy described in Lemma 1. In particular, the cascade size is
given by
![]() .
.
If
![]() , then the crisis in the free-information economy would cascade to and stop at bank with distance 3, which would choose
, then the crisis in the free-information economy would cascade to and stop at bank with distance 3, which would choose
![]() to avert insolvency. Thus each bank
to avert insolvency. Thus each bank ![]() with distance
with distance
![]() chooses
chooses
![]() . The equilibrium cascade size is still the same as the free-information economy, i.e.,
. The equilibrium cascade size is still the same as the free-information economy, i.e.,
![]() , but the banks' actions and payments are different.
, but the banks' actions and payments are different.
If
![]() , then bank with distance 3 would be insolvent in the
free-information economy and would choose
, then bank with distance 3 would be insolvent in the
free-information economy and would choose
![]() . Thus, all banks choose
. Thus, all banks choose
![]() and they are all insolvent, i.e., the cascade size is given by
and they are all insolvent, i.e., the cascade size is given by
![]() .
.
Note that the loan trade decisions of the banks with distance ![]() depend on the free-information cascade size
depend on the free-information cascade size
![]() . In particular, if
. In particular, if
![]() , these banks are potential buyers in the loan market, while if
, these banks are potential buyers in the loan market, while if
![]() , they are either neutral in the loan market (if
, they are either neutral in the loan market (if
![]() ) or they are potential sellers (if
) or they are potential sellers (if
![]() ). This dependence of the banks' loan trades on the free-information cascade size
). This dependence of the banks' loan trades on the free-information cascade size
![]() (which itself depends on the loan price) plays a key role in subsequent analysis, where we endogenize the loan prices and complete the characterization of the
equilibrium.
(which itself depends on the loan price) plays a key role in subsequent analysis, where we endogenize the loan prices and complete the characterization of the
equilibrium.
We next solve the equilibrium level of loan prices in the costly information setting and present our main results. There are three cases to consider depending on the cascade size
![]() over the price range
over the price range
![]() .
.
Case (i).
If
![]() , then we conjecture that there is a unique symmetric equilibrium, that we refer to as the fair-price equilibrium, in which loan
markets endogenously clear and loans trade at their fair price
, then we conjecture that there is a unique symmetric equilibrium, that we refer to as the fair-price equilibrium, in which loan
markets endogenously clear and loans trade at their fair price
![]() . To verify this conjecture, recall that
. To verify this conjecture, recall that
![]() is a decreasing function so that
is a decreasing function so that
![]() for all
for all
![]() . Hence, regardless of the endogenous price
. Hence, regardless of the endogenous price ![]() , Lemma 2 implies that all banks with
, Lemma 2 implies that all banks with ![]() choose
choose
![]() and as such, these banks are potential buyers of loans. Thus, under the deep secondary market assumption
and as such, these banks are potential buyers of loans. Thus, under the deep secondary market assumption
![]() , the unique equilibrium price is given by
, the unique equilibrium price is given by
![]() . Once the equilibrium price is determined, the remaining equilibrium allocations are uniquely determined as described in Lemma 2, proving our
conjecture for this case.
. Once the equilibrium price is determined, the remaining equilibrium allocations are uniquely determined as described in Lemma 2, proving our
conjecture for this case.
Case (ii).
If
![]() , we conjecture that there is a unique symmetric equilibrium, which we refer to as the fire-sale equilibrium, in which there is a
breakdown in the loan market and
, we conjecture that there is a unique symmetric equilibrium, which we refer to as the fire-sale equilibrium, in which there is a
breakdown in the loan market and
![]() . To see this, note that
. To see this, note that
![]() for all
for all
![]() , thus Lemma 2 implies that all banks with
, thus Lemma 2 implies that all banks with ![]() choose either
choose either
![]() (if
(if
![]() ), or
), or
![]() (if
(if
![]() ). In words, these banks are either neutral in the legacy loan market or they are sellers, in particular, they are not potential buyers.
Using Lemma 2 once more, note that the banks with distance
). In words, these banks are either neutral in the legacy loan market or they are sellers, in particular, they are not potential buyers.
Using Lemma 2 once more, note that the banks with distance ![]() are necessarily insolvent, so they choose
are necessarily insolvent, so they choose
![]() and become sellers in the legacy loan market. Thus, the legacy loan market features at least 3 sellers but no buyers. The market clearing condition
and become sellers in the legacy loan market. Thus, the legacy loan market features at least 3 sellers but no buyers. The market clearing condition
![]() implies that
implies that
![]() , i.e., there is a breakdown in the secondary loan market.
, i.e., there is a breakdown in the secondary loan market.
Case (iii).
If
![]() , we conjecture that there are two stable equilibria: one fair-price equilibrium and one
fire-sale equilibrium. To see this, first suppose that the price of loans is given by
, we conjecture that there are two stable equilibria: one fair-price equilibrium and one
fire-sale equilibrium. To see this, first suppose that the price of loans is given by
![]() so that the cascade size satisfies
so that the cascade size satisfies
![]() . Then, the analysis for case (i) applies unchanged, in particular, all banks with distance
. Then, the analysis for case (i) applies unchanged, in particular, all banks with distance ![]() are potential buyers and the price
are potential buyers and the price ![]() clears the market, verifying that there is a fair-price equilibrium. Next suppose that the price of
loans is given by
clears the market, verifying that there is a fair-price equilibrium. Next suppose that the price of
loans is given by
![]() so that the cascade size satisfies
so that the cascade size satisfies
![]() . Then, the analysis for case (ii) applies unchanged, in particular, all banks with distance
. Then, the analysis for case (ii) applies unchanged, in particular, all banks with distance ![]() are either neutral in the loan market or they sell their loans, and loan prices collapse to
are either neutral in the loan market or they sell their loans, and loan prices collapse to
![]() , verifying that there is a fire-sale equilibrium.
, verifying that there is a fire-sale equilibrium.
We summarize these results in the following, and main, proposition.
(i) Fair-price equilibrium: If
![]() , there is a unique equilibrium in which loans trade at their fair price
, there is a unique equilibrium in which loans trade at their fair price
![]() .
.
The cascade size is the same as the free-information benchmark, i.e.,
![]() . The insolvent banks (with distance
. The insolvent banks (with distance
![]() ) choose
) choose
![]() and sell their loans, while the solvent banks with distance
and sell their loans, while the solvent banks with distance
![]() choose
choose
![]() and are indifferent between using their reserves to make new loans or to buy legacy loans in the secondary market. The aggregate level of new loans is equal to the benchmark Eq.
and are indifferent between using their reserves to make new loans or to buy legacy loans in the secondary market. The aggregate level of new loans is equal to the benchmark Eq.
![]() .
.
(ii) Fire sale equilibrium: If
![]() , then there is a unique equilibrium in which there is a breakdown in the secondary loan market, i.e., there is an excess supply of loans and
, then there is a unique equilibrium in which there is a breakdown in the secondary loan market, i.e., there is an excess supply of loans and
![]() .
.
(ii.1) If
![]() , all banks with distance
, all banks with distance ![]() choose
choose
![]() . These banks remain solvent and the cascade size is
. These banks remain solvent and the cascade size is
![]() .
.
(ii.2) If
![]() , all banks with distance
, all banks with distance ![]() choose
choose
![]() . These banks go under and the cascade size in this case is
. These banks go under and the cascade size in this case is ![]() .
.
In either sub-case, all flexible reserves are hoarded as liquidity and there are no new loans,
![]() .
.
(iii) Multiple equilibria: If
![]() , there are two stable equilibria.
, there are two stable equilibria.
In the fair-price equilibrium, loans trade at their fair price
![]() , the cascade size is
, the cascade size is
![]() , the solvent banks are indifferent between making new loans or purchasing loans in the secondary market, and the aggregate level of new loans
, the solvent banks are indifferent between making new loans or purchasing loans in the secondary market, and the aggregate level of new loans
![]() is given by the benchmark Eq.
is given by the benchmark Eq.
![]() .
.
In the fire sale equilibrium,
![]() , the cascade size is given by either
, the cascade size is given by either ![]() (if
(if
![]() ) or
) or ![]() (if
(if
![]() ), all banks hoard liquidity and (if
), all banks hoard liquidity and (if
![]() ) dump their loans in the secondary market, and there are no new loans,
) dump their loans in the secondary market, and there are no new loans,
![]() .
.
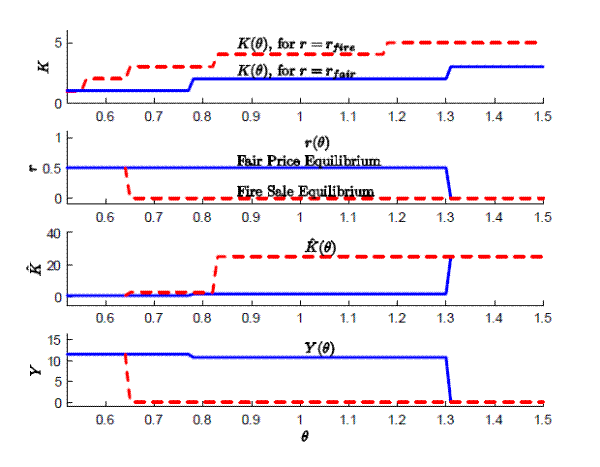
Discussion. Figure 4 displays the equilibria with network uncertainty for a particular parameterization of the model. The top panel reproduces the cascade size
![]() in the free-information benchmark as a function of the losses in the originating bank
in the free-information benchmark as a function of the losses in the originating bank ![]() , when loan prices are fixed at
, when loan prices are fixed at
![]() and
and
![]() . The remaining three panels display the equilibria with network uncertainty, illustrating the characterization in Proposition 2. Note that there is a unique
equilibrium for small and large levels of
. The remaining three panels display the equilibria with network uncertainty, illustrating the characterization in Proposition 2. Note that there is a unique
equilibrium for small and large levels of ![]() , however, there are multiple equilibria for intermediate levels of
, however, there are multiple equilibria for intermediate levels of ![]() .
.
When ![]() is sufficiently small so that
is sufficiently small so that
![]() , i.e., when the free-information benchmark features a short cascade even for the price level
, i.e., when the free-information benchmark features a short cascade even for the price level
![]() , there is a unique fair price equilibrium. This equilibrium features a low level of complexity thus the banks that are uncertain about their distance to the distressed bank can
rule out an indirect hit. Consequently, these banks use their reserves to make new loans and to demand assets. The aggregate level of new loans is the same as in the free-information benchmark, and assets trade at their fair prices.
, there is a unique fair price equilibrium. This equilibrium features a low level of complexity thus the banks that are uncertain about their distance to the distressed bank can
rule out an indirect hit. Consequently, these banks use their reserves to make new loans and to demand assets. The aggregate level of new loans is the same as in the free-information benchmark, and assets trade at their fair prices.
In contrast, when ![]() is sufficiently large so that
is sufficiently large so that
![]() , i.e., when the cascade size in the free-information benchmark is sufficiently large, there is a unique fire-sale equilibrium. In this equilibrium, the
aggregate level of new loans makes a very large and discontinuous drop to zero. That is, when the losses (measuring the severity of the initial shock) are beyond a threshold, the cascade size becomes so large that banks are unable to tell whether they are connected to the distressed bank or not.
All uncertain banks act as if they are closer to the distressed bank than they actually are, hoarding much more liquidity than in the free-information benchmark and leading to a severe credit crunch episode. Moreover, these banks, some of which would be potential buyers in the free-information
benchmark, become sellers and this leads to a collapse in asset prices. This result provides a rationale for the collapse of asset prices in an environment in which complexity suddenly (and endogenously) rises. Furthermore, it is possible (if
, i.e., when the cascade size in the free-information benchmark is sufficiently large, there is a unique fire-sale equilibrium. In this equilibrium, the
aggregate level of new loans makes a very large and discontinuous drop to zero. That is, when the losses (measuring the severity of the initial shock) are beyond a threshold, the cascade size becomes so large that banks are unable to tell whether they are connected to the distressed bank or not.
All uncertain banks act as if they are closer to the distressed bank than they actually are, hoarding much more liquidity than in the free-information benchmark and leading to a severe credit crunch episode. Moreover, these banks, some of which would be potential buyers in the free-information
benchmark, become sellers and this leads to a collapse in asset prices. This result provides a rationale for the collapse of asset prices in an environment in which complexity suddenly (and endogenously) rises. Furthermore, it is possible (if
![]() ) that the uncertain banks panic so much that they take an extremely precautionary action to increase their liquidation outcome. However, ex-post, this action
ensures that the uncertain banks become insolvent.
) that the uncertain banks panic so much that they take an extremely precautionary action to increase their liquidation outcome. However, ex-post, this action
ensures that the uncertain banks become insolvent.
When ![]() is in an intermediate range, the cascade size is manageable if price of loans is high (i.e.,
is in an intermediate range, the cascade size is manageable if price of loans is high (i.e.,
![]() ), however it becomes unmanageable if loans trade at the fire-sale price (i.e.,
), however it becomes unmanageable if loans trade at the fire-sale price (i.e.,
![]() ). In this case, the interaction between asset prices and the endogenous level of complexity generates multiple equilibria.
). In this case, the interaction between asset prices and the endogenous level of complexity generates multiple equilibria.
In the fair-price equilibrium, loans trade at a higher price and the cascade size is relatively small, which reduces the level of complexity. With the lower level of complexity, the banks that are uncertain about their distance to the distressed bank become potential buyers of loans, which ensures that loans trade at the higher price and that the cascade is shorter.
Set against this benign scenario is the possibility of a fire-sale equilibrium, in which the price of loans collapses and there is a longer cascade, which increases the level of complexity. As the level of complexity increases, banks that are uncertain about their distances panic and sell their loans, which reinforces the collapse of loan prices.
Note also that, whenever there are multiple equilibria, the fair-price equilibrium Pareto dominates the fire-sale equilibrium for all banks and their depositors. Intuitively, the fire-sale equilibrium entails two distinct social costs: fewer new loans are made and more banks become insolvent. In the next section, we identify the negative externalities in our setup that account for these social costs.
4 Three Externalities
In this section, we discuss the various externalities present in our setup and we highlight the role they play in our main results. Our model features three distinct externalities, which we call the network-liquidity externality, the fire-sale externality and the complexity externality. The first of these emerges directly from the interlinkages between banks. The second externality stems from the interaction of loan prices and the endogenous determination of bank runs. These two externalities are relatively standard. Models of interconnected banks typically feature externalities akin to our network-liquidity externality (see, for example, Rotemberg (2009)), while models based on the Diamond and Dybvig (1983) setup typically lead to fire-sale externalities whenever prices affect the likelihood of bank runs (see, for example, Allen and Gale (2005)). The complexity externality is novel to our analysis, and it emerges from the interaction of loan prices and the complexity of the financial network.
4.1 Network-liquidity Externality
In our setup, a distressed bank can obtain liquidity through two distinct sources: It can either withdraw its deposits on the forward neighbor bank, or it can hoard its liquid reserves (or it can sell its legacy loans, as a last measure). Since aggregate liquidity is scarce, a bank that chooses the former option puts its forward neighbor bank also in distress, imposing a liquidity externality on it. In particular, if the bank decides to withdraw its cross deposits, the forward neighbor bank scrambles for liquidity and faces insolvency if it is unable to meet this liquidity demand. A distressed bank in our setup always (weakly) prefers to withdraw deposits (cf. assumption (LBO)).9 In Appendix A.2, we study the polar opposite case, enforced by the government, in which a bank that needs liquidity first hoards its own liquid reserves, and thus avoids inflicting a liquidity externality whenever it can. Our analysis shows that internalizing the liquidity externalities in this fashion leads to shorter cascades in aggregate (see Proposition A.2 in the appendix).
Intuitively, the scramble for liquidity is like a hot potato which the banks can either pass straight to their neighbors, or which they can cool down a bit using their resources before passing it on. When all banks pass it without cooling it, the hot potato eventually reaches a vulnerable bank, i.e., a bank which is sufficiently close to the original distressed bank. This bank cannot pass the potato to its neighbor, which is already bankrupt. Moreover, the resources of this bank alone are not sufficient to cool down the potato hence the bank burns (i.e., it cannot meet the liquidity demand and becomes insolvent), which lengthens the cascade. In contrast, when each bank cools down the potato before passing it on, then the potato is cold before it reaches the vulnerable bank, leading to a much shorter cascade.
4.2 Fire Sale Externality
Consider a bank that decides to sell some loans, leading to a small decline in loan prices. This action has a small positive effect on the net budgets of the banks that buy legacy loans, while it has a small negative effect on the net budgets of the banks that sell legacy loans. Absent further effects, the welfare impacts of these budget changes would typically "net out," which is the content of the first welfare theorem. However, a small decline also increases the likelihood of a bank run in our setup, leading to a further decline in the welfare of these banks and their depositors. Consequently, the effects of price changes do not necessarily "net out," and loan prices feature a negative pecuniary externality.
To formalize this point, let us consider the benchmark economy analyzed in Section 2.2. This setting shuts down the complexity externality (since the banks know the financial network) which we will analyze in the next subsection.
Recall that the cascade size
![]() is decreasing in
is decreasing in ![]() : with a lower loan price, the liquidation
payment of each bank is greater (cf. Eq.
: with a lower loan price, the liquidation
payment of each bank is greater (cf. Eq.
![]() ), thus the crisis is contained after a smaller number of insolvencies (cf. Eq.
), thus the crisis is contained after a smaller number of insolvencies (cf. Eq.
![]() ). In particular, there exists some
). In particular, there exists some
![]() such that, for any
such that, for any
![]() we have
we have
The general intuition behind this externality is that a drop in asset prices lowers the liquidation value of an insolvent bank, which increases the probability of a bank run in the counterparties of this bank.
4.3 Complexity Externality
Consider next the model analyzed in Section 3 in which banks only have local information about the financial network. Similar to the above analysis for the fire sale externality, a bank that sells a loan has a small negative impact on loan prices, which in turn increases the length of the cascade. However, in this case, longer cascades also increase the complexity of the financial network. Since banks are averse to complexity (which we model as infinite risk aversion with respect to the financial network), an increase in complexity leads to a welfare reduction for banks that are uncertain about the financial network.
To formalize this point, consider the set of parameters that lead to multiple equilibria in Proposition 3,
![]() . Then, there exists
. Then, there exists
![]() such that, for any
such that, for any
![]() we have
we have
In contrast, when the loans trade at price
![]() , the banks with distance
, the banks with distance
![]() are worried that they might suffer an indirect hit from the cascade. Since these banks are infinitely risk averse, their welfare is greatly reduced. Moreover,
these banks hoard liquidity to precaution against the worst case scenario, and they end up paying
are worried that they might suffer an indirect hit from the cascade. Since these banks are infinitely risk averse, their welfare is greatly reduced. Moreover,
these banks hoard liquidity to precaution against the worst case scenario, and they end up paying
![]() to their depositors. Hence, a small drop in prices inflicts a discrete negative effect on all of the banks with distance
to their depositors. Hence, a small drop in prices inflicts a discrete negative effect on all of the banks with distance
![]() and their depositors, demonstrating the complexity externality.
and their depositors, demonstrating the complexity externality.
The complexity externality may also lead to multiple Pareto-ranked equilibria in our setup, as we have already seen in Proposition 3. In particular, an increase in the level of complexity due to a reduction in the price of assets not only lowers the welfare of many banks and their depositors, but also induces these banks to take extreme precautionary measures, which, in some instances, includes further asset sales. The sale of assets by banks in panic mode reduces asset prices further, which leads to a vicious cycle culminating in the fire-sale equilibrium. In contrast, an increase in asset prices reduces the complexity externality, which may mitigate the precautionary measures and turn more sellers into buyers, leading to a virtuous spiral towards the fair price equilibrium.
Finally, note that the complexity externality is potentially much more potent than the fire sale externality analyzed in the previous subsection and highlighted in the literature. The reason is that the fire-sale externality affects banks that are on the verge of insolvency. In contrast, the complexity externality affects all banks that are uncertain about the financial network, which, in practice, includes virtually all financial institutions. The greater scope of the complexity externality also leads to widespread (precautionary) actions, which has the potential to create aggregate effects, price changes, and multiple equilibria.
5 Conclusion
In this paper we provide a model that illustrates how fire sales and complexity can trigger a very powerful negative feedback loop within a financial network. More severe fire sales lengthen the potential cascades, and raise the complexity of the environment exponentially. This triggers confusion among potential asset buyers, which pull back and exacerbate the fire sale. In extreme scenarios these potential buyers can turn into sellers, leading to a complete collapse in secondary markets.
In our model, the distressed institutions' motive for fire sales is to improve their outcome in the worst case scenario of insolvency. This is an extreme assumption made only to simplify the exposition. In reality, the distressed institutions may sell assets for a multitude of reasons that do not imply anticipating insolvency. E.g., they may be forced to do so by regulatory requirements, or they may hope to avoid a run by obtaining more liquidity. These reasons can be incorporated into our framework while preserving our main conclusions.
Having said this, the particular insolvency motive we consider also raises the question of what would happen if the distressed institutions chose to gamble for resurrection by not selling their assets, which would improve their outcome in good states at the cost of a greater bankruptcy risk. Our model suggests that gambling for resurrection may be a mixed blessing for the aggregate. Gambling by potential buyers, that is, institutions that are far from the cascade but that do not know this, would limit the fire sales and the downward spiral of prices. On the other hand, gambling by institutions near the cascade would increase the cascade size and trigger the complexity mechanism.
We did not explore policy questions, but it is apparent that our environment creates many policy opportunities during crises. Supporting secondary markets, insulating financial institutions from counterparty risk, and stress testing (increasing transparency and supporting if needed) systemically important financial institutions, are all policies practiced during the current financial crisis and supported by our framework.
Case (i): 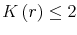 .
.
To prove that the conjectured actions and payments constitute an equilibrium, first note that the original distressed bank optimally chooses ![]() and pays out the same level
and pays out the same level ![]() that it would pay in the free-information economy (since it receives the full amount
that it would pay in the free-information economy (since it receives the full amount ![]() from its forward neighbor,
from its forward neighbor, ![]() , which is solvent in the conjectured equilibrium). Next consider a bank with distance
, which is solvent in the conjectured equilibrium). Next consider a bank with distance ![]() . Under the conjectured equilibrium, this bank knows that it will receive
. Under the conjectured equilibrium, this bank knows that it will receive ![]() from its forward neighbor, which is equal to what it would receive in the free-information economy. Hence, it optimally chooses the same action it would choose when information is free.
from its forward neighbor, which is equal to what it would receive in the free-information economy. Hence, it optimally chooses the same action it would choose when information is free.
Consider next a bank with distance ![]() . This bank is uncertain about its distance, thus it chooses its date 0 action as if it will receive
. This bank is uncertain about its distance, thus it chooses its date 0 action as if it will receive
![]() from its forward neighbor. Under the conjectured equilibrium, the cascade size is
from its forward neighbor. Under the conjectured equilibrium, the cascade size is
![]() , thus we have
, thus we have
![]() . Since the bank makes no losses in cross deposits (even in the worst case scenario of
. Since the bank makes no losses in cross deposits (even in the worst case scenario of
![]() ), it optimally chooses
), it optimally chooses
![]() , verifying the optimality of the conjectured action.
, verifying the optimality of the conjectured action.
Since the banks' actions are the same as the free-information economy, their payments are also identical to that case, which verifies (by Lemma 1) that the equilibrium is distance based and monotonic.
Case (ii):  .
.
Similar to the previous case, the original distressed bank and the banks with distance ![]() optimally choose the same action and make the same payments as in the free-information economy.
optimally choose the same action and make the same payments as in the free-information economy.
Consider next a bank with distance ![]() . This bank is uncertain about its distance, thus it chooses its date 0 action as if it will receive
. This bank is uncertain about its distance, thus it chooses its date 0 action as if it will receive
![]() from its forward neighbor. Since
from its forward neighbor. Since
![]() , under the conjectured equilibrium, we have
, under the conjectured equilibrium, we have
![]() (which is equal to its level in the free-information benchmark) lies in the interval
(which is equal to its level in the free-information benchmark) lies in the interval
![]() . Hence, the bank with distance
. Hence, the bank with distance ![]() expects (with some
probability) to make losses less than its buffer, thus it chooses
expects (with some
probability) to make losses less than its buffer, thus it chooses
![]() to counter these losses, verifying the optimality of its conjectured action.
to counter these losses, verifying the optimality of its conjectured action.
These banks with distance ![]() are solvent, but they pay potentially less than the free-information economy. In particular, the bank with distance
are solvent, but they pay potentially less than the free-information economy. In particular, the bank with distance ![]() pays the same amount
pays the same amount ![]() that it would pay in the free-information case, while the banks with distance
that it would pay in the free-information case, while the banks with distance ![]() end up paying
end up paying
Case (iii):  .
.
In this case, note that the banks' payments, given the conjectured actions, are the solutions to the following system of equations:
![\displaystyle =\frac{y+\left( 1-y\right) r-\theta+zQ_{1}\left[ n-1\right] }{1+z}](img248.gif) |
(12) | |
![\displaystyle =\frac{y+\left( 1-y\right) r+zQ_{1}\left[ k-1\right] }{1+z}](img250.gif) , for , for |
Note that, by condition
To verify the optimality of banks' actions, first note that Eq.
![]() implies the payments
implies the payments
![]() are lower than what they would be in the free-information economy, because the forward neighbor of the original distressed
bank pays
are lower than what they would be in the free-information economy, because the forward neighbor of the original distressed
bank pays
![]() in this case (while it would be solvent and would pay
in this case (while it would be solvent and would pay ![]() unit
unit![]() per deposit in the free-information economy). Consider a bank with distance
per deposit in the free-information economy). Consider a bank with distance
![]() , and recall that this bank chooses its date 0 action knowing that it will receive
, and recall that this bank chooses its date 0 action knowing that it will receive
![]() from its forward neighbor. Since
from its forward neighbor. Since
![]() , this bank would be insolvent in the free-information economy. In the present case,
, this bank would be insolvent in the free-information economy. In the present case,
![]() is even lower than what it would be in the free-information economy. Thus the bank with distance
is even lower than what it would be in the free-information economy. Thus the bank with distance
![]() is necessarily insolvent, and it optimally chooses
is necessarily insolvent, and it optimally chooses
![]() .
.
Consider next a bank with distance ![]() . This bank is uncertain about its distance and thus it chooses its date 0 action as if it will receive
. This bank is uncertain about its distance and thus it chooses its date 0 action as if it will receive
![]() from its forward neighbor. Since
from its forward neighbor. Since
![]() , and since the payments
, and since the payments
![]() are even lower than the free-information economy, we necessarily have
are even lower than the free-information economy, we necessarily have
![]() . In other words, the bank with distance
. In other words, the bank with distance ![]() believes that it might experience losses beyond its buffer and go bankrupt. Consequently, it chooses the most extreme precautionary action
believes that it might experience losses beyond its buffer and go bankrupt. Consequently, it chooses the most extreme precautionary action
![]() to improve their liquidation outcome, verifying the optimality of the conjectured action.
to improve their liquidation outcome, verifying the optimality of the conjectured action.
A.2 Equilibrium without Liquidity Externalities
In the main text, the bank always considers deposit withdrawal as the first source of liquidity (cf. assumption (LBO)), thus imposing a liquidity externality on its forward neighbor bank. To clarify the role of liquidity externalities, in this appendix we analyze the equilibrium under a government policy that prevents banks from withdrawing cross deposits unless they have used all of their liquid reserves.
To facilitate the analysis, it helps to consider a slightly greater action space for banks:
where
Assumption (LPO-R). Consider a bank that needs liquidity at date 1 and whose forward neighbor bank is solvent. The government imposed liquidity pecking order
for this bank is such that the bank first considers hoarding its flexible reserves, i.e., it considers the action
![]() . The bank withdraws some of its cross deposits (chooses
. The bank withdraws some of its cross deposits (chooses
![]() ) only if
) only if
![]() is not sufficient to meet its liquidity demand.
is not sufficient to meet its liquidity demand.
Finally, we strengthen the right hand side of condition
![]() to
to
so that a bank's own legacy loans are enough to promise all depositors (including the backward neighbor bank) at least 1 unit at date 2.
Under these assumptions and when ![]() is sufficiently large, we conjecture that there is an equilibrium in which all banks with distance
is sufficiently large, we conjecture that there is an equilibrium in which all banks with distance ![]() (i.e., all banks except potentially the original distressed bank) are solvent. In other words, the cascade size is at most 1, in
stark contrast with the equilibria characterized in Propositions 1 and 2.
(i.e., all banks except potentially the original distressed bank) are solvent. In other words, the cascade size is at most 1, in
stark contrast with the equilibria characterized in Propositions 1 and 2.
In the conjectured equilibrium, the original bank
![]() hoards all of its liquid reserves and also withdraws its deposits on bank
hoards all of its liquid reserves and also withdraws its deposits on bank
![]() , i.e., it chooses
, i.e., it chooses
![]() and
and
![]() , which puts bank
, which puts bank
![]() in need of
in need of ![]() units of liquidity. Under the
new assumption for the liquidity pecking order, bank
units of liquidity. Under the
new assumption for the liquidity pecking order, bank
![]() (with distance
(with distance ![]() ) first resorts to hoarding
its flexible reserves. If
) first resorts to hoarding
its flexible reserves. If ![]() , then this bank chooses
, then this bank chooses
![]() , that is, the bank meets its liquidity payments purely by hoarding
its flexible reserves, and it does not withdraw any cross deposits. Otherwise
, that is, the bank meets its liquidity payments purely by hoarding
its flexible reserves, and it does not withdraw any cross deposits. Otherwise ![]() and this bank chooses
and this bank chooses
![]() . In this case, consider bank
. In this case, consider bank
![]() with distance
with distance ![]() , which needs to find
, which needs to find
![]() units of liquidity. This bank's response is similar to bank
units of liquidity. This bank's response is similar to bank
![]() : if
: if ![]() , then the bank meets its
liquidity payment purely by hoarding its flexible reserves, and otherwise it withdraws an even smaller amount from its forward neighbor.
, then the bank meets its
liquidity payment purely by hoarding its flexible reserves, and otherwise it withdraws an even smaller amount from its forward neighbor.
It follows that a pattern emerges for the banks' cross withdrawal decisions. In particular, let
![]() denote the unique integer such that
denote the unique integer such that
Going back to the original distressed bank
![]() , note that, unlike in the previous sections, this bank obtains a total of
, note that, unlike in the previous sections, this bank obtains a total of ![]() units of liquidity:
units of liquidity: ![]() units from its buffer and
units from its buffer and ![]() units from cross deposits (if it remains solvent). Hence, this bank is insolvent if and only if
units from cross deposits (if it remains solvent). Hence, this bank is insolvent if and only if
which is a stronger condition than
Note also that there is at most one seller in the conjectured equilibrium (the original distressed bank
![]() ) while the banks with distance
) while the banks with distance
![]() are potential buyers of loans. Hence, under the deep secondary market assumption (i.e., the analogue of condition
are potential buyers of loans. Hence, under the deep secondary market assumption (i.e., the analogue of condition
![]() for this setup),
for this setup),
the unique equilibrium price is given by
Proposition 3 establishes our main result in this appendix: If the banks avoid inflicting a liquidity externality, then the cascade size is much
shorter relative to the cases analyzed in Propositions 1 and 2. To see the intuition, consider the equilibrium in Proposition 3 and consider what the banks would do if we removed the government imposed liquidity pecking order in assumption (LPO-R). Consider bank ![]() , which meets its liquidity demand from its backward neighbor purely by hoarding its flexible reserves. For this bank, hoarding reserves delivers
1 unit of liquidity at an opportunity cost of
, which meets its liquidity demand from its backward neighbor purely by hoarding its flexible reserves. For this bank, hoarding reserves delivers
1 unit of liquidity at an opportunity cost of ![]() (in period
(in period ![]() ), while withdrawing cross deposits would deliver 1 unit of liquidity at an opportunity cost
of
), while withdrawing cross deposits would deliver 1 unit of liquidity at an opportunity cost
of ![]() . Given the characterization in 3, it can be checked that
. Given the characterization in 3, it can be checked that
![]() (as some of the losses in the original bank will spillover to bank
(as some of the losses in the original bank will spillover to bank
![]() ). Hence, if not restricted by government policy, bank
). Hence, if not restricted by government policy, bank
![]() would strictly prefer to withdraw its cross deposits to hoarding liquidity, which would put bank
would strictly prefer to withdraw its cross deposits to hoarding liquidity, which would put bank
![]() in distress. Similarly, absent government policy, bank
in distress. Similarly, absent government policy, bank
![]() would prefer to withdraw its cross deposits and the scramble for liquidity would continue to cascade in similar fashion. Eventually, a vulnerable bank,
would prefer to withdraw its cross deposits and the scramble for liquidity would continue to cascade in similar fashion. Eventually, a vulnerable bank, ![]() , which is sufficiently close to the original distressed bank (and thus has incurred some losses) would become distressed. This bank might be unable to find the required liquidity and might become insolvent. Hence, the liquidity externalities have the potential to make vulnerable banks go insolvent. The government imposed liquidity order in assumption (LPO-R) internalizes these liquidity externalities, which in turn ensures that the cascade size is shorter.
, which is sufficiently close to the original distressed bank (and thus has incurred some losses) would become distressed. This bank might be unable to find the required liquidity and might become insolvent. Hence, the liquidity externalities have the potential to make vulnerable banks go insolvent. The government imposed liquidity order in assumption (LPO-R) internalizes these liquidity externalities, which in turn ensures that the cascade size is shorter.
![\displaystyle \left( 1-y\right) \sum_{j}\mathbf{1}\left\{ A_{0}^{j}=HS\right\} -\frac {y}{r}\sum_{j}\mathbf{1}\left\{ A_{0}^{j}=B\right\} \quad\left\{ \begin{array}[c]{c}% \geq0\text{ if }r=r_{fire}\\ =0\text{ if }r\in\left( r_{fire},r_{fair}\right) \\ \leq0\text{ if }r=r_{fair}% \end{array} \right.](img53.gif) .
.
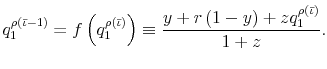
![Cascade size in the free-information benchmark. The plot displays the cascade size K(r) when the loan prices are exogenously fixed at r in [0,r_fair] (for a given level of theta). The x-axis indicates r, ranging from 0.05 to 0.5. The y-axis indicates K, ranging from 0 to 6. The curve behaves similar to a descending stepwise function. From r =0.05 to about r=0.1, K is at a level of 5. For r=0.1 to about r=0.2, K is at a level of 4. For r=0.2 to r=0.45, K is at a level of 3. Finally, for r=0.45 to 0.5, K is at a level of 2.](figure2.gif)