Figure 1 is titled "Probability Distribution of Potential Losses." The vertical axis is labeled "Probability" and the horizontal axis is labeled "Losses." The probability distribution shown in the chart begins at zero, increases steeply to a peak, than decreases asymptotically toward the horizontal axis. The mean and the 99.9th percentile of the probability distribution are labeled. The horizontal axis from zero to the mean is labeled expected losses and the horizontal axis from the mean to the 99.9th percentile of losses is labeled unexpected losses. The text that follows discusses this chart in more depth.
Table A is titled "QIS-4 Results: Changes in Minimum Required Capital." The table shows the changes in Minimum Required Capital or MRC by portfolio, aggregated across all QIS-4 participants. Entries in parentheses denote negative numbers. The term "portfolio" is used here to identify discrete segments of capital requirements. For example, operational risk is listed as a separate line item in this table, which means that all risk-based capital requirements associated with operational risk have been captured within this line item. It is important to note that operational risk has been segregated in this way when considering the changes in MRC for the various credit portfolios. For most institutions, at least some portion of the operational risk charge would be associated with various credit-related activities. However, Table A makes no attempt to allocate operational risk to the various portfolios, as any such allocation would require arbitrary assumptions. There are no percentage change numbers for operational risk because it is not separated out as a specific charge under current rules.
Column 1 shows the dollar-weighted (Each institution's contribution to
the aggregate is equal to the dollar amount of its MRC.) average percentage
change in MRC by portfolio. Some of the largest changes in MRC occur for
mortgages – both home equity lines of credit (HELOCs) and all other
residential mortgages – and for qualifying revolving exposures (QREs),
which mostly consist of credit card exposures. However, it is important
to consider the relative size of portfolios as well as the percentage change
when attempting to understand the drivers of the 12.5 percent aggregate
decrease in MRC. Columns 5 and 6 show the share each portfolio contributes
to MRC, under the current framework (Column 5) and the QIS-4 interpretation
of Basel II as defined in the QIS-4 instructions (Column 6).
Column 2 shows the percentage point contribution of each portfolio to the
overall average percentage change (of 12.5%). From this column, we
can see that operational risk, Corporate-Bank-Sovereign, HELOCs, Residential
Mortgages, and QREs were key drivers of the aggregate change in MRC.
Column 3 shows that risk-based capital requirements declined by more than 26 percent in half the institutions in the study. Most portfolios showed double-digit declines in minimum risk-based capital requirements for over half the banking organizations, with the exception of credit cards. It should be noted that Column 3 gives every participating institution equal weight. Column 4 shows the analogous weighted median change, using total exposures as weights.
Table B is titled "Transitional Floors," and shows the transitional floor percent for each of the three transitional floor periods. During the first transitional floor period, the transitional floor percentage will be 95 percent; the second period will have a floor of 90 percent; and the third period will have a floor of 85 percent.
Table C is titled "IRB Risk-Based Capital Formulas for Wholesale Exposures to Non-Defaulted Obligors and Segments of Non-Defaulted Retail Exposures" and outlines the supervisory formulas necessary to calculate the capital requirement for non-defaulted retail and wholesale exposures.
Within the Retail section, the formula for the Capital Requirement (K) for Non-Defaulted Exposures reads as follows:
Also within the Retail section, the formulas for Correlation (R) include residential mortgages, qualifying revolving exposures and other retail exposures. For residential mortgage exposures: R = 0.15. For qualifying revolving exposures: R = 0.04. For other retail exposures: R = 0.03 x e−35×PD.
Within the Wholesale section, the formula for the Capital Requirement (K) for Non-Defaulted Exposures reads as follows:
Also within the Wholesale section, the formulas for Correlation (R) include HVCRE exposures and wholesale exposures other than HVCRE exposures. For HVCRE exposures:
For wholesale exposures other than HVCRE exposures:
Also within the Wholesale section, there is a formula for Maturity Adjustment (b) which reads as follows:
Table D illustrates which EAD estimation methodologies may be applied to particular types of exposure. OTC Derivatives may apply the Current exposure methodology or Internal models methodology. Collateralized OTC derivatives may apply the collateral haircut methodology (in conjunction with the current exposure methodology) or internal models methodology. Both repo-style transactions and eligible margin loans may apply the collateral haircut methodology, simple VaR methodology or the internal models methodology. Cross-product netting sets can apply only the internal models methodology. Footnote 55 is applicable to the Simple VaR methodology and states "... (o)nly repo-style transactions and eligible margin loans subject to a single-product qualifying master netting agreement are eligible for the simple VaR methodology."
Figure 2 is titled "EAD and LGD for Eligible Margin Loans and Repo-Style Transactions." It is a flow chart with several potential paths. All paths begin with "Eligible Margin Loans and Repo-Style Transactions" with two options. The first is "Notional Exposure with Adjusted LGD" which concludes with "Plug PD, Adjusted LGD, and Notional EAD into wholesale function." The other path is "Adjusted Exposure at Default Approach" and can flow in two directions. The first, "Models Approach," then asks the question, "Is there a Master Netting Agreement?" If "no," then the path flows to "Internal Models Methodology" and concludes with "Plug PD, Unsecured LGD, and Adjusted EAD into wholesale function." If "yes," the path can flow the same as the "no" answer, or it can flow to "Simple VaR Methodology." Heading back to "Adjusted Exposure at Default Approach," the path can also flow to "Haircut Approach" with again two options, "Standardized" and "Own Estimates," both of which lead to "Repo-Style Transaction?" Simple "VaR" Methodology from the "Master Netting Agreement" question also has a dotted connection to "Repo-Style Transaction") From "Repo-Style Transaction?," if "yes," the path leads to "5 day holding period," and then concludes with "Plug PD, Unsecured LGD, and Adjusted EAD into wholesale function." If "no," the path leads to "10 day holding period" and again concludes with "Plug PD, Unsecured LGD, and Adjusted EAD into wholesale function."
Table E is titled "Standard Supervisory Market Price Volatility Haircuts" and allows the bank to locate the appropriate haircut to be used for a security based on its rating and residual maturity. There are four primary columns titled "External rating grade category for debt securities," "Residual maturity for debt securities," "Issuers exempt from the 3 basis point floor," and "Other Issuers." The rows contain various ranges of ratings and the first two of these rows also have 3 sub-rows within each to account for the varying residual maturities within each rating category.
Following these first primary rows, the table gives specific haircuts for four other assets that may not be rated. These include main index equities, other publicly traded equities, mutual funds, and cash on deposit with the bank.
H subscript m equals H subscript n multiplied by the square root of (T subscript M divided by T subscript N).
Figure 3 is titled "EAD and LGD for OTC Derivative Contracts." It is a flow chart with several potential paths. All paths begin with "EAD for OTC Derivatives" with two potential methods to choose from: "Current Exposure Methodology" or "Internal Models Methodology." If the Current Exposure Methodology is chosen, the path then leads to "Master Netting Agreement." From here, the path follows either "yes" or "no." If yes, the path follows to "Net Replacement Cost + Adjusted Potential Future Exposure." If no, the path follows to "Transaction Replacement Cost + Potential Future Exposure." Both of these paths then lead to the question, "Is Collateral Posted?" and if "yes," there are two options. The first option is "Adjust LGD" leading to "Plug PD, Adjusted LGD, and EAD into Wholesale Function." The second option for "yes" is "Haircut Collateral to Adjust EAD" with again two options, "Standardized Haircuts" and "Own Estimates," both of which conclude to "Plug PD, Unsecured LGD, and Adjusted EAD into Wholesale Function." Going back to "Is Collateral Posted?," if "no" is selected, the path concludes with "Plug PD, Unsecured LGD, and EAD into Wholesale Function." Heading all the way back to the first box, "EAD for OTC Derivatives," the second option is "Internal Models Methodology," which flows to "Collateral Considered in Internal Models Methodology" and concludes with "Plug PD, Unsecured LGD, and Adjusted EAD into Wholesale Function."
The maturity of the expected positive exposure equals 1 plus the ratio of A over B, where:
A equals the summation of the quantities (effective expected exposure for future time periods t subscript k multiplied by delta for future time periods t subscript k multiplied by the risk-free discount factor for future time periods t subscript k) over all values of k for which t subscript k is greater than one year; and
B equals the summation of the quantities (effective expected exposure for future time periods t subscript k multiplied by delta for future time periods t subscript k multiplied by the risk-free discount factor for future time periods t subscript k) over all values of k for which t subscript k is one year or less.
Table F is titled "Risk Weights for Unsettled DvP and PvP Transactions" and shows the risk weight to be applied to positive current exposure for various ranges of the number of business days after contractual settlement date for DvP and PvP transactions. For business days from 5 to 15, the risk weight is 100 percent; for business days from 16 to 30, the risk weight is 625 percent; for business days 31 to 45, the risk weight is 937.5 percent; and for business days 46 or more, the risk weight is 1,250 percent.
Table G is titled "Long-Term Credit Rating Risk Weights under RBA and IAA." It consists of 4 primary columns with headings of "Applicable Rating (Illustrative rating example)," "Column 1: Risk weights for senior securitization exposures backed by granular pools," "Column 2: Risk weights for non-senior securitization exposures backed by granular pools," and "Column 3: Risk weights for securitization exposures backed by non-granular pools." Overall, this table allows banks to apply the correct risk weight for different types of securitization exposures based on the applicable long-term credit rating.
Table H is titled "Short-Term Credit Rating Risk Weights under RBA and IAA" and consists of 4 primary columns with headings of "Applicable Rating (Illustrative rating example)," "Column 1: Risk weights for senior securitization exposures backed by granular pools," "Column 2: Risk weights for non-senior securitization exposures backed by granular pools," and "Column 3: Risk weights for securitization exposures backed by non-granular pools." Overall, this table allows banks to apply the correct risk weight for different types of securitization exposures based on the applicable short-term credit rating.
When Y is less than K subscript IRB, the function S[Y] is equal to Y, where K subscript IRB is defined as the ratio of the risk-based capital requirement for the underlying exposures plus the expected credit loss of the underlying exposures (all as determined as if the underlying exposures were directly held by the bank) to the amount of the underlying exposures
When Y is greater than K subscript IRB, the function S[Y] is equal to K subscript IRB plus the function K[Y] minus the function K[K subscript IRB] plus the product of ((d multiplied by K subscript IRB) divided by 20) multiplied by (1 minus e) raised to the power of (20 minus (K subscript IRB minus Y) divided by K subscript IRB))
The function K[Y] is equal to (1 minus h) multiplied by [(1 minus the cumulative beta distribution with parameters [a and b evaluated at Y]) multiplied by Y, plus the cumulative beta distribution with parameters [a plus 1 and b evaluated at Y] multiplied by c]
h equals (1 minus the quantity (K subscript IRB divided by the securitization's exposure-weighted average loss given default)) raised to the power of N
b equals g multiplied by (1 minus c)
c equals K subscript IRB divided by (1 minus h)
g equals ((1 minus c) multiplied by c) divided by f) minus 1
f equals the quantity ((v plus K subscript IRB raised to the second power) divided by (1 minus h)) minus c to the second power plus (1 minus K subscript IRB) multiplied by K subscript IRB minus v) divided by ((1 minus h) multiplied by 1000))
v equals K subscript IRB multiplied by ((the securitization's exposure-weighted average loss given default minus K subscript IRB) plus 0.25 multiplied by (1 minus the securitization's exposure-weighted average loss given default)) divided by N))
d equals 1 minus (1 minus h) multiplied by (1 minus the cumulative beta distribution with parameters a and b evaluated at K subscript IRB)
N equals (the summation of exposure at
default subscript i for all values of i) raised to the power of two divided
by (the summation of exposure at default subscript i raised to the power
of two) for all values of i![]()
N equals ((100 plus 1 plus 1 plus 1)
raised to the power of 2) divided by (100 raised to the power of 2 plus
1 raised to the power of two plus 1 raised to the power of two plus one
raised to the power of 2) equals 10,609 divided by 10,003 equals 1.06
![]()
The securitization's exposure-weighted average loss given default equals the summation of the loss given default subscript i multiplied by the exposure at default subscript i for all values of i.
N equals 1 divided by C subscript 1 multiplied by C subscript m plus ((C subscript m minus C subscript 1) divided by m minus 1)) multiplied by the greater of {1 minus m multiplied by C subscript 1 and zero}
H equals the summation of (a subscript
i multiplied by H subscript i) for all values of i ![]()
Table I is titled "Controlled Early Amortization
Provisions" and consists of two main sections, "Retail Credit
Lines" and "Non-retail Credit Lines." Within both sections,
there are two columns, "Uncommitted" and "Committed."
This table allows banks to determine the appropriate 3-month average excess
spread credit conversion factor (CCF) for both uncommitted and committed,
retail and non-retail credit lines.![]()
Table J is titled "Non-Controlled Early
Amortization Provisions" and consists of two main sections, "Retail
Credit Lines" and "Non-retail Credit Lines." Within both
sections, there are two columns, "Uncommitted" and "Committed."
This table allows banks to determine the appropriate 3-month average excess
spread credit conversion factor (CCF) for both uncommitted and committed,
retail and non-retail credit lines. ![]()
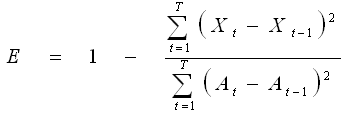
E equals 1 minus (the summation of t
from t equals 1 to T of the quantity (X subscript t minus X subscript t
minus 1) raised to the power of two), divided by (the summation of t from
t equals 1 to T of the quantity (A subscript t minus A subscript t minus
1) raised to the power of two) ![]()
Table 1 is titled "Transitional
Floors," and shows the transitional floor percent for each of the
three transitional floor periods. During the first transitional floor period,
the transitional floor percentage will be 95 percent; the second period
will have a floor of 90 percent; and the third period will have a
floor of 85 percent.![]()
Table 2 is titled "IRB Risk-Based Capital Formulas for Wholesale Exposures to Non-Defaulted Obligors and Segments of Non-Defaulted Retail Exposures" and outlines the supervisory formulas necessary to calculate the capital requirement for non-defaulted retail and wholesale exposures.
Within the Retail section, the formula for the Capital Requirement (K) for Non-Defaulted Exposures reads as follows:
Also within the Retail section, the formulas for Correlation (R) include residential mortgages, qualifying revolving exposures and other retail exposures. For residential mortgage exposures: R = 0.15. For qualifying revolving exposures: R = 0.04. For other retail exposures: R = 0.03 x e−35×PD.
Within the Wholesale section, the formula for the Capital Requirement (K) for Non-Defaulted Exposures reads as follows:
Also within the Wholesale section, the formulas for Correlation (R) include HVCRE exposures and wholesale exposures other than HVCRE exposures. For HVCRE exposures:
For wholesale exposures other than HVCRE exposures:
Also within the Wholesale section, there is a formula for Maturity Adjustment (b) which reads as follows:
Table 3 is titled "Standard Supervisory Market Price Volatility Haircuts" and allows the bank to locate the appropriate haircut to be used for a security based on its rating and residual maturity. There are four primary columns titled "External rating grade category for debt securities," "Residual maturity for debt securities," "Issuers exempt from the 3 basis point floor," and "Other Issuers." The rows contain various ranges of ratings and the first two of these rows also have 3 sub-rows within each to account for the varying residual maturities within each rating category.
Following these first primary rows, the table gives specific haircuts for
four other assets that may not be rated. These include main index equities,
other publicly traded equities, mutual funds, and cash on deposit with
the bank.![]()
H subscript m equals H subscript n multiplied by the square root of (T subscript
M divided by T subscript N). ![]()
The maturity of the expected positive exposure equals 1 plus the ratio of A over B, where:
A equals the summation of the quantities (effective expected exposure for future time periods t subscript k multiplied by delta for future time periods t subscript k multiplied by the risk-free discount factor for future time periods t subscript k) over all values of k for which t subscript k is greater than one year; and
B equals the summation of the quantities (effective expected exposure for
future time periods t subscript k multiplied by delta for future time periods
t subscript k multiplied by the risk-free discount factor for future time
periods t subscript k) over all values of k for which t subscript k is
one year or less.![]()
K subscript o equals [the Loss Given
Default subscript g multiplied by N multiplied by ((N raised to the negative
1 power multiplied by (the Probability of Default subscript o) plus N raised
to the negative 1 power multiplied by (0.999) times the square root of
the asset value correlation of the obligor) divided by (the square root
of 1 minus the asset value correlation of the obligor)) minus (the Expected
Loss Given Default subscript g multiplied by the Probability of Default
subscript o)] multiplied by [(1 plus (M minus 2.5) multiplied by b) divided
by 1 minus 1.5 multiplied by b] ![]()
Table 5 is titled "Risk Weights
for Unsettled DvP and PvP Transactions" and shows the risk weight
to be applied to positive current exposure for various ranges of the number
of business days after contractual settlement date for DvP and PvP transactions.
For business days from 5 to 15, the risk weight is 100 percent;
for business days from 16 to 30, the risk weight is 625 percent;
for business days 31 to 45, the risk weight is 937.5 percent; and
for business days 46 or more, the risk weight is 1,250 percent.![]()
Table 6 is titled "Long-Term Credit
Rating Risk Weights under RBA and IAA." It consists of 4 primary columns
with headings of "Applicable Rating (Illustrative rating example),"
"Column 1: Risk weights for senior securitization exposures backed
by granular pools," "Column 2: Risk weights for non-senior
securitization exposures backed by granular pools," and "Column 3:
Risk weights for securitization exposures backed by non-granular pools."
Overall, this table allows banks to apply the correct risk weight for different
types of securitization exposures based on the applicable long-term credit
rating.![]()
Table 7 is titled "Short-Term Credit
Rating Risk Weights under RBA and IAA" and consists of 4 primary
columns with headings of "Applicable Rating (Illustrative rating example),"
"Column 1: Risk weights for senior securitization exposures backed
by granular pools," "Column 2: Risk weights for non-senior
securitization exposures backed by granular pools," and "Column
3: Risk weights for securitization exposures backed by non-granular pools."
Overall, this table allows banks to apply the correct risk weight for different
types of securitization exposures based on the applicable short-term credit
rating. ![]()
When Y is less than K subscript IRB, the function S[Y] is equal to Y, where K subscript IRB is defined as the ratio of the risk-based capital requirement for the underlying exposures plus the expected credit loss of the underlying exposures (all as determined as if the underlying exposures were directly held by the bank) to the amount of the underlying exposures
When Y is greater than K subscript IRB, the function S[Y] is equal to K subscript IRB plus the function K[Y] minus the function K[K subscript IRB] plus the product of ((d multiplied by K subscript IRB) divided by 20) multiplied by (1 minus e) raised to the power of (20 minus (K subscript IRB minus Y) divided by K subscript IRB))
The function K[Y] is equal to (1 minus h) multiplied by [(1 minus the cumulative beta distribution with parameters [a and b evaluated at Y]) multiplied by Y, plus the cumulative beta distribution with parameters [a plus 1 and b evaluated at Y] multiplied by c]
h equals (1 minus the quantity (K subscript IRB divided by the securitization's exposure-weighted average loss given default)) raised to the power of N
b equals g multiplied by (1 minus c)
c equals K subscript IRB divided by (1 minus h)
g equals ((1 minus c) multiplied by c) divided by f) minus 1
f equals the quantity ((v plus K subscript IRB raised to the second power) divided by (1 minus h)) minus c to the second power plus (1 minus K subscript IRB) multiplied by K subscript IRB minus v) divided by ((1 minus h) multiplied by 1000))
v equals K subscript IRB multiplied by ((the securitization's exposure-weighted average loss given default minus K subscript IRB) plus 0.25 multiplied by (1 minus the securitization's exposure-weighted average loss given default)) divided by N))
d equals 1 minus (1 minus h) multiplied by (1 minus the cumulative beta distribution with parameters a and b evaluated at K subscript IRB)
N equals (the summation of exposure at
default subscript i for all values of i) raised to the power of two divided
by (the summation of exposure at default subscript i raised to the power
of two) for all values of i![]()
The securitization's exposure-weighted
average loss given default equals the summation of the loss given default
subscript i multiplied by the exposure at default subscript i for all values
of i.![]()
N equals 1 divided by C subscript 1 multiplied
by C subscript m plus ((C subscript m minus C subscript 1) divided by m
minus 1)) multiplied by the greater of {1 minus m multiplied by C subscript
1 and zero}![]()
H equals the summation of (a subscript
i multiplied by H subscript i) for all values of i ![]()
Table 8 is titled "Controlled Early Amortization
Provisions" and consists of two main sections, "Retail Credit
Lines" and "Non-retail Credit Lines." Within both sections,
there are two columns, "Uncommitted" and "Committed."
This table allows banks to determine the appropriate 3-month average excess
spread credit conversion factor (CCF) for both uncommitted and committed,
retail and non-retail credit lines.![]()
Table 9 is titled "Non-Controlled Early
Amortization Provisions" and consists of two main sections, "Retail
Credit Lines" and "Non-retail Credit Lines." Within both
sections, there are two columns, "Uncommitted" and "Committed."
This table allows banks to determine the appropriate 3-month average excess
spread credit conversion factor (CCF) for both uncommitted and committed,
retail and non-retail credit lines. ![]()
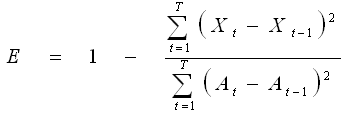
E equals 1 minus (the summation of t
from t equals 1 to T of the quantity (X subscript t minus X subscript t
minus 1) raised to the power of two), divided by (the summation of t from
t equals 1 to T of the quantity (A subscript t minus A subscript t minus
1) raised to the power of two) ![]()
