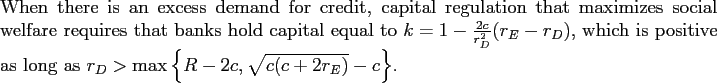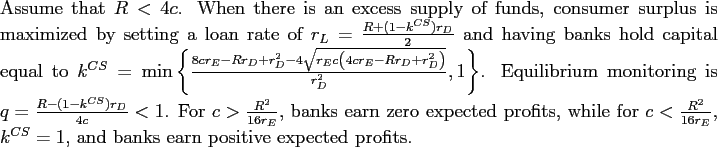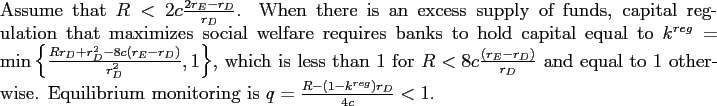Credit Market Competition and Capital Regulation1
Keywords: Capital regulation, credit market competition
Abstract:
1 Introduction
A common justification for capital regulation for banks is the reduction of bank moral hazard. Given the presence of deposit insurance, banks have easy access to deposit funds. If they hold a low level of capital, there is an incentive for them to take on excessive risk. If the risky investment pays off, the banks' shareholders receive the payoff. On the other hand, if it does not, the bulk of the losses are borne either by depositors or by the body providing deposit insurance. Given the widely accepted view that equity capital is more costly for banks than other forms of funds, the common assumption in much of the extant analyses of bank regulation is that capital adequacy standards should be binding as banks attempt to economize on the use of this costly input.
In practice, however, it appears that the amount of capital held by banks has varied substantially over time in a way that is difficult to explain as a function of regulatory changes. For example, Berger et al. (1995) report that in the 1840's and 1850's banks in the U.S. had capital ratios of around 40 to 50 percent. These ratios fell dramatically throughout the twentieth century, reaching a range of 6 to 8 percent in the 1940's where they stayed until the end of the 1980's. More recent evidence in Flannery and Rangan (2004) suggests that bank capital ratios have again increased, with banks in the U.S. now holding capital that is 75% in excess of the regulatory minimum (see also Barth et al., 2005, for international evidence).2 Given that capital adequacy standards were not in existence during much of the nineteenth century, and have not fluctuated much since their inception, it is hard to find a regulatory rationale to explain movements in banks' capital holdings.
To better understand the role of bank capital and regulation, we present a simple model of bank lending that incorporates two features widely believed to be important for banking markets. First, we incorporate a consideration related to banks' lending behavior into their choice of financing, recognizing that banks' capital structures may have implications for their ability to attract clients (e.g., borrowers). Second, we assume that banks perform a special role as monitors or as producers of information. With these two features, we show that costly capital is not a sufficient condition to guarantee that banks will minimize how much capital they hold, implying that capital requirements need not be binding if banks operate in a competitive market. Moreover, our model is static in nature, so we obtain this result even abstracting from other, possibly important, dynamic considerations, such as those found in Blum and Hellwig (1995), Bolton and Freixas (2005), or Peura and Keppo (2005).
The starting point of our model is that firms face an agency problem between shareholders and managers, which banks can help resolve by monitoring. Specifically, we assume that the more monitoring a bank does, the greater is the probability that a firm's investment is successful. Bank monitoring therefore has two effects in our model. First, it increases the probability that the firm's loan is repaid, thus increasing the return to the bank. Second, it benefits the firm's owners since it increases the return on their investments. Firms therefore find bank loans more desirable the greater is the underlying agency problem between shareholders and managers of the firm.3
Given limited liability for the bank, we argue that borrowers can use two different tools to provide their lending bank with an incentive to monitor. One instrument is embodied in the interest rate on the loan, since a marginal increase in the loan rate gives the bank a greater incentive to monitor in order to receive the higher payoff if the project succeeds. This increased payoff for the bank can also benefit the firm's owners if it exceeds the extra amount they pay the bank for the loan. A borrower can therefore use the interest payment on the loan to pay for bank monitoring in a way that is contingent on the success of the project. The second instrument is the amount of equity capital a bank has. The more capital a bank holds, the greater the loss the bank's owners will face if the loan is not repaid and so the greater is the incentive to monitor. Put differently, capital helps solve the limited liability problem banks face due to their extensive reliance on deposit-based financing.4
We consider two distinct cases regarding the structure of the credit market in our analysis. In the first case, we assume that the demand for loans by firms with good projects exceeds banks' supply of funds so that borrowers must compete for funds. In the second case, we assume instead that there is a shortage of good projects relative to the funds available so that banks must compete for firms' business and tailor their contracts so as to attract this business.
When there is a shortage of bank funds available, we show that banks optimally choose to hold no capital since equity is more costly than deposits, and limited liability protects them from having to repay depositors when their loans are not repaid. Banks also raise the interest rates on loans to the highest level that is consistent with firms being willing to borrow, and it is this which provides them with an incentive to monitor. We also show that when the cost of equity is not too much greater than the cost of deposits, a regulator interested in maximizing social welfare would impose a requirement that banks hold a positive amount of capital. This "capital requirement" leads to improved monitoring and reduces the cost to the deposit insurance fund, an aspect which is not internalized by the banks. The banks, however, would like to have as low a level of capital as possible so that any capital constraint imposed by a regulator will be binding.
The case where there is an excess supply of bank funds is more complex. In equilibrium, we find that even in the absence of a regulator, banks will hold a positive amount of capital in order to attract borrowers' business. The reason is that capital acts as a commitment device for banks to monitor, which is good for borrowers. Moreover, we also find that the loan rate most attractive to borrowers is also one that is sufficiently high to induce banks to monitor. These findings suggest that market discipline can be imposed not only from the liability side, as has been stressed in the literature on the use of subordinated debt (for a review, see Flannery and Nikolova, 2004), but also from the asset side of the bank's balance sheet (see Kim et al., 2005, for evidence that borrowers may indeed exert a disciplinary influence on banks' behavior).
In this setting, we show that a regulator will in general want to choose a different level of capital than that obtained in the market equilibrium. Specifically, when the cost of equity capital is relatively low, and is just above the cost of deposits, the regulator will want to impose a capital requirement that is above the level of capital obtained in the market. This occurs for the same reason as above, in that the cost of deposit insurance is not fully internalized by banks or borrowers. By contrast, when the cost of equity capital is high relative to the cost of deposits, the regulator may want to impose a capital requirement that is lower than that in the market. The reason is that the borrowers do not fully internalize the cost of equity capital and demand a high level of capital as a commitment for banks to monitor. In this instance, any capital requirement set by a regulator would not be binding, because competition for borrowers leads banks to hold greater amounts of capital than is socially optimal.
We extend our model to the case where there is no deposit insurance and show that the qualitative results of the base model are unaffected. Specifically, banks may have incentives to hold capital above what would be socially optimal when there is an excess supply of funds and banks have to compete for borrowers. Interestingly, in the absence of deposit insurance, banks may prefer to hold a positive level of capital even in the case where there is an excess demand for credit as a way of reducing their cost of borrowing from depositors.
The implications of our model are consistent with recent empirical observations, including the capital buildup of banks during the 90's, when the competitiveness of credit markets is thought to have increased significantly (for a discussion of this issue, see Boot and Thakor, 2000). Our model also offers the surprising prediction that, ceteris paribus, borrowers should be willing to pay higher interest rates to less-capitalized banks in order to provide them an alternative incentive to monitor. This is consistent with recent work by Hubbard et al. (2002), who find that borrowing from poorly-capitalized banks is more expensive, but only for informationally-sensitive borrowers (see also Kim et al., 2005). Moreover, our model offers other cross-sectional implications concerning firms' sources of borrowing. An implication of our analysis is that borrowing from a well-capitalized bank that thus commits to monitoring, is of greater value to firms with high agency problems. Firms for which monitoring adds little value should prefer to borrow either from an arm's length source of financing or from a bank with low capital. Billett et al. (1995) finds that lender "identity," in the sense of the lender's credit rating, is an important determinant of the market's reaction to the announcement of a loan. To the extent that capitalization improves a lender's rating and reputation, these results are in line with the predictions of our model.
Recent research on the role of bank capital has studied the interaction between capital and liquidity creation (Diamond and Rajan, 2000) and the role of capital in determining banks' lending capacities and providing incentives to monitor (Holmstrom and Tirole, 1997). Our approach is complementary to these, but instead focuses on how borrower demand for monitoring services can itself lead banks to hold capital. Our paper is also related to studies of the role of capital in reducing risk-taking, recent examples of which are Hellmann et al. (2000) and Repullo (2004).
Section 2 outlines the model. Section 3 considers firms' financing choice and banks' choice of monitoring taking the loan rates and capital amounts as given. The case where there is an excess demand for credit is considered in Section 4, while the case where there is an excess supply of funds is analyzed in Section 5. Section 6 extends the analysis to the case where there is no deposit insurance, and where banks can engage in risk-shifting via their monitoring decisions. Section 7 contains concluding remarks.
2 Model
Consider a simple one-period economy, with ![]() banks and
banks and ![]() firms. There are three
parties: firms (borrowers), an arm's length credit market, and banks. We describe each of these below.
firms. There are three
parties: firms (borrowers), an arm's length credit market, and banks. We describe each of these below.
Borrowers: Each firm can invest in a risky project with gross payoff of ![]() when successful and 0 when not, and will choose to do so as
long as the expected return from the project is greater than what it can earn in its next best alternative,
when successful and 0 when not, and will choose to do so as
long as the expected return from the project is greater than what it can earn in its next best alternative,
![]() . The manager of the firm can choose how much effort
. The manager of the firm can choose how much effort ![]() to spend in running
the project and increase its success probability at a cost of
to spend in running
the project and increase its success probability at a cost of
![]() , and how much time to spend on other activities,
, and how much time to spend on other activities, ![]() , for which he
enjoys a private benefit
, for which he
enjoys a private benefit ![]() . For simplicity, we also let
. For simplicity, we also let ![]() represent the probability
of success of the investment project, so that effort increases the expected return of the project and reduces the probability of failure. The firm's shareholders can choose between financing the project with an arm's length loan or with a bank loan.
represent the probability
of success of the investment project, so that effort increases the expected return of the project and reduces the probability of failure. The firm's shareholders can choose between financing the project with an arm's length loan or with a bank loan.
Credit market financing: A competitive arm's length market provides financing at a gross interest rate of ![]() . This loan is unmonitored, giving the firm's
manager full discretion in choosing how much effort to exert.
. This loan is unmonitored, giving the firm's
manager full discretion in choosing how much effort to exert.
Banks: Banks finance themselves with an amount of capital ![]() at a cost
at a cost ![]() per unit, and an amount of deposits
per unit, and an amount of deposits ![]() at a cost
at a cost ![]() ,
with
,
with
![]() . Deposits are fully insured so that the deposit rate
. Deposits are fully insured so that the deposit rate ![]() does not
depend on the risk of bank portfolios. (We analyze the case where there is no deposit insurance in Section 6.1.) This assumption captures the idea that bank capital is a particularly expensive form of financing, and that depositors don't have the specialized skills necessary to
become bankers, therefore having a lower opportunity cost (see Berger et al., 1995, for a discussion of this issue. Hellmann et al., 2000, and Repullo, 2004, make a similar assumption).5
does not
depend on the risk of bank portfolios. (We analyze the case where there is no deposit insurance in Section 6.1.) This assumption captures the idea that bank capital is a particularly expensive form of financing, and that depositors don't have the specialized skills necessary to
become bankers, therefore having a lower opportunity cost (see Berger et al., 1995, for a discussion of this issue. Hellmann et al., 2000, and Repullo, 2004, make a similar assumption).5
Banks can monitor their borrowers and by doing so influence managerial effort. Specifically, each bank chooses a monitoring effort ![]() and can constrain the manager's actions so that he
exerts effort
and can constrain the manager's actions so that he
exerts effort ![]() , but this comes at a cost of
, but this comes at a cost of ![]() for the bank. The convex cost
function reflects the fact that it is increasingly difficult for a bank to control the actions of a borrower. Our modelling of bank monitoring captures the idea that banks can help to reduce an agency problem between the shareholders and managers of the firm, and thus increase value.6 We note, however, that there are other equally plausible interpretations of the influence banks have on firms that are consistent with our model. For example, banks may instead have to
choose how much effort to dedicate to screening borrowers. Firms would benefit from such screening by enjoying more accurate pricing of the risk associated with their loans and avoiding cross-subsidies to less-efficient borrowers.
for the bank. The convex cost
function reflects the fact that it is increasingly difficult for a bank to control the actions of a borrower. Our modelling of bank monitoring captures the idea that banks can help to reduce an agency problem between the shareholders and managers of the firm, and thus increase value.6 We note, however, that there are other equally plausible interpretations of the influence banks have on firms that are consistent with our model. For example, banks may instead have to
choose how much effort to dedicate to screening borrowers. Firms would benefit from such screening by enjoying more accurate pricing of the risk associated with their loans and avoiding cross-subsidies to less-efficient borrowers.
Market structure: The loan rate ![]() and the amount of capital
and the amount of capital ![]() are determined endogenously, and can be set in one of two ways. They can either both be determined by the bank or the amount of capital can be set by a regulator who maximizes social welfare. The market is always competitive, but the solution will depend on the division of surplus
between banks and borrowers. We will distinguish between two cases for the allocation of surplus: first, the case where there is a shortage of funds available to lend (
are determined endogenously, and can be set in one of two ways. They can either both be determined by the bank or the amount of capital can be set by a regulator who maximizes social welfare. The market is always competitive, but the solution will depend on the division of surplus
between banks and borrowers. We will distinguish between two cases for the allocation of surplus: first, the case where there is a shortage of funds available to lend (![]() ), and second the
case where there is a shortage of firms with good investment projects (
), and second the
case where there is a shortage of firms with good investment projects (![]() ).
).
Timing: The model can be divided into 4 stages. First, the level of bank capital ![]() is determined, either by the bank or by a regulator. Second, banks set the
loan rate
is determined, either by the bank or by a regulator. Second, banks set the
loan rate ![]() .7 Third, borrowers choose the loan that is most
attractive to them. Finally, banks choose their monitoring effort
.7 Third, borrowers choose the loan that is most
attractive to them. Finally, banks choose their monitoring effort ![]() once the terms of the loan have been set and they have raised capital and deposits.
once the terms of the loan have been set and they have raised capital and deposits.
3 Financing choice and bank monitoring
Before proceeding to the main analysis, it is useful to characterize the borrowers' choice of financing source, as well as the banks' choice of monitoring effort taking as given the amount of capital, ![]() , and the pricing of the loans,
, and the pricing of the loans, ![]() . With an unmonitored (i.e., arm's length) loan, the manager of each firm chooses effort
. With an unmonitored (i.e., arm's length) loan, the manager of each firm chooses effort ![]() to maximize
to maximize
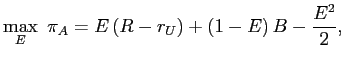 |
(1) |
where
| (2) |
with the additional condition that
The firm chooses the source of financing that maximizes its value. That is, the firm chooses to obtain a bank loan as long as the return,
![]() , is greater than if the loan is unmonitored,
, is greater than if the loan is unmonitored,
![]() . This can be expressed as
. This can be expressed as
Condition 3 shows that the choice between an unmonitored loan from the arm's length market and a monitored loan from a bank depends on the level of private benefit for the manager as well as the loan rates. Firms where managers have large private benefits, so that there is a severe agency problem, will prefer to borrow from banks as a way to solve the manager's agency problem and commit to a higher level of monitoring. Also, a bank loan will be preferred if the arm's length market is not very attractive (if
To find the optimal level of monitoring for the banks, note that each of them chooses a monitoring effort so as to maximize expected profits. Since the bank's revenues is
![]() if the loan is repaid and zero if the loan defaults, the expected profit can be expressed as
if the loan is repaid and zero if the loan defaults, the expected profit can be expressed as
| (4) |
The solution to this problem yields
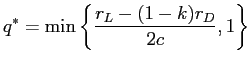 |
(5) |
as the optimal level of monitoring for each bank. Note that, when
We note that this framework implies a moral hazard problem in the choice of monitoring when banks raise a positive amount of deposits. Since banks repay depositors only when their portfolios succeed, they do not internalize the full cost of default on depositors. This limited liability biases
bank monitoring downwards. Capital forces banks to bear some of the burden associated with non-performing loans, and therefore provides an incentive for banks to monitor. Thus, a possible rationale for regulation is to limit moral hazard and raise the level of monitoring. This is illustrated by
noting that, in the absence of limited liability, the equilibrium level of monitoring would be
![]() , with the inequality strict whenever
, with the inequality strict whenever
![]() . Since our focus is on bank monitoring and regulation, in what follows we restrict attention to the case where firms find it optimal to borrow from a bank.
. Since our focus is on bank monitoring and regulation, in what follows we restrict attention to the case where firms find it optimal to borrow from a bank.
4 Excess demand for credit
We begin with the case where there is a shortage of loanable funds relative to the demand for credit, which implies that banks will be able to obtain their preferred terms. This case reflects a situation where there are fewer banks than investment projects (![]() ), so that borrowers compete away the return on their projects in order to attract funding.
), so that borrowers compete away the return on their projects in order to attract funding.
Banks set ![]() and
and ![]() so as to maximize their expected profits, taking into
account their subsequent monitoring choice and the fact that borrowers accept the loans only if they have a non-negative surplus. Thus, the profit-maximizing contract solves the following problem:
so as to maximize their expected profits, taking into
account their subsequent monitoring choice and the fact that borrowers accept the loans only if they have a non-negative surplus. Thus, the profit-maximizing contract solves the following problem:
| (6) |
subject to
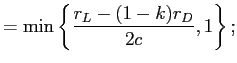 |
||
| 0 |
The first constraint represents the monitoring effort that banks choose in order to maximize expected profits after lending to borrowers, which was obtained above. The second constraint is the participation constraint of borrowers, labelled as consumer surplus (
The solution to this maximization problem yields the following result.
Proof: See the appendix. ![]()
The intuition behind Proposition 1 is simple. When there is an excess supply of profitable lending opportunities, banks will retain all the surplus from investment projects as borrowers compete away their own returns in order to attract funds. Since equity is more costly to banks, they choose to finance themselves entirely with deposits. Banks benefit from a high loan rate in two ways. First, a high loan rate provides them with a large return, all things equal. Second, a high loan rate also give banks greater incentives to monitor. Loan rates and capital are indeed two alternative ways to provide banks with monitoring incentives, but they differ in their impact. Raising capital entails a direct cost only for banks, whereas increasing loan rates has a negative impact only for borrowers. Banks therefore offer to lend at the highest rate that borrowers' are willing to accept.
Given banks' desire to minimize their holdings of capital, there may be scope for capital regulation in this context. Due to limited liability, banks do not internalize the full cost of default, and simply choose their level of capital and loan prices so as to maximize their expected profits. By contrast, a regulator interested in maximizing social welfare, which includes the cost borne by the deposit insurance fund, would solve the following problem:
| (7) |
subject to
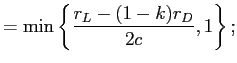 |
||
| 0 |
The optimization problem is similar to before, with the important difference that the regulator chooses only the level of capital, and that it does so in order to maximize social welfare. The loan rate is still set as part of the market solution, as given in Proposition 4.
Proof: See the appendix. ![]()
Proposition 2 implies that welfare-maximizing capital regulation requires a positive level of capital due to its positive incentive effect on bank monitoring. This occurs when the required return for depositors ![]() is sufficiently high that banks would not monitor fully when they have no capital (i.e., when
is sufficiently high that banks would not monitor fully when they have no capital (i.e., when ![]()
![]() ), and also high enough that the positive incentive effect on social welfare of raising capital outweighs the cost
), and also high enough that the positive incentive effect on social welfare of raising capital outweighs the cost ![]() (i.e., when
(i.e., when ![]()
![]() ).
).
Comparing Propositions 1 and 2 leads to the following immediate result.
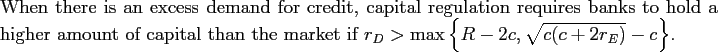
This result establishes that a regulator will often require a higher amount of capital than the amount that maximizes banks' profits, and never a lower amount. Regulation can thus be beneficial as it increases social welfare relative to what would be obtained under the market solution. In these instances, there is a rationale for capital regulation as a way of providing banks with incentives to monitor.
5 Excess supply of funds
We now turn to the case where there is a shortage of good lending opportunities for banks relative to the funds the banking system has available to lend. In this case, banks will have to set contract terms competitively in order to attract borrowers, who will generally be able to appropriate
most, if not all, of the surplus associated with their projects. In contrast to the previous section, this case reflects the situation where there are fewer investment projects than banks (![]() ).
).
The capital holdings and interest rate that maximize borrower surplus solve the following problem:
| (8) |
subject to
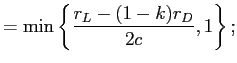 |
||
| 0 | ||
where, as before,
Proof: See the appendix, which contains a full characterization of the equilibrium. ![]()
The results in Proposition 4 highlight the incentive mechanisms for bank monitoring provided by a competitive credit market. There are two ways of providing banks with incentives to monitor: by requiring that they hold a minimum amount of capital ![]() , and by setting the rate
, and by setting the rate ![]() on the loan so as to compensate them for their monitoring when the project is successful and
the loan is repaid. Both of these variables increase bank monitoring, but differ in terms of their costs and their effects on consumer surplus and bank profits. Borrowers would like banks to hold large amounts of capital so as to commit to exert a high level of monitoring, as borrowers' returns
increase with
on the loan so as to compensate them for their monitoring when the project is successful and
the loan is repaid. Both of these variables increase bank monitoring, but differ in terms of their costs and their effects on consumer surplus and bank profits. Borrowers would like banks to hold large amounts of capital so as to commit to exert a high level of monitoring, as borrowers' returns
increase with ![]() but they do not fully internalize the costs of capital and of monitoring. By contrast, since capital is a costly input (i.e.,
but they do not fully internalize the costs of capital and of monitoring. By contrast, since capital is a costly input (i.e.,
![]() ), banks would prefer to minimize its use and to instead receive incentives through a higher loan rate,
), banks would prefer to minimize its use and to instead receive incentives through a higher loan rate, ![]() . However, while increasing
. However, while increasing ![]() is good for incentive purposes, its direct effect is to reduce the surplus to the borrowers. Raising
is good for incentive purposes, its direct effect is to reduce the surplus to the borrowers. Raising ![]() will therefore eventually reduce borrower surplus, and this occurs when the positive incentive effect of a higher loan rate on bank monitoring is dominated by the negative direct effect on consumer
surplus,
will therefore eventually reduce borrower surplus, and this occurs when the positive incentive effect of a higher loan rate on bank monitoring is dominated by the negative direct effect on consumer
surplus, ![]() . Thus, when borrowers obtain the surplus, banks have to raise a positive amount of capital to attract borrowers.
. Thus, when borrowers obtain the surplus, banks have to raise a positive amount of capital to attract borrowers.
The exact amounts of monitoring and capital in equilibrium depend on the return of investment projects ![]() , the cost of capital
, the cost of capital ![]() , and the cost of monitoring
, and the cost of monitoring ![]() . When projects are not very profitable (
. When projects are not very profitable (![]() ) but capital is not too costly (
) but capital is not too costly (![]() ), banks raise the highest level of capital, but do not monitor fully since the cost of doing so would
be too high. If capital is relatively costly, however, so that
), banks raise the highest level of capital, but do not monitor fully since the cost of doing so would
be too high. If capital is relatively costly, however, so that ![]() , market incentives lead banks to choose a lower level of capital (
, market incentives lead banks to choose a lower level of capital (![]() ), less monitoring (
), less monitoring (![]() ), or both. The participation constraint of banks prevents them from raising the highest
level of capital, thus leading to a lower level of monitoring. In the appendix, we also present the case where projects are highly profitable (
), or both. The participation constraint of banks prevents them from raising the highest
level of capital, thus leading to a lower level of monitoring. In the appendix, we also present the case where projects are highly profitable (![]() ), and show that, when capital is not too
costly, banks exert the maximum effort,
), and show that, when capital is not too
costly, banks exert the maximum effort, ![]() , and raise the highest level of capital,
, and raise the highest level of capital, ![]() . Borrowers want banks to monitor fully as projects are very profitable, and can induce banks to do so by raising only capital, as long as this is not too costly and banks' profits are positive. When capital is costly, however, banks will again choose a lower level of capital
and/or less monitoring.
. Borrowers want banks to monitor fully as projects are very profitable, and can induce banks to do so by raising only capital, as long as this is not too costly and banks' profits are positive. When capital is costly, however, banks will again choose a lower level of capital
and/or less monitoring.
Interestingly, borrowers may be willing to give up some of the return on the loans to the banks in order to provide them with incentives to monitor. They accomplish this by allowing the loan rates to reflect the returns of the projects, and to be increasing in such returns as long as there are
incentive effects from doing so (as long as ![]() ):
):
![]() . In other words, the loan's price need not be set only to compensate banks for the credit risk associated with granting the loan, but also to induce
them to exert effort in monitoring the projects and thus improve the expected returns of the loans. Furthermore, since capital and loan rates are alternative instruments for providing banks with an incentive to monitor, we note that the equilibrium value of
. In other words, the loan's price need not be set only to compensate banks for the credit risk associated with granting the loan, but also to induce
them to exert effort in monitoring the projects and thus improve the expected returns of the loans. Furthermore, since capital and loan rates are alternative instruments for providing banks with an incentive to monitor, we note that the equilibrium value of ![]() is decreasing in the level of capital
is decreasing in the level of capital ![]() . This implies that these are substitute instruments from the point of
view of borrowers, who only trade off their relative costs from the perspective of reducing consumer surplus. The findings in Hubbard et al. (2002) and Kim et al. (2005) lend support to this result, in that they find that interest rates are higher on loans from less-capitalized banks.
. This implies that these are substitute instruments from the point of
view of borrowers, who only trade off their relative costs from the perspective of reducing consumer surplus. The findings in Hubbard et al. (2002) and Kim et al. (2005) lend support to this result, in that they find that interest rates are higher on loans from less-capitalized banks.
The complement to Proposition 2 from the previous section is to analyze the optimal choice of capital from a social welfare perspective when we assume that there is an excess supply of funds, and rates are set as part of a market solution to maximize the return to borrowers. In other words, a regulator would solve the following problem.
| (9) |
subject to
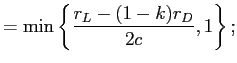 |
||
| 0 |
Again, we focus here on the case of an interior solution, and leave the other cases, which are qualitatively similar, to the appendix.
Proof: See the appendix, which contains a full characterization of the equilibrium. ![]()
While the interest rate on the loan is determined in a competitive market setting and not subject to regulatory interference, a regulator may want to impose a capital requirement for banks in order to ensure they have sufficient incentives to monitor. In contrast to Proposition 2, now the
regulator is more likely to require that banks hold a positive amount of capital, and this amount is greater than in the case where bank funds are in short supply. The reason is that the market sets a lower loan rate when borrowers obtain the surplus than when banks obtain it and, therefore, the
regulator has to use more capital to provide banks with incentives to monitor. Optimal regulation, however, does not necessarily call for "narrow banking" in the sense of having fully capitalized intermediaries, but rather allows for a mix between capital and deposit-based financing. This will
generally be true when the cost of capital relative to deposits,
![]() , is high, or when the aggregate return from encouraging greater monitoring,
, is high, or when the aggregate return from encouraging greater monitoring, ![]() , is relatively low.
, is relatively low.
We now turn to one of the main results in the paper, which is whether a pure market-based system is likely to provide sufficient incentives for bank discipline and monitoring, and whether capital regulation can be an effective tool for providing such incentives. For that, we have the following:
Proof: See the appendix. ![]()
While the exact expressions for
![]() are provided in the proof, the interpretation of this result can be stated quite generally for all parameter values as follows. When capital is much more expensive than
deposits (
are provided in the proof, the interpretation of this result can be stated quite generally for all parameter values as follows. When capital is much more expensive than
deposits (
![]() ), it is socially optimal to economize on capital and instead rely more heavily on deposits for financing the bank. The market solution, by contrast, will demand that banks
hold an excessive level of capital when there is a shortage of good lending opportunities and credit markets are competitive. At the other extreme, when bank capital is not significantly more costly than deposits, regulators desire that banks hold more capital than the market requires. The reason
is that the regulator internalizes both the cost of raising capital as well as the cost to the deposit insurance fund. Thus, when the difference
), it is socially optimal to economize on capital and instead rely more heavily on deposits for financing the bank. The market solution, by contrast, will demand that banks
hold an excessive level of capital when there is a shortage of good lending opportunities and credit markets are competitive. At the other extreme, when bank capital is not significantly more costly than deposits, regulators desire that banks hold more capital than the market requires. The reason
is that the regulator internalizes both the cost of raising capital as well as the cost to the deposit insurance fund. Thus, when the difference
![]() is high, the regulator chooses to impose a lower capital requirement because capital is socially more costly than repaying depositors in case of bank default. By contrast, when
the difference
is high, the regulator chooses to impose a lower capital requirement because capital is socially more costly than repaying depositors in case of bank default. By contrast, when
the difference
![]() is low, the regulator prefers to require a high level of capital and reduce the costs of bank default.
is low, the regulator prefers to require a high level of capital and reduce the costs of bank default.
The result of Proposition 5 also suggests that, when capital is relatively expensive, capital regulation is not likely to be binding as market incentives will induce banks to hold greater amounts of capital than is socially optimal. In other words, a minimum capital requirement imposed by a regulator, as well as changes in this requirement, would have no effect on banks' aggregate holdings of capital.8 In fact, social welfare maximization would call for a ceiling being placed on the level of capital, or a tax on its use so as to discourage banks from holding excessive capital.
The contrast between the finding in Proposition 5 and that in Proposition 3 is clear. When there is a shortage of bank funds and banks are able to appropriate most of the surplus from lending, capital regulation plays a clear role in increasing bank monitoring and reducing the probability of failure. However, when there is an excess supply of funds and loan rates are relatively low, the market may demand bank monitoring by requiring that banks hold a higher amount of capital. The effectiveness of capital regulation, therefore, clearly depends on the structure of the market for bank credit. When there is an excess demand for credit, establishing a capital adequacy requirement can be a useful way of imposing bank discipline, reducing the burden to the insurance fund and raising social welfare. By contrast, when there is an excess supply of funds, the incentives provided in the market as banks compete to attract borrowers may lead banks to hold excessive amounts of capital, so that capital adequacy requirements become ineffective and unnecessary.
6 Extensions
In this section we look at two important extensions. First, we consider the case where there is no deposit insurance, so that banks must internalize the cost imposed on depositors of their inability to repay deposits when their projects fail. Second, we consider a simple extension to allow for banks to shift risk in their choice of investments.
6.1 The Case Without Deposit Insurance
Up to now we have considered only the case where deposits are fully insured, so that the interest rate paid on deposits is determined entirely by depositors' opportunity cost, given by ![]() . A concern, however, is that banks' incentives to economize on the use of capital may be driven by the fixed-cost nature of deposits, which are not sensitive to risk when they are fully insured. In this section we analyze the case where deposits are not insured, so that the
promised repayment must compensate depositors for the risk they face when placing their money in banks that may not repay. This introduces a liability-side disciplining force on bank behavior and capital holdings since banks will have to bear the cost of their risk-taking through a higher deposit
rate.
. A concern, however, is that banks' incentives to economize on the use of capital may be driven by the fixed-cost nature of deposits, which are not sensitive to risk when they are fully insured. In this section we analyze the case where deposits are not insured, so that the
promised repayment must compensate depositors for the risk they face when placing their money in banks that may not repay. This introduces a liability-side disciplining force on bank behavior and capital holdings since banks will have to bear the cost of their risk-taking through a higher deposit
rate.
Consider the following slight change to the model. The timing is modified as follows. First, banks choose how much to raise in deposits (![]() ) and capital (
) and capital (![]() ); the promised repayment on deposits (i.e., the deposit rate)
); the promised repayment on deposits (i.e., the deposit rate) ![]() is then also set. Second, the loan rate
is then also set. Second, the loan rate
![]() is determined. Third, borrowers choose the loan that is most attractive to them. Fourth, banks choose their monitoring effort
is determined. Third, borrowers choose the loan that is most attractive to them. Fourth, banks choose their monitoring effort ![]() once the terms of the loan have been set. Note that the only change is the introduction of the setting of the deposit rate
once the terms of the loan have been set. Note that the only change is the introduction of the setting of the deposit rate ![]() in
stage 1.
in
stage 1.
Deposits are uninsured, so that the expected value of their promised payment ![]() must be equal to depositors' opportunity cost
must be equal to depositors' opportunity cost ![]() . Given
. Given ![]() , depositors conjecture a level of monitoring for the bank,
, depositors conjecture a level of monitoring for the bank, ![]() , and set the deposit rate to meet their reservation return, which is given by
, and set the deposit rate to meet their reservation return, which is given by ![]() . This implies that
. This implies that
![]() , or that
, or that
![]() .
.
We now solve the model by backward induction. For a given ![]() , banks choose monitoring to maximize
, banks choose monitoring to maximize
| (10) |
For an interior solution, this problem yields
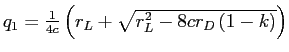 and
and
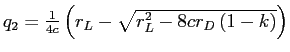 , with
, with
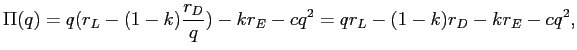 |
(11) |
which is strictly increasing in
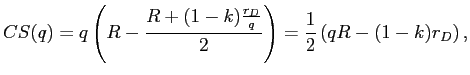 |
(12) |
which again is strictly increasing in
Having solved the last stage, stages 2 and 3 follow along the lines of the previous sections. The rate on the loan, ![]() , is given either by the maximum rate that is consistent with
borrowers' participation constraints when there is an excess supply of projects, or by the rate that maximizes the return to borrowers,
, is given either by the maximum rate that is consistent with
borrowers' participation constraints when there is an excess supply of projects, or by the rate that maximizes the return to borrowers,
![]() , when there is an excess supply of funds. Solving the first stage, where banks or the regulator choose the level of capital, we obtain the following result.
, when there is an excess supply of funds. Solving the first stage, where banks or the regulator choose the level of capital, we obtain the following result.
Proof: See the appendix. ![]()
The proposition establishes that one of our main results, that market-driven incentives can lead banks to hold more capital than is socially optimal, continues to hold even for the case where deposits are not insured. Moreover, it holds under similar conditions as before: when the opportunity cost of deposits is low relative to the cost of bank capital. The intuition is similar to that in the previous section, in that the market solution does not fully internalize all the costs and benefits associated with holding capital. Specifically, when there is an excess supply of funds banks need to adjust their offers to attract borrowers, and end up competing their return away. However, the trade-off between the benefit of increased monitoring and the cost of capital is not the same for borrowers as it is for the society. From a social welfare perspective, requiring that banks hold large amounts of capital has a large negative impact on bank profits when capital is relatively costly, and this reduction in profits may more than offset any gains to borrowers from increased monitoring. Borrowers, of course, do not fully internalize this effect, and may demand a higher level of capital than what is socially optimal.
It is also worth pointing out that, unlike the case with deposit insurance, banks may now wish to hold some capital even when funding is in short supply and borrowers must compete for funding. The following proposition formalizes this result.
Proof: See the appendix. ![]()
The intuition for this result is as follows. When the deposit rate is constant, banks have no incentive to hold any capital since capital is a costly form of financing. In the absence of deposit insurance, however, capital signals a commitment to monitor on the part of the bank. Depositors
recognize this greater incentive to monitor by banks and reduce the interest payment they demand on their deposits. Banks may therefore have an incentive to hold capital as a way of reducing their cost of funding, and this incentive is greatest when the cost of deposits is high relative to the cost
of equity (i.e., when ![]() is close to
is close to ![]() ). One way of interpreting this
finding is that capital can be valuable even when the payment to depositors accurately reflects the risk they bear, so that banks internalize the cost of their risk-taking. In other words, there is scope for bank capital to improve welfare even when there is a clear channel for discipline from the
liability side of the bank's balance sheet. Finally, we note that since borrowers compete away their surplus, the regulator's maximization problem is equivalent to the market's problem, so there is no additional role for regulation.
). One way of interpreting this
finding is that capital can be valuable even when the payment to depositors accurately reflects the risk they bear, so that banks internalize the cost of their risk-taking. In other words, there is scope for bank capital to improve welfare even when there is a clear channel for discipline from the
liability side of the bank's balance sheet. Finally, we note that since borrowers compete away their surplus, the regulator's maximization problem is equivalent to the market's problem, so there is no additional role for regulation.
6.2 Banks and Asset Substitution
In the analysis above, we have assumed throughout that bank monitoring is strictly value-increasing, in that greater monitoring increases the expected return of the projects at the same time that it reduces the probability of failure. Here, we briefly analyze the case where banks may suffer from
an asset substitution problem due to limited liability: since they are highly leveraged, they may have an incentive to take on risky projects, shifting some of the risk onto creditors. Specifically, we assume that the maximum return on the projects, ![]() , is a decreasing function of
, is a decreasing function of ![]() ,
,
![]() , so that for low monitoring, the return on the projects is high but risky. By contrast, when a bank monitors a lot and
, so that for low monitoring, the return on the projects is high but risky. By contrast, when a bank monitors a lot and ![]() is high, the return on the project is lower, but the project is safer. For simplicity, we focus only on the case where there is a shortage of funds.
is high, the return on the project is lower, but the project is safer. For simplicity, we focus only on the case where there is a shortage of funds.
Given ![]() , expected profits for the bank can be expressed as
, expected profits for the bank can be expressed as
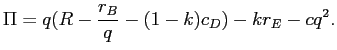 |
(13) |
The FOC for an interior solution is
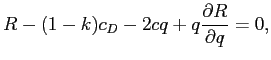 |
(14) |
which defines the equilibrium value of monitoring,
We can now use the FOC to find
![]() by use of the implicit function theorem (IFT). Define
by use of the implicit function theorem (IFT). Define
![]() , which is identically equal to 0. By the IFT,
, which is identically equal to 0. By the IFT,
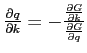 . However, since the problem is concave in
. However, since the problem is concave in ![]() , we have that
, we have that
![]() , which means that the sign of
, which means that the sign of
![]() is the same as the sign of
is the same as the sign of
![]() . Therefore,
. Therefore,
![]() , implying that capital provides incentives to monitor. Therefore, we conclude that our results continue to hold even in the case where limited liability
for banks creates a risk-shifting problem.
, implying that capital provides incentives to monitor. Therefore, we conclude that our results continue to hold even in the case where limited liability
for banks creates a risk-shifting problem.
7 Concluding remarks
A standard view of capital regulation is that it offsets the risk-taking incentives provided by deposit insurance. A common approach in the study of bank regulation has been to assume that any capital requirements will be binding, since equity capital is generally believed to more costly than other forms of finance. However, in many cases such as the U.S. in the 1990's they appear not to be binding. In this paper we have developed an alternative view of capital that is consistent with the observation that capital constraints may or may not be binding. In particular, when there is an excess supply of funds relative to the number of attractive projects available so that banks compete for projects, the level of capital determined by the market can be higher than the level required by a regulator that maximizes social welfare.
Our main results continue to hold even in the absence of deposit insurance. First, we show that the market equilibrium can still involve a positive level of capital, whether there is an excess supply or a shortage of bank funds. In addition, the optimal amount of capital from a social welfare point of view can be above or below the equilibrium level in the market.
Our model has a number of implications which are in line with recent empirical observations. First, it suggests that capital requirements may not bind when, as in the last decade (see, e.g., Boot and Thakor, 2000), the competitiveness of credit markets increases. Second, in line with the results in Kim et al. (2005), the model shows that also borrowers can impose discipline on banks by demanding they hold capital as a commitment devise to exert monitoring. Finally, an interesting empirical implication of our analysis is that bank monitoring, and thus capital holdings, are of more value to firms with high agency problems. Firms for which monitoring has little value should prefer to borrow either from an arm's length source of financing, or from a bank with low capital, and thus lower costs. Billett et al. (1995) finds that lender "identity", in the sense of the lender's credit rating, is an important determinant of the market's reaction to the announcement of a loan. To the extent that capitalization improves a lender's rating and reputation, these results are consistent with the predictions of our model.
A. Proofs
Proof of Proposition 4: Substituting ![]() in bank profits, we obtain
in bank profits, we obtain
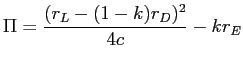 .
.Differentiating profits with respect to ![]() gives
gives
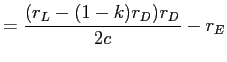 |
||
This implies that ![]() . Furthermore, for
. Furthermore, for
![]() ,
,
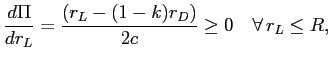
Proof of Proposition 4: Substituting
![]() and
and ![]() in the expression for
in the expression for ![]() gives
gives
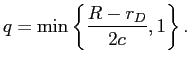
Substituting
![]() and keeping
and keeping ![]() , social welfare becomes
, social welfare becomes
r_{D}.](img136.gif)
Differentiating SW with respect to ![]() , we have
, we have
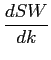 |
![LaTex Encoded Math: \displaystyle =\frac{(R-(1-k)r_{D})r_{D}}{2c}-r_{E}-[-\frac{(1-k)r_{D}% ^{2}}{2c}-r_{D}+\frac{(R-(1-k)r_{D})r_{D}}{2c}]=0](img138.gif) |
|
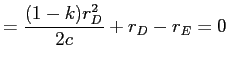 . . |
Calculating this expression at the two extreme levels of capital gives
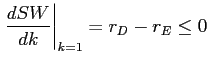 ,
,and
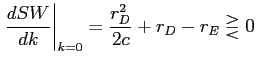 ,
,implying that the welfare-maximizing level of capital is
![]() if
if
![]() , and is given by
, and is given by
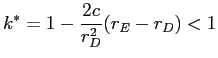 ,
,Proposition 5B When there is an excess supply of funds, maximizing borrower surplus yields the following equilibrium:
1) For ![]() , monitoring is
, monitoring is ![]() . The loan rate is
. The loan rate is
![]() , and banks are required to hold capital
, and banks are required to hold capital ![]() equal
to
equal
to
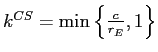 . For
. For ![]() (i.e., if
(i.e., if
![]() ), banks earn profits
), banks earn profits
![]() , otherwise
, otherwise ![]() .
.
2) For ![]() , monitoring is
, monitoring is
![]() . The loan rate is
. The loan rate is
![]() , and banks hold capital equal to
, and banks hold capital equal to
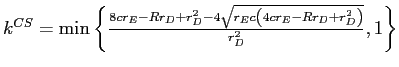 , which is less than
, which is less than ![]() for
for
![]() and equal to one otherwise. For
and equal to one otherwise. For ![]() ,
,
![]() , and
, and ![]() for
for ![]() .
.
Proof: Start by noting that, since
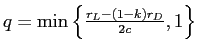 , if
, if
![]() then
then
![]() . Since
. Since
![]() , we have that
, we have that
![]() for
for ![]() . Therefore, more capital increases consumer surplus.
. Therefore, more capital increases consumer surplus.
We proceed in two stages, starting by maximizing ![]() with respect to the loan's price,
with respect to the loan's price, ![]() , for a fixed
, for a fixed ![]() , which yields
, which yields
![]()
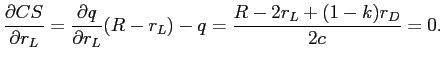
We can now maximize ![]() with respect to the choice of capital,
with respect to the choice of capital, ![]() . However, we
know from above that the combination of
. However, we
know from above that the combination of
![]() and the highest possible
and the highest possible ![]() will be optimal for
borrowers. We therefore introduce the participation constraint for the bank, that
will be optimal for
borrowers. We therefore introduce the participation constraint for the bank, that
![]() . Substituting for
. Substituting for
![]() as well as for
as well as for ![]() , we obtain
, we obtain
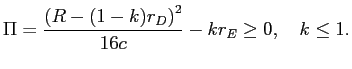
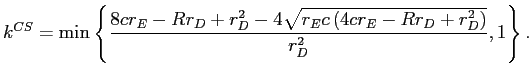
We now check when in fact ![]() . From the definition of the optimal level of monitoring
. From the definition of the optimal level of monitoring
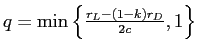 , we see that, for
, we see that, for
![]() ,
, ![]() . Substituting in the optimal value for
. Substituting in the optimal value for ![]() gives the following condition:
gives the following condition:
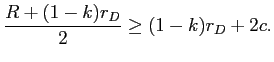
Otherwise, for ![]() ,
, ![]() , which implies that
, which implies that ![]() . Moreover, substituting this value of
. Moreover, substituting this value of ![]() into
into
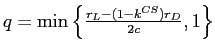 and observing that
and observing that ![]() , we obtain that
, we obtain that ![]() and
and
![]() for
for ![]() , and is less than 1
otherwise. All together, this implies that
, and is less than 1
otherwise. All together, this implies that ![]() for
for ![]() , and
, and ![]() for
for ![]() .
. ![]()
Proposition 5B When there is an excess supply of funds, capital regulation that maximizes social welfare requires:
1) For
![]() , monitoring is
, monitoring is
![]() , and capital equals
, and capital equals
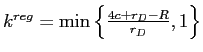 , which is less than 1 for
, which is less than 1 for ![]() and equal to 1 otherwise.
and equal to 1 otherwise.
2) For
![]() , monitoring is
, monitoring is
![]() and capital equals
and capital equals
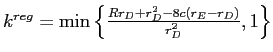 , which is less than 1 for
, which is less than 1 for
![]() and equal to 1 otherwise.
and equal to 1 otherwise.
Proof: Start by maximizing social welfare with respect to ![]() , assuming that the loan rate is set to maximize
, assuming that the loan rate is set to maximize ![]() , i.e., that
, i.e., that
![]() . Social welfare is given by
. Social welfare is given by
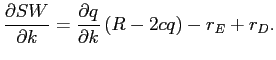
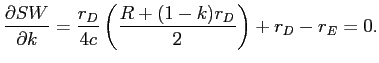
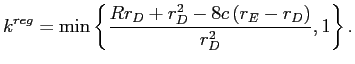
The previous solution assumed that ![]() . To get the bounds on when
. To get the bounds on when ![]() ,
substitute the solution for
,
substitute the solution for ![]() , assuming
, assuming ![]() , into
, into
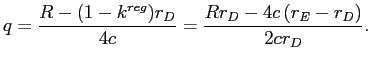
One final point that needs to be verified is that, for
![]() , then
, then
![]() , but that for
, but that for
![]() , we have that
, we have that ![]() , which
would imply that
, which
would imply that
![]() . Note, however, that for both of these conditions to be true at the same time requires that
. Note, however, that for both of these conditions to be true at the same time requires that
![]() . This will be satisfied if and only if
. This will be satisfied if and only if
![]()
![]() . We can now use this in the necessary condition for
. We can now use this in the necessary condition for ![]() , which is
, which is
![]() . Given the restriction on
. Given the restriction on ![]() and
and
![]() , the right hand side must be less than
, the right hand side must be less than
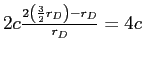 . Therefore, the joint assumption that
. Therefore, the joint assumption that
![]() and
and
![]() implies that
implies that ![]() , and
consequently that
, and
consequently that
![]() , as desired.
, as desired. ![]()
Proof of Proposition 5: We begin with the case of parameter values such that ![]() , and show that there exists a value
, and show that there exists a value
![]() such that
such that
![]() if and only if
if and only if
![]() . Consider the solution that maximizes consumer surplus,
. Consider the solution that maximizes consumer surplus, ![]() , and assume that
, and assume that ![]() and
and
![]() , which implies that
, which implies that
![]() . From the condition defining
. From the condition defining ![]() ,
,
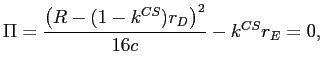
By contrast, ![]() is defined by
is defined by
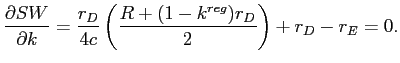
At the other extreme, we consider the solutions as
![]() . For
. For
![]() ,
,
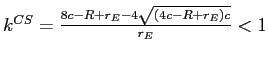 . By comparison,
. By comparison,
![]() as
as
![]() for all parameter values. Therefore, we can also conclude that there must exist some threshold
for all parameter values. Therefore, we can also conclude that there must exist some threshold
![]() such that, for
such that, for
![]() ,
,
![]() .
.
Comparing the two values of ![]() ,
,
![]() if and only if
if and only if
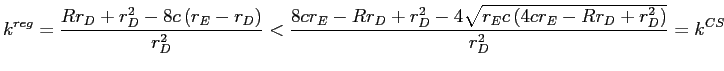
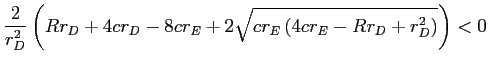
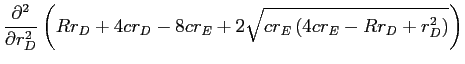 |
||
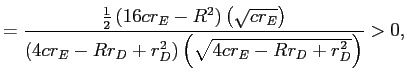 |
since by assumption
The finding that the function
![]() is convex implies that
is convex implies that
![]() can at most cross zero twice, the first time from above and the second from below. However, two crossings are inconsistent with the finding in the proposition above that for
low values of
can at most cross zero twice, the first time from above and the second from below. However, two crossings are inconsistent with the finding in the proposition above that for
low values of ![]() ,
,
![]() , while for high values of
, while for high values of ![]() ,
,
![]() . Therefore,
. Therefore,
![]() at one unique point, which implies that
at one unique point, which implies that
![]() , and we have just one threshold, as desired.
, and we have just one threshold, as desired.
We next proceed to the case where ![]() in both cases, which is true for sufficiently large
in both cases, which is true for sufficiently large ![]() , but that
, but that ![]() . Start with the case of consumer surplus maximization, where, for
. Start with the case of consumer surplus maximization, where, for ![]() ,
, ![]() and
and
![]() . For the case with regulation, we have that for
. For the case with regulation, we have that for
![]() ,
, ![]() and
and
![]() . Therefore,
. Therefore,
![]()
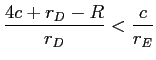
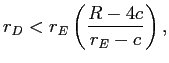
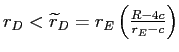 , as desired.
, as desired.
The last case is a possible "mixed" case, in which monitoring may be at a maximum for one solution but not the other. It is straightforward to show that the only case of relevance is where, with a slight abuse of notation, ![]() but
but ![]() . This occurs for
. This occurs for
![]() , and in this range
, and in this range
![]() and
and
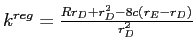 . The difference
. The difference
![]() simplifies to
simplifies to
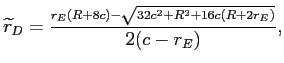
Proof of Proposition 6.1: Assume that there is an excess supply of funds so that, as before, consumer surplus is maximized by setting
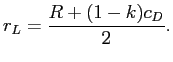
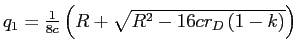 and
and
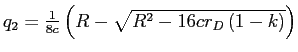 . We focus again on the Pareto dominant equilibrium with a higher level of monitoring (
. We focus again on the Pareto dominant equilibrium with a higher level of monitoring (We proceed by maximizing ![]() with respect to the choice of capital,
with respect to the choice of capital, ![]() . However,
we know from above that the combination of
. However,
we know from above that the combination of
![]() and the highest possible
and the highest possible ![]() will be optimal for
borrowers. We therefore introduce the participation constraint for the bank, that
will be optimal for
borrowers. We therefore introduce the participation constraint for the bank, that
![]() . Substituting for
. Substituting for ![]() gives
gives
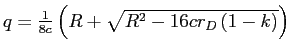 , and we obtain
, and we obtain
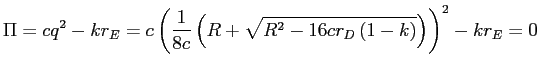
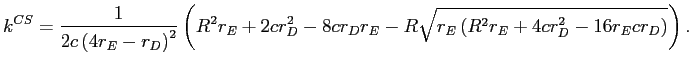
To maximize social welfare in the absence of deposit insurance, we need to solve
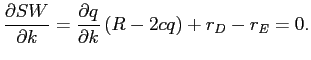
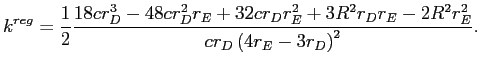
Comparing these two solutions, we note that as
![]() , we have that, as before,
, we have that, as before,
![]() . By contrast, for the case of social welfare maximization it is easy to see from the FOC that as
. By contrast, for the case of social welfare maximization it is easy to see from the FOC that as
![]() ,
,
![]() as well. Therefore, for
as well. Therefore, for ![]() sufficiently small, we have that
sufficiently small, we have that
![]() , as desired.
, as desired. ![]()
Proof of Proposition 6.1: Note that bank profit maximization with respect to ![]() yields the following FOC:
yields the following FOC:
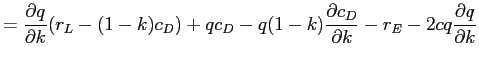 |
||
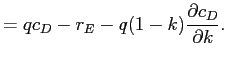 |
Since
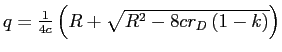 when
when
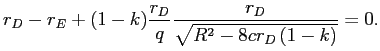
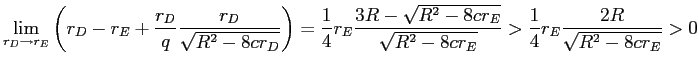
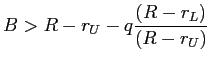 .
.