Skip to: [Printable Version (PDF)] [Bibliography] [Footnotes]

Finance and Economics Discussion Series: 2006-20 Screen Reader version*

Inflation Targeting under Imperfect Knowledge*

Athanasios Orphanides
Board of Governors of the Federal Reserve System
and
John C. Williams
Federal Reserve Bank of San Francisco

April 2006

Keywords: Learning, Natural rate of interest, natural rate of unemployment, rational expectations, monetary policy rules, uncertainty, bond prices.

Abstract:

A central tenet of inflation targeting is that establishing and maintaining well-anchored inflation expectations are essential. In this paper, we reexamine the role of key elements of the inflation targeting framework towards this end, in the context of an economy where economic agents have an imperfect understanding of the macroeconomic landscape within which the public forms expectations and policymakers must formulate and implement monetary policy. Using an estimated model of the U.S. economy, we show that monetary policy rules that would perform well under the assumption of rational expectations can perform very poorly when we introduce imperfect knowledge. We then examine the performance of an easily implemented policy rule that incorporates three key characteristics of inflation targeting: transparency, commitment to maintaining price stability, and close monitoring of inflation expectations, and find that all three play an important role in assuring its success. Our analysis suggests that simple difference rules in the spirit of Knut Wicksell excel at tethering inflation expectations to the central bank's goal and in so doing achieve superior stabilization of inflation and economic activity in an environment of imperfect knowledge.

JEL Classification: D83, D84, E52, E58.

1 Introduction

A central tenet of inflation targeting is that establishing and maintaining well-anchored inflation expectations are essential. Well-anchored expectations enables inflation-targeting central banks to achieve greater stability of output and employment in the short-run, while ensuring price stability in the long-run. Three elements of inflation targeting have been critically important for the successful implementation of this framework.¹ First and foremost is the announcement of an explicit quantitative inflation target and the acknowledgment that low and stable inflation is the primary objective and responsibility of the central bank. Second is the clear communication of the central bank's policy strategy and the rationale for its decisions, which enhances the predictability of the central bank's actions and its accountability to the public. Third is a forward-looking policy orientation, characterized by the vigilant monitoring of inflation expectations at both short-term and longer-term horizons. Together, these elements provide a focal point for inflation, facilitate the formation of the public's inflation expectations, and provide guidance as to actions that may be needed to foster price stability.

Although inflation-targeting (IT) central banks have stressed these key elements, the literature that has studied inflation targeting in the context of formal models has largely described inflation targeting in terms of the solution to an optimization problem within the confines of a linear rational expectations model. This approach is limited in its appreciation of the special features of the inflation-targeting framework, as emphasized by Faust and Henderson (2004), and strips from IT its raison d'être. In an environment of rational expectations with perfect knowledge, for instance, inflation expectations are anchored as long as policy satisfies a minimum test of stability. Furthermore, with the possible exception of a one-time statement of the central bank's objectives, central bank communication loses any independent role because the public already knows all it needs in order to form expectations relevant for its decisions. In such an environment, the public's expectations of inflation and other variables are characterized by a linear combination of lags of observed macroeconomic variables and, as such, they do not merit special monitoring by the central bank or provide useful information to the policymaker for guiding policy decisions.

In this paper, we argue that in order to understand the attraction of IT to central bankers and its effectiveness relative to other monetary policy strategies, it is essential to recognize economic agents' imperfect understanding of the macroeconomic landscape within which the public forms expectations and policymakers must formulate and implement monetary policy. To this end, we consider two modest deviations from the perfect knowledge rational expectations benchmark, and reexamine the role of the key elements of the inflation targeting framework in the context of an economy with imperfect knowledge. We find that including these modifications provides a rich framework in which to analyze inflation targeting strategies and their implementation.

The first relaxation of perfect knowledge that we incorporate is to recognize that policymakers face uncertainty regarding the evolution of key natural rates. In the United States, for example, estimates of the natural rates of interest and unemployment are remarkably imprecise.² Indeed, this problem is arguably even more dramatic for small open economies and transitional economies that have tended to adopt IT. As is well known, policymaker misperceptions regarding the evolution of natural rates can result in persistent policy errors, hindering successful stabilization policy.³

The second modification that we allow for is the presence of imperfections in expectations formation that arise when economic agents have incomplete knowledge of the economy's structure. We assume that agents rely on an adaptive learning technology to update their beliefs and form expectations based on incoming data. Recent research has highlighted the ways in which imperfect knowledge can act as a propagation mechanism for macroeconomic disturbances in terms of amplification and persistence that have first-order implications for monetary policy.⁴Agents may rely on a learning technology to guard against numerous potential sources of uncertainty. One source could be the evolution of natural rates in the economy, paralleling the uncertainty faced by policymakers. But another might be uncertainty regarding the policymaker's understanding of the economy, and likely response to economic developments, and perhaps the precise quantification of policy objectives. Recognition of this latter element in the economy highlights a role for central bank communications, including that of an explicit quantitative inflation target, that would be absent in an environment of perfect knowledge.

We investigate the role of inflation targeting in an environment of imperfect knowledge using an estimated quarterly model of the U.S. economy. Specifically, we compare the performance of the economy subject to shocks with characteristics similar to those observed in the data over the past four decades under alternative informational assumptions and policy strategies. Following McCallum (1988) and Taylor (1993), we focus our attention on implementable policy rules that, nonetheless, capture the key characteristics of IT. Our analysis shows that some monetary policy rules that would perform well under the assumption of rational expectations with perfect knowledge can perform very poorly when we introduce imperfect knowledge. In particular, rules that rely on estimates of natural rates for the setting of policy are susceptible to making persistent errors. Under certain conditions, these errors can give rise to endogenous "inflation scares" whereby inflation expectations become unmoored from the central bank's desired anchor. These results illustrate the potential shortcomings of such standard policy rules and the desirability of identifying an alternative monetary policy framework when knowledge is imperfect.

We then examine the performance of an easily implemented policy rule that incorporates the three key characteristics of inflation targeting highlighted above in an economy with imperfect knowledge, and find that all three play an important role in assuring its success. First, central bank transparency, including explicit communication of the inflation target, can lessen the burden placed on agents to infer central bank intentions and can thereby improve macroeconomic performance. Second, policies that do not rely on estimates of natural rates are easier to communicate and better designed to ensuring medium-run inflation control when natural rates are highly uncertain. Finally, policies that respond to the public's near-term inflation expectations help the central bank avoid falling "behind the curve" in terms of controlling inflation, and result in better stabilization outcomes than policies that rely only on past realizations of data and ignore information contained in private agent expectations.

A reassuring aspect of our analysis is that despite the environment of imperfect knowledge and the associated complexity of the economic environment, successful policy can be remarkably simple to implement and communicate. We find that simple "difference" rules that do not require any knowledge of the economy's natural rates are particularly well suited to assure medium-run inflation control when natural rates are highly uncertain. These rules share commonalities with the simple robust strategy first proposed by Wicksell (1898), who, after defining the natural rate of interest, also pointed out that precise knowledge about it, though desirable, was neither feasible nor necessary for policy implementation aimed towards maintaining price stability.

"This does not mean that the bank ought actually to ascertain the natural rate before fixing their own rates of interest. That would, of course, be impracticable, and would also be quite unnecessary. For the current level of commodity prices provides a reliable test of the agreement or diversion of the two rates. The procedure should rather be simply as follows: So long as prices remain unchanged, the bank's rate of interest is to remain unaltered. If prices rise, the rate of interest is to be raised; and if prices fall, the rate of interest is to be lowered; and the rate of interest is henceforth to be maintained at its new level until a further movement in prices calls for a further change in one direction or the other. ...

In my opinion, the main cause of the instability of prices resides in the instability of the banks to follow this rule."

Wicksell (1898, 1936), p. 189 (emphasis in original)

Our analysis confirms that simple difference rules that implicitly target the price level in the spirit of Wicksell excel at tethering inflation expectations to the central bank's goal and in so doing achieve superior stabilization of inflation and economic activity.

The remainder of the paper is organized as follows. Section II describes the estimated model of the economy. Section III lays out the model of perpetual learning and its calibration. Section IV analyzes key features of the model under rational expectations and imperfect knowledge. Section V examines the performance of alternative monetary policy strategies, including our implementation of inflation targeting. Section VI concludes.

2 A Simple Estimated Model of the U.S. Economy

We use a simple estimated quarterly model of the U.S. economy from Orphanides and Williams (2002), the core of which consists of the following two equations:

$\begin{displaymath} \pi_{t} = \phi_\pi \pi^e_{t+1} + (1-\phi_\pi) \pi_{t-1} + \alpha_\pi (u^e_t-u^*_t) + e_{\pi,t}, \; \; \; e_\pi \sim {\rm iid} (0,\sigma^2_{e_\pi}), \end{displaymath}$

(1)

$\begin{displaymath} u_t = \phi_u u_{t+1}^e + \chi_1 u_{t-1} + \chi_2 u_{t-2} + \chi_3 u^*_t + \alpha_u \, ( r^a_{t-1} - r^*_t) + e_{u,t}, \; \; \; e_{u} \sim {\rm iid} (0,\sigma^2_{e_u}). \end{displaymath}$

(2)

Here $\pi$ denotes the annualized percent change in the aggregate output price deflator,

denotes the unemployment rate,

denotes the (true) natural rate of unemployment,

denotes the (ex ante) real interest rate with one year maturity, and

the (true) natural real rate of interest. The superscript

denotes the public's expectations formed during

. This model combines forward-looking elements of the New Synthesis model studied by Goodfriend and King (1997), Rotemberg and Woodford (1999), Clarida, Galí and Gertler (1999), and McCallum and Nelson (1999), with intrinsic inflation and unemployment inertia as in Fuhrer and Moore (1995a), Batini and Haldane (1999), Smets (2003), and Woodford (2003).

The "Phillips curve" in this model (1) relates inflation during quarter to lagged inflation, expected future inflation, and expectations of the unemployment gap during the quarter, using retrospective estimates of the natural rate discussed below. The estimated parameter $\phi_\pi$ measures the importance of expected inflation for the determination of inflation. The unemployment equation (2) relates unemployment during quarter to the expected future unemployment rate, two lags of the unemployment rate, the natural rate of unemployment, and the lagged real interest rate gap. Here, two elements importantly reflect forward-looking behavior. The first element is the estimated parameter $\phi_u$ , which measures the importance of expected unemployment, and the second is the duration of the real interest rate, which serves as a summary of the influence of interest rates of various maturities on economic activity. We restrict the coefficient $\chi_3$ to equal $1-\phi_u-\chi_1-\chi_2$ so that the equation can be equivalently written in terms of the unemployment gap.

In estimating this model, we are confronted with the difficulty that expected inflation and unemployment are not directly observed. Instrumental variable and full-information maximum likelihood methods impose the restriction that the behavior of monetary policy and the formation of expectations be constant over time, neither of which appears tenable over the sample period that we consider (1969-2002). Instead, we follow the approach of Roberts (1997) and use survey data as proxies for expectations. (See also Rudebusch (2002) and Orphanides and Williams (2005b).) In particular, we use the median forecasts from the Survey of Professional Forecasters from the prior quarter as the expectations relevant for the determination of inflation and unemployment in period ; that is, we assume expectations are based on information available at time . In addition, to match the inflation and unemployment data as well as possible with the forecasts, we employ first-announced estimates of these series in our estimation. Our primary sources for these data are the Real-Time Dataset for Macroeconomists and the Survey of Professional Forecasters, both currently maintained by the Federal Reserve Bank of Philadelphia (Zarnowitz and Braun (1993), Croushore (1993), and Croushore and Stark (2001)). Using least squares over the sample 1969:1 to 2002:2, we obtain the following estimates:

$\begin{displaymath} \pi_{t} = \putb 0.540 (0.086) \pi^e_{t+1} \putb +0.460 ~~(--) \pi_{t-1} \putb -\,0.341 ~(0.099) ( u^e_t - u^*_t) + e_{\pi,t}, \end{displaymath}$

(3)

, ,

$\begin{displaymath} u_t = \putb 0.257 (0.084) u_{t+1}^e \putb +\,1.170 ~(0.107) u_{t-1} \putb -\,0.459 ~(0.071) u_{t-2} \putb -\,0.032 ~~(--) u^*_t \putb +\,0.043 ~(0.013) (r^a_{t-1} - r^*_t) + e_{u,t}, \end{displaymath}$

(4)

The numbers in parentheses are the estimated standard errors of the corresponding regression coefficients. (Dashes are shown under the restricted parameters.) The estimated unemployment equation also includes a constant term (not shown) that captures the average premium of the one-year Treasury bill rate we use for estimation over the average of the federal funds rate, which corresponds to the natural rate of interest estimates we employ in the model. For simplicity, we make no attempt to model the evolution of risk premia. In the model simulations, we impose the expectations theory of the term structure whereby the one-year rate equals the expected average of the federal funds rate over four quarters.

2.1 Natural Rates

We assume that the true processes governing natural rates in the economy follow highly persistent autoregressions. Specifically, we posit that the natural rates follow:

$\begin{displaymath}u^*_t = 0.01 \bar u^* + 0.99 \; u^*_{t-1} + e_{u^*,t}, \end{displaymath}$

$\begin{displaymath}r^*_t = 0.01 \bar r^* + 0.99 \; r^*_{t-1} + e_{r^*,t},\end{displaymath}$

where $\bar u^*$ and $\bar r^*$ denote the unconditional means of the natural rates of unemployment and interest, respectively. The assumption that these processes are stationary is justified by the finding based on a standard ADF test that one can reject the null of nonstationarity of both the unemployment rate and the ex post real federal funds rate over 1950-2003 at the 5 percent level. To capture the assumed high persistence of these series, we set the AR(1) coefficient to 0.99 and and then calibrate the innovation variances to be consistent with estimates of time variation in the natural rates in postwar U.S. data.

As discussed in Orphanides and Williams (2002), there exists a wide range of estimates of the variances of the innovations to the natural rates. Indeed, owing to the imprecision in estimates of these variances, the postwar U.S. data do not provide clear guidance regarding these parameters. Therefore, we consider three alternative calibrations of these variances, which we index by . The case of corresponds to constant and known natural rates, where $\sigma_{e_{u^*}} = \sigma_{e_{r^*}} = 0$ . For the case of , we assume $\sigma_{e_{u^*}} = 0.070$ and $\sigma_{e_{r^*}} = 0.085$ . These values imply an unconditional standard deviation of the natural rate of unemployment (interest) of 0.50 (0.60), in the low end of the range of standard deviations of smoothed estimates of these natural rates suggested by various estimation methods (see Orphanides and Williams 2002 for details). Finally, the case of corresponds to the high end of the range of estimates, for which case we assume $\sigma_{e_{u^*}} = 0.140$ and $\sigma_{e_{r^*}} = 0.170$ . Arguably, given the stability of the post-war U.S. economy relative to many small open economies and transitional economies, for those countries the relevant values of may be higher than those based on U.S. data.

2.2 Monetary Policy

We consider two classes of simple monetary policy rules. First, we analyze versions of the "Taylor Rule" (Taylor 1993), where the level of the nominal interest rate is determined by the perceived natural rate of interest, $\hat r^*_t$ , the inflation rate, and a measure of the level of the perceived unemployment gap, the difference between the unemployment rate and the perceived natural rate of unemployment, $\hat u^*_t$ ,

$\begin{displaymath} i_t = \hat r^*_t + \bar\pi^e_{t+j} + \theta_\pi (\bar\pi^e_{t+j} - \pi^*) + \theta_u (u^e_{t+k} - \hat u_t^*), \end{displaymath}$

(5)

where $\bar\pi$ denotes the four-quarter average of the inflation rate, $\pi^*$ is the central bank's inflation objective,

is the forecast horizon of inflation, and

is the forecast horizon of the unemployment rate forecast. We consider a range of values for the forecast horizons from

, in which case policy responds to the latest observed data (for quarter

), to a forecast horizon up to three years into the future. When policy is based on forecasts, we assume that the central bank uses the same forecasts of inflation and unemployment rate as available to private agents.

We refer to this class of rules as "level rules" because they relate the level of the interest rate to the level of the unemployment gap. Rules of this type have been found to perform quite well in terms of stabilizing economic fluctuations, at least when the natural rates of interest and unemployment are accurately measured. Note that here we consider a variant of the Taylor rule that responds to the unemployment gap instead of the output gap for our analysis, recognizing that the two are related by Okun's (1962) law. In his 1993 exposition, Taylor examined response parameters equal to 1/2 for the inflation gap and the output gap, which, using an Okun's coefficient of 2, corresponds to setting $\theta_\pi=0.5$ and $\theta_u=-1.0$ .

If policy follows a level rule given by equation (5), then the "policy error" introduced in period by natural rate misperceptions is given by

$\begin{displaymath} (\hat r^*_t - r^*_t) - \theta_u (\hat u^{*}_t - u^{*}_t). \end{displaymath}$

Although unintentional, these errors could subsequently induce undesirable fluctuations in the economy, worsening stabilization performance. The extent to which misperceptions regarding the natural rates translate into policy induced fluctuations depends on the parameters of the policy rule. As is evident from the expression above, policies that are relatively unresponsive to real-time assessments of the unemployment gap, that is, those with small $\theta_u$ , minimize the impact of misperceptions regarding the natural rate of unemployment.

As discussed in Orphanides and Williams (2002), one policy rule that is immune to natural rate mismeasurement of the kind considered here is a "difference" rule where the change in the nominal interest rate is determined by the inflation rate and the change in the unemployment rate:

$\begin{displaymath} \Delta i_t = \theta_\pi (\bar\pi^e_{t+j} - \pi^*) + \theta_{\Delta u} \Delta u_{t+k}. \end{displaymath}$

(6)

This rule is closely related to price level targeting strategies and corresponds to the first difference of the rule that would be obtained if the price level were substituted for inflation in the level rule (5).⁵We note that this policy rule is as simple, in terms of the number of parameters, as the original formulation of the Taylor rule. However, the difference rule is simpler to communicate and implement in practice than the Taylor rule because it does not require knowledge of the natural rates of interest or unemployment. In this sense, policy guided by a difference rule can be more transparent than policy guided by a level rule.

3 Perpetual Learning

Expectations play a central role in the determination of inflation, the unemployment rate, and the interest rate in the model. We consider two alternative models of expectations formation. One model, used in most monetary policy research, is rational expectations, that is, expectations that are consistent with the model. The second model is one of perpetual learning, where agents continuously reestimate a forecasting model and form expectations using that model.

In the case of learning, we follow Orphanides and Williams (2005b) and posit that agents obtain forecasts for inflation, unemployment, and interest rates by estimating a restricted VAR of the form corresponding to the reduced form of the rational expectations equilibrium with constant natural rates. We assume that this VAR is estimated recursively with constant gain least squares.⁶ Each period, agents use the resulting VAR to construct one-step-ahead and multi-step-ahead forecasts. This learning model can be justified in two ways. First, in practice agents have only finite quantities of data to work with, and rational expectations may be seen as an assumption that holds only in the distant future when sufficient data have been collected. Alternatively, agents may allow for the possibility of structural change and therefore place less weight on older data, in which case learning is a never-ending process.

Specifically, let denote the $1 \times 3$ vector consisting of the inflation rate, the unemployment rate, and the federal funds rate, each measured at time : $Y_t = (\pi_t, u_t, i_t)$ , and let be the $j \times 1$ vector of a constant and lags of that serve as regressors in the forecast model. The precise number of lags of elements of that appear in may depend on the policy rule. For example, consider the difference rule (6) when policy responds to the 3-quarter ahead forecast of inflation, , and the lagged change in the unemployment rate, . (This is one of the policies for which we present detailed simulation results later on). In this case, two lags of the unemployment rate and one lag each of inflation and the interest rate suffice to capture the reduced form dynamics under rational expectations with constant natural rates, so $X_t = (1, \pi_{t-1}, u_{t-1},u_{t-2}, i_{t-1})'$

The recursive estimation can be described as follows: Let be the $j \times 3$ vector of coefficients of the forecasting model. Then, using data through period , the parameters for the constant-gain least squares forecasting model can be written as:

$LaTex Encoded Math: \displaystyle c_t =$	$\textstyle c_{t-1} + \kappa R^{-1}_t X_t (Y_t - X'_t c_{t-1}),$		(7)
$LaTex Encoded Math: \displaystyle R_t =$	$\textstyle R_{t-1} + \kappa (X_t X'_t - R_{t-1}),$		(8)

where $\kappa>0$ is a small constant gain.

Note that this algorithm estimates all parameters of the agent's forecasting system and does not explicitly incorporate any information regarding the central bank's numerical inflation objective. Later on, we introduce this element of inflation targeting by positing that the announcement and explicit commitment to a quantitative inflation target simplifies the agent's forecasting problem by reducing by one the number of parameters requiring estimation and updating.

A key parameter for the constant-gain-learning algorithm is the updating rate $\kappa$ . To calibrate the relevant range for this parameter, we examined how well different values of $\kappa$ fit the expectations data from the Survey of Professional Forecasters, following Orphanides and Williams (2005b). To examine the fit of the Survey of Professional Forecasters (SPF), we generated a time series of forecasts using a recursively estimated VAR for the inflation rate, the unemployment rate, and the federal funds rate. In each quarter we reestimated the model using all historical data available during that quarter (generally from 1948 through the most recent observation). We allowed for discounting of past observations by using geometrically declining weights. This procedure resulted in reasonably accurate forecasts of inflation and unemployment, with root mean squared errors (RMSE) comparable to the residual standard errors from the estimated structural equations, (3) and (4). We found that discounting past data with values corresponding to $\kappa$ in the range 0.01 to 0.04 yielded forecasts closest, on average, to the SPF than the forecasts obtained with lower or higher values of $\kappa$ . Milani (2005), finds a similar range of values in an estimated DSGE model with learning. In light of these results, we consider three alternative calibrations of the gain, $\kappa = \{0.01, 0.02, 0.03 \}$ , with $\kappa = 0.02$ serving as a "baseline" value.⁷ As in the case of natural rate variation, given the stability of the post-war U.S. economy relative to many small open economies and transitional economies, the relevant values of $\kappa$ may be higher for these countries than those based on U.S. data.

Given this calibration of the model, this learning mechanism represents a relatively modest deviation from rational expectations and yields reasonable forecasts. Indeed, agents' average forecasting performance in the model is close to the optimal forecast.

3.1 Central Bank Learning

In the case of "level rules," policymakers need a procedure to compute real-time estimates of the natural rates. If policymakers knew the true data-generating processes governing the evolution of natural rates, they could use this knowledge to design the optimal estimator. But, in practice, there is considerable uncertainty about these processes, and the optimal estimator for one process may perform poorly if the process is misspecified. Williams (2005) shows that a simple constant gain method to update natural rate estimates based on the observed rates of unemployment and (ex post) real interest rates is reasonably robust to natural rate model misspecification. We follow this approach and assume that policymakers update their estimates of natural rates using simple constant gain estimators given by:

$\begin{displaymath}\hat r^*_t = \hat r^*_{t-1} + 0.005 (i_{t-1} - \pi_{t-1} - \hat r_{t-1}^*), \end{displaymath}$

$\begin{displaymath}\hat u^*_t = \hat u^*_{t-1} + 0.005 (u_{t-1} - \hat u_{t-1}^*). \end{displaymath}$

4 Effects of Imperfect Knowledge on Economic Dynamics

We first present some simple comparisons of the behavior of the economy under rational expectations with known natural rates and under learning with time-varying and unobservable natural rates. Under learning, the economy is governed by nonlinear dynamics, so we use numerical simulations to illustrate the properties of the model economy, conditional on the policymaker following a specific policy rule.

4.1 Simulation Methodology

In the case of rational expectations with constant and known natural rates, we compute all model moments and impulse responses numerically as described in Levin, Wieland, and Williams (1999). In all other cases, we compute approximations of the unconditional moments and impulse responses using simulations of the model.

For model stochastic simulations used to compute estimates of unconditional moments, the initial conditions for each simulation are given by the rational expectations equilibrium with known and constant natural rates. Specifically, all model variables are initialized to their steady-state values, assumed without loss of generality to be zero. The central bank's initial perceived levels of the natural rates are set to their true values, likewise equal to zero. Finally, the initial values of the and matrices describing the private agents' forecasting model are initialized to their respective values corresponding to the reduced form of the rational equilibrium solution to the structural model assuming constant and known natural rates.

Each period, innovations are generated from Gaussian distributions with variances reported above. The innovations are serially and contemporaneously uncorrelated. For each period, the structural model is simulated, the private agent's forecasting model is updated resulting in a new set of forecasts, and the central bank's natural rate estimate is updated. To estimate model moments, we simulate the model for 41,000 periods and discard the first 1000 periods to mitigate the effects of initial conditions. We compute the unconditional moments from sample root mean squares from the remaining 40,000 periods (10,000 years) of simulation data.⁸

Private agents' learning process injects a nonlinear structure into the model that may generate explosive behavior in a stochastic simulation of sufficient length for some policy rules that would have been stable under rational expectations. One source of instability is due to the possibility that the forecasting model itself may become unstable. We take the view that in practice private forecasters reject unstable models. Each period of the simulation, we compute the root of maximum modulus of the forecasting VAR excluding the constants. If the modulus of this root falls below the critical value of 1, the forecast model is updated as described above; if not, we assume that the forecast model is not updated and the matrices and are held at their respective previous period values.⁹

Stability of the forecasting model is not sufficient to assure stability in all simulations. For this reason, we impose a second condition that restrains explosive behavior. In particular, if the inflation rate or the unemployment gap exceeds, in absolute value, five times their respective unconditional standard deviations (computed under the assumption of rational expectations and known and constant natural rates), then the variables that exceed this bound are constrained to equal the corresponding limit in that period. These constraints on the model are sufficient to avoid explosive behavior for the exercises that we consider in this paper and are rarely invoked for most of the policy rules we study, particularly for optimized policy rules.

For impulse responses, we first compute an approximation of the steady-state distribution of the model state vector by running a stochastic simulation of 100,000 periods. We then draw 1001 sample state vectors from this distribution and compute the IRF for each of these draws. From these 1001 IRFS, we compute an estimate of the distribution of the model IRFS.

4.2 Impulse Responses

We use model impulse responses to illustrate the effects of learning on macroeconomic dynamics. For this purpose, let monetary policy follow a level policy rule similar to that proposed by Taylor (1993), with $\theta_\pi=0.5$ and $\theta_u =-1$ , where the inflation forecast horizon is three quarters ahead and that of the unemployment rate is the last observed quarter, that is .

Figure 1 compares the impulse responses of inflation, the nominal interest rate, and the unemployment rate in our model to one standard deviation shocks to inflation and unemployment under perfect knowledge, that is, rational expectations with known natural rates (RE), to the impulse responses under imperfect knowledge with time variation in the natural rates, , and perpetual learning with gain $\kappa = 0.02$ . Each period corresponds to one quarter. Under learning, the impulse responses to a specific shock vary with the state of the economy and the state of beliefs governing the formation of expectations. That is, the responses vary with the initial conditions, $\{X,c,R\}$ , at the time the shock occurs. To summarize the range of possible outcomes in the figure, we plot the median and the 70% range of the distribution of impulse responses corresponding to the stationary distribution of $\{X,c,R\}$ . Under rational expectations, the responses are invariant to the state of the economy.

The dynamic impulse responses to a specific shock exhibit considerable variation under learning. Further, the distribution of responses is not symmetric around the impulse response that obtains under rational expectations. For example, the impulse responses of inflation and unemployment to an inflation shock are noticeably skewed in a direction that yields greater persistence. Indeed, with some probability this persistence may be quite extreme, indicating that under learning transitory shocks can have very long-lasting effects.

4.3 Macroeconomic Variability and Persistence

Perpetual learning provides a powerful propagation mechanism for economic shocks in the economy, resulting in greater volatility and persistence. A summary comparison of the asymptotic variances and persistence for this experiment is presented in Table 1, which includes the full range of natural range variation and values of $\kappa$ that we consider here.

Learning on the part of the public increases the variability and persistence of key macroeconomic variables. Even absent natural rate misperceptions, the case of , shocks to inflation and unemployment engender time variation in private agents' estimates of the VAR used for forecasting. This time variation in the VAR coefficients adds persistent noise to the economy relative to the perfect knowledge benchmark. As a result, the unconditional variances and the serial correlations of inflation, unemployment, and the interest rate rise under learning. These effects are larger for higher values of $\kappa$ , for which the sensitivity of the VAR coefficients to incoming data is greater.

**Table 1:** Performance under the Taylor Rule
Expectations		Standard Deviation $\pi$	Standard Deviation	Standard Deviation $\Delta i$	First-order Autocorrelation $\pi$	First-order Autocorrelation	First-order Autocorrelation
RE	0	2.93	0.87	2.33	0.81	0.88	0.78
RE	1	3.22	0.88	2.35	0.84	0.88	0.82
RE	2	3.94	0.89	2.39	0.89	0.88	0.89

$\kappa = 0.01$	0	3.29	0.93	2.57	0.84	0.89	0.81
$\kappa = 0.01$	1	4.16	1.10	2.89	0.89	0.92	0.86
$\kappa = 0.01$	2	5.00	1.22	3.10	0.93	0.93	0.89

$\kappa = 0.02$	0	3.66	0.99	2.80	0.86	0.90	0.83
$\kappa = 0.02$	1	4.35	1.11	3.01	0.90	0.92	0.87
$\kappa = 0.02$	2	5.21	1.24	3.29	0.93	0.93	0.89

$\kappa = 0.03$	0	3.95	1.04	3.00	0.87	0.91	0.84
$\kappa = 0.03$	1	4.57	1.15	3.22	0.90	0.92	0.87
$\kappa = 0.03$	2	5.37	1.29	3.48	0.92	0.93	0.89

The presence of natural rate variation amplifies the effects of private sector learning on macroeconomic variability and persistence. Under rational expectations and the Taylor Rule, time-varying natural rates and the associated misperceptions increase the variability of inflation, but have relatively little effect on the variability of the unemployment gap and interest rates. But, the combination of private sector learning and natural rate variation (and misperceptions) can dramatically increase macroeconomic variability and persistence. For example, under the Taylor Rule, the standard deviation of the unemployment gap rises from 0.87 percent under rational expectations with constant natural rates to 1.11 percent under learning with and $\kappa = 0.02$ . For inflation, the increase in the standard deviation is even more dramatic, from 2.93 percent to 4.35 percent. Similarly, the first-order autocorrelation of the unemployment gap rises from 0.88 to 0.92 and that of inflation rises from 0.81 to 0.90. The presence of natural rate variation and misperceptions interferes with the public's ability to forecast inflation, unemployment, and interest rates accurately. These forecast errors contribute to a worsening of macroeconomic performance.

4.4 Excess Sensitivity of Long-Horizon Expectations

The adaptive learning algorithm that economic agents employ to form expectations under imperfect knowledge in our model also allows us to investigate the behavior of long-horizon expectations. This is of interest in that it allows examination of the apparent excess sensitivity of yields on long-run government bonds to shocks--a phenomenon that appears puzzling in standard models when knowledge is perfect. Shiller (1979) and Mankiw and Summers (1984) point out that long-term interest rates appear to move in the same direction following changes in short-term interest rates and "overreact" relative to what would be expected if the expectations hypothesis held and expectations were assumed to be rational. Changes in the federal funds rate appear to cause long-term interest rates to generally move considerably and in the same direction (Cook and Hahn, 1989, Roley and Sellon, 1995, Kuttner, 2001). Kozicki and Tinsley (2001a,b), Cogley (2005), and Gürkaynak, Sack, and Swanson (2005) suggest that this sensitivity could be attributed to movements in long-run inflation expectations that differ from those implied by standard linear rational expectations macro models with fixed and known parameters.

Learning-induced expectations dynamics provide a potential explanation for these phenomena.¹⁰ Figure 2 shows the 1-, 2-, and 10-year-ahead forecasts of the inflation and nominal interest rates from the impulse response to a one standard deviation inflation shock, based on the same shocks used in computing Figure 1; Figure 3 shows the same for a one standard deviation shock to the unemployment rate. Note that these measure the annualized quarterly inflation or interest rate expected to prevail quarters in the future, not the average inflation or interest rate over the next quarters. These forward rates are computed by projecting ahead using the agents' forecasting model. Under perfect knowledge, inflation is expected to be only a few basis points above baseline two years after the shock, and expectations of inflation 10 years in the future are nearly unmoved. The same pattern is seen in forward interest rates.

In contrast to the stability of longer-run expectations found under perfect knowledge, the median response under imperfect knowledge shows inflation and interest rate expectations at the 2- and 10-year horizons rising by nearly 10 basis points in response to a transitory inflation shock. Moreover, the excess sensitivity of longer-run inflation expectations to transitory shocks exhibited by the median response is on the lower end of the 70% range of impulse responses, indicating that the response of longer-run expectations is on average even larger and depends crucially on the conditions in which the shock occurs. Indeed, under unfavorable conditions, the inflation expectations process can become unmoored for an extended period. Such episodes correspond to endogenously generated "inflation scares" and are similar to historical episodes for the United States described in Goodfriend (1993). In these episodes, inflation expectations and long-term interest rates appear to react excessively and persistently to some event that would not warrant such a reaction if expectations were well anchored. These results also serve to highlight one of the crucial concerns regarding the behavior of expectations that the practice of inflation targeting attempts to address, and that cannot appear in an environment of rational expectations with perfect knowledge. Under perfect conditions, expectations always remain well-anchored.

5 Implications for Monetary Policy Design

In this section, we explore the ways in which monetary policy can be improved in an environment of imperfect knowledge. We consider three issues, all of which are closely related key characteristics of inflation targeting. First, we compare the performance of the economy under the level policy rule framework and under the easier to communicate and more transparent difference policy framework. As we discuss, the difference rule strategy appears superior for assuring achievement of the policymaker's inflation objective, especially in an environment with uncertainty regarding natural rates--a situation in which level rules that rely on "gaps" from natural rate concepts for policy implementation run into substantial difficulties. Next, we consider the optimal horizon for expectations of inflation and unemployment rates to which policy reacts in the policy rule as well as some robustness characteristics of policy under alternative preferences for inflation stabilization versus stabilization of real economic activity. Finally, we turn to the role of communicating an explicit numerical long-run inflation objective to the public for the performance of the economy under alternative policies.

To ease comparisons, in what follows, we compare the performance of the economy using a loss function as a summary statistic. Specifically, we assume that the policymakers' objective is to minimize the weighted sum of the unconditional variances of inflation, the unemployment gap, and the change in the nominal federal funds rate:

$\begin{displaymath} \mathcal{L} = Var(\pi-\pi^*) + \lambda Var( u - u^*) + \nu Var(\Delta(i)), \end{displaymath}$

(9)

where

denotes the unconditional variance of variable

. As a benchmark, we consider $\lambda = 4$ and $\nu= 1$ but also consider alternatives for the relative weight of real-activity stabilization, $\lambda$ . (Note that $\lambda=4=2^2$ corresponds to the case of equal weights on inflation and output gap variability--based on Okun's law with coefficient 2.)

5.1 Comparing the Level and Difference Rule Approaches

Up to this point, we have assumed that policy follows a specific formulation of the Taylor Rule. As emphasized in Orphanides and Williams (2002), such policies are particularly prone to making errors when there is considerable uncertainty regarding natural rates. In particular, persistent misperceptions of the natural rates of unemployment or interest translate into persistent deviations of inflation from its target value. Perpetual learning on the part of economic agents amplifies the effect of such errors and further complicates the design of policy. It is thus instructive to also study alternative monetary policy rules that are robust to natural rate misperceptions and are therefore better designed for achieving medium-run inflation stability as in an inflation targeting framework.

We start by examining more closely the performance of alternative parameterizations of the Taylor rule. Figure 4 presents iso-loss contours of the economy with the above loss function for alternative parameterizations of the level rule with and :

$\begin{displaymath} i_t = \hat r^*_t + \bar\pi^e_{t+3} + \theta_\pi (\bar\pi^e_{t+3} - \pi^*) + \theta_u (u^e_{t-1} - \hat u_t^*), \end{displaymath}$

(10)

The top left panel shows the loss under rational expectations with constant natural rates, referred to in the following as "perfect knowledge," while the other panels show the loss under learning with $\kappa = 0.02$ and time-varying natural rates for values of $s= \{0, 1, 2\}$ . In each panel, the horizontal axis shows the value of the inflation response, $\theta_\pi$ , and the vertical axis shows the value of the unemployment response, $\theta_u$ . The contour charts are constructed by computing the loss for each pair of policy rule coefficients along a grid. The contour surface traces the losses corresponding to the values of these response coefficients. The coordinates corresponding to the minimum loss (marked with an "x") identify the optimal parameters, among the set of values along the grid that we evaluated, for the underlying rule.¹¹ Thus, from the top-left panel, the optimal level rule under perfect knowledge is given by: $i_t = \hat r_{t}^*+\bar\pi^e_{t+3} { + 0.6} (\bar\pi^e_{t+3} - \pi^*) { -3.2} (u_{t-1} - \hat u^*_{t}).$

As can be seen, the level rule optimized under the assumption of perfect knowledge is not robust to uncertainty regarding the formation of expectations or natural rate variation. Comparison of the two left panels, for example, indicates that if the optimal level policy under perfect knowledge were implemented when the economy is governed by and $\kappa = 0.02$ , the loss would be very high relative to the loss associated with the best policy under learning. (The same is true for the classic Taylor rule, with $\theta_\pi=0.5$ and $\theta_u=-1.0$ .) One problem with the optimal level rule under perfect knowledge is that policymaker misperceptions of the natural rates of interest and unemployment translate into persistent overly expansionary or contractionary policy mistakes. In such circumstances, the policy rule's rather timid response to inflation is insufficient to contain inflation expectations near the policymaker's target. This is seen in the autocorrelation of inflation, shown in contours plots in Figure 5. The combination of private sector learning and natural rate misperceptions yield an autocorrelation of inflation dangerously close to unity when the optimal policy under perfect knowledge is followed.

For level rules of this type, there is a tradeoff between achieving optimal performance in one model specification and being robust to model misspecification. We have seen that the optimal rule under perfect knowledge is not robust to the presence of imperfect knowledge. For our benchmark case with imperfect knowledge, and $\kappa = 0.02$ , a rule with response coefficients close to $\theta_\pi=1.5$ , $\theta_u=-1.5$ would be best in this family. The greater responsiveness to inflation in this parameterization proves particularly helpful for improving economic stability in this case. But this policy performs noticeably worse if in fact knowledge is perfect.

Next we turn to the alternative policy that avoids gaps from natural concepts altogether. Figure 6 presents comparable iso-loss contours for the difference rule (6) with and :

$\begin{displaymath} i_t = i_{t-1} + \theta_\pi (\bar\pi^e_{t+3} - \pi^*)+ \theta_{\Delta u} \Delta u_{t-1}. \end{displaymath}$

(11)

The structure of this figure is comparable to Figure 4, except that here, the vertical axis in each panel reflects the responsiveness to the change in unemployment, $\theta_{\Delta u}$ . Comparison of Figure 6 with Figure 4 suggests that the difference rule generally yields superior performance, especially when knowledge is imperfect. Further, note that in sharp contrast to the level rule optimized assuming perfect knowledge, the difference rule optimized assuming perfect knowledge appears to be robust to learning and natural rate variation. A difference rule with a response coefficient to inflation of about 1 and to the change in the unemployment rate of about

is nearly optimal both under perfect knowledge and under imperfect knowledge. Indeed, the loss surface is relatively flat in the region of parameters close to this policy.¹² By avoiding policy mistakes related to natural rate misperceptions, this rule keeps inflation--and thereby inflation expectations--under tight control despite the presence of imperfect knowledge.

To get a better sense of how the economy behaves under imperfect knowledge with a well-designed difference rule, Figures 7, 8 and 9 present impulse responses for the difference rule with $\theta_\pi=1$ , $\theta_{\Delta u}=-3$ . The three figures are directly comparable to the impulse responses for the Taylor rule shown earlier in Figures 1, 2, and 3. These responses exhibit some overshooting and secondary cycling as is typical of difference rules. Still, as shown above, the resulting loss is significantly lower than that resulting under the level rules that may not exhibit such oscillations. In contrast to the impulse responses under the Taylor rule, the 70% range of impulse responses under the difference rule shown in these figures is much tighter and concentrated around the impulse response under perfect knowledge. This serves to demonstrate the relative usefulness of this strategy for mitigating the role of imperfect knowledge in the economy. In particular, Figures 8 and 9 show that even without incorporating explicit information about the policymaker's objective in the formation of expectations, this policy rule succeeds in anchoring long-horizon expectations, especially of inflation, quite well under imperfect knowledge.

5.2 Forecast Horizons

Throughout the analysis so far, we have assumed that the policy rule responds to expected inflation at a three-quarter-ahead horizon and to the lagged unemployment rate or the lagged change in the unemployment rate. We also explicitly examine the choice of horizon for the class of difference rules.

We find that under perfect knowledge an outcome-based difference rule that responds to lagged inflation and unemployment performs about as well as forward-looking alternatives, consistent with the findings of Levin, Wieland, and Williams (2003). But, under imperfect knowledge, an optimized difference rule that responds to the three-quarter horizon for expected inflation outperforms its outcome-based counterpart. As discussed in Orphanides and Williams (2005a), under learning, inflation expectations represent an important state variable for the determination of actual inflation that is not collinear with lagged inflation. Thus, expected inflation can be a more useful summary statistic for inflation in terms of a policy rule.¹³

The inflation forecast horizon in the policy rule should not, however, be too far into the future. Rules that respond to inflation expected two or more years ahead generally perform very poorly. Indeed, such rules are prone to generating indeterminacy, as discussed by Levin, Wieland, and Williams (2003). In contrast to inflation, we find that the optimal horizon for the change in the unemployment rate is , meaning that policy should respond to the most recent observed change in unemployment (that for the previous quarter), as opposed to a forecast of the change in the unemployment rate in subsequent periods.

5.3 Alternative Preferences

Next, we explore the sensitivity of the simple policy rules we advocate as a benchmark for successful policy implementation to the assumed underlying policymaker preferences. Recall that in our benchmark parameterization we examined preferences with a unit weight on inflation variability and a weight, $\lambda = 4$ , on unemployment variability, noting that from Okun's law this implies equal weights on inflation and output gap variability. But, as with various other aspects of the policy problem we examine, it is unrealistic to assume that policymakers can have much confidence on the appropriate relative weights they should attach to inflation and employment stabilization in the economy from a public welfare perspective. It is therefore important to know whether a policy under consideration performs well across a range of reasonable alternative preferences. Indeed, robustness to such a range of preferences would appear to be essential for successful implementation of inflation targeting in practice.

Figures 10 and 11 present the iso-loss contours of the benchmark difference rule with weights $\lambda = 1$ and $\lambda = 8$ respectively, comparable to that in Figure 6 with $\lambda = 4$ . The iso-loss contours associated with placing greater emphasis on price stability (Figure 10) or employment stability (Figure 11) suggest that policies derived based on our benchmark loss function would do rather well under either alternative. This speaks well for the robustness of our benchmark difference rules as guides for policy, as a robust policy guide ought to perform well across a range of reasonable alternative preferences.

5.4 Explicit Numerical Inflation Objective

The features of policy we described so far may be important not just for characterizing policy under inflation targeting but also for characterizing policy for non-IT central banks that may not have an explicit quantitative inflation target but, nonetheless, also recognize the value of price stability and well-anchored inflation expectations for fostering overall economic stability. Next, we turn to the examination of what is arguably the most important distinguishing characteristic of inflation targeting, relative to alternative policy frameworks, namely the specification of an explicit numerical inflation objective.

As in Orphanides and Williams (2004, 2005a), we formalize this element of transparency by positing that announcement of an explicit target is taken at face value by economic agents who incorporate this information directly into their recursive forecasting algorithm. We implement the idea of a known numerical inflation target by modifying the learning model used by agents in forecasting to have the property that inflation asymptotically returns to target. No other changes are made to the model or the learning algorithm. In essence, with a known inflation target, agents need to estimate one fewer parameter in their forecasting model for inflation than what they would need to do if they did not know the precise numerical value of the central bank's inflation objective. More precisely, we assume that agents estimate reduced-form forecasting equations for the unemployment rate and the inflation rate just as before. We then solve the resulting two-equation system for its steady-state values of the unemployment rate and the interest rate, assuming that the steady-state inflation rate equals its target value. We then modify the forecast equation for the interest rate by subtracting the steady-state values of each variable from the observed values on both sides of the equation and by eliminating the constant term. This equation is estimated using the constant-gain algorithm. The resulting three-equation system has the property that inflation asymptotically goes to target. This system is used for forecasting as before.

To trace the role of a known target in the economy under alternative policy rules, we compute impulse responses corresponding to the same policy rules examined earlier. Figure 12 shows the impulse responses to the inflation and unemployment shocks for the classic parameterization of the Taylor rule, assuming that the central bank has communicated its inflation objective to the public. Compared to Figure 1, the responses of inflation under imperfect knowledge are more tightly centered around the responses under perfect knowledge. The differences are more noticeable when examining long-run inflation expectations. Figures 13 and 14 show the impulse responses of longer-run inflation and interest rate expectations, following the format of Figures 2 and 3. Communication of an explicit numerical inflation objective yields a much tighter range of responses of longer-run inflation expectations that are centered around the actual target. Absent here is the upward bias in the response of inflation expectations evident in the case where agents do not know the target. Interestingly, although knowledge of the long-term inflation objective anchors long-term inflation expectations much better, it is unclear whether this translates to a much reduced sensitivity of forward interest rates to economic shocks.¹⁴

Figures 15, 16, and 17 show the impulse responses corresponding to the difference rule specified as above and assuming the central bank has successfully communicated its objective to the public as described above. Short-run expectations tend to cluster around those that obtain under perfect knowledge. The median responses are remarkably close to those under rational expectations and the 70% ranges tend to be quite narrow, especially for inflation. Long-horizon inflation expectations are extremely stable under the difference rule coupled with an explicit numerical inflation objective. For instance, the behavior of 10-year ahead inflation expectations is virtually indistinguishable from what would be expected under perfect knowledge. Forward interest rates, however, continue to show some small movements.

Based on these impulse responses, the expected benefits of announcing an explicit inflation target may be quite different depending on the policy rule in place. In terms of anchoring long-horizon inflation expectations, for example, the benefits of a known target seem considerably larger if policy follows the classic parameterization of the Taylor rule than if policy is based on a well-designed difference rule. The extent of these benefits also depends on the precise degree of imperfections in the economy, that is the learning rate, $\kappa$ , and variation in natural rates, , in our model. In the limiting case of rational expectations, for instance, the "announcement" of the policymaker's target in our model does not make any difference at all, as agents already know the policymaker's preferences and objectives, by assumption.

To obtain a clearer picture of the stabilization benefits of a known inflation target in an environment of imperfect knowledge, we can compare the performance of an economy with a known target to that with an unknown target for a given set of policies.

**Table 2:** The Role of An Explicit Quantitative Inflation Objective - A: Taylor Rule ( $\theta_\pi=0.5$ , $\theta_u=-1.0$ )
	Unknown $\pi^*$ Standard Deviation $\pi$	Unknown $\pi^*$ Standard Deviation	Unknown $\pi^*$ Standard Deviation $\Delta i$	Unknown $\pi^*$ Loss	Known $\pi^*$ Standard Deviation $\pi$	Known $\pi^*$ Standard Deviation	Known $\pi^*$ Standard Deviation $\Delta i$	Known $\pi^*$ Loss
0	3.66	0.99	2.80	25.1	3.37	0.95	2.67	22.1
1	4.35	1.11	3.01	32.9	3.76	1.04	2.80	26.4
2	5.21	1.24	3.29	44.2	4.21	1.18	3.02	32.5

**Table 2 (continued):** The Role of An Explicit Quantitative Inflation Objective - B: Taylor Rule ( $\theta_\pi=1.5$ , $\theta_u=-1.5$ )
	Unknown $\pi^*$ Standard Deviation $\pi$	Unknown $\pi^*$ Standard Deviation	Unknown $\pi^*$ Standard Deviation $\Delta i$	Unknown $\pi^*$ Loss	Known $\pi^*$ Standard Deviation $\pi$	Known $\pi^*$ Standard Deviation	Known $\pi^*$ Standard Deviation $\Delta i$	Known $\pi^*$ Loss
0	2.43	0.84	3.15	18.6	2.34	0.82	3.02	17.2
1	2.62	0.96	3.31	21.5	2.37	0.89	3.05	18.1
2	2.93	1.13	3.58	26.5	2.65	1.08	3.29	22.5

**Table 2 (continued):** The Role of An Explicit Quantitative Inflation Objective - C: Difference Rule ( $\theta_\pi=1$ , $\theta_{\Delta u}=-3$ )
	Unknown $\pi^*$ Standard Deviation $\pi$	Unknown $\pi^*$ Standard Deviation	Unknown $\pi^*$ Standard Deviation $\Delta i$	Unknown $\pi^*$ Loss	Known $\pi^*$ Standard Deviation $\pi$	Known $\pi^*$ Standard Deviation	Known $\pi^*$ Standard Deviation $\Delta i$	Known $\pi^*$ Loss
0	2.15	0.89	2.20	12.6	2.03	0.80	2.08	11.0
1	2.20	0.98	2.26	13.7	2.08	0.90	2.11	12.0
2	2.35	1.18	2.36	16.6	2.26	1.13	2.23	15.2

Note: All evaluations are for the case of learning with $\kappa = 0.02$ .

Table 2 presents such a comparison when expectations are formed with our benchmark learning rate, $\kappa = 0.02$ . In the top panel, we present the results for the classic Taylor rule with $\theta_\pi=0.5$ and $\theta_u=-1.0$ , whose properties under learning without a known inflation target were examined in detail in section 4. In the middle panel, we present the results for the Taylor rule with $\theta_\pi=1.5$ and $\theta_u=-1.5$ , which, as described before, performs best within this family of level rules when $\kappa = 0.02$ and

. In the bottom panel, we present comparable results for the difference rule with $\theta_\pi=1$ and $\theta_{\Delta u}=-3$ , which, as shown earlier, performs well even under learning with an unknown inflation target.

The stabilization performance of the economy uniformly improves with a known inflation target under all three rules. For each rule, the variability of inflation, real activity, and interest rates is smaller when the central bank successfully communicates its numerical inflation objective to the public. But there are noticeable differences in the extent of this improvement. The gains of making the target known appear substantial under the classic Taylor rule. A more modest reduction in volatility is evident for the more aggressive level rule while the gains associated with a known target are quite small when policy is based on the more robust difference rule.

Indeed, an important lesson suggested by these results is that the improvement associated with successfully communicating a target can be rather small, compared to the improvement that could be expected from adopting the other elements of robust policies. For example, abandoning policy based on even the best parameterization of the level Taylor rule in favor of the robust difference rule yields a larger benefit than communicating a numerical inflation objective but continuing to follow a level rule.

6 Conclusion

Inflation targeting has been a very popular strategy among central banks, particularly in small open economies. However, researchers have struggled with pinning down exactly what IT means in terms of an implementable policy rule. To some, the Taylor Rule, or any monetary policy rule with a fixed long-run inflation target, is a form of IT; to others, IT is identified with solution to a central bank optimization problem in a rational expectations model. One shortcoming of these approaches is that they abstract from the very cause that gave rise to IT in the first place: the loss of a nominal anchor that transpired under previous policy regimes in many countries.

This paper has attempted to put IT strategy back into the context in which it was born, namely one where inflation expectations can endogenously drift away from the central bank's goal. We assume that private agents and the central bank have imperfect knowledge of the economy; in particular, private agents attempt to infer the central bank's goals and reactions through past actions. In such an environment, key characteristics of IT in practice--including transparency, a commitment to price stability, and close attention to inflation expectations--can influence the evolution of inflation expectations and the behavior of the economy.

The problem of imperfect knowledge may be especially acute in small open economies and transition economies that have been drawn to IT. For these countries, many of which have undergone dramatic structural change over the past few decades, conclusions regarding the characteristics of optimal monetary policy rules that are based on rational expectations models with perfect knowledge cannot provide trustworthy guidance. Our analysis suggests that policies formulated and communicated in terms of gaps from natural rate concepts that are fundamentally unknowable may be particularly problematic. A more reliable approach to successful implementation of inflation targeting is to search for monetary policy strategies that are robust to imperfect knowledge.

References

Batini, Nicoletta and Andrew Haldane (1999), "Forward-looking Rules for Monetary Policy." In Monetary Policy Rules, edited by John B. Taylor. Chicago: University of Chicago.

Beechey, Meredith (2004). "Learning and the Term Structure of Interest Rates." University of California, Berkeley, mimeo, April.

Bernanke, Ben S. and Frederic S. Mishkin (1997). "Inflation Targeting: A New Framework for Monetary Policy?" Journal of Economic Perspectives, Spring, 11(2), pp. 97-116.

Bernanke, Ben S., Thomas Laubach, Frederic S. Mishkin, and Adam Posen (1999). Inflation Targeting: Lessons from the International Experience, Princeton, NJ: Princeton University Press.

Clarida, Richard, Jordi Galí, and Mark Gertler (1999), "The Science of Monetary Policy," Journal of Economic Literature, 37(4), 1661-1707, December.

Clark, Todd, and Sharon Kozicki (2005). "Estimating Equilibrium Interest Rates in Real Time," The North American Journal of Economics and Finance, 16(3), 395-413.

Cogley, Timothy (2005). "Changing Beliefs and the Term Structure of Interest Rates: Cross-Equation Restrictions with Drifting Parameters." Review of Economic Dynamics, 8(2), 420-451, April.

Cook, T. and T. Hahn (1989), "The Effect of Changes in the Federal Funds Rate Target on Market Interest Rates in the 1970s." Journal of Monetary Economics, 24, pp. 331-351.

Cukierman, A. and F. Lippi (2005), "Endogenous Monetary Policy with Unobserved Potential Output," Journal of Economic Dynamics and Control, 29(11), 1951-1983, November.

Croushore, Dean (1993). "Introducing: The Survey of Professional Forecasters," Federal Reserve Bank of Philadelphia Business Review, November/December, 3-13.

Croushore, Dean and Tom Stark (2001). "A Real-Time Data Set for Macroeconomists," Journal of Econometrics, 105, 111-130, November.

Evans, George and Seppo Honkapohja (2001). Learning and Expectations in Macroeconomics. Princeton: Princeton University Press.

Faust, Jon and Dale W. Henderson (2004). "Is Inflation Targeting Best-Practice Monetary Policy?" Federal Reserve Bank of St. Louis Review, 86(4), 117-144.

Fuhrer, Jeffrey C. and George R. Moore (1995a) "Inflation Persistence," Quarterly Journal of Economics, 110(1), 127-59.

Fuhrer, Jeffrey C. and George R. Moore (1995b) "Forward-Looking Behavior and the Stability of a Conventional Monetary Policy Rule," Journal of Money, Credit and Banking, 27(4, Part 1), 1060-1070, November.

Gaspar, Vitor and Frank Smets(2002). "Monetary Policy, Price Stability and Output Gap Stabilisation," International Finance, 5(2), Summer, 193-211.

Gaspar, Vitor, Frank Smets, and David Vestin (2005). "Monetary Policy under Adaptive Learning." Working paper, March.

Goodfriend, Marvin (1993). "Interest Rate Policy and the inflation Scare Problem: 1979-1992." Economic Quarterly, Federal Reserve Bank of Richmond, 79 (1), Winter, pp. 1-23.

Goodfriend, Marvin (2004). "Inflation Targeting in the United States?" In The Inflation Targeting Debate, edited by Ben Bernanke and Michael Woodford, University of Chicago Press.

Goodfriend, Marvin and Robert King (1997). "The New Neoclassical Synthesis and the Role of Monetary Policy," NBER Macroeconomics Annual, (12), 231-283.

Gürkaynak, Refet, Brian Sack, and Eric Swanson (2005). "The Excess Sensitivity of Long Term Interest Rates: Evidence and Implication for Macroeconomic Models." American Economic Review.

Judd, John P. and Brian Motley (1992), "Controlling Inflation with an Interest Rate Instrument," Federal Reserve Bank of San Francisco Economic Review, No. 3, 3-22.

Laubach, Thomas and John C. Williams (2003). "Measuring the Natural Rate of Interest," Review of Economics and Statistics, 85(4), 1063-1070.

Kuttner, Kenneth N. (2001). "Monetary policy surprises and interest rates: Evidence from the Fed funds futures market." Journal of Monetary Economics, June, 47(3), pp. 523-544.

Kozicki, Sharon and Peter A. Tinsley (2001a). "Term Structure Views of Monetary Policy Under Alternative Models of Agent Expectations." Journal of Economic Dynamics and Control, 25, pp. 149-184.

Kozicki, Sharon and Peter A. Tinsley(2001b). "What Do You Expect? Imperfect Policy Credibility and Tests of the Expectations Hypothesis." Federal Reserve Bank of Kansas City Working Paper 01-02, April.

Leiderman, Leonardo and Lars E. O. Svensson, eds. (1995), Inflation Targets, London: Centre for Economic Policy Research.

Levin, Andrew, Volker Wieland and John Williams (1999), "Robustness of Simple Monetary Policy Rules under Model Uncertainty." In Monetary Policy Rules, edited by John B. Taylor. Chicago: University of Chicago.

Levin, Andrew, Volker Wieland and John Williams (2003). "The Performance of Forecast-Based Policy Rules under Model Uncertainty." American Economic Review, 93(3), 622-645, June.

Mankiw, N. Gregory and Lawrence H. Summers (1984). "Do Long-Term Interest Rates Overreact to Short-Term Interest Rates?" Brookings Papers on Economic Activity, 1, pp. 223-242.

McCallum, Bennett T. (1988). "Robustness Properties of a Rule for Monetary Policy." Carnegie-Rochester Conference Series on Public Policy, 29, Autumn, 173-203.

McCallum, Bennett T. and Edward Nelson (1999), "Performance of Operational Policy Rules in an Estimated Semiclassical Structural Model." In Monetary Policy Rules, edited by John B. Taylor. Chicago: University of Chicago.

Milani, Fabio (2005). "Expectations, Learning, and Macroeconomic Persitence." mimeo, Univeristy of California, Irvine.

Okun, Arthur (1962). "Potential Output: Its Measurement and Significance," in American Statistical Association 1962 Proceedings of the Business and Economic Section, Washington, D.C.: American Statistical Association.

Orphanides, Athanasios (2003a). "Monetary Policy Evaluation with Noisy Information." Journal of Monetary Economics, 50(3), 605-631, April.

Orphanides, Athanasios (2003b), "Historical Monetary Policy Analysis and the Taylor Rule," Journal of Monetary Economics, 50(5), 983-1022, July.

Orphanides, Athanasios and Simon van Norden (2002), "The Unreliability of Output Gap Estimates in Real Time," Review of Economics and Statistics, 84(4), 569-583, November.

Orphanides, Athanasios and John C. Williams (2002). "Robust Monetary Policy Rules with Unknown Natural Rates." Brookings Papers on Economic Activity, 2:2002, 63-118.

Orphanides, Athanasios and John C. Williams (2004). "Imperfect Knowledge, Inflation Expectations and Monetary Policy." In The Inflation Targeting Debate, edited by Ben Bernanke and Michael Woodford, University of Chicago Press.

Orphanides, Athanasios and John C. Williams (2005a). "Inflation Scares and Forecast-Based Monetary Policy." Review of Economic Dynamics, 8, 498-527.

Orphanides, Athanasios and John C. Williams (2005b). "The Decline of Activist Stabilization Policy: Natural Rate Misperceptions, Learning, and Expectations." Journal of Economic Dynamics and Control, 29(11), 1927-1950, November.

Orphanides, Athanasios and John C. Williams (2005c). "Robust Monetary Policy with Imperfect Knowledge." Working paper.

Orphanides, Athanasios and John C. Williams (2006)."Monetary Policy with Imperfect Knowledge." Journal of the European Economics Association, forthcoming.

Roberts, John M. (1997), "Is Inflation Sticky?" Journal of Monetary Economics, 39, 173-196.

Roley, V.V. and G. H. Sellon (1995). "Monetary Policy Actions and Long Term Interest Rates." Federal Reserve Bank of Kansas City Economic Quarterly, 80, pp. 77-89.

Rotemberg, Julio J. and Michael Woodford (1999), "Interest Rate Rules in an Estimated Sticky Price Model." In Monetary Policy Rules, edited by John B. Taylor. Chicago: University of Chicago.

Rudebusch, Glenn (2002) "Assessing Nominal Income Rules for Monetary policy with Model and Data Uncertainty," Economic Journal, 112, 402-432, April.

Sargent, Thomas J (1993). Bounded Rationality in Macroeconomics. Oxford and New York: Oxford University Press, Clarendon Press.

Sargent, Thomas J. (1999). The Conquest of American Inflation. Princeton: Princeton University Press.

Sheridan, Niamh (2003). "Forming Inflation Expectations," Johns Hopkins University, mimeo, April.

Shiller, Robert J. (1979), "The Volatility of Long-Term Interest Rates and Expectations Models of the Term Structure." Journal of Political Economy December, 87(6), 1190-1219.

Smets, Frank (2003). "Maintaining Price Stability: How Long Is the Medium Term?" Journal of Monetary Economics, September, 50(6), 1293-1309.

Taylor, John B. (1993). "Discretion versus Policy Rules in Practice." Carnegie-Rochester Conference Series on Public Policy, 39, 195-214.

Wicksell, Knut (1898), Interest and Prices, 1936 translation from the German by R. F. Kahn, London: Macmillan.

Williams, John C. (2005). "Robust Estimation and Monetary Policy with Unobserved Structural Change." In Models and Monetary Policy: Research in the Tradition of Dale Henderson, Richard Porter and Peter Tinsley, edited by Jon Faust, Athanasios Orphanides and David L. Reifschneider. Washington: Board of Governors of the Federal Reserve System.

Woodford, Michael (2003). Interest and Prices: Foundations of a Theory of Monetary Policy. Princeton: Princeton University Press.

Zarnowitz, Victor and Phillip A. Braun (1993), "Twenty-two Years of the NBER-ASA Quarterly Economic Outlook Surveys: Aspects and Comparisons of Forecasting Performance." In Business Cycles, Indicators, and Forecasting. Edited by James H. Stock and Mark W. Watson. Chicago: University of Chicago Press.

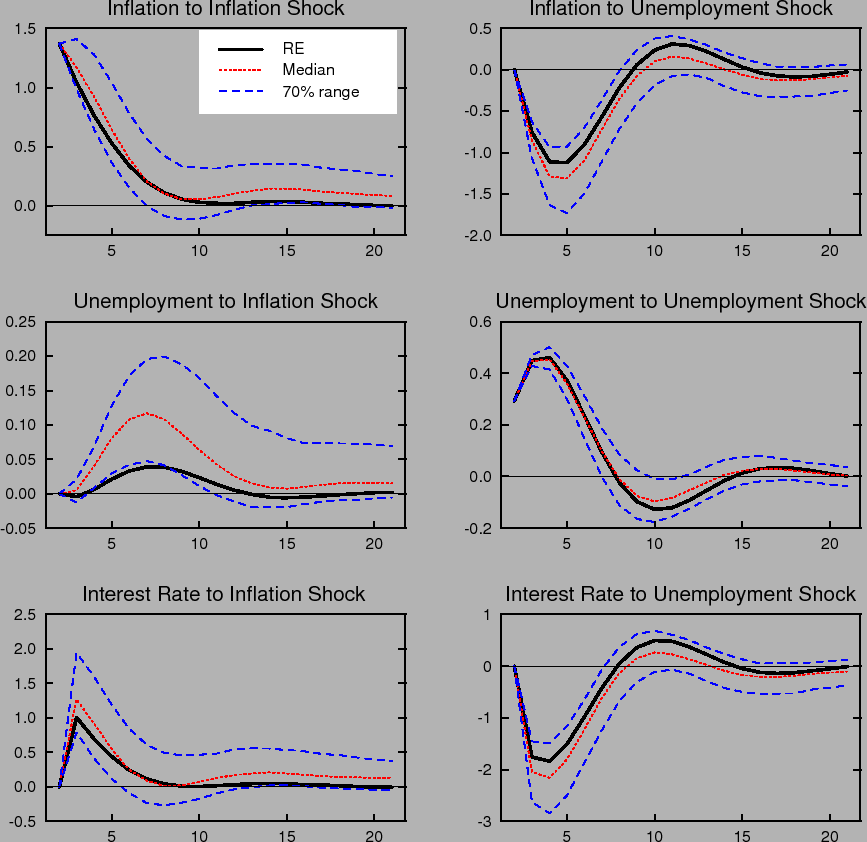
Figure 1: Shows dynamic impulse responses of inflation (top panels), unemployment (middle panels) and interest rate (bottom panels) under the classic Taylor rule. The three panels on the left show the responses to an inflation shock. The panels on the right show the corresponding responses to an unemployment shock. Each panel shows the response with rational expectations and perfect knowledge and the median and 70% range of outcomes under learning.

Figure 1: Impulse Responses under the Taylor Rule: $i_t = \hat r^*_t + \bar\pi^e_{t+3} + 0.5 (\bar \pi^e_{t+3} - \pi^*) - (u_{t-1} - \hat u_t^*).$ Rational expectations with perfect knowledge (RE), and median and 70% range of outcomes under learning with , $\kappa = 0.02$ .

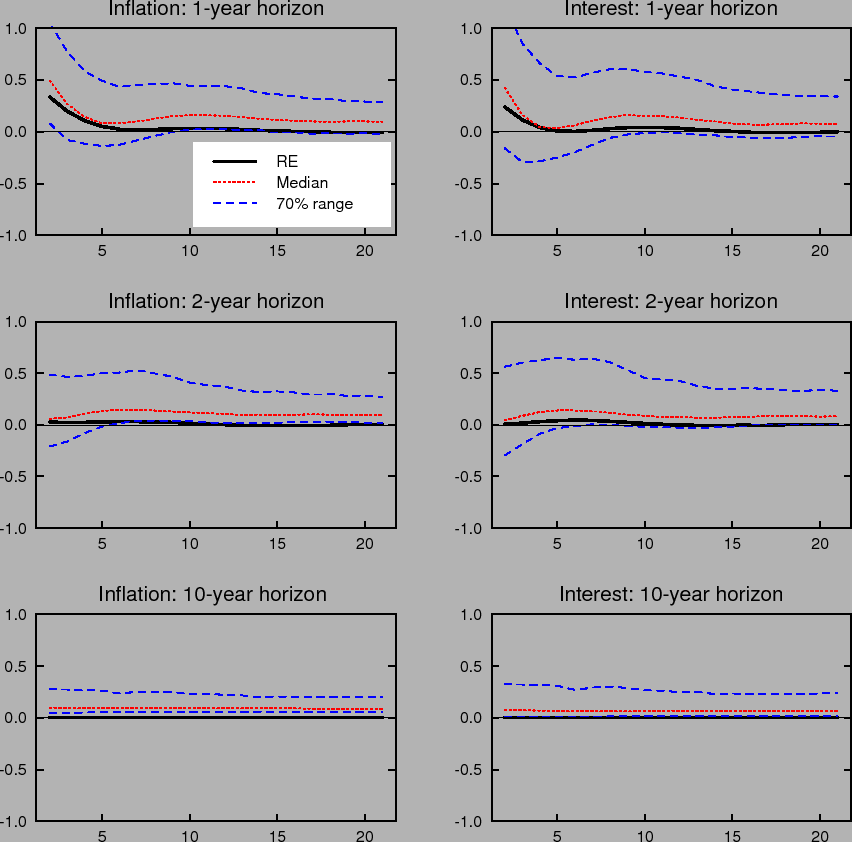
Figure 2: Shows dynamic impulse responses of inflation (top panels), unemployment(middle panels) and interest rate (bottom panels) under the classic Taylor rule. The three panels on the left show the responses to an inflation shock. The panels on the right show the corresponding responses to an unemployment shock. Each panel shows the response with rational expectations and perfect knowledge and the median and 70% range of outcomes under learning.

Figure 2: Impulse Response to Inflation Shock under the Taylor Rule: $i_t = \hat r^*_t + \bar\pi^e_{t+3} + 0.5 (\bar \pi^e_{t+3} - \pi^*) - (u_{t-1} - \hat u_t^*).$ Rational expectations with perfect knowledge (RE), and median and 70% range of outcomes under learning with , $\kappa = 0.02$ .

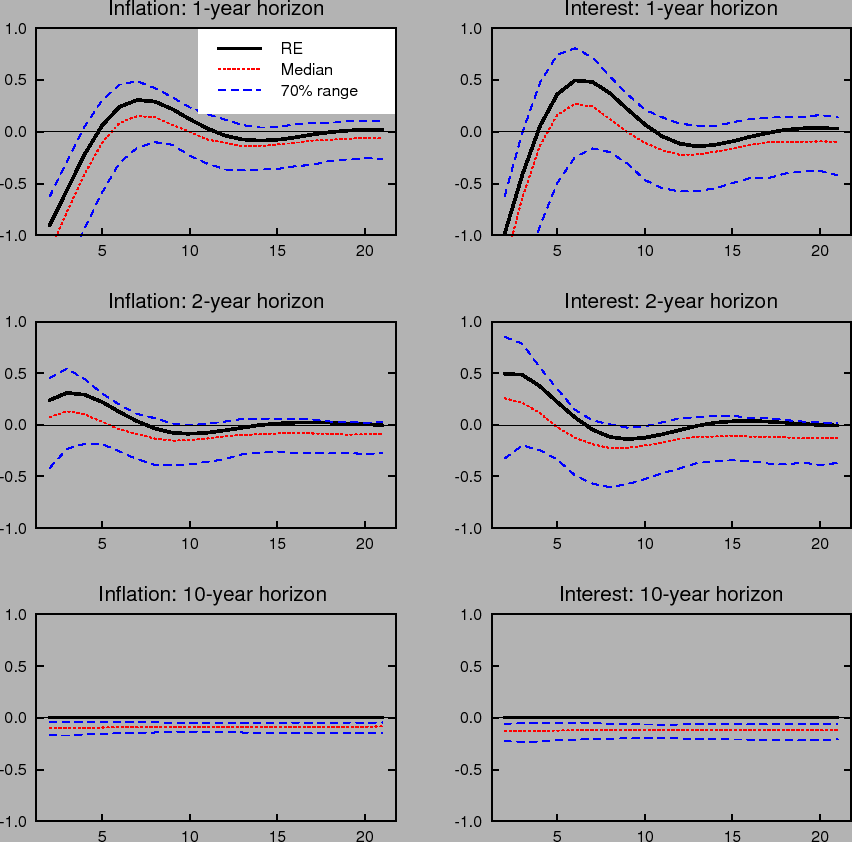
Figure 3: Shows dynamic impulse responses to an unemployment shock for inflation expectations (left column) and interest rate expectations (right column)under the classic Taylor rule. The three panels in each column correspond to 1-year, 2-year and 10-year ahead horizons. Each panel shows the response with rational expectations and perfect knowledge and the median and 70% range of outcomes under learning.

Figure 3: Impulse Response to Unemployment Shock under the Taylor Rule: $i_t = \hat r^*_t + \bar\pi^e_{t+3} + 0.5 (\bar \pi^e_{t+3} - \pi^*) - (u_{t-1} - \hat u_t^*).$ Rational expectations with perfect knowledge (RE), and median and 70% range of outcomes under learning with , $\kappa = 0.02$ .

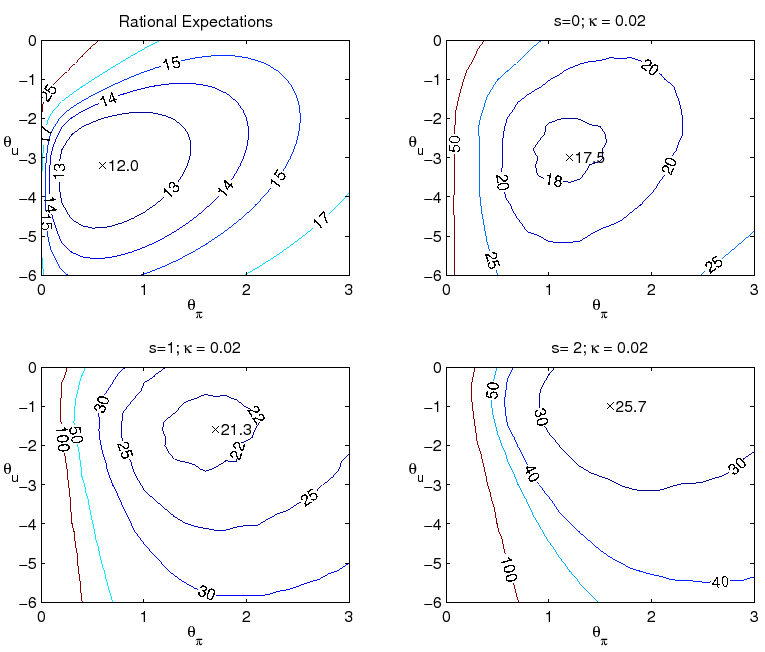
Figure 4: Shows iso-loss contours of the economy with the loss function described in equation 9 with lambda=4 and nu=1 under the level rule. The top left panel shows the loss under rational expectations with constant natural rates while the other panels show the loss under learning with kappa=0.02 and time-varying natural rates for values of s= {0, 1, 2}, respectively.

Figure 4: Performance of Level Rule. $i_t = \hat r^*_t + \bar\pi^e_{t+3} + \theta_\pi (\bar\pi^e_{t+3} - \pi^*) +\theta_u (u_{t-1} - \hat u_t^*)$

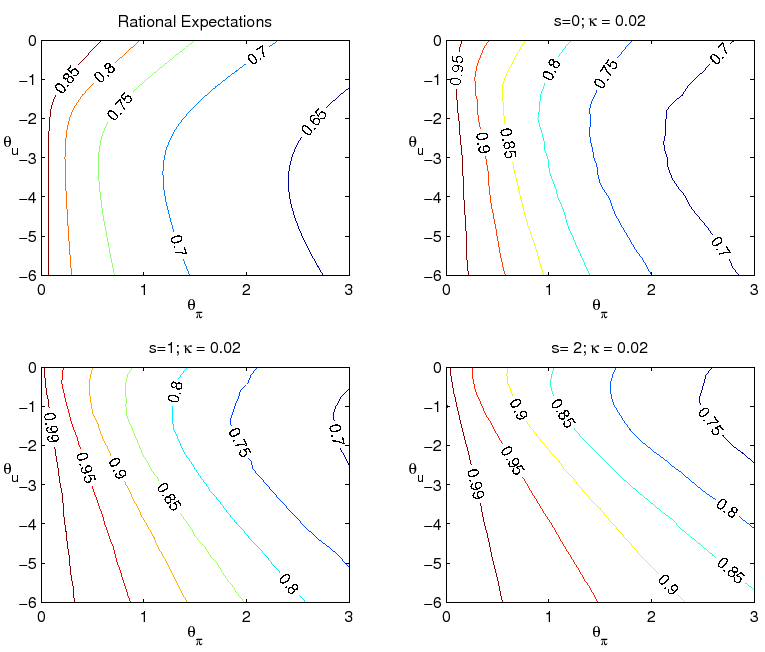
Figure 5: Shows the autocorrelation of inflation under the level rule for alternative assumptions as shown in Figure 4.

Figure 5: Autocorrelation of Inflation under Level Rule. $i_t = \hat r^*_t + \bar\pi^e_{t+3} + \theta_\pi (\bar\pi^e_{t+3} - \pi^*) +\theta_u (u_{t-1} - \hat u_t^*)$

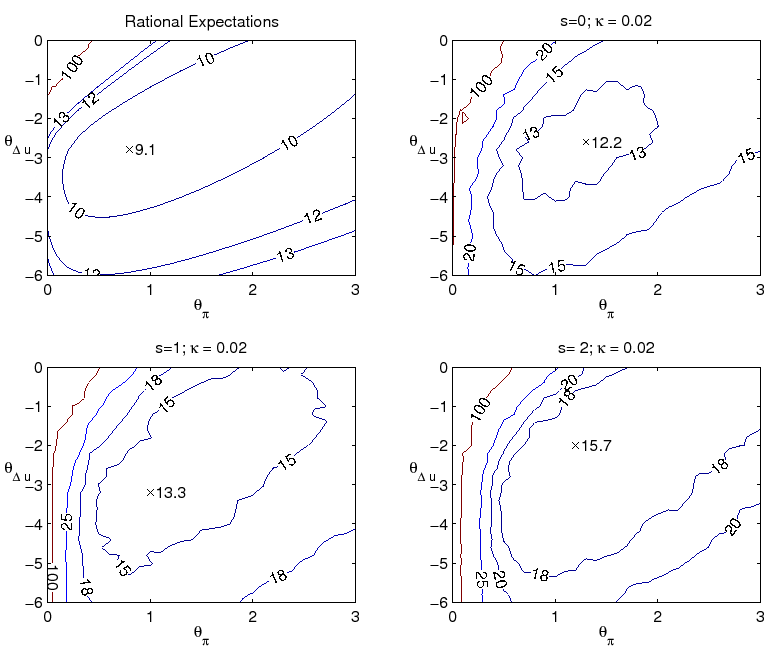
Figure 6: Shows iso-loss contours of the economy with the loss function described in equation 9 with lambda=4 and nu=1 under the difference rule. The top left panel shows the loss under rational expectations with constant natural rates while the other panels show the loss under learning with kappa=0.02 and time-varying natural rates for values of s= {0, 1, 2}, respectively.

Figure 6: Performance of Difference Rule. $i_t = i_{t-1} + \theta_\pi (\bar\pi^e_{t+3} - \pi^*) + \theta_{\Delta u} \Delta u_{t-1}$ .

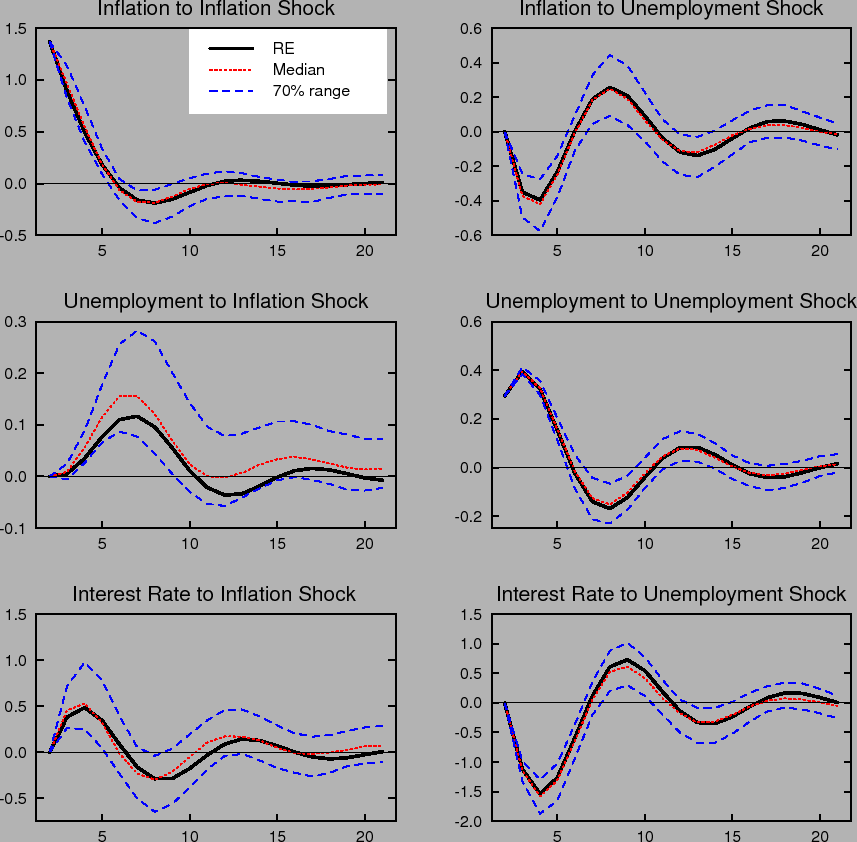
Figure 7: Shows dynamic impulse responses of inflation (top panels), unemployment(middle panels) and interest rate (bottom panels) under the baseline difference rule. The three panels on the left show the responses to an inflation shock. The panels on the right show the corresponding responses to an unemployment shock. Each panel shows the response with rational expectations and perfect knowledge and the median and 70% range of outcomes under learning.

Figure 7: Impulse Response Functions under the Difference Rule: $i_t = i_{t-1} + 1 \, (\bar\pi^e_{t+3} - \pi^*) -3 \, \Delta u_{t-1}.$ Rational expectations with perfect knowledge (RE), and median and 70% range of outcomes under learning with , $\kappa = 0.02$ .

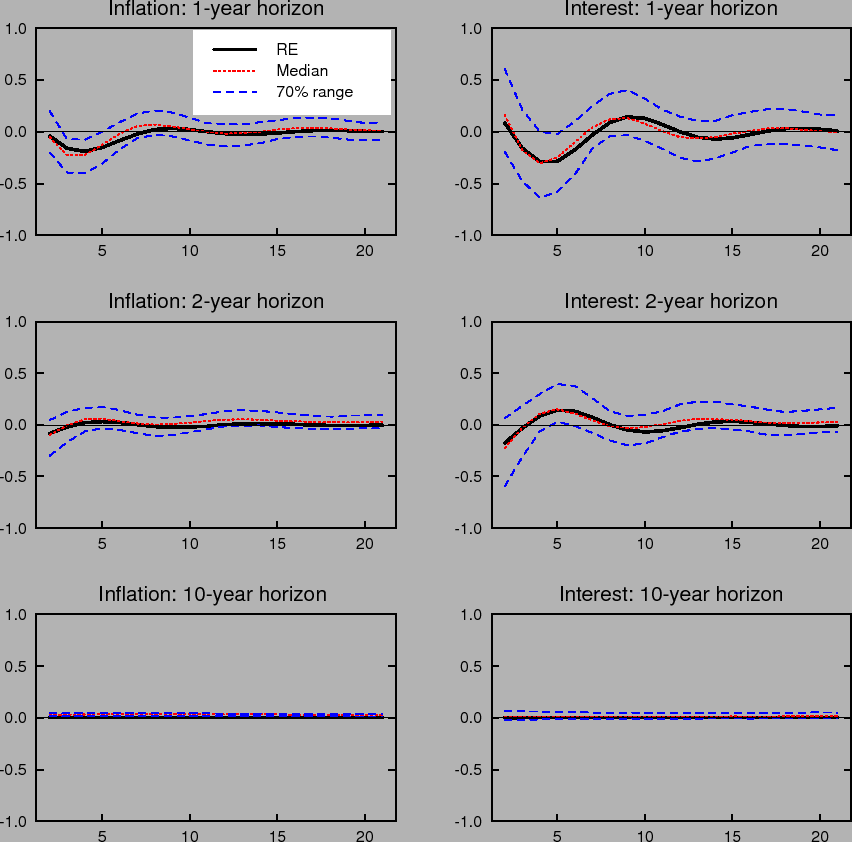
Figure 8: Shows dynamic impulse responses to an inflation shock for inflation expectations (left column) and interest rate expectations (right column)under the baseline difference rule. The three panels in each column correspond to 1-year, 2-year and 10-year ahead horizons. Each panel shows the response with rational expectations and perfect knowledge and the median and 70% range of outcomes under learning.

Figure 8: Impulse Response to Inflation Shock under the Difference Rule: $i_t = i_{t-1} + 1 \, (\bar\pi^e_{t+3} - \pi^*) -3 \, \Delta u_{t-1}.$ Rational expectations with perfect knowledge (RE), and median and 70% range of outcomes under learning with , $\kappa = 0.02$ .

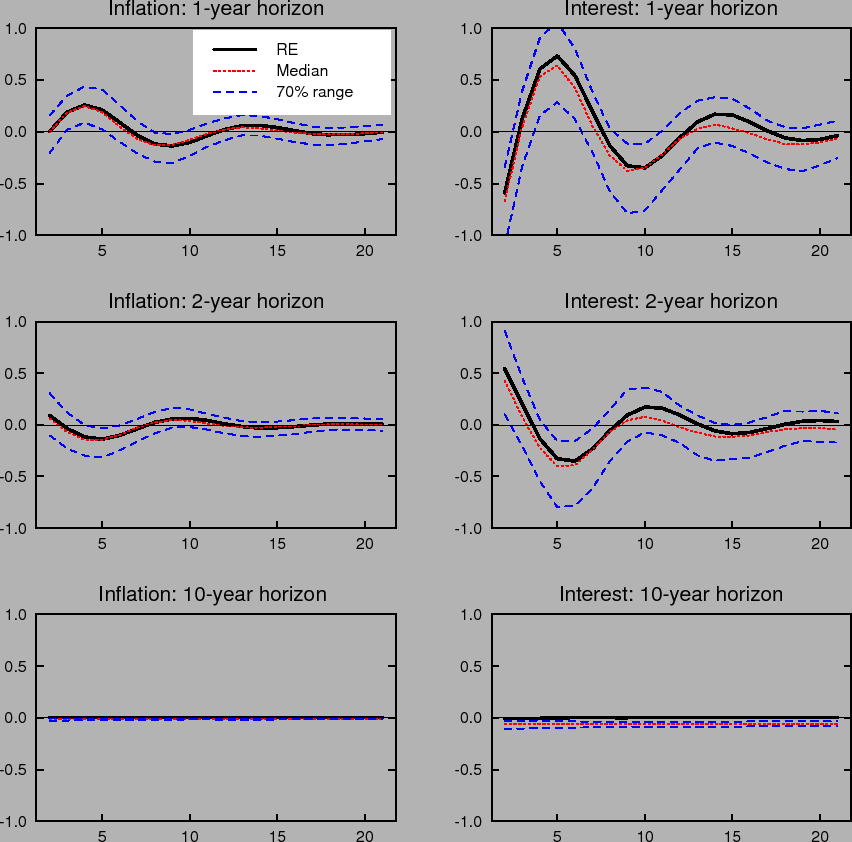
Figure 9: Shows dynamic impulse responses to an unemployment shock for inflation expectations (left column) and interest rate expectations (right column)under the baseline difference rule. The three panels in each column correspond to 1-year, 2-year and 10-year ahead horizons. Each panel shows the response with rational expectations and perfect knowledge and the median and 70% range of outcomes under learning.

Figure 9: Impulse Response to Inflation Shock under the Difference Rule: $i_t = i_{t-1} + 1 \, (\bar\pi^e_{t+3} - \pi^*) -3 \, \Delta u_{t-1}.$ Rational expectations with perfect knowledge (RE), and median and 70% range of outcomes under learning with , $\kappa = 0.02$ .

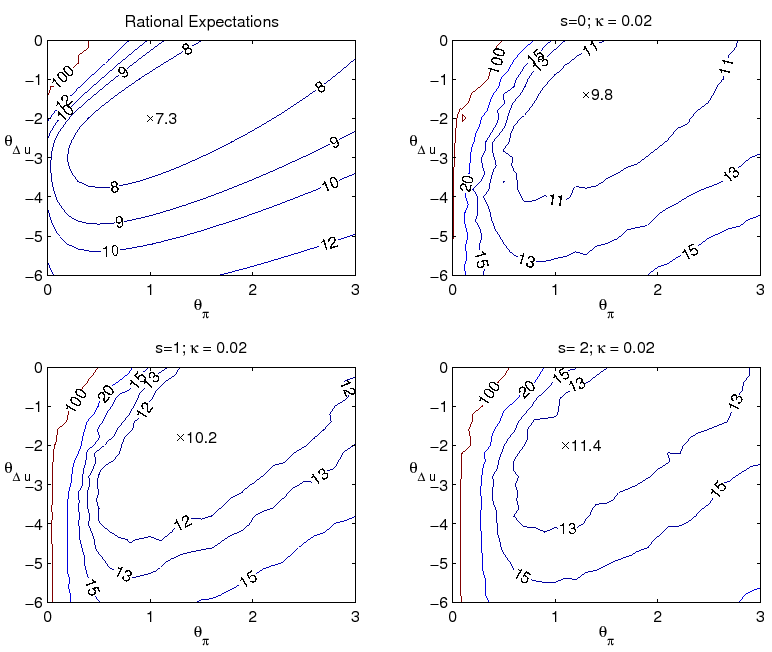
Figure 10: Shows iso-loss contours of the economy with the loss function described in equation 9 with lambda=1 and nu=1 under the difference rule. The top left panel shows the loss under rational expectations with constant natural rates while the other panels show the loss under learning with kappa=0.02 and time-varying natural rates for values of s= {0, 1, 2}, respectively.

Figure 10: Performance of Difference Rule with Greater Emphasis on Inflation Stability ( $\lambda = 1$ ). $i_t = i_{t-1} + \theta_\pi (\bar\pi^e_{t+3} - \pi^*) + \theta_{\Delta u} \Delta u_{t-1}$

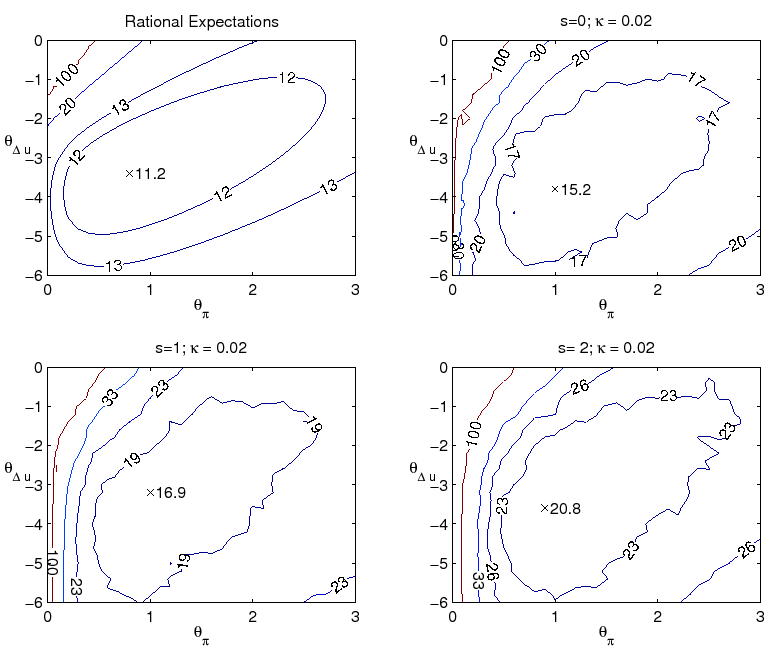
Figure 11: Shows iso-loss contours of the economy with the loss function described in equation 9 with lambda=8 and nu=1 under the difference rule. The top left panel shows the loss under rational expectations with constant natural rates while the other panels show the loss under learning with kappa=0.02 and time-varying natural rates for values of s= {0, 1, 2}, respectively.

Figure 11: Performance of Difference Rule with Greater Emphasis on Employment Stability ( $\lambda = 8$ ). $i_t = i_{t-1} + \theta_\pi (\bar\pi^e_{t+3} - \pi^*) + \theta_{\Delta u} \Delta u_{t-1}$

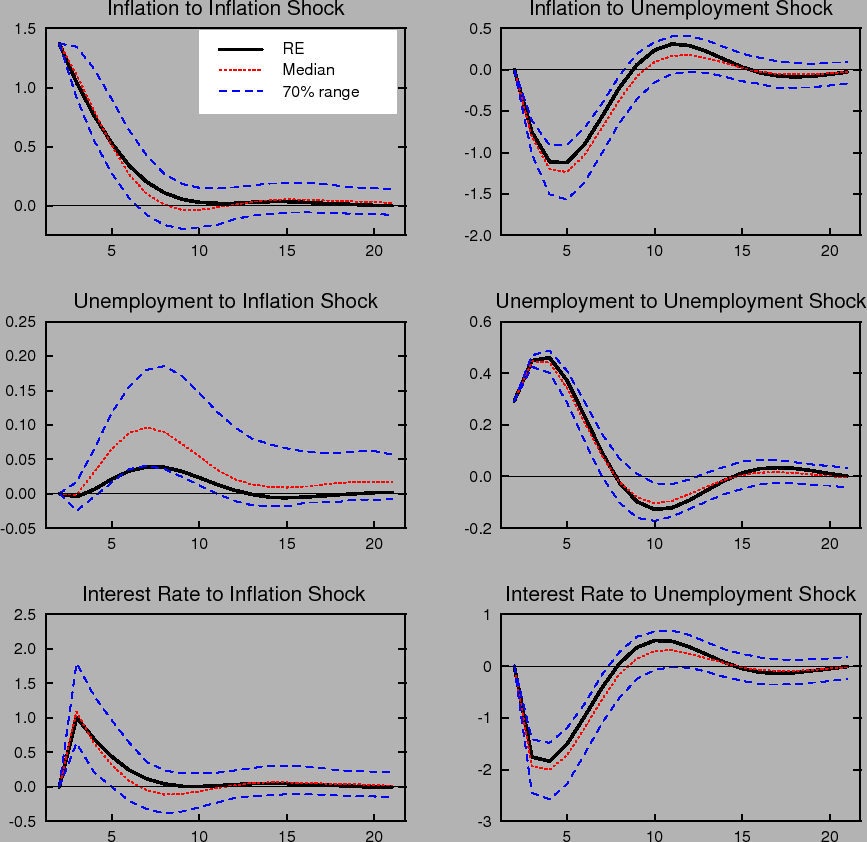
Figure 12: Shows dynamic impulse responses of inflation (top panels), unemployment(middle panels) and interest rate (bottom panels) under the classic Taylor rule when the inflation target is known. The three panels on the left show the responses to an inflation shock. The panels on the right show the corresponding responses to an unemployment shock. Each panel shows the response with rational expectations and perfect knowledge and the median and 70% range of outcomes under learning.

Figure 12: Impulse Response to Inflation Shock with Known $\pi^*$ under the Taylor Rule: $i_t = \hat r^*_t + \bar\pi^e_{t+3} + 0.5 (\bar \pi^e_{t+3} - \pi^*) - (u_{t-1} - \hat u_t^*).$ Rational expectations with perfect knowledge (RE), and median and 70% range of outcomes under learning with , $\kappa = 0.02$ .

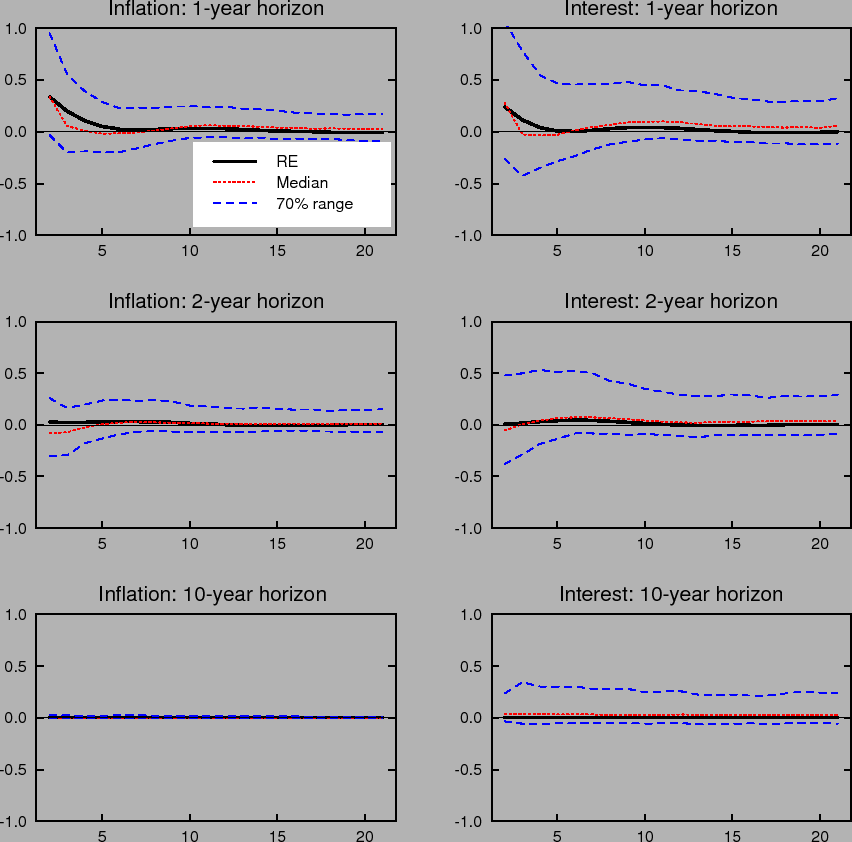
Figure 13: Shows dynamic impulse responses to an inflation shock for inflation expectations (left column) and interest rate expectations (right column)under the classic Taylor rule when the inflation target is known. The three panels in each column correspond to 1-year, 2-year and 10-year ahead horizons. Each panel shows the response with rational expectations and perfect knowledge and the median and 70% range of outcomes under learning.

Figure 13: Impulse Responses to Inflation Shock with Known $\pi^*$ under the Taylor Rule: $i_t = \hat r^*_t + \bar\pi^e_{t+3} + 0.5 (\bar \pi^e_{t+3} - \pi^*) - (u_{t-1} - \hat u_t^*).$ Rational expectations with perfect knowledge (RE), and median and 70% range of outcomes under learning with , $\kappa = 0.02$ .

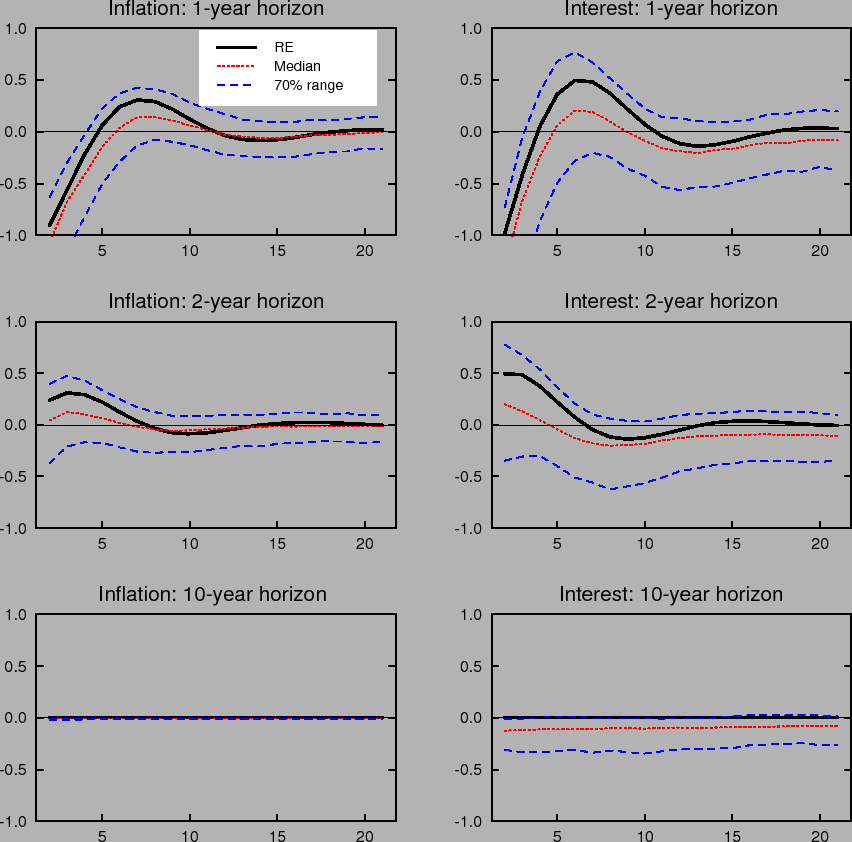
Figure 14: Shows dynamic impulse responses to an unemployment shock for inflation expectations (left column) and interest rate expectations (right column)under the classic Taylor rule when the inflation target is known. The three panels in each column correspond to 1-year, 2-year and 10-year ahead horizons. Each panel shows the response with rational expectations and perfect knowledge and the median and 70% range of outcomes under learning.

Figure 14: Impulse Responses to Unemployment Shock with Known $\pi^*$ under the Taylor Rule: $i_t = \hat r^*_t + \bar\pi^e_{t+3} + 0.5 (\bar \pi^e_{t+3} - \pi^*) - (u_{t-1} - \hat u_t^*).$ Rational expectations with perfect knowledge (RE), and median and 70% range of outcomes under learning with , $\kappa = 0.02$ .

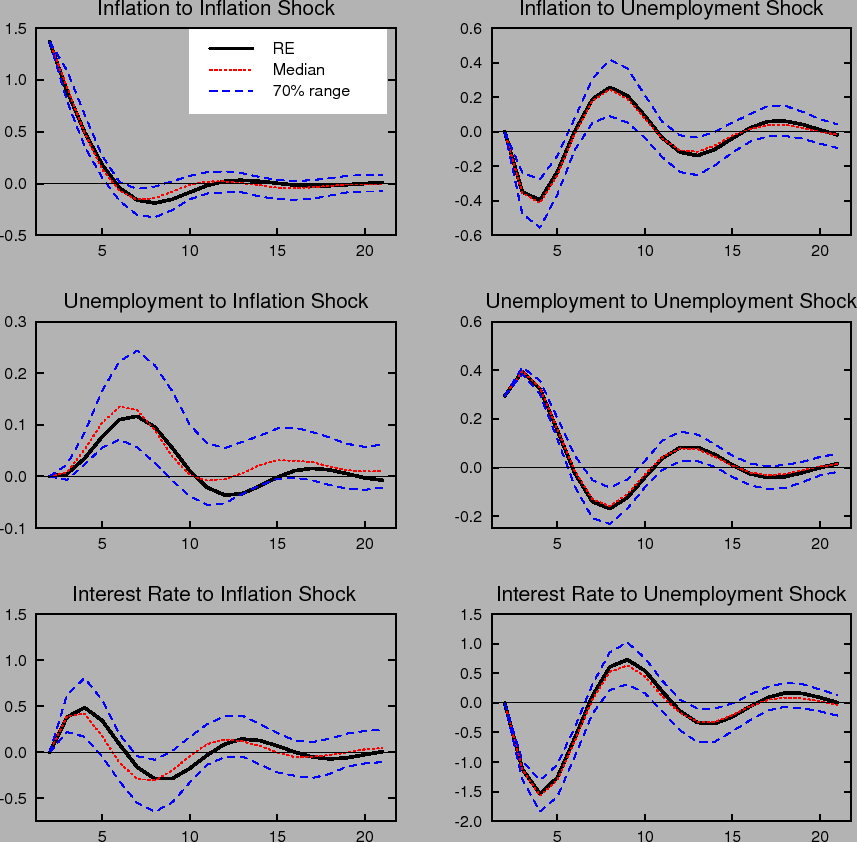
Figure 15: Shows dynamic impulse responses of inflation (top panels), unemployment(middle panels) and interest rate (bottom panels) under the baseline difference rule when the inflation target is known. The three panels on the left show the responses to an inflation shock. The panels on the right show the corresponding responses to an unemployment shock. Each panel shows the response with rational expectations and perfect knowledge and the median and 70% range of outcomes under learning.

Figure 15: Impulse Responses with Known $\pi^*$ under the Difference Rule: $i_t = i_{t-1} + (\bar\pi^e_{t+3} - \pi^*) - 3 \Delta u_{t-1}$ . Rational expectations with perfect knowledge (RE), and median and 70% range of outcomes under learning with , $\kappa = 0.02$ .

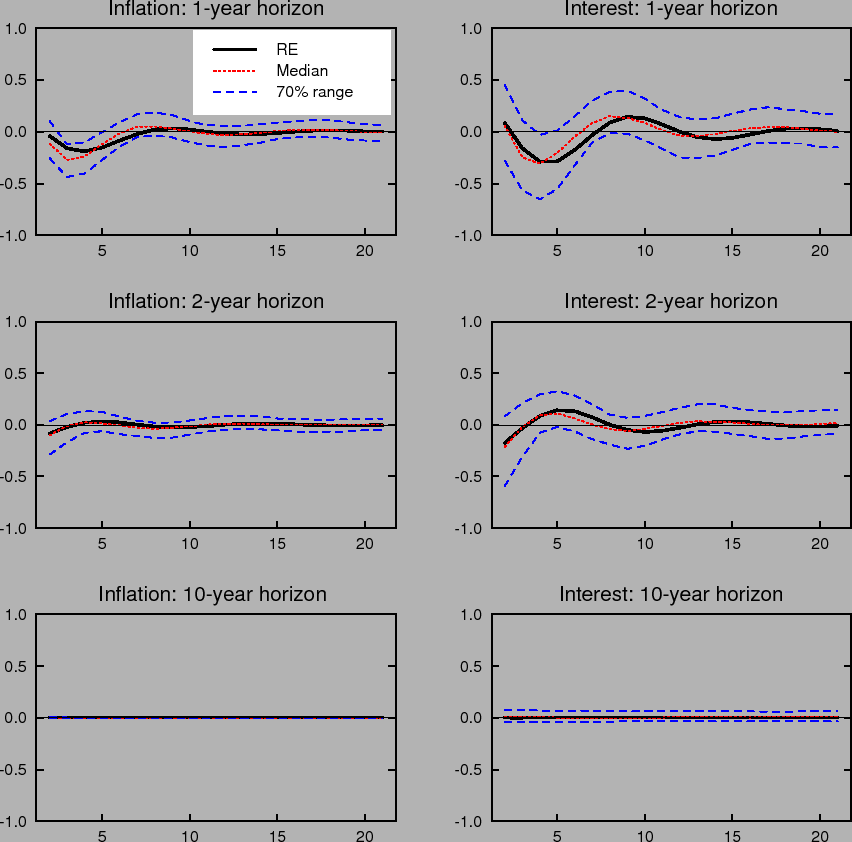
Figure 16: Shows dynamic impulse responses to an inflation shock for inflation expectations (left column) and interest rate expectations (right column)under the baseline difference rule when the inflation target is known. The three panels in each column correspond to 1-year, 2-year and 10-year ahead horizons. Each panel shows the response with rational expectations and perfect knowledge and the median and 70% range of outcomes under learning.

Figure 16: Impulse Responses to Inflation Shock with Known $\pi^*$ under the Difference Rule: $i_t = i_{t-1} + (\bar\pi^e_{t+3} - \pi^*) - 3 \Delta u_{t-1}$ . Rational expectations with perfect knowledge (RE), and median and 70% range of outcomes under learning with , $\kappa = 0.02$ .

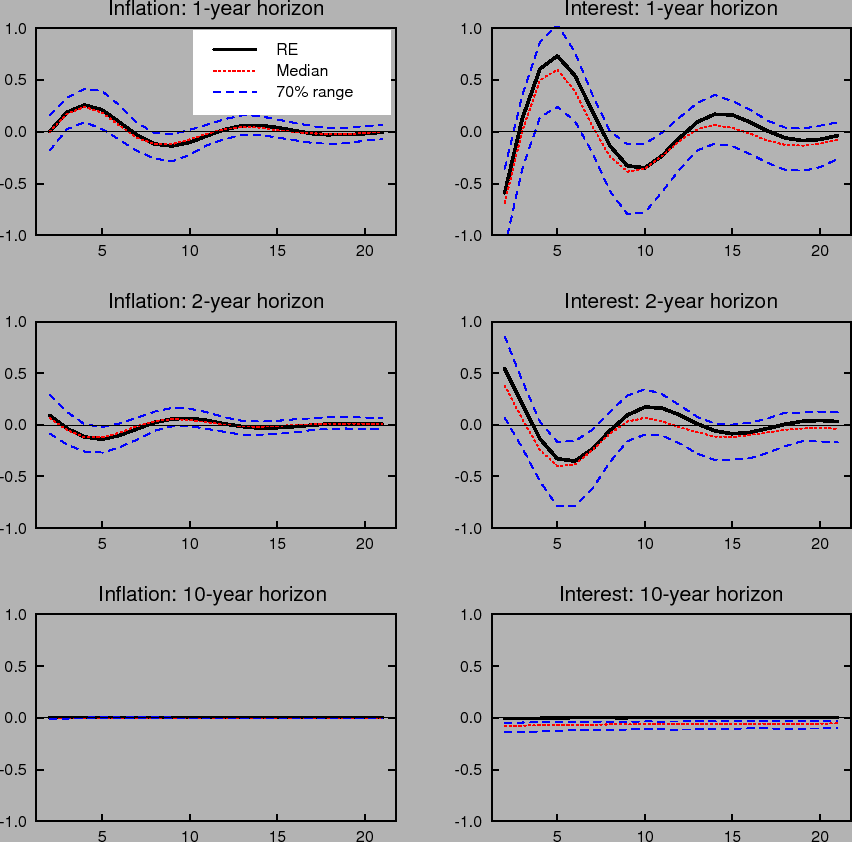
Figure 17: Shows dynamic impulse responses to an unemployment shock for inflation expectations (left column) and interest rate expectations (right column)under the baseline difference rule when the inflation target is known. The three panels in each column correspond to 1-year, 2-year and 10-year ahead horizons. Each panel shows the response with rational expectations and perfect knowledge and the median and 70% range of outcomes under learning.

Figure 17: Impulse Responses to Unemployment Shock with Known $\pi^*$ under the Difference rule: $i_t = i_{t-1} + (\bar\pi^e_{t+3} - \pi^*) - 3 \Delta u_{t-1}$ . Rational expectations with perfect knowledge (RE), and median and 70% range of outcomes under learning with , $\kappa = 0.02$ .

Footnotes

* We would like to thank Richard Dennis, Bill English, Ali Hakan Kara, Thomas Laubach, Nissan Liviatan, John Murray, Rodrigo Vergara, and participants of presentations at the Federal Reserve Board, the Bundesbank, the Federal Reserve Banks of Chicago and New York, the American University, the conference on "Monetary Policy under Inflation Targeting," Santiago, October 20-21, 2005, the conference in honor of Alex Cukierman on "New Developments in the Analysis of Monetary Policy and Institutions," Tel Aviv, December 15-16, 2005, and the British Columbia Macro/Bank of Canada conference, Vancouver, April 7-8, 2006, for useful comments. The opinions expressed are those of the authors and do not necessarily reflect the views of the Board of Governors of the Federal Reserve System or the management of the Federal Reserve Bank of San Francisco.
Correspondence: Orphanides: Federal Reserve Board, Washington, D.C. 20551, Tel.: (202) 452-2654, e-mail: [email protected]. Williams: Federal Reserve Bank of San Francisco, 101 Market Street, San Francisco, CA 94105, Tel.: (415) 974-2240, e-mail: [email protected].org. Return to Text

1. A number of studies have examined in detail the defining characteristics of inflation targeting. See Leiderman and Svensson (1995), Bernanke and Mishkin (1997), Bernanke et al (1999), Goodfriend (2004), and citations therein. Return to Text

2. For discussion and documentation of this imprecision see Orphanides and Williams (2002), Laubach and Williams (2003), Clark and Kozicki (2005) and references therein. See also Orphanides and van Norden (2002) for the related unreliability regarding the measurement of the natural rate of output and implied output gap. Return to Text

3. For analyses of the implications of misperceptions for policy design see Orphanides and Williams (2002); Orphanides (2003a); Cukierman and Lippi (2005); and references therein. Return to Text

4. See Orphanides and Williams (2004, 2005a,b,c); Gaspar and Smets (2002); Gaspar, Smets and Vestin (2005); Milani 2005; and references in these papers. Return to Text

5. See also Judd and Motley (1992), Fuhrer and Moore (1995b), and Orphanides (2003b) for related policy rule specifications and Orphanides and Williams (2002, 2005c) for analyses of a generalization that nests the level rule (5) and difference rule (6). Return to Text

6. Sargent (1993,1999), and Evans and Honkapohja (2001) discuss properties of constant gain learning. Return to Text

7. The value $\kappa = 0.02$ is also in line with the discounting reported by Sheridan (2003) as best for explaining the inflation expectations data reported in the Livingston Survey. Return to Text

8. Based on simulations under rational expectations in which we can compute the moments directly, this sample size is sufficient to yield very accurate estimates of the unconditional variances. In addition, testing indicates that 1000 periods is sufficient to remove the effects of initial conditions on simulated second moments. Return to Text

9. We chose this critical value so that the test would have a small effect on model simulation behavior while eliminating explosive behavior in the forecasting model. Return to Text

10. See Orphanides and Williams 2005a and Beechey 2004 for analysis of the reaction of the term structure of expectations to news in the presence of perpetual learning. Return to Text

11. In constructing the loss contour charts, we only evaluate the losses along the points of the grid. Thus, the minima reported in the charts are approximate and do not correspond precisely to the true minimum values. In cases where the true optimal policy rule coefficients lie near the midpoint between two grid points, the true optimal policy will yield a loss that may be slightly lower than that reported in the chart, even after rounding to one decimal place. Return to Text

12. In Orphanides and Williams (2006), we compute the optimal Bayesian policy assuming equal weights across the specifications of learning and natural rate variability considered here. We find that a difference rule with $\theta_{\pi} = 1.1$ and $\theta_{\Delta u} =2.6$ is remarkably robust to uncertainty regarding the degree of imperfect knowledge. Return to Text

13. Using a simpler model, Orphanides and Williams (2005a) show that with certain parameterizations of the loss function it is better to respond to actual inflation and in others, it pays to respond to expected inflation. A hybrid rule that responds to both actual and expected inflation outperforms either type of simple rule that responds to one or the other. Return to Text

14. Note, however, that these comparisons are based on the assumption that forecasts of these rates are governed by the same learning process governing the expectations for inflation and economic activity at shorter-horizons that matter for the determination of economic outcomes in the model. If, instead, the long-horizon interest rate expectations embedded in financial markets reflect additional knowledge, that could result in smaller deviations from the perfect knowledge benchmark than those presented here. Return to Text