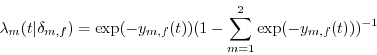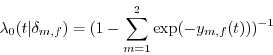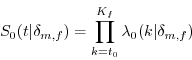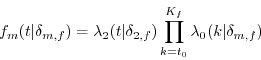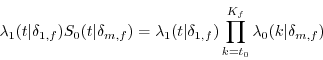FRB: Finance and Economics Discussion Series: Screen Reader Version - The relocation decisions of working couples

Skip to: [Printable Version (PDF)] [Bibliography] [Footnotes]

Finance and Economics Discussion Series: 2006-33 Screen Reader version ^♣

The Relocation Decisions of Working Couples

Jonathan F. Pingle *

August 2006

Keywords: Relocation, domestic migration

Abstract

Most prime-age married couples in the U.S. today have two labor force participants. Migration decisions are more complicated for two-earner couples than for one-earner couples because any gain from moving that accrues to one spouse must be great enough to offset any loss to the other spouse. This paper estimates the extent to which internal migration is depressed by rising earnings equality among spouses. The results indicate that couples' migration propensities are substantially lower the more equal spouses' labor incomes.

1. Introduction

Most professional couples eventually face a co-location decision: whether or not to relocate when one spouse receives a job offer. Accepting a job offered to one spouse increasingly depends on whether the other spouse can relocate too, without compromising career aspirations or family income. A 2004 survey by the outplacement firm, Challenger, Gray & Christmas showed a sharp drop in the willingness of displaced managers and executives to relocate--the primary concern cited was a working spouse. According to the study, the relocation rate of displaced executives with employed spouses declined 54 percent between 1995 and 2004. In addition, two-earner couples are not limited to professionals. Among blue-collar workers, the job of one spouse can tie the other spouse to a location.

The analysis in this paper shows that as the labor incomes from husbands and wives have become more equal, the probability of migration has fallen dramatically. The empirical specifications are duration models that estimate the influence of relative labor incomes of spouses on their hazard rate of migration out of U.S. states and metropolitan statistical areas (MSA). Admittedly, relative incomes are endogenous, which can not be satisfactorily addressed in an instrumental variables setting. However, several specifications are considered, and several complications addressed, which altogether reveal a surprisingly robust relationship, even conditional on labor supply decisions on the extensive margin or intensive margin (part-time work). The fact that the relative labor income of spouses is such a robust predictor of migration propensities is consistent with several economic models of household decisions.

During the last 30 years wives' contributions to married couples' incomes has risen noticeably. The research literature suggests that this happened for a host of reasons ranging from the diffusion of the birth control pill to the implementation of child and family leave policies.¹ Intuitively, as labor incomes of husbands and wives become more equal--or the contribution of their wages to household consumption becomes more equal--then the relative wage gain one spouse receives from relocation needs to be increasingly large in order to offset any disruption to the earnings stream provided by the other spouse, in particular large enough to offset the earnings lost by moving. This suggests that the more equal the contributions of each spouse's labor income to household income, the less likely a couple will migrate.

This empirical result is an important contribution to the migration and labor supply literatures because less worker migration implies stickier labor supply adjustment. Migration among prime age workers is, in general, very sticky, and two-earner couples with school-age children are extremely unlikely to relocate. Changes in migration propensities for these workers have important implications for how workers are distributed across urban areas. As male and female earnings converge, location decisions may increasingly become an absorbing state, which has implications for the ability of cities to attract working couples.

2. Literature review²

The common economic model of migration, built in the framework of a human capital model by Larry Sjaastad (1962), implies that in order to relocate, the present value of all future gains from moving need to outweigh the costs. Jacob Mincer (1978) extended that framework to model a family migration decision. He noted that to undertake a move, the future gains to one spouse would need to be large enough to offset any lost income (or utility) to the other. The model assumed a joint distribution for husband and wife wage shocks, and implied that married couples' migration probabilities rise the more highly correlated the arrival probabilities of two (net) positive wage offers. In other words, larger urban areas provide more wage offers, and thus it is more likely that both spouses instead of just one draw a beneficial wage offer from that location. Further, Mincer's model implies that migration for two-earner couples should move closely with vacancy rates at a business cycle frequency as the relative abundance of vacancies is likely to increase the odds of two beneficial offers reaching the couple.³

Few contributions to the literature on the migration propensities of two-earner couples in the U.S. have been made since Mincer (1978), in particular whether two-earner couples are in fact less likely to move than one-earner couples. Also, Mincer's paper is based on early 1970s data, an era with very different household labor supply patterns than today. Even the most recent studies of other aspects of couples' location choice are based on pre-1994 data. This paper revisits the influence of having two earners in a couple on the couple's migration decisions and finds that relative income is an important determinant. The relative contributions of wives labor income to household income has risen dramatically since the 1970s, depressing migration rates.

More recent work has evaluated the location choices of educated married couples, dubbed "power couples" by Dora Costa and Matthew Kahn (2001). Costa and Kahn note that by the 1990 decennial census, couples composed of two college graduates were increasingly concentrated in large metropolitan statistical areas (MSA). In theory, a larger city would have more employers, and thus be more likely to satisfy the career desires of both members of a well-educated couple. Less populated areas, with a narrower array of job vacancies, would be less likely satisfy both members of the couple.⁴ The hypothesis that pairs of acceptable job offers for married couples are more prevalent in larger cities coincides with the traditional theories of family migration of Mincer (1978) and Robert H. Frank (1978).

Of course, cities want to lure the educated. No city wants "brain drain"--the out-migration of the most productive labor and part of a city tax base. As Costa and Kahn (2001) point out, the propensity of skilled workers to migrate would determine the ability of cities to adjust to positive regional labor market shocks--some smaller cities might find it difficult to lure skilled workers if co-location decisions matter. If the migration of working couples is limited, firms may be less likely to locate in cities that are small or that have fewer college graduates. This would reinforce the negative effects of the out-migration of skilled workers.

Understanding whether the rise of two-earner couples depresses labor supply adjustment is not only interesting because of the implications for regional or urban economic development, but also because this is a source of aggregate friction. Robert Shimer (2006) recently proposed a macroeconomic model of the labor market based on mismatch which overcomes the empirical shortcomings of the often-used Mortenson-Pissarides model (Dale Mortensen and Christopher Pissarides, 1999), which has difficulty explaining the relative volatility of unemployment during business cycles. The mismatch is generated in part by stickiness in regional migration which inhibits labor supply adjustment, and the results below suggest this mechanism is indeed an important labor market feature, as Shimer assumes.⁵ Not only is urban development influenced by two-earner couples' migration, but the aggregate matching function and unemployment durations are influenced by how collocation decisions are made by the nation's 33 million dual-earner married couples.

3. Migration and earnings trends

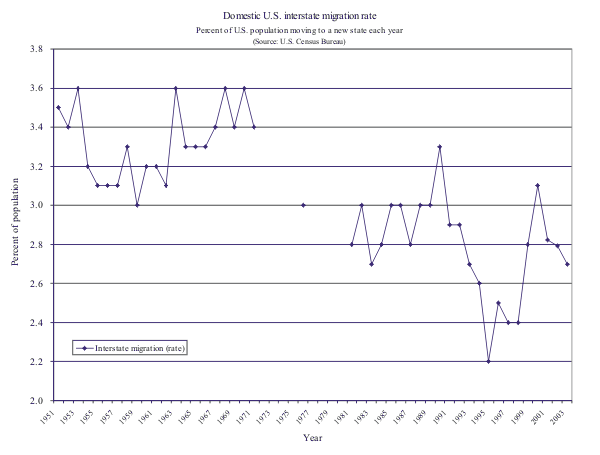
Figure 1: Domestic U.S. interstate migration rate. ⁶

$Figure 1: Domestic U.S. interstate migration rate. Figure 1 depicts the Census Bureau estimate of the fraction of the U.S. population that moves to a new U.S. state each year. On balance the fraction of the population who undertakes an interstate move each year has declined since the 1950s and 1960s when 3.4 percent of the population was moving each year. Recently, about 2.8 percent of the population has been moving to a new state each year.$

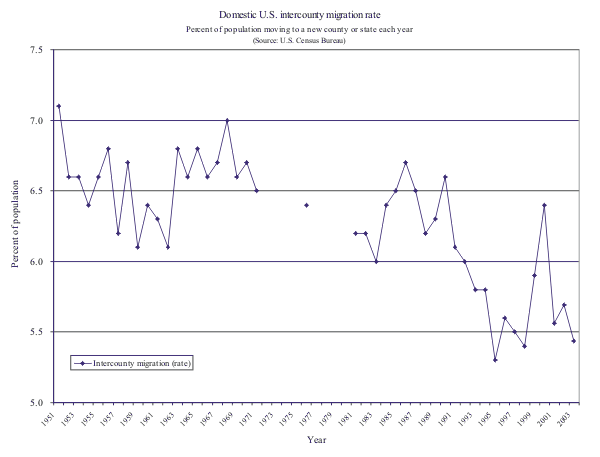
Figures 1 and 2 show the trends in domestic migration during the past 50 years. The migration rates are those reported by the U.S. Census Bureau and show the fraction of the population that moves to a new state each year (Figure 1) or moves to a new county or new state each year (Figure 2). Both migration rates have trended down during the post-war period (as a share of the 2003 population, a percentage point represents nearly 3 million people). A substantial fraction of the decline can be explained by the dwindling presence of the military (and military families) in the U.S. population since the Vietnam war (see Pingle, 2006). When individuals not associated with the military are removed from the rates, migration trends do not decline as steeply. In addition, the aging of the baby-boomers has put slight downward pressure on migration rates because migration is highest among young adults.

Figure 2 Domestic U.S. intercounty migration rate.

$Figure 2: Domestic U.S. intercounty migration rate. Figure 2 depicts the Census Bureau estimate of the fraction of the U.S. population that moves to a new county or U.S. state each year. On balance the fraction of the population who undertakes a move to a location outside their initial county of residence each year has declined since the 1950s and 1960s when 6.5 percent of the population was moving each year. Recently, about 5.5 percent of the population has been moving to a new county or state each year.$

However, in an era of high-speed communication, higher levels of education, interstate media coverage, and cheap air travel, even flat migration trends are a bit of a surprise. For example, education levels have been shown to raise migration propensities, and the average level of educational attainment in the population has risen over time. In addition, macroeconomists generally think that job search has become more efficient which should facilitate acquiring out-of-state information and lead to more job-related relocation. Similarly, smaller families and the later ages at which people marry should increase migration rates. One only has to look at the incredible growth in the Southwest and Southeast portions of the country to acknowledge that migration remains a vibrant part of American economic development.

Table 1: Married-couple earnings (selected years, in thousands)
Year	Married-couple families	Husbands and wives both with earnings	Percent husband and wives both with earnings	Wives earning more than husband	Percent wives earning more than husband	Full-time women's earnings as a percent of men's*	Contribution of wives' earnings to family income (median pct.) *
2003	57,725	33,189	57.5	8,355	25.2	79.4	35.2
2002	57,327	33,531	58.5	8,394	25.0	77.9	34.8
2001	56,755	33,666	59.3	8,109	24.1	76.4	34.4
2000	56,598	33,876	59.9	7,906	23.3	76.9	33.5
1999	55,315	33,344	60.3	7,420	22.3	76.5	32.8
1998	54,778	32,783	59.8	7,435	22.7	76.3	32.8
1997	54,321	32,745	60.3	7,446	22.7	74.4	32.7
1996	53,604	32,390	60.4	7,327	22.6	75.0	32.6
1995	53,570	32,030	59.8	7,028	21.9	75.5	31.9
1994	53,865	32,093	59.6	7,218	22.5	76.4	31.9
1993	53,181	31,267	58.8	6,960	22.3	77.1	32.2
1992	53,090	31,224	58.8	6,979	22.4	75.8	32.4
1991	52,457	31,003	59.1	6,499	21.0	74.2	31.3
1987	51,675	29,079	56.3	5,266	18.1	69.8	29.5
1983	50,090	26,120	52.1	4,800	18.4	66.5	28.8
1981	49,630	25,744	51.9	4,088	15.9	64.4	27.3

Source: U.S. Census Bureau, Current Population Survey, Annual Social and Economic Supplements. Table and additional footnotes describing data available at http://www.census.gov/hhes/www/income/histinc/f22.html. Earnings refer to wage or labor earnings.

* Taken from separate data releases. Data on wives' contributions to family income is also based on Current Population Survey data and is available on-line (with more description) at http://www.bls.gov/cps/wlf-table24-2005.pdf. Women's earnings as a percent of men's based on median usual weekly earnings of full-time wage and salary workers, available at http://www.bls.gov/cps/wlf-table16-2005.pdf Return to Table

Table 1 shows data on recent earnings trends among married-couple families. Since the early 1980s, two-earner married couples have become more common than one-earner married couples. In addition, the share of married couples where wives are earning more than husbands has topped one-quarter--up dramatically from the 16 percent in 1981. During that time, the contribution of wives earnings to family income has moved up from 27.3 percent to 35.2 percent, as the wages of full-time women workers have risen relative to full time working men. The bottom line is that wives' labor income comprises an increasing share of the earnings within American families.

Katherine Bradbury and Jane Katz (2005) recently outlined the changes in employment, hours and earnings of married women during the last three decades. The literature on labor supply notes that married women's employment and labor force participation rates have risen in the post-war period along with women's education levels, employment opportunities, and wages. The labor supply literature relates these changes to a long list of possible reasons, including the introduction of the birth control pill, well-developed child care markets, less discrimination, rising skill levels among women, lower marriage rates, rising age at first marriage, less fertility, and child and family leave policies. Although Bradbury and Katz do not try to explain the changes in the contribution of women's earnings to households, the authors note that combining the rise in work and wages, married women's contribution to household earnings have risen dramatically. Among under-55 couples, the ratio of wives' labor earnings to husbands' labor earnings went from 0.14 at the start of the 1970s to 0.36 by the late 1990s. To the extent that the contributions of wives' earnings continues to rise, understanding how these changes lower aggregate migration will help characterize this source of aggregate labor market friction.

4. Data.

The 1996 and 2001 Survey of Income and Program Participation (SIPP) panels were combined for the empirical analysis, together creating a dataset of nearly 40,000 households observed at four-month intervals for up to four years. The survey contains detailed household and individual characteristics at a monthly frequency. Every four months a household is re-interviewed about the preceding four months. For the analysis below, each observation is based on the fourth month of the reference period, so that each household has three observations a year, spaced four months apart.⁷ Although the empirical models have been estimated on data that includes one-person households, the analysis below focuses on about 17,000 couples--defined as pairs of respondents who described themselves as married or as unmarried partners between the ages of 25 and 45, either same or opposite gender couples. Sample means and brief descriptions of the variables are shown in table 2.

Geographic locations of households are observed by the survey staff at the initial interview date, follow-up interviews are sometimes done over the phone, and respondents fill in information for the missing months in between interviews. In addition, the SIPP makes an effort to follow movers and obtain an exit interview--which helps sort out migration and attrition. The quality of SIPP data for evaluating migration has been noted by Diana DeAre (1993) and Rebecca Clark and Alden Speare (1988). David Neumark and Daiji Kawaguchi (2001) used the SIPP to evaluate attrition in the Current Population Survey, noting the SIPP staff's "substantial" efforts to follow movers. By comparison, publicly available data from the National Longitudinal Surveys and the Panel Study of Income Dynamics are released with a longer lag and do not include location information, (and when confidential access is granted, the remaining information provided can be limited).

Table 2: Sample means and variable descriptions
Variable	Mean	St. Dev.	Description
Lqmove	0.01	(0.092)	Indicator for interstate move at time t+1
Lmsqmove	0.02	(0.124)	Indicator move to another MSA at time t+1
Index	0.33	(0.331)	Within-couple ratio of high to low earner's labor income
Duration (residence)	2.95	(0.893)	Log of length of time lived in state of residence
Age	3.55	(0.172)	Log age of male in couple or survey respondent
Schild	0.60	(0.489)	= 1 if couple has a school age child
Owner	0.69	(0.462)	= 1 if couple is a homeowner
Unemp	0.05	(1.018)	Gap between state unemployment rate and national average
Vacancy	0.77	(0.724)	Conference Board Help Wanted Index $\div$ 100
Degree	0.36	(0.481)	= 1 if one spouse has college degree
Degree2	0.18	(0.383)	= 1 if both spouses have college degree
Black	0.08	(0.264)	= 1 if one spouse is black
Hispanic	0.15	(0.359)	= 1 if one spouse claims Hispanic ethnicity
Two_work	0.68	(0.465)	= 1 if both spouses work one week during month or more
Pt	0.40	(0.490)	= 1 if one spouse worked part time during month
W/partner	0.09	(0.293)	Unmarried partner, same or opposite gender

n: 17,018 couples contributing 106,400 observations.

(The MSA sub-sample has 10,522 couples contributing 62,357 observations.)

Notes: sample means are shown as of the end of the first wave, which would be the beginning of 1996, or the beginning of 2001 for each of the respective panels.

The SIPP also has drawbacks. For example, weekly hours worked can not be easily tabulated, although part-time workers are identified. The panel nature of the data provides necessary pre-move characteristics, but suffers from sample attrition. Also, while every household has a state identifier, only a fraction of the survey respondents have their MSA status identified (an MSA sub-sample). Thus, the empirical framework models out of state moves (interstate migration) for the entire sample, and moves among states and MSAs for the MSA sub-sample.⁸

The dependent variable in the empirical analysis is an indicator for a family move that represents the end of a spell of residence in the couple's initially observed location. Two types of moves are considered. First, an indicator variable "qmove" was set to equal one if a couple undertook a move that crossed state lines between survey interviews. Second, for the sub-sample for which MSA status is identified, an indicator variable "msqmove" was set to one if a couple in the MSA sub-sample relocated to outside their MSA of initial residence between survey interviews.

Note that in order to avoid the contemporaneous correlation between earnings and migration, the four-month lead of the moving indicator, labeled "lqmove" or "lmqmove," was used as the dependent variable in the empirical analysis. For example, people might quit a job prior to a move, thus influencing the contemporaneous relationship between the RHS variables and "qmove." Tests for Granger causality failed to show any significant relationship between the independent variables of interest and the variables "lqmove" nor "lmsqmove". In addition, there was little change in coefficient estimates whether a four-month lead of the migration indicator or an eight-month lead of the migration indicator was used as the dependent variable. Thus, the analysis assumes that there is no contemporaneous simultaneity between the lead of migration and relative earnings.

The independent variable of interest is the ratio of spouses' labor incomes. Presumably most asset income--stocks, bonds, dividends, and interest--is largely portable (although there are some exceptions like defined benefit plans which will be linked to an employer). In contrast, labor earnings usually require someone to show up somewhere, and thus require location decisions. The variable "index" is the ratio of the monthly earnings of the couple's "low" earner to the monthly earnings of the couple's "high" earner. In other words, the monthly earnings of the spouse who made less that month, was divided by the monthly earnings of the spouse who made more that month. The responses for the fourth month of the reference period (the month prior to the interview) were used. The variable ranges from a value of 0, which is a one-earner couple, to a value of 1, where each spouse has equal labor income. If both spouses have no labor income their index is assigned to be zero--they are not tied.

A variable reflecting spell duration, "duration", is defined as the number of years one of the couple's members has lived in the state of residence (the longer of the two) in which they are observed. The survey asks when people moved into their current state of residence, but not MSA. However, the duration variable will help control for the unobserved preferences for family networks and for being a long-time resident that likely contributes substantially to migration decisions, even though it is an imperfect control in the specifications for the MSA sub-sample. In addition, an indicator variable for homeownership models another important tie to a location. There are costs to buying and selling a home, and owning a home is an important signal that a couple is putting down roots. House prices were not considered.

The remaining variables used in the empirical model are shown in table 2. The specifications are parsimonious to lower the estimation burden, but do not ignore other influences. For example, the number of children did not contribute significantly to likelihood functions in the empirical analysis, conditional on having a school age child, and was excluded. Also, parameterizations of age, other than log-linear, made little difference in the empirical analysis. An indicator for "with partner" equals one if the couple identified each other as an "unmarried partner" in the household relationship field of the SIPP, and allows the analysis to include cohabiting and same-sex couples in addition to married couples. There are race indicators, and indicators for level of education of each spouse.

As will be discussed later, data on couples in which one member suffers an involuntary separation from an employer are used to construct spells of non-employment--consecutive months without a job--in order to explore whether being tied to a location by a working spouse might prolong periods of non-employment for spouses exogenously separated from work due to a labor demand shock. Also, measures of income used in specification tests are deflated by the personal consumption expenditure deflator. Finally, the SIPP over-samples households in demographic groups that are likely to be program participants. However, the use of sample weights was inconsequential in several specifications so for simplicity the weights are not used.

5. Empirical framework

The empirical models are semi-parametric hazard rate models and competing risks models that relate the migration indicator to spouses' relative labor incomes and other characteristics. The duration models are the dynamic extension of the static model which has been the workhorse of the migration literature. For example, the probability of moving is often modeled in a latent variable framework, where a probit equation relates an indicator variable, which equals one if someone moves, to observable characteristics. One recent example is Antonio Spilimbergo and Luis Ubeda (2004) who analyzed racial differences in migration propensities.

Several economic models suggest that the relative earnings of spouses might influence household decisions more than simply the levels of earnings. For example, Martin Browning, Francois Bourguignon, Pierre-Andre Chiappori and Valerie Lechene (1994) suggest a structural model of household allocation that differs from the basic neoclassical model of family labor supply by including a "sharing rule" that determines intra-household allocation based on relative incomes. The authors estimate the parameters of their structural model and reject the traditional model in which income among family members is pooled (and everyone's utility is maximized) in favor of their sharing rule in which decision "power" is weighted by relative income.

Bargaining power is not the only mechanism through which relative earnings of spouses influences decisions. For example, Casey Mulligan and Yona Rubinstein (2006) use a model of household specialization to analyze the labor supply of married women.⁹ Their work shows that a substantial number of the features of the aggregate time series data on married women's labor supply can be explained by the ratio of wives' wages to husbands' wages. The wage ratio depends on household specialization, which, in turn, depends on which spouse has a comparative advantage at market work. Like labor supply, relocation might depend on whether that comparative advantage is great enough that moving for one spouse's career and not the other is optimal.

The simplest migration decision, where the cost is the income forsaken due to relocation, will fix ideas. A household is considering a move in between two periods, and , with a utility function $U_{t}(q_{t})$ in each period, defined over consumption ( which is equal to total household income, $I_{t}$ , in each period, and income w $_{m}$ and w $_{f}$ for each spouse ( and . The objective function, with discount parameter, $\delta$ , would be, $V=U(q_{1})$ + $\delta$ U( $q_{2})$ , maximized subject to the income constraints: $q_{1 }=I_{1}$ & q $_{2}=I_{2 }$ . In the first period income is $I_{1} = w_{m}+w_{f}$ .

In the second period, assume that the gains to moving accrue to member , who is offered some percentage increase ( $\alpha$ ) on her current income as a raise in order to induce the member to move to another location. Assume the other spouse, , needs to forsake his income, $w_{m}$ , in the second period if the move takes place. The probability of a move reduces to a simple function of relative incomes:

Prob(Move=1) $= f(w_{m}+ w_{f}$ < $w_{f}$ + $\alpha$ w $_{f}$ )

(( $w_{m}/ w_{f})$ $< \quad \alpha$ )

(1)

The empirical model uses panel data so that migration propensities are estimated as a function of pre-move characteristics. However, moves out of state or out of an MSA may not be observed for individuals who leave the panel due to attrition. Although the results will reveal that attrition is playing little role, there is no way of knowing how sensitive the results are to panel attrition until its effect is estimated. Simply assuming that people who attrit are the same as people who are observed seems unsatisfactory when there is likely some correlation between migration and attrition. Thus a general model of transitions is written out that can be specified as either a model of the hazard rate of exit from current location, or a competing risks model that allows a spell to end in a move, attrition or neither--a right censored spell.

The indicator variable reflecting a family's ( migration decision, move $_{f}$ , is a function of the spouses' wage ratio and observable characteristics interpreted as the costs of moving. An error term, $\varepsilon$ $_{t}$ , could be interpreted as an exogenous shock to the couple each period that reflects their draw from a distribution of wage offers. The probability of a move, or more specifically, the probability of a transition from one location to another, at time , is approximated by the following transition rates:

$\begin{displaymath} \Pr (move_{t,f} >0)=\Pr (\varepsilon _{t,f} >-(\beta _1 X_{t,f} +\alpha \delta _f ))=\lambda (t\vert \delta _f ) \end{displaymath}$

(2)

If $\varepsilon$ $_{t}$ follows a log weibull distribution (type I extreme value) the transition rate equations are logistic regressions. The empirical framework is an approximation to the structural decision which relates relocation to observed costs, observed characteristics, uncorrelated unobserved costs, $\varepsilon$ $_{t,f}$ , and all the couple-specific persistent costs and characteristics, $\delta$ $_{f}$ . The matrix

includes the following controls representing the costs and benefits of migration: the wage ratio ("index"), age, school-age children, home ownership, unemployment, job vacancies, education, race, couple type, and the duration of residence in that U.S. state--all described in section 4 and table 2.

The problem of attrition stems from an "unmeasured risk factor". For example, an estimate of the effect of relative earnings on migration is likely to be biased upward if spouses with more equal earnings are more responsible, and thus less likely to attrit, but are thus systematically more likely to be observed migrating. The solution to this problem is similar to relaxing the independence of irrelevant alternatives (IIA) assumption in the multinomial logit model. Under IIA, if we have three outcome possibilities, and each are generated by an independent stochastic process, then the ratio of the probabilities of being in any two states will not depend on even the existence of the third or remaining state. If the characteristics of the third state change, this will not influence the relative probabilities of the two other states. In order to allow the probability of migration to depend on the probability of attriting, the empirical framework adds a random effect to represent the unmeasured risk factor which models the correlation across the processes. More specifically, a random effect is added to each stochastic process, migration and attrition, but the pairs of values of the realized random effects are drawn from a joint distribution where the correlation relating the marginal distributions is freely estimated. Thus, the IIA's independence assumption is relaxed, and through the unobserved heterogeneity, the features of each process can influence the relative probability of the other outcomes.

This method of handling panel data attrition was originally proposed by Daniel Hill (1994) who elaborated on the specification in several papers. Although Hill assumed a Gumbel's Type B bivariate extreme-value distribution, one specification employed below assumes a discrete distribution for the joint distribution of the random effect. The mass points and probabilities of the joint distribution are estimated along with the coefficients in the likelihood function.¹⁰ This specification was used on the MSA subsample. Because of difficulty in evaluating the likelihood on the full sample, however, a normal distribution was imposed on the unmeasured risk factor and Gaussian quadrature was used to evaluate the integral over the distribution of the random effect.¹¹ As Hill (1994) notes, period-by-period correlation between the two stochastic processes could be identified (in other words the correlation parameter of a bivariate distribution). However, the computational demands are already substantial and the correlation parameter is assumed to be constant for all periods, t=1,...,T.

To clarify the specification, in the case of attrition, define two types of transition rates, moving ( and attrition (:

$\begin{displaymath} \lambda _m (t\vert \delta _{m,f} )=\exp (-y_{m,f} (t))(1-\sum\limits_{m=1}^2 {\exp (-y_{m,f} (t)))^{-1}} \end{displaymath}$

(3)

where:

$\begin{displaymath} y_{m,f} =\beta _m X_{m,f} +{\gamma }'_m f(t)+\delta _{m,f} \end{displaymath}$

(4)

Equations (2) and (3) are the result of rewriting (1) using the distributional assumption. Define the probability of not transitioning to a new location or out of the sample as $\lambda _{0}$ , one minus the probability of the other options:

$\begin{displaymath} \lambda _0 (t\vert \delta _{m,f} )=1-\lambda _1 (t\vert \delta _{1,f} )-\lambda _2 (t\vert \delta _{2,f} ) \end{displaymath}$

(5)

or:

$\begin{displaymath} \lambda _0 (t\vert \delta _{m,f} )=(1-\sum\limits_{m=1}^2 {\exp (-y_{m,f} (t)))^{-1}} \end{displaymath}$

(6)

The survivor function, the joint probability of not having yet left the sample due to attrition and prior to any move is given by:

$\begin{displaymath} S_0 (t\vert \delta _{m,f} )=\prod\limits_{k=t_0 }^{K_f } {\lambda _0 (k\vert \delta _{m,f} )} \end{displaymath}$

(7)

The contribution to the likelihood function, of a spell that ends in a move is given by:

$\begin{displaymath} f_m (t\vert \delta _{m,f} )=\lambda _2 (t\vert \delta _{2,f} )\prod\limits_{k=t_0 }^{K_f } {\lambda _0 (k\vert \delta _{m,f} )} \end{displaymath}$

(8)

Then, the joint probability of remaining in the sample and then attriting prior to censoring, conditional on the unobserved heterogeneity is given by:

$\begin{displaymath} \lambda _1 (t\vert \delta _{1,f} )S_0 (t\vert \delta _{m,f} )=\lambda _1 (t\vert \delta _{1,f} )\prod\limits_{k=t_0 }^{K_f } {\lambda _0 (k\vert \delta _{m,f} )} \end{displaymath}$

(9)

Finally, the contribution to the likelihood function of an observed mover:

$\begin{displaymath} L(t)=\int_{-\infty }^\infty {f_m (t\vert \delta _{m,f} )S_0 (t\vert \delta _{m,f} )dG(\delta _1 ,\delta _2 )} \end{displaymath}$

(10)

where

( $\delta$ $_{1}$ , $\delta$ $_{2})$ is the joint distribution of the heterogeneity parameters, with unrestricted variance and correlation parameter, rho. The specifications include a constant, and the nonparametric heterogeneity distribution is assumed to be mean zero for identification.

The costs of moving parameterized in the matrix in (1) are assumed to include a function of the duration of time spent in the state of residence ( in equation (3)). Following John Ham and Robert Lalonde (1996) and Steven Nickell (1979), duration is parameterized within the equations for the transition rates $\lambda$ ( as a polynomial, in this case a cubic polynomial.¹² The variation in durations, the lengthy gap between what would be long and short spells, and the computational burden made a simple functional form more attractive than nonparametric estimation of the baseline hazard, as proposed by Bruce Meyer (1990), or grouping durations in the estimation as in John Newman and Charles McCulloch (1984). However, the model allows spell length to influence the hazard, which produces a declining hazard rate over most spell durations or duration dependence. Presumably, a household's preferences for staying in the initial location are reflected in the duration dependence, which is identified by the panel nature of the data and the functional form assumption.

In addition, initial conditions are ignored even though all spells are in progress. Although the distribution of couples across locations may have some second-order effect on the results, the initial conditions problem in this context is not the same as in the context of unemployment durations, where stock sampling causes a sample selection problem based on who has or has not exited--a certain type of person is more likely to be sampled because they are more likely to have long spells. In migration, everyone needs to start somewhere. Unobserved preferences for starting location that are reflected in the duration of residence will be captured by the duration polynomial.

The estimate of interest is the coefficient on the variable "index", the ratio of labor earnings, in the matrix . As discussed earlier, contemporaneous feedback from the migration indicator to the variable "index" was ruled out with tests for Granger causality. However, decisions on labor supply may be forward looking and thus "index" may be endogenous. Some couples may have only one earner because they know they are going to move, which might influence this relationship. However, if that were true, why would a couple forsake current period labor earnings even if that income stream would be lost later? This kind of foresight implies the couple was not optimizing in the first place. The endogeneity problem would stem from a couple being a highly mobile "type" and the influence of past mobility might have lowered the current value of the variable "index" which then would predict high mobility, but which would instead be the result of the couple's "type." As a test of the correlation between "index" and this type of permanent characteristic, the wage ratio "index" passed a Hausman test for exogeneity from the random effects. For the test, the dependent variable was the migration indicator, and the specification included only the variable "index". Estimates of both random and fixed effects specifications produced almost no difference in the coefficient estimates and the Chi-squared test statistic was zero at two decimal places. With contemporaneous simultaneity ruled out, and to the extent that the aggregate changes in spousal earnings equality have been driven by exogenous influences, the empirical framework will provide an accurate assessment of the influence of the changes in family labor supply, specialization and the importance of partners' earnings on migration.

6. Empirical results

Two sets of estimates are presented. The hazard model parameter estimates are shown in table 3 and the competing risks model estimates are shown in table 4. In columns (1) and (2) of table 3, basic hazard rate specifications are shown for interstate migration and MSA migration, respectively. In columns (3) and (4) an indicator for a two-earner couple is added to the specifications. Table 4 shows the results when attrition is modeled, and column (1) contains the results for the model of interstate migration using the full sample, and column (2) contains the results for the model of MSA migration using the MSA sub-sample. Standard errors are in parentheses. For the wage ratio, denoted "index", a marginal effect is also shown. The marginal effect was calculated by resetting the variable "index" to one, integrating over the heterogeneity distribution to compute the sample predictions, then resetting the variable "index" to zero, and integrating again to compute new predicted probabilities. The differences in the predicted probabilities are the marginal effects.

On balance, the coefficient estimates are reasonable, consistent with theory, and consistent with the literature. The educated are more likely to move.¹³ Homeowner's are less likely to move--either because preferences to stay in one place are correlated with owning a home, or because the costs of moving are higher for homeowners. Not surprisingly, there is negative duration dependence; the longer an individual remains in their state of residence, the less likely they will move. Older people are less likely to move. Unmarried couples are less likely to move--which could be because people marry, then move.

Table 3: Model results
Variable:	Outcome 1 Migrate (Interstate)	Outcome 2 Migrate (MSA)	Outcome 3 Migrate (Interstate)	Outcome 4 Migrate (MSA)
Index	-0.614^**	-0.356^**	-0.391^**	-0.361^**
(std. er.)	(0.123)	(0.088)	(0.123)	(0.120)
P $>\vert$ z $\vert$	0.000	0.000	0.018	0.003
dy/dx	-0.0034	-0.0067	-0.0022	-0.0069
Two_work			-0.224^**	0.006
Two_work (std. er.)			(0.111)	(0.081)
Duration (residence)	-0.173	-0.364^**	-0.165	-0.364^**
Duration (residence) (std. er.)	(0.191)	(0.093)	(0.192)	(0.093)
Duration^2	-2.085^*	0.062	-2.149^*	0.062
Duration^2 (std. er.)	(1.238)	(0.198)	(1.252)	(0.198)
Duration^3	0.237	0.047	0.247	0.047
Duration^3 (std. er.)	(0.231)	(0.038)	(0.234)	(0.038)
Age	-0.942^**	-1.205^**	-0.938^**	-1.205^**
Age (std. er.)	(0.269)	(0.193)	(0.271)	(0.193)
Schild	-0.165^*	-0.135^**	-0.167^*	-0.134^**
Schild (std. er.)	(0.088)	(0.064)	(0.089)	(0.064)
Owner	-0.894^**	-1.349^**	-0.889^**	-1.349^**
Owner (std. er.)	(0.090)	(0.071)	(0.092)	(0.071)
Unemp	-0.041	0.083^**	-0.043	0.083^**
Unemp (std. er.)	(0.039)	(0.029)	(0.039)	(0.029)
Vacancy	-0.029	2.502^**	-0.014	2.501^**
Vacancy (std. er.)	(0.213)	(0.197)	(0.217)	(0.197)
Degree	0.710^**	0.242^**	0.725^**	0.241^**
Degree (std. er.)	(0.104)	(0.077)	(0.106)	(0.077)
Degree2	0.225^**	0.182^**	0.223^**	0.182^**
Degree2 (std. er.)	(0.107)	(0.086)	(0.108)	(0.086)
Black	0.150	-0.119	0.147	-0.119
Black (std. er.)	(0.154)	(0.110)	(0.155)	(0.110)
Hispanic	-0.460^**	-0.130^*	-0.481^**	-0.129^*
Hispanic (std. er.)	(0.127)	(0.077)	(0.129)	(0.077)
W/partner	-0.549^**	-0.296^**	-0.551^**	-0.296^**
W/partner (std. er.)	(0.167)	(0.108)	(0.169)	(0.108)
Constant	-5.086	0.228	-5.121	0.227
Constant (std. er.)	(230.3)	(0.681)	(226.8)	(0.681)
Mass points	(-7.40,6.25)	(-0.38,0.55)	(-6.85,6.38)	(-0.37,0.57)
Variance	46.26	0.211	43.7	0.207
Probabilities (1,2)	(0.46,0.54)	(0.59,0.41)	(0.48,0.52)	(0.61,0.39)
Covariance (2,1)	-	-	-	-
L:	-4,147.23	-6,147.01	-4,145.10	-6,147.01
N:	106,400	62,357	106,400	62,357

Notes: ^**Significant at the 5 percent level. Return to Table ^*Significant at the 10 percent level. Return to Table Standard errors are shown in parentheses. Columns one and two show coefficient estimates of hazard rate models of the probability of moving conditional on the spell of not moving/ Columns three and four show competing risks models that allow one outcome to be attrition in addition to migration.

Table 4: Model results: with attrition
Variable	Outcome 1 Attrit	Outcome 1 Migrate (Interstate)	Outcome 2 Attrit	Outcome 2 Migrate (MSA)
Index	-0.141^*	-0.622^**	-0.140	-0.356^**
(std. er.)	(0.066)	(0.122)	(0.098)	(0.086)
P $>\vert$ z $\vert$	0.032	0.000	0.151	0.000
dy/dx	-0.0020	-0.0036	-0.0017	-0.0072
Duration (residence)	-0.917	-0.144	0.067	-0.381^**
Duration (residence) (std. er.)	(0.095)	(0.190)	(0.152)	(0.094)
Duration^2	-0.096	-1.927	-0.162	0.080
Duration^2 (std. er.)	(0.233)	(1.257)	(0.359)	(0.192)
Duration^3	0.099	1.854	-0.036	0.053
Duration^3 (std. er.)	(0.043)	(2.369)	(0.066)	(0.038)
Age	-0.024	-0.093^**	0.008	-1.180^**
Age (std. er.)	(0.015)	(0.027)	(0.249)	(0.186)
Schild	-0.217^**	-0.186^**	-0.154	-0.143^**
Schild (std. er.)	(0.050)	(0.087)	(0.076)	(0.062)
Owner	-0.434^**	-0.891^**	-0.460^**	-1.323^**
Owner (std. er.)	(0.053)	(0.095)	(0.088)	(0.062)
Unemp	-0.026	-0.046	-0.009	0.080^**
Unemp (std. er.)	(0.022)	(0.039)	(0.035)	(0.028)
Vacancy	0.573	0.070	0.609^**	2.422^**
Vacancy (std. er.)	(0.123)	(0.215)	(0.204)	(0.184)
Degree	-0.235^**	0.674^**	-0.187^**	0.231^**
Degree (std. er.)	(0.063)	(0.107)	(0.094)	(0.075)
Degree2	-0.034	0.213^**	-0.091	0.175^**
Degree2 (std. er.)	(0.079)	(0.106)	(0.112)	(0.083)
Black	0.335^**	0.183	0.326^**	-0.95^**
Black (std. er.)	(0.083)	(0.153)	(0.135)	(0.106)
Hispanic	-0.020	-0.447^**	-0.026	-0.119
Hispanic (std. er.)	(0.067)	(0.127)	(0.095)	(0.074)
W/partner	0.242^**	-0.504^**	0.358^**	-0.255^**
W/partner (std. er.)	(0.077)	(0.169)	(0.126)	(0.103)
Constant	-9.416^**	0.001	-4.154^**	0.309
Constant (std. er.)	(27.16)	(0.988)	(1.062)	(0.662)
Mass points			(-0.67,2.51)	(0.01,-0.05)
Variance	64.52	1.082	1.676	0.001
Probabilities (1,2)			(0.79,0.21)	(0.79,0.21)
Covariance (2,1)	4.193	4.193	-0.032	-0.032
L:			-13,710.516	-13,710.516
N:	106,400	106,400	62,357	62,357

Notes: ^**Significant at the 5 percent level.Return to Table ^*Significant at the 10 percent level.Return to Table Standard errors are shown in parentheses. Columns one and two show coefficient estimates of hazard rate models of the probability of moving conditional on the spell of not moving/ Columns three and four show competing risks models that allow one outcome to be attrition in addition to migration. Note that age and duration coefficients were scaled and then un-scaled for presentation in the interstate sample for computational ease.

The variable "index," the ratio of the couple's labor income, is estimated to significantly lower the hazard rate of out-migration for states and MSAs in all the specifications. The marginal effects suggest that relative equality of spousal income prevents relocations. Consider the estimates of the effect of relative wages on the probability of moving from an MSA. The MSA sub-sample's annual MSA migration rate is 6.7 percent. The estimates imply that if spousal wage inequality narrowed by 5 percent, from the 0.33 sample average to 0.35, the MSA migration rate would fall from 6.7 percent to 6.6 percent. In other words, every five percent increase in the wage gap would reduce the migration rate by 0.1 percentage point. If we went back to 1970 intra-family earnings, migration would be a full percentage point higher. Although that only loosely translates into population figures, 0.1 percentage point on the aggregate U.S. migration rate would represent 300,000 people annually who would not move because they are in households tied by a spouse's income.

The wage ratio is also significant conditional on an indicator for whether or not the couple has two workers as opposed to only one or no workers. Having two workers significantly lowers the probability of an interstate move, but does not help in predicting an MSA move. Why the results for these two types of moves would be so different is unclear, although this could reveal some differences in the decision processes related to the distance of moves which are likely on average longer in the case of interstate moves. In addition, specifications with part-time work indicators and variables with the levels of income did not alter the results. Table 4 shows the two specifications that allow the marginal effect of the index on migration to depend on the probability of attrition, which had little influence on the results--a little surprising given attrition should be related to the likelihood of observing migration. In specification not shown, inverse probability weights were used to address the panel attrition, with little influence also. The evidence suggests that that the observed covariates control for attrition. Altogether, the results appear robust to a variety of considerations.

Empirically the variable "index" was a much more significant predictor of migration than either the levels of income or hours of labor supply. For example, in logistic regressions like those in table 3 that modeled the probability of observing a move as a function of the covariates, the coefficient on the wage ratio ("index") in one logistic specification was -0.6067. After an indicator for whether either spouse had worked part-time during the month was added to the specification, the coefficient on "index" became -0.6051, the part-time indicator was not significantly different from zero, and the marginal effect of "index" was the same at four decimal places.¹⁴ Similarly, adding the levels of each spouse's monthly labor income in alternative specifications essentially did not change the coefficient on relative wages. The part-time indicators and the levels of income did not contribute significantly to the likelihood functions of several specifications, as revealed by likelihood ratio tests, except for one case. In that case, the primary wage earner's level of income was positively correlated with the probability of moving out of an MSA at the 10 percent level of significance, although the levels were not a statistically significant predictor of an interstate move in other specifications.

The robustness of relative earnings in predicting migration may be an indication that a model of household specialization or bargaining might describe the moving decision of households better than the human capital model. The empirical model is a general reduced-form parameterization, so the lack of theoretical framework does not necessarily imply any particular specification error, but instead suggests that future structural modeling of migration decisions might consider the husband-wife decision-making mechanism more carefully.

The discussion purposely avoids several points. For example, assets were ignored. Presumably most assets are transferable around the country--a savings account, stocks, portable retirement accounts, etc., are as accessible in Manhattan (New York) as Manhattan, Kansas. So the primary determinant of the process will be labor income, and potential wages. Of course, different regions offer different types of consumption. For example, leisure time in Jackson Hole, Wyoming may not quite provide the same utility as leisure time in Chicago. Distance and post-move location choice are also not discussed.¹⁵ Divorce was ignored. These considerations would add substantial complexity, but would probably not add much to the basic conclusion that more equal spousal labor earnings substantially reduce migration propensities.

Other economic outcomes might be influenced by the reduced migration. For example, workers may be forming bad matches by forgoing relocation. Workers may be accepting lower wages to remain in one specific location. Lowering migration may lengthen spells of non-employment. Additional specifications of hazard rate models were estimated to evaluate some alternatives, however, the samples of couples with involuntary job loss was not large enough to identify whether the reduction in migration was also lengthening unemployment durations, which would be an interesting analysis. Specifications were estimated which included an indicator variable for when the couple's primary wage earner was in a spell of non-employment which began with an involuntary separation from employment. The spell indicator was interacted with the wage ratio observed at the household's initial interview to prevent the job loss from directly influencing the spousal wage ratio. The interaction term estimated that even among households in which the primary wage earner suffers involuntary job loss, previously observed equal spousal earnings are lowering migration. However, the coefficient on the interaction between job loss and the earnings ratio was statistically significant at only the 30 percent level of significance--a bit above the conventional 5 or 10 percent levels. ¹⁶

7. Conclusion

The results suggest that cities which succeed in attracting the young and educated will likely end up with the educated couples who put down roots. Migration often corresponds to early career job offers, or the end of a period in school. Following these decisions, the couples in which both workers contribute substantially to household income become much less likely to move, particularly as they age, have children, and buy homes. This implies early-career location choice is something of an absorbing state for many of these couples with two careers. Thus, the cities attracting young, high income couples will likely keep them--cities like Washington, San Francisco, or Seattle. As migration continues to decline, this could sort the most productive labor away from cities that can not find ways of attracting the young and the educated before they marry, form dual-worker households, or have children--after which relocation becomes difficult even if one of the spouses gets a good job offer elsewhere.

In addition, Mincer's model implies that the relative abundance of vacancies in good economic times increases the likelihood that couples together get attractive offers (the coefficient estimates suggest that the vacancy rate is positively correlated with some migration among couples). Thus, going forward it seems likely that the share of couples that need two attractive job offers in order to move is going to continue to rise. This implies that couples will reallocate their labor across regions relatively more in good economic times than bad. Overall, the results suggest that the importance of wives' earnings have held down some adjustment.

Finally, these dynamics have implications for the couples themselves. Forsaking relocation due to a spouse's job might hold down wage growth for the spouse who has to turn down a job offer in another part of the county. The compromised spouse lowers their lifetime utility. That is the relocation problem couples today increasingly face, and the problem will probably become more common. In the future, technology and telecommuting might help spouses bridge the geographic gap between location of residence and location of work. But for many couples, relocation decisions will force them to make difficult choices, and likely limit the extent to which migration of labor moves across the country.

9. References

Blau, David M. 1994. "Labor Force Dynamics of Older Men," Econometrica. 62:1, January, 117-156.

Bradbury, Katherine and Jane Katz. 2005. "Wives' Work and Family Income Mobility," Public Policy Discussion Papers, Federal Reserve Bank of Boston, No. 04-3, May.

Browning, Martin, and Francois Bourguignon, Pierre-Adnre Chiappori and Valerie Lechene. 1994. "Incomes and Outcomes: A Structural Model of Intrahousehold Allocation," Journal of Political Economy, 102:5, December, pp. 1067-1096.

Compton, Janice, and Robert A. Pollak. 2004. "Why Are Power Couples Increasingly Concentrated in Large Metropolitan Areas," National Bureau of Economic Research, Working Paper w10919, November.

Costa, Dora L. and Matthew E. Kahn. 2000. "Power Couples: Changes in the Locational Choice of the College Educated," Quarterly Journal of Economics. 115:4, November, 1287-1315.

Eberwein, Curtis, John C. Ham, and Robert J. LaLonde. 2002. "Alternative methods of estimating program effects in event history models," Labour Economics, 9, 249-278.

Frank, Robert H. 1978. "Family Location Constraints and the Geographic Distribution of Female Professionals," The Journal of Political Economy, 86:1, February, 117-130.

Goldin, Claudia and Lawrence F. Katz. (2002). "The Power of the Pill: Oral Contraceptives and Women's Career and Marriage Decisions," The Journal of Political Economy, 110:4, August, 730-770.

Greenwood, Michael J. 1997. "Internal migration in developed countries," Handbook of Population and Family Economics, Volume 1, Part 2, Mark R. Rosenzweig and Oded Stark, eds., pp. 647-720

Ham, John C., and Robert J. LaLonde. 1996. "The Effect of Sample Selection and Initial Conditions in Duration Models: Evidence from Experimental Data on Training," Econometrica, 64:1, January, 175-205.

Heckman, James J., and Burton Singer. 1984(a). "A Method for Minimizing the Impact of Distributional Assumptions in Econometric Models for Duration Data," Econometrica, 52:2, March, 1984.

Heckman, James J., and Burton Singer. 1984(b). "Econometric Duration Analysis," Journal of Econometrics, 24, 63-132.

Hill, Daniel H. 1994. ""Adjusting for Attrition in Event History Analysis," Proceedings of the American Statistical Association Section on Survey Research Methods, August, 1994.

Meyer, Bruce D. 1990. "Unemployment Insurance and Unemployment Spell," Econometrica, 58:4, April,757-782.

Mincer, Jacob. 1978. "Family Migration Decisions," Journal of Political Economy, 86:5, 749-773.

Mortenson, Dale T., and Christopher A. Pissarides. 1999. "Job reallocation, employment fluctuations and unemployment," Handbook of Macroeconomics, Volume 1, Part 2, John B. Taylor and Michael Woodford, eds., pp. 1171-1128.

Mulligan, Casey B., and Yona Rubinstein. 2006. "Specialization, Inequality, and the Labor Market for Women," unpublished manuscript, January.

Neumark, David, and Daiji Kawaguchi. 2001. "Attrition Bias in Economic Relationships Estimated with Matched CPS Files," National Bureau of Economic Research, Working Paper #8663, December.

Newman, John L., and Charles E. McCulloch. 1984. "A Hazard Rate Approach to the Timing of Births," Econometrica, 52:4, July, 939-961.

Nickell, Stephen. 1979. "Estimating the Probability of Leaving Unemployment," Econometrica, 47:5, September, 1249-1266.

Pencavel, John. (2004). "The Association between Earnings Inequality and Labor Supply in Husband-Wife Families," http://client.norc.org/jole/SOLEweb/pencavel2005.pdf, unpublished manuscript, December.

Pingle, Jonathan F. 2006. "A Note on Measuring Internal Migration in the U.S.," Economics Letters, forthcoming.

Pissarides, Christopher A., and Ian McMaster. 1990. "Regional Migration, Wages and Unemployment: Empirical Evidence and Implications for Policy," Oxford Economic Papers, New Series, 42:4, October, pp. 812-831.

Pissarides, Christopher A., and Jonathan Wadsworth. 1989. "Unemployment and the Inter-Regional Mobility of Labour," The Economic Journal, 99:397, September, pp. 739-755.

Rabe-Hesketh, Sophia, Anders Skrondal, and Andrew Pickles. 2005. "Maximum Likelihood Estimation of Limited and Discrete Dependent Variable Models with Nested Random Effects," Journal of Econometrics, 128, 301-323

Schwartz, Aba. 1973. "Interpreting the Effect of Distance on Migration," The Journal of Political Economy, 81:5, September-October, 1153-1169.

Schwartz, Aba. 1976. "Migration, Age and Education," The Journal of Political Economy, 84:4, Part 1, August, 701-720.

Sjaastad, Larry A. 1962. "The Costs and Returns of Human Migration," The Journal of Political Economy, 70:5, Part 2, October, 80-93.

Shimer, Robert. 2005. "Mismatch," NBER Working Paper, w11888, December.

Spilimbergo, Antonio, and Luis Ubeda. 2004. "Family attachment and the decision to move by race," Journal of Urban Economics, 55, 478-497.

Tuma, Nancy Brandon, and Philip K. Robins. 1980. "A Dynamic Model of Employment Behavior: An Application to the Seattle and Denver Income Maintenance Experiments," Econometrica, 48:4, 1031-1052.

Footnotes

* The views expressed here are the author's and do not necessarily reflect those of the Federal Reserve Board or its staff. Thanks to Marianne Bitler, Joseph Lupton, Tom Tallarini and William Wascher for helpful comments and Blake Bailey for research assistance.
Contact: [email protected] or (202) 452-3816. Return to Text

1. Claudia Goldin and Lawrence F. Katz (2002) note the importance of the pill in raising education levels and the age at first marriage for U.S. women. Return to Text

2. For a more detailed overview of the migration literature, discussion of the determinants of migration, and review of the models, see Michael J. Greenwood (1997). Return to Text

3. Christopher Pissarides and Jonathan Wadsworth (1989) note there are reasons why migration may be either positively or negatively correlated with the business cycle. Return to Text

4. Compton and Pollack (2004) argue MSA size is uncorrelated with migration of educated married couples and the reason they populate urban areas is because they are single there and then marry. Return to Text

5. Christopher Pissarides and Ian McMaster (1990) note that labor supply adjustment to correct regional imbalances in Great Britain can be slow--they discuss adjustment in terms of decades. Return to Text

6. The data is available at: http://www.census.gov/population/www/socdemo/migrate.html. The data source is the Current Population Survey, in which the migration questions were not asked for most years in the 1970s. Further, the migration questions have remained reasonably consistent, but the survey has undergone numerous other changes and population weights have changed over time. Return to Text

7. This avoids the well-known seam problem in the SIPP. Return to Text

8. The SIPP identifies the MSA for respondents in large states, but does not identify respondents by MSA for individuals in small states with few MSAs to inhibit the ability to track down survey respondents. Among states, North Dakota, South Dakota and Montana together are labeled with one state identifier, as are New Hampshire and Maine. Return to Text

9. See also John Pencavel (2004) for another recent contribution to the literature on specialization and relative wages of husbands and wives. Return to Text

10. Similar integration in duration models has been described by James J. Heckman and Burton Singer (1984a,1984b) and David M. Blau (1994). A related multiple state transition framework is detailed by Nancy Brandon Tuma and Philip K. Robins (1980). Return to Text

11. The Newton-Raphson algorithm and description of the integration are discussed in Sophia Rabe-Hesketh, Anders Skrondal and Andrew Pickles (2005). Return to Text

12. Curtis Eberwein, Ham and Lalonde (2002) propose adding higher order polynomial terms until the model fit fails to show much improvement. In the results below, the addition of the cubic term to the polynomial did not significantly increase the model fit. Return to Text

13. See Aba Schwartz (1976). Return to Text

14. The specification tests use the same variables as the empirical framework, except that correlation over time in the error terms was modeled as individual-specific random effects, which were integrated out of the likelihood function using Gaussian quadrature with 12 points of support--the standard panel data logistic regression specification in STATA. Quadrature was used in the hazard model framework because of the computational speed relative to the model that corrects for attrition, which took several days to estimate. Return to Text

15. See Aba Schwartz (1973) for the influence of distance on migration. Return to Text

16. Pissarides and Wadsworth (1989) note that individuals who experience unemployment in Britain are significantly more likely to migrate. Return to Text