Incorporating Judgement in Fan Charts *
Within a decision-making group, such as the monetary-policy committee of a central bank, group members often hold differing views about the future of key economic variables. Such differences of opinion can be thought of as reflecting differing sets of judgement. This paper suggests modelling each agent's judgement as one scenario in a macroeconomic model. Each judgement set has a specific dynamic impact on the system, and accordingly, a particular predictive density - or fan chart - associated with it. A weighted linear combination of the predictive densities yields a final predictive density that correctly reflects the uncertainty perceived by the agents generating the forecast. In a model-based environment, this framework allows judgement to be incorporated into fan charts in a formalised manner.
JEL Classification: C15, C53, E17, E50
1. Introduction
Most economists agree that there is no such thing as a perfect model. In the absence of such, it is widely accepted that incorporating judgement into forecasting and policy analysis is both desirable and necessary.1 The aim of this paper is to present a framework in which judgement can be incorporated in a formal and model-consistent manner into a model-based forecasting process. Specifically, we show how predictive densities associated with differing sets of judgement can be combined to achieve the overall goal of one final predictive density for each macroeconomic variable of interest.
Predictive densities are most familiarly represented as fan charts, which are used in a range of applications, the best known probably being the inflation fan charts published by the Bank of England. The nature of monetary policy and its lags demand that central banks devote much time and energy to forecasting, and addressing how to incorporate judgement into their forecasts is paramount. Consider the following situation: The monetary policy committee at a central bank is about to make a decision regarding the policy interest rate. A main scenario - generated, perhaps, by the staff responsible for macroeconomic forecasting - is presented. One member of the committee is concerned that upcoming wage negotiations will lead to faster wage growth the coming year, while another member believes that foreign demand will be stronger than predicted in the main scenario. How can these views be accommodated in the forecasting process?
The methodology put forward in this paper takes its starting point from the suggestion that judgement should be modelled as a scenario in a general-equilibrium type macroeconomic model. A scenario is defined by laying down the probability density function for a number of future observations for one or more variables in the system. Thus the way in which judgement is modelled in this paper resembles the way in which Sims (1982) and Leeper and Zha (2003) model policy interventions. The main methodological distinction between the current paper and previous studies is that we allow specification of distributions for future values of any variable instead of just those under the control of the policy maker. This modelling choice allows us to observe the dynamic effect of judgement upon the system. The dynamic impact is encapsulated in a predictive density corresponding to each judgement set. We suggest that the predictive densities associated with the different scenarios be combined into one final fan chart via a weighted linear combination, a method also referred to as the linear opinion pool. This allows judgement to be incorporated in the final fan chart in a model-consistent manner that correctly reflects the uncertainty perceived by the agents generating the forecasts.
In the previous literature, the typical way to address judgement has been to adjust the level of a chosen variable with "intercept corrections" or "add factors"; for examples of this, see Reifschneider et al. (1997), Clements and Hendry (1998) and Svensson (2005). Such adjustments may be based on systematic historical forecast errors, rules of thumb, alternative models or other, more or less ad hoc, methods. The methodology suggested in this paper aims to formalise the incorporation of judgement to some extent.2 The motivation for turning away from ad hoc methods is that whilst judgement may improve forecasting performance, it can also introduce inconsistencies and shortcomings in the process, such as forecast bias and damaged forecast accuracy (Armstrong, 1985; Hogarth, 1987). An example of such shortcomings can be found in the Riksbank's fan charts. Because of the way in which judgement is incorporated, the fan charts have the undesirable property that inflation and its determinants can always be more uncertain than usual.3 While the methodology proposed in this paper is not immune to all potential problems that judgement can introduce to the forecasting process, it alleviates several through the use of general-equilibrium type models - such as DSGE or VAR models - that ensure the equilibrium properties of the system are taken into account.
Another advantage of the method proposed in this paper is its ability to address several conflicting scenarios, a practical issue noted by Svensson and Tetlow (2005).4 From an empirical point of view, this is an appealing feature given the complexity of many forecasting processes and it is made feasible by the use of model-averaging techniques. Model averaging has frequently been employed in the forecasting literature - see, for example, Diebold and Pauly (1990) and Garratt et al. (2003) - but not in the way presently suggested. We argue that model-averaging techniques, such as the linear opinion pool, are a valuable tool to address judgement and forecast uncertainty.5
The remainder of this paper is organised as follows: Section 2 presents the background and terminology regarding judgement and lays down some notation. Section 3 discusses the combination of forecast densities, with extra attention paid to the issue of how to determine the weights for the linear opinion pool. In Section 4, the method is employed in an empirical application using a Bayesian VAR model. Finally, Section 5 concludes.
2. Modelling judgement
As stated in the introduction, the aim of this paper is to suggest a framework through which judgement can be incorporated in a forecasting process. In order to present the statistical methodology upon which the analysis relies, it will be useful to first describe what we mean by judgement and how this will be modelled. One potential definition is that by Svensson (2005, p. 2), who describes judgement as "information, knowledge, and views outside the scope of a particular model". This is an appealingly broad description and roughly in line with economists' conception of judgement in forecasting.
As a typical example of what could be seen as judgement in this framework, consider the task of forecasting future CPI inflation using a VAR model four periods ahead standing at time ![]() .
Assume next that a substantial cut in the value-added tax is decided upon by the parliament and announced to take place at
.
Assume next that a substantial cut in the value-added tax is decided upon by the parliament and announced to take place at ![]() +1. Since the VAR model is purely backward looking, it will never be
able to take the effects of this tax cut into account by itself (unless it is a recurring event). Given that we have this information, it is desirable to incorporate it into the forecast though.
+1. Since the VAR model is purely backward looking, it will never be
able to take the effects of this tax cut into account by itself (unless it is a recurring event). Given that we have this information, it is desirable to incorporate it into the forecast though.
Based on Svensson's qualitative definition of judgement, it will be useful to look more closely at four cases of interest:
![]() There are known future values for one or more variables in the system and these are different from those suggested by the model.6
There are known future values for one or more variables in the system and these are different from those suggested by the model.6
ii) There are known future values for one or more variables not in the system, but which will affect the system, and these are different to those implicitly used by the model.
iii) An agent's perceived probability density function (PDF) for predictions for one or more variables in the system differs from that suggested by the model.
iv) An agent's perceived PDF for predictions for one or more variables not in the system, but which will affect the system, differs from that implicitly used by the model.
The first case is usually reasonably straightforward to deal with since we often simply can condition on the known values in the model. It is not completely trivial though as the forecaster typically has to decide how to generate the conditioning. Put differently, it must be decided upon which combination of shocks that caused the outcome. The question of which combination of shocks to use in order to generate a particular outcome or distribution is an equally important issue in all four cases above though and we will therefore discuss this issue in more detail below. From now on the discussion will, however, focus on the last three cases which are more interesting and they will be treated in the same way methodologically.
Turning to the way in which judgement will be modelled in this paper, we will initially denote by
![]() the
the ![]() x1 vector of variables being modelled. We assume that there is a
main scenario in the forecasting process, given, for example, by a macroeconomic model's endogenous forecast. Judgement - as described in cases ii), iii) and iv) above - is then represented as
x1 vector of variables being modelled. We assume that there is a
main scenario in the forecasting process, given, for example, by a macroeconomic model's endogenous forecast. Judgement - as described in cases ii), iii) and iv) above - is then represented as ![]() -1 alternative scenarios, where a particular alternative scenario is defined as the PDF for the predictions of the
-1 alternative scenarios, where a particular alternative scenario is defined as the PDF for the predictions of the ![]() x1 vector
x1 vector
![]() over the horizon
over the horizon ![]() to
to ![]() , where
, where
![]() is a subset of the variables in
is a subset of the variables in
![]() with
with
![]() and
and
![]() for
for
![]() . Stacking our predictions in the
. Stacking our predictions in the
![]() x1 vector
x1 vector
![]() , each scenario accordingly describes the PDF for the vector
, each scenario accordingly describes the PDF for the vector
![]() , denoted
, denoted
![]() . In empirical applications, we would typically expect
. In empirical applications, we would typically expect ![]() to equal one - or at least be small - since it is at short horizons that we think that judgement may be superior to models.7 It also appears reasonable to expect
to equal one - or at least be small - since it is at short horizons that we think that judgement may be superior to models.7 It also appears reasonable to expect
![]() to be of fairly low dimension as it seems non-trivial to specify a distribution for a large number of variables over a long forecasting horizon.
to be of fairly low dimension as it seems non-trivial to specify a distribution for a large number of variables over a long forecasting horizon.
Having specified
![]() , the practical issue of how to generate the predictive density associated with that scenario remains. A number of methods for such conditional
forecasting have been used in the literature - see for example Sims (1982), Doan et al. (1984), Waggoner and Zha (1999), Leeper and Zha (2003), Adolfson, Laséen, Lindé and Villani (2005), Cogley et al. (2005) and Robertson et al. (2005) - where stochastic
simulation typically is an important feature. As the purpose of this paper is to evaluate judgement using the dynamic impact on the system, we will follow the line of research relying on repeated simulation of the model. In this framework, forecasts are generated by feeding shocks into the system
and after making sure that the restrictions defined by
, the practical issue of how to generate the predictive density associated with that scenario remains. A number of methods for such conditional
forecasting have been used in the literature - see for example Sims (1982), Doan et al. (1984), Waggoner and Zha (1999), Leeper and Zha (2003), Adolfson, Laséen, Lindé and Villani (2005), Cogley et al. (2005) and Robertson et al. (2005) - where stochastic
simulation typically is an important feature. As the purpose of this paper is to evaluate judgement using the dynamic impact on the system, we will follow the line of research relying on repeated simulation of the model. In this framework, forecasts are generated by feeding shocks into the system
and after making sure that the restrictions defined by
![]() are met we can observe the dynamic effects that a particular scenario has.8
are met we can observe the dynamic effects that a particular scenario has.8
We will not dwell on the technical details regarding the different ways of generating predictive densities from different scenarios here - instead the reader is referred to the above mentioned articles for details. One method will also be more closely described in the empirical application in Section 4. However, it is worth pointing out that when a scenario is generated we should - depending on application and, in particular, the information available - carefully consider if any shock(s) should be given a more pronounced position. For example, a scenario that describes a higher wage growth than suggested by the model could be generated in a number of ways depending on what the underlying causes are judged to be: Higher productivity or stronger labour unions might be the answer, but it could also be a weaker real exchange rate, a higher inflation rate or strong foreign demand. If we are fairly sure that the driving force in a particular scenario is a certain shock (or combination of shocks), this information should clearly be used when generating the scenario. Intuitively, it seems preferable to use as detailed information as possible as this should generate the highest accuracy. Empirical work along this line of reasoning can be found in Leeper and Zha (2003) and Adolfson, Laséen, Lindé and Villani (2005); in both articles was a constant future interest rate path generated by a monetary policy shock. Needless to say, we could on the other hand also be in the situation where we are almost completely agnostic regarding the underlying causes in a particular scenario. In such a case, it might be more reasonable to "plead ignorant" and a method such as that of Sims' (1982) - in which the sum of squares of the shocks is minimised - could be one reasonable alternative.
3. Combining predictive densities
The way in which judgement is modelled is a key element in the methodological framework presented in this paper. An equally important issue though is how to generate a single predictive density which takes the ![]() -1 sets of potentially conflicting judgement into account in a sensible way. In this paper we suggest that the linear opinion pool should be used for this purpose. This is a method to combine probability distributions with a strong support in the literature; see for
example McKonway (1981) and Wallis (2005).9
-1 sets of potentially conflicting judgement into account in a sensible way. In this paper we suggest that the linear opinion pool should be used for this purpose. This is a method to combine probability distributions with a strong support in the literature; see for
example McKonway (1981) and Wallis (2005).9
Our goal is to generate the PDF for the stacked ![]() x1vector of predictions
x1vector of predictions
![]() , where
the
, where
the ![]() x1 vector
x1 vector
![]() is a subset of the variables in
is a subset of the variables in
![]() with
with ![]() . Employing the linear opinion pool, this is
accomplished by taking a weighted average of the predictive densities under the main and alternative scenarios according to
. Employing the linear opinion pool, this is
accomplished by taking a weighted average of the predictive densities under the main and alternative scenarios according to
The linear opinion pool has a number of appealing features; the weighted density automatically integrates to one and, as pointed out by Clemen and Winkler (1999, p. 189), the method also "satisfies a number of seemingly reasonable axioms" such as the unanimity property and marginalisation property. Most importantly though, it allows us to in a straightforward way combine the predictive densities from all scenarios under consideration and this can be done regardless of whether they are compatible or at odds with each other.
The weighted density is not necessarily easy to describe though, as
![]() typically is not of the same form as the distributions that were weighted together. For example, weighting together
typically is not of the same form as the distributions that were weighted together. For example, weighting together ![]() normal distributions,
normal distributions,
![]() is in general not a normal distribution even though this assumption is not uncommon in the literature.10 But whilst this could be a potential problem when aiming for analytical expressions, it need not impose much of a problem in empirical applications.11 The potentially complicated form of
is in general not a normal distribution even though this assumption is not uncommon in the literature.10 But whilst this could be a potential problem when aiming for analytical expressions, it need not impose much of a problem in empirical applications.11 The potentially complicated form of
![]() should, however, not only be considered a problem. Clearly, it is also an advantage of the linear opinion pool that it - despite its simplicity - is able to
generate for example bimodal distributions or distributions with fat tails.
should, however, not only be considered a problem. Clearly, it is also an advantage of the linear opinion pool that it - despite its simplicity - is able to
generate for example bimodal distributions or distributions with fat tails.
What we have seen so far is that the suggested method to weight together the ![]() different predictive densities as such obviously is very straightforward and easy to implement. However, one
key question still remains, namely that of how to determine the weights
different predictive densities as such obviously is very straightforward and easy to implement. However, one
key question still remains, namely that of how to determine the weights ![]() .
.
3.1 Arbitrary weights
One solution to the problem of which weights to use in equation (1) is to simply employ an arbitrary set of weights which reflect the forecasters' or decision makers' probabilities over the different scenarios. This solution has a certain appeal and has the advantage that it generates a weighted predictive density that correctly reflects the risk picture as perceived by the forecasters or decision makers. In some cases it should also be unproblematic to determine such arbitrary weights: Several sets of judgement could for example reflect several models used by the same agent - an agent that alone has all the power in the decision making process. In such a case the agent obviously just has to decide herself which weights to employ in equation (1).
However, different sets of judgement will often reflect the views of different agents; recall that the framework presented is intended as a potential tool for groups such as the monetary policy committee of a central bank. Needless to say, different agents need not necessarily agree upon which weights to assign to the different scenarios and formalised procedures to establish the weights are therefore of interest. Methods that describe decision making in a group in a formalised way include DeGroot (1974) and Öller (1978), where the former article describes a method to reach consensus and the latter suggests a voting procedure. In Öller's voting procedure, the votes could be evenly distributed over the agents involved in the process or also take additional information - such as each agent's previous forecast performance - into account. Relying on such procedures to establish the weights in equation (1) could clearly be of interest both to the equivalent of a monetary policy committee or a group responsible for generating forecasts at a lower level.
Usage of arbitrary weights obviously has some advantages, but the literature on model averaging and forecasting has typically relied on more formal methods to address the issue of forecast combination. Equal weights over models - that is,
![]() for all
for all ![]() - is one method that has been commonly employed; see, for example, Diebold and Pauly (1990) and Hendry and Clements (2004). Optimal weights, derived by minimising the mean square error of the point forecast, was used by Granger and Ramanathan (1984) and Diebold and Pauly (1990).
Akaike and Schwarz weights were used by Garratt et al. (2003) and Pesaran and Zaffaroni (2004) and Hall and Mitchell (2004) suggested that a data driven approach - aiming to minimise a test statistic - should be employed. In line with these more data-based methods to determine weights, we
will next suggest an alternative to arbitrary weights.
- is one method that has been commonly employed; see, for example, Diebold and Pauly (1990) and Hendry and Clements (2004). Optimal weights, derived by minimising the mean square error of the point forecast, was used by Granger and Ramanathan (1984) and Diebold and Pauly (1990).
Akaike and Schwarz weights were used by Garratt et al. (2003) and Pesaran and Zaffaroni (2004) and Hall and Mitchell (2004) suggested that a data driven approach - aiming to minimise a test statistic - should be employed. In line with these more data-based methods to determine weights, we
will next suggest an alternative to arbitrary weights.
3.2 Distance-based weights
Despite the relatively good supply of methods to determine weights for forecast combination, an additional approach will nevertheless be suggested here.12 The suggested
method takes its starting point in the idea that the main scenario in the forecasting process should be a forecast that there is quite some confidence in; this could for example be the endogenous forecast from a DSGE or VAR model with well-established forecasting properties. We next note that
imposition of a certain PDF on
![]() typically has effects on the rest of the variables in the system at horizons beyond
typically has effects on the rest of the variables in the system at horizons beyond ![]() . These effects can be large or small and the predictive density from an alternative scenario can accordingly have been shifted substantially or negligibly relative to the predictive density of the main scenario. A substantial shift implies a forceful intervention and we
therefore argue that a substantial shift typically should render a scenario to be judged less likely.13 A small shift in the predictive density on the other hand implies that
the added judgement was largely consistent with the benchmark density.
. These effects can be large or small and the predictive density from an alternative scenario can accordingly have been shifted substantially or negligibly relative to the predictive density of the main scenario. A substantial shift implies a forceful intervention and we
therefore argue that a substantial shift typically should render a scenario to be judged less likely.13 A small shift in the predictive density on the other hand implies that
the added judgement was largely consistent with the benchmark density.
In line with the above arguments, we suggest that the weights in equation (1) could be set in such a way that deviations from the forecast density of the main scenario are penalised; the larger the distance between an alternative scenario's predictive density and the
predictive density of the main scenario, the lower is the weight assigned to that scenario. In order to implement this principle for determining the weights, we need a measure of the distance between two densities though. The Kullback-Leibler information criterion (Kullback and Leibler,
1951) is a highly useful tool for this task; it measures the distance between two (potentially time-varying) distributions - one "reference distribution" (![]() and one "alternative
distribution" (
and one "alternative
distribution" (![]() - and is defined as
- and is defined as
The empirical usefulness of the Kullback-Leibler information criterion (KLIC) has been thoroughly established and it has been employed as an evaluation measure in recent work by for example Cogley et al. (2005) and Robertson et al. (2005). The work of Cogley et al. is similar in spirit to this paper; employing a Bayesian VAR to generate fan charts for U.K. inflation, they then investigated - using the KLIC as one of several measures - how much the model needed to be "twisted" in order to match the Bank of England's fan charts. They concluded that large values of the KLIC, implying large deviations from the benchmark VAR, would require convincing arguments by the monetary policy committee.
Armed with a method to measure the distance between different predictive densities, we can next turn to the issue of exactly how deviations from the main scenario's predictive density should be penalised and, accordingly, the weights for the different scenarios determined. We propose that the
weights for the different scenarios, ![]() , could be given by
, could be given by
Equation (3) penalises deviations from the main scenario's predictive density in a non-linear fashion; other things equal, scenarios will receive a higher weight the smaller the deviations of their predictive densities are relative to the benchmark density. As such, the suggested method is based on the same principle as when Akaike or Schwarz weights are used, except that the true distribution is treated as known in this case.15 The relationship between KLIC and Akaike weights can be seen by noting that the Akaike information criterion is a function of an estimator of the expected Kullback-Leibler information criterion; see Burnham and Anderson (2004).
Regarding the specification of equation (3), we would like to point out that reasonably often when Schwarz weights are calculated - and almost always when Akaike weights are calculated - a uniform prior over models is used. This means that the weights are strictly data determined. However, instead of letting the weights be completely data determined, we argue that it is reasonable to assume that forecasters or decision makers a priori will have an opinion regarding how likely a particular scenario is. We accordingly want to incorporate this opinion into the analysis and therefore allow for non-uniform priors over scenarios in equation (3).16
Relying on the distance-based weighting scheme presented above introduces both benefits and shortcomings through the way in which deviations from the predictive density under the main scenario are being penalised. On the one hand, it means that an "extreme" scenario - which at a certain point in time may actually have a large probability of occurring - will receive a disproportionately low weight since it typically will be judged highly unlikely by the data. Using the distance-based weighting scheme in such cases would lead to an incorrectly assessed uncertainty and a misleading final fan chart. On the other hand, equation (3) implies an additional safeguard against bad judgement as the procedure can be seen as a way of "shrinking" the weighted predictive density towards that of the main scenario. Since the main scenario here by assumption is free from judgement, the suggested method thereby mildly favours the views of Armstrong (1985) and Makridakis (1988). However, instead of following Armstrong and Makridakis - and actually exclude judgement whenever statistical models are available - judgement is only penalised in the present framework.
The distance-based weights also imply that we in practice are evaluating the judgement provided and conclude that scenarios associated with a large KLIC are less likely that those with a small KLIC. Whilst the application is this paper is new, the suggested methodology is, however, clearly related to the policy evaluation conducted in Sims (1982), Doan et al. (1984), Leeper and Zha (2003) and Hamilton and Herrera (2004). In Sims, Doan et al. and Hamilton and Herrera, policy is evaluated by calculating how likely the sequence of structural shocks needed to generate a particular scenario is. Leeper and Zha on the other hand - whose methodology also was employed by Hamilton and Herrera - proposed that policy could be evaluated by constructing linear projections of macro variables conditional on hypothetical paths of monetary policy. These projections were judged reliable if the impact of an intervention was within plus/minus two standard deviations of the historical fluctuations. If not, the intervention was judged to be inconsistent with the prevailing policy regime, leading potentially to changes in private agents' decision rules. As such, Leeper and Zha's work could be seen as a way of empirically testing the relevance of the Lucas critique. The fact that the suggested methodology in this paper emphasises the dynamic impact on the system - rather than the size and sign of the intervention itself - makes it more closely related to the work of Leeper and Zha (2003) than that of Sims (1982) though.
Summing up before we turn to the empirical application, we now have the following procedure to generate a final fan chart which takes judgement into account:
![]() A main scenario for the coming
A main scenario for the coming ![]() quarters is generated in a macroeconomic
model. This main scenario has a predictive density for the
quarters is generated in a macroeconomic
model. This main scenario has a predictive density for the ![]() variables that are being forecasted.
variables that are being forecasted.
![]() Judgement is presented in terms of
Judgement is presented in terms of ![]() -1 alternative scenarios which are defined
as PDFs for future values for one or more variables in the system. Each alternative scenario has a predictive density for the
-1 alternative scenarios which are defined
as PDFs for future values for one or more variables in the system. Each alternative scenario has a predictive density for the ![]() variables that are being forecasted associated with it.
variables that are being forecasted associated with it.
![]() weights are determined for the linear opinion pool. These weights could be generated in a number of ways; we have in this paper suggested
weights are determined for the linear opinion pool. These weights could be generated in a number of ways; we have in this paper suggested ![]() arbitrary weights and ii) a data-based method which takes the KLIC into account in a formalised fashion.
arbitrary weights and ii) a data-based method which takes the KLIC into account in a formalised fashion.
![]() The final predictive density (fan chart) is achieved by weighting together the predictive densities of the different scenarios.
The final predictive density (fan chart) is achieved by weighting together the predictive densities of the different scenarios.
4. Empirical application
In order to illustrate the method presented above, we next turn to an empirical application using Swedish macroeconomic data. Two completely hypothetical alternative scenarios will be presented and a final fan chart then generated by weighting together the predictive densities from the alternative scenarios to that from the model's endogenous forecast. The empirical analysis will be carried out with a standard reduced form Bayesian VAR model. Such a model obviously has limitations as it is more or less impossible to associate behavioural explanations to the scenarios. In many practical applications this shortcoming is serious enough to warrant usage of structural VAR or DSGE models instead as such models can incorporate judgement in a more precise way. However, the purpose of the present exercise is merely to illustrate the principle behind the suggested methodology. For this purpose the reduced form VAR is quite sufficient and the simplicity of the model is appealing as it should maximise transparency.
Turning to the model, it is given by
The numerical evaluation of the posterior distributions is conducted using the Gibbs sampler - see for example Tierny (1994) - with the number of draws set to 10 000. The chain is serially dependent but there has been no thinning of it. Whilst this could be done in order to increase efficiency, it is largely a matter of taste since at convergence the draws are identically distributed according to the posterior distribution; see for example Gelman et al. (2003).
We apply the model to Swedish data from 1980Q2 to 2004Q4 and define
The judgement that is to be included is defined as one scenario for the real exchange rate and one for the unemployment rate. In both cases we lay down paths from 2005Q1 to 2005Q4 and we accordingly let ![]() and
and ![]() in both scenarios. The real exchange rate path is given by [465 460 457 452], which can be compared to the endogenous median forecast from
the model of [473 474 474 474]. We can note that the last observation for the real exchange rate in (non-transformed) TCW terms was 112.85. The conditioning path implies an appreciation to 91.84 - or 18.6 percent - in 2005Q4. For the unemployment rate, the conditioning path is [4.5 4.0 3.7
3.5], which is a substantially stronger development for the labour market than the endogenous median forecast of [5.2 5.1 4.9 4.7].
in both scenarios. The real exchange rate path is given by [465 460 457 452], which can be compared to the endogenous median forecast from
the model of [473 474 474 474]. We can note that the last observation for the real exchange rate in (non-transformed) TCW terms was 112.85. The conditioning path implies an appreciation to 91.84 - or 18.6 percent - in 2005Q4. For the unemployment rate, the conditioning path is [4.5 4.0 3.7
3.5], which is a substantially stronger development for the labour market than the endogenous median forecast of [5.2 5.1 4.9 4.7].
By laying down particular paths for the real exchange rate and the unemployment rate, we are imposing distributions
![]() which have all mass in one point each, just like in Sims (1982), Leeper and Zha (2003) and Adolfson, Laséen, Lindé and Villani (2005).
Such exact imposition of particular paths is called hard conditions using the terminology of Waggoner and Zha (1999). This choice of how to model the scenarios is a simplification in some aspects. For example, it is typically easier to generate the desired distribution; since the variance
is zero, we in practice only have to match the first moment.20
which have all mass in one point each, just like in Sims (1982), Leeper and Zha (2003) and Adolfson, Laséen, Lindé and Villani (2005).
Such exact imposition of particular paths is called hard conditions using the terminology of Waggoner and Zha (1999). This choice of how to model the scenarios is a simplification in some aspects. For example, it is typically easier to generate the desired distribution; since the variance
is zero, we in practice only have to match the first moment.20
We use the model to generate forecasts twelve quarters ahead from 2004Q4. This is slightly longer than the Riksbank's traditional horizon of two years but in line with recent statements by the former governor Lars Heikensten (Sveriges Riksbank, 2005). The forecasts, and thereby the scenarios,
are generated the following way: for every draw from the posterior distribution, a sequence of independent standard normal shocks,
![]() , are drawn. These shocks are then used together with the definition
, are drawn. These shocks are then used together with the definition
![]() - where
- where ![]() is obtained from the standard Cholesky decomposition of
is obtained from the standard Cholesky decomposition of
![]() as
as
![]() - to generate the reduced form shocks and thereby the future data. When a variable has been conditioned upon - that is, it has to take on a particular
value at a certain horizon - the forecasts are obviously still generated sequentially one horizon at a time. However, one shock in each scenario -
- to generate the reduced form shocks and thereby the future data. When a variable has been conditioned upon - that is, it has to take on a particular
value at a certain horizon - the forecasts are obviously still generated sequentially one horizon at a time. However, one shock in each scenario -
![]() in the real exchange rate scenario and
in the real exchange rate scenario and
![]() in the unemployment scenario - is used to generate the conditioning. This means that this shock is generated last for each horizon and its value is set such that given the
elements in
in the unemployment scenario - is used to generate the conditioning. This means that this shock is generated last for each horizon and its value is set such that given the
elements in
![]() , the forecast of the variable in question is exactly that specified in the scenario.21 This choice of generating the conditionings is obviously arbitrary, but it can probably also be described as one of the most intuitive alternatives. As our goal is to illustrate a principle, we argue that it therefore is
well-suited for the purpose.
, the forecast of the variable in question is exactly that specified in the scenario.21 This choice of generating the conditionings is obviously arbitrary, but it can probably also be described as one of the most intuitive alternatives. As our goal is to illustrate a principle, we argue that it therefore is
well-suited for the purpose.
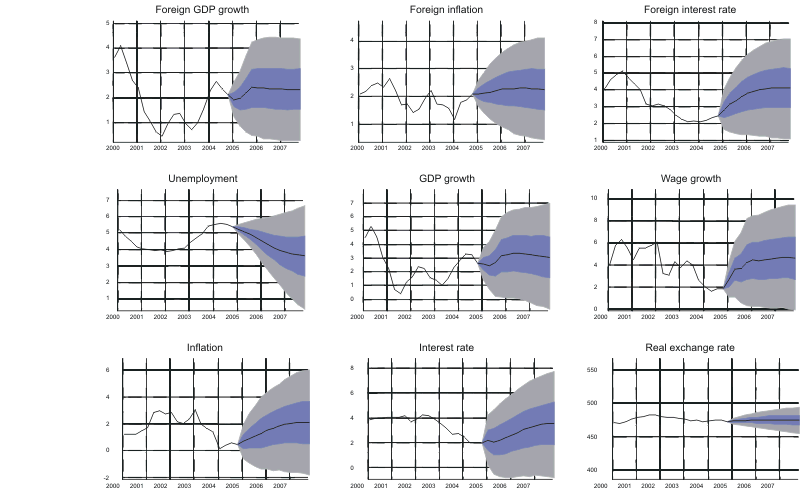
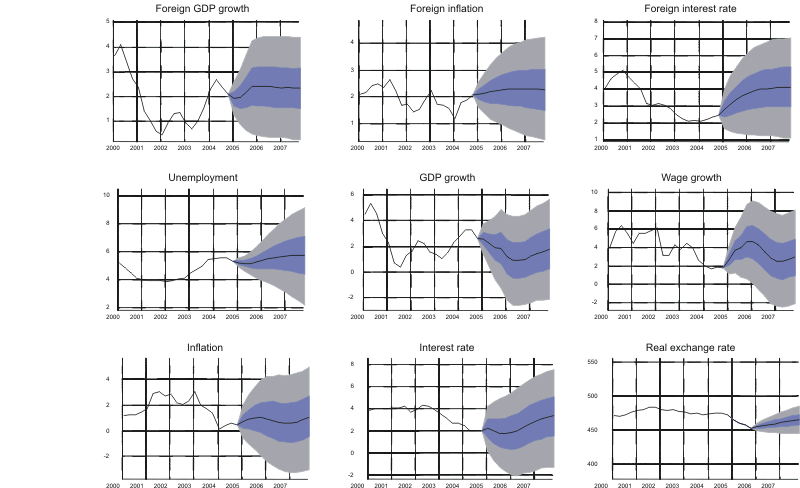
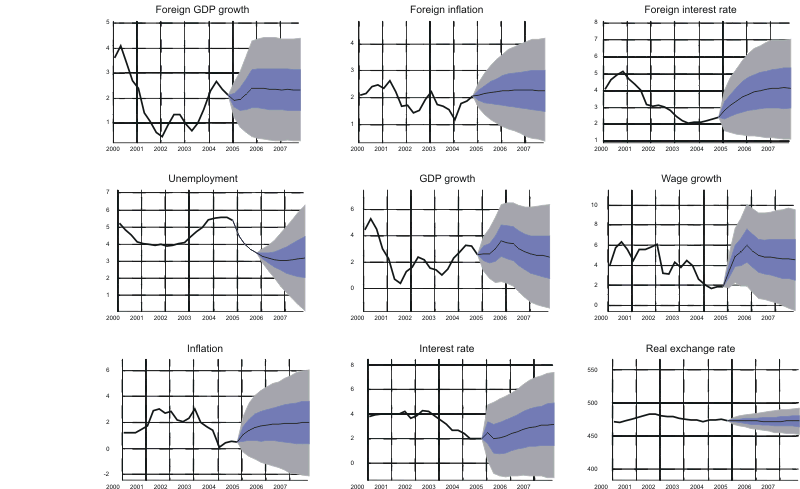
Based on the above described routine, we get as many paths for each variable as we have iterations in the Gibbs sampling algorithm except for the variable we have conditioned upon which takes on the same value every iteration. The predictive densities from the respective scenarios are given in Figures A1 to A3 in Appendix A; the black line is the median forecast and the coloured bands are 50 and 90 percent confidence bands.22
Turning to the issue of how to combine the predictive densities under consideration, we will initially use a set of arbitrary weights and simply employ these to weight the predictive densities according to equation (1). Second, we will also make use of equation (3) - in which deviations from the benchmark predictive density are penalised - in the weighting procedure, thereby allowing both data and a set of arbitrary prior weights to influence the weights in equation (1).
4.1 Combination of predictive densities using arbitrary weights
Figures 1 and 2 show predictive densities for Swedish GDP growth, CPI inflation and the three month treasury bill rate.23 The plots give the median forecast and 50 and 90
percent confidence bands for different sets of weights.24 The solid lines in both figures represent the predictive densities from the model's endogenous forecast, that is,
weights have been set to
![]() where
where ![]() is the weight given to the model's endogenous forecast,
is the weight given to the model's endogenous forecast, ![]() the weight on the
real exchange rate scenario and
the weight on the
real exchange rate scenario and ![]() the weight on the unemployment scenario. The predictive densities given by the dashed lines have been generated by weighting the three different
predictive densities using the arbitrary weights
the weight on the unemployment scenario. The predictive densities given by the dashed lines have been generated by weighting the three different
predictive densities using the arbitrary weights
![]() in Figure 1 and
in Figure 1 and
![]() in Figure 2.25
in Figure 2.25
Looking at Figures 1 and 2 it is obvious that by taking the two alternative scenarios into account the shape of the predictive densities has been changed substantially. In practice, this means that the risk picture - as perceived by the agents producing the forecast - can be significantly
altered when judgement is included. Considering the way in which the shape of the predictive densities has been changed, we note that there appears to have been a downward shift at the longer horizons for all variables regardless of whether the weight vector is
![]() or
or
![]() . The predictive densities using
. The predictive densities using
![]() do clearly deviate more from the benchmark, but this is only
to be expected since
do clearly deviate more from the benchmark, but this is only
to be expected since
![]() is a linear combination of
is a linear combination of
![]() and
and
![]() .
.
The shifts in the predictive densities are consistent with a stronger real exchange rate generating lower GDP growth and inflation and thereby a lower interest rate. At the shorter horizons though, the confidence bands for GDP growth are approximately the same for the weighted predictive densities as those for the endogenous forecast; it can also be noted that the predictive density for inflation has been shifted up slightly. This reflects the increase in GDP growth and inflation that initially follows a negative shock to the unemployment rate and this effect counteracts the decrease that the negative real exchange rate shock has. Another feature worth mentioning is that for all variables - but maybe most obviously so for GDP growth - the weighted predictive density is skewed relative to that from the endogenous forecast. Put differently, by taking a linear combination of the predictive densities from the three scenarios we have generated predictive densities that have not just been shifted in a symmetric way. This serves as an empirical illustration of the claim in Section 3 that the weighted densities potentially can have complicated forms.
We have now seen the predictive densities that were the outcome of an arbitrary choice of weights. Keep in mind though that these weights for example could have been the outcome of a consensus decision or voting procedure in a group and therefore potentially highly legitimate. Next we will investigate the effect of letting data influence the weights and accordingly turn to predictive density combination using the weights from equation (3).
Figure 1. Fan charts from model's endogenous forecast compared to weighted fan charts generated with weight vector [1/3 1/3 1/3].
Solid lines are fan charts from model's endogenous forecast; dashed lines are weighted fan charts.
Figure 2. Fan charts from model's endogenous forecast compared to weighted fan charts generated with weight vector [0.0 0.5 0.5].
Solid lines are fan charts from model's endogenous forecast; dashed lines are weighted fan charts.
4.2 Combination of predictive densities using distance-based weights
The weights generated by equation (3) are functions of the KLIC for the different scenarios and we must therefore first calculate the KLIC for each scenario. As pointed out above, the two hypothetical alternative scenarios impose paths for the real exchange rate and unemployment rate respectively which are reasonably far from the model's endogenous median forecasts. However, our method is based on an evaluation of the dynamic impact on the system from this conditioning and we therefore turn to the KLIC to find out how large this is. The KLIC for each scenario is calculated relative to the predictive density from the endogenous forecast from the model; using the definition in equation (2), we see that this implies that the KLIC for the endogenous forecast is zero.
The practical calculation of the KLIC is described in Appendix C. Before the KLIC can be calculated though,
![]() - that is, the subset of the variables in
- that is, the subset of the variables in
![]() employed in the calculation of the KLIC - must be established. This issue will matter for the weights and attention should therefore be paid to it in practical applications. In
principle, as many variables as possible should be included in
employed in the calculation of the KLIC - must be established. This issue will matter for the weights and attention should therefore be paid to it in practical applications. In
principle, as many variables as possible should be included in
![]() if one wants to take into account the dynamic effects in all dimensions. However, it is also possible to picture a situation in which only a few variables are included in
if one wants to take into account the dynamic effects in all dimensions. However, it is also possible to picture a situation in which only a few variables are included in
![]() ; this might be the case for example if deviations in some dimensions are judged unimportant by the decision makers. In order to illustrate the importance of this question,
the KLIC has here been calculated using three different sets of variables. Letting numbers denote the variables' position in
; this might be the case for example if deviations in some dimensions are judged unimportant by the decision makers. In order to illustrate the importance of this question,
the KLIC has here been calculated using three different sets of variables. Letting numbers denote the variables' position in
![]() in equation (5), the three alternatives are given by
in equation (5), the three alternatives are given by
![]() ,
,
![]() and
and
![]() .26 Note that the first vector is
the largest possible given that we have used hard conditions. As pointed out in Appendix C, the calculations would not be fruitful if the real exchange rate and/or the unemployment rate were included. Values for the various combinations are given in Table 1.
.26 Note that the first vector is
the largest possible given that we have used hard conditions. As pointed out in Appendix C, the calculations would not be fruitful if the real exchange rate and/or the unemployment rate were included. Values for the various combinations are given in Table 1.
| Variables used for evaluation : Prior weight
|
Endogenous forecast KLIC |
Endogenous forecast |
Real exchange rate scenario KLIC |
Real exchange rate scenario |
Unemployment scenario KLIC |
Unemployment scenario |
|---|---|---|---|---|---|---|
| [1 2 3 5 6 7 8] : [1/3 1/3 1/3] |
0.0000 | 0.7300 | 2.5871 | 0.0549 | 1.2213 | 0.2150 |
| [5 6 7 8] : [1/3 1/3 1/3] |
0.0000 | 0.6127 | 1.5174 | 0.1343 | 0.8845 | 0.2530 |
| [7] : [1/3 1/3 1/3] |
0.0000 | 0.3788 | 0.2613 | 0.2917 | 0.1397 | 0.3294 |
| [1 2 3 5 6 7 8] : [0.0 0.5 0.5] |
0.0000 | 0.0000 | 2.5871 | 0.2035 | 1.2213 | 0.7965 |
| [5 6 7 8] : [0.0 0.5 0.5] |
0.0000 | 0.0000 | 1.5174 | 0.3468 | 0.8845 | 0.6532 |
| [7] : [0.0 0.5 0.5] |
0.0000 | 0.0000 | 0.2613 | 0.4696 | 0.1397 | 0.5304 |
The order in which scenarios are referred to in prior weight vector is [endogenous forecast, real exchange rate scenario, unemployment scenario].
The KLIC values obviously tell us something about how likely the different scenarios are in light of the model and the data. In this particular application, we can for example tell that the unemployment scenario is judged more likely than the real exchange rate scenario; regardless of which variables are included in the calculation of the KLIC, the value for the unemployment scenario is approximately half of that for the real exchange rate scenario. However, the KLIC values are difficult to interpret - it is not obvious what constitutes a "small" or "large" deviation from the reference distribution. By next turning to the distance-based weights, we instead face non-negative numbers that sum to one. These weights accordingly tell us in a straightforward way how deviations from the reference distribution are penalised.
The weights have been calculated by assuming that the prior weights over scenarios are given either by
![]() or
or
![]() , where
, where ![]() is the prior weight given to the model's endogenous forecast,
is the prior weight given to the model's endogenous forecast, ![]() the prior weight on the real exchange rate scenario and
the prior weight on the real exchange rate scenario and
![]() the prior weight on the unemployment scenario. This choice of weights was made so that the fan charts are directly comparable to those in Figures 1 and 2; through this setup any
difference between the weighted predictive densities is due to the KLIC. Note that the KLIC is calculated using three different subset of variables:
the prior weight on the unemployment scenario. This choice of weights was made so that the fan charts are directly comparable to those in Figures 1 and 2; through this setup any
difference between the weighted predictive densities is due to the KLIC. Note that the KLIC is calculated using three different subset of variables:
![]() ,
,
![]() and
and
![]() . Weights for the scenarios - calculated with the two sets of prior weights and three sets of variables for evaluation - are given in Table 1.
. Weights for the scenarios - calculated with the two sets of prior weights and three sets of variables for evaluation - are given in Table 1.
Figures 3 to 5 show the predictive densities from the endogenous forecast and those generated by weighting predictive densities according to the weights from equation (3), where
![]() were used as prior weights; just like above, solid lines represent the former and dashed lines the latter. As can be seen, the weights generated by equation (3) are always highest for the endogenous forecast but as the number of variables used for calculation of the KLIC
is reduced, more weight is put on the alternative scenarios. This is clearly illustrated in Figures 3 to 5 where there are only minor differences between the predictive density of the endogenous forecast and the weighted predictive density when all variables except unemployment and the real
exchange rate are used to calculate the KLIC. Using fewer variables in the evaluation though, the weighted predictive densities look more and more different from that of the endogenous forecast. When only inflation is used to calculate the KLIC, the weights given by equation (3)
are actually fairly close to 1/3 for all scenarios and Figure 5 accordingly looks a lot like Figure 1. The fact that weights are more evenly distributed over scenarios as fever variables are used to calculate the KLIC is in line with our expectations. It can intuitively be explained by the fact
that as fewer variables are included in
were used as prior weights; just like above, solid lines represent the former and dashed lines the latter. As can be seen, the weights generated by equation (3) are always highest for the endogenous forecast but as the number of variables used for calculation of the KLIC
is reduced, more weight is put on the alternative scenarios. This is clearly illustrated in Figures 3 to 5 where there are only minor differences between the predictive density of the endogenous forecast and the weighted predictive density when all variables except unemployment and the real
exchange rate are used to calculate the KLIC. Using fewer variables in the evaluation though, the weighted predictive densities look more and more different from that of the endogenous forecast. When only inflation is used to calculate the KLIC, the weights given by equation (3)
are actually fairly close to 1/3 for all scenarios and Figure 5 accordingly looks a lot like Figure 1. The fact that weights are more evenly distributed over scenarios as fever variables are used to calculate the KLIC is in line with our expectations. It can intuitively be explained by the fact
that as fewer variables are included in
![]() , there are fewer dimensions in which the densities can deviate from each other.
, there are fewer dimensions in which the densities can deviate from each other.
We next turn to the case where
![]() in which the benchmark model - whilst we might not be interested
in it per se - can be seen as a "neutral" way of evaluating two conflicting views regarding the economy before weighting the predictive densities together. It can then be seen in Figures 6 to 8 that the influence of the unemployment scenario - which was judged more likely by the KLIC -
is reduced as the KLIC is being calculated using fewer variables. As only inflation is used to calculate the KLIC, the predictive densities in Figure 8 are virtually identical to those in Figure 2. This is of course precisely what we expect since the weights according to equation (3) in that case are very close to 0.5 for both scenarios.
in which the benchmark model - whilst we might not be interested
in it per se - can be seen as a "neutral" way of evaluating two conflicting views regarding the economy before weighting the predictive densities together. It can then be seen in Figures 6 to 8 that the influence of the unemployment scenario - which was judged more likely by the KLIC -
is reduced as the KLIC is being calculated using fewer variables. As only inflation is used to calculate the KLIC, the predictive densities in Figure 8 are virtually identical to those in Figure 2. This is of course precisely what we expect since the weights according to equation (3) in that case are very close to 0.5 for both scenarios.
Summing up, we think that the above exercise has shown that judgement can be introduced in the analysis in a formal and reasonably straightforward way. The linear opinion pool allows us to combine the predictive densities from several scenarios and conflicting sets of judgement can thereby be accounted for in the forecasting process. In the empirical analysis we used arbitrary weights and weights based on the KLIC of a scenario's predictive density relative to a benchmark predictive density. Both of these approaches seem reasonable in practice. A combination of these two methods, in which arbitrary weights are used but where the decision makers can use the KLIC values as input in the decision making process, is also a potential solution. However, the method to determine weights should probably be made application and institution specific in order to generate the best possible result. More work is therefore needed on this particular issue.
Figure 3. Fan charts from model's endogenous forecast compared to weighted fan charts generated with prior vector [1/3 1/3 1/3] and evaluated using all possible variables.
Solid lines are fan charts from model's endogenous forecast; dashed lines are weighted fan charts.
Figure 4. Fan charts from model's endogenous forecast compared to weighted fan charts generated with prior vector [1/3 1/3 1/3] and evaluated using GDP, wage, inflation and interest rate.
Solid lines are fan charts from model's endogenous forecast; dashed lines are weighted fan charts.
Figure 5. Fan charts from model's endogenous forecast compared to weighted fan charts generated with prior vector [1/3 1/3 1/3] and evaluated using inflation.
Solid lines are fan charts from model's endogenous forecast; dashed lines are weighted fan charts.
Figure 6. Fan charts from model's endogenous forecast compared to weighted fan charts generated with prior vector [0.0 0.5 0.5] and evaluated using all possible variables.
Solid lines are fan charts from model's endogenous forecast; dashed lines are weighted fan charts.
Figure 7. Fan charts from model's endogenous forecast compared to weighted fan charts generated with prior vector [0 0.5 0.5] and evaluated using GDP, wage, inflation and interest rate.
Solid lines are fan charts from model's endogenous forecast; dashed lines are weighted fan charts.
Figure 8. Fan charts from model's endogenous forecast compared to weighted fan charts generated with prior vector [0 0.5 0.5] and evaluated using inflation.
Solid lines are fan charts from model's endogenous forecast; dashed lines are weighted fan charts.
5. Conclusions
This paper has outlined a new method to incorporate judgement into a forecasting process. We have suggested that each judgement set be modelled as an alternative scenario in a macroeconomic model, with its dynamic effect on the system described by a predictive density. Specifically, we suggest combining the predictive densities stemming from the different sets of judgement into one final predictive density. This final density thereby reflects the judgemental views within the context of the macroeconomic model.
Forecasters in general, and central banks in particular, often wish to provide an accurate predictive density for a number of macroeconomic variables. The framework offers a formalised and model-consistent way to incorporate judgement into predictive densities in a model-based environment. The methodology is best suited to a forecasting process that places a great deal of emphasis on one model which, given recent improvements in the forecasting ability of DSGE models, increasingly describes the forecasting practices of several central banks.27 As policy institutions head further along the path of incorporating models into the policy process, a new and straightforward way to address judgement when generating predictive densities is available.
Although the empirical application in this paper focused upon marginal predictive densities for one variable at a time, the method also yields joint predictive densities, facilitating answering joint-probability questions of the type posed by Leeper and Zha (2003). For example, knowing the probability with which inflation may exceed a target and output growth may be negative at the same time is clearly of interest to policy makers, as it reveals the policy tradeoff they face in a particular scenario or across all scenarios. This issue can be readily addressed in the proposed framework, increasing its appeal in applied policy work. The framework also explicitly addresses how conflicting sets of judgement can be taken into account in the forecasting process, as it is rarely the case in practice that judgement sets are completely compatible with each other. The paper thus extends related literature on predictive densities and judgement, such as Svensson and Tetlow (2005).
Finally, it is important to stress that although the framework put forward in this paper places a model in the prominent position, this does not detract from the value of judgement. Rather, our goal is to step away from ad hoc judgemental adjustments and toward a more formal framework, thereby generating more accurate predictive densities. The use of fan charts is a relatively new development and the implementation at different policy institutions suffers from various shortcomings, as pointed out by Leeper (2003), Clements (2004) and Hall and Mitchell (2004). As interest in fan charts and model-based forecasting increases, there is reason for improvement and refinement of the techniques.
References
Adolfson, M., Andersson, M. K., Lindé, J., Villani, M. and Vredin, A. (2005), "Modern Forecasting Models in Action: Improving Macro Economic Analyses at Central Banks", Working Paper No. 190, Sveriges Riksbank.
Adolfson, M., Laséen, S., Lindé, J. and Villani, M. (2005), "Are Constant Interest Rate Forecasts Modest Interventions? Evidence from a Dynamic Open Economy Model", International Finance 8, 509-535.
Armstrong, J. S. (1985), Long-Range Forecasting. 2nd edition. John Wiley, New York.
Blix, M. and Sellin, P. (1998), "Uncertainty Bands for Inflation Forecasts", Working Paper No. 65, Sveriges Riksbank.
Brock, W. A., Durlauf, S. N. and West, K. D. (2003), "Policy Evaluation in Uncertain Economic Environments", Brookings Papers on Economic Activity 2003:1, 235-301.
Burnham, K. P. and Anderson, D. R. (2004), "Multimodel Inference: Understanding AIC and BIC in Model Selection", Sociological Methods and Research 33, 261-304.
Clemen, R. T. (1989), "Combining Forecasts: A Review and Annotated Bibliography", International Journal of Forecasting 5, 559-583.
Clemen, R. T. and Winkler, R. L. (1999), "Combining Probability Distributions from Experts in Risk Analysis", Risk Analysis 19, 187-203.
Clements, M. P. (2004), "Evaluating the Bank of England Density Forecasts of Inflation", Economic Journal 114, 844-866.
Clements, M. P. and Hendry, D. F. (1998), Forecasting Economic Time Series. Cambridge University Press, Cambridge.
Cogley, T., Morozov, S. and Sargent, T. J. (2005), "Bayesian Fan Charts for U.K. Inflation: Forecasting and Sources of Uncertainty in an Evolving Monetary System", Journal of Economic Dynamics and Control 29, 1893-1925.
DeGroot, M. H. (1974), "Reaching a Consensus", Journal of the American Statistical Association 69, 118-121.
Diebold, F. X. and Pauly, P. (1990), "The Use of Prior Information in Forecast Combination", Journal of Forecasting 6, 503-508.
Doan, T., Litterman, R. and Sims, C. (1984), "Forecasting and Conditional Projection Using Realistic Prior Distributions", Econometric Reviews 3, 1-100.
Garratt, A., Lee, K., Pesaran, M. H. and Shin, Y. (2003), "Forecast Uncertainties in Macroeconomic Modeling: An Application to the U.K. Economy", Journal of the American Statistical Association 98, 829-838.
Gelman, A., Carlin, J. B., Stern, H. S. and Rubin, D. B. (2003), Bayesian Data Analysis, 2nd edition. Chapman and Hall, New York.
Granger, C. W. J. and Ramanathan, R. (1984), "Improved Methods of Combining Forecasts", Journal of Forecasting 3, 197-204.
Hall, S. G. and Mitchell, J. (2004), "Optimal Combination of Density Forecasts", Tanaka Business School Discussion Papers TBS/DP04/16.
Hamilton, J. D. and Herrera, A. M. (2004), "Oil Shocks and Aggregate Macroeconomic Behavior: The Role of Monetary Policy", Journal of Money, Credit, and Banking 36, 265-286.
Hendry, D. F. and Clements, M. P. (2004), "Pooling of Forecasts", Econometrics Journal 7, 1-31.
Hogarth, R. M. (1987), Judgment and Choice. John Wiley, New York.
Kullback, S. and Leibler, R. A. (1951), "On Information and Sufficiency", Annals of Mathematical Statistics 22, 79-86.
Lawrence, M. J., Edmundson, R. H. and O'Connor, M. J. (1985), "An Examination of the Accuracy of Judgemental Extrapolation of Time Series", International Journal of Forecasting 1, 14-25.
Lawrence, M. J., Edmundson, R. H. and O'Connor, M. J. (1986), "The Accuracy of Combining Judgemental and Statistical Forecasts", Management Science 32, 1521-1532.
Leeper, E. M. (2003), "An Inflation Reports Report", Sveriges Riksbank Economic Review 2003:3, 94-118.
Leeper, E. M. and Zha, T. (2003), "Modest Policy Interventions", Journal of Monetary Economics 50, 1673-1700.
Litterman, R. B. (1986), "Forecasting with Bayesian Vector Autoregressions - Five Years of Experience", Journal of Business and Economic Statistics 5, 25-38.
Makridakis, S. (1988), "Metaforecasting", International Journal of Forecasting 4, 467-491.
McKonway, K. J. (1981), "Marginalization and Linear Opinion Pools", Journal of the American Statistical Association 76, 410-414.
McNees, S. K. (1990), "The Role of Judgment in Macroeconomic Forecasting Accuracy", International Journal of Forecasting 6, 287-299.
Mitchell, J. and Hall, S. G. (2005), "Evaluating, Comparing and Combining Density Forecasts Using KLIC with an Application to the Bank of England and NIESR "Fan" Charts of Inflation", Oxford Bulletin of Economics and Statistics 67, 995-1033.
Öller, L.-E. (1978), "A Method for Pooling Forecasts", Journal of the Operational Research Society 29, 55-63.
Reifschneider, D. L., Stockton, D. J. and Wilcox, D. W. (1997), "Econometric Models and the Monetary Policy Process", Carnegie-Rochester Conference Series on Public Policy 47, 1-37,
Robertson, J. C., Tallman, E. W. and Whiteman, C. H. (2005), "Forecasting Using Relative Entropy", Journal of Money, Credit, and Banking 37, 383-401.
Sanders, N. R. and Ritzman, L. P. (1999), "Judgmental Adjustments of Statistical Forecasts". In: Armstrong, J. S. (ed), Principles of Forecasting. Kluwer Academic Publishers, Norwell.
Schorfheide, F. (2000), "Loss Function-Based Evaluation of DSGE Models", Journal of Applied Econometrics 15, 645-670.
Schott, J. R. (1997), Matrix Analysis for Statistics. Wiley, New York.
Sims, C. A. (1982), "Policy Analysis with Econometric Models", Brookings Papers on Economic Activity 1982:1, 107-164.
Smets, F. and Wouters, R. (2004), "Forecasting with a Bayesian DSGE Model - An Application to the Euro Area", Working Paper No. 389, European Central Bank.
Svensson, L. E. O. (2005), "Monetary Policy with Judgement: Forecast Targeting", International Journal of Central Banking 1, 1-54.
Svensson, L. E. O. and Tetlow, R. J. (2005), "Optimal Policy Projections", International Journal of Central Banking 1, 177-207.
Svensson, L. E. O. and Williams, N. (2005), "Monetary Policy with Model Uncertainty: Distribution Forecast Targeting", NBER Working Paper No. 11733.
Sveriges Riksbank. (2005), Tankar om hur det penningpolitiska arbetet kan utvecklas. Speech by Governor Lars Heikensten on February 22 at Nationalekonomiska Föreningen. Retreived from www.riksbank.se/templates/Page.aspx?id=15783.
Tierny, L. (1994), "Markov Chains for Exploring Posterior Distributions", Annals of Statistics 22, 1701-1762.
Villani, M. and Warne, A. (2003), "Monetary Policy Analysis in a Small Open Economy Using Bayesian Cointegrated Structural VARs", Working Paper No. 296, European Central Bank.
Wallis, K. F. (2005), "Combining Density and Interval Forecasts: A Modest Proposal", Oxford Bulletin of Economics and Statistics 67, 983-994.
Waggoner, D. F. and Zha, T. (1999), "Conditional Forecasts in Dynamic Multivariate Models", Review of Economics and Statistics 81, 639-651.
Appendix A - Predictive densities
Figure A1. Endogenous forecast from Bayesian VAR model using Swedish data.
Figure A2. Forecasts from real exchange rate scenario in Bayesian VAR model using Swedish data.
Figure A3. Forecasts from unemployment scenario in Bayesian VAR model using Swedish data.
Appendix B - Generating weighted predictive densities
This appendix shortly describes how the weighted predictive densities are generated in this paper. Clearly, this is only one of many potential ways in which the weighting can be conducted.
The predictive density from each scenario is generated using a Gibbs sampling algorithm as described in Section 4. For each scenario - ![]() - we have a three dimensional matrix
- we have a three dimensional matrix
![]() of dimensions
of dimensions ![]() x
x![]() x
x![]() which contains all predictions generated under that scenario. Using the
which contains all predictions generated under that scenario. Using the ![]() matrices
matrices
![]() , a weighted predictive density - stored in the
, a weighted predictive density - stored in the ![]() x
x![]() x
x![]() matrix A - can be produced the following way:
matrix A - can be produced the following way:
1. Decide which of the ![]() matrices to sample a 1x
matrices to sample a 1x![]() x
x![]() plane from. The probability of matrix
plane from. The probability of matrix
![]() being chosen is given by the weight of that scenario,
being chosen is given by the weight of that scenario, ![]() .
.
2. Sample, with a probability given by
![]() for all planes in the matrix, a 1x
for all planes in the matrix, a 1x![]() x
x![]() plane from the chosen
plane from the chosen
![]() .
.
3. Store the plane in A.
4. Return to 1. Repeat the procedure ![]() times.
times.
Appendix C - Calculating the Kullback-Leibler information criterion
From a practical point of view, the integral in equation (2) could be very difficult to solve analytically in many cases. This can of course be circumvented by relying on numerical methods, but a numerical calculation of the integral could potentially come at a high computational cost if the system is of high dimension. A simplification which will be used in this paper is therefore to assume that we have a simple known form for the densities in question which yields a convenient analytical solution. We describe this assumption in this appendix.
Initially, define
![]() as the
stacked
as the
stacked ![]() x1 vector of forecasts, where the
x1 vector of forecasts, where the ![]() x1 vector
x1 vector
![]() is the subset of the variables in
is the subset of the variables in
![]() employed in the calculation of the KLIC,
employed in the calculation of the KLIC,
![]() and
and ![]() is the forecast horizon. We next assume that
is the forecast horizon. We next assume that ![]() follows a multivariate normal distribution which implies that knowledge of the mean
follows a multivariate normal distribution which implies that knowledge of the mean
![]() and covariance
and covariance
![]() of the distribution is sufficient to completely describe it.28 The distributions
of the distribution is sufficient to completely describe it.28 The distributions ![]() and
and ![]() are hence given by
are hence given by
![]() (A1)
(A1)
![]() (A2)
(A2)
Relying on the above assumptions, the KLIC can be calculated as
![]() (A3)
(A3)
where we have made use of the following lemma:
Lemma 1
Let ![]() be a p-dimensional vector with mean
be a p-dimensional vector with mean
![]() and covariance matrix
and covariance matrix
![]() , then
, then
![]() (A4)
(A4)
for every p vector b and symmetric pxp matrix B![]() [Proof: Schott (1997).]
[Proof: Schott (1997).]
Whilst equation (A3) is a simple expression, we still need means and covariance matrices of the distributions in question to implement it. These moments could be calculated in numerous ways depending upon the chosen framework but one convenient solution in empirical applications is to once again
rely on stochastic simulation. Using numerical techniques, ![]() values taken on by
values taken on by ![]() are generated as the predictive densities for the main and alternative scenarios are simulated. The
are generated as the predictive densities for the main and alternative scenarios are simulated. The ![]() x1 vectors
x1 vectors
![]() and
and
![]() and the
and the ![]() x
x![]() covariance matrices
covariance matrices
![]() and
and
![]() can then be estimated using maximum likelihood by employing equations (A5) and (A6) respectively.
can then be estimated using maximum likelihood by employing equations (A5) and (A6) respectively.
![]() (A5)
(A5)
![]() (A6)
(A6)
for
![]() and where
and where ![]() is the number of iterations in the numerical
algorithm. The KLIC is then computed by simply replacing the true parameters in equation (A3) with their maximum likelihood estimates.
is the number of iterations in the numerical
algorithm. The KLIC is then computed by simply replacing the true parameters in equation (A3) with their maximum likelihood estimates.
A technical issue that we want to point out here is that relying on the above described method and hard conditions, any variable included in
![]() cannot be included in
cannot be included in
![]() since
since
![]() in that case would be singular. Put differently, we cannot include variables that we have imposed hard conditions on in the calculation of the KLIC.
in that case would be singular. Put differently, we cannot include variables that we have imposed hard conditions on in the calculation of the KLIC.
Footnotes
Board of Governors of the Federal Reserve System,
Division of Monetary Affairs,
Washington, DC 20551, USA.
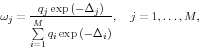
![Figure 1. The figure shows the endogenous and weighted fan charts for GDP growth, inflation and interest rate. Weighted fan charts were generated using the weight vector [1/3 1/3 1/3]. The fan charts are presented as plots of the 5th, 25th, 50th, 75th and 95th percentiles from the predictive densities. There appears to have been a downward shift at the longer horizons for all variables. At the shorter horizons though, the confidence bands for GDP growth are approximately the same for the weighted predictive density as those for the endogenous forecast and the predictive density for inflation has been shifted up slightly.](figure_1.gif)
![Figure 2. The figure shows the endogenous and weighted fan charts for GDP growth, inflation and interest rate. Weighted fan charts were generated using the weight vector [0 0.5 0.5]. The fan charts are presented as plots of the 5th, 25th, 50th, 75th and 95th percentiles from the predictive densities. The effects shown in Figure 2 are similar to those in Figure 1 but more pronounced, that is, the shifts between endogenous and weighted fan charts are larger.](figure_2.gif)
![Figure 3. The figure shows the endogenous and weighted fan charts for GDP growth, inflation and interest rate. Weighted fan charts were generated using KLIC weights evaluated over all possible variables and prior vector [1/3 1/3 1/3]. The fan charts are presented as plots of the 5th, 25th, 50th, 75th and 95th percentiles from the predictive densities. Only minor differences between the predictive density of the endogenous forecast and the weighted predictive density can be seen when all variables except unemployment and the real exchange rate are used to calculate the KLIC.](figure_3.gif)
![Figure 4. The figure shows the endogenous and weighted fan charts for GDP growth, inflation and interest rate. Weighted fan charts were generated using KLIC weights evaluated over GDP, wage, inflation and interest rate and prior vector [1/3 1/3 1/3]. The fan charts are presented as plots of the 5th, 25th, 50th, 75th and 95th percentiles from the predictive densities. There appears to have been a downward shift at the longer horizons for all variables, though it is not particularly large. At the shorter horizons, there is a very minor upward shift in inflation.](figure_4.gif)
![Figure 5. The figure shows the endogenous and weighted fan charts for GDP growth, inflation and interest rate. Weighted fan charts were generated using KLIC weights evaluated over inflation and prior vector [1/3 1/3 1/3]. The fan charts are presented as plots of the 5th, 25th, 50th, 75th and 95th percentiles from the predictive densities. The weights given by equation (3) are fairly close to 1/3 for all scenarios and Figure 5 accordingly looks a lot like Figure 1.](figure_5.gif)
![Figure 6. The figure shows the endogenous and weighted fan charts for GDP growth, inflation and interest rate. Weighted fan charts were generated using KLIC weights evaluated over all possible variables and prior vector [0 0.5 0.5]. The fan charts are presented as plots of the 5th, 25th, 50th, 75th and 95th percentiles from the predictive densities. There has been a substantial downward shift at the longer horizons for all variables. At the shorter horizons on the other hand, the confidence bands tend to be shifted upward sligthly.](figure_6.gif)
![Figure 7. The figure shows the endogenous and weighted fan charts for GDP growth, inflation and interest rate. Weighted fan charts were generated using KLIC weights evaluated over GDP, wage, inflation and interest rate and prior vector [0 0.5 0.5]. The fan charts are presented as plots of the 5th, 25th, 50th, 75th and 95th percentiles from the predictive densities. Like in Figure 6, there has been a substantial downward shift at the longer horizons for all variables and a small upward shift at the shorter horizons. The effects are sligthly more pronounced than in Figure 6 though.](figure_7.gif)
![Figure 8. The figure shows the endogenous and weighted fan charts for GDP growth, inflation and interest rate. Weighted fan charts were generated using KLIC weights evaluated over inflation and prior vector [0 0.5 0.5]. The fan charts are presented as plots of the 5th, 25th, 50th, 75th and 95th percentiles from the predictive densities. The predictive densities are virtually identical to those in Figure 2; this is of course precisely what we expect since the weights according to equation (3) in this case are very close to 0.5 for both scenarios.](figure_8.gif)