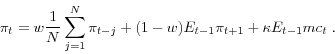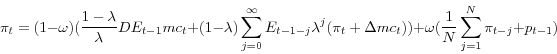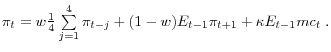FRB: Finance and Economics Discussion Series: Screen Reader Version - A QUANTITATIVE COMPARISON OF STICKY-PRICE AND STICKY-INFORMATION MODELS OF PRICE SETTING

Skip to: [Printable Version (PDF)] [Bibliography] [Footnotes]

Finance and Economics Discussion Series: 2006-45 Screen Reader version ^♣

A QUANTITATIVE COMPARISON OF STICKY-PRICE AND STICKY-INFORMATION MODELS OF PRICE SETTING^*

AUGUST 2006

MICHAEL T. KILEY

FEDERAL RESERVE BOARD

WASHINGTON, DC 20551

202.452.2448

[email protected]

Keywords: Phillips curve, New-Keynesian model, Inflation persistence

Abstract

I estimate sticky-price and sticky-information models of price setting for the United States via maximum-likelihood techniques, reaching several conclusions. First, the sticky-price model fits best, and captures inflation dynamics as well as reduced-form equations once hybrid-behavior is allowed. Second, the importance of hybrid behavior in sticky-price models is potentially consistent with a role for some information imperfections, such as sticky information, as a complement to nominal price rigidities. Finally, the favorable results herein for the hybrid sticky-price model when evaluated by statistics that summarize the relative fit of different models is consistent with the existing literature that is both supportive and dismissive of such models, as this literature has largely ignored fit in evaluating such models. Many previous studies have focused on ancillary issues, such as the standard errors associated with certain parameters or Granger-causality tests that may not provide much information about sticky-price models.

JEL Codes: E3

1. Introduction

There is a great deal of disagreement over how to best model inflation dynamics, and rival views are often only weakly contrasted empirically. Our analysis provides a quantitative evaluation of two leading structural models of inflation dynamics - the sticky-price model and the sticky-information model - and considers their performance relative to reduced-form regressions. The analysis differs from much previous work in its focus on measures of fit and explicit consideration of alternative models. Three conclusions are reached: The sticky-price model appears to fit best, particularly over the recent sample and if allowance is made for what has been termed "hybrid" behavior; in addition, the presence of "hybrid" behavior is consistent with the types of information imperfections emphasized in the sticky-information model, implying that the data's preference for a sticky-price hybrid model provides support to some role for such information imperfections as a complement to sticky prices; and, finally, the results herein are consistent with previous research that has reached quite diverse conclusions. For example, authors have used similar results to support rational expectations sticky-price models (e.g., Gali and Gertler (1999) or Sbordone (2005)), or to criticize such models (e.g., Rudd and Whelan (2003, 2005a, 2005b, 2005c)). Our discussions will take pains to illustrate how emphasis on particular stylized facts by other authors has led to the range of conclusions they have offered.

Before turning to the substantive analysis, it is useful to compare our analysis to the themes covered thirty-five years ago in a conference at the Federal Reserve Board on a broadly similar theme, The Econometrics of Price Determination (Board of Governors of the Federal Reserve System (1971)). The research at that earlier conference largely focused on the "wage-price" sectors of a number of macroeconometric models; our focus on sticky-price and sticky-information models of price setting, increasingly employed as the price and/or wage specification in dynamic general equilibrium models, falls directly within that earlier tradition. But significant differences in approach, reflecting the results of decades of research, are also apparent. Most importantly, the research at the earlier conference made at most ad hoc attempts to distinguish between dynamics induced by expectations and those intrinsic to price or wage setting (although the contributions of Robert Lucas and Peter von zur Muehlen emphasized the importance of separating the impact of expectations from other factors in a manner immediately familiar to the modern reader). This distinction is the hallmark of rational expectations models and remains the central area of disagreement in empirical work on inflation dynamics.

The next section discusses our empirical strategy. The analysis then turns to baseline and hybrid versions of a standard sticky-price model. The sticky-information model is considered next, with a special focus on comparing the sticky-information and sticky-price models. The final two sections discuss the interpretation of our results, with particular emphasis on linking the findings herein to other research.

2. Empirical strategy

The empirical analysis will focus on the price level for the nonfarm business sector of the United States. The primary estimation sample is 1965Q1 to 2002Q4; I will also consider the more recent 1983Q1 to 2002Q4 sample separately. The price level (P) is given by the nonfarm output deflator. In each model below, prices will depend upon a measure of marginal cost. In practice, I measure nominal marginal cost (P*MC) by unit labor costs.¹ Unit labor costs are the theoretically correct measure of nominal marginal cost under some reasonable assumptions and are the standard in models of price-setting (e.g., Gali and Gertler (1999), Sbordone (2002)). The literature on reduced-form price equations has traditionally focused on output gap measures as the cost measure (e.g., Fuhrer and Moore (1995), Roberts (1997), Rudd and Whelan (2005c)), and our discussion later will examine the consistency of the estimated models with the reduced-form correlation between detrended output and inflation. Real marginal cost is nominal marginal labor cost divided by the price level, or the labor share of income (MC). Other data used in the estimation include the level of real output (Y) in the nonfarm business sector and the nominal effective federal funds rate (r); the manner in which these variables enter the system is discussed below. The data on prices (P) and the labor share (MC) are logged and linearly detrended prior to estimation; the data on real output is logged and linearly-detrended with a break in the trend in 1973Q1; and the nominal federal funds rate is demeaned.

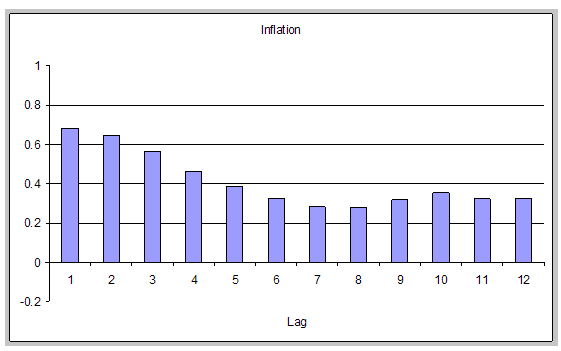
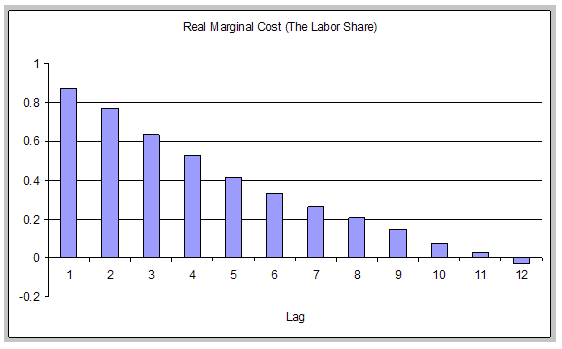
The persistence of inflation will prove important in model comparisons. Figure 1 graphs the autocorrelation functions of inflation and real marginal cost (the labor share) over the sample period (for the first 12 lags). Inflation is quite persistent, and the autocorrelations decay very slowly. Real marginal cost is also very highly autocorrelated. As marginal cost is the key driver of inflation in the models examined, such models will have no difficulty predicting persistent inflation, a point emphasized for the sticky-price model in, for example, Rudd and Whelan (2005a) and Fuhrer (2005).

Each of the models presented below is estimated via maximum likelihood (ML). The system of equations consists of the structural pricing equation and three reduced-form equations for (log) nominal marginal cost (p+mc), the nominal funds rate (r), and (log) real output (y)

$\begin{displaymath} p_t & = & F(p_{t-1} ,p_{t-2} ,...,E_{t-1} mc_t ,E_{t-2} mc_t ,...,E_{t-1} p_t ,E_{t-2} p_t ,E_{t-1} p_{t+1} )+v_t \end{displaymath}$

$\begin{displaymath} X_t & = & A(L)Z_t +e_t ,\quad X_t =[\Delta (p_t +mc_t ),r_t ,y_t ]',\quad Z_t =[mc_t ,r_t ,y_t ,\Delta p_t ]' \end{displaymath}$

where F is a structural pricing equation,

is a structural shock to the pricing equation (a cost-push shock, in the language of Gali and Gertler (1999) and others), A(L) are the reduced-form coefficients governing dynamics for the remainder of the system (where L is the lag polynomial), and

is a vector of reduced-form shocks to the non-price equations.

A reduced-form system for marginal cost and any of its determinants is necessary to form the expectations that enter the structural pricing equation for ML estimation. I assume that the reduced-form process governing (the change in) nominal marginal cost is well described by lags of real marginal cost, output, the nominal interest rate, and inflation. Output is similarly well-captured by reduced-form equations containing lags of each variable in the system, while the reduced-form for the nominal interest rate contains contemporaneous values as well, consistent with the literature on monetary policy reaction functions and the typical identifying assumption in vector autoregressions used for monetary policy analysis.² A reduced-form system can quite accurately summarize the information in past data for current-period realizations and is the correct reduced form in many structural models, limiting the degree of concern regarding mis-specification.³ Combining the reduced-form equations for marginal cost, output, and the nominal interest rate with a structural pricing equation results in a restricted reduced-form representation for inflation, in which inflation depends upon lags of itself and all the other variables.

In the estimation, the likelihood was formed solely based on the one-step-ahead inflation forecast errors derived via the Kalman filter using the Anderson-Moore AIM algorithm (see Anderson (2000)); the reduced-form coefficients in the system and the disturbances were estimated separately and held fixed during the maximization of the likelihood constructed from the one-step-ahead inflation errors.⁴ Consequently, the differences in estimated likelihoods reflect only the different fits of the inflation equations, facilitating their comparison. The one-step-ahead forecast errors ignore any information in contemporaneous variables that would be useful in forecasting inflation and hence are comparable to the errors from reduced-form equations relating inflation to its own lags and lags of other variables.⁵

An alternative estimation strategy would be to instrument for expectations and find the structural parameters via an instrumental variables (IV) estimator (e.g., the Generalized Method of Moments). However, limited-information estimators have been shown to have some poor properties in the context of forward-looking equations like the price-setting models examined herein; examples include Ma (2002), Jondeau and Le Bihan (2003), Eichenbaum and Fisher (2003), Fuhrer and Olivei (2004), and Rudd and Whelan (2005a, 2005b, 2005c).

ML estimation provides a measure of fit through the likelihood function, facilitating model comparisons. In the current analysis, the set of models examined are non-nested. It is also likely that none of the models considered is literally true. Even when the models are not true, the likelihood will concentrate in the neighborhood of the "best" parameter vector and provide a summary measure of the congruence between the data and model under reasonable regularity conditions, as discussed in the literature on pseudo-ML estimation (e.g., White (1994)). The comparison across models can be made by penalizing the individual likelihoods by the number of parameters as in the Bayesian information criterion (BIC). BIC for model j equals

$\begin{displaymath} BIC(j)=L(j)-\frac{N(j)}{2}\ln (T), \end{displaymath}$

where L(j) is the log-likelihood of model j, N(j) is the number of parameters in model j, and T is the sample size used in estimating the models. BIC has been shown to be a consistent model-selection criterion under quite general conditions; it is an asymptotic approximation to the marginal-likelihood of a model, and is thus independent of the priors a Bayesian might place on the parameters of a model. It is consistent with a Bayesian approach where the data are allowed to dominate priors over the parameters.

Consistent with this latter observation on the similarity between BIC and a Bayesian approach in large samples, a pseudo-posterior odds measure can be found by using the BIC in place of the marginal likelihood, yielding the data-determined probability of model j, $\rho$ (j),

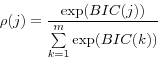
$\begin{displaymath} \rho (j) & = & \frac{\exp (BIC(j))}{\sum\limits_{k=1}^m {\exp (BIC(k))} } \end{displaymath}$

where m refers to the number of models in the set considered plausible. This pseudo-odds measure implicitly places equal priors on each model, which - in conjunction with the independence of the BIC from priors over parameters within each model - implies that the relative odds are driven by the congruence between model and data, adjusted for degrees of freedom. Econometricians outside the Bayesian tradition have used such measures as reasonable tools for model comparisons (e.g., Doppelhoffer, Miller and Sala-i-Martin (2000), Brock, Durlauf, and West (2003)). It is important to emphasize that these pseudo-odds do not correspond to the relative odds that would result from some set of "flat" priors over models and their parameters (Sims (2002)). Rather, they are an intuitive ad hoc way to assess relative fit that will choose the true model in a large sample and provide some indication of the preferred model given the available data.

3. Sticky-price models

Specifications

The sticky-price models will follow relatively standard specifications. For our current purposes, I only present the equations that are estimated; a discussion of the behavioral practices underlying the baseline and hybrid specifications is deferred to section 5 and the appendix.⁶ Following common practice, our baseline sticky-price model is derived from the Calvo sticky-price model and relates current inflation to expected inflation next period and to real marginal cost,

Baseline SP $\pi _t & = & E_{t-1} \pi _{t+1} +\kappa E_{t-1} mc_t$ .⁷

In the hybrid sticky-price model, inflation is related to a lead of inflation, a lag of inflation, and real marginal cost - with the sum of the coefficients on the lead and lag of inflation equaling one (see footnote 7):

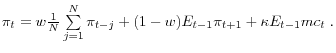
Hybrid SP $\pi _t & = & w\frac{1}{N}\sum\limits_{j=1}^N {\pi _{t-j} } +(1-w)E_{t-1} \pi _{t+1} +\kappa E_{t-1} mc_t \;.$

As discussed later, the presence of a lag can be justified through a number of amendments to the baseline model - such as the presence of rule-of-thumb price-setters as in Gali and Gertler (1999) or dynamic indexation as in Christiano et al (2005). This hybrid model is the natural extension that allows for indexing or rule-of-thumb behavior to a measure of inflation that smoothes through some of the quarterly volatility in inflation. Roberts (2005) also considers hybrids with a moving average of inflation lags, although he does not consider the behavioral assumptions that would generate such a specification that I discuss later. For now, the inclusion of the moving-average term is motivated solely by the observation that reduced-form Phillips curves that fit well are often specified to include long moving averages of inflation (e.g., Gordon (1998)).

Results

Table 1 presents estimates of the baseline and hybrid sticky-price models for the full sample, 1965Q1 to 2002Q4. Two hybrid models are considered: a one-lag model (e.g., that of Gali and Gertler (1999)), and a four-lag model. For each model, I present estimates of the parameters of the model and their standard errors; the Q-statistic that examines the degree of serial correlation over 12 lags in the one-step-ahead forecast errors (and its p-value); the log-likelihood and BIC for the model; and the R² for the model, computed as one minus the sum of squared forecast errors divided by the sum of squared deviations of inflation from its sample mean.

Turning first to the baseline sticky-price model, the estimated sensitivity to marginal cost ( $\kappa )$ falls in the range typical of the literature, and the R² for the model is about 0.4 (line 1). Nonetheless, it is clear the model fails to track inflation very well, as the Q-statistic reveals a very large degree of autocorrelation in the forecast errors or cost-push shocks. This does not imply that the model does not predict very persistent inflation even in the absence of serially-correlated cost-push shocks. Because the baseline model essentially has inflation track real marginal cost (or the labor share) and real marginal cost is very persistent (with a first-order autocorrelation near 0.9), the baseline model predicts persistent inflation. The poor performance of the model and extreme serial correlation of the residuals rather reflects the fact that the predictions of the model result in large and persistent forecast errors. In economic terms, the baseline model expects inflation to track real marginal cost closely, and it does not. This failure is the source of Fuhrer's (2005) critique, in which he emphasizes that the errors in baseline and simple hybrid sticky-price models are large and persistent.

One way to quickly see how poorly the baseline sticky-price model performs is to compare it to a reduced-form regression. In particular, rows 4 through 6 of table 1 report the likelihood, BIC, and R² for regressions of the following form:

$\begin{displaymath} \pi _t & = & A(L)Z_t +e_t ,\quad Z_t =[mc_t ,r_t ,y_t ,\pi _t ]', \end{displaymath}$

where the number of lags of each variable in Z equals one, two, or three. The likelihood and BIC for the reduced-form models are much larger than those of the baseline sticky-price model; consequently, a pseudo-odds criterion places essentially no weight on the baseline sticky-price model (rows 7 to 10 of table 1). According to this criterion, the baseline sticky-price model provides a poor summary of the time-series properties of U.S. inflation.

The hybrid sticky-price models fit substantially better than the baseline models over the 1965Q1 to 2002Q4 sample (as indicated by the likelihood and BIC values), with the model using a four-quarter average of lagged inflation (N equal to four) dominating the one-lag model. The parameter estimates show that the weight on the sum of inflation lags ( falls to just above $\raise.5ex\hbox{$\scriptstyle 1$}\kern-.1em/ \kern-.15em\lower.25ex\hbox{$\scriptstyle 4$}$ as N increases from one to four. Interpretation of this parameter value is tricky and depends on the behavioral assumptions used to motivate the inclusion of additional lags. However, this value suggests that in a model with rule-of-thumb price-setters (like that presented in the appendix) about $\raise.5ex\hbox{$\scriptstyle 1$}\kern-.1em/ \kern-.15em\lower.25ex\hbox{$\scriptstyle 2$}$ of price-setters use a rule-of-thumb, similar to the value implied by the one-lag hybrid model. This seems large enough to suggest that a search for micro-foundations motivating such behavior is valuable.

Turning back to the empirical results, the R² for the best-fitting model lies very close to that of the reduced-form regressions reported in table 1. In addition, there is only marginal evidence of serial correlation in the residuals of the best-fitting model; this suggests that the inclusion of long lags allows for sufficient intrinsic inflation inertia to account for inflation dynamics, in contrast to the baseline and one-period-lag hybrid critiqued in Fuhrer (2005). The Bayesian information criterion indicates that the hybrid sticky-price model (with N equal to four) fits the data as well or better than the reduced-form regressions in table 1, and the pseudo-odds measure places nearly all the weight on the hybrid sticky-price model with four lags.

Table 2 presents estimation results for the sticky-price models over the 1983Q1 to 2002Q4 period. Some may view this period as more appropriate for evaluation of each structural model, as the monetary policy regime has arguably been more stable during this period. With regard to which structural model fits the data best, the change in sample period has no effect; the sticky-price hybrid model with a four-quarter moving average of inflation (N equal to four) remains the best-fitting model. It also remains the case that the best-fitting sticky-price model is preferred to the reduced-form regressions by the BIC criterion. On other dimensions, the change in sample period alters the results a bit. In particular, the baseline and one-period indexation sticky-price hybrids both fit as well or better than reduced-form models over the 1983Q1 to 2002Q4 period according to the BIC criterion. In addition, the estimated sensitivity of inflation to marginal cost in the sticky-price models is much lower in the recent sample.

Combining the results from both sample periods, I reach three conclusions. First, hybrid sticky-price models of price setting fit the data as well as simple reduced forms, after correcting for degrees of freedom by the BIC criterion, if long lags are included in the hybrid model; this begs the question, considered in section 5, of what behavioral assumptions could justify such long lags. Second, it is clear that the hybrid sticky-price model with a one-period lag (N equal to 1) - the standard specification of Christiano et al (2005) and similar to the specification of Gali and Gertler (1999) - performs poorly relative to a reduced-form regression over the last four decades. Finally, this model - and the baseline model - performs relatively better over the last two decades - a period of greater stability in monetary policy behavior.

4. Sticky-information models

Specifications

Sticky-information models assume that prices are reset optimally every period, but that the information gathering activities of firms - on which prices are based - are costly and occur only infrequently. Sims (2003) discusses an optimization problem confronting a firm that faces such costs. Our analysis follows a more ad hoc, but empirically tractable, direction. In the baseline sticky-information model, firms reset price in every period, subject to their constrained information set. In particular, some firms have access only to stale, i.e., lagged, information. An information-set-updating rule analogous to the Calvo price-setting rule is employed, as in Mankiw and Reis (2002). Each firm faces a probability 1- $\lambda$ in period t that it will update its information set through the previous period, t-1; with probability $\lambda$ , the firm does not update its information set. This process repeats itself for each period t, implying a geometric distribution of periods since last updating of the information set across the population of firms. The implied average information lag equals 1/(1- $\lambda )$ .

As shown in Mankiw and Reis (2002), inflation is governed by the following equation (ignoring constants)

Baseline SI $\pi _t & = & \frac{1-\lambda }{\lambda }DE_{t-1} mc_t +(1-\lambda )\sum\limits_{j=0}^\infty {E_{t-1-j} \lambda ^j(\pi _t +\Delta } mc_t )$ .⁸

where the parameter D measures the sensitivity of the desired relative price absent information imperfections to real marginal cost..

In the hybrid sticky-information model, there exist two types of firms. The first set, a fraction 1- $\omega$ of firms, choose the optimal price given their information set (which is determined in the same manner as that in the baseline model). A second set follow a "rule-of-thumb", setting their period-t price equal to the aggregate price level last period, plus the rate of inflation over the previous N quarters (expressed at a quarterly rate). Allowance for such indexation may appear odd, in that it assumes that the "rule-of-thumb" firms have information on recent inflation and the aggregate price level when some of the optimizing firms do not. However, the information problem associated with estimating current-period marginal cost, which depends on productivity, input costs, and potentially other factors, may be more severe than that of finding recent inflation data. More importantly, the pricing scheme provides a simple hybrid extension of the sticky-information model that can be taken to the data; if such an amendment to the baseline sticky-information model finds empirical support, further work could focus more finely on the consistency of the specification with plausible assumptions regarding information acquisition and firm behavior.

Given these assumptions, inflation is governed by the following equation

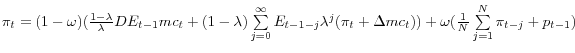
Hybrid SI $\pi _t & = & (1-\omega )( & \frac{1-\lambda }{\lambda }DE_{t-1} mc_t +(1-\lambda )\sum\limits_{j=0}^\infty {E_{t-1-j} \lambda ^j(\pi _t +\Delta } mc_t ))+\omega (\frac{1}{N}\sum\limits_{j=1}^N {\pi _{t-j} } +p_{t-1} )$

Results

Table 3 presents estimates of the sticky-information models for the full sample, 1965Q1 to 2002Q4. As for the sticky-price models, I present estimates of the parameters of the model and their standard errors; the Q-statistic that examines the degree of serial correlation over 12 lags in the one-step-ahead forecast errors (and its p-value); the log-likelihood and BIC for the model; and the R² for the model, computed as one minus the sum of squared forecast errors divided by the sum of squared deviations of inflation from its sample mean.⁹

The baseline sticky-information model (line 1) fits much better than the baseline sticky-price model reported in table 1 and matches the fit of a one-lag reduced-form for inflation (line 4). The residuals are only moderately serially-correlated (see the Q-statistic). And the estimated information lag appears reasonable at between one and two quarters (column 3), a bit below the four quarters assumed by Mankiw and Reis (2002) and the estimates presented by Carroll (2003) and Khan and Zhu (2004), all obtained via quite different methods. However, the baseline sticky-information model provides a poor fit to the data compared to well-fitting reduced-form regressions with two or more lags, as can be seen by comparing the likelihood, BIC, and R² for the reduced-form regressions reported in lines 5 and 6 of table 3.

The hybrid models, lines 2 and 3, fit only modestly better than the baseline model (as indicated by the likelihood and BIC values reported in the right-hand columns). The best-fitting sticky-information model uses a four lags of inflation for rule-of-thumb price setters (N equal to four). In this case, the estimated average information lag is about 1-1/2 quarters. The estimated parameters suggest that the share of rule-of-thumb price setters is high at near $\raise.5ex\hbox{$\scriptstyle 1$}\kern-.1em/ \kern-.15em\lower.25ex\hbox{$\scriptstyle 2$}$ . This result illustrates that the sticky-information model has the same problem as the sticky-price model in generating the importance of lagged inflation for forecasting inflation in the absence of some ad hoc adjustment to the model. The importance of hybrid dynamics for both the sticky-price and sticky-information models highlights the need for sources of richer dynamics, a point pursued in section 5 below.

The Bayesian information criterion indicates that the hybrid sticky-information models (with N equal to one) fit the data worse than the reduced-form regression in table 1, although the degrees-of-freedom adjusted fits are pretty close to each other. However, comparison to table 1 indicates that the hybrid sticky-price model appears to fit better than the hybrid sticky-information model. This highlights how the typical empirical strategy - look at one model and if it performs acceptably along some metric, stop - will not help discriminate across different model specifications that both perform relatively well.

Table 4 presents estimation results for the sticky-information models over the 1983Q1 to 2002Q4 period. The sticky-information models fit much better (relative to reduced forms) in this sample. The best-fitting model is again the four-lag hybrid. Interestingly, in this sample the baseline sticky-information model fits slightly worse than the baseline sticky-price model from table 2.

Combining the results from the sticky-price and sticky-information models, I conclude that the sticky-price hybrid model with a long-indexation lag matches the data on inflation better than the sticky-information alternatives. The next section considers behavioral assumptions that may help us understand the role of sticky prices and sticky information in the hybrid sticky-price model.

5. How should the results be interpreted?

The empirical results show a preference for hybrid sticky-price models both over the full sample and in the more recent period. One interpretation of this finding is that the sticky-price model fails to account for the behavior of inflation, as ad hoc amendments to the baseline sticky-price model are needed to match the data. Moreover, the findings in favor of sticky-price models seem to contradict the need for "sticky information" emphasized in analyses of the costs of disinflations or the slow, hump-shaped response of inflation to certain economic shocks.

Our interpretation differs from this pessimistic assessment: in our view, the results support the importance of both sticky-information and sticky-prices. As discussed in the appendix, the sticky-price hybrid with four lags can be rationalized by different behavioral assumptions. One plausible set of assumptions leading to this model is the following modification of the "rule-of-thumb" story from Gali and Gertler (1999):

Individual firms adjust prices infrequently, consistent with the microeconomic evidence on nominal price rigidity (and in contrast to the dynamic indexation model of Christiano et al (2005) or the sticky-information model of Mankiw and Reis (2002)).
A fraction of these firms adjust prices optimally - i.e., in a forward-looking manner and based on all available information.
The remainder adjust prices using a rule-of-thumb that links their price to lagged information sets on optimal prices and the average rate of inflation that has occurred since the period of the lagged information set. When the lagged information set is one period, this is simply the model of Gali and Gertler (1999). When the lagged information sets include four lags and the fraction of firms at each lag is declining at an appropriate rate, the four-lags model (preferred in our estimation results) arises.

The last assumption used to justify the hybrid sticky-price model with either one or four lags clearly shows that the model is a type of "sticky-information model" - it simply has not been called such to date, perhaps because some might argue the model is more "ad hoc" than the sticky-information model of Mankiw and Reis (2002) or Sims (2003). While compared to the latter paper this is clearly true, this argument seems quite weak when the reference point is the popular model of Mankiw and Reis (2002). As a version of a "sticky-information" model, the hybrid sticky-price model captures the aspects of inflation dynamics absent from the baseline sticky-price model while preserving consistency with the evidence on price-rigidity. In the end, our finding that the hybrid sticky-price model with four lags fits the data well is consistent with sticky prices and moderate information lags that differ across price setters (sticky-information).

Of course, the specific manner in which "sticky information" is incorporated into the sticky-price model in our N-lag hybrid remains ad hoc. Future research integrating the sticky-price and sticky-information models should focus on plausible behavioral stories motivated from first principles. At least two approaches appear promising. Kumhof and Laxton (2005) integrate information and price-adjustment costs in an optimizing model to explain inflation inertia; while their implementation does not have infrequent nominal price changes as in the sticky-price literature, the basic thrust of their research appears promising.

Finally, a comparison of the post-1982 results with the full sample results may provide a clue as to an important source of imperfect information over the last forty years. The results for the most recent sample period for a baseline sticky-price model were more favorable - although the hybrid models were still preferred. This suggests that imperfect information - a source of hybrid-type behavior - may have been less important over the past two decades. One potential explanation is that monetary policy has been more stable - especially with respect to its inflation goal - over the more recent period and that this has lowered the importance for inflation dynamics of learning about the inflation goal. Erceg and Levin (2003) formalize this intuition.

6. Comparison to earlier results

The set of results from estimates of sticky-price models and, to a lesser extent, sticky-information models, has exploded in recent years. Nonetheless, there seems to have been only modest convergence of opinion, and a researcher lacking direct contact with the data and range of techniques applied by different authors could find summarizing the results of this research difficult. The remainder of our discussion relates the findings herein to those of previous authors.

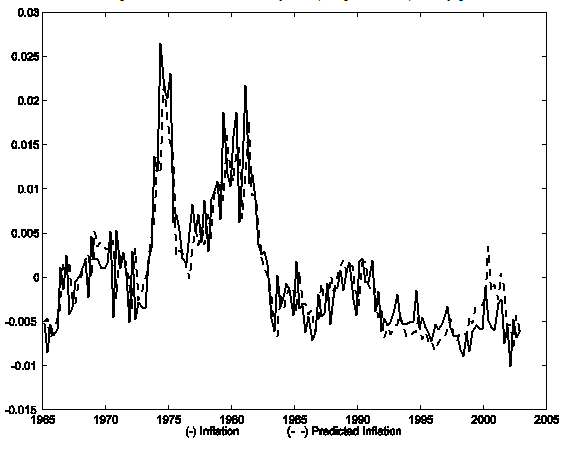
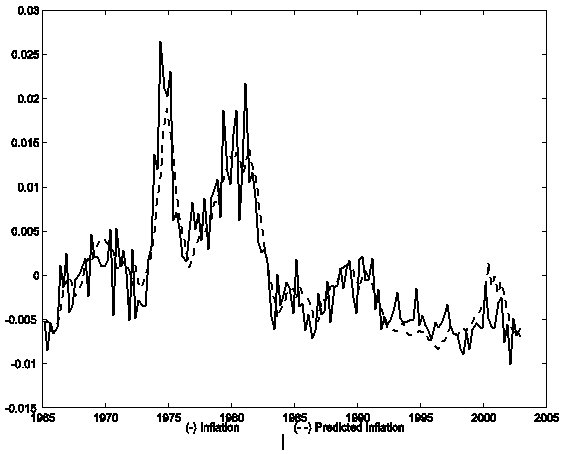
Gali, Gertler, and Lopez-Salido (2005) and Sbordone (2005) (building on Gali and Gertler (1999) and Sbordone (2002)) both suggest that a hybrid sticky-price model adequately describes inflation dynamics in the United States. While these authors use different estimation techniques, their conclusions are partially driven by an informal consideration of the tracking performance of their models. In particular, Gali and Gertler (1999) and subsequent researchers have presented a graph like figure 2, which plots (demeaned) inflation and the one-step-ahead forecast of inflation from the estimated hybrid (N equal to one) model over 1965Q1 to 2002Q4. As is clear, the series move together, especially before 1998 - as should have been apparent from the R² statistic in table 1. Nonetheless, this model was soundly rejected by the BIC criterion. As shown in figure 3, the graph of actual and predicted inflation for the hybrid model with N equal to four is hard to compare visually to figure 2; at least to this author's eye, the figures look pretty similar. One lesson from this exercise is that "ocular" regressions of the form emphasized by previous research provide little information.

Rudd and Whelan (2003, 2005b, 2005c) also examine the hybrid sticky-price model; in contrast to the previous authors, they conclude that it provides a poor approximation to inflation dynamics. This different conclusion does not arise because Rudd and Whelan estimate parameters of the hybrid sticky-price model that are very different from those presented by supporters of such models. Rather, they also emphasize informal measures of fit like figure 2, and note that the marginal improvement in fit from real marginal cost (the labor share) in such equations is small. This interpretation is completely consistent with the results reported by supporters of the sticky-price model; it is also consistent with our previous conclusion that such informal metrics provide little information.

The different conclusions of these supporters and detractors of the sticky-price model are partly related to three other considerations. First, there has been some debate over whether the coefficient on real marginal cost ( $\kappa$ in the hybrid sticky-price model) is different from zero in the statistical sense. The estimated value of this parameter is (largely) consistent across studies, but standard errors differ. Our estimates are statistically different from zero, using maximum likelihood; estimates via GMM using the same data tend to have larger standard errors and to not differ from zero in a statistical sense. We performed a Monte Carlo experiment in which our preferred sticky-price model, the four-lag hybrid, was simulated to create artificial samples of 152 periods (with 500 replications), drawing from the shocks estimated for the model over 1965-2002. The hybrid model was then estimated via GMM, with statistics from the simulations reported in table 5.¹⁰ As shown in the upper rows, the simulations tend to estimate fairly accurately the coefficient on lags of inflation (. While the coefficient on real marginal cost ( $\kappa )$ lies quite close to its true value on average, its standard error is sizable. This suggests that a focus on the standard error of this parameter is not a useful way to assess this model.

There has also been debate about whether inflation Granger-causes real marginal cost (the labor share), with Rudd and Whelan (2005a, 2005c) differing from, for example, Sbordone (2005). Results from our Monte Carlos exercises suggest this is not a useful test; as reported in the middle panel of table 5, the simulations failed to find Granger-causality at the 10-percent significance level in 41.4 percent of the simulations. This occurs largely because the cost-push shocks ( from the equations in section 2) cause inflation to move in ways independent of the labor share and lower the ability of the regressions to find Granger causality from inflation to the labor share. Alternative Monte Carlo exercises (not reported) in which the cost-push shocks are made much smaller almost always detected Granger Causality of the type emphasized in previous research.

Finally, Rudd and Whelan (2005c) emphasize that detrended output enters reduced-form regressions for inflation with a highly-significant coefficient. This is completely consistent with our sticky-price hybrid model. As reported in the lower panel of table 5, estimation of an inflation regression including four lags of the dependent variable and lagged detrended output on the simulated data yielded a coefficient significantly greater than zero (at the 10-percent level) in 99.8 percent of the simulations. This occurs because detrended output is an important factor in the reduced-form equations for marginal cost (the labor share) and the federal funds rate.

To summarize, most of the reported results in Gali, Gertler, and Lopez-Salido (2005), Sbordone (2005), and Rudd and Whelan (2005c) echo those reported herein. Estimated parameters for the one-lag hybrid are in the same neighborhood, and tracking exercises like figure 2 are very similar in each study. However, none of these earlier studies focus on formal metrics of fit; rather, they focus on ancillary issues like standard errors of parameters, Granger-causality of the labor share by inflation, and the partial correlation of inflation and lagged detrended output. None of these ancillary issues is likely to provide much information about the ability of a hybrid sticky-price model to track inflation according to our Monte Carlo simulation. And perhaps more importantly, only Gali and Gertler (1999) emphasize the economic story behind a hybrid model - an emphasis of our section 5 - and none of these earlier investigations formally considers a more complex, but better-fitting, hybrid with four inflation lags.

Our focus on the fit of alternative models is most closely related to a long series of papers by Jeff Fuhrer. However, his evaluations do not consider relative fit as measured by BIC. A typical strategy, pursued, for example, in Fuhrer (1997), is to consider whether the likelihood-ratio statistic rejects the null hypothesis that the restrictions imposed by the model under consideration are satisfied by a baseline reduced form. Table 6 considers tests of this type: it reports the likelihoods for the baseline and hybrid sticky-price models for each sample period as well as that of a reduced form with four lags of inflation, detrended output, the nominal federal funds rate, and real marginal cost¹¹; the likelihood ratio statistic; and the p-value of the null hypothesis that the restrictions of the structural model considered are satisfied. Turning first to the set of results for the 1965Q1 to 2002Q4 period, the likelihood ratio statistics clearly reject the null hypothesis that the restrictions of the sticky-price models are satisfied for the baseline and one-period hybrid models, with p-values essentially equal to zero. In the four-lag case, the null is not rejected at the one-percent level and barely rejected at the five-percent level. On balance, these results echo those in Fuhrer, who argues that classical tests of this type suggest failures of sticky-price models.

Our interpretation is quite different for two reasons. First, even the baseline model's restrictions are not rejected at the five-percent level for the 1983Q1 to 2002Q4 period. More importantly, I have been assessing the relative performance by the BIC criterion, not likelihood-ratio statistics. To see the different implications of these approaches, consider first the likelihood-ratio statistic; with a critical value of five-percent, this criterion chooses the reduced-form model over the sticky-price model - i.e., rejects the restrictions of the sticky-price model - when the likelihood ratio statistic exceeds 23.7. By contrast, the BIC criterion prefers the reduced-form model when the LR statistic exceeds 67.6.¹² Obviously, the BIC criterion requires much larger "violations" of the sticky-price model's restrictions in order to prefer the reduced-form model. This occurs for two reasons: first, the BIC criterion is derived as an asymptotic approximation to a Bayesian analysis that prefers parsimony; and second, this approximation requires stronger evidence from the data as the sample size increases - as more data should lead to stronger rejections of false hypotheses. The first reason seems a desirable feature. The second, as emphasized by Leamer (1983) and Sims (2002), corresponds to the notion that the significance level of a classical test should decrease with the sample size because, for any prior views regarding null hypotheses, the data should speak more loudly with a larger sample.

Our discussion of previous work has focused largely on sticky-price models, as sticky-information models have received far less attention.¹³ Consistent with the research that has motivated the sticky-information model, we find that the baseline version of this model can generate intrinsically persistent inflation and hence fits better than the pure sticky-price model over the 1965-2002 period, but this advantage disappears in the recent period. With regard to empirical work, Khan and Zhu (2004) estimate a sticky-information model via limited-information methods and find plausible parameters; however, they do not assess fit relative to other models of inflation dynamics. Korenok (2004) compares baseline sticky-price and sticky-information models using Bayesian methods, and finds that the baseline sticky-price model fits better than the baseline sticky-information model. Laforte (2006) compares hybrid sticky-price models to a sticky-information model in a setup that assumes that the remainder of the system is given by a simple dynamic general equilibrium model. His estimation strategy uses Bayesian methods; as in this research, the sticky-price models he considers dominate the sticky-information models.

7. Conclusions

I have estimated sticky-price and sticky-information models for the United States via maximum-likelihood techniques. While the baseline sticky-information model generates greater serial correlation in inflation and hence dominates the baseline sticky-price model over the 1965-2002 sample, this advantage disappears in the recent period. In addition, hybrid sticky-price models empirically dominate sticky-information alternatives - particularly when hybrid behavior is tied to lags up to one year.

The finding that hybrid sticky-price models provide a better summary of inflation dynamics than a sticky-information model does not imply that sticky-information stories, or more generally information imperfections, are unimportant. Rather, it confirms the importance for inflation dynamics of factors in addition to nominal price rigidities, perhaps including sticky information. For example, the hybrid sticky-price model, under some assumptions, relies on an imperfect information element to generate a form of backward-looking behavior. But clearly stronger micro-foundations and a more careful understanding of any changes in the importance of price rigidities or information imperfections across time periods are needed in future research.

Finally, our discussion has attempted to show the links between the results reported herein and those in the very large related literature. While it is impossible to summarize all previous work, it is noteworthy that our findings for sticky-price models are very similar to those in earlier work that has reached a range of different conclusions. The range of conclusions in other work stems to an important extent from a focus in such research on issues unrelated to model fit. Our comparison of sticky-price models to sticky-information and reduced-form models of inflation suggest that hybrid sticky-price models can match inflation dynamics in the United States over the past forty years.

Appendix: Behavioral Assumptions Behind a Hybrid Sticky-Price Model

There are a large number of symmetric, monopolistically-competitive intermediate-goods firms that set nominal prices; preferences over varieties take the Dixit-Stiglitz form. Firm j's marginal cost in period t is denoted by MC $_{t}$ , its nominal price by $P_{jt}$ , its demand by $Y_{jt}$ , and the economy-wide average price index by $P_{t}$ . The firm's profit in period t is then

$\begin{displaymath}[\frac{P_{jt} }{P_t }-MC_t ]P_t Y_{jt} . \end{displaymath}$

As in Gali and Gertler (1999), intermediate-good firms set prices via a procedure similar to that of Calvo (1983). In each period, a firm faces a constant probability, 1 - $\theta$ , of being able to reset its nominal price; absent receipt of a "reset signal", the firm's nominal price remains fixed, consistent with evidence of nominal price rigidities. A firm that resets its price falls in to one of two groups: a group of optimizing firms, and a group of "rule-of-thumb" firms. Optimizing firms set their price (denoted Pf $_{t}$ , where f refers to forward-looking) at a level that maximizes expected profits over the period for which their nominal price is fixed

$\begin{displaymath} \mathop {\max }\limits_{Pf_{jt} } \;E_{t-1} \sum\limits_{k=1}^\infty {(\beta \theta )^kv_{t+k} [Pf_{jt} -MC_{t+k} ]Y_{jt+k} } \end{displaymath}$

where $\beta$ is the constant portion of the firms discount factor,

is the time-varying portion, $\theta$ captures the effect of the random nature of price-adjustment on discounting, and E is the expectations operator. The first-order condition for the optimal price is given by

$\begin{displaymath} E_{t-1} \sum\limits_{k=1}^\infty {(\beta \theta )^kv_{t+k} [Pf_{jt} -\lambda MC_{t+k} P_{t+k} ]Y_{jt+k} } \;=0 \end{displaymath}$

where $\lambda$ is the static markup (i.e., the markup absent price rigidity).

Rule-of-thumb firms are themselves split into N groups. Members of the kth group set their nominal price equal to the economywide average price reset in period t-k ( $P*_{jt-k})$ plus the change in the aggregate price level between period t-k-1 and period t-1. In this sense, the firms have different amounts of "sticky-information". Gali and Gertler (1999) assume N equals one.

Following the same steps as in Gali and Gertler (1999), the log-linearized equations for the aggregate price level, the economywide average reset price, the reset price of forward-looking firms, and the average reset price of rule-of-thumb firms are given by

Price index p $_{t}: p_t =\theta p_{t-1} +(1-\theta )p_t^\ast$ (A.1)

Index of newly re-set prices p* $_{t}: p_t^\ast =(1-\omega )pf_t +(1-\theta )pb_t^$ (A.2)

Forward-looking re-set price pf $_{t}: pf_t =(1-\beta \theta )E_{t-1} \sum\limits_{k=1}^\infty {(\beta \theta )^k[mc_{t+k} +p_{t+k} ]} \;=0$ (A.3)

Average of rule-of-thumb reset prices: 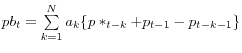$pb_t =\sum\limits_{k=1}^N {a_k \{p\ast _{t-k} +p_{t-1} -p_{t-k-1} \}}$ (A.4)

where $\omega$ is the fraction of rule-of-thumb price setters and a $_{k}$ is the fraction of rule-of-thumb price setters in the kth group.

Combining (A.1) through (A.4), and some algebra, yields

$\begin{array}{l} \pi _t =\frac{\omega }{\theta +\omega [1-\theta (1-\beta a_1 )]}\sum\limits_{k=1}^N {(a_k -\beta \theta a_{k+1} )\pi _{t-k} } +\frac{\beta \theta }{\theta +\omega [1-\theta (1-\beta a_1 )]}E_{t-1} \pi _{t+1} ... \ \quad +\frac{(1-\omega )(1-\theta )(1-\beta \theta )}{\theta +\omega [1-\theta (1-\beta a_1 )]}E_{t-1} s_t . \ \end{array}$ (A.5)

This equation is of the basic form of the N lag hybrid sticky-price model; if the fraction of firms in the kth group of rule-of-thumb firms declines by the appropriate amount between k and k+1, the hybrid presented in the main text arises when the discount factor equals one.

References

Anderson, Gary (2000) The Anderson-Moore Algorithm. Federal Reserve Board Occasional Staff Study 4, http://www.federalreserve.gov/pubs/oss/oss4/aimindex.html.

Brock, William, Steven Durlauf and Kenneth West (2003) Policy Evaluation in Uncertain Economic Environments. Brookings Papers on Economic Activity.

Calvo, G.A. (1983) Staggered Prices in a Utility Maximizing Framework. Journal of Monetary Economics 12:383-398.

Carroll, Christopher (2003) The Epidemiology of Macroeconomic Expectations. In Larry Blume and Steven Durlauf, eds., The Economy as an Evolving Complex System, III, Oxford University Press, forthcoming.

Christiano, Lawrence J., Martin Eichenbaum and Charles Evans (2005) Nominal Rigidities and the Dynamic Effects of a Shock to Monetary Policy. Journal of Political Economy.

Corrado, Carol and Laurence Slifman, "Decomposition of Productivity and Costs" American Economic Review, 89 (1999), pp. 328-32.

Dopplehoffer, Gernot, Ronald I. Miller and Xavier Sala-i-Martin (2000) Determinants of Long-Run Growth: A Bayesian Averaging of Classical Estimates (BACE) Approach. NBER Working Paper No. 7750, June.

Eichenbaum, Martin and Jonas D.M. Fisher (2003) Time Series Implications of the Calvo Model of Sticky Prices. Federal Reserve Bank of Chicago Working Paper 2003-23.

Erceg, Christopher J. and Andrew T. Levin (2003) Imperfect Credibility and Inflation Persistence. Journal of Monetary Economics, v. 50, iss. 4, pp. 915-44

Fuhrer, Jeffrey (1997) "The (Un)Importance of Forward-Looking Behavior in Price Specifications," Journal of Money, Credit, and Banking 29, 338-50.

Fuhrer, Jeffrey (2002) Habit Formation in Consumption and Its Implications for Monetary Policy Models. American Economic Review, 90, 367-390.

Fuhrer, Jeffrey (2005) Intrinsic and Inherited Inflation Persistence. Federal Reserve Bank of Boston Working Paper 05-08.

Fuhrer, Jeffrey and Geoffrey Moore (1995) Inflation Persistence. Quarterly Journal of Economics.

Fuhrer, Jeffrey and Giovanni P. Olivei (2004) Estimating Forward-Looking Euler Equations with GMM and Maximum Likelihood Estimators: An Optimal Instruments Approach. Mimeo, March 2004.

Galí, Jordi and Mark Gertler (1999) Inflation Dynamics: A Structural Econometric Approach. Journal of Monetary Economics, 44(2), October, 195-222.

Gali, J., Gertler, M. and J.D. Lopez-Salido (2005) Robustness of the Estimates of the Hybrid New Keynesian Phillips Curve, Journal of Monetary Economics.

Gordon, Robert J. (1998) Foundations of the Goldilocks Economy: Supply Shocks and the Time-Varying NAIRU. Brookings Papers on Economic Activity, 1998 Issue 2, p297-333

Jondeau, Eric and Hervé Le Bihan (2003) ML VS GMM Estimates of Hybrid Macroeconomic Models (with an Application to the New Phillips Curve). Banque de France Working Paper NER#103, October 2003.

Khan, Hashmat and Zhenhua Zhu (2004) Estimates of the Sticky-Information Phillips Curve for the United States, Canada, and the United Kingdom. Revised Version of Bank of Canada Working paper 2002-19, forthcoming Journal of Money, Credit and Banking.

Kiley, Michael T. (2002) Partial Adjustment and Staggered Price Setting. Journal of Money, Credit, and Banking 34(2), May, pages 283-298

Kiley, Michael T. (2004) Is Moderate-to-High Inflation Inherently Unstable? Federal Reserve Board FEDS Working Paper 2004-43

Korenok, Oleg (2004) Empirical Comparison of Sticky Price and Sticky Information Models. Department of Economics, Rutgers University. Mimeo.

Kumhof, Michael and Douglas Laxton (2005) A Rational Expectations Model of Optimal Inflation Inertia. Mimeo, International Monetary Fund.

Laforte, Jean-Philippe (2006) Pricing Models: A Bayesian DSGE Approach to the U.S. Economy. Federal Reserve Board.

Leamer, Edward (1983) Model Choice and Specification Analysis. In Griliches, Zvi and Michael D. Intriligator, eds., Handbook of Econometrics, Volume 1. Elsevier.

Ma, Adrian (2002) GMM Estimation of the New Phillips Curve. Economics Letters, 76, 411-417.

Mankiw, N. Gregory and Ricardo Reis (2002) Sticky Information Versus Sticky Prices: A Proposal to Replace the New Keynesian Phillips Curve. Quarterly Journal of Economics, vol. 117 (4), pp. 1295-1328.

Mankiw, N. Gregory, Ricardo Reis and Justin Wolfers (2003) Disagreement About Inflation Expectations. National Bureau of Economic Research Macroeconomics Annual.

Roberts, John (1997) Is Inflation Sticky? Journal of Monetary Economics, vol. 39 (July 1997), pp. 173-96.

Roberts, John (2005) How Well Does the New Keynesian Phillips Curve Fit the Data? Mimeo, Federal Reserve Board.

Rudd, Jeremy and Karl Whelan (2003) "Can Rational Expectations Sticky-Price Models Explain Inflation Dynamics?" Forthcoming in the American Economic Review.

Rudd, Jeremy and Karl Whelan (2005a) "Does Labor's Share Drive Inflation?" Journal of Money, Credit, and Banking, 37, 297-312.

Rudd, Jeremy and Karl Whelan (2005b) "Modelling Inflation Dynamics: A Critical Review of Recent Research." Federal Reserve Board Finance and Economics Discussion Papers 2005-66.

Rudd, Jeremy and Karl Whelan (2005c) "New Tests of the New-Keynesian Phillips Curve," Journal of Monetary Economics, 52, 1167-1181.

SbordoneArgia M. (2002) Prices and Unit Labor Costs: A New Test of Price Stickiness. Journal of Monetary Economics, March 2002, v. 49, iss. 2, pp. 265-92

SbordoneArgia M. (2005) Do Expected Future Marginal Costs Drive Inflation Dynamics? Journal of Monetary Economics.

Sims, Christopher A. (2002) Testing Restrictions and Comparing Models. Mimeo, Princeton University.

Sims, Christopher A. (2003) Implications of Rational Inattention. Journal of Monetary Economics, 50, 665-690.

White, Halbert (1994) Estimation, inference, and specification analysis. Cambridge; New York: Cambridge University Press.

Table 1
Sticky-Price Models, 1965Q1 to 2002Q4 Sample

$\begin{displaymath} \pi _t & = & w\frac{1}{N}\sum\limits_{j=1}^N {\pi _{t-j} } +(1-w)E_{t-1} \pi _{t+1} +\kappa E_{t-1} mc_t \;. \end{displaymath}$
	$\kappa$		Q Statistic (p-value)	Log-likelihood	BIC	R²
1. Baseline (N=0)	0.0477 (0.006)	0.00	371.62 (0.000)	409.94	404.92	0.41
2. Hybrid with N=1	0.0112 (0.003)	0.42 (0.019)	39.02 (0.000)	468.52	460.99	0.73
3. Hybrid with N=4	0.0168 (0.003)	0.26 (0.016)	23.75 (0.022)	483.66	476.13	0.78
4. Reduced-form model, N equals 1				464.19	451.63	0.71
5. Reduced-form model, N equals 2				490.26	467.66	0.80
6. Reduced-form model, N equals 3				492.87	460.22	0.80

Pseudo-odds measures
7. Baseline Sticky-Price model	0.00
8. Hybrid Sticky-Price model with N = 1	0.00
9. Hybrid Sticky-Price model with N = 4	1.00
10. Reduced-form model (N equals 2)	0.00

Table 2
Sticky-Price Models, 1983Q1 to 2002Q4 Sample

$\begin{displaymath} \pi _t & = & w\frac{1}{N}\sum\limits_{j=1}^N {\pi _{t-j} } +(1-w)E_{t-1} \pi _{t+1} +\kappa E_{t-1} mc_t \;. \end{displaymath}$
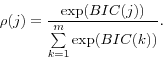
	$\kappa$		Q Statistic (p-value)	Log-likelihood	BIC	R²
1. Baseline (N=0)	0.0063 (0.0016)	0.00	66.39 (0.000)	309.61	305.23	0.26
2. Hybrid with N=1	0.0036 (0.0014)	0.24 (0.059)	24.27 (0.019)	314.25	307.68	0.34
3. Hybrid with N=4	0.0036 (0.0017)	0.17 (0.039)	10.83 (0.543)	316.49	309.91	0.38
4. Reduced-form model, N equals 1				313.58	302.63	0.33
5. Reduced-form model, N equals 2				317.06	297.34	0.38
6. Reduced-form model, N equals 3				319.67	291.18	0.42

Pseudo-odds measures
7. Baseline Sticky-Price model	0.01
8. Hybrid Sticky-Price model with N = 1	0.10
9. Hybrid Sticky-Price model with N = 4	0.90
10. Reduced-form model (N equals 1)	0.00

Table 3
Sticky-Information Models, 1965Q1 to 2002Q4 Sample

$\begin{displaymath} \pi _t & = & (1-\omega )( & \frac{1-\lambda }{\lambda }DE_{t-1} mc_t +(1-\lambda )\sum\limits_{j=0}^\infty {E_{t-1-j} \lambda ^j(\pi _t +\Delta } mc_t ))+\omega (\frac{1}{N}\sum\limits_{j=1}^N {\pi _{t-j} } +p_{t-1} ) \end{displaymath}$
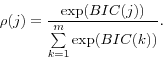
	$\lambda$	$\omega$		Q Statistic (p-value)	Log-likelihood	BIC	R²
1. Baseline (N=0)	0.408 (0.063)	0	0.050 (0.001)	25.50 (0.013)	462.26	457.24	0.70
2. Hybrid with N=1	0.577 (0.105)	0.344 (0.128)	0.235 (0.119)	27.04 (0.008)	463.37	455.83	0.71
3. Hybrid with N=4	0.319 (0.128)	0.456 (0.128)	0.090 (0.058)	18.62 (0.098)	468.00	460.46	0.73
4. Reduced-form model, N equals 1					464.19	451.63	0.71
5. Reduced-form model, N equals 2					490.26	467.66	0.80
6. Reduced-form model, N equals 3					492.87	460.22	0.80

Pseudo-odds measures
7. Baseline Sticky-Information model	0.00
8. Hybrid Sticky-Information model with N = 1	0.00
9. Hybrid Sticky-Information model with N = 4	0.00
10. Reduced-form model (N equals 2)	1.00

Table 4
Sticky-Information Models, 1983Q1 to 2002Q4 Sample

$\begin{displaymath} \pi _t & = & (1-\omega )( & \frac{1-\lambda }{\lambda }DE_{t-1} mc_t +(1-\lambda )\sum\limits_{j=0}^\infty {E_{t-1-j} \lambda ^j(\pi _t +\Delta } mc_t ))+\omega (\frac{1}{N}\sum\limits_{j=1}^N {\pi _{t-j} } +p_{t-1} ) \end{displaymath}$
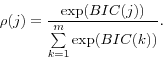
	$\lambda$	$\omega$	D	Q Statistic (p-value)	Log-likelihood	BIC	R²
1. Baseline (N=0)	0.610 (0.086)	0	0.199 (0.133)	12.84 (0.381)	308.70	304.32	0.25
2. Hybrid with N=1	0.694 (0.073)	0.280 (0.112)	0.376 (0.122)	20.83 (0.053)	311.24	304.67	0.29
3. Hybrid with N=4	0.647 (0.088)	0.337 (0.118)	0.355 (0.128)	12.86 (0.379)	312.29	305.72	0.34
4. Reduced-form model, N equals 1					313.58	302.63	0.33
5. Reduced-form model, N equals 2					317.06	297.34	0.38
6. Reduced-form model, N equals 3					319.67	291.18	0.42

Pseudo-odds measures
7. Baseline Sticky-Information model	0.15
8. Hybrid Sticky-Information model with N = 1	0.21
9. Hybrid Sticky-Information model with N = 4	0.61
10. Reduced-form model (N equals 2)	0.03

Notes: S.E. stands for standard error. Estimates for constant term are excluded. Q-statistic refers to test for serial correlation in residuals, based on 12 lags. BIC is the Bayesian information criterion. The pseudo-odds measure follows Dopplehoffer, Miller and Sala-i-Martin (2000) and Brock, Durlauf, and West (2003) by defining the ex post weight on model j, $\rho$ (j), as

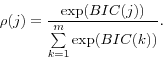
$\begin{displaymath} \rho (j) & = & \frac{\exp (BIC(j))}{\sum\limits_{k=1}^m {\exp (BIC(k))} }. \end{displaymath}$

Table 5
Monte Carlos Simulations of Hybrid Sticky-Price Model
Model:
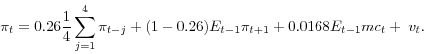
$\begin{displaymath} \pi _t & = & 0.26\frac{1}{4}\sum\limits_{j=1}^4 {\pi _{t-j} } +(1-0.26)E_{t-1} \pi _{t+1} +0.0168E_{t-1} mc_t +\;v_t . \end{displaymath}$
$\begin{displaymath} X_t & = & A(L)Z_t +e_t ,\quad X_t =[\Delta (p_t +mc_t ),r_t ,y_t ]',\quad Z_t =[mc_t ,r_t ,y_t ,\Delta p_t ]' \end{displaymath}$

Panel A: GMM estimation of $\pi _t & = & w\frac{1}{4}\sum\limits_{j=1}^4 {\pi _{t-j} } +(1-w)E_{t-1} \pi _{t+1} +\kappa E_{t-1} mc_t \;.$
	w	$\kappa$
Mean	0.28	0.020
Standard Error	0.07	0.014

Panel B: Does Inflation Granger-Cause Real Marginal Cost in the Simulated Data?
Percent of simulations in which inflation does not Granger-cause real marginal cost at the 10-percent significance level or better	41.4%

Panel C: Is Detrended Output Significant in a Reduced-Form for Inflation?
Percent of simulations in which detrended output is significant at the 10-percent level in the reduced-form inflation equation	99.8%

Notes: The parameters of A(L) were fixed at the values estimated by ordinary least squares regressions over the 1965Q1 to 2002Q4 sample (with two lags of each variable). The Monte Carlo simulations involved 500 artificial samples of 152 periods, generating via repeated sampling with replacement of the errors (

and

and simulation of the system of equations for inflation, output, nominal marginal cost, and the nominal federal funds rate. The estimated parameters and standard errors reported in panel A are the results of GMM estimation using two lags of each variable in the system. The Granger-causality tests summarized in panel B come from a reduced-form equation for real marginal cost (the labor share) involving two lags of the dependent variable and inflation. The tests for the significance of detrended output in the reduced form for inflation were conducted in a regression of inflation on four of its own lags and one lag of detrended output.

Table 6
Likelihood Ratio Tests of Sticky-Price Model Restrictions

1965Q1 to 2002Q4 Sample Period
	Log-likelihood	LR statistic	P-value
Baseline Sticky-Price Model	409.94	171.18	0.000
Hybrid Sticky-Price Model with N = 1	468.52	54.02	0.000
Hybrid Sticky-Price Model with N = 4	483.66	23.74	0.049
Reduced-Form with four lags	495.53	-	-

1983Q1 to 2002Q4 Sample Period
	Log-likelihood	LR statistic	P-value
Baseline Sticky-Price Model	309.61	24.36	0.059
Hybrid Sticky-Price Model with N = 1	314.25	15.08	0.373
Hybrid Sticky-Price Model with N = 4	316.49	10.61	0.716
Reduced-Form with four lags	321.79	-	-

Notes: LR statistic equals the difference between the likelihood of the reduced form and the structural model multiplied by 2. The P-value is the probability that a $\chi ^{2}$ random variable with the appropriate degrees of freedom is greater than or equal to the LR statistic. The reduced form for inflation contains four lags of inflation, output, the nominal federal funds rate, and real marginal cost.

Figure 1:

Autocorrelation Functions for Inflation and Real Marginal Cost (The Labor Share)

Figure 2:

Inflation and predicted inflation from hybrid (N equal to one) sticky-price model

Figure 3:

Inflation and predicted inflation from hybrid (N equal to four) sticky-price model