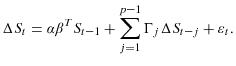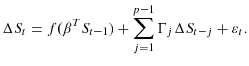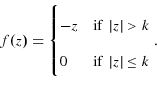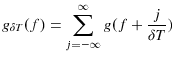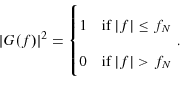Linear Cointegration of Nonlinear Time Series with an Application to Interest Rate Dynamics
November 29, 2006
Keywords: cointegration; nonlinearity; interest rates; nonparametric estimation
Abstract:
JEL Classification: C14; C32; C51; C82; E4
1 Introduction
Cointegration is the primary econometric model of system dynamics for nonstationary time series. Cointegration is normally defined as the existence of a stationary linear combination of nonstationary time series. The fact that the combination is linear does not necessarily imply linear dynamics for the resulting stationary stochastic process. Cointegration is nevertheless strongly associated with linear dynamics, because cointegration was initially developed within the linear Box-Jenkins framework. In particular, the standard model of cointegration--the vector error correction model (VECM)--does assume linear dynamics. Linearity makes econometric models tractable, but linear models can only reproduce a restricted class of dynamic behavior. Most economic models are nonlinear: producing richer dynamics.
A broader definition of cointegration is necessary in order to incorporate nonlinear dynamics. Our motivation for broadening the class of dynamics is based on the simple observation that nonlinearity is a dominant property in the sense that a linear combination of nonlinear processes is itself
generally nonlinear. Nonstationarity is similarly dominant. Cointegration is a special case where adding two or more nonstationary processes together results in a stationary process. But if any of the cointegrated series are nonlinear, the linear combination generally produces a nonlinear
stationary process. For example, let
![]() so that
so that ![]() is a random walk and let
is a random walk and let
![]() where
where ![]() is a stationary and nonlinear stochastic process. Then
is a stationary and nonlinear stochastic process. Then
![]() is a linear cointegrating vector for
is a linear cointegrating vector for
![]() as
as
![]() and
and ![]() is stationary. Since
is stationary. Since ![]() , is nonlinear, the cointegrating relation
, is nonlinear, the cointegrating relation
![]() is a nonlinear stochastic process.
is a nonlinear stochastic process.
We developed this motivation in Barnett et al. (2000), mainly as a critique of Johansen's maximum likelihood cointegration estimator which assumes linearity.2 Although we start from the same observation--that linear combinations of nonlinear series are generally nonlinear--this paper is more constructive. We derive a definition of linear cointegration from Hall and Heyde's (1980) martingale representation theorem for stationary stochastic processes. This extended definition, suggested by Bierens (1997), does not a priori restrict the dynamic behavior to be linear as did previous definitions of cointegration. As a result, the stationary dynamics of the cointegrated system may exhibit nonlinear dynamics. We also develop an asymptotically valid procedure to test linear cointegrations for the nonlinear stationary dynamics.
Our definition of cointegration, and the associated concept of nonlinear dynamics, differs from nonlinear cointegration introduced by Granger (1991). Intuitively, nonlinear cointegration occurs when a nontrivial nonlinear combination of nonstationary time series is stationary. In contrast, our extended definition still uses linear combinations to produce stationarity. The definition of nonlinear cointegration actually says nothing about the dynamics of the resulting stationary process, which is our focus. In practice, nonlinear cointegration has been defined by a VECM model with a nonlinear error correction term. Consequently, nonlinear cointegration has been predicated on the assumption that the stationary dynamics are linear. The martingale based definition could be further extended to allow for nonlinear cointegration with potentially nonlinear stationary dynamics, but testing for such complicated dynamics would be challenging.
To test for the presence of nonlinear dynamics in a linearly cointegrated system, we implement a sequential procedure. In the first stage, cointegrating vectors are estimated using Bierens's (1997,2005) nonparametric test for cointegration. Although Bierens (1997) assumed linearity for clearer exposition, the test is still valid when applied to nonlinear processes. If a cointegration is found, it defines a new stationary process representing the long-run economic equilibrium. In the second stage, the stationary cointegration is tested for nonlinearity. At this stage we are testing a system of economic variables, or an equilibrium economic relation, for nonlinear dynamics even though existing tests for nonlinearity are univariate.
The nonlinearity test used in the second stage should be conservative. A conservative test reduces the chances of finding nonlinearity due to inappropriately accepting the hypothesis of stationarity in the first stage. The possibility that a nonstationary linear time series could be identified as nonlinear is not a new problem. Tests for nonlinearity require stationarity as a maintained assumption. Given the strong evidence that many economic series are nonstationary, this requirement implies that tests for nonlinearity are almost always conditional on the correct removal of nonstationarity, for example through correct detrending or differencing. Failure to remove any nonstationarity can lead to spurious acceptance of nonlinearity (Lee et al., 2005/6).
Based on Monte Carlo comparisons of various tests for nonlinearity, we use Hinich's (1982) nonparametric bispectral test, which was found to be conservative.3 We do not, however, implement the surrogate data and bootstrap methods introduced by Hinich et al. (2005) to improve the power of Hinich's test, as the theoretical validity of the sequential testing rests on an asymptotic argument. Furthermore, bootstrapping only the second-stage estimator would be inappropriate.4
To demonstrate the two-stage nonparametric testing method, we test a system of short-term U.S. interest rates: specifically the rates for short-term Commercial Paper, short-term Treasury Bills, and Federal Funds. Short-term interest rates on Federal Funds and on unsecured corporate and government debts are frequently included in studies of the business cycle, money demand, and the monetary transmission mechanism. Since short-term interest rates are likely to respond more quickly to monetary policy than other economic variables, the dynamic interaction between Federal Funds and other short-term rates is critical to understanding how changes in monetary policy are transmitted through the economy.
Besides their economic relevance, interest rates are available on a daily basis for a long period of time and the nonparametric tests perform better with more data. Using the business day data does, however cause difficulties with missing values due to holidays. To avoid this problem, we sample the daily data at a weekly frequency, but only after appropriately filtering the data to prevent aliasing. This multirate filter, produced by applying the anti-aliasing filter and resampling, appears to be a new approach in econometrics and improves the performance of both Bierens' and Hinich's tests.
Correcting for aliasing may also be the reason we unequivocally find that U.S. interest rates contain a unit root. Whether or not interest rates contain unit roots has been heavily debated. Although many authors have found that U.S. interest rates are integrated (Nelson and Plosser, 1982, Psaradakis et al., 2006, Rapach and Weber, 2004, Rose, 1988), other research has suggested that interest rates are better described as long-memory or fractionally integrated series (Backus and Zin, 1993, Gil-Alana, 2004, Tsay, 2000). The empirical case for long-memory is usually based on conflicting results from various tests of the unit root and stationarity hypotheses. In contrast, we find uniform agreement among a variety of univariate tests that the levels of the interest rates are nonstationary and the differences are stationary. Other authors, such as Pfann et al. (1996) and Maki (2003), have suggested that interest rates exhibit nonlinear dynamics which affect the power of stationarity tests. Our results do not seem to suffer from low power, despite finding evidence of nonlinearity.
Since the interest rates are both integrated and nonlinear, we apply our two-stage method. Bierens' nonparametric test shows that the weekly interest rates are linearly cointegrated. For comparison, we also perform Johansen (1988)'s standard parametric tests. The
nonparametric and parametric results are very similar: identifying the same two cointegrating vectors. In addition, the cointegration estimates are robust to removing the period starting near the third quarter of ![]() through the first quarter of 1984 when the Federal Reserve shifted its monetary policy instrument away from interest rates (Rudebusch, 1995). Estimates for the prior and subsequent sub-sample find the same cointegrating vectors as the estimates for the full sample.
through the first quarter of 1984 when the Federal Reserve shifted its monetary policy instrument away from interest rates (Rudebusch, 1995). Estimates for the prior and subsequent sub-sample find the same cointegrating vectors as the estimates for the full sample.
After identifying two cointegrations in the first stage, we subsequently test each cointegration for nonlinearity. Linearity is rejected for both using the full data set. This result is not completely robust as linearity can be accepted for the first sub-sample. This result may stem from the reduction in the power of Hinich's test that stems from the relatively short span of data. However linearity can be rejected for the second sub-sample, which suggests that the nonlinearity is not produced only by switching regimes.5
We conclude that stationary interest rate dynamics are nonlinear. A simple explanation is that the adjustment mechanism that corrects deviations from the long-run interest rate equilibrium is nonlinear. Since we find two cointegrations, it is possible that nonlinearity also describes movements within the cointegration space. Regardless of whether nonlinearity can be isolated as a disequilibrium phenomena or not, the equilibrium dynamics are not simply characterized by the individual dynamics as would be expected from a linear system. This complexity points to the need for further work modeling the interest rate dynamics.
The paper is organized as follows. Section 2 clarifies the difference between linearity and nonlinearity for stationary processes. We also discuss the bispectrum to provide intuition for Hinich's test. Section 3 contains the theoretical contribution. Using a martingale representation for integrated processes, we derive a definition of cointegration that is applicable to nonlinear stochastic processes. This extended definition of linear cointegration is compared to the standard VECM model of both linear and nonlinear cointegration. Section 4 contains the empirical results and Section 5 concludes. The appendix reviews the aliasing problem and our multirate anti-aliasing filter design.
2 Nonlinear Processes
Whether a process is linear or nonlinear is determined by its serial dependence structure. For stationary processes, the difference between linear and nonlinear dynamics can be clarified by looking at the restrictions implied by linearity for both the Wold decomposition and the Volterra representation. The discussion in this section assumes stationarity. We defer formally defining stationarity until the discussion of integration and cointegration in the next section.
Under mild regularity conditions, a stationary stochastic process ![]() has a representation of the form:
has a representation of the form:
where
At first glance, this representation seems to suggest that every stationary process can be represented as an infinite-order moving average process. This impression is misleading. The process may be nonlinear because the input process is uncorrelated but is not necessarily stochastically
independent. ![]() can be represented as the output of a time-invariant linear filter applied to white noise input, but
can be represented as the output of a time-invariant linear filter applied to white noise input, but ![]() is a linear process only if
is a linear process only if
![]() is stochastically independent.6 In general, whiteness
is not sufficient for stochastic independence unless the white noise sequence is Gaussian.
is stochastically independent.6 In general, whiteness
is not sufficient for stochastic independence unless the white noise sequence is Gaussian.
For linear models, the coefficients of the moving average representation completely characterize the effect of a shock. The response of a linear sequence to a shock is completely characterized by the transfer function of the filter:
If the input to a linear sequence is a sine wave of frequency
A general model for a stationary stochastic process is
where, unlike the Wold representation
If ![]() is linear then only the first term in the Volterra representation
exists; for linear processes the Wold and Volterra representations are
identical implying that the impulse process in the Wold decomposition must be
independent in this case.
is linear then only the first term in the Volterra representation
exists; for linear processes the Wold and Volterra representations are
identical implying that the impulse process in the Wold decomposition must be
independent in this case.
The existence of higher-order terms in the Volterra expansion implies that
![]() is a nonlinear process. Unlike a linear process, the response
of the nonlinear sequence to a shock will depend on generalized transfer
functions of the form:
is a nonlinear process. Unlike a linear process, the response
of the nonlinear sequence to a shock will depend on generalized transfer
functions of the form:
If the input to a nonlinear sequence contains components with frequencies
Tests for linearity and Gaussianity can be based on the properties of these generalized transfer functions as reflected in a process' higher-order polyspectra. In general, the ![]() -order
polyspectrum is the Fourier transform of the
-order
polyspectrum is the Fourier transform of the ![]() -order cumulant function. The first three cumulants are defined by
-order cumulant function. The first three cumulants are defined by
![]() ,
,
![]() , and
, and
![]() .8 Strict
stationarity (or even third-order stationarity) implies
.8 Strict
stationarity (or even third-order stationarity) implies
![]() for all
for all ![]() ,
,
![]() is a function only of
is a function only of
![]() , and
, and
![]() is a function only of
is a function only of
![]() and
and
![]() . The second and third-order cumulant functions for stationary processes can be denoted by
. The second and third-order cumulant functions for stationary processes can be denoted by
![]() and
and
![]() respectively. These functions are assumed to be absolutely summable.
respectively. These functions are assumed to be absolutely summable.
The power spectrum is then defined as the Fourier transform of
![]() :
:
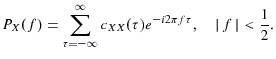 |
(2.6) |
where f denotes the frequency measured in units of inverse time.9 The bispectrum is defined as the second-order Fourier transform of
Define the skewness function,
![]() , as the normalized square modulus of the bispectrum:
, as the normalized square modulus of the bispectrum:
Let
These properties form the basis of Hinich's (1982) tests of Gaussianity and linearity. The intuition is that the skewness function will be flat for linear processes and identically zero for Gaussian processes. If the skewness function is significantly rough then linearity is rejected.
Hinich's test is conservative, not only in practice but also in theory. The test is conservative in theory because the null hypothesis that
![]() is constant for all frequency pairs is a necessary, but not sufficient condition for linearity. Nonlinearity could be detected in higher order polyspectra, even if the
normalized bispectrum is flat.10 Nevertheless, Ashley et al. (1986) found that Hinich's bispectral test had substantial power against many common
nonlinear time series models including bilinear models, nonlinear moving-average and autoregressive models, and linear and nonlinear threshold autoregressive models.
is constant for all frequency pairs is a necessary, but not sufficient condition for linearity. Nonlinearity could be detected in higher order polyspectra, even if the
normalized bispectrum is flat.10 Nevertheless, Ashley et al. (1986) found that Hinich's bispectral test had substantial power against many common
nonlinear time series models including bilinear models, nonlinear moving-average and autoregressive models, and linear and nonlinear threshold autoregressive models.
A key aspect of Hinich's tests is that (at least third-order) stationarity is assumed. However, economic time series often appear to be subject to permanent shocks, and it has become a standard practice to model these time series as non-stationary integrated processes. As is the norm in testing for nonlinearity, if the process is nonstationary Hinich's test can falsely reject linearity. Consequently, individual economic series are usually differenced or detrended before being tested for nonlinearity. Cointegration can provide a richer model of nonstationarity and an alternate method to recover stationary dynamics for a system of economic variables.
3 Integration and Cointegration
Cointegration as it is normally defined is incompatible with nonlinear dynamics. Cointegration was developed within the framework of vector error-correction models. Linearity of the stationary dynamics was explicitly assumed, because the VECM model is linear and the innovation process was assumed to be independent or Gaussian. However, there is no compelling reason for this restriction.
Using Hall and Heyde's martingale representation, we show that the innovation process of a integrated series is not in general a linear stochastic process. It is then straightforward to define cointegration for a vector of integrated processes using the martingale representation.
For clarity, our martingale-based definition is contrasted with the standard VECM definition of cointegration including the extension to nonlinear cointegration. The representation theorem shows that nonlinearity is more general than just nonlinear cointegration, as nonlinear dynamics can be present even when the cointegrating relationship is linear.
Initially, we establish some definitions and notational conventions. The definitions are standard and can be found in a number of references. For all time periods, let ![]() denote a
denote a
![]() -dimensional vector random sequence,
-dimensional vector random sequence,
![]() on a probability space
on a probability space
![]() .
.
Let
![]() denote a one to one ergodic measure-preserving shift transformation. If
denote a one to one ergodic measure-preserving shift transformation. If
![]() is a random variable on the probability space, then
is a random variable on the probability space, then
![]() defines a strictly stationary ergodic sequence. A stochastic sequence is said to be integrated of order
one,
defines a strictly stationary ergodic sequence. A stochastic sequence is said to be integrated of order
one, ![]() , if the first difference of the sequence is strictly stationary.11 A martingale difference sequence is strictly stationary by definition, so martingales are
, if the first difference of the sequence is strictly stationary.11 A martingale difference sequence is strictly stationary by definition, so martingales are ![]() The concept of integration can be extended to higher orders.
The concept of integration can be extended to higher orders.
Hall and Heyde (1980, pp. 136) prove the following representation theorem:
where
and,
where
From the Hall and Heyde representation, we derive a representation for an
![]() sequence:
sequence:
From (3.2) and (3.3), both
A system of integrated time series is cointegrated if some linear combinations of the time series are stationary. Cointegration can be defined as a reduced rank condition involving the covariance matrix of the vector martingale difference. We need the following lemma for the form of the covariance matrix for a vector martingale difference sequence.
Cointegrating vectors for an
![]() sequence that are based on the martingale representation are defined by:
sequence that are based on the martingale representation are defined by:
![\begin{displaymath}\begin{split}E_{0}\bigg[\Big( {\sum\limits_{s=0}^{t}{\beta _{j}^{T}Y_{s}}}\Big) \Bigl( {\sum\limits_{s=0}^{t}{\beta _{j}^{T}Y_{s}}}\Bigr) ^{T}\bigg] &= \beta_{j}^{T}E_{0}\bigg[\Big( {\sum\limits_{s=0}^{t}{Y_{s}}}\Big) \Big( {\sum\limits_{s=0}^{t}{Y_{s}}}\Big) ^{T} \bigg] \beta _{j} \\ &=\beta _{j}^{T}\mathbf{CC}^{T}\beta _{j}=\mathbf{0}^{T}\mathbf{0}=0. \end{split}\end{displaymath}](img111.gif)
|
(3.7) |
The proof also supports the following corollary:
Corollary 2. Denote the q by (q - r) orthogonal compliment matrix of 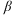 by
by 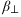 , so that
, so that 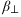 has the property
has the property 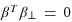 . The common stochastic trend
. The common stochastic trend 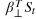 , which
has dimension (q - r), is integrated but not cointegrated. The q
-dimensional sequences
, which
has dimension (q - r), is integrated but not cointegrated. The q
-dimensional sequences 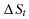 and
and
![\left[ {{\begin{array}{*{20}c} {\beta ^T } \hfill & {\beta _\bot ^T \Delta } \hfill \\ \end{array}}}\right] S_{t}](img1_6.gif) are both stationary. In the absence of
cointegration, the two transformations are equivalent. If r = 0, then
are both stationary. In the absence of
cointegration, the two transformations are equivalent. If r = 0, then 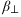 is full rank and can be taken as the identity matrix.
is full rank and can be taken as the identity matrix.
In contrast to extant definitions, the martingale based definition of cointegration does not require independence, Gaussianity, or linearity of the stationary components of the process. Previous definitions of linear cointegration are a special case, much like independence is a special case of the martingale property. The difference can be made clearer by looking at the expectation of the cointegration relations,
These expectations have been purged of the effects of the permanent shocks generated by the martingale difference and are stationary. When viewed as a new stochastic process, there are no restrictions on the dependence structure of
Our method contrasts with the standard approach to cointegration. Stationary linear combinations of integrated variables are usually specified to follow a linear ARMA process or are included in linear structural models. The standard linear VECM has the form:
If the model is cointegrated then the
Granger (1991) proposes three nonlinear generalizations of cointegration. The first generalization is that nonlinear functions of the time series may be cointegrated in the sense that
![]() and
and
![]() have a dominant property that the linear combination of nonlinearly transformed variables
have a dominant property that the linear combination of nonlinearly transformed variables
![]() does not exhibit. A second generalization is to allow time-varying cointegration vectors. A third generalization is nonlinear error correction, in which
the cointegration relations would enter the error-correction model through a nonlinear function
does not exhibit. A second generalization is to allow time-varying cointegration vectors. A third generalization is nonlinear error correction, in which
the cointegration relations would enter the error-correction model through a nonlinear function ![]() , i.e.
, i.e.
Granger (1991) gives conditions under which
A natural nonlinear error-correction specification is to allow mean reversion only for large deviations, so that ![]() has the form:
has the form:
In this case,
Although, the extended definition of cointegration could be further extended to allow for nonlinear cointegration, we limit ourselves to the case where the linear combination is stationary. Such stationary linear combinations can exhibit nonlinear dynamics. Differentiating between nonlinear error correction and stationary nonlinear dynamics is likely difficult in practice.
Our proposed method for testing for whether a cointegration is nonlinear is sequential. This sequential method allows us to test the stationary components of the system for nonlinear dynamics. We first estimate cointegrating vectors using Bierens' (1997) non-parametric test. Bierens' test is asymptotically valid for a nonlinear data generating processes due to Hall and Heyde's representation theorem. We then test the estimated cointegrating relations for Gaussianity and linearity using Hinich's (1982) tests. Asymptotically, Hinich's test is also valid as the cointegrating vectors are stationary. In practice, as is the norm, the results of Hinich's tests are conditional on whether the first stage estimates do eliminate any nonstationarity.
4 Empirical Results
We apply our sequential procedure to a system of short-term U.S. interest rates. Short-term interest rates are available at a high frequency over an extended time period: constituting a larger sample size than many other business cycle variables, such as real output and inflation. In addition, interest rates directly capture the dynamics caused by monetary policy changes.
We use business daily data for the interest rates on one-month Commercial Paper (![]() ), the secondary market rate on one-month Treasury Bills (
), the secondary market rate on one-month Treasury Bills (![]() ), and the Federal Funds (
), and the Federal Funds (![]() ) from
) from ![]() to
to ![]() . The commercial paper and Federal Funds rates are available from the Federal Reserve Board's website. The commercial paper rate series was
discontinued in August 1997. The Federal Reserve Bank of St. Louis provided us with the secondary market rate on one-month Treasury Bills. These interest rates are converted to one-month
holding period yields on a bond interest basis, and are passed through an anti-aliasing filter. The anti-aliasing filter is designed to remove the high-frequency power in the daily rate series to minimize the bias caused by converting the daily time series to weekly time series either by direct
sampling or weekly averaging. The daily rates are converted to weekly rates by sampling the filtered daily rates once per week. Figure 1 displays the natural logarithms of the filtered interest rates.
. The commercial paper and Federal Funds rates are available from the Federal Reserve Board's website. The commercial paper rate series was
discontinued in August 1997. The Federal Reserve Bank of St. Louis provided us with the secondary market rate on one-month Treasury Bills. These interest rates are converted to one-month
holding period yields on a bond interest basis, and are passed through an anti-aliasing filter. The anti-aliasing filter is designed to remove the high-frequency power in the daily rate series to minimize the bias caused by converting the daily time series to weekly time series either by direct
sampling or weekly averaging. The daily rates are converted to weekly rates by sampling the filtered daily rates once per week. Figure 1 displays the natural logarithms of the filtered interest rates.
Correcting for aliasing does not impact the asymptotics of the cointegration estimator, because cointegration is related to the long-run dynamics while aliasing distorts higher frequency dynamics. Nevertheless, correcting for aliasing might improve the power of the cointegration estimators in a finite sample. In addition, Hinich and Patterson (1985,1989) showed that aliasing does bias tests for nonlinearity towards accepting linearity. Aliasing is discussed in the appendix.
After applying the multirate filter, we test this data with our two-stage method: first testing for cointegration and then testing for nonlinearity. Two cointegrating vectors are found for the system of three interest rates over the period ![]() . We then run several tests on each cointegrating relation. We first test the cointegrations for an alternative form of nonstationarity considered by Hinich and Wild (2001). This alternative type of
nonstationarity is rejected, so we test for Gaussianity. Gaussianity of both the real and imaginary parts of the bispectrum is strongly rejected. Finally, we test for nonlinearity. We find strong evidence that the cointegrations exhibit nonlinear dynamics.
. We then run several tests on each cointegrating relation. We first test the cointegrations for an alternative form of nonstationarity considered by Hinich and Wild (2001). This alternative type of
nonstationarity is rejected, so we test for Gaussianity. Gaussianity of both the real and imaginary parts of the bispectrum is strongly rejected. Finally, we test for nonlinearity. We find strong evidence that the cointegrations exhibit nonlinear dynamics.
4.1 Univariate Tests
Before estimating cointegration relations, we run a battery of univariate tests. We first test the unit root and stationarity hypotheses on ![]() ,
, ![]() ,
, ![]() , and their first differences
, and their first differences ![]() using several tests with different nulls. These tests include: an augmented Dickey-Fuller (ADF) test and a Phillips-Perron (PP) test of the unit root hypotheses against the alternative of stationarity; the KPSS test of the null of stationarity
against the alternative of nonstationarity; and the Bierens (1997) non-parametric test for the existence of cointegration run as a univariate test of the unit root with drift hypothesis against trend stationarity on each variable.14 For the ADF test, the lag length,
using several tests with different nulls. These tests include: an augmented Dickey-Fuller (ADF) test and a Phillips-Perron (PP) test of the unit root hypotheses against the alternative of stationarity; the KPSS test of the null of stationarity
against the alternative of nonstationarity; and the Bierens (1997) non-parametric test for the existence of cointegration run as a univariate test of the unit root with drift hypothesis against trend stationarity on each variable.14 For the ADF test, the lag length, ![]() , is chosen by the formula
, is chosen by the formula
![]() . For the PP and KPSS tests, the truncation lag for the Newey-West estimator is also set with this formula. The test results are shown in Table 1 Stationarity Tests along
with a mnemonic for the tests' hypotheses and the 5 and 10 percent critical
values.
. For the PP and KPSS tests, the truncation lag for the Newey-West estimator is also set with this formula. The test results are shown in Table 1 Stationarity Tests along
with a mnemonic for the tests' hypotheses and the 5 and 10 percent critical
values.
| Variable | ADF | PP | KPSS1 | Bierens |
|---|---|---|---|---|
| -1.9132 | -8.6587 | 0.9272 | 1.1441 | |
| -1.8289 | -9.4498 | 1.0186 | 0.7741 | |
| -1.8174 | -8.8747 | 1.0027 | 1.0203 | |
|
|
-7.4386 | -740.9803 | 0.1120 | 0.0000 |
|
|
-8.0123 | -877.6077 | 0.1210 | 0.0000 |
|
|
-7.3217 | -2118.753 | 0.1249 | 0.0000 |
| UR | UR | S | URD | |
| S | S | NS | TS | |
| <-3.86 | <-14.0 | >.436 | <.025 | |
| <-2.57 | <-11.2 | >.347 | <.006 |
The logged interest rates are clearly ![]() processes: every test rejects stationarity of the levels at well above the
processes: every test rejects stationarity of the levels at well above the ![]() confidence level and fails to reject stationarity of the first differences even at the
confidence level and fails to reject stationarity of the first differences even at the ![]() confidence level. The consistency of the test results
is important, because differences in these tests can be interpreted as evidence of long-memory rather than integration. For example, Karanasos et al. (2006) interpret their simultaneous rejection of both the unit root hypothesis and stationarity as evidence for
fractional integration and long-memory in real U.S. interest rates. Our results are not open to such interpretation.
confidence level. The consistency of the test results
is important, because differences in these tests can be interpreted as evidence of long-memory rather than integration. For example, Karanasos et al. (2006) interpret their simultaneous rejection of both the unit root hypothesis and stationarity as evidence for
fractional integration and long-memory in real U.S. interest rates. Our results are not open to such interpretation.
Given the results of the stationarity tests, we test the stationary first difference of each interest rate for nonlinearity. We pre-whiten each of the components using an ![]() filter to
eliminate bias in the spectral estimation prior to testing and to decrease the likelihood of falsely rejecting the null of linearity. The tests (available on request) provide overwhelming evidence of nonlinear dynamics for the first differences of these short-term interest rates over the full
sample.
filter to
eliminate bias in the spectral estimation prior to testing and to decrease the likelihood of falsely rejecting the null of linearity. The tests (available on request) provide overwhelming evidence of nonlinear dynamics for the first differences of these short-term interest rates over the full
sample.
We also tested the first differences for nonlinearity over two sub-periods: Sept. 13, ![]() through Sept. 19, 1979 and March
through Sept. 19, 1979 and March ![]() , 1984 through Dec.
, 1984 through Dec. ![]() , 1996. These are periods over which a target for the federal funds rate can be constructed, see Rudebusch (1995).
Effectively, we are dropping the period when the Federal Reserve shifted its intermediate target away from interest rates. This period is also when many interest rates were deregulated.
, 1996. These are periods over which a target for the federal funds rate can be constructed, see Rudebusch (1995).
Effectively, we are dropping the period when the Federal Reserve shifted its intermediate target away from interest rates. This period is also when many interest rates were deregulated.
For these sub-samples, we can accept the null of linearity in the first sub-sample, but reject linearity in the second. The number of data points for the first sub-sample is 258 versus
669 for the second sub-sample and ![]() for the full sample. The evidence
reported in Ashley et al. (1986) would indicate that the power of these tests is substantially higher over both the second sub-sample and over the full sample. This provides one explanation for the inability to reject linearity in the first sub-sample. Another possible
explanation for finding nonlinearity only in the second sub-sample could be that deregulation of interest rates transformed the dynamics going forward.
for the full sample. The evidence
reported in Ashley et al. (1986) would indicate that the power of these tests is substantially higher over both the second sub-sample and over the full sample. This provides one explanation for the inability to reject linearity in the first sub-sample. Another possible
explanation for finding nonlinearity only in the second sub-sample could be that deregulation of interest rates transformed the dynamics going forward.
Regardless for the reasons for accepting linearity in the first sub-sample, finding evidence of nonlinearity in the second sub-sample is crucial. If linearity was rejected for both sub-samples, it would appear that the nonlinearity found over the full sample was driven solely by a regime shift. Rejecting linearity in the second sub-sample does not rule out a break in the dynamics due to the policy, but it does rule out the shift being the only source of nonlinearity. Consequently, we continue analyzing the full sample, although we also check the results for the two sub-samples.
4.2 Cointegration
The cointegration analysis used the system
The number of cointegrations determined by both the ![]() -min test and estimating
-min test and estimating
![]() is
is ![]() . The
. The ![]() -min tests are reported in Table 2.
-min tests are reported in Table 2. ![]() is the smoothing parameter; the value is set
optimally for the different confidence levels following Bierens (1997). The tests are run in sequence, starting with the null hypothesis that the number of cointegrating vectors is zero, followed by a test of the null hypothesis that there is one cointegrating vector, and
so on until the null cannot be rejected. We find that
is the smoothing parameter; the value is set
optimally for the different confidence levels following Bierens (1997). The tests are run in sequence, starting with the null hypothesis that the number of cointegrating vectors is zero, followed by a test of the null hypothesis that there is one cointegrating vector, and
so on until the null cannot be rejected. We find that ![]() (no cointegration) is decisively rejected, as is the hypothesis that
(no cointegration) is decisively rejected, as is the hypothesis that ![]() (one cointegrating vector), but we cannot reject the hypothesis that
(one cointegrating vector), but we cannot reject the hypothesis that ![]() (two cointegrating vectors).
(two cointegrating vectors).
| Null Hypothesis | Alternative Hypothesis | Test Stat | Critical Region | M | Conclusion |
|---|---|---|---|---|---|
| r = 0 | r = 1 | 0.00000 |
|
3 | Reject |
| r = 0 | r = 1 | 0.00000 |
|
Reject | |
| r = 0 | r = 1 | 0.00000 |
|
Reject | |
| r = 1 | r = 2 | 0.00054 |
|
3 | Reject |
| r = 1 | r = 2 | 0.00054 |
|
3 | Reject |
| r = 1 | r = 2 | 0.00054 |
|
3 | Reject |
| r = 2 | r = 3 | 0.76618 |
|
3 | Accept |
| r = 2 | r = 3 | 0.76618 |
|
3 | Accept |
| r = 2 | r = 3 | 0.76618 |
|
3 | Accept |
M is the smoothing parameter for the nonparametric estimator
For comparison, we also estimate the parametric maximum likelihood ![]() -max and trace tests of Johansen (1988) using the CATS
package (Hansen and Juselius, 2006). The
-max and trace tests of Johansen (1988) using the CATS
package (Hansen and Juselius, 2006). The ![]() maximum likelihood method estimates a finite-order VECM, as in (3.9), where the coefficient matrices
maximum likelihood method estimates a finite-order VECM, as in (3.9), where the coefficient matrices
![]() are
are ![]() . If the system is cointegrated then
the matrix
. If the system is cointegrated then
the matrix ![]() has reduced rank
has reduced rank ![]() , and can be decomposed into
, and can be decomposed into
![]() . The matrices
. The matrices ![]() and
and ![]() are full rank 3 by
are full rank 3 by ![]() matrices, and the columns of
matrices, and the columns of ![]() are the cointegration vectors.
are the cointegration vectors.
Pantula (1989) and Johansen (1992) suggested a procedure to jointly identify the deterministic components and the rank of ![]() . The idea
is to test the models sequentially, beginning with the most restrictive model considered. Each hypothesis can be tested using either the trace or
. The idea
is to test the models sequentially, beginning with the most restrictive model considered. Each hypothesis can be tested using either the trace or ![]() -max test statistics. We conducted
these tests for a set of lag lengths
-max test statistics. We conducted
these tests for a set of lag lengths
![]() . These tests uniformly find that there are two cointegration vectors and that the correct deterministic component is a constant that is restricted to the cointegration space.
This specification is therefore extremely robust to the lag length and agrees with the rank determination of the non-parametric test. Table 3 reports these tests for a lag length of
. These tests uniformly find that there are two cointegration vectors and that the correct deterministic component is a constant that is restricted to the cointegration space.
This specification is therefore extremely robust to the lag length and agrees with the rank determination of the non-parametric test. Table 3 reports these tests for a lag length of ![]() .15
.15
| Hypothesis |
|
Trace | |||
|---|---|---|---|---|---|
|
|
103.48 | 14.09 | 158.63 | 31.88 | 34.78 |
|
|
103.47 | 13.39 | 158.60 | 26.70 | 29.38 |
|
|
114.26 | 16.13 | 172.02 | 39.08 | 42.20 |
|
|
50.59 | 10.29 | 55.15 | 17.79 | 19.99 |
|
|
50.59 | 10.60 | 55.13 | 13.31 | 15.34 |
|
|
51.41 | 12.39 | 57.77 | 22.95 | 25.47 |
|
|
4.55 | 7.50 | 4.55 | 7.50 | 9.13 |
The results from the nonparametric and parametric estimators are very similar. The non-parametric estimate of the cointegration vectors is
![]() , where
, where
![]() and
and
![]() . The parametric estimate of the cointegration vectors is
. The parametric estimate of the cointegration vectors is
![]() , where
, where
![]() and
and
![]() .16 The parametric estimate is
statistically equivalent to the nonparametric estimate. For both estimators, the first basis vector
.16 The parametric estimate is
statistically equivalent to the nonparametric estimate. For both estimators, the first basis vector ![]() reflects the near stationarity of the spread between the logarithms of the
Commercial Paper and Treasury Bill rates. Similarly, the second basis vector
reflects the near stationarity of the spread between the logarithms of the
Commercial Paper and Treasury Bill rates. Similarly, the second basis vector ![]() reflects the near stationarity of the spread between the Treasury Bill rate and Federal Funds
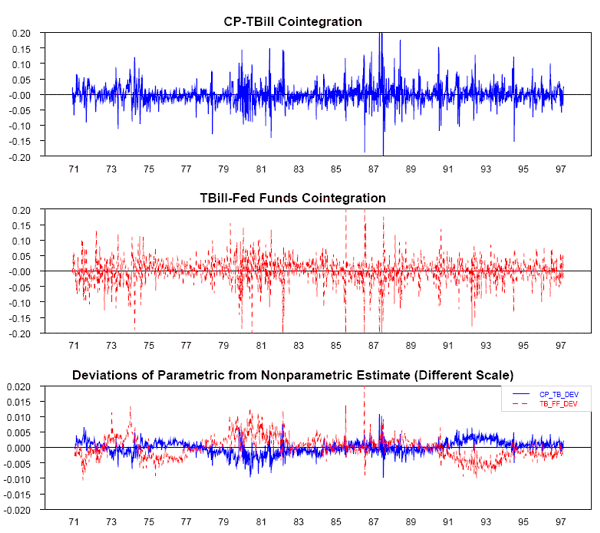
rates.17 The nonparametric estimates of the two cointegration relations are shown in Figure 2. The differences between the nonparametric and parametric estimates,
also included in the figure, are an order of magnitude smaller.
reflects the near stationarity of the spread between the Treasury Bill rate and Federal Funds
rates.17 The nonparametric estimates of the two cointegration relations are shown in Figure 2. The differences between the nonparametric and parametric estimates,
also included in the figure, are an order of magnitude smaller.
This consistency of the nonparametric and parametric contrasts with the results of Coakley and Fuertes (2001) and Calza and Sousa (2006) where the parametric and nonparametric results differ. In these papers, the authors argue for accepting the nonparametric results because Bierens estimator is valid for a broader range of data generating processes. In particular, Coakley and Fuertes (2001) argue that the maximum likelihood estimates are distorted due to nonlinear mean reversion in exchange rates which would imply nonlinear cointegration. The consistency between our nonparametric and parametric estimates reveals no evidence of nonlinear cointegration between interest rates.
Bierens (1997) argued that hypothesis tests in the parametric model have higher power than comparable tests in the non-parametric model. This argument does not necessarily hold because the argument and the hypothesis tests are predicated on linearity. Despite the parametric estimator's consistency with the nonparametric estimates, the parametric estimator is likely misspecified since the individual interest rates are nonlinear. Since the nonparametric and parametric cointegrations are indistinguishable, we can safely sidestep the issue of misspecification by focusing solely on the nonparametric results.
4.2.1 Robustness
As already discussed, our results are robust to the type of estimator and lag length. Before moving to the second stage of our approach and testing for nonlinearity, we also tested the results for robustness to the Federal Reserve's choice of policy instrument, by examining the integration and
cointegration properties of the data over two sub-periods: Sept. 13, 1974 through
Sept. 19, 1979 and March ![]() , 1984 through Dec. 31,
1996.
, 1984 through Dec. 31,
1996.
The results of the non-parametric cointegration tests for the two sub-samples are reported in Table 4. The results show that the rank identifications are consistent with those from the full sample. The parametric estimators also identified
two cointegrating vectors for each sub-period. Further, the estimated cointegration vectors are consistent with the estimated vectors from the full sample; we cannot reject the joint hypothesis,
![]() and
and
![]() , for either sub-sample. These tests are
, for either sub-sample. These tests are
![]() . For the 1974-
. For the 1974-![]() sub-sample, the test statistic is 3.26 (p-value of
sub-sample, the test statistic is 3.26 (p-value of ![]() ), and for the 1984- 1996
sub-sample, the test statistic is .38 (p-value of .83).
), and for the 1984- 1996
sub-sample, the test statistic is .38 (p-value of .83).
| Null Hypothesis | Alternative Hypothesis | Test Stat: 1974-1979 |
Test Stat: 1984-1996 |
Critical Region | M | Conclusion |
|---|---|---|---|---|---|---|
| r = 0 | r = 1 | 0.00000 | 0.00000 |
|
3 | Reject |
| r = 0 | r = 1 | 0.00000 | 0.00000 |
|
Reject | |
| r = 0 | r = 1 | 0.00000 | 0.00000 |
|
Reject | |
| r = 1 | r = 2 | 0.00523 | 0.00008 |
|
3 | Reject |
| r = 1 | r = 2 | 0.00523 | 0.00008 |
|
3 | Reject |
| r = 1 | r = 2 | 0.00523 | 0.00008 |
|
3 | Reject |
| r = 2 | r = 3 | 1.33438 | 2.33982 |
|
3 | Accept |
| r = 2 | r = 3 | 1.33438 | 2.33982 |
|
3 | Accept |
| r = 2 | r = 3 | 1.33438 | 2.33982 |
|
3 | Accept |
M is the smoothing parameter for the nonparametric estimator
4.3 Tests for Nonlinearity of the Cointegration Relations
The stationary components of the system consist of the two cointegration relations and the first difference of the common stochastic trend. We test the estimated cointegration relations for nonlinear serial dependence using the bispectrum tests. The cointegration vectors, ![]() and
and ![]() are basis vectors for the cointegration space, so that any linear
combination of
are basis vectors for the cointegration space, so that any linear
combination of ![]() and
and ![]() are also stationary. Thus, evidence of
nonlinearity in one of the cointegration relations is actually evidence that the stationary components of the system are nonlinear. Prior to testing for nonlinearity, each of the cointegration relations is pre-whitened by an
are also stationary. Thus, evidence of
nonlinearity in one of the cointegration relations is actually evidence that the stationary components of the system are nonlinear. Prior to testing for nonlinearity, each of the cointegration relations is pre-whitened by an ![]() filter to eliminate bias in the spectral estimation prior and to decrease the likelihood of falsely rejecting the null of linearity.
filter to eliminate bias in the spectral estimation prior and to decrease the likelihood of falsely rejecting the null of linearity.
For robustness, we test these relations for stationarity using the frequency domain test derived by Hinich and Wild (2001). The Hinich and Wild (HW) test checks for residual non-stationarity due to the existence of a waveform with random phase and amplitude. This test has
a very different alternative hypothesis than the cointegration test, and should detect nonstationarity at seasonal frequencies. The test is
![]() under the null of stationarity. The HW-stationarity tests, reported in Table 5, confirm that the cointegration relations are stationary.
under the null of stationarity. The HW-stationarity tests, reported in Table 5, confirm that the cointegration relations are stationary.
| Cointegration (Nonparametric) |
HW | Gauss1 | Gauss2 |
|---|---|---|---|
|
|
|
|
|
|
|
|
|
|
HW test statistic is
![]() under
under ![]() stationarity
stationarity
Gauss1 test statistic is
![]() under
under
![]()
Gauss2 test statistic is
![]() under
under
![]()
If the time series are Gaussian, then the real and imaginary components of the bispectrum are zero. The test statistics for these two hypotheses, called Gauss1 and Gauss2 respectively, are also reported in Table 5. If either the real or imaginary components of the bispectrum are non-zero then Gaussianity is rejected. If the imaginary component is non-zero then the sequence is not time-reversible. The results indicate that the stationary components of the system are highly non-Gaussian and are not time-reversible.
Rejecting Gaussianity is necessary but not sufficient to reject linearity. Table 6 gives the results of Hinich's test for nonlinearity over the full sample. The ![]() test statistics are independent and normally distributed under the null of linearity, and we treat these tests as two-tailed, as Ashley et al. (1986) found that one-tailed tests may fail to detect certain types of nonlinearity
test statistics are independent and normally distributed under the null of linearity, and we treat these tests as two-tailed, as Ashley et al. (1986) found that one-tailed tests may fail to detect certain types of nonlinearity
| Cointegration (Nonparametric) |
||||||
|---|---|---|---|---|---|---|
|
|
-2.81 | -4.09 | -5.39 | -2.65 | 2.78 | 2.19 |
|
|
-2.26 | -2.66 | -0.93 | -0.38 | 1.29 | 1.94 |
![]() is
is
![]() under
under ![]() is constant
is constant
![]()
Linearity is rejected if
![]() exceeds the critical value.
exceeds the critical value.
c.v.
![]()
The tests are computed for the non-parametric estimates of the cointegrations
The strongest evidence of nonlinearity is found in the first cointegration relation. Linearity is rejected for
![]() by
by ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() using the
using the ![]() critical values and by
critical values and by
![]() using the
using the ![]() critical values. Flatness of the skewness function is a
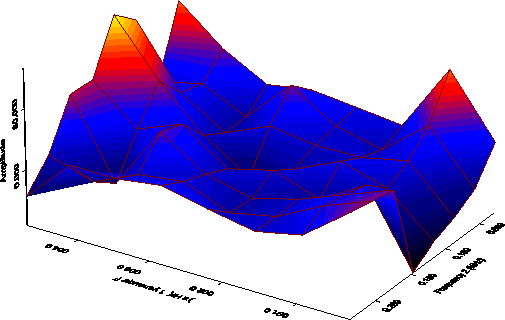
necessary condition for linearity. Figure 3 shows that the skewness function for the first cointegration is clearly far from flat, which is what should be expected from the statistical tests.
critical values. Flatness of the skewness function is a
necessary condition for linearity. Figure 3 shows that the skewness function for the first cointegration is clearly far from flat, which is what should be expected from the statistical tests.
Evidence of nonlinearity is also found in the second cointegration, although this evidence is somewhat weaker. Linearity is rejected for
![]() by
by ![]() and by
and by ![]() using the
using the ![]() critical values, and by
critical values, and by ![]() using the
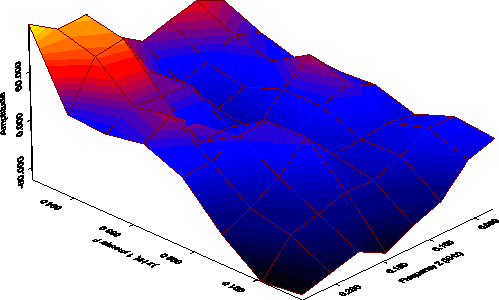
using the ![]() critical values. Figure 4 shows the skewness function for the second cointegration. Again, the
skewness function is not flat, but it is flatter than the skewness function of the first cointegration, reflecting weaker evidence of nonlinearity in the second cointegration. However, nonlinearity in either cointegration implies that the cointegrated system exhibits nonlinear dynamics.
critical values. Figure 4 shows the skewness function for the second cointegration. Again, the
skewness function is not flat, but it is flatter than the skewness function of the first cointegration, reflecting weaker evidence of nonlinearity in the second cointegration. However, nonlinearity in either cointegration implies that the cointegrated system exhibits nonlinear dynamics.
4.3.1 Robustness
Structural shifts over the long period being analyzed could be mistaken for nonlinear dynamics. As previously discussed, to address this issue we delete the period 1979-1983 and consider the two sub-samples. Table 7 presents the test for nonlinearity over these two sub-samples. Similar to the univariate results, linearity cannot be rejected for the first subsample but can for the second. As previously mentioned, Hinich's test has relatively low power for the first sub-sample. Rejecting linearity for the second sub-sample implies that the shift in policy regime does not cause the nonlinearity per se. The results could alternatively be interpreted as the result of interest rate deregulation rather than low power. Post-deregulation, the interest rate dynamics seem to become more complex, even though the long-run equilibrium relations were unchanged.
Table 7: Linearity Tests for Sub-Samples
| Cointegration | ||||||
|---|---|---|---|---|---|---|
|
|
-1.07 | -1.39 | -1.99 | -0.36 | 0.98 | 1.12 |
|
|
-1.15 | -1.72 | 0.50 | 0.79 | 0.15 | 0.67 |
| Cointegration | ||||||
|---|---|---|---|---|---|---|
|
|
-2.00 | -2.95 | -4.43 | -3.88 | 1.95 | 1.96 |
|
|
-1.99 | -2.82 | -2.14 | 0.05 | 2.40 | 1.91 |
![]() is
is
![]() under
under ![]() is constant
is constant
![]()
Linearity is rejected if
![]() exceeds the critical value.
exceeds the critical value.
c.v.
![]()
There is strong evidence of nonlinearity in the stationary components of the system. Although the evidence is not completely robust to the sample of data tested, the nonlinearity does not stem solely from a structural break caused by the change in targeting approach in the early ![]() s or the deregulation of interest rates, as the second sub-sample shows strong evidence of nonlinearity.
s or the deregulation of interest rates, as the second sub-sample shows strong evidence of nonlinearity.
5 Conclusion
We have shown that cointegration relations in ![]() systems generally produce nonlinear dynamics. Our approach follows advancements in probability theory where many results that required
independence, and therefore implied linearity, have been extended using martingales to allow for more general dependence or nonlinearity. Because the cointegration relations derived from
systems generally produce nonlinear dynamics. Our approach follows advancements in probability theory where many results that required
independence, and therefore implied linearity, have been extended using martingales to allow for more general dependence or nonlinearity. Because the cointegration relations derived from ![]() systems are stationary, they can be tested for nonlinear serial dependence using standard polyspectral techniques. A feature of our two-stage method is that it tests a system of economic variables, or an equilibrium economic relation, for nonlinearity even though existing tests for nonlinearity,
including the bispectrum test, are univariate.
systems are stationary, they can be tested for nonlinear serial dependence using standard polyspectral techniques. A feature of our two-stage method is that it tests a system of economic variables, or an equilibrium economic relation, for nonlinearity even though existing tests for nonlinearity,
including the bispectrum test, are univariate.
Tests for the existence of nonlinear dynamics require large sample sizes and may be adversely affected by aliasing and other problems associated with time aggregation. Interest rates are measured with high frequency and aliasing can be controlled by adequate attention to filter design. For these reasons, the conditions are more favorable to testing interest rate data for nonlinear dynamics than for most other variables that are important to the business cycle, money demand, and the monetary transmission mechanism. We found that short-term US interest rates are cointegrated and that the stationary components of the system are nonlinear. The Hinich nonlinearity test is conservative, which strengthens our finding of nonlinear interest rate dynamics.
These results suggest that the untested assumption of linearity may be incorrect. The failure to find robust evidence of nonlinearity in lower frequency macroeconomic time series may be due to the small sample sizes that can be obtained for those time series, in addition to problems associated with sampling and time aggregation. Our particular example shows that the spreads between the Commercial Paper, Treasury Bill, and Federal Funds rates exhibit nonlinear dynamics. Our results are consistent with work that suggests there are asymmetric effects of monetary policy on interest rates, such as Choi (1999). Our results suggest that better forecasts of these spreads might be obtained with nonlinear models, such as bilinear models.
Appendix: Aliasing and Constructing Anti-Aliasing Filters
Let ![]() be a stationary continuous-time series that is sampled at regular intervals of time,
be a stationary continuous-time series that is sampled at regular intervals of time,
![]() .
. ![]() is called the sampling
interval, and
is called the sampling
interval, and
![]() is the sampling rate. The sampled sequence is denoted
is the sampling rate. The sampled sequence is denoted
![]() ,
,
![]() .
.
The power spectrum of the continuous-time series is
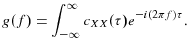
for
It is very important to eliminate any power in a time series at frequencies that exceed the Nyquist folding frequency prior to sampling, because failure to do so will lead to biased estimation due to aliasing. Aliasing has traditionally been described in the frequency domain, but Hinich and Rothman (1998) showed that aliasing corrupts the impulse response functions in the time domain and therefore leads to serious identification problems.
The same problem results if a discrete-time sequence is sampled at a lower frequency, such as sampling a daily interest rate at weekly intervals. In this case, the sampling interval is
![]() and the Nyquist folding frequency is
and the Nyquist folding frequency is
![]() . If the daily interest rates have power at frequencies exceeding
. If the daily interest rates have power at frequencies exceeding ![]() then aliasing will occur. The solution to this problem is to filter the daily interest rates in such a way that the power spectrum of the filtered rates will be zero at frequencies exceeding the Nyquist. If
then aliasing will occur. The solution to this problem is to filter the daily interest rates in such a way that the power spectrum of the filtered rates will be zero at frequencies exceeding the Nyquist. If
![]() are the filter weights then the power spectrum of the filtered sequence equals the power spectrum of the underlying sequence multiplied by the gain of the filter
are the filter weights then the power spectrum of the filtered sequence equals the power spectrum of the underlying sequence multiplied by the gain of the filter
![]() where
where
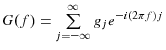 . The solution to the aliasing problem would be to design a filter with gain:
. The solution to the aliasing problem would be to design a filter with gain:
This gain function corresponds to the ideal symmetric low-pass filter with weights
which cannot be realized with a finite data sample. In fact, the rate of decrease of the filter weights is too slow to simply truncate the filter at some finite number of leads and lags. The usual solution is to taper the weights of the ideal filter. We taper the ideal weights using a Hanning cosine taper. This filter is referred to as an anti-aliasing filter in the text.
Applying the anti-aliasing filter produces a business day series that should not contain power at frequencies higher than every two weeks. This series still suffers from problems created by missing values caused by holidays. We subsequently resample our series on every Wednesday to avoid the missing value problem. Since the Nyquist frequency is then every two weeks, the resulting weekly series should avoid aliasing. The combination of applying the anti-aliasing filter and then decimating to the weekly sample produces a multi-rate filter.
The common approach in economics is to report unweighted weekly averages of daily interest rates. Weekly averages are also effectively produced by a multi-rate filter: combining a filter with decimation. The filter is an unweighted averaging filter that has a wider main lob and much larger side lobes than the anti-aliasing filter we use. Weekly averages therefore potentially are strongly aliased. Monthly and quarterly averages that are often used in studies of the real interest rate are similarly aliased.
Bibliography
Footnotes
E-mail: [email protected]
Melvin Hinich provided technical advice on his bispectrum computer program. Hermann Bierens provided technical advice on implementing his nonparametric cointegration tests. We thank William Barnett, Florenz Plassmann, Eric Verhoogen and seminar participants at George Washington University, the IMF Institute, the 2006 Midwest Macroeconomics Conference, and the 2006 Udine Workshop for helpful comments and suggestions. We also thank Samia Husain for research assistance. The views presented are solely those of the authors and do not necessarily represent those of the Federal Reserve Board or its staff. Any remaining errors are the responsibility of the authors. Return to Text
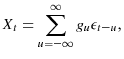
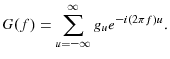
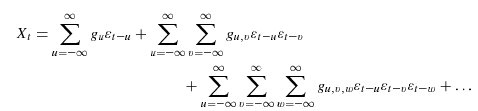
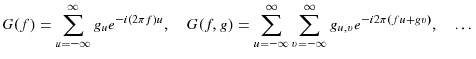
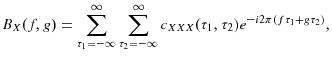
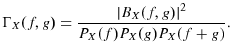
![\displaystyle Y_{0}=\sum\limits_{k=-\infty}^{\infty}{(E[X_{k}\mid F_{0}]-E[X_{k}\mid F_{-1}])};%](img85.gif)
![\displaystyle Z_{0}=\sum\limits_{k=0}^{\infty}{(E[X_{k}\mid F_{-1}])}-\sum\limits_{k=-\infty }^{-1}{(X_{k}-E[X_{k}\mid F_{-1}])},%](img86.gif)
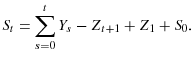
![\begin{displaymath} % latex2html id marker 4197 E[Y_{t}Y_{s}^{T}]=% \begin{cases}\mathbf{CC}^{T} & \text{if $s=t$}\\ \mathbf{0} & \text{if $s \neq t$}% \end{cases} % \end{displaymath}](img100.gif)