Diagnosing and Treating Bifurcations in Perturbation Analysis of Dynamic Macro Models*
Keywords: bifurcation, perturbation, relative price distortion, optimal monetary policy
Abstract:
JEL Classification: C63; C61; E52.
1 Introduction
In recent analysis of nonlinear dynamic macroeconomic models, the characterization of their first-order dynamics has been an important step for understanding theoretical implications and evaluating empirical success. However, the presence of a bifurcation in perturbation analysis of nonlinear dynamic systems implies that the first-order behavior of the economy cannot be characterized solely in terms of the first-order derivatives of the model equations.
In this paper, we use two simple macroeconomic models to address several issues regarding bifurcations. In particular, the bifurcation problem would emerge in conjunction with the price dispersion generated by staggered price setting in the part of firms. We then show how to apply l'Hospital's rule to characterize the solution of each model in terms of its higher-order derivatives. We also show that in some cases the bifurcation can be eliminated through renormalization of model variables; furthermore, renormalization may yield a more accurate first-order solution than applying l'Hospital's rule to the original formulation.
Before presenting our results, it is noteworthy that our definition of bifurcation is distinct from the one analyzed in Benhabib and Nishimura (1979). In particular, their analysis on bifurcation is associated with time evolution of dynamic systems. However, our concern with bifurcation arises in the process of approximating nonlinear equations, as discussed in Judd (1998).
We proceed as follows. Section 2 describes the two examples and illustrates how to detect the existence of a bifurcation problem. Section 3 follows the general approach of Judd (1998) and applies l'Hospital's rule to characterize the first-order behavior of each model. Section 4 shows how the bifurcation can be eliminated through renormalization of model variables. Section 5 concludes.
2 Diagnosis of Bifurcations
This section discusses how we can detect the existence of bifurcation in two simple economies. In both models, Calvo-style price setting behavior of firms can be summarized by the following law of motion for the relative price distortion:
where the distortion index is defined as
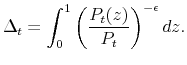
2.1 A Single-Equation Setting
To discuss the issue of bifurcation, we have to close the model with another equation. In the first example, we simply assume that inflation follows an exogenous stochastic process,
By combining the two equations, we now have a single-equation model:
Since this equation is backward looking, this exact nonlinear form can be used for any dynamic analysis. However, we suppose that we have to rely on approximation methods to analyze this model as would be the case when there are forward-looking equations.
Woodford (2003) and Benigno and Woodford (2005) pointed out that, when deviations of the (net) inflation rate from its zero steady state are of first order in terms of exogenous variations, deviations of the distortion index from one is of second order. Based on this observation, one can naturally approximate the system with respect to the square root of the logarithm of the relative price distortion index. Note that this distortion index is unity at the steady state with zero inflation rate. We follow the convention of using lower cases for log deviations,
Specifically,
Under the choice of
![]() as the approximation variable, (2.2) can be rewritten as follows:
as the approximation variable, (2.2) can be rewritten as follows:
Now let's see what happens if we try a Taylor approximation of this system with respect to
It is noteworthy to find out what would happen if we feed this case into computer codes commonly available for dynamic macroeconomic analysis. The Dynare package (version 3.05) produces an message saying `Warning: Matrix is singular to working precision', and AIM (developed by Gary Anderson and George Moore, and widely used at the Federal Reserve Board) returns a code indicating `Aim: too many exact shiftrights'. The routine developed by Christopher Sims (gensys.m) ends without any output or error message.
2.2 A Multi-Dimensional Setting
The second example is a case with multiple equations. Our example is a prototypical Calvo-style sticky-price model, and the optimal policy problem is to maximize the household welfare subject to the following four constraints: the law of motion for relative price distortions, the social resource constraint, the firms' profit maximization condition, and the present-value budget constraint of the household. However, it is shown in Yun (2005) that the optimal policy problem can be reduced to minimizing the index for relative price distortion (2.1). At the optimum, we have the following relationship:
Therefore, the solution to the optimal policy problem can be represented with the following bivariate nonlinear system:
As in the single-equation case, we start with a normalization according to which
![]() and
and ![]() are endogenous variables and
are endogenous variables and
![]() is exogenous:
is exogenous:
![\begin{displaymath} \left[ \begin{array}[c]{c}% \exp\left( \gamma_{t}^{2}\right) -\left( 1-\alpha\right) \left[ \frac{1-\alpha\left( \exp\pi_{t}\right) ^{\epsilon-1}}{1-\alpha}\right] ^{\frac{\epsilon}{\epsilon-1}}-\alpha\exp\left( \gamma_{t-1}^{2}\right) \left( \exp\pi_{t}\right) ^{\epsilon}\ \exp\left( \gamma_{t}^{2}\right) -\exp\left( \gamma_{t-1}^{2}\right) \left( \exp\pi_{t}\right) \end{array}\right] =\left[ \begin{array}[c]{c}% 0\ 0 \end{array}\right] , \end{displaymath}](img25.gif)
![\begin{displaymath} \left\vert J_{\left( \gamma_{t},\pi_{t};\gamma_{t-1}\right) }\right\vert =\left\vert \begin{array}[c]{cc}% 0 & 0\ 0 & -1 \end{array}\right\vert =0. \end{displaymath}](img27.gif)
3 Resolution of Bifurcations
As explained in Judd (1998) and Judd and Guu (2001), the bifurcation problem can be resolved by using l'Hospital's rule.
3.1 A Single-Equation Setting
To understand the approximated behavior of
![]() in the singe-equation example, we need to compute
in the singe-equation example, we need to compute
![]() and
and
![]() where
where
![]() is defined as an implicit function as follows:
is defined as an implicit function as follows:
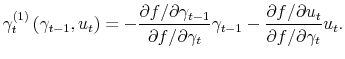
Noting that the derivatives in the numerators are also zero at the steady state, we apply l'Hospital's rule to the two ratios in the form of ![]() and obtain the following first-order
approximation:1
and obtain the following first-order
approximation:1
This is an example of the transcritical bifurcation.2
In this single-equation model, it is easy to avoid the bifurcation problem when we consider the following equation that is equivalent to (2.3),
![\displaystyle \tilde{f}\left( \gamma_{t};\gamma_{t-1},u_{t}\right) \equiv\gamma_{t}% -\sqrt{\log\left\{ \left( 1-\alpha\right) \left[ \frac{1-\alpha\left( \exp u_{t}\right) ^{\epsilon-1}}{1-\alpha}\right] ^{\frac{\epsilon}% {\epsilon-1}}+\alpha\exp\left( \gamma_{t-1}^{2}\right) \left( \exp u_{t}\right) ^{\epsilon}\right\} }=0.](img36.gif)
3.2 A Multi-Dimensional Setting
To illustrate how we can invoke the bifurcation method in the multi-dimensional example, we substitute the second equation in (2.5) into the first to obtain:
| 0 | ||
![\displaystyle \equiv\exp\left( \gamma_{t}^{2}\right) -\left( 1-\alpha\right) \left[ \frac{1-\alpha\left( \frac{\exp\left( \gamma_{t}^{2}\right) }{\exp\left( \gamma_{t-1}^{2}\right) }\right) ^{\epsilon-1}}{1-\alpha}\right] ^{\frac{\epsilon}{\epsilon-1}}-\alpha\exp\left( \gamma_{t-1}^{2}\right) \left( \frac{\exp\left( \gamma_{t}^{2}\right) }{\exp\left( \gamma _{t-1}^{2}\right) }\right) ^{\epsilon}.](img41.gif)
|
Were the assumptions of the bifurcation theorem to hold, then differentiation of the implicit expression
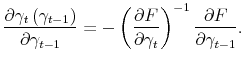
However, since both derivatives on the right-hand side are zero at the steady state, we need to apply l'Hospital's rule to compute
![]() . The first-order solution for
. The first-order solution for
![]() is
is
Note that the dependence of
4 Renormalization of Model Variables
The presence of bifurcations is not only related to the economic model in hand, but also to the choice of the variable with respect to which the Taylor approximation is applied. This section shows that the bifurcation can be eliminated through renormalization of model variables; furthermore, renormalization may yield a more accurate first-order solution than applying l'Hospital's rule to the original formulation.
4.1 A Single-Equation Setting
In the single-equation setting, if we can approximate the model with respect to
![]() and
and
![]() instead of
instead of
![]() and
and
![]() , then the bifurcation problem would not emerge.3 To see this, rewrite (2.2) as follows:
, then the bifurcation problem would not emerge.3 To see this, rewrite (2.2) as follows:
![\displaystyle g\left( \delta_{t};\delta_{t-1},u_{t}\right) \equiv\exp\delta_{t}-\left( 1-\alpha\right) \left[ \frac{1-\alpha\left( \exp u_{t}\right) ^{\epsilon-1}}{1-\alpha}\right] ^{\frac{\epsilon}{\epsilon-1}}-\alpha\left( \exp\delta_{t-1}\right) \left( \exp u_{t}\right) ^{\epsilon}=0.](img49.gif)
Under this renormalization, the expression for the relative price distortion is richer--and more accurate--than (3.6) derived using l'Hospital's rule. Another renormalization that produces a solution similar to (3.6) is to approximate with respect to
![]() (instead of
(instead of
![]() ). This alternative way is based on the interpretation that the initial relative price distortion is of second order. Specifically, we rewrite the model as
). This alternative way is based on the interpretation that the initial relative price distortion is of second order. Specifically, we rewrite the model as
![\displaystyle h\left( \delta_{t};\gamma_{t-1},u_{t}\right) \equiv\exp\delta_{t}-\left( 1-\alpha\right) \left[ \frac{1-\alpha\left( \exp u_{t}\right) ^{\epsilon-1}}{1-\alpha}\right] ^{\frac{\epsilon}{\epsilon-1}}-\alpha\left( \exp\gamma_{t-1}^{2}\right) \left( \exp u_{t}\right) ^{\epsilon}=0,](img52.gif)
4.2 A Multi-Dimensional Setting
In the multi-dimensional case, the two ways of renormalization would correspond to
![\begin{displaymath} \left[ \begin{array}[c]{c}% \exp\delta_{t}-\left( 1-\alpha\right) \left[ \frac{1-\alpha\left( \exp \pi_{t}\right) ^{\epsilon-1}}{1-\alpha}\right] ^{\frac{\epsilon}{\epsilon -1}}-\alpha\left( \exp\delta_{t-1}\right) \left( \exp\pi_{t}\right) ^{\epsilon}\ \exp\delta_{t}-\left( \exp\delta_{t-1}\right) \left( \exp\pi_{t}\right) \end{array}\right] =\left[ \begin{array}[c]{c}% 0\ 0 \end{array}\right] \end{displaymath}](img54.gif)
![\begin{displaymath} \left[ \begin{array}[c]{c}% \exp\delta_{t}-\left( 1-\alpha\right) \left[ \frac{1-\alpha\left( \exp \pi_{t}\right) ^{\epsilon-1}}{1-\alpha}\right] ^{\frac{\epsilon}{\epsilon -1}}-\alpha\left( \exp\gamma_{t-1}^{2}\right) \left( \exp\pi_{t}\right) ^{\epsilon}\ \exp\delta_{t}-\left( \exp\gamma_{t-1}^{2}\right) \left( \exp\pi _{t}\right) \end{array}\right] =\left[ \begin{array}[c]{c}% 0\ 0 \end{array}\right] . \end{displaymath}](img55.gif)
![\begin{displaymath} \left\vert J_{\left( \delta_{t},\pi_{t}\right) }\right\vert =\left\vert \begin{array}[c]{cc}% 1 & 0\ 1 & -1 \end{array}\right\vert =-1, \end{displaymath}](img56.gif)
According to the first renormalization, the second-order approximation of (2.1) is
and the logarithmic transformation of (2.4) is
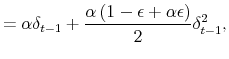 |
||
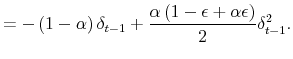 |
It is noteworthy to point out that, according to this renormalization, the first-order relationship between inflation and relative price distortions (
The alternative renormalization consistent with the timeless perspective is to adopt
![]() (instead of
(instead of
![]() ) as an exogenous variable. Based on this choice of an expansion parameter, Woodford (2003) concluded that the optimal inflation rate is zero to the first order in the absence of
cost-push shocks. Under this normalization, the two model equations are approximated as follows:
) as an exogenous variable. Based on this choice of an expansion parameter, Woodford (2003) concluded that the optimal inflation rate is zero to the first order in the absence of
cost-push shocks. Under this normalization, the two model equations are approximated as follows:
The second-order solution to this system of equations would be purely quadratic5
The first-order approximation of this solution is consistent with the optimality of zero inflation, as derived in the linear-quadratic approximation by Woodford (2003), Benigno and Woodford (2005), and Levine, Pearlman and Pierse (2006). Furthermore, the second-order solution for inflation is equivalent to the one via the bifurcation method, (3.7).
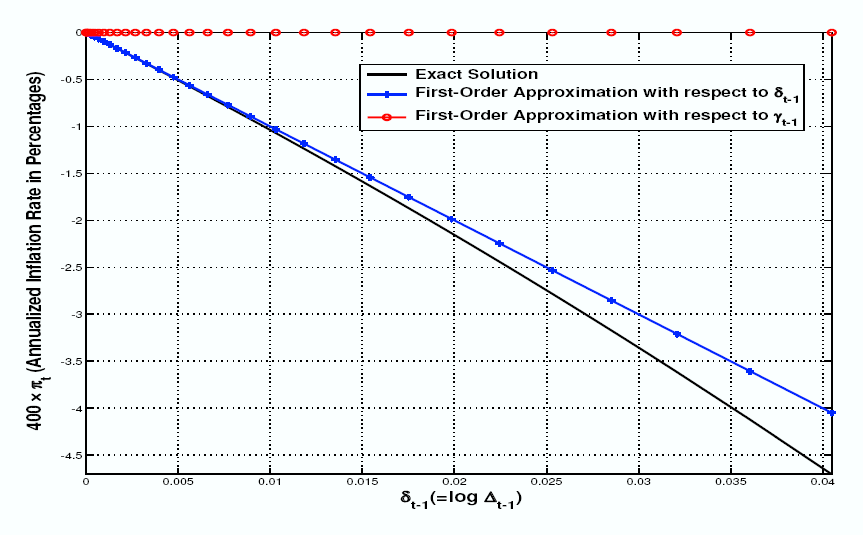
4.3 Accuracy Comparison
After presenting two different renormalizations, it is natural to compare approximation errors for these two methods.6 For this purpose, we use as a reference point the closed-form solution to the optimal policy problem (2.5). Specifically, as shown in Yun (2005), the exact nonlinear solution for the optimal inflation rate is
It is noteworthy that this closed-form solution is feasible only when the relative price distortion is the only distortion--due to the assumption that there is an optimal subsidy and there are no cost-push shocks. The optimal rate of inflation is less than zero
The difference between the two methods is that the expansion parameter of the first renormalization is
![]() , while that of the second is
, while that of the second is
![]() . Figure 1 compares the accuracy of the two normalizations based on the first-order solution under each normalization.7 The black solid line represents the exact closed-form solution for annualized inflation (
. Figure 1 compares the accuracy of the two normalizations based on the first-order solution under each normalization.7 The black solid line represents the exact closed-form solution for annualized inflation (
![]() ) in terms of initial relative distortion (
) in terms of initial relative distortion (
![]() ). The blue line with crosses is the linear approximation of this nonlinear solution. This corresponds to the first-order approximation of
). The blue line with crosses is the linear approximation of this nonlinear solution. This corresponds to the first-order approximation of ![]() when the expansion parameter is
when the expansion parameter is
![]() --that is,
--that is,
![]() . It is evident that this approximation is more accurate than
. It is evident that this approximation is more accurate than
![]() : the first-order approximation with
: the first-order approximation with
![]() as the expansion parameter, depicted by the red circles.
as the expansion parameter, depicted by the red circles.
We can provide an intuitive understanding about the improved accuracy of the approximation with respect to
![]() as follows. Since
as follows. Since
![]() is the square of
is the square of
![]() , the first-order approximation with respect to
, the first-order approximation with respect to
![]() is equivalent to the second-order approximation with respect to
is equivalent to the second-order approximation with respect to
![]() :
:
5 Conclusion
We have illustrated how to detect the existence of a bifurcation and demonstrated how to apply l'Hospital's rule to characterize the solution. We have also shown that the bifurcation can be eliminated through renormalization of model variables; furthermore, renormalization may yield a more accurate first-order solution than applying l'Hospital's rule to the original formulation. This paper has focused on the consequences of renormalization on the treatment of bifurcations. However, the renormalization is also associated with the welfare evaluation of different policies as in Benigno and Woodford (2005).
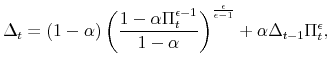
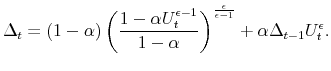
![\displaystyle f\left( \gamma_{t};\gamma_{t-1},u_{t}\right) \equiv\exp\left( \gamma _{t}^{2}\right) -\left( 1-\alpha\right) \left[ \frac{1-\alpha\left( \exp u_{t}\right) ^{\epsilon-1}}{1-\alpha}\right] ^{\frac{\epsilon}{\epsilon-1}% }-\alpha\exp\left( \gamma_{t-1}^{2}\right) \left( \exp u_{t}\right) ^{\epsilon}=0.%](img18.gif)
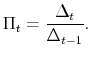
![\displaystyle \left[ \begin{array}[c]{c}% \Delta_{t}-\left( 1-\alpha\right) \left( \frac{1-\alpha\Pi_{t}^{\epsilon -1}}{1-\alpha}\right) ^{\frac{\epsilon}{\epsilon-1}}-\alpha\Delta_{t-1}% \Pi_{t}^{\epsilon} \Delta_{t}-\Delta_{t-1}\Pi_{t}% \end{array} \right] =\left[ \begin{array}[c]{c}% 0 0 \end{array} \right] .%](img22.gif)
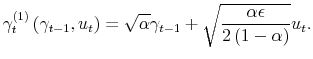
![\displaystyle \Pi_{t}\left( \Delta_{t-1}\right) =\left[ \alpha+\left( 1-\alpha\right) \Delta_{t-1}^{\epsilon-1}\right] ^{\frac{-1}{\epsilon-1}}.%](img75.gif)