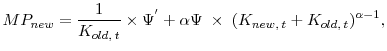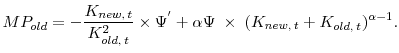Learning By Investing
Embodied Technology and Business Cycles
Keywords: Embodied Technology, Learning, Overinvestment
Abstract:
In the last decade of the 20th century, the U.S. economy witnessed a persistent and substantial increase in private investment. The boom was sharply reversed in 2001, and a great deal of evidence suggests that the capital stock had become excessive. Standard equilibrium business cycle models have difficulties in predicting the investment boom and overshooting. An embodied technology model is constructed to replicate the pattern of investment boom and collapse. Unlike previous models of embodiment, the present model assumes that new technology increases the productivity of capital of all vintages, but only new capital can facilitate the adoption of the new technology. Further, although agents in this model know about the advent of a new technology, they have imperfect information about its magnitude. Agents learn the magnitude by investing in new capital. I present a sufficient condition for having a persistent investment boom and overshooting. I also solve the model numerically in a dynamic general equilibrium (DGE) setup. The model presented in this paper extends the standard DGE business cycle models in two ways: First, it presents a strong internal propagation mechanism with respect to technology shocks; second, it generates endogenous recessions without invoking technological regress. The model also offers a possible explanation on why consumption growth was strong during the last recession.
JEL Classification: E22, E32
1 Introduction
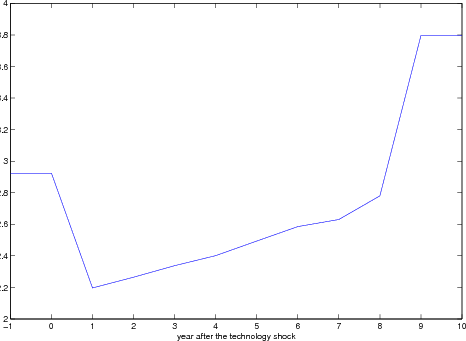
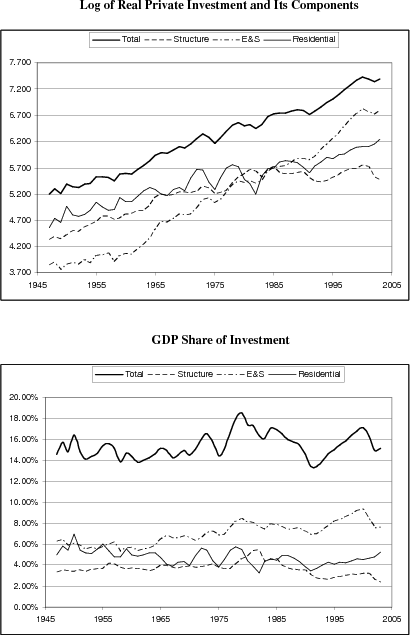
The most recent business cycle demonstrated many unique characteristics that are at variance with previous cycles. One of the most remarkable features of the economic expansion in the 1990s was the persistent and substantial increase in private investment, in terms of both its level and its
share in GDP. ![]() Investment growth stopped abruptly in the second half of the year 2000. In the subsequent years, investment decreased sharply and at the same time the economy as a whole
experienced a recession.
Investment growth stopped abruptly in the second half of the year 2000. In the subsequent years, investment decreased sharply and at the same time the economy as a whole
experienced a recession.
One of the distinguishing characteristics of this investment boom is that the economy may have accumulated too much capital and overinvested, especially in certain sectors. For instance, more than 90 percent of the optical fiber cables installed during the 1990s were left unused in the years that followed, resulting in thousands of miles of "dark fiber."1 At the moment when the investment boom was about to crash, the overinvestment phenomenon had already drawn much attention from entrepreneurs and policy makers. On July 14, 2000, close to the peak of the boom, Microsoft President and CEO Steve Ballmer commented that, "A lot of people are overinvesting in dot-com start-ups ... There has been a hysteria. There is too much money chasing Internet ideas in the short run."2 Similarly, one year later, after the investment spending boom collapsed and the economy was in a recession, the vice chairman of the Federal Reserve Board, Roger W. Ferguson, commented on July 18, 2001, that " ... for a variety of reasons ... firms may be holding considerably more capital now than they would prefer . . . although it is difficult to determine how large the overhangs of capital might be at present, they seem likely to exert at least a modest amount of drag on the economy over the near term, even as growth picks up."3
Another aspect of the last cycle is that consumption did not show as much weakness as it had (on average) in prior downturns. Consumption growth, especially for durable goods, was much stronger than GDP growth during the years of 2001 and 2002.
In this paper I construct an embodied technology model to explain why the last business cycle exhibited the unique characteristics described above. In my model, new technology has to be embodied into new capital goods before it can increase total factor productivity (TFP). Different from the traditional embodiment models, a la Solow (1959), my model assumes that new technology increases the productivity of capital of all vintages, instead of only the new vintage. The more the economy has invested in new capital, the higher is the TFP, up to a point. In addition, I assume that although the agents know about the advent of a new technology, they have imperfect information about the magnitude of the new technology shock. Agents have to learn the magnitude of the new technology by investing in new capital goods.4 They observe the output and evaluate whether they have invested beyond the optimal amount. If they have not, they revise up their beliefs about the magnitude of the technological innovation and invest more in subsequent periods, hence an investment boom follows. If they find that investment has overshot, they will sharply reduce subsequent investment, and thereby trigger a recession. During the recession, resources are reallocated from investment to consumption. Therefore, even though GDP does not increase, we may still observe healthy growth in consumption.
I first set up the firm's capital demand problem under the proposed embodiment and learning mechanisms and contrast the capital demand in this model with that in the standard models. Then I provide a sufficient condition on the prior belief over the technology shock distribution that generates persistent investment booms and overshooting. I also solve the model numerically in a stochastic dynamic general equilibrium setup to study the business cycle dynamics. The model can qualitatively replicate what happened during the last business cycle. I find that after a reasonably large permanent technology shock, investment can keep increasing for as long as nine years. Naturally, the model also predicts an output boom as persistent as the investment boom. Investment overshoots at its peak and is sharply reduced subsequently. When investment is cut back, output stops growing. Under certain calibrations, output decreases in absolute terms. However, during the recession, consumption rises to a higher level, even relative to the level in the boom.
Standard dynamic general equilibrium (DGE) models have often been criticized on two grounds. First, in many DGE models, if the shock process is not very persistent, the output, investment, and consumption dynamics typically are not very persistent either. Put differently, these models lack strong internal propagation mechanisms.5 Second, DGE models usually demand certain levels of technological regress to generate significant recessions.6 This paper addresses these two problems. In my model, output does not jump in response to a technology shock, as the economy has to invest in new capital to take advantage of the new technology. Because the agents have to learn the magnitude of the technology shock, they are cautious in making investment decisions before they have learned much about the underlying technology. Consequently, GDP growth is gradual, which stretches out the length of booms. In addition, the model generates endogenous recessions. Under certain assumptions, the investment boom caused by the new technology will eventually overshoot the optimal level. It is the favorable technology shock that leads the economy into a recession. In this sense, a favorable technology shock already contains the seed of a future recession. There is no need for any negative technology shocks to trigger recessions.
Finally, it is worthwhile to point out that if one technology shock can generate a persistent investment and output boom as well as sizable overinvestment, this shock should be sufficiently large. It should have a significant contribution to TFP. ![]() Such technology shocks can be motivated as General Purpose Technology (GPT)-shocks, which have been found empirically to impact most industries of the economy.7 The point of view that the recent boom was at least partially driven by a GPT shock finds support in many recent empirical studies.8
Such technology shocks can be motivated as General Purpose Technology (GPT)-shocks, which have been found empirically to impact most industries of the economy.7 The point of view that the recent boom was at least partially driven by a GPT shock finds support in many recent empirical studies.8
2.1 Production Function with Embodiment and Learning
I study investment dynamics in a model in which new technology has to be embodied in new capital before it can increase TFP, and the agents have only imperfect information about the new technology. First I summarize the assumptions I make and introduce the production function under these assumptions.
A technological innovation arrives at ![]() . Before then, the production function of a typical firm is
. Before then, the production function of a typical firm is
where ![]() is output,
is output, ![]() is the pre-shock level of capital, and
is the pre-shock level of capital, and ![]() is the pre-shock level of technology. The post-shock level of technology is denoted by,
is the pre-shock level of technology. The post-shock level of technology is denoted by, ![]() .
The shock is multiplicative,
.
The shock is multiplicative,
We normalize ![]() to 1, and hence
to 1, and hence
![]() . After the technology shock arrives, the production function becomes
. After the technology shock arrives, the production function becomes
Capital accumulations follow
and
In production function (3),
![]() is the effective TFP level at period
is the effective TFP level at period ![]() . It is equal to the minimum
of
. It is equal to the minimum
of ![]() , the underlying post-shock level of technology, and
, the underlying post-shock level of technology, and
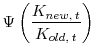 , an embodiment function.
, an embodiment function. ![]() is the capital stock combining old and new capital. Old capital is available before and after the arrival of the new technology, whereas new capital is available only after the technological innovation, that is, when
is the capital stock combining old and new capital. Old capital is available before and after the arrival of the new technology, whereas new capital is available only after the technological innovation, that is, when ![]() . We assume that there is a transformation technology that can transform one unit of output into one unit of either old or new capital. The capital accumulation equations and their initial levels are given by equations (5) and (6). I impose two very general restrictions on
. We assume that there is a transformation technology that can transform one unit of output into one unit of either old or new capital. The capital accumulation equations and their initial levels are given by equations (5) and (6). I impose two very general restrictions on ![]()
and
Restriction (7) satisfies Assumption 1. To see this, notice that if there is no new capital invested after the innovation,
![]() , and
, and
![]() . Restriction (8) establishes that the
. Restriction (8) establishes that the ![]() function is strictly monotonically increasing and concave.
function is strictly monotonically increasing and concave.
In each period, the firm may convert its output into investment in old capital, which embodies no new technology, or it may convert its output into investment in new capital, which embodies the technology and potentially increases TFP. Therefore the firm has to simultaneously determine the amount of old and new investment. To simplify the analysis, I assume that there is a minimum level of investment in old capital that equals its the maintenance cost
| (9) |
It is straightforward to show that the marginal product of new capital is always at least weakly larger than that of the old capital. We then have the following lemma:
Proof: Refer to Appendix A.
Subsequently, we have
Therefore, we have to focus only on the investment decisions on new capital. Note that although the firms have to replenish their depreciated old capital, they may choose to sell their old capital if a market for it exists. However, in our analysis we do not have to model this directly because at equilibrium, the price of old capital will adjust to such a level that makes the firms indifferent between selling and buying a marginal unit of capital. Because all firms are the same in our model, there will be no transactions in the market. It is useful to keep in mind, however, that the shadow price of old capital is pinned down by the marginal product of old capital relative to new capital and by the adjustment cost associated with the resale of capital.
Because of the monotonicity of ![]() and because the level of
and because the level of
![]() is fixed along the optimal investment path, there exists a level of
is fixed along the optimal investment path, there exists a level of
![]() such that
such that
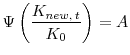 . Denote this level of
. Denote this level of
![]() by
by ![]() , and introduce the notation
, and introduce the notation
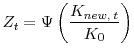 . We can rewrite the production function (3) as
. We can rewrite the production function (3) as
and
By Assumption 4, the firm does not know how big ![]() is after the new technology arrives. It does know the distribution of
is after the new technology arrives. It does know the distribution of ![]() . The firm learns how big the shock is by continuously investing in new capital and evaluating whether adding new capital keeps contributing to increasing TFP. Denote the probability density function (PDF) and cumulative
density function (CDF) of
. The firm learns how big the shock is by continuously investing in new capital and evaluating whether adding new capital keeps contributing to increasing TFP. Denote the probability density function (PDF) and cumulative
density function (CDF) of ![]() by
by ![]() and
and ![]() respectively. Mechanically, learning is carried out as follows: The firm observes the output and the levels of both old and new capital and computes the value of
respectively. Mechanically, learning is carried out as follows: The firm observes the output and the levels of both old and new capital and computes the value of ![]() . By equation (11) the firm can infer the conditional distribution of
. By equation (11) the firm can infer the conditional distribution of ![]() by applying
by applying
The idea is simple: If the firm has not invested enough to completely embody the new technology,
![]() , and in turn,
, and in turn,
![]() . The firm therefore is able to infer that
. The firm therefore is able to infer that ![]() is greater
than
is greater
than ![]() and that the conditional distribution of
and that the conditional distribution of ![]() is
is
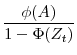 . Conversely, if the invested new capital is sufficient to embody the new technology in the sense that
. Conversely, if the invested new capital is sufficient to embody the new technology in the sense that
![]() , the exact magnitude of
, the exact magnitude of ![]() can be inferred as
can be inferred as
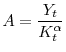 .
.
2.2 The Firm's Problem and Capital Demand
In this section, I set up the firm's profit maximization problem and derive a sufficient condition under which investment will accelerate after the technological innovation. As we have shown, investment in old capital is a constant and equal to the amount of old capital depreciation. However,
investment in new capital includes the part that replenishes depreciated new capital, which grows with the stock of new capital. Therefore, if, under some conditions, investment accelerates from ![]() to
to ![]() in an economy of zero depreciation, the same set of conditions should also lead to accelerating investment in an economy of positive depreciation.10 Hence, without loss of generality, I assume that
in an economy of zero depreciation, the same set of conditions should also lead to accelerating investment in an economy of positive depreciation.10 Hence, without loss of generality, I assume that
![]() . In this case, all investment along the optimal path will be the net increase of new capital.
. In this case, all investment along the optimal path will be the net increase of new capital.
Consider a firm that maximizes the discounted sum of dividend flows under the constant interest rate, ![]() . Immediately after the arrival of the technology shock, the cum
dividend value function of the firm is
. Immediately after the arrival of the technology shock, the cum
dividend value function of the firm is
![\displaystyle V(K_0) = \max_{[I_{t}]_{t=0}^\infty} \; E_0 \; \sum^\infty_{t=0} \; \left( \frac{1}{1+r} \right) ^t(Y_t - I_t),](img55.gif) |
(14) |
subject to the production function (3), the information update function (13), and the modified capital accumulation function
To capture the unique characteristics of capital demand in the underlying model, consider an auxiliary problem in which the firm has a standard production function but has to invest before the magnitude of a technological innovation is revealed. To fix the idea, consider a firm that anticipates
a shock of unknown magnitude will arrive at ![]() . The firm has to make an investment at
. The firm has to make an investment at ![]() . In this case, the firm's optimality condition is simply to invest up to such a level that the expected marginal product of capital is equal to the borrowing cost,
. In this case, the firm's optimality condition is simply to invest up to such a level that the expected marginal product of capital is equal to the borrowing cost, ![]() .
That is
.
That is
or
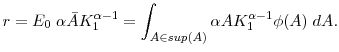 |
where
In contrast, in our model with ![]() -type embodiment and learning, the first-order condition for capital is more complex, and, in turn, the investment dynamics are very different. In such a
model, the cum dividend value of the firm is the sum of current period payoffs and the discounted weighted average of future value in two regimes,
-type embodiment and learning, the first-order condition for capital is more complex, and, in turn, the investment dynamics are very different. In such a
model, the cum dividend value of the firm is the sum of current period payoffs and the discounted weighted average of future value in two regimes, ![]() and
and
![]() . In the first regime, with capital
. In the first regime, with capital ![]() , the true magnitude of
, the true magnitude of
![]() has not been revealed, and the learning process will continue. Let
has not been revealed, and the learning process will continue. Let ![]() be the
value of the firm in this regime. In the second regime, the firm finds that
be the
value of the firm in this regime. In the second regime, the firm finds that ![]() is sufficient to entirely pick up the new technology, and
is sufficient to entirely pick up the new technology, and ![]() is learned. The firm value is given by
is learned. The firm value is given by
![]() .
.
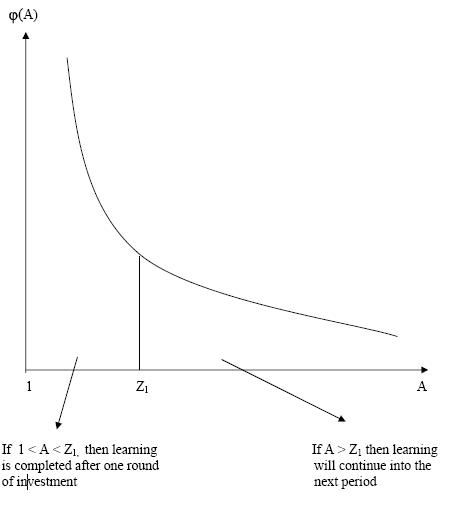
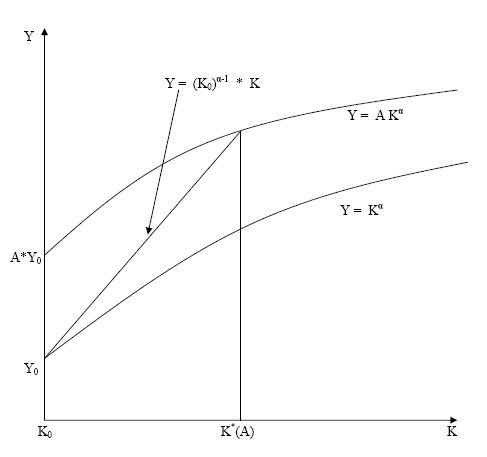
Note that ![]() is a function of
is a function of ![]() only, whereas
only, whereas ![]() is a function of both
is a function of both ![]() and
and ![]() (figure 1). Suppose a firm in the middle of the learning process with capital
(figure 1). Suppose a firm in the middle of the learning process with capital ![]() finds that
finds that ![]() has not been revealed yet. In such a scenario, the firm learns that
has not been revealed yet. In such a scenario, the firm learns that ![]() . The current capital stock
. The current capital stock ![]() contains all the information available about the conditional distribution of
contains all the information available about the conditional distribution of ![]() . Therefore,
. Therefore, ![]() contains all information available about the value of the firm. However, if the same firm realizes that
contains all information available about the value of the firm. However, if the same firm realizes that ![]() is completely revealed with capital
is completely revealed with capital ![]() , then all levels of
, then all levels of ![]() that
are between 1 and
that
are between 1 and ![]() can induce this.
can induce this. ![]() can be either very close to the true level of
can be either very close to the true level of ![]() or much bigger than
or much bigger than ![]() , and the corresponding values of the firms are very different. Therefore, the value of a firm that has completed the learning process depends on both the capital level
, and the corresponding values of the firms are very different. Therefore, the value of a firm that has completed the learning process depends on both the capital level ![]() as well as the value of
as well as the value of ![]() . Ex ante, the firm can compute the probability of being in each regime when it increases capital
stock from
. Ex ante, the firm can compute the probability of being in each regime when it increases capital
stock from ![]() to
to ![]() , but it does not know the exact magnitude of the shock. The
firm has to compute the expectation of
, but it does not know the exact magnitude of the shock. The
firm has to compute the expectation of ![]() conditioned on
conditioned on ![]() being between
being between ![]() and
and ![]() .
.
Define
![]() to be the probability of the firm remaining in the learning process after it increases its capital stock from
to be the probability of the firm remaining in the learning process after it increases its capital stock from ![]() to
to ![]() , then
, then
![]() can be computed as
can be computed as
The firm's problem can be rewritten as the following Bellman equation system
where
and
In equation (18) the term
![]() is the expected value of a firm that has learned the value of
is the expected value of a firm that has learned the value of ![]() . The expectation is taken with respect to
. The expectation is taken with respect to ![]() conditional on
conditional on
![]() because only when
because only when ![]() is within this range can a firm with capital
level of
is within this range can a firm with capital
level of ![]() have completed the learning process.
have completed the learning process.
I now introduce a useful lemma:
Proof: Refer to Appendix A. Appendix A also discusses in detail the economic interpretation of the first-order condition for capital demand in the model with learning and embodiment.
The intuition of Lemma 2 is simple. In a model with the ![]() type embodiment and learning, new capital has additional roles besides production: First, new
capital embodies new technology and increases TFP; second, new capital helps learning. Conditional on the value of
type embodiment and learning, new capital has additional roles besides production: First, new
capital embodies new technology and increases TFP; second, new capital helps learning. Conditional on the value of ![]() not being completely learned, more investment leads to a higher value of
not being completely learned, more investment leads to a higher value of
![]() and in turn leads to a tighter conditional distribution of
and in turn leads to a tighter conditional distribution of ![]() . Hence, the marginal
value of investment is higher than in a conventional model, and the firm will invest more.
. Hence, the marginal
value of investment is higher than in a conventional model, and the firm will invest more.
Now we discuss the conditions under which investment accelerates persistently as we observed in the 1990s. Heuristically, this requires some properties related to the distribution of ![]() . In
particular, conditional on the current capital stock not completely revealing the level of
. In
particular, conditional on the current capital stock not completely revealing the level of ![]() , the posterior expectation of
, the posterior expectation of ![]() should increase at a sufficiently fast rate. I will provide a sufficient condition on the distribution of
should increase at a sufficiently fast rate. I will provide a sufficient condition on the distribution of ![]() so that investment will be increasing over
time, that is,
so that investment will be increasing over
time, that is,
![]() .
.
I focus on the condition under which the optimal ![]() is greater than the optimal
is greater than the optimal ![]() , or
, or
![]() .11 The result can be
extended to
.11 The result can be
extended to
![]() . As shown in Lemma 1, the stock of old capital is a constant; therefore, in order to have
. As shown in Lemma 1, the stock of old capital is a constant; therefore, in order to have ![]() , it is sufficient to show that the increment of the effective TFP associated with capital increasing from
, it is sufficient to show that the increment of the effective TFP associated with capital increasing from ![]() to
to
![]() is bigger than the increment of the effective TFP associated with capital increasing from
is bigger than the increment of the effective TFP associated with capital increasing from ![]() to
to ![]() . This is due to the concavity of the
. This is due to the concavity of the ![]() function.
Specifically, we have
function.
Specifically, we have
and, of course,
![]() .
.
Let
![]() be the level of capital that satisfies
be the level of capital that satisfies
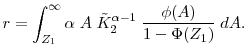 |
(22) |
We recognize that
![]() is the optimal capital level of in our auxiliary problem if
is the optimal capital level of in our auxiliary problem if ![]() follows the truncated distribution
follows the truncated distribution
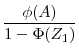 .12 By
.12 By
![]() , we know that the optimal capital level under the
, we know that the optimal capital level under the ![]() -type
embodiment and learning,
-type
embodiment and learning, ![]() , should be greater than
, should be greater than
![]() . Therefore, we have
. Therefore, we have
Finally, combining the relationship (21) and (23) and letting
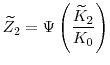 , we have
, we have
where
We have a lemma to characterize
![]() :
:
Proof: By applying the FOC of the auxiliary problem and the steady state relationship, it is straightforward to have (25).
Now we reach the following proposition:
Because ![]() is an increasing concave function, Proposition 1 basically argues that if an increasing and concave transformation, which is pinned down by the
function
is an increasing concave function, Proposition 1 basically argues that if an increasing and concave transformation, which is pinned down by the
function ![]() , of the conditional expectation of the technology shock is at least twice as big as the lower bound of the support of the conditional distribution, investment will
accelerate.
, of the conditional expectation of the technology shock is at least twice as big as the lower bound of the support of the conditional distribution, investment will
accelerate.
An Example
A particularly interesting example is
If ![]() has such a functional form, the model will have some desirable properties. We will defer more careful discussion of the properties to the next section. For now, notice that if
has such a functional form, the model will have some desirable properties. We will defer more careful discussion of the properties to the next section. For now, notice that if
![]() is chosen to be as in (27), the sufficient condition given in (26) will be reduced to
is chosen to be as in (27), the sufficient condition given in (26) will be reduced to
which is simply that the conditional expectation is at least twice as big as the lower bound. It is not difficult to locate a distribution with such properties. For example, let ![]() follow
the Pareto distribution
follow
the Pareto distribution
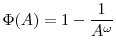 ,
,
![]() , where
, where ![]() is the
distribution parameter. For the conditional expectation, if
is the
distribution parameter. For the conditional expectation, if ![]() , we have
, we have
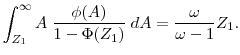 |
(29) |
For
![]() ,
,
![]() ,
,
![]() .
.
This example gives us some hints about the shape of the distributions that are likely to induce increasing investment. The Pareto distribution is heavily tailed. The fat-tail property is particularly pronounced for the cases in which
![]() . In addition, the Pareto distribution has a decreasing hazard rate. Let
. In addition, the Pareto distribution has a decreasing hazard rate. Let ![]() denote the hazard rate of the distribution. For the Pareto distribution we have
denote the hazard rate of the distribution. For the Pareto distribution we have
which is decreasing with ![]() . Why does the hazard rate affect how much a firm should invest? The hazard rate is positively related to the probability of ending learning. If the probability is
high, the firm should be more cautious about investment. A decreasing hazard rate implies a decreasing probability of being able to complete the learning process. In this scenario, the firm will choose to engage in a more aggressive investment plan.
. Why does the hazard rate affect how much a firm should invest? The hazard rate is positively related to the probability of ending learning. If the probability is
high, the firm should be more cautious about investment. A decreasing hazard rate implies a decreasing probability of being able to complete the learning process. In this scenario, the firm will choose to engage in a more aggressive investment plan.
It is worthwhile to point out that what is required in Proposition 1 is a very strong condition. Indeed, because the concavity of the ![]() function can be quite powerful and the difference
between
function can be quite powerful and the difference
between ![]() and
and
![]() can be quite large, a distribution that does not have a tail as fat as that of the Pareto distribution can generate the investment acceleration as well. I have not found an
analytical expression for the necessary condition for accelerating investment.
can be quite large, a distribution that does not have a tail as fat as that of the Pareto distribution can generate the investment acceleration as well. I have not found an
analytical expression for the necessary condition for accelerating investment.
2.3 Discussion
In this section, I explain more carefully the assumptions I made and contrast my model with other familiar models in the literature.
Technology is not like fertilizer in most cases. Better fertilizer increases the harvest on the same land with the same farmers and tractors being used. Better technology typically requires producers to invest in new capital before they may enjoy the higher productivity brought by the new technology. In the polar case, new technology and new capital can be complements in a Leontief sense. Output does not increase after a new technology arrives if no new capital investment has been made. The empirical relevance of embodied technology has been established in many studies (for example, Hercowitz 1998).
Roughly speaking, there are two types of technological innovation. One is the small, incremental innovation that happens probably every day. This type of progress might increase the productivity of only one sector or even one production unit. The other type is the large, revolutionary innovation, such as the invention of electricity and the introduction of information technology (IT). This type of progress is what is usually referred to as GPT, and occurs infrequently. In this paper, I focus on the second type of technological progress, the GPT.
The model introduced in this paper differs from the standard embodied technology models in many aspects. Solow (1959) is one of the classical contributions to the idea of embodied technology. In his model, capital of a particular vintage embodies the technology of the same vintage, and total
output is the sum of the output produced by capital of various vintages. Letting
![]() denote the output produced by capital and technology of vintage
denote the output produced by capital and technology of vintage ![]() in time
in time ![]() , we have
, we have
The aggregated output at time ![]() is given by
is given by
| (32) |
One important property of the Solow-type embodiment is that a new technology makes capital of only the same vintage more productive. The productivity of capital of older vintages does not change. This can be shown by observing that
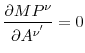 for
for
![]() , where
, where ![]() is the marginal product of capital of vintage
is the marginal product of capital of vintage
![]() . Put differently, old capital is not able to benefit from the innovations.13 In contrast, in a
. Put differently, old capital is not able to benefit from the innovations.13 In contrast, in a ![]() -embodiment model, it is the new capital that facilitates the adoption of the innovations. However,
once adopted, the new technology increases the productivity of all capital, old and new.
-embodiment model, it is the new capital that facilitates the adoption of the innovations. However,
once adopted, the new technology increases the productivity of all capital, old and new.
The contrast between ![]() -embodied and Solow-embodied technology reflects two categories of technological innovation. One type of innovation does require substantial replacement of old
capital with new capital, whereas the other type of innovation requires adding new capital but does not require replacing old capital. Now consider the following hypothetical example. An automobile company produces cars using assembly lines, controlled by a mechanical system. A new technology that
controls assembly lines with computers is then introduced in the market. If the old assembly lines cannot be adapted to the computer system and have to be replaced with new assembly lines, the scenario is best described by a Solow model. If the computer system can be used to operate the old
assembly lines, the scenario is consistent with the
-embodied and Solow-embodied technology reflects two categories of technological innovation. One type of innovation does require substantial replacement of old
capital with new capital, whereas the other type of innovation requires adding new capital but does not require replacing old capital. Now consider the following hypothetical example. An automobile company produces cars using assembly lines, controlled by a mechanical system. A new technology that
controls assembly lines with computers is then introduced in the market. If the old assembly lines cannot be adapted to the computer system and have to be replaced with new assembly lines, the scenario is best described by a Solow model. If the computer system can be used to operate the old
assembly lines, the scenario is consistent with the ![]() -embodied technology. In this setup, it is the productivity of the entire firm (both the assembly lines and the controlling computer
system) that will increase. I will provide more examples in Section 5 to show that the
-embodied technology. In this setup, it is the productivity of the entire firm (both the assembly lines and the controlling computer
system) that will increase. I will provide more examples in Section 5 to show that the ![]() -model captures important characteristics of the 1990s expansion.
-model captures important characteristics of the 1990s expansion.
In addition, our model also differs from the Solow embodiment because the latter does not distinguish between the concepts of effective TFP and potential TFP introduced in this paper. The Solow model assumes that new technology is entirely
embodied in the first slice of new capital. The marginal productivity level is irrelevant to the amount of new capital invested. In contrast, in Assumption 2, our model explicitly assumes that, subject to a certain limit, ![]() , a monotonically increasing functional relationship exists between the amount of new investment and the extent to which new technology is transformed into TFP.
, a monotonically increasing functional relationship exists between the amount of new investment and the extent to which new technology is transformed into TFP.
In the Solow-type embodied technology model, the firm will replace old capital with new capital because only capital of the latest vintage has higher productivity. When there are convex investment adjustment costs, or capital is not completely reversible, this replacement will be carried out
over time. The observed TFP averaging across capital of all vintages converges to the state-of-the-art technology level at ![]() . At the other extreme, if technology is disembodied as in
the fertilizer example, a technology innovation would imply an immediate jump of TFP to the post-shock level. The
. At the other extreme, if technology is disembodied as in
the fertilizer example, a technology innovation would imply an immediate jump of TFP to the post-shock level. The ![]() -type embodiment introduced in this paper implies a time series path of
effective TFP lying between the above two polar cases.
-type embodiment introduced in this paper implies a time series path of
effective TFP lying between the above two polar cases.
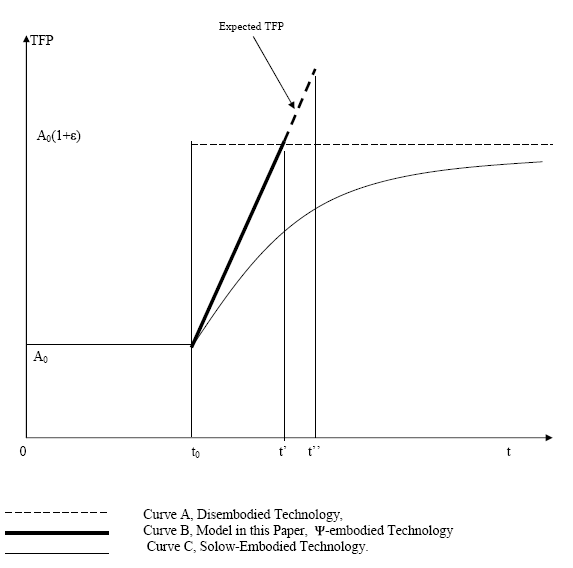
Figure 2 illustrates this contrast. Curve A is the TFP path after a technology shock in a disembodied model. It jumps to ![]() from
from ![]() right after the shock arrives at time
right after the shock arrives at time ![]() . Curve C is the path of the Solow-type embodiment with partially irreversible capital. The
TFP only asymptotically converges to
. Curve C is the path of the Solow-type embodiment with partially irreversible capital. The
TFP only asymptotically converges to ![]() because old capital is gradually replaced by the capital that embodies the new technology. Curve B represents the TFP path implied by the
because old capital is gradually replaced by the capital that embodies the new technology. Curve B represents the TFP path implied by the
![]() -type embodiment. At time
-type embodiment. At time ![]() , the firm learns the news about a technology
innovation and starts to invest. It accumulates a sufficient amount of capital at
, the firm learns the news about a technology
innovation and starts to invest. It accumulates a sufficient amount of capital at ![]() to pick up all of the new technology, and from then on curve B coincides with curve A. However, the firm
does not realize that it has invested enough in new capital until it observes that learning is completed at
to pick up all of the new technology, and from then on curve B coincides with curve A. However, the firm
does not realize that it has invested enough in new capital until it observes that learning is completed at ![]() . Therefore the expected TFP level between
. Therefore the expected TFP level between ![]() and
and ![]() exceeds the true level of the underlying technology.
exceeds the true level of the underlying technology.
The model assumes - simply for convenience - a standard lag of one period between the time of the investment and the time when the new capital becomes productive. One consequence is that the firm can make an investment that leads to a suboptimal level of capital for at most one period. However,
the model can be generalized to allow for a ![]() -period gestation delay, which can be either time-to-build or time-to-plan. Then the firm may make what are ex post
suboptimal investments for multiple periods. As long as the investment decisions are irreversible, the extent to which the firm may accumulate capital beyond the first best level is largely irrelevant to the choice of investment-decision-making frequency (including continuous time modelling).
Consider a
-period gestation delay, which can be either time-to-build or time-to-plan. Then the firm may make what are ex post
suboptimal investments for multiple periods. As long as the investment decisions are irreversible, the extent to which the firm may accumulate capital beyond the first best level is largely irrelevant to the choice of investment-decision-making frequency (including continuous time modelling).
Consider a ![]() -period time-to-build setup as an example. Suppose that, at time
-period time-to-build setup as an example. Suppose that, at time ![]() ,
the capital invested
,
the capital invested ![]() periods before becomes productive and the firm realizes that the capital stock is above the optimal level. The firm wishes that it had not invested any new capital
after
periods before becomes productive and the firm realizes that the capital stock is above the optimal level. The firm wishes that it had not invested any new capital
after ![]() . However, since it cannot reverse the capital that has already been invested, the capital of the firm will keep rising for the next
. However, since it cannot reverse the capital that has already been invested, the capital of the firm will keep rising for the next ![]() periods. To sum up, in a high frequency model, the investment per period can be infinitesimally small, but the total amount of capital overinvested can still be substantial if the time-to-build is sufficiently long.
periods. To sum up, in a high frequency model, the investment per period can be infinitesimally small, but the total amount of capital overinvested can still be substantial if the time-to-build is sufficiently long.
Finally, Assumption 5 assumes away the possibility of learning from other firms. Should this assumption be relaxed, firms can strategically choose the timing for investment. In particular, firms can delay their own investment until other firms
have invested enough and the true magnitude of ![]() is completely revealed. This will further complicate the analysis. I leave the discussion of this to a separate appendix available from the
author.14On the other hand, this assumption is not wildly unrealistic. It captures the notion that the technology shock may have hit firms in various
industries in very different ways even if it is a GPT. An auto producer may learn very little about how much IT would increase its productivity by observing by how much IT has increased the productivity in the food industry. In addition, even within the same industry, the integration of the new
capital and new technology with existing capital may require firm-specific knowledge.
is completely revealed. This will further complicate the analysis. I leave the discussion of this to a separate appendix available from the
author.14On the other hand, this assumption is not wildly unrealistic. It captures the notion that the technology shock may have hit firms in various
industries in very different ways even if it is a GPT. An auto producer may learn very little about how much IT would increase its productivity by observing by how much IT has increased the productivity in the food industry. In addition, even within the same industry, the integration of the new
capital and new technology with existing capital may require firm-specific knowledge.
3 A Numerical Example: Dynamic General Equilibrium
This section gives an example to show quantitatively how ![]() -type embodiment and learning lead to overinvestment and affect the investment and output impulse response functions (IRF) with
respect to the technology innovation. The computational details are in Appendix B. In the example, the
-type embodiment and learning lead to overinvestment and affect the investment and output impulse response functions (IRF) with
respect to the technology innovation. The computational details are in Appendix B. In the example, the ![]() function is explicitly calibrated and the model is set up in a dynamic general
equilibrium (DGE) environment.
function is explicitly calibrated and the model is set up in a dynamic general
equilibrium (DGE) environment.
3.1 Embodiment Function Calibration
In the previous section, we require only that ![]() be monotonically increasing and concave. In this section, we calibrate the functional form of
be monotonically increasing and concave. In this section, we calibrate the functional form of ![]() explicitly. We assume that pre-shock old capital,
explicitly. We assume that pre-shock old capital, ![]() , is the steady state level vis-à-vis
, is the steady state level vis-à-vis ![]() , and we impose only two conditions that
, and we impose only two conditions that ![]() should satisfy: First, the minimum amount of
new capital required to completely embody the new technology is the steady state level of capital. Second, the
should satisfy: First, the minimum amount of
new capital required to completely embody the new technology is the steady state level of capital. Second, the ![]() -embodied technology production function has the same long-run steady state
as in a standard neoclassical production function with disembodied technology for any level of
-embodied technology production function has the same long-run steady state
as in a standard neoclassical production function with disembodied technology for any level of ![]() . The first condition requires that if
. The first condition requires that if ![]() is the steady state level of new capital, we have
is the steady state level of new capital, we have
In a standard Cobb-Douglas production function of disembodied technology,
![]() , let
, let
![]() and
and
![]() be the steady state level of capital associated with two levels of technology,
be the steady state level of capital associated with two levels of technology, ![]() and
and ![]() . Then we have the well-known relationship
. Then we have the well-known relationship
Because the above relation holds regarding all pairs of ![]() and
and ![]() , we can let
, we can let
![]() and
and ![]() as the pre- and post-shock level of technology specified in
(2). By (33) and (34), and keeping in mind
as the pre- and post-shock level of technology specified in
(2). By (33) and (34), and keeping in mind ![]() by normalization, we have
by normalization, we have
If we rearrange and notice that the above relationship holds for any ![]() , then for any
, then for any
![]() , the embodiment function reads
, the embodiment function reads
This is exactly what we used as the example to illustrate the sufficient condition for accelerating investment. Indeed, this surprisingly concise functional relationship requires only the two sensible conditions we introduced in the beginning paragraph of this section. Finally, plugging equation (36) into the production function (11), we reach
Figure 3 contrasts production function (37) with a standard disembodied production function. In the latter, output jumps from ![]() to
to
![]() when technology increases from 1 to
when technology increases from 1 to ![]() , even without any investment in
new capital. The entire production function shifts up. For the
, even without any investment in
new capital. The entire production function shifts up. For the ![]() -type embodied technology, the production function is linear before the capital stock approaches the new steady state
-type embodied technology, the production function is linear before the capital stock approaches the new steady state
![]() . Beyond
. Beyond ![]() , the
, the ![]() -type production function coincides with the disembodied production function.
-type production function coincides with the disembodied production function.
One key feature that this ![]() function delivers is that sufficient learning is closely related to overinvestment. On the one hand, the firm wants to have a sufficient amount of capital to
make the new technology completely embodied. On the other hand, with such an embodiment function, the firm will not learn the true value of
function delivers is that sufficient learning is closely related to overinvestment. On the one hand, the firm wants to have a sufficient amount of capital to
make the new technology completely embodied. On the other hand, with such an embodiment function, the firm will not learn the true value of ![]() until it has accumulated capital above the steady
state level. This pattern very much resembles the last business cycle. The economy heavily invested in IT-related capital to test the boundary of this great new technology. After each wave of investment, it seemed that adding more new capital would further advance productivity. However by the time
the economy understood the potential of IT, it had invested too much. Investment then subsequently reversed, and a recession occured.
until it has accumulated capital above the steady
state level. This pattern very much resembles the last business cycle. The economy heavily invested in IT-related capital to test the boundary of this great new technology. After each wave of investment, it seemed that adding more new capital would further advance productivity. However by the time
the economy understood the potential of IT, it had invested too much. Investment then subsequently reversed, and a recession occured.
3.2 A Dynamic General Equilibrium Model
The Household
A representative agent maximizes the discounted sum of future utility over an infinite time horizon. The agent owns the shares of the firm, receives dividend payments each period, and can trade the shares to smooth consumption. The representative household's problem is
subject to
where
![]() is the consumption level in period
is the consumption level in period ![]() ,
,
![]() is the share holdings at the end of period
is the share holdings at the end of period ![]() ,
,
![]() is the per-share dividend payment in period
is the per-share dividend payment in period ![]() ,
,
![]() is the ex-dividend share price of the firm at the end of period
is the ex-dividend share price of the firm at the end of period ![]() .
.
The Firm
A fixed number of firms maximize the sum of discounted dividend flows
subject to
where output
It is the investment adjustment cost, and ![]() is a convex
is a convex
![]() function. In this numerical example, we assume that the depreciation rate is positive. The information structure is the same as in Section 2.2 such that the post-shock level of
the underlying technology is
function. In this numerical example, we assume that the depreciation rate is positive. The information structure is the same as in Section 2.2 such that the post-shock level of
the underlying technology is ![]() , the CDF and PDF of which are
, the CDF and PDF of which are ![]() and
and
![]() respectively.
respectively.
Equilibrium
Given the initial state of the economy, ![]() ,
, ![]() , and the unconditional
distribution of
, and the unconditional
distribution of ![]() , the equilibrium conditions are familiar to us and are shared by many DGE models. An equilibrium is given by a sequence of quantities
, the equilibrium conditions are familiar to us and are shared by many DGE models. An equilibrium is given by a sequence of quantities
![]() and prices
and prices
![]() such that given prices
such that given prices
![]() , the representative household solves (38); the firm solves (40) subject to underlying constraints. The markets for
equity shares and goods clear.
, the representative household solves (38); the firm solves (40) subject to underlying constraints. The markets for
equity shares and goods clear.
The equity market clearing condition is
The optimal consumption in this model is therefore trivially determined as
Let the marginal value of capital be
![\displaystyle E_t \; \left[\beta \frac{U^\prime(C_{t+1})}{U^\prime(C_{t})} (MPK_{t+1}+1-\delta) \right] = 1.](img166.gif) |
(45) |
An Equivalent Social Planner's Problem
It is usually hard to compute the numerical results in a decentralized model. The equilibrium path of the quantities that are interesting,
![]() , in the decentralized model can be replicated by a planner's problem. The social planner will solve the following problem
, in the decentralized model can be replicated by a planner's problem. The social planner will solve the following problem
subject to
as well as the same capital accumulation and production functions.
In a manner similar to the Bellman equations (18)-(20), the social planner's problem can be written as
| (48) |
where
| (49) |
and
![\displaystyle W(K_1, \; A) = \max_{[I_t]} \; \sum^\infty_{t=1} \; \beta^{t-1} U(A \; K^\alpha_t - I_t - \Theta_t) \; .](img174.gif) |
(50) |
The analytical solution to this problem is not tractable. This Bellman equation system, however, can be solved numerically by iterating both the value functions ![]() and
and ![]() . Appendix B provides the computational details.
. Appendix B provides the computational details.
3.3 Parameters Choices and Numerical Results
The model is calibrated annually, and the values of most parameters are set to the standard values in the literature. First, preferences are assumed to be CRRA,
where
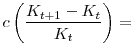 |
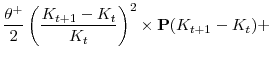 |
(52) | |
![\displaystyle \displaystyle\frac{\theta^-}{2}\left(\frac{K_{t+1}-K_t}{K_t}\right)^2 \times [1-\mathbf{P}(K_{t+1}-K_t)],](img179.gif) |
where
The calibration of ![]() and
and ![]() follows Hall (2001). As Hall (2001)
points out,
follows Hall (2001). As Hall (2001)
points out, ![]() , the adjustment cost coefficient for positive capital stock changes, can be related to the time needed to double the capital stock. Summers (1981) and Shapiro (1986)
provide some empirical evidence on the size of
, the adjustment cost coefficient for positive capital stock changes, can be related to the time needed to double the capital stock. Summers (1981) and Shapiro (1986)
provide some empirical evidence on the size of ![]() . Shapiro reports
. Shapiro reports ![]() is equal to eight quarters, or two years. Summers reports a much larger number for
is equal to eight quarters, or two years. Summers reports a much larger number for ![]() . His findings suggest that
. His findings suggest that ![]() is equal to thirty-two years! Summers's finding has been viewed as unrealistic by many authors (for example, see Tobin 1981). Therefore, Hall (2001) adopts two values for this parameter. He uses the value that Shapiro (1986) reports (two years) as
the lower bound and eight years as the upper bound. I synthesize Hall's calibration by using the geometric average of the lower and upper value he used, which leads to
is equal to thirty-two years! Summers's finding has been viewed as unrealistic by many authors (for example, see Tobin 1981). Therefore, Hall (2001) adopts two values for this parameter. He uses the value that Shapiro (1986) reports (two years) as
the lower bound and eight years as the upper bound. I synthesize Hall's calibration by using the geometric average of the lower and upper value he used, which leads to
![]() . The parameter
. The parameter ![]() is then chosen to be equal to 40, which is ten
times
is then chosen to be equal to 40, which is ten
times ![]() , to capture the irreversibility of installed capital. The level of the adjustment cost plays an important role in determining the length of the period of increasing
investment. Because it is possible to have increasing investment only before the true magnitude of
, to capture the irreversibility of installed capital. The level of the adjustment cost plays an important role in determining the length of the period of increasing
investment. Because it is possible to have increasing investment only before the true magnitude of ![]() is learned, then faster investment can accelerate the learning process. A higher adjustment
cost keeps the firm from investing too fast and prolongs the learning process. At the pre-shock steady state, the investment share is 21 percent, which is higher than the investment share in the data. The reason for this discrepancy is that I chose
is learned, then faster investment can accelerate the learning process. A higher adjustment
cost keeps the firm from investing too fast and prolongs the learning process. At the pre-shock steady state, the investment share is 21 percent, which is higher than the investment share in the data. The reason for this discrepancy is that I chose
![]() , whereas the economywide depreciation rate can be considerably lower.
, whereas the economywide depreciation rate can be considerably lower.
What is still left to be "calibrated" is the distribution of the technological innovation. One restriction we impose is that the support of ![]() is
is
![]() to reflect the notion that there is no technological regress. To begin, I constrain that the difference between
to reflect the notion that there is no technological regress. To begin, I constrain that the difference between ![]() and
and ![]() , denoted by
, denoted by ![]() , to
follow an exponential distribution. The PDF for
, to
follow an exponential distribution. The PDF for ![]() is
is
![]() , whereas the CDF is
, whereas the CDF is
![]() . One reason for choosing an exponential distribution is that it has an analytical closed-form CDF, which is convenient when computing the
. One reason for choosing an exponential distribution is that it has an analytical closed-form CDF, which is convenient when computing the
![]() probability of overshooting. Another consideration is that the exponential distribution has a constant hazard rate, which is the border case between an increasing and decreasing
hazard rate. If an exponential distribution generates the desired dynamics, namely, accelerating investment, then for the families of distributions that have a decreasing hazard rate, the acceleration should be more pronounced.
probability of overshooting. Another consideration is that the exponential distribution has a constant hazard rate, which is the border case between an increasing and decreasing
hazard rate. If an exponential distribution generates the desired dynamics, namely, accelerating investment, then for the families of distributions that have a decreasing hazard rate, the acceleration should be more pronounced.
The exponential distribution has only one parameter, ![]() , and
, and
 . Because the new technology in this paper is set to be a GPT, the innovation is not expected to take place every single year. Rather, it arrives
once in a long period. The postwar data suggest that, measured by the Solow residual, the average annual percentage growth of TFP is 0.79 percent. After controlling for the variations in capital utilization and nonconstant returns to scale, Basu, Fernald, and Kimball (2004) report that the
"purified" residual increases on average 0.35 percent annually. Suppose that a GPT innovation takes place once every decade, and that all the productivity increase is due to the GPT progress; the mean of
. Because the new technology in this paper is set to be a GPT, the innovation is not expected to take place every single year. Rather, it arrives
once in a long period. The postwar data suggest that, measured by the Solow residual, the average annual percentage growth of TFP is 0.79 percent. After controlling for the variations in capital utilization and nonconstant returns to scale, Basu, Fernald, and Kimball (2004) report that the
"purified" residual increases on average 0.35 percent annually. Suppose that a GPT innovation takes place once every decade, and that all the productivity increase is due to the GPT progress; the mean of ![]() should then be between 8.19 percent and 3.56 percent.15 If we postulate that only a fraction of the productivity growth is due to
the GPT progress, then the mean of
should then be between 8.19 percent and 3.56 percent.15 If we postulate that only a fraction of the productivity growth is due to
the GPT progress, then the mean of ![]() should be correspondingly lower. As a benchmark, I choose the mean of
should be correspondingly lower. As a benchmark, I choose the mean of ![]() to be 4 percent and
to be 4 percent and
![]() .
.
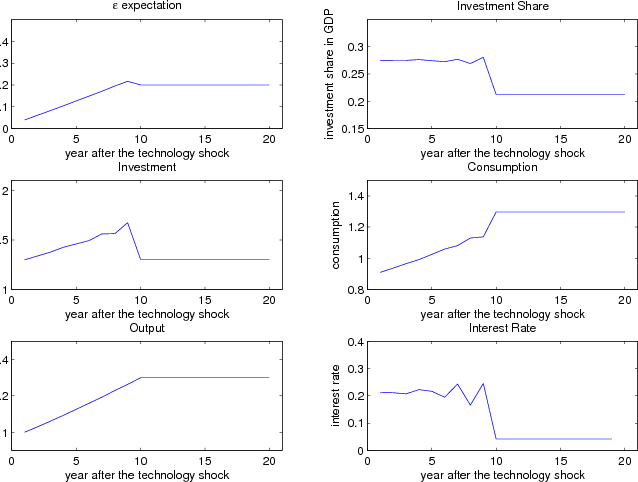
Figure 4 illustrates the impulse-response dynamics of the economy after a new technology arrives. The magnitude of this technology shock is equal to 0.2. This is close to the cumulative productivity growth during the 1990s. The upper-left panel shows the conditional expectation of the magnitude
of the technology shock. We see that right after the shock arrives, the expectation is simply equal to the unconditional mean, 0.04. After the agent invests in new capital and some of the new technology has been embodied, the agent learns that the technology shock is at least as large as what has
already been embodied and revises the conditional belief about the magnitude of the shock. Therefore, the conditional expectation of ![]() keeps increasing until the investment overshoots.
In the period before overshooting, the conditional expectation of
keeps increasing until the investment overshoots.
In the period before overshooting, the conditional expectation of ![]() is equal to 0.24, which is higher than the true magnitude of the shock. After overshooting, the true magnitude of
the shock is completely learned and the conditional expectation goes back to 0.2, which is the true value of the shock. In this setup, we find that investment finally overshoots in the tenth year after the arrival of the new technology.
is equal to 0.24, which is higher than the true magnitude of the shock. After overshooting, the true magnitude of
the shock is completely learned and the conditional expectation goes back to 0.2, which is the true value of the shock. In this setup, we find that investment finally overshoots in the tenth year after the arrival of the new technology.
The investment dynamics, in the middle-left panel, show that in the nine consecutive years, in which investment has been increasing since the innovation, the annual growth rate is 3 percent and the cumulative growth is 28.5 percent. In the tenth year, when the agent learns that capital stock has overshot, investment is reduced dramatically, to 1.31, a decrease of 22 percent.
The output dynamics, in the bottom-left panel, indicate a long-lasting output boom and an endogenous recession. Before the magnitude of the shock has been learned completely, investment keeps increasing and fuels the output boom. Output climbs from 1.00 to 1.30, with an average annual growth rate of about 3.0 percent. The collapse of the investment boom also ends the output boom. We see a sharp decrease in the output growth, though the level of output does not decrease in absolute terms.
One way in which the benchmark result is at variance with the data is that although investment increases quite persistently, the growth rate of investment is not as high as that of output. Consequently, the investment share is flat. In contrast, the data indicate that the share of private fixed investment (PFI) increases from 13.4 percent to 17.1 percent during the 1990s.
The consumption dynamics, in the middle-right panel, largely replicate the pattern of the output IRF before overshooting. At the moment of overshooting, consumption actually increases substantially because investment is sharply reduced while output is largely unchanged. This pattern is
consistent with the most recent recession, during which investment crashed but consumption was sustained. This is one of the characteristics that makes the most recent business cycle unique. Typically, consumption is significantly procyclical. However, in the two years following the cyclical peak,
real GDP grew a cumulative 2.6 percent, whereas real consumption grew almost 5.7 percent. I will discuss the dynamics of the implied (shadow) risk free interest rate, ![]() (bottom-right
panel) in the next section.
(bottom-right
panel) in the next section.
The substantial adjustment cost assumed in this model contributed to the long-lasting boom through two channels. First, high ![]() slows new investment. Second, high
slows new investment. Second, high ![]() leads to a large cost of overshooting and makes the firm invest in new capital more cautiously. If we use the lower value adopted by Hall (2001), namely
leads to a large cost of overshooting and makes the firm invest in new capital more cautiously. If we use the lower value adopted by Hall (2001), namely
![]() and
and
![]() , the investment path will be almost 10 percent higher than that in figure 4. Consequently, the boom period is shorter, only seven years. In addition, in the low adjustment cost
model, the economy overshoots by a large amount of new capital, which makes the investment crash and recession more pronounced.
, the investment path will be almost 10 percent higher than that in figure 4. Consequently, the boom period is shorter, only seven years. In addition, in the low adjustment cost
model, the economy overshoots by a large amount of new capital, which makes the investment crash and recession more pronounced.
To summarize, the model generates persistent investment and output booms and endogenous overinvesting and recession. However, the investment share of GDP does not increase as much as we observe in the data. Meanwhile the investment growth rate is lower than that in the data. One potential reason
for this is that the revision of the firm's conditional expectation of ![]() is not climbing very fast. Therefore, one round of successful investment does not prompt a round of sharply
more aggressive investment. A distribution that induces a larger leap of conditional expectations also induces a larger leap of investment. I introduce an alternative distribution of technology shocks to allow for a fatter tail. Assume that the PDF of
is not climbing very fast. Therefore, one round of successful investment does not prompt a round of sharply
more aggressive investment. A distribution that induces a larger leap of conditional expectations also induces a larger leap of investment. I introduce an alternative distribution of technology shocks to allow for a fatter tail. Assume that the PDF of ![]() is
is
![]() and
and
![]() . This is a weighted average of two exponential distributions. Unlike the standard exponential distribution that has a constant hazard rate, this distribution has a
decreasing hazard rate. We choose the parameters
. This is a weighted average of two exponential distributions. Unlike the standard exponential distribution that has a constant hazard rate, this distribution has a
decreasing hazard rate. We choose the parameters ![]() ,
, ![]() , and
, and
![]() to make this distribution have the same mean as the previous one. Figure 5 illustrates the IRF after a shock of
to make this distribution have the same mean as the previous one. Figure 5 illustrates the IRF after a shock of
![]() in this setup.
in this setup.
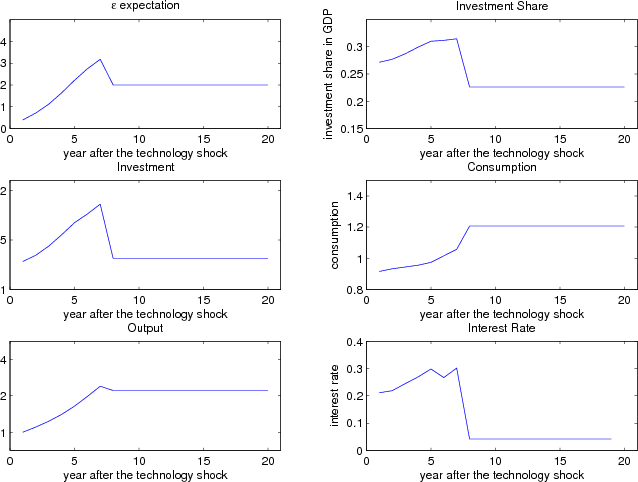
In contrast to the previous case, the conditional expectation of ![]() increases much more rapidly. Within eight years, it jumps from 0.04, the unconditional mean, to near 0.4 before
the economy overshoots. This rapidly revised belief about the magnitude of the technology shock induces a similarly rapid increase in investment. It grows from 1.28, a level lower than but close to the previous case in the first year, to 1.86, which reflects a 5.5 percent average annual increase.
The initial investment in this setup is similar to the previous one because the two distributions have the same mean, whereas the investment grows faster in this setup because of the decreasing hazard rate.
increases much more rapidly. Within eight years, it jumps from 0.04, the unconditional mean, to near 0.4 before
the economy overshoots. This rapidly revised belief about the magnitude of the technology shock induces a similarly rapid increase in investment. It grows from 1.28, a level lower than but close to the previous case in the first year, to 1.86, which reflects a 5.5 percent average annual increase.
The initial investment in this setup is similar to the previous one because the two distributions have the same mean, whereas the investment grows faster in this setup because of the decreasing hazard rate.
During the same period, output grows at a slower rate of 3.3 percent. Therefore, the investment share increases from about 27.15 percent to nearly 31.44 percent over seven periods. Because investment grows faster, the boom lasts a shorter time. The economy overshoots after eight years. An
important distinction is that the recession is more pronounced in this setup, and we are able to visualize the decrease in output because the economy has overshot by a large amount and has to decumulate excess capital in a more aggressive way. For the same reason the output and investment dynamics
in this model are not linear in ![]() .
.
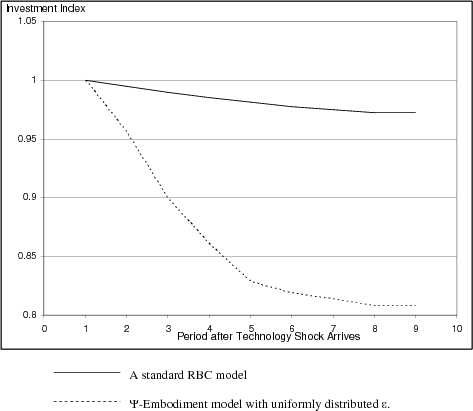
Second, to highlight how the hazard rate and infinite support of the distribution of ![]() matter, I slightly change the model. I assume that
matter, I slightly change the model. I assume that ![]() follows a uniform distribution, which has an increasing hazard rate and a well defined upper bound. The dashed curve in figure 6 shows that in this scenario, if a shock of same magnitude arrives, investment is high at the early
stage of the boom but diminishes over time even if the investment has not overshot. The intuition is simple: Because of the known upper bound as well as the increasing probability of overshooting, the firm invests at an increasingly cautious pace.
follows a uniform distribution, which has an increasing hazard rate and a well defined upper bound. The dashed curve in figure 6 shows that in this scenario, if a shock of same magnitude arrives, investment is high at the early
stage of the boom but diminishes over time even if the investment has not overshot. The intuition is simple: Because of the known upper bound as well as the increasing probability of overshooting, the firm invests at an increasingly cautious pace.
3.4 Discussion on Interest Rate and Firm Value Dynamics
The bottom-right panel of figures 4 and 5 show the dynamics of the implied (shadow) risk-free interest rate, ![]() . Recall that the following familiar Euler equation should hold in the
decentralized model, if the consumer can borrow and lend at a risk-free interest rate to smooth consumption16
. Recall that the following familiar Euler equation should hold in the
decentralized model, if the consumer can borrow and lend at a risk-free interest rate to smooth consumption16
which implies that
where the last equality follows because
 . The interest rate before the economy overshoots is very high in this model because of high expected consumption growth. High consumption growth is expected
because before investment overshoots, some consumption has been sacrificed to increase investment. In the next period, if the economy remains undershot, consumption will remain low. When the economy overshoots, consumption will bounce back dramatically. Expected consumption growth is the average of
the two scenarios weighted by the probability of overshooting. Because the probability of overshooting is not trivially small, expected consumption growth is quite high. After overshooting, the interest rate jumps down to the ordinary level, which is close to the steady state level,
. The interest rate before the economy overshoots is very high in this model because of high expected consumption growth. High consumption growth is expected
because before investment overshoots, some consumption has been sacrificed to increase investment. In the next period, if the economy remains undershot, consumption will remain low. When the economy overshoots, consumption will bounce back dramatically. Expected consumption growth is the average of
the two scenarios weighted by the probability of overshooting. Because the probability of overshooting is not trivially small, expected consumption growth is quite high. After overshooting, the interest rate jumps down to the ordinary level, which is close to the steady state level,
One implication of the high discount rate is the substantial decline of firm value. Indeed, during the learning phase of the transition, firm value decreases upon the arrival of the GPT innovation and remains low until the economy overshoots (figure 7). When the economy overshoots, the interest rate is adjusted to its normal level, as does firm value.
This scenario is apparently at odds with what happened in the 1990s. We did not see interest rates as high, or firm value as weak, as the present model predicts. One important reason for this gap is the present model is a closed economy model. Every dollar of increase in investment is at the cost of contemporaneous consumption, which will lift expected consumption growth and the interest rate. However, during the 1990s, especially during the later part of the decade, large amounts of foreign capital flowed in and helped keep the interest rate low. The interest rate and firm value puzzle can thus be reconciled in an open economy setup. The caveat of that approach is that if the interest rate is kept low because of the sufficient foreign asset supplies, investment will jump faster because capital is cheaper, and the investment boom may be shorter. Ceteris paribus, to keep interest rates low and the investment boom long-lasting, we need either faster depreciation of new capital or a larger adjustment cost or a combination of the two forces.
4 Related Literature
The learning mechanism employed in this paper is closely related to the literature often referred to as "Bayesian learning by doing." Aghion, Bolton, Harris, and Jullien (1991) study the problem of optimal learning through sequential experimentation by a single decision maker. In an application of the theory, Aghion, Bolton, and Jullien (1987) investigate experimental price setting by a monopolist facing uncertainty about demand.
Zeira (1987), Rob (1991) and Barbarino and Jovanovic (forthcoming) study uncertainty about some types of underlying capacity limits. For example, Rob (1991) proposes a mechanism for learning about market capacity through sequential entry of firms. Barbarino and Jovanovic (forthcoming) study a related learning problem in which the market capacity is learned through capacity expansion at firm level. One restrictive assumption in their models is that overshooting happens at an industry level. Within an industry, any firm level expansions on the margin do not alter the probability of overshooting of the industry because firms are infinitesimally small. Hence, when a firm decides to expand, it does not have to take into account the increased likelihood of overshooting that such an expansion would cause.
In addition, my model differs from those in previous studies in that it is a DGE model and can be used to study aggregated fluctuations, whereas Zeira (1987), Rob (1991) and Barbarino and Jovanovic (forthcoming) are partial equilibrium models that focus on firm or industry-level dynamics.
As for the origin of the uncertainty, my model is similar in spirit to that of Zeira (1987). Zeira sets forth the idea of productive capital and assumes that output is not a function of existing capital but a function of the minimum value between existing capital and productive capital. The
level of the productive capital is unknown to the producers. In my model, the ![]() -type embodiment suggests that the effective TFP is equal to the minimum between the level of underlying
technology and the TFP that can be embodied in the current amount of net new investment. In a certain sense, my model can be viewed as an extension and articulation of Zeira (1987). However, because of complexities elsewhere in my model, my analytical results are not as elegant as those in Zeira
(1987).
-type embodiment suggests that the effective TFP is equal to the minimum between the level of underlying
technology and the TFP that can be embodied in the current amount of net new investment. In a certain sense, my model can be viewed as an extension and articulation of Zeira (1987). However, because of complexities elsewhere in my model, my analytical results are not as elegant as those in Zeira
(1987).
In recent studies of business cycles, various authors have proposed mechanisms to make DGE business cycle models exhibit impulse response functions that are more consistent with the data. Much of this effort has focused on imperfect information and expectations. Beaudry and Portier (2004) revitalized the idea of Pigou (1926) and argued that an upward-biased expectation of future productivity growth will lead to a current expansion. Similar to their work, Jaimovich and Rebelo (2006) show that "recessions are caused not by contemporaneous negative shocks but by lackluster news about future TFP or investment-specific technical change." Unlike my model, Beaudry and Portier (2004) and Jaimovich and Rebelo (2006) do not explicitly model learning. As time progresses, the agents should be able to collect additional information about future productivity growth. If the agents are allowed to revise their expectations about future productivity growth conditional on the evolving information set, as long as new information arrives at a sufficiently slow rate, it is less likely that recessions of the scale in their papers will happen.
Learning plays a central role in Van Nieuwerburgh and Veldkamp (2006). They focus on the asymmetry of business cycles, that is, why booms usually last a long period while recessions are short and sharp. In their model, the production function is characterized by exogenous noise, which makes it hard to tell if high output is due to better technology or lucky output shocks. In contrast to my model, their learning mechanism is more like a signal-extraction device. When productivity is expected to be high, production is higher and this will thereby lead to a flow of more precise information. When the economy passes the peak of a productivity boom, precise estimates of the slowdown prompt investment and labor to fall sharply. Conversely, at the end of a slump, low production impedes learning, slows the recovery, and makes booms more gradual than crashes. Thus booms and recessions in their model are still exogenous, and boom does not have to induce a recession. Learning in their model affects the duration of booms and recessions only and does not lead to any overshooting.
5 A Closer Look at the Last Business Cycle
The model in this paper generates a persistent investment boom as well as a surge in observed TFP. ![]() In this section, I document the pattern of the cycle in the 1990s in greater detail. I
present several stylized examples to highlight the relevance of the
In this section, I document the pattern of the cycle in the 1990s in greater detail. I
present several stylized examples to highlight the relevance of the ![]() -embodied technology in that era. I also provide examples of other historical episodes that share characteristics
similar to the most recent one.
-embodied technology in that era. I also provide examples of other historical episodes that share characteristics
similar to the most recent one.
The lower panel of figure 8 plots investment as a share of GDP. Starting in 1991, the share of PFI largely increased in parallel to the share of E&S investment. The share of real PFI increased from 13.4 percent to 17.1 percent by 2000, whereas the share of E&S investment increased from 6.9 percent to 9.5 percent.17 In respect to real PFI, only four other years in history saw higher investment share, 18 whereas for E&S investment reached new historical highs every year from 1995 to 2000.
Another well-documented characteristic of the 1991-2000 period is a rapid increase in productivity. Productivity growth was particularly strong during the second part of the decade. Oliner and Sichel (2000) report that from 1995 to 1999, output per hour increased 2.5 percent annually, which is almost double the average growth rate in the previous twenty-five years. They estimate that about two thirds of this increase was due to the contribution of information technology. Furthermore, they estimate that about 1 percentage point of the annual increase in labor productivity was due to computer hardware and software.
Indeed, a substantial part of the increase in productivity in the 1990s did not require replacing old capital with new capital. On the contrary, old capital benefitted from being operated with new capital that embodied new technology. One celebrated example comes from Wal-Mart (See, for example, Tsao 2003). The retailer did not replace its truck fleet but equipped itself with better inventory control and logistics technology, which are rooted in the IT revolution. Similarly, businesses that expand their e-commerce operation only have to install better information processing and telecom equipment but the productivity of all its buildings and physical structures benefit. If we interpret capital broadly and include human capital, we can see that the IT-related knowledge is most valuable when it is combined with the existing base of knowledge and the old human capital has not been completely substituted with IT-based human capital.
Returning to the most recent recession, although real GDP increased only 0.8 percent in 2001, real personal consumption increased 2.5 percent. The dispersion between GDP and consumption growth was quite persistent in the next year as well. Real GDP increased 1.9 percent in 2002, whereas real consumption grew 3.1 percent. Consumption growth in that year was particularly strong for durable goods - 6.6 percent.
Several important episodes in history share similar patterns of investment. Jovanovic and Rousseau (2005) document that the share of total power generated by electricity increased sharply between 1900 and 1929. This suggests an investment boom in electricity generating and related industries. The growth of electric power share slowed down abruptly in 1929, the first year of the Great Depression, and electricity expansion never returned to its previous strength, even after the end of the depression. This pattern indicates a certain degree of capital overhang. Similar anecdotes can be found in the studies of canal and railroad expansions in the 19th century. Each boom started with the advent of a revolutionary technology and ended with overinvestment. Canal building boomed after the invention of the steamboat, and by the year 1860 more than 4,000 miles of canal had been completed. However, many of these canals did not live up to the expectations of their promoters. Many of these projects eventually turned out to be financial failures.19 Later in the same century, the railroad expansion shared a similar fate. Thousands of miles of railroad were built and left unused or under used, a phenomenon described by Schumpeter (1949) as construction "ahead of demand." Fogel's investigation (1964) found that the ex post return in the railroad industry in the early 1870s turned out to be too low to attract capital. Overall, the steamboat, the railroad, and electricity all contributed to productivity increases to a great extent, but investors eventually overshot.
6 Conclusion and Future Research
In this paper, I propose a new model in which, once new technology has been embodied into new capital, it increases the productivity of capital of all vintages. Subject to the limits of the available new technology, the more new capital that has been installed, the higher is the productivity level. Agents in the economy do not know exactly the magnitude of the new technology shock and therefore have to learn it by investing in new capital. The true magnitude is learned after their investments overshoot the optimal level. I provide a sufficient condition under which investment increases persistently and overshoots at the end. After overshooting, investment is sharply reduced and a recession is triggered. On the other hand, consumption can increase during recessions because output is reallocated from investment to consumption.
The investment, consumption, and output dynamics derived from the model match qualitatively what we observed in the data of the last business cycle. I argue that the model adds a strong internal propagation mechanism to the standard DGE models. In addition, it generates endogenous recessions without invoking technological regress.
Some extensions to the model seem promising. One is to allow for a more flexible and generalized learning structure. In particular, a "learning from others" framework where firms can learn from other firms might be more realistic. As Bolton and Harris (1999) point out, if we extended the single-agent problem of optimal learning by experimentation into a multi-agent setup, the free-rider problem would arise. In the context of my model, this implies that if one firm invests more, not only this firm but all other firms can potentially acquire better information about the underlying new technology. Therefore, a typical firm will strategically delay its investment in the absence of additional incentives. One such incentive for investment would be in a monopolistic environment. Because a firm's profit is a function of its productivity level, a firm that invests quickly acquires a higher level of productivity relative to those firms investing slowly. The tradeoff in such a model would be between investing quickly and acquiring higher productivity sooner versus investing slowly and avoiding the potential costs due to overshooting. This might result in a Nash equilibrium at which a fraction of the firms choose to be leaders and invest quickly and others choose to be followers.
A. Proof of Lemmas
Proof of Lemma 1: By the production function (3), if
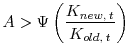 , then
, then
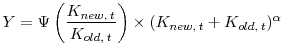 . The marginal product of
. The marginal product of ![]() and
and ![]() are
are
and
If
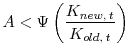 , then
, then
![]() . The marginal product of
. The marginal product of ![]() and
and ![]() are equal. Remember
are equal. Remember
![]() , therefore,
, therefore,
| (A.3) |
![]()
Proof of Lemma 2 The first order condition of Bellman equations (18) - (20) is
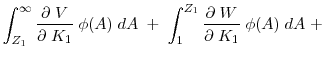 |
|||
| (A.4) |
By the envelope theorem and repeated use of the Newton-Leibnitz Theorem we have
![\displaystyle + \frac{1}{1+r}\times\frac{\phi(Z_1) \; \Psi^\prime(K_1)}{[1-\Phi(Z_1)]^2} \times \left[\int_{Z_2}^\infty V(K_2)\; \phi(A) \; d A \; + \; \int_{Z_1}^{Z_2}W(K_2,A) \; \phi(A)\; dA\right]](img227.gif) |
|||
![\displaystyle + \frac{1}{1+r}\times\frac{1}{1-\Phi(Z_1)}\times\left[\int_{Z_2}^\infty \frac{\partial \; V}{\partial \; K_2}\; \phi(A) \; d A \; + \; \int_{Z_1}^{Z_2}\frac{\partial \; W}{\partial \; K_2} \; \phi(A)\; d A \right]](img228.gif) |
|||
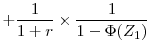 |
|||
| (A.5) |
The first order condition for (19) provides that
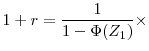 |
(A.6) | ||
![\displaystyle \left\{\int_{Z_2}^\infty \frac{\partial \; V}{\partial \; K_2}\; \phi(A) \; d A \; + \; \int_{Z_1}^{Z_2}\frac{\partial \; W}{\partial \; K_2} \; \phi(A)\; dA +[W(K_2, Z_2)-V(K_2)]\phi(Z_2)\;\Psi^\prime(K_2) \right\}.](img233.gif) |
Plug (A.6) into (A.5) we have
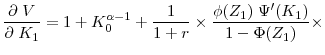 |
(A.7) | ||
![\displaystyle \left[ \frac{\displaystyle \int^\infty_{Z_2} V(K_2) \phi(A) \; dA + \int^{Z_2}_{Z_1} W(K_2, A) \phi(A) \; dA}{1-\Phi(Z_1)} - W(K_2, Z_1)\right].](img235.gif) |
However, we still have
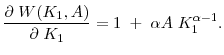 |
(A.8) |
Finally, plug (A.7) and (A.8) into (A.4) we reach
![\displaystyle \left[ K_0^{\alpha-1}[1-\Phi(Z_1)] + \alpha K_1^{\alpha-1} \; \int_1^{Z_1} A \; \phi(A)\; d A \;\right] \;\; +](img238.gif) |
|||
| (A.9) | |||
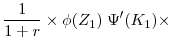 |
|||
![\displaystyle \left[ \frac{\displaystyle \int^\infty_{Z_2} V(K_2) \; \phi(A) \; d A + \int^{Z_2}_{Z_1} W(K_2, \; Z_2) \;\phi(A) \; d A}{1-\Phi(Z_1)} - W(K_2, Z_1)\right].](img241.gif) |
Keep in mind that the optimality condition of the auxiliary problem is
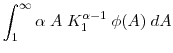 |
|||
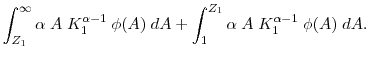 |
(A.10) |
Notice that in (A.9) and (A.10), the common part is
![]() . We can show that
. We can show that
![]() , the value of the RHS of (A.9) excluding the common part has a larger value than the RHS of (A.10) excluding the common part. In order to make the RHS of (A.9) equal to the
RHS of (A.10), we must have the optimal
, the value of the RHS of (A.9) excluding the common part has a larger value than the RHS of (A.10) excluding the common part. In order to make the RHS of (A.9) equal to the
RHS of (A.10), we must have the optimal ![]() in (A.9) greater than the optimal
in (A.9) greater than the optimal ![]() in
(A.10)
in
(A.10)
![]()
The Economic Interpretation of (A.9)
The RHS of equation (A.9) has three components, and here is an intuitive interpretation of them.
1.
![K_0^{\alpha-1}[1-\Phi(Z_1)] + \displaystyle \alpha K_1^{\alpha-1} \int_1^{Z_1} A \; \phi(A)\; d A \;](img247.gif) is the expected marginal productivity that incorporates the
is the expected marginal productivity that incorporates the ![]() -type embodiment.
-type embodiment.
2. As illustrated in figure 4, the extent to which investment overshoots varies, hence the ![]() loss of overshooting varies. The marginal gain due to the
reduction of the loss of overshooting in the subsequent periods is
loss of overshooting varies. The marginal gain due to the
reduction of the loss of overshooting in the subsequent periods is
![]() . To see this, assume that the firm has capital
. To see this, assume that the firm has capital ![]() and that the true size of
and that the true size of ![]() is equal to
is equal to
![]() , where
, where ![]() is a sufficiently small positive number. Because
is a sufficiently small positive number. Because
![]() ; the firm would have found undershooting and the continuation value would be
; the firm would have found undershooting and the continuation value would be ![]() . However, because
. However, because ![]() is so close to
is so close to ![]() and the firm has not
realized this, the cost of overshooting will be quite big. Suppose that the firm increases investment on the margin and pushes
and the firm has not
realized this, the cost of overshooting will be quite big. Suppose that the firm increases investment on the margin and pushes ![]() up so that
up so that ![]() , investment will overshoot and learn the true size of
, investment will overshoot and learn the true size of ![]() . The continuation value will be
. The continuation value will be
![]() . Because
. Because ![]() is sufficiently small, we then should have
is sufficiently small, we then should have
![]() . Because
. Because ![]() is the steady state level of
capital corresponding to the technology level
is the steady state level of
capital corresponding to the technology level ![]() , we have
, we have
![]() . The difference measures the loss reduced by avoiding large overshooting in the subsequent period. The gain is weighted by the change of the probability of
overshooting on the margin,
. The difference measures the loss reduced by avoiding large overshooting in the subsequent period. The gain is weighted by the change of the probability of
overshooting on the margin,
![]() .
.
3. Finally, suppose the firm has undershot with ![]() , the term
, the term
![\displaystyle \frac{1}{1+r} \times \phi(Z_1) \; \Psi'(K_1)\times \left[ \displaystyle \frac{\displaystyle \int^\infty_{Z_2} V(K_2) \; \phi(A) \; d A + \int^{Z_2}_{Z_1} W(K_2, \; A) \; \phi(A) \; d A}{1-\Phi(Z_1)} - W(K_2, \; Z_1)\right]](img255.gif)
captures the value of the additional information provided by the marginal investment. Recall that the firm updates the belief about ![]() conditional on
conditional on ![]() after observing undershooting. The firm should be better off if instead it learns that
after observing undershooting. The firm should be better off if instead it learns that
![]() , where
, where
![]() , because tighter conditional distribution provides more precise information about
, because tighter conditional distribution provides more precise information about ![]() . Since this helps to increase the firm's value only after the next period, the value of information has to be discounted by
. Since this helps to increase the firm's value only after the next period, the value of information has to be discounted by ![]() . The fraction term in the bracket is the
expected value of the firm conditional on
. The fraction term in the bracket is the
expected value of the firm conditional on ![]() , and the second term in the bracket,
, and the second term in the bracket,
![]() , is the value of the firm if the true size of the shock is
, is the value of the firm if the true size of the shock is ![]() but
the firm overshoots its capital to
but
the firm overshoots its capital to ![]() . The difference between these two terms is the gain from pushing up the lower bound of the conditional distribution of
. The difference between these two terms is the gain from pushing up the lower bound of the conditional distribution of ![]() .
.
B. Computation Method
I use value function iteration over a discrete grid to compute the value functions. I discretize the ![]() distribution with
distribution with ![]() points, and each point has weight equal to
points, and each point has weight equal to
![]() . Depending on the shape of the distribution,
. Depending on the shape of the distribution, ![]() may have to be rather
large to capture the tail properties. Meanwhile I discretize the state variable,
may have to be rather
large to capture the tail properties. Meanwhile I discretize the state variable, ![]() .
.
I begin by computing the value function
![]() because it does not involve
because it does not involve ![]() . This can be computed with the
standard value function iteration technique. I iterate the value functions until the average gap between two consecutive iterations is smaller than 0.0001. Because the computation process is time consuming and
. This can be computed with the
standard value function iteration technique. I iterate the value functions until the average gap between two consecutive iterations is smaller than 0.0001. Because the computation process is time consuming and ![]() is large, I do not compute
is large, I do not compute
![]() for each
for each ![]() I simulated in the discretized distribution. Instead, I
compute
I simulated in the discretized distribution. Instead, I
compute
![]() on a rougher grid of
on a rougher grid of ![]() and interpolate the value function
for all
and interpolate the value function
for all ![]() grids.
grids.
I then compute
![]() for all possible pairs
for all possible pairs
![]() on the
on the ![]() grid. With
grid. With ![]() and
and ![]() in hand, I iterate
in hand, I iterate ![]() until the gap is smaller than 0.0001. Thus, we have a value function of the economy with capital level
until the gap is smaller than 0.0001. Thus, we have a value function of the economy with capital level ![]() without having overshot.
without having overshot.
![\displaystyle \widetilde{A}_t = \min \; \left[A , \; \Psi\left(\frac{K_{new, \: t}}{K_{old, \: t}}\right)\right].](img13.gif)
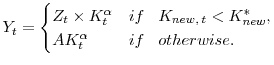
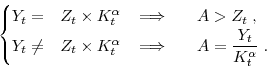
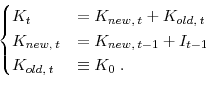
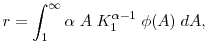
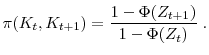
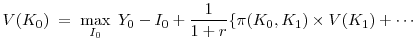
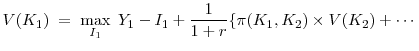
![\displaystyle W(K_1, \; A) = \max_{[I_t]} \; \sum^\infty_{t=1} \; \left(\frac{1}{1+r}\right)^{t-1} [A K^\alpha_t\ - I_t].](img79.gif)
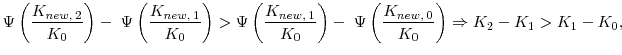
![\displaystyle \widetilde{Z}_2 = \Psi\left[\left(\displaystyle \int^\infty_{Z_1} A \; \frac{\phi(A)}{1-\Phi(Z_1)} \; d A\right)^{\frac{1}{1-\alpha}} - 1 \right].](img104.gif)
![\displaystyle \Psi\left[\left(\displaystyle \int^\infty_{Z_1} A \; \frac{\phi(A)}{1-\Phi(Z_1)} \; d A\right)^{\frac{1}{1-\alpha}} - 1 \right] > 2 Z_1 \;\;\;\;\;\;\;\;\; \forall \;\;\; Z_1 \; .](img105.gif)
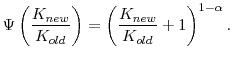
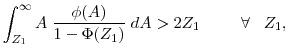
![\displaystyle \min\left[A, \; \Psi\left(\frac{K^*_{new}}{K_0}\right)\right] = A = \Psi\left(\frac{K^*_{new}}{K_0}\right).](img133.gif)
![$\displaystyle \frac{A''}{A'} = \left[\frac{K^{^*}(A'')}{K^{^*}(A')}\right]^{1-\alpha} \;\;\;\;\;\;\;\;\; \forall \;\; A' \;\;$](img139.gif) and
and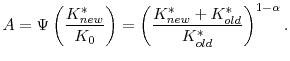
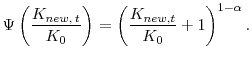
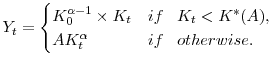
![\displaystyle \max_{[C_t, S_t]} E_0 \; \sum^\infty_{t=0} \; \beta^t U(C_t),](img149.gif)
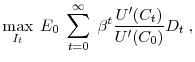
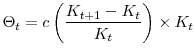
![\displaystyle \max_{[C_t]} E_0 \; \sum^\infty_{t=0} \; \beta^t U(C_t),](img168.gif)
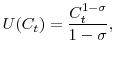
![\displaystyle r^f_t = \frac{U^\prime(C_t)}{\beta E_t \; U^\prime(C_{t+1})} - 1 = \frac{1}{\beta} \frac{C_t^{-2}}{E_t \; [C_{t+1}^{-2}]} -1,](img208.gif)