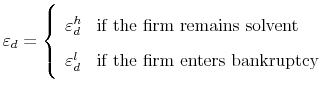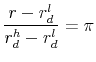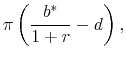Why Do Firms Offer Risky Defined Benefit Pension Plans?
Keywords: Pensions, risk, compensation, corporate finance
Abstract:
1 Introduction
In the aggregate, private defined-benefit pension plans in the United States are underfunded by a considerable margin. The Pension Benefit Guaranty Corporation, the federal insurer of such plans, puts the aggregate shortfall of assets from liabilities among insured single-employer plans at about $350 billion as of September 30, 2006 (PBGC 2006, p. 8). In addition, the characteristics of the assets that these plans hold are very different from the characteristics of their liabilities. Coronado and Liang (2006) find that the typical pension trust holds 60 percent to 70 percent of its value in equities. In contrast, by at least one definition, liability is fixed and known with certainty in nominal terms.1 These two factors--the substantial shortfall of assets from liabilities and the mismatch between assets and liabilities--imply that private DB plans are a risky proposition for both workers and firms.2
As Bodie (1990) and others have pointed out, even risky firms could greatly reduce the risk of their pension promises by contributing a sufficient level of resources to their pension trust funds and by investing those resources in fixed-income securities designed to deliver their payoffs just as pension obligations are coming due. This strategy would immunize the pension fund from market fluctuations, because stock returns would be irrelevant and interest-rate changes would affect pension assets (through bond values) and liabilities (through the present value of future obligations) at the same time and by the same amounts.3 Despite this possibility, almost all firms choose to make their pension promises risky.4 Thus the question motivating this paper: Is it optimal for firms to introduce more than the minimum amount of risk into their pension promises? In particular, can firms really gain value by making their pension promises risky rather than free of risk? In this paper, we develop a model of pension financing in which the total compensation offered to workers must clear the labor market, an approach that formalizes some of the ideas suggested by Bulow (1982) and Bodie (1988, 1990, inter alia). The firms in our model maximize their value by making their pension promises free of risk.
Many readers will find this conclusion to be highly counterintuitive. How could a firm improve its financial position by offering a riskless pension promise rather than a risky one? Aren't risky promises discounted at higher rates of return than riskless ones, ensuring that the present-discounted value (PDV) of a riskless promise exceeds the PDV of a risky one? By making the pension promise riskless, won't firms therefore be taking on additional cost?
The answer is yes, firms that eliminate the risk from previously risky pension promises will take on additional pension cost. But minimizing pension cost alone is not the appropriate objective for firms to pursue: Firms should aim to minimize the market value of total compensation cost, not pension cost in isolation (holding the real activity of the firm constant). We show that if workers understand the implications of pension risk, they will demand greater compensation for riskier pension promises than for safer ones, all else being equal. Thus while riskier pension promises may reduce pension cost, they do not reduce the total compensation cost of the firms in our model.
One way to see the economic intuition for this result is to think of workers as disadvantaged bondholders of the firm--"bondholders" because they hold promises of future payments just as ordinary bondholders do, but "disadvantaged" because, unlike ordinary bondholders, workers are assumed to be unable to diversify away the company-specific risk to which they are exposed through risky pension promises. In return for the promise of a risky DB pension, workers offer their employers a lower "pric" (in the form of wage concessions) than the employers could obtain from bond-market investors in return for the same promised cash flows. Thus, we generate a violation of the standard Modigliani-Miller result that purely financial operations do not affect the value of the firm: Firms that offer a risky pension plan are committing a form of financial inefficiency because they are obtaining part of their financing on worse-than-market terms. The more they avail themselves of this source of financing, the more they reduce their own value. Taking the risk out of the pension promise eliminates the financial inefficiency because in that case--and that case only--workers are willing to provide financing on terms that are as good as the ones that the firm could obtain from financial markets.
This paper is only a first step because, for the sake of transparency and simplicity, we focus explicitly on a single source of pension risk--the employer's funding (i.e., contribution) decision, abstracting from the portfolio allocation decision. In addition, we suppress a number of important features of the pension landscape, some of which would reinforce the argument in favor of making the pension promise riskless, and some of which would weaken it. One of these factors is the PBGC, which offers insurance against downside risk, and--in return--charges premiums far below the economically fair level. Another factor that we suppress is the tax code, and its associated influence on portfolio allocation. A third factor is the empirical regularity--noted by Bodie (1990), that workers seem to hold a call option on part of the surplus in pension trust funds. The way for firms to minimize the market value of this call option is to eliminate the upside potential associated with the trust fund; this, in turn is accomplished by matching the characteristics of the assets in the trust fund to the characteristics of the plan's liabilities. So again, this consideration strengthens the argument for making the pension promise free of risk. In work in progress, we are extending the model to include the portfolio allocation decision, and to capture some of the additional factors omitted here.
Our paper proceeds as follows: In the next section, we briefly review the literature that has considered whether firms should offer a risky pension promise or one that is free of risk. Then we present a bare-bones model with a consumer that lives for two periods, earning cash wages when young and a pension when old. We find that, in this model, the firm's optimal strategy is to fund the pension promise fully. We also begin the process of exploring the robustness of this result to variations in model specification and calibration. We close by revisiting the question of why no real-world firm follows the prescription of our model.
2 Related literature
Early work on pension funding recognized that pension obligations represent contingent liabilities for shareholders and contingent assets for employees, where the contingency is the solvency of the firm. Sharpe (1976), Black (1976), and Treynor (1977) demonstrate that this structure implies that a firm's pension obligation can be analyzed in an options-pricing framework: Firms effectively own an option that entitles them to put the funding gap to their employees if and when the firms become insolvent.5 The value of the pension obligation in an economic balance sheet therefore consists of promised benefits (a liability) and a put option on the difference between promised benefits and the value of the trust fund (an asset).
Using standard options theory, Treynor shows that increasing the risk of the underlying assets increases the value of the put option and therefore--holding other forms of compensation constant--the value of shareholder equity. As a result, again ignoring any changes in other components of compensation, the put option provides an explanation for why corporations might prefer that pension fund managers invest in risky assets. Sharpe (1976) demonstrates that if workers have access to perfect capital markets and if there is no firm-specific risk, workers can offset the pension funding decisions of the firm so long as the firm is guaranteed to survive. In this case, the funding decision is irrelevant: A firm can either fully fund its pension, or it can underfund it and pay employees an additional amount equal to the put value of the shortfall.
Harrison and Sharpe (1983) analyze pension asset allocation and funding decisions in the presence of potentially mispriced pension insurance. Following Tepper (1981), they allow tax considerations to affect the investment of pension assets. Abstracting from mispriced pension insurance, they confirm Tepper's result that firms will optimally invest pension assets (which are tax-exempt) entirely in the higher-taxed assets (bonds). They demonstrate, however, that presence of mispriced pension insurance can overturn this result. In particular, if equities are a more effective vehicle for taking advantage of naive insurance pricing, the optimal pension strategy may involve a combination of equities and debt. A common feature of these studies is that they tend to focus almost exclusively on the decisions of firms without reference to the economic decisions of employees. For example, Treynor ignores the labor-market response to the effect of the put option on the value of compensation, and Sharpe does not consider the effect of undiversifiable firm-specific risk on employee compensation demands. Bulow (1982) brings the idea of market-clearing compensation into the model: in his words, "[a]t each point in time, the firm should be willing to pay its employees their marginal product, in the form of a combination of salary and benefits." Implicit in this condition is that risk transfers between firms and employees must be compensated--an insight that is central to our argument.
A few recent studies have moved beyond the effect of pension investments on the value of the put option and examined other factors affecting pension funding and investments. As noted earlier, Bodie (1990) argues that employees may have an implicit call option on a portion of the returns in the trust fund if they can bargain for higher salary or more-generous pensions in high-return states of the world. If this is the case, the pension allocation decision is tilted toward assets that more nearly mimic the characteristics of liabilities because the firm is obligated to make up for any shortfall as long as it remains solvent but is also pressured into distributing a portion of upside realizations to workers in the form of higher compensation.6
Rauh (2006) focuses on what he calls the firm's risk-management incentive: If a firm survives, it must make up any shortfall between the trust fund and promised benefits. As a result, pension investment decisions affect liquidity and cash flow as well as the value of its put option. If these effects are strong enough, they can outweigh the put-option incentive, leading firms to move away from risky pension assets. Indeed, looking at small to medium sized firms, Rauh finds that firms with the strongest put-option incentive to shift risks to employees--those closest to default--tend to invest in safer assets than firms with well-funded pensions.
Another factor, identified by Lucas and Zeldes (2006), is that firms may invest pension assets in equity as a hedge against future wage growth (and thus future pension obligations). In this framework, equities provide a hedge against wage growth as long as wage growth and equity returns are sufficiently correlated. Finally, a number of authors, including Bader (2003), Bodie (1998, 2000), Gold and Hudson (2003), Ralfe et al. (2004), and Wilcox (2006), have recently argued that pension funds should hold only bonds for various reasons, including immunization against interest rate movements, reduced balance-sheet risk, improved pension security for employees, improved tax efficiency and reduced administrative costs. However, none of these papers offers an explicit model of pension funding and investment in the context of an equilibrium model of employee compensation. This paper aims to begin filling that gap by developing a model of pension funding.7
3 The model
The representative worker in our model lives for two periods. The worker consumes in both periods, and supplies one unit of labor when young. Compensation comes in two forms: wages, denoted by ![]() , received when the worker is young, and benefits, denoted by
, received when the worker is young, and benefits, denoted by ![]() , received when the worker is old.8 The budget constraint is given by:
, received when the worker is old.8 The budget constraint is given by:
where
The firm that employs the representative worker is at risk of declaring bankruptcy at the end of the first period; let ![]() be the probability that bankruptcy occurs. In general, the
probability of bankruptcy is correlated with the state of the macroeconomy and hence with the performance of the risky asset; when times are good and the risky asset enjoys a high return, the probability of bankruptcy presumably is relatively low, on average. To simplify the model, however, we
assume that the probability of bankruptcy of the firm we study is uncorrelated with the state of the economy.9
be the probability that bankruptcy occurs. In general, the
probability of bankruptcy is correlated with the state of the macroeconomy and hence with the performance of the risky asset; when times are good and the risky asset enjoys a high return, the probability of bankruptcy presumably is relatively low, on average. To simplify the model, however, we
assume that the probability of bankruptcy of the firm we study is uncorrelated with the state of the economy.9
The level of benefits actually received, ![]() , depends on the level of benefits promised,
, depends on the level of benefits promised, ![]() ; the amount that the firm contributes into the trust fund in the first period,
; the amount that the firm contributes into the trust fund in the first period, ![]() ; and the stochastic characteristics of bankruptcy. If the firm survives into the second
period, the worker receives the full amount of promised benefits. From the worker's perspective, this implies:
; and the stochastic characteristics of bankruptcy. If the firm survives into the second
period, the worker receives the full amount of promised benefits. From the worker's perspective, this implies:
From the firm's perspective, it implies that if the firm survives and the value of the trust fund falls short of
paid in the second period.
On the other hand, if the firm declares bankruptcy at the end of the first period, the worker receives whichever is the lesser of the promised benefit and the proceeds of the trust fund:
In this case, the firm's compensation costs are still reduced by any surplus in the trust fund over promised benefits; but a consequence of declaring bankruptcy is that the firm escapes responsibility for making up any shortfall in trust-fund assets. Thus, when the firm goes bankrupt in the second period, its total compensation costs consist of
paid in the second period.
Note that even though, in this simplified version of the model, the firm is compelled to invest the trust fund entirely in the risk-free asset, the pension benefit is certain only if the firm contributes enough to the pension trust in the first period to fully prefund the pension liability at
the risk-free rate (
![]() ). If the firm contributes less than enough to fund the promised pension benefit at the risk-free rate, the benefit is at risk because the firm might declare bankruptcy and
therefore fail to top up the pension trust in the second period.
). If the firm contributes less than enough to fund the promised pension benefit at the risk-free rate, the benefit is at risk because the firm might declare bankruptcy and
therefore fail to top up the pension trust in the second period.
Let the period utility function be denoted by ![]() . Expected lifetime utility is given by:
. Expected lifetime utility is given by:
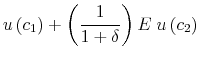 |
(1) |
where
The worker chooses ![]() and
and ![]() to maximize expected utility. The first-order
conditions for consumption imply:
to maximize expected utility. The first-order
conditions for consumption imply:
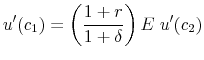 |
(2) |
A critical assumption is that the labor market is perfectly competitive and that workers fully understand the implications of the risk embedded in the promised pension benefit for their expected utility. As a result of that understanding, firms are unable to employ any workers unless the compensation package they offer provides the market-clearing level of expected utility.
The firm minimizes the market value of compensation. The firm's choice variables are the wage paid in the first period, the promised benefit paid in the second period, and the contribution into the trust fund in the first period.
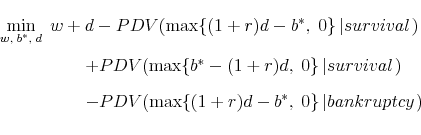
|
(3) |
The expression can be simplified by noting that the trust-fund surplus, if any, reverts to the plan sponsor regardless of whether the firm declares bankruptcy. Thus, the cost minimization problem can be stated as:
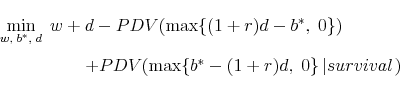 |
(4) |
Because the cash flow associated with the first maximum term is known with certainty once the firm chooses ![]() and
and ![]() , it can be discounted at the risk-free rate, and the term can be simplified as follows:
, it can be discounted at the risk-free rate, and the term can be simplified as follows:
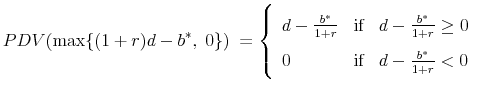
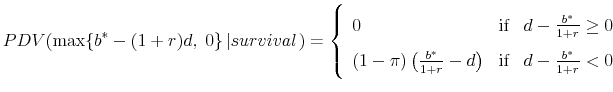 |
(5) |
Collecting terms, we have:
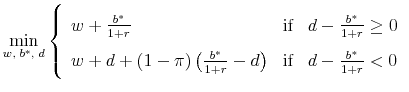
|
(6) |
Note that the direct incentive to the firm, ignoring any adjustment in the compensation demands of the worker, is to minimize the prefunding of the pension obligation by setting
The firm conducts this cost minimization subject to the constraint that the compensation it pays must provide the market-clearing level of utility.12 The firm also assumes that the worker arranges consumption in the optimal manner between the first and second period, and that the budget constraint is binding. For convenience, we record these constraints here:
Minimum utility:
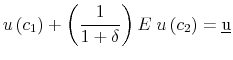
Optimal saving/consumption decision:
![\displaystyle u'(c_1 ) = E\left[ {\frac{{(1 + r)}}{{1 + \delta }}} \right]\;u'(c_2 )](img26.gif)
Budget constraint:
4 Results
We find that the firm minimizes its total compensation cost by contributing at least the full amount of the promised benefit in the first period,
![]() . In this case, the firm's minimized cost is given by:
. In this case, the firm's minimized cost is given by:
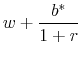
We demonstrate this result both numerically and analytically. To show the result numerically, we implement and solve a simple numerical model. In this model, utility exhibits exhibit constant relative risk aversion and the subjective rate of discount is assumed to be equal to the interest rate.
To solve the model, we first compute the level of utility associated with an initial set of compensation parameters ![]() ,
, ![]() , and
, and ![]() and then search for the combination of
and then search for the combination of ![]() and
and ![]() that minimizes costs for a given pension obligation
that minimizes costs for a given pension obligation ![]() and subject to the
constraint that utility equals
and subject to the
constraint that utility equals
![]() . We solve the model for both plausible and extreme specifications of risk aversion and the risk-free return,13 and with the exception of linear utility, all of our specifications produce the same result: The firm optimally selects
. We solve the model for both plausible and extreme specifications of risk aversion and the risk-free return,13 and with the exception of linear utility, all of our specifications produce the same result: The firm optimally selects
![]() .
.
We can also demonstrate the result analytically. If the firm makes the pension benefit risky, the worker will receive (in present-value terms)
![]() with probability
with probability ![]() and
and ![]() with probability
with probability ![]() . Of course, this is an inferior offer from the worker's perspective relative to
receiving
. Of course, this is an inferior offer from the worker's perspective relative to
receiving
![]() with certainty, and the worker will demand to be compensated for that loss. Does any level of compensation exist that both (a) the firm would be willing to pay in return for
being allowed to make the pension promise risky, and (b) the worker would see as sufficiently generous as to rationalize accepting a risky promise rather than a risk-free one? At most, the firm would be willing to pay
with certainty, and the worker will demand to be compensated for that loss. Does any level of compensation exist that both (a) the firm would be willing to pay in return for
being allowed to make the pension promise risky, and (b) the worker would see as sufficiently generous as to rationalize accepting a risky promise rather than a risk-free one? At most, the firm would be willing to pay
![]() because that is the market value of the direct financial benefit to the firm from making the benefit risky rather than risk-free (as can be seen from equation (6)). To
see whether the firm could ever get workers to accept a risky benefit, consider the extreme case in which the firm transfers all of that value back to workers with certainty, in return for being allowed to make the pension promise risky. In that case, the payments to the
worker would have the following structure:
because that is the market value of the direct financial benefit to the firm from making the benefit risky rather than risk-free (as can be seen from equation (6)). To
see whether the firm could ever get workers to accept a risky benefit, consider the extreme case in which the firm transfers all of that value back to workers with certainty, in return for being allowed to make the pension promise risky. In that case, the payments to the
worker would have the following structure:
![]() with certainty, plus
with certainty, plus
![]() when the firm does not declare bankruptcy--that is, in
when the firm does not declare bankruptcy--that is, in ![]() percent of the outcomes in the second period, and
percent of the outcomes in the second period, and ![]() in the other
in the other ![]() percent of
the outcomes. From the perspective of the worker, the deficiency of this even this offer--the most generous one the firm would be willing to make--is clear: Even with the greatest compensation the firm would be willing to make, the expected value of the payment to the
worker is only
percent of
the outcomes. From the perspective of the worker, the deficiency of this even this offer--the most generous one the firm would be willing to make--is clear: Even with the greatest compensation the firm would be willing to make, the expected value of the payment to the
worker is only
![]() ; but the payment under this risky approach has positive variance, a characteristic that makes the proposition strictly inferior to receiving
; but the payment under this risky approach has positive variance, a characteristic that makes the proposition strictly inferior to receiving
![]() for sure. In other words, the firm is offering the worker a lottery that has an expected value of zero. A straightforward application of Jensen's inequality
demonstrates that as long as utility is strictly concave, this lottery must decrease utility.14 To make the worker indifferent between this lottery and a
fully funded pension with
for sure. In other words, the firm is offering the worker a lottery that has an expected value of zero. A straightforward application of Jensen's inequality
demonstrates that as long as utility is strictly concave, this lottery must decrease utility.14 To make the worker indifferent between this lottery and a
fully funded pension with
![]() , the firm would therefore have to increase compensation by more than
, the firm would therefore have to increase compensation by more than
![]() , the value of the cost reduction. We conclude that the firm cannot reduce total costs by underfunding its pension.
, the value of the cost reduction. We conclude that the firm cannot reduce total costs by underfunding its pension.
The analytical and numerical results follow inevitably from the curvature of the utility function and from the fact that the worker is unable to diversify away the idiosyncratic risks associated with bankruptcy. The concavity of utility implies that workers are risk averse, and the inability to diversify away the idiosyncratic risk means that the worker will demand a wage premium in excess of what would be required by participants in the bond market who can, by hypothesis, diversify away all idiosyncratic risk. Thus, the most efficient funding strategy for the firm must be to contribute the full present discounted value of promised benefits.
5 Interpretation
Our model provides a clear result that firms minimize their costs when they fully fund their pension promise (and preliminary work underway suggests an equally clear result that the cost-minimizing investment strategy is an all-bond portfolio). While these results may be consistent with some of the prior literature, they are unquestionably at odds with the current practice of private DB funds. This gap raises the question of what elements of reality are missing from our model. In this section we consider a few of the leading possibilities.
The frictions we examine can be summarized by a simple taxonomy: one or more of the key players in the model (employees, employers, shareholders, or taxpayers) face informational or other barriers that prevent the equilibrium result from obtaining. We examine these possibilities one at a time.
Employees. A key assumption of our model is that employees fully understand and value the effects of the risk characteristics of the pension plan on their own utility. If informational costs or other frictions prevent workers from demanding additional compensation when the risk of their DB promise goes up, then our result will not hold. Prior to the recent spate of DB terminations and freezes, plan failures were quite rare, so it is plausible that many workers were not accustomed to thinking of a pension promise as a risky asset.15
An additional possibility is that employees understand but do not value the pension risk in the way that we model. For example, perhaps workers are indifferent toward a risky pension promise because they are also shareholders and they feel that whatever is good for the company is good for them (despite the undiversifiable risk they face from the firm's fortunes).16
Employers. Even if employees understand and value the risk they face from their pension promise, the mechanism may break down if employers face institutional rigidities or other considerations in managing their pension funds. For example, debt instruments do not go out as many years into the future as pension liabilities do, making it impossible to literally immunize all pension liabilities. These rigidities may prevent firms from offering risk-free pension promises even when it is in their long-term interest to do so.17 Over time, firms might offer more debt at very long maturities if they perceived the market as demanding it.
Shareholders. Another key assumption in the model is that firms are minimizing costs in order to maximize shareholder value. If informational costs prevent shareholders from properly assessing the risk of the pension promise (and hence the total economic costs facing the firm), then again the mechanism cam break down and the result may not hold. The most likely margin for this scenario to take place in reality is related to the arcane and difficult set of accounting rules that apply to pension obligations. As we noted in the introduction, current accounting rules allow firms to book expected pension fund earnings as income, while smoothing any discrepancy between expected and actual earnings over five years. This treatment effectively allows firms to book the equity premium as an asset while displaying only a fraction of the associated variance in its reported earnings, providing an incentive to invest the pension fund significantly in risky assets. While market values of pension assets and liabilities are reported in footnotes, Coronado and Sharpe (2003) show that investors appear to be fooled by the balance sheet and income statements and to factor in only a portion of the detail provided in the footnotes. The Financial Accounting Standards Board is currently undertaking a long-term project to revisit pension accounting, so this informational friction may be reduced in the relatively near future.
Taxpayers. Finally, an additional breakdown of the model can occur through the last key economic player, which is the taxpayer. Our current model provides no role for taxpayers because there is no pension insurance. Our result would disappear if employees were fully insured against the loss of benefits in the event of bankruptcy, because in that case, worker compensation would not depend on the firm's pension funding policy and the firm would be either indifferent over funding strategies (if PBGC premiums were economically fair) or would strictly prefer a risky funding strategy (if PBGC premiums were less than economically fair). In reality, the PBGC does not fully insure pension benefits (giving workers an incentive to monitor funding strategies), but their premiums are not fairly priced, both because they are too low in general (CBO, 2005), and because they do not depend on the risk of the pension promise.18 In principle, the mispricing could be severe enough to cause the firm in our model to prefer a risky pension promise--despite the surcharge assessed by workers--because some of the risk is shared with taxpayers.
6 Conclusion
It has long been recognized that underfunded pensions allow firms to shed cost in times of bankruptcy. At first blush, this form of implicit insurance seems to raise the possibility of moral hazard, with firms maximizing pension risk at the employees' expense. In the model we present here, the firm's optimal pension funding strategy is not to shift pension risk to employees, but rather to structure the pension fund so that it will deliver promised benefits in all states of the world. Our argument relies entirely on the principle that workers will demand to receive sufficient total compensation to allow them to achieve a market-clearing level of utility. In our model, risk-averse workers faced with a risky pension will bargain for a wage increase that ends up costing the firm more than the reduction in the market value of pension costs due to underfunding.
In work underway, we are extending our model to generalize the asset-pricing assumptions we use here, incorporate a portfolio-allocation decision by the pension fund, and allow additional richness such as mispriced PBGC insurance. In addition, we seek to explore conditions under which risky pensions could be part of an equilibrium compensation package.
Bibliography
Appendix
The value of the pension put can be calculated using standard binomial methods. To price the option, it turns out to be helpful to distinguish between two regimes: one where the firm contributes an amount to the pension fund sufficient to guarantee promised benefits in all states, and one where the pension fund will always fall short of promised benefits if the firm goes bankrupt. In the first case, the value of the pension put is simply 0 since the contingent liability does not alter the firm's costs. In this case, total compensation costs are simply given by
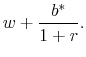
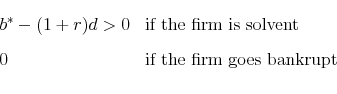
![\displaystyle \left[ {\begin{array}{*{20}c} {b^* - (1 + r)d} \ 0 \ \end{array}} \right] = \left[ {\begin{array}{*{20}c} {1 + r} & {1 + r_d^h } \ {1 + r} & {1 + r_d^l } \ \end{array}} \right]\left[ {\begin{array}{*{20}c} {\omega _1 } \ {\omega _2 } \ \end{array}} \right]](img46.gif)
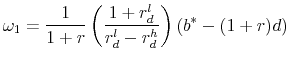
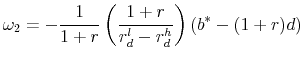
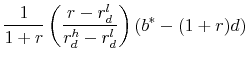
We assume that own-firm debt pays ![]() if the firm remains solvent and
if the firm remains solvent and ![]() if the firm goes bankrupt. The mean-zero error term can therefore take on the following two values. The mean-zero error term can therefore take on the following two values.
if the firm goes bankrupt. The mean-zero error term can therefore take on the following two values. The mean-zero error term can therefore take on the following two values.