Implied Interest Rate Skew, Term Premiums, and the "Conundrum"
The skew, irrespective of the mean and variance, of investors' interest rate expectations may affect required bond yields over expected short rates. Indeed, evidence suggests that the near-term skew of the option-implied distribution of short-term interest rates correlates with distant-horizon term premiums, as derived from a latent-factor affine term structure model (ATSM). Reduced-form models that include skew generally fit the data well and actually better "explain" variation in the term premium during the so-called "conundrum" than during other periods of the May 1989 to May 2006 sample. Moreover, estimates suggest that skew accounts for over half of the movement in term premiums during the "conundrum," considerably more than any other correlate. Caveats regard the term structure of skew as well as alternative measures of the term premium. Indeed, regression analysis of movements in term premiums is plagued by specification bias on both the left- and right-hand-side of the equation.
1. Introduction
Alan Greenspan, then Federal Reserve Chairman, lodged "conundrum" into the lexicon of fixed income analysts with his February 2005 testimony to Congress, as the substantial drop in global bond yields amid increases in the federal funds rate puzzled many financial market participants. Subsequent analysis, particularly the application of latent-factor affine term structure models (ATSMs) (Kim and Wright, 2005),2 suggests that the drop in longer-term yields during the last tightening cycle appears to reflect declines in term premiums, as opposed to expected short rates, which actually increased somewhat over the episode. In addition to the general motivation for linking the output of latent factor models to observable variables, the "conundrum" has unleashed considerable interest in explaining movements in term premiums, defined as the required yield on a bond above the expected path of interest rates through its maturity.
This paper extends previous research (Kim and Wright, 2005; Backus and Wright, 2007; Durham, 2006a) that addresses time-varying ATSM-based term premiums by focusing on a possible correlate absent from the literature, option-implied interest rate skew. As outlined further below, the skew, irrespective of the mean and variance, of investors' interest rate expectations potentially affects required bond yields over the anticipated short rate path. Briefly, if the risks to rates are skewed to the downside (upside), borrowers will pay a lower (higher) premium to lock in borrowing costs over a given horizon. From the perspective of investors, long-term bonds are more (less) attractive if the distribution of rates is skewed to the downside (upside), because expected capital appreciation is therefore skewed to the upside (downside), all else equal. To invoke informally a consumption-based CAPM approach, skew may capture investors' propensity to pay more for assets that are expected to provide compensation during broader economic downturns.
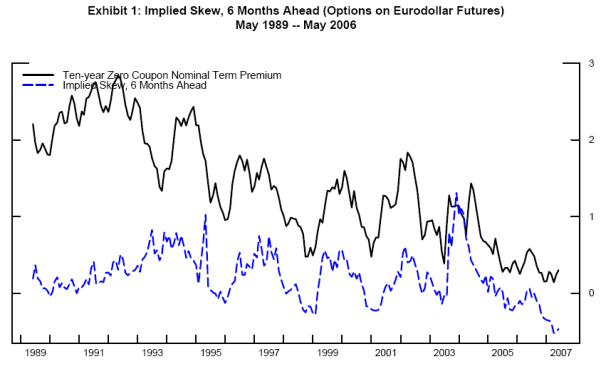
Some evidence strongly supports this hypothesis, as the correlation between six-month-ahead skew derived from options on Eurodollar futures and the ATSM-based ten-year zero-coupon term premium is positive and statistically significant over the monthly sample from May 1989 through May 2007 as well as alternative periods. In particular, the "conundrum" does not seem to be particularly problematic for the complete regression model, as the residuals are actually lower on average during this episode, which raises the issue of just why this particular period is so puzzling. Moreover, variation in near-term skew helps account for more of the decline in term premiums during the "conundrum" period than any other correlate. Specifically, an out-of-sample prediction based on a reduced-form model estimated notably before the most recent tightening cycle (i.e. using data only through May 2004) suggests that the subsequent variation in skew would correspond to an approximate 35 basis point decline in the premium between June 2004 and June 2006. The actual net decline was about 70 basis points.
There are some strong caveats. For example, the horizons of implied skew and term premiums should largely correspond, and, possible liquidity issues and limited data aside, estimates of skew derived from longer-dated interest rate caps generally do not corroborate the result. Also, the estimate of the term premium is based on a Gaussian ATSM in which the skew of the disturbances is necessarily zero, and therefore the correlation perhaps fundamentally contradicts the underlying model. And, non-model based estimates of the term premium do not similarly seem to correlate with skew estimates. These caveats aside, no other variable is robust to such sensitivity analysis, and therefore the findings with respect to skew do not seem comparatively fragile. Indeed, there seems to be considerable specification bias on both the left- and right-hand-sides of the equation in reduced-form models of the term premium.
Section 2 discusses other possible determinates of the term premium, and Section 3 outlines the arguments regarding implied skew and some baseline empirical results. Section 4 discusses the "conundrum" in more detail with particular respect to developments in skew during the episode. Section 5 describes the sensitivity analyses regarding sample selection, the term structures of skew and term premiums, and alternative measures of the term premium. Section 6 concludes.
2. What drives term premiums?
Latent factor arbitrage-free models of the term structure are understandably unsatisfying to some, insofar as the underlying factors are by construction unobservable. ATSMs may fit the data well, but they provide no direct economic interpretation or intuition. However, one can get a sense of what economic and financial variables are relevant to yield curve movements by examining the empirical correlates of the output of the model--namely, the expected path of the short rate and term premiums.3 With respect to the latter, term premiums derived from some ATSMs are a function of the volatility and market price of risk parameters. Therefore, empirically speaking, time variation in the term premium should be related to observable proxies for perceived uncertainty and attitudes toward risk.
To broadly guide the specification search, consider the closed-form expression of the term premium from a (single-factor) Vasicek (1977) model in which the market price of risk is a function of the underlying latent factors. The underlying stochastic process is
where
And finally, given the closed-form solution to the model, the expression for the term premium--in this case the difference between the forward rate at some horizon,
Therefore, the term premium is a function of
For example, previous papers report an empirical link between interest rate option-implied volatility and ATSM-based term premium estimates (Kim and Wright, 2005; Backus and Wright, 2007; Durham, 2006a). Therefore, the specifications (of ten-year zero coupon term premiums) below include the implied volatility derived from options on ten-year Treasury note futures. Notably, this captures the implied volatility of the underlying over the life of the option and not the horizon of the term premium,6 but nonetheless, the coefficient should be positive.7
The use of observed implied volatility measures necessitates two caveats. First, implied volatility can be thought of as expected volatility and a premium for volatility risk and therefore with respect to (3) can be related to either ![]() or
or ![]() . Second, although there are alternatives, the primary measure of the term premium below again is based on
an ATSM in which
. Second, although there are alternatives, the primary measure of the term premium below again is based on
an ATSM in which ![]() does not vary. Therefore, any correlation between the term premium and implied volatility may seem somewhat coincidental, although again the premium for
volatility risk embedded in implied volatility and
does not vary. Therefore, any correlation between the term premium and implied volatility may seem somewhat coincidental, although again the premium for
volatility risk embedded in implied volatility and ![]() are still time-varying.
are still time-varying.
Also under the general volatility rubric, the model includes the variance of responses from the Michigan survey of short-run inflation expectations. This is strictly a measure of disagreement among respondents and not a measure of individual uncertainty. However, disagreement and uncertainty tend to be positively correlated in survey data. Presumably, the inflation risk premium component of the nominal term premium should be positively correlated with uncertainty about future inflation, and the estimated coefficient should be positive (Durham, 2006a). Of course, uncertainty regarding the outlook for the real economy is also relevant on this score. However, inflation and output dispersion among survey respondents is quite closely correlated, for example, using Blue Chip data.8
A number of other variables might track attitudes toward risk or relative preferences for Treasury securities. For example, the implied volatility on the S&P 500 might affect the demand for safe assets, insofar as increased (decreased) uncertainty in the stock market prompts investors to allocate from equities (Treasuries) into Treasuries (equities). Assuming no change in the expected path of short rates, term premiums should decline (increase), and therefore the estimated parameter should be negative. Also under this rubric, foreign demand for U.S. assets, specifically Treasury securities, might potentially have an effect.9 There are no obvious choices for proxies, but the correlation between foreign custody holdings of U.S. Treasury securities (as a ratio of Treasury securities outstanding) and the term premium should be negative.
Finally, there is some evidence that term premiums are countercyclical (Backus and Wright, 2007), as uncertainty and/or the market price of risk could conceivably be greater during economic downturns. There are a number of possible proxies--Backus and Wright (2007) document the positive correlation between unemployment and distant-horizon forward rates--but the following regressions include the contemporaneous value of capacity utilization in the regressions,10 and the expected sign is negative.11
Turning to some initial results, Regression 1 in Table 1, which covers average monthly data from May 1989 through May 2007, largely reconfirms some of these previous findings. For example, ten-year Treasury note implied volatility and the (dispersion) variance of Michigan survey respondents are both positively correlated with the ATSM-based ten-year zero-coupon term premium, as expected, although the parameter on the survey data is only significant with 10 percent confidence.12 The volatility on the S&P 500 and foreign custody holdings of U.S. Treasuries enter with negative coefficients, again as anticipated, that are statistically significant. Finally, the coefficient for capacity utilization has the expected negative sign, but the estimate is statistically insignificant, and the R-squared for the model is 0.726.
Before turning to skew, note that this overall result--from the individual coefficients to the overall fit of the model--is somewhat reassuring in the context of a latent-factor model. That is, the underlying factors are of course not observable, but the output of the model, at least with respect to term premiums, seems to be consistent with some economic interpretation.13
3. Why might skew affect term premiums?
The intuition regarding skew and term premiums can be expressed from different perspectives. Consider first the borrower and think of the term premium as the relative price of locking in borrowing costs over some fixed horizon. If the implied distribution of expected short rates is skewed to the downside, then irrespective of the mean or variance of that density, borrowers are more inclined to roll over short-term obligations, because the odds are tilted toward lower future funding costs, and therefore the relative price of securing rates over longer horizons drops. Conversely, borrowers would pay more to avoid rolling over debt if the risks were skewed toward higher borrowing costs over the horizon. This implies a positive correlation between skew and term premiums.
The implications are identical, but now consider the perspective of the lender or investor. Longer-term bonds are more attractive, all else equal, if the distribution of expected rates over a given horizon is skewed to the downside, because, simply given the inverse relation between yields and bond prices, capital appreciation is skewed to the upside, all else equal. With negative interest rate skew, investors are willing to pay more to hold longer-dated bonds, bond prices are comparatively higher, and the term premium component of yields is lower. One could also add some consumption-based CAPM flavor to this logic if downside skew in rate expectations is associated with deleterious macroeconomic outcomes. The investor conceivably pays more for an asset (e.g. a longer-term bond) that hedges (by way of capital appreciation) against unfavorable states of the world.14
Turning to measurement, similar to implied volatilities, the skew of the distribution of expected interest rates is derived from options prices, but notably using quotes both at-the-money and otherwise. Following Breeden and Litzenberger (1978), the value of an option can be expressed as its discounted expected value under the risk-neutral measure, as in
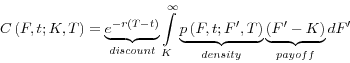
where
One can of course recover moments given the density, and this paper uses two measures of skew that are closely correlated in practice.15 Perhaps the most standard calculation,
where
where
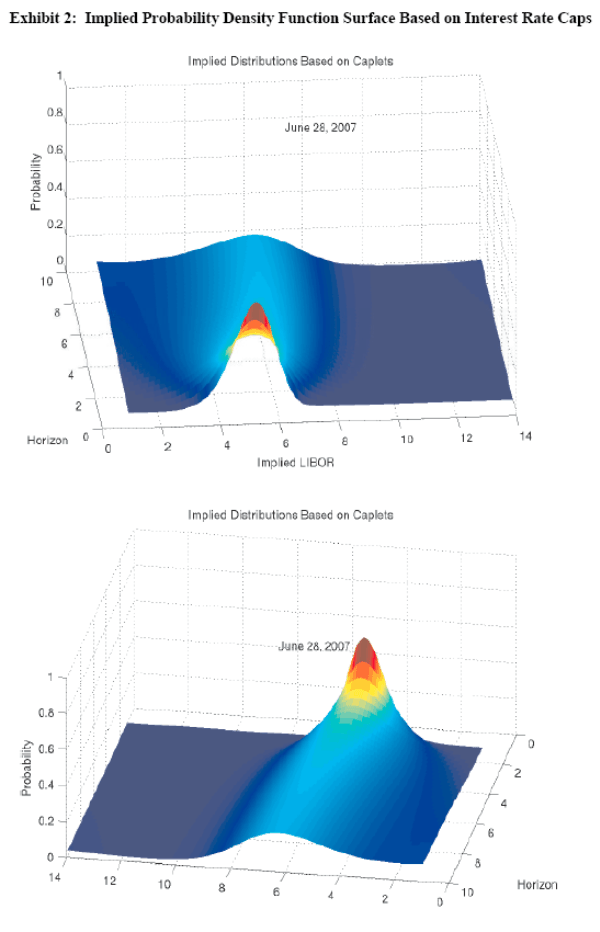
This paper uses two derivative instruments. First, options on Eurodollar futures measure near-term skew at the six-, nine-, and twelve-month horizons. To reflect the fact that the FOMC moves in 25-basis-point increments, the underlying densities are actually point distributions in 25-basis-point increments.18 Exhibit 1 shows the time series of skew at the six-month horizon, along with the ATSM-based estimate of the term premium. Interest rate cap(let)s provide a read on skew at longer horizons, and the underlying distributions are continuous. Exhibit 2 illustrates the implied probability density surface based on interest rate caps on June 28, 2007.19
Turning to empirical results, Regression 2 in Table 1 adds the implied skew from the six-month-ahead Eurodollar implied PDF. Notably, the coefficient is safely statistically significant, and the magnitude of the coefficient is considerable. The R-squared values increase from 0.726 to 0.764.
4. Where's the "Conundrum?"
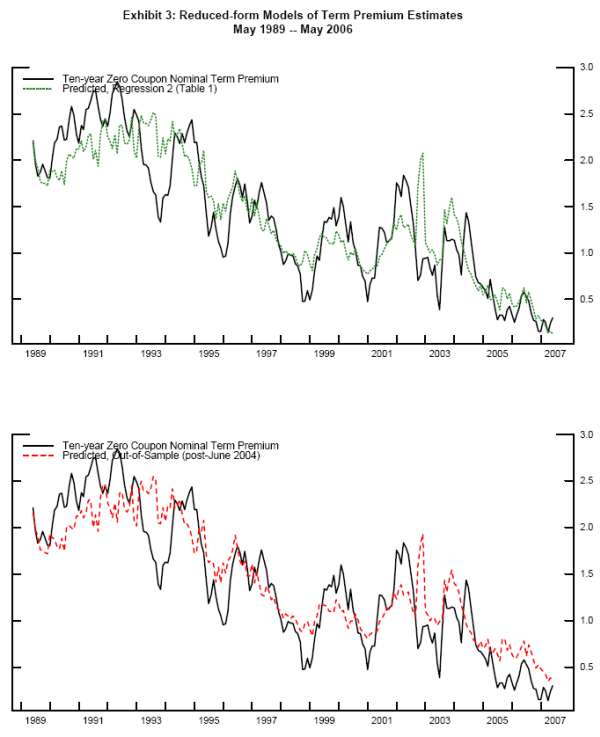
As noted in Exhibit 3, the model that includes skew notably plugs some of the gap between the predicted and actual values during the so-called "conundrum" period. Visual inspection suggests that the model does not seem to fit the conundrum period any worse than any other part of the sample. Indeed, the model actually performs comparatively better during this period--the average absolute value of the size of the residual in the complete sample is about 26 basis points,20 but the average absolute value of the residual from July 2004 through June 2006--the period of the most recent tightening cycle--was about 16 basis points. Moreover, the average residual, at one basis point, is not even negative over this period, and therefore term premiums do not appear consistently to be "too low."
The coefficients from Regression 2 and variation in the underlying independent variables suggest that skew may have played a notable role during this particular period, even though in general the contribution of skew to variance "explained" over the complete sample is perhaps somewhat modest. From the day before the FOMC first raised rates on June 30, 2004 through the day of the last tightening on June 29, 2006, the estimated zero-coupon term premium declined 71 basis points on net (from 128 to 57 basis points). The estimated parameter suggests that the move in skew over the same period implies a 38 basis point drop in the term premium,21 greater than half the total net decline. Also, skew "accounts" for much more of the decline in the term premium during the period than any other variable. The drop in ten-year Treasury note implied volatility and the increase in capacity utilization during the conundrum period suggest 12 and 5 basis point declines in the term premium, respectively, and the underlying movements in Michigan inflation survey variance, S&P 500 implied volatility, and foreign custody holdings of U.S. Treasuries all contrarily suggests very modest increases in term premiums.22
One natural suspicion regarding these results is that the coefficients are in-sample and derived using data from the conundrum period. However, estimation of the coefficients using the May 1989 - May 2004 sample, notably before the first tightening of the most recent cycle, nonetheless suggests that the model performs well out-of-sample from June 2004 through May 2007. The average absolute value of the residual, at 21 basis points, over the last tightening cycle is actually lower than the total sample average of 27 basis points. Also, the predicted change in the term premium given the variation in skew over the cycle, at 34 basis points, is only slightly lower than the in-sample estimate. Therefore, this simple model would have performed reasonably well before the onset of the last tightening cycle and the ensuing fall in long rates.
To digress somewhat, if the "conundrum" is simply about why the term premium component of longer-dated yields declined over the most recent tightening cycle, then strong caveats regarding econometric correlations and true causation aside, the model goes some way toward addressing the puzzle in general, and skew seems to play an important role in particular. In fact, judging again from the relative size of the residuals, any "conundrum" over this particular period, even on an out-of-sample basis, is not readily apparent.
But perhaps the move in term premiums per se is not regarded as particularly curious. Is the conundrum simply that long term rates fell as the FOMC raised short rates (or removed policy accommodation), which does contrast with the rise in long rates during the 1986, 1994, and 1999 tightening episodes? But of course, the starting and ending points of tightening episodes are inherently different. And in principle, longer rates could move either up or down or if policy firming is greater or less than expected, respectively.23 Put more broadly, that movements along the yield curve are not perfectly correlated hardly constitutes a new puzzle for fixed income analysts.
Could the conundrum also regard the particular constellation of movements in expected short rates (up only slightly) and term premiums (down considerably) over the period? However, at least the (multi-factor) ATSM employed here certainly does not restrict expected short rates and term premiums from moving in opposite directions, which does not seem inconsistent with theory and too uncommon in practice, even at a daily frequency. As on February 27, 2007, for example, investors can revise down sharply their outlook for policy amid greater uncertainty and higher term premiums. Conversely, market participants may revise the path for policy rates upward slightly amid decreased uncertainty and less aversion to risk.
Perhaps analysts should be more precise about where, exactly, the conundrum lies.24 To claim that interest rates (or term premiums) are "too low" is a judgment that ultimately requires some underlying model, reduced form or otherwise. But if variation in term premiums generally accords with developments in other factors, then possibly the "conundrum" actually regards the expected path of the short rate. That is, perhaps the puzzle regards the "dogs that did not bark" as opposed to those that did. Whether or not the expected path of short rates implied by ATSMs or survey data was "too low" vis-à-vis investors' forecasts for inflation and output during the period is an unanswered question beyond the scope of this paper.
5. Some sensitivity analysis and caveats
Before inferences get too far afield, some sensitivity analysis and caveats regarding the relation between skew and term premiums more generally is instructive. These regard parameter stability, the horizon of skew, and alternative measures of the term premium.
5.1. Sample selection
The relation seems fairly robust to sample selection, particularly with respect to more recent periods. Regression 3 includes data only from May 1998 through May 2007,25 and the safely significant coefficient on six-month-ahead skew is actually larger than in the complete sample (0.740 vs. 0.545). None of the other possible correlates of the term premium are statistically significant in the regression--only skew seems to matter. In addition, at noted in Row 1 in Table 2, given daily data from May 10, 2005 through June 21, 2007, the (univarite) correlation between the term premium and skew is still significant and highly positive.
5.2. Horizons of skew and term premiums
The results outlined previously specifically document the relation between skew at the six-month horizon and ten-year zero-coupon term premiums. True, options at shorter horizons are generally much more liquid, but ideally distant-horizon skew is more relevant for longer-dated term premiums, and near-term skew is more germane to shorter-dated term premiums. To address this issue, some alternative specifications examine whether the result is robust when the horizons for skew and the term premium more closely correspond. For example, Regressions 4 and 5, which cover the May 1998 - May 2007 sample, include the implied skew from distributions derived from options on Eurodollar futures that expire nine and twelve months ahead on the left-hand-side.26
Even though these horizons still hardly match that of the term premium, the results cast some doubt on the general relation. Regression 4 produces a positive coefficient for nine-month-ahead skew that narrowly misses the 10 percent confidence level, and the parameter for twelve-month ahead skew from Regression 5 is statistically insignificant. Also, as Rows 2 and 3 of Table 2 indicate, the daily univariate correlations between skew at these horizons and the term premium are statistically significant, but the magnitude is notably less than that for the six-month horizon.
Although liquidity may be an issue and data are limited, a more direct assessment uses skew from implied distributions derived from interest rate caplets at distant horizons. Data are only available from May 10, 2005 through June 21, 2007, but as Rows 4 and 5 in Table 2 suggest, the correlation between the term premium and implied skew five and ten years ahead is actually slightly negative.
The negative correlation, although based on few data, is somewhat curious, perhaps especially given that six-month-ahead skew from options on Eurodollar futures is still positively correlated with ten-year-ahead estimates from caplets, with a pairwise coefficient of about 0.38 over the sample. There are also differing views among practitioners as to whether one can extract "fundamental" signals from far-dated out-of-the-money interest rate caps, as flows might be more related to transient "technical" hedging demands as opposed to views on the distribution of expected policy rates in the very distant future. Indeed, at least over this sample, caplet-based skew at more distant horizons is just as volatile as skew in the near-term,27 which presents a "sensitivity puzzle" under the assumption that expectations for the path for policy are more stable than estimates of the equilibrium policy rate well beyond the current business cycle. Nonetheless, taken at face value, and for these immediate purposes, limited available data suggest that skew at longer-horizons supports the hypothesis.
Although longer-dated term premiums may be of primary interest in the context of the "conundrum," one can also more closely match horizons by considering near-term skew and term premiums at the shorter end of the curve. Toward that end, Regression 6 includes the ATSM-based estimate of the instantaneous forward (Treasury) term premium one year ahead on the left-hand-side. The coefficient on six-month-ahead skew is statistically significant, but interestingly the magnitude is somewhat less than that for the ten-year zero coupon term premium (0.533 vs. 0.740). Moreover, perhaps more germane to the expected path for monetary policy, Regression 7 includes on the left-hand-side the year-ahead forward term premium from an ATSM calibrated exclusively to near-term forward rate agreements.28 This model produces a statistically insignificant coefficient for skew. Therefore, these models curiously suggest that longer-dated term premiums respond more than shorter-dated premiums (if at all) to near-term skew.
5.3. Alternative measures of the term premium
Another critical caveat regards the particular measure of the term premium under consideration. In closed-form, the term premium from the Gaussian three-factor model ATSM is a function of volatility and the market price of volatility risk, notably not skew. All disturbances are normally distributed and have zero skew by definition, and therefore the positive correlation between six-month-ahead Eurodollar option-implied skew and ten-year zero-coupon term premiums, while perhaps intuitive and robust econometrically, is formally perplexing within the confines of this particular term premium estimate.
Therefore, the question is whether alternative non-model-based measures of the term premium also produce a statistically significant relation. These measures are perhaps generally not preferable the ATSM-based estimate, largely given the absence of the no-arbitrage constraint, but at least they do not rest on some of the key (Gaussian) assumptions that are particularly restrictive in the case of skew. There are surely other worthy metrics, but such alternatives include the slope of the Eurodollar futures curve between four and five years ahead (Regression 8), the slope of the instantaneous Treasury forward curve between nine and ten years ahead (Regression 9),29 and the predicted excess return of five-year over one-year Treasury securities from Cochrane and Piazzesi (2005).30
Even though each measure notably declined during the "conundrum" period,31 the covariance matrix of these various estimates over the May 1998 - May 2007 sample suggests considerable uncertainty about measures of the term premium in general, as the (pairwise) correlation coefficients between the ATSM ten-year zero-coupon measure and these alternatives is 0.220, -0.307, and 0.273, respectively. Perhaps unsurprisingly, therefore, Regressions 8, 9, and 10 produce statistically insignificant coefficients for six-month-ahead skew. Thus, the result does in fact seem sensitive to the specification of the term premium on the left-hand-side, and the model that explicitly suggests that skew is not priced actually produces the robust result.
6. Discussion
Insofar as the "conundrum" in interest rates over the most recent Federal Reserve tightening cycle reduces to a puzzle about the level of term premiums, one measure of implied interest rate skew goes some way in addressing the issue. This is not to suggest that skew "explains" the "conundrum," as the query might simply shift to an examination of why expected skew and the market price of skew moved considerably over the period. And, again, this paper makes no progress in delineating changing expectations from changing risk tolerances with respect to skew, although the same can be said for implied volatility. Also, the general performance of the reduced-form model does not imply that accounting for movements in term premiums is trivial--explaining movements in yields over any period is hardly a precise science.
The empirical relation between skew and term premiums seems sensitive both to the horizon of skew and to the precise measure of the term premium. But before jettisoning the notion that skew matters, note that few other potential correlates of the term premium are likely to be too robust under this analysis, either. For example, as Table 1 indicates, the proxy for implied volatility, which is also subject to the same issues related to matching horizons, is only statistically significant in three of the ten models. In addition, there are both statistically significant positive and negative coefficients across the ten regressions for inflation survey variance, and S&P 500 implied volatility, foreign custody holdings of U.S. Treasuries, and capacity utilization are not consistently robust. Therefore, comparatively speaking, the results for skew are not exceptionally fragile. The fact that term premium estimates are not very closely correlated is also noteworthy on this score. Unlike, say, empirical studies of excess stock returns or economic growth, concepts for which there is little disagreement regarding measurement, there should also be a healthy dose of suspicion about the left-hand-side when regressing term premiums on possible correlates. To say the least, there is room for empirical progress, and meanwhile inferences should tread carefully.
With respect to future research and analysis, a more ideal measure of the term premium might be derived from a no-arbitrage model of the term structure that somehow includes a time-varying skew parameter, which in turn relates in an intuitive way to term premiums. Such a model is unlikely to be very tractable, but meanwhile, perhaps some non-Gaussian models might be somewhat better suited for these purposes.32
References
Backus, David K. and Jonathan H. Wright, 2007, "Cracking the Conundrum,"
Cochrane, John H. and Monika Piazzesi, 2005, "Bond Risk Premia," American Economic Review, Vol. 95, pp. 138-160.
Dai, Q. and K. J. Singleton, 2002, "Expectations Puzzles, Time-Varying Risk Premia, and Dynamic Models of the Term Structure," Journal of Financial Economics, Vol. 63, pp. 415-441.
Durham, J. Benson, 2006a, "An Estimate of the Inflation Risk Premium Using a Three-Factor Affine Term Structure Model," Finance and Economics Discussion Series, No. 42.
Durham, J. Benson, 2006b, "Additional Analytical Approximations of the Term Structure and Distributional Assumptions for Jump-Diffusion Processes," Journal of Fixed Income, Vol. 15 No. 4 (March), pp. 61-73.
Harvey, Campbell R. and Akhtar Siddique, 2000, "Conditional Skewness in Asset Pricing Tests, Journal of Finance, Vol. 55 No. 3 (June), pp. 1263-1295.
Kim, Don and Athanasios Orphanides, 2005, "Term Structure Estimation with Survey Data on Interest Rate Forecasts," Finance and Economics Discussion Series, No. 48.
Kim, Don and Jonathan Wright, 2005, "An Arbitrage-Free Three-Factor Term Structure Model and the Recent Behavior of Long-Term Yields and Distant-Horizon Forward Rates," Finance and Economics Discussion Series, No. 33.
Shimko, David, 1993, "Bounds of Probability," Risk, vol. 6 no. 4, pp. 33-37.
Vasicek, O., 1977, "An Equilibrium Characterization of the Term Structure of Interest Rates," Journal of Financial Economics, Vol. 5, pp. 177-188.
Warnock, F., and V. Warnock, 2006, "International Capital Flows and U.S. Interest Rates," NBER Working Paper Series, No. 12560.
| Independent Variable | (1)
5/1989 - 5/2007 10-year Zero Coupon Nominal Term Premium |
(2)
5/1989 - 5/2007 10-year Zero Coupon Nominal Term Premium |
(3)
5/1998 - 5/2007 10-year Zero Coupon Nominal Term Premium |
(4)
5/1998 - 5/2007 10-year Zero Coupon Nominal Term Premium |
(5)
5/1998 - 5/2007 10-year Zero Coupon Nominal Term Premium |
(6)
5/1998 - 5/2007 1-year Instantaneous Forward Nominal Term Premium |
(7)
5/1998 - 5/2007 FRA Term Premium, 1 Year Ahead |
(8)
5/1998 - 5/2007 Eurodollar Futures Slope, 4 to 5 Years Ahead |
(9)
5/1998 - 5/2007 Treasury Forward Curve Slope, 9 to 10 Years Ahead |
(10)
5/1998 - 5/2007 Excess 5- vs. 1-year bond return, Cochrane and Piazzesi (2005) |
|---|---|---|---|---|---|---|---|---|---|---|
| 10-year Treasury Note Implied Volatility | 0.1207 | 0.0434 | 0.0029 | 0.1217 | 0.1677 | -0.0322 | 0.0636 | 0.0375 | 0.0075 | -0.0015 |
| 10-year Treasury Note Implied Volatility (standard error) | (0.009)** | (0.450) | (0.952) | (0.172) | (0.071)+ | (0.488) | (0.300) | (0.002)** | (0.514) | (0.716) |
| Michigan Inflation Survey Variance | 0.0099 | 0.0122 | -0.0011 | -0.0054 | -0.0081 | 0.0061 | 0.0148 | -0.0082 | -0.0039 | -0.0022 |
| Michigan Inflation Survey Variance (standard error) | (0.051)+ | (0.022)* | (0.837) | (0.507) | (0.322) | (0.297) | (0.233) | (0.003)** | (0.028)* | (0.006)** |
| S&P 500 Implied Volatility | -0.0169 | -0.0079 | 0.0108 | -0.0041 | -0.0074 | 0.0045 | 0.0160 | 0.0012 | 0.0003 | 0.0008 |
| S&P 500 Implied Volatility (standard error) | (0.045)* | (0.266) | (0.190) | (0.614) | (0.340) | (0.603) | (0.073)+ | (0.669) | (0.833) | (0.123) |
| Foreign Custody Holdings of U.S. Treasuries | -0.0761 | -0.0693 | -0.0156 | -0.0259 | -0.0251 | -0.0235 | -0.0221 | 0.0075 | 0.0032 | -0.0006 |
| Foreign Custody Holdings of U.S. Treasuries (standard error) | (0.001)** | (0.001)** | (0.465) | (0.317) | (0.386) | (0.271) | (0.176) | (0.304) | (0.345) | (0.491) |
| Capacity Utilization | -0.0073 | -0.0111 | -0.0197 | -0.0082 | -0.0062 | 0.0507 | 0.0080 | -0.0283 | -0.0071 | -0.0076 |
| Capacity Utilization (standard error) | (0.813) | (0.689) | (0.548) | (0.861) | (0.895) | (0.172) | (0.763) | (0.016)* | (0.388) | (0.002)** |
| Eurodollar Implied Skew, 6 Months Ahead | 0.5437 | 0.7400 | 0.5330 | -0.2069 | -0.0030 | -0.0357 | -0.0088 | |||
| Eurodollar Implied Skew, 6 Months Ahead (standard error) | (0.007)** | (0.002)** | (0.018)* | (0.343) | (0.954) | (0.281) | (0.515) | |||
| Eurodollar Implied Skew, 9 Months Ahead | 0.1968 | |||||||||
| Eurodollar Implied Skew, 9 Months Ahead (standard error) | (0.443) | |||||||||
| Eurodollar Implied Skew, 12 Months Ahead | -0.0016 | |||||||||
| Eurodollar Implied Skew, 12 Months Ahead (standard error) | (0.990) | |||||||||
| Constant | 2.6197 | 2.9595 | 2.4308 | 1.4258 | 1.0931 | -3.2831 | -0.6449 | 2.1587 | 0.5868 | 0.6435 |
| Constant (standard error) | (0.024)* | (0.006)** | (0.076)+ | (0.376) | (0.499) | (0.021)* | (0.686) | (0.000)** | (0.027)* | (0.000)** |
| Observations | 217 | 217 | 109 | 109 | 109 | 109 | 109 | 109 | 109 | 109 |
| Adjusted R-squared | 0.726 | 0.764 | 0.614 | 0.459 | 0.445 | 0.341 | 0.424 | 0.641 | 0.162 | 0.461 |
| Durbin-Watson | 0.310 | 0.379 | 0.496 | 0.281 | 0.285 | 0.346 | 0.537 | 0.334 | 0.282 | 0.610 |
p values in parentheses
+ significant at 10%; * significant at 5%; ** significant at 1% (Based on Newey-West standard errors)
| Skew Horizon | Correlation Coefficient | |
|---|---|---|
| (1) | 6 months | 0.6335* |
| (2) | 9 months | 0.3704* |
| (3) | 12 months | 0.2326* |
| (4) | 5 years | -0.2573* |
| (5) | 10 years | -0.1962* |