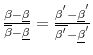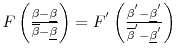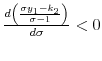Hyperbolic Discounting and Uniform Savings Floors
Keywords: Hyperbolic discounting, general equilibrium, commitment
Abstract:
Previous research suggests that, in partial equilibrium, individuals whose decision-making exhibits a present-bias - such as hyperbolic discounters who tend to over-consume - will be in favor of having a floor imposed on their savings. In this paper, I show it is quite difficult for the introduction of a savings floor to be Pareto-improving in general equilibrium. Indeed, a necessary condition for the floor to be Pareto-improving is that it is high enough to be binding for all individuals. Even in that case, because the equilibrium interest rate is affected by the level of the savings floor, some individuals may prefer to commit to a future time path of consumption by facing a high interest rate (and no floor) rather than a high floor.
JEL: E21, H4, H55
1 Introduction
One common explanation for the widespread support of the provision of retirement income through Social Security is that people realize they will not save adequately on their own, and thus, they prefer to have a mandatory program in place that effectively saves for them. Modelling such
preferences requires a deviation from the standard economic model - for example, assuming that individuals discount future consumption using a hyperbolic function rather than an exponential one. A hyperbolic discounting function induces time-inconsistent preferences that impart a bias for present
consumption: from today's perspective, the discount rate between two future periods, ![]() and
and ![]() , is low, but from the time-
, is low, but from the time-![]() perspective, the discount rate between
perspective, the discount rate between ![]() and
and ![]() is high.
is high.
George Akerlof (1998) articulates this line of thought succinctly: "the hyperbolic model explains the uniform popularity of Social Security, which acts as a pre-commitment device to redistribute consumption from times when people would be tempted to overspend - during their working lives - to times when they would otherwise be spending too little - in retirement. ... The hyperbolic discounting model explains, as the standard model will not, why the young as well as the old should be particularly enthusiastic about Social Security" (p. 187).
Although Akerlof was commenting on the model of Laibson et al. (1998), his reasoning follows more generally from the class of hyperbolic discounting models that focuses on an individual's decision problem given exogenously fixed prices. In these models, individuals value commitment devices that restrict their ability to take certain actions: examples include minimum savings requirements (Amador et al., 2006) and illiquid assets which are particularly costly to use to finance current consumption (Laibson et al., 1998).1 The assumption of fixed prices is appropriate given that the question these models are being used to address is whether an individual will choose to use an available commitment device. The rationale for this assumption is that the decision of any one individual will have a negligible impact on market prices.
The assumption of fixed prices may be less appropriate when the question of interest is whether an individual will support legislation that creates (or preserves) a public commitment device - that is, a commitment device that affects all members of society. A state-mandated retirement savings program like Social Security is a public commitment device in that individuals cannot choose whether to participate in or opt out of Social Security. To the extent Social Security alters the savings of many individuals, it will affect aggregate variables such as the capital stock, and hence, prices such as wages and interest rates. This motivates this paper's general equilibrium analysis of the desirability of Social Security as a commitment device. In particular, I investigate whether the predicted popularity of Social Security based upon fixed-price reasoning is robust to the plausible alternative that individuals consider Social Security's impact on prices.
Modern public retirement savings programs have many complex features: some are pay-as-you-go, others are fully-funded, and most redistribute wealth across generations. A common feature, however, is that they redistribute resources across time for any particular individual. From an individual's perspective, a state-mandated retirement savings program reduces disposable income when she is young and provides resources to help finance consumption in old age. Thus, it works like a savings floor. To focus on the role of a legislated retirement savings program as a commitment device, I will model it as a uniform savings floor, where "uniform" means that the same savings floor applies to all individuals in the population.2
I study the desirability of a uniform savings floor in an economy populated by individuals who are hyperbolic discounters but differ in the intensity of their bias for present consumption. To capture the fact that changes in Social Security are infrequent while savings decisions occur continuously, the savings floor in the model is voted upon and set in an initial period, and individuals earn income and make consumption and savings decisions subject to this floor in subsequent periods. When voting, individuals consider the impact the savings floor will have on future equilibrium interest rates and wages. I use this model to characterize individual preferences over the savings floor and to establish conditions under which individuals unanimously agree that a savings floor is welfare improving.
I find that, in general equilibrium, preferences over the savings floor are (a) extreme - each individual either prefers having no savings floor or having a floor so high that it is a binding constraint on all individuals; and (b) quite often divergent - individuals prefer different extreme floors. Consequently, a necessary condition for the introduction of a savings floor to be Pareto improving is that it is high enough to be binding for all individuals. Even in that case, because the equilibrium interest rate adjusts with the savings floor, some voters may prefer to commit to a future time path of consumption by facing a high interest rate (and no floor) rather than a high floor.
The intuition behind the differences in preferences over the savings floor is as follows. Consider an economy without a savings floor (i.e., no constraint on borrowing). All else equal, individuals who have relatively less present-bias will save more than average in order to supply loans in the debt market to those who have more desire for present consumption. The introduction of a savings floor will reduce the aggregate demand for loans, the interest rate, and thus, the wealth of lenders. This negative wealth effect will counteract the welfare gains from the mitigation of the time-inconsistency for these individuals. On the other hand, individuals who were originally borrowers will benefit from the positive wealth effect that accompanies the decreased interest rate and directly from the constraint itself. It turns out that the wealth effect's opposite impact on lenders' and borrowers' welfare is often strong enough to generate disagreement over the preferred savings floor.3 The one reason disagreement might not occur is if the increase in aggregate production (from increased capital/savings) is large enough to compensate any losses from the shift in the distribution of wealth caused by the changing interest rate. Agreement is more likely to occur the closer the strength of the present-bias of the individual with least present-bias is to that of the average individual.
That each individual's preferred savings floor is an extreme is a result of the hyperbolic discounting. Individuals who have a bias for present consumption lack self-control, can benefit from being constrained, and, in the basic model, cannot become overly constrained. Alternatively, if individuals had time-consistent preferences, then they would suffer from being constrained and might not prefer an extreme policy. In an extension of the model that allows for heterogeneity in both self-control (i.e., the time-inconsistency parameter) and patience (i.e., the long-run discount factor), I show that the extreme result continues to hold if commitment is valued more than the ability to trade with others.
After characterizing individual preferences, I describe how the equilibrium savings floor is chosen and consider some comparative statics with respect to the average amount of self-control in the population. I find that a decrease in average self-control that leaves the median voter unchanged may lead to a less stringent public commitment program. Based on the extreme-preference result, individuals are basically deciding whether to vote for a high savings floor that constrains everybody or a low floor that constrains nobody. Under the high floor, the average level of self-control has no impact on welfare since all agents are constrained. With no floor, on the other hand, lower average self-control implies that the equilibrium interest rate must be higher for the debt market to clear. The substitution effect of the higher interest rate increases welfare because, as a hyperbolic discounter, the median voter overconsumes from the perspective of her initial-period preferences. Thus, as long as the wealth effect of the higher interest rate is not too negative, the median voter is more likely to vote for no savings floor.4 The high interest rate associated with having no floor effectively enables the median voter to commit to less future borrowing.
Selected Literature Review
Laibson (1997) analyzes the desire for commitment devices in general equilibrium but within a representative agent framework in which all agents, by construction, respond to the commitment device in the same way. I depart from the representative agent framework for a couple of reasons. First, for the purpose of investigating the conditions under which individuals reach a consensus on the desirability of Social Security, the representative agent assumption is clearly not compelling. Second, because Social Security is not tailored to fit each individual (rather the same tax and benefit schedules apply to all), it almost certainly will affect different people differently, depending on their response to program parameters and relative prices. Adding heterogeneity across agents in time-inconsistency is a simple way to depart from the representative agent framework.5
Furthermore, adding heterogeneity seems like a natural way to enrich models of hyperbolic discounting preferences. First, the experimental studies from the psychology literature that suggest discount functions are approximately hyperbolic also provide evidence of heterogeneity (Kirby and Herrnstein, 1995). In recent work, Ameriks and coauthors (2004) document differences across individuals in their level of self-control and find a link between self-control and wealth accumulation. Further evidence of heterogeneity of discount factors comes from the enormous dispersion in the accumulated wealth of families approaching retirement, even after conditioning on lifetime earnings, lifetime financial resources, and portfolio choice (Venti and Wise, 2000).6
To my knowledge, Ludmer (2004) is the only other paper which analyzes the welfare implications of commitment devices in a general equilibrium environment that does not admit a representative agent. He considers hyperbolic discounting agents who are ex-ante identical and trade a limited supply of illiquid assets. After characterizing asset prices and the portfolio holdings of agents, he shows that the availability of illiquid assets will generally not lead to welfare improvements. These welfare results arise through changes in equilibrium asset prices in a manner similar to the interest-rate channel described above. My analysis differs from Ludmer's in at least two ways. First, in my model all individuals can make use of the uniform savings floor, whereas only a fraction of agents in his model can utilize the illiquid assets. Second, the savings floor is endogenously determined, while in his paper the supply of illiquid assets is exogenously set.
The rest of the paper is organized as follows. Section 2 lays out the basic model and derives equilibrium conditions, while individual preferences regarding a uniform savings floor are characterized in Section 3. In Section 4, I generalize the extreme-preference result of Section 3 by considering richer forms of agent heterogeneity; specifically, agents differ in their self-control and patience. Section 5 analyzes how the selection of the equilibrium savings floor is affected by changes in the distribution of types. Section 6 concludes, and an Appendix contains all proofs.
2 Basic Model
In this section, I set up the model, describe the agents' decision problems, and derive conditions that must hold in equilibrium. In Section 3, I use these equilibrium conditions to characterize individuals' preferences over a uniform savings floor.
2.1 Environment
The economy lasts for three periods, ![]() . In period 0, the only thing that happens is that the uniform savings floor is voted upon and set. In periods 1 and 2, individuals supply labor
and capital services to firms, receive rent and wage income in return, and decide how much to consume or save subject to the savings floor. A debt market exists in which individuals can borrow from and lend to each other, so it is possible to have negative savings.
. In period 0, the only thing that happens is that the uniform savings floor is voted upon and set. In periods 1 and 2, individuals supply labor
and capital services to firms, receive rent and wage income in return, and decide how much to consume or save subject to the savings floor. A debt market exists in which individuals can borrow from and lend to each other, so it is possible to have negative savings.
There is a unit measure of individuals, who differ only by their time-inconsistency parameter,
![]() , and a type-
, and a type-
![]() agent has preferences represented by the following utility functions:
agent has preferences represented by the following utility functions:
| Period 0 | |||
| Period 1 | |||
| Period 2 |
where
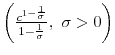 form7 and note that
form7 and note that
There are many identical firms, each with a constant returns to scale production technology, ![]() .8 I let
.8 I let
![]() and assume that
and assume that ![]() is strictly concave. Firms take
prices as given, rent the services of capital and labor, and produce output.
is strictly concave. Firms take
prices as given, rent the services of capital and labor, and produce output.
2.2 Decision Problems
Firms maximize profits at each point in time. Letting ![]() be the rental rate of capital and
be the rental rate of capital and ![]() be the wage rate, first-order conditions for profit maximization imply that
be the wage rate, first-order conditions for profit maximization imply that
Individuals supply both capital and labor services inelastically,9 and thus, they have only two decisions: a period-0 vote and a period-1
consumption-savings decision. Let ![]() denote the price in period 1 of a claim to consumption in period 2,
denote the price in period 1 of a claim to consumption in period 2, ![]() denote period-1 income, and
denote period-1 income, and ![]() be a savings floor (i.e., borrowing constraint). In period 1, given
be a savings floor (i.e., borrowing constraint). In period 1, given ![]() ,
, ![]() ,
, ![]() and
and ![]() each agent chooses savings,
each agent chooses savings, ![]() , to solve
, to solve
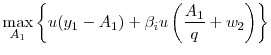 |
|||
| s.t. |
Let
In period 0, agents vote over the period-1 savings floor. Each individual's most preferred policy is given by the solution to
![\displaystyle \max_{\phi }\left\{ u\left[ y_{1}-A_{1}^{\ast }(\beta _{i};\phi , q(\phi ), w_2(\phi))\right] +u\left[\frac{A_{1}^{\ast }(\beta _{i};\phi ,q(\phi ),w_2(\phi))}{q(\phi)} +w_{2}(\phi)\right] \right\}](img38.gif) |
|||
| s.t. |
where
A few comments are in order concerning the period-0 voting problem. First, note that agents consider how the savings floor will impact both the equilibrium interest rate,
![]() , and period-2 wage rate,
, and period-2 wage rate, ![]() , through its impact on the
aggregate capital stock
, through its impact on the
aggregate capital stock ![]() . Agents know that the aggregate capital stock will be equal to the sum of individual holdings of capital, and that the equilibrium interest rate will adjust
so that the aggregate supply of loans equals the quantity demanded by borrowers in period 1. Second, the bounds on the policy space
. Agents know that the aggregate capital stock will be equal to the sum of individual holdings of capital, and that the equilibrium interest rate will adjust
so that the aggregate supply of loans equals the quantity demanded by borrowers in period 1. Second, the bounds on the policy space
![]() will not be binding in the following sense: any savings floor less than the natural borrowing limit,
will not be binding in the following sense: any savings floor less than the natural borrowing limit,
![]() , is equivalent to
, is equivalent to
![]() because all agents are unconstrained at
because all agents are unconstrained at
![]() , and the upper bound of
, and the upper bound of
![]() only rules out savings floors that are Pareto inferior to
only rules out savings floors that are Pareto inferior to
![]() .
.
2.3 Equilibrium Conditions
Necessary conditions for an equilibrium include profit maximization by firms, constrained optimality of individual choices, and market clearing. Thus, given ![]() and
and ![]() , the interest rate and period-2 wage rate are functions of the period-2 capital stock as given by equations (1) and (2). Individuals are indifferent
to the composition of their savings,
, the interest rate and period-2 wage rate are functions of the period-2 capital stock as given by equations (1) and (2). Individuals are indifferent
to the composition of their savings, ![]() , which implies that the interest rate on debt must equal the rental rate on capital:
, which implies that the interest rate on debt must equal the rental rate on capital:
Individual savings must satisfy
where for constrained agents, (4) holds with strict inequality and (5) with equality, and for unconstrained agents, (4) holds with equality. Finally, at the equilibrium interest rate, markets must also clear. That is,
where
For any ![]() , equations
, equations
![]() jointly determine
jointly determine
![]()
![]() ,
,
![]() ,
, ![]() ,
,
![]() , and
, and
![]() .
.
![]() is the cut-off between constrained and unconstrained individuals. Agents of type
is the cut-off between constrained and unconstrained individuals. Agents of type
![]() optimally choose to save
optimally choose to save ![]() ;
;
![]()
![]() are unconstrained; and
are unconstrained; and
![]()
![]() are constrained. As I am primarily interested in characterizing individual preferences over
are constrained. As I am primarily interested in characterizing individual preferences over ![]() , it is not yet necessary to specify the procedure by which these preferences are aggregated to determine the savings floor for the economy. In Section 5, the aggregation process will be made explicit.
, it is not yet necessary to specify the procedure by which these preferences are aggregated to determine the savings floor for the economy. In Section 5, the aggregation process will be made explicit.
To rule out multiple equilibria, I assume that the equilibrium period-2 capital stock, ![]() , is a function. I also make the following assumption:
, is a function. I also make the following assumption:
Assumption 1 The period-2 capital stock, ![]() , is a (weakly) increasing function of the savings floor
, is a (weakly) increasing function of the savings floor
![]() .
.
The intuition for Assumption 1 is relatively straight-forward. If the savings floor is not a binding constraint for any agent, the period-2 capital stock will not change with a marginal increase in the savings floor. If, on the other hand, the savings floor constrains some agents, an increase in the savings floor will directly increase the period-2 capital stock through the savings of those constrained individuals. This would cause the period-2 wage to increase and the interest rate to decline, so unconstrained agents may save less. They will not, however, save so much less that the period-2 capital stock declines below its initial level, because that would reverse the movements in the wage and interest rate.11
Assumption 1 holds quite generally. For example, I show in the appendix that sufficient conditions for Assumption 1 to hold include:
- for CRRA preferences
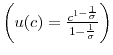 ,
,
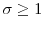 .
. - for CARA preferences
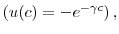
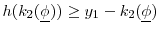 and either
and either
-
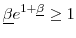 (that is,
(that is,
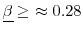 ), or
), or  is the uniform distribution.
is the uniform distribution.
-
As described in the appendix, these conditions guarantee that an unconstrained agent saves less in response to an increase in the aggregate capital stock
![]() , which is weaker than ensuring that her savings fall in response to a decrease in the rate of return
, which is weaker than ensuring that her savings fall in response to a decrease in the rate of return
![]() . Bernheim (2002) describes how, in theory, savings can either rise or fall in response to a decrease in the rate of return. Savings can rise
if (a) an individual has a low enough elasticity of intertemporal substitution that the desire to smooth consumption leads to more savings in response to a smaller rate of return; or (b) an individual has large enough savings that the negative wealth effect associated with the decreased interest
rate causes her to consume less (save more) in the first period. The second situation could occur, for example, if the distribution of earnings through time is heavily front-loaded. The conditions for Assumption 1 are sufficient to ensure neither situation occurs for any agent.
. Bernheim (2002) describes how, in theory, savings can either rise or fall in response to a decrease in the rate of return. Savings can rise
if (a) an individual has a low enough elasticity of intertemporal substitution that the desire to smooth consumption leads to more savings in response to a smaller rate of return; or (b) an individual has large enough savings that the negative wealth effect associated with the decreased interest
rate causes her to consume less (save more) in the first period. The second situation could occur, for example, if the distribution of earnings through time is heavily front-loaded. The conditions for Assumption 1 are sufficient to ensure neither situation occurs for any agent.
3 Preferences for Public Commitment
I now characterize the period-0 preferences of individuals for a public commitment device, namely ![]() , the period-1 savings floor. I find that all individuals prefer an extreme policy
but, for many type distributions, they do not all prefer the same extreme: some prefer no savings floor and others prefer a floor so high that it is a binding constraint for all individuals. Moreover, that the floor constrains all individuals (and hence eliminates all borrowing) is a necessary, but
not sufficient, condition for the introduction of a savings floor to be a Pareto improvement. This is the paper's key result, as it adds important qualifications to the conventional wisdom that ubiquitous lack of self-control will lead to a consensus opinion on the desirability of a
government-mandated savings floor.
, the period-1 savings floor. I find that all individuals prefer an extreme policy
but, for many type distributions, they do not all prefer the same extreme: some prefer no savings floor and others prefer a floor so high that it is a binding constraint for all individuals. Moreover, that the floor constrains all individuals (and hence eliminates all borrowing) is a necessary, but
not sufficient, condition for the introduction of a savings floor to be a Pareto improvement. This is the paper's key result, as it adds important qualifications to the conventional wisdom that ubiquitous lack of self-control will lead to a consensus opinion on the desirability of a
government-mandated savings floor.
Let
![]() denote the period-0 indirect utility of an agent of type
denote the period-0 indirect utility of an agent of type
![]() when the savings floor is
when the savings floor is ![]() :
:
![\displaystyle U(\beta _{i};\phi )\equiv u[y_{1}-A_{1}^{\ast }(\beta _{i};\phi )]+u\left[ \frac{A_{1}^{\ast }(\beta _{i};\phi )}{q(\phi )}+w_{2}(\phi)\right].](img82.gif) |
Changes in ![]() can affect
can affect
![]() through four channels: the direct effect of constrained borrowing, the substitution and wealth effects associated with a change in the equilibrium interest rate, and the
income effect of a change in the period-2 wage. I characterize
through four channels: the direct effect of constrained borrowing, the substitution and wealth effects associated with a change in the equilibrium interest rate, and the
income effect of a change in the period-2 wage. I characterize
![]() in a series of lemmas to pinpoint the channels through which changes in
in a series of lemmas to pinpoint the channels through which changes in ![]() are operating. As
are operating. As ![]() changes, the entire equilibrium changes to be consistent with equations (1) - (7).
changes, the entire equilibrium changes to be consistent with equations (1) - (7).
3.1 Regions of the Policy Space
For a given level of the savings floor, some individuals will be constrained and others unconstrained. The first lemma says that if an agent is constrained for some level of the savings floor, she will also be constrained by any higher savings floor.
Lemma 1 An increase in the savings floor, ![]() must increase the cut-off between constrained and unconstrained agents,
must increase the cut-off between constrained and unconstrained agents,
![]() .
.
Another classification of individuals is by whether they save more or less than the per-capita capital stock. I will refer to agents with
![]() as lenders and agents with
as lenders and agents with
![]() as borrowers.13 The second lemma
implies that if an individual is a borrower for some savings floor, then in an equilibrium with a higher savings floor, the individual will not be a lender. For a constrained agent, this follows immediately from Lemma 1 and
as borrowers.13 The second lemma
implies that if an individual is a borrower for some savings floor, then in an equilibrium with a higher savings floor, the individual will not be a lender. For a constrained agent, this follows immediately from Lemma 1 and
![]() .
.
Lemma 2 If an agent is an unconstrained borrower for some ![]() , she will not be a lender for any higher savings floor.
, she will not be a lender for any higher savings floor.
The intuition for Lemma 2 is as follows: an unconstrained borrower will not be affected by the constraint directly but will be affected by the decreased equilibrium interest rate and increased period-2 wage. The substitution effect associated with the interest rate change causes her to borrow
more. If she had negative net savings, ![]() , the wealth effect would be positive and reinforce the desire to borrow. If instead she had positive net savings,
, the wealth effect would be positive and reinforce the desire to borrow. If instead she had positive net savings,
![]() , her interest income would decrease (i.e., negative wealth effect), but it turns out that her wage income would increase more than enough to offset the decreased
interest income. Thus, an unconstrained borrower will borrow more.
, her interest income would decrease (i.e., negative wealth effect), but it turns out that her wage income would increase more than enough to offset the decreased
interest income. Thus, an unconstrained borrower will borrow more.
Figure 1 illustrates the implications of Lemmas 1 and 2 for a particular agent. At the highest savings floor,
![]() , the agent is certainly constrained. As the floor is lowered, she moves from being constrained to unconstrained, and as the interest rate rises and period-2 wage falls, she
possibly moves from being a borrower to being a lender. Note that some individuals will never be in certain regions. For example, the individual with the most self-control (
, the agent is certainly constrained. As the floor is lowered, she moves from being constrained to unconstrained, and as the interest rate rises and period-2 wage falls, she
possibly moves from being a borrower to being a lender. Note that some individuals will never be in certain regions. For example, the individual with the most self-control (
![]() ) will never be an unconstrained borrower because she never saves less than the per capita capital stock. Other individuals (consider
) will never be an unconstrained borrower because she never saves less than the per capita capital stock. Other individuals (consider
![]() ) will never be lenders.
) will never be lenders.
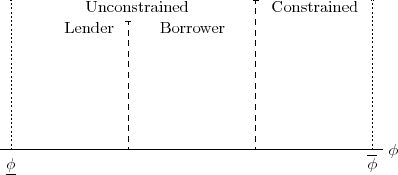
3.2 The Indirect Utility Function
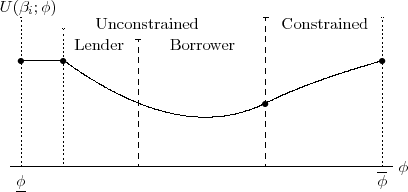
I now proceed to characterize the shape of a given agent's indirect utility function with respect to the level of the uniform savings floor. I move from the left to the right of Figure 1: first considering the unconstrained region and then the constrained region. Figure 2 will show the shape of the indirect utility function for any given agent.
For sufficiently low values of ![]() , no agents will be constrained (i.e.,
, no agents will be constrained (i.e.,
![]() ). Thus, a small increase in the savings floor will have no impact on equilibrium quantities nor on the utility of the agents. This is shown by the flat portion of the indirect
utility function in Figure 2. Figure 2 also graphically depicts Lemmas 3 and 4, which characterize the preferences of unconstrained and constrained agents over the savings floor when some agents are constrained (i.e.,
). Thus, a small increase in the savings floor will have no impact on equilibrium quantities nor on the utility of the agents. This is shown by the flat portion of the indirect
utility function in Figure 2. Figure 2 also graphically depicts Lemmas 3 and 4, which characterize the preferences of unconstrained and constrained agents over the savings floor when some agents are constrained (i.e.,
![]() ).
).
Lemma 3
![]() is quasiconvex in
is quasiconvex in ![]() over the unconstrained region of the policy
space.
over the unconstrained region of the policy
space.
To gain some intuition for Lemma 3, consider the slope of the indirect utility function14:
Utility will be increasing if and only if the expression within the brackets is positive. The second term in this expression,
The first term within the brackets,
![]() , can be positive or negative depending on the sign of
, can be positive or negative depending on the sign of
![]() . If the agent is a lender,
. If the agent is a lender,
![]() , the loss in interest income due to an interest rate decrease is greater than the increased wage income, so wealth and utility decline. If the agent is a borrower, however,
utility can increase because the change in interest income is less important than the change in wage income. In fact, if the agent has negative net savings,
, the loss in interest income due to an interest rate decrease is greater than the increased wage income, so wealth and utility decline. If the agent is a borrower, however,
utility can increase because the change in interest income is less important than the change in wage income. In fact, if the agent has negative net savings, ![]() , the reduction in
interest payments and increase in wage income both increase wealth.
, the reduction in
interest payments and increase in wage income both increase wealth.
Thus, a lender's utility unambiguously decreases with an increase in the savings floor, while a borrower views the increased floor as a mixed blessing. On the one hand, the borrower becomes wealthier due to the price changes, but on the other hand, the decreased interest rate and steeper earnings trajectory exacerbate her commitment problem. One can rewrite the bracketed expression in (8) to see that it has the opposite sign of
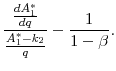 |
Thus, something like the price elasticity of savings determines which force is more important for the borrower. If the "price elasticity of savings" is large
Having characterized the preferences over the savings floor for an unconstrained individual, Lemma 4 describes how the indirect utility of a constrained agent changes with an increase in the savings floor.
Lemma 4
![]() is increasing over the constrained region of the policy space.
is increasing over the constrained region of the policy space.
The slope of the indirect utility function is
An increase in the savings floor directly benefits agents who are borrowing constrained through giving them more commitment. This is reflected by the term in square brackets in (9). The term outside of the brackets shows that an increase in the period-2 capital stock also makes these agents better off because they are borrowers,
One might at first be surprised by Lemma 4. As ![]() increases, the equilibrium interest rate decreases, and it may seem that for low enough values of the interest rate, a tighter
constraint cannot possibly be welfare improving. The resolution is that, in equilibrium, the interest rate will never get too low. As long as there is one unconstrained individual, the interest rate is bounded below:
increases, the equilibrium interest rate decreases, and it may seem that for low enough values of the interest rate, a tighter
constraint cannot possibly be welfare improving. The resolution is that, in equilibrium, the interest rate will never get too low. As long as there is one unconstrained individual, the interest rate is bounded below:
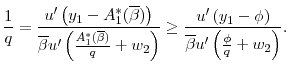 |
3.3 Extreme Preferences
The preceding characterization of the indirect utility function for any particular agent leads to a two-part "Extreme Preferences" result for the entire distribution of agents. First, Proposition 1 establishes that all individuals prefer an extreme policy. Second, Proposition 2 shows that, for many distributions, agents will not all prefer the same extreme: some individuals prefer no savings floor while others prefer a floor so high that it is a binding constraint for all agents.
Proposition 1 Each individual's preferred policy is either (effectively) no savings floor,
![]() , or the maximum savings floor,
, or the maximum savings floor,
![]() .
.
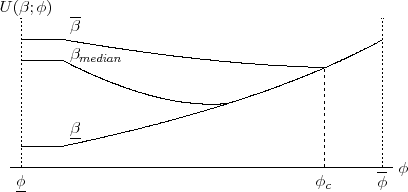
Figure 3 plots the quasiconvex indirect utility functions of three individuals over the policy space. The individual with least self-control,
![]() , will prefer maximum constraint, as he always directly benefits from the constraint of the savings floor. The one with most control,
, will prefer maximum constraint, as he always directly benefits from the constraint of the savings floor. The one with most control,
![]() , is a lender while she is unconstrained and thus has decreasing utility until she becomes constrained.
, is a lender while she is unconstrained and thus has decreasing utility until she becomes constrained. ![]() denotes the lowest savings floor that constrains all individuals. In the case that
denotes the lowest savings floor that constrains all individuals. In the case that
![]() ,
,
![]() and agents will not all prefer the same extreme.15 More generally, whether all agents prefer the same extreme depends upon the entire distribution of types, as demonstrated by Proposition 2.
and agents will not all prefer the same extreme.15 More generally, whether all agents prefer the same extreme depends upon the entire distribution of types, as demonstrated by Proposition 2.
Proposition 2 There exists a type
![]() who is indifferent between
who is indifferent between
![]() and
and
![]() , and
, and
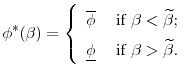 |
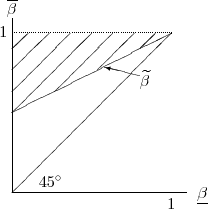
A few lessons can be gleaned from Proposition 2 and Figure 3. First, as long as there are some agents who suffer relatively little from a lack of self-control (i.e.,
![]() ), individuals will disagree over optimal policy. This is evident from Figure 4 which qualitatively illustrates combinations of
), individuals will disagree over optimal policy. This is evident from Figure 4 which qualitatively illustrates combinations of
![]() and
and
![]() that will result in individuals preferring different extremes.16 The region above the
that will result in individuals preferring different extremes.16 The region above the
![]() locus denotes such distributions.
locus denotes such distributions.
Second, Figure 3 shows that a marginal increase in the savings floor is only Pareto improving if the floor already constrains all agents. If it does not, those agents with less self-control problems (high ![]() ) prefer to get their commitment from the high interest rate associated with a low savings floor, rather than having a marginally higher floor but a lower interest rate. The key is that equilibrium prices adjust with the savings floor. In contrast, a tighter constraint is
always a Pareto improvement in a partial equilibrium setting. Because prices are fixed in partial equilibrium, period-0 utility only changes with an increasing savings floor if the floor is binding, in which case utility increases.17
) prefer to get their commitment from the high interest rate associated with a low savings floor, rather than having a marginally higher floor but a lower interest rate. The key is that equilibrium prices adjust with the savings floor. In contrast, a tighter constraint is
always a Pareto improvement in a partial equilibrium setting. Because prices are fixed in partial equilibrium, period-0 utility only changes with an increasing savings floor if the floor is binding, in which case utility increases.17
To understand the previous lesson more clearly, it may help to consider how an endowment economy would differ from the production economy that has been analyzed so far.18 In an endowment economy, the level of aggregate savings is fixed (i.e., 0) regardless of the savings floor. An increase in the floor changes the interest rate and the consumption distribution (across individuals) but does not alter the aggregate amount of consumption
nor the distribution of aggregate consumption through time. Thus, no change in the savings floor can be Pareto improving. Mathematically,
![]() , which implies that no savings floor is a binding constraint on all agents. As a result, any heterogeneity in self-control leads to large differences in
the preferred savings floor of agents.
, which implies that no savings floor is a binding constraint on all agents. As a result, any heterogeneity in self-control leads to large differences in
the preferred savings floor of agents.
In comparison, in a production economy, an increase in the savings floor increases the level of aggregate savings and hence the period-2 capital stock. Similarly to the endowment economy, as long as the savings floor is not binding for all agents, the cross-sectional distribution of consumption changes as a decrease in the interest rate is good for borrowers and bad for lenders. Differently, the profile of aggregate consumption through time also changes as more consumption is shifted to period 2. When the savings floor is binding for all individuals, a marginal increase in the floor is Pareto improving because it moves the consumption profile of each individual more in line with period-0 preferences without affecting the cross-sectional distribution.
A final note is that the magnitude of the welfare loss due to changes in the interest rate is not trivial. Under a reasonable calibration - log utility, a Cobb-Douglas production function with capital share of 0.33, and a uniform distribution of types between [0.25,0.9] - the individual with
most self-control would suffer a welfare loss of approximately 1.5% of lifetime wealth when moving from no savings floor to the lowest savings floor that constrains her, ![]() . Thus, in the
model, the incentive for individuals to consider general equilibrium effects when voting for their preferred savings floor is quantitatively significant.
. Thus, in the
model, the incentive for individuals to consider general equilibrium effects when voting for their preferred savings floor is quantitatively significant.
4 Extended Model: Heterogeneity in Self-Control and Patience
In the basic model of Section 2, individuals differed only by their lack of self-control (i.e., the strength of their present-bias, ![]() ). In this
section, I extend the model to allow for heterogeneity in patience as well. I will then derive conditions under which all individuals prefer either a savings floor low enough to not provide any constraint or one high enough to be binding for all individuals. A second use of the extended model is to
isolate the role of time-inconsistency in driving the extreme-preferences result of Section 3.
). In this
section, I extend the model to allow for heterogeneity in patience as well. I will then derive conditions under which all individuals prefer either a savings floor low enough to not provide any constraint or one high enough to be binding for all individuals. A second use of the extended model is to
isolate the role of time-inconsistency in driving the extreme-preferences result of Section 3.
The only difference from the basic model is that individuals, indexed by ![]() , are heterogeneous in both their long-run discount factor,
, are heterogeneous in both their long-run discount factor,
![]() , and their time-inconsistency parameter,
, and their time-inconsistency parameter,
![]() . Preferences are represented by
. Preferences are represented by
| Period 0 | |||
| Period 1 | |||
| Period 2 |
where
Let
![]() be the
time-0 indirect utility of an agent of type
be the
time-0 indirect utility of an agent of type
![]() when the savings floor is
when the savings floor is ![]() . Thus,
. Thus,
Proposition 3 give sufficient conditions for an extreme policy to be the most preferred policy of an individual.
Proposition 3 If
![]() , individual i will prefer either a savings floor low enough to not provide any constraint or one high
enough to be binding for all individuals.
, individual i will prefer either a savings floor low enough to not provide any constraint or one high
enough to be binding for all individuals.
Note that a savings floor that constrains all individuals eliminates all borrowing and hence all lending - that is, it eliminates all trade between agents. Thus, when choosing the level of the uniform savings floor, individuals make a trade-off between gains from trade and gains from commitment.
All individuals prefer an extreme constraint when (a) there are smaller gains from trade because individuals have similar period-0 preferences (i.e., less variation in ![]() ); or (b) there
is a greater need for commitment (i.e., lower levels of
); or (b) there
is a greater need for commitment (i.e., lower levels of
![]() ).
).
Proposition 3 is a generalized version of Proposition 1 as it is clear that, in the special case of heterogeneity only in ![]() , all individuals prefer an extreme policy. In another
special case, a model with standard time-consistent preferences where
, all individuals prefer an extreme policy. In another
special case, a model with standard time-consistent preferences where ![]() and
and ![]() is the only form of variation, Proposition 3 establishes that an individual can have an interior policy as his most-preferred policy. When individuals had time-inconsistent preferences, it was not possible for them to be overly constrained, but with standard preferences, the
direct effect of a constraint is to decrease utility. A small amount of constraint may be welfare improving due to the wealth effect (the second term in equation (10)), but this effect is overwhelmed by the distortion of optimal choice that becomes more severe as the constraint
increases (the first term in equation (10)). The extreme-preferences result, therefore, crucially depends on the presence of time-inconsistency in preferences.
is the only form of variation, Proposition 3 establishes that an individual can have an interior policy as his most-preferred policy. When individuals had time-inconsistent preferences, it was not possible for them to be overly constrained, but with standard preferences, the
direct effect of a constraint is to decrease utility. A small amount of constraint may be welfare improving due to the wealth effect (the second term in equation (10)), but this effect is overwhelmed by the distortion of optimal choice that becomes more severe as the constraint
increases (the first term in equation (10)). The extreme-preferences result, therefore, crucially depends on the presence of time-inconsistency in preferences.
5 Comparative Statics
Having characterized individual preferences for a uniform savings floor, I now consider some comparative statics of the model. I return to the baseline model from Section 2 and consider how a shift in the distribution of types affects the outcome of the voting over the savings floor. To do so, it becomes necessary to specify how individual preferences are aggregated.
Because, as shown by Proposition 2, all individuals prefer either
![]() or
or
![]() and the preferred savings floor of an individual is a monotonic function of her type, the savings floor preferred by the median type is clearly a Condorcet winner. Thus, I
assume that
and the preferred savings floor of an individual is a monotonic function of her type, the savings floor preferred by the median type is clearly a Condorcet winner. Thus, I
assume that
![]() and evaluate how changes in the distribution of types,
and evaluate how changes in the distribution of types,
![]() affect
affect
![]() . The following proposition shows that a decrease in the average amount of self-control in the economy can actually lead to a policy providing less commitment.
. The following proposition shows that a decrease in the average amount of self-control in the economy can actually lead to a policy providing less commitment.
Proposition 4 Consider two distributions,
![]() and
and
![]() , such that
, such that ![]() first-order stochastically dominates
first-order stochastically dominates ![]() and
and
![]() . The equilibrium savings floor chosen under
. The equilibrium savings floor chosen under ![]() is lower than the one chosen under
is lower than the one chosen under ![]() ; that is,
; that is,
![]() .
.
Thus, a shift in the distribution of agents that increases the average bias for present consumption may lead to policies that provide less commitment, not more as typically suggested by models that feature a time-inconsistent representative agent. If the median voter's self-control does not
change while average self-control decreases, the median voter benefits more from others' lack of constraint and may vote for less public commitment. Of course, if the shift also leads to the new median voter having less self-control, ![]() may increase. Each individual considers the direct effect of the savings floor on their own savings decision and the impact it will have on prices because it affects others' savings decisions as well.
may increase. Each individual considers the direct effect of the savings floor on their own savings decision and the impact it will have on prices because it affects others' savings decisions as well.
6 Conclusion
I have extended the analysis of the economics of commitment to a general equilibrium setting in which individuals vote for their preferred level of a uniform savings floor. The model adds important qualifications to the partial equilibrium intuition that lack of self-control will lead to unanimous support for a savings floor. In particular, the model identifies interest rate changes as an ever-present force that could lead to disagreement over the floor's level. Even if all individuals suffer from a bias for present consumption, those who have relatively more self-control benefit from lending at a high equilibrium interest rate to those who wish to borrow. A savings floor restricts the demand of borrowers, causes the interest rate to fall, and, for some individuals, leads to decreased savings and possibly decreased welfare.
If, for some level of the savings floor, there are individuals who choose to save more than the minimum required, some of these individuals are certainly worse off than they would have been without the savings floor due to the negative substitution and wealth effects of a reduced interest rate on their utility. On the other hand, if the savings floor is binding for all individuals, all may be better off because a binding savings floor also shifts the profile of aggregate consumption through time to be more in line with period-0 preferences. Whether all individuals are made better off by the introduction of the savings floor depends on whether this shift - which benefits all individuals - is enough to compensate those individuals whose wealth decreases with the reduced interest rate.
Thus, there is a clear analogy to the well-known point about the benefits of free trade: reducing trade barriers is a Pareto improvement only after the losers are compensated. A contribution of this paper is to demonstrate in a stylized general equilibrium model what conditions can be expected to involve some agents being made worse off from a public commitment policy over savings. Generally, if the agents with least present bias have sufficiently more self-control than the average agent, they will be worse off with a savings floor.
This does not necessarily mean that public commitment policies will not have broad-based support. Although a vote over a single policy of a savings floor is likely to produce disagreement, a combined policy package might not. For example, a policy package that included both a savings floor and a tax cut on interest income would be more likely to pass in a median voter setup, because it would compensate the lenders for the decreased interest rate.19
The model also has implications for other aspects of financial decision making when individuals suffer from a lack of self-control. Because a higher interest rate must lead to a more upward-sloping consumption profile, interest rates can provide commitment to agents who lack self-control. For example, Agarwal et al. (2005) analyze a market experiment where consumers are given the choice between two credit card contracts, one with an annual fee but a lower interest rate and one with no annual fee but a higher interest rate. To minimize their interest costs net of the fee, consumers who expect to borrow a lot should choose the low interest rate contract, and vice-versa. Although the majority of consumers either immediately choose or eventually switch to the contract that ex post minimizes their net costs, Agarwal and co-authors find that a small number of consumers persists in holding a contract that does not minimize net interest costs.
One potential explanation for the behavior of these consumers is that they have time-inconsistent preferences. The contract that minimizes interest costs is not necessarily the one that maximizes utility because a consumer may benefit from a more upward-sloping consumption profile associated with a higher interest rate.20 Thus, in the same way that lack of self-control has been used to explain the popularity of low-return illiquid assets, it might explain why individuals would be willing to pay a fee in order to face a higher interest rate on future borrowing.
7.1 Some Useful Expressions
I start by deriving some expressions that will be used over and over again in the proofs to follow.
From equations
![]() , it is straight-forward to show how equilibrium prices respond to a change in the period-2 capital stock:
, it is straight-forward to show how equilibrium prices respond to a change in the period-2 capital stock:
The savings of an unconstrained agent,
![]() , is implicitly defined by equation (4). Using the implicit function theorem yields
, is implicitly defined by equation (4). Using the implicit function theorem yields
where
7.2 Sufficient Conditions for Assumption 1
I will first show that
![]() is a sufficient condition for
is a sufficient condition for
![]() , and I will then derive conditions on preferences such that
, and I will then derive conditions on preferences such that
![]() for all
for all ![]() and all
and all ![]() .
.
The first point is proved by contradiction. Let
![]() , but assume
, but assume
![]() . If
. If ![]() increases, the left-hand side of equation
increases, the left-hand side of equation
![]() increases because
increases because
![]() for constrained agents and
for constrained agents and
![]() for unconstrained agents, but the right-hand side of equation
for unconstrained agents, but the right-hand side of equation
![]() decreases because
decreases because
![]() .
.
![]()
I now derive sufficient conditions for
![]() . From equation
. From equation
![]() ,
,
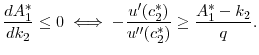 |
CRRA Preferences:
![]() and
and
![]() , so
, so
![]() clearly holds if
clearly holds if
![]() because
because
![]() . For
. For
![]() , rearrange
, rearrange
![]() to get
to get
![]() , which holds because
, which holds because
![]() .
.
CARA Preferences:
![]() , so
, so
From the first-order condition for an unconstrained agent,
![]() or
or
![e^{\gamma \left[ h(k_2) - (y_1 - k_2) + \left(\frac{1}{q} + 1 \right) (A_1^* - k_2)\right]} = \frac{\beta}{q}](img199.gif) . Thus,
. Thus,
![]() can be written as
can be written as
Normalize ![]() so that
so that
![]() , then
, then
![]() will guarantee
will guarantee
![]() when
when
![]() . Also, note that with
. Also, note that with
![]() ,
,
![]() because all individuals would have
because all individuals would have
![]() if
if
![]() and all individuals would have
and all individuals would have
![]() if
if
![]() .
.
Therefore, one sufficient condition is
![]() because it ensures that
because it ensures that
![]() when no agents are constrained. As
when no agents are constrained. As ![]() increases,
increases, ![]() increases and
increases and
![]() increases, so equation
increases, so equation
![]() will continue to hold.
will continue to hold.
An alternative way to derive a sufficient condition is to solve for ![]() directly from the market-clearing condition and check that
directly from the market-clearing condition and check that
![]() , or equivalently, that
, or equivalently, that
![]() . Assuming a uniform distribution of types and continuing to normalize
. Assuming a uniform distribution of types and continuing to normalize ![]() so that
so that
![]() , equation
, equation
![]() becomes
becomes
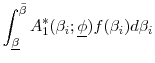 |
![\displaystyle \int_{\underline{\beta }}^{\bar{\beta}} \left [ \frac{ln \left( \frac{\beta_i}{q}\right )}{\gamma} \frac{q}{q+1} + k_2 \right ] \frac{1}{\overline{\beta} - \underline{\beta}}d\beta _{i}](img217.gif) |
||
![\displaystyle \frac{q}{(\overline{\beta} - \underline{\beta})(q+1)\gamma} \left [ \beta_i \left [ ln \left ( \frac{\beta_i}{q}\right ) -1 \right] \right ]_{\underline{\beta}}^{\overline{\beta}} + k_2](img218.gif) |
|||
![\displaystyle \frac{\overline{\beta}[ln(\overline{\beta})-1] - \underline{\beta}[ln(\underline{\beta})-1] + (\underline{\beta} - \overline{\beta})ln(q)}{(\overline{\beta} - \underline{\beta})(1+ q^{-1})\gamma} + k_2 = k_2.](img219.gif) |
Thus,
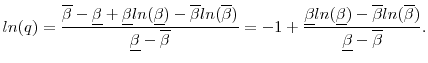
Then, we have
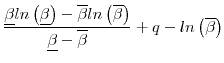 |
|||
which clearly holds. Therefore,
7.3 Proof of Proposition 1
Proposition 1 follows directly from Lemmas 1-4, which together demonstrate that
![]() is quasiconvex in
is quasiconvex in ![]() ,
,
![]() .
.
7.3.1 Proof of Lemma 1
Assume ![]() increases. The left-hand side of (7) must strictly increase. On the right-hand side, note that
increases. The left-hand side of (7) must strictly increase. On the right-hand side, note that
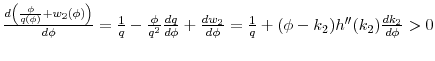 because
because
![]() by equation (6),
by equation (6), ![]() is concave, and
is concave, and
![]() by Assumption 1. Therefore,
by Assumption 1. Therefore,
![]() must strictly decrease, and
must strictly decrease, and
![]() is also decreasing by Assumption 1, equation (1), and equation (3). Therefore,
is also decreasing by Assumption 1, equation (1), and equation (3). Therefore,
![]() must increase for (7) to hold. QED
must increase for (7) to hold. QED
7.3.2 Proof of Lemma 2
I show that
![]() .
.
![]() and from equation
and from equation
![]() , it is clear that
, it is clear that
Finally, note that
7.3.3 Proof of Lemma 3
I need to show that
![]() is quasiconvex in
is quasiconvex in ![]() ; that is, if
; that is, if
![]() for some
for some ![]() ,
,
![]() for all greater
for all greater ![]() . The sign of
. The sign of
![]() depends crucially on the level of savings,
depends crucially on the level of savings, ![]() . In this proof, I will first show how
. In this proof, I will first show how ![]() changes with
changes with ![]() and then sign
and then sign
![]() conditional on
conditional on ![]() .
.
![]() will be in one of three regions:
will be in one of three regions:
-
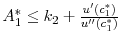 ,
, -
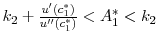 ,
, -
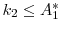 .
.
First, I show that if ![]() is in region 1 for some
is in region 1 for some ![]() , it will be in region
1 for any higher
, it will be in region
1 for any higher ![]() . Let
. Let
![]() . From Lemma 2,
. From Lemma 2,
![]() . Then,
. Then,
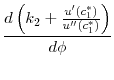 |
![$\displaystyle \left [ 1 + \left [1 - \frac{u'(c_1^*) u^{\prime\prime\prime}(c_1^*)}{[u^{\prime\prime}(c_1^*)]^2} \right] \frac{d c_1^*}{d k_2} \right ] \frac{d k_2}{d \phi}$](img246.gif) |
||
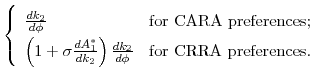 |
Thus, with CARA preferences,
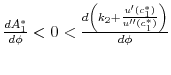 because
because
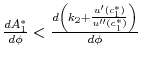 because
because
Moving to region 2, it is clear from the proof of Lemma 2 that if ![]() is in region 2 for some
is in region 2 for some ![]() , it will not be in region 3 for any higher
, it will not be in region 3 for any higher ![]() . It will decrease (see equation
. It will decrease (see equation
![]() ) and either stay within region 2 or move into region 1.
) and either stay within region 2 or move into region 1.
Finally, if ![]() is in region 3, as
is in region 3, as ![]() increases it will either stay in
region 3 or decrease and move into region 2.
increases it will either stay in
region 3 or decrease and move into region 2.
Now that I have shown how the level of savings, ![]() , moves with
, moves with ![]() , I sign
, I sign
![]() in each of the three regions. I will show that in region 3, utility is decreasing in
in each of the three regions. I will show that in region 3, utility is decreasing in ![]() . In region 2, there is a threshold level of savings above which utility is decreasing in
. In region 2, there is a threshold level of savings above which utility is decreasing in ![]() and below which it is increasing. Finally, in region
1, utility is always increasing. Thus,
and below which it is increasing. Finally, in region
1, utility is always increasing. Thus,
![]() is quasiconvex in
is quasiconvex in ![]() .
.
The slope of the indirect utility function is given by
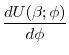 |
![\displaystyle \left[ u^{\prime } \left( \frac{A_{1}^{\ast }}{q} + w_{2} \right) \left( \frac{\frac{dA_{1}^{\ast }}{d k_2}}{q} - \frac{A_{1}^{\ast } }{q^2} \frac{d q}{d k_2} + \frac{d w_2}{d k_2}\right) - u^{\prime }(y_{1}-A_{1}^{\ast}) \frac{dA_{1}^{\ast }}{d k_2} \right] \frac{d k_2}{d\phi }](img259.gif)
|
||
![$\displaystyle \left[ u^{\prime } \left( c_2^* \right) \left( \frac{\frac{dA_{1}^{\ast }}{d k_2}}{q} + \left(A_1^* - k_2 \right) h^{\prime\prime}(k_2) \right) - u^{\prime }(c_{1}^*) \frac{dA_{1}^{\ast }}{d k_2} \right] \frac{d k_2}{d\phi }$](img260.gif) |
|||
![$\displaystyle \left[ \left(A_1^* - k_2 \right) q h^{\prime\prime}(k_2) + (1 - \beta) \frac{dA_{1}^{\ast }}{d k_2} \right] \frac{u'(c_2^*)}{q} \frac{d k_2}{d\phi }.$](img261.gif) |
The third equality comes from substituting the first-order condition of the agent's period-1 decision problem
![]() into the expression and collecting like terms. Therefore,
into the expression and collecting like terms. Therefore,
![]() has the same sign as
has the same sign as
In region 3
![]() ,
,
![]() is negative. If savings is extremely high
is negative. If savings is extremely high
![]() , consumption in both periods decreases with an increase in
, consumption in both periods decreases with an increase in ![]() . This is apparent from inspecting equations
. This is apparent from inspecting equations
![]() and
and
![]() . If
. If
![]() ,
,
![]() is negative as both terms in
is negative as both terms in
![]() are negative.
are negative.
In region 2
![]() , the first term in
, the first term in
![]() is positive and the second term is negative. I show below (Section 7.3.5) that under the sufficient conditions for
Assumption 1, it will be the case that if (21) is positive for some
is positive and the second term is negative. I show below (Section 7.3.5) that under the sufficient conditions for
Assumption 1, it will be the case that if (21) is positive for some ![]() it will be positive for any greater
it will be positive for any greater ![]() . Thus, there is a cutoff level,
. Thus, there is a cutoff level,
![]() , above which
, above which
![]() is positive. Since
is positive. Since
![]() in region 2, once
in region 2, once
![]() is positive for some
is positive for some ![]() , it will be positive
for any greater
, it will be positive
for any greater ![]() .
.
Finally, in region 1
![]() ,
,
![]() is positive as consumption in both periods increases with an increase in
is positive as consumption in both periods increases with an increase in ![]() . This is apparent from equations
. This is apparent from equations
![]() and
and
![]() . QED
. QED
7.3.4 Proof of Lemma 4
First, consider the case that at least one agent is unconstrained, so that
![]() . Recall that
. Recall that
![]() .
.
For an unconstrained agent,
![]() and
and
![]() . Thus,
. Thus,
![]() . Rewriting (22), it is easy to see that
. Rewriting (22), it is easy to see that
![$\displaystyle \frac{dU(\beta _{con};\phi )}{d\phi } = \left[ \frac{1}{q}u^{\prime }\left( \frac{\phi }{q}+w_{2}\right) -u^{\prime }(y_{1}-\phi )\right] + u^{\prime }\left( \frac{\phi }{q}+w_{2}\right) \left[ \phi - k_2 \right] h^{\prime\prime}(k_2) \frac{d k_2}{d \phi} >0.$](img285.gif) |
In the case that all agents are constrained, utility is increasing in ![]() by definition of
by definition of
![]() . QED
. QED
7.3.5 Sufficient conditions which ensure that if equation (21) is positive for 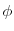 it
will be positive for any greater
it
will be positive for any greater 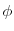 .
.
Combining equations (15) and (21) yields
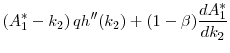 |
|||
![$\displaystyle \frac{\left \{\frac{k_2 - A_1^*}{q}\left [ \frac{q^2} {\beta} u^{\prime\prime}(c_1^*) + u^{\prime\prime}(c_2^*) \right ] + \left [ u'(c_2^*)+\frac{A_1^* - k_2}{q} u^{\prime\prime}(c_2^*) \right ] (1-\beta) \right \} \left [ -q^2 h^{\prime\prime}(k_2)\right] } {\frac{q^2} {\beta} u^{\prime\prime}(c_1^*) + u^{\prime\prime}(c_2^*)}$](img287.gif) |
|||
![$\displaystyle \frac{\left \{ [A_1^* - k_2] \left[ u^{\prime\prime}(c_1^*) + \frac{\beta^2}{q^2} u^{\prime\prime}(c_2^*) \right ] - (1-\beta) \frac{\beta}{q} u'(c_2^*) \right \}\left [ q h^{\prime\prime}(k_2)\right]} {u^{\prime\prime}(c_1^*) + \frac{\beta}{q^2} u^{\prime\prime}(c_2^*)}$](img288.gif) |
|||
![$\displaystyle \frac{\left \{ [A_1^* - k_2] \left[ \frac{u^{\prime\prime}(c_1^*)}{u'(c_1^*)} + \frac{u'(c_1^*)}{u'(c_2^*)} \frac{u^{\prime\prime}(c_2^*)}{u'(c_2^*)} \right ] - (1-\beta) \right \}\left [ q h^{\prime\prime}(k_2) u'(c_1^*)\right]} {u^{\prime\prime}(c_1^*) + \frac{\beta}{q^2} u^{\prime\prime}(c_2^*)},$](img289.gif) |
where the last equality used
CRRA Preferences: In this case,
![$\displaystyle [A_1^* - k_2] \left[ \frac{u^{\prime\prime}(c_1^*)}{u'(c_1^*)} + \frac{u'(c_1^*)}{u'(c_2^*)} \frac{u^{\prime\prime}(c_2^*)}{u'(c_2^*)} \right ]$](img291.gif) |
![\displaystyle [A_1^* - k_2]\left[ \frac{-1}{\sigma c_1^*} + \frac{\beta}{q} \frac{(-1)}{\sigma c_2^*} \right ]](img292.gif) |
||
![\displaystyle \frac{k_2 - A_1^*}{\sigma c_1^*} \left[ 1 + \left(\frac{\beta}{q} \right)^{1-\sigma} \right].](img293.gif) |
Then,
In region 2,
![]() and
and
![]() , so if
, so if
![]() , the expression in equation
, the expression in equation
![]() is positive.
is positive.
CARA Preferences: In this case,
![$\displaystyle [A_1^* - k_2] \left[ \frac{u^{\prime\prime}(c_1^*)}{u'(c_1^*)} + \frac{u'(c_1^*)}{u'(c_2^*)} \frac{u^{\prime\prime}(c_2^*)}{u'(c_2^*)} \right ]$](img291.gif) |
![\displaystyle [A_1^* - k_2]\left[ - \gamma + \frac{\beta}{q} (- \gamma) \right ]](img299.gif) |
||
![\displaystyle \gamma [k_2 - A_1^*]\left[ 1 + \frac{\beta}{q} \right ].](img300.gif) |
Then,
![\displaystyle \frac{d \left( \gamma (k_2 - A_1^*) \left[ 1 + \frac{\beta}{q} \right] \right)}{d \phi}](img301.gif) |
![\displaystyle \left \{ \left[ 1- \frac{d A_1^*}{d k_2}\right] \left[1 + \frac{\beta}{q} \right]+ \frac{- \beta}{q^2} \frac{d q}{d k_2}[k_2 - A_1^*]\right\} \gamma \frac{d k_2}{d \phi}.](img302.gif) |
Substituting in equation
![]() for
for
![]() and collecting like terms yields
and collecting like terms yields
Finally, note that
![$\displaystyle u'(c_1^*) \left [ q \frac{u^{\prime\prime}(c_1^*)}{u'(c_1^*)} - \frac{u^{\prime\prime}(c_2^*)}{u'(c_1^*)} \right ]$](img307.gif) |
|||
![$\displaystyle u'(c_1^*) \left [ q \frac{u^{\prime\prime}(c_1^*)}{u'(c_1^*)} - \frac{u^{\prime\prime}(c_2^*) q}{u'(c_2^*) \beta} \right ]$](img308.gif) |
|||
![\displaystyle u'(c_1^*) q \gamma \left [\frac{1}{\beta} - 1 \right] > 0,](img309.gif) |
so all three terms in the curly brackets in (24) are negative. Thus, (24) is positive for CARA preferences as long as
![]() (i.e., Assumption 1 holds).
(i.e., Assumption 1 holds).
7.4 Proof of Proposition 2
By Proposition 1,
![]()
If
![]() , all agents have the same utility since they have identical endowments and period-0 preferences. That is,
, all agents have the same utility since they have identical endowments and period-0 preferences. That is,
If
![]() , all agents are unconstrained, and period-0 utility is denoted by
, all agents are unconstrained, and period-0 utility is denoted by
![]() . Furthermore,
. Furthermore,
![]() since an agent of type
since an agent of type
![]() is the first to become constrained, and hence, his utility is nondecreasing over the policy space. At the other extreme, if
is the first to become constrained, and hence, his utility is nondecreasing over the policy space. At the other extreme, if
![]() ,
,
![]() since a type
since a type
![]() agent will always be an unconstrained lender, and thus, her utility is nonincreasing over the policy space. Finally,
agent will always be an unconstrained lender, and thus, her utility is nonincreasing over the policy space. Finally,
![]() is strictly increasing in
is strictly increasing in ![]() :
:
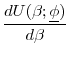 |
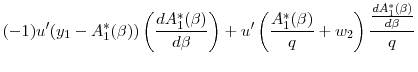 |
||
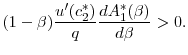 |
Thus, there exists some
![]() such that
such that
![]() has the same sign as
has the same sign as
![]()
Finally, note that
![]() depends on the entire distribution of types because
depends on the entire distribution of types because
![]() QED
QED
7.5 Proof of Proposition 3
This proof closely follows the proof of Proposition 1. Extending Lemmas 1 and 2 to this more general case is straight-forward and omitted. For Lemma 3, the slope of the indirect utility function is given by
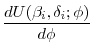 |
![$\displaystyle \left \{ \left[ \frac{\delta_i }{q}u^{\prime }(c_{2}^{\ast }) - u^{\prime }(c_{1}^{\ast })\right] \frac{dA_{1}^{\ast }}{ d k_2 } + \delta_i u^{\prime }(c_{2}^{\ast }) h^{\prime\prime}(k_2) \left [ A_1^* - k_2 \right ] \right \} \frac{d k_2}{d \phi}$](img326.gif) |
||
![$\displaystyle \left[ (1 - \beta_i) \frac{dA_{1}^{\ast }}{d k_2} + \left(A_1^* - k_2 \right) q h^{\prime\prime}(k_2) \right] \frac{ \delta_i u'(c_2^*)}{q} \frac{d k_2}{d \phi }.$](img327.gif) |
Thus, under the sufficient conditions for Assumption 1,
For a constrained agent,
![\displaystyle \frac{d U (\beta _{i},\delta _{i};\phi )}{d\phi } = \underbrace{ \left[ \frac{ \delta _{i}}{q}u^{\prime }\left( \frac{\phi }{q} + w_{2}\right) - u^{\prime }(y_{1}-\phi )\right] }](img329.gif) |
![$\displaystyle \underbrace{\left[ \delta _{i}u^{\prime }\left( \frac{\phi }{q}+w_{2}\right)[\phi - k_2] h^{\prime\prime}(k_2) \frac{d k_2}{d \phi}\right]. }$](img331.gif) |
||
| substitution effect |
wealth effect |
The wealth effect is always positive but approaches 0 as
![]() . (Recall that
. (Recall that ![]() is the lowest savings floor that
constrains all agents.) The substitution effect is non-negative for a `just-constrained' individual and becomes smaller as
is the lowest savings floor that
constrains all agents.) The substitution effect is non-negative for a `just-constrained' individual and becomes smaller as ![]() increases. If the substitution effect remains non-negative as
increases. If the substitution effect remains non-negative as
![]() , then the individual's most preferred policy will either be no constraint or a savings floor that is a binding constraint for all individuals. Thus, we need to check
the sign of
, then the individual's most preferred policy will either be no constraint or a savings floor that is a binding constraint for all individuals. Thus, we need to check
the sign of
![]() as
as
![]() .
.
The equilibrium price when
![]() must satisfy
must satisfy
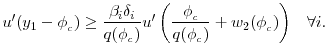
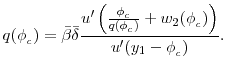
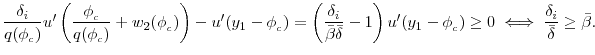 QED
QED7.6 Proof of Proposition 4
From market clearing
![]() ,
,
![]() , and
, and
![]() , it must be that
, it must be that
![]() ,
,
![]() . This claim can be proven by contradiction. Assume
. This claim can be proven by contradiction. Assume
![]() for some
for some ![]() . If the market clearing
condition held for distribution
. If the market clearing
condition held for distribution ![]() , it would not hold for distribution
, it would not hold for distribution ![]() because the right-hand side would increase but the left-hand side would decrease.
because the right-hand side would increase but the left-hand side would decrease.
Let
![]()
![]() denote the individual who is indifferent between no savings floor and a maximum savings floor for distribution
denote the individual who is indifferent between no savings floor and a maximum savings floor for distribution ![]()
![]() . Note that
. Note that
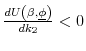 for
for
![]() (otherwise,
(otherwise,
![]() would clearly prefer the maximum savings floor to no savings floor) and that
would clearly prefer the maximum savings floor to no savings floor) and that
![]() is constant regardless of the distribution of types. Thus,
is constant regardless of the distribution of types. Thus,
![]() because
because
![]() . If
. If
![]() ,
,
![]() . Otherwise,
. Otherwise,
![]() . QED
. QED
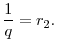
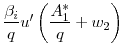
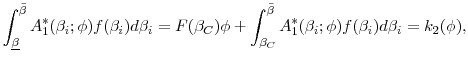
![\displaystyle u^{\prime }[y_{1}-\phi]=\frac{\beta _{C}}{q(\phi )}u^{\prime }\left[\frac{ \phi}{q(\phi )}+w_{2}(\phi )\right].](img58.gif)
![$\displaystyle \frac{dU(\beta ;\phi )}{d\phi } = \left[ \left(A_1^* - k_2 \right) q h^{\prime\prime}(k_2) + (1 - \beta) \frac{dA_{1}^{\ast }}{d k_2} \right] \frac{u'(c_2^*)}{q} \frac{d k_2}{d\phi }.$](img99.gif)
![$\displaystyle \frac{dU(\beta _{con};\phi )}{d\phi } = \left[ \frac{1}{q}u^{\prime }\left( \frac{\phi }{q}+w_{2}\right) -u^{\prime }(y_{1}-\phi )\right] + u^{\prime }\left( \frac{\phi }{q}+w_{2}\right) \left[ \phi - k_2 \right] h^{\prime\prime}(k_2) \frac{d k_2}{d \phi}.$](img109.gif)
![$\displaystyle \frac{dU(\beta_i, \delta_i ;\phi )}{d\phi }=\left[ \frac{\delta_i }{q}u^{\prime }(c_{2}^{\ast })-u^{\prime }(c_{1}^{\ast })\right] \frac{dA_{1}^{\ast }}{ d\phi } + \delta_i u^{\prime }(c_{2}^{\ast }) \left [ A_1^* - k_2 \right ] h^{\prime\prime}(k_2) \frac{d k_2}{d \phi}.$](img135.gif)
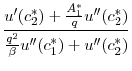
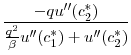
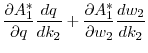
![$\displaystyle \frac{\left [ u'(c_2^*)+\frac{A_1^* - k_2}{q} u^{\prime\prime}(c_2^*) \right ] \left [ -q^2 h^{\prime\prime}(k_2)\right]} {\frac{q^2}{\beta}u^{\prime\prime}(c_1^*) + u^{\prime\prime}(c_2^*)}$](img169.gif)
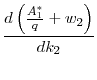
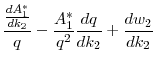
![$\displaystyle \frac{\left [ (A_1^* - k_2) u^{\prime\prime}(c_1^*) - u'(c_1^*) \right ] \frac{q^2}{\beta} h^{\prime\prime}(k_2)} {\frac{q^2}{\beta}u^{\prime\prime}(c_1^*) + u^{\prime\prime}(c_2^*)}$](img172.gif)
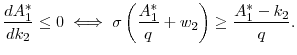
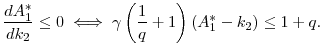
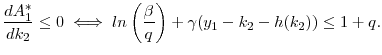
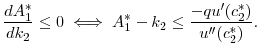
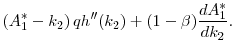
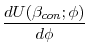
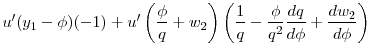
![$\displaystyle u^{\prime }\left( \frac{\phi }{q}+w_{2}\right) \left( \frac{1}{q} + \left [ \phi - k_2 \right ] h^{\prime\prime}(k_2) \frac{d k_2}{d \phi} \right) - u^{\prime }(y_{1}- \phi).$](img281.gif)
![\displaystyle \frac{d \left( \frac{k_2 - A_1^*}{\sigma c_1^*} \left[ 1 + \left(\frac{\beta}{q} \right)^{1-\sigma} \right] \right)}{d \phi} =](img294.gif)
![\displaystyle \left [ \left[ c_1^* + [k_2 - y_1] \frac{dA_1^*}{dk_2}\right] \left[1 + \left( \frac{\beta}{q} \right)^{1-\sigma} \right] + c_1^* [k_2 - A_1^*] [\sigma - 1] \left(\frac{\beta}{q} \right)^{1 - \sigma} \frac{1}{q} \frac{d q}{d k_2} \right] \frac{1}{\sigma (c_1^*)^2} \frac{d k_2}{d \phi}.](img295.gif)
![$\displaystyle \frac{\left \{ \left [ \frac{q^2}{\beta} u^{\prime\prime}(c_1^*) + u^{\prime\prime}(c_2^*) \right ] \left[ 1 + \frac{\beta}{q}\right] - u'(c_2^*) \left[ 1 + \frac{\beta}{q}\right] \frac{d q}{d k_2} + \frac{A_1^* - k_2}{q} \frac{d q}{d k_2} \left [q u^{\prime\prime}(c_1^*) - u^{\prime\prime}(c_2^*) \right] \right\}\gamma \frac{d k_2}{d \phi}}{\frac{q^2}{\beta} u^{\prime\prime}(c_1^*) + u^{\prime\prime}(c_2^*)}.$](img305.gif)