Skip to: [Printable Version (PDF)] [Bibliography] [Footnotes]

Finance and Economics Discussion Series: 2007-62 Screen Reader version ^♣

Risk and Concentration in Payment and Securities Settlement Systems

David C. Mills, Jr.^†

[email protected]

Travis D. Nesmith

[email protected]

Keywords: Interbank payments, securities settlement, strategic games, bank behavior

Abstract:

Large value payment and securities settlement systems are important components of an economy's financial system. Many such systems are operated by central banks and are liquidity intensive. Central banks often provide inexpensive liquidity to facilitate settlement. This leads to a number of policy questions about the provision of such liquidity. To answer these questions, central banks need to understand what factors influence the timing of settlement. This paper offers a model to better understand intraday patterns of settlement and identifies three factors that influence the timing of settlement: the cost of intraday liquidity, a participant's exposure to settlement risk, and system design. Incorporating all three factors enables our model to explain a number of stylized facts concerning behavior within the Federal Reserve's Fedwire fund and securities systems around a major policy change. In particular, the model captures the different responses of the two systems in both the pattern of settlement and the use of intraday liquidity. The results map out how policy interacts with participants' incentives to influence the use of intraday liquidity and the resultant credit exposure of a central bank. The model, therefore, can inform decision-making at central banks.

JEL classification: E58, G21, D81

Large-value payment and securities settlement systems facilitate the exchange of goods and services and the transfer of funds between borrowers and lenders. In many countries, the central bank operates at least one of these types of systems. The volume and value of payments and securities transferred across these systems necessitate that they be designed to operate both safely and efficiently.

In the United States, the Federal Reserve operates a large-value payment system, the Fedwire funds service, and a securities settlement system for government securities and other assets, the Fedwire securities service.¹ On average in 2005, it took just seven days for the value of payments settled in Fedwire funds--the smaller of the two systems by value--to exceed nominal GDP.

The Fedwire funds system, like many large-value payment systems, is a real-time gross settlement (RTGS) system. In an RTGS system, payments are made one at a time with finality. In securities settlement systems, payments are exchanged for financial securities. Many securities settlement systems settle each transaction individually on a delivery-versus-payment (DVP) basis, so that the securities and funds are exchanged between counterparties simultaneously with finality. The Fedwire securities service is a DVP system.² Because RTGS and DVP systems settle payments and securities one at a time, liquidity is needed to complete each transaction.

One solution to this liquidity problem is for participants to concentrate settlement at a focal period during the day so that transactions can partially offset each other, thereby economizing on the amount of needed liquidity. Such a solution requires participants to coordinate the time when transactions are settled, which may or may not be costly.

Another solution--one that is employed by many central banks including the Federal Reserve--is to provide relatively inexpensive liquidity through intraday overdrafts. The availability of inexpensive liquidity can improve the efficiency of payment and securities settlement systems by making it less costly for participants to settle transactions when outgoing transactions are not offset by incoming transactions. This solution, however, may provide less incentive for participants to concentrate payments. Moreover, the provision of liquidity means that the central bank is exposed to credit risk that it must manage.

Central banks, therefore, face a number of important policy questions regarding whether and how to provide intraday liquidity in RTGS payment and DVP settlement systems: 1) To what extent do the cost of acquiring intraday liquidity and other factors influence the time when participants submit transactions to the system? 2) How do these factors contribute to the concentration (or lack thereof) of transactions during the day? 3) If there is concentration, how do these factors affect the selection of the specific focal period during the day? 4) How do these factors impact the amount of intraday overdrafts and the central banks' credit exposure? 5) How do these factors affect the efficiency of a system? 6) How do they affect other risks in a system, such as the risk of settlement delay?

The key policy question from which the others are derived is the first one. There is limited evidence to help central banks identify what factors influence participants' timing decisions. Policy analysis is often based on numerical simulations of submission patterns that assume no change in participants' behavior. But such analysis is subject to a type of Lucas critique, making it difficult to predict the effects of potential policy changes.

Our goal in this paper is to model the strategic interaction of participants in both payment and settlement systems to better understand the intraday patterns of settlement. With this better understanding, the model is able to make a number of predictions regarding the policy questions posed above.

To identify the factors that influence a participant's timing decision for transactions, our model is designed to capture a number of stylized facts about settlement on the Federal Reserve's Fedwire funds and securities systems. The stylized facts summarize the observed intraday pattern of settlement and the use of intraday overdrafts both before and after the imposition of intraday overdraft fees by the Fed in April 1994 and the subsequent increase in those fees in April 1995.³ These facts, which emphasize different responses to the policy change for Fedwire funds and securities, are:

The initial intraday overdraft fee did not significantly impact the timing of Fedwire funds settlement. Both before and after the fee, funds settlement was concentrated later in the day.
The initial intraday overdraft fee did not significantly affect the amount of overdrafts related to Fedwire funds.
The initial intraday overdraft fee significantly impacted the timing of Fedwire securities settlement. Before the fee, securities settlement was not significantly concentrated. After the fee, securities settlement became concentrated early in the day.
The initial intraday overdraft fee significantly reduced the amount of overdrafts related to Fedwire securities.
The subsequent increase in the intraday overdraft fee had no discernible impact on Fedwire funds or securities settlement. Neither the timing of settlement nor the use of overdrafts was significantly affected for either service.

In order to match the stylized facts, our model allows for three factors that influence the timing of transactions: the cost of intraday liquidity, the extent of settlement risk, and the overall design of a system.

The cost of intraday liquidity captures the direct cost of going into overdraft at the central bank. The effect of such direct costs has been the focus of earlier research on large-value payments systems. In particular, Bech and Garratt (2003)--hereafter Bech03-- examined the effect these costs have on RTGS participants' behavior and the timing of transactions. In their model, the imposition of an intraday overdraft fee encourages participants to noncooperatively coordinate payments either early or late whenever the cost of acquiring liquidity exceeds an assumed social cost of delaying payments. If intraday liquidity is free (or sufficiently inexpensive), however, then there is equilibrium concentration of payments early, motivated by this social cost of delay. This result is inconsistent with stylized fact 1.

Our model is in the spirit of Bech03. System participants behave noncooperatively but interdependently and can obtain intraday liquidity from a central bank at a cost.⁴ Participants time submissions so as to minimize all relevant costs involved in settling transactions. The game-theoretic framework of Bech03 is a useful starting point to understand how changes in policies provide different incentives for banks regarding the timing of transactions settlement.⁵

The main innovation of our model is the inclusion of settlement risk as a significant factor that influences the timing of transactions. Furfine (2003) emphasizes that settlement risk is an important factor in payment and securities settlement systems because it can be a channel for bank contagion and consequently a source of systemic risk. To our knowledge, no one has considered the effects of settlement risk on participants' transactions timing decisions.⁶ Nor has there been any work in applying this framework to securities settlement systems.

Our inclusion of settlement risk is based on the following intuition. When a sender of a payment initiates a transaction, the participant's balance at the central bank is reduced, which may cause an overdraft. This payment may have been sent with the expectation it would be offset with incoming payments. However, if there is uncertainty regarding the receipt of such payments, participants face settlement risk and have an incentive to delay sending payments until such uncertainty is resolved. In effect, delaying transactions provides some insurance against settlement risk. This incentive encourages later day concentration of payments regardless of the cost of intraday overdrafts; the imposition of an intraday overdraft fee only strengthens the existing incentive to delay payments. As a result, the impact of such a fee on overdrafts would be marginal. Thus, the inclusion of settlement risk in the model can explain stylized facts 1-2 and 5 for Fedwire funds.

Factoring settlement risk into participants' timing decisions implies that late-day coordination in RTGS payment systems may be optimal. If participants limit their risk exposure by delaying payments, the potential for contagion may be smaller ex post than might otherwise be the case. This conclusion is consistent with Furfine's (2003) findings for the U.S. and those of Angelini et al. (1996) for the Italian payment system.

The final factor that we add to the model which can influence participants' decisions on the timing of transactions is system design. We extend the payments framework to study DVP securities settlement systems. The DVP nature of settlement suggests that the settlement risk of a participant is diminished because it receives funds (or securities) at the same time it sends securities (or funds). As a result, the impact of settlement risk on strategic interaction is marginal for these systems.

Unlike in an RTGS system, settlement risk does not provide an incentive to concentrate transactions in a DVP securities settlement system. In Fedwire securities, the sender of the securities initiates the transaction, consequently the sender of funds has less control over the management of intraday overdrafts. This lack of control is not costly when there is no intraday overdraft fee, but becomes more of an issue when there is a positive fee. The fee, therefore, creates an incentive to send securities and receive funds early, encouraging early concentration of settlement activity. This is consistent with the stylized fact 3. The imposition of an intraday overdraft fee reduces overdrafts as it encourages more concentration, consistent with stylized fact 4. Raising the intraday overdraft fee only strengthens the incentive and has little marginal impact, which is consistent with stylized fact 5 for securities.

The models' ability to match the dramatically different reactions induced by the introduction of an intraday overdraft fee suggest that settlement risk is an important factor in participants' decisions regarding the timing of payments. Policy makers need to consider the impact that system design and other policy changes have on settlement risk and how that impacts participants' incentives. Our model provides a starting point from which to evaluate possible policy alternatives.

The remainder of our paper is organized as follows. Section 1 documents the stylized facts. Section 2 presents the model of the funds system. We derive the equilibrium behavior in the model and discuss the implications for overdrafts. This analysis is then repeated for the securities model in Section 3 The final section concludes.

1 Stylized Facts

The stylized facts are derived from the intraday pattern of settlement in Fedwire funds and securities both before and after the April 1994 introduction of an intraday overdraft fee and its subsequent increase in April 1995. Some of the evidence was observed by Richards (1995), which provides a history of the Federal Reserve's credit risk management policies.⁷ The impact of this policy change can be summarized as the timing of settlement and the amount of overdrafts across the Fedwire funds service was largely unchanged, whereas the timing of settlement and the amount of overdrafts related to Fedwire securities changed significantly in response to the initial fee but not for the fee increase.

We begin by documenting the timing and extent of concentration. Unfortunately, data limitations require that we rely on Richards (1995) for evidence on intraday timing. Figure 1, reproduced from Richards (1995),

**Figure 1:** Funds Timing (Richards, 1995, pp. 1074)

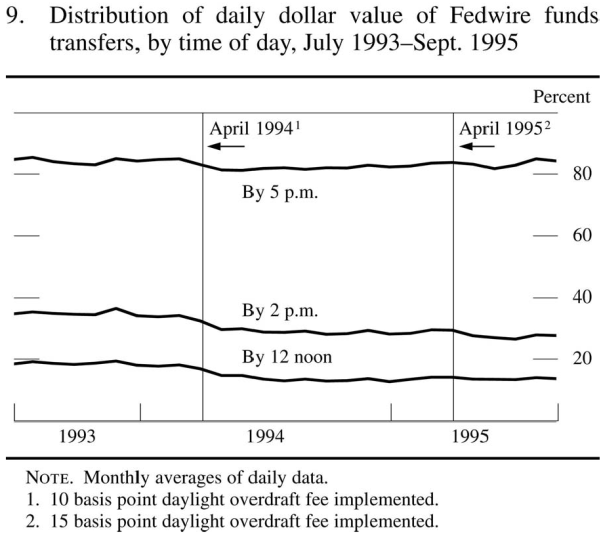
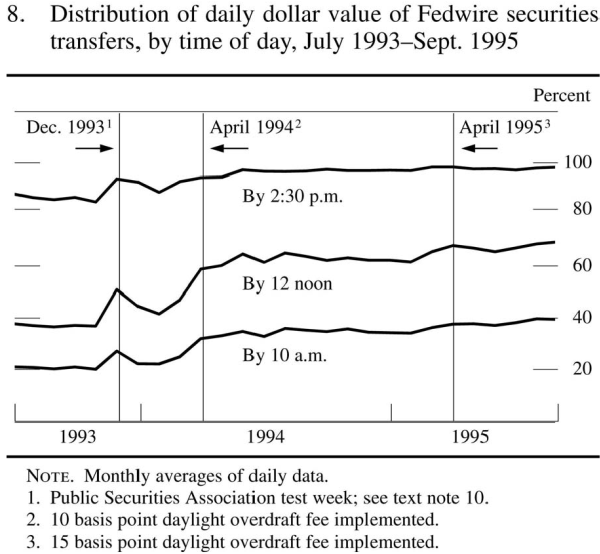
shows little change in the timing of Fedwire funds transactions in 1994. The percent of value settled prior to 2:00 p.m. trended down somewhat, falling around 7 percent from 1993 to 1995. This evidence is consistent with stylized facts 1. This trend towards later concentration of settlement has continued in more recent data (see PSR06, 2006).

Fedwire securities responded to the fee more strongly, as shown in Figure 2, also reproduced from Richards (1995).

**Figure 2:** Securities Timing (Richards, 1995, pp. 1074)

From 1993 to 1995, the percentage of value settled by 10:00 a.m. increased 20% and the percentage settled by noon increased around 30%. Comparing these figures shows that securities settlement tends to occur much earlier than funds settlement and that the difference became accentuated after the fee was imposed in April 1994. Figure 2 thus documents stylized fact 3.

Inspection of Figures 1 and 2 also reveals that the April 1995 fee increase had a negligible effect on both funds and securities, as summarized in fact 5.

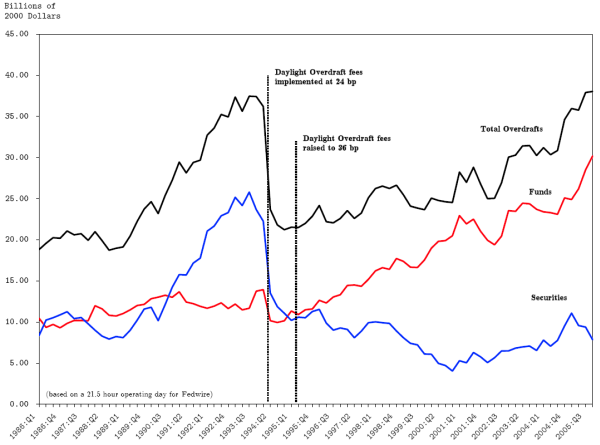
Data are available that details the impact of the policy change on the use of overdrafts. In the aggregate, average daily overdrafts in 1994 fell from $32.4 billion in the first quarter to $19.3 billion in the fourth quarter: more than a 40% drop in the Federal Reserve's credit exposure. The 1995 increase in the fee had little impact on overdrafts.

The decline in total overdrafts masks a strong asymmetry between the responses of Fedwire funds and Fedwire securities respectively. The asymmetric response can been seen in Figure 3. This figure shows the quarterly average of average daily overdrafts for Fedwire funds, Fedwire securities, and their sum in constant 2000 dollars. The large decline in total overdrafts was almost entirely driven by a reduction in the use of overdrafts to settle securities. While Fedwire funds overdrafts do dip somewhat after the fee is initially imposed, the change is small relative to that of overdrafts from securities.

**Figure 3:** Average Daily Overdrafts per Quarter

In addition to the relatively small drop in funds-related overdrafts when the fee was imposed, the funds overdrafts continued to grow at roughly the same rate after the policy change. More formally, as shown in Table 1, the first Chow (1960) test rejects a structural break in funds overdrafts in response to the initial fee. The Chow test's null hypothesis is that the coefficients of a linear regression are constant before and after a possible break point. In this case, we regressed the first difference of the quarterly average of overdrafts in the Fedwire funds system on a constant and a trend.⁸ Correcting for heteroscedasticity and serial correlation in the errors further strengthens the result. The structural stability of funds' overdrafts supports stylized fact 2.

Table 1: Chow Tests for Structural Stability
Variable	Test Statistic	Probability Value
$\Delta$ (Avg. Funds Overdrafts)	0.70512	49.73%
$\Delta$ (Avg. Secs. Overdrafts)	5.56071	0.56%

In contrast, the clearest feature of Fedwire securities overdrafts is the dramatic fall after the fee is imposed. Furthermore, the strong upward growth trend is reversed after the policy takes effect and securities overdrafts continue to decline albeit more slowly for a considerable period. Not surprisingly, as shown in Table 1, the Chow test for securities overdrafts confirms a structural break following the pricing change. Correcting for heteroscedasticity and serial correlation further strengthens the result. The evidence for a structural break in securities' overdrafts supports stylized fact 4

Turning to the effect of the subsequent fee increase, Figure 3 shows no signs of any significant impact in April 1995 on either funds or securities overdrafts. Chow tests (not shown) strongly reject a structural break for both funds' and securities overdrafts, supporting stylized fact 5.

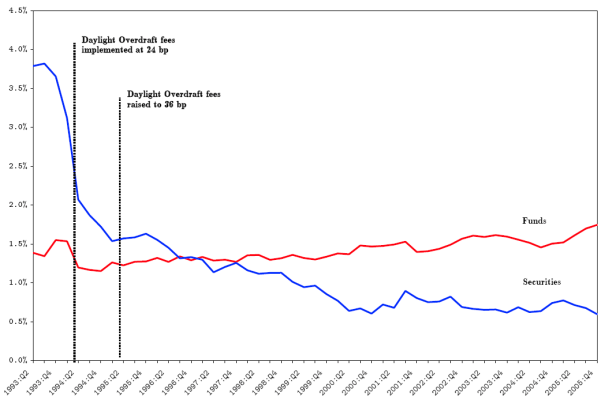
Further evidence of the asymmetric impact of the Federal Reserve's policy change is provided by Figure 4. This figure shows the quarterly average of the ratio of daily overdrafts to the daily value of settled transactions.⁹ Since the fee was imposed, the ratio for Fedwire funds has remained remarkably stable, while the ratio has fallen substantially for Fedwire securities.

**Figure 4:** Quarterly Turnover Ratios

As shown in Table 2, we can accept the hypothesis that the turnover ratio for funds is stationary using any of the Dickey-Fuller (DF), Augmented Dickey-Fuller (ADF), or Phillips-Perron (PP) tests¹⁰ (for other changes that could affect the two services, see BIS2005, 2005).

Table 2: Stationarity Test Results
Variable	Test Statistic	Stationarity
Funds Turnover Ratio: DF	-1.20020	Accept 10%
Funds Turnover Ratio: ADF	-0.82498	Accept 10%
Funds Turnover Ratio: PP	-1.22495	Accept 10%
Secs. Turnover Ratio: DF	-4.69688	Reject 1%
Secs. Turnover Ratio: ADF	-6.29156	Reject 1%
Secs. Turnover Ratio: PP	-4.79373	Reject 1%
Secs. Turnover Ratio: DF(t)	-3.46409	Reject 10%
Secs. Turnover Ratio: ADF(t)	-7.19960	Reject 1%
Secs. Turnover Ratio: PP(t)	-3.57294	Reject 5%
Secs. Turnover Ratio: Perron (A)	1.289	Accept 10%

These tests are run with an intercept, but no trend. The hypothesis of stationarity is accepted for any reasonable confidence level.

Stationarity of the turnover ratio implies the value of funds settled over Fedwire and the overdrafts used in that settlement are cointegrated. The interpretation is that in the long-run the value of payments drives the use of overdrafts. This equilibrium relationship is stable in the long-run despite the many changes in the payment system environment including the policy changes in 1994 and 1995.

The turnover ratio for securities is more complicated. From Table 2, stationarity of the securities turnover ratio can be rejected at the 99 percent confidence level. Trend stationarity can also be rejected but not at the same uniform strength; the rejection level is somewhat sensitive to the number of lags included in the test.

The results can be clarified by looking at the last line in the table which reports results from Perron's (1989) test. Perron's test has a null of stationarity with a single shift in level in the series. This hypothesis is overwhelmingly accepted for the securities ratio, implying the existence of a cointegration between the value of securities settled and the corresponding overdrafts. However unlike for the funds, the policy change caused the cointegration for securities to suffer a structural break. The asymmetric impact of the fee imposition on the causal relationship for funds and securities provides further support for stylized facts 2 and 4.

Having provided empirical support for the stylized facts, we now present our models, first for funds and then for securities.

2 The Funds Model

1 Environment

The baseline model shares many characteristics with Bech03's model. There are three periods denoted which can be interpreted as morning, afternoon and overnight. There are two agents called banks indexed by $i\in\{1,2\}$ whose objective is to minimize the expected cost of making payments to one another.¹¹ In addition to the banks, there is an institution which can be interpreted as a central bank that provides payment services to the banks.¹²Specifically, banks can send and receive payments by moving balances across accounts that they have with the central bank. In doing so, the banks are able to access liquidity from the central bank by overdrawing their account.

The timing of events is as follows. Banks start period 0 with a zero account balance from which to make payments.¹³ Then with probability , bank $i\in\{1,2\}$ receives an instruction to make a payment of 1 dollar to bank . The realization of this payment shock is independent of whether the other bank also receives a payment instruction. Moreover, the realization of the payment shock is private information to the bank. That is, the banks cannot communicate with one another and so coordinate payments cooperatively in order to reduce the expected costs of making payments.¹⁴

If bank receives a payment instruction, it then decides whether to make the payment in the morning (period 0) or in the afternoon (period ). We assume that banks do not strategically delay payments until the overnight period (period 2) unless it receives information concerning the ability of the other bank to send payments (see below).¹⁵ Banks can overdraw on their central bank accounts to make payments at a fee $r\geq0$ for each period $t\in\{0,1\}$ in which their account is in overdraft status. An account is in overdraft status whenever it has a negative balance at the end of a period. If a bank's account is in overdraft status at the end of period 1, it must borrow funds in the overnight market at interest rate to return to a zero balance.¹⁶

At the beginning of period 1, a bank may receive a settlement shock. Specifically, with a small probability $\varepsilon>0$ , bank cannot receive a payment from bank during period 1, but will receive it in period 2. The realization of the settlement shock is independent across banks. Moreover, the realization of the settlement shocks is common information among the banks, but the realization of whether a bank is to receive a payment from the affected bank remains private. Thus if a bank finds out that it cannot receive a payment from the other bank, it can delay any outstanding payments that must be sent to the affected bank until period 2.

The settlement shock represents a certain type of settlement risk to the receiving bank--defined as the risk that a payment is not sent by the expected time, in this case by the end of the intraday period.¹⁷ Such a shock could occur, for example, when the sending bank has an operational disruption or has a lack of available liquidity to send a payment at a particular point in time. This restricts the receiving bank's incoming source of liquidity that could offset outgoing payments and reduce their own costs of sending payments. The settlement shock can be thought of as a proxy for uncertainty regarding incoming funds to offset outgoing funds. While such a shock is relatively small in scope, it does have a cost by raising the probability that a bank needs to borrow in the overnight market (see below). More severe types of settlement shocks, such as those arising from insolvency, would have the effect of strengthening this cost.

Finally, during period 2 any outstanding payments are made and any outstanding overdraft balances are repaid by borrowing overnight at interest rate .

Three noticeable differences exist between this model and that in Bech03. The first is that banks do not receive a second payment instruction shock in the afternoon. A second shock would complicate the analysis without fundamentally changing our results. The second difference is that we do not assume that there is a social cost of payment delay. In the Bech03 model this assumption directly suggests that late-day concentration of payments is suboptimal. Relaxing that assumption does not ex-ante imply that early payments are socially optimal.¹⁸ The third difference is the introduction of the settlement shock, which we shall demonstrate below, is an important addition for matching the model with the stylized facts for Fedwire.

2 Cost Functions

As in Bech03, a bank's objective is to minimize the expected cost of making a payment. This objective only becomes relevant when a bank receives a payment shock at the beginning of period 0. Thus, we can focus on a bank's payment strategy in the state of the world in which it receives a payment instruction.

In what follows, we focus on pure strategies. Let $s_{i}$ denote the strategy of bank given that it received a payment instruction. The set of possible pure strategies is $s_{i}\in\{m,a\}$ , where denotes a morning payment (at period 0) and denotes an afternoon payment (at period 1). A strategy profile is a pair of timing strategies $(s_{i},s_{j})$ .

The expected cost of making a payment, , is a function of its payment timing strategy, $s_{i}$ , the timing strategy of the other bank, $s_{j}$ , the probability that the bank is to receive a payment, , the intraday overdraft fee, , the overnight interest rate, , and the probability of settlement risk, $\varepsilon$ . Let $c(s_{i},s_{j})$ denote bank 's expected cost of making a payment when it plays the timing strategy $s_{i}$ while bank plays the timing strategy $s_{j}$ . Then there are four possible realizations of expected costs:

$\displaystyle c(m,m)=(1-p)(2r+R)$

(1)

$\displaystyle c(m,a)=p(1-\varepsilon)r+p\varepsilon(2r+R)+(1-p)(2r+R)$

(2)

$\displaystyle c(a,m)=(1-p)(1-\varepsilon)(r+R)+(1-p)\varepsilon R$

(3)

$\displaystyle c(a,a)=(1-p)(1-\varepsilon)(r+R)+(1-p)\varepsilon R.$

(4)

Equation (2.2) pertains to bank 's cost if both it and bank send their payments in the morning (period 0). With probability , bank also receives a payment instruction and sends it in the morning. Thus, both payments offset and there is no overdraft fee and no need for bank to borrow in the overnight market. With probability , bank does not receive a payment. In that case, bank must pay the overdraft fee, , both in the morning and the afternoon. It then must borrow in the overnight market to cover its overdraft. Bank 's total cost in this case is .

Equation (2.2) pertains to bank 's cost if it sends a payment in the morning and bank , if it receives a payment instruction, sends it in the afternoon. With probability , bank receives a payment instruction and delays until the afternoon. Bank sends its payment and goes into overdraft for the morning (period 0). In the afternoon, bank sends its payment. With probability $(1-\varepsilon)$ , the payment is received by bank and no further overdraft charges are incurred. In such a scenario, bank 's total cost is . With probability $\varepsilon$ , there is a settlement shock and so bank must incur an additional overdraft fee for the afternoon, ends the day with an account balance of -1, and must borrow in the overnight market to bring the account balance back to zero. In this scenario, the bank's total cost is $\left( 2r+R\right)$ . Finally, with probability , bank does not receive a payment instruction, and, as before bank 's total cost is .

Equation (2.2) pertains to bank 's costs if it sends a payment in the afternoon while bank sends its payment in the morning if bank receives an instruction. With probability bank receives a payment instruction and sends the payment in the morning. Bank 's account balance goes to 1. Bank then sends its payment in the afternoon. Regardless of whether there is a settlement shock, bank does not face any settlement costs because it enters the afternoon with a positive account balance. Either the payment goes out in the afternoon (with probability $(1-\varepsilon)$ ) or it goes out in the overnight market. In that case, bank would not have to borrow in the overnight market. With probability , bank does not receive an instruction. Bank sends its payment in the afternoon and it goes through with probability $(1-\varepsilon)$ . In that case, bank 's costs are $\left( r+R\right)$ because the payment requires an afternoon overdraft and a loan in the overnight market. If there is a settlement shock (with probability $\varepsilon$ ), then bank does not pay an overdraft fee, but must borrow in the overnight market to make the late payment and so its cost is .

Finally, equation (2.2) pertains to bank 's cost if both banks send payments in the afternoon. With probability , bank receives an instruction. Both banks delay payments until the afternoon. If there is no settlement shock, then both payments offset each other and there are no overdraft charges. If there is a settlement shock, both banks send payments overnight and these offset each other so that there are no overnight loan charges.¹⁹ With probability , bank does not receive a payment instruction, and bank 's cost is determined in the same manner as in equation (2.2).

3 Equilibrium

In this subsection, we solve for the Bayesian Nash equilibria of the payment coordination game.

Free Intraday Overdrafts.--We first solve for the Bayesian Nash equilibrium when there is no intraday overdraft fee () as was the case for Fedwire before 1994. Table 3 represents the game in a $2\times2$ normal form. From Table 3 we have the following proposition.

Table 3: Payment Game with Free Overdrafts
	Bank 2:	Bank 2:
Bank 1:		$p\varepsilon R+(1-p)R$
Bank 1:	$p\varepsilon R+(1-p)R$

Proposition 1 For any $\varepsilon>0$ , and

, the strategy profiles

and

are Bayesian Nash equilibria, but only

survives the elimination of weakly dominated strategies.

Proof. If bank

plays

then bank

is indifferent to playing

; both strategies yield a cost of

. Thus

is a Bayesian Nash equilibrium. If bank

plays

, then

strongly dominates

for bank

because

has a higher expected cost by $p\varepsilon R$ . Thus

is also a Bayesian Nash equilibrium. Moreover

weakly dominates

so that

is the equilibrium that survives the elimination of weakly dominated strategies. $\qedsymbol$

Proposition 2.3 shows that in the presence of settlement risk, even a small risk, banks wish to concentrate their payments in order to reduce the expected costs related to settlement. Although banks are indifferent as to when such concentration takes place, the settlement risk encourages banks to delay payments. The model predicts that payments are concentrated in the afternoon, consistent with the pre-price observations in Fedwire funds documented in stylized fact 1. By delaying payments, information is revealed that can help the banks minimize their costs. If information pertaining to a shock is revealed, a bank can delay outgoing payments until period 2 in order to reduce the likelihood of having to borrow in the overnight market.

Costly Intraday Overdrafts.--We now turn to the pure strategy equilibria of the payments game when there is a positive overdraft fee (), as is the case in Fedwire starting in 1994. Table 4 represents the game in a $2\times2$ normal form with equations (2.2-2.2) simplified where appropriate.

Table 4: Payment Game with Costly Overdrafts
	Bank 2:	Bank 2:
Bank 1:		$(1-p+p\varepsilon)\left( R+r\right) +r$ $(1-p)R+(1-p)(1-\varepsilon)r$
Bank 1:	$(1-p)R+(1-p)(1-\varepsilon)r$ $(1-p+p\varepsilon)\left( R+r\right) +r$ $(1-p+p\varepsilon)\left( R+r\right) +r$	$(1-p)R+(1-p)(1-\varepsilon)r$ $(1-p)R+(1-p)(1-\varepsilon)r$

The inclusion of a positive value of

in the expected cost functions leads to the following proposition.

Proposition 2 For any $\varepsilon>0$ , and

, the strategy profile

is the unique equilibrium.

Proof. First we show that

dominates

for bank

when bank

plays

. Bank

's expected cost is less when playing

$\displaystyle (1-p)(2r+R)>(1-p)R+(1-p)(1-\varepsilon )r$

(5)

which can be seen by inspection. Next, we show that

dominates

for bank

when bank

plays

. Bank

's expected cost is less when playing

$\displaystyle p(1-\varepsilon )r+(1-p+p\varepsilon )(2r+R)>(1-p)R+(1-p)(1-\varepsilon )r.$

(6)

Rearranging (6) gives

$\displaystyle p(1-\varepsilon )r+p\varepsilon (2r+R)+(1-p)(2r+R)>(1-p)[r+(1-\varepsilon )R].$

(7)

Because the last term on the left-hand side of (7) is greater than the right-hand side, the inequality holds. $\qedsymbol$

Proposition 2.3 states that charging a price for intraday overdrafts eliminates the equilibrium that existed without pricing and strengthens the banks' preferences to concentrate payments later in the day. However, because the banks already had a preference for late day concentration due to settlement risk with free intraday overdrafts, empirically we would not expect much of a change in the timing and concentration of Fedwire funds once intraday overdrafts became costly. Thus, the model is consistent with stylized fact 1.

4 Efficiency and Risk in the Funds Model

In the introduction we noted that central banks face a number of policy questions regarding the efficiency and riskiness of payment systems. Bank behavior on the timing of payments directly impacts these policy questions. Our model is equipped to provide some insights on a number of such questions relating to the impact of introducing a price on intraday overdrafts.

Consider efficiency. We say an equilibrium is efficient if it minimizes the joint expected costs of the two banks. In the payment game without pricing, inspection of Table 3 shows that both equilibria minimize the joint cost of the two banks. This result contrasts with Bech03. When intraday overdrafts are free, Bech03's assumption of a social cost of delay implies that only is efficient.

In the payment game with the pricing of overdrafts, the unique equilibrium is efficient. A bank's expected cost at is less than its cost under any other outcome. This result again contrasts with Bech03. In our model, delaying payments partially insures a bank against the possibility that incoming payments are not settled, which adds to a bank's cost of sending payments. The introduction of an overdraft fee does add to the cost of making payments even with concentration because some banks will need to send outgoing payments without receiving incoming payments, go into overdraft in the afternoon, and pay an overdraft fee. Thus, the greater the fee, the greater the expected cost of making payments.

Central banks are also concerned about their own exposure to credit risk which is related to the aggregate size of intraday overdrafts. As the size of an individual overdraft is one, the amount of expected intraday overdrafts in the funds model without pricing is simply , which is the probability that one bank receives a payment times the probability that the other does not (a situation where payments cannot offset).

As in the case of free intraday overdrafts, the amount of expected intraday overdrafts in the model with a positive price is . Thus, the model predicts no change in the aggregate amount of expected overdrafts.²⁰ Thus, we should not expect to see much change in overdrafts for Fedwire funds in response to the introduction of overdraft pricing. This is consistent with stylized fact 2.

Additionally, the equilibria in the model with pricing are not sensitive to the level of the fee. Proposition 2.3 holds for any . Thus, the model predicts that neither the amount nor timing of overdrafts should be sensitive to the level of a positive intraday overdraft fee when that fee is less than the overnight rate (as is assumed). Consequently, changes in the fee will have the effect of raising the cost of making payments without significantly lowering the aggregate amount of overdrafts. This matches the experience in Fedwire funds as summarized by stylized fact 5.

Finally, the incentive to concentrate payments late in the day suggests that more payments may be susceptible to a settlement shock in aggregate. If a settlement shock occurs, the fact that both banks delay payments until period 1 means that more payments face the risk that they will not settle until the overnight period. This risk posed by late day payments has been a recent issue of interest for central banks.²¹

3 The Securities Model

1 Environment

The securities model is very similar to the funds model. There are three periods, two banks, and a central bank that provides payment services to the banks. The main differences between the two models are: i) the bank sending securities decides when to initiate the transaction and ii) the delivery-versus-payment (DVP) feature of securities settlement affects the cost of initiating transactions.

The timing of events is as follows. Banks start period 0 with a zero account balance from which to make payments. Then, with probability bank $i\in\{1,2\}$ receives an instruction to send securities valued at 1 dollar to bank . As before, the realization of this payment shock is independent of whether the other bank also receives an instruction and is private information to the bank.

If bank receives a payment instruction, it then decides whether to send the securities in the morning (period 0) or in the afternoon (period ). It is assumed that banks do not strategically delay the sending of securities until the overnight period (period 2) unless it receives information concerning the ability of the other bank to send securities and/or payments (see below). The DVP nature of securities settlement automatically forces the bank receiving the securities to send the equivalent payment (of dollar) at the same time as it receives the securities. Banks will overdraw on their central bank accounts to send these funds at a fee $r\geq0$ for each period $t\in\{0,1\}$ when their account is in overdraft status. An account is in overdraft status whenever it has a negative balance at the end of a period. If a bank's account is in overdraft status at the end of period 1, it must borrow funds in the overnight market at interest rate to return to a zero balance.

As in the funds model a bank may receive a settlement shock at the beginning of period 1. Specifically, with a small probability $\varepsilon>0$ , bank cannot settle a securities transaction with bank during period 1, but will be able to in period 2. The realization of the settlement shock is independent across banks. Moreover, the realization of the settlement shocks is common information among the banks, but the realization of whether a bank is to receive securities from the affected bank remains private. Thus if a bank finds out that it cannot receive securities from the other bank, it can delay any outstanding transactions that must be sent to the affected bank until period 2. As in the funds model, this shock represents a certain type of liquidity risk to the receiving bank.

Finally during period 2, any outstanding securities settlement transactions are made and any outstanding overdraft balances are repaid by borrowing overnight at interest rate .

2 Cost Functions

A bank's objective is to minimize the expected cost of securities settlement. As before, this only becomes relevant when a bank receives a payment shock at the beginning of period 0. Thus, we can focus attention on a bank's securities settlement strategy in the state of the world in which it receives a securities settlement instruction.

As before, we focus on pure strategies. The notation is similar to that in the funds model. The expected cost of a securities transaction, , is a function of its timing strategy, $s_{i}$ , the timing strategy of the other bank, $s_{j}$ , the probability that the bank is to receive securities, , the intraday overdraft fee, , the overnight interest rate, , and the probability of settlement risk, $\varepsilon$ . Let $c(s_{i},s_{j})$ denote bank 's expected cost of initiating a securities transaction when it plays the timing strategy $s_{i}$ while bank plays the timing strategy $s_{j}$ . Then there are four possible realizations of expected costs:

$\displaystyle c(m,m)=0%$

(8)

$\displaystyle c(m,a)=0%$

(9)

$\displaystyle c(a,m)=p\varepsilon2r+p(1-\varepsilon)r%$

(10)

$\displaystyle c(a,a)=0.%$

(11)

Equation (8) pertains to bank 's cost if both it and bank send their securities in the morning (period 0). Regardless of whether bank also receives a securities settlement instruction or not bank sends its securities in the morning and receives a payment at the same time. Thus, there is no overdraft fee and no need for bank to borrow in the overnight market so its cost are always 0.

Equation (9) pertains to bank 's cost if it sends its securities in the morning and bank , if it receives a securities settlement instruction, sends it in the afternoon. As in equation (8) there is no cost to bank .

Equation (10) pertains to bank 's costs if it sends securities in the afternoon while bank sends securities in the morning if it receives an instruction. With probability bank receives a securities settlement instruction and sends it in the morning. Bank 's funds account balance goes to . Bank then sends its securities in the afternoon. If the transaction is completed in the afternoon (with probability $(1-\varepsilon)$ ) then bank must pay an overdraft fee for the morning. If there is a settlement shock (with probability $\varepsilon$ ), the bank must pay for overdrafts in the morning and the afternoon. In that case, bank will not have to borrow in the overnight market to send its securities as it will get a dollar in return and its funds balance will return to 0.

Finally equation (11) pertains to bank 's cost if both banks send securities in the afternoon. As with and , bank has no cost to send its securities.

3 Equilibrium

We now solve for the Bayesian Nash equilibria of the securities settlement coordination game.

Free Intraday Overdrafts.--As with the funds model, we begin with the Bayesian Nash equilibrium when there is no intraday overdraft fee () as was the case for Fedwire before 1994. Table 5 represents the game in a $2\times2$ normal form.

Table 5: Securities Settlement Game with Free Overdrafts
	Bank 2:	Bank 2:
Bank 1:	0 0	0 0
Bank 1:	0 0	0 0

The main implication is that without overdraft fees, there is no cost to securities settlement. The settlement risk is completely eliminated by the DVP nature of the securities settlement system. Banks that send securities do not have to incur overdrafts. Those that receive securities may incur overdrafts but face no cost in doing so. Thus, we have the following.

Proposition 3 For any $\varepsilon>0$ , and

, all strategy profiles are Bayesian Nash equilibria.

The key implication of the proposition is that banks have no incentive to coordinate payments. Thus, Proposition 3.3 suggests no empirically significant concentration of payments in a DVP securities settlement system with no intraday overdraft fee. Such is the observation for Fedwire securities before pricing in stylized fact 3.

Costly Intraday Overdrafts.--We now turn to the pure strategy equilibria of the securities game when there is a positive overdraft fee () as is the case in Fedwire starting in 1994. Table 6 represents the game in a $2\times2$ normal form.

Table 6: Securities Settlement Game with Costly Overdrafts
	Bank 2:	Bank 2:
Bank 1:	0 0	0 $p\varepsilon 2r+p(1-\varepsilon)r$
Bank 1:	$p\varepsilon 2r+p(1-\varepsilon)r$ 0	0 0

With

we have the following proposition.

Proposition 4 For any $\varepsilon>0$ and

, the strategy profiles

and

are Bayesian Nash equilibria, but only

survives the elimination of weakly dominated strategies.

Proof. If bank

plays

then bank

is indifferent to playing

; both strategies yield a cost of 0. Thus

is a Bayesian Nash equilibrium. If bank

plays

, then

strongly dominates

for bank

because

has a positive expected cost whereas

does not. Thus

is also a Bayesian Nash equilibrium. Moreover

weakly dominates

so that

is the equilibrium that survives the elimination of weakly dominated strategies. $\qedsymbol$

The main intuition for Proposition 3.3 is that banks have no incentive to delay sending securities. If they delay, then there is a good chance that the other bank sends securities earlier and causes the receiving bank to go into overdraft which is now costly. Thus, banks prefer to send their securities early and receive the equivalent funds early. This funding can then be used to offset current or future payments due to the receipt of securities and to avoid overdrafts. Thus, the DVP nature of the securities settlement system provides an incentive for early securities settlement only if there is a positive price for overdrafts. This is consistent with stylized fact 3 as securities transactions over Fedwire became much more concentrated earlier in the day after the introduction of an overdraft fee.

4 Efficiency and Risk in the Securities Model

As with the funds model, we now turn to the policy questions regarding the efficiency and riskiness of securities settlement systems.

First, consider efficiency. Recall that an equilibrium is efficient if it jointly minimizes the expected costs of the two banks. Any equilibrium of the settlement game with no overdraft fee is going to be efficient from this perspective. In the securities game with the pricing of overdrafts, both Bayesian Nash equilibria are efficient. Note that the introduction of an overdraft fee does add to the cost of settlement as it did in the funds model. The greater the fee, the greater the expected cost of securities settlement.

Next, consider risk. In the model with no fee, the expected amount of overdrafts is indeterminate. It will be at least as large as the amount of overdrafts found in the funds game, . It is likely higher, however, because the securities game supports more equilibria with no incentive to economize on the need for overdrafts; that is, there is no incentive to concentrate securities transactions. In the model with a positive price, both Bayesian Nash equilibria have the tendency to lower overdrafts. Because pricing encourages coordination, expected overdrafts are which is likely lower than that without an overdraft fee because it encourages equilibria with the concentration of settlement transactions. This is consistent with stylized fact 4 that the introduction of an intraday overdraft fee reduced the overdrafts from securities transactions.

As with the funds model, the equilibrium outcomes in the model are not sensitive to the level of the fee. Proposition 3.3 holds for any . Thus, the model predicts that neither the amount or timing of overdrafts should be sensitive to the level of a positive intraday overdraft fee. Consequently, changes in the fee will raise the costs of settlement without further reductions in the aggregate level of overdrafts. This matches the experience in Fedwire securities as summarized by stylized fact 5.

Finally, the early equilibrium, which survives the elimination of weakly dominated strategies, suggests that less securities transactions are susceptible to the settlement shock after the overdraft fee is imposed. Thus, fewer securities transactions are likely to have to be scheduled during the overnight period. This poses less risk that securities transactions will be delayed until the overnight period.

4 Conclusion

This paper models the strategic interaction of participants in both payment and settlement systems to better understand the intraday patterns of settlement. We identify factors that influence a participant's timing decision for transactions. We develop a model that has three possible factors: the cost of intraday liquidity, the extent of settlement risk, and the overall design of a system. We then demonstrate how the model successfully matches a number of stylized facts about the timing of transactions in the Federal Reserve's Fedwire funds and securities services.

As mentioned in the introduction, predictions about future policy changes typically assume no change in participants' behavior. By using observed responses to policy changes to extract the factors that influence the timing of transactions, our model provides a solid starting point for future policy analysis. A key insight is that settlement risk and the design of payment and settlement systems matters. For example, the framework can be used to evaluate how alternatives to real-time gross settlement systems might impact concentration in payments systems or to evaluate the impact in securities settlement of having the sender of funds initiate a transaction. Future work could also focus on how participants may respond in times of stress so that policy makers can anticipate the likelihood of financial contagion and crises.

Another useful extension is to combine the two models presented in the paper into a single, comprehensive model. Settlement of funds and securities affect the same account balance that determines overdrafts and their associated fees. Thus, it would seem natural to model the timing decisions of banks regarding the sending of funds and securities as a joint decision. Indeed, we have worked out a such a version of the model and the results in this paper are robust. Offering two separate models instead of one comprehensive model greatly simplifies the presentation of the main ideas.²² Future work that focuses on the interrelationship of multiple systems and its impact on risk and efficiency would benefit from a single, comprehensive model.

While our model is focused on matching facts in response to a particular policy change, the framework could be applied to other policies as well. For example, many RTGS systems in the European Union and elsewhere provide free intraday liquidity but require the credit to be collateralized. As shown in Bech03, collateralized intraday overdrafts can have an implicit cost to acquiring liquidity that can lead to different outcomes regarding concentration. Their analysis, however, did not account for settlement risk or look at securities settlement systems.

While our model does well in qualitatively explaining the stylized facts concerning Fedwire, other features that we have not modeled may also contribute to those facts. For example, banks receive many payment instructions later in the day rather than just at the beginning of the day. Because these payment instructions arrive at the bank late in the day, the payments are sent with very little delay. Thus, late-day concentration of payments may be because the majority of payment instructions are late-day. In this paper, our focus is on payment instructions about which banks are informed early in the day and so have a choice regarding the timing of settlement. Adding some new late-day instructions can easily be accommodated in the model without altering the basic intuition of our paper.²³ Whether late-day concentration of payments is mainly driven by the delay of payments to avoid expected costs, or is simply an artifact of new payment instructions received late is an as yet unsolved empirical question. Nonetheless, we expect both explanations for late-day concentration to have some explanatory power.

Acknowledgements

The authors thank James Chapman, Elizabeth Klee, Antoine Martin, Robert Reed, and Neil Wallace and seminar participants at the Payments Workshop at the Federal Reserve Bank of New York and the 2007 Midwest Macroeconomic Meetings for comments and suggestions. We also thank Samia Y. Husain for valuable research assistance.

Bibliography

Angelini, P., Maresca, G., Russo, D., Jun., 1996.

Systemic risk in the netting system. Journal of Banking and Finance 20 (5), 853-68.

Bech, M. L., Garratt, R., Apr., 2003.

The intraday liquidity management game. Journal of Economic Theory 109 (2), 198-219.

Bech, M. L., Speight, G., Willison, M., Yang, J., 2005.

The optimal supply of central bank money intra-day, paper presented at the Future of Payments Conference, Bank of England, London, UK.

Board of Governors of the Federal Reserve System, Jun., 2006.

Policy on payments system risk: Docket no. op-1259. Federal Register 71 (124), 36800-11.

Chow, G. C., Jul., 1960.

Tests of equality between sets of coefficients in two linear regressions. Econometrica 28 (3), 591-605.

Coleman, S. P., Feb., 2002.

The evolution of the federal reserve's intraday credit policies. Federal Reserve Bulletin 88 (2), 67-84.

Committee on Payment and Settlement Systems, 1992.

Delivery versus Payment in Securities Settlement Systems. Vol. CPSS Publications No. 6. Bank for International Settlements, Basel.

Committee on Payment and Settlement Systems, 2005.

New developments in large-value payment systems. Vol. CPSS Publications No. 67. Bank for International Settlements, Basel.

Dickey, D. A., Fuller, W., Jun., 1979.

Distribution of the estimators for autoregressive time series with a unit root. Journal of the American Statistical Association 74 (366), 427-31.

Furfine, C., Feb., 2003.

Interbank exposures: Quantifying the risk of contagion. Journal of Money, Credit, and Banking 35 (1), 111-128.

Green, E. J., 1997.

Money and debt in the structure of payments. Bank of Japan Monetary and Economic Studies 215, 63-87.

Green, E. J., 2005.

The role of the central bank in payment systems, paper presented at the Future of Payments Conference, Bank of England, London, UK.

Kahn, C. M., McAndrews, J., Roberds, W., Aug., 2003.

Settlement risk under gross and net settlement. Journal of Money, Credit, and Banking 35 (4), 591-608.

Perron, P., Nov., 1989.

The great crash, the oil price shock, and the unit root hypothesis. Econometrica 57 (6), 1361-1401.

Phillips, P. C. B., Mar., 1987.

Time series regression with a unit root. Econometrica 55 (2), 277-301.

Phillips, P. C. B., Perron, P., Jun., 1988.

Testing for a unit root in time series regression. Biometrika 75 (2), 335-346.

Richards, H. W., Dec., 1995.

Daylight overdraft fees and the federal reserve's payment system risk policy. Federal Reserve Bulletin 81 (12), 1065-77.

Footnotes

† Corresponding author. Phone: 202-530-6265. Fax: 202-872-7533.
The views in this paper are soley the responsibility of the authors and do not necessarily reflect the views of the Board of Governors or other staff of the Federal Reserve System. Any errors are our responsibility. Return to Text

1. Eligible securities include those issued by the U.S. Treasury, federal agencies, government sponsered enterprises (such as Fannie Mae and Freddie Mac), and certain international organizations (such as the World Bank and International Monetary Fund). Return to Text

2. The Fedwire securities service is a "Model 1" DVP system. See BIS1992 (1992) for two other models for DVP systems. Return to Text

3. In April 1994 the intraday overdraft fee went from 0 to 24 basis points (using a 24-hour rate). In April 1995 the fee increased from 24 to the current fee of 36 basis points. Return to Text

4. Their model considers two different types of policies that affect the cost of acquiring intraday liquidity: an explicit price or interest rate due to be paid at the end of the day for an unsecured overdraft, or an implicit price due to the opportunity cost of collateral posted to secure an overdraft. Our model focuses only on the first type of policy because it closely resembles the policy of the Federal Reserve. Our model could be extended to look at collateral-based policies. Return to Text

5. While the need to economize on liquidity may encourage cooperation over noncooperative behavior, the size and scale of large value payment and securities settlement systems suggest that a noncooperative framework is an appropriate one. There are over 7500 participants in Fedwire. Cooperative behavior from such a large number of players would be extremely difficult. Return to Text

6. Kahn et al. (2003) model settlement risk within payment systems to compare the riskiness of net and gross settlement payment systems. They do not model participants' timing decisions, but allow participants to strategically default, and not send payments. In our model, participants do not strategically default on payments, but can strategically decide when to send payments.

Bech et al. (2005) model operational risk in payment systems where timing of payments is studied. In their model, a disruption that causes an inability for a bank to send payments it has agreed to send leads to some social cost. In our model, a disruption that makes a bank unable to receive payments leads a bank with an overdraft position to incur a cost because it needs to borrow in the overnight market to return their account balance to a nonnegative position. Return to Text

7. See also Coleman (2002) for updates to the policy history after 1995. Return to Text

8. We first differenced the data due to nonstationarity. The constant and trend are individually insignificant, but jointly significant. We include the trend as it is significant for securities overdrafts. If the trend is dropped, the Chow test has a value of 1.10954 with a probability of 29.55 percent. Return to Text

9. The data on the value of transactions settled is only available from 1993 onwards. Return to Text

10. For3 the Dickey-Fuller and Augmented Dickey-Fuller tests, see Dickey and Fuller (1979). The lag length in the ADF tests is 2, which minimizes the Akaike Information Criterion. The Bayesian Information Criterion uniformly chooses a lag length of zero: equivalent to the DF test. For the Phillips-Perron test, see Phillips (1987) and Phillips and Perron (1988). The results are presented for zero lags in the error process based on a Ljung-Box test for serial correlation, but the conclusions are not sensitive to the inclusion of more lags. Return to Text

11. Participants in payment and settlement systems are typically depository institutions, with some exceptions. For simplicity, we refer to participants as banks. Return to Text

12. There is nothing in the model that suggests that these payment services should be provided by a central bank instead of a private clearinghouse. Green (1997) discusses this issue. Return to Text

13. It is implicitly assumed that the cost of "pre-funding" a payments account is greater than the expected cost of overdrawing accounts to make payments. In an environment where overnight reserves on account at a central bank pays no interest, this is a reasonable assumption. Return to Text

14. While the inability to communicate seems extreme when there are only two banks, such an assumption serves as a proxy for systems such as the Federal Reserve's Fedwire service, in which there are thousands of daily participants and many periods within a day to send and receive payments. Return to Text

15. Banks have an interest in making payments on behalf of their customers on the day they are requested. Return to Text

16. The assumption that the overnight interest rate

is greater than the price for intraday overdrafts

is consistent with the historical relationship between the Federal Reserve's price for intraday overdrafts and the Federal Funds rate. Moreover, if

then banks would have an incentive to avoid overdrafts completely and prefund their payment and settlement accounts. Thus,

serves as an upper bound on the policy choice of

. Return to Text

17. For more detailed information on settlement risk see BIS1992 (2005). Return to Text

18. We can easily include some cost to the delay of payments, but that cost will have to be sufficiently small enough for the models to match the stylized facts for Fedwire. Moreover, Green (2005) argues that there is no evidence of such a social cost in Fedwire. Return to Text

19. This is true regardless of which bank receives the shock. Information regarding the shock will allow the other bank to delay its payment until period 2. Return to Text

20. Recall that the addition of an intraday overdraft fee eliminates the weakly dominated equilibirium

. It also eliminates any possible mixed strategy equilibria that could have resulted in higher expected overdrafts (as banks are less likely to concentrate payments when they mix strategies). If mixed strategies are considered, the model would predict a slight reduction in overdrafts as a result of increased incentive to concentrate payments in the afternoon period. Return to Text

21. See, for example, PSR06 (2006). Return to Text

22. For example, banks are more hetergenous than they are here. In a unified model, banks would either by one of three basic types: send only payments, send only securities, send both payments and securities. This leads to a larger number of games to consider. Return to Text

23. See Bech03 for an example. Return to Text

^♣ This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to Text