Skip to: [Printable Version (PDF)] [Bibliography] [Footnotes]

Finance and Economics Discussion Series: 2007-63 Screen Reader version ^♣

Explaining a Productive Decade

STEPHEN D. OLINER

Board of Governors of the Federal Reserve System

DANIEL E. SICHEL

Board of Governors of the Federal Reserve System

KEVIN J. STIROH

Federal Reserve Bank of New York

August 2007

We thank Martin Baily, John Fernald, Andrew Figura, Dale Jorgenson, Gregory Mankiw, participants at the March 2007 Brookings Panel conference, and participants at the March 2007 Productivity Meeting at the National Bureau of Economic Research for useful comments and discussions; we also thank John Roberts for providing code and assistance to implement his Kalman filter model, George Smith and Robert Yuskavage of the Bureau of Economic Analysis for help with the industry data, and David Byrne for assistance with semiconductor data. The views expressed in this paper are those of the authors and do not necessarily reflect the views of the Federal Reserve Bank of New York, the Board of Governors of the Federal Reserve System, or other staff members at either organization.

Keywords: Productivity, information technology, total factor productivity, sources of growth, intangible capital

Abstract:

This paper analyzes the sources of U.S. productivity growth in recent years using both aggregate and industry-level data. We confirm the central role for information technology (IT) in the productivity revival during 1995-2000 and show that IT played a significant, though smaller, role after 2000. Productivity growth after 2000 appears to have been boosted by industry restructuring and cost cutting in response to profit pressures, an unlikely source of future strength. In addition, the incorporation of intangible capital into the growth accounting framework takes some of the luster off the performance of labor productivity since 2000 and makes the gain during 1995-2000 look larger than in the official data. Finally, we examine the outlook for trend growth in labor productivity; our estimate, though subject to much uncertainty, is centered at 2-1/4 percent a year, faster than the lackluster pace that prevailed before 1995 but somewhat slower than the 1995-2006 average.

Productivity growth in the United States rose sharply in the mid-1990s, after a quarter century of sluggish gains. That pickup was widely documented, and a relatively broad consensus emerged that the speedup in the second half of the 1990s was importantly driven by information technology (IT).¹ After 2000, however, the economic picture changed dramatically, with a sharp pullback in IT investment, the collapse in the technology sector, the terrorist attacks of September 11, 2001, and the 2001 recession. Given the general belief that IT was a key factor in the growth resurgence in the mid-1990s, many analysts expected that labor productivity growth would slow as IT investment retreated after 2000. Instead labor productivity accelerated further over the next several years. More recently, however, the pace of labor productivity growth has slowed considerably.

In light of these developments, researchers and other commentators have been intensely interested in the course of productivity growth since 2000. Distinguishing among the possible explanations for the continued strength in productivity growth is challenging, because much of that strength appeared in measured multifactor productivity (MFP), the unexplained residual in the standard growth accounting setup. Nevertheless, potential explanations can be divided into two broad categories: those centered on IT and those unrelated or only loosely related to IT.

The simplest IT-centered story--that rapid technological progress in the production of IT and the induced accumulation of IT capital raised productivity growth--does not work for the period after 2000, because the contributions to growth from both the production and the use of IT declined. A second IT-related story that has received a great deal of attention is that IT investment proxies for complementary investments in intangible capital, and a growing body of research has highlighted the important role played by such intangibles.² A third IT-related story identifies IT as a general-purpose technology that spurs further innovation over time in a wide range of industries, ultimately boosting growth in MFP.³ Because this process takes time, the gains in MFP observed since 2000 could reflect the follow-on innovations from the heavy investment in IT in the second half of the 1990s.

Another broad set of explanations highlights forces not specific to IT. Gains in labor productivity since 2000 could have been driven by fundamental technological progress outside of IT production, as implied by the strong growth in MFP in other sectors.⁴ Alternatively, the robust advance in labor productivity could reflect broader macroeconomic factors such as normal cyclical dynamics, a decline in adjustment costs after 2000 as investment spending dropped back, greater-than-usual business caution in hiring and investment, or increased competitive pressures on firms to restructure, cut costs, raise profits, and boost productivity. The profit-driven cost-cutting hypothesis, in particular, has received considerable attention in the business press.⁵

In this paper we try to sort out these issues using both aggregate and industry-level data.⁶ We investigate four specific questions. First, given the latest data and some important extensions to the standard growth accounting framework, is an IT-centered story still the right explanation for the resurgence in productivity growth over 1995-2000, and does IT play a significant role when considering the entire decade since 1995? Second, what accounts for the continued strength in productivity growth after 2000? Third, how has investment in intangible capital influenced productivity developments? Finally, what are the prospects for labor productivity growth in coming years?

Our analysis relies in part on neoclassical growth accounting, a methodology that researchers and policymakers have used for many years to gain insights into the sources of economic growth. Notably, the Council of Economic Advisers, the Congressional Budget Office, and the Federal Reserve Board routinely use growth accounting as part of their analytical apparatus to assess growth trends.⁷

Of course, growth accounting is subject to limitations, and in recent years many analysts have leveled critiques at this methodology. For example, the standard neoclassical framework does not explicitly account for adjustment costs, variable factor utilization, deviations from perfect competition and constant returns to scale, outsourcing and offshoring, management expertise, or the intangibles that are omitted from published data. In addition, researchers have raised a host of measurement issues that could affect the standard framework.⁸ It is well beyond the scope of this paper to deal with all of these critiques, but we augment the standard framework to account for some of the most salient ones. In particular, we take on board time-varying utilization of inputs, adjustment costs for capital, and intangibles. Our intention is to broaden the standard framework to get a fuller view of productivity developments during the past decade.

Briefly, our answers to the four questions we pose are as follows. Both the aggregate and the industry-level results indicate that IT was indeed a key driver of the pickup in labor productivity growth over 1995-2000. IT also is a substantial contributor to labor productivity growth over the full decade since 1995, although its contribution is smaller after 2000. In the aggregate data, this conclusion stands even after accounting for variable factor utilization, adjustment costs, and intangible capital.

Regarding the continued strength in labor productivity growth since 2000 in the published data, our answer has a number of elements. As a matter of growth accounting arithmetic, the smaller--although still sizable--contribution of IT after 2000 was more than offset by several factors, the most important being faster MFP growth outside the IT-producing sector. Just as the aggregate data highlight different sources of productivity growth during 1995-2000 than since 2000, so do the industry data. The industry composition of labor productivity growth across these periods shifted significantly, and we report evidence that IT capital was linked to changes in industry productivity growth in the 1990s but not in the period since 2000.

The industry data also suggest that the rapid post-2000 productivity gains were due, at least in part, to restructuring and cost cutting in some industries as highlighted by Robert Gordon.⁹ In particular, those industries that saw the sharpest declines in profits from the late 1990s through 2001 also tended to post the largest gains in labor productivity in the early 2000s. Because these restructuring-induced advances probably were one-time events (and could be reversed), they are unlikely to be a source of ongoing support to productivity growth.

In addition, the industry evidence indicates that reallocations of both material and labor inputs have been important contributors to labor productivity growth since 2000, a point that Barry Bosworth and Jack Triplett also note.¹⁰ Although it is difficult to pin a precise interpretation on the reallocation results, the importance of these reallocations could be viewed as evidence that the flexibility of the U.S. economy has supported aggregate productivity growth in recent years by facilitating the shifting of resources among industries.

The incorporation of intangibles into the aggregate growth accounting framework takes some of the luster off the performance of labor productivity since 2000 and makes the gains in the 1995-2000 period look better than in the published data. In addition, the step-up after 2000 in MFP growth outside the IT-producing sector is smaller after accounting for intangibles than in the published data. Thus any stories tied to a pickup in MFP growth (such as IT as a general-purpose technology) may apply to the entire decade since 1995 and not simply to recent years. This framework also implies that intangible investment has been quite sluggish since 2000, coinciding with the soft path for IT capital spending. All else equal, this pattern could be a negative for labor productivity growth in the future to the extent that these investments are seed corn for future productivity gains.

Finally, our analysis of the prospects for labor productivity growth highlights the wide range of possible outcomes. We report updated estimates of trend growth in labor productivity from a Kalman filter model developed by John Roberts;¹¹ these results generate a 2-standard-error confidence band extending from 1 $\raise.5ex\hbox{$\scriptstyle 1$}\kern-.1em/ \kern-.15em\lower.25ex\hbox{$\scriptstyle 4$}$ percent to 3 $\raise.5ex\hbox{$\scriptstyle 1$}\kern-.1em/ \kern-.15em\lower.25ex\hbox{$\scriptstyle 4$}$ percent at an annual rate, with a point estimate of 2 $\raise.5ex\hbox{$\scriptstyle 1$}\kern-.1em/ \kern-.15em\lower.25ex\hbox{$\scriptstyle 4$}$ percent. In addition, we solve for the steady-state growth of labor productivity in a multisector model under a range of conditioning assumptions. This machinery also suggests a wide range of outcomes, extending from about 1 $\raise.5ex\hbox{$\scriptstyle 1$}\kern-.1em/ \kern-.15em\lower.25ex\hbox{$\scriptstyle 2$}$ percent to just above 3 percent, with a midpoint of 2 $\raise.5ex\hbox{$\scriptstyle 1$}\kern-.1em/ \kern-.15em\lower.25ex\hbox{$\scriptstyle 4$}$ percent. Notwithstanding the wide band of uncertainty, these estimates are consistent with productivity growth remaining significantly above the pace that prevailed in the twenty-five years before 1995, but falling short of the very rapid gains recorded over the past decade.

The paper is organized as follows. The next section reviews the aggregate growth accounting framework and presents baseline results that account for variable factor utilization and adjustment costs. The section that follows uses the approach of Susanto Basu and coauthors to generate time series for intangible investment and capital services and presents growth accounting results for the augmented framework.¹² This approach complements that in the 2005 and 2006 papers by Carol Corrado, Charles Hulten, and Daniel Sichel, who also developed time series of intangible investment and capital and incorporated those estimates into a standard growth accounting framework. We then turn to the industry data to supplement the insights that can be drawn from the aggregate data. Finally, we discuss the outlook for productivity growth and present some brief conclusions.

Aggregate Growth Accounting: Analytical Framework and Baseline Results

We use an extension of the growth accounting framework developed by Oliner and Sichel to analyze the sources of aggregate productivity growth in the United States.¹³ That framework was designed to measure the growth contributions from the production and use of IT capital, key factors that emerged in the second half of the 1990s. The framework has some limitations, however. It excludes intangible capital, which has received much attention in recent research on the sources of productivity gains. It also imposes the strict neoclassical assumption of a frictionless economy and thus abstracts from cyclical influences on productivity growth and from the effects of adjustment costs arising from the installation of new capital goods.

The growth accounting framework in this paper incorporates all of these considerations. We meld the original Oliner-Sichel model with the treatment of adjustment costs and cyclical factor utilization developed by Basu, John Fernald, and Matthew Shapiro.¹⁴ In addition, we take account of intangible capital by drawing on the model of Basu, Fernald, Nicholas Oulton, and Sylaja Srinivasan.¹⁵

Analytical Framework

The model that underlies our analytical framework includes six sectors. Four of these produce the final nonfarm business output included in the National Income and Product Accounts (NIPAs): computer hardware, software, communications equipment, and a large non-IT-producing sector. The NIPAs omit production of virtually all intangible capital other than software. Our model accounts for this capital by adding a fifth final-output sector that produces the intangible assets excluded from the NIPAs. In addition to the five final-output sectors, our model includes a sector that produces semiconductors, which are either consumed as an intermediate input by the final-output sectors or exported to foreign firms. To focus on the role of semiconductors in the economy, the model abstracts from all other intermediate inputs.

Following BFS, we allow the length of the workweek, labor effort, and the utilization of capital to vary over time. We also assume that the installation of new capital diverts resources from the production of market output. As in BFS, these adjustment costs depend on the amount of investment relative to existing capital. Boosting the ratio of investment to capital increases the fraction of output that is lost to adjustment costs.¹⁶ To complete the model specification, we assume that the production function in every sector exhibits constant returns to scale and that the economy is perfectly competitive.¹⁷

Given this model, the appendix shows that growth in aggregate labor productivity can be expressed as

(1) $A\dot {L}P\equiv \dot {V}-\dot {H}= \sum\limits_j {\left( {\alpha _j^K -\phi _j } \right)\left( {\dot {K}_j -\dot {H}} \right)} {\kern 1pt}{\kern 1pt} +\alpha ^L\dot {q} +M\dot {F}P,{\kern 1pt}$

where a dot over a variable signifies the growth rate of that variable, is aggregate value added in nonfarm business, is aggregate hours worked, $_{j}$ is the aggregate amount of type- capital used in the nonfarm business sector, $\alpha ^L$ and $\alpha _j^K$ are, respectively, the income shares for labor and each type of capital, $\phi _j$ is the adjustment cost elasticity of output with respect to type- capital, is an index of labor quality, and MFP denotes multifactor productivity. The various types of capital include computer hardware, software, communications equipment, other tangible capital, and intangible capital other than software; each type of capital is produced by the corresponding final-output sector in our model. Except for the adjustment cost effect captured by $\phi _j ,$ equation 1 is a standard growth decomposition. It expresses growth in labor productivity as the sum of the contribution from the increase in capital per hour worked (capital deepening), the contribution from the improvement in labor quality, and growth in aggregate MFP.¹⁸

Aggregate MFP growth, in turn, equals a share-weighted sum of the sectoral MFP growth rates:

(2) $M\dot {F}P=\sum\limits_i {\mu _i M\dot {F}P_i } + \mu _S M\dot {F}P_S ,$

where denotes the semiconductor sector and indexes the final-output sectors in our model (listed above). The weight for each sector equals its gross output divided by aggregate value added. These are the usual Domar weights that take account of the input-output relationships among industries.¹⁹ Equation 2 has the same structure as its counterpart in an earlier paper by Oliner and Sichel.²⁰ The only formal difference is that including intangible capital increases the number of final-output sectors from four to five.²¹

Finally, the sectoral MFP growth rates in equation 2 can be expressed as

(3) $M\dot {F}P_i =\xi _i {\kern 1pt}\dot {W}_i -\mathop \sum \limits_j^ {\kern 1pt}\phi _{j,i} \left( {\dot {I}_{j,i} -\dot {K}_{j,i} } \right)+\dot {z}_i$

for the final-output sectors and

(4) $M\dot {F}P_S =\xi _S {\kern 1pt}\dot {W}_S -\mathop \sum \limits_j^ {\kern 1pt}\phi _{j,S} \left( {\dot {I}_{j,S} -\dot {K}_{j,S} } \right)+\dot {z}_S$

for semiconductor producers, where the $\xi '\mbox{s}$ represent the elasticity of sectoral output with respect to the workweek (, the $I'\mbox{s}$ and $K'\mbox{s}$ denote sectoral investment and capital services for each type of capital, the $\phi '\mbox{s}$ represent the sectoral adjustment cost elasticities for each type of capital, and the $z'\mbox{s}$ represent the true level of technology. All of the $\xi '\mbox{s}$ and $\phi '\mbox{s}$ take positive values.

In the BFS model that we adopt, firms vary the intensity of their factor use along all margins simultaneously, which makes the workweek a sufficient statistic for factor utilization in general. Lengthening the workweek boosts measured MFP growth in equations 3 and 4 as firms obtain more output from their capital and labor. Regarding adjustment costs, faster growth of investment spending relative to that of capital depresses measured MFP growth as firms divert resources from producing market output to installing new plant and equipment. The effects of factor utilization and adjustment costs drive a wedge between measured MFP growth and the true pace of improvement in technology $\dot {z}.$

Data, Calibration, and Measurement Issues

This section provides a brief overview of the data used for our aggregate growth accounting, discusses the calibration of key parameters, and addresses some important measurement issues.²² The national accounts data that we discuss here exclude virtually all forms of intangible capital except for investment in computer software. We defer the consideration of intangible capital until the next section.

Our dataset represents an up-to-date reading on productivity developments through 2006 based on data available as of the end of March 2007. We rely heavily on the dataset assembled by the Bureau of Labor Statistics (BLS) for its estimates of MFP in the private nonfarm business sector. This dataset extended through 2005 at the time we conducted the analysis for this paper. We extrapolated the series required for our framework through 2006, drawing largely on corresponding series in the NIPAs.

To calculate the income share for each type of capital in our framework, we follow the BLS procedure that distributes total capital income across assets by assuming that each asset earns the same rate of return net of depreciation.²³ This is the same method used by Oliner and Sichel and by Jorgenson, Ho, and Stiroh.²⁴ Consistent with the standard practice in the productivity literature, we allow these income shares to vary year by year.²⁵

These data and procedures generate a series for aggregate MFP growth via equation 1. Given this series as a top-line control, we estimate MFP growth in each sector with the "dual" method employed by various researchers in the past.²⁶ This method uses data on the prices of output and inputs, rather than their quantities, to calculate sectoral MFP growth. We opt for the dual approach because the sectoral data on prices are available on a more timely basis than the corresponding quantity data. Roughly speaking, the dual method compares the rate of change in a sector's output price with that of its input costs. Sectors in which prices fall quickly compared with their input costs are estimated to have experienced relatively rapid MFP growth.²⁷

The expression that links aggregate and sectoral MFP growth (equation 2) involves the Domar weight for each sector, the ratio of the sector's gross output to aggregate value added. For the four NIPA-based final-output sectors, gross output simply equals the value of the sector's final sales, which we estimate using data from the Bureau of Economic Analysis (BEA). For the semiconductor sector we calculate gross output based on data from the Semiconductor Industry Association as well as data constructed by Federal Reserve Board staff to support the Federal Reserve's published data on U.S. industrial production.

The final step is to calculate the influence of adjustment costs and factor utilization on the growth of both aggregate and sectoral MFP. In principle, we could use equations 3 and 4 to calculate the effects at the sectoral level and then aggregate those effects using equation 2. However, as equations 3 and 4 show, this bottom-up approach requires highly disaggregated data on investment and the workweek and equally disaggregated output elasticities with respect to adjustment costs and the workweek (the $\phi '\mbox{s}$ and the $\xi '\mbox{s).}$ Unfortunately, estimates of the required sectoral elasticities are not available.

To make use of readily available estimates, we work instead from the top down. That is, we model the effects of adjustment costs and the workweek for the nonfarm business sector as a whole and then distribute the aggregate effects across sectors. Let $\dot {W}\mbox{ and }\xi$ denote, respectively, the percentage change in the workweek for aggregate nonfarm business and the elasticity of nonfarm business output with respect to this aggregate workweek. Then the workweek effect for aggregate nonfarm business equals $\xi \dot {W}.$ Similarly, we measure the aggregate effect of adjustment costs as $\phi (\dot {I}-\dot {K}),$ where $\dot {I},\dot {K},\mbox{ and }\phi$ denote, respectively, growth in aggregate real investment spending, growth in aggregate real capital services, and the aggregate adjustment cost elasticity. To complete the top-down approach, we assume that the adjustment cost and workweek effects are uniform across sectors. Under this assumption, the top-down version of equations 2 through 4 is as follows (starting with the sectoral equations):

(5) $M\dot {F}P_i =\frac{1}{\bar {\mu }}\left( {\xi {\kern 1pt}\dot {W}-{\kern 1pt} \phi (\dot {I}-\dot {K})} \right)+\dot {z}_i$

(6) $M\dot {F}P_S =\frac{1}{\bar {\mu }}\left( {\xi {\kern 1pt}\dot {W}-{\kern 1pt} \phi (\dot {I}-\dot {K})} \right)+\dot {z}_S$

(7) $M\dot {F}P=\sum\limits_i {\mu _i M\dot {F}P_i } + \mu _S M\dot {F}P_S =\xi \dot {W} - \phi (\dot {I}-\dot {K}) + \sum\limits_i {\mu _i \dot {z}_i } + \mu _S \dot {z}_S ,$

where $\bar {\mu }\equiv \sum\nolimits_i {\mu _i } +\mu _S .$ One can easily verify that the second equality holds in equation 7 by substituting for MFP $_{i}$ and MFP $_{S}$ from equations 5 and 6. Equations 5 through 7 serve as our empirical counterpart to equations 2 through 4.

We follow BFS in specifying $\xi ,$ , and $\phi .$ Starting with the workweek effect, we specify the aggregate elasticity $\xi$ to be a weighted average of BFS's sectoral estimates of $\xi$ for durable manufacturing, nondurable manufacturing, and nonmanufacturing. Using weights that reflect current-dollar output shares in these sectors, we obtain an aggregate value of $\xi$ equal to 1.24. To measure the workweek itself, we use the BLS series for production or nonsupervisory workers from the monthly survey of establishments. Because the workweek in equations 5 through 7 is intended to measure cyclical variation in factor use, we detrend the log of this monthly series with the Hodrick-Prescott filter (with $\lambda$ = 10,000,000 as in BFS) and use the detrended series to calculate $\dot {W}$ on an annual basis.

With regard to adjustment costs, we set the output elasticity $\phi$ equal to 0.035.²⁸ This elasticity is based on estimates of capital adjustment costs by Shapiro.²⁹ More recent studies provide estimates of adjustment costs on both sides of $\phi$ = 0.035. Robert Hall estimates capital adjustment costs in an Euler equation framework similar to Shapiro's but uses more-disaggregated data and a different set of instruments for estimation.³⁰ Hall cannot reject the hypothesis that $\phi$ = 0. In contrast, Charlotta Groth, using industry-level data for the United Kingdom, estimates $\phi$ to be about 0.055.³¹ The divergent results in these studies highlight the uncertainty surrounding estimates of capital adjustment costs but do not suggest the need to move away from a baseline estimate of $\phi$ = 0.035. We apply this elasticity to the difference between the growth rates of aggregate real business fixed investment from the NIPAs and the corresponding capital services series $(\dot {I}-\dot {K}).$

To summarize, we use annual data from BEA and BLS through 2006 to implement the aggregate growth accounting framework in equation 1. This framework yields an annual time series for aggregate MFP growth. We then use the dual method to allocate this aggregate MFP growth across sectors. Finally, we calculate the effects of adjustment costs and changes in factor utilization on both aggregate and sectoral MFP growth, drawing heavily on parameter values reported by BFS.

Results

Table 1 presents our decomposition of labor productivity growth in the nonfarm business sector using the published data described above. These data exclude intangible capital other than business investment in software, which, again, is already treated as an investment good in the NIPAs. The next section fully incorporates intangible capital into our measurement system and presents an augmented set of growth accounting results.

Focusing first on the published data, table 1 shows that average annual growth in labor productivity picked up from about 1.5 percent a year during 1973-95 to about 2.5 percent during the second half of the 1990s and then rose further, to more than 2.8 percent, in the period after 2000. Our results indicate that an important part of the initial acceleration (about 0.6 percentage point of the total speedup of just over 1 percentage point) reflected the greater use of IT capital. In addition, growth of MFP rose notably in the IT-producing sectors, with an especially large increase for producers of semiconductors. The pickup for the semiconductor sector mirrors the unusually rapid decline in semiconductor prices from 1995 to 2000, which the model interprets as a speedup in MFP growth.³² The last line of the table shows that, all told, IT capital deepening and faster MFP growth for IT producers more than accounted for the total speedup in labor productivity growth during 1995-2000. These results confirm that the IT-centric story for the late 1990s holds up after incorporating the latest vintage of data and extending the framework to account for adjustment costs and utilization effects.

The table also quantifies the influence of adjustment costs and changes in utilization during this period (the two lines under "Growth of MFP"). These two factors, on net, do not explain any of the upward swing in MFP growth from 1973-95 to 1995-2000, consistent with the results in BFS. Although the greater utilization of capital and labor had a positive effect on MFP growth during 1995-2000, this influence was offset by the negative effect from the higher adjustment costs induced by the investment boom of that period.

Table 1 tells a sharply different story for the period since 2000. Even though labor productivity accelerated another 0.35 percentage point, the growth contributions from IT capital deepening and MFP advances in IT-producing sectors dropped back substantially. At the same time, MFP growth strengthened in the rest of nonfarm business, adding roughly $\raise.5ex\hbox{$\scriptstyle 3$}\kern-.1em/ \kern-.15em\lower.25ex\hbox{$\scriptstyle 3$}$ percentage point to annual labor productivity growth during 2000-06 from its 1995-2000 average. And, given the minimal growth in hours worked after 2000, even the anemic advance in investment outlays led to a positive swing in the growth contribution from non-IT capital deepening ("Other tangible capital").³³

All in all, table 1 indicates that IT-related factors retreated from center stage after 2000 and that other factors--most notably, a surge in MFP growth outside the IT-producing sectors--were responsible for the continued rapid advance in labor productivity as reported in the published data.³⁴ Nonetheless, for the entire period since 1995, the use and production of IT capital are important, accounting for roughly two-thirds of the post-1995 step-up in labor productivity growth. The next section of the paper examines whether the inclusion of intangible capital changes this characterization.

We conclude this discussion with two points. The first concerns the use of the year 2000 as the breakpoint for comparing the boom period of the late 1990s with more recent years. We chose 2000 rather than 2001 to avoid splitting the two periods at a recession year, which would have accentuated the need for cyclical adjustments. However, our main findings are robust to breaking the two periods at 2001. Second, our big-picture results are very similar to those in Jorgenson, Ho, and Stiroh,³⁵ which contains the latest estimates from the framework pioneered by Dale Jorgenson. Consistent with our findings, their framework emphasizes the role of IT in explaining the step-up in labor productivity growth during 1995-2000. It also shows a reduced contribution from IT after 2000, which was more than offset by other factors. The differences in results are relatively minor and largely stem from the broader sectoral coverage in the Jorgenson, Ho, and Stiroh framework. In particular, their framework incorporates the flow of services from owner-occupied housing and consumer durable goods into both output and capital input. The stocks of these assets have grown rapidly since the mid-1990s, and so Jorgenson, Ho, and Stiroh's estimates of non-IT capital deepening are larger than those reported here.

Aggregate Growth Accounting with Intangible Capital

The growth accounting analysis in the previous section relies on published data, which exclude virtually all types of intangible capital except software. As argued by Corrado, Hulten, and Sichel,³⁶ any intangible asset that generates a service flow beyond the current period should be included in the capital stock, and the production of such assets should be included in current-period output. Applying this standard, in their 2006 paper (henceforth CHS) Corrado, Hulten, and Sichel estimated that the intangible investment excluded from the NIPAs amounted to roughly $1 trillion annually over 2000-03, an amount nearly equal to outlays for business fixed investment included in the national accounts, and they constructed a growth accounting system that includes a broad set of intangibles through 2003.

Of total business investment in intangibles, CHS estimate that scientific and nonscientific R&D each accounted for about 19 percent during 2000-03; computerized information, which is comprised mostly of the software category already included in the NIPAs, accounted for 14 percent; brand equity accounted for 13 percent; and firm-specific organizational capital accounted for about 35 percent. The last category contains many well-known examples of the successful deployment of intangible capital, including Wal-Mart's supply-chain technology, Dell's build-to-order business model, and Intel's expertise in organizing semiconductor production.³⁷

The CHS estimates of intangible investment and capital are a valuable addition to the literature, but the source data for their series are currently available only through 2004 or 2005. Thus their approach cannot be used to develop growth accounting estimates that are as timely as those based on published data. As an alternative, we construct a data system for intangibles that runs through 2006, based on the framework in BFOS. In the BFOS model, firms use intangible capital as a complement to their IT capital. Because of this connection to IT capital, we can generate estimates of intangible investment and capital from published data on IT capital and related series.

BFOS used their model for a more limited purpose: to specify and estimate regressions to discern whether intangibles could explain the MFP growth patterns in published industry data. They did not formally build intangibles into an integrated growth accounting framework along the lines of CHS. That is precisely what we do here.³⁸

Description of the Model

The basic features of the BFOS model are as follows. Firms have a (value-added) production function in which IT capital and intangible capital are complementary inputs:

(8) $V_t =F\left[ {G\left( {K_t^{IT} ,R_t } \right),K_t^{NT} ,L_t ,z_t } \right],$

where $_{t}$ $^{IT}$ , $_{t}$ , and $_{t}$ $^{NT}$ denote IT capital, intangible capital, and tangible capital other than IT capital, respectively; is labor input; andis the level of technology. For simplicity, BFOS assume that there are no adjustment costs and that factor utilization does not vary. The function that combines IT capital and intangible capital is assumed to take the constant elasticity of substitution form:

(9) $G\left( {K_t^{IT} ,R_t } \right)=\left[ {a\left( {K_t^{IT} } \right)^{{(\sigma -1)} \mathord{\left/ {\vphantom {{(\sigma -1)} \sigma }} \right. \kern-\nulldelimiterspace} \sigma }+\left( {1-a} \right)\left( {R_t } \right)^{{(\sigma -1)} \mathord{\left/ {\vphantom {{(\sigma -1)} \sigma }} \right. \kern-\nulldelimiterspace} \sigma }} \right]^{\sigma \mathord{\left/ {\vphantom {\sigma {(\sigma -1)}}} \right. \kern-\nulldelimiterspace} {(\sigma -1)}}$

where $\sigma$ is the elasticity of substitution between $K_t^{IT} \mbox{and }R_t ,$ and governs the income share of each type of capital.

Because $K_t^{IT} \mbox{and }R_t$ are separable from other inputs, firms minimize costs by first choosing the optimal combination of $K_t^{IT} \mbox{and }R_t$ and then selecting other inputs conditional on this choice. For the first-stage optimization, the usual first-order condition sets the ratio of the marginal products of $K_t^{IT} \mbox{and }R_t$ equal to the ratio of their user costs, which implies

(10) $R_t =K_t^{IT} \left( {\frac{1-a}{a}} \right)^\sigma \left( {\frac{r_t^{IT} }{r_t^R }} \right)^\sigma$ ,

where $_{t}$ $^{IT}$ and $_{t}$ $^{R}$ denote the respective user costs. Equation 10 implies the following expression for the growth of intangible capital:

(11) $\dot {R}_{_t } =\dot {K}_t^{IT} +\sigma \left( {\dot {r}_t^{IT} -\dot {r}_t^R } \right).$

Importantly, equation 11 enables us to calculate a model-implied series for the growth rate of intangible capital based solely on data for IT capital and user costs and on an assumed value for the elasticity of substitution between intangible capital and IT capital. No direct data on intangible capital are required. We chain together the time series of growth rates from equation 11 to produce an indexed series for the level of real intangible capital, .

To implement equation 11, we calculate $\dot {K}_t^{IT} \mbox{and }\dot {r}_t^{IT}$ from the same BLS data that we used in the previous section. We also need to specify the user cost for intangible capital ( $_{t}$ $^{R})$ and the elasticity of substitution between IT capital and intangible capital $(\sigma ).$ We use data from CHS to calculate $\dot {r}_t^R$ and $\sigma ,$ as described next.

CHS measure the user cost of intangible capital in accord with the standard Hall and Jorgenson formulation:³⁹

(12) $r^{R} =p^{R} \left( {\rho +\delta^{R} -\Pi^{R} } \right)T^{R},$

where $^{R}$ is the price index for this type of capital, $\rho$ is the nominal rate of return net of depreciation, $\delta$ $^{R}$ is the depreciation rate, $\Pi$ $^{R}$ is the expected capital gain over and above that captured in the depreciation rate, and $^{R}$ accounts for the tax treatment of intangible assets. Equation 12 is identical to the user cost formula that we employ for all other types of capital in our growth accounting framework. We adopt CHS's specification of each term in the user cost formula.

To select a value for the elasticity of substitution $\sigma ,$ we examined the CHS series for the income shares of IT capital and intangible capital.⁴⁰ If $\sigma$ were equal to one (the Cobb-Douglas case), the ratio of the IT income share to the intangible income share drawn from data in CHS (which we denote by $\alpha$ $_{t}$ $^{R,CHS})$ would be constant. In fact, the ratio of the IT income share to the intangible income share trends upward in the CHS data. Given that the user cost of IT capital has fallen relative to that of intangible capital, the upward trend in the share ratio implies more substitution toward IT capital than would occur in the Cobb-Douglas case. We find that setting $\sigma$ to 1.25 approximates the upward trend in the share ratio.

To complete the system, we need a nominal anchor to convert the indexed series for $_{t}$ to dollar values. For the nominal anchor, we require that the average income share of intangible capital in our framework over 1973-2003 (denoted $\bar {\alpha }_t^{R,BFOS} )$ equal the average value of the CHS-based share over the same period:⁴¹

(13) $\bar {\alpha }^{R,BFOS}=\bar {\alpha }^{R,CHS}$ .

To satisfy equation 13, we scale the indexed levels series for intangible capital, $_{t}$ , by $\psi$ . The income share for intangible capital in year is then

(14) $\alpha _t^{R,BFOS} =\frac{r_t^R R_t \psi }{p_t V_t +r_t^R R_t \psi }$ ,

where the denominator equals the sum of published nonfarm business income and the income accruing to intangible capital. We average equation 14 over the period 1973-2003, substitute the average share into the left-hand side of equation 13, and solve for the scaling factor $\psi$ . We then apply this scaling factor to the indexed levels series for $_{t}$ and denote the resulting series for real intangible capital by $_{t}$ ^*. Given $_{t}$ ^*, the associated series for real intangible investment comes from the standard perpetual inventory equation:

(15) $N_t^\ast =R_t^\ast -\left( {1-\delta ^R} \right)R_{t-1}^\ast$ .

We calculate growth in real intangible investment from the series for $_{t}$ ^*.

We now have all the pieces we need to incorporate intangibles into our growth accounting framework. An important point is that including intangible assets affects both the output and the input sides of the production accounts. On the output side, the growth of production equals a weighted average of growth in real intangible investment $\dot {N}^\ast$ and growth in published real nonfarm business output. The weight for each component equals its share in the augmented measure of current-dollar output. On the input side, the total contribution from capital now includes a term for intangible capital, calculated as the income share for intangible capital times the growth rate of this capital in real terms, $\alpha _t^{R,BFOS} \times \dot {R}^\ast .$ The income shares for all other inputs are scaled down so that the shares (including that for intangible capital) sum to one.⁴²

Results

The results from this augmented growth accounting framework, shown in table 2, differ in important respects from the results based on published data. As can be seen by comparing the first two lines, labor productivity growth during 1995-2000 becomes stronger once we include intangibles, but it becomes less robust during 2000-06. Indeed, in the augmented framework, the productivity advance since 2000 is estimated to be well below that posted during 1995-2000, reversing the relative growth rates for the two periods based on published data. This reversal arises from the time profile for real investment in intangibles. As shown in the lower part of the table, real intangible investment is estimated to have surged during 1995-2000, boosting growth in aggregate output, and then retreated during 2000-06.

The growth contribution from intangible capital deepening ("New intangible capital" in table 2) follows the general pattern for IT capital, moving higher during 1995-2000 and then falling back. This similarity reflects the explicit link between intangible capital and IT capital in the BFOS model. The lower part of the table provides full detail on the growth of intangible capital and its determinants from equation 11. Despite the broadly similar growth contour for intangible capital and IT capital across periods, intangible capital increases much less rapidly than IT capital in each period, because of the quality-adjusted declines in IT prices that cause the user cost of IT capital to trend lower. This user cost effect became more pronounced during 1995-2000--when the prices for IT capital goods fell especially rapidly--restraining the growth of intangible capital even though the growth of IT capital jumped.

Taken together, the revisions to the output and the input sides of the growth accounting equation imply a revised path for MFP growth, after controlling for the effects of adjustment costs and factor utilization ("Growth of MFP excl. above effects"). The inclusion of intangibles leaves a somewhat smaller imprint on MFP growth than on the growth of labor productivity, as the revisions to the two sides of the growth accounting equation are partly offsetting. Consistent with the more muted revision from the published data, the path for MFP continues to show the fastest growth after 2000. However, the pickup in MFP growth from 1995-2000 to 2000-06, at 0.04 percentage point, is negligible compared with that indicated by published data (see the equivalent line in table 1).

Robustness Checks

The BFOS model imposes a strictly contemporaneous relationship between the growth of intangible capital and the growth of IT capital. This relationship may be too tight, as the two forms of capital accumulation may be subject to (unmodeled) adjustment costs and differences in project length from the planning stage to final rollout.

To examine the robustness of our results, we consider alternative timing assumptions for the growth of intangible capital. The first two alternatives smooth the growth of intangible capital without introducing leads or lags relative to the growth in IT capital. The idea is that some projects to produce intangible capital may be long-lived and thus may not display the same stops and starts as purchases of IT capital. We implement this timing change by using a three-year or a five-year centered moving average for the growth rate of IT capital and its user cost on the right-hand side of equation 11. The third timing change allows intangible capital growth to lag IT capital growth by a year but does not affect the relative volatility of the series. This timing assumption embeds the often-expressed view that firms take time to accumulate the intangible capital needed to fully leverage their IT investments.

Our reading of the literature suggests that the first two alternatives fit the facts better than the introduction of a systematic lag from IT capital to intangible capital. Case studies published elsewhere portray the installation of IT capital and associated changes in business practices and organization as being interwoven rather than strictly sequential.⁴³ Sinan Aral, Erik Brynjolfsson, and D. J. Wu support this view, noting that "... [as] firms successfully implement IT (and complementary intangible investments) and experience greater marginal benefits from IT investments, they react by investing in more IT," a process they characterize as a "virtuous cycle."⁴⁴ Nonetheless, we consider the scenario with the lagged accumulation of intangible capital for the sake of completeness.

As the top panel of table 3 shows, these alternative timing assumptions have some effect on the period-by-period growth of real intangible capital but do not change the basic result, namely, that this type of capital essentially has not grown since 2000. The series for intangible investment, shown in the bottom panel of the table, is also reasonably robust to alternative timing assumptions. In each case, real intangible investment is estimated to have declined since 2000. As a further robustness check, the table also displays the CHS series for intangible capital and intangible investment, which we have extended through 2005 based on some of the key source data in their framework. (This is a preliminary extension of the CHS series for illustrative purposes only and should not be regarded as official CHS data.) The extended CHS series for intangible investment and capital exhibit patterns across periods that are broadly similar to those in our series. Notably, the CHS series decelerate sharply after 2000, and the growth rates for 2000-05 are the weakest for the three periods shown, confirming an important qualitative feature of our estimates. Because the CHS series are constructed independently from the series in this paper, the qualitative correspondence between them lends credibility to the basic thrust of our results, if not to the precise figures.

Table 4 explores the growth accounting implications of the alternative timing assumptions for intangible capital. For each timing assumption we show three key variables: growth in labor productivity, the growth contribution from intangible capital deepening, and MFP growth (after controlling for the effects of adjustment costs and factor utilization). Most features of the baseline results are robust to the alternative assumptions. In every case, labor productivity is estimated to have grown more rapidly during 1995-2000 than during 2000-06, reversing the relative growth rates based on published data. In addition, the growth contribution from intangible capital deepening is always largest during 1995-2000 and then drops back to essentially zero during 2000-06. Finally, although the alternative timing assumptions generate a larger step-up in MFP growth after 2000 than in the baseline, they nonetheless temper the increase by 0.2 to 0.3 percentage point relative to the published data.

Industry-Level Productivity

We now turn to the industry origins of U.S. productivity growth during the late 1990s and after 2000. The aggregate data show that the sources of productivity growth changed after 2000, which suggests that the industry-level origins of aggregate productivity growth and the underlying forces may have also changed. To explore this, we construct productivity accounts for sixty industries that span the U.S. private economy from 1988 to 2005. Although measurement error, omitted variables, and endogeneity problems always make it difficult to identify the sources of productivity gains, we make some progress by exploiting cross-sectional variation in industry productivity over time and by examining the link between productivity and observable factors such as IT intensity and changing profit shares.

The industry analysis presented here focuses on labor productivity, reflecting our interest in understanding the industry origins of aggregate labor productivity growth. Moreover, we do not have the detailed data on labor quality, intangible investment, or adjustment costs at the industry level necessary to create comparable estimates of MFP growth. To the extent that intangible capital is correlated with IT investment, however, one can interpret the IT intensity results as broadly indicative of the whole suite of activities that are complementary to IT.

Output Measures, Data, and Summary Statistics

Output Measures. Industry output can be measured using either a gross output or a value-added concept, each with its advantages and disadvantages.⁴⁵ Gross output corresponds closely to the conventional idea of output or sales and reflects all inputs including capital, labor, and intermediate energy, materials, and services. Value added, by contrast, is a somewhat artificial concept that strips out the contribution of intermediate inputs and incorporates only capital and labor.

Although both value added and gross output are used for productivity analysis, we favor gross output. Empirical work by, among others, Michael Bruno; J. R. Norsworthy and David Malmquist; Jorgenson, Frank Gollop, and Barbara Fraumeni rejects the existence of value-added functions on separability grounds.⁴⁶ Basu and Fernald show that using value-added data leads to biased estimates and incorrect inferences about production parameters.⁴⁷ A later contribution by the same authors argues against the value-added function because failure of the neoclassical assumption about perfect competition implies that some of the contribution of intermediate inputs remains in measured value-added growth.⁴⁸ Value added has the advantage, however, that it aggregates directly to GDP.

Data. We use three pieces of U.S. industry-level data--output, hours, and capital stock--from government sources. The first two create a panel of average labor productivity (ALP) across U.S. industries, and the third is used to develop measures of the intensity of the use of IT. One practical difficulty is the recent conversion of the industry data from the Standard Industrial Classification (SIC) system to the North American Industrial Classification (NAICS) system, which makes it difficult to construct long historical time series or to directly compare the most recent data with earlier results.

BEA publishes annual data on value added and gross output for sixty-five industries that together make up the private U.S. economy.⁴⁹ These data, which are based on an integrated set of input-output and industry production accounts, span 1947-2005 for real value added and 1987-2005 for real gross output. Although BEA also publishes various measures of employment by industry, it does not provide industry-level series on hours worked. We obtain hours by industry from the Output and Employment database maintained by the Office of Occupational Statistics and Employment Projections at BLS. Complete data on total hours for all industries begin in 1988.⁵⁰ Because these hours data are currently available only to 2004, we use the growth rate of full-time equivalent employees for the disaggregated industries, from BEA data, to proxy for hours growth in 2005.

We create two measures of industry ALP--real value added per hour worked and real gross output per hour worked--by combining the BEA output data with the BLS hours data across industries for 1988 to 2005.

The third data source is the Fixed Asset accounts from BEA for nonresidential capital. These data include forty-six different types of nonresidential capital for sixty-three disaggregated NAICS industries since 1987. To estimate capital services we map the asset-specific service prices from Jorgenson, Ho, and Stiroh onto these assets and employ Tornqvist aggregation using the service price and a two-period average of the capital stock for each asset in each industry.⁵¹ The resulting measure of capital services is an approximation, because we miss industry variation in rates of return, asset-specific inflation, and tax code parameters. Nevertheless, it captures the relatively high service prices for short-lived assets such as IT capital, defined as above to include computer hardware, software, and communications equipment.

We combine these three sources of data to form a panel from 1988 to 2005 for a private industry aggregate, fifteen broad sectors, and sixty disaggregated industries. The fifteen-sector breakdown follows BEA's convention, except that manufacturing is broken into durables and nondurables. The number of disaggregated industries is smaller than that available from either BEA or BLS, because of the need to generate consistently defined industries across all data sources. All aggregation is done via Tornqvist indices, except for hours, which are simply summed. Both the broad sectors and the disaggregated industries sum to the private industry aggregates of nominal output from BEA, hours from BLS, and nominal nonresidential capital from BEA. The list of industries and their 2005 value added are reported in appendix table A-1.

Summary Statistics. Table 5 reports estimates of labor productivity growth from our industry data and compares them with the latest estimates from BLS. The first two lines of the top panel report average annual growth of ALP for the BLS business and nonfarm business sectors, and the third line reports the private industry aggregate described above. Although our private industry aggregate grows somewhat less rapidly than the BLS aggregates, all three series show similar trends: a pickup of ALP growth of about 1 percentage point after 1995 and a smaller increase after 2000.

The second panel of table 5 reports estimates for the fifteen broad NAICS sectors. These sectors range in size from the very large finance, insurance, real estate, rental, and leasing sector, at 23.3 percent of 2005 value added, to the very small agriculture, forestry, fishing, and hunting sector, at only 1.1 percent. In terms of ALP growth, eight of these fifteen sectors, which accounted for 73 percent of value added in 2005, showed faster productivity growth over 1995-2000 than over 1988-95.⁵² The further acceleration in aggregate productivity after 2000 occurred in seven sectors, which accounted for only 44 percent of 2005 value added. Although productivity in the large retail trade, wholesale trade, and finance sectors all decelerated after 2000, the two trade sectors continued to post impressive productivity gains through 2005.

The pickup in aggregate productivity growth in the mid-1990s appears to have originated in different sectors than did the subsequent step-up in 2000. Six sectors (agriculture, durable goods, wholesale trade, retail trade, finance, and arts and entertainment) show an acceleration after 1995 but a deceleration after 2000, whereas five sectors (construction, nondurables, utilities, information, and other services) show the opposite pattern. Together these eleven sectors produced 72 percent of value added in 2005. In their analysis of MFP growth, Corrado and others reach a similar conclusion, although Bosworth and Triplett emphasize the continued importance of service industries as a source of aggregate productivity growth.⁵³

Table 5 also summarizes, in the third and fourth panels, the disaggregated industry data by reporting the mean, median, and hours-weighted mean productivity growth rates across these industries for gross output and value added, respectively. One interesting observation is the divergence in trends between gross output and value-added measures of productivity: the post-1995 gains are strongest for gross output, whereas the post-2000 gains are strongest for value added. Both series incorporate the same hours data, so that this divergence directly reflects differences between the gross output and value-added output measures.

It is beyond the scope of this paper to investigate this divergence further. For completeness, we report results for both gross output and value added, although, again, we prefer gross output because it is a more fundamental measure of production and does not require additional assumptions about the nature of the production function.

Finally, we emphasize that there is enormous heterogeneity among the disaggregated industries that lie beneath these summary statistics, both within time periods and across time. For example, thirty-seven of the sixty industries, which accounted for nearly 60 percent of aggregate output, experienced an acceleration of productivity after 1995 but a decline after 2000, or vice versa. This highlights the widespread churning and reallocation of resources among industries, which we show to be an important source of aggregate productivity gains.

Industry Origins of the Aggregate Productivity Gains

We now review how the data for the disaggregated industries can be aggregated to form economywide productivity estimates, and we employ this familiar framework to identify the industry origins of the aggregate productivity gains over 1988-2005.

Decomposition and Reallocations. At the industry level, real value added is defined implicitly from a gross output production function as

(16) $\dot {Y}_i =\alpha _i^V \dot {V}_i +(1-\alpha _i^V )\dot {M}_i ,$

where $\alpha$ $_{i}$ $^{V}$ is the average share of nominal value added in nominal gross output for industry and $_{i}$ denotes real intermediate inputs.⁵⁴ One attractive property of industry value added is that it aggregates to a simple expression for growth in aggregate value added:

(17) $\dot {V}=\sum\limits_i {v_i \dot {V}_i } ,$

where $_{i}$ is the average share of industry 's nominal value added in aggregate nominal value added. Aggregate hours worked, , is the simple sum of industry hours,

(18) $H=\sum\limits_i {H_i } ,$

and aggregate labor productivity is defined as ALP $^{V}$ .

Equations 16, 17, and 18 can be combined to yield the following decomposition of ALP growth:⁵⁵

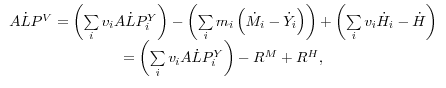
(19) $\begin{array}{c} A\dot {L}P^V=\left( {\sum\limits_i {v_i A\dot {L}P_i^Y } } \right)-\left( {\sum\limits_i {m_i \left( {\dot {M}_i -\dot {Y}_i } \right)} } \right)+\left( {\sum\limits_i {v_i \dot {H}_i -\dot {H}} } \right) \ =\left( {\sum\limits_i {v_i A\dot {L}P_i^Y } } \right)-R^M+R^H, \ \end{array}$

where ALP $^{Y}$ is industry labor productivity based on gross output and $_{i}$ is the average ratio of nominal industry intermediate inputs to nominal aggregate value added. This equation simplifies to

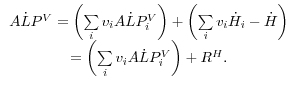
(20) $\begin{array}{c} A\dot {L}P^V=\left( {\sum\limits_i {v_i A\dot {L}P_i^V } } \right)+\left( {\sum\limits_i {v_i \dot {H}_i -\dot {H}} } \right) \ =\left( {\sum\limits_i {v_i A\dot {L}P_i^V } } \right)+R^H. \ \end{array}$

The first term in equation 19 is a "direct productivity effect" equal to the weighted average of growth in gross output labor productivity in the component industries. The second term, $^{M}$ , is a "reallocation of materials," which reflects variation in intermediate input intensity across industries. It enters with a negative sign because when more intermediate inputs are used to raise gross output, $\dot {M}>\dot {Y},$ these must be netted out to reach aggregate productivity. The third term, $^{H}$ , is a "reallocation of hours." Aggregate hours growth, $\dot {H},$ approximately weights industries by their (lagged) share of aggregate hours, and so aggregate productivity rises if industries with value-added shares above their hours shares--that is, those industries with relatively high (nominal) productivity levels--experience growth in hours. Equation 20 is a simplification using value-added labor productivity at the industry level.⁵⁶

Table 6 reports estimates of the decomposition framework in equations 16 to 20. The first row in the top panel repeats the productivity estimates that come from the BEA data on aggregate private industry output and the sum of hours worked from BLS. The second row reports the estimates we derive by explicitly aggregating the detailed industries as in equations 17 and 18. There is a small divergence for the middle period, but the two estimates tell the same story of a large productivity acceleration after 1995 and a smaller one after 2000.⁵⁷

The second and third panels of table 6 report the decomposition from equations 19 and 20 using gross output data and value-added data, respectively. Both panels indicate a substantial increase in the direct contribution of industry-level productivity after 1995 (1.31 percentage points for gross output and 0.83 percentage point for value added), followed by a large decline after 2000 for gross output (-0.94 percentage point) and no change for value added.

Both the materials and hours reallocation terms turn positive after 2000, boosting the aggregates and suggesting that an important part of the post-2000 productivity gains stemmed from the shifting of inputs among industries.⁵⁸ In fact, we do not observe an increase in productivity growth after 2000 when looking at the direct industry contributions, an insight that is only possible with industry-level data.⁵⁹

The materials reallocation term contributes positively to aggregate productivity growth when gross output is growing faster than materials, which implies that value added is growing faster than gross output (see equation 16). This pattern has held since 2000 and likely reflects some combination of substitution among inputs, biased technical change, and new production opportunities such as outsourcing. Better understanding of these forces is an important area for future work.

The reallocation of hours is positive when industries with relatively high productivity (in nominal terms) have strong hours growth. Growing reallocations are consistent with the notion that increased competitive pressures, flexible labor markets, and restructuring were part of the productivity story in recent years. Elsewhere Stiroh discusses some evidence of increased flexibility of U.S. labor markets and reports evidence of increased reallocation across industries.⁶⁰

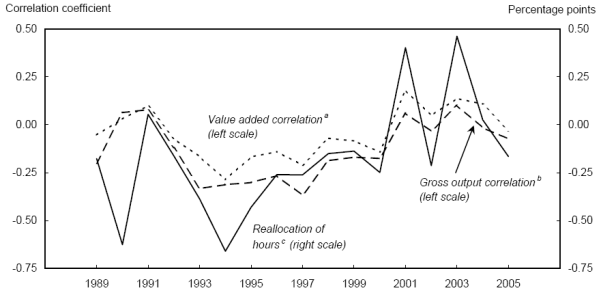
To provide an alternative perspective, we calculate the annual cross-sectional correlation between hours growth and the lagged level of ALP for the sixty disaggregated industries. Figure 1 plots the estimated correlations for both the value-added and gross output measures of labor productivity; the figure also shows the term from equation 19 for the annual reallocation of hours. All three series seem to have trended upward, particularly since the early 1990s, which suggests that industries with relatively high productivity have become more likely to show strong hours growth in the following year. There also seems to be a cyclical component, as the correlations and hours reallocations rise during recessions, consistent with the notion of a cleansing effect of recessions.⁶¹

This interpretation of the reallocation of hours is suggestive; we have provided neither a deep economic explanation nor sophisticated econometric evidence that might identify the causal factors. Rather we are highlighting what appears to be an increasingly important source of aggregate productivity growth and pointing toward further research.

Role of IT Classifications. Table 6 also quantifies the direct contributions from IT-producing, IT-using, and other industries. Consistent with the classification scheme used by BEA,⁶² we identify four industries as IT-producing: computer and electronic products, publishing including software, information and data processing services, and computer system design and related services. Following Stiroh,⁶³ we identify industries as IT-using if their IT capital income share (nominal IT capital income as a share of nominal nonresidential capital income) is above the median for all industries, excluding the four IT-producing industries. All remaining industries are labeled "other industries." This leaves four IT-producing industries with nearly 5 percent of aggregate value added in the most recent period, twenty-six IT-using industries with 59 percent, and thirty "other industries" with the remainder.⁶⁴

As shown in table 6, the IT-producing and IT-using industries more than account for the direct contribution from individual industries to the productivity acceleration during 1995-2000. After 2000, however, the impact of IT is much less clear-cut, with the swing in the growth contributions from all three groups of industries concentrated in a fairly narrow range.

For the full decade from 1995 to 2005, the direct contribution from the IT-using industries was far larger than it had been over 1988-1995, despite the decline after 2000 based on gross output data. In contrast, the direct contribution from "other industries" remained smaller throughout 1995-2005 than it had been before 1995. This distinction highlights the important role for IT use in driving the faster growth in productivity that has prevailed over the entire period since the mid-1990s.

The contribution from the IT-producing industries moved up during 1995-2000 and back down during 2000-05, with the size of the swing depending on which output measure one uses. That said, both output measures show that the IT-producing industries made relatively large contributions to aggregate productivity growth throughout the sample period. For example, using the value added figures, the four IT-producing industries accounted for 19 percent (0.47 $\div$ 2.52) of aggregate productivity growth over 2000-05, far above their 4 percent share of value added.

Potential Explanations for the Industry Variation

We now explore two specific questions about the cross-sectional distribution of productivity growth. First, was the link between IT and productivity growth after 2000 as strong as in the second half of the 1990s? The simple decompositions presented above suggest that it was not, but we examine this more formally here. Second, is there evidence for the idea that competition and restructuring contributed to the strong productivity gains after 2000?

IT and Productivity Growth. This section examines the link between industry-level productivity growth and IT intensity. The intuition is straightforward: if IT plays an important role in productivity growth through either the direct capital deepening effect, a complementary but omitted input, or productivity spillovers, one should expect the most IT-intensive industries to show the largest productivity gains. We estimate cross-sectional regressions that relate the change in productivity growth over two periods to IT intensity at the end of the first period as

(21) $\Delta A\dot {L}P_i =\alpha +\beta IT_i +\varepsilon _i ,$

where $\Delta A\dot {L}P$ is the change in productivity growth between two periods (from 1988-95 to 1995-2000, from 1988-95 to 1995-2005, or from 1995-2000 to 2000-05).

We use two alternative measures of IT intensity. The first is a qualitative indicator of relative intensity: a dummy variable equal to one if the IT share of total nonresidential capital income exceeds the industry median and zero otherwise.⁶⁵ This qualitative approach allows a broad interpretation of IT as a proxy for related investments such as intangible capital and the improved management practices that typically accompany IT. Moreover, this type of indicator variable is robust to the type of measurement error in the capital stock described by Randy Becker and coauthors,⁶⁶ but it misses the variation in IT intensity across industries. Our second measure is the actual share of IT capital services in total nonresidential capital services. This quantitative measure better captures differences in IT intensity but is more prone to measurement error. We estimate the IT share regressions with data from all sixty industries and from fifty-six industries after dropping the four IT-producing industries; the latter sample removes some outliers and focuses on the impact of the use of IT.

We define IT intensity as that just before the period of acceleration, for example in 1995 when analyzing the change in productivity growth after 1995, and in 2000 when examining the change after 2000. Although this procedure is not perfect, it helps control for the endogeneity of investment. In the dummy variable specification, $\beta$ represents the change in productivity growth across periods for IT-intensive industries relative to the change for other industries; in the quantitative specification, $\beta$ represents the increase in the change of productivity growth associated with a marginal increase in IT intensity.

Table 7 presents the results. The first three columns examine changes in the second half of the 1990s by comparing 1995-2000 with 1988-95. The middle three columns extend the data to 2005 but keep the breakpoint and the measure of IT intensity at 1995. The final three columns focus on the post-2000 gains by comparing the change in productivity from 2000 to 2005 with that from 1995 to 2000. The top panel uses gross output as the output measure, and the bottom panel uses value added. All estimates use ordinary least squares (OLS) with robust standard errors.⁶⁷

The estimates through 2000 suggest a link between IT intensity and the change in productivity growth using the gross output data, but the results are weaker using the value-added data. When we extend the data to include the post-2000 period and compare 1995-2005 with 1988-95, both sets of estimates show large and significant IT effects. The final three columns indicate that IT intensity in 2000 is not a useful predictor of the change in productivity growth after 2000.⁶⁸

These results show that the most IT-intensive industries in 1995 experienced larger increases in productivity growth after 1995 and that these gains lasted through 2005. Although the IT intensity variable explains only a relatively small portion of the overall variation across industries, the size of the IT effect is economically large: IT-intensive industries showed an increase in productivity growth that was between 1.5 and 2.0 percentage points greater than other industries when 1995-2005 is compared with 1988-95. Despite data revisions and the shift to NAICS, these results are similar to those in earlier work, indicating strong support for the view that IT use mattered for the productivity gains after 1995. Of course, to the extent that IT capital is correlated with other factors such as management skills or intangible capital, these gains should be attributed to the whole suite of business activities that accompany IT investment, and not narrowly to changes in physical capital.

By contrast, the post-2000 acceleration in productivity does not appear to be tied to the accumulation of IT assets in the late 1990s. In particular, we find no evidence that industries that sowed lots of IT capital in the late 1990s reaped a particularly large productivity payoff after 2000. Although these results are surely confounded by cyclical dynamics that were especially severe in the high-technology sectors, analysis of an earlier vintage of the industry data by Stiroh shows that the reduced correlation between IT and productivity is not due solely to the high-technology slowdown in 2001.⁶⁹

Competitive Pressures and Productivity Growth. One idea that has received considerable attention is that U.S. firms may have been under increased pressure in the 2000s to cut costs and raise efficiency in order to maintain profitability in a more globalized and competitive environment.⁷⁰ Robert Gordon, for example, concludes that the "savage cost cutting and layoffs" that followed the profit boom of the late 1990s likely explain the unusual surge of productivity in the early 2000s.⁷¹ Mark Schweitzer notes that managers have stressed the need to realign business processes without hiring additional workers, although he admits that empirical support is limited.⁷² Erica Groshen and Simon Potter raise the possibility that new management strategies promoted lean staffing in order to increase efficiency.⁷³ Firms may have been better able to carry out these strategies in an environment of more flexible and efficient labor markets.⁷⁴

If the cost-cutting hypothesis is true, productivity growth should have been relatively strong and hours growth relatively weak after 2000 in those industries that experienced the biggest decline in profits in earlier years and thus were under the most intense pressure to restructure. To identify those industries, we examine the change in the profit share derived from the BEA industry data, where the profit share is defined as gross operating surplus (consumption of fixed capital; business transfers; other gross operating surplus such as profits before tax; net interest; and miscellaneous payments) as a share of value added. Although one might want to remove the consumption of fixed capital and the normal return to capital, those data are not available at a detailed level. Our profit share measure should be viewed as a broad measure that includes the gross return to capital.

We then compared industry growth from 2001 to 2004--the period of extremely rapid aggregate productivity gains--with changes in industry-level profit shares from the 1997 peak in the aggregate profit share to the 2001 trough. As a first pass, figures 2 and 3 plot the growth of hours and labor productivity from 2001 to 2004 against the change in the profit share from 1997 to 2001 for sixty industries. These scatterplots offer some support for the restructuring hypothesis, as a decline in the profit share is associated (significantly) with slower hours growth and faster ALP growth.⁷⁵ To gauge the magnitude of this effect, note that industries with below-median changes in the profit share experienced hours growth 2 percentage points slower on average than did other industries and labor productivity growth about 3 percentage points faster.⁷⁶

We also estimate cross-sectional regressions that relate growth in the early 2000s to the lagged change in the profit share as

(22) $\dot {X}_i =\alpha +\beta \Delta PR_i +{\rm {\bf\gamma Z}}_i +\varepsilon _i ,$

where $\dot {X}$ is average annual growth of either hours, intermediate inputs, labor productivity, or output from 2001 to 2004, $\Delta$ PR is the change in the profit share from 1997 to 2001, and Z are controls. Equation 22 is obviously a reduced-form regression, and the controls are therefore intended to soak up variation attributable to other factors. Z includes the contemporaneous change in the profit share from 2001 to 2004, to control for demand effects; lagged growth in the dependent variable from 1997 to 2001, to control for longer-run trends (for example, the possibility that some industries may be in secular decline); and the IT service share, to control for IT intensity. Finally, we interacted the IT service share with the lagged change in the profit share, to examine whether IT intensity facilitated adjustment to competitive pressures.

Table 8 reports estimates of equation 22 without and with these controls. The top panel uses input growth (either hours or intermediate inputs) as the dependent variable, the middle panel uses labor productivity measures based on gross output or value added, and the bottom panel uses the two output measures. All estimates use OLS with robust standard errors.

The hours growth regressions reveal a strong positive link, as industries with large declines in the profit share over 1997-2001 experienced significantly slower hours growth from 2001 to 2004. There is no similar link with intermediate inputs. Firms might have been expected to economize on all margins, but differences in adjustment costs could explain the different results for hours and intermediate inputs. The results in the middle panel show a strong negative link between the lagged change in the profit share and productivity growth. Finally, the bottom panel reports some evidence that output growth was faster in the industries with a declining profit share, but the link is weaker and far less robust than that between labor productivity and the profit share.⁷⁷

These results support the hypothesis that competitive pressure and restructuring help explain the post-2000 productivity gains. One interpretation is that firms in those industries where profits fell most dramatically through 2001 became cautious, hired fewer workers, and improved productivity and efficiency after 2001. Moreover, the absence of strongly significant effects in the output regressions, together with the robustness of the results to the inclusion of the contemporaneous change in the profit share, suggests that this was not just a demand story, but rather reflects how firms chose to produce a given amount of output. Similarly, the results are robust to including a lagged dependent variable, and so it does not appear that we are merely capturing long-run trends. Finally, these estimates provide additional evidence that IT was not a driving factor in the early 2000s, as both the level of IT intensity and the interaction term are insignificant in all except the hours regressions.

Productivity Trends and Outlook

This section turns to the outlook for productivity growth. After highlighting issues with the recent data, we report long-period averages of labor productivity growth to provide a benchmark for assessing the strength of recent growth. We also present trend estimates from a Kalman filter model and estimates of the steady-state growth implicit in our aggregate growth accounting model. Finally, we compare these trend estimates with those reported by other analysts.

What Do the Recent Data Say?

Assessing the underlying trend in labor productivity growth since 2000 has been complicated by major data revisions to both output and hours worked and by swings in actual productivity growth. Table 9 displays both dimensions of the recent data. Moving down a column in the table shows the effect of revisions across successive vintages of data, while moving across a row shows the effect of adding additional years to the period covered by the data.⁷⁸

For 2000-03, the average growth of labor productivity was reported initially in March 2004 to have been 3.8 percent. This surprisingly robust gain led many analysts to ask why labor productivity growth had accelerated further despite sluggish investment spending, the 2001 recession, and other adverse shocks. However, subsequent revisions reduced the rate of advance to 3.4 percent.⁷⁹ The initial estimates for 2000-04 and 2000-05 were revised downward in a similar fashion, tempering some of the earlier optimism about the underlying trend. In addition to these revisions, smaller gains in labor productivity over the past few years have brought down the average growth rate, reported in the bottom row of the table. In the current vintage of data (March 2007), growth over 2000-06 averaged 2.8 percent, a full percentage point below the initial reading for the first three years of this period.

Long-Period Averages

Long-period averages of labor productivity growth provide one way to put the recent figures into perspective. The first column of table 10, using data from BLS, shows productivity growth rates over several periods extending back to 1909. These data cover a broader sector of the economy than nonfarm business and so do not line up perfectly with the estimates presented earlier in the paper. That said, labor productivity growth according to these figures has averaged 2.2 percent a year since 1909.⁸⁰ The second column shows productivity growth rates over selected periods since 1950 for the nonfarm business sector; here growth averaged 2.7 percent a year during 1995-2006, similar to that during the so-called "golden era" of productivity from 1950 to 1973 and well above the postwar average of 2.1 percent a year. Thus by historical standards the performance of labor productivity since 1995 has been quite strong.

Kalman Filter Estimates

As one approach to obtaining time-varying estimates of the trend in labor productivity, we use a slightly modified version of the Kalman filter model developed by John Roberts.⁸¹ Although alternative implementations could yield answers that differ from the one presented here, the Roberts model has some appealing features.⁸² In particular, it allows for shocks to both the level and the growth rate of trend productivity, and it controls for cyclical changes in productivity growth by assuming that hours adjust gradually to output following a cyclical shock. We estimate the model by the maximum likelihood method, using standard BLS data on labor productivity in the nonfarm business sector from the first quarter of 1953 to the fourth quarter of 2006.

For the fourth quarter of 2006, this procedure estimates that the trend in labor productivity growth was 2 $\raise.5ex\hbox{$\scriptstyle 1$}\kern-.1em/ \kern-.15em\lower.25ex\hbox{$\scriptstyle 4$}$ percent a year, roughly $\raise.5ex\hbox{$\scriptstyle 1$}\kern-.1em/ \kern-.15em\lower.25ex\hbox{$\scriptstyle 2$}$ percentage point below the average pace of productivity growth since 2000. Put another way, the model interprets some of the extraordinary growth in the years immediately after the 2001 recession as transitory. The model also delivers a 2-standard-error confidence band around the estimated trend, ranging from 1.3 percent to 3.2 percent. Thus considerable uncertainty surrounds this estimate of trend productivity growth.

teady-State Analysis of Labor Productivity Growth

As a complement to the Kalman filter estimate of the trend in labor productivity growth, we calculate the growth rate that would prevail in the steady state of our aggregate growth accounting model. For this exercise we use the version of the model that excludes our added intangibles, so that our estimates can be compared with those of other researchers. We stress at the outset that we do not regard these steady-state results as forecasts of productivity growth over any period. Rather this exercise yields "structured guesses" for growth in labor productivity consistent with alternative scenarios for certain key features of the economy.

The steady state in our model is characterized by the following conditions. Real output in each sector grows at a constant rate (which can differ across sectors), and real investment in each type of capital grows at the same constant rate as the real stock of that capital. Because $\dot {I}=\dot {K}$ for each type of capital, adjustment costs have no effect on MFP growth (sectoral or aggregate) in the steady state. On the labor side, we require that hours worked grow at the same constant rate in every sector, that the workweek be fixed, and that labor quality improve at a constant rate.

Under these conditions the steady-state growth rate of aggregate labor productivity can be written as follows (see the appendix for details):

(23) $A\dot {L}P= \sum\limits_i {\left[ {\left( {{(\alpha _i^K -\phi _i )} \mathord{\left/ {\vphantom {{(\alpha _i^K -\phi _i )} {\alpha ^L}}} \right. \kern-\nulldelimiterspace} {\alpha ^L}} \right)\left( {\dot {z}_i +\beta _i^S \dot {z}_S } \right)} \right]} {\kern 1pt}{\kern 1pt} +\dot {q} +\dot {z},{\kern 1pt}$

where the $\alpha '\mbox{s}$ denote income shares, the $\phi '\mbox{s}$ denote the adjustment cost elasticity of output with respect to each type of capital, $\beta _i^S$ is the share of total costs in final-output sector represented by purchases of semiconductors, $\dot {q}{\kern 1pt}$ is the rate of increase in labor quality, $\dot {z}_i$ and $\dot {z}_S$ denote the rates of improvement in sectoral technology, and $\dot {z}{\kern 1pt}$ is the Domar share-weighted sum of these sectoral rates of improvement. Recall that the $\dot {z}{\kern 1pt}$ terms (sectoral or aggregate) equal the growth of MFP after controlling for the effects of changes in factor utilization and adjustment costs. No explicit terms for capital deepening appear in equation 23. However, capital deepening is determined endogenously from the improvement in technology, and the terms in brackets account for the growth contribution from this induced capital deepening.⁸³

The steady-state equation depends on a large number of parameters (income shares, sectoral output shares, semiconductor cost shares, and so on.) We consider a range of parameter values, which are listed in appendix table A-2. For the most part, steady-state growth is not very sensitive to these parameters individually. However, the results do depend importantly on two parameters: the rate of improvement in labor quality and the rate of advance in technology outside the IT-producing sectors ("other nonfarm business").⁸⁴ Following Jorgenson, Ho, and Stiroh,⁸⁵ we assume that labor quality will improve by 0.15 percent a year, well below the historical rate of increase, as the educational attainment of new labor force entrants rises more slowly than in the past and experienced workers reach retirement age. For the value of $\dot {z}{\kern 1pt}$ in other nonfarm business, we consider values ranging from 0.19 to 0.98 percent a year. The lower-bound figure equals the average annual growth of $\dot {z}{\kern 1pt}$ in this sector over 1973-2000, which allows for reversion to the longer-term average prevailing before the recent period of rapid gains. The upper-bound figure equals the average annual increase over 2000-06, minus $\raise.5ex\hbox{$\scriptstyle 1$}\kern-.1em/ \kern-.15em\lower.25ex\hbox{$\scriptstyle 4$}$ percentage point to account for the likelihood that some of the advance during this period was transitory.

Table 11 presents the results from the steady-state exercise using equation 23. The estimated range for steady-state labor productivity growth runs from 1.46 percent at an annual rate to 3.09 percent. The wide range reflects our uncertainty about the values of the parameters that determine steady-state growth. The center of the range is 2 $\raise.5ex\hbox{$\scriptstyle 1$}\kern-.1em/ \kern-.15em\lower.25ex\hbox{$\scriptstyle 4$}$ percent, about $\raise.5ex\hbox{$\scriptstyle 1$}\kern-.1em/ \kern-.15em\lower.25ex\hbox{$\scriptstyle 2$}$ percentage point below the average rate of labor productivity growth since 2000. This step-down from the recent average largely reflects the assumption that improvements in labor quality will slow and that gains in MFP, after controlling for adjustment costs and factor utilization, will not be as robust as the average pace since 2000.

Comparing Results

Table 12 compares the results from our steady-state and Kalman filter analyses with forecasts of labor productivity growth from a variety of sources. All but three of these forecasts have a horizon of ten years. The other three have shorter horizons.⁸⁶ These forecasts for average annual growth in labor productivity range from 2 percent to 2.6 percent. As noted above, the midpoint of our estimated range for steady-state growth and the estimated trend from the Kalman filter are both 2 $\raise.5ex\hbox{$\scriptstyle 1$}\kern-.1em/ \kern-.15em\lower.25ex\hbox{$\scriptstyle 4$}$ percent, near the center of the range of these forecasts. Thus there seems to be considerable agreement that labor productivity growth will remain reasonably strong over a medium-term horizon.

That said, one should be humble about this type of exercise, for a number of reasons. First, both the Kalman filter and our steady-state machinery point to a very wide confidence band around the point estimates. Second, the data on labor productivity through 2006 still could be revised significantly. In the future we might be looking at a different picture of actual labor productivity growth for recent years than the one we see today. Finally, as a general matter, economists do not have a stellar track record in forecasting trends in labor productivity. Although we think the analysis here moves the debate forward, we are acutely aware of the inherent limitations.

Conclusion

Productivity developments since 1995 have raised many important and interesting questions for productivity analysts and policymakers, four of which we address in this paper. First, given the data now available and the various critiques of neoclassical growth accounting that have arisen in recent years, is IT still a critical part of the story for the observed acceleration in productivity growth over 1995-2000? Second, what is the source of the continued strength in productivity growth since 2000? Third, how has the accumulation of intangible capital influenced recent productivity developments? And, finally, based on our answers to these questions, what is the outlook for productivity growth? We have used a variety of techniques to address these questions, including aggregate growth accounting augmented to incorporate variable utilization, adjustment costs, and intangible asset accumulation; an assessment of industry-level productivity patterns; and Kalman filter and steady-state analysis to gauge trend productivity.

Both the aggregate and the industry-level results confirm the central role of IT in the productivity revival during 1995-2000. IT also plays a significant role after 2000, although its impact appears smaller than it was during 1995-2000. These results stand even after accounting for variable factor utilization, adjustment costs, and intangible capital and so provide strong support for the consensus view that IT was a key source of growth for the U.S. economy over the past decade.

Our results suggest that the sources of the productivity gains since 2000 differ in important ways from those during 1995-2000. Along with the smaller direct role for IT in the latest period, aggregate productivity growth since 2000 appears to have been boosted by industry restructuring in response to profit pressures and by a reallocation of material and labor inputs across industries. We also find considerable churning among industries, with some industries showing accelerating productivity in the second half of the 1990s and different ones accelerating in the most recent period.

Adding intangible capital to our aggregate growth accounting framework changes the time profile for productivity growth since 1995 relative to the published data. The measure of intangible assets used in this paper implies that the fastest gains in labor productivity occurred during 1995-2000, with some step-down after 2000. In addition, the inclusion of intangibles tempers the size of the pickup in MFP growth from 1995-2000 to 2000-06.

Finally, in terms of the productivity outlook, both the Kalman filter and the steady-state analyses deliver broadly similar results and highlight the wide range of uncertainty surrounding estimates of growth in trend labor productivity. In both cases the central tendencies suggest a rate for trend productivity gains of around 2 $\raise.5ex\hbox{$\scriptstyle 1$}\kern-.1em/ \kern-.15em\lower.25ex\hbox{$\scriptstyle 4$}$ percent a year, a rate that is consistent with productivity growth remaining well above the lackluster pace that prevailed during the twenty-five years before 1995, but somewhat slower than the 1995-2006 average.

References

Aaronson, Daniel, Ellen R. Rissman, and Daniel G. Sullivan. 2004. "Assessing the Jobless Recovery." Federal Reserve Bank of Chicago Economic Perspectives (Second Quarter): 2-20.

Aizcorbe, Ana, Stephen D. Oliner, and Daniel E. Sichel. 2006. "Shifting Trends in Semiconductor Prices and the Pace of Technological Progress." Finance and Discussion Series Working Paper 2006-44. Board of Governors of the Federal Reserve System.

Aral, Sinan, Erik Brynjolfsson, and D. J. Wu. 2006. "Which Came First, IT or Productivity? The Virtuous Cycle of Investment and Use in Enterprise Systems." Paper presented at the 27^th International Conference on Information Systems, Milwaukee, December 10-13.

Baily, Martin Neil. 2003. "Comment." Brookings Papers on Economic Activity, no. 2: 280-7.

Baily, Martin N. 2004. "Recent Productivity Growth: The Role of Information Technology and Other Innovations," Federal Reserve Bank of San Francisco Economic Review (April): 35-42.

Baily, Martin N., and Robert Z. Lawrence. 2001. "Do We Have a New E-conomy?" American Economic Review, Papers and Proceedings 91(2): 308-12.

Basu, Susanto, and John G. Fernald. 1995. "Are Apparent Productive Spillovers a Figment of Specification Error?" Journal of Monetary Economics 36(1): 165-88.

_____. 1997. "Returns to Scale in U.S. Production: Estimates and Implications." Journal of Political Economy 105(2): 249-83.

_____. 2001. "Why is Productivity Procyclical? Why Do We Care?" In New Developments in Productivity Analysis, edited by Charles R. Hulten, Edwin R. Dean, and Michael J. Harper. National Bureau of Economic Research Studies in Income and Wealth, vol. 63. University of Chicago Press.

_____. 2007. "Information and Communications Technology as a General-Purpose Technology: Evidence from US Industry Data." German Economic Review 8(2): 146-73.

Basu, Susanto, John G. Fernald, and Miles S. Kimball. 2006. "Are Technology Improvements Contractionary?" American Economic Review 96(5): 1418-48.

Basu, Susanto, John G. Fernald, Nicholas Oulton, and Sylaja Srinivasan. 2004. "The Case of the Missing Productivity Growth, or Does Information Technology Explain Why Productivity Accelerated in the United States But Not in the United Kingdom?" In NBER Macroeconomics Annual 2003, edited by Mark Gertler and Kenneth Rogoff. MIT Press.

Basu, Susanto, John G. Fernald, and Matthew D. Shapiro. 2001. "Productivity Growth in the 1990s: Technology, Utilization, or Adjustment?" Carnegie-Rochester Conference Series on Public Policy 55: 117-65.

Becker, Randy, and others. 2005. "Micro and Macro Data Integration: The Case of Capital." Center for Economic Studies Working Paper 2005-02. U.S. Census Bureau (May).

Black, Sandra E., and Lisa M. Lynch. 2001. "How to Compete: The Impact of Workplace Practices and Information Technology on Productivity." Review of Economics and Statistics 83(3): 434-45.

_____. 2004. "What's Driving the New Economy: The Benefits of Workplace Innovation." Economic Journal, 114(493): F97-F116.

Bloom, Nicholas, and John Van Reenen. 2006. "Measuring and Explaining Management Practices Across Firms and Countries." Discussion Paper 5581. London: Centre for Economic Policy Research (March).

Board of Governors of the Federal Reserve System. 2001. Federal Open Market Committee Transcripts. Available at www.federalreserve.gov/fomc/transcripts.

Bosworth, Barry P. and Jack E. Triplett. 2007. "The Early 21^st Century Productivity Expansion is Still in Services." International Productivity Monitor, no. 14 (Spring): 3-19.

Brainard, William C., and George L. Perry. 2000. "Making Policy in a Changing World." In Economic Events, Ideas, and Policies: The 1960s and After, edited by George L. Perry and James Tobin. Washington, D.C.: Brookings Institution Press.

Bresnahan, Timothy F., Erik Brynjolfsson, and Lorin Hitt. 2002. "Information Technology, Workplace Organization, and the Demand for Skilled Labor: Firm-Level Evidence." Quarterly Journal of Economics 117(1): 339-76.

Bresnahan, Timothy F., and M. Trajtenberg. 1995. "General Purpose Technologies: Engines of Growth?" Journal of Econometrics 65(1): 83-108.

Bruno, Michael. 1978. "Duality, Intermediate Inputs, and Value Added." In Production Economics: A Dual Approach to Theory and Applications, vol. 2, edited by Melvyn Fuss and Daniel McFadden. Amsterdam: North Holland.

Brynjolfsson, Erik, and Lorin M. Hitt. 2000. "Beyond Computation: Information Technology, Organizational Transformation and Business Performance." Journal of Economic Perspectives 14(4): 23-48.

_____. 2003. "Computing Productivity: Firm-Level Evidence." Review of Economics and Statistics 85(4): 793-808.

Brynjolfsson, Erik, Lorin M. Hitt, and Shinkyu Yang. 2002. "Intangible Assets: Computers and Organizational Capital." Brookings Papers on Economic Activity, no. 1: 137-98.

Caballero, Ricardo J., and Mohamad L. Hammour. 1994. "The Cleansing Effect of Recessions." American Economic Review 84(5): 1350-68.

Congressional Budget Office. 2007a. The Budget and Economic Outlook: Fiscal Years 2008 to 2017. Washington, D.C. (January).

_____. 2007b. Labor Productivity: Developments since 1995. Washington, D.C. (March).

Corrado, Carol, Charles Hulten, and Daniel Sichel. 2005. "Measuring Capital and Technology: An Expanded Framework." In Measuring Capital in the New Economy, edited by Carol Corrado, John Haltiwanger, and Daniel Sichel. National Bureau of Economic Research Studies in Income and Wealth, vol. 65. University of Chicago Press.

_____. 2006. "Intangible Capital and Economic Growth." Working Paper 11948. Cambridge, MA: National Bureau of Economic Research (January).

Corrado, Carol, and others. 2007. "Sectoral Productivity in the United States: Recent Developments and the Role of IT." German Economic Review 8(2): 188-210.

Daveri, Francesco, and Andrea Mascotto. 2002. "The I.T. Revolution across the U.S. States." Working Paper 226. Milan: Innocenzo Gasparini Institute for Economic Research (November).

Domar, Evsey D. 1961. "On the Measurement of Technological Change." Economic Journal 71(284): 709-29.

Farrell, Diana, Martin Baily, and Jaana Remes. 2005. "U.S. Productivity After the Dot Com Bust." Washington, D.C.: McKinsey Global Institute.

Foster, Lucia, John Haltiwanger, and C.J. Krizan. 2002. "The Link Between Aggregate and Micro Productivity Growth: Evidence from Retail Trade," Working Paper 9120. Cambridge: MA: National Bureau of Economic Research (August).

Global Insight. 2007. "U.S. Executive Summary" (March).

Gordon, Robert J. 2003. "Exploding Productivity Growth: Context, Causes, and Implications." Brookings Papers on Economic Activity, no. 2: 207-79.

_____. 2006. "Future U.S. Productivity Growth: Looking Ahead by Looking Back." Paper presented at the Workshop at the Occasion of Angus Maddison's 80^th Birthday, World Economic Performance: Past, Present, and Future. University of Groningen (October 27).

_____. 2007. "Was the Post-1995 Productivity Growth Upsurge a Will-o'-the Wisp?" Presentation at the NBER Productivity Program Meetings. Cambridge, MA (March 9).

Groshen Erica L., and Simon Potter. 2003. "Has Structural Change Contributed to a Jobless Recovery?" Current Issues in Economics and Finance 9(8). Federal Reserve Bank of New York (August).

Groth, Charlotta. 2005. "Estimating UK Capital Adjustment Costs." Working Paper 258. Bank of England.

Groth, Charlotta, Soledad Nunez, and Sylaja Srinivasan. 2006. "Productivity Growth, Adjustment Costs, and Variable Factor Utilization: The UK Case." Working Paper 295. Bank of England (April).

Hall, Robert E. 2004. "Measuring Factor Adjustment Costs." Quarterly Journal of Economics 119(3): 899-927.

Hall, Robert E., and Dale W. Jorgenson. 1967. "Tax Policy and Economic Behavior." American Economic Review 57(3): 391-414.

Houseman, Susan. 2007. "Outsourcing, Offshoring, and Productivity Measurement in U.S. Manufacturing." Working Paper 06-130. Kalamazoo, Mich.: W. E. Upjohn Institute for Employment Research (April).

Howells, Thomas F., Kevin B. Barefoot, and Brian M. Lindberg. 2006. "Annual Industry Accounts: Revised Estimates for 2003-2005." Survey of Current Business 86 (December): 45-55.

Inklaar, Robert, Mary O'Mahony, and Marcel Timmer. 2005. "ICT and Europe's Productivity Performance: Industry-level Growth Account Comparisons with the United States." Review of Income and Wealth 51(4): 505-36.

Jorgenson, Dale W. 2001. "Information Technology and the U.S. Economy." American Economic Review 91(1): 1-32.

Jorgenson, Dale, Frank Gollop, and Barbara Fraumeni. 1987. Productivity and U.S. Economic Growth. Harvard Economic Studies, vol. 159. Cambridge, MA: Harvard University Press.

Jorgenson, Dale W., Mun S. Ho, and Kevin J. Stiroh. 2002. "Projecting Productivity Growth: Lessons from the U.S. Growth Resurgence. Federal Reserve Bank of Atlanta Economic Review 87 (Fall): 1-14.

_____. 2005. Productivity, vol. 3: Information Technology and the American Growth Resurgence. Cambridge, MA: MIT Press.

_____. 2007. "A Retrospective Look at the U.S. Productivity Growth Resurgence." Staff Report 277. Federal Reserve Bank of New York (February).

Jorgenson, Dale W., and others. 2006. "The Industry Origins of the American Productivity Resurgence." Federal Reserve Bank of New York (October). Forthcoming in Economic Systems Research.

Jorgenson, Dale W., and Stiroh, Kevin J. 2000. "Raising the Speed Limit: U.S. Economic Growth in the Information Age." Brookings Papers on Economic Activity, no. 1: 125-211.

Kahn, James A., and Jong-Soo Lim. 1998. "Skilled Labor-Augmenting Technical Progress in U.S. Manufacturing." Quarterly Journal of Economics 113(4): 1281-1308.

Kahn, James A., and Robert W. Rich. 2006. "Tracking Productivity in Real Time." Current Issues in Economics and Finance 12(8). Federal Reserve Bank of New York (November).

Kiley, Michael T. 2001. "Computers and Growth with Frictions: Aggregate and Disaggregate Evidence." Carnegie-Rochester Conference Series on Public Policy 55: 171-215.

Macroeconomic Advisers. 2007. Macro Focus. March 22.

McKinsey Global Institute. 2001. U.S. Productivity Growth, 1995-2000: Understanding the Contribution of Information Technology Relative to Other Factors. Washington, D.C.: McKinsey Global Institute (October).

_____. 2002. How IT Enables Productivity Growth: The US Experience Across Three Sectors in the 1990s. Washington, D.C.: McKinsey Global Institute (November).

Nakamura, Leonard. 1999. "Intangibles: What Put the New in the New Economy?" Federal Reserve Bank of Philadelphia Business Review (July/August): 3-16.

_____. 2001. "What is the U.S. Gross Investment in Intangibles? (At Least) One Trillion Dollars a Year!" Working Paper 01-15. Federal Reserve Bank of Philadelphia (October).

_____. 2003. "The Rise in Gross Private Investment in Intangible Assets Since 1978. Federal Reserve Bank of Philadelphia (June).

Nordhaus, William D. 2002a. "The Recent Recession, the Current Recovery, and Stock Prices," Brookings Papers on Economic Activity, no. 1: 199-220.

_____. 2002b. "Productivity Growth and the New Economy." Brookings Papers on Economic Activity, no. 2: 211-44.

Norsworthy, J. R., and David H. Malmquist. 1983. "Input Measurement and Productivity Growth in Japanese and U.S. Manufacturing." American Economic Review 73(5): 947-67.

Okubo, Sumiye, and others. 2006. "BEA's 2006 Research and Development Satellite Account: Preliminary Estimates for 1959-2002 and Effect on GDP and Other Measures." Survey of Current Business 86 (December): 14-27.

Oliner, Stephen D., and Daniel E. Sichel. 2000. "The Resurgence of Growth in the Late 1990s: Is Information Technology the Story? Journal of Economic Perspectives 14(4): 3-22.

_____. 2002. "Information Technology and Productivity: Where Are We Now and Where Are We Going?" Federal Reserve Bank of Atlanta Economic Review 87 (Fall): 15-44.

O'Mahony, Mary, and Bart van Ark, editors. 2003. EU Productivity and Competitiveness: An Industry Perspective. Can Europe Resume the Catching-up Process? Luxembourg: Office for Official Publications of the European Communities.

Organization for Economic Cooperation and Development. 2000. A New Economy? The Changing Role of Innovation and Information Technology in Growth. Paris.

_____. 2006. Economic Policy Reforms - Going for Growth. Paris.

Roberts, John M. 2001. "Estimates of the Productivity Trend Using Time-Varying Parameter Techniques," Contributions to Macroeconomics 1(1), Article 3. Available at: http://www.bepress.com/bejm/contributions/vol1/iss1/art3.

Schreft, Stacey L., and Aarti Singh. 2003. "A Closer Look at Jobless Recoveries." Federal Reserve Bank of Kansas City Economic Review (Second Quarter): 46-73.

Schreyer, Paul. 2000. "The Contribution of Information and Communication Technology to Output Growth: A Study of the G7 Countries." OECD Science, Technology, and Industry Working Paper 2000/2. Paris (March).

Schweitzer, Mark. 2004. "Economic Restructuring and the Slow Recovery of Employment." Federal Reserve Bank of Cleveland (December 31).

Shapiro, Matthew D. 1986. "The Dynamic Demand for Capital and Labor." Quarterly Journal of Economics 101(3): 513-42.

Sichel, Daniel E. 2003. "Comment." Brookings Papers on Economic Activity, no. 2: 287-93.

Smith, George M., and Sherlene K. S. Lum. 2005. "Annual Industry Accounts, Revised Estimates for 2002-2004." Survey of Current Business 85 (December): 18-69.

Stiroh, Kevin J. 2001. "Investing in Information Technology: Productivity Payoffs for U.S. Industries." Current Issues in Economics and Finance 7(6). Federal Reserve Bank of New York (April).

_____. 2002a. "Are ICT Spillovers Driving the New Economy?" Review of Income and Wealth 48(1): 33-57.

_____. 2002b. "Information Technology and the U.S. Productivity Revival: What Do the Industry Data Say?" American Economic Review 92(5): 1559-76.

_____. 2006a. "Volatility Accounting: A Production Perspective on Increased Economic Stability." Staff Report 245. Federal Reserve Bank of New York (April). Forthcoming in the Journal of the European Economic Association.

_____. 2006b. "The Industry Origins of the Second Surge of U.S. Productivity Growth." Federal Reserve Bank of New York (July).

Stiroh, Kevin J., and Matthew Botsch. 2007. "Information Technology and Productivity Growth in the 2000s." German Economic Review 8(2): 255-80.

Survey of Professional Forecasters. 2007. Federal Reserve Bank of Philadelphia. February 13. Downloaded from www.philadelphiafed.org/econ/spf/index.html.

Triplett, Jack E. 1996. "High-Tech Industry Productivity and Hedonic Price Indices." In Industry Productivity: International Comparison and Measurement Issues. Proceedings of May 2-3, 1996 OECD workshop. Paris: OECD.

Triplett, Jack E., and Barry P. Bosworth. 2004. Productivity in the U.S. Services Sector: New Sources of Economic Growth. Washington, D.C.: Brookings Institution Press.

van Ark, Bart. 2000. "Measuring Productivity in the `New Economy': Towards a European Perspective." De Economist (Quarterly Review of the Royal Netherlands Economic Association) 148(1): 87-105.

van Ark, Bart, and Robert Inklaar. 2005. "Catching Up or Getting Stuck? Europe's Troubles to Exploit ICT's Productivity Potential." Research Memorandum GD-79. Groningen Growth and Development Center (September).

van Ark, Bart, Robert Inklaar, and Robert H. McGuckin. 2003. "ICT and Productivity in Europe and the United States: Where Do the Differences Come From?" CESifo Economic Studies 49 (March): 295-318.

Yang, Shinkyu, and Erik Brynjolfsson. 2001. "Intangible Assets and Growth Accounting: Evidence from Computer Investments." Unpublished paper. MIT.

Table 1. Contributions to Growth in Labor Productivity Based on Published Data $^{a}$
Item / Contributions from (percentage points)	1973- 1995 (1)	1995- 2000 (2)	2000- 2006 (3)	Change at 1995 (2)-(1)	Change at 2000 (3)-(2)
Growth of labor productivity in the nonfarm business sector (percent a year) $^{b}$	1.47	2.51	2.86	1.04	.35
Capital deepening	.76	1.11	.85	.35	-.26
Capital deepening: IT capital	.46	1.09	.61	.63	-.48
Capital deepening: IT capital, Computer hardware	.25	.60	.28	.35	-.32
Capital deepening: IT capital, Software	.13	.34	.20	.21	-.14
Capital deepening: IT capital, Communications equipment	.07	.15	.14	.08	-.01
Capital deepening: Other tangible capital	.30	.02	.24	-.28	.22
Improvement in labor quality	.27	.26	.34	-.01	.08
Growth of MFP	.44	1.14	1.67	.70	.53
Growth of MFP: Effect of adjustment costs	.04	-.11	.08	-.15	.19
Growth of MFP: Effect of utilization	-.03	.13	-.09	.16	-.22
Growth of MFP excl above effects	.42	1.11	1.68	.69	.57
Growth of MFP excl above effects: IT-producing sectors,	.28	.75	.51	.47	-.24
Growth of MFP excl above effects: IT-producing sectors, Semiconductors	.09	.45	.23	.36	-.22
Growth of MFP excl above effects: IT-producing sectors, Computer hardware	.12	.19	.10	.07	-.09
Growth of MFP excl above effects: IT-producing sectors, Software	.04	.08	.13	.04	.05
Growth of MFP excl above effects: IT-producing sectors, Communications equipment	.04	.04	.05	.00	.01
Growth of MFP excl above effects: Other nonfarm business	.15	.36	1.17	.21	.81
Memorandum: total IT contribution $^{c}$	.74	1.84	1.12	1.10	-.72

Source: Authors' calculations.

(a) Detail may not sum to total because of rounding.

(b) Measured as 100 times the average annual log difference for the indicated years.

Table 2. Contributions to Growth in Labor Productivity: Accounting for Intangibles $^{a}$
Item	1973- 1995 (1)	1995- 2000 (2)	2000- 2006 (3)	Change at 1995 (2)-(1)	Change at 2000 (3)-(2)
Growth of labor productivity In the nonfarm business sector (percent a year) $^{b}$
Growth of labor productivity In the nonfarm business sector: Based on published data $^{c}$	1.47	2.51	2.86	1.04	.35
Growth of labor productivity In the nonfarm business sector: Accounting for intangibles $^{d}$	1.58	2.95	2.43	1.37	-.52
(Contributions from, percentage points $^{e}$ )
Capital deepening (Contributions from, percentage points $^{e})$	.94	1.40	.75	.46	-.65
Capital deepening: IT capital (Contributions from, percentage points $^{e})$	.44	1.02	.57	.58	-.45
Capital deepening: Other tangible capital (Contributions from, percentage points $^{e})$	.29	.02	.22	-.27	.20
Capital deepening: New intangible capital (Contributions from, percentage points $^{e})$	.22	.36	-.04	.14	-.40
Improvement in labor quality (Contributions from, percentage points $^{e})$	.26	.25	.32	-.01	.07
Growth of MFP (Contributions from, percentage points $^{e})$	.37	1.31	1.36	.94	.05
Growth of MFP: Effect of adjustment costs (Contributions from, percentage points $^{e})$	.04	-.12	.10	-.16	.22
Growth of MFP: Effect of utilization (Contributions from, percentage points $^{e})$	-.03	.13	-.09	.16	-.22
Growth of MFP excl above effects (Contributions from, percentage points $^{e})$	.36	1.30	1.34	.94	.04
Growth of MFP excl above effects: IT-producing sectors (Contributions from, percentage points $^{e})$	.26	.72	.47	.46	-.25
Growth of MFP excl above effects: Intangible sector (Contributions from, percentage points $^{e})$	.01	.08	.07	.07	-.01
Growth of MFP excl above effects: Other nonfarm business (Contributions from, percentage points $^{e})$	.09	.50	.81	.41	.31
Memorandum: Real intangible investment (Growth rates, percent a year $^{b})$	5.7	12.0	-4.6	6.3	-16.6
Memorandum: Real intangible capital services (Growth rates, percent a year $^{b})$	6.8	7.7	-.7	.9	-8.4
Memorandum: Real IT capital services (Growth rates, percent a year $^{b})$	15.6	20.4	8.9	4.8	-11.5
Memorandum: User cost, intangible capital (Growth rates, percent a year $^{b})$	4.6	1.2	3.6	-3.4	2.4
Memorandum: User cost, IT capital (Growth rates, percent a year $^{b})$	-2.4	-9.0	-4.1	-6.6	4.9
Expenditure share, intangible investment (Nominal shares, percent)	4.6	6.2	5.1	1.6	-1.1
Income share, intangible capital (Nominal shares, percent)	4.7	6.4	6.5	1.7	.1

Source: Authors' calculations.

(a) Detail may not sum to total because of rounding. (b) Measured as 100 times the average annual log difference for the indicated years. (c) From table 1. (d) Derived using methodology discussed in text. (e) Contributions to growth of nonfarm business labor productivity with accounting for intangibles.

Table 3. Growth of Intangible Capital and Investment Under Alternative Timing Assumptions for Intangible Capital $^{a,b}$
Timing assumption	1973- 1995	1995- 2000	2000- 2005
Intangible Capital Services: Baseline timing for intangible capital growth	6.8	7.7	-.9
Intangible Capital Services: Three-year centered moving average	6.9	7.1	-.3
Intangible Capital Services: Five-year centered moving average	6.8	6.7	.4
Intangible Capital Services: One-year lag relative to baseline	7.4	7.1	-.2
Intangible Capital Services: Memorandum: Corrado, Hulten, and Sichel series $^{c}$	5.2	7.3	2.8
Intangible investment: Baseline timing for intangible capital growth	5.7	12.0	-6.2
Intangible investment: Three-year centered moving average	6.1	9.1	-5.2
Intangible investment: Five-year centered moving average	6.1	8.5	-4.1
Intangible investment: One-year lag relative to baseline	6.9	8.8	-8.7
Intangible investment: Memorandum: Corrado, Hulten, and Sichel series $^{c}$	5.2	8.3	1.1

Source: Authors' calculations.

a. The alternative timing assumptions pertain to growth of intangible capital. The effect on intangible investment is calculated through the perpetual inventory relationship linking investment and capital.

b. Measured as 100 times the average annual log difference for the indicated years.

c. From Corrado, Hulten, and Sichel (2006), series for "New CHS intangibles," with preliminary extension to 2005 estimated by the authors.

Table 4. Growth in Labor Productivity and Selected Growth Contributions Under Alternative Timing assumptions for Intangible Capital $^{a}$
	1973- 1995 (1)	1995- 2000 (2)	2000- 2006 (3)	Change at 1995 (2)-(1)	Change at 2000 (3)-(2)
Baseline $^{b}$ : Labor productivity growth	1.58	2.95	2.43	1.37	-.52
Baseline $^{b}$ : Labor productivity growth, Contribution from intangible capital	.22	.36	-.04	.14	-.40
Baseline $^{b}$ : Labor productivity growth, Contribution from MFP growth $^{c}$	.36	1.30	1.34	.94	.04
Three-year centered moving average: Labor productivity growth,	1.59	2.77	2.56	1.18	-.21
Three-year centered moving average: Labor productivity growth, Contribution from intangible capital	.22	.32	.00	.10	-.32
Three-year centered moving average: Labor productivity growth, Contribution from MFP growth $^{c}$	.38	1.13	1.45	.75	.32
Five-year centered moving average: Labor productivity growth	1.59	2.72	2.59	1.31	-.13
Five-year centered moving average: Labor productivity growth, Contribution from intangible capital	.22	.29	.02	.07	-.27
Five-year centered moving average: Labor productivity growth, Contribution from MFP growth $^{c}$	.38	1.11	1.46	.73	.35
On-year lag relative to baseline: Labor productivity growth,	1.62	2.77	2.51	1.15	-.26
On-year lag relative to baseline: Labor productivity growth, Contribution from intangible capital	.23	.32	.01	.09	-.31
On-year lag relative to baseline: Labor productivity growth, Contribution from MFP growth $^{c}$	.39	1.13	1.39	.74	.26

Source: Authors' calculations.

(a) Growth of labor productivity is in percent a year and is measured as 100 times the average annual log difference for the indicated years. Growth contributions are in percentage points.

(b) From table 2.

Table 5. Estimates of Labor Productivity Growth in the Aggregate and by Sector
	Value Added, 2005: Billions of dollars	Value Added, 2005: Share (percent)	Average Growth rate of labor productivity (percent a year): 1988-95	Average Growth rate of labor productivity (percent a year): 1995-2000	Average Growth rate of labor productivity (percent a year): 2000-05	Change in productivity growth rate (percentage points): 1988-95 to 1995-2000	Change in productivity growth rate (percentage points): 1995-2000 to 2000-05
Value added, aggregate measures $^{a}$ : BLS business sector			1.48	2.69	3.07	1.21	0.38
Value added, aggregate measures $^{a}$ : BLS nonfarm business sector			1.46	2.52	3.02	1.06	0.50
Value added, aggregate measures $^{a}$ : Private industry aggregate, this paper	10,892	100.0	1.25	2.24	2.52	0.99	0.28
Value added by broad sector $^{a}$ : Agriculture, forestry, fishing, and hunting	123	1.1	1.95	5.31	5.13	3.36	-0.19
Value added by broad sector $^{a}$ : Mining	233	2.1	3.54	0.59	-4.59	-2.95	-5.19
Value added by broad sector $^{a}$ : Construction	611	5.6	-0.32	-1.19	-0.98	-0.87	0.22
Value added by broad sector $^{a}$ : Durable goods	854	7.8	3.57	7.69	6.04	4.13	-1.65
Value added by broad sector $^{a}$ : Nondurable goods	658	6.0	2.26	1.78	4.26	-0.48	2.49
Value added by broad sector $^{a}$ : Utilities	248	2.3	5.14	3.43	4.03	-1.70	0.60
Value added by broad sector $^{a}$ : Wholesale trade	743	6.8	2.24	5.41	3.64	3.17	-1.77
Value added by broad sector $^{a}$ : Retail trade	824	7.6	2.69	4.66	4.00	1.97	-0.66
Value added by broad sector $^{a}$ : Transportation and warehousing	345	3.2	3.00	2.48	2.12	-0.52	-0.36
Value added by broad sector $^{a}$ : Information	555	5.1	3.70	2.48	8.85	-1.23	6.37
Value added by broad sector $^{a}$ : Finance, insurance, real estate, rental, and leasing	2,536	23.3	1.77	1.83	1.73	0.07	-0.11
Value added by broad sector $^{a}$ : Professional and business services	1,459	13.4	-0.94	0.16	2.33	1.11	2.16
Value added by broad sector $^{a}$ : Education services, health care, social assistance	975	9.0	-2.40	-1.22	0.84	1.18	2.07
Value added by broad sector $^{a}$ : Arts, entertainment, recreation, accommodation, and food services	445	4.1	0.65	1.12	0.13	0.46	-0.99
Value added by broad sector $^{a}$ : Other services, except government	283	2.6	-0.31	-1.45	-0.32	-1.14	1.13
Gross output by detailed industry $^{b}$ : Mean			1.80	2.95	2.28	1.15	-0.68
Gross output by detailed industry $^{b}$ :Median			1.62	2.19	1.88	0.57	-0.30
Gross output by detailed industry $^{b}$ : Weighted mean $^{c}$			1.59	2.68	2.19	1.09	-0.49
Value added by detailed industry $^{b}$ : Mean			1.78	2.02	2.80	0.24	0.78
Value added by detailed industry $^{b}$ :Median			1.74	1.16	2.82	-0.58	1.66
Value added by detailed industry $^{b}$ : Weighted mean $^{c}$			1.33	1.94	2.46	0.62	0.51

Source: Authors' calculations.

a. Growth of real value added per hour worked, measured as 100 times the average log difference for the indicated years.

b. Calculated across the sixty observations in each period using real gross output or real value added per hour worked.

c. Industries are weighted by hours at the beginning of each period.

Table 6. Decompositions of Aggregate Labor Productivity Growth
Item	No. of industries	1988-95: Share of total value added $^{a}$ (%)	1988-95: Contribution to ALP growth $^{b}$ (% pts)	1995-2000: Share of total value added (%)	1995-2000: Contribution to ALP growth (% pts)	2000-05: Share of total value added (%)	2000-05: Contribution to ALP growth (% pts)	Change in contribution (percentage points): 1988-95 to 1995-2000	Change in contribution (percentage points): 1995-2000 to 2000-05
Aggregates: Private industry aggregate $^{c}$			1.25		2.24		2.52	0.99	0.28
Aggregates: Aggregated industries $^{d}$	60		1.24		2.2		2.52	0.96	0.32
Decomposition using industry real gross output per hour worked:
Decomposition using industry real gross output per hour worked: Industry contribution	60	100	1.79	100	3.1	100	2.16	1.31	-0.94
Decomposition using industry real gross output per hour worked: Industry contribution, IT-producing industries $^{e}$	4	4	0.33	5	0.5	4.5	0.25	0.17	-0.25
Decomposition using industry real gross output per hour worked: Industry contribution, IT-using industries $^{f}$	26	57.3	0.71	58.6	1.99	59.1	1.54	1.28	-0.45
Decomposition using industry real gross output per hour worked: Industry contribution, Other industries	30	38.7	0.75	36.4	0.61	36.4	0.37	-0.14	-0.23
Decomposition using industry real gross output per hour worked: Reallocation of materials, - $^{M g}$			-0.2		-0.68		0.26	-0.48	0.94
Decomposition using industry real gross output per hour worked: Reallocation of hours, $^{H}$			-0.34		-0.21		0.1	0.13	0.31
Decomposition using industry real value-added per hour worked: Industry contribution			1.59		2.41		2.41	0.83	0
Decomposition using industry real value-added per hour worked: Industry contribution, IT-producing industries			0.36		0.7		0.47	0.34	-0.23
Decomposition using industry real value-added per hour worked: Industry contribution, IT-using industries			0.48		1.31		1.54	0.82	0.24
Decomposition using industry real value-added per hour worked: Industry contribution, Other industries			0.74		0.41		0.4	-0.33	0
Decomposition using industry real value-added per hour worked: Reallocation of hours, $^{H}$			-0.34		-0.21		0.1	0.13	0.31

Source: Authors' calculations.

a. Nominal value added in indicated industries divided by aggregate nominal value added for each period, multiplied by 100.

b. Growth of industry productivity, weighted by nominal value-added shares in each year.

c. Based on BEA and BLS aggregate data from table 5.

d. Weighted aggregate of industry output and hours data.

e. Includes computer and electronic products, publishing including software, information and data processing services, and computer system design and related services, as defined by BEA.

f. Includes all non-IT-producing industries with a 1995 IT capital services share above the 1995 median.

g. Reallocations are defined as in equations 19 and 20.

Table 7. Regressions Relating Labor Productivity Growth to IT Capital Intensity $^{a}$
Output measure and independent variable	1988-95 to 1995-2000 (1)	1988-95 to 1995-2000 (2)	1988-95 to 1995-2000 (3)	1988-95 to 1995-2005 (1)	1988-95 to 1995-2005 (2)	1988-95 to 1995-2005 (3)	1995-2000 to 2000-05 (1)	1995-2000 to 2000-05 (2)	1995-2000 to 2000-05 (3)
Gross output: 1995 IT dummy $^{b}$	1.277**			1.478***
Gross output: 1995 IT dummy $^{b}$ (robust standard error)	(0.585)			(0.491)
Gross output: 1995 IT share $^{c}$		0.038	0.081***		0.037*	0.060***
Gross output: 1995 IT share $^{c}$ (robust standard error)		(0.028)	(0.027)		(0.020)	(0.019)
Gross output: 2000 IT dummy							0.156
Gross output: 2000 IT dummy (robust standard error)							(0.931)
Gross output: 2000 IT share								0.010	-0.031
Gross output: 2000 IT share (robust standard error)								(0.044)	(0.048)
Gross output: Constant	0.513	0.543	0.009	0.074	0.216	-0.040	-0.756	-0.865	-0.206
Gross output: Constant (robust standard error)	(0.438)	(0.478)	(0.478)	(0.371)	(0.401)	(0.382)	(0.480)	(0.650)	(0.651)
Gross output: IT-producing industries included in sample?	No	No	Yes	No	No	Yes	No	No	Yes
Gross output: ²	0.08	0.06	0.18	0.14	0.07	0.12	0.00	0.00	0.02
Value Added: 1995 IT dummy	1.904			1.967**
Value Added: 1995 IT dummy	(1.173)			(0.893)
Value Added: 1995 IT share		0.029	0.066		0.051*	0.048
Value Added: 1995 IT share		(0.044)	(0.054)		(0.026)	(0.035)
Value Added: 2000 IT dummy							0.095
Value Added: 2000 IT dummy							(1.448)
Value Added: 2000 IT share								0.046	-0.041
Value Added: 2000 IT share								(0.066)	(0.055)
Value Added: Constant	-0.709	-0.227	-0.828	-0.352	-0.198	-0.284	0.730	-0.056	1.225
Value Added: Constant	(0.913)	(0.915)	(1.009)	(0.709)	(0.667)	(0.725)	(0.944)	(1.149)	(1.017)
Value Added: IT-producing industries included in sample?	No	No	Yes	No	No	Yes	No	No	Yes
Value Added: ²	0.04	0.01	0.03	0.08	0.05	0.026	0.00	0.02	0.01

Source: Authors' regressions.

a. Data are for the sixty industries listed in appendix table A-1 (fifty-six industries when the four IT-producing industries are dropped). Numbers

in parentheses are robust standard errors. Asterisks indicate statistical significance at the ***1 percent, **5 percent, and *10 percent level.

b. Dummy variable equal to 1 for industries with an IT capital share above the median in the indicated year, and zero otherwise.

c. IT capital services as a share of nonresidential capital services in the indicated year.

Table 8a Regressions Relating Growth in Inputs, Productivity, and Output to Earlier Changes in the Profit Share $^{a}$ (Dependent variable: average annual growth rate of indicated input type)
Independent variable	Hours (1)	Hours (2)	Hours (3)	Intermediate inputs (1)	Intermediate inputs (2)	Intermediate inputs (3)
Change in profit share, $^{b}$ 1997-2001	19.212***	16.413***	16.170***	-0.069	1.864	1.502
Change in profit share, $^{b}$ 1997-2001 (robust standard error)	(4.940)	(5.126)	(5.273)	(10.339)	(10.789)	(11.398)
Change in profit share, 2001-04		-0.115	13.389*		8.244	22.546
Change in profit share, 2001-04 (robust standard error)		(6.159)	(7.952)		(12.592)	(22.270)
Lagged dependent variable, 1997-2001		0.722***	0.782***		0.255	0.280
Lagged dependent variable, 1997-2001 (robust standard error)		(0.155)	(0.128)		(0.165)	(0.168)
IT service share, $^{c}$ 2001		-0.089***	-0.069***		-0.032	-0.009
IT service share, $^{c}$ 2001 (robust standard error)		(0.027)	(0.025)		(0.064)	(0.067)
Change in profit share, 1997-2001 $\times$ IT service share, 2001			-0.444**			-0.474
Change in profit share, 1997-2001 $\times$ IT service share, 2001 (robust standard error)			(0.173)			(0.522)
Constant	-1.175**	0.239	-0.193	0.533	0.104	-0.459
Constant (robust standard error)	(0.459)	(0.478)	(0.463)	(0.733)	(1.076)	(1.499)
R2	0.17	0.51	0.57	0.00	0.10	0.12

Table 8b Regressions Relating Growth in Inputs, Productivity, and Output to Earlier Changes in the Profit Share $^{a}$ (Dependent variable: average annual growth rate of labor productivity)
	Value added (1)	Value added (2)	Value added (3)	Gross output (1)	Gross output (2)	Gross output (3)
Change in profit share, 1997-2001	-38.487***	-40.655***	-39.835***	-28.456***	-20.929***	-20.851***
Change in profit share, 1997-2001 (standard error)	(11.253)	(14.067)	(14.230)	(6.437)	(7.116)	(7.379)
Change in profit share, 1997-2001		5.703	0.563		7.013	4.655
Change in profit share, 1997-2001(standard error)		(11.962)	(15.520)		(8.705)	(8.353)
Lagged dependent variable, 1997-2001		-0.055	-0.041		0.169	0.176
Lagged dependent variable, 1997-2001 (standard error)		(0.186)	(0.195)		(0.168)	(0.178)
IT service share, 2001		-0.008	-0.018		0.030	0.025
IT service share, 2001 (standard error)		(0.035)	(0.041)		(0.028)	(0.037)
Change in profit share, 1997-2001 $\times$ IT service share, 2001			0.177			0.077
Change in profit share, 1997-2001 $\times$ IT service share, 2001 (standard error)			(0.297)			(0.294)
Constant	3.283***	3.332***	3.540***	2.279***	1.319**	1.404**
Constant (standard error)	(0.745)	(0.882)	(0.871)	(0.341)	(0.522)	(0.555)
²	0.26	0.27	0.28	0.37	0.44	0.44

Table 8c Regressions Relating Growth in Inputs, Productivity, and Output to Earlier Changes in the Profit Share $^{a}$ (Dependent variable: average annual growth rate of output )
	Value added (1)	Value added (2)	Value added (3)	Gross output (1)	Gross output (2)	Gross output (3)
Change in profit share, 1997-2001	-19.274**	-19.781*	-19.826*	-9.243	-0.785	-0.707
Change in profit share, 1997-2001 (standard error)	(9.511)	(10.820)	(10.794)	(6.933)	(7.645)	(7.729)
Change in profit share, 1997-2001		10.770	11.472		10.342	16.689
Change in profit share, 1997-2001(standard error)		(11.257)	(17.752)		(10.943)	(16.531)
Lagged dependent variable, 1997-2001		-0.043	-0.044		0.294	0.300
Lagged dependent variable, 1997-2001 (standard error)		(0.150)	(0.152)		(0.211)	(0.216)
IT service share, 2001		-0.006	-0.005		-0.014	-0.002
IT service share, 2001 (standard error)		(0.028)	(0.034)		(0.041)	(0.040)
Change in profit share, 1997-2001 $\times$ IT service share, 2001			-0.023			-0.203
Change in profit share, 1997-2001 $\times$ IT service share, 2001 (standard error)			(0.290)			(0.356)
Constant	2.108***	2.058***	2.029**	1.105**	0.529	0.281
Constant (standard error)	(0.679)	(0.680)	(0.780)	(0.486)	(0.552)	(0.867)
²	0.11	0.15	0.15	0.04	0.22	0.23

Table 9. Effects of Data Revisions and Data for Additional Years on Measured Growth of Labor Productivity $^{a}$
Vintage of data	Period covered by the data: 1995-2000	Period covered by the data: 2000-03	Period covered by the data: 2000-04	Period covered by the data: 2000-05	Period covered by the data: 2000-06
March 2004	2.4	3.8
August 2004	2.5	3.7
March 2005	2.5	3.7	3.7
August 2005	2.5	3.4	3.4
March 2006	2.5	3.4	3.4	3.3
August 2006	2.5	3.4	3.3	3.1
March 2007	2.5	3.4	3.3	3.0	2.8

Source: Authors' calculations using BLS data.

a. Measured as 100 times the average log difference over indicated period, based on annual average data.

Table 10. Growth of Labor Productivity: Long-Period Averages $^{a}$
Period	Private economy/ business sector	Nonfarm business sector
1909-1928	1.4
1928-1950	2.5
1950-1973	2.9	2.6
1973-1995	1.5	1.4
1995-2006	2.8	2.7
1909-2006	2.2
1950-2006	2.3	2.1

Source: Authors' calculations using BLS data.

Measured as 100 times the average log difference over indicated period, based on annual average data.

Data before 1947 pertain to the private economy (defined as gross national product less general government), whereas data for 1947 and later years pertain to the business sector.

Table 11. Growth of Labor Productivity: Steady-State Results $^{a}$
	Using lower- bound parameters	Using upper- bound parameters
Growth of labor productivity in the nonfarm business sector (percent a year)	1.46	3.09
Contributions from (percentage points): Induced capital deepening	0.75	1.39
Contributions from (percentage points):Improvement in labor quality	0.15	0.15
Contributions from (percentage points):Growth of MFP	0.56	1.55
Memorandum: MPF growth, other nonfarm business (percent a year)	0.19	0.98

Source: Authors' calculations.

Calculated from equation 23 in the text. Values for the parameters that appear in equation 23 are listed in the appendix.

Table 12. Alternative Estimates of Future Growth in Labor Productivity (percent a year)
Source	Date of projection	Estimate
This paper: steady-state analysis	March 2007	1.5 to 3.1
This paper: Kalman-filter analysis	March 2007	1.3 to 3.2
Robert Gordon	March 2007	2.0
Survey of Professional Forecasters $^{a}$	February 2007	2.2
Global Insight	March 2007	2.2
Macroeconomic Advisers	March 2007	2.2
Congressional Budget Office	January 2007	2.3
Dale Jorgenson, Mun Ho, and Kevin Stiroh $^{b}$	October 2006	2.5
James Kahn and Robert Rich	March 2007	2.5
Council of Economic Advisers	January 2007	2.6

Sources: Gordon (2007, slide 24); Survey of Professional Forecasters (2007, table 7); Global Insight (2007, page 6); Macroeconomic Advisers (2007, page 11); Congressional Budget Office (2007a, table 2-2); Jorgenson, Ho, and Stiroh (2007, table 3); Kahn and Rich (2006), updated to March 2007 based on the productivity model update posted at http://www.newyorkfed.org/research/national_economy/richkahn_prodmod.pdf; Council of Economic Advisers, Economic Report of the President 2007, table 1-2.

(a) Median of the thirty-eight forecasts in the survey. (b) "Base-case" projection.

Figure 1. Link Between Productivity and Hours Reallocation, 1989-2005

Figure 1 Data

Source: Authors' calculations using BLS and BEA data. a. Annual cross-sectional correlation between hours growth and the lagged level of productivity for the sixty industries in appendix table A-1, calculated using industry value added.

b. Above correlation calculated using industry gross output.

c. Reallocation of hours to high-productivity industries, as defined in equation 19. This is the difference between the aggregate growth rate of hours weighted by industry value added and the aggregate growth rate of hours weighted by hours in each of the sixty industries.

Figure 2. Hours Growth over 2001-04 versus Changes in the Profit Share over 1997-2001, by Industry

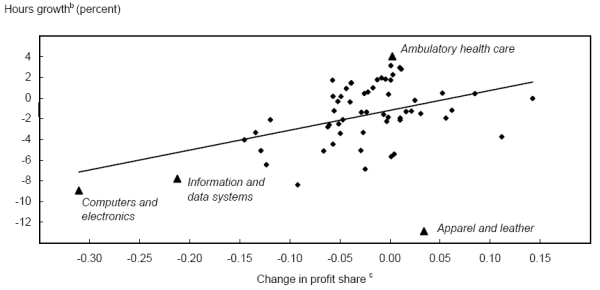Figure 2 Data

Source: Authors' calculations using BLS and BEA data.

a. Each point is one of sixty industry observations; line plots fitted values from an OLS regression.

b. Average annual rate of growth in hours worked from 2001 to 2004.

c. Change in the ratio of gross operating surplus to value added from 1997 to 2001.

Figure 3. Labor Productivity Growth over 2001-04 versus Changes in the Profit Share over 1997-2001, by Industry

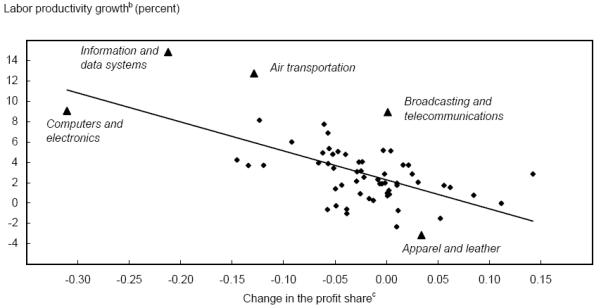Figure 3 Data

Source: Authors' calculations using BLS and BEA data.

a. Each point is one of sixty industry observations; line plots fitted values from an OLS regression.

b. Average annual rate of growth of labor productivity from 2001 to 2004 based on gross output.

c. Change in the ratio of gross operating surplus to value added from 1997 to 2001.

APPENDIX FOR AGGREGATE GROWTH ACCOUNTING MODEL

This appendix presents the model that generates our aggregate growth accounting equation and derives the key results from the model. As described in the text, the model divides nonfarm business into six sectors. Five of the sectors produce final output (computer hardware, communications equipment, software, other final output included in the NIPAs, and intangible assets excluded from the NIPAs). The remaining sector produces semiconductors, which are either consumed as an intermediate input by the final-output sectors or exported to foreign firms. The model includes adjustment costs for capital and allows the utilization of capital and labor to vary over time.

The Model

Let $_{i}$ denote the real gross output produced by final-output sector . To produce this output, sector employs labor ( $_{i})$ and various types of capital $(K_{j, i} ).$ Sector also buys semiconductors ( $_{i})$ as an intermediate input. The production of each final-output sector, $_{i}$ , is allocated to an investment good for domestic use ( $_{i})$ , a consumption good for domestic use ( $_{i})$ , and exports ( $_{i})$ , where $I_i , C_i ,\mbox{ and }X_i$ are identical goods sold to different agents (businesses buyhouseholds buy and foreigners buy $_{i})$ . We also identify the destination within the nonfarm business sector of the investment good produced by sector . Let $_{i,j}$ and $I_{i,S}$ denote, respectively, the purchases of $_{i}$ by final-output sector ( = 1,...,5) and by semiconductor producers, with $_{ }=\sum$ $_{j}$ $I_{i,j}$ + $I_{i,S}$ .⁸⁷

Following Basu, Fernald, and Shapiro (2001), we model the rate of utilization for each type of capital in each sector $(u_{j, i} )$ , the level of labor effort in each sector ( $_{i})$ , and the adjustment costs imposed by each type of capital.⁸⁸ The adjustment-cost function for each sector, $\Phi _i \left( {{I_{1,i} } \mathord{\left/ {\vphantom {{I_{1,i} } {K_{1,i} }}} \right. \kern-\nulldelimiterspace} {K_{1,i} },...,{I_{5,i} } \mathord{\left/ {\vphantom {{I_{5,i} } {K_{5,i} }}} \right. \kern-\nulldelimiterspace} {K_{5,i} }} \right),$ represents the resources that are diverted from producing market output to installing new capital. Adjustment costs depend positively on the amount of investment spending relative to installed capital. Doubling for a given would increase adjustment costs, but doubling the level of both and would leave adjustment costs unchanged.

With this notation, production for each final-output sector can be written as(A1) $Y_i =C_i +\sum\nolimits_j {I_{i,j} } +I_{i,S} +X_i =$ $F_i \left( {u_{1,i} K_{1,i} ,...,u_{5,i} K_{5,i} ,E_i L_i ,S_i ,Z_i } \right)\left[ {1-\Phi _i \left( {{I_{1,i} } \mathord{\left/ {\vphantom {{I_{1,i} } {K_{1,i} }}} \right. \kern-\nulldelimiterspace} {K_{1,i} },...,{I_{5,i} } \mathord{\left/ {\vphantom {{I_{5,i} } {K_{5,i} }}} \right. \kern-\nulldelimiterspace} {K_{5,i} }} \right)} \right]$ ,

where $F_i (\cdot )$ is the production function and $_{i}$ measures the level of technology. $F_i (\cdot )$ is assumed to exhibit constant returns to scale in capital, labor, and semiconductor inputs. To ease the notational burden, we have suppressed time subscripts in equation A1 and will do so throughout this appendix. We also will suppress explicit reference to the number of sectors in summations involving the final-output sectors, unless needed for clarity.⁸⁹

The gross output of the semiconductor sector ( $_{s})$ is either sold as intermediate input to the domestic final-output sectors ( $_{d})$ or is exported ( $_{x})$ , so that $_{s}=S$ $_{d}+S$ $_{x}$ . Moreover, because the semiconductors used by the final-output sectors ( $_{i})$ include imported semiconductors ( $_{m})$ , $\sum$ $_{i}$ $_{i }=S$ $_{d}+S$ $_{m}$ . Accordingly, $_{s}=\sum$ $_{i}$ $_{i }+S$ $_{x}-S$ $_{m}$ . On the input side, we assume that the semiconductor sector employs labor and the same set of capital inputs as the final-output sectors. We also allow, as in the final-output sectors, for variation in factor utilization and for adjustment costs. With these assumptions,

(A2) $Y_S =S_d +S_x =\sum\nolimits_i {S_i } +S_x -S_m =F_S \left( {u_{1,S} K_{1,S} ,...,u_{5,S} K_{5,S} ,E_S L_S ,Z_S } \right)\left[ {1-\Phi _S \left( {{I_{1,S} } \mathord{\left/ {\vphantom {{I_{1,S} } {K_{1,S} }}} \right. \kern-\nulldelimiterspace} {K_{1,S} },...,{I_{5,S} } \mathord{\left/ {\vphantom {{I_{5,S} } {K_{5,S} }}} \right. \kern-\nulldelimiterspace} {K_{5,S} }} \right)} \right]$ .

Because we assume that semiconductor producers use no intermediate inputs, gross output and value added for this sector are identical. $F_S (\cdot )\mbox{ and }\Phi _S (\cdot )$ exhibit the same properties as their counterparts for the final-output sectors. We also assume that perfect competition prevails throughout the economy.

The next step is to define the relationship between the sectoral variables and their aggregate counterparts. We express the growth in aggregate final output as a superlative index of growth in sectoral final output. Let $\dot {B}\equiv \frac{\partial B/\partial t}{B}$ denote the growth in any variable . Then, the growth of aggregate real value added in nonfarm business ( is

(A3) $\dot {V}=\sum\nolimits_i {\mu _i \dot {Y}} +\mu _{S,x} \dot {S}_x -\mu _{S,m} \dot {S}_m ,$

where $\mu _i$ $\equiv \quad p$ $_{i}$ $_{i}$ /pV, $\mu _{S,x}$ $\equiv$ $_{s}$ $_{x}$ /pV, $\mu _{S,m}$ $\equiv \quad p$ $_{s}$ $_{m}$ /pV, and pV $\equiv$ $\sum\nolimits_i {p_i } Y_i +p$ $_{s}$ $_{x}- p$ $_{s}$ $_{m}$ .⁹⁰ $_{i}$ and $_{s}$ denote the prices of final output and semiconductors, respectively, and pV represents aggregate current-dollar value added. Equation A3 expresses the growth in aggregate real value added as a share-weighted average of real growth for each type of final output and net exports of semiconductors. Note that the domestically produced semiconductors sold to final-output sectors are an intermediate input for those sectors and thus do not appear in equation A3, consistent with the treatment of semiconductors in the NIPAs.

We assume that labor used in a given sector is identical to labor used in any other sector, so that aggregate labor input is

(A4) $L=\sum\nolimits_i {L_i } +L_S .$

We also assume that each type of capital is homogeneous, implying that

(A5) $K_j =\sum\nolimits_i {K_{j,i} } +K_{j,S} .$

Given equations A4 and A5, plus the assumption that the markets for labor and capital are perfectly competitive, there is a common hourly wage rate ( for labor across every sector and, likewise, a common rental rate $(\tilde {r}_j )$ for all capital of type . However, in the presence of adjustment costs, the shadow value of type- capital need not equal the market rental rate, a point we discuss in more detail below.

Labor input in each sector ( $_{i})$ is the product of the number of workers employed ( $_{i})$ , the length of the workweek ( $_{i})$ , and an index of labor quality ( $_{i})$ that reflects the characteristics of the workers employed in that sector. We allow labor quality to change over time, but given our assumption of identical labor input across sectors, we restrict $_{i}$ to equal a common value in every sector at a given point in time. Using equation A4, and noting that the number of hours worked ( $_{i})$ equals the product of the number of workers and the workweek, we obtain

(A6) $L=\sum\nolimits_i {qW_i N_i } +qW_S N_S =q\left( {\sum\nolimits_i {W_i N_i } +W_S N_S } \right)=q\left( {\sum\nolimits_i {H_i } +H_S } \right)=qH,$

where represents the aggregate number of hours worked.

As noted above, we impose the standard neoclassical assumptions of perfect competition and constant returns to scale. Under these assumptions and our additional assumption that there are no adjustment costs for labor or the use of semiconductor input, profit-maximizing firms set the marginal revenue product of each of these inputs equal to its one-period cost. Using equations A1 and A2, these first-order conditions for labor and semiconductor input are:

(A7) $w=p_h \frac{\partial F_h }{\partial (E_h L_h )}\frac{\partial (E_h L_h )}{\partial L_h }\left( {1-\Phi _h } \right)=p_h \frac{\partial F_h }{\partial (E_h L_h )}E_h \left( {1-\Phi _h } \right)$ for = all and

(A8) $p_S =p_i \frac{\partial F_i }{\partial S_i }\left( {1-\Phi _i } \right){\kern 1pt}{\kern 1pt}$ for all .

For capital, the presence of adjustment costs alters the first-order conditions. In particular, the marginal value of an additional unit of capital this period (its shadow value) can differ from the prevailing one-period rental cost, and the extent of this divergence can vary across sectors. Let $r_{j,h}$ denote the shadow value of type- capital for sector , where as above, indexes the final-output sectors and the semiconductor sector. Following Groth, Nunez, and Srinivasan (2006), the first-order condition for capital in our model can be written as

(A9) $r_{j,h} =p_h \left( {\frac{\partial F_h }{\partial (u_{j,h} K_{j,h} )}u_{j,h} \left( {1-\Phi _h } \right)+F_h \frac{\partial \Phi _h }{\partial ({I_{j,h} } \mathord{\left/ {\vphantom {{I_{j,h} } {K_{j,h} }}} \right. \kern-\nulldelimiterspace} {K_{j,h} })}\frac{I_{j,h} }{K_{j,h}^2 }} \right)$ for all and for = all and .⁹¹ Equation A9 differs from the first-order conditions for labor and semiconductor use in two ways. First, the sector-specific shadow value appears in the equation rather than an economywide wage rate or semiconductor price. Second, the shadow value of capital encompasses not only the marginal revenue product of an additional unit of capital but also its effect on adjustment costs.

To derive the growth accounting expressions, totally differentiate equations A1 and A2, which produces:

(A10) $\dot {Y}_i = \sum\nolimits_j {\frac{\partial F_i }{\partial (u_{j,i} K_{j,i} )}\frac{u_{j,i} K_{j,i} }{F_i }\left( {\dot {u}_{j,i} +\dot {K}_{j,i} } \right)} +\frac{\partial F_i }{\partial (E_i L_i )}\frac{E_i L_i }{F_i }\left( {\dot {E}_i +\dot {L}_i } \right) +\frac{\partial F_i }{\partial S_i }\frac{S_i }{F_i } \dot {S}_i -\sum\nolimits_j {\phi _{j,i} \left( {\dot {I}_{j,i} -\dot {K}_{j,i} } \right)} + \dot {z}_i {\kern 1pt}{\kern 1pt}{\kern 1pt}{\kern 1pt}{\kern 1pt}$

(A11) $\dot {Y}_S = \sum\nolimits_j {\frac{\partial F_S }{\partial (u_{j,S} K_{j,S} )}\frac{u_{j,S} K_{j,S} }{F_S }\left( {\dot {u}_{j,S} +\dot {K}_{j,S} } \right)} +\frac{\partial F_S }{\partial (E_S L_S )}\frac{E_S L_S }{F_S }\left( {\dot {E}_S +\dot {L}_S } \right) -\sum\nolimits_j {\phi _{j,S} \left( {\dot {I}_{j,S} -\dot {K}_{j,S} } \right)} + \dot {z}_S {\kern 1pt}{\kern 1pt}{\kern 1pt}{\kern 1pt}{\kern 1pt}$

where $\phi _{j,h} \equiv \frac{\partial \Phi _h }{\partial ({I_{j,h} } \mathord{\left/ {\vphantom {{I_{j,h} } {K_{j,h} }}} \right. \kern-\nulldelimiterspace} {K_{j,h} })}\frac{1}{1-\Phi _h }\frac{I_{j,h} }{K_{j,h} }\mbox{ and} \dot {z}_h \equiv \frac{\partial F_h }{\partial Z_h }\frac{Z_h }{F_h }\dot {Z}_h {\kern 1pt}\mbox{for}{\kern 1pt}{\kern 1pt}{\kern 1pt}h=\mbox{all }i \mbox{and }S.$ The output elasticities in equations A10 and A11 are unobserved but can be expressed in terms of income shares. For labor, use equation A7, along with the fact that $Y_h =F_h \left( {1-\Phi _h } \right)$ from equations A1 and A2, to obtain:

(A12) $\frac{wL_h }{p_h Y_h } =\frac{\partial F_h }{\partial (E_h L_h )}\frac{E_h L_h }{Y_h }\left( {1-\Phi _h } \right)=\frac{\partial F_h }{\partial (E_h L_h )}\frac{E_h L_h }{F_h }$ for = all and .

Similarly, for semiconductors used as an input in the final-goods industries, equation A8 implies that

(A13) $\frac{p_S S_i }{p_i Y_i } =\frac{\partial F_i }{\partial S_i }\frac{S_i }{Y_i }\left( {1-\Phi _i } \right)=\frac{\partial F_i }{\partial S_i }\frac{S_i }{F_i }$ .

Finally, for capital, equation A9 implies that

(A14) $\frac{r_{j,h} K_{j,h} }{p_h Y_h }=\frac{\partial F_h }{\partial (u_{j,h} K_{j,h} )}\frac{u_{j,h} K_{j,h} }{Y_h }\left( {1-\Phi _h } \right)+\frac{F_h }{Y_h }\frac{\partial \Phi _h }{\partial ({I_{j,h} } \mathord{\left/ {\vphantom {{I_{j,h} } {K_{j,h} }}} \right. \kern-\nulldelimiterspace} {K_{j,h} })}\frac{I_{j,h} }{K_{j,h} }\equiv \frac{\partial F_h }{\partial (u_{j,h} K_{j,h} )}\frac{u_{j,h} K_{j,h} }{F_h }+\phi _{j,h}$

for = all and Now, substitute equations A12 through A14 into equations A10 and A11 to obtain:

(A15) $\dot {Y}_i ={\kern 1pt}\sum\nolimits_j {{\kern 1pt}\left( {\frac{r_{j,i} K_{j,i} }{p_i Y_i }-\phi _{j,i} } \right)\left( {\dot {u}_{j,i} +\dot {K}_{j,i} } \right)} +\frac{wL_i }{p_i Y_i }\left( {\dot {E}_i +\dot {L}_i } \right) +\frac{p_S S_i }{p_i Y_i }\dot {S}_i -\sum\nolimits_j {\phi _{j,i} \left( {\dot {I}_{j,i} -\dot {K}_{j,i} } \right)} +\dot {z}_i {\kern 1pt}$

(A16) $\dot {Y}_S ={\kern 1pt}\sum\nolimits_j {{\kern 1pt}\left( {\frac{r_{j,S} K_{j,S} }{p_S Y_S }-\phi _{j,S} } \right)\left( {\dot {u}_{j,S} +\dot {K}_{j,S} } \right)} +\frac{wL_S }{p_S Y_S }\left( {\dot {E}_S +\dot {L}_S } \right) -\sum\nolimits_j {\phi _{j,S} \left( {\dot {I}_{j,S} -\dot {K}_{j,S} } \right)} +\dot {z}_S {\kern 1pt}.$

To simplify the notation, let $\beta _{j,i}^K$ $\equiv$ $_{j,i}$ $_{j,i}$ / $_{i}$ $_{i}$ , the income share for type- capital in final-output sector ; $\beta _i^L$ $\equiv$ wL $_{i}$ / $_{i}$ $_{i}$ , the income share for labor in final-output sector ;

$\beta _i^S \equiv \quad p$ $_{s}$ $_{i}$ / $_{i}$ $_{i}$ , the income share for semiconductor input in final-output sector ;

$\gamma^{L} \equiv$ wL $_{s}$ / $_{s}$ $_{s}$ , the income share for labor in the semiconductor sector; and $\gamma _j^K$ $\equiv$ $_{j,s}$ $_{j,s}$ / $_{s}$ $_{s}$ , the income share for type- capital in the semiconductor sector. Substitute this notation into equations A15 and A16 and rearrange terms to obtain:

(A17) $\dot {Y}_i = \sum\nolimits_j {\left( {\beta _{j,i}^K -\phi _{j,i} } \right)\dot {K}_{j,i} } {\kern 1pt}{\kern 1pt} +\beta _i^L \dot {L}_i +\beta _i^S \dot {S}_i + {\kern 1pt}\left[ {\beta _i^L \dot {E}_i +\sum\nolimits_j {\left( {\beta _{j,i}^K -\phi _{j,i} } \right)\dot {u}_{j,i} } } \right] -\sum\nolimits_j {\phi _{j,i} \left( {\dot {I}_{j,i} -\dot {K}_{j,i} } \right)} {\kern 1pt}{\kern 1pt}+ \dot {z}_i {\kern 1pt}$

(A18) $\dot {Y}_S = {\kern 1pt}{\kern 1pt}\sum\nolimits_j {\left( {\gamma _j^K -\phi _{j,S} } \right)\dot {K}_{j,S} } +\gamma ^L\dot {L}_S +\left[ {\gamma ^L\dot {E}_S +{\kern 1pt}{\kern 1pt}\sum\nolimits_j {\left( {\gamma _j^K -\phi _{j,S} } \right)\dot {u}_{j,S} } } \right]{\kern 1pt} -\sum\nolimits_j {\phi _{j,S} \left( {\dot {I}_{j,S} -\dot {K}_{j,S} } \right)} {\kern 1pt} + \dot {z}_S {\kern 1pt}{\kern 1pt}.$

The terms in brackets represent the effects of changes in labor effort and capital utilization on output growth. Basu, Fernald, and Shapiro (2001) show that, in their model, labor effort and capital utilization vary linearly with the workweek of labor, . Thus the terms in brackets can be condensed to $\xi _i {\kern 1pt}\dot {W}_i$ and $\xi _S \dot {W}_S$ , where the $\xi$ coefficients embed the $\beta , \gamma , \mbox{and} \phi$ parameters. Accordingly,

(A19) $\dot {Y}_i ={\kern 1pt}{\kern 1pt}\sum\nolimits_j {\left( {\beta _{j,i}^K -\phi _{j,i} } \right)\dot {K}_{j,i} } +\beta _i^L \dot {L}_i +\beta _i^S \dot {S}_i + {\kern 1pt}\xi _i \dot {W}_i -\sum\nolimits_j {\phi _{j,i} \left( {\dot {I}_{j,i} -\dot {K}_{j,i} } \right)} + {\kern 1pt}{\kern 1pt}\dot {z}_i$

(A20) $\dot {Y}_S = {\kern 1pt}{\kern 1pt}\sum\nolimits_j {\left( {\gamma _j^K -\phi _{j,S} } \right)\dot {K}_{j,S} } +\gamma ^L\dot {L}_S +\xi _S \dot {W}_S {\kern 1pt} -\sum\nolimits_j {\phi _{j,S} \left( {\dot {I}_{j,S} -\dot {K}_{j,S} } \right)} {\kern 1pt}{\kern 1pt} + \dot {z}_S .{\kern 1pt}$

The notation in A19 and A20 can be simplified further. In the model developed here, multifactor productivity (MFP) captures the combined effect of improvements in technology, changes in factor utilization, and adjustment costs. That is,

(A21) $M\dot {F}P_i = {\kern 1pt}\xi _i \dot {W}_i -\sum\nolimits_j {\phi _{j,i} \left( {\dot {I}_{j,i} -\dot {K}_{j,i} } \right)} {\kern 1pt}{\kern 1pt}+ \dot {z}_i {\kern 1pt}{\kern 1pt}$

(A22) $M\dot {F}P_S = {\kern 1pt}\xi _S \dot {W}_S -\sum\nolimits_j {\phi _{j,S} \left( {\dot {I}_{j,S} -\dot {K}_{j,S} } \right)} {\kern 1pt}{\kern 1pt}+ \dot {z}_S {\kern 1pt}{\kern 1pt}.$

Equations A19 and A20 then can be expressed as:

(A23) $\dot {Y}_i ={\kern 1pt}{\kern 1pt}\sum\nolimits_j {\left( {\beta _{j,i}^K -\phi _{j,i} } \right)\dot {K}_{j,i} } +\beta _i^L \dot {L}_i +\beta _i^S \dot {S}_i + {\kern 1pt}M\dot {F}P_i$

(A24) $\dot {Y}_S = {\kern 1pt}{\kern 1pt}\sum\nolimits_j {\left( {\gamma _j^K -\phi _{j,S} } \right)\dot {K}_{j,S} } +\gamma ^L\dot {L}_S +M\dot {F}P_S .{\kern 1pt}$

Income Shares

In a standard growth accounting model with constant returns to scale in production, perfect competition, and no adjustment costs, the income shares for the various inputs sum to one. Our model imposes constant returns to scale and perfect competition but includes adjustment costs for capital. The following proposition shows how the inclusion of these adjustment costs affects the sum of the income shares.

Proposition 1 In the model described above (equations A1 through A24), the income shares for each final-output sector satisfy

$\sum\nolimits_j {\left( {\beta _{j,i}^K -\phi _{j,i} } \right)+ } \beta _i^L +\beta _i^S =1.$

Similarly, the income shares for the semiconductor sector satisfy

$\sum\nolimits_j {\left( {\gamma _j^K -\phi _{j,S} } \right)+ \gamma ^L} =1.$

Proof.

We present the proof for the final-output sectors. The derivation for the semiconductor sector is identical and is omitted to save space.⁹² By assumption, the production function for each final-output sector, $F_i \left( {u_{1,i} K_{1,i} ,...,u_{5,i} K_{5,i} ,E_i L_i ,S_i ,Z_i } \right)$ from equation A1, exhibits constant returns to scale in the inputs $K_{1,i} ,...,K_{5,i} ,L_i ,\mbox{and }S_i .$ Accordingly, Euler's theorem implies that

(A25) $\sum\nolimits_j {\frac{\partial F_i }{\partial (u_{j,i} K_{j,i} )}\frac{u_{j,i} K_{j,i} }{F_i }+\frac{\partial F_i }{\partial (E_i L_i )}\frac{E_i L_i }{F_i }} +\frac{\partial F_i }{\partial S_i }\frac{S_i }{F_i }=1$ .

Now substitute the first-order conditions A12 through A14 into equation A25, which yields

(A26) $\sum\nolimits_j {\left( {\frac{r_{j,i} K_{j,i} }{p_i Y_i }-\phi _{j,i} } \right)+\frac{wL_i }{p_i Y_i }} +\frac{p_S S_i }{p_i Y_i }=1$ ,

or equivalently,

(A27) $\sum\nolimits_j {(\beta _{j,i}^K -\phi _{j,i} )+\beta _i^L } +\beta _i^S =1$ . $_{?}$

Additional Assumptions

The other propositions proved in this appendix require assumptions beyond those in the model described above. We list these assumptions here and refer back to them as needed. As indicated below, the derivation of the aggregate growth accounting equation (proposition 2) relies on assumptions 1 through 3, whereas the algorithm for measuring sectoral MFP growth (proposition 3) and the steady-state results (proposition 4) both rely on assumption 4.

Assumption 1

The shadow value for type- capital is the same in every sector: $r_{j,i} =r_{j,S} =r_j$ . This assumption imposes an equal gap for all sectors between the shadow value of type- capital and the economywide user cost $(\tilde {r}_j )$ for this capital. It does not force the shadow value to equal the user cost.

Assumption 2

The adjustment cost elasticity for type- capital is the same across all sectors and equals the corresponding elasticity for the aggregate economy scaled to enforce consistency between sectoral and aggregate production. Let $\mu _i ={p_i Y_i } \mathord{\left/ {\vphantom {{p_i Y_i } {pV\mbox{ and }}}} \right. \kern-\nulldelimiterspace} {pV\mbox{ and }}\mu _S ={p_S Y_S } \mathord{\left/ {\vphantom {{p_S Y_S } {pV}}} \right. \kern-\nulldelimiterspace} {pV}$ represent the Domar share weights for the various sectors. With this notation, we assume that $\phi _{j,i} =\phi _{j,S} ={\phi _j } \mathord{\left/ {\vphantom {{\phi _j } {\bar {\mu }}}} \right. \kern-\nulldelimiterspace} {\bar {\mu }}$ , where $\bar {\mu }\equiv \sum\nolimits_i {\mu _i +\mu _S } .$ This scaling parallels that imposed in equations 5 through 7 in the text.

Assumption 3

The stock of type- capital grows at the same rate in every sector: $\dot {K}_{j,i} =\dot {K}_{j,S} =\dot {K}_j$ .

Assumption 4

The labor share in each sector is the same up to a scaling factor that reflects the intensity of semiconductor use; similarly, the capital share (net of adjustment costs) is the same in each sector after this scaling. That is,

$\frac{\beta _1^L }{1-\beta _1^S }\quad =\quad \ldots \quad = \quad \frac{\beta _5^L }{1-\beta _5^S }\quad = \quad \gamma^{L}$ and $\frac{\beta _{j, 1}^K -\phi _{j, 1} }{1-\beta _1^S }$ = ... = $\frac{\beta _{j, 5}^K -\phi _{j, 5} }{1-\beta _5^S }=\gamma _j^K -\phi _{j,S}$ for = 1,...,5.

One can easily verify that the restricted factor shares sum to one in each sector. Also, one can show that the labor share and the capital share (net of adjustment costs) for aggregate nonfarm business equal their counterparts in the semiconductor sector. That is, if we let $\alpha^{L} \mbox{ and }\alpha _j^K$ denote the labor and capital shares for aggregate nonfarm business, then $\alpha^{L} \mbox{=}\gamma ^L\mbox{ and }\alpha _j^K -\phi _j =\gamma _j^K -\phi _{j,S}$ .

Aggregate Labor Productivity

Proposition 2 derives the expression for growth in aggregate labor productivity in our model.

Proposition 2 Given the model described by equations A1 through A24 and given assumptions 1 through 3, the growth accounting equation for aggregate labor productivity is:

$\dot {V}-\dot {H}={\kern 1pt}{\kern 1pt}\sum\nolimits_j {\left( {\alpha _j^K -\phi _j } \right)\left( {\dot {K}_j -\dot {H}} \right)} +\alpha ^L\dot {q} +M\dot {F}P{\kern 1pt}$

where $M\dot {F}P=\sum\nolimits_i {\mu _i M\dot {F}P} + \mu _S M\dot {F}P_S$

$M\dot {F}P_i =\xi _i {\kern 1pt}\dot {W}_i -\sum\nolimits_j {{\kern 1pt}\phi _{j,i} \left( {\dot {I}_{j,i} -\dot {K}_{j,i} } \right)} +\dot {z}_i$

$M\dot {F}P_S =\xi _S {\kern 1pt}\dot {W}_S -\sum\nolimits_j {\phi _{j,S} } \left( {\dot {I}_{j,S} -\dot {K}_{j,S} } \right){\kern 1pt}+\dot {z}_S$

$\alpha^{L} =$ wL/pV and $\alpha _j^K$ = $_{j}$ $_{j}$ /pV.

Proof.

To begin, substitute the expression for $\dot {Y}_i$ from equation A23 into equation A3:

(A28) $\dot {V}=\sum\nolimits_i {\mu _i \left( {{\kern 1pt}\sum\nolimits_j {(\beta _{j,i}^K -\phi _{j,i} )\dot {K}_{j,i} } {\kern 1pt} + \beta _i^L \dot {L}_i + \beta _i^S \dot {S}_i +M\dot {F}P_i } \right)} + \mu_{S,x} \dot {S}_x - \mu _{S,m} \dot {S}_m$

$\begin{displaymath} = \sum\nolimits_j {\sum\nolimits_i {\left( {\mu _i \beta _{j,i}^K -\mu _i \phi _{j,i} } \right)\dot {K}_{j,i} } } + \sum\nolimits_i {\mu _i \beta _i^L \dot {L}_i } + \sum\nolimits_i {\mu _i \beta _i^S \dot {S}_i } {\kern 1pt} + \sum\nolimits_i {\mu _i M\dot {F}P} + \mu _{S,x} \dot {S}_x - \mu _{S,m} \dot {S}_{m}. \end{displaymath}$

The definitions of the $\alpha$ 's, $\beta$ 's, and $\mu$ 's imply that

(A29) $\mu _i \beta _{j,i}^K \equiv \frac{p_i Y_i }{pV}\frac{r_{j,i} K_{j,i} }{p_i Y_i }=\frac{r_{j,i} K_j }{pV}\frac{K_{j,i} }{K_j }=\frac{\left( {r_j +(r_{j,i} -r_j )} \right)K_j }{pV}\frac{K_{j,i} }{K_j }=\left( {\alpha _j^K +\frac{(r_{j,i} -r_j )K_j }{pV}} \right)\frac{K_{j,i} }{K_j }$

(A30) $\mu _i \beta _i^L \equiv \frac{p_i Y_i }{pV}\frac{wL_i }{p_i Y_i }=\frac{wL}{pV}\frac{L_i }{L}=\alpha ^L\frac{L_i }{L}$

(A31) $\mu _i \beta _i^S \equiv \frac{p_i Y_i }{pV}\frac{p_S S_i }{p_i Y_i }=\frac{p_S Y_S }{pV}\frac{S_i }{Y_S }=\mu _S \frac{S_i }{Y_S }$ .

Substitute equations (A29) through (A31) into the second line of equation (A28) to obtain

(A32) $\dot {V} = \sum\nolimits_j {\sum\nolimits_i {\left( {\alpha _j^K \frac{K_{j,i} }{K_j }-\mu _i \phi _{j,i} } \right)\dot {K}_{j,i} } } + \sum\nolimits_i {\alpha ^L\frac{L_i }{L}\dot {L}_i } + \sum\nolimits_i {\mu _S \frac{S_i }{Y_S }\dot {S}_i } {\kern 1pt}$

$\begin{displaymath} + \sum\nolimits_i {\mu _i M\dot {F}P} + \mu _{S,x} \dot {S}_x - \mu _{S,m} \dot {S}_m + \sum\nolimits_j {\sum\nolimits_i {\frac{\left( {r_{j,i} -r_j } \right)K_j }{pV}\frac{K_{j,i} }{K_j }\dot {K}_{j,i} } } . \end{displaymath}$

The final term captures the effect on output growth of reallocating type-

capital across sectors when the shadow value of this capital differs from one sector to the next. This term equals zero under assumption 1 and will not appear in the remainder of the derivation.

Next, totally differentiate $Y_S =\sum\nolimits_i {S_i } +S_x -S_m$ from equation A2 to obtain

(A33) $\dot {Y}_S =\sum\nolimits_i {\frac{S_i }{Y_S }\dot {S}_i } + \frac{S_x }{Y_S }\dot {S}_x - \frac{S_m }{Y_S }\dot {S}_m$ .

Multiplying equation A33 by $\mu _S$ and using the definitions of $\mu _S$ , $\mu _{S,x}$ , and $\mu _{S,m}$ ,

(A34) $\sum\nolimits_i {\mu _S \frac{S_i }{Y_S }\dot {S}_i } =\mu _S \dot {Y}_S - \mu _{S,x} \dot {S}_x + \mu _{S,m} \dot {S}_m$ .

In addition, totally differentiate equations A4 and A5:

(A35) $\dot {L} = \sum\nolimits_i {\frac{L_i }{L}\dot {L}_i } + \frac{L_S }{L}\dot {L}_S$

(A36) $\dot {K}_j = \sum\nolimits_i {\frac{K_{j, i} }{K_j }\dot {K}_{j,i} } + \frac{K_{j,S} }{K_j }\dot {K}_{j,S}$ .

Now, substitute equation A34 through A36 into equation A32 (after zeroing out the reallocation term), which yields

(A37) $\dot {V} =\sum\nolimits_j {\alpha _j^K \left( {\dot {K}_j - \frac{K_{j,S} }{K_j }\dot {K}_{j,S} } \right)} {\kern 1pt} -\sum\nolimits_j {\sum\nolimits_i {\mu _i \phi _{j,i} \dot {K}_{j,i} } } + \alpha ^L \left( {\dot {L} - \frac{L_S }{L}\dot {L}_S } \right) + \sum\nolimits_i {\mu _i M\dot {F}P_i } + {\kern 1pt}\mu _S \dot {Y}_S$

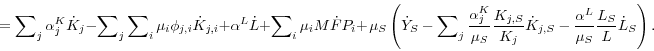
$\begin{displaymath} = \sum\nolimits_j {\alpha _j^K \dot {K}_j } -\sum\nolimits_j {\sum\nolimits_i {\mu _i \phi _{j,i} \dot {K}_{j,i} } } + \alpha ^L\dot {L} +\sum\nolimits_i {\mu _i M\dot {F}P_i } + {\kern 1pt}\mu _S \left( {\dot {Y}_S - \sum\nolimits_j {\frac{\alpha _j^K }{\mu _S } \frac{K_{j,S} }{K_j }\dot {K}_{j,S} } - \frac{\alpha ^L}{\mu _S } \frac{L_S }{L}\dot {L}_S } \right). \end{displaymath}$

The definitions of the $\alpha$ 's, $\gamma$ 's, and $\mu$ 's imply that

(A38) $\frac{\alpha _j^K }{\mu _S } \frac{K_{j,S} }{K_j }\equiv \frac{{r_j K_j } \mathord{\left/ {\vphantom {{r_j K_j } {pV}}} \right. \kern-\nulldelimiterspace} {pV}}{{p_S Y_S } \mathord{\left/ {\vphantom {{p_S Y_S } {pV}}} \right. \kern-\nulldelimiterspace} {pV}}\frac{K_{j,S} }{K_j }=\frac{r_j K_{j,S} }{p_S Y_S }=\gamma _j^K$

(A39) $\frac{\alpha ^L}{\mu _S } \frac{L_S }{L}\equiv \frac{{wL} \mathord{\left/ {\vphantom {{wL} {pV}}} \right. \kern-\nulldelimiterspace} {pV}}{{p_S Y_S } \mathord{\left/ {\vphantom {{p_S Y_S } {pV}}} \right. \kern-\nulldelimiterspace} {pV}}\frac{L_S }{L}=\frac{wL_S }{p_S Y_S }=\gamma ^L.$

Substituting equations (A38) and (A39) into equation (A37), we obtain

(A40) $\dot {V}= \sum\nolimits_j {\alpha _j^K \dot {K}_j } -\sum\nolimits_j {\sum\nolimits_i {\mu _i \phi _{j,i} \dot {K}_{j,i} } } + \alpha ^L\dot {L} + \sum\nolimits_i {\mu _i M\dot {F}P_i } + {\kern 1pt}\mu _S \left( {\dot {Y}_S - \sum\nolimits_j {\gamma _j^K \dot {K}_{j,S} } - \gamma ^L\dot {L}_S } \right)$

$\begin{displaymath} = \sum\nolimits_j {\alpha _j^K \dot {K}_j } -\sum\nolimits_j {\sum\nolimits_i {\mu _i \phi _{j,i} \dot {K}_{j,i} } } + \alpha ^L\dot {L} + \sum\nolimits_i {\mu _i M\dot {F}P_i } + {\kern 1pt}\mu _S M\dot {F}P_S -\sum\nolimits_j {\mu _S \phi _{j,S} \dot {K}_{j,S} } , \end{displaymath}$

where the second line follows from equation A24. Collecting the terms that involve the adjustment cost elasticities, equation A40 can be written as

(A41) $\dot {V} =\sum\nolimits_j {\alpha _j^K \dot {K}_j } -\sum\nolimits_j {\left( {\sum\nolimits_i {\mu _i \phi _{j,i} \dot {K}_{j,i} } +\mu _S \phi _{j,S} \dot {K}_{j,S} } \right)} + \alpha ^L\dot {L} + \sum\nolimits_i {\mu _i M\dot {F}P_i } + {\kern 1pt}\mu _S M\dot {F}P_S .$

We now invoke assumptions 2 and 3 to simplify the terms in adjustment costs, yielding

(A42) $\dot {V} =\sum\nolimits_j {\left( {\alpha _j^K -\phi _j } \right)\dot {K}_j } + \alpha ^L\dot {L} + \sum\nolimits_i {\mu _i M\dot {F}P_i } + {\kern 1pt}\mu _S M\dot {F}P_S .$

To complete the proof, note that equation A6 implies that $\dot {L}=\dot {H}+\dot {q}$ and recall that proposition 1 applied to aggregate nonfarm business implies that $\sum\nolimits_j {\left( {\alpha _j^K -\phi _j } \right)+ \alpha ^L} =1.$ Hence,

(A43) $\alpha^{L} \dot {L} = \alpha^{L} \left( {\dot {H}+\dot {q}} \right) = \dot {H}-{\kern 1pt}\sum\nolimits_j {\left( {\alpha _j^K -\phi _j } \right)\dot {H}} + \alpha^{L} \dot {q}$ .

Substitute equation A43 into A42, which produces

(A44) $\dot {V} - \dot {H} = \sum\nolimits_j {\left( {\alpha _j^K -\phi _j } \right)\left( {\dot {K}_j - \dot {H}} \right)} {\kern 1pt} + \alpha ^L\dot {q} + \sum\nolimits_i {\mu _i M\dot {F}P_i } + {\kern 1pt}\mu _S M\dot {F}P_S ,$

where $M\dot {F}P_i$ and $M\dot {F}P_S$ are defined in equations A21 and A22, respectively. $_{?}$

Measuring Sectoral MFP

To make use of proposition 2, we need to estimate MFP growth in each sector. This can be done either from the sectoral production functions, as in equations A23 and A24, or from the sectoral cost functions - the "dual" approach. We opt for the dual approach because the required data are more readily available. The dual counterparts to equations A23 and A24 are:

(A45) $\dot {p}_i =\beta _i^L \dot {w} +\mathop \sum \limits_{j=1}^5 \left( {\beta _{j,i}^K -\phi _{j,i} } \right)\dot {r}_j +\beta _i^S \dot {p}_S -M\dot {F}P_i$ $_{ }$ for = 1,...,5

(A46) $\dot {p}_S =\gamma ^L\dot {w} +\mathop \sum \limits_{j=1}^5 \left( {\gamma _j^K -\phi _{j,S} } \right)\dot {r}_j -M\dot {F}P_S$ .⁹³

These equations state that the growth in each sector's output price equals the growth in the share-weighted average of its input costs (modified to account for the adjustment cost elasticities), minus the growth in MFP. MFP growth enters with a negative sign because efficiency gains hold down a sector's output price given its input costs.

To reduce the amount of data needed to estimate MFP growth from equations A45 and A46, we invoke assumption 4 regarding the restrictions on income shares across sectors. Applying this assumption to equation A45 and making use of the resulting correspondence between the $\gamma$ 's and the $\alpha$ 's $(\alpha^{L} \mbox{=}\gamma ^L\mbox{ and }\alpha _j^K -\phi _j =\gamma _j^K -\phi _{j,S} )$ , we obtain

(A47) $\dot {p}_i = (1-\beta _i^S )\left[ {\alpha ^L\dot {w}+ \mathop \sum \limits_{j=1}^5 \left( {\alpha _j^K -\phi _j } \right)\dot {r}_j } \right] + \beta _i^S \dot {p}_S -M\dot {F}P_i$ for = 1,...,5.

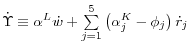Let $\dot {\Upsilon }\equiv \alpha ^L\dot {w}+ \mathop \sum \limits_{j=1}^5 \left( {\alpha _j^K -\phi _j } \right)\dot {r}_j$ denote the share-weighted growth in labor and capital costs for the nonfarm business sector as a whole. Substitute $\dot {\Upsilon }$ into the dual equations A46 and A47, with $\gamma^{L} =\alpha^{L}$ and $\gamma _j^K -\phi _{j,S} =\alpha _j^K -\phi _j$ in equation A46. The result is

(A48) $\dot {p}_i = (1-\beta _i^S )\dot {\Upsilon } + \beta _i^S \dot {p}_S -M\dot {F}P_i$ $_{ }$ for = 1,...,4

(A49) $\dot {p}_5 = (1-\beta _5^S )\dot {\Upsilon } + \beta _5^S \dot {p}_S -M\dot {F}P_5$ $_{ }$

(A50) $\dot {p}_S = \dot {\Upsilon }-M\dot {F}P_S$

where we have specifically identified final-output sector 5, which will serve as the numeraire sector.⁹⁴

We now use the dual equations to derive expressions for MFP growth in two cases. In the first case, we infer the rates of sectoral MFP growth that are consistent with an independent estimate of aggregate MFP growth (from our aggregate growth accounting system). This case represents the methodology we use to compute growth contributions through history. In the second case, which we use for our forward-looking steady-state analysis, we solve for aggregate MFP growth and MFP growth in sectors 1 through 4 conditional on an assumed pace of MFP growth in sector 5. The next proposition derives the expressions for sectoral MFP growth in both cases.

Proposition 3

Let $\pi _S \equiv \dot {p}_S -\dot {p}_5$ and $\pi _i \equiv \dot {p}_i -\dot {p}_5$ (= 1,...,4) denote price changes relative to sector 5. Given the dual equations A48 through 50 (which make use of assumption 4), the solutions for sectoral and aggregate MFP growth are as follows.

Case I: Conditioning on Aggregate MFP Growth

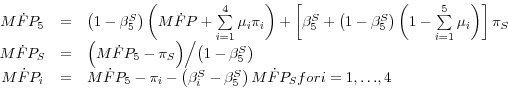
$\begin{displaymath}\begin{array}{cccl} & M\dot {F}P_5 &=&\left( {1-\beta _5^S } ... ...t {F}P_S \HTMLcode{EM}{ for } i = 1,{\ldots},4 \ \end{array}\end{displaymath}$

Case II: Conditioning on MFP Growth in Sector 5

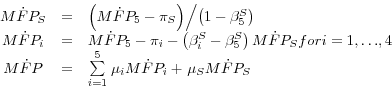
$\begin{displaymath}\begin{array}{cccl} &M\dot {F}P_S &=& {\left( {M\dot {F}P_5 -\pi _S } \right)} \mathord{\left/ {\vphantom {{\left( {M\dot {F}P_5 -\pi _S } \right)} {\left( {1-\beta _5^S } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {1-\beta _5^S } \right)} \ &M\dot {F}P_i &=& M\dot {F}P_5 -\pi _i -\left( {\beta _i^S -\beta _5^S } \right)M\dot {F}P_S \HTMLcode{EM}{ for } i = 1,{\ldots},4 \ &M\dot {F}P &=& \mathop \sum \limits_{i= 1}^5 {\kern 1pt}\mu _i M\dot {F}P_i + {\kern 1pt}\mu _S M\dot {F}P_S \end{array}\end{displaymath}$

Proof.

The proof for Case II is nearly immediate. Subtract equation A49 from equations A48 and A50. After rearranging terms and using equation A50 to substitute $M\dot {F}P_S$ for $\dot {\Upsilon }-\dot {p}_S ,$ we obtain:

(A51) $M\dot {F}P_i =M\dot {F}P_5 -\pi _i -\left( {\beta _i^S -\beta _5^S } \right)M\dot {F}P_S$ for = 1,...,4

(A52) $M\dot {F}P_S ={\left( {M\dot {F}P_5 -\pi _S } \right)} \mathord{\left/ {\vphantom {{\left( {M\dot {F}P_5 -\pi _S } \right)} {\left( {1-\beta _5^S } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {1-\beta _5^S } \right)}.$

Equations A51 and A52, plus the expression for $M\dot {F}P$ derived in Proposition 2, establish the results for Case II. Note that the solution is recursive - first solve for $M\dot {F}P_S$ from equation A52, then substitute the result into equation A51, and finally substitute all the sectoral MFP growth rates into the expression for aggregate MFP growth.

To prove the result for Case I, substitute equations A51 and A52 into the expression for aggregate MFP growth. After rearranging terms, this yields:

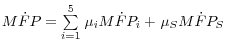
(A53) $M\dot {F}P= \mathop \sum \limits_{i= 1}^5 {\kern 1pt}\mu _i M\dot {F}P_i + {\kern 1pt}\mu _S M\dot {F}P_S$

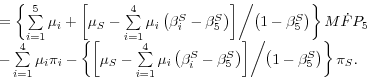
$\begin{displaymath} \begin{array}{l} =\left\{ {\mathop \sum \limits_{i=1}^5 \mu... ...ft( {1-\beta _5^S } \right)}} \right\}\pi _S . \ \end{array}\end{displaymath}$

Let $\Omega \quad \equiv$ $\mathop \sum \limits_{i=1}^5 \mu _i + {\left[ {\mu _S -\mathop \sum \limits_{i=1}^4 \mu _i \left( {\beta _i^S -\beta _5^S } \right)} \right]} \mathord{\left/ {\vphantom {{\left[ {\mu _S -\mathop \sum \limits_{i=1}^4 \mu _i \left( {\beta _i^S -\beta _5^S } \right)} \right]} {\left( {1-\beta _5^S } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {1-\beta _5^S } \right)}$ . Equation A53 then becomes

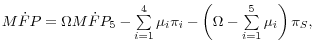
(A54) $M\dot {F}P=\Omega M\dot {F}P_5 - \mathop \sum \limits_{i=1}^4 \mu _i \pi _i -\left( {\Omega - \mathop \sum \limits_{i=1}^5 \mu _i } \right)\pi _S \mbox{,}$

which implies

(A55) $M\dot {F}P_5 ={\left[ {\left( {M\dot {F}P + \mathop \sum \limits_{i=1}^4 \mu _i \pi _i } \right)+\left( {\Omega - \mathop \sum \limits_{i=1}^5 \mu _i } \right)\pi _S } \right]} \mathord{\left/ {\vphantom {{\left[ {\left( {M\dot {F}P + \mathop \sum \limits_{i=1}^4 \mu _i \pi _i } \right)+\left( {\Omega - \mathop \sum \limits_{i=1}^5 \mu _i } \right)\pi _S } \right]} \Omega }} \right. \kern-\nulldelimiterspace} \Omega .$

One can easily verify that $\mu _S =\sum\nolimits_i {\mu _i } \beta _i^S +\mu _{S,x} -\mu _{S,m}$ from the definitions of the $\mu$ 's and the $\beta$ 's. Substituting this equation for $\mu _S$ into the expression above for $\Omega$ , one can show that $\Omega$ simplifies to be 1/(1 - $\beta _5^S )$ . Using $\Omega$ = 1/(1 - $\beta _5^S )$ , equation A55 becomes

(A56) $M\dot {F}P_5 =\left( {1-\beta _5^S } \right)\left( {M\dot {F}P + \mathop \sum \limits_{i=1}^4 \mu _i \pi _i } \right)+\left[ {\beta _5^S +\left( {1-\beta _5^S } \right)\left( {1-\mathop \sum \limits_{i=1}^5 \mu _i } \right)} \right]\pi _S .$

This equation, combined with equations A51 and A52, completes the proof for Case I. As in Case II, the solution is recursive. First, obtain $M\dot {F}P_5$ from equation A56. Then, substitute the result into equations A51 and A52. $_{?}$

Analysis of the Steady State

The results presented so far do not require the economy to have reached a steady state. We now impose additional conditions to derive the growth accounting equation for aggregate labor productivity in the steady state. First, we require that real output in each sector grow at a constant rate (which can differ across sectors). For each final-output sector, we also require that all components of the sector's output (consumption goods, investment goods, and exports) grow at the same constant rate in the steady state as total output for the sector:

(A57) $\dot {Y}_j =\dot {C}_j =\dot {X}_j =\dot {I}_{j,S} =\dot {I}_{j,i} .$

For example, the output of computers sold as an investment good grows at the same rate as the output of computers sold as a consumer good. For the semiconductor sector, we require that domestic output, exports, imports, and semiconductor use in each final-output sector all grow at the same constant rate:

(A58) $\dot {Y}_S =\dot {S}_x =\dot {S}_m =\dot {S}_i .$

With $\dot {I}_{j,S}$ and $\dot {I}_{j,i}$ forced to be constant from equation A57, investment spending and the capital stock will grow at the same rate for each type of capital:

(A59) $\dot {I}_{j,i} =\dot {K}_{j,i}$ and $\dot {I}_{j,S} =\dot {K}_{j,S}$ for all and .

Combining equations A57 and A59, we obtain

(A60) $\dot {Y}_j =\dot {K}_{j,i} =\dot {K}_{j,S}$ for all and .⁹⁵

Because $\dot {I}=\dot {K}$ for each type of capital, adjustment costs have no effect on MFP growth (sectoral or aggregate) in the steady state. Finally, we require that hours worked grow at the same constant rate in every sector,

(A61) $\dot {H}_h =\dot {H}$ for = all and;

that the workweek is fixed,

(A62) $\dot {W}_h =0$ for = all and ;

and that the economywide measure of labor quality ( improves at a constant rate.

Proposition 4

Under the steady-state conditions in equations A57 through A59 and assumption 4 (which restricts the income shares across sectors), the growth accounting equation for aggregate labor productivity is

$\dot {V}-\dot {H}=\sum\nolimits_i {\left( {\frac{\alpha _i^K -\phi _i }{\alpha ^L}} \right)\left( {M\dot {F}P_i +\beta _i^S M\dot {F}P_S } \right)} {\kern 1pt}{\kern 1pt} +\dot {q} +M\dot {F}P,$

where

$M\dot {F}P=\sum\nolimits_i {\mu _i M\dot {F}P_i } + {\kern 1pt}\mu _S M\dot {F}P_S$ with $M\dot {F}P_i =\dot {z}_i$ and $M\dot {F}P_S =\dot {z}_S .$

Proof.

Substitute A59 and A62 into equations A21 and A22 to establish that $M\dot {F}P_i =\dot {z}_i$ and $M\dot {F}P_S =\dot {z}_S .$ Next, equation A61 implies that labor input in each sector grows at the same rate as labor input for aggregate nonfarm business; that is,

(A63) $\dot {L}_h =\dot {q}+\dot {H}_h =\dot {q}+\dot {H}=\dot {L}\mbox{ for }h=\mbox{all }i\mbox{ and }S.$

Substitute equations A58, A60, and A63 into the growth accounting equations A23 and A24, restrict the income shares in accord with assumption 4, and recall that $\gamma^{L} =\alpha^{L}$ and $\alpha _j^K -\phi _j =\gamma _j^K -\phi _{j,S}$ when we impose these restrictions. The result is:

(A64) $\dot {Y}_i =\sum\nolimits_j {\left( {1-\beta _i^S } \right)} \left( {\alpha _j^K -\phi _j } \right)\dot {Y}_j +\left( {1-\beta _i^S } \right)\alpha ^L\dot {L}+\beta _i^S \dot {Y}_S +M\dot {F}P_i \quad _{ }$ for all

(A65) $\dot {Y}_S =\sum\nolimits_j {\left( {\alpha _j^K -\phi _j } \right)\dot {Y}_j } +\alpha ^L\dot {L}+M\dot {F}P_S$ .

Equations A64 and A65 form a system of equations in $\dot {Y}_i$ for all and $\dot {Y}_S$ . Solving this system yields

(A66) 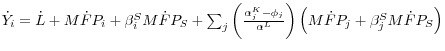$\dot {Y}_i =\dot {L} +M\dot {F}P_i + \beta _i^S M\dot {F}P_S +\sum\nolimits_j {\left( {\frac{\alpha _j^K -\phi _j }{\alpha ^L}} \right)\left( {M\dot {F}P_j +\beta _j^S M\dot {F}P_S } \right)}$ for all

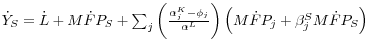(A67) $\dot {Y}_S =\dot {L} + M\dot {F}P_S +\sum\nolimits_j {\left( {\frac{\alpha _j^K -\phi _j }{\alpha ^L}} \right)\left( {M\dot {F}P_j +\beta _j^S M\dot {F}P_S } \right)}$ .

Now, substitute equations A58, A66, and A67 into equation A3 (the expression for growth in aggregate output) and rearrange terms:

(A68) $\dot {V} = \sum\nolimits_i {\mu _i } \dot {Y}_i +\mu _{S,x} \dot {S}_x -\mu _{S,m} \dot {S}_m = \sum\nolimits_i {\mu _i } \dot {Y}_i +\left( {\mu _{S,x} -\mu _{S,m} } \right)\dot {Y}_S$

$\begin{displaymath} = \left( {\sum\nolimits_i {\mu _i } +\mu _{S,x} -\mu _{S,m} } \right)\left[ {\dot {L} + \sum\nolimits_j {\left( {\frac{\alpha _j^K -\phi _j }{\alpha ^L}} \right)\left( {M\dot {F}P_j +\beta _j^S M\dot {F}P_S } \right)} } \right] +\sum\nolimits_i {\mu _i } M\dot {F}P_i \end{displaymath}$

$\begin{displaymath} + \left( { \sum\nolimits_i {\mu _i } \beta _i^S +\mu _{S,x} -\mu _{S,m} } \right)M\dot {F}P_S . \end{displaymath}$

The definition of current-dollar output in our model, $\sum\nolimits_i {p_i Y_i } +p$ $_{s}$

$_{x}- p$ $_{s}$

$_{m}$ = pV, implies that $\sum\nolimits_i {\frac{p_i Y_i }{pV}} +\frac{p_S S_x }{pV}-\frac{p_S S_m }{pV}=1$ , or

(A69) $\sum\nolimits_i {\mu _i } +\mu _{S,x} -\mu _{S,m} =1$ .

In addition, recall from above that $\mu _S =\sum\nolimits_i {\mu _i } \beta _i^S +\mu _{S,x} -\mu _{S,m}$ . Substituting equation A69 and this expression for $\mu _S$ into equation A68 yields

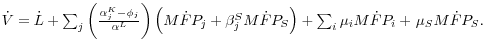
(A70) $\dot {V}=\dot {L} + \sum\nolimits_j {\left( {\frac{\alpha _j^K -\phi _j }{\alpha ^L}} \right)\left( {M\dot {F}P_j +\beta _j^S M\dot {F}P_S } \right)} + \sum\nolimits_i {\mu _i M\dot {F}P_i } + {\kern 1pt}\mu _S M\dot {F}P_S .$

Finally, recall that $\dot {L}=\dot {H}+\dot {q}$ from equation A6 and use to index the final-output sectors in every term, producing:

(A71) $\dot {V}-\dot {H}=\sum\nolimits_i {\left( {\frac{\alpha _i^K -\phi _i }{\alpha ^L}} \right)\left( {M\dot {F}P_i +\beta _i^S M\dot {F}P_S } \right)} {\kern 1pt}{\kern 1pt} +\dot {q} +\sum\nolimits_i {\mu _i M\dot {F}P_i } + {\kern 1pt}\mu _S M\dot {F}P_S .$ $_{?}$

Appendix Table A-1. Value Added, IT Share, and IT Classification of U.S. Industries
Name	Value added, 2005 (millions of dollars	IT share, 2005 $^{a}$	IT classification: IT $_{1995}$ $^{b}$	IT classification: IT $_{2000}$ $^{c}$	IT classification: IT-producing $^{d}$
Agriculture, forestry, fishing, and hunting	123.1	1.4	0	0	0
Oil and gas extraction	159.6	1.8	0	0	0
Mining, except oil and gas	31.5	6.0	0	0	0
Support activities for mining	42.2	8.9	0	0	0
Construction	611.1	19.0	1	1	0
Wood products	39.0	6.4	0	0	0
Nonmetallic mineral products	53.3	9.1	0	0	0
Primary metals	61.1	5.3	0	0	0
Fabricated metal products	130.5	9.3	0	0	0
Machinery	111.1	23.3	1	1	0
Computer and electronic products	135.3	23.4	1	1	1
Electrical equipment, appliances, and components	47.8	12.8	1	1	0
Motor vehicles, bodies and trailers, and parts	95.4	15.2	1	1	0
Other transportation equipment	71.1	28.4	1	1	0
Furniture and related products	37.1	9.6	0	0	0
Miscellaneous manufacturing	72.6	16.0	1	1	0
Food and beverage and tobacco products	175.7	8.8	0	0	0
Textile mills and textile product mills	23.8	4.0	0	0	0
Apparel and leather and allied products	16.8	7.2	0	0	0
Paper products	54.6	6.5	0	0	0
Printing and related support activities	46.9	12.4	0	1	0
Petroleum and coal products	63.5	9.4	0	0	0
Chemical products	209.2	17.1	1	1	0
Plastics and rubber products	67.7	5.6	0	0	0
Utilities	248.0	5.5	0	0	0
Wholesale trade	743.2	25.4	1	1	0
Retail trade	823.5	14.6	1	0	0
Air transportation	41.0	42.7	1	1	0
Rail transportation	32.3	2.0	0	0	0
Water transportation	9.0	42.3	1	1	0
Truck transportation	114.1	11.5	0	0	0
Transit and ground passenger transportation	17.1	16.8	1	1	0
Pipeline transportation	9.3	27.6	1	1	0
Other transportation and support activities	89.1	15.1	0	1	0
Warehousing and storage	32.7	19.0	0	0	0
Publishing industries (includes software)	150.2	49.8	1	1	1
Motion picture and sound recording industries	40.5	16.5	1	1	0
Broadcasting and telecommunications	304.1	46.5	1	1	0
Information and data processing services	60.4	81.7	1	1	1
Federal Reserve banks, credit intermediation, and related activities	474.7	28.6	1	1	0
Securities, commodity contracts, and investments	167.4	51.8	1	1	0
Insurance carriers and related activities	296.1	38.9	1	1	0
Funds, trusts, and other financial vehicles	19.5	6.6	0	0	0
Real estate	1472.6	8.7	0	0	0

(continued)

Appendix Table A-1. Value Added, IT Share, and IT Classification of U.S. Industries (continued)
Name	Value added, 2005 (millions of dollars	IT share, 2005 $^{a}$	IT classification: IT $_{1995}$ $^{b}$	IT classification: IT $_{2000}$ $^{c}$	IT classification: IT-producing $^{d}$
Rental and leasing services and lessors of intangible assets	105.8	23.1	1	1	0
Legal services	180.9	47.7	1	1	0
Computer systems design and related services	140.8	89.3	1	1	1
Miscellaneous professional, scientific, and technical services	542.5	67.5	1	1	0
Management of companies and enterprises	225.8	45.6	1	1	0
Administrative and support services	336.6	45.5	1	1	0
Waste management and remediation services	32.3	6.2	0	0	0
Educational services	115.8	22.1	0	1	0
Ambulatory health care services	441.9	14.5	1	0	0
Hospitals and nursing and residential care facilities	342.2	13.1	1	0	0
Social assistance	75.4	21.3	1	1	0
Performing arts, spectator sports, museums, and related activities	54.0	10.2	0	0	0
Amusements, gambling, and recreation industries	60.1	4.8	0	0	0
Accommodation	104.6	5.0	0	0	0
Food services and drinking places	225.9	5.8	0	0	0
Other services, except government	282.8	13.8	0	0	0

Source: Authors' calculations based on BEA data.

a. Nominal value of IT capital services divided by nominal value of total nonresidential capital services.

b. Equals 1 if 1995 IT capital service share is greater than 1995 median, and zero otherwise.

c. Equals 1 if 2000 IT capital service share is greater than 2000 median, and zero otherwise.

d. As defined by BEA.

Appendix Table A-2. Parameter Values for Steady-State Calculations
	Historical Averages: 1973-1995	Historical Averages: 1995-2000	Historical Averages: 2000-2006	Steady-State: Lower Bound	Steady-State: Upper Bound	Method for Setting Bounds
Output shares¹ ( $\mu$ ): 1. Computer hardware	1.08	1.47	1.02	0.7	1.2	A
Output shares¹ ( $\mu$ ): 2. Software	0.97	2.38	2.59	2.4	2.8	A
Output shares¹ ( $\mu$ ): 3. Communication equipment	1.54	1.89	1.34	1.2	1.5	A
Output shares¹ ( $\mu$ ): 4. Other final-output sectors	96.42	94.21	94.87	95.52	94.32	B
Output shares¹ ( $\mu$ ): 5. Net exports of semiconductors	-0.01	0.05	0.18	0.18	0.18	C
Output shares¹ ( $\mu$ ): 6. Total semiconductor output	0.36	0.93	0.67	0.65	0.8	A
Semiconductor cost shares¹ ( $\beta$ ): 7. Computer hardware	30	30	30	30	30	D
Semiconductor cost shares¹ ( $\beta$ ): 8. Software	0	0	0	0	0	D
Semiconductor cost shares¹ ( $\beta$ ): 9. Communication equipment	2.15	8.45	8.4	8	11	A
Semiconductor cost shares¹ ( $\beta$ ): 10. Other final-output sectors	0.01	0.29	0.08	0.18	0.07	B
Relative inflation rates² ( $\pi$ ): 11. Semiconductors	-27.29	-48.27	-31.75	-28.15	-34.41	E
Relative inflation rates² ( $\pi$ ): 12. Computer hardware	-19	-27.23	-18.13	-18.08	-22.1	E
Relative inflation rates² ( $\pi$ ): 13. Software	-3.96	-3.15	-3.55	-3.39	-4.14	E
Relative inflation rates² ( $\pi$ ): 14. Communication equipment	-2.76	-5.29	-5.62	-5	-6.1	F
Depreciation rates³ ( $\delta$ ): 15. Computer hardware	30.34	31.49	31.54	31.54	31.54	C
Depreciation rates³ ( $\delta$ ): 16. Software	35.59	38.12	37.76	37.76	37.76	C
Depreciation rates³ ( $\delta$ ): 17. Communication equipment	13	13	13	13	13	C
Depreciation rates³ ( $\delta$ ): 18. Other business fixed capital	5.96	6.04	5.76	5.76	5.76	C
Expected capital gains/losses⁴ ( $\Pi$ ): 19. Computer hardware	-14.73	-23.94	-13.57	-14.32	-17.51	E
Expected capital gains/ losses⁴ ( $\Pi$ ): 20. Software	0.16	-1.07	-0.04	-0.06	-0.07	E
Expected capital gains/ losses⁴ ( $\Pi$ ): 21. Communication equipment	-0.16	-3.13	-3.07	-3	-4.1	G
Expected capital gains/ losses⁴ ( $\Pi$ ): 22. Other business fixed capital	5.5	2.73	3.71	4.28	5.23	E
Capital-output ratios (TpKK /pY): 23. Computer hardware	0.021	0.03	0.032	0.028	0.033	A
Capital-output ratios (TpKK /pY): 24. Software	0.023	0.055	0.075	0.075	0.09	A
Capital-output ratios (TpKK /pY): 25. Communication equipment	0.075	0.085	0.09	0.084	0.095	A
Capital-output ratios (TpKK /pY): 26. Other business fixed capital	2.38	2.14	2.19	2.2	2.4	A
Income shares¹ ( $\alpha$ ): 27. Computer hardware	1.11	1.84	1.64	1.44	1.8	B
Income shares¹ ( $\alpha$ ): 28. Software	0.97	2.42	3.26	3.26	3.91	B
Income shares¹ ( $\alpha$ ): 29. Communication equipment	1.57	1.81	1.98	1.81	2.16	B
Income shares¹ ( $\alpha$ ): 30. Other business fixed capital	19.77	18.22	17.39	15.57	14.7	B
Income shares¹ ( $\alpha$ ): 31. Other capital5	8.07	6.81	6.59	6.59	6.59	C
Income shares1 ( $\alpha$ ): 32. Labor	68.52	68.9	69.13	71.33	70.84	B
Other parameters: 33. Growth of "other" sector MFP³	0.15	0.38	1.23	0.19	0.98	H
Other parameters: 34. Growth of labor quality³ (q)	0.4	0.38	0.48	0.15	0.15	I
Other parameters: 35. Nominal return on capital³ (R)	7.84	5.22	5.91	5.6	5.6	J
Other parameters: 36. Ratio of domestic semiconductor output to domestic use (1+ $\theta$ )	0.99	1.06	1.35	1.35	1.35	C

1. Current-dollar shares, in percent.

2. Output price inflation in each sector minus that in the "other final-output" sector, in percentage points.

3. In percent.

4. Three-year moving average of price inflation for each asset, in percent.

5. Includes land, inventories, and tenant-occupied housing.

Key: Methods for setting steady-state bounds.

A. Range around recent values based on visual inspection of the series.

B. Implied by other series.

C. Average value over 2000-2006.

D. Assumed constant value.

E. The lower and upper bounds equal, respectively, 0.9 and 1.1 times the average rate of change over 1973-2006.

F. Calibrated to keep the sector's MFP growth rate near the average pace over 1995-2006.

G. The lower and upper bounds equal the corresponding values for the relative inflation rate of communication equipment (line 14), plus 2 percentage points - the assumed rate of inflation in the "other final-output" sector.

H. The lower bound equals the average rate of improvement in technology $(\dot {z})$ in this sector over 1973-2000; the upper bound equals the average rate of improvement over 2000-2006 minus $\raise.5ex\hbox{$\scriptstyle 1$}\kern-.1em/ \kern-.15em\lower.25ex\hbox{$\scriptstyle 4$}$ percentage point.

I. From Jorgenson, Ho, and Stiroh (2007).

J. Average value over 1995-2006.

Footnotes

1. . See Economic Report of the President

Basu, Fernald, and Shapiro (2001), Brynjolffson and Hitt (2000, 2003), Jorgenson and Stiroh (2000), Jorgenson, Ho, and Stiroh (2002, 2005), and Oliner and Sichel (2000, 2002). In these papers IT refers to computer hardware, software, and communications equipment. This category often also is referred to as information and communications technology, or ICT. For industry-level evidence supporting the role of IT in the productivity resurgence, see Stiroh (2002b). For an interpretation of the industry evidence that puts less emphasis on IT, see Bosworth and Triplett (2007) and McKinsey Global Institute (2001). Return to Text

2. . See Corrado, Hulten, and Sichel (2005, 2006), Brynjolfsson and Hitt (2003), Bresnahan, Brynjolfsson, and Hitt (2002), Basu and others (2004), Black and Lynch (2001, 2004), and Nakamura (1999, 2001, 2003). The National Income and Product Accounts (NIPAs) exclude virtually all intangibles other than software, although the Bureau of Economic Analysis, which produces the NIPA data, recently released a satellite account for scientific research and development; see Okubo and others (2006). Return to Text

3. . Bresnahan and Trajtenberg (1995) were the first to write about IT as a general-purpose technology. Also, see Organization for Economic Cooperation and Development (2000), Schreyer (2000), van Ark (2000), Basu and others (2004), and Basu and Fernald (2007). Return to Text

4. . Jorgenson, Ho, and Stiroh (2007); Bosworth and Triplett (2007). Return to Text

5. . See Gordon (2003), Baily (2003), Schweitzer (2004), and Stiroh (2006a). For references to the business press, see Gordon (2003) and Stiroh (2006a). Return to Text

6. . Several other researchers have examined industry data, including Baily and Lawrence (2001), Stiroh (2002b), Nordhaus (2002b), Corrado and others (2007), and Bosworth and Triplett (2007). For references to the literature on industry-level data in Europe, see van Ark and Inklaar (2005). Return to Text

7. . See Economic Report of the President 2007, Congressional Budget Office (2007a, 2007b), and the latest available transcripts of the meetings of the Federal Open Market Committee (FOMC; Board of Governors of the Federal Reserve System, 2001). The 2001 FOMC transcripts show that staff presentations on the economic outlook featured growth accounting in the discussion of productivity trends. Private sector analysts also rely on growth accounting; see, for example, Global Insight (2007) and Macroeconomic Advisers (2007). Return to Text

8. . Much has been written about the link between management expertise and productivity, including Bloom and van Reenen (2006), McKinsey Global Institute (2001), and Farrell, Baily, and Remes (2005). Gordon (2003) and Sichel (2003) provide reasons why offshoring and hours mismeasurement may have had a relatively limited effect on labor productivity growth, whereas Houseman (2007) argues that these factors could have had a significant effect in the U.S. manufacturing sector. For a discussion of measurement issues related to the pace of technical progress in the semiconductor industry, see Aizcorbe, Oliner, and Sichel (2006). For further discussion of issues related to critiques of the neoclassical framework, see Congressional Budget Office (2007b). Return to Text

9. . Gordon (2003). Return to Text

10. . Bosworth and Triplett (2007). Return to Text

11. . Roberts (2001). Return to Text

12. . Basu and others (2004). Return to Text

13. . Oliner and Sichel (2000, 2002). Return to Text

14. . Basu, Fernald, and Shapiro (2001; hereafter BFS) Return to Text

15. . Basu and others (2004; hereafter BFOS). Return to Text

16. . Although BFS also include adjustment costs for labor in their model, they zero out these costs in their empirical work. We simply omit labor adjustment costs from the start. For additional discussion of capital adjustment costs and productivity growth, see Kiley (2001). Return to Text

17. . The results in BFS and in Basu, Fernald, and Kimball (2006) strongly support the assumption of constant returns for the economy as a whole. We invoke perfect competition as a convenience in a model that already has many moving parts. Return to Text

18. . The weight on $\dot {K}_j -\dot {H}$ represents the output elasticity of type-

capital. In the case without adjustment costs,

$\phi _j$ = 0, and so the income share $\alpha _j^K$ proxies for this output elasticity. However, in the presence of adjustment costs, the first-order condition for the optimal choice of capital yields the more general result shown in equation 1. In effect, the income share captures both the direct contribution of capital to production and the benefit of having an extra unit of capital to absorb adjustment costs. The weight in equation 1 nets out the portion of the income share that relates to adjustment costs, as this effect is embedded in the MFP term discussed below. Return to Text

19. . Domar (1961). Return to Text

20. . Oliner and Sichel (2002). Return to Text

21. . In contrast to the expression for aggregate MFP growth in BFS, equation 2 contains no terms to account for reallocations of output, labor, or capital across sectors. The particularly clean form of equation 2 arises, in large part, from our assumption of constant returns to scale and the absence of adjustment costs for labor (which implies that competitive forces equate the marginal product of labor in all sectors). In addition, we have assumed that any wedge between the shadow value of capital and its user cost owing to adjustment costs is the same in all sectors. Given this assumption, reallocations of capital across sectors do not affect aggregate output. Return to Text

22. . For details on data sources, see the data appendix to Oliner and Sichel (2002). Return to Text

23. . The weight on the capital deepening term in equation 1 for type-

capital equals its income share minus its adjustment cost elasticity. As discussed below, empirical estimates of these asset-specific elasticities are not available, which forces us to approximate the theoretically correct weights. Note that the weights on the capital deepening terms in equation 1 sum to one minus the labor share under constant returns to scale. We replace the theoretically correct weights with standard income-share weights that also sum to one minus the labor share. This approximation attaches the correct weight to aggregate capital deepening but may result in some misallocation of the weights across asset types. Return to Text

24. . Oliner and Sichel (2000, 2002); Jorgenson, Ho, and Stiroh (2002, 2007). Return to Text

25. . Year-by-year share weighting embeds the implicit assumption that firms satisfy the static first-order condition that equates the marginal product of capital with its user cost. Strictly speaking, this assumption is not valid in the presence of adjustment costs, as noted by BFS and by Groth, Nunez, and Srinivasan (2006). Both of those studies replace the year-by-year share weights with the average shares over periods of five years or more, in an effort to approximate a steady-state relationship that might be expected to hold on average over longer periods. We found, however, that our results were little changed by replacing year-by-year shares with period-average shares. Accordingly, we adhere to the usual share weighting practice in the literature. Return to Text

26. . Jorgenson and Stiroh (2000), Jorgenson, Ho, and Stiroh (2002, 2007), Oliner and Sichel (2000, 2002), and Triplett (1996), among others. Return to Text

27. . Oliner and Sichel (2002) give a nontechnical description of the way in which we implement the dual method, and the appendix to this paper provides the algebraic details. Return to Text

28. . BFS used a larger value for $\phi$ , 0.05, but subsequently corrected some errors that had affected that figure. These corrections caused the value of $\phi$ to be revised to 0.035. Return to Text

29. . Shapiro (1986). Return to Text

30. . Hall (2004). Return to Text

31. . Groth (2005). Return to Text

32. . Jorgenson (2001) argues that the steeper declines in semiconductor prices reflected a shift from three-year to two-year technology cycles starting in the mid-1990s. Aizcorbe, Oliner, and Sichel (2006) report that shorter technology cycles drove semiconductor prices down more rapidly after 1995, but they also estimated that price-cost markups for semiconductor producers narrowed from 1995 to 2001. Accordingly, the faster price declines in the late 1990s--and the associated pickup in MFP growth--partly reflected true improvements in technology and partly changes in markups. These results suggest some caution in interpreting price-based swings in MFP growth as a proxy for corresponding swings in the pace of technological advance. Return to Text

33. . The combined effect of adjustment costs and factor utilization remained essentially zero after 2000. Although the deceleration in investment spending after 2000 eliminated the negative effect of adjustment costs, the net decline in the workweek pushed the utilization effect into negative territory. Return to Text

34. . Of course, MFP growth is a residual, so this result speaks only to the proximate sources of growth and does not shed light on the more fundamental forces driving MFP growth. Return to Text

35. . Jorgenson, Ho, and Stiroh (2007). Return to Text

36. . Corrado, Hulten, and Sichel (2005, 2006). Return to Text

37. . See Brynjolfsson and Hitt (2000), Brynjolfsson, Hitt, and Yang (2002), and McKinsey Global Institute (2002) for interesting case studies regarding the creation of organizational capital. Return to Text

38. . The BFOS model focuses on intangibles that are related to information technology. This is a narrower purview than in Corrado, Hulten, and Sichel (2005, 2006), who develop estimates for a full range of intangible assets, regardless of their connection to IT. Although we do not provide a comprehensive accounting for intangibles, we highlight the intangible assets that are central to an assessment of the contribution of information technology to economic growth. Return to Text

39. . Hall and Jorgenson (1967). Return to Text

40. . Specifically, for the income share of intangible capital, we use the income share series for "New CHS intangibles," that is, those intangibles over and above those included in the NIPAs. We then adjust this series downward to account for the fact that some CHS intangibles are not related to IT and thus do not fit in the BFOS framework. As a crude adjustment, we remove the income share associated with brand equity and one-third of the income share for other components of "New CHS intangibles." Return to Text

41. . We use 2003 as the final year for this calculation because that is the last year of data in CHS. Return to Text

42. . See Yang and Brynjolfsson (2001) for an alternative approach to incorporating intangibles into a standard growth accounting framework. Their approach relies on financial market valuations to infer the amount of unmeasured intangible investment and shows that, through 1999, the inclusion of intangibles had potentially sizable effects on the measured growth of MFP. Return to Text

43. . Brynjolfsson and Hitt (2000), Brynjolfsson, Hitt, and Yang (2002), and McKinsey Global Institute (2002). Return to Text

44. . Aral, Brynjolfsson, and Wu (2006, p. 2). Some interpret the econometric results in Brynjolfsson and Hitt (2003) as support for a lag between the installation of IT capital and the accumulation of complementary capital. We believe this interpretation is incorrect. Brynjolfsson and Hitt show that the firm-level effect of computerization on MFP growth is much stronger when evaluated over multiyear periods than when evaluated on a year-by-year basis. Importantly, however, the variables in their regression are all measured contemporaneously, whether over single-year or multiyear periods. Accordingly, their results suggest that the correlation between the growth of IT capital and intangible capital may be low on a year-by-year basis, but that a stronger contemporaneous correlation holds over longer periods, boosting the measured effect on MFP growth. Return to Text

45. . For background on industry productivity analysis, see Jorgenson, Gollop, and Fraumeni (1987), Basu and Fernald (1995, 1997, 2001, 2007), Nordhaus (2002b), Stiroh (2002a, 2002b), Triplett and Bosworth (2004), and Bosworth and Triplett (2007). Return to Text

46. . Bruno (1978); Norsworthy and Malmquist (1983); Jorgenson, Gollop, and Fraumeni (1987). Return to Text

47. . Basu and Fernald (1995, 1997). Return to Text

48. . Basu and Fernald (2001). Return to Text

49. . Howells, Barefoot, and Lindberg (2006). Return to Text

50. . The underlying sources of these data are the BLS Current Employment Survey (for wage and salary jobs and average weekly hours), the Current Population Survey (for self-employed and unpaid workers, agricultural workers, and household employment), and unemployment insurance tax records. Return to Text

51. . Jorgenson, Ho, and Stiroh (2007). Return to Text

52. . As a comparison, Stiroh (2001, 2002b) reported an acceleration of ALP after 1995 for six of ten broad sectors, which accounted for the majority of output using earlier vintages of SIC data. Return to Text

53. . Corrado and others (2007); Bosworth and Triplett (2007). Return to Text

54. . BEA uses the "double deflation" method to estimate real value added for all industries as the difference between real gross output and real intermediate inputs (Howells, Barefoot, and Lindberg, 2006). Basu and Fernald (2001) show that this can be approximated, as in equation 16, by defining gross output as a weighted average of value added and intermediate input growth. Return to Text

55. . As in Stiroh (2002b). Return to Text

56. . This value-added approach is similar to the decomposition in Nordhaus (2002b). Return to Text

57. . We also aggregated the industry output data using a Fisher (rather than the Tornqvist) index and still found a small difference for the period 1995-2000. We do not have an explanation for this. Return to Text

58. . Jorgenson and others (2006) show an increase in both the intermediate input and hours reallocation terms, although both are slightly negative through 2004. The results in Bosworth and Triplett (2007) are similar to ours in some respects (rising direct contribution of gross output productivity through 2000 followed by a substantial fall, and an intermediate reallocation term that switches from negative to positive after 2000), but their hours reallocation term remains negative through 2005. This divergence reflects differences in the estimation of the hours series. Bosworth and Triplett (2007) use the BEA series on full-time/part-time employees, which they scale by total hours per employee from BLS for 1987 to 2004. They hold hours per full-time/part-time employee constant from 2004 to 2005. Return to Text

59. . This is analogous to the analysis of the sources of productivity growth within the U.S. retail trade sector by Foster, Haltiwanger, and Krizan (2002), who report that the majority of productivity gains reflect entry and exit, with a very small contribution from productivity gains within continuing establishments. Return to Text

60. . Stiroh (2006a). Return to Text

61. . Caballero and Hammour (1994). Return to Text

62. . See, for example, Smith and Lum (2005) and Howells, Barefoot, and Lindberg (2006). Return to Text

63. . Stiroh (2002b). Return to Text

64. . Appendix table A-1 shows this classification scheme for the sixty detailed industries based on both 1995 and 2000 IT capital income shares and reports the 2005 share. Baily and Lawrence (2001), Stiroh (2001), and Jorgenson, Ho, and Stiroh (2005) also use relative shares of IT capital in total capital to identify IT-intensive industries in the United States, and Daveri and Mascotto (2002), Inklaar, O'Mahony, and Timmer (2005), O'Mahony and van Ark (2003), and van Ark, Inklaar, and McGuckin (2003) do so in international studies. Return to Text

65. . This specification is identical to a difference-in-difference-style regression with a post-1995 or post-2000 dummy variable, an IT intensity dummy, and the interaction estimated with annual data for the full period. Return to Text

66. . Becker and others (2005). Return to Text

67. . We also estimated (but do not report) weighted least squares estimates, which are appropriate if the somewhat arbitrary nature of the industry classification system makes measurement error more severe in the relatively small industries. See Kahn and Lim (1998) for a more detailed discussion of weights in industry regressions. These weighted estimates are similar to those reported in table 7. Return to Text

68. . Stiroh and Botsch (2007) report similar results. Return to Text

69. . Stiroh (2006b). These results could be consistent with an IT-based explanation if the pervasiveness of IT makes it difficult to identify a link econometrically. That is, if IT is integral for all industries, then measures of IT intensity may not be useful for classification purposes. This view, however, is inherently untestable. Return to Text

70. . Baily (2004) discusses the case study evidence of the impact of competitive intensity on firms' need to innovate and increase productivity and argues that competitive pressure gradually increased during the 1970s and 1980s. Return to Text

71. . Gordon (2003, p. 274). See Nordhaus (2002a) for details on profit trends over this period. Return to Text

72. . Schweitzer (2004). Return to Text

73. . Groshen and Potter (2003). Return to Text

74. . This has been documented by Schreft and Singh (2003) and by Aaronson, Rissman, and Sullivan (2004). Return to Text

75. . The significance of the cross-sectional correlation is robust to dropping the two major outliers--computers and electronics, and information and data systems--on the far left of figures 2 and 3. Return to Text

76. . t-tests for differences in the mean growth rates between the two groups of industries reject the hypothesis that the two had equal growth rates for hours and productivity, but fail to reject the hypothesis that the two had equal output growth rates. Return to Text

77. . As a robustness check, we estimated difference-in-difference regressions and found that industries with a below-median change in the profit share from 1997 to 2001 had a bigger decline in the growth of hours and a bigger increase in the growth of gross output labor productivity than did other industries. No significant difference emerged for value-added labor productivity growth. We also ran regressions with more detailed measures of intermediate inputs, including energy, materials, and purchased service inputs, as the dependent variable, but those results were uniformly insignificant and are not reported. As a second robustness check, we compared hours, productivity, and output growth for 1992 with the change in the profit share from 1989 to 1991 and found largely insignificant results, suggesting that the latest cyclical episode was different from the previous one. Return to Text

78. . The figures in table 9 are calculated from BLS's quarterly Productivity and Costs data. The definition of nonfarm business in these data includes government enterprises. In contrast, the definition of nonfarm business in BLS's MFP data, the data we use to calculate the labor productivity growth rates in table 1, excludes government enterprises. This slight difference in sectoral coverage explains why labor productivity growth for 2000-06 differs by 0.1 percentage point across the two tables. The same explanation accounts for the slight difference in the average growth rate for 1973-95 between table 1 and the column for nonfarm business in table 10 below. Return to Text

79. . Jorgenson, Ho, and Stiroh (2007) show that such revisions are not unusual; for example, there was a steady stream of upward revisions to productivity growth in the mid-1990s. Return to Text

80. . There are a number of alternative historical series for labor productivity. Although they yield different results in some periods, the patterns of growth and long-run averages are qualitatively similar to the BLS data presented here. For example, see Gordon (2006). Return to Text

81. . In Roberts (2001) the Kalman filter is used to obtain time-varying estimates of trend growth in both potential output and labor productivity. Our implementation first uses a Hodrick-Prescott filter to estimate the trend in hours and then feeds this exogenous trend to the model. Hence we need to estimate a trend only for labor productivity. Return to Text

82. . For other estimates of trend productivity using Kalman filter techniques, see Brainard and Perry (2000) and Gordon (2003). Return to Text

83. . Even though adjustment costs have no direct effect on growth in the steady state, the adjustment cost elasticities ( $\phi$ $_{i})$ appear in the weights on the capital deepening terms in equation 23, just as they did in the growth accounting equation that applies outside the steady state (equation 1). As in that case, we lack the information to specify these asset-specific elasticities. We proceed as we did before, by replacing the theoretically correct weights with standard income-share weights that sum to the same value (one minus the labor share). Return to Text

84. . For the IT-producing sectors, the rate of advance in technology is determined endogenously from the assumed rates of change in prices for IT capital and a variety of other parameters. Return to Text

85. . Jorgenson, Ho, and Stiroh (2007). Return to Text

86. . The horizon in Kahn and Rich (2006) is five years, that in Economic Report of the President 2007 is six years, and that in Macroeconomic Advisers (2007) is eight years. Return to Text

87. For both

and

, the first subscript refers to the sector producing the capital good, whereas the second subscript refers to the sector using the capital good as an input to production. Thus $I_{i,j}$ denotes the amount of the investment good produced by sector

that is sold to sector

. Likewise, $K_{j, i}$ denotes the stock of the investment good produced by sector

that is used by sector

. Return to Text

88. As noted in the text, Basu, Fernald, and Shapiro (2001) include adjustment costs for labor in their model but zero out these adjustment costs for their empirical work. We simply exclude adjustment costs for labor from the start. Return to Text

89. As noted above, the model includes a sector for the production of intangible assets omitted from the NIPAs. If we were to exclude that sector - to be consistent with the coverage of the published NIPA data - all the results presented here would continue to hold. Formally, the only change would be that the summations over the final-output sectors would run from 1 to 4 rather than from 1 to 5. Return to Text

90. Equation A3 is just one of several possible superlative indexes of output growth. It differs slightly from the Fisher chain index used in the NIPAs. Return to Text

91. Equation A9 is the counterpart using our notation to equation A.9 in Groth, Nunez, and Srinivasan (2006, p. 27). The markup term in that equation disappears under our assumption of perfect competition. Return to Text

92. Indeed, the proof applies to any sector or the aggregate economy as long as one assumes constant returns to scale and perfect competition. Return to Text

93. This part of the appendix explicitly indexes the sectors because proposition 3 below makes use of a numeraire sector to measure changes in relative prices. Return to Text

94. We use the NIPA sector producing goods other than IT as the numeraire sector. Return to Text

95. To interpret equation A60, consider an example in which sector

produces software. Equation A60 says that the output of the software sector will grow at the same rate as the software used as an input by every final-output sector and the semiconductor sector. Equation A60 does not have any implications for the growth of software output relative to the growth of output in any other sector. Return to Text

^♣ This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to Text