Skip to: [Printable Version (PDF)] [Bibliography] [Footnotes]

Finance and Economics Discussion Series: 2008-03 Screen Reader version ^♣

Monetary Policy Actions and Long-Run Inflation Expectations

Michael T. Kiley¹

December 2007

Version 3

Keywords: Inflation objective, learning

Abstract:

The degree to which inflation expectations are anchored at long horizons is important for many issues in macroeconomics and finance. There has been little research examining observable measures of long-run inflation expectations. We investigate the evolution of survey measures of long-run inflation expectations in the United States. Our analysis emphasizes the role of a time-varying inflation objective of monetary policymakers. This focus makes monetary policy actions a key determinant of long-run inflation expectations. Our results have important implications for work on inflation dynamics, monetary policy rules, the costs of disinflation, and the term structure of interest rates.

JEL Codes: E3, E4

1. Introduction

The degree to which inflation expectations are tied down at long horizons, or anchored, is central to many of the key issues in macroeconomics, monetary policy, and finance. An incomplete list of topics influenced by the extent of anchoring in long-run inflation expectations includes

the nature of fluctuations in inflation and in the economy more generally;
the setting of monetary policy;
and the behavior of the term structure of interest rates and other asset prices.

Despite its potential importance, there has been relatively little research on the factors driving observable measures of expectations for inflation at distant horizons.² We fill in this gap (or gaping hole?) by examining the evolution of survey measures of long-run inflation expectations in the United States. We focus on the factors that determine the level of inflation expectations and their movements over time. Our analysis emphasizes the role of a potentially time-varying inflation objective of monetary policymakers. This focus makes monetary policy actions a key determinant of long-run inflation expectations.

Before turning to our conceptual framework and results, we will note a few important strands of recent research that highlight the role of fluctuations in long-run inflation expectations.

With regard to inflation dynamics, the degree of anchoring of inflation expectations is central in most empirical and theoretical applications - as inflation is a function of inflation expectations in most treatments. On the empirical front, Roberts (2006) and Hooker (2002) have suggested that better anchoring of inflation expectations in the United States has made inflation less sensitive to variations in aggregate demand and to supply shocks (such as sharp increases in energy prices), respectively.. Also, Stock and Watson (2007) and Cogley and Sargent (2007) have suggested that inflation in the United States has become more stable, in the sense of a smaller variance of permanent shocks to inflation; this type of reduced-form evidence points to changes in the stability of long-run inflation expectations (either because long-run inflation expectations are an important determinant of inflation, or vice versa). On the theoretical front, standard models of price adjustment, such as those underlying the New-Keynesian Phillips Curve, imply an important role for the long-run or steady-state inflation rate. Empirical investigations of these models show the importance of time-variation in long-run inflation for the ability of such models to capture inflation dynamics (e.g., Cogley and Sbordone (2006) and the sub-sample analysis of Kiley (2007a)). However, this line of research has not examined observable measures of the public's expectations for inflation at long horizons.

The degree to which public perceptions of the monetary authority's long-run inflation objective fluctuates also has important implications for monetary policy. For example, Ball (1995), Bomfim at al (1997), Erceg and Levin (2003), Roberts (2007), and Kiley (2007b) show that the cost of disinflation in many small- and large-scale macroeconomic models hinges on the degree to which long-run inflation expectations move in response to policy actions. The interaction between policy actions and the evolution of the public's perceptions of policy objectives plays an important role in many other recent investigations of the interaction between learning and monetary policy (e.g., Bullard and Mitra (2002), Orphanides and Williams (2005), and Gaspar, Smets, and Vestin, (2006)). While Erceg and Levin (2003) and Orphanides and Williams (2005) make some reference to inflation expectations at long horizons, none of this research examines the evolution of survey measures of long-run inflation expectations at more than a superficial level.

Finally, a number of studies have emphasized the potential importance of shifts in long-run inflation expectations for the behavior of the term structure of interest rates. For example, Gürkaynak, Sack, and Swanson (2005) found that long-run inflation expectations, as measured by the difference in yields between nominal and inflation-indexed bonds, move in response to news about the economy, rather than remaining unaffected as would be implied by some simple models. More generally, models of the term structure of interest rates fit the data better under the assumption that both inflation expectations and beliefs about the central bank's reaction function are drifting (Kozicki and Tinsley (2001), Rudebusch and Wu (2003); and Cogley (2005)). Most of this research has also ignored available survey measures of long-run inflation expectations. Kozicki and Tinsley (2001) is an important exception. They include an analysis of a survey measure of long-run inflation expectations.³ But their work assumes that long-run inflation expectations are a function of an adaptive-learning algorithm, implying that these expectations are solely a function of past inflation. We take a different tack, and consider a model in which monetary policy actions are the key determinant of long-run inflation expectations. Given that inflation at long horizons is (in most models) solely a function of monetary policy choices, our approach seems likely to provide important insights. Our empirical work will compare our approach with an adaptive-learning specification.

The next section discusses our conceptual framework. Section 3 presents the basic empirical results. Section 4 compares our approach to an adaptive learning approach, examines the implications of our results for work on inertia in monetary policy rules, and briefly discusses the link between our findings and work on the cost of disinflation. The final section summarizes our findings and suggests areas for further investigation.

2. The conceptual framework

Suppose that monetary policymakers pursued a policy with a time-varying inflation target consistent with a generalized Taylor-style nominal interest rate rule. Specifically, the nominal interest rate (i) is a linear function of its own lags, the long-run real interest rate (r*, assumed to be constant), inflation ( $\Delta$ p), the gap between inflation and a time-varying goal for inflation ( $\Delta$ p- $\Delta$ p*), a measure of the output gap or economic activity (y), and a residual (e):

Equation 1

$\begin{displaymath} i(t)=\sum\limits_{j=1}^N {a_j i(t-j)} +[1-\sum\limits_{j=1}^N {a_j } ][r\ast +\Delta p(t)+\gamma^{\Delta p} (\Delta p(t)-\Delta p\ast (t))+\gamma^y y(t)]+e(t). \end{displaymath}$

The time variation in the long-run inflation goal is clear in equation 1; also, we have restricted the nominal interest rate rule to a form that only depends on contemporaneous values of inflation and the output gap, but this restriction could easily be relaxed. Conventional wisdom suggests that the coefficients on the deviation of inflation from its targeted value and the output gap should be positive. In particular, a positive value for the coefficient on the inflation gap is consistent with the Taylor principle - the idea that the real interest rate should be higher when inflation is above its desired level, ceteris paribus.⁴

Our focus will be on possible variation in the inflation goal. Following much previous work (e.g., Bomfim et al (1997), Erceg and Levin (2003), Kozicki and Tinsley (2001), and Cogley and Sbordone (2006)), we assume that the long-run inflation goal shifts over time in a random-walk manner, i.e.,

Equation 2

$\begin{displaymath} \Delta p\ast (t)=\Delta p\ast (t-1)+v(t), \end{displaymath}$

where v(t) is the innovation to the inflation goal at time t. We assume that v(t) and e(t) are independent. Importantly, we assume also that the long-run inflation goal is not announced, but must be inferred by some method.

Of course, the random-walk specification for the long-run inflation goal is not meant to suggest that monetary policy has allowed for "random" variation in the long-run inflation objective. Rather, this specification is a convenient mathematical representation of the notion that the long-run objective for inflation may have shifted over time in response to changes in economist's and policymaker's understanding of the nature of inflation fluctuations and the costs associated, in the long run, with different levels of inflation. Ireland (2007) provides a reduced-form model in which some macroeconomic fundamentals drive time variation in the long-run inflation goal.

With this basic framework, we can derive the efficient method that private agents would use to infer the long-run inflation goal. If agents form their inference so as to minimize the quadratic difference between the true long-run goal for inflation and their estimate, or if the shocks to the policy rule (e(t) in equation 1) and inflation goal (v(t) in equation 2) are governed by a Normal distribution, then the estimate of the inflation goal derived from observations on nominal interest rates, inflation, and the output gap via the Kalman filter is the optimal one.

The solution to this signal extraction problem is standard (e.g., Muth (1961) and Sargent (1987)). We focus on the steady-state, or long-run, equation governing the evolution of the public's beliefs. The implied evolution of the perceived inflation goal E $\Delta$ p(t) is governed by

Equation 3

$\begin{displaymath} \begin{array}{l} E\Delta p\ast (t)=E\Delta p\ast (t-1)-\kap... ...mits_{j=1}^N {a_j } ]\gamma^{\Delta p} \}^2} \ \end{array}. \end{displaymath}$

In equation 3, the evolution of the inflation target is governed by the public's perceptions of monetary policy actions. The degree to which agent's perception of the inflation goal are updated depends on $\kappa$ , a positive constant that is itself a function of the parameters of the nominal interest rate rule and the variances of the transitory shock to the policy rule ( $\sigma _e^2 )$ and the shock to the inflation goal ( $\sigma _v^2 )$ . Tighter-than-expected policy, i.e., a nominal interest rate higher than expected given the policy rule and agents perception of the inflation goal, leads to an updated, lower, value of the inflation goal. In particular, a higher variance of shocks to the inflation target ( $\sigma _v^2 )$ would imply more substantial updating of agent's perception of the inflation goal in response to any perceived deviation from the nominal interest rate rule because agents would attribute a greater portion of such a perceived deviation to a change in inflation goal.

If the econometrician has available data on the public's perception of the long-run goal for inflation, Equation 3 is estimable directly. However, more efficient coefficient estimates could be obtained by estimating the updating equation (equation 3) with the policy rule (equation 1). But equation 1 is not directly estimable, as it involves the true inflation goal - i.e., any available data on the public's perception should not be inserted into the policy rule. This difficulty can be overcome by first differencing equation 1, yielding

Equation 4

$\begin{displaymath} \begin{array}{c} \Delta i(t)=\sum\limits_{j=1}^N {a_j \Delta i(t-j)} +[1-\sum\limits_{j=1}^N {a_j } ][(1+\gamma^{\Delta p} )\Delta \Delta p(t)+\gamma^y \Delta y(t)]+... \ e(t)-e(t-1)-[1-\sum\limits_{j=1}^N {a_j } ]\gamma^{\Delta p} u(t) \ \end{array}. \end{displaymath}$

Equation 4 can be estimated, as the unobservable inflation goal disappears from the policy rule on first-differencing. The resulting policy rule has a moving average error, which is easily accounted for in estimation. We will estimate equation 3 and a system involving equations 3 and 4 in the next section. (Of course, an alternative but modestly more involved procedure would involve estimating equations 1 and 3 together, taking into account the unobserved nature of the inflation goal by forming the likelihood function using the Kalman filter. We avoid this procedure because our alternative is more direct, simpler, and yields fairly precise coefficient estimates, as shown below).

3. Empirical results

3.1 Data

We present empirical results using two measures of the public's expectations of inflation at long horizons. The first measure is from surveys of professional forecasters. These surveys measure expectations of the average rate of change in the Consumer Price Index (CPI) over the next ten years. The summary measure we construct splices together observations from surveys by the private firms Drexel-Burnham-Lambert and Barclays de Zoete Wedd covering the period from September 1978 to September 1991 with the observations from the Survey of Professional Forecasters covering the period after September 1991. We will call this measure the professional forecasters' measure.

The second measure is from the Reuters-Michigan Survey Research Center Survey of Consumers. This series measures the rate of price change expected over the next five-to-ten years; we use the median of the responses collected in the survey as our measure of the central tendency of household's long-run expectations. (Of course, there is some dispersion in expectations in both surveys; we do not exploit this dispersion, and view future investigations of the cross-sectional variation in the survey measures as an interesting topic for research, as in Mankiw, Reis, and Wolfers (2003)). We will call this measure the household measure.

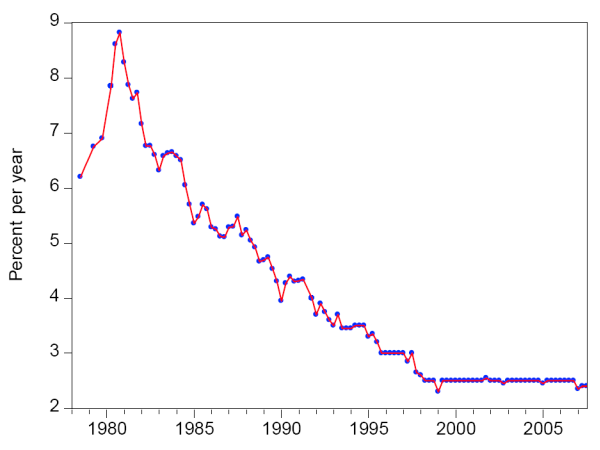
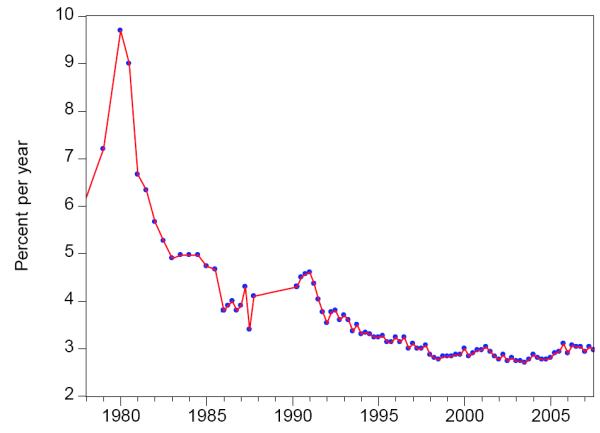
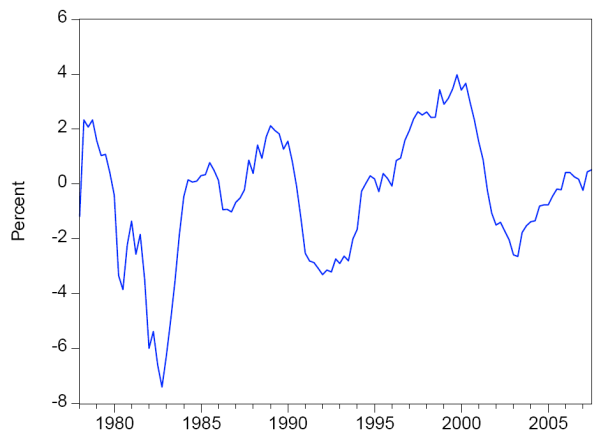
Both measures of long-run inflation expectations contain a number of missing observations, as the survey questions were only posed at irregular intervals early in our sample period. We linearly interpolate between missing observations. Figure 1 presents the raw and interpolated series for the professional forecasters' measure in the upper panel (with the raw series denoted by the dots and the interpolated series by the line) and the raw and interpolated series for the household measure in the lower panel (with the raw series denoted by the dots and the interpolated series by the line); the period is 1978Q1 to 2007Q3. The raw and interpolated data look very similar; in particular, inflation expectations over the longer-run rose early in the sample, then began a long downward trend beginning around 1981, and appear to have stabilized in the late 1990s. Our empirical analysis will consider both the interpolated and raw series.

In addition, the data from the Survey of Professional Forecasters and the Survey of Consumers refer to inflation expectations over some range of future years, including expectations for the near-term. As a result, these survey measures depend on both near- and long-term expectations. In order to focus on long-term expectations, we assume that inflation expectations converge to long-run expectations after three years (a reasonable horizon in models of inflation dynamics like the New-Keynesian Phillips curve, where inflation persistence is not very high - see, for example, Cogley and Sbordone (2006)). With the survey measures (roughly) referring to inflation expectations over the next 10 years (40 quarters), our assumption about convergence to long-run expectations implies that the survey measure of inflation ( $\Delta$ p $^{S})$ is related to near-term expectations of inflation ( $\Delta$ p) and long-run expected inflation ( $\Delta$ p $^{LR})$ by

Equation 5

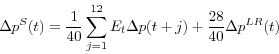
$\begin{displaymath} \Delta p^S(t)=\frac{1}{40}\sum\limits_{j=1}^{12} {E_t \Delta p(t+j)} +\frac{28}{40}\Delta p^{LR}(t) \end{displaymath}$

We construct long-run expected inflation by using actual realizations of inflation over the next 12 quarters and the survey measures of expected inflation to solve for long-run expected inflation in equation 5. Our empirical analysis will instrument for this long-run measure using the survey measure and lags of inflation in order to take account of the expectations operator in equation 5. We will also consider the results when the survey measure is used as the measure of long-run expected inflation without these adjustments.

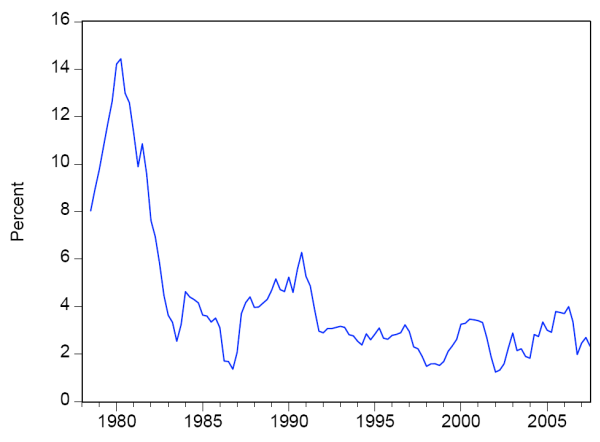
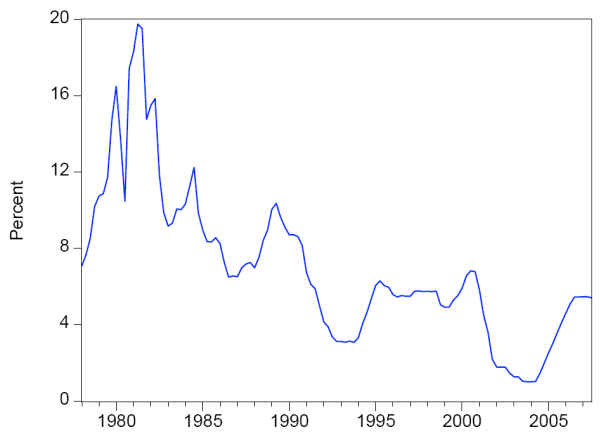
Our model assigns monetary policy actions the central role in guiding long-run expectations; in particular, the updating of private sector beliefs is determined by the influence of movements in the policy-determined nominal interest rate relative to movements in inflation and economic activity, where the latter is captured by the output gap. The nominal interest rate is measured by the effective nominal federal funds rate (at an annual rate); inflation is measured by the percent change in the Consumer Price Index over the past four quarters (where the emphasis on a four-quarter change follows Taylor (1993) and most other empirical work); and the output gap is given by the percent deviation of Gross Domestic Product (GDP, in chain-weighted 2000 dollars) from trend GDP as measured in the Federal Reserve Board's FRB/US model.

Figure 2 presents the data for CPI inflation, the nominal federal funds rate, and the output gap since 1978. The low-frequency movements in inflation and the nominal interest rate are readily apparent: inflation and nominal interest rates rose early in the sample and have trended down since the early 1980s. The data for the output gap clearly show the recessions in the early 1980s, early 1990s, and early 2000s.

Our final set of statistics before turning to our analysis examines the basic moments of the data for CPI inflation and our two survey measures of inflation expectations in table 1. We report the mean, median, and standard deviation of each series (where we include interpolated observations for our survey measures). The means and medians for inflation and expected inflation at longer horizons are very similar, while actual inflation is much more volatile than expected inflation at longer horizons (as measured by the standard deviation). Each is these facts is broadly consistent with the ideas underlying our model of the determination of long-run inflation expectations, with relies on updating via the Kalman filter and hence will tend to imply that long-run expectations have the same central tendency as actual inflation but are less volatile.

3.2 Basic results

We now turn to our formal analysis of the determinants of long-run expectations. Our initial results rely simply on estimating the updating equation for long-horizon expectations - equation 3; we defer joint estimation of the updating equation and monetary policy rule for later. For our baseline empirical results, we restrict attention to a simple Taylor-rule specification without lags of nominal interest rates. In this specification, the nominal interest rate rule depends only on the long-run real interest rate (r*), inflation, the inflation gap, and the output gap. As in Taylor (1993), we fix the long-run real interest rate (r*) at 2 percent. With these restrictions and the replacement of the public's beliefs about the long-run goal for inflation (E $\Delta$ p*) with the data for the long-run expectation derived from equation 5 ( $\Delta$ p $^{LR})$ in equation 3, the estimated equation is

Equation 6

$\begin{displaymath} \Delta p^{LR}(t)-\{\Delta p^{LR}(t-1)-\kappa \left( {i(t-1)-[2+\Delta p(t-1)+\gamma^{\Delta p} (\Delta p(t-1)-\Delta p^{LR}(t-1))+\gamma^y y(t-1)]} \right)\}=w(t) \end{displaymath}$

Note that we have added an error term to the updating equation in equation 6 and written the updating rule as an orthogonality condition, to emphasize that we will instrument for $\Delta$ p $^{LR}$ . While the theory does not include an error, its presence could be motivated by three considerations: measurement error in the surveys of long-horizon expectations, the error induced by our adjustment using future inflation in equation 5, and approximation error in the underlying theory.

We present results for four versions of equation 6 in table 2. The first two (in columns 1 and 2) use the long-horizon measure of expectations ( $\Delta$ p $^{LR}$ from equation 5) based on the professional forecasters' measure. The first specification jointly estimates the updating coefficient ( $\kappa )$ and the coefficients from the policy rule ( $\gamma$ $^{\Delta p}$ and $\gamma$ $^{y})$ . The second specification sets the coefficients in the policy rule at the values suggested by Taylor (1993), i.e., 0.5 on both the inflation deviation from target ( $\gamma$ $^{\Delta p})$ and the output gap ( $\gamma$ $^{y})$ ; these values are both consistent with a long literature and provide a robustness check on the results. The last two specifications reported in columns 3 and 4 of table 2 are the same as those in columns 1 and 2, with the long-horizon measure of expectations based on the household measure replacing the professional forecasters' measure. In all cases, the equation is estimated by the generalized method of moments. The instruments used include the current and lagged values for the unadjusted survey measure of long-horizon inflation expectations ( $\Delta$ p $^{ S}$ (t) and $\Delta$ p $^{ S}$ (t-1)), the lagged four-quarter change in the overall CPI ( $\Delta$ p(t-1)), the lagged four-quarter change in the CPI excluding food and energy ( $\Delta$ p $^{Core}$ (t-1)), the lagged nominal federal funds rate (r(t-1)), and the lagged output gap (y(t-1)). Standard errors are corrected for heteroskedasticity. The sample extends from 1979Q1 to 2004Q2 (where the last three years of data drop out because of the adjustments to the survey measure induced by equation 5).

The results are very similar for each survey measure. Consider first the cases where the updating and policy rule coefficients are each estimated (columns 1 and 3). In both cases, the updating coefficient ( $\kappa )$ is around 0.015 and the policy rule coefficients ( $\gamma$ $^{\Delta p}$ and $\gamma$ $^{y})$ are large (e.g., uniformly exceeding 1). In addition, the standard errors are large; as a result, none of the coefficients differ from zero in a statistically significant manner, although all have the sign suggested by the model in section 2.

Columns 2 and 4 set the policy rule coefficients at their Taylor (1993) values. As a result, the updating coefficient ( $\kappa )$ is estimated to be slightly larger - at 0.020 for the professional forecasters' measure and 0.016 for the household measure - and the standard errors are smaller, implying that the coefficients are significant at the 1 percent or 5 percent level, respectively. We will defer discussion of the economic implications of the magnitude of the updating coefficient for section 4. For now, we note that the results from estimating the updating rule (equation 6) provide some support for the basic framework, in that the coefficients have the signs consistent with

tighter monetary policy (a higher nominal funds rate, all else equal) lowering long-run inflation expectations
and higher inflation or economic activity (all else equal) raising long-run inflation expectations.

The statistical significance of the coefficients depended on whether the coefficients of the policy rule were estimated or pre-specified. This sensitivity suggests that there may be gains in efficiency from jointly estimating the updating equation and the policy rule (the system of equations 3 and 4). We next consider joint estimation of the system

Equation 7

Equation 8

$\begin{displaymath} \Delta i(t)=(1+\gamma^{\Delta p} )\Delta \Delta p(t)+\gamma^y \Delta y(t)+e(t)-e(t-1)-\gamma^{\Delta p} u(t) \end{displaymath}$

We use the same instruments for equation 7 as when estimating the updating rule in isolation. For equation 8, the instrument set includes the following, all lagged one period: the first difference of the unadjusted survey measure of long-horizon inflation expectations ( $\Delta$ $\Delta$ p $^{ S}$ (t-1)), the first difference of the four-quarter change in the overall CPI ( $\Delta$ $\Delta$ p(t-1)), the first difference of the four-quarter change in the CPI excluding food and energy ( $\Delta$ $\Delta$ p $^{Core}$ (t-1)), the first difference of the nominal federal funds rate ( $\Delta$ r(t-1)), and the first difference of the output gap ( $\Delta$ y(t-1)). Standard errors are adjusted for first-order serial correlation, as indicated by the error structure in equation 8.

Table 3 presents these results; column 1 reports the estimates based on the professional forecasters' measure of expectations, while column 2 reports the results based on the household measure. The updating coefficient ( $\kappa )$ is estimated at 0.020 and 0.026 for the professional forecasters and household data, respectively, and each is statistically significant at better than the 1 percent level. The coefficient on the output gap ( $\gamma$ $^{y})$ is large and highly statistically significant for the systems based on both survey measures; however, the coefficient on inflation ( $\gamma$ $^{\Delta p})$ is imprecisely estimated in each case. Overall, the results strengthen those based on the updating equation alone, in that the significance of deviations from the policy rule in influencing long-run inflation expectations - i.e., the size and statistical significance of the updating coefficient $\kappa$ - is greater under the system approach.

3.3. Robustness checks

We now turn to some robustness checks. In particular, our analysis so far has been based on the interpolated data and the measure of long horizon inflation expectations that adjusts for realized CPI inflation over the next twelve quarters, $\Delta$ p $^{LR}$ .

We first consider the robustness of the results to measuring long-run expectations by the unadjusted survey measure $\Delta$ p $^{ S}$ (while preserving the interpolations). The results are reported in table 4. Columns 1 and 2 report results from joint estimation of the updating equation and the policy rule (the system of equations 7 and 8) with the unadjusted survey measure. The results are essentially the same as those using the adjusted survey measure for long-horizon inflation expectations: the updating coefficient $\kappa$ is highly significant as is the policy-rule coefficient on the output gap $\gamma$ $^{y}$ , while the coefficient on inflation $\gamma$ $^{\Delta p}$ is imprecisely estimated.

Our final robustness check drops the interpolations to the survey measures of expectations (and the adjustment for the next twelve quarters of inflation). Dropping interpolations greatly reduces the sample sizes, as the updating equation is dynamic and hence relies on consecutive non-missing observations. Table 5 reports the results based on system estimation of the updating and policy rule equations (the system of equations 7 and 8). For the professional forecasters' measure, dropping interpolations has little effect on the estimated coefficients (which remain at values similar to those reported previously). However, the results based on the household measure are no longer supportive of updating of expectations based on monetary policy actions; in particular, the updating coefficient $\kappa$ is not significantly different from zero and has the wrong sign. This result is not too surprising, as the sample for the household measure with interpolations includes no observations prior to 1986:Q2 and much of the variation in the data occurs during that earlier period.

To summarize the results, our estimates of the relationship between changes in long-run inflation expectations and deviations of monetary policy from a perceived rule provide some support for the idea that long-run inflation expectations depend importantly on monetary policy actions and the evolution of actual inflation and real economic activity. In particular, the coefficients from estimates of an updating equation for long-run inflation expectations based on our Kalman-filtering model imply that

a tighter monetary policy (a higher nominal funds rate, all else equal) lowers long-run inflation expectations
and higher inflation or economic activity (all else equal) raise long-run inflation expectations.

4. Implications of our results

4.1 Comparison to adaptive learning

We have pursued a very focused empirical approach that emphasizes the idea that the public's assessment of the long-run inflation goal of the monetary authority will be influenced by the perceived discrepancy between policy actions and those consistent with the public's previous perception of the long-run inflation goal. Some earlier work has taken a different approach, and suggested that inflation expectations mainly depend on past realizations of inflation. For example, Kozicki and Tinsley (2001) assume that the data on the professional forecasters' measure of long-horizon inflation expectations depends on past inflation and call this assumption an adaptive-learning algorithm. Levin, Natalucci, and Piger (2004) examine the correlation between long-horizon inflation expectations and inflation, but do not consider the role of other factors in influencing long-run inflation expectations.

Our approach and the adaptive learning approach share the feature that private agents' assessment of the long-run goal for inflation is not fixed and depends on incoming data because the inflation goal is not directly observable. The central difference between the adaptive learning approach and our approach is that our emphasis on monetary policy actions gives a role for nominal interest rates and the output gap in the updating of long-horizon inflation expectations. To see the empirical relevance of our approach, we estimate by least squares the following reduced-form regressions for the change in both the professional forecasters and household survey measures of long-horizon inflation expectations:

Equation 9

$\begin{displaymath} \Delta \Delta p^S(t)=a_0 +a_1 [p(t-1)-\Delta p^S(t-1)]+a_2 i(t-1)+a_3 y(t-1)+\varepsilon (t) \end{displaymath}$

The results are reported in table 6. The coefficient estimates do not support the adaptive learning approach. In particular, the equation for professional forecasters' measure yields a highly significant negative coefficient on the nominal interest rate, suggesting the tighter monetary policy lowers this measure of inflation expectations. For the household measure, the coefficient on the output gap is positive and highly significant - suggesting that higher levels of economic activity raise this measure of inflation expectations. These reduced-form findings are consistent with our more structured examination above. In this regard, the tight structure we impose in section 3 allows for an easier economic interpretation.

4.2 Estimation of monetary policy rules

We have already noted that the behavior of inflation expectations at long horizons has important implications for a number of important issues in macroeconomics, monetary policy, and finance. We will discuss in detail one area where the model and empirical analysis can provide new insights into an unresolved controversy: the degree of smoothing of monetary policy actions since 1979.

Our empirical results in section 3 ignored a role for lagged nominal interest rates in the policy rule. A more general nominal interest rate rule that allows for smoothing takes the form shown in equation 1, i.e.,

$\begin{displaymath} i(t)=\sum\limits_{j=1}^N {a_j i(t-j)} +[1-\sum\limits_{j=1}^N {a_j } ][r\ast +\Delta p(t)+\gamma^{\Delta p} (\Delta p(t)-\Delta p\ast (t))+\gamma^y y(t)]+e(t) \end{displaymath}$

Many of the studies that assume smoothing motivate their choice by noting the high degree of serial correlation in the residuals of equations that do not include smoothing (e.g., the discussion of nominal interest rate rules in Orphanides (2007)).

It should be clear that our model of policymaker behavior implies serial correlation in the errors of policy rules that ignore time-variation in the inflation goal, because the inflation goal is a persistent omitted variable from such equations according to our model. In fact, our model implies that such specifications ignore a unit-root component in the policy rule, indicating that specifications with smoothing but without a time-varying inflation goal are quite likely to estimate large coefficients on the lagged dependent variable. This occurs because, according to our model, the policy rules estimated by many researchers omit an important variable by ignoring time-variation in the inflation target. Rudebusch (2002, 2006) has previously suggested that findings of policy smoothing probably reflect an omitted variable from the policy rule.

To examine a separate role for smoothing and a time-varying inflation target, we estimate the following system of equations:

Equation 10

$\begin{displaymath} \Delta p^{LR}(t)-\{\Delta p^{LR}(t-1)-\kappa \left( {\begin{array}{l} i(t-1)-\{a_1 i(t-2)+[1-a_1 ][2+... \ \Delta p(t-1)+\gamma^{\Delta p} (\Delta p(t-1)-\Delta p^{LR}(t-1))+\gamma^y y(t-1)]\} \ \end{array}} \right)\}=w(t) \end{displaymath}$

Equation 11

$\begin{displaymath} \begin{array}{c} \Delta i(t)=a_1 \Delta i(t-1)+[1-a_1 ][(1+\gamma^{\Delta p} )\Delta \Delta p(t)+\gamma^y \Delta y(t)]+... \ e(t)-e(t-1)-[1-a_1 ]\gamma^{\Delta p} u(t) \ \end{array}\end{displaymath}$

As before, we estimate this system using the generalized method of moments and allow for first-order serial correlation in the residuals. The instruments are the same as for the system of equation 7 and 8, with one addition: the second lag of the nominal interest rate is added to the instrument set for equation 10, consistent with the addition of that lag to the equation.

Table 7 reports the results for the professional forecasters and household measures (in columns 1 and 2, respectively). In both cases, there is no support for interest rate smoothing, as the coefficient a $_{1}$ is estimated to lie very close to or below zero. The inclusion of the additional variable also lowers the size and significance of the updating coefficient $\kappa$ ; given that there is no support for smoothing, the lower size and significance of the updating coefficient $\kappa$ may simply reflect the added noise induced into the system by inclusion of the lagged nominal interest rate. We readily admit that this test is a bit weak - it is extremely difficult to differentiate between a lag of the interest rate and a moving average error in a specification like equation 11.

Nonetheless, we interpret these findings as consistent with the idea that empirical evidence for a high degree of interest rate smoothing may stem from omitted variable bias as suggested by Rudebusch. Time-variation in the long-run goal for inflation, as suggested by the variation in long-horizon inflation expectations, seems a likely source of this omitted variable bias. This view is consistent with the variation in long-horizon inflation expectations in figure 1.

4.3 The cost of disinflation

In an economy in which the long-run inflation goal is varying over time, the speed with which the public's perception of the inflation goal is updated is a key determinant of the cost of disinflation, or the sacrifice ratio (Bomfim et al (1997), Erceg and Levin (2003), Kiley (2007b) and Roberts (2007)). Our empirical work captures this speed in the coefficient $\kappa$ , and we estimated $\kappa$ at a value near 0.02, give or take a bit.

Let's define the sacrifice ratio as the sum of the output gap over a period of disinflation divided by the change in inflation. Previous work has suggested a wide range of values for this measure - from about 2 to 4 over the last forty years in the United States (see Bomfim et al (1997)). In order to go from our estimate of $\kappa$ to a value for the sacrifice ratio requires a complete general-equilibrium model, and such an exercise is well beyond the scope of this paper. But Roberts (2007) considers this question in a fairly standard New-Keynesian general equilibrium model (that is not too dissimilar to that used in Erceg and Levin (2003)). He reports that a value for $\kappa$ near 0.02 is consistent with a sacrifice ratio near 2 over a five-year horizon.

5. Summary

An understanding of the historical variation in inflation expectations, especially at long horizons, is important for questions in macroeconomics and finance such as the nature of inflation dynamics, the costs of disinflation, and the relationship between yields on long-term bonds and short-term interest rates. We have provided an empirical examination of the variation in long-run inflation expectations that emphasizes the role of monetary policy actions.

We reach three conclusions regarding the experience in the United States since the late 1970s. First, long-run inflation expectations are not a function of past inflation alone, but depend on monetary policy actions, inflation, and economic activity. Reduced-form regressions provide weak evidence for these conclusions; our structural model provides stronger evidence. These results point to straightforward and easily interpretable results: tighter monetary policy lowers long-run inflation expectations, and higher inflation and stronger economic activity raise long-run inflation expectations absent a monetary policy response. Second, previous work that finds large interest-rate smoothing in monetary policy reaction functions has largely ignored time-variation in the inflation goal of the monetary authority; when such variation is taken into account, there appears to be little support for interest rate smoothing. And finally, our estimates for the speed with which monetary policy actions may influence long-horizon inflation expectations appears to be consistent with reduced-form evidence on the cost of disinflation, or the size of the sacrifice ratio, that has been reported in other studies.

Our research raises a number of interesting questions for further research. Examples include the following:

Is the experience in the United States regarding long-horizon inflation expectations similar to that in other countries?
How is the relationship between monetary policy actions and long-horizon inflation expectations affected by regimes that announce the inflation goal, like inflation targeting?
What are the related effects on inflation dynamics?
How might the available data on long-horizon inflation expectations, and their relationship to monetary policy actions, affect our understanding of fluctuations in the yield curve.

Some of these questions have been asked. But the answers to all of these questions may be more easily found through a greater attention to available data on long-horizon inflation expectations.

References

Ball, Laurence M. (1995) "Disinflation with Imperfect Credibility," Journal of Monetary Economics, February 1995, pp. 5-23.

Bernanke, Ben (2007) "Inflation Expectations and Inflation Forecasting." Speech at the Monetary Economics Workshop of the National Bureau of Economic Research Summer Institute, Cambridge, Massachusetts, July 10.

Bomfim, Antulio; Tetlow, Robert; Muehlen, Peter Von Zur; Williams, John (1997) Expectations, Learning and the Costs of Disinflation: Experiments using the FRB/US Model. Federal Reserve Board Finance and Economics Discussion Series 1997-42.

Bullard, James, and Kaushik Mitra (2002). "Learning about Monetary Policy Rules," Journal of Monetary Economics, vol. 49(September), pp. 1105-29.

Carroll, Christopher D. (2003). "Macroeconomic Expectations of Households and Professional Forecasters," Quarterly Journal of Economics, vol. 118 (February), pp. 269-98.

Cogley, Timothy (2005). "Changing Beliefs and the Term Structure of Interest Rates: Cross-Equation Restrictions with Drifting Parameters," Review of Economic Dynamics, vol. 8 (April), pp. 420-51.

Cogley, Timothy and Argia M. Sbordone (2006) Trend Inflation and Inflation Persistence in the New Keynesian Phillips Curve. Mimeo, University of California, Davis, July.

Cogley, Timothy, and Thomas J. Sargent (2007). "Inflation Gap Persistence in the U.S. (5.7 MB PDF)" University of California, Davis, working paper, January.

Croushore, Dean (1998) "Evaluating Inflation Forecasts," Federal Reserve Bank of Philadelphia Working Paper Number 98-14.

Erceg, Christopher, and Andrew Levin (2003). "Imperfect Credibility and Inflation Persistence," Journal of Monetary Economics, vol. 50 (May), pp. 915-44.

Gaspar, Vitor, Frank Smets, and David Vestin (2006). "Adaptive Learning, Persistence, and Optimal Monetary Policy," Journal of the European Economic Association, vol. 4 (April-May), pp. 376-85.

Gürkaynak, Refet, Brian Sack, and Eric Swanson (2005). "The Sensitivity of Long-term Interest Rates to Economic News: Evidence and Implications for Macroeconomic Models," American Economic Review, vol. 95 (March), pp. 425-36.

Hooker, Mark A. (2002) "Are Oil Shocks Inflationary? Asymmetric and Nonlinear Specifications versus Changes in Regime." Journal of Money, Credit, and Banking, May 2002, v. 34, iss. 2, pp. 540-61.

Ireland, Peter N. (2007) "Changes in the Federal Reserve's Inflation Target: Causes and Consequences," Journal of Money, Credit, and Banking, December 2007.

Kiley, Michael T. (2007a) "A Quantitative Comparison of Sticky-Price and Sticky-Information Models of Price Setting," Journal of Money, Credit, and Banking, vol. 39 (February), pp. 101-125.

Kiley, Michael T. (2007b) Inflation Dynamics and Monetary Policy: Comparing Small and Large-Scale Policy Models. Paper presented at the Federal Reserve System policy Conference, May 16, 2007, St. Louis, MO.

Kozicki, Sharon, and Peter Tinsley (2001). "Shifting Endpoints in the Term Structure of Interest Rates," Journal of Monetary Economics, vol. 47(June), pp. 613-52.

Levin, Andrew, Fabio Natalucci, and Jeremy Piger (2004). "The Macroeconomic Effects of Inflation Targeting (406 KB PDF)," Federal Reserve Bank of St. Louis, Review, vol. 86 (July), pp. 51-80.

Mankiw, N. Gregory, Ricardo Reis, and Justin Wolfers (2003). "Disagreement about Inflation Expectations," NBER Macroeconomics Annual, pp. 209-248.

Orphanides, Athanasios, and John C. Williams (2005). "Inflation Scares and Forecast-based Monetary Policy," Review of Economic Dynamics, vol. 8 (April), pp. 498-527.

Orphanides, Athanasios (2007) "Taylor Rules." Federal Reserve Board Finance and Economics Discussion Series 2007-18.

Roberts, John (1998) "Inflation Expectations and the Transmission of Monetary Policy." Federal Reserve Board Finance and Economics Discussion Series 1998-43.

Roberts, John (2006). "Monetary Policy and Inflation Dynamics," International Journal of Central Banking, vol. 2 (September), pp. 193-230.

Roberts, John (2007) "Learning, Sticky Inflation, and the Sacrifice Ratio." Mimeo, Federal Reserve Board.

Rudebusch, Glenn (2002) "Term Structure Evidence on Interest Rate Smoothing and Monetary Policy Inertia." Journal of Monetary Economics 49(6), September, 1161-1187.

Rudebusch, Glenn (2006) "Monetary Policy Inertia: Fact or Fiction?" International Journal of Central Banking 2 (4), December 2006, 85-135.

Rudebusch, Glenn, and Tao Wu (2003). "A Macro-Finance Model of the Term Structure, Monetary Policy, and the Economy (562 KB PDF)," Federal Reserve Bank of San Francisco Working Paper 2003-17, September.

Stock, James, and Mark Watson (2007). "Why Has U.S. Inflation Become Harder to Forecast?" Journal of Money, Credit, and Banking, vol. 39 (February), pp. 3-34.

Thomas Jr., Lloyd B. (1999) "Survey Measures of Expected U. S. Inflation," Journal of Economic Perspectives, 13, 125-144.

Taylor, John B. (1993) "Discretion versus Policy Rules in Practice." Carnegie Rochester Conference Series on Public Policy, December, 39, pp. 195-214.

Figure 1

A. Expected CPI inflation over the next 10 years from surveys of professional forecasters

Figure 1, Panel A Data

Figure 1

B. Expected inflation over the next 5 to 10 years from the Reuters/Michigan Survey of Consumers

(Raw data: dots; Interpolated data: line)
Figure 1, Panel B Data

Figure 2

A. CPI inflation (Four-quarter percent change in the CPI)

Figure 2, Panel A Data

Figure 2

B. Nominal federal funds rate (annual rate)

Figure 2, Panel B Data

Figure 2, continued

C. Output gap (percent deviation of GDP from trend, FRB/US model estimate)

Figure 2, Panel C Data

Table 1

Basic statistics for inflation and long-horizon inflation expectations

(Sample: 1978Q1 to 2007Q3)

	CPI inflation	Long-horizon expectation, professional forecasters	Long-horizon expectation, households
Mean	4.1	4.2	4.1
Median	3.4	3.6	3.5
Std. Dev.	3.2	1.8	1.6

Note: CPI inflation is measured by the percent change in the Consumer Price Index from the previous quarter, at an annual rate. The long-run expectations refer to the interpolated series presented in figure 1 based on several different surveys, as discussed in the text.

Table 2

Estimation results

(Sample: 1979Q1 to 2004Q2)

Parameter	(1) Professional Forecasters	(2) Professional Forecasters	(3) Household Measure	(3) Household Measure
$\kappa$	0.017 (0.011)	***0.020 (0.007)	0.013 (0.013)	**0.016 (0.007)
$\gamma$ $^{\Delta p}$	1.03 (1.52)	0.5	1.76 (2.55)	0.5
$\gamma$ $^{y}$	2.24 (1.51)	0.5	3.27 (3.30)	0.5

Note: Estimated via GMM. See text for discussion of instruments. Standard errors reported in parentheses (corrected for heteroskedasticity). ***, **, * denotes statistically different from zero at the 1, 5, and 10 percent levels, respectively.

Table 3

Estimation results

$\begin{displaymath} \Delta i(t)=(1+\gamma^{\Delta p} )\Delta \Delta p(t)+\gamma^y \Delta y(t)+e(t)-e(t-1)-\gamma^{\Delta p} u(t) \end{displaymath}$

(Sample: 1979Q1 to 2004Q2)

Parameter	(1) Professional Forecasters	(2) Household Measure
$\kappa$	***0.020 (0.006)	***0.026 (0.005)
$\gamma$ $^{\Delta p}$	0.30 (0.38)	-0.22 (0.32)
$\gamma$ $^{y}$	***1.22 (0.26)	***1.59 (0.31)

Table 4

Estimation results

$\begin{displaymath} \Delta p^S(t)-\{\Delta p^S(t-1)-\kappa \left( {i(t-1)-[2+\Delta p(t-1)+\gamma^{\Delta p} (\Delta p(t-1)-\Delta p^S(t-1))+\gamma^y y(t-1)]} \right)\}=w(t) \end{displaymath}$

$\begin{displaymath} \Delta i(t)=(1+\gamma^{\Delta p} )\Delta \Delta p(t)+\gamma^y \Delta y(t)+e(t)-e(t-1)-\gamma^{\Delta p} u(t) \end{displaymath}$

(Sample: 1979Q1 to 2004Q2)

Parameter	(1) Professional Forecasters	(2) Household Measure
$\kappa$	***0.015 (0.005)	***0.019 (0.004)
$\gamma$ $^{\Delta p}$	0.30 (0.45)	-0.20 (0.37)
$\gamma$ $^{y}$	***1.00 (0.26)	***1.44 (0.31)

Table 5

Estimation results (no interpolations)

$\begin{displaymath} \Delta p^S(t)-\{\Delta p^S(t-1)-\kappa \left( {i(t-1)-[2+\Delta p(t-1)+\gamma^{\Delta p} (\Delta p(t-1)-\Delta p^S(t-1))+\gamma^y y(t-1)]} \right)\}=w(t) \end{displaymath}$

$\begin{displaymath} \Delta i(t)=(1+\gamma^{\Delta p} )\Delta \Delta p(t)+\gamma^y \Delta y(t)+e(t)-e(t-1)-\gamma^{\Delta p} u(t) \end{displaymath}$

(Sample: 1979Q1 to 2004Q2)

Parameter	(1) Professional Forecasters	(2) Household Measure
$\kappa$	***0.015 (0.005)	-0.007 (0.010)
$\gamma$ $^{\Delta p}$	-0.02 (0.52)	0.30 (0.31)
$\gamma$ $^{y}$	***0.83 (0.29)	***0.62 (0.19)

Note: Estimated via GMM. See text for discussion of instruments. Standard errors reported in parentheses (corrected for heteroskedasticity and first-order serial correlation). ***, **, * denotes statistically different from zero at the 1, 5, and 10 percent levels, respectively. Dropping interpolations changes the sample periods. In column 1, the sample for the updating equation is 1980Q3 to 2004Q2, with observations missing in 1991Q3 and 1991Q4; the sample for the rule equation is 1980Q4 to 2004Q2, with observations missing in 1991Q4 and 1992Q1. In column 2, the sample for the updating equation is 1986Q2 to 2004Q2, with observations missing from 1988Q1 to 1990Q2; the sample for the rule equation is 1986Q3 to 2004Q2, with observations missing from 1988Q2 and 1990Q3.

Table 6

Reduced-form equation for survey measures

$\begin{displaymath} \Delta \Delta p^S(t)=a_0 +a_1 [\Delta p(t-1)-\Delta p^S(t-1)]+a_2 i(t-1)+a_3 y(t-1)+\varepsilon (t) \end{displaymath}$

(Sample: 1979Q1 to 2004Q2)

Parameter	Professional Forecasters	Households
a $_{1}$	***0.044 (0.011)	-0.015 (0.022)
a $_{2}$	***-0.014 (0.005)	-0.005 (0.009)
a $_{3}$	-0.001 (0.007)	***0.031 (0.011)

Table 7

Estimation results

(Sample: 1979Q1 to 2004Q2)

Parameter	(1) Professional Forecasters	(2) Household Measure
a $_{1}$	-0.21 (0.23)	-0.02 (0.13)
$\kappa$	0.003 (0.002)	0.001 (0.003)
$\gamma$ $^{\Delta p}$	0.27 (0.39)	-0.32 (0.33)
$\gamma$ $^{y}$	***1.26 (0.32)	***1.07 (0.33)

Footnotes

1. Address: Mail Stop 76, Federal Reserve Board, Washington, DC 20551. Email: [email protected]. I would like to thank Alan Kackmeister, David Lebow, Dave Reifschneider and John Roberts for comments on this research. Any remaining errors are the sole responsibility of the author. The views expressed herein are those of the author, and do not reflect the views of the Board of Governors of the Federal Reserve System or its staff. Return to Text

2. . In contrast, a large literature has examined the behavior of near-term inflation expectations, largely to examine the degree to which such expectations are unbiased and efficient; Croushore (1998) and Thomas (1999) discuss the literature in some detail. Roberts (1998) and Carroll (2003) examine models of near-term expectations. Mankiw, Reis, and Wolfers (2002) recently considered the dispersion in inflation expectations - a novel and potentially important topic. Levin, Natalucci, and Piger (2004) show that long-run inflation expectations fluctuate and are correlated with recent readings on inflation, but do not investigate the behavior of long-run inflation expectations more generally. Bernanke (2007) suggests that a better understanding of the learning rule that governs inflation expectations at long-horizons may help policymakers in their forecasting of inflation and monetary policy deliberations. Return to Text

3. In particular, they consider one of the measures we analyze below (the measure we call the professional forecasters' measure) for a subsample of the period we consider. Return to Text

4. While the Taylor principle is not a central concern herein, it is important to the properties of the basic New-Keynesian model of fluctuations. Return to Text

^♣ This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to Text