
The TIPS Yield Curve and Inflation Compensation 1
Keywords: Yield curve, treasury market, inflation compensation, risk premia
Abstract:
For over ten years, the U.S. Treasury has issued index-linked debt. Federal Reserve Board staff have fitted a yield curve to these indexed securities at the daily frequency from the start of 1999 to the present. This paper describes the methodology that is used and makes the estimates public. Comparison with the corresponding nominal yield curve allows measures of inflation compensation (or breakeven inflation rates) to be computed. We discuss the interpretation of inflation compensation and its relationship to inflation expectations and uncertainty, offering some empirical evidence that these measures are affected by an inflation risk premium that varies considerably at high frequency. In addition, we also find evidence that inflation compensation was held down in the early years of the sample by a premium associated with the illiquidity of TIPS at the time. We hope that the TIPS yield curve and inflation compensation data, which are posted here and will be updated periodically, will provide a useful tool to applied economists.
1. Introduction
For over ten years, the U.S. Treasury has issued Treasury inflation-protected securities (TIPS) - debt securities for which the coupon and principal payments are indexed to the Consumer Price Index (CPI) - in addition to conventional nominal bonds. However, for both nominal securities and TIPS, the Treasury issues only securities with particular maturities and coupon rates. Thus, it is not possible to directly observe the nominal or real discount factors from these issues.
In our previous paper (Gürkaynak, Sack and Wright, 2007), we estimated a smoothed nominal Treasury yield curve from the outstanding off-the-run nominal Treasury notes and bonds. The results allowed us to compute the nominal discount factor, as well as to compute nominal Treasury yields and forward rates at any horizon. The first part of this paper is the sequel that fits a similar yield curve to outstanding TIPS. The results allow us to recover the real discount function as well as real Treasury yields and forward rates at a daily frequency back to 1999. These data are available online and will be updated periodically.
A comparison of the nominal and TIPS smoothed yield curves allows us to compute measures of inflation compensation-the rate of inflation that would give an investor the same return at maturity on a nominal security and a TIPS. These measures are also known as breakeven inflation rates among
financial market participants. These yield curves (nominal, TIPS and inflation compensation) can be expressed in terms of zero-coupon yields, par yields, instantaneous forward rates, or ![]() -by-
-by-![]() forward rates (that is, the
forward rates (that is, the ![]() -year rate beginning
-year rate beginning ![]() years ahead) for any
years ahead) for any ![]() and
and ![]() .
.
In addition to describing how we fit the real yield curve, the paper provides some discussion on how to interpret the resulting measures. In the second part of the paper, we pay particular attention to the measures of inflation compensation in this regard. These measures are driven to a great extent by investors' expectations of inflation. However, we argue that high-frequency movements in inflation compensation are considerably too volatile to represent revisions to rational expectations of inflation alone: Inflation compensation provides information about agents' inflation expectations but its interpretation is complicated by inflation risk premia and the differential liquidity premia between TIPS and nominal securities. We provide support of this view by analyzing the time series properties of inflation compensation and actual inflation and by comparing inflation compensation to survey respondents' inflation forecasts. Among other results, we show that inflation risk premia are related to the dispersion of survey forecasts.
Section 2 describes the mechanics of TIPS and briefly discusses the operation of the TIPS market. Section 3 describes the yield curve fitting exercise. Section 4 shows the results of our estimation, including an assessment of the fit of the TIPS curve. Section 5 provides some empirical analysis that is pertinent to the interpretation of inflation compensation. Section 6 provides a proxy for inflation compensation that can be extended back to 1971. Section 7 offers some concluding thoughts. The data are posted as an appendix to the paper on the FEDS website.
2. The TIPS market
A nominal Treasury security pays the holder a coupon twice a year and the principal value at maturity. The coupon and principal value are fixed in nominal terms, and their value will be eroded over time by inflation. For TIPS, on the other hand, the principal payment is multiplied by the ratio
of the reference CPI on the date of maturity to the reference CPI on the date of issue.3 If the maturity or issue date falls on day ![]() of a month with
of a month with ![]() days, then the reference CPI is
days, then the reference CPI is
where
The first TIPS were issued in 1997. Treasury initially sold five-, ten-, and thirty-year TIPS. The five-year TIPS was dropped in September 1998 and the thirty-year TIPS was dropped in October 2001. Subsequently, the five-year TIPS was reintroduced and a twenty-year TIPS was added in May 2004. As of the time of writing, there are 24 outstanding TIPS with maturity dates ranging from 2008 to 2032.
Liquidity in TIPS was initially poor, and investor participation in the market was limited, either due to lack of familiarity with the asset class or in some cases institutional rules preventing these securities from being held. Another important factor shaping the market was that, for a time, the long-term future of TIPS was unclear. For example, in May 2001, the Treasury Advisory Committee of the Bond Market Association recommended that the TIPS program be discontinued. However, the Treasury subsequently reaffirmed its commitment to the program, and liquidity improved substantially. TIPS now represent about 10 percent of the outstanding supply of Treasury coupon securities and trading volumes in TIPS are now generally comparable to those on off-the-run nominal Treasury securities.6 More detail on the history and liquidity of the TIPS market is provided by Sack and Elsasser (2004).
3. Yield curve fitting
This section begins by reviewing the fundamental concepts of the yield curve, including the necessary "bond math" for determining both nominal and TIPS yields. It then describes the specific estimation method employed in this paper.
textit3.1 Discount Function and Zero-Coupon Yields: Nominal and Real
The starting point for pricing any nominal fixed-income asset is the nominal discount function, or the price of a nominal zero-coupon bond. This represents the value today to an investor of a $1 nominal payment ![]() years hence. We denote this as
years hence. We denote this as ![]() . The continuously compounded yield on this nominal zero-coupon bond can be written as
. The continuously compounded yield on this nominal zero-coupon bond can be written as
Here and throughout, yields and coupon rates are expressed in percentage points; for example, 5 percent is written 0.05.
In the same way, we consider a real discount function, or the price of a real zero-coupon bond. We denote this as
![]() . This represents the value today to an investor of a $
. This represents the value today to an investor of a $
![]() payment
payment ![]() years hence where
years hence where ![]() denotes the price index at time
denotes the price index at time ![]() .7 The continuously compounded nominal yield on this bond is
.7 The continuously compounded nominal yield on this bond is
![]() . The continuously compounded real yield on this bond can be written as
. The continuously compounded real yield on this bond can be written as
![]() . Our convention henceforth throughout this paper is that we shall discuss real bonds in terms of their real yields and nominal bonds in terms of their
nominal yields.
. Our convention henceforth throughout this paper is that we shall discuss real bonds in terms of their real yields and nominal bonds in terms of their
nominal yields.
3.2 Par yields and forward rates.
As discussed in our earlier paper (Gürkaynak, Sack and Wright, 2007), there are a number of ways of expressing the information in the nominal yield curve in addition to continuously compounded zero-coupon yields. One way is to solve for the coupon rate which ensures that the price of the bond today will equal its maturity price. This is known as the par yield and is the market convention used to describe bond yields. Par yields are quoted with semiannual compounding because coupons on U.S. Treasury securities are paid twice per year. An alternative way of describing the yield curve is in terms of forward rates. We can solve for continuously-compounded instantaneous forward rates at all horizons. Or we can solve for m-year forward rates beginning n-years hence.8
All of these concepts apply to both TIPS and nominal securities, giving us two parallel sets of yields. In this paper, let ![]() and
and
![]() denote the n-period ahead nominal and real instantaneous forward rates, and let
denote the n-period ahead nominal and real instantaneous forward rates, and let
![]() and
and
![]() denote the
denote the ![]() -year nominal and real forward rates beginning
-year nominal and real forward rates beginning
![]() years hence, respectively. In addition, we will use
years hence, respectively. In addition, we will use
![]() and
and
![]() to denote the
to denote the ![]() -year nominal and real par yields, respectively.
-year nominal and real par yields, respectively.
3.3 The Nelson-Siegel-Svensson yield curve
Rather than fitting a spline-based, nonparametric curve, we impose some structure on the shape by imposing a parametric form that fits the TIPS yields remarkably well. The benefit of the parametric approach is that it smoothes through the idiosyncratic movements in yields of individual securities and accurately represents the underlying shape of the (real) discount function.
The yield curves that we fit assume that the instantaneous forward rates (whether real or nominal) follow the functional form
The assumed functional form of the forward rates (and hence yields) has some intuitive characteristics. As discussed in more detail in our earlier paper, it allows the forward rate curve the flexibility to start and end at estimated parameters, and to have a hump-shaped pattern in-between. The Nelson-Siegel functional form effectively allows for only one hump, whereas the Svensson curve allows for two humps. Below we will show that allowing the second hump is important to capture convexity effects at longer horizons. The estimated parameters will determine the magnitude and location of these humps.
Given any candidate set of parameters, we can use (4) to solve for the nominal and real discount factors. With these discount factors, we can construct a predicted price for any Treasury security (nominal or real) with a given maturity date and coupon rate by considering it to be a bundle of zero-coupon securities, one corresponding to each payment on the security, with the value of each payment determined by the appropriate discount factor. We then estimate the nominal and TIPS yield curves by numerically choosing the set of parameters so as to minimize the weighted sum of squared deviations between actual and predicted prices. The weights are the inverse of the durations of each individual security.9
The ranges of maturities available for estimation over our sample are shown graphically in Figure 1, which takes the same form as a figure reported by Bliss (1996). The date is shown on the horizontal axis, the remaining maturity is shown on the vertical axis, and each outstanding TIPS security is represented by a dot showing its remaining maturity on that date. For example, a dot at a ten-year maturity in 2000 denotes a security that is to mature ten years later, in 2010. The remaining maturity of that security will be traced out by a downward-sloping line, with the maturity shrinking as time passes.
As noted before, the Svensson curve allows for two humps, while the original Nelson-Siegel functional form allows for just one hump. The second hump is however not well identified unless we have enough long-term securities. As discussed in Gürkaynak, Sack and Wright (2007), for the nominal yield curve we used the restricted functional form up to 1980, but then we switched to the Svensson parameterization after that point because more long-term nominal Treasury securities became available to estimate the shape of more distant forward rates. Following similar reasoning, and given the maturities available as shown in Figure 1, for the TIPS yield curve we used the more restricted functional form up to the end of 2003, and we switch to the Svensson parameterization after that point as the issuance of 20-year TIPS helped the estimation.
TIPS with less than 18 months to maturity are dropped from the estimation of the TIPS yield curve, because the effect of the indexation lag makes the prices of these securities erratic. TIPS with remaining maturity between 18 and 24 months are downweighted linearly for smooth behavior of the short-end of the curve over time. All other TIPS are included in estimation of the TIPS yield curve, as there is no particular liquidity premium in on-the-run TIPS securities. (By comparison, for the nominal yield curve we excluded on-the-run and first-off-the-run securities because they often command a premium for liquidity that pushes them away from the yield curve.)
3.4 Inflation Compensation
Having computed nominal and TIPS yields, it is straightforward to solve for rates of inflation compensation, or what market participants typically refer to as breakeven inflation rates. These rates are defined as the inflation rates which, if realized, would leave an investor indifferent between holding a TIPS and a nominal Treasury security.
The formula is simplest for the continuously compounded zero-coupon inflation compensation rate:
It simply states that the cumulative amount of inflation needed to equalize the return on nominal and real zero-coupon securities, expressed as an annual inflation rate on a continuously-compounded basis, is given by the difference in the nominal and real yields. Similarly, the continuously compound instantaneous forward inflation compensation rate is as follows:
For par securities, the semi-annually compounded inflation compensation rate is as follows:
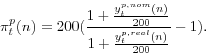
To be more precise, inflation compensation represents the increase in the index ratio required to equalize the returns on the securities. Because of the indexation lag in the construction of TIPS, this will not correspond exactly to the rate of inflation required over that period. Instead, it represents the rate of inflation required from about 2
4. Yield curve results
Using the above methodology, we estimate the U.S. TIPS yield curve using daily data from January 1999 to the present. Our underlying quotes on individual TIPS are kindly provided to us by Barclays Capital Markets.11
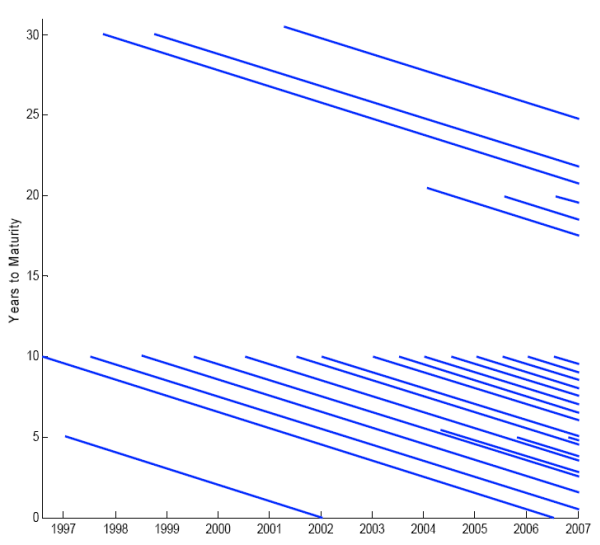
As an example of the results, Figure 2 shows the estimated TIPS yield curve on June 1, 2005. The solid line is the continuously compounded par yield curve, the open circles are the actual quotes on all outstanding coupon securities included in the estimation, and the crosses are the predicted yields for these issues.12
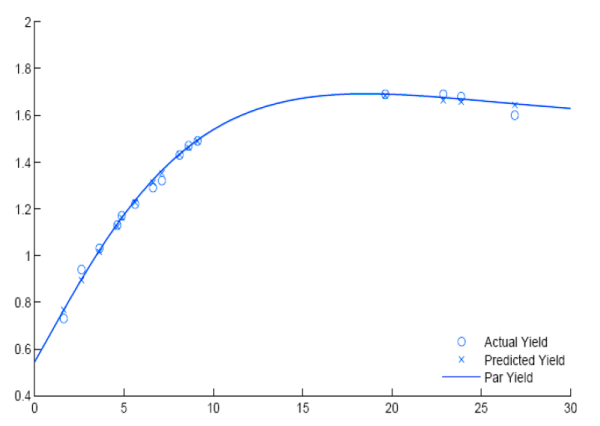
As can be seen, the yield curve generally does an impressive job fitting the entire cross-section of TIPS issues with a function of only six parameters. The success at fitting TIPS yields on this date is repeated throughout the sample. Figure 3 shows the average absolute yield prediction error in different maturity buckets over time. As can be seen, all of the errors are quite small over the entire sample. The largest fitting errors tend to be seen in the very shortest (2-5 year) and longest (20-30 year) maturity buckets, and even there the typical errors are only a few basis points.
Figure 4 returns to the specific date considered in Figure 3, only now showing the zero-coupon TIPS yield curve and the instantaneous forward rates at all horizons, as well as the corresponding measures for inflation compensation. In June 2005, the Federal Reserve was in the middle of a tightening cycle. The TIPS yield curve sloped up at that time, reflecting expectations for the continued removal of monetary policy accommodation and perhaps a real-interest-rate risk premium that was increasing in maturity. Most likely because of convexity effects, the upward slope of the zero-coupon TIPS yield curve tapers off at long horizons and eventually turns down. Accordingly, the forward rates turn down earlier and much more sharply. Inflation compensation slopes down at short to intermediate maturities, perhaps reflecting expectations for a moderation in headline inflation, but then slopes up at intermediate and longer maturities, presumably owing in part to an inflation risk premium that is increasing in maturity.
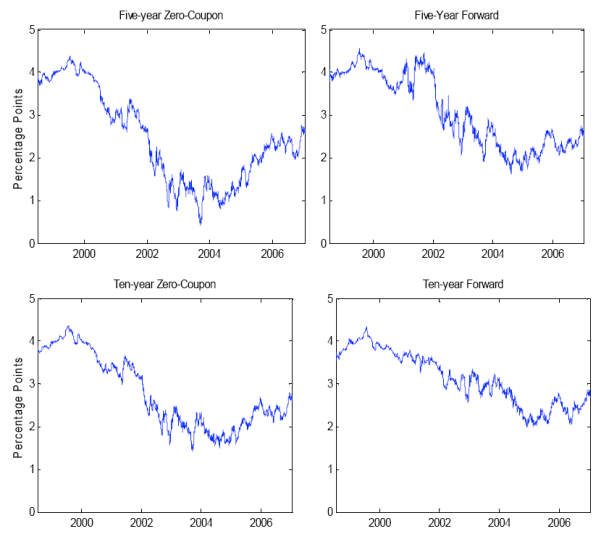
The history of five- and ten-year zero-coupon and instantaneous forward TIPS yields is shown in Figure 5. As can be seen in the figure, in 1999, TIPS yields were high reflecting in part the premium that investors demanded to induce them to hold these assets that were then quite illiquid. TIPS yields subsequently declined sharply, as liquidity improved and the FOMC eased monetary policy to combat the most recent recession. The FOMC began to tighten monetary policy again in the middle of 2004. Five-year zero-coupon TIPS yields began to rise, as expected, but ten-year instantaneous forward TIPS yields fell over 2004 and remained quite low through 2006. The fall in distant-horizons forward (nominal) rates over this period was famously termed the "conundrum" by former Fed Chairman Greenspan and is discussed in Kim and Wright (2005) and Backus and Wright (2007). Here we see the same phenomenon in real rates.
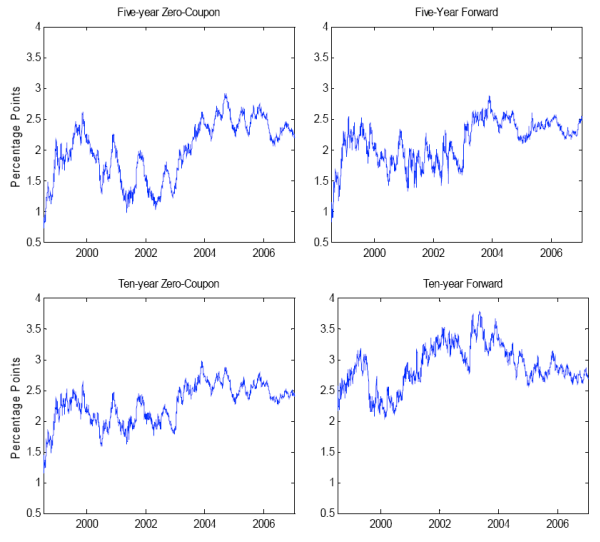
The behavior of five- and ten-year zero-coupon and instantaneous forward inflation compensation over the sample is shown in Figure 6. Inflation compensation was quite low in 1999, reflecting the poor liquidity of TIPS relative to nominal securities (the counterpart of the high TIPS yields at that time). Breakeven inflation rates tended to drift higher through 2003, a pattern that is most apparent in the ten-year forward rate, in part because of the improvement in TIPS liquidity. In addition, investors may have become more concerned about upside inflation risks by early 2004, in light of the updrift in realized inflation, the rebound in growth, and the accommodative stance of monetary policy. Since 2004, inflation compensation has remained in a fairly narrow range at all horizons, with forward rates drifting down some.
One measure that is of particular interest is the five-year forward five-year inflation compensation rate (also known as the five-year five-year forward breakeven inflation rate), because it has been explicitly mentioned by a number of Fed policymakers in their speeches. The behavior of this measure is often taken as a gauge of the Fed's inflation-fighting credibility. Policymakers seem to look to this measure to help judge whether near-term inflation pressures are working their way into longer-term expectations. The concern is that such leakage would create a more persistent inflation problem that would then be costly to reverse. If the Fed maintains its credibility, then the forward inflation compensation measure should be relatively unresponsive to information about the near-term outlook.13 This measure, which can be derived from our yield curves as a par forward rate over a five-year horizon, is shown in Figure 7. It shares many of the same properties of the instantaneous forward rates discussed above.
The yield curve estimated above is intended to be flexible enough to capture the general shape of TIPS yields while smoothing through some of the factors that might affect individual securities. One such factor is the seasonality of CPI. Because TIPS are indexed to non-seasonally adjusted CPI, the yield on an individual security will reflect the expected seasonal change in the index ratio between the quote date (or more specifically the settlement date) and the maturity date of the security. This has two effects; it causes some variation in yields over time as the seasonality of the quote date changes, and it causes some variation across individual securities. For example, TIPS securities that mature in April tend to have higher yields and lower breakeven rates than those maturing in January, because the CPI seasonal corresponding to the April maturity is much lower than that corresponding to the January maturity (reducing the price of the April TIPS and hence raising their yield). At longer maturities, the impact of the seasonal pattern gets amortized over a longer period and is negligible, but it can be important at shorter horizons. The Svensson yield curve, however, smoothes through this variation across maturity months. This feature is desirable for our curve, as it is designed to extract information about macroeconomic expectations and risks.14
The appendix that accompanies this paper provides data on zero-coupon yields (continuously compounded), instantaneous forward rates (continuously compounded), and par yields (coupon-equivalent) for TIPS securities at a range of maturities as well as the five-year forward par five-year TIPS yield (coupon-equivalent). The maturities included span from 5 to 20 years for the period through 2004, and from 2 to 20 years for the period since then (when we use the more flexible specification, as discussed above). Yields at maturities below 5 years are not reported before the end of 2004 because, as can be seen in Figure 1, this would at times have entailed extrapolating the TIPS yield curve outside of the range of maturities that were actually outstanding. Meanwhile, yields for maturities below 2 years are never reported because the shortest maturity TIPS are excluded from our smoothed yield curve on account of the indexation lag and other near-term carry considerations.
The data are daily and are available back to January 4, 1999. The appendix also includes estimates of the six parameters of the Svensson TIPS yield curve and the zero-coupon, instantaneous forward and par rates of inflation compensation, and the five-year forward five-year rate of inflation compensation. This appendix is posted on the website http://www.federalreserve.gov/pubs/feds/2008/200805/feds200805.xls, using the mnemonics described in Table 1. We intend to update the data regularly, as a resource for academic researchers and financial market practitioners.
5. The behavior of inflation compensation
Armed with the TIPS yields and inflation compensation rates constructed above, we can now conduct some empirical analysis that is relevant for interpreting these measures. We focus specifically on inflation compensation rates.
Inflation compensation is a mechanical calculation of the level of inflation which, if realized, would give investors the same return on TIPS and nominal Treasury securities. It is often used as a measure of inflation expectations, but this is correct only if investors are risk-neutral and there is no liquidity premium. In this section we provide several strands of analysis supporting the notion that variation in the inflation risk premium and the liquidity premium constitute an important part of the behavior of inflation compensation.
5.1 The volatility of forward inflation compensation rates
In this subsection we address whether distant-horizon forward rates of inflation compensation can be viewed simply as measures of the long-run expected level of inflation, or the implicit inflation target of the central bank. If a ten-year forward rate of inflation compensation really is the rational long-run expectation of inflation, then it should be a martingale. Otherwise, the expectation of the long-run expectation of inflation tomorrow would differ from the long-run expectation of inflation today, which is impossible by the law of iterated expectations.
Table 2 shows the standard deviation of one-day and one-, three- and six-month changes in ten-year ahead forward instantaneous inflation compensation. The standard deviation of a one-day change in forward inflation compensation is a bit less than 5 basis points. If this ten-year forward
inflation compensation really is a martingale, then the volatility of ![]() -period changes must be
-period changes must be ![]() times the volatility of one-period changes. This can be tested by a variance ratio test. Accordingly, Table 2 also reports variance ratio statistics testing the hypothesis that ten-year forward inflation compensation is a martingale. The test statistic is
times the volatility of one-period changes. This can be tested by a variance ratio test. Accordingly, Table 2 also reports variance ratio statistics testing the hypothesis that ten-year forward inflation compensation is a martingale. The test statistic is ![]() in the notation of Lo and MacKinlay (1998), which means that it is the variance ratio statistic that allows for time-varying conditional heteroskedasticity. Under the martingale hypothesis,
this test statistic has a standard normal asymptotic distribution. However, we see in Table 2 that the test rejects in the left tail, meaning that the volatility of longer-term changes in inflation compensation is too small relative to the volatility of daily changes for inflation compensation to
be a martingale.15
in the notation of Lo and MacKinlay (1998), which means that it is the variance ratio statistic that allows for time-varying conditional heteroskedasticity. Under the martingale hypothesis,
this test statistic has a standard normal asymptotic distribution. However, we see in Table 2 that the test rejects in the left tail, meaning that the volatility of longer-term changes in inflation compensation is too small relative to the volatility of daily changes for inflation compensation to
be a martingale.15
Stock and Watson (2007) find that an unobserved components model with stochastic volatility provides good forecasts for inflation. The model is a univariate model in which inflation is the sum of a martingale permanent component and a martingale difference sequence transitory component. The variance of the innovations to both components is allowed to be time-varying. At any point in time, the forecast of future inflation at any horizon is equal to the estimated permanent component. And the volatility of that forecast is the volatility of the permanent component. Stock and Watson find that the volatility of the permanent component was high in the early 1980s but has fallen since then and is now about 19 basis points per quarter. The standard deviation of one-day changes in ten-year inflation compensation is 4.8 basis points. So if we interpret ten-year inflation compensation as a long-run inflation measure and appeal to the martingale property that this implies, then the volatility of quarterly changes in long-run inflation expectations should be 38 basis points per quarter, which is twice as big as Stock and Watson estimate. We conclude from these exercises that inflation compensation is too volatile at high frequency to represent inflation expectations alone.
5.2 Comparison to surveys of inflation expectations
Twice a year, in March and October, Blue Chip Economic Indicators collects long-range forecasts of CPI inflation five-to-ten years hence from a large number of professional forecasters. It seems worthwhile to compare the survey results with average five-to-ten year forward inflation compensation in each of the survey months. After all, at least at shorter horizons, surveys have been remarkably accurate predictors of future inflation (Ang, Bekaert and Wei, 2007).
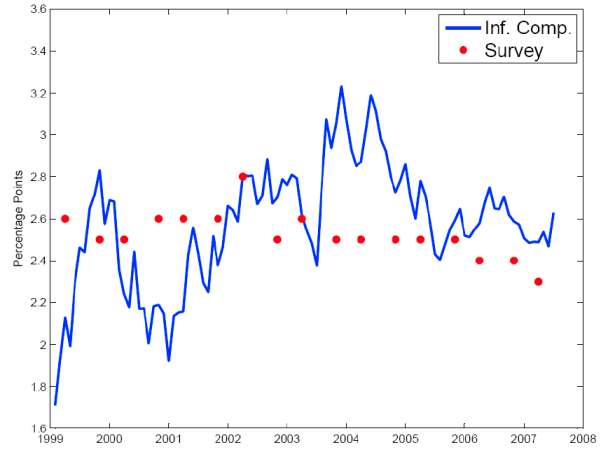
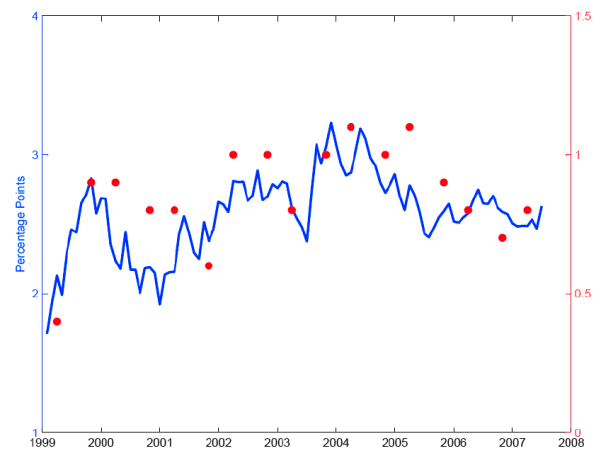
Figure 8 plots the time series of the mean survey forecast and five-to-ten year forward inflation. Inflation compensation has been far more volatile than survey expectations, and the two have no consistent relationship with each other. Since 2002, survey expectations have been consistently below
inflation compensation, suggesting that the inflation risk premium (which pushes inflation compensation up) now outweighs the TIPS liquidity premium (which pushes inflation compensation down). 16![]() 17
17
It is also of interest to study the association between inflation compensation and investors' uncertainty about inflation. Macroeconomic uncertainty is very hard to measure and we are not aware of any survey asking respondents for density forecasts at long horizons. But, the dispersion of long-horizon survey responses may serve as a crude proxy for uncertainty.18 The Blue Chip surveys report a simple dispersion measure for their long-horizon survey questions, which is the difference between the average of the ten highest forecasts and the average of the ten lowest forecasts. Figure 9 plots the time series of this dispersion measure for CPI and five-to-ten year forward inflation compensation. There is a moderately strong positive association between these two variables. In fact, the correlation between the survey dispersion and five-to-ten year forward inflation compensation in the survey months is 0.71, which seems reasonable if inflation compensation represents in part a risk premium: compensation for uncertainty about future inflation.
In 2003 and 2004 both the survey dispersion and forward inflation compensation increased and subsequently declined. Arguably, during the period when the federal funds rate was kept at 1 percent to forestall the possibility that the U.S. might enter into a deflationary period, investors were quite uncertain about the long-run inflation level and accordingly demanded a relatively big inflation risk premium. As monetary policy accommodation was removed, uncertainty and inflation risk premia fell. Declining uncertainty about inflation is one of the candidate explanations for the "conundrum" proposed by Backus and Wright (2007).19
5.3 Take-aways on inflation compensation
The evidence presented in this section suggests that it would be a mistake to interpret every change in inflation compensation as a pure change in inflation expectations. Rather, as an accounting equation, inflation compensation represents inflation expectations plus an inflation risk premium minus the TIPS liquidity premium. The liquidity premium moves slowly over time (as will be shown below). However, the evidence above suggests that the inflation risk premium may exhibit considerable volatility even over relatively short horizons.
Variation of the inflation risk premium should not be surprising, especially considering that the expectations hypothesis of the nominal term structure is routinely rejected (meaning that nominal term premiums vary over time). It is intuitive to think of the inflation risk premium as depending on uncertainty about inflation. This is consistent with the positive association between inflation compensation and the dispersion of survey forecasts of inflation. It may also help to account for the apparent excess volatility of inflation compensation relative to rational expectations of inflation. A consideration that may further boost the volatility of inflation compensation is a positive correlation between the level of inflation and uncertainty about inflation (as found by Friedman (1977) and Ball (1992)), in which case an increase in inflation expectations would also cause the inflation risk premium to rise and hence prompt an outsized movement in inflation compensation.20
Even though inflation compensation conflates investors' inflation expectations with the price and quantity of inflation risk, it is nonetheless a very useful indicator of investors' inflation concerns. Moreover, it is the only inflation indicator that is available at high frequency, which makes it quite useful in a range of applications. To obtain model-based decompositions of TIPS-based inflation compensation into its inflation expectation, risk premium and liquidity premium components, one would have to turn to a structural yield curve model, such as the affine model presented in D'Amico, Kim and Wei (2007).
6. Backcasting inflation compensation
The TIPS yield curve and the associated inflation compensation term structure have many applications for practitioners and researchers, but their usefulness is limited by the relatively short sample over which data are available to study their properties. Indeed, TIPS have been available for only about a decade, while nominal Treasury securities have a much longer history. But the longer history of nominal yields raises an interesting possibility: If the relationship between nominal yields and inflation compensation has been relatively stable over time, it should be possible to backcast inflation compensation using the observed relationship between the nominal yields and inflation compensation in the recent sample. That is, we can find the combination of nominal yields that best proxies a particular breakeven measure over the period for which we have TIPS, and we can then compute this proxy over a much longer sample.
Before doing the backcasting, we take a related intermediate step and focus on the factor structure of the nominal yield curve and its components--the TIPS and inflation compensation curves. It is well known that the term structure of nominal yields can be well explained by a small number of principal components. These factors are often interpreted as having to do with macroeconomic factors such as the business cycle, inflation prospects, and the steady-state level of real rates. Most of the variation in nominal yields can be explained by the first principal component which, given the factor loadings, can be interpreted as the level of yields. Including two more principal components--commonly interpreted as the slope and curvature, respectively--accounts for nearly all of the variation in yields.
Using month-end data since January 2003, Table 3 shows the fraction of the variance in zero-coupon nominal yields at annual maturities from two to twenty years that can be explained by the first few principal components. Of course, the fact that our Svensson yield curves are tightly parameterized functional forms with just 6 parameters guarantees that the smoothed yields will have a low-dimensional representation, but the nominal yield curve fits remarkably well so it seems very likely that the same would be true for a spline-based curve as well. The first principal component (that we think of as the level) explains 61 percent of the variation in nominal yields, and the first three factors together account for essentially 100% of the variation.21 Thus, any information contained in the nominal yield curve (such as the information contained in inflation compensation) should be well represented by the first three factors.
As an aside, we run the same principal components decomposition on the TIPS yields and inflation compensation at the same maturities. Interestingly, the same result holds, with almost all of the variation accounted for by several factors. Indeed, the first factor alone explains even a greater share of the TIPS yields and inflation compensation than it does for the nominal yields. Thus, the parsimonious representation of the nominal yield curve seems to hold up once one digs into the various components of the nominal yields. This is a topic that we hope to return to in future research.
If nominal Treasury yields in fact embed much of the information contained in inflation compensation, we can create a proxy by regressing inflation compensation on the first three principal components of the nominal term structure.22 Specifically, we do so for the five-year forward five-year inflation compensation rate shown earlier in Figure 7. However, the exercise is complicated by the poor liquidity of TIPS in the early years of the TIPS program. Accordingly, we estimate the regression using month-end data that starts only in 2003.
The R-squared from this regression is 79 percent, indicating a fairly tight relationship between inflation compensation and the nominal term structure. Of course the relationship is not perfect. Note that an R-squared too close to unity would imply that inflation compensation (and therefore the TIPS yield) can be perfectly synthesized from the nominal term structure and therefore that TIPS are redundant securities. The R-squared we find is high enough to let us confidently assert that there exists a strong time series relationship between the nominal yield curve and inflation compensation, but it is not so high as to diminish the relevance of TIPS.
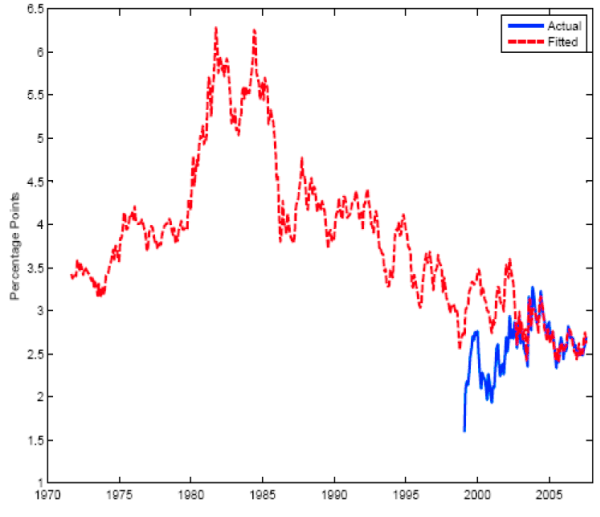
In the backcasting exercise we used the coefficients from the regression and the longer history of nominal term structure data to obtain fitted five-to-ten-year forward inflation compensation back to 1971. This sample covers both the period before index linked securities existed (before 1997) and the period in which TIPS liquidity was poor (1997 to 2002). Figure 10 shows the actual and fitted inflation compensation series.
One result that emerges from this exercise is an estimate of the liquidity premium for TIPS over the period from 1999 to 2002. As can be seen from the figure, actual inflation compensation was well below fitted inflation compensation, consistent with investors demanding a higher yield on TIPS (relative to nominal yields) to compensate them for the poor liquidity of these securities. This estimated liquidity premium is big, but it is also very inertial. Indeed, throughout this period the higher-frequency movements in inflation compensation tracked those of its fitted value, suggesting that these movements were not generated by the liquidity premium. The liquidity premium instead remained big in the early years and then gradually faded by 2003.
The assumption that the relationship between hypothetical inflation compensation and nominal yields has been stable over the period since 1971 is a very strong one, and the fitted values from this regression should be treated as only a crude proxy for inflation compensation, especially in the early part of the sample. Nonetheless, the behavior of the fitted value of inflation compensation over the longer period since 1971 appears qualitatively reasonable. It rose in the late 1970s and exceeded 6 percent in the early 1980s, presumably reflecting both a high level of longer-term inflation expectations and a sizable inflation risk premium. It declined sharply in the mid 1980s and drifted lower over the next 15 years, likely because investors were revising down both their inflation expectations and the compensation that they demanded for inflation risk over that period. In recent years, inflation compensation has shown much more stability, remaining in a tight range by historical standards. This likely reflects the fact that longer-term inflation expectations have stabilized and that the inflation risk premium has remained relatively low (and thus has not swung over a big range).
7. Conclusion
In this paper we have estimated the U.S. TIPS yield curve using an approach that is simple and parsimonious. The methodology is quite effective at capturing the general shape of the yield curve while smoothing through idiosyncratic variation in the yields of individual inflation-protected securities. The estimated yield curve can be expressed in a variety of ways, including zero-coupon yields, par yields, and forward rates. And it can be compared to the corresponding nominal yield curve to obtain estimates of inflation compensation.
Having the real yield curve should provide tremendous benefits to our efforts to better understand the behavior of nominal yields. It allows us to parse nominal yields and forward rates into their real rate component and their inflation compensation component. These two components may behave quite differently, in which case simply looking at a nominal yield might mask important information. Accordingly, we hope that our TIPS yield curve will be useful to researchers. It is to this end that we have made the full dataset available to be downloaded from http://www.federalreserve.gov/pubs/feds/2008/200805/feds200805.xls and will update it regularly.
Ang, Andrew, Geert Bekaert and Min Wei (2007): "Do Macro Variables, Asset Markets or Surveys Forecast Inflation Better?," Journal of Monetary Economics, 54, pp.1163-1212.
Backus, David K. and Jonathan H. Wright (2007): "Cracking the Conundrum," Brookings Papers on Economic Activity, 1, pp.293-329.
Ball, Laurence (1992): "Why does Higher Inflation Raise Inflation Uncertainty?" Journal of Monetary Economics, 29, pp.371-378.
Barr, David G. and John Y. Campbell (1997): "Inflation, Real Interest Rates and the Bond Market: A Study of UK Nominal and Index-Linked Government Bond Prices," Journal of Monetary Economics, 39, pp.361-383.
Beechey, Meredith J. (2007): "Lowering the Anchor: How the Bank of England's Inflation Targeting Policies Have Shaped Inflation Expectations and Perceptions of Inflation Risk," manuscript, Federal Reserve Board.
Bliss, Robert R. (1996), "Testing Term Structure Estimation Methods," Advances in Futures and Options Research, 9, 197-231.
D'Amico, Stefania, Don H. Kim and Min Wei (2006): "TIPS from TIPS," manuscript, Federal Reserve Board.
Ejsing, Jacob, Juan Angel Garcia and Thomas Werner (2007): "The Term Structure of Euro Area Break-Even Inflation Rates: The Impact of Seasonality," manuscript, European Central Bank.
Friedman, Milton (1977): "Nobel Lecture: Inflation and Unemployment," Journal of Political Economy, 85, pp.451-472.
Gürkaynak, Refet S., Brian Sack and Jonathan H. Wright (2007), "The U.S. Treasury Yield Curve: 1961 to the Present," Journal of Monetary Economics, forthcoming.
Gürkaynak, Refet S. and Justin Wolfers (2007), "Macroeconomic Derivatives: An Initial Analysis of Market-Based Macro Forecasts, Uncertainty, and Risk." NBER International Seminar on Macroeconomics 2005, pp. 11-50.
Kim, Don H. and Jonathan H. Wright (2005), "An Arbitrage-Free Three-Factor Term Structure Model and the Recent Behavior of Long-Term Yields and Distant-Horizon Forward Rates," Finance and Economics Discussion Series, 2005-33.
Lo, Andrew W. and A.Craig Mackinlay (1988): "Stock Prices Do Not Follow Random Walks: Evidence from a Simple Specification Test," Review of Financial Studies, 1, pp. 41-66.
Nelson, C. R. and A. F. Siegel (1987), "Parsimonious Modeling of Yield Curves," Journal of Business, 60, pp.473-489.
Richardson, Matthew and James H. Stock (1991): "Drawing Inferences from Statistics Based on Multiyear Asset Returns," Journal of Financial Economics, 25, pp.323-348.
Roush, Jennifer E. (2007): "The Cost of TIPS Issuance," manuscript, Federal Reserve Board.
Sack, Brian and Robert Elsasser (2004): "Treasury Inflation-Indexed Debt: A Review of the U.S. Experience," Economic Policy Review, 10, pp.47-63.
Stock, James H. and Mark W. Watson (2007): "Why has U.S. Inflation Become Harder to Forecast?" Journal of Money, Credit and Banking, 39, pp.3-33.
Svensson, Lars E. O. (1994): "Estimating and Interpreting Forward Rates: Sweden 1992-1994," National Bureau of Economic Research Working Paper 4871.
| Series | Compounding Convention | Mnemonics | Maturities Reported (max) |
|---|---|---|---|
| TIPS yields: Zero-coupon | Continuously Comp. | TIPSYXX | All integers 2-20 |
| TIPS yields: Par | Coupon-Equivalent | TIPSPYXX | All integers 2-20 |
| TIPS yields: Instantaneous forward | Continuously Comp. | TIPSFXX | All integers 2-20 |
| TIPS yields: One-year forward | Coupon-Equivalent | TIPS1FXX | 4, and 9 |
| TIPS yields: Five-to-ten-year forward | Coupon-Equvalent | TIPS5F5 | |
| TIPS yields: Parameters | N/A | BETA0 to
TAU2 |
N/A |
| Inflation compensation: Zero-coupon | Coupon-Equivalent | BKEVENYXX | All integers 2-20 |
| Inflation compensation: Par | Continuously Comp. | BKEVENXX | All integers 2-20 |
| Inflation compensation: Instantaneous forward | Coupon-Equivalent | BKEVENFXX | All integers 2-20 |
| Inflation compensation: One-year forward | Coupon-Equivalent | BKEVEN1FXX | 4, and 9 |
| Inflation compensation: Five-to-ten-year forward | BKEVEN5F5 |
Notes: XX in each case denotes the maturity in years. For example, TIPSY10 denotes the ten-year zero-coupon yield. The one-year forward rates XX years hence denote the one-year forward rates beginning XX years hence. For example, TIPS1F09 is the one-year forward rate from nine to ten years hence. The parameters are labeled BETA0, BETA1, BETA2, BETA3, TAU1, and TAU2, corresponding to the equations in the text. Note that the parameters BETA3 and TAU2 are restricted to zero in the earlier part of the sample, as discussed in the text.
Notes: This table shows the standard deviation of one-day and one-, three- and six-month changes in the ten-year instantaneous forward rate of inflation compensation. They are computed assuming 22 days per month. The variance ratio statistic is the heteroskedasticity robust test statistic of Lo and MacKinlay (1988) and has a standard normal asymptotic distribution. *, ** and *** denote significance at the 10, 5 and 1 percent significance levels respectively.
Notes: This table shows the fraction of the variance in zero-coupon nominal yields at annual maturities from two to twenty years that is accounted for by the first m principal components of those yields (cumulatively). The same information is included for TIPS yields and inflation compensation. The data are end-of-month from January 2003 to June 2006, inclusive.

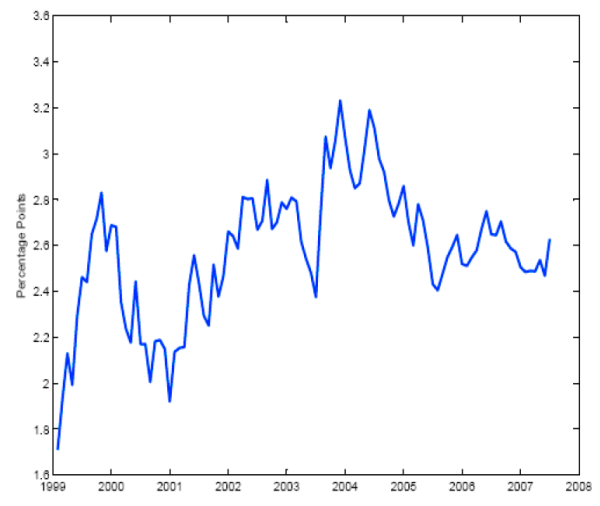
Notes: Forward par inflation compensation.
Footnotes
Sack: Macroeconomic Advisers, LLC, Washington DC 20006; [email protected]
Wright: Federal Reserve Board, Washington DC 20551; [email protected] Return to Text