The Federal Reserve Board eagle logo links to home page
Skip to: [Printable Version (PDF)] [Bibliography] [Footnotes]
Finance and Economics Discussion Series: 2008-16 Screen Reader version ♣

Corporate Hedging, Investment and Value*

Jose M. Berrospide*
Amiyatosh Purnanandam*
Uday Rajan*
February 2008


Keywords: Currency derivatives, firm value, underinvestment, debt capacity, cost of capital.

Abstract:

We consider the effect of hedging with foreign currency derivatives on Brazilian firms in the period 1997 through 2004, a period that includes the Brazilian currency crisis of 1999. We find that, derivative users have valuations that are 6.7-7.8% higher than non-user firms. Hedging with currency derivatives allows firms to sustain larger capital investments, and also removes the sensitivity of investment to internally generated funds. Thus, it mitigates the underinvestment friction of Froot, Scharfstein, and Stein (1993), at a time when capital in the economy as a whole is scarce. We further show that hedging increases the foreign currency debt capacity of a firm, and that foreign debt is a cheaper source of capital than domestic debt during our period of study.


JEL Codes: G30, G32.





1 Introduction

Despite the widespread use of derivatives by firms, and the impressive growth in the derivatives market in the last two decades, empirical evidence on the effect of derivative usage on firm value is limited and often mixed. There are several reasons for this. First, there is a lack of data on the extent and direction of a firm's exposure to risk. It is often non-trivial to even identify the frictions that hedging may help overcome. Second, data on the kinds of derivatives used by a firm, and indeed on whether firms are hedging or speculating, may be unavailable. Finally, hidden or unobservable firm characteristics introduce additional complications that affect the interpretation of empirical results.

For example, suppose we find that a firm using derivatives has a higher value than an observationally identical non-user firm. It is possible that derivative usage is correlated with an omitted variable that has a positive effect on firm value, such as managerial skill. We may then incorrectly conclude that derivative usage has a positive effect on firm value. Therefore, if one finds a link between firm value and derivative usage, it is an equally important empirical task to identify the specific channels via which derivatives might add value to a firm.

We study the effect of derivative usage on firm value and financial policy in a setting that is less likely to suffer from some of these concerns. We consider a panel of Brazilian firms in a period surrounding the 1999 currency crisis. Until January 1999, Brazil had a managed exchange rate policy (a "crawling peg") for its currency, the real. Following a severe currency crisis, the policy was abandoned in favor of a fully floating exchange rate in January, 1999. The economy suffered through a large recession as a result of the crisis. In this period, many firms in Brazil had liabilities denominated in foreign currency, primarily US dollars. During the managed exchange rate regime these firms faced minimal exposure to foreign currency risk. However, this exposure increased dramatically in the floating exchange rate regime. While only a handful of firms hedged their currency exposure prior to 1999, the usage of currency derivatives increased steadily from 1997 to 2004, our period of study, with over 40% of firms in the sample using currency derivatives by the end of the period.1

Our setting has three noticeable advantages. First, following the radical change in exchange rate policy and the upheaval in the economy, Brazilian firms were in a state of disequilibrium. It would require some time for firms to determine what their optimal policies should be in the new environment. If all firms are behaving optimally, the effect of hedging on value may be hard to detect in equilibrium.2 That is, if hedging does appear to be of value, firms that do not hedge must either be behaving sub-optimally, or perhaps have some hidden cost to hedging relative to hedged firms that is unobserved by the econometrician.

Second, the nature of the risk faced by firms in our study is clear. A large number of firms in our sample had some liabilities denominated in foreign currency over the period of study. In the managed exchange rate period, such positions were implicitly hedged via government policy. Once the exchange rate was floated, firms were required to hedge on their own to protect against a further fall in the Brazilian real. Thus, both the source of risk and the direction of the hedge are immediate to deduce.

Finally, the crisis itself was exogenous to the actions of any particular firm, though of course it came about as a result of a weakness in the overall economy. A typical problem in any regression model of firm value is the issue of endogeneity between firm value and the decision variable of interest, such as the hedging decision in our case. A natural experiment that randomly assigns firms to be hedgers or non-hedgers would be an ideal research design to get around this problem. Since the decision to hedge is endogenous, our setting does not represent a pure natural experiment. Nevertheless, it is a setting in which the exogenous change in the exchange rate regime led to a corresponding exogenous change in the marginal value of currency hedging, which was close to zero in the managed exchange rate period. If hedging has any value, its value should be demonstrable when such a large shock occurs. By comparing hedgers and non-hedgers as well as by comparing a firm's own value before and after it started hedging, our experiment design is less likely to be affected by endogeneity issues.

We find in pooled regressions that hedgers have significantly higher market valuations (as measured by the market-to-book ratio or Tobin's q) than their non-hedger counterparts, after controlling for key drivers of firm value such as firm size, profitability and growth potential. To reduce the likelihood that the result is due to unobservable factors correlated with derivative usage, we estimate a firm fixed effects model, which by design controls for any omitted variables as long as they remain constant over time. We continue to find a large valuation premium (of 6.7-7.8%) for currency derivative usage. This suggests that a substantial portion of the valuation effect that we document in the pooled regressions is causal in nature.

We then explore the reasons behind the valuation premium we obtain. The theoretical literature posits that hedging allows firms to overcome frictions due to bankruptcy costs (Smith and Stulz (1985)). Stulz (1996) suggests that the primary reason to hedge is to reduce the likelihood of costly "left-tail" events such as financial distress or an inability to carry out an investment policy. In a dynamic setting, Leland (1998) shows that the reduction in the probability of financial distress leads to increased debt capacity and thus to a higher firm value via increased interest tax shields. A different approach is offered by Froot, Scharfstein and Stein (1993), who show that, when external financing is costly, hedging can remove inefficiencies from a firm's investment decisions by providing capital in low cash flow states. At the empirical level, the extant literature has provided significant insights into the debt capacity channel of hedging using data from the US (see Graham and Rogers (2002)), but the investment channel has largely remained unexplored.

Our study contributes to the literature by showing that hedging helps firms smooth their investment policies. We find that hedgers invest considerably more than non-hedgers, controlling for the investment opportunity set at the industry level. Just as importantly, we find that a hedged firm's investment is not sensitive to its operating cash flow. A non-hedger, on the other hand, is significantly dependent on its internal funds for investment. This provides direct evidence in support of the Froot, Scharfstein, and Stein (1993) model. A basic friction faced by Brazilian firms in our period of study is a shortage of capital, which results in underinvestment by non-hedged firms.3 Hedging enables firms to maintain capital expenditure at a time of overall economic stress, and thus mitigates the underinvestment friction.

To examine why the level of investment is higher for hedgers in our sample, we consider the effects of derivative usage on leverage. In our setting, the debt channel has an additional effect on firm value as compared to the Leland model. As we show in Section 2.2, the intermediation capability of the domestic banking sector was severely hampered during the period of our study, with low bank credit availability and a high spread between lending and deposit rates. In such an environment, foreign currency debt can be a cheaper source of capital than domestic debt. Thus, in addition to the extra tax-shields generated by additional debt, currency derivatives may add value through their effect on the cost of capital to the firm. While we do not have direct data on the cost of domestic and foreign debt, we can infer their relative costs from the financial expenses and net incomes reported by firms. We show that a real of foreign currency debt is cheaper for a hedger firm than a real of domestic debt. We further demonstrate, both in univariate analysis and via regressions, that hedged firms have significantly greater foreign leverage, and a greater proportion of foreign currency debt.4 The level of domestic debt is the same across hedged and unhedged firms. Thus, overall, hedged firms do have higher leverage, as in the Leland (1998) model.

Finally, we account for the likely endogeneity between the decision to hedge and the extent of foreign currency debt taken on by a firm. We first model the hedging decision of a firm via a hazard rate process. We then use the key determinants of hedging in an instrumental variable estimation of derivative usage and foreign currency debt. Even after accounting for the endogeneity of these decisions, we find that hedged firms have significantly higher foreign currency debt than non-hedgers. Overall, therefore, our results show that in a segmented capital market, derivative usage can add value by increasing the firm's access to a cheaper source of capital.

There has been much empirical work on the effect of derivative usage on firm value in recent years. Using a sample of US firms over the period 1990-95, Allayanis and Weston (2002) estimate that users of foreign currency derivatives command an average premium of 4.87% in firm value. However, Guay and Kothari (2003) suggest that the extent of derivative usage by US firms is too small to justify such a large value premium. They show via simulation that a simultaneous three standard deviation adverse change in exchange rates, interest rates, and commodity prices will generate enough cash flow via derivatives holdings to add only 1.3% to the the equity value of the median US firm. Of course, we have not observed such large negative shocks to the US economy over the last few decades. In Brazil, on the other hand, the economy suffered extreme economic conditions during our study period, allowing us to directly estimate the effect of hedging on firm value in an adverse economic scenario. Graham and Rogers (2002) examine a sample of US firms in the period 1994-95, and find that firms indeed hedge to increase debt capacity; the resultant tax benefits add about 1.1% to firm value. Our findings support their key conclusions that derivatives result in higher debt capacity and therefore higher value.

Since we analyze the economy in a setting of disequilibrium, and exploit the panel nature of our data to control for unobservable firm-specific factors, our results are one step closer to establishing causal effects of hedging. We document two channels that have not been explored in the empirical literature through which derivatives add to firm-value; specifically, derivatives (i) alleviate the underinvestment problem, which increases the expected growth rate of cash flows, and (ii) increase a firm's access to a cheaper source of capital. As a result, our estimates that hedging via derivatives adds 6.7-7.8% to firm value are larger than those of Graham and Rogers (2002).

Since using derivatives is an endogenous decision, it is possible that non-users have devised other methods of hedging. Indeed, Tufano (1996) points out that gold firms employ many different methods of operational and financial hedging. Petersen and Thiagarajan (2000) demonstrate the case of two gold firms with similar eventual risk exposures, though one uses derivatives and the other a mix of methods. Mackay and Moeller (2007) consider hedging by real (as opposed to financial) means, and show that hedging concave revenues while letting concave costs remain unhedged adds 2-3% to the value of oil refiners. To the extent that firms which do not use derivatives hedge via other means, we are less likely to find a valuation effect of derivative usage. Further, our firm fixed effect regressions are less susceptible to this bias as long as firms do not frequently change their non-derivatives hedging policy.

Our results on the financial performance of hedged versus unhedged firms contrast somewhat with those of Allayannis, Brown, and Klapper (2002), who find that, following the East Asian currency crisis, hedged foreign currency debt is associated with worse financial performance of East Asian firms, whereas unhedged debt is not. In their work, the worse performance of firms with hedged debt is attributed in part to illiquidity of derivative markets following the currency crisis. The difference in our results is perhaps attributable to the longer period of our study as well as the sample from a different market. In related work, Rossi (2007) examines the decision of Brazilian firms to hedge, and their choice of instruments, over the period 1996 to 2004, using a data set that is substantially similar to ours. Our results on the driving factors behind the hedging decision are similar: this decision depends on the size of the firm and the extent of foreign currency debt. While our focus is on the effect of hedging on firm value and financial performance, in the last section of the paper, we account for the endogeneity in the decision to hedge.

Our paper also provides insights on the ambiguous results in the literature on balance sheet effects and currency crisis. A series of empirical studies using firm-level data for some Latin American countries find ambiguous results on the impact of a currency depreciation on the investment and output of firms with dollar-denominated debt (see, for example, Cowan, Hansen, and Herrera, 2005, and the references therein). Some studies find evidence of strong balance sheet effects, while others find the opposite, i.e., following a devaluation, firms heavily indebted in dollars do not invest less than their counterparts with local currency debt. Cowan, Hansen, and Herrera (2005) argue that the currency composition of debt is endogenous, and recover balance sheet effects in Chilean firms after controlling for the endogeneity. In our paper, we account for the possibility that both the currency composition of debt and hedging are endogenous and simultaneously determined.

The rest of the paper is organized as follows. We review the literature in Section 1. We provide some background information on the Brazilian economy and the currency crisis in Section 2. Section 3 briefly describes our data and sources, while Section 4 contains the empirical results. We conclude with Section 5.


2 Brazil: Macroeconomic environment

In late 1998 and early 1999, Brazil suffered from a financial crisis that led to its currency, the real, being fully floated on January 15, 1999. The real (denoted as R$; plural reais) was introduced in July 1994, as part of a stabilization package known as the Real Plan (see Averbug, 2002). The package included elements of privatisation and dollarisation, and was primarily intended to control inflation (which had averaged 1,403% per year from 1990 to 1993) and foster economic growth. The plan successfully reduced inflation to 20% by 1995.

As part of the plan, important regulatory changes were introduced in the financial markets to reduce controls on capital flows and improve the access of corporations to foreign currency debt from international capital markets. A crawling peg exchange rate regime was adopted for the real, with preannounced narrow bands within which the exchange rate was maintained. In this paper, we refer to the period before January 1999 as the "fixed exchange rate regime."

The years leading up to 1999 saw financial crises affect Mexico (1994), East Asia (1997), and Russia (1998). The Brazilian economy was severely affected by the Russian crisis of August, 1998, and suffered substantial capital outflows. External aid from the IMF and the G-7 provided a breather, but capital outflows increased again in January, 1999, leading to the fixed exchange rate regime being abandoned in favor of a floating regime. There were continued shocks to the economy in the floating exchange rate period, with the Argentinian crisis of 2001-02 having a ripple effect throughout Latin America, and a presidential election in 2002 contributing to political uncertainty.

2.1 Exchange rate, GDP growth, and inflation

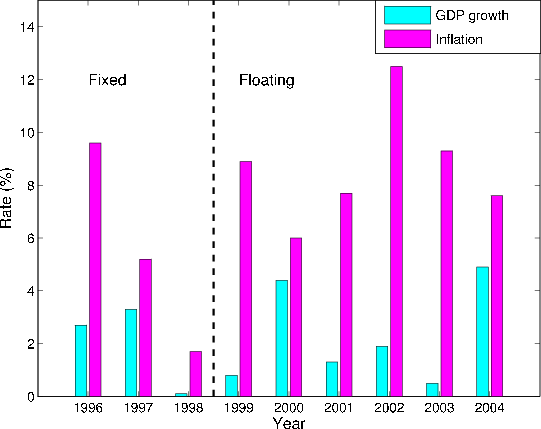
Figure 1 displays the exchange rate (in reais/US dollar) of Brazil over the period 1996 through 2005. As seen from the figure, the exchange rate surged immediately after the real was floated in January, 1999, with the value of the real falling by about 65% within two weeks. The real/US dollar rate increased sharply again in 2001 and 2002. Further, compared to the orderly change in the value of the real in the fixed exchange rate regime, in the floating era the real was significantly more volatile. Figure 2 displays Brazil's annual real GDP growth and the inflation rate, as measured by the CPI, from 1996 to 2004. As seen from the figure, GDP growth was very low immediately before and after the decision to float the real (1998 and 1999, respectively) as well as in the period 2001-03, but was stronger in 2000 and 2004. Conversely, inflation was high throughout the period, averaging over 8% per year in the floating exchange rate years.


Figure 1: Exchange rate (reais per US dollar)
Figure 1. Refer to link below for figure data.
Figure 1 Data


Figure 2: GDP growth and inflation
Figure 2. Refer to link below for figure data.}
Figure 2 Data



2.2 Domestic banking sector

The intermediation efficiency of the domestic banking sector in Brazil has typically been poor, compared both to developed markets as well as other comparable developing economies. The spread between the lending and deposit rates, a measure of efficiency and competition in the banking market, has averaged about 30% in Brazil. This is about ten times higher than the average spread in developed countries and about three times higher than the average spread in Latin American countries (Sobrinho (2007)). As a consequence, the nominal interest rate charged to commercial borrowers has remained high as compared to other countries. Inflation-adjusted short-term interest rates in Brazil have also been high. For example, based on IMF data, Rogoff (2005) shows that the inflation-adjusted short-term interest rate in Brazil was 9.6% in 2004, significantly higher than many other developed and developing countries.

Several reasons have been proposed for the inefficiency of banking sector in Brazil. Nakane, Afanasieff and Lhacer (2002) and Gelos (2006) point to a government subsidy to poorly performing sectors of the economy, high default rates on corporate loans, high operating costs of banks, and onerous reserve requirements in addition to overall macroeconomic instability. Sobrinho (2007) shows that a government policy requiring banks to make unprofitable loans to selected riskier borrowers leads to disproportionately higher rates on the other loans. Belaisch (2003) finds some evidence of oligopolistic behavior in the Brazilian banking sector. Arida, Bacha, and Lara-Resende (2005) suggest that high credit spreads for Brazilian firms are a result of a crowding-out effect due to rising government debt in the aftermath of the currency crisis.

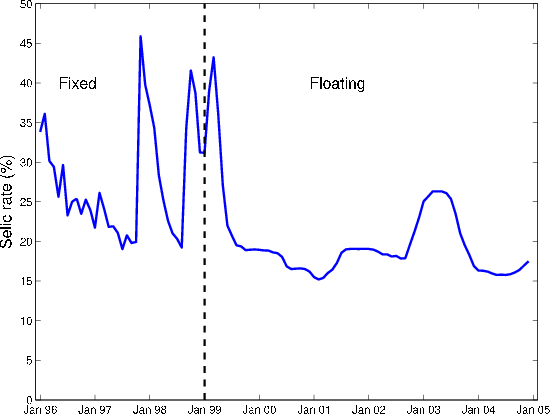
Inefficiencies in the banking sector have resulted in limited access to bank credit as well as a high cost of bank loans. Gelos (2006) shows that on average the bank credit-to-GDP ratio was less than 30% in Brazil in 2003, compared to about 60% for Chile and the U.S. Figure 3 displays the evolution of the "Selic," the Brazilian Central Bank's overnight lending rate, from the period 1996 through 2005. For much of this period, the Selic hovered around 20-25%, with a few spikes corresponding to the East Asian (1997) and Russian (1998) currency crises.

Figure 3: Domestic interest rate (Selic)
Figure 3. Refer to link below for figure data.
Figure 3 Data


Overall, during the period of our study, the Brazilian economy was passing through an extremely turbulent phase. The change in exchange rate regime especially provides us with a well-structured setting to study the effect of currency risk hedging on firm value.


3 Data

We collect data from two sources. First, we obtain financial statement and market value information for all Brazilian firms listed in the Economatica database as of August, 2006. This comprises a list of more than 350 firms. The database over-represents large firms and potentially suffer from a survivorship bias: we have no data on firms that may have gone bankrupt or been acquired. If non-hedgers are more likely to fail, the bias works against our finding any value to hedging. We exclude financial firms, which may use currency derivatives to hedge operational rather than financial risk. We also exclude state-owned and foreign-owned firms, both of which may have deep pockets. For each of the firms contained in the database in 2006, we obtain annual financial statements and equity market values for the period 1997 through 2004 from Economatica.

While Economatica computes equity market values for many firms, there are several missing values. As a second way of determining equity values, we also determine for each firm, and each class of share it has issued, the average daily closing price for the last five trading days of each year. We then determine the value of each class of share for each firm by multiplying the average price times the number of shares outstanding, and add across the classes to determine the overall market value of equity for the firm. As a cross-check, we find a high correlation between the market values from the two methods, when both are available.

Our second source of data is BOVESPA, the São Paolo stock exchange. The BOVESPA web site provides the footnotes to the annual financial statements over our period of study. Since the sets of firms listed in Economatica and BOVESPA are different, our overall dataset is the intersection of these two sources of information. We obtain the following items of information for each firm-year from the footnotes to the balance sheet: whether a firm uses foreign exchange derivatives, whether it is an exporter, whether it has dollar assets, and the amount of foreign debt outstanding.

Following regulation CVM No. 235, introduced on March 23, 1995, in the footnotes to the balance sheet a publicly traded company is required to disclose whether it uses derivative contracts, and also the nature and face value of the contracts.5 Thus, for many firms, we can identify whether they use currency derivatives. Many non-users explicitly mention that they do not use derivatives, whereas many firms do not mention derivatives at all. The latter are treated as missing values. Since we only know the kinds of derivative contracts used (e.g., exchange rate or currency derivatives, and swaps, options, or forward contracts) and their notional value, but not the terms of the contracts themselves, we create a dummy variable dderiv set to 1 if firms use foreign exchange derivatives, and zero otherwise. The most common hedge contracts among firms in our sample are currency swaps and forward contracts.

Similarly, we create a dummy variable export set to 1 if a firm is an exporter, and zero otherwise. On exports, some firms disclose data on exports as part of the annual report. In other cases, firms mention they are exporters but do not disclose information about foreign sales. The export dummy is set to 1 in each case. We also create a dummy variable dol set to 1 if a firm holds assets denominated in or indexed to US dollars. Such assets include cash and deposits in foreign currency and government bonds (treasury notes and central bank bonds indexed to the dollar). Finally, in many cases, firms report the currency composition of their debt, from which we determine the foreign to total debt ratio for each firm.

Our basic measure of value is Tobin's q, or the ratio of a firm's market value to its book value, where market value is determined as the sum of book value of debt and market value of equity, and book value is the sum of book value of debt and book value of equity. We remove observations with missing values for market value of equity, book equity, cash holdings, and derivative usage. Our final data set is an unbalanced panel containing 167 firms and 1,023 observations (firm-year pairs). We winsorize all variables in both tails at the 1% level to control for outliers.

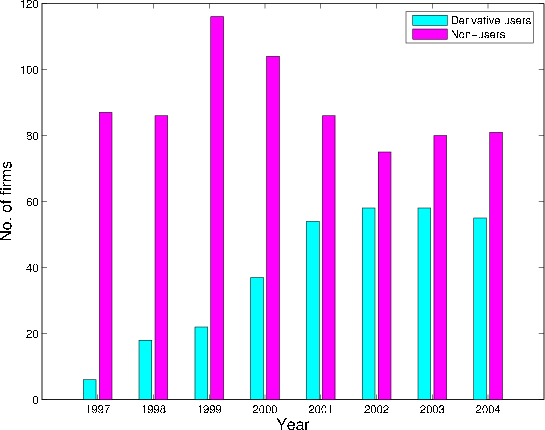
Figure 4 shows the number of firms in each year of our sample. The number of derivative users grows for the first four years and levels out between 53 and 58 over the last four years. The total number of firms grows for the first three years, and is between 133 and 141 over the last five years.

Figure 4: Number of firms in sample
Figure 4. Refer to link below for figure data.
Figure 4 Data


4 Results

We start with a description of the key statistics of our sample firms and a univariate comparison of derivative users and non-users. Table 1 presents some descriptive statistics. Panels A and B provide the mean, median and standard deviation of key firm characteristics of hedgers and non-hedgers respectively, and Panel C provides the corresponding statistics for all firms. Apart from the usual caveats that apply to univariate tests, in our exercise we also need to keep in mind the effect of pooling observations across different years. There was considerable inflation in Brazil during the period of analysis. In our formal empirical analysis, we explicitly control for this effect.

The univariate analysis shows some obvious differences in firm characteristics across the two groups. Hedgers are much larger firms, both in terms of their revenue and market capitalization. The median hedger firm's revenue (R$ 1,214 million) is more than five times that of the median non-hedger firm (R$ 228 million). The median hedger firm's book leverage (33.69%) is about 10% higher than that of the median non-hedger firm (22.39%). Noticeably, while the domestic leverage (i.e., the ratio of local currency debt to book value of assets) is similar at about 10% for the median firm across the two groups, hedgers have a substantially higher foreign currency leverage (defined as the ratio of foreign currency debt to book value of assets). The median hedger firm has a foreign currency leverage of 20.96% as against 4.93% for the median non-hedger firm. The differences in firm size, book leverage and foreign leverage across the two groups are all significant at 1% level. Further, we find that hedgers keep significantly higher cash-balances as compared to non-hedgers.

We also investigate the operating profitability and capital expenditures of the two groups. While the earnings before interest and taxes (scaled by total assets), called margin in the table, is similar (about 20%) across the two groups, we find that hedgers have a net income to assets ratio approximately double that of non-hedgers, and a capital expenditures to assets ratio almost 50% higher than non-hedgers. Finally, we find that the median market-to-book ratio for hedgers is 1.01 as against 0.71 for the median non-hedger firm. This difference is significant at 1% level.

Overall, our univariate results show that hedgers are large firms with high leverage, especially high foreign currency debt. They seem to have similar operating profitability as non-hedgers, but are able to invest more via capital expenditures. In addition, their market value is significantly higher compared to their non-hedger counterparts. In the rest of this Section, we try to tease out the effect of derivatives on firm value more precisely.

4.1 Valuation effects

To isolate the effects of derivatives on firm value, we need to control for other known drivers of value. Consider a simple dividend or earnings growth model of firm valuation. Any variables that potentially affect either the firm's current or future cash-flows or its cost of capital may in turn affect value. In particular, we include the following controls: (i) the firm's operating profit margin, which is a measure of its current earnings (ii) the log of sales revenue, which we use as a proxy for firm size throughout the paper (iii) the growth in sales revenue, which proxies for the current growth rate of the firm, (iv) capital expenditure, which proxies for the expected future growth rate, (v) the cash balance of the firm, which accounts for an important alternative means of hedging (vi) financial income to total assets, which captures the mechanical effects of increased cash flow in bad states due to the hedge (vii) financial expenses (which include interest expenses) to total assets, which proxies for the extent of debt, and (viii) industry and year fixed effects. We now describe the role of each of these.

The operating profit margin of a firm measures its profitability prior to financial income or expenses, and corresponds to the numerator in an earnings growth model of firm value. Since derivatives directly affect financial income, we use operational earnings as our profitability control. The particular measure we use is a firm's earnings before interest and taxes scaled by total assets.

Next, we control for firm size. Large firms are likely to have lower risk, and thus a lower cost of capital. Especially during an economic downturn, large firms are expected to better withstand adverse shocks. This could happen, for example, due to their ability to access external capital markets relatively easily or due to their more competitive positions in product markets, as compared to small firms. We include the log of the firm's sales revenue as a control for market size. We find similar results for an alternative definition of firm size based on the log of total assets of the firm.

In the spirit of the dividend growth model, we need a proxy for the expected growth rate in the firm's earnings. In the absence of direct growth forecasts, we use two proxies to capture growth rates. First, we consider the firm's sales growth, which is computed by measuring the year-by-year percentage growth in a firm's sales revenue. This measure is a proxy for the current growth rate of a firm and to the extent current growth rate is correlated with future growth rate, it controls for expected growth in firm's earnings. Our second measure of growth is the capital expenditure of the firm scaled by its total assets. Higher levels of capital expenditure are typically associated with better investment opportunities and a higher anticipated earnings growth rate for a firm.

Cash represents the ultimate hedge, suggesting that hedging via derivatives will be less valuable to firms with high cash balances. To control for this, we include the ratio of cash to total assets as a right-hand side variable in the regression.

Through the bulk of our sample period, the value of the real was falling relative to the US dollar (see Figure 1). Thus, firms that hedged against such a fall will have increased cash flow as a result of the hedge, and hence a higher value. Gains from financial derivative transactions are reported in financial income (losses are reported in financial expense). We include the ratio of financial income to total assets as a variable, to account for the extra cash flow generated by the hedge as the real depreciates.

The capital structure of a firm can affect its value through several channels. An immediate effect of debt is its impact on firm-value through higher tax-shields. In addition, leverage can have indirect valuation implications through its effect on agency costs. To control for these effects, we include the firm's financial expense to total assets on the right-hand side. Since our dependent variable includes the book value of debt in both numerator and denominator, we prefer this variable over a direct leverage ratio in our regression specification, to avoid any mechanical correlation between the dependent and explanatory variable. Financial expense includes interest expense, losses from derivatives, and bank fees.

Finally, we control for industry and year fixed effects. Based on their primary industry classification, we group firms into 16 industry groups and include these dummies in the model. It is very likely that industry affiliation captures a large component of a firm's growth opportunities as well as its risk, and therefore its cost of capital. Year dummies are included to control for significant changes in macro-economic conditions from year-to-year, most notably inflation.

Table 2 provides the basic regression results for the effect of currency derivative usage on value. In Models 1 and 2, we provide results from pooled OLS regression estimation with firm-level clustered standard errors. For both of these models, we find that firm value is higher for large firms and firms with better operating profitability. High sales growth firms and firms with high capital expenditure also have higher value, but these results are statistically weak. In Model 2 that includes the effects of cash balance, financial income, and leverage, we find that firms with higher cash balances have larger value.

In both models, we find a positive and significant coefficient on dderiv, the dummy variable representing the hedger firms. The coefficient estimates from the OLS model are large, in the range of 14.3-16.5%, and statistically significant (at the 5% level for Model 1 and the 10% level for Model 2). Since these effects are economically large, we next turn to identifying their source. An immediate possibility is an omitted variable problem; that is, we find these effects because we have not controlled for some firm-specific factor that creates higher value and that is also positively correlated with derivative usage. For example, better managerial ability, which is unobservable, could be one potential candidate for an alternative interpretation of our results.

To deal with this concern, we exploit the panel nature of our data and estimate a firm fixed effects model. In such a model, any firm-specific omitted factor that is constant from year-to-year, including unobservable managerial skill, is automatically controlled for. Models 3 and 4 of Table 2 provide regression estimates from the fixed effects model. Since we have firm fixed effects, we drop industry dummies from these models. To account for correlated errors across firms in the same industry, we adjust standard errors for clustering of residuals at the industry level.

We find a positive coefficient of 7.82% on the dderiv dummy in Model 3, and 6.71% in Model 4. Both coefficients are statistically significant at the 10% level. The fixed effects model suggests that derivative users seem to gain value when they begin using derivatives. Since firm fixed effects implicitly control for various unobserved characteristics of the firm, we are closer to a causal link from hedging to firm value. Compared to the OLS models, we find that the point estimate of dderiv has dropped by approximately a half in this specification, consistent with the idea that the firm-specific unobservable factors do contribute significantly to the OLS point estimates.

The fixed effects regressions also show that firm value increases significantly with operating profitability, capital expenditure, and cash balance. Unlike the pooled OLS model, the effect of size has become insignificant in the fixed-effect model. This suggests that some unobservable firm-specific characteristic is correlated both with value and size.

Overall, then, we establish a significant association between firm value and derivative usage. Why should hedging add value? Motivated by previous studies, we now explore two channels via which this value creation may be taking place: (a) the effect of derivatives on a firm's capital expenditure plans (Froot, Scharfstein, and Stein (1993)), and (b) its effect on a firm's debt capacity (Leland (1998)).

4.2 Effect of derivatives on capital expenditures

Froot, Scharfstein, and Stein (1993) suggest that hedging minimizes the frictions associated with volatile cash flows and thereby allows a firm to maintain a smooth investment policy. In particular, the sensitivity of investment to a firm's internal profit before hedging should be lower for hedgers as compared to non-hedgers. The key assumption of costly external financing underpinning the theoretical model of Froot, Scharfstein and Stein is likely to be especially true in our sample, when the entire economy was passing through a major transition. During such a period, scarcity of internal funds and poor health of the domestic banking sector have the potential to severely hamper a firm's investment policy.

We estimate the effect of currency derivative usage on a firm's capital expenditure scaled by beginning-of-the-year total assets. In these OLS regressions, we control for the firm's operating profit (EBIT), size (the log of sales revenue), and leverage. We include year and industry dummies to capture the effects of the macroeconomic environment and industry-specific investment opportunities. The results are presented in Table 3.

The coefficient on dderiv in Model 1 suggests that hedgers invest about 1.3% (as a proportion of total assets) more than non-hedgers. The univariate results in Table 1 show that the mean level of capital expenditure for non-hedger firms in our sample is about 5.6%. Therefore, after controlling for other factors that affect capital expenditure, the mean hedger firm invests about 23% more than the mean non-hedger firm. The other coefficients in Model 1 indicate that firms invest more when they have higher internal profits and higher size, though the latter results is statistically insignificant.

In Model 2, we drop the operating margin from the regression, and instead include two interaction variables in the model: (a) operating margin interacted with dderiv and (b) operating margin interacted with 1-dderiv. The first interaction term captures the sensitivity of capital expenditures to internal profits for derivative users, whereas the second term does that for non-users.6 This allows us to estimate the sensitivity of investments to internal pre-hedging profits across the two groups and provides a cleaner test of the theory of Froot, Scharfstein, and Stein (1993).

With this model specification, the coefficient on dderiv is larger and significant at the 1% level. More importantly, we find a positive and significant (at the 1% level) coefficient of 6.26% on the interaction of margin with the non-hedger dummy, and statistically zero coefficient on the interaction with the hedger dummy. That is, the investment-cash-flow sensitivity of derivative users is zero, whereas it is positive for the non-users. Consistent with Froot, Scharfstein, and Stein (1993), we find that derivative users' capital expenditure policy is insulated from the availability of internal funds, whereas the same is not true for non-users.

A large literature has investigated the sensitivity of investments to cash flows. Alternative interpretations have been offered to the empirical finding of a positive coefficient on internal cash flows in an investment regression, including (i) firms face financial constraints, and therefore depend on internal funds to undertake capital expenditures, and (ii) when cash-flows are high, firms have better investment opportunities, which in turn produces a positive correlation between investments and cash flow. In our regressions, we control for industry-specific effects, so it is hard to argue that high cash flow proxies for a better investment opportunity set only for non-hedgers.

Summarizing the results from capital expenditure regressions, we find that (a) derivative users invest more than non-users, and (b) their investment plans are less sensitive to their own operating funds before the effect of hedging. In the next sections, we explore a channel via which derivative usage may allow a firm to smooth its investment policy. We show first that foreign currency debt is a cheaper source of capital than domestic debt for firms in our sample. Then, we show that derivative users have better access to foreign currency debt. Access to the local currency debt market may be limited for all firms in the period of the economic crisis, so that access to foreign currency debt mitigates the effects of credit rationing. This, in turn, allows them to invest more and make their investment less sensitive to internal cash-flows. Since foreign debt is cheaper, derivative users can further avail of a larger proportion of operating profit. We explore this channel of value creation in detail in the rest of the paper.

4.3 Foreign currency debt: price and quantity

As discussed earlier, at the macroeconomic level there is evidence that (a) domestic credit was scarce in Brazil during the period of study, and (b) domestic interest rates were very high during this period. Thus, access to foreign debt can allow firms to benefit both via the greater quantity and reduced cost of debt financing. In the remainder of the paper, we explore these two channels in more detail at the micro-economic level using our sample. We proceed in two steps. First, we show that foreign currency debt is indeed a cheaper source of capital as compared to domestic debt. Next, we show that hedging not only leads to a greater proportion of foreign debt for firms (as a proportion of total debt), but also allows firms to increase their foreign leverage (i.e., the ratio of foreign currency debt to total assets).

We do not have direct data on the interest rates or loan spreads charged to firms for foreign versus domestic loans, or, indeed, on the cost of the foreign currency hedge. We therefore adopt a different approach: we analyze the income statements of firms and relate their interest expenses and net profitability to their domestic and foreign leverage.

4.3.1 Cost of domestic and foreign debt

Our first test is designed to directly assess the costs of domestic and foreign debt. Brazilian firms report their interest expenses under the item "financial expenses." This item may also include other items such as bank fees and losses on account of derivative transactions. Lacking a finer break-up of interest expenses, we take financial expenses as a proxy in our empirical exercise. We regress the R$ amount of financial expenses in a year on the firm's domestic and foreign debt, both measured in R$. We take the average values of the beginning and the end of the year debt levels since we are regressing a flow variable (interest expense) on level variables. The estimated coefficient in this model can be interpreted as the average firm's interest cost for every real of debt. Thus the estimated coefficients are closer in interpretation to interest rate on the debt of an average firm.

We provide estimation results in Table 4. In all three models, we include year dummies to remove time-specific variation in the cost of debt, and industry dummies to partly control for variation in operational risk. Across the three models, the average cost of domestic debt varies from 25.35% to 28.65% per year. In Model 1, the cost of foreign debt is estimated at a much lower value of 11.50% per year. The difference between these estimates is highly significant (unreported in the table). In Model 2, we break foreign currency debt into two groups by interacting the level of foreign currency debt with the currency hedging dummy. We include two variables in the regression: (i) fordebt*dderiv, which takes the value of foreign currency debt for hedgers, and zero otherwise, and (ii) fordebt*(1-dderiv), which takes the value of foreign currency debt for non-hedgers, and zero otherwise. In Model 3, we include measures of tangibility (PPE) and earnings (EBIT) to proxy for credit risk and profitability. While the estimated cost of foreign debt for hedgers is higher in Model 3, in both Models 2 and 3, at the 5% level we reject the hypothesis that domestic debt has the same cost as foreign debt for hedgers, but cannot reject it for non-hedgers.

Overall these results show that during our estimation period, the domestic debt cost about 25-28% per annum. Though approximate, our estimates of interest rates are in line with the overall interest rate environment in the economy. As shown earlier in Figure 3, the benchmark Selic rate was around 20% in Brazil during most of the period of our study. Our estimate is in line with this number. The cost of foreign debt for hedged firms is significantly lower.

As a further test, we analyze the effect of foreign currency debt on net profit, given a level of operating profit. We regress a firm's net income to total asset ratio on domestic leverage, foreign leverage of hedgers and non-hedgers, and several control variables. We compute domestic leverage ( domlevavg) as the ratio of local currency debt to the book value of total assets. Foreign leverage, forlevavg, is constructed as the ratio of foreign currency debt to total assets. Again, we take the beginning and the end of the year average values of these leverage ratios for our regression model, and we interact forlevavg with dderiv and its complement.

In these regressions, we control for other components of net income, including EBITDA, depreciation and amortization, and investment income from subsidiaries, all scaled by total assets. We include firm size on the right-hand size to account for the effect of economies of scale: Larger firms may have a lower per dollar cost of raising external funds, which in turn may lead to better profitability.

Table 5 provides the regression results. The associated t-statistics are reported after clustering standard errors at the firm level. As expected, we find that firms with higher operating profits, lower depreciation and amortization expenses and higher investment income have higher net income. In Model 1, the coefficient on dderiv implies that, controlling for these effects, derivative users have a net income to total assets ratio higher by 1.59%, compared to non-users. The mean ratio for non-users is 2%, as reported in Table 1. In Models 2 and 3, we explore the effect of the cost of domestic and foreign debt on profitability. The estimated coefficient on domlevavg, the average ratio of domestic debt to total assets, is about -14%. That is, for every dollar of operating profit, domestic debt reduces net income by about 14% through its effect on the financial expenses. For non-hedgers, foreign currency debt reduces profitability by 11-12%, whereas for hedgers it reduces profitability by just 3-4%. At the 5% level, we reject the hypothesis that the coefficient on domestic leverage equals the coefficient on foreign debt for hedgers, but cannot reject the null hypothesis on a similar test using non-hedgers.

Overall, therefore, our results suggest that the foreign debt of hedger firms has a lower cost than either domestic debt or the foreign debt of non-hedgers. In the long run, the cost of the hedge should equalize the effective cost of foreign debt for hedgers and non-hedgers. However, we analyze a short period of time and especially a period during which the Brazilian currency underwent large depreciation, which may have led to high costs of foreign debt for non-hedgers. Of course, in a frictionless market, the cost of hedged foreign debt and domestic debt should also be equal. The high spread between lending and domestic rates, mentioned in Section 2.2, will allow the possibility that hedged foreign debt is indeed cheaper than domestic debt. Note that firms were selling reais and buying US dollars. It is likely that a foreign bank taking the other side of the transaction also had branches in Brazil, and thus benefitted from acquiring reais at low deposit rates.

4.4 Derivatives and foreign debt capacity

Next, we analyze the effect of hedging on the debt-mix (i.e., the ratio of foreign debt to total debt) and the foreign debt capacity (i.e., the ratio of foreign debt to total assets) of a firm. We note that firms are likely to use dollar derivatives and foreign currency debt in conjunction, and therefore these two decisions are determined jointly. Later in the paper, in Section 4.5, we carefully account for this possibility. We defer a serious discussion of endogeneity to the later section.

We model the ratio of foreign debt to total debt for each firm in each year as a function of currency derivative usage and several control variables. Our control variables are motivated by two broad economic arguments. First, a firm may have natural hedges in the form of foreign currency cash flows that reduce the dollar risk arising from its debt portfolio. We include a dummy variable export that equals one if a firm reports export income in its footnotes, zero otherwise. Several Brazilian firms also hold financial assets linked to the US dollar. These include foreign currency accounts as well as domestic bonds indexed to the US dollar. We include a dummy variable dol that equals one for firms with dollar assets, zero otherwise.

Our second set of controls are motivated by the studies on the determinants of leverage in general (see Titman and Wessels (1988) and Graham, Lemmon and Schallheim (1998) for example), and are included in the regression to ensure that our results are not simply driven by incentives to raise more debt. These control variables capture the effects of firm size, growth options, profitability, asset tangibility and non-debt tax shields enjoyed by the firm. As a proxy for growth options, we include sales growth, measured as the year-by-year percentage growth in sales revenue. Asset tangibility is captured by the ratio of property, plant and equipment (PPE) to total assets. We include depreciation and amortization scaled by total assets as a control for non-debt tax shields.

Table 6 provides the regression estimates. In Models 1-3, we provide OLS estimates with standard errors adjusted for clustering at the firm level. Industry and year fixed effects are included as well. We find a positive and significant coefficient on dderiv suggesting that derivative users have higher foreign debt in their liability. The point estimates suggest that derivative users have about a 17-18% higher foreign currency debt ratio than their non-user counterparts. In Model 4, we estimate a firm fixed effects model and obtain a coefficient of 6.77% on dderiv, which is significant at the 1% level. The firm fixed effects model suggests that our results are not driven by a firm-specific omitted variable.

Having established that foreign currency debt for hedger firms is cheaper than domestic debt and that hedgers use more foreign debt in their debt-mix, we now turn to the level of debt for hedged firms. Our univariate results in Table 1 indicate clearly that hedgers have greater foreign leverage and approximately similar domestic leverage as compared to non-hedgers. For a more formal analysis, we regress foreign currency leverage (foreign currency debt scaled by total assets) on dderiv and other control variables.

The regression results are provided in Table 7. In the regression, we control for the well-known determinants of leverage described earlier for the debt-mix regression. In Models 1 and 2 we regress the ratio of foreign currency debt to total assets on dderiv and control variables. We include year and industry dummies in the estimation and report standard errors clustered at firm-level. The coefficient on dderiv, significant at the 1% level in both models, indicates the difference in foreign leverage between hedgers and non-hedgers. We find that hedgers have approximately 7% larger foreign leverage than non-hedgers.

In the univariate tests of Table 1, we find that the total leverage of the average hedger firm is 34.46%, significantly higher than the leverage of 23.79% for the average non-hedger firm. Thus, it is unlikely that the foreign leverage is substituting domestic debt. To rule out this possibility, we regress domestic leverage on dderiv and control variables and report the results in Table 7, under Models 3 and 4. We do not find any meaningful association between the hedging dummy and domestic leverage.

These results, taken together with the debt-mix results, suggest that hedger firms have a higher leverage than non-hedgers. Further, fixing the level of leverage they have a larger quantity of foreign currency debt in their liabilities. Thus hedging seems to benefit the firm both through the well-known higher debt capacity channel as well as through a lower cost of debt.


4.5 Derivatives and foreign debt: Controlling for endogeneity

It is plausible that our results relating debt-mix and debt-capacity to hedging suffer from a simultaneous equations bias: Firms with large foreign debt are more likely to hedge. We next use an instrumental variable model to address this issue and to estimate the effect of derivatives on foreign currency debt net of a reverse causation effect. We model the foreign currency debt ratio and currency derivative usage both as endogenous variables. The first-stage regression (the dderiv equation) requires a reasonable model of the derivative usage decision. As a precursor to our instrumental variable regression, therefore, we next estimate a hazard rate model of the determinants of derivative usage.

4.5.1 Hazard rate model of derivative usage

Much of our empirical understanding about why firms use derivatives is driven by studies based on US firms (such as Geczy et al. (1997) and Purnanandam (2007)). Bartram, Brown, and Fehle (2007) provide evidence from international data by investigating derivative usage across number of countries. Many empirical studies in this area are based on cross-sectional data or data points with a limited time-series. Since we have panel data, as a by-product we estimate a richer model of a firm's hedging decision. There are likely to be high fixed costs to establishing a hedging program, which include hiring sophisticated managers and learning about various hedging options. Once these costs are incurred, it is likely that a firm will continue to hedge in the future.

We therefore model a firm's decision to hedge in a Cox-proportional hazard rate framework (see Cox (1972)). This framework, often used in the bankruptcy prediction literature (see Shumway (1997)), estimates the probability of hedging by a firm conditional on the fact that it has not hedged as yet. The hazard rate for firm j at time t (i.e., firm j's probability of using derivatives at time t conditional on it being a non-user so far) is modeled as:

\displaystyle h(t\vert x_{j})=h_{0}(t)exp(x_{j,t-1}\beta_{j})    

Here, x_{j,t-1} refers to the firm characteristics at the end of year t-1 that are likely to be associated with a firm's decision to hedge using derivatives in year t. h_{0}, called the baseline hazard function, represents the hazard ratio for a hypothetical firm that assumes a value of zero uniformly for all x_{j}. The model is estimated via maximum likelihood to obtain the \beta coefficients. The coefficient estimates tell us the effect of various firm characteristics on a firm's decision to begin hedging in the next year, given that it has not hedged in the past.

For this estimation, all level variables (such as firm size and leverage) are measured as of the beginning of the year. Thus, the interpretation of our results is in a predictive sense. Among the explanatory variables, we include firm size as a proxy for economies of scale and access to derivatives markets, and leverage as a control for hedging due to financial distress concerns. We also include the squared value of leverage in our model, since the decision to hedge may be concave in leverage: firms with very high leverage may have no incentive to hedge even when faced with higher expected bankruptcy costs (see Purnanandam (2007)). Since holding cash is an alternative way to hedge, we control for a firm's cash balance. Annual sales growth captures the effects of growth opportunities in the spirit of Froot, et al. (1993). Finally, we include dol, the dollar asset dummy, and export, the export dummy, to account for natural hedges the firm may have.

Table 8 presents the estimation results. We find that larger firms and high growth firms are more likely to use derivatives, as reported by Geczy, et al. (1997) in their sample of large US firms. Further, firms with high cash balances are more likely to use derivatives, suggesting that these two hedging methods are complementary. Finally, we find a strong non-monotonic relation between leverage and derivative usage. At low leverage levels, the likelihood of using derivatives is increasing in leverage, but the pattern reverses for highly-levered firms. This finding is consistent with the theoretical and empirical findings of Purnanandam (2007), who reports a similar non-monotonic relation between leverage and hedging for US firms.

Therefore, the key drivers of a firm's hedging decision in Brazil seem to be in line with what other authors have found among US firms. Our results provides an econometric improvement over earlier studies as they exploit the panel nature of our data, and can be taken as an out-of-sample evidence for some of the earlier work on derivative usage.

4.5.2 Instrumental variable regression

Our hazard rate regressions demonstrate that variables such as leverage and leverage-squared are strong predictors of derivative usage in our sample. In unreported analysis, we find that leverage terms (especially the square) do not have strong explanatory power in explaining a firm's foreign currency debt to total debt ratio, after we control for the effect of derivatives and other variables that enter various models in Table 6. Thus, we exploit the non-monotonicity between leverage and hedging and use leverage and leverage-squared as instruments for derivative usage in the first stage regression. We also include the cash balance (as a ratio of total assets) as an instrument.

Since derivative usage is a binary variable, at the first stage, we estimate a Probit model for the choice of derivative usage. This ensures that the fitted values will lie between zero and one. As suggested by Maddala (1983, pages 244-245), we then take the linear projection of first stage estimates and substitute it into a second stage OLS regression with foreign debt to total debt ratio as the dependent variable. The second stage standard errors are corrected for the two-stage estimation bias. Table 9 presents the second-stage results for IV model. Our first stage estimates (not reported) are similar to the estimates from the Cox-model. In addition, we check for the validity and strength of our instruments. The partial R-squared measures the improvement obtained in the model's fit in the first-stage regression by including the instruments. As reported in the table, we are able to explain over 7% of variation in the first stage regression by the addition of our instruments. The \chi^2 statistic confirms that the excluded instruments are jointly significant at 1%.

Models 1 and 2 of Table 9 show that, controlling for endogeneity, we obtain a point estimate of approximately 6-6.5% on the effect of derivative usage on the foreign currency debt ratio. As in the OLS model, the coefficient is significant at the 1% level. The magnitude of the coefficients is in line with that reported in Table 6 in the firm fixed effects specification (Model 4).

In Model 3, we present the IV regression estimates from the second stage for the foreign currency leverage model, using the same instruments for the hedging decision and the same right-hand side variables as in Models 1 and 2. The point estimate on dderiv dummy is a significant 5.38%, which is slightly lower than the estimate of 6.96% that we obtained in the base model without endogeneity correction (see Model 2 of Table 7). Thus, both the foreign currency to total debt mix as well as foreign currency leverage ratio results are unlikely to be completely driven by reverse causation argument. We do not model domestic leverage in the IV regression framework since that will necessitate a specification with three endogenous variables, namely hedging, foreign debt and domestic debt, and in the absence of a rich theoretical model and more data, it is a challenging task to achieve identification in such a model. As shown earlier via both univariate tests and a regression model, hedger firms do not have significantly lower levels of domestic debt, which alleviates concern regarding substitution between the two sources of debt.

4.6 Economic significance of results

Our firm fixed effect regressions in Table 2 control for firm-specific unobservables, and suggest that the valuation effect of derivative usage is in the range of 6.7-7.8%. Are these economic magnitudes plausible? We show that derivative users have higher capital expenditures than non-users, and their investments are insensitive to operating profitability, or internally generated cash flow. Thus, derivative usage is directly associated with a higher expected growth rate for the firm. Further, we argue that, in our setting, derivatives also add value both via their effect on foreign debt capacity, and thus the cost of capital for a firm. The currency shocks faced by the Brazilian economy in the period following the switch to the floating exchange rate regime in early 1999 are substantial. With segmented capital markets, foreign capital, if available to a firm, is cheaper and thus of value.

In terms of quantitative magnitudes, we find that derivative users invest about 1.3% more than the non-user firms, an increase of more than 20% compared to the average non-user. On the financial side, derivative users have a ratio of net income to total assets that is higher by about 1.6% compared to non-users, after controlling for operating profits, investment income and level of debt. The average non-user has a net income to total asset ratio of about 2% in our sample. Thus, the derivative users are able to generate about an 80% higher income than non-users, which is an economically large number. We find that at least a part of this can be explained by higher foreign debt, which is cheaper than domestic debt, in their debt mix. Derivative users have about a 6% higher ratio of foreign to total debt compared to non-users. The average ratio for non-users in the sample is about 42% (unreported), implying an increase in the ratio of about 15%.

Overall, therefore, we find derivative usage to be associated with an 80% higher net profit after controlling for operating profits, a 15% higher foreign to total debt ratio and a 20% higher capital expenditure as compared to the average non-user firm. These are all economically large numbers. While the net profit and capital expenditures directly capture the effects on current and future cash flow, the foreign to total debt ratio affects the cost of capital for firms as well. Given the magnitudes of these numbers, the 7-8% value difference that we report for derivative users is certainly plausible. In our context, when the economy passes through extreme adverse shocks, derivative usage becomes particularly important, and add considerable value to a firm by allowing it to have smooth financing and operating policies.


5 Conclusion

The Brazilian currency crisis of 1999 represents a natural setting to study the effects of corporate financial policy on firm performance and value. The switch to a floating exchange rate in January 1999 was followed by periods of high volatility and rapid depreciation of the real. We analyze the valuation effect of risk-management policies in a panel of 167 Brazilian firms from 1997 to 2004. Our empirical design allows us to identify the source of risk and the direction of the hedge that we study. Further, by focusing on an economy in disequilibrium, econometrically we are more likely to establish a causal effect of hedging on firm value. Further, we are able to address some concerns that often plague the interpretation of results of similar studies based on a sample of US firms.

We find that foreign currency hedging is positively correlated with the value of a firm, as measured by the ratio of market value to book value of its assets. Using a firm fixed effects specification, we estimate a valuation premium in the range of 6.7-7.8% for currency hedging. We identify a specific channel, hitherto unexplored in the literature, via which hedging is valuable: It allows a firm to continue making capital expenditures regardless of its current pre-hedging profitability as measured by EBIT. We further document that hedging increases the ability of a firm to take on foreign currency debt. It is likely that, in the aftermath of the economic crisis, domestic capital is scarce, and costlier than hedged foreign debt. Overall, therefore, we provide evidence that risk-management policies add significant value to firms during a period of economic turmoil.

Bibliography

Adam, T., S. Dasgupta, and S. Titman, 2007
, Financial Constraints, Competition and Hedging in Industry equilibrium, forthcoming, Journal of Finance.
Allayannis, G. and J. Weston, 2001
, The Use of Foreign Currency Derivatives and Firm Market Value, Review of Financial Studies 14, 243-276.
Allayannis, G., G. Brown, and L. Klapper, 2002
, Capital Structure and Financial Risk: Evidence from Foreign Debt Use in East Asia, Journal of Finance 58(6), 2667-2709.
Arida, P., E. L. Bacha, and A. Lara-Resende, 2005
, Credit, Interest, and Jurisdictional Uncertainty: Conjectures on the Case of Brazil, in F. Giavazzi, I. Goldfajn, and S. Herrera (eds) Inflation Targeting, Debt, and the Brazilian Experience, 1999 to 2003, MIT Press, Cambridge, MA.
Averbug, A., 2002
, The Brazilian Economy in 1994: From the Real Plan to Inflation Targets, The World Economy 25 (7), 925-944.
Bartram, S., G. Brown, and F. Fehle, 2006
, International Evidence on Financial Derivative Usage, Working paper.
Belaisch, A., 2003
, Do Brazilian banks compete? IMF Working Paper 03/113.
Berrospide, J., 2007
, Exchange Rates, Optimal Debt Composition and Hedging in Small Open Economies, Working paper, University of Michigan.
Bonomo M., B. Martins and R. Pinto, 2003
, Debt composition and exchange rate balance sheet effect in Brazil, a firm level analysis, Emerging Markets Review 4(4), 368-396.
Cowan, K., E. Hansen and Luis O. Herrera, 2005
, Currency Mismatches, Balance Sheet Effects and Hedging in Chilean Non-Financial Corporations, Central Bank of Chile Working Paper No. 346.
Cox, D. R, 1972
, Regression models and life tables, Journal of the Royal Statistical Society, 34 (2), 187-220.
Froot, K., D. Scharfstein, and J. Stein, 1993
, Risk Management: Coordinating Corporate Investment and Financing Policies, Journal of Finance, 48, 1629-1658.
Gelos, R. G., 2006
, Banking Spreads in Latin America, The IMF Working Paper, 06/44.
Geczy, C., B. A. Minton and C. Schrand, 1997
, Why Do Firms Use Currency Derivatives? Journal of Finance 52, 1323-1354.
Graham, John R., and Daniel A. Rogers, 2002
, Do Firms Hedge in Response to Tax Incentives? Journal of Finance 57, 815-839.
Guay, W. and S. Kothari, 2003
, How Much Do Firms Hedge with Derivatives? Journal of Financial Economics 70, 423-461.
Holmstrom, B. and J. Tirole, 1997
, Financial Intermediation, Loanable Funds, and the Real Sector, Quarterly Journal of Economics 112(3), 663-691.
Leland, H. E., 1998
, Agency Costs, Risk Management, and Capital Structure, Journal of Finance 53, 1213-1243.
Mackay, P. and S. Moeller, 2007
, The Vale of Corporate Risk Management, Journal of Finance 62, 1379-1419.
Nakane, M., T. Afanasieff and P. V. Lhacer, 2002
, The Determinants of Bank Interest Spread in Brazil, Central Bank of Brazil Working Paper Series, 46.
Petersen, M. and S. Thiagarajan, 2000
, Risk Measurement and Hedging, With and Without Derivatives, Financial Management 29, 5-30.
Rossi, J. L., 2007
, The Use of Currency Derivatives by Brazilian Companies: An Empirical Investigation, Working paper, IBMEC, São Paulo.
Purnanandam, A., 2007
, Financial distress and corporate risk management: Theory & Evidence, Forthcoming, Journal of Financial Economics.
Rogoff, K., 2005
, Strategies for Bringing Down Long-Term Real Interest Rates in Brazil, Central Bank of Brazil Presentation on August 30, 2005.
Smith, C.W., and R. Stulz, 1985
, The determinants of firms' hedging policies, Journal of Financial and Quantitative Analysis 28, 391-405.
Sobrinho, N. F. S., 2007
, The Macroeconomics of Bank Interest Spreads: Evidence from Brazil, Working Paper, University of California, Los Angeles, Department of Economics.
Stulz, R., 1984
, Optimal hedging policies, Journal of Financial and Quantitative Analysis 19, 127-140.
Stulz, R., 1996
, Rethinking Risk Management, Journal of Applied Corporate Finance 9(3), 8-24.
Tufano, P., 1996
, Who Manages Risk? An Empirical Examination of Risk Management Practices in the Gold Mining Industry, Journal of Finance 51(4), 1097-1137.



6.1 Description of Variables

The following variables are defined for each firm and each year.

logsize: natural logarithm of sales revenues.

salesgrowth: growth rate of revenues from year t-1 to year t.

margin: ratio of EBIT to total assets.

ebitda: ratio of EBITDA to total assets.

dep/TA: ratio of depreciation and amortization to total assets.

ppe/TA: ratio of permanent assets (the bulk of which are plant, property, and equipment) to total assets.

leverage: ratio of total debt to total assets.

forlev: ratio of foreign currency debt to total assets.

domlev: ratio of domestic currency debt to total assets.

cash: ratio of cash and short-term investments to total assets.

invinc: income from equity investments in other firms.

dderiv: dummy variable set to 1 if firm uses foreign currency derivatives, and zero otherwise.

export: dummy variable set to 1 if firm reports export sales, and zero otherwise.

dol: dummy variable set to 1 if firm reports foreign currency asset holdings, and zero otherwise.

6.2 Example Firm

To illustrate the data collection process, we consider the firm Acesita S.A. in the year 2001. Financial information (i.e., the balance sheet and income statement) is obtained from Economatica, as is the market value of equity. Most of the variables we need (including, for example, book value of debt, revenues, net profit) are thus easily obtained.

Data on hedging and the extent of foreign currency debt are in the explanatory notes to the financial statements (the "Notas Explicativas") maintained on the Bovespa (the São Paolo stock exchange) web site at www.bovespa.br.


From the Notas Explicativas for Acesita S.A. in 2001, we extract the following information:

Table A: Information obtained from financial statement for Acesita S.A. in 2001

Item Number, Page Item (in Portuguese) Translation to English Amount (thousands of R$)
13., 17-18 Financiamentos Financing  
13., 17-18 (continued 1) Moeda estrangeira Foreign currency 2,074,809
13., 17-18 (continued 2) Moeda nacional Domestic currency 330,411
21., 24-26 Instrumentos Financeiros Financial Instruments  
21., 24-26 (continued) Operacoes de Swap Swap operations 995,404

The text on Item 21 (page 25), Instrumentos Financeiros, explains that the firm engages in currency swap operations to reduce the effects of exchange rate variation. Similarly, the text on page 5 (Item 4, Disponibilidades or Short-term assets) explains that a specified amount of the short-term assets are indexed to the US dollar.

Based on this information, we set dderiv = 1 (since it has a foreign currency derivative position) and dol = 1 (since it holds foreign currency assets) for Acesita in 2001.


Table 1: Firm characteristics Across Derivative Users and Non-Users This table provides the descriptive statistics for the sample firms. Panels A and B provide the descriptive statistics for the non-users and users of derivatives, respectively. Panel C provides the corresponding number for all firms pooled across the two groups. All the summary statistics are pooled across sample years starting in year 1998 and ending in 2004. Revenue is the sales of a firm represented in millions of R$. Market Cap denotes the market capitalization of the firm's equity in millions of R$ computed by multiplying the number of shares by year end share price. Leverage is the ratio of book value of debt to book value of assets. Domestic and Foreign leverage represent the ratio of local currency borrowings and foreign currency borrowings to the book value of total assets, respectively. Market/Book ratio of assets is computed as the ratio of (book value of debt + market value of equity) to (book value of debt + book value of equity). Margin denotes the ratio of earnings before interest and taxes to the book value of total assets. Net Income/TA denotes the ratio of net income to book value of total assets. Cash/TA measures the cash-holdings as a fraction of book value of total assets. Capex represents the ratio of capital expenditure to the one-year lagged value of total assets. The number of observations for Capex variable is lower than other variables as it is missing for some observations and it requires total assets from the previous year in denominator. Columns labeled as N, Median and Mean represent the number of observations, median and mean, respectively. Std.Dev. represents the standard deviation.



Table 1: Firm characteristics Across Derivative Users and Non-Users
Variable N Median Mean Std.Dev.
Panel A: Non-Users, Revenue 715 228.2370 523.6458 856.4104
Panel A: Non-Users, Market Cap 715 66.7580 322.2439 871.4893
Panel A: Non-Users, Leverage 715 0.2239 0.2378 0.1781
Panel A: Non-Users, Domestic Leverage 715 0.1085 0.1415 0.1407
Panel A: Non-Users, Foreign Leverage 715 0.0493 0.0964 0.1194
Panel A: Non-Users, Market/Book (Asset) 715 0.7131 0.8303 0.5687
Panel A: Non-Users, Margin 715 0.1987 0.2216 0.1537
Panel A: Non-Users, Net Income/TA 715 0.0200 0.0187 0.0954
Panel A: Non-Users, Cash/TA 715 0.0327 0.0711 0.0926
Panel A: Non-Users, Capex 625 0.0401 0.0555 0.0625
Panel B: Users, Revenue 308 1214.3945 2553.1309 3530.5675
Panel B: Users, Market Cap 308 617.4578 2108.4502 3811.1485
Panel B: Users, Leverage 308 0.3369 0.3447 0.1296
Panel B: Users, Domestic Leverage 308 0.1028 0.1213 0.0852
Panel B: Users, Foreign Leverage 308 0.2096 0.2233 0.1243
Panel B: Users, Market/Book (Asset) 308 1.0122 1.1957 0.6746
Panel B: Users, Margin 308 0.2165 0.2437 0.1364
Panel B: Users, Net Income/TA 308 0.0410 0.0391 0.0710
Panel B: Users, Cash 308 0.0613 0.1074 0.1124
Panel B: Users, Capex 284 0.0602 0.0784 0.0678
Panel C: All Firms, Revenue 1023 411.2240 1134.6736 2263.6956
Panel C: All Firms, Market Cap 1023 134.7062 860.0264 2359.1912
Panel C: All Firms, Leverage 1023 0.2744 0.2700 0.1721
Panel C: All Firms, Domestic Leverage 1023 0.1055 0.1354 0.1269
Panel C: All Firms, Foreign Leverage 1023 0.1052 0.1346 0.1341
Panel C: All Firms, Market/Book (Asset) 1023 0.8025 0.9403 0.6251
Panel C: All Firms, Margin 1023 0.2043 0.2283 0.1490
Panel C: All Firms, Net Income/TA 1023 0.0268 0.0248 0.0892
Panel C: All Firms, Cash 1023 0.0391 0.0820 0.1003
Panel C: All Firms, Capex 909 0.0459 0.0626 0.0650


Table 2: Firm Value and Derivative Usage This table presents the regression estimates from a regression of market-to-book value on derivative usage and other control variables. The dependent variable in the regression is the market-to-book value of the firm's asset defined as the ratio of the (book value of total debt plus market value of equity) to the (book value of debt plus book value of equity). The explanatory variables are defined as follows: dderiv is a binary variable that equals one for the users of currency derivatives. logsize is the natural logarithm of the firm's total revenue for the year. margin measures the operating profit of the firm and is measured as the ratio os Earnings before interest and Taxes to the book value of total assets. salesgrowth represents the percentage growth in year-by-year revenue of the firm. capex/TA is measured as the ratio of firm's capital expenditure to the book value of total assets. cash/TA is the ratio of the firm's cash balance to the book value of total assets. fininc/TA is the ratio of the firm's financial income (which includes gains on derivative transactions) to total assets. finexp/TA is the ratio of firm's financial expenses (such as interest expense, bank fees, and losses on derivative transactions) to the book value of total assets. All regressions include year dummies. Models 1 and 2 are estimated using OLS regression with pooled data, whereas Models 3 and 4 are estimated using a firm fixed effects model. Robust t-statistics adjusted for firm-level clustering for OLS models and industry-level clustering for fixed effects models are given in brackets in the column t-stat. Other estimation details are provided in the last six rows of the table. R^{2} reported for the fixed effects model is the within group R^{2}, i.e., based on the estimation model that uses deviations from the mean. ** denotes significance at the 5% level and * at the 10% level.



Table 2: Firm Value and Derivative Usage
  OLS Regression Model 1: Estimate OLS Regression Model 1: t-stat OLS Regression Model 2: Estimate OLS Regression Model 2: t-stat Firm Fixed Effects Regression Model 3: Estimate Firm Fixed Effects Regression Model 3: t-stat Firm Fixed Effects Regression Model 4: Estimate Firm Fixed Effects Regression Model 4: t-stat
dderiv 0.1655** (2.18) 0.1426* (1.89) 0.0782* (2.00) 0.0671* (1.77)
logsize 0.0975** (2.95) 0.0897** (2.63) 0.0012 (0.03) 0.0003 (0.01)
margin 0.7864** (2.27) 0.7719** (2.19) 1.6084** (4.41) 1.6038** (4.35)
salesgrowth 0.0677 (0.90) 0.0844 (1.11) -0.0308 (-0.58) -0.0231 (-0.45)
capex/TA 0.7867 (1.18) 0.9792 (1.44) 1.5414** (3.25) 1.6534** (3.59)
cash/TA     0.4625 (1.48)     0.4005** (3.60)
fininc/TA     -0.5803 (-0.93)     0.1362 (0.25)
finexp/TA     1.1490* (1.82)     0.2800 (0.81)
intercept -0.8123* (-1.84) -0.8061* (-1.75) 0.3872 (0.72) 0.3252 (0.61)
R^2 0.269   0.278   0.325   0.325  
N 909   905   909   905  
Year dummies yes   yes   yes   yes  
Industry dummies yes   yes   no   no  
Clustering unit firm   firm   industry   industry  
Firm Fixed Effects no   no   yes   yes  


Table 3: Derivatives and Capital Expenditure This table presents regression estimates from a regression of firm's capital expenditure on derivative usage and control variables. The dependent variable in the regression is the ratio of capital expenditure to beginning of the year total assets of the firm. The explanatory variables are defined as follows: dderiv is a binary variable that equals one for the users of currency derivatives. logsize is the natural logarithm of the firm's total revenue for the prior year. margin is computed as the ratio of Earnings before Interest and Taxes for the same fiscal year scaled by the year end total assets. levavg represents the average of the beginning and end of year book leverage. margin*dderiv is the interaction of margin and derivative dummy variables described earlier, which means that it takes the value of margin for the users of derivative zero otherwise. margin*(1-dderiv) takes the value of margin for non-hedgers and zero otherwise. Both models 1 and 2 are estimated using the OLS method. Robust t-statistics adjusted for firm level clustering are given in brackets in the column t-Statistic. We provide other estimation details in the last four rows. ** denotes significance at the 5% level and * at the 10% level.



Table 3: Derivatives and Capital Expenditure
  Model 1: Estimate Model 1: t-stat Model 2: Estimate Model 2: t-stat
dderiv 0.0132* (1.80) 0.0309** (2.45)
margin 0.0430** (2.33)    
margin*dderiv     -0.0093 (-0.27)
margin*(1-dderiv)     0.0626** (2.94)
logsize 0.0025 (1.37) 0.0021 (1.14)
levavg -0.0154 (-0.95) -0.0127 (-0.79)
intercept 0.0372 (1.46) 0.0359 (1.45)
R^2 0.179   0.182  
N 889   889  
Year dummies yes   yes  
Industry dummies yes   yes  


Table 4: InterestExpense and Foreign Currency Debt This table presents OLS regression estimates from a regression of financial expenses of firm on the level of domestic and foreign currency debt. The dependent variable in the regression is the financial expense of the firm in R$ obtained from the firm's income statement. domdebt is the average of the beginning and end of the year domestic debt in R$. fordebt is the average of the beginning and end of the year foreign currency debt. dderiv is a dummy variable that takes a value of one for derivative users, zero otherwise. ppe is the property, plant and equipment at the end of the year in R$. EBIT is the earnings before interest and taxes during the year in R$. Robust t-statistics adjusted for firm level clustering are given in brackets under column t-Statistic. All models include year dummies as well. ** denotes significance at the 5% level and * at the 10% level.



Table 4: InterestExpense and Foreign Currency Debt
  Model 1: Estimate Model 1: t-stat Model 2: Estimate Model 2: t-stat Model 3: Estimate Model 3: t-stat
domdebt 0.2560** (8.19) 0.2535** (8.12) 0.2865** (11.11)
fordebt 0.1160** (4.94)        
fordebt*dderiv     0.1119** (5.12) 0.2002** (6.05)
fordebt*(1-deriv)     0.1736** (6.04) 0.2375** (5.91)
ppe         -0.0148 (-1.02)
EBIT         -0.1250* (-1.72)
R^2 0.628   0.633   0.658  
N 998   998   998  
Year dummies yes   yes   yes  
Industry dummies yes   yes   yes  
Clustering unit firm   firm   firm  


Table 5: Profitability and Foreign Currency Debt This table presents regression estimates from a regression of firm's net profitability on derivative usage, foreign currency debt, and control variables. The dependent variable in the regression is the ratio of net income to total assets of the firm. The explanatory variables are defined as follows: logsize is the natural logarithm of the firm's total revenue for the prior year. ebitda/TA is computed as Earnings before interest, Taxes and Depreciation for the same fiscal year scaled by total assets. dep/TA measures the Depreciation and Amortization scaled by the beginning of the year book value of total assets. invinc/TA measures the firm's income from investment in equity of other firms scaled by total assets. dderiv is a binary variable that equals one for the users of currency derivatives. levavg is the average value of the beginning and end of year ratios of total debt to book value of total assets. forlevavg is the average of the beginning and end of year ratios of foreign currency debt to book value of total assets. domlevavg represents the average of the beginning and end of year ratios of domestic debt to book value of total assets. All three models are estimated using the OLS method. Robust t-statistics adjusted for firm level clustering are given in brackets in the column t-Statistic. We provide other estimation details in the last three rows. ** denotes significance at the 5% level and * at the 10% level.



Table 5: Profitability and Foreign Currency Debt
  Model 1: Estimate Model 1: t-stat Model 2: Estimate Model 2: t-stat Model 3: Estimate Model 3: t-stat
dderiv 0.0159** (1.97)     -0.0044 (-0.30)
forlevavg*dderiv     -0.0404 (-1.17) -0.0295 (-0.67)
forlevavg*(1-dderiv)     -0.1174** (-3.01) -0.1208** (-2.86)
logsize 0.0057* (1.81) 0.0046 (1.42) 0.0048 (1.40)
ebitda/TA 0.1837** (4.92) 0.1873** (5.02) 0.1876** (5.02)
levavg -0.1201** (-4.47)        
domlevavg     -0.1403** (-4.04) -0.1400** (-4.04)
invinc/TA 1.4825** (6.07) 1.4885** (6.06) 1.4882** (6.09)
dep/TA -0.8168** (-3.42) -0.8075** (-3.32) -0.8057** (-3.30)
intercept -0.0488 (-1.18) -0.0358 (-0.87) -0.0383 (-0.89)
R^2 0.350   0.335   0.334  
N 953   953   953  
Year dummies yes   yes   yes  
Industry dummies yes   yes   yes  
Clustering unit firm   firm   firm  


Table 6: Foreign Currency Debt-Mix and Derivative Usage This table presents regression estimates from a regression of firm's foreign currency debt on derivative usage and control variables. The dependent variable in the regression is the ratio of foreign currency debt to the total debt of the firm. The explanatory variables are defined as follows: dderiv is a binary variable that equals one for the users of currency derivatives. logsize is the natural logarithm of the firm's total revenue for the prior year. margin is computed as the ratio of Earnings before Interest and Taxes for the same fiscal year scaled by the year end total assets. salesgrowth represents the percentage growth in year-by-year revenue of the firm. dep/TA measures the Depreciation and Amortization scaled by the beginning of the year book value of total assets. export is a dummy variable that equals one for the exporters, zero otherwise. dol is a dummy variable that equals one for firms that hold dollar assets, zero otherwise. ppe/TA is the ratio of firm's permanent assets (plant,property and equipment) to the total assets. Models 1-3 are estimated using OLS method, whereas Model 4 is based on firm fixed-effects. Robust t-statistics adjusted for firm-level clustering for Models 1-3 and industry-level clustering for Model 4 are given in brackets under the columns labelled t-stat. ** denotes significance at the 5% level and * at the 10% level.



Table 6: Foreign Currency Debt-Mix and Derivative Usage
  Model 1: Estimate Model 1: t-stat Model 2: Estimate Model 2: t-stat Model 3: Estimate Model 3: t-stat Model 4: Estimate Model 4: t-stat
dderiv 0.1805** (5.89) 0.1816** (5.96) 0.1688** (5.66) 0.0677** (2.59)
logsize 0.0719** (6.81) 0.0659** (5.92) 0.0578** (4.45) 0.0350* (1.66)
margin -0.2136 (-1.57) -0.2190* (-1.65) -0.2054 (-1.40) -0.1640 (-1.06)
export     0.0779** (2.00) 0.0656* (1.66) -0.0331 (-0.63)
dol         0.1083** (2.45)    
salesgrowth         -0.0606* (-1.94)    
ppe/TA         -0.1439 (-1.34)    
dep/TA         0.2876 (0.38)    
intercept -0.3369** (-2.30) -0.3222** (-2.23) -0.1601 (-0.92) 0.0578 (0.22)
R^2 0.361   0.369   0.393   0.057  
N 992   992   947   992  
Year dummies yes   yes   yes   yes  
Industry dummies yes   yes   yes   no  
Firm fixed-effects no   no   no   yes  


Table 7: Leverage and Derivative Usage This table presents regression estimates from a regression of firm's foreign currency and domestic leverage on derivative usage and control variables. The dependent variable in the regression is the ratio of foreign currency debt to the total assets of the firm in Models 1 and 2, and domestic currency debt to total assets in Models 3 and 4. The explanatory variables are defined as follows: dderiv is a binary variable that equals one for the users of currency derivatives. logsize is the natural logarithm of the firm's total revenue for the prior year. margin is computed as the ratio of Earnings before Interest and Taxes for the same fiscal year scaled by the year end total assets. salesgrowth represents the percentage growth in year-by-year revenue of the firm. dep/TA measures the Depreciation and Amortization scaled by the beginning of the year book value of total assets. export is a dummy variable that equals one for the exporters, zero otherwise. dol is a dummy variable that equals one for firms that hold dollar assets, zero otherwise. ppe/TA is the ratio of firm's permanent assets (plant,property and equipment) to the total assets. All models are estimated using OLS method. Robust t-statistics adjusted for firm-level clustering are given in brackets under the columns labeled t-stat. ** denotes significance at the 5% level and * at the 10% level.



Table 7: Leverage and Derivative Usage
Dependent Variable Foreign Debt / Total Assets, Model 1: Estimate Foreign Debt / Total Assets, Model 1: t-stat Foreign Debt / Total Assets, Model 2: Estimate Foreign Debt / Total Assets, Model 2: t-stat Domestic Debt / Total Assets, Model 3: Estimate Domestic Debt / Total Assets, Model 3: t-stat Domestic Debt / Total Assets, Model 4: Estimate Domestic Debt / Total Assets, Model 4: t-stat
dderiv 0.0765** (5.06) 0.0696** (4.68) -0.0070 (-0.44) -0.0072 (-0.44)
logsize 0.0321** (7.19) 0.0221** (4.39) -0.0142 (-1.63) -0.0176* (-1.87)
margin -0.2213** (-4.04) -0.1962** (-3.91) -0.1092** (-2.15) -0.1195** (-2.06)
export     0.0240 (1.63)     0.0115 (0.68)
dol     0.0785** (4.35)     0.0100 (0.56)
salesgrowth     -0.0169 (-1.49)     0.0037 (0.24)
ppe/TA -0.0109 (-0.31) -0.0287 (-1.00) 0.0403 (0.82) 0.0281 (0.47)
dep/TA     0.2218 (0.63)     0.3598 (0.99)
intercept -0.2141** (-3.33) -0.1277** (-2.04) 0.2833** (2.52) 0.3096** (2.65)
R^2 0.392   0.455   0.161   0.160  
N 1023   978   1023   978  
Year dummies yes   yes   yes   yes  
Industry dummies yes   yes   yes   yes  
Clustering unit firm   firm   firm   firm  


Table 8: Cox Proportional Hazard Model for Derivative Usage This table presents Cox Proportional Hazard Model regression estimates from a regression of firm's decision to use derivatives for the first time on various firm-level characteristics. The dependent variable in the regression is a binary variable that equals one in the year when firms start using derivatives, and zero otherwise. After the first year in which derivative-usage is reported by a firm, it is not used for estimation in the subsequent years. In particular we estimate the following model: h(t\vert x_{j})=h_{0}(t)exp(x_{j}\beta_{x}); where h stands for the hazard rate of derivative usage, meaning it is the probability of using derivatives next year conditional on not having used derivatives in the past. h_{0} is the baseline hazard rate and h_{t} reports hazard rate conditional on set of covariates given by x_{j} at time t. In this table, we report the \beta coefficients of this regression. The explanatory variables ( x_{i}s) are defined as follows: logsize is the natural logarithm of the firm's total revenue for the prior year. leverage is computed as the ratio of total debt to total assets measured as of the beginning of the year. levsquare is the squared value of leverage described above. cash/TA measures the cash holdings of the firm scaled by the total assets for the prior year end. export is a dummy variable that equals one for the exporters, zero otherwise. dol is a dummy variable that equals one for firms that hold dollar assets, zero otherwise. Both these variables are also measured as of the prior year. salesgrowth is the percentage increase in firm's sales during the year. In model 2 and 4, we also control for year dummies. ** denotes significance at the 5% level and * at the 10% level.



Table 8: Cox Proportional Hazard Model for Derivative Usage
  Model 1: Estimate Model 1: t-stat Model 2: Estimate Model 2: t-stat Model 3: Estimate Model 3: t-stat Model 4: Estimate Model 4: t-stat
logsize 0.5932** (7.13) 0.6121** (7.79) 0.5382** (5.79) 0.5368** (6.31)
leverage 8.3866** (2.95) 10.4364** (3.11) 8.5328** (2.95) 10.2344** (3.00)
levsquare -12.4736** (-2.88) -15.7130** (-3.04) -12.8876** (-2.89) -15.9289** (-3.02)
cash/TA 2.3976** (2.69) 2.6091** (2.32) 2.5124** (2.71) 2.3940** (2.26)
salesgrowth 0.9553** (3.14) 0.5490* (1.65) 0.8918** (2.85) 0.4460 (1.38)
dol         0.4503 (1.53) 0.6784** (2.05)
export         -0.1144 (-0.50) 0.0190 (0.06)
N 719   719   719   719  
Year dummies no   yes   no   yes  
Industry dummies no   yes   no   yes  


Table 9: Derivatives and Foreign Currency Debt: IV Regression This table presents regression estimates from Instrumental Variable regressions of firm's foreign currency debt on derivative usage and control variables. In Models 1 and 2, the dependent variable in the regression is the ratio of foreign currency debt to the total debt of the firm. In Model 3, the dependent variable is the foreign currency leverage defined as the ratio of foreign currency debt to total assets of the firm. The endogenous variable is the derivative usage of firm, dderiv. We estimate the model using IV regression technique. In the first stage dderiv is instrumented with firm's leverage, its squared term, lev- squared and firm's cash holdings, cash/TA. The explanatory variables are defined as follows: logsize is the natural logarithm of the firm's total revenue for the prior year. margin is computed as the ratio of Earnings before Interest and Taxes for the same fiscal year scaled by the year end total assets. dep/TA measures the Depreciation and Amortization scaled by the beginning of the year book value of total assets. export is a dummy variable that equals one for the exporters, zero otherwise. dol is a dummy variable that equals one for firms that hold dollar assets, zero otherwise. salesgrowth represents the percentage growth in year-by-year revenue of the firm. ppe/TA is the ratio of firm's permanent assets (plant,property and equipment) to the total assets. Robust t-statistics adjusted for firm level clustering are given in brackets under column t-Statistic. We provide the statistics from the first-stage estimation in the last three rows. Partial R^{2} measures the improvement in adjusted (pseudo) R-squared obtained by including the instruments in the first stage Probit model of derivative usage. Chi-squared statistics test for the joint significance of all excluded instruments. ** denotes significance at the 5% level and * at the 10% level.



Table 9: Derivatives and Foreign Currency Debt: IV Regression
Dependent Variable Foreign Debt/Total Debt, Model 1: Estimate Foreign Debt/Total Debt, Model 1: t-stat Foreign Debt/Total Debt, Model 2: Estimate Foreign Debt/Total Debt, Model 2: t-stat Foreign Debt/Total Assets, Model 3: Estimate Foreign Debt/Total Assets, Model 3: t-stat
dderiv 0.06565** (3.78) 0.0580** (3.11) 0.0487** (5.96)
logsize 0.0304** (2.20) 0.0372** (2.46) -0.0050 (-0.76)
margin -0.1662** (-2.10) -0.1904** (-1.99) -0.1861** (-4.67)
export 0.06353** (2.62) 0.0628** (2.14) 0.0211* (1.93)
dol 0.1038** (4.12) 0.1115** (4.13) 0.0742** (6.76)
salesgrowth     -0.0632* (-1.77) -0.0150 (-1.00)
ppe/TA     -0.1403* (-1.77) -0.1051 (-0.32)
dep/TA     0.1627 (0.77) 0.0084 (0.04)
intercept 0.2696 (1.25) 0.2661 (1.10) 0.3528** (3.38)
R^2 0.3579   0.3676   0.4644  
N 992   947   978  
Partial R^{2} 0.0729   0.0651   0.0651  
Chi-squared Stat 74.70   64.92   64.92  
Year dummies yes   yes   yes  
Industry dummies yes   yes   yes  


Footnotes

* Federal Reserve Board; Tel: (202) 452-3590, E-mail: [email protected] Return to Text
* Ross School of Business, University of Michigan; Tel: (734) 764-6886, E-mail: [email protected] Return to Text
* Ross School of Business, University of Michigan; Tel: (734) 764-2310, E-mail: [email protected] Return to Text
* We would like to thank Tim Adam, Sudheer Chava, Kathryn Dominguez, Jie Gan, Han Kim, Peter Mackay, Paige Parker, Amit Seru, Rene Stulz, Linda Tesar, Jing Zhang, and seminar participants at CSSS (Calcutta), Hong Kong UST, Michigan, National University of Singapore, Notre Dame, and Singapore Management University for helpful comments. All errors remain our own. The views expressed are those of the authors and do not necessarily reflect those of the Board of Governors of the Federal Reserve System or its staff. Return to Text
1. We use the terms "hedging" and "using derivatives" synonymously in this paper. Return to Text
2. For example, in the model of Adam, Dasgupta, and Titman (2007), in equilibrium some firms hedge and others do not, but each firm is indifferent between hedging and not and has the same value in either case. Return to Text
3. Over a different period of study, Bonomo, Martins, and Pinto (2003) find a significant drop in corporate investment after a 1991 devaluation in Brazil. Return to Text
4. Berrospide (2007) extends the Holmstrom and Tirole (1997) model of external financing to an open economy, and demonstrates theoretically that hedging can increase foreign debt capacity. Return to Text
5. The CVM is the Brazilian analog of the SEC in the US. Return to Text
6. We obtain similar results when we interact derivative usage with EBITDA rather than EBIT. Both these measures capture the pre-hedging cash-flows of the firm since the effect of currency hedging is reported under financial expenses and income item, which comes after EBIT on the profit and loss statement. Return to Text

♣ This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to Text
Home | Economic Research and Data | Accessibility | Contact us
Last update: April 11, 2008