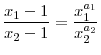Happiness Maintenance and Asset Prices
Keywords: State-dependent utility, affect and decisionmaking, equity premium puzzle
Abstract:
JEL Codes: D81, D91, E44, G12.
I. Introduction
Empirical research in finance has extensively documented the failure of traditional asset pricing models to account for the historically observed level, volatility, and cyclical behavior of asset returns. The last decade has witnessed some progress in bringing theory closer to the data (see, for example, Campbell and Cochrane (1999) and Bansal and Yaron (2004)). Nevertheless, the identification of the fundamental sources of aggregate risk that drive expected returns remains an open challenge.
This paper proposes a new analytical framework based on the link between immediate emotions and risk preferences. The starting point of my analysis is the well replicated finding that individuals who feel good are more risk averse than individuals who feel neutral (see Isen (1999) for a thorough review of the evidence). This finding is consistent with the notion that individuals have a preference for happiness maintenance: accepting a gamble when happy puts their happiness, in addition to any tangible stake, at risk.
I embed happiness maintenance preferences into an otherwise standard equilibrium asset pricing model along the lines of Lucas (1978) and Mehra and Prescott (1985). In my model, investors derive direct utility from both consumption and financial wealth. The current state of the economy changes their attitude toward wealth gambles, which I refer to as "hedonic" risk aversion: in good times investors prefer not to "push their luck" - i.e., they become more conservative toward their portfolio risk.
I show, both analytically and numerically, that happiness maintenance goes a long way toward accounting for stock market facts. With a realistic consumption growth process and reasonable risk aversion and time preference parameters, my model delivers a sizable equity premium, a low and stable risk-free rate, volatile and predictable stock returns, and price-dividend and Sharpe ratios in line with the data.
What is the economic mechanism behind these results? In essence, it is a "leverage effect" that makes equity riskier for an investor with happiness maintenance preferences. To see this point, consider that changes in hedonic risk aversion induce changes in investors' views about how valuable wealth is relative to consumption. This is the reason why the level of the wealth to consumption ratio, rather than its volatility, emerges as an extra source of risk: even if wealth were to stay constant, investors in my model would consider equity risky, due to the need to hedge swings in their hedonic risk aversion. Thus, changes in hedonic risk aversion increase the standard deviation of investors' intertemporal marginal rate of substitution. The increase in perceived risk leads investors to require a higher return on risky assets for any given level of consumption and wealth risk.
It is worth stressing the two main features that distinguish happiness maintenance from previous models. First, in contrast to previous models that add a second term to the utility function, such as financial or housing wealth (e.g. Bakshi and Chen (1996), Piazzesi et al (2005), Barberis et al (2001)), happiness maintenance generates a large equity premium without the need for financial wealth to be too volatile. This is the case since the leverage effect depends on the level, rather than the volatility, of the wealth-consumption ratio. Second, in contrast with habit persistence models that rely on high and strongly counter-cyclical effective risk aversion (e.g. Campbell and Cochrane (1999), but also Barberis, Huang and Santos (2001) who need strongly counter-cyclical loss aversion), low and mildly pro-cyclical hedonic risk aversion is sufficient for the leverage effect to be operative. Thus, my results highlight that counter-cyclical risk aversion is not a necessary condition for equilibrium asset pricing models to replicate stock market facts.
Happiness maintenance differs from the standard consumption-based approach of Campbell and Cochrane (1999) also in terms of the predictions of the model. In the consumption-based model, stock return volatility is generated through changes in risk aversion that are driven by consumption. Thus, in contrast with the data, stock returns and consumption are strongly correlated. My wealth-based framework weakens the correlation between returns and consumption since stock return volatility is driven not only by consumption, but also by wealth. Thus, the multi-factor structure of my model distinguishes it from standard consumption-based approaches.
My study makes the following four additional contributions to the literature. First, I identify a fundamentally different source of equity risk, which is complementary to standard consumption and wealth volatility (see Kocherlakota (1996) for a comprehensive survey).
Second, my model contributes to the literature on predictability (for a survey see Cochrane (2000)). In fact, in my model the consumption-wealth ratio predicts expected returns. Lettau and Ludvigson (2001) provide empirical evidence of a common component in expected returns and the consumption-wealth ratio. With happiness maintenance preferences, such common component emerges in equilibrium, as the level of the consumption-wealth ratio directly affects the riskiness of stocks. Thus, my model offers a general equilibrium perspective over the earlier empirical findings.
Third, my work contributes to the wealth-based asset pricing literature (e.g. Bakshi and Chen (1996), Epstein and Zin (1989, 1991)) by addressing the Campbell (1993) critique. This class of models identifies the volatility of wealth as a risk factor. However, these models do not generate volatile wealth with low risk aversion since they imply a constant price/dividend ratio. In other words, the fact that consumption is smooth and wealth is volatile is itself a puzzle that must be explained. My full-fledged general equilibrium setting directly address this issue: even with low risk aversion, the leverage effect allows me to generate endogenously a realistic volatility of wealth.
Finally, my paper contributes to the growing literature on emotions and investor behavior (e.g. Lo and Repin (2001), Mehra and Sah (2001); see Loewenstein (2000) for a survey). Saunders (1993) and Kamstra, Kramer and Levi (2000) document an empirical relationship between weather or length of the day and asset returns, which they interpret as evidence of an impact of moods on asset prices. Lo and Repin (2001) offer direct evidence of an emotional reaction of investors to risk by documenting significant correlation between changes in stock market traders' cardiovascular variables and market volatility. Mehra and Sah (2001) formally explore the role of small fluctuations in investors' preferences within a non-rational expectations framework. To the best of my knowledge, my paper represents the first comprehensive equilibrium treatment of emotions and asset prices.
Outline of the paper
The first section develops a formal representation of happiness-maintenance preferences which are then embedded into an otherwise standard equilibrium asset pricing model. The second section characterizes equilibrium returns in an economy populated by investors with happiness-maintenance preferences. The results of a simple calibration exercise are in the third section, which investigates the quantitative implications of happiness maintenance. The fourth section concludes. Algebraic derivations and proofs are in Appendix A. Tables and Figures are in Appendix B.
II. A wealth-based capital asset pricing model
In this section I develop a formal representation of investors' happiness maintenance preferences and embed into an otherwise standard dynamic equilibrium asset pricing model.
II.1 Setup
Mine is a standard "endowment economy" (Lucas (1978), Mehra and Prescott (1985)) populated by a large number of infinitely-lived investors, who are identical with respect to their preferences, endowments and expectations and face a standard consumption/saving problem. Given these assumptions,
it is customary to aggregate investors into a representative agent. There is one consumption good. The only source of income is a large number of identical and infinitely-lived fruit trees, each in fixed supply. Without loss of generality, the supply of trees is normalized to unity and it is
assumed that there exists one tree per individual, so that the amount of fruit produced by a tree in period ![]() , denoted
, denoted ![]() , represents the output or dividend per capita. Fruits are non-storable, cannot be used to increase the number of trees and can only be used for consumption. They are uncertain and evolve according to
, represents the output or dividend per capita. Fruits are non-storable, cannot be used to increase the number of trees and can only be used for consumption. They are uncertain and evolve according to
![]() , where
, where
![]() ... ,
... ,
![]() is the growth rate of output which follows a given stationary stochastic process to be detailed on later. Each tree has a single perfectly divisible equity claim outstanding on
it. In each period there is a spot market for the consumption good and a financial market in which equity shares are exchanged at a price
is the growth rate of output which follows a given stationary stochastic process to be detailed on later. Each tree has a single perfectly divisible equity claim outstanding on
it. In each period there is a spot market for the consumption good and a financial market in which equity shares are exchanged at a price ![]() Consequently, the gross rate of return on
equity holdings from period
Consequently, the gross rate of return on
equity holdings from period ![]() to period
to period ![]() is defined as
is defined as
![]() A one-period risk-free asset in zero net supply at a price
A one-period risk-free asset in zero net supply at a price ![]() completes the description of the "technology" side of the economy. It pays a gross interest rate
completes the description of the "technology" side of the economy. It pays a gross interest rate
![]() .
.
Investor preferences
Investors derive utility from a composite good, ![]() which includes both current (per-capita) consumption,
which includes both current (per-capita) consumption, ![]() and current (per-capita) financial wealth,
and current (per-capita) financial wealth, ![]() . They rank random sequences of the composite good according to
. They rank random sequences of the composite good according to
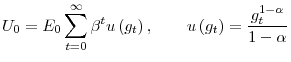
In contrast to standard models, investors' financial wealth, ![]() enters their preferences directly over and above the indirect utility of the consumption services it
provides
enters their preferences directly over and above the indirect utility of the consumption services it
provides![]() 1 that is
1 that is
Affect-maintenance preferences are modelled as an instance of state-dependent preferences by postulating a state-dependent demand for financial happiness. Appendix A gives a standard set of axioms and a representation theorem for these preferences. To facilitate intuition on the connection
between
![]() and happiness maintenance, it is useful to rewrite the utility function as
and happiness maintenance, it is useful to rewrite the utility function as
Investors' expected utility has a decision component, which depends on current consumption, and a hedonic component, which depends on the performance of their portfolios. Financial income relative to consumption is assumed to provide a first approximation indicator of this performance and, hence, a direct source of happiness with respect to financial wealth. Thus, the term
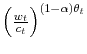 formalizes the intuition that investors' utility depends on their experienced happiness. If
formalizes the intuition that investors' utility depends on their experienced happiness. If
One important implication of
![]() is that a mean preserving spread of financial wealth (relative to consumption) directly reduces investors' utility. If financial
wealth is a source of happiness, the desire to maintain happiness should determine the size of the reduction of investors' utility. In fact, while investors' relative risk aversion over
is that a mean preserving spread of financial wealth (relative to consumption) directly reduces investors' utility. If financial
wealth is a source of happiness, the desire to maintain happiness should determine the size of the reduction of investors' utility. In fact, while investors' relative risk aversion over ![]() gambles,
gambles, ![]() is constant, investors' hedonic risk aversion,
is constant, investors' hedonic risk aversion, ![]() that is
their risk aversion2 over portfolio risk, is a simple function of their demand for financial happiness. By definition,3 hedonic risk aversion is
that is
their risk aversion2 over portfolio risk, is a simple function of their demand for financial happiness. By definition,3 hedonic risk aversion is
where
The parameter ![]() controls how far back in the past investors look to determine whether times are good or bad. When
controls how far back in the past investors look to determine whether times are good or bad. When ![]() definition
definition
![]() simplifies to
simplifies to
![]() In this case good times are measured simply by the current state of the economy. If
In this case good times are measured simply by the current state of the economy. If ![]() a mean of the recent past states of the economy measures investors' hedonic risk aversion. This is broadly consistent with the psychological evidence on incidental emotions, which documents the existence of a durability or
projection effect (see Loewenstein et al. (2001) for a survey): investors' current moods are affected by the recent economic trend. An alternative interpretation is that investors' views about current times are formed by extrapolating from the recent past.
a mean of the recent past states of the economy measures investors' hedonic risk aversion. This is broadly consistent with the psychological evidence on incidental emotions, which documents the existence of a durability or
projection effect (see Loewenstein et al. (2001) for a survey): investors' current moods are affected by the recent economic trend. An alternative interpretation is that investors' views about current times are formed by extrapolating from the recent past.
In summary, the choices of an investor with affect-dependent preferences are fully characterized by the triple
![]() i.e., respectively, by his subjective rate of time preference,
i.e., respectively, by his subjective rate of time preference, ![]() his relative risk aversion,
his relative risk aversion, ![]() and his relative demand for financial happiness,
and his relative demand for financial happiness,
![]() Variables
Variables
![]() are sufficient relative to the entire history of shocks up to, and including, time
are sufficient relative to the entire history of shocks up to, and including, time ![]() for predicting the subsequent evolution of the economy. They thus constitute legitimate state variables for the model.
for predicting the subsequent evolution of the economy. They thus constitute legitimate state variables for the model.
Further discussion of assumptions
Happiness maintenance is a well replicated finding (for a detailed overview of the experimental psychology findings see Isen (1999) and Appendix A). While earlier studies indicate a tendency toward conservatism for individuals in a good mood, the study by Isen et al. (1988) is most relevant since it focuses directly on the notion of risk aversion typically employed in economics and finance. The study examined the slope of the utility associated with various outcomes, as a function of positive affect induced by means of a small bag of candy. Participants were asked to make choices between pairs of simple 50-50 gambles in such a way that a set of indifference points could be found and individual utility functions constructed. The average utility curves were computed for the two groups and people in whom positive affect had been induced displayed steeper utility function than controls.
Finally, notice that in my specification
![]() is iso-elastic, which insures stationarity of returns and is broadly consistent with an established stylized fact of the relationship between individual emotional
well-being and aggregate economic conditions (see Easterlin (2000) and Frey and Stutzer (2002) for recent surveys): there is no clear cut trend, positive or negative, in self-reported subjective well-being over periods of 20 to 30 years in rich countries. In particular, in the United States between
1946 and 1991, per capita real income has risen by a factor of 2.5, but happiness, on average, remained constant.
is iso-elastic, which insures stationarity of returns and is broadly consistent with an established stylized fact of the relationship between individual emotional
well-being and aggregate economic conditions (see Easterlin (2000) and Frey and Stutzer (2002) for recent surveys): there is no clear cut trend, positive or negative, in self-reported subjective well-being over periods of 20 to 30 years in rich countries. In particular, in the United States between
1946 and 1991, per capita real income has risen by a factor of 2.5, but happiness, on average, remained constant.
II.2 The consumption-saving problem
Given the asset price function,
![]() initial asset holdings,
initial asset holdings, ![]() the
initial state of the economy,
the
initial state of the economy, ![]() and initial affective state,
and initial affective state,
![]() the problem of the "stand-in" investor is to choose a sequence of plans for consumption,
the problem of the "stand-in" investor is to choose a sequence of plans for consumption, ![]() and end-of-period asset holdings,
and end-of-period asset holdings, ![]() that maximizes her present discounted expected utility subject to the budget constraint. Formally, the investor chooses
consumption and asset holdings that solve the following
that maximizes her present discounted expected utility subject to the budget constraint. Formally, the investor chooses
consumption and asset holdings that solve the following
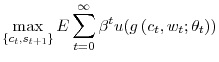 |
(3) | |
where
This problem admits a recursive formulation which, through standard perturbation arguments, delivers5 the following Euler equation:
where
The Euler equation is derived using only the preferences and budget constraint of the investor. Before exploiting the restrictions imposed by equilibrium on asset returns, it is useful to consider the consequences of the individual budget constraint and preferences for asset returns. The risk-free interest rate is given by
where
Under
![\displaystyle R_{f}=\frac{1}{\beta E\left[ \left( \frac{c_{t+1}}{c_{t}}\right) ^{\left( 1-\alpha\right) \left( 1-\theta\right) -1}\left( \frac{w_{t+1}}{w_{t}% }\right) ^{\left( 1-\alpha\right) \theta}\tilde{k}_{t+1}\right] }%](img94.gif)
Happiness maintenance adds an extra source of volatility, ![]() which is fundamentally different from standard consumption and wealth uncertainty. To see this, consider the last term in
the denominator of
which is fundamentally different from standard consumption and wealth uncertainty. To see this, consider the last term in
the denominator of
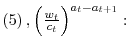 since hedonic risk aversion changes, investors' marginal utility varies even if
there is no consumption or wealth uncertainty. Importantly, large consumption or wealth swings are not needed to generate enough volatility since happiness maintenance introduces a "leverage effect," which depends on the level, rather than the growth rate, of the wealth/consumption ratio. It is
this leverage effect that gives to mild variation in hedonic risk aversion potency for asset pricing.
since hedonic risk aversion changes, investors' marginal utility varies even if
there is no consumption or wealth uncertainty. Importantly, large consumption or wealth swings are not needed to generate enough volatility since happiness maintenance introduces a "leverage effect," which depends on the level, rather than the growth rate, of the wealth/consumption ratio. It is
this leverage effect that gives to mild variation in hedonic risk aversion potency for asset pricing.
The intuition for how the leverage effect works is straightforward: changes in hedonic risk aversion make
![]() stochastically negative or positive. Thus, in contrast to other models with state-dependent preferences such as Campbell and Cochrane (1999), even small changes in hedonic risk
aversion can generate substantial volatility as the wealth to consumption ratio operates as either a discount or a compound factor depending on whether
stochastically negative or positive. Thus, in contrast to other models with state-dependent preferences such as Campbell and Cochrane (1999), even small changes in hedonic risk
aversion can generate substantial volatility as the wealth to consumption ratio operates as either a discount or a compound factor depending on whether
![]() is negative or positive. This effect magnifies the contribution of consumption and wealth volatility to the standard deviation of investors' intertemporal marginal rate of
substitution, thus increasing investors' perceived risk. As a result, investors seeking safety in the risk-free asset bid its price up, which lowers the risk-free return.
is negative or positive. This effect magnifies the contribution of consumption and wealth volatility to the standard deviation of investors' intertemporal marginal rate of
substitution, thus increasing investors' perceived risk. As a result, investors seeking safety in the risk-free asset bid its price up, which lowers the risk-free return.
In summary, since the main mechanism in my model operates through changes in hedonic risk aversion, I do not need high curvature of the utility function to match the equity premium. This is the way my model contributes to the resolution of the risk-free rate puzzle. Moreover, since I only need small changes in hedonic risk aversion, I can maintain a relatively stable interest rate.
The leverage effect implied by happiness maintenance depresses the price of risky assets. In fact, the expected return on equity is
and the implied (conditional) expected premium demanded by the investor to hold her wealth in equities,
The expected premium, as stated in
To see the intuition for this last point, consider the term
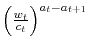 in
in
![]() equity is riskier for an investor with happiness maintenance preferences since she fears that changes in hedonic risk aversion will
change her views about how valuable wealth is relative to consumption. This is the reason why the level of the wealth to consumption ratio matters for risk: as
equity is riskier for an investor with happiness maintenance preferences since she fears that changes in hedonic risk aversion will
change her views about how valuable wealth is relative to consumption. This is the reason why the level of the wealth to consumption ratio matters for risk: as
![]() stochastically changes from negative to positive, the wealth to consumption ratio induces lower discounting. Thus, happiness maintenance introduces a leverage effect that
increases the standard deviation of investors' intertemporal marginal rate of substitution. The increase in perceived risk leads investors to require a higher return on risky assets for any given level of consumption and wealth risk.
stochastically changes from negative to positive, the wealth to consumption ratio induces lower discounting. Thus, happiness maintenance introduces a leverage effect that
increases the standard deviation of investors' intertemporal marginal rate of substitution. The increase in perceived risk leads investors to require a higher return on risky assets for any given level of consumption and wealth risk.
It is worth stressing three important features that distinguish happiness maintenance from previous resolutions of the equity premium puzzle. First, the wealth to consumption ratio is bounded even in a growing economy, since the budget constraint of the investor holds. Thus, in contrast to previous consumption-based models with state-dependent preferences (e.g. Danthine et al. (2003) and Gordon and St-Amour (2000)), happiness maintenance preferences preserve stationarity of returns. Second, in contrast to previous models that add a second term to the utility function, such as financial or housing wealth (e.g. Bakshi and Chen (1996) and Piazzesi et al (2005)), happiness maintenance does not need financial wealth to be too volatile to be able to generate large enough premiums. This is the case since the leverage effect increases the impact of wealth volatility on the volatility of the pricing kernel. Finally, in contrast with most habit persistence models that rely on a strongly counter-cyclical risk aversion,6 as the next section will make clearer, I only need mild variation in hedonic risk aversion for the leverage effect to be operative. Thus, happiness maintenance does not need to make interest rates counterfactually volatile.
III. Aggregate asset pricing implications
of happiness maintenance
Can affect maintenance provide a satisfactory analytical account of the main stylized facts of financial markets? To address this question, I characterize equilibrium asset prices and returns in an economy populated by investors with happiness maintenance preferences. I then study the quantitative properties of the model vis-a-vis the historical record of US stock returns in the post-war period.
III.1 Equilibrium characterization of returns
Given the fixed supplies of goods and assets, it is trivial to determine quantity choices in a competitive equilibrium: all fruits are consumed during the period in which they are produced, i.e.,
![]() , and the representative investor holds all her wealth in the risky asset,
, and the representative investor holds all her wealth in the risky asset,
![]() . Since consumer-investors are assumed to have identical preferences, per-capita consumption of the representative investor equals aggregate consumption, which then equals
aggregate output.
. Since consumer-investors are assumed to have identical preferences, per-capita consumption of the representative investor equals aggregate consumption, which then equals
aggregate output.
Equilibrium is characterized by the asset price function that supports this allocation, that is by the function
![]() that solves
that solves
![]() Loosely speaking, the optimality conditions that correspond to the solution of the investor's problem defined in
Loosely speaking, the optimality conditions that correspond to the solution of the investor's problem defined in
![]() and the requirement of market clearing in the aggregate provide the equilibrium pricing equation for the risk-free and risky assets.
For the probability structure specified in the next section, Appendix A contains a proof of the existence of equilibrium. The following proposition offers a characterization of equilibrium asset returns.
and the requirement of market clearing in the aggregate provide the equilibrium pricing equation for the risk-free and risky assets.
For the probability structure specified in the next section, Appendix A contains a proof of the existence of equilibrium. The following proposition offers a characterization of equilibrium asset returns.
and
where
An important qualification of my results transpires from this characterization of equilibrium returns. Since all the investor's wealth is financial, in equilibrium there is a tight mapping between the properties of the wealth to consumption ratio and the price-dividend ratio. However, recent empirical work by Menzly, Santos and Veronesi (2004) and Lustig, Van Nieuwerburgh and Verdelhan (2007) has shown that these two ratios behave quite differently in the presence of human capital, government transfers or, in general, non financial income. While beyond the scope of this paper, integrating non-financial wealth into the model is an important question for future research.
A Note on Aggregation
The equilibrium pricing equations in
![]() and
and
![]() are derived under the assumption that investors are homogeneous. This is certainly a strong assumption. Investors may be heterogeneous
along a variety of dimensions, which raises the question of aggregation.
are derived under the assumption that investors are homogeneous. This is certainly a strong assumption. Investors may be heterogeneous
along a variety of dimensions, which raises the question of aggregation.
Since in my economy financial markets are competitive and complete, and investors' preferences satisfy the axioms of expected utility (see Appendix A for a formal proof), existence of a representative (single agent) economy with the same aggregate consumption series as the heterogeneous agent economy and the same asset price functions is guaranteed by construction (Prescott and Mehra (1980)). However, it is well known that these properties do not guarantee strict-aggregation, i.e. that the representative agent can be constructed independent of the underlying heterogeneous agent economy's initial wealth distribution.
The question of whether happiness maintenance admits strict-aggregation is important but beyond the scope of this paper. However, there are reasons to believe that the intuition of my model is likely to go through under several types of investor heterogeneity. The results should generalize to any particular form of heterogeneity such that aggregate hedonic risk aversion still varies with the aggregate state of the economy. Another form of heterogeneity that does aggregate is when investors have different wealth levels, but identical wealth to income ratios, a case that can be modelled by having several cohorts of investors, each with a continuum of equally wealthy investors.
While this is speculative, there are good reasons to believe that my intuition will survive more extreme forms of heterogeneity, such as, for example, when investors differ in their hedonic risk aversion, ![]() . Even if
. Even if ![]() varies across investors, as far as each individual investor has pro-cyclical hedonic risk aversion there is no reason to believe that this property will be
lost in the aggregate.
varies across investors, as far as each individual investor has pro-cyclical hedonic risk aversion there is no reason to believe that this property will be
lost in the aggregate.
III.2 Quantitative assessment
In order to gain insight into the quantitative effect of affect maintenance on aggregate asset returns, I compute numerical solutions to the problem of the investor defined in
![]() for various parameter choices and use these solutions to compute the associated time averaged risk-free rate, market rate, and risk
premium as implied by equations
for various parameter choices and use these solutions to compute the associated time averaged risk-free rate, market rate, and risk
premium as implied by equations
![]() and
and
![]() . The choice of specific values for the behavioral parameters and the aggregate growth rate of output,
. The choice of specific values for the behavioral parameters and the aggregate growth rate of output, ![]() , is crucial for the empirical evaluation of the model.
, is crucial for the empirical evaluation of the model.
Calibration of the "technology" side of the model is standard. I consider two alternative stochastic processes for the aggregate output growth, ![]() . In the first case, as in Mehra and
Prescott (1985),
. In the first case, as in Mehra and
Prescott (1985), ![]() follows a Markov chain and the number of states
follows a Markov chain and the number of states ![]() is
limited to two
is
limited to two
![]() with transition probabilities given by
with transition probabilities given by ![]() and defined as
and defined as
The parameters ![]()
![]() and
and ![]() are chosen to match respectively the mean, standard deviation and first order autocorrelation of aggregate consumption growth in the US economy between 1889 and 1985. The values required are
are chosen to match respectively the mean, standard deviation and first order autocorrelation of aggregate consumption growth in the US economy between 1889 and 1985. The values required are
![]()
![]()
![]()
In the second case, aggregate output growth follows an iid lognormal process (as in Campbell and Cochrane (1999)), i.e.
Investor preference parameters,
![]() are chosen based on evidence from field studies and the consensus view in the previous literature. It is customary to choose a time preference
coefficient,
are chosen based on evidence from field studies and the consensus view in the previous literature. It is customary to choose a time preference
coefficient, ![]() close to and lower than one. A negative rate of time preference has been shown to be effective in "solving" the risk-free rate puzzle, but introspection provides a
strong argument in support of a positive rate of time preference. Consequently, I choose the
close to and lower than one. A negative rate of time preference has been shown to be effective in "solving" the risk-free rate puzzle, but introspection provides a
strong argument in support of a positive rate of time preference. Consequently, I choose the ![]() lower than one that optimizes the performance of the model with respect to the risk-free
rate.
lower than one that optimizes the performance of the model with respect to the risk-free
rate.
The literature after Mehra and Prescott (1985) deems reasonable risk aversion coefficients within the
![]() interval. Field studies support this choice, since an
interval. Field studies support this choice, since an ![]() beyond 10 would imply rejections of consumption (and wealth) bets that most subjects in experiments do not turn down. I choose risk aversion close to the lower bound of the interval
beyond 10 would imply rejections of consumption (and wealth) bets that most subjects in experiments do not turn down. I choose risk aversion close to the lower bound of the interval
![]() to explore the full extent to which happiness maintenance can account for stock market facts without resorting to high risk aversion. Given that
to explore the full extent to which happiness maintenance can account for stock market facts without resorting to high risk aversion. Given that ![]() is needed to satisfy the transversality condition of the infinite horizon problem, I take
is needed to satisfy the transversality condition of the infinite horizon problem, I take ![]() to be equal to 3.
to be equal to 3.
Given the simple specification of
![]() in
in
![]() I need to determine reasonable ranges of two parameters,
I need to determine reasonable ranges of two parameters, ![]() and
and ![]() . Recall that, for the composite good
. Recall that, for the composite good ![]() to be well defined,
to be well defined,
![]() has to lie at every point of time within the
has to lie at every point of time within the
![]() interval. This suggests a first restriction for
interval. This suggests a first restriction for
![]() Neither psychological experiments nor introspection provide guidance on how to further restrict
Neither psychological experiments nor introspection provide guidance on how to further restrict ![]() I take a pragmatic stand and consider the interval
I take a pragmatic stand and consider the interval
![]() . This is a conservative choice, since it constrains the demand for happiness to be lower than that for consumption, and hedonic risk aversion to be always lower than
. This is a conservative choice, since it constrains the demand for happiness to be lower than that for consumption, and hedonic risk aversion to be always lower than
![]() and less volatile than the underlying state of the economy. In fact, with
and less volatile than the underlying state of the economy. In fact, with ![]() hedonic risk aversion is
hedonic risk aversion is
![]() and its standard deviation is
and its standard deviation is
![]() Thus,
Thus,
![]() implies
implies
![]() and
and
![]() Finally, since the model is calibrated on yearly frequency, I constrain
Finally, since the model is calibrated on yearly frequency, I constrain ![]() within the
within the
![]() interval so as to roughly span the average length of a business cycle. This restriction implies that investors span at most an entire cycle in their assessment of recent
economic conditions. In summary, my preference parameter values are
interval so as to roughly span the average length of a business cycle. This restriction implies that investors span at most an entire cycle in their assessment of recent
economic conditions. In summary, my preference parameter values are
![]()
![]() and
and
![]()
Two features of my calibration are worth emphasizing. First, my parametrization implies low and mildly volatile hedonic risk aversion, which is consistent with the emphasis of happiness maintenance experiments on mild everyday emotions. Second, my two-parameter
specification of
![]() is relatively parsimonious in that it allows for fewer free parameters than previous wealth-based models (see, for example, Barberis et al. (2001)). Finally, in contrast to
Campbell and Cochrane (1999), I am not forcing the
is relatively parsimonious in that it allows for fewer free parameters than previous wealth-based models (see, for example, Barberis et al. (2001)). Finally, in contrast to
Campbell and Cochrane (1999), I am not forcing the
![]() process to match the stochastic properties of returns.
process to match the stochastic properties of returns.
Computing returns
Expected returns cannot be solved for in closed form and need to be computed using numerical methods. As in Mehra and Prescott (1985), the definition of returns can be used to rewrite equation
![]() in terms of the price-dividend ratio. Since the pricing kernel does not depend on the level of consumption, I do not expect asset prices
to depend on consumption levels either. Thus, it is natural to assume that the price of equities is
in terms of the price-dividend ratio. Since the pricing kernel does not depend on the level of consumption, I do not expect asset prices
to depend on consumption levels either. Thus, it is natural to assume that the price of equities is
![]()
![]() where
where
![]() is a price-dividend ratio function related to
is a price-dividend ratio function related to
![]() , the growth rate of output, both directly and through the dependence of
, the growth rate of output, both directly and through the dependence of
![]() on
on
![]() . Under probability structure
. Under probability structure
![]() the Euler equation defines a system of (nonlinear) first-order difference equations in unknown price-dividend ratios (see
Appendix A for details) . Using these price relationships, I can compute the conditional and unconditional expectation of asset returns.7
the Euler equation defines a system of (nonlinear) first-order difference equations in unknown price-dividend ratios (see
Appendix A for details) . Using these price relationships, I can compute the conditional and unconditional expectation of asset returns.7
The number of first-order difference equations and price-dividend ratios defined by the Euler and the methods adopted to actually solve these equations depend on the value of ![]() In
particular, when
In
particular, when ![]()
![]() the price-dividend ratio,
the price-dividend ratio,
![]() depends only on the growth rate of output, and the Euler equation defines a system of two equations in two unknowns which can be solved as in
Mehra and Prescott (1985). When
depends only on the growth rate of output, and the Euler equation defines a system of two equations in two unknowns which can be solved as in
Mehra and Prescott (1985). When
![]() the Euler in general defines more than two equations. This is the case since
the Euler in general defines more than two equations. This is the case since
![]() depends on past realizations of aggregate dividend growth, which induces time-variation in expected returns and makes the price-dividend ratio,
depends on past realizations of aggregate dividend growth, which induces time-variation in expected returns and makes the price-dividend ratio,
![]() depend effectively on two states,
depend effectively on two states,
![]() and
and
![]() . Since the traditional solution methodology is not applicable to this case, I employ standard simulation methods . In particular, I employ a simple parametrized expectation algorithm (see Marcet and Marshall (2002) for a detailed description of the algorithm) and then compute summary statistics by simulating the solved system to generate a long times series of
50,000 data points.8
. Since the traditional solution methodology is not applicable to this case, I employ standard simulation methods . In particular, I employ a simple parametrized expectation algorithm (see Marcet and Marshall (2002) for a detailed description of the algorithm) and then compute summary statistics by simulating the solved system to generate a long times series of
50,000 data points.8
Volatility bounds and the market price of risk.
To fully explore the quantitative effects of happiness maintenance on returns, it is useful to consider Hansen and Jagannathan (1991)'s statement of the equity premium puzzle, according to which the largest possible Sharpe ratio is given by the conditional standard deviation of the log stochastic discount factor. More formally,
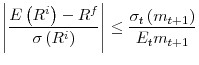
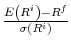 is the Sharpe ratio,
is the Sharpe ratio,
I have argued in the previous section that happiness maintenance increases the volatility of the pricing kernel through a leverage effect,
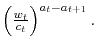 Panels B-D of Figure 1 show that, even with low and moderately procyclical hedonic risk aversion, the leverage effect is strong enough to bring
the equilibrium pricing kernel well within Hansen-Jagannathan bounds. This is in sharp contrast to Panel A, which shows that, even with a risk aversion of 10, the market prices of risk
implied by power utility falls short from satisfying the bounds.
Panels B-D of Figure 1 show that, even with low and moderately procyclical hedonic risk aversion, the leverage effect is strong enough to bring
the equilibrium pricing kernel well within Hansen-Jagannathan bounds. This is in sharp contrast to Panel A, which shows that, even with a risk aversion of 10, the market prices of risk
implied by power utility falls short from satisfying the bounds.
Inspecting the mechanism.
In contrast to the habit-persistence preferences of Campbell and Cochrane (1999), happiness maintenance matches the equity premium without high implied risk aversion. In fact, risk aversion in my model is constant and equal to ![]() Moreover, while the elasticity of intertemporal substitution is different from
Moreover, while the elasticity of intertemporal substitution is different from
![]() and is a complicated function of the other parameters of the model, in my benchmark calibration it is equal to 0.4, a value which is well within the range commonly assumed
in the literature.10
and is a complicated function of the other parameters of the model, in my benchmark calibration it is equal to 0.4, a value which is well within the range commonly assumed
in the literature.10
The comparative dynamics of the coefficient of relative risk aversion, ![]() and the rate of time preference,
and the rate of time preference, ![]() under happiness maintenance are standard and, thus, omitted for brevity .Not surprisingly, the value of hedonic risk aversion is key for the empirical
performance of the model. Table 3 illustrates this point by experimenting with several different combinations of values for
under happiness maintenance are standard and, thus, omitted for brevity .Not surprisingly, the value of hedonic risk aversion is key for the empirical
performance of the model. Table 3 illustrates this point by experimenting with several different combinations of values for ![]() and
and ![]() that, however, imply the same mean and volatility of hedonic risk aversion as in my benchmark calibration. The message is that, as far as hedonic risk aversion preserves the features of my baseline calibration, the model can match the
Sharpe ratio for a wide range of combinations of values of
that, however, imply the same mean and volatility of hedonic risk aversion as in my benchmark calibration. The message is that, as far as hedonic risk aversion preserves the features of my baseline calibration, the model can match the
Sharpe ratio for a wide range of combinations of values of ![]() and
and ![]() . Even
with risk aversion as low as 2, the model can deliver a premium in line with the data.
. Even
with risk aversion as low as 2, the model can deliver a premium in line with the data.
III.2.b Cyclicality and the correlation puzzle
The first column of Table 4 reports stylized facts about the price-dividend ratio over the business cycle: the price-dividend ratio is procyclical and displays positive auto-correlation. In contrast to standard consumption-based models that imply a counter-cyclical price-dividend ratio, the cyclicality and autocorrelations of the price-dividend ratio implied by my model are in line with the data. In the next section, I discuss the intuition for this result in the context of predictability.
Before moving on, though, it is worth contrasting another dimension along which happiness maintenance improves the fit with the data. It is well known that standard consumption-based models imply a correlation between stock returns and consumption growth equal to one, which is much higher than in the data. This is the "correlation puzzle" of Cochrane and Hansen (1992). Happiness maintenance alleviates the puzzle since it predicts a correlation well below 1. To understand this, note that in my model stock returns are made up of two standard components, news about consumption and wealth, and a novel component, changes in hedonic risk aversion. Although changes in hedonic risk aversion are ultimately caused by changes in consumption, the rich multi-factor structure of the model lowers the correlation between returns and consumption.
III.2.c Long-horizon predictability and volatility
Can pro-cyclical changes in hedonic risk aversion reproduce the observed patterns of predictability of asset returns? To develop intuition about this question, it is helpful to start by considering the implications of happiness maintenance for the volatility of equity prices. To this end, Table 5 presents the results of regressions of long-horizon log stock price changes on long-horizon log consumption changes. The first column shows that in the data these regressions yield coefficients invariably greater than one, and as high as 1.61 at a 20-year horizon. Barsky and DeLong (1993) characterize this finding as the "excess volatility" of stock prices. In contrast to traditional consumption-based asset pricing models, happiness maintenance generates stock prices that are more volatile than underlying consumption fundamentals (as evidenced by the coefficients in the third and forth columns which are consistently greater than one).
To see how the model generates prices that are more volatile than the underlying dividends, suppose that there is a positive consumption innovation this period. This shock increases current hedonic risk aversion, ![]() which is pro-cyclical. However, as indicated by the term
which is pro-cyclical. However, as indicated by the term
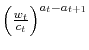 in
in
![]() what matters for a forward-looking investor is the anticipated
change in hedonic risk aversion,
what matters for a forward-looking investor is the anticipated
change in hedonic risk aversion,
![]() Thus, a positive consumption innovation makes the future look relatively brighter, i.e. it actually implies a lower expected change in hedonic risk aversion. This increases the
value of wealth relative to consumption for the investor (recall from
Thus, a positive consumption innovation makes the future look relatively brighter, i.e. it actually implies a lower expected change in hedonic risk aversion. This increases the
value of wealth relative to consumption for the investor (recall from
![]() that
that ![]() and,
thus,
and,
thus, ![]() control the relative demand for wealth). As a result, as it is clear from
control the relative demand for wealth). As a result, as it is clear from
![]() the investor discounts the future dividend stream at a lower rate, giving stock prices an extra jolt upward. A similar mechanism works
for a negative shock, which generates low current hedonic risk aversion and pushes prices lower. The ultimate effect is that prices are more volatile than consumption growth.
the investor discounts the future dividend stream at a lower rate, giving stock prices an extra jolt upward. A similar mechanism works
for a negative shock, which generates low current hedonic risk aversion and pushes prices lower. The ultimate effect is that prices are more volatile than consumption growth.
This mechanism is also underlying long horizon predictability: since the investor's hedonic risk aversion varies over time depending on the state of the economy, expected returns on the risky asset also vary. To understand this in more detail, suppose once again that there is a positive shock to
consumption, which increases the investor's current hedonic risk aversion. This makes wealth relatively more valuable with respect to consumption, since the investor expect a lower change in hedonic risk aversion. The higher demand for wealth pushes the stock price still higher, leading to a higher
price-dividend ratio. At the same time, higher demand for wealth implies that subsequent stock returns will be lower on average, since the investor demands a lower premium to bear equity risk. Price-dividend ratios are therefore inversely related to future returns. Notice that, although my model
generates predictability through state-dependent preference as Campbell and Cochrane (1999), the economic mechanism is distinct from theirs. One advantage of my leverage effect is its non-linearity in risk aversion changes - i.e. small switches in risk aversion are sufficient for the term
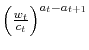 to operate as either a discount or a compound factor. Thus, I only need mild, rather than strong, cyclicality of risk aversion.
to operate as either a discount or a compound factor. Thus, I only need mild, rather than strong, cyclicality of risk aversion.
The results reported in Table 6 confirm this intuition about predictability. In particular, I report the slope coefficients,
![]() and
and ![]() obtained from running the following regression of
cumulative log returns over a k-year horizon on lagged price-dividend ratio:
obtained from running the following regression of
cumulative log returns over a k-year horizon on lagged price-dividend ratio:
III.3 Robustness checks
The results in Table 7 show that the model is robust to alternative specifications of the happiness demand process which preserve the pro-cyclicality of hedonic risk aversion. In particular, the third column of Table 7 shows that replacing specification
![]() with a different pro-cyclical process for
with a different pro-cyclical process for
![]() produces returns that are virtually indistinguishable from the benchmark calibration.
produces returns that are virtually indistinguishable from the benchmark calibration.
Finally, the second column of Table 7 contrasts the implication of happiness maintenance (reported, for ease of comparison, in the first column) with those of a model where hedonic risk aversion is counter-cyclical. I report summary statistics of asset returns when
the happiness demand process
![]() is perfectly negatively correlated with consumption growth. This departure from the baseline model makes the premium shrink to about a quarter of its benchmark value, mostly due to
the fact that the risk-free rate is four times as high.
is perfectly negatively correlated with consumption growth. This departure from the baseline model makes the premium shrink to about a quarter of its benchmark value, mostly due to
the fact that the risk-free rate is four times as high.
IV. Conclusion
Drawing on ingredients from outside the usual domain of finance and economics can help to understand several otherwise puzzling features of financial markets. In particular, I use an equilibrium model simple to the extreme and show that mild everyday feelings have rich implications for aggregate asset returns. Happiness maintenance, a well documented feature of the immediate emotional perception of risk, increases the risk associated with equity, thus contributing to resolve some of the most prominent documented asset pricing puzzles. Further, it provides a novel perspective over a broad set of important stylized features of financial markets, such as, the predictability of asset returns and the volatility of asset prices at long horizons.
An important feature of my model is that it does not depart from conventional asset pricing wisdom along any dimensions other than investors' preferences. Moreover, my two-parameter specification of happiness maintenance preferences is relatively parsimonious with respect to other wealth-based models. Overall, my results strongly suggest that pro-cyclical risk aversion provides a potentially useful construct to understand stock market facts.
Appendix A: Evidence of Happiness Maintenance, Derivations, and Proofs
Happiness maintenance is a well replicated finding. For example, Isen and Patrick (1983) conducted an experiment to study the influence of positive affect on choices under uncertainty. Participants, a large sample of college students, were randomly assigned to two groups: positive affect was induced only in participants in one group by receipt of a small gift, a McDonald's gift certificate worth $.50. Subjects were given ten poker chips and told that these chips represented their credit for participating in the study. Risk preferences were measured in terms of the amount of chips actually bet by the two groups of participants in a game of roulette. They found that individuals in a positive mood bet significantly less than controls on gambles with a meaningful probability of losing (about 20% chance of winning). In particular, individuals in a neutral state bet on average about six times as many chips as individuals in a positive mood11. Isen and Geva (1987) used the level of the probability of winning before accepting a bet of fixed amount and found again that, when a meaningful amount was at stake, namely their whole endowment of chips, individuals in a positive mood, in contrast to those in a control group, set a level for the probability of winning as a cutoff point for accepting a given gamble on average about 30% higher than controls. Isen et al. (1984) documented that individuals in whom a positive mood had been induced by receipt of a small gift expressed greater preference in a lottery choice for a $1 ticket rather than a $10 ticket relative to a control group. Nygren et al. (1996) provided stronger support for an influence of affect on risk taking: they asked participants in whom positive affect had been induced, as well as no manipulation controls, to make actual betting decisions in twelve different three-outcome gambles. The mean bet value of affect condition participants was found to be consistently lower of about 30% than controls, regardless of the riskiness of the gambles, i.e. the ratio of the probability of winning and loosing or of the amounts.
While these early results indicated a tendency toward conservatism in risk preferences, Fong and McCabe (1999) replicate their essence within a very careful experimental setup that through the adoption of auction theoretic techniques (see Kagel (1995)) enables them to avoid potential difficulties with the studies mentioned so far, especially associated with the possible role of uncontrolled variables, the lack of monetary incentives and the lack of mechanism to ensure that truthful revelation of private values of the lottery was a dominant strategy. They endowed their subjects with lottery tickets and let them bid for the tickets in both a sealed-bid and an English auction. Subjects could earn up to $10 in each lottery or as little as zero in each. They found that average exit price is significantly lower for subjects whose mood had been improved by a minor manipulation, indicated a higher risk aversion in affect subjects.
The perspective suggested by these findings is well described by the idiom: don't push your luck. It is worth contrasting it with the findings of illusion of control or "gambling with the house money" of Thaler and Johnson (1990), which motivate the work of Barberis et al. (2001). As suggested in Arkes et al. (1988), the presence of a meaningful loss might be the crucial determinant of the discrepancy between the findings of the two classes of experiments. In one experiment, where a meaningful loss was nonexistent, affect participants exhibited relatively more risk-prone behavior compared to controls. In a second experiment dealing with insurance buying behavior where participants were forced to focus on potential loss, positive affect participants displayed a greater risk aversion than did controls. Nygren et al. (1996) further illustrates this point: positive affect participants significantly overestimated the probability of winning while participants in the control group did not, in accord with the findings of studies such as Johnson and Tversky (1983). Nevertheless, in actual gambling situations, affect condition participants were much less likely to gamble than were controls.
Axioms and representation theorems for state-dependent utility
Technically, the specification chosen for the affect-dependent utility belongs to the wider class of state-dependent utility functions. The structure of the preferences underlying state-dependent utility functions is relatively well understood. Karni (1985) and more recently Dreze and Rustichini (2001) present a thorough analysis of alternative axiomatizations. I follow Myerson (1991) and give a list of axioms and a representation theorem for state-dependent preferences of the type informally illustrated in the text.
Notation
For any finite set ![]() let
let
![]() denote the set of probability distributions over
denote the set of probability distributions over ![]() That
is, define:
That
is, define:
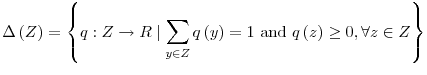
Let ![]() denote the set of possible prizes that the decision maker could ultimately get,
denote the set of possible prizes that the decision maker could ultimately get, ![]() denote the set of possible states of the world, and assume both
denote the set of possible states of the world, and assume both ![]() and
and ![]() are finite. Define a lottery to be any function
are finite. Define a lottery to be any function ![]() that specifies a nonnegative real number
that specifies a nonnegative real number
![]() for every prize
for every prize ![]() in
in ![]() and every state
and every state ![]() in
in ![]() such that
such that
![]() for every
for every ![]() in
in ![]()
Let ![]() denote the set of all such lotteries. That is,
denote the set of all such lotteries. That is,
For any state ![]() in
in ![]() and any lottery
and any lottery ![]() in
in ![]()
![]() denotes the probability distribution over
denotes the probability distribution over ![]() designated by
designated by ![]() in state
in state ![]() . That is,
. That is,
Let ![]() denote the set of all events,
denote the set of all events, ![]() , so that
, so that
For any two lotteries ![]() and
and ![]() in
in ![]() and any event
and any event ![]() in
in ![]() I write
I write
![]() if and only if (iff) the lottery
if and only if (iff) the lottery ![]() would be at least as desirable
as
would be at least as desirable
as ![]() in the opinion of the decision-maker, if he knew that the true state of the world was in the set
in the opinion of the decision-maker, if he knew that the true state of the world was in the set ![]() In other words,
In other words,
![]() iff the decision-maker would be willing to choose the lottery
iff the decision-maker would be willing to choose the lottery ![]() when he has to choose between
when he has to choose between ![]() and
and ![]() and he knows only that the event
and he knows only that the event
![]() has occurred. Given the relation
has occurred. Given the relation
![]() I can define
I can define
where
For any number ![]() such that
such that
![]() and for any two lotteries
and for any two lotteries ![]() and
and ![]() in
in ![]()
![]() denotes the lottery in
denotes the lottery in ![]() such that
such that
Finally, a conditional-probability function on ![]() is any function
is any function
![]() that specifies nonnegative conditional probabilities
that specifies nonnegative conditional probabilities
![]() for every state
for every state ![]() in
in ![]() and every event
and every event ![]() , such that
, such that
![]() if
if ![]() and
and
![]()
Axioms
The axioms are to hold for all lotteries ![]() and
and ![]() in
in ![]() , for all events
, for all events ![]() and
and ![]() in
in ![]() and for all numbers
and for all numbers ![]() and
and
![]() between 0 and 1:
between 0 and 1:
A representation theorem
A utility function can be any function from
![]() into the real numbers,
into the real numbers, ![]() A utility function is state-independent
iff there exists some function
A utility function is state-independent
iff there exists some function
![]() , such that
, such that
![]() for all
for all ![]() and
and ![]()
where
Discussion and caveats
Definition, existence and uniqueness of the equilibrium solution
This Appendix provides a more formal definition of equilibrium for an exchange economy populated by investors with happiness maintenance preferences. It also contains a proof that such equilibrium exists.
Definition of equilibrium
Equilibrium is defined by a pair of functions,
![]() the asset pricing function, and
the asset pricing function, and
![]() , a value function, such that:
, a value function, such that:
-
![v:\Re^{+}\times\Re^{+}\rightarrow\Re^{+};v(s,y,\theta;p(\circ))=\max E_{0}\left[ \sum_{t=0}^{\infty}\beta^{t}u\left( g_{t}\right) \right] ,](img292.gif) subject to
subject to
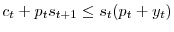 given
given
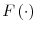 ,
,
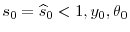 .
. -
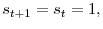
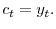
Euler equations and returns
The functional equation associated with the investor's maximization problem is:
where
where
Substituting back for consumption from the budget constraint and using the definition of ![]() , the Euler equation
, the Euler equation
![]() can be written as
can be written as
![\displaystyle =\beta E_{t}\left\{ \left[ \begin{array}[c]{c}% \left( 1-\theta_{t+1}\right) c_{t+1}^{\left( 1-\alpha\right) \left( 1-\theta_{t+1}\right) -1}w_{t+1}^{\left( 1-\alpha\right) \theta_{t+1}}\\ +\theta_{t+1}c_{t+1}^{\left( 1-\alpha\right) \left( 1-\theta_{t+1}\right) }w_{t+1}^{\left( 1-\alpha\right) \theta_{t+1}-1}% \end{array} \right] \left( p_{t+1}+y_{t+1}\right) \right\}](img309.gif)
|
||
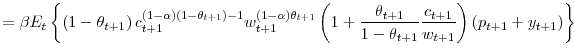 |
Simple algebraic manipulations deliver the Euler equation
![]() that appears in the text.
that appears in the text.
Existence of equilibrium
This section proves the existence of a (bounded and strictly positive) equilibrium price-dividend function for probability structure
![]() The main complication in establishing existence derives from the endogeneity of the pricing kernel induced by the dependence of
the utility function on wealth and, in equilibrium, on the price-dividend function. Such endogeneity prevents us from characterizing the Euler equation as a non-linear counterpart of the linear Fredholm equations much studied in the consumption-based asset pricing tradition.
The main complication in establishing existence derives from the endogeneity of the pricing kernel induced by the dependence of
the utility function on wealth and, in equilibrium, on the price-dividend function. Such endogeneity prevents us from characterizing the Euler equation as a non-linear counterpart of the linear Fredholm equations much studied in the consumption-based asset pricing tradition.
Under the assumed probability structure, the Euler equation defines the following system of two non-linear equations in two unknown price-dividend ratio functions:
where
![\begin{displaymath} \left[ \begin{array}[c]{cc}% \pi_{11} & \pi_{12}\ \pi_{21} & \pi_{22}% \end{array}\right] \equiv\left[ \begin{array}[c]{cc}% \pi & 1-\pi\ 1-\pi & \pi \end{array}\right] \end{displaymath}](img325.gif)
To simplify notation, I notice that
![]() can be rewritten as
can be rewritten as
![\displaystyle f_{1}\left( f_{1}+1\right) ^{-a_{1}}-\beta\left[ \begin{array}[c]{c}% \pi_{11}\lambda_{1}^{1-\alpha}\left( f_{1}+1+\gamma_{1}\right) \left( f_{1}+1\right) ^{-a_{1}}\\ +\pi_{12}\lambda_{2}^{1-\alpha}\left( f_{2}+1+\gamma_{2}\right) \left( f_{2}+1\right) ^{-a_{2}}% \end{array} \right]](img327.gif)
|
||
![\displaystyle f_{2}\left( f_{2}+1\right) ^{-a_{2}}-\beta\left[ \begin{array}[c]{c}% \pi_{21}\lambda_{1}^{1-\alpha}\left( f_{1}+1+\gamma_{1}\right) \left( f_{1}+1\right) ^{-a_{1}}\\ +\pi_{22}\lambda_{2}^{1-\alpha}\left( f_{2}+1+\gamma_{2}\right) \left( f_{2}+1\right) ^{-a_{2}}% \end{array} \right]](img328.gif)
|
![\displaystyle f_{1}-\beta\left[ \pi_{11}\lambda_{1}^{1-\alpha}\left( f_{1}+1+\gamma _{1}\right) +\pi_{12}\lambda_{2}^{1-\alpha}\left( f_{2}+1+\gamma_{2}\right) \frac{\left( f_{2}+1\right) ^{-a_{2}}}{\left( f_{1}+1\right) ^{-a_{1}}% }\right]](img329.gif) |
||
![\displaystyle f_{2}-\beta\left[ \pi_{21}\lambda_{1}^{1-\alpha}\left( f_{1}+1+\gamma _{1}\right) \frac{\left( f_{1}+1\right) ^{-a_{1}}}{\left( f_{2}+1\right) ^{-a_{2}}}+\pi_{22}\lambda_{2}^{1-\alpha}\left( f_{2}+1+\gamma_{2}\right) \right]](img330.gif) |
![\displaystyle x_{1}-\beta\left[ \pi_{11}\lambda_{1}^{1-\alpha}\left( x_{1}+\gamma _{1}\right) +\pi_{12}\lambda_{2}^{1-\alpha}\left( x_{2}+\gamma_{2}\right) \frac{x_{2}^{-a_{2}}}{x_{1}^{-a_{1}}}\right] -1](img331.gif) |
||
![\displaystyle x_{2}-\beta\left[ \pi_{21}\lambda_{1}^{1-\alpha}\left( x_{1}+\gamma _{1}\right) \frac{x_{1}^{-a_{1}}}{x_{2}^{-a_{2}}}+\pi_{22}\lambda _{2}^{1-\alpha}\left( x_{2}+\gamma_{2}\right) \right] -1](img332.gif) |
![\displaystyle x_{1}-\beta\left[ \pi_{11}\lambda_{1}^{1-\alpha}\left( x_{1}+\gamma _{1}\right) +\left( 1-\pi_{11}\right) \lambda_{2}^{1-\alpha}\left( x_{2}+\gamma_{2}\right) \frac{x_{1}^{a_{1}}}{x_{2}^{a_{2}}}\right] -1](img333.gif) |
||
![\displaystyle x_{2}-\beta\left[ \pi_{21}\lambda_{1}^{1-\alpha}\left( x_{1}+\gamma _{1}\right) \frac{x_{2}^{a_{2}}}{x_{1}^{a_{1}}}+\left( 1-\pi_{21}\right) \lambda_{2}^{1-\alpha}\left( x_{2}+\gamma_{2}\right) \right] -1](img334.gif) |
where
![\begin{displaymath} G\left( x,\phi\right) =\left[ \begin{array}[c]{c}% G_{1}\left( x,\pi_{1}\right) \ G_{2}\left( x,\pi_{2}\right) \end{array}\right] =0 \end{displaymath}](img338.gif)
I resort to a fixed point argument (see Milnor (1997) for a detailed treatment) to show that a solution to ![]() exists.
exists.
It is understood that all parameters other than the probabilities are taken as given. Let
I start by proving the following
![\begin{displaymath} D_{\pi,x}G=\left[ \begin{array}[c]{cc}% \alpha\left( \lambda_{1}\right) -\alpha\left( \lambda_{2}\right) & 0\ 0 & \hat{\alpha}\left( \lambda_{1}\right) -\hat{\alpha}\left( \lambda _{2}\right) \end{array}\right] \end{displaymath}](img351.gif)
where I define
![]()
![]() ,
,
![]()
![]()
Evidently,
![]() is onto if
is onto if
![]() (or, equivalently,
(or, equivalently,
![]() and
and
![]() (or, equivalently,
(or, equivalently,
![]() However,
However,
Suppose, then, that these equalities hold.
![]() simplifies to
simplifies to
 |
By taking the ratio, I obtain
I need to verify the existence of an open and full Lebesgue measure set of parameter values such that
When
![]() and
and
![]()
![]() simplifies to
simplifies to
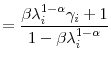 |
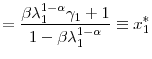 |
||
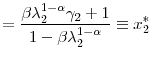 |
and
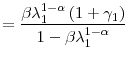 |
||
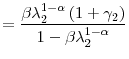 |
Thus
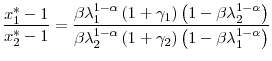
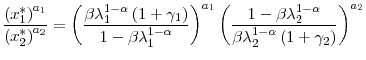
Consider now the function
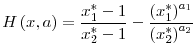
It is straightforward to show that
![]() In fact, I have
In fact, I have
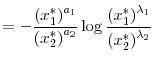 |
||
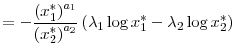 |
Clearly, there exists an open and full Lebesgue measure set of parameter values
![]() such that
such that
![]() or, equivalently,
or, equivalently, ![]() is a smooth manifold.
is a smooth manifold.
![]()
![]()
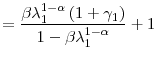 |
||
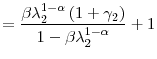 |
Clearly, the solution is unique. ![]()
Suppose that (without loss of generality) ![]() Then
Then
![\displaystyle \beta\left[ \pi_{11}\lambda_{1}^{1-\alpha}\left( 1+\gamma_{1}\right) +\left( 1-\pi_{11}\right) \lambda_{2}^{1-\alpha}\left( x_{2}+\gamma _{2}\right) \frac{1}{x_{2}^{a_{2}}}\right] =0](img409.gif)
Suppose, by contradiction, that
![]() such that
such that
![]() I distinguish two cases (
I distinguish two cases (![]() is symmetric to zero and therefore ignored):
is symmetric to zero and therefore ignored):
-
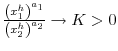
The second equation becomes
thus in the limit![\displaystyle 1=\beta\left[ \pi_{21}\lambda_{1}^{1-\alpha}\left( \frac{x_{1}^{h}}% {x_{2}^{h}}+\frac{\gamma_{1}}{x_{2}^{h}}\right) \frac{\left( x_{2}% ^{h}\right) ^{a_{2}}}{\left( x_{1}^{h}\right) ^{a_{1}}}+\left( 1-\pi _{21}\right) \lambda_{2}^{1-\alpha}\left( 1+\frac{\gamma_{2}}{x_{2}^{h}% }\right) \right] +\frac{1}{x_{2}^{h}}%](img414.gif)
![\displaystyle 1=\beta\left[ \pi_{21}\lambda_{1}^{1-\alpha}\lim_{h\rightarrow\infty}\left( \frac{x_{1}^{h}}{x_{2}^{h}}\right) K^{-1}+\left( 1-\pi_{21}\right) \lambda_{2}^{1-\alpha}\right]](img415.gif)
The first equation (again dividing by
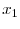 and taking the limit) becomes
and taking the limit) becomes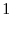
![\displaystyle =\beta\left[ \pi_{11}\lambda_{1}^{1-\alpha}\left( 1+\frac{\gamma_{1}% }{x_{1}^{h}}\right) +\left( 1-\pi_{11}\right) \lambda_{2}^{1-\alpha}\left( \frac{x_{2}^{h}}{x_{1}^{h}}+\frac{\gamma_{2}}{x_{1}^{h}}\right) \frac{\left( x_{1}^{h}\right) ^{a_{1}}}{\left( x_{2}^{h}\right) ^{a_{2}}}\right] +\frac{1}{x_{1}^{h}}](img417.gif)
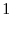
![\displaystyle =\beta\left[ \pi_{11}\lambda_{1}^{1-\alpha}+\left( 1-\pi_{11}\right) \lambda_{2}^{1-\alpha}\lim_{h\rightarrow\infty}\left( \frac{x_{2}^{h}}% {x_{1}^{h}}\right) K\right]](img418.gif)
Since
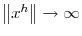 and
and
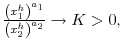 then
then
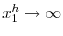 and
and
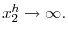 Since
Since
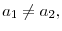 either
either
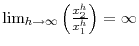 or
or
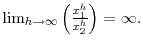 Hence,
Hence,
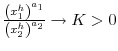 is impossible.
is impossible. -
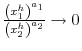
By repeating the same procedure, I have
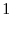
![\displaystyle =\beta\left[ \pi_{11}\lambda_{1}^{1-\alpha}+\left( 1-\pi_{11}\right) \lambda_{2}^{1-\alpha}\lim_{h\rightarrow\infty}\frac{\left( x_{1}^{h}\right) ^{a_{1}-1}}{\left( x_{2}^{h}\right) ^{a_{2}-1}}\right]](img428.gif)
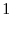
![\displaystyle =\beta\left[ \pi_{21}\lambda_{1}^{1-\alpha}\lim_{h\rightarrow\infty }\frac{\left( x_{2}^{h}\right) ^{a_{2}-1}}{\left( x_{1}^{h}\right) ^{a_{1}-1}}+\left( 1-\pi_{21}\right) \lambda_{2}^{1-\alpha}\right]](img429.gif)
If
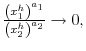 then either
then either
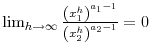 or
or
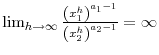 . Hence
. Hence
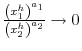 is impossible.
is impossible.
I are now in a position to state the following
Computation of returns
To write the Euler as a (nonlinear) first order difference equation in the price-dividend ratio, recall
![\displaystyle 1=\beta E\left[ \frac{1-\theta_{t+1}}{1-\theta_{t}}\left( \frac{c_{t+1}% }{c_{t}}\right) ^{-\alpha}\frac{\left( w_{t+1}/c_{t+1}\right) ^{-a_{t+1}}% }{\left( w_{t}/c_{t}\right) ^{-a_{t}}}\left( 1+\frac{\theta_{t+1}}% {1-\theta_{t+1}}\frac{c_{t+1}}{w_{t+1}}\right) R_{t+1}\right]](img434.gif)
Define
![]() to be the price-dividend ratio and observe that in equilibrium I can write
to be the price-dividend ratio and observe that in equilibrium I can write
![]() The Euler, then, becomes
The Euler, then, becomes
![\displaystyle 1=\beta E\left[ \frac{1-\theta_{t+1}}{1-\theta_{t}}\left( \frac{c_{t+1}% }{c_{t}}\right) ^{-\alpha}\frac{\left( f_{t+1}+1\right) ^{-a_{t+1}}% }{\left( f_{t}+1\right) ^{-a_{t}}}\left( 1+\frac{\theta_{t+1}}% {1-\theta_{t+1}}\frac{c_{t+1}}{\left( f_{t+1}+1\right) y_{t+1}}\right) R_{t+1}\right]](img436.gif)
|
|
![\displaystyle 1=\beta E\left[ \frac{1-\theta_{t+1}}{1-\theta_{t}}\left( \frac{c_{t+1}% }{c_{t}}\right) ^{-\alpha}\frac{\left( f_{t+1}+1\right) ^{-a_{t+1}}% }{\left( f_{t}+1\right) ^{-a_{t}}}\left( 1+\frac{1-\theta_{t+1}}% {1-\theta_{t}}\frac{1}{f_{t+1}+1}\right) R_{t+1}\right]](img437.gif) |
since by definition returns are
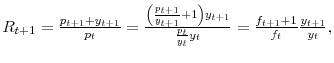 I have
I have
![\displaystyle 1=\beta E\left[ \frac{1-\theta_{t+1}}{1-\theta_{t}}\left( \frac{c_{t+1}% }{c_{t}}\right) ^{-\alpha}\frac{\left( f_{t+1}+1\right) ^{-a_{t+1}}% }{\left( f_{t}+1\right) ^{-a_{t}}}\left( 1+\frac{1-\theta_{t+1}}% {1-\theta_{t}}\frac{1}{f_{t+1}+1}\right) \frac{f_{t+1}+1}{f_{t}}\frac {y_{t+1}}{y_{t}}\right]](img439.gif)
|
|
![\displaystyle 1=\beta E\left[ \frac{1-\theta_{t+1}}{1-\theta_{t}}\left( \frac{c_{t+1}% }{c_{t}}\right) ^{1-\alpha}\frac{\left( f_{t+1}+1\right) ^{-a_{t+1}}% }{\left( f_{t}+1\right) ^{-a_{t}}}\left( 1+\frac{1-\theta_{t+1}}% {1-\theta_{t}}\frac{1}{f_{t+1}+1}\right) \frac{f_{t+1}+1}{f_{t}}\right]](img440.gif)
|
Hence, the Euler can be rewritten as
![\displaystyle f_{t}\left( f_{t}+1\right) ^{-a_{t}}=\beta E\left[ \frac{1-\theta_{t+1}% }{1-\theta_{t}}\left( \frac{c_{t+1}}{c_{t}}\right) ^{1-\alpha}\left( 1+\frac{1-\theta_{t+1}}{1-\theta_{t}}\frac{1}{f_{t+1}+1}\right) \left( f_{t+1}+1\right) ^{1-a_{t+1}}\right]](img441.gif)
Hedonic Relative Risk Aversion
Consider the a-temporal case where the outcome ![]() is independent of the preference state
is independent of the preference state ![]() with probabilities given by
with probabilities given by ![]() and
and ![]() respectively.
It is straightforward to derive the hedonic risk aversion of the investor by using the definition of relative risk aversion . In fact,
respectively.
It is straightforward to derive the hedonic risk aversion of the investor by using the definition of relative risk aversion . In fact,
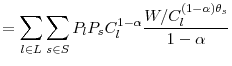 |
||
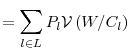 |
where
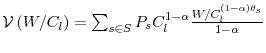 is the state independent utility function, that is a linear
combination with positive weights of conditionally isoelastic concave functions, and thus concave. Moreover, given that
is the state independent utility function, that is a linear
combination with positive weights of conditionally isoelastic concave functions, and thus concave. Moreover, given that 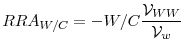
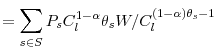 |
||
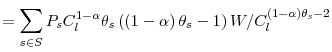 |
||
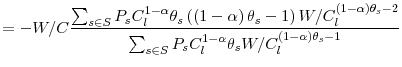 |
||
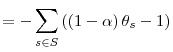 |
||
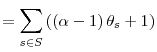 |
If preferences are state-independent, i.e.
Intertemporal elasticity of substitution
Recall the Euler
![\displaystyle 1=\beta E\left[ g_{c}^{\left( 1-\alpha\right) \left( 1-\theta_{t}\right) -1}g_{w}^{\left( 1-\alpha\right) \theta_{t}}k_{t+1}\left( \frac{c_{t+1}% }{w_{t+1}}\right) ^{\left( 1-\alpha\right) \left( \theta_{t}-\theta _{t+1}\right) }R_{t+1}\right]](img467.gif)
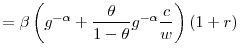 |
||
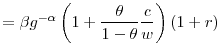 |
It is straightforward to observe that if I take the term
![]() as exogenous and ignore the dependence of wealth on returns, then
as exogenous and ignore the dependence of wealth on returns, then
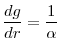
Nevertheless, using the investors' budget constraint
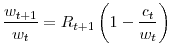
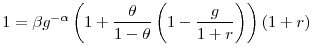
Taking logs I have
| 0 | 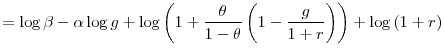 |
|
| 0 | 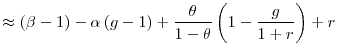 |
|
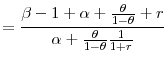 |
Hence, the elasticity of intertemporal substitution is
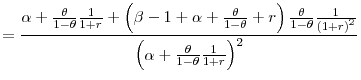 |
||
![\displaystyle =\frac{1}{\alpha+\frac{\theta}{1-\theta}\frac{1}{1+r}}\left[ 1+\frac{\theta}{1-\theta}\frac{\beta-1+\alpha+\frac{\theta}{1-\theta}% +r}{\left( \alpha+\frac{\theta}{1-\theta}\frac{1}{1+r}\right) \left( 1+r\right) ^{2}}\right]](img486.gif) |
Appendix B: Tables and Figures
Table 1 - Summary of unconditional first and second moments of returns in the benchmark calibration
| US data (MP sample) |
US data 1891-1998 |
US data 1947-1998 |
HM, iid:
|
HM, Markov:
|
|
|---|---|---|---|---|---|
|
|
0.80 | 1.91 | 0.90 | 1.77 | 0.84 |
|
|
6.98 | 7.91 | 8.08 | 7.81 | 6.95 |
|
|
6.18 | 6.00 | 7.18 | 6.03 | 6.11 |
|
|
5.44 | 5.44 | 1.75 | 2.22 | 5.55 |
|
|
19.02 | 18.60 | 15.65 | 22.82 | 23.17 |
|
|
18.53 | 18.50 | 15.27 | 22.61 | 22.57 |
|
|
23.75 | 23.75 | 28.31 | 28.34 | 38.12 |
|
|
7.6 | 7.6 | 11.5 | 7.16 | 6.4 |
|
|
0.33 | 0.32 | 0.47 | 0.34 | 0.27 |
Note: This table reports historical data and model-implied moments of financial variables for various assets. All statistics are annualized and in percent terms. The financial variables are the riskfree rate, ![]() , the equity return,
, the equity return, ![]() the excess return of equity over the riskfree rate,
the excess return of equity over the riskfree rate, ![]() , and the price to dividend ratio,
, and the price to dividend ratio, ![]() The moments are mean,
The moments are mean, ![]() , and standard deviation,
, and standard deviation, ![]() . The historical data for the MP sample is from Mehra and Prescott (1985) and covers the 1889-1985 period. Otherwise,
historical data is from Campbell (1999). The only difference in the calibration of columns "HM, iid" and "HM, Markov" is the specification of the process for (log) consumption growth under which the happiness maintenance model is solved. The process is specified as iid lognormal for "HM, iid"
(specification
. The historical data for the MP sample is from Mehra and Prescott (1985) and covers the 1889-1985 period. Otherwise,
historical data is from Campbell (1999). The only difference in the calibration of columns "HM, iid" and "HM, Markov" is the specification of the process for (log) consumption growth under which the happiness maintenance model is solved. The process is specified as iid lognormal for "HM, iid"
(specification
![]() in the text) and Markov for "HM, Markov" (specification
in the text) and Markov for "HM, Markov" (specification
![]() in the text).
in the text).
Parameter values: ![]()
![]()
![]()
![]()
Implied hedonic risk aversion:
![]()
![]()
![]()
![]()
Table 2 - Summary of unconditional first and second moments of returns when
![]()
| US data: (MP sample) | US data: 1891-1998 | US data: 1947-1998 | No Happiness: (
|
No HM: (
|
|
|---|---|---|---|---|---|
|
|
0.80 | 1.91 | 0.90 | 5.74 | 4.64 |
|
|
6.98 | 7.91 | 8.08 | 6.22 | 5.24 |
|
|
6.18 | 6.00 | 7.18 | 0.48 | 0.60 |
|
|
5.44 | 5.44 | 1.75 | 1.57 | 2.20 |
|
|
19.02 | 18.60 | 15.65 | 4.87 | 5.65 |
|
|
18.53 | 18.50 | 15.27 | 4.60 | 5.20 |
|
|
0.33 | 0.32 | 0.47 | 0.10 | 0.11 |
Note: This table reports historical data and model-implied moments of financial variables for various assets. All statistics are annualized and in percent terms. The financial variables are the riskfree rate, ![]() , the equity return,
, the equity return, ![]() the excess return of equity over the riskfree rate,
the excess return of equity over the riskfree rate, ![]() , and the price to dividend ratio,
, and the price to dividend ratio, ![]() The moments are mean,
The moments are mean, ![]() , and standard deviation,
, and standard deviation, ![]() . The historical data for the MP sample is from Mehra and Prescott (1985) and covers the 1889-1985 period. Otherwise,
historical data is from Campbell (1999). The difference between columns "No Happiness" and "No HM" is in the calibration of the hedonic risk aversion parameter,
. The historical data for the MP sample is from Mehra and Prescott (1985) and covers the 1889-1985 period. Otherwise,
historical data is from Campbell (1999). The difference between columns "No Happiness" and "No HM" is in the calibration of the hedonic risk aversion parameter,
![]() under which the happiness maintenance model is solved. The parameter is set equal to zero in column "No Happiness" and as a constant equal to 0.25 in column "No HM".
under which the happiness maintenance model is solved. The parameter is set equal to zero in column "No Happiness" and as a constant equal to 0.25 in column "No HM".
Parameter values: ![]()
![]()
![]()
![]()
Table 3 - Inspecting the mechanism: ![]()
|
|
|
|
|
|---|---|---|---|
| US data | 0.80 | 6.18 | 0.32 |
| 0.21 | 4.27 | 0.23 | |
| 0.84 | 6.11 | 0.27 | |
| 2.36 | 6.12 | 0.28 | |
| 3.71 | 6.19 | 0.30 | |
| 5.05 | 6.16 | 0.32 | |
| 6.22 | 6.23 | 0.33 | |
| 7.41 | 6.18 | 0.35 | |
| 8.44 | 6.24 | 0.37 | |
| 9.54 | 6.11 | 0.39 |
Note: This table reports historical data and model-implied moments of financial variables for various assets. All statistics are annualized and in percent terms. The financial variables are the riskfree rate, ![]() , and the excess return of equity over the riskfree rate,
, and the excess return of equity over the riskfree rate, ![]() The moments are mean,
The moments are mean, ![]() , and standard deviation,
, and standard deviation, ![]() . The historical data is from Mehra and Prescott (1985) and covers the 1889-1985 period. Model-implied
moments are from the Happiness Maintenance model for various values of hedonic risk aversion,
. The historical data is from Mehra and Prescott (1985) and covers the 1889-1985 period. Model-implied
moments are from the Happiness Maintenance model for various values of hedonic risk aversion, ![]() .
.
Parameter values:
![]()
![]()
![]()
![]()
![]()
Table 4 - Cyclicality and Correlations
| US data | No Happiness:
|
HM-1: |
HM-2: |
|
|---|---|---|---|---|
|
|
p-cyclical | -0.15 | 0.08 | 0.09 |
|
|
0.78 | -0.15 | 0.55 | 0.63 |
|
|
0.59 | 0.01 | 0.33 | 0.54 |
|
|
0.54 | 0.00 | -0.04 | 0.43 |
|
|
0.36 | 0.00 | 0.00 | 0.21 |
Note: This table reports historical data and model-implied moments of financial variables for various assets. All statistics are annualized and in percent terms. The financial variables are the price to dividend ratios, ![]() and its lags up to 5 years . The moments are correlations,
and its lags up to 5 years . The moments are correlations, ![]() . The historical data is from Campbell (1999) and covers the 1889-1985 period. The only difference among columns "No Happiness," "HM-1," and "HM-2" is the calibration of the hedonic risk aversion parameter,
. The historical data is from Campbell (1999) and covers the 1889-1985 period. The only difference among columns "No Happiness," "HM-1," and "HM-2" is the calibration of the hedonic risk aversion parameter,
![]() under which the happiness maintenance model is solved. The parameter is set equal to zero in column "No Happiness" and as in the benchmark parametrization (specification
under which the happiness maintenance model is solved. The parameter is set equal to zero in column "No Happiness" and as in the benchmark parametrization (specification
![]() in the text) for columns "HM-1" and "HM-2" with 2 and 5 lags, respectively.
in the text) for columns "HM-1" and "HM-2" with 2 and 5 lags, respectively.
Parameter values: ![]()
![]()
![]()
![]()
Table 5 - Long-horizon volatility
| US Data | No Happiness:
|
HM-1: |
HM-2: |
|
|---|---|---|---|---|
| 1.14 | 1.0 | 4.9 | 2.0 | |
|
|
1.5 | 1.0 | 4.5 | 2.0 |
|
|
1.61 | 1.0 | 3.9 | 1.7 |
|
|
1.42 | 1.0 | 2.8 | 1.4 |
| 60% | 98% | 61% | 80% | |
|
|
76% | 98% | 52% | 80% |
|
|
70% | 98% | 40% | 75% |
|
|
61% | 98% | 36% | 75% |
Note: This table reports regression results of the change in (log) prices,
![]() on a constant and the change in (log) consumption,
on a constant and the change in (log) consumption,
![]() for
for
![]() years using historical and model-implied data. The reported statistics are the estimated slope coefficient,
years using historical and model-implied data. The reported statistics are the estimated slope coefficient, ![]() and
and ![]() of these regressions. The "US data" column runs regressions with annual NYSE data for the 1889-1985 period. The only difference
among columns "No Happiness," "HM-1," and "HM-2" is that the regressions are run on model-generated data under alternative calibrations of the hedonic risk aversion parameter,
of these regressions. The "US data" column runs regressions with annual NYSE data for the 1889-1985 period. The only difference
among columns "No Happiness," "HM-1," and "HM-2" is that the regressions are run on model-generated data under alternative calibrations of the hedonic risk aversion parameter,
![]() . The parameter is set equal to zero in column "No Happiness," and as in the benchmark parametrization (specification
. The parameter is set equal to zero in column "No Happiness," and as in the benchmark parametrization (specification
![]() in the text) for columns "HM-1" and "HM-2" with 2 and 5 lags, respectively.
in the text) for columns "HM-1" and "HM-2" with 2 and 5 lags, respectively.
Parameter values:
![]()
![]()
![]()
![]()
![]()
![]()
Table 6 - Long-horizon predictability
| US data | No Happiness:
|
HM-1: |
HM-2: |
|
|---|---|---|---|---|
| -1.5 | -15.6 | -6.9 | -5.2 | |
| -3.0 | -15.6 | -10.8 | -6.5 | |
| -3.7 | -15.7 | -10.2 | -7.7 | |
| -6.6 | -15.1 | -10.4 | -11.1 | |
|
|
-12.1 | -14.7 | -10.2 | -10.5 |
| 4% | 7% | 28% | 13% | |
| 8% | 5% | 44% | 15% | |
| 10% | 4% | 41% | 18% | |
| 19% | 3% | 42% | 25% | |
|
|
39% | 2% | 40% | 21% |
Note: This table reports regression results of log stock returns,
![]() on a constant and the log price-dividend ratio for
on a constant and the log price-dividend ratio for
![]() years using historical and model-implied data. The reported statistics are the estimated slope coefficient,
years using historical and model-implied data. The reported statistics are the estimated slope coefficient, ![]() and
and ![]() of these regressions. The "US data" column runs regressions with annual NYSE data for the 1889-1985 period. The only difference
among columns "No Happiness," "HM-1," and "HM-2" is that the regressions are run on model-generated data under alternative calibrations of the hedonic risk aversion parameter,
of these regressions. The "US data" column runs regressions with annual NYSE data for the 1889-1985 period. The only difference
among columns "No Happiness," "HM-1," and "HM-2" is that the regressions are run on model-generated data under alternative calibrations of the hedonic risk aversion parameter,
![]() . The parameter is set equal to zero in column "No Happiness," and as in the benchmark parametrization (specification
. The parameter is set equal to zero in column "No Happiness," and as in the benchmark parametrization (specification
![]() in the text) for columns "HM-1" and "HM-2" with 2 and 5 lags, respectively.
in the text) for columns "HM-1" and "HM-2" with 2 and 5 lags, respectively.
Parameter values:
![]()
![]()
![]()
![]()
![]()
![]()
Table 7 - Summary of unconditional first and second moments of returns under alternative specifications of the happiness demand process
| HM:
(
|
Countercyclical:
(
|
HM-1:
(
|
|
|---|---|---|---|
|
|
0.84 | 3.85 | 0.84 |
|
|
6.95 | 5.41 | 6.95 |
|
|
6.11 | 1.55 | 6.11 |
|
|
5.55 | 2.89 | 5.55 |
|
|
23.17 | 13.84 | 23.17 |
|
|
22.57 | 13.50 | 22.57 |
|
|
0.27 | 0.11 | 0.27 |
Note: This table reports model-implied moments of financial variables for various assets. All statistics are annualized and in percent terms. The financial variables are the riskfree rate, ![]() , the equity return,
, the equity return, ![]() the excess return of equity over the riskfree rate,
the excess return of equity over the riskfree rate, ![]() , and the price to dividend ratio,
, and the price to dividend ratio, ![]() The moments are mean,
The moments are mean, ![]() , and standard deviation,
, and standard deviation, ![]() . The difference between columns "HM," "Countercyclical," and "HM-1" is in the calibration of the hedonic risk aversion parameter,
. The difference between columns "HM," "Countercyclical," and "HM-1" is in the calibration of the hedonic risk aversion parameter,
![]() under which the happiness maintenance model is solved. The parameter is set as in the standard parametrization (specification
under which the happiness maintenance model is solved. The parameter is set as in the standard parametrization (specification
![]() in the text) for column "HM," as perfectly negatively correlated with consumption growth for column "Countercyclical," and as a
two-state Markov-process that takes values 0.25 and 0.23 in expansions and recessions, respectively.
in the text) for column "HM," as perfectly negatively correlated with consumption growth for column "Countercyclical," and as a
two-state Markov-process that takes values 0.25 and 0.23 in expansions and recessions, respectively.
Parameter values: ![]()
![]()
![]()
![]()
Figure 1 - Hansen-Jagannathan Bounds
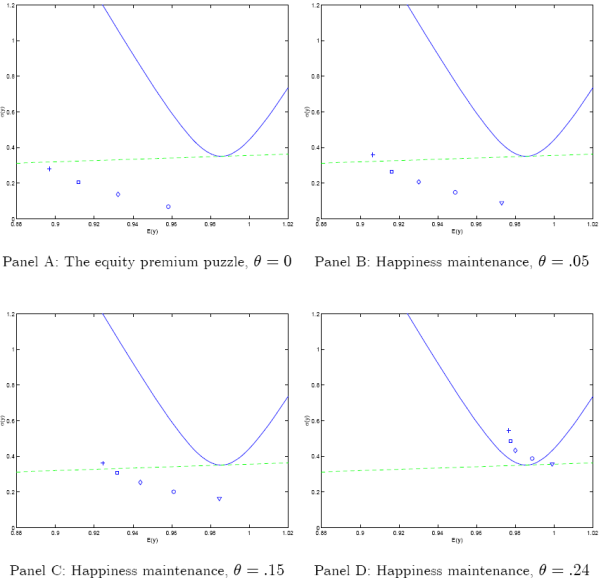
Note: The Figure plots Hansen and Jagannathan (1991)'s bounds and the model implied market price of risk for different values hedonic risk aversion. The market price of risk is the ratio of conditional standard deviation to mean of the model implied pricing kernel. X axis displays the conditional mean, Y axis displays conditional standard deviation.
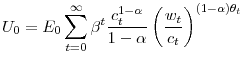
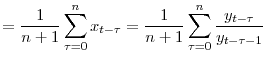
![\displaystyle R_{f}=\frac{1}{\beta E\left[ \left( \frac{c_{t+1}}{c_{t}}\right) ^{-\alpha }\left( \frac{w_{t+1}/c_{t+1}}{w_{t}/c_{t}}\right) ^{1-a_{t+1}}% k_{t+1}\left( \frac{w_{t}}{c_{t}}\right) ^{a_{t}-a_{t+1}}\right] } %](img84.gif)
![\displaystyle R_{f}=\frac{1}{\beta E\left[ \left( \frac{c_{t+1}}{c_{t}}\right) ^{-\alpha }\right] }%](img90.gif)
![\displaystyle 1=\beta E\left[ \left( \frac{c_{t+1}}{c_{t}}\right) ^{-\alpha}\left( \frac{w_{t+1}/c_{t+1}}{w_{t}/c_{t}}\right) ^{1-a_{t+1}}k_{t+1}\left( \frac{w_{t}}{c_{t}}\right) ^{a_{t}-a_{t+1}}R_{t+1}\right] ,%](img99.gif)
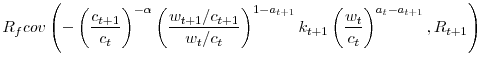
![\displaystyle R_{f}=\frac{1}{\beta E\left[ x_{t+1}^{-\alpha}\left( \frac{f_{t+1}+1}% {f_{t}+1}\right) ^{\left( 1-\alpha\right) \theta_{t}}k\left( f_{t+1}\right) \left( f_{t+1}+1\right) ^{\left( 1-\alpha\right) \left( \theta_{t+1}-\theta_{t}\right) }\right] }%](img112.gif)
![\displaystyle 1=\beta E\left[ x_{t+1}^{-\alpha}\left( \frac{f_{t+1}+1}{f_{t}+1}\right) ^{\left( 1-\alpha\right) \theta_{t}}k\left( f_{t+1}\right) \left( f_{t+1}+1\right) ^{\left( 1-\alpha\right) \left( \theta_{t+1}-\theta _{t}\right) }R_{t+1}\right]%](img113.gif)
![\displaystyle =\left[ \begin{array}[c]{cc}% \pi & 1-\pi\\ 1-\pi & \pi \end{array} \right]](img130.gif)
![\displaystyle =\beta E\left[ \left( \frac{c_{t+1}}{c_{t}}\right) ^{\left( 1-\alpha\right) \left( 1-\theta_{t}\right) -1}\left( \frac{w_{t+1}}{w_{t}% }\right) ^{\left( 1-\alpha\right) \theta_{t}}k_{t+1}\left( \frac{c_{t+1}% }{w_{t+1}}\right) ^{\left( 1-\alpha\right) \left( \theta_{t}-\theta _{t+1}\right) }\right] ER_{t+1}](img313.gif)
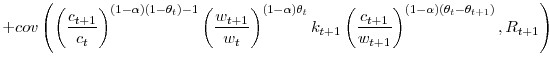
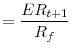
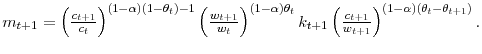
![\displaystyle f_{1}\left( f_{1}+1\right) ^{-a_{1}}-\beta\left[ \begin{array}[c]{c}% \pi_{11}\lambda_{1}^{1-\alpha}\left( 1-\frac{a_{1}}{1-\alpha}\frac{1}% {f_{1}+1}\right) \left( f_{1}+1\right) ^{1-a_{1}}\\ +\pi_{12}\lambda_{2}^{1-\alpha}\left( 1-\frac{a_{2}}{1-\alpha}\frac{1}% {f_{2}+1}\right) \left( f_{2}+1\right) ^{1-a_{2}}% \end{array} \right]](img322.gif)
![\displaystyle f_{2}\left( f_{2}+1\right) ^{-a_{2}}-\beta\left[ \begin{array}[c]{c}% \pi_{21}\lambda_{1}^{1-\alpha}\left( 1-\frac{a_{1}}{1-\alpha}\frac{1}% {f_{1}+1}\right) \left( f_{1}+1\right) ^{1-a_{1}}\\ +\pi_{22}\lambda_{2}^{1-\alpha}\left( 1-\frac{a_{2}}{1-\alpha}\frac{1}% {f_{2}+1}\right) \left( f_{2}+1\right) ^{1-a_{2}}% \end{array} \right]](img324.gif)