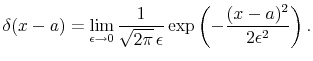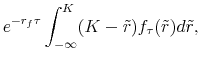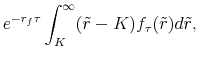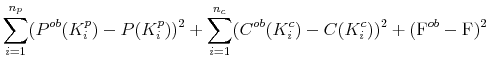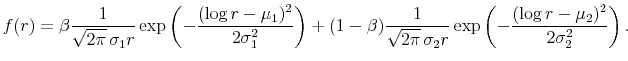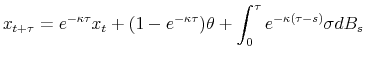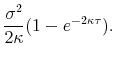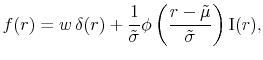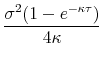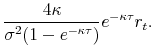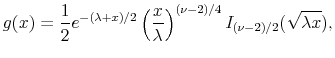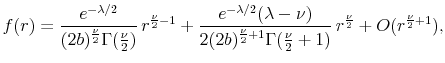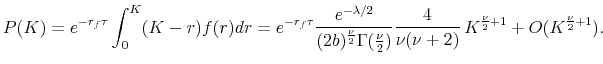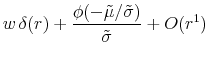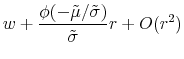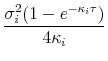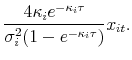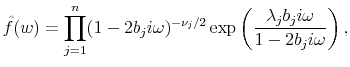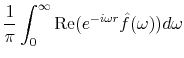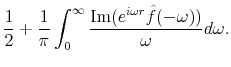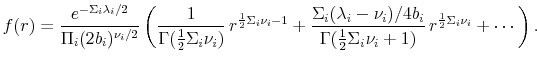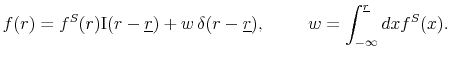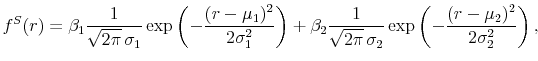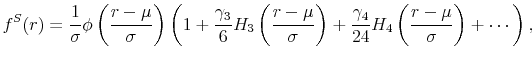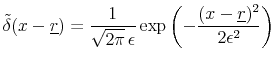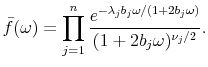Zero Bound, Option-Implied PDFs, and
Term Structure Models
Keywords: Zero bound, term structure of interest rates, options, probability density functions
Abstract:
This paper points out that several known ways of modeling non-negative nominal interest rates lead to different implications for the risk-neutral distribution of the short rate that can be checked with options data. In particular, Black's boundary models ("interest rates as options") imply a probability density function (pdf) that contains a Dirac delta function and a cumulative distribution function (cdf) that is nonzero at the zero boundary, while models like the CIR and positive-definite quadratic-Gaussian (QG) models have a zero cdf at the boundary. Eurodollar futures options data are found to favor Black's boundary models: the CIR/QG models, even multifactor versions, have difficulty capturing option prices accurately not only in low interest rate environments but also in higher interest rate environments, and data in early 2008 provide an almost tangible signature of the Dirac delta function in Black's boundary pdf models. Options data also contradict the prediction of well-known models whose cdf is zero at the zero boundary, namely that the risk-neutral pdf is always positively skewed.
1 Introduction
It is well known, at least since Breeden and Litzenberger (1978), that options at a broad range of strikes can provide information about the whole risk-neutral distribution of the underlying security prices, not just mean and variance. Policy makers and market participants have utilized this fact to deduce the risk-neutral distribution of short-term interest rates from eurodollar futures options or federal funds futures options, and many studies have explored techniques that are useful in this regard and discussed their applications to various settings.1However, this literature so far has not made much connection with the vast literature on dynamic term structure models, i.e., relatively little work has been done to investigate what the option-implied risk-neutral distribution tells about the underlying stochastic process of interest rates and whether known term structure models can capture the risk neutral distribution implicit in option prices.2 The present paper is a contribution toward filling this gap.
We shall be focusing in particular on the the zero boundary behavior of the short rate and its ramifications for term structure models. Perhaps the best known model that recognizes the presence of the zero bound is the CIR model, written down by Cox, Ingersoll, and Ross in their seminal paper
(1985). This type of model has the feature that the cumulative distribution function (cdf) of the short rate vanishes as the short rate approaches zero. A different treatment of zero-boundary behavior was proposed by Fischer Black in his last paper (1995), in which the nominal short rate is modeled
as
![]() , where
, where ![]() is a "shadow-rate" process that can go below zero. As
we shall see, this type of model implies a short rate cdf that is nonzero at the zero boundary. Proper modeling of the behavior near the zero boundary (e.g., whether it is better described as CIR-like, Black-like, or something else) is a basic and historically important problem in term structure
modeling, but it has significance beyond that, as different boundary behaviors could signify different underlying macroeconomic mechanism of the interest rate determination.
is a "shadow-rate" process that can go below zero. As
we shall see, this type of model implies a short rate cdf that is nonzero at the zero boundary. Proper modeling of the behavior near the zero boundary (e.g., whether it is better described as CIR-like, Black-like, or something else) is a basic and historically important problem in term structure
modeling, but it has significance beyond that, as different boundary behaviors could signify different underlying macroeconomic mechanism of the interest rate determination.
In the case of Japan, studies by Gorovoi and Linetsky (2004) and Ueno, Baba, and Sakurai (2006) using yields data give strong support for Black-type models. However, some might argue that this conclusion does not necessarily carry over to the postwar US economy.3 Indeed, non-negative interest rate modeling with US data has so far been predominantly in terms of models whose short rate cdf is zero at the zero boundary, e.g., the BGM model (Brace, Gutarek, and Musiela (1997)), the multifactor CIR model, the quadratic-Gaussian (QG) model, and the non-affine model of Ahn and Gao (1999).4As the US short rate in the past 50 years has not been low enough to see a significant effect of the zero bound on the yield curve,5the distinction between the two types of models is difficult to discern from yields data. A key point of the present paper is that data on out-of-money options can help, as the models may imply strong enough differences in risk-neutral distributions, especially near the zero bound. Recently (early 2008), short-term interest rates have come down to a fairly low level while uncertainty about interest rates has remained relatively high, thus it is particularly interesting to explore what the options data from this episode tell about term structure models. Beyond fundamental theoretical interest, modeling of risk-neutral distribution in such environment is an important practical problem for market participants as well.
This paper makes largely two contributions. The first is to explore the implications of well-known and tractable term structure models that respect the non-negativity condition for nominal interest rates (e.g., the multifactor positive-definite CIR/QG models) for the risk-neutral distribution of the short rate. In particular, this paper derives the asymptotic form of their risk-neutral probability density function (pdf) at vanishing interest rates (relevant for the discussion of the behavior near the zero boundary), which does not seem to have been explored in the literature. This paper also develops a method for fast computation of option prices for the risk-neutral distribution implied by the multifactor CIR model and (positive-definite) QG model, and explores how well these models perform in matching the observed out-of-money eurodollar futures option prices. In addition, this paper points out that known models which have zero cdf at the zero boundary imply a fairly strong restriction on the shape of the distribution, namely that the distribution is always positively skewed, and examines whether this prediction is born out in the options data. The second contribution is to examine the implications of Black-type boundary models for option prices and option-implied pdfs. After deriving the risk-neutral pdf of the simplest Black's boundary model ("Black-Vasicek model"), this paper develops flexible parametric models of risk-neutral pdf that are consistent with Black's boundary behavior and lead to convenient calculation of option prices, and explore their practical performance.
The main findings are as follows. A flexible parametric pdf model with Black's boundary behavior (normal-mixture shadow rate model) is found to perform quite well in matching the option prices across various strikes in a variety of interest rate environment from 1998 to 2008. The model produces implied prices of the 1-year-maturity 0.5%-strike eurodollar futures option in February and March of 2008 that agree fairly well with actual settlement prices. On the other hand, the traditional lognormal-mixture pdf model and 2-factor and 3-factor (positive-definite) CIR/QG models substantially underprice this "low-strike" put option. The CIR/QG models have difficulty matching the option prices accurately not only in low interest rate environments but also in higher interest rate environments, often generating large and biased pricing errors. In addition, options data contradict these models' prediction that the skewness of the pdf is always positive.
The remainder of this paper is organized as follows. Section 2 sets up the stage for the later parts of the paper, discussing empirically important zero boundary behaviors and reviewing the risk-neutral pdf extraction techniques. It also introduces a mathematical object called the Dirac
![]() -function, which seldom appears in finance literature but is needed for the discussion of the pdfs with Black's boundary behavior. Section 3 examines the pdfs and option prices in
one-factor models, comparing Black's boundary model with CIR/QG models. Section 4 examines richer pdf models and develops useful techniques for them; the application of these models to actual options data and the empirical results are discussed in Section 5. Section 6 concludes.
-function, which seldom appears in finance literature but is needed for the discussion of the pdfs with Black's boundary behavior. Section 3 examines the pdfs and option prices in
one-factor models, comparing Black's boundary model with CIR/QG models. Section 4 examines richer pdf models and develops useful techniques for them; the application of these models to actual options data and the empirical results are discussed in Section 5. Section 6 concludes.
2.1 "Zero-cdf model" vs Black's model
Nominal interest rates cannot go below zero. The best known model that respects this condition is the CIR model. This model is nested by the so-called CEV model6
| (1) |
which admits two kinds of boundary behavior: when
| (2) |
is satisfied, the zero boundary is inaccessible, and if not, it is accessible.
In the accessible boundary case (
![]() , or
, or
![]() and
and
![]() ), zero is a regular boundary (according to the terminology of Feller (1952)),7 and additional conditions at the boundary can be imposed. For example, requiring that
), zero is a regular boundary (according to the terminology of Feller (1952)),7 and additional conditions at the boundary can be imposed. For example, requiring that ![]() stay at zero forever after it
hits the zero boundary amounts to having an absorbing boundary. As the permanent stay of the short rate at zero would not be a promising description of the actual economy, we shall not consider the absorbing boundary scenario further in this paper, and instead focus on the regular "unrestricted
boundary behavior", after Longstaff (1992).8
stay at zero forever after it
hits the zero boundary amounts to having an absorbing boundary. As the permanent stay of the short rate at zero would not be a promising description of the actual economy, we shall not consider the absorbing boundary scenario further in this paper, and instead focus on the regular "unrestricted
boundary behavior", after Longstaff (1992).8
Most of the non-negative interest rate models applied to the US data have been either inaccessible boundary models or regular unrestricted boundary models. The former include the CIR model with
![]() , the BGM model, and Ahn and Gao (1999)'s non-affine model. The latter include the CIR model with
, the BGM model, and Ahn and Gao (1999)'s non-affine model. The latter include the CIR model with
![]() and (positive-definite) quadratic-Gaussian model (Beaglehole and Tenney (1992)). All these models (i.e., both the inaccessible boundary models and regular
unrestricted boundary models) share the feature that the cdf of the conditional distribution of the short rate is zero at the zero boundary. Therefore, in this paper we shall refer to these models collectively as "zero-cdf models", for brevity.
and (positive-definite) quadratic-Gaussian model (Beaglehole and Tenney (1992)). All these models (i.e., both the inaccessible boundary models and regular
unrestricted boundary models) share the feature that the cdf of the conditional distribution of the short rate is zero at the zero boundary. Therefore, in this paper we shall refer to these models collectively as "zero-cdf models", for brevity.
Let us now discuss Black's boundary models. As the short rate in these models can stay at the zero boundary for an extended period, they have the feature that a finite probability mass is concentrated at the point ![]() ; this means that the probability density function of the conditional distribution,
; this means that the probability density function of the conditional distribution, ![]() , is infinite at
, is infinite at ![]() . Mathematically,
. Mathematically,
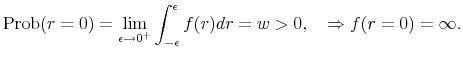 |
(3) |
A natural way to describe such a distribution is to use the Dirac
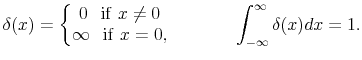 |
(4) |
It has the property
Using the ![]() -function, the pdf of Black's boundary models can be expressed as10
-function, the pdf of Black's boundary models can be expressed as10
where
The cumulative distribution function of the short rate,
![]() , takes the form
, takes the form
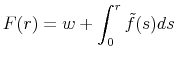 |
(7) |
(for
2.2 Option-implied risk-neutral pdfs
Consider a eurodollar futures option with strike ![]() and maturity
and maturity ![]() .11Let
.11Let ![]() denote the futures rate at the maturity
of the option, and let
denote the futures rate at the maturity
of the option, and let
![]() be the risk-neutral pdf of
be the risk-neutral pdf of ![]() . The put option price
. The put option price
![]() and the call option price
and the call option price
![]() can be expressed in terms of
can be expressed in terms of ![]() as
as
where the prefactor
Taking successive derivatives of both sides of eq. (8) gives a simple formula for the pdf,
where the double prime notation denotes second derivatives; the maturity index
where the superscript
There are many possibilities for parametrizing
![]() . The general wisdom is that a flexible parametric form with 4 to 6 parameters is sufficient to match observed option prices at various strikes.14 A parametrization substantially richer than this can often lead to strange implications at minimal improvements in the fit of option prices (overfitting). Perhaps the most popular
parametric form is the "mixture of lognormals":15
. The general wisdom is that a flexible parametric form with 4 to 6 parameters is sufficient to match observed option prices at various strikes.14 A parametrization substantially richer than this can often lead to strange implications at minimal improvements in the fit of option prices (overfitting). Perhaps the most popular
parametric form is the "mixture of lognormals":15
Note that if
It is also worth noting that despite the typically good performance, forms like (11) do have a limitation that is particularly relevant to our problem (pdf modeling in the proximity of the zero bound). Because the lognormal distribution has the feature that
![]() as
as
![]() , the form (11) can have difficulty when the actual distribution contains a
, the form (11) can have difficulty when the actual distribution contains a ![]() -function at
-function at ![]() . As noted earlier (eq. (5)), the delta function
. As noted earlier (eq. (5)), the delta function ![]() can be approximated by a lognormal distribution with mean and variance close to zero, which can be achieved by having a small
can be approximated by a lognormal distribution with mean and variance close to zero, which can be achieved by having a small ![]() and a large and negative
and a large and negative ![]() in eq. (11), but in such a two-component mixture model this may incur a substantial cost in the fit of other aspects of the pdf. Section 4.2
develops parametric forms for
in eq. (11), but in such a two-component mixture model this may incur a substantial cost in the fit of other aspects of the pdf. Section 4.2
develops parametric forms for ![]() that can describe Black's boundary behavior more easily and naturally.
that can describe Black's boundary behavior more easily and naturally.
To have a manageable scope, this paper will be focusing only on the processes and distributions in the risk-neutral measure (which determines pricing), and not the physical (real world) measure.16Therefore, henceforth we shall often drop the adjective "risk-neutral" for brevity.
3.1 Black-Vasicek model
Let us now derive the pdf and option prices for the simplest Black's boundary model, which has the shadow rate described by the one-factor Vasicek process:
This model, which we shall refer to as the "Black-Vasicek model," has been theoretically and empirically studied by Gorovoi and Linetsky (2004) and Ueno, Baba, and Sakurai (2006) and others, but its risk-neutral pdf has not been discussed in the literature, to my knowledge.17
The conditional distribution of this model, i.e., the transition density
![]() , can be easily obtained if one thinks in terms of the shadow rate process
, can be easily obtained if one thinks in terms of the shadow rate process ![]() rather than the
rather than the ![]() process. Note that if
process. Note that if
![]() , we have
, we have
![]() ; hence in this case, the distribution of
; hence in this case, the distribution of
![]() equals that of
equals that of
![]() . On the other hand, if
. On the other hand, if
![]() , we have
, we have
![]() . Thus all scenarios in which
. Thus all scenarios in which
![]() is non-positive maps to a single point
is non-positive maps to a single point
![]() . Therefore, we have
. Therefore, we have
where
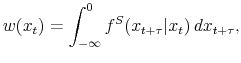 |
(15) |
and
The transition density function
![]() for the Vasicek process is well-known: Since the stochastic differential equation (13) has the solution
for the Vasicek process is well-known: Since the stochastic differential equation (13) has the solution
the random variable
with conditional mean and variance given by
 |
Thus, suppressing time indices and simplifying notations, we have the conditional distribution of the short rate given by
where
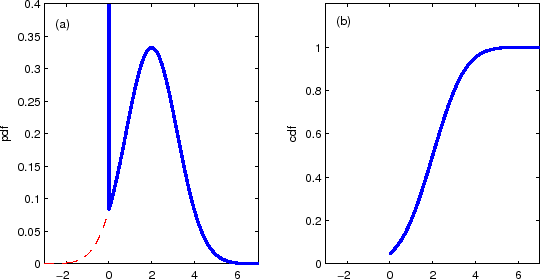
The pdf and cdf of the short rate in the Black-Vasicek model are illustrated in Figure 1a,b. The dashed line in Figure 1b is the part of the shadow rate distribution that collapses onto the delta function at
The prices of ![]() -maturity put/call options with strike
-maturity put/call options with strike ![]() are straightforward
to evaluate. Substituting eq. (19) into eq. (8), we have
are straightforward
to evaluate. Substituting eq. (19) into eq. (8), we have
| (21) | |||
| (22) |
where
3.2 Two zero-cdf models
Let us now consider two well-known and tractable positive interest rate models: the CIR model and the QG model. The CIR model is given by
It is well known (CIR, 1985) that the random variable
where
Consider now the positive-definite 1-factor QG model
Since the random variable
| (27) | |||
where
The pdf of the
![]() distribution (CIR/QG models) is given by
distribution (CIR/QG models) is given by
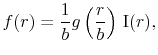 |
(28) |
with
where
3.3 Comparing the model implications
To get a feel for the qualitative difference between Black's boundary models and zero-cdf (CIR/QG) models, it is instructive compare the behavior of the pdf ![]() in the
in the
![]() limit.
limit.
For the CIR/QG model, expanding the expression (29) in powers of ![]() , using the well-known series expansion of the modified Bessel function of the first kind
, using the well-known series expansion of the modified Bessel function of the first kind
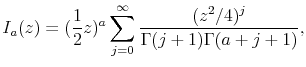 |
(30) |
gives
where the notation
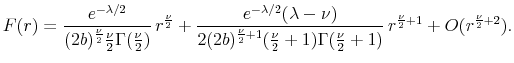 |
(32) |
From eq. (31) it can be seen that depending on ![]() , we can expect qualitatively different behavior of
, we can expect qualitatively different behavior of ![]() :
:
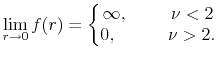 |
(33) |
Recall that, for the CIR model (eq. (23)),
Note also that since ![]() for the QG model, we have
for the QG model, we have
![]() for the QG model. As the zero boundary is accessible in the QG model (since
for the QG model. As the zero boundary is accessible in the QG model (since ![]() in eq. (26) is unrestricted, it can reach zero), it shows a qualitatively similar small-
in eq. (26) is unrestricted, it can reach zero), it shows a qualitatively similar small-![]() behavior as the CIR model with violated
Feller condition. It should be noted, however, that an accessible zero boundary does not always imply
behavior as the CIR model with violated
Feller condition. It should be noted, however, that an accessible zero boundary does not always imply
![]() , as we shall see with the case of the 3-factor QG model (Sec. 4.1). Note also that even in the case
, as we shall see with the case of the 3-factor QG model (Sec. 4.1). Note also that even in the case
![]() (one-factor CIR model with violated Feller condition and the QG model), the cdf is zero at
(one-factor CIR model with violated Feller condition and the QG model), the cdf is zero at ![]() , since
, since
![]() in the
in the
![]() limit.
limit.
The small-![]() behavior of the pdf in eq. (31) implies that the put option price for small strike
behavior of the pdf in eq. (31) implies that the put option price for small strike ![]() is given by
is given by
These asymptotic behaviors of CIR/QG models can be compared with the those of the Black-Vasicek model:
(for
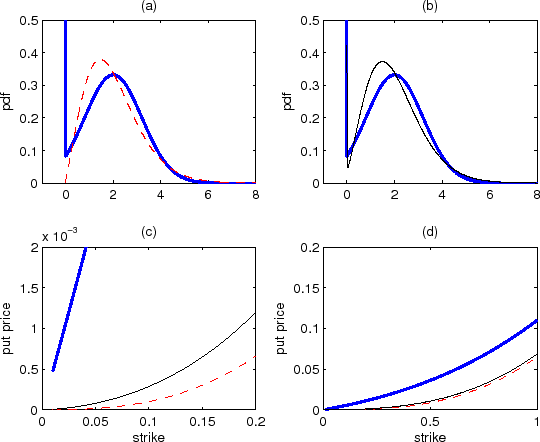 |
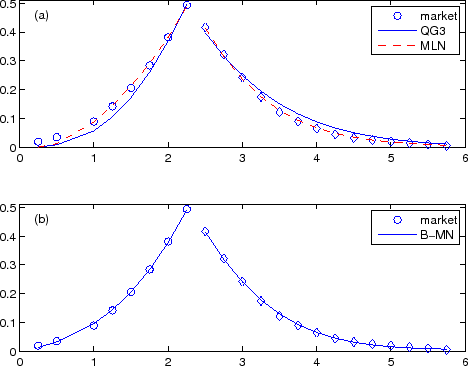
Figure 2 graphically illustrates the qualitative difference between Black's boundary models and CIR/QG models. Figure 2a plots, in thick solid line, the pdf of the Black-Vasicek model with parameters in eq. (19) given by
![]() , which imply
, which imply ![]() . It also shows, in thin
dashed line, the pdf of the
. It also shows, in thin
dashed line, the pdf of the
![]() model with
model with ![]() (corresponding to the CIR model
satisfying the Feller condition), whose
(corresponding to the CIR model
satisfying the Feller condition), whose ![]() and
and ![]() were determined such that
the model matches the mean and variance of the Black-Vasicek model;22 requiring the means and variances of the distributions be similar amounts to having
comparable at-the-money option prices. Figure 2b shows the pdf of the
were determined such that
the model matches the mean and variance of the Black-Vasicek model;22 requiring the means and variances of the distributions be similar amounts to having
comparable at-the-money option prices. Figure 2b shows the pdf of the
![]() model with
model with ![]() (corresponding to the CIR model
violating the Feller condition and the QG model) in thin solid line. As discussed with eq. (31), this pdf has a singularity of the form
(corresponding to the CIR model
violating the Feller condition and the QG model) in thin solid line. As discussed with eq. (31), this pdf has a singularity of the form ![]() , but it has a local
minimum at a point very close to zero,23 and above that it looks similar to the pdf of the
, but it has a local
minimum at a point very close to zero,23 and above that it looks similar to the pdf of the
![]() distribution with
distribution with ![]() (i.e., Figure 2a).
(i.e., Figure 2a).
Despite the rough similarity in the shape of the pdf of the Black-Vasicek model and the
![]() model, the model-implied put prices are drastically different, with the Black-Vasicek model producing far larger numbers, as shown in Figure 2c. This is because the
model, the model-implied put prices are drastically different, with the Black-Vasicek model producing far larger numbers, as shown in Figure 2c. This is because the ![]() singularity in the
singularity in the
![]() model is a much weaker singularity than the
model is a much weaker singularity than the ![]() -function singularity in the Black-Vasicek model; to put it simply, Black's boundary model has a much larger probability weight at or near zero than the CIR/QG model. Note also that in the low interest rate region the Black-Vasicek model shows a linear dependence on
-function singularity in the Black-Vasicek model; to put it simply, Black's boundary model has a much larger probability weight at or near zero than the CIR/QG model. Note also that in the low interest rate region the Black-Vasicek model shows a linear dependence on
![]() , as predicted by eq. (35).
, as predicted by eq. (35).
Although the
![]() behavior of the pdfs and put option prices derived above for the one-factor Black-Vasicek and CIR/QG models are useful for getting a firm handle on the zero boundary
behavior of these models, these predictions might not be cleanly testable empirically, as options might not exist (trade) at very low strikes, and even if they existed their quality may be in doubt. Furthermore, certain market realities (to be discussed at the end of Sec. 5.2) may blur the clean
asymptotic behaviors. Still, even if one moves onto regions where the asymptotic behaviors like (34) and (35) are no longer accurate, the basic intuition would still carry over, and one would expect Black's boundary model to produce higher put option
prices for small
behavior of the pdfs and put option prices derived above for the one-factor Black-Vasicek and CIR/QG models are useful for getting a firm handle on the zero boundary
behavior of these models, these predictions might not be cleanly testable empirically, as options might not exist (trade) at very low strikes, and even if they existed their quality may be in doubt. Furthermore, certain market realities (to be discussed at the end of Sec. 5.2) may blur the clean
asymptotic behaviors. Still, even if one moves onto regions where the asymptotic behaviors like (34) and (35) are no longer accurate, the basic intuition would still carry over, and one would expect Black's boundary model to produce higher put option
prices for small ![]() 's than zero-cdf models (with comparable mean and variance) when the rates are low enough (or the distribution is wide enough) that the weight of the
's than zero-cdf models (with comparable mean and variance) when the rates are low enough (or the distribution is wide enough) that the weight of the ![]() -function piece in Black's boundary model is non-negligible. This is illustrated in Figure 2d (which plots the same objects as Figure 2c but on a
larger scale). It is also interesting to note that the put option prices for the
-function piece in Black's boundary model is non-negligible. This is illustrated in Figure 2d (which plots the same objects as Figure 2c but on a
larger scale). It is also interesting to note that the put option prices for the
![]() model (inaccessible boundary) and the
model (inaccessible boundary) and the
![]() model (accessible boundary) are quite similar, beyond the very small
model (accessible boundary) are quite similar, beyond the very small ![]() region.
region.
4 Richer parametric forms
The one-factor models considered in the previous section, though instructive, may be too parsimonious to capture option prices accurately for a broad range of strikes. Let us now therefore consider richer versions of zero-cdf models and Black's boundary models.
4.1 Multifactor zero-cdf models
A non-negative, multifactor version of the CIR model can be constructed by adding up independent CIR factors:
| (36) | |||
where the Brownian motions
Because ![]() 's are independent, the results about the 1-factor CIR model carries over easily; it is straightforward to show that the distribution of
's are independent, the results about the 1-factor CIR model carries over easily; it is straightforward to show that the distribution of
![]() is given by
is given by
where
Let us now consider the general ![]() -factor positive-definite QG model,
-factor positive-definite QG model,
where the superscript T denotes matrix transpose;
It is straightforward to show that the conditional distribution of the short rate in the positive-definite QG model also takes the form (37),25 with
where
| (41) | |||
| (42) | |||
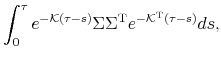 |
(43) |
(the notation
| (44) |
where
Models like the multifactor CIR model have been criticized for the restrictive nature of the factor correlation structure. However, the positive-definite QG models have been widely believed to accommodate a rich factor correlation structure, due to the ability to specify
![]() and
and ![]() flexibly; see, e.g., Ahn, Dittmar, and Gallant (2002).
Therefore, it bears emphasizing that not only the multifactor CIR model but also the positive-definite QG model has a short rate distribution given by a positive linear combination of independent noncentral
flexibly; see, e.g., Ahn, Dittmar, and Gallant (2002).
Therefore, it bears emphasizing that not only the multifactor CIR model but also the positive-definite QG model has a short rate distribution given by a positive linear combination of independent noncentral ![]() random variables, and that this holds no matter how flexible the model is and no matter how many factors it has.
random variables, and that this holds no matter how flexible the model is and no matter how many factors it has.
The pdf ![]() and cdf
and cdf ![]() of the distribution for the multifactor CIR/QG model
(eq. (37)) do not have simple closed-form expressions in general, but the characteristic function
of the distribution for the multifactor CIR/QG model
(eq. (37)) do not have simple closed-form expressions in general, but the characteristic function
![]() has a simple expression
has a simple expression
due to the independence of the noncentral
The option prices
Let us now consider the small-![]() behavior of
behavior of ![]() . Appendix A shows that
. Appendix A shows that
This form has an interesting dependence on the number of factors: the exponent in the leading term increases with number of factors. For the QG model, we have
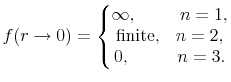 |
(49) |
This pattern is due to the fact that when there are more factors it is less likely for
To get further insights into the distribution described by eq. (37), it is useful to examine its cumulants (hence moments), which is straightforward to calculate from the cumulant generating function (
![]() ). The mean, variance, and the third central moment of this distribution are easily derived from the cumulants of the noncentral
). The mean, variance, and the third central moment of this distribution are easily derived from the cumulants of the noncentral ![]() variables (see, e.g., Johnson, Kotz, Balakrishnan (1994, p447)):
variables (see, e.g., Johnson, Kotz, Balakrishnan (1994, p447)):
It can be seen that because
More generally speaking, one cannot create a negatively skewed distribution by forming a positive linear combination of independent, positive-skewed random variables. Therefore, a model like
| (51) |
where
4.2 Flexible pdfs with Black's boundary behavior
This section develops flexible parametric forms for the risk-neutral pdf that are consistent with Black's boundary behavior. The earlier discussion with the Black-Vasicek model points to the way: write down a flexible form for the shadow rate distribution ![]() that has some weight below zero, and take
that has some weight below zero, and take
Here we have a slightly more general expression in which the lower boundary
The distribution ![]() can be modeled with similar degree of parsimony as the pdfs that are in use in the extant literature. A natural candidate for
can be modeled with similar degree of parsimony as the pdfs that are in use in the extant literature. A natural candidate for ![]() is the "mixture of normals" form, i.e.,
is the "mixture of normals" form, i.e.,
where
where
These forms, which are richer than that of the Black-Vasicek model (eq. (19)), can be viewed as accommodating a more complicated process for the shadow rate, e.g., a multifactor model with stochastic volatility.
The formula for ![]() ,
, ![]() and F for the mixture-of-normals shadow rate model
(eq. (53)) and the Gram-Charlier/Edgeworth shadow rate model (eq. (54)) are provided in Appendix C.
and F for the mixture-of-normals shadow rate model
(eq. (53)) and the Gram-Charlier/Edgeworth shadow rate model (eq. (54)) are provided in Appendix C.
5.1 Empirical strategy
To examine how well zero-cdf models perform in matching option prices, I have implemented two versions of pdf models, which we shall refer to as the QG3 model and the CIR2 model:
|
|---|
The QG3 model covers all possible 3-factor positive-definite QG models, but it also includes a special case of the 3-factor CIR model (
![]() ). The CIR2 model covers all possible cases of the 2-factor CIR models, but it also nests the 2-factor QG model. This model also nests the
Longstaff-Schwartz (1992) model, which was regarded by at least H
). The CIR2 model covers all possible cases of the 2-factor CIR models, but it also nests the 2-factor QG model. This model also nests the
Longstaff-Schwartz (1992) model, which was regarded by at least H![]() rdahl (2000) as a promising model for describing the short rate distribution. In terms of the number of parameters, the QG3 and CIR2
models are richer than the B-MN and MLN models by one parameter.
rdahl (2000) as a promising model for describing the short rate distribution. In terms of the number of parameters, the QG3 and CIR2
models are richer than the B-MN and MLN models by one parameter.
It is also worth noting that, because the QG3 and CIR2 models originate from specific term structure models, the pdf parameters
![]() (
(![]() for QG3) are linked to the elementary parameters of
the term structure model and the state variables
for QG3) are linked to the elementary parameters of
the term structure model and the state variables ![]() .28Therefore the pdf parameters can be obtained from an estimated term structure model. However, there are many ways of estimating term structure models,29which could lead to different estimated elementary parameters and state variables, and in turn, different pdfs. Therefore, in this paper we shall simply treat the pdf parameters for the QG3 model and the CIR2 model as free parameters to be determined in the optimization
problem (10), in the same way as the pdf parameters for the B-MN and MLN models are determined. This way can be viewed as giving the QG3 and CIR2 model a maximum chance to fit options data.30
.28Therefore the pdf parameters can be obtained from an estimated term structure model. However, there are many ways of estimating term structure models,29which could lead to different estimated elementary parameters and state variables, and in turn, different pdfs. Therefore, in this paper we shall simply treat the pdf parameters for the QG3 model and the CIR2 model as free parameters to be determined in the optimization
problem (10), in the same way as the pdf parameters for the B-MN and MLN models are determined. This way can be viewed as giving the QG3 and CIR2 model a maximum chance to fit options data.30
Lastly, note that the estimation of multifactor CIR and QG models in the literature have often included a constant term in the short rate, i.e.,
![]() and
and
![]() . Empirically, Duffie and Singleton (1997) obtained a negative
. Empirically, Duffie and Singleton (1997) obtained a negative ![]() for the multifactor CIR model, but in that case it is no longer a non-negative interest rate model. Ahn, Dittmar, and Gallant (2002) obtained a positive
for the multifactor CIR model, but in that case it is no longer a non-negative interest rate model. Ahn, Dittmar, and Gallant (2002) obtained a positive ![]() in their estimation of the QG model; in this case, there is no probability weight in the region
in their estimation of the QG model; in this case, there is no probability weight in the region ![]() . In any case, the inclusion of the constant term does not change major
qualitative behaviors of these models, including the prediction that the pdfs are always positively skewed.
. In any case, the inclusion of the constant term does not change major
qualitative behaviors of these models, including the prediction that the pdfs are always positively skewed.
5.2 Data
For the empirical investigation, we shall confine attention to the eurodollar futures option with maturity of about 1 year. The 1-year maturity was chosen so as to have a horizon that is reasonably short but at the same time long enough to have a sizeable width of the distribution.
To get a sense of the performance of the models in a variety of contingencies, I have computed the pdfs for the above four models for every last business day of the month from May 1998 to March 2008. Besides these monthly data, I also have computed the pdfs from a second dataset consisting of daily data from Feb 4, 2008 to April 28, 2008. As we shall see, this period is particularly interesting as regards the zero boundary behavior question.
The options data used in this paper are from CME (Chicago Mercantile Exchange). The prefactor
![]() in eq. (8) was computed using the 1-year LIBOR. The CME eurodollar futures options are American options. I have converted their price into corresponding
European price by subtracting the early excercise premium computed based on Baroni-Adesi and Whaley (1987)'s formula; these corrections tended to be fairly small.
in eq. (8) was computed using the 1-year LIBOR. The CME eurodollar futures options are American options. I have converted their price into corresponding
European price by subtracting the early excercise premium computed based on Baroni-Adesi and Whaley (1987)'s formula; these corrections tended to be fairly small.
The eurodollar futures options markets have fixed maturity dates (identical to maturity dates for the eurodollar futures contracts, 4 days a year); for each date in the sample, I chose the option maturity that is closest to 365.25 days. This creates a saw-tooth behavior of the time series of option maturities (oscillating between approximately 7/8 and 9/8 year) for the monthly sample.
The options are typically available at strikes with multiples of 25 basis points, but sometimes there are options with strikes at odd multiples of 12.5 basis points, which are dropped as they tend to be not as liquid as the even multiples. Also, in order to avoid illiquid options, only the options with strikes at which there is a nonzero open interest are used. Thus the number of call and put options used in the pdf computations varies over time.
Figure 3 shows the minimum put strike and the maximum call strike that were available on each day of the monthly sample. Also shown is the put strike rate that corresponds to the current futures rate minus
![]() , and the call strike rate that corresponds to the futures rate plus
, and the call strike rate that corresponds to the futures rate plus
![]() , where the proxy
, where the proxy ![]() for the standard deviation of the pdf is
computed as
for the standard deviation of the pdf is
computed as
| (57) |
where
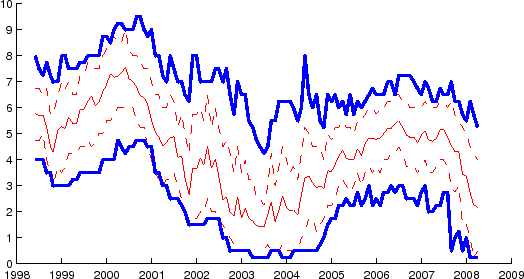 |
Table 2 provides some statistics regarding the liquidity of options proxied by open interest, for strikes
![]() away from the mean.32Options about
1/2 standard deviation from the current futures rate are the most active, but the whole strike range (at least up to
away from the mean.32Options about
1/2 standard deviation from the current futures rate are the most active, but the whole strike range (at least up to
![]() standard deviation) is fairly active; e.g., the median open interest in the
standard deviation) is fairly active; e.g., the median open interest in the
![]() put option is more than a third of that of the
put option is more than a third of that of the
![]() option.
option.
Lastly, as a caveat, note that since the ![]() here is taken to be the 3-month LIBOR, the "zero bound" (more precisely, the lower bound) is not exactly at zero, as the 3-month LIBOR
contains a premium for credit/liquidity risk, besides some differential between the 3-month rate and the instantaneous rate. This means that the proper location of the delta function for the Black's boundary model pdf (
here is taken to be the 3-month LIBOR, the "zero bound" (more precisely, the lower bound) is not exactly at zero, as the 3-month LIBOR
contains a premium for credit/liquidity risk, besides some differential between the 3-month rate and the instantaneous rate. This means that the proper location of the delta function for the Black's boundary model pdf (
![]() ) should be a small but nonzero number. Furthermore, the delta function itself would be smudged out a bit, in other words,
) should be a small but nonzero number. Furthermore, the delta function itself would be smudged out a bit, in other words,
where
It is difficult to get a precise sense of
![]() for the 3-month LIBOR, but the recent Japanese experience can provide some guidance: even at the height of Bank of Japan's Quantitative Easing Program, the 3-month yen TIBOR
rate (an analogue of the US dollar LIBOR) did not go below 8 basis points. For simplicity, the main computations in this paper assumed that the lower bound
for the 3-month LIBOR, but the recent Japanese experience can provide some guidance: even at the height of Bank of Japan's Quantitative Easing Program, the 3-month yen TIBOR
rate (an analogue of the US dollar LIBOR) did not go below 8 basis points. For simplicity, the main computations in this paper assumed that the lower bound
![]() is at 0, but I have also computed the pdf for the B-MN model with
is at 0, but I have also computed the pdf for the B-MN model with
![]() 0.15% to check the robustness of the results. Intuitively one would expect that the difference between these two settings would be immaterial for option strikes that are
substantially larger than the effective lower bound (i.e.,
0.15% to check the robustness of the results. Intuitively one would expect that the difference between these two settings would be immaterial for option strikes that are
substantially larger than the effective lower bound (i.e.,
![]() ), but at a very low strike (e.g., 25 basis points), there may be a more visible difference between
), but at a very low strike (e.g., 25 basis points), there may be a more visible difference between
![]() vs
vs
![]() .
.
5.3 Option pricing performance
To get a sense of the overall fit across strikes, it is useful to look at the root-mean-square errors, i.e.,
| (59) |
where
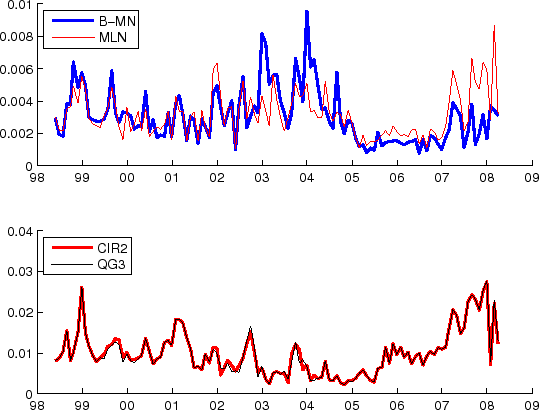 |
Figure 4 shows the time series of RMSEs based on the four models (B-MN, MLN, CIR2, QG3) for the 1998-2008 period. As can be seen in the top panel, the B-MN model (Black's boundary model) and the MLN model (conventional benchmark) performed similarly well, the MLN model
producing a somewhat smaller RMSE in 2003-2004 and larger RMSE in 2007-2008. Note that during most of the data period, with the exceptions around 2003 and 2008, the distributions were sufficiently away from the zero bound (as can be seen in Figure 3), thus the B-MN model was
simply the "mixture of normals" model (i.e., ![]() ); the results indicate that there is little practical difference between the normal-mixture model and the lognormal-mixture model most of
the times. On the other hand, the QG3 model and CIR2 model led to notably larger RMSEs. (Note the difference in the y-axis scales in top panel and bottom panel). Between the two models, the RMSE numbers were very similar, practically lying on top of each other.
); the results indicate that there is little practical difference between the normal-mixture model and the lognormal-mixture model most of
the times. On the other hand, the QG3 model and CIR2 model led to notably larger RMSEs. (Note the difference in the y-axis scales in top panel and bottom panel). Between the two models, the RMSE numbers were very similar, practically lying on top of each other.
|
|---|
It is also useful to examine the individual (strike-specific) pricing errors,
![]() and
and
![]() . Table 3 displays summary statistics for the pricing errors for put options with strikes
. Table 3 displays summary statistics for the pricing errors for put options with strikes
![]() and
and
![]() units below F and call options with strikes
units below F and call options with strikes
![]() and
and
![]() units above F. It can be seen that the errors for the QG3 and CIR2 models are not only large, but they also deviate systematically from zero. For example, even the 75-percentile
value of the pricing error for the put option at the strike of F
units above F. It can be seen that the errors for the QG3 and CIR2 models are not only large, but they also deviate systematically from zero. For example, even the 75-percentile
value of the pricing error for the put option at the strike of F
![]() is negative; this negative bias means that the QG3 and CIR2 models tend to systematically underprice the farther-out-of-money put options. On the other hand, they tend to
overprice the near-the-money call options.
is negative; this negative bias means that the QG3 and CIR2 models tend to systematically underprice the farther-out-of-money put options. On the other hand, they tend to
overprice the near-the-money call options.
In sum, the pdfs based on zero-cdf term structure models (CIR2 and QG3 models) perform notably worse than the MLN and B-MN models despite having one more parameter, suggesting that the kind of restrictions on the shape of the risk-neutral distribution implied by these models are not well supported by data.
5.4 Is the pdf always positively skewed?
 |
A test of skewness that does not need an assumption about the functional form of the pdf can be constructed as follows. Note that a negatively skewed distribution has
![]() , while a positively skewed distribution has
, while a positively skewed distribution has
![]() .33 Since the cumulative
distribution function
.33 Since the cumulative
distribution function ![]() at the median is 1/2 by definition, one can check whether the skewness is always positive by examining whether the condition
at the median is 1/2 by definition, one can check whether the skewness is always positive by examining whether the condition
holds, where we have used the fact that the mean of the risk-neutral distribution is the current futures rate. Since
| (61) |
we can check the condition (60) by evaluating the first derivatives
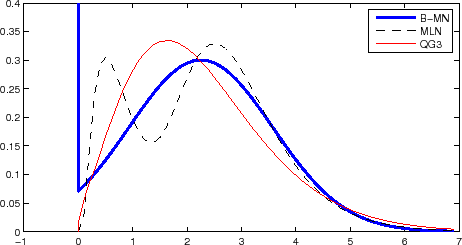
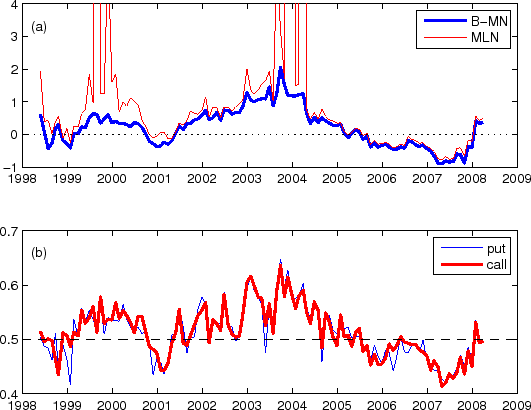
An example of negatively skewed pdf (April 30, 2007) is shown in Figure 6. The B-MN and MLN models produce fairly similar pdf (except for a small "wiggle" in the MLN pdf), and both clearly show a notable negative skew. As discussed earlier, since zero-cdf models like the QG3 model cannot produce a negatively skewed distribution, the estimated pdf from this model is a nearly symmetric distribution instead. Not surprisingly, pricing errors of the QG3 and CIR2 models tend to be particular large during the times of negatively skewed pdfs (as can be seen in Figure 4b).
5.5 Financial market turmoil of 2008
In early 2008, the turmoil in financial markets that had begun in mid-2007 intensified, posing considerable systemic risk and raising much concern about the broader economy. This lead to a substantial lowering of the federal funds target rate (and of the market's expectation of the future target rate). In March, the 1-year-ahead eurodollar futures rate had dropped to levels as low as 1.9%. Amid heightened uncertainty about the path of the interest rate, eurodollar futures options with very low strikes, in particular 0.25% and 0.5%, had begun to trade. This section explores whether the above models, if any, can explain the prices observed for these options.
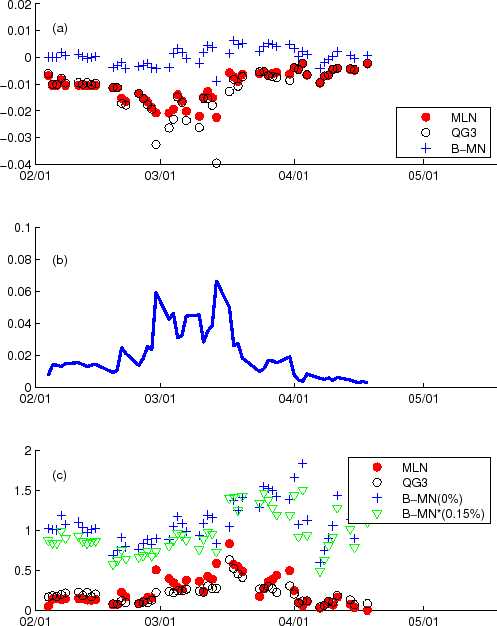 |
It befits to start with a cautionary remark that the liquidity in these put options was significantly lower than near-the-money options. The 1-year-maturity 0.25%-strike option, in particular, had an open interest of only about 30. However, the market in the 0.5%-strike option was more active,
with decent open interest (ranging from 2000 to 8000 in the months of February and March, comparable to the 25 percentile open interest in the put options with strikes ![]() to
to
![]() away from the current futures rate in Table 2). Therefore, at least the 0.5%-strike option merits a serious look.
away from the current futures rate in Table 2). Therefore, at least the 0.5%-strike option merits a serious look.
Figure 7a shows the pricing error
![]() for the 0.5%-strike option from the B-MN, MLN, and QG3 models, for every business day from February 4 to April 28, 2008. The MLN and QG3 models (and the CIR2 model, not
shown) generated much larger errors than the B-MN model in this period, and these errors were systematically negative, i.e., the QG3 and MLN models tended to underprice the option. These errors were particularly large during the first half of March; this is precisely the period where the B-MN model
indicates a substantial weight of the
for the 0.5%-strike option from the B-MN, MLN, and QG3 models, for every business day from February 4 to April 28, 2008. The MLN and QG3 models (and the CIR2 model, not
shown) generated much larger errors than the B-MN model in this period, and these errors were systematically negative, i.e., the QG3 and MLN models tended to underprice the option. These errors were particularly large during the first half of March; this is precisely the period where the B-MN model
indicates a substantial weight of the ![]() -function piece (
-function piece (![]() in eq. (52)), shown in Figure 7b. Although not shown, the pricing errors for
in eq. (52)), shown in Figure 7b. Although not shown, the pricing errors for ![]() tell a similar story. Figure 7c shows the ratio
tell a similar story. Figure 7c shows the ratio
![]() for the B-MN, MLN, and QG3 models. Note that the ratio is much smaller than 1 (sometimes orders of magnitude smaller) for the MLN and QG3 models, i.e., these models grossly
underpriced the
for the B-MN, MLN, and QG3 models. Note that the ratio is much smaller than 1 (sometimes orders of magnitude smaller) for the MLN and QG3 models, i.e., these models grossly
underpriced the ![]() option.
option.
 |
To show a representative day from this period, the fit of put and call option prices on March 10, 2008 is shown in Figure 8. Note that the QG3 model fits the put and call option prices rather poorly; the CIR2 model (not shown) gives similar results. The B-MN model prices put and call options fairly well across strikes. The MLN model also prices put and call option price well, except at the strikes of 0.25% and 0.5%.
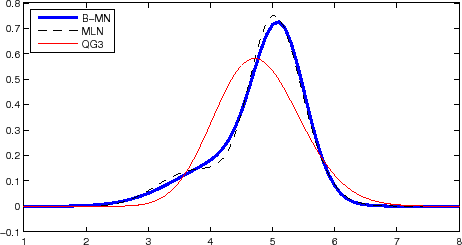
The model-implied pdfs for this date, shown in Figure 9, help explain this result. The MLN model pdf has a bimodal structure with a pronounced peak in the low interest rate region (centered at about 0.5%) and a broader peak at about 2.5%. This produces a fairly good fit of
option prices for most of the strikes, but since the left tails of both peaks have to vanish at 0, it leads to low prices of put options at strikes of 0.5% and 0.25%. The QG3 model also has a pdf that vanishes in the zero limit (recall from Section 4.1 that the pdf of the 3-factor positive-definite
QG model has the behavior
![]() ,
,
![]() ), thus producing much lower prices of low-strike options than the B-MN model which has a delta function singularity with weight of about 0.04. It is also interesting to note
that the modal implications of the pdfs are quite different, e.g., the QG3 pdf indicates that the most likely value is less than 2%, while the B-MN pdf indicates that the most likely value is larger than 2%.
), thus producing much lower prices of low-strike options than the B-MN model which has a delta function singularity with weight of about 0.04. It is also interesting to note
that the modal implications of the pdfs are quite different, e.g., the QG3 pdf indicates that the most likely value is less than 2%, while the B-MN pdf indicates that the most likely value is larger than 2%.
Several alternative computations of the pdf were done to check the robustness of the results. For example, put options with strikes below 1% were dropped in the computation (10), but this led to very similar results as the original computations. In other words, the good fit of the low-strike put option in the B-MN model is not due to their inclusion in the computation.
Another robustness check is with respect to the choice of the lower-boundary; as discussed in Section 5.2, there are reasons to consider a nonzero
![]() . The computation of the B-MN model pdf with
. The computation of the B-MN model pdf with
![]() again matched the price of the 0.5%-strike put option reasonably well. Figure 7c shows, with inverted triangle symbols, the
again matched the price of the 0.5%-strike put option reasonably well. Figure 7c shows, with inverted triangle symbols, the
![]() ratio for this case (this computation also dropped options with strikes less than 1%); it can be seen that the ratio is still fairly close to 1, and much larger than the
values predicted by the QG3 and MLN models.34
ratio for this case (this computation also dropped options with strikes less than 1%); it can be seen that the ratio is still fairly close to 1, and much larger than the
values predicted by the QG3 and MLN models.34
Lastly, note that 2002-3 is another interesting period from which the near-zero behavior of the risk-neutral pdf can be studied, but this paper forgoes a treatment comparable to that given to the 2008 episode, for space considerations.
6 Concluding remarks
The main conclusions of this paper can be summarized as follows. (1) Black's boundary model can capture the low-strike put option prices in February and March of 2008, which would have seemed puzzlingly high from the viewpoint of the popular zero-cdf term structure models. While some might alternatively argue that the "high" prices of these options are due to low liquidity or irrational pricing, we can say, at least, that the Black's boundary behavior provides one possible rational explanation for them. (2) Well-known non-negative interest rate models like the multifactor (positive-definite) CIR/QG models not only have difficulty capturing the low-strike option prices in early 2008 but also generate large and biased option pricing errors at other times as well. We have seen this specifically in the context of 2-factor and 3-factor CIR/QG models, but the theoretical arguments presented in Sec 4.1 suggest that having more factors would not change this conclusion. We have also seen that options data contradict the prediction that the pdf is always positively skewed. These constitute strong evidence against well-known term structure models that have zero cdf at the zero boundary.
This paper also has broader implications:
(a) The encouraging results from the flexible parametric pdf model with Black's boundary behavior developed here suggests that such a model may be useful for practical applications to other settings, for example, the extraction of risk-neutral pdfs from the Japanese interest rate options market (euroyen futures options).
(b) The evidence against zero-cdf models (and evidence for Black's boundary models) documented here indicates that, in modeling the postwar US economy there is little motivation to search for "special" macroeconomic mechanisms that would generate behaviors in which the short rate always stays above zero or "bounces off" from zero.35
(c) While the tractability of the affine and QG models may provide some incentive to consider the positive-definite versions of these models as approximate models (even if the true boundary behavior were Black's boundary behavior), the results in this paper cautions that they would be poor approximations, at least in certain contexts.
(d) This paper provides some justification for favoring models that can have negative nominal interest rates. It may appear counter-intuitive to deliberately ignore a clearly reasonable constraint about nominal interests (positive-definiteness). Indeed, Ahn, Dittmar, and Gallant (2002) and Leippold and Wu (2003) considered it a virtue that the QG model's parameters can be restricted so as to guarantee the positivity of nominal interest rates, and to my knowledge, all published papers that studied the QG model empirically have imposed such restriction. In so doing, however, they rule out specifications such as
Though it allows negative nominal rates, a specification like this accommodates negatively skewed pdfs (as observed in Sec. 5.4). The key point is that such specification is very similar to Black's model specification (which guarantees non-negative interest)
except when rates are close enough to zero for the zero bound to have substantial effects;36 hence most of the times it corresponds to Black's boundary model. In situations in which the zero bound matters, eq. (62) would no longer be a good approximation of (63), but in this case the positive-definite versions of the QG model would not be a good approximation of (63) either.
The empirical design of this paper had the following features: (i) the focus on the risk-neutral measure, and (ii) day-by-day implementations using only options data (and the current futures rate) for that day. Though this design was sufficient for detecting the problems with zero-cdf models (such as the multifactor positive-definite CIR/QG models) and yielded useful techniques for modeling pdfs for low interest rate scenarios, in the future it would be useful to extend the design to also examine the physical-measure processes and distributions, and utilize the time-series as well as the cross-sectional aspects of both options data and yield curve data, to achieve a more detailed understanding of the near-zero boundary processes.
7 The
 behavior of the pdf for
behavior of the pdf for
multifactor CIR/QG models
This appendix derives the small-![]() asymptotic expansion of the probability density function
asymptotic expansion of the probability density function ![]() for the distribution
for the distribution
![]() .
.
For this, we will use the Laplace transform of the probability density function
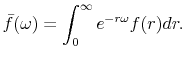 |
(64) |
The inverse Laplace transform
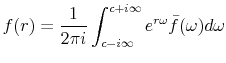 |
(65) |
gives back the pdf from
The Laplace transform of the pdf, i.e.
![]() , is simply related to the characteristic function
, is simply related to the characteristic function
![]() as
as
![]() . Therefore, from eq. (45), we have
. Therefore, from eq. (45), we have
The basic idea is to expand this in powers of
Note that the exponent in the exponential in eq. (66) can be written
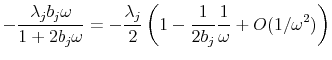 |
(67) |
and that
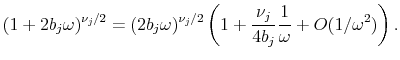 |
(68) |
Therefore,
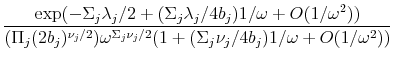 |
(69) | ||
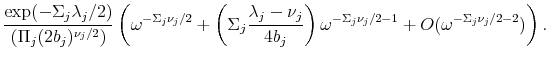 |
Because the inverse Laplace transform of
8 Option prices for risk-neutral distribution described by positive linear combination of independent noncentral 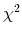 random variables
random variables
This appendix derives an approximate (but very accurate) formula for option prices for the distribution of short rate implied by CIR/QG models.
We want to evaluate the expressions
| (70) | |||
| (71) |
where
| (72) | |||
Thus we need to evaluate
| (73) |
therefore
| (74) | |||
where
It thus remains to derive expressions for cdfs ![]() and
and
![]() . This can be done using the saddle-point formula of Lugannani and Rice (1980) for cdfs,37 which uses the cumulant generating function
. This can be done using the saddle-point formula of Lugannani and Rice (1980) for cdfs,37 which uses the cumulant generating function
![]() :
:
where
Note that
![]() is related to the characteristic function as
is related to the characteristic function as
![]() . Thus, from eq. (45), we have
. Thus, from eq. (45), we have
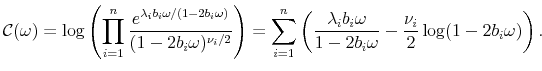 |
(76) |
The cumulative distribution function in the new measure
![]() is given by the same expression as that of
is given by the same expression as that of ![]() , except that the
cumulant generating function
, except that the
cumulant generating function
![]() in eq. (75) is replaced by the cumulant generating function for the new measure,
in eq. (75) is replaced by the cumulant generating function for the new measure,
![]() , which is given by
, which is given by
| (77) |
Using the identity
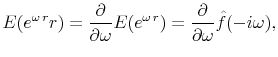 |
(78) |
it is straightforward to show
![\displaystyle {\mathcal C}^{\dag }(\omega)={\mathcal C}(\omega)+\log\left[\sum_{i=1}^n\left(\frac{\lambda_i b_i}{(1-2b_i\omega)^2}+\frac{\nu_i b_i}{1-2b_i\omega}\right)\right] -\log(\sum_{i=1}^n b_i(\lambda_i+\nu_i)).](img379.gif) |
(79) |
I have checked the Lugannani-Rice formula for the cumulant generating functions
![]() against the Fourier-inversion formula for cdf (eq. (47)) at several sets of parameter values, and found that in all cases the
agreements were excellent across the entire range of
against the Fourier-inversion formula for cdf (eq. (47)) at several sets of parameter values, and found that in all cases the
agreements were excellent across the entire range of ![]() , i.e., both in the tail and center regions of the distribution. One caveat is that the formula can be numerically unstable when
, i.e., both in the tail and center regions of the distribution. One caveat is that the formula can be numerically unstable when
![]() happens to be the mean of the distribution (i.e.,
happens to be the mean of the distribution (i.e.,
![]() ,
,
![]() ). However, such situation occurs rarely in our optimization problem (eq. (10)); if it does occur, one can find a nearby parameter vector
that does not have the problem but has a very similar pdf content, or use the conventional (slower) formula (47) with characteristic functions corresponding to
). However, such situation occurs rarely in our optimization problem (eq. (10)); if it does occur, one can find a nearby parameter vector
that does not have the problem but has a very similar pdf content, or use the conventional (slower) formula (47) with characteristic functions corresponding to
![]() .
.
9 Options and futures prices for flexible pdfs with Black's boundary behavior
This appendix provides formulae that are useful for the implementation of flexible pdf models with Black's boundary behavior.
It is straightforward to show that the option prices for the normal-mixture shadow rate distribution ![]() (eq. (53)) and lower boundary
(eq. (53)) and lower boundary
![]() are given by
are given by
![\displaystyle e^{-r_f\tau}[w\,(K-\underline{r}) +\sum_{i=1}^2 \beta_i \sigma_i(k_i(\Phi(k_i)-\Phi(\underline{\rho}_i))+\phi(k_i)- \phi(\underline{\rho}_i))]](img383.gif) |
(80) | ||
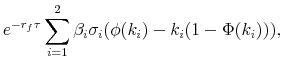 |
where
| (81) | |||
| (82) |
The current futures rate F
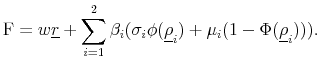 |
(83) |
The option prices for the Gram-Charlier/Edgeworth shadow rate distribution (eq. (54)) and lower boundary
![]() are given by
are given by
| (84) | |||
| (85) |
where
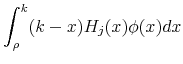 |
(86) | ||
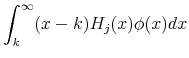 |
(87) | ||
| (88) |
Using the property of Hermite polynomials that
![]() , it is straightforward to show
, it is straightforward to show
| (89) |
Similarly, and using integration by parts, we have
| (90) | |||
| (91) |
for
| (92) | |||
| (93) |
The current futures rate is given by
| (94) |
Bibliography
Ahn, D. -H., R. F. Dittmar, and A. R. Gallant (2002), "Quadratic term structure models: theory and evidence", Review of Financial Studies, 15, pp243-88.
Ahn, D. -H., and B. Gao (1999), "A parametric nonlinear model of term structure dynamics," Review of Financial Studies, 12, pp721-62.
Ait-Sahalia, Y. (1996), "Testing continuous-time models of the spot interest rate," Review of Financial Studies, 9, pp385-426.
Bank for International Settlements (1999), Estimating and Interpreting Probability Density Functions (Proceedings of the workshop held at the BIS on 14 June 1999).
Baroni-Adesi, G. and R. Whaley (1987), "Efficient analytic approximation of American option values," Journal of Finance, 42, pp301-20.
Beaglehole, D. and M. Tenney (1992), "Corrections and additions to 'A nonlinear equilibrium model of the term structure of interest rates' " Journal of Financial Economics, 32, pp345-53.
Black, F. (1976), "The pricing of commodity contracts", Journal of Financial Economics, 3, pp167-79.
Black, F. (1995), "Interest rates as options", Journal of Finance, 50, pp1371-76.
Bomfim, A. (2003), "Interest rate as options: Assessing the markets' view of the liquidity trap", FEDS working paper No 2003-45.
Brace, A., D. Gatarek, and M. Musiela (1997), "The market model of interest rate dynamics", Mathematical Finance 7, 127-55.
Breeden, D. T. and R. H. Litzenberger (1978), "Prices of state-contingent claims implicit in option prices", Journal of Business, 51, 621-51.
Cecchetti, S. G. (1988), "The case of the negative nominal interest rates: new estimates of the term structure of interest rates during the Great Depression", Journal of Political Economy, 96, pp1111-41.
Chan, K. C., G. A. Karolyi, F. A. Longstaff, and A. B. Sanders, "An empirical comparison of alternative models of the short-term interest rate", Journal of Finance, 47, pp1209-27.
Cox, J.C., J. Ingersoll, and S. A. Ross (1985), "A theory of the term structure of interest rates", Econometrica, 53, pp385-407.
Daniels, H. E. (1987), "Tail probability approximations", International Statistical Review, 55, pp37-48.
Dirac, P. A. M. (1958), Principles of Quantum Mechanics, (4th ed.) Oxford Univ. Press.
Duffie, D. and K. Singleton (1997), "An econometric model of the term structure of interest rate swap yields", Journal of Finance, 52, pp1287-1321.
Feldh![]() tter, P., and D. Lando (2007), "Decomposing the swap spread", working paper.
tter, P., and D. Lando (2007), "Decomposing the swap spread", working paper.
Feller, W. (1952), "The parabolic differential equations and the associated semi-groups of transformations", Annals of Mathematics, 55, pp468-519.
Goldstein, R. S. and W. P. Kierstead (1997), "On the term structure of interest rates in the presence of reflecting and absorbing boundaries", working paper.
Gorovoi, V. and V. Linetsky (2004), "Black's model of interest rates as options, eigenfunction expansions, and Japanese interest rates", Mathematical Finance, 14, pp49-78.
H![]() rdahl, P. (2000), "Estimating the implied distribution of the future short-term interest rate using the Longstaff-Schwartz model", working paper.
rdahl, P. (2000), "Estimating the implied distribution of the future short-term interest rate using the Longstaff-Schwartz model", working paper.
H![]() rdahl, P. and D. Vestin (2005), "Interpreting implied risk-neutral densities: the role of risk premia", Review of Finance, 9, pp97-137.
rdahl, P. and D. Vestin (2005), "Interpreting implied risk-neutral densities: the role of risk premia", Review of Finance, 9, pp97-137.
Jackwerth, J. C. (2004), Option-Implied Risk-Neutral Distributions and Risk Aversion, The Research Foundation of AIMR.
Johnson, N., S. Kotz, and N. Balakrishnan (1994), Continuous Univariate Distributions, Volume 2, Wiley.
Karlin, S. and H. M. Taylor (1981), A Second Course in Stochastic Processes, Academic Press.
Leippold, M. and L. Wu (2003), "Design and estimation of quadratic term structure models", European Finance Review, 7, pp47-73.
Longstaff, F. A. (1992), "Multiple equilibria and term structure models", Journal of Financial Economics, 32, pp333-44.
Longstaff, F. A. and E. S. Schwartz (1992), "Interest rate volatility and term structure: a two-factor general equilibrium model", Journal of Finance, 47, pp1259-82.
Lugannani, R. and S. Rice (1980), "Saddlepoint approximations for the distribution of the sum of independent random variables", Advances in Applied Probability, 12, pp475-90.
McManus, D. J. (1999), "The information content of interest rate futures options", working paper.
Rogers, L. C. G. and O. Zane (1999), "Saddlepoint approximations to option prices", Annals of Applied Probability, 9, pp493-503.
Shimko, D. (1993), "Bounds of probability", RISK, 6(April), 33-37.
Stuart, A. and K. Ord (1994), Kendall's Advanced Theory of Statistics, Volume 1, Halsted Press.
Ueno, Y., N. Baba, and Y. Sakurai (2006), "The use of the Black model of interest rates as options for monitoring the JGB market expectations", Bank of Japan Working Paper Series.