
Temporal Risk Aversion and Asset Prices
Keywords: Temporal risk aversion, Intertemporal substitution, Equity premium, Risk free rate
Abstract:
JEL Classification: G12
1. Introduction
Agents with standard, time-separable preferences do not care about the temporal distribution of risk. This is a strong assumption. For example, it seems plausible that in reality a consumer may find persistent shocks to consumption less desirable than uncorrelated fluctuations. Such a consumer is said to exhibit temporal risk aversion. This type of risk aversion is lacking from standard preferences, because, with additive separability, expected utility is independent of the correlation of consumption in two different time periods. However, other than mathematical convenience, there is no compelling reason for assuming that temporal risk aversion is exactly zero and that consumers do not care about the temporal distribution of risk.
This paper works with an alternative specification for preferences to investigate the implications of temporal risk aversion for asset prices. Allowing for temporal risk aversion is achieved by abandoning time-separability, while staying within the expecteutility framework. This has two additional and closely related consequences. First, a separation of risk aversion from the intertemporal elasticity of substitution is attained. As is well known, with standard preferences the two are tightly linked, yet separating them can be crucial in explaining asset prices. Second, relative risk aversion can depend on the duration of the consumption gamble and this leads to notions of short-run and long-run risk aversion. This is also central to understanding the asset pricing implications. In particular, for the economy studied here, the equity premium is found to depend only on long-run risk aversion.
The preferences are specialized so as to yield stationary asset returns. To study the asset pricing implications, the present paper focuses on an endowment economy with ![]() consumption
growth. For this case, closed form solutions are derived for the risk-free rate and the equity premium. The risk-free rate depends primarily on a parameter indexing the desire to smooth consumption and the rate of time preference. By contrast, as mentioned, the equity premium depends only the
coefficient of long-run relative risk aversion, which is equal to a separate preference parameter.
consumption
growth. For this case, closed form solutions are derived for the risk-free rate and the equity premium. The risk-free rate depends primarily on a parameter indexing the desire to smooth consumption and the rate of time preference. By contrast, as mentioned, the equity premium depends only the
coefficient of long-run relative risk aversion, which is equal to a separate preference parameter.
The rest of this paper is organized as follows. The next section briefly covers the basics of temporal risk aversion. After that, the paper will present and discuss the preferences studied here, derive the pricing kernel for the endowment economy and, finally, present some asset pricing implications. Some of the related literature is discussed throughout the paper.
2. Temporal risk aversion
Following Richard (1975), temporal risk aversion can be defined in the following way.1 Consider a consumer who lives for two periods and is faced with a
choice between two consumption gambles. In the first gamble, consumption in the two periods is either
![]() or, with equal probability,
or, with equal probability,
![]() , where
, where
![]() . The second gamble results in either
. The second gamble results in either
![]() or
or
![]() , again with equal probability 0.5. If the consumer prefers the second lottery to the first for all values of
, again with equal probability 0.5. If the consumer prefers the second lottery to the first for all values of ![]() and
and ![]()
![]() , then
the consumer is considered to be temporally risk averse. If the first lottery is preferred, then the consumer is said to be temporally risk loving, while temporal risk neutrality applies in the case of indifference. An equivalent definition of temporal risk aversion replaces the second, preferred
gamble by independent draws in each period. That is, consumption is uncorrelated over time and, in each period, is either
, then
the consumer is considered to be temporally risk averse. If the first lottery is preferred, then the consumer is said to be temporally risk loving, while temporal risk neutrality applies in the case of indifference. An equivalent definition of temporal risk aversion replaces the second, preferred
gamble by independent draws in each period. That is, consumption is uncorrelated over time and, in each period, is either ![]() or
or ![]() , with equal probability. The equivalence of the definitions follows directly from the additive properties of expected utility. A straightforward extension of the definition to
, with equal probability. The equivalence of the definitions follows directly from the additive properties of expected utility. A straightforward extension of the definition to ![]() periods is presented in Richard (1975).2
periods is presented in Richard (1975).2
It seems reasonable to regard the second gamble as less risky - there is no risk of a `lifetime of misery' due to permanently low consumption (or less risk of that outcome, in the case of the second definition). In contrast, any consumer with time-separable preferences is indifferent between
these two gambles and so is temporally risk neutral, because the serial correlation of consumption does not matter for expected utility under additive separability. (With time-separability expected utility is
![]() which is trivially equal to
which is trivially equal to
![]() .)
.)
Richard (1975) shows that a consumer with a twice differentiable utility function
![]() is temporally risk averse if and only if the cross-partial derivative is negative, i.e. if and only if
is temporally risk averse if and only if the cross-partial derivative is negative, i.e. if and only if
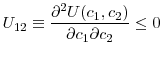
3. Preferences
Preferences are ordered by
with
As a consequence of time-consistency, past choices will matter for decisions over current and future consumption, except for some special cases (such as additive separability). This feature is not unusual in the literature on consumption-based asset pricing: it is also present in models with
habit or durability in consumption. A recent paper by Kihlstrom (2007) focuses on the alternative case that the consumer ignores past consumption in
![]() . With that approach, current choices are independent of past choices, but that also implies that the preferences are dynamically inconsistent.3
. With that approach, current choices are independent of past choices, but that also implies that the preferences are dynamically inconsistent.3
Time-separable preferences (and therefore temporal risk neutrality) can be obtained as a special case by setting ![]() . Otherwise, assuming that
. Otherwise, assuming that ![]() and
and ![]() are both twice differentiable and checking the cross-partial derivative, it is easy to show that
are both twice differentiable and checking the cross-partial derivative, it is easy to show that
![]() is temporally risk averse (loving) if
is temporally risk averse (loving) if ![]() is concave (convex).
Further algebra shows that this is in turn equivalent to
is concave (convex).
Further algebra shows that this is in turn equivalent to ![]() being more (less) risk averse than
being more (less) risk averse than ![]() in the sense of Arrow and Pratt. That is, the following statements are equivalent:
in the sense of Arrow and Pratt. That is, the following statements are equivalent:
- (i)
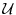 is temporally risk averse (loving);
is temporally risk averse (loving); - (ii)
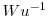 is concave (convex); and
is concave (convex); and - (iii)
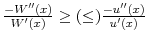 , for
, for
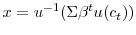 .
.
As the second statement suggests, this approach follows naturally from Kihlstrom and Mirman's (1974) analysis of risk aversion with multiple goods.
To obtain stationary asset pricing implications in the context of a growth economy, (1) is specialized to iso-elastic functional forms:
![]() and
and
![]() . Then
. Then
In a deterministic setting,
To illustrate the role of the parameter ![]() , suppose consumption is constant over time and equal to
, suppose consumption is constant over time and equal to ![]() (so that
(so that
![]() constant
constant ![]()
![]() ), then
), then ![]() is the coefficient of relative risk aversion with
respect to gambles over
is the coefficient of relative risk aversion with
respect to gambles over ![]() , i.e. lifetime consumption gambles. For this reason, I will refer to
, i.e. lifetime consumption gambles. For this reason, I will refer to ![]() as long-run (relative) risk aversion.
as long-run (relative) risk aversion.
3.1 Long-run risk aversion
To further understand the role of long-run risk aversion ![]() , it useful to define a lifetime consumption gamble as a lottery that changes consumption in each period by a common factor
, it useful to define a lifetime consumption gamble as a lottery that changes consumption in each period by a common factor
![]() , where
, where
![]() is a random variable that has zero mean and is orthogonal to the initial consumption process. Formally, let
is a random variable that has zero mean and is orthogonal to the initial consumption process. Formally, let
![]() be a given stochastic process for consumption without the gamble. With the gamble, consumption is
be a given stochastic process for consumption without the gamble. With the gamble, consumption is
![\displaystyle E\mathcal{U}=E[\frac{1}{1-\alpha}(\Sigma_{t=0}^{T}\beta^{t}c_{t}^{1-\gamma })^{(1-\alpha)/(1-\gamma)}]](img46.gif)
![\displaystyle E\mathcal{\tilde{U}}\equiv E[\frac{1}{1-\alpha}(\Sigma_{t=0}^{T}\beta ^{t}\tilde{c}_{t}^{1-\gamma})^{(1-\alpha)/(1-\gamma)}]=E[(1+\tilde {\varepsilon})^{1-\alpha}]E\mathcal{U}%](img47.gif)
3.2 Short-run risk aversion
It is more common to consider risk aversion with respect to one period consumption gambles. Although with time-separable, iso-elastic utility there is no difference with between this and the long-run concept, with the preferences postulated in (2) there generally is. For
this reason, I will use the term short-run risk aversion to refer to risk aversion with respect to one period consumption gambles. To characterize short-run risk aversion, the marginal utility of consumption during period ![]() is:
is:
with
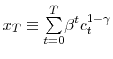
Short-run risk aversion is the sum of two terms. If the consumer is temporally risk neutral (the time-separable case, with
In that case, it is also clear from equation (4) that short-run relative risk aversion is generally not constant. To gain insight into this, let us first consider the case that future consumption is known at time ![]() . Then
. Then
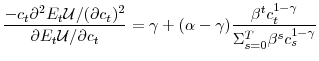
The case of stochastic future consumption will be analyzed in more detail after the presentation the endowment economy. It will be shown for that economy that, under certain conditions, short-run risk aversion converges to ![]() as
as ![]() goes to infinity.
goes to infinity.
3.3 Discussion
With the intertemporal elasticity of substitution (IES) equal to ![]() , and long-run risk aversion equal to
, and long-run risk aversion equal to ![]() , these preferences separate, to some degree, consumption smoothing from risk aversion. This contrasts sharply with time-separable preferences for which, as mentioned, the IES is the inverse of the coefficient of relative risk aversion. Epstein-Zin-Weil
preferences also provide a separation between the two concepts (see Epstein and Zin (1989) and Weil (1989)). The key difference with the approach taken here is that Epstein-Zin-Weil preferences are non-expected utility preferences. They do not satisfy the axioms of von Neumann and Morgenstern for
consumption gambles extending over multiple periods. As discussed by Epstein and Zin, this is manifested by an associated preference for early or late resolution of uncertainty. An open question is to what extent the accomplishments of Epstein-Zin-Weil preferences in the asset pricing literature
are due to the fact that they lie outside the traditional expected utility framework.5 For example, is the preference for early or late resolution of
uncertainty crucial? Or is it `just' the separation of risk aversion from consumption smoothing that matters? As illustrated by the preferences used here, by introducing temporal risk aversion, it is possible to have that separation without leaving the expected utility framework and, as a
consequence, without relying on any preference for early or late resolution of uncertainty. In this sense, the approach taken here is also a smaller departure from the standard time-separable preferences.
, these preferences separate, to some degree, consumption smoothing from risk aversion. This contrasts sharply with time-separable preferences for which, as mentioned, the IES is the inverse of the coefficient of relative risk aversion. Epstein-Zin-Weil
preferences also provide a separation between the two concepts (see Epstein and Zin (1989) and Weil (1989)). The key difference with the approach taken here is that Epstein-Zin-Weil preferences are non-expected utility preferences. They do not satisfy the axioms of von Neumann and Morgenstern for
consumption gambles extending over multiple periods. As discussed by Epstein and Zin, this is manifested by an associated preference for early or late resolution of uncertainty. An open question is to what extent the accomplishments of Epstein-Zin-Weil preferences in the asset pricing literature
are due to the fact that they lie outside the traditional expected utility framework.5 For example, is the preference for early or late resolution of
uncertainty crucial? Or is it `just' the separation of risk aversion from consumption smoothing that matters? As illustrated by the preferences used here, by introducing temporal risk aversion, it is possible to have that separation without leaving the expected utility framework and, as a
consequence, without relying on any preference for early or late resolution of uncertainty. In this sense, the approach taken here is also a smaller departure from the standard time-separable preferences.
4. The Pricing Kernel
Suppose that the consumer reduces consumption in period ![]() by 1 unit, purchases an asset with gross return
by 1 unit, purchases an asset with gross return ![]() and then uses the proceeds to increase consumption in period
and then uses the proceeds to increase consumption in period ![]() . Equilibrium asset prices have to be such that for the consumer the net marginal effect
of this action on expected utility is zero. This perturbation argument implies the following Euler equation:
. Equilibrium asset prices have to be such that for the consumer the net marginal effect
of this action on expected utility is zero. This perturbation argument implies the following Euler equation:
Using equation (3) and the law of iterated expectations, the following version of the intertemporal marginal rate of substitution is a valid pricing kernel:6
The first two factors equal the pricing kernel for the time-separable case (
The goal is now to obtain a convenient expression for this new factor. It will be possible to do this for an economy with a long horizon, ![]() . Formally, I will consider a sequence of
economies indexed by
. Formally, I will consider a sequence of
economies indexed by ![]() and then derive a result characterizing the limit of the pricing kernel as
and then derive a result characterizing the limit of the pricing kernel as ![]() approaches infinity.7 Focusing on the infinite horizon case in this way will also have the advantage that the pricing kernel will not depend
on on the `time remaining',
approaches infinity.7 Focusing on the infinite horizon case in this way will also have the advantage that the pricing kernel will not depend
on on the `time remaining', ![]() , as a state variable, which would have the undesirable consequence of generating nonstationary asset returns.
, as a state variable, which would have the undesirable consequence of generating nonstationary asset returns.
It is convenient to split up ![]() into realized and future terms:
into realized and future terms:
where the second step introduces a convenient normalization, with
Denoting the growth rate of consumption by
At the same time
so, exploiting the
![\displaystyle E_{t}[f_{T}^{t+1}]=% {\textstyle\sum\nolimits_{s=0}^{T-(t+1)}} \left( E[\beta g_{t}^{1-\gamma}]\right) ^{s+1}=\frac{\beta E[g_{t}% ^{1-\gamma}]\{1-(\beta E[g_{t}^{1-\gamma}])^{T-t}\}}{1-\beta E[g_{t}% ^{1-\gamma}]}%](img88.gif)
In contrast, if ![]() (more precisely, if
(more precisely, if
![]() ), then
), then
![]() remains bounded for arbitrarily large
remains bounded for arbitrarily large ![]() . At the same time,
. At the same time,
![]() grows exponentially as time passes. Thus, even if
grows exponentially as time passes. Thus, even if ![]() is very large, after a
few periods,
is very large, after a
few periods, ![]() is likely to be large relative to
is likely to be large relative to
![]() , as the former diverges in expectation and the latter does not, if
, as the former diverges in expectation and the latter does not, if ![]() . This suggests that, at that point in time,
. This suggests that, at that point in time,
![\displaystyle \frac{E_{t+1}\left[ x_{T}^{\delta}\right] }{E_{t}\left[ x_{T}^{\delta }\right] }=\frac{E_{t+1}\left[ (1+f_{T}^{t+1}/z_{t})^{\delta}\right] }{E_{t}\left[ (1+f_{T}^{t+1}/z_{t})^{\delta}\right] }\approx\frac{1}{1}=1](img94.gif)
Since I am interested in temporal risk aversion, and since in any case the asset pricing implications of the standard preferences are well understood, I will focus on the alternative case that ![]() . Note that if
. Note that if
![]() this is realistic only if
this is realistic only if ![]() , i.e. if the intertemporal
elasticity of substitution exceeds unity. Intuitively,
, i.e. if the intertemporal
elasticity of substitution exceeds unity. Intuitively, ![]() means that, unless
means that, unless ![]() is close to
is close to ![]() , the future is more important than the past for current decisions.
, the future is more important than the past for current decisions.
Epstein and Zin (1989) have critiqued the kind of preferences postulated in (2) by pointing out that, if ![]() and without growth, the dependence of the marginal
utility of current consumption on past consumption is greater as the past becomes more distant. However, this is not true under condition (9) (
and without growth, the dependence of the marginal
utility of current consumption on past consumption is greater as the past becomes more distant. However, this is not true under condition (9) (![]() ). This
condition can be satisfied even with a constant consumption profile, provided
). This
condition can be satisfied even with a constant consumption profile, provided
![]() ; with growth
; with growth ![]() may be less than 1 provided
may be less than 1 provided ![]() . Interestingly, the parameter restriction under which temporal risk aversion turns out to have
novel asset pricing implications also addresses the critique of Epstein and Zin.
. Interestingly, the parameter restriction under which temporal risk aversion turns out to have
novel asset pricing implications also addresses the critique of Epstein and Zin.
Using (7), the new factor in the pricing kernel can be written as
Intuitively, and informally, for large
![\displaystyle \underset{T\rightarrow\infty}{\lim}\frac{E_{t+1}\left[ x_{T}^{\delta}\right] }{E_{t}\left[ x_{T}^{\delta}\right] }=(\beta g_{t+1}^{1-\gamma})^{\delta }\Lambda=\beta^{\delta}g_{t+1}^{\gamma-\alpha}\Lambda](img109.gif)
![\displaystyle \underset{T\rightarrow\infty}{\lim}E_{t}\left[ \frac{E_{t+1}\left[ x_{T}^{\delta}\right] }{E_{t}\left[ x_{T}^{\delta}\right] }\right] =1=E_{t}\left[ \beta^{\delta}g_{t+1}^{\gamma-\alpha}\right] \Lambda ~\implies\Lambda=\frac{1}{\beta^{\delta}E_{t}[g_{t+1}^{\gamma-\alpha}]}%](img111.gif)
If this informal line of reasoning is correct, then substituting this limiting value into (6) yields a very simple expression for the limiting pricing kernel - see equation (13) below. The following proposition, the main result of the paper, shows that under certain conditions this argument can indeed be formalized.
Remark 1: ![]() requires that either
requires that either ![]() and
and
![]() , or
, or ![]() and
and
![]() . If (realistically)
. If (realistically) ![]() , then, given assumption (12), only the first possibility is consistent with
, then, given assumption (12), only the first possibility is consistent with
![]() . As mentioned,
. As mentioned,
![]() implies positive temporal risk aversion.
implies positive temporal risk aversion.
Remark 2: condition (12) implies ![]() (since
(since ![]() and
and
![]() by (12)).
by (12)).
The proof employs the mean value theorem and the reflection principle for Brownian motion to show that the history of past consumption, summarized in ![]() , is asymptotically unimportant
in
, is asymptotically unimportant
in
![]() . Then, the dominated convergence theorem is used to to interchange the limit
and expectations operators. The conditions stated in the theorem are sufficient. I suspect that they are not all necessary, but I have not shown this (except for the conditions outlined in footnote 13 and the following trivial case).
. Then, the dominated convergence theorem is used to to interchange the limit
and expectations operators. The conditions stated in the theorem are sufficient. I suspect that they are not all necessary, but I have not shown this (except for the conditions outlined in footnote 13 and the following trivial case).
It is worth pointing out that if
![]() , so that the utility function is time-separable, then equation (13) specializes to the standard pricing kernel for time-separable utility with
constant relative risk aversion:
, so that the utility function is time-separable, then equation (13) specializes to the standard pricing kernel for time-separable utility with
constant relative risk aversion:
![]() .
.
An increase in long-run risk aversion ![]() makes marginal utility, and therefore the pricing kernel, more responsive to realized growth rates, but without having a big impact on its
expected value due to the correction
makes marginal utility, and therefore the pricing kernel, more responsive to realized growth rates, but without having a big impact on its
expected value due to the correction
![]() . (In the special case
. (In the special case ![]() , the impact is
exactly zero; for positive but small
, the impact is
exactly zero; for positive but small ![]() the impact is small, as will be shown more explicitly below.) This is important for the asset pricing implications, since, loosely speaking, the
equity premium depends on the volatility of the pricing kernel, while the risk free rate depends on its conditional mean.
the impact is small, as will be shown more explicitly below.) This is important for the asset pricing implications, since, loosely speaking, the
equity premium depends on the volatility of the pricing kernel, while the risk free rate depends on its conditional mean.
The following proposition characterizes short-run risk aversion in this economy:
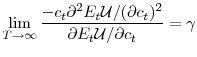
Thus, for this stochastic economy, a similar result applies as for the deterministic case: when the horizon ![]() is large, short-run risk aversion is close to
is large, short-run risk aversion is close to ![]() . In this sense, the separation between the intertemporal elasticity of substitution and short-run risk aversion vanishes in the limit. This separation remains, however, for long-run risk aversion, which is always
equal to
. In this sense, the separation between the intertemporal elasticity of substitution and short-run risk aversion vanishes in the limit. This separation remains, however, for long-run risk aversion, which is always
equal to ![]() . The next section shows how this affects asset prices.
. The next section shows how this affects asset prices.
5. Asset Prices
Using the expression for the limiting pricing kernel in (13), pricing assets is straightforward, using the optimality condition
![]() , where
, where
![]() is the gross realized return to any tradeable asset, between period
is the gross realized return to any tradeable asset, between period ![]() and
and ![]() . In what follows it is assumed that the conditions to theorem 1 are satisfied. This is consistent with temporal risk aversion (
. In what follows it is assumed that the conditions to theorem 1 are satisfied. This is consistent with temporal risk aversion (
![]() ) only if
) only if ![]() is less than 1, so that the intertemporal elasticity of substitution exceeds unity (and short-run risk aversion is less than 1 in
the limit).
is less than 1, so that the intertemporal elasticity of substitution exceeds unity (and short-run risk aversion is less than 1 in
the limit).
It should be stated at the outset that, with ![]() consumption growth and the asymptotic irrelevance of past consumption to the pricing kernel (see (13)), the
model will imply constant values for the risk-free rate and the equity premium. This is also true for for standard preferences combined with
consumption growth and the asymptotic irrelevance of past consumption to the pricing kernel (see (13)), the
model will imply constant values for the risk-free rate and the equity premium. This is also true for for standard preferences combined with ![]() consumption growth.
consumption growth.
5.1 Risk-free rate
Denote the risk-free one period real interest rate between period ![]() and
and ![]() by
by
![]() . In the limiting economy,
. In the limiting economy,
The constant short-rate implies a flat real term structure. That is, real yields on all long bonds are constant and equal to the short rate. Again, this is also true for standard preferences with ![]() consumption growth.
consumption growth.
5.2 Consumption claim
Lucas (1978) and Mehra and Prescott (1985) define equity as a claim to aggregate consumption. Deriving the expected return to such a consumption claim using
![]() is standard. The resulting `consumption equity premium' is:
is standard. The resulting `consumption equity premium' is:
As can be seen, the risk premium depends only long-run risk aversion. For the preferences used here, temporal risk aversion implies that long-run risk aversion exceeds short-run risk aversion. In this sense, therefore, temporal risk aversion increases the risk premium on a consumption claim.
5.3 Equity
Extending the formulation by Abel (1999), equity is modelled as a claim to dividends equal to
![]() in period
in period ![]() . The parameter
. The parameter ![]() is a modeling device that closely approximates the effect of leverage on returns (see Abel (1999)), with positive leverage corresponding to
is a modeling device that closely approximates the effect of leverage on returns (see Abel (1999)), with positive leverage corresponding to ![]() .
.
![]() is a shock which assumed to be uncorrelated with consumption and is distributed
is a shock which assumed to be uncorrelated with consumption and is distributed
![]() . It is included because in the data dividend volatility exceeds consumption volatility and because the dividend and consumption growth rates are
imperfectly correlated. Finally,
. It is included because in the data dividend volatility exceeds consumption volatility and because the dividend and consumption growth rates are
imperfectly correlated. Finally, ![]() is a convenient way of considering the effect of the duration of the equity claim.
is a convenient way of considering the effect of the duration of the equity claim. ![]() or
or
![]() are standard choices. The resulting equity premium is:
are standard choices. The resulting equity premium is:
As finance theory predicts, nonsystematic risk (
Why does the equity premium depend on long-run risk aversion, as opposed the short-run concept? The intuition for this result is that the risk in this economy stems from the ![]() shocks
to the growth rate of consumption (and therefore dividends). These innovations act as permanent shocks to the level of consumption. A positive innovation to the growth rate raises consumption in all remaining periods by the same ratio. It is
therefore similar to the lifetime consumption gamble discussed in section 3.1. Loosely speaking, it is also more similar the lottery that the consumer dislikes in the definition of temporal risk aversion than the alternative (see section 2).
shocks
to the growth rate of consumption (and therefore dividends). These innovations act as permanent shocks to the level of consumption. A positive innovation to the growth rate raises consumption in all remaining periods by the same ratio. It is
therefore similar to the lifetime consumption gamble discussed in section 3.1. Loosely speaking, it is also more similar the lottery that the consumer dislikes in the definition of temporal risk aversion than the alternative (see section 2).
This result is not driven by the fact that equity is a long-lived claim, as it holds even for a very short-duration equity claim (small![]() ) and even, it can be shown, for a one period
equity strip. Rather, it is due to the fact that the economic risk inherent in equity is `long-run risk' to the level of consumption.
) and even, it can be shown, for a one period
equity strip. Rather, it is due to the fact that the economic risk inherent in equity is `long-run risk' to the level of consumption.
5.4 Numerical examples
As Mehra and Prescott (1985) and others have shown, it is difficult for standard models with time-separable preferences to account for the 6% equity premium and the low risk-free rate with conventional levels for risk aversion.8 In this subsection, I examine whether it is easier to do so with temporal risk aversion. I use the values calculated by Mehra and Prescott for the mean and standard deviation of the growth rate of real per capita
consumption of nondurables and services: ![]() and
and
![]() . Following Abel (1999) and Bansal and Yaron (2004), I set the leverage parameter at
. Following Abel (1999) and Bansal and Yaron (2004), I set the leverage parameter at ![]() . The average U.S. equity premium reported by Mehra and Prescott is
. The average U.S. equity premium reported by Mehra and Prescott is ![]() per annum, and the average real risk-free rate is
per annum, and the average real risk-free rate is ![]() .
.
First, I ask what equity premium the model can generate subject to matching the risk-free rate exactly and subject to the parameter restrictions needed for theorem 1 to hold (most importantly, condition (12)). Under those restrictions, the model can account for
about half the equity premium (![]() ). Parameter values that accomplish this are, for example,
). Parameter values that accomplish this are, for example, ![]() ,
,
![]() and
and
![]() . That is, with risk aversion ranging from 0.75 for the short run to
8 for the long run, the model can match the risk-free rate and about half the equity premium. Note that with
. That is, with risk aversion ranging from 0.75 for the short run to
8 for the long run, the model can match the risk-free rate and about half the equity premium. Note that with
![]() the intertemporal elasticity of substitution is
the intertemporal elasticity of substitution is
![]() . Incidentally, the predicted equity premium is well within two standard deviations of the historical average. For comparison, with time-separable preferences the result
is an equity premium of only
. Incidentally, the predicted equity premium is well within two standard deviations of the historical average. For comparison, with time-separable preferences the result
is an equity premium of only ![]() .9 This is the
well-know equity premium puzzle.
.9 This is the
well-know equity premium puzzle.
Alternatively, one can ask how close the model can get to matching the risk-free rate while replicating the point estimate of the equity premium. Using equation (15), to match the equity premium exactly, long-run risk aversion must equal
![]() . However, that value results in a risk-free rate that is too low, because, as mentioned, temporal risk aversion lowers the risk-free rate. Assuming a high rate of time preference
(a low
. However, that value results in a risk-free rate that is too low, because, as mentioned, temporal risk aversion lowers the risk-free rate. Assuming a high rate of time preference
(a low ![]() ) would help, but this is ruled out by the parameter restriction to the theorem (12). Under that restriction and with
) would help, but this is ruled out by the parameter restriction to the theorem (12). Under that restriction and with
![]() , the model can generate a risk-free rate that is about 1 percentage point below the historical average. For example, with permissible parameter values
, the model can generate a risk-free rate that is about 1 percentage point below the historical average. For example, with permissible parameter values
![]() ,
,
![]() and
and
![]() , the risk-free rate is
, the risk-free rate is
![]() .10
.10
The low risk-free rate contrasts sharply with the case of time-separable preferences, for which high levels of risk aversion imply counterfactually high values for the risk-free rate.11 For example, setting
![]() to match the equity premium results in a risk-free rate near
to match the equity premium results in a risk-free rate near ![]() with standard preferences, if
with standard preferences, if
![]() . The reason is that with time separability high risk aversion implies a strong desire for consumption smoothing, which in the presence of growth results in a high interest rate
in equilibrium.
. The reason is that with time separability high risk aversion implies a strong desire for consumption smoothing, which in the presence of growth results in a high interest rate
in equilibrium.
More important is that the preferences with temporal risk aversion can generate sizable risk premia without suffering from what can be called the `Lucas-Murphy critique'. As Robert Lucas (1990) has observed,12 two countries that differ in their growth rate (![]() ) by 1 percent, differ in their interest rate by
) by 1 percent, differ in their interest rate by ![]() percent, where
percent, where ![]() is the reciprocal of the intertemporal elasticity of substitution
(assuming the same preferences and variance of consumption growth). With time separable preferences
is the reciprocal of the intertemporal elasticity of substitution
(assuming the same preferences and variance of consumption growth). With time separable preferences ![]() is also risk aversion, so then levels of risk aversion in excess of
is also risk aversion, so then levels of risk aversion in excess of ![]() , in Lucas' estimate, would then imply counterfactually large differences in real interest rates across countries (think of South Korea and the U.S.). In his 2003 presidential address, Lucas revisits
this argument and concludes that the IES should in fact be close to one. The preferences used in this paper can combine higher long-run risk aversion with a relatively high intertemporal elasticity of substitution (i.e. a low
, in Lucas' estimate, would then imply counterfactually large differences in real interest rates across countries (think of South Korea and the U.S.). In his 2003 presidential address, Lucas revisits
this argument and concludes that the IES should in fact be close to one. The preferences used in this paper can combine higher long-run risk aversion with a relatively high intertemporal elasticity of substitution (i.e. a low ![]() ), thus avoiding the prediction of enormous cross-country real interest rate differentials.
), thus avoiding the prediction of enormous cross-country real interest rate differentials.
6. Conclusion
The starting point of this paper has been the idea that consumers may care about the temporal distribution of risk; in particular, they may find persistent shocks to consumption less desirable than uncorrelated fluctuations. I have formulated expected utility preferences that exhibit such
temporal risk aversion and studied their asset pricing implications. I found that temporal risk aversion leads naturally to a separation of risk aversion from the intertemporal elasticity of substitution, as well as a distinction between short-run and long-run risk aversion. For an endowment
economy with ![]() consumption growth, I derived a simple expression for the limiting pricing kernel, which yields stationary implications for asset returns. In that economy, closed form
solutions show that the equity premium depends only on a parameter indexing long-run risk aversion, while the risk-free rate instead depends primarily on a separate parameter indexing the desire to smooth consumption over time and the rate of time preference. Quantitatively, the model improves upon
the ability of standard preferences to simultaneously account for the historical averages of the equity premium and the risk-free rate.
consumption growth, I derived a simple expression for the limiting pricing kernel, which yields stationary implications for asset returns. In that economy, closed form
solutions show that the equity premium depends only on a parameter indexing long-run risk aversion, while the risk-free rate instead depends primarily on a separate parameter indexing the desire to smooth consumption over time and the rate of time preference. Quantitatively, the model improves upon
the ability of standard preferences to simultaneously account for the historical averages of the equity premium and the risk-free rate.
At least two open questions remain. First, is the pricing kernel valid under a wider set of conditions than for which it has been derived here? And, second, what additional asset pricing implications of temporal risk aversion are there for the case of non-![]() consumption growth? For example, it seems interesting to investigate the effect of long-run risk (Bansal and Yaron (2004)) in the presence of temporal risk aversion. I leave these questions for future research.
consumption growth? For example, it seems interesting to investigate the effect of long-run risk (Bansal and Yaron (2004)) in the presence of temporal risk aversion. I leave these questions for future research.
Appendix 1. Proof of Theorem 1
Define
Using (7), (10) and the assumption that
so that, introducing a convenient normalization,
![\displaystyle \frac{E_{t+1}[x_{T}^{\delta}]}{(\beta^{t+1}c_{t+1}^{1-\gamma})^{\delta}% \xi^{\delta}(1,T-t-1)}=\frac{\xi^{\delta}(z_{t+1},T-t-1)}{\xi^{\delta }(1,T-t-1)}%](img181.gif)
Next, since
![]() , we have, using (17) and a slightly different normalization,
, we have, using (17) and a slightly different normalization,
where I have introduced the following notation:
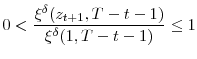
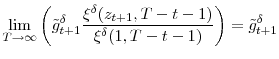
Combining equations (18), (19) and (20) yields
Finally, combining this with equation (6),
![\displaystyle \underset{T\rightarrow\infty}{\lim}M_{t+1}^{T}=\frac{\beta g_{t+1}^{-\alpha}% }{E_{t}[g_{t+1}^{\gamma-\alpha}]}%](img195.gif)
Proof of lemma 1. The proof proceeds in several steps.
1. [Upper bound on ![]() ] First, recall the definition
] First, recall the definition
Since ![]() , and exploiting the
, and exploiting the ![]() assumption,
assumption,
Because assumption (12) implies that
2. [Applying the mean value theorem] To proceed, differentiate ![]() with respect to
with respect to ![]() :
:
Now, since
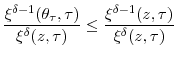
3. [Lower bound on ![]() ]13 To bound the
ratio
]13 To bound the
ratio
![]() from above, a lower bound for
from above, a lower bound for
![]() is needed in addition to the upper bound. Using the notation from step 1, we can write
is needed in addition to the upper bound. Using the notation from step 1, we can write
![]() . Since
. Since
![]() ,
,
![]() , where
, where ![]() is the running sum of independent standard normals:
is the running sum of independent standard normals:
![]() where
where ![]() are
are ![]()
![]() random variables. (The notation
random variables. (The notation
![]() stands for `is equal in distribution to'.) Thus,
stands for `is equal in distribution to'.) Thus,
where
![\displaystyle \frac{1}{\tilde{\mu}+0.5\delta\tilde{\sigma}^{2}}\left\{ (\tilde{\mu}% +\delta\tilde{\sigma}^{2})\exp[(\delta\tilde{\mu}+0.5\delta^{2}\tilde{\sigma }^{2})\tau]\Phi\left( \frac{\tilde{\mu}+\delta\tilde{\sigma}^{2}}% {\tilde{\sigma}}\sqrt{\tau}\right) +\tilde{\mu}\Phi\left( -\frac{\tilde{\mu }}{\tilde{\sigma}}\sqrt{\tau}\right) \right\}](img255.gif)
4. [Showing that
![]() and
and
![]() ] Applying the lower and upper bounds on
] Applying the lower and upper bounds on ![]() ((24) and (26)) yields, for
((24) and (26)) yields, for
![]() :
:
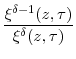 |
![\displaystyle \leq\frac{\exp [(\tilde{\mu}(\delta-1)+0.5(\delta-1)^{2}\tilde{\sigma}^{2})\tau]}% {(2\tau)^{\delta}\left( \frac{\tilde{\mu}+\delta\tilde{\sigma}^{2}}% {2\tilde{\mu}+\delta\tilde{\sigma}^{2}}\right) \exp[(\delta\tilde{\mu }+0.5\delta^{2}\tilde{\sigma}^{2})\tau]}](img265.gif) |
|
![\displaystyle =(2\tau)^{-\delta}\left( \frac{2\tilde{\mu}+\delta\tilde{\sigma}^{2}% }{\tilde{\mu}+\delta\tilde{\sigma}^{2}}\right) \exp[-(\tilde{\mu}% +(\delta-0.5)\tilde{\sigma}^{2})\tau]](img266.gif) |
Assumption (12) to the theorem states that
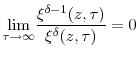
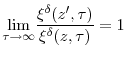
Appendix 2. Proof of Theorem 2
From equations (4), (7) and (16), and the assumption that ![]() is
is ![]() ,
,
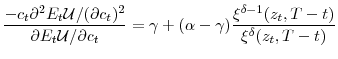
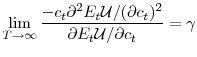
References
Abel, Andrew B., 1999. "Risk premia and term premia in general equilibrium," Journal of Monetary Economics 43, 3-33.
Bansal, Ravi and Amir Yaron, 2004. "Risks for the Long Run: A Potential Resolution of Asset Pricing Puzzles," The Journal of Finance, Vol. LIX, No. 4.
Bommier, Antoine, 2003. "Risk Aversion, Intertemporal Elasticity of Substitution and Correlation Aversion," working paper, University of Toulouse.
Bommier, Antoine, and Jean-Charles Rochet, 2006. "Risk aversion and planning horizons," Journal of the European Economic Association 4(4):708-734.
Borodin, Andrei N, and Paavo Salminen, 2002. "Handbook of Brownian Motion - Fatcs and Formulae," Second Edition, Birkhauser Verlag, Basel.
Eden, Benjamin, 2008. "Substitution, Risk Aversion and Asset Prices," working paper, Vanderbilt University.
Epstein, Larry G. and Stephen M. Tanny, 1980. " Increasing Generalized Correlation: A Definition and Some Economic Consequences," The Canadian Journal of Economics / Revue canadienne d'Economique, Vol. 13, No. 1. (Feb., 1980), pp. 16-34.
Epstein, Larry G., and Stanley Zin, 1989. " Substitution, Risk Aversion, and the Temporal Behavior of Asset Returns: A Theoretical Framework," Econometrica, Vol. 57, No. 4, 937-969.
Gomes, Francisco and Alexander Michaelides, 2008. " Asset Pricing with Limited Risk Sharing and Heterogeneous Agents," Review of Financial Studies, 2008, 21(1): 415-448.
Hansen, Lars Peter, John C. Heaton, and Nan Li, 2008. "Consumption Strikes Back? Measuring Long-Run Risk," Journal of Political Economy, Vol. 116, No. 2.
Ingersoll, Jonathan E., 1987. "Theory of Financial Decision Making," Rowan and Littlefield Publishers.
Kandel, Shmuel and Robert F. Stambaugh, 1991. "Asset Returns and Intertemporal Preferences," Journal of Monetary Economics, 27,1, pp. 39-71.
Kihlstrom, Richard E., 2007. "Risk Aversion and the Elasticity of Substitution in General Dynamic Portfolio Theory: Consistent Planning by Forward Looking, Expected Utility Maximizing Investors," working paper, University of Pennsylvania.
Kihlstrom, Richard E. and Leonard J. Mirman, 1974. " Risk Aversion with Many Commodities," Journal of Economic Theory 8, 361-388.
Lucas, Robert E. , Jr., 1978. "Asset Prices in an Exchange Economy," Econometrica, Vol. 46, No. 6., pp. 1429-1445.
Lucas, Robert E., Jr., 1990. "Supply-Side Economics: An Analytical Review," Oxford Economic Papers, 42 (2).
Lucas, Robert E., Jr., 2003. "Macroeconomic Priorities," American Economic Review, March.
Mehra, Rajnish, and Edward C. Prescott, 1985. "The Equity Premium," Journal of Monetary Economics 15, 145-161.
Modigliani, Franco and Merton H. Miller, 1958. "The Cost of Capital, Corporation Finance and the Theory of Investment," The American Economic Review, Vol. 48, No. 3., pp. 261-297.
Piazzesi, Monika, and Martin Schneider, 2006. " Equilibrium Yield Curves," NBER Macroeconomics Annual 2006.
Pratt, John W., 1964. "Risk Aversion in the Small and in the Large," Econometrica, Vol. 32, No. 1-2.
Richard, Scott F., 1975. "Multivariate Risk Aversion, Utility Independence and Separable Utility Functions," Management Science, Vol. 22, No. 1. (Sep.), pp. 12-21.
Routledge, Bryan R., and Stanley E. Zin, 2003. " Generalized Disappointment Aversion and Asset Prices", NBER working paper 10107.
Tallarini, Thomas D., 2000. "Risk-Sensitive Real Business Cycles," Journal of Monetary Economics, vol. 45, pp. 507-32.
Weil, Philippe, 1989. "The equity premium puzzle and the risk-free rate puzzle," Journal of Monetary Economics 24, 401-421.
Footnotes
Since
![]() is a convex mapping (
is a convex mapping (![]() ), Jensen's inequality
implies that
), Jensen's inequality
implies that
![\displaystyle \xi^{\delta}(z,\tau)\geq\left( E[z+f_{\tau}^{1}\vert z]\right) ^{\delta}=\left( z+% {\textstyle\sum\nolimits_{s=1}^{\tau}} \left( E[\tilde{g}]\right) ^{s}\right) ^{\delta}=\left( z+\frac {E[\tilde{g}]}{E[\tilde{g}]-1}((E[\tilde{g}])^{\tau}-1)\right) ^{\delta}%](img228.gif)
![\displaystyle \frac{\xi^{\delta-1}(z,\tau)}{\xi^{\delta}(z,\tau)}\leq\frac{(E[\tilde {g}^{\delta-1}])^{\tau}}{\left( z+\frac{E[\tilde{g}]}{E[\tilde{g}% ]-1}((E[\tilde{g}])^{\tau}-1)\right) ^{\delta}}%](img229.gif)
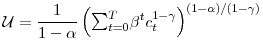
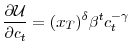
![\displaystyle \frac{-c_{t}\partial^{2}E_{t}\mathcal{U}/(\partial c_{t})^{2}}{\partial E_{t}\mathcal{U}/\partial c_{t}}=\gamma+(\alpha-\gamma)\frac{E_{t}% [x_{T}^{\delta-1}]}{E_{t}[x_{T}^{\delta}]}\beta^{t}c_{t}^{1-\gamma }%](img54.gif)
![\displaystyle M_{t+1}^{T}=\frac{E_{t+1}[\partial\mathcal{U}/\partial c_{t+1}]}% {E_{t}[\partial\mathcal{U}/\partial c_{t}]}=\beta\left( \frac{c_{t+1}}{c_{t}% }\right) ^{-\gamma}\frac{E_{t+1}\left[ x_{T}^{\delta}\right] }{E_{t}\left[ x_{T}^{\delta}\right] }%](img66.gif)
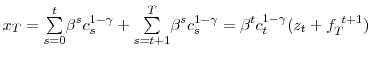
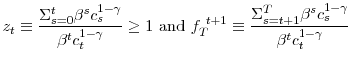
![\displaystyle \frac{E_{t+1}\left[ x_{T}^{\delta}\right] }{E_{t}\left[ x_{T}^{\delta }\right] }=(\beta g_{t+1}^{1-\gamma})^{\delta}\frac{E_{t+1}\left[ (z_{t+1}+f_{T}^{t+2})^{\delta}\right] }{E_{t}\left[ (z_{t}+f_{T}% ^{t+1})^{\delta}\right] }%](img101.gif)
![\displaystyle M_{t+1}^{\ast}\equiv\underset{T\rightarrow\infty}{\lim}M_{t+1}^{T}=\frac{\beta g_{t+1}^{-\alpha}}{E_{t}[g_{t+1}^{\gamma-\alpha}]}%](img118.gif)
![\displaystyle \lim_{T\rightarrow\infty}\frac{E_{t+1}[x_{T}^{\delta}]}{(\beta^{t+1}% c_{t+1}^{1-\gamma})^{\delta}\xi^{\delta}(1,T-t-1)}=1%](img183.gif)
![\displaystyle \frac{E_{t}[x_{T}^{\delta}]}{(\beta^{t}c_{t}^{1-\gamma})^{\delta}\xi^{\delta }(1,T-t-1)}=E_{t}\left[ \tilde{g}_{t+1}^{\delta}\frac{\xi^{\delta}% (z_{t+1},T-t-1)}{\xi^{\delta}(1,T-t-1)}\right]%](img185.gif)
![\displaystyle \lim_{T\rightarrow\infty}E_{t}\left[ \tilde{g}_{t+1}^{\delta}\frac {\xi^{\delta}(z_{t+1},T-t-1)}{\xi^{\delta}(1,T-t-1)}\right] =E_{t}\left[ \lim_{T\rightarrow\infty}\left( \tilde{g}_{t+1}^{\delta}\frac{\xi^{\delta }(z_{t+1},T-t-1)}{\xi^{\delta}(1,T-t-1)}\right) \right] =E_{t}\left[ \tilde{g}_{t+1}^{\delta}\right]%](img193.gif)
![\displaystyle \lim_{T\rightarrow\infty}\frac{E_{t+1}[x_{T}^{\delta}]}{E_{t}[x_{T}^{\delta}% ]}=\lim_{T\rightarrow\infty}\left( \frac{\frac{E_{t+1}[x_{T}^{\delta}% ]}{(\beta^{t+1}c_{t+1}^{1-\gamma})^{\delta}\xi^{\delta}(1,T-t-1)}}{\frac {E_{t}[x_{T}^{\delta}]}{(\beta^{t}c_{t}^{1-\gamma})^{\delta}\xi^{\delta }(1,T-t-1)}}\frac{(\beta^{t+1}c_{t+1}^{1-\gamma})^{\delta}}{(\beta^{t}% c_{t}^{1-\gamma})^{\delta}}\right) =\frac{\tilde{g}_{t+1}^{\delta}}% {E_{t}\left[ \tilde{g}_{t+1}^{\delta}\right] }=\frac{g_{t+1}^{\gamma-\alpha }}{E_{t}[g_{t+1}^{\gamma-\alpha}]}%](img194.gif)
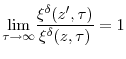
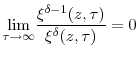
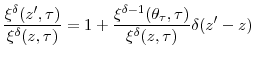
![\displaystyle \xi^{\delta}(z,\tau)\geq(2\tau)^{\delta}\left( \frac{\tilde{\mu}+\delta \tilde{\sigma}^{2}}{2\tilde{\mu}+\delta\tilde{\sigma}^{2}}\right) \exp[(\delta\tilde{\mu}+0.5\delta^{2}\tilde{\sigma}^{2})\tau ]%](img263.gif)