
Property Taxes and Elderly Mobility
Keywords: Property tax, elderly mobility, property tax relief program
Abstract:
JEL classification: H31, H71, R21
1 Introduction
During the late 1990s and early 2000s, the housing market in the United States experienced a remarkable boom. As housing prices increased, property taxes rose significantly in many parts of the country. Increases in property taxes have drawn attention from both the general public and policy makers. The public and politicians are particularly concerned that elderly homeowners who live on fixed incomes will be driven out of their homes because they can no longer afford increasing property taxes. In response, many states are looking for new ways of providing property tax relief to elderly homeowners. Although policy makers have assumed that rising property taxes cause elderly homeowners to move, researchers have provided little empirical evidence of such a link.
Apart from its policy implications, studying property taxes' effect on elderly mobility is also of great economic importance. The simplest version of the life-cycle model, which assumes away capital market imperfection, transaction costs, bequest motives, and uncertainty, predicts that utility-maximizing agents accumulate wealth while working and deplete wealth after retirement. If elderly homeowners view their housing wealth as a part of retirement savings to be used for general consumption, then we would expect elderly homeowners to trade down and consume their housing wealth after retirement. However, studies including Feinstein and McFadden (1989) and Venti and Wise (1989, 1990, 2001) find little evidence of downsizing behavior among elderly homeowners in the absence of precipitating shocks such as health decline and loss of spouse. Because residential mobility is directly linked to housing adjustment and downsizing decisions, studying how factors such as property taxes affect elderly mobility may help us build richer models to describe household life-cycle saving and consumption patterns.
Despite its policy and economic significance, the question whether property taxes have caused elderly homeowners to move is difficult to address empirically for two reasons. First, reliable household-level measures of property tax payments and mobility outcomes are scarce. Hence, many earlier studies use aggregated measures such as property tax per capita and state to state or county to county migration flows. These studies include Cebula (1974), Clark and Hunter (1992), Dresher (1994), Conway and Houtenville(2001), and Duncombe et al (2003). Second, property taxes are likely to be endogenous to individuals' moving decisions. For example, many local public services are financed through property taxes. Hence, elderly homeowners who value local public services (e.g. nice parks, low crime rates, and new senior centers) are likely to live in areas with high property taxes. Because tastes for local public services may be correlated with mobility outcomes and because econometricians do not observe individual tastes, studies that fail to instrument for property taxes often suffer from omitted variable bias.
In this paper, I use the 1992 to 2004 waves of the Health and Retirement Survey (HRS) panel data. This dataset has household-level measures of property tax payments and mobility outcomes in addition to extensive information on demographics and socio-economic characteristics. To address the endogeneity problem associated with property taxes, I exploit the variation in state-provided property tax relief programs and use simulated relief benefits to instrument for property tax payments. By construction, these simulated relief benefits contain only the variation in program rules and depend exclusively on state of residence, year, and age of homeowners. More generous relief programs reduce property tax payments of eligible homeowners, and these state-provided programs are arguably exogenous to individual homeowners' unobserved tendency to move. Therefore, simulated relief benefits serve as a valid instrument for property taxes in studying elderly mobility.
I also use the variation in effective property tax rates and housing value appreciation rates as an alternative strategy to study whether higher property taxes cause elderly homeowners to move. The thought experiment is to compare two observably identical homeowners, one living in a place with a high effective property tax rate and the other living in a place with a low effective property tax rate. When housing values in both places go up, the person who lives in the area with a high effective tax rate will experience a larger increase in property taxes. Thus, he would be more likely to move if property taxes affect homeowners' mobility. The key identification assumption here is that in the absence of a property tax effect, mobility in areas with high effective tax rates responds to rising property values the same way as mobility in areas with low effective tax rates, after controlling for observable characteristics. For example, if increases in housing wealth affect mobility, this identification strategy assumes that such a wealth effect is symmetric for homeowners in both areas with high effective tax rates and areas with low effective tax rates.
I find that higher property taxes have a significant impact on elderly homeowners' moving decisions. My central instrumental variable estimates suggest that a $100 increase in annual property taxes causes the two-year mobility rate to increase by 0.76 percentage points, which represents an eight percent increase from a baseline two-year mobility rate of nine percent. The results are robust to various model specifications. Individuals living in areas where the effective property tax rate is high and housing values have been appreciating rapidly are the most affected. Moreover, I find mixed evidence on whether liquidity constraints may play a role in the effect of property taxes on elderly mobility. This paper's findings provide indispensable evidence for normative welfare analysis of the impact of property taxes and property tax relief programs on elderly homeowners.
This paper proceeds as follows. The next section outlines the background and reviews previous research on property taxes and elderly mobility. Section 3 then describes the data used in this paper. In section 4, I explain the empirical strategies that I use to identify the effect of property taxes on elderly mobility. I also show estimation results using these strategies. The last section concludes and provides directions for future research.
2 Background and Previous Research
In 2004, property tax collections in the U.S. exceeded $300 billion. Property taxes are responsible for approximately 72% of all local tax revenues, representing the most important tax revenue source for local governments.1 The housing market boom of the late 1990s and early 2000s led to significant increases in residential property taxes. Figure 1 shows that from 2000 to 2005, median house value rose by 47% in real terms and median property tax payments by homeowners increased by 30%.2
Rising property taxes may be particularly burdensome to elderly homeowners. Following notations in Poterba (1992), the user cost faced by a homeowner under the current U.S. tax system can be written as
![\displaystyle uc = \begin{cases}(1-\tau_{inc})[\tau_p + \alpha i + (1-\alpha)r] + m + \delta - \pi^H & \text{for itemizers} \\ \tau_p + \alpha i + (1-\tau_{inc})(1-\alpha)r + m + \delta - \pi^H & \text{for non-itemizers} \end{cases}](img3.gif) |
where
![\displaystyle burden = \begin{cases}\frac{\displaystyle (1-\tau_{inc})\tau_p}{\displaystyle (1-\tau_{inc})[\tau_p + \alpha i + (1-\alpha)r] + m + \delta - \pi^H} & \text{for itemizers} \\ \frac{\displaystyle \tau_p}{\displaystyle \tau_p + \alpha i + (1-\tau_{inc})(1-\alpha)r + m + \delta - \pi^H} & \text{for non-itemizers} \end{cases}](img12.gif)
|
According to the 2004 Survey of Consumer Finances, the median homeowner of age 65 or above is a non-itemizer who faces a marginal tax rate of 15% and who has paid off his mortgages. In contrast, the median homeowner of age below 65 is an itemizer with a marginal tax rate of 25% and a loan to value ratio of 0.5. Assuming that
State and local governments may be concerned that elderly homeowners in the face of rising property tax burdens decide to relocate to areas with low property taxes. Given that around half of property tax revenues are used to finance public schools and that elderly homeowners usually do not consume school services, elderly homeowners may find that the local public services that they receive are not worth their costs. In response, they decide to adjust their housing consumption bundles and relocate to areas with both fewer public services and lower property taxes. Precisely because elderly homeowners in general consume fewer public services but expand the state and local tax base, they are attractive to state and local governments except when they reach the end of their lives and demand expensive medical care services through Medicaid. They are even called "pure gold" in Longino and Crown (1989). As discussed in Mackey and Carter (1994), many states in the U.S. provide a wide range of tax preferences to entice elderly migrants.
Alternatively, increasing property taxes may raise mobility rates among elderly homeowners through liquidity constraints. Because the elderly typically rely on fixed incomes such as Social Security benefits and pension benefits, and because many of them do not have many liquid assets, rising property taxes may cause elderly homeowners to be liquidity-constrained. Even if an elderly homeowner has great psychological attachment to his house and prefers not to move as long as he can afford it, significant increases in property taxes may eventually cause the homeowner to liquidate his housing wealth. This liquidity constraint mechanism and the demand adjustment mechanism mentioned earlier have very different welfare implications as to whether property tax relief programs should be provided by state and local governments.
A few papers investigate property taxes and elderly mobility using household-level data. The studies closest to this paper are Farnham and Sevak (2006) and Seslen (2005). The former study is a test of a life-cycle Tiebout model using the 1992-2000 HRS data and local fiscal data. It finds that cross-state, empty-nest movers experience reduced exposure to local school spending and property taxes. Although their study examines both property taxes and elderly mobility, Farnham and Sevak (2006) addresses the question from a different angle than the current study. Their study focuses on testing whether property tax payments decline after an elderly homeowner makes a move, whereas my study asks whether rising property taxes induce elderly homeowners to move. Moreover, their paper presents a correlation study, while my paper tackles the causality question using instrumental variable strategies.
Seslen (2005) examines the effect of property taxes on elderly homeowners' downsizing decisions in a competing risk framework. Using the Retirement History Survey from 1969 to 1979, she finds little evidence that property taxes affect elderly homeowners' decisions to move and to liquidate their housing wealth. Thus, she concludes that property tax relief programs are likely to solely transfer resources to the wealthy without achieving the goal of protecting the needy. Although Seslen (2005) employs sophisticated econometric tools, the data she studies were collected about 30 years ago, and they may not bear on the current situation. She uses self-reported property tax payments as the key explanatory variable, but she ignores the potential endogeneity problem where some unobserved factor drives both property tax payments and mobility decisions.
My paper advances the prior literature in several ways. First, I use the HRS data, a nationally representative panel of elderly households that contains rich information on individual and household characteristics, including actual annual property tax payments. The panel structure also provides an opportunity for me to look at the dynamic relationship between the last period's property tax payments and the next period's mobility outcomes, which is impossible to do with cross-sectional data. Second, during my sample period, the United States experienced significant increases in property taxes. The recent trend of rising property taxes provides a good opportunity to study the effect of property taxes on elderly homeowners' moving decisions. Third, I obtained access to the HRS restricted geographic identifiers and collected data on state-provided property tax relief programs for the past 15 years. With these data, I am able to calculate the amount of eligible property tax relief benefits for each household in each survey year. Lastly, I address the potential endogeneity problem using instrumental variable approaches. To my knowledge, this is the first study to examine the causal effect of property taxes on elderly mobility and to measure property tax relief benefits at the household level. The innovations in both data and estimation methodology allow this paper to present more compelling evidence than currently exists on the effect of property taxes on elderly mobility.
3.1 HRS Household Level Panel Data
The Health and Retirement Study (HRS) is biannual panel data of the elderly and near-elderly in the United States. At present, seven waves of the survey (1992-2004) have been released to researchers. The HRS includes households from four different cohorts.3 The original HRS cohort consists of individuals born between 1931 and 1941. They appear in all seven waves of my sample. The AHEAD cohort (born before 1924) was interviewed in 1993 first and then in 1995. Since 1998, the AHEAD cohort has been interviewed concurrently with the HRS cohort biannually. In 1998, two other cohorts were added to the sample: the "Children of the Depression" (CODA) cohort (born between 1924 and 1930), and the "War Baby" (WB) cohort (born between 1942 and 1947). Hence, these two cohorts appear only in the last four waves (1998-2004) in my sample.
In addition to the publicly available HRS data, I obtained restricted access to household level geographic identifiers. These identifiers allow me to identify the state of residence for each household at each survey interview time. The state identifier is crucial in my analysis because it links households with the state-provided property tax relief programs for which they are eligible. Because of the ambiguity associated with mobility for people living in mobile homes, I exclude them from my analysis. Because farms and ranches may be treated as agricultural rather than residential properties for property tax purposes, I also exclude people living on farms or ranches from my sample. Households residing in mobile homes or on farms and ranches combined constitute around 10 percent of the entire HRS sample. I also dropped individuals who are newly separated or divorced because mobility becomes complicated for these individuals. Newly separated or divorced homeowners represent less than 1 percent of the sample.
Except for the very first survey conducted on each household, every subsequent survey asks respondents whether they have moved since their last survey interview. I use respondents' answers as my mobility measure. I contacted HRS staff to confirm that this mobility measure is a valid and consistent measure across waves. Panel A of Table 5 displays the two-year mobility rates of the HRS cohort households from 1992 to 2004. In earlier years when those respondents were relatively young, their two-year moving probability was around 7%. Toward the end of the panel, the probability increases to 12%. In contrast, the average one-year mobility rate among homeowners of age below 65 is about 10% during the 1990s and early 2000s. Panel B of Table 5 shows that homeownership rates of HRS cohort households stay steady at around 80% during the 12-year sample period. Panel C of Table 5 presents a tenure transition matrix for all moves made by HRS cohort households between 1992 and 2004. Over 80% of homeowners remain homeowners after they relocate, and 70% of renters stay renters after they move. In summary, Table 5 shows evidence consistent with the conclusion drawn by Venti and Wise (2001) that mobility rates among elderly homeowners are low, and that elderly homeowners do not seem to trade down and consume their housing wealth in the absence of precipitating shocks.
In all seven waves, respondents were requested to report the amount of property taxes paid on their primary residence during the past year. I assume the self-reported property tax payments are the actual payments after all relevant exemptions, rebates or refunds provided by relief programs have been applied. Such an assumption is crucial for the first-stage regression in my IV strategy. For programs where participation is automatic and property tax bills are mailed to homeowners after benefits have been netted out, this assumption seems justified. For programs where homeowners receive rebate checks soon after paying property taxes, it is unclear whether respondents report their before-relief property tax payments or after-relief property tax payments. For programs that are implemented by state personal income tax credits, respondents are likely to report their before-relief benefits for two reasons. First, relief benefits are usually received long after homeowners have paid their property taxes. Second, property tax relief benefits may appear less salient on state personal income tax returns. For example, filers may view property tax credits that they claim against income tax liabilities as income tax relief benefits rather than property tax relief benefits. Recent studies including Chetty, Looney and Kroft (2007) and Finkelstein (2007) suggest that tax salience could have a significant impact on behavior. Regression results presented in an earlier version of this paper suggest that respondents in states that use income tax credits to grant property tax relief benefits do not report lower property tax payments when they are eligible for more generous relief benefits. Therefore, I exclude in my main regression analysis states where relief benefits are granted by tax credits on state personal income tax returns.4 The dropped observations represent about 25% of the sample.
Table 2 presents the summary statistics of demographic and socio-economic variables. Note that only about 17% of moves in the sample are cross-state moves, which implies a 3.8% five-year cross-state mobility rate (i.e.
![]() ). This rate is very similar to what other studies on elderly migration find.5 Given that the majority of moves are within-state relocations, results produced by studies focusing on cross-state mobilities could be misleading.
). This rate is very similar to what other studies on elderly migration find.5 Given that the majority of moves are within-state relocations, results produced by studies focusing on cross-state mobilities could be misleading.
3.2.1 Background on Property Tax Relief Programs
As of 2005, all 50 states and District of Columbia have some form of property tax relief programs for homeowners, especially for low-income and elderly homeowners. Many of these programs were first established well before my sample period started.6 Broadly speaking, there are four categories of relief programs. The first includes Homestead Exemptions and Credits. This is the most widely used form of property tax relief. Homestead exemption programs usually reduce assessed property value by a certain amount.7 Homestead credit programs either refund a certain percentage of taxes due or provide a fixed credit to qualifying homeowners.8 These homestead exemption and credit programs usually require homeowners to file an application to local property tax authorities.
The second category is Circuit-Breakers. Some of these programs are for homeowners only, and others are for homeowners as well as renters. Since these programs are designed to help people who need assistance, benefits are typically a decreasing function of income. Circuit-breaker programs can work either on a sliding scale or through a threshold mechanism. For example, District of Columbia has a circuit-breaker program where homeowners whose income is $20,000 or less can receive up to a $750 tax credit using a threshold mechanism. In 2007, Idaho's circuit-breaker program refunded up to $1320 for homeowners of age 65 or above with income below $28,000 using a sliding scale mechanism.9
The third category is Property Tax Deferral Programs. These programs allow qualified homeowners, typically low-income elderly homeowners, to defer property tax payments at a low interest rate. Effectively, they become a lien against the taxpayer's house. When the homeowner sells the house or dies, deferred taxes must be paid when the estate is settled. Deferral programs are considered by academics the most targeted and cost-effective way of providing property tax relief. Nevertheless, very few qualified homeowners take up such programs in practice. Anecdotal evidence suggests that elderly homeowners are reluctant to put a lien on their houses. This is consistent with the observation that very few elderly homeowners purchase reverse mortgages in the United States.
The last broad category is Property Tax Limits. Property tax limits include rate limits, assessment limits, revenue rollbacks, expenditure limits, and property tax freezes. Depending on the state, any one or a combination of the above limits can be used. Proposition 13 in California and Proposition 2.5 in Massachusetts are among the most prominent examples of property tax limits. Although almost all states have property tax limits of one kind or another, many of these programs do not guarantee that individual homeowners' property tax bills will not go up significantly from year to year. Because property taxes are the product of taxable values and tax rates, the amount of property taxes homeowners pay will be limited only when both assessment values and tax rates are limited. Rate limits or assessment limits alone are insufficient in curbing property tax growths. Moreover, states usually allow for override and bonded indebtedness so that local governments can still increase property taxes. For example, if non-elderly homeowners want to spend more on schools, they may approve an override, in which event the elderly will face rising property taxes. However, two kinds of limits apply to individual homeowners: "assessment value freezes" and "property tax freezes."10
Participation rates of property tax relief programs vary across states and programs. In mid-1990s, the American Association of Retired Persons (AARP) obtained numbers of program participants from various state administering offices and estimated participation rates for these programs.11 The median estimated participation rate among the eligible is the highest for homestead exemptions - around 90%. In contrast, the median estimated participation rate is only about 40% for homestead credits and circuit-breakers and less than 1% for deferral programs. It is puzzling why participation rates for homestead credits and circuit-breakers are so low among elderly households. Some have suggested that social stigma and program complexity may play a role.12
Since state-provided property tax relief programs are extremely complicated and vary tremendously across states, I focus on three types of relief programs in this paper.13 The first type includes homestead exemptions, homestead credits, and circuit-breakers. Relief benefits from these programs can be quantified for individual homeowners. The second and the third types refer to assessment value freezes and property tax freezes, respectively. For these two types, it is difficult to quantify their benefits for individual homeowners. Hence, I use dummy variables to indicate whether a homeowner is eligible for "assessment value freezes" or "property tax freezes."
3.2.2 Data Collection on Property Tax Relief Programs
First, I collected descriptive information from a range of publications by the U.S. Advisory Commission on Intergovernmental Relations (ACIR), the American Association of Retired Persons (AARP) and the National Conference of State Legislatures (NCSL) from 1990 to 2005. Then I compiled and organized such information by state and year. In my effort to confirm changes in these state programs over years and to resolve inconsistencies reported in various ACIR, AARP, and NCSL publications, I read state statutes that define these programs in legal terms. I searched for historical local news on property tax relief program changes. I studied program application forms, homeowners' brochures, and Q&As on state and/or local government websites. I contacted Connecticut, Delaware, Georgia, Florida, Hawaii, Illinois, Indiana, Louisiana, Maine, Maryland, Massachusetts, Mississippi, Nevada, New Jersey, North Dakota, Texas, Utah, Virginia, and Wyoming state and/or local governments for further explanation and confirmation of program details.
After obtaining accurate program descriptions, I calculated eligible benefits as a function of state of residence, year, age, income, house value, Social Security income, marital status, household size, and wealth. This calculation generates three output variables: the amount of benefits from homestead exemption, homestead credit, and circuit-breaker programs that a homeowner is eligible for, whether eligible for an "assessment value freeze" program, and whether eligible for an "property tax freeze" program. Such output parameters can be calculated for any homeowner in the U.S. in any year between 1990 and 2004.
Table 3 shows year 2000 formulas used in calculating property tax relief benefits for the ten states with the most observations in my sample. The amount of eligible benefits are calculated for a hypothetical married homeowner of age 65 with an annual total household income of $20,000, Social Security income of $10,000, and house value of $100,000. The amount of eligible benefits for this hypothetical homeowner varies from zero in Pennsylvania to $1,000 in New Jersey. The formulas shown in Table 3 suggest that eligible benefits vary considerably across states, and they are sensitive to individual characteristics such as income and house value.
The first two columns in Table 4 show the percentage of homeowners eligible for relief benefits and the average benefits conditional on eligibility by age groups, income quintiles, and house value quintiles. A number of interesting patterns emerge. The percentage of homeowners eligible for relief benefits increases monotonically in age and decreases monotonically in income and housing value. Conditional on eligibility, average benefits decrease in income. Given that property taxes relief programs target low-income and elderly homeowners, such patterns are expected. The conditional average benefits increases monotonically in housing value. This pattern is likely due to the threshold design of circuit-breakers. For example, if a circuit-breaker refunds property taxes exceeding 3% of a homeowner's income, then homeowners living in more expensive houses would receive higher refunds ceteris paribus. The conditional average benefits do not appear to change monotonically in age. This pattern is likely caused by complicated correlations between age and household characteristics. For example, the younger elderly homeowners tend to have higher income, which leads to lower relief benefits. The younger elderly homeowners also tend to live in more expensive houses, which leads to higher relief benefits.
The first part of Figure 2 plots conditional average benefits by state. South Dakota and Utah are missing from the map because no homeowners in the sample are from these two states. Delaware, Idaho, Maine, Montana, and Vermont each have fewer than 10 households in the sample. Because access to state identifiers is restricted, I cannot show them on this map for confidentiality reasons. This map also shows that District of Columbia, Iowa, Maryland, Michigan, Nebraska, Washington and Wisconsin have the highest average conditional benefits.
4 Empirical Strategy and Results
In this section, I present the empirical models and estimation results in studying the effect of property taxes on elderly mobility. Specifically, I first use property tax relief benefits as instruments to identify the impact of property taxes on elderly mobility. Then I use variations in housing value appreciation rates across geographic areas and years to identify such impact. I also explore whether liquidity constraints play a role in property taxes' effect on elderly homeowners' moving decisions.
4.1.1 Probit and IV Probit Estimation
To investigate whether property taxes have an impact on elderly mobility, I start with the following probit model:14
where
The first column in Table 5 displays estimation results of equation (1). To make the results interpretable, I show marginal effects of independent variables by calculating the marginal effect for each household and then averaging them across all households. To be consistent with results presented later in this section, standard errors shown in parenthesis are bootstrapped by 500 random draws with replacement. I implement a block-bootstrap scheme to make certain that observations are clustered at state level in estimating standard errors.16
The estimated effect of property taxes shown in column (1) is positive but insignificant both statistically and economically. The magnitude suggests that a $100 increase in property taxes is associated with a mere 0.0065 percentage points increase in two-year mobility rates. It is unsurprising
that the probit estimate of ![]() is small and insignificant since property taxes are likely to be endogenous to elderly homeowners' moving decisions. For instance, if there exists
heterogeneity among elderly homeowners in their tastes for local public services, then homeowners who desire good local public services may choose to stay in areas that provide excellent local public services. Since such services are financed partially by property taxes, homeowners in these areas
also pay high property taxes. Therefore, the unobserved tastes for local public services are correlated with both property tax payments and mobility outcomes, which causes the probit estimate of
is small and insignificant since property taxes are likely to be endogenous to elderly homeowners' moving decisions. For instance, if there exists
heterogeneity among elderly homeowners in their tastes for local public services, then homeowners who desire good local public services may choose to stay in areas that provide excellent local public services. Since such services are financed partially by property taxes, homeowners in these areas
also pay high property taxes. Therefore, the unobserved tastes for local public services are correlated with both property tax payments and mobility outcomes, which causes the probit estimate of ![]() to be biased. An appropriate instrumental variable strategy has to be used to address such an endogeneity problem and to generate an consistent estimate of
to be biased. An appropriate instrumental variable strategy has to be used to address such an endogeneity problem and to generate an consistent estimate of ![]() .
.
Since eligibility for higher relief benefits means lower property tax payments, one potential candidate as an instrument for property taxes is eligible benefits for property tax relief programs. Recall that my property tax relief program Benefit Calculator imputes
![]() (i.e. the amount of eligible benefits from homestead exemptions, homestead credits, and circuit-breakers) for each household in each survey year.
(i.e. the amount of eligible benefits from homestead exemptions, homestead credits, and circuit-breakers) for each household in each survey year.
![]() , however, is a nonlinear function of state, age, year, household income, house value, marital status, Social Security benefits, pension benefits, household size, and total
assets. To the extent that any of these factors influences elderly homeowners' moving decisions through channels other than property taxes,
, however, is a nonlinear function of state, age, year, household income, house value, marital status, Social Security benefits, pension benefits, household size, and total
assets. To the extent that any of these factors influences elderly homeowners' moving decisions through channels other than property taxes,
![]() would correlate with both property taxes and unobserved moving tendencies, and hence, would violate the exclusion restriction. For example, homeowners who receive high Social
Security benefits and pension benefits may have strong ties with local labor markets, which reduces their moving probabilities. In other words,
would correlate with both property taxes and unobserved moving tendencies, and hence, would violate the exclusion restriction. For example, homeowners who receive high Social
Security benefits and pension benefits may have strong ties with local labor markets, which reduces their moving probabilities. In other words,
![]() has two sources of variation: the variation caused by relief program rules and the variation stemming from individual characteristics. The latter source of variation may be
endogenous and cause probit estimates to be biased. To deal with such an endogeneity problem, I use a simulated IV approach.17
has two sources of variation: the variation caused by relief program rules and the variation stemming from individual characteristics. The latter source of variation may be
endogenous and cause probit estimates to be biased. To deal with such an endogeneity problem, I use a simulated IV approach.17
To simulate program generosity in state ![]() in year
in year ![]() for homeowners of age
for homeowners of age
![]() , I take the national sample of homeowners of age
, I take the national sample of homeowners of age ![]() who responded to HRS in year
who responded to HRS in year
![]() and run them through state
and run them through state ![]() 's relief programs. The weighted average eligible
benefits for these homeowners becomes the simulated measure of program generosity for state
's relief programs. The weighted average eligible
benefits for these homeowners becomes the simulated measure of program generosity for state ![]() in year
in year ![]() for homeowners of age
for homeowners of age ![]() . Essentially, I measure state program generosity using a national representative sample that does not correlate with any individual homeowner's
characteristics, but only with the exogenous variation in state, age, and year. Mathematically,
. Essentially, I measure state program generosity using a national representative sample that does not correlate with any individual homeowner's
characteristics, but only with the exogenous variation in state, age, and year. Mathematically,
![]() is constructed as follows:
is constructed as follows:
where
![]() isolates the exogenous variation due to relief program rules from the potentially endogenous variation due to individual homeowners' socio-economic characteristics.
Comparing column (2) with column (4) of Table 4 illustrates this point. Even though the conditional average benefit calculated using individual characteristics has no clear
relationship with age, the simulated conditional average benefit increases monotonically in age, reflecting the fact that property tax relief programs are more generous for the oldest homeowners. In addition, column (2) shows that the conditional average benefit calculated using individual
characteristics decreases monotonically in income and increases monotonically in house value. In contrast, the simulated conditional average benefit does not exhibit any relationship with either income or house value, suggesting that the simulated benefit measure
isolates the exogenous variation due to relief program rules from the potentially endogenous variation due to individual homeowners' socio-economic characteristics.
Comparing column (2) with column (4) of Table 4 illustrates this point. Even though the conditional average benefit calculated using individual characteristics has no clear
relationship with age, the simulated conditional average benefit increases monotonically in age, reflecting the fact that property tax relief programs are more generous for the oldest homeowners. In addition, column (2) shows that the conditional average benefit calculated using individual
characteristics decreases monotonically in income and increases monotonically in house value. In contrast, the simulated conditional average benefit does not exhibit any relationship with either income or house value, suggesting that the simulated benefit measure
![]() is rid of variations stemming from individual characteristics. In summary, the simulated benefits contain only the variation in program rules and depend exclusively
on state, age, and year by construction. Even though a homeowner's unobserved tendencies to move can be correlated with factors that determine his benefit eligibility, such unobserved tendencies to move are orthogonal to relief program rules and thus, orthogonal to simulated benefits.
is rid of variations stemming from individual characteristics. In summary, the simulated benefits contain only the variation in program rules and depend exclusively
on state, age, and year by construction. Even though a homeowner's unobserved tendencies to move can be correlated with factors that determine his benefit eligibility, such unobserved tendencies to move are orthogonal to relief program rules and thus, orthogonal to simulated benefits.
The second map in Figure 2 plots simulated conditional average benefits by state. South Dakota and Utah are missing from the map because no homeowners in the sample are from these two states. Comparing the two maps in Figure 2, we observe that
simulated eligible benefits are highly correlated with eligible benefits calculated using individual characteristics. Nevertheless, they are noticeably different from each other. For example, the conditional average benefits based on individual characteristics are higher in Colorado than in
Minnesota and North Dakota, while the simulated conditional average benefits are higher in Minnesota and North Dakota than in Colorado.
![]() is measured using residents in state
is measured using residents in state ![]() , whereas
, whereas
![]() is measured using a national representative sample. To the extent that residents in state
is measured using a national representative sample. To the extent that residents in state ![]() is different from the national representative sample, it is unsurprising for the two maps in Figure 2 to exhibit different patterns.
is different from the national representative sample, it is unsurprising for the two maps in Figure 2 to exhibit different patterns.
I also use two other relief benefit eligibility measures,
![]() (i.e. whether eligible for an assessment value freeze program) and
(i.e. whether eligible for an assessment value freeze program) and
![]() (i.e. whether eligible for a property tax freeze program) to instrument for property tax payments. Because eligibilities for assessment value freeze programs and property tax
freeze programs depend only on state, age, year, and household income, and because state, age, year, and household income are arguably exogenous covariates,
(i.e. whether eligible for a property tax freeze program) to instrument for property tax payments. Because eligibilities for assessment value freeze programs and property tax
freeze programs depend only on state, age, year, and household income, and because state, age, year, and household income are arguably exogenous covariates,
![]() and
and
![]() satisfy the exclusion restriction and may be used as valid instruments for property tax payments.18
satisfy the exclusion restriction and may be used as valid instruments for property tax payments.18
To implement the simulated IV strategy in a probit framework, I use the two-step estimator suggested by Rivers and Vuong (1988).19 Beside computational
ease, the Rivers-Vuong two-step IV approach has another appealing feature. The usual probit ![]() -test on
-test on ![]() , which is a consistent estimate of the first-stage error term, is a valid test of the null hypothesis that
, which is a consistent estimate of the first-stage error term, is a valid test of the null hypothesis that ![]() is exogenous. Such a test is equivalent to the
Hausman specification test suggested by Hausman (1978). Because I use a two-step procedure to estimate the IV probit model, standard errors need to be adjusted accordingly. I choose to obtain consistent estimates of standard errors by bootstrapping in lieu of the delta-method for two reasons.
First, bootstrapping is computationally easier to implement. Second, bootstrapping provides higher-order refinements while the delta-method is only a first-order approximation (Horowitz (2001)).
is exogenous. Such a test is equivalent to the
Hausman specification test suggested by Hausman (1978). Because I use a two-step procedure to estimate the IV probit model, standard errors need to be adjusted accordingly. I choose to obtain consistent estimates of standard errors by bootstrapping in lieu of the delta-method for two reasons.
First, bootstrapping is computationally easier to implement. Second, bootstrapping provides higher-order refinements while the delta-method is only a first-order approximation (Horowitz (2001)).
Column (2) of Table 5 shows the IV probit estimation results. The estimated marginal effect of property taxes is both statistically and economically significant. The point estimate suggests that a $100 increase in annual property tax payments induces the two-year
mobility rate to increase by 0.76 percentage points. Given that the baseline two-year mobility rate among elderly homeowners is 9%, the IV probit estimate implies that a $100 increase in annual property taxes induces mobility to rise by 8 percent. Moreover, the coefficient on ![]() is statistically different from zero at 0.01 level, rejecting the null hypothesis that
is statistically different from zero at 0.01 level, rejecting the null hypothesis that ![]() is exogenous and confirming the necessity of an IV strategy.
is exogenous and confirming the necessity of an IV strategy.
Table 5 also shows that the instruments used here -
![]() ,
,
![]() , and
, and ![]() - are quite strong in the first-stage regression.
The first-stage F-stat is 43 and the concentration parameter is 126. Stock, Wright and Yogo (2002) suggest that the rule of thumb for detecting weak instruments is to check whether the first-stage F-stat exceeds 10. Hansen, Hausman and Newey (2006) conclude that a concentration parameter of 30 or
above suggests that there is no weak instruments problem. By either standard,
- are quite strong in the first-stage regression.
The first-stage F-stat is 43 and the concentration parameter is 126. Stock, Wright and Yogo (2002) suggest that the rule of thumb for detecting weak instruments is to check whether the first-stage F-stat exceeds 10. Hansen, Hausman and Newey (2006) conclude that a concentration parameter of 30 or
above suggests that there is no weak instruments problem. By either standard,
![]() ,
,
![]() , and
, and ![]() are strong instruments for
are strong instruments for ![]() .
.
The estimated marginal effects of other covariates are mostly consistent with our expectation and the previous literature's findings. For instance, homeowners who are currently working are less likely to move. Homeowners who are recently widowed have higher moving probabilities. Large families are less prone to move, supposedly due to high moving costs. Negative health shocks and number of living children are associated with higher mobility rates, which echoes the finding by Silverstein and Angelelli (1998) that older parents engage in return migration in order to live closer to children from whom they receive care.
4.1.2 Allowing for Household Heterogeneity - Random Effects Probit Model
An advantage of using panel data is that we can take into account unobserved individual heterogeneity. To simplify notations, I denote ![]() as the mobility outcome,
as the mobility outcome,
![]() as a vector of all explanatory variables, and
as a vector of all explanatory variables, and ![]() as the
time-constant unobserved household effects. The probit model assumes
as the
time-constant unobserved household effects. The probit model assumes
The density of
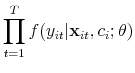 |
|||
![\displaystyle \prod_{t=1}^T \Phi(\mathbf{x}_{it}\theta + c_i)^{y_{it}}[1-\Phi(\mathbf{x}_{it}\theta + c_i)]^{1-y_{it}}](img55.gif) |
Ideally, we would prefer estimating a fixed effects probit model where no assumption is made about the distribution of
The traditional random effects probit model imposes the assumption that ![]() are normally distributed conditional on
are normally distributed conditional on
![]() :
:
Because
![\displaystyle \int_{-\infty}^{\infty} \left[ \prod_{t=1}^T f(y_{it} \vert \mathbf{x}_{it},c_i,\theta) \right] \frac{1}{\sigma_c} \phi \left(\frac{c}{\sigma_c}\right) dc](img64.gif) |
|||
![\displaystyle \int_{-\infty}^{\infty} \left[ \prod_{t=1}^T \Phi(\mathbf{x}_{it}\theta + c_i)^{y_{it}} [1-\Phi(\mathbf{x}_{it}\theta + c_i)]^{1-y_{it}} \right] \frac{1}{\sigma_c} \phi \left(\frac{c}{\sigma_c}\right) dc](img65.gif) |
The log-likelihood function for the entire sample of
Columns (3) and (4) in Table 6 present the estimation results of the random effects probit model and that of the two-step IV random effects probit model. The marginal effects are very close to those estimated by the probit and IV probit models. The point estimate of the
IV random effects probit model suggests that a $100 increase in annual property tax payments causes the two-year mobility rate to go up by 0.73 percentage points. The estimated coefficient on ![]() is statistically different from zero at 0.01 level, suggesting that
is statistically different from zero at 0.01 level, suggesting that ![]() is endogenous to mobility outcomes. As a robustness check, OLS and 2SLS estimation results
are shown in columns (5) and (6). The LPM also generates similar results.
is endogenous to mobility outcomes. As a robustness check, OLS and 2SLS estimation results
are shown in columns (5) and (6). The LPM also generates similar results.
4.1.3 Robustness Checks across Sub-samples and Specifications
In this section, I estimate the effect of property taxes on elderly mobility using different sub-samples and different model specifications. The purpose of this exercise is to check whether my findings are driven by some peculiar sub-population and whether the estimated results are robust to various regression specifications. I first exclude the AHEAD cohort. The AHEAD cohort were born before 1924 and are the oldest cohort in the sample. Even though I have included in the main specification a full set of age dummies and year dummies, which effectively controls for cohort fixed effects, coefficients on all covariates have been restricted to be the same across cohorts. If the oldest elderly move for reasons completely different from those of the younger elderly, they may respond to property taxes and relief programs distinctively from other cohorts. The regression results excluding the AHEAD cohort are shown in columns (3) and (4) of panel A in Table 7. The IV probit point estimate is similar to the one obtained when the AHEAD cohort is included.
Next, I drop households living in California because Proposition 13 creates a very unusual institutional setting. Proposition 13 in California was adopted in 1978. It limits property tax rate at 1% and requires assessment values grow no more than 2% per year unless the house is sold and re-assessment is carried out. Wasi and White (2005) find that Proposition 13 has a lock-in effect on homeowners in California. In the late 1980s, two amendments to Proposition 13 were passed. They allow any homeowner of age 55 or above who move to another house of equal or less market value within the same county to pay property taxes on the previous house' assessment value. Ferreira (2005) use a regression discontinuity strategy to show that mobility rates of 55-year-old homeowners are 25% higher than those of 54-year-old homeowners in California after those amendments were enacted. Proposition 13 may cause elderly homeowners in California to respond differently to property taxes and relief programs than elderly homeowners in other states. The regression results without California observations are shown in columns (5) and (6) of panel A in Table 7. They appear to be very similar to the results obtained for the entire sample.
I then investigate whether the results I find are driven by a small fraction of households who made multiple moves during the sample period. Specifically, I drop households who moved three or more times between 1992 and 2004.20 Columns (7) and (8) of panel A in Table 7 present the probit and IV probit estimation results. The reported marginal effects remain unchanged, suggesting that the estimated marginal effect of property taxes on elderly mobility is not driven by frequent movers.
By construction, the variation in the simulated benefits comes from state, age, and year. To ascertain that the results I have found in my main regressions do not originate from uncontrolled two-way interactions between state, age and year, I add two-way interaction fixed effects in the property
tax regression. The first two columns of panel B in Table 7 display the original estimation results without controlling for any two-way interactions. In columns (3) and (4), I add controls for state![]() year fixed effects. In columns (5) and (6), I add controls for year
year fixed effects. In columns (5) and (6), I add controls for year![]() age fixed effects. In columns (7) and (8), I add controls for state
age fixed effects. In columns (7) and (8), I add controls for state![]() age fixed effects.
age fixed effects.
In the case of adding state![]() age fixed effects, around 1,500 additional fixed effects are controlled for in the regression model. Not surprisingly, estimated standard error becomes
considerably larger and the marginal effect is significant only at 0.10 level. Nevertheless, the estimated coefficient on property tax payments always remains positive and of roughly the same magnitude.
age fixed effects, around 1,500 additional fixed effects are controlled for in the regression model. Not surprisingly, estimated standard error becomes
considerably larger and the marginal effect is significant only at 0.10 level. Nevertheless, the estimated coefficient on property tax payments always remains positive and of roughly the same magnitude.
In summary, estimation results from the probit model, the random effects probit model, and the LPM all suggest that property taxes play an important role in elderly homeowners' moving decisions. The results do not appear to be driven by some peculiar sub-sample and are robust to adding two-way interaction fixed effects. These estimation results also demonstrate that it is essential to recognize that property taxes are endogenous to the probability of moving. The central IV estimate suggests that a $100 increase in property taxes induces the two-year mobility rate to rise by 0.76 percentage points, representing a 8% increase from the baseline average two-year mobility rate of 9 percent. Such a large estimated impact of property taxes may be a manifestation of the local average treatment effects (LATE) formulated by Imbens and Angrist (1994). The instruments used to identify the causal effect of property taxes - simulated benefits, eligibility for assessment value freeze program, and eligibility for property tax freeze program - affect property taxes only of homeowners who both are eligible for and actually take up property tax relief. Because property tax relief programs are designed to assist low-income and elderly homeowners, and because people who actually take up these programs tend to be more sensitive to property taxes, it is not surprising that the IV estimates are large in magnitude. The estimates shown here measure the mobility response to property taxes among the compliers (i.e. eligible homeowners who actually receive benefits from property tax relief programs), so one must be cautious when generalizing these results to the overall population.
4.2 Using Variations in Housing Appreciation Rates
In the previous section, I used eligible benefits for property tax relief programs as instruments and find that higher property taxes induce elderly homeowners to move. To the extent that these instruments affect property tax payments only of homeowners who are both eligible for and actually
enroll in property tax relief programs, the effect found may be specific to such homeowners. In this section, I use a different empirical strategy to identify the effect of property taxes on mobility rates of all elderly homeowners. Specifically, I make use of the intuition that homeowners living
in places with high Effective Tax Rates (i.e. the property tax payment to house value ratio) and high housing appreciation rates will be the most affected by rising property taxes. If increasing property taxes induce elderly homeowners to move, individuals subject to high
![]() are more likely to move than those subject to low
are more likely to move than those subject to low
![]() , where
, where ![]() is the housing appreciation rate for
Metropolitan Statistical Area (MSA)
is the housing appreciation rate for
Metropolitan Statistical Area (MSA) ![]() at time
at time ![]() .21 In particular, I estimate the following probit model:
.21 In particular, I estimate the following probit model:
If property taxes are important in elderly homeowners' moving decisions, then we would expect
Note that individual level variables ![]() may be endogenous for the same reasons that property tax payments may be endogenous. Hence, estimates of equation (3)
are inconsistent without an appropriate instrumental variable strategy. I use state-year level median effective tax rates
may be endogenous for the same reasons that property tax payments may be endogenous. Hence, estimates of equation (3)
are inconsistent without an appropriate instrumental variable strategy. I use state-year level median effective tax rates ![]() , and the interaction between
, and the interaction between ![]() and
and ![]() to instrument for their individual level counterparts.22 The regression outcomes are reported in columns (1) and (2) of Table 8.
to instrument for their individual level counterparts.22 The regression outcomes are reported in columns (1) and (2) of Table 8.
The results in Table 8 show a number of interesting patterns. The estimated marginal effect of
![]() in the IV probit model is positive and statistically significant, suggesting that higher property taxes induces elderly homeowners to relocate.23 The estimated marginal effect of
in the IV probit model is positive and statistically significant, suggesting that higher property taxes induces elderly homeowners to relocate.23 The estimated marginal effect of ![]() is negative
and marginally significant. The variable
is negative
and marginally significant. The variable ![]() measures how much housing values have changed from last year to this year. If homeowners extrapolate housing price movements, they would expect
housing value to continue increasing in a housing market boom and to continue declining in a housing market bust.
measures how much housing values have changed from last year to this year. If homeowners extrapolate housing price movements, they would expect
housing value to continue increasing in a housing market boom and to continue declining in a housing market bust. ![]() being negative implies that in times when housing prices keep
rising, homeowners decide to delay moving and cash in the expected capital gains later. The Hausman test appears to reject the exogeneity assumption and suggests that an instrumental variable approach is necessary for consistent estimates. In addition, the LPM generates very similar results.
being negative implies that in times when housing prices keep
rising, homeowners decide to delay moving and cash in the expected capital gains later. The Hausman test appears to reject the exogeneity assumption and suggests that an instrumental variable approach is necessary for consistent estimates. In addition, the LPM generates very similar results.
I interpret the estimated marginal effects using the following example: Take ![]() to be 0.01 and
to be 0.01 and ![]() to be 5% as the benchmark scenario. These numbers are chosen because they are close to the sample medians. Consider an increase in annual housing appreciation rate from 5% to 10%. The direct housing appreciation effect,
to be 5% as the benchmark scenario. These numbers are chosen because they are close to the sample medians. Consider an increase in annual housing appreciation rate from 5% to 10%. The direct housing appreciation effect,
![]() , implies a decrease in the two-year mobility rate by 1.3 (
, implies a decrease in the two-year mobility rate by 1.3 (
![]() ) percentage points. The indirect property-tax-increase effect,
) percentage points. The indirect property-tax-increase effect,
![]() , suggests a rise in the mobility rate by 1.2 (
, suggests a rise in the mobility rate by 1.2 (
![]() ) percentage points. Therefore, the net effect of an increase in the housing appreciation rate from 5% to 10% is a decrease of 0.1 (
) percentage points. Therefore, the net effect of an increase in the housing appreciation rate from 5% to 10% is a decrease of 0.1 (![]() ) percentage points in the two-year mobility rate. Now take
) percentage points in the two-year mobility rate. Now take ![]() to be 0.02 and
consider the same increase in
to be 0.02 and
consider the same increase in ![]() from 5% to 10%. The direct housing appreciation effect is still a 1.3 percentage point decrease in the two-year mobility rate. The indirect
property-tax-increase effect, however, will increase mobility by 2.4 (
from 5% to 10%. The direct housing appreciation effect is still a 1.3 percentage point decrease in the two-year mobility rate. The indirect
property-tax-increase effect, however, will increase mobility by 2.4 (
![]() ) percentage points. Therefore, the net effect is a 1.1 (
) percentage points. Therefore, the net effect is a 1.1 (![]() ) percentage point increase in the two-year mobility rate.
) percentage point increase in the two-year mobility rate.
The IV probit estimation results suggest that homeowners living in places with both high effective property tax rates and rapid housing value appreciation are the most affected by rising property taxes. Exploiting variations in housing value appreciation rates rather than in state-provided
property tax relief programs, the results shown in this section complement and reinforce the previous finding that property taxes play an important role in elderly homeowners' moving decisions. Furthermore, finding a large and statistically significant effect of
![]() on elderly mobility suggests that increasing demand for local public services cannot fully explain the sharp increases in property taxes during the recent years, at
least not for elderly homeowners. If property tax increases are entirely driven by elderly homeowners' demand for more and better local public services, then we would not expect elderly mobility to rise in areas with high ETR and fast housing price appreciation.
on elderly mobility suggests that increasing demand for local public services cannot fully explain the sharp increases in property taxes during the recent years, at
least not for elderly homeowners. If property tax increases are entirely driven by elderly homeowners' demand for more and better local public services, then we would not expect elderly mobility to rise in areas with high ETR and fast housing price appreciation.
4.3 Do Liquidity Constraints Matter?
There are two potential explanations for why elderly homeowners move when property taxes increase. The first focuses on liquidity constraints. Under the assumption that elderly homeowners have substantial emotional and psychological attachment to their homes, they do not wish to move unless they become liquidity-constrained and have to trade down. This explanation implies that elderly homeowners do not perceive their housing wealth in the same way they perceive their financial wealth. It also suggests that providing property tax relief programs may be welfare-improving for elderly homeowners with difficulties accessing the credit market and cashing out their housing wealth.
The second explanation is a demand adjustment story. When homeowners were in their prime-age living with school-aged children, they were willing to pay high property taxes and receive local services including public schools. As homeowners grow older, they no longer have school-age children and, consequently, they do not value school services as much. When property taxes increase, elderly homeowners may decide to relocate to places with lower property taxes and fewer, or different public services. This explanation suggests that property tax relief programs may have distorted elderly homeowners' mobility decisions and locked in people who optimally should have moved.
The liquidity constraint explanation and demand adjustment explanation have distinct policy implications. Pioneered by Zeldes (1989), a sizable literature shows both theoretically and empirically that liquidity constraints may have a significant impact on household consumption and saving
trajectories. If there exist impediments in the credit market that prevent elderly homeowners from borrowing against their housing wealth, providing property tax relief to them may help to smooth consumption and to enhance welfare. On the other hand, if moving from a place with high property taxes
to a place with low property taxes gives elderly homeowners higher utility, then property tax relief may artificially lock elderly homeowners into their long-time home. To explore whether liquidity constraints explain the effect of property taxes on elderly mobility, I estimate
where
Using eligible benefits for property tax relief programs as instruments for
![]() and
and
![]() , I find mixed evidence on whether liquidity constraints may have played a role in property taxes' impact on elderly homeowners' moving decisions. The estimates
of
, I find mixed evidence on whether liquidity constraints may have played a role in property taxes' impact on elderly homeowners' moving decisions. The estimates
of ![]() are larger than that of
are larger than that of ![]() regardless of whether being
liquidity-constrained is defined by income, financial wealth, or education. For example, for households in the bottom two income quintiles, the IV-probit estimates suggest that a $100 increase in property taxes induces the two-year mobility rate to increase by 0.92 percentage points. In contrast,
it induces the two-year mobility rate to increase by only 0.58 percentage points for households in the top three income quintiles. Unfortunately, standard errors of the estimated marginal effects are large and the null hypothesis that
regardless of whether being
liquidity-constrained is defined by income, financial wealth, or education. For example, for households in the bottom two income quintiles, the IV-probit estimates suggest that a $100 increase in property taxes induces the two-year mobility rate to increase by 0.92 percentage points. In contrast,
it induces the two-year mobility rate to increase by only 0.58 percentage points for households in the top three income quintiles. Unfortunately, standard errors of the estimated marginal effects are large and the null hypothesis that
![]() cannot be rejected.
cannot be rejected.
5 Conclusion
Property taxes are the most important tax revenue source for local governments. The recent housing market boom led to significant increases in homeowners' property tax liabilities. Both policy-makers and the general public are concerned by the prospect that house-rich but income-poor elderly homeowners are overburdened by rising property taxes. The goal of this paper is to provide empirical evidence on whether property taxes play an important role in elderly homeowners' moving decisions.
Using instrumental variable approaches, this paper finds that property taxes are important in elderly homeowners' moving decisions. The central point estimates suggest that a $100 increase in annual property taxes leads to a 0.76 percentage point increase on average in two-year mobility rates. The median annual property tax payment in my sample is $1200, and the average two-year mobility rate of elderly homeowners is 9 percent. My point estimates suggest that the impact of property taxes on elderly mobility is economically significant. In addition, the effect of property taxes is most pronounced for homeowners living in areas that rely heavily on property taxes and that experience remarkable housing value appreciation. A variety of robustness checks are performed to test the stability of the found effects.
According to the 2004 data, property tax relief programs cost about $10 billion a year in the United States.24 In some states, these relief programs are provided at a great expense of lost revenues. For example, circuit-breakers in Vermont cost about 10% of total property tax revenues every year. Is the money well spent? Does the benefit of having these programs justify their cost? If the effect of property taxes on mobility is driven by demand adjustment, property tax relief programs would keep elderly homeowners from relocating to places where the marginal price of local services matches the marginal benefit. Thus, we essentially spend valuable resources locking homeowners in their houses and preventing them from following an optimal housing consumption path. In contrast, if the effect is due to liquidity constraints, providing generous property tax relief programs may alleviate such constraints and allow people who value the house the most to stay in it. This paper offers mixed evidence on whether liquidity constraints serve as a driving force behind the effect of increasing property taxes on elderly mobility. More empirical studies are needed before we can fully assess the welfare implication of property tax relief programs.
Many intriguing and important questions remain unexplored with regard to the impact of property taxes on elderly homeowners. At present, little empirical analysis has been conducted to address the question why effective tax rates did not decline in proportion to the increases in housing prices. Dye and Reschovsky (2007) suggests that cuts in state school aid caused by state fiscal crisis may be partially responsible for rising property taxes in recent years. Furthermore, virtually no evidence has been presented to rationalize the prevalence of property tax relief programs and the political popularity associated with expanding these programs. Do elderly homeowners enjoy more political power by voting more often than non-elderly homeowners? Do state and local governments use property tax relief programs to entice retiree migrants? Do population aging and baby-boomers' entering retirement age imply diminishing support for public-school spending? Poterba (1998) discusses issues related to demographic change and the political economy of public education. More research is called for to address such questions.
The second set of research questions includes investigating the best way of providing property tax relief. Economists believe that reverse mortgages are an efficient mechanism for elderly homeowners to tap into their housing wealth and to achieve consumption smoothing toward the end of their life-cycle. The fact that very few eligible elderly homeowners take up property tax deferral programs is consistent with the observation that the reverse mortgage market in the U.S. is tiny. Studying why property tax deferral programs are unpopular among elderly homeowners could help us better understand whether elderly homeowners perceive their housing wealth in the same way they perceive their financial wealth, and whether the absence of a thriving reverse mortgage market is due to a lack of demand. The third set of questions extends beyond mobility and asks whether property taxes induce other behavior responses among elderly homeowners. These remaining questions are left for future study.
![\includegraphics[height=18cm, width=14cm]{fig2.eps}](img22.gif) |
| Mean | SE | No. Obs. | |
|---|---|---|---|
| Wave: 1992-1994 | 0.063 | 0.004 | 3641 |
| Wave: 1994-1996 | 0.082 | 0.005 | 2764 |
| Wave: 1996-1998 | 0.075 | 0.005 | 3264 |
| Wave: 1998-2000 | 0.092 | 0.005 | 3084 |
| Wave: 2000-2002 | 0.133 | 0.006 | 2851 |
| Wave: 2002-2004 | 0.119 | 0.006 | 2643 |
Note: This table refers to HRS cohort (born between 1931 and 1941) households only. Household weights are used.
| Homeowner | Renter | Other | No. Obs. | |
|---|---|---|---|---|
| Wave: 1992 | 0.771 | 0.194 | 0.035 | 6726 |
| Wave: 1994 | 0.788 | 0.180 | 0.031 | 5999 |
| Wave: 1996 | 0.800 | 0.177 | 0.024 | 5712 |
| Wave: 1998 | 0.804 | 0.164 | 0.032 | 5432 |
| Wave: 2000 | 0.809 | 0.157 | 0.034 | 5071 |
| Wave: 2002 | 0.817 | 0.148 | 0.035 | 4826 |
| Wave: 2004 | 0.807 | 0.147 | 0.046 | 4645 |
| To Own(%) | To Rent(%) | To Other(%) | No. Obs. | |
|---|---|---|---|---|
| From Own | 80.66 | 14.37 | 4.97 | 1909 |
| From Rent | 21.98 | 70.68 | 7.34 | 1266 |
| From Other | 22.87 | 44.58 | 32.54 | 206 |
| Mean | Median | SD | |
|---|---|---|---|
|
Moved between Waves |
0.09 | 0.29 | |
| Fraction of Cross-State Moves | 0.17 | 0.38 | |
| Property Tax | 1,756 | 1,200 | 2,693 |
| House Value | 149,811 | 110,849 | 179,146 |
| Income | 63,776 | 41,900 | 102,144 |
| Financial Wealth | 126,526 | 26,000 | 528,838 |
| Having Mortgage or Home Loan | 0.46 | 0.50 | |
| Age | 64.5 | 9.8 | |
| Male | 0.52 | 0.50 | |
| White | 0.91 | 0.29 | |
| Household Size | 2.25 | 1.15 | |
| Number of Children | 3.06 | 1.93 | |
| Less than High School | 0.22 | 0.41 | |
| High School Graduates | 0.32 | 0.47 | |
| Some College | 0.22 | 0.42 | |
| College Graduates | 0.24 | 0.43 | |
| Currently Working | 0.43 | 0.49 | |
| Currently Retired | 0.48 | 0.50 | |
| Currently Disabled | 0.02 | 0.13 | |
| Newly Retired | 0.08 | 0.28 | |
| Married | 0.66 | 0.47 | |
| Separated or Divorced | 0.12 | 0.32 | |
| Widowed | 0.20 | 0.40 | |
| Newly Widowed | 0.02 | 0.14 | |
| Recently Hospitalized | 0.30 | 0.46 |
Note: ![]() . The sample is restricted to households who were homeowners in the current wave and who have valid data for all variables. Property tax, income, house value, and financial wealth are in 2000 dollars. Household weights are used.
. The sample is restricted to households who were homeowners in the current wave and who have valid data for all variables. Property tax, income, house value, and financial wealth are in 2000 dollars. Household weights are used.
| Formula Used For a Hypothetical Homeowner: (year=2000, age=65, married, Income=$20,000, SSB=$10,000, HV=$100,000) |
Benefit | |
|---|---|---|
| State: FL |
|
$146 |
| State: CA |
|
$186 |
| State: MI |
|
$536 |
| State: TX |
|
$119 |
| State: NY |
|
$367 |
| State: IL |
|
$166 |
| State: PA |
|
$0 |
| State: NJ |
|
$1000 |
| State: GA |
|
$150 |
| State: MN |
|
$510 |
Note: ![]() is the state-year specific average effective property tax rate.
is the state-year specific average effective property tax rate. ![]() is house value.
is house value. ![]() is Social Security benefit. Benefits shown here refer to eligible benefits from state-provided homestead exemptions, homestead credits, and circuit-breakers.
is Social Security benefit. Benefits shown here refer to eligible benefits from state-provided homestead exemptions, homestead credits, and circuit-breakers.
| Eligible Benefits: Percentage Eligible (1) |
Eligible Benefits: Conditional Avg Benefit (2) |
Simulated Benefits: Percentage Eligible (3) |
Simulated Benefits: Conditional Avg Benefit (4) |
|
|---|---|---|---|---|
| age |
5% | 363 | 6% | 248 |
| 55-59 | 6% | 382 | 7% | 262 |
| 60-64 | 13% | 332 | 14% | 274 |
| 65-74 | 45% | 313 | 45% | 305 |
| 53% | 350 | 53% | 319 |
| Eligible Benefits: Percentage Eligible (1) | Eligible Benefits: Conditional Avg Benefit (2) | Simulated Benefits: Percentage Eligible (3) | Simulated Benefits: Conditional Avg Benefit (4) | |
|---|---|---|---|---|
| Lowest | 55% | 359 | 34% | 275 |
| 2nd Quintile | 33% | 338 | 31% | 294 |
| 3rd Quintile | 18% | 330 | 26% | 287 |
| 4th Quintile | 11% | 300 | 20% | 283 |
| Highest | 5% | 158 | 16% | 281 |
| Eligible Benefits: Percentage Eligible (1) | Eligible Benefits: Conditional Avg Benefit (2) | Simulated Benefits: Percentage Eligible (3) | Simulated Benefits: Conditional Avg Benefit (4) | |
|---|---|---|---|---|
| Lowest | 34% | 187 | 29% | 253 |
| 2nd Quintile | 25% | 272 | 25% | 272 |
| 3rd Quintile | 23% | 380 | 25% | 230 |
| 4th Quintile | 22% | 427 | 24% | 302 |
| Highest | 15% | 458 | 23% | 285 |
Note: All dollar amounts are in 2000 dollars. Eligible benefits are calculated based on individual homeowners' characteristics. Simulated benefits are calculated by simulation for each state-age-year cell. "Percentage Eligible" is the percentage of homeowners who are eligible for homestead exemptions, homestead credits, or circuit-breakers. "Conditional Avg Benefit" is the average benefit from homestead exemptions, homestead credits, and circuit-breakers conditional on being eligible for these programs. Household weights are used.
| Probit (1) | IV Probit (2) | |
|---|---|---|
| Property Taxes (in 10,000) | 0.0065 | 0.7624*** |
| Property Taxes (in 10,000) (Standard Error) | (0.0115) | (0.2692) |
| Male | 0.0021 | -0.0010 |
| Male (Standard Error) | (0.0060) | (0.0067) |
| White | 0.0458*** | 0.0385*** |
| White (Standard Error) | (0.0086) | (0.0101) |
| Household Size | -0.0105*** | -0.0104*** |
| Household Size (Standard Error) | (0.0026) | (0.0028) |
| Number of Children | 0.0070*** | 0.0070*** |
| Number of Children (Standard Error) | (0.0013) | (0.0014) |
| Married | -0.0363 | -0.0413 |
| Married (Standard Error) | (0.0370) | (0.0394) |
| Newly Widowed | 0.0391*** | 0.0453*** |
| Newly Widowed (Standard Error) | (0.0131) | (0.0140) |
| Currently Working | -0.0186*** | -0.0264*** |
| Currently Working (Standard Error) | (0.0064) | (0.0076) |
| Newly Retired | 0.0236*** | 0.0129 |
| Newly Retired (Standard Error) | (0.0076) | (0.0114) |
| Spouse Currently Working | -0.0196** | -0.0188* |
| Spouse Currently Working (Standard Error) | (0.0077) | (0.0101) |
| Spouse Newly Retired | -0.0013 | 0.0052 |
| Spouse Newly Retired (Standard Error) | (0.0098) | (0.0109) |
| Recently Hospitalized | 0.0108** | 0.0096 |
| Recently Hospitalized (Standard Error) | (0.0051) | (0.0060) |
| Hausman Test | -4.1179*** | |
| (Coef on first-stage residual |
(1.3602) | |
| First Stage F-Stat | 43 | |
| Concentration Parameter | 126 |
Note: This table reports marginal effects derived from estimates of equation (1). ![]() In addition to the variables shown in the table, the regressions also include income quintile dummies, house value quintile dummies, financial wealth quintile dummies, age dummies, spouse age dummies, states fixed effects and year fixed effects. The simulated benefit measure
In addition to the variables shown in the table, the regressions also include income quintile dummies, house value quintile dummies, financial wealth quintile dummies, age dummies, spouse age dummies, states fixed effects and year fixed effects. The simulated benefit measure
![]() and binary variables
and binary variables
![]() and
and
![]() are used as instruments in the IV specification. Marginal effects shown are weighted averages across the population. Standard errors are bootstrapped by 500 random draws with
replacement clustered at state level. Household weights are used. ***, **, * denote significance at the 1%, 5%, and 10% levels respectively.
are used as instruments in the IV specification. Marginal effects shown are weighted averages across the population. Standard errors are bootstrapped by 500 random draws with
replacement clustered at state level. Household weights are used. ***, **, * denote significance at the 1%, 5%, and 10% levels respectively.
| Probit (1) | Probit IV (2) | RE Probit (3) | RE Probit IV (4) | LPM (5) | LPM IV (6) | |
|---|---|---|---|---|---|---|
| Property Taxes | 0.0065 | 0.7624*** | 0.0046 | 0.7260** | 0.0068 | 0.6058** |
| Property Taxes: (in 10,000) | (0.0115) | (0.2692) | (0.0054) | (0.2901) | (0.0095) | (0.2398) |
| Hausman Test | -4.0079*** | -4.9617*** | ||||
| Hausman Test: (Coef on first-stage residual |
(1.3602) | (1.7912) |
Note: ![]() . In addition to the variables shown in the table, the regressions also include income quintile dummies, house value quintile dummies, financial wealth quintile dummies, male, white, household size, number of children, whether married, whether newly widowed, education categories, whether currently working, whether newly retired, whether spouse is currently working, whether spouse is newly retired, whether hospitalized, age dummies, spouse age dummies, state fixed effects, and year fixed effects. The simulated benefit measure
. In addition to the variables shown in the table, the regressions also include income quintile dummies, house value quintile dummies, financial wealth quintile dummies, male, white, household size, number of children, whether married, whether newly widowed, education categories, whether currently working, whether newly retired, whether spouse is currently working, whether spouse is newly retired, whether hospitalized, age dummies, spouse age dummies, state fixed effects, and year fixed effects. The simulated benefit measure
![]() and binary variables
and binary variables
![]() and
and
![]() are used as instruments in the IV specifications. Marginal effects shown are weighted averages across the population. Standard errors in column (1)-(4) are bootstrapped with
500 random draws with replacement clustered at state level. Standard errors in column (5) and (6) are clustered at state level. Household weights are used. ***, **, * denote significance at the 1%, 5%, and 10% levels respectively.
are used as instruments in the IV specifications. Marginal effects shown are weighted averages across the population. Standard errors in column (1)-(4) are bootstrapped with
500 random draws with replacement clustered at state level. Standard errors in column (5) and (6) are clustered at state level. Household weights are used. ***, **, * denote significance at the 1%, 5%, and 10% levels respectively.
| Orig. Sample (1) | Orig. Sample IV (2) | Drop AHEAD (3) | Drop AHEAD IV (4) | Drop CA (5) | Drop CA IV (6) | Drop Freq. Movers (7) | Drop Freq. Movers IV (8) | |
|---|---|---|---|---|---|---|---|---|
| Property Taxes | 0.0065 | 0.7624*** | 0.0039 | 0.7565** | 0.0010 | 0.7697*** | 0.0084 | 0.7676*** |
| (in 10,000) | (0.0115) | (0.2692) | (0.0124) | (0.3172) | (0.0114) | (0.2590) | (0.0098) | (0.2670) |
| N | 22,520 | 22,520 | 17,082 | 17,082 | 19,963 | 19,963 | 21,691 | 21,691 |
| Orig. Specification (1) | Orig. Specification IV (2) | Add State*Year (3) | Add State*Year IV (4) | Add Year*Age (5) | Add Year*Age IV (6) | Add State*Age (7) | Add State*Age IV (8) | |
|---|---|---|---|---|---|---|---|---|
| Property Taxes | 0.0065 | 0.7624*** | 0.0054 | 0.5242** | 0.0057 | 0.7726*** | 0.0091 | 0.8716* |
| (in 10,000) | (0.0115) | (0.2692) | (0.0117) | (0.2649) | (0.0120) | (0.2555) | (0.0206) | (0.4570) |
| N | 22,520 | 22,520 | 22,520 | 22,520 | 22,520 | 22,520 | 22,520 | 22,520 |
Note: This table reports the robustness checks of equation (1). In addition to the variables shown in the table, the regressions also include income quintile dummies, house value quintile dummies, financial wealth quintile dummies, male, white, household size, number of children, whether married, whether newly widowed, education categories, whether currently working, whether newly retired, whether spouse is currently working, whether spouse is newly retired, whether hospitalized, age dummies, spouse age dummies, state fixed effects, and year fixed effects. The simulated benefit measure
![]() and binary variables
and binary variables
![]() and
and
![]() are used as instruments in the IV specification. Marginal effects shown are weighted averages across the population. Standard errors are bootstrapped by 500 random draws with
replacement clustered at state level. Household weights are used. ***, **, * denote significance at the 1%, 5%, and 10% levels respectively.
are used as instruments in the IV specification. Marginal effects shown are weighted averages across the population. Standard errors are bootstrapped by 500 random draws with
replacement clustered at state level. Household weights are used. ***, **, * denote significance at the 1%, 5%, and 10% levels respectively.
| Probit (1) | IV Probit (2) | OLS (3) | 2SLS (4) | |
|---|---|---|---|---|
|
|
0.031 | 0.235** | 0.026 | 0.234** |
|
|
0.053 | (0.107) | (0.082) | (0.093) |
| 0.181 | 2.81 | 0.169 | 2.93 | |
| (0.303) | (2.70) | (0.276) | (2.90) | |
| -0.042 | -0.262* | -0.036 | -0.260** | |
| (0.087) | (0.137) | (0.142) | (0.102) |
| Probit (1) | IV Probit (2) | OLS (3) | 2SLS (4) | |
|---|---|---|---|---|
| (Coef on first-stage residual |
-1.67*** | |||
| (Coef on first-stage residual |
(0.52) | |||
| (Coef on first-stage residual |
-15.5 | |||
| (Coef on first-stage residual |
(19.0) | |||
| N | 29,102 | 29,102 | 29,102 | 29,102 |
Note: This table reports marginal effects derived from estimates of equation 3. In addition to the variables shown in the table, the regressions also include income quintile dummies, house value quintile dummies, financial wealth quintile dummies, male, white, household size, number of children, whether married, whether newly widowed, education categories, whether currently working, whether newly retired, whether spouse is currently working, whether spouse is newly retired, whether hospitalized,age dummies, spouse age dummies, states fixed effects and year fixed effects. ![]() is MSA level housing value appreciation rates. State effective tax rate
is MSA level housing value appreciation rates. State effective tax rate ![]() and the interaction between
and the interaction between ![]() and
and ![]() are used as instruments for
are used as instruments for ![]() and
and
![]() in the IV specifications. Marginal effects shown are weighted averages across the population. Standard errors in column (1) and (2) are bootstrapped by 500 random
draws with replacement clustered at state level. Standard errors in column (3) and (4) are clustered at state level. Household weights are used. ***, **, * denote significance at the 1%, 5%, and 10% levels respectively.
in the IV specifications. Marginal effects shown are weighted averages across the population. Standard errors in column (1) and (2) are bootstrapped by 500 random
draws with replacement clustered at state level. Standard errors in column (3) and (4) are clustered at state level. Household weights are used. ***, **, * denote significance at the 1%, 5%, and 10% levels respectively.
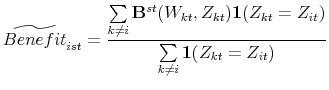
![\includegraphics[scale=1]{fig1.eps}](img2.gif)