
A Structural Estimation
Missaka Warusawitharana *
Board of Governors of the Federal Reserve System
Is the return to private R&D as high as believed? This study identifies a flaw in the production function approach to estimating the return to R&D. I provide new estimates based on a structural estimation approach that incorporates uncertainty about the outcome from R&D. The results shed light on the rate of innovation, the impact of an innovation on profits, and the market value of the R&D stock. The parameter estimates imply a mean return to R&D of 3.7-5.5%, much lower than previous values. The analysis also demonstrates the unsuitability of using the return to R&D as a basis for policy decisions on tax subsidies to R&D.
1 Introduction
Estimating the returns to research and development (R&D) expenditures has value from an economic growth perspective (Romer (1990)) and a macro fluctuations perspective (Comin and Gertler (2006) and Barlevy (2007)). A substantial literature employs the production function based approach of Griliches (1979) and finds returns to private R&D in the range of 25 - 60%. Based partly on this finding, Jones and Williams (1998) argue that optimal R&D investment is two to four times the observed level. However, is the return to R&D as high as believed and should the return be used as a basis for policy decisions?
This study begins by demonstrating that the production function approach to estimating the return to R&D suffers from an indeterminacy flaw: the estimated returns vary sharply with the assumed obsolescence rates. The production function approach estimates the elasticity of value-added with respect to R&D using regressions of log value-added on factor inputs. This literature finds that different obsolescence rates lead to similar elasticity estimates. Therefore, the literature focuses on the estimates obtained assuming an obsolescence rate of 15%, as in Griliches and Mairesse (1984). However, the estimated next period return equals the elasticity estimate times the ratio of value-added to R&D stocks, which varies with the obsolescence rate. Thus, different assumptions for the obsolescence rate lead to different estimates for the return to R&D.
This study tackles the above problem by using structural estimation to estimate the return to R&D.1 The underlying model incorporates uncertainty in the outcome to R&D, unlike the production function approach. Such uncertainty is arguably a key economic feature of R&D investment as neither researchers nor managers know the outcome of an R&D project when they initiate it. The model incorporates uncertainty from R&D in a manner similar to the endogenous growth literature (Romer (1990), Grossman and Helpman (1991), and Aghion and Howitt (1992)) by assuming that the R&D stock impacts the probability of an innovation, which results in higher profits in the future. The model thus departs from the production based literature, which treats R&D stocks as simply another input in the production function.
The model economy consists of firms in an R&D sector and non-R&D sector. This follows the Compustat data set as most firms either report positive R&D for all years or report no R&D at all. Firms in the non-R&D sector are modelled following the Q-theoretic approach, with a downward sloping demand curve (Gomes (2001) and Eberly, Rebelo, and Vincent (2008)). In addition to physical investment, firms in the R&D sector also accumulate an R&D stock. The R&D stock does not reflect the stock of ideas applicable for production, as in Griliches (1979). Instead, the R&D stock measures the degree of investments made by the firm towards generating the next innovation. In each period, a firm may successfully innovate, leading to a jump in the firm's profits that dissipates over time. Prior innovations by the firm are reflected in the current profitability level. A firm would realize a negative return from R&D investment in a year in which it failed to innovate, thereby enabling the model to capture failed R&D outcomes.
The model yields an explicit characterization of the R&D policy function in terms of the expected increase in firm value from an innovation and the residual value of R&D investment in the next period. An unexpected feature of the model is that the optimal R&D policy does not necessarily increase with the return. The return to R&D measures the increase in next period profits from an innovation, which is only one aspect of the impact of R&D on firm value, which determines optimal R&D investment. Parameter changes can simultaneously yield higher returns to R&D and lower optimal R&D investment.
Identification of the model parameters follows from matching moments on R&D, profits, and valuations for both R&D and non-R&D sector firms. The estimates reveal that an innovation leads to increases in profitability of 13% to 19%. The fraction of firms innovating each year ranges from 0.41 to 0.51. These estimates indicate that firms generate a substantial increase in profits from an innovation but also face significant uncertainty on the outcome of their R&D investments. The estimated mean annual return to private R&D ranges from 3.7% to 5.5%, much lower than the production function estimates. These low returns are partly explained by a high autocorrelation term that implies the benefit of an innovation lasts many periods into the future. The low returns do not, however, deter firms from generating the high R&D investment levels observed in the data.
The model also enables an estimation of the market value of the R&D stock. Hall (2001) highlights the growing importance of intangible capital in the US economy. The estimates indicate that the market value of R&D stocks as a fraction of all capital ranges from 16.7% to 23.1%. Combined with the high level of R&D investment, this demonstrates the prominent role of R&D in understanding capital accumulation.
Counterfactual experiments on a additional 5% tax subsidy to R&D generate economically significant increases in R&D investment and the rate of innovation for all the estimated models. This demonstrates that the low return to R&D does not invalidate prior arguments for robust policy actions in favor of R&D investment, particularly given the evidence of technology spillovers found by Bloom, Schankerman, and van Reenen (2007). Taken together, these results demonstrate that the return to R&D is much lower than commonly believed and should not be used for forming R&D related policy decisions.
2 Model
The model economy consists of a large number of heterogeneous firms. The firms operate in either an R&D sector or a non-R&D sector. The two sectors differ only in that firms in the R&D sector can engage in R&D and potentially obtain an improvement in their profitability while firms in the non-R&D sector cannot do so. Firms are exogenously assigned to each sector and do not switch from one to another (see Klette and Kortum (2004) for a model where firms endogenously decide whether to engage in R&D or not). These assumptions correspond to the data on US firms, where some firms report positive R&D activity for most or all periods and others report zero R&D for all periods. The model does not incorporate leverage.
A The non-R&D sector
Non-R&D firms operate as standard Q-theory firms facing a downward sloping demand curve.2 In each period, the output of the ![]() firm follows a Cobb-Douglas specification with
firm follows a Cobb-Douglas specification with
where
The parameters of the above process are identical across firms in the non-R&D sector. Thus, heterogeneity across firms is driven by heterogeneity in shocks to profitability. Let
The results given in (Stokey and Lucas, 1989, Chapter 9) ensure the existence and uniqueness of
B The R&D sector
Firms in the R&D sector are similar to those in the non-R&D sector, except for their R&D activity. These firms also invest in a stock of R&D. The R&D stock of the firm does not directly impact the production function as in Griliches (1979) and others. Instead, the R&D stock stochastically affects the transition of profitability across periods. The model views R&D stocks as measuring the potential for future innovations rather than a measure of the stock of ideas applicable for production. When a firm's R&D activity is successful, the firm realizes a profitability jump in the next period.5 If the R&D effort was not successful, the firm will not realize a jump in profitability. These innovations reflect discoveries by firms that lead to an increased profitability of the firm's capital stock.6 A fraction of the R&D stock becomes obsolete each period reflecting the conclusion or abandonment of R&D projects. The model attempts to capture the inherently uncertain nature of the innovation process through this mechanism as a firm would realize a negative return from its R&D investment in a year in which it failed to innovate.
Denote the accumulated R&D stock of the firm at the end of each period by
![]() . Let
. Let ![]() equal the investment in R&D activity. The law of motion
for R&D stocks is given by
equal the investment in R&D activity. The law of motion
for R&D stocks is given by
where
where
The distribution for
The model is agnostic on the source of the jump in profits from a successful innovation. This may arise from either improvements in the current products of the firm, the introduction of entirely new products, or cost reductions. More formally, a successful innovation may result in an increase in
the productivity parameter ![]() or the demand shifter
or the demand shifter ![]() . The model does not take a
stand on whether patent protection is necessary for generating an increase in profitability (see Boldrin and Levine (2008)). While the inability to link R&D investment directly to total factor productivity may be a drawback, the above approach has the benefit of
allowing R&D to have a broader impact. Correspondingly, the endogenous growth literature highlights both quality improvements and new product introductions as the outcome of innovations.
. The model does not take a
stand on whether patent protection is necessary for generating an increase in profitability (see Boldrin and Levine (2008)). While the inability to link R&D investment directly to total factor productivity may be a drawback, the above approach has the benefit of
allowing R&D to have a broader impact. Correspondingly, the endogenous growth literature highlights both quality improvements and new product introductions as the outcome of innovations.
The timing of the firm's decisions warrant clarification. R&D sector firms enter each period with an R&D stock, a capital stock, and a profitability level. The firms invest in R&D and capital during the period. At the end of the period, each firm discovers whether it successfully
innovated or not. If a firm succeeds, its next period profitability will be higher than if it did not. The accumulated R&D stock carries over to the next period and a fraction of it becomes obsolete after the realization of the profitability level
![]() . Note that this timing sequence differs from the law of motion for capital: the current period R&D investment adds to the R&D stock which impacts the realization of the
next profitability level. This timing structure was chosen as it yields a value function that is separable in the R&D stock. It also captures the idea that R&D investment in the current period impacts the firm's profitability in the next period.
. Note that this timing sequence differs from the law of motion for capital: the current period R&D investment adds to the R&D stock which impacts the realization of the
next profitability level. This timing structure was chosen as it yields a value function that is separable in the R&D stock. It also captures the idea that R&D investment in the current period impacts the firm's profitability in the next period.
The dividends paid by the firm in each period is given by
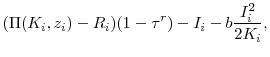
Denote the value of the firm after the realization of ![]() but prior to the obsolescence of the R&D stock as
but prior to the obsolescence of the R&D stock as
![]() .9 For notational convenience,
define
.9 For notational convenience,
define
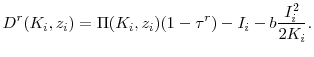 |
(A.11) |
The value of the firm can be expressed as a solution to the following Bellman equation:
The lack of a non-negativity constraint on R&D investment implies that firms can sell their R&D if necessary. While firms do so infrequently in the simulation, this assumption is necessary for the subsequent characterization of the R&D policy function. The reversibility assumption is also supported by anecdotal evidence of firms selling partially developed products to other firms, particularly in the pharmaceutical sector. The expectation in the Bellman equation is taken over the joint distribution for
Observe that
The value of the R&D stock equals
This establishes our conjecture and demonstrates that the value function is separable in the R&D stock. Note that this is not a general result, and it arose from the particular assumptions made about the timing and structure of the optimization problem. The separability ensures that the return to R&D investment is negative in periods where the firm does not innovate.
C R&D policy
The above analysis simplifies the solution of the optimal R&D policy of the firms. The optimal choice of
![]() impacts the current period dividend payment, the level of R&D stock carried over to the next period, as well as the transition equation for profitability
impacts the current period dividend payment, the level of R&D stock carried over to the next period, as well as the transition equation for profitability ![]() . The first two pieces are linear in
. The first two pieces are linear in
![]() . Let
. Let
![]() be the optimal policy in the interior region, where the
be the optimal policy in the interior region, where the
![]() constraint does not bind. The following proposition characterizes the optimal R&D stock in this region:
constraint does not bind. The following proposition characterizes the optimal R&D stock in this region:
Therefore, the optimal policy function for R&D stocks is given by
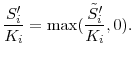
The separability of the value function into its R&D stock and the above characterization of the R&D policy both simplify and improve the accuracy of the numerical solution of the value function in the subsequent estimation. The next section examines the return to R&D in this setting.
D Return to R&D
A key objective of estimating the above structural model is to identify the private return to R&D, defined as the marginal impact of R&D investment on next period after-tax profits. This definition closely mirrors that employed in the production function literature, where the return equals the marginal impact of R&D investment on next period value added. From an accounting perspective, the profits measure employed in the study equals the value added measure minus selling and administrative expenses. The impact of R&D on profits would be a more relevant variable for a firm's optimization decision than the impact of R&D on value added. Some algebra, detailed in Appendix B, yields the following expression for the expected return to R&D investment.
The above expression lends itself to a natural interpretation in the context of the model. The first term equals the expected increase in next period profits from an innovation divided by the expected increase in firm value from an innovation. The
The intuition for the above formula arises from the fact that R&D policies are derived from optimality conditions. This implies that the discounted total marginal expected return to R&D investment equals its marginal cost, 1. Current period R&D investment affects the firm in the next period by increasing profits if the firm innovated and by increasing the residual R&D stock. An innovation also increases firm value, as expected profitability in subsequent periods
increases, and as the firm optimally readjusts its capital stock in response to the innovation. The estimated return focuses only on the component of the total return measured in next period profits. Parameter changes that shift the total return from next period profits to an increase in firm value
or that increase the residual value of R&D result in a lower estimated return. The maximum return of
![]() is obtained when
is obtained when ![]() and
and
![]() . The estimated return increases with the obsolescence rate
. The estimated return increases with the obsolescence rate ![]() . Note
that changes in the parameter that influences the success probability,
. Note
that changes in the parameter that influences the success probability, ![]() , impact the return indirectly through the
, impact the return indirectly through the
![]() terms.
terms.
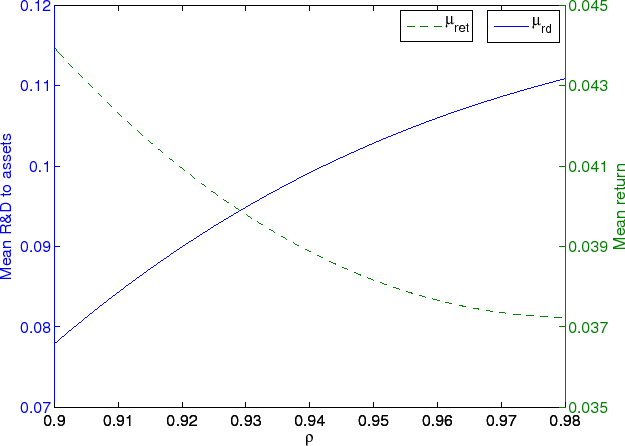
The return to R&D does not directly affect the optimal R&D policy in this setting, as they are both jointly determined. Figure 1 demonstrates the non-monotone relationship between optimal R&D investment and the return in the model. The figure plots the mean
level of R&D investment on the left y-axis and the mean return to R&D on the right y-axis as the autocorrelation parameter, ![]() , increases from 0.90 to 0.98. The other parameters are
fixed at the estimates obtained in Section 4.1. An increase in
, increases from 0.90 to 0.98. The other parameters are
fixed at the estimates obtained in Section 4.1. An increase in ![]() increases the benefit of an innovation and leads to an increase in the expected firm value from an
innovation. This results in higher R&D investment. However, an increase in
increases the benefit of an innovation and leads to an increase in the expected firm value from an
innovation. This results in higher R&D investment. However, an increase in ![]() has no impact on the expected increase in next period profits from an innovation, leading to a decrease in
the ratio of the expected increase in profits to firm value. This results in a reduction of the return as defined above.
has no impact on the expected increase in next period profits from an innovation, leading to a decrease in
the ratio of the expected increase in profits to firm value. This results in a reduction of the return as defined above.
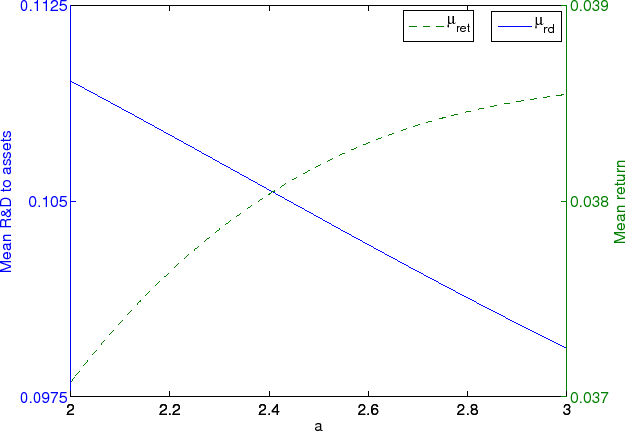
The non-monotone relationship between R&D investment and the return to R&D extends to changes in the parameter driving the success rate, ![]() . Figure 2 plots
the mean level of R&D investment on the left y-axis and the mean return to R&D on the right y-axis as
. Figure 2 plots
the mean level of R&D investment on the left y-axis and the mean return to R&D on the right y-axis as ![]() increases from 2 to 3. The other parameters are fixed at the estimates obtained
in Section 4.1. For these parameters, an increase in
increases from 2 to 3. The other parameters are fixed at the estimates obtained
in Section 4.1. For these parameters, an increase in ![]() leads to a decrease in optimal R&D as it lowers the probability of a successful innovation. This also lowers
the growth options associated with R&D investment, thereby reducing the increase in firm value from an innovation while having no impact on the expected increase in profits from an innovation. Thus, an increase in
leads to a decrease in optimal R&D as it lowers the probability of a successful innovation. This also lowers
the growth options associated with R&D investment, thereby reducing the increase in firm value from an innovation while having no impact on the expected increase in profits from an innovation. Thus, an increase in ![]() leads to an increased return to R&D.
leads to an increased return to R&D.
The above figures demonstrate that a high return to R&D does not imply a high level of R&D investment in this setting, or vice versa. Therefore, the return to R&D does not provide an appropriate statistic for forming R&D policies in the context of the model. The intuition for this result is that the R&D policy is determined by the expected total return to R&D, while the return focuses only on the expected impact on next period profits, which is only one component of the total return.
E Statistics of economic interest
The above analysis focuses on the return to R&D. The model also enables the computation of other statistics that may either be of independent interest or be useful in understanding R&D decisions.
The optimal R&D policy increases with the expected jump in firm value from an innovation. The percentage jump in firm value equals
![\displaystyle \frac{E_z[V^r(K_i^{\prime }, S_i^{\prime }, z_i^{\prime })\vert j_i=1] - E_z[V^r(K_i^{\prime }, S_i^{\prime }, z_i^{\prime })\vert j_i=0]}{E_z[V^r(K_i^{\prime }, S_i^{\prime }, z_i^{\prime })]}.](img83.gif)
The ![]() parameter estimates the impact of an innovation on next period profits. The total impact of an innovation also depends on the speed at which the increase in profitability mean
reverts. The present value equivalent permanent increase in profitability from an innovation provides an alternate method of evaluating the impact of an innovation on profits. This is given by:
parameter estimates the impact of an innovation on next period profits. The total impact of an innovation also depends on the speed at which the increase in profitability mean
reverts. The present value equivalent permanent increase in profitability from an innovation provides an alternate method of evaluating the impact of an innovation on profits. This is given by:
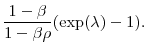
The model also provides an estimate of the value of the aggregate capital stock, which includes both physical capital and R&D stocks. The expected value of the R&D stock of each firm is given by
![\displaystyle \frac{\sum_i \left(E_z[V^r(K^{\prime }_i, S^{\prime }_i, z^{\prime }_i)] - E_z[V^n(K^{\prime }_i, z^{\prime }_i)\vert z_i]\right)}{\sum_i E_z[V^r(K^{\prime }_i, S^{\prime }_i, z^{\prime }_i)\vert z_i]}.](img86.gif)
3 Estimation
The study estimates the above models using indirect inference, a variant of simulated methods of moments estimation (see Gourieroux, Monfort, and Renault (1993) for details). This method involves comparing a selected set of data moments with the same moments from artificial data obtained by simulating the model for a given set of parameters. The parameter estimates are obtained as the solution to the minimization of a quadratic form of the difference between the data and simulated moments. Appendices C and D discuss the estimation in more detail.
A Data
The data for the estimation is obtained from the Compustat Annual data set. The data set includes information on profits, capital expenditures, and balance sheet items for listed US corporations. The market value of equity is obtained from the linked CRSP data set. The sample period extends from 1987 to 2006, and was chosen to provide a stable tax environment for research and development expenditures. The sample excludes financial firms and regulated utilities.
Figure 3 plots R&D investment as a fraction of the sum of R&D and physical investment over time. The figure demonstrates the substantial level of investment in R&D conducted by US corporations. This provides suggestive evidence that the return to R&D is lower than widely believed as it would be difficult to reconcile the high level of R&D investment with the substantial private returns reported in the literature (Griliches (1994)) under standard concavity assumptions. The high level of R&D investment also suggests that calibrations and estimations of RBC models may be misspecified when they do not take into account R&D investment.
The data on research and development expenditures (Compustat Annual data item 46) is available for more than half the observations. This series measures company funded R&D and excludes those funded by the government. As such, the results in this study measure the return to private R&D. About 11% of the sample reports a zero value for R&D spending. One key choice in this paper is to treat firm-year observations with missing or zero values for R&D expenditures as firms in the non-R&D sector. The results would be biased if some of these firms engage in substantial R&D activity. Accounting rules provide some comfort in this regard, as they clearly specify the classification and reporting of R&D expenditures. Furthermore, most firms that report positive values for R&D expenditures do so for all years, while many firms do not engage in any R&D expenditures at all. The fraction of such observations in the data equals 87.75%.10 This indicates that the data can be separated into two sectors: an R&D sector with positive R&D expenditures and a non-R&D sector with zero spending on R&D. The method of moments estimation matches first and second moments on data from the two sectors.
The production function regressions require the construction of the R&D stock for each firm. The R&D stock for an assumed obsolescence rate was constructed using a perpetual inventory method, with historical R&D expenditures from 1975 onwards. The initial R&D stock was obtained assuming a real growth rate of 5%. The initial assumptions have little impact, as the regressions use observations from 1987 onwards, matching the sample selection for the structural estimation. The log value added measure is obtained as net sales (data item 12) minus cost of goods sold (data item 41). All variables except employment are adjusted for inflation using the GDP deflator for non-residential investment.
Table 1 provides summary statistics for firms in the R&D and non-R&D sectors. Total assets equals the book value of assets (data item 6). Profits equals operating income before depreciation (data item 13) scaled by book assets. Investment is defined as capital expenditure on plant, property, and equipment (data item 30) minus retirements of plant, property, and equipment (data item 184). Tobin's Q is computed as the market value of assets scaled by the book value of assets.11 An alternative definition would be to define Q as the market value of capital scaled by the replacement value of capital. While this definition may be preferred where measurement error is a concern (Erickson and Whited (2000)), it also leads to large outliers, particularly in the R&D sector, that may bias the comparison between the two sectors. The variables are Winsorized at the 99% level to eliminate outliers. The data used to compute the matched moments are adjusted for firm and year fixed effects within the R&D and non-R&D sectors, respectively.
The moments demonstrate a sharp contrast between these two sectors, indicating fundamental differences between firms that engage in R&D activity and those that do not. These differences are statistically significant at the 1% level. Firms in the R&D sector have an average Tobin's Q value almost 50% greater than firms in the non-R&D sector (Chan, Lakonishok, and Sougiannis (2001) find that the market value of the firm reflect R&D activity). On the other hand, these firms exhibit much lower average earnings after accounting for their R&D expenditures. The level of R&D spending is quite substantial when compared to total assets and larger than the rate of investment. However, aggregate expenditures on R&D are lower than total capital expenditures within the R&D sector, as small firms do a disproportionately larger level of R&D spending. This is consistent with the R&D policy function given in Proposition 1 as smaller firm capture a greater increase in firm value per unit of capital from an innovation.
B Identification
The results obtained from indirect inference methods are sensitive to the choice of which specifics moments are to be matched. In particular, it is important to select moments that are informative about the parameters of interest. Intuitively, if a given simulated moment varies strongly with a parameter, matching this moment to the data will be informative about the underlying parameter.
The moments I match include the first moment of profits for the R&D and non-R&D sectors. This will be informative about the parameters of the profitability process, as well as the parameters influencing the success rate and impact of R&D spending. The second moments of profits for
both sectors help identify ![]() . The first and second moments of R&D spending provide information on the R&D parameters
. The first and second moments of R&D spending provide information on the R&D parameters
![]() and
and![]() . The first moments of Tobin's Q for each sector help inform the returns to
scale parameter
. The first moments of Tobin's Q for each sector help inform the returns to
scale parameter ![]() and the R&D parameters. The second moments of Q for both sectors also help identify
and the R&D parameters. The second moments of Q for both sectors also help identify ![]() and the volatility of profits. The autocorrelation coefficient for profits and R&D spending helps inform the
and the volatility of profits. The autocorrelation coefficient for profits and R&D spending helps inform the ![]() parameter. Finally, the second
moment of investment identifies the level of adjustment cost parameter
parameter. Finally, the second
moment of investment identifies the level of adjustment cost parameter ![]() . It should be noted that each moment provides information on almost all of the parameters.
. It should be noted that each moment provides information on almost all of the parameters.
All moments do not have the same weight in the estimation. The optimal weighting matrix is obtained as the inverse of the covariance matrix of the chosen moments. Intuitively, the GMM estimation works harder to match the more precisely estimated moments. Standardizing the chosen moments by their standard errors reveals that the estimation places little weight on matching the autocorrelation for R&D, and emphasizes the first moment of R&D, the first moment of Q for both sectors, and the first moment of operating income for the non-R&D sector.
Some of the auxiliary parameters in the model are calibrated to simplify the estimation of the parameters of interest. The calibrated parameters are the discount factor ![]() , the per
period fixed cost of operations
, the per
period fixed cost of operations ![]() and the depreciation rate
and the depreciation rate ![]() . The calibrated
value of
. The calibrated
value of
![]() follows Gomes (2001), Hennessy and Whited (2005), and Bloom (2008) and reflects an equity premium of
6%. The fixed cost of operation is set at 15% of the profits prior to R&D expenditure for the median firm in each sector.12 The depreciation rate
follows Gomes (2001), Hennessy and Whited (2005), and Bloom (2008) and reflects an equity premium of
6%. The fixed cost of operation is set at 15% of the profits prior to R&D expenditure for the median firm in each sector.12 The depreciation rate
![]() , a value which equals the mean investment rate for all firms from the data. Setting the depreciation rate equal to the investment rate in the data ensures that the steady state
investment rate in the simulated data, which equals the depreciation rate, matches the actual data. One could easily match the mean investment rates for the two sectors separately by specifying different depreciation rates. The fraction of firms in the R&D sector equals 0.48, the fraction of
observations with positive R&D values in the data set. The
, a value which equals the mean investment rate for all firms from the data. Setting the depreciation rate equal to the investment rate in the data ensures that the steady state
investment rate in the simulated data, which equals the depreciation rate, matches the actual data. One could easily match the mean investment rates for the two sectors separately by specifying different depreciation rates. The fraction of firms in the R&D sector equals 0.48, the fraction of
observations with positive R&D values in the data set. The ![]() parameter is not identified with the chosen moments as it functions as a scaling parameter. As such, fix
parameter is not identified with the chosen moments as it functions as a scaling parameter. As such, fix ![]() for both sectors. The chosen moments do not include the relative firm size between R&D and non-R&D firms. This could be matched by allowing
for both sectors. The chosen moments do not include the relative firm size between R&D and non-R&D firms. This could be matched by allowing ![]() to vary across the two sectors.
to vary across the two sectors.
C Estimating the return using production functions
This section details the observation that the production function approach pioneered by Griliches (1979) suffers from an indeterminacy flaw when applied to estimating the return to R&D. This approach specifies value-added by the firm as a multiplicative function of factor inputs, including the R&D stock:
| (A.21) |
A linear regression of log value-added on log inputs yields the elasticity of value-added with respect to the R&D stock
The return to R&D in this framework equals the marginal product of R&D on value-added and is given by:
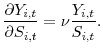
Table 2 presents the results of the above regression for different assumptions on ![]() using the Compustat data set. Note that even though the notation is
identical,
using the Compustat data set. Note that even though the notation is
identical, ![]() may not be comparable across the two approaches as the R&D stock concept in the production function regression differs from the R&D stock concept in the structural
model. The sample ranges from 1987 to 2006, and all variables except employment are adjusted for inflation using the GDP deflator for non-residential investment. The pooled regression includes year and industry dummies, and the standard errors are robust to clustering at the firm level. The assumed
obsolescence rates range from 0 to 0.25.
may not be comparable across the two approaches as the R&D stock concept in the production function regression differs from the R&D stock concept in the structural
model. The sample ranges from 1987 to 2006, and all variables except employment are adjusted for inflation using the GDP deflator for non-residential investment. The pooled regression includes year and industry dummies, and the standard errors are robust to clustering at the firm level. The assumed
obsolescence rates range from 0 to 0.25.
The regressions reveal that the estimated elasticity of value-added with respect to R&D varies little with the obsolescence rate ![]() , as commonly found in the literature. The point
estimate implies an economically and statistically significant contribution of R&D to value-added by firms. The adjusted R-square values indicate that the model fit does not vary much with
, as commonly found in the literature. The point
estimate implies an economically and statistically significant contribution of R&D to value-added by firms. The adjusted R-square values indicate that the model fit does not vary much with ![]() .
.
The table reports the sample median steady state return for a hypothetical firm with a constant R&D policy and the sample median return using the computed R&D stocks. Both return estimates vary sharply with the obsolescence rate ![]() . Using the standard assumption of
. Using the standard assumption of
![]() leads to an estimated median return of 45.2%, similar to the high rates of return reported in the literature (see Griliches (1986) and Hall and Mairesse (1995)). However, changing the assumed value of
leads to an estimated median return of 45.2%, similar to the high rates of return reported in the literature (see Griliches (1986) and Hall and Mairesse (1995)). However, changing the assumed value of ![]() to 0 yields a much lower return (12.6%), and assuming
to 0 yields a much lower return (12.6%), and assuming
![]() yields an even higher return. The steady state returns with a fixed R&D policy exhibit similar variation. Thus, the return estimates obtained from production function
regressions vary sharply with the assumed obsolescence rates, a difficulty compounded by the lack of evidence on the appropriate value for
yields an even higher return. The steady state returns with a fixed R&D policy exhibit similar variation. Thus, the return estimates obtained from production function
regressions vary sharply with the assumed obsolescence rates, a difficulty compounded by the lack of evidence on the appropriate value for ![]() .
.
A Baseline model
The estimation begins with the baseline model, which identifies the impact of R&D on profits, the success rate from R&D, and the rate of depreciation for R&D stocks. Table 3 presents the results of estimating the model by indirect inference. Panel A reports the matched moments for the data and simulations, respectively. Panel B reports the estimated parameter values. Panel C reports some statistics of economic interest from the simulated data set.
The low value for the J-statistic demonstrates that the model matches the chosen moments well. Examination of the matched moments indicates that the model succeeds in matching the first and second moments of R&D to assets. The model also matches the first moment
of Tobin's Q for both sectors, and matches the second moment of Tobin's Q for the non-R&D sector. While the measure of Tobin's Q in the simulated data incorporates the R&D stock it also reflects differences in growth options due to potential innovations. The model fares less well at
matching the first and second moments of income for both sectors. The estimation yields a ![]() value that is much higher than regression estimates, thereby resulting in higher
autocorrelations for both profits and R&D expenditures.
value that is much higher than regression estimates, thereby resulting in higher
autocorrelations for both profits and R&D expenditures.
The model has trouble generating the high level of Tobin's Q given the observed levels of profits. A related difficulty arises from matching the variation in Tobin's Q given the variation in profits. A high autocorrelation value helps with both of these challenges. For a given distribution of profits, an increase in persistence will increase Tobin's Q for high profitability firms and lower it for low profitability firms. This impact will be greater for high Q firms, resulting in higher first and second moments for Tobin's Q. A high autocorrelation value also increases R&D investment by extending the benefit of an innovation further into the future.
The results indicate that firms in the R&D sector generate an economically and statistically significant increase in profitability from a successful innovation. The point estimate for ![]() of 0.123 implies that a successful innovation increases the profitability of the firm by 13.1%. Ignoring any changes in the capital stock, this is equivalent in present value terms to a 9.0% permanent increase in profitability. In the steady state, 50.7% of firms in the
R&D sector innovate each period. However, there is sharp cross-sectional variation in the probability of innovation, reflecting the sensitivity of the R&D policy function on the current profitability and size of the firm.
of 0.123 implies that a successful innovation increases the profitability of the firm by 13.1%. Ignoring any changes in the capital stock, this is equivalent in present value terms to a 9.0% permanent increase in profitability. In the steady state, 50.7% of firms in the
R&D sector innovate each period. However, there is sharp cross-sectional variation in the probability of innovation, reflecting the sensitivity of the R&D policy function on the current profitability and size of the firm.
An application of equation (12) yields the distribution of the expected return to R&D in the simulations. The simulations yield a mean return of only 3.7%, with a 95th percentile value of 8.2% (multiplying by
![]() yields the pre-tax return). These values are substantially lower than commonly believed. The residual value of R&D investment at the end of the next period equals
yields the pre-tax return). These values are substantially lower than commonly believed. The residual value of R&D investment at the end of the next period equals
![]() , implying a maximum expected return of 30.5%. The return is driven lower by the high
, implying a maximum expected return of 30.5%. The return is driven lower by the high ![]() parameter, which shifts the benefits of an innovation further into the future. This decreases the ratio of expected increase in next period profits from an innovation to the expected increase in firm value. While the return is much lower than those reported in
the literature, that does not deter firms from maintaining a high level of R&D investment.
parameter, which shifts the benefits of an innovation further into the future. This decreases the ratio of expected increase in next period profits from an innovation to the expected increase in firm value. While the return is much lower than those reported in
the literature, that does not deter firms from maintaining a high level of R&D investment.
The estimated obsolescence rate of
![]() is not directly comparable to the values employed in the production function approach. The R&D stock in the model pertains only to the R&D investments applicable to
generating the next innovation. Prior innovations from R&D would be reflected in a higher level of profitability
is not directly comparable to the values employed in the production function approach. The R&D stock in the model pertains only to the R&D investments applicable to
generating the next innovation. Prior innovations from R&D would be reflected in a higher level of profitability ![]() . In contrast, the R&D stock in the production function approach
reflects all the accumulated knowledge application for production. The estimated high obsolescence rate indicates that a substantial proportion of a firm's R&D expenditures ceases to have any value if the firm fails to innovate. Hall (2007) obtains obtains similarly high
estimates of
. In contrast, the R&D stock in the production function approach
reflects all the accumulated knowledge application for production. The estimated high obsolescence rate indicates that a substantial proportion of a firm's R&D expenditures ceases to have any value if the firm fails to innovate. Hall (2007) obtains obtains similarly high
estimates of ![]() using a valuation based approach, thus providing support for this study's view of R&D stocks as measuring the stock of experiments towards the next innovation. It is
less plausible to view the stock of ideas applicable for production becoming obsolete at these rates. The
using a valuation based approach, thus providing support for this study's view of R&D stocks as measuring the stock of experiments towards the next innovation. It is
less plausible to view the stock of ideas applicable for production becoming obsolete at these rates. The ![]() estimate implies a half-life of R&D expenditures of 2.53 years, indicating
a moderate lifespan for R&D projects. The point estimate for the adjustment cost parameter
estimate implies a half-life of R&D expenditures of 2.53 years, indicating
a moderate lifespan for R&D projects. The point estimate for the adjustment cost parameter ![]() matches those found by Whited (1992), Cooper and
Haltiwanger (2006), and Eberly, Rebelo, and Vincent (2008).
matches those found by Whited (1992), Cooper and
Haltiwanger (2006), and Eberly, Rebelo, and Vincent (2008).
The steady state mean expected increase in firm value equals ![]() , with a high degree of cross-sectional variation. A high impact of innovation on firm value induces firms to incur the
high level of R&D expenditures observed in the data and the simulations despite the low return estimates. While the appropriate sample counterpart is unclear, the estimate is consistent with anecdotal evidence of sudden jumps in firm value upon the release of news about potential
innovations.
, with a high degree of cross-sectional variation. A high impact of innovation on firm value induces firms to incur the
high level of R&D expenditures observed in the data and the simulations despite the low return estimates. While the appropriate sample counterpart is unclear, the estimate is consistent with anecdotal evidence of sudden jumps in firm value upon the release of news about potential
innovations.
The estimation yields a value of the aggregate R&D stock equal to 17.9% of the value of all capital.13 In comparison, the aggregate value of R&D investment to all investment in the sample period equals 24.6%. This indicates that a substantial portion of the aggregate capital stock consists of R&D stocks. As R&D stocks comprise a large fraction of all intangible capital, these findings support the argument of Hall (2001) that intangible capital accumulation forms an important component of US investment.
B Estimates with a lower discount rate
The estimates of the baseline model indicate that the model has difficulty reconciling the profit and valuation levels. This has the effect of yielding a very high autocorrelation parameter, as the model strives to reconcile a low level of profits with the observed valuations. One solution to
this difficulty is to assume a lower discount rate. The value of
![]() used in the baseline estimation is calibrated assuming a 6% equity premium. Recent evidence indicates that the equity premium may have been sharply lower for this sample
period, motivating a higher value for
used in the baseline estimation is calibrated assuming a 6% equity premium. Recent evidence indicates that the equity premium may have been sharply lower for this sample
period, motivating a higher value for ![]() . This section reports the results using a discount rate of
. This section reports the results using a discount rate of
![]() to estimate the model.14
to estimate the model.14
Table 4 presents the results using the lower discount rate. Panel A reports the matched moments for the data and simulations, respectively. Panel B reports the estimated parameter values. Panel C reports some statistics of economic interest from the simulated data set.
The value of the J-statistic is lower than that for the baseline model. As suggested above, this model has better success reconciling the moments on profits with the valuation moments. The lower discount rate also leads to a lower autocorrelation parameter. The estimates continue to have difficulty with the second moment of Tobin's Q, as the model does not generate as many observations with high Tobin's Q as found in the data. Overall, the lower discount rate improves the performance of the model.
The point estimate for ![]() implies a 18.9% increase in profitability from a successful innovation. This is larger than the corresponding value obtained in the baseline estimation
because the lower value of
implies a 18.9% increase in profitability from a successful innovation. This is larger than the corresponding value obtained in the baseline estimation
because the lower value of ![]() requires an innovation to have a greater initial impact on profits, as the benefit dissipates faster. In present value terms, the estimate corresponds to a
4.63% permanent increase in profitability, lower than the comparable estimate for the baseline model. The smaller permanent increase in profits generates a similar level of R&D expenditures, as the firms discount future dividends less than before. The steady state rate of innovation is lower,
with a mean probability of success of 0.450.15 This is partly due to the higher obsolescence rate
requires an innovation to have a greater initial impact on profits, as the benefit dissipates faster. In present value terms, the estimate corresponds to a
4.63% permanent increase in profitability, lower than the comparable estimate for the baseline model. The smaller permanent increase in profits generates a similar level of R&D expenditures, as the firms discount future dividends less than before. The steady state rate of innovation is lower,
with a mean probability of success of 0.450.15 This is partly due to the higher obsolescence rate ![]() , which implies a lower steady state R&D stock than in the baseline model.
, which implies a lower steady state R&D stock than in the baseline model.
The steady state mean return to R&D expenditures equals 5.5%, higher than the estimated value from the baseline model. Nonetheless, this estimate is much lower than the values reported in the literature. Intuitively, the lower estimate for ![]() implies that more of the benefit of an innovation is realized in the next period, thereby increasing the ratio of expected increase in profits from an innovation to the expected increase in firm value. The higher estimate of
implies that more of the benefit of an innovation is realized in the next period, thereby increasing the ratio of expected increase in profits from an innovation to the expected increase in firm value. The higher estimate of
![]() decreases the residual value of R&D expenditures, also resulting in a higher return. However, the higher return does not translate to a higher level of R&D expenditures.
decreases the residual value of R&D expenditures, also resulting in a higher return. However, the higher return does not translate to a higher level of R&D expenditures.
The difference in expected firm value from innovating versus not-innovating has a direct impact on R&D policy in the model. The mean expected increase in firm value of ![]() is lower
than the corresponding value in the baseline model. There is also much less cross-sectional variation in the increase in firm value. The higher impact of a successful innovation on profits does not translate to firm values, as the benefit dissipates faster.
is lower
than the corresponding value in the baseline model. There is also much less cross-sectional variation in the increase in firm value. The higher impact of a successful innovation on profits does not translate to firm values, as the benefit dissipates faster.
C Estimates using only R&D sector data
The results presented in the baseline model assume that the non-R&D related parameters are identical across both sectors and use non-R&D sector data to help estimate these parameters. However, these parameters may vary across the two sectors. This section presents the results of estimating the model using data only on R&D sector firms. This leads to a decrease in the number of matched moments and provides a robustness check to differences in model parameters across the two sectors.
Table 5 presents the results of estimating the model using indirect inference with data on R&D sector firms only. Panel A reports the matched moments for the data and simulations, respectively. Panel B reports the estimated parameter values. Panel C reports some
statistics of economic interest from the simulated data set. The calibrated value of
![]() , the mean capital investment rate for R&D sector firms. The discount rate
, the mean capital investment rate for R&D sector firms. The discount rate
![]() , as in the baseline model.
, as in the baseline model.
The matched moments exhibit a similar pattern to that observed in Table 3. The model matches the first and second moments of R&D and has difficulty reconciling the level of profitability with the level of Tobin's Q. The model also implies a higher autocorrelation
level for profits and R&D than found in the data. The ![]() -statistic increases and its
-statistic increases and its ![]() -value decreases, as the number of data points and the degrees of freedom decrease. However, the data does not reject the model.
-value decreases, as the number of data points and the degrees of freedom decrease. However, the data does not reject the model.
The point estimates imply a higher impact of an innovation on profits and a higher obsolescence rate for R&D expenditures. The lower point estimate for ![]() suggests that mark-ups
may be slightly higher in the R&D sector. Somewhat surprisingly, the measures of economic interest are quite similar to those obtained using data on both sectors. The return to R&D is, as before, much lower than that reported in the literature. The probability of an innovation exhibits
sharp cross-sectional variation and is slightly lower than the baseline model estimate.
suggests that mark-ups
may be slightly higher in the R&D sector. Somewhat surprisingly, the measures of economic interest are quite similar to those obtained using data on both sectors. The return to R&D is, as before, much lower than that reported in the literature. The probability of an innovation exhibits
sharp cross-sectional variation and is slightly lower than the baseline model estimate.
The above estimates indicate that firms capture an economically and statistically significant increase in profits from innovation. They also face significant uncertainty regarding the outcome of their R&D expenditures. This uncertainty does not, however, deter firms from undertaking the substantial level of R&D expenditures observed in the data.
5 Policy experiments
This section presents the results of counterfactual experiments on the following: a subsidy on R&D spending and an increase in the impact of a successful innovation on profits. The policy experiments reflect the model and are partial equilibrium in nature. They do not take into account possible responses by consumers or changes in government spending arising from these exogenous changes. As such, substantial care needs to be taken in using these experiments to argue for policy changes. The analysis provides a method to quantify the impact of changes in key parameters on the level of R&D spending, profits, firm value, and the rate of innovation within the context of the model.
A A subsidy to R&D spending
There exists an active policy debate about using the tax code to subsidize R&D investment. The research and experimentation tax credit uses a complex formula based on growth rates in these expenditures, which comprise only a subset of total R&D expenditures. The estimation presented in
the previous section accounts for the tax credit through the calibration of the gross tax rate on operating income, ![]() . The tax credit amounted to about 2.5% of all spending on R&D by
firms from 1990 to 2001 (Moris (2005)). Currently, the tax credit is not permanent and requires Congressional authorization every few years. This counterfactual experiment studies the impact of a further 5% R&D tax credit within the context of the model (see Bloom, Griffith, and van Reenen (2002) for a cross-country study on the impact of tax subsidies on innovation). Table 6 reports the moments of interest using the actual estimates and with a 5% subsidy on R&D expenditures. Panel A reports the values
for the baseline model, Panel B reports the values with the lower discount rate parameter, and Panel C reports the results with the R&D sector only estimates. While the analysis does not impose any other taxes to offset the drop in tax revenue, it can provide a basis for a cost-benefit analysis
of R&D tax credits.
. The tax credit amounted to about 2.5% of all spending on R&D by
firms from 1990 to 2001 (Moris (2005)). Currently, the tax credit is not permanent and requires Congressional authorization every few years. This counterfactual experiment studies the impact of a further 5% R&D tax credit within the context of the model (see Bloom, Griffith, and van Reenen (2002) for a cross-country study on the impact of tax subsidies on innovation). Table 6 reports the moments of interest using the actual estimates and with a 5% subsidy on R&D expenditures. Panel A reports the values
for the baseline model, Panel B reports the values with the lower discount rate parameter, and Panel C reports the results with the R&D sector only estimates. While the analysis does not impose any other taxes to offset the drop in tax revenue, it can provide a basis for a cost-benefit analysis
of R&D tax credits.
The subsidy for R&D expenditures leads to higher spending and a greater level of innovation under all models. The tax subsidy increases the rate of innovation by 4.4, 3.6, and 4.4 percentage points for the models estimated in Sections 4.1, 4.2, and 4.3, respectively. This is driven by an approximately 1% increase in the rate of R&D expenditures in response to the additional tax credit. The findings imply a mean increase in R&D expenditures of 1.72 to 2.15 dollars for a dollar increase in the R&D tax credit. This is higher than the 1 to 1 impact of R&D tax credits on R&D expenditures estimated by Hall and van Reenen (2000). The similar impact of the tax subsidy for all models contrasts with the different rates of return. This provides further evidence that using the return to R&D for policy prescriptions leads to erroneous conclusions in this setting.
B An increase in the impact of a successful innovation
An increase in the impact of a successful innovation provides a method to incorporate changes in patent policy that favor innovators into the model. Eaton and Kortum (1999) directly estimate a model of international research and patenting and find a strong effect of
strengthening patent rights on productivity growth. While such an analysis does not shed much light on the optimal level of patent protection, it can help quantify the impact of a change in patent policy on R&D expenditures and the rate of innovation. Gilbert and Shapiro
(1990) argue for viewing patent policy in terms of the degree of profits accruing to the innovator. In the context of this study, increased patent protection can be viewed as an exogenous increase in ![]() . Table 7 reports the moments of interest using the actual estimates and the new values obtained with a 5% increase in
. Table 7 reports the moments of interest using the actual estimates and the new values obtained with a 5% increase in ![]() . Panel A
reports the values for the baseline model, Panel B reports the values with the lower discount rate parameter, and Panel C reports the results with the R&D sector only estimates.
. Panel A
reports the values for the baseline model, Panel B reports the values with the lower discount rate parameter, and Panel C reports the results with the R&D sector only estimates.
The increase in the impact of a successful innovation on profits leads to higher investment in R&D for all models. The rate of innovation increases by 3.7, 3.2, and 3.6 percentage points, respectively. The increase in ![]() has a similar impact on the rate of innovation as the R&D tax subsidy. However, this experiment has a larger impact on valuation compared to the tax subsidy. The tax subsidy benefits all R&D firms, while the increase in
has a similar impact on the rate of innovation as the R&D tax subsidy. However, this experiment has a larger impact on valuation compared to the tax subsidy. The tax subsidy benefits all R&D firms, while the increase in ![]() benefits only firms that innovate. As firms with higher valuations invest more in R&D and are more likely to innovate, the change in
benefits only firms that innovate. As firms with higher valuations invest more in R&D and are more likely to innovate, the change in ![]() has a bigger impact on these firms, as reflected in the larger increase in the mean value of Tobin's Q.
has a bigger impact on these firms, as reflected in the larger increase in the mean value of Tobin's Q.
6 Conclusion
An empirical analysis demonstrates that the high returns to R&D found in much of the literature are sensitive to assumptions of the obsolescence rate. This study estimates the return to R&D by simultaneously estimating all the key structural parameters of a dynamic model. The underlying model differs from that used in the production based approach as it incorporates uncertainty in the outcome of R&D projects, an arguably key economic feature of R&D investment. Further, the R&D stock in the model measures investment made towards generating the next innovation instead of the knowledge stock applicable for production. The identified variables of interest include the impact of an innovation on profits, the rate of innovation, the return to R&D, and the expected increase in firm value from an innovation.
The estimates reveal an economically and statistically significant impact of an innovation on profits. In present value terms, an innovation leads to an increase in profitability of 4.6-9.0%. This translates to an expected increase in firm value from innovating of 14.1-21.3%. The estimated rates of innovation suggest a significant probability of failure for R&D projects, highlighting the importance of uncertainty in estimating the return to R&D. The estimated returns to R&D are much lower than those found in the literature. However, this does not deter firms from maintaining a high level of R&D investment.
Counterfactual experiments examine the impact of a subsidy to R&D expenditures and an increase in profits from a successful innovation. A tax subsidy yields a clear increase in the rate of innovation even though the estimates imply a low return. These findings suggests that, as it focuses only on the short-term impact, the return to R&D would not be an appropriate tool for R&D policy analysis.
The analysis in this study employs a partial equilibrium approach that does not incorporate economic growth. Combining the findings of this study with endogenous growth models, such as that by Klette and Kortum (2004), may provide a rich framework for further research and policy analysis.
A Proofs
![\displaystyle \frac{\tilde{S}_i^{\prime }}{K_i} = \frac{1}{a} \left[\log(a) - \log\left((1-\tau^r)(1-\beta(1-\gamma))\right) + \log\left(\frac{\beta( E_z[G(K_i^{\prime }, z_i^{\prime })\vert j_i=1] - E_z[G(K_i^{\prime }, z_i^{\prime })\vert j_i=0])}{K_i}\right) \right].](img72.gif) |
The impact of R&D spending on the expected value of the firm in the next period can be clarified by an application of the law of iterated expectations,
The derivative of the above expression with respect to
![\displaystyle \frac{\partial{E_z[G(K_i^{\prime }, z_i^{\prime })]}}{\partial{S_i^{\prime }}} = \frac{a}{K_i}\exp(-a\frac{S_i^{\prime }}{K_i})\left(E_z[G(K_i^{\prime }, z_i^{\prime })\vert j_i=1] - E_z[G(K_i^{\prime }, z_i^{\prime })\vert j_i=0]\right).](img114.gif)
Some algebra reveals that the second order condition with respect to
B Expected return to R&D
The after-tax expected return to R&D expenditures is given by:
The conditional expectation of
| (B.2) |
Using the transition equation for
The partial derivative of the probability of an innovation equals:
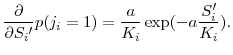 |
(B.3) |
The above expressions yield the following:
![\displaystyle \frac{\partial}{\partial{S_i{^\prime }}} E_z\left[\Pi(K_i^{\prime }, z_i^{\prime })\right]](img126.gif) |
![\displaystyle (K_i^{\prime })^{\theta} \left[z_i^{\rho} \exp\left(\mu + \sigma^2/2 + \lambda \right) \frac{a}{K_i} \exp(-a\frac{S_i^{\prime }}{K_i}) - z_i^{\rho} \exp\left(\mu + \sigma^2/2 \right) \frac{a}{K_i} \exp(-a\frac{S_i^{\prime }}{K_i}) \right]](img127.gif) |
||
![\displaystyle (K_i^{\prime })^{\theta} \frac{a}{K_i} \exp(-a\frac{S_i^{\prime }}{K_i}) z_i^{\rho} \exp\left(\mu + \sigma^2/2 \right) [\exp(\lambda) - 1].](img128.gif) |
Substituting the expression for
![\displaystyle \frac{\partial}{\partial{S_i{^\prime }}} E_z\left[ \Pi(K_i^{\prime }, z_i^{\prime })\right] = \left(\frac{(K_i^{\prime })^{\theta} z_i^{\rho} \exp\left(\mu + \sigma^2/2 \right) [\exp(\lambda) - 1]}{E_z[G(K_i^{\prime }, z_i^{\prime })\vert j_i=1] - E_z[G(K_i^{\prime }, z_i^{\prime })\vert j_i=0]}\right) \frac{\left(1 - \beta(1 - \gamma)\right)}{\beta}.](img77.gif)
|
C Simulated method of moments
The indirect inference method of Gourieroux, Monfort, and Renault (1993) obtains parameter estimates by matching a set of selected moments from the data to those obtained by simulation. Denote the structural parameters by ![]() . The matched moments can be written as a solution to a minimization problem
. The matched moments can be written as a solution to a minimization problem ![]() , where
, where ![]() denotes the data and
denotes the data and ![]() the moments to be matched. The data moments are then given by
the moments to be matched. The data moments are then given by
| (C.1) |
where
| (C.2) |
The study picks
The structural parameters are then obtained by minimizing a quadratic form of the distance between the data and simulated moments.
| (C.3) |
where
![\displaystyle \hat{W} = \left[N \text{var}(\hat{M}) \right]^{-1}.](img143.gif) |
(C.4) |
The above covariance matrix is calculated with the actual data set using the influence function method of Erickson and Whited (2000). The estimator is asymptotically normal for fixed
| (C.5) | |||
![\displaystyle (1 + \frac{1}{S}) \left[\frac{\partial^2{Q}}{\partial{\Psi}\partial{M}'} \left(\frac{\partial{Q}}{\partial{M}}\frac{\partial{Q}}{\partial{M}}'\right)^{-1} \frac{\partial^2{Q}}{\partial{M}\partial{\Psi}'}\right]^{-1}. \notag](img149.gif) |
(C.6) |
While
The indirect inference method also yields a GMM-style test of the over-identifying restrictions. The ![]() -statistic adjusted for the simulation size converges in distribution to a
-statistic adjusted for the simulation size converges in distribution to a
![]() distribution, with degrees of freedom equal to the number of moments minus the number of parameters:
distribution, with degrees of freedom equal to the number of moments minus the number of parameters:
![\displaystyle J = \frac{NS}{1+S} \left[\hat{M} - \hat{m}(\Psi)\right]' \hat{W} \left[\hat{M} - \hat{m}(\Psi) \right].](img153.gif) |
(C.7) |
D Numerical Solution
The simulations require numerical solution of the value function for firms in the R&D and non-R&D sectors. The capital grid has 61 points and the profits grid has 10 points. The capital grid is centered around an approximation of the median size of the firm given the parameters.
Simulations which result in steady state firm sizes near the boundaries of the grid are discarded in the estimation. The profit grid is formed using the quadrature method of Tauchen and Hussey (1991), with a mean value obtained by guessing the success rate. The endogenous
jumps in ![]() from an innovation are handled by interpolating firm value over two more grids constructed using the transition equation for profitability conditional on whether the firm
innovates. The expected value of the firm is obtained using the law of iterated expectations.
from an innovation are handled by interpolating firm value over two more grids constructed using the transition equation for profitability conditional on whether the firm
innovates. The expected value of the firm is obtained using the law of iterated expectations.
The simulated sample is generated using the value and policy functions for the R&D and non-R&D sectors. The law of motion for profitability is generated directly using the transition equations (6) and (2). The firm's decisions are obtained using linear interpolation of the policy functions. The simulations maintain the same fraction of firms in the R&D sector as in the data. The simulation is run for 100 years, with the initial 50 discarded as a burn-in sample. This yields the value of the quadratic form of the difference in the data moments and simulated moments. The program searches for the parameters that minimize this distance using the simulated annealing algorithm. Each estimation involved evaluating more than 100,000 candidate parameter sets.
Bibliography
| R&D sector | Non-R&D sector | |||
|---|---|---|---|---|
| Variable | Mean | Std. Dev. | Mean | Std. Dev. |
| Log assets | 5.034 | 2.131 | 5.193 | 1.860 |
| Tobin's Q | 2.174 | 1.224 | 1.528 | 0.680 |
| Profits | 0.072 | 0.146 | 0.144 | 0.100 |
| R&D to assets | 0.112 | 0.082 | ||
| Investment to assets | 0.063 | 0.062 | 0.094 | 0.089 |
| Number of observations | 35409 | 38207 | ||
| Obsolescence rate | |||||
|---|---|---|---|---|---|
| Regressor |
|
|
|
|
|
| Labor | 0.656 | 0.650 | 0.649 | 0.648 | 0.648 |
| (0.016) | (0.016) | (0.016) | (0.016) | (0.016) | |
| Capital stock | 0.181 | 0.169 | 0.162 | 0.157 | 0.152 |
| (0.012) | (0.012) | (0.012) | (0.012) | (0.012) | |
| R&d stock | 0.197 | 0.216 | 0.225 | 0.229 | 0.234 |
| (0.008) | (0.009) | (0.008) | (0.008) | (0.008) | |
| Number of Observations | 39582 | 39582 | 39582 | 39582 | 39582 |
| Adjusted R-squared | 0.892 | 0.894 | 0.895 | 0.896 | 0.896 |
| Steady state return
|
- | 9.3% | 19.4% | 29.7% | 50.4% |
| Estimated return
|
12.6% | 24.1% | 34.8% | 45.2% | 65.0% |
| Moment | Data | Model |
|---|---|---|
| First moment of R&D to assets | 0.112 | 0.108 |
| Second moment of R&D to assets | 0.019 | 0.024 |
| First moment of Q (R&D sector) | 2.174 | 1.876 |
| First moment of Q (non-R&D sector) | 1.528 | 1.573 |
| Second moment of Q (R&D sector) | 6.224 | 4.582 |
| Second moment of Q (non-R&D sector) | 2.799 | 2.833 |
| First moment of profits (R&D sector) | 0.072 | 0.132 |
| First moment of profits (non-R&D sector) | 0.144 | 0.180 |
| Second moment of profits (R&D sector) | 0.027 | 0.052 |
| Second moment of profits (non-R&D sector) | 0.031 | 0.046 |
| Autocorrelation of profits | 0.469 | 0.871 |
| Autocorrelation of R&D to assets | 0.289 | 0.439 |
| Second moment of investment to assets | 0.012 | 0.021 |
| J-statistic | 0.375 | |
| p-value | 0.999 |
Panel B: Parameter estimates
| Parameter | |||||||
|---|---|---|---|---|---|---|---|
| Estimate | 0.837 | 0.970 | 0.188 | 0.123 | 2.094 | 1.591 | 0.240 |
| Standard error | 0.002 | 0.002 | 0.002 | 0.001 | 0.014 | 0.010 | 0.002 |
Panel C: Economic impact
| Variable of interest | 5th Percentile | Mean | 95th Percentile |
|---|---|---|---|
| Probability of innovation |
0.017 | 0.507 | 0.822 |
| Expected rate of return from R&D | 1.6% | 3.7% | 8.2% |
| Expected increase in firm value from an innovation | 7.8% | 21.3% | 74.7% |
| Equivalent permanent profit increase | - | 8.96% | - |
| Ratio of aggregate R&D value to the value of all capital | - | 17.9% | - |
| Moment | Data | Model |
|---|---|---|
| First moment of R&D to assets | 0.112 | 0.106 |
| Second moment of R&D to assets | 0.019 | 0.023 |
| First moment of Q (R&D sector) | 2.174 | 1.857 |
| First moment of Q (non-R&D sector) | 1.528 | 1.583 |
| Second moment of Q (R&D sector) | 6.224 | 4.048 |
| Second moment of Q (non-R&D sector) | 2.799 | 2.634 |
| First moment of profits (R&D sector) | 0.072 | 0.112 |
| First moment of profits (non-R&D sector) | 0.144 | 0.168 |
| Second moment of profits (R&D sector) | 0.027 | 0.040 |
| Second moment of profits (non-R&D sector) | 0.031 | 0.041 |
| Autocorrelation of profits | 0.469 | 0.859 |
| Autocorrelation of R&D to assets | 0.289 | 0.449 |
| Second moment of investment to assets | 0.012 | 0.017 |
| J-statistic | 0.293 | |
| p-value | 1.000 |
Panel B: Parameter estimates
| Parameter | |||||||
|---|---|---|---|---|---|---|---|
| Estimate | 0.870 | 0.861 | 0.296 | 0.173 | 2.461 | 2.492 | 0.335 |
| Standard error | 0.001 | 0.001 | 0.001 | 0.001 | 0.017 | 0.020 | 0.002 |
Panel C: Economic impact
| Variable of interest | 5th Percentile | Mean | 95th Percentile |
|---|---|---|---|
| Probability of innovation |
0.000 | 0.450 | 0.772 |
| Expected rate of return from R&D | 2.9% | 5.5% | 10.0% |
| Expected increase in firm value from an innovation | 10.3% | 14.1% | 20.6% |
| Equivalent permanent profit increase | - | 4.63% | - |
| Ratio of aggregate R&D value to the value of all capital | - | 23.1% | - |
| Moment | Data | Model |
|---|---|---|
| First moment of R&D to assets | 0.112 | 0.108 |
| Second moment of R&D to assets | 0.019 | 0.022 |
| First moment of Q | 2.174 | 1.885 |
| Second moment of Q | 6.224 | 4.538 |
| First moment of profits | 0.072 | 0.143 |
| Second moment of profits | 0.027 | 0.053 |
| Autocorrelation of profits | 0.435 | 0.889 |
| Autocorrelation of R&D to assets | 0.289 | 0.536 |
| Second moment of investment to assets | 0.008 | 0.014 |
| J-statistic | 0.502 | |
| p-value | 0.778 |
Panel B: Parameter estimates
| Parameter | |||||||
|---|---|---|---|---|---|---|---|
| Estimate | 0.795 | 0.944 | 0.233 | 0.150 | 2.079 | 2.348 | 0.338 |
| Standard error | 0.019 | 0.012 | 0.014 | 0.003 | 0.171 | 0.161 | 0.017 |
Panel C: Economic impact
| Variable of interest | 5th Percentile | Mean | 95th Percentile |
|---|---|---|---|
| Probability of innovation |
0.000 | 0.413 | 0.736 |
| Expected rate of return from R&D | 2.8% | 5.2% | 11.2% |
| Expected increase in firm value from an innovation | 9.1% | 19.7% | 52.8% |
| Equivalent permanent profit increase | - | 8.74% | - |
| R&D to assets | Profits | Tobin's Q | |||
|---|---|---|---|---|---|
| Estimate | 0.000 | 0.108 | 0.132 | 1.876 | 0.507 |
| Experiment | 0.050 | 0.119 | 0.140 | 2.053 | 0.551 |
Panel B: Model with lower discount rate
| R&D to assets | Profits | Tobin's Q | |||
|---|---|---|---|---|---|
| Estimate | 0.000 | 0.106 | 0.112 | 1.857 | 0.450 |
| Experiment | 0.050 | 0.117 | 0.113 | 2.044 | 0.486 |
Panel C: R&D sector only model
| R&D to assets | Profits | Tobin's Q | |||
|---|---|---|---|---|---|
| Estimate | 0.000 | 0.108 | 0.143 | 1.885 | 0.413 |
| Experiment | 0.050 | 0.121 | 0.148 | 2.077 | 0.457 |
| R&D to assets | Profits | Tobin's Q | |||
|---|---|---|---|---|---|
| Estimate | 0.123 | 0.108 | 0.132 | 1.876 | 0.507 |
| Experiment | 0.129 | 0.117 | 0.140 | 2.368 | 0.544 |
Panel B: Model with lower discount rate
| R&D to assets | Profits | Tobin's Q | |||
|---|---|---|---|---|---|
| Estimate | 0.173 | 0.106 | 0.112 | 1.857 | 0.450 |
| Experiment | 0.182 | 0.116 | 0.113 | 2.172 | 0.482 |
Panel C: R&D sector only model
| R&D to assets | Profits | Tobin's Q | |||
|---|---|---|---|---|---|
| Estimate | 0.150 | 0.108 | 0.143 | 1.885 | 0.413 |
| Experiment | 0.158 | 0.119 | 0.149 | 2.180 | 0.449 |
 |
 |
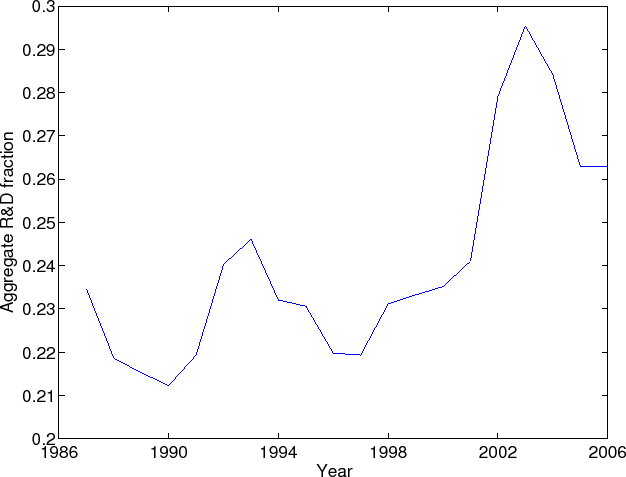 |
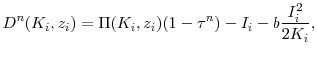
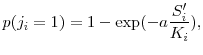
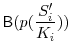
![\displaystyle -(1-\tau^r) + (1-\tau^r)\beta(1 - \gamma) + \beta \frac{\partial{E_z[G(K_i^{\prime }, z_i^{\prime })]}}{\partial{S_i^{\prime }}} = 0.](img110.gif)
![\displaystyle E_z[G(K_i^{\prime }, z_i^{\prime })] = E_z[G(K_i^{\prime }, z_i^{\prime })\vert j_i=1](1-\exp(-a\frac{S_i^{\prime }}{K_i})) + E_z[G(K_i^{\prime }, z_i^{\prime })\vert j_i=0]\exp(-a\frac{S_i^{\prime }}{K_i}).](img113.gif)
![\displaystyle (1-\tau^r)(1 - \beta(1 - \gamma)) = \beta \frac{a}{K_i}\exp(-a\frac{\tilde{S}_i^{\prime }}{K_i})\left(E_z[G(K_i^{\prime }, z_i^{\prime })\vert j_i=1] - E_z[G(K_i^{\prime }, z_i^{\prime })\vert j_i=0]\right)](img115.gif)
![\displaystyle \Rightarrow \frac{\tilde{S}_i^{\prime }}{K_i} = \frac{1}{a} \left[\log(a) - \log\left((1-\tau^r)(1-\beta(1-\gamma))\right) + \log\left(\frac{\beta( E_z[G(K_i^{\prime }, z_i^{\prime })\vert j_i=1] - E_z[G(K_i^{\prime }, z_i^{\prime })\vert j_i=0])}{K_i}\right) \right]. \notag](img116.gif)
![\displaystyle \frac{\partial}{\partial{S_i{^\prime }}} E_z\left[ \Pi(K_i^{\prime }, z_i^{\prime })(1-\tau^r)\right] = \frac{\partial}{\partial{S_i{^\prime }}} E_z\left[ z_i^{\prime }(K_i^{\prime })^{\theta}(1-\tau^r)\right].](img117.gif)