
The Rigidity of Choice.
Lifecycle savings with information-processing limits
Keywords: Rational inattention, dynamic programming, consumption
Abstract:
Information is, we must steadily remember, a measure of one's freedom of choice in selecting a message. The greater this freedom of choice, and hence the greater the information, the greater is the uncertainty that the message actually selected is some particular one. Thus greater freedom of choice, greater uncertainty, greater information go hand in hand. (Claude Shannon, sic.)
1 Introduction
Every day people face an overwhelming amount of data. Every day, though, people use these for their decisions. In selecting useful information, people face a trade off between reacting quickly and precisely to news about their financial possibilities and not spending time crunching numbers to figure out their exact net worth. To match these facts, macroeconomists have adopted a number of modelling strategies able to inject inertia within the rational expectation framework. These devices, such as the costly acquisition and diffusion of information, largely rely on ad-hoc technology to generate smooth and delayed responses of consumption to a shock to income consistent with observed data. Contrary to this approach, this paper proposes a way to relate inertial behavior in consumption and savings based on people's preferences.
To this end, the paper offers a micro-founded explanation on the nature of inertia in consumption and savings. Following Rational Inattention (Sims, 2003, 2006), I model the limits of people to process information at an infinite rate by using Shannon channels.
Under this information processing constraint, individuals choose a signal that conveys information about their financial possibilities. The signal can provide any kind of information as long as its overall content is within the channel's capacity. Consumers base their expectations of the economic conditions on the signal and decide how much to consume. Thus, in my framework, the delayed and smoothed responses of savings to changes in wealth are the result of a slow information flow due to processing constraints. Combining the standard utility maximization framework subject to a budget constraint with information processing limits leads to a departure from rational expectations. My paper shows how to model this formally in an intertemporal setting. In particular, I assume that people do not know the exact value of their wealth but have an idea of their net worth. A way of thinking about this hypothesis is that people do not know exactly of what the dollar value of their paycheck (nominal) corresponds to in terms of cups of coffee (real), assuming that this is what they care about. People process information to sharpen their knowledge of how much consumption their wealth can purchase. I model initial uncertainty as a probability distribution over the possible realizations of wealth. In such a framework, it is possible to study how choices of information play out with people's preferences when they decide on consumption throughout their life time.
The challenge of this model and, more generally, of models of rational inattention is dealing with the infinite dimensional state space implied by having a prior as state. For this reason, the applications of rational inattention have been limited to either a linear quadratic framework where Gaussian uncertainty has been considered (such as Sims 1998, 2003, Luo 2007, Mackowiak and Wiederholt 2007, Mondria, 2006, Moscarini 2004) or a two-period consumption-saving problem (Sims 2006) where the choice of optimal ex post uncertainty is analyzed for the case of log utility and two Constant Relative Risk Aversion (CRRA) utility specifications. The linear quadratic Gaussian (LQG) framework can be seen as a particular instance of rational inattention in which the optimal distribution chosen by the household turns out to be Gaussian. Gaussianity has two main advantages. First, it allows an explicit analytical solution for these models. One can show that the problem can be solved in two steps. First, the information gathering scheme is found and then, given the optimal information, the consumption profile. Second, it is easy to compare the results to a signal extraction problem. When looking at the behavior of rational inattentive consumers, it is impossible to separate an exogenously given Gaussian noise in the signal extraction model from an endogenous noise that is optimally chosen to be Gaussian.
The tractability of rational inattention LQG models comes at the cost of restrictive assumptions on preferences and the nature of the signal. Constraining uncertainty of the individual to a quadratic loss / certainty equivalent setting does not take into account the possibility that the agent is very uncertain about his economic environment; ceteris paribus, more uncertainty generates second-order effects of information that have first order impact on individuals' decisions. In this sense, rational inattention LQG models are subject to the same limits as methods that use linear approximation of optimality conditions to study stochastic dynamic models.1 With little uncertainty about the economic environment, linear approximations of the optimality conditions may provide a fairly adequate description of the exact solution of the system. This fact suggests that the uncertainty at the individual level might actually be large, undermining the accuracy of both linearized and rational inattention LQG models. To assess the importance of information choices for people' expectations, it is important to let consumers select their information from a wider set of distributions that includes but it is not limited to the Gaussian family.
The theoretical contribution of this paper is to provide the analytical and computational tools necessary to apply information theory in a dynamic context with optimal choice of ex-post uncertainty. I propose a methodology to handle the additional complexity without the LQG setting. I propose a discretization of the framework and derive its theoretical properties. Then, I provide a computational strategy that is able to solve the model.
Several predictions emerge from the model. Evaluating the unconditional moments of the time series of consumption for a given degree of risk aversion, the first result of the paper is that higher information costs are associated with more persistence and higher volatility. The seemingly paradoxical results of having sluggish and volatile consumption at the same time can be reconciled if one considers that information-processing constraints prevent the consumers to respond promptly to fluctuations in wealth. To make a concrete example, suppose a person starts off with low wealth and initially chooses to consume a little. If he is risk averse, he may decide not to modify his consumption profile until he acquires more information about his wealth. As he processes information through time, he gets more and more data about his high value of wealth and changes his consumption when he is sure that he has saved enough to afford a higher consumption expenditure. The more risk averse the consumer is, the longer he waits. The longer the wait, the more wealth grows because of the accumulation of savings and current income. The combination of waiting while processing information and sharp changes once information has been processed through time generates sluggishness and volatility in consumption.
Second, by looking at the life-cycle profile of consumption I find that the behavior of consumption is smooth and persistent with several peaks along the simulated path. These peaks in consumption occur later in life for people that have access to low information flow. This effect is stronger as risk aversion increases. The logic behind this result is that risk averse consumers react to uncertainty by processing more information on their low values of wealth and keep their consumption low as a precaution until the uncertainty is diminished. They accumulate more savings throughout early adult life than their infinite-information-processing counterparts. They keep saving until the accumulation of wealth and information indicates that they can enjoy a high consumption profile.
This leads also to the finding that individual consumption can have more than one hump along its path as wealth accumulates through time. The key point is that individuals can vary their information flow during their life time. To see why, suppose that a person receives signals that his wealth is low. In this case, he wants to pay attention to his expenses and closely monitor the activity of his account. Once he makes sure that he has saved enough, he may decide to spend less effort monitoring his balance and enjoy consumption. Decumulation of savings continues until he receives information that he has emptied his checking account. This news call for his attention again, so he starts saving and monitor his balance more frequently than before. These results combined are suggestive of a precautionary motive for savings driven by information processing limits.
Third, I find that consumers with processing capacity constraints have asymmetric responses to income fluctuations, with negative shocks producing sharper and more persistent effects than positive ones. This effect is stronger as the degree of risk aversion increases. Compared with a situation in which there are no information-processing limits, in a rational-inattention consumption-savings model, an adverse temporary income shock makes consumers reduce their consumption for a longer period of time. This happens because risk-averse people who receive bad news about their finances save right away to hedge against the possibility of running out of wealth in the future. Once they have enough savings and information, they gradually increase their consumption and smooth the remaining effect of the shock over time. This result also points toward precautionary motive due to information-processing limits.
Finally, I find that the predictions of the model can be used to address important policy questions. In the context of fiscal reforms of consumer spending, I show that, as wealth decreases, rationally inattentive consumers respond faster to a tax rebate that increases their income by
![]() . For a given level of wealth, the lower the processing capacity, the longer it takes for consumption to react to shocks to disposable income. These findings make intuitive sense. A tax
rebate matters more for people with lower income and, as a result, tighter budgetary constraints than for wealthy people.2 As a result, poorer people
acknowledge and react faster to the positive income shocks. By contrast, wealthy people do not perceive the increase in disposable income as a significant change in their financial position. Thus, consumption for wealthy people does not change significantly, instead it adjusts slowly over time.
Consider an individual that has wealth and infinite processing capacities. The reaction of consumption to a temporary positive income shock would be to adjust immediately to a new higher value of consumption so to smooth out the effect of the shock throughout time. With limited processing capacity,
the individual smooths consumption slowly over time because the effect of the increase in disposable income on wealth spread out slowly through time. These predictions are in line with the empircal evidence on tax rebate (e.g., Johnson, Parker, and Soules (2006)).
. For a given level of wealth, the lower the processing capacity, the longer it takes for consumption to react to shocks to disposable income. These findings make intuitive sense. A tax
rebate matters more for people with lower income and, as a result, tighter budgetary constraints than for wealthy people.2 As a result, poorer people
acknowledge and react faster to the positive income shocks. By contrast, wealthy people do not perceive the increase in disposable income as a significant change in their financial position. Thus, consumption for wealthy people does not change significantly, instead it adjusts slowly over time.
Consider an individual that has wealth and infinite processing capacities. The reaction of consumption to a temporary positive income shock would be to adjust immediately to a new higher value of consumption so to smooth out the effect of the shock throughout time. With limited processing capacity,
the individual smooths consumption slowly over time because the effect of the increase in disposable income on wealth spread out slowly through time. These predictions are in line with the empircal evidence on tax rebate (e.g., Johnson, Parker, and Soules (2006)).
My results are observational distinct from the previous literature on consumption and information (e.g., Reis (2006)). The distinguishing feature of my model with respect to previous works is its ability to generate endogenously asymmetric response of consumption to shocks.3 Finally, my paper contributes to the literature that models how people form endogenously expectations and react to the economy on the basis of their rationally chosen information.4
The paper is organized as follows. Section 2 lays out the theoretical basis of rational inattention and informally introduces the model. Section 3 states the problem of the consumers as a discrete stochastic dynamic programming problem, while Section 4 derives the properties of the Bellman function. Section 5 provides the numerical methodology used to solve the model. Section 6 delivers its main results. By comparing the predictions of the model on the preliminary evidence on tax rebates, I find that the model can be a valid instrument to address the impact of tax reforms on consumer spending. Section 7 concludes.
2 Foundations of Rational Inattention
Rational inattention (Sims 1988,5 1998, 2003, 2005, 2006) blends two main fields: Information Theory and Economics. The first draws mainly on the work of Shannon (1948). The main contribution is to define a measure of the choice involved in the selection of the message and the uncertainty regarding the outcome. The measure used is entropy. Details on this part are in Appendix F. Based on Shannon's apparatus, the economic contribution is that of using Shannon capacity as a technological constraint to capture individuals' inability of processing information about the economy at infinite rate. Given these limits, people reduce their uncertainty by selecting the focus of their attention. The resulting behavior depends on the choices of what to observe of the environment once the information-processing frictions are acknowledged.
2.1 The Economics of Rational Inattention
Consider a person who wants to buy lunch. He doesn't know his exact wealth but he knows that he has some cash and a credit card. Not recalling the expenses charged on the credit card up to that point, he can go to the bank or simply check his wallet. Going to the bank to figure out his wealth for lunch is beyond his time and interest, so he decides to check his wallet. He browses through it thinking about what he wants and what he can afford to buy for lunch. Mapping dollar bills into his knowledge of prices from previous consumption, he realizes he can only afford a sandwich instead of his favorite sushi roll. Then, he uses the receipt to update his prior on the price of sandwiches, what he thinks he has left in his wallet and, ultimately, his wealth. This updated knowledge will be used for his next purchase. Such a story can be directly mapped into a rational inattention framework.
First, the person does not know his wealth, ![]() , but he has a prior on it,
, but he has a prior on it,
![]() . Before processing any information, his uncertainty about wealth is the entropy of his prior,
. Before processing any information, his uncertainty about wealth is the entropy of his prior,
![]() , where
, where
![]() denotes the expectation operator.6 Before processing any information, lunch too is a random variable,
denotes the expectation operator.6 Before processing any information, lunch too is a random variable, ![]() , ranging from sandwiches to sushi. To reduce entropy, he can choose whether to have a detailed
report from the bank or to look at his wallet. The two options differ in amount of information and effort in processing their content. The choice of the option (signal) together with consumption result in a joint probability
, ranging from sandwiches to sushi. To reduce entropy, he can choose whether to have a detailed
report from the bank or to look at his wallet. The two options differ in amount of information and effort in processing their content. The choice of the option (signal) together with consumption result in a joint probability
![]() . Both dollars in the wallet and knowledge of prices of sandwiches and sushi contribute to the reduction of uncertainty in wealth of an amount equal to
. Both dollars in the wallet and knowledge of prices of sandwiches and sushi contribute to the reduction of uncertainty in wealth of an amount equal to
![]() , which is the entropy of
, which is the entropy of ![]() that remains given the knowledge of
that remains given the knowledge of ![]() . The information flow, or maximum reduction of uncertainty about the prior on wealth, is bounded by the
information that the selected signal conveys. In formulae:
. The information flow, or maximum reduction of uncertainty about the prior on wealth, is bounded by the
information that the selected signal conveys. In formulae:
where
The example illustrates how people handle everyday decision weighing the effort of processing all the available information (personal net worth), against the precision of the information they can absorb (walking to the bank versus checking the wallet) guided by their interest (buying lunch). This is the core of rational inattention: information is freely available but people can only process it at finite rate. Information-processing limits make attention a scarce resource. As for any other scarce resource, rational people use attention optimally according to what they have at stake. By appending an information-processing constraint to an otherwise standard optimization framework, the theory explains why people react to changes in the economic environment with delays and errors.
The appeal of Shannon capacity as a constraint to attention is that it provides a measure of uncertainty which does not depend on the characteristics of the channel. The quantity (1) is a probabilistic measure of the information shared by two random variables and it applies to any channel. Thus, the Shannon capacity does not require explicit modelling of how individuals process information. Moreover, treating processing capacity as a constraint to utility maximization produces inertial reactions to the environment as a result of individual rational choices. A rational person may not find it worthy to look beyond his wallet when deciding what to buy for lunch. The dollar bills in his wallet provide little information about current and future activities of his balance. Thus, if something happened to his current account, for example, a sudden drop in his investment, checking his wallet would give him no acknowledgement of the event. Nevertheless, the signal is capable of guiding the consumer on his lunch decision. Over time and through expenses, the person would figure out the drop in his investment and modify his behavior even with respect to lunch.
3.1 The problem of the household
To understand the implications of the limits to information processing, I start with the full information problem.
Let
![]() be the measurable space where
be the measurable space where ![]() represents
the sample set and
represents
the sample set and
![]() the event set. States and actions are defined on
the event set. States and actions are defined on
![]() . Let
. Let
![]() be the
be the ![]() algebra generated by
algebra generated by
![]() up to time
up to time ![]() , i.e.,
, i.e.,
![]() . Then, the collection
. Then, the collection
![]() such that
such that
![]()
![]() is a filtration. Let
is a filtration. Let
![]() be the utility of the household defined over a consumption good,
be the utility of the household defined over a consumption good, ![]() . I assume that the utility belongs to the CRRA family,
. I assume that the utility belongs to the CRRA family,
![]() with
with ![]() the coefficient
of risk aversion. Consumer's problem is:
the coefficient
of risk aversion. Consumer's problem is:
s.t.
where
Consider now a consumer who cannot process all the information available in the economy to track his wealth precisely. This not only adds a constraint to the decision problem but fundamentally affects each constraint (3)-(4).
First, because the consumer doesn't know his wealth, (4) no longer holds. His uncertainty about wealth is given by the prior
![]() . Second, before processing any information, consumption is also a random variable. This is because the uncertainty about wealth translates into a number of possible
consumption profiles with various levels of affordability. It follows that to maximize lifetime utility, consumer needs to reduce uncertainty about wealth and, at the same time, to choose consumption. Hence, when information cannot flow at an infinite rate, the choice of the consumer is the
distribution
. Second, before processing any information, consumption is also a random variable. This is because the uncertainty about wealth translates into a number of possible
consumption profiles with various levels of affordability. It follows that to maximize lifetime utility, consumer needs to reduce uncertainty about wealth and, at the same time, to choose consumption. Hence, when information cannot flow at an infinite rate, the choice of the consumer is the
distribution
![]() as opposite to the stream of consumption
as opposite to the stream of consumption
![]() in (2). Another way of looking at this is that the consumer chooses a noisy signal on wealth where the noise can assume any
distribution selected by the consumer. Given that the agent has a probability distribution over wealth, choosing this signal is akin to choosing
in (2). Another way of looking at this is that the consumer chooses a noisy signal on wealth where the noise can assume any
distribution selected by the consumer. Given that the agent has a probability distribution over wealth, choosing this signal is akin to choosing
![]() . The optimal choice of this distribution is the one that makes the distribution of consumption conditional on wealth as close to the wealth as the limits imposed by the
Shannon capacity allow.
. The optimal choice of this distribution is the one that makes the distribution of consumption conditional on wealth as close to the wealth as the limits imposed by the
Shannon capacity allow.
Third, with respect to the program (2)-(4), there is a new constraint on the amount of information the consumer can process. The reduction in uncertainty conveyed by the signal depends on the attention allocated by the consumer to track his wealth. Paying
attention to reduce uncertainty requires spending some time and effort to process information. I model the task of thinking by appending a Shannon channel to the constraint sets. Limits in the capacity of the consumers are captured by the fact that the reduction in uncertainty conveyed by the
signal cannot be higher than a given number,
![]() The information flow available to the consumer is a function of the signal, i.e., the joint distribution
The information flow available to the consumer is a function of the signal, i.e., the joint distribution
![]() . In formulae:
. In formulae:
Fourth, the update of the prior replaces the law of motion of wealth by using the budget constraint in (3). To describe the way individuals transit across states, define the operator
![]() which combines the expectation in period
which combines the expectation in period ![]() of a variable in period
of a variable in period ![]() with the knowledge of consumption in period
with the knowledge of consumption in period ![]() ,
, ![]() , and the remaining uncertainty over wealth. Applying
, and the remaining uncertainty over wealth. Applying
![]() to equation (3) leads to:
to equation (3) leads to:
where,
To fully characterize the transition from the prior
which is known as Bayesian conditioning. In (7), the function
Let ![]() be the shadow cost of using the channel (5), and combine all these four ingredients. Then, the program of the household under information frictions
is:
be the shadow cost of using the channel (5), and combine all these four ingredients. Then, the program of the household under information frictions
is:
s.t.
![]()
where
This problem is a well-posed mathematical problem with convex objective function and concave constraint sets. What makes it hard to solve is that both the state and the control variables are infinite dimensional. To make progress in solving it, I implement two simplifications: a) I discretize the framework and b) I show that the resulting setting admits a recursive formulation. Then, I study the properties of the Bellman recursion and solve the problem.
Before turning to the solution, I present a brief digression about how constraint (9) operates and how the difference between this model and the existing literature on rational inattention may help to build up the intuition for the solution methodology and the results.
3.2.1 Shannon's constraint in action
To get a sense of how the Shannon capacity constraints affect the decision of the household, I contrast the optimal policy function
![]() for consumers that have identical characteristics but differ in their limits of information-processing.
for consumers that have identical characteristics but differ in their limits of information-processing.
A caveat is in order. In order to explore the interaction between information flow and coefficient of risk aversion, I solve the model in (8)-(12) information flow by fixing the shadow cost of processing information, ![]() , attached to (9) and let
, attached to (9) and let ![]() vary endogenously every period. In this section, I follow a
different route. In order to clarify the mechanisms behind Shannon capacity as a constraint for information transmission, I fix the number of bits,
vary endogenously every period. In this section, I follow a
different route. In order to clarify the mechanisms behind Shannon capacity as a constraint for information transmission, I fix the number of bits, ![]() , across utilities and adjust the
shadow cost
, across utilities and adjust the
shadow cost ![]() to map different coefficients of risk aversion to the same information flow.8 First consider
to map different coefficients of risk aversion to the same information flow.8 First consider
![]() . In the full information case,9 the distribution
. In the full information case,9 the distribution
![]() is degenerate, the choice of
is degenerate, the choice of
![]() reduces to that of
reduces to that of
![]() in (8).10 The resulting optimal policy is given by
in (8).10 The resulting optimal policy is given by
For comparison with the case with finite
![Figure 1: In order to clarify the mechanisms behind Shannon capacity\ as a constraint for information transmission, I fix the number of bits, $\kappa $, across utilities and adjust the shadow cost $\theta $ to map different coefficient of risk aversion to the same information flow. To be more specific, I solve the model with CRRA consumer assuming the same parameters as the baseline model ($\beta ,R,\bar{y}$)$\equiv $($0.9881,1.012,1,1$), the same simplex point (prior) $g\left( \tilde{w}\right) $ and adjusting the shadow cost of processing capacity, $\theta $, to get roughly the same information capacity ($\kappa _{\log }=2.08$ and $\kappa _{crra}=2.13$). The latter implies that the difference in allocation of probabilities within the grid are attributable solely on the coefficient of risk aversion $\gamma $. \ As I will explain in more details in the solution methodologies, the same shadow cost ($\theta $) does deliver different information flow ($\kappa $) according to the degree of risk aversion of the agents with more risk averse agents having higher $\kappa $ for a given $\theta $ than less risk averse ones. To get $\kappa _{\log }\thickapprox \kappa _{crra}$ , I set $\theta _{\log }=0.02$ in Figure 3 while $\theta _{crra}=0.08$ in Figure 4. First consider $u\left( c\right) =\log \left( c\right) $. In the full information case, or, in the wording of my model, when information flows at infinite rate, $\kappa \rightarrow \infty $ in (9). the distribution $g\left( w\right) $ is degenerate, the choice of $p\left( c_{t},w_{t}\right) $ reduces to that of $c\left( w_{t}\right) $ in (8). More formally, for $I\left( p\left( \cdot _{w};\cdot _{c}\right) \right) \rightarrow \infty $, the probabilities $g\left( w\right) $ and $p\left( \cdot _{w},\cdot _{c}\right) $ are degenerate. Using Fano's inequality (Thomas and Cover 1991), \[ c\left( \mathcal{I}\left( p\left( \cdot _{w};\cdot _{c}\right) \right) \right) =c\left( w\right) \] which makes the first order conditions for this case the full information solutions. The resulting optimal policy is given by \begin{equation} c_{t}^{\ast }\left( w_{t}\right) =\left( 1-\beta \right) w_{t}+\beta \bar{y}. \label{full_info_optpol} \end{equation} For comparison with the case with finite $\kappa $, I plot the policy function for the (discretized) full information case as the joint distribution $p\left( c,w\right) \delta _{c^{\ast }\left( w\right) }\left( c,w\right) $ with $\delta _{c^{\ast }\left( w\right) }$ the Dirac measure. Figure 1 plots such a distribution for a $20x20$ grid where the equi-spaced vector $c$ ranges from $0.8$ to $3$ and $w$ is also equi-spaced with support in $\left[ 1,10\right] $.](img98.gif)
Suppose now that capacity is low. In this case, rational consumers limit their processing effort by concentrating probability on the highest feasible value(s) of consumption. To see why, recall that consumers are risk averse (log-utility). They process the necessary information to learn where
the boundary ![]() is and avoid infeasible consumption bundles.11 Since the Shannon capacity places high restriction on information-processing, this individual consumes roughly the same amount each period, independently of his level of wealth.
is and avoid infeasible consumption bundles.11 Since the Shannon capacity places high restriction on information-processing, this individual consumes roughly the same amount each period, independently of his level of wealth.
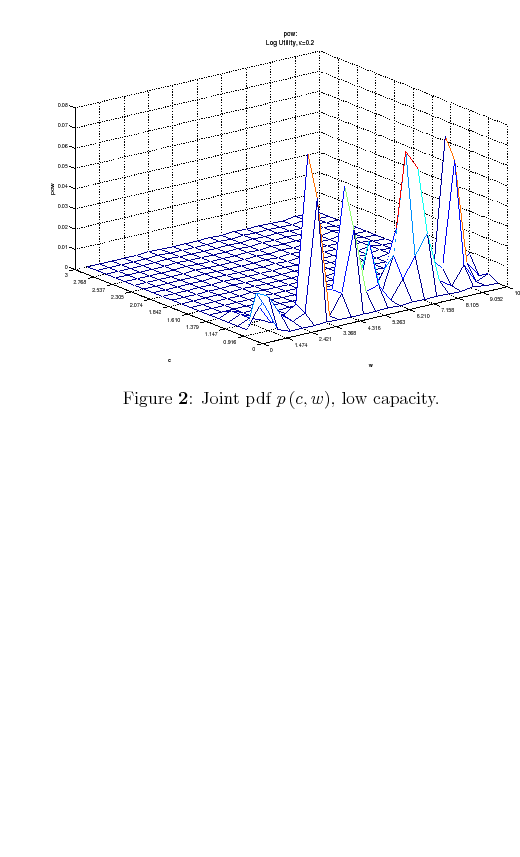
This case describes situations in which people have a vague idea of their wealth and prefer default savings/spending options (whether it is a pension plan or health insurance) rather than figuring out the exact consistency of their net worth. Figure 2 displays the
resulting optimal policy. Finally, Figure 3 displays the optimal joint distribution for an intermediate case,
![]() . The first observation is that a person with a finite information flow tries to make
. The first observation is that a person with a finite information flow tries to make
![]() as close to
as close to ![]() as the information constraint
allows him to.
as the information constraint
allows him to.
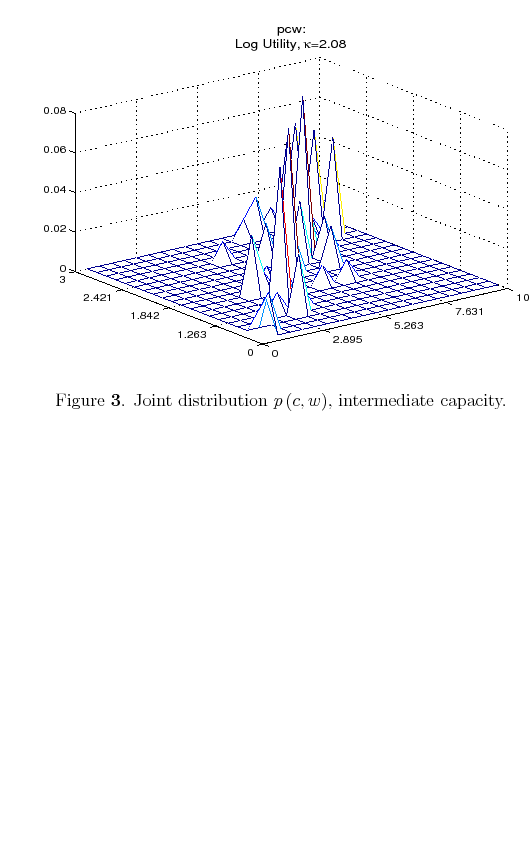
The second observation is that the optimal policy function for the information-constrained consumer places low weight, even no weight, on low values of consumption for high values of wealth. The reason why this happens depends on the utility function. A consumer with log-utility wants to maintain a consumption profile that is fairly smooth throughout the lifetime, as can be seen from (13). To avoid values of consumption that are either too low or too high, he needs to be well informed about such events to reduce the probability of their occurrence. The resulting optimal policy places a higher probability mass on the central values of consumption and wealth.
To see how the allocation of probability changes with the utility function, consider a consumer that differs from the previous only in the utility specification which now assume a CRRA form,
![]() with
with ![]() . As in the
previous case, the optimal policy function still places a close-to-zero probability on low values of consumption for high values of wealth but now the CRRA consumer trade off probabilities about modest values of consumption and wealth so that he can have high probability mass on high values of
consumption when wealth is high.
. As in the
previous case, the optimal policy function still places a close-to-zero probability on low values of consumption for high values of wealth but now the CRRA consumer trade off probabilities about modest values of consumption and wealth so that he can have high probability mass on high values of
consumption when wealth is high.
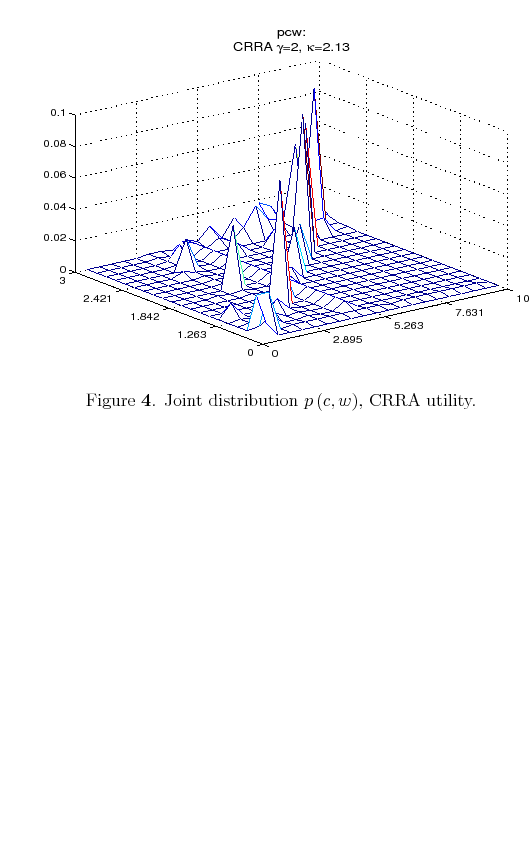
In other words, with CRRA preferences, individuals want to be better informed on low and middle values of wealth to enjoy high consumption in every period. Figure 4 illustrates this case.
3.2.2 Shannon's channel through the economic literature
The goal of this section is to compare my model with the literature in rational inattention. The first comparison is with the consumption saving model in the linear quadratic Gaussian (LQG) case 12 Sims(2003) fully characterizes the analytical solution of a consumption saving model where utility is quadratic,
![]() , constraints are linear and ex-ante optimal shape of uncertainty is Gaussian. In this LQG setting, the optimal distribution of ex-post uncertainty is
also Gaussian. The Gaussian solution make a model with rational inattention in the LQG case observationally equivalent to a signal extraction problem a la Lucas.
, constraints are linear and ex-ante optimal shape of uncertainty is Gaussian. In this LQG setting, the optimal distribution of ex-post uncertainty is
also Gaussian. The Gaussian solution make a model with rational inattention in the LQG case observationally equivalent to a signal extraction problem a la Lucas.
Note that the analytical solution in Sims (2003) cannot be recovered if one assume a restriction in the support of either ![]() or
or ![]() (e.g., the conventional
(e.g., the conventional ![]() ) or a no-borrowing constraint (e.g.,
) or a no-borrowing constraint (e.g.,
![]()
![]() ). This is because both constraints break the LQ
framework, necessary to obtain Gaussianity in the optimal ex-post uncertainty.
). This is because both constraints break the LQ
framework, necessary to obtain Gaussianity in the optimal ex-post uncertainty.
The second issue with the LQG approach is that the linear quadratic approximation gives valid predictions when uncertainty is small. This is similar to the argument for linearizing the first order condition of a problem and getting locally a good approximation. However, if one wants to explain an observed consumption and savings time series through limited processing constraints, the inertial behavior that we see in the data suggests that uncertainty is fairly big. Thus, the tractability of the LQG framework comes at the expense of effectiveness in matching the data.
The third issue, which is the most important for the purpose of this paper, is that rational inattention LQG models do not allow to explain different speed and amounts of reactions of people to different news about their wealth. For instance, consumption drops faster following a sudden layoff
than in the event of a tax break. Moreover, the magnitude of the change in consumption depends on people's attitude towards risk13 and their income
level14. The certainty equivalence framework that arises with Gaussian ex ante uncertainty and quadratic utility does not allow for endogenous
differentiation amongst these events. In such a setting, the speed and amount of households' reactions to different news are created by sources of inertia exogenous to the model. This has been one of the criticisms to signal extraction models a la Lucas and applies also to rational inattention
LQG.15 For instance, different reactions are generated by assuming that people have immediate access to some signals and not others, as in Lucas (1973) or
they receive independent information about different news, as in Ma![]() kowiak and Wiederholt (2008). In this paper, I choose another approach. I assume that information is freely available and I do not constrain
ex-ante uncertainty to be Gaussian. Moreover, I explore the link between risk aversion and information-processing limits by allowing utility specifications of the CRRA family.
kowiak and Wiederholt (2008). In this paper, I choose another approach. I assume that information is freely available and I do not constrain
ex-ante uncertainty to be Gaussian. Moreover, I explore the link between risk aversion and information-processing limits by allowing utility specifications of the CRRA family.
Before this paper, Sims (2006) solves a two period model with non-Gaussian ex-ante uncertainty and CRRA preferences. Sims (2006) assumes that agents live two periods, the first of which they are inattentive while the second period their uncertainty is resolved. This paper focuses on a fully dynamic rational inattention model. I depart from the work of Sims (2006) in two main dimensions. The first is conceptual. A fully dynamic model with rational inattention allows the researcher to investigate time series properties of consumption and savings. The resulting behavior reveals endogenous noise and delays of consumption in response to shock to income, with negative income shocks producing faster reactions effects as the risk aversion increases. The intuition for this result is the reaction of risk adverse individuals to signals that indicate a reduction in wealth is to immediately decrease their consumption for precautionary motives while collecting information over time about the consistency of their net worth. Complementary to these findings, richer dynamic makes the model suitable to address policy questions such as reaction to fiscal policy stimulus as I will show in the last section. This paper is also distinct from the one of Lewis (2008) . The most prominent differences are that, in Lewis (2008), households do not see consumption over time and they optimize over a finite horizon. Not observing consumption in turn implies that once the stream of probabilities is chosen at the beginning of period, the update of the beliefs is deterministic in the choice of the signal. While Lewis (2008)'s framework does deliver upward-sloping age profiles as average consumption over a fixed time length, it does not allow to study unconditional moments of consumption nor conditional response of consumption to shocks as in my framework.
The second contribution is methodological. A fully dynamic rational inattention model involves facing an infinite dimensional problem as displayed in (8)-(12). To work with this framework, I developed analytical and computation tools that are suitable to address the dynamics of a non-LQG model.
Moreover, my results are observational distinct from the previous literature on sticky information (Mankiw and Reis (2002)) and consumption and information (Reis (2006)). Mankiw and Reis (2002) assume that every period an exogenous fraction of agents (firms) obtain perfect information concerning all current and past disturbances, while all other firms set prices based on old information. Reis (2006) shows that a model with a fixed cost of obtaining perfect information can provide a microfoundation for this kind of slow diffusion of information. My model differs from the literature on inattentiveness in that I assume that information is freely available in each period but the bounds on information processing given by the Shannon channel force consumers to choose the scope of their information within the limit of their capacity. The interaction of information flow and risk aversion in my model delivers endogenous asymmetry in the response of consumption to shocks both in terms of speed and amount. This prediction constitutes a distinguishing feature of my model with respect to the literature of inattentiveness and, more generally, to the consumption-saving literature.
4.1 Discretizing the Framework
I consider wealth and consumption as defined on compact sets. In particular, admissible consumption profiles belong to
![]() Likewise, wealth has support
Likewise, wealth has support
![]() . I identify by
. I identify by ![]() the
elements of set
the
elements of set
![]() and by
and by ![]() the elements in
the elements in
![]() I approximate the state of the problem, i.e., the distribution of wealth by using the simplex:
I approximate the state of the problem, i.e., the distribution of wealth by using the simplex:
- Definition
- The set
 of all mappings
of all mappings
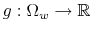 fulfilling
fulfilling
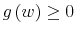 for all
for all
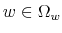 and
and
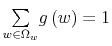 is called a simplex. Elements
is called a simplex. Elements 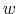 of
of
 are called vertices of the simplex
are called vertices of the simplex 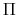 ,
functions
,
functions 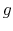 are called points of
are called points of 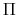 .
.
Let
![]() be the dimension of the belief simplex which approximates the distribution
be the dimension of the belief simplex which approximates the distribution
![]() and let
and let
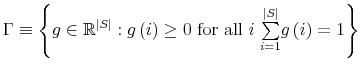 denote the set of all probability distribution on
denote the set of all probability distribution on ![]() . The initial condition for the problem is
. The initial condition for the problem is
![]()
The consumer enters each period choosing the joint distribution of consumption and financial possibilities. From the previous section, the control variable for the discretized set up as the probability mass function
![]() where
where
![]() and
and
![]() , constrained to belong to the set of distributions. Given
, constrained to belong to the set of distributions. Given
![]() and
and
![]() and the observation of
and the observation of ![]() consumed in period
consumed in period
![]() the belief state is updated using Bayesian conditioning:
the belief state is updated using Bayesian conditioning:
where
The interpretation of (15) is akin to its continuous counterpart. The capacity of the agents to process information is constrained by a number,
4.2 Recursive Formulation
The purpose of this section is to show that the discrete dynamic programming problem has a solution and to recast it into a Bellman recursion. To show that a solution exists, first note that the set of constraints for the problem is a compact-valued concave correspondence. Second, I need to show
that the state space is compact. Compactness comes from the curvature of the utility function and the fact that the belief space has a bounded support in
![]() . The compact domain of the state and the fact that Bayesian conditioning for the update preserves the Markovianity of the belief state ensures that the transition
. The compact domain of the state and the fact that Bayesian conditioning for the update preserves the Markovianity of the belief state ensures that the transition
![]() and (14) has the Feller property. Then, the conditions for applying the Theorem of
the Maximum are fulfilled which guarantees the existence of a solution. In the next section, I provide sufficient conditions to guarantee uniqueness.
and (14) has the Feller property. Then, the conditions for applying the Theorem of
the Maximum are fulfilled which guarantees the existence of a solution. In the next section, I provide sufficient conditions to guarantee uniqueness.
Casting the problem of the consumer in a recursive Bellman equation formulation, the full discrete-time Markov program amounts to:
subject to:
![]()
where
The Bellman equation in (17) takes up as its argument the marginal distribution of wealth
![]() and uses as the control variable the joint distribution of wealth and consumption,
and uses as the control variable the joint distribution of wealth and consumption,
![]() . The latter links the behavior of the agent with respect to consumption
. The latter links the behavior of the agent with respect to consumption
![]() , on one hand, and income
, on one hand, and income
![]() on the other, hence specifying the actions over time. The first term on the right hand side of (17) is the utility function
on the other, hence specifying the actions over time. The first term on the right hand side of (17) is the utility function
![]() . The second term,
. The second term,
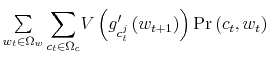 , represents the
expected continuation value of being in state
, represents the
expected continuation value of being in state
![]() discounted by the factor
discounted by the factor
![]() . This corresponds to interest rate
. This corresponds to interest rate ![]() which gives an
annualized gross real rate of investment
which gives an
annualized gross real rate of investment
![]() , with a quarterly frequency of the data. The expectation is taken with respect to the endogenously chosen distribution
, with a quarterly frequency of the data. The expectation is taken with respect to the endogenously chosen distribution
![]() . I have discussed the relations in (18)-(21) earlier. Moreover, I appended the equation in (20) which constrains the choice of the distribution to be consistent with the initial prior
. I have discussed the relations in (18)-(21) earlier. Moreover, I appended the equation in (20) which constrains the choice of the distribution to be consistent with the initial prior
![]()
Next, I analyze the main properties of the Bellman recursion (17) and derive conditions under which it is a contraction mapping and show that the mapping is isotone.
4.3 Properties of the Bellman Recursion
To prove that the value function is a contraction and an isotonic mapping, I shall introduce the relevant definitions. Let me restrict attention to choices of probability distributions that satisfy the constraints (18)-(21). To make the notation
more compact, let
![]() ,
,
![]() ,
,
![]() and let
and let ![]() be the set that contains (18)-(21). I introduce the following definitions:
be the set that contains (18)-(21). I introduce the following definitions:
- D1.
- A control probability distribution
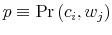 is feasible for the problem (17)-(21) if
is feasible for the problem (17)-(21) if
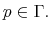 Let
Let
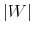 be the cardinality of
be the cardinality of
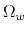 and let
denote the set of all probability distributions on
and let
denote the set of all probability distributions on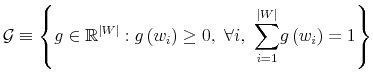
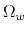 . An optimal policy has a value function that satisfies the Bellman optimality equation in (17):
. An optimal policy has a value function that satisfies the Bellman optimality equation in (17):
The Bellman optimality equation can be expressed in value function mapping form. Let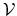 be the set of all bounded real-valued functions
be the set of all bounded real-valued functions 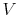 on
on
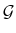 and let
and let
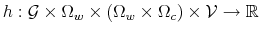 be defined as follows:
Define the value function mapping
be defined as follows:
Define the value function mapping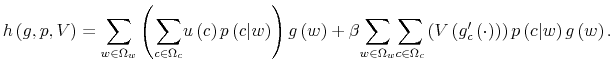
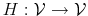 as
as
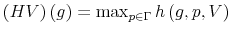 .
. - D2.
- A value function
 dominates another value function
dominates another value function  if
if
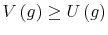 for all
for all
- D3.
- A mapping
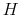 is isotone if
is isotone if 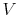 ,
,
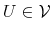 and
and 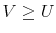 imply
imply
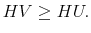
- D4.
- A supremum norm of two value functions
 ,
,
 over
over
 is defined as
is defined as
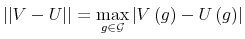
- D5.
- A mapping
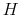 is a contraction under the supremum norm if for all
is a contraction under the supremum norm if for all 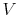 ,
,
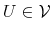 ,
holds for some
,
holds for some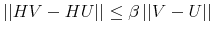
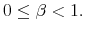
Endowed with these notion, it is possible to derive some properties of the solution to the Bellman equation.
First, note that the uniqueness of the solution to which the value function converges to requires concavity of the constraints and convexity of the objective function. It is immediate to see that all the constraints but (18) are actually linear in
![]() and
and
![]() . For (18), the concavity of
. For (18), the concavity of
![]() is guaranteed by Theorem (16.1.6) of Thomas and Cover (1991). The concavity of
is guaranteed by Theorem (16.1.6) of Thomas and Cover (1991). The concavity of
![]() is the result of the following:
is the result of the following:
- Lemma 1.
- For a given
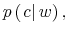 the expression (18) is concave in
the expression (18) is concave in
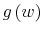 .
.
Next, I need to prove the convexity of the value function and the fact that the value iteration is a contraction mapping. All the proofs are in Appendix A.
- Proposition 1.
- For the discrete Rational Inattention Consumption Saving value recursion
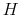 and two given functions
and two given functions 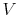 and
and 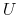 , it holds that
with
, it holds that
with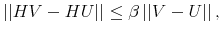
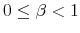 and
and
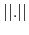 the supreme norm. That is, the value recursion
the supreme norm. That is, the value recursion  is a contraction mapping.
is a contraction mapping.
Proposition 1 can be explained as follows. The space of value functions defines a vector space and the contraction property ensures that the space is complete. Therefore, the space of the value functions together with the supreme norm form a Banach space; the Banach fixed-point theorem ensures (a) the existence of a single fixed point and (b) that the value recursion always converges to this fixed point (see Theorem 6 of Alvarez and Stockey, 1998 and Theorem 6.2.3 of Puterman, 1994).
- Corollary
- For the discrete Rational Inattention Consumption Saving value recursion
 and two given functions
and two given functions 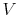 and
and 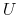 , it holds that
that is the value recursion
, it holds that
that is the value recursion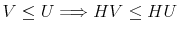
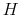 is an isotonic mapping.
is an isotonic mapping.
The isotonic property of the value recursion ensures that the value iteration converges monotonically.
These theoretical results establish that in principle there is no barrier in defining value iteration algorithms for the Bellman recursion for the discrete rational inattention consumption-savings model.
5 Numerical Technique and its Predictions
I solve the model by transforming the underlying partially observable Markov decision process into an equivalent, fully observable Markov decision process with a state space that consists of all probability distributions over the core 17 state of the model (wealth).
For a model with ![]() core states,
core states,
![]() , the transformed state space is the
, the transformed state space is the
![]() -dimensional simplex, or belief simplex. Expressed in plain terms, a belief simplex is a point, a line segment, a triangle or a tethraedon in a
single, two, three or four-dimensional space, respectively. Formally, a belief simplex is defined as the convex hull18 of
belief states from an affinely independent19 set
-dimensional simplex, or belief simplex. Expressed in plain terms, a belief simplex is a point, a line segment, a triangle or a tethraedon in a
single, two, three or four-dimensional space, respectively. Formally, a belief simplex is defined as the convex hull18 of
belief states from an affinely independent19 set ![]() . The points of
. The points of ![]() are the vertices of the belief simplex. The convex hull formed by any subset of
are the vertices of the belief simplex. The convex hull formed by any subset of ![]() is a face of the belief simplex. To address the issue of dimensionality in the state space of my model, I use a grid-based approximation approach. The idea of a grid based approach is to use a finite grid to discretize the uncountably
infinite continuous state space. The implementation has the following steps: I place a finite grid over the simplex point, I compute the values for points in the grid, and I use a kernel regression to interpolate solution points that fall outside the grid.
is a face of the belief simplex. To address the issue of dimensionality in the state space of my model, I use a grid-based approximation approach. The idea of a grid based approach is to use a finite grid to discretize the uncountably
infinite continuous state space. The implementation has the following steps: I place a finite grid over the simplex point, I compute the values for points in the grid, and I use a kernel regression to interpolate solution points that fall outside the grid.
5.1 Belief Simplex and Dynamic Programming
If full information were available, previous history of the process would be irrelevant to the problem. However, because the consumer cannot completely observe wealth, he may require all the past information about the system to behave optimally. The most general approach is to keep track of the
entire history of his previous consumption purchases up to time ![]() , denoted
, denoted
![]() . For any given initial state probability distribution
. For any given initial state probability distribution ![]() , the number of possible histories is
, the number of possible histories is
![]() with
with
![]() denoting the set of consumption behavior up to time
denoting the set of consumption behavior up to time ![]() . This number
goes to infinity as the decision horizon approaches infinity, which makes this method of representing history useless for infinite-horizon problems.
. This number
goes to infinity as the decision horizon approaches infinity, which makes this method of representing history useless for infinite-horizon problems.
To overcome this issue, Astrom (1965) proposed an information state approach. It is based upon the idea that all the information needed to act optimally can be summarized by a vector of probabilities over the system, the belief state. Let
![]() denote the probability that the wealth is in state
denote the probability that the wealth is in state
![]() where
where
![]() is assumed to be a finite set. Probability distributions such as
is assumed to be a finite set. Probability distributions such as
![]() that are defined on finite sets are in fact simplices. Let
that are defined on finite sets are in fact simplices. Let ![]() be the possible values that
be the possible values that ![]() can assume. The discretization of the core state is an equi-spaced grid with
can assume. The discretization of the core state is an equi-spaced grid with ![]() values of
values of ![]() ranging from 1 to 10. The points in the simplex
ranging from 1 to 10. The points in the simplex ![]() are
are ![]() distinct values for the marginal pdf
distinct values for the marginal pdf
![]() in the interval
in the interval
![]() . The simplex is constructed using uniform random samples from the unit simplex. The reason why I use this methodology is that it is computationally faster than
non-uniform grid and it is able to handle higher dimensional space.20 In my model, each point in the simplex is an
. The simplex is constructed using uniform random samples from the unit simplex. The reason why I use this methodology is that it is computationally faster than
non-uniform grid and it is able to handle higher dimensional space.20 In my model, each point in the simplex is an ![]() -array whose column contains
-array whose column contains ![]() random values in the
random values in the
![]() range and whose sum per row is 1. To span the simplex I use
range and whose sum per row is 1. To span the simplex I use
![]() .21 The distribution of
values within the simplex is uniform in the sense that it has the conditional probability of a uniform distribution over the whole
.21 The distribution of
values within the simplex is uniform in the sense that it has the conditional probability of a uniform distribution over the whole ![]() -cube, given that the sum per row is
-cube, given that the sum per row is ![]() . The algorithm calls three types of random processes that determine the placement of random points in the
. The algorithm calls three types of random processes that determine the placement of random points in the ![]() dimensional simplex. The first process considers values uniformly within each simplex. The second random process selects samples of different types of simplex in proportion to their volume. Finally, the third process implements a random permutation in order to have an even
distribution of simplex choices among types.
dimensional simplex. The first process considers values uniformly within each simplex. The second random process selects samples of different types of simplex in proportion to their volume. Finally, the third process implements a random permutation in order to have an even
distribution of simplex choices among types.
For each simplex point, I initialize the corresponding joint distribution of consumption ![]() and wealth
and wealth ![]() . I assume
. I assume ![]() equi-spaced values for
equi-spaced values for ![]() ranging
in
ranging
in
![]() . The values in
. The values in
![]() are chosen so that
are chosen so that ![]() is about 3 times
is about 3 times ![]() , roughly consistent with individual data on consumption and wealth.
, roughly consistent with individual data on consumption and wealth.
Let core states and behavior states be sorted in descending order. I impose the constraint ![]() ,22. Then, given the symmetry in the dimensionality of
,22. Then, given the symmetry in the dimensionality of
![]() and
and
![]() , the joint distribution of consumption and wealth for a given multidimensional grid point is square matrix with rows corresponding to levels of consumption. Summing the matrix per
row results in the marginal distribution of consumption,
, the joint distribution of consumption and wealth for a given multidimensional grid point is square matrix with rows corresponding to levels of consumption. Summing the matrix per
row results in the marginal distribution of consumption,
![]() . Likewise, the columns of the matrix correspond to levels of wealth. Evaluating the sum per columns of the matrix amounts to the marginal pdf of wealth,
. Likewise, the columns of the matrix correspond to levels of wealth. Evaluating the sum per columns of the matrix amounts to the marginal pdf of wealth,
![]() . Given the initial belief simplex, its successor belief states can be determined by Bayesian conditioning at each multidimensional point of the simplex and gives the
expression:
. Given the initial belief simplex, its successor belief states can be determined by Bayesian conditioning at each multidimensional point of the simplex and gives the
expression:
Let
![]() be the set of all bounded real-valued function
be the set of all bounded real-valued function ![]() on
on ![]() . Then, the Bellman optimality equation of the household is described by (17)-(21).
. Then, the Bellman optimality equation of the household is described by (17)-(21).
Without loss of generality, I restrict the columns of the matrix
![]() to sum to the marginal pdf of wealth in the main diagonal. Moreover, because some of the values of the marginal
to sum to the marginal pdf of wealth in the main diagonal. Moreover, because some of the values of the marginal
![]() per simplex-point are exactly zero given the definition of the envelope for the simplex, I constrain the choices of the joint distributions corresponding to those values to
be zero. This handling of the zeroes makes the parameter vector being optimized over have different lengths for different rows of the simplex. Hence the degrees of freedom in the choice of the control variables for simplex points vary from a minimum of 0 to a maximum of
per simplex-point are exactly zero given the definition of the envelope for the simplex, I constrain the choices of the joint distributions corresponding to those values to
be zero. This handling of the zeroes makes the parameter vector being optimized over have different lengths for different rows of the simplex. Hence the degrees of freedom in the choice of the control variables for simplex points vary from a minimum of 0 to a maximum of
![]() .23 Once the
belief simplex is set up, I initialize the joint probability distribution of consumption and wealth per belief point and solve the program of the household by backward induction iterating on the value function
.23 Once the
belief simplex is set up, I initialize the joint probability distribution of consumption and wealth per belief point and solve the program of the household by backward induction iterating on the value function
![]() . To map the finer state space into Matlab possibilities, I interpolate the value function with the new values of (23) using a
kernel regression of
. To map the finer state space into Matlab possibilities, I interpolate the value function with the new values of (23) using a
kernel regression of
![]() into
into
![]() I use an Epanechnikov kernel with smoothing parameter
I use an Epanechnikov kernel with smoothing parameter ![]() . 24 A kernel regression approximates the exact non linear value function in (17) with a
piece-wise linear function. The following propositions illustrate this point.
. 24 A kernel regression approximates the exact non linear value function in (17) with a
piece-wise linear function. The following propositions illustrate this point.
- Proposition 2.
- If the utility is CRRA with a parameter of risk aversion
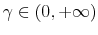 and if
and if 
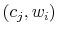 satisfies (18)-(21), then the optimal
satisfies (18)-(21), then the optimal  value function
value function
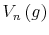 defined over
defined over  can be expressed as:
where the
can be expressed as:
where the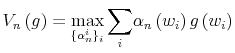
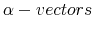 ,
,
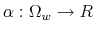 , are
, are
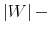 dimensional hyperplanes.
dimensional hyperplanes.
Intuitively, each
![]() vector corresponds to a plan and the action associated with a given
vector corresponds to a plan and the action associated with a given
![]() vector is the optimal action for planning horizon
vector is the optimal action for planning horizon ![]() for all priors
that have such a function as the maximizing one. With the above definition, the value function amounts to:
for all priors
that have such a function as the maximizing one. With the above definition, the value function amounts to:
Using the above proposition and the fact that the set of all consumption profiles
![]() is discrete, it is possible to show directly the convex properties for the value function. For fixed
is discrete, it is possible to show directly the convex properties for the value function. For fixed
![]() vectors, the
vectors, the
![]() operator is linear in the belief space. Therefore, the convex property is given by the fact that
operator is linear in the belief space. Therefore, the convex property is given by the fact that ![]() is defined as the maximum of a set of convex (linear) functions and, thus, obtains a convex function as a result. The optimal value function
is defined as the maximum of a set of convex (linear) functions and, thus, obtains a convex function as a result. The optimal value function ![]() is the limit for
is the limit for
![]() and, becuase all the
and, becuase all the ![]() are convex function, so is
are convex function, so is
![]() .
.
- Proposition 3.
- Assuming the CRRA utility function and the conditions of Proposition 1, let
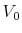 be an initial value function that is piecewise linear
and convex. Then the
be an initial value function that is piecewise linear
and convex. Then the 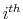 value function obtained after a finite number of update steps for a rational inattention consumption-saving problem is also finite,
piecewise linear and convex (PCWL).
value function obtained after a finite number of update steps for a rational inattention consumption-saving problem is also finite,
piecewise linear and convex (PCWL).
To implement numerically the optimization of the value function at each point of the simplex, I use Sims' CSMINWEL as a gradient-based search method and iterate on the value function up to convergence. The value iteration converges in about 202 iterations. Table 1 reports the benchmark parameter values and the grids.
I simulate the model for ![]() periods by drawing from the optimal policy function,
periods by drawing from the optimal policy function,
![]() , and generate the time series path of consumption, wealth and expected wealth. For each
, and generate the time series path of consumption, wealth and expected wealth. For each ![]() , I use the joint distribution
, I use the joint distribution
![]() to evaluate the time path of information flow (
to evaluate the time path of information flow (
![]() ). Finally, I derive the impulse response functions for the economy by
assuming temporary shocks to the mean of income,
). Finally, I derive the impulse response functions for the economy by
assuming temporary shocks to the mean of income, ![]() . A pseudocode that implements the procedure is in Appendix C.
. A pseudocode that implements the procedure is in Appendix C.
| Discretization | |
|---|---|
| Wealth Space |
|
| Consumption Space |
|
| Mean of Income, |
1.1 |
| Joint Distribution per simplex point,
|
20 |
| Marginal |
20 |
| Marginal |
20 |
| Coeff. risk aversion, |
1 |
| Interest rate, |
1.012 |
| Discount Factor, |
0.9881 |
6 Results
In this section, I investigate the dynamic interplay of information flow and degree of risk aversion. In particular, I study different specifications of the baseline model changing degrees of risk aversion,
![]() , and different Lagrange multipliers,
, and different Lagrange multipliers,
![]() , representing the shadow costs of processing information in (18). Time path for each individual are average across simplex points. For the
time series of the aggregate economy, I perform
, representing the shadow costs of processing information in (18). Time path for each individual are average across simplex points. For the
time series of the aggregate economy, I perform ![]() Monte Carlo runs and simulate the model for each path for
Monte Carlo runs and simulate the model for each path for ![]() periods. Then, I compute average across runs and simplex-points. Sample statistics are calculated after I compute these averages. I choose this way of calculating average to compare my model, tailored for individual behavior, to aggregate data. I divide the
results into three parts: (1) interaction of information flow and risk aversion; (2) implications of information constraint on lifetime consumption; and (3) consumption reaction to temporary income shocks.
periods. Then, I compute average across runs and simplex-points. Sample statistics are calculated after I compute these averages. I choose this way of calculating average to compare my model, tailored for individual behavior, to aggregate data. I divide the
results into three parts: (1) interaction of information flow and risk aversion; (2) implications of information constraint on lifetime consumption; and (3) consumption reaction to temporary income shocks.
| CRRA |
CRRA |
Log Utility | CRRA |
|
|---|---|---|---|---|
|
|
1.01 | 0.98 | 0.91 | 0.83 |
|
|
0.15 | 0.18 | 0.21 | 0.33 |
|
|
1.41 | 1.20 | 0.86 | 0.78 |
| 1.14 | 1.09 | 1.08 | 1.02 | |
| 0.08 | 0.09 | 0.11 | 0.14 | |
| 2.03 | 1.99 | 1.87 | 1.72 |
- Result 1. Information flow and risk aversion
- In the discrete rational inattention consumption-savings model, higher degrees of risk aversion result in a higher amount of information processed for a given processing cost. Moreover, for a given degree of risk aversion, as the information flow decreases, the volatility of consumption increases.
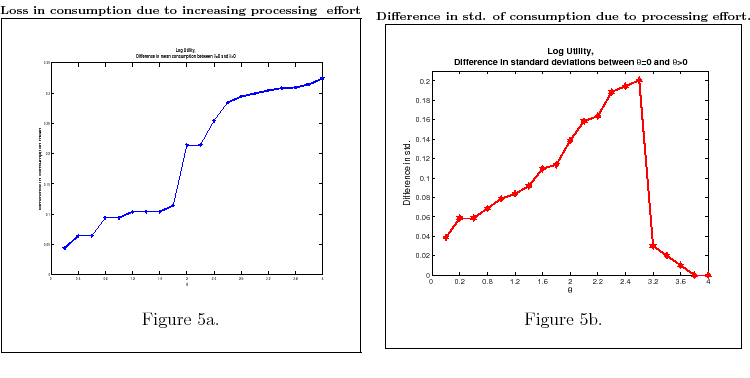
This finding is documented in Table 2 and in Figures 5-6. Figure 5a plots the difference between the mean of the time series of consumption between ![]() and
and ![]() . After deriving the time path of consumption as described above, I calculate the mean and standard deviation of the average of the time path and subtract from it the mean of the time path
for the full information equivalent (
. After deriving the time path of consumption as described above, I calculate the mean and standard deviation of the average of the time path and subtract from it the mean of the time path
for the full information equivalent (![]() ).25 Figure 5a shows how this difference changes as
).25 Figure 5a shows how this difference changes as ![]() varies and when utility is logarithmic. Figure 5b plots the corresponding difference in standard deviation
of consumption as a function of
varies and when utility is logarithmic. Figure 5b plots the corresponding difference in standard deviation
of consumption as a function of ![]() .
.
To understand this result, consider what happens in the full information (![]() ) case. With
) case. With ![]() , the agent smooths consumption regardless of his utility. To appreciate how preferences towards risk play out with processing limits (
, the agent smooths consumption regardless of his utility. To appreciate how preferences towards risk play out with processing limits (![]() ), consider
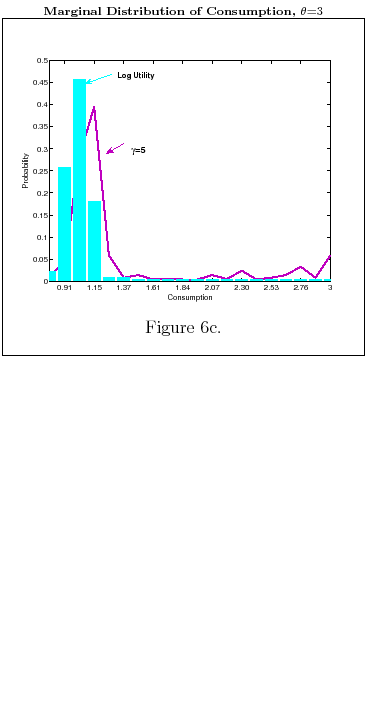
Figure 6c. It plots the optimal distribution of consumption for two individuals (
), consider
Figure 6c. It plots the optimal distribution of consumption for two individuals (
![]() and
and ![]() ) when information is very costly to process
(
) when information is very costly to process
(![]() ). In this case, a rational agent consumes a fixed amount every period in the limits of his net worth. This requires very little bits of information. In Figure 6c note how a person
with log-utility puts probability mass mostly on the lower values of consumption while a more risk averse agent sacrifices smoothing consumption to allocate some probability on higher values of consumption. Assuming the same
). In this case, a rational agent consumes a fixed amount every period in the limits of his net worth. This requires very little bits of information. In Figure 6c note how a person
with log-utility puts probability mass mostly on the lower values of consumption while a more risk averse agent sacrifices smoothing consumption to allocate some probability on higher values of consumption. Assuming the same ![]() the resulting effect is solely due to consumer preference. Now consider Table 2 and Figures 6a-6b.
the resulting effect is solely due to consumer preference. Now consider Table 2 and Figures 6a-6b.
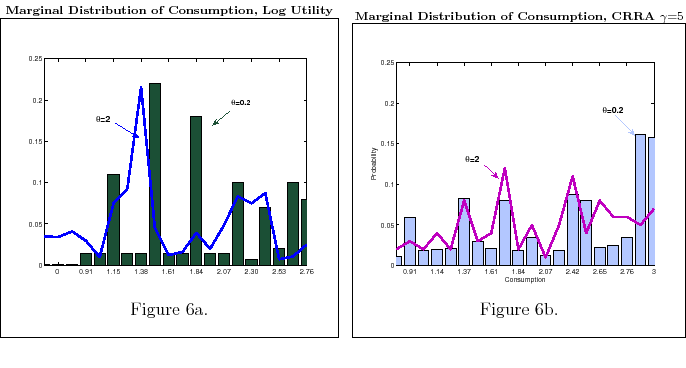
When ![]() , people select how much information they want to process and which values of wealth to be better informed about according to their utility. Also in this case, the higher the
degree of risk aversion, the higher the quest for information (
, people select how much information they want to process and which values of wealth to be better informed about according to their utility. Also in this case, the higher the
degree of risk aversion, the higher the quest for information (![]() ). This is exactly what Table 2 shows. In the table, the higher the coefficient of risk aversion,
). This is exactly what Table 2 shows. In the table, the higher the coefficient of risk aversion, ![]() , the higher the information collected by the agent,
, the higher the information collected by the agent, ![]() , and the higher the mean of
consumption. The same story can be told in terms of probability distribution as in 6a-6c. For a given level of
, and the higher the mean of
consumption. The same story can be told in terms of probability distribution as in 6a-6c. For a given level of ![]() , a person with log utility would be better informed on extreme values of
wealth to avoid such values. This knowledge makes it possible to assign high probability to the middle value of consumption, as his utility commands. By contrast, a consumer with CRRA,
, a person with log utility would be better informed on extreme values of
wealth to avoid such values. This knowledge makes it possible to assign high probability to the middle value of consumption, as his utility commands. By contrast, a consumer with CRRA, ![]() , wants to avoid low values of consumption for high values of wealth. Processing information about these events decreases the likelihood of their occurrence and makes it possible to place high probability on high value of consumption. This mechanism makes consumption more
persistent for people with a higher degree of risk aversion (cfr. Figure 6a-6c).
, wants to avoid low values of consumption for high values of wealth. Processing information about these events decreases the likelihood of their occurrence and makes it possible to place high probability on high value of consumption. This mechanism makes consumption more
persistent for people with a higher degree of risk aversion (cfr. Figure 6a-6c).
Processing capacity (![]() ) strengthens this effect. This is because high information flow allows consumers to enjoy high and smooth consumption throughout their life time. If information
flows at very low rate, households update their knowledge slowly over time and wait to modify their behavior until they have sufficient knowledge of their financial possibilities. Inertial behavior of consumption due to low information flow induces sharp changes in consumption after the consumer
accumulates information. This mechanism makes consumption more volatile for people with lower information flow.
) strengthens this effect. This is because high information flow allows consumers to enjoy high and smooth consumption throughout their life time. If information
flows at very low rate, households update their knowledge slowly over time and wait to modify their behavior until they have sufficient knowledge of their financial possibilities. Inertial behavior of consumption due to low information flow induces sharp changes in consumption after the consumer
accumulates information. This mechanism makes consumption more volatile for people with lower information flow.
Figure 5b plots the standard deviation of consumption for several values of ![]() . As pointed out, for very high shadow cost of processing information
. As pointed out, for very high shadow cost of processing information ![]() , consumption does not vary over time. For
, consumption does not vary over time. For
![]() , the volatility of consumption increases with
, the volatility of consumption increases with ![]() . This result
makes sense. To see why, consider again the full information version of the model. People's will to smooth consumption in full information is limited by the finite flow of information available. When deciding on the precision of their signals, risk averse people trade off lower volatility in
consumption for better knowledge of low value of wealth.
. This result
makes sense. To see why, consider again the full information version of the model. People's will to smooth consumption in full information is limited by the finite flow of information available. When deciding on the precision of their signals, risk averse people trade off lower volatility in
consumption for better knowledge of low value of wealth.
The time series path of consumption, wealth and information flow drawn from the optimal policy
![]() confirm this result and offer further insights on the properties of the model.
confirm this result and offer further insights on the properties of the model.
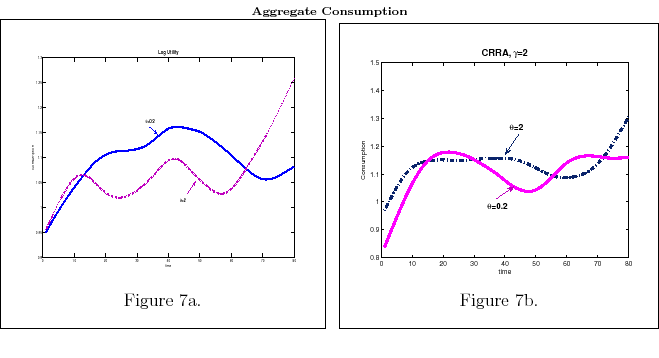
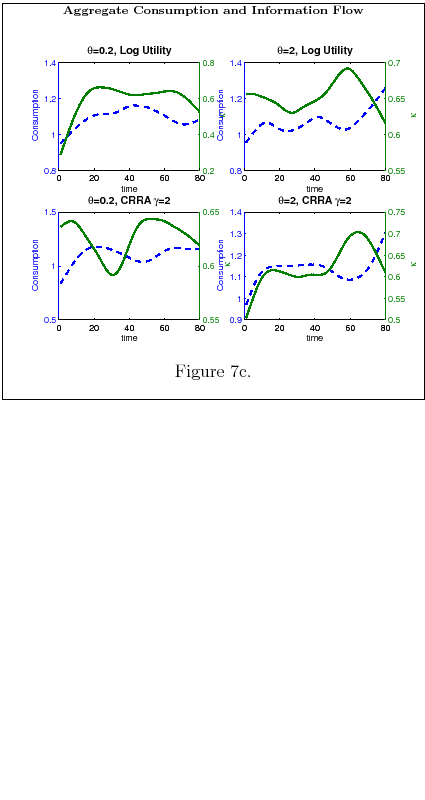
- Result 2. Time path of consumption and savings.
- Changes in consumption over time are infrequent and significant. Moreover:
- Consumption is hump-shamped. It gets to its peak later for individual that have low information flow. The effect is stronger as the degree of risk aversion increases..
- Individuals with high information flow, by having sharper signals on their wealth, have savings behavior that follows closely their wealth. Furthermore, the lower the degree of risk aversion, the higher the fluctuations of savings per period.
- Individuals with low information flow, tend to consume a constant amount every period. They increase their consumption only if the information they process points them towards a significant increase in wealth. The higher the degree of risk aversion, the less volatile the time path of consumption for these types.
Figures 7-8 illustrate these points for aggregate and individual time series behavior, respectively. The simulations are derived by drawing the time path of consumption and wealth from
![]() , after the value iteration has converged. Figures 7a-7c plot the average across the Monte Carlo runs and simplex points (i.e., initial beliefs about wealth).
Individual time series (Figures 8a-8b) are an average of initial beliefs. To have some interesting transitional dynamics, I begin the simulation with an initial condition for wealth far from the steady state26.
, after the value iteration has converged. Figures 7a-7c plot the average across the Monte Carlo runs and simplex points (i.e., initial beliefs about wealth).
Individual time series (Figures 8a-8b) are an average of initial beliefs. To have some interesting transitional dynamics, I begin the simulation with an initial condition for wealth far from the steady state26.
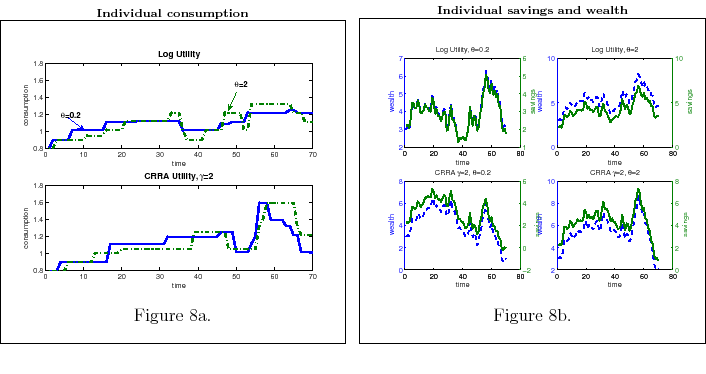
To appreciate the results, consider what would happen with full information. In such a case, consumption smoothing (![]() ) implies an immediate (
) implies an immediate (![]() ) adjustment of consumption to its long-run optimal values and no transient behavior. Thus, in that case from
) adjustment of consumption to its long-run optimal values and no transient behavior. Thus, in that case from ![]() onwards, the simulations lead to a constant time path. Now consider Figures 7(a-c)-8(a,b). The hump in consumption comes from Result 1 and a simple intuition: information-constrained people are cautious (degree of risk aversion
onwards, the simulations lead to a constant time path. Now consider Figures 7(a-c)-8(a,b). The hump in consumption comes from Result 1 and a simple intuition: information-constrained people are cautious (degree of risk aversion
![]() ), consume a little and collect information about wealth before they change consumption. For a fixed
), consume a little and collect information about wealth before they change consumption. For a fixed ![]() , the more risk averse they are (cfr. Figure 7a with log utility and Figure 7b with CRRA,
, the more risk averse they are (cfr. Figure 7a with log utility and Figure 7b with CRRA, ![]() ), the longer they wait before increasing their
consumption. This inertial behavior in consumption leads to an increase in savings and, as a result, in wealth (cfr. Figure 8a-8b). Processed information keeps signaling the increase in wealth until households realize that they are wealthy enough to increase their consumption. Thus, the hump in
consumption is the mirrored image of the rise (until people know they rich) and fall (once people know they are rich) in wealth. Note that, depending on the history of income shocks, consumption can have more than one hump in its path. To see why, consider a high realization of income occurring
after a hump in consumption. Over time, signals about wealth convey such information, consumers start saving and history as well as humps repeat themselves. These effects are enhanced by the shadow cost of processing information,
), the longer they wait before increasing their
consumption. This inertial behavior in consumption leads to an increase in savings and, as a result, in wealth (cfr. Figure 8a-8b). Processed information keeps signaling the increase in wealth until households realize that they are wealthy enough to increase their consumption. Thus, the hump in
consumption is the mirrored image of the rise (until people know they rich) and fall (once people know they are rich) in wealth. Note that, depending on the history of income shocks, consumption can have more than one hump in its path. To see why, consider a high realization of income occurring
after a hump in consumption. Over time, signals about wealth convey such information, consumers start saving and history as well as humps repeat themselves. These effects are enhanced by the shadow cost of processing information, ![]() , with higher costs forcing long periods of inertia in consumption followed by sizeable changes. Note also the relationship between consumption and information flow (Figure 7c): risk averse agents would rather push forward consumption in times in which
they are processing information about wealth. Finally, note from 7(a-b)-8(a,b) how the peak in consumption occurs later for an individual with higher degree of risk aversion and lower information flow. The rationale for this result is that more cautious people wait to be better informed about their
wealth before modifying their consumption behavior. In particular, since a consumer with CRRA utility (
, with higher costs forcing long periods of inertia in consumption followed by sizeable changes. Note also the relationship between consumption and information flow (Figure 7c): risk averse agents would rather push forward consumption in times in which
they are processing information about wealth. Finally, note from 7(a-b)-8(a,b) how the peak in consumption occurs later for an individual with higher degree of risk aversion and lower information flow. The rationale for this result is that more cautious people wait to be better informed about their
wealth before modifying their consumption behavior. In particular, since a consumer with CRRA utility (![]() ) chooses to be better informed about low values of wealth than a log utility
consumer (cfr. Figures 7a and 7b), he processes news about high value of wealth slower than his log counterpart. The resulting additional savings for precautionary motives are triggered by both the curvature of the utility function and the bound on information-processing constraint.
) chooses to be better informed about low values of wealth than a log utility
consumer (cfr. Figures 7a and 7b), he processes news about high value of wealth slower than his log counterpart. The resulting additional savings for precautionary motives are triggered by both the curvature of the utility function and the bound on information-processing constraint.
The last result comes from studying how consumers with limited processing capacity react to temporary shocks to income (![]() ). Before stating the result, it is worth comparing to the
predictions of standard consumption-saving literature. With full information, the response of consumption to either negative and positive temporary income shocks are immediate: consumption adjust in period
). Before stating the result, it is worth comparing to the
predictions of standard consumption-saving literature. With full information, the response of consumption to either negative and positive temporary income shocks are immediate: consumption adjust in period ![]() to an amount exactly equal to the discounted present value of the shock,
to an amount exactly equal to the discounted present value of the shock,
![]() . This is the case regardless whether the shock is adverse or favorable, so long as the absolute value of these shocks match. The same holds true under
certainty-equivalence with a linear constraints and quadratic utility (LQ) framework. With risk averse agents and information-processing limits, it happens that:
. This is the case regardless whether the shock is adverse or favorable, so long as the absolute value of these shocks match. The same holds true under
certainty-equivalence with a linear constraints and quadratic utility (LQ) framework. With risk averse agents and information-processing limits, it happens that:
- Result 3. Persistent stickiness and asymmetric response to shocks.
- Consumption's response to temporary fluctuations of wealth is asymmetric: Negative shocks trigger a sharper reaction and higher persistence of consumption than positive ones.
The logic behind this result is easily understood by considering the interdependence of information flow and coefficient of risk aversion. A risk averse person is more likely to be affected by negative events than positive ones. As soon as he receives signals that his wealth is lower than what he thought, he reacts by decreasing his consumption. The change in behavior and its persistence are more consistent the more risk averse and uninformed the consumer is. This occurs because consumers wait to gather more information before changing their behavior and, in the meanwhile, build up a savings buffer. Thus, the temporary change in income propagates slowly over time. A positive temporary income shock triggers the opposite behavior in a risk averse uninformed person. The intuition is that this type of consumer is concerned about negative wealth fluctuations and allocates most of his information capacity to prevent this event. A signal that indicates positive wealth may be ignored, generating extra savings in the meanwhile. Once this is acknowledged, a prudent consumer distributes the additional consumption driven by the income shock plus savings throughout his lifetime. This pattern of consumption behavior matches what we observe in macro data on consumption and documented in the literature as excess smoothness. Furthermore, the discrete rational inattention consumption-saving model provides a rationale for excess sensitivity in response to news on wealth.27
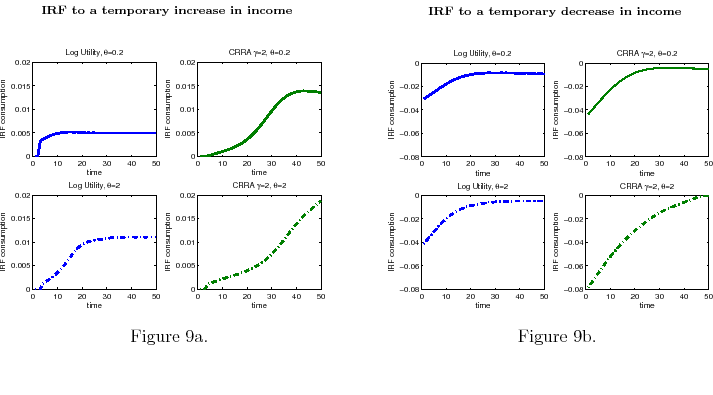
Since the model is non-linear, let me first explain how the impulse responses are generated and then focus on the intuition that the graphs suggest. I simulate the model drawing ![]() times from the same optimal policy distribution under two scenarios. In the first, I draw from a distribution with constant mean of the shock to income. In the second, I assume that the mean of the shocks increase/decrease in the very first period (one-time shocks) and then revert back to its
original distribution. Impulse responses of consumption are the difference between the two income paths averaged over simplex-points and
times from the same optimal policy distribution under two scenarios. In the first, I draw from a distribution with constant mean of the shock to income. In the second, I assume that the mean of the shocks increase/decrease in the very first period (one-time shocks) and then revert back to its
original distribution. Impulse responses of consumption are the difference between the two income paths averaged over simplex-points and ![]() Monte Carlo draws of income. The impulse
response functions are plotted in Figures 9a-9b. Consider Figures 9a first. They display a positive (Figure 9a) and a negative (Figure 9b) shock to income respectively. Note that for both log and CRRA
Monte Carlo draws of income. The impulse
response functions are plotted in Figures 9a-9b. Consider Figures 9a first. They display a positive (Figure 9a) and a negative (Figure 9b) shock to income respectively. Note that for both log and CRRA ![]() and for different value of the shadow cost (
and for different value of the shadow cost (
![]()
![]()
![]() ) the reaction to a negative shocks (
) the reaction to a negative shocks (
![]() ) starts from the very first period. However, the extent of the reaction varies across utilities and information costs. When
) starts from the very first period. However, the extent of the reaction varies across utilities and information costs. When
![]() , a log utility-type consumer reacts on impact by increasing savings to an extent lower than the shock. He then adjust savings and consumption so to distribute the averse shock
throughout time. The same log-type but with
, a log utility-type consumer reacts on impact by increasing savings to an extent lower than the shock. He then adjust savings and consumption so to distribute the averse shock
throughout time. The same log-type but with ![]() decreases more consumption on impact than his
decreases more consumption on impact than his
![]() counterpart. He increases consumption slowly over time until it reaches its new long-run value. Likewise, a consumer with risk aversion
counterpart. He increases consumption slowly over time until it reaches its new long-run value. Likewise, a consumer with risk aversion ![]() varies his saving when the shock hits to an extent that depends on his information flow. In particular, note that for
varies his saving when the shock hits to an extent that depends on his information flow. In particular, note that for ![]() the decrease in consumption on impact and in the following periods is so significant that consumers can use the accumulated savings to restore their original consumption plan. The endogenous asymmetric response to shocks, even in this very simple setting, makes rational
inattention models observationally distinct from any other standard macroeconomic model. In those frameworks, either there is no asymmetric reaction (as in LQG) or the asymmetric response is due to the asymmetric magnitude of the shocks (as in models a la Lucas). These implications make the theory
appealing from an empirical standpoint (e.g., think about consumers' reactions to a tax break vs. being fired from the job). Moreover, they make the theory suitable to study the impact of policy changes on private sectors decision. The 2008 Tax Rebate provides one such example.
the decrease in consumption on impact and in the following periods is so significant that consumers can use the accumulated savings to restore their original consumption plan. The endogenous asymmetric response to shocks, even in this very simple setting, makes rational
inattention models observationally distinct from any other standard macroeconomic model. In those frameworks, either there is no asymmetric reaction (as in LQG) or the asymmetric response is due to the asymmetric magnitude of the shocks (as in models a la Lucas). These implications make the theory
appealing from an empirical standpoint (e.g., think about consumers' reactions to a tax break vs. being fired from the job). Moreover, they make the theory suitable to study the impact of policy changes on private sectors decision. The 2008 Tax Rebate provides one such example.
6.1 Policy implications
A feature of the model worth exploring is how consumption's reaction to shocks depends on the initial value of wealth.
Drawing a time series from the probability distribution that solves the model, it is natural that the farther away wealth is from its steady state, the more consumption reacts to a shock to wealth. The interesting prediction of the model with an information-processing constraint is that for
either the log or the CRRA, ![]() utility, it does matter for the impulse response whether we start from a value of wealth above or below the steady state. In both cases, the reactions
are faster in case of a negative shock than a positive one. However, extent and timing are different with wealthier people reacting faster and with sharper decrease in consumption to a negative shock than poorer people do when facing the same kind of shock. This is due to the fact that poorer
people already consume small amount so that when a negative shock hits, even if they receive immediately signal of the news, they only gradually reduce their consumption. Savings slowly accumulate over time until the shock is absorbed. For a given processing capacity, wealthier people can afford to
reduce their consumption as soon as they acknowledge the negative shock. The jump start in savings makes it possible for them to absorb the shock faster. By contrast, a positive shock has a stronger effect on poorer people than wealthier one. To see why, consider a tax rebate. Taking two
individuals with the same characteristics in terms of risk aversion and information-processing constraints but different initial net worth, the wealthier person takes longer to change his consumption behavior. When the change does occur, the magnitude is smaller than the one for a poorer person.
The intuition for this result is that an increase in disposable income for a less wealthy person .implies a more sizeable financial break than the same amount does to a wealthy person. Risk aversion prevents both types of consumers from immediately disposing of the additional credit but it has a
bigger effect on impact for the more constrained consumer.
utility, it does matter for the impulse response whether we start from a value of wealth above or below the steady state. In both cases, the reactions
are faster in case of a negative shock than a positive one. However, extent and timing are different with wealthier people reacting faster and with sharper decrease in consumption to a negative shock than poorer people do when facing the same kind of shock. This is due to the fact that poorer
people already consume small amount so that when a negative shock hits, even if they receive immediately signal of the news, they only gradually reduce their consumption. Savings slowly accumulate over time until the shock is absorbed. For a given processing capacity, wealthier people can afford to
reduce their consumption as soon as they acknowledge the negative shock. The jump start in savings makes it possible for them to absorb the shock faster. By contrast, a positive shock has a stronger effect on poorer people than wealthier one. To see why, consider a tax rebate. Taking two
individuals with the same characteristics in terms of risk aversion and information-processing constraints but different initial net worth, the wealthier person takes longer to change his consumption behavior. When the change does occur, the magnitude is smaller than the one for a poorer person.
The intuition for this result is that an increase in disposable income for a less wealthy person .implies a more sizeable financial break than the same amount does to a wealthy person. Risk aversion prevents both types of consumers from immediately disposing of the additional credit but it has a
bigger effect on impact for the more constrained consumer.
![Figure 10: Even in its simplicity the model can be used to\ address important\ policy questions. In particular, it can be used to analyze the effectiveness of tax policy reforms on individual consumption and savings decisions. Figure 10 displays the impulse response function of consumption to a stimulus payment which increases income of $2\%$ with respect to its(constant) long run level. The discretized solutions are generated using equi-spaced grid of consumption and wealth, with $50$ points each . Consumption takes up value in $\left[ 0.5,3\right] $ while wealth ranges from $1$ to $10$. I use the same parameters ($R=1.012$ and $\beta =1/R$) of the baseline model and a simplex of size $\left( 50!\right) \ast \left( 49\right) $ and two specifications of utility functions. In both cases I choose $\theta $ so that the capacities corresponds to $\cong 2.5$ bits and $0.88$ bits. The constraint $\kappa =2.5$ corresponds to $\theta _{\log }=0.01$ and $\theta _{crra}=0.05$ for the log case and the crra, $\gamma =2$ case respectively, while $\kappa =0.88$ is given by $\theta _{\log }=0.1$ and $\theta _{crra}=0.9.$ Once the value iteration converged, I generate the impulse response function by simulating time series path of consumption and wealth with $10,000$ Monte Carlo runs for each initial condition on wealth. I consider three initial values of wealth as a proxy of population with low, middle and low net worth. I then average the time series per quarters and simplex points. Figure 10 gives interesting insights on the effect of the stimulus on consumer spending. For the degrees of risk aversion considered and information capacity, the reaction of the stimulus is higher the lower the initial wealth. This is not surprising, as the stimulus payments have bigger impact on the disposable income of credit constrained consumers than richer people. For a given amount of information capacity and wealth, the higher the risk aversion the lower the spending in the first quarters. This result also makes sense. If a consumer is risk averse and have no credit frictions, it allocates more attention in processing information about low values of wealth. This leads to processing slower and, in turn, reacting slower to positive news to income (Result 3). Finally for a given wealth and degree of risk aversion, the lower the information processing capacity, the lower the response of consumption spending to the rebate. The insights one can gather from the model have strong policy implications on the effectiveness of tax reform on people's behavior. The 2008 tax rebate provides one such example. The model predicts that such a policy has greater response on impact for individual with low net worth. Figure 10 also suggests that the effects will be mild and spread out through several quarters for middle-high income households.](img304.gif)
Even in its simplicity, the model can be used to address important policy questions. In particular, it can be used to analyze the effectiveness of tax policy reforms on individual consumption and savings decisions. Figure 10 displays the impulse response function of consumption to a stimulus
payment which increases income of ![]() with respect to its (constant) long run level. The discretized solutions are generated using equi-spaced grid of consumption and wealth, with
50 points each. Consumption takes up value in
with respect to its (constant) long run level. The discretized solutions are generated using equi-spaced grid of consumption and wealth, with
50 points each. Consumption takes up value in
![]() while wealth ranges from 1 to 10. I use the same parameters (
while wealth ranges from 1 to 10. I use the same parameters (![]() and
and ![]() ) of the baseline model and a simplex of size
) of the baseline model and a simplex of size
![]() and two specifications of utility functions. In both cases I choose
and two specifications of utility functions. In both cases I choose ![]() so that the capacities corresponds to
so that the capacities corresponds to ![]() bits and 0.88 bits28. Once the value iteration converged, I generate the impulse response function by simulating a time series path of consumption
and wealth with
bits and 0.88 bits28. Once the value iteration converged, I generate the impulse response function by simulating a time series path of consumption
and wealth with ![]() Monte Carlo runs for each initial condition on wealth. I consider three initial values of wealth as a proxy of population with low, middle and low net worth. I then
average the time series per quarters and simplex points. Figure 10 gives interesting insights on the effect of the stimulus on consumer spending. For the degrees of risk aversion considered and information capacity, the reaction of the stimulus is higher the lower the initial wealth. This is not
surprising, as the stimulus payments have bigger impact on the disposable income of credit constrained consumers than richer people. For a given amount of information capacity and wealth, the higher the risk aversion, the lower the spending in the first quarter. This result also makes sense. If a
consumer is risk averse and have no credit frictions, he allocates more attention in processing information about low values of wealth. This leads to processing information slower and, in turn, reacting slower to positive news to income (Result 3). Finally for a given wealth and degree of risk
aversion, the lower the information processing capacity, the lower the response of consumption spending to the rebate. The findings in Figure 10 can be summarized as:
Monte Carlo runs for each initial condition on wealth. I consider three initial values of wealth as a proxy of population with low, middle and low net worth. I then
average the time series per quarters and simplex points. Figure 10 gives interesting insights on the effect of the stimulus on consumer spending. For the degrees of risk aversion considered and information capacity, the reaction of the stimulus is higher the lower the initial wealth. This is not
surprising, as the stimulus payments have bigger impact on the disposable income of credit constrained consumers than richer people. For a given amount of information capacity and wealth, the higher the risk aversion, the lower the spending in the first quarter. This result also makes sense. If a
consumer is risk averse and have no credit frictions, he allocates more attention in processing information about low values of wealth. This leads to processing information slower and, in turn, reacting slower to positive news to income (Result 3). Finally for a given wealth and degree of risk
aversion, the lower the information processing capacity, the lower the response of consumption spending to the rebate. The findings in Figure 10 can be summarized as:
- Result 4. Economic stimulus and rational inattention.
- The impact of a one time tax rebate on rational inattentive consumers:
- 1.
- is stronger the lower the initial net worth.
- 2.
- is more delayed the higher the degree of risk aversion.
- 3.
- is more persistent but less effective the lower the information-processing capacity.
The insights one can gather from the model have strong policy implications on the effectiveness of tax reform on people's behavior. The 2001 tax rebate provides one such example. The model predicts that such a policy has greater response on impact for individual with low net worth. Figure 10 also suggests that the effect will be mild and spread out through several quarters for middle-high income households. These findings are consistent with the empircal evidence on consumers spending of 2001 tax rebates (cfr., Johnson, Parker and Soules (2006)).
7 Conclusions
This paper applies rational inattention to a dynamic model of consumption and savings. Consumers rationally choose the nature of the signal they want to acquire subject to the limits of their information processing capacity. The dynamic interaction of risk aversion and endogenous choice of information flow enhances precautionary savings.
I showed that for a given degree of risk aversion, the lower the information flow, the flatter the consumption path. The model predicts that for a given information flow, the higher the degree of risk aversion, the more persistent consumption. Also, for a given degree of risk aversion, the lower the information flow, the more volatile consumption.
Furthermore, the model predicts that consumption path has humps. Under information-processing constraints, an hump occurs when people consume a little and save a lot while collecting information about wealth. When consumers realize that they are rich, they increase consumption and decumulate savings. This increase stops when they acknowledge that their wealth is low again: they start to save and process more information. Thus, consumption decreases. Consistent with the previous two results, I find that the peak in consumption is delayed the more the individual becomes risk averse.
Differing from other life-cycle models, in my model there could be more than one hump in the consumption path. Depending on the history of the income shocks, a very low or very high realization of income affects consumers' signal through its effect on wealth. Consumers react to the news by varying savings and information over time, thereby generating another hump.
Finally, the model predicts that consumers with processing capacity constraints have asymmetric responses to shocks, with negative shocks producing more persistent effects than positive ones. This asymmetry, observed in actual data, is novel to the theoretical literature of consumption and savings. Studying the reactions of rational inattentive people to temporary income shocks can also be used to assess the effectiveness of policy reforms on consumption spending. The model predicts that, for a given level of wealth, the speed and magnitude of the consumption adjustment to the income shock depends on their processing capacity. Moreover, consumers with low wealth react faster to temporary tax relief than wealthier people. The results agree with both intuition and preliminary data on consumer spending.
The results seem to suggest that enriching the standard macroeconomic toolbox with rational inattention theory is a step worth taking.
8.1 Proof of Proposition 1.
The Bellman Recursion in the discrete Rational Inattention Consumption-Saving Model is a Contraction Mapping.
![\displaystyle H^{p}V\left( g\right) =\left[ {\displaystyle\sum\limits_{w\in\Omega_{w}}% }\left( {\displaystyle\sum\limits_{c\in\Omega_{c}}}u\left( c\right) p\left( c\vert w\right) \right) g\left( w\right) +\beta{\displaystyle\sum \limits_{w\in\Omega_{w}}}{\displaystyle\sum\limits_{c\in\Omega_{c}}}\left( V\left( g_{c}^{\prime}\left( \cdot\right) \right) \right) p\left( c\vert w\right) g\left( w\right) \right] .](img319.gif)
Then it holds
![\displaystyle \beta{\displaystyle\sum\limits_{w\in\Omega_{w}}}{\displaystyle\sum \limits_{c\in\Omega_{c}}}\left[ \left( V^{p_{2}}\left( g_{c}^{\prime }\left( \cdot\right) \right) \right) -\left( U^{p_{2}}\left( g_{c}^{\prime}\left( \cdot\right) \right) \right) \right] p_{2}g\left( w\right)](img338.gif) |
||
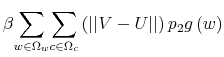 |
8.2 Proof of Corollary.
The Bellman Recursion in the discrete Rational Inattention Consumption-Saving Model is an Isotonic Mapping.
By definition,
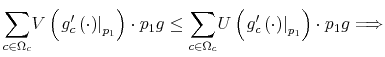
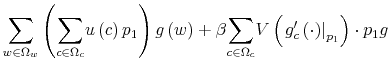
|
||
 |
8.3 Proof of Proposition 2.
The Optimal Value Function in the discrete Rational Inattention Consumption-Saving Model is Piecewise Linear and Convex (PCWL).
and therefore if I define the vectors
I have the desired
where
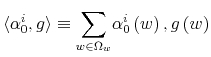 . For the general case, using equation
(22):
. For the general case, using equation
(22):
by the induction hypothesis
Plugging into the above equation (19) and by definition of
With the above:
At this point, it is possible to define
Note that these hyperplanes are independent on the prior
and define:
Note that
Now
is a finite set of linear function parametrized in the action set.
8.4 Proof of Proposition 3.
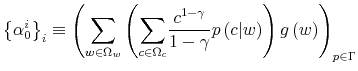
9.1 Concavity of Mutual information in the Belief State.
For a given
![]() , Mutual Information is concave in
, Mutual Information is concave in
![]()
Condition on
Q.E.D.
10 Appendix C
Pseudocode
Let ![]() be the shadow cost associated to
be the shadow cost associated to
![]() . Define a Model as a pair
. Define a Model as a pair
![]() . For a given specification :
. For a given specification :
- Step 1: Build the simplex. Construct an equi-spaced grid to approximate each
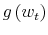 -simplex point.
-simplex point. - Step 2: For each simplex point, define
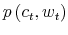 . and Initialize with
. and Initialize with
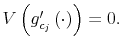
- Step 3: For each simplex point, find
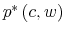 s.t.
s.t.
![]()
![]()
![\max_{_{p\left( c_{t},w_{t}\right) }% }\left\{ {\sum\limits_{w_{t}\in\Omega_{w}}\sum\limits_{c_{t}\in\Omega_{c}}% }\left( \frac{c_{t}^{1-\gamma}}{1-\gamma}\right) p^{\ast}\left( c_{t}% ,w_{t}\right) -\theta\left[ I_{t}\left( C_{t},W_{t}\right) \right] \right\} .](img402.gif)
- Step 4: For each simplex point, compute
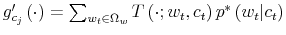 . Use a kernel regression to interpolate
. Use a kernel regression to interpolate
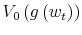 into
into
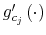 .
. - Step 5: Optimize using csminwel and iterate on the value function up to convergence.
- Obs.
- Convergence and Computation Time vary with the specification
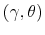 .
. -
- 180-320 iterations each taking 8min-20min
- Step 6. For each model
 , draw from the ergodic
, draw from the ergodic
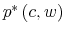 a sample
a sample
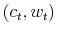 and simulate the time series of consumption, wealth, expected wealth and information flow by averaging over 1000 draws.
and simulate the time series of consumption, wealth, expected wealth and information flow by averaging over 1000 draws. - Step 7. Generate histograms of consumption and impulse response function of consumption to temporary positive and negative shocks to income.
11.1 Optimality Conditions
In this section I incorporate explicitly the constraint on information processing and derive the Euler Equations that characterize its solution.
The main feature of this section is to relate the link between the output of the channel consumption, with the capacity chosen by the agent. In deriving the optimality conditions, I incorporate the consistency assumption (20) in the main diagonal of the joint
distribution to be chosen, ![]()
![]() . Note that such a restriction is WLOG. I then show the analytical details of the derivatives with respect to control and
states.
. Note that such a restriction is WLOG. I then show the analytical details of the derivatives with respect to control and
states.
11.2 First Order Conditions
To evaluate the derivative of the Bellman equation with respect to a generic distribution
![]() , define the differential operator
, define the differential operator
![]() and
and ![]() as the shadow cost of processing information . Then, the optimal control for the program (17)-(21) amounts to:
as the shadow cost of processing information . Then, the optimal control for the program (17)-(21) amounts to:
![]()
This expression states that the optimal distribution depends on the weighted difference of two consumption profiles, ![]() and
and ![]() where the weights are given by current and future discounted utilities. Note that the differential of the marginal utility of current consumption is also weighted by the conditional optimal distribution of consumption and wealth.
where the weights are given by current and future discounted utilities. Note that the differential of the marginal utility of current consumption is also weighted by the conditional optimal distribution of consumption and wealth.
The interpretation of (36) is that the optimal probability of consumption and wealth depends on both levels of current and intertemporal utility and marginal utility. In particular, there is an intertemporal trade-off by consuming the maximum value of wealth allowed by
the signal, ![]() and a lower consumption
and a lower consumption ![]() . To illustrate the
argument, suppose a consumer believes that his wealth is
. To illustrate the
argument, suppose a consumer believes that his wealth is ![]() with high probability. Suppose for simplicity that
with high probability. Suppose for simplicity that
![]() allows him to spend
allows him to spend ![]() or
or ![]() . The decision of shifting probability from
. The decision of shifting probability from
![]() to
to
![]() depends on four variables. First, the current difference in utility levels,
depends on four variables. First, the current difference in utility levels,
![]() which tells the immediate satisfaction of consuming
which tells the immediate satisfaction of consuming
![]() rather than
rather than ![]() . However, consuming more today has a cost
in future consumption and wealth levels tomorrow,
. However, consuming more today has a cost
in future consumption and wealth levels tomorrow,
![]() . Optimal allocation of probabilities requires trading off not only intertemporal levels of utility but also marginal
intertemporal utilities where now the current marginal utility of consumption is weighted by the effort required to process information today.
. Optimal allocation of probabilities requires trading off not only intertemporal levels of utility but also marginal
intertemporal utilities where now the current marginal utility of consumption is weighted by the effort required to process information today.
To explore this relation further, I evaluate the derivative of the continuation value for a given optimal
![]() , that is
, that is
![]() . To this end, define the ratio between differential in utilities (current and discounted future) and
differential in marginal current utility as
. To this end, define the ratio between differential in utilities (current and discounted future) and
differential in marginal current utility as
![]() . Also,
let
. Also,
let
![]() be the ratio
be the ratio
![]() when current level of utilities are equalized and future differential utilities are constant, i.e.,
when current level of utilities are equalized and future differential utilities are constant, i.e.,
![]() and
and
![]() or,
or,
![]() . Then, an
application of Chain rule and point-wise differentiation leads to
. Then, an
application of Chain rule and point-wise differentiation leads to
where
![]()
Let me focus on the explanation for the terms
![]() which characterize the optimal solution of the conditional distribution
which characterize the optimal solution of the conditional distribution
![]()
The first term
![]() states
that the optimal choice of the distribution balances differentials between current and future levels of utilities between high (
states
that the optimal choice of the distribution balances differentials between current and future levels of utilities between high (![]() ) and low (
) and low (![]() ) values of consumption. In case of log utility, the term
) values of consumption. In case of log utility, the term
![]() is a likelihood ratio between utilities in the two states of the word (
is a likelihood ratio between utilities in the two states of the word (![]() and
and ![]() ) and the interpretation is that the higher is the value of the state of the world
) and the interpretation is that the higher is the value of the state of the world ![]() with respect to
with respect to ![]() as measured by the utility of consumption, the lower is the optimal
as measured by the utility of consumption, the lower is the optimal
![]() . This matches the intuition because the consumer would like to place more probability on the occurrence of
. This matches the intuition because the consumer would like to place more probability on the occurrence of ![]() the wider the difference between
the wider the difference between ![]() and
and ![]() . A perhaps more interesting intertemporal relation is captured by the terms
. A perhaps more interesting intertemporal relation is captured by the terms
![]() and
and
![]() , both of which display the occurrence of the update distribution
, both of which display the occurrence of the update distribution
![]() ,
, ![]() . To disentangle the
contribution of each argument of
. To disentangle the
contribution of each argument of
![]() and
and
![]() , I combine the derivative of the control with the envelope condition. Let
, I combine the derivative of the control with the envelope condition. Let
![]() be the term
be the term
![]() led one period and define the differential between transition from one particular state to another and transition from one particular state to all the possible states as
led one period and define the differential between transition from one particular state to another and transition from one particular state to all the possible states as
![]()
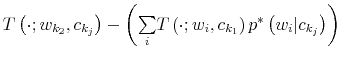 for
for ![]() . Evaluating the derivative with respect to the state almost surely reveals that
. Evaluating the derivative with respect to the state almost surely reveals that
![]() while
while
![]() . The terms
. The terms
![]() and
and
![]() reveal that in setting the optimal distribution
reveal that in setting the optimal distribution
![]() consumers take into account not only differential between levels and marginal utilities but also how the choice of the distribution shrinks or
widens the spectrum of states that are reachable after observing the realized consumption profile.
consumers take into account not only differential between levels and marginal utilities but also how the choice of the distribution shrinks or
widens the spectrum of states that are reachable after observing the realized consumption profile.
An interesting special case that admits a closed form solution is when the agent is risk neutral. Consider the framework in Section (3.2) and let utility take up the form
![]() , then in the region of admissible solution
, then in the region of admissible solution
![]() , the optimal probability distribution makes
, the optimal probability distribution makes ![]() independent on
independent on
![]() . To see this, it is easy to check that in the two period case with no discounting, the utility function reduces to
. To see this, it is easy to check that in the two period case with no discounting, the utility function reduces to
![]() , which implies
, which implies
![]() . That is, since all the uncertainty is driven by
. That is, since all the uncertainty is driven by ![]() , the consumer does not bother processing information beyond the knowledge of where the limit of
, the consumer does not bother processing information beyond the knowledge of where the limit of ![]() lies. In other word, the constraint on information flow does not
bind. With the continuation value, exploiting risk neutrality, the optimal policy function amounts to:
lies. In other word, the constraint on information flow does not
bind. With the continuation value, exploiting risk neutrality, the optimal policy function amounts to:
The solution uncovers some important properties of the interplay between risk neutrality and information flow. First of all, households with linear utility do not spend extra consumption units in sharpening their knowledge of wealth. This is due to the fact that because the consumer is risk neutral and, at the margin, costs and benefits of information flows are equalized amongst periods, there is no necessity to gather more information than the boundaries of current consumption possibilities. In each period, the presence of information processing constraint forces the consumer to allocate some utils to learn just enough to prevent violating the non-borrowing constraint. Once those limits are figured out, the consumption profiles in the region
11.2.0.1 Derivative with Respect to Controls
In the main text, I state that the optimal control amounts to :
![]()
which can be rewritten, opening up the operator
![]() as:
as:
![\displaystyle \varphi_{\left( c_{k_{1}},c_{k_{2}}\right) }^{\kappa}=\Pr\left( c_{k_{1}% },w_{k_{2}}\right) \left( \psi_{\left( c_{k_{1}},c_{k_{2}},\theta\right) }^{\kappa}\ln\frac{\Pr\left( c_{k_{1}},w_{k_{2}}\right) }{\Pr\left( c_{k_{1}}\right) }+\beta\left[ \frac{\partial V^{\prime}\left( g_{c_{k_{1}% }}^{\prime}\left( \cdot\right) \right) }{\partial\Pr\left( c_{k_{1}% },w_{k_{2}}\right) }-\frac{\partial V^{\prime}\left( g_{c_{k_{2}}}^{\prime }\left( \cdot\right) \right) }{\partial\Pr\left( c_{k_{1}},w_{k_{2}% }\right) }\right] \right)](img459.gif)
where
-
![\varphi_{\left( c_{k_{1}},c_{k_{2}}\right) }^{\kappa}\equiv-\left[ u\left( c_{k_{1}}\left( \kappa\right) \right) -u\left( c_{k_{2}}\left( \kappa\right) \right) +\beta\left( V\left( g_{c_{k_{1}}}^{\prime}\left( \cdot\right) \right) -V\left( g_{c_{k_{2}}}^{\prime}\left( \cdot\right) \right) \right) \right]](img460.gif) , and
, and -
![\psi_{\left( c_{k_{1}},c_{k_{2}},\theta\right) }^{\kappa}% \equiv-\theta\left[ u^{\prime}\left( c_{k_{1}}\left( \kappa\right) \right) -u^{\prime}\left( c_{k_{2}}\left( \kappa\right) \right) \right] .](img461.gif)
Note that by Chain rule
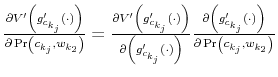 , for
, for ![]() Plug (36) in the second term of the above expression and evaluating point-wise the derivatives delivers
Plug (36) in the second term of the above expression and evaluating point-wise the derivatives delivers
In
![]()
-
-
![\frac{\partial g\left( \left. \cdot\right\vert _{c_{k_{1}}}\right) }{\partial\Pr\left( c_{k_{1}},w_{k_{2}}\right) }% =\frac{\partial\left[ \frac{1}{p\left( c_{k_{1}}\right) }\left( {\textstyle\sum\limits_{i}} T\left( \cdot;w_{i},c_{k_{1}}\right) \Pr\left( w_{i},c_{k_{1}}\right) \right) \right] }{\partial\Pr\left( c_{k_{1}},w_{k_{2}}\right) }=](img466.gif) Define
Define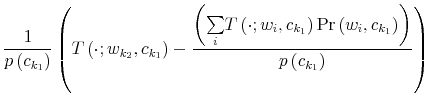
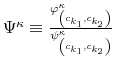 and
and
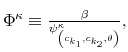 to get rid of cumbersome notation, let
to get rid of cumbersome notation, let
 Then the first order conditions result into
Then the first order conditions result into
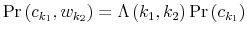
(40)
wherewhile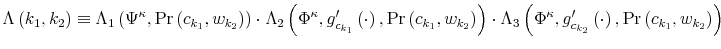
11.2.0.2 Derivative with Respect to States
To derive the envelope condition with respect to a generic state
![]() for
for ![]() , let me start by placing the restrictions on
the marginal distribution of wealth in the main diagonal of the joint distribution
, let me start by placing the restrictions on
the marginal distribution of wealth in the main diagonal of the joint distribution
![]() . The derivative then amounts to:
. The derivative then amounts to:
![\begin{displaymath}\frac{\partial\Pr\text{ }_{t}\left( c_{j},w_{k}\right) }{\partial g\left( w_{k}\right) }=\frac{\partial\Pr\text{ }_{t}\left( c_{j}\right) }{\partial g\left( w_{k}\right) }=\left\{ \begin{array}[c]{cc}% 1 & \left\{ \left( j=k\right) \cap\left( j\neq\max l\in\Omega_{c}\right) \right\} \ -1 & \left\{ j=\max l\in\Omega_{c}\right\} \ 0 & \text{o/whise}% \end{array}\right. .\end{displaymath}](img478.gif)
Let ![]() denote the maximum indicator
denote the maximum indicator ![]() belonging to
belonging to
![]() Then the derivative of the state
Then the derivative of the state
![]() displays:
displays:
![]()
![]()
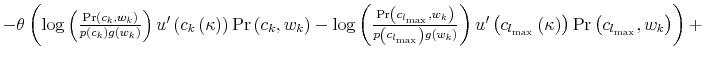
![+\beta\sum_{j}\left[ \frac{\partial V\left( g_{c_{k_{j}}}^{\prime}\left( \cdot\right) \right) }{\partial\left( g_{c_{k_{j}}}^{\prime}\left( \cdot\right) \right) }\left( \frac{\partial\left( g_{c_{k_{j}}}^{\prime }\left( \cdot\right) \right) }{\partial g\left( w_{k}\right) }\right) \Pr\left( c_{j},w_{k}\right) \right] .](img485.gif)
Combining first order conditions and the envelope condition after some algebra leads to the result in (40).
12.1 A simple example
To illustrate how a consumer with information constraints differs from a consumer with full information and a consumer with no information, consider the following model of consumer's choice.
Suppose the household has three wealth possibilities,
![]() , and three consumption possibilities
, and three consumption possibilities
![]() . Before any observation is made, the consumer has the following prior on wealth,
. Before any observation is made, the consumer has the following prior on wealth,
![]() ,
,
![]() ,
,
![]() . Moreover the consumer cannot borrow,
. Moreover the consumer cannot borrow, ![]() and, if
his check bounces he suffers
and, if
his check bounces he suffers ![]() . He derives utility from consumption defined as
. He derives utility from consumption defined as
![]() . His payoff matrix is summarized in Figure a.
. His payoff matrix is summarized in Figure a.
If uncertainty in the payoff can be reduced at no cost, the consumer would set ![]()
![]()
![]() .
.
In contrast, if he cannot gather any information about wealth besides that provided by the prior, the consumer will avoid unpleasant surprises by setting ![]() whatever the wealth.
whatever the wealth.
The difference in bits in the two policies is measured by the mutual information between ![]() and
and ![]() . The ex-ante uncertainty embedded in the prior for
. The ex-ante uncertainty embedded in the prior for ![]() is calculated by evaluating its entropy in bits, i.e.,
is calculated by evaluating its entropy in bits, i.e.,
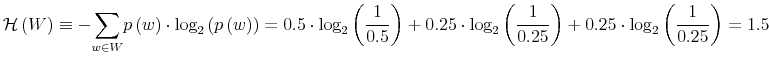
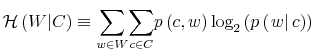 . The mutual information between
. The mutual information between 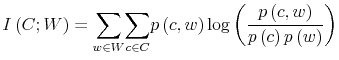
To see what this formula implies, consider first the situation in which information can flow at infinite rate. In this case ex-post uncertainty is fully resolved. Moreover, note that
![]()
![]()
![]() since the consumer is setting positive probability on one and only one value of consumption per value of wealth. This in turns implies
since the consumer is setting positive probability on one and only one value of consumption per value of wealth. This in turns implies
![]() , so the mutual information in this case will be
, so the mutual information in this case will be
![]() .
.
Instead, if the consumer has zero information flow or, equivalently, if processing information is prohibitively hard for him, his optimal policy of setting ![]() at all times makes
consumption and wealth independent of each other. This implies that
at all times makes
consumption and wealth independent of each other. This implies that
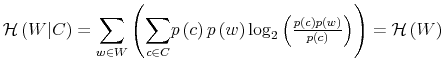 . Hence, in
this case
. Hence, in
this case
![]() and no reduction in the uncertainty about wealth occurs upon observing consumption. The intuition is that if a consumer decides to spend the same amount in consumption
regardless of his wealth level, his purchase will tell him nothing about his financial possibilities. The expected utility in the first case is
and no reduction in the uncertainty about wealth occurs upon observing consumption. The intuition is that if a consumer decides to spend the same amount in consumption
regardless of his wealth level, his purchase will tell him nothing about his financial possibilities. The expected utility in the first case is
![]() while in the second case
while in the second case
![]() .
.
Now, assume that the consumer can allocate some effort in choosing size and scope of information about his wealth he wants to process, under the limits imposed by his processing capacity. Let
![]() be the maximum amount of information flow that the consumer can process. Let the probability matrix of the consumer be:
be the maximum amount of information flow that the consumer can process. Let the probability matrix of the consumer be:
Figure b: Probability Matrix
where the zeroes on the lower left corner of the matrix encode a non-borrowing constraint ![]() .29 The program of the consumer is:30
.29 The program of the consumer is:30
Note that the result of trading information for the highest value to gain a more precise knowledge of the lower value of wealth is driven by the functional form of utility. For instance, a consumer with the same bound on processing capacity but CRRA utility with coefficient of risk aversion,
say, ![]() , would have chosen a probability
, would have chosen a probability
![]() lower than his log-utility counterpart. This is because higher degrees of risk aversion induce the consumers to be better informed about low values of wealth to avoid
such occurrences. The intuition is that because the attention of the consumer within the limits of the Shannon capacity is allocated according to his utility, the degree of risk aversion plays an important role in determining what events receive the consumer's attention. A log-utility consumer
wants to be well informed about the middle values of his wealth, while a high risk averse consumer selects a signal which provides sharper information about the lower values of wealth, so that he can avoid high disutility. The opposite direction is taken by the less risk-averse agent.
lower than his log-utility counterpart. This is because higher degrees of risk aversion induce the consumers to be better informed about low values of wealth to avoid
such occurrences. The intuition is that because the attention of the consumer within the limits of the Shannon capacity is allocated according to his utility, the degree of risk aversion plays an important role in determining what events receive the consumer's attention. A log-utility consumer
wants to be well informed about the middle values of his wealth, while a high risk averse consumer selects a signal which provides sharper information about the lower values of wealth, so that he can avoid high disutility. The opposite direction is taken by the less risk-averse agent.
12.2 Analytical Results for a three-point distribution
In this section I will focus on the optimality conditions derived above for a three point distribution. The goal is to fully characterize the solution for this particular case and explore its insights.32
Let me assume the wealth to be a random variable that takes up values in ![]()
![]() with distribution
with distribution
![]() described by:
described by:
The equation describing the evolution of the wealth is displayed by the budget constraint
![\displaystyle _{t}\left( c_{j},w_{i}\right) \begin{tabular}[c]{\vert\vert c\vert\vert c\vert c\vert c\vert}\hline\hline $C\backslash W$\ & $w_{1}$\ & \multicolumn{1}{\vert\vert c\vert}{$w_{2}$} & \multicolumn{1}{\vert\vert c\vert\vert}{$w_{3}$} \\ \hline\hline $c_{1}$\ & $x_{1}$\ & $x_{2}$\ & $x_{3}$\\ \hline $c_{2}$\ & $0$\ & $x_{4}$\ & $x_{5}$\\ \hline $c_{3}$\ & $0$\ & $0$\ & $x_{6}$\\ \hline \end{tabular}](img559.gif)
where the zeros in the SW end of the matrix encodes the feasibility constraint
![]()
![]()
![]() and
and
![]() . The additional restrictions to the above matrix are the ones commanded by the marginal on wealth. That is:
. The additional restrictions to the above matrix are the ones commanded by the marginal on wealth. That is:
Without loss of generality, I place the marginal distribution of wealth in the main diagonal of
![]()
The resulting marginal distribution of consumption that endogenously depends on the choices of
![\begin{displaymath} \Pr\left( C=c_{j}\right) =\left\{ \begin{array}[c]{ccc}% c_{1} & \text{w.p } & g_{1}+p_{1}+p_{2}\ c_{2} & \text{w.p } & g_{2}-p_{1}+p_{3}\ c_{3} & \text{w.p} & 1-\left( g_{1}+g_{2}\right) -\left( p_{2}% +p_{3}\right) \end{array}\right. . \end{displaymath}](img574.gif)
The specification of
The approximation is necessary since (43) cannot hold exactly at the boundaries of the support of the wealth,
12.2.0.1 Euler Equations.
Making use of the marginal distribution of wealth described above and making use of (42) together with the specifications of
![]() and
and
![]() , I can explicitly evaluate
, I can explicitly evaluate
![]() point-wise. To illustrate this point, using the numerical values of
point-wise. To illustrate this point, using the numerical values of
![]() above, the derivatives point-wise are as follows.
above, the derivatives point-wise are as follows.
In
![]()
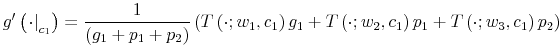
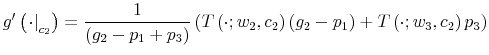
![]()
![\displaystyle =p_{1}\left( \begin{array}[c]{c}% \theta\left( \left[ u^{\prime}\... ...l g_{c_{2}}^{\prime }\left( \cdot\right) }{\partial p_{1}}% \end{array} \right)](img608.gif) |
Note that
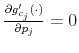 for
for
![]() .33 This result is
not driven by the specification chosen for the transition function
.33 This result is
not driven by the specification chosen for the transition function
![]() , but it is a feature of the three point distribution. Indeed, because two of the three values of wealth are at the boundaries of
, but it is a feature of the three point distribution. Indeed, because two of the three values of wealth are at the boundaries of
![]() , the absorbing states
, the absorbing states ![]() and
and ![]() place tight restrictions on the continuation value
place tight restrictions on the continuation value
![]() through the transition function and, as a result, the update for the marginal
through the transition function and, as a result, the update for the marginal
![]() according to (42). That is, the marginal probability on wealth
according to (42). That is, the marginal probability on wealth
![]() in this case tends to its ergodic value
in this case tends to its ergodic value
![]() . It follows that
. It follows that
![]() which is a constant since the
functional argument is. This is what makes the 3-point distribution tractable.
which is a constant since the
functional argument is. This is what makes the 3-point distribution tractable.
For the general case, the first order condition with respect to the first control amounts to:
![]()
Similarly, for the second control
![]()
And finally:
![]()
Using the result that the value function converges to
![\begin{displaymath} u\left( c_{j}\left( \kappa\right) \right) =\left\{ \begin{array}[c]{cc}% -\frac{e^{-\gamma\left( c_{j}\left( \kappa\right) \right) }}{\gamma} & \text{for }\gamma>0\ \log\left( c_{j}\left( \kappa\right) \right) & \text{for }\lim _{\gamma\rightarrow0}\left( -\frac{e^{-\gamma\left( c_{j}\left( \kappa\right) \right) }}{\gamma}\right) \end{array}\right. \end{displaymath}](img630.gif)
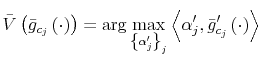
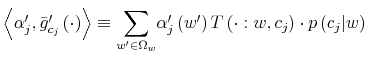 . To get a close form
solution, I need to represent the probability distribution of the prior. One of the possibilities is to use a particle based representation. The latter is performed by using
. To get a close form
solution, I need to represent the probability distribution of the prior. One of the possibilities is to use a particle based representation. The latter is performed by using 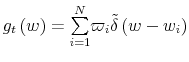
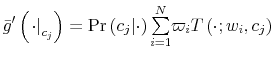
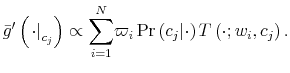
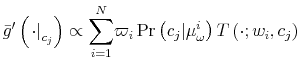
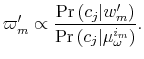
![\displaystyle =% {\displaystyle\sum\limits_{w\in\Omega_{w}}} \left[ {\displaystyle\sum\limits_{k}} \varpi_{k}\tau\left( w\vert w_{k},\Sigma_{k}\right) \right] \left[ {\displaystyle\sum\limits_{l}} \varpi_{l}^{\prime}\tilde{\delta}\left( w-w_{l}\right) \right]](img655.gif) |
||
![\displaystyle =% {\displaystyle\sum\limits_{k}} \varpi_{k}% {\displaystyle\sum\limits_{w\in\Omega_{w}}} \left( \tau\left( w\vert w_{k},\Sigma_{k}\right) \left[ {\displaystyle\sum\limits_{l}} \varpi_{l}\tilde{\delta}\left( w-w_{l}\right) \right] \right)](img656.gif) |
||
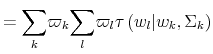 |
||
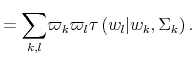 |
where
Representing priors in this fashion allows an explicit evaluation of the differences in the value functions in the first order conditions, since
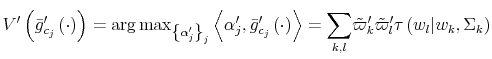 , where
, where
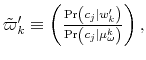
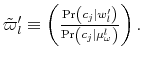 Since the result of the
Since the result of the ![]() is just one of the member of the set
is just one of the member of the set
![]() and all the elements involved in the definition of
and all the elements involved in the definition of
![]() function in
function in
![]() are a finite set of linear function parametrized in the action set, so is the final result.
are a finite set of linear function parametrized in the action set, so is the final result.
Let a prime (" ![]() ") denote the variables led one period ahead, algebraic manipulation delivers the following optimal control functions:
") denote the variables led one period ahead, algebraic manipulation delivers the following optimal control functions:
where
-
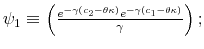
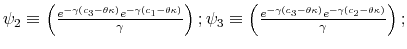
-
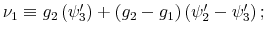
-
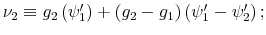
-
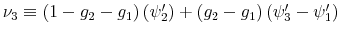
-
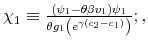
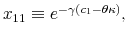
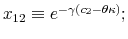
-
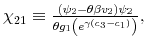
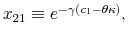
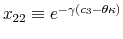 and
and -
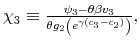
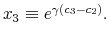
and
![]() is the
is the
![]() function that satisfies
function that satisfies
![]() 34. The argument of the
34. The argument of the
![]() is always positive for the first order conditions derived, implying that for each of the optimal policies the function returns a real solution amongst other complex
roots, which is unique and positive. Since
is always positive for the first order conditions derived, implying that for each of the optimal policies the function returns a real solution amongst other complex
roots, which is unique and positive. Since
![]() it is possible
to calculate the derivatives of the above expression with respect to
it is possible
to calculate the derivatives of the above expression with respect to
![]() . However, the sign of the derivatives with respect to those variables is indeterminate. The rationale behind this result is quite simple. Consider the
joint probability distribution
. However, the sign of the derivatives with respect to those variables is indeterminate. The rationale behind this result is quite simple. Consider the
joint probability distribution
![]() . The overall effect of an increase in this probability results from the interplay of several factors. In general, if
. The overall effect of an increase in this probability results from the interplay of several factors. In general, if ![]() is low (or, equivalently, the capacity of the channel,
is low (or, equivalently, the capacity of the channel,
![]() , in (18) is high), a risk averse consumer will try to reduce the off diagonal term of the joint as much as possible. That is, he would set
, in (18) is high), a risk averse consumer will try to reduce the off diagonal term of the joint as much as possible. That is, he would set
![]()
![]() and
and
![]() as low as its capacity allows him to sharpen his knowledge of the state. On the opposite extreme, for very high value of the cost associated to
information processing,
as low as its capacity allows him to sharpen his knowledge of the state. On the opposite extreme, for very high value of the cost associated to
information processing, ![]() ,
, ![]() and
and ![]() will be higher, the higher the prior
will be higher, the higher the prior
![]() with respect to
with respect to
![]() and
and
![]() . This is due to the fact that when the capacity of the channel is low -or, equivalently, the effort of processing information is high-, the first order conditions
indicate that it is optimal for the consumer to shift probabilities towards the higher belief state. The intuition is that when it is costly to process information, the household cannot reduce the uncertainty about his wealth. If the individual is risk adverse as implied by the CRRA utility
function, in each period, he would rather specialize in the consumption associated to the higher prior than attempt to consume a different quantity and running out of wealth in the following periods. This intuition leads to an optimal policy of the consumer that commands high probability to one
particular consumption profile and set the remaining probabilities as low as possible. To illustrate this, consider a consumer who has a high value of
. This is due to the fact that when the capacity of the channel is low -or, equivalently, the effort of processing information is high-, the first order conditions
indicate that it is optimal for the consumer to shift probabilities towards the higher belief state. The intuition is that when it is costly to process information, the household cannot reduce the uncertainty about his wealth. If the individual is risk adverse as implied by the CRRA utility
function, in each period, he would rather specialize in the consumption associated to the higher prior than attempt to consume a different quantity and running out of wealth in the following periods. This intuition leads to an optimal policy of the consumer that commands high probability to one
particular consumption profile and set the remaining probabilities as low as possible. To illustrate this, consider a consumer who has a high value of ![]() and a prior on
and a prior on ![]() higher than the other priors. If he cannot sharpen his knowledge of the wealth due to prohibitively information processing effort, he will optimize its dynamic problem by placing very high
probability on
higher than the other priors. If he cannot sharpen his knowledge of the wealth due to prohibitively information processing effort, he will optimize its dynamic problem by placing very high
probability on
![]() , i.e., increase
, i.e., increase ![]() and
and ![]() and decrease
and decrease ![]() . Likewise, if
. Likewise, if ![]() is higher than the other priors and
is higher than the other priors and ![]() is high -
is high -![]() is low-, optimality commands to decrease both
is low-, optimality commands to decrease both ![]() and
and ![]() and increase
and increase ![]() .
.
13.1 The Mathematics of Rational Inattention
This part addresses the mathematical foundations of rational inattention. The main reference is the seminal work of Shannon (1948). Drawing from the information theory literature, I provide an overview Shannon's axiomatic characterization of entropy and mutual information and show the main theoretical features of these two quantities.
Formally, the starting point is a set of possible events whose probabilities of occurrence are
![]() . Suppose for a moment that these probabilities are known but that is all we know concerning which event will occur. The quantity
. Suppose for a moment that these probabilities are known but that is all we know concerning which event will occur. The quantity
![]() is called the entropy of the set of probabilities
is called the entropy of the set of probabilities
![]() . If
. If ![]() is a chance variable, then
is a chance variable, then
![]() indicates its entropy; thus
indicates its entropy; thus ![]() is not an argument of a function
but a label for a number, to differentiate it from
is not an argument of a function
but a label for a number, to differentiate it from
![]() say, the entropy of the chance variable
say, the entropy of the chance variable ![]() .
.
Quantities of the form
![]() play a central role in Information Theory as measures of information, choice and uncertainty. The quantity
play a central role in Information Theory as measures of information, choice and uncertainty. The quantity ![]() goes by the name of entropy 35 and
goes by the name of entropy 35 and ![]() is the probability of a system being in cell
is the probability of a system being in cell ![]() of its phase space.
of its phase space.
The measure of how much choice is involved in the selection of the events is
![]() and it has the following properties:
and it has the following properties:
- Axiom 1
 is continuous in the
is continuous in the 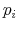 .
.- Axiom 2
- If all the
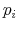 are equal,
are equal,
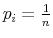 , then
, then 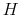 should be a monotonic increasing function of
should be a monotonic increasing function of
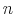 . With equally likely events there is more choice, or uncertainty, when there are more possible events.
. With equally likely events there is more choice, or uncertainty, when there are more possible events. - Axiom 3
- If a choice is broken down into two successive choices, the original
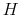 should be the weighted sum of the individual values of
should be the weighted sum of the individual values of 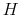 .
.
Theorem 2 of Shannon (1948) establishes the following results:
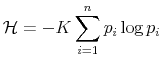
- Remark 1.
- .
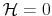 if and only if all the
if and only if all the 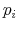 but one are zero, with the one
remaining having the value unity. Thus only when we are certain of the outcome does
but one are zero, with the one
remaining having the value unity. Thus only when we are certain of the outcome does
 vanish. Otherwise
vanish. Otherwise
 is positive.
is positive. - Remark 2.
- For a given
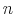 ,
,
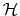 is a maximum and equal to
is a maximum and equal to 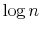 when all the
when all the 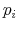 are equal (i.e.,
are equal (i.e.,
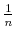 ). This is also intuitively the most uncertain situation.
). This is also intuitively the most uncertain situation. - Remark 3.
- Suppose there are two random variables,
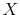 and
and 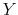 ,
Moreover,
,
Moreover,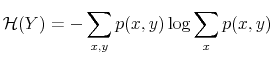 with equality only if the events are independent (i.e.,
with equality only if the events are independent (i.e.,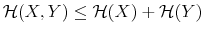
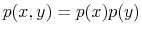 ). This means that the uncertainty of a joint event is less than or equal to the sum of the individual uncertainties.
). This means that the uncertainty of a joint event is less than or equal to the sum of the individual uncertainties. - Remark 4.
- Any change toward equalization of the probabilities
 increases
increases
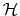 . Thus if
. Thus if
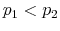 an increase in
an increase in 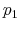 , or a decrease in
, or a decrease in 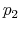 that makes the two probabilities more alike results into an increase in
that makes the two probabilities more alike results into an increase in
 . The intuition is trivial since equalizing the probabilities of two events makes them indistinguishable and therefore increases uncertainty on their occurrence. More generally,
if we perform any "averaging" operation on the
. The intuition is trivial since equalizing the probabilities of two events makes them indistinguishable and therefore increases uncertainty on their occurrence. More generally,
if we perform any "averaging" operation on the 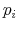 of the form
of the form
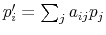 where
where
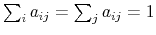 , and all
, and all
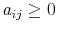 , then in general
, then in general
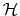 increases36.
increases36. - Remark 5.
- Given two random variables
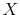 and
and 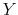 as in Remark 3, not necessarily
independent, for any particular value
as in Remark 3, not necessarily
independent, for any particular value 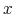 that
that 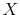 can assume there is a conditional
probability
can assume there is a conditional
probability 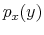 that
that 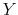 has the value
has the value 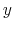 . This is given by
The conditional entropy of
. This is given by
The conditional entropy of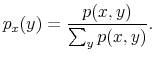
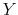 , is then defined as
, is then defined as
 and it is the average of the entropy of
and it is the average of the entropy of  for each possible
realization the random variable
for each possible
realization the random variable 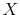 , weighted according to the probability of getting a particular realization
, weighted according to the probability of getting a particular realization 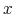 . In formulae,
This quantity measures the average amount of uncertainty in
. In formulae,
This quantity measures the average amount of uncertainty in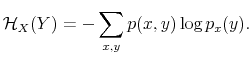
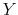 after knowing
after knowing 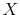 .
Substituting the value of
.
Substituting the value of 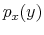 , delivers
, delivers
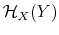
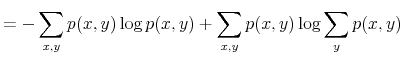
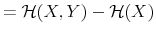
or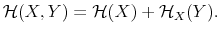
This formula has a simple interpretation. The uncertainty (or entropy) of the joint event ![]() is the uncertainty of
is the uncertainty of ![]() plus the uncertainty of
plus the uncertainty of ![]() after learning the realization of
after learning the realization of ![]() .
.
- Remark 6.
- Combining the results in Axiom 3 and remark 5, it is possible to recover
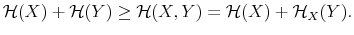
This reads
![]() and implies that the uncertainty of
and implies that the uncertainty of ![]() is
never increased by knowledge of
is
never increased by knowledge of ![]() . If the two random variables are independent, then the entropy will remain unchanged.
. If the two random variables are independent, then the entropy will remain unchanged.
To substantiate the interpretation of entropy as the rate of generating information, it is necessary to link
![]() with the notion of a channel. A channel is simply the medium used to transmit information from the source to the destination, and its capacity is defined as the rate at which the channel transmits information. A discrete channel is a system through which a sequence of choices from a finite set of elementary symbols
with the notion of a channel. A channel is simply the medium used to transmit information from the source to the destination, and its capacity is defined as the rate at which the channel transmits information. A discrete channel is a system through which a sequence of choices from a finite set of elementary symbols
![]() can be transmitted from one point to another. Each of the symbols
can be transmitted from one point to another. Each of the symbols ![]() is assumed to have a certain duration in time
is assumed to have a certain duration in time ![]() seconds. It is not required that all possible sequences of the
seconds. It is not required that all possible sequences of the ![]() be capable of transmission on the system; certain sequences only may be allowed. These sequeences will be possible signals for the channel. Given a channel, one may be interested in measuring its capacity to transmit information. In
general, with different lengths of symbols and constraints on the allowed sequences, the capacity of the channel is defined as:
be capable of transmission on the system; certain sequences only may be allowed. These sequeences will be possible signals for the channel. Given a channel, one may be interested in measuring its capacity to transmit information. In
general, with different lengths of symbols and constraints on the allowed sequences, the capacity of the channel is defined as:
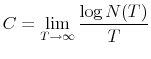
To explain the argument in a very simple case, consider transmitting files via computers. The speed at which one can exchange documents depends on the internet connection and it is expressed in bits per seconds. The maximum amount of bits per second that can be transmitted is negotiated with the provider. However, this does not mean that the computer will always be transmitting data at this rate; this is the maximum possible rate and whether or not the actual rate reaches this maximum depends on the usage and the source of information which feeds the channel. The link between channel capacity and entropy is illustrated by the following Theorem 9 of Shannon:
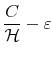 symbols per second over the channel where
symbols per second over the channel where
The intuition behind this result is that by selecting an appropriate coding scheme, the entropy of the symbols on a channel achieves its maximum at the channel capacity. Alternatively, channel capacity can be related to mutual information.
In formulae:
Intuitively,
![]()
![]() measures the amount of information
that two random variables have in common. The capacity of the channel is then alternatively defined by
measures the amount of information
that two random variables have in common. The capacity of the channel is then alternatively defined by
Footnotes
Note also that this constraint is computationally convenient reducing the number of choice variables from ![]() to
to
![]() per iteration. Return to Text
per iteration. Return to Text
![\begin{displaymath}p\left( c,w\right) =\left[ \begin{array}[c]{ccc}% 1 & 0 & 0\ & 0 & 0\ & & 0 \end{array}\right] \end{displaymath}](img224.gif) leaving zero degrees of freedom. If, instead, e.g.,
leaving zero degrees of freedom. If, instead, e.g.,
This function allows to solve the functional equation
![\displaystyle \max_{\left\{ c_{t}\right\} _{t=0}^{\infty}}E_{0}\left\{ \left. {\displaystyle\sum\limits_{t=0}^{\infty}} \beta^{t}\left[ \left( \frac{c_{t}^{1-\gamma}}{1-\gamma}\right) \right] \right\vert \mathcal{I}_{0}\right\}%](img33.gif)
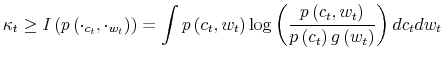
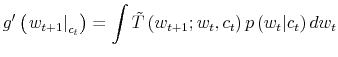
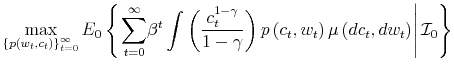
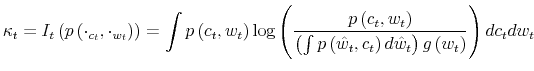
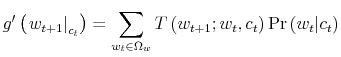
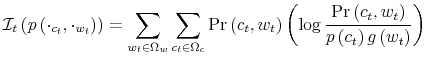
![\displaystyle \max_{\left\{ p\left( w_{t},c_{t}\right) \right\} _{t=0}^{\infty}}% E_{0}\left\{ \left. {\displaystyle\sum\limits_{t=0}^{\infty}} \beta^{t}\left[ {\displaystyle\sum\limits_{w_{t}\in\Omega_{w}}} {\displaystyle\sum\limits_{c_{t}\in\Omega_{w}}} \left( \frac{c_{t}^{1-\gamma}}{1-\gamma}\right) \Pr\left( c_{t}% ,w_{t}\right) \right] \right\vert \mathcal{I}_{0}\right\} .%](img137.gif)
![\displaystyle V\left( g\left( w_{t}\right) \right) =\max_{\Pr\left( c_{t},w_{t}\right) } \left[ \begin{array}[c]{c}% {\displaystyle\sum\limits_{w_{t}\in\Omega_{w}}}\left( {\displaystyle\sum \limits_{c_{t}\in\Omega_{c}}}u\left( c_{t}\right) \Pr\left( c_{t}% ,w_{t}\right) \right) +\\ +\beta\sum\limits_{w_{t}\in\Omega_{w}}{\displaystyle\sum\limits_{c_{t}% \in\Omega_{c}}}V\left( g_{c_{t}^{j}}^{\prime}\left( w_{t+1}\right) \right) \Pr\left( c_{t},w_{t}\right) \end{array} \right]%](img140.gif)
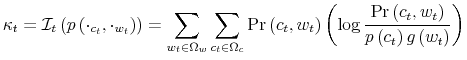
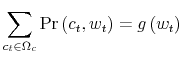
![\displaystyle V^{\ast}\left( g\right) =\max_{p\in\Gamma}\left[ {\displaystyle\sum \limits_{w\in\Omega_{w}}}\left( {\displaystyle\sum\limits_{c\in\Omega_{c}}% }u\left( c\right) p\left( c\vert w\right) \right) g\left( w\right) +\beta\sum\limits_{w\in\Omega_{w}}{\displaystyle\sum\limits_{c\in\Omega_{c}}% }\left( V^{\ast}\left( g_{c}^{\prime}\left( \cdot\right) \right) \right) p\left( c\vert w\right) g\left( w\right) \right]%](img164.gif)
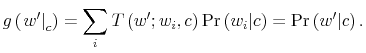
![\displaystyle V_{0}\left( g\right) =\max_{p\in\Gamma}\left[ {\displaystyle\sum \limits_{w\in\Omega_{w}}}\left( {\displaystyle\sum\limits_{c\in\Omega_{c}}% }u\left( c\right) p\right) g\left( w\right) \right]%](img354.gif)
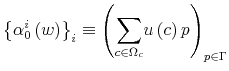
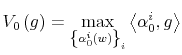
![\displaystyle V_{n}\left( g\right) =\max_{p\in\Gamma}\left[ \begin{array}[c]{c}% {\displaystyle\sum\limits_{w\in\Omega_{w}}}\left( {\displaystyle\sum \limits_{c\in\Omega_{c}}}u\left( c\right) p\left( c\vert w\right) \right) g\left( w\right) +\\ +\beta{\displaystyle\sum\limits_{w\in\Omega_{w}}}{\displaystyle\sum \limits_{c\in\Omega_{c}}}\left( V_{n-1}\left( g_{c}^{\prime}\left( \cdot\right) _{c}\right) \right) p\left( c\vert w\right) g\left( w\right) \end{array} \right]%](img359.gif)
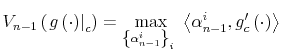
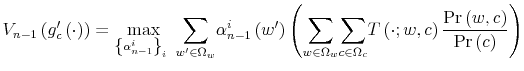
![\displaystyle =\max_{p\in\Gamma}\left[ \begin{array}[c]{c}% {\displaystyle\sum\limits_{w\in\Omega_{w}}}\left( {\displaystyle\sum \limits_{c\in\Omega_{c}}}u\left( c\right) p\right) g\left( w\right) +\\ +\beta\max_{\left\{ \alpha_{n-1}^{i}\right\} _{i}\ }{\displaystyle\sum \limits_{w^{\prime}\in\Omega_{w}}}\alpha_{n-1}^{i}\left( w^{\prime}\right) \left( {\displaystyle\sum\limits_{w\in\Omega_{w}}}\left( {\displaystyle\sum \limits_{c\in\Omega_{c}}}\frac{T\left( \cdot;w,c\right) }{\Pr\left( c\right) }\cdot p\right) g\left( w\right) \right) \end{array} \right]](img363.gif)
![\displaystyle =\max_{p\in\Gamma}\left[ \left\langle u\left( c\right) \cdot p,\text{ }g\left( w\right) \right\rangle +\beta{\displaystyle\sum\limits_{c\in \Omega_{c}}}\frac{1}{\Pr\left( c\right) }\max_{\left\{ \alpha_{n-1}% ^{i}\right\} _{i}\ }\left\langle {\displaystyle\sum\limits_{w^{\prime}% \in\Omega_{w}}}\alpha_{n-1}^{i}\left( w^{\prime}\right) T\left( \cdot;w,c\right) \cdot p,\text{ }g\right\rangle \right]%](img364.gif)
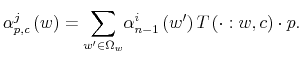
![\displaystyle V_{n}\left( g\right) =\max_{p\in\Gamma}\left[ \left\langle u\left( c\right) \cdot p,\text{ }g\right\rangle +\beta{\displaystyle\sum \limits_{c\in\Omega_{c}}}\frac{1}{\Pr\left( c\right) }\max_{\left\{ \alpha_{p,c}^{j}\right\} _{j}\ }\left\langle \alpha_{p,c}^{j},g\right\rangle \right] ,%](img367.gif)
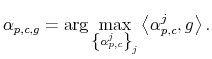
![\displaystyle =\max_{p\in\Gamma}\left[ \left\langle u\left( c\right) \cdot p,\text{ }g\right\rangle +\beta{\displaystyle\sum \limits_{c\in\Omega_{c}}}\frac{1}{\Pr\left( c\right) }\left\langle \alpha_{p,c,g},\text{{}}g\right\rangle \right]](img371.gif)
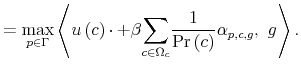
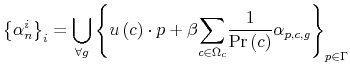
![\displaystyle p^{\ast}\left( w_{k_{2}}\vert c_{k_{1}}\right) =\frac{e^{\left( \frac{\left[ \left( c_{k_{1}}-c_{k_{2}}\right) +\beta\Delta_{k}\bar{V}\left( g_{c}^{\prime}\left( .\right) \right) \right] }{\theta}\right) }}{% {\textstyle\sum\limits_{j}} \tilde{\Delta}T_{j}}%](img456.gif)
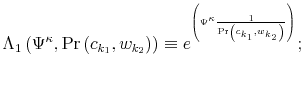
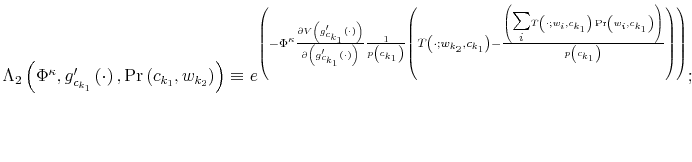
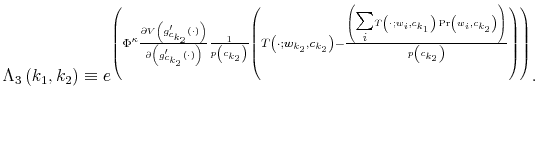
![\displaystyle % \begin{tabular}[c]{\vert\vert c\vert\vert c\vert c\vert c\vert}\hline\hline $C\backslash W$\ & $w_{1}$\ & \multicolumn{1}{\vert\vert c\vert}{$w_{2}$} & \multicolumn{1}{\vert\vert c\vert\vert}{$w_{3}$}\\ \hline\hline $c_{1}$\ & $g_{1}$\ & $p_{1}$\ & $p_{2}$\\ \hline $c_{2}$\ & $0$\ & $g_{2}-p_{1}$\ & $p_{3}$\\ \hline $c_{3}$\ & $0$\ & $0$\ & $1-\left( g_{1}+g_{2}\right) -\left( p_{2}% +p_{3}\right) $\\ \hline \end{tabular} \ \ \%](img571.gif)
![\displaystyle =p_{1}\left( \theta\left( \left[ u^{\prime}\left( c_{1}\left( \kappa\right) \right) -u^{\prime}\left( c_{2}\left( \kappa\right) \right) \right] \right) \ln\left( \frac{p_{1}}{\left( g_{1}+p_{1}% +p_{2}\right) }\right) \right)%](img623.gif)
![\displaystyle =p_{2}\left( \theta\left( \left[ u^{\prime}\left( c_{1}\left( \kappa\right) \right) -u^{\prime}\left( c_{3}\left( \kappa\right) \right) \right] \right) \ln\left( \frac{p_{2}}{\left( g_{1}+p_{1}% +p_{2}\right) }\right) \right)%](img626.gif)
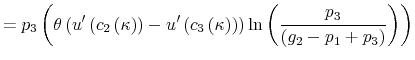
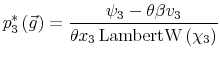
![\begin{displaymath}p\left( c,w\right) =\left[ \begin{array}[c]{ccc}% \frac{1}{3} & p_{1} & p_{2}\ & \frac{1}{3} & p_{3}\ & & \frac{1}{3}% \end{array}\right] .\end{displaymath}](img228.gif)
![\begin{displaymath} \frac{1}{\left( g_{1}+p_{1}+p_{2}\right) ^{2}}\left[ \begin{array}[c]{c}% 0.81p_{2}-0.15g_{1}\ -\left( 0.56p_{2}-0.15g_{1}\right) \ -0.25p_{2}% \end{array}\right] =0 \end{displaymath}](img614.gif)
![\begin{displaymath} \frac{p_{3}}{\left( g_{2}-p_{1}+p_{3}\right) ^{2}}\left[ \begin{array}[c]{c}% -0.15\ 0.15\ 0 \end{array}\right] =0 \end{displaymath}](img616.gif)