Skip to: [Printable Version (PDF)] [Bibliography] [Footnotes]

Finance and Economics Discussion Series: 2008-63 Screen Reader version ^♣

Fluctuations in Individual Labor Income: A Panel VAR Analysis*

Ivan Vidangos

Federal Reserve Board

Keywords: Earnings dynamics, income determination, wage shocks, unemployment

Abstract:

This paper studies variation in individual labor income over time using a panel vector autoregression (PVAR) in income, the wage rate, hours of work, and hours of unemployment. The framework is used to investigate how much of the residual variation in labor income is due to residual variation in the wage rate, work hours, and unemployment hours. I also explore the dynamic effects of unanticipated changes in each of the variables in the system, investigate their interactions, and assess their contribution to short-run and long-run income movements. The model is estimated on a sample of male household heads from the Panel Study of Income Dynamics (PSID). I find that innovations in the wage rate and work hours (conditional on unemployment) are about equally important in the short run. Wage innovations are very persistent, while the effect of changes in hours is mostly transitory. As a result, the wage rate is much more important in the determination of income movements in the long run. Innovations in unemployment have a relatively small, but very persistent effect on income which operates through the wage rate.

1 Introduction

This paper studies variation in labor income over time using an extended panel vector autoregression (PVAR) in income, the wage rate, hours of work, and hours of unemployment. More precisely, the framework is a restricted PVAR extended to allow for contemporaneous effects among some of the variables in the system. For consistency with the income dynamics literature, all variables used are residuals from " Mincer-type" regressions. The framework is used to investigate how much of the residual variation in labor income is due to residual variation in the wage rate, work hours, and unemployment hours. I also explore the dynamic effects of unanticipated changes in each of the variables in the system, investigate their interactions, and assess their contribution to short-run and long-run income movements. The model is estimated on a sample of male household heads from the Panel Study of Income Dynamics (PSID).

Understanding the behavior of income over time is important for a variety of lines of research in economics. Notable examples are the consumption-saving literature, and a class of dynamic stochastic general equilibrium models used to explore a variety of issues in macroeconomics, including the distribution of wealth and consumption, the welfare costs of business cycles, and asset pricing.¹ Additional examples include studies of intergenerational earnings correlations and studies of the effects of training programs or job displacement.

Not surprisingly, there is a large empirical literature that studies income dynamics. The goal of these studies is to fit the residual of a Mincer-type income regression to an appropriate time-series statistical model. The specifications typically used are combinations of components-of-variance and autoregressive moving-average (ARMA) models. Almost all of the existing studies use exclusively univariate income processes. Univariate models, however, have several important limitations:

(i) They provide little information on specific sources of variation. Such information can be important: understanding the dynamic effects of unemployment on income, for instance, provides useful information about the potential benefits of unemployment insurance.

(ii) Different types of shocks may have different properties and different dynamic effects on income. For instance, shocks may differ in their persistence and degree of predictability. Effects may also vary: a shock that affects both hours and the wage rate may have a very different effect on income than a shock that affects only hours.

(iii) The channels through which different shocks operate might contain useful information. For instance, does unemployment affect labor income only through an effect on work hours or also through an effect on the wage rate? What is the relative importance of each effect? Addressing such questions requires the use of multivariate models.

(iv) One might also be interested in decomposing the variation in income at different horizons into parts attributable to different shocks. Such a decomposition would provide useful information about the role that different shocks play for income distribution and inequality. This cannot be accomplished with univariate processes.

(v) Finally, in many decision models, such as models of consumption and saving, economic agents form expectations about future income. These expectations are likely to be conditioned on variables such as the wage, employment status, and health, as these variables contain important information about future income. Univariate income processes used as inputs to decision models do not exploit such conditioning information.

The multivariate approach in this paper overcomes some of these limitations. The framework used here allows me to study specific, economically interpretable types of shocks which play a central role in the determination of income fluctuations. This framework also allows me to investigate the dynamic properties of these shocks, their interactions, their effects on income, and their relative contribution to short-run and long-run income movements. The main goal is to illustrate the advantages of using a multivariate approach. The framework presented here can be expanded and refined along several dimensions. Some of these extensions are addressed in separate work², and are discussed in a later section.

The main results of this paper are as follows. Most of the variation in income in the very short run is due to innovations not related to the other variables in the model. These "income" innovations (which are likely to reflect largely measurement error, but also capture changes in non-wage labor income, such as bonuses and commissions) account for almost 80 percent of the variation in income within one period. These innovations, however, have a very short-lived effect, and consequently explain only 37 - 38 percent of the long-run income variance. Most of the remaining long-run variation in income is due to innovations in the wage rate. Wage innovations, which account for only 8 percent of the variation of (measured) income within one period, are very persistent and are responsible for more than 40 percent of the long-run income variance. Wage innovations are thus the most important factor affecting long-run movements in income. Consequently, any shock that affects the wage rate is also likely to have a long-lasting effect on income. Innovations in work hours have a similar effect to wage innovations in the very short run. However, hours innovations have a largely transitory effect on income, and therefore account for only 10 - 13 percent of the long-run income variance. Accordingly, any shock that affects labor income only through an effect on hours is likely to have a short-lived effect on income. Finally, innovations in unemployment explain a relatively small fraction of income variance but have a very persistent effect on income. The persistence of the effect of unemployment on income is due to a large, negative, and very persistent effect of unemployment on the wage rate. Unemployment innovations account for less than 5 percent of the income variation in the very short run, and for about 10 percent in the long run.

Very few previous studies have investigated income variation using a multivariate approach. One exception is Altonji, Martins, and Siow (2002; hereafter AMS), who use a vector moving-average framework for the first differences of family income, the wage rate, hours of work, and unemployment. Their results are not directly comparable to mine because I work with data in levels. However, a later section in this paper presents some results from estimation of the models used here in first differences rather than in levels, and discusses some of the differences between the two studies.³

The paper is organized as follows. Section 2 reviews the existing empirical literature on income dynamics. Section 3 presents the extended PVAR models. Section 4 discusses the estimation methods. Section 5 describes the data used. Section 6 presents the estimation results. Section 7 presents impulse responses and variance decompositions, and discusses and interprets the results. Finally, section 8 discusses the limitations of the work presented here, as well as extensions of this work that are addressed in separate research.

2 Review of the Empirical Literature

There is an extensive body of research that analyzes the dynamics of income in the U.S. population using longitudinal data. This literature typically removes the variation in income due to demographic characteristics, education, and economy-wide effects, and fits the residual income variance to an appropriate time-series statistical model. There are two general approaches to modeling the residual income variance followed in the literature. In the first approach, which is often referred to as the " unit-root" approach, the income residuals $u_{it}$ are modeled as either (i) $u_{it}=\mu_{i}+v_{it}$ where $\mu_{i}$ is an individual-specific, time-invariant unobserved effect and $v_{it}$ follows an $\ ARMA(p,q)$ process, or (ii) $u_{it}=\mu_{i}+p_{it}+e_{it}$ where $p_{it}\sim AR(p)$ is a permanent component and $e_{it}\sim MA(q)$ is a transitory component. The parameters and are determined from the covariance structure of the income residuals. A fairly widely accepted result is that $v_{it}\sim ARMA(1,1)$ or (or, alternatively, that $p_{it}\sim AR(1)$ and $e_{it}\sim MA(1)$ or ), with the autoregressive coefficient near 1, provide a good description of the data. See, for instance, MaCurdy (1982), Abowd and Card (1989), Topel (1991), Topel and Ward (1992), and Meghir and Pistaferri (2004). In the second approach, sometimes called the "profile heterogeneity" approach, the income residuals $u_{it}$ are modeled as $u_{it}=\alpha _{i}+\lambda_{i}EXP_{it}+\varepsilon_{it}$ , where $\alpha_{i}\$ and $\lambda_{i}\$ are correlated individual-specific, time-invariant unobserved components, $EXP_{it}$ represents labor market experience or potential experience, and $\varepsilon_{it}$ is a transitory error component. See, for instance, Lillard and Weiss (1979), Hause (1980), Baker (1997), and Guvenen (2007).

Almost all models of income in the literature are univariate models and do not consider other variables that are related to income. One early exception is Abowd and Card (1989), who study the bivariate process of changes in labor income and hours of work.⁴ Another exception is Altonji, Martins, and Siow (2002; hereafter AMS). AMS consider a second-order vector-moving-average system, where changes in income depend on current and past shocks to income, hours, the wage rate, and unemployment. Their estimation results attribute 70.8 percent of the variation in income (in first differences) to measurement error, and 82.9 percent of the remaining variation to the income shock. AMS also find that innovations in the wage rate are mostly permanent, while innovations in unemployment are mostly transitory. The degree of persistence of hours shocks is somewhere in between.

3 Model Specification

This section introduces the models used in this paper to analyze fluctuations in labor income. The models are essentially restricted panel vector autoregressions (PVAR), extended to allow for contemporaneous effects among some of the variables in the system. The variables considered in the PVAR are labor income, the real wage rate, hours of work, and hours of unemployment, all in logarithms. All variation in these variables that is due to any (common) deterministic time trend, economy-wide effects, age, and education, was removed prior to the analysis. The analysis here uses, thus, the residuals from regressions of each of the four system variables against year indicators, education, and a third-degree polynomial in age. Two features of the models presented require special discussion. First, the basic specifications do not include fixed effects in the income, wage, hours, or unemployment equations. This modeling choice has both advantages and disadvantages and is justified below. Second, the basic specifications do not allow for specific forms of serial correlation in the errors. A later section in the paper considers a specification that includes fixed effects in all equations and one that allows for moving-average errors. I present estimation results for those specifications and briefly discuss some of their implications. The results from these two alternative specifications, however, are not the central focus of the paper, for reasons discussed below. A more in-depth analysis of these specifications is left for future research.

3.1 Models without Unemployment

The first model I consider essentially defines labor income as the product of the wage rate and hours. Income is additionally allowed to depend on one lag of itself in order to account for state dependence in non-wage labor income. In this model, the wage and hours are specified as autonomous time-series processes that do not depend on the other variables in the system. In Model 1, both variables follow an autoregressive process of order one, ignoring the possibility that the errors may be serially correlated. Letting $y_{it}$ , $w_{it}$ , and $h_{it}$ denote income, the wage rate, and hours, respectively, model 1 is thus:

(1)	$\displaystyle w_{it}$	$\displaystyle =\gamma_{1ww}w_{i,t-1}+u_{it}^{w}$
(2)	$\displaystyle h_{it}$	$\displaystyle =\gamma_{1hh}h_{i,t-1}+u_{it}^{h}$
(3)	$\displaystyle y_{it}$	$\displaystyle =\gamma_{0yw}w_{it}+\gamma_{0yh}h_{it}+\gamma_{1yy}y_{i,t-1}% +u_{it}^{y}%$

Model 2 allows for some additional interactions among income, the wage rate, and hours. Specifically, hours are allowed to depend contemporaneously on the wage rate, and they are also allowed to depend on two lags of income. The inclusion of the wage in the hours equation reflects the labor supply response to changes in the current wage. The inclusion of lagged income in the hours equation intends to capture the dependence of the choice of hours worked by an individual on wealth, which should depend on past income. The first and third equations are exactly as in model 1. Model 2 is thus:

(4)	$\displaystyle w_{it}$	$\displaystyle =\gamma_{1ww}w_{i,t-1}+u_{it}^{w}$
(5)	$\displaystyle h_{it}$	$\displaystyle =\gamma_{0hw}w_{it}+\gamma_{1hh}h_{i,t-1}+\gamma_{1hy}% y_{i,t-1}+\gamma_{2hy}y_{i,t-2}+u_{it}^{h}$
(6)	$\displaystyle y_{it}$	$\displaystyle =\gamma_{0yw}w_{it}+\gamma_{0yh}h_{it}+\gamma_{1yy}y_{i,t-1}% +u_{it}^{y}%$

Model 3 includes some additional lags of some of the variables in all equations. Specifically, the wage rate is now allowed to depend on three lags of itself, rather than just one; hours and income are now allowed to depend on two lags of themselves. Model 3 may be viewed as a slightly more "atheoretical", but also more dynamically complete model, and is given by:

(7)	$\displaystyle w_{it}$	$\displaystyle =\gamma_{1ww}w_{i,t-1}+\gamma_{2ww}w_{i,t-2}+\gamma_{3ww}% w_{i,t-3}+u_{it}^{w}$
(8)	$\displaystyle h_{it}$	$\displaystyle =\gamma_{0hw}w_{it}+\gamma_{1hh}h_{i,t-1}+\gamma_{1hy}% y_{i,t-1}+\gamma_{2hh}h_{i,t-2}+\gamma_{2hy}y_{i,t-2}+u_{it}^{h}$
(9)	$\displaystyle y_{it}$	$\displaystyle =\gamma_{0yw}w_{it}+\gamma_{0yh}h_{it}+\gamma_{1yy}y_{i,t-1}% +\gamma_{2yy}y_{i,t-2}+u_{it}^{y}%$

Model 4, included as a benchmark, is essentially an unrestricted PVAR of order 2, except for the contemporaneous dependence of income on the wage and hours, and of hours on the wage rate. Here I impose no restrictions on the PVAR(2) on the basis of economic considerations. Model 4 is thus given by:

(10)	$\displaystyle w_{it}$	$\displaystyle =\gamma_{1ww}w_{i,t-1}+\gamma_{1wh}h_{i,t-1}+\gamma_{1wy}% y_{i,t-1}+\gamma_{2ww}w_{i,t-2}$
		$\displaystyle +\gamma_{2wh}h_{i,t-2}+\gamma_{2wy}y_{i,t-2}+u_{it}^{w}$
(11)	$\displaystyle h_{it}$	$\displaystyle =\gamma_{0hw}w_{it}+\gamma_{1hw}w_{i,t-1}+\gamma_{1hh}% h_{i,t-1}+\gamma_{1hy}y_{i,t-1}$
		$\displaystyle +\gamma_{2hw}w_{i,t-2}+\gamma_{2hh}h_{i,t-2}+\gamma_{2hy}y_{i,t-2}% +u_{it}^{h}$
(12)	$\displaystyle y_{it}$	$\displaystyle =\gamma_{0yw}w_{it}+\gamma_{0yh}h_{it}+\gamma_{1yw}w_{i,t-1}% +\gamma_{1yh}h_{i,t-1}$
		$\displaystyle +\gamma_{1yy}y_{i,t-1}+\gamma_{2yw}w_{i,t-2}+\gamma_{2yh}h_{i,t-2}% +\gamma_{2yy}y_{i,t-2}+u_{it}^{y}.$

3.2 Models with Unemployment

The last two specifications that I consider here extend the three-variable system above to include unemployment. Note that the interpretation of shocks to hours in these models will differ relative to their interpretation in the previous models. In the models without unemployment, a large part of unanticipated changes in hours is likely to be due to innovations in unemployment. In the models with unemployment, by contrast, hours shocks will represent all unanticipated changes in hours of work for reasons other than changes in unemployment.

Since model 3 is more "dynamically complete" than models 1 and 2, and theoretically more satisfactory than model 4, I use model 3 as the basis for introducing unemployment; this choice, however, has no bearing on the results. Models 5 and 6 specify unemployment as following a univariate autoregressive process of order three; unemployment is thus treated as exogenous in the system. The wage rate, on the other hand, is allowed to depend on one lag of unemployment. This is intended to capture part of the negative effect that a spell of unemployment may have on an individual's wage once he or she becomes reemployed. Hours are allowed to depend on current and lagged unemployment. Finally, model 5 allows income to depend contemporaneously on unemployment, whereas model 6 restricts the effect of unemployment on income to occur only through hours and the wage, so unemployment does not enter the income equation directly. Model 5 is:

(13)	$\displaystyle u_{it}$	$\displaystyle =\gamma_{1\operatorname{u}% u}u_{i,t-1}+\gamma_{2\operatorname{u}% u}u_{i,t-2}+\gamma_{3\operatorname{u}% u}u_{i,t-3}+u_{it}^{u}$
(14)	$\displaystyle w_{it}$	$\displaystyle =\gamma_{1ww}w_{i,t-1}+\gamma_{1wu}u_{i,t-1}+\gamma_{2ww}% w_{i,t-2}+\gamma_{3ww}w_{i,t-3}+u_{it}^{w}$
(15)	$\displaystyle h_{it}$	$\displaystyle =\gamma_{0hu}u_{it}+\gamma_{0hw}w_{it}+\gamma_{1hu}u_{i,t-1}% +\gamma_{1hh}h_{i,t-1}+\gamma_{1hy}y_{i,t-1}$
		$\displaystyle +\gamma_{2hh}h_{i,t-2}+\gamma_{2hy}y_{i,t-2}+u_{it}^{h}$
(16)	$\displaystyle y_{it}$	$\displaystyle =\gamma_{0yu}u_{it}+\gamma_{0yw}w_{it}+\gamma_{0yh}h_{it}% +\gamma_{1yy}y_{i,t-1}+\gamma_{2yy}y_{i,t-2}+u_{it}^{y}.%$

Model 6 is almost identical, with the only difference that unemployment does not enter the income equation:

(17)	$\displaystyle y_{it}=\gamma_{0yw}w_{it}+\gamma_{0yh}h_{it}+\gamma_{1yy}y_{i,t-1}% +\gamma_{2yy}y_{i,t-2}+u_{it}^{y}.%$

I also experimented with a purely atheoretical model where the wage rate, hours, and income are allowed to depend on current and several lags of unemployment. In that model, the only coefficients on unemployment that are strongly significantly different from zero correspond exactly to the lags of unemployment included in model 5. Thus, the purely empirical dependence of income, wage, and hours on unemployment in the PSID sample agrees exactly with this specification.

3.3 Heterogeneity

One important feature of the models just presented is that they do not include fixed effects in the income, wage, hours, and unemployment equations. Even though unobserved heterogeneity is likely to be important, there are reasons why introducing fixed effects in the present context may be more harmful than beneficial, and there is merit in starting with the simpler specifications introduced above.

First, introducing fixed effects would require estimating the models in first differences (or using a similar transformation of the data). As will be discussed later, an analysis in first differences in this context is likely to be considerably less robust because of timing problems in the measurement of the variables. Additionally, introducing fixed effects in the models above would require estimating the models by generalized method of moments (GMM), which is problematic here because the available instruments are likely to be very weak (this is particularly likely to be a problem in the case of the wage equations). Second, previous studies, including MaCurdy (1982) and Meghir and Pistaferri (2004) have rejected specifications with fixed effects, using PSID data.⁵ Third, in the case of hours of work and unemployment, note that since these variables are modeled here as autoregressive processes, unless the influence of the fixed effect is fully reflected in the distribution of the initial conditions, a fixed effect would play the role of a person-specific drift. It is not clear that a drift is a reasonable element to have in a representation of the behavior of hours of work and unemployment over time.

For the reasons laid out above, I focus here on specifications without fixed effects, which allows me to work with the levels of the variables and is likely to lead to more robust results. A later section presents some results using a specification with fixed effects and discusses the main implications of using such a specification. Altonji, Smith, and Vidangos (2008) estimate richer dynamic multivariate models that include employment status and job changes as well as multiple sources of unobserved heterogeneity using simulation-based estimation techniques.

4 Estimation

Letting and represent, in this section, two arbitrary variables, the general form of each equation in the PVAR systems presented above is:

(18)	$\displaystyle y_{it}=\alpha_{1}y_{i,t-1}+...+\alpha_{p}y_{i,t-p}+\beta_{0}x_{it}+\beta _{1}x_{i,t-1}+...+\beta_{m}x_{i,t-m}+u_{it}^{y},%$

where the error, $u_{it}^{y}$ , is for now assumed to be serially uncorrelated.

The form of feedback considered in models 1 - 6 does not introduce simultaneity into the system; therefore, models 1-6 are estimated equation by equation. The generic equation (18) is a standard linear dynamic panel data model without a fixed effect. Under the assumption of no serial correlation in $u_{it}^{y}$ , equation (18) can be estimated consistently by pooled least squares. The only restriction required for consistency of this estimator is that all regressors included in equation (18) be orthogonal to the error term $u_{it}^{y}$ . A sufficient (and considerably stronger) condition is that $y_{i,t-1}$ and $x_{it}$ be predetermined; that is, that they satisfy the sequential moment restriction:

(19)	$\displaystyle E[u_{it}^{y}\vert x_{it},y_{i,t-1},x_{i,t-1},...,y_{i1,}x_{i1}]=0.%$

This condition is consistent with all forms of feedback among variables considered in models 1-6. Thus, if we are willing to assume that $u_{it}% ^{y}$ is serially uncorrelated as in condition (8), pooled least squares is a consistent estimator for all models presented above.

The assumption that $u_{it}^{y}$ is serially uncorrelated is, however, restrictive, especially for the models including a smaller number of lags. In section 6, I allow $u_{it}^{y}$ to follow a moving-average process. I check the covariance structure of the residuals from equation (18) for the presence of serially correlated errors. Since the presence of moving-average errors would introduce bias in the least-squares estimator, estimation of the more general models proceeds differently. The estimation strategy is discussed in section 6.

5 Data

The sample used is from the Panel Study of Income Dynamics (PSID). The sample period is 1978 to 1992, covering an interval of 15 years. The sample does not include earlier years because the wage variable used was not available for salaried workers prior to 1976, and for the first two years it was right-censored at $9.98. The sample was restricted to male individuals who were heads of household each year between 1978 and 1992, who had not retired, and who were employed, unemployed, or temporarily laid off at the time of the interview. Only individuals with observations on all variables in all years were included. These criteria yielded a sample of 479 household heads. For comparability of results, the treatment of outliers is similar to that of Altonji, Martins, and Siow (2002; AMS). In particular, if the head's wage or labor income showed an increase of more than 500 percent, or a decrease of more than 80 percent from the previous year, the new value was set to 500 percent, or 20 percent, of its previous value. Observations with a reported level of hours above 5,000 were eliminated.

I now discuss the variables used in the study. The income variable is total labor income of the head. This variable includes income from wages, bonuses, overtime, commissions, and professional trade or practice, as well as the labor part of farm income, business income, market gardening income, and roomers and boarders income. The wage variable used is the hourly wage rate for hourly workers and salaried workers at the time of the interview. The rate for hourly workers is directly recorded from the respondents' answers, while the rate for salaried workers is constructed from total salary, using a fixed number of hours. In both cases, the variables are based on questions that are independent of those used to calculate labor income. Although wage data are generally available for temporarily laidoff workers, they are generally not available for the unemployed. As a result, the sample will tend to pick workers with more stable careers. Work hours are simply the total number of hours worked by the head of the household, and unemployment is measured as 2,000 plus hours of unemployment of the head (this rescaling is done to prevent percentage changes in unemployment hours at low levels from being implicitly assigned an inordinately large weight). Finally, all monetary variables were deflated by the Consumer Price Index, and all variables are in natural logarithms.

6 Estimation Results

This section presents the estimation results. Subsection 6.1 presents results from least-squares estimation of the various models presented in section 3, while subsection 6.2 presents estimation results for two alternative specifications of models 1-6: the specification with moving-average errors and the specification with fixed effects.

6.1 Baseline Specifications

Table 1 presents the least-squares estimates of the parameters of the various models presented in section 3. I discuss first the income equation in all six models. With the only exception of model 4 (the "unrestricted" PVAR) all variables included in all models have coefficients significantly different from zero at a 0.1 percent level. This suggests that the specifications are appropriate and that model 3 may be more informative than models 1 and 2. The lags of wage and hours included in the unrestricted PVAR are all insignificant, which lends support to the restrictions imposed in the other specifications. In all six models, the R squared in the income equation is between 0.84 and 0.85. These simple models are thus able to explain a large part of the variation in income. This is not surprising since wage income is a central component of labor income. Income, however, also contains non-wage income components and measurement error.⁶ Consider now the magnitude of the estimated coefficients. The coefficient on the wage rate (between 0.34 and 0.42) is in all cases, except for model 4, slightly larger than the coefficient on hours (between 0.29 and 0.33). These two coefficients are, in general, slightly smaller than the coefficient on lagged income (between 0.42 and 0.55). Finally, in the models with unemployment, the coefficient on unemployment, -0.55, is the largest in absolute value.

I now turn to the hours equation. The models for hours do not explain much of the hours variation: the R squared ranges between 0.23 in the univariate model (model 1) and 0.37 in the models with unemployment. The coefficient on the current wage is negative and significant at a 1 percent level in all cases, although the magnitude of the coefficient varies considerably across models, between -0.07 and -0.18. This significant negative coefficient would imply that the income effect from a change in the wage rate dominates the substitution effect. In model 4, the lagged wage also has a significant negative effect on hours, controlling for the current wage. This result can be rationalized by an intertemporal labor supply model. The coefficient on lagged income, which is intended to capture wealth, is positive and significant at a 1 percent level in all cases. Thus, either lagged income does not reflect wealth or it is not the case that more wealth induce people to work less. Unemployment, as expected, has a large negative contemporaneous effect on hours (the coefficient is -1.23). Lagged unemployment has a positive and significant effect on hours. Finally, lagged hours are, as expected, informative in predicting current hours. The second lag of hours is also important, so we may slightly prefer model 3 to models 1 and 2. In conclusion, the model for hours does not explain much of the hours variation and appears to contradict some of the implications of economic theory. This may be due to the fact that hours are largely a choice variable of economic agents, and therefore are affected by a variety of factors not accounted for in the analysis.

I now turn to the wage equations. In constrast to hours, the simple models for the wage rate explain a large fraction of the wage variation. Even in the univariate model, which includes one lag of the wage as the only explanatory variable, the R Squared is 0.79. In that model, the coefficient on lagged wage is 0.90, so the wage rate is very persistent. Further lags of the wage are also strongly significant and seem informative in predicting wages. In the models with unemployment, lagged unemployment has a very significant negative effect on the wage rate. Unemployment, thus, seems to lead to losses in income not only because of the earnings lost while unemployed, but also because it depresses the wage the individual receives in his or her next job.⁷ In the unrestricted PVAR model, the coefficients on lagged income and lagged hours are also significant in the wage equation. Due to the lack of theoretical support for this relationship, I disregard this as not representing a causal link and lacking much interpretative value.

Finally, consider the unemployment equation. Unemployment is modeled here as a univariate autoregressive process of order three. Note that, in contrast to the wage rate, the model does not explain much of the variation in unemployment: the R squared is only 0.23. The estimated coefficient on the first lag of unemployment is 0.37, so unemployment hours are not very persistent. The coefficients on the second and third lags of unemployment are fairly small and are significant at a 5 percent level, but not at a 1 percent level. Unemployment is thus not very predictable, at least not with this simple descriptive model.

6.2 Alternative Specifications: Moving-Average Errors and Fixed Effects

This subsection presents estimation results for two alternative specifications of models 1-6: a specification that allows for moving-average errors and a specification that includes fixed effects.

6.2.1 Moving-Average Errors

Here I consider a more general specification of models 1-6, in which the error term $u_{it}^{j}$ from equation (18) is allowed to follow a moving-average process of order q:

(20)	$\displaystyle u_{it}^{j}=\varepsilon_{it}^{j}+\theta_{1}\varepsilon_{i,t-1}^{j}% +...+\theta_{q}\varepsilon_{i,t-q}^{j},$ for $\displaystyle j=u,w,h,y.%$

To determine whether a moving-average specification for the error term $u_{it}^{j}$ is consistent with the data, I analyze the covariance structure of the residuals from equation (18), and compare it with the theoretical implications of a moving-average process. For instance, an process implies nonzero serial correlation of order less than or equal to , and no serial correlation of orders greater than . Inspection of the covariance structure thus allows one to determine whether a moving-average specification seems appropriate, and it also allows one to determine the order of the moving-average process. The covariance structure of the residuals, not presented here, is available upon request. For models 3-6, the residuals show no sign of serial correlation; thus, I do not allow for moving-average residuals in those models. For models 1 and 2, on the other hand, the residuals seem to exhibit nonzero first-order serial correlation. I therefore consider an representation of the errors of models 1 and 2.

Moving-average errors make some of the regressors in the various equations correlated with the error term, rendering least-squares estimation inconsistent. For instance, in the income equation of models 1 and 2, errors imply that income lagged one period is endogenous. This implies that the least squares estimates of models 1 and 2 presented above are likely to be affected by some bias. Consequently, I reestimate models 1 and 2 by instrumental variables, where the endogenous variables are instrumented by further lagged levels of the variables in the system, provided that they are uncorrelated with the error term. The estimation results are presented in Table 2. Following estimation of the coefficients by instrumental variables, I estimate the moving-average parameters by fitting the theoretical auto-covariances implied by the MA model to the corresponding sample moments of the variables, using an equally-weighted minimum distance estimator. For a simple discussion of this method, see Abowd and Card (1989, Appendix A). The estimated moving-average parameters are also presented in Table 2.

To see the effect of allowing moving-average errors and using instrumental-variables estimation, consider first model 1 in Table 2. In the income equation, the coefficients on the wage rate and hours become smaller, and the coefficient on lagged income becomes larger, relative to the least-squares estimates discussed before. In the hours equation, the coefficient on lagged hours increases from 0.49 to 0.92. In the wage equation, the autoregressive coefficient increases from 0.90 to 0.98. Thus, both the wage rate and hours appear more persistent here. We must however also account for the moving-average coefficients: these are -0.29, -0.50, and -0.38 in the income, hours, and wage equations, respectively.

In model 2, the feedback between equations results in a larger number of endogenous variables in the equations. Thus, hours are endogenous in the wage equation and lagged income is endogenous in the hours equation. In the income equation, the estimated coefficient on the wage rate is even smaller than in model 1, and the coefficient on hours is essentially zero. Similarly, in the hours equation, the coefficients on current wage and lagged income are statistically zero; the only nonzero coefficient in the hours equation is the coefficient on lagged hours. The wage equation is the same as in model 1, and the moving-average coefficients are also essentially the same as in model 1.

The results presented in Table 2 will not be the focus of the subsequent analysis. The central results come from the preferred models 3, 5, and 6; for these specifications, there is no evidence of serial correlation in the residuals. I will, however, mention the most important implications of the estimates of the models with moving-average errors.

6.2.2 Models with Fixed Effects

This subsection presents estimation results from models 1-6 when all equations, in all six models, are specified with individual-specific, time-invariant, unobservable effects. Equation (18), the generic equation, becomes:

(21)	$\displaystyle y_{it}=\alpha_{1}y_{i,t-1}+...+\alpha_{p}y_{i,t-p}+\beta_{0}x_{it}+\beta _{1}x_{i,t-1}+...+\beta_{m}x_{i,t-m}+\mu_{i}+u_{it}^{y},%$

where $\mu_{i}$ is an individual-specific, unobservable, fixed effect. The important implication of this specification is that the presence of $\mu_{i}%$ renders least squares estimation of equation (21) inconsistent, even if the transitory error $u_{it}^{y}$ is serially uncorrelated. There is an extensive literature on estimation of dynamic linear models with fixed effects such as equation (21). Consistent estimation of (21) typically requires transforming the equation to eliminate $\mu_{i}$ prior to estimation, and then exploiting moment conditions that relate transformed or untransformed variables to the transformed errors. I estimate equation (21) using the linear generalized method of moments (GMM) estimator discussed in Arellano and Bond (1991). This method estimates equation (21) in first differences, using as instruments lagged levels of the dependent variable and any other endogenous predetermined variables. One problem with estimators of this type is that they require that the error component $u_{it}^{y}$ be serially uncorrelated. This is a potential problem for models 1 and 2, where the error seems to be serially correlated. A more serious potential problem here is that this estimator (as well as most traditional estimators of linear dynamic panel data models) may suffer from severe small-sample bias in the presence of autoregressive unit roots due to a weak instruments problem. In the context of my analysis, this problem is likely to be present at least in the wage equations.⁸

Table 3 presents the GMM estimates of models 1-6 with fixed effects. In interpreting the results, it should be kept in mind that the estimates presented here are estimates of the equations in first differences, in contrast to the least-squares estimates presented in Table 1, which are estimates of the equations in levels. Consider first the income equation in Table 3. In all six models, the most important difference relative to the least-squares estimates is that the coefficient on the wage rate is very small and not significantly different from zero. This makes little intuitive sense, and would significantly affect the analysis of the next sections of the paper. Considering the high persistence in the wage, this is likely to be due to a weak instruments problem, as discussed above. Another possible reason is the time inconsistency in the measurement of income and wages. Specifically, the wage rate measure refers to the time of the survey, while labor income and hours refer to the calendar year of the survey. This inconsistency may weaken the relationship between a change in the wage and a change in labor income. For a detailed discussion of this problem, see AMS, p.15.

In the hours equation, the coefficient on lagged hours is around 0.12, much smaller than before. Other than lagged hours, the only variable that is significantly different from zero is current hours of unemployment, which continue to have a large negative effect on work hours. The remaining variables have essentially insignificant coefficients. In the wage equation, the coefficients on lagged wage are around 0.30 and 0.40, and are thus also considerably smaller than before in all models. An important result is that lagged unemployment continues to be significantly negatively related to the wage rate. Another interesting result in model 4 is that lagged income and lagged hours continue to be strongly related to the wage rate, just as they were in Table 1. Finally, we may also note that the tests for serial correlation suggest that models 1 and 2 (in levels) have serially correlated errors; whereas models 3-6 have serially uncorrelated errors; this agrees with the discussion of the covariance structure in the previous section.

Given the problems with the coefficient on the wage in the income equations, the results presented in Table 3 will not be the focus of the subsequent analysis. Nevertheless, I will briefly discuss the main implications of these estimates for the analysis in the following sections.

7 Analysis of Results

This section uses the model estimates to simulate the PVAR system and analyze some implications of the estimates. Subsection 7.1 presents impulse-response functions, 7.2 decomposes the short-run and long-run variation in income into parts due to the various shocks in the system, and subsection 7.3 summarizes and interprets the results.

7.1 Response of Income to Shocks

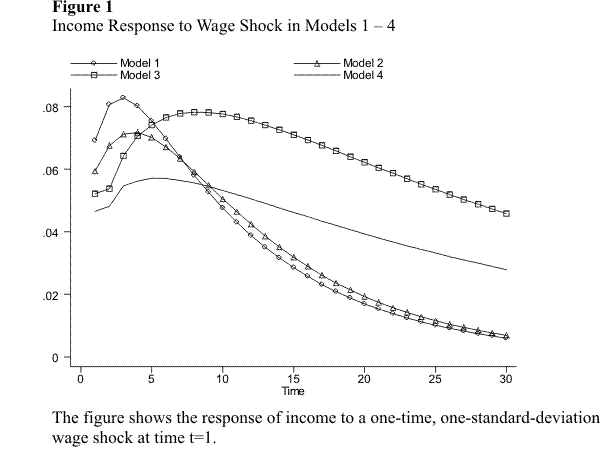
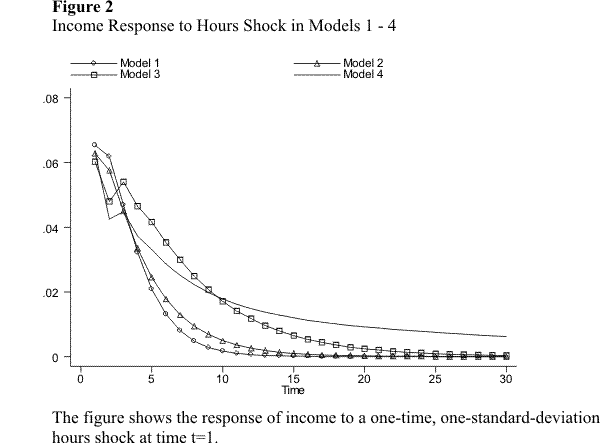
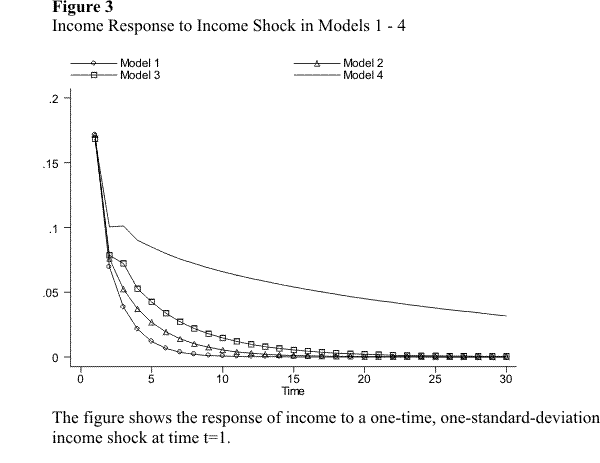
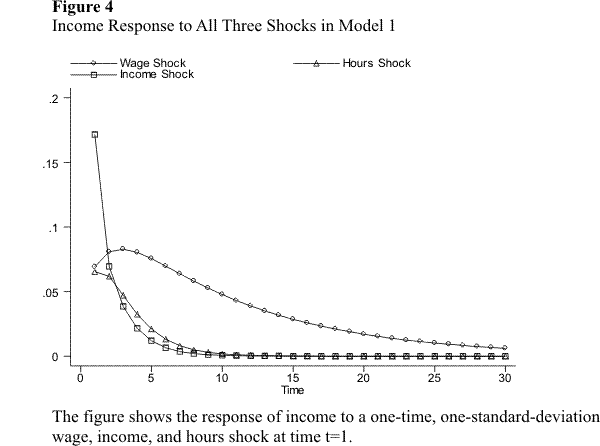
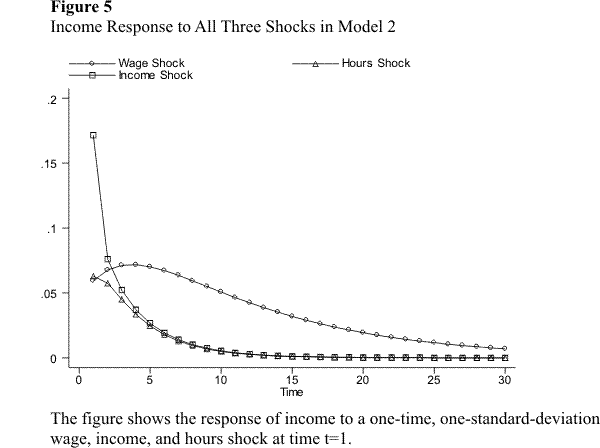
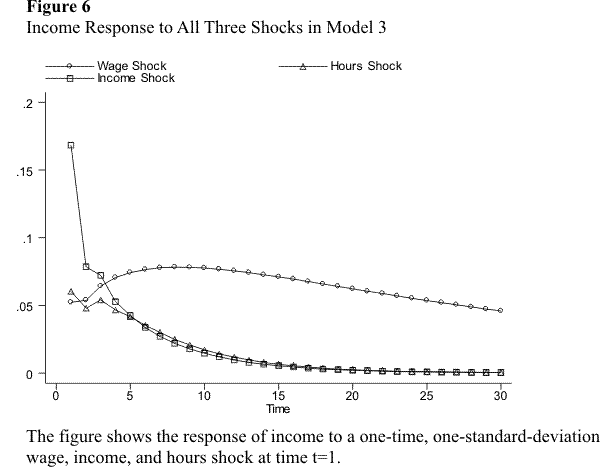
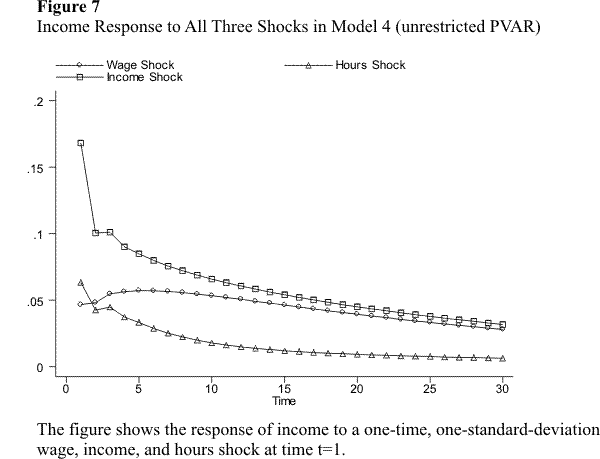
This subsection simulates the response of income to unanticipated changes in the wage rate, hours of work, and hours of unemployment. I perform the simulations for the preferred specification of each of the six models discussed above. Specifically, I simulate separately the response of income over time to a one-time, one-standard-deviation innovation in each of the variables. The response of income is presented in figures 2.1 through 2.9. Figures 2.1 - 2.3 compare the income response to a single shock across models 1 - 4. Figures 2.4 - 2.7 compare the income response to different shocks for a given model, for the models without unemployment. Figures 2.8 - 2.9 do the same for the models with unemployment.

Consider first the effect on income of an innovation in the wage rate in the models without unemployment. Figure 2.1 shows the response of income to a single wage shock for models 1, 2, 3, and 4 (the unrestricted PVAR), while figures 2.4 - 2.7 compare this response against the response to the other shocks for each model. Notice first that all models lead to similar qualitative results: the response of labor income to a wage shock is hump-shaped and very persistent. The immediate response is a jump in income of between one half and one third of the size of the wage shock itself. After the immediate reaction, income continues to increase for a few periods, until it eventually peaks and begins to decline. The eventual decline is, however, very slow, so the effect of the wage shock is very persistent. Models 1 and 2 imply a larger immediate response of income to the wage shock, but also a somewhat faster decline. Model 3, the "more dynamically complete" specification, implies a somewhat smaller immediate response of income, but an even more persistent effect of the shock. The response in the unrestricted PVAR lies somewhere in between.

We now turn to the income effect of the hours shock. As figure 2.2 and figures 2.4 - 2.7 show, all four models yield again very similar results. Hours shocks have a much less persistent effect on income than wage shocks. In all four models, the immediate response of income is a jump of about one third of the size of the hours shock itself. This immediate response is almost identical to the instantaneous response to the wage shock. The effect of the hours shock after the initial period, however, is very different. In all models, income declines towards zero fairly quickly. In models 1 and 2, this decline is monotonic; in models 3 and the PVAR, there is an initial decrease followed by a small one-period increase, before a monotonic decline toward zero. In all cases, most of the effect of the hours shock is transitory.

Finally, consider the effect of the income shock. Recall that this shock captures unexpected changes in components of labor income other than wages income, as well as measurement error. Models 1, 2, and 3 yield essentially identical results: (i) the immediate effect of the income shock is considerably larger than the effect of the wage and hours shocks; (ii) this effect is very transitory.

Let us first discuss the immediate effect of the shock. Technically, the reason that the contemporaneous effect of the income shock is larger than the effect of the other two shocks is the following: the wage and hours shocks affect income contemporaneously through the coefficients of wage and hours in the income equation, which are smaller than one, whereas the income shock enters the income equation directly, thus with an implied coefficient of one. Since the variance of all three shocks is very similar, the instantaneous response of income to the income shock is larger. The variance of the income shock may seem excessively large: once we account for current wage and hours, and some lags of income, we might expect the variance of the income shock to be significantly smaller than the variance of the wage and hours shocks. The fact that the variance is large appears to be an indication that measurement error in income is large. One possible empirical strategy to deal with this problem is to use an external estimate of the variance of measurement error from validation studies on the PSID, and estimate the model using a simulation-based estimator. This is the strategy followed in the companion paper Altonji, Smith, and Vidangos (2008).

The effect of the income shock, although large in the initial period, is very transitory. In fact, more than half of the immediate response of income to the shock dissipates in just one period, after which the effect of the shock continues to decline at a fast rate towards zero. This highly transitory effect of the income shock seems, again, consistent with the interpretation of the shock as consisting largely of (unsystematic) measurement error. The small fraction of the effect of the shocks that does persist for a few periods may reflect a small degree of permanence in surprise changes in the components of labor income other than wage income.

Finally, note that the results from the unrestricted PVAR (model 4) are slightly different from those of the other models and imply a more persistent effect of the income shock. This result is due to the feedback in the PVAR from lagged income to the wage rate. As discussed above, I disregard this relationship, because it seems very unlikely to have any causal or economic content.

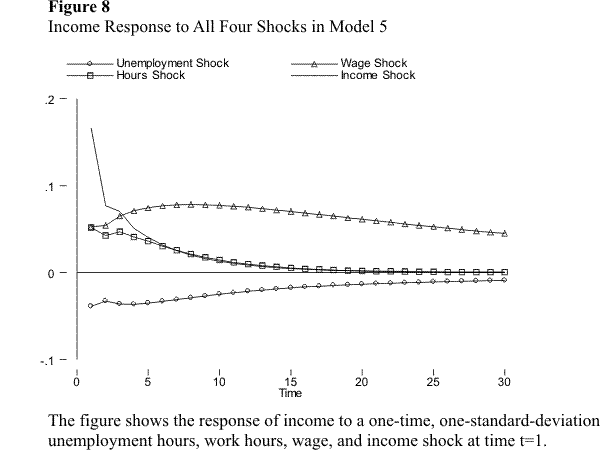
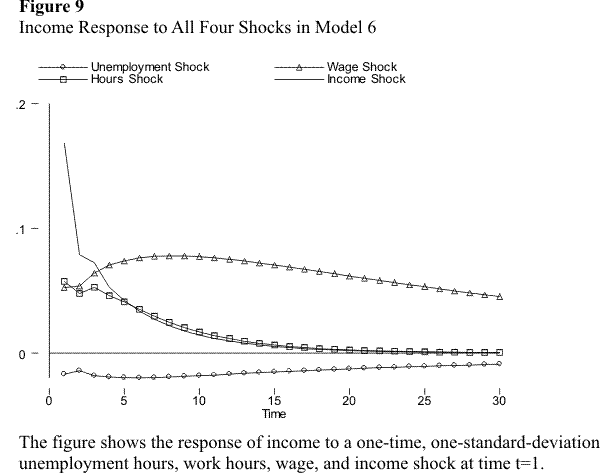
Figures 2.8 and 2.9 display the response of income to each of the four shocks in the systems with unemployment. Figure 2.8 refers to model 5, where unemployment enters the income equation, whereas figure 2.9 refers to model 6. As the figures show, the introduction of hours of unemployment into the system does not affect the response of income to the wage, hours, and income shocks relative to my previous results, so I concentrate here on the effect of the unemployment shock on income. The first thing to note is that the explicit inclusion or exclusion of unemployment in the income equation does not affect, at least qualitatively, the response of income to the unemployment shock in an important way. Including unemployment in the income equation leads, of course, to a larger response, especially in the early periods, but otherwise the response is very similar. In both cases, the response of income to the unemployment shock has two noteworthy features: (i) the response is rather small; (ii) the effect of the unemployment shock seems to be quite persistent. The reason for the first of these two features is simply that the variance of the unemployment shock is very small. In fact, as was discussed above, unemployment enters the income equation with a larger coefficient (in absolute value) than wage, hours, and lagged income. However, the standard deviation of the unemployment shock is approximately one fourth of the standard deviation of the other three shocks. Thus, the reason that the response of income to the unemployment shock is small is simply that the size of the unemployment shock is small.

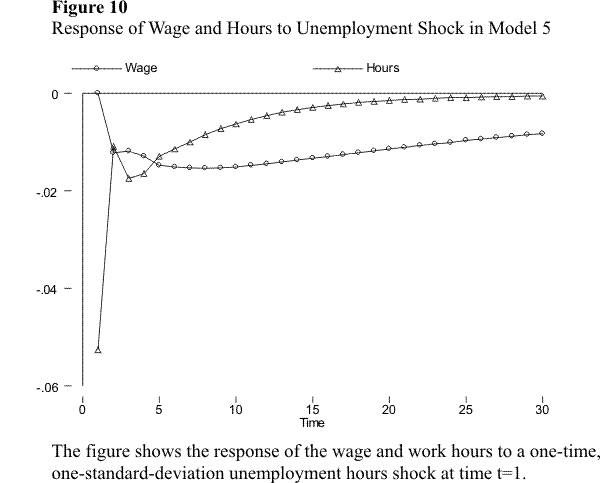
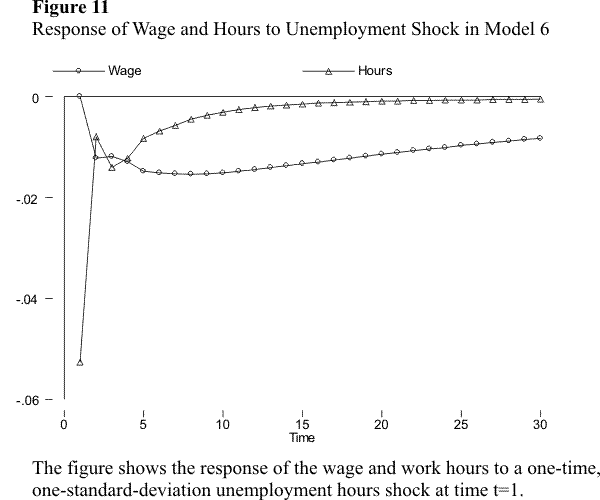
The second feature, namely that the effect of the unemployment shock on income is very persistent, is more interesting. One might expect that most of the effect of an unemployment shock on income occurs through its contemporaneous effect on hours. However, we have seen that the effect of hours shocks on income is very transitory, which might lead us to expect that unemployment shocks are also transitory. The result that they are not suggests that unemployment has a significant and persistent (negative) effect on the wage rate. I explore this in figures 2.10 and 2.11, which display the response of the wage and hours to the unemployment shock, in models 5 and 6. The figures show that, in both models, the unemployment shock has a transitory effect on hours, but a very persistent effect on the wage rate. Unemployment thus affects income not only because an individual foregoes labor income during periods of unemployment, but also because the wage that the individual receives when he or she becomes reemployed is lower than the pre-unemployment wage. The effect operating through hours is short-lived; in fact, as figures 2.10 and 2.11 show, most of this effect vanishes after only one period (one year). However, the effect operating via the wage rate is very persistent.

7.2 Decomposition of Income Variation

The next natural question raised by the previous analysis is: how much of the variation in income at different horizons is due to each of the four shocks in the system? This subsection attempts to provide an answer to this question. For clarity of exposition, the discussion concentrates on the results from model 5, which includes unemployment, and where unemployment enters the income equation directly. The results implied by the other models are very similar and are not discussed in detail. Table 4 presents the results for model 5. Panels a and b decompose the variation in income that results from a one-time simultaneous shock in each of the four variables in period 1. Panel a focuses on the departure of income, in the current period, from the value it would have taken in the absence of the four shocks in period 1; Panel b focuses on the total (cumulative) variation in income that has taken place between period 1 and the current period, in response to the four shocks. Panels c and d are defined similarly, but for a different experiment. There, I consider a situation in which the system receives one-standard-deviation shocks to each of the variables every period, starting with period 1. That is, the innovations continue to shock the system after period 1. I decompose the resulting variation in income just as in Panels a and b. Tables 5 and 6 display the results for models 6 and 3, respectively.

Consider Table 4, Panel a first. In period 1, when all four shocks hit, the income shock is responsible for 79.9 percent of the variation in income. The wage, hours, and unemployment shocks account for only 8.1, 7.7, and 4.4 percent of this variation, respectively. These results are driven by the large impact of the income shock in the initial period, as was already discussed above. Five years after the shocks, however, the income shock is responsible for only 16.8 percent of the continuing variation in income due to the shocks. The wage shock, by contrast, explains most (57.1 percent) of the persisting variation. The hours and unemployment shocks account for about 13 percent each. Ten years after the shocks, practically all surviving variation in income is due to the wage and unemployment shocks: the wage shock accounts for 85.6 percent of this variation, while the unemployment shock accounts for 9.1 percent. The hours and income shocks are responsible for less than 3 percent of the departure in income from its level without the shocks.

As a better measure of the decomposition of the variance of income due to the shocks, one might want to consider not only the variation in income in the current period, but rather the total (cumulative) variation between the shock period and the current period. This is presented in Panel b. The fifth row of the table shows that, five years after the shocks, the income shock accounts for 53.8 percent of the variance, while the wage shock accounts for 25.9 percent. The figures for the unemployment and hours shocks are 8.2 and 12.1 percent, respectively. Ten years after the shock, the wage innovation explains 42.6 percent of the variance, compared with 38.0 percent explained by the income shock. The unemployment and hours shocks explain 9.1 and 10.2 percent. This is my preferred measure of decomposition of income variation.

Consider now the experiment of subjecting the system to a series of one-standard-deviation shocks every period, starting with period 1. This may be a more appropriate way of analyzing and decomposing the variation in income, since, in reality, income evolves over time in response to changes in the wage rate, hours of work, and unemployment shocks that take place every period. I concentrate on the cumulative variation in income, which, as above, should provide a better measure of variance. Table 4, Panel d decomposes the cumulative variation into parts attributable to the series of shocks in each of the four different variables. The important point to note in Panel d is that the decomposition of income variance is very similar to the results presented in Panel b. The conclusions resulting from Panel d are essentially the same as the ones discussed before. The results from this subsection will be further discussed, in conjunction with all the previous analysis, in the following subsection.

7.3 Summary and Interpretation of Results

The purpose of this subsection is to summarize and interpret the results presented above. Consider first the income shock. By far, most of the short-run variation in income is due to the income shock. Innovations in income explain about 80 percent of the variance of measured income in the initial period and about 70 percent one period later. The income shock is likely to consist largely of measurement error and I therefore interpret the result above as an indication that measurement error in labor income is significant. Extending the framework to explicitly account for measurement error would allow a more precise interpretation of the results.⁹ A second very important property of the income shock here is that its effect is mostly transitory. In fact, over half of the effect disappears after only one period. This is, again, consistent with the interpretation that the income shock consists primarily of (unsystematic) measurement error. The combination of the large initial effect and the low persistence of the income shock imply that, in the long run (after ten years), the income shock accounts for between 37 and 38 percent of the variation in income.¹⁰

Consider now the wage shock. In the very short run, innovations in the wage rate account for about 8 percent of the variation in income. This effect is comparable with the immediate effect of the hours shock. Wage shocks, however, are very persistent (and hump-shaped). As a result, innovations in the wage rate account for more than 40 percent of the long-run (after ten years) variation in income, making wage shocks the most important factor determining the long-run variance of income.

Let us now turn to the effect of the hours shock. The short-run effect of innovations in hours depends somewhat on whether or not unemployment is included in the system. In the system with unemployment, the immediate effect of an hours shock is essentially the same as that of the wage shock: it accounts for about 8 percent of the income variation. In the system without unemployment, the immediate effect is slightly larger: hours shocks account for between 10 and 11 percent of the short-run variation in income. In either case, hours shocks are not very persistent. Hence, their long-run effect is considerably smaller than the long-run effect of wage shocks. This long run effect depends, again, on whether or not the system includes unemployment. In model 5, where unemployment is present and enters the income equation directly, hours shocks account for between 10 and 13 percent of the long run (after 10 years) variation in income. In the models without unemployment, hours become slightly more important: in model 3, for instance, they account for between 14 and 17 percent of the long-run variation in income.

The interpretation of hours shocks also depends on whether or not unemployment is included. When unemployment is not included, changes in unemployment hours are likely to be an important component of hours shocks. Therefore, the results from the models with unemployment should be more informative. In these models in particular, innovations in hours appear not to be very important. It is reasonable to expect, however, that explicitly accounting for measurement error in income would reduce the role played by the income shock in the very short run, magnifying the relative role played by hours shocks, at least in the short run.

Perhaps the most interesting result from the analysis above regards the effect of the unemployment shock on income. Consider model 5, where unemployment is allowed to affect income directly, as well as through its effect on hours and the wage rate. In this model, unemployment shocks account for less than 5 percent of the income variation in the very short run, and for about 10 percent in the long run (10 years after the shocks). The effect of the unemployment shock is small in the short run because the size of the unemployment shock is small (i.e., the estimated variance of the error in the unemployment equation is small). On the other hand, the importance of the unemployment shock increases with time, because the unemployment shock has a very persistent effect on income. As was discussed above, the reason for the high degree of persistence of unemployment shocks is that lagged unemployment (lagged by one period) has a large, negative, and very persistent effect on the wage rate, which translates into a persistent effect on income.¹¹ ¹²

Finally, I briefly discuss the results that would obtain from the two alternative specifications discussed above: the specification with moving-average errors and the specification with fixed effects. Consider first the instrumental-variables estimates presented in Table 2, where the errors in models 1 and 2 follow MA(1) processes. The main implications of those estimates for the behavior of income over time are as follows. In model 1, the income and wage shocks have essentially the same effect as in the analysis above. The hours shock, on the other hand, behaves very similarly to the wage shock: the response of income is hump-shaped, and the effect of the shock is very persistent. As a result, although in the short run the income shock accounts for almost 90 percent of the income variation, in the long run, each shock accounts for roughly one third of the variation in income. In model 2, by contrast, hours have essentially no effect on income; innovations in hours account for less than 2 percent of the variation in income in both the short and long run. This result is not very sensible and is due to the fact that the estimated coefficient on hours in the income equation in model 2 is close to zero.

Consider now the GMM estimates presented in Table 3 for models 1-6 with fixed effects, estimated in first differences. The results from Table 3 have the following implications. First of all, no shock has a permanent effect. The effect of all shocks is transitory and vanishes completely after four periods. Second, the wage shock has essentially no effect on income. In both the short and long run, the wage shock accounts for less than 1 percent of the variation in income. The reason for these results is that the estimated coefficient on the wage in the income equation is close to zero in almost all models, as was discussed above. Third, the income shock continues to behave as before. Consequently, the income shock accounts for almost 90 percent of the short-run variation of income, and almost 85 percent of its long-run variance.¹³ Finally, unemployment shocks account for about 6 percent of the short-run variation and 9 percent of the long-run variation, while hours account for about 5 percent of the short-run variation and 6 percent of the long-run variation. As discussed above, the small coefficient on the wage in the income equation is problematic and is likely to be caused by a weak instruments problem and by time inconsistencies in the measurement of income and wages. Consequently, I stick to the estimation in levels presented above, which looks more robust.

8 Conclusions

This paper studies variation in individual labor income over time using an extended panel vector autoregression (PVAR) framework in income, the wage rate, hours of work, and hours of unemployment. For consistency with the income dynamics literature, all variables used are residuals from "Mincer-type" regressions. The framework is used to investigate how much of the residual variation in labor income is due to residual variation in the wage rate, work hours, and hours of unemployment. I also explore the dynamic effects of unanticipated changes in each of the variables in the system, investigate their interactions, and assess their relative importance in the determination of short-run and long-run income movements.

I find that, in the very short run, most of the variation in labor income is due to a factor other than innovations in the wage rate, hours, or unemployment. Measurement error is likely to be a major component of this factor, but the factor might also reflect unexpected changes in non-wage labor income such as bonuses and commissions, and the fact that for salaried workers the PSID wage measure is constructed using schedules with a fixed number of hours. Most of the effect of this factor (which includes measurement error) is short-lived and accounts for 37 - 38 percent of (residual) income variation in the long run. I also find that, in the short run, innovations in the wage rate and work hours have a very similar effect on income, conditional on unemployment. Wage innovations, however, are very persistent, while the effect of changes in hours is mostly transitory. As a result, the wage rate is the most important factor in the determination of (residual) income movements in the long run, explaining more than 40 percent of the variation. Hours, by contrast, are responsible for only 10-13 percent of the long-run variance. Finally, I find that innovations in unemployment have a relatively small, but very persistent effect on income. In the long run, they account for 10 percent of the variation in income. The persistence of the effect of unemployment on income is due to a large, negative, and very persistent effect of unemployment on the wage rate.

The multivariate approach pursued in this paper stands in contrast with most of the existing empirical literature on income dynamics, which studies income variation over time without regard to income components or to specific factors that drive the income fluctuations. The approach followed here offers several advantages: (i) It allows me to distinguish specific sources of income variation. In this paper I consider wage shocks, hours shocks, unemployment shocks, and shocks to non-wage labor income (including measurement error). It would be straightforward to incorporate additional shocks, such as health shocks; (ii) It allows different types of shocks to have different dynamic properties and different effects on income. For instance, the results show that wage shocks are very persistent, while hours shocks are mostly transitory. Consequently, factors that affect the wage rate are likely to have a long-lasting effect on income, while factors that affect only hours are likely to have only short-lived effects; (iii) It allows me to investigate the dynamic interactions among different shocks. One example are unemployment shocks, which are seen to have a long-lasting effect on income because of their persistent effect on the wage rate. One could also use this framework to investigate the effect of, for instance, health shocks on income, and their dynamic interactions with hours, the wage rate, and employment status; (iv) It allows me to decompose the variation in income at different horizons into parts attributable to different shocks. This decomposition provides useful information about the role that different shocks play for income distribution and inequality; (v) Finally, the multivariate approach can also be advantageous when using the income process as an input to decision models, as used in the consumption-saving literature, or in macroeconomics or public finance. Specifically, this framework allows specifications in which agents condition their expectations of future income on variables such as health and employment status, which contain important information about future income.

Although this paper illustrates important advantages of taking a multivariate approach to study fluctuations in labor income, the work presented here has some important limitations. First, as discussed above, measurement error is likely to be an important component of the income shock considered in the PVAR system. A more complete analysis must explicitly account for measurement error and distinguish it from actual innovations to non-wage labor income. Second, variables such as labor income, the wage rate, work hours, and unemployment are likely to be importantly influenced by unobservable characteristics of individuals such as different preferences over work and leisure as well as ability and productivity in the labor market. Such unobservable factors should be accounted for in a flexible manner. Third, the only sources of risk to labor income considered in this paper are unemployment and unanticipated shocks to the wage rate, hours of work, and non-wage labor income. There are additional sources of risk that are also likely to be important and should be included in a more complete analysis, including disability and other health-related shocks. Fourth, this paper does not study the income or wage effects of discrete events such as job changes or accidents. Illness and unemployment could also be modeled as discrete events. Altonji, Smith, and Vidangos (2008) addresses some of the above limitations.¹⁴ Finally, it was claimed above that the multivariate approach can be of value when using the income process as an input to decision models. This is explored in Vidangos (2008), which studies the implications of a related multivariate model of family income-which allows for unemployment, disability, health, and wage shocks-for precautionary behavior and welfare in the context of a lifecycle consumption model.

References

Abowd, J.M. and Card, D.E. (1987). "Intertemporal labor supply and long-term employment contracts." American Economic Review, 77(1), 50-68.

Abowd, J.M. and Card, D.E. (1989). "On the covariance structure of hours and earnings changes." Econometrica, 57(2), 411-445.

Aiyagari, S.R. (1994). "Uninsured idiosyncratic risk and aggregate saving." Quarterly Journal of Economics 109, 659-684.

Altonji, J.G., Martins, A.P., and Siow, A. (2002). "Dynamic factor models of consumption, hours, and income." Research in Economics, 56, 3-59.

Altonji, J.G., Smith Jr., A.A., and Vidangos, I. (2008). " Modeling Earnings Dynamics." Unpublished Manuscript. Yale University and Federal Reserve Board.

Arellano, M. and Bond, S.R. (1991). "Some tests of specification for panel data: Monte Carlo evidence and an application to employment equations." Review of Economic Studies, 58, 277-297.

Arellano, M. and Bover, O. (1995). "Another look at the instrumental-variable estimation of error-components models." Journal of Econometrics, 68, 29-52.

Baker, M. (1997). "Growth-rate heterogeneity and the covariance structure of life cycle earnings." Journal of Labour Economics, 15(2), 338-375.

Baker, M. and Solon, G. (2003). "Earnings dynamics and inequality among Canadian men, 1976-1992: evidence from longitudinal income tax records." Journal of Labor Economics 21(2), 289-321.

Binder, M., Hsiao, C., and Pesaran, M.H. (2005). "Estimation and Inference in Short Panel Vector Autoregressions with Unit Roots and Cointegration", Econometric Theory, 21(4), 795-837.

Blundell, R.W. and Bond, S.R. (1998). "Initial conditions and moment restrictions in dynamic panel data models." Journal of Econometrics, 87, 115-143.

Castañeda, A., Díaz-Giménez, J., and Ríos-Rull V. (2003). "Accounting for the U.S. Earnings and Wealth Inequaility." Journal of Political Economy, 111(4), 818-857.

Deaton, A. (1991). "Saving and liquidity constraints." Econometrica, 59(5), 1221-1248.

Geweke, J. and Keane, M. (2000). "An empirical analysis of earnings dynamics among men in the PSID: 1968-1989." Journal of Econometrics, 96, 293-356.

Guvenen, F. (2007). "Learning Your Earning: Are Labor Income Shocks Really Very Persistent?" American Economic Review 97(3), 687-712.

Haider, S.J. (2001). "Earnings Instability and Earnings Inequality of Males in the United States: 1967-1991." Journal of Labor Economics, 19(4), 799-836.

Hause, J.C. (1980). "The fine structure of earnings and the on-the-job training hypothesis." Econometrica, 48(4), 1013-1029.

Heaton, J. and Lucas, D.J. (1996). "Evaluating the effects of incomplete markets on risk sharing and asset pricing." Journal of Political Economy, 104(3), 443-487.

Holtz-Eakin, D., Newey, W., and Rosen, H.S. (1988). " Estimating vector autoregressions with panel data." Econometrica, 56(6), 1371-1395.

Imrohoroglu, A. (1989). "Cost of Business Cycles with Indivisibilities and Liquidity Constraints." Journal of Political Economy, 97(6), 1364-1383.

Krusell, P. and Smith Jr., A . A. (1998). "Income and Wealth Heterogeneity in the Macroeconomy." Journal of Political Economy, 106(5), 867-896.

Krusell, P. and Smith Jr., A . A. (1999). "On the welfare effects of eliminating business cycles." Review of Economic Dynamics 2, 254-272.

Lillard, L. and Weiss, Y. (1979). "Components of variation in panel earnings data: American scientists 1960-1970." Econometrica 47(2), 437-454.

Lillard, L. and Willis, R. (1978). "Dynamic aspects of earning mobility." Econometrica 46(5), 985-1012.

Low, H., Meghir, C., and Pistaferri, L. (2006). "Wage risk, employment risk, and precautionary saving." Unpublished Manuscript. Cambridge University, University College London, and Stanford University.

MaCurdy, T.E. (1982). "The use of time series processes to model the error structure of earnings in a longitudinal data analysis." Journal of Econometrics, 18, 83-114.

Meghir, C. and Pistaferri, L. (2004). "Income variance dynamics and heterogeneity." Econometrica, 72(1), 1-32.

Storesletten, K., Telmer, C., and Yaron, A. (2001a). "The Welfare Costs of Business Cycles Revisited: Finite Lives and Cyclical Variation in Idiosyncratic Risk." European Economic Review, 45, 1311-1339.

Storesletten, K., Telmer, C., and Yaron, A. (2001b). "How Important are Idiosyncratic Shocks? Evidence from Labor Supply." American Economic Review (Papers and Proceedings), 91, 413-417.

Storesletten, K., Telmer, C., and Yaron, A. (2007). "Asset Pricing with Idiosyncratic Risk and Overlapping Generations." Review of Economic Dynamics, 10(4), 519-548.

Storesletten, K., Telmer, C., and Yaron, A. (2004a). " Consumption and Risk Sharing Over the Life Cycle." Journal of Monetary Economics, 51(3), 609-633.

Storesletten, K., Telmer, C., and Yaron, A. (2004b). " Cyclical Dynamics in Idiosyncratic Labor Market Risk." Journal of Political Economy, 112(3), 695-717.

Telmer, C. (1993). "Asset-Pricing Puzzles and Incomplete Markets." Journal of Finance, 48(5), 1803-1832.

Topel, R. (1991). Specific Capital, Mobility, and Wages: Wages Rise with Job Seniority." Journal of Political Economy, 99(1), 145-176.

Topel, R. and Ward, M. (1992). "Job Mobility and the Careers of Young Men." Quarterly Journal of Economics, 107(2), 439-479.

Vidangos, I. (2008). "Household Welfare, Precautionary Saving, and Social Insurance under Multiple Sources of Risk." Unpublished Manuscript. Federal Reserve Board.

Table 1 Pooled Least Squares Estimates of Models 1-6.
Income Equation:	Model 1	Model 2	Model 3	Model 4	Model 5	Model 6
Income Equation: Wage_t	0.4151	0.4151	0.3650	0.3358	0.3637	0.3650
Income Equation: Wage_t (Robust Standard Error)	(0.0239)	(0.0239)	(0.0248)	(0.0268)	(0.0231)	(0.0248)
Income Equation: Wage_t (p value)	*0.000	*0.000	*0.000	*0.000	*0.000	*0.000
Income Equation: Hours_t	0.3315	0.3315	0.3240	0.3417	0.2903	0.3240
Income Equation: Hours_t (Robust Standard Error)	(0.0350)	(0.0350)	(0.0370)	(0.0466)	(0.0343)	(0.0370)
Income Equation: Hours_t (p value)	*0.000	*0.000	*0.000	*0.000	*0.000	*0.000
Income Equation: Unemployment_t					-0.5530
Income Equation: Unemployment_t (Robust Standard Error)					(0.0854)
Income Equation: Unemployment_t (p value)					*0.000
Income Equation: Income_t-1	0.5541	0.5541	0.4249	0.4332	0.4222	0.4249
Income Equation: Income_t-1 (Robust Standard Error)	(0.0245)	(0.0245)	(0.0232)	(0.0223)	(0.0222)	(0.0232)
Income Equation: Income_t-1 (p value)	*0.000	*0.000	*0.000	*0.000	*0.000	*0.000
Income Equation: Income_t-2			0.1938	0.1916	0.1961	0.1938
Income Equation: Income_t-2 (Robust Standard Error)			(0.0170)	(0.0176)	(0.0168)	(0.0170)
Income Equation: Income_t-2 (p value)			*0.000	*0.000	*0.000	*0.000
Income Equation: Hours_t-1				-0.0269
Income Equation: Hours_t-1 (Robust Standard Error)				(0.0244)
Income Equation: Hours_t-1 (p value)				*0.270
Income Equation: Hours_t-2				-0.0164
Income Equation: Hours_t-2 (Robust Standard Error)				(0.0160)
Income Equation: Hours_t-2 (p value)				*0.304
Income Equation: Wage_t-1				0.0405
Income Equation: Wage_t-1 (Robust Standard Error)				(0.0232)
Income Equation: Wage_t-1 (p value)				*0.081
Income Equation: Wage_t-2				-0.0147
Income Equation: Wage_t-2 (Robust Standard Error)				(0.0194)
Income Equation: Wage_t-2 (p value)				*0.448
Income Equation: Root MSE	0.1732	0.1732	0.1684	0.1682	0.1663	0.1684
Income Equation: R-Squared	0.841	0.841	0.851	0.8514	0.8547	0.851
Hours Equation: Wage_t		-0.1770	-0.1317	-0.0682	-0.1252	-0.1252
Hours Equation: Wage_t (Robust Standard Error)		(0.0300)	(0.0276)	(0.0267)	(0.0275)	(0.0275)
Hours Equation: Wage_t (p value)		*0.000	*0.000	*0.011	*0.000	*0.000
Hours Equation: Unemployment_t					-1.2274	-1.2274
Hours Equation: Unemployment_t (Robust Standard Error)					(0.1315)	(0.1315)
Hours Equation: Unemployment_t (p value)					*0.000	*0.000
Hours Equation: Unemployment_t-1					0.7293	0.7293
Hours Equation: Unemployment_t-1 (Robust Standard Error)					(0.1505)	(0.1505)
Hours Equation: Unemployment_t-1 (p value)					*0.000	*0.000
Hours Equation: Income_t-1		0.1173	0.1271	0.1390	0.1331	0.1331
Hours Equation: Income_t-1 (Robust Standard Error)		(0.0336)	(0.0291)	(0.0307)	(0.0286)	(0.0286)
Hours Equation: Income_t-1 (p value)		*0.001	*0.000	*0.000	*0.000	*0.000
Hours Equation: Income_t-2		0.0779	0.0142	0.0581	0.0021	0.0021
Hours Equation: Income_t-2 (Robust Standard Error)		(0.0213)	(0.0219)	(0.0215)	(0.0222)	(0.0222)
Hours Equation: Income_t-2 (p value)		*0.000	*0.517	*0.007	*0.924	*0.924
Hours Equation: Hours_t-1	0.4914	0.4065	0.3281	0.3158	0.3632	0.3632
Hours Equation: Hours_t-1 (Robust Standard Error)	(0.0469)	(0.0529)	(0.0386)	(0.0404)	(0.0462)	(0.0462)
Hours Equation: Hours_t-1 (p value)	*0.000	*0.000	*0.000	*0.000	*0.000	*0.000
Hours Equation: Hours_t-2			0.2063	0.1820	0.1860	0.1860
Hours Equation: Hours_t-2 (Robust Standard Error)			(0.0232)	(0.0231)	(0.0234)	(0.0234)
Hours Equation: Hours_t-2 (p value)			*0.000	*0.000	*0.000	*0.000
Hours Equation: Wage_t-1				-0.1075
Hours Equation: Wage_t-1 (Robust Standard Error)				(0.0345)
Hours Equation: Wage_t-1 (p value)				*0.002
Hours Equation: Wage_t-2				-0.0221
Hours Equation: Wage_t-2 (Robust Standard Error)				(0.0178)
Hours Equation: Wage_t-2 (p value)				*0.214
Hours Equation: Root MSE	0.1978	0.1899	0.1862	0.1854	0.1775	0.1775
Hours Equation: R-Squared	0.2306	0.2753	0.3033	0.3094	0.3667	0.3667
Wage Equation: Wage_t-1	0.9014	0.9014	0.6078	0.4321	0.6038	0.6038
Wage Equation: Wage_t-1 (Robust Standard Error)	(0.0111)	(0.0111)	(0.0285)	(0.0261)	(0.0284)	(0.0284)
Wage Equation: Wage_t-1 (p value)	*0.000	*0.000	*0.000	*0.000	*0.000	*0.000
Wage Equation: Wage_t-2			0.2381	0.2108	0.2385	0.2385
Wage Equation: Wage_t-2 (Robust Standard Error)			(0.0300)	(0.0225)	(0.0297)	(0.0297)
Wage Equation: Wage_t-2 (p value)			*0.000	*0.000	*0.000	*0.000
Wage Equation: Wage_t-3			0.1070		0.1102	0.1102
Wage Equation: Wage_t-3 (Robust Standard Error)			(0.0186)		(0.0185)	(0.0185)
Wage Equation: Wage_t-3 (p value)			*0.000		*0.000	*0.000
Wage Equation: Unemployment_t-1					-0.2845	-0.2845
Wage Equation: Unemployment_t-1 (Robust Standard Error)					(0.0677)	(0.0677)
Wage Equation: Unemployment_t-1 (p value)					*0.000	*0.000
Wage Equation: Income_t-1				0.3724
Wage Equation: Income_t-1 (Robust Standard Error)				(0.0258)
Wage Equation: Income_t-1 (p value)				*0.000
Wage Equation: Income_t-2				-0.0699
Wage Equation: Income_t-2 (Robust Standard Error)				(0.0161)
Wage Equation: Income_t-2 (p value)				*0.000
Wage Equation: Hours_t-1				-0.1778
Wage Equation: Hours_t-1(Robust Standard Error)				(0.0340)
Wage Equation: Hours_t-1(p value)				*0.000
Wage Equation: Hours_t-2				-0.0264
Wage Equation: Hours_t-2(Robust Standard Error)				(0.0158)
Wage Equation: Hours_t-2 (p value)				*0.095
Wage Equation: Root MSE	0.1732	0.1732	0.1619	0.1487	0.1613	0.1613
Wage Equation: R-Squared	0.7927	0.7927	0.8227	0.8483	0.8241	0.8241
Unemployment Equation: Unemployment_t-1					0.3689	0.3689
Unemployment Equation: Unemployment_t-1 (Robust Standard Error)					(0.0502)	(0.0502)
Unemployment Equation: Unemployment_t-1(p value)					*0.000	*0.000
Unemployment Equation: Unemployment_t-2					0.0988	0.0988
Unemployment Equation: Unemployment_t-2 (Robust Standard Error)					(0.0411)	(0.0411)
Unemployment Equation: Unemployment_t-2(p value)					*0.017	*0.017
Unemployment Equation: Unemployment_t-3					0.1073	0.1073
Unemployment Equation: Unemployment_t-3 (Robust Standard Error)					(0.0446)	(0.0446)
Unemployment Equation: Unemployment_t-3(p value)					*0.017	*0.017
Unemployment Equation: Root MSE					0.0429	0.0429
Unemployment Equation: R-Squared					0.2336	0.2336

Asterisks (*) denote p values.

Table 2 Estimates of Models 1-2 with Moving-Average Errors.
	Model 1	Model 2
Income Equation: Wage_t	0.2613	0.1466
Income Equation: Wage_t (Robust Standard Error)	-0.0324	-0.0392
Income Equation: Wage_t (p value)	*0.000	*0.000
Income Equation: Hours_t	0.2662	0.0397
Income Equation: Hours_t (Robust Standard Error)	-0.0375	-0.0497
Income Equation: Hours_t (p value)	*0.000	*0.425
Income Equation: Income_t-1	0.7204	0.8425
Income Equation: Income_t-1 (Robust Standard Error)	-0.031	-0.0373
Income Equation: Income_t-1 (p value)	*0.000	*0.000
Income Equation: Instrumented	Income_t-1	Income_t-1 Hours_t
Income Equation: Instruments:	Income_t-2 Income_t-3 Hours_t-1 Wage_t-1	Income_t-2 Income_t-3 Hours_t-1 Hours_t-2 Hours_t-3 Wage_t-1
Income Equation: MA(1) Coefficient	-0.2917	-0.3018
Income Equation: MA(1) Coefficient (Robust Standard Error)	-0.0672	-0.0704
Income Equation: MA(1) Coefficient (p value)	*0.000	*0.000
Income Equation: Estimated Error Variance	0.03	0.0327
Income Equation: Estimated Error Variance (Robust Standard Error)	-0.002	-0.0023
Income Equation: Estimated Error Variance (p value)	*0.000	*0.000
Hours Equation: Wage_t		0.0211
Hours Equation: Wage_t (Robust Standard Error)		-0.052
Hours Equation: Wage_t(p value)		*0.686
Hours Equation: Income_t-1		-0.0478
Hours Equation: Income_t-1 (Robust Standard Error)		-0.0913
Hours Equation: Income_t-1(p value)		*0.601
Hours Equation: Income_t-2		0.0328
Hours Equation: Income_t-2 (Robust Standard Error)		-0.0468
Hours Equation: Income_t-2(p value)		*0.483
Hours Equation: Hours_t-1	0.9167	0.9242
Hours Equation: Hours_t-1 (Robust Standard Error)	-0.0265	-0.0564
Hours Equation: Hours_t-1(p value)	*0.000	*0.000
Hours Equation: Instrumented:	Hours_t-1	Hours_t-1 Income_t-1
Hours Equation: Instruments:	Hours_t-2 Hours_t-3	Income_t-2 Income_t-3 Hours_t-2 Hours_t-3
Hours Equation: MA(1) Coefficient	-0.4968	-0.4702
Hours Equation: MA(1) Coefficient (Robust Standard Error)	-0.2112	-0.2023
Hours Equation: MA(1) Coefficient (p value)	*0.027	*0.029
Hours Equation: Estimated Error Variance	0.0385	0.0373
Hours Equation: Estimated Error Variance (Robust Standard Error)	-0.0084	-0.0078
Hours Equation: Estimated Error Variance (p value)	*0.000	*0.000
Wage Equation: Wage_t-1	0.9776	0.9776
Wage Equation: Wage_t-1 (Robust Standard Error)	-0.0055	-0.0055
Wage Equation: Wage_t-1	*0.000	*0.000
Wage Equation: Instrumented:	Wage_t-1	Wage_t-1
Wage Equation: Instruments:	Wage_t-2 Wage_t-3	Wage_t-2 Wage_t-3
Wage Equation: MA(1) Coefficient	-0.3792	-0.3792
Wage Equation: MA(1) Coefficient (Robust Standard Error)	-0.0642	-0.0642
Wage Equation: MA(1) Coefficient	*0.000	*0.000
Wage Equation: Estimated Error Variance	0.027	0.027
Wage Equation: Estimated Error Variance (Robust Standard Error)	-0.0018	-0.0018
Wage Equation: Estimated Error Variance	*0.000	*0.000

Estimation of coefficients of the system's variables by instrumental variables.
Estimation of moving-average parameters by equally-weighted minimum distance.

Table 3 Estimates of Models with Fixed Effects.
Income Equation	Model 1	Model 2	Model 3	Model 4	Model 5	Model 6
Income Equation: Wage_t	0.0338	0.0484	0.0244	0.168	0.0249	0.0161
Income Equation: Wage_t (Robust Standard Error)	-0.0318	-0.0302	-0.0343	-0.0567	-0.0355	-0.035
Income Equation: Wage_t (p value)	*0.287	*0.109	*0.477	*0.003	*0.483	*0.646
Income Equation: Hours_t	0.2902	0.2638	0.2846	0.2848	0.2365	0.3002
Income Equation: Hours_t (Standard Error)	-0.0542	-0.0586	-0.0657	-0.0686	-0.0712	-0.0738
Income Equation: Hours_t (p value)	*0.000	*0.000	*0.000	*0.000	*0.001	*0.000
Income Equation: Unemployment_t					-0.6512
Income Equation: Unemployment_t (Standard Error)					-0.1646
Income Equation: Unemployment_t (p value)					*0.000
Income Equation: Income_t-1	0.2967	0.2502	0.2911	0.2533	0.2987	0.3092
Income Equation: Income_t-1 (Standard Error)	-0.0437	-0.0426	-0.0557	-0.0472	-0.058	-0.0588
Income Equation: Income_t-1 (p value)	*0.000	*0.000	*0.000	*0.000	*0.000	*0.000
Income Equation: Income_t-2			0.0766	0.0719	0.0827	0.0824
Income Equation: Income_t-2 (Standard Error)			-0.0251	-0.0264	-0.0256	-0.026
Income Equation: Income_t-2 (p value)			*0.002	*0.006	*0.001	*0.002
Income Equation: Hours_t-1				-0.0159
Income Equation: Hours_t-1 (Standard Error)				-0.0269
Income Equation: Hours_t-1 (p value)				*0.554
Income Equation: Hours_t-2				0.0008
Income Equation: Hours_t-2 (Standard Error)				-0.0162
Income Equation: Hours_t-2 (p value)				*0.958
Income Equation: Wage_t-1				0.0016
Income Equation: Wage_t-1 (Standard Error)				-0.0295
Income Equation: Wage_t-1 (p value)				*0.956
Income Equation: Wage_t-2				-0.0467
Income Equation: Wage_t-2 (Standard Error)				-0.0246
Income Equation: Wage_t-2 (p value)				*0.058
Income Equation: Test for 1st order Serial Corr.	-10.13	-10.21	-9.41	-9.29	-9.11	-9.33
Income Equation: Test for 1st order Serial Corr. (p value)	*0.000	*0.000	*0.000	*0.000	*0.000	*0.000
Income Equation: Test for 2nd order Serial Corr.	2.39	2.1	-0.84	-1.21	-1.13	-0.93
Income Equation: Test for 2nd order Serial Corr. (p value)	*0.017	*0.035	*0.400	*0.228	*0.258	*0.353
Hours Equation: Wage_t		0.0148	0.0128	-0.0105	0.0376	0.0376
Hours Equation: Wage_t (Standard Error)		-0.0392	-0.0389	-0.063	-0.0381	-0.0381
Hours Equation: Wage_t		*0.706	*0.742	*0.868	*0.325	*0.325
Hours Equation: Unemployment_t					-1.3842	-1.3842
Hours Equation: Unemployment_t (Standard Error)					-0.1252	-0.1252
Hours Equation: Unemployment_t					*0.000	*0.000
Hours Equation: Unemployment_t-1					0.1823	0.1823
Hours Equation: Unemployment_t-1 (Standard Error)					-0.105	-0.105
Hours Equation: Unemployment_t-1					*0.083	*0.083
Hours Equation: Income_t-1		0.0516	0.0477	0.0592	0.0209	0.0209
Hours Equation: Income_t-1 (Standard Error)		-0.0625	-0.066	-0.0405	-0.0643	-0.0643
Hours Equation: Income_t-1		*0.410	*0.469	*0.144	*0.745	*0.745
Hours Equation: Income_t-2		0.0457	0.0324	0.0475	0.0264	0.0264
Hours Equation: Income_t-2 (Standard Error)		-0.024	-0.0264	-0.0227	-0.0293	-0.0293
Hours Equation: Income_t-2		*0.056	*0.219	*0.036	*0.368	*0.368
Hours Equation: Hours_t-1	0.1248	0.119	0.137	0.1302	0.1318	0.1318
Hours Equation: Hours_t-1 (Standard Error)	-0.0341	-0.0337	-0.0356	-0.0326	-0.037	-0.037
Hours Equation: Hours_t-1	*0.000	*0.000	*0.000	*0.000	*0.000	*0.000
Hours Equation: Hours_t-2			0.0399	0.032	0.0173	0.0173
Hours Equation: Hours_t-2 (Standard Error)			-0.0174	-0.0162	-0.022	-0.022
Hours Equation: Hours_t-2			*0.022	*0.048	*0.433	*0.433
Hours Equation: Wage_t-1				-0.0491
Hours Equation: Wage_t-1 (Standard Error)				-0.0347
Hours Equation: Wage_t-1				*0.157
Hours Equation: Wage_t-2				0.0119
Hours Equation: Wage_t-2 (Standard Error)				-0.0246
Hours Equation: Wage_t-2				*0.629
Hours Equation: Test for 1st order Serial Corr.	-5.04	-4.61	-4.61	-4.62	-4.2	-4.2
Hours Equation: Test for 1st order Serial Corr. (p values)	*0	*0	*0	*0	*0	*0
Hours Equation: Test for 2nd order Serial Corr.	1.72	1.48	0.36	0.37	0.26	0.26
Hours Equation: Test for 2nd order Serial Corr. (p values)	*0.085	*0.140	*0.722	*0.709	*0.794	*0.794
Wage Equation: Wage_t-1	0.2985	0.2985	0.4154	0.2409	0.4145	0.4145
Wage Equation: Wage_t-1 (Standard Error)	-0.0474	-0.0474	-0.0524	-0.0351	-0.0527	-0.0527
Wage Equation: Waget-1	*0.000	*0.000	*0.000	*0.000	*0.000	*0.000
Wage Equation: Wage_t-2			0.1409	0.0825	0.1429	0.1429
Wage Equation: Wage_t-2 (Standard Error)			-0.0326	-0.0241	-0.0324	-0.0324
Wage Equation: Wage_t-2			*0.000	*0.001	*0.000	*0.000
Wage Equation: Wage_t-3			0.0293		0.0333	0.0333
Wage Equation: Wage_t-3 (Standard Error)			-0.0222		-0.0222	-0.0222
Wage Equation: Wage_t-3			*0.188		*0.133	*0.133
Wage Equation: Unemployment_t-1					-0.3048	-0.3048
Wage Equation: Unemployment_t-1 (Standard Error)					-0.1116	-0.1116
Wage Equation: Unemployment_t-1					*0.006	*0.006
Wage Equation: Income_t-1				0.3425
Wage Equation: Income_t-1 (Standard Error)				-0.0447
Wage Equation: Income_t-1				*0.000
Wage Equation: Income_t-2				0.0023
Wage Equation: Income_t-2 (Standard Error)				-0.0198
Wage Equation: Income_t-2				*0.907
Wage Equation: Hours_t-1				-0.1438
Wage Equation: Hours_t-1 (Standard Error)				-0.0407
Wage Equation: Hours_t-1				*0.000
Wage Equation: Hours_t-2				-0.0179
Wage Equation: Hours_t-2 (Standard Error)				-0.0164
Wage Equation: Hours_t-2				*0.275
Wage Equation: Test for 1st order Serial Corr.	-10.26	-10.26	-9.73	-11.23	-9.71	-9.71
Wage Equation: Test for 1st order Serial Corr. (p values)	*0	*0	*0	*0	*0	*0
Wage Equation: Test for 2nd order Serial Corr.	2.94	2.94	-0.84	-0.05	-1.03	-1.03
Wage Equation: Test for 2nd order Serial Corr. (p values)	*0.003	*0.003	*0.399	*0.964	*0.304	*0.304
Unemployment Equation: Unemployment_t-1					0.295	0.295
Unemployment Equation: Unemployment_t-1 (Standard Error)					-0.0441	-0.0441
Unemployment Equation: Unemployment_t-1					*0.000	*0.000
Unemployment Equation: Unemployment_t-2					0.046	0.046
Unemployment Equation: Unemployment_t-2 (Standard Error)					-0.0334	-0.0334
Unemployment Equation: Unemployment_t-2					*0.169	*0.169
Unemployment Equation: Unemployment_t-3					0.0474	0.0474
Unemployment Equation: Unemployment_t-3 (Standard Error)					-0.0474	-0.0474
Unemployment Equation: Unemployment_t-3					*0.317	*0.317
Unemployment Equation: Test for 1st order Serial Corr.					-6.03	-6.03
Unemployment Equation: Test for 1st order Serial Corr. (p values)					*0	*0
Unemployment Equation: Test for 2nd order Serial Corr.					1.11	1.11
Unemployment Equation: Test for 2nd order Serial Corr. (p values)					*0.266	*0.266

Estimation of all equations by linear GMM.
Tests for serial correlation use the first-differenced residuals. See Arellano and Bond (1991).

Table 4 Decomposition of Income Variance in Model 5:
Panel A Income Variation: Departure in Current Period from Level Absent Innovations
Innovation: One-time innovation in period 1
	Percent of variation in income due to: Unemployment Innovation	Percent of variation in income due to: Wage Innovation	Percent of variation in income due to: Hours Innovation	Percent of variation in income due to: Income Innovation
Horizon (Years): 1	4.4	8.1	7.7	79.9
Horizon (Years): 2	9.2	25.0	15.4	50.3
Horizon (Years): 3	10.5	33.1	17.3	39.1
Horizon (Years): 4	12.8	47.6	15.5	24.2
Horizon (Years): 5	12.9	57.1	13.3	16.8
Horizon (Years): 6	12.5	66.0	10.3	11.1
Horizon (Years): 7	11.8	72.8	7.8	7.6
Horizon (Years): 8	10.9	78.3	5.7	5.1
Horizon (Years): 9	10.0	82.4	4.1	3.5
Horizon (Years): 10	9.1	85.6	2.9	2.4

Table 4 Decomposition of Income Variance in Model 5:
Panel B Income Variation: Cumulative Variation Between Period 1 and Current Period
Innovation: One-time innovation in period 1
	Percent of variation in income due to: Unemployment Innovation	Percent of variation in income due to: Wage Innovation	Percent of variation in income due to: Hours Innovation	Percent of variation in income due to: Income Innovation
Horizon (Years): 1	4.4	8.1	7.7	79.9
Horizon (Years): 2	5.6	12.3	9.6	72.4
Horizon (Years): 3	6.7	16.8	11.3	65.3
Horizon (Years): 4	7.6	21.5	11.9	59.0
Horizon (Years): 5	8.2	25.9	12.1	53.8
Horizon (Years): 6	8.7	29.9	11.9	49.5
Horizon (Years): 7	8.9	33.6	11.6	45.9
Horizon (Years): 8	9.1	37.0	11.1	42.8
Horizon (Years): 9	9.1	40.0	10.7	40.2
Horizon (Years): 10	9.1	42.6	10.2	38.0

Table 4 Decomposition of Income Variance in Model 5:
Panel C Income Variation: Departure in Current Period from Level Absent Innovations
Innovation: Innovations in every period starting in period 1
	Percent of variation in income due to: Unemployment Innovation	Percent of variation in income due to: Wage Innovation	Percent of variation in income due to: Hours Innovation	Percent of variation in income due to: Income Innovation
Horizon (Years): 1	4.4	8.1	7.7	79.9
Horizon (Years): 2	6.1	13.5	10.5	69.9
Horizon (Years): 3	7.4	18.5	12.5	61.7
Horizon (Years): 4	8.6	24.0	13.4	54.0
Horizon (Years): 5	9.5	29.3	13.7	47.5
Horizon (Years): 6	10.1	34.3	13.6	42.0
Horizon (Years): 7	10.6	39.1	13.1	37.3
Horizon (Years): 8	10.8	43.5	12.5	33.2
Horizon (Years): 9	11.0	47.5	11.7	29.8
Horizon (Years): 10	11.0	51.3	11.0	26.8

Table 4 Decomposition of Income Variance in Model 5:
Panel D Income Variation: Cumulative Variation Between Period 1 and Current Period:
Innovation: Innovations in every period starting in period 1
	Percent of variation in income due to: Unemployment Innovation	Percent of variation in income due to: Wage Innovation	Percent of variation in income due to: Hours Innovation	Percent of variation in income due to: Income Innovation
Horizon (Years): 1	4.4	8.1	7.7	79.9
Horizon (Years): 2	5.6	11.9	9.7	72.8
Horizon (Years): 3	6.6	15.7	11.3	66.4
Horizon (Years): 4	7.5	19.6	12.3	60.6
Horizon (Years): 5	8.3	23.4	12.9	55.4
Horizon (Years): 6	8.9	27.2	13.1	50.8
Horizon (Years): 7	9.4	30.7	13.1	46.7
Horizon (Years): 8	9.8	34.2	12.9	43.1
Horizon (Years): 9	10.1	37.4	12.6	39.9
Horizon (Years): 10	10.3	40.5	12.3	37.0

Table 5 Decomposition of Income Variance in Model 6:
Panel A Income Variation: Departure in Current Period from Level Absent Innovations
Innovation: One-time innovation in period 1
	Percent of variation in income due to: Unemployment Innovation	Percent of variation in income due to: Wage Innovation	Percent of variation in income due to: Hours Innovation	Percent of variation in income due to: Income Innovation
Horizon (Years): 1	0.8	7.9	9.5	81.7
Horizon (Years): 2	1.8	24.9	19.7	53.6
Horizon (Years): 3	2.7	33.1	22.3	41.9
Horizon (Years): 4	3.6	48.5	20.7	27.2
Horizon (Years): 5	4.2	58.6	18.0	19.2
Horizon (Years): 6	4.6	68.0	14.2	13.1
Horizon (Years): 7	4.9	75.2	10.9	9.1
Horizon (Years): 8	5.0	80.7	8.0	6.3
Horizon (Years): 9	5.0	84.8	5.9	4.3
Horizon (Years): 10	4.9	87.9	4.2	3.0

Table 5 Decomposition of Income Variance in Model 6:
Panel B Income Variation: Income Variation: Cumulative Variation Between Period 1 and Current Period
Innovation: One-time innovation in period 1
	Percent of variation in income due to: Unemployment Innovation	Percent of variation in income due to: Wage Innovation	Percent of variation in income due to: Hours Innovation	Percent of variation in income due to: Income Innovation
Horizon (Years): 1	0.8	7.9	9.5	81.7
Horizon (Years): 2	1.1	12.1	12.1	74.7
Horizon (Years): 3	1.4	16.6	14.3	67.7
Horizon (Years): 4	1.7	21.3	15.2	61.7
Horizon (Years): 5	2.0	25.8	15.5	56.7
Horizon (Years): 6	2.3	29.9	15.4	52.4
Horizon (Years): 7	2.5	33.7	15.0	48.7
Horizon (Years): 8	2.7	37.2	14.5	45.6
Horizon (Years): 9	2.8	40.3	14.0	42.9
Horizon (Years): 10	3.0	43.1	13.4	40.6

Table 5 Decomposition of Income Variance in Model 6:
Panel C Income Variation: Departure in Current Period from Level Absent Innovations
Innovation: Innovations in every period starting in period 1
	Percent of variation in income due to: Unemployment Innovation	Percent of variation in income due to: Wage Innovation	Percent of variation in income due to: Hours Innovation	Percent of variation in income due to: Income Innovation
Horizon (Years): 1	0.8	7.9	9.5	81.7
Horizon (Years): 2	1.2	13.3	13.1	72.4
Horizon (Years): 3	1.6	18.3	15.8	64.4
Horizon (Years): 4	1.9	23.9	17.2	57.0
Horizon (Years): 5	2.3	29.2	17.7	50.7
Horizon (Years): 6	2.6	34.4	17.7	45.2
Horizon (Years): 7	2.9	39.4	17.2	40.5
Horizon (Years): 8	3.2	44.0	16.4	36.4
Horizon (Years): 9	3.4	48.3	15.6	32.8
Horizon (Years): 10	3.6	52.1	14.6	29.6

Table 5 Decomposition of Income Variance in Model 6:
Panel D Income Variation: Cumulative Variation Between Period 1 and Current Period
Innovation: Innovations in every period starting in period
	Percent of variation in income due to: Unemployment Innovation	Percent of variation in income due to: Wage Innovation	Percent of variation in income due to: Hours Innovation	Percent of variation in income due to: Income Innovation
Horizon (Years): 1	0.8	7.9	9.5	81.7
Horizon (Years): 2	1.1	11.7	12.1	75.1
Horizon (Years): 3	1.3	15.5	14.2	69.0
Horizon (Years): 4	1.6	19.4	15.6	63.4
Horizon (Years): 5	1.9	23.3	16.4	58.4
Horizon (Years): 6	2.2	27.1	16.8	53.9
Horizon (Years): 7	2.4	30.8	16.9	49.9
Horizon (Years): 8	2.6	34.3	16.8	46.3
Horizon (Years): 9	2.8	37.7	16.5	43.0
Horizon (Years): 10	3.0	40.9	16.1	40.1

Table 6 Decomposition of Income Variance in Model 3:
Panel A Income Variation: Departure in Current Period from Level Absent Innovations
Innovation: One-time innovation in period 1
	Percent of variation in income due to: Wage Innovation	Percent of variation in income due to: Hours Innovation	Percent of variation in income due to: Income Innovation
Horizon (Years): 1	7.8	10.5	81.7
Horizon (Years): 2	25.5	20.2	54.3
Horizon (Years): 3	33.7	23.8	42.5
Horizon (Years): 4	50.2	21.8	28.0
Horizon (Years): 5	60.8	19.2	20.0
Horizon (Years): 6	71.1	15.1	13.7
Horizon (Years): 7	78.8	11.6	9.6
Horizon (Years): 8	84.7	8.6	6.6
Horizon (Years): 9	89.1	6.3	4.6
Horizon (Years): 10	92.3	4.5	3.2

Table 6 Decomposition of Income Variance in Model 3:
Panel B Income Variation: Cumulative Variation Between Period 1 and Current Period
Innovation: One-time innovation in period 1
	Percent of variation in income due to: Wage Innovation	Percent of variation in income due to: Hours Innovation	Percent of variation in income due to: Income Innovation
Horizon (Years): 1	7.8	10.5	81.7
Horizon (Years): 2	12.2	12.9	74.9
Horizon (Years): 3	16.7	15.2	68.1
Horizon (Years): 4	21.6	16.1	62.3
Horizon (Years): 5	26.2	16.5	57.3
Horizon (Years): 6	30.5	16.4	53.1
Horizon (Years): 7	34.5	16.0	49.6
Horizon (Years): 8	38.1	15.4	46.5
Horizon (Years): 9	41.4	14.9	43.8
Horizon (Years): 10	44.3	14.3	41.5

Table 6 Decomposition of Income Variance in Model 3:
Panel C Income Variation: Departure in Current Period from Level Absent Innovations
Innovation: Innovations in every period starting in period 1
	Percent of variation in income due to: Wage Innovation	Percent of variation in income due to: Hours Innovation	Percent of variation in income due to: Income Innovation
Horizon (Years): 1	7.8	10.5	81.7
Horizon (Years): 2	13.4	14.0	72.7
Horizon (Years): 3	18.4	16.8	64.8
Horizon (Years): 4	24.2	18.2	57.6
Horizon (Years): 5	29.7	18.8	51.5
Horizon (Years): 6	35.2	18.7	46.1
Horizon (Years): 7	40.4	18.3	41.4
Horizon (Years): 8	45.2	17.5	37.3
Horizon (Years): 9	49.7	16.6	33.7
Horizon (Years): 10	53.9	15.6	30.5

Table 6 Decomposition of Income Variance in Model 3:
Panel D Income Variation: Cumulative Variation Between Period 1 and Current Period
Innovation: Innovations in every period starting in period 1
	Percent of variation in income due to: Wage Innovation	Percent of variation in income due to: Hours Innovation	Percent of variation in income due to: Income Innovation
Horizon (Years): 1	7.8	10.5	81.7
Horizon (Years): 2	11.8	12.9	75.3
Horizon (Years): 3	15.6	15.1	69.3
Horizon (Years): 4	19.6	16.5	63.9
Horizon (Years): 5	23.6	17.4	59.0
Horizon (Years): 6	27.5	17.9	54.6
Horizon (Years): 7	31.3	18.0	50.7
Horizon (Years): 8	35.0	17.9	47.1
Horizon (Years): 9	38.6	17.6	43.9
Horizon (Years): 10	41.9	17.1	41.0

The figure shows the response of income to a one-time, one-standard-deviation wage shock at time t=1 in models 1 through 4. For all models, the response of income to the wage shock is hump-shaped and persistent. The immediate response is a jump in income of between 0.04 and 0.07. After the immediate reaction, income continues to increase for a few periods, until it eventually peaks and begins to decline. The eventual decline is slow, making the effect of the wage shock persistent. Models 1 and 2 show a somewhat larger immediate response and a faster subsequent decline. Model 3 and 4 decline very slowly, making the effect of the shock very persistent. Model 4 peaks at a lower level than the other three models.

The figure shows the response of income to a one-time, one-standard-deviation hours shock at time t=1 in models 1 through 4. For all models, the figure shows that hours shocks have a much less persistent effect on income than wage shocks. The immediate response of income is a jump of about 0.06. After the initial period, income declines towards zero fairly quickly. In models 1 and 2, the decline is monotonic; in models 3 and 4, the initial decrease is followed by a small one-period increase, before a monotonic decline toward zero. In all cases, most of the effect of the hours shock is transitory. The effect is slightly more persistent for Model 4.

The figure shows the response of income to a one-time, one-standard-deviation income shock at time t=1 in models 1 through 4. Models 1, 2, and 3 show essentially the same response: a large immediate jump of income followed by a fast decline. For these models, more than half of the immediate response of income to the shock dissipates in just one period, and the subsequent decline to zero is fast. For model 4, slightly less than one half of the initial response dissipates in one period and the subsequent decline is significantly slower, with almost one third of the initial response still present after 30 periods.

The figure shows the response of income to one-time, one-standard-deviation shocks to the wage, hours, and income at time t=1 in Model 1. The response of income to the wage shock is hump-shaped and persistent. The immediate response is a jump in income of about 0.07. After the immediate reaction, income continues to increase for a few periods, until it eventually peaks and begins to decline. The eventual decline is slow, making the effect of the shock persistent. The response to the hours shock is much less persistent. The immediate reaction is a jump of about the same size as for the wage shock. After the initial period, income declines towards zero monotonically and fairly quickly. Finally, the initial response to the income shock is considerably larger than the response to the other two shocks (about 0.17) and is very transitory. More than half of the immediate response dissipates in just one period, after which the effect of the shock continues to decline fast towards zero.

The figure shows the response of income to one-time, one-standard-deviation shocks to the wage, hours, and income at time t=1 in Model 2. The results are almost identical to those of Model 1 in Figure 4. The response of income to the wage shock is hump-shaped and persistent. The immediate response is a jump in income of about 0.06. After the immediate reaction, income continues to increase for a few periods, until it eventually peaks and begins to decline. The eventual decline is slow, making the effect of the shock persistent. The response to the hours shock is much less persistent than the response to the wage shock. The immediate reaction is a jump of the same size as for the wage shock. After the initial period, income declines towards zero monotonically and fairly quickly. Finally, the initial response to the income shock is considerably larger than the response to the other two shocks (about 0.17) and is very transitory. More than half of the immediate response dissipates in just one period, after which the effect of the shock continues to decline fast towards zero.

The figure shows the response of income to one-time, one-standard-deviation shocks to the wage, hours, and income at time t=1 in Model 3. The results are for the most part similar to those of Models 1 and 2. The response of income to the wage shock is hump-shaped and persistent. The immediate response is a jump in income of about 0.05. After the immediate reaction, income continues to increase for a few periods, until it eventually peaks and begins to decline. The eventual decline is slow, making the effect of the shock very persistent (more persistent than in models 1 and 2). For the hours shock, the immediate reaction is a jump of about the same size as for the wage shock. Following the jump, income drops for one period, then increases slightly, and then declines monotonically toward zero. Finally, the initial response to the income shock is considerably larger than the response to the other two shocks (about 0.17) and is very transitory. More than half of the immediate response dissipates in just one period, after which the effect of the shock continues to decline fast towards zero.

The figure shows the response of income to one-time, one-standard-deviation shocks to the wage, hours, and income at time t=1 in Model 4 (the unrestricted PVAR). The response of income to the wage shock is hump-shaped (but flatter than in the previous models) and persistent. The immediate response is a jump in income of about 0.05. After the immediate reaction, income increases for a few periods, until it peaks and begins a very slow decline. For the hours shock, the immediate reaction is a jump of about 0.06. Following the jump, income drops for one period, then increases slightly, and then declines monotonically toward zero. Finally, the initial response to the income shock is considerably larger than the response to the other two shocks (about 0.17) and is very transitory. Slightly less than one half of the immediate reaction dissipates in just one period, after which income stays roughly constant for one period, and then declines monotonically, but is still at about one third of the initial jump after 30 periods.

The figure shows the response of income to one-time, one-standard-deviation shocks to unemployment hours, the wage, work hours, and income at time t=1 in Model 5. The response of income to the unemployment hours shock is small but persistent. After an initial drop of about 0.04, income recovers slowly toward zero. The response of income to the wage shock is hump-shaped and very persistent. After an initial jump of about 0.05, income continues to increase for a few periods, until it eventually peaks and begins to decline slowly. The response to the hours shock is much less persistent. After an initial jump of the same size as for the wage shock, income declines towards zero fairly quickly. Finally, the initial response to the income shock is considerably larger than the response to the other shocks and is very transitory. More than one half of the immediate response of income--a jump of about 0.17--dissipates in just one period, after which the effect of the shock continues to decline towards zero at a fast rate.

The figure shows the response of the wage and work hours to a one-time, one-standard-deviation unemployment hours shock at time t=1 in Model 5. The response of hours to the unemployment shock is large but transitory. After an initial drop of about 0.053, about three fourths of the drop dissipate in just one period. This recovery is followed by a second small drop, which is followed by a fairly quick monotonic recovery towards zero. The response of the wage to the unemployment shock is persistent. Following no response in period 1, the wage drops by about 0.01 in the second period, continues to decline for a few periods, and then starts recovering very slowly. Most of the initial effect persists even after 30 periods.

The figure shows the response of the wage and work hours to a one-time, one-standard-deviation unemployment hours shock at time t=1 in Model 6. The results are very similar to those for Model 5 in Figure 10. The response of hours to the unemployment shock is large but transitory. After an initial drop of about 0.053, more than three fourths of the drop dissipate in just one period. This recovery is followed by a second small drop, which is followed by a fairly quick monotonic recovery towards zero. The response of the wage to the unemployment shock is persistent. Following no reaction in period 1, the wage drops by about 0.01 in the second period, continues to decline for a few periods, and then starts recovering very slowly. Most of the initial effect persists even after 30 periods.

Footnotes

* I am grateful to Joe Altonji and George Hall for helpful discussions and suggestions. All remaining errors are my own. The views expressed in this paper are solely the responsibility of the author and should not be interpreted as reflecting the views of the Board of Governors of the Federal Reserve System or of any other employee of the Federal Reserve System. Return to Text

1. See Krusell and Smith (1998), Castañeda, Díaz-Giménez, and Ríos-Rull (2003), Storesletten, Telmer, and Yaron (2004a) on the distribution of wealth and consumption, Imrohoroglu (1989), Krusell and Smith (1999), Storesletten, Telmer, and Yaron (2001a) on the welfare costs of business cycles, and Telmer (1993), Heaton and Lucas (1996), Storesletten, Telmer, and Yaron (2007) on asset pricing. Return to Text

2. See Altonji, Smith, and Vidangos (2008) and Vidangos (2008). Return to Text

3. A companion paper, Altonji, Smith, and Vidangos (2008), extends the analysis presented here to include discrete variables like employment status and job changes, and to control for measurement error. The multivariate income model in that paper is estimated by indirect inference on PSID data. Return to Text

4. Abowd and Card (1989) propose a fairly simple components-of-variance model, in which changes in income and hours are driven by three factors (in addition to measurement error). One of these factors affects both income and hours, while the remaining two factors affect only the variance of and contemporaneous covariance between income and hours. The estimated model is quite successful in reproducing the covariance structure observed in the data, but it is not clear what the statistical factors driving the income and hours processes might represent. Return to Text

5. For both income and the wage rate, the high degree of persistence in the levels of both variables, along with the low persistence in their first differences, could be accounted for either by an autoregressive process without fixed effects but with a unit root, or by a stationary autoregressive process with a fixed effect. MaCurdy (1982) allows for the presence of a fixed effect but his estimates lead him to accept the hypothesis that the variance of the fixed effect is zero, both for earnings and the wage rate. He thus eliminates the fixed effect from his models. Meghir and Pistaferri (2004) conduct a similar test for labor income using data from the PSID. They also reject the specification with fixed effects, concluding that the permanent component of income is more likely to follow a martingale process. Return to Text

6. In my sample, a simple regression that explains income in terms of only the current wage and hours (without lagged income) yields an R squared of 0.75. Return to Text

7. In principle, the negative effect could also be due to the existence of permanent heterogeneity in wages, correlated with unemployment risk. However, as I show below, the strong negative effect of unemployment on the wage rate remains when I introduce fixed effects. Return to Text

8. One possibility to get around this problem is to use a simulation-based estimator, as in Altonji, Smith, and Vidangos (2008). Return to Text

9. As was mentioned above, one way to do this would be to introduce an external estimate of the variance of measurement error and estimate the model using a simulation-based estimator. This is the strategy followed in Altonji, Smith, and Vidangos (2008). Return to Text

10. Altonji, Martins, and Siow (2002; AMS) estimate vector-moving-average models of family income, the wage rate, hours of work, and unemployment (their models do not include autoregressive components). The variables are in first differences. AMS find that measurement error is responsible for 70.8 percent of the variance of income (in first differences), and that 82.9 percent of the remaining 29.2 percent of the variance is due to the income shock. Return to Text

11. If unemployment is left out of the wage equation, the persistence of the effect of the unemployment shock on income essentially vanishes. Return to Text

12. AMS find that the long-run effect of innovations in unemployment on income is near zero. In their findings, even after only two years, a shock to unemployment of the head of the household has essentially no effect on income. In their models, the wage depends on lagged values of itself only; in particular, it is not allowed to depend on current or lagged values of unemployment. Their analysis thus does not capture the persistent effect of unemployment on the wage rate. Return to Text

13. These results are quite similar to AMS, who also work with the variables in first differences. Return to Text

14. They estimate a joint model of earnings, employment, job changes, wages, and work hours. The model accounts for measurement error and multiple sources of permanent unobserved heterogeneity. In addition to wage shocks and hours shocks, earnings are affected by employment and job change shocks. Return to Text

^♣ This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to Text