
Salience and Taxation: Theory and Evidence
| Raj Chetty | Adam Looney | Kory Kroft |
|---|---|---|
| UC-Berkeley and NBER | Federal Reserve Board | UC-Berkeley |
Keywords: Tax, behavioral economics
Abstract:
This paper presents evidence that consumers underreact to taxes that are not salient and characterizes the welfare consequences of tax policies when agents make such optimization errors. The empirical evidence is based on two complementary strategies. First, we conducted an experiment at a grocery store posting tax inclusive prices for 750 products subject to sales tax for a three week period. Scanner data show that this intervention reduced demand for the treated products by 8 percent. Second, we find that state-level increases in excise taxes (which are included in posted prices) reduce alcohol consumption significantly more than increases in sales taxes (which are added at the register and are hence less salient). We develop simple, empirically implementable formulas for the incidence and efficiency costs of taxation that account for salience effects as well as other optimization errors. Contrary to conventional wisdom, the formulas imply that the economic incidence of a tax depends on its statutory incidence and that a tax can create deadweight loss even if it induces no change in demand. Our method of welfare analysis yields robust results because it does not require specification of a positive theory for why agents fail to optimize with respect to tax policies.
A central assumption in public economics is that agents optimize fully with respect to tax policies. For example, Frank P. Ramsey's (1927) seminal analysis of optimal commodity taxation assumes that agents respond to tax changes in the same way as price changes. Canonical results on tax incidence, efficiency costs, and optimal income taxation (e.g. Arnold C. Harberger 1964, James A. Mirrlees 1971, Anthony B. Atkinson and Joseph E. Stiglitz 1976) all rely on full optimization with respect to taxes.
Contrary to the full optimization assumption, there is accumulating evidence which suggests that individuals are inattentive to some types of incentives.1Inattention and imperfect optimization could be particularly important in the case of taxation because tax systems are complex and nontransparent in practice. Income tax schedules are typically highly nonlinear, benefit-tax linkages for social insurance programs are opaque (e.g. social security taxes and benefits), and taxes on commodities are often not displayed in posted prices (sales taxes, hotel city taxes, vehicle excise fees).
In the first half of this paper, we investigate empirically whether individuals optimize fully with respect to taxes by analyzing the effect of "salience" on behavioral responses to commodity taxation. Specifically, we show that commodity taxes that are included in the posted prices that consumers see when shopping (and are thus more salient) have larger effects on demand.2 In Xavier Gabaix and David I. Laibson's (2006) terminology, our empirical analysis shows that some types of taxes are " shrouded attributes." In the second half of the paper, we develop a simple method of characterizing the welfare consequences of taxation when agents optimize imperfectly with respect to taxes.
We study the importance of salience empirically using two complementary strategies: (1) an experiment in a grocery store and (2) an observational study of the effect of alcohol taxes on alcohol consumption. The experiment was implemented at a supermarket over a three-week period in early 2006. In this store, prices posted on the shelf exclude sales tax of 7.375 percent. If a product is subject to sales tax, it is added to the bill only at the register, as in most other retail stores in the United States.3 To test if people underreact to the sales tax because it is not included in the posted price, we posted tags showing the tax inclusive price below the original pretax price tags (shown in Exhibit 1). We posted these tags for all products (roughly 750 total) in three taxable groups: cosmetics, hair care accessories, and deodorants. A preliminary survey-based evaluation of the tags indicates that they succeed in reminding consumers of actual tax inclusive prices. Without the tags, nearly all survey respondents ignored taxes when calculating the total price of a basket of goods whereas with the tags, the vast majority computed the total tax inclusive price correctly.
We analyze the effect of posting tax inclusive prices on demand using a differences-in-differences research design. Scanner data show that quantity sold and total revenue in the treated group of products fell by about 8 percent during the intervention relative to two "control groups" - other products in the same aisle of the treatment store that were not tagged and products in two other stores in nearby cities. The null hypothesis that posting tax inclusive prices has no effect on demand is rejected using both t-tests and nonparametric permutation tests. To interpret the magnitude of the treatment effect, we compare it with the price elasticity of demand for these categories, which is in the range of 1 to 1.5. Since showing the tax inclusive price reduced demand by nearly the same amount as a 7.375 percent price increase, we infer that most consumers do not normally take the sales tax into account.
A concern with the experiment is that posting 750 new tags may have reduced demand because of a "Hawthorne effect" or a short-run violation of norms. This issue motivates our second empirical strategy, which compares the effect of price changes with tax changes using observational data over a longer horizon. To implement this test, we focus on alcohol consumption because alcohol is subject to two state-level taxes in the U.S.: an excise tax that is included in the posted price and a sales tax that is added at the register (and hence is less salient). Exploiting state-level changes in these two tax rates between 1970 and 2003 coupled with annual data on total beer consumption by state, we find that increases in the excise tax reduce beer consumption by an order of magnitude more than similar increases in the sales tax. A simple calibration shows that the magnitude of the difference in the elasticity estimates cannot be explained purely by the fact that the sales tax applies to a broader base, especially since food and nonalcoholic beverages are exempt from sales tax in most states. The difference in elasticities persists over time, indicating that behavioral responses to taxes and prices differ even in the long run.
Why do consumers underreact to taxes that are not included in posted prices? One explanation is that customers are uninformed about the sales tax rate or which goods are subject to sales tax. An alternative hypothesis is that salience matters: the customers know what is taxed, but focus on the posted price when shopping. To distinguish between these hypotheses, we surveyed grocery shoppers about their knowledge of sales taxes. The median individual correctly reported the tax status of 7 out of the 8 products on the survey, indicating that our empirical findings are driven by salience effects. A key feature of salience is that it matters in steady state, and not just on the transition path after tax changes.
Our empirical results contradict the basic assumptions of the neoclassical models currently used to guide tax policy. To understand the implications of the empirical evidence for tax policy, we need a method of characterizing the welfare consequences of taxation when agents do not optimize perfectly relative to taxes. The objective of the second half of the paper is to develop such a method. The main challenge we confront, which is central to behavioral public economics more generally, is the recovery of true preferences when behavior is inconsistent with full optimization. We characterize the welfare consequences of taxation using an approach that does not rely on a specific positive model of behavior, as in B. Douglas Bernheim and Antonio Rangel (2008). Our method relies on two assumptions: (1) taxes affect welfare only through their effects on the consumption bundles chosen by agents and (2) consumption choices when prices are perfectly salient are optimal. Under these assumptions, we derive formulas for the effect of taxes on social surplus (deadweight loss) and distribution (incidence) that depend only on the empirically observed demand function and not on the underlying model which generates that demand function. Intuitively, there are two demand curves that together are sufficient statistics for welfare calculations when individuals make optimization errors: the tax-demand curve, which tells us how demand varies as a function of (non salient) taxes, and the price-demand curve, which tells us how demand varies as (fully salient) posted prices change. We use the tax-demand curve to determine the effect of the tax on behavior and then use the price-demand curve to calculate the effect of that change in behavior on welfare. The price-demand curve can be used to recover the agent's preferences and calculate welfare changes because it is generated by optimizing behavior.
The benefits of this approach to welfare analysis are its simplicity and adaptability. The formulas for deadweight loss and incidence can be derived using supply and demand diagrams and familiar notions of consumer and producer surplus. The formulas differ from Harberger's (1964) widely applied
formulas by a single factor - the ratio of the compensated tax elasticity to the compensated price elasticity. Thus, one can calculate the (partial equilibrium) deadweight cost and incidence of any tax policy by estimating both the tax and price elasticities instead of just the tax elasticity as in
the existing empirical literature. Although we motivate our welfare analysis by evidence of salience effects, the formulas account for all errors that consumers may make when optimizing with respect to taxes.4 For example, confusion between average and marginal income tax rates (Charles de Bartolome (1995), Jeffrey B. Liebman and Richard J. Zeckhauser (2004), Naomi E. Feldman and Peter Katuš![]() ák (2006)) or overestimation of estate tax rates (Robert J. Blendon et al. (2003), Joel B. Slemrod (2006)) can be handled using exactly the same formulas, without requiring knowledge of individuals' tax perceptions and
information set.
ák (2006)) or overestimation of estate tax rates (Robert J. Blendon et al. (2003), Joel B. Slemrod (2006)) can be handled using exactly the same formulas, without requiring knowledge of individuals' tax perceptions and
information set.
The results of the welfare analysis challenge widely held intuitions based on the full optimization model. First, the agent who bears the statutory incidence of a tax bears more of the economic incidence, violating the classic tax neutrality result in competitive markets. Second, a tax increase can have an efficiency cost even when demand for the taxed good does not change by distorting budget allocations. Finally, holding fixed the tax elasticity of demand, we show that an increase in the price elasticity of demand reduces deadweight loss and increases incidence on consumers.
This paper builds on and relates to several recent papers in public economics. Our theoretical analysis can be viewed as an application of Bernheim and Rangel's (2008) choice-based approach to welfare, where the choices when taxes are salient reveal an agent's true rankings (see section IV for more details). Our analysis also relates to the work of Liebman and Zeckhauser (2004), who analyze optimal income taxation in a model where individuals misperceive tax schedules because of " ironing" or "spotlighting" behavior. Our approach does not require assumptions about whether individuals iron, spotlight, or respond in some other way to the tax schedule, as any of these behaviors are captured in the empirically observed tax and wage elasticities of labor supply.
Our empirical results are consistent with those of Amy N. Finkelstein (2007) and Tomer Blumkin, Bradley J. Ruffle, and Yosi Ganun (2008), who find evidence of salience effects in toll collection and a lab experiment on consumption vs. income taxes. One notable study that does not find that salience matters is Harvey S. Rosen (1976), who shows that the cross-sectional correlation between marginal tax rates and work hours is similar to the correlation between wage rates and work hours. The cross-sectional approach to estimation of wage elasticities has since been shown to suffer from identification problems, which could explain why our use of exogenous variation to identify salience effects yields different results.
The remainder of the paper is organized as follows. Section I presents an organizing framework for our empirical analysis. Section II discusses the grocery experiment. Section III presents the evidence on alcohol sales. Section IV explores why consumers underreact to taxes. Section V presents the theoretical welfare analysis. Section VI concludes.
I Empirical Framework
To motivate the empirical analysis, consider consumer behavior in an economy with two goods, ![]() and
and ![]() , that are supplied perfectly elastically.5 Normalize the price of
, that are supplied perfectly elastically.5 Normalize the price of ![]() to 1 and let
to 1 and let ![]() denote the pretax price of
denote the pretax price of ![]() .
Assume that
.
Assume that ![]() is untaxed and
is untaxed and ![]() is subject to an ad valorem sales tax
is subject to an ad valorem sales tax ![]() . The total price of
. The total price of ![]() is
is
![]() . The price that consumers see when deciding what to purchase is
. The price that consumers see when deciding what to purchase is ![]() ;
the sales tax is not included in the posted price. Since consumers must calculate
;
the sales tax is not included in the posted price. Since consumers must calculate ![]() themselves but can see
themselves but can see ![]() directly, we will say that the tax inclusive price
directly, we will say that the tax inclusive price ![]() is less " salient" than the pretax price
is less " salient" than the pretax price ![]() .
.
Let
![]() denote demand as a function of the posted price and the ad-valorem sales tax. In the neoclassical full-optimization model, demand depends only on the total tax inclusive price:
denote demand as a function of the posted price and the ad-valorem sales tax. In the neoclassical full-optimization model, demand depends only on the total tax inclusive price:
![]()
![]() .
. ![]() If consumers optimize fully, a 1 percent increase in
If consumers optimize fully, a 1 percent increase in
![]() and a 1 percent increase in the gross-of-tax price (
and a 1 percent increase in the gross-of-tax price (
![]() ) reduce demand by the same amount:
) reduce demand by the same amount:
![]() . We hypothesize that in practice consumers
underreact to the tax
. We hypothesize that in practice consumers
underreact to the tax ![]() because it is less salient:
because it is less salient:
![]() . To test this hypothesis, we log-linearize the demand function
. To test this hypothesis, we log-linearize the demand function
![]() to obtain the following estimating equation:
to obtain the following estimating equation:
In this equation, the parameter
The null hypothesis of full optimization implies
Strategy 1: Manipulate Tax Salience. Our first empirical strategy is to make the sales tax as salient as the pretax price by posting the tax inclusive price ![]() on
the shelf. When tax inclusive prices are posted, consumers presumably optimize relative to the tax inclusive price and set demand to
on
the shelf. When tax inclusive prices are posted, consumers presumably optimize relative to the tax inclusive price and set demand to
![]() . Hence, the effect of posting the tax inclusive price on demand is
. Hence, the effect of posting the tax inclusive price on demand is
The right hand side of this equation measures the effect of posting tax inclusive prices on demand divided by the effect of a price increase corresponding to the size of the tax. This ratio measures the degree of misperception of total prices when taxes are not included in posted prices. If all consumers normally take the sales tax into account, posting
Strategy 2: Manipulate Tax Rate. An alternative method of estimating
![]() is to exploit independent variation in
is to exploit independent variation in ![]() and
and ![]() to estimate the sales tax elasticity
to estimate the sales tax elasticity
![]() and the price elasticity
and the price elasticity
![]() , as in Rosen (1976). As shown in (2), the ratio of the two elasticities
, as in Rosen (1976). As shown in (2), the ratio of the two elasticities
![]() identifies
identifies
![]() .
.
In the next section, we implement strategy 1 using a field experiment at a grocery store. In section III, we implement strategy 2 using observational data on alcohol consumption.
II.A Research Design
We conducted an experiment posting tax inclusive prices at one store of a national grocery chain. The store is a 37,000 square foot supermarket with annual revenue of approximately $25 million and is located in a middle-income suburb in Northern California. Approximately 30 percent of the products sold in the store are subject to the local sales tax of 7.375 percent, which is added at the register. Price tags on the shelves display only pretax prices, as in the upper half of the tag shown in Exhibit 1.
The grocery chain's managers expected that posting tax inclusive prices would reduce sales.7 To limit revenue losses, they asked us to restrict our intervention to three product groups that were not "sales leaders" and to limit the duration of the intervention to three weeks. We looked for three product groups that met this requirement as well as two additional criteria: (1) products with relatively high prices so that the dollar amount of the sales tax is nontrivial; and (2) products belonging to "impulse purchase categories" - goods that exhibit high price elasticities - so that the demand response to the intervention would be detectable. We chose three groups of taxable toiletries: cosmetics, hair care accessories, and deodorants. These three product groups take up half an aisle of the store and together include about 750 distinct products.
We posted tax inclusive prices for all products in the three groups beginning on February 22, 2006 and ending on March 15, 2006.8 Exhibit 1 shows how the
price tags were altered. The original tags, which show pretax prices, were left untouched on the shelf. A tag showing the tax inclusive price was attached directly below this tag for each product. The added tag stated "Total Price: $![]() + Sales Tax = $
+ Sales Tax = $![]() ," where
," where ![]() denotes
the pretax price (repeating the information in the original tag) and
denotes
the pretax price (repeating the information in the original tag) and ![]() denotes the tax inclusive price. The original pretax price was repeated on the new tag to avoid giving the impression
that the price of the product had increased. For the same reason, the fonts used for
denotes the tax inclusive price. The original pretax price was repeated on the new tag to avoid giving the impression
that the price of the product had increased. For the same reason, the fonts used for ![]() ,
, ![]() , and the words "Sales Tax" exactly matched the font used by the store for the original price. Additional details on experiment implementation are given in Appendix A.
, and the words "Sales Tax" exactly matched the font used by the store for the original price. Additional details on experiment implementation are given in Appendix A.
Evaluation of Tags. To determine whether the tags are effective in increasing tax salience and are understood by consumers, we conducted a preliminary survey-based evaluation in an undergraduate class. We showed the students a photograph of taxable products on the shelf at the grocery store similar to that in Exhibit 1. We distributed surveys (shown in Appendix Exhibit 1) asking each student to choose two goods and write down "the total bill due at the register for these two items." We first showed the photograph with the regular tags displaying only the pretax prices. After collecting the survey responses, we showed a second photograph of products with our tax inclusive price tags and asked students to repeat the exercise. The results are summarized in the first panel of Table 1. When presented with the first photo, the modal response was the total pretax bill for the two products. Only 18 percent of students reported a total price within $0.25 of the total tax inclusive amount. When presented with the second photo, the modal response included the sales tax, and 75 percent wrote down an amount within $0.25 of the true tax inclusive total. This evidence shows that posting tax inclusive price tags does indeed have a strong "first stage" effect on tax salience. Moreover, the results allay concerns that the tags confused consumers into believing that these items were subject to an additional tax or that the pretax price of the product had been increased.
Although we are confident that the tags increased tax salience substantially, we cannot rule out the possibility that they also affected demand through other channels or "Hawthorne effects." For instance, the very fact that 750 new tags were posted on the shelves could have deterred customers from the aisle. We are only able to estimate the effect of posting the tags on demand, and have no means of decomposing the effect of the intervention into the various mechanisms through which the tags may have had an effect. The large first-stage effect of the tags on perceived prices leads us to believe that the primary mechanism is increased tax salience, but we ultimately rely on evidence from the second empirical approach (see section III) to address such concerns.
Empirical Strategy. To estimate the effect of our intervention on demand, we compare changes in quantity sold in the " treatment" group of products whose tags were modified with two "control" groups. We define the treatment group as products that belong to the cosmetics, hair care accessories, or deodorants product groups in the store where we conducted the experiment. The first control group is a set of products in the same aisles as the treatment products for which we did not change tags within the experimental store. These products include similar (taxable) toiletries such as toothpaste, skin care, and shaving products; see Appendix Table 1 for the full list. The second control group consists of all the toiletry products sold in a pair of stores in nearby cities. These control stores were selected to match the treatment store prior to the experiment on the demographic and store characteristics shown in Appendix Table 2. Using these two control groups, we implement a standard difference-in-difference methodology to test whether sales of the treated products fell during the intervention relative to the controls.
II.B Data and Summary Statistics
We use scanner data from the treatment store and the two control stores, spanning week 1 of 2005 to week 13 of 2006. The dataset contains weekly information on price and quantity sold for all toiletry (treatment and control) products in each store. See Appendix A for details on the dataset.
Within the treatment group, there are 13 product " categories" (e.g. lipsticks, eye cosmetics, roll-on deodorants, body spray deodorants). The control product group contains 95 categories, which are listed in Appendix Table 1. We analyze the data at the category level (summing quantity sold and revenue over the individual products within categories) rather than the product level for two reasons. First, the intervention was done at the category level. Second, we cannot distinguish products that were on the shelf but did not sell (true zeros) from products that were not on the shelf. Analyzing the data at the category level circumvents this problem because there are relatively few category-weeks with missing data (4.7 percent of all observations). Since all the categories always existed in all stores throughout the sample period, we believe that these observations are true zeros, and code them as such.
Table 2 presents summary statistics for the treatment and control product groups in each store. The treatment store sold an average of 25 items per category and earned $98 of revenue per week per category over the sample period (column 1 of Table 2). The treatment products thus account for approximately $1,300 of revenue per week as a whole. Average weekly quantity sold per category is similar for the control products in the treatment store, but products in these categories are somewhat more expensive on average (column 2). Sales and revenue for the same categories in the control stores are very similar to those in the treatment store (columns 3-4).
II.C Results
Comparison of Means. We begin our analysis with a cross-tabulation of mean quantity sold in Table 3. The upper panel of the table shows data for the treatment store. The data is split into four cells. The rows split the data by time: pre experiment (week 1 of 2005 to week 6 of 2006) vs. the intervention period (weeks 8 to 10 of 2006).9 The columns split the data by product group: treated vs. control categories. Each cell shows the mean quantity sold for the group labelled on the axes, along with the standard error and the number of observations. All standard errors reported in this and subsequent tables in this section are clustered by week to adjust for correlation of errors across products.10
The mean quantity sold in the treatment categories fell by an average of 1.30 units per week during the experimental period relative to the pre period baseline. Meanwhile, quantity sold in the control categories within the treatment store went up by 0.84 units. Hence, sales fell in the treatment
categories relative to the control categories by 2.14 units on average, with a standard error of 0.64. This change of
![]() units is the "within treatment store" difference-in-difference estimate of the impact of posting tax inclusive prices. The identification assumption necessary for consistency
of
units is the "within treatment store" difference-in-difference estimate of the impact of posting tax inclusive prices. The identification assumption necessary for consistency
of ![]() is the standard "common trends" condition (Bruce D. Meyer 1995), which in this case requires that sales of the treatment and control products would have evolved similarly absent
our intervention.
is the standard "common trends" condition (Bruce D. Meyer 1995), which in this case requires that sales of the treatment and control products would have evolved similarly absent
our intervention.
One natural way of evaluating the validity of this identification assumption is to compare the change in sales of treatment and control products in the control stores, where no intervention took place. The lower panel of Table 3 presents such a comparison. In the control stores, sales of
treatment products increased by a (statistically insignificant)
![]() units relative to sales of control products. The fact that
units relative to sales of control products. The fact that ![]() is
not significantly different from zero suggests that sales of the treatment and control products would in fact have evolved similarly in the treatment store had the intervention not taken place.
is
not significantly different from zero suggests that sales of the treatment and control products would in fact have evolved similarly in the treatment store had the intervention not taken place.
Putting together the upper and lower panels of Table 3, one can construct a "triple difference" (DDD) estimate of the effect of the intervention, as in Jonathan Gruber (1994). This estimate is ![]()
![]() . This estimate is statistically significant with
. This estimate is statistically significant with ![]() ,
rejecting the null of full-optimization (
,
rejecting the null of full-optimization (
![]() ). Note that both within-store and within-product time trends are differenced out in the DDD. The DDD estimate is therefore immune to both store-specific shocks - such as a
transitory increase in customer traffic - and product-specific shocks - such as fluctuations in demand for certain goods. Hence, the identification assumption for consistency of the DDD estimate is that there was no shock during our experimental intervention that differentially affected sales of
only the treatment products in the treatment store. In view of the planned, exogenous nature of the intervention, we believe that this condition is likely to be satisfied.
). Note that both within-store and within-product time trends are differenced out in the DDD. The DDD estimate is therefore immune to both store-specific shocks - such as a
transitory increase in customer traffic - and product-specific shocks - such as fluctuations in demand for certain goods. Hence, the identification assumption for consistency of the DDD estimate is that there was no shock during our experimental intervention that differentially affected sales of
only the treatment products in the treatment store. In view of the planned, exogenous nature of the intervention, we believe that this condition is likely to be satisfied.
We gauge the magnitude of the treatment effect using the framework in section I. The mean quantity sold per category fell by 2.2 units per week, relative to a base of 29 units sold per
week. Making the sales tax salient thus reduces demand by 7.6 percent. We show below that the estimated price elasticity of demand at the category level is
![]() . Given the sales tax rate of 7.375 percent, plugging these values into (3) yields a point estimate of
. Given the sales tax rate of 7.375 percent, plugging these values into (3) yields a point estimate of
![]() . That is, a 10 percent tax increase reduces demand by the same amount as a 3.5 percent price increase.
. That is, a 10 percent tax increase reduces demand by the same amount as a 3.5 percent price increase.
Regression Estimates. We evaluate the robustness of the DDD estimate by estimating a series of regression models with various covariate sets and sample specifications in Table 4. Let the outcome of interest (e.g. quantity, log quantity, revenue) be denoted by
![]() . Let the variables
. Let the variables ![]() (treatment store),
(treatment store), ![]() (treatment categories), and
(treatment categories), and ![]() (treatment time) denote indicators for whether an observation is in the experimental
store, categories, and time, respectively. Let
(treatment time) denote indicators for whether an observation is in the experimental
store, categories, and time, respectively. Let ![]() denote a vector of additional covariates. We estimate variants of the following linear model, which generalizes the DDD method above (see
Gruber 1994):
denote a vector of additional covariates. We estimate variants of the following linear model, which generalizes the DDD method above (see
Gruber 1994):
In this specification, the third-level interaction (
Specification 1 of Table 4 estimates (4) for quantity sold, controlling for the mean price of the products in each category using a quadratic specification and including category, week, and store fixed effects.11 The estimated effect of the treatment is essentially the same as in the comparison of means, which is not surprising since there were no unusual price changes during our intervention period. Specification 2 shows
that the intervention led to a significant reduction in revenue (price![]() quantity) from the treated products.12
quantity) from the treated products.12
In specification 3, we estimate an analogous model in logs instead of levels. In this specification, we weight each observation by the mean revenue over time by category by store, placing greater weight on the larger categories as in the levels regressions. The log specification is perhaps a
better model for comparisons across categories with different baseline quantities, but it forces us to omit observations that have zero quantity sold. It yields a slightly larger estimate than the levels model for the reduction in quantity sold (10.1 percent). The estimated category-level price
elasticity - the effect of a 1 percent increase in the prices of all goods within a category - is
![]() . This elasticity is identified by the variation in average category-level prices across weeks within the stores. The estimate is consistent with those of Stephen J.
Hoch et al. (1995), who estimate a full product-level demand system and obtain category-level price elasticities of 1 to 1.5 for similar products using scanner data from the same grocery chain.
. This elasticity is identified by the variation in average category-level prices across weeks within the stores. The estimate is consistent with those of Stephen J.
Hoch et al. (1995), who estimate a full product-level demand system and obtain category-level price elasticities of 1 to 1.5 for similar products using scanner data from the same grocery chain.
Placebo and Permutation Tests. To further evaluate the "common trends" identification assumption, we check for unusual patterns in demand immediately before and after the experiment. We replicate specification 1 including indicator variables for the three week
periods before the intervention began (![]() : weeks 4 to 6 of 2006) and after the intervention ended (
: weeks 4 to 6 of 2006) and after the intervention ended (![]() : weeks 11 to 13). We also include second- and third-level interactions of
: weeks 11 to 13). We also include second- and third-level interactions of ![]() and
and ![]() with the
with the ![]() and
and ![]() variables, as for the
variables, as for the ![]() variable in (4). Column 4 of Table 4 reports estimates of the third-level interactions for the periods before, during, and after the experiment. Consistent with the other results
in Table 4, quantity sold in the treatment group is estimated to change by
variable in (4). Column 4 of Table 4 reports estimates of the third-level interactions for the periods before, during, and after the experiment. Consistent with the other results
in Table 4, quantity sold in the treatment group is estimated to change by
![]() units during the intervention. The corresponding "placebo" estimates for the periods before and after the treatment are close to zero, indicating that the fall in demand
coincides precisely with the intervention period.
units during the intervention. The corresponding "placebo" estimates for the periods before and after the treatment are close to zero, indicating that the fall in demand
coincides precisely with the intervention period.
A concern in DD analysis is that serial correlation can bias standard errors, leading to overrejection of the null hypothesis of no effect (Marianne Bertrand, Esther Duflo, and Sendhil Mullainathan 2002). To address this concern, we implement a nonparametric permutation test for ![]() . We first choose a "placebo triplet" consisting of a store, three week time period, and a randomly selected set of 13 product categories. We then estimate (4), pretending
that the placebo triplet is the treatment triplet. We repeat this procedure for all permutations of stores and contiguous three week periods and 25 different randomly selected groups of 13 categories, obtaining
. We first choose a "placebo triplet" consisting of a store, three week time period, and a randomly selected set of 13 product categories. We then estimate (4), pretending
that the placebo triplet is the treatment triplet. We repeat this procedure for all permutations of stores and contiguous three week periods and 25 different randomly selected groups of 13 categories, obtaining
![]() placebo estimates. Defining
placebo estimates. Defining
![]() to be the empirical cdf of these placebo effects, the statistic
to be the empirical cdf of these placebo effects, the statistic ![]() gives a p-value for the hypothesis that
gives a p-value for the hypothesis that ![]() . Intuitively, if the experiment had a significant effect on demand, we would expect the estimated coefficient to be
in the lower tail of estimated placebo effects.13 Since this test does not make parametric assumptions about the error structure, it does not suffer from
the overrejection bias of the t-test.
. Intuitively, if the experiment had a significant effect on demand, we would expect the estimated coefficient to be
in the lower tail of estimated placebo effects.13 Since this test does not make parametric assumptions about the error structure, it does not suffer from
the overrejection bias of the t-test.
Figure 1 illustrates the results of the permutation test by plotting the empirical distribution of placebo effects ![]() for log quantity (specification 3 of Table 4). The vertical line in the
figure denotes the treatment effect reported in Table 4. For log quantity,
for log quantity (specification 3 of Table 4). The vertical line in the
figure denotes the treatment effect reported in Table 4. For log quantity, ![]() (
(
![]() . An analogous test for log revenue yields
. An analogous test for log revenue yields ![]() (
(
![]() . Although these p-values are larger than those obtained using the t-tests, they confirm that the intervention led to an unusually low level of demand.
. Although these p-values are larger than those obtained using the t-tests, they confirm that the intervention led to an unusually low level of demand.
Finally, we consider subsets of the large set of counterfactuals across time, categories, and stores. In column 5 of Table 4, we restrict the sample to the treatment product categories and compare across time and stores. This DD estimate is quite similar to the DDD estimates. Results are also similar when we restrict the sample to the treatment store or limit the pre experiment sample to the three months immediately before the intervention.
III.A Research Design
We turn now to the second empirical test: comparing the effect of increases in posted prices and taxes on demand. We implement this strategy by focusing on alcohol consumption. Alcohol is subject to two taxes in most states: (1) an excise tax that is levied at the
wholesale level and is included in the price posted on the shelf or restaurant menu and (2) a sales tax, which is added at the register (except in Hawaii, which we exclude). The total price of alcohol is therefore
![]() where
where ![]() is the pretax price,
is the pretax price, ![]() is the excise tax, and
is the excise tax, and ![]() is the sales tax. Since the excise tax is included in
the posted price, it is more salient than the sales tax.
is the sales tax. Since the excise tax is included in
the posted price, it is more salient than the sales tax.
We estimate the effect of ![]() and
and ![]() on alcohol consumption by
exploiting the many state-level changes in the two taxes between 1970 and 2003. Our estimating equation is based on the demand specification in (1):
on alcohol consumption by
exploiting the many state-level changes in the two taxes between 1970 and 2003. Our estimating equation is based on the demand specification in (1):
We estimate (5) in first-differences because both the tax rates and alcohol consumption are highly autocorrelated series. Letting
We estimate variants of (6) using OLS and test the hypothesis that
III.B Data and Summary Statistics
Tax rates on alcohol vary across beer, wine, and spirits. In the interest of space, we present results for beer, which accounts for the largest share of alcohol consumption in the U.S. As we discuss below, the results for total alcohol consumption are similar, because changes in tax rates across the three types of alcohol are very highly correlated.
We use data on aggregate annual beer consumption by state from the National Institute of Alcohol Abuse and Alcoholism (NIAAA) (2006) from 1970-2003. These data are compiled from administrative state tax records, and are more precise than data from surveys because they reflect total consumption in each state. We obtain data on beer excise tax and sales tax rates and revenues by state from the Brewer's Almanac (various years), World Tax Database (2006), and other sources.15 The state sales tax is an ad valorem tax (proportional to price), while the excise tax is typically a specific tax (dollars per gallon of beer). We convert the excise tax rate into percentage units comparable to the sales tax by dividing the beer excise tax per case in year 2000 dollars by the average cost of a case of beer in the United States in the year 2000.16 We normalize the excise tax by the average national price because each state's price is endogenous to its tax rate. Details on the data sources and construction of tax rates are given in Appendix A.
Table 5 shows summary statistics for the pooled dataset. Between 1970 and 2003, mean per capita consumption of beer is roughly 240 cans per year. The average state excise tax rate is 6.4 percent of the average price, while the mean state sales tax rate is 4.3 percent.17 There is considerable independent variation within states in the two taxes over the sample period. There are 153 legislated changes to the sales tax and 131 legislated changes to excise taxes; the correlation between excise tax changes and sales tax changes is 0.06.
III.C Results
We begin with a graphical analysis to illustrate the relationship between alcohol consumption and taxes in Figures 2a and 2b. These figures plot annual state-level changes in log beer consumption per capita against log changes in the gross-of-excise-tax price
![]() and the gross-of-sales-tax price
and the gross-of-sales-tax price
![]() . To construct Figure 2a, we first round each state excise tax change to the nearest tenth of a percent. We then compute the mean change in log beer consumption for
observations with the same rounded excise tax change. Finally, we plot the mean consumption change against the rounded excise tax rates, superimposing a best-fit line on the points as a visual aid. Figure 2b is constructed analogously using sales tax changes. To make the range of changes in the
excise tax comparable to the smaller range of changes in the sales tax, we restrict the range of both tax changes to
. To construct Figure 2a, we first round each state excise tax change to the nearest tenth of a percent. We then compute the mean change in log beer consumption for
observations with the same rounded excise tax change. Finally, we plot the mean consumption change against the rounded excise tax rates, superimposing a best-fit line on the points as a visual aid. Figure 2b is constructed analogously using sales tax changes. To make the range of changes in the
excise tax comparable to the smaller range of changes in the sales tax, we restrict the range of both tax changes to ![]() log points. Figure 2a shows that increases in the beer excise tax
sharply reduce beer consumption. Figure 2b shows that increases in the sales tax have a much smaller effect on beer consumption.
log points. Figure 2a shows that increases in the beer excise tax
sharply reduce beer consumption. Figure 2b shows that increases in the sales tax have a much smaller effect on beer consumption.
Regression Estimates. Table 6 presents estimates of the model for the state-level growth rate of alcohol consumption in (6). In these and all subsequent specifications, we adjust for potential serial correlation in errors by clustering the
standard errors by state. Column 1 reports estimates of a baseline model that includes only year fixed effects (which remove aggregate trends) and log state population growth as covariates. In this specification, a 1 percent increase in the gross-of-excise-tax price is estimated to reduce beer
consumption by 0.87 percent (
![]() ).18 In
contrast, a 1 percent increase in the gross-of-sales-tax price is estimated to reduce beer consumption by 0.20 percent (
).18 In
contrast, a 1 percent increase in the gross-of-sales-tax price is estimated to reduce beer consumption by 0.20 percent (
![]() ). The null hypothesis that the excise and sales tax elasticities are equal is rejected with
). The null hypothesis that the excise and sales tax elasticities are equal is rejected with ![]() .
.
Columns 2-4 control for factors that may be correlated with the tax changes. One concern is that sales tax changes are correlated with the business cycle. In column 2, we control for the state-level business cycle by including changes in log state per capita income and the state unemployment
rate as covariates. Introducing these controls reduces the estimated sales tax coefficient, and as a result the null hypothesis of equal elasticities is rejected with ![]() . The sales tax
effect is smaller because sales taxes are sometimes raised during budgetary shortfalls that occur in recessions. Since alcohol is a normal good (as indicated by the coefficients on per capita income and unemployment rate), failing to control for the business cycle biases the correlation between
alcohol consumption and sales tax changes upward in magnitude. Hence, the endogeneity of sales tax rate appears to work against rejecting the null hypothesis that
. The sales tax
effect is smaller because sales taxes are sometimes raised during budgetary shortfalls that occur in recessions. Since alcohol is a normal good (as indicated by the coefficients on per capita income and unemployment rate), failing to control for the business cycle biases the correlation between
alcohol consumption and sales tax changes upward in magnitude. Hence, the endogeneity of sales tax rate appears to work against rejecting the null hypothesis that
![]() .19
.19
Another concern is that excise tax increases are sometimes associated with contemporaneous tightening of alcohol regulations. We evaluate this concern using data on four regulations: the legal drinking age, the blood alcohol content limit, implementation of stricter drunk driving regulations for youths, and introduction of administrative license revocation laws. We control for the change in the legal drinking age (in years) and separate indicator variables for a shift toward stricter regulations in each of the other three measures in column 3. The coefficient on the excise tax rate does not change significantly because regulation changes have modest effects on total beer consumption; on average, beer consumption falls by only 0.5 percent when one of the four regulations is tightened.
A third concern is that trends in excise tax rates may be correlated with changes in social norms, which directly influence alcohol consumption. For example, rising acceptance of alcohol consumption in historically conservative regions such as the South may have led to both a reduction in the excise tax as a percentage of price and an increase in alcohol consumption. To assess whether such trends lead to significant bias, we include region fixed effects in column 4 of Table 6, effectively identifying the model from changes in taxes in geographically adjacent states. The coefficient on the excise rate remains substantially larger than the coefficient on the sales tax, suggesting that our results are not spuriously generated by region-specific trends.
There are two sources of variation identifying the excise tax coefficient: (1) policy changes in the nominal tax rate, which produce sharp jumps in tax rates and (2) gradual erosion of the nominal value of the tax by inflation, which creates differential changes in excise tax rates across states because they have different initial tax rates.20 To test whether the two sources of variation yield similar results, we isolate the effect of the policy changes using an instrumental variables strategy. We fix the price of beer at its sample average and compute the implied ad valorem excise tax as the nominal tax divided by this time-invariant price. The only variation in this simulated tax rate is due to policy changes. Using the simulated excise tax rate to instrument for the actual excise tax rate, we replicate the specification in column 3 of Table 6. The point estimates of both tax elasticities, reported in column 1 of Table 7, are similar to those in previous specifications. The standard errors rise as expected since part of the variation in excise tax rates has been excluded.
Thus far, we have focused on changes in tax rates and alcohol consumption at an annual frequency. One explanation of the difference between the sales and excise tax effects at the annual frequency is learning: people might immediately perceive excise taxes, but learn about changes in the sales tax over time. To test for such learning effects, we estimated specifications including lags and leads of the tax variables and differences over longer horizons. For example, Column 2 of Table 7 shows the effect of sales and excise tax changes on consumption over a three-year horizon (as in Jonathan Gruber and Emmanuel Saez (2002)). An increase in the excise tax rate continues to have a large negative effect on alcohol consumption after three years, whereas an equivalent increase in the sales tax still does not. This evidence suggests that consumers underreact to taxes that are not salient even in the long run.
The premise underlying our analysis is that firms pass changes in the state excise tax through to consumers so that they are reflected in the posted price of beer. We expect full pass through of state-level tax changes because each state constitutes a small share of the national market,
effectively making the state-level supply curves flat. We check this mechanism using data on posted prices of beer from the ACCRA cost of living survey from 1982 to 2000. Using these data, we estimate the price elasticity of demand for beer, instrumenting for changes in the posted price using
changes in the excise tax rate. The estimated price elasticity of demand, reported in column 3 of Table 7, is
![]() , almost identical to the estimates of
, almost identical to the estimates of
![]() in the previous specifications. The standard error rises because we have price data for only 55 percent of the observations. The reason that
in the previous specifications. The standard error rises because we have price data for only 55 percent of the observations. The reason that
![]() is that state-level excise tax increases are fully passed through to consumers as expected - the coefficient on the excise tax variable in the
first-stage regression is approximately 1. This finding supports the claim that the excise tax has a larger effect on demand than the sales tax because it is fully salient.
is that state-level excise tax increases are fully passed through to consumers as expected - the coefficient on the excise tax variable in the
first-stage regression is approximately 1. This finding supports the claim that the excise tax has a larger effect on demand than the sales tax because it is fully salient.
Relative Price Changes and Excise vs. Sales Taxes. An important concern in the comparison of sales and excise tax effects is that the sales tax applies to a broader set of goods than alcohol. Approximately 40 percent of consumption is subject to sales
taxation.21 A 1 percent increase in ![]() changes the relative price of alcohol and all other goods less than a 1 percent increase in
changes the relative price of alcohol and all other goods less than a 1 percent increase in ![]() , which could potentially explain why the sales tax effect is smaller than the excise tax
effect even absent salience effects.
, which could potentially explain why the sales tax effect is smaller than the excise tax
effect even absent salience effects.
We evaluate the magnitude of the bias due to this problem in two ways. First, we estimate the model using only the thirty states that fully exempted all food items from the sales tax in 2000.22 In these states, changes in the sales tax always affect the relative price of alcohol and food (and nonalcoholic beverages), which is the most plausible substitute for alcohol. Column 4 of Table 7 shows that the sales tax elasticity remains quite small in this subsample.
As an alternative approach, we calibrate the effect of a 1 percent increase in a (hypothetical) tax ![]() that applies solely to alcohol (
that applies solely to alcohol (![]() ) and is excluded from the posted price. Treating all goods other than alcohol as a composite commodity (
) and is excluded from the posted price. Treating all goods other than alcohol as a composite commodity (![]() ) of which 40 percent is
subject to sales tax, observe that a 1 percent increase in the gross-of-sales-tax price
) of which 40 percent is
subject to sales tax, observe that a 1 percent increase in the gross-of-sales-tax price
![]() increases the price of
increases the price of ![]() relative to
relative to ![]() by
by
![]() percent. It follows that the effect of a 1 percent increase in the tax
percent. It follows that the effect of a 1 percent increase in the tax ![]() that applies solely to alcohol is given by
that applies solely to alcohol is given by
![]() . Scaling up the largest estimated response to the sales tax in Table 6 of -0.20 by
. Scaling up the largest estimated response to the sales tax in Table 6 of -0.20 by
![]() yields an estimate of
yields an estimate of
![]() , which remains substantially below the excise tax elasticity estimates.
, which remains substantially below the excise tax elasticity estimates.
A related concern is that increases in the beer excise tax may induce substitution to wine and spirits, thereby biasing the beer tax elasticity up relative to the sales tax elasticity. To assess the extent of substitution, we estimate the effect of the beer excise tax on the share of beer in total alcohol (ethanol) consumption. The estimates in column 5 of Table 7 show that the beer share is insensitive to the beer tax rate. The reason is that excise tax rates on beer, wine, and spirits are highly correlated. For example, the correlation coefficient of changes in beer and wine tax rates is 0.94; in 86 percent of the instances in which a state changes its beer excise tax, it also changes its wine excise tax rate. We also find that the effect of changes in beer excise taxes on total ethanol consumption is much larger than the effect of changes in sales tax rates. We conclude that differences in tax bases are unlikely to explain the substantial gap between the estimated sales and excise tax elasticities.
Summary. Averaging across the estimates in Tables 6 and 7, the mean estimate of the gross-of-excise-tax elasticity is 0.84. The mean estimate of the gross-of-sales-tax elasticity is 0.03. Scaling up the sales tax coefficient by
![]() , we obtain an implied elasticity of 0.05 for a tax
, we obtain an implied elasticity of 0.05 for a tax ![]() that is
applied solely to alcohol at the register. Combining these estimates yields a point estimate of
that is
applied solely to alcohol at the register. Combining these estimates yields a point estimate of
![]() .
.
IV Why Do Consumers Underreact to Taxes?
There are two potential explanations for the finding that consumers underreact substantially to taxes that are not included in posted prices. One is that customers are uninformed about sales tax rates. Showing the tax inclusive price tags may have provided new information about tax rates. An alternative explanation is that salience matters: individuals know about taxes when their attention is drawn to the subject, but do not pay attention to taxes that are not transparent while deciding what to buy.
A few pieces of auxiliary evidence from the empirical analysis cast doubt on the information hypothesis. First, sales of the (taxable) toiletries adjacent to those that were tagged in the grocery store experiment did not change significantly during the intervention. The fact that posting tax inclusive prices had no "spillover effects" suggests that individuals did not simply learn that toiletries are subject to sales tax. Second, demand returned to pre experiment levels after the intervention ended, suggesting that there were no persistent learning effects.23 Third, the finding the sales and excise tax elasticities for alcohol demand do not converge over time suggests that the underreaction to the sales tax is not caused by delays in acquiring information.
To distinguish between information and salience more directly, we surveyed 91 customers entering the store where we conducted the experiment about their knowledge of sales taxes. See Appendix A for details on survey implementation and Appendix Exhibit 2 for the survey instrument. We asked individuals the local sales tax rate and whether various products (e.g. milk, magazines, toothpaste) were subject to sales tax. Summary statistics for the survey data are displayed in Panel B of Table 1. 75 percent of those surveyed reported the sales tax rate within 0.5 percentage points of the true rate, and 97 percent reported a rate between 6.75 percent and 8.75 percent. The modal answer was exactly 7.375 percent. The median respondent answered 7 out of 8 questions about taxable status of the goods correctly. The respondents generally believe that food is not taxed, but inedible items and "sin" goods are taxed. Exceptions to this heuristic led to the most errors. In California, carbonated beverages are subject to sales tax, while cookies are not. Among respondents who got one question wrong, Coca Cola and cookies accounted for more than half the mistakes.
In summary, most consumers are well informed about commodity tax rates when their attention is drawn to the subject. However, they do not remember to include the tax when making consumption decisions, as shown by the survey of students discussed in section II. The two surveys and two strands of empirical evidence together indicate that salience and inattention are a central determinant of consumer responses to taxation in steady state.
Positive Theories. There are many positive theories that can explain underreaction to taxation. In a companion paper (Chetty, Looney, and Kroft 2007), we propose a bounded-rationality model in which agents pay cognitive costs to calculate tax inclusive prices. We show
that small cognitive costs can generate substantial inattention to taxes because the utility loss from ignoring taxes is a second-order function of the tax rate. For example, an agent who spends
![]() , has
, has
![]() , and linear utility in
, and linear utility in ![]() , loses only
, loses only ![]() by ignoring a 10 percent sales tax. An economy populated by individuals who face small
cognitive or time costs of paying attention to taxes can thus generate
by ignoring a 10 percent sales tax. An economy populated by individuals who face small
cognitive or time costs of paying attention to taxes can thus generate
![]() .
.
More generally, agents with limited attention may use heuristics to achieve a consumption allocation that approximates the fully optimal bundle, but leads them to underreact to taxes. For example, consumers may apply a tax rate of 5 percent or 10 percent instead of 7.375, percent or compute 7 percent of ![]() instead of
7 percent of the exact price
instead of
7 percent of the exact price ![]() . A more sophisticated heuristic is to keep a
separate shadow value of money in mind for taxed and untaxed goods. An entirely different theory of attention is a psychological model in which allocation of attention is triggered by cues (e.g. the visibility or color of pricing information) rather than economic optimization.
. A more sophisticated heuristic is to keep a
separate shadow value of money in mind for taxed and untaxed goods. An entirely different theory of attention is a psychological model in which allocation of attention is triggered by cues (e.g. the visibility or color of pricing information) rather than economic optimization.
Our data does not allow us to distinguish between these models. We therefore proceed to analyze the welfare consequences of taxation in a manner that does not depend on a specific positive theory of underreaction to taxes.
V Welfare Analysis
This section explores the implications of our empirical results for tax policy. In particular, we generalize Harberger's (1964) canonical partial-equilibrium formulas for incidence and deadweight loss to allow for salience effects and other optimization errors with respect to taxes. The formulas we develop can be used to analyze the effects of taxes in the specific commodity markets that we analyzed empirically, as well as other policies such as labor and capital income taxation.
We first characterize tax incidence, which is essentially a mechanical calculation of price changes. We then characterize efficiency costs, which is a more complex problem because additional assumptions are required to calculate welfare changes when agents optimize imperfectly. We restrict attention to tax policies designed to raise revenue (e.g. to finance a public good).24 The tools developed below can be adapted to analyze Pigouvian taxes intended to correct behavior, but we defer that analysis to future work.
V.A Setup
We use the same two good model as in section I, but assume from this point onward that the sales tax levied on good ![]() is a specific (unit) tax
is a specific (unit) tax ![]() rather than an ad-valorem tax for consistency with the theoretical literature on commodity taxation.25 Let
rather than an ad-valorem tax for consistency with the theoretical literature on commodity taxation.25 Let ![]() denote the pretax price of
denote the pretax price of ![]() and
and ![]() denote the tax inclusive price of
denote the tax inclusive price of ![]() . Good
. Good ![]() , the numeraire, is untaxed. As is standard in partial equilibrium analysis, assume that tax revenue is not spent on the taxed good (i.e. it is used to buy
, the numeraire, is untaxed. As is standard in partial equilibrium analysis, assume that tax revenue is not spent on the taxed good (i.e. it is used to buy ![]() or thrown away).
or thrown away).
Consumption. The representative consumer has wealth ![]() and has utility
and has utility ![]() . Let
. Let
![]() denote the bundle chosen by a fully optimizing consumer as a function of the posted price, tax, and wealth. Full optimization implies
denote the bundle chosen by a fully optimizing consumer as a function of the posted price, tax, and wealth. Full optimization implies
![]() , contradicting our empirical findings. Let
, contradicting our empirical findings. Let
![]() denote the empirically observed demand functions, which permit
denote the empirically observed demand functions, which permit
![]() . We do not place structure on the positive model that generates
. We do not place structure on the positive model that generates
![]() other than to assume that the demand functions are smooth and that the choices are feasible:
other than to assume that the demand functions are smooth and that the choices are feasible:
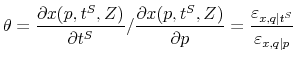
Production. Price-taking firms use ![]() units of the numeraire
units of the numeraire ![]() to produce
to produce ![]() units of
units of ![]() . The marginal cost of production is weakly
increasing:
. The marginal cost of production is weakly
increasing:
![]() and
and
![]() . The representative firm's profit at pretax price
. The representative firm's profit at pretax price ![]() and
level of supply
and
level of supply ![]() is
is ![]() . Assuming that firms optimize perfectly, the supply
function for good
. Assuming that firms optimize perfectly, the supply
function for good ![]() is implicitly defined by the marginal condition
is implicitly defined by the marginal condition
![]() .28 Let
.28 Let
![]() denote the price elasticity of supply.
denote the price elasticity of supply.
V.B Incidence
How is the burden of a tax shared between consumers and producers in competitive equilibrium when consumers optimize imperfectly with respect to taxes? We derive formulas for the incidence of the sales tax on producers and consumers which parallel the derivations of Laurence J. Kotlikoff and
Lawrence H. Summers (1987) for the full-optimization case. As is standard in the literature on tax incidence, we use
![]() instead of
instead of
![]() to refer to the demand curve in this subsection. Let
to refer to the demand curve in this subsection. Let
![]() denote the equilibrium pretax price that clears the market for good
denote the equilibrium pretax price that clears the market for good ![]() as
a function of the tax rate. The market clearing price
as
a function of the tax rate. The market clearing price ![]() satisfies
satisfies
Implicit differentiation of (7) yields the following results.
and the incidence on consumers is
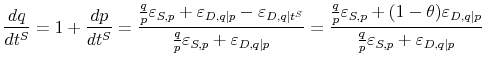
Figure 3 illustrates the incidence of introducing a sales tax ![]() in a market that is initially untaxed. The figure plots supply and demand as a function of the pretax price
in a market that is initially untaxed. The figure plots supply and demand as a function of the pretax price
![]() . The market initially clears at a price
. The market initially clears at a price
![]() . When the tax is levied, the demand curve shifts inward by
. When the tax is levied, the demand curve shifts inward by
![]() units, creating an excess supply of
units, creating an excess supply of
![]() units of the good at the initial price
units of the good at the initial price ![]() .
To re-equilibriate the market, producers cut the pretax price by
.
To re-equilibriate the market, producers cut the pretax price by
![]() units. The only difference in the incidence diagram in Figure 3 relative to the traditional model without salience effects is that the demand
curve shifts inward by
units. The only difference in the incidence diagram in Figure 3 relative to the traditional model without salience effects is that the demand
curve shifts inward by
![]() instead of
instead of
![]() . With salience effects, the shift in the demand curve is determined by the tax elasticity, while the price adjustment needed to clear the market is determined by
the price elasticity. This is why one must estimate both the tax and price elasticities to calculate incidence.
. With salience effects, the shift in the demand curve is determined by the tax elasticity, while the price adjustment needed to clear the market is determined by
the price elasticity. This is why one must estimate both the tax and price elasticities to calculate incidence.
Three general lessons about tax incidence emerge from the formulas in Proposition 1.
1. [Attenuated Incidence on Producers] Incidence on producers is attenuated by
![]() relative to the traditional model. Intuitively, producers face less pressure to reduce the pretax price when consumers
underreact to the sales tax. In the extreme case where
relative to the traditional model. Intuitively, producers face less pressure to reduce the pretax price when consumers
underreact to the sales tax. In the extreme case where
![]() , consumers bear all of the tax, because there is no need to change the pretax price to clear the market. More generally, the incidence of a tax on consumers is
inversely related to the degree of attention to the tax (
, consumers bear all of the tax, because there is no need to change the pretax price to clear the market. More generally, the incidence of a tax on consumers is
inversely related to the degree of attention to the tax (![]() ).
).
One interpretation of this result is that the demand curve becomes more inelastic when individuals are inattentive. Though changes in inattention and the price elasticity both affect the gross-of-tax-elasticity
![]() in the same way, their effects on incidence are not equivalent. To see this, consider two markets,
in the same way, their effects on incidence are not equivalent. To see this, consider two markets, ![]() and
and ![]() , where
, where
![]() . In market
. In market ![]() , demand is inelastic
and consumers are fully attentive to taxes:
, demand is inelastic
and consumers are fully attentive to taxes:
![]() and
and
![]() . In market
. In market ![]() , demand is elastic but consumers are inattentive:
, demand is elastic but consumers are inattentive:
![]() and
and
![]() . An econometrician would estimate the same tax elasticity in both markets:
. An econometrician would estimate the same tax elasticity in both markets:
![]() . However,
. However,
![]() whereas
whereas
![]() . In market
. In market ![]() , suppliers bear most of the incidence
since demand is 3 times more elastic to price than supply. In market
, suppliers bear most of the incidence
since demand is 3 times more elastic to price than supply. In market ![]() , even
though demand is 10 times as price elastic as supply, producers are able to shift most of the incidence of the tax to consumers because of inattention.
, even
though demand is 10 times as price elastic as supply, producers are able to shift most of the incidence of the tax to consumers because of inattention.
Intuitively, a low price elasticity of demand has two effects on incidence: it reduces the shift in the demand curve but increases the size of the price cut needed to re-equilibriate the market for a given level of excess supply. Inattention to the tax also reduces the shift in the demand curve,
but does not have the second offsetting effect. This difference is apparent in the formula for
![]() in (8), where
in (8), where
![]() appears in both the numerator and denominator whereas
appears in both the numerator and denominator whereas ![]() appears only in the numerator. As a result, a 1 percent reduction in attention leads to greater incidence on consumers than a 1 percent reduction in the price elasticity. As
appears only in the numerator. As a result, a 1 percent reduction in attention leads to greater incidence on consumers than a 1 percent reduction in the price elasticity. As
![]() approaches 0,
approaches 0,
![]() approaches
approaches ![]() irrespective of
irrespective of
![]() . If consumers are sufficiently inattentive, they bear most of the incidence of a tax even if supply is inelastic.
. If consumers are sufficiently inattentive, they bear most of the incidence of a tax even if supply is inelastic.
2. [No Tax Neutrality] Taxes that are included in posted prices - such as the alcohol excise tax - have greater incidence on producers because they are fully salient (![]() ).
).
![]() Taxes levied on producers are more likely to be included in posted prices than taxes levied on consumers because producers must actively "shroud" a tax levied on them in order to reduce
its salience. Together, these observations imply that producers will generally bear more of the incidence when a tax is levied on them than when it is levied on the consumers. Statutory incidence affects economic incidence, contrary to intuition based on the full-optimization model.29
Taxes levied on producers are more likely to be included in posted prices than taxes levied on consumers because producers must actively "shroud" a tax levied on them in order to reduce
its salience. Together, these observations imply that producers will generally bear more of the incidence when a tax is levied on them than when it is levied on the consumers. Statutory incidence affects economic incidence, contrary to intuition based on the full-optimization model.29
3. [Effect of Price Elasticity] Holding fixed the size of the tax elasticity
![]() , an increase in the price elasticity of demand raises incidence on consumers (
, an increase in the price elasticity of demand raises incidence on consumers (
![]() ). This is because holding fixed the shift in the demand curve created by the introduction of the tax, a smaller
price reduction is needed to clear the market if demand is very price elastic. In contrast, if the degree of inattention
). This is because holding fixed the shift in the demand curve created by the introduction of the tax, a smaller
price reduction is needed to clear the market if demand is very price elastic. In contrast, if the degree of inattention ![]() is held fixed as
is held fixed as
![]() varies, we obtain the conventional result
varies, we obtain the conventional result
![]() because
because
![]() and
and
![]() vary at the same rate. Thus, taxing markets with more elastic demand could lead to greater or lesser incidence on consumers, depending on the extent to which the tax
elasticity
vary at the same rate. Thus, taxing markets with more elastic demand could lead to greater or lesser incidence on consumers, depending on the extent to which the tax
elasticity
![]() covaries with the price elasticity
covaries with the price elasticity
![]() .
.
V.C Efficiency Cost
In the interest of space, we formally characterize the excess burden of introducing a sales tax in a market where there are no pre existing taxes and production is constant-returns-to-scale (
![]() ). In this case, the pretax price of
). In this case, the pretax price of ![]() is fixed at
is fixed at
![]() . Moreover, since firms earn zero profits, only consumer welfare matters for excess burden. We briefly discuss the effects of endogenous producer prices and pre existing taxes
at the end of this section.
. Moreover, since firms earn zero profits, only consumer welfare matters for excess burden. We briefly discuss the effects of endogenous producer prices and pre existing taxes
at the end of this section.
V.C.1 Definitions
Let
![]() denote the agent's indirect utility as a function of the posted price of good
denote the agent's indirect utility as a function of the posted price of good ![]() , the sales tax, and wealth. Let
, the sales tax, and wealth. Let
![]() denote the agent's expenditure function, which represents the minimum wealth necessary to attain utility
denote the agent's expenditure function, which represents the minimum wealth necessary to attain utility ![]() at a given posted price and sales tax. Let
at a given posted price and sales tax. Let
![]() denote tax revenue.
denote tax revenue.
Following Herbert Mohring (1971) and Alan J. Auerbach (1985), we measure the excess burden (deadweight cost) of a tax using the concept of equivalent variation. When ![]() is fixed, the excess
burden of introducing a sales tax
is fixed, the excess
burden of introducing a sales tax ![]() in a previously untaxed market is
in a previously untaxed market is
The value
V.C.2 Preference Recovery
The efficiency cost of a tax policy depends on two elements: (1) the change in behavior induced by the tax and (2) the effect of that change in behavior on the consumer's utility. The first element is observed empirically. The second element is the key challenge for behavioral welfare economics.
How do we compute indirect utility
![]() when the agent's behavior is not consistent with optimization? The following two assumptions allow us to recover
when the agent's behavior is not consistent with optimization? The following two assumptions allow us to recover ![]() without specifying a positive model for the demand function
without specifying a positive model for the demand function
![]() .
.
A1 Taxes affect utility only through their effects on the chosen consumption bundle. The agent's indirect utility given a tax of ![]() is
is
A2 When tax inclusive prices are fully salient, the agent chooses the same allocation as a fully-optimizing agent:
Assumption A1 requires that consumption is a sufficient statistic for utility - that is, holding fixed the consumption bundle ![]() , the tax rate or its salience has no effect on
, the tax rate or its salience has no effect on
![]() To understand the content of this assumption, consider the following situation in which it is violated. In a bounded rationality model, the cognitive cost that the agent pays to calculate
the total price when
To understand the content of this assumption, consider the following situation in which it is violated. In a bounded rationality model, the cognitive cost that the agent pays to calculate
the total price when ![]() makes his utility lower than pure consumption utility. Taxes that are not included in posted prices therefore generate deadweight burden beyond that due to
the distortion in the consumption bundle (Chetty, Looney, and Kroft 2007). In such models, the excess burden computations in this paper correspond to the deadweight cost net of any increase in cognitive costs.30
makes his utility lower than pure consumption utility. Taxes that are not included in posted prices therefore generate deadweight burden beyond that due to
the distortion in the consumption bundle (Chetty, Looney, and Kroft 2007). In such models, the excess burden computations in this paper correspond to the deadweight cost net of any increase in cognitive costs.30
Assumption A2 requires that the agent behaves like a fully-optimizing agent when all taxes are fully salient. That is, the agent's choices when total prices are fully salient reveal his true rankings. This assumption is violated when the agent's choices are suboptimal even without taxes. For
example, if there are other "shrouded attributes" or if agents suffer from biases when optimizing relative to prices (Nina Mazar, Botond Koszegi, and Dan Ariely 2008), we would not directly recover true preferences from ![]() . The excess burden formulas derived below ignore errors in optimization relative to prices.
. The excess burden formulas derived below ignore errors in optimization relative to prices.
Using assumptions A1 and A2, we calculate consumer welfare and excess burden in two steps. We first use the demand function without taxes ![]() to recover the agent's underlying
preferences (
to recover the agent's underlying
preferences (![]() ) as in the full-optimization model. We then use the demand function with taxes
) as in the full-optimization model. We then use the demand function with taxes
![]() to calculate the agent's indirect utility
to calculate the agent's indirect utility
![]() as a function of the tax rate. Conceptually, this method pairs the libertarian criterion of calculating welfare from individual choice with the assumption that the agent
optimizes relative to true incentives only when tax inclusive prices are perfectly salient.
as a function of the tax rate. Conceptually, this method pairs the libertarian criterion of calculating welfare from individual choice with the assumption that the agent
optimizes relative to true incentives only when tax inclusive prices are perfectly salient.
Our calculation of excess burden can be viewed as an application of Bernheim and Rangel's (2008) choice-based approach to welfare analysis. Bernheim and Rangel show that one can obtain bounds on welfare without specifying a positive theory of behavior by separating the inputs that matter for
utility from "ancillary conditions" that do not. By applying a "refinement" to identify ancillary conditions under which an agent's choices reveal his true rankings, one can sharpen the bounds. In Bernheim and Rangel's terminology, our assumption A1 is that tax salience is an "ancillary
condition" that affects choices but not true utility. Assumption A2 is a "refinement" which posits that the choices made when the tax is not perfectly salient are "suspect," and should be discarded when inferring the utility relevant for welfare analysis. This refinement allows us to obtain
exact measures of equivalent variation and efficiency costs without placing specific structure on the model that generates
![]() .
.
V.C.3 Formula for Excess Burden
We derive a formula for excess burden using quadratic approximations analogous to those used by Harberger (1964) and Edgar K. Browning (1987). To state the formula compactly, we introduce notation for income-compensated elasticities. Let
![]()
![]() denote the income-compensated (Hicksian) price effect. Define
denote the income-compensated (Hicksian) price effect. Define
![]() as the analogous income-compensated tax effect. Note that this "compensated tax effect" does not necessarily
satisfy the Slutsky condition
as the analogous income-compensated tax effect. Note that this "compensated tax effect" does not necessarily
satisfy the Slutsky condition
![]() . It is possible to have an upward-sloping compensated tax-demand curve because
. It is possible to have an upward-sloping compensated tax-demand curve because
![]() is not generated by utility maximization. In contrast, assumption A2 guarantees
is not generated by utility maximization. In contrast, assumption A2 guarantees
![]() through the Slutsky condition. Let
through the Slutsky condition. Let
![]() and
and
![]() denote the compensated price and tax elasticities.
denote the compensated price and tax elasticities.
where
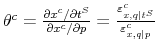 is the ratio of the compensated tax and
price effects.
is the ratio of the compensated tax and
price effects.Proof. See Appendix B. Chetty (2008) gives an instructive proof for the quasilinear case.
Figure 4 illustrates the calculation of deadweight loss for the quasilinear case. The initial price of the good is ![]() and the price after the imposition of the sales tax is
and the price after the imposition of the sales tax is
![]() . The figure plots two demand curves. The first is the standard Marshallian demand curve as a function of the total price of the good,
. The figure plots two demand curves. The first is the standard Marshallian demand curve as a function of the total price of the good, ![]() . This price-demand curve coincides with the marginal utility
. This price-demand curve coincides with the marginal utility
![]() under assumption A2. The second,
under assumption A2. The second,
![]() represents how demand varies with the tax on
represents how demand varies with the tax on ![]() . This tax-demand curve is drawn assuming
. This tax-demand curve is drawn assuming
![]() , consistent with the empirical evidence.
, consistent with the empirical evidence.
The agent's initial consumption choice prior to the introduction of the tax is depicted by
![]() . Initial consumer surplus is given by triangle
. Initial consumer surplus is given by triangle ![]() , which
equals total utility (up to a constant). When the tax
, which
equals total utility (up to a constant). When the tax ![]() is introduced, the agent cuts consumption of
is introduced, the agent cuts consumption of ![]() by
by
![]() . Notice that at the new consumption choice
. Notice that at the new consumption choice ![]() , the agent's marginal willingness-to-pay for
, the agent's marginal willingness-to-pay for ![]() is below the total price
is below the total price
![]() because he underreacts to the tax. This optimization error leads to a loss of surplus corresponding to triangle
because he underreacts to the tax. This optimization error leads to a loss of surplus corresponding to triangle ![]() . The consumer's surplus after the implementation of the tax is therefore given by triangle
. The consumer's surplus after the implementation of the tax is therefore given by triangle ![]() minus triangle
minus triangle ![]() . The revenue raised from the tax corresponds to the rectangle
. The revenue raised from the tax corresponds to the rectangle ![]() It follows that the
change in total surplus - government revenue plus consumer surplus - equals the shaded triangle
It follows that the
change in total surplus - government revenue plus consumer surplus - equals the shaded triangle ![]() , whose area is given by (10) when utility is quasilinear.31
, whose area is given by (10) when utility is quasilinear.31
When utility is not quasilinear (
![]() ), the form of the formula remains exactly the same, but all the inputs are replaced by income-compensated effects, exactly as in the Harberger formula. The
intuition for this difference is analogous to that in the full-optimization model: behavioral responses due to pure income effects are nondistortionary, since they would occur under lump sum taxation as well. Deadweight loss is determined by difference between the actual behavioral response (
), the form of the formula remains exactly the same, but all the inputs are replaced by income-compensated effects, exactly as in the Harberger formula. The
intuition for this difference is analogous to that in the full-optimization model: behavioral responses due to pure income effects are nondistortionary, since they would occur under lump sum taxation as well. Deadweight loss is determined by difference between the actual behavioral response (
![]() ) and the socially optimal response given the reduction in net-of-tax income
) and the socially optimal response given the reduction in net-of-tax income
![]() , which is
, which is
![]() .
.
Like the Harberger formula, (10) ignores the third- and higher-order terms in the Taylor expansion for ![]() . Hence, it provides an accurate measure of excess burden
for small tax changes. In addition, note that
. Hence, it provides an accurate measure of excess burden
for small tax changes. In addition, note that
![]() must be evaluated at a point with zero sales tax
must be evaluated at a point with zero sales tax ![]() .
.
![]() The reason is that we recover true preferences only when the posted price equals the total price:
The reason is that we recover true preferences only when the posted price equals the total price:
![]() if and only if
if and only if ![]() . If an environment
without sales tax is not observed, one could implement the formula by assuming that the price elasticity does not depend on the tax rate (
. If an environment
without sales tax is not observed, one could implement the formula by assuming that the price elasticity does not depend on the tax rate (
![]() ) and using an estimate of
) and using an estimate of
![]() .
.
Discussion. The only difference between (10) and the canonical Harberger formula (
![]() ) is the introduction of the parameter
) is the introduction of the parameter
![]() . Three general lessons about excess burden emerge from this new parameter.
. Three general lessons about excess burden emerge from this new parameter.
1. [Inattention Reduces Excess Burden if
![]() ] When utility is quasilinear, the tax
] When utility is quasilinear, the tax ![]() generates deadweight loss equivalent to that created by a perfectly salient tax of
generates deadweight loss equivalent to that created by a perfectly salient tax of
![]() . If agents ignore the tax completely and
. If agents ignore the tax completely and ![]() , then
, then ![]() . Taxation creates no inefficiency when
. Taxation creates no inefficiency when ![]() because the agent's consumption
allocation coincides with the first-best bundle that he would have chosen under lump sum taxation.32 As the degree of attention to the tax rises, excess
burden rises at a quadratic rate:
because the agent's consumption
allocation coincides with the first-best bundle that he would have chosen under lump sum taxation.32 As the degree of attention to the tax rises, excess
burden rises at a quadratic rate:
![]() . Excess burden rises with the square of
. Excess burden rises with the square of ![]() for the same
reason that it rises with the square of the
for the same
reason that it rises with the square of the ![]() - the increasing marginal social cost of deviating from the first-best. Because
- the increasing marginal social cost of deviating from the first-best. Because ![]() is a quadratic function of
is a quadratic function of ![]() but a linear function of
but a linear function of
![]() , inattention (reductions in
, inattention (reductions in ![]() ) and inelasticity
(reductions in
) and inelasticity
(reductions in
![]() ) have different effects on excess burden, as in the incidence analysis. Like incidence, excess burden depends on which side of the market is taxed. Since a tax on
producers is likely to be included in posted prices, it leads to a larger reduction in demand and more deadweight loss than an equivalent tax levied on consumers when utility is quasilinear.
) have different effects on excess burden, as in the incidence analysis. Like incidence, excess burden depends on which side of the market is taxed. Since a tax on
producers is likely to be included in posted prices, it leads to a larger reduction in demand and more deadweight loss than an equivalent tax levied on consumers when utility is quasilinear.
2. [Inattention Can Raise Excess Burden if
![]() ] Unlike in the quasilinear case, making a tax less salient to reduce
] Unlike in the quasilinear case, making a tax less salient to reduce
![]() can increase deadweight loss when there are income effects. In fact, a tax can create deadweight cost even if the agent
completely ignores it and demand for the taxed good does not change, i.e.
can increase deadweight loss when there are income effects. In fact, a tax can create deadweight cost even if the agent
completely ignores it and demand for the taxed good does not change, i.e.
![]() . This result contradicts the canonical intuition that taxes generate deadweight costs only if they induce changes in demand. In the full-optimization
model, taxation of a normal good creates a deadweight cost only if
. This result contradicts the canonical intuition that taxes generate deadweight costs only if they induce changes in demand. In the full-optimization
model, taxation of a normal good creates a deadweight cost only if
![]() since
since
![]() given
given
![]() . This reasoning fails when the tax-demand is not the outcome of perfect optimization, because there is no Slutsky condition for
. This reasoning fails when the tax-demand is not the outcome of perfect optimization, because there is no Slutsky condition for
![]() . A zero uncompensated tax elasticity does not imply that the compensated tax elasticity is zero. Instead, when
. A zero uncompensated tax elasticity does not imply that the compensated tax elasticity is zero. Instead, when
![]() ,
,
![]() and (10) becomes
and (10) becomes
As a concrete example, consider an individual who consumes cars (![]() ) and food (
) and food (![]() ).
Suppose he chooses the same car he would have bought at a total price of
).
Suppose he chooses the same car he would have bought at a total price of ![]() because he does not perceive the tax (
because he does not perceive the tax (
![]() ) and therefore has to cut back on food to meet his budget. This inefficient allocation of net-of-tax income leads to a loss in surplus. The lost surplus
is proportional to the income effect on cars
) and therefore has to cut back on food to meet his budget. This inefficient allocation of net-of-tax income leads to a loss in surplus. The lost surplus
is proportional to the income effect on cars
![]() because this elasticity determines how much the agent should have cut spending on the car to reach the social optimum given the tax. This example illustrates
that policies which " hide" taxes can potentially create substantial deadweight loss despite attenuating behavioral responses, particularly when the income elasticity and expenditure on the taxed good are large.
because this elasticity determines how much the agent should have cut spending on the car to reach the social optimum given the tax. This example illustrates
that policies which " hide" taxes can potentially create substantial deadweight loss despite attenuating behavioral responses, particularly when the income elasticity and expenditure on the taxed good are large.
Note that inattention to a tax on ![]() need not necessarily lead to
need not necessarily lead to
![]() . The effect of inattention on
. The effect of inattention on
![]() depends on how the agent meets his budget given the tax. The agent must reduce consumption of at least one of the goods to meet his budget when the tax on
depends on how the agent meets his budget given the tax. The agent must reduce consumption of at least one of the goods to meet his budget when the tax on
![]() is introduced:
is introduced:
![]() . The way in which agents meet their budget may vary across individuals (Chetty, Looney, and Kroft 2007). For example,
credit-constrained agents may be forced to cut back on consumption of
. The way in which agents meet their budget may vary across individuals (Chetty, Looney, and Kroft 2007). For example,
credit-constrained agents may be forced to cut back on consumption of ![]() if they ignore the tax when buying
if they ignore the tax when buying ![]() , as in the car purchase example above, leading to
, as in the car purchase example above, leading to
![]() and
and ![]() . Agents who smooth
intertemporally, in contrast, may cut both
. Agents who smooth
intertemporally, in contrast, may cut both ![]() as well as future purchases of
as well as future purchases of ![]() (buying
a cheaper car next time). Such intertemporal smoothing could lead to a long-run allocation closer to the socially optimal response
(buying
a cheaper car next time). Such intertemporal smoothing could lead to a long-run allocation closer to the socially optimal response
![]() , in which case hidden taxes would lead to
, in which case hidden taxes would lead to
![]() and
and ![]() . Importantly, Proposition 2 holds irrespective of how the
agent meets his budget. Variations in the budget adjustment process are captured in the value of
. Importantly, Proposition 2 holds irrespective of how the
agent meets his budget. Variations in the budget adjustment process are captured in the value of
![]() .
.
3. [Role of Price Elasticity] Holding fixed
![]() , excess burden is inversely related to
, excess burden is inversely related to
![]() . As demand becomes less price-elastic,
. As demand becomes less price-elastic, ![]() increases. This can be seen in Figure 4, where the shaded triangle becomes larger as
increases. This can be seen in Figure 4, where the shaded triangle becomes larger as ![]() becomes steeper, holding
becomes steeper, holding
![]() fixed. Intuitively, an agent with price-inelastic consumption has rapidly increasing marginal utility as his consumption level deviates from the first-best level. A given
reduction in demand thus leads to a larger loss of surplus for an agent with more price-inelastic demand. As in the incidence analysis, taxing markets with more elastic demand could lead to greater or lesser excess burden, depending on the covariance between
fixed. Intuitively, an agent with price-inelastic consumption has rapidly increasing marginal utility as his consumption level deviates from the first-best level. A given
reduction in demand thus leads to a larger loss of surplus for an agent with more price-inelastic demand. As in the incidence analysis, taxing markets with more elastic demand could lead to greater or lesser excess burden, depending on the covariance between
![]() and
and
![]() .
.
It is straightforward to extend the preceding results to allow for pre-existing taxes and endogenous producer prices; see Chetty (2008) for a complete analysis and discussion of these cases. When ![]() is fixed and the initial sales tax rate is
is fixed and the initial sales tax rate is ![]() , the excess burden of a sales tax increase
, the excess burden of a sales tax increase ![]() is approximately
is approximately
where
VI Conclusion
This paper has shown empirically that commodity taxes that are included in posted prices reduce demand significantly more than taxes that are not included in posted prices. Individuals appear to be well informed about commodity taxes when their attention is drawn to the topic, suggesting that salience is an important determinant of behavioral responses to taxation. The finding that individuals make systematic optimization errors even with respect to relatively simple, linear commodity taxes suggests that more complex policies such as income taxes or transfers could generate very different behavioral responses from those predicted by standard models.33 Moreover, the standard method of using variation in tax rates as instruments to estimate wage and price elasticities cannot be applied unless the tax is perfectly salient.
Our empirical results contradict the basic assumptions of the canonical theory of taxation used for policy analysis. As an alternative, we have proposed a method of welfare analysis that does not rely on a specific positive model of how agents make choices when faced with taxes. This approach
accommodates salience effects as well as other optimization errors with respect to taxes. The formulas we obtain for the incidence and excess burden of commodity taxes are simple variants of those in introductory textbooks and can be easily adapted to analyze other tax policies, such as income or
capital taxation. Much as Harberger (1964) identified the compensated price elasticity as the key parameter to be estimated in subsequent work, our analysis identifies the compensated tax and price elasticities (
![]() and
and
![]() ) as "sufficient statistics" for empirical studies in behavioral public economics.
) as "sufficient statistics" for empirical studies in behavioral public economics.
A natural next step would be to characterize optimal taxation when agents optimize imperfectly, generalizing the results of Ramsey (1927) and Mirrlees (1971). For this purpose, it will be important to extend the welfare analysis to a general equilibrium model with more than two markets. Combining the formulas developed here with a positive theory of tax salience could be useful in characterizing the optimal structure of the tax system. For example, Chetty, Looney, and Kroft's (2007) bounded-rationality model predicts that attention and behavioral responses to taxation are larger when (1) tax rates are high, (2) the price-elasticity of demand is large, and (3) the amount spent on the good is large. Combined with the welfare analysis here, these predictions suggest that in markets with these three characteristics, tax incidence should fall more heavily on producers and excess burden should be closer to the Harberger measure.
Finally, the approach to welfare analysis proposed here - using a domain where incentives are fully salient to characterize the welfare consequences of policies that are not salient - can be applied in other contexts. Many social insurance and transfer programs (e.g. Medicare and Social Security) have complex features and may induce suboptimal behaviors. One can characterize the welfare consequences of these programs more accurately by estimating behavioral responses to analogous programs whose incentives are more salient. Another potential application is to optimal regulation (e.g. consumer protection laws, financial market regulations). By identifying "suboptimal" transactions using data on consumer's choices in domains where incentives are more salient, one could develop rules to maximize consumer welfare that do not rely on paternalistic judgements.
Bibliography
Grocery Experiment. The store changes product prices on Wednesday nights and leaves the prices fixed (with rare exceptions) for the following week, termed a "promotional week." To synchronize our intervention with this pricing cycle, a team of researchers and research assistants printed tags every Wednesday night and attached them to each of the 750 products. The tags were changed between 11 pm and 2 am, which are low-traffic times at the store. The tags were printed using a template and card stock supplied by the store (often used for sales or other additional information on a product) in order to match the color scheme and layout familiar to customers. The two control stores were chosen by a minimum-distance criterion based on the characteristics listed in Appendix Table 1.
The raw scanner data provided by the grocery chain contains information on weekly revenue and quantity sold for each product (UPC id) that was sold among the 108 categories listed in Appendix Table 2 in the three stores from 2005 week 1 to 2006 week 15. The original dataset contains 331,508 product-week-store observations. The quantity and revenue variables are measured net of returns (i.e., returns count as negative sales). We exclude 1,756 observations where the weekly quantity or revenue was zero or negative, which are cases where as many or more items were returned than purchased in that week. Including these observations does not affect the results. Finally, we aggregate to the category-week-store level by summing quantity and revenue across products, setting the sum to zero if no products were sold in a given category-week-store.
The average price for each category of goods is defined as
![]() where
where ![]() indexes the category,
indexes the category, ![]() time, and
time, and ![]() products,
products, ![]() is the price of good
is the price of good ![]() at time
at time ![]() , and
, and
![]() is the average quantity sold of good
is the average quantity sold of good ![]() . This "category price" is
effectively a price index for a fixed basket of products where each product's weight in the basket is determined by its average weekly sales over the period before and during the experiment. Since the scanner data reports only items that have sold each week, we impute prices for unsold items when
constructing
. This "category price" is
effectively a price index for a fixed basket of products where each product's weight in the basket is determined by its average weekly sales over the period before and during the experiment. Since the scanner data reports only items that have sold each week, we impute prices for unsold items when
constructing ![]() . In particular, we use the price in the last observed transaction for unsold products; if no previous price is available, we use the next available price. Alternative
imputation methods - such as using the closest observed price, or an average of previous and subsequent prices - give similar results. Varying the imputation technique has little impact on the estimates in Tables 4 and 5 because items requiring imputation have low sales volume, and therefore
receive little weight in the category-level price variable.
. In particular, we use the price in the last observed transaction for unsold products; if no previous price is available, we use the next available price. Alternative
imputation methods - such as using the closest observed price, or an average of previous and subsequent prices - give similar results. Varying the imputation technique has little impact on the estimates in Tables 4 and 5 because items requiring imputation have low sales volume, and therefore
receive little weight in the category-level price variable.
Grocery Store Survey. We surveyed 91 customers entering the treatment store in August 2006 about their knowledge of sales taxes. Survey respondents were offered candy bars and sodas to spend a few minutes filling out the survey displayed in Appendix Exhibit 2. After collecting basic demographic information, the survey asked individuals to report whether each of eight goods were subject to sales tax or not. Many individuals remarked while filling out the survey that they did not think about taxes while shopping, and therefore were hesitant to report which goods were taxed. These individuals were asked to mark their best guess to avoid nonresponse bias. To assess whether knowledge of taxes is correlated with experience, we also asked whether individuals had purchased each of these goods recently. Finally, we asked questions about tax rates and bases - the sales tax rate in the city where the store is located, the state income tax rate, and the tax base for the federal estate tax.
Alcohol Analysis. Data on aggregate annual beer, wine, spirits, and ethanol consumption by state are available from the NIAAA (2006) from 1970-2003. These data contain information on total gallons of beer sold by wholesalers because this measure determines tax liabilities. See Thomas M. Nephew et al. (2004) and Nekisha E. Lakins et al. (2004) for details on data construction.
State excise tax rates on beer are primarily obtained from the Brewer's Almanac (various years), published annually by the Beer Institute. These rates were verified and corrected using the Tax Foundation's State Tax Collections and Rates (various years) and the State Tax Handbook. Our measure of the excise rate includes taxes that are statutorily `local' excise taxes - which are sometime excluded from state statistics available in the Brewer's Almanac - that are applied state-wide. Specifically, in Alabama, Georgia, and Louisiana all counties or localities levy an excise tax in addition to the state excise tax.
Excise taxes on alcohol frequently differ by product, packaging, and whether sold for on- or off-premise consumption. In states where rates differ, our measure corresponds to the excise tax on packaged 12oz. beer, sold for off-premise consumption, with an alcohol content of 3.2 percent or more. Excise rates on other beer products are highly correlated with this measure across states, and the timing of tax changes for different categories of alcoholic beverages within a state are virtually identical. Per-gallon taxes are converted to per-case rates by multiplying by 2.25, the number of gallons in 24 12oz. cans or bottles. The excise tax rate is converted into an ad valorem rate by dividing the real CPI-adjusted beer excise tax per case in year 2000 dollars by the average cost of a case of beer in the United States in 2000, as measured by the Beer Institute. Since Alaska has a higher price level than the continental United States, we follow Census Bureau practice and adjust its price level up by 25 percent when calculating the percentage excise tax rate. None of our results are affected by this adjustment, or by excluding Alaska entirely. For a subset of years (1982-2000) and states, we have actual beer price data from the ACCRA cost of living index survey, which samples the price of a six pack of beer (Budweiser, Schlitz, or Miller Lite) in large cities. We define the ACCRA price variable as the annual average of all prices in each state.
State sales taxes are obtained primarily from the World Tax Database (2006) at the University of Michigan. These data were verified and corrected using state Department of Revenue websites and the State Tax Handbook. Four states (KS, VT, DC, MN) apply a higher sales tax rate to alcohol than other products. In those states we include the alcohol rate rather than the general sales rate when they differ. We supplement the data on state-level sales taxes with data on average local sales tax rates, which are imputed from data on local revenues from the Census Bureau's Survey of State and Local Government Finances and a tax base defined as state revenues divided by the state rate.
Since our estimation strategy relies on the timing and magnitude of the tax changes, we evaluate the precision of the data by regressing the change in the log of state tax revenues on the change in the log of the sales tax rate, controlling for state income. In the full sample, the coefficient estimate on the sales tax rate is 0.76 (s.e. 0.03). A state-by-state analysis of changes in rates and changes in revenues also yields similarly high correlations, with the exception of West Virginia. In WV, the correlation between sales tax rates and revenues is near zero and statistically insignificant, perhaps because the tax base is often changed at the same time as the rate. Since this problem could artificially attenuate the sales tax elasticity, we exclude West Virginia from our analysis.
Appendix B: Proof of Proposition 2
We derive an expression for ![]() using Taylor expansions that ignore third and higher-order terms, i.e. terms proportional to
using Taylor expansions that ignore third and higher-order terms, i.e. terms proportional to
![]() for
for ![]() . Let
. Let
![]() denote the utility attained by a fully optimizing agent who consumes the optimal bundle
denote the utility attained by a fully optimizing agent who consumes the optimal bundle
![]() . Let
. Let
![]() denote tax revenue obtained from a fully optimizing agent.
denote tax revenue obtained from a fully optimizing agent.
The agent's loss from failing to optimize relative to the tax is
We will use Taylor expansions to obtain simple expressions for each of these three terms below.
i) Auerbach (1985) shows that ignoring third-order terms, excess burden for an optimizing agent is
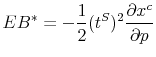
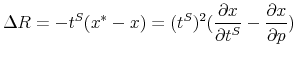
iii) Simplifying the expression for ![]() requires more work. First recall that the expenditure function is
requires more work. First recall that the expenditure function is
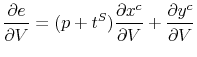 .
.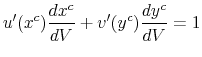
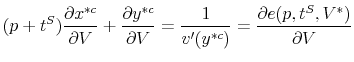
![\displaystyle G=\frac{\partial e(p,t^{S},V^{\ast})}{\partial V}[V^{\ast}(p,t^{S}% ,Z)-V(p,t^{S},Z)]-\frac{1}{2}\frac{\partial^{2}e(p,t^{S},V^{\ast})}{\partial V^{2}}[V^{\ast}-V]^{2}+...](img287.gif)
![\displaystyle G=\frac{[V^{\ast}(p,t^{S},Z)-V(p,t^{S},Z)]}{v^{\prime}(y^{\ast c}% (p,t^{S},V^{\ast}))}%](img291.gif)
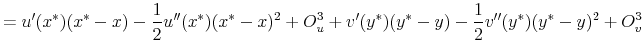 |
where
Using the first-order-condition that characterizes the choice of the fully-optimizing agent,
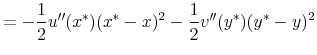 |
||
![\displaystyle =-\frac{1}{2}(x^{\ast}-x)^{2}[u^{\prime\prime}(x^{\ast})+v^{\prime\prime }(y^{\ast})(p+t^{S})^{2}]](img305.gif) |
(13) |
Totally differentiating the fully-optimizing agent's first-order-condition with respect to
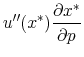 |
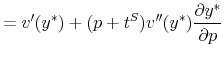 |
|
![\displaystyle =v^{\prime}(y^{\ast})+(p+t^{S})[-(p+t^{S})\frac{\partial x^{\ast}}{\partial p}-x^{\ast}]v^{\prime\prime}(y^{\ast})](img308.gif) . . |
It follows that
![\displaystyle \lbrack u^{\prime\prime}(x^{\ast})+(p+t^{S})^{2}v^{\prime\prime}(y^{\ast })]\frac{\partial x^{\ast}}{\partial p}=v^{\prime}(y^{\ast})-(p+t^{S})x^{\ast }v^{\prime\prime}(y^{\ast})](img309.gif)
![\displaystyle \widetilde{G}=-\frac{1}{2}(x^{\ast}-x)^{2}\frac{[v^{\prime}(y^{\ast}% )-(p+t^{S})x^{\ast}v^{\prime\prime}(y^{\ast})]}{\partial x^{\ast}/\partial p}\text{.}%](img310.gif) |
(14) |
Defining
Finally, we use a result from Chetty (2006) which relates the coefficient of relative risk aversion
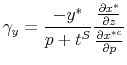 . . |
(16) |
Inserting this expression into (15) yields
![\displaystyle \simeq-\frac{1}{2}(x^{\ast}-x)^{2}\frac{1}{\partial x^{\ast}/\partial p}[1-x^{\ast}\frac{\frac{\partial x^{\ast}}{\partial z}}{\frac{\partial x^{\ast c}}{\partial p}}]](img316.gif) |
||
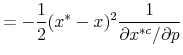 |
||
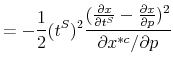 |
Combining the expressions for ![]() ,
, ![]() , and
, and ![]() above using (12) and collecting terms yields
above using (12) and collecting terms yields
![\displaystyle EB(t^{S})=(t^{S})^{2}\frac{1}{\frac{\partial x^{c}}{\partial p}}% \{\frac{\partial x}{\partial t^{S}}[\frac{\partial x}{\partial p}-\frac{1}% {2}\frac{\partial x}{\partial t^{S}}-\frac{\partial x^{c}}{\partial p}% ]-\frac{1}{2}[\frac{\partial x}{\partial p}-\frac{\partial x^{c}}{\partial p}]^{2}\}](img319.gif)
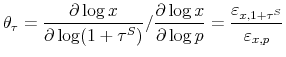
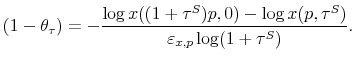
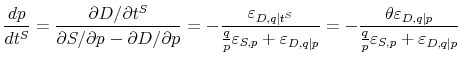
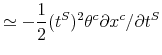
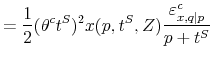
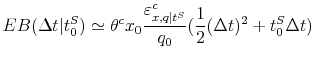
![\displaystyle G\simeq\frac{\widetilde{G}}{v^{\prime}(y^{\ast})}=-\frac{1}{2}(x^{\ast}% -x)^{2}\frac{1}{\partial x^{\ast}/\partial p}[1+(p+t^{S})\frac{x^{\ast}% }{y^{\ast}}\gamma_{y}]\text{.}%](img312.gif)