Skip to: [Printable Version (PDF)] [Bibliography] [Footnotes]

Finance and Economics Discussion Series: 2009-14 Screen Reader version ^♣

Household Welfare, Precautionary Saving, and Social Insurance under Multiple Sources of Risk*

Ivan Viggdangos*

Federal Reserve Board

Keywords: Income risk, consumption, lifecycle models, precautionary savings, social insurance

Abstract:

This paper assesses the quantitative importance of a number of sources of income risk for household welfare and precautionary saving. To that end I construct a lifecycle consumption model in which household income is subject to shocks associated with disability, health, unemployment, job changes, wages, work hours, and a residual component of household income. I use PSID data to estimate the key processes that drive and affect household income, and then use the consumption model to: (i) quantify the welfare value to consumers of providing full, actuarially fair insurance against each source of risk and (ii) measure the contribution of each type of shock to the accumulation of precautionary savings. I find that the value of fully insuring disability, health, and unemployment shocks is extremely small (well below 1/10 of 1% of lifetime consumption in the baseline model). The gains from insuring shocks to the wage and to the residual component of household income are significantly larger (above 1% and 2% of lifetime consumption, respectively). These two shocks account for more than 60% of precautionary wealth.

1 Introduction

A great deal of attention has been devoted to modeling dynamics and measuring risk in individual and household income. On one front, there is a substantial empirical literature in labor economics which has studied the dynamic properties of labor income.¹ On a different front, a large number of studies in macroeconomics and public finance, which require the specification of an income process and measures of income uncertainty, have used a variety of strategies to quantify income risk.²

In spite of these large bodies of work, surprisingly little is known about the specific sources underlying income risk and their importance for households' economic well-being. Almost all existing studies model income risk by means of one or two statistical innovations in a univariate time-series income process. Such innovations are difficult to interpret since they capture variation in income that may be due to a number of rather different factors including unemployment, illness, job changes, unexpected changes in wages and hours of work, etc. It is impossible to tell from such formulations which of the many possible sources drive the unexplained variation in income, or what the relative importance of the different sources is. Yet, identifying the sources of variation and risk is essential for addressing questions about insurance of risk, since most insurance programs-whether public or private-typically address specific risks, as in the case of unemployment insurance and disability insurance.

Identifying the various sources of risk and quantifying their effects on household welfare necessitates extending the usual treatment and modeling of income. First, we need to explicitly account for the fact that households face a large number of risks which are likely to differ in key aspects such as their predictability, insurability, relative importance over the lifecycle, etc. Second, one needs to recognize that households can affect their income by adjusting their behavior along a number of margins, including their labor supply, saving, job-search effort, and timing of retirement. Unfortunately, introducing both multiple risks and multiple choice variables into a decision model as the one considered here makes the computational cost of solving the model too burdensome. This paper thus follows most previous studies in treating income as exogenous, and advances the existing literature by considering a significantly richer specification of income risk.

More specifically, I propose a lifecycle consumption model in which households optimally choose consumption and saving, and where household income is subject to shocks associated with disability, health, unemployment, job changes, wages, hours, and a residual component of household income.³ The specification allows for complex dynamic relationships which are difficult to capture in a simple reduced-form approach. An unemployment shock, for instance, affects household income via several channels: it has a direct negative effect on current earnings operating through work hours; it also has a positive effect on household income which reflects both the labor supply response of other household members as well as unemployment insurance benefits; it affects the new wage of the worker upon finding a new job after the spell of unemployment; and finally, it affects social security benefits during retirement through the effect on lifetime average earnings.

I use PSID data to estimate the processes which govern the joint evolution of variables that drive and affect income. Estimation is complicated by the presence of both discrete and continuous variables, state dependence in several equations, and the need to control for unobserved heterogeneity in all equations. I address these issues by using a variety of estimation techniques including generalized indirect inference.⁴ The parameterized model is then used to quantify the welfare value to consumers (in terms of the equivalent variation in lifetime consumption) of providing full, actuarially fair insurance against each of the sources of uninsured income risk, and to measure the contribution of each source of uncertainty to the accumulation of precautionary savings.⁵

Very few previous studies have analyzed the welfare effects of multiple sources of risk in a unified framework. One exception is Low, Meghir, and Pistaferri (2006), who consider a consumption model with endogenous participation and job-mobility decisions, and two sources of uncertainty: unemployment and wage risk. They find that wage risk has important welfare effects but that unemployment risk does not.

One related line of research has examined a variety of mechanisms to insure household consumption, including unemployment insurance (Gruber, 1997; Browning and Crossley, 2001), food stamps (Blundell and Pistaferri, 2003), and Medicaid (Gruber and Yelowitz, 1999).⁶ Some of the empirical studies in this literature have looked at the effects of specific income shocks and of specific forms of insurance (such as unemployment and unemployment insurance) on the levels of consumption. One important difference between this paper and those studies is that this paper captures, and focuses on, the uncertainty in consumption introduced by specific sources of income risk, rather than on the levels of consumption.

My main findings are as follows. The welfare gains from fully insuring disability, health, and unemployment shocks are extremely small (well below 1/10 of 1% of lifetime consumption in the baseline model). The gains from insuring wage shocks and the additional component of household income are significantly larger (above 1% and 2% of lifetime consumption, respectively). These two shocks account for more than 60% of precautionary wealth.

The paper is organized as follows. The next section presents the lifecycle consumption model and discusses its implementation. Section 3 describes the data. Section 4 presents estimation results and an evaluation of the fit of the model. Section 5 discusses the solution of the parameterized lifecycle model. Section 6 presents the welfare and precautionary saving analysis, and section 7 concludes.

2 Model

2.1 Overview

This section introduces a lifecycle model of consumption in which households face multiple income shocks. The decision unit is the household and a period corresponds to one year. Households are part of the labor force for $T_{W}$ years, retire at an exogenously specified date, and live in retirement for up to $T_{R}$ years.⁷ Years in the model are indexed by the variable , where indicates the first period of a worker's career. During working years, thus represents potential experience, although sometimes will also be referred to as age, especially when refering to the retirement years. After retirement, households face mortality risk.

The choice problem facing the household is standard: every period, households choose consumption and saving with the objective of maximizing expected discounted utility over their remaining periods of life: $\mathit{E}_{t}% [\sum_{s=t}^{T}\beta^{s-t}\pi_{s}u(c_{s})]$ , where $\mathit{E}_{t}[\cdot]$ is the expectations operator conditional on information available in period , $\beta\leq1$ is the discount factor, $\pi_{t}$ are conditional survival probabilities⁸, is the per-period utility function satisfying $u^{\prime}>0$ , $u^{\prime\prime}\leq0$ , and $\lim_{c\rightarrow0}u^{\prime }(c_{t})=\infty$ , $c_{t}$ is household consumption, and $T=T_{W}+T_{R}$ is the maximum age attainable. The household is assumed to have no bequest motives.

The dynamic budget constraint is $z_{t+1}=(1+r)(z_{t}-c_{t})+y_{t+1}$ , where $z_{t}$ is cash on hand, is the real interest rate, and $y_{t+1}$ is total household nonasset income. Each period, households receive an exogenous stream of nonasset income $y_{t}$ . During the working years, $y_{t}$ should be thought of as encompassing all labor and transfer income of the household.⁹During the retirement years, $y_{t}$ consists of social security benefits.¹⁰ Nonasset income depends on a number of stochastic variables and shocks: $y_{t+1}=f(s_{t+1},\varepsilon_{1,t+1})$ , where $\varepsilon _{1,t+1}$ is a vector of shocks and $s_{t+1}$ is a vector of state variables which describe household characteristics such as health, employment, wage rate, etc. State variables $s_{t}$ evolve stochastically over time according to the law of motion $s_{t+1}=g(s_{t},\varepsilon_{2,t+1})$ , where $\varepsilon_{2,t+1}$ is a vector of shocks. I next describe separately, and in more detail, the problem faced by the household in the working years and in the retirement years.

2.2 Working Years

During the household's working years, the state variables that affect income and are included in vector $s_{t}$ are: (i) an indicator of disability $D_{t}$ ; (ii) an indicator of other health limitations $H_{t}$ ; (iii) an indicator of employment status $E_{t}$ ; (iv) a persistent component of the wage $p_{t}^{w}$ ; and (v) a persistent component of household income $p_{t}^{y}$ , which captures all residual variation in household income not explained by earnings of the head or state variables $D_{t}$ , $H_{t}$ , and $E_{t}$ . This residual component turns out to play a large role in explaining the variation of household income in the PSID.¹¹Households in the model take into account their current health status, employment status, and non-transitory aspects of wages and household income when forming expectations about uncertain future nonasset income.

The household's decision problem during the working years is:

Maximize

$\displaystyle \mathit{E}_{t}[\sum_{s=t}^{T}\beta^{s-t}\pi_{s}u(c_{s})]$

subject to

$\displaystyle D_{t+1}$	$\displaystyle =g_{D}(t,D_{t},H_{t},\varepsilon_{t+1}^{D},\tau)$	(1)
$\displaystyle H_{t+1}$	$\displaystyle =g_{H}(t,D_{t+1},D_{t},H_{t},\varepsilon_{t+1}^{H},\tau )$	(2)
$\displaystyle E_{t+1}$	$\displaystyle =g_{E}(t,D_{t+1},H_{t+1},E_{t},\varepsilon_{t+1}^{EE}% ,\varepsilon_{t+1}^{UE},\varepsilon_{t+1}^{DE},\tau)$	(3)
$\displaystyle p_{t+1}^{w}$	$\displaystyle =g_{w}(E_{t+1},E_{t},p_{t}^{w},\varepsilon_{t+1}^{w}% ,\varepsilon_{t+1}^{J},\tau)$	(4)
$\displaystyle p_{t+1}^{y}$	$\displaystyle =g_{y}(p_{t}^{y},\varepsilon_{t+1}^{y},\tau)%$	(5)
$\displaystyle z_{t+1}$	$\displaystyle =(1+r)(z_{t}-c_{t})+y_{t+1}(t,D_{t+1},H_{t+1},E_{t+1},p_{t+1}% ^{w},p_{t+1}^{y},\varepsilon_{t+1}^{J},\varepsilon_{t+1}^{h};\tau )$	(6)
$\displaystyle c_{t}$	$\displaystyle \geq0;$ $\displaystyle (z_{t}-c_{t})\geq-\overline{b}$

Above, equation (1) describes the evolution of the indicator of disability $D_{t+1}$ . The value of $D_{t+1}$ depends on age , on whether the household (head) was disabled in the previous period $D_{t}$ , on any other previous-period health limitations $H_{t}$ , and on an shock $\varepsilon_{t+1}^{D}$ . Index $\tau$ indicates a specific household type.¹² Equation (2) describes the evolution of the health limitations indicator $H_{t+1}$ , which depends on age, lagged disability, lagged health, and an shock $\varepsilon_{t+1}^{H}$ . In addition, $H_{t+1}$ depends on current disability, since $H_{t+1}$ is defined to be 1 whenever $D_{t+1}$ equals 1. Equation (3) describes the evolution of employment status $E_{t+1}$ , which depends on potential experience , current disability status, current health limitations, previous-period employment status, and a set of shocks.¹³

Equation (4) determines the evolution of the persistent wage component $p_{t+1}^{w}$ , which depends on current and previous-period employment status (i.e., on the employment transition between the two periods), on its own lagged value, on an shock $\varepsilon_{t+1}^{w}$ , and on whether there was a job change between periods and .¹⁴ Equation (5) shows the dependence of the persistent component $p_{t+1}^{y}$ on its own lagged value and a stochastic shock. Equation (6) describes the evolution of cash on hand, making explicit that the value of household nonasset income $y_{t+1}$ depends on the realizations of variables , $D_{t+1}$ , $H_{t+1}$ , $E_{t+1}$ , $p_{t+1}^{w}$ , $p_{t+1}% ^{y}$ , $\varepsilon_{t+1}^{J}$ , and $\varepsilon_{t+1}^{h}$ .¹⁵ Finally, households cannot borrow more than amount $\overline{b}$ in any given period.

2.3 Retirement Years

In all periods following retirement labor income is zero. Retired households receive nonasset income from social security only. The level of social security benefits, $SS_{t+1}$ , is determined in the last year of work, according to the formula

$\displaystyle SS_{t+1}=PIA(ALE(D_{t},H_{t},E_{t},p_{t}^{w},p_{t}^{y})),%$

(7)

where

stands for principal insurance amount and

stands for average lifetime earnings. In the last working year, state variables $D_{t}$ , $H_{t}$ , $E_{t}$ , $p_{t}^{w}$ , and $p_{t}^{y}$ are used to predict average lifetime earnings. Predicted

are then used, along with the rules of the Social Security Administration, to determine the

. Households are assumed to receive a level of benefits equal to their

. Details of the calculation of both

and

are given in Appendix 2. Once the level of social security benefits has been determined, it is assumed to stay constant for as long as the household is alive.¹⁶Households also receive asset income, which is determined endogenously within the model.

Retired households in the model may additionally face out-of-pocket medical expenditures $M_{t+1}$ , which reduce net income disposable for consumption. The household's decision problem during the retirement years is thus:

Maximize

$\displaystyle \mathit{E}_{t}[\sum_{s=t}^{T}\beta^{s-t}\pi_{s}u(c_{s})]$

subject to

$\displaystyle H_{t+1}$	$\displaystyle =g_{H}(t,D_{t+1},D_{t},H_{t},\varepsilon_{t+1}^{H},\tau )$	(2)
$\displaystyle p_{t+1}^{M}$	$\displaystyle =g_{M}(p_{t}^{M},\varepsilon_{t+1}^{M},\tau)%$	(8)
$\displaystyle SS_{t+1}$	$\displaystyle =g_{S}(SS_{t})$	(9)
$\displaystyle z_{t+1}$	$\displaystyle =(1+r)(z_{t}-c_{t})+SS_{t+1}-M_{t+1}(t,H_{t+1},p_{t+1}^{M}% )+I_{t+1}%$	(10)

Above, equation (8) describes the evolution of $p_{t+1}^{M}$ , the persistent component of out-of-pocket medical expenditures. Equation (9) describes the evolution of social security benefits. Finally, equation (10) describes the evolution of cash on hand during retirement, reflecting the fact that exogenous nonasset income now comes from social security benefits $SS_{t+1}$ and that there may be out-of-pocket medical expenses $M_{t+1}$ which would reduce income available for consumption. Additionally, households may receive insurance transfers $I_{t+1}$ .

Transfers for retired households are intended to provide a minimum level of consumption after accounting for medical expenditures. These transfers capture the combined effects of programs such as Food Stamps, Supplemental Security Income, and Medicaid. A common specification for such transfers is $I_{t+1}=\max\{0,$ ${\b{c\/}}$ $+M_{t+1}-[SS_{t+1}+(1+r)(z_{t}-c_{t})]\}$ (see Hubbard, Skinner, and Zeldes (1994, 1995) and Scholz, Seshadri, and Khitatrakun (2006)). The introduction of medical expenditures and transfers $I_{t+1}$ , however, complicates the solution of the consumption decisions because they introduce nonconvexities which lead to the existence of multiple local maxima in the solution of the Bellman equation. This problem can be addressed by using a global search in the optimization involved in the solution of the Bellman equation as in Hubbard, Skinner, and Zeldes (1994, 1995), but it increases the computation time required to solve the problem significantly. This will be left for future research. This version makes the simplifying assumption that medical expenditures can wipe out current income but cannot affect accumulated wealth. This assumption preserves the concavity of the righ-hand-side of the Bellman equation and guarantees that the unique local maximum is also the global maximum. It also preserves the monotonicity (in wealth) of the consumption policy functions. On the other hand, this simplifying assumption significantly restricts the potential importance of medical expenditures. The treatment of medical expenditures here is thus preliminary and the results should be interpreted with caution. Several studies suggest that medical expenditures are important for saving behavior and potentially for welfare. Examples include Palumbo (1999) and De Nardi, French, and Jones (2006).

2.4 Model Implementation

This section discusses two points about implementing the model presented above. The first point regards index $\tau$ . As mentioned earlier, $\tau$ indexes the household type. Types can be defined based on observed characteristics (education, race) and unobserved characteristics (unobserved permanent heterogeneity). Different household types will face different processes (different parameter values) governing the evolution of the various state variables and income. The parameterized lifecycle model will be evaluated here for one specific household type: households whose head is white, who have the mean level of education in the PSID sample, and who are at the mean of the distribution of the unobserved permanent heterogeneity components. One important assumption maintained throughout the analysis is that unobserved heterogeneity is known at the beginning of a worker's career. Under this assumption, these permanent components do not constitute risk (i.e., uncertainty).

The second point regards the definition of the state variables in the model and their correspondence to variables in the PSID. Most of the variables included in the state vector, such as those refering to health or employment, will refer to characteristics of the household head in the PSID. The reason is that these variables are likely to be the most important determinants and predictors of income. Household income, on the other hand, will refer to a household aggregate in the PSID which includes labor income and transfer income from all members of the household. I use this variable to construct predicted income for a household of the average size and composition in the PSID sample. The household income process is estimated using this predicted income measure (which has been purged from variation due to differences in household size and composition).

2.5 Model Parameterization

All parameters that appear in the parameterized form of transition equations (1) - (5) and (8) are estimated using PSID data. Estimation is discussed in section 4. On the other hand, model parameters such as the coefficient or relative risk aversion, the real interest rate, and the discount factor are chosen based on values found elsewhere in the literature. The sensitivity of results to alternative assumptions about these parameters is examined in a later section.

Preferences are assumed to be of the constant relative risk aversion (CRRA) form, $u(c_{t})=\frac{c_{t}^{1-\alpha}-1}{1-\alpha}$ , where $\alpha$ is the coefficient of relative risk aversion. The baseline model assumes a value of $\alpha=3.0$ .¹⁷The interest rate is assumed to be fixed at the value (Gourinchas and Parker, 2002). The discount factor $\beta$ is set such that the discount rate equals the interest rate, as in Low, Meghir, and Pistaferri (2006) and many other studies.¹⁸Conditional survival probabilities are obtained from the Life Tables published by the Center for Disease and Control Prevention of the U.S. Department of Health and Human Services. Finally, households in the baseline model are assumed to be credit-constrained ( $\overline{b}=0$ ).

3 Data

Estimation is conducted using data from the PSID. I start here by giving a brief description of the key variables. Appendix 1 provides a detailed explanation of all variables used. The disability indicator $D_{t}$ equals 1 if an individual is disabled and 0 otherwise. It is constructed from the respondent's self-reported employment status at the survey date, where "disabled"is one of the possible answers in the questionnaire. A currently disabled individual is by definition not currently employed. This variable is thus likely to capture severe forms of disability. Indicator $H_{t}$ , on the other hand, is constructed based on the survey question: "Do you have any physical or nervous condition that limits the type of work or the amount of work you can do?" $H_{t}$ equals 1 when a respondent answers "yes", and 0 otherwise. This variable is thus likely to capture both serious and less serious health limitations, including temporary illness and other conditions that affect work. Additionally, $H_{t}$ is set to 1 whenever $D_{t}$ equals 1. Employment $E_{t}$ , like disability, is based on self-reported employment status at the survey date. It equals 1 for employed and temporarily laidoff workers, and zero for disabled and unemployed individuals. Finally, household income $y_{t}$ includes all labor and transfer income of the household head and, if present, of the spouse and any other family members. As was discussed in the previous section, I construct and use predicted income for a household of the average size and composition in the PSID sample, in order to account for heterogeneity in household size and composition which is not present in the consumpion model.

As will be discussed below, estimation is conducted in four parts, where each of the following four subsets of equations is estimated separately: (i) disability; (ii) health; (iii) employment, wage, and household income; (iv) medical expenditures. Some sample restrictions imposed vary slightly across the different estimation samples. Estimation of all equations other than medical expenditures uses data from the 1975-1997 PSID waves. Medical expenditures, on the other hand, use the 1999, 2001, and 2003 waves. The reason is that earlier waves did not contain information on medical expenses (note also that interviews have been conducted only every two years since 1997).

In all cases, the data include members of both the SRC and SEO samples, as well as nonsample members who married PSID sample members. I consider only households with a male head who is living in the household at the time of the interview. Both single and married individuals are included. I exclude a small fraction of person-year observations in which the head reports being a full-time student or "keeping house"at the time of the interview. These observations are discarded because in the lifecycle model household heads cannot be out of the labor force except when disabled. I also exclude individuals who are missing data on education. Only observations where the head is at least 18 years old are used.

Some additional sample restrictions, including restrictions based on potential experience (or age) differ according to the process being estimated. For estimation of the health limitations process, I use observations where potential experience ranges from 1 to 65. The corresponding age range is 18 to 87. This sample has observations. Table 1A (bottom panel) displays the number of observations and the mean of the health limitations indicator for different levels of potential experience. The column labeled All t refers to all levels of potential experience, while the next columns report values for the ranges of potential experience indicated in the top row. The overall mean of the indicator is 0.136 and increases from 0.052 for low experience ( $1\leq t\leq10$ ) to 0.497 for high experience ().

Estimation of disability and of the joint process of employment, wage, and household income excludes retired individuals and observations where age exceeds 64 (the resulting range of potential experience is 1-48, with very few values above 45. Table 1A (top panel) displays the number of observations and the mean of the disability indicator for different levels of potential experience. The overall mean of the indicator is 0.022 and increases from 0.022 for $1\leq t\leq10$ to 0.110 for $t\geq41$ .

In addition, for estimation of the employment, wage, and household income equations (which also uses data on work hours and labor earnings, as will be discussed below), I censor reported work hours at 4000, add 200 to reported hours before taking logs to reduce the impact of very low values on the variation in the logarithm, and I restrict observed wage rates and household income (in levels) to increase by no more than 500% and decrease to no less than 20% of their previous-year values.¹⁹ I also censor the wage to be no less than $3.50/hour and household income to be no less than $1,000/year in year-2000 dollars.²⁰ Table 1B displays the number of observations, mean, standard deviation, minimum, and maximum values of all key variables used in the estimation of the joint model of income. The second-to-last row displays the raw household income data, while the last row displays the predicted value for a household of the average size and composition, which is the variable actually used in estimation.

Finally, estimation of the out-of-pocket medical expenditures process uses observations where potential experience is above 43, in correspondence with the model's assumption that medical costs are zero during working years. The PSID variable used here consists of all out-of-pocket payments made by the household over the course of the two years prior to the interview year (see Appendix 1). Table 1C provides summary statistics in thousands of year-2000 dollars. The sample consists of 2,831 observations and has a mean of 3.25, a standard deviation of 10.76, a 99th percentile of 38.63, and a maximum value of 317.47.

4 Parameter Estimation

This section presents the parametric models specified for the various transition equations introduced in section 2 and discusses their estimation. As was mentioned above, the estimation strategy involves estimating the various equations of the model in four parts. Specifically, the equations for medical expenditures, health limitations, and disability are estimated separately from the rest of the equations (employment, wage rates, and household income). The reasons for estimating these equations separately are the following: (i) Out-of-Pocket Medical Expenditures: As discussed above, estimation of medical expenditures uses PSID waves 1999, 2001, and 2003, while all other equations use data from waves 1975-1997. (ii) Health: In the lifecycle model, health appears as a state variable both before and after retirement. Estimation of the health process is therefore based on a sample which includes all levels of potential experience (and age). Most other state variables in the consumption model (including disability) relate to the labor market and their estimation therefore excludes high levels of potential experience (and age). (iii) Disability: I initially attempted to estimate the disability process jointly with all other labor market and income processes. However, the fact that the disability indicator in the PSID sample is zero more than 97% of the time introduces numerical instabilities in the implementation of indirect inference.²¹ Estimating the disability equation individually allows the use of standard maximum likelihood methods and sidesteps the numerical difficulties. The following subsections introduce the parametric forms used and discuss estimation as well as estimation results.

4.1 Disability

The transition equation for the disability indicator $D_{t}$ is assumed to have the following form

$\displaystyle D_{t+1}=I[\gamma_{0}^{D}+\gamma_{1}^{D}(t+1)+\gamma_{2}^{D}(t+1)^{2}% +\gamma_{3}^{D}(t+1)^{3}+\gamma_{4}^{D}D_{t}+\gamma_{5}^{D}H_{t}+\zeta ^{D}+\varepsilon_{t+1}^{D}>0],%$

(11)

where $\zeta^{D}$ is an individual-specific, permanent component. In estimation, it is assumed that $\zeta^{D}\sim N(0,\sigma_{\zeta^{D}}^{2})$ and $\varepsilon_{t+1}^{D}\sim N(0,1)$ so equation (11) is a dynamic probit with permanent unobserved heterogeneity. The parameters of equation (11) are estimated by maximum likelihood. The unobserved component $\zeta^{D}$ is integrated out of the (conditional) likelihood function by Gauss-Hermite quadrature. The initial condition for $D_{t}$ is assumed to be zero, since in the PSID sample $D_{t}=0$ for all individuals for

Table 2A presents estimation results for equation (11). The probability that $D_{t+1}=1$ is monotonically increasing in experience (the slope of the polynomial is positive for between 1 and 40). The coefficient of $\hat{\gamma}_{4}^{D}=1.611$ on $D_{t}$ indicates a fairly high degree of state dependence.²² Unobserved heterogeneity, with an estimated standard deviation of $\hat{\sigma}_{\zeta^{D}}=0.934$ , also plays a significant role.

4.2 Health

The transition equation for the health indicator is assumed to take the form

$\displaystyle H_{t+1}=I[\gamma_{0}^{H}+\gamma_{1}^{H}(t+1)+\gamma_{2}^{H}(t+1)^{2}% +\gamma_{3}^{H}(t+1)^{3}+\gamma_{4}^{H}H_{t}+\zeta^{H}+\varepsilon_{t+1}% ^{H}>0],%$

(12)

where $\zeta^{H}$ is an individual-specific permanent component.²³ In addition, $H_{t+1}$ is set to 1 whenever $D_{t+1}$ equals 1.²⁴ The parameters of equation (12) are also estimated by maximum likelihood, where $\zeta^{H}%$ is assumed to be $\sim N(0,\sigma_{\zeta^{H}}^{2})$ and is integrated out of the conditional likelihood by numerical quadrature. The equation is estimated on the sample of observations where $D_{t+1}\neq1$ (since $H_{t+1}$ is defined to be 1 whenever $D_{t+1}$ equals 1). The initial realization of $H_{t+1}$ is assumed to be independent of $\zeta^{H}$ ²⁵, but the distribution of $H_{1}$ in the model is set such that its mean equals the mean of $H_{1}$ in the PSID.

Table 2B presents estimation results (which are conditional on an individual not being disabled). The probability that $H_{t+1}=1$ increases monotonically with age. Lagged health limitations have a fairly large and strongly significant effect on the probability of current health limitations ( $\hat{\gamma}_{4}^{H}=1.119$ ). Unobserved heterogeneity also plays an important role ( $\hat{\sigma}_{\zeta^{H}}$ ).

4.3 Employment, Wage Rates, and Household Income

Employment, wage rates, and household income are determined jointly by a set of recursive equations. The system also includes an equation for job changes and an equation for work hours. Although job changes and work hours are not state variables in the lifecycle model, they are key variables in the determination of income. Therefore, the lifecycle model includes two shocks which capture job changes and innovations in work hours, respectively. The evolution of job changes and hours, and their effects on income, are thus estimated as part of the recursive system that drives household income. The following subsection presents the joint model of employment, job changes, wage rates, work hours, and household income. Additional details are provided in Appendix 3.

4.3.1 Functional Forms

Employment - Employment Transition

Conditional on being employed, next-period employment is determined by

$\displaystyle E_{t+1}=I[\gamma_{0}^{EE}+\gamma_{1}^{EE}t+\gamma_{2}^{EE}t^{2}+\gamma _{3}^{EE}H_{t+1}+\gamma_{4}^{EE}ED_{t}+\zeta^{EE}+\varepsilon_{t+1}% ^{EE}>0].%$

(13)

Employment-employment transitions are thus determined by a latent variable which depends on a quadratic polynomial in potential experience

, current health limitations $H_{t+1}$ , employment duration $ED_{t}$ , and the error term $\zeta^{EE}+\varepsilon_{t+1}^{EE}$ . The definition of $ED_{t}$ and its treatment is discussed below. The error component $\zeta^{EE}$ is an individual-specific permanent component and $\varepsilon_{t+1}^{EE}$ is an

idiosyncratic shock. It is assumed that $\zeta^{EE}\sim N(0,\sigma _{\zeta^{EE}}^{2})$ and $\varepsilon_{t+1}^{EE}\sim N(0,1)$ . Component $\zeta^{EE}$ is allowed to be correlated with unobserved permanent components in the other equations. The factor structure of the permanent components in the different equations is also specified below.

Unemployment - Employment Transition

Conditional on being unemployed, next-period employment is given by

$\displaystyle E_{t+1}=I[\gamma_{0}^{UE}+\gamma_{1}^{UE}t+\gamma_{2}^{UE}t^{2}+\gamma _{3}^{UE}H_{t+1}+\gamma_{4}^{UE}UD_{t}+\zeta^{UE}+\varepsilon_{t+1}% ^{UE}>0].%$

(14)

Transitions from unemployment into employment are thus determined by a latent variable which depends on a quadratic polynomial in potential experience

, current health limitations $H_{t+1}$ , unemployment duration $UD_{t}$ (discussed below), an individual-specific permanent component $\zeta^{UE}$ , and the

idiosyncratic shock $\varepsilon_{t+1}^{UE}\sim N(0,1)$ . The term $\zeta^{UE}$ is assumed to be $\sim N(0,\sigma_{\zeta^{UE}}^{2})$ and may be correlated with the permanent components in the other equations.

Disability - Employment Transition

Transitions from disability back into employment are rather infrequent in the PSID sample. These transitions are modeled as

$\displaystyle E_{t+1}=I[\gamma_{0}^{DE}+\varepsilon_{t+1}^{DE}>0]$ where $\displaystyle \varepsilon_{t+1}^{DE}\sim N(0,1)$ . $\displaystyle %$

(15)

The fact that these transitions are infrequent in the data makes it difficult to estimate their dependence on experience or on permanent unobserved components.

Job Changes

Conditional on being employed in both and , the occurrence of a job change between the two periods is determined by

$\displaystyle J_{t+1}=I[\gamma_{0}^{J}+\gamma_{1}^{J}t+\gamma_{2}^{J}t^{2}+\gamma_{3}% ^{J}JD_{t}+\zeta^{J}+\varepsilon_{t+1}^{J}>0],%$

(16)

where $JD_{t}$ is job duration (discussed in the next paragraph), $\zeta ^{J}\sim N(0,\sigma_{\zeta^{J}}^{2})$ is an individual-specific permanent component, and $\varepsilon_{t+1}^{J}\sim N(0,1)$ is

Employment-, Unemployment-, and Job Duration

Estimation of equations (13), (14), and (16) controls for duration dependence in employment and job mobility by including the variables $ED_{t}$ , $UD_{t}$ , and $JD_{t}$ , respectively. Here, $ED_{t}$ is defined as the number of consecutive periods that an employed individual has been employed up to period , $UD_{t}$ is the number of consecutive periods that an unemployed individual has been unemployed up to period , and $JD_{t}%$ is the number of periods that an employed individual has been at their current job. It would be straightforward to introduce $ED_{t}$ , $UD_{t}$ , and $JD_{t}$ as state variables in the lifecycle consumption model from section 2. This is not done here because of the computational burden of the additional state variables. Instead, the approach is to control for duration dependence in estimation, but to set the duration variables to their sample mean (by year of potential experience) when parameterizing the employment and job-change equations. I also experimented with estimating equations (13), (14), and (16) without controlling for duration dependence. In this case the potential-experience profiles of the transition probabilities do not match the data well, but the results for welfare and precautionary saving are not affected.

Wage Equation²⁶

Log wages are assumed to follow the process

$\displaystyle \ln wage_{t+1}=\beta^{w}X_{t+1}^{w}+w_{t+1},$

where $wage_{t+1}$ is a latent wage which is equal to the actual wage for employed individuals, but is also defined for individuals who are not employed.²⁷ Vector $X_{t+1}^{w}$ is a vector of exogenous variables including a polynomial in experience, and $w_{t+1}$ is specified as

$\displaystyle w_{t+1}=\gamma_{1}^{w}H_{t+1}+p_{t+1}^{w}.$

In the above equation $p_{t+1}^{w}$ is a persistent component of the wage and is given by

$\displaystyle p_{t+1}^{w}=\rho_{w}(1+\phi_{1}\cdot\Psi_{t+1})p_{t}^{w}+\gamma_{2}^{w}% J_{t+1}+\gamma_{3}^{w}(1-E_{t+1})+\zeta^{w}+(1+\phi_{2}\cdot\Psi_{t+1}% )\cdot\varepsilon_{t+1}^{w},$

(17)

where $\displaystyle \Psi_{t+1}\equiv J_{t+1}+E_{t+1}\cdot(1-E_{t})$ and $\displaystyle \varepsilon_{t+1}^{w}\sim N(0,\sigma_{w}^{2})$ . $\displaystyle %$

The persistent wage component $p_{t+1}^{w}$ depends on the previous-period (latent) wage via the autoregressive coefficient $\rho_{w}$ . The degree of dependence on $p_{t}^{w}$ is allowed to change according to whether indicator $\Psi_{t+1}$ equals 0 or 1. Indicator $\Psi_{t+1}$ equals 1 if either (i) there is a job change between periods

and

or (ii) a worker who is unemployed or disabled at

is reemployed at

. The variance of the shock $\varepsilon_{t+1}^{w}$ also depends on the value of $\Psi_{t+1}$ . This dependence captures the increased level of wage uncertainty associated with new jobs, which is present whether the worker was previously employed or not. The term $\zeta^{w}\sim N(0,\sigma_{\zeta^{w}}^{2})$ is a person-specific permanent component which is allowed to be correlated with the permanent components present in the employment, job-change, hours, and household income equations.²⁸ A job change and a job loss are also allowed to affect the mean of the persistent component $p_{t+1}^{w}$ via the coefficients $\gamma_{2}^{w}$ and $\gamma_{3}^{w}$ .

Hours Equation

Log hours are assumed to follow the process

$\displaystyle \ln hours_{t+1}=\beta^{h}X_{t+1}^{h}+h_{t+1},$

where $X_{t+1}^{h}$ is defined similarly to $X_{t+1}^{w}$ and $h_{t+1}$ is given by

$\displaystyle h_{t+1}=\gamma_{0}^{h}+\gamma_{1}^{h}E_{t+1}+\gamma_{2}^{h}w_{t+1}+\gamma _{3}^{h}D_{t+1}+\gamma_{4}^{h}H_{t+1}+\zeta^{h}+\varepsilon_{t+1}^{h}.$

(18)

That is, annual hours of work are allowed to depend on employment status at the survey date, the wage rate, disability, and health. The term $\zeta ^{h}$ is person-specific and time-invariant, and may be correlated with the unobserved permanent components in the previous equations. The error $\varepsilon_{t+1}^{h}\sim N(0,\sigma_{h}^{2})$ is .

Household Income Equation

Log household income is assumed to follow the process

$\displaystyle \ln income_{t+1}=\beta_{1}^{y}X_{t+1}^{y}+y_{t+1},$

where $X_{t+1}^{y}$ is defined similarly to $X_{t+1}^{w}$ and $X_{t+1}^{h}$ , and $y_{t+1}$ is given by

$\displaystyle y_{t+1}=\gamma_{0}^{y}+\gamma_{1}^{y}w_{t+1}+\gamma_{2}^{y}h_{t+1}+\gamma _{3}^{y}D_{t+1}+\gamma_{4}^{y}H_{t+1}+\gamma_{5}^{y}U_{t+1}+\zeta^{y}% +p_{t+1}^{y},%$

(19)

$\displaystyle p_{t+1}^{y}=\rho_{y}p_{t}^{y}+\varepsilon_{t+1}^{y}.$

Above, $U_{t+1}$ is an indicator of unemployment defined by $U_{t+1}% =1-$ $E_{t+1}-D_{t+1}$ . The household income equation states first that household income depends on the wage and work hours of the head.²⁹ The reason for this dependence is simply that labor earnings of the head are typically the main component of household income. In addition, (19) allows $D_{t+1}$ , $H_{t+1}$ , and $U_{t+1}$ to affect household income via components of household income other than the head's earnings, such as public and private transfers received by the family or labor income of other family members. Parameters $\gamma_{3}^{y}$ , $\gamma_{4}^{y}$ , and $\gamma_{5}^{y}$ are thus likely to capture insurance to shocks to the head's ability to work, health, or employment status. The household-specific permanent component $\zeta^{y}$ is allowed to be correlated with the permanent components in the employment transitions, job changes, wage rate, and work hours equations. The factor structure of the various unobserved permanent components is described below. The component $p_{t+1}^{y}$ captures the residual unexplained variation in household income. This residual exhibits important persistence in the data and is thus modeled as an AR(1) process. The shock $\varepsilon_{t+1}^{y}\sim N(0,1)$ is

Permanent Unobserved Heterogeneity

The permanent unobserved components in the above equations are assumed to follow the factor structure

$\displaystyle \zeta^{EE}$	$\displaystyle =\delta_{\mu}^{EE}\mu+\delta_{\eta}^{EE}\eta$
$\displaystyle \zeta^{UE}$	$\displaystyle =\delta_{\mu}^{UE}\mu+\delta_{\eta}^{UE}\eta$
$\displaystyle \zeta^{JC}$	$\displaystyle =\delta_{\mu}^{JC}\mu+\delta_{\eta}^{JC}\eta$	(20)
$\displaystyle \zeta^{w}$	$\displaystyle =\delta_{\mu}^{w}\mu$
$\displaystyle \zeta^{h}$	$\displaystyle =\delta_{\mu}^{h}\mu+\delta_{\eta}^{h}\eta$
$\displaystyle \zeta^{y}$	$\displaystyle =\delta_{\lambda}^{y}\lambda,$

where $\mu\sim N(0,1)$ , $\eta\sim N(0,1)$ , and $\upsilon\sim N(0,1)$ (introduced below) are mutually independent, individual-specific permanent components, and all $\delta$ coefficients are factor loadings to be estimated. Factor $\mu$ is defined as the unobserved heterogeneity component in wages, but it is also allowed to influence employment, job changes, and hours. Factor $\eta$ also affects employment, job changes, and hours, but is assumed to have no influence on wages. The latter component is intended to capture factors related to labor supply and to job and employment mobility preferences. Factor $\lambda$ in the income equation is defined as $\lambda=\kappa\mu+\sqrt{1-\kappa^{2}}\upsilon$ and is thus $\sim N(0,1)$ and correlated with $\mu$ , with correlation coefficient $\kappa$ (which is also estimated).

4.3.2 Estimates of the Income Model

The employment, job mobility, wage rate, work hours, and household income equations presented above are estimated jointly by generalized indirect inference.³⁰ Appendix 4 describes implementation of the estimation method used here.³¹ In order to estimate the effects of disability and health in equations (13) - (19) I simulate $D_{t}$ and $H_{t}$ using the estimates of equations (11) and (12) presented above. Estimation in this section is thus conditional on the estimated parameters of the disability and health processes.

Estimation results for equations (13) - (19) are presented in Table 2C. I will not discuss the estimated parameters of all equations here. Instead, I will focus on the main features of the estimates of the wage and household income equations only. The next section will use simulations to provide an informal evaluation of the fit of all estimated equations and will thus illustrate some of the implications of the estimated parameters in the employment, job change, and hours equations.

Panel (d) in Table 2C presents estimates of the wage equation. The most important features of the estimates are the following. Persistence in the wage rate is high but well below unity (the autoregressive coefficient $\hat{\rho}_{w}$ is 0.939). The standard deviation $\hat{\sigma}_{w}$ of the wage shock $\varepsilon_{t+1}^{w}$ for job stayers is fairly large (0.097). When wage shocks involve a new job (whether the job change involves going through a period of nonemployment or not) the standard deviation of the wage shock more than triples to 0.298 ( $\hat{\phi}% _{1}=2.054$ ), and the dependence on the lagged wage falls to 0.794 ( $\hat{\phi}_{2}=-0.154$ ). New jobs are thus associated with substantial wage risk. Finally, nonemployment is negatively related to the persistent wage component through the coefficient $\widehat{\gamma}_{3}^{w}=-0.140$ .

Panel (f) presents the estimated parameters of the household income equation. The most important features of the estimates are the following. Wages and hours have a strong positive association with household income (coefficients $\hat{\gamma}_{1}^{y}$ and $\hat{\gamma}_{2}^{y}$ are 0.592 and 0.454, respectively). Conditional on the wage and hours, disability is positively related to household income (coefficient $\hat{\gamma}_{3}^{y}$ is 0.186). This positive relationship is likely to reflect transfers from disability insurance but could also reflect a positive labor supply response of a spouse or other family members to disability of the head. In either case, the positive coefficient suggests the presence of substantial insurance against disability shocks.

Contrary to disability, health limitations do not have a positive association with household income conditional on the wage and hours (coefficient $\hat{\gamma}_{4}^{y}$ is -0.007). There is thus no evidence of insurance against health limitations captured by . Unemployment does have have a positive relationship, but the coefficient is small ( $\hat{\gamma}_{5}% ^{y}=0.027$ ).

The results further indicate that permanent unobserved heterogeneity in household income is important ( $\hat{\delta}_{\lambda}^{y}=0.248$ ) and negatively correlated with unobserved heterogeneity in the employment, job mobility, wage rate, and hours equations ( $\hat{\kappa}=-0.148$ ). One possible explanation is that households who do permanently better in the labor market may also receive permanently less transfers from public programs. Another possible explanation is that permanently higher earnings of the head may permanently reduce the labor supply of a spouse if present. Finally, the serially correlated error in household income $p_{t}^{y}$ (i.e., the residual household income component) has an autoregressive coefficient of $\hat{\rho }_{y}=0.449$ and a large standard deviation of $\hat{\sigma}_{y}=0.168$ .

4.4 Medical Expenditures

Out-of-pocket medical expenditures in old age are assumed to be given by³²

$\displaystyle M_{t+1}=\exp(\gamma_{0}^{M}+\gamma_{1}^{M}(t+1)+\gamma_{2}^{M}(t+1)^{2}% +\gamma_{3}^{M}(t+1)^{3}+\gamma_{4}^{M}H_{t+1}+p_{t+1}^{M})%$

(21)

$\displaystyle p_{t+1}^{M}=\rho_{M}\cdot p_{t}^{M}+\varepsilon_{t+1}^{M},$

where $Var[\varepsilon_{t+1}^{M}]= \sigma_{M}^{2}$ . The log of medical expenditures $\ln M_{t+1}$ thus depends on a deterministic polynomial in age, health status, and a persistent component $p_{t+1}^{M}$ which follows an AR(1) process.³³ The $\gamma$ coefficients in equation (21) are estimated by fitting a least-squares regression of $\ln M_{t+1}$ . Any unobserved permanent component affecting medical expenditures is assumed to be captured by the permanent component in health.³⁴ Parameters $\rho_{M}$ and $\sigma_{M}^{2}$ are estimated by fitting sample autocovariances of the least-squares regression residuals to theoretical autocovariances implied by the first-order autoregressive assumption on the error term. Autocovariances are fitted using an equally-weighted minimum distance estimator.³⁵

Table 2D presents the estimated parameters. The age profile is not very pronounced: the polynomial in is initially increasing, then decreasing, and then increasing again. Health limitations have a significant positive relationship with medical expenditures. If one sets the persistent shock $p_{t+1}^{M}$ to zero, for instance, expected medical expenditures at are $\$413$ for someone in good health and $\$640$ for someone in poor health. Uncertainty in medical expenditures is large ( $\hat{\sigma}% _{M}=0.936$ ) and the shocks are fairly persistent (the autoregressive coefficient is $\hat{\rho}_{M}=0.745$ ).³⁶

4.5 Evaluation of Fit

This section provides an informal evaluation of the fit of the processes estimated in the previous section by simulating data from the estimated processes, and then comparing sample statistics of the simulated data against sample statistics of the PSID data. I simulate data from the estimated equations for a large number of individuals and then randomly select a subsample of the simulated data in such a way that its demographic pattern matches that of the PSID sample.

Table 3A presents the sample mean of the disability and health limitations indicators for different levels of potential experience. The column under the "Overall" heading displays statistics for all levels of potential experience. The next columns report results for the level of indicated in the top row. For each reported level of experience, the results combine data for periods , , and . For instance, uses data for and 6. As the figures show, the simulated data match the PSID data fairly closely. The overall mean of is 0.02 in both the PSID and the simulated data. The probability that equals 1 increases steadily with experience. For health limitations, the overall mean is 0.13 in the PSID and in the simulations. The probability that also increases steadily with experience. For high levels of experience ( around 60), these probabilities are in the PSID and 0.54 in the simulated data.

Table 3B presents similar statistics for all variables used in the estimation of the joint household income process.³⁷ I will not attempt to discuss all statistics here. The main points to notice in Table 3B are the following. (i) The overall fit of the simulated data is good. (ii) The main aspect that is missed by the simulations is a fairly strong and steady increase in the standard deviation of log hours with potential experience. This increase translates into a similar rise in the standard deviation of labor earnings of the head and, to a lesser extent, of household income. This feature of the PSID data appears to reflect the fact that exceptionally low levels of reported hours become more common with large values of potential experience. This, in turn, is likely to be the result of workers retiring gradually and significantly reducing their hours of work prior to full retirement.

Finally, Table 3C presents statistics for the estimated medical expenditures process. Overall, the fit seems fair given the somewhat erratic pattern observed in the data. The overall mean is 1.576 in the PSID and 1.342 in the simulated data. The overall standard deviation is 3.758 in the PSID and 3.519 in the simulations.

5 Solution to the Lifecycle Model

Once parameterized, the lifecycle model is solved by numerical dynamic programming. The model gives rise to three different forms of Bellman equations, corresponding to (i) the working years, (ii) the transition between work and retirement, and (iii) the retirement years, respectively. The Bellman equations are as follows:

Working years

$\displaystyle V(t,D_{t},H_{t},E_{t},p_{t}^{w},p_{t}^{y},z_{t})$	$\displaystyle =\max\{u(c_{t})$
	$\displaystyle +\beta\mathit{E}[V(t+1,D_{t+1},H_{t+1},E_{t+1},p_{t+1}^{w},p_{t+1}% ^{y},z_{t+1})$
	$\displaystyle \vert t,D_{t},H_{t},E_{t},p_{t}^{w},p_{t}^{y},z_{t}]\},%$	(22)

where the expectation, given transition equations (1) - (6), is taken over shocks $\varepsilon_{t+1}^{D}$ , $\varepsilon_{t+1}^{H}$ , $\varepsilon_{t+1}^{EE}$ , $\varepsilon_{t+1}^{UE}$ , $\varepsilon_{t+1}^{DE}$ , $\varepsilon_{t+1}^{J}$ , $\varepsilon_{t+1}^{w}$ , $\varepsilon_{t+1}^{h}$ , $\varepsilon_{t+1}^{y}$ .

Last working year

$\displaystyle V(t,D_{t},H_{t},E_{t},p_{t}^{w},p_{t}^{y},z_{t})$	$\displaystyle =\max\{u(c_{t})$
	$\displaystyle +\beta\pi_{t}\mathit{E}_{t}[V(t+1,H_{t+1},p_{t+1}^{M},SS_{t+1}% ,z_{t+1})$
	$\displaystyle \vert t,D_{t},H_{t},E_{t},p_{t}^{w},p_{t}^{y},z_{t}]\},%$	(23)

where the expectation, given transition equations (2), (7), and (10) is taken over shocks $\varepsilon_{t+1}^{H}$ and $\varepsilon_{t+1}^{M}$ .

Retirement years

$\displaystyle V(t,H_{t},p_{t}^{M},SS_{t},z_{t})$	$\displaystyle =\max\{u(c_{t})$
	$\displaystyle +\beta\pi_{t}\mathit{E}_{t}[V(t+1,H_{t+1},p_{t+1}^{M},SS_{t+1}% ,z_{t+1})$
	$\displaystyle \vert t,H_{t},p_{t}^{M},SS_{t},z_{t}]\},%$	(24)

where the expectation, given transition equations (2) and (8) - (10) is taken over $\varepsilon_{t+1}^{H}$ and $\varepsilon_{t+1}^{M}$ .

In solving the model, cash on hand $z_{t}$ and the persistent wage component $p_{t}^{w}$ are treated as continuous state variables. Consumption $c_{t}$ is also continuous. State variables $p_{t}^{y}$ and $p_{t}^{M}$ are approximated by Markov chains, and $SS_{t+1}$ is also discretized. Since the dynamic programming problem has a finite horizon, the Bellman equations are solved by value function iteration. The largest computational costs of solving the Bellman equations in this model arise from computing the expectations of the next-period value function. Expectations are computed as follows: For state variables $D_{t}$ , $H_{t}$ , and $E_{t}$ , I use estimated equations (11)-(15), and pseudo-random draws of $\varepsilon_{t+1}^{D}$ , $\varepsilon_{t+1}^{H}$ , $\varepsilon_{t+1}^{EE}$ , $\varepsilon_{t+1}^{UE}$ , $\varepsilon_{t+1}^{DE}$ , to simulate the joint behavior of $D_{t}$ , $H_{t}$ , and $E_{t}$ . From the simulation, I compute matrices of transition probabilities for a vector $(D_{t}$ , $H_{t}$ , $E_{t})$ and use these transition matrices to compute the expectations. For state $p_{t}^{y}%$ , I use the transition probabilities associated with the Markov chain approximation. Finally, I use Gauss-Hermite quadrature to compute expectations with respect to $\varepsilon_{t+1}^{J}$ , $\varepsilon_{t+1}^{h}$ , and $\varepsilon_{t+1}^{w}$ .

Treating cash on hand and the persistent wage component as continuous requires the use of an interpolation scheme to evaluate next-period's value function at arbitrary values of the continuous state variables. I use bicubic interpolation. This preserves differentiability of the right-hand side of the Bellman equation and allows solving each optimization problem using Newton-Raphson, which is convenient because of its fast (quadratic) convergence. All programs are written in Fortran 90 and parallelized using MPI (Message Passing Interface).

5.1 Optimal Consumption Behavior

This section discusses some of the properties of the solution to the lifecycle consumption model presented above. The data were treated, and the model was parameterized, so that income and consumption are in thousands of year-2000 dollars. The model corresponds to a household of mean size and composition, with mean years of education, whose head is white, and who is at the mean of the distribution of permanent unobserved heterogeneity components. All aggregate risk is abstracted from in the model.³⁸

Figure 1 presents mean experience profiles for household nonasset income and consumption, both simulated from the baseline lifecycle model. The nonasset income profile has a humped shape, with a significant drop at the time of retirement. The drop at retirement is particularly pronounced because the current parameterization of nonasset retirement income in the model uses only social security benefits of the household head.³⁹ The mean profile of (optimal) consumption is also hump-shaped, but smoother than income. Mean consumption in the figure never exceeds mean income. This is because of the presence of borrowing constraints along with the assumption in the simulations that households begin their career with zero initial assets.⁴⁰

Figures 2 - 5 display optimal consumption rules and their dependence on the value of the various state variables in the model. Figure 2 exhibits optimal consumption as a function of cash on hand for an employed household in good health in period 1 (first year of career) who is at the mean of the distribution of the persistent wage and household income components $p_{t}% ^{w}$ and $p_{t}^{y}$ . At low levels of cash on hand, households are credit-constrained and consume their entire wealth. Above a certain threshold, households begin to save. This behavior is typical of consumption models with precautionary motives.⁴¹

Figure 3 illustrates the dependence of optimal consumption on the level of the residual component of household income $p_{t}^{y}$ in period 1 (first year of career) for an employed individual in good health who is at the mean of the wage distribution. The figure displays consumption policy functions for values of $p_{t}^{y}$ ranging from 2 standard deviations above to 2 standard deviations below the mean. The figure indicates that, conditional on having $20,000 in cash on hand in its first year of career, a household with component $p_{t}^{y}$ two standard deviations above the mean will spend about $3,000 more on consumption than a household with $p_{t}^{y}$ two standard deviations below the mean.

Figure 4 shows the dependence of consumption on the persistent wage component $p_{t}^{w}$ . The figure refers to a household who is employed, in good health, and at the mean of the household income component $p_{t}^{y}$ in period 1. A higher current wage leads to a higher level of consumption for a given level of resources. The figure corresponds to values of $p_{t}^{w}%$ ranging from 2.8 standard deviations above to 2.8 standard deviations below the mean. Conditional on having $30,000 in total resources in its first year of career, a household with component $p_{t}^{w}$ 2.8 standard deviations above the mean will spend about $12,000 more on consumption than a household with $p_{t}^{w}$ 2.8 standard deviations below the mean. Figure 5 displays the optimal consumption rule over the entire range of possible realizations that $p_{t}^{w}$ may take in the simulations.⁴²

The figures give a sense of the effects on optimal consumption of changes in a particular state variable, holding the rest constant. Changes in most state variables, such as a change in employment status, however, lead to same-period changes in other state variables. The next section uses simulations to analyze various implications of the lifecycle model, accounting for all interactions among the different variables.

6 Simulation Analysis

This section uses simulations to investigate the implications of the consumption and income models for the importance of the various sources of income risk for household welfare and precautionary saving. The analysis is based on numerically solving and then simulating the consumption model for a large number of households under a variety of scenarios. The scenarios differ in the number and type of shocks facing the households, who behave optimally under each scenario. In all simulations, households are assumed to begin their career with zero initial assets. The determination of initial conditions for the key simulated processes is discussed in more detail in Appendix 3.

6.1 Welfare Gains of Insuring Specific Sources of Risk

This subsection evaluates the welfare gains to the household from fully insuring against each specific source of income risk. We will consider two different insurance schemes. In the first, which will be called the unadjusted case, full insurance means the following: For any given shock, an insured household is compensated (by a lumpsum transfer) upon the realization of the shock in such a way that the realization of the shock has no effect on the realization of income. For instance, insuring unemployment risk means that in the event of unemployment the household receives a transfer that exactly offsets the income lost due to the unemployment shock. Thus, income after the insurance transfer is exactly the same as it would have been had the worker remained employed. As another example, fully insuring wage risk means that the insured household's income after the transfer will be the same, regardless of the actual realization of the wage shock, as it would have been had the realization of the wage shock been zero.

Insuring risk in this way has two effects. First, insurance reduces the variance (uncertainty) in income associated with a particular source of risk. Second, insurance may also affect the mean of income.⁴³ This bring us to the second insurance scheme, which will be called the adjusted case. In this case, mean income in the insured scenario will be adjusted so that it equals mean income in the uninsured scenario for each year in the lifecycle. That is, the household is required to pay an actuarially fair premium for insurance, and as a result expected household income is the same under both the insured and uninsured scenarios. In this sense the insurance considered here is actuarially fair. Insurance is also full or complete in that it eliminates all uncertainty in income created by the presence of a particular source of risk. Most of the discussion that follows will focus on the adjusted case, although for completeness, I will also present results for the unadjusted case (where mean income in the insured scenario is allowed to be different from mean income in the uninsured scenario).

Two additional points about the insurance experiment and welfare analysis are worth stressing. First, the insurance considered here is in addition to already existing insurance mechanisms which are captured by the household nonasset income process estimated on PSID data.⁴⁴ Second, in all cases, households in the model adjust their behavior optimally to the provision of the additional insurance.

The welfare gains of insurance are calculated in terms of the "equivalent compensating variation" in consumption. That is, the welfare calculations ask the following question: What percentage of current lifetime consumption would households be willing to pay in order to be fully insured against a particular source of risk? The metric used for welfare comparisons is expected lifetime utility at time zero. This is the expected lifetime utility right before an individual begins their career and before any uncertainty (other than the household's type) is resolved. This metric is given by:

$\displaystyle W=\mathit{E}_{0}[\sum_{t=1}^{T}\beta^{t-1}\pi_{t}u(c^{\ast}(\Omega_{t}% ))]=\int[\sum_{t=1}^{T}\beta^{t-1}\pi_{t}u(c^{\ast}(\Omega_{t}))]d\Phi,$

(25)

where $\Omega_{t}$ is the state vector, $c^{\ast}(\Omega_{t})$ is the consumption policy function, which prescribes the optimal level of consumption at any given point in the state space (i.e., at any possible contingency that the household may encounter), and $\Phi$ denotes the joint distribution of the random state vector $\Omega=(\Omega_{1},...,\Omega_{T})$ .⁴⁵

6.1.1 Results

Table 4 presents results for the welfare gains of insuring each source of risk for the baseline consumption model. Panel (a) presents adjusted results (the case of actuarially fair insurance), while panel (b) shows unadjusted results. The entries in columns (1), (2), and (3) of panel (a) indicate that the welfare gains of fully insuring disability, health, and unemployment risk are extremely small. According to the table, households are willing to pay no more than 0.04 of $1\%$ of lifetime consumption in exchange for full insurance against these risks. The welfare value of insurance is small even if one does not adjust for the effect of insurance on mean income. As panel (b) shows, the value of insuring disability and health risks in the unadjusted case is still no larger than 0.04 of $1\%$ of lifetime consumption. The value of insuring unemployment in the unadjusted case is 0.62 of $1\%$ of lifetime consumption.

Column (5) displays the results for wage shocks. These shocks are innovations in the hourly wage which are not related to changes in employment status or in employer. As the table shows, households in the baseline model would be willing to pay up to $1.20\%$ of their lifetime consumption in order to be insured against such shocks.

Columns (6), (7), and (8) present the gains of insuring shocks associated with job changes, hours of work, and the residual component of household income. The equivalent compensating variation in these cases is $0.72\%$ , $0.45\%$ , and $2.19\%$ , respectively.⁴⁶ I don't discuss the results for medical expenditures here, as these are preliminary (see discussion in section 2).

6.1.2 Discussion

Overall, the results in Table 4 indicate that the value of insuring most sources of risk in the model is small. Particularly striking is how minuscule consumers' willingness to pay for insurance against disability, health, and unemployment risks turns out to be. It is also remarkable how much more valuable insurance against wage shocks is. These results, however, are consistent with Low, Meghir, and Pistaferri (2006), who study the welfare effects of unemployment and wage shocks, and find that wage risk is important, but that unemployment risk is not.

The shock to the residual component of household income turns out to play a very important role. This is perhaps not surprising, considering that this shock captures all variation in household income which is not explained by earnings, disability, health, or unemployment of the head, and that household income includes spousal labor income and all transfer income.⁴⁷ An important part of this residual component is thus likely to capture factors that are not really risk, but rather reflect choice, such as spousal labor supply. The approach used here does not allow to determine what part of a given shock actually represents risk. It is interesting, nevertheless, that the shock to residual household income turns out to play the largest role of all shocks in the welfare analysis, which suggests that this component constitutes an important part of the shock estimated in simple univariate models of household income, where income is driven by a single shock to the income process.

Regarding the very small welfare value of insuring disability, health, and unemployment risk, it should be stressed again that all insurance considered here is insurance over and above existing insurance provided by government transfers (already included in the household income process), self-insurance provided by saving, and insurance within the family (also included in the household income process). The results from Table 4 thus seem to suggest that existing insurance mechanisms do a good job of protecting households against the sources of risk considered here. They also suggest that even a small deadweight loss created by additional insurance would be sufficient to wipe out much of the gains of such additional insurance.

One important caveat that should be emphasized is that the value of insurance is measured here from an ex-ante point of view, that is, before any uncertainty other than a household's type is realized. Measuring the value of insurance conditional on, for instance, being disabled or unemployed would yield higher benefits of additional insurance.

Still, the value of insuring some of these risks may seem surprisingly low in light of the estimation results, which would appear to imply that their effects are important. In the case of disability, for instance, the estimates presented in Table 2C suggest that becoming disabled has a very strong negative effect on earnings ( enters the equation of log work hours with coefficient $\widehat{\gamma}_{3}^{h}=-0.896$ and the persistent wage equation with coefficient $\widehat{\gamma}_{3}^{w}=-0.280$ ).⁴⁸

However, even if disability has a large effect on income when it occurs, it is still a low-probability event and hence, from an ex-ante point of view, it does not account for much of the variation in lifetime income and does not contribute greatly to income uncertainty. The same is true of unemployment. Health limitations, as measured here, are on the other hand more frequent, but their estimated effect on income is rather small. It should also be noted that the framework used here only considers the effects of disability and health on income and abstracts from direct effects on utility. Such effects are likely to be important for welfare.

One additional reason that helps explain the small value of insurance obtained and which should be mentioned here is that for the broad measure of household income taken from the PSID, income very rarely falls below $\$1,000$ (in year-2000 dollars). Consequently, income shocks in the lifecycle model are discretized in such a way that household income in the model can never fall below $\$1,000$ . This is important for welfare because under constant relative risk aversion (CRRA) utility the really painful events occur when consumption drops to extremely low levels. The presence of an income floor effectively provides a consumption floor, ruling out situations where consumption is near zero. The view taken here is that the floor of $\$1,000$ per year used in the calculations is very conservative, given that people have access to a wide array of transfers. Thus, a more precise way to interpret the results in this paper may be that, if one is willing to assume that constant relative risk aversion utility is a reasonable representation of preferences and that existing safety nets provide a minimum level of income and consumption as low as $\$1,000$ a year, then the value of insuring risk over and above already existing insurance is small.

It may also be worth mentioning that ignoring some margins of choice in the model, such as labor supply, has an ambiguous impact on the value of insurance. In the simulated model, treating labor supply as fixed forces consumption to take on the full effects of the shocks, which thus turn out to be more painful than they would otherwise be. However, keeping labor supplied fixed in estimation of the income process also affects the estimates of risk. A given observed variation in income may reflect demand shocks that are partially absorbed and offset by an adjustment in labor supply, and this adjustment has a welfare cost. Thus, allowing for flexible labor supply in the estimation and in the simulation could make the results change either way.

Finally, Table 7A presents results obtained under alternative assumptions regarding the household's degree of risk aversion and patience. Panel (a) (second row) displays results for households with a coefficient of relative risk aversion of 5.0.⁴⁹ As should be expected, the higher degree of risk aversion increases the value of insurance for all sources of risk. However, the increase in the coefficient of relative risk aversion to a value as high as 5.0 does not change any of the main results or conclusions drawn from the analysis above. In particular, the value of insuring disability, health, and unemployment risk remains minuscule, and the relative importance of the various sources of risk does not change. Panel (b) displays results for different values of the discount factor. The numbers in the table suggest that the importance of the residual component of household income increases as impatience increases, while the wage component appears to become less important. One possible reason for this is that the wage affects social security benefits, and thus may affect future periods more than the residual component of household income does. Most importantly, the results regarding disability, health, and unemployment do not change significantly. Overall, we conclude that the most important features of the results are robust to alternative, empirically plausible assumptions about household preferences.

6.2 Precautionary Saving

This section investigates the contribution of the various sources of uncertainty to the accumulation of precautionary savings. Figure 6 displays the mean level of assets held by simulated households, by year of potential experience. The upper curve represents mean asset holdings under the full-uncertainty scenario, while the lower curve displays mean asset holdings under no uncertainty. The mean profile of net income is identical under both scenarios. The difference between the two curves is mean precautionary wealth, that is, the mean level of assets held only because of the presence of uncertainty. Figure 7 displays this difference.⁵⁰

Figure 8 displays mean precautionary wealth as a fraction of total wealth. The figure shows that precautionary savings make up the entirety of savings for the first 11-12 years of a worker's career. Workers start saving for lifecycle reasons (retirement) only after this point. Even 20 years into a worker's career, precautionary wealth continues to make up 50% or more of total savings. The exact point at which retirement saving begins to matter will depend on how substantial the drop in income at retirement is. The current version of the lifecycle model analyzed here does not account for defined benefit pensions or social security benefits received by family members other than the household head. As a result, income drops significantly at retirement and workers start saving for retirement relatively early in their career.

Table 5 decomposes precautionary wealth into components attributable to various sources of risk. Specifically, the table calculates the difference between mean precautionary wealth under full uncertainty and mean precautionary wealth under a scenario in which one particular source of risk is fully insured, and then expresses this difference as a percentage of mean precautionary wealth. Contributions are normalized to sum to 100% of precautionary wealth⁵¹. The results in the table show that the largest contribution by far is made by shocks to the residual component of household income ( $43\%$ of precautionary wealth). Wage shocks are also very important, contributing almost $20\%$ of precautionary wealth. Together, these two sources thus account for about $63\%$ . The individual contribution of all other shocks is below $20\%$ . Among these, job-mobility shocks make the largest contribution ( $9.34\%$ ) and disability shocks the smallest ( $2.34\%$ ).

Table 7B presents results from a similar decomposition under alternative assumptions about the coefficient of relative risk aversion and discount factor. As above, Panel (a) considers households with a coefficient of risk aversion of 5.0, while Panel (b) considers households with an increasing degree of impatience. As the numbers in the table show, the relative importance of the various sources of risk for the accumulation of precautionary saving does not appear to be sensitive to alternative assumptions about risk aversion and patience. More generally, the results for precautionary saving seem consistent with the welfare results from the previous section, and the general discussion presented in that section also applies here.

7 Conclusions and Research Agenda

This paper uses a lifecycle consumption model to quantify the effects of a number of sources of income risk on household welfare and precautionary saving. The model includes income shocks associated with disability, health, unemployment, job changes, wages, work hours, and a residual component of household income. I estimate the processes driving the evolution of these variables using PSID data, accounting for permanent unobserved heterogeneity -which is assumed to be known at the beginning of a worker's career- and a rich set of dynamic interactions among the variables. I then use the consumption model to quantify the welfare value of providing full, actuarially fair insurance against each source of risk and measure the contribution of each shock to the accumulation of precautionary savings.

The main findings are that: (i) the value of insuring disability, health, and unemployment shocks is extremely small (well below 1/10 of 1% of lifetime consumption in the baseline model); (ii) the gains from insuring shocks to the wage and to the residual component of household income are significantly larger (above 1% and 2% of lifetime consumption, respectively); and (iii) the latter two shocks account for more than 60% of precautionary wealth.

The insurance evaluated in this paper is insurance over and above existing insurance provided by government transfers, self-insurance through saving, and insurance within the family, all of which are already captured in the baseline model. The results thus seem to suggest that existing insurance mechanisms do a good job of protecting households against the sources of risk considered here. They also suggest that even a small deadweight loss created by additional insurance would be sufficient to wipe out much of the gains of such additional insurance.

It should be noted, however, that the value of insurance is measured from an ex-ante point of view, that is, before any uncertainty other than a household's type is realized. Measuring the value of insurance conditional on, for instance, being disabled or unemployed should yield higher benefits. Even more importantly, the model analyzed in this paper corresponds to households who are at the mean of the distribution of the permanent unobserved components. Although the framework developed here permits analyzing households over the entire distribution of these components, this is left for future research because of the computational costs of these calculations. It is important to bear in mind, however, that a clear understanding of the role of heterogeneity is required in order to draw definitive conclusions.

An interesting question that arises from the results presented here regards the value and relative role of different existing insurance mechanisms. For instance, to what extent are transfers from disability insurance and unemployment insurance responsible for the small welfare effects of disability and unemployment risk? This particular question may be addressed using this paper's framework in the following way: (i) remove payments received from disability insurance (alternatively, unemployment insurance) from the income data constructed from the PSID; (ii) estimate the household income equation presented in section 4 using the modified household income data; (iii) solve the lifecycle consumption model using the new estimated income process and perform a welfare analysis. An analysis of the role of these and other sources of insurance is left for future research.

One potentially important source of risk that is only partially addressed in this paper is the risk associated with catastrophic medical-expenditure shocks in old age. As discussed earlier, the treatment in this paper does not allow medical-expenditure shocks to wipe out a household's accumulated wealth. Some studies, including Palumbo (1999) and De Nardi, French, and Jones (2006), suggest that the risk of catastrophic medical expenditures may be important for saving behavior and welfare. A more flexible treatment of medical expenditures and their effects on accumulated wealth will be pursued in future work.

8 Appendix 1: Definition of PSID Variables

Potential Experience: Potential labor market experience is defined as 10)-5 where is years of education. Labor market experience obtained with less than 10 years of education (which is unusual in the data and typically corresponds to very young individuals) is not counted as work experience.

Employment Status: The employment indicator is constructed from the reported employment status of the head of household at the survey date. The "employment status" PSID variable has eight possible categories: (1) working now; (2) only temporarily laid off, sick leave or maternity leave; (3) looking for work, unemployed; (4) retired; (5) permanently disabled; temporarily disabled; (6) keeping house; (7) student; (8) other; "workfare"; in prison or jail. Indicator is set to 1 for categories (1) and (2); it is set to 0 otherwise.

Disability: The disability indicator is also based on reported employment status at the survey date. Indicator is set to 1 whenever employment status is (5) and it is set to 0 otherwise.

Health Limitations: The health limitations indicator is constructed from the survey question: "Do you have any physical or nervous condition that limits the type of work or the amount of work you can do?"Indictor is set to 1 when a respondent answers "yes" to the above question, and it is set to 0 otherwise.

Wage: For hourly workers, the wage variable used is the reported hourly wage at the survey date. For salaried workers, the variable is constructed from reported weekly, monthly, or yearly salary, divided by an appropriate standard number of hours. The measure used here further accounts for the fact that the PSID variable is capped at $9.98 per hour prior to 1978. This is done by replacing capped values for the years 1975-1977 with predicted values constructed by Altonji and Williams (2005). Predicted values are based on a regression of the log of the reported wage on a constant and the log of annual earnings divided by annual hours using the sample of individuals in 1978 for whom the reported wage exceeds $9.98.

Hours: The hours variable is the reported total annual hours of work (in all jobs).

Household income: Household income is defined as the sum of (i) total labor income of the head; (ii) total labor income of the wife; (iii) total transfer income of the head and wife; (iv) taxable income of others; and (v) total transfers of others. In most waves, the PSID does not separately report labor and asset income of other family unit members.

Out-of-Pocket Medical Expenditures: Total out-of-pocket medical expenditures are the sum of out-of-pocket payments for (i) nursing home and hospital bills; (ii) doctor, outpatient surgery, dental bills; and (iii) prescriptions, in-home medical care, special facilities, and other services. The payments refer to the two-year period prior to the survey year. Detailed medical expenditures data are provided by the PSID starting with the 1999 wave.

9 Appendix 2: Determination of Social Security Benefits

This appendix describes the determination of the level of social security benefits. Social security benefits in the model are determined in the last year of work according to the formula:

$\displaystyle S_{t+1}=PIA(ALE(D_{t},H_{t},E_{t},p_{t}^{w},p_{t}^{y}))$

where stands for principal insurance amount and stands for average lifetime earnings. Households are assumed to receive a level of benefits equal to their . and are determined as follows.

Average Lifetime Earnings:

In the last working year, the state variables are used to predict average lifetime earnings according to a forecasting equation. The coefficients of the forecasting equation are determined by simulations of the income (earnings) model using the following procedure:

1. Use the model of disability, health, employment, job changes, wages and hours (which imply earnings) to simulate a large number of careers.

2. Use the simulated earnings data to compute average lifetime earnings for each simulated career as calculated by the Social Security Administration. In particular, yearly earnings are censored from above to the maximum yearly earnings subject to the social security tax. In 1996, for instance, the maximum taxable yearly amount was $62,700. are then computed as the average of such censored earnings over the 35 years of highest earnings.

3. Regress against all (simulated) variables that would be known to the agent in the last year of career in the lifecycle model. These include all state variables in the last working year (disability, health, employment, persistent wage, persistent household income) as well as all permanent heterogeneity components (which define the household type). This regression uses a flexible specification which includes a number of higher-order terms and interactions among the different variables. Several alternatives specifications were tried and the regression with the best fit was selected as the forecasting equation. Estimation results for this forecasting regression are presented in Table 6. Notice in particular the high $R^{2}$ in the regression (0.88).

Principal Insurance Amount

Once average lifetime earnings have been determined, the principal insurance amount is determined by the rules of the Social Security Administration. I use "bend points" for the year 1996 (the last year of the sample used in estimation). The 1996 monthly "bend points", in current dollars, are $\$437$ and $\$2,635$ . The corresponding yearly bend points in thousands of year-2000 dollars are $b_{1}=5.606$ and $b_{2}=33.801$ . The , in thousands of year-2000 dollars, is then calculated as

$\displaystyle PIA=0.90\cdot\min\{ALE,b_{1}\}+0.32\cdot\min\{\max\{ALE-b_{1},0\},b_{2}% -b_{1}\}+0.15\cdot\max\{ALE-b_{2},0\}.$

10 Appendix 3: Further Details of Model Specification and Estimation - Employment, Job Changes, Wage, Hours, and Household Income

This appendix provides some additional details about the joint model of employment, job changes, wage rate, work hours, and household income, its estimation, and its relation to the income process in the lifecycle model.

First Stage Regression and Household Income in Levels

Recall that log household income is given by

$\displaystyle \ln income_{t+1}=\beta^{y}X_{t+1}^{y}+y_{t+1}.$

Let $X_{t+1}^{y}=[X_{1,t+1}^{y},X_{2,t+1}^{y},X_{3,t+1}^{y}]$ be a partition of $X_{t+1}^{y}$ where (i) $X_{1,t+1}^{y}$ contains a quadratic polynomial in age (of the head); (ii) $X_{2,t+1}^{y}$ contains years of education of the head and wife as well as variables describing household size and composition (number of major adults, number of additional adults, number of children under 6, and number of children between 6 and 18); and (iii) $X_{3,t+1}^{y}$ contains year indicators and race indicators for black and other nonwhite. Vector $\beta^{y}=[\beta_{1}^{y},\beta_{2}^{y},\beta_{3}^{y}]$ is estimated in a first-stage least-squares regression. Variation in income due to $[X_{2,t+1}^{y},X_{3,t+1}^{y}]$ is then removed from the data prior to estimation by GII (where the coefficients of component $y_{t+1}$ in equation (19) are estimated). The level of household nonasset income in the lifecycle model $Y_{t+1}$ is determined as $\hat{Y}_{t+1}=\exp(\ln \widehat{income}_{t+1})=\exp(\hat{\beta}_{1}^{y}X_{1,t+1}^{y}+\hat{\beta}% _{2}^{y}\overline{X}_{2,t+1}^{y}+\hat{y}_{t+1})$ , where $\overline{X}% _{2,t+1}^{y}$ is the average of vector $X_{2,t+1}^{y}$ in the PSID sample and where $\hat{y}_{t+1}$ is the predicted value of component $y_{t+1}$ .

Initial Conditions

Initial conditions in employment, job changes, the wage, hours, and household income are explicitly modeled and estimated. For a discussion of related models and further details about estimation, see Altonji, Smith, and Vidangos (2008).

Employment: Initial employment status is assumed to be determined by $\mathit{ }E_{1}=I[\hat{b}_{0}+\delta_{\mu}^{EE}\mu+\delta _{\eta}^{EE}\eta+\varepsilon_{1}^{EE}>0]$ where $\hat{b}_{0}\equiv\hat{b}% _{0}^{\ast}\cdot\hat{\sigma}_{E1}$ , $\hat{\sigma}_{E1}\equiv\sqrt{(\hat {\delta}_{\mu}^{EE})^{2}+(\hat{\delta}_{\eta}^{EE})^{2}+1}$ , $\delta_{\mu }^{EE}\mu$ and $\delta_{\eta}^{EE}$ are defined as before, $\varepsilon _{1}^{EE}\sim N(0,1)$ , and $\hat{b}_{0}^{\ast}$ is the coefficient estimate from a Probit of $E_{t}$ on a constant estimated on PSID data for $t\leq3$ . I use the first three years here rather than just the first year because there are relatively few observations when .

Wages: The initial condition of the persistent wage component is modeled as $p_{1}^{w}=\theta_{w}\zeta^{w}+u_{w1},$ where $\theta_{w}$ is a free parameter estimated with GII and $u_{w1}\sim N(0,\sigma_{w1}^{2}),$ where $\sigma_{w1}^{2}$ is set such that $Var(\theta_{w}\zeta^{w}+u_{w1})$ equals the variance of the residual of regression for low levels of .

Household Income: The initial condition of the residual component of household income is determined as $p_{1}^{y}=\theta_{y}\zeta^{y}+u_{y1},$ where $\theta_{y}$ is a free parameter estimated with GII and $u_{y1}\sim N(0,\sigma_{y1}^{2}),$ where $\sigma_{y1}^{2}$ is set such that $Var(\theta_{y}\zeta^{y}+u_{y1})$ equals the variance of the residual of regression for low levels of .

Measurement Error

Estimation accounts for measurement error in wages, hours, earnings, and household income. The treatment of measurement error here follows the treatment in Altonji, Smith, and Vidangos (2008). For household income, measurement error is set to account for 25% of the variance of the first difference in observed household income, after accounting for the effect of measurement error in earnings. Since earnings are a component of household income, one additionally needs to account for the effect of measurement error in earnings on observed household income. Altonji, Smith, and Vidangos (2008) shows that there is a residual component in earnings which is not accounted for by wages and hours. This component is assumed here to consist entirely of measurement error. The system estimated by generalized indirect inference includes an auxiliary equation of earnings in order to identify this component. Estimates of the household income process account for the effect of this measurement error component.

11 Appendix 4: Estimation Mechanics - GII

The equations that determine the evolution of employment, job changes, wage, hours, and household income are estimated by generalized indirect inference (GII). The implementation of GII used here is akin to that used in Altonji, Smith, and Vidangos (2008), which provides a detailed discussion. This appendix gives some further details of the implementation used in this paper. The auxiliary model consists of a system of seemingly unrelated regressions (SUR) with 8 equations and 27 covariates that are common to all 8 equations. The model is implemented under the assumption that the errors follow a multivariate normal distribution with unrestricted covariance matrix. The auxiliary model effectively used⁵² may be written as

$\displaystyle y_{it}=Z_{it}\Pi+u_{it};$ $\displaystyle u_{it}\sim N(0,\Sigma);{ }u_{it}$ iid over $\displaystyle i$ and $\displaystyle t,\qquad$

(26)

where

$\displaystyle y_{it}$	$\displaystyle =[E_{it}E_{i,t-1},E_{it}U_{i,t-1},J_{it}E_{it}E_{i,t-1},$	(27)
	$\displaystyle w_{it},h_{it},e_{it},\ln(1+w_{it}{}^{2}),y_{it}]^{\prime},\qquad$

and

$\displaystyle Z_{it}=[cons,(t-1),(t-1)^{2},ED_{i,t-1},UD_{i,t-1},JD_{i,t-1},$	(28)
$\displaystyle E_{i,t-1}E_{i,t-2},E_{i,t-2}E_{i,t-3},$
$\displaystyle E_{i,t-1}U_{i,t-2},E_{i,t-2}U_{i,t-3},$
$\displaystyle J_{i,t-1}\cdot E_{i,t-1}\cdot E_{i,t-2},J_{i,t-2}\cdot E_{i,t-2}\cdot E_{i,t-3},$
$\displaystyle w_{i,t-1},w_{i,t-2},h_{i,t-1},h_{i,t-2},e_{i,t-1},e_{i,t-2},y_{i,t-1}% ,y_{i,t-2},$
$\displaystyle w_{i,t-1}(t-1),w_{i,t-1}(t-1)^{2},w_{i,t-1}J_{it}$
$\displaystyle D_{it},D_{i,t-1},H_{it},H_{i,t-1}]^{\prime}.$

Above, $U_{it}$ is an indicator of unemployment defined as $U_{it}% =1-E_{it}-D_{it}$ . All other variables are defined as before.

Bibliography

Abowd, J.M. and Card, D.E. , (1987)

"Intertemporal Labor Supply and Long-Term Employment Contracts", American Economic Review, 77(1), 50-68.

Abowd, J.M. and Card, D.E. , (1989)

"On the Covariance Structure of Hours and Earnings Changes", Econometrica, 57(2), 411-445.

Aiyagari, S.R. , (1994)

"Uninsured Idiosyncratic Risk and Aggregate Saving", Quarterly Journal of Economics 109(3), 659-684.

Altonji, J.G., Martins, A.P., and Siow, A. , (2002)

"Dynamic Factor Models of Wages, Hours, and Earnings", Research in Economics 56(1), 3-59.

Altonji, J.G. and Segal, L.M. , (1996)

"Small Sample Bias in GMM Estimation of Covariance Structures", Journal of Business and Economic Statistics, 14(3), 353-366.

Altonji, J.G., Smith, A.A., Jr., and Vidangos, I. , (2008)

"Modeling Earnings Dynamics", unpublished manuscript, Yale University and Federal Reserve Board.

Altonji, J.G. and Williams, N. , (2005)

"Do Wages Rise With Job Seniority? A Reassessment", Industrial and Labor Relations Review, 58(3), 370-397.

Attanasio, O.P., Banks, J., Meghir, C., and Weber, G. , (1999)

"Humps and Bumps in Lifetime Consumption", Journal of Business and Economic Statistics, 17(1), 22-35.

Baker, M. , (1997)

"Growth-rate heterogeneity and the covariance structure of life cycle earnings", Journal of Labour Economics, 15(2), 338-375.

Baker, M. and Solon, G. , (2003)

"Earnings Dynamics and Inequality among Canadian Men, 1976-1992: Evidence from Longitudinal Income Tax Records", Journal of Labor Economics, 21(2), 289-321.

Blundell, R. and Pistaferri, L. , (2003)

"Income Volatility and Household Consumption: The Impact of Food Assistance Programs", Journal of Human Resources, 38:S, 1032-1050.

Blundell, R., Pistaferri, L., and Preston, I. , (2008)

"Consumption Inequality and Partial Insurance", American Economic Review, forthcoming.

Blundell, R. and Preston, I. , (1998)

"Consumption Inequality and Income Uncertainty", Quarterly Journal of Economics, 113(2), 603-640.

Browning, M. and Crossley, T.F. , (2001)

"Unemployment Insurance Benefit Levels and Consumption Changes,"Journal of Public Economics, 80(1), 1-23.

Burkhauser, R.V., Daly, M.C., Houtenville, A.J., and Nargis, N. , (2002)

"Self-Reported Work Limitation Data: What They Can and Cannot Tell Us", Demography, 39(3), 541-555.

Cagetti, M., (2003)

"Wealth Accumulation Over the Life Cycle and Precautionary Savings", Journal of Business and Economic Statistics, 21(3), 339-353.

Castañeda, A., Díaz-Giménez, J., and Ríos-Rull V. , (2003)

"Accounting for the U.S. Earnings and Wealth Inequality", Journal of Political Economy, 111(4), 818-857.

Carroll, C. , (2001)

"A Theory of the Consumption Function, with and without Liquidity Constraints", Journal of Economic Perspectives, 15(3), 23-45.

Carroll, C. , (1997)

"Buffer-Stock Saving and the Life Cycle/Permanent Income Hypothesis", Quarterly Journal of Economics, 112(1), 1-55.

Carroll, C. , (1992)

"The Buffer-Stock Theory of Saving: Some Macroeconomic Evidence", Brookings Papers on Economic Activity, 1992(2), 61-156.

Carroll, C. and Samwick, A. , (1998)

"How Important is Precautionary Saving?", Review of Economics and Statistics, 1992(2), 61-156.

Center for Disease Control and Prevention. , 2002

Life Tables. U.S. Department of Health and Human Services. Available at (http://www.cdc.gov/nchs/data/nvsr/nvsr53/nvsr53_06.pdf).

Chetty, R. , (2006)

"A New Method of Estimating Risk Aversion", American Economic Review, 96(5), 1821-1834.

Cullen, J.B. and Gruber, J. , (2000)

"Does Unemployment Insurance Crowd Out Spousal Labor Supply?, Journal of Labor Economics 18(3), 546-72.

Cunha, F., Heckman, J.J., and Navarro, S. , (2005)

"Separating Uncertainty from Heterogeneity in Life Cycle Earnings, The 2004 Hicks Lecture", Oxford Economic Papers 57(2), 191-261.

Cunha, F. and Heckman, J.J. , (2006)

"Identifying and Estimating the Distributions of Ex Post and Ex Ante Returns to Schooling: A Survey of Recent Developments", unpublished manuscript, University of Chicago.

Daly, M.C. and Burkhauser, R.V. , (2003)

"The Supplemental Security Income Program"in Means-Tested Programs in the United States, edited by R. Moffitt. National Bureau of Economic Research and University of Chicago Press: Chicago, IL.

Daly, M.C. and Houtenville, A. , (2003)

"Employment Declines Among People with Disabilities"in The Decline in Employment of People with Disabilities: A Policy Puzzle, edited by R. V. Burkhauser and D. Stapleton. Upjohn Press, March 2003.

Deaton, A. , (1991)

"Saving and Liquidity Constraints", Econometrica, 59(5), 1221-1248.

De Nardi, M., French, E., and Jones, J. , (2006)

"Differential Mortality, Uncertain Medical Expenses, and the Saving of Elderly Singles", Federal Reserve Bank of Chicago WP 2005-13.

Dynan, K.E., Skinner, J., and Zeldes, S.P. , (2004)

"Do the Rich Save More?", Journal of Political Economy, 112(2), 397-444.

Dynarski, S. and Gruber, J. , (1997)

"Can Families Smooth Variable Earnings?", Brookings Papers on Economic Activity, 1, 229-303.

Engen, E.M., Gale, W.G., and Uccello, C.E. , (1999)

"The Adequacy of Household Saving", Brookings Papers on Economic Activity, 1999:2, 65-165.

Engen, E.M., and Gale, W.G. , (1993)

"IRAs and Saving in a Stochastic Life-Cycle Model", mimeo, Brookings Institution.

Engen, E.M., Gale, W.G., and Scholz, J.K. , (1994)

"Do Saving Incentives Work?", Brookings Papers on Economic Activity, 1994:1, 85-151.

Geweke, J. and Keane, M. , (2000)

"An empirical analysis of earnings dynamics among men in the PSID: 1968-1989", Journal of Econometrics, 96, 293-356.

Gourieroux, C., Monfort, A., and Renault, E. , (1993)

"Indirect Inference", Journal of Applied Econometrics, 8, S85-S118.

Gourinchas, P.O., and Parker, J. , (2002)

"Consumption over the Life Cycle", Econometrica, 70(1) 47-89.

Gouveia, M. and Strauss, R. , (1994)

"Effective Federal Individual Income Tax Functions: An Exploratory Empirical Analysis", National Tax Journal 47(2), 317-339.

Gouveia, M. and Strauss, R. , (2000)

"Effective Tax Functions for the U.S. Individual Income Tax: 1966-89", Proceedings of the 92nd Annual Conference on Taxation, Atlanta, October 24-26. Washington, DC: National Tax Association.

Gruber, J. , (1997)

"The Consumption Smoothing Benefits of Unemployment Insurance", American Economic Review, 87(1) 192-205.

Gruber, J. , (1998)

"Unemployment Insurance, Consumption Smoothing, and Private Insurance: Evidence from the PSID and CEX", Research in Employment Policy, 1, 3-32.

Gruber, J. and Yelowitz, A. , (1999)

"Public Health Insurance and Private Savings", Journal of Political Economy, 107(6), 1249-74.

Guvenen, F. , (2006)

"Learning Your Earning: Are Labor Income Shocks Really Very Persistent?", American Economic Review, 97(3), 687-712.

Haider, S.J. , (2001)

"Earnings Instability and Earnings Inequality of Males in the United States: 1967-1991", Journal of Labor Economics, 19(4), 799-836.

Hall, R.E. and Mishkin, F. , (1982)

"The Sensitivity of Consumption to Transitory Income: Estimates from Panel Data on Households", Econometrica, 50(2), 461-481.

Hause, J.C. , (1980)

"The fine structure of earnings and the on-the-job training hypothesis", Econometrica, 48(4), 1013-1029.

Heaton, J. and Lucas, D.J. , (1996)

"Evaluating the effects of incomplete markets on risk sharing and asset pricing", Journal of Political Economy, 104(3), 443-487.

Heckman, J. J. , (1981)

"The Incidental Parameters Problem and the Problem of Initial Conditions in Estimating a Discrete Time - Discrete Data Stochastic Process", in Structural Analysis of Discrete Data with Econometric Applications, edited by C.F. Manski and D. McFadden, pp. 179-95. Cambridge: MIT Press.

Hubbard, G., Skinner, J., and Zeldes, S. , (1994)

"The importance of precautionary motives in explaining individual and aggregate saving", Carnegie-Rochester Conference Series on Public Policy, 40, 59-125.

Hubbard, G., Skinner, J., and Zeldes, S. , (1995)

"Precautionary Saving and Social Insurance", Journal of Political Economy, 103(2), 360-399.

Huggett, M. , (1996)

"Wealth Distribution in Life-Cycle Economies", Journal of Monetary Economics, 38(3), 469-494.

Hurst, E. and Stafford, F. , (2004),

"Home is Where the Equity Is: Liquidity Constraints, Refinancing and Consumption,"Journal of Money, Credit and Banking, 36(6), 985-1014.

Jacobson, L., LaLonde, R., and Sullivan, D. , (1993)

"Earnings Losses of Displaced Workers", American Economic Review, 83(4), 685-709.

Keane, M. and Smith Jr., A.A. , (2003)

"Generalized Indirect Inference for Discrete Choice Models", unpublished manuscript, Yale University.

Kniesner, T.J. and Ziliak, J.P. , (2002)

"Tax Reform and Automatic Stabilization", American Economic Review, 92(3), 590-612.

Krusell, P. and Smith Jr., A.A. , (1997)

"Income and Wealth Heterogeneity, Portfolio Selection, and Equilibrium Asset Returns", Macroeconomic Dynamics, 1, 387-422.

Krusell, P. and Smith Jr., A.A. , (1998)

"Income and Wealth Heterogeneity in the Macroeconomy", Journal of Political Economy, 106(5), 867-896.

Lillard, L. and Weiss, Y. , (1979)

"Components of variation in panel earnings data: American scientists 1960-1970", Econometrica, 47(2), 437-454.

Lillard, L. and Willis, R. , (1978)

"Dynamic aspects of earning mobility", Econometrica, 46(5), 985-1012.

Low, H., Meghir, C., and Pistaferri, L. , (2006)

"Wage Risk and Employment Risk over the Life Cycle", unpublished manuscript, Cambridge University, University College London, and Stanford University.

MaCurdy, T.E. , (1982)

"The use of time series processes to model the error structure of earnings in a longitudinal data analysis", Journal of Econometrics, 18, 83-114.

Meghir, C. and Pistaferri, L. , (2004)

"Income variance dynamics and heterogeneity", Econometrica, 72(1), 1-32.

Moffitt, R. , (2002)

"Documentation for Moffitt Welfare Benefits File", manuscript (February 22), Johns Hopkins University, http://www.econ.jhu.edu/People/Moffitt/DataSets.html.

Palumbo, M.G. , (1999)

"Uncertain Medical Expenses and Precautionary Saving Near the End of the Life Cycle", Review of Economic Studies, 66 (April), 395-421.

Scholz, J.K., Seshadri, A., and Khitatrakun, S. , (2006)

"Are Americans Saving "Optimally" for Retirement?", Journal of Political Economy, 114(4), 607-643.

Smith, A.A., Jr. , (1990)

"Three Essays on the Solution and Estimation of Dynamic Macroeconomic Models", Ph.D. thesis (Duke University).

Smith, A.A., Jr. , (1993)

"Estimating Nonlinear Time-Series Models using Simulated Vector Autoregressions", Journal of Applied Econometrics, 8, S63-S84.

Stephens, M., Jr. , (2002)

"Worker Displacement and the Added Worker Effect", Journal of Labor Economics, 20(3), 504-37.

Storesletten, K., Telmer, C., and Yaron, A. (2004a). "Consumption and Risk Sharing Over the Life Cycle", Journal of Monetary Economics, 51(3), 609-633.

Storesletten, K., Telmer, C., and Yaron, A. (2004b). "Cyclical Dynamics in Idiosyncratic Labor Market Risk", Journal of Political Economy, 112(3), 695-717.

Storesletten, K., Telmer, C., and Yaron, A. , (2007)

"Asset Pricing with Idiosyncratic Risk and Overlapping Generations", Review of Economic Dynamics 10(4), 519-548.

Sullivan, J.X. , (2008)

"Borrowing During Unemployment: Unsecured Debt as a Safety Net", Journal of Human Resources, forthcoming.

Topel, R. , (1991)

"Specific Capital, Mobility, and Wages: Wages Rise with Job Seniority", Journal of Political Economy, 99(1), 145-176.

Vidangos, I. , (2008)

"Fluctuations in Individual Labor Income: A Panel VAR Analysis", unpublished manuscript, Federal Reserve Board.

Wooldridge, J.M., (2005),

"Simple Solutions to the Initial Conditions Problem for Dynamic, Nonlinear Panel Data Models with Unobserved Heterogeneity", Journal of Applied Econometrics, 20, 39-54.

Table 1A Descriptive Statistics - Disability and Health Samples.

	All t	1 $\le$ t $\le$ 10	11 $\le$ t $\le$ 20	21 $\le$ t $\le$ 30	31 $\le$ t $\le$ 40	41 $\le$ t $\le$ 50	51 $\le$ t $\le$ 60	61 $\le$ t $\le$ 65
Disability: Obs.	76,075	15,950	28,908	17,234	9,833	4,150
Disability: Mean	0.020	0.002	0.009	0.025	0.045	0.095
Health: Obs.	88,928	17,376	30,009	18,067	11,039	8,230	3,736	471
Health: Mean	0.137	0.053	0.083	0.128	0.190	0.316	0.418	0.495

The table displays the number of observations and mean of the disability and health limitations indicator, by cells of potential experience. All cells contain ten years except for the last one, which contains only 5. The statistics displayed correspond to the samples used in estimation of the disability and health models, respectively. The disability sample excludes retired individuals, and all individuals above 64 years of age. After this restriction, the maximum level of potential experience in the sample is 49. All variables are constructed from the PSID.

Table 1B Descriptive Statistics - Employment, Job Changes, Wage, Hours, and Household Income.

Variable	Obs.	Mean	StDev	Min	Max
E $_{t}$	41,840	0.94	0.24	0	1
J $_{t}$	41,840	0.09	0.28	0	1
wage $_{t}$	39,337	16.80	9.07	3.50	145.20
hours $_{t}$	41,840	2101	646	0	4000
earnings $_{t}$	41,840	38.84	25.43	0	785.83
income $_{t}$ (raw)	41,840	56.77	33.11	0	809.75
income $_{t}$ (predicted)	41,840	48.77	24.20	0.65	618.53

The table presents descriptive statistics for variables in the PSID sample used in the estimation of the joint model of employment, job changes, wage, hours, and household income. "Predicted" household income is the level of household income predicted for a household of the average size and composition in the PSID sample. This is the household income variable used in estimation (see Appendix 3).

Table 1C.1 Descriptive Statistics - Medical Expenditures.

Obs.	Mean	St. Dev.	Min	Max
2,831	3.25	10.76	0.00	317.47

The table displays descriptive statistics for reported out-of-pocket medical expenditures in the 1999, 2001, and 2003 PSID waves. Expenditures refer to total outlays over the two calendar years preceding the survey year and are measured in thousands of year-2000 dollars. The sample was restricted to individuals with more than 43 years of potential experience.

Table 1C.2 Descriptive Statistics - Medical Expenditures.

Percentiles: 1%	Percentiles: 5%	Percentiles: 10%	Percentiles: 25%	Percentiles: 50%	Percentiles: 75%	Percentiles: 90%	Percentiles: 95%	Percentiles: 99%
0.00	0.00	0.00	0.25	1.10	2.92	6.47	10.21	38.63

Table 2A Point Estimates and Standard Errors - Disability Indicator (D $_{t+1}$ ).

Variable	cons	t+1	(t+1)²/100	D $_{t}$	H $_{t}$	$\zeta$ $^{D}$
Parameter	$\gamma$ $^{D}$ $_{0}$	$\gamma$ $^{D}$ $_{1}$	$\gamma$ $^{D}$ $_{2}$	$\gamma$ $^{D}$ $_{4}$	$\gamma$ $^{D}$ $_{5}$	$\sigma$ $_{\zeta D }$
Estimate	-3.6580	0.0377	-0.0195	2.2043	0.9579	0.4748
SE	(0.1197)	(0.0081)	(0.0146)	(0.0719)	(0.0423)	(0.0497)
Obs.	76,075

The table displays parameter estimates and standard errors of the disability indicator equation. All parameters were estimated by maximum likelihood. The person-specific permanent unobserved component was integrated out of the conditional likelihood function by numerical quadrature. The sample excludes retired individuals, and individuals above 64 years of age.

Table 2B Point Estimates and Standard Errors - Health Limitations Indicator (H $_{t+1}$ ).

Variable	cons	t+1	(t+1)²/100	H $_{t}$	$\zeta$ $^{H}$
Parameter	$\gamma$ $^{H}$ $_{0}$	$\gamma$ $^{H}$ $_{1}$	$\gamma$ $^{H}$ $_{2}$	$\gamma$ $^{H}$ $_{4}$	$\sigma$ $_{\zeta H }$
Estimate	-2.6763	0.0267	0.0203	1.1244	0.9657
SE	(0.0449)	(0.0029)	(0.0048)	(0.0203)	(0.0198)
Obs.	88,928

The table displays parameter estimates and standard errors for the health limitations indicator equation. All parameters were estimated by maximum likelihood. The person-specific permanent unobserved component was integrated out of the conditional likelihood function by numerical quadrature. The sample was restricted to observations where the disability indicator is zero.

Table 2C Point Estimates and Standard Errors - Employment, Job Mobility, Wage, Hours, and Household Income.

Panel (a) - Employment-to-Employment Transitions( $E_{t+1}$ )

Variable	cons	t	t²/100	H $_{t+1}$	ED $_{t}$	$\mu$	$\eta$
Parameter	$\gamma$ $^{EE}$ $_{0}$	$\gamma$ $^{EE}$ $_{1}$	$\gamma$ $^{EE}$ $_{2}$	$\gamma$ $^{EE}$ $_{3}$	$\gamma$ $^{EE}$ $_{4}$	$\delta$ $^{EE}$ $_{\mu }$	$\delta$ $^{EE}$ $_{\eta }$
Estimate	2.3858	0.0327	-0.0482	-0.0622	-0.0337	0.8720	-0.6124
SE	(0.0682)	(0.0089)	(0.0206)	(0.0045)	(0.0595)	(0.0568)	(0.0514)

The table displays point estimates for the Employment, Job Mobility, Wage, Hours, and Household Income equations. All equations were estimated jointly by generalized indirect inference. Parametric bootstrap standard errors are in parentheses. When parameterizing the employment and job-change equations in the lifecycle model, the duration variables EDt, UDt, and JDt are evaluated at their sample mean (by year of potential experience).

Table 2C: Point Estimates and Standard Errors - Employment, Job Mobility, Wage, Hours, and Household Income.

Panel (b) - Unemployment-to-Employment Transitions (E $_{t+1}$ )

Variable	cons	t	t²/100	H $_{t+1}$	UD $_{t}$	$\mu$	$\eta$
Parameter	$\gamma$ $^{UE}$ $_{0}$	$\gamma$ $^{UE}$ $_{1}$	$\gamma$ $^{UE}$ $_{2}$	$\gamma$ $^{UE}$ $_{3}$	$\gamma$ $^{UE}$ $_{4}$	$\delta$ $^{UE}$ $_{\mu }$	$\delta$ $^{UE}$ $_{\eta }$
Estimate	0.9398	0.0090	-0.0480	-0.0456	-0.0556	0.7598	0.4925
SE	(0.0737)	(0.0011)	(0.0350)	(0.0263)	(0.0448)	(0.1138)	(0.1014)

Table 2C Point Estimates and Standard Errors - Employment, Job Mobility, Wage, Hours, and Household Income.

Panel (c) - Job Changes (J $_{t+1}$ )

Variable	cons	t	t²/100	JD $_{t}$	$\mu$	$\eta$
Parameter	$\gamma$ $^{J}$ $_{0}$	$\gamma$ $^{J}$ $_{1}$	$\gamma$ $^{J}$ $_{2}$	$\gamma$ $^{J}$ $_{3}$	$\delta$ $^{J}$ $_{\mu }$	$\delta$ $^{J}$ $_{\eta }$
Estimate	-0.6054	-0.0111	-0.0374	-0.1034	-0.3882	0.2828
SE	(0.0553)	(0.0051)	(0.0166)	(0.0120)	(0.0433)	(0.0310)

Table 2C (continued) Point Estimates and Standard Errors - Employment, Job Mobility, Wage, Hours, and Household Income.

Panel (d) - Wage (w $_{t+1}$ )

Variable	H $_{t+1}$	p $^{w}$ $_{t}$	$\Psi$ $_{t+1}$	J $_{t+1}$	1-E $_{t+1}$	$\mu$	$\varepsilon$ $^{w}$	$\Psi$ $_{t+1}$
Parameter	$\gamma$ $^{w}$ $_{1}$	$\rho$ $_{w }$	$\Phi _{1}$	$\gamma$ $^{w}$ $_{2}$	$\gamma$ $^{w}$ $_{3}$	$\delta$ $^{w}$ $_{\mu }$	$\sigma$ $_{w }$	$\Phi _{2}$
Estimate	-0.0015	0.9389	-0.1538	0.0197	-0.1400	0.0160	0.0975	2.0535
SE	(0.0421)	(0.0029)	(0.0093)	(0.0045)	(0.0089)	(0.0019)	(0.0020)	(0.2766)

Table 2C (continued) Point Estimates and Standard Errors - Employment, Job Mobility, Wage, Hours, and Household Income.

Panel (e) - Work Hours (h $_{t+1}$ )

Variable	cons	E $_{t+1}$	w $_{t+1}$	D $_{t+1}$	H $_{t+1}$	$\mu$	$\eta$	$\varepsilon$ $^{h}$
Parameter	$\gamma$ $^{h}$ $_{0}$	$\gamma$ $^{h}$ $_{1}$	$\gamma$ $^{h}$ $_{2}$	$\gamma$ $^{h}$ $_{3}$	$\gamma$ $^{h}$ $_{4}$	$\delta$ $^{h}$ $_{\mu }$	$\delta$ $^{h}$ $_{\eta }$	$\sigma$ $_{h}$
Estimate	-0.5258	0.5921	-0.1948	-0.8957	-0.1085	0.2436	0.1284	0.2269
SE	(0.0089)	(0.0080)	(0.0160)	(0.0192)	(0.0065)	(0.0093)	(0.0114)	(0.0014)

Table 2C (continued) Point Estimates and Standard Errors - Employment, Job Mobility, Wage, Hours, and Household Income.

Panel (f) - Household Income (y $_{t+1}$ )

Variable	cons	w $_{t+1}$	h $_{t+1}$	D $_{t+1}$	H $_{t+1}$	U $_{t+1}$	$\lambda$	p $^{y}$ $_{t}$	$\varepsilon$ $^{y}$
Parameter	$\gamma$ $^{y}$ $_{0}$	$\gamma$ $^{y}$ $_{1}$	$\gamma$ $^{y}$ $_{2}$	$\gamma$ $^{y}$ $_{3}$	$\gamma$ $^{y}$ $_{4}$	$\gamma$ $^{y}$ $_{5}$	$\delta$ $^{y}$ $_{\lambda }$	$\rho$ $_{y }$	$\sigma$ $_{y }$	$\kappa$
Estimate	0.1447	0.5919	0.4535	0.1862	-0.0068	0.0269	0.2478	0.4486	0.1677	-0.1478
SE	(0.0046)	(0.0096)	(0.0113)	(0.0327)	(0.0024)	(0.0085)	(0.0877)	(0.0965)	(0.0088)	(0.0134)

Table 2D Point Estimates and Standard Errors - Medical Expenditures (lnM $_{t+1}$ )

Variable	cons	t+1	(t+1)²	(t+1)³	H $_{t+1}$	Family Size	year 2001	year 2003
Parameter	$\gamma$ $^{M}$ $_{0}$	$\gamma$ $^{M}$ $_{1}$	$\gamma$ $^{M}$ $_{2}$	$\gamma$ $^{M}$ $_{3}$	$\gamma$ $^{M}$ $_{4}$	$\gamma$ $^{M}$ $_{5}$	$\gamma$ $^{M}$ $_{6}$	$\gamma$ $^{M}$ $_{7}$	$\rho$ $_{M}$ $^{(1)}$	$\sigma$ $_{M}$ $^{(1)}$
Estimate	-19.9013	1.1011	-0.0209	0.0001	0.4394	-0.1266	0.1391	0.2520	0.7455	0.9356
SE	(7.5830)	(0.3903)	(0.0066)	(0.0000)	(0.0612)	(0.0367)	(0.0712)	(0.0715)
Obs.	2,426
Adj R-squared	0.09

The table displays point estimates and standard errors for the medical expenditures equation. The parameters were estimated by least-squares, unless indicated otherwise. Parameters indicated by (1) were estimated by equally-weighted minimum distance matching the 0th, 2nd, and 4th order autocovariances of the residuals of the least-squares equation to those impied by an AR(1) process (the data on medical expenditures are available in two-year intervals only). The sample was restricted to individuals who were retired or had more than 43 years of potential experience. The least-squares regression includes year indicators and controls for family size.

Table 3A Evaluation of Fit: Disability and Health Descriptive Statistics - PSID Sample and Simulated Data

Sample Statistic	Overall	t=5	t=10	t=20	t=30	t=40	t=50	t=60
Mean Disability PSID	0.02	0.001	0.004	0.016	0.030	0.075
Mean Disability Simulated	0.02	0.002	0.004	0.014	0.034	0.090
Mean Health Limitations PSID	0.13	0.05	0.06	0.11	0.14	0.24	0.37	0.50
Mean Health Limitations Simulated	0.14	0.05	0.06	0.10	0.17	0.27	0.40	0.54

The table presents descriptive statistics of the PSID sample, and of data simulated from the estimated model. The descriptive statistics of simulated data are based on a simulated sample which is 10 times as large as the PSID sample, but has the same demographic structure (by potential experience) as the PSID sample. All statistics are computed using 3-year windows around the indicated value of t. For instance, t=10 corresponds to sample moments computed over all observations where t=9,10,11. The only exception is t=60, which uses only two years: t=59,60.

Table 3B Evaluation of Fit: Working-Years Variables Descriptive Statistics - PSID Sample and Simulated Data

Sample Statistic	Overall	t=5	t=10	t=20	t=30	t=40
Mean Employment PSID	0.93	0.94	0.94	0.94	0.94	0.88
Mean Employment Simulated	0.93	0.93	0.94	0.93	0.92	0.86
Mean Emp. To Emp. Transition PSID	0.97	0.98	0.97	0.97	0.98	0.96
Mean Emp. To Emp. Transition Simulated	0.96	0.96	0.96	0.96	0.96	0.93
Mean Unemp. To Emp. Transition PSID	0.55	0.56	0.59	0.55	0.46	0.42
Mean Unemp. To Emp. Transition Simulated	0.53	0.57	0.58	0.57	0.47	0.37
Mean Job Change if Employed PSID	0.08	0.21	0.15	0.07	0.05	0.04
Mean Job Change if Employed Simulated	0.10	0.18	0.15	0.09	0.05	0.02
Mean Employment Duration PSID	11.87	4.21	6.61	12.49	17.34	21.22
Mean Employment Duration Simulated	14.49	5.05	8.78	15.57	20.85	22.55
Mean Unemployment Duration PSID	1.88	1.65	1.82	2.11	1.75	1.70
Mean Unemployment Duration Simulated	1.35	1.68	1.73	1.42	1.07	0.68
Mean Job Duration PSID	9.60	3.00	4.78	9.88	14.98	19.26
Mean Job Duration Simulated	9.35	2.44	4.53	9.73	15.18	18.14
St. Dev. Log Wage PSID	0.39	0.35	0.37	0.40	0.40	0.41
St. Dev. Log Wage Simulated	0.41	0.39	0.40	0.41	0.41	0.42
St. Dev. Log Hours PSID	0.49	0.35	0.42	0.49	0.55	0.75
St. Dev. Log Hours Simulated	0.45	0.43	0.43	0.44	0.48	0.57
St. Dev. Log Earnings PSID	0.78	0.55	0.68	0.79	0.85	1.09
St. Dev. Log Earnings Simulated	0.70	0.63	0.66	0.70	0.75	0.82
St. Dev. Log Household Nonasset PSID	0.49	0.45	0.47	0.50	0.51	0.56
Income Simulated	0.48	0.45	0.47	0.49	0.49	0.50

Table 3C Evaluation of Fit: Out-of-Pocket Medical Expenditures Descriptive Statistics - PSID Sample and Simulated Data

Sample Statistic	Overall	44 $\le$ t $\le$ 48	49 $\le$ t $\le$ 53	54 $\le$ t $\le$ 58	59 $\le$ t $\le$ 63	64 $\le$ t $\le$ 68
Mean PSID	1.576	1.446	1.290	1.651	1.904	1.886
Mean Simulated	1.342	1.397	1.352	1.266	1.260	1.436
Standard Deviation PSID	3.758	2.260	1.781	4.266	5.847	4.494
Standard Deviation Simulated	3.519	3.540	3.916	3.117	3.363	3.606

The table presents descriptive statistics of the PSID sample, and of data simulated from the estimated model. The numbers refer to yearly figures, measured in thousands of year 2000 dollars. The descriptive statistics of simulated data are based on a simulated sample which is 10 times as large as the PSID sample, but has the same demographic structure (by potential experience) as the PSID sample. Statistics are displayed for the entire sample and for 5-year cells of potential experience. For instance, 44 $\le$ t $\le$ 48 includes all years between 44 and 48. For the PSID sample, only observations with strictly positive levels of medical expenditures are included in the table (only this subset of the data was used in estimation).

Table 4, Panel (a) - Effect ADJUSTED for Variation in Mean Income Profile (Actuarially Fair Insurance)

Insured Source of Risk	Disability	Health	Unemp.	MedCosts	Wage	Job Change	Hours	Res. Income
Equivalent Variation (% of Lifetime Consumption)	0.02%	0.00%	0.04%	0.01%	1.20%	0.72%	0.45%	2.19%

The table presents the welfare gains from fully insuring individual sources of risk. For each source, the calculation compares expected lifetime utility under the full-uncertainty scenario versus a scenario in which one particular source of risk is fully insured so that its realization has no effect on net income. Welfare gains are expressed in terms of the "equivalent compensating variation", that is, the percentage variation of lifetime consumption (in the full-uncertainty world) that would make the household indifferent between living in that compensated full-uncertainty world versus living in the alternative insured scenario. Panel (b) adjusts mean income under the insured scenario so that it equals mean income under the uncompensated, full-uncertainty scenario.

Table 4, Panel (b) - Effect NOT Adjusted for Variation in Mean Income Profile

Insured Source of Risk	Disability	Health	Unemp.	MedCosts	Wage	Job Change	Hours	Res. Income
Equivalent Variation (% of Lifetime Consumption)	0.04%	0.01%	0.62%	0.24%	0.62%	-0.35%	-0.13%	0.28%

Table 5 Contribution of Individual Sources of Risk to Precautionary Saving - Baseline Case

Source of Risk	Disability	Health	Unemp.	MedCosts	Wage	Job Change	Hours	Res. Income
Contribution	2.34%	8.56%	3.77%	5.57%	19.13%	9.34%	8.15%	43.14%

The table displays the contribution of individual sources of risk to the accumulation of precautionary wealth. Precautionary wealth is defined here as the difference between mean precautionary wealth under full uncertainty and mean precautionary wealth under no uncertainty. The calculation then computes the difference between mean precautionary wealth under full uncertainty and mean precautionary wealth under a scenario in which one particular source of risk is fully insured so that its realization has no effect on net income. This difference is then expressed as a percentage of mean precautionary wealth. The contributions are normalized to sum to 100%.

Table 6 Average Lifetime Earnings Regression Dependent Variable: (Simulated) Average Lifetime Earnings

Variable	cons	$\zeta$ $^{D}$	( $\zeta$ $^{D})$ $^{2}$	( $\zeta$ $^{D})$ $^{3}$	$\zeta$ $^{H}$	( $\zeta$ $^{H})$ $^{2}$	$\mu$	$\mu ^{2}$	$\mu ^{3}$	$\eta$	$\eta ^{2}$	p $^{w}$ $_{T}$	(p $^{w}$ $_{T})$ $^{2}$ $_{ }$	(p $^{w}$ $_{T})$ $^{3}$ $_{ }$	D $_{T}$	H $_{T}$	E $_{T}$	$\mu \ast$ p $^{w}$ $_{T}$
Estimate	3.358	-0.003	-0.016	-0.006	-0.015	-0.007	0.357	-0.038	0.005	0.149	-0.007	0.240	0.008	-0.018	-0.108	0.000	-0.040	-0.011
SE	(0.004)	(0.001)	(0.001)	(0.000)	(0.001)	(0.001)	(0.002)	(0.001)	(0.000)	(0.001)	(0.001)	(0.004)	(0.005)	(0.004)	(0.005)	(0.003)	(0.004)	(0.004)
Obs.	48,030
Root MSE	0.184
Adj R-squared	0.88

The table presents estimation results for the average lifetime earnings regression. The regression uses data simulated from a joint model of labor earnings to determine the predictive power of variables known in the last year of a worker's career for his/her average lifetime earnings, as calculated by the Social Security Administration (taking, for instance, only the 35 years with highest earnings to calculate the average). The dependent variable is simulated average lifetime earnings. The independent variables are all permanent variables variables in the joint model of earnings, all time-varying variables in the last year of career only (year T), and some interactions. After experimentation with different specifications, only the interactions with a significant predictive power were included in the equation.

Table 7A Welfare Gains of Full Insurance: Sensitivity to Degree of Risk Aversion and Discount Factor Equivalent Variation in Lifetime Consumption - Effect Adjusted for Variation in Mean Income Profile (Actuarially Fair Insurance).

Panel (a) - Coefficient of Relative Risk Aversion

Source of Risk:	Disability	Health	Unemp.	MedCosts	Wage	Job Change	Hours	Res.Income
$\alpha$ = 3.0	0.02%	0.00%	0.04%	0.01%	1.20%	0.72%	0.45%	2.19%
$\alpha$ = 5.0 $^{(1)}$	0.03%	0.01%	0.07%	0.02%	1.95%	1.17%	0.72%	4.79%

The table presents the welfare gains from fully insuring individual sources of risk (see Table 4.4A, Panel a) for different values of the coefficient of risk aversion $\alpha$ and the discount factor $\beta$ . (1) All other parameters are held at their baseline value. (2) $\beta$ = 1/(1+r).

Panel (b) - Discount Factor

Source of Risk:	Disability	Health	Unemp.	MedCosts	Wage	Job Change	Hours	Res.Income
$\beta$ = 0.967 $^{(2)}$	0.02%	0.00%	0.04%	0.01%	1.20%	0.72%	0.45%	2.19%
$\beta$ = 0.94 $^{(1)}$	0.01%	0.00%	0.05%	0.02%	0.97%	0.75%	0.44%	3.15%
$\beta$ = 0.90 $^{(1)}$	0.01%	0.00%	0.05%	0.02%	0.73%	0.77%	0.42%	4.19%

Table 7B Contribution of Individual Sources of Risk to Precautionary Saving: Sensitivity to Degree of Risk Aversion and Discount Factor Panel (a) - Coefficient of Relative Risk Aversion

Source of Risk:	Disability	Health	Unemp.	MedCosts	Wage	Job Change	Hours	Res.Income
$\alpha$ = 3.0	2.34%	8.56%	3.77%	5.57%	19.13%	9.34%	8.15%	43.14%
$\alpha$ = 5.0 $^{(1)}$	2.26%	8.14%	3.21%	5.11%	19.71%	9.37%	8.16%	44.04%

The table presents the contribution of individual sources of risk to the accumulation of precautionary wealth (see Table 4.5A) for different values of the coefficient of risk aversion $\alpha$ and the discount factor $\beta$ . (1) All other parameters are held at their baseline value. (2) $\beta$ = 1/(1+r).

Table 7B Contribution of Individual Sources of Risk to Precautionary Saving: Sensitivity to Degree of Risk Aversion and Discount Factor Panel (b) - Discount Factor

Source of Risk:	Disability	Health	Unemp.	MedCosts	Wage	Job Change	Hours	Res.Income
$\beta$ = 0.967 $^{(2)}$	2.34%	8.56%	3.77%	5.57%	19.13%	9.34%	8.15%	43.14%
$\beta$ = 0.94 $^{(1)}$	2.14%	10.44%	2.93%	8.77%	16.82%	6.91%	8.03%	43.96%
$\beta$ = 0.90 $^{(1)}$	2.03%	10.79%	2.80%	8.81%	15.62%	7.61%	7.86%	44.48%

Figure 1

Figure 2
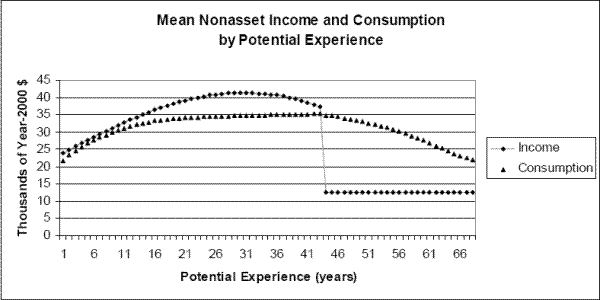
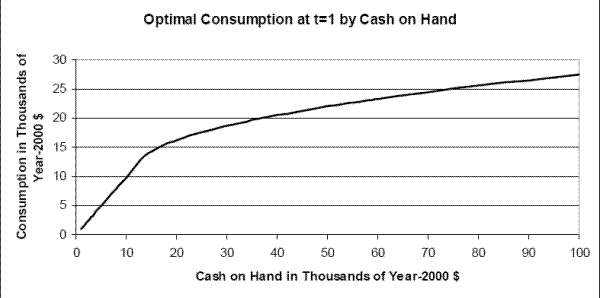
$Figure 2: Optimal Consumption at t=1 by Cash on Hand. The figure shows the optimal level of consumption as a function of cash on hand for an employed, healthy individual with mean persistent wage and household income components, who is in the first period of their career. At low levels of cash on hand (below about {\$}15,000), households are credit-constrained and consume their entire wealth (optimal consumption falls on a 45-degree line). Above the threshold, households begin to save (the line becomes flatter than a 45-degree line). As cash on hand increases, the fraction that is consumed falls (the slope of the consumption function decreases).$

Figure 3
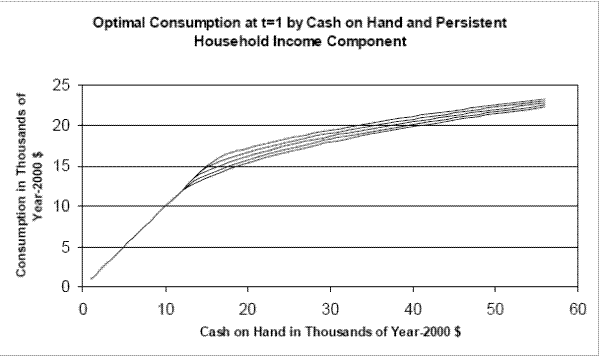
$Figure 3: Optimal Consumption at t=1 by Cash on Hand and Persistent Household Income Component. The figure shows the optimal level of consumption as a function of cash on hand for an employed, healthy individual with mean (persistent) wage, who is in the first period of their career. The figure displays five lines, each corresponding to a different level of the persistent household income component p$^{y}$$_{t}$, which ranges from 2 standard deviations above to 2 standard deviations below the mean. At low levels of cash on hand (below about {\$}12,000 to {\$}15,000), households are credit-constrained and consume their entire wealth (optimal consumption falls on a 45-degree line). Above the threshold, households begin to save (the consumption function becomes flatter than a 45-degree line) and, as cash on hand increases, the fraction that is consumed falls (the slope of the consumption function decreases). Once above the threshold, a household with component p$^{y}$$_{t}$ two standard deviations above the mean spends about {\$}3,000 more on consumption than a household with p$^{y}$$_{t}$ two standard deviations below the mean.$

Figure 4
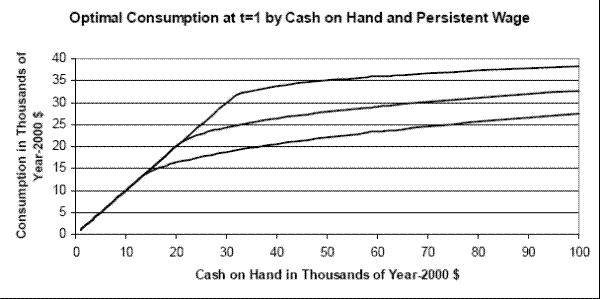
$Figure 4: Optimal Consumption at t=1 by Cash on Hand and Persistent Wage. The figure shows the optimal level of consumption as a function of cash on hand for an employed, healthy individual with mean persistent household income component, who is in the first period of their career. The figure displays three lines, each corresponding to a different level of the of the persistent wage component p$^{w}$$_{t}$, which ranges from 2.8 standard deviations above to 2.8 standard deviations below the mean. At low levels of cash on hand (below about {\$}15,000 to {\$}30,000), households are credit-constrained and consume their entire wealth (optimal consumption falls on a 45-degree line). Above the threshold, households begin to save (the consumption function becomes flatter than a 45-degree line) and, as cash on hand increases, the fraction that is consumed falls (the slope of the consumption function decreases). Once above the threshold, and conditional on having {\$}30,000 in total resources in its first year of career, a household with component p$^{w}$$_{t}$ that is 2.8 standard deviations above the mean will spend about {\$}12,000 more on consumption than a household with p$^{w}$$_{t}$ that is 2.8 standard deviations below the mean.$

Figure 5
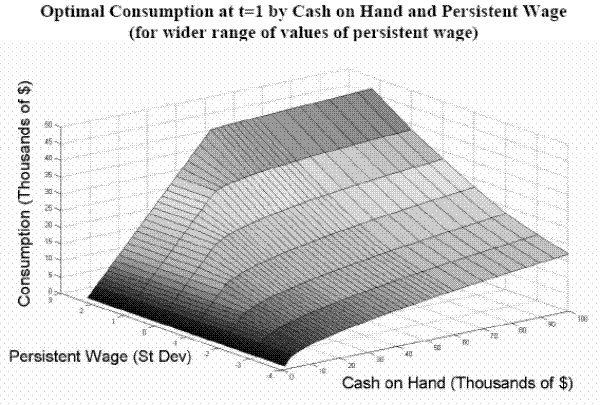
$Figure 5: Optimal Consumption at t=1 by Cash on Hand and Persistent Wage (for wider range of values of persistent wage). The 3-dimensional figure shows the optimal level of consumption (an optimal consumption surface) as a function of two continuous state variables: cash on hand and the persistent wage component. The surface corresponds to an employed individual in good health, with mean persistent household income component, and who is in the first period of their career. The figure displays the optimal consumption rule over the entire range of possible realizations that p$^{w}$$_{t}$ and cash on hand may take in the simulations. For any given value of p$^{w}$$_{t}$, low levels of cash on hand lead to credit-constrained households who consume their entire wealth (optimal consumption falls on a 45-degree line). Above the threshold, households begin to save (the consumption function becomes flatter than a 45-degree line) and, as cash on hand increases, the fraction that is consumed falls (the slope of the consumption function decreases). The higher p$^{w}$$_{t}$ is, the higher the threshold level of cash on hand.$

Figure 6

Figure 7
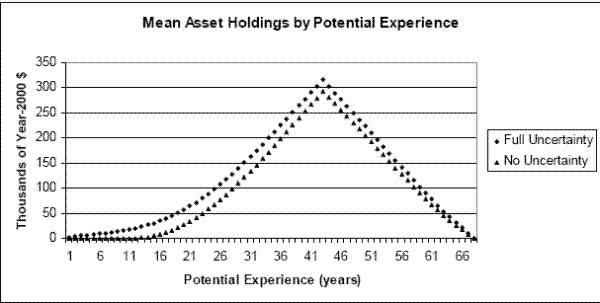
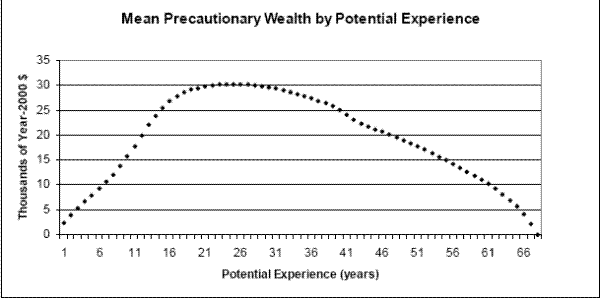
$Figure 7: Mean Precautionary Wealth by Potential Experience. The figure shows mean precautionary wealth by year in the lifecycle. Specifically, I simulate the careers of 50,000 households and compute the cross-sectional mean of assets for each period t both for the benchmark model and for a model without uncertainty. The figure plots the difference between the full-uncertainty scenario and the no-uncertainty scenario (which is, by definition, mean precautionary wealth) against t. As the figure shows, mean precautionary wealth is about {\$}2,000 at t=1, increases monotonically until it reaches a peak at about {\$}30,000 around t=23, and then slowly decreases until it reaches zero at the end of the lifecycle.$

Figure 8

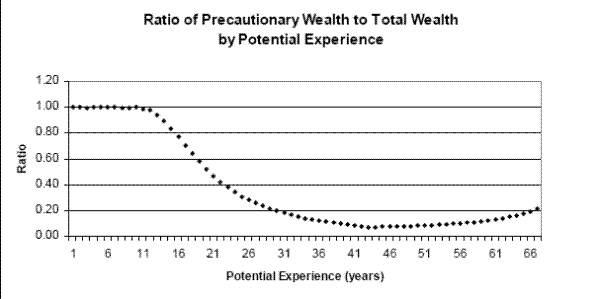
Footnotes

* I am indebted to Joe Altonji for his continuous support and encouragement. I would also like to thank Tony Smith, Fabian Lange, George Hall, Giuseppe Moscarini, Luigi Pistaferri, Bjoern Bruegemann, Melissa Tartari, and Mary Daly for helpful discussions. I am responsible for all remaining shortcomings of the paper. The views expressed here are my own and do not necessarily represent those of the Board of Governors or the staff of the Federal Reserve System. Return to Text

* E-mail: [email protected]. Return to Text

1. This literature includes Lillard and Willis (1978), Lillard and Weiss (1979), Hause (1980), MaCurdy (1982), Hall and Mishkin (1982), Abowd and Card (1987, 1989), Topel (1991), Baker (1997), Geweke and Keane (2000), Haider (2001), Meghir and Pistaferri (2004). Return to Text

2. Models that require a measure of income uncertainty or risk have been used to study a wide range of issues, including the following. In macroeconomics: consumption and precautionary saving (Carroll, 1992, 1997; Gourinchas and Parker, 2002; Cagetti, 2003); the distribution of wealth and consumption (Huggett, 1996; Krusell and Smith, 1998; Castañeda, Díaz-Giménez and Ríos-Rull, 2003; Storesletten, Telmer, and Yaron, 2004a); asset pricing (Heaton and Lucas, 1996; Krusell and Smith, 1997; Storesletten, Telmer, and Yaron, 2007). In public finance: the adequacy of private saving (Engen, Gale, and Uccello, 1999; Scholz, Seshadri, and Khitatrakun, 2006); tax-sheltered accounts and saving (Engen and Gale, 1993; Engen, Gale, and Scholz, 1994); wealth accumulation (Hubbard, Skinner, and Zeldes, 1994, 1995; Dynan, Skinner, and Zeldes, 2004). Return to Text

3. I also consider out-of-pocket medical expenditure shocks. However, a proper treatment of these shocks requires introducing means-tested transfers, and this complicates the solution of the consumption model significantly. The current version of the model thus makes the simplifying assumption that medical expenditures can wipe out current income but cannot wipe out accumulated wealth, and excludes means-tested transfers. This simplifies the solution of the model but it also restricts the potential importance of medical expenditures significantly. Hence, the results related to medical expenditures are viewed here as very preliminary and are excluded from much of the analysis and discussion. A full treatment, including means-tested transfers, is left for future research. Return to Text

4. The implementation of generalized indirect inference in this paper builds on the implementation used in Altonji, Smith, and Vidangos (2008). Return to Text

5. The insurance considered here is additional to already-existing insurance provided by government transfers, self-insurance through saving, and insurance within the family. This will be further discussed below. Return to Text

6. Other mechanisms that have been studied include spousal earnings (Cullen and Gruber, 2000; Stephens, 2002), the delay of durable goods purchases (Browning and Crossley, 2001), mortgage refinancing (Hurst and Stafford, 2004), progressive income taxation (Kniesner and Ziliak, 2002), and unsecured debt (Sullivan, 2008). Return to Text

7. In implementing the model, $T_{W}$ and $T_{R}%$ will be set to 43 and 25, respectively. Return to Text

8. Survival probabilities may be allowed to depend not only on age, but also on any other state variable considered in the model, such as health status. Return to Text

9. The appropriate measure of income to use here is after-tax income. The current version of the model does not distinguish between pre-tax and after-tax income. Future versions will make this distinction, and use after-tax income, by introducing estimated tax functions that approximate effective income taxes. Such tax functions are estimated, for instance, by Gouveia and Strauss (1994, 2000) for the years 1966-1989. Return to Text

10. One could also allow $y_{t}$ to include a defined benefit pension. Return to Text

11. After accounting for variation in household income due to earnings of the head, household size and composition (including variables that might affect the labor supply of a spouse, such as number of children under 6), a polynomial in age, education, race, year indicators, disability, health, employment, and permanent heterogeneity the residual that remains in household income is large and persistent. This component is represented by $p_{t}^{y}$ and is modeled here as an AR(1) process. This component consists primarily of unexplained variation in spousal labor earnings and transfers from public programs. Return to Text

12. Types can be defined according to permanent observed characteristics (such as education and race) or unobserved characteristics (such as unobserved permanent heterogeneity in ability or preferences). The baseline model will be evaluated for one specific household type, which will be defined below. Return to Text

13. These three shocks will determine the transition into employment from three possible states in the previous period: employment, unemployment, and disability. Return to Text

14. Shock $\varepsilon_{t+1}^{J}$ is a job-change shock. Section 4 discusses how job changes are determined. Return to Text

15. Some of these variables, in turn, depend on the shocks $\varepsilon_{t+1}^{D}$ , $\varepsilon_{t+1}^{H}$ , $\varepsilon_{t+1}^{EE}$ , $\varepsilon_{t+1}^{UE}$ , $\varepsilon_{t+1}^{DE}$ , $\varepsilon_{t+1}^{w}$ , and $\varepsilon_{t+1}^{y}%$ . Return to Text

16. In the current version of the model, $y_{t}$ during retirement is calibrated using only social security benefits of the household head. A later section discusses how this might affect the analysis and results presented here. Return to Text

17. The range of values usually considered empirically plausible is 0.5-5.0. Gourinchas and Parker (2002) estimate $\alpha$ to be around 0.5-1.4 in a lifecycle consumption model. Cagetti (2003) obtains considerably higher estimates, around 4.0. Chetty (2006), using a model with consumption and leisure in the utility function, estimates $\alpha$ to be around 1.0 and argues that values of $\alpha$ above 2.0 are inconsistent with the evidence on labor supply behavior. Return to Text

18. Notice that models with finite horizon do not face the restrictions on the relative values of the discount factor and the real interest rate that infinite horizon models have. Smaller values of the discount factor (greater impatience), however, will lead to less saving. Return to Text

19. Increases above 500% and declines to less than 20% of the previous value are very uncommon and are likely to represent reporting errors in most cases. Return to Text

20. Given the existence of minimum-wage legislation, reported hourly wages below $3.50/hour are likely to be misreports. Similarly, for a measure of household income as broad as the one used here, very low values of household income are likely to be misreports. Return to Text

21. See discussion of estimation mechanics in Appendix 4. The introduction of disability leads to flat regions near the global optimum of the objective function. Return to Text

22. To get a sense of the magnitude of this coefficient, note that the transitory shock $\varepsilon_{t+1}^{D}$ in the equation has a standard deviation of 1. Return to Text

23. Since the equations for $D_{t}$ and $H_{t}$ are estimated separately, I do not estimate the correlation between $\zeta^{D}$ and $\zeta^{H}$ . This is of no consequence here, however, since I consider households at the mean of the distribution of the various permanent heterogeneity components, which is normalized to zero. The important issue is to control for variation due to permanent components, both because this variation should not represent risk and to avoid bias in coefficients on lagged dependent variables. Return to Text

24. The equation can thus be expressed as $H_{t+1}=D_{t+1}+(1-D_{t+1})\cdot I[\gamma_{0}^{H}+\gamma_{1}^{H}% (t+1)+\gamma_{2}^{H}(t+1)^{2}+\gamma_{3}^{H}(t+1)^{3}+\gamma_{4}^{H}% H_{t}+\zeta^{H}+\varepsilon_{t+1}^{H}>0]$ . Return to Text

25. Methods that deal with the initial-conditions problem such as that proposed in Wooldridge (2005) are not applicable here because of the highly unbalanced nature of the sample. I experimented with correcting for initial conditions using the method suggested in Heckman (1981), but the reduced-form approximation of the initial value of the latent variable invariably showed very little explanatory power, and hence was not helpful. All dynamic equations other than equation (12), however, deal with the initial-conditions problem (see Appendix 3). Return to Text

26. The specification of the wage process proposed here is similar to one of the specifications studied in Altonji, Smith, and Vidangos (2008). A more detailed description of the process is provided in that paper. That paper also studies alternative specifications of the wage process which include job-specific components. The reason that specifications with job-specific wage components are not used in this paper is that the job-specific wage component would introduce an additional state variable in the consumption model, adding to the computational requirements of its solution. Return to Text

27. For a discussion of the concept of a latent wage used here, see Altonji, Smith, and Vidangos (2008). Return to Text

28. Notice that the permanent component is inside the autoregressive part of the persistent wage component. Consequently, its effect on the wage may change with

. This specification may be thought of as an alternative to the "heterogeneous-profile" types of models for wages and earnings often used in the literature. For a discussion of the "heterogeneous profiles" literature in earnings dynamics see Baker (1997) or Guvenen (2006). Return to Text

29. Recall that when taking the model to the data, $w_{t+1}$ , $h_{t+1}$ , $D_{t+1}$ , $H_{t+1}$ , and $U_{t+1}$ refer to the head of the household. Return to Text

30. The coefficients on the variables in vectors $X_{t}^{w}$ , $X_{t}^{h}$ , and $X_{t}^{y}$ , however, are not estimated by indirect inference. Variation due to variables in the $X_{t}$ vectors is removed from the data using a first-stage regression prior to estimation by indirect inference. Vectors $X_{t}^{w}$ and $X_{t}^{h}$ contain a polynomial in experience, education, race, and year indicators. Vector $X_{t}^{y}$ contains a number of additional variables (see Appendix 3). The experience polynomial and the sample average of most of the variables in vector $X_{t}^{y}$ are added back to the household income equation when calculating levels of household income to be used in the consumption model. Return to Text

31. For a general discussion of the method see Keane and Smith (2003). Return to Text

32. Similar specifications are used in Hubbard, Skinner, and Zeldes (1994, 1995) and Scholz, Seshadri, and Khitatrakun (2006), among others. Return to Text

33. Notice that the disability indicator $D_{t}$ does not enter equation (21). The reason is that $D_{t}$ is a variable related to employment status and is not a state variable in old age in the lifecycle model. Return to Text

34. Equation (21) does not allow for permanent unobserved heterogeneity other than that entering through health. The reason is that from the point of view of the lifecycle, medical expenditures in old age are assumed to be unknown early in life and are thus treated as risk. Return to Text

35. For evidence in favor of using equal weights rather than an optimal weighting scheme see Altonji and Segal (1996). Return to Text

36. Scholz, Seshadri, and Khitatrakun (2006) use a model similar to equation (21) and a measure of medical expenditures similar to the one used here but constructed from the Health and Retirement Study. They estimate the persistence parameter to be around 0.84 and 0.86, and a standard deviation of the shock which ranges from 0.512 for married households with college education to 2.081 for single households with no college. Reported medical expenditures of zero are set in their analysis to $1.00 (i.e., 0 in logs). I find that setting expenditures of zero to $1 considerably inflates the persistence of shocks. The reason is that very low values of expenditures (such as zero expenditures) tend to be more persistent than large values. This turns out to affect the estimates of persistence significantly. Setting zero expenditures to $1 in a log specification also implies that percentage changes at very low levels of expenditures have the same effect as similar percentage changes at high levels of expenditures. It would generally be more appropriate to set zero expenditures in a log model to some higher minimum level, say $300. However, in the case of medical expenditures, this distorts the estimates significantly because of the large number of zeros in the distribution. The approach taken here is to use only positive values of expenditures in the estimation. This will overestimate the probabilities of facing medical expenditures. However, this approach still implies smaller expenditures (and smaller persistence) than setting $0 observations to any amount that is below about $300. Return to Text

37. The table also displays statistics for employment duration, unemployment duration, job duration, and labor earnings. Even though these variables do not appear in the consumption model, they are used in estimation of the joint model of employment, job changes, wage, hours, and income. See Appendix 3 and Appendix 4. Return to Text

38. Year effects are removed from the wage, hours, earnings, and household income data prior to estimation. Return to Text

39. It is straightforward to include social security benefits of a spouse and dependents. One could also consider a second type of household which additionally receives defined benefit pensions. The inclusion of additional components of retirement income will make the drop less pronounced and will tend to reduce saving for retirement purposes. It will not affect uncertainty, however, which is the main object of interest here. The important aspects of retirement nonasset income here are that (i) income drops at the time of retirement, and (ii) there is no uncertainty after retirement in social security receipts. One possible extension that would introduce an additional source of uncertainty during retirement which seems relevant would be to account for uncertainty in rates of return and hence in endogenous asset income. One important aspect to consider in such an extension is that a high degree of heterogeneity in participation in the stock market implies that uncertainty in rates of return is likely to be highly heterogeneous across households. Return to Text

40. All assumptions used in the simulations are discussed in more detail in the next section. Return to Text

41. See, for instance, Deaton (1991), Carroll (2001), Gourinchas and Parker (2002), or Cagetti (2003). Optimal behavior is qualitatively similar whether borrowing constraints are exogenously imposed or arise as "natural" constraints, using the terminology introduced by Aiyagari (1994). Return to Text

42. Recall that both the persistent wage $p_{t}^{w}$ and cash on hand $z_{t}$ are treated as continuous state variables in the numerical solution of the model. Return to Text

43. The reason why insurance affects mean income varies somewhat across different shocks. For instance, the occurrence of disability, health, and unemployment shocks always affects income negatively. Hence, fully insuring against these risks raises expected income. Wage, hours, and household income shocks, on the other hand, affect expected wage, hours and household income because these variables have log-normal distributions. Hence, although the shocks are symmetric around zero, a change in the variance of the processes also affects their mean. Return to Text

44. Recall that the household nonasset income data used to estimate the income process includes labor income of all household members and transfers from outside the household, whether from public or private sources. Return to Text

45. Let $W_{U}$ denote welfare under the full-uncertainty scenario and $W_{I}$ denote welfare under the insured scenario. As explained above, the insured scenario compensates the effects of a particular source of risk such that the risk has no effect on net income. The "equivalent compensating variation" is then defined as the value of parameter $\xi$ which solves the equation $W((1+\xi)c^{\ast}(\Omega_{t}))=W_{I}$ . 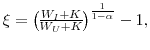Solving for $\xi$ yields $\xi=% \genfrac{(}{)}{}{}{W_{I}+K}{W_{U}+K}% ^{\frac{1}{1-\alpha}}-1,$ where $K=\frac{1}{1-\alpha}\sum_{t=1}^{T}% \beta^{t-1}\pi_{t}$ . This is the measure of welfare gains of insurance (alternatively, welfare costs of risk) used below. Return to Text

46. Notice that job-mobility shocks also operate mostly through an effect on the wage rate. The difference with wage shocks is that the latter do not involve a change of employer. Return to Text

47. Recall that variation due to potential experience, education, race, and other demographic variables was also removed from the data in a first-stage regression. Return to Text

48. Recall, however, that there is also an important insurance component captured by the coefficient $\widehat{\gamma}_{3}^{y}=0.186$ in the household income equation. Return to Text

49. As noted above, the value 5.0 is at the high end of values generally considered empirically plausible. See discussion in note 17. I do not consider values of the coefficient of risk aversion smaller than 3.0 because they would lead to an even smaller value of insurance than in the baseline case. Return to Text

50. Like most consumption models, the model used here does not distinguish between liquid and illiquid assets. In particular, the model does not separately allow for real estate wealth. Intergenerational transfers are also ignored. Return to Text

51. Without the normalization, their sum slightly exceeds 100% because of interactions among the different sources of uncertainty (for instance, the dependence of disability on lagged health limitations). Return to Text

52. In practice, the auxiliary model actually used in estimation included a few additional covariates. Due to an error in one of the programs, however, the sorting of the data in the additional covariates was different from the sorting of the data in the rest of the variables, rendering the additional covariates uncorrelated with the rest of the variables in the SUR system. Consequently, the auxiliary model effectively used is the model described in this appendix. Excluding the additional covariates altogether from estimation yields estimates that are very close to the ones reported in this paper. The additional covariates that were initially intended to be included are $\overline{E}_{i}$ , $\overline {J}_{i}$ , $\overline{ED}_{i}$ , $\overline{UD}_{i}$ , $\overline{JD}_{i}$ , $w_{i,t-1}-\overline{w_{i}}$ , $h_{i,t-1}-\overline{h_{i}}$ , $e_{i,t-1}% -\overline{e_{i}}$ , and $y_{i,t-1}-\overline{y_{i}}$ , where a bar over a variable indicates a person-specific time average. Return to Text

^♣ This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to Text