Reset Price Inflation and the Impact of Monetary Policy Shocks
Keywords: Reset price inflation, strategic complementarities, contract multiplier, time-dependent pricing, state-dependent pricing
Abstract:
A standard state-dependent pricing model implies very limited scope for using active monetary policy to stabilize real activity. Two modeling strategies which expand the role of monetary policy are time-dependent pricing and strategic complementarities between price-setting firms. These mechanisms have telltale implications for the persistence and volatility of "reset price inflation." Reset price inflation is the rate of change of all desired prices (including for goods that have not changed price in the current period). Using the micro data underpinning the CPI, we construct an empirical measure of reset price inflation and use this measure to assess the validity of the modeling approaches. We find that time-dependent models imply unrealistically high persistence and stability of reset price inflation. This discrepancy is exacerbated by adding strategic complementarities, even under state-dependent pricing. A state-dependent model with no strategic complementarities aligns most closely with the CPI data.
This research was conducted with restricted access to U.S. Bureau of Labor Statistics (BLS) data. Rob McClelland provided us invaluable assistance and guidance in using BLS data. We thank Jose Mustre Del Rio for excellent research assistance. The views expressed here are those of the authors and do not necessarily reflect the views of the BLS or the Federal Reserve System. We are grateful to Carlos Carvalho, Jon Steinsson, and numerous seminar participants for helpful comments.
Consumer prices change every seven or eight months in the U.S.1 Yet the real effects of monetary shocks have been estimated to last around thirty months.2 These figures suggest real effects lasting roughly four times longer than nominal price stickiness - i.e., using Taylor's (1980) terminology, the "contract multiplier" in the U.S. is around four. In contrast, research on calibrated DSGE models obtains much lower contract multipliers, at least in the absence of strategic complementarities and sticky information. Chari, Kehoe and McGrattan (2000) report contract multipliers around one in a variety of time-dependent pricing models. Caballero and Engel (2007) and Golosov and Lucas (2007) arrive at contract multipliers well below one in their state-dependent pricing models. Dotsey, King and Wolman (1999) and Midrigan (2008) obtain intermediate contract multipliers in their state-dependent models.
As has been well-known since Ball and Romer (1990) and Kimball (1995), strategic complementarities in the pricing decisions of individual sellers can produce large contract multipliers.3 A starting point for these models is that the nominal stickiness be staggered, to create the possibility of coordination failure among price setters.4 In response to an aggregate shock, strategic complementarities mute the size of price changes for those changing prices, as price setters wait for the average price to respond.
We show that models with high contract multipliers at the macro level display slow-moving "reset" prices at the micro level. A reset price for an individual seller is that price it would choose if it implemented a price change in the current period. Actual prices often differ from reset prices, of course, because of nominal price stickiness. We define "theoretical reset price inflation" as the weighted average change of all reset prices, including those of current price changers and non-changers alike. We denote "reset price inflation" as the weighted average change of reset prices for price changers only. In the Calvo (1983) time-dependent pricing model, the probability of changing price is independent of the desired reset price change, so reset price inflation is a pure reflection of theoretical reset price inflation. In state-dependent models, sellers weigh the benefits of moving to the reset price against the (menu) costs of doing so. For these models reset price inflation can depart importantly from theoretical reset price inflation.
Strategic complementarities should dampen the volatility of reset price inflation and boost its persistence. An individual seller will move by smaller amounts, requiring multiple price changes to fully respond to a shock. We confirm this intuition by simulating DSGE models featuring time-dependent pricing (TDP) or state-dependent pricing (SDP), with or without strategic complementarities. The models feature a single aggregate shock (to money or productivity) plus idiosyncratic shocks to each seller's productivity. The complementarities take the form of intermediate goods, as in Basu (1995). Intermediates can slow down "monetary pass-through" because price changers have not seen their intermediate costs fully adjust due to the sticky prices of their suppliers. Sellers are grouped into one of two sectors: the flexible price sector (low menu cost, bigger idiosyncratic shocks) or the sticky price sector (high menu cost, smaller shocks).
Using the micro data on prices collected by the U.S. Bureau of Labor Statistics for the Consumer Price Index, we construct an empirical index of reset price inflation for the months January 1989 through May 2008. We impute to all items, both those changing and not, the reset price changes exhibited by price changers. To arrive at the reset price change for an item changing price, we compare the item's new price to its estimated reset price the previous month - not the item's last new price, set perhaps months earlier. A useful analogy is to home price indices constructed from repeat sales (e.g., Shiller 1991 and Zillow.com). These indices estimate the value of residential homes even when they are not sold. Once a home is sold, the difference between the transacted price and the previous period's estimated value is used to update the estimated value of other homes that were not sold. Our reset price index is the analogue for all consumer items to these home price indices.
We compare the behavior of our empirical measure of reset price inflation to that of an identically-constructed measure from simulated TDP and SDP models. As mentioned previously, reset price inflation is the exact counterpart to theoretical reset price inflation in the Calvo model. Even though our constructed reset price inflation is not the same as theoretical reset price inflation for SDP models, we find that simulated SDP models yield clear predictions for our constructed reset price inflation.
To delve further into the role played by price rigidity, we partition the CPI goods into "flexible" and "sticky" groups. The former represents 30 percent of consumer spending and displays an average monthly frequency of price changes of 1/3. The latter constitutes 70 percent of spending and displays an average monthly frequency of around 1/10. Our simulated models feature flexible and sticky-price sectors, with each sector's frequency and absolute size of price changes matching those statistics in the CPI data.
We find the models with big contract multipliers are fundamentally at odds with the data. TDP models, with or without strategic complementarities, and the SDP models with strategic complementarities, generate unrealistically high persistence and low volatility of reset price inflation. These models predict that the impact of a nominal shock on reset prices will build over time. But in the data we see the opposite. An increase in reset price inflation predicts lower, not higher, reset price inflation in subsequent months, so that an index of reset prices responds more on impact than over time. Another model prediction is that goods with infrequent price changes (the sticky-price goods) will display relatively more persistent inflation (overall, not reset). But we do not see this in the data.
The SDP model with no complementarities comes closest to matching the empirical patterns. It features broadly realistic volatility and persistence of reset and actual price inflation for all goods, flexible goods, and sticky goods. Related, a way to rescue strategic complementarities might be to incorporate endogenous monetary policy. If monetary policy quickly offsets the aggregate shock (to money itself or to aggregate productivity), then models with complementarities no longer imply outsized persistence of reset and actual inflation. This solution creates two problems, however. First, endogenous monetary policy essentially gets rid of the contract multiplier. Second, this solution reduces reset inflation volatility to around one-fifth of the observed level, and the variance of actual inflation to less than one-tenth the observed level. If monetary policy offsets shocks, price setters respond little to these shocks and inflation becomes much too smooth.
The literature on monetary policy has coalesced on strategic complementarities in order to rationalize a large contract multiplier. But our results strongly reject the predictions of those sticky-price models we examine that feature sufficient complementarities to produce an important contract multiplier.
The rest of the paper proceeds as follows. Section 2 describes the dataset and the empirical properties of reset price inflation. Section 3 lays out the models and compares statistics from the simulated models to their empirical counterparts. Section 4 concludes.
2. An empirical measure of reset price inflation
The CPI Research Database
We use the micro data underlying the non-shelter portion of the CPI to construct our measure of reset price inflation. The BLS surveys about 85,000 items a month in its Commodities and Services Survey. Individual prices are collected at around 20,000 retail outlets across 45 large urban areas.5 The survey covers all goods and services other than shelter, or about 70 percent of the CPI based on BLS consumer expenditure weights. The CPI Research Database (hereafter CPI-RDB) maintained by the BLS Division of Price and Index Number Research contains all prices in the Commodities and Services Survey since January 1988. We use the CPI-RDB through May 2008, for a sample of "1988-2008".
The BLS collects consumer prices monthly for food and fuel items in all areas. The BLS also collects prices monthly for all items in the three largest metropolitan areas (New York, Los Angeles, and Chicago). The BLS collects prices for items in other categories and other urban areas only bimonthly. For our competing models, the impulse responses for reset price inflation differ markedly in the initial periods after a shock, making it valuable to have an empirical counterpart that captures the data at high frequency. For this reason, we restrict our analysis to the top three areas that have monthly data on all goods.
The BLS defines 300 or so categories of consumption as Entry Level Items (ELIs). Within these categories are prices for particular items (we call a longitudinal series of individual price quotes at the micro level a "quote-line"). The BLS provided us with unpublished ELI weights for each year
from 1988-1995 and 1999-2004 based on Consumer Expenditure Surveys in each of those years. We normalize the nonshelter portion of the weights to sum to 1 in each year. We set the 1996 and 1997 ELI weights to the 1995 weights, and the 1998 weights to their 1999 level. We set the 2005 and onward
weights to their 2004 level. The CPI-RDB also contains weights for each price within an ELI. We allocate each ELI's weight to individual prices in each month in proportion to these item weights to arrive at weights ![]() that sum to 1 across items (
that sum to 1 across items (![]() 's) in each month.
's) in each month.
The BLS labels each price as either a "sale" price or a "regular" price. Sale prices are temporarily low prices (including clearance prices). Golosov and Lucas (2007), Nakamura and Steinsson (2008a), and others filter out such sale prices on the grounds that they are idiosyncratic deviations from stickier regular prices. Related, in classifying goods as "flexible" or "sticky" and in calibrating the model economies, we do so based on the frequency of regular price changes. We adopt this treatment because it yields more conservative results with respect to our conclusions. If, alternatively, we encompass the higher rate of price changes involving prices labeled by the BLS as sales prices, we would obtain an average frequency of price change of a little over 25 percent monthly rather than 22 percent. In turn, this would require even larger contract multipliers for our model economies to generate the same persistence in the impact of monetary shocks. But we find that the data do not support large contract multipliers. We use all prices, including sale prices, when constructing our inflation and reset price inflation series. To the extent sales are truly idiosyncratic their impact on the time series for price inflation, given the large samples of price quotes in each sector, will average close to zero. To the extent sales do affect aggregate price inflation, they are not idiosyncratic and so should not be excluded. That said, we will show that our results are robust to excluding sales prices from the series for price inflation.
Forced item substitutions occur when an item in the sample has been discontinued from its outlet and the price collector identifies a similar replacement item (e.g., new model) in the outlet to price going forward. The monthly rate of forced item substitutions is consistently about 3 percent in the sample. Essentially all item substitutions involve price changes. We include these price changes at substitutions in our statistics.6 But our results are extremely robust to treating all price changes as zero at forced substitutions.
About 12 percent of the prices the BLS attempts to collect are unavailable in a given month. The BLS classifies roughly 5 percent of items as out-of-season. We put zero weight on out-of-season items when calculating both inflation and the frequency of price changes. The BLS classifies the other 7 percent as temporarily unavailable. As these items may be only intermittently unavailable during the month, we treat items out of stock as available at the previously collected price. We employ this treatment both for calculating frequency of price changes and time series of inflation rates.
Although the BLS requires its price collectors to explain large price changes to limit measurement errors, some price changes in the dataset appear implausibly large. We exclude price changes that exceed a factor of five. Such price jumps constitute less than one-tenth of one percent of all price changes.
Defining Reset Price Inflation
Section 3 below illustrates how models with high contract multipliers exhibit inertia not only in price inflation, but also in reset price inflation -- so the behavior of reset price inflation is a barometer for lasting real effects of monetary shocks.
Whether pricing is time-dependent or state-dependent, the desired price level for item ![]() in month
in month ![]() ,
,
![]() , satisfies an Euler equation taking into account effects on current and future prices. Following Dotsey et al. (1999), the Euler equation is
, satisfies an Euler equation taking into account effects on current and future prices. Following Dotsey et al. (1999), the Euler equation is
![\begin{displaymath} \frac{\partial \Pi _{i,t} }{\partial P_{i,t}^\ast }=-E_t \left[ {\beta \frac{u'(c_{t+1} )}{u'(c_t )}(1-\lambda _{i,t+1} )\frac{\partial V_{i,t+1} }{\partial P_{i,t}^\ast }} \right] \end{displaymath}](img5.gif)
where
Reset price inflation for a given seller is the log first difference of its reset price:
This definition does not require a price change at either
(2.1)
![]() ,
,
where the weights ![]() add to 1. By comparison actual inflation is
add to 1. By comparison actual inflation is
![]() where
where
![]() and
and ![]() denotes the log
of the actual BLS price of item
denotes the log
of the actual BLS price of item ![]() at time
at time ![]() .
.
Whereas starred variables denote reset values, those without stars represent actual values. Let ![]() be a price-change indicator:
be a price-change indicator:
To construct an empirical measure of aggregate reset price inflation, each month we divide items into those that change price (
where ^'s denote our estimates. In turn, our estimate of aggregate reset price inflation is
(2.2)
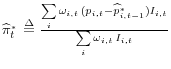 .
.
Although the estimate
![]() only employs time
only employs time ![]() price changers, price changes from
previous months are captured in the base values of
price changers, price changes from
previous months are captured in the base values of
![]() , which are indexed to reflect prior changes.7
, which are indexed to reflect prior changes.7
In Table 1 we present a stylized example useful for contrasting the rate of reset price inflation (
![]() ) to actual inflation (
) to actual inflation (![]() ) and the average inflation of
price changers (call this
) and the average inflation of
price changers (call this
![]() ). The example has two goods. Both goods change price in period 0, establishing base prices for calculating reset price inflation. Good A's price increases by 20% in period
1, with Good B's unchanged. This yields a rate of 20% for reset price inflation, same as the average rate of price increase conditional on changing price, while actual inflation is 10%. But note that it also kicks up the base price for calculating reset price inflation by 20%, not only for Good A,
but also for Good B. Thus, when B's price increases by 20% in period 2, while A's remain unchanged, B's price just meets its updated reset price from period 1. As a result, reset price inflation for period 2 equals zero, despite the same actual inflation rate and rate of increase for price
changers, respectively 10% and 20%, as in period 1. More generally, the average rates of reset price inflation and actual inflation will be equal over the "medium-run", but their time-series properties (volatility, persistence) can be quite different.
). The example has two goods. Both goods change price in period 0, establishing base prices for calculating reset price inflation. Good A's price increases by 20% in period
1, with Good B's unchanged. This yields a rate of 20% for reset price inflation, same as the average rate of price increase conditional on changing price, while actual inflation is 10%. But note that it also kicks up the base price for calculating reset price inflation by 20%, not only for Good A,
but also for Good B. Thus, when B's price increases by 20% in period 2, while A's remain unchanged, B's price just meets its updated reset price from period 1. As a result, reset price inflation for period 2 equals zero, despite the same actual inflation rate and rate of increase for price
changers, respectively 10% and 20%, as in period 1. More generally, the average rates of reset price inflation and actual inflation will be equal over the "medium-run", but their time-series properties (volatility, persistence) can be quite different.
Our estimated reset price inflation is equivalent to theoretical reset price inflation under the special case of Calvo pricing. By contrast, under SDP the decision to change a price reflects selection on the idiosyncratic component in a seller's desired price change. For this reason, estimated
reset price inflation
![]() can differ markedly from theoretical reset price inflation
can differ markedly from theoretical reset price inflation ![]() . We illustrate this difference for SDP models in Section 3 as a means of discriminating between the TDP and SDP models.
. We illustrate this difference for SDP models in Section 3 as a means of discriminating between the TDP and SDP models.
A key question for us is what extra information is contained in
![]() that cannot be gleaned from
that cannot be gleaned from ![]() alone. Under Calvo, one
can infer
alone. Under Calvo, one
can infer
![]() from
from ![]() if one also knows the price-change frequency.8 But endogenous price changing, and especially selection of changers, breaks the simple translation from
if one also knows the price-change frequency.8 But endogenous price changing, and especially selection of changers, breaks the simple translation from
![]() to
to ![]() . By endogenous price changing we mean any
response in the fraction of goods changing price to underlying shocks. By selection of changers we mean that, in contrast to Calvo, the changers may be those with larger gaps between actual and reset prices. Related,
. By endogenous price changing we mean any
response in the fraction of goods changing price to underlying shocks. By selection of changers we mean that, in contrast to Calvo, the changers may be those with larger gaps between actual and reset prices. Related,
![]() should be directly revealing about strategic complementarities, whereas
should be directly revealing about strategic complementarities, whereas ![]() is also affected by any response of the fraction changing. Some forces for a low contract multiplier (selection) or a high contract multiplier (strategic complementarities) operate on
is also affected by any response of the fraction changing. Some forces for a low contract multiplier (selection) or a high contract multiplier (strategic complementarities) operate on
![]() directly, whereas their effect on
directly, whereas their effect on ![]() can be clouded by
movements in frequency. The persistence of
can be clouded by
movements in frequency. The persistence of ![]() may be informative about the contract multiplier, but does not say where it is coming from (frequency or reset price inflation).
may be informative about the contract multiplier, but does not say where it is coming from (frequency or reset price inflation).
Similarly, we could focus on the average price change among changers (
![]() ) rather than constructing the less direct measure
) rather than constructing the less direct measure
![]() . In models we simulate, however, we find that the volatility of
. In models we simulate, however, we find that the volatility of
![]() /
/![]() does not vary with the contract multiplier (e.g., SDP
with or without complementarities), whereas the volatility of
does not vary with the contract multiplier (e.g., SDP
with or without complementarities), whereas the volatility of
![]() /
/![]() falls sharply with the contract multiplier. We will
revisit this issue in Section 3 below.
falls sharply with the contract multiplier. We will
revisit this issue in Section 3 below.
Evidence on Reset Price Inflation
Table 2 contains summary statistics on our constructed measure of reset price inflation, as well as on actual inflation for comparison. All the monthly series are HP-filtered and seasonally adjusted.9 Our measure of "all goods" excludes not only shelter, which is missing from the CPI-RDB, but also energy, fresh fruit and vegetables, and eggs. We exclude these for two reasons. First, they are arguably subject to big "sectoral" shocks that are absent from our models. If these shocks are temporary, then they artificially lower aggregate inflation persistence. Second, these goods involve little or no processing, and hence lack the strategic complementarities through slow-moving input prices.
In addition to the aggregate statistics, we examine actual and reset price inflation for two sub-aggregates: "flexible" goods and "sticky" goods. As mentioned, the BLS places individual price quote-lines into one of about 300 categories (ELIs). We calculate the average frequency of regular price changes within each ELI, then classify quote-lines as "flexible" or "sticky" based on their ELI's frequency. We choose a threshold frequency separating the two groups of 1/6, similar to the overall mean (weighted) frequency of 16.8 percent. This generates a 70 percent share of spending on the sticky group compared to 30 percent on the flexible group. We put more price quotes in the sticky group to mitigate sampling error there, given its smaller number of price changes per observed price. The flexible goods average 3,100 price quotes per month, compared to 8,300 for the sticky goods. The mean frequency of price changes is 33.3 percent in the flexible group, while only 9.5 percent for the sticky.
We calculate reset price inflation using formula (2.2) for flexible goods and sticky goods separately. We then calculate aggregate reset price inflation as the weighted average of reset price inflation for the two groups, with weights 0.3 on the flexible and 0.7 on the sticky, consistent with their expenditure shares. We do the same in calculating actual inflation at the aggregate level. Constructing reset price inflation at the group level first avoids overweighting frequent changers in calculating aggregate reset price inflation.10
The first row of Table 2 reports a standard deviation of monthly reset price inflation of almost 1.0 percent.11 There is no persistence in reset price inflation as measured by its first-order autocorrelation. In fact this serial correlation is notably negative, at -0.44. We provide more evidence on persistence below. The third and fourth rows report the comparable statistics for actual inflation. Actual inflation is much less volatile than reset price inflation, with a standard deviation, at 0.18%, less than one-fifth that for reset price inflation. This lower volatility for actual inflation follows mechanically from its including many zero price changes, unless variations in the frequency of changes play a major role in inflation movements - but we know from Klenow and Kryvtsov (2008) that frequency changes do not play that role. Actual inflation (serial correlation -0.12) is more persistent than reset price inflation (serial correlation -0.44). Again, this is expected under nominal price stickiness unless the frequency of price changes is highly responsive to the inflation rate; in fact, all models in Section 3 predict this result.
Our serial correlation for actual inflation is lower than reported in many studies for several reasons. First is our use of an HP filter (in addition to monthly dummies to capture seasonality). If we do not HP-filter, the serial correlation in actual inflation is modestly higher (+0.06 rather than -0.12). We also exclude energy and raw food items. Incorporating these categories would noticeably raise the serial correlation of unfiltered inflation to 0.30. Finally, longer time series - extending back to the 1970s or earlier - exhibit much more persistence. Persistence fell markedly by the time our sample began in the late 1980s. See Stock and Watson (2006) or Nason (2006), for example. Even for recent samples Stock and Watson find inflation has a persistent component. When we estimate an ARMA(1,1) for inflation we get an AR(1) coefficient of 0.89 (s.e. 0.03) and an MA(1) coefficient of -0.99 (.01). We highlight the AR(1) specification in our tables to be concise and to underscore that transitory components dominate the variance of recent inflation, just as Stock and Watson find. When estimating impulse response functions we consider less restricted specifications.
The second and third columns of Table 2 repeat the statistics from the first column for the flexible and sticky groups separately. We see that reset price inflation is volatile in both the flexible and sticky sectors, with standard deviations of 1.3 and 1.2 percent, respectively. Actual inflation is more than twice as volatile in the flexible vs. sticky sector, reflecting the important smoothing effect of many unchanging prices in the sticky sector. 12
Table 2 also shows the persistence in reset and actual price inflation across the two sectors. The flexible and sticky sectors have similar persistence in reset and actual price inflation as all goods. This runs counter to the prediction of many sticky price models that infrequent price changes act as a force for actual inflation inertia.13
The price series (reset and actual) described in Table 2 reflect sale prices as well as regular prices. The results, however, do not hinge on this treatment. Table 3 repeats all the statistics from Table 2 but treats sales prices as temporarily missing, carrying forward the most recent regular price as the price for that month. The patterns highlighted from Table 2 are nearly unchanged in Table 3. In particular, reset price inflation continues to show a strong negative serial correlation of -0.43 (vs. -0.44 in Table 2), and the serial correlation of actual inflation increases only modestly to -0.06 (vs. -0.12 in Table 2). This means that sale prices either wash out in the aggregate or mimic the movements in regular prices. Inflation is modestly more persistent at 0.15 (vs. -0.09) for sticky goods under this treatment.
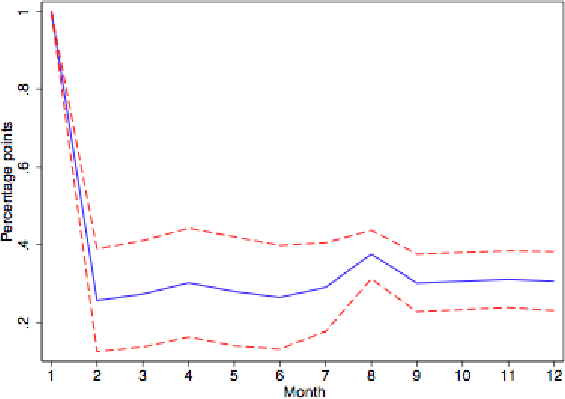
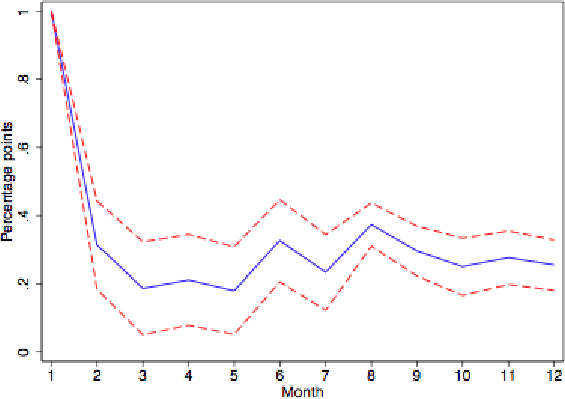
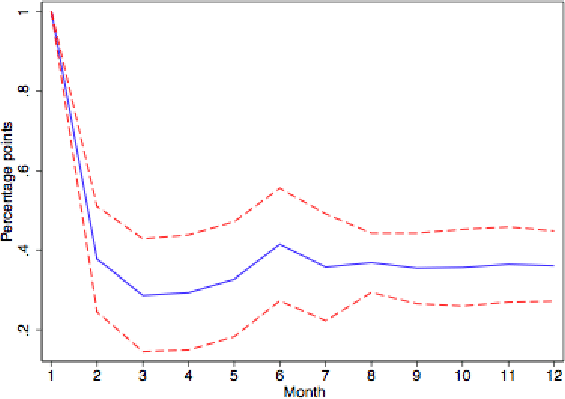
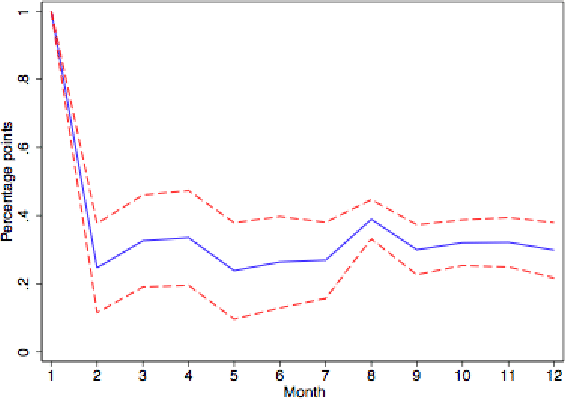
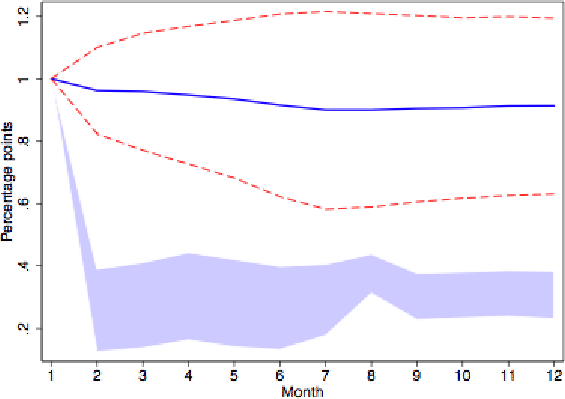
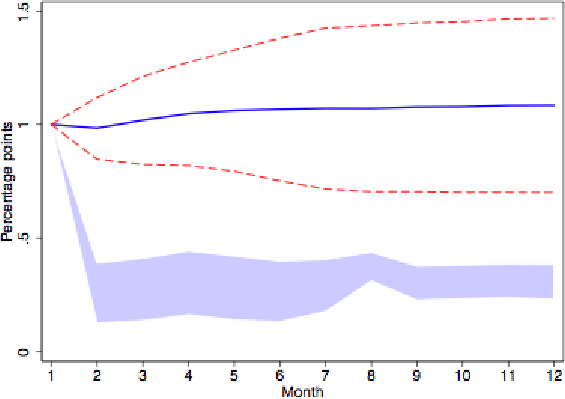
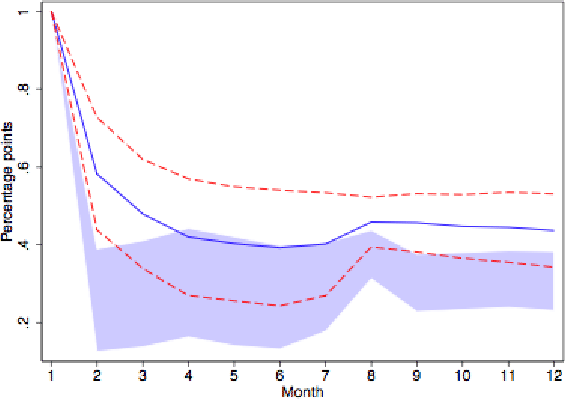
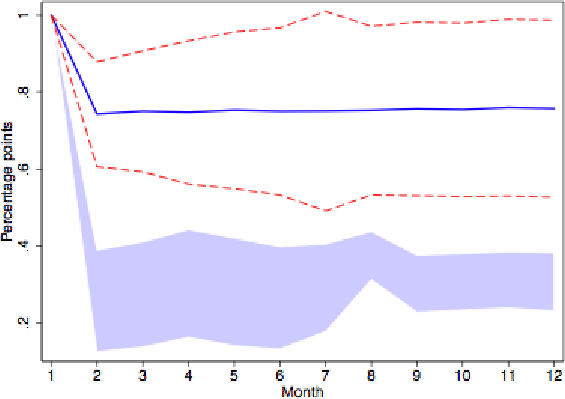
To further investigate the persistence properties of these inflation rates, we next show impulse responses derived from univariate AR(6) regressions. (The choice of 6 monthly lags is based on the Akaike criterion.) Figure 1 gives the response of reset prices to a 1% impulse for all goods. The (level) response in reset prices is much greater on impact than over time. The impact effect is more than double the long-run response. This mean reversion in reset prices does not reflect temporarily sales, as the patterns are very similar for series purged of sale prices as shown in Figure 2. The shape also holds separately for flexible and sticky goods, as depicted in Figures 3 and 4.14
One concern about Figures 1-4 is that the shocks themselves may be transitory. Responses to permanent shocks may exhibit far greater persistence. We therefore estimated the response of reset prices to a shock with a permanent 1% impact on actual prices, identified by imposing a long run restriction on a bivariate VAR with reset and actual price inflation. Reset prices overshoot their long run response just as much in this case.
We carried out a number of data robustness checks. Unless noted, the serial correlations and impulse functions were virtually unaffected. We aggregated the monthly time series up to the bi-monthly, quarterly, or even annual level. We split the monthly time series into two time periods, January 1989 through December 1998 and January 1999 through May 2008. We split the panel to create two samples (both going from January 1989 through May 2008) with half as many prices in each. The variance of reset price inflation was modestly higher in the two subsamples, as one would expect given greater sampling error. We dropped all price changes associated with product turnover (i.e., item substitutions). We looked only at services, whose prices are stickiest and whose spending exhibits little volatility (sectoral shocks thus being less of a concern). In each of these deviations from our baseline case, our findings remain intact. Finally, we looked at bi-monthly data for all areas (45 cities, as opposed to the monthly data for just New York, Los Angeles, and Chicago areas). This important robustness check incorporates much more data (68,500 quotes per bi-month vs. the 11,400 per month in our baseline dataset). Doing so materially lowers volatility by mitigating sampling error. We will return to these all-area results when comparing models to the data.
3. Sticky price models and reset price inflation
The leading TDP and SDP models have predictions for the behavior of reset price inflation. We will illustrate using a Calvo TDP model and an SDP model in the spirit of Golosov and Lucas (2007), respectively. They will be two-sector models with and without strategic complementarities, so Carvalho (2006) and Nakamura and Steinsson (2008b) are even closer antecedents. We first sketch the models, then report statistics from model simulations for comparison with the facts documented in the previous section.
The Models
Infinitely-lived households have preferences over labor supply and a composite consumption good, where composite consumption is a CES aggregate of individual consumption varieties. They also have access to state-contingent bonds (in zero net supply) for transferring resources across time periods, and they choose bond holdings, consumption, and labor supply to maximize discounted utility subject to a lifetime budget constraint.
Individual varieties are supplied by a continuum of monopolistically competitive firms. The production function of a particular firm (good) ![]()
![]() is given by
is given by
(3.1)
![]()
where ![]() denotes productivity,
denotes productivity, ![]() labor,
labor, ![]() a CES aggregate of individual intermediate goods, and
a CES aggregate of individual intermediate goods, and ![]() the share of the composite intermediate good.
Firms are grouped into one of two sectors distinguished by how frequently firms change price.
the share of the composite intermediate good.
Firms are grouped into one of two sectors distinguished by how frequently firms change price.
Production function (3.1) exhibits two key features commonly used in macro models of price stickiness. Following Danziger (1999) and Golosov and Lucas (2007), a firm's productivity is subject to idiosyncratic shocks, which will be important for capturing the dispersion of individual price
changes seen in the data. A second key feature is the inclusion of intermediate goods, following Basu (1995) and Dotsey and King (2006). For![]() , each firm uses intermediate inputs
produced by all other firms in the economy. Intermediates are a way of generating strategic complementarities in price-setting, as costs fully respond to a shock only when other firms' prices respond. In an excellent survey, Mackowiak and Smets (2008) suggest such "macro rigidities" are promising
for obtaining high contract multipliers.
, each firm uses intermediate inputs
produced by all other firms in the economy. Intermediates are a way of generating strategic complementarities in price-setting, as costs fully respond to a shock only when other firms' prices respond. In an excellent survey, Mackowiak and Smets (2008) suggest such "macro rigidities" are promising
for obtaining high contract multipliers.
Firms hire inputs and set prices to maximize expected discounted profits subject to a fixed cost of changing price. In the SDP models, the cost is constant over time for each firm, but does vary across firms depending on the firm's sector. For the TDP models, firms receive a menu cost draw of
either 0 or ![]() in each period, with the sector-specific probability of a menu cost of zero being fixed over time.
in each period, with the sector-specific probability of a menu cost of zero being fixed over time.
Finally, we assume a cash-in-advance constraint on a household's nominal spending
In turn, we assume the money supply evolves as follows:
(3.2)
![]()
where ![]() is a monetary policy shock and
is a monetary policy shock and
![]() is steady-state aggregate real demand. When
is steady-state aggregate real demand. When ![]() , the money supply evolves exogenously according to a geometric random walk with drift. We will also consider an "endogenous monetary policy" case, in which
, the money supply evolves exogenously according to a geometric random walk with drift. We will also consider an "endogenous monetary policy" case, in which ![]() and money growth is inversely related to lagged aggregate real demand.
and money growth is inversely related to lagged aggregate real demand.
An appendix provides a more thorough mathematical exposition of the model,
including its key parameters, and describes the solution method.15
Calibration
Table 4 reports the values of economy-wide parameters in the TDP and SDP models. We consider three specifications: a baseline case featuring no strategic complementarities, a strategic complementarities specification that generates a "contract multiplier" of 4, and a specification with
strategic complementarities and "endogenous monetary policy." Most parameters remain constant across the three specifications. The monthly discount factor is
![]() . We consider log utility in consumption (
. We consider log utility in consumption (![]() ) and linear
labor supply (
) and linear
labor supply (![]() ), while the parameter governing the disutility of labor supply (
), while the parameter governing the disutility of labor supply (![]() ) is set so that steady state labor supply is 1/3. The elasticity of demand for consumption varieties is
) is set so that steady state labor supply is 1/3. The elasticity of demand for consumption varieties is ![]() , within the range of values estimated in the trade and
IO literatures, e.g., Broda and Weinstein (2006) and Hendel and Nevo (2006).16 We set the parameters for the money growth process (
, within the range of values estimated in the trade and
IO literatures, e.g., Broda and Weinstein (2006) and Hendel and Nevo (2006).16 We set the parameters for the money growth process (
![]() ) to match the mean growth rate of inflation (0.2%), the standard deviation of nominal non-shelter PCE growth (0.48%), and, for the "endogenous monetary policy" case,
the serial correlation of nominal PCE growth (-0.31) over our sample period.17 The serial correlation of the idiosyncratic productivity shock is set to
) to match the mean growth rate of inflation (0.2%), the standard deviation of nominal non-shelter PCE growth (0.48%), and, for the "endogenous monetary policy" case,
the serial correlation of nominal PCE growth (-0.31) over our sample period.17 The serial correlation of the idiosyncratic productivity shock is set to
![]() , based on estimates in Klenow and Willis (2006) using the serial correlation of new relative prices in the CPI-RDB.
, based on estimates in Klenow and Willis (2006) using the serial correlation of new relative prices in the CPI-RDB.
Table 4 also presents parameter values determining the degree of strategic complementarity in pricing. Following Ball and Romer (1990), we define strong real rigidities (more strategic complementarities in this model) as low responsiveness of a firm's real price to changes in aggregate real demand. The firm's optimal price in the absence of menu costs can be expressed (ignoring constants) as
(3.3)
![]() .
.
As in Woodford (2003), we define strategic complementarity as a positive weight on the aggregate price, rather than having all weight on the aggregate money stock. Thus, when
![]() is small, prices exhibit greater complementarity. Our baseline model has log utility in consumption (
is small, prices exhibit greater complementarity. Our baseline model has log utility in consumption (![]() ), linear labor supply (
), linear labor supply (![]() ), and no intermediate goods (
), and no intermediate goods (![]() ), so that
), so that
![]() . This baseline case has no strategic complementarity (the coefficient is 0 on the aggregate price level). In our "strategic complementarities" case, we choose
the intermediate input share to generate a contract multiplier of 4, where the contract multiplier is calculated as the ratio of the duration of real effects of a monetary policy shock to the number of periods in a typical contract.18 This requires an intermediate share of
. This baseline case has no strategic complementarity (the coefficient is 0 on the aggregate price level). In our "strategic complementarities" case, we choose
the intermediate input share to generate a contract multiplier of 4, where the contract multiplier is calculated as the ratio of the duration of real effects of a monetary policy shock to the number of periods in a typical contract.18 This requires an intermediate share of ![]() in the SDP model (
in the SDP model (![]() for TDP) and yields
for TDP) and yields
![]() , or strong strategic complementarities (a coefficient of 0.95 on the aggregate price level).19 As emphasized by Basu (1995), more intensive use of intermediate inputs makes the response of marginal cost to monetary shocks a function of not only the nominal wage but the extent of price adjustment at other
firms - a strategic complementarity.
, or strong strategic complementarities (a coefficient of 0.95 on the aggregate price level).19 As emphasized by Basu (1995), more intensive use of intermediate inputs makes the response of marginal cost to monetary shocks a function of not only the nominal wage but the extent of price adjustment at other
firms - a strategic complementarity.
Table 5 reports the values of sector-specific parameters in our models. In the SDP model, we calibrate the standard deviation of each sector's idiosyncratic productivity shock and each sector's menu costs to generate frequencies of price change by sector of 0.33 (flexible) and 0.10 (sticky), as well as an average size of price change of 8% and 9.5% in the respective sectors. These figures correspond closely to the frequency and average size of price changes in the BLS data by sector, excluding energy and raw food. The required shocks have standard deviations of 4.94% for the flexible sector and 4.75% for the sticky sector. Expended menu costs average about 0.20% of revenue, somewhat lower than the estimates of Levy et al. (1997) and Zbaracki et al. (2004). Finally, 30% of firms are in the flexible sector and 70% are in the sticky, to match the BLS expenditure shares on these two groups.
For the TDP model, only the menu cost parameters differ from the SDP model. We actually embed Calvo in an SDP model with time-varying menu costs. Each period, the menu cost is zero for a fraction ![]() of firms, while prohibitively large for a fraction
of firms, while prohibitively large for a fraction![]() of firms.
of firms.
Results and Interpretation
We now compare statistics from model simulations to the data statistics. To match the
data sample, we simulate economies with 3,100 firms in the flexible sector and 8,300 firms in the sticky sector for 233 periods. We run 100 such simulations and report the average and standard deviation of the statistics across the simulations. We find that models generating large contract multipliers, either through the use of TDP or strategic complementarities, display unrealistically high persistence and low volatility of reset price inflation. Compared to the empirical data, reset price inflation in the models is way too persistent and stable.
In Table 6 we present statistics for the Calvo TDP model without strategic complementarities. This model has a contract multiplier around two.20 Model
reset inflation rates are too smooth relative to the data, exhibiting only one-fourth the observed variance. Reset price inflation is also too persistent (-0.04 in the model vs. -0.44 in the data), and the discrepancy is even greater for actual inflation (0.73 in the model vs. -0.12 in the data).
Figure 5 presents the univariate IRF for model reset prices for all goods. The model IRF is flat, meaning the average desired price fully responds on impact. Equation (3.3) shows why: the average desired price, washing out idiosyncratic shocks ![]() , moves one-for-one with a change in money supply in the absence of strategic complementarities. Because money growth follows a random walk, the result is a flat impulse response function. Figure 5 also shows the confidence intervals from
the data for comparison; the empirical IRFs are, in contrast, highly transitory. The model and empirical bands do not overlap despite each representing +/- two standard deviations. The contrast is similarly stark for flexible and sticky goods separately (not shown).
, moves one-for-one with a change in money supply in the absence of strategic complementarities. Because money growth follows a random walk, the result is a flat impulse response function. Figure 5 also shows the confidence intervals from
the data for comparison; the empirical IRFs are, in contrast, highly transitory. The model and empirical bands do not overlap despite each representing +/- two standard deviations. The contrast is similarly stark for flexible and sticky goods separately (not shown).
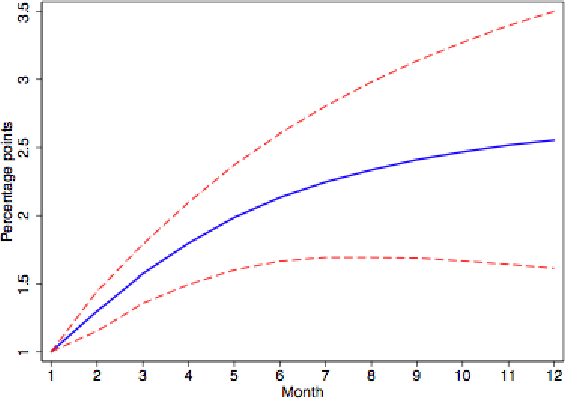
Table 7 presents results from a Calvo TDP model with strategic complementarities. The contract multiplier here is approximately four. The complementarities further depress the volatility of reset price inflation, so that the model variance is now more than an order of magnitude smaller than the empirical variance. The excess persistence problems seen in Table 6 (TDP without strategic complementarities) remain. Figure 6 shows that, if anything, the univariate IRF for reset prices builds because of the strategic complementarities, in contrast to the falling empirical IRF. The model IRF would build more briskly if not for the sampling error from the finite sample of firms, as in the data.
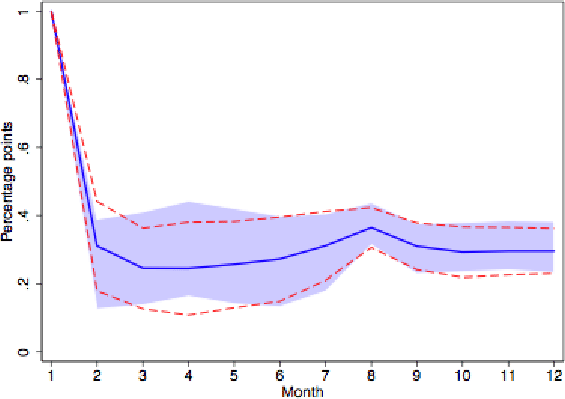
Table 8 presents the SDP model without strategic complementarities. As in Golosov and Lucas (2007), the contract multiplier in this model is well below one at 0.4. Inflation persistence is markedly reduced relative to the TDP models--a result anticipated by Caballero and Engel (2007). The persistence of reset price inflation is now within striking distance of the data (-0.31 model vs. -0.44 data). And Figure 7 shows that the model impulse response function for reset prices is much closer to the empirical pattern. The selection effect stressed by Golosov and Lucas means first-responders actually overshoot the long run response after selection effects have faded. But the persistence of actual inflation is still too high (0.38 model vs. -0.12 data for actual inflation). The gap is even larger for sticky goods (0.53 model vs. -0.15 data). Finally, the volatility of reset price inflation is too high in this model relative to the data, with variances more than double the actual ones for all goods and sticky goods. Still, the discrepancies are notably smaller than for the TDP models.
The reduced persistence and greater volatility of actual inflation for the SDP model do not reflect important fluctuations in the frequency of price changes under the SDP model. The standard deviation of the frequency of price changes is very low for the SDP model, equaling about 0.2 and 0.4
percentage points, respectively, for flexible and sticky goods. Directly related, the average rate of price increase conditional on changing,
![]() , provides little information beyond that in actual inflation. For instance, for sticky goods under TDP the standard deviation of
, provides little information beyond that in actual inflation. For instance, for sticky goods under TDP the standard deviation of
![]() is exactly 10 times the standard deviation of actual inflation with or without complementarities. For the SDP models this ratio remains very similar, equaling 9.4. Reset
price inflation, in contrast, is much more volatile for the SDP model than under TDP, making it a more discriminating statistic. In particular, for the TDP model with strategic complements, the standard deviation of reset inflation for sticky goods is only 4.6 times its standard deviation for
actual inflation, whereas for the SDP model without complementarities this ratio is 8.0. Based on the CPI data (Table 2), the observed ratio is 7.6.
is exactly 10 times the standard deviation of actual inflation with or without complementarities. For the SDP models this ratio remains very similar, equaling 9.4. Reset
price inflation, in contrast, is much more volatile for the SDP model than under TDP, making it a more discriminating statistic. In particular, for the TDP model with strategic complements, the standard deviation of reset inflation for sticky goods is only 4.6 times its standard deviation for
actual inflation, whereas for the SDP model without complementarities this ratio is 8.0. Based on the CPI data (Table 2), the observed ratio is 7.6.
In Table 9 we add strategic complementarities (intermediate share
![]() ) to produce a contract multiplier of around four. Doing so makes reset inflation much smoother, to the point that empirical reset price inflation is almost four times as
volatile as reset price inflation in the model. Model inflation rates become more persistent as well, moving away from the data (e.g., serial correlation -0.24 in the model vs. -0.44 in the data). Model inflation becomes too stable; for flexible goods the model variance is less than one-eighth its
empirical counterpart. Perhaps most problematic, inflation persistence is 0.73 in the model, about 16 standard errors from the empirical counterparts of -0.12. In short, a big contract multiplier makes reset and actual inflation rates way too stable and persistent.
) to produce a contract multiplier of around four. Doing so makes reset inflation much smoother, to the point that empirical reset price inflation is almost four times as
volatile as reset price inflation in the model. Model inflation rates become more persistent as well, moving away from the data (e.g., serial correlation -0.24 in the model vs. -0.44 in the data). Model inflation becomes too stable; for flexible goods the model variance is less than one-eighth its
empirical counterpart. Perhaps most problematic, inflation persistence is 0.73 in the model, about 16 standard errors from the empirical counterparts of -0.12. In short, a big contract multiplier makes reset and actual inflation rates way too stable and persistent.
Figure 8 plots the IRF for reset prices in the SDP model with strategic complementarities. The trajectory is largely flat, in sharp contrast to the plunging profiles in the SDP model without complementarities (Figure 7) and in the data (Figures 1-4).
Because we can produce time series for theoretical reset price inflation in model economies, we can use its IRF to document the impact of the "selection effect" and sampling error on our estimated reset price inflation in the model. Figure 9 displays the response of the theoretical reset price in the SDP model with complementarities. Note its upward sloping trajectory. Strategic complementarities mute the size of price changes for those changing prices, as price setters wait for the average price to respond. Thus, theoretical reset price inflation is small on impact but accumulates over time as more firms change price.
Constructed reset price inflation in Figure 8 differs sharply from theoretical reset price inflation in Figure 9 in part because of a strong "selection effect" (see Caballero and Engel, 2007, and Golosov and Lucas, 2007). The firms changing price in a given period are not an unbiased sample of the population, but rather those who most benefit from a price change. The response of reset price inflation is much greater on impact because only firms in the tails of the distribution change price. For example, in response to a positive monetary shock, the average productivity of the price changers is below the average productivity of all firms, causing the measured reset price inflation (which depends only on price changers) to be much higher than theoretical reset price inflation. In the long-run, the response of these two measures is the same. As a result the selection effect also explains much of the greater volatility found in the SDP models relative to the TDP models.
Sampling error is another reason the IRF for measured reset price inflation is flatter than that for theoretical reset price inflation. Our theoretical plot (Figure 9) is for the population (continuum) of firms in the model economy, whereas Figure 8 is from simulations with a finite sample of firms to mimic the data. Our idiosyncratic shocks (serial correlation 0.7) are less persistent than our aggregate shocks, which follow a random walk. In finite samples the idiosyncratic shocks do not wash out, imparting less persistence to reset price inflation.21 Below we present results with bi-monthly data from all cities, a much larger
sample with correspondingly lesser sampling error.
A potential explanation for our negative findings (too persistent IRFs in models with big contract multipliers) is that we have neglected endogenous monetary policy, which can reduce persistence in the presence of permanent shocks. The literature has estimated big contract multipliers over long periods (such as 1950 to 2000), but the Fed may have reduced inflation persistence and volatility dramatically in the 20 years covered by our sample (1988-2008). Authors have documented regime changes in U.S. inflation over the past two decades (e.g., Nason, 2006), as well as for many inflation targeting countries (e.g., Benati, 2008).
In this spirit, we simulate the SDP model with complementarities and a version of endogenous monetary policy. Specifically, we set ![]() (the response of money growth to
lagged real money balances) in equation (3.2) to match the serial correlation of nominal PCE growth (-0.31) over our sample period. Here money growth offsets movements in the real money stock. As shown in Table 10 (summary statistics) and Figure 10 (univariate IRFs for flexible and sticky groups),
this specification succeeds in driving down the persistence of reset price inflation to levels observed in the data (e.g., -0.43 in the model vs. -0.44 in the data for all goods). Moreover, Figure 10 depicts a model IRF for reset prices that is spot on with the empirical estimates. The required
endogenous monetary policy involves price level targeting rather than more conventional inflation targeting. Gorodnichenko and Shapiro (2007) argue that the Greenspan Fed did target the price level.
(the response of money growth to
lagged real money balances) in equation (3.2) to match the serial correlation of nominal PCE growth (-0.31) over our sample period. Here money growth offsets movements in the real money stock. As shown in Table 10 (summary statistics) and Figure 10 (univariate IRFs for flexible and sticky groups),
this specification succeeds in driving down the persistence of reset price inflation to levels observed in the data (e.g., -0.43 in the model vs. -0.44 in the data for all goods). Moreover, Figure 10 depicts a model IRF for reset prices that is spot on with the empirical estimates. The required
endogenous monetary policy involves price level targeting rather than more conventional inflation targeting. Gorodnichenko and Shapiro (2007) argue that the Greenspan Fed did target the price level.
Still, there are two problems with this endogenous monetary policy scenario. First, there is no longer a contract multiplier above one.22 Second and more problematic, endogenous money growth saps inflation of most of its volatility. Empirical reset price inflation has six times the variance in the endogenous money model, and empirical inflation has thirteen times the variance in the model. The intuition is this: if endogenous monetary policy undoes the impact of complementarities on inflation persistence, then there is little reason for reset and actual prices to respond. If prices are sticky, one will not want to incorporate very transitory shocks into new prices. Thus we are left with the problem of reconciling a model with strong complementarities simultaneously with the observed persistence and volatility of empirical inflation rates. This "excess smoothness" problem is even worse for the population of prices than for finite samples presented in Table 10. Sampling error dominates the variances in finite simulations, whereas it appears to account for a much smaller fraction of the empirical variances.
Another robustness check we perform is to replace the aggregate monetary shock with an aggregate productivity shock. Indeed, Altig et al. (2005) argue that shocks to aggregate productivity are more important for inflation movements than are monetary policy shocks. With random walk aggregate productivity, instead of random walk money, our results are virtually identical (e.g., for SDP with complementarities, with or without endogenous money).
Finally, one could argue that we failed to entertain large, temporary sectoral shocks that do not wash out in the aggregate. Boivin, Giannoni and Mihov (2009) provide evidence that disaggregated inflation rates are much more volatile and transitory than aggregate inflation. But strong strategic complementarities make it hard to explain large responses to transitory shocks, whether they be aggregate or sectoral. And we calibrated our aggregate shocks to generate the observed variability of nominal consumption growth. Thus adding sectoral shocks (or more aggregate shocks) to generate more realistic volatility of reset price inflation may require unrealistically high volatility of real consumption growth and/or its covariance with inflation.
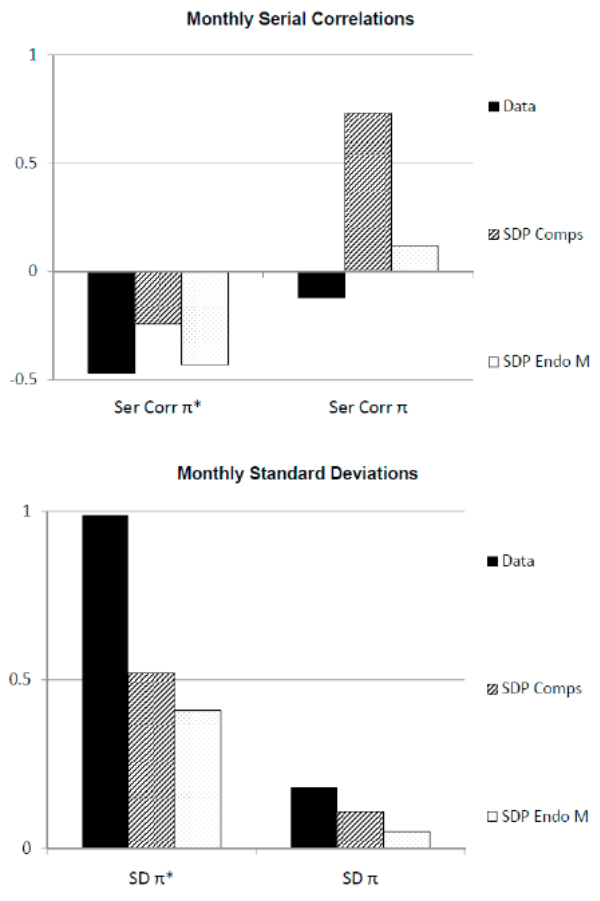
We now recap some of our key findings. Figure 11 contains bar charts of data moments vs. moments from finite sample simulations of the SDP model with strong complementarities. The top panel contains serial correlations, and the bottom panel standard deviations. Without endogenous monetary policy ("SDP Comps"), the model seriously overstates the persistence and understates the volatility of reset and actual inflation. Endogenous monetary policy ("SDP Endo M") largely closes the persistence gaps, but widens the volatility gaps.
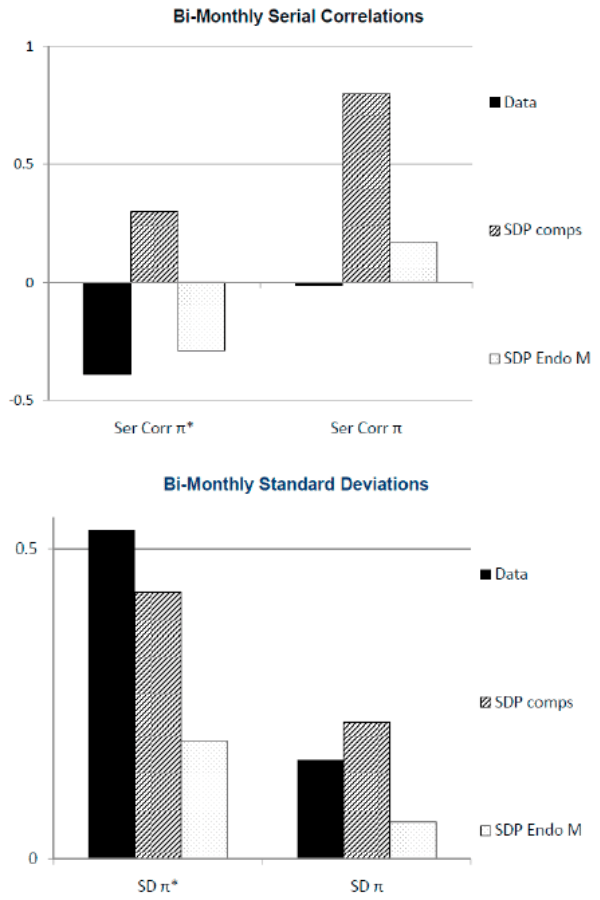
In Figure 12 we provide the same model vs. data statistics, only for much larger bi-monthly samples. Recall that we have roughly six times the prices per bi-month from all cities as we have monthly prices per month from the top three cities. (So this greatly reduces the impact of sampling error for both the data and model statistics.) The bi-monthly serial correlations (top panel of Figure 12) are similar to those in the monthly samples. Without endogenous monetary policy the SDP model with strong complementarities exhibits excessive persistence, with endogenous monetary policy it does not.23 But, again, endogenous monetary policy drains most of the volatility out of both reset and actual inflation rates (bottom panel of Figure 12). We are unable to reconcile strong complementarities with both the transitory and volatile behavior we observe in reset price inflation.
Although not shown, a model that comes closest to fitting all the empirical moments in Table 2 is an SDP model with endogenous monetary policy and an intermediate goods share of only 1/3. This degree of complementarities is not sufficient to produce a contract multiplier above 1, however, even in the absence of endogenous monetary policy.
4. Conclusion
A large empirical literature has estimated that monetary policy shocks affect real variables for several years, much longer than the duration of nominal prices. A popular explanation for this contract multiplier combines sticky prices and strategic complementarities. The complementarities make reset prices build slowly after permanent shocks, prolonging the real effects beyond the duration of nominal prices. That is, strategic complementarities impart persistence to reset price inflation. However, using data underlying the U.S. CPI from 1988-2008, we do not see the persistence in reset price inflation that models with complementarities predict.
Temporary shocks (or endogenous monetary policy) might explain the low persistence of reset price inflation, but at the expense of failing to generate as much volatility as seen in reset price inflation in the U.S. from 1988-2008. Strong strategic complementarities severely dampen the volatility of reset price inflation when shocks are transitory. In short, we fail to find a model specification with strong complementarities that fits both the low persistence and nontrivial volatility of observed reset price inflation. This is true whether we entertain monetary or productivity shocks, and even accounting for how sampling error and temporary sales affect the persistence and volatility of reset price inflation.
Models of complementarities not explored here might be able to reconcile low persistence of reset price inflation with a high contract multiplier. But our intuition is that other complementarities (e.g., sticky wages rather than sticky intermediates) have similar predictions for the persistence of reset price inflation. A more promising reconciliation may involve sticky information rather than strategic complementarities. The contract multiplier might be high in response to a subset of shocks about which firms have sticky information. Meanwhile, the variance and persistence of reset price inflation may be dominated by shocks about which firms have more flexible information. Mackowiak and Wiederholt (2008) present a DSGE model in which this is precisely the case.24
Alternatively, the contract multiplier may not be so high after all. Perhaps the high inflation persistence over longer samples reflects the persistence of monetary shocks rather than complementarities. The low inflation persistence of recent decades could be because the Fed stopped adding persistence, revealing low endogenous persistence.
Our conclusions overlap with those of several recent studies. Cogley and Sargent (2001), Primiceri (2006), and Cogley and Sbordone (2008) all argue that U.S. inflation persistence over long samples stems from changes in trend inflation (i.e., monetary regime changes). They do not rely on a high contract multiplier per se. Klenow and Willis (2006) and Kryvtsov and Midrigan (2008) find it difficult to reconcile specific types of strategic complementarities with, respectively, large idiosyncratic price changes and countercyclical inventories/sales. Gopinath, Itskhoki and Rigobon (2007) and Gopinath and Itskhoki (2008), in contrast, see strategic complementarities behind the incomplete pass-through of exchange rates to import prices.
This appendix provides a more detailed exposition of the price-setting models and discusses the solution method we used.
A representative household has discounted utility
![\begin{displaymath} U_0 =E_0 \sum\limits_{t=0}^\infty {\beta ^{\,t}\left[ {\frac{C_t^{1-\gamma } }{1-\gamma }-\omega \frac{L_t^{1+\psi } }{1+\psi }} \right]} \end{displaymath}](img73.gif)
where
(A1)
![C=\left[ {\int\limits_0^1 {c(i)^{\,1-1/\theta }di} } \right]^{\,\frac{\theta }{\theta -1}}](img77.gif) .
.
The household's budget constraint is
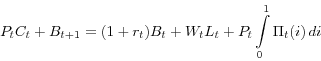
where
The household chooses bond holdings, labor supply, and consumption of individual varieties to satisfy the following first-order conditions:
(A2)
![1=\beta E_t \left[ {\left( {1+r_{t+1} } \right)\left( {\frac{C_{t+1} }{C_t }} \right)^{-\gamma }\frac{P_t }{P_{t+1} }} \right]](img85.gif)
(A3)
![]()
(A4)
![]() .
.
Turning to production, there are a continuum of monopolistically competitive firms indexed by ![]() , which denotes the one variety each produces. Firm
, which denotes the one variety each produces. Firm![]() has productivity
has productivity![]() and combines labor
and combines labor![]() and a composite intermediate good
and a composite intermediate good ![]() to produce good
to produce good ![]() :
:
(A5)
![]()
where![]() denotes the share of the composite intermediate good. The intermediate composite is a CES aggregate of individual intermediate goods:
denotes the share of the composite intermediate good. The intermediate composite is a CES aggregate of individual intermediate goods:
(A6)
![X(i)=\left[ {\int\limits_0^1 {x_t (i,j)^{1-1/\theta }} dj} \right]^{\,\frac{\theta }{\theta -1}}](img88.gif)
where ![]() is the quantity of intermediate good
is the quantity of intermediate good ![]() used by firm
used by firm ![]() . Note that symmetry between (A6) and the consumption aggregator (A1) means that the unit price of
. Note that symmetry between (A6) and the consumption aggregator (A1) means that the unit price of ![]() is equal to
is equal to ![]() , the unit price of the consumption composite. Firms are grouped into one of two sectors, to be indexed by
, the unit price of the consumption composite. Firms are grouped into one of two sectors, to be indexed by ![]() , with the main difference between sectors being how frequently firms change price. A firm's productivity is subject to idiosyncratic shocks of the following form:
, with the main difference between sectors being how frequently firms change price. A firm's productivity is subject to idiosyncratic shocks of the following form:
where
Firm ![]() in sector
in sector ![]() maximizes its discounted (real) profits
maximizes its discounted (real) profits
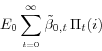
where
(A7)
![]() .
.
A firm's profits equal revenue less input costs, including the cost of changing prices (the last term). ![]() is an indicator function for whether firm
is an indicator function for whether firm ![]() changes its price in period
changes its price in period ![]() at a cost of
at a cost of ![]() units of labor. For the SDP models, we set
units of labor. For the SDP models, we set
![]() . That is, in the SDP models the menu cost is fixed over time for each firm, but does vary across firms depending on the firm's sector. For the TDP models,
. That is, in the SDP models the menu cost is fixed over time for each firm, but does vary across firms depending on the firm's sector. For the TDP models,
![]() . Specifically, we mimic the Calvo model by having firms in sector
. Specifically, we mimic the Calvo model by having firms in sector ![]() face a menu cost of 0 with probability
face a menu cost of 0 with probability ![]() and a menu cost of
and a menu cost of ![]() with probability
with probability ![]() . These Calvo menu cost realizations are independent both across firms within sectors and over time.
. These Calvo menu cost realizations are independent both across firms within sectors and over time.
Firm choices of intermediates satisfy a first-order condition comparable to consumer choices of final consumption varieties:
(A8)
![]() .
.
Setting production equal to total demand (from consumers and others firms) for firm ![]() yields
yields
(A9)
![y_t (i)=c_t (i)+\int\limits_0^1 {x_t (j,i)\,dj} =\,\,\left[ {\frac{p_t (i)}{P_t }} \right]^{\,-\theta }\left( {C_t +X_t } \right)](img103.gif)
where
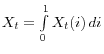 . The aggregate resource constraints for output and labor are then
. The aggregate resource constraints for output and labor are then
(A10)
![C_t +X_t =\left[ {\int\limits_0^1 {y_t (i)^{1-1/\theta }} di} \right]^{\,\frac{\theta }{\theta -1}}\equiv Y_t \mbox{ and }\,L_t =\int\limits_0^1 {\left[ {L_t (i)+k_t (i)I_t (i)} \right]\,} di](img105.gif) .
.
Finally, we assume a cash-in-advance constraint on a consumer's nominal spending
In turn, we assume the money supply evolves as follows:
where
For setting up the firm's value function, it is useful to substitute a few variables out of the firm's profit function. This (along with one assumption described below) will allow us to express the firm's value as a function of only three states:
![]() . First, we use firm cost-minimization to substitute
. First, we use firm cost-minimization to substitute ![]() out of profits (A7) using
out of profits (A7) using
(A11)
![]() .
.
Second, we use the firm's production function to substitute ![]() out of profits:
out of profits:
We next substitute
(A12)
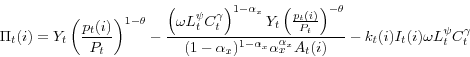
.
We then log-linearize the production function (A5), labor supply (A3), resource constraints (A10), and equation (A11) around the flexible-price steady state to express ![]() and
and
![]() as linear functions of
as linear functions of ![]() , where ^'s denote log deviations
from steady state values. Specifically,
, where ^'s denote log deviations
from steady state values. Specifically,
![\begin{displaymath} \hat {L}_t =\left[ {\frac{\frac{C}{Y}+\gamma \left( {\frac{X}{Y}-\alpha _x } \right)}{1+\psi \alpha _x -\left( {1+\psi } \right)\left( {\frac{X}{Y}} \right)}} \right]\hat {C}_t \end{displaymath}](img120.gif)
where
Finally, the cash-in-advance constraint implies
To write the firm's value function in terms of these same three state variables, we must make one more simplifying assumption. The state space of the firm's problem is actually infinite dimensional since the evolution of the price level depends on the entire distribution of all firms' prices and productivity levels. In the spirit of Krusell and Smith
(1998), we assume that firms perceive the evolution of the price level as being a function of a
single moment of this distribution. Specifically,
Nakamura and Steinsson (2008b) show that this assumption makes the model tractable while still providing highly accurate forecasts of the price level.
In the end, the firm's value function takes the recursive form
where
![]() is the stochastic discount factor between periods
is the stochastic discount factor between periods ![]() and
and
![]() . The model is then solved using value function iteration, with the additional requirement that the forecast rule
. The model is then solved using value function iteration, with the additional requirement that the forecast rule ![]() be consistent with the aggregation of firm pricing decisions.
be consistent with the aggregation of firm pricing decisions.
| Period 0 | Period 1 | Period 2 | |
|---|---|---|---|
| Price of Good A | 1 | 1.22 | 1.22 |
| Inflation for Good A | 20% | 0% | |
| Reset price for Good A | 1 | 1.22 | 1.22 |
| Reset Inflation for Good A | 20% | 0% | |
| Price of Good B | 1 | 1 | 1.22 |
| Inflation for Good B | 0% | 20% | |
| Reset price for Good B | 1 | 1.22 | 1.22 |
| Reset Inflation for Good B | 20% | 0% | |
| Inflation ( |
10% | 10% | |
| Inflation for changers (
|
20% | 20% | |
| Reset inflation (
|
20% | 0% |
Note: The example assumes equal expenditure shares, equaling one half, for both goods. It also assumes that both Good A and Good B exhibited a price change in period 0, establishing the base price for calculating reset price inflation for period 1. The number 1.22 in the table represents exp(0.2) to two decimal places.
| Statistic | All Goods |
Flexible Goods |
Sticky Goods |
|---|---|---|---|
| Standard deviation of |
0.99%
(0.05) |
1.30%
(0.06) |
1.21%
(0.06) |
| Serial correlation of |
-0.47
(0.05) |
-0.41
(0.05) |
-0.49
(0.06) |
| Standard deviation of |
0.18%
(0.01) |
0.41%
(0.02) |
0.16%
(0.01) |
| Serial correlation of |
-0.12
(0.06) |
-0.10
(0.06) |
-0.15
(0.08) |
Notes: All data are from the CPI-RDB. Samples run from January 1989 through May 2008. The threshold frequency of regular price changes is one-sixth per month: quote-lines in ELIs with average frequency higher than one-sixth are in the flexible group, and those with lower frequency are in the sticky group. All series are monthly, are HP-filtered with smoothing parameter 1,000,000, and are seasonally adjusted. Standard errors are in parentheses.
| Statistic | All Goods |
Flexible Goods |
Sticky Goods |
|---|---|---|---|
| Standard deviation of |
0.95%
(0.04) |
1.38%
(0.06) |
1.13%
(0.05) |
| Serial correlation of |
-0.41
(0.05) |
-0.42
(0.05) |
-0.40
(0.04) |
| Standard deviation of |
0.14%
(0.01) |
0.39%
(0.02) |
0.10%
(0.01) |
| Serial correlation of |
-0.05
(0.06) |
-0.05
(0.06) |
0.09
(0.08) |
Notes: All data are from the CPI-RDB. Samples run from January 1989 through May 2008. The threshold frequency of regular price changes is one-sixth per month: quote-lines in ELIs with average frequency higher than one-sixth are in the flexible group, and those with lower frequency are in the sticky group. All series are monthly, are HP-filtered with smoothing parameter 1,000,000, and are seasonally adjusted. Standard errors are in parentheses.
| Parameter | Baseline | Strategic Complements |
Endogenous
Monetary Policy |
|---|---|---|---|
| Monthly Discount Factor ( |
0.96 |
Same | Same |
| Coefficient of Relative Risk Aversion ( |
1 | Same | Same |
| Inverse of Frisch elasticity of labor supply ( |
0 | Same | Same |
| Steady-state Labor Supply ( |
0.333 | Same | Same |
| Elasticity of demand ( |
4 | Same | Same |
| Intermediate Input Share ( SDP TDP |
0
0 |
0.95
0.67 |
0.95
- |
| Persistence of Idio. Productivity Shock ( |
0.7 | Same | Same |
| Mean Growth Rate of Money ( |
0.2% | Same | Same |
| S.D. of Innovation to Money Growth ( |
0.48% | 0.48% | 0.41% |
| Money Growth's reaction to M/P ( |
0 | 0 | -0.6 |
Notes: Parameter values apply to both the TDP and SDP models, unless otherwise noted. As shown in the text, prices are strategic complements if
![]() . The target steady state labor supply is obtained by varying the utility function parameter
. The target steady state labor supply is obtained by varying the utility function parameter ![]() . The intermediate input share in the non-baseline cases is chosen to generate a contract multiplier of 4. The parameters for the money growth process are chosen to match the mean growth rate of inflation, the standard deviation of nominal
non-shelter PCE, and, for the "endogenous monetary policy" case, the serial correlation of nominal PCE.
. The intermediate input share in the non-baseline cases is chosen to generate a contract multiplier of 4. The parameters for the money growth process are chosen to match the mean growth rate of inflation, the standard deviation of nominal
non-shelter PCE, and, for the "endogenous monetary policy" case, the serial correlation of nominal PCE.
| Parameter | Baseline | Strategic Complements |
Endogenous
Monetary Policy |
|---|---|---|---|
| Menu Costs (SDP Only): Flexible | 0.168% | Same | Same |
| Menu Costs (SDP Only): Sticky | 0.218% | Same | Same |
| S.D. of Idiosyncratic Productivity Shocks: Flexible ( |
4.93% | 4.94% | 4.94% |
| S.D. of Idiosyncratic Productivity Shocks: Sticky ( |
4.70% | 4.75% | 4.75% |
| Probability of Zero Menu Cost (TDP Only): Flexible ( |
0.333 | Same | - |
| Probability of Zero Menu Cost (TDP Only): Sticky ( |
0.100 | Same | - |
| Sector Weights: Flexible | 0.3000 | Same | Same |
| Sector Weights: Sticky | 0.7000 | Same | Same |
Notes: Expended menu costs are evaluated at the steady state wage and scaled by steady state revenue,
. Although the expended menu costs are similar across sectors, the labor cost (
| Statistic | All Goods |
Flexible Goods |
Sticky Goods |
|---|---|---|---|
| Standard deviation of |
0.49%
(0.03) |
0.51%
(0.03) |
0.49%
(0.03) |
| Serial correlation of |
-0.04
(0.07) |
-0.07
(0.07) |
-0.04
(0.07) |
| Standard deviation of |
0.12%
(0.01) |
0.21%
(0.02) |
0.10%
(0.01) |
| Serial correlation of |
0.73
(0.05) |
0.60
(0.05) |
0.84
(0.04) |
Notes: Statistics are averages across 100 model simulations, each of 233 periods. Standard deviations across simulations are in parentheses. Each simulation consists of 3,100 firms in the flexible sector and 8,300 firms in the sticky sector.
| Statistic | All Goods |
Flexible Goods |
Sticky Goods |
|---|---|---|---|
| Standard deviation of |
0.29%
(0.02) |
0.28%
(0.01) |
0.32%
(0.02) |
| Serial correlation of |
-0.02
(0.07) |
-0.12
(0.07) |
-0.04
(0.07) |
| Standard deviation of |
0.08%
(0.01) |
0.12%
(0.01) |
0.07%
(0.01) |
| Serial correlation of |
0.80
(0.05) |
0.62
(0.06) |
0.87
(0.04) |
Notes: Statistics are averages across 100 model simulations, each of 233 periods. Standard deviations across simulations are in parentheses. Each simulation consists of 3,100 firms in the flexible sector and 8,300 firms in the sticky sector.
| Statistic | All Goods |
Flexible Goods |
Sticky Goods |
|---|---|---|---|
| Standard deviation of |
1.79%
(0.08) |
1.34%
(0.07) |
2.01%
(0.10) |
| Serial correlation of |
-0.31
(0.06) |
-0.38
(0.06) |
-0.29
(0.06) |
| Standard deviation of |
0.28%
(0.02) |
0.40%
(0.02) |
0.25%
(0.02) |
| Serial correlation of |
0.38
(0.07) |
0.16
(0.07) |
0.53
(0.06) |
Notes: Statistics are averages across 100 model simulations, each of 233 periods. Standard deviations across simulations are in parentheses. Each simulation consists of 3,100 firms in the flexible sector and 8,300 firms in the sticky sector.
| Statistic | All Goods |
Flexible Goods |
Sticky Goods |
|---|---|---|---|
| Standard deviation of |
0.52%
(0.02) |
0.40%
(0.02) |
0.67%
(0.03) |
| Serial correlation of |
-0.24
(0.06) |
-0.34
(0.05) |
-0.27
(0.06) |
| Standard deviation of |
0.11%
(0.01) |
0.14%
(0.01) |
0.11%
(0.01) |
| Serial correlation of |
0.73
(0.05) |
0.43
(0.08) |
0.76
(0.05) |
Notes: Statistics are averages across 100 model simulations, each of 233 periods. Standard deviations across simulations are in parentheses. Each simulation consists of 3,100 firms in the flexible sector and 8,300 firms in the sticky sector.
| Statistic | All Goods |
Flexible Goods |
Sticky Goods |
|---|---|---|---|
| Standard deviation of |
0.41%
(0.02) |
0.37%
(0.02) |
0.53%
(0.03) |
| Serial correlation of |
-0.43
(0.05) |
-0.46
(0.05) |
-0.45
(0.04) |
| Standard deviation of |
0.05%
(0.002) |
0.10%
(0.004) |
0.04%
(0.002) |
| Serial correlation of |
0.12
(0.06) |
-0.04
(0.06) |
0.17
(0.07) |
Notes: Statistics are averages across 100 model simulations, each of 233 periods. Standard deviations across simulations are in parentheses. Each simulation consists of 3,100 firms in the flexible sector and 8,300 firms in the sticky sector.
Notes for Figures 1 and 2: Dashed lines denote 95% confidence interval. Estimates reflect
accumulated responses to a univariate VAR for reset price inflation with 6 monthly lags.
Notes for Figures 3 and 4: Dashed lines denote 95% confidence interval. Estimates reflect accumulated responses to a univariate VAR for reset price inflation with 6 monthly lags.
Notes for Figures 5 and 6: Dashed lines denote 95% confidence interval. Estimates reflect accumulated responses to a univariate VAR for reset price inflation with 6 monthly lags. Shaded area denotes the 95% confidence interval for estimates based on CPI-RDB data.
Notes for Figures 7 and 8: Dashed lines denote 95% confidence interval. Estimates reflect accumulated responses to a univariate VAR for reset price inflation with 6 monthly lags. Shaded area denotes the 95% confidence interval for estimates based on CPI-RDB data.
Note for Figure 9: Estimates reflect accumulated responses to a univariate VAR for reset price inflation with 6 monthly lags.
Notes for Figure 10: Dashed lines denote 95% confidence interval. Estimates reflect accumulated responses to a univariate VAR for reset price inflation with 6 monthly lags. Shaded area denotes the 95% confidence interval for estimates based on CPI-RDB data.
Altig, David, Lawrence Christiano, Martin Eichenbaum and Jesper Linde (2005), "Firm-Specific Capital, Nominal Rigidities and the Business Cycle," NBER Working Paper 11034 (January).
Ball, Laurence and David Romer (1990), "Real Rigidities and the Non-neutrality of Money," Review of Economic Studies 57 (April): 183-203.
Basu, Susanto (1995), "Intermediate Goods and Business Cycles: Implications for Productivity and Welfare," American Economic Review 85 (June): 512-531.
Bernanke, Ben S., Jean Boivin, and Piotr Eliasz (2005), "Measuring the Effects of Monetary Policy: A Factor-Augmented Vector Autoregressive (FAVAR) Approach," Quarterly Journal of Economics 120 (February): 387-422.
Benati, Luca (2008), "Investigating Inflation Persistence across Monetary Regimes," Quarterly Journal of Economics 123 (January): 1005-1060.
Blanchard, Olivier and Jordi Gali (2007), "Real Rigidities and the New Keynesian Model," Journal of Money, Credit and Banking, Proceedings of the Conference on Quantitative Evidence on Price Determination, 39 (February): 35-65.
Boivin, Jean, Marc Giannoni and Ilian Mihov (2009), "Sticky Prices and Monetary Policy: Evidence from Disaggregated U.S. Data," forthcoming in the American Economic Review.
Broda, Christian and David E. Weinstein (2006), "Globalization and the Gains from Variety," Quarterly Journal of Economics 121 (May): 541-585.
Caballero, Ricardo J. and Eduardo M.R.A. Engel (2007), "Price Stickiness in Ss Models: New Intrepretations of Old Results," Journal of Monetary Economics 54 (September): 100-121.
Calvo, Guillermo A. (1983), "Staggered Prices in a Utility-Maximizing Framework," Journal of Monetary Economics 12 (September): 383-398.
Carvalho, Carlos (2006), "Heterogeneity in Price Stickiness and the Real Effects of Monetary Shocks," Frontiers of Macroeconomics 2 (Article 1). Available at : http://www.bepress.com/bejm/frontiers/vol2/iss1/art1.
Chari, V. V., Patrick J. Kehoe, and Ellen R. McGrattan (2000), "Sticky Price Models of the Business Cycle: Can the Contract Multiplier Solve the Persistence Problem?"
Econometrica 68 (September): 1151-1179.
Christiano, Lawrence J., Martin Eichenbaum, and Charles Evans (1999), "Monetary Policy Shocks: What Have We Learned and to What End?," Handbook of Macroeconomics, volume 1A, Elsevier: New York, John B. Taylor and Michael Woodford, eds.
Christiano, Lawrence J., Martin Eichenbaum, and Charles Evans (2005), "Nominal Rigidities and the Dynamic Effects of Shocks to Monetary Policy," Journal of Political Economy 113 (February): 1-45.
Cogley, Timothy and Thomas J. Sargent (2001), "Evolving Post World War II U.S. Inflation Dynamics," NBER Macroeconomics Annual 16: 331-373.
Cogley, Timothy and Argia M. Sbordone (2008), "Trend Inflation, Indexation, and Inflation Persistence in the New Keynesian Phillips Curve," American Economic Review 98 (December): 2101-2126.
Danziger, Leif (1999), "A Dynamic Economy with Costly Price Adjustments," American Economic Review 89 (September): 878-901.
Dotsey, Michael and Robert King (2006), "Pricing, Production, and Persistence," Journal of the European Economic Association 4 (September): 893-928.
Dotsey, Michael, Robert King and Alexander Wolman (1999), "State-Dependent Pricing and the General Equilibrium Dynamics of Money and Output," Quarterly Journal of Economics 114 (May): 655-690.
Gertler, Mark and John Leahy (2008), "A Phillips Curve with an Ss Foundation," Journal of Political Economy 116 (June): 533-572.
Golosov, Mikhail and Robert E. Lucas, Jr. (2007), "Menu Costs and Phillips Curves," Journal of Political Economy 115 (April): 171-199.
Gopinath, Gita, Oleg Itskhoki, and Roberto Rigobon (2007), "Currency Choice and Exchange Rate Pass-through," NBER Working Paper 13432 (September).
Gopinath, Gita and Oleg Itskhoki (2008), "Frequency of Price Adjustment and Pass-through," NBER Working Paper 14200 (July).
Gorodnichenko, Yuriy and Matthew D. Shapiro (2007), "Monetary Policy When Potential Output is Uncertain: Understanding the Growth Gamble of the 1990s," Journal of Monetary Economics 54 (May): 1132-1162.
Hendel, Igal and Aviv Nevo (2006), "Measuring the Implications of Consumer Inventory Behavior," Econometrica 74 (November): 1637-1673.
Kimball, Miles S. (1995), "The Quantitative Analytics of the Basic Neomonetarist Model," Journal of Money, Credit, and Banking 27 (November): 1241-1277.
Klenow, Peter J. and Kryvtsov, Oleksiy (2008), "State-Dependent or Time-Dependent Pricing: Does It Matter For Recent U.S. Inflation?" Quarterly Journal of Economics 123 (August): 863-904.
Klenow, Peter J. and Jonathan L. Willis (2006), "Real Rigidities and Nominal Price Changes," unpublished paper (March).
Klenow, Peter J. and Jonathan L. Willis (2007), "Sticky Information and Sticky Prices," Journal of Monetary Economics 54 (September): 79-99.
Krusell, Per and Anthony Smith (1998), "Income and Wealth Heterogeneity and the Macroeconomy," Journal of Political Economy 106 (October): 867-896.
Kryvtsov, Oleksiy and Virgiliu Midrigan (2008), "Inventories, Markups, and Real Rigidities in Menu Cost Models," unpubished paper (April).
Levy, Daniel, Mark Bergen, Shantanu Dutta, and Robert Venable (1997), "The Magnitude of Menu Costs: Direct Evidence from Large U.S. Supermarket Chains," Quarterly Journal of Economics 112 (August): 791-825.
Mackowiak, Bartosz and Frank Smets (2008), "Implications of Micro Price Data for Macroeconomic Models," CEPR Discussion Paper 6961.
Mackowiak, Bartosz and Mirko Wiederholt (2008), "Business Cycle Dynamics Under Rational Inattention," unpublished paper (November).
Midrigan, Virgiliu (2008), "Menu Costs, Multiproduct Firms, and Aggregate Fluctuations," unpublished paper, New York University.
Nakamura, Emi and Jon Steinsson (2008a), "Five Facts About Prices: A Reevaluation of Menu Cost Models," Quarterly Journal of Economics 123 (November): 1415-1464.
Nakamura, Emi and Jon Steinsson (2008b), "Monetary Non-Neutrality in a Multi-Sector Menu Cost Model," NBER Working Paper 14001 (May).
Nason, James M. (2006), "Instability in U.S. Inflation: 1967-2005," Federal Reserve Bank of Atlanta Economic Review (2nd quarter): 39-59.
Primiceri, Giorgio E. (2006), "Why Inflation Rose and Fell: Policymakers' Beliefs and US Postwar Stabilization Policy," Quarterly Journal of Economics 121 (August): 867-901.
Romer, David H. and Christina D. Romer (2004), "A New Measure of Monetary Shocks: Derivation and Implications," American Economic Review 94 (September): 1055-1084.
Shiller, Robert J. (1991), "Arithmetic Repeat Sales Price Estimators," Journal of Housing Economics 1 (March): 110-126.
Stock, James H. and Mark W. Watson (2006), "Why Has U.S. Inflation Become Harder to Forecast?", NBER Working Paper 12324 (June).
Taylor, John B. (1980), "Aggregated Dynamics and Staggered Contracts," Journal of Political Economy 88 (February): 1-24.
Woodford, Michael (2003), Interest and Prices: Foundations of a Theory of Monetary Policy, Princeton University Press.
Zbaracki, Mark J., Mark Ritson, Daniel Levy, Shantanu Dutta, and Mark Bergen (2004) "Managerial and Customer Costs of Price Adjustment: Direct Evidence from Industrial Markets," Review of Economics and Statistics 86 (May): 514-533.
Footnotes
![P_t =\left[ {\int\limits_0^1 {p_t (i)^{\,1-\theta }di} } \right]^{\,\frac{1}{1-\theta }}](img84.gif) . Return to Text
. Return to Text