
Demand-driven Job Separation
Reconciling Search Models with the Ins and Outs of Unemployment
Keywords: Search and matching model, gross worker flows, job finding rate, job separation rate
Abstract:
JEL classifications: J63, J64, E24, E32
1 Introduction
The Mortensen-Pissarides (1994, henceforth MP) search and matching model has emerged as a powerful tool to study unemployment and the labor market, and an extensive literature has introduced equilibrium unemployment into general equilibrium models through a search framework.1 In parallel to these theoretical developments, many studies have documented the empirical properties of job and worker flows over the business cycle.2 In particular, Shimer (2007) focuses on individual workers' transition rates and finds that the contribution of the job separation rate (JS) to unemployment's variance is small over the post-war period and even smaller since the mid-80s. Movements in the job finding rate (JF), on the other hand, account for three-quarters of unemployment's variance over the post-war period.3
However, the MP model has difficulties explaining the low contribution of the job separation rate as well as other stylized facts about unemployment and its transition probabilities. Instead, I present a search and matching model with a new mechanism of job separation based on firms' demand constraints that is remarkably successful at matching the data. Despite a small number of parameters, the model is consistent with the behavior of labor market variables, can rationalize a low, yet non-trivial, contribution of the job separation rate and can explain the declining contribution of JS since 1985.
Shimer's (2007) evidence on the low contribution of the job separation rate led to a recent modeling trend that treats the job separation rate as acyclical.4 However, such a conclusion may be too hasty. First, while the jury is still out on the precise contribution of JS to unemployment fluctuations, Shimer's (2007) estimate amounts to a non-trivial 25 percent over the post-war period.5 The contribution of JS indeed drops to only 5 percent over 1985-2007, but it is important to understand the reasons behind this decline. In addition, as Blanchard and Diamond (1990) first showed, the number of hires tends to increase in recessions while the job finding rate decreases. This happens because the pool of unemployed increases proportionally more than unemployment outflows and suggests that unemployment inflows play an important role in recessions. Finally, an important characteristic of unemployment is its asymmetric behavior, the fact that increases in the unemployment rate are steeper than decreases, and I find that this asymmetry disappears after 1985. Again, this suggests that an asymmetric mechanism such as job separation is driving the response of unemployment to shocks, but that this mechanism is weaker since the mid-80s.
A natural candidate to account for both unemployment outflows and inflows is the MP model with endogenous separation, but the model has difficulties generating three stylized facts about cyclical unemployment and its transition probabilities: (i) the unemployment-vacancy correlation is negative, (ii) JS is half as volatile as JF but is three times more volatile than detrended real GDP and (iii) movements in JS are sharp and short-lived while movements in JF are persistent and mirror the behavior of unemployment. Indeed, Ramey (2008) and Elsby and Michaels (2008) show that for plausible parameter values, the MP model generates an upward-sloping Beveridge curve as well as too much volatility in JS relative to JF.6 Moreover, I simulate a MP model with AR(1) productivity shocks and find that it generates counterfactually similar dynamic properties for the job finding rate and the job separation rate. These empirical issues arise because in a MP model calibrated with plausible idiosyncratic productivity shocks, job destruction is the main margin of adjustment in employment and " drives" the job creation margin; a burst of layoffs generates higher unemployment, makes workers easier to find and stimulates the posting of vacancies. This mechanism explains why the MP model can generate a counterfactually positive unemployment-vacancy correlation and counterfactually similar impulse responses for -JF and JS.
The main contribution of this paper is to present a new model of endogenous separation that is consistent with the three stylized facts about unemployment and its transition probabilities. In a search and matching model of the labor market, demand-constrained firms have the choice between two labor inputs; an extensive margin (number of workers) subject to hiring frictions and a flexible but more expensive intensive margin (hours per worker). Moreover, while hiring is costly and time consuming, firing is costless and instantaneous. The model is closest to Krause and Lubik's (2007) New-Keynesian search model with endogenous job destruction à la Mortensen-Pissarides (1994), but with one important difference: there are no match-specific productivity shocks and job separation does not depend on the productivity of each match.7 Instead, when faced with lower than expected demand, firms can choose to layoff extra workers to save on labor costs. With demand-driven job separation, I show that endogenous job separation is zero in steady-state, so that firms cannot reduce firing but must post vacancies to increase employment. Because of hiring frictions, firms hoard labor and only use the job separation margin for large negative shocks. Consistent with fact (ii), JS is less volatile than JF, and the contribution of JS to unemployment fluctuations is not necessarily large. In fact, the model can closely match an empirical contribution of JS of 25 percent over the post-war period. Further, contrary to a standard MP model, vacancy posting is the main variable of adjustment of employment, and job separation is only used in exceptional circumstances. As a result, and consistent with fact (iii), adjustments in JS are sharp and short-lived while JF inherits the persistence of aggregate demand shocks. As in the MP model, a burst of layoffs increases unemployment and decreases the expected cost of filling a vacancy, so that firms want to profit from exceptionally low labor market tightness to increase their number of new hires. However, because of demand constraints, the incentive is much weaker than in the MP model; gross hires may go up in recessions, in line with Blanchard and Diamond (1990), but consistent with fact (i), firms post fewer vacancies, and the unemployment-vacancy correlation is negative.
Another contribution of the paper is to provide an explanation for the decline in the contribution of JS and the weaker asymmetry in unemployment since 1985. The model implies that these two findings are by-products of the Great Moderation.8 Because of hiring frictions, firms hoard labor and do not lay-off workers in small recessions, preferring to reduce hours per worker. Since the last two recessions (1991 and 2001) were relatively mild, firms made little use of the job separation margin, and the contribution of JS, as well as the asymmetric behavior of unemployment, declined.9 Interestingly, the current recession that started in December 2007 is a lot more pronounced and is witnessing a large increase in the job separation rate (see Barnichon, 2009), consistent with the model's prediction. Therefore, treating JS as acyclical may be especially inappropriate in times of higher macroeconomic volatility.
The remainder of the paper is organized as follows: Section 2 discusses the importance of understanding fluctuations in the job separation rate; Section 3 documents three stylized facts about unemployment and its flows that the MP model has difficulties explaining; Section 4 presents a search model with demand-driven job separation and Section 5 confronts it with the data; Section 6 reviews the literature on the empirical performance of MP models with endogenous job destruction, and Section 7 offers some concluding remarks.
2 The importance of understanding unemployment inflows
In this section, I highlight a number of empirical points that suggest that layoffs play an important role in unemployment fluctuations and that assuming a constant job separation rate can lead to misinformed conclusions about the behavior of unemployment.
2.1 The small and declining contribution of unemployment inflows
In two influential papers, Shimer (2007) and Hall (2005) argue that the contribution of unemployment inflows to unemployment fluctuations is much smaller than the contribution of unemployment outflows, and more dramatically that fluctuations in the employment exit probability are quantitatively irrelevant in the last two decades. Indeed, Shimer (2007) shows that fluctuations in the job separation rate accounts for 25% of the variance of the cyclical component of unemployment over 1948-2007 but for only 5% over the last 20 years.10 As a result, a large number of recent papers assume a constant separation rate when modeling search unemployment.11 However, a contribution of 25 percent is not trivial.12Furthermore, if assuming a constant separation rate seems reasonable over the last two decades, it brushes aside the reasons behind the decline in the contribution of JS since the mid-80s. Since the assumption's validity depends on whether the smaller contribution of JS is a permanent or temporary phenomenon, one needs to understand the reasons behind the decline in the importance of unemployment inflows.
2.2 Gross hires tend to increase in recessions
Analyzing gross flows data, Blanchard and Diamond (1990), Fujita and Ramey (2006) and Elsby, Michaels and Solon (2008) show that the number of hires tends to increase in recessions while the job finding rate decreases. Since the flow from unemployment to employment is equal to the job finding probability times the number of unemployed, this implies that the pool of unemployed increases proportionately more than the flow. This observation is hard to reconcile with a constant job separation rate, but a burst of layoffs would increase unemployment independently of JF and could explain why unemployment increases faster than the job finding rate in recessions.
2.3 Unemployment displays asymmetry in steepness
An important characteristic of unemployment is its asymmetric behavior, and a large literature has documented a non-trivial asymmetry in steepness for the cyclical component of unemployment.13 Put differently, increases in unemployment are steeper than decreases. Table 1 presents the skewness coefficients for the first-differences of monthly unemployment and industrial production.14 Unemployment presents strong evidence of asymmetry in steepness but this is not the case of industrial production. This suggests that an asymmetric mechanism such as job separation is driving the response of unemployment to shocks. Further, we can see in Table 1 that the asymmetric behavior of unemployment is much weaker over 1985-2007. Again, before assuming a constant separation rate and thus no asymmetry in unemployment, it is important to understand the reasons behind this phenomenon.
3 Unemployment transition probabilities and the MP model
The evidence presented in the previous section underscores the importance of understanding both unemployment flows; the outflows as well as the inflows. The Mortensen-Pissarides (1994) search and matching model with endogenous separation explicitly model both flows and is therefore a natural candidate to study the determinants of unemployment. In this section, I study the empirical performances of the MP model with respect to unemployment and its flows.
3.1 Three facts about unemployment and its transition probabilities
I now highlight three stylized facts about unemployment and its transition probabilities. Table 2 summarizes the detrended US data for unemployment, vacancies, labor market tightness, job finding probability, job separation probability, hours per worker and real GDP over 1951-2006.15
Fact 1: The Beveridge Curve and the correlations between JF, JS and unemployment
A well documented fact about the labor market is the strong negative relationship between unemployment and vacancies, the so-called Beveridge curve. At quarterly frequencies, Table 2 shows that the correlation equals -0.90 over 1951-2006. A point that has attracted less attention is the fact that JF is very highly correlated with unemployment (-0.95) but that this is less the case for the JS-unemployment correlation (0.61). Finally, the JF-JS correlation is negative and equals -0.48.
Fact 2: The employment exit probability is half as volatile as the job finding probability and is three times more volatile than output
As Shimer (2007) first emphasized and as Table 2 shows, the employment exit probability is about 55% less volatile than the job finding probability. Moreover, JS and JF are respectively three times and six times more volatile than detrended real GDP.16
Fact 3: Movements in the job separation rate are sharp and short-lived while movements in the job finding rate are persistent and mirror the behavior of unemployment.
Looking at the autocorrelation coefficients for the flow probability series from Shimer (2007) over 1951-2006, Table 2 shows that the employment exit probability is much less persistent than the job finding probability with respective coefficients equal to 0.65 and 0.91.
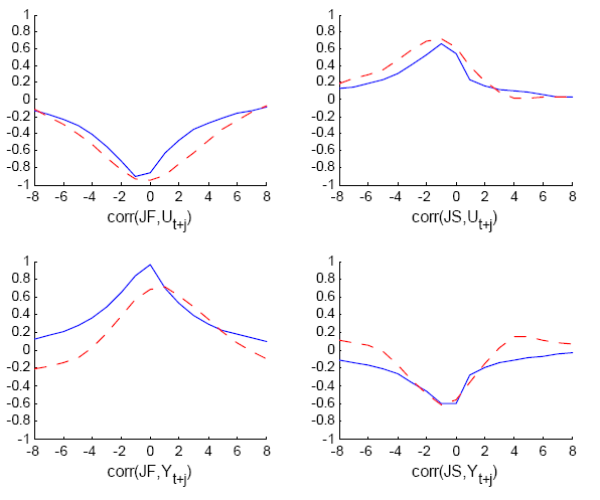
Fujita and Ramey (2007) document the cross-correlations of the job separation rate, the job finding rate, and unemployment at various leads and lags, and observe that while the job finding rate seems to move contemporaneously with unemployment, the job separation rate leads unemployment. This is apparent in Figure 1 which plots the cross-correlations using Shimer's (2007) data for the job separation probability and the job finding probability. In addition, while correlations with JF are spread symmetrically around zero, correlations with JS display a very strong asymmetry. The unemployment-job separation rate correlation decreases very fast at positive lags of unemployment and is virtually nil after one year. Using real GDP instead of unemployment, similar conclusions emerge. In addition, we can see that the employment exit probability leads GDP while the job separation probability lags GDP.17
Another way to assess the dynamic properties of unemployment and its transition probabilities is to consider the impulse response functions to technology shocks and monetary policy shocks in structural VARs. Following Barnichon (2008), Canova, Michelacci and Lopez-Salido (2008) and Fujita (2009), I use long-run restrictions in a VAR with output per hour, unemployment, job finding probability and employment exit probability over 1951-2006 as in Gali (1999) to identify the impact of technology shocks, and I use a VAR with a recursive ordering with unemployment, job finding probability, employment exit probability and the federal funds rate over 1960-2006 to estimate the effect of monetary policy shocks.18 Figure 2 plots the impulse response functions to a positive technology shock and a monetary shock. In both cases, the employment exit probability is much less persistent than the job finding probability. Moreover, the job finding probability response mirrors that of unemployment while the employment exit probability response leads the response of unemployment and reverts to its long-run value a year before the other variables.
3.2 Confronting the MP models with the Facts
In this section, I examine whether the MP model can account for the stylized facts. A number of variants of the MP model have been developed since the seminal work of Mortensen and Pissarides (1994). This section focuses on the standard MP model but in Section 6, I review the different variants and study how they fare relative to the standard MP model.
To illustrate my statements, I log-linearize and simulate a calibrated version of a MP model with AR(1) productivity shocks. The model and its calibration are standard, and I leave the details for the Appendix.19 Figure 3 plots the impulse responses of labor market variables to a negative productivity shock, and Table 3 presents summary statistics for simulated data.
Fact 1 and 2 are difficult to reproduce, a point forcefully made by Ramey (2008) and Elsby and Michaels (2008). After calibrating the MP model with plausible idiosyncratic productivity shocks and parameter values, these authors find that the model generates a positive correlation between unemployment and vacancies and too much fluctuation in JS relative to JF. Indeed, Figure 3 shows a simultaneous increase in unemployment and vacancy posting. This positive correlation emerges because a (large) burst of layoffs generates higher unemployment which makes workers easier to find and stimulates the posting of vacancies. Table 3 confirms this result and shows that the unemployment-vacancy correlation is positive at 0.96. Figure 3 also shows the much stronger response of the job separation rate relative to that of the job finding rate, and looking at Table 3, the standard deviation of JF is only 0.013 while the standard deviation of JS is much higher at 0.096.
Turning to Fact 3, MP models generate counterfactually similar dynamic properties for the job finding rate and the job separation rate in response to AR(1) productivity shocks. As Figure 3 shows, the response of the productivity threshold
![]() below which firm and worker decide to separate mirrors the response of the aggregate productivity shock
below which firm and worker decide to separate mirrors the response of the aggregate productivity shock ![]() , and JS inherits the persistence of the aggregate shock. Further, the job finding probability depends directly on the vacancy-unemployment ratio via the matching function. As a result, the large and persistent increase in job separation leads to a persistent
decrease in labor market tightness, and hence to a persistent fall in JF. Thus, JF and JS display very similar impulse responses and share the same autocorrelation coefficient (Table 3). However, Figure 2 shows that in the data, the job separation rate returns faster to its long run level than the
job finding rate, and Table 2 shows that JS is a lot less persistent than JF.
, and JS inherits the persistence of the aggregate shock. Further, the job finding probability depends directly on the vacancy-unemployment ratio via the matching function. As a result, the large and persistent increase in job separation leads to a persistent
decrease in labor market tightness, and hence to a persistent fall in JF. Thus, JF and JS display very similar impulse responses and share the same autocorrelation coefficient (Table 3). However, Figure 2 shows that in the data, the job separation rate returns faster to its long run level than the
job finding rate, and Table 2 shows that JS is a lot less persistent than JF.
4 A search and matching model with endogenous separation
In this section, I present a search and matching model in which endogenous separation is driven by demand constraints.
4.1 The model
I develop a partial equilibrium model in which firms are demand constrained. Since my goal is to evaluate the model along the labor market dimension, I follow a reduced-form approach that allows for more tractability and facilitates computation.20
This search model is similar to Krause and Lubik (2007) in that it assumes large demand-constrained firms with many workers. However, unlike Krause and Lubik (2007), there are no match-specific productivity shocks, and job separation does not depend on the productivity of each match. Instead, when faced with lower than expected demand, firms can choose to layoff extra workers to save on labor costs.
Firms and the labor market
I consider an economy populated by a continuum of households of measure one and a continuum of firms of measure one. At each point in time, firm ![]() needs to satisfy demand for its product
needs to satisfy demand for its product
![]() and hires
and hires ![]() workers to produce a quantity
workers to produce a quantity
| (1) |
where I normalize the aggregate technology index to one, and
In a search and matching model of the labor market, workers must be hired from the unemployment pool through a costly and time-consuming job creation process. Firms post vacancies at a unitary cost ![]() (in units of utility of consumption), and unemployed workers search for jobs. Vacancies are matched to searching workers at a rate that depends on the number of searchers on each side of the market. I assume that the matching function takes the usual Cobb-Douglas form so that the
flow
(in units of utility of consumption), and unemployed workers search for jobs. Vacancies are matched to searching workers at a rate that depends on the number of searchers on each side of the market. I assume that the matching function takes the usual Cobb-Douglas form so that the
flow ![]() of successful matches within period
of successful matches within period ![]() is given by
is given by
![]() where
where ![]() is a positive constant,
is a positive constant,
![]() ,
, ![]() denotes the number of unemployed and
denotes the number of unemployed and ![]() =
=
![]() the total number of vacancies posted by all firms. Accordingly, the probability of a vacancy being filled in the next period is
the total number of vacancies posted by all firms. Accordingly, the probability of a vacancy being filled in the next period is
![]() where
where
![]() is the labor market tightness. Similarly, the probability for an unemployed worker to find a job is
is the labor market tightness. Similarly, the probability for an unemployed worker to find a job is
![]() . Because of hiring frictions, a match formed at
. Because of hiring frictions, a match formed at ![]() will only start producing at
will only start producing at ![]() . Matches are terminated at an exogenous rate
. Matches are terminated at an exogenous rate
![]() but the firm can also choose to destroy an additional fraction
but the firm can also choose to destroy an additional fraction ![]() of its jobs, so that the job separation rate
of its jobs, so that the job separation rate
![]() .
.
The timing of the model is similar to that of Krause and Lubik (2007). Denote
![]() the employment of firm
the employment of firm ![]() at the beginning of period
at the beginning of period ![]() . Once the uncertainty is resolved, firms can decide whether to lay-off a fraction
. Once the uncertainty is resolved, firms can decide whether to lay-off a fraction ![]() of its employment
of its employment
![]() in order to begin production with
in order to begin production with
![]() workers and pay the corresponding wage bill. At the end of the period,
workers and pay the corresponding wage bill. At the end of the period,
![]() matches are created but an additional fraction
matches are created but an additional fraction
![]() of firm's beginning of period employment
of firm's beginning of period employment
![]() is destroyed.22 The firm enters next
period with
is destroyed.22 The firm enters next
period with
![]() workers.
workers.
From now on, I will only consider the beginning of period employment
![]() , so that for a firm
, so that for a firm ![]() posting
posting ![]() vacancies at date
vacancies at date ![]() , its the law of motion for employment is given by
, its the law of motion for employment is given by
Households
I follow Merz (1995) and Andolfatto (1996) in assuming that households form an extended family that pools its income. There are ![]() unemployed workers who receive unemployment benefits
unemployed workers who receive unemployment benefits
![]() in units of utility of consumption, and
in units of utility of consumption, and ![]() employed workers who receive the
wage payment
employed workers who receive the
wage payment ![]() from firm
from firm ![]() for providing hours
for providing hours ![]() . Consequently, the value of unemployment
. Consequently, the value of unemployment ![]() in terms of current consumption is
in terms of current consumption is
![\displaystyle U_{t}=\frac{b}{\lambda_{t}}+\beta E_{t}\left[ JF_{t+1}W_{t+1}+(1-JF_{t+1} )U_{t+1}\right]](img52.gif)
![\displaystyle W_{it}=w_{it}-\frac{\lambda_{h}}{\lambda_{t}\left( 1+\sigma_{h}\right) }h_{it}^{1+\sigma_{h}}+\beta E_{t}\left[ \left( 1-JS_{t+1}\right) W_{it+1}+JS_{t+1}U_{t+1}\right]](img54.gif)
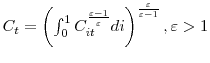 .
.Wage bill setting
The firms and workers bargain individually about the real wage. To keep the model simple, I assume that the firm owns all the bargaining power and pays a wage equal to the worker's reservation wage ![]()
![]() .23 That way, I can
show:24
.23 That way, I can
show:24
The firm's problem
Firm ![]() will choose a sequence of vacancies
will choose a sequence of vacancies
![]() and job separation
and job separation
![]() to minimize its expected present discounted cost of satisfying demand for its product
to minimize its expected present discounted cost of satisfying demand for its product
![]() subject to the law of motion for employment. Formally, the firm minimizes
subject to the law of motion for employment. Formally, the firm minimizes
![\displaystyle \min_{v_{it},\rho_{it}}E_{t}\sum_{j}\beta^{j}\frac{u^{\prime}(C_{t+j} )}{u^{\prime}(C_{t})}\left[ \left( 1-\rho_{it+j}\right) n_{i,t+j} w_{i,t+j}+\frac{c}{\lambda_{t+j}}v_{i,t+j}\right]](img67.gif)
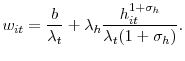
Closing the model
The law of motion for aggregate demand is
4.2 Dynamics of the model
I now present the first-order conditions for vacancy posting and job separation and discuss some properties of the model. I show that, with aggregate demand constraints, endogenous job separation is zero in steady-state, so that firms cannot reduce firing but must post vacancies to increase employment. Because hiring is costly and time consuming, a trade-off emerges between the intensive and the extensive margin. Consequently, firms hoard labor and only fire workers when demand falls below a certain threshold. An increase in output volatility raises the contribution of unemployment inflows since firms are more likely to face large negative shocks and resort to the job separation margin.
The vacancy posting condition
The optimal vacancy posting condition takes the form
![\displaystyle \frac{c_{t}}{q(\theta_{t})}=E_{t}\beta_{t+1}\left[ (1-\rho_{it+1})\chi _{it+1}+\frac{c_{t+1}}{q(\theta_{t+1})}(1-\bar{\rho}-\rho_{it+1})\right]](img76.gif) |
(3) |
with
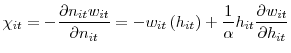
Using the wage equation (2), I can rewrite the marginal worker's value as
Since
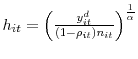 and
and The job separation condition
For the job separation condition, I get the first-order condition
![\displaystyle \frac{\partial(1-\rho_{it})n_{it}w_{it}}{\partial\rho_{it}}=-n_{it}E_{t} \beta_{t+1}\left[ (1-\rho_{it+1})\chi_{it+1}+\frac{c_{t+1}}{q(\theta_{t+1} )}(1-\bar{\rho}-\rho_{it+1})\right]](img91.gif)
Because hiring is costly, the firm hoards labor and does not lay-off workers with a small negative marginal value. It will only fire workers when demand is so low that the marginal value of firing a worker
![]() is large enough to equal the cost of hiring a worker (or equivalently, the expected benefit of keeping that worker).
is large enough to equal the cost of hiring a worker (or equivalently, the expected benefit of keeping that worker).
Furthermore, (5) implies that there cannot be any endogenous separation in steady state, and the firm must post vacancies to increase employment. In steady-state, because of a constant rate of attrition
![]() , the firm must replenish its stock of workers by constantly posting a minimal number of vacancies. This implies that the firm is satisfying its vacancy posting condition and the
steady-state marginal value of a worker is
, the firm must replenish its stock of workers by constantly posting a minimal number of vacancies. This implies that the firm is satisfying its vacancy posting condition and the
steady-state marginal value of a worker is
![]() Since
Since
![]() , the firm does not satisfy its job separation condition and
, the firm does not satisfy its job separation condition and ![]() , so that
, so that
![]() . Starting from the steady-state equilibrium, a positive shock does not lead to a burst of "unfiring" as the firm cannot lower
. Starting from the steady-state equilibrium, a positive shock does not lead to a burst of "unfiring" as the firm cannot lower
![]() (i.e. keep workers that it would have otherwise fired) and must use the job creation margin.
(i.e. keep workers that it would have otherwise fired) and must use the job creation margin.
To visualize the mechanisms driving vacancy posting and job separation, Figure 4 plots the relationship between the marginal value of a worker and hours per worker, a proxy for "demand pressure". In steady-state, the value of a marginal worker is positive and equals the net cost of hiring.
When demand goes up, hours per worker increase and with them the marginal value of a worker, leading the firm to post more vacancies. For small negative shocks such that
![]() , the firm hoards labor and posts fewer vacancies. For large negative shocks, however,
, the firm hoards labor and posts fewer vacancies. For large negative shocks, however,
![]() , and the firm uses the job separation margin, and one can observe a burst of layoffs.25
, and the firm uses the job separation margin, and one can observe a burst of layoffs.25
Finally, an implication of labor hoarding is that an increase in output volatility raises the contribution of the job separation rate to unemployment fluctuations since the firm is more likely to face large negative shocks and resort to the job separation margin. For the same reason, the asymmetric behavior of unemployment will be less pronounced in times of lower output volatility.
5 Confronting the model with the data
In this section, I study whether a calibrated version of the model generates realistic impulse response functions, can quantitatively account for the stylized facts about unemployment and its transition probabilities, and can rationalize the small and declining contribution of unemployment inflows, the increase in gross hiring during recessions as well as the weaker asymmetry in unemployment since 1985.
5.1 Calibration
First, I discuss the calibration of the model; and Table 4 lists the parameter values. An attractive feature of the model is its small number of (standard) parameters. Whenever possible, I use the values typically used in the literature. I assume a monthly frequency, as a monthly calibration is
better able to capture the high rate of job finding in the US. I set the monthly discount factor ![]() to
to ![]() and the returns to hours
and the returns to hours ![]() to 0.65. Turning to the labor market, I set the matching function elasticity to
to 0.65. Turning to the labor market, I set the matching function elasticity to ![]() as in Shimer (2005). I set the exogenous component of the separation rate to 0.032, which is the average value of the 5-year rolling lower-bound of Shimer's (2007) employment exit probability series.26A worker finds a job with probability
as in Shimer (2005). I set the exogenous component of the separation rate to 0.032, which is the average value of the 5-year rolling lower-bound of Shimer's (2007) employment exit probability series.26A worker finds a job with probability
![]() so that equilibrium unemployment equals 10 percent.27 The scale parameter of the matching functions
so that equilibrium unemployment equals 10 percent.27 The scale parameter of the matching functions ![]() is chosen such that, as in den Haan and Kaltenbrunner (2009), a firm fills a vacancy with a probability
is chosen such that, as in den Haan and Kaltenbrunner (2009), a firm fills a vacancy with a probability
![]() . Shimer (2005) sets the income replacement ratio to 40 percent, so that with a labor income share of 65 percent, the unemployment benefits-output ratio
. Shimer (2005) sets the income replacement ratio to 40 percent, so that with a labor income share of 65 percent, the unemployment benefits-output ratio ![]() . The steady-state ratio of vacancy-posting costs to GDP is set to 1% following most of the literature.28 As in Trigari (2009) and Christoffel, Kuester and Linzert (2006), I choose
. The steady-state ratio of vacancy-posting costs to GDP is set to 1% following most of the literature.28 As in Trigari (2009) and Christoffel, Kuester and Linzert (2006), I choose
![]() , i.e. an hours per worker elasticity of 0.1. Finally, I set the standard deviation of output
, i.e. an hours per worker elasticity of 0.1. Finally, I set the standard deviation of output
![]() and the first-order coefficient
and the first-order coefficient
![]() in order to match the persistence and volatility of HP-detrended real GDP, converted to monthly frequency. I numerically solve the model using policy function iterations with
intergrid cubic spline interpolation on a grid with (30,30) points for
in order to match the persistence and volatility of HP-detrended real GDP, converted to monthly frequency. I numerically solve the model using policy function iterations with
intergrid cubic spline interpolation on a grid with (30,30) points for ![]()
![]() . Employment
. Employment ![]() is discretized over
is discretized over
![]() , and I follow Tauchen (1986) to construct the transition matrix for
, and I follow Tauchen (1986) to construct the transition matrix for ![]() . In the Appendix, I describe the numerical algorithm used to solve the firm's problem
. In the Appendix, I describe the numerical algorithm used to solve the firm's problem
5.2 Impulse response functions
Figure 5 and 6 show the simulated impulse response functions of unemployment, hours per worker, the job finding rate, and the job separation rate after respectively a positive and a negative one standard-deviation aggregate demand shock. The asymmetric nature of the labor market is clearly apparent. Following a positive aggregate demand shock, unemployment declines progressively while hours per worker react on impact. After two quarters, hours per worker are back to their long-run value while unemployment starts its mean reversion. After a negative shock, however, unemployment responds on impact because of a burst of layoffs. Thanks to the strong response of the job separation rate, firms rely less on their intensive margin and make a smaller adjustment to their number of posted vacancies. Note that vacancy posting decreases but does not drop to zero, so that the firms are simultaneously firing and posting vacancy.29 This is due to the AR(1) structure of the shocks hitting the economy. Since hiring takes one period and since shocks are mean-reverting, the firm anticipates the need for future higher employment and post vacancies (albeit less so than in normal times) to satisfy the expected increase in demand next period.30
Because it is costless to adjust the number of workers through the separation margin, layoffs show no persistence: firms fire as many workers as necessary, and endogenous job separation reverts quickly to zero. The job finding rate, on the other hand, is persistent and mirrors the behavior of unemployment after two quarters.
Unlike a standard MP model (see Figure 3) or Krause and Lubik (2007), an increase in job separation does not lead to an increase in vacancy postings, and unemployment and vacancy are negatively correlated. The intuition for these results is as follows. Looking at Figure 4, firms use the job
separation margin when the marginal value of a worker falls below
![]() . However, after this burst of layoffs, the marginal value of a worker lies at the boundary between the labor hoarding region and the lay-off region since
. However, after this burst of layoffs, the marginal value of a worker lies at the boundary between the labor hoarding region and the lay-off region since
![]() . This implies that if aggregate demand is persistent, the worker's marginal value in the next period will not be far off the labor hoarding-layoff
threshold, and there will not be another large burst of layoffs. Further, since the labor hoarding-layoff boundary is located in a region in which firms lower the number of posted vacancies, the firm is unlikely to post more vacancies as it lays off workers.31
. This implies that if aggregate demand is persistent, the worker's marginal value in the next period will not be far off the labor hoarding-layoff
threshold, and there will not be another large burst of layoffs. Further, since the labor hoarding-layoff boundary is located in a region in which firms lower the number of posted vacancies, the firm is unlikely to post more vacancies as it lays off workers.31
Finally, Figure 7 shows that the model is consistent with the fact that gross hiring tends to increase during recessions as well as with Fujita's (2009) empirical impulse response for gross hires. A burst of layoffs decreases labor market tightness and lowers hiring costs as the expected cost of filling a vacancy declines. This leads the firm to profit from an exceptionally low labor market tightness to increase new hires: the job finding rate goes down but less than unemployment, and hiring increases. An interesting implication of the model is that this phenomenon becomes stronger with the size of the shock. As Figure 7 illustrates, the larger the adverse demand shock, the more the firm resorts to the job separation margin, the more labor market tightness decreases and the stronger is the firm's incentive to profit from lower hiring costs by increasing gross hires.
5.3 Simulation
Using a calibrated version of the model, I simulate 600 months (i.e. 50 years) of data, and I repeat this exercise 500 times. I first evaluate the model by considering the moments of simulated data to test whether the model is consistent with the three facts about unemployment and its transition probabilities. Then I study whether the model can account for the small and declining contribution of unemployment inflows, as well as the fact that unemployment displays no steepness asymmetry since 1985.
Table 5 presents the summary statistics for quarterly averages of the monthly series. A general conclusion is that given the model simplicity and its small number of parameters, the model is remarkably successful at explaining the behavior of labor market variables: the moments all have the correct sign and are close to their empirical values.32 First, the model has no problem generating Fact 1, i.e. a Beveridge curve and a negative job finding rate-job separation rate correlation. The model can also explain the strong unemployment-vacancies correlation (-0.81 versus -0.90 in the data) as well as the weaker JF-JS correlation (-0.59 versus -0.48 in the data). Similarly, and consistent with the data, the model generates a high job finding rate-unemployment correlation (-0.91 versus -0.95 in the data) and a smaller job separation rate-unemployment correlation (0.47 versus 0.61 in the data). These results stem from the asymmetric nature of the labor market and the fact that firms can adjust employment with the job creation margin at all times but can only use the job separation margin for negative demand shocks. For positive demand shocks, the job separation rate does not move and the correlation with unemployment or the job finding rate is nil. As a result, the JS-unemployment correlation and the JF-JS correlation are closer to a half than to one.
Table 5 also shows that the model is consistent with Fact 2, as the job finding rate is more volatile than the job separation rate. The fact that the model has no problem matching the volatility of the job finding rate is a result of the demand constraints faced by firms. In order to satisfy an expanding demand, firms must increase either their extensive or their intensive margin. Since the intensive margin is relatively costly because of the high disutility cost of longer hours, most of the adjustment occurs through employment.33 Thus, the model does not suffer from a Shimer (2005) type puzzle as it generates enough fluctuations in unemployment given plausible movements in output. Nonetheless, JF is slightly too volatile, a problem with search models of unemployment already pointed out by Fujita and Ramey (2004). This is due to the excessively rapid response of vacancies; and incorporating sunk costs for vacancy creation as in Fujita and Ramey (2004) would presumably correct this shortcoming. Finally, the job separation rate's volatility is close to its empirical value. Unlike standard MP models, the separation margin is only used for large negative shocks as firms hoard labor and only use the job separation margin for large negative shocks.
Turning to Fact 3 and the dynamic properties of JF and JS, Figure 8 shows that the model is very successful at reproducing the cross-correlograms of JF, JS and unemployment. JS is not persistent enough as most of the adjustment along the job separation margin takes place in one period, but assuming convex costs in firing would probably correct this shortcoming. JF is slightly less persistent than in the data, and this is again due to excessively rapid response of vacancies. Finally, the low persistence of model JF and JS explains the low persistence of model hours per worker as the intensive margin adjusts to movements in employment to ensure that the firm satisfies demand at all times.
Finally, in Table 6, I follow Shimer (2007), Elsby, Michaels and Solon (2008) and Fujita and Ramey (2008) and measure the contribution of JF and JS. I find that the contribution of JS amounts to ![]() , only slightly lower than the contribution measured by Shimer (2007).
, only slightly lower than the contribution measured by Shimer (2007).
5.4 The weaker contribution of JS since 1985
We saw in Section 2 that the contribution of JS to the variance of unemployment declined from about 25 percent during the post-war period to only 5 percent over the last 20 years (Shimer, 2007). Moreover, the steepness asymmetry in unemployment disappeared after 1985.
The model implies that these two findings are by-products of the Great Moderation, the period of low macroeconomic volatility enjoyed by the US (and other developed countries) over 1985-2007. One insight from section 4 was that a decrease in output volatility lowers the contribution of JS and the asymmetry in unemployment as firms are less likely to face large negative shocks and resort to the job separation margin. Figure 6 shows this effect quantitatively. As the size of the shock doubles from one half to one standard-deviation of detrended GDP, the response of JS on impact more than doubles, and unemployment shows a stronger initial response. The hours per worker response, on the other hand, does not increase with the size of the shock.
To evaluate whether the decline in macroeconomic volatility can explain the weaker contribution of JS, I estimate the contribution of JS and JF on simulated data with an output volatility of
![]() , consistent with the drop in volatility experienced by the US during the Great Moderation. As Table 6 shows, the contribution of JS decreases to
, consistent with the drop in volatility experienced by the US during the Great Moderation. As Table 6 shows, the contribution of JS decreases to ![]() , suggesting that the Great Moderation is responsible for some of the decline in the contribution of JS.34
, suggesting that the Great Moderation is responsible for some of the decline in the contribution of JS.34
Finally, looking at Table 6, the skewness of model unemployment also declines sharply when the volatility of output decreases, suggesting that the Great Moderation is responsible for some of the decline in the asymmetry of unemployment. With an output volatility of
![]() , the skewness of model unemployment is 0.53, close to its empirical counterpart of 0.62. But with a standard-deviation of output is
, the skewness of model unemployment is 0.53, close to its empirical counterpart of 0.62. But with a standard-deviation of output is
![]() , model unemployment shows no evidence of asymmetry, just as in the data.
, model unemployment shows no evidence of asymmetry, just as in the data.
6 Related literature
In Section 2, I mainly focused on the canonical Mortensen-Pissarides (1994) search and matching model. However, a number of variants of the MP framework have been used to model unemployment. In this section, I review the literature on the different variants and their empirical performances.
First, while the original MP model assumes persistent idiosyncratic productivity shocks, the computational cost associated with keeping track of the jobs' productivity distribution lead many researchers to assume instead i.i.d. idiosyncratic productivity shocks. Indeed, only a few papers solved the original MP model with endogenous separation (Mortensen-Pissarides (1994), Ramey (2008), Elsby and Michaels (2008), Pissarides (2008)), but a vast literature has solved rich general equilibrium models with search unemployment and i.i.d. idiosyncratic productivity shocks: Den Haan, Ramey and Watson (2000), Costain and Reiter (2005), Walsh (2005), Thomas (2006), Krause and Lubik (2007), Cooper, Haltiwanger and Willis (2008), Thomas and Zanetti (2008), Trigari (2009) among others.
Second, variants of the MP model can be classified in two categories, depending on whether firms are atomistic with only one worker or large with many workers. In their seminal paper, Mortensen and Pissarides (1994) assume the existence of a finite mass of workers and of an infinite mass of atomistic firms. Each non-matched firm can post a vacancy to form a match with one worker only. Another line of research departs from the assumption of free entry and atomistic firms to model instead a finite number of large firms with a continuum of jobs.35 This approach has the advantage of allowing for a more realistic representation of the firm as well as providing a framework to study the interaction of labor market frictions with other frictions such as nominal rigidities. While the majority of papers pursued the first approach, Krause and Lubik (2007) provide a tractable example of the second approach in which the firms' production function displays constant returns to employment. While aggregation is more difficult with decreasing returns to employment, Elsby and Michaels (2008) present an analytically tractable model while Cooper, Haltiwanger and Willis (2008) solve and estimate a similar model with numerical methods.
Krause and Lubik (2007), for MP models with large firms, and Costain and Reiter (2005), Thomas (2006), Ramey (2008) and Elsby and Michaels (2008), for MP models with atomistic firms, make the case that Fact 1 is difficult to reproduce. Standard MP models are unable to replicate the Beveridge curve because a burst of layoffs generates higher unemployment which makes workers easier to find, stimulating the posting of vacancies. Krause and Lubik (2007) show that introducing real wage rigidity allows the model to generate a Beveridge curve. However, the model cannot reproduce Fact 2 as "firms adjust almost exclusively via the separation rate and job creation does not play a quantitatively significant role" (Krause and Lubik, 2007, p724). Ramey (2008) shows that a search model with on the job search can generate a Beveridge curve. However, that model cannot reproduce Fact 2 as it generates too much volatility in the job destruction rate compared to the job finding rate (Ramey, 2007, Figure 1). Thomas (2006) shows how firing costs help the MP model in generating a Beveridge curve. However, his model cannot generate Fact 3 as the impulse response of JF counterfactually mirrors that of JS.
While fewer papers other than Ramey (2008) and Elsby and Michaels (2008) focused on Fact 2, Krause and Lubik (2007) show that in MP models with large firms, the job separation rate moves too much compared to the job finding rate. This is not the case in MP models with instantaneous hiring and firing costs (Thomas and Zanetti, 2008) and in MP models with an intensive labor margin (Trigari, 2009). However, both of these models cannot generate Fact 3: the impulse response of JF counterfactually mirrors that of JS, displays no persistence and overshoots its long-run value.
Finally, a very promising line of research is the work from Cooper, Haltiwanger and Willis (2008) and Elsby and Michaels (2008). By considering large firms with decreasing returns to employment and idiosyncratic productivity shocks, they show that such generalized MP models can generate a Beveridge curve. Elsby and Michaels (2008) show that their model can generate elasticities of JS and JF with respect to productivity that are consistent with the data. However, it is difficult to confront these models with the last two stylized Facts as Cooper et al (2008) do not focus on unemployment flows and Elsby and Michaels' (2008) model has only two aggregate productivity states.
7 Conclusion
This paper presents a search model with a demand-driven job separation mechanism that can account for both the outflows and the inflows of unemployment. Despite a relatively small number of parameters, the model is successful at explaining the behavior of labor market variables and is consistent with a low, but non-trivial, contribution of JS to unemployment fluctuations. On the other hand, the benchmark framework, the Mortensen-Pissarides search and matching model with endogenous separation, has difficulties explaining the low contribution of JS as well as other stylized facts.
In addition, my model attributes the decrease in the contribution of JS since 1985 to the Great Moderation, the dramatic drop in macroeconomic volatility enjoyed by the US economy from the mid 80s until 2007. It also implies that the lower contribution of JS was a temporary phenomenon and that the importance of JS would increase in times of higher macroeconomic volatility such as the in current (since December 2007) recession.36
While a demand-driven job separation mechanism shows promises towards an equilibrium model of unemployment with endogenous outflows and inflows, an important extension of this model would be to incorporate idiosyncratic (productivity or demand) shocks to allow for firm heterogeneity. Moreover, embedding the model in a general equilibrium framework would allow me to study the implications of labor market asymmetries on output and inflation. Because increasing employment is more costly than lowering employment, firms tend to adjust prices rather than quantities after positive monetary shocks but do the opposite after monetary contractions. As a result, monetary policy would have a stronger ability to lower, than to raise, output. I leave these topics for future research.
A.1 A Mortensen-Pissarides (1994) model with i.i.d. idiosyncratic productivity shocks
I follow Thomas (2006), and I present an MP model with a finite mass of workers and an infinite mass of atomistic firms. Each non-matched firm can post a vacancy to form a match with one worker only. Workers are hired from the unemployment pool through a costly and
time-consuming job creation process. Firms post vacancies at a unitary cost ![]() , and unemployed workers search for jobs. Vacancies are matched to searching workers at a rate that depends on the
number of searchers on each side of the market. The matching function takes the usual Cobb-Douglas form so that the flow
, and unemployed workers search for jobs. Vacancies are matched to searching workers at a rate that depends on the
number of searchers on each side of the market. The matching function takes the usual Cobb-Douglas form so that the flow ![]() of successful matches within period
of successful matches within period ![]() is given by
is given by
![]() Accordingly, the probability of a vacancy being filled in the next period is
Accordingly, the probability of a vacancy being filled in the next period is
![]() where
where
![]() , and the probability for an unemployed worker to find a job is
, and the probability for an unemployed worker to find a job is
![]() .
.
In this economy, jobs are subject to idiosyncratic productivity shocks drawn from a distribution with the log-normal cdf ![]() , and there exists a threshold productivity
, and there exists a threshold productivity
![]() such that all jobs with productivity below it yield a negative surplus are destroyed. Therefore, total separation rate is
such that all jobs with productivity below it yield a negative surplus are destroyed. Therefore, total separation rate is
![]() with
with
![]() the exogenous separation rate, and the law of motion for employment is
the exogenous separation rate, and the law of motion for employment is
![]() .
.
New jobs have maximum productivity ![]() . The value of continuing a match with idiosyncratic productivity
. The value of continuing a match with idiosyncratic productivity ![]() and aggregate productivity
and aggregate productivity ![]() is given by
is given by
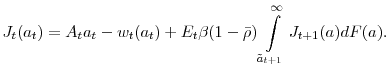
![\displaystyle W_{t}(a_{t})=w_{t}(a_{t})+E_{t}\beta\left[ (1-\bar{\rho})\int\limits_{\tilde {a}_{t+1}}^{\infty}J_{t+1}(a)dF(a)+\rho_{t+1}U_{t+1}\right]](img135.gif)
The familiar job destruction condition is then given by
![]() or
or
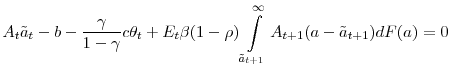
I then solve the model by log-linearizing around the steady-state. For the calibration, I use the same parameter values as in this paper's model (see Table 4) whenever possible. For other parameters, I follow Thomas (2006). The aggregate productivity shock ![]() follows an AR(1) process such that
follows an AR(1) process such that
![]() with
with
![]() and the standard-deviation
and the standard-deviation
![]() calibrated to match the cyclical volatility of detrended US real output. Idiosyncratic productivity
calibrated to match the cyclical volatility of detrended US real output. Idiosyncratic productivity ![]() has mean
has mean ![]() and standard-deviation
and standard-deviation
![]() as in Ramey (2008) and Elsby and Michaels (2008).
as in Ramey (2008) and Elsby and Michaels (2008).
Households
I consider an economy populated by a continuum of households of measure one and a continuum of firms of measure one. With equilibrium unemployment, ex-ante homogenous workers become heterogeneous in the absence of perfect income insurance because each individual's wealth differs based on his
employment history. To avoid distributional issues, I follow Merz (1995) and Andolfatto (1996) in assuming that households form an extended family that pools its income and chooses per capita consumption and assets holding to maximize its expected lifetime utility. There are ![]() unemployed workers who receive unemployment benefits
unemployed workers who receive unemployment benefits ![]() in units of utility of
consumption, and
in units of utility of
consumption, and ![]() employed workers who receive the wage payment
employed workers who receive the wage payment ![]() from
firm
from
firm ![]() for providing hours
for providing hours ![]() . Denoting
. Denoting ![]() the individual disutility from working, the representative family seeks to maximize
the individual disutility from working, the representative family seeks to maximize
![\displaystyle E_{0}\sum\limits_{t=0}^{\infty}\beta^{t}\left[ \ln\left( C_{t}\right) +\lambda_{m}\ln(\frac{M_{t}}{P_{t}})-\frac{\lambda_{h}}{1+\sigma_{h}}\int _{0}^{1}n_{it}h_{it}^{1+\sigma_{h}}di\right]](img149.gif)
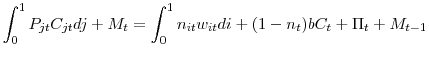
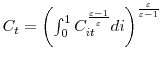 where
where 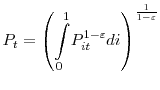 .
.Firms and the labor market
Each differentiated good is produced by a monopolistically competitive firm using labor as the only input. As in the reduced-form model of the paper, at date ![]() , each firm
, each firm ![]() produces a quantity
produces a quantity
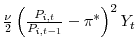 with
with The firm's problem
Since the wage and the law of motion for employment take the same expression as in the reduced-form model, I can now state the firm's problem. Firm ![]() will choose a sequence of price
will choose a sequence of price
![]() , vacancies
, vacancies
![]() and endogenous separation rate
and endogenous separation rate
![]() to maximize its value
to maximize its value
![\displaystyle \max_{P_{it},v_{it},\rho_{it}}E_{t}\sum_{j}\beta^{j}\frac{u^{\prime}(C_{t+j} )}{u^{\prime}(C_{t})}\left[ \frac{P_{i,t+j}}{P_{t+j}}y_{i,t+j}^{d}-\left( 1-\rho_{it+j}\right) n_{i,t+j}w_{i,t+j}-\frac{c}{\lambda_{t+j}} v_{i,t+j}-\frac{\nu}{2}\left( \frac{P_{i,t+j}}{P_{i,t+j-1}}-\pi^{\ast }\right) ^{2}Y_{t+j}\right]](img171.gif)
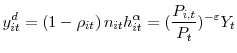
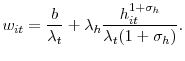
The central bank
The money supply evolves according to
![]() with
with
![]() ,
,
![]() and
and
![]() I interpret
I interpret
![]() as an aggregate demand shock.
as an aggregate demand shock.
Closing the model
Averaging firms' employment, total employment evolves according to
![]() The labor force being normalized to one, the number of unemployed workers is
The labor force being normalized to one, the number of unemployed workers is
![]() Finally, as in Krause and Lubik (2007), vacancy posting costs are distributed to the aggregate households so that
Finally, as in Krause and Lubik (2007), vacancy posting costs are distributed to the aggregate households so that
![]() in equilibrium.
in equilibrium.
The price setting condition
The vacancy posting condition and the job separation condition are identical to the ones I report in the paper, and I do not repeat them here. For the price-setting condition, I get the standard result for models with quadratic price adjustment
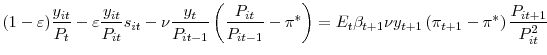
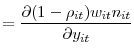 |
||
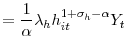 |
In order to produce an extra unit of output, the firm needs to increase hours since employment is a state variable. As a result, the wage response to changes in hours is driving the firm's real marginal cost. To get some intuition, I consider very small perturbations around the zero-inflation steady-state. For very small shocks,
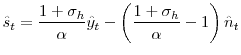
With
![]() , the real marginal cost increases with demand but decreases with the employment level. As a result, firms can lower the impact of shocks on their real
marginal cost and optimal price by adjusting their extensive margin. Inflation will be less responsive to shocks than in a standard New-Keynesian model without unemployment but will display more persistence. Following an increase in demand, the value of a marginal worker goes up and leads the firm
to increase its level of employment. But this decreases future real marginal cost and leads the firm to post lower prices, which itself increases demand and output next period. This in turn leads to a future rise in employment, and, as the process goes on, the response to a demand shock will die
out more slowly than in the standard New-Keynesian case.
, the real marginal cost increases with demand but decreases with the employment level. As a result, firms can lower the impact of shocks on their real
marginal cost and optimal price by adjusting their extensive margin. Inflation will be less responsive to shocks than in a standard New-Keynesian model without unemployment but will display more persistence. Following an increase in demand, the value of a marginal worker goes up and leads the firm
to increase its level of employment. But this decreases future real marginal cost and leads the firm to post lower prices, which itself increases demand and output next period. This in turn leads to a future rise in employment, and, as the process goes on, the response to a demand shock will die
out more slowly than in the standard New-Keynesian case.
The possibility to lay-off workers creates an asymmetry in the behavior of employment that generates asymmetry in real marginal cost and in inflation. Because it is easier to fire than hire workers, firms can more easily smooth fluctuations in their real marginal cost after negative shocks than after positive shocks. As a result, a monetary policy shock has a different impact depending on its sign. Following a negative monetary policy shock, firms can more easily adjust quantities than prices, but after a negative shock, the opposite happens because of hiring frictions. Inflation will behave asymmetrically; displaying large and short lived responses following positive nominal shocks but displaying small and more persistent responses following positive shocks.
A.3 Computation
I solve the model with policy function iteration by simultaneously solving the two first-order conditions for vacancy posting and job destruction:
with
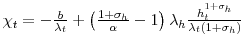 the value of a marginal worker.
the value of a marginal worker.
I use policy function iterations with intergrid cubic spline interpolation on a grid with ![]() points for the two state variables
points for the two state variables ![]() and
and ![]() . Employment
. Employment ![]() is discretized over
is discretized over
![]() , and I follow Tauchen's method (1986) to represent the AR(1) process
, and I follow Tauchen's method (1986) to represent the AR(1) process ![]() as a Markov chain. Since employment will only rarely take extreme values, I allow for a higher grid density for employment around its steady-state value.
as a Markov chain. Since employment will only rarely take extreme values, I allow for a higher grid density for employment around its steady-state value.
The general algorithm is as follows:
1. Guess policy functions for
![]() and
and
![]() and interpolate their values with intergrid cubic spline interpolation for points not on the grid
and interpolate their values with intergrid cubic spline interpolation for points not on the grid
2. For all ![]() and
and ![]() :
:
a. If
![]()
![]() and find
and find
![]() to satisfy (6) using interpolated
to satisfy (6) using interpolated
![]() and
and ![]() to compute the right-hand side of (6).
to compute the right-hand side of (6).
b. Otherwise, solve jointly (6) and (7) for
![]() and
and
![]()
3. Repeat 2. until
![]() and
and
![]()
Since it is computationally demanding to jointly solve for ![]() and
and ![]() , I
restrict this joint calculation to the first and latter steps of the computation loop. More precisely, I start with a loose value for
, I
restrict this joint calculation to the first and latter steps of the computation loop. More precisely, I start with a loose value for
![]() so that once I obtain a decent approximation for
so that once I obtain a decent approximation for ![]() , I only
iterate on
, I only
iterate on ![]() taking the policy rule
taking the policy rule ![]() as given. When
as given. When ![]() converges to a good approximation, I resume solving for both
converges to a good approximation, I resume solving for both ![]() and
and ![]() simultaneously.
simultaneously.
Table 1: Skewness, Monthly data
Notes: Monthly unemployment u is constructed by the BLS from the CPS, and y is logged real GDP. Both series are seasonally adjusted. Newey-West standard errors are reported in parentheses. ** indicates significance at the 5% level.
Table 2: US Data, 1951-2006
| jf | js | ||||||
|---|---|---|---|---|---|---|---|
| Standard deviation | 0.187 | 0.198 | 0.378 | 0.116 | 0.065 | 0.007 | 0.021 |
| Quarterly autocorrelation | 0.938 | 0.948 | 0.946 | 0.912 | 0.648 | 0.83 | 0.84 |
| Correlation matrix: |
1 | -0.90 | -0.97 | -0.95 | 0.61 | -0.50 | -0.69 |
| Correlation matrix: |
- | 1 | 0.98 | 0.92 | -0.55 | 0.63 | 0.78 |
| Correlation matrix: |
- | - | 1 | 0.96 | -0.62 | 0.60 | 0.76 |
| Correlation matrix: jf | - | - | - | 1 | -0.48 | 0.51 | 0.69 |
| Correlation matrix: js | - | - | - | - | 1 | -0.55 | -0.56 |
| Correlation matrix: |
- | - | - | - | - | 1 | 0.81 |
| Correlation matrix: |
- | - | - | - | - | - | 1 |
Table 3: Mortensen-Pissarides (1994) model with productivity shocks
| jf | js | |||||
|---|---|---|---|---|---|---|
| Standard deviation | 0.084
(0.01) |
0.044
(0.004) |
0.044
(0.003) |
0.012
(0.001) |
0.096
(0.009) |
0.021
(0.002) |
| Quarterly autocorrelation | 0.88
(0.02) |
0.91
(0.02) |
0.76
(0.04) |
0.76
(0.05) |
0.76
(0.05) |
0.84
(0.03) |
| Correlation matrix: |
1 | 0.96
(0.01) |
-0.96
(0.01) |
-0.97
(0.06) |
0.97
(0.06) |
-0.99
(0.00) |
| Correlation matrix: |
1 | -0.87
(0.02) |
0.86
(0.03) |
0.86
(0.03) |
-0.93
(0.01) |
|
| Correlation matrix: |
1 | 0.99
(0.00) |
-0.99
(0.00) |
0.99
(0.00) |
||
| Correlation matrix: jf | 1 | -0.99
(0.00) |
-0.99
(0.00) |
|||
| Correlation matrix: js | 1 | -0.96
(0.00) |
||||
| Correlation matrix: |
1 |
Notes: Standard errors -the standard deviation across 500 model simulations over 600 months- are reported in parentheses.
Table 4: Calibration, monthly frequency
| Discount rate |
|
|
|---|---|---|
| Matching function elasticity |
|
Shimer (2005) |
| Bargaining weight |
|
|
| Probability vacancy is filled | q( |
den Haan, Ramey and Watson (2000) |
| Job finding probability | u=10% | |
| Exogenous separation rate |
|
u=10% |
| Income replacement ratio | b=0.28 | Shimer (2005) |
| Vacancy posting cost | c=0.01 | Andolfatto (1996) |
| Returns to hours |
|
|
| Disutility of hours |
|
Trigari (Forthcoming) |
| AR(1) process for output | ||
| Standard-deviation of AD shock |
|
Table 5: MP model with demand constraints, Aggregate Demand shocks
| jf | js | ||||||
|---|---|---|---|---|---|---|---|
| Standard deviation | 0.174
(0.021) |
0.470
(0.046) |
0.623
(0.069) |
0.173
(0.019) |
0.061
(0.006) |
0.007
(0.001) |
0.020
(0.002) |
| Quarterly autocorrelation | 0.86
(0.03) |
0.65
(0.06) |
0.75
(0.05) |
0.75
(0.05) |
0.15
(0.08) |
0.14
(0.08) |
0.84
(0.04) |
| Correlation matrix: |
1 | -0.83
(0.03) |
-0.90
(0.02) |
-0.91
(0.02) |
0.47
(0.04) |
-0.30
(0.07) |
-0.97
(0.01) |
| Correlation matrix: |
- | 1 | 0.98
(0.00) |
0.98
(0.00) |
-0.60
(0.03) |
0.76
(0.02) |
0.92
(0.01) |
| Correlation matrix: |
- | - | 1 | 0.99
(0.00) |
-0.58
(0.03) |
0.66
(0.03) |
0.97
(0.01) |
| Correlation matrix: jf | - | - | - | 1 | -0.59
(0.03) |
0.65
(0.03) |
0.97
(0.01) |
| Correlation matrix: js | - | - | - | - | 1 | -0.50
(0.03) |
-0.60
(0.03) |
| Correlation matrix: |
- | - | - | - | - | 1 | 0.48
(0.05) |
| Correlation matrix: |
- | - | - | - | - | - | 1 |
Table 6: Contribution of JF/JS and Skewness, model data
| Size of AD shocks | ? |
|
|---|---|---|
| Contribution of JS | 22 %
(0.03) |
13 %
(0.02) |
| Contribution of JF | 78 %
(0.03) |
87 %
(0.02) |
| Skewness(dU) | 0.53**
(0.16)) |
0.14
(0.17)) |
Notes: u and y are monthly model unemployment and output. The contributions of JF and JS are calculated using the method from Shimer (2007) and Fujita and Ramey (2007). Standard errors -the standard deviation across 500 model simulations over 600 months (50 years)- are reported in parentheses.
Figure 1: Empirical Cross-Correlograms of the Job Finding rate and the Job Separation rate with Unemployment and Output over 1951-2006.
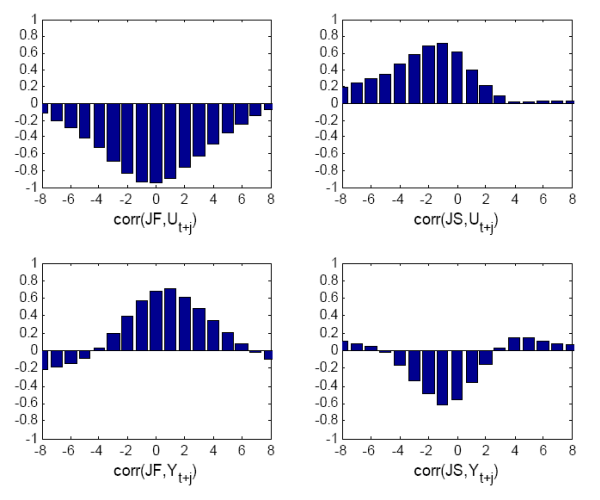
Figure 2: Impulse response functions of Unemployment, the (minus) Job Finding probability and the Job Separation probability to monetary and technology shocks. Solid circles indicate that the response is signicant at the 5% level and open circles at the 10% level.
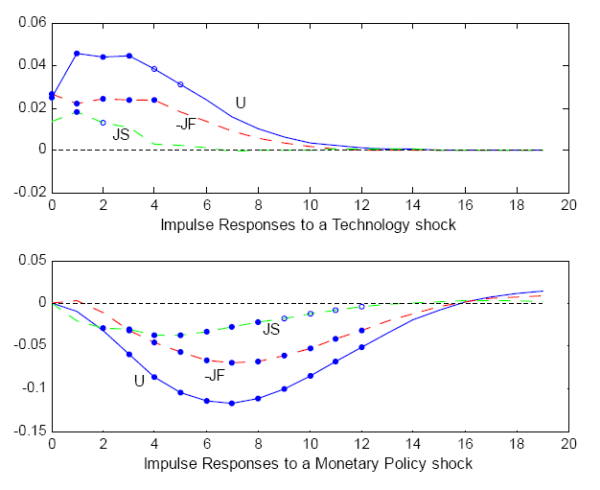
Figure 3: Mortensen-Pissarides (1994) model impulse response functions to a negative one standard-deviation productivity shock.
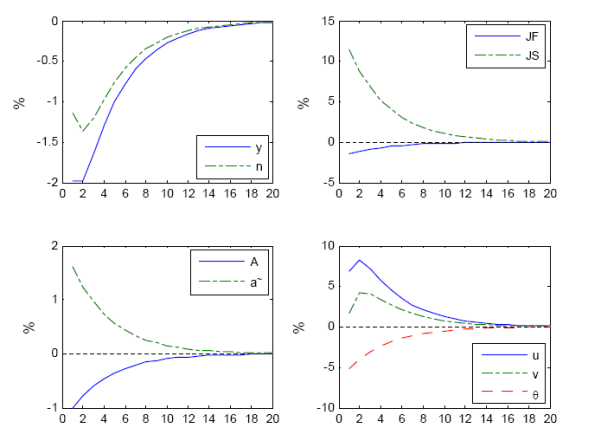
Figure 4: Aggregate Demand and the value of a marginal worker. Δv indicates changes in posted vacancies, and ρ>0 indicates use of the job separation margin.
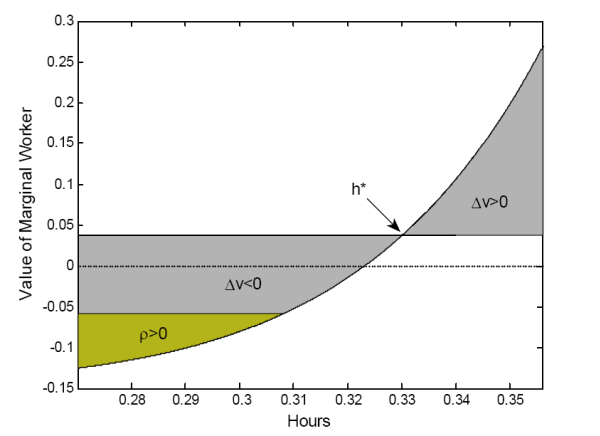
Figure 5: Model impulse response functions to a positive one standard-deviation aggregate demand shock.
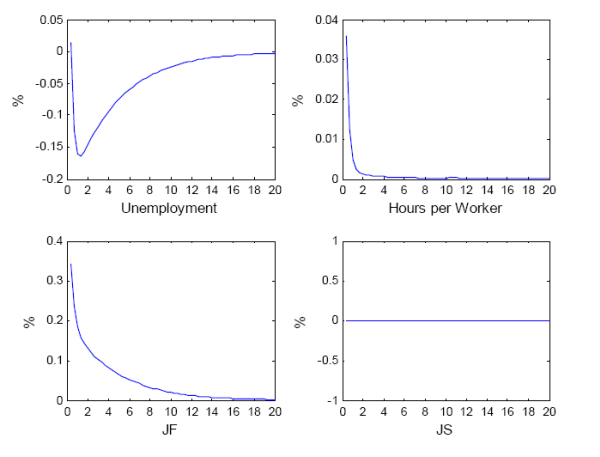
Figure 6: Model impulse response functions to negative aggregate demand shocks with respective size of one and one-half standard-deviation.
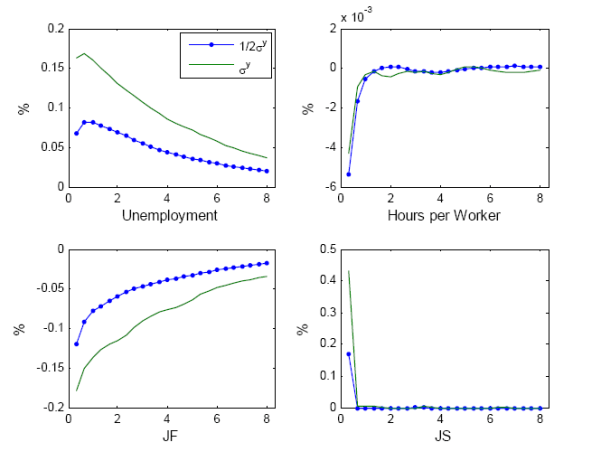
Figure 7: Model impulse response functions of gross hires to negative aggregate demand shocks of different size.
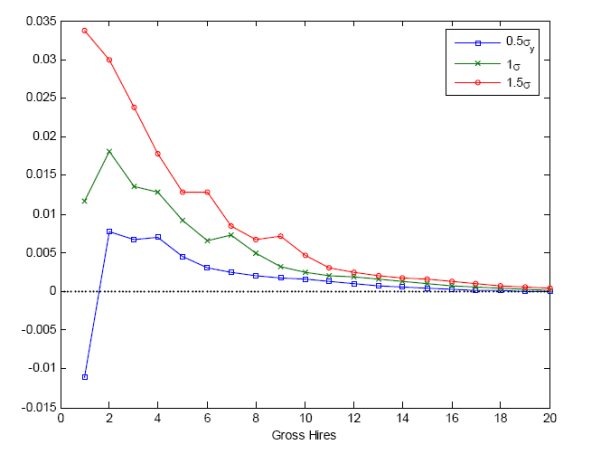
Figure 8: Model (plain line) and empirical (dotted line) cross-correlograms of the Job Finding rate and the Job Separation rate with Unemployment and Output.
Footnotes
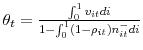 . Return to Text
. Return to Text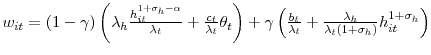 and the rest of the
analysis goes through. Return to Text
and the rest of the
analysis goes through. Return to Text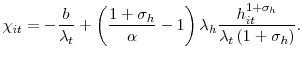
![\displaystyle =E_{t}\beta_{t+1}\left[ (1-\rho_{t+1} )\chi_{t+1}+\frac{c_{t+1}}{q(\theta_{t+1})}(1-\bar{\rho}-\rho_{t+1})\right]](img190.gif)