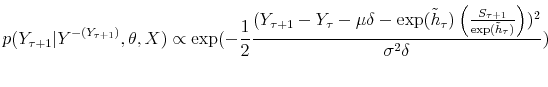Bayesian Analysis of Stochastic Volatility Models with Lévy Jumps: Application to Risk Analysis
Keywords: Bayesian estimation, stochastic volatility, Lévy jumps, density forecast
Abstract:
JEL classification: C1, C11, G1, G12
1 Introduction
In this paper I estimate a broad class of asset pricing models. I evaluate their performance with respect to goodness of fit, density forecast and Value at Risk (VaR) analysis. This is not trivial since there is a need for a balance between a level of model complexity - which always has a
positive effect on the goodness of fit, and a possible extent of model overfiting - which decreases the forecasting power of the model. Specifically, I consider the family of continuous-time, time-changed jump diffusion models developed in Carr and Wu (2004). Stochastic volatility, or time-change,
can arise either from a diffusion part, or a jump part, or both. The leverage effect is assumed to arise from the diffusion part if diffusion is a source of stochastic volatility. The jump component includes either finite activity compound Poisson or infinite activity Lévy ![]() -stable jumps. I consider an estimation under the statistical measure, since it allows to perform density forecast and VaR analysis and use data on daily S&P 500 index returns. I choose this
data for empirical study since it is a broad indicator of the equity market and it has been used in other comparable studies in the literature. An important advantage of my empirical analysis is that I consider a large family of models. Therefore I can study in depth the marginal effects of
different jump structures and source of stochastic volatility with respect to goodness of fit and density forecast performance.
-stable jumps. I consider an estimation under the statistical measure, since it allows to perform density forecast and VaR analysis and use data on daily S&P 500 index returns. I choose this
data for empirical study since it is a broad indicator of the equity market and it has been used in other comparable studies in the literature. An important advantage of my empirical analysis is that I consider a large family of models. Therefore I can study in depth the marginal effects of
different jump structures and source of stochastic volatility with respect to goodness of fit and density forecast performance.
My contribution to the literature is two-folded. First, I propose a Bayesian estimation method to estimate the general continuous-time, time-changed jump diffusion models with compound Poisson or, most importantly, infinite activity Lévy ![]() -stable jumps. Second, I analyze the marginal contribution of jumps and volatility specifications in goodness of fit and density forecast. Intuitively, the more general jump structure with infinite activity should fit the data
better than the finite activity compound Poisson jumps as found in Li, Wells and Yu (2008). However, it has not been studied in the literature, what the effect of infinite activity jumps is on the density forecast and VaR analysis. Moreover, it is important to address the choice of the source of
stochastic volatility when we condition on the jump structure. How, if at all, the specification of stochastic volatility contributes to goodness of fit and density forecast?
-stable jumps. Second, I analyze the marginal contribution of jumps and volatility specifications in goodness of fit and density forecast. Intuitively, the more general jump structure with infinite activity should fit the data
better than the finite activity compound Poisson jumps as found in Li, Wells and Yu (2008). However, it has not been studied in the literature, what the effect of infinite activity jumps is on the density forecast and VaR analysis. Moreover, it is important to address the choice of the source of
stochastic volatility when we condition on the jump structure. How, if at all, the specification of stochastic volatility contributes to goodness of fit and density forecast?
I estimate my models by MCMC Bayesian methods and directly address the problem of parameter estimation in the presence of both latent volatility and latent jump sizes. The recent attempt to estimate models with latent Lévy ![]() -stable jumps in returns by Li, Wells and Yu (2008) constitutes the foundation to solve this problem but it also introduces separability on the Markov chain state-space. I fill this gap in the literature by constructing an MCMC algorithm free of
the separability flaw. The proposed algorithm is applicable in any stochastic volatility specification and is based on the Buckle's (1995) Bayesian method.
-stable jumps in returns by Li, Wells and Yu (2008) constitutes the foundation to solve this problem but it also introduces separability on the Markov chain state-space. I fill this gap in the literature by constructing an MCMC algorithm free of
the separability flaw. The proposed algorithm is applicable in any stochastic volatility specification and is based on the Buckle's (1995) Bayesian method.
In my empirical analysis of the S&P 500 returns, I find that the models with Lévy ![]() -stable jumps in returns are able to represent well excess kurtosis and skewness of
return distribution, if diffusion is included as a source of stochastic volatility. Lévy
-stable jumps in returns are able to represent well excess kurtosis and skewness of
return distribution, if diffusion is included as a source of stochastic volatility. Lévy ![]() -stable jumps dominate Poisson jumps specifications with respect to goodness of fit
analysis, since the latter are only suited to fit big jumps. Most importantly, models with stochastic volatility coming only from pure jumps do not fit the asset returns well. Nevertheless, based only on goodness of fit measure, one cannot in a decisive way point out if there is a need for the jump
component as the second source of stochastic volatility. This conclusion holds for the models with all considered jump structures including infinite activity Lévy
-stable jumps dominate Poisson jumps specifications with respect to goodness of fit
analysis, since the latter are only suited to fit big jumps. Most importantly, models with stochastic volatility coming only from pure jumps do not fit the asset returns well. Nevertheless, based only on goodness of fit measure, one cannot in a decisive way point out if there is a need for the jump
component as the second source of stochastic volatility. This conclusion holds for the models with all considered jump structures including infinite activity Lévy ![]() -stable
jumps.
-stable
jumps.
The density forecast and VaR analysis shed new light on the application of continuous-time jump diffusion models of asset returns. I find that correct specification of the source of stochastic volatility is of fundamental importance in the density forecast and VaR analysis. The performance of
the compound Poisson jump models do not significantly change with the addition of the jump component to the diffusion as the source of stochastic volatility. On the contrary, models with Lévy ![]() -stable jumps improve in the density forecast and VaR performance with the inclusion of both sources of stochastic volatility, thus dominating all other model specifications. The joint stochastic volatility enables us to extract information about latent volatility from both
diffusion and jumps, where the jumps are more informative with its infinite activity property. However, one cannot go further and exclude the diffusion from the source of stochastic volatility. This conclusion does not depend on the jump structure and agrees with the goodness of fit analysis.
-stable jumps improve in the density forecast and VaR performance with the inclusion of both sources of stochastic volatility, thus dominating all other model specifications. The joint stochastic volatility enables us to extract information about latent volatility from both
diffusion and jumps, where the jumps are more informative with its infinite activity property. However, one cannot go further and exclude the diffusion from the source of stochastic volatility. This conclusion does not depend on the jump structure and agrees with the goodness of fit analysis.
The most difficult problem that arises in the density forecast analysis involves approximation of the filtering density. I follow the auxiliary particle filter approach, as developed in Pitt and Shephard (1999), and modify it to allow for the new features of my model. Durham (2006) extends the
basic particle filter for models with leverage effect but does not include jumps in returns. Moreover, he works with particle filter and does not apply auxiliary particle filter involving index parameter draws. Johannes, Polson and Stroud (2008) offer further refinements to the auxiliary particle
filter algorithm for models with jumps and stochastic volatility. However, their algorithm cannot be applied to specifications with Lévy ![]() -stable jumps. I refine auxiliary
particle filter to study jump-diffusion models with leverage effect. Moreover, I allow for various sources of stochastic volatility and most importantly for Lévy
-stable jumps. I refine auxiliary
particle filter to study jump-diffusion models with leverage effect. Moreover, I allow for various sources of stochastic volatility and most importantly for Lévy ![]() -stable jumps in
returns.
-stable jumps in
returns.
My model specifications are not new and are based on the continuous-time, time-changed jump diffusion framework, which is the direct outcome of the evolution in the asset pricing literature that started with Black and Scholes (1973). However, their model produces disappointing results both in fitting time-series of returns and cross section of option prices, since it lacks the ability to represent non-normality of asset returns. In recent asset pricing literature, stochastic volatility and jumps are found to be important, allowing to represent skewness and excess kurtosis both in unconditional and conditional return distribution. Merton (1976) was the first to consider jump-diffusion models. Heston (1993) assumed volatility to be stochastic and followed the square-root Cox, Ingersoll and Ross (1985) (CIR) specification, while Jacquier, Polson and Rossi (1994) (JPR) assumed log-volatility specification. In this paper I follow JPR specification, since it does not require additional constraints on the parameters, satisfies non-negativity after discretization and allows for convenient interpretation of the parameters in the models with joint stochastic volatility.
Das and Sundaram (1999) found that jumps and stochastic volatility have different effects on the conditional asset return distribution and hence they play complimentary role in the option pricing literature. The generalized version of the model with both stochastic volatility and jumps required
different techniques of estimation under statistical measure, where estimation problems arise from the unobservable stochastic volatility. This was partially resolved with development of efficient method of moments (EMM) estimation of Gallant and Tauchen (1996) and Bayesian Markov chain Monte Carlo
(MCMC) methods. However, the class of models with Lévy ![]() -stable jumps in returns and the class of models with various sources of stochastic volatility lack a robust estimation
method under the statistical measure. I construct a new MCMC method to estimate these models.
-stable jumps in returns and the class of models with various sources of stochastic volatility lack a robust estimation
method under the statistical measure. I construct a new MCMC method to estimate these models.
The next generalization allowed for instantaneous correlation between increments of returns and volatility, the relation called leverage effect. Empirical results of Jacquier, Polson and Rossi (2004), Jones (2003), Andersen, Benzoni and Lund (2002) among others found the respective correlation to be significantly negative. The negative leverage effect has a deep intuitive explanation, since periods of high volatility on the market coincides more often with market crashes. The leverage effect helps in capturing the skewness of the stock returns and corrects estimates of parameters governing volatility as stated in Jacquier, Polson and Rossi (2004). Moreover, Jones (2003) included in one of his model specifications the leverage effect as a function of volatility. His findings suggest, that as volatility increases, the leverage effect is higher in magnitude. Hence, in periods of high volatility the probability of market crashes is higher than in periods with low volatility. Andersen, Benzoni and Lund (2002) estimated stochastic volatility models with compound Poisson jumps in returns and leverage effect under the statistical measure. They found that jumps, stochastic volatility and leverage effect are all important features of asset return models and generate skewness, excess kurtosis and conditional heteroscedasticity. Eraker, Johannes and Polson (2003) further extended the jump-diffusion model with stochastic volatility and studied jumps not only in returns but also in volatility. Although jumps in volatility are found to be an important feature in fitting the data on the 1987 crash, the discrete jumps in returns cannot be modeled successfully by jumps in volatility.
Since the arrival rate of Poisson jumps under the statistical measure was found to be small (about few jumps per year), the more subtle jumps cannot be modeled by rare and big compound Poisson jumps. This in turn is one of the main critiques of finite activity jumps in returns. The solution to
this problem lies in the introduction of infinite activity Lévy jumps, that is the process with infinite number of "small" jumps in a finite time interval. The latest specifications include infinite activity jumps as in the case of variance-gamma (VG) model of Madan, Carr and Chang (1998)
and CGMY class of models by Carr, Geman, Madan and Yor (2002). Li, Wells and Yu (2008) estimate the jump-diffusion model with VG jumps in returns and stochastic volatility from diffusion under the statistical measure and found its superior goodness of fit over the models with finite activity
compound Poisson jumps. Lévy ![]() -stable jumps, which are also of infinite activity, have already been studied in the literature under the risk-neutral measure in Huang and Wu (2004)
and Carr and Wu (2003) but there has been so far no successful application of this jump structure under the statistical measure. A recent approach by Li, Wells and Yu (2008) introduces separability on the Markov chain state-space in the MCMC algorithm. I construct a robust MCMC algorithm to
estimate models with Lévy
-stable jumps, which are also of infinite activity, have already been studied in the literature under the risk-neutral measure in Huang and Wu (2004)
and Carr and Wu (2003) but there has been so far no successful application of this jump structure under the statistical measure. A recent approach by Li, Wells and Yu (2008) introduces separability on the Markov chain state-space in the MCMC algorithm. I construct a robust MCMC algorithm to
estimate models with Lévy ![]() -stable jumps. In addition, I relax the assumption required in the option pricing approach that imposes maximum negative skewness on Lévy
-stable jumps. In addition, I relax the assumption required in the option pricing approach that imposes maximum negative skewness on Lévy
![]() -stable jumps, required to price options in a model with infinite second and higher moments. This allows modelling of the degree of skewness and the algorithm by Buckle (1995) is a
suitable foundation to develop a method of estimation under the statistical measure. Finally, my analysis is based both on goodness of fit and density forecast. The latter is missing in the literature under the statistical measure for infinite activity jumps and hence I fill this gap in the
literature. This lets us find how the models with infinite activity jumps perform in risk management. Finally, I allow for stochastic volatility to arise from diffusion, jumps or both and also look at its implications on the density forecast.
-stable jumps, required to price options in a model with infinite second and higher moments. This allows modelling of the degree of skewness and the algorithm by Buckle (1995) is a
suitable foundation to develop a method of estimation under the statistical measure. Finally, my analysis is based both on goodness of fit and density forecast. The latter is missing in the literature under the statistical measure for infinite activity jumps and hence I fill this gap in the
literature. This lets us find how the models with infinite activity jumps perform in risk management. Finally, I allow for stochastic volatility to arise from diffusion, jumps or both and also look at its implications on the density forecast.
Another important issue in the literature has been the type of data used in the estimation. There are two general approaches to model asset returns. The first approach specifies models under the statistical measure, which allows for direct analysis of the return series and therefore density forecast and value at risk (VaR) analysis. The second approach uses options data and specifies models under the risk-neutral measure. There is also a way to utilize information from both worlds as in Chernov and Ghysels (2000) and Eraker (2004), however, it results in even further technical difficulties. Moreover, estimation under both the statistical and the risk-neutral measures requires definition of market risk premia, which can also be a potential source of misspecification as noted by Andersen, Benzoni and Lund (2002). Therefore I estimate the models under statistical measure which allows the study of density forecast and VaR analysis.
The rest of this paper is organized as follows, Section 2 introduces the concept of Lévy process and describes estimated model specifications, Section 3 describes MCMC estimation algorithm and the auxiliary particle filter, Section 4 gives a brief overview of the data used in the estimation and presents the results of the estimation with goodness of fit, density forecast and VaR performance analysis, and Section 5 concludes. The tables are presented at the end of the paper.
2.1 Lévy Processes
In this section I closely follow Applebaum (2004) and Bertoin (1998). Let
![]() be a scalar Lévy process defined on a probability space
be a scalar Lévy process defined on a probability space
![]() with given filtration
with given filtration
![]() . From definition, a Lévy process
. From definition, a Lévy process ![]() has
independent and stationary increments, or more precisely,
has
independent and stationary increments, or more precisely,
![]() is independent of
is independent of
![]() and has the same distribution as
and has the same distribution as
![]() for all
for all
![]() . It is also stochastically continuous. I restrict my analysis to the modification of
. It is also stochastically continuous. I restrict my analysis to the modification of ![]() which exhibits cádlág paths and hence its sample paths are right-continuous with left limits. By the Lévy-Ito decomposition every Lévy process can be decomposed as the sum of three independent processes: a linear drift, Brownian motion and a pure
jump part. Accordingly, the log-characteristic function of a Lévy process is the sum of the log-characteristic functions of its Lévy components and is given by the Lévy-Khintchine formula. The characteristic function of the Lévy process is given by
which exhibits cádlág paths and hence its sample paths are right-continuous with left limits. By the Lévy-Ito decomposition every Lévy process can be decomposed as the sum of three independent processes: a linear drift, Brownian motion and a pure
jump part. Accordingly, the log-characteristic function of a Lévy process is the sum of the log-characteristic functions of its Lévy components and is given by the Lévy-Khintchine formula. The characteristic function of the Lévy process is given by
where
where
The above condition implies finite quadratic variation of any Lévy process. We can extend the Lévy measure
This class of processes is very general and contains Brownian motion and compound Poisson process as two special cases. Brownian motion is the only Lévy process with continuous sample paths and hence does not allow for discontinuous jumps. The compound Poisson jump process, however, represents special jump characteristics with its finite activity property. The sum of the Brownian part and the compound Poisson part, although a Lévy Process, does not allow for more general jump structures and is one of the main critiques of asset returns models based on them. In this work I allow for more general properties of the jump structure by redefining the jump part of the underlying asset returns process and allowing for infinite activity. The pure jump Lévy process with infinite activity, however, can also be classified into two general sub-classes with respect to the total absolute variation of the process. The Lévy pure jump process is of finite total variation if the following condition is satisfied by its Lévy measure:
otherwise it is of infinite total variation.
Since infinite variation jumps resemble Brownian motion much closer than other types of jumps, I restrict my analysis to the Lévy ![]() stable pure jump process with index of
stability
stable pure jump process with index of
stability
![]() , the Lévy process with infinite total variation1. I also investigate another extreme case with finite activity Poisson type jumps, since its simplicity decreases an extent of possible overfitting problems.
, the Lévy process with infinite total variation1. I also investigate another extreme case with finite activity Poisson type jumps, since its simplicity decreases an extent of possible overfitting problems.
2.2 Lévy  stable Process
stable Process
The building block of ![]() stable process is a stable distribution. Let
stable process is a stable distribution. Let
![]() denote a stable distributed random variable with index of stability
denote a stable distributed random variable with index of stability
![]() , skewness
, skewness
![]() , scale parameter
, scale parameter ![]() , and location parameter
, and location parameter
![]()
![]() . In this paper I use the characteristic function specification as in Buckle (1995):
. In this paper I use the characteristic function specification as in Buckle (1995):
In this parametrization, parameter
The most widely used parametrization is given by Samorodnitsky and Taqqu (1994) and Zolotarev (1986) and denoted by
![]() , where:
, where:
and
Since the stable distribution is infinitely divisible there exists a Lévy process
![]() with stable distributed increments - the Lévy
with stable distributed increments - the Lévy ![]() stable
process2:
stable
process2:
Since
2.3 Dynamics of the Asset Returns Process
Let ![]() denote the logarithm of asset price or logarithm of the index level at time
denote the logarithm of asset price or logarithm of the index level at time ![]() and
and
![]() be the corresponding log-return. I consider several specifications that differ in the source of stochastic volatility in the returns process and the type of jump component in
returns. In the following,
be the corresponding log-return. I consider several specifications that differ in the source of stochastic volatility in the returns process and the type of jump component in
returns. In the following,
![]() defines a two-dimensional standard Brownian motion on
defines a two-dimensional standard Brownian motion on
![]() probability space defined above. Carr and Wu (2004) noted that stochastic volatility can be alternatively interpreted as the stochastic time change of the underlying
processes. I define the following time-changed process
probability space defined above. Carr and Wu (2004) noted that stochastic volatility can be alternatively interpreted as the stochastic time change of the underlying
processes. I define the following time-changed process ![]() , being a semimartingale:
, being a semimartingale:
where
It can be shown, that
- Models with Poisson jumps.
My model specifications with Poisson jumps draw from the work of Andersen, Benzoni and Lund (2002) and Eraker, Johannes and Polson (2003) among others. The compound Poisson jump process
![]() is characterized by its normally distributed jumps with mean
is characterized by its normally distributed jumps with mean
![]() , variance
, variance
![]() and unit jump intensity. The time changed process
and unit jump intensity. The time changed process
![]() has an instantaneous Poisson arrival intensity
has an instantaneous Poisson arrival intensity
![]() and the jump compensator
and the jump compensator
![]() , where
, where
![]() is a pdf of normal distribution with mean
is a pdf of normal distribution with mean ![]() and variance
and variance
![]() and hence
and hence
![]() is a Lévy measure of jumps of the compound Poisson process
is a Lévy measure of jumps of the compound Poisson process
![]() .
.
- Models with Lévy
 -stable jumps.
-stable jumps.
The idea of modelling asset returns with Lévy ![]() -stable jumps is not new to the asset pricing literature. Carr and Wu (2003) and Huang and Wu (2004) applied models with both the
diffusion and Lévy
-stable jumps is not new to the asset pricing literature. Carr and Wu (2003) and Huang and Wu (2004) applied models with both the
diffusion and Lévy ![]() -stable jumps to model asset returns under risk-neutral measure. I pursue similar specification with its application under statistical measure and I loosen up
their assumption of maximum negative skewness. In the model above
-stable jumps to model asset returns under risk-neutral measure. I pursue similar specification with its application under statistical measure and I loosen up
their assumption of maximum negative skewness. In the model above
![]() is a Lévy
is a Lévy ![]() -stable process with stable distributed
increments:
-stable process with stable distributed
increments:
- Restrictions defining all model specifications.
The restrictions on the parameter ![]() and the predictable functions
and the predictable functions
![]() ,
,
![]() completely characterize all model specifications and are provided in Table I. I specify six model specifications, where the models (1), (2) and (3) have a Poisson jump component,
and the models (4), (5) and (6) have a Lévy
completely characterize all model specifications and are provided in Table I. I specify six model specifications, where the models (1), (2) and (3) have a Poisson jump component,
and the models (4), (5) and (6) have a Lévy ![]() -stable jump component. For each jump type I distinguish three sources of stochastic volatility: from diffusion, jumps and jointly:
from the diffusion and jumps. For models with stochastic volatility only from the jump component, I consider specification without leverage effect and I impose the restriction
-stable jump component. For each jump type I distinguish three sources of stochastic volatility: from diffusion, jumps and jointly:
from the diffusion and jumps. For models with stochastic volatility only from the jump component, I consider specification without leverage effect and I impose the restriction ![]() . In the
other specifications I model the leverage effect and estimate
. In the
other specifications I model the leverage effect and estimate
![]() . In order to model the source of stochastic volatility I have to define the functions
. In order to model the source of stochastic volatility I have to define the functions
![]() and
and
![]() governing the instantaneous "speed", or the time rate, of the business time respectively
governing the instantaneous "speed", or the time rate, of the business time respectively ![]() and
and ![]() . The affix
. The affix ![]() denotes Poisson type
jumps and
denotes Poisson type
jumps and ![]() denotes Lévy
denotes Lévy ![]() -stable jumps.
-stable jumps.
In models with stochastic volatility only from diffusion (PJ, SJ), I specify
![]() to be a positive constant, given by
to be a positive constant, given by
![]() for the model with Poisson jumps (PJ) and
for the model with Poisson jumps (PJ) and
![]() for the model with Lévy
for the model with Lévy ![]() -stable jumps (SJ) with
-stable jumps (SJ) with
![]() . I define the constant volatility from Lévy
. I define the constant volatility from Lévy ![]() -stable
jumps to be a function of
-stable
jumps to be a function of ![]() , since the model simplifies significantly after discretization presented in Section 3.1. In order to specify stochastic
volatility from diffusion in models PJ and SJ, I assume the log-volatility specification with
, since the model simplifies significantly after discretization presented in Section 3.1. In order to specify stochastic
volatility from diffusion in models PJ and SJ, I assume the log-volatility specification with
![]() .3
.3
In models with stochastic volatility from jumps (PJSV, SJSV), I specify
![]() and
and
![]() as a constant volatility from diffusion. In these models
as a constant volatility from diffusion. In these models ![]() , since the pure jump part is independent from OU process governing the stochastic volatility and I do not model the leverage effect. Finally, in the class of models with joint stochastic volatility from both the diffusion and jumps (DiffPJSV, DiffSJSV), I specify
, since the pure jump part is independent from OU process governing the stochastic volatility and I do not model the leverage effect. Finally, in the class of models with joint stochastic volatility from both the diffusion and jumps (DiffPJSV, DiffSJSV), I specify
![]() ,
,
![]() ,
,
![]() ,
,
![]() and
and ![]()
![]() . In these models the parameters
. In these models the parameters ![]() and
and
![]() are identified, since stochastic volatility process
are identified, since stochastic volatility process ![]() drives both the diffusion and jumps, and hence drives the wedge between levels of log-volatilities for the diffusion and jump components. Without loss of generality I assume that
drives both the diffusion and jumps, and hence drives the wedge between levels of log-volatilities for the diffusion and jump components. Without loss of generality I assume that ![]() drives this wedge via shift in the stochastic volatility from diffusion
drives this wedge via shift in the stochastic volatility from diffusion
![]() in the model with Poisson jumps and
in the model with Poisson jumps and
![]() drives this wedge via stochastic volatility from jumps
drives this wedge via stochastic volatility from jumps
![]() in the model with Lévy
in the model with Lévy ![]() -stable jumps. This
overcomes several estimation issues in models DiffPJSV and DiffSJSV.4
-stable jumps. This
overcomes several estimation issues in models DiffPJSV and DiffSJSV.4
Summing up, I define three model specifications with Poisson jumps: model (1) PJ, model (2) PJSV and model (3) DiffPJSV. Accordingly, I have other three specifications with Lévy ![]() -stable jumps: model (4) SJ, model (5) SJSV and model (6) DiffSJSV. The summary of all restrictions, defining each specification, is presented in Table I.
-stable jumps: model (4) SJ, model (5) SJSV and model (6) DiffSJSV. The summary of all restrictions, defining each specification, is presented in Table I.
3.1 Discretization scheme
In order to estimate the parameters of the continuous-time specifications I need to discreticize the models. In the following I use first order Euler scheme5.
![]() are independent
are independent ![]()
![]() distributed and all other random variables are also independent:
distributed and all other random variables are also independent:
- Models (1) - (3) with Poisson jumps:
- Models (4) - (6) with Lévy
 -stable jumps:
-stable jumps:
In the above
![]() and
and
![]() , given
, given
![]() , is centered stable distributed with index of stability
, is centered stable distributed with index of stability
![]() , skewness coefficient
, skewness coefficient
![]() and with respective scale parameters
and with respective scale parameters
![]() in the parametrization given by the characteristic function in (5). For notational simplicity I define
in the parametrization given by the characteristic function in (5). For notational simplicity I define
![]() and
and
![]() . All other variables and parameters are defined in Section 2.3 with the respective constraints on the parameter
. All other variables and parameters are defined in Section 2.3 with the respective constraints on the parameter ![]() and the functions
and the functions
![]() and
and ![]() defining all model specifications.
defining all model specifications.
The problem I face concerns a choice of ![]() parameter, which governs the extent of the discretization bias. In this paper I fix
parameter, which governs the extent of the discretization bias. In this paper I fix ![]() and use the data at daily frequency. As noted by Eraker, Johannes and Polson (2003) the discretization bias of daily data is not significant6.
and use the data at daily frequency. As noted by Eraker, Johannes and Polson (2003) the discretization bias of daily data is not significant6.
Since my models are estimated at the daily frequency, in models (2) and (3) with Poisson jumps and stochastic volatility component from jumps, the volatility levels
![]() are close to zero. Hence, following Johannes and Polson (2003), I allow for maximum one jump per day. I consider the following approximation of the function
governing stochastic volatility from Poisson jumps:
are close to zero. Hence, following Johannes and Polson (2003), I allow for maximum one jump per day. I consider the following approximation of the function
governing stochastic volatility from Poisson jumps:
The relative error of this approximation is given by
Since models with infinite activity jumps in returns have an infinite number of small jumps in a finite time, an identification problem arises if we are able to disentangle them from the continuous-path Brownian part. The recent work by Aït-Sahalia (2003) provides the positive theoretical
answer for the simple model of asset returns with Cauchy jumps (stable jumps with ![]() and
and ![]() ) and with constant volatility from diffusion. Finally, in Aït-Sahalia and Jacod (2008) a test is constructed to verify existence of jumps in the discretely observed continuous-time process. Since discretely sampled data allows to disentangle infinite activity jumps from
diffusion, the test provides positive identification answer for models with infinite activity jumps and the diffusion.
) and with constant volatility from diffusion. Finally, in Aït-Sahalia and Jacod (2008) a test is constructed to verify existence of jumps in the discretely observed continuous-time process. Since discretely sampled data allows to disentangle infinite activity jumps from
diffusion, the test provides positive identification answer for models with infinite activity jumps and the diffusion.
3.2 Markov chain Monte Carlo methods
In this section I briefly describe Markov chain Monte Carlo (MCMC) methods, with more detailed exposition in Chib and Greenberg (1996), Johannes and Polson (2003) and Jones (1998).
Let
![]() denote the observations,
denote the observations, ![]() are the unobserved (latent) state
variables and
are the unobserved (latent) state
variables and ![]() are the parameters of the model. In the Bayesian inference we utilize the prior information on the parameters to derive the joint posterior distribution for both
parameters and state variables. By the Bayes rule, we have:
are the parameters of the model. In the Bayesian inference we utilize the prior information on the parameters to derive the joint posterior distribution for both
parameters and state variables. By the Bayes rule, we have:
where
The Gibbs sampler provides useful methods to draw samples from complicated and non-standard distributions. However, it assumes that we can sample directly from the set of all complete conditional distributions. If we face a problem of sampling from intractable distribution, we can replace the particular Gibbs sampler step by the Metropolis-Hastings (MH) step in Metropolis, Rosenbluth and Rosenbluth (1953). Further details about the MH algorithm can be found in Chib and Greenberg (1996).
In my work I am interested in obtaining random samples from the posterior distribution
![]() . This allows for computation of several statistics including the sample means and higher moments from the desired marginal posterior distributions. The sample mean from
the posterior distribution of the parameters is taken to be the population parameter estimate. Moreover, the ergodic averaging theorem guarantees almost sure convergence to the true population moments (Johannes and Polson (2003)).
. This allows for computation of several statistics including the sample means and higher moments from the desired marginal posterior distributions. The sample mean from
the posterior distribution of the parameters is taken to be the population parameter estimate. Moreover, the ergodic averaging theorem guarantees almost sure convergence to the true population moments (Johannes and Polson (2003)).
3.3 Bayesian Inference for Stable Distributions
In my application with latent Lévy ![]() -stable jumps one of the sufficient conditions for the Gibbs sampler to converge needs to be carefully addressed. The constructed Markov
chain should be constructed in a way, that guarantees strictly positive probability of visiting any subspace of the support of the target density. If Markov chain does not satisfy this condition, I call it a separability problem. Li, Wells and Yu (2008) do not correct
for the separability problem in their MCMC algorithm derived for the latent stable jumps. This leaves their results questionable and demands alternative approach to the estimation of the latent stable distributed jumps.
-stable jumps one of the sufficient conditions for the Gibbs sampler to converge needs to be carefully addressed. The constructed Markov
chain should be constructed in a way, that guarantees strictly positive probability of visiting any subspace of the support of the target density. If Markov chain does not satisfy this condition, I call it a separability problem. Li, Wells and Yu (2008) do not correct
for the separability problem in their MCMC algorithm derived for the latent stable jumps. This leaves their results questionable and demands alternative approach to the estimation of the latent stable distributed jumps.
The main problem in the application of the Bayesian MCMC methods for stable distributions is the nonexistence of its density function for index of stability
![]() . Buckle (1995) found a solution to this problem by introducing auxiliary variable, such that the joint density of the auxiliary variable and the stable distributed random
variable exists. Let
. Buckle (1995) found a solution to this problem by introducing auxiliary variable, such that the joint density of the auxiliary variable and the stable distributed random
variable exists. Let ![]() and
and ![]() be the random variables with their
joint density
be the random variables with their
joint density ![]() , conditional on
, conditional on ![]()
![]()
![]() and
and ![]() : given by:
: given by:
where
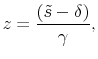
and
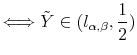 |
(16) |
and
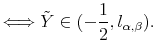 |
(17) |
In my application I have to draw ![]() for all
for all ![]() conditional on all other state
variables and parameters as in the Gibbs sampler. Since one of the conditioning state variables is the auxiliary variable
conditional on all other state
variables and parameters as in the Gibbs sampler. Since one of the conditioning state variables is the auxiliary variable
![]() , it uniquely determines the sign of the draw
, it uniquely determines the sign of the draw
![]() at the
at the ![]() step of the Gibbs sampler. This violates one of the main
assumptions of the MCMC method since the state space cannot be separated into two subspaces according to the sign of the starting value of
step of the Gibbs sampler. This violates one of the main
assumptions of the MCMC method since the state space cannot be separated into two subspaces according to the sign of the starting value of
![]() - the sign that it would never leave. To illustrate the problem, let the starting values in the Gibbs sampler specify
- the sign that it would never leave. To illustrate the problem, let the starting values in the Gibbs sampler specify
![]() ,
,
![]() for some
for some ![]() ,
and all other parameters, including
,
and all other parameters, including
![]() ,
,
![]() ,
,
![]() ,
,
![]() (consistent with chosen values
(consistent with chosen values
![]() and
and
![]() , in the support of the joint distribution and with other state variables). Suppose, without loss of generality, that we have to first update the jump size
, in the support of the joint distribution and with other state variables). Suppose, without loss of generality, that we have to first update the jump size ![]() in the algorithm. Since
in the algorithm. Since
![]() we have to draw
we have to draw
![]() . In the next step the draw of all other jump specific parameters
. In the next step the draw of all other jump specific parameters
![]() ,
,
![]() ,
,
![]() ,
,
![]() have to be consistent with
have to be consistent with
![]() and
and
![]() . At the end we have to update the auxiliary variable
. At the end we have to update the auxiliary variable
![]() in support of the joint distribution, hence
in support of the joint distribution, hence
![]() . Continuing in this manner we construct an MCMC chain that never visits negative values of jump sizes at time
. Continuing in this manner we construct an MCMC chain that never visits negative values of jump sizes at time ![]() . The algorithm has to draw
. The algorithm has to draw
![]() for all iterations
for all iterations ![]() with the same sign as the starting value
with the same sign as the starting value
![]() . However, if we do not treat the jump variables as latent and we observe the jump sizes
. However, if we do not treat the jump variables as latent and we observe the jump sizes ![]() for all
for all ![]() as in the Buckle (1995), there is no update step of the jump sizes and there are no MCMC separability issues.
as in the Buckle (1995), there is no update step of the jump sizes and there are no MCMC separability issues.
In this paper I offer a solution to this problem by construction of the mixture distribution of two, truncated at zero, stable distributions. Lets define the following probability:
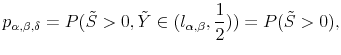 |
(18) |
which for
where
where the density
This specification complicates the MCMC algorithm by introducing mixing variable
3.4 Estimation Algorithm
In this section I briefly describe the set of complete conditional distributions to be used in the MCMC algorithm. My algorithm allows for the most general stochastic volatility specifications, both from the diffusion and infinite activity jumps, the new feature in the asset pricing literature under statistical measure. Since models with Poisson jumps in returns have already been studied in the literature, I postpone their model specific derivations to the appendix.
In the following I concentrate attention on the jump specific parameters and state variables in the model with Lévy ![]() stable jumps, joint stochastic volatility and leverage
effect - DiffSJSV specification. Other model specifications can be approached in a similar way with specific constraints on the parameters
stable jumps, joint stochastic volatility and leverage
effect - DiffSJSV specification. Other model specifications can be approached in a similar way with specific constraints on the parameters ![]() and the functions governing stochastic
volatility
and the functions governing stochastic
volatility ![]() and
and
![]() described in Section 2.3 and Table I.7
described in Section 2.3 and Table I.7
In the sequel I assume the number of daily observations ![]() and discretization parameter
and discretization parameter ![]() . I present the detailed discussion of updating pure jump sizes
. I present the detailed discussion of updating pure jump sizes
![]() ,
,
![]() , their respective auxiliary variables
, their respective auxiliary variables
![]()
![]() , the mixing variables
, the mixing variables
![]() and the jump specific parameters
and the jump specific parameters ![]() ,
,
![]() .
.
Let
![]() for sets
for sets ![]() and
and ![]() ,
,
![]() with truncation at zero defined above for
with truncation at zero defined above for ![]() with Lévy
with Lévy ![]() -stable distribution, and
-stable distribution, and
![]() .
.
Note that in model DiffSJSV, given ![]()
![]() ,
,
![]() ,
, ![]() we have
we have ![]()
![]()
![]() . Hence,
. Hence,
![]() and
and
![]() are, given
are, given ![]() ,
, ![]() ,
,
![]() ,
, ![]() , the respective jointly independent, truncated (at zero)
parts of
, the respective jointly independent, truncated (at zero)
parts of ![]() . Moreover, the realization of
. Moreover, the realization of ![]() , having its impact only on
the scale parameter, does not affect the distribution governing the mixing variables
, having its impact only on
the scale parameter, does not affect the distribution governing the mixing variables
![]() which are still Bernoulli with parameter
which are still Bernoulli with parameter
![]() in eq. (19).
in eq. (19).
Let
![]() ,
,
![]() and
and
be respectively the vector of parameters, the observed log-asset prices and the vector of state variables.
3.4.1 Updating auxiliary variables
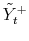 ,
,
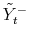
Define the following change of variables
![]() . As proved in Buckle (1995), function
. As proved in Buckle (1995), function
![]() in eq. (15) is increasing for given parameters
in eq. (15) is increasing for given parameters
![]() and
and
![]() . Moreover, for
. Moreover, for
![]() ,
,
![]() as
as
![]() and
and
![]() as
as
![]() .
.
From (14) the conditional posterior for
![]() ,
, ![]() , is given by:
, is given by:
The support of the above distribution is given by
and hence
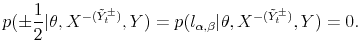 |
(26) |
Moreover, since
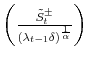 and value at maximum
and value at maximum
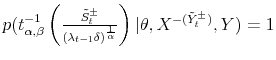 . This makes the rejection sampling
algorithm a suitable method to draw from the distribution in (24). For details on the rejection sampling please see Devroye (1986). In this paper, however, I use adaptive rejection sampling algorithm (ARS) of Gilks and Wild (1992), which utilizes rejected draws8. This makes the sampling much more efficient especially in the case where the distribution is highly spiked around the mode. Since
. This makes the rejection sampling
algorithm a suitable method to draw from the distribution in (24). For details on the rejection sampling please see Devroye (1986). In this paper, however, I use adaptive rejection sampling algorithm (ARS) of Gilks and Wild (1992), which utilizes rejected draws8. This makes the sampling much more efficient especially in the case where the distribution is highly spiked around the mode. Since
Note that in the above
![]() and some of the properties in eq. (25) do not hold for
and some of the properties in eq. (25) do not hold for
![]() . Since we are interested in the negative skewness, we have the following proposition for the maximum negative skewness
. Since we are interested in the negative skewness, we have the following proposition for the maximum negative skewness ![]() :
:
This result shows, that the update procedure described above cannot be directly applied for ![]() . Since Li, Wells and Yu (2008) applied a similar update procedure for the model with
stochastic volatility from diffusion and the maximum negative skewness
. Since Li, Wells and Yu (2008) applied a similar update procedure for the model with
stochastic volatility from diffusion and the maximum negative skewness ![]() , this leaves their update method incorrect.10 The first source of their misspecification is the separability problem of the MCMC and the second is their application of the Buckle (1995) updating method for
, this leaves their update method incorrect.10 The first source of their misspecification is the separability problem of the MCMC and the second is their application of the Buckle (1995) updating method for ![]() . My algorithm corrects for both of these problems in the models with Lévy
. My algorithm corrects for both of these problems in the models with Lévy ![]() -stable jumps by construction of
the MCMC free of the separability issue and by estimation of
-stable jumps by construction of
the MCMC free of the separability issue and by estimation of
![]() .
.
3.4.2 Updating jump size variables
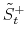 ,
,
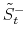
By application of the Bayes rule the conditional posterior distribution for
![]() and
and
![]() is given by:
is given by:
| (28) |
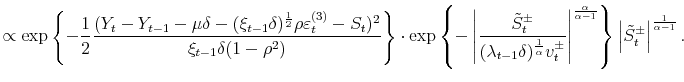
Using the change of variable formula, the density of
3.4.3 Updating index of stability parameter 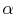
The next problem is the choice of bounds for the parameter
![]() . This is a delicate matter since as
. This is a delicate matter since as
![]() the power coefficient
the power coefficient
![]() in eq. (14) approaches infinity. Moreover, as
in eq. (14) approaches infinity. Moreover, as
![]() we approach normal distribution and lose identification. Taking the above into account, I assume the uniform prior distribution on
we approach normal distribution and lose identification. Taking the above into account, I assume the uniform prior distribution on
![]() to avoid overflow computation problems. This not a restrictive assumption, since bounds are barely (or not at all) hit by the sampler.
to avoid overflow computation problems. This not a restrictive assumption, since bounds are barely (or not at all) hit by the sampler.
As noted by Buckle (1995) updating the index of stability ![]() is the most difficult part in the Bayesian inference of stable jumps. I modify his approach to accommodate for the mixture
of truncated stable distributions. He solved the problem of multimodality of complete conditional distribution by the above described change of variables from the auxiliary variables
is the most difficult part in the Bayesian inference of stable jumps. I modify his approach to accommodate for the mixture
of truncated stable distributions. He solved the problem of multimodality of complete conditional distribution by the above described change of variables from the auxiliary variables
![]() to
to
![]() using the transformation
using the transformation
![]()
![]() . If we condition not on
. If we condition not on
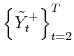 and
and
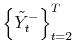 but instead on
but instead on
![]() and
and
![]() , the complete conditional distribution of
, the complete conditional distribution of ![]() is given by:
is given by:
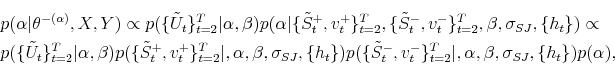
where
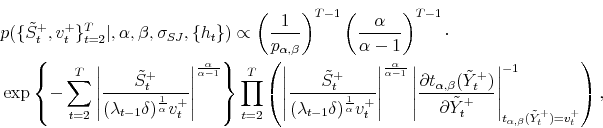
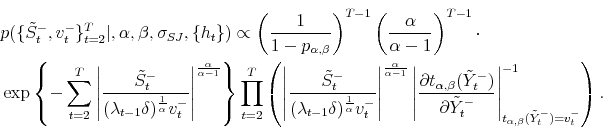
Note that the state vector
3.4.4 Updating skewness parameter 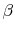
Since I want to model the negative skewness of asset returns, I consider the restriction ![]() . In order to control the degree of skewness, I relax the maximum negative skewness
(
. In order to control the degree of skewness, I relax the maximum negative skewness
(![]() ) assumption of Carr and Wu (2003). Their assumption is needed to price derivative securities but is not required under statistical measure.
) assumption of Carr and Wu (2003). Their assumption is needed to price derivative securities but is not required under statistical measure.
In my setting I have to restrict
![]() , since according to proposition (1), one cannot guarantee unimodality of the distribution in eq. (24) for
, since according to proposition (1), one cannot guarantee unimodality of the distribution in eq. (24) for
![]() . The choice of the uniform, independent prior distribution
. The choice of the uniform, independent prior distribution
![]() addresses these issues and avoids overflow computation problems.
addresses these issues and avoids overflow computation problems.
Updating skewness parameter ![]() is similar to updating
is similar to updating ![]() :
:
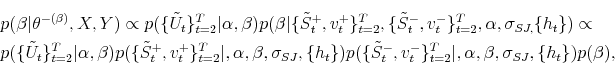
where all components are derived in the updating procedure for
3.4.5 Updating mixing variables
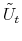
Since
![]() is a Bernoulli distribution with probability of success
is a Bernoulli distribution with probability of success
![]() , the complete conditional posterior is also Bernoulli and is given by:
, the complete conditional posterior is also Bernoulli and is given by:
and:
We can directly calculate the above probabilities and normalize their sum to unity. The draw from this distribution is then straightforward.
3.5 Auxiliary Particle Filter
In order to perform density forecast analysis, I fix vector of parameters ![]() for each model at the respective posterior mean and calculate the following probabilities:
for each model at the respective posterior mean and calculate the following probabilities:
where
Note that I condition on the estimate of parameter value ![]() and do not integrate it out. Hence, I do not take into account the parameter estimation uncertainty. Since I have a
relatively long sample size, the parameters are estimated with high precision11. The effect of parameter estimation uncertainty is beyond the scope of this
paper. In the notation below, I omit the explicit dependence on the model
and do not integrate it out. Hence, I do not take into account the parameter estimation uncertainty. Since I have a
relatively long sample size, the parameters are estimated with high precision11. The effect of parameter estimation uncertainty is beyond the scope of this
paper. In the notation below, I omit the explicit dependence on the model ![]() specification, since it suffices to induce it from
specification, since it suffices to induce it from ![]() vector of parameter estimates.
vector of parameter estimates.
In this work I consider one-day ahead ![]() time horizon for density forecast analysis, which makes it possible to assess a model ability to forecast one-day ahead daily log-return
distribution. Note that (32) can be calculated not only for the in-sample period but also for the out-of sample period, whenever we have data available. We can study quantile forecast (VaR) performance of the model by comparison of given significance levels and
unconditional covering frequencies of each model implied by the probabilities in (32). Moreover, if the model is correctly specified, binary variables indicating if the data points are contained in the VaR interval, should be independently distributed. Hence, there
should be no "clustering" in time of their respective realizations.
time horizon for density forecast analysis, which makes it possible to assess a model ability to forecast one-day ahead daily log-return
distribution. Note that (32) can be calculated not only for the in-sample period but also for the out-of sample period, whenever we have data available. We can study quantile forecast (VaR) performance of the model by comparison of given significance levels and
unconditional covering frequencies of each model implied by the probabilities in (32). Moreover, if the model is correctly specified, binary variables indicating if the data points are contained in the VaR interval, should be independently distributed. Hence, there
should be no "clustering" in time of their respective realizations.
We can estimate values in eq. (32) by:
where
The draws from this distribution can be performed by utilizing the following condition:
By discarding draws for variables that do not directly enter in equation (33), we have draws from the desired
The work of Christoffersen (1998) on the evaluation of the interval forecasts and its further extension by Diebold, Gunther and Tay (1998) to the context of the density forecast allow us to draw conclusions based on the following criterion. A given model is correctly specified if
![]() (for
(for
![]() is
is ![]()
![]() distributed. By transformation using the inverse cdf of the standard normal distribution, I define:
distributed. By transformation using the inverse cdf of the standard normal distribution, I define:
The distribution of
In order to sample from distributions in eq. (34) we have to sample from filtering density
![]() and then, conditional on this draw, sample from all predicting densities
and then, conditional on this draw, sample from all predicting densities
![]() and
and
![]() . Sampling from these densities is rather straightforward. The most difficult problem involves approximation of the filtering density
. Sampling from these densities is rather straightforward. The most difficult problem involves approximation of the filtering density
![]() by the auxiliary particle filter, as developed in Pitt and Shephard (1999). Chib, Nardari and Shephard (2002) extend basic auxiliary particle filter of Pitt and
Shephard (1999) for Poisson type jumps in returns but do not include leverage effect. Johannes, Polson and Stroud (2008) offer further refinements to the auxiliary particle filter algorithm for models with jumps and stochastic volatility. However, their algorithm cannot be applied to the
specifications with Lévy
by the auxiliary particle filter, as developed in Pitt and Shephard (1999). Chib, Nardari and Shephard (2002) extend basic auxiliary particle filter of Pitt and
Shephard (1999) for Poisson type jumps in returns but do not include leverage effect. Johannes, Polson and Stroud (2008) offer further refinements to the auxiliary particle filter algorithm for models with jumps and stochastic volatility. However, their algorithm cannot be applied to the
specifications with Lévy ![]() -stable jumps.12 Durham (2006) extends the basic particle filter for models with leverage effect but does not include jumps in returns, moreover, he works with particle filter and does not apply auxiliary particle filter involving index parameters draws13. In this paper I present auxiliary particle filter for jump-diffusion models with the leverage effect. Moreover, I allow for different sources of stochastic volatility and most
importantly for Lévy
-stable jumps.12 Durham (2006) extends the basic particle filter for models with leverage effect but does not include jumps in returns, moreover, he works with particle filter and does not apply auxiliary particle filter involving index parameters draws13. In this paper I present auxiliary particle filter for jump-diffusion models with the leverage effect. Moreover, I allow for different sources of stochastic volatility and most
importantly for Lévy ![]() -stable jumps in returns.
-stable jumps in returns.
Lets first notice, that:
and
Substituting (38) into (37) we have:
Auxiliary particle filter is a recursive algorithm to approximate filtering densities
![]() for
for ![]() by a finite number
by a finite number ![]() of "particles" for each
of "particles" for each ![]() . These particles define discrete probability distribution filter
. These particles define discrete probability distribution filter
![]() . I denote particles for filter at time
. I denote particles for filter at time ![]() as
as
![]() , where
, where
![]() . Given
. Given ![]() particles defining discrete probability distribution filter
at time
particles defining discrete probability distribution filter
at time ![]() , we obtain approximation
, we obtain approximation
![]() for
for ![]() defined by its respective
defined by its respective
![]() particles using relation in (39):
particles using relation in (39):
- draw
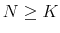 indexes
indexes
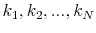 from the discrete probability distribution
from the discrete probability distribution
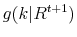 with support of
with support of
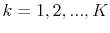 . The choice of
. The choice of
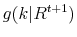 should reflect an information content of the future return
should reflect an information content of the future return 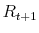 on the choice of index mixture
on the choice of index mixture 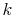 and hence the particle
and hence the particle
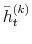 . Note that
. Note that 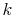 represents an index on mixture in (39) as in Pitt and Shephard (1999). I specify the weights to be proportional to:
represents an index on mixture in (39) as in Pitt and Shephard (1999). I specify the weights to be proportional to:
where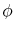 denotes normal pdf calculated at
denotes normal pdf calculated at
 with mean
with mean 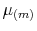 and variance
and variance
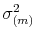 given by:
given by:
![\begin{displaymath} \mu_{(m)}=\left\{ \begin{array}[c]{c}% \mu+\lambda_{t}\mu_{j}\text{ \ \ for models with Poisson jumps}\ \mu\text{ \ \ \ \ for models with L\'{e}vy }\alpha\text{-stable jumps}% \end{array}\right. \end{displaymath}](img390.gif) and where we substitute all constraints as in Table I. My choice of
and where we substitute all constraints as in Table I. My choice of![\begin{displaymath} \sigma_{(m)}^{2}=\left\{ \begin{array}[c]{c}% (1-\rho^{2})\xi_{t}+\lambda_{t}(\sigma_{j}^{2}+\mu_{j}^{2})-(\lambda_{t}% \mu_{j})^{2}\text{ for models with Poisson jumps}\ (1-\rho^{2})\xi_{t}+\lambda_{t}^{\frac{2}{\alpha}}\text{ for models with L\'{e}vy }\alpha\text{-stable jumps}% \end{array}\right. \end{displaymath}](img391.gif)
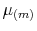 and
and
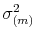 for models with Poisson jumps coincides respectively with
for models with Poisson jumps coincides respectively with
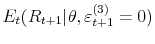 and
and
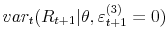 . In case of models with Lévy
. In case of models with Lévy 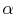 -stable jumps I pursue the same strategy as for Poisson models, but in the first step I approximate the distribution
-stable jumps I pursue the same strategy as for Poisson models, but in the first step I approximate the distribution
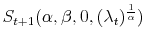 , given
, given
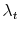 , by
, by
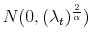 . Hence, I simply replace
. Hence, I simply replace  -stable
distribution by normal distribution with the same scale parameter. Finally, I denote the index draws as
-stable
distribution by normal distribution with the same scale parameter. Finally, I denote the index draws as
 and record the respective values of
and record the respective values of
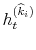 for
for  , where
, where
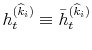 . Note that the above specification of
. Note that the above specification of
 allows to draw the indexes
allows to draw the indexes 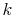 on particles
on particles
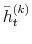 and this draw is consistent with the scale and mean implied by the next-period return
and this draw is consistent with the scale and mean implied by the next-period return 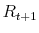 . This makes my algorithm efficient and easy to implement for all considered models.
. This makes my algorithm efficient and easy to implement for all considered models. - Draw proposal particles
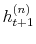 ,
,
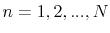 , given mixture index and particle from the preceding filter using the respective prediction density:
, given mixture index and particle from the preceding filter using the respective prediction density:
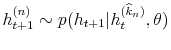
- Draw jump increments
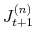 ,
,
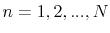 , from
, from
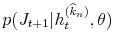 .
. - Reweight the draws
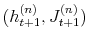 ,
,
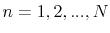 , by drawing
, by drawing 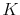 times (with replacement) from the discrete probability
distribution with weights proportional to:
times (with replacement) from the discrete probability
distribution with weights proportional to:
for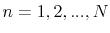 . We finally get
. We finally get 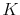 draws defining discrete filter distribution
draws defining discrete filter distribution
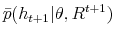 by discarding draws on
by discarding draws on 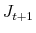 . Denote the
new particles as
. Denote the
new particles as
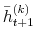 , where
, where
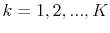 .
. - Go to point 1. and increment
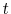 .
.
By comparing weights in (41) to the first integrand component in (39), the validity of the whole algorithm is based on the importance sampling principle. In my applications I take
![]() and
and
![]() . I do not draw from the discrete auxiliary particle filter distribution
. I do not draw from the discrete auxiliary particle filter distribution
![]() but directly utilize all derived particles from the filter. The above choice of
but directly utilize all derived particles from the filter. The above choice of ![]() and
and ![]() is sufficient to induce a low variability of statistics calculated using derived particles among different starting seeds of random number
generator.
is sufficient to induce a low variability of statistics calculated using derived particles among different starting seeds of random number
generator.
4.1 The Data
In this paper the data on the S&P 500 index extends from 01/02/1981 to 12/31/2007 and comprises of 6813 daily observations available from CRSP database. The S&P 500 index levels are reported at the closing times in each business day. All six model specifications are estimated using this data set. It allows for modelling the market crash of 1987 and the "dot.com" corrections from 1999-2001.
In Table II and Figure 1, I present respectively the descriptive statistics of daily log-returns on the S&P 500 index and graphs of S&P 500 index log-level and S&P 500 index log-returns. The data on the S&P log-returns indicate that there exists significant negative skewness of
-1.7465 and kurtosis of 42.79. In Figure 1, I also report the skewness and
kurtosis as a term structure of S&P 500 returns. The term structure of skewness and kurtosis determine volatility smiles for options across all maturities.14 Carr and Wu (2003) find that the volatility smiles do not flatten completely as maturity increases and propose the log-stable model of asset returns, where asset returns have infinite variance and higher moments, and the CLT does not work. This also motivates my
specification with Lévy ![]() -stable jumps15.
-stable jumps15.
4.2 Estimation Procedure
Since MCMC algorithms require a choice of starting values for all parameters and latent variables, I first list them for all estimated models. The parameter estimates were found not to be affected by different choice of starting values for the MCMC algorithms. I take the posterior mean for each
model to be an estimate of the respective parameters and reported in Table III for all model specifications. In Figures 2 and 3, I present respectively the smoothed estimates of jump sizes in eq. (35) and stochastic volatility ![]() .
.
For models with Lévy ![]() -stable jumps in returns, the starting values for mean/drift parameters
-stable jumps in returns, the starting values for mean/drift parameters ![]() ,
,
![]() are zero, for the scale parameters
are zero, for the scale parameters
![]() ,
,
![]() ,
, ![]() are one, for the correlation parameter
are one, for the correlation parameter ![]() is zero, for
is zero, for
![]() is one. For jump specific parameters I specify
is one. For jump specific parameters I specify
![]() and
and
![]() . The choice of starting values for the latent variables involves the choice of
. The choice of starting values for the latent variables involves the choice of
![]() (only positive jumps),
(only positive jumps),
![]() , and finally
, and finally
![]() and
and
![]() for all
for all ![]() . Since I update stable jumps auxiliary
variables
. Since I update stable jumps auxiliary
variables
![]() and
and
![]() at the beginning of the MCMC algorithm, I do not need to specify their starting values. In all models the choice of starting values for the MCMC does not affect the
estimation results. In models SJ and SJSV with stochastic volatility from either diffusion or jumps but not both, I draw
at the beginning of the MCMC algorithm, I do not need to specify their starting values. In all models the choice of starting values for the MCMC does not affect the
estimation results. In models SJ and SJSV with stochastic volatility from either diffusion or jumps but not both, I draw ![]() realizations from the MCMC chains, where the first
realizations from the MCMC chains, where the first
![]() draws are treated as the burn-in period and the last
draws are treated as the burn-in period and the last ![]() as draws
from the stationary distribution. In the model with joint stochastic volatility DiffSJSV, I choose the same starting values but draw
as draws
from the stationary distribution. In the model with joint stochastic volatility DiffSJSV, I choose the same starting values but draw ![]() realizations and I double the size of the burn-in
period to the first
realizations and I double the size of the burn-in
period to the first ![]() draws compared to other models with Lévy
draws compared to other models with Lévy ![]() -stable jumps. I run simulation in model PJ for
-stable jumps. I run simulation in model PJ for ![]() draws, in model PJSV for
draws, in model PJSV for ![]() draws and in model DiffPJSV for
draws and in model DiffPJSV for ![]() draws where I treat the first
draws where I treat the first ![]() ,
, ![]() and
and ![]() draws as the
burn-in period, respectively.16 For models with Poisson jumps the drift and log-volatility related parameters and latent variables are given the same
starting values as for models with infinite activity jumps.
draws as the
burn-in period, respectively.16 For models with Poisson jumps the drift and log-volatility related parameters and latent variables are given the same
starting values as for models with infinite activity jumps.
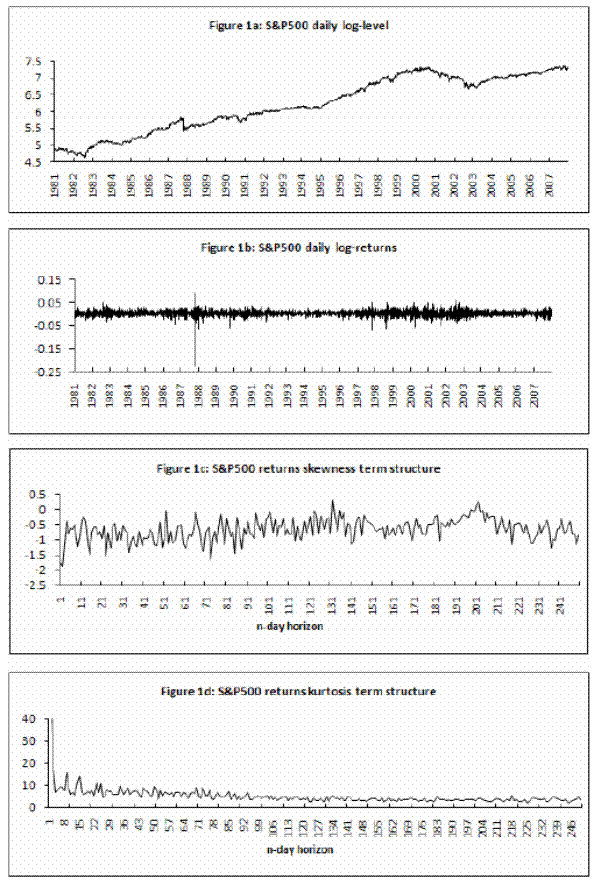
Figure 1 Data
Poisson jump specific parameters are given starting values
![]() ,
,
![]() and
and
![]() and for latent variables I assume no jumps
and for latent variables I assume no jumps
![]() for all
for all ![]() . Moreover, in the model with joint
stochastic volatility I choose
. Moreover, in the model with joint
stochastic volatility I choose
![]() .
.
In the following I implement the model selection criteria developed in Jones (2003). Recall that in all model specifications
![]() and
and
![]() are assumed to be jointly independent and
are assumed to be jointly independent and ![]()
![]() . In the following lets call
. In the following lets call
![]() the residuals from returns equation and
the residuals from returns equation and
![]() the residuals from the log-volatility equation. We may view those residuals as latent variables.
Hence, we can construct posterior distributions for functions of these latent variables by evaluating these functions at each step of the MCMC algorithm. Since model residuals are
the residuals from the log-volatility equation. We may view those residuals as latent variables.
Hence, we can construct posterior distributions for functions of these latent variables by evaluating these functions at each step of the MCMC algorithm. Since model residuals are ![]()
![]() I calculate mean, standard deviation, skewness, kurtosis and first-order autocorrelation. Then I calculate the median and
I calculate mean, standard deviation, skewness, kurtosis and first-order autocorrelation. Then I calculate the median and ![]() confidence intervals for those statistics reported in Table IV. A correct model specification implies that mean is zero, standard deviation one, skewness zero, kurtosis three and autocorrelation zero.
confidence intervals for those statistics reported in Table IV. A correct model specification implies that mean is zero, standard deviation one, skewness zero, kurtosis three and autocorrelation zero.
4.3 Estimation Results for S&P 500 Data
Since I have the same log-volatility specification as in Jacquier, Polson and Rossi (2004), their results shed light on the importance of the leverage effect. In their work, the leverage effect is found to correct for a possible misspecification resulting in the biased estimates of the
volatility states and the parameters of the log-volatility process. Hence, in my work I consider specifications with leverage effect and focus attention on the source of stochastic volatility and the jump structure. In models with either joint stochastic volatility or stochastic volatility from
diffusion I find the leverage effect to be statistically significant with the estimates of -0.5891, -0.5880, -0.7496, -0.6428 respectively for models PJ,
DiffPJSV, SJ and DiffSJSV. Since the only models that do not allow for the leverage effect are the models with stochastic volatility from jumps, I restrict ![]() for these
specifications.17 In my analysis the estimation of all six model specifications allows us to draw conclusions about the marginal importance of the
different jump structures and the source of stochastic volatility.
for these
specifications.17 In my analysis the estimation of all six model specifications allows us to draw conclusions about the marginal importance of the
different jump structures and the source of stochastic volatility.
In all models the parameters are precisely estimated with an exception of the parameters governing skewness of returns ![]() and
and ![]() , for models with Poisson and Lévy
, for models with Poisson and Lévy ![]() -stable jumps respectively. In model PJ the parameter
-stable jumps respectively. In model PJ the parameter
![]() is estimated at the level 0.0022, which gives approximately one jump
per two calendar years. Similarily, in models PJSV and DiffPJSV the activity rate of the Poisson jumps, governed by
is estimated at the level 0.0022, which gives approximately one jump
per two calendar years. Similarily, in models PJSV and DiffPJSV the activity rate of the Poisson jumps, governed by
![]() process, also indicates a similar average jump intensity. The small number of realized Poisson jumps limits the ability to precisely estimate the mean of the jump
sizes
process, also indicates a similar average jump intensity. The small number of realized Poisson jumps limits the ability to precisely estimate the mean of the jump
sizes ![]() and results in the relative estimation errors of
and results in the relative estimation errors of ![]() ,
,
![]() ,
, ![]() for models PJ, PJSV and DiffPJSV, respectively. In models with
Lévy
for models PJ, PJSV and DiffPJSV, respectively. In models with
Lévy ![]() -stable jumps, the lack of precision in the estimation of
-stable jumps, the lack of precision in the estimation of ![]() is also a consequence of limited information in the sample about the tails of the returns distribution and implies that the relative estimation errors for parameter
is also a consequence of limited information in the sample about the tails of the returns distribution and implies that the relative estimation errors for parameter ![]() are
are ![]() ,
, ![]() and
and ![]() for specifications SJ, SJSV and DiffSJSV, respectively. In model DiffSJSV the parameter
for specifications SJ, SJSV and DiffSJSV, respectively. In model DiffSJSV the parameter
![]() controls for the relative importance of diffusion and Lévy
controls for the relative importance of diffusion and Lévy ![]() -stable jumps to the total volatility of returns. The relative error of estimation of
-stable jumps to the total volatility of returns. The relative error of estimation of ![]() suggests that there is enough information in the sample to disentangle
diffusion from infinite activity Lévy
suggests that there is enough information in the sample to disentangle
diffusion from infinite activity Lévy ![]() -stable jumps. In Figures 2 and 3, I present smoothed jump sizes and log-volatility estimates respectively, where the former are defined in
(35). The models with stochastic volatility arising only from diffusion violate
-stable jumps. In Figures 2 and 3, I present smoothed jump sizes and log-volatility estimates respectively, where the former are defined in
(35). The models with stochastic volatility arising only from diffusion violate ![]() property of jumps, since in models PJ and SJ I visually find an
evidence of jump clustering. In specifications with joint stochastic volatility DiffPJSV (DiffSJSV) a jump clustering is a built-in characteristic of the model but clustering is allowed to arise only from the stochastic volatility.
property of jumps, since in models PJ and SJ I visually find an
evidence of jump clustering. In specifications with joint stochastic volatility DiffPJSV (DiffSJSV) a jump clustering is a built-in characteristic of the model but clustering is allowed to arise only from the stochastic volatility.
I test for independence of the jump increments by using the standard Ljung-Box test.18
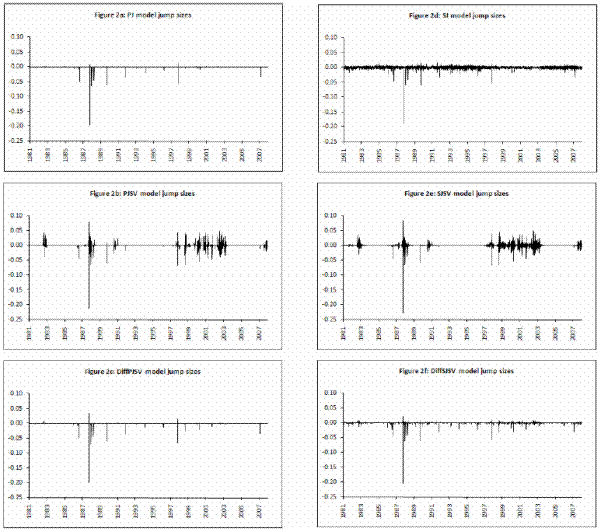
Figure 2 Data
Since Poisson jumps are rare events I concentrate attention only on the Lévy ![]() -stable jumps specifications SJ and DiffSJSV. In Figure 4, I illustrate smoothed jump increments for
models SJ and DiffSJSV, where the latter are corrected for the varying intensity, or in other words, are scaled by the stochastic volatility. I present smoothed estimates of
-stable jumps specifications SJ and DiffSJSV. In Figure 4, I illustrate smoothed jump increments for
models SJ and DiffSJSV, where the latter are corrected for the varying intensity, or in other words, are scaled by the stochastic volatility. I present smoothed estimates of
![]() for model DiffSJSV and call it in the sequel as descaled jump increments. The descaled
jump increments are
for model DiffSJSV and call it in the sequel as descaled jump increments. The descaled
jump increments are ![]() by construction. By using the scalability property for stable distribution and applying it
by construction. By using the scalability property for stable distribution and applying it
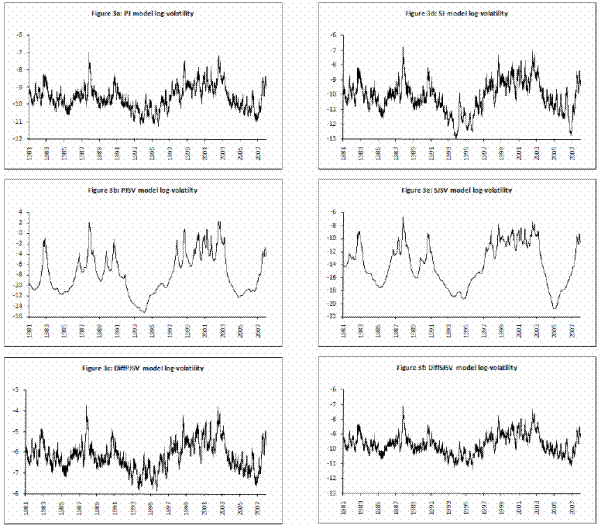
Figure 3 Data
to the discretized version of the model in eq. (11) we have
where the descaled jumps are the jump sizes divided by the instantaneous volatility. In model SJ I do not have to follow this procedure, since
![]() is constant and hence for this model I present the jump size estimates as in Figure 2 and eq. (35). I find that model DiffSJSV produces in
general higher
is constant and hence for this model I present the jump size estimates as in Figure 2 and eq. (35). I find that model DiffSJSV produces in
general higher ![]() -values at lags 1-500 than model SJ.19 Hence, there is less degree of dependence between
-values at lags 1-500 than model SJ.19 Hence, there is less degree of dependence between
Figure 4 Data
the neighboring jumps with distance of up to 2 years in model DiffSJSV. At horizons ranging from 500-2500 both models perform poorly, although model SJ performs somewhat better. However,
none of these models reach the ![]() -value of 0.05 at lags 500-2000. Since in the
following sections I am mostly interested in the short-horizon density forecasts, model DiffSJSV having superior fit at shorter lags is better suited for this task.
-value of 0.05 at lags 500-2000. Since in the
following sections I am mostly interested in the short-horizon density forecasts, model DiffSJSV having superior fit at shorter lags is better suited for this task.
4.3.1 The Source of Stochastic Volatility
Focusing attention on models with stochastic volatility from jumps PJSV and SJSV, we can evidently eliminate them as they are outperformed by other models with the same jump structure. In both models the parameters governing skewness of returns ![]() and
and ![]() are estimated with the lowest precision among all specifications. Moreover, the speed of mean reversion
parameters
are estimated with the lowest precision among all specifications. Moreover, the speed of mean reversion
parameters
![]() are much closer to the non-stationarity level and have the highest relative estimation errors among all stochastic volatility specifications of
are much closer to the non-stationarity level and have the highest relative estimation errors among all stochastic volatility specifications of ![]() and
and ![]() for models PJSV and SJSV, respectively. There are also significantly higher relative errors of
estimation of parameters
for models PJSV and SJSV, respectively. There are also significantly higher relative errors of
estimation of parameters
![]() of respectively
of respectively ![]() and
and ![]() .
.
In terms of goodness of fit analysis presented in Table IV, models PJSV and SJSV perform much worse than their counterparts with the same jump specification. Although they perform relatively well with respect to the skewness of returns, they cannot represent leptokurtic property of returns. This
is documented by too small standard deviation of residuals of 0.9084 for model PJSV and 0.8965 for models SJSV, as well as by too high kurtosis of residuals, respectively 3.7349 and 3.7059. Note that even much richer specification of infinite activity Lévy ![]() -stable jumps do not alleviate these problems since model SJSV do not
fit the data better than the simple Poisson jump model PJSV.
-stable jumps do not alleviate these problems since model SJSV do not
fit the data better than the simple Poisson jump model PJSV.
I find almost perfect fit with respect to the log-volatility equation for all model specifications irrespective of the source of stochastic volatility and jump structure.
In models with stochastic volatility from diffusion (PJ) and joint stochastic volatility (DiffPJSV) with Poisson jumps I do not find significant differences with respect to the precision of parameter estimates and goodness of fit, that can in a decisive way point out the best stochastic
volatility specification. However, in models SJ and DiffSJSV with Lévy ![]() -stable jumps the differences in goodness of fit can be found in the degree of kurtosis
-stable jumps the differences in goodness of fit can be found in the degree of kurtosis ![]() and 3.1397, respectively, in Table IV. However, the latter still dominates all other
models including all specifications with Poisson jumps. On the other hand, I find in the previous section that model SJ is dominated by model DiffSJSV with joint stochastic volatility when satisfying the independence assumption of descaled jump increments at shorter autocorrelation horizons of up
to 2 years.
and 3.1397, respectively, in Table IV. However, the latter still dominates all other
models including all specifications with Poisson jumps. On the other hand, I find in the previous section that model SJ is dominated by model DiffSJSV with joint stochastic volatility when satisfying the independence assumption of descaled jump increments at shorter autocorrelation horizons of up
to 2 years.
Summing up, I reject models with stochastic volatility from jumps and find that diffusion is an important feature, since it has to be a source of stochastic volatility. I postpone the final choice between models with stochastic volatility from diffusion and joint stochastic volatility to density forecast and VaR analysis in Section 4.4.
4.3.2 Modelling Jumps in Returns
In this section I provide an evidence in favor of models with infinite activity Lévy ![]() -stable jumps. I restrict my analysis to models with either joint stochastic volatility or
stochastic volatility from diffusion, since they dominate the models with stochastic volatility from jumps with respect to the estimation precision and goodness of fit. Since all considered models are estimated with high degree of precision with the exception of parameters governing skewness of
returns, I concentrate attention on the goodness of fit analysis presented in Table IV.
-stable jumps. I restrict my analysis to models with either joint stochastic volatility or
stochastic volatility from diffusion, since they dominate the models with stochastic volatility from jumps with respect to the estimation precision and goodness of fit. Since all considered models are estimated with high degree of precision with the exception of parameters governing skewness of
returns, I concentrate attention on the goodness of fit analysis presented in Table IV.
I find that Poisson jumps are suited to fit only big jumps, which agrees with findings in Li, Wells and Yu (2008). My estimates of jump intensity
![]() for models with stochastic volatility from diffusion and
for models with stochastic volatility from diffusion and
![]() for joint stochastic volatility imply only about one jump per two years. Hence "small", frequent, and more subtle jumps are simply not represented by the models with
Poisson jumps in returns, even if we include joint stochastic volatility. The above can be seen by a comparison of smoothed jump size estimates for Poisson models with the respective estimates for Lévy
for joint stochastic volatility imply only about one jump per two years. Hence "small", frequent, and more subtle jumps are simply not represented by the models with
Poisson jumps in returns, even if we include joint stochastic volatility. The above can be seen by a comparison of smoothed jump size estimates for Poisson models with the respective estimates for Lévy ![]() -stable models in Figure 2. As expected the skewness, affected by large jumps in the very left tail of the return distribution, is much better represented than kurtosis of returns in models with Poisson jumps. This is documented by the skewness of residuals of
-stable models in Figure 2. As expected the skewness, affected by large jumps in the very left tail of the return distribution, is much better represented than kurtosis of returns in models with Poisson jumps. This is documented by the skewness of residuals of ![]() and -0.0470, and kurtosis of residuals of 3.2578 and 3.2481 respectively for models PJ and DiffPJSV. Models SJ and DiffSJSV, with Lévy
and -0.0470, and kurtosis of residuals of 3.2578 and 3.2481 respectively for models PJ and DiffPJSV. Models SJ and DiffSJSV, with Lévy ![]() -stable jumps in returns and infinite number of "small" jumps in the finite time interval, have a very good fit both with respect to skewness and kurtosis of returns and dominate other model
specifications.
-stable jumps in returns and infinite number of "small" jumps in the finite time interval, have a very good fit both with respect to skewness and kurtosis of returns and dominate other model
specifications.
4.4 Density Forecast and VaR analysis
In this section I apply auxiliary particle filter described in Section 3.5 to evaluate one-day horizon forecast and quantile forecast (VaR) performance of all models. In Table V, I present descriptive statistics of
![]() distribution
distribution ![]() , with
, with
![]() defined in eq. (36) calculated for different model specifications with their respective parameters fixed at the MCMC estimates as in
Table III for S&P500 data on the period 01/02/1981-12/31/2007. S&P500 daily log-returns, used for
defined in eq. (36) calculated for different model specifications with their respective parameters fixed at the MCMC estimates as in
Table III for S&P500 data on the period 01/02/1981-12/31/2007. S&P500 daily log-returns, used for
![]() calculation, are derived from S&P500 index level for all available observations. A correct specification implies that
calculation, are derived from S&P500 index level for all available observations. A correct specification implies that
![]() is
is ![]()
![]() distributed, hence the mean is zero, standard deviation one, skewness zero, kurtosis three. Note that excess kurtosis and negative skewness of generalized residuals
distributed, hence the mean is zero, standard deviation one, skewness zero, kurtosis three. Note that excess kurtosis and negative skewness of generalized residuals
![]() implies respectively too small kurtosis and not enough negative skewness in the model implied forecasting distribution only if the scale of the generalized residuals
is correctly represented and close to one.20Moreover, there should be no autocorrelation in the levels and the squares of generalized residuals.
implies respectively too small kurtosis and not enough negative skewness in the model implied forecasting distribution only if the scale of the generalized residuals
is correctly represented and close to one.20Moreover, there should be no autocorrelation in the levels and the squares of generalized residuals.
In Figure 5, I present quantile-quantile plots (qq-plots) of generalized residuals, that show all deviations from assumption of normality. In Table V, I present the calculated statistics (and the ![]() -values) of Jarque-Bera test for normality. In Figures 6 and 7, I include autocorrelation functions for levels and squares of generalized residuals respectively. This allows us to draw conclusions on whether the independence assumption is satisfied. Serial correlation in the squares
of generalized residuals is an indication of the lack of ability of the model to represent the volatility of returns. In Figures 8 and 9, I present
-values) of Jarque-Bera test for normality. In Figures 6 and 7, I include autocorrelation functions for levels and squares of generalized residuals respectively. This allows us to draw conclusions on whether the independence assumption is satisfied. Serial correlation in the squares
of generalized residuals is an indication of the lack of ability of the model to represent the volatility of returns. In Figures 8 and 9, I present ![]() -values of the Ljung-Box test for
dependence calculated at different maximum number of lags in the autocorrelation expansion for levels and squares of generalized residuals. In Table VI, I also present one-day horizon VaR performance. I calculate values of
-values of the Ljung-Box test for
dependence calculated at different maximum number of lags in the autocorrelation expansion for levels and squares of generalized residuals. In Table VI, I also present one-day horizon VaR performance. I calculate values of
![]() defined in equation (33), given estimated model parameters, and then compute empirical coverage frequencies for significance levels of
defined in equation (33), given estimated model parameters, and then compute empirical coverage frequencies for significance levels of ![]() ,
, ![]() and
and ![]() . Note that the density forecast analysis deals with the whole shape of the predictive density, while VaR analysis refers only to its very left tail.
. Note that the density forecast analysis deals with the whole shape of the predictive density, while VaR analysis refers only to its very left tail.
The density forecast analysis in general, and VaR analysis in specific, stress the importance of correct specification of stochastic volatility. If model misspecifies stochastic volatility, it also performs poorly in density forecast and VaR analysis. To illustrate this, note that for goodness of fit analysis we utilize all available information in the sample, conditioning on all observed asset returns, while in the forecast and VaR analysis we only condition on the filtered volatility states and have available only current and past values of returns determining latent volatility. Hence, the behavior of stochastic volatility, as a state variable, and an ability to filter its values, is of fundamental importance in the density forecast. In this light a correct specification of the source of stochastic volatility determines a forecasting ability of the model.
4.4.1 Models with Poisson Jumps
I reject model PJSV with stochastic volatility from jumps, since it is outperformed by other specifications and has poor performance with respect to both skewness -0.2335 and kurtosis 4.9226 in the density forecast analysis in Table V. Most importantly, the scale of the forecast is incorrect at 0.8834. The above results in the rejection of normality by the Jarque-Bera test.
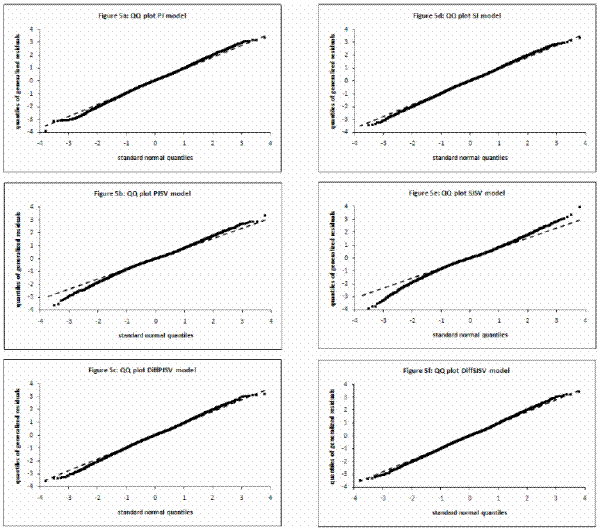
Figure 5 Data
The qq-plot in Figure 5b illustrates the problem in the tails of the forecasting distribution21. Ljung-Box test statistics for the levels of
![]() in Figure 8b do not differ from the other model specifications and accept independence in the levels at
in Figure 8b do not differ from the other model specifications and accept independence in the levels at ![]() significance level if we include small number of lags in the test of up to 2 years apart. However, in the test for squared
residuals the model completely falls behind other specifications with the
significance level if we include small number of lags in the test of up to 2 years apart. However, in the test for squared
residuals the model completely falls behind other specifications with the ![]() -values of the Ljung-Box test close to 0 in Figure 9b. This is an evidence of model
PJSV's inability to represent not only the distribution of one-day ahead forecasted returns but also the dynamics of volatility. In Figures 6b and 7b an inspection of autocorrelation functions of levels and squares of generalized residuals visualizes the problem.
-values of the Ljung-Box test close to 0 in Figure 9b. This is an evidence of model
PJSV's inability to represent not only the distribution of one-day ahead forecasted returns but also the dynamics of volatility. In Figures 6b and 7b an inspection of autocorrelation functions of levels and squares of generalized residuals visualizes the problem.
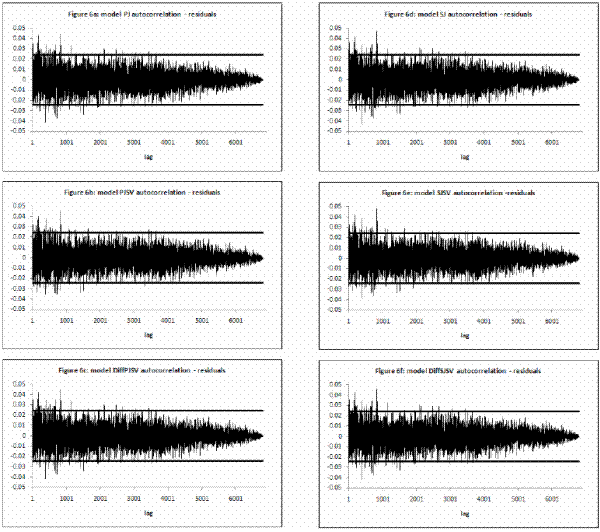
Figure 6 Data
One of the possible explanations is an incorrect source of stochastic volatility.
Models PJ and DiffPJSV with diffusion included as a source of stochastic volatility dominate model PJSV. An inspection of the qq-plots in Figure 5 and descriptive statistics of generalized residuals in Table V reveal the clear advantage of models PJ and DiffPJSV over model PJSV in representing
forecasting distribution. However, there is no significant difference in performance between models PJ and DiffPJSV. In the density forecast analysis presented in Table V both models perform on par and dominate model PJSV. Although they represent better forecasting distribution compared to model
PJSV, they still fall short in this respect with Jarque-Bera ![]() -values of 0.0061
and 0.0027 respectively. Hence, it still does not suffice to accept the null hypothesis of normally distributed generalized residuals even at the
-values of 0.0061
and 0.0027 respectively. Hence, it still does not suffice to accept the null hypothesis of normally distributed generalized residuals even at the ![]() level. In order to identify a source of the problem I inspect descriptive statistics of generalized residuals and find that both models
level. In order to identify a source of the problem I inspect descriptive statistics of generalized residuals and find that both models
 for models with Poisson jumps, respectively PJ, PJSV, DiffPJSV; (d, e, f) autocorrelation function of the squared generalized residuals
for models with Poisson jumps, respectively PJ, PJSV, DiffPJSV; (d, e, f) autocorrelation function of the squared generalized residuals
 for models with Lévy
for models with Lévy 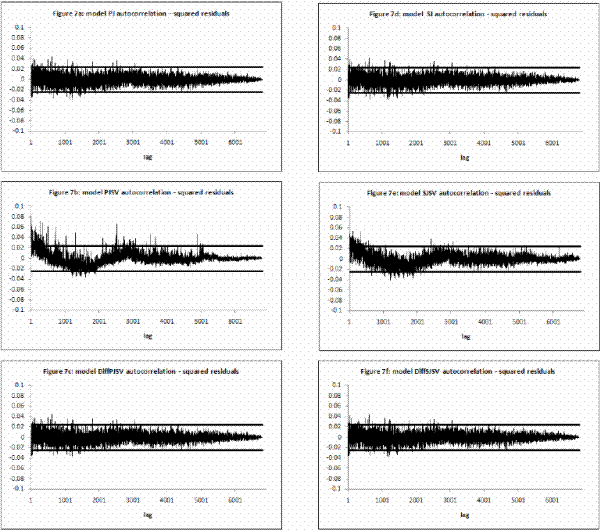
Figure 7 Data
fail with respect to kurtosis of the forecasting distribution but represent skewness slighlty better. The high kurtosis values of 3.1517 and 3.1642, for models PJ and DiffPJSV respectively, are the main driving factor of high Jarque-Bera test statistics found in both models. This result stays in line with my previous findings from goodness of fit analysis in Section 4.3.2, where the models with Poisson jumps PJ and DiffPJSV represent skewness better than kurtosis of returns. Since the scale of the forecasting distribution is well represented we can draw conclusion that there is too small kurtosis in the PJ and DiffPJSV
model implied forecasting distribution which is later verified in the VaR analysis. In the Ljung-Box test for dependence in the squares of generalized residuals presented in Figure 9 the test ![]() -values are higher than
-values are higher than ![]() with an exception for the maximum lags of approximately 25-400 and 1200-1800 business days. This constitutes a colossal improvement compared to model PJSV in representing the dynamics of volatility. The same conclusions can be
drawn from an inspection of autocorrelation functions for the squares of generalized residuals in Figure 7. Most importantly, I do not find significant differences between models PJ and DiffPJSV.
with an exception for the maximum lags of approximately 25-400 and 1200-1800 business days. This constitutes a colossal improvement compared to model PJSV in representing the dynamics of volatility. The same conclusions can be
drawn from an inspection of autocorrelation functions for the squares of generalized residuals in Figure 7. Most importantly, I do not find significant differences between models PJ and DiffPJSV.
Finally, model PJSV is outperformed by models PJ and DiffPJSV in the VaR analysis presented in Table VI. Model PJSV overestimates VaR values in the estimation sample and therefore underestimates the empirical coverage frequencies by inducing too high skewness and kurtosis in the forecasting
distribution. Both models PJ and DiffPJSV perform on par in the VaR analysis underestimating VaR values at ![]() with coverage frequencies of approximately
with coverage frequencies of approximately ![]() . Both models produce very good results at the
. Both models produce very good results at the ![]() and
and ![]() levels with a general tendency to perform better at higher significance levels.
levels with a general tendency to perform better at higher significance levels.
Since models PJ and DiffPJSV include diffusion component as a source of stochastic volatility, it is the diffusion that contains the most information about latent stochastic volatility. I conclude that diffusion is the primary source of stochastic volatility in models with Poisson jumps which is intuitive, since Poisson jumps are rare. As discussed in the previous section, the correct specification of stochastic volatility is of major importance. It affects how the model performs in the density forecast and VaR analysis.
Summing up, model PJSV with stochastic volatility only from jumps is rejected not only with respect to the goodness of fit but also with respect to the density forecast and VaR performance, since it is outperformed by other specifications with Poisson jumps. Models PJ and DiffPJSV both perform on par and hence the benefits of additional source of stochastic volatility from the Poisson jumps in model DiffPJSV are rather minor, if any. The diffusion component serves as the primary source of stochastic volatility in the models with Poisson jumps.
4.4.2 Models with Lévy  -stable Jumps
-stable Jumps
In forecast analysis the main objective is to correctly represent the forecasting distribution, where filtered latent volatility states play the first role. Since Lévy ![]() -stable
jumps have infinite activity property, they are able to represent not only big and rare Poisson type jumps, but also more frequent and subtle jumps. Hence, when the Lévy
-stable
jumps have infinite activity property, they are able to represent not only big and rare Poisson type jumps, but also more frequent and subtle jumps. Hence, when the Lévy ![]() -stable
jumps component is included as a source of stochastic volatility, it should provide additional information about latent stochastic volatility and therefore improve the density forecast performance. I also analyze an extreme case where stochastic volatility arises only from the pure jump Lévy
-stable
jumps component is included as a source of stochastic volatility, it should provide additional information about latent stochastic volatility and therefore improve the density forecast performance. I also analyze an extreme case where stochastic volatility arises only from the pure jump Lévy
![]() -stable process. It allows to verify if diffusion still plays the fundamental role as a source of stochastic volatility in the models with infinite activity, infinite variation
jumps.
-stable process. It allows to verify if diffusion still plays the fundamental role as a source of stochastic volatility in the models with infinite activity, infinite variation
jumps.
I find that we cannot simply exclude the diffusion as a component driving stochastic volatility even with Lévy ![]() -stable jumps in returns. This is illustrated by the poor
performance of model SJSV with respect to the density forecast and VaR analysis presented in Tables V and VI respectively. In the density forecast model SJSV shares similarities with model PJSV. It fails to represent scale, skewness and kurtosis of the forecasting distribution with the respective
statistics of 0.891, -0.1221 and 3.7942 calculated for generalized residuals. This implies the high value of Jarque-Bera test statistic of 195.96 and rejection
of normality, although this statistic is significantly improved compared to model PJSV. In Figure 5e, I present qq-plot that visualizes the failure of the SJSV specification to represent the forecasting distribution. Since the scale of the forecasting distribution is misspecified as in model PJSV,
I have to postpone a conclusion about skewness
-stable jumps in returns. This is illustrated by the poor
performance of model SJSV with respect to the density forecast and VaR analysis presented in Tables V and VI respectively. In the density forecast model SJSV shares similarities with model PJSV. It fails to represent scale, skewness and kurtosis of the forecasting distribution with the respective
statistics of 0.891, -0.1221 and 3.7942 calculated for generalized residuals. This implies the high value of Jarque-Bera test statistic of 195.96 and rejection
of normality, although this statistic is significantly improved compared to model PJSV. In Figure 5e, I present qq-plot that visualizes the failure of the SJSV specification to represent the forecasting distribution. Since the scale of the forecasting distribution is misspecified as in model PJSV,
I have to postpone a conclusion about skewness
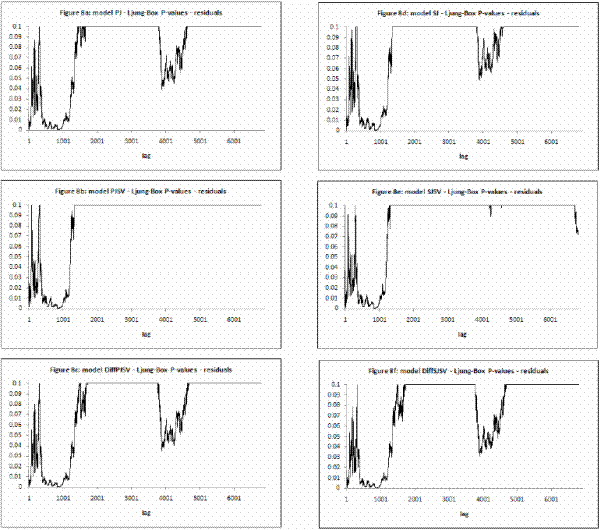
Figure 8 Data
and kurtosis of the implied forecasting distribution to the VaR analysis. In the test for dependence in the squared generalized residuals in Figure (9) model SJSV completely falls behind other specifications with its Ljung-Box test ![]() -values close to zero at all maximum lags considered ( 2-6811) with an exception of only one lag ( 1), where it equals 0.15. Hence, model SJSV can neither represent the distribution of one-day ahead forecasted returns nor
the dynamics of volatility. However, both models PJSV and SJSV produce similar results to other specifications in the Ljung-Box test for dependence in levels of the generalized residuals in Figure (8). In Figures 6 and 7 an inspection of autocorrelation functions of levels and squares of
generalized residuals visualize these findings.
-values close to zero at all maximum lags considered ( 2-6811) with an exception of only one lag ( 1), where it equals 0.15. Hence, model SJSV can neither represent the distribution of one-day ahead forecasted returns nor
the dynamics of volatility. However, both models PJSV and SJSV produce similar results to other specifications in the Ljung-Box test for dependence in levels of the generalized residuals in Figure (8). In Figures 6 and 7 an inspection of autocorrelation functions of levels and squares of
generalized residuals visualize these findings.
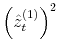 for models with Poisson jumps, respectively PJ, PJSV, DiffPJSV, calculated as a function of different maximum number of lags; (d, e, f) Ljung-Box test
for models with Poisson jumps, respectively PJ, PJSV, DiffPJSV, calculated as a function of different maximum number of lags; (d, e, f) Ljung-Box test
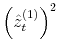 for models with Lévy
for models with Lévy 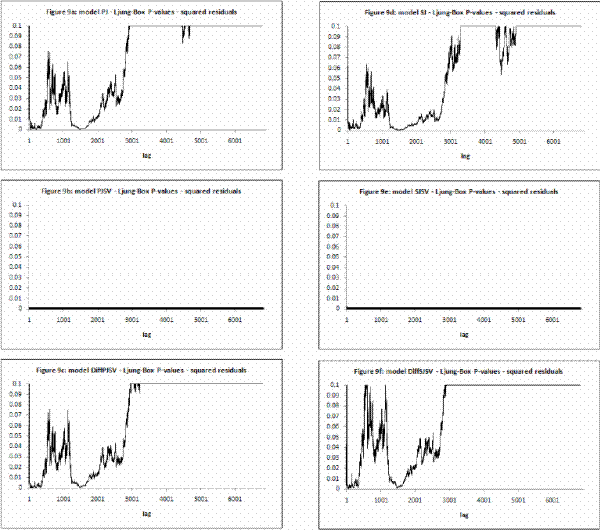
Figure 9 Data
Finally, I concentrate on models with diffusion as a source of stochastic volatility. In model DiffSJSV the joint stochastic volatility enables us to extract information about latent volatility from both diffusion and infinite activity jumps. The above produces the best performance in the
density forecast analysis across all model specifications. This model performs the best in terms of representing skewness and kurtosis of predictive distribution with skewness of -0.0014 and
kurtosis of 3.0981 compared to -0.0266 and 3.1042 respectively for model SJ. The Jarque-Bera ![]() -value of 0.255 confirms superiority of model DiffSJSV in representing the forecasting distribution, although model SJ with the
-value of 0.255 confirms superiority of model DiffSJSV in representing the forecasting distribution, although model SJ with the ![]() -value of
0.1432 also performs well. Both mean and standard deviation of generalized residuals are close to the theoretical values in models SJ and DiffSJSV. An inspection of qq-plot in Figure 5
verifies normality assumption of generalized residuals for both considered models. Model DiffSJSV's advantage over other models, including the SJ specification, shows up in the very left tail of the generalized residuals. As I find above, the autocorrelation functions in Figure 6 for levels of
generalized residuals are not significantly affected by the model specification and all models perform similarily in the Ljung-Box test for levels of generalized residuals in Figure 8. On the other hand, I find significant differences between models SJ and DiffSJSV in the analysis of the squared
generalized residuals and hence the model implied dynamics of volatility. Even tough the autocorrelation functions in Figure 7 do not provide any significant proof of this, in Figure 9 I find that model DiffSJSV performs superior to any other model and has the highest Ljung-Box test
-value of
0.1432 also performs well. Both mean and standard deviation of generalized residuals are close to the theoretical values in models SJ and DiffSJSV. An inspection of qq-plot in Figure 5
verifies normality assumption of generalized residuals for both considered models. Model DiffSJSV's advantage over other models, including the SJ specification, shows up in the very left tail of the generalized residuals. As I find above, the autocorrelation functions in Figure 6 for levels of
generalized residuals are not significantly affected by the model specification and all models perform similarily in the Ljung-Box test for levels of generalized residuals in Figure 8. On the other hand, I find significant differences between models SJ and DiffSJSV in the analysis of the squared
generalized residuals and hence the model implied dynamics of volatility. Even tough the autocorrelation functions in Figure 7 do not provide any significant proof of this, in Figure 9 I find that model DiffSJSV performs superior to any other model and has the highest Ljung-Box test ![]() -values. Most importantly, comparing directly models SJ and DiffSJSV in Figures 9d,f I find that model DiffSJSV outperforms model SJ especially at maximum lags in the Ljung-Box test of up to about
5 years. This implies that model DiffSJSV is superior in representing the dynamics of volatility, which shows up in its density forecast performance.
-values. Most importantly, comparing directly models SJ and DiffSJSV in Figures 9d,f I find that model DiffSJSV outperforms model SJ especially at maximum lags in the Ljung-Box test of up to about
5 years. This implies that model DiffSJSV is superior in representing the dynamics of volatility, which shows up in its density forecast performance.
In the VaR analysis in Table VI models SJ and DiffSJSV produce very good results among all specifications. Model DiffSJSV dominates all other specifications in the VaR analysis in the very left tail at ![]() and
and ![]() levels with empirical coverage frequencies of 0.98% and
levels with empirical coverage frequencies of 0.98% and ![]() . At
. At ![]() level it produces second best result with the coverage frequency of
level it produces second best result with the coverage frequency of ![]() comparing to
comparing to ![]() in model PJ. I also find that model SJ performs very well in the VaR analysis but is dominated by model DiffSJSV with a joint stochastic
volatility specification.
in model PJ. I also find that model SJ performs very well in the VaR analysis but is dominated by model DiffSJSV with a joint stochastic
volatility specification.
The biggest problem in the VaR analysis arises in model SJSV at the ![]() and
and ![]() levels and this result is similar to model PJSV. The model improves at the
levels and this result is similar to model PJSV. The model improves at the ![]() level. Model SJSV, although dominated in the VaR analysis by other models with Lévy
level. Model SJSV, although dominated in the VaR analysis by other models with Lévy
![]() -stable jumps, performs better than model PJSV.
-stable jumps, performs better than model PJSV.
Summing up, the jump component cannot serve as the only source of stochastic volatility even in the models with Lévy ![]() -stable jumps. In case of models SJ and DiffSJSV with
diffusion as a source of stochastic volatility, I find evidence in favor of model DiffSJSV with stochastic volatility arising from both diffusion and jump components. This stays in contrast to the results for the Poisson jumps, where the marginal importance of the stochastic volatility from the
jump component does not have a first order importance in the density forecast analysis.
-stable jumps. In case of models SJ and DiffSJSV with
diffusion as a source of stochastic volatility, I find evidence in favor of model DiffSJSV with stochastic volatility arising from both diffusion and jump components. This stays in contrast to the results for the Poisson jumps, where the marginal importance of the stochastic volatility from the
jump component does not have a first order importance in the density forecast analysis.
4.4.3 Poisson or Lévy 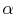 -stable Jumps?
-stable Jumps?
I focus attention on the choice of the jumps specification: compound Poisson or Lévy ![]() -stable jumps. The model with Lévy
-stable jumps. The model with Lévy ![]() -stable jumps and joint stochastic volatility DiffSJSV outperforms all other models with respect to the density forecast and VaR analysis, which stems from the fact that it offers one important advantage in the modelling of asset
returns. Since joint stochastic volatility makes possible to extract information about latent volatility from both diffusion and jumps and since jumps have infinite activity, they are more informative about the latent volatility. The infinite activity guarantees that it can represent small and
frequent jumps as oppose to the Poisson jumps model, which is found to fit only big and rare jumps in returns. Since Poisson jumps occur very rarely, they have only limited information about latent stochastic volatility and even if this information is extracted in the form of stochastic volatility
arising from both the diffusion and the jumps in model DiffPJSV, its forecasting performance is dominated by model DiffSJSV.
-stable jumps and joint stochastic volatility DiffSJSV outperforms all other models with respect to the density forecast and VaR analysis, which stems from the fact that it offers one important advantage in the modelling of asset
returns. Since joint stochastic volatility makes possible to extract information about latent volatility from both diffusion and jumps and since jumps have infinite activity, they are more informative about the latent volatility. The infinite activity guarantees that it can represent small and
frequent jumps as oppose to the Poisson jumps model, which is found to fit only big and rare jumps in returns. Since Poisson jumps occur very rarely, they have only limited information about latent stochastic volatility and even if this information is extracted in the form of stochastic volatility
arising from both the diffusion and the jumps in model DiffPJSV, its forecasting performance is dominated by model DiffSJSV.
5 Conclusions
In this paper I address the choice of jump structure and source of stochastic volatility in the continuous-time jump diffusion models of asset returns. I consider two types of jump structures - compound Poisson and infinite activity Lévy ![]() -stable jumps. The source of stochastic volatility comes from the diffusion component, the pure jump component or both. I use data on daily S&P500 index returns since it is a broad indicator of the equity markets. I perform
estimation under statistical measure - this allows us to not only answer how the models fit the data but also how they perform in the density forecast and VaR analysis. The large family of models considered lets us marginalize the effects of different jump structures and source of stochastic
volatility with respect to goodness of fit and density forecast performance.
-stable jumps. The source of stochastic volatility comes from the diffusion component, the pure jump component or both. I use data on daily S&P500 index returns since it is a broad indicator of the equity markets. I perform
estimation under statistical measure - this allows us to not only answer how the models fit the data but also how they perform in the density forecast and VaR analysis. The large family of models considered lets us marginalize the effects of different jump structures and source of stochastic
volatility with respect to goodness of fit and density forecast performance.
I face the problem of parameters estimation in the presence of latent stochastic volatility and latent jump sizes. I perform estimation using Bayesian methods and propose a new algorithm for models with Lévy ![]() -stable jumps. My method solves the problem of MCMC state-space separability and thus allows for the estimation of a broad class of contiuous-time jump diffusion models with Lévy
-stable jumps. My method solves the problem of MCMC state-space separability and thus allows for the estimation of a broad class of contiuous-time jump diffusion models with Lévy ![]() -stable jumps and various sources of stochastic volatility.
-stable jumps and various sources of stochastic volatility.
Lévy ![]() -stable jumps dominate compound Poisson jumps specifications with respect to goodness of fit analysis, since the latter are only suited to fit big and rare jumps.
Moreover, models with Lévy
-stable jumps dominate compound Poisson jumps specifications with respect to goodness of fit analysis, since the latter are only suited to fit big and rare jumps.
Moreover, models with Lévy ![]() -stable jumps can adequately represent kurtosis of the underlying data and skewness of the returns distribution but only if diffusion is included as a
source of stochastic volatility. It is important to note that models with stochastic volatility arising only from the pure jump component fail to fit the returns and this feature is irrespective of the jump structure specification. On the other hand, one cannot in a decisive way point out if there
is a need for jump component as the second source of stochastic volatility by restricting analysis only to goodness of fit. This conclusion holds for the models with all considered jump structures including infinite activity Lévy
-stable jumps can adequately represent kurtosis of the underlying data and skewness of the returns distribution but only if diffusion is included as a
source of stochastic volatility. It is important to note that models with stochastic volatility arising only from the pure jump component fail to fit the returns and this feature is irrespective of the jump structure specification. On the other hand, one cannot in a decisive way point out if there
is a need for jump component as the second source of stochastic volatility by restricting analysis only to goodness of fit. This conclusion holds for the models with all considered jump structures including infinite activity Lévy ![]() -stable jumps.
-stable jumps.
The density forecast and VaR analysis shed new light on the application of continuous-time jump diffusion models of asset returns. I find that correct specification of the source of stochastic volatility is of fundamental importance in the density forecast and VaR analysis. The performance of
the compound Poisson jump models do not significantly change with the addition of the jump component to the diffusion as the source of stochastic volatility. On the contrary, the models with Lévy ![]() -stable jumps improve in the density forecast and VaR performance with the inclusion of both sources of stochastic volatility, thus dominating all other model specifications. The joint stochastic volatility enables us to extract information about latent volatility from both
diffusion and jumps, where the jumps are more informative with their infinite activity property. However, we cannot go further and exclude the diffusion from the source of stochastic volatility. This conclusion does not depend on the jump structure and agrees with the goodness of fit analysis.
-stable jumps improve in the density forecast and VaR performance with the inclusion of both sources of stochastic volatility, thus dominating all other model specifications. The joint stochastic volatility enables us to extract information about latent volatility from both
diffusion and jumps, where the jumps are more informative with their infinite activity property. However, we cannot go further and exclude the diffusion from the source of stochastic volatility. This conclusion does not depend on the jump structure and agrees with the goodness of fit analysis.
A line for future research is to study the density forecast and VaR performance using data from the underlying and option prices. Since option prices contain information about latent volatility, it is important to investigate their potential explanatory power. Moreover, in this paper I analyze diffusion as the only source of leverage effect and further research could involve removing this restriction. This can help to answer a question of whether diffusion is still an important feature of the model when jump component is a source of leverage effect.
6 Appendix: Complete Conditional Posteriors
Since models DiffPJSV and DiffSJSV contain both: stochastic volatility from diffusion and jumps, we can derive complete conditional distributions for them and then apply the constraints in order to employ the derived distributions for other model specifications. However, note that they are not simple generalizations of the other specifications.
6.1 Models DiffPJSV and DiffSJSV - complete conditional posteriors for non-jump specific parameters and latent variables
Let use the notation from Sections 3.1 and 3.4. Let denote the jump specific parameters and latent variables depending on the model specification with Poisson or Lévy ![]() -stable jumps by the index
-stable jumps by the index
![]() . In the following
. In the following
![]() ,
,
![]() are the vectors of non-jump specific parameters,
are the vectors of non-jump specific parameters,
![]() latent log-volatility states and
latent log-volatility states and
![]() the jump sizes defined in (35). Moreover, let define the jump specific parameters and latent variables:
the jump sizes defined in (35). Moreover, let define the jump specific parameters and latent variables:
and define
- updating
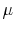
I choose the following prior distribution on ![]()
![]() I set
I set ![]() and
and ![]() , which is a relatively flat prior for the mean of asset returns. The conditional posterior distribution is conjugate to prior and given by:
, which is a relatively flat prior for the mean of asset returns. The conditional posterior distribution is conjugate to prior and given by:
![a^{\ast}=A^{\ast}\cdot(A^{-1}a+\frac{1}{1-\rho^{2}% }\sum_{t=1}^{T-1}\left[ \frac{(Y_{t+1}-Y_{t}-J_{t+1})}{\xi_{t}}-\frac {\rho\varepsilon_{t+1}^{(3)}\delta^{0.5}}{\xi_{t}^{0.5}}\right]](img546.gif) .
.
- 2.
- updating
The prior on
![]() is
is
![]() truncated
truncated ![]() with the support
with the support
![]() and
and
![]()
![]() , which is also a relatively flat prior that imposes stationarity on the log-volatility process
, which is also a relatively flat prior that imposes stationarity on the log-volatility process ![]() . Hence, the conditional posterior is also truncated and conjugate to prior:
. Hence, the conditional posterior is also truncated and conjugate to prior:
- 3.
- updating
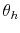
The prior on
![]() is
is
![]() , with
, with ![]() and
and ![]() . The conditional posterior is conjugate to prior:
. The conditional posterior is conjugate to prior:
- 4.
- updating
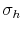 and
and 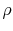
I update
![]() and
and ![]() as a block following Jacquier, Polson and Rossi (2004) (JPR).
Let define the following bijective correspondence:
as a block following Jacquier, Polson and Rossi (2004) (JPR).
Let define the following bijective correspondence:
I choose the joint prior distribution on the transformed parameters
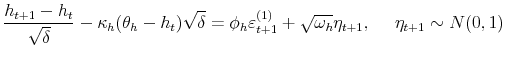
- 5.
- updating volatility states
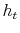 for
for 
By application of the Bayes rule, we have:
where
![]() and the last term
and the last term
![]() depends on the model specification:
depends on the model specification:
I apply MH algorithm, with a proposal density given by
- 6.
- updating volatility state
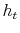 for
for 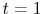
By application of the Bayes rule, we have:
- 7.
- updating volatility state
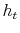 for
for 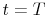
By application of the Bayes rule, we have:
- 8.
- updating parameter
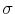 (models PJSV, SJSV and DiffPJSV only)
(models PJSV, SJSV and DiffPJSV only)
Lets define the function
![]() for models
for models
![]() ,
, ![]() and
and
![]() for model
for model
![]() . Update of parameter
. Update of parameter ![]() is equivalent to update in the
following regression model:
is equivalent to update in the
following regression model:
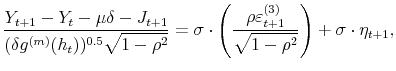
where
![]()
![]() . Lets define
. Lets define
![]() and
and ![]()
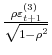 . We have the following complete conditional posterior for
. We have the following complete conditional posterior for
![]() :
:
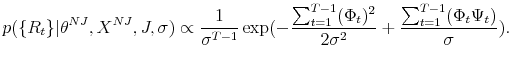
- 9.
- updating
 (models SJ and DiffSJSV)
(models SJ and DiffSJSV)
In the model SJ let assume an inverse gamma prior on
![]() ,
,
![]() where
where ![]() and
and
![]() . In the model DiffSJSV I assume completely flat prior
. In the model DiffSJSV I assume completely flat prior
![]() . Let define the function
. Let define the function
![]() for model
for model ![]() and
and
![]() for model
for model
![]() . We have the following complete conditional posterior for
. We have the following complete conditional posterior for
![]() :
:
![\displaystyle \exp\left\{ -\left( \frac{1}{\sigma_{SJ}}\right) ^{\frac{\alpha}{\alpha-1}% }\left[ \sum_{t=2}^{T}\left( \left\vert \frac{\tilde{S}_{t}^{-}}% {(g^{(m)}(h_{t-1})\delta)^{\frac{1}{\alpha}}v_{t}^{-}}\right\vert ^{\frac{\alpha}{\alpha-1}}+\left\vert \frac{\tilde{S}_{t}^{+}}{(g^{(m)}% (h_{t-1})\delta)^{\frac{1}{\alpha}}v_{t}^{+}}\right\vert ^{\frac{\alpha }{\alpha-1}}\right) \right] \right\} \left( \frac{1}{\sigma_{SJ}% ^{\frac{\alpha}{\alpha-1}}}\right) ^{2(T-1)}\cdot p(\sigma_{SJ}).](img634.gif)
![\displaystyle q(\sigma_{SJ})\propto\exp\left\{ -\left( \frac{1}{\sigma_{SJ}}\right) ^{\frac{\alpha}{\alpha-1}}\left[ \sum_{t=2}^{T}\left( \left\vert \frac{\tilde{S}_{t}^{-}}{(g^{(m)}(h_{t-1})\delta)^{\frac{1}{\alpha}}v_{t}^{-}% }\right\vert ^{\frac{\alpha}{\alpha-1}}+\left\vert \frac{\tilde{S}_{t}^{+}% }{(g^{(m)}(h_{t-1})\delta)^{\frac{1}{\alpha}}v_{t}^{+}}\right\vert ^{\frac{\alpha}{\alpha-1}}\right) \right] \right\} \left( \frac{1}% {\sigma_{SJ}^{\frac{\alpha}{\alpha-1}}}\right) ^{2(T-1)}.](img635.gif)
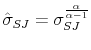 , then by the change of variable formula:
, then by the change of variable formula:
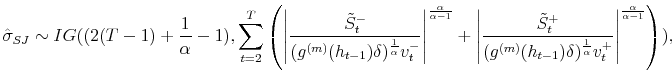
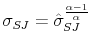 . In the model SJ I use MH algorithm with the above choice of proposal density, which is very efficient with acceptance rate of above
. In the model SJ I use MH algorithm with the above choice of proposal density, which is very efficient with acceptance rate of above
6.2 Models with Poisson Jumps: complete conditional posteriors for jump specific parameters and latent variables
- updating latent jump times
Since
![]() is
is
![]() , the conditional posterior is also
, the conditional posterior is also ![]() :
:
![\displaystyle p(Y_{t+1}\vert Y_{t},\theta,X)\propto\exp(-\frac{1}{2}\frac{[Y_{t+1}-Y_{t}% -\mu\delta-q_{t+1}\varkappa_{t+1}-(\xi_{t}\delta)^{\frac{1}{2}}\rho \varepsilon_{t+1}^{(3)}]^{2}}{\delta(1-\rho^{2})\xi_{t}}).](img649.gif)
- 2.
- updating latent jump sizes
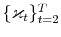
By application of the Bayes rule, we have:
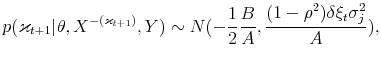
- 3.
- updating mean jump size parameter
I take the prior
![]() with
with ![]()
![]() . By application of the Bayes rule, we have:
. By application of the Bayes rule, we have:
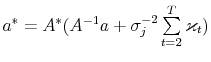 .
.
- 4.
- updating variance jump size parameter
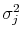
I take the inverse gamma prior
![]() with
with ![]() and
and
![]() . By application of the Bayes rule, we have:
. By application of the Bayes rule, we have:
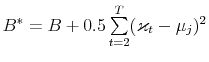 .
.
- 5.
- updating constant jump intensity
 in model PJ
in model PJ
I specify the beta prior distribution on
![]() . Then the conditional posterior is conjugate to prior:
. Then the conditional posterior is conjugate to prior:
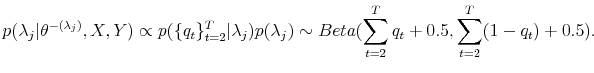
6.3 Models with Lévy 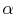 -stable Jumps: complete
conditional posteriors for jump specific parameters and latent variables
-stable Jumps: complete
conditional posteriors for jump specific parameters and latent variables
- 1.
- updating volatility states
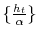 in model SJSV
in model SJSV
Since in this model ![]() process drives only jumps, I redefine SJSV model to simplify its update procedure by using a change of variable
process drives only jumps, I redefine SJSV model to simplify its update procedure by using a change of variable
![]() and then directly update
and then directly update
![]() . I also redefine the set
. I also redefine the set ![]() to replace
to replace ![]() by
by
![]() .23 The OU process
.23 The OU process
![]() is given by:
is given by:
The complete conditional posterior for
![]() ,
, ![]() , is given by:
, is given by:
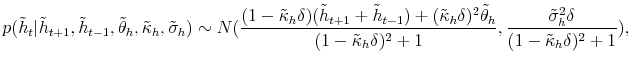
for
|
|
|||
|---|---|---|---|
| Stoch. Volatility from Diffusion: model (1) PJ | -1< |
exp(x) |
|
| Stoch. Volatility from Diffusion: model (4) SJ | -1< |
exp(x) |
|
| Stoch. Volatility from Jumps: model (2) PJSV | 0 |
|
exp(x) |
| Stoch. Volatility from Jumps: model (5) SJSV | 0 |
|
exp(x) |
| Joint Stochastic Volatility: model (3) DiffPJS | -1< |
|
exp(x) |
| Joint Stochastic Volatility: model (6) DiffSJS | -1< |
exp(x) |
|
The table reports the list of restrictions for models presented in SDE (8).
The table reports the mean, standard deviation, skewness and kurtosis of S&P500 daily log-returns (x100).
| Mean | Std. Deviation | Skewness | Kurtosis | Daily autocorr | |
|---|---|---|---|---|---|
| PJ | 0.0035 | 1.0002 | -0.048 | 3.2578 | 0.0226 |
| PJ Standard Error | (-0.0190;0.0260) | (0.9826;1.0164) | (-0.0869;-0.0081) | (3.1666;3.3654) | (0.016;0.0284) |
| PJSV | 3.97E-05 | 0.9084 | -0.0382 | 3.7349 | 0.0166 |
| PJSV Standard Error | (-0.0237;0.0237) | (0.8929;0.9241) | (-0.0831;0.0076) | (3.6179;3.8528) | (0.0046;0.0286) |
| DiffPJSV | 0.0035 | 1.0002 | -0.047 | 3.2481 | 0.0232 |
| DiffPJSV Standard Error | (-0.0191;0.0261) | (0.9834;1.0169) | (-0.0860;-0.0082)) | (3.1528;3.3590) | (0.0175;0.0291) |
| SJ | 0.005 | 0.9995 | -0.0074 | 3.059 | 0.0101 |
| SJ Standard Error | (-0.0172;0.0271) | (0.9829;1.0168) | (-0.0630;0.0482) | (2.9532;3.1779) | (-0.0080;0.0279) |
| SJSV | 0.0001 | 0.8965 | -0.0301 | 3.7059 | 0.0209 |
| SJSV Standard Error | (-0.0236;0.0238) | (0.8812;0.9119) | (-0.0825;0.0227) | (3.5671;3.8480) | (0.0061;0.0356) |
| DiffSJSV | 0.0024 | 0.9999 | 0.0076 | 3.1397 | 0.0198 |
| DiffSJSV Standard Error | (-0.0203;0.0251) | (0.9835;1.0165) | (-0.0416;0.0561) | (3.0444;3.2429) | (0.0078;0.0307) |
| Mean | Std. Deviation | Skewness | Kurtosis | Daily autocorr | |
|---|---|---|---|---|---|
| PJ | -0.003 | 0.9998 | 0.0064 | 3.0302 | 0.0077 |
| PJ Standard Error | (-0.0263;0.0203) | (0.9832;1.0166) | (-0.0521;0.0651) | (2.9168;3.1570) | (-0.0145;0.0295 ) |
| PJSV | -1.07E-02 | 1.0003 | 0.0003 | 2.9974 | 0.0005 |
| PJSV Standard Error | (-0.0319;0.0116) | (0.9835;1.0171) | (-0.0578;0.0585) | (2.8878;3.1202) | (-0.0233;0.0242) |
| DiffPJSV | -0.0027 | 0.9999 | 0.0057 | 3.0284 | 0.0078 |
| DiffPJSV Standard Error | (-0.0260;0.0207) | (0.9832;1.0167) | (-0.0525;0.0642) | (2.9148;3.1566) | (-0.0144;0.0298) |
| SJ | -0.0049 | 0.9998 | 0.001 | 3.0186 | 0.0052 |
| SJ Standard Error | (-0.0277;0.0180) | (0.9830;1.0168) | (-0.0568;0.0592) | (2.907;3.1428) | (-0.0168;0.0271) |
| SJSV | -0.0063 | 1 | 0.0011 | 2.998 | 0.0001 |
| SJSV Standard Error | (-0.0289;0.0173) | (0.983;1.0169) | (-0.0571;0.0592) | (2.888;3.1213) | (-0.0237;0.0239) |
| DiffSJSV | -0.0023 | 0.9998 | -0.0045 | 3.0269 | 0.0067 |
| DiffSJSV Standard Error | (-0.0257;0.0210) | (0.9831;1.0166) | (-0.0624;0.0539) | (2.9150;3.1522) | (-0.0151;0.0285) |
The table reports posterior medians and 95% confidence intervals (in parentheses) of mean, std. deviation, skewness, kurtosis and daily autocorrelation of model residuals calculated at each step of MCMC algorithms for different model specifications. A correct specification implies, that mean is zero, standard deviation one, skewness zero, kurtosis three and daily autocorrelation zero.
| Mean | Std. Deviation | Skewness | Kurtosis | Jarque-Ber | |
|---|---|---|---|---|---|
| PJ | 0.0022 | 0.9937 | -0.0569 | 3.1517 | 10.2113 |
| PJ p-value | (0.0061) | ||||
| PJSV | -0.0054 | 0.8834 | -0.2335 | 4.9226 | 1.11E+03 |
| PJSV p-value | (0) | ||||
| DiffPJSV | 0.0022 | 0.9922 | -0.0608 | 3.1642 | 11.8461 |
| DiffPJSV p-value | (0.0027) | ||||
| SJ | 0.0033 | 0.9829 | -0.0266 | 3.1042 | 3.8866 |
| SJ p-value | (0.1432) | ||||
| SJSV | -0.013 | 0.8910 | -0.1221 | 3.7942 | 195.9642 |
| SJSV p-value | (0) | ||||
| DiffSJSV | 0.0024 | 0.9931 | -0.0014 | 3.0981 | 2.7327 |
| DiffSJSV p-value | (0.2550) |
Descriptive statistics of
![\displaystyle \psi_{x}(u)=ibu-\frac{1}{2}u^{2}\sigma^{2}+\int_{% \mathbb{R} \backslash\left\{ 0\right\} }[\exp(iuz)-1-iuz1_{\vert z\vert<1}% ]v(dz),%](img21.gif)
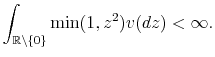
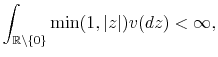
![\displaystyle E(\exp(uiS)=\left\{ \begin{array}[c]{c}% \exp\{i\delta u-\gamma^{\alpha}\vert u\vert^{\alpha}\exp[-i\frac{\pi\beta}{2}% sgn(u)\min(\alpha,2-\alpha)]\}\text{ \ for }\alpha\neq1\\ \exp\{i\delta u-\gamma\vert u\vert[1+i\beta\frac{2}{\pi}sgn(u)\log(\gamma\vert u\vert)]\}\text{ for }\alpha=1, \end{array} \right.%](img48.gif)
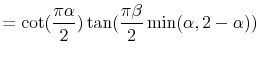
![\displaystyle =\gamma\lbrack\cos(\frac{\pi\beta}{2}\min(\alpha ,2-\alpha))]^{1/\alpha},](img57.gif)
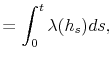
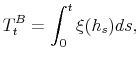
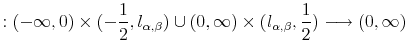
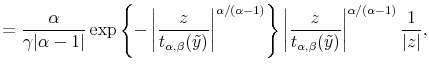
![\displaystyle t_{\alpha,\beta}(\tilde{y})=\left( \frac{\sin[\pi\alpha\tilde{y}+\eta _{\alpha,\beta}]}{\cos\pi\tilde{y}}\right) \left( \frac{\cos\pi\tilde{y}% }{\cos[\pi(\alpha-1)\tilde{y}+\eta_{\alpha,\beta}]}\right) ^{(\alpha -1)/\alpha},%](img193.gif)
![\displaystyle p_{\alpha,\beta}=p_{\alpha,\beta,\delta=0}=0.5+\frac{\arctan[\hat{\beta}% \tan(\pi\alpha/2)]}{\pi\alpha},%](img228.gif)
![\displaystyle =\left\{ \begin{array}[c]{c}% \frac{1}{p_{\alpha,\beta}}f(\tilde{s}^{+},\tilde{y}^{+};\delta=0)\text{ if }\tilde{s}^{+}>0\text{ }and\text{ }\tilde{y}^{+}\in(l_{\alpha,\beta},\frac {1}{2})\\ 0\text{ otherwise}% \end{array} \right. ,](img238.gif)
![\displaystyle =\left\{ \begin{array}[c]{c}% \frac{1}{1-p_{\alpha,\beta}}f(\tilde{s}^{-},\tilde{y}^{-};\delta=0)\text{ if }\tilde{s}^{-}<0\text{ }and\text{ }\tilde{y}^{-}\in(-\frac{1}{2}% ,l_{\alpha,\beta})\\ 0\text{ otherwise}% \end{array} \right. ,%](img240.gif)
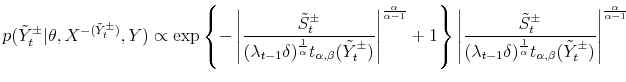
 and
and 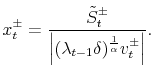
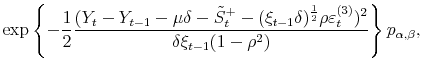
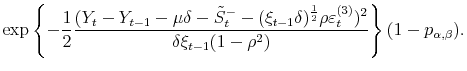
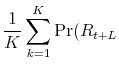
![\displaystyle J_{t}(m)=\left\{ \begin{array}[c]{c}% q_{t}\varkappa_{t}\text{ : models with Poisson jumps}\\ S_{t}(\alpha,\beta,0,(\lambda_{t-1}\delta)^{1/\alpha})\text{ : models with L\'{e}vy }\alpha\text{-stable jumps}% \end{array} \right.%](img358.gif)
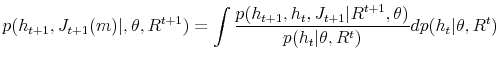
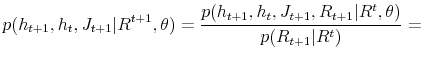
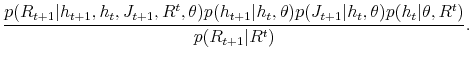
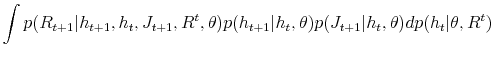
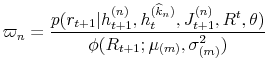
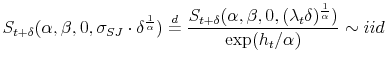
![\displaystyle p(Y_{\tau+1}\vert\theta^{NJ},X^{NJ},Y_{\tau},J)\propto\frac{1}{\xi_{\tau}^{0.5}% }\exp\left\{ -\frac{1}{2}\frac{[Y_{\tau+1}-Y_{\tau}-\mu\delta-J_{\tau+1}% -(\xi_{\tau}\delta)^{\frac{1}{2}}\rho\varepsilon_{\tau+1}^{(3)}]^{2}}% {\delta(1-\rho^{2})\xi_{\tau}}\right\} ,%](img588.gif)