Skip to: [Printable Version (PDF)] [Bibliography] [Footnotes]

Finance and Economics Discussion Series: 2010-04 Screen Reader version ^♣

Income Taxes, Compensating Differentials, and Occupational Choice: How Taxes Distort the Wage-Amenity Decision

David Powell*

Hui Shan**

Keywords: Income taxes, occupational choice, compensating differentials

Abstract:

The link between taxes and occupational choices is central for understanding the welfare impacts of income taxes. Just as taxes distort the labor-leisure decision, they also distort the wage-amenity decision. Yet, there are no estimates of the full response on this margin. When tax rates increase, workers favor jobs with lower wages and more non-taxable amenities. We introduce a two-step methodology which uses compensating differentials to characterize the tax elasticity of occupational choice. We estimate a significant compensated elasticity of 0.05, implying that a 10% increase in the net-of-tax rate causes workers to change to a 0.5% higher wage job.

JEL classification: H24, H31, J24

1 Introduction

It is well-known that taxes can distort individual labor supply decisions. Numerous studies have estimated the impact of income taxes on the labor-leisure tradeoff by looking at the effect of taxes on the number of hours worked. Fewer papers have studied another central component of income tax distortion - the tradeoff between wages and non-taxable amenities. This tradeoff manifests itself through occupational choice. The tax system may alter how workers choose between different jobs in the labor market, and studying this link is critical in our understanding of the welfare impacts of income taxes. By distorting occupational choices, income taxes can lead to inefficiently allocated workers with potentially long-term economic consequences. While a few studies estimate the effect of taxes on specific amenities, there are - to our knowledge - no estimates of the full response on the wage-amenity decision.

Workers are paid in both taxable monetary wages and non-taxable amenities. These amenities are very broadly defined, including qualities such as difficulty of the job, convenience of the hours, etc. By reducing the return to monetary wages, a high tax rate diminishes the benefit to high wage occupations. The tradeoff, then, is between non-taxable amenities and a taxable compensating differential for the level of amenities provided.

A vast literature has studied the effect of income taxes on the number of hours worked while fewer have looked at the occupational-choice facet of individual labor supply. The probable reason for this relative interest in "hours worked" is that hours are measurable and knowable. Furthermore, the counterfactual is obvious. An extra hour of work translates into one less hour of leisure. The tradeoff between wages and amenities is much harder to study for two reasons. First, non-taxable amenities vary on many dimensions and there is no comprehensive index of all occupational amenities. Second, the counterfactual - the compensating differential - is not immediately known or reported in any data set.

In this paper, we introduce a novel two-step estimation procedure to study the relationship between income taxes and occupational choice. This methodology first characterizes the wage-amenity decision that workers make and then estimates the impact of tax rate changes on those decisions. In the first step, we estimate the compensating differential for each occupation in each year. These estimates are then used as the dependent variable in the second step. The main specification relates the difference in the compensating differentials of the new occupation and the old occupation to the change in a worker's marginal net-of-tax rate. Basic theory would suggest that when the net-of-tax rate increases, the return to a high wage occupation increases and, consequently, workers should move to high wage occupations.

This strategy studies job transitions resulting from tax schedule changes. When the tax schedule changes, some workers may experience a tax increase relative to other workers and move to lower wage occupations. Similarly, other workers may experience a relative tax decrease and move to higher wage occupations. Our identification strategy relies on the differential impact that tax schedule changes have on workers in the same occupation but with different initial tax-related characteristics such as capital income and secondary earnings. When the tax schedule changes, a person with high secondary earnings may experience a different tax change than another worker with the same job but low secondary earnings. By analyzing these relative movements within an occupation, we avoid the confounding factors of tax-driven general equilibrium effects changing wages and amenity provision in an occupation.

The findings in this paper suggest that occupational choice is a component of income tax distortion. We find statistically significant, though economically modest, occupational-choice responses to tax changes. Our preferred estimates suggest a compensated elasticity of 0.05, implying that a 10% increase in the net-of-tax rate causes workers, on average, to switch to an occupation paying 0.5% higher wages. Interestingly, we estimate similar elasticities for both men and women. We also find no evidence that younger workers are more responsive to tax changes than older workers in choosing occupations with different wages and non-taxable amenities.

This paper asks and studies the question, "When net-of-tax rates increase, do workers move to occupations with higher compensating differentials?" To the best of our knowledge, this is the first paper that examines the impact of taxes on the individual's choice of jobs with different compensating differentials. A previous literature has studied the effect of tax changes on the provision of specific amenities. For example, Gruber and Lettau (2004) investigate the tax effect on health insurance provision by employers. However, no study has estimated the tax elasticity of all amenities. We see the results of this paper as direct complements to the tax elasticity of working hours literature. The wage-amenity choice with respect to taxes is a critical component of the individual labor supply response to taxes.

The rest of this paper proceeds as follows. In section 2, we review the existing research. We then present a theoretical framework on the effect of income taxes on the demand for wage and non-taxable amenities in section 3. Section 4 introduces our two-step methodology and explains our identification strategy. In section 5, we discuss the data used in this paper. Section 6 presents the estimation procedure and results, and section 7 concludes.

2 Previous Research

Our paper complements the existing literature on labor supply and taxes. This vast literature is summarized in Hausman (1985) and Blundell and MaCurdy (1999) and focuses primarily on the impact of taxes on number of hours worked. Another set of papers, such as Eissa and Hoynes (2004), examine the effect of taxes on the extensive margin of labor supply, labor force participation. The consensus of the literature is that women appear to change working hours and labor force participation status in response to taxes, whereas prime-age men do not. While working hours and labor force participation are important aspects of labor supply, there are other margins where taxes could play an important role. Feldstein (1997) highlights the importance of understanding other facets of labor supply:

The relevant distortion to labor supply is not only the effect of tax rates on participation rates and hours but also their effect on education, occupational choice, effort, location, and all of the other aspects of behavior that affect the short-run and long-run productivity and income of the individual. Unfortunately, we still know very little about how taxes affect labor supply defined in this broad way.

A related set of studies has looked at the effect of taxes on self-employment and entrepreneurship. Gentry and Hubbard (2002) study the impact of tax progressivity on the decision to become an "entrepreneur." They find evidence suggesting that a progressive tax schedule with imperfect loss offsets discourages entry to entrepreneurship. Bruce (2000, 2002) investigates the link between tax rates and transitions into and out of self-employment. He finds higher marginal tax rates increase the probability of self-employment. He interprets this counter-intuitive finding as evidence of tax evasion among the self-employed.

Few studies have examined the relationship between taxes and occupational choice. Gentry and Hubbard (2004) look at the effect of tax rates and tax progressivity on changing to a self-reported "better" job. They argue that a more progressive tax system reduces the return to job search and discourages upward job mobility. They find that both higher tax rates and increased tax progressivity decrease the probability that a head of household will move to a better job in the coming year.

This paper is also closely related to the literature on the elasticity of taxable income. Feldstein (1999) argues that the compensated elasticity of taxable income is the central parameter needed to calculate the deadweight loss associated with income taxes. Given its importance, many studies have estimated the elasticity of taxable income using different data and empirical strategies.¹ We use a specification that is similar to the one used in Gruber and Saez (2002) and Auten et al. (2008). Our parameter of interest is, theoretically, a component of the overall tax elasticity. We specify this relationship in section 4. We believe that understanding the magnitude of the components is especially important. The tax system can tax different types of income differently so an aggregate elasticity is not sufficient. The component elasticities help us understand the mechanisms through which the distortions occur. The economic consequences can be very different if workers respond to taxes by changing the number of hours they work than if they respond by changing occupations.

3 Theoretical Framework

In this section, we illustrate the intuition behind our empirical test using a simple model. Assume that a worker chooses from a continuum of job options. Each job offers a combination of wage compensation () and non-taxable compensation () where higher non-taxable amenities imply relatively lower wages (), all else equal. The worker values both wages and non-taxable amenities. Let denote the worker's other income, and the total tax liability given taxable income . The worker maximizes his utility over consumption () and non-taxable amenities () subject to his budget constraint.

$\displaystyle \max_{c,n} U(c, n)$

s.t. $\displaystyle c = w(n) + y - T[w(n)+y]$

The first order condition of this maximization problem can be expressed as

FOC: $\displaystyle w'(n)(1-T')=-\frac{U_n}{U_c}$

(1)

First, assume that

is unchanged by tax changes for the worker. Equation (1) suggests that when the tax rate increases, the left hand side of the equation increases, implying that $\frac{U_n}{U_c}$ decreases. Under the standard assumption that the utility function is concave, the demand for

must increase relative to the demand for

. Thus, the relative demand for wage compensation decreases when the tax rate increases.² In practice, tax changes may induce changes to

. Our empirical strategy, however, will account for such general equilibrium effects.

This paper focuses specifically on the individual occupational decision and does not explicitly model the firm-level decisions concerning wages and amenity provision. It is helpful, however, to discuss why an individual may face heterogeneity in in the above model. Variation in amenities can originate from two sources. First, there can be sorting among workers such that some occupations become "high amenity occupations" simply because the workers in those occupations tend to demand lots of amenities. Second, some jobs are, by their nature, high amenity jobs. For example, workers prefer safe working environments and firms can potentially respond to workers' preferences, but it is unlikely that construction workers are ever going to have on-the-job fatality rates as low as accountants. Our model and empirical strategy are agnostic to the reason for or type of amenity heterogeneity.

The key insight of this model is that, for any given after-tax income , we expect $\frac{\partial n}{\partial (1-\tau)}\vert _I <0$ . Since we do not observe , however, our empirical strategy focuses on the relationship between the marginal net-of-tax rate and the choice of wage. Because , $\frac{\partial n}{\partial (1-\tau)}\vert _I <0$ implies $\frac{\partial w}{\partial (1-\tau)}\vert _I >0$ . When a worker's marginal net-of-tax rate increases, we expect to see her move to a higher wage job with fewer amenities, all else equal. This model prediction guides our empirical specification where we study the relationship between the change in the individual's wage and the change in the tax rate, holding the after-tax income constant.

4 A Two-Step Estimation Method

4.1 The Setup of the Two-Step Procedure

The key question that we address in this paper is whether workers move to higher wage jobs when net-of-tax rates increase. Suppose individual worked in occupation at time . At time , she worked in occupation . If we could observe individuals' counterfactual wages in occupations they are not working in, our ideal specification to estimate the magnitude of $\frac{\partial w}{\partial (1-\tau)}\vert _I$ would be the following:

$\displaystyle \ln w_{ijt}- \ln w_{ikt}=\gamma+\beta_1 \ln \left( \frac{1-\tau_{ijt}}{1-\tau_{ik,t-1}} \right) + \beta_2 \ln \left( \frac{z_{ik,t-1}-T_{t}[z_{ik,t-1}]}{z_{ik,t-1}-T_{t-1}[z_{ik,t-1}]} \right) + \nu_{ijt} - \nu_{ikt}$

(2)

where $\tau$ is the marginal tax rate and

is the tax liability under the tax schedule at time

for total pre-tax income

The left-hand side of equation (2) is the wage that individual receives in his new occupation at time relative to the wage he would have received in his old occupation at time . If , then individual worked in the same occupation at both time and , and the dependent variable equals zero. It is important to use the time wage for the old occupation since tax changes potentially have nontrivial general equilibrium effects. To understand the potential general equilibrium effects of taxes in our context, consider an unpleasant job as tax rates increase. There are two possible firm-level responses now that workers want to leave this job. First, the job can become more pleasant. To some extent, however, this might not be possible due to the nature of the job. Alternatively, wages can increase. There is empirical evidence of both of these effects caused by tax changes. Gruber and Lettau (2004) document changes in health insurance provision in response to tax changes. Powell (2009a) estimates wage responses to tax changes in industries with different injury and fatality risks. Because general equilibrium effects may cause wages to adjust from time to , comparing wages in two different time periods will likely result in estimation bias due to confounding general equilibrium effects. By comparing contemporaneous wages in equation (2), we account for the general equilibrium effects without imposing any assumptions on specific labor demand functional forms.

The right-hand side of equation (2) is similar to the Gruber and Saez (2002) specification and separately estimates the substitution and income effects.³ By separately estimating the income effect, we can interpret the coefficient on the marginal tax rate variable ( $\beta_1$ ) as a compensated elasticity. When the marginal net-of-tax rate increases, we expect workers to move to higher wage jobs. An increase in after-tax income should cause workers to move to lower wage jobs due to an increased demand for amenities. Therefore, we expect $\beta_1>0, \beta_2<0$ .

Equation (2) looks at whether tax rate increases cause workers to move to occupations with lower wages and presumably more non-taxable amenities, holding after-tax income constant. In practice, we do not observe $w_{ikt}$ , the wage that individual would have earned at time in occupation had he not switched to occupation . Furthermore, $w_{ijt}$ includes other individual-level responses to taxes, such as effort regardless of occupational choice, that we want to exclude. To address these problems, we use the compensating differentials of these occupations instead of the wages themselves.

The wage received by individual in occupation at time can be decomposed into two parts.

$\displaystyle \ln w_{ijt} = \alpha_{it} + \phi_{it}(n_{ijt})$

(3)

$\alpha_{it}$ is the return to the individual's ability and effort at time

. It represents the wage earned by the individual regardless of occupation and can include behavioral responses to taxes unrelated to job-specific amenities. For example, when tax rates decrease, workers may decide to work harder and earn a higher wage. If this is true regardless of occupation, then we want this effort included in $\alpha_{it}$ . $\phi_{it}(n_{ijt})$ represents the tradeoff between wages and amenities across occupations. A higher $n_{ijt}$ means that the worker receives more amenities in occupation

. As a result, the worker is willing to accept lower wages in occupation

. $\phi_{it}(n_{ijt})$ can be interpreted as the individual-specific compensating differential.

Let $n_{jt}$ denote the average level of amenities received by individuals working in occupation at time and $\phi_{jt}(\cdot)$ the average price function for amenities. If there are $M_{jt}$ workers in occupation at time , then

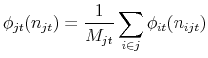$\displaystyle \phi_{jt}(n_{jt})=\frac{1}{M_{jt}} \sum_{i \in j} \phi_{it}(n_{ijt})$

We rewrite the wage equation as

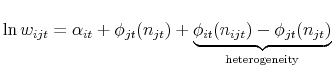$\displaystyle \ln w_{ijt} = \alpha_{it} + \phi_{jt}(n_{jt}) + \underbrace{\phi_{it}(n_{ijt}) - \phi_{jt}(n_{jt})}_{\text{heterogeneity}}$

where $\phi_{jt}(n_{jt})$ is the average compensating differential for occupation

at time

. An individual may receive a compensating differential, $\phi_{it}(n_{ijt})$ , which is different from the occupation average, $\phi_{jt}(n_{jt})$ , for two reasons. First, the worker may receive a different level of amenities ( $n_{ijt} \neq n_{jt}$ ). Second, the worker may face a different price function for amenities ( $\phi_{it}(\cdot) \neq \phi_{jt}(\cdot)$ ). Put differently, a worker may get more amenities than the average worker in an occupation and the worker may get paid a higher wage for a given level of amenities. Our wage model allows for such individual heterogeneity in the compensating differential term within an occupation.

To simplify notation, we define $\phi_{jt} \equiv \phi_{jt}(n_{jt})$ and $\mu_{ijt} \equiv \phi_{it}(n_{ijt}) - \phi_{jt}(n_{jt})$ . The wage equation now becomes

$\displaystyle \ln w_{ijt}=\alpha_{it} + \phi_{jt} + \mu_{ijt}$

(4)

Note that equation (4) places no real restrictions on the wage function and is essentially tautological. The purpose is simply to divide each person's wage into separate components.

Using the compensating differentials in place of wages, we plug equation (4) into equation (2) and get

$\displaystyle \phi_{jt}-\phi_{kt}=\gamma+\beta_1 \ln \left( \frac{1-\tau_{ijt}}{1-\tau_{ik,t-1}} \right) + \beta_2 \ln \left( \frac{z_{ik,t-1}-T_{t}[z_{ik,t-1}]}{z_{ik,t-1}-T_{t-1}[z_{ik,t-1}]} \right) + \epsilon_{ijt}-\epsilon_{ikt}$

(5)

$\phi_{jt}-\phi_{kt}$ is the difference in the compensating differentials between the old and new occupations at time

and should reflect differences in amenity levels. The individual ability term $\alpha_{it}$ conveniently drops out in this equation. If we have measures of $\phi_{jt}$ and $\phi_{kt}$ , we can estimate our parameter of interest $\beta_1$ . Note that the $\mu$ terms are now included in the total residual, $\epsilon$ . It is important to realize that the error term includes this heterogeneity as we must make sure that our instruments, discussed in the next section, are orthogonal to $\mu$ .

Equation (4) cannot be estimated because there is only one observation per person-year and $\alpha_{it}$ is not identified. Instead, we use $\alpha_{it}=\alpha_i+X_{it}'\delta$ and rewrite equation (4) as

$\displaystyle \ln w_{ijt}=\alpha_i+\phi_{jt}+X_{it}'\delta+\mu_{ijt}$

(6)

where

is a vector of age group fixed effects. Because we focus on $(\ln w_{ijt}-\ln w_{ikt})$ and the $\alpha_{it}$ term cancels out, the form of this term is largely irrelevant. Identifying $\alpha_{it}$ would certainly help the precision of our estimates, but it is unnecessary for our purposes. We include the age group fixed effects to improve the precision of the estimated compensating differential terms.

To summarize, we have presented a two-step estimation method to study the effect of tax rate changes on individuals' decisions to choose among occupations with different wages and non-taxable amenities. This method allows us to account for general equilibrium effects and to model wages in a flexible manner. In step one, we estimate equation (6) to obtain a set of compensating differentials.⁴ In step two, we relate these estimated compensating differentials to tax changes.

4.2 Instruments

Our main specification in equation (5) cannot be estimated consistently using ordinary least squares (OLS) because the tax variables are endogenous. Tax rates and tax liabilities are functions of wages and, similarly, compensating differentials. Workers who switch to high wage occupations will see their tax rates and tax liabilities increase. As a result, we may find that increases in taxes correlate with increases in compensating differentials. To solve the endogeneity problem, we need to construct valid instruments for these tax variables.

Gruber and Saez (2002) instrument actual tax rates with predicted tax rates which are a function of a household's initial income and tax schedule changes. We also use tax schedule changes as a shock to tax rates, but we have to go one step further and shut down tax change variation based on initial labor income. When the tax schedule changes, the rates of different brackets change by different amounts. We want to use the fact that workers A and B within an occupation may experience different tax rate changes because they are in different brackets. However, if worker A is in a higher bracket than worker B because he has a higher wage, then this source of variation is problematic for our empirical strategy. A higher wage may imply a higher-than-average compensating differential (a positive $\mu_{ikt}$ ), which is a part of the residual term. Instead, our identification relies on differential tax changes resulting from workers being in different tax brackets due to "other tax-related characteristics" in the initial period. Such tax-related characteristics include marital status, number of dependents, secondary earning, capital income, etc.

To implement this strategy, we create "predicted tax changes" (represented by $\hat{\tau}$ ) and "counterfactual tax changes" (represented by $\tilde{\tau}$ ) using NBER's TAXSIM program. The predicted tax rate is simply the Gruber-Saez instrument. First, we inflate the worker's income to year terms so that his real income remains constant. Then, we find his time tax rate using the inflated income and the time tax schedule. We call this predicted tax rate $\hat{\tau}_{ikt}$ .

The counterfactual tax rate is the tax rate that an individual would experience given his labor income and the initial (non-labor income) tax-related characteristics of other workers in his occupation. For the counterfactual tax rate for individual at time , assume there are people in his occupation at time and index each person by . First, we find the tax rate individual would have faced if he had person 's tax-related characteristics but his own labor income at time for each of the workers. Then we average the hypothetical tax rates. We call this counterfactual tax rate $\tilde{\tau}_{ik,t-1}$ . For the counterfactual tax rate at time , the steps are similar. We inflate the income to time so that the income is constant in real terms and repeat the process using the time tax schedule. We call this counterfactual tax rate $\tilde{\tau}_{ikt}$ .

To summarize, we have obtained the predicted tax rate $\hat{\tau}_{ikt}$ , which is the tax rate based on own initial labor and non-labor income. We have also obtained the counterfactual tax rates $\tilde{\tau}_{ik,t-1}$ and $\tilde{\tau}_{ikt}$ , which are the tax rates based on own labor income and others' non-labor income. In addition, we have the actual tax rate $\tau_{ik, t-1}$ faced by individual at time .

		$\displaystyle \hat{\tau}_{ik,t-1}=\tau_{ik,t-1}$
		$\displaystyle \hat{\tau}_{ikt}=E\left[\tau_{ikt}\vert\mbox{Labor Income}_{ik,t-1},\mbox{Other Income}_{ik,t-1}\right]$
		$\displaystyle \tilde{\tau}_{ik,t-1}=\frac{1}{M} \sum_{m=1}^{M} E\left[\tau_{mk,t-1}\vert\mbox{Labor Income}_{ik,t-1},\mbox{Other Income}_{mk,t-1}\right]$
		$\displaystyle \tilde{\tau}_{ikt}=\frac{1}{M} \sum_{m=1}^{M} E\left[\tau_{mkt}\vert\mbox{Labor Income}_{ik,t-1},\mbox{Other Income}_{mk,t-1}\right]$

Our instrument for the tax rate change variable is

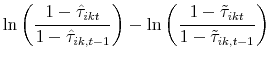$\displaystyle \ln \left( \frac{1-\hat{\tau}_{ikt}}{1-\hat{\tau}_{ik,t-1}} \right) - \ln \left( \frac{1-\tilde{\tau}_{ikt}}{1-\tilde{\tau}_{ik,t-1}} \right)$

The first term refers to individual

's predicted tax rate change. The second term refers to the average tax rate change the worker would have experienced given his initial labor income and the initial "other tax-related characteristics" of other workers in his occupation. The difference between the two represents the predicted tax rate change experienced by individual

solely due to his initial tax-related characteristics other than labor income. Similarly, our instrument for the after-tax income change variable is

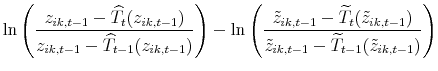$\displaystyle \ln \left( \frac{z_{ik,t-1} - \widehat{T}_t(z_{ik,t-1})}{z_{ik,t-1} - \widehat{T}_{t-1}(z_{ik,t-1})} \right) - \ln \left( \frac{\tilde{z}_{ik,t-1} - \widetilde{T}_t(\tilde{z}_{ik,t-1})}{\tilde{z}_{ik,t-1} - \widetilde{T}_{t-1}(\tilde{z}_{ik,t-1})} \right)$

Thus, our tax instruments calculate how each person's taxes change relative to how his taxes would change if he had the same "other tax-related characteristics" as other workers in the occupation. The variation in the tax instruments originates from tax schedule changes interacting with workers' "other tax-related characteristics." Compared to the existing tax elasticity literature, our instruments eliminate the tax change variation based on workers' initial labor income and provide a cleaner experiment. The literature has a dependent variable of all taxable income and uses differential tax changes based on initial taxable income as the identifying variation. Our dependent variable is a labor measure, and we use tax changes based on the part of initial taxable income not attributed to labor income as the identifying variation.

4.3 Further Discussion of the Methodology

There are several benefits to our two-step methodology for studying the impact of taxes on occupational choice. We believe there would be a natural tendency to study how taxes affect job turnover using, for example, an indicator variable for "changing jobs." This alternative specification is an instructive baseline to discuss the benefits of our approach.⁵

First, data on occupations can be very noisy and some "job changes" are potentially the same job categorized differently in various years. Using a dummy variable for "changing jobs" would be econometrically problematic because these coding errors cannot be modeled as classical measurement error. Our methodology assigns compensating differentials to each occupation and, consequently, turns these coding errors into classical measurement error in the dependent variable. While our strategy benefits from more accurate coding systems and we carefully considered the level of our coding system to minimize misclassification errors, inaccuracies should not bias the estimation results in our model.

Second, our methodology flexibly accounts for general equilibrium effects. At no point did we specify any functional form concerning the general equilibrium impact of taxes on wages or amenities. Furthermore, there are substantial wage trends occurring during the sample period, but our methodology does not require us to model them because we compare occupational choices made by workers in the same job at the same time.

Third, we explicitly estimate a parameter of economic interest. This point can best be illustrated by introducing an instructive framework. Denote as the total income, which is the sum of labor income and capital income . Denote and as the share of labor income and capital income respectively. As discussed before, a vast literature has attempted to estimate the elasticity of taxable income with respect to the net-of-tax rate $\epsilon_{I,1-\tau}$ . This aggregate elasticity is a weighted average of the labor income elasticity and capital income elasticity:

$\displaystyle \epsilon_{I,1-\tau} = \epsilon_{L,1-\tau}s_L + \epsilon_{K,1-\tau}s_K$

Labor income can be expressed as where is the wage and is number of hours worked. Plugging in equation (3), we can write the labor income elasticity $\epsilon_{L,1-\tau}$ as

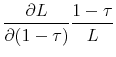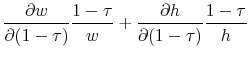$\displaystyle \frac{\partial L}{\partial (1-\tau)} \frac{1-\tau}{L}$	$\displaystyle =$	$\displaystyle \frac{\partial w}{\partial (1-\tau)} \frac{1-\tau}{w} + \frac{\partial h}{\partial (1-\tau)} \frac{1-\tau}{h}$
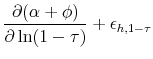	$\displaystyle =$	$\displaystyle \frac{\partial (\alpha+\phi)}{\partial \ln (1-\tau)} + \epsilon_{h,1-\tau}$
	$\displaystyle =$	$\displaystyle \epsilon_{w,1-\tau}\vert _{\phi} + \epsilon_{w,1-\tau}\vert _{\alpha} + \epsilon_{h,1-\tau}$

The above equation indicates that the elasticity of labor income consists of three components. The first component is the elasticity of the individual-specific return ( $\alpha$ ). For example, workers may decide to work harder when the tax rate changes, so we can think of this term as an elasticity of "effort." The second component is the choice of non-taxable amenities ( $\phi$ ). This is the margin we study. The third component is the hours worked. By focusing on wages and compensating differentials, we are able to quantify the relative importance of $\epsilon_{w,1-\tau}\vert _{\alpha}$ in the tax elasticity of labor income. In contrast, the estimates from the alternative specification cannot be easily interpreted in the context of labor income elasticity.

Like most of the labor supply and tax literatures, we have modeled the individual response in a static framework. One may be concerned that workers adjust their current labor supply not only to the current tax rate but also to the tax rates of other brackets which, they believe, they will be subject to in the future. In other words, "future taxes" is an omitted variable and may bias our estimates. Recall that our experiment is to compare one worker with high secondary earnings to another worker in the same job with low secondary earnings before and after a tax change which differentially affects their tax brackets. These two workers may expect that, in the future, they'll be in different tax brackets than they currently are in and make current occupational choice decisions based on that expectation. As long as these two workers' expectations of their "future brackets" do not change in a systematic manner relative to each other, our estimates will not be biased. Relative to the existing literature which has tended to ignore future tax rates entirely, our empirical strategy should be robust to individuals' dynamic responses to tax changes.

4.3.1 Sorting and Matching

In our two-step methodology, we estimate the empirical compensating differential for each occupation and year. The empirical compensating differentials vary across occupations for two reasons. First, they vary because of variation in the "amenity level" of the occupations in that year. Second, they vary in the market value of those amenities. The market value is partially a function of the preferences of the workers in that occupation. Workers are likely to have heterogeneous preferences for specific amenities, and they may sort into different occupations based on these preferences. For example, teachers may value a decrease in on-the-job injury rates differently than engineers value the exact same decrease. We are not using the labor market's average valuation of occupation safety. Instead, we care about the empirical valuation of occupation safety and all other amenities among teachers and, separately, among engineers. By remaining agnostic about the driving forces of the compensating differentials, our method allows the estimated values of the amenities to be different if the market prices vary across occupations. The relevant metric, then, is the difference in compensating differentials faced by the worker. This is the market value of the amenities, not the average value placed on such amenities by the general population. Thus, our strategy uses the right measure for the dependent variable.

It is also worth emphasizing that the dependent variable in specification (5) is not the difference in compensating differentials of two random occupations, but the difference for the new occupation and the old occupation chosen by individual . Such a "selection," however, should not introduce bias in our estimates. The individuals in an occupation are likely good fits for that occupation relative to the average worker in the labor market. But the individual wage component, $\mu_{ijt}$ , is the individual's "fit" relative to the other workers in the occupation. On average, there should be no systematic bias introduced at the occupation level. In summary, our model allows for both "sorting" and "matching" in the labor market. We simply use the empirical compensating differential as a summary measure of the additional wages paid to a worker who has already (1) sorted into the occupation based on amenity preferences and (2) matched to a job which is a good fit.

This empirical strategy may not seem transparent or intuitive because it does not study any specific non-taxable amenities. Unfortunately, no methodology that seeks to study the full effect of taxes on job choice can do so transparently, due to the lack of a comprehensive measure of all job amenities. We believe that arriving at an elasticity of the full compensating differential is worth this cost since it informs us of the complete job choice response with respect to taxes.

5 Data

We use the Panel Study of Income Dynamics (PSID), a longitudinal data set containing household- and individual-level variables on a wide range of topics. Starting with the 1981 data, the PSID provides consistent occupation and industry codes using the 1970 3-digit Census coding. After the 1997 survey, the PSID becomes a biannual survey and we can no longer observe individuals' annual income in a continuous manner. Our final data set, therefore, includes the years 1981-1997. We limit our data set to workers between the ages of 25 and 55. We exclude the self-employed from the sample because they may face a very different set of amenities than other workers in the same occupation. In our main specification, we define and to be three years apart. We also try alternative time intervals as robustness checks. In all analysis, we use sample weights to obtain nationally-representative estimates.

There are three sets of variables in the PSID that we use in our analysis. The first set includes income and family composition variables. NBER's TAXSIM program estimates the tax liabilities and marginal tax rates given these variables. Butrica and Burkhauser (1997) show that the tax rates and tax liabilities calculated by NBER's TAXSIM are similar to tax burden values supplied by the PSID staff from 1980 through 1991, the last year the PSID staff provided such information. As shown in Table 1, the average household income in our sample is $57,056 in 1997 dollars. The average tax liability faced by PSID respondents, which is the sum of federal, state, and half of the FICA taxes, is $14,813 in 1997 dollars. The average marginal tax rate is 35.2% in the sample.

Second, the PSID provides detailed information on labor supply. We have information on the hourly wage rate for each worker in each year, which is used in the estimation of the compensating differentials. Table 1 shows that the average hourly wage is $17.35 in 1997 dollars in the analysis sample.

Third, the PSID contains 3-digit occupation and industry codes from the 1970 Census coding system. We use the occupation and industry codes that refer to each person's main job. One concern with the 3-digit coding system is that it may be too detailed and have a great deal of misclassification problems. For example, "Machine operatives, miscellaneous specified," "Machine operatives, not specified," "Miscellaneous operatives," and "Not specified operatives" are four different occupations under the 3-digit coding system. If we use this coding system, many of the observed transitions between occupations are likely to be misclassifications. To minimize these errors while still capturing meaningful transitions between jobs with different non-taxable amenities, we categorize workers by the 2-digit occupation codes⁶ interacted with the 1-digit industry codes. We believe that it is important and interesting to distinguish the same occupation by industry. For example, accountants in the finance industry and accountants in public administration may receive very different amenities. In addition, this type of job transition may be relatively easy to make, providing a rich source of occupational changes in response to taxes. Some occupation-industry combinations are not possible. In the end, we are left with 115 occupation-industries. In the rest of this paper, we refer to occupation-industry combinations simply as "occupations."

Panel A of Table 2 lists the most frequent occupation changes observed in our data. Many of the listings occur twice, and the original jobs and new jobs look similar. It is possible that these observed transitions are driven by coding errors in the data. In this case, specifications using an indicator variable for "changing jobs" as the dependent variable would suffer biases due to non-classical measurement errors on the left-hand side. It is also possible that workers freely move across similar jobs and these observed transitions are real. Panel B of Table 2 lists the most frequent transitions as a percentage of the original occupation population.

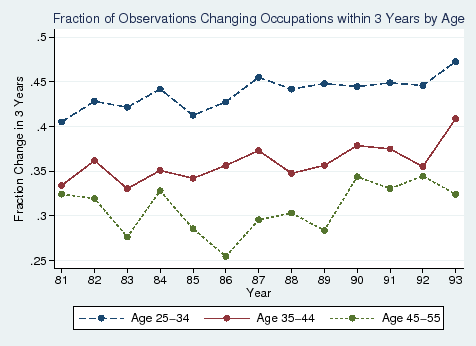
On average, we observe 38.2% of the respondents change their occupations within the next three years. We are not the first to find such a large occupation change rate in the PSID. Kambourov and Manovskii (2009) provide an extensive discussion on this issue. The possibility of misclassification is high. As mentioned before, while misclassifications are unfortunate, they should not bias our estimates because they are transformed into classical measurement error in the dependent variable in our model. Figure 1 shows the occupation change rate across years by age group. It is reassuring that the younger workers appear to have higher occupational change rates than older workers.

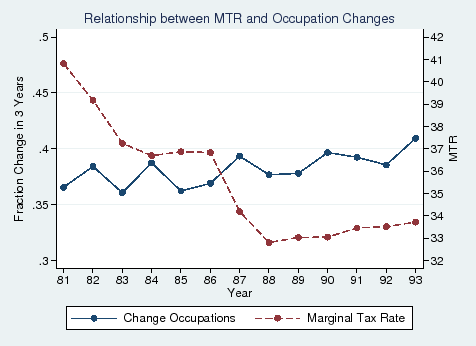
In Figure 2, we graph the sample-average marginal tax rate and occupation change rate together. We are not suggesting that any relationship from this graph should be interpreted as causal. The overall occupation change rate during the sample period remains relatively stable. The Economic Recovery Tax Act of 1981 and the Tax Reform Act of 1986 are the major tax changes during our sample period. Because they both generated significant differential tax changes, they are the main identifying forces of our estimation strategy.

6 Estimation Results

6.1 Estimating Compensating Differentials

As introduced in section 4, the first step of our two-step methodology is to obtain compensating differentials for each occupation in each year by estimating the following equation:

$\displaystyle \ln w_{ijt}=\alpha_i+\phi_{jt}+X_{it}'\delta+\mu_{ijt}$

where $\alpha_i$ is an individual fixed effect and $X_{it}$ is a vector of age-group fixed effects. We require an occupation-year cell to contain at least 5 observations to be included in the sample. We use the PSID sample weights and cluster the standard errors at the individual level when estimating this equation.

Estimating the above equation produces a full set of estimated compensating differentials ( $\hat{\phi}_{jt}$ ). Our measure of compensating differentials is a summary statistic of all non-taxable amenities associated with an occupation and the market value of those amenities. Since we cannot create a full list of all amenities, it would be impossible to know the true compensating differential function. Furthermore, the value placed on these amenities may vary based on workers' preferences, implying that a cross-sectional difference in any specific amenity may not correlate with differences in the wages. As a result, it is impossible to verify whether $\hat{\phi}_{jt}$ is the "right" compensating differential estimate. However, there are ways for us to indirectly check whether these estimates are sensible.

We previously presented the most frequent occupation transitions observed in the sample in Table 2. Because of the apparent fluidity between some occupations, we would think that these occupations may have very similar compensating differentials. We find it comforting that this seems to, in fact, be the case. For example, the two most frequent transitions are between "Operatives (Manufacturing)" and "Craftsmen (Manufacturing)." "Operatives (Manufacturing)" is estimated to have the 47th (out of 115) highest average compensating differential while "Craftsmen (Manufacturing)" has the 45th highest. The similarity of these estimates suggests that these jobs are close substitutes. Additionally, the most frequent transition as a fraction of original occupation population is the move from "Accountants (Finance)" to "Managers (Finance)." These two occupations also have very similar compensating differentials as "Accountants (Finance)" are ranked 36th while "Managers (Finance)" are ranked 39th.

We can also check the internal consistency of the compensating differential estimates. It is not necessary that the compensating differentials for occupations remain constant over time. Firm-level responses and worker re-sorting can change the compensating differential for an occupation from one year to the next. However, the compensating differential of the same occupation should have some correlation over time since occupations have a certain level of fixed characteristics. Thus, we estimate the following equation for all .

$\displaystyle \hat{\phi}_{jt}=\lambda + \rho \hat{\phi}_{js} + \zeta$

(7)

The OLS estimates of $\rho$ may be biased towards 0 because of measurement error in the explanatory variable. The obvious candidates for instruments are the lags (or leads) of the predicted compensating differentials. Table 3 presents the IV estimates of $\rho$ . We use $\hat{\phi}_{j,s-1}$ as the instrument for $\hat{\phi}_{js}$ when

. When

and

, we use $\hat{\phi}_{j,s+1}$ . When

and

, we use $\hat{\phi}_{j,s+2}$ . Note that the choice of leads or lags does not change the main conclusions of this exercise. The average 1-year relationship (i.e. the coefficient on the diagonal) is 0.962 in the IV estimates, suggesting occupations have relatively stable predicted compensating differentials over time. Overall, the coefficients shown in Table 3 suggest that the estimated compensating differentials are reasonable.

6.2 Estimating the Effect of Tax Changes

The second step of our two-step estimation procedure is to regress the change in predicted compensating differentials on tax changes. Define $\hat{\phi}^{i}_{jt}$ as the compensating different for individual 's chosen occupation at time , and $\hat{\phi}^{i}_{kt}$ as the compensating differential at time for individual 's previous occupation . Our main specification is

$\displaystyle \hat{\phi}^{i}_{jt}-\hat{\phi}^{i}_{kt} = \lambda_{kt} + X'_{i, t-1}\Pi + \beta_1 \ln \left( \frac{1-\tau_{ijt}}{1-\tau_{ik,t-1}} \right) + \beta_2 \ln \left( \frac{z_{ik,t-1}-T_{t}[z_{ik,t-1}]}{z_{ik,t-1}-T_{t-1}[z_{ik,t-1}]} \right) + \epsilon_{ijt}-\epsilon_{ikt}$

(8)

where $\lambda_{kt}$ are occupation-year fixed effects that account for the general equilibrium effects experienced by everyone in the original occupation-year. $X_{i,t-1}$ is a vector of control variables, including race, sex, marital status, education, number of dependents, job tenure, (job tenure)

, and age group fixed effects. When the net-of-tax rate increases, wages become relatively more valuable to workers and workers tend to move to high wage occupations. When the after-tax income increases, the demand for non-taxable amenities should increase and workers tend to move to low wage occupations. Therefore, we expect $\beta_1$ to be positive and $\beta_2$ to be negative.

As mentioned in section 4, we use instrumental variables to deal with the potential endogeneity problem associated with the tax variables. The underlying experiment implied by our instruments is to compare the behavior of a worker who experiences a large tax increase (for reasons unrelated to the heterogeneity in the received compensating differential) relative to the other workers in his occupation. This experiment is more intuitive when we control for occupation-year fixed effects. The inclusion of these fixed effects allows us to compare the relative behavior of one individual to other workers in the same occupation. We should highlight that the inclusion of $\lambda_{kt}$ makes the estimation of (8) equivalent whether the dependent variable is $\hat{\phi}^{i}_{jt}-\hat{\phi}^{i}_{kt}$ or $\hat{\phi}^{i}_{jt}$ .

Note that the occupation-year fixed effect term also accounts for any common or "typical" job changes for people in that occupation-year. If most workers in that occupation-year were, for example, going to move to a higher wage job regardless of the tax change, the fixed effect term will pick it up. We are defining the $\phi$ terms as "compensating differentials," but it is possible that there are non-amenity forces or simple estimation errors included in the estimates of $\phi$ . These "other factors" are only problematic if they correlate with the tax changes. The inclusion of the occupation-year fixed effects makes this potential problem much less likely because the "other factors" must disproportionately affect the workers experiencing relatively larger tax changes than other workers in the same occupation. In other words, the correlation between the tax changes and the errors in the compensating differentials must occur within the occupation-year for our identification strategy to fail.

The dependent variable is equal to 0 for any person who does not change occupations. Essentially, our specification simultaneously examines whether people change jobs when taxes changes and what "direction" and "magnitude" that they move in terms of the compensating differential. These non-movers are an important component of the overall elasticity. If people simply do not change occupations in response to taxes, we want to capture that in our estimate.

The dependent variable, the difference in compensating differentials, is estimated rather than observed. In the second step of our estimation, we use the variance-covariance matrix of the first-step regression to adjust the sample weights. Specifically, we weight each observation by the inverse of the standard error of the dependent variable. In addition, we also incorporate the PSID weights to ensure that our sample is nationally representative.

Because our sample observations are not independent of each other, we need to adjust the estimated standard errors accordingly. The PSID is a panel data set, so we must adjust the standard errors by clustering at the individual level. Furthermore, we estimate compensating differentials for each occupation in each year, and these compensating differentials appear to be serially correlated. Therefore, we also adjust the standard errors by clustering at the occupation level. We use the multi-way clustering procedure introduced by Cameron et al. (2006) to account for clustering at both the individual and occupation levels.

6.2.1 Illustrative Exercise

Before presenting our main estimates, we do a heuristic exercise to illustrate the thought experiment behind our estimation strategy. We divide the sample into workers that our instrument predicts will experience a tax rate increase relative to other workers in their occupation-year and workers that our instrument predicts will experience a relative tax rate decrease. Since most predicted tax rate changes in our data are rather small, we only use the top 25% predicted tax rate increases and top 25% predicted tax rate decreases for this exercise.⁷ We then look at whether these people change to a higher compensating differential job, do not change jobs, or move to a lower compensating differential job. We are interested in the "difference" in the percentage of workers moving to higher wage occupations and lower wage occupations. We also re-scale these differences by the implicit "first stage" to get the correct estimate.⁸

There are several limitations to this exercise. Most importantly, the exercise completely ignores the income effect. Workers that experience a tax increase may want to move to a low amenity job simply because their after-tax income has decreased, biasing this exercise against finding an effect. Second, estimation error in the predicted compensating differentials may cause bias because categories are used here. Third, this exercise only looks at the direction of the tax change and the job change. It does not relate the magnitude of the tax change to the job change.

Table 4 reports the results of this exercise. We indeed find evidence that workers move to higher wage occupations when the instrument predicts a relative decrease in the marginal tax rate. The magnitude suggests that a tax change could result in 3-4% of the entire labor force shifting jobs. Given that many people are not changing jobs and many of the job changes we do see are potentially not real or not made for tax reasons (i.e. natural job transitions), this number is rather large relative to the overall percentage of occupation changes. When compared to the entire labor force, however, the results suggest that we should expect the total tax distortion to be rather modest.

6.2.2 Regression Results

Although the above exercise highlights the intuition behind our IV strategy, the IV estimates provide a more rigorous measure of the impact of tax changes on choices over occupations with different amenities. The first column of Panel A in Table 6 presents the OLS estimates of the key coefficients. In our model, we hypothesize that workers will choose higher wage jobs when their net-of-tax rate increases and $\beta_1$ should be positive. However, the OLS estimate of $\beta_1$ is negative and statistically significant. This finding is consistent with our suspicion that the change in the net-of-tax rate is endogenous. For example, a worker who moves to a higher wage job will probably also face a higher tax rate because of his higher income. We need to use the instruments constructed in section 4 to isolate the causal effect of tax changes on occupational choice.

Table 5 presents the first stage results for our main specification. We report the relevant coefficients and Shea's Partial statistic which indicates the strength of the first stage. Note that our instruments strongly predict the endogenous variables.⁹ The second column in Table 6 presents the IV estimates. Unlike the OLS estimates, the IV estimates of $\beta_1$ have the expected sign. Its magnitude suggests that a 10% increase in the net-of-tax rate would cause individuals to move to an occupation with a wage that is 0.49% higher. This elasticity is economically modest, though statistically significant. The IV estimate of $\beta_2$ , the effect of changes in after-tax income on occupation choices, is small and statistically insignificant.

It is well-known that male and female labor markets may have different dynamics. Hence, we study the male and female samples separately in addition to studying the full PSID sample. Note that whenever we use a different sub-sample in this paper, we estimate the compensating differentials using only the relevant sub-sample. In other words, we estimate compensating differentials separately by gender in these regressions. Also, the tax instruments are formed using only the relevant sub-sample. The gender-specific IV estimates suggest that women and men are equally responsive to tax changes when it comes to wage-amenity decisions.¹⁰ The literature on the tax elasticity of working hours and labor force participation typically finds that women are more responsive than men. However, it is not clear that this result should extend to the wage-amenity margin. Men's choice sets may have a higher variation in non-taxable amenities than women's. For example, Hersch (1998) documents that jobs with high injury rates are male-dominated. This difference suggests that men may be actively choosing between safe and risky jobs while women are less likely to make a job decision along the safety margin, regardless of taxes.

6.3 Robustness Checks and Extensions

We have so far focused on a 3-year interval length. Even though the 3-year interval length is our preferred specification because it allows the worker ample time to respond to taxes by searching and moving to a different occupation, we believe the adjustment time itself is of interest. In Table 7, we present IV results with 1-, 2-, 3- and 4-year intervals. In the full sample, the estimate of $\beta_1$ is small and statistically insignificant in the 1-year interval specification. However, it is positive and statistically significant in the 2-, 3-, and 4-year specifications. This pattern suggests that the occupation adjustment is not immediate, but that by the second year, the full adjustment has occurred. The same pattern holds for women. For men, the adjustment appears to be immediate as the 1-year specification produces an estimate in line with the other estimates.

We might think that the coefficients of interest vary by age. We cut the sample into "young" (25-34) and "old" (35-55) to explore the potential heterogeneity across age groups. Table 8 presents the IV estimation results. For simplicity, we only report the coefficient on the marginal net-of-tax rate, though the estimated specification is the same. Again, the compensating differentials and the instruments are generated using only the sub-sample in question. Overall, the results provide mixed evidence. In the full sample and the female sample, we find evidence suggesting that older workers are more responsive to tax changes than younger workers when looking at 3- or 4-year intervals. In the male sample, we find young workers responding more for some interval lengths, but not for others. The main conclusion drawn from Table 8 is that our main results are not being driven by young workers, as some might expect. Even though young workers are more likely to change occupations, as shown in Figure 1, they do not seem to be more responsive to taxes when making these changes. This may be because older workers understand their marginal tax rates better than younger workers.

Finally, we look at the effect of our weighting method on the estimates. Recall that we weight each observation by the inverse of the standard error of the estimated compensating differentials. In Table 9, we do not use these weights obtained from the first step of the two-step estimation procedure. We do, however, still use the PSID sample weights. The results are largely unchanged, although the standard errors are slightly bigger. This robustness check suggests that our weighting procedure, while improving the precision of our estimates, is not driving the main results as we would come to the same conclusions without the weighting.

7 Conclusion

Taxes can affect occupational choice by distorting the return to monetary wages relative to non-taxable amenities. In this paper, we study the effect of tax changes on wage-amenity decisions where amenities are defined in a broad and agnostic manner. Non-taxable amenities of a job include both observable characteristics such as health insurance provision and unobservable characteristics such as stress and workplace environment. We introduce a two-step estimation procedure and use compensating differentials as the summary statistic of the non-taxable amenities associated with a job. We believe that this methodology offers a fruitful means of characterizing the amenity decision faced by workers and can be extended to other contexts where occupational choice or non-taxable amenities play a significant role.

We find that when the net-of-tax rate increases, workers move to higher wage jobs, implicitly sacrificing non-taxable amenities. We estimate a statistically significant compensated elasticity of 0.05, suggesting that a 10% increase in the marginal net-of-tax rate leads workers to choose an occupation with a 0.5% higher wage. In related work, Powell (2009b) focuses on the tax elasticity of labor income and reports a mean elasticity of 0.5. Our paper, then, suggests that the wage-amenity tradeoff accounts for 10% of the overall labor tax distortion. While our estimated elasticity is modest, it is possible that the true long-term distortion is larger than this elasticity suggests.

This paper contributes to the tax literature on several fronts. First, we look beyond working hours and labor force participation and provide evidence on other aspects of labor supply. Second, this paper complements existing studies by looking at all non-taxable amenities as opposed to one single dimension of amenities. Third, we use identification sources unavailable to the existing tax literature, resulting in a potentially cleaner experiment. Our instruments can be easily applied to other studies examining the tax effect on labor market outcomes. In summary, we believe that occupational choice is an important mechanism of distortion resulting from income taxes that has been generally ignored by the literature. Our paper focuses on this important margin and provides critical evidence for the understanding of how taxes impact economic welfare.

Appendix A: Models with Intensive Labor Supply

Adding the intensive labor supply decision ( = hours worked) does not change the FOC for the wage-amenity tradeoff in a meaningful way. We can model amenities in two different ways. First, we can think of each job as having a fixed level of amenities . The worker maximizes a utility function which now contains hours worked. Previously, we used to represent labor income. After adding the intensive margin of labor supply in the model, we think of labor income as equal to the wage $\omega(n)$ times hours worked :

$\displaystyle \max_{c,h,n} U(c, h, n)$

s.t. $\displaystyle c = \omega(n)h + y - T[w(n)h+y]$

The first order conditions of this maximization problem can be expressed as

		FOC1: 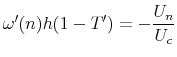$\displaystyle \omega'(n)h(1-T') = -\frac{U_n}{U_c}$
		FOC2: 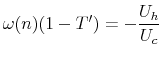$\displaystyle \omega(n)(1-T') = -\frac{U_h}{U_c}$

Note that the FOC regarding to the choice of non-taxable amenities is essentially the same as the model shown in section 3 of the paper.

Alternatively, we can think of amenity consumption as proportional to the number of hours worked. For example, a safe working environment decreases fatality rates per hour. Each hour worked, then, is extra consumption of this safety. We can model amenities as instead of :

$\displaystyle \max_{c,h,n} U(c, h, nh)$

s.t. $\displaystyle c = \omega(n)h + y - T[w(n)h+y]$

The first order condition of this maximization problem can be expressed as

		FOC1: 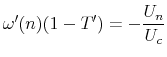$\displaystyle \omega'(n)(1-T') = -\frac{U_n}{U_c}$
		FOC2: 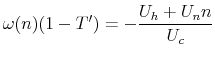$\displaystyle \omega(n)(1-T') = -\frac{U_h+U_nn}{U_c}$

The relevant FOC is, again, essentially the same.

References

Auten, Gerald, Robert Carroll, and Geoffrey Gee. 2008. "The 2001 and 2003 Tax Rate Reductions: An Overview and Estimate of the Taxable Income Response." National Tax Journal, 61(3): 345-364.

Blundell, Richard, and Thomas MaCurdy. 1999. "Labor supply: A Review of Alternative Approaches." In Handbook of Labor Economics, Vol 3, ed. Orley Ashenfelter and David Card, 1559-1695. New York: Elsevier.

Bruce, Donald. 2000. "Effects of the United States Tax System on Transitions into Self-Employment." Labour Economics, 7(5): 545-574.

Bruce, Donald. 2002. "Taxes and Entrepreneurship Endurance: Evidence from the Self-Employed." National Tax Journal, 54(1): 5-24.

Butrica, Barbara A., and Richard V. Burkhauser. 1997. "Estimating Federal Income Tax Burdens for Panel Study of Income Dynamics (PSID) Families Using the National Bureau of Economic Research TAXSIM Model." Syracuse University Center for Policy Research Aging Studies Program Paper 12.

Cameron, Colin A., Jonah B. Gelbach, and Douglas L. Miller. 2006. "Robust Inference with Multi-way Clustering." NBER Technical Working Paper 327.

Eissa, Nada, and Hilary Hoynes. 2004. "Taxes and the Labor Market Participation of Married Couples: The Earned Income Tax Credit." Journal of Public Economics, 88(9-10): 1931-1958.

Feldstein, Martin. 1997. "How Big Should Government Be?" National Tax Journal, 50(2) 197-213.

Feldstein, Martin. 1999. "Tax Avoidance And The Deadweight Loss Of The Income Tax." The Review of Economics and Statistics, 81(4): 674-680.

Gentry, William M., and R. Glenn Hubbard. 2002. "Tax Policy and Entry into Entrepreneurship." Mimeograph, Columbia University.

Gentry, William M., and R. Glenn Hubbard. 2004. "The Effects of Progressive Income Taxation on Job Turnover." Journal of Public Economics, 88(11): 2301-2322.

Gruber, Jonathan, and Michael Lettau. 2004. "How Elastic is the Firm's Demand for Health Insurance?" Journal of Public Economics, 88(7-8): 1273-1293.

Gruber, Jonathan, and Emmanuel Saez. 2002. "The Elasticity of Taxable Income: Evidence and Implications." Journal of Public Economics, 84(1): 1-32.

Hausman, Jerry A. 1985. "Taxes and Labor Supply." In Handbook of Public Economics, Vol 1, ed. Alan J. Auerbach and Martin Feldstein, 213-263. New York: Elsevier.

Hersch, Joni. 1998. "Compensating Differentials for Gender-Specific Job Injury Risks." American Economic Review, 88(3): 598-627.

Kambourov, Gueorgui, and Iourii Manovskii. 2009. "Occupational Specificity of Human Capital." International Economic Review, 50(1): 63-115.

Powell, David M. 2009. "Using Income Tax Changes to Identify the Value of a Statistical Life." PhD diss. MIT.

Powell, David M. 2009. "The Tax Elasticity of Labor Income Throughout the Income Distribution: The Introduction of a Fixed Effects Quantile Estimator." PhD diss. MIT.

Saez, Emmanuel, Joel Slemrod, and Seth H. Giertz. 2009. "The Elasticity of Taxable Income with Respect to Marginal Tax Rates: A Critical Review." NBER Working Paper 15012.

Figure 1:

Figure 2:

Table 1: Summary Statistics of the PSID Analysis Sample
	Mean	SD
Change Occupation within 3 years (%)	38.2	48.6
Wage ($)	17.35	11.10
Age	37.2	7.5
Male (%)	50.4	50.0
Married (%)	70.3	45.7
Less than High School (%)	10.1	30.2
High School Graduates (%)	39.5	48.9
Some College (%)	22.0	41.5
College Graduates (%)	28.3	45.1
Total Income ($)	57,056	36,490
Marginal Tax Rate (%)	35.2	9.3
Tax Liability ($)	14,813	13,851

Note: N=42,310. Wage, total income, and tax liability are in 1997 dollars.

Table 2: Most Frequent Occupation (Industry) Changes with 3 Years
A. Most Frequent in Number of Observations
Original	New
Operatives (Manufacturing)	Craftsmen (Manufacturing)
Craftsmen (Manufacturing)	Operatives (Manufacturing)
Sales (Retail)	Managers (Retail)
Managers (Retail)	Sales (Retail)
Operatives (Manufacturing)	Unskilled Laborers (Manufacturing)
Unskilled Laborers (Manufacturing)	Operatives (Manufacturing)
Service Workers (Service)	Clerical (Service)
Clerical (Service)	Managers (Service)
Secretaries (Service)	Clerical (Service)
Service Workers (Service)	Other Medical (Service)

Table 2: Most Frequent Occupation (Industry) Changes with 3 Years
B. Most Frequent in Percentage of Workers in Original Occupation
Original	New	%
Accountants (Finance)	Managers (Finance)	30.6
Sales (Services)	Managers (Services)	30.2
Unskilled Laborers (Manufacturing)	Operatives (Manufacturing)	29.4
Sales (Manufacturing)	Sales (Retail)	29.3
Foremen (Construction)	Craftsmen (Manufacturing)	27.7

Note: Must have at least 40 observations in the original occupation to be considered in Panel B.

Table 3: Pairwise Comparisons of Predicted Compensating Differentials: IV Estimates
	1985	1986	1987	1988	1989	1990	1991	1992	1993	1994	1995	1996
1984	0.904***	0.954***	1.012***	1.079***	0.385**	0.167	-0.459	0.113	-0.014	0.083	-0.353	0.17
1984	(0.208)	(0.219)	(0.255)	(0.283)	(0.166)	(0.232)	(0.307)	(0.191)	(0.210)	(0.210)	(0.227)	(0.213)
1985	.	1.056***	0.734***	0.622***	0.672***	-0.014	0.458	-0.231	-0.077	0.343	-0.531**	-0.122
1985	.	(0.242)	(0.202)	(0.201)	(0.210)	(0.236)	(0.315)	(0.201)	(0.217)	(0.230)	(0.251)	(0.222)
1986	.	.	1.138***	1.228***	0.667**	0.228	-0.43	0.242	0.055	0.01	-0.478	0.417
1986	.	.	(0.235)	(0.325)	(0.276)	(0.282)	(0.332)	(0.255)	(0.278)	(0.253)	(0.299)	(0.291)
1987	.	.	.	0.648***	0.281*	0.035	-0.155	-0.229	-0.247	0.033	-0.166	0.122
1987	.	.	.	(0.128)	(0.144)	(0.164)	(0.194)	(0.144)	(0.158)	(0.159)	(0.178)	(0.176)
1988	.	.	.	.	0.339**	0.268*	-0.097	-0.011	-0.259	0.118	0.095	0.379**
1988	.	.	.	.	(0.147)	(0.151)	(0.202)	(0.132)	(0.164)	(0.149)	(0.169)	(0.159)
1989	.	.	.	.	.	0.826***	0.624*	0.373	0.143	1.056***	0.667**	1.184***
1989	.	.	.	.	.	(0.292)	(0.339)	(0.256)	(0.278)	(0.308)	(0.312)	(0.332)
1990	.	.	.	.	.	.	1.334***	0.43	1.159**	1.434***	1.271**	1.222**
1990	.	.	.	.	.	.	(0.441)	(0.450)	(0.484)	(0.507)	(0.504)	(0.573)
1991	.	.	.	.	.	.	.	0.291	1.010***	1.123***	0.986***	0.562***
1991	.	.	.	.	.	.	.	(0.213)	(0.275)	(0.296)	(0.321)	(0.159)
1992	.	.	.	.	.	.	.	.	1.878**	1.759**	1.186**	1.548***
1992	.	.	.	.	.	.	.	.	(0.749)	(0.688)	(0.578)	(0.409)
1993	.	.	.	.	.	.	.	.	.	1.116**	1.310**	1.906**
1993	.	.	.	.	.	.	.	.	.	(0.470)	(0.560)	(0.731)
1994	.	.	.	.	.	.	.	.	.	.	1.016***	0.907***
1994	.	.	.	.	.	.	.	.	.	.	(0.246)	(0.223)
1995	.	.	.	.	.	.	.	.	.	.	.	0.992***
1995	.	.	.	.	.	.	.	.	.	.	.	(0.209)

Note: Each cell represents a separate regression $\hat{\phi}_{jt}=\lambda + \rho \hat{\phi}_{js} + \zeta$ . Column headings refer to year of predicted compensating differential variable for the dependent variable ( $\hat{\phi}_{jt}$ ). Row headings refer to year of explanatory variable in the regression ( $\hat{\phi}_{js}$ ). Significance levels: * 10%, ** 5%, *** 1%.

Table 4: Predicted Tax Changes and Occupation Changes
Change in Compensating Differentials	% Decrease	% Same	% Increase
All Predicted MTR Decrease	18.88	59.19	21.92
All Predicted MTR Increase	20.35	58.80	20.85
All Difference	-1.47		1.07
All Scaled Difference	$\framebox{-4.05}$		$\framebox{2.95}$
Male Predicted MTR Decrease	17.47	61.66	20.87
Male Predicted MTR Increase	17.64	63.44	18.92
Male Difference	-0.17		1.95
Male Scaled Difference	$\framebox{-0.46}$		$\framebox{5.32}$
Female Predicted MTR Decrease	20.08	57.12	22.80
Female Predicted MTR Increase	23.12	54.44	22.44
Female Difference	-3.04		0.36
Female Scaled Difference	$\framebox{-8.36}$		$\framebox{0.99}$

Note: "Predicted MTR Decrease" refers to the top 25% of MTR decreases predicted by the instrument. "Predicted MTR Increase" refers to the top 25% of MTR increases predicted by the instrument. "Scaled Difference" equals "Difference" divided by the first stage relationship between the instrument and the endogenous explanatory variable.

Table 5: First-Stage Estimation Results for 3-Year Occupation (Industry) Changes
	All $\Delta \ln(1-\tau)$	All $\Delta \ln(z-T)$	Male $\Delta \ln(1-\tau)$	Male $\Delta \ln(z-T)$	Female $\Delta \ln(1-\tau)$	Female $\Delta \ln(z-T)$
MTR Instrument	0.475***	0.009***	0.544***	0.019***	0.402***	0.006**
MTR Instrument (Standard error)	(0.020)	(0.002)	(0.023)	(0.004)	(0.032)	(0.003)
After-tax Income Instrument	0.367***	0.908***	0.534***	0.718***	-0.002	0.924***
After-tax Income Instrument (Standard error)	(0.101)	(0.012)	(0.109)	(0.030)	(0.138)	(0.015)
Occupation*Year Fixed Effects	Yes	Yes	Yes	Yes	Yes	Yes
Shea's	0.0502	0.5688	0.0582	0.3618	0.0393	0.7029
N	42,310	42,310	21,666	21,666	18,917	18,917

Note: Covariates included but not shown in this table are gender, race, education, job tenure, (job tenure)

, number of dependents, marital status, and age group dummies. Standard errors in parentheses are clustered by occupation and individual using the two-way clustering technique. Significance levels: * 10%, ** 5%, *** 1%.

Table 6A: OLS and IV Estimation Results for 3-Year Occupation (Industry) Changes
A. All (N=42,310)	OLS	IV
$\Delta \ln(1-\tau)$	-0.019***	0.049***
$\Delta \ln(1-\tau)$ (Standard errors)	(0.004)	(0.014)
$\Delta \ln(z-T)$	0.118***	0.024
$\Delta \ln(z-T)$ (Standard errors)	(0.028)	(0.035)
Occupation*Year Fixed Effects	Yes	Yes

Table 6B: OLS and IV Estimation Results for 3-Year Occupation (Industry) Changes
B. Male (N=21,666)	OLS	IV
$\Delta \ln(1-\tau)$	-0.019***	0.050**
$\Delta \ln(1-\tau)$ (Standard errors)	(0.006)	(0.021)
$\Delta \ln(z-T)$	0.047	-0.105*
$\Delta \ln(z-T)$ (Standard errors)	(0.036)	(0.060)
Occupation*Year Fixed Effects	Yes	Yes

Table 6C: OLS and IV Estimation Results for 3-Year Occupation (Industry) Changes
C. Female (N=18,917)	OLS	IV
$\Delta \ln(1-\tau)$	-0.029***	0.067**
$\Delta \ln(1-\tau)$ (Standard errors)	(0.006)	(0.027)
$\Delta \ln(z-T)$	0.161***	0.048
$\Delta \ln(z-T)$ (Standard errors)	(0.043)	(0.052)
Occupation*Year Fixed Effects	Yes	Yes

Note: The dependent variable is the difference in predicted compensating differentials between the old and new occupations at time

. Covariates included but not shown in this table are gender, race, education, job tenure, (job tenure)

Table 7: IV Estimation Results of Occupation (Industry) Changes with Different Interval Lengths
	1-Year	2-Year	3-Year	4-Year
A. All $\Delta \ln(1-\tau)$	0.005	0.035**	0.049***	0.037***
A. All $\Delta \ln(1-\tau)$ (Standard error)	(0.015)	(0.015)	(0.014)	(0.014)
A. All $\Delta \ln(z-T)$	-0.092*	-0.057	0.024	-0.008
A. All $\Delta \ln(z-T)$ (Standard error)	(0.051)	(0.035)	(0.035)	(0.033)
A. All Occupation*Year Fixed Effects	Yes	Yes	Yes	Yes
A. All N	57,957	49,181	42,310	36,486
B. Male $\Delta \ln(1-\tau)$	0.048**	0.036*	0.050**	0.041*
B. Male $\Delta \ln(1-\tau)$ (Standard error)	(0.023)	(0.020)	(0.021)	(0.022)
B. Male $\Delta \ln(z-T)$	-0.503***	-0.168***	-0.105*	-0.136**
B. Male $\Delta \ln(z-T)$ (Standard error)	(0.136)	(0.064)	(0.060)	(0.066)
B. Male Occupation*Year Fixed Effects	Yes	Yes	Yes	Yes
B. Male N	29,821	25,479	21,666	18,953
C. Female $\Delta \ln(1-\tau)$	0.006	0.055**	0.067**	0.042*
C. Female $\Delta \ln(1-\tau)$ (Standard error)	(0.025)	(0.028)	(0.027)	(0.024)
C. Female $\Delta \ln(z-T)$	-0.224***	-0.062	0.048	0.063
C. Female $\Delta \ln(z-T)$ (Standard error)	(0.078)	(0.055)	(0.052)	(0.042)
C. Female Occupation*Year Fixed Effects	Yes	Yes	Yes	Yes
C. Female N	26,889	22,635	18,917	16,591

Note: The dependent variable is the difference in predicted compensating differentials between the old and new occupations at time

. Covariates included but not shown in this table are gender, race, education, job tenure, (job tenure)

Table 8: IV Estimation Results of the Marginal Tax Rate Effect on Occupation (Industry) Changes by Interval Length and Age Group
	All Young	All Old	Male Young	Male Old	Female Young	Female Old
1-Year	0.006	-0.001	0.081**	-0.009	-0.024	0.040
1-Year (Standard error)	(0.031)	(0.033)	(0.039)	(0.056)	(0.065)	(0.037)
N	24,997	30,737	13,198	15,474	11,706	15,167
2-Year	0.027	0.029	0.015	0.038	0.052	0.053
2-Year (Standard error)	(0.023)	(0.293)	(0.030)	(0.049)	(0.052)	(0.049)
N	21,886	25,235	11,647	12,745	10,170	12,407
3-Year	0.000	0.049**	-0.040	0.066	0.036	0.100**
3-Year (Standard error)	(0.024)	(0.025)	(0.029)	(0.046)	(0.070)	(0.042)
N	19,527	20,853	10,436	10,542	8,950	10,138
4-Year	0.031	0.053**	0.094***	0.027	-0.041	0.105**
4-Year (Standard error)	(0.025)	(0.026)	(0.031)	(0.044)	(0.054)	(0.045)
N	17,436	17,265	9,340	8,724	8,039	8,478

Note: The dependent variable is the difference in predicted compensating differentials between the old and new occupations at time

. Covariates included but not shown in this table are gender, race, education, job tenure, (job tenure)

Table 9: IV Estimation Results: Effect of Weighting
	All	All	Male	Male	Female	Female
$\Delta \ln(1-\tau)$	0.049***	0.054***	0.050**	0.063**	0.067**	0.057*
$\Delta \ln(1-\tau)$ (Standard error)	(0.014)	(0.017)	(0.021)	(0.026)	(0.027)	(0.031)
$\Delta \ln(z-T)$	0.024	0.019	-0.105*	-0.142*	0.048	0.038
$\Delta \ln(z-T)$ (Standard error)	(0.035)	(0.045)	(0.060)	(0.080)	(0.052)	(0.064)
Occupation*Year Fixed Effects	Yes	Yes	Yes	Yes	Yes	Yes
Weighted by Standard Errors	Yes	No	Yes	No	Yes	No
N	42,310	42,310	21,666	21,666	18,917	18,917

Note: The dependent variable is the difference in predicted compensating differentials between the old and new occupations at time

. Covariates included but not shown in this table are gender, race, education, job tenure, (job tenure)

Footnotes

* RAND, [email protected] Return to Text

** Federal Reserve Board of Governors, [email protected]. We are grateful to Gerald Auten, David Autor, Neil Bhutta, Tonja Bowen Bishop, Tom Garrett, Jon Gruber, Jerry Hausman, Amanda Pallais, Jim Poterba, Nirupama Rao, Claudia Sahm, and Chris Smith for their comments, advice, and support. We thank Dan Feenberg and Inna Shapiro for their help with NBER's TAXSIM program and Donald Bruce for graciously sharing his PSID code. This research was supported by the National Institute on Aging, Grant Number P01-AG05842. The findings and conclusions expressed are solely those of the authors and do not represent the views of the Federal Reserve System or the National Institute on Aging. Return to Text

1. See Saez et al. (2009) for a survey of the literature. Return to Text

2. In Appendix A, we also consider models where the worker chooses occupation and working hours simultaneously. The tradeoff between wage and non-taxable amenities remains the same when the hours decision is included, and these models also predict that workers will demand more non-taxable compensation when the tax rate increases. Return to Text

3. Our income effect variable ( $\ln \left( \frac{z_{ik,t-1}-T_{t}[z_{ik,t-1}]}{z_{ik,t-1}-T_{t-1}[z_{ik,t-1}]} \right)$ ) is slightly different than the Gruber-Saez variable. Our specification holds the taxable income at time

fixed, whereas the Gruber-Saez specification lets taxable income change between periods

and

. We hold

constant because taxable income is a choice variable. The income effect is the response to the budget constraint shift. The Gruber-Saez variable includes the budget constraint shift and the household's labor supply choices, modeling taxable income as a function of both of these effects. In this paper, we hold

constant so that households are responding only to the budget constraint shift. Return to Text

4. We interpret the resulting $\phi$ terms as the compensating differentials. It is possible that these terms include factors unrelated to the market price of non-taxable amenities and it is certain that the terms will be measured with error. These "contaminations" should not bias our estimates, however, unless they are correlated with our tax instruments. We discuss the robustness of our empirical strategy to different interpretations of the $\phi$ terms in section 6. Return to Text

5. Note that the relationship between "changing jobs" and the tax rate is non-linear because both tax rate increases and decreases should induce job changes. Return to Text

6. We follow Kambourov and Manovskii (2009) in constructing the 2-digit occupation codes. Return to Text

7. Note that this sample still includes workers that experience tax rate changes as small as 1%. Return to Text

8. In general, if our instrument predicts a tax rate increase, the probability that the worker's tax rate actually increased is about 35% higher than if the instrument predicts a tax rate decrease. We scale by the appropriate factor in each cell. Return to Text

9. The strength of the prediction of the after-tax income variable is a side effect of holding initial pre-tax income constant in the endogenous variable, as discussed in section 4. Return to Text

10. Note that the coefficient of interest is larger for each sub-sample than the aggregate sample. Because the tax instruments and compensating differentials are constructed differently in the sub-samples and in the entire sample and because we do not include occupation*year*gender interactions in the full-sample regression, this is not worrisome. It is not guaranteed that the full sample estimate will be between the male and female estimates and simple estimation imprecision can lead to this "inconsistency." Return to Text

^♣ This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to Text