Variance Risk Premia, Asset Predictability Puzzles, and Macroeconomic Uncertainty1
Keywords: Short-run predictability, variance premium dynamics, equity premium puzzle, bond risk premia, credit spread puzzle, macroeconomic uncertainty, recursive preference.
Abstract:
This paper presents predictability evidence from the difference between implied and expected variances or variance risk premium that: (1) the variance difference measure predicts a significant positive risk premium across equity, bond, and credit markets; (2) the predictability is short-run, in that it peaks around one to four months and dies out as the horizon increases; and (3) such a short-run predictability is complementary to that of the standard predictor variables--P/E ratio, forward spread, and short rate. These findings are potentially justifiable by a general equilibrium model with recursive preference that incorporates stochastic economic uncertainty. Calibration evidence suggests that such a framework is capable of reproducing the variance premium dynamics, especially its high skewness and kurtosis, without introducing jumps. The calibrated model can also qualitatively explain the equity premium puzzle and the bond risk premia in short horizons.
JEL classification: G12, G13, G14.
1 Introduction
Option implied volatility, such as the Chicago Board Option Exchange's VIX index, is widely viewed by investors as the market gauge of fear (Whaley, 2000).3 In recent research, the difference between the implied and expected volatilities has been interpreted as an indicator of the representative agent's risk aversion (Rosenberg and Engle, 2002; Bollerslev, Gibson, and Zhou, 2008a; Bakshi and Madan, 2006). An alternative interpretation is that the implied-expected variance difference, as a proxy for variance risk premium, is due to the macroeconomic uncertainty risk (Bollerslev, Tauchen, and Zhou, 2009; Drechsler and Yaron, 2008). Such an approach relies on the non-standard recursive utility framework of Epstein and Zin (1991) and Weil (1989), such that the consumption uncertainty risk commands a time-varying risk premium. This method follows the spirit of the long-run risks models as pioneered by Bansal and Yaron (2004), but focuses on the independent consumption volatility as a primary source of the time variation in market risk premia, while shutting down the long-run risk channel completely.
This paper demonstrates that the difference between implied and expected variances, as a measure for variance risk premium, provides a significant predictability for short-run equity returns, bond returns, and credit spreads. The documented return predictability peaks around one-to-four month horizons across these markets, and then dies out as the forecasting horizon increases. More importantly, such a short-term forecastability of market risk premia is complementary to the standard established predictors--P/E ratio, forward spread, and short rate, which are indicated by the asset pricing theory or empirical evidence; in that when combined together, the statistical significance of the variance risk premium proxy is rather increased or at least stable, instead of being crowded out by the standard predictor variables. This constitutes an important evidence that risk premia across major financial markets comove in the short-run, and such a common component seems to be intimately related to the variance risk premium, which is constructed from the high quality derivatives market data and high-frequency underlying market prices.
This type of common short-run risk factor may be a proxy for stochastic economic uncertainty or consumption volatility risk that varies independently with the consumption growth rate--the latter being the main focus of the long-run risk models (Bansal and Yaron, 2004).4 These empirical results may be consistent with a self-contained general equilibrium model incorporating the effects of such a time-varying economic uncertainty, where the uncertainty risk is priced only under the recursive utility function. Calibration evidence shows that such a framework can replicate quantitatively the observed skewness and kurtosis in variance premium dynamics, without introducing jumps into the endowment process and/or the volatility process (as in, e.g., Eraker and Shaliastovich, 2008; Drechsler and Yaron, 2008). More importantly, within such a calibration parameter setting, the model can qualitatively explain the equity premium puzzle and bond risk premia in short-horizons.
There is a fundamental link between the notion of option-implied volatility risk premium and the notion of variance risk premium embedded in underlying assets. Within the arbitrage pricing framework, stochastic volatility of equity market can only be priced, if its innovation is correlated with the market return innovation (Bates, 1996; Bakshi and Kapadia, 2003; Heston, 1993). There is a great deal of empirical evidence that equity volatility is negatively correlated with the equity returns, such that the negative volatility risk premium embedded in equity options provides a vital hedging service for the average investors. However, within a consumption-based asset pricing framework, without assuming any arbitrary statistical correlation between the volatility and consumption innovations, one need to endow the economic agents with a preference for an earlier resolution of uncertainty and a stochastic volatility-of-volatility. Under such a setup the variance risk premium embedded in equity, bond, and credit markets must be positive, as more risk requires more return compensation. And the positive variance risk premium embedded in underlying assets is entirely consistent with the negative volatility risk premium implied from option prices.
Economic uncertainty and its effect on asset prices can be examined with other techniques under the recursive preference structure. Bansal and Shaliastovich (2008a) and Shaliastovich (2008) introduce information learning into the long-run risk model, such that endogenously asset prices requires a compensation for jump risks. Chen and Pakos (2008) model the endowment growth rate as a Markov switching process with a constant volatility, where learning brings about an endogenous uncertainty premium. Drechsler (2008) applies the Knightian uncertainty about model misspecification with realistic asset dynamics to explain the observed option pricing puzzles. Lettau, Ludvigson, and Wachter (2008) use a Markov switching model to describe the long-swing changes in the constant consumption volatility--Great Moderation--and to draw implications for the declining equity risk premiums.5
In contrast, the approach taken here shuts down the the long-run component in consumption growth, and attributes the higher order time-variation in financial market risk premia to the stochastic volatility-of-volatility in consumption growth. Conceptually, the root of macroeconomic or consumption uncertainty can be traced back to the volatility shocks in total factor productivity and firm-specific technology in a real business cycle model (Bloom, Floetotto, and Jaimovich, 2009; Bloom, 2009). Such an approach treats the short-run economic uncertainty as a fundamental priced risk factor, without relying on informational learning, heterogeneous beliefs, or behavioral assumptions. The emphasis here is also complementary to the long-run risk perspective (Bansal and Yaron, 2004) or rare disaster angle (Gabaix, 2009; Barro, 2006), and is orthogonal to the channel of time-varying risk aversion (Campbell and Cochrane, 1999). Lastly, but not the least, this framework has sharp empirical testable hypotheses, since the economic uncertainty factor or stochastic volatility-of-volatility is uniquely identified by the variance risk premium.6
The rest of the paper will be organized as the follows, the next section defines the variance risk premium and describes its empirical measurement; Section 3 presents the main empirical evidence of the short-run predictability from implied-expected variance difference for risk premia in asset markets; the following section discusses a general equilibrium model with stochastic economic uncertainty and provides some calibration implications for explaining the short-run risk premia dynamics; and Section 5 concludes.
2 Variance Risk Premium and Empirical Measurement
The central empirical finding of this paper is that market risk premia have a common short-run component--variance risk premium--that is not directly observable. However, an empirical proxy can be constructed from the difference between model-free option-implied variance and the conditional expectation of model-free realized variance.
2.1 Variance Risk Premium: Definition and Measurement
To define the procedure in quantifying the model-free implied variance, let ![]() denote the price of a European call option maturing at time
denote the price of a European call option maturing at time ![]() with strike price
with strike price ![]() , and
, and ![]() denote the price of a time
denote the price of a time ![]() zero-coupon bond maturing at time
zero-coupon bond maturing at time ![]() . As shown by Carr and Madan (1998); Britten-Jones and Neuberger (2000) among others, the market's risk-neutral expectation of the return variance between time
. As shown by Carr and Madan (1998); Britten-Jones and Neuberger (2000) among others, the market's risk-neutral expectation of the return variance between time ![]() and
and ![]() conditional on time
conditional on time ![]() information, or the implied variance
information, or the implied variance
![]() , can be expressed in a "model-free" fashion as the a portfolio of European calls,
, can be expressed in a "model-free" fashion as the a portfolio of European calls,
which relies on an ever increasing number of calls with strikes spanning from zero to infinity.7
This equation follows directly from the classical result in Breeden and Litzenberger (1978), that the second derivative of the option call price with respect to strike equals the risk-neutral density, such that all risk neutral moments payoff can be replicated by the
basic option prices (Bakshi and Madan, 2000). In practice,
![]() must be constructed on the basis of a finite number of strikes; which turns out to be a fairly accurate approximation to the true (unobserved) risk-neutral expectation of the future
market variance, under reasonable assumptions about the underlying asset dynamics (Carr and Wu, 2008; Bollerslev, Gibson, and Zhou, 2008a; Jiang and Tian, 2005).
must be constructed on the basis of a finite number of strikes; which turns out to be a fairly accurate approximation to the true (unobserved) risk-neutral expectation of the future
market variance, under reasonable assumptions about the underlying asset dynamics (Carr and Wu, 2008; Bollerslev, Gibson, and Zhou, 2008a; Jiang and Tian, 2005).
In order to define the measure in quantifying the actual return variation, let ![]() denote the logarithmic price of the asset. The realized variance over the discrete
denote the logarithmic price of the asset. The realized variance over the discrete ![]() to
to ![]() time interval can be measured in a "model-free" fashion by
time interval can be measured in a "model-free" fashion by
where the convergence relies on
As demonstrated in the literature (see, e.g., Barndorff-Nielsen and Shephard, 2002; Andersen, Bollerslev, Diebold, and Ebens, 2001), this "model-free" realized variance measure based on high-frequency intraday data offers a
much more accurate ex-post observation of the true (unobserved) return variance than the traditional ones based on daily or coarser frequency returns. In practice, various market microstructure frictions invariably limit the highest sampling frequency that may be used in reliably estimating
![]() .
.
The variance risk premium is defined as the difference between the ex-ante risk neutral expectation of the future return variance and the objective or statistical expectation of the return variance over the ![]() time interval,
time interval,
which is not directly observable in practice. To construct an empirical proxy for such a variance risk premium concept (3), one need to estimate various reduced-form counterparts of the risk neutral and physical expectations, i.e.,
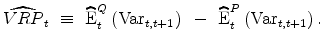 In practice, the
risk-neutral expectation
In practice, the
risk-neutral expectation
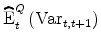 is typically replaced by the CBOE implied variance or VIX
is typically replaced by the CBOE implied variance or VIXOne approach is to estimate a reduced-form multi-frequency auto-regression with multiple lags for
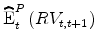 (Bollerslev, Tauchen, and Zhou, 2009). For more specific structural jump-diffusion processes, one could use
the model-implied objective expectation (Todorov, 2009). Based on the evidence of implied-realized variance forecast efficiency and a potential two-factor structure in variance dynamics, Drechsler and Yaron (2008) use lagged implied and realized
variances to forecast the expected variance. For forecasting purposes only, one could use time-
(Bollerslev, Tauchen, and Zhou, 2009). For more specific structural jump-diffusion processes, one could use
the model-implied objective expectation (Todorov, 2009). Based on the evidence of implied-realized variance forecast efficiency and a potential two-factor structure in variance dynamics, Drechsler and Yaron (2008) use lagged implied and realized
variances to forecast the expected variance. For forecasting purposes only, one could use time-![]() realized variance
realized variance
![]() (Bollerslev, Tauchen, and Zhou, 2009), which ensures that the variance risk premium proxy is in the time
(Bollerslev, Tauchen, and Zhou, 2009), which ensures that the variance risk premium proxy is in the time ![]() information set. Following the common practice in the variance swap market, Carr and Wu (2008) use the ex-post forward realized variance to substitute for the expected variance in characterizing the variance
risk premium. When presenting the empirical findings, I will focus on the method that uses the twelve lag auto-regressive estimate.
information set. Following the common practice in the variance swap market, Carr and Wu (2008) use the ex-post forward realized variance to substitute for the expected variance in characterizing the variance
risk premium. When presenting the empirical findings, I will focus on the method that uses the twelve lag auto-regressive estimate.
2.2 Data Description and Summary Statistics
For the option-implied variance of the S&P500 market return, I use the end-of-month data of the Chicago Board of Options Exchange (CBOE) volatility index VIX![]() on a monthly basis, as a
risk-neutral expectation of return variance for the next 30 days. Following the literature, the monthly realized variance measure for the S&P500 index is the summation of the 78 within
day five-minute squared returns covering the normal trading hours from 9:30am to 4:00pm plus the close-to-open return.
on a monthly basis, as a
risk-neutral expectation of return variance for the next 30 days. Following the literature, the monthly realized variance measure for the S&P500 index is the summation of the 78 within
day five-minute squared returns covering the normal trading hours from 9:30am to 4:00pm plus the close-to-open return.
Here I consider three market risk premium measures with their traditional predictor variables. Specifically, monthly P/E ratios and index returns for the S&P500 are obtained from Standard & Poor's, bond returns and forward rates are from the monthly CRSP Fama t-bill data set with 1 to 6 month maturities, and AAA and BAA corporate bond spreads are from Moody's with Fama-Bliss risk-free interest rates from CRSP. The empirical analysis here is for the sample period from January 1990 to December 2008, when the new VIX index based on S&P500 index becomes available.
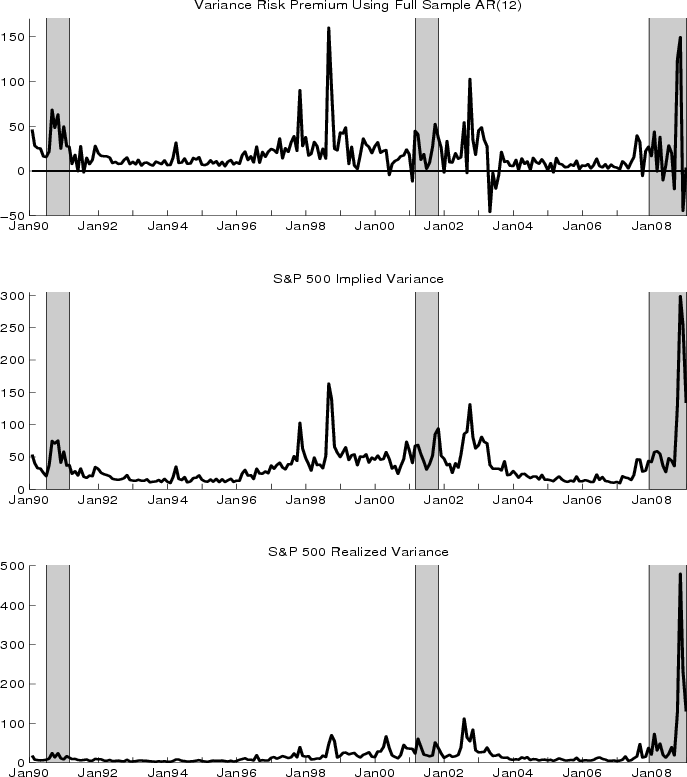
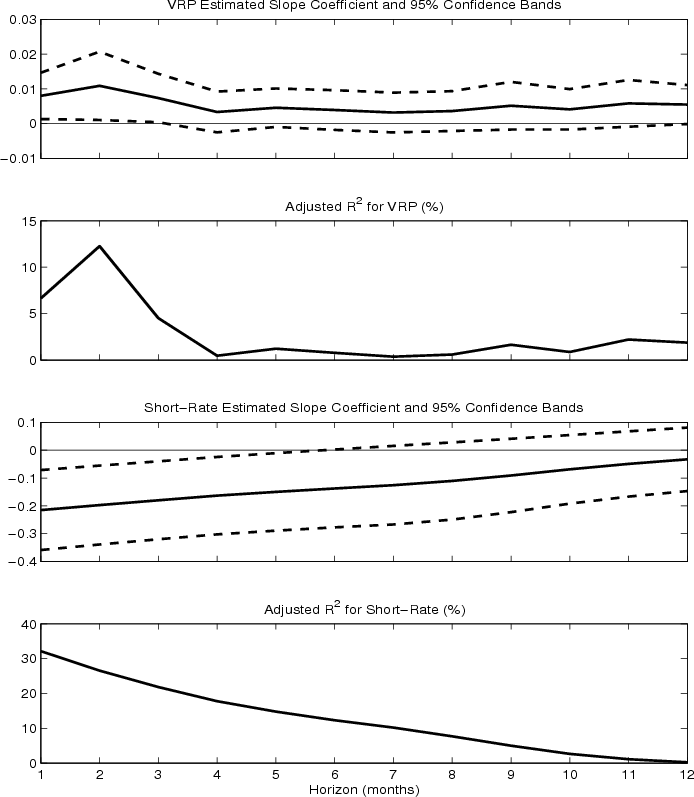
To give a visual illustration, Figure 1 plots the monthly time series of variance risk premium, implied variance, and realized variance.The variance risk premium proxy is moderately high during the 1990 and 2001 recessions, and much higher around the 1997-1998 Asia-Russia-LTCM crisis and the 2002-2003 corporate accounting scandals. The variance spikes during October 2008 already surpasses the initial shock of the Great Depression in October 1929. The huge run-up of variance risk premium in the fourth quarter of 2008 actually leads an equity market bottom in the first quarter of 2009.
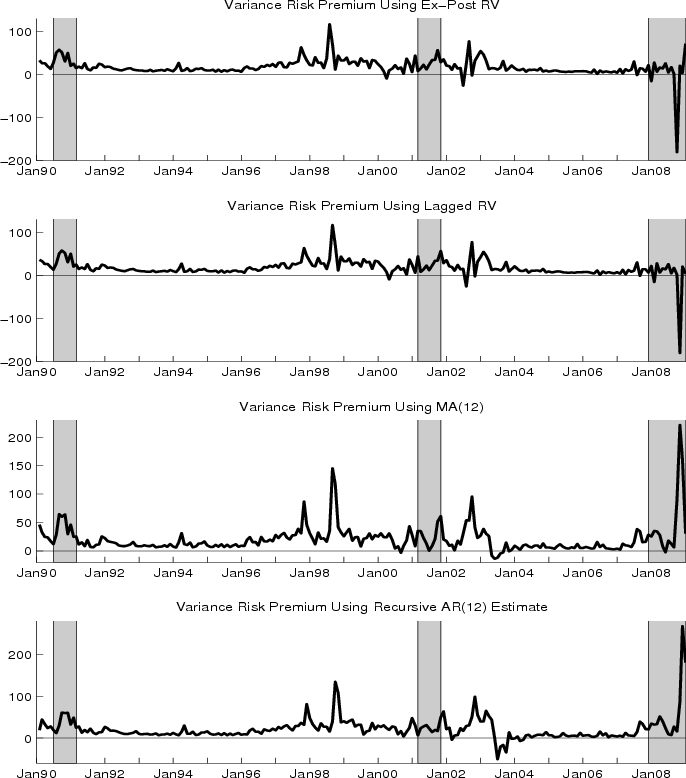
Table 1 Panel A compares the summary statistics of different variance risk premium proxies based on alternative ways to estimate the conditional expectation of realized variances. The mean level of variance risk premium is around 17 to 22 (in percentage-squared, monthly basis) across five different estimates, with a standard deviation around 22-28. Not surprisingly, the variance risk premiums based on current and lagged realized variance have the highest kurtosis of 44 to 46, while the full sample AR(12) estimate has the lowest of 17. Also noteworthy is that the variance risk premium estimates based on raw current and lag realized variance has a skewness of -3, while others are all positive skewed. The negative skewness is entirely driven by one monthly observation of a negative spike in October 2008 (Figure 2 upper two panels) and by not using the expected variance in constructing the variance risk premium. Finally, the auto-regressive coefficient of order one is generally low between 0.26 and 0.76, with the full sample AR (12) achieves the lowest value. Figure 2 also shows the variance risk premia based on other estimates of the expected variance, where the recursive AR(12) and MA(12) approaches both suggest that the variance risk premium had achieved the unprecedented historical level around October-November 2008.
Basic summary statistics for the monthly returns and predictor variables are given in Table 1 Panels B to D. The mean excess return on the S&P500 over the sample period equals 3.58 percent annually, reflecting the significantly lowered market returns during the 2007-2008 financial crisis and economic downturn. The one month holding period returns for 2-6 month t-bills are ranging from 0.44 to 0.86 percent annually, and the credit spread for Moody's AAA rating is 1.25 percent and BAA 2.14 percent. The sample means for the variance risk premium is about 18.30 (in percentages squared). P/E ratio and short rate are very persistent with first order autocorrelations 0.97 and 0.99. While forward spread and variance risk premium are rather stationary, with a serial correlation between -0.10 to 0.39. Of particular interests, is that the variance risk premium variable generally has very small correlations with standard long-run predictor variables--0.07 with P/E ratio, around 0.04 to 0.06 with forward spreads, and -0.09 with short rate--which may partially explain why the short-run predictability of the variance premium variable is complementary to those of the established standard predictors.
3 Short-Run Predictability Puzzles of Financial Assets
This section presents new predictability evidence of the variance risk premium proxy for equity returns, bond return, and credit spreads, with and without the standard predictor variables--P/E ratio, forward spread, and short rate. Data are monthly observations with horizons up to one year. All
of the reported ![]() -statistics are based on heteroskedasticity and serial correlation consistent standard errors (Newey and West, 1987). The discussion focuses on the
estimated slope coefficients and their statistical significance as determined by the robust
-statistics are based on heteroskedasticity and serial correlation consistent standard errors (Newey and West, 1987). The discussion focuses on the
estimated slope coefficients and their statistical significance as determined by the robust ![]() -statistics. The forecasts accuracy of the regressions are also measured by the corresponding
adjusted
-statistics. The forecasts accuracy of the regressions are also measured by the corresponding
adjusted ![]() 's.8
's.8
3.1 Equity Returns
For equity returns, I focus on the regression of S&P500 returns on a long-run predictor--P/E ratio and a short-run predictor--variance risk premium,
where
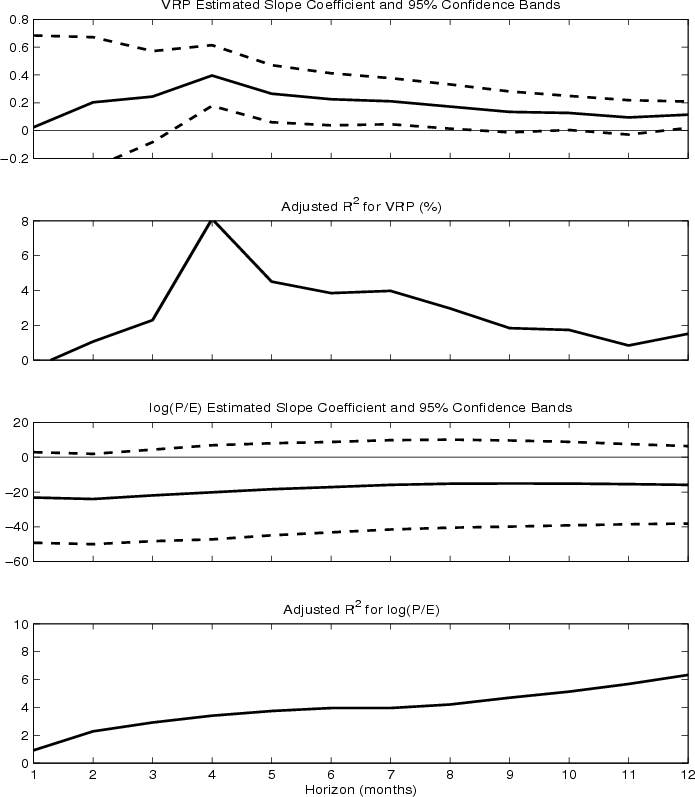
Table 2 top row shows that the predictability or ![]() of the variance risk premium
of the variance risk premium ![]() , starts out at -0.43 percent at monthly, peaks around 8 percent at four month, and then gradually decreases toward zero with longer forecasting horizons. The robust
, starts out at -0.43 percent at monthly, peaks around 8 percent at four month, and then gradually decreases toward zero with longer forecasting horizons. The robust ![]() -statistic is the highest at four month at 3.56 and remains marginally significant at the ten month horizon. On the other hand, as shown in the middle row in Table 2, the usual long-run predictor,
-statistic is the highest at four month at 3.56 and remains marginally significant at the ten month horizon. On the other hand, as shown in the middle row in Table 2, the usual long-run predictor,
![]() ratio, starts out barely significant at 10 percent level from one to three month, and then becomes insignificant. However, the adjusted
ratio, starts out barely significant at 10 percent level from one to three month, and then becomes insignificant. However, the adjusted ![]() of P/E ratio monotonically increases from 0.92 percent at one month to 6.34 percent at twelve month.
of P/E ratio monotonically increases from 0.92 percent at one month to 6.34 percent at twelve month.
Turning to the joint regressions reported in the bottom row of Table 2, it is clear that combining the variance premium with the P/E ratio results in an even higher ![]() of 12.59 percent at four month horizon, which is higher than the sum of two
of 12.59 percent at four month horizon, which is higher than the sum of two ![]() 's in the respective univariate regressions. The
's in the respective univariate regressions. The ![]() -statistics for
-statistics for ![]() and
and
![]() are also somewhat higher at four month, 3.61 and -1.60, than their univariate counterparts respectively.
are also somewhat higher at four month, 3.61 and -1.60, than their univariate counterparts respectively.
Figure 3 visualizes such a short-run predictability pattern in ![]() and
and ![]() -statistics. The predictability of variance premium has a tent shape pattern maximizes at four month horizon. While P/E ratio has no statistical significance at one-to-twelve month horizons.
-statistics. The predictability of variance premium has a tent shape pattern maximizes at four month horizon. While P/E ratio has no statistical significance at one-to-twelve month horizons.
3.2 Bond Returns
The failure of the Expectations Hypothesis (EH) of interest rates can be best characterized as that bond excess return, estimated from forward rates, is largely predictable and time-varying countercyclically (Fama, 1984,1986; Stambaugh, 1988).9Here I adopt the conventional forward rate setup as in Fama (1984) and augment it with the variance risk premium variable,
where
As shown in Table 3, the variance risk premium can significantly forecast the one month holding period excess returns of the two-six month t-bills, with a positive slope coefficient around 0.006 to 0.013. Considering the average level of variance risk premium of 18.30,
this magnitude translates to an average bond risk premium induced by variance risk around 11 to 24 basis points. More importantly, the Newey-West ![]() -statistics are all well above the 1 percent
significance level, with an
-statistics are all well above the 1 percent
significance level, with an ![]() around 2.77 to 4.57 percent. Moving to the two month holding period, the
around 2.77 to 4.57 percent. Moving to the two month holding period, the ![]() -ratios reduce to a marginal significance of 1.22 to 2.05, and the
-ratios reduce to a marginal significance of 1.22 to 2.05, and the ![]() decreases to 0.86 to 3.54 percent. The predictability of variance premium converges to zero as the
holding period increase to three-five months.
decreases to 0.86 to 3.54 percent. The predictability of variance premium converges to zero as the
holding period increase to three-five months.
As Table 4 indicates, the forward rate (spread) is indeed a powerful predictor for excess bond returns for two-to-six month bonds with one-to-five month holding periods--![]() -statistics all above 1 percent level and
-statistics all above 1 percent level and ![]() between 2.06 and 30.88 percent. Another pattern is that the magnitudes of
between 2.06 and 30.88 percent. Another pattern is that the magnitudes of ![]() -statistics and
-statistics and ![]() are generally higher at the one-month horizon and lower toward the five-month horizon. Overall, the predictability of
forward spreads for short-term bills reported here are similar to those reported by Fama (1984).
are generally higher at the one-month horizon and lower toward the five-month horizon. Overall, the predictability of
forward spreads for short-term bills reported here are similar to those reported by Fama (1984).
More importantly, when variance risk premium is combined with forward rates, as shown in Table 5, the predictability of the variance risk premium remains intact. For example, at one month horizon, the ![]() -statistics are much higher for 3, 5, 6 month t-bills; and slightly lower for 2 and 4 month t-bills. Note that the adjusted
-statistics are much higher for 3, 5, 6 month t-bills; and slightly lower for 2 and 4 month t-bills. Note that the adjusted ![]() 's for the one month
horizon with both variance premium and forward spread are all higher than the ones with forward spreads alone (Table 4 top row), suggesting that variance premium variable indeed contributes to the short-run bond return predictability, independent of that provided by
the forward spread.
's for the one month
horizon with both variance premium and forward spread are all higher than the ones with forward spreads alone (Table 4 top row), suggesting that variance premium variable indeed contributes to the short-run bond return predictability, independent of that provided by
the forward spread.
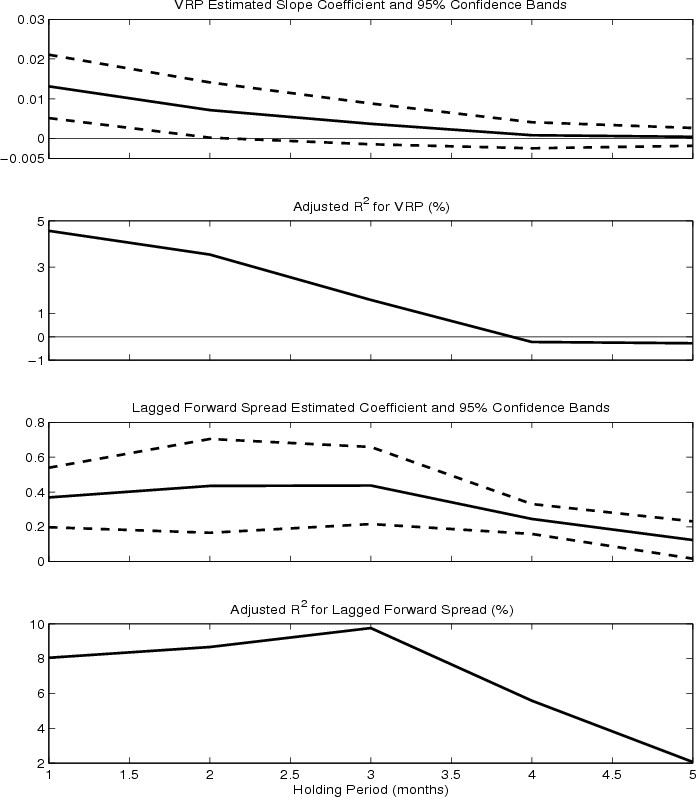
These results can be visualized in Figure 4, where for six month t-bill returns, the predictability of the variance premium variable is significant at one month but is monotonically decreasing with the holding period. While for the forward spread variable, although being significant at all one-to-five month horizons, its predictability seems to have a tent shape pattern that peaks at three month. This result suggests that the variance difference and forward spread are proxies for different components in bond risk premia.
3.3 Credit Spreads
The relatively large and time-varying credit spread on corporate bond has long been viewed as an anomaly in the literature (see, e.g., Huang and Huang, 2003). Here I provide some new evidence that, in additional to the standard predictor, namely the interest rate level (Longstaff and Schwartz, 1995), the variance risk premium proxy also helps to explain the short-run movement in credit spreads, with the following standard forecasting regression,
where the credit spread CS
As shown in Table 6, short term interest rate is indeed a predominant predictor of the future credit spread levels, with ![]() -statistics of -3.94 for investment grade
(Moody's AAA rating) and -2.94 for speculative grade (Moody's BAA rating). The adjusted
-statistics of -3.94 for investment grade
(Moody's AAA rating) and -2.94 for speculative grade (Moody's BAA rating). The adjusted ![]() is around 32 percent, and the negative sign of the slope coefficient is consistent with the
risk-neutral drift interpretation in Longstaff and Schwartz (1995).11 Although the significance of the short rate level extends to
the six-month horizon, it is a very persistent variable with an AR(1) coefficient of 0.99 (Panel E in Table 1). As shown in the lower two panels of Figure 5, the predictability of short rate for credit spread shows a monotonic pattern of
decreasing, even though the slope coefficient value seems to be increasing.
is around 32 percent, and the negative sign of the slope coefficient is consistent with the
risk-neutral drift interpretation in Longstaff and Schwartz (1995).11 Although the significance of the short rate level extends to
the six-month horizon, it is a very persistent variable with an AR(1) coefficient of 0.99 (Panel E in Table 1). As shown in the lower two panels of Figure 5, the predictability of short rate for credit spread shows a monotonic pattern of
decreasing, even though the slope coefficient value seems to be increasing.
Note that if we include the variance risk premium alone in the forecasting regressions, its statistical significance is above the 1 percent level at one month horizon, with ![]() -statistic
being 2.49 for AAA grade and 2.35 for BAA grade. Given the average level of variance risk premium of 18.30, that translates into an average effect on credit spread in the order of 9 to 15 basis points. Once the forecasting horizons increase to 3, 6, 9, and 12 months, the
-statistic
being 2.49 for AAA grade and 2.35 for BAA grade. Given the average level of variance risk premium of 18.30, that translates into an average effect on credit spread in the order of 9 to 15 basis points. Once the forecasting horizons increase to 3, 6, 9, and 12 months, the ![]() -statistic for the variance difference variable become insignificant or marginal. As shown in the upper two panels of Figure 5, the predictability of variance premium for credit
spread shows a hump-shape pattern, which peaks at two month horizon and then becomes generally insignificant.
-statistic for the variance difference variable become insignificant or marginal. As shown in the upper two panels of Figure 5, the predictability of variance premium for credit
spread shows a hump-shape pattern, which peaks at two month horizon and then becomes generally insignificant.
When the variance risk premium is combined with the short rate, both become more significant at the short horizons. For example, at one month horizon, the ![]() -statistics for short rate is
-4.59 for AAA and -3.53 for BAA; while for variance premium it is 4.26 and 3.77 respectively. In fact, the variance risk premium variable maintains at least a marginal significance in the joint regressions even at the 12 month horizon, even though the short rate drops out as insignificant beyond
the 6 month horizon. Judging from the
-statistics for short rate is
-4.59 for AAA and -3.53 for BAA; while for variance premium it is 4.26 and 3.77 respectively. In fact, the variance risk premium variable maintains at least a marginal significance in the joint regressions even at the 12 month horizon, even though the short rate drops out as insignificant beyond
the 6 month horizon. Judging from the ![]() perspective, e.g., at the one month horizon, the univariate
perspective, e.g., at the one month horizon, the univariate ![]() for variance risk premium is about 5-7 percent, but its contribution to the joint
for variance risk premium is about 5-7 percent, but its contribution to the joint ![]() is about 9-10 percent, on top of what the short rate level has already achieved--32
percent.
is about 9-10 percent, on top of what the short rate level has already achieved--32
percent.
This is an important finding, in that the variance risk premium or implied-expected variance difference captures an important component in credit risk premium that is independent with and complementary to the systematic risk risk factor that has already been captured by the short-term interest rate. Section 4 tries to provide some economic interpretation for such an effect.
3.4 Correlations between Different Markets
There is a valid concern that if the different financial markets exhibit a high degree of (positive) correlation among the residuals, then as a joint statistical inference issue, the conventional ![]() -statistics of the regression slope coefficient may have to be discounted, even if they are highly significant in the univariate regressions (Boudoukh, Richardson, and Whitelaw, 2008). This concern can be alleviated by the fact that the variance risk
premium variable is not persistent at all, with an AR(1) coefficient being 0.26; and that neither the
-statistics of the regression slope coefficient may have to be discounted, even if they are highly significant in the univariate regressions (Boudoukh, Richardson, and Whitelaw, 2008). This concern can be alleviated by the fact that the variance risk
premium variable is not persistent at all, with an AR(1) coefficient being 0.26; and that neither the ![]() -statistics nor the
-statistics nor the ![]() 's for variance premium are monotonically increasing with the forecasting horizons, although the P/E ratio does show such a pattern in its adjusted
's for variance premium are monotonically increasing with the forecasting horizons, although the P/E ratio does show such a pattern in its adjusted ![]() 's.
's.
One still need to address the remaining concern on whether the residuals of different markets are heavily correlated with each other. As shown in Panel A of Table 7, the raw return correlations between these three markets are generally low--ranging from -0.18 to 0.09--and are mostly close to zero. However, the concern about join statistical inference does bite for the securities in the same market--t-bills returns have correlations between 0.61 and 0.95 and two credit spreads have a correlation of 0.91. One should note that this paper focuses on the short-run predictability pattern of the variance premium variable across different markets, but not for the instruments in the same market.
Furthermore, once regressed on the variance risk premium variable, as shown in Panel B of Table 7, the residual correlations between different markets are either closer to zero or become slightly more negative in all cases, except one where the correlation between equity return and 2 month t-bill return increases from 0.04 to 0.08, albeit still a very small number indeed. Therefore, it seems that no strong positive comovement among these regressions residuals can be detected. Nonetheless, the high positive correlations among t-bill returns and between credit spreads remain largely unchanged.
Even if there is a high degree of positive correlation among the same instruments of a particular market, it does not necessarily mean that the univariate significant ![]() -statistics need to
be discounted. An alternative interpretation could be that there is another common risk factor missing, in addition to the short-run variance premium variable; which should be incorporated in explaining the time-variations in these risk premiums.12
-statistics need to
be discounted. An alternative interpretation could be that there is another common risk factor missing, in addition to the short-run variance premium variable; which should be incorporated in explaining the time-variations in these risk premiums.12
4 A Model of Macroeconomic Uncertainty
It is very challenging to provide a conceptual framework to jointly explain the risk premium dynamics in equity, bond, and credit markets. Here I draw from a self-contained general equilibrium model with stochastic consumption volatility-of-volatility (Bollerslev, Tauchen, and Zhou, 2009), and try to give a unified qualitative interpretation of these short-term risk premia puzzles. One should admit upfront that such a stylized model cannot provide satisfactory quantitative explanation for various aspects of asset pricing puzzles, within the same parameter setting and being constrained by matching the consumption dynamics.13
To be more specific, I will try to calibrate a model with macroeconomic uncertainty, by matching the equity risk premium as in Bansal and Yaron (2004) and short-run equity risk premium as in Bollerslev, Tauchen, and Zhou (2009), constrained by reasonable preference structure and consumption dynamics. And then I explore how far such a unified parameter setting can go for jointly explaining some salient features in variance risk premium and bond risk premium. One can learn by knowing why such a model is successful for explaining some risk premium dynamics across markets and why it cannot simultaneously explain the short-run predictability pattern in these markets.
4.1 Model Assumptions and Price-Dividend Ratio
The representative agent in the economy is equipped with Epstein-Zin-Weil recursive preferences, and has the value function ![]() of her life-time utility as
of her life-time utility as
where
Suppose that log consumption growth and its volatility follow the joint dynamics
where
Let ![]() denote the logarithm of the price-dividend or wealth-consumption ratio, of the asset that pays the consumption endowment,
denote the logarithm of the price-dividend or wealth-consumption ratio, of the asset that pays the consumption endowment,
![]() ; and conjecture a solution for
; and conjecture a solution for ![]() as an affine function
of the state variables,
as an affine function
of the state variables,
![]() and
and ![]() ,
,
One can solve for the coefficients
4.2 Model-Implied Equity, Variance, Bond Risk Premia
Given the solution of the price-dividend ratio, one can easily solve for the variables of interest, like equity return and risk-free rate (see, Bollerslev, Tauchen, and Zhou, 2009, for details), the model-implied equity risk premium can be shown as
The premium is composed of two separate terms. The first term,
The conditional variance of the time ![]() to
to ![]() return,
return,
![]() Var
Var![]() , can be shown as
, can be shown as
![]() The variance risk premium can be defined as the difference between risk-neutral and
objective expectations of the return variance,
The variance risk premium can be defined as the difference between risk-neutral and
objective expectations of the return variance,
where the approximation comes from the fact that the model-implied risk-neutral conditional expectation cannot be computed in closed form, and a log-linear approximation is applied. One key observation here is that any temporal variation in the endogenously generated variance risk premium, is due solely to the volatility-of-volatility or economic uncertainty risk,
The bond yield in this economy can be shown as an affine function of the state variables,
![y_t(n)= - \frac{1}{n} \left[\begin{array}{ccc} A(n) & B(n) & C(n) \end{array} \right] \left[\begin{array}{ccc} 1 & \sigma^2_{g,t} & q_t \end{array} \right]',](img96.gif) where the
coefficients
where the
coefficients ![]() ,
, ![]() , and
, and ![]() are given in Zhou (2008). Let
are given in Zhou (2008). Let
![]() be the bond excess return from
be the bond excess return from ![]() to
to ![]() for an
for an ![]() -period bond holding for one period, then its expected value
-period bond holding for one period, then its expected value ![]() or bond risk premium is given by,
or bond risk premium is given by,
where the risk premia genuinely has two time-varying components--consumption risk and uncertainty risk, but they are co-linear in the same state variable
4.3 Calibrating Equity, Variance, and Bond Risk Premia
To more directly gauge how the model adopted here can explain the documented risk premium dynamics, I perform a limited calibration exercise. The basic strategy is to find the preference and distribution parameters that are constrained by reasonable consumption dynamics and can simultaneously match the observed equity, bond, and variance premia as much as possible.
4.3.1 Calibration Design and Parameter Setting
As shown in Table 8, the benchmark parameter settings are adapted from Bansal and Yaron (2004) such that the consumption growth rate (
![]() ) is 2.4 percent annually and the consumption volatility is highly persistent (
) is 2.4 percent annually and the consumption volatility is highly persistent (
![]() at monthly), same across the two calibration settings in both this paper and Bollerslev, Tauchen, and Zhou (2009). I also use the same
intertemporal elasticity of substitution (IES) parameter (
at monthly), same across the two calibration settings in both this paper and Bollerslev, Tauchen, and Zhou (2009). I also use the same
intertemporal elasticity of substitution (IES) parameter (
![]() ) such that agents have the same preference for an earlier resolution of economic uncertainty. The time preference is also the same as
) such that agents have the same preference for an earlier resolution of economic uncertainty. The time preference is also the same as
![]() across two scenarios. The Campbell-Shiller approximation constants are chosen as
across two scenarios. The Campbell-Shiller approximation constants are chosen as
![]() hence
hence
![]() , similar as those in Bansal and Yaron (2004).
, similar as those in Bansal and Yaron (2004).
However, these two papers differ dramatically in terms of both risk aversion and volatility risk. In Bollerslev, Tauchen, and Zhou (2009), the risk aversion coefficient is
![]() , same as in Bansal and Yaron (2004); but in this paper, I choose
, same as in Bansal and Yaron (2004); but in this paper, I choose ![]() . On the other hand, in Bollerslev, Tauchen, and Zhou (2009), the consumption volatility is
. On the other hand, in Bollerslev, Tauchen, and Zhou (2009), the consumption volatility is
![]() , similar as that in Bansal and Yaron (2004), while here it increases to
, similar as that in Bansal and Yaron (2004), while here it increases to
![]() . A material implication of these parameter values is that the consumption volatility is increased to 4 times of the 2.7 percent annually, which may be
justifiable if one "leverages" up the dividend shocks several times larger than the consumption shocks (Abel, 1999).14
. A material implication of these parameter values is that the consumption volatility is increased to 4 times of the 2.7 percent annually, which may be
justifiable if one "leverages" up the dividend shocks several times larger than the consumption shocks (Abel, 1999).14
Furthermore, Bollerslev, Tauchen, and Zhou (2009) choose the stochastic economic uncertainty process, ![]() , to have monthly persistence level of
, to have monthly persistence level of
![]() , long-run mean of
, long-run mean of
![]() , and volatility-of-volatility parameter as
, and volatility-of-volatility parameter as
![]() ; but here I choose
; but here I choose
![]() ,
,
![]() , and
, and
![]() , implying that the
, implying that the ![]() process is not only magnified but also
more persistent and volatile. As demonstrated bellow, such a modification is critical in balancing the needs of jointly matching the equity, variance, and bond risk premia in the short-run.
process is not only magnified but also
more persistent and volatile. As demonstrated bellow, such a modification is critical in balancing the needs of jointly matching the equity, variance, and bond risk premia in the short-run.
4.3.2 Calibrated Equity, Variance, and Bond Risk Premia
The calibration results in Table 9 indicate that one can achieve a reasonable compromise to simultaneously match the equity, variance, bond risk premium puzzles, without relying on introducing jumps into the endowment and/or its volatility process (as in Eraker and Shaliastovich, 2008; Drechsler and Yaron, 2008) or introducing exogenous inflation process for the nominal bonds (Bansal and Shaliastovich, 2008b; Gallmeyer, Hollifield, Palomino, and Zin, 2008; Wachter, 2006). It can be achieved if one would be willing to "levered" up the volatility-of-volatility process and to lower risk aversion to a moderate level. Admittedly such a "short-run" risk model lacks the long-run component to match the consumption growth predictability, which is subject to some debate due to the consumption data measurement problem.
The resulting equity risk premium is 5.11 percent and real interest rate 1.86 percent, which are different than Bollerslev, Tauchen, and Zhou (2009) (7.79 and 0.69 percent) but similar to the observed premiums of 3.58 and 1.13 percent for the sample period 1990-2008 (as opposed to 7.84 and 0.87 percent for 1930-2008). The parameter choice here has a advantage of getting a better equity volatility of 13.24 percent, as opposed to 4 percent in Bollerslev, Tauchen, and Zhou (2009), comparing to 14.60 percent observed in the recent period. On the other hand, this paper overfits the volatility of risk-free rate at 8.83 percent, versus 3.37 percent in recent data and 2.95 percent in Bollerslev, Tauchen, and Zhou (2009). This sacrifice in matching the equity risk premium has gained in explaining the variance and bond risk premia. However, the underfitting of equity risk premium (5.11 percent) and the overfitting of short rate volatility (7.83 percent) disappear if one considers the earlier sample period of 1891-1949 (4.97 and 7.83 percent respectively).
The model-implied variance risk premium has a mean of 18.30 and a standard deviation of 25.12, which are very close to observed values of 18.30 and 22.69. More importantly, the model produces quite reasonable values in skewness (2.48) and kurtosis (13.18), which are slightly less than the
observed values of 2.79 and 16.62. On the other hand, the parameter specification in Bollerslev, Tauchen, and Zhou (2009) would completely miss the level and standard deviation of variance premium and underfit the the skewness and kurtosis. These results are non-trivial
in that a stochastic volatility-of-volatility model can generate realistic skewness and kurtosis in variance risk premium, similar to the result provided in Drechsler and Yaron (2008), where the common jumps have been introduced into the consumption growth and its
volatility processes. Finally, the model-implied persistence level--equal to ![]() --is as high as 0.95, as opposed to the low value of 0.26 reflected in the data and 0.80 in Bollerslev, Tauchen, and Zhou (2009). It turns out that such a high level of persistence is necessary to generate high enough variance risk premium, without sacrificing too much in matching the equity risk premium and risk-free rate, but with overfitting of the interest rate
volatility and bond risk premia.
--is as high as 0.95, as opposed to the low value of 0.26 reflected in the data and 0.80 in Bollerslev, Tauchen, and Zhou (2009). It turns out that such a high level of persistence is necessary to generate high enough variance risk premium, without sacrificing too much in matching the equity risk premium and risk-free rate, but with overfitting of the interest rate
volatility and bond risk premia.
The observed bond risk premium for 2-6 month t-bills holding one month are positive but only mildly upward sloping around 0.44 to 0.86 percent. If one chooses the specification in Bollerslev, Tauchen, and Zhou (2009), the bond risk premia would be extremely hump-shaped
with about 3 percent at 2 month, 7 percent at 4 month, and
![]() percent at 6 month.15 In
contrast, the specification chosen in this paper would produce a term structure of bond risk premia from 2.92 percent to 13.90 percent for 2-6 month t-bills holding one month, which is certainty more steep than the observed data, but is quite closer to the observed term structure or bond risk
premiums than Bollerslev, Tauchen, and Zhou (2009). Again, this is a non-trivial result because one has not introduced the inflation dynamics or monetary distortion yet into the model.
percent at 6 month.15 In
contrast, the specification chosen in this paper would produce a term structure of bond risk premia from 2.92 percent to 13.90 percent for 2-6 month t-bills holding one month, which is certainty more steep than the observed data, but is quite closer to the observed term structure or bond risk
premiums than Bollerslev, Tauchen, and Zhou (2009). Again, this is a non-trivial result because one has not introduced the inflation dynamics or monetary distortion yet into the model.
4.3.3 Challenge for Explaining the Term Structure of Predictability
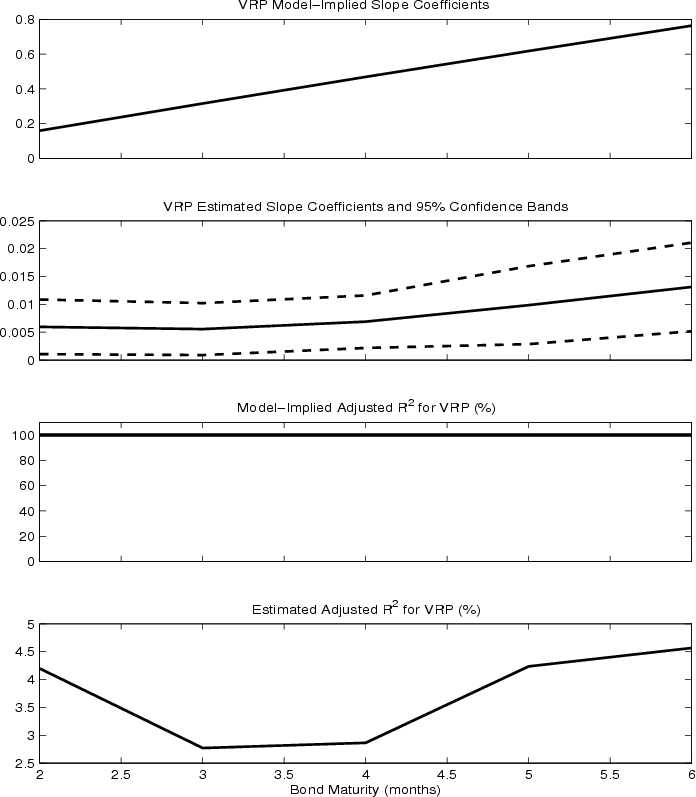
The current modeling framework has been shown (Bollerslev, Tauchen, and Zhou, 2009, Figure 1) to be able to replicate the short-run predictability pattern in equity returns (top two panels in Figure 3). However, such a model implies that the
bond risk premium is entirely driven by the uncertainty risk factor, ![]() , (equation 14), which is also the only state variable in the variance risk premium (equation
13). Therefore, as shown in Figure 6, the prediction
, (equation 14), which is also the only state variable in the variance risk premium (equation
13). Therefore, as shown in Figure 6, the prediction ![]() 's should be always equal to one, as opposed to the low single digit; and the
(deterministic) slope coefficients, although upward sloping, are many times larger than their empirical counterparts. Therefore it remains a challenge to simultaneously reproduce the short-run predictability patterns of the variance risk premium for both equity and bond returns, and for credit
spreads the current model still lacks a defaultable sector.
's should be always equal to one, as opposed to the low single digit; and the
(deterministic) slope coefficients, although upward sloping, are many times larger than their empirical counterparts. Therefore it remains a challenge to simultaneously reproduce the short-run predictability patterns of the variance risk premium for both equity and bond returns, and for credit
spreads the current model still lacks a defaultable sector.
4.4 Extension to Credit Spread Puzzles
It is also challenging to incorporate the default risk of a representative firm into the current modeling framework. The strategy could follow Chen (2008) and Bhamra, Kuehn, and Strebulaev (2009), where the recursive preference plus macroeconomic
uncertainty generate richer dynamics in the credit spread dynamics. To fix the idea, assume that in a Merton (1974) type model as in Chen, Collin-Dufresne, and Goldstein (2008), the credit spread of a discount bond for a defaultable firm with
![]() maturity can be shown as
maturity can be shown as
where LGD is the loss given default, PD is the real default probability,
The equilibrium structural approach (as in, e.g., Chen, 2008; Bhamra,
Kuehn, and Strebulaev, 2009, among others) can be viewed as letting the real default probability
PD![]() to be time-varying and countercyclical, with possible business cycle fluctuations of the firm's refinancing decision or default barrier. It is also possible to model the recovery rate
to be time-varying and countercyclical, with possible business cycle fluctuations of the firm's refinancing decision or default barrier. It is also possible to model the recovery rate
![]() LGD
LGD![]() as stochastic to help explain the cyclical behavior in credit spreads, but the quantitative
improvement could be marginal in this angle. Chen, Collin-Dufresne, and Goldstein (2008) take a novel approach to allow for the market price of risk
as stochastic to help explain the cyclical behavior in credit spreads, but the quantitative
improvement could be marginal in this angle. Chen, Collin-Dufresne, and Goldstein (2008) take a novel approach to allow for the market price of risk ![]() to be
driven by a countercyclical risk aversion motivated by the Campbell and Cochrane (1999) external habit model. Finally, one can allow the asset volatility
to be
driven by a countercyclical risk aversion motivated by the Campbell and Cochrane (1999) external habit model. Finally, one can allow the asset volatility ![]() to be time-varying and countercyclical. Such an extension may be consistent with the empirical and calibration evidence in Zhang, Zhou, and Zhu (2009), where the stochastic asset volatility can help structural models to explain the credit spread puzzles.16
to be time-varying and countercyclical. Such an extension may be consistent with the empirical and calibration evidence in Zhang, Zhou, and Zhu (2009), where the stochastic asset volatility can help structural models to explain the credit spread puzzles.16
5 Conclusion
The implied-expected variance difference can be viewed as a measure for the variance risk premium. This paper provides consistent empirical evidence that the variance risk premium can significantly predict short-run equity returns, bond returns, and credit spreads. The documented return predictability peaks around one-to-four month and decline with the forecasting horizon. Importantly, such a short-term forecastability of risk premia is complementary to the established predictors--P/E ratio, forward spread, and short rate. This constitutes an important evidence that risk premia across major financial markets co-vary in short-term, and such a comovement seems to be driven by a common risk factor, measured by the implied-expected variance difference.
Such a common short-run risk factor may be a proxy for the macroeconomic uncertainty or consumption volatility risk that varies independently with the consumption growth risk--the latter being the main focus of the long-run risks model (Bansal and Yaron, 2004). The empirical results may be consistent with a general equilibrium model incorporating the effects of such a time-varying economic uncertainty component, where the uncertainty risk is priced only under the recursive preference. This paper provides calibration evidence that the equity premium puzzle, variance premium dynamics, and bond risk premia in short-horizon may be qualitatively explained by the proposed model with the same calibration parameter setting. Extension to credit spread puzzle requires a defaultable sector in the modeling framework.
Although the stylized model examined here can provide qualitative justification for the short-run predictability of asset market returns from the variance risk premium, it is not rich enough to simultaneously explain such effects within the same parameter setting. More importantly, to jointly interpret the long-run and short-run comovements in asset markets, a consumption growth factor may be needed to quantitatively replicate various predictability puzzles established in the literature. Finally, the short-run forecastability of variance risk premium documented here as in the time-series domain need to be reconciled with the cross-sectional evidence of asset market returns. I leave these challenging issues for future research.
Bibliography
"Risk Premia and Term Premia in General Equilibrium," Journal of Monetary Economics, vol. 43, 3-33. "The Distribution of Realized Stock Return Volatility," Journal of Financial Economics, vol. 61, 43-76. "Delta-Hedged Gains and the Negative Market Volatility Risk Premium," Review of Financial Studies, vol. 16, 527-566. "Spanning and Derivative-Security Valuation," Journal of Financial Economics, vol. 55, 205-238. "A Theory of Volatility Spread," Management Science, vol. 52, 1945-1956. "A Note on the Economics and Statistics of Predictability: A Long Run Risks Perspective," Working Paper, Duke University and University of Pennsylvania. "An Empirical Evaluation of the Long-Run Risks Model for Asset Prices," Duke University and University of Pennsylvania. "Learning and Asset-Price Jumps," Working Paper, Duke University. "A Long-Run Risks Explanation of Preditability Puzzles in Bond and Currency Markets," Working Paper, Duke University. "Risks for the Long Run: A Potential Resolution of Asset Pricing Puzzles," Journal of Finance, vol. 59, 1481-1509. "Econometric Analysis of Realised Volatility and Its Use in Estimating Stochastic Volatility Models," Journal of Royal Statistical Society, Series B, vol. 64, 253-280. "Rare Disasters and Asset Markets in the Twentieth Century," Quarterly Journal of Economics, vol. 121, 823-866. "Jumps and Stochastic Volatility: Exchange Rate Process Implicit in Deutsche Mark Options," The Review of Financial Studies, vol. 9, 69-107. "The Long-Run Risks Model and Aggregate Asset Prices: An Empirical Assessment," Working Paper, Harvard University. "What Do Asset Prices Have to Say about Risk Appetite and Uncertainty?" Working Paper, European Central Bank.Table 1: Summary statistics
The sample period extends from January 1990 to December 2008. All variables are reported in annualized percentage form whenever appropriate. Panel A reports the variance risk premiums using different methods for estimating the physical expectation of the realized variance: (1) ex post realized variance, (2) lagged realized variance, (3) 12 month moving average, (4) recursive AR(12) forecast, and (5) full sample AR(12) forecast. Panel B reports S&P500 market returns, log price-earning ratio. Panel C reports the 1 month excess holding period return and forward minus spot rate spreads for Treasury zero coupon bond with 1-6 month maturities. Panel D reports the Moody's AAA and BAA credit spread indices with the US short rate level.| Lag |
Recursive |
Full Sample |
|||
| Summary Statistics: Mean | 17.22 | 17.07 | 20.49 | 21.81 | 18.30 |
| Summary Statistics: Std Dev | 20.27 | 19.99 | 25.03 | 27.86 | 22.69 |
| Summary Statistics: Skewness | -3.12 | -3.32 | 4.19 | 4.39 | 2.79 |
| Summary Statistics: Kurtosis | 44.20 | 46.41 | 27.51 | 34.15 | 16.62 |
| Summary Statistics: AR(1) | 0.28 | 0.76 | 0.66 | 0.76 | 0.26 |
| Correlation Matrix: |
1.00 | 0.28 | 0.11 | 0.23 | 0.04 |
| Correlation Matrix: Lag |
1.00 | 0.06 | 0.12 | 0.18 | |
| Correlation Matrix: |
1.00 | 0.63 | 0.75 | ||
| Correlation Matrix: Recursive |
1.00 | 0.21 | |||
| Correlation Matrix: Full Sample |
1.00 |
|
|
|
||
| Summary Statistics: Mean | 3.58 | 18.30 | 3.12 |
| Summary Statistics: Std Dev | 50.58 | 22.69 | 0.25 |
| Summary Statistics: Skewness | -0.90 | 2.79 | 0.48 |
| Summary Statistics: Kurtosis | 50.08 | 16.62 | 2.53 |
| Summary Statistics: AR(1) | 0.07 | 0.26 | 0.97 |
| Correlation Matrix:
|
1.00 | 0.01 | -0.11 |
| Correlation Matrix: |
1.00 | 0.07 | |
| Correlation Matrix:
|
1.00 |
|
|
|
|
|
|
|||||||
| Summary Statistics: Mean | 0.44 | 0.57 | 0.56 | 0.78 | 0.86 | 18.30 | 0.41 | 0.46 | 0.46 | 0.50 | 0.54 |
| Summary Statistics: Std Dev | 0.63 | 0.70 | 0.86 | 1.03 | 1.33 | 22.69 | 0.96 | 0.76 | 0.69 | 0.69 | 0.69 |
| Summary Statistics: Skewness | 0.91 | 0.74 | 1.16 | 1.18 | 0.65 | 2.79 | 1.15 | 0.51 | 0.97 | 0.88 | 0.74 |
| Summary Statistics: Kurtosis | 4.85 | 4.59 | 6.05 | 5.88 | 8.87 | 16.62 | 5.31 | 4.05 | 6.26 | 5.29 | 5.19 |
| Summary Statistics: AR(1) | 0.47 | 0.36 | 0.29 | 0.32 | 0.30 | 0.26 | -0.10 | 0.26 | 0.35 | 0.37 | 0.39 |
| Correlation Matrix:
|
1.00 | 0.91 | 0.80 | 0.73 | 0.61 | 0.22 | 0.71 | 0.76 | 0.75 | 0.74 | 0.71 |
| Correlation Matrix:
|
1.00 | 0.92 | 0.88 | 0.77 | 0.18 | 0.57 | 0.66 | 0.64 | 0.62 | 0.60 | |
| Correlation Matrix:
|
1.00 | 0.95 | 0.86 | 0.18 | 0.46 | 0.52 | 0.53 | 0.51 | 0.50 | ||
| Correlation Matrix:
|
1.00 | 0.92 | 0.21 | 0.37 | 0.44 | 0.43 | 0.44 | 0.43 | |||
| Correlation Matrix:
|
1.00 | 0.22 | 0.27 | 0.33 | 0.33 | 0.33 | 0.38 | ||||
| Correlation Matrix: |
1.00 | 0.06 | 0.04 | 0.05 | 0.05 | 0.06 | |||||
| Correlation Matrix:
|
1.00 | 0.88 | 0.88 | 0.88 | 0.84 | ||||||
| Correlation Matrix:
|
1.00 | 0.94 | 0.94 | 0.93 | |||||||
| Correlation Matrix:
|
1.00 | 0.97 | 0.95 | ||||||||
| Correlation Matrix:
|
1.00 | 0.97 | |||||||||
| Correlation Matrix:
|
1.00 |
| AAA | BAA | Short Rate | ||
| Summary Statistics: Mean | 1.25 | 2.14 | 18.30 | 4.24 |
| Summary Statistics: Std Dev | 0.45 | 0.68 | 22.69 | 1.83 |
| Summary Statistics: Skewness | 0.89 | 2.15 | 2.79 | -0.20 |
| Summary Statistics: Kurtosis | 3.18 | 10.50 | 16.62 | 2.37 |
| Summary Statistics: AR(1) | 0.98 | 1.05 | 0.26 | 0.99 |
| Correlation Matrix: AAA | 1.00 | 0.91 | 0.16 | -0.61 |
| Correlation Matrix: BAA | 1.00 | 0.17 | -0.62 | |
| Correlation Matrix: |
1.00 | 0.10 | ||
| Correlation Matrix: Short Rate | 1.00 |
Table 2: Equity Returns, Variance Risk Premia, and P/E ratios
The sample period extends from January 1990 to December 2008. All of the regressions are based on monthly observations. Robust| Monthly Horizon | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| (1) Constant | 3.13 | 1.74 | -0.69 | -2.90 | -0.43 | 0.44 | 0.82 | 1.72 | 2.60 | 2.90 | 3.56 | 3.33 |
| (1) Constant (t-statistic) | (0.55) | (0.34) | (-0.14) | (-0.56) | (-0.09) | (0.10) | (0.19) | (0.41) | (0.64) | (0.72) | (0.93) | (0.86) |
| (1) |
0.02 | 0.20 | 0.24 | 0.40 | 0.27 | 0.23 | 0.21 | 0.17 | 0.13 | 0.13 | 0.10 | 0.11 |
| (1) |
(0.07) | (0.85) | (1.47) | (3.56) | (2.54) | (2.36) | (2.50) | (2.13) | (1.80) | (2.04) | (1.51) | (2.38) |
| (1) Adj. |
-0.43 | 1.06 | 2.29 | 8.11 | 4.50 | 3.85 | 3.97 | 2.97 | 1.83 | 1.73 | 0.83 | 1.51 |
| (2) Constant | 75.94 | 80.65 | 72.44 | 67.22 | 61.90 | 58.25 | 54.26 | 52.42 | 52.36 | 52.70 | 53.83 | 55.11 |
| (2) Constant (t-statistic) | (1.84) | (1.95) | (1.73) | (1.56) | (1.48) | (1.42) | (1.34) | (1.31) | (1.34) | (1.39) | (1.48) | (1.57) |
| (2) log(P/E) | -23.18 | -24.06 | -22.00 | -20.22 | -18.44 | -17.23 | -15.91 | -15.24 | -15.15 | -15.21 | -15.53 | -15.90 |
| (2) log(P/E) (t-statistic) | (-1.75) | (-1.82) | (-1.64) | (-1.47) | (-1.37) | (-1.30) | (-1.22) | (-1.18) | (-1.20) | (-1.24) | (-1.32) | (-1.40) |
| (2) Adj. |
0.92 | 2.28 | 2.92 | 3.40 | 3.74 | 3.96 | 3.95 | 4.21 | 4.70 | 5.13 | 5.69 | 6.34 |
| (3) Constant | 75.94 | 79.84 | 72.98 | 67.96 | 62.20 | 58.53 | 54.60 | 52.65 | 52.44 | 52.90 | 53.87 | 55.38 |
| (3) Constant (t-statistic) | (1.83) | (1.90) | (1.70) | (1.50) | (1.43) | (1.38) | (1.31) | (1.29) | (1.32) | (1.38) | (1.47) | (1.56) |
| (3) log(P/E) | -23.42 | -25.10 | -23.72 | -22.83 | -20.17 | -18.71 | (-17.31) | -16.40 | -16.04 | -16.10 | -16.18 | -16.74 |
| (3) log(P/E) (t-statistic) | (-1.65) | (-1.80) | (-1.70) | (-1.60) | (-1.44) | (-1.37) | (-1.28) | (-1.24) | (-1.24) | (-1.29) | (-1.36) | (-1.46) |
| (3) |
0.04 | 3.59 | 0.27 | 0.42 | 0.29 | 0.24 | 0.23 | 0.19 | 0.15 | 0.14 | 0.11 | 0.13 |
| (3) |
(0.12) | (1.50) | (1.51) | (3.61) | (2.67) | (2.52) | (2.61) | (2.21) | (1.86) | (2.17) | (1.69) | (2.77) |
| (3) Adj. |
0.51 | 5.59 | 5.76 | 12.59 | 9.08 | 8.60 | 8.75 | 7.91 | 7.15 | 7.52 | 7.04 | 8.57 |
Table 3: Bond Returns and Variance Risk Premia
The sample period extends from January 1990 to December 2008. All of the regressions are based on monthly observations. The regression takes the formwhere
| Holding Period | 2 Month Bill | 3 Month Bill | 4 Month Bill | 5 Month Bill | 6 Month Bill |
| 1 Month/Const. | 0.33 | 0.47 | 0.43 | 0.60 | 0.62 |
| 1 Month/Const. (t-statistic) | (4.00) | (5.66) | (4.67) | (5.35) | (4.34) |
| 1 Month/Const. |
5.96e-3 | 5.55e-3 | 6.88e-3 | 9.85e-3 | 13.12e-3 |
| 1 Month/Const. |
(2.38) | (2.33) | (2.86) | (2.76) | (3.23) |
| 1 Month/Const. Adj. |
4.20 | 2.77 | 2.86 | 4.24 | 4.57 |
| 2 Months/Const. | 0.25 | 0.22 | 0.22 | 0.29 | |
| 2 Months/Const. (t-statistic) | (5.69) | (5.69) | (5.23) | (4.53) | |
| 2 Months/Const. |
1.76e-3 | 2.58e-3 | 4.26e-3 | 7.17e-3 | |
| 2 Months/Const. |
(1.22) | (2.05) | (1.95) | (2.03) | |
| 2 Months/Const. Adj. |
0.86 | 1.34 | 2.23 | 3.54 | |
| 3 Months/Const. | 0.16 | 0.26 | 0.32 | ||
| 3 Months/Const. (t-statistic) | (4.97) | (5.39) | (4.23) | ||
| 3 Months/Const. |
1.28e-3 | 1.98e-3 | 3.70e-3 | ||
| 3 Months/Const. |
(1.19) | (1.24) | (1.42) | ||
| 3 Months/Const. Adj. |
0.70 | 0.93 | 1.59 | ||
| 4 Months/Const. | 0.18 | 0.28 | |||
| 4 Months/Const. (t-statistic) | (5.74) | (4.74) | |||
| 4 Months/Const. |
0.57e-3 | 0.84e-3 | |||
| 4 Months/Const. |
(0.50) | (0.50) | |||
| 4 Months/Const. Adj. |
-0.17 | -0.22 | |||
| 5 Months/Const. | 0.16 | ||||
| 5 Months/Const. (t-statistic) | (4.31) | ||||
| 5 Months/Const. |
0.44e-3 | ||||
| 5 Months/Const. |
(0.38) | ||||
| 5 Months/Const. Adj. |
-0.28 |
Table 4: Bond Returns and Lagged Forward Spreads
The sample period extends from January 1990 to December 2008. All of the regressions are based on monthly observations. Regression takes the formwhere
| Holding Period | 2 Month Bill | 3 Month Bill | 4 Month Bill | 5 Month Bill | 6 Month Bill |
| 1 Month/Const. | 0.23 | 0.36 | 0.34 | 0.51 | 0.59 |
| 1 Month/Const. (t-statistic) | (4.90) | (5.91) | (4.35) | (4.28) | (4.54) |
| 1 Month/Const. Forward Spread | 0.47 | 0.39 | 0.44 | 0.41 | 0.37 |
| 1 Month/Const. Forward Spread (t-statistic) | (7.22) | (7.93) | (5.59) | (4.83) | (4.23) |
| 1 Month/Const. Adj. |
21.64 | 30.88 | 17.99 | 11.75 | 8.05 |
| 2 Months/Const. | 0.22 | 0.26 | 0.27 | 0.39 | |
| 2 Months/Const. (t-statistic) | (5.86) | (5.74) | (4.02) | (4.11) | |
| 2 Months/Const. Forward Spread | 0.24 | 0.29 | 0.47 | 0.43 | |
| 2 Months/Const. Forward Spread (t-statistic) | (3.45) | (4.92) | (5.57) | (3.16) | |
| 2 Months/Const. Adj. |
5.59 | 9.13 | 18.07 | 8.67 | |
| 3 Months/Const. | 0.14 | 0.20 | 0.25 | ||
| 3 Months/Const. (t-statistic) | (4.54) | (4.60) | (3.85) | ||
| 3 Months/Const. Forward Spread | 0.23 | 0.36 | 0.44 | ||
| 3 Months/Const. Forward Spread (t-statistic) | (3.25) | (5.96) | (3.87) | ||
| 3 Months/Const. Adj. |
6.70 | 12.01 | 9.76 | ||
| 4 Months/Const. | 0.15 | 0.23 | |||
| 4 Months/Const. (t-statistic) | (5.51) | (5.03) | |||
| 4 Months/Const. Forward Spread | 0.18 | 0.24 | |||
| 4 Months/Const. Forward Spread (t-statistic) | (3.18) | (5.60) | |||
| 4 Months/Const. Adj. |
4.53 | 5.59 | |||
| 5 Months/Const. | 0.14 | ||||
| 5 Months/Const. (t-statistic) | (5.01) | ||||
| 5 Months/Const. Forward Spread | 0.12 | ||||
| 5 Months/Const. Forward Spread (t-statistic) | (2.26) | ||||
| 5 Months/Const. Adj. |
2.06 |
Table 5: Bond Returns, Variance Risk Premia, and Lagged Forward Spreads
The sample period extends from January 1990 to December 2008. All of the regressions are based on monthly observations. Regression takes the formwhere
| Holding Period | 2 Month Bill | 3 Month Bill | 4 Month Bill | 5 Month Bill | 6 Month Bill |
| 1 Month/Const. | 0.18 | 0.27 | 0.26 | 0.34 | 0.41 |
| 1 Month/Const. (t-statistic) | (3.62) | (4.51) | (3.17) | (3.37) | (3.13) |
| 1 Month/Const. Forward Spread | 0.44 | 0.39 | 0.42 | 0.40 | 0.34 |
| 1 Month/Const. Forward Spread (t-statistic) | (7.08) | (7.99) | (5.29) | (4.79) | (4.06) |
| 1 Month/Const. |
3.65e-3 | 5.04e-3 | 4.85e-3 | 9.23e-3 | 11.10e-3 |
| 1 Month/Const. |
(2.07) | (3.02) | (2.75) | (2.99) | (3.29) |
| 1 Month/Const. Adj. |
22.98 | 33.23 | 19.25 | 15.47 | 11.18 |
| 2 Months/Const. | 0.20 | 0.22 | 0.22 | 0.29 | |
| 2 Months/Const. (t-statistic) | (4.86) | (4.52) | (3.35) | (3.08) | |
| 2 Months/Const. Forward Spread | 0.23 | 0.28 | 0.46 | 0.40 | |
| 2 Months/Const. Forward Spread (t-statistic) | (3.46) | (4.84) | (5.67) | (3.34) | |
| 2 Months/Const. |
1.25e-3 | 2.00e-3 | 3.11e-3 | 5.82e-3 | |
| 2 Months/Const. |
(0.99) | (1.92) | (1.89) | (2.11) | |
| 2 Months/Const. Adj. |
5.82 | 9.80 | 19.11 | 10.86 | |
| 3 Months/Const. | 0.13 | 0.18 | 0.21 | ||
| 3 Months/Const. (t-statistic) | (4.31) | (4.07) | (2.86) | ||
| 3 Months/Const. Forward Spread | 0.22 | 0.35 | 0.42 | ||
| 3 Months/Const. Forward Spread (t-statistic) | (3.24) | (5.98) | (4.03) | ||
| 3 Months/Const. |
0.58e-3 | 1.37e-3 | 2.85e-3 | ||
| 3 Months/Const. |
(0.67) | (1.08) | (1.28) | ||
| 3 Months/Const. Adj. |
6.51 | 12.27 | 10.55 | ||
| 4 Months/Const. | 0.15 | 0.22 | |||
| 4 Months/Const. (t-statistic) | (4.85) | (3.91) | |||
| 4 Months/Const. Forward Spread | 0.18 | 0.24 | |||
| 4 Months/Const. Forward Spread (t-statistic) | (3.38) | (5.72) | |||
| 4 Months/Const. |
0.18e-3 | 0.52e-3 | |||
| 4 Months/Const. |
(0.18) | (0.33) | |||
| 4 Months/Const. Adj. |
4.13 | 5.25 | |||
| 5 Months/Const. | 0.14 | ||||
| 5 Months/Const. (t-statistic) | (3.18) | ||||
| 5 Months/Const. Forward Spread | 0.12 | ||||
| 5 Months/Const. Forward Spread (t-statistic) | (2.45) | ||||
| 5 Months/Const. |
0.15e-3 | ||||
| 5 Months/Const. |
(0.15) | ||||
| 5 Months/Const. Adj. |
1.64 |
Table 6, Part 1 of 5: Credit Spreads, Variance Risk Premia, and Interest Rates - 1 Month Horizon
The sample period extends from January 1999 to December 2008. All of the regressions are based on monthly observations. Regression takes the form| CS |
where the credit spread of
|
Moody's AAA Bond Yield Spread: Constant |
Moody's AAA Bond Yield Spread: |
Moody's AAA Bond Yield Spread: |
Moody's AAA Bond Yield Spread: Adj. |
Moody's BAA Bond Yield Spread: Constant | Moody's BAA Bond Yield Spread: |
Moody's BAA Bond Yield Spread: |
Moody's BAA Bond Yield Spread: Adj. |
| 1.86 | -0.14 | 32.68 | 3.06 | -0.22 | 32.15 | ||
| (10.56) | (-3.94) | (8.18) | (-2.94) | ||||
| 1.17 | 4.68e-3 | 5.19 | 2.00 | 7.99e-3 | 6.64 | ||
| (11.19) | (2.49) | (14.21) | (2.35) | ||||
| 1.78 | -0.15 | 5.85e-3 | 41.13 | 2.93 | -0.23 | 9.76e-3 | 42.37 |
| (11.74) | (-4.59) | (4.26) | (9.10) | (-3.53) | (3.77) |
| Moody's AAA Bond Yield Spread: Constant | Moody's AAA Bond Yield Spread: |
Moody's AAA Bond Yield Spread: |
Moody's AAA Bond Yield Spread: Adj. |
Moody's BAA Bond Yield Spread: Constant | Moody's BAA Bond Yield Spread: |
Moody's BAA Bond Yield Spread: |
Moody's BAA Bond Yield Spread: Adj. |
| 1.77 | -0.12 | 22.33 | 2.92 | -0.18 | 21.83 | ||
| (9.33) | (-3.11) | (7.66) | (-2.52) | ||||
| 1.19 | 3.79e-3 | 2.61 | 2.01 | 7.37e-3 | 4.52 | ||
| (10.63) | (1.84) | (13.56) | (2.08) | ||||
| 1.71 | -0.13 | 5.24e-3 | 27.75 | 2.81 | -0.19 | 9.58e-3 | 29.77 |
| (10.00) | (-3.49) | (3.09) | (8.39) | (-3.00) | (2.87) |
| Moody's AAA Bond Yield Spread: Constant | Moody's AAA Bond Yield Spread: |
Moody's AAA Bond Yield Spread: |
Moody's AAA Bond Yield Spread: Adj. |
Moody's BAA Bond Yield Spread: Constant | Moody's BAA Bond Yield Spread: |
Moody's BAA Bond Yield Spread: |
Moody's BAA Bond Yield Spread: Adj. |
| 1.66 | -0.09 | 12.78 | 2.75 | -0.14 | 12.32 | ||
| (7.80) | (-2.17) | (6.92) | (-1.93) | ||||
| 1.21 | 2.72e-3 | 0.93 | 2.08 | 3.93e-3 | 0.77 | ||
| (10.37) | (1.19) | (12.31) | (1.35) | ||||
| 1.61 | -0.10 | 4.26e-3 | 15.71 | 2.69 | -0.15 | 6.25e-3 | 14.95 |
| (7.94) | (-2.43) | (2.17) | (7.08) | (-2.21) | (2.28) |
| Moody's AAA Bond Yield Spread: Constant | Moody's AAA Bond Yield Spread: |
Moody's AAA Bond Yield Spread: |
Moody's AAA Bond Yield Spread: Adj. |
Moody's BAA Bond Yield Spread: Constant | Moody's BAA Bond Yield Spread: |
Moody's BAA Bond Yield Spread: |
Moody's BAA Bond Yield Spread: Adj. |
| 1.53 | -0.06 | 4.97 | 2.55 | -0.09 | 5.00 | ||
| (6.65) | (-1.30) | (6.59) | (-1.35) | ||||
| 1.22 | 2.94e-3 | 1.17 | 2.07 | 5.15 | 1.64 | ||
| (9.89) | (1.29) | (12.36) | (1.48) | ||||
| 1.49 | -0.07 | 3.90e-3 | 7.35 | 2.49 | -0.10 | 6.67e-3 | 8.00 |
| (6.71) | (-1.49) | (1.86) | (6.92) | (-1.60) | (1.85) |
| Moody's AAA Bond Yield Spread: Constant | Moody's AAA Bond Yield Spread: |
Moody's AAA Bond Yield Spread: |
Moody's AAA Bond Yield Spread: Adj. |
Moody's BAA Bond Yield Spread: Constant | Moody's BAA Bond Yield Spread: |
Moody's BAA Bond Yield Spread: |
Moody's BAA Bond Yield Spread: Adj. |
| 1.37 | -0.02 | 0.25 | 2.30 | -0.03 | 0.23 | ||
| (5.82) | (-0.45) | (6.92) | (-0.57) | ||||
| 1.20 | 4.20e-3 | 2.85 | 2.06 | 5.49e-3 | 1.88 | ||
| (9.66) | (2.05) | 11.49 | (1.92) | ||||
| 1.33 | -0.03 | 4.67e-3 | 3.78 | 2.24 | -0.04 | 6.19e-3 | 2.67 |
| (5.88) | (-0.66) | (2.50) | (7.22) | (-0.80) | (2.10) |
Table 7: Correlations between Different Markets
This table reports the correlations between equity, bond, and credit markets for the raw excess returns and the residual excess returns after regressing on the variance risk premium (VRP) variable. The correlations are for the monthly sample period 1990-2008.| Equity | 2 M. Bill | 3 M. Bill | 4 M. Bill | 5 M. Bill | 6 M. Bill | AAA | BAA | |
| Equity | 1.00 | 0.04 | 0.03 | -0.06 | -0.06 | -0.12 | -0.15 | -0.18 |
| 2 M. Bill | 1.00 | 0.91 | 0.80 | 0.73 | 0.61 | -0.17 | -0.16 | |
| 3 M. Bill | 1.00 | 0.92 | 0.88 | 0.77 | -0.11 | -0.09 | ||
| 4 M. Bill | 1.00 | 0.95 | 0.86 | -0.07 | -0.01 | |||
| 5 M. Bill | 1.00 | 0.92 | -0.09 | 0.06 | ||||
| 6 M. Bill | 1.00 | 0.01 | 0.09 | |||||
| AAA | 1.00 | 0.91 | ||||||
| BAA | 1.00 |
| Equity | 2 M. Bill | 3 M. Bill | 4 M. Bill | 5 M. Bill | 6 M. Bill | AAA | BAA | |
| Equity | 1.00 | 0.08 | 0.03 | -0.04 | -0.09 | -0.08 | -0.21 | -0.29 |
| 2 M. Bill | 1.00 | 0.91 | 0.79 | 0.71 | 0.59 | -0.24 | -0.25 | |
| 3 M. Bill | 1.00 | 0.92 | 0.87 | 0.76 | -0.18 | -0.16 | ||
| 4 M. Bill | 1.00 | 0.95 | 0.86 | -0.12 | -0.07 | |||
| 5 M. Bill | 1.00 | 0.92 | -0.07 | 0.01 | ||||
| 6 M. Bill | 1.00 | -0.05 | 0.02 | |||||
| AAA | 1.00 | 0.90 | ||||||
| BAA | 1.00 |
Table 8: Model Calibration Parameter Setting
This table reports the calibration parameter values for the stochastic volatility-of-volatility model used in this paper. BTZ2009 refers to the calibration setting of Bollerslev, Tauchen, and Zhou (2009), with an emphasis on equity risk premium and its short-run predictability. The Campbell-Shiller linearization constants areTable 9: Calibrated Equity, Variance, and Bond Risk Premia
This table reports the calibration output values for the stochastic volatility-of-volatility model used in this paper. BTZ2009 refers to the calibration setting of Bollerslev, Tauchen, and Zhou (2009). For equity risk premiums, the long historical sample is based on the annual CRSP data from 1930 to 2008 (Bansal, Kiku, and Yaron, 2009), and the short historical sample is based on the annual S&P data from 1891 to 1949 (Gvozdeva and Kumar, 2009). While the short data sample is based on the monthly data from 1990 to 2008 used in this paper. The calibrated equity premiums and bond risk premia are analytical results, while the variance premium moments are based a simulated sample of 1,000,000 months.| Calibration Target Variables | 1930-2008 | 1891-1949 | 1990-2008 | BTZ2009 | This Paper |
| Equity Risk Premium (%): Equity Risk Premium | 7.84 | 4.97 | 3.58 | 7.79 | 5.11 |
| Equity Risk Premium (%): Equity Premium Volatility | 20.16 | 20.36 | 14.60 | 4.02 | 13.24 |
| Equity Risk Premium (%): Risk-Free Rate | 0.86 | 1.96 | 1.13 | 0.69 | 1.86 |
| Equity Risk Premium (%): Risk-Free Rate Volatility | 1.74 | 7.83 | 3.37 | 2.95 | 8.83 |
| Variance Risk Premium(% |
--- | --- | 18.30 | 3.70 | 18.30 |
| Variance Risk Premium(% |
--- | --- | 22.69 | 7.29 | 25.12 |
| Variance Risk Premium(% |
--- | --- | 2.79 | 1.70 | 2.48 |
| Variance Risk Premium(% |
--- | --- | 16.62 | 11.42 | 13.18 |
| Variance Risk Premium(% |
--- | --- | 0.26 | 0.80 | 0.95 |
| Bond Risk Premium (%): 2 Month Bill | --- | --- | 0.44 | 2.99 | 2.92 |
| Bond Risk Premium (%): 3 Month Bill | --- | --- | 0.57 | 5.81 | 5.78 |
| Bond Risk Premium (%): 4 Month Bill | --- | --- | 0.56 | 7.08 | 8.56 |
| Bond Risk Premium (%): 5 Month Bill | --- | --- | 0.78 | -1.41
|
11.27 |
| Bond Risk Premium (%): 6 Month Bill | --- | --- | 0.86 | -1.06
|
13.90 |
This figure plots the variance risk premium or implied-expected variance difference (top panel), the implied variance (middle panel), and the realized variance (bottom panel) for the S&P500 market index from January 1990 to December 2008. The variance risk premium is based on the realized variance forecast from a full sample AR(12). The shaded areas represent NBER recessions.
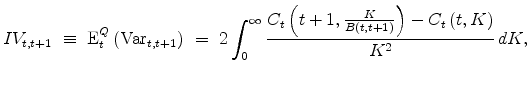
![\displaystyle RV_{t,t+1} \equiv \sum_{j=1}^{n}\left[p_{t+\frac{j}{n}} - p_{t+\frac{j-1}{n}}\right]^2 \longrightarrow](img12.gif) Var
Var![\displaystyle V_t ~ = ~ \left[\left(1-\delta\right)C_t^{\frac{1-\gamma}{\theta}} +\delta\left(E_t\left[V_{t+1}^{1-\gamma}\right]\right)^{\frac{1}{\theta}}\right]^{\frac{\theta}{1-\gamma}},](img42.gif)
![\displaystyle _t(T) = - \frac{1}{T} \log\left\{1-\mbox{LGD} \times \mbox{Normal} \left[\mbox{Normal}^{-1} \left(\mbox{PD}\right)+\lambda\sigma \sqrt{T}\right] \right\},](img122.gif)