Real-time Model Uncertainty in the United States:
'Robust' Policies Put to the Test*
Keywords: monetary policy, model uncertainty, real-time analysis.
Abstract:
JEL Classifications: E37, E5, C5, C6.
1 Introduction
We have involved ourselves in a colossal muddle, having blundered in the control of a delicate machine, the working of which we do not understand.
-John Maynard Keynes, "The Great Slump of 1930" (December 1930).
Over the past decade or so, there has been an explosion of work studying the characteristics of monetary policy rules in general and interest-rate feedback rules in particular. While considerable insight has come out of this literature, so has a fundamental critique, namely that results formulated
in this way may not be robust to misspecification of the underlying model. Keynes's metaphor of the economy as a "delicate machine...which we do not understand" seems as apt today as it was in 1930.
It follows that a principal concern for policy makers is uncertainty, and how to deal with it. The fast growing literature on model uncertainty seeks answers to this question; see, inter alia,Levin, Wieland and Williams (1999), Tetlow and von zur Muehlen (2001), Onatski and Williams (2003), Levin et al. (2005), Brock, Durlauf and West (2007) and Taylor and Wieland (2009).1 This strand often employs the rival models method of analysis wherein the researcher posits two or more alternative models of the economy and employs statistical or decision theoretic techniques to find a policy rule that performs "well" in each of the posited models; see, e.g., McCallum (1988). While this approach to the problem has produced interesting and useful results, it is hampered by the artificiality of the environment in which it which it has been employed. In nearly all cases, the models under consideration are either highly abstract or "toy" models that do not fit the data well, useful perhaps for making narrow points, but not to be taken seriously as tools of monetary policy design.2
Virtually absent from the above characterization of the literature is the real-time analysis of model uncertainty. At one level, this is not surprising; after all, while it is easy to conceptualize changing views about what the true model might be, it is more difficult to imagine the laboratory in which such an analysis could be conducted. That is, however, exactly what this paper provides. Our laboratory is the Federal Reserve Board staff and the FRB/US model. We examine time variation in model properties, and hence model uncertainty, as it was seen in real time by the Federal Reserve Board staff. We do this using 46 of the vintages of the Board staff's FRB/US model, or four per year, that were actually used for forecasting and policy analysis during the period from July 1996 to October 2007, examining how the model specification, coefficients, databases and stochastic shock sets changed from vintage to vintage as new and revised data came in. The advantage provided is that we can focus on those aspects of model uncertainty that are germane to policy decisions, using a model that is used to formulate advice for those decisions.
The relevance of the model is unquestionable: since its introduction in July 1996, the FRB/US model has been used continuously for communicating ideas to the Board of Governors and the Federal Open Market Committee (FOMC). All of the Greenbook's alternative scenarios focusing on domestic economic issues are conducted using the model, forecast confidence intervals are computed using FRB/US, as are optimal policy exercises that appear in the Bluebook; see Svensson and Tetlow (2005).3 In his 1987 monograph on his time as Vice Chairman of the Federal Reserve Board, Alan Blinder notes (p. 12) the important role that FRB/US simulations played in guiding his thinking; and Blinder and Yellen (2001), explain what happened in the US economy in the 1990s, using extensive simulations of the FRB/US model.
As we shall show, the US economy was buffeted by a range of economic forces over this period, including a productivity boom, a stock market boom and bust, a recession, and an abrupt change in fiscal policy. There were also 40 changes in the intended federal funds rate, 24 increases and 16 decreases.4 These events turned out to have important implications for how the Board's staff saw the economy and how they embraced those views in the model's structure. This, in turn, had important implications for what policies would, and would not, work well in such an environment.
Armed with these 46 vintages of the model, we ask whether the policy rules that have been promoted as robust in one environment or another are in fact robust in this real-world context. In other words, if the federal funds rate had followed rules that were optimized within the context of the Fed staff's FRB/US model, how would the economy have performed?
We study eight particular rules. The first is the familiar Taylor (1993) rule, although we use parameterizations that are optimal for the model vintages we are interested in. We also consider three rules that take up the argument of Orphanides (2001) and Orphanides and van Norden (2002) that the inherent difficulty in conditioning policy on unobservable constructed variables like output gaps, policy should eschew feedback on latent variables altogether. Two candidate rules follow Bennett McCallum (1988), by keying off of nominal output growth. A nominal output growth rule establishes a nominal anchor but unlike, say, an inflation targeting rule, makes no explicit call on whether shocks are real or nominal; because of this, it is arguably less susceptible to supply-side misspecifications. Two rules pick up the finding of Levin, Onatski, Williams and Williams (2005)--henceforth LOWW--to the effect that policy should respond to nominal wage inflation instead of price inflation. In this way, the policymaker pays particular attention to the labor market, arguably the part of the economy that, from a neoclassical perspective, is the most distorted.
This paper goes a number of steps beyond previous contributions to the literature. As already noted, it goes beyond the extant rival models literature through its novel and efficacious focus on models that are actually used in a policy environment. It also goes beyond the literature on parameter uncertainty. That literature assumes that parameters are random but the model is fixed over time: misspecification is simply a matter of sampling error. Model uncertainty is a thornier problem, in large part because it often does not readily lend itself to statistical methods of analysis. We explicitly allow the models to change over time in response not just to the data but to the economic issues of the day.5 Finally, as already noted, it does all this within a class of possible models that is undeniably realistic.
The analysis presented herein is, of course, based on the US economy and the FRB/US model. It should be clear, however, that the problems under study are more general than this. Uncertainty, in its various forms, is of concern for monetary authorities the world over as it is for other decision makers. Real-time data issues and data uncertainty more generally have garnered a great deal of attention in the U.K.; see, e.g., Garratt and Vahey (2006) and Garratt, Koop and Vahey (2008) and references therein. On the continent, Giannone, Reichlin and Sala (2005) study real-time uncertainty for its implications for monetary policy while Cimadomo (2008) and Giuliodori and Beetsma (2008) uncover important implications of real-time data uncertainty and, indirectly, model uncertainty for the measurement of fiscal stance and the conduct of fiscal policy for the OECD countries and the Euro area, respectively.6 The relevance of the topic for the Euroarea is particularly striking because a large part of the raison d'etre of its creation was about inducing changes in economic structure that would, as a biproduct, introduce even more model uncertainty, at least for a time.
The rest of this paper proceeds as follows. The second section begins with a discussion of the FRB/US model in generic terms, and the model's historical archives. The third section compares model properties by vintage. To do this, we document changes in real-time "model multipliers" and compare them with their ex post counterparts. The succeeding section computes optimized Taylor-type rules and compares these to commonly accepted alternative policies in a stochastic environment. The fifth section examines the stochastic performance of candidate rules for two selected vintages, the December 1998 and October 2007 models. A sixth and final section sums up and concludes.
2.1 The real-time data
In describing model uncertainty, it pays to start at the beginning; in present circumstances, the beginning is the data. It is the data, and the staff's view of those data back in 1996 that determined how the first vintage of FRB/US was structured. And it is the surprises from those data, and how they were interpreted as the series were revised and extended with each successive vintage, that conditioned the model's evaluation and refinement. To that end, in this subsection we examine key data series by vintage. We also provide some evidence on the model's forecast record during the period of interest. And we reflect on the events of the time, the shocks they engendered, and the revisions to the data. Our treatment of the subject is subjective--it comes, in part, from the archives of the FRB/US model--and incomplete. It is beyond the scope of this part of the paper to provide an comprehensive survey of data revisions over the period from 1996 to 2007. Fortunately, however, Anderson and Kliesen (2005) provide just such a summary.
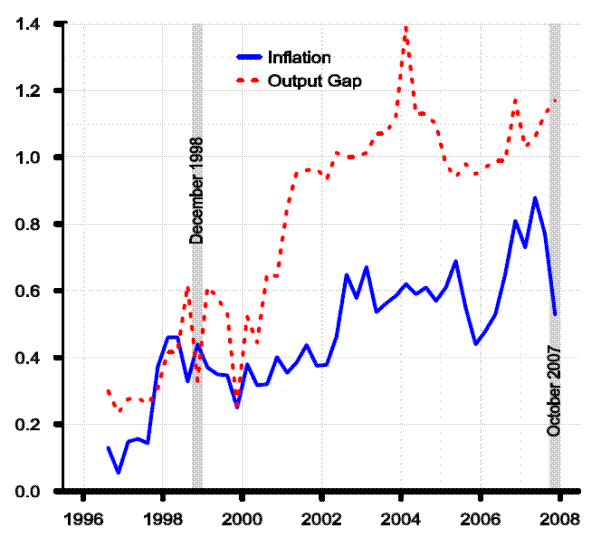
Figure 2.1 shows the four-quarter growth rate of the GDP price index, for selected vintages. (Note we show only real-time historical data because of rules restricting the publication of forecast data.) The inflation rate moves around some, but the various vintages for the most part are highly correlated. In any event, our reading of the literature is that data uncertainty, narrowly defined to include revisions of published data series, is not a first-order source of problems for monetary policy design; see, e.g., Croushore and Stark (2001). Figure 2.2 shows the more empirically important case of model measures of growth in potential non-farm business output.7
Unlike the case of inflation, potential output growth is a latent variable the definition and interpretation of which depends on model concepts. This means is the historical measures of potential are themselves a part of the model, and so we should expect significant revisions.8 Even so, the magnitudes of the revisions shown in Figure 2.2 are remarkable. The July 1996 vintage shows growth in potential output of about 2 percent, typical of the estimates of models at the time. For the next several years, succeeding vintages show both higher potential output growth rates and more responsiveness to the economic cycle. By January 2001, growth in potential was estimated at over 5 percent for some dates, before subsequent changes resulted in a path that was lower and more variable. The very concept of potential growth had changed. Why did potential undergo such dramatic revision? Table 1 reminds us about how extraordinary the late 1990s were. The table shows selected FRB/US model forecasts for the four-quarter growth in real GDP, on the left-hand side of the table, and PCE price inflation, on the right-hand side, for the period for which public availability of the data are not restricted.9 The table shows the substantial underprediction of GDP growth over most of the period, together with underpredictions of inflation.
Table 1: Four-quarter growth in real GDP and PCE prices: selected FRB/US model forecasts
| forecast date | Real GDP: forecast | Real GDP: data | Real GDP: data - forecast* | GDP price index: forecast | GDP price index: data | GDP price index: data - forecast* |
| July 1996 | 2.2 | 4.0 | 1.8 | 2.3 | 1.9 | -0.4 |
| July 1997 | 2.0 | 3.5 | 1.5 | 2.2 | 0.9 | -1.3 |
| Aug. 1998 | 1.7 | 4.1 | 2.4 | 1.8 | 1.3 | -0.5 |
| Aug. 1999 | 3.2 | 5.3 | 2.1 | 2.3 | 2.3 | 0.0 |
| Aug. 2000 | 4.5 | 0.8 | -3.7 | 2.1 | 2.3 | 0.2 |
| Aug. 2001 | 2.2 | 3.0 | 0.8 | 2.7 | 0.8 | -2.0 |
| Aug 2002 | 3.6 | 3.1 | -0.5 | 1.3 | 1.7 | 0.3 |
The more recent historical measures shown in Figure 2.2 for the August 2002 and October 2007 vintages show paths that differ in two important ways from the others. First, these series are the only ones shown that are less optimistic than their predecessors. In part, this reflects the onset of the 2001 recession, particularly for the August 2002 series. Second, these two latter series show considerably more volatility over time. This is a manifestation of a change in thinking that arose in response to economic conditions of the day. In its early vintages, the modeling of potential output in FRB/US was traditional for large-scale econometric models: trend labor productivity and trend labor input, were based on exogenous split time trends. In essence, the model took the typical Keynesian view that nearly all shocks affecting aggregate output were demand-side phenomena. Then, in the late 1990s, as under-predictions of GDP growth were experienced without concomitant underpredictions in inflation, these priors were updated. The staff began adding model code to allow the supply side of the model to respond to output surprises by projecting forward revised profiles for productivity growth; what had been an essentially deterministic view of potential output was evolving into a stochastic one.10
Further insight on the origins and persistence of these forecast errors can be gleaned from Figure 2.3, which focuses attention on a single year, 1996, and shows forecasts and "actual" four-quarter GDP growth, non-farm business potential output growth, and PCE inflation for that year. Each date on the horizontal axis corresponds with a database, so that the first observation on the far left of the black line is what the FRB/US model database for the 1996:Q3 (July) vintage showed for four-quarter GDP growth for 1996. (The black line is broken over the first two observations to indicate that some observations for 1996 were forecast data at the time; after the receipt of the advance release of the NIPA for 1996:Q4 on January 31, 1997, the figures are treated as data.) Similarly, the last observation of the same solid black line shows what the 2006:Q4 database has for historical GDP growth in 1996. The black line shows that the data combined with the model predicted four-quarter GDP growth of 2.2 percent for 1996 as of July 1996. However when the first final data for the 1996:Q4 were released on January 31, 1997, GDP growth for the year was 3.1 percent, a sizable forecast error of 0.8 percentage points.11 The black line shows that GDP growth was revised up in small steps and large jumps right up until late in 2003 and to stand by the end of 2006 at 4.4 percent; so by the (unfair) metric of recent data, the forecast error from the July 1996 projection is 2.2 percentage points. Comparisons of the black line, measuring real GDP growth, with the red line, measuring potential output growth, show the influence that data revisions had on the FRB/US measures of potential. The slow response of the red line and the resulting gap between it and the black line in 1996 and 1997 reflects the strong Keynesian prior of the day. Then, as can be seen, in 1998 a more profound change in view was undertaken, and by 1999 nearly all real growth in 1996 was seen as emanating from supply shocks. All told, given the long climb of the black line, the revisions to potential output growth shown by the red line seem explicable, at least until about 2001. After that point, the emerging recession resulted in wholesale revisions of potential output growth going well back into history. The blue line shows that there was a revision in PCE inflation that coincided with substantial changes in both actual GDP and potential, in 1998:Q3. This reflects the annual revision of the NIPA data and with it some updates in source data.12
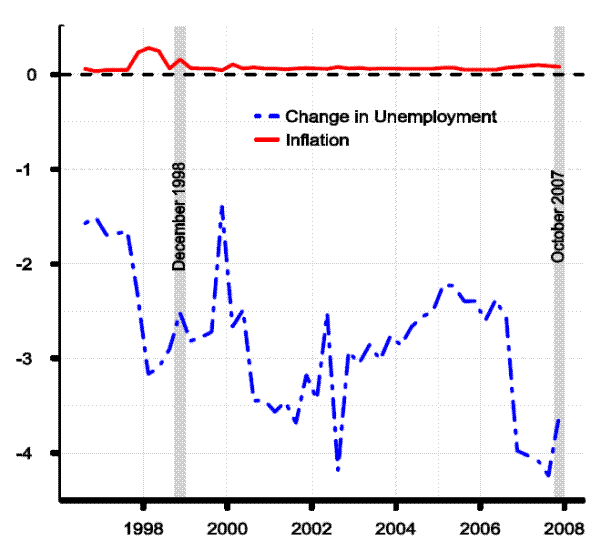
Despite the volatility of potential output growth, the resulting output gaps, shown in Figure 2.4, show considerable covariation, albeit with non-trivial revisions. This observation underscores the underappreciated fact that output gaps (or unemployment gaps) are not the sole driver of fluctuations in inflation; other forces are also at work, particularly trend productivity which affects unit labor costs, and relative price shocks such those affecting food, energy and non-oil import prices.
2.2 A generic description of the FRB/US model
The FRB/US model came into production in July 1996 as a replacement for the venerable MIT-Penn-SSRC (MPS) model that had been in use at the Board of Governors for many years.
The main objectives guiding the development of the model were that it be useful for both forecasting and policy analysis; that expectations be explicit; that important equations represent the decision rules of optimizing agents; that the model be estimated and have satisfactory statistical properties; and that the full-model simulation properties match the "established rules of thumb regarding economic relationships under appropriate circumstances" as Brayton and Tinsley (1996, p. 2) put it.
To address these challenges, the staff included within the FRB/US model a specific expectations block, and with it, a fundamental distinction between intrinsic model dynamics (dynamics that are immutable to policy) and expectational dynamics (which policy can affect). In most instances, the intrinsic dynamics of the model were designed around representative agents choosing optimal paths for decision variables facing adjustment costs.13
Ignoring asset pricing equations for which adjustment costs were assumed to be negligible, a generic model equation would look something like:
where
From the outset, FRB/US has been a significantly smaller model than was MPS, but it is still quite large. At inception, it contained some 300 equations and identities of which perhaps 50 were behavioral. About half of the behavioral equations in the first vintage of the model were modeled using formal specifications of optimizing behavior. Among the identities are the expectations equations.
Two versions of expectations formation were envisioned: VAR-based expectations and perfect foresight. The concept of perfect foresight is well understood, but VAR-based expectations probably requires some explanation. In part, the story has the flavor of the Phelps-Lucas "island paradigm":
agents live on different islands where they have access to a limited set of core macroeconomic variables, knowledge they share with everyone in the economy. The core macroeconomic variables are the output gap,
![]() the inflation rate,
the inflation rate, ![]() and the federal funds rate,
and the federal funds rate,
![]() as well as agents' beliefs of the long-run target rate of inflation,
as well as agents' beliefs of the long-run target rate of inflation,
![]() and the equilibrium real rate of interest in the long run,
and the equilibrium real rate of interest in the long run,
![]() . These variables comprise the model's core VAR expectations block which we can write as follows:
. These variables comprise the model's core VAR expectations block which we can write as follows:
![\begin{displaymath} w=\left[ \begin{array}[c]{c}% \widetilde{y}-\widetilde{y}^{\infty}\ \pi-\pi^{\infty}\ r-r^{\infty}% \end{array}\right] \varepsilon=\left[ \begin{array}[c]{c}% u^{y}\ u^{\pi}\ u^{r}% \end{array}\right] . \end{displaymath}](img26.gif)
![\begin{displaymath}w^{\infty}=\left[ \begin{array}[c]{ccc}% 0 & \pi^{\infty} & r^{\infty}% \end{array}\right] ^{/}\end{displaymath}](img29.gif) .
.
In addition to variables of this core VAR, agents have information that is germane to their island, or sector. Consumers, for example, augment their core VAR model with information about potential output growth and the ratio of household income to GDP, which forms the consumer's auxiliary VAR. Two features of this set-up are worth noting. First, the set of variables agents are assumed to use in formulating forecasts is restricted to a set that is smaller than under rational expectations. (By definition, under perfect-foresight expectations, the information set includes all the states in the model with all the cross-equation restrictions implied by the model.) Second, agents are allowed to update their beliefs, but only in a restricted way. In particular, for any given vintage, the coefficients of the VARs are taken as fixed, while agents' perceptions of long-run values for the inflation target and the equilibrium real interest rate are continually updated using simple learning rules.14
In this paper, we will be working exclusively with the VAR-based expectations version of the model. Typically it is the multipliers of this version of the model that are reported to Board members when they ask "what-if questions". This is the version that is used for forecasting and most of the policy analysis by the Fed staff, including, as Svensson and Tetlow (2005) demonstrate, policy optimization experiments. Thus, the pertinence of using this version of the model for the question at hand is unquestionable. What might be questioned, on standard Lucas-critique grounds, is the validity of the Taylor-rule optimizations carried out below. However, the period under study is one entirely under the leadership of a single Chairman, and we are aware of no evidence to suggest that there was a change in regime during this period. So as Sims and Zha (2006) have argued, it seems likely that the perturbations to policies encompassed by the range of policies studied below are not large enough to induce a change in expectations formation other than that can be captured by changes in the endpoints. Moreover, in an environment such as the one under study, where changes in the non-monetary part of the economy are likely to dwarf the monetary-policy perturbations, it seems safe to assume that private agents were no more rational with regard to their anticipations of policy than the Fed staff was about private-sector decision making.15 In their study of the evolution of the Fed beliefs over a longer period of time, Romer and Romer (2002), ascribe no role to the idea of rational expectations. Moreover, Rudebusch (2002) shows that issues of model uncertainty are often of second-order importance in linear rational expectations models. Thus the VAR-based expectations case is arguably the more quantitatively interesting one. Finally, what matters for this real-time study is that it is certainly the case that the model buiiders believe in VAR-based expectations formation and the model was, in fact, used for forecasting and policy analysis alike; see, e.g. Svensson and Tetlow (2005). Later on we will have more to say about the implications of assuming VAR-based expectations for our results and those in the rest of the literature
There is not the space here for a complete description of the model. Readers interested in detailed descriptions of the model are invited to consult papers on the subject, including Brayton and Tinsley (1996), Brayton, Levin, Tryon and Williams (1997), and Reifschneider, Tetlow and Williams (1999). However, before leaving this section it is important to note that the structure of macroeconomic models at the Fed have always responded to economic events and the different questions that those events evoke, even before FRB/US. Brayton, Levin, Tryon and Williams (1997) note, for example, how the presence of financial market regulations meant that for years a substantial portion of the MPS model dealt specifically with mortgage credit and financial markets more broadly. The repeal of Regulation Q induced the elimination of much of that detailed model code. Earlier, the oil price shocks of the 1970s and the collapse of Bretton Woods gave the model a more international flavor than it had previously. We shall see that this responsiveness of models to economic conditions and questions continued with the FRB/US model in the 1990s. The key features influencing the monetary policy transmission mechanism in the FRB/US model are the effects of changes in the funds rate on asset prices and from there to expenditures. Philosophically, the model has not changed much in this area: all vintages of the model have had expectations of future economic conditions in general, and the federal funds rate in particular, affecting long-term interest rates and inflation. From this, real interest rates are determined and this in turn affects stock prices and exchange rates, and from there, real expenditures. Similarly, the model has always had a wage-price block, with the same basic features: sticky wages and prices, expected future excess demand in the goods and labor markets influencing price and wage setting, and a channel through which productivity affects real and nominal wages. That said, as we shall see, there have been substantial changes over time in both (what we may call) the interest elasticity of aggregate demand and the effect of excess demand on inflation.
Over the years, equations have come and gone in reflection of the needs, and data, of the day. The model began with an automotive sector but this block was later dropped. Business fixed investment was originally disaggregated into just non-residential structures and producers' durable equipment, but the latter is now disaggregated into high-tech equipment and "other". The key consumer decision rules and wage-price block have undergone frequent modification over the period. On the other hand, the model has always had an equation for consumer non-durables and services, consumer durables expenditures, and housing. There has always been a trade block, with aggregate exports and non-oil and oil imports, and equations for foreign variables. The model has always had a three-factor, constant-returns-to-scale Cobb-Douglas production function with capital, labor hours and energy as factor inputs.
2.3 The model archive
Since its inception in July 1996, the FRB/US model code, the equation coefficients, the baseline forecast database, and the list of stochastic shocks with which the model would be stochastically simulated, have all been stored for each of the eight forecasts the Board staff conducts every year. Because it is releases of National Income and Product Accounts (NIPA) data that typically induce re-assessments of the model, we use four archives per year, or 46 in total, the ones immediately following NIPA preliminary releases.16
In what follows, we experiment with each vintage of model, comparing their properties in selected experiments. Consistent with the real-time philosophy of this endeavor, the experiments we choose are typical of those used to assess models by policy institutions in general and the Federal Reserve Board in particular. They fall into two broad classes. One set of experiments, model multipliers, attempts to isolate the behavior of particular parts of the model. A multiplier is the response of a key endogenous variable to an exogenous shock after a fixed period of time. An example is the response of the level of output after eight quarters to a persistent increase in the federal funds rate. The other set of experiments judge the stochastic performance of the model and are designed to capture the full-model properties under fairly general conditions. So, for example, we will compute by stochastic simulation the optimal coefficients and economic performance of simple rules, conditional on a model vintage, a baseline database, and a set of stochastic shocks.17
Model multipliers have been routinely reported to, and used by, members of the FOMC. Indeed, the model's sacrifice ratio--about which we will have more to say below--was used in the very first FOMC meeting following the model's introduction. Similarly, model simulations of alternative policies have been carried out and reported to the FOMC in a number of memos and official FOMC documents.18
The archives document model changes and provide a unique record of model uncertainty. As we shall see, the answers to questions a policy maker might ask differ depending on the vintage of the model. The seemingly generic issue of the output cost of bringing down inflation, for example, can be subdivided into several more precise questions, including: (i) what would the model say is the output cost of bringing down inflation today?; (ii) what would the model of today say the output cost of bringing down inflation would have been in December 1998?; and (iii) what would the model have said in December 1998 was the output cost of disinflation at that time? These questions introduce a time dependency to the issue that rarely appears in other contexts.
The answers to these and other related questions depend on the model vintage and everything that goes along with it: the model itself, the policy rule, the baseline database and the set of stochastic shocks.
3 Model multipliers in real time and ex post
In this section, we consider the variation in real time of selected model multipliers. In the interests of brevity, we devote space to just four multipliers. The first is the sacrifice ratio; that is, the cumulative annualized cost measured in terms of increased unemployment over five years of permanently reducing the inflation rate by one percentage point. The second is the funds rate multiplier, defined here as the percentage change in the level of real output after eight quarters that is induced by a persistent 100-basis-point increase in the nominal federal funds rate.19 In the parlance of an undergraduate textbook closed-economy model, these two multipliers represent the slope of the Phillips curve and the slope of the aggregate demand curve, respectively. To add an international element, we add an exchange-rate multiplier-specifically, the percentage change in real GDP associated with a 10-percent appreciated of the trade-weight exchange value of the US dollar, and a non-oil import price multiplier: namely, the effect on PCE inflation of a persistent 10-percent increase in the relative price of non-oil imports. The sacrifice ratio is the outcome of a five-year simulation experiment; the other multipliers are measured in terms of their effects after eight quarters, except the import-price passthrough scenario which is computed over a 12-quarter horizon.
It is easiest to show the results graphically. But before turning to specific results, it is useful to outline how these figures are constructed and how they should be interpreted. In all cases, we show two lines. The black solid line is the real-time multiplier by vintage. Each point on the line represents the outcome of the same experiment, conducted on the model vintage of that date, using the baseline database at that point in history. So at each point shown by the black line, the model, its coefficients and the baseline all differ. The red dashed line shows what we call the ex post multiplier. The ex post multiplier is computed using the most recent model vintage for each date; the only thing that changes for each point on the dashed red line is the initial conditions under which the experiment is conducted. Differences over time in the red line reveal the extent to which the model is nonlinear with respect to the phenomenon under study, because the multipliers for linear models are independent of initial conditions.
Now let us look at Figure 3.1, which shows the sacrifice ratio.20 Let us focus on the red dashed line first. It shows
that for the October 2007 model, the sacrifice ratio is essentially constant over time. So if the staff were asked to assess the sacrifice ratio, or what the sacrifice ratio would have been in, say, December 1998, the answer based on the October 2007 model would be the same: about
![]() , meaning that it would take that many percentage-point-years of unemployment to bring down inflation by one percentage point. Now, however, look at the black solid line. Since
each point on the line represents a different model, and the last point on the far right of the line is the October 2007 model, the red dashed line and the black solid line must meet at the right-hand side in this and all other figures in this section. But notice how much the real-time sacrifice
ratio has changed over the 12-year period of study. Had the model builders been asked in December 1998 what the sacrifice ratio was, the answer based on the February 1997 model would have been about
, meaning that it would take that many percentage-point-years of unemployment to bring down inflation by one percentage point. Now, however, look at the black solid line. Since
each point on the line represents a different model, and the last point on the far right of the line is the October 2007 model, the red dashed line and the black solid line must meet at the right-hand side in this and all other figures in this section. But notice how much the real-time sacrifice
ratio has changed over the 12-year period of study. Had the model builders been asked in December 1998 what the sacrifice ratio was, the answer based on the February 1997 model would have been about
![]() . Prior to a revision in mid-2007 that was undertaken in large part expressly to reduce it, the sacrifice ratio for vintages from 2004 to 2006 was of the order of
. Prior to a revision in mid-2007 that was undertaken in large part expressly to reduce it, the sacrifice ratio for vintages from 2004 to 2006 was of the order of
![]() , or more than double what it was in the 1990s.21
, or more than double what it was in the 1990s.21
The sacrifice ratio is a crucial statistic for any central bank model. On the one hand, it describes the cost of bringing down inflation, given that one inherits a higher inflation rate than is desired because of, say, having incurred a supply shock. From this perspective, a high sacrifice ratio is a bad thing. On the other hand, however, a high sacrifice ratio reflects a flat Phillips curve, which is to say that shocks to aggregate demand of a given magnitude will manifest themselves in smaller change in inflation than would otherwise be the case. From this perspective, a high sacrifice ratio is a good thing. Which effect dominates depends on the incidence of supply and demand shocks.
The primacy of the model's sacrifice ratio to policy debates is clear from FOMC transcripts. It was, for example, a topic of discussion at the first FOMC meeting following the introduction of the model.22 Similarly, the February 1, 2000, meeting of the FOMC produced this exchange between Federal Reserve Bank of Minneapolis President Gary Stern and then FOMC Secretary (now Federal Reserve Board Vice Chairman) Donald Kohn:23
Mr. Stern: Let me ask about the Bluebook [FRB/US model simulation] sacrifice ratio. I don't know what your credibility assumption is, but it seems really high.
Mr. Kohn: It is a little higher than we've had in the past, but not much. It is consistent with the model looking out over the longer run. It is a fairly high sacrifice ratio, I think, compared to some other models, but it is not out of the bounds...
Kohn was clearly aware that the model's sacrifice ratio had undergone some change and was rightfully cognizant of how it compares against alternative models. As it happens, the increases already incurred in the sacrifice ratio were only the beginning.
The climb in the model sacrifice ratio is striking, particularly as it was incurred over such a short period of time among model vintages with substantial overlap in their estimation periods. One might be forgiven for thinking that this phenomenon is idiosyncratic to the model under study. But other work shows that this result is not a fluke.24 At the same time, as we have already noted, the model builders did incorporate shifts in the NAIRU (and in potential output), but found that leaning exclusively on this one story for macroeconomic dynamics in the late 1990s was insufficient. Thus, the revealed view of the model builders contrasts with idea advanced by Staiger, Stock and Watson (2001), among others, that changes in the Phillips curve are best accounted for entirely by shifts in the NAIRU. Toward the end of the decade, a reduction in the sacrifice ratio became an important objective of the specification and estimation of the model's wage-price block; success on this front was achieved through respecification of how long-term inflation expectations evolve over time. .
Figure 3.2 shows the funds-rate multiplier; that is, the percentage decrease in the level of real GDP after eight quarters in response to a persistent 100-basis-point increase in the funds rate. This time, the red dashed line shows important time variation: the ex post funds rate multiplier varies with initial conditions, it is largest, in absolute terms, at about 1.6 percentage point in late 2000, and lowest at the beginning and at the end of the period, at about 1 percent. The nonlinearity stems entirely from the specification of the model's stock market equation, which is written in levels, rather than in logs, a feature that makes the interest elasticity of aggregate demand an increasing function of the ratio of stock market wealth to total wealth. The mechanism is that an increase in the funds rate raises long-term bond rates, which in turn bring about a drop in stock market valuation operating through the arbitrage relationship between expected risk-adjusted bond and equity returns. The larger the stock market, the stronger the effect.25
The real-time multiplier, shown by the solid black line is harder to characterize. Two observations stand out. The first is the sheer volatility of the multiplier. In a large-scale model such as the FRB/US model, where the transmission of monetary policy operates through a number of channels, time variation in the interest elasticity of aggregate demand depends on a large variety of parameters. Second, the real-time multiplier is almost always smaller than the ex post multiplier. The gap between the two is particularly marked in 2000, when the business cycle reached a peak, as did stock prices. At the time, concerns about possible stock market bubbles were rampant. One aspect of the debate between proponents and detractors of the active approach to stock market bubbles concerns the feasibility of policy prescriptions in a world of model uncertainty.26 The considerable difference between the real-time and ex post multipliers during this period demonstrates the difficulty in carrying out historical analyses of the role of monetary policy; today's assessment of the strength of those monetary policy actions can differ substantially from what the FRB/US model implied in real time.
The final two multipliers covered in this section cover real and nominal aspects of the international economy. The first is the effect of a sustained 10-percent appreciation of the real exchange value of the US dollar on real output in the United States. The second is the effect of a lasting 10-percent change in the relative price of non-oil import goods on PCE inflation.27 Without belaboring the details, the salient fact to take from these two figures is first and foremost the variability of the elasticities.28 In the case of non-oil import prices, the figure also shows quite clearly another aspect of the so-called great moderation, namely a sharp reduction over time in the influence of shocks on inflation; the phenomenon of diminished pass-through of exchange-rate shocks into inflation in particular has been documented by Campa and Goldberg (200) and Gagnon and Ihrig (2004).
To summarize this section, real-time multipliers show substantial variation over time, and differ considerably from what one would say ex post the multipliers would be. Moreover, the discrepancies between the two multiplier concepts have often been large at critical junctures in recent economic history. It follows that real-time model uncertainty is an important problem for policy makers. The next section quantifies this point by characterizing optimal policy, and its time variation, conditional on these model vintages.
4.1 The rules
In the current context, a monetary policy rule can be described as robust if: (i), the optimized policy coefficients do not differ in important ways across models; or (ii) the performance of the economy does not depend in an economically important way on rule parameterization. A robust policy rule can also be described as effective if (iii) it performs "well," relative to some benchmark policy rule.
A popular simple monetary policy rule is the canonical Taylor (1993) rule. One reason the Taylor rule is advocated for monetary policy because of its simplicity in that it calls for feedback on only those variables that would be central to nearly all macro models. Because of this, it is often suggested that the Taylor rule will be robust to model misspecification; see, e.g., Williams (2003) for an argument along these lines. And indeed many central banks use simple rules of one sort or another, including Taylor rules, in the assessment of monetary policy and for formulating policy advice, including in the Federal Reserve Board staff's Bluebook which describes policy options for the FOMC. In the US case, Giannone et al. (2005) show that the good fit of simple two-argument Taylor-type rules can be attributed to the small number of fundamental factors driving the US economy; that is, the two arguments that appear in Taylor rules encompass all that one needs to know to summarize monetary policy in history. We shall use the Taylor rule, appropriately parameterized, as out benchmark.
Taylor rules have their detractors. Much of the earlier work on robust policy rules has focussed on the importance of estimation and misperception of potential output and the associated mismeasurement of the output gap.29 Accordingly, some of the rules we consider are those that have been suggested as prophylactics for this problem. In other instances, it is a broader class of latent variables that have been the object of concern. For example, as
we have already noted, the productivity boom in the U.S. in the second half of the 1990s, brought about misperceptions not just of the level of the output gap, but also of potential output growth going ahead; these concepts in turn have a
bearing on the equilibrium real interest rate since in all but the smallest of open economies, the equilibrium real interest rate is determined, in part, by the steady-state growth rate of the economy. The two problems are related but different. Mismeasurement of the level of potential output,
without corresponding errors in potential output growth, and associated ![]() errors, are a stationary process. Missing a shift in trend growth is much more persistent and affects a wider
range of variables in a fully articulated macromodel. Accordingly, some of the rules we consider stem from the addressing of the latter, more complicated problem.
errors, are a stationary process. Missing a shift in trend growth is much more persistent and affects a wider
range of variables in a fully articulated macromodel. Accordingly, some of the rules we consider stem from the addressing of the latter, more complicated problem.
Most of our analysis is restricted to the class of optimized two-parameter policy rules. This keeps the rules on equal footing in that it is to be expected that adding extra optimized parameters should improve performance, at least for a given model. It also makes keeps the already onerous computational costs to a manageable level. However, as a check against possible idiosyncrasies in results, we do consider a few three-parameter specifications.
4.1.1 Two-parameter policy rules
Our first rule is the most familiar: the Taylor rule. Formally, the Taylor rule--which for short we will often refer to as "TR"--is written:
where
In our first bow to the output-gap mismeasurement problem, we also study an inflation targeting rule (ITR); that is, a rule that eschews feedback on the output gap altogether in order to avoid problems from the sort of data and conceptual revisions described in Section 2 above, as suggested by Orphanides (2001):
For this rule and several others, we allow for instrument smoothing, with the parameter
where it should be understood that
We will also analyze a Taylor-type rule that substitutes the change in the unemployment rate for the traditional output gap in order to allow a real variable to enter the rule while still minimizing the effects of misperceptions of potential output; see, e.g., Orphanides and Williams (2002):
Notice that this rule, designated URR, is written in the first-difference of the funds rate, a configuration that eliminates the need to condition on the equilibrium real interest rate. As such, the URR takes a step towards insulation against persistent shocks to productivity and associated mismeasurements of
Another much touted rule is the nominal output growth rule, along the lines suggested by Bennett McCallum (1988) and Feldstein and Stock (1994) and revisited recently by Dennis (2001) and Rudebusch (2002). Its purported advantage is that it parsimoniously includes both prices and real output growth but without taking a stand on the split between the two; for this reason it is said to be able to withstand productivity shocks. Detractors note that because output typically leads inflation, responding to the sum of the two is not as obviously beneficial as presumed. We experiment with two versions. The first is designated with the rubric "YNR I", and is written as:
where
This version, which we designate as "YNR II," has the virtue of being comparable to TR in that other than substituting nominal output growth for inflation, it is identical.
We also pick up on the finding of LOWW (2005) to the effect that a policy that responds to nominal wage inflation (WR I) instead of nominal price inflation, performs well. In this way, the policymaker pays particular attention to that part of the economy that, from a neoclassical perspective, is arguably is the most distorted. Like the nominal output growth targeting rule, because wage setting is supposed to reflect both price inflation and labor productivity, the nominal wage growth rule also has the merit of implicitly incorporating changes in trend productivity.
where
4.1.2 Three-parameter policy rules
As noted, the benchmark from which all our rules are to be compared is the optimized version of the Taylor rule. There is, however, a chance that this choice is inappropriate. It is possible that the two-parameter Taylor rule is too parsimonious to adequately respond to the myriad economic disturbances to which the economy is subjected. In recognition of this possibility, we also explore a dynamic Taylor rule--let us call it "xTR" where the "x" means "extended" to add the lagged instrument as an argument:
This rule is the most commonly studied extension on the static Taylor rule; Williams (2003) argues that the inclusion of the lagged instrument can provide significant benefits in terms of economic outcomes in linearized New Keynesian models.
We also consider the same extension applied to some of the other rules so that each has a different nominal anchor but contains both the output gap and the lagged instrument, and to the URR so that it too carries a lagged instrument term plus an inflation term.
Lastly, because it is possible that concepts like the output gap cannot do justice to the real-side phenomena that buffet the economy in a world of where productivity shocks are prevalent, it seems prudent to consider conditioning policy specifically on potential output growth. At the same time, to be realistic, one should use not ex post measures of potential growth but rather the estimates that modelers were working with in real time. We can do so with the following rule, which we call the potential growth rule (Y*R):
where
Together, these rules encompass a broad range of the rules that have been proposed as robust to model misspecification, and do so in a generic way in that their arguments do not depend on idiosyncrasies of the FRB/US model.
4.2 The policy problem
Formally, a policy rule is optimized by choosing the parameters of the rule,
![]()
![]() , to minimize a loss function subject to a given model vintage,
, to minimize a loss function subject to a given model vintage,
![]() and a given set of stochastic shocks,
and a given set of stochastic shocks, ![]() In our case, this is:
In our case, this is:
subject to:
and
where
The optimal coefficients of a given rule are a function of the model's stochastic shocks, as equation (5) indicates.34 The optimized coefficient on the output gap, for example, represents not only the fact that unemployment-rate stabilization--and hence, indirectly, output-gap stabilization--is an objective of monetary policy, but also that in economies where demand shocks play a significant role, the output gap will statistically lead changes in inflation in the data; so the output gap will appear because of its role in forecasting future inflation. However, if the shocks for which the rule is optimized turn out not to be representative of those that the economy will ultimately bear, performance will suffer. As we shall see, this dependence will turn out to be significant for our results.35
4.3 Computation
Solving a problem like this is easily done for small, linear models; FRB/US, however, is a large, non-linear model. Given the size the model, and the differences across vintages, we optimized the policy rule coefficients employing a sophisticated derivative-free optimization procedure with distributed processing. Specifically, each vintage of the model is subjected to bootstrapped shocks from its stochastic shock archive. Historical shocks from the estimation period of the key behavioral equations are drawn.36 In all, 1500 draws of 80 periods each are used for each vintage to evaluate candidate parameterizations. The target rate of inflation is taken to be two percent as measured by the annualized rate of change of the personal consumption expenditure price index.37 The algorithm is described in detail in Gray and Kolda (2004) and Kolda (2004); here we provide just a thumbnail sketch. In the first step, the rule is initialized with a starting guess; that guess and some neighboring points are evaluated. Since all our rules are two-parameter rules, we need only investigate four neighboring points: higher and lower, by some step size, for each of the two parameters, with the initial guess in the middle. The loss function is evaluated for each of the five points and one with the lowest loss becomes the center of the next cluster of five points. As the five points become less and less distinguishable from one another, the step size is reduced until the convergence criterion is satisfied.
Optimization of a two-parameter policy rule using a single Intel Xeon 2.8 GHz machine can take over ten hours, depending on the rule; distributed processing speeds things up. Because this is exercise is computationally intensive we are limited in the range of preferences we can investigate. Accordingly, we discuss only one set of preferences: equal weights on output, inflation and the change in the federal funds rate. This is the same set of preferences that have been used in optimal policy simulations carried out for the FOMC; see Svensson and Tetlow (2005).
5.1 The Taylor rule
Let us begin with the Taylor rule (TR). In this instance, we provide a full set of results--that is, optimized parameters for each of the 46 vintages; later we will narrow our focus. The results are best summarized graphically. In Figure 5.1,
the blue solid line is the optimized coefficient for the TR on inflation,
![]() , while the red dashed line is feedback coefficient on the output gap,
, while the red dashed line is feedback coefficient on the output gap,
![]() . Perhaps the most noteworthy observation from 5.1 is the distinct upward creep, on average, in both parameters. The inflation response coefficient
never actually gets very large: it starts out quite low and only in the new century does it climb above the 0.5 percent level of the traditional Taylor rule. The rise over time in the output gap coefficient is more impressive. It too starts out low with the first vintage in July 1996 at about 0.1,
but then rises more-or-less steadily thereafter-the late 1999 dip aside-reaching values generally above 1 with the later vintages.38
. Perhaps the most noteworthy observation from 5.1 is the distinct upward creep, on average, in both parameters. The inflation response coefficient
never actually gets very large: it starts out quite low and only in the new century does it climb above the 0.5 percent level of the traditional Taylor rule. The rise over time in the output gap coefficient is more impressive. It too starts out low with the first vintage in July 1996 at about 0.1,
but then rises more-or-less steadily thereafter-the late 1999 dip aside-reaching values generally above 1 with the later vintages.38
The sharp increase in the gap coefficient in 2001 coincides with the inclusion of a new investment block which, in conjunction with changes to the supply block, tightened the relationship between supply-side disturbances and subsequent effects on aggregate demand, particularly over the longer term.39 The new investment block, in turn, was driven by two factors: the earlier inclusion by the Bureau of Economic Analysis of software in the definition of equipment spending and the capital stock, and associated enhanced appreciation on the part of the staff of the importance of the ongoing productivity and investment boom. In any case, while the upward jump in the gap coefficient stands out, it bears recognizing that the rise in the gap coefficient was a continual process.
The point to be taken from Figure 5.1 is that the time variation in model properties, described in Section 3, carries over into substantial variation in the optimized TR policy parameters. At the same time, it is clear that time variation in the multipliers is not the sole reason why optimized TR coefficients change. In fact, changes in the stochastic structure of the economy are also in play. To the extent these differences in optimized parameters, conditional on the stochastic shocks, imply significant differences in economic performance, we can say that model uncertainty is a significant problem. We can examine this question by comparing the performance of the optimized TR against other plausible parameterizations. For this exercise and nearly all that follow, we narrow our focus to just two vintages: the December 1998 vintage and the October 2007 vintage. (The optimized Taylor rule coefficients associated with these vintages are indicated in the figure by the gray bars.) These particular vintages were chosen because they were far apart in time, thereby reflecting as different views of the world as this environment allows, and because their properties are among the most different of any in the set.
In the next section we examine the implications for economic performance of the TR and the other optimized simple rules for two selected model vintages.
5.2.1 Two-parameter rules
To this point, we have compared model properties and optimized policies but have had nothing directly to say about performance. This section fills this void. We consider the performance, on average of the model economies under stochastic simulation. We also expand our study to encompass the wider range of simple rules introduced in sections 4.1.1 and 4.1.2. At the same time, in order to make the computational costs feasible, we focus on results for the two selected vintages. Table 2 shows the performance for the complete set two-parameter rules. The table is divided into two panels, one for each of the December 1998 and October 2007 vintages. In both panels, losses have been normalized on the performance of the optimized Taylor rule so that the efficacy of other rules can be interpreted as multiples of the TR loss.
Table 2: FRB/US model performance in stochastic simulation![]()
(2-parameter rule optimizations, selected vintages)
| line | policy rule | parameter: anchor, |
parameter: real, |
December 1998:
|
December 1998:
|
December 1998:
|
October 2007:
|
October 2007:
|
October 2007:
|
| 1. | Taylor rule | 0.44 | 0.33 | 1 | 0.53 | 1.17 | 1 | ||
| 2. | Inflation | 0.87 | -0.32 | 1.44 | -0.30 | -0.81 | 4.51 | ||
| 3. | Price level | 8.14 | 0.46 | 1.03 | 14.7 | 1.14 | 0.96 | ||
| 4. | U-rate | 0.16 | -2.52 | 1.19 | 0.08 | -3.60 | 0.88 | ||
| 5. | Nom. output I | 0.20 | 0.93 | 1.35 | 0.37 | 0.90 | 1.42 | ||
| 6. | Nom output II | 0.02 | 0.43 | 1.26 | 0.02 | 1.12 | 1.06 | ||
| 7. | Wage growth I | 1.05 | -0.41 | 1.46 | 0.63 | -0.71 | 1.57 | ||
| 8. | Wage growth II | 0.72 | 0.39 | 0.92 | 0.09 | 1.16 | 1.03 |
![]() Average value for eq. (2) from 1500 stochastic simulations over 20 years, normalized so that losses are interpretable as multiples of the loss under the optimized
Taylor rule.
Average value for eq. (2) from 1500 stochastic simulations over 20 years, normalized so that losses are interpretable as multiples of the loss under the optimized
Taylor rule.
Before delving into the numbers, it is useful to recall that the results in this table pertain to monetary authorities that understand the nature of the economy they control, including the shocks to which the economy is subject. That is, we are setting aside, for the moment, the issue of model uncertainty, which we take up in the next section. With this in mind let us focus for the moment on the optimized parameters and normalized losses for the December 1998 vintage shown in left-hand panel of Table 2. The results show, first, why the TR has been a popular specification for policy design: it renders a very good performance with losses that are lower than nearly all of the alternatives. The one rule that outperforms TR is WR II which is identical to the Taylor rule but replaces price inflation with wage inflation, shown on line 8. This rule is a version of the rule championed by LOWW (2005) on the grounds that in many models, it is wages that is the source of most nominal stickiness. It is not simply feedback on wages that is important to this result, however; the performance of WR I, on line 7, shows that a rule that replaces price inflation with wage inflation as the nominal anchor, but omits direct feedback on the output gap in favor of persistence in funds-rate setting through the presence of a lagged funds rate is the worst rule among those shown. There are other rules that are not far behind the TR in terms of performance, including the (change in) unemployment rate rule, URR, line 4, with a loss only of 19 percent more than the Taylor rule, and the price-level targeting rule, line 3, which carries a loss only slightly above that of the Taylor rule. This latter result may seem familiar to results seen elsewhere that show strong performance of price-level targets. However, to the best of our knowledge, prior results have been exclusively for linear rational expectations models where the powerful role of expectations in strengthening the error-correcting properties of such rules is paramount. That good performance arises from a price-level target in our VAR-based expectations approach is remarkable. Of related interest is the fact that the price-level rule significantly outperforms the ITR. Inflation targeting allows "bygones to be bygones" in the control of the price level, whereas price-level errors have to be reversed in price-level targeting regimes. Reversing price-level errors is a good thing when agents know that the central bank will do this, because anticipated reversals of the price level implies strongly anchored expectations for the inflation rate. When expectations are "boundedly rational," however, the conventional wisdom has been that bringing the price level back to some predetermined path will be all cost and no benefit. We see here that this is not so for the VAR-based expectations of the FRB/US model.
More generally, the performances of the other rules are not greatly different from the Taylor rule; as noted, the WR I performs the worst, but its loss is only about 1-1/2 times that of the TR, not a good performance but not disastrous either. Evidently, controlling the economy of the December 1998 vintage is a relatively straightforward task.
Let us turn now to the right-hand panel where we show parallel results for the October 2007 vintage. Here, once again, the TR does pretty well, on average, but in this instance there are two rules that do better, the price-level rule and the URR. We have already noted that parameterizations of these rules did well in the December 1998 vintage. In addition, two other rules also performed almost as well as the TR: the YNR II and WR II. These rules share two important features. First, they employ feedback on a nominal variable that attempts to correct, albeit indirectly, for trend productivity growth and errors in its measurement. Second, they maintain feedback on the output gap. Thus, notwithstanding the mismeasurement issues associated with persistent changes in productivity growth, feedback on the output gap, which is subject to errors in productivity levels, is still beneficial, as can be seen by comparing line 6 with line 5, on the one hand, and line 8 with line 7, on the other. In other words, these two rules produce good results but not entirely for the reasons for which these rules were originally advocated.
The last word on this panel concerns, once again, the ITR. Its performance controlling the October 2007 vintage could fairly be described as terrible, at 4-1/2 times the loss of the Taylor rule. Qualitatively, this is similar to the results for the December 1998 vintage, but quantitatively much worse. The reasons for this stem from the forementioned tightening of the linkages between the supply block of the model and subsequent aggregate demand fluctuations, together with the nature of the shocks that were incurred during the period over which the two rules are optimized. The rules for the December 1998 vintage are conditioned on shocks 1981 to 1995, while the October 2007 vintage is conditioned on shocks from 1988 to 2002. The former period was dominated by garden-variety demand shocks, whereas the latter had large and persistent disturbances to aggregate supply; in particular, the productivity boom of the second half of the 1990s. Moreover, many of the key shocks borne during the more recent period were larger than was the case in the earlier period.40 An implication of productivity booms is that they disrupt the "normal" time-series relationship between output (or employment) and inflation: when output fluctuations are dominated by demand shocks, and prices are sticky, output will statistically lead inflation and the optimized parameters of rules like the Taylor rule will reflect that relationship. When demand shocks are the prevalent force behind output fluctuations there is no dilemma for monetary policy: stabilizing output and stabilizing inflation are simultaneously achievable because they are one and the same. It follows that one can feedback on output (or its proxies) or inflation, and achieve good results either way. However when supply shocks drive cycles, inflation and output will tend to move in opposite directions, setting up a dilemma for the policymaker. Under these circumstances, responding to output and to inflation or no longer good substitutes for the purposes of minimizing losses and responding strictly to inflation is insufficient for controlling output.
5.2.2 Three-parameter rules
Table 3 tests the appropriateness of using the two-parameter Taylor rule as our benchmark by considering the simple extensions noted in section 4.1.2. In particular, the second row of the table shows that the performance of a Taylor extended to allow an optimized parameter on the lagged instrument renders only slightly better performance the TR itself, for either vintage. Moreover, the attempt through the use of a productivity growth term in the Y*R fares worse, as shown in the third line.41 The final two lines of the table exhibit the advantage of allowing feedback on the lagged instrument relative to the YNR II.
Table 3
FRB/US model performance in stochastic simulation![]()
(3-parameter rule optimizations, selected vintages)
| line | rule |
|
|
|
December 1998:
|
December 1998:
|
December 1998:
|
December 1998:
|
October 2007:
|
October 2007:
|
October 2007:
|
October 2007:
|
| 1. | TR | - | 0.44 | 0.33 | - | 1 | 0.53 | 1.17 | - | 1 | ||
| 2. | xTR | 0.33 | 0.29 | 0.33 | 0.98 | 0.22 | 1.07 | 0.22 | 0.98 | |||
| 3. | Y*R |
|
0.38 | 0.36 | 0.10 | 1.04 | 0.41 | 1.23 | 0.29 | 1.02 | ||
| 4. | YNR II | 0.02 | 0.43 | - | 1.26 | 0.02 | 1.12 | - | 1.06 | |||
| 5. | xYNR |
0.13 | 0.10 | 0.88 | 1.04 | 0.23 | 0.36 | 0.73 | 0.97 |
This is the one case where adding the lagged instrument to a rule that already has a nominal anchor variable and an aggregate demand term pays off in a significant way. Still, none of these rules do markedly better than the Taylor rule despite the advantage of an added parameter. We thus conclude
that using the Taylor rule as our benchmark is not erecting a straw man. We also satisfied that focussing our attention, henceforth, on two-parameter policy rules is a suitable restriction.
Our goal in this paper has been to uncover policies that are robust across models. To this point, we have identified rules which when properly specified, perform well in contexts where they should perform well. The ones that do not--the inflation targeting rule, and nominal income and wage growth rules that include the lagged instrument as their second argument--are not candidates as robust performers. Whether those rules that are strong performers in their own environments are also robust is the subject of the next section.
6 Robustness
We now turn our principal issue, the robustness of optimized policies to model misspecification. The thought experiment is to imagine a policymaker that believes she is controlling the December 1998 economy model, but in half of the instances we discuss below, it turns out that it is the October 2007 vintage that is the true model. Those results are presented in Table 4. Then, in Table 5, we reverse the exercise by having that our central banker assume she is controlling the October 2007 vintage but it turns out that half of the time, it is the December 1998 vintage that is the correct model.
The same eight two-parameter rules as before are considered, with 16 parameterizations. We subject both of these models to same set of stochastic shocks as in the optimization exercise, for each candidate rule. As before, we are mostly interested in normalized losses where the normalization sets the loss under the appropriate optimized TR policy to unity (although we do show the absolute losses, for completeness). Before we proceed with the results, it is worth recalling that, at the risk of oversimplication, that the December 1998 vintage is a model that sees the US economy as being relatively stable and easy to control: rule parameterizations that are optimal for the December 1998 vintage are generally less aggressive than their October 2007 counterparts.
Table 4
Normalized model performance for optimized 2-parmeter rules under stochastic simulation*
(December 1998 model vintage)
| line | rule | vin. | anchor variables
|
anchor variables
|
anchor variables
|
anchor variables
|
real variables
|
real variables
|
real variables
|
Dec. 98 loss: abs. | Dec. 98 loss: norm. |
| 1. | Taylor | D98 | 0.44 | 0.33 | 17.6 | 1 | |||||
| 2. | Taylor | O07 | 0.53 | 1.17 | 29.2 | 1.66 | |||||
| 3. | Inflation | D98 | 0.87 | -0.32 | 25.4 | 1.44 | |||||
| 4. | Inflation | O07 | -0.30 | -0.81 | 406 | 23.0 | |||||
| 5. | Price level | D98 | 8.14 | 0.46 | 18.3 | 1.04 | |||||
| 6. | Price level | O07 | 14.7 | 1.14 | 26.9 | 1.53 | |||||
| 7. | Nom. output I | D98 | 0.20 | 0.93 | 23.7 | 1.35 | |||||
| 8. | Nom. output I | O07 | 0.37 | 0.90 | 33.5 | 1.90 | |||||
| 9. | Nom. Output II | D98 | 0.02 | 0.43 | 22.2 | 1.26 | |||||
| 10. | Nom. Output II | O07 | 0.02 | 1.12 | 31.0 | 1.76 | |||||
| 11. | U-rate | D98 | 0.16 | -2.52 | 21.0 | 1.19 | |||||
| 12. | U-rate | O07 | 0.08 | -3.60 | 24.3 | 1.38 | |||||
| 13. | Wage growth I | D98 | 1.05 | -0.41 | 25.7 | 1.57 | |||||
| 14. | Wage growth I | O07 | 0.63 | -0.71 | 27.8 | 1.58 | |||||
| 15. | Wage growth II | D98 | 0.72 | 0.39 | 16.2 | 0.92 | |||||
| 16. | Wage growth II | O07 | 0.09 | 1.16 | 29.4 | 1.67 |
Beginning with the TR, where the normalized loss is unity by definition, we see that a policymaker who uses the October 2007 parameterization of that rule incurs losses about two-thirds higher what she could have achieved had she known the true model; the Taylor rule is not particularly robust in this sense. The inflation-targeting rule, not a particularly good performer at the best of circumstances, is disastrous when misspecified, as shown on line 4. Among the top performers--at least when the true economy turns out to be the December 1998 vintage--are the price-level rule, lines 5 and 6, the change-in-unemployment rule, lines 11 and 12, and the wage-growth rule that includes the gap, lines 15 and 16. Each of these rules performs at least as well as the Taylor rule when misspecified, and provides performance that is close to that of the Taylor when properly specified.42 The YNR II is not far off the mark set by the optimized Taylor rule.
Table 5 turns the exercise around by considering the case where the October 2007 vintage turns out to be the correct one. Misspecification of the Taylor rule is more costly here: the deterioration relative to the best policy parameterization is 80 percent. Once again, the ITR performs very poorly, while most of the rules that do include feedback on the output gap-the Taylor rule, the price-level rule, one of the nominal-output rules, and the change-in-unemployment rule, all perform well. The one notable exception to the conclusion that feedback on the output gap is always a good thing is the WR II where misspecification of the rule, as in line 16, results in large losses relative to the Taylor and most alternatives to it. Even here, though, its seems that it is feedback on wage growth that is the key to this result as the rules in lines 13 and 14, which respond to wage growth and the lagged instrument, but not the output gap, perform even worse. What this tells us is that while a wage-growth rule can turn in a very good performance, as it does when paired with the output gap on line 15, a good calibration is critical to its performance; the rule is not robust.
The PLR turns in an even stronger performance for the October 2007 vintage than it did for the December 1998 one. This result obtains notwithstanding that the parameterizations of the two rules differ significantly: the feedback parameters on the output gap are 1.14 and 0.46. As in rational expectations models, an important contribution to economic performance under this rule is that constraining the drift in the price level anchors inflation fluctuations. In both vintages of the FRB/US model, keeping inflation in check also limits cycling in long-term expected inflation. The stability of long-term inflation expectations reinforces the stabilizing force of policy making output stabilization less critical than would otherwise be the case.43
This case contrasts sharply with the URR. For this rule, feedback on inflation itself is slight at 0.08 and 0.16. But feedback on the change in the unemployment rate is vigorous: -3.60 and -2.52. Thus, aggressively tempering fluctuations in unemployment is substituting for inflation (and price-level) control. The fact that the URR is written in the first-difference of the instrument, and therefore does not depend on estimates of the equilibrium real rate of interest is also a factor; this means that the instrument can find the right level even when a productivity shock changes what that level should be. The URR is the one rule of which we are aware that was tested, by Orphanides and Williams (2002), in an environment that allowed for persistent, unobserved shocks to the "natural rate of interest," and found to execute well.
Table 5
Normalized model performance for optimized simple rules under stochastic simulation*
(October 2007 model vintage)
| line | rule | vin. | anchor variables
|
anchor variables
|
anchor variables
|
anchor variables
|
real variables
|
real variables
|
real variables
|
Oct. 07 loss: abs. | Oct. 07 loss: norm. |
| 1. | Taylor | O07 | 0.53 | 1.17 | 17.7 | 1 | |||||
| 2. | Taylor | D98 | 0.44 | 0.33 | 31.9 | 1.80 | |||||
| 3. | Inflation | O07 | -0.30 | -0.81 | 79.9 | 4.51 | |||||
| 4. | Inflation | D98 | 0.87 | -0.32 | 134 | 7.57 | |||||
| 5. | Price level | O07 | 14.7 | 1.14 | 17.0 | 0.96 | |||||
| 6. | Price level | D98 | 8.14 | 0.46 | 22.8 | 1.29 | |||||
| 7. | Nom. output I | O07 | 0.37 | 0.90 | 25.2 | 1.42 | |||||
| 8. | Nom. output I | D98 | 0.20 | 0.93 | 29.8 | 1.68 | |||||
| 9. | Nom. Output II | O07 | 0.02 | 1.12 | 18.7 | 1.06 | |||||
| 10. | Nom. Output II | D98 | 0.02 | 0.42 | 24.6 | 1.39 | |||||
| 11. | U-rate | O07 | 0.08 | -3.60 | 15.6 | 0.88 | |||||
| 12. | U-rate | D98 | 0.16 | -2.52 | 18.9 | 1.07 | |||||
| 13. | Wage growth I | O07 | 0.63 | -0.71 | 104 | 5.89 | |||||
| 14. | Wage growth I | D98 | 1.05 | -0.41 | 41.9 | 6.38 | |||||
| 15. | Wage growth II | O07 | 0.09 | 1.16 | 18.3 | 1.03 | |||||
| 16. | Wage growth II | D98 | 0.72 | 0.39 | 57.1 | 3.22 |
The results for URR is Tables 4 and 5 suggest that it could be a robust rule. We can take a closer look at the robustness of URR by computing its optimized parameters for all vintages. The results of this exercise are shown in Figure 6.1.
The figure shows that the coefficient on inflation, the solid red line, is never much above zero, regardless of the vintage. By contrast, the coefficient on the change in the unemployment rate, the dashed blue line, jumps around somewhat with perhaps a slight tendency to increase, in absolute terms, over time. The range over the complete set of vintages for the coefficient on the change in the unemployment rate spans from a low of -1.4 for the November 1999 vintage, to a high of -4.2 for the August 2007 vintage, considerably wider the range encompassed by the December 1998 and October 2007 vintages, shown by the gray bars. The computations underlying 6.1 allow us to expand on the robustness analysis of Tables 4 and 5 while focussing on the unemployment rate rule. We do this it Table 6 below where we consider the performance of the most extreme parameterizations of the rule in our two benchmark vintages.
Table 6
Performance of selected parameterizations of change-in-unemployment rate rule
| line | rule parameterization | coefficients:
|
coefficients:
|
losses for model, December 1998: absolute | losses for model, December 1998: normalized | losses for model, October 2007: absolute | losses for model, October 2007: normalized |
| 1. | December 1998 | -2.56 | 0.16 | 20.97 | 1 | 26.85 | 1.28 |
| 2. | November 1999 | -1.40 | 0.04 | 33.12 | 1.58 | 31.71 | 1.52 |
| 3. | August 2007 | -4.24 | 0.09 | 26.63 | 1.27 | 21.05 | 1.01 |
| 4. | October 2007 | -3.94 | 0.08 | 25.62 | 1.22 | 20.85 | 1 |
The table shows that when either of our benchmark models is subjected controlled by the most extreme parameterization of the URR, the small absolute coefficient on the (change in the) unemployment rate in the November 1999 vintage, the deterioration in control increases the loss relative to the best possible parameterization by a bit over 50 percent, as shown on line 2 of the table. The parameterization that rendered the largest coefficient on the change in the unemployment rate, the August 2007 vintage, gave coefficients that are not much different from the (chronologically close) October 2007 vintage. Thus lines 3 and 4 of the table are similar. Incremental losses, relative to the best possible URR parameterization, of 50-some percent, are not particularly large in comparison with the results in Tables 4 and 5.
7 Concluding remarks
For central banks, the appropriate design of monetary policy under uncertainty is a critical issue. Many conferences are devoted to the subject and the list of papers is lengthy and still growing. In nearly all instances, however, the articles, whether they originate from central banks themselves or from academia, have tended to be abstract applications. One posits an idealized model, or several models, of the economy and investigates, in some way, how missperceptions of, or perturbations to, the model affect outcomes. A good deal has been learned from these exercises, but results have tended to be specific to the environment of the chosen models. Moreover, the models themselves typically have not been representative of the models upon which central banks rely. It is difficult to know how serious a problem model uncertainty is if one cannot give a concrete and meaningful measure of uncertainty.
This paper has cast some light on model uncertainty and the design of policy in a much different context from the extant literature. We have examined 46 vintages of the model the Federal Reserve Board staff has used to carry out forecasts and policy analysis from 1996 to 2007. And we have done so in a real-time context that focusses on the real problems that the Fed faced over this period. Our examination looked at a number of simple policy rules that have been marketed as "robust." In the end, we uncovered a number of useful observations. First, model uncertainty is a substantial problem. Changes to the FRB/US model over the period of study were frequent and often important in their implications. The ensuing optimized policies also differed significantly in their parameterizations. Second, many simple rules that have been touted as robust, turn out to be less appealing than one might have suspected. In particular, pure inflation targeting rules and indeed nearly all rules that fail to respond to measures of aggregate demand turn out not to be robust. Third, adding an instrument smoothing term to rule that already had a nominal anchor and a real variable contributes little to the robustness and efficiency of rules. Fourth, notwithstanding problems of mismeasurement of output gaps, it generally pays for policy to feedback on some measure of excess demand. Fifth, a case can be made for designing simple rules that minimize the use of latent variables like potential output and the equilibrium real interest rate as arguments.
So why are simple rules not as reliable in the current context, when they have been in others? Levin et al. (1999) argue that simple rules do a good job of controlling economies, even in models for which their parameterizations are incorrect. The reason is because Levin et al. (1999) restricted their attention to full-information linear rational expectations models, which tend to be forgiving of wide ranges of policy rule misspecification. Loosely speaking, linear rational expectations models have loss surfaces that tend to be very flat in a large neighborhood around the optimized rule parameterization; see, e.g., Levin and Williams (2003). Economists are fond of rational expectations, and for good reason: it removes a free parameter from the model, and ensures that policy decisions are not founded on what amounts to money illusion. Nonetheless, the sense in which agents are rational is questionable. In environments such as the US economy of the 1990s and 2000s, with bubbles and financial crises, amid a broader economy that has produced fewer and milder recessions than before, it seems plausible that the economy has undergone structure shifts. To the extent that this is so, it seems reasonable to consider expectations that are somewhat less than fully rational-such models may include agents in the process of learning, as Primiceri (2005) and Milani (2007) have done, for example.
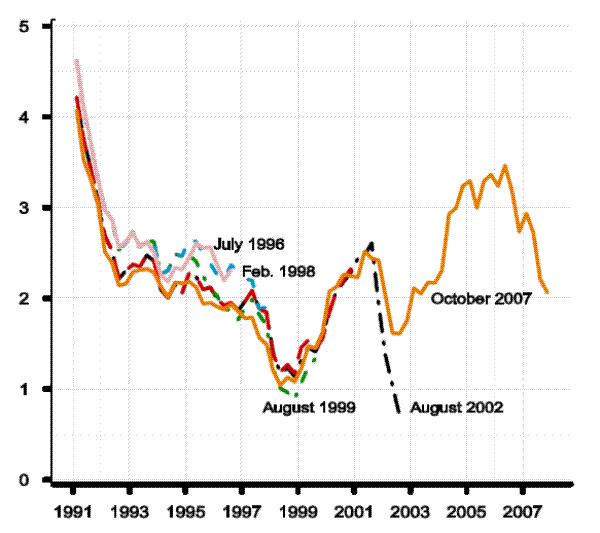
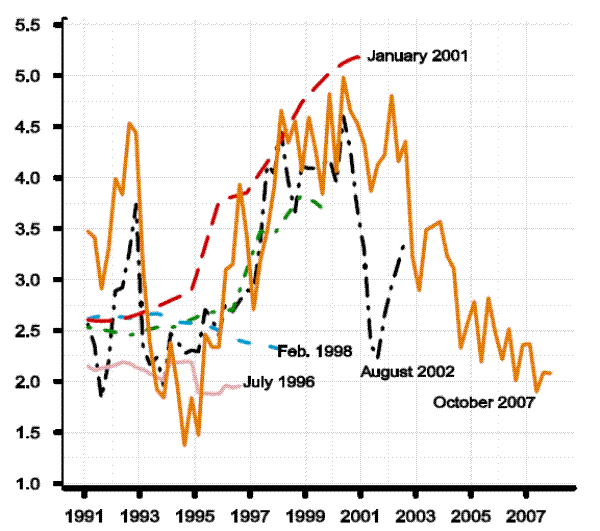
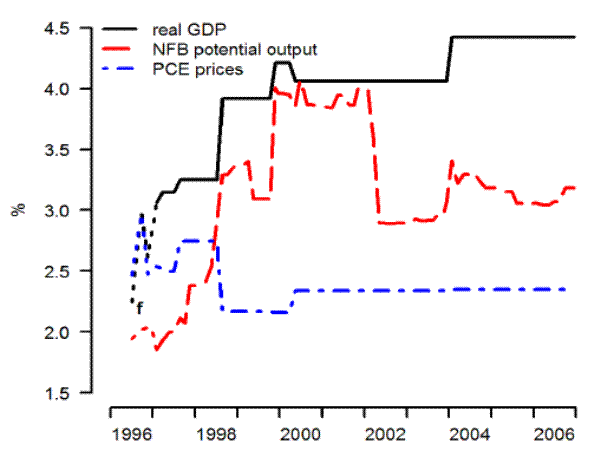
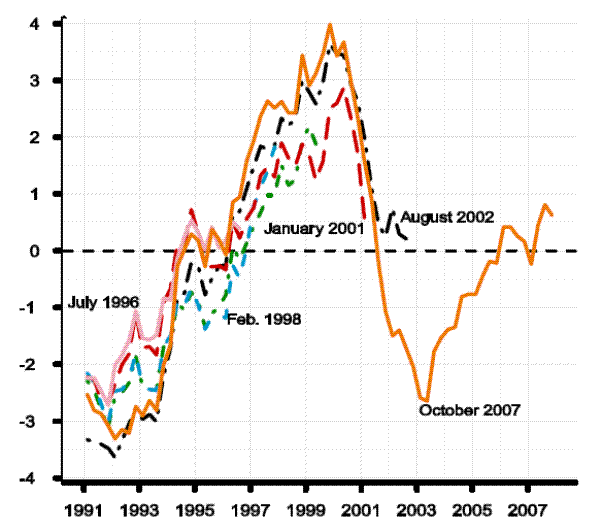
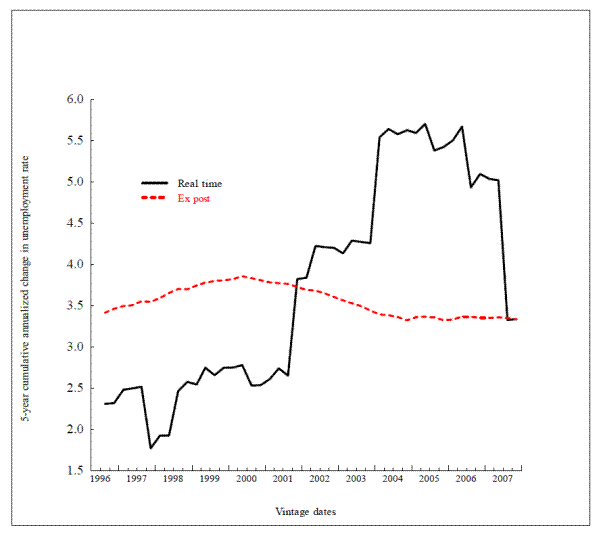
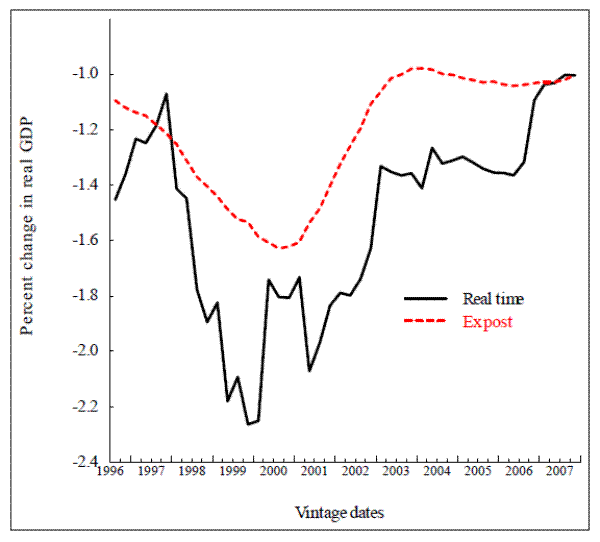
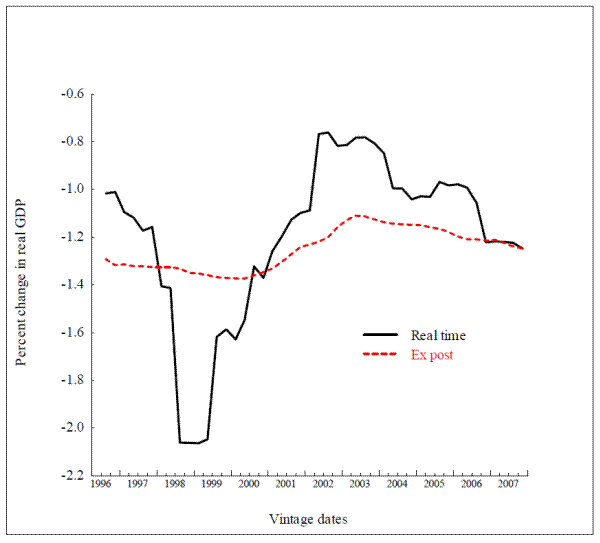
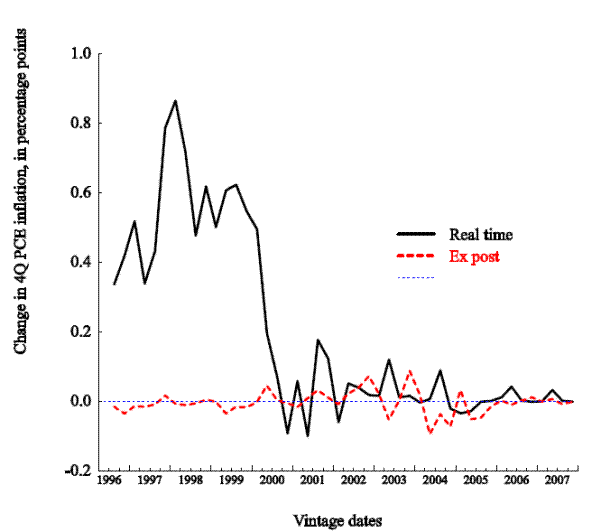
![\displaystyle \underset{\langle\Phi\rangle}{MIN}\;% {\displaystyle\sum\limits_{i=0}^{T}} \beta^{i}\left[ \left( \pi_{t+i}-\pi_{t+i}^{\ast}\right) ^{2}+\lambda _{y}\left( u_{t+i}-u_{t+i}^{\ast}\right) ^{2}+\lambda_{\Delta r}(\Delta r_{t+i})^{2}\right] %](img67.gif)