
Tips from TIPS: the informational content of Treasury Inflation-Protected Security prices†
Keywords: Treasury inflation-protected securities (TIPS), expected inflation, inflation risk premium, liquidity, SPF, term structure
Abstract:
1 Introduction
This paper presents a joint study of yields on nominal Treasury securities and those on Treasury Inflation-Protected Securities (TIPS) in a no-arbitrage asset pricing framework. Since its inception in 1997, the market for TIPS has grown substantially and now comprises about 8% of the outstanding Treasury debt market. More than a decade's TIPS data thus accumulated is a rich source of information to academic researchers and market participants alike. Because TIPS are securities whose coupon and principal payments are indexed to the price level, information about yields on these "real bonds" has direct implications for asset pricing models, many of which are written in terms of real consumption. Meanwhile, real-time TIPS data has attracted much attention from policy makers and market participants as a source of information about the state of the economy. In particular, the differential between yields on nominal Treasury securities and on TIPS of comparable maturities, often called the "breakeven inflation rate" (BEI) or "inflation compensation", has been used by policy makers and market participants as a proxy for market's inflation expectation. For example, the minutes of FOMC meetings often take note of changes in TIPS yields since the previous meeting,1 and explicit references to TIPS breakeven rates in speeches by Fed officials are common.2 Similarly, financial press frequently cite TIPS breakeven rates when discussing inflation expectations.
However, two difficulties arise in such interpretation of the TIPS breakeven inflation. First, TIPS breakeven inflation contains the inflation risk premium, which is the extra compensation investors in nominal bonds demand for bearing inflation risks. Second, TIPS has only been introduced recently and during its existence has been a less liquid instrument compared to nominal Treasury securities. The additional "liquidity premium" TIPS investors require for holding such instruments will drive up TIPS yields and depress the TIPS breakeven inflation. While the inflation risk premium has been studied by many researchers,3 the liquidity premium embedded in TIPS breakeven inflation has to our knowledge never been examined in the asset pricing literature.
The goal of this paper is to document the existence of liquidity premium in TIPS yields and to quantitatively characterize its behavior. To this end, we estimate and contrast several models for real and nominal yields, where the liquidity premium is either ignored or modeled as following different processes. All models we use are from the affine-Gaussian no-arbitrage term structure family and allow a rich dynamics in both the inflation risk premium and in nominal and real term premia.
Our main findings can be summarized as follows. First, a general 3-factor affine term structure model that ignores the liquidity premium generates large pricing errors for TIPS as well as counterfactual implications for inflation expectations and inflation risk premiums. In comparison, after incorporating an additional liquidity factor, the three 4-factor models that we estimate lead to notably smaller TIPS pricing errors, generate reasonable inflation risk premiums, and produce model-implied inflation expectations that agree well with survey inflation forecasts. Second, the liquidity premium estimates from all 4-factor models share the feature that it was large (1-2%) in the early years but declined in recent years, consistent with the notion that TIPS market liquidity conditions have improved over time and that TIPS pricing has possibly become more "efficient". In particular, around 80% of the variations in our estimates of TIPS liquidity premiums can be explained by variables related to the liquidity conditions in the TIPS market. Third, our best model for TIPS liquidity premiums has three parts, including a deterministic trend that captures the gradual but steady decline in TIPS liquidity premiums from the early years, a TIPS-specific factor that is independent of the nominal bond factors, as well as a component that is correlated with the rest of the economy. Finally, a variance decomposition shows that TIPS liquidity premiums explain more than 40% of variations in TIPS breakeven inflation, while that percentage declines to about one quarter in the long run.
The results in this paper shows that one needs to be careful in using the TIPS breakeven inflation rate as a proxy for inflation expectation, since an economically significant TIPS liquidity premium, on top of the inflation risk premium, could drive a large wedge between the TIPS breakeven inflation and inflation expectation. This problem seems to be especially severe in the early years of the TIPS market.
The remainder of this paper is organized as follows. In Section 2, we provide evidence that TIPS yields and TIPS breakeven inflation contain an additional factor, likely reflecting the illiquidity of TIPS, beyond those driving the nominal interest rates. Section 3 spells out the details of the no-arbitrage models we use, including the specification of the additional liquidity factor, and Section 4 explains the empirical methodology. Section 5 presents the main empirical results based on one model assuming zero TIPS liquidity premium and three models in which the TIPS liquidity premium is assumed to follow different specifications. Section 6 provides further discussions on the model estimates of the TIPS liquidity premiums and shows that they are indeed linked to the liquidity conditions in the TIPS markets. Section 7 provides some variance decomposition results for TIPS yields, TIPS breakeven inflation and nominal yields. Finally, Section 8 concludes.
2 A TIPS Liquidity Factor: Simple Analysis
In this section we present some simple analysis suggesting there exists a factor that is important for explaining the variations in TIPS yields but not as crucial for modeling nominal interest rates. We further argue that this factor is related to the illiquidity of the TIPS market. This serves as the motivation for introducing a TIPS-specific factor when we model nominal and TIPS yields jointly in later sections.
Simple Regression Analysis
In our first analysis, we regress the 10-year TIPS breakeven inflation rate, defined as the spread between the 10-year nominal yield and the 10-year TIPS yield, on 3-month, 2-year and 10-year nominal yields plus a constant:4
Standard finance theory suggests that nominal yield of any maturity can be decomposed into the underlying real yield, inflation expectation and the inflation risk premium: where
Principal Components Analysis
Next, we conduct a principal component analysis (PCA) of the cross section of the nominal and TIPS yields. It is well known that, in the case of nominal yields, three factors explain most of the nominal yield curve movements. This is confirmed in Panel B of Table 1, which shows that more than 97% of the variations in weekly changes of 3- and 6-month and 1-, 2-, 4-, 7- and 10-year nominal yields can be explained by the first three principal components. However, once we add the 5-, 7- and 10-year TIPS yields, at least four factors are needed to explain the same amount of variance. Panel C of Table 1 reports the correlations between the first four PCA factors extracted from nominal yields alone and the first four PCA factors extracted from nominal and TIPS yields combined. It is interesting to note that, once we add TIPS yields to the analysis, the first, the second and the fourth factors largely retain their interpretations as the level, slope and curvature of the nominal yields curve, as can be seen from their high correlation with the first, the second and the third nominal factors, respectively. However, the third PCA factor extracted from nominal and TIPS yields combined is not highly correlated with any of the nominal PCA factors. The results shown here and the simple regression analysis shown above have an interesting parallel with the literature on the unspanned stochastic volatility (USV) effect: using a simple regression analysis, Collin-Dufresne and Goldstein (2002) argued that bond derivatives contain a factor that is not spanned by the yield curve factors, and Heidari and Wu (2003) reported evidence for unspanned stochastic volatility using a PCA analysis.5
A Case for TIPS Liquidity Premium
A promising interpretation of the TIPS-specific factor we found above is that it reflects a "liquidity premium": investors would demand a compensation for holding a relative new and illiquid instrument like TIPS, especially in the early years.
Indeed, several measures related to TIPS market liquidity conditions, as well as anecdotal reports, indicate that the liquidity in TIPS market was much poorer than that of nominal securities, and that TIPS market liquidity improved over time, although this improvement was not a smooth, steady process. The top panel of Figure 1 shows the gross TIPS issuance over the period 1997-2007. The TIPS issuance dipped slightly in 2000-2001 before rising substantially in 2004. According to Sack and Elsasser (2004), there were talks around 2001 that the Treasury might discontinue the TIPS due to the relatively weak demand for TIPS. TIPS outstanding, shown in the bottom panel of Figure 1, began to grow at a faster pace from 2004 onward and now exceeds 400 billion dollars. Figure 2 tells a similar story from the demand side: TIPS transaction volumes grew by sixfold during our sample period and TIPS mutual funds also experienced significant growth.6 In view of this institutional history, it is not unreasonable to suppose that TIPS contained a significant liquidity premium at least in its early years and that the liquidity premium have edged lower over time.
A liquidity premium in TIPS can help resolve a seeming inconsistency between survey inflation forecasts (10-year SPF survey and Michigan long-term survey) and the 10-year TIPS breakeven inflation, all of which are plotted in Figure 3. Recall that the true breakeven inflation, defined as the yield differential between nominal and real bonds of comparable maturities and liquidity features, is the sum of expected inflation and the inflation risk premium, and can be considered as a good measure of the former if the second term is relatively small and does not vary too much over time. However, Figure 3 shows that this is not the case: the TIPS breakeven inflation lied below both measures of survey inflation forecasts almost all the time before 2004.7 8 9 Such disparity cannot be attributed solely to the existence of inflation risk premium, as such an explanation would require the inflation risk premium to be mostly negative in the 1999-2007 period and highly volatile, which stands in contrast with most studies in the literature that find inflation risk premiums to be positive on average and relatively smooth.10
On the other hand, a positive TIPS liquidity premium would push the TIPS-based breakeven inflation below the true breakeven inflation and, if the TIPS liquidity premium exceeds the inflation risk premium in absolute terms, even lower than survey inflation forecasts. Furthermore, part of the volatility of the TIPS breakeven inflation rate may be due to the volatility of the TIPS liquidity premium.
In order to study these issues quantitatively, we need a framework for identifying and measuring the relevant components, including the TIPS liquidity premium, inflation expectations, and inflation risk premium. For this purpose, we use the no-arbitrage term structure modeling framework, to which we now turn.
3 A Joint Model of Nominal and TIPS yields
This section details the no-arbitrage framework that we use to model nominal and TIPS yields jointly. The no-arbitrage approach has the benefit of avoiding the tight assumptions that go into structural, utility-based models while still allowing term structure variations to be modeled in a dynamically consistent manner by requiring the cross section of yields to satisfy the no-arbitrage restrictions.
3.1 State Variable Dynamics and the Nominal Pricing Kernel
We assume that real yields, expected inflation and nominal yields are driven by a vector of three latent variables,
![]() , which follows a multivariate Gaussian process,
, which follows a multivariate Gaussian process,
where
The nominal short rate is specified as
where
The nominal pricing kernel takes the form
where the vector of nominal prices of risk is given by
in which
3.2 Inflation and the Real Pricing Kernel
The price level processes takes the form:
where the instantaneous expected inflation,
and the unexpected inflation,
A real bond can be thought of as a nominal asset paying realized inflation upon maturity. Therefore, the real and the nominal pricing kernels are linked by the no-arbitrage relation
Applying Ito's lemma to Equation (8) and using Equations (3) to (7), the real pricing kernel can be derived as following the process
| (9) | |||
| (10) |
where the real short rate is given by
| (11) |
and the vector of real prices of risk is given by
| (12) |
in which the coefficients are linked to their nominal counterparts by
3.3 Nominal and Real Bond Prices
By the definition of nominal and real pricing kernels, the time-![]() prices of
prices of ![]() -period nominal and real bonds,
-period nominal and real bonds,
![]() and
and
![]() , are given by
, are given by
| (17) |
The bond prices can be also expressed in terms of a risk-neutral expectation as
where the superscript
Following the standard literature,11 it is straightforward to derive a closed-form solution for the bond prices:
| (19) |
where
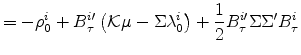 |
(20) | |
| (21) |
with initial conditions
Nominal and real yields therefore both take the affine form,
where the factor loadings
3.4 Inflation Expectations and Inflation Risk Premiums
In this model, inflation expectations also take an affine form,
where the factor loadings
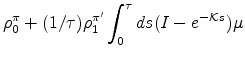 |
|||
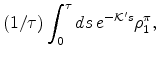 |
From equations (22)-(24), it can be seen that both the breakeven inflation rate, defined as the difference between zero coupon nominal and real yields of identical maturities, and the inflation risk premium, defined as the difference between the breakeven inflation rate and the expected log inflation over the same horizon, are affine in the state variables:
and
Using Equation (8) we can write the price of a ![]() -period nominal bond as
-period nominal bond as
It is then straightforward to show that the inflation risk premium
| (28) |
where
In practice, the Jensen's inequality term is fairly small, and the inflation risk premium is mainly determined by the covariance between the real pricing kernel and inflation,12 and can assume either a positive or a negative sign depending on how the two terms covaries over time.
3.5 A Four-Factor Model of TIPS Yields
Given the evidence presented in Section 2 on the existence of a TIPS-specific factor, we allow the TIPS yield to deviate from the true underlying real yield. The spread between the TIPS yields and the true real yield,
mainly captures the liquidity premium TIPS investors demand for holding a less liquid instrument, but could also reflect other factors that can potentially drive a wedge between the TIPS yield and the true real yield.13 Since the relative illiquidity of TIPS would lower TIPS prices and raise TIPS yields, we would in general expect
We model
![]() as containing a stochastic component and a deterministic component. To model the stochastic part, we assume that the investors discount TIPS cash flows by adjusting the true
instantaneous real short rate with a positive liquidity spread, resulting in a TIPS yield that exceeds the true real yield by
as containing a stochastic component and a deterministic component. To model the stochastic part, we assume that the investors discount TIPS cash flows by adjusting the true
instantaneous real short rate with a positive liquidity spread, resulting in a TIPS yield that exceeds the true real yield by
where
The instantaneous liquidity spread ![]() is given by
is given by
where
in which
| (33) |
Appendix B shows that the stochastic part of the TIPS liquidity premium takes the affine form
Note that although we focus on a one-factor specification for the liquidity factor
To accommodate potential nonstationarities associated with the inception of the TIPS market, we also allow for a maturity-independent downward-trending deterministic component in the liquidity premium, which takes the form
where
The total liquidity premium on a ![]() -year TIPS in our "full model" is then the sum of the two components:
-year TIPS in our "full model" is then the sum of the two components:
| (36) |
with the TIPS yields given by
We shall refer to this model as Model L-IId. In the empirical part, we also estimate three restricted versions of the full model. The model with the least restrictions, which we shall call Model L-II, sets
This is the model studied by Chen, Liu, Cheng (2005), although their specification differ from ours along other dimensions.
3.6 Discussions and Related Literature
Besides its tractability, the affine-Gaussian bond pricing framework used here allows for a flexible correlation structure between the factors. As inflation risk premiums arise from the correlation between the real pricing kernel and inflation, it is important to allow for a general correlation structure. On the other hand, the affine-Gaussian setup does not capture the time-varying inflation uncertainty and therefore cannot further decompose inflation risk premiums into the part due to time-varying inflation risks and time-varying prices of inflation risk. Nonetheless, the affine-Gaussian model could still provide a reasonable estimate of inflation risk premium, similar to the way it generates reasonable measures of term premia despite its inability to capture time-varying interest rate volatilities. We view the general affine-Gaussian model as an important benchmark to be investigated before more sophisticated models can be explored.
Some of the models studied in the earlier literature, such as Pennacchi (1991) and Campbell and Viceira (2001), can be viewed as a special case of this model. For example, Pennacchi (1991)'s model corresponds to a two-factor version of our model with constant market price of risk. Campbell and Viceira (2001) is also a special case of this model, but their real term structure has a lower dimension than the nominal term structure (nominal yields are described by 2 factors and real yields are described by 1 factor). In this paper, we let the real term structure have as many factors as the nominal term structure; if the real term structure is truly lower-dimensional than nominal term structure, we let the data decide on that. A related point is that in a reduced-form setup like ours, one cannot make a distinction between real and nominal factors, as correlation effects in the general model make such a distinction meaningless.
To our knowledge, this is the first paper to model liquidity premium in TIPS in a no-arbitrage framework. There is a large literature studying the pricing implications of indexed bonds using data from other countries with longer histories of issuing inflation linked securities,16 There have also been studies of US real yields and inflation risk premia that use realized inflation17 or survey inflation forecasts18 without incorporating information from indexed bonds. Due to the short data history, studies using U.S. inflation-linked assets, including TIPS or inflation swaps, are fairly recent and relatively few.19 In addition, most of these studies take TIPS at their face value, and typically find a real yield that seems too high as well as inflation risk premium estimates that are insignificant or negative in the early sample when TIPS was first introduced. In contrast, this paper shows that there is a persistent liquidity premium component in TIPS prices, which, if not properly taken account of, will bias the results.
4.1 Identification and Summary of Models
We only impose restrictions that are necessary for achieving identification so as to allow a maximally flexible correlation structure between the factors, which has shown to be critical in fitting the rich behavior in risk premiums that we observe in the data.20 In particular, we employ the following normalization:
and leave all other parameters unrestricted. It can be shown that any specification of the affine Gaussian model that has a
To summarize, we estimate four models that differ in how TIPS liquidity premium is modeled, including one model that equates TIPS yields with true real yields and assumes zero liquidity premium on TIPS (Model NL), a model with an independent liquidity factor (Model L-I), a model allowing the TIPS liquidity premium to be correlated with other state variables (Model L-II), and the most general model (Model L-IId) in which TIPS liquidity premiums also contain a deterministic trend. Table 2 summarizes the models and the parameter restrictions. Two things are worth noting here: First, as shown in Section 3.5, Models NL, L-I and L-II can all be considered as special cases of Model L-IId. Second, Model NL has a 3-factor representation of TIPS yields, while in all other models TIPS yields have a 4-factor specification.
4.2 Data
We use 3- and 6-month, 1-, 2-, 4-, 7-, and 10-year nominal yields and CPI-U data from January 1990 to March 2007. In contrast, our TIPS yields are restricted by data availability and cover a shorter period from January 1999 to March 2007, with the earlier period without TIPS data (1990-1998) treated as missing observations. Both nominal and TIPS yields, shown in Figure 4, are based on zero-coupon yield curves fitted at the Federal Reserve Board22 and are sampled at the weekly frequency, while CPI-U inflation is available monthly and assumed to be observed on the last Wednesday of the current month.23 As discussed in more details in Appendix A, shorter-maturity TIPS yields are affected to a larger degree by the problem of indexation lags. In addition, no more than one TIPS with a maturity of below 5 years existed before 2002, hence near-maturity zero-coupon TIPS yields cannot be reliably estimated during that period. We therefore only use 5-, 7-, and 10-year TIPS yields in our estimation. Because the models we estimate do not accommodate seasonalities, we use seasonally-adjusted CPI inflation in the estimation. TIPS are indexed to non-seasonally-adjusted CPI; however, our use of seasonally-adjusted CPI is not expected to matter much for the relatively long maturities that we examine.
The sample period 1990-2007 was chosen as a compromise between having more data in order to improve the efficiency of estimation, and having a more homogeneous sample so as to avoid possible structural breaks24 in the relation between term structure variables and inflation. This sample period roughly spans Greenspan's tenure and a little bit of Bernanke's as well.
Results from Kim and Orphanides (2006) suggest that the standard technique of estimating our models using only nominal and TIPS yields and inflation data for a relative short sample period of 1990-2007 will almost surely run into small sample problems: variables like
![]() and
and ![]() may not be reliably estimated, and the estimated model
typically generates a path of expected future short rate over the next 5 to 10 years that is too smooth compared to survey-based measures of market expectations.25 Therefore, we supplement the aforementioned data with survey forecasts of 3-month T-bill yields to help stabilize the estimation and to better pin down some of the model parameters. Note that survey inflation forecast data are not used in the estimation,
as we would like to get a measure of inflation expectations from yields data, independently of other sources of information about inflation expectation.
may not be reliably estimated, and the estimated model
typically generates a path of expected future short rate over the next 5 to 10 years that is too smooth compared to survey-based measures of market expectations.25 Therefore, we supplement the aforementioned data with survey forecasts of 3-month T-bill yields to help stabilize the estimation and to better pin down some of the model parameters. Note that survey inflation forecast data are not used in the estimation,
as we would like to get a measure of inflation expectations from yields data, independently of other sources of information about inflation expectation.
To be specific, we use the 6-month- and 12-month-ahead forecasts of the 3-month T-bill yield from Blue Chip Financial Forecasts, which are available monthly, and allow the size of the measurement errors to be determined within the estimation. We also use long-range forecast of 3-month T-bill yield over the next 5 to 10 years from the same survey, which are available twice a year, with the standard deviation of its measurement error fixed at a fairly large value of 0.75% at an annual rate. This is done to prevent the long-horizon survey forecasts from having unduly strong influence on the estimation, and can be viewed as similar to a quasi-informative prior in a Bayesian estimation.
We denote the short-horizon survey forecasts by ![]() and
and ![]() and the
long-range forecast by
and the
long-range forecast by
![]() . The standard deviation of their measurement errors are denoted denoted
. The standard deviation of their measurement errors are denoted denoted
![]() and
and
![]() , respectively. These survey-based forecasts are taken as noisy measures of corresponding true market expectations. More specifically, we have that for the short-term survey
forecasts,
, respectively. These survey-based forecasts are taken as noisy measures of corresponding true market expectations. More specifically, we have that for the short-term survey
forecasts,
| (40) |
for
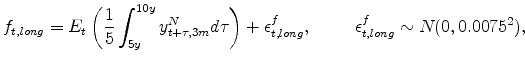 |
(41) |
where the corresponding model forecasts,
| (42) |
where the factor loadings
4.3 Estimation Methodology
We rewrite the model in a state-space form and estimate it by the Kalman filter. Denote by
![]() the augmented state vector including the log price level,
the augmented state vector including the log price level,
![]() , and the TIPS liquidity factor,
, and the TIPS liquidity factor,
![]() . The state equation is derived as Euler discretization of equations (2), (6) and (33) and can be
written in a matrix form as
. The state equation is derived as Euler discretization of equations (2), (6) and (33) and can be
written in a matrix form as
where
![\displaystyle G_{h}=% \left[\begin{matrix}\rho_0^{\pi} h \\ \mathcal{K}\mu h \\ \tilde{\kappa}\tilde{\mu} h \end{matrix}\right],](img132.gif) ![\displaystyle \Gamma _{h}=% \left[\begin{matrix}1 & \rho^{\pi\prime}_{1} h & 0\\ 0 & I_{3\times 3}-\mathcal{K} h & 0 \\ 0 & 0 & 1-\tilde{\kappa} h \end{matrix}\right]](img133.gif) and and 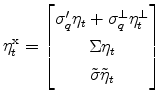 |
in which
| (46) |
We specify the set of nominal yields as
![]() , and the set of TIPS yields as
, and the set of TIPS yields as
![]() , and collect in
, and collect in ![]() all
data used in the estimation, including the log price level
all
data used in the estimation, including the log price level ![]() , all nominal yields
, all nominal yields ![]() , all TIPS yields
, all TIPS yields
![]() , and 6 month-ahead, 12 month-ahead, and long-horizon forecasts of future 3-month nominal yield:
, and 6 month-ahead, 12 month-ahead, and long-horizon forecasts of future 3-month nominal yield:
| (47) |
We assume that all nominal and TIPS yields and survey forecasts of nominal short rate are observed with error. The observation equation therefore takes the form
where
![\displaystyle A=\left[\begin{matrix}0\\ A^N \\ \tilde{a} + A^{\cal T}\\ a^f_{6m}\\ a^f_{12m}\\ a^f_{long}\end{matrix}\right], \,\,\, B = \left[\begin{matrix}1 & 0 & 0 \\ 0 & B^{N\prime} & 0 \\ 0 & B^{\cal T \prime} & \tilde{b}^{\prime} \\ 0 & b^{f \prime}_{6m} & 0 \\ 0 & b^{f\prime}_{12m} & 0 \\ 0 & b^{f \prime}_{long} & 0 \end{matrix}\right],\,\,\, {\rm e}_t=\left[\begin{matrix}0\\ e^N_{t} \\ e^{\cal T}_{t}\\ e^f_{t,6m}\\ e^f_{t,12m}\\ e^f_{t,long}\end{matrix}\right],](img147.gif)
|
(49) |
in which
Based on the state equation (46) and the observation equation (49), it is straightforward to implement the Kalman-filter and perform the maximum likelihood estimation. The details are given in Appendix C. Two aspects
are worth noting here: first, the log price level ![]() is nonstationary, so we use a diffuse prior for
is nonstationary, so we use a diffuse prior for ![]() when initializing the Kalman filter. Second, inflation, survey forecast and TIPS yields are not available for all dates, which introduces missing data in the observation equation and are handled in the standard way by allowing the dimensions of the matrices
when initializing the Kalman filter. Second, inflation, survey forecast and TIPS yields are not available for all dates, which introduces missing data in the observation equation and are handled in the standard way by allowing the dimensions of the matrices
![]() and
and ![]() in Equation (49) to be time-dependent (see, for
example, Harvey (1989, sec. 3.4.7)).
in Equation (49) to be time-dependent (see, for
example, Harvey (1989, sec. 3.4.7)).
Note that all four versions of our models can be accommodated in the above setup. To implement Model NL without the liquidity premium, one simply set
![]() and
and
![]() , and fix
, and fix
![]() ,
,
![]() ,
,
![]() and
and
![]() at arbitrary values as those variables do not enter the likelihood function of Model NL. To implement Model L-I with the independent liquidity factor only, one would fix
at arbitrary values as those variables do not enter the likelihood function of Model NL. To implement Model L-I with the independent liquidity factor only, one would fix
![]() .
.
To facilitate the estimation and also to make the results easily replicable, we follow the following steps in estimating all our models:
- We first perform a " pre"-estimation where a set of preliminary estimates of the parameters governing the nominal term structure is obtained using nominal yields and survey forecasts of 3-month T-bill yield alone.
- Based on these estimates and data on nominal yields, we can obtain a preliminary estimate of the state variables,
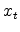 .
. - A regression of the monthly inflation onto estimates of
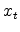 obtained in the second step gives a preliminary set of estimates of the parameters governing the inflation dynamics.
obtained in the second step gives a preliminary set of estimates of the parameters governing the inflation dynamics. - Finally, these preliminary estimates are used as starting values in the full, one-step estimation of all model parameters.
5 Empirical Results
In this Section, we discuss and compare the empirical performance of the various Models. As we shall see, there are notable differences between the model equating TIPS yields with the true real yields (Model NL) and the models that allow the two sets of yields to differ by a liquidity premium component (Models L-I, L-II and L-IId).
5.1 Parameter Estimates and Overall Fit
Parameter Estimates
Table 3 reports the parameter estimates for all four models. Four things are worth noting here: First, estimates of parameters governing the nominal term structure are almost identical across the three models; under our set-up, these parameters seem to be fairly
robustly estimated. In particular, all estimations uncover a very persistent factor with a half life of about 13 years. Note also that all four models exhibit a similar fit to nominal yields and survey forecasts of nominal short-term interest rates. For example, the nominal yield fitting errors (
![]() ) are fairly small in all four models: except for the 3-month yield which has
) are fairly small in all four models: except for the 3-month yield which has ![]() of about 10 basis points, other maturity yields have
of about 10 basis points, other maturity yields have ![]() of 5 basis points or less.
of 5 basis points or less.
Second, there are notable differences in the estimates of parameters governing the expected inflation process. In particular, the loading of the instantaneous inflation on the second and the most persistent factor is negligible in the model without a TIPS liquidity factor (Model NL) but becomes positive and significant in the three models with a TIPS liquidity factor (Models L-I, L-II and L-IId). As a result, the monthly autocorrelation of one-year-ahead inflation expectation is about 0.9 in Model NL but above 0.99 in all other models. As we will see later, the lack of persistence in the inflation expectation process prevents Model NL from generating meaningful variations in longer-term inflation expectations as we observe in the data.
Third, parameter estimates for the TIPS liquidity factor process are significant in both Models L-I and L-II and assume similar values. The estimated market price of liquidity risk carries the expected negative sign, as one would generally expect any deterioration of liquidity conditions to
occur during bad economic times. In Models L-II and L-IId, the loading of the instantaneous TIPS liquidity premium on each of the three state variables, ![]() , is estimated to be
indistinguishable from zero; however, a Wald test shows that they are jointly significant.
, is estimated to be
indistinguishable from zero; however, a Wald test shows that they are jointly significant.
Finally, the fit to TIPS yields are significantly better in models with a TIPS liquidity factor, as can be seen from the smaller estimates of the standard deviations of TIPS measurement errors. For example, for the 10-year TIPS, the fitting errors from the L-I and L-II models are 6 basis points, while the fitting error from Model NL is 35 basis points. The fitting errors are found to have a substantial serial correlation. For example, in the case of the 5-year TIPS, we obtain a weekly AR(1) coefficient of 0.96, 0.91, and 0.91 for Model NL, L-I model, and L-II model, respectively. The finding of serial correlation in term structure fitting errors are however a fairly common phenomenon, and have been noted by Chen and Scott (1993) and others.
Overall Fit
Panel A of Table 8 reports some test statistics that compare the overall fit of the three models. We first report two information criteria commonly used for model selection, the Akaike Information Criterion (AIC) and the Bayesian Information Criterion (BIC). Both information criteria are minimized by the most general model, Model L-IId.
We also report results from likelihood ratio (LR) tests of the three restricted models, Models NL, L-I and L-II, against their more general counterparts, Model L-I, L-II and L-IId, respectively. Compared to Model L-I, Model NL imposes the restriction
![]() . The standard likelihood ratio test does not apply here because the nuisance parameters,
. The standard likelihood ratio test does not apply here because the nuisance parameters,
![]() ,
,
![]() ,
,
![]() and
and
![]() , are not identified under the null (Model NL) and appear only under the alternative (Model L-I).26 Here we follow Garcia and Perron (1996) and calculate a conservative upper bound for the significance of the likelihood ratio test statistic as suggested by Davies (1987). In particular, denote by
, are not identified under the null (Model NL) and appear only under the alternative (Model L-I).26 Here we follow Garcia and Perron (1996) and calculate a conservative upper bound for the significance of the likelihood ratio test statistic as suggested by Davies (1987). In particular, denote by ![]() the vector of nuisance parameters of size
the vector of nuisance parameters of size ![]() , and define the likelihood ratio statistic as a function of
, and define the likelihood ratio statistic as a function of
![]() :
:
![\displaystyle \Pr\left[ \sup_{\theta\in\Omega}LR\left(\theta\right) >M\right] <\Pr\left[ LR\left( \theta\right) >M\right] +VM^{\frac{1}{2}\left( s-1\right) }\exp^{-\left( M/2\right) }\frac{2^{-s/2}}{\Gamma\left( s/2\right) }%](img171.gif)
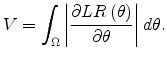
The LR test of Model L-I against Model L-II, on the other hand, is fairly standard. Based on the likelihood estimates of the two models, we obtain a LR statistic of
Finally, Model L-II is rejected in favor of the full model, Model L-IId, based on the Davies (1987) procedure, with a large LR test value of 433.41.
5.2 Fitting TIPS Yields and TIPS Breakeven Inflation
The estimated standard deviations of TIPS measurement errors reported in the previous section suggest that Model NL has trouble fitting the TIPS yields. This section looks at the fit of TIPS yields and TIPS breakeven inflation across models in more details.
The three left (right) panels of Figures 5 plot the actual and the model-implied TIPS yields (TIPS breakeven inflation) based on Models NL, L-I and L-IId, respectively, together with the real yields (the true breakeven inflation) as implied by the three models.27 By construction, the model-implied TIPS yields and the model-implied real yields coincide under Model NL.
The top left panel of Figures 5 shows that, according to Model NL, the downward path of 10-year TIPS yields from 1999 to 2004 is part of a broader decline in real yields since the early 1990's, with real yields estimated to have come down from a level as high as
![]() in the early 90's to about
in the early 90's to about ![]() around 2003. During the same period, the
10-year nominal yield declined from around
around 2003. During the same period, the
10-year nominal yield declined from around ![]() to a little over
to a little over ![]() . Therefore,
Model NL attributes the decline of 10-year nominal yield entirely to a lower real yield, leaving little room for lower inflation expectation or lower inflation risk premiums. While there is some empirical evidence suggesting that long-term inflation expectations may have edged down during this
period,28 it is hard to imagine economic mechanisms that would generate such a large decline in long-term real yields. Furthermore, although Model NL
matches the general trend of TIPS yields during this period, it has problem fitting the time variations, frequently resulting in large fitting errors. In contrast, the decline in real yields as implied by Models L-I and L-IId, plotted in the middle and the bottom left panels, is less pronounced and
more gradual. With the flexibility brought by the additional liquidity premium factor, these two models are also able to fit TIPS yields almost perfectly.
. Therefore,
Model NL attributes the decline of 10-year nominal yield entirely to a lower real yield, leaving little room for lower inflation expectation or lower inflation risk premiums. While there is some empirical evidence suggesting that long-term inflation expectations may have edged down during this
period,28 it is hard to imagine economic mechanisms that would generate such a large decline in long-term real yields. Furthermore, although Model NL
matches the general trend of TIPS yields during this period, it has problem fitting the time variations, frequently resulting in large fitting errors. In contrast, the decline in real yields as implied by Models L-I and L-IId, plotted in the middle and the bottom left panels, is less pronounced and
more gradual. With the flexibility brought by the additional liquidity premium factor, these two models are also able to fit TIPS yields almost perfectly.
The problem with Model NL can be further seen by looking at the model-implied 10-year breakeven inflation, as shown in the upper right panel of Figures 5. The 10-year breakeven rate implied by Model NL, which by construction should equal the 10-year TIPS breakeven inflation, appears too smooth compared to its data counterpart and misses most of the short-run variations in the actual series. The poor fitting of the TIPS breakeven inflation rates highlights the difficulty that the 3-factor model has in fitting nominal and TIPS yields simultaneously.29 In contrast, the 10-year breakeven inflation rates implied by Models L-I and L-IId, shown in the middle and bottom left panels, show substantial variations that roughly match those of the actual TIPS breakeven inflation rate. In particular, the model-implied and the TIPS-based breakeven inflation rates peak locally at the beginning of 2000, in the middle of 2001 and 2002, and so on, and the magnitude of their variation are also similar. In these two models, the gap between the model-implied and the TIPS-based breakeven inflation rates is the sum of TIPS liquidity premium and TIPS measurement errors.
To quantify the improvement in terms of the model fit, Panels B and C of Table 8 provide three goodness-of-fit statistics for TIPS yields at the 5-, 7- and 10-year maturities and TIPS breakeven inflation at the 7- and 10-year maturities, respectively. The first
statistic, CORR, is simply the sample correlation between the fitted series and its data counterpart. Consistent with the visual impression from Figure 5, allowing a TIPS liquidity premium component improves the model fit for raw TIPS yields and even more so for TIPS
breakeven inflation, with the correlation between model-implied 10-year TIPS breakeven and the data counterpart rising from ![]() to over
to over ![]() once we move from Model NL to the other models. The next two statistics are based on one-step-ahead model prediction errors from the Kalman Filter,
once we move from Model NL to the other models. The next two statistics are based on one-step-ahead model prediction errors from the Kalman Filter, ![]() , defined in Equation (15) in Appendix C, and are designed to capture how well each model can explain the data without resorting to large exogenous shocks or measurement errors. More specifically, the second statistic is
the root mean squared prediction errors (RMSE), and the third statistic is the coefficient of determination (
, defined in Equation (15) in Appendix C, and are designed to capture how well each model can explain the data without resorting to large exogenous shocks or measurement errors. More specifically, the second statistic is
the root mean squared prediction errors (RMSE), and the third statistic is the coefficient of determination (![]() ), defined as the percentage of in-sample variations of each data series
explained by the model:
), defined as the percentage of in-sample variations of each data series
explained by the model:
where
5.3 Matching Survey Inflation Forecasts
It is conceivable that a model with more parameters like Model L-IId could generate smaller in-sample fitting errors for variables whose fit is explicitly optimized, but produce undesirable implications for variables not used in the estimation. To check this possibility, we examine the model fit for a variable that is not used in our estimation but is of enormous economic interest, the expected inflation. In particular, we examine how closely the model-implied inflation expectations mimic survey-based inflation forecasts. Ang, Bekaert, and Wei (2007) recently provide evidence that survey inflation forecasts outperforms various other measures of inflation expectations in predicting future inflation. In addition, survey inflation forecast has the benefit of being a real-time, model-free measure, and hence not subject to model estimation errors or look-ahead biases that could affect measures based on in-sample fitting of realized inflation.31
Panel D of Table 8 reports the three goodness-of-fit statistics, CORR, RMSE and ![]() , for 1- and 10-year ahead inflation forecasts from the SPF. Among the
models, Model NL generates inflation expectations that agree least well with survey inflation forecasts, producing large RMSEs and small
, for 1- and 10-year ahead inflation forecasts from the SPF. Among the
models, Model NL generates inflation expectations that agree least well with survey inflation forecasts, producing large RMSEs and small ![]() statistics at both horizons. This poor fit is
especially prominent at the 1-year horizon: the RMSE is large, the correlation between the model and survey forecast is essentially 0, and the
statistics at both horizons. This poor fit is
especially prominent at the 1-year horizon: the RMSE is large, the correlation between the model and survey forecast is essentially 0, and the ![]() is highly negative at
is highly negative at ![]() . In contrast, all other models, which have a liquidity factor, generate a reasonable fit with the survey forecasts at both horizons. The best fit is achieved by Models L-II and L-IId, both of
which generate correlations above
. In contrast, all other models, which have a liquidity factor, generate a reasonable fit with the survey forecasts at both horizons. The best fit is achieved by Models L-II and L-IId, both of
which generate correlations above ![]() and small RMSEs at both horizons and explain a large amount of sample variations in survey inflation forecasts. Models L-II and L-IId also improve
notably upon Model L-I, suggesting that some cyclical variations in TIPS yields might not be due to movements in the real yields. Overall, Model L-IId does not seem to suffer from an overfitting problem. As we will see from later sections, this model also generate sensible implications for TIPS
liquidity premiums and inflation risk premiums, further supporting our conclusion.
and small RMSEs at both horizons and explain a large amount of sample variations in survey inflation forecasts. Models L-II and L-IId also improve
notably upon Model L-I, suggesting that some cyclical variations in TIPS yields might not be due to movements in the real yields. Overall, Model L-IId does not seem to suffer from an overfitting problem. As we will see from later sections, this model also generate sensible implications for TIPS
liquidity premiums and inflation risk premiums, further supporting our conclusion.
A visual comparison of the model-implied inflation expectations and survey forecasts can help us understand the results in Table 8. The left panels of Figure 6 plot the 1-year inflation expectation based on Models NL, L-I and L-IId, together with the survey forecast. It can be seen that the Model-NL-implied 1-year inflation expectation contains a large amount of short-run fluctuations that are not shared by its survey counterpart. It also fails to capture the downward trend in survey inflation forecasts during much of the sample period. In comparison, implied 1-year inflation expectation based on the other models show a visible downward trend, consistent with the survey evidence. It is interesting that although Models L-I and L-IId exhibit similar fit to TIPS yields and TIPS breakevens, as can be seen from Figure 5, they are more differentiable based on their implications for inflation expectations. In particular, while the 1-year inflation expectation implied by Model L-IId bears a high resemblance to the 1-year survey forecast, the same series implied by Model L-I appears to be much more variable than the survey counterpart.
It is also not surprising that Model NL produces a larger RMSEs for 10-year inflation expectations than the L-I and L-II models: the upper middle panel of Figure 6 shows that Model NL completely misses the downward trend in the 10-year survey inflation forecast since the early 1990s and implies a 10-year inflation expectations that moved little over the sample period. This is the flip side of the discussions in Section 5.2, where we see a Model-NL-implied 10-year real rate that is too variable and is used by the model to explain the entire decline in nominal yields in the 1990s. Overall, the near-constancy of the long-term inflation expectation is the most problematic feature of Model NL. Models L-I and L-IId, on the other hand, produce 10-year inflation expectations that are clearly downward trending, though the model-implied values are a bit lower than the survey forecast in the early 1990s, as shown in the two lower panels in the middle column of Figure 6. As can be recalled from Figure 5, the long-term real yields in these models also display a downward trend, but a much weaker one compared to that in Model NL.
Finally, the three right panels of Figure 6 plot the model-implied inflation risk premiums at the 1- and 10-year horizons for the three models under consideration. One immediately notable feature is that Model-NL implies an inflation risk premium, shown in the upper right panel, that is negative and increasing over time in the 1990-2007 period. In contrast, as mentioned in Section 2, most of the existing studies not using TIPS find that average inflation risk premium has been positive historically. Furthermore, studies such as Clarida/Friedman:84:JF indicate that the inflation risk premium likely was positive and substantial in the early 1980s and probably has come down since then. As can be seen from Figure 7, which plots the 10-year inflation risk premium estimates together with the 95% confidence bands for the three models, even after we take into account sampling uncertainties, long-term inflation risk premiums implied by Model NL remain negative over most of the sample period. In comparison, the two models that allow for a liquidity premium, Models L-I and L-IId, both generate 10-year inflation risk premiums that are positive and fluctuate in the 0 to 1% range over the same sample period. The short-term inflation risk premiums implied by these two models, on the other hand, are fairly small, consistent with our intuition.
5.4 Summary
In summary, we find that Model NL, which equates TIPS yields with true underlying real yields, fares poorly along a number of dimensions, including generating a poor fit with the TIPS data as well as unreasonable implications for inflation expectations and inflation risk premiums. This underscores the need to take into account a liquidity premium in modeling TIPS yields. In contrast, models that allows for a TIPS liquidity premium, Models L-I and L-II, improves upon Model NL in all three aspects and in particular produce long-term inflation expectations that agree quite well with survey forecasts.
Among models allowing a liquidity premium in TIPS yields, Models L-II and Model L-IId generate short-term inflation expectations that matches survey counterparts better than Model L-I, suggesting it is important to allow for a systematic component in TIPS liquidity premiums.
Finally, a likelihood ratio test rejects Models L-II in favor of our preferred model, Model L-IId, which features a deterministic trend in TIPS liquidity premium that is designed to capture the "newness effect" during the early years of TIPS. In the remainder of our analysis we'll be mainly focusing on this model.
6.1 Model Estimates of TIPS Liquidity Premiums
Once we estimate the model parameters and the state variables, we can calculate the TIPS liquidity premiums at various maturities based on Equation (35). The top and the middle panels of Figure 8 plot the 5-, 7- and 10-year liquidity premiums implied by Models L-I and L-II, respectively, while the bottom panel shows the the deterministic and the stochastic components of the liquidity premiums based on Model L-IId.
Three things are worth noting from this graph: First, all three panels show that liquidity premiums exhibit substantial time variations at all maturities. The substantial variabilities at maturities as long as 10 years are in part due to the fact that the independent liquidity factor is
estimated to be very persistent under the risk-neutral measure. As can be seen from Table 8, the risk-neutral persistence of the liquidity factor,
![]() , is estimated to be very small at around 0.1 in all models and is tightly estimated, with a standard error of about 0.006.
In contrast, the persistence parameter under the physical measure,
, is estimated to be very small at around 0.1 in all models and is tightly estimated, with a standard error of about 0.006.
In contrast, the persistence parameter under the physical measure,
![]() , is not as precisely estimated, with typical values of around 0.20 and typical standard errors of around 0.27.
, is not as precisely estimated, with typical values of around 0.20 and typical standard errors of around 0.27.
Second, the term structure of TIPS liquidity premiums is relatively flat at all times under Model L-I, while under Model L-II, the term structure has a mild downward-sloping behavior during the 2001-2004 period. Technically, a market price of risk on the independent liquidity factor that is on
average positive, as is the case in all three models here, would contribute to a downward-sloping term structure of TIPS liquidity premium.32 This is in
contrast to the standard one-factor interest rate models, where the market price of interest rate risk is typically found to be negative. Although the TIPS liquidity premiums in Models L-II and L-IId are also driven by the nominal bond factors, ![]() , in addition to
, in addition to
![]() , a variance decomposition indicates that the TIPS-specific factor
, a variance decomposition indicates that the TIPS-specific factor
![]() drives most of the variations in TIPS liquidity premium. Nonetheless, as we've seen in Section 5, allowing the TIPS liquidity premiums to depend on
nominal bond factors seems important in explaining the dynamics of TIPS yields.
drives most of the variations in TIPS liquidity premium. Nonetheless, as we've seen in Section 5, allowing the TIPS liquidity premiums to depend on
nominal bond factors seems important in explaining the dynamics of TIPS yields.
Finally, all three models imply that the TIPS liquidity premiums were fairly high (1-2 %) when TIPS were first introduced, had been on a downward trajectory until around 2004, and have stayed at a relatively low level from 2005 onwards. The deterministic trend implied by Model L-IId came down from about 120 basis points in 1999 to below 10 basis points by the end of 2004. After removing the downward trend, the stochastic liquidity premiums appear more stationary and largely vary between -50 and 50 basis points.
6.2 What Drives the TIPS Liquidity Premiums?
The behavior of the liquidity premiums we have seen in Figure 8 seems broadly consistent with the perception that TIPS market liquidity conditions have improved over time. In this section, we examine this issue more closely. One difficulty in this regard is the lack of precise, real-time measures of the TIPS market liquidity. One measure that has been used in the literature33 is the 13-week moving average of weekly TIPS turnover, defined as the weekly average of daily TIPS transaction volumes divided by the TIPS outstanding at the end of the current month.34 As can be seen in the top panel of Figure 3, the turnover in TIPS remained low up to mid 2002 and then rose substantially, suggesting an improvement in the liquidity conditions of the TIPS market in recent years.35 The rise coincides roughly with the decline in our TIPS liquidity premium estimates. In particular, all our model-based TIPS liquidity premiums (Model L-I, L-II, L-IId) have correlations with this measure more negative than -73%.
However, the turnover may be affected by factors other than the liquidity conditions in the TIPS market. For example, there is a large empirical literature documenting a positive contemporaneous correlation between price volatility and trading volumes, independent of current market liquidity conditions.36 In particular, as shown in the middle panel of Figure 9, interest rate volatilities declined markedly during the latter half of the sample period, which might have contributed to the drop in TIPS turnover after 2005. Indeed, evidence from TIPS bid-ask spreads, arguably a better measure of liquidity conditions in the TIPS market, indicates that the early improvement in TIPS liquidity may not have been largely reversed in the most recent sample period, as one might assume based on the rapid decline in TIPS turnover since 2005. For example, two informal surveys of the primary dealers conducted by the Federal Reserve Bank of New York in 2003 and 2007, shown in Table 8, find that the average bid-ask spreads on TIPS continue to narrow across all maturities during this period.37 Unfortunately, a long history of this measure is unavailable.
To quantify the effects of various factors on our estimates of TIPS liquidity premiums, we therefore regress the 5-, 7- and 10-year TIPS liquidity premiums from Model L-IId onto three explanatory variables, the first of which being the TIPS turnover ratio.
The second explanatory variable, IMPVOL, is the implied volatility from options on 10-year Treasury note futures and is included to control for the positive contemporaneous correlation between price volatility and trading volumes. The last variable, ASW, represents the difference between the on-the-run and the off-the-run 10-year Treasuries par asset swap spreads and can be considered as a market-based measure of the liquidity premiums on the nominal Treasury market. In a fixed-income asset swap, one party exchanges the fixed-rate cash flows from the underlying security for a floating-rate cash flow where the floating rate is typically quoted as 6-month LIBOR plus a spread, the asset swap spread. Asset swap spreads varies over time and across securities according to the perceived default and liquidity risk of the underlying security. Because both nominal Treasury and TIPS are usually considered free of default risks, their asset swap spreads can be regarded as a good measure of the liquidity premiums in those assets. Consistent with their relative liquidity, we usually observe increasingly more negative spreads as we move across asset classes in the order of TIPS, off-the-run nominal Treasuries and on-the-run nominal Treasuries. For our purposes, an ideal measure of the relative illiquidity of TIPS compared to off-the-run nominal Treasuries would be the difference between the TIPS and the off-the-run nominal asset swap spreads.38 Unfortunately TIPS asset swaps only started trading in 2006; we therefore use the difference between the off-the-run and the on-the-run 10-year nominal Treasuries as an approximation. The daily correlation between the two spreads is 0.90 over the period of March 16, 2006 to November 13, 2009.
Figure 9 plots all three explanatory variables; their correlations with TIPS liquidity premium estimates from Model LII-d and with each other are reported in Panel B of Table 8. The three variables are not highly correlated with each other, but all have large correlations with the liquidity premium estimates. The results from this regression are reported in Panel A of Table 8. The coefficients on all three variables are statistically significant and carry the expected sign. In particular, a lower TIPS turnover raises the TIPS liquidity premiums, but the effect will be smaller if the lower turnover is accompanied by a lower volatility.39 Together these three variables explain about 80% of the variations in TIPS liquidity premium estimates at all maturities.40 It remains an interesting topic for future research to see whether our model-based measures of TIPS liquidity premiums correlate with other measures of TIPS market liquidity.41
The results in Table 8 suggest one simple way to adjust the TIPS breakeven inflation for the liquidity effects. Consider the difference between the SPF forecast of average inflation over the next ten years,
![]() , and the 10-year TIPS breakeven inflation,
, and the 10-year TIPS breakeven inflation,
![]() , and regress it on the same three right-hand-side variables as in Equation (53):42
, and regress it on the same three right-hand-side variables as in Equation (53):42
Assuming that the 10-year inflation risk premiums do not vary too much over time, the fitted values from this regression can be thought of as a rough gauge of the liquidity premium component in the difference between the TIPS breakeven inflation and the survey counterpart, the other components being inflation risk premiums and measurement errors. Using the coefficient estimates, one can generate a real-time estimate of TIPS liquidity premiums, which can be added to the observed TIPS breakeven inflation to produce a liquidity-adjusted series. The results from such an exercise are plotted in Figure 10, which shows the adjusted 10-year TIPS breakeven inflation together with the raw series as well as the model-implied true breakeven inflation. The adjusted BEI using this simple method is much closer to the true BEI based on our full model. It is much more variable than the true BEI, especially in the early years, although the difference has narrowed towards the end of our sample period.
While the qualitative behavior of TIPS liquidity premium thus seems reasonable, our estimates of ![]() does seem large in comparison with that of the corporate bonds. Corporate bonds,
including those with the highest credit rating (AAA/AA), tend to trade infrequently at once a day or less; TIPS, in comparison, trade more often than AAA/AA corporate bonds even during the early years when liquidity was the poorest. The bid-ask spread in TIPS has also been substantially smaller
than those of corporate bonds. In this regard, our estimates of TIPS liquidity premium around 1.5% in the early years seems puzzlingly high, in comparison with investment-grade corporate bonds which typically trade at a liquidity premiums of about 50 basis points.43 The high value of the TIPS liquidity premium in the early years may partly reflect a depressed demand for TIPS due to the newness of the security and the relative complexity of TIPS
payoff structure. Furthermore, a popular belief that TIPS are tax-disadvantageous for taxable investors44 may have further depressed the demand for
TIPS.
does seem large in comparison with that of the corporate bonds. Corporate bonds,
including those with the highest credit rating (AAA/AA), tend to trade infrequently at once a day or less; TIPS, in comparison, trade more often than AAA/AA corporate bonds even during the early years when liquidity was the poorest. The bid-ask spread in TIPS has also been substantially smaller
than those of corporate bonds. In this regard, our estimates of TIPS liquidity premium around 1.5% in the early years seems puzzlingly high, in comparison with investment-grade corporate bonds which typically trade at a liquidity premiums of about 50 basis points.43 The high value of the TIPS liquidity premium in the early years may partly reflect a depressed demand for TIPS due to the newness of the security and the relative complexity of TIPS
payoff structure. Furthermore, a popular belief that TIPS are tax-disadvantageous for taxable investors44 may have further depressed the demand for
TIPS.
7.1 Decomposing TIPS Yields and TIPS Breakeven Inflation
In this section we examine how much variations in TIPS yields and TIPS breakeven inflation rate can be attributed to variations in TIPS liquidity premiums. Using Equations (2) and (30), we can decompose TIPS yields,
![]() , and TIPS breakven inflation,
, and TIPS breakven inflation,
![]() , into different components:
, into different components:
where
Table 8 reports the variance decomposition results based on Equation (55) and Model L-IId estimates, using either the unconditional (Panel A) or the instantaneous (Panel B) variance-covariance matrix of the state variables. A time series plot of the decomposition is shown in Figure 11.
For TIPS yields, real yields dominate TIPS liquidity premiums in accounting for the time variations both unconditionally and instantaneously. In comparison, TIPS liquidity premiums are more important in driving TIPS breakeven inflation, explaining about 23% of its unconditional variations at all three maturities, although expected inflation still accounts for the majority of time variations in TIPS breakeven inflation. The contribution of TIPS liquidity premiums is even larger instantaneously and explains about 43% of the short-run variations in TIPS breakeven inflation. The last observation suggests that one should be especially cautious in interpreting short-run variations in TIPS breakeven inflation solely in terms of changes in inflation expectation or inflation risk premiums.
7.2 Decomposing Nominal Yields
Although it is not the focus of the current paper, our models can also be used to separate nominal yields into real yields, expected inflation and inflation risk premiums:
Figure 12 plots the 1- and 10-year nominal yields and their constituents, whereas Table 8 reports the variance decomposition results.
These results indicate that, at least during our sample period, real yield changes explain more than half of the variations in nominal yields at all maturities. Inflation expectation explains about 40% (20%) of the variations in the 1-quarter (10-year) nominal yield. Inflation risk premiums account for the remaining 10% of the nominal yield changes. This stands in contrast to previous studies using a longer sample period but not using TIPS yields, which typically find relatively smooth real yields but volatile inflation expectation or inflation risk premiums.45 The limited evidence we have so far from TIPS seems to suggest that real yields may also vary considerably over time.
8 Conclusion
In this paper, we document that there exists a TIPS-specific factor that is important for explaining TIPS yield variations but not as crucial for explaining nominal interest rate movement, and provide evidence that this factor might be reflecting a liquidity premium in TIPS yields.
We then develop a joint no-arbitrage term structure model of nominal and TIPS yields incorporating a rich specification of the TIPS liquidity premiums. The main findings can be summarized as the following. First, we find that our estimated liquidity premium was quite large
![]() until about 2003 but has come down in recent years, consistent with the common perception that TIPS market liquidity has improved in recent years. Second, our TIPS liquidity
premium estimates contain a persistent downward trend in its early years, that is best modeled as a deterministic trend reflecting gradual market acceptance of TIPS as a new debt instrument. Finally, we show that ignoring the liquidity premium components leads to a poor model fit of TIPS yields,
TIPS breakeven inflation and survey inflation forecasts.
until about 2003 but has come down in recent years, consistent with the common perception that TIPS market liquidity has improved in recent years. Second, our TIPS liquidity
premium estimates contain a persistent downward trend in its early years, that is best modeled as a deterministic trend reflecting gradual market acceptance of TIPS as a new debt instrument. Finally, we show that ignoring the liquidity premium components leads to a poor model fit of TIPS yields,
TIPS breakeven inflation and survey inflation forecasts.
TIPS breakeven inflation has been increasingly gaining attention as a measure of investors' inflation expectations that is available in real-time and at high frequencies. However, our results raise caution in interpreting movement in TIPS breakeven inflation solely in terms of changing inflation expectations, as substantial liquidity premiums and inflation risk premiums could at times drive a large wedge between between the two. In an encouraging note, the reduced liquidity premium that we find for the most recent period (2005-2007) raises the possibility that, going forward, the TIPS yields may be a better gauge of the true real yields. However, given that TIPS is less liquid than nominal Treasury securities, we caution that TIPS liquidity premiums might rise again in times of financial market stress. A better understanding of the determinants of TIPS liquidity premiums and the sources of its variation remains an interesting topic for future research.
Appendix
A More on the TIPS Data
This appendix is devoted to a more detailed discussion of the TIPS data. Figure A1 shows the smoothed TIPS par yield curves on June 9, 2005 in the top panel and on June 9, 1999 in the bottom panel, together with the actual traded TIPS yields that were used to create the smoothed TIPS par-yield and zero-coupon curves. The smoothing is done by assuming that the zero-coupon TIPS yield curve follows the 4-parameter Nelson-Siegel (1987) functional form up to the end of 2003 and the 6-parameter Svensson (1994) functional form thereafter,46 and minimizing the fitting error for the actual traded TIPS securities. The substantial increase in the number of points in the top panel reflects the growth of the TIPS market. Note that in 1999 there is essentially one data point on the curve between the 0 and 5 years maturity (corresponding to the 5-year TIPS issued in 1997), thus the TIPS term structure in the short-maturity region of 0-5 years cannot be determined reliably. With more points across the maturity spectrum in 2005, shorter maturity TIPS yields can be determined more reliably than in 1999.
Still, the analysis of the short-maturity TIPS are complicated by the indexation lag and seasonality issues. Note that the TIPS payments are indexed to the CPI 2.5 months earlier, thus TIPS yields contain some amount of realized inflation, often referred to as the "carry effect". The yield that is more relevant to policy makers is the one that takes out this realized inflation - the so-called carry-adjusted yields, which can be heuristically represented as
where
As noted in the main text, since data reliability and indexation lags pose larger problems to shorter-maturity TIPS, in this paper we focus on long-maturity TIPS yield for which the effects of indexation lag and seasonality are less important. While the analysis of shorter-maturity TIPS yields is an important problem in itself, it deserves a fuller treatment elsewhere.49 The 5-, 7- and 10-year carry-unadjusted TIPS yields used in this analysis can be viewed as the carry-corrected TIPS yield plus a measurement error, as suggested by Equation (1).
B Stochastic TIPS Liquidity Premium
Since
![]() is independent of the other state variables in
is independent of the other state variables in ![]() , the first term on
the right-hand side of Equation (31) can be written as the sum of two components:
, the first term on
the right-hand side of Equation (31) can be written as the sum of two components:
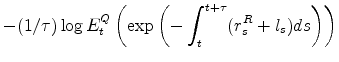 |
||
| (B-2) |
The first component can be solved to be
| (B-3) |
where
![\displaystyle \tilde{\gamma} \left[(\tilde{\mu}^*-\frac{\tilde{\sigma}^2}{2\tilde{\kappa}^*})(1-\tilde{b}_{\tau})+\frac{\tilde{\sigma}^2}{4\tilde{\kappa}^*}\tau\tilde{b}_{\tau}^2\right]](img224.gif) |
(B-4) | ||
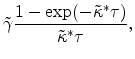 |
(B-5) |
in which the risk-neutral
The second component can be shown to take the form
| (B-7) |
where
where
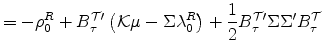 |
(B-10) | |
| (B-11) |
with initial conditions
Taken together, we have that
![\displaystyle =\left( \tilde{a}+a_{\tau}^{\mathcal{T}}\right) +\left[ \begin{array}[c]{cc}% b_{\tau}^{\mathcal{T}^{\prime}} & \tilde{b}% \end{array} \right] \left[ \begin{array}[c]{c}% x_{t}\\ \tilde{x}_{t}% \end{array} \right] -y_{t}^{R}](img243.gif) |
||
![\displaystyle =\left[ \tilde{a}_{\tau}+(a_{\tau}^{\mathcal{T}}-a_{\tau}^{R})\right] +\left[ \begin{array}[c]{cc}% (b_{\tau}^{\mathcal{T}}-b_{\tau}^{R})^{\prime} & \tilde{b}_{\tau}% \end{array} \right] \left[ \begin{array}[c]{c}% x_{t}\\ \tilde{x}_{t}% \end{array} \right]](img244.gif) |
(B-12) |
where the second equality comes from Equation (23).
C Kalman Filter and Likelihood Function
We use the Kalman filter to compute optimal estimates of the unobservable state factors based on all available information. For example, given the initial guess for the state factors
![]() , it follows from the state equation (46) that the optimal estimate of the state factor
, it follows from the state equation (46) that the optimal estimate of the state factor ![]() at time
at time ![]() is given by
is given by
for any time period
The variance-covariance matrix of the estimation error can be derived as
where
Given any forecast for ![]() , we can compute a forecast for the observable variables based on all time
, we can compute a forecast for the observable variables based on all time ![]() information:
information:
The conditional variance-covariance matrix of this estimation error can then be computed as
where
The next step is to update the equation for the state variables. Before doing this, we need to recover the distribution of
![]() The conditional covariance between the forecasting errors for state variables and that for observation variables takes the form of
The conditional covariance between the forecasting errors for state variables and that for observation variables takes the form of
The conditional joint distribution for ![]() and
and ![]() is therefore
is therefore
![\displaystyle % \begin{bmatrix} \rm y_{t}\ \rm x_t\end{bmatrix}\mid\Im_{t-h}\sim N\left( \genfrac{[}{]}{0pt}{}{a+F\widehat{\rm x}_{t,t-h}}{\widehat{\rm x}_{t,t-h\text{ }}}% ,% \begin{bmatrix} B Q_{t,t-h} B^{\prime}+\Omega_{t}^{e} & B Q_{t,t-h}\ Q_{t,t-h} B^{\prime} & Q_{t,t-h}% \end{bmatrix}\right) ,](img269.gif)
The variance-covariance matrix of the updated state vector,
We estimate the parameters by maximizing the log-likelihood function
Bibliography
| Coefficient: Constant | Coefficient: 3-month | Coefficient: 2-year | Coefficient: 10-year | Adj. |
|
| In Level | 3.4637 | -0.4519 | 0.6516 | -0.4384 | 32.3% |
| In Level (standard error) | (0.1138) | (0.0345) | (0.0479) | (0.0346) | |
| In Weekly Changes | 0.0032 | 0.0110 | -0.0850 | 0.5687 | 59.0% |
| In Weekly Changes (standard error) | (0.0025) | (0.0334) | (0.0409) | (0.0366) |
| PC | nominal yields only | nominal and TIPS yields |
| 1st | 75.17 | 71.11 |
| 2nd | 93.25 | 87.26 |
| 3rd | 97.44 | 94.72 |
| 4th | 99.36 | 97.58 |
| PC1 (nominal and TIPS yield) | PC2 (nominal and TIPS yield) | PC3 (nominal and TIPS yield) | PC4 (nominal and TIPS yield) | |
| PC1 (nominal yield alone) | 0.97 | -0.21 | -0.15 | 0.01 |
| PC2 (nominal yield alone) | 0.12 | 0.86 | -0.49 | 0.02 |
| PC3 (nominal yield alone) | 0.04 | 0.08 | 0.20 | 0.97 |
| PC4 (nominal yield alone) | -0.01 | -0.03 | -0.06 | 0.01 |
Panel A regresses 10-year TIPS breakevens on 3-month, 2-year and 10-year nominal yields using weekly data from Jan. 6, 1999 to Mar. 14, 2007. Panel B report the cumulative percentage of total variance of weekly yield changes explained by the first four principal components, where the second and the third column report results for nominal yields alone and nominal and TIPS yields combined, respectively. The in-sample correlation between the two sets of principal components are reported in Panel C.
| Model | Restrictions and Idenfications |
| Model NL |
|
| Model L-I |
|
| Model L-II |
|
| Model L-IId |
|
| Model NL (parameter estimate) | Model NL (standard error) | Model L-I (parameter estimate) | Model L-I (standard error) | Model L-II (parameter estimate) | Model L-II (standard error) | Model L-IId: parameter estimate | Model L-IId: standard error | |
|
|
0.8587 | (0.5206) | 0.8676 | (0.5227) | 0.8573 | (0.4948) | 0.8374 | (0.4606) |
|
|
0.0529 | (0.0787) | 0.0573 | (0.0793) | 0.0555 | (0.0794) | 0.0529 | (0.0781) |
|
|
1.5219 | (0.8048) | 1.5321 | (0.8040) | 1.5394 | (0.7729) | 1.5672 | (0.7574) |
|
|
-0.3346 | (0.3200) | -0.3098 | (0.3105) | -0.3232 | (0.3101) | -0.3175 | (0.3101) |
|
|
-4.5682 | (9.1343) | -4.5353 | (9.0421) | -4.4144 | (8.1903) | -4.0846 | (6.7681) |
|
|
-0.5524 | (0.2581) | -0.5449 | (0.2522) | -0.5494 | (0.2538) | -0.5362 | (0.2469) |
| Model NL (parameter estimate) | Model NL (standard error) | Model L-I (parameter estimate) | Model L-I (standard error) | Model L-II (parameter estimate) | Model L-II (standard error) | Model L-IId: parameter estimate | Model L-IId: standard error | |
| 0.0419 | (0.0135) | 0.0434 | (0.0116) | 0.0428 | (0.0125) | 0.0422 | (0.0132) | |
|
|
2.8343 | (5.2462) | 2.8318 | (5.2564) | 2.7671 | (4.7530) | 2.5726 | (3.9118) |
|
|
0.4825 | (0.1249) | 0.4797 | (0.1239) | 0.4809 | (0.1248) | 0.4675 | (0.1207) |
|
|
0.6089 | (0.0378) | 0.6177 | (0.0403) | 0.6180 | (0.0387) | 0.6195 | (0.0377) |
|
|
0.4362 | (0.2228) | 0.4107 | (0.1807) | 0.4147 | (0.1946) | 0.4236 | (0.2449) |
|
|
-0.1818 | (0.8732) | -0.2933 | (0.7752) | -0.2447 | (0.8142) | -0.2049 | (0.8544) |
|
|
-0.0471 | (3.3761) | -0.4308 | (2.8805) | -0.2597 | (3.1019) | -0.1136 | (3.3049) |
|
|
-0.5330 | (1.7491) | -0.5489 | (1.7874) | -0.5288 | (1.6390) | -0.4592 | (1.3462) |
|
|
1.7508 | (4.9179) | 1.7894 | (4.9932) | 1.7104 | (4.5060) | 1.5341 | (3.7315) |
|
|
3.7651 | (15.9132) | 3.8379 | (16.1348) | 3.6471 | (14.3685) | 3.1187 | (11.0801) |
|
|
-0.0274 | (0.2452) | -0.0277 | (0.2406) | -0.0272 | (0.2370) | -0.0419 | (0.2252) |
|
|
-0.2865 | (0.1339) | -0.2854 | (0.1318) | -0.2849 | (0.1330) | -0.2752 | (0.1326) |
|
|
-0.6948 | (0.8960) | -0.6677 | (0.8587) | -0.6854 | (0.8420) | -0.6296 | (0.6714) |
|
|
-0.0717 | (0.3145) | -0.0749 | (0.3224) | -0.0725 | (0.3155) | -0.0551 | (0.3238) |
|
|
0.6171 | (0.2355) | 0.6329 | (0.2429) | 0.6303 | (0.2397) | 0.6314 | (0.2404) |
|
|
0.6551 | (2.1043) | 0.6812 | (2.1309) | 0.6634 | (1.9803) | 0.5887 | (1.7096) |
| Model NL (parameter estimate) | Model NL (standard error) | Model L-I (parameter estimate) | Model L-I (standard error) | Model L-II (parameter estimate) | Model L-II (standard error) | Model L-IId: parameter estimate | Model L-IId: standard error | |
|
|
0.0271 | (0.0035) | 0.0280 | (0.0069) | 0.0239 | (0.0082) | 0.0236 | (0.0084) |
|
|
-0.7843 | (2.8227) | 0.8836 | (1.4332) | 0.0746 | (0.6436) | 0.0729 | (0.5890) |
|
|
0.0766 | (0.1062) | 0.2563 | (0.0707) | 0.2575 | (0.1262) | 0.2443 | (0.1248) |
|
|
-0.5094 | (0.3937) | 0.1216 | (0.1276) | -0.0165 | (0.2079) | -0.0221 | (0.2107) |
|
|
-0.1724 | (0.0651) | -0.1176 | (0.0720) | -0.1050 | (0.0763) | -0.1076 | (0.0757) |
|
|
-0.0231 | (0.0803) | 0.0597 | (0.0750) | 0.0651 | (0.0757) | 0.0506 | (0.0750) |
|
|
-0.0016 | (0.0656) | 0.0354 | (0.0594) | 0.0306 | (0.0611) | 0.0358 | (0.0609) |
|
|
0.7795 | (0.0288) | 0.7279 | (0.0241) | 0.7144 | (0.0245) | 0.7144 | (0.0245) |
| Model NL (parameter estimate) | Model NL (standard error) | Model L-I (parameter estimate) | Model L-I (standard error) | Model L-II (parameter estimate) | Model L-II (standard error) | Model L-IId: parameter estimate | Model L-IId: standard error | |
|
|
0.6114 | (0.0411) | 0.6152 | (0.0415) | 1.2545 | (0.0914) | ||
|
|
0.2083 | (0.2655) | 0.2206 | (0.2630) | 0.6037 | (0.3973) | ||
|
|
0.0218 | (0.0113) | 0.0157 | (0.0115) | 0.0003 | (0.0105) | ||
|
|
0.3213 | (0.6657) | 0.2851 | (0.5090) | -0.0263 | (0.3356) | ||
|
|
-0.1091 | (0.2652) | -0.1209 | (0.2627) | -0.1472 | (0.4020) | ||
| -0.6765 | (1.2459) | -2.9521 | (5.7532) | |||||
| -0.0179 | (0.1547) | 0.2739 | (0.1717) | |||||
| -0.0833 | (0.2509) | -1.0137 | (0.3285) | |||||
| 1.1871 | (0.0310) | |||||||
| 0.0014 | (0.0001) | |||||||
| 731467.911 | (25.2593) |
| Model NL (parameter estimate) | Model NL (standard error) | Model L-I (parameter estimate) | Model L-I (standard error) | Model L-II (parameter estimate) | Model L-II (standard error) | Model L-IId: parameter estimate | Model L-IId: standard error | |
|
|
0.1005 | (0.0026) | 0.1012 | (0.0027) | 0.1012 | (0.0027) | 0.1013 | (0.0027) |
|
|
0.0231 | (0.0016) | 0.0221 | (0.0016) | -0.0222 | (0.0016) | -0.0224 | (0.0017) |
|
|
0.0532 | (0.0017) | 0.0530 | (0.0018) | 0.0530 | (0.0018) | 0.0531 | (0.0017) |
|
|
0.0000 | (140.6008) | -0.0000 | (59.2489) | -0.0000 | (50.6589) | -0.0000 | (27.7162) |
|
|
0.0293 | (0.0012) | 0.0294 | (0.0012) | 0.0294 | (0.0013) | 0.0294 | (0.0012) |
|
|
0.0000 | (120.1913) | 0.0000 | (0.9395) | 0.0000 | (44.6608) | -0.0000 | (0.9058) |
|
|
0.0489 | (0.0018) | 0.0490 | (0.0019) | 0.0490 | (0.0019) | 0.0489 | (0.0018) |
| Model NL (parameter estimate) | Model NL (standard error) | Model L-I (parameter estimate) | Model L-I (standard error) | Model L-II (parameter estimate) | Model L-II (standard error) | Model L-IId: parameter estimate | Model L-IId: standard error | |
|
|
0.4307 | (0.0953) | 0.0654 | (0.0059) | 0.0657 | (0.0060) | -0.0000 | (4.8466) |
|
|
0.3511 | (0.0832) | -0.0021 | (0.0414) | -0.0004 | (0.2385) | -0.0428 | (0.0035) |
|
|
0.3578 | (0.0802) | 0.0647 | (0.0060) | -0.0643 | (0.0059) | -0.0520 | (0.0038) |
| Model NL (parameter estimate) | Model NL (standard error) | Model L-I (parameter estimate) | Model L-I (standard error) | Model L-II (parameter estimate) | Model L-II (standard error) | Model L-IId: parameter estimate | Model L-IId: standard error | |
|
|
0.1760 | (0.0135) | 0.1758 | (0.0134) | 0.1758 | (0.0134) | 0.1758 | (0.0134) |
|
|
0.2261 | (0.0197) | 0.2260 | (0.0196) | 0.2260 | (0.0197) | 0.2261 | (0.0196) |
This table reports parameter estimates and standard errors for all four models we estimate. Standard errors are calculated using the BHHH formula and are reported in parentheses.
| Model NL | Model L-I | Model L-II | Model L-IId | |
| No. of parameters | 42 | 47 | 50 | 53 |
| Log likelihood | 53,663.65 | 55,972.49 | 55,976.70 | 56,193.41 |
| AIC | -107,243.30 | -111,850.97 | -111,853.40 | -112,280.81 |
| BIC | -107,041.70 | -111,625.37 | -111,613.39 | -112,026.41 |
| LR p-value | 0.04 |
| Model NL | Model L-I | Model L-II | Model L-IId | |
| 5-year CORR (in %) | 93.14 | 99.41 | 99.42 | 99.53 |
| 5-year RMSE | 0.43 | 0.13 | 0.13 | 0.11 |
| 5-year |
83.93 | 98.61 | 98.62 | 99.06 |
| 7-year CORR (in %) | 92.99 | 99.45 | 99.46 | 99.50 |
| 7-year RMSE | 0.36 | 0.10 | 0.10 | 0.10 |
| 7-year |
85.96 | 98.91 | 98.92 | 98.93 |
| 10-year CORR (in %) | 92.52 | 99.19 | 99.20 | 99.42 |
| 10-year RMSE | 0.37 | 0.12 | 0.11 | 0.10 |
| 10-year |
80.90 | 98.18 | 98.21 | 98.76 |
| Model NL | Model L-I | Model L-II | Model L-IId | |
| 7-year CORR (in %) | 51.61 | 97.21 | 97.24 | 97.35 |
| 7-year RMSE | 0.35 | 0.09 | 0.09 | 0.10 |
| 7-year |
23.44 | 94.47 | 94.54 | 94.21 |
| 10-year CORR (in %) | 32.08 | 94.76 | 94.80 | 95.11 |
| 10-year RMSE | 0.35 | 0.11 | 0.11 | 0.10 |
| 10-year |
-18.12 | 88.71 | 88.85 | 89.74 |
| Model NL | Model L-I | Model L-II | Model L-IId | |
| 1-year CORR (in %) | 2.07 | 62.94 | 88.65 | 88.08 |
| 1-year RMSE | 0.78 | 0.58 | 0.33 | 0.34 |
| 1-year |
-52.21 | 17.45 | 72.93 | 70.71 |
| 10-year CORR (in %) | 73.34 | 72.72 | 83.86 | 83.92 |
| 10-year RMSE | 0.51 | 0.40 | 0.42 | 0.42 |
| 10-year |
17.36 | 49.46 | 44.35 | 42.22 |
This table reports various diagnostic statistics for the four models estimated. Panel A reports the number of parameters, the log likelihood, the Akaike information criterion (AIC), the Bayesian information criterion (BIC) values, and the p-value from a Likelihood Ratio test of the current model against the more general Model to its right, where the p-values reported for Models NL and L-II are the Davie (1987) upper bounds. Panels B to D report three goodness-of-fit statistics for the 5-, 7- and 10-year TIPS yields, 7- and 10-year TIPS breakeven inflation and 1- and 10-year survey inflation forecasts, respetively, including the root mean squared fitted errors (RMSE), the correlation between the fitted series and the data counterpart (CORR), and the coefficient of determination (
| Less than five years | Five to Ten Years | Above ten years | |
| 2003 | 1 to 2 | 2 | 4 to 16 |
| Two-year | Five-year | Ten-Year | Twenty-Year | Thirty-year | |
| 2007 | 1/2 to 1 | 1 | 1-2 | 4-6 | 6-10 |
This table reports the TIPS bid-ask spread at various maturities based on two informal survey conducted by the Federal Reserve Bank of New York in 2003 and 2007, respectively. One tick is 1/32s of a point where a point roughly equals one percent of the security's par value.
| Maturity | Coefficients: Constant | Coefficients: Turnover | Coefficients: Imp Vol | Coefficients: ASW Spread | Adjusted |
| 5-year | 0.3074 | -0.4309 | 0.1196 | 0.0258 | 79.52% |
| 5-year (standard error) | (0.0771) | (0.0275) | (0.0095) | (0.0025) | |
| 7-year | 0.4139 | -0.3752 | 0.0824 | 0.0253 | 80.95% |
| 7-year (standard error) | (0.0641) | (0.0229) | (0.0079) | (0.0020) | |
| 10-year | 0.5076 | -0.3337 | 0.0465 | 0.0251 | 82.30% |
| 10-year (standard error) | (0.0541) | (0.0193) | (0.0067) | (0.0017) |
| Liquidity Premiums: 5-year | Liquidity Premiums: 7-year | Liquidity Premiums: 10-year | TIPS Turnover | 10-Year Imp Vol | |
| TIPS Turnover | -0.7286 | -0.7547 | -0.7850 | ||
| 10-year implied volatility | 0.5515 | 0.5098 | 0.4449 | -0.1314 | |
| On/off ASW spread | 0.7996 | 0.8189 | 0.8340 | -0.6374 | 0.4742 |
Panel A regresses 5, 7- and 10-year TIPS liquidity premium estimates based on Model L-IId on TIPS turnover, implied volatility of 10-year nominal Treasury future options and the difference between the on-the-run and the off-the-run 10-year Treasuries par asset swap spreads using weekly data from either Jan. 6, 1999 to Mar. 14, 2007. Their in-sample pairwise correlations are reported in Panel B.
| Maturity | TIPS yield: real yield | TIPS yield: liq prem | TIPS BEI: inf exp | TIPS BEI: inf risk prem | TIPS BEI: liq prem |
| 5-year | 1.1717 | -0.1717 | 0.5870 | 0.1890 | 0.2240 |
| 5-year (standard error) | (0.2836) | (0.2836) | (0.3050) | (0.2386) | (0.3170) |
| 7-year | 1.1819 | -0.1819 | 0.5659 | 0.1994 | 0.2347 |
| 7-year (standard error) | (0.2690) | (0.2690) | (0.3065) | (0.2616) | (0.3131) |
| 10-year | 1.1910 | -0.1910 | 0.5453 | 0.2090 | 0.2458 |
| 10-year(standard error) | (0.2581) | (0.2581) | (0.3192) | (0.2944) | (0.3095) |
| Maturity | TIPS yield: real yield | TIPS yield: liq prem | TIPS BEI: inf exp | TIPS BEI: inf risk prem | TIPS BEI: liq prem |
| 5-year | 1.1596 | -0.1596 | 0.5447 | 0.0167 | 0.4386 |
| 5-year (standard error) | (0.2963) | (0.2963) | (0.2473) | (0.2064) | (0.2639) |
| 7-year | 1.2285 | -0.2285 | 0.5500 | 0.0239 | 0.4261 |
| 7-year (standard error) | (0.3040) | (0.3040) | (0.2710) | (0.2397) | (0.2597) |
| 10-year | 1.3024 | -0.3024 | 0.5431 | 0.0348 | 0.4221 |
| 10-year(standard error) | (0.3073) | (0.3073) | (0.2984) | (0.2740) | (0.2556) |
Note: This table reports the unconditional and the instantaneous variance decompositions of TIPS yields into real yields and TIPS liquidity premiums, and of nominal yields into expected inflation, the inflation risk premiums and the negative of TIPS liquidity premiums, all based on Model L-IId estimates. The variance decompositions of TIPS yields are calculated according to
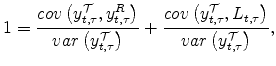
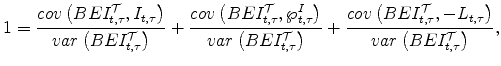
| Maturity | real yield | inf exp | inf risk prem |
| 1-quarter | 0.5108 | 0.4156 | 0.0736 |
| 1-quarter (standard error) | (0.2541) | (0.2281) | (0.0927) |
| 1-year | 0.5715 | 0.3497 | 0.0787 |
| 1-year (standard error) | (0.1930) | (0.1843) | (0.0924) |
| 5-year | 0.6503 | 0.2609 | 0.0888 |
| 5-year (standard error) | (0.1486) | (0.1417) | (0.1146) |
| 10-year | 0.6715 | 0.2347 | 0.0938 |
| 10-year (standard error) | (0.1401) | (0.1429) | (0.1362) |
| Maturity | real yield | inf exp | inf risk prem |
| 1-quarter | 0.7719 | 0.2252 | 0.0029 |
| 1-quarter (standard error) | (0.1090) | (0.1009) | (0.0312) |
| 1-year | 0.7692 | 0.2172 | 0.0137 |
| 1-year (standard error) | (0.1082) | (0.0915) | (0.0365) |
| 5-year | 0.7132 | 0.2496 | 0.0372 |
| 5-year (standard error) | (0.1231) | (0.1154) | (0.0970) |
| 10-year | 0.6892 | 0.2494 | 0.0614 |
| 10-year (standard error) | (0.1331) | (0.1438) | (0.1345) |
Note: This table reports the unconditional and the instantaneous variance decompositions of nominal yields into real yields, expected inflation, the inflation risk premiums, all based on Model L-IId estimates. The variance decomposition is calculated according to
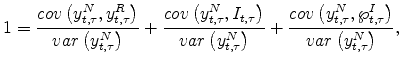
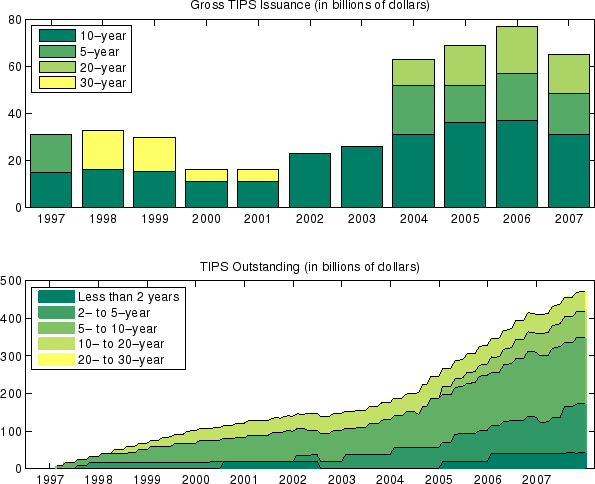 The top panel plots gross TIPS issuance broken down by initial maturities of 10, 5, 20 and 30 years. The bottom panel plots TIPS outstanding broken down by remaining maturities, based on data reported in the Treasury's Monthly Statement of the Public Debt (MSPD). |
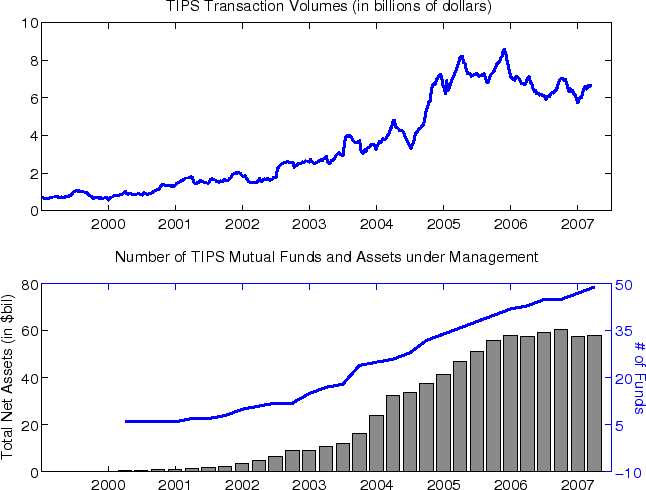 Top top panel plots the weekly TIPS transaction volumes, defined as 13-week moving average of weekly averages of daily TIPS transaction volumes reported by primary dealers in Government Securities Dealers Reports (FR-2004). The bottom panels plots number of TIPS mutual funds (left axis) and the total net assets under management (left axis).) |
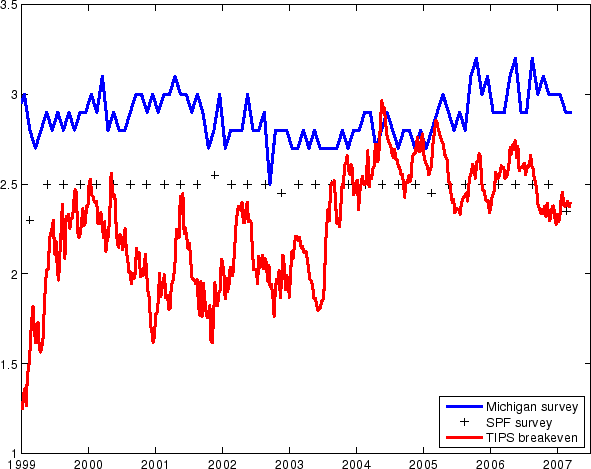 This chart shows the 10-year TIPS breakeven inflation (red line), long-horizon Michigan inflation forecast (blue line), and 10-year SPF inflation forecast (black pluses). |
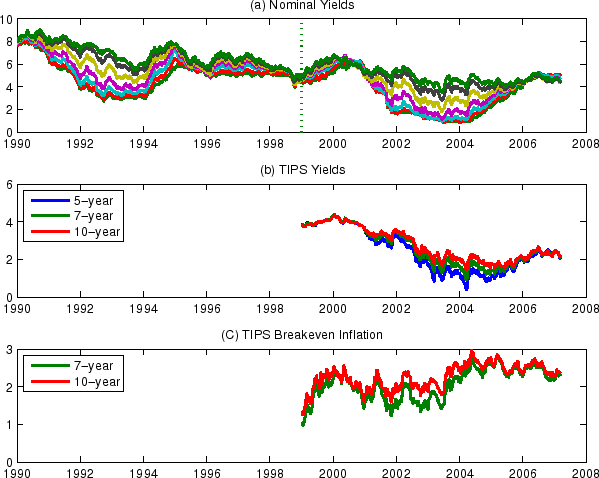 Top top panel plots the 3- and 6-month, 1-, 2-, 4-, 7- and 10-year nominal yields. The middle panel plots the 5-, 7- and 10-year TIPS yields. The bottom panels plots the 5- and 7-year TIPS breakeven inflation.) |
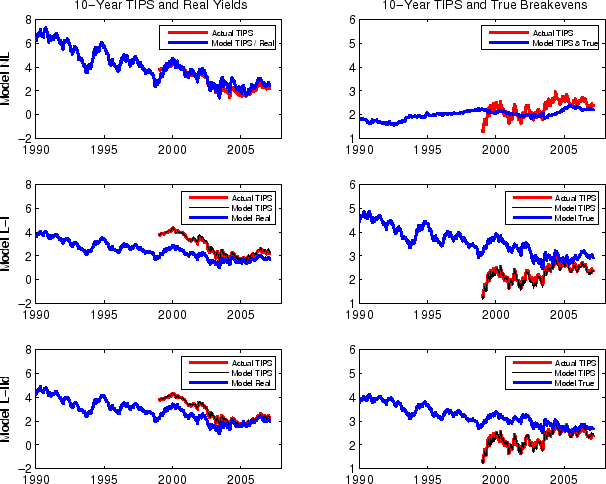 The panels on the left plot the 10-year actual TIPS yields (red), the 10-year model-implied TIPS yields (black) and the 10-year model-implied real yields (blue). The panels on the right plot the 10-year actual TIPS breakevens (red), the 10-year model-implied TIPS breakevens (black) and the 10-year model-implied true breakevens (blue). The model estimates are based on Model NL (upper panels), Model L-I (middle panels), and Model L-IId (lower panels), respectively. |
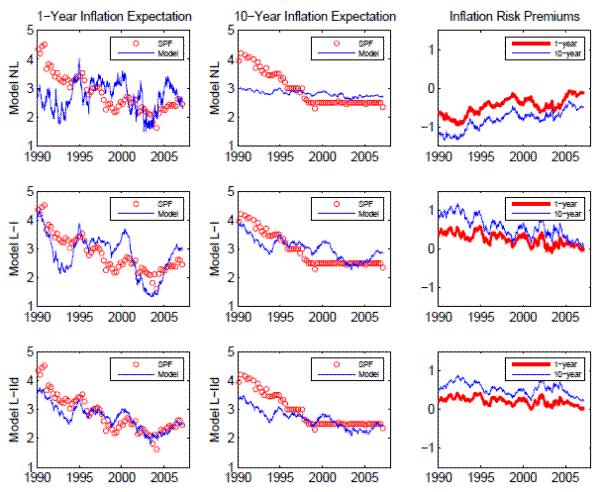 The left and middle panels plot the 1- and 10-year model-implied inflation expectation, respectively, together with the survey counterparts from Survey of Professional Forecasters (SPF), while the right panels plot the 1- and 10-year model-implied inflation risk premiums. The model estimates are based on Model NL (upper panels), Model L-I (middle panels), and Model L-IId (lower panels), respectively. |
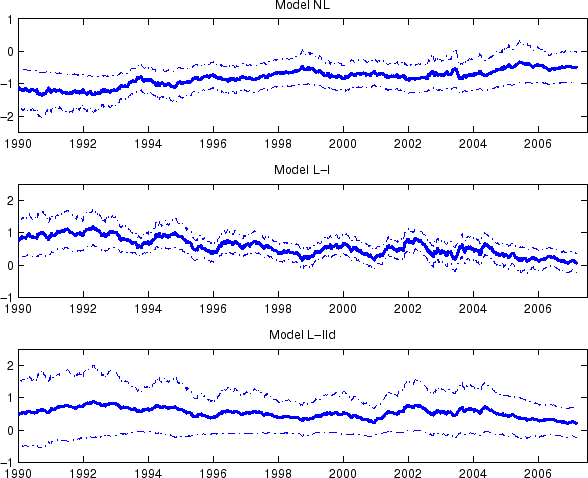 The three panels plot the model-implied 10-year inflation risk premiums with 2 BHHH standard error bands based on Model NL (top panel), Model L-I (middle panel) and Model L-IId (bottom panel), respectively. |
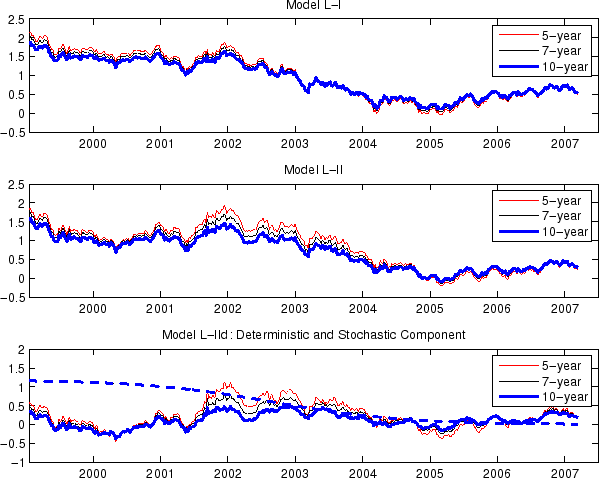 The top panel plot the 5-, 7- and 10-year TIPS liquidity premiums based on Model NL estimates. The bottom two panels plots the same series based on Model L-IId estimates, as well as a decomposition of these series into a deterministic component (dashed line in the middle panel) and a stochastic component (bottom panel). |
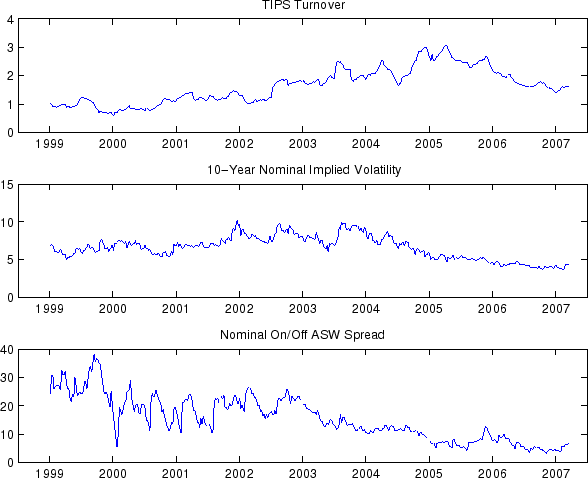 This chart plots various measures that potentially reflect liquidity conditions in the TIPS market, including the TIPS turnover ratio as defined in Section 6.2 (top panel), implied volatilities from options on the 10-year nominal Treasury note futures (middle panel) and the difference between the on-the-run and the off-the-run 10-year Treasuries par asset swap spreads (bottom panel). |
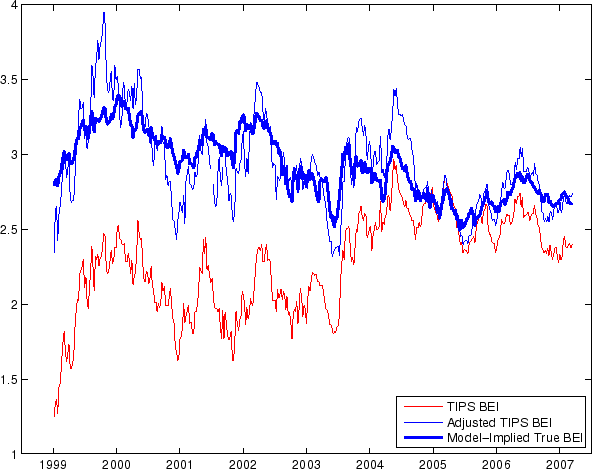 This chart plots the liquidity-adjusted 10-year TIPS BEI base on Equation (54) (thin blue line) together with the unadjusted series (red line) and the model-implied true TIPS BEI from Model L-IId (thick blue line). |
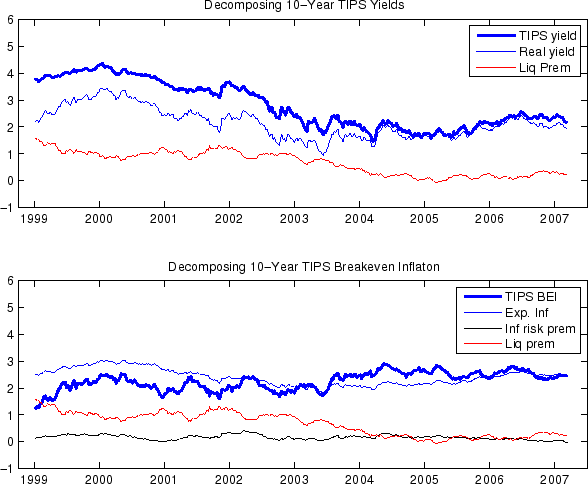 The top panel decomposes the 10-year TIPS yields into the real yield and the TIPS liquidity premiums, while the bottom panel decomposes the 10-year TIPS breakeven inflation into the expected inflation, the inflation risk premium and the TIPS liquidity premium, all according to Equation (55). |
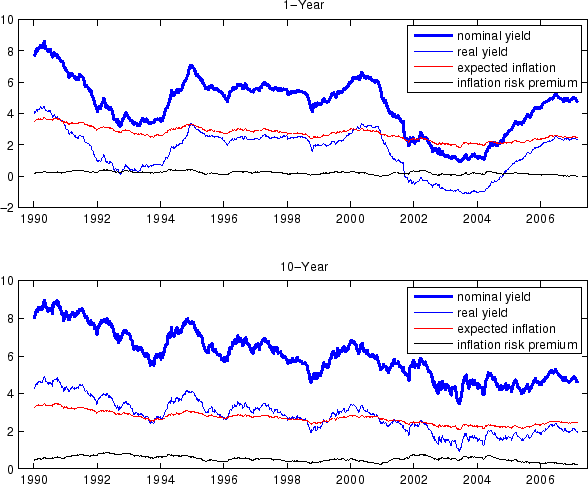 This chart decomposes the 1- and 10-year nominal yields into real yields, expected inflation and inflation risk premiums according to Equation (56). |
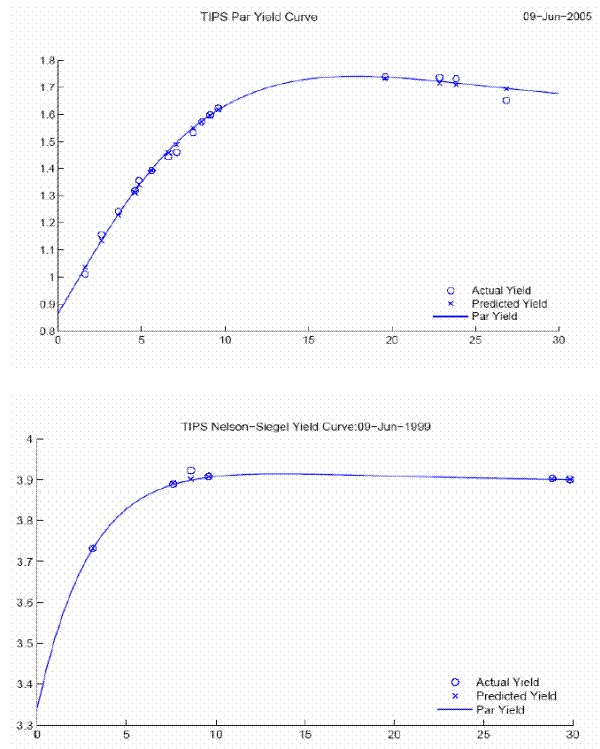
|
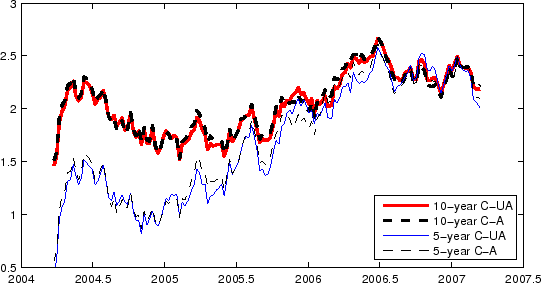 Note: This figure plots 10-year carry-unadjusted (carry-adjusted) TIPS yields in red solid (black dashed) line and 5-year carry-unadjusted (carry-adjusted) TIPS
yields in blue solid (gray dashed) line. Note: This figure plots 10-year carry-unadjusted (carry-adjusted) TIPS yields in red solid (black dashed) line and 5-year carry-unadjusted (carry-adjusted) TIPS
yields in blue solid (gray dashed) line. |
Footnotes
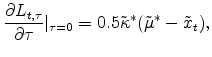
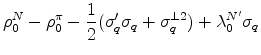
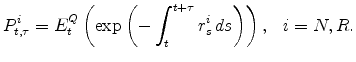
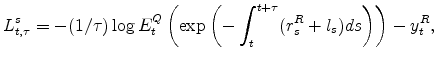
![\displaystyle L^s_{t,\tau}= \left[ \tilde{a}_{\tau} + (a^{\cal T}_{\tau} - a^R_{\tau}) \right] + \left[ \begin{array}[c]{cc}% (b^{\cal T}_{\tau}-b^R_{\tau})' & \tilde{b}_{\tau}% \end{array} \right] \left[ \begin{array}[c]{c}% x_{t}\\ \tilde{x}_{t}% \end{array} \right]](img101.gif)
![\displaystyle \mu = 0_{3\times1}, \,\,\, \Sigma = \left[\begin{matrix}0.01 & 0 & 0 \\ \Sigma_{21} & 0.01 & 0\\ \Sigma_{31} & \Sigma_{32} & 0.01 \end{matrix}\right], \,\,\, \mathcal{K}= \left[\begin{matrix}\mathcal{K}_{11} & 0 & 0 \\ 0 & \mathcal{K}_{22} & 0\\ 0 & 0 & \mathcal{K}_{33} \end{matrix}\right], \,\,\, \tilde{\sigma}=0.01.](img110.gif)
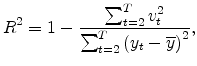
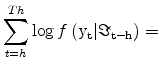
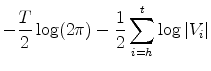
![\displaystyle -\frac{1}{2}\sum_{i=h}^{t}\left[ \left( \rm y_{t}-A-B\widehat{\rm x}% _{t,t-h}\right) ^{\prime}V_{t}^{-1}\left( \rm y_{t}-A-B\widehat{\rm x}% _{t,t-h}\right) \right].](img279.gif)