Output Gaps
Keywords: Business cycles, potential output
Abstract:
JEL classification: E32; O41.
1 Introduction
"The world is complicated enough without introducing further confusion and ambiguities because two different names are unknowingly being used for the same thing, or because the same word is being applied to quite different phenomena" Paul Samuelson (1948), page 6.
What is the output gap? The question is simple. But the answer is not, in part because economist's employ quite different definitions; indeed, Paul Samuelson noted the troublesome tendency of economists to talk at, rather than to, each other by using the same term for different phenomena more than half a century ago.
I consider three definitions of the output gap:
- The deviation of output from its long-run stochastic trend (i.e., the "Beveridge-Nelson cycle", as defined in Beveridge and Nelson (1981));
- The deviation of output from the level consistent with current technologies and normal utilization of capital and labor input (i.e., the "production-function approach", as employed, for example, by the Congressional Budget Office (CBO) (CBO (2001)));
- The deviation of output from a "flexible-price" or "natural rate" level.1
This research presents estimates of each concept from a dynamic-stochastic-general-equilibrium (DSGE) model developed at the Federal Reserve Board and discusses the correspondence between these estimates and those produced elsewhere; the uses of each concept are also highlighted. The EDO model can produce estimates of each concept. However, the concepts, in and of themselves, do not play a central role in EDO (where decisions are based on utility and profit maximization problems, and the gap measures are determined from definitions "outside the model" which do not enter private agents' decisions). As a result, it is important to consider the question at hand before deciding on a given output gap concept: The Beveridge-Nelson gap provides answers to some questions, the production-function approach provides answers to other questions, and the flexible-price/natural-rate gaps provide yet again different information.
Key results from the analysis are the the following.
- The DSGE model's estimate of the output gap (according to either a Beveridge-Nelson or production-function approach) is very similar to gaps from the Congressional Budget Office or the Federal Reserve's large-scale macro-econometric model (FRB/US) model, but the DSGE model's estimate of potential growth is considerably more variable; the latter result stems from the significant degree of fluctuation in aggregate technology estimated by the DSGE model, a result consistent with the significant role such fluctuations play in model's descended from those of the real-business-cycle tradition (from Kydland and Prescott (1982)). Moreover, potential growth from the DSGE model co-varies with GDP growth to a much more significant degree than does potential from either the CBO or the FRB/US model; this is again consistent with the model's roots in the quantitative tradition initiated by Kydland and Prescott (1982), and closely related to a large time-series literature on the covariance between potential and actual GDP growth.
- The flexible-price/natural-rate gaps are highly dependent on modeling assumptions, and their use in policy applications or forecasting requires a deep understanding of a specific model's structure. (This result is closely related to the critique of DSGE models of Chari, Kehoe, and McGrattan (2009), who highlight the sensitivity of policy applications of such models to controversial modeling assumptions). In particular, a natural-rate gap does not provide the same type of guidance to a "Taylor" rule for nominal interest rates as other concepts of gaps; indeed, the signals from the Beveridge-Nelson gap provide a better sense of movements in the "natural rate of interest" than do the signals from the natural rate of output gap.
- "Equilibrium" or trend expected growth is highly variable in the flex-price/natural-rate case, implying that a focus on the current level of such gaps can be misleading in a policy discussion. In contrast, expected trend growth for the Beveridge-Nelson concept is exogenous and constant; moreover, all other notions of "trend" converge to the Beveridge-Nelson trend (by definition).
- The DSGE model's estimate of the Beveridge-Nelson gap is as closely related to unemployment fluctuations as those from policy institutions (e.g., obeys Okun's law) and has more predictive ability for inflation (e.g., has a tighter reduced-form Phillips curve relationship).
Before proceeding to the main discussion, a brief introduction to the primary model considered in the analysis helps frame the discussion. The DSGE model employed is the EDO (Estimated, Dynamic, Optimization-based) model developed in (see Edge, Kiley, and Laforte (2007, 2008, 2009) and Chung, Kiley, and Laforte (2010)). This model is ideally suited to address the questions of interest, as it includes
- A two-sector structure emphasizing the importance of fluctuations in aggregate and investment-specific technology for explaining long-run growth and cyclical fluctuations - implying a stochastic trend in production and expenditure;
- A rich array of other shocks to pricing decisions, preferences, and the desirability of smoothing consumption over time through capital accumulation that allow for temporary fluctuations in activity;
- A New-Keynesian structure with nominal rigidities in both prices and wages and variable utilization of capital input; and
- An empirical approach that ensures the model can provide a reasonable characterization of the sources of fluctuations over history.
Section 2 summarizes some related recent research. The third discusses the structure of the EDO model. The fourth section examines each output gap concept within EDO, and highlights the projection implications of the model-dependent (flexible-price/natural-rate) concepts and the guidance from output gaps to "Taylor" rules for the nominal interest rate. The fifth section compares estimates from EDO to those of the CBO and from the Federal Reserve's FRB/US model - a traditional, large-scale econometric model. A concluding section provides some thoughts for future research.
2 Related Research
Despite the ambiguity associated with the concept of the output gap suggested by the quite different concepts highlighted above, the related literature is deep and influential in policy circles.
Perhaps the cleanest definition of an output gap is that associated with the cycle in output introduced by Beveridge and Nelson (1981). According to this definition, the cycle in output, or the output gap, is the deviation of output from the level expected to prevail in the long run (i.e., as
time, t, approaches ![]() ), with the effect of any deterministic aspects of the growth in output on its long-run level removed. This definition of the output gap has several advantages.
First, it is not model-specific: Any approach capable of capturing the reduced-form time-series characteristics of output can provide an estimate of this definition of the output gap; as a result, univariate or multivariate time-series methods as well as structural economic models can, in
principle, estimate the output gap.2 Second, the Beveridge-Nelson approach provides information related to a very specific forecasting problem - in particular,
the current estimate of the Beveridge-Nelson gap provides an estimate of how much economic growth will deviate from its deterministic (or, in some models, "steady-state") level going forward: An answer to this forecasting problem forms the basis of a long-standing academic approach to discussions
of the gap (e.g., the discussions in Nelson (1964) and Thurow and Taylor (1966) of the growth outlook for the 1960s in the United States, or the discussion in CBO (2010) of the growth outlook from 2010-2020). Finally, this method often provides estimates of the output gap that correspond to widely
held views on what is "reasonable", although this result depends on assumptions (e.g., the discussion in Morley, Nelson, and Zivot (2003)).
), with the effect of any deterministic aspects of the growth in output on its long-run level removed. This definition of the output gap has several advantages.
First, it is not model-specific: Any approach capable of capturing the reduced-form time-series characteristics of output can provide an estimate of this definition of the output gap; as a result, univariate or multivariate time-series methods as well as structural economic models can, in
principle, estimate the output gap.2 Second, the Beveridge-Nelson approach provides information related to a very specific forecasting problem - in particular,
the current estimate of the Beveridge-Nelson gap provides an estimate of how much economic growth will deviate from its deterministic (or, in some models, "steady-state") level going forward: An answer to this forecasting problem forms the basis of a long-standing academic approach to discussions
of the gap (e.g., the discussions in Nelson (1964) and Thurow and Taylor (1966) of the growth outlook for the 1960s in the United States, or the discussion in CBO (2010) of the growth outlook from 2010-2020). Finally, this method often provides estimates of the output gap that correspond to widely
held views on what is "reasonable", although this result depends on assumptions (e.g., the discussion in Morley, Nelson, and Zivot (2003)).
The EDO model provides an excellent framework for computation of the Beveridge-Nelson gap. As highlighted in the introduction, the inclusion of stochastic trends in both aggregate and investment-specific technology implies the model has a non-trivial Beveridge-Nelson permanent component to output, and connects the model to the burgeoning literature on empirical two-sector growth models (see Edge, Kiley, and Laforte (2008, 2009)). The neoclassical core of the model ensures that the model captures the long-run relationships between output, investment, and consumption: King, Plosser, Stock, and Watson (1991) demonstrated the usefulness of such information for estimation of the Beveridge-Nelson gap in a multivariate context; similarly, Cochrane (1994) emphasized the potential role for consumption in identifying trends in output (due to the dependence of consumption on permanent income). The estimation of EDO includes information on output and several components of consumption and investment, yielding a rich, multivariate information set for output gap estimation. Indeed, the information set is quite broad, including expenditure variables, labor input, real wages, inflation, and the federal funds rate. Previous work has highlighted how time-series decompositions of output into permanent and transitory components can exploit information on hours (e.g., Rotemberg and Woodford (1996)) and inflation (e.g., Kuttner (1994)).
While the Beveridge-Nelson concept is perhaps the cleanest definition, the most prevalent definition at policy institutions appears to be the production-function approach (e.g., the approach used at the CBO (2001) and in the Federal Reserve's FRB/US model). In this approach, the output gap is defined as the deviation of output from the level that would occur if capital and labor input were utilized at "normal" rates, given current technology. In general, this approach, as employed at policy institutions, involves some smoothing of measured total factor productivity in order to estimate "true" technology. In contrast, the level of true technology in EDO is estimated to be consistent with the observed behavior of a broad range of economic variables and the underlying structure of the model. In principle, EDO could deliver very volatile estimated levels of "true" technology; however, this result is not predetermined, as the EDO model includes features that could cause measured total factor productivity to deviate from underlying technology (such as variable capital utilization, which could cause measured capital input to deviate from true capital input, and imperfect competition which could distort total factor productivity computations). The primary advantage of considering the EDO estimate of this concept is to compare it to estimates of the same concept produced by policy institutions. While the preferences of policy institutions for this approach is quite clear from their modeling efforts, it is not obvious what question motivates this particular focus.
The last approach considered (the flexible-price/natural-rate approach) is the focus of some discussions in the research literature using DSGE models. Most prominently, the "natural-rate" approach in Woodford (2003) and Edge, Kiley, and Laforte (2008) has been widely discussed. The natural-rate approach defines the gap as one that would arise in the absence of nominal rigidities and shocks to "markups"; this approach is motivated in simple New-Keynesian models by the structure of such simple models, in which nominal rigidities are the only (significant) distortion, implying that the removal of such distortions provides an estimate of the level of output that is economically efficient. However, a focus on flexible-price or natural output will not, in general, be directly related to economic efficiency. Specifically, the behavior of a flexible-price/natural-rate gap and its relationship to an efficiency gap measure will be highly dependent on the model's structure - specifically, on the types of imperfections and shocks included in the model. For example, EDO has two sectors, and nominal rigidities in the prices and wages prevailing in both sectors; as a result, its estimate of the natural rate of output may differ substantially from those of a model with one sector or with only nominal rigidities in prices or wages. Justiniano and Primiceri (2008) also discuss the factors that influence efficiency gaps relative to those that simply remove wage and price rigidities in a simpler model.
As an important aside, this discussion highlights how consideration of the implications of the efficiency gap are complex. In a simple one-sector model without markup or other distortionary shocks, stabilization of the natural-rate gap would imply stabilization of inflation (e.g., Woodford (2003)). In EDO, the world is more complicated. There are two sectors, both with nominal rigidities and which are not symmetric (as one produces only a capital good and the other produces a good that can be used for consumption and as a capital good). As a result, stabilization of aggregate output at the natural level level is not, by itself, sufficient for efficiency (as the distribution of output across sectors matters as well, e.g. Aoki (2001) and Erceg and Levin (2006)). In addition, EDO has nominal wage rigidities in each sector, again implying that stabilization of the efficiency gap need not imply efficiency (e.g., Erceg, Henderson, and Levin (2000)). Finally, EDO has markup shocks, which also induce a tradeoff between output gap and inflation stabilization (e.g., Clarida, Gali, and Gertler (1999)). Each of these features seems at least potentially important, implying that great care should be taken when considering the implications of a given estimate of the natural rate gap for economic efficiency.
3 The EDO Model
The EDO model contains a detailed description of domestic production and expenditures decisions. The heart of the model is a two-sector production structure. In particular, the economy consists of a consumption goods and an investment goods sector. The motivation for this basic structure is discussed in detail in Edge, Kiley, and Laforte (2007, 2008, 2009). I present the most recent version of the EDO model; more complete documentation is available in Chung, Kiley, and Laforte (2010).
Figure 1 provides a graphical overview of the economy described by the model. The model possesses two final good sectors in order to capture key long-run growth facts and to differentiate between the cyclical properties of different categories of durable expenditure (e.g., housing, consumer durables, and nonresidential investment). For example, technological progress has been faster in the production of business capital and consumer durables (such as computers and electronics). Edge, Kiley, and Laforte (2008 and 2010) discuss this motivation in greater detail. The first sector is the slow-growing sector--called "CBI" because most of these goods are used for consumption (C) and because they are produced by the business and institutions (BI) sector--and the second is the fast-growing sector--called "KB" because these goods are used for capital (K) accumulation and are produced by the business (B) sector. The goods are produced in two stages by intermediate- and then final-goods producing firms (shown in the center of the figure). As in most new-Keynesian models, the introduction of intermediate and final goods producers facilitates the specification of nominal rigidities.
The disaggregation of production (aggregate supply) leads naturally to some disaggregation of expenditures (aggregate demand). EDO moves beyond the typical model with just two categories of (private domestic) demand (consumption and investment) and distinguishes between four categories of private demand: consumer non-durable goods and non-housing services, consumer durable goods, residential investment, and non-residential investment. The boxes surrounding the producers in the figure illustrate the sources of each demand for each category. Consumer non-durable goods and services are sold directly to households; consumer durable goods, residential capital goods, and non-residential capital goods are intermediated through capital-goods intermediaries (owned by the households), who then rent these capital stocks to households. Consumer non-durable goods and services and residential capital goods are purchased (by households and residential capital goods owners, respectively) from the first of economy's two final goods producing sectors, while consumer durable goods and non-residential capital goods are purchased (by consumer durable and residential capital goods owners, respectively) from the second sector. In addition to consuming the non-durable goods and services that they purchase, households supply labor to the intermediate goods-producing firms in both sectors of the economy.
This remainder of this section provides an overview of the decisions made by each of the agents in the economy. Given some of the broad similarities between the model and others, the presentation is selective.
3.1 The Final Goods Producers' Problem
The economy produces two final goods and services: slow-growing "consumption" goods and services,
![]() , and fast-growing "capital" goods,
, and fast-growing "capital" goods,
![]() . These final goods are produced by aggregating (according to a Dixit-Stiglitz technology) an infinite number of sector-specific differentiated intermediate inputs,
. These final goods are produced by aggregating (according to a Dixit-Stiglitz technology) an infinite number of sector-specific differentiated intermediate inputs,
![]() for
for
![]() , distributed over the unit interval. The representative firm in each of the consumption and capital goods producing sectors chooses the optimal level of each intermediate input,
taking as given the prices for each of the differentiated intermediate inputs,
, distributed over the unit interval. The representative firm in each of the consumption and capital goods producing sectors chooses the optimal level of each intermediate input,
taking as given the prices for each of the differentiated intermediate inputs,
![]() , to solve the cost-minimization problem:
, to solve the cost-minimization problem:
The term
where
3.2 The Intermediate Goods Producers' Problem
The intermediate goods entering each final goods technology are produced by aggregating (according to a Dixit-Stiglitz technology) an infinite number of differentiated labor inputs,
![]() for
for ![]() , distributed over the unit interval and combining this
aggregate labor input (via a Cobb-Douglas production function) with utilized non-residential capital,
, distributed over the unit interval and combining this
aggregate labor input (via a Cobb-Douglas production function) with utilized non-residential capital,
![]() . Each intermediate-good producing firm effectively solves three problems: two factor-input cost-minimization problems (over differentiated labor inputs and the aggregate
labor and capital) and one price-setting profit-maximization problem.
. Each intermediate-good producing firm effectively solves three problems: two factor-input cost-minimization problems (over differentiated labor inputs and the aggregate
labor and capital) and one price-setting profit-maximization problem.
In its first cost-minimization problem, an intermediate goods producing firm chooses the optimal level of each type of differential labor input, taking as given the wages for each of the differentiated types of labor,
![]() , to solve:
, to solve:
The term
where
In its second cost-minimization problem, an intermediate-goods producing firm chooses the optimal levels of aggregated labor input and utilized capital, taking as given the wage, ![]() , for aggregated labor,
, for aggregated labor,
![]() (which is generated by the cost function derived the previous problem), and the rental rate,
(which is generated by the cost function derived the previous problem), and the rental rate,
![]() , on utilized capital,
, on utilized capital,
![]() , to solve:
, to solve:
The parameter
The exogenous productivity terms contain a unit root, that is, they exhibit permanent movements in their levels. The stochastic processes ![]() and
and
![]() evolve according to
evolve according to
where
The unit-root in technology in both sectors yields a non-trivial Beveridge-Nelson permanent/transitory decomposition. The presence of capital-specific technological progress allows the model to generate differential trend growth rates in the economy's two production sectors. In line with
historical experience, a more rapid rate of technological progress in capital goods production is accomodated by calibrating
![]() , where (as is the case for all model variables) an asterisk on a variable denotes its steady-state value.
, where (as is the case for all model variables) an asterisk on a variable denotes its steady-state value.
In its price-setting (or profit-maximization) problem, an intermediate goods producing firm chooses its optimal nominal price and the quantity it will supply consistent with that price. In doing so it takes as given the marginal cost,
![]() , of producing a unit of output,
, of producing a unit of output,
![]() , the aggregate price level for its sector,
, the aggregate price level for its sector, ![]() , and households'
valuation of a unit of nominal profits income in each period, which is given by
, and households'
valuation of a unit of nominal profits income in each period, which is given by
![]() where
where
![]() denotes the marginal utility of non-durables and non-housing services consumption. Specifically, firms solve:
denotes the marginal utility of non-durables and non-housing services consumption. Specifically, firms solve:
The profit function reflects price-setting adjustment costs (the size which depend on the parameter
3.3 The Capital Owners' Problem
I now shift from producers' decisions to spending decisions. There exists a unit mass of non-residential capital owners (individually denoted by k, with k distributed over the unit interval) who choose investment in non-residential capital,
![]() , the stock of non-residential capital,
, the stock of non-residential capital,
![]() (which is linked to the investment decision via the capital accumulation identity), and the amount and utilization of non-residential capital in each production sector,
(which is linked to the investment decision via the capital accumulation identity), and the amount and utilization of non-residential capital in each production sector,
![]() ,
,
![]() ,
,
![]() , and
, and
![]() . (Recall, that the firm's choice variables in equation 5 is utilized capital
. (Recall, that the firm's choice variables in equation 5 is utilized capital
![]() .) The mathematical representation of this decision is described by the following maximization problem (in which capital owners take as given the rental
rate on non-residential capital,
.) The mathematical representation of this decision is described by the following maximization problem (in which capital owners take as given the rental
rate on non-residential capital,
![]() , the price of non-residential capital goods,
, the price of non-residential capital goods,
![]() , and households' valuation of nominal capital income in each period,
, and households' valuation of nominal capital income in each period,
![]() , and the exogenous risk premium specific to non-residential investment,
, and the exogenous risk premium specific to non-residential investment,
![]() ):
):
The parameter
Higher rates of utilization incur a cost (reflected in the last two terms in the capital owner's profit function). Utilization is unity in the steady-state, implying
The time-variation in utilization, along with the imperfect competition in product and labor markets, implies that direct measurement of total factor productivity may not provide an accurate estimate of technology; as a result, the EDO model can deliver smoother estimates of technology that might be implied by a real-business-cycle model.
The problems solved by the consumer durables and residential capital owners are slightly simpler than the non-residential capital owner's problems. Since utilization rates are not variable for these types of capital, their owners make only investment and capital accumulation decisions. Taking as
given the rental rate on consumer durables capital,
![]() , the price of consumer-durable goods,
, the price of consumer-durable goods,
![]() , and households' valuation of nominal capital income,
, and households' valuation of nominal capital income,
![]() , and the exogenous risk premium specific to consumer durables investment,
, and the exogenous risk premium specific to consumer durables investment,
![]() , the capital owner chooses investment in consumer durables,
, the capital owner chooses investment in consumer durables,
![]() , and its implied capital stock,
, and its implied capital stock,
![]() , to solve:
, to solve:
The residential capital owner's decision is analogous:
The notation for the consumer durables and residential capital stock problems parallels that of non-residential capital. In particular, the asset-specific risk premia shocks,
3.4 The Households' Problem
The final group of private agents in the model are households who make both expenditure and labor-supply decisions. Households derive utility from four sources: their purchases of the consumer non-durable goods and non-housing services, the flow of services from their rental of consumer-durable
capital, the flow of services from their rental of residential capital, and their leisure time, which is equal to what remains of their time endowment after labor is supplied to the market. Preferences are separable over all arguments of the utility function. The utility that households derive from
the three components of goods and services consumption is influenced by the habit stock for each of these consumption components, a feature that has been shown to be important for consumption dynamics in similar models. A household's habit stock for its consumption of non-durable goods and
non-housing services is equal to a factor ![]() multiplied by its consumption last period
multiplied by its consumption last period
![]() . Its habit stock for the other components of consumption is defined similarly.
. Its habit stock for the other components of consumption is defined similarly.
Each household chooses its purchases of consumer non-durable goods and services,
![]() , the quantities of residential and consumer durable capital it wishes to rent,
, the quantities of residential and consumer durable capital it wishes to rent, ![]() and
and
![]() , its holdings of bonds,
, its holdings of bonds, ![]() , its wage for each sector,
, its wage for each sector,
![]() and
and
![]() , and the supply of labor consistent with each wage,
, and the supply of labor consistent with each wage,
![]() and
and
![]() . This decision is made subject to the household's budget constraint, which reflects the costs of adjusting wages and the mix of labor supplied to each sector, as well as the demand
curve the household faces for its differentiated labor. Specifically, the
. This decision is made subject to the household's budget constraint, which reflects the costs of adjusting wages and the mix of labor supplied to each sector, as well as the demand
curve the household faces for its differentiated labor. Specifically, the ![]() th household solves:
th household solves:
In the utility function the parameter
The stationary, unit-mean, stochastic variable
![]() represents an aggregate risk-premium shock that drives a wedge between the policy short-term interest rate and the return to bonds received by a household. Letting
represents an aggregate risk-premium shock that drives a wedge between the policy short-term interest rate and the return to bonds received by a household. Letting
![]() denote the log-deviation of
denote the log-deviation of
![]() from its steady-state value of
from its steady-state value of
![]() , the process is
, the process is
The variable
The household's budget constraint reflects wage setting adjustment costs, which depend on the parameter ![]() and the lagged and steady-state wage inflation rate, and the costs in
changing the mix of labor supplied to each sector, which depend on the parameter
and the lagged and steady-state wage inflation rate, and the costs in
changing the mix of labor supplied to each sector, which depend on the parameter ![]() . The costs incurred by households when the mix of labor input across sectors changes may be
important for sectoral co-movements.
. The costs incurred by households when the mix of labor input across sectors changes may be
important for sectoral co-movements.
3.5 Gross Domestic Product
The demand and production aspects of the model are closed through the exogenous process for demand other than private domestic demand and the GDP identity.
![]() represents exogenous demand (i.e., GDP other than private domestic demand, the aggregate of
represents exogenous demand (i.e., GDP other than private domestic demand, the aggregate of
![]() ,
,
![]() ,
, ![]() , and
, and
![]() ). Exogenous demand is assumed to follow the process:
). Exogenous demand is assumed to follow the process:
Exogenous demand impinges on each sector symmetrically, and specifically that the percent deviation of exogenous demand proportionally affects demand for each sector's (
The rate of change of Gross Domestic Product (real GDP) equals the Divisia (share-weighted) aggregate of production in the two sectors (and of final spending across each expenditures category), as given by the identity:
3.6 Monetary Authority
The last important agent in the model is the monetary authority. It sets monetary policy in accordance with an Taylor-type interest-rate feedback rule. Policymakers smoothly adjust the actual interest rate ![]() to its target level
to its target level
![]()
where the parameter
In equation 16, the deterministic, or steady-state, levels of growth are suppressed. Consumer price inflation and the change in the output gap also enter the target. The target equation is:
In equation (17),
| (40) |
The parameter ![]() is the share of the durable goods in nominal consumption expenditures.
is the share of the durable goods in nominal consumption expenditures.
3.7 Summary of Model Specification
The brief presentation of the model highlights several important points. First, although the model considers production and expenditure decisions in a bit more detail, it shares many similar features with other DSGE models in the literature, such as imperfect competition, nominal price and wage rigidities, and real frictions like adjustment costs and habit-persistence. The rich specification of structural shocks (to aggregate and investment-specific productivity, aggregate and sector-specific risk premiums, and mark-ups) and adjustment costs allows the model to be brought to the data with some chance of finding empirical validation.
Within EDO, fluctuations in all economic variables are driven by eleven structural shocks. For the discussion of each concept of the output gap, it is most convenient to summarize these shocks into four broad categories:
- Permanent technology shocks: This category consists of shocks to aggregate and investment-specific (or fast-growing sector) technology.
- Financial, or intertemporal, shocks: This category consists of shocks to risk premia. In EDO, variation in risk premia - both the premium households' receive relative to the federal funds rate on nominal bond holdings and the additional variation in discount rates applied to the investment decisions of capital intermediaries - are purely exogenous. Nonetheless, the specification captures important aspects of related models with more explicit financial sectors (e.g., Bernanke, Gertler, and Gilchrist (1999)).
- Markup shocks: This category includes the price (two shocks) and wage (one shock) markup shocks.
- Other demand shocks: This category includes the shock to autonomous demand and a monetary policy shock.
Using this categorization, only technology shocks affect the Beveridge-Nelson permanent component. The Beveridge-Nelson gap reflects the influence of all shocks (and technology shocks imply movements in the gap, as the economy does not instantaneous adjust to the long-run implications of a shock to technology for standard neoclassical adjustment reasons and because of the short-run impediments to adjustment created by wage and price rigidities).
Several shocks do not influence the flexible-price or natural-rate of output (defined as the flexible price and constant markup outcome): markup shocks, by definition; the monetary policy shock, as such shocks are neutral under price and wage flexibility; and the aggregate risk premium shock driving a wedge between the household return to a nominal bond and the policy interest rate, which enters everywhere the nominal funds rate enters and hence affects the natural rate of interest but not the natural rate of output (as in related models, e.g., Smets and Wouters (2007)). The last point will be important in discussion prescriptions for policy from gaps and policy rules. It will also be quite important in examining the historical fluctuations in the natural rate of interest and the natural rate of output, as this is an important shock in EDO and was the shock that emerged as central in the 2008-2009 recession where the link between the funds rate and other bond yields broke due to a jump in risk spreads.
Finally, the relation between the natural rate of output and economic efficiency depends upon whether certain shocks are distortionary - a point on which theory is ambiguous, a standard feature of New-Keynesian DSGE models (discussed, for example, in Smets and Wouters (2007)). For example, EDO labels certain shocks as shocks to markups introduced through stochastic elasticities of substitution between goods or labor input, but other models enter shocks in the same equilibrium conditions through labor supply or other shocks; shocks to markups are distortionary, and shocks to preferences are not. Theory does not distinguish between such observationally equivalent shocks, which are (after all) simply appended to a model to generate variation in the data. Chari, Kehoe, and McGrattan (2009) are highly critical of this ambiguity, and suggest that DSGE models must find some method for identifying whether such shocks are distortionary or non-distortionary before such models can be used in policy applications; one possibility they mention is to explore microeconomic implications of these shocks/distortions. While I agree that such research is essential to definitively answer some questions of policy interest, I view the forecast performance (e.g., Edge, Kiley, and Laforte (2009)) and range of policy-relevant stories that can be discussed with such models (e.g., Edge, Kiley, and Laforte (2008)) as suggesting that such models are currently useful, when analyzed with care. (As an aside, the critique of Chari, Kehoe, and McGrattan (2009) is not particularly novel; for example, Clarida, Gali, and Gertler (1999) emphasize how New-Keynesian models may provide a useful guide to underlying structural relationships even if their welfare implications and the interpretation of structural disturbances in such models may be somewhat controversial).
3.8 Estimation Strategy and Results
The empirical implementation of the model takes a log-linear approximation to the first-order conditions and constraints that describe the economy's equilibrium, casts this resulting system in its state-space representation for the set of (in this case 11) observable variables, uses the Kalman filter to evaluate the likelihood of the observed variables, and forms the posterior distribution of the parameters of interest by combining the likelihood function with a joint density characterizing some prior beliefs. Since a closed-form solution of the posterior is not available, Markov-Chain Monte Carlo (MCMC) methods are used.
The model is estimated using 11 data series over the sample period from 1984:Q4 to 2008:Q4. The series are:
- The growth rate of real gross domestic product;
- The growth rate of real consumption expenditure on non-durables and services excluding housing services;
- The growth rate of real consumption expenditure on durables;
- The growth rate of real residential investment expenditure;
- The growth rate of real business investment expenditure;
- Consumer price inflation, as measured by the growth rate of the Personal Consumption Expenditure price index;
- Consumer price inflation, as measured by the growth rate of the Personal Consumption Expenditure price index excluding food and energy prices;
- Inflation for consumer durable goods, as measured by the growth rate of the Personal Consumption Expenditure price index for durable goods;
- Hours, which equals hours of all persons in the non-farm business sector from the Bureau of Labor Statistics;3
- The growth rate of real wages, as given by compensation per hour in the non-farm business sector from the Bureau of Labor Statistics divided by the GDP price index;
- The federal funds rate.
The estimation results depend upon the specification of priors and calibration of certain parameters. A number of parameters are calibrated. As reported in table 1, these include the household's discount factor (![]() ), the Cobb-Douglas share of capital input (
), the Cobb-Douglas share of capital input (![]() ), the curvature parameter associated with costs of varying capital utilization
(
), the curvature parameter associated with costs of varying capital utilization
(![]() ), the depreciation rates (
), the depreciation rates (
![]() ,
,
![]() ,
,
![]() ), and the elasticities of substitution between differentiated intermediate goods and labor input (
), and the elasticities of substitution between differentiated intermediate goods and labor input (
![]() ,
,
![]() ,
,
![]() ). The share of exogenous demand in overall expenditure (
). The share of exogenous demand in overall expenditure (
![]() ) equals 20 percent. Other calibrated parameters include the steady-state growth rates of aggregate technology, investment-specific technology, and the rate of consumer price
inflation (at 0 percent, 4.5 percent, and 2
1/4 percent (all at annual rates), respectively); these calibrations ensure the model matches the average behavior of the data over the estimation sample.
) equals 20 percent. Other calibrated parameters include the steady-state growth rates of aggregate technology, investment-specific technology, and the rate of consumer price
inflation (at 0 percent, 4.5 percent, and 2
1/4 percent (all at annual rates), respectively); these calibrations ensure the model matches the average behavior of the data over the estimation sample.
Tables 2 and 3 present the prior distributions assumed for the estimated parameters and the posterior mode and standard deviation about that mode from the estimation. The parameter values echo results elsewhere in the literature. With
regard to monetary policy, smoothing is important (![]() near 0.7), the coefficient on the change in the output gap is large (
near 0.7), the coefficient on the change in the output gap is large (
![]() near 0.3), and the coefficients on inflation and the level of the output gap take values near those of Taylor (
near 0.3), and the coefficients on inflation and the level of the output gap take values near those of Taylor (![]() near 1.5,
near 1.5, ![]() near 1/4, where the division by 4 converts from annual rates to quarterly rates). There is only modest "indexation"
in the price and wage Phillips curves (
near 1/4, where the division by 4 converts from annual rates to quarterly rates). There is only modest "indexation"
in the price and wage Phillips curves (![]() and
and ![]() near 1/4). Finally,
habits and adjustment costs are important (e.g.,
near 1/4). Finally,
habits and adjustment costs are important (e.g., ![]() near 0.6).
near 0.6).
| Parameter | Prior Distribution Type | Prior Distribution Mean | Prior Distribution S.D. | Posterior Distribution Mode | Posterior Distribution S.D. | Posterior Distribution 10th perc. | Posterior Distribution 50th perc. | Posterior Distribution 90th perc. |
| N | 0.000 | 0.3300 | 0.6024 | 0.0350 | 0.5917 | 0.6392 | 0.6807 | |
| G | 2.000 | 1.0000 | 0.1918 | 0.2514 | 0.1409 | 0.3860 | 0.7701 | |
| G | 4.000 | 1.0000 | 2.5028 | 1.0797 | 2.2321 | 3.2782 | 4.8710 | |
| G | 4.000 | 1.0000 | 3.8424 | 1.9715 | 1.9764 | 3.9778 | 6.8915 | |
| G | 4.000 | 1.0000 | 2.1868 | 1.0576 | 2.1997 | 3.3348 | 4.8769 | |
| G | 4.000 | 1.0000 | 0.2411 | 0.0911 | 0.2239 | 0.3180 | 0.4504 | |
| G | 4.000 | 1.0000 | 0.3702 | 0.5521 | 0.4485 | 0.9534 | 1.8840 | |
| G | 4.000 | 1.0000 | 8.6694 | 2.3585 | 7.4588 | 9.9908 | 13.3231 | |
| N | 0.000 | 0.5000 | 0.3006 | 0.1343 | 0.2325 | 0.4056 | 0.5779 | |
| N | 0.000 | 0.5000 | 0.2542 | 0.1318 | 0.0823 | 0.2505 | 0.4207 | |
|
|
N | 1.500 | 0.0625 | 1.4562 | 0.0606 | 1.3776 | 1.4548 | 1.5331 |
| N | 0.250 | 0.1250 | 0.2096 | 0.0283 | 0.1769 | 0.2101 | 0.2486 | |
|
|
N | 0.000 | 0.1250 | 0.3310 | 0.0936 | 0.2104 | 0.3273 | 0.4488 |
| N | 0.500 | 0.2500 | 0.6593 | 0.0453 | 0.5949 | 0.6559 | 0.7116 |
| Parameter | Prior Distribution Type | Prior Distribution Mean | Prior Distribution S.D. | Posterior Distribution Mode | Posterior Distribution S.D. | Posterior Distribution 10th perc. | Posterior Distribution 50th perc. | Posterior Distribution 90th perc. |
|
|
N | 0.000 | 0.3300 | 0.7930 | 0.0364 | 0.7579 | 0.8070 | 0.8502 |
| N | 0.000 | 0.3300 | 0.8297 | 0.0302 | 0.8076 | 0.8496 | 0.8836 | |
| N | 0.000 | 0.3300 | -0.2110 | 0.1422 | -0.4099 | -0.2412 | -0.0469 | |
| B | 0.500 | 0.0150 | 0.9173 | 0.1637 | 0.4577 | 0.6821 | 0.8969 | |
| N | 0.000 | 0.3300 | 0.8328 | 0.0285 | 0.7914 | 0.8324 | 0.8637 | |
|
|
I | 1.000 | 2.0000 | 0.3742 | 0.0597 | 0.3234 | 0.3881 | 0.4737 |
|
|
I | 1.000 | 2.0000 | 1.4573 | 0.3374 | 0.5267 | 0.7994 | 1.3940 |
|
|
I | 1.000 | 2.0000 | 1.5877 | 0.7145 | 1.6168 | 2.4055 | 3.4337 |
|
|
I | 0.200 | 2.0000 | 0.1572 | 0.0134 | 0.1437 | 0.1595 | 0.1778 |
|
|
I | 0.250 | 2.0000 | 0.8771 | 0.1321 | 0.7181 | 0.8748 | 1.0533 |
|
|
I | 0.250 | 2.0000 | 0.4036 | 0.0663 | 0.3751 | 0.4551 | 0.5437 |
|
|
I | 0.200 | 2.0000 | 0.3125 | 0.1576 | 0.2845 | 0.4296 | 0.6678 |
|
|
I | 0.200 | 2.0000 | 0.4621 | 0.2747 | 0.3926 | 0.6584 | 1.0556 |
|
|
I | 1.000 | 2.0000 | 0.4921 | 0.1562 | 0.4102 | 0.5433 | 0.7742 |
|
|
I | 1.000 | 2.0000 | 7.2703 | 11.9676 | 8.8443 | 18.8741 | 38.5473 |
|
|
I | 1.000 | 2.0000 | 0.4788 | 0.0866 | 0.3984 | 0.4922 | 0.6190 |
4.1 The Beveridge-Nelson Gap
As implicit in the definition of the Beveridge-Nelson trend above, the Beveridge-Nelson gap is defined as
i.e., as the forecast of GDP growth in excess of its steady-state level going forward. This measure is computed for the EDO model given the implied reduced-form vector autoregressive/moving average representation of the model in terms of the observable variables used in its estimation.
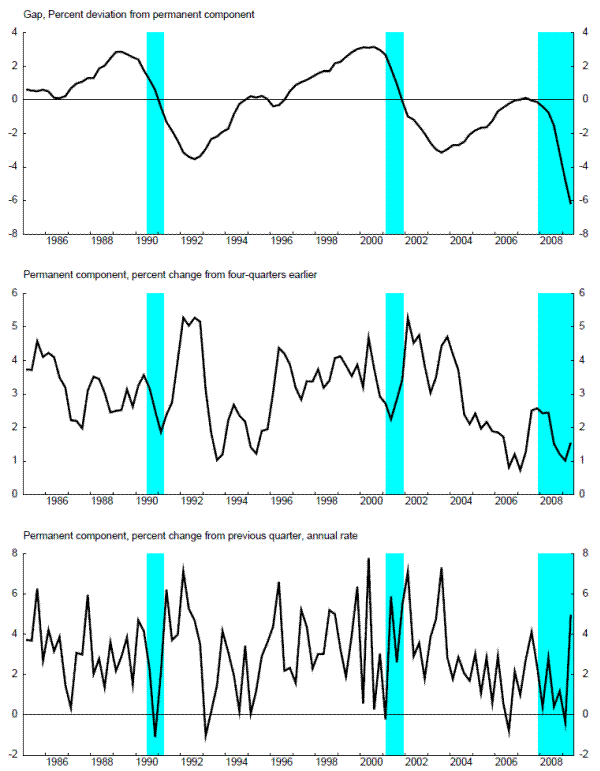
Figure 2 presents the estimate of the Beveridge-Nelson gap from the EDO model in the upper panel; the shading represents National Bureau of Economic Research (NBER) recession periods. It is clear that this measure of the gap captures the cyclical peaks in activity as identified by the NBER well; it is also clear that the EDO Beveridge-Nelson output gap has continue to widen following the NBER-identified end of recent recessions - consistent with the generally agreed upon view that these periods have been sluggish or "jobless" recoveries. The picture of the Beveridge-Nelson gap implied by EDO also shows a fairly smooth evolution of the gap; this contrasts with much of the literature on univariate time-series estimates of the Beveridge-Nelson gap (e.g., the discussion in Morley, Nelson, and Zivot (2003)), but echoes the result from (at least some) multivariate time series approaches (e.g., Rotemberg and Woodford (1996)).
The middle panel of figure 2 presents the percent change from four-quarters earlier in the Beveridge-Nelson permanent component implied by these gap estimates; the bottom panel presents the one-quarter percent change (at an annual rate). These panels show that the variation in the growth rate of the permanent component is considerable. Of course, the permanent component depends solely on the technology shocks - implying that the variation shown is consistent with a view that permanent technology shocks have considerable quarter-to-quarter volatility. The figures also show that recession periods do not appear very tied to low realizations of technology - that is, recessions are not primarily driven by technology shocks in this DSGE model; Chung, Kiley, and Laforte (2010)) discuss the sources of business cycles in more detail, and there results highlight only a moderate role for technology shocks in cyclical fluctuations, despite the considerable volatility of technology relative to the smooth view embedded in some production-function approaches to potential GDP (as discussed in the section 5).
4.2 The Production-Function Approach
Production in each sector of the EDO model is governed by a Cobb-Douglas production function for each sector. In the production function approach to measuring the output gap, the gap is defined as the deviation of output from the level that would occur if labor input (per capita) and utilization
rates equaled their steady-state values (where these steady-state values, denoted with a ![]() , are constant, with the latter equal to one). As a result, the production-function gap is given
by the Divisia-weighted (i.e., share-weighted) aggregate of the production-function gaps in each sector, which are defined by
, are constant, with the latter equal to one). As a result, the production-function gap is given
by the Divisia-weighted (i.e., share-weighted) aggregate of the production-function gaps in each sector, which are defined by
Several points are noteworthy. First, variable utilization of capital and capital adjustment costs, in addition to imperfect competition in product and labor markets, imply that simple "growth acccounting" may not accurately measure the production-function gap. For EDO, the production function gap is inferred by imposing the model's structural restrictions and using the data on all unobservables to infer this gap. In addition, the production function gap, as written above, does not depend on any smoothing of technology: In EDO, the cyclical movements in total factor productivity (properly measured, after accounting for imperfect competition and the effects of variable utilization and capital adjustment costs) are solely a function of utilization, which enters equation 20; production-function based methods that do not rely on an entire model's structure to control for cyclical movements in total factor productivity, such as those of the CBO or the Federal Reserve's FRB/US model, may smooth their measures of total factor productivity according to some method, and such effects would enter equation 20 through the utilization term (although alternative presentations of the production-function method may include such adjustments as a separate term in their accounting). Because labor input and utilization move to their steady-state values in the long run and production always lies on the production function for each sector (by definition), the production function gap differs from the Beveridge-Nelson gap solely because of deviations of the (aggregate productive) capital stock from its long-run level. To the extent that the contribution of capital stock deviations from long-run levels contribute only moderately to overall deviations of production from its long-run level, it is reasonable to expect that the production function gap and the Beveridge-Nelson gaps will be similar.
Figure 3 presents the estimate of the production function gap from EDO, along with the Beveridge-Nelson gap. It is clear that these measures of the gap move together, and both capture the cycle identified by the NBER.
The middle and bottom panels of figure 2 presents the percent changes from four-quarters earlier and from the previous period in the production-function approach and the Beveridge-Nelson permanent components. These series move together in broad terms. But the magnitude of quarter-to-quarter fluctuations in the Beveridge-Nelson permanent component is a bit higher than that for the production-function approach. This occurs because long-run capital stock levels are strongly affected by quarter-to-quarter movements in technology, but actual capital stock levels move slowly; as a result, capital stock deviations from long-run levels can move considerably, boosting the volatility of the Beveridge-Nelson permanent component.
4.3 The Natural-rate Approach
The final definition is the natural-rate gap, which is the gap between output and the level that would prevail absent wage and price rigidities and markup shocks. This is the concept emphasized in Woodford (2003), largely because the analysis of Woodford considers only distortions associated with nominal rigidities and markup shocks (so that the natural rate is the efficient rate).
As can be seen in figure 4, the natural-gap is closely related to the Beveridge-Nelson cycle, but to a notably lesser degree late in the sample. For example, the natural-rate gap is positive in 2008, whereas the Beveridge-Nelson gap is deep in negative territory. This is consistent with the idea that the downturn in economic activity was driven by an increase factors that could not have been perfectly offset by monetary policy alone - that is, that the increase in risk premia and distortions in financial markets that arose in this period reflected real (as well as nominal) factors (such as information asymmetries, etc.). Of course, simply because such fluctuations were "natural" - that is, not nominal in origin - does not imply that such fluctuations were desirable (e.g., pareto optimal). Pareto optimality depends on the degree to which the movements in risk premia reflect, for example, preferences or distortions associated with informational asymmetries.
The risk premia wedges are related to the investment wedge of Chari, Kehoe, and McGrattan (2007), which represents a wedge between the marginal rates of substitution and technical substitution between current and future consumption.4 Interpreting such wedges as inefficient is consistent with the idea that fluctuations in such premia reflect, for example, information imperfections that make external finance more costly than internal funds, as in Bernanke, Gertler, and Gilchrist (1999). A social planner aware of such information imperfections would ignore such factors in its efficient allocations. It is important to remember in a monetary policy discussion that the presence of such wedges need not imply that monetary policy should act forcefully to counteract the effects of such wedges, even if a social planner would. A policymaker constrained to induce allocations through a given set of instruments may not be able to implement such allocations, and such implementation constraints are central in practical policy design. For example, Carlstrom and Fuerst (2009) present a simple model of financing frictions and examine the optimal monetary policy given such frictions; their analysis presents examples where monetary policy acts to mitigate only a small portion of the (output) effects of financial frictions, because monetary policy does not have the tools to implement the efficient allocation. 5
With that said, we will see below the central role in typical recessions of the aggregate risk premium, which (as discussed above) should be offset one-for-one by monetary policy in the EDO model to implement the natural rate of output. Indeed, the importance of this shock will be a key reason why the natural rate of output does not provide the commonly expected information for a "Taylor" policy rule even though the Beveridge-Nelson gap and the natural rate of interest do provide such information. Given the divergence between the Beveridge-Nelson and natural rate gaps shown in figure 4, this issue is especially important in the financial crisis period beginning in 2007.
4.4 Using The Natural-Rate Approach
Two issues arise in any practical use of the flexible-price/natural-rate approach.
First, the natural rate of output provides a point-in-time estimate, but the natural rate follows a complicated time series process and hence the current point-in-time estimate does not provide the same type of "trend" information as the Beveridge-Nelson trend. This occurs because the natural-rate measure depends on the evolution of all exogenous and endogenous state variables in the model used to estimate the concept, and any model capable of explaining the data and stock-flow dynamics (associated with investments in many different types of business and household capital) will have a complex state space.
Second, the natural rate of output gap does not provide "Taylor" rule relevant information without also considering the natural rate of interest. In contrast, the Beveridge-Nelson gap will provide this information, at least within the EDO model.
4.4.1 Point-in-time estimates and forecasts of the natural rate
Turning to the first issue and as emphasized by Beveridge and Nelson (1981), their definition of trend implies that the growth of the trend going forward is a constant (which, in the EDO DSGE model, is a function of the expected rate of aggregate and investment-specific technological progress
and the expected population growth rate). As a result, the EDO model, at the parameter estimates presented above for the growth rates of technological progress and assuming a population growth rate of ![]() percent per year, implies that the expected growth rate of the Beveridge-Nelson trend is
percent per year, implies that the expected growth rate of the Beveridge-Nelson trend is ![]() percent per year.
percent per year.
All other concepts of "equilibrium" output must converge to the Beveridge-Nelson trend at some far horizon (as that is the definition of the Beveridge-Nelson trend). And the projection of output from a DSGE model like EDO is a function of economic fundamentals (e.g., capital stocks, technology, markups, risk premia, etc.) and is not affected by "equilibrium" concepts of output like the natural-rate of output (which is simply a construct of the economic analysts focus, not the concern of utility-maximizing households and profit-maximizing firms). Consequently, the projections of the natural rate of output will tend to fluctuate significantly over time. As a result, discussions of the economic outlook or the potential policy implications of alternative measures of "equilibrium" output must take into account both the current level of such concepts and their projected evolution.
Table 4 illustrates these points by presenting, for the Beveridge-Nelson definition and the natural-rate definition, the 2009Q2 measures of the output gap and the projected change in the "equilibrium" or trend output level associated with those definitions for 2009 and 2010 (on a Q4/Q4 basis).
| Definition | Trends |
Trends |
Trends |
Trends |
|
| Beveridge-Nelson | -6.2 | 2.8 | 2.8 | 2.8 | 2.8 |
| Natural-rate | -0.3 | 1.3 | 3.2 | 4.2 | 4.3 |
- Gap in percent. Figures for projected trends in 2009 refer to percent changes over the second half of the year (at an annual rate); figures for 2010, 2011, and 2012 refer to Q4/Q4 percent changes.
The Beveridge-Nelson gap is -6.2 percent of GDP as of the second quarter of 2009, and projected growth in the associated trend is 2.8 percent - the constant expected growth rate associated with this concept. In contrast, the natural-rate gap is -0.3 percent - output in the second quarter of 2009 (after real GDP had fallen for four consecutive quarters) was about in line with the flexible-price, constant-markup level consistent with the EDO model and other estimated shocks.
In considering these different gaps, the level of actual GDP is the same across definitions. Moreover, output converges to the Beveridge-Nelson trend; as a result, the "trend" or "equilibrium" level of output associated with the natural rate definition (which must also converge to the Beveridge-Nelson trend) is projected to rise slowly in the second half of 2009 (about 1.3 percent) and then to accelerate considerably over the 2010 to 2012 period, to about 4 1/4 percent in 2011 and 2012.
It is fairly clear that policy discussions tend to (at least implicitly) assume that future expected "equilibrium" or trend growth is relatively steady (in the way that policy institutions estimates of trend growth tend to be smooth, as discussed for the CBO below). Such a presumption is not warranted if one is considering the natural rate of output from typical DSGE models, a point emphasized in other research (e.g., Edge, Kiley, and Laforte (2008)). To the extent these concepts are increasingly entering policy discussions, there may need to be an increased appreciation for the possibility that such a definition of trend output may move significantly over a projection period.
4.4.2 The natural rate in interest-rate rules
The role of the output gap plays a central role in monetary policy discussions, as even a cursory consideration of the prominence "Taylor" rules (Taylor (1993)) in such discussions reveals.6 Such a policy rule appears in EDO (equation 17).
For discussion purposes, let's consider a simple benchmark rule, in which the nominal interest rate (![]() ) is a function of its natural rate(
) is a function of its natural rate(![]() ), inflation (
), inflation (![]() ), and a measure of the output gap (
), and a measure of the output gap (![]() )
)
Traditional rules (e.g., Taylor (1993) and Taylor (1999)) ignore the model-specific predictions for the natural rate (i.e., set ![]() equal to zero) and consider deviations of output
from trend as the gap measure; as discussed above, the Beveridge-Nelson cycle is the most straightforward definition of such a gap. As a result, such traditional descriptions would imply very accomodative monetary policy in the middle of 2009: With
equal to zero) and consider deviations of output
from trend as the gap measure; as discussed above, the Beveridge-Nelson cycle is the most straightforward definition of such a gap. As a result, such traditional descriptions would imply very accomodative monetary policy in the middle of 2009: With
![]() equal to 0.5 or 1.0 (the values in Taylor (1993) and Taylor (1999), at annual rates) and the Beveridge-Nelson gap at -6.2 percent, the nominal interest rate would be prescribed
by 21 to be more than 3 or 6 percentage points lower than in the absence of a gap.
equal to 0.5 or 1.0 (the values in Taylor (1993) and Taylor (1999), at annual rates) and the Beveridge-Nelson gap at -6.2 percent, the nominal interest rate would be prescribed
by 21 to be more than 3 or 6 percentage points lower than in the absence of a gap.
Naive application of a natural rate gap in such a policy rule would have implied essentially no downward pressure from the natural rate gap on the nominal interest rate, as the natural rate gap was estimated to be approximately zero in the middle of 2009. But such an application would be
inappropriate. As emphasized by Woodford (2003), the natural rate framework aims to stabilize inflation and output at its natural rate by allowing the nominal interest rate to track the natural rate of interest (for example, by setting ![]() to one). Indeed, such stabilization could be perfectly successful in simple models like those presented in Woodford (2003), implying stable inflation and no output gap in any period; nonetheless, the nominal interest
rate would vary considerably with the determinants of the natural rate.
to one). Indeed, such stabilization could be perfectly successful in simple models like those presented in Woodford (2003), implying stable inflation and no output gap in any period; nonetheless, the nominal interest
rate would vary considerably with the determinants of the natural rate.
In the event, the natural rate of interest from the EDO model is very highly correlated with the Beveridge-Nelson gap from the model, with a simple correlation coefficient of 0.88. As shown in figure 5, the Beveridge-Nelson gap and the natural rate of interest were both extremely low in the middle of 2009. As a result, the natural rate framework for a policy rule of Woodford (2003) and the traditional framework of Taylor (1993) both prescribed accomodative policy. Some discussions have confused the information from Beveridge-Nelson gaps, natural rate of output gaps, and the natural rate of interest.7
5.1 Estimates
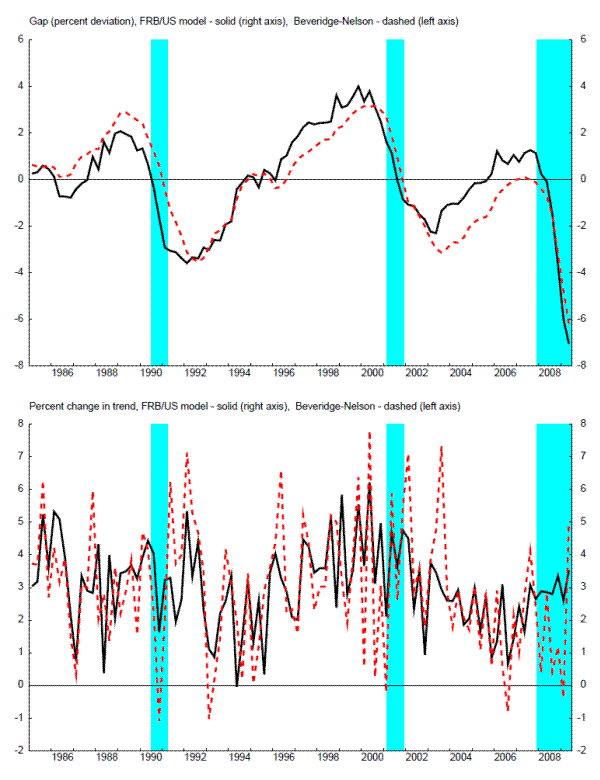
Figure 6 and 7 present the production-function based output gaps from the CBO (CBO (2010) and from the Federal Reserve's FRB/US model, along with the Beveridge-Nelson cycle from the EDO model, in the upper panels. The CBO gap is widely used by economists. These gaps are both highly correlated with the Beveridge-Nelson cycle from the EDO model (with correlation coefficients exceeding 0.84 for both measures).
The lower panels of these figures present the percent change from the previous quarter in the estimate of trend (at an annual rate), along with the change in the Beveridge-Nelson permanent component from EDO. While the gaps in the upper panels are highly correlated, the trend estimates from the FRB/US model and especially from the CBO are much smoother. In short, EDO has a much more variable "potential" growth rate.
Of course, the data on GDP is the same for the EDO Beveridge-Nelson gap, the CBO gap, and the FRB/US model gap. Moreover, the growth rate of GDP equals the sum of the change in the gap and potential GDP growth. As a result, similar movements in the gap for all three measures, and quite different movements in potential, must imply quite different covariances between actual growth, the change in the gap, and potential growth. (For example, the variance of GDP growth equals the sum of the variance of the change in the gap, the variance of potential growth, and twice the covariance of the change in the gap and potential growth; similar mixes of variances and covariances could be done for other combinations of actual/gap/potential). The structural implications of DSGE models like EDO for the covariance between the Beveridge-Nelson trend and cycle could be used to inform the related time-series literature. For example, Beveridge and Nelson (1981) simply assumed an ARIMA representation of GDP growth, which imposes no restrictions on the covariances between innovations to the trend and cycle; Clark (1987) and other research assumed an unobserved components structure for GDP growth with an assumption of zero correlation between the (true) innovations to the trend and cycle; and Morley, Nelson, and Zivot (2003) discuss in detail the role of such assumptions and the strength of evidence for/against a correlation between innovations to trend and cycle.
5.2 Granger causality
A final subject that is important in policy discussions related to the output gap or economic slack concerns the relationship of slack, in a projection or reduced-form sense, to other key economic variables such as unemployment and inflation. Indeed, such correlations are two of the most important reduced-form relationships in empirical macroeconomics (i.e., the unemployment/output gap relationship known as Okun's law (Okun (1962)) and the inflation/output gap relationship in reduced-form Phillips curves).
The simplest summary measure of a forecast relationship asks whether a variable helps predict another after accounting for lags of the variable itself - i.e., whether a variable Granger causes another (Granger (1969)). Table 5 presents the p-values associated with Granger causality tests running from each gap measure to the change in the unemployment rate and core inflation.
| Gap measure | Change in Unemployment rate | Core PCE inflation |
| Beveridge-Nelson | 0.00 | 0.08 |
| Natural rate | 0.00 | 0.36 |
| CBO | 0.01 | 0.19 |
| FRB/US | 0.00 | 0.18 |
- Each column contains the p-value associated with the null that the variable does not Granger cause the change in the unemployment rate (Sample 1986q1-2009q2, with four lags).
All the measures of the output gap show the Okun's law relationship - that is, lagged values of these measures of the output gap Granger cause changes in the unemployment rate over the 1986Q1 to 2009Q2 period. This should not be surprising - deviations of output from long-run levels must be associated with movements in labor input, and the lead of hours over unemployment is a well-known regularity.
The Phillips curves relationships are less clear for some of the measures. In particular, the FRB/US model and CBO estimates do not appear to Granger cause core inflation; neither does the natural rate measure. In contrast, the Beveridge-Nelson gap from the EDO model does appear to Granger cause core inflation, at least at the 10 percent statistical significance level. Given that, for example, one of the motivations for the CBO measure is a Phillips curve motivation (see Congressional Budget Office (2001, 2002)), the relative success of the DSGE model's Beveridge-Nelson gap is a victory.8 It also highlights the potential policy information from this type of DSGE model, as a Phillips curve relation looms large in some policy discussions.9
6 Conclusion
The review of alternative output gap definitions and estimates, both from the EDO DSGE model and from policy institutions, suggests that care must be taken in defining concepts in any discussion of economic slack and related policy implications.
Looking back, my analysis suggests four conclusions:
- The EDO model's estimate of the output gap (according to either a Beveridge-Nelson or production-function approach) is very similar to gaps from the Congressional Budget Office or the Federal Reserve's large-scale macro-econometric model (FRB/US) model, but the DSGE model's estimate of potential growth is considerably more variable; the latter result stems from the significant degree of fluctuation in aggregate technology estimated by the DSGE model, a result consistent with the significant role such fluctuations play in model's descended from those of the real-business-cycle tradition (from Kydland and Prescott (1982)).
- The flexible-price/natural-rate gaps are highly dependent on modeling assumptions, and their use in policy applications or forecasting requires a deep understanding of a specific model's structure. (This result is closely related to the critique of DSGE models of Chari, Kehoe, and McGrattan (2009), who highlight the sensitivity of policy applications of such models to controversial modeling assumptions). In particular, a natural-rate gap does not provide the same type of guidance to a "Taylor" rule for nominal interest rates as other concepts of gaps; indeed, the signals from the Beveridge-Nelson gap provide a better sense of movements in the "natural rate of interest" than do the signals from the natural rate of output gap.
- "Equilibrium" or trend expected growth is highly variable in the flex-price/natural-rate case, implying that a focus on the current level of such gaps can be misleading in a policy discussion. In contrast, expected trend growth for the Beveridge-Nelson concept is exogenous and constant; moreover, all other notions of "trend" converge to the Beveridge- Nelson trend.
- The DSGE model's estimate of the Beveridge-Nelson gap is as closely related to unemployment fluctuations as those from policy institutions (e.g., obeys Okun's law) and has more predictive ability for inflation (e.g., has a tighter reduced-form Phillips curve relationship).
On balance, the results suggest that the ability of a DSGE model like EDO to capture the trend/cycle decomposition of output that drives much of the discussion of macroeconomic stabilization policy is quite good - as should be suspected given the forecasting performance of such models (e.g., Edge, Kiley, and Laforte (2009)). An interesting topic for future research involves using the structural model's implications for the covariances between trend and cycle innovations in order to bridge the distance between a structural analysis of output gaps such as herein and the time-series literature of, for example, Morley, Nelson, and Zivot (2003).
Bibliography
- Aoki, K. (2001), Optimal Monetary Policy Responses to Relative-Price Changes, Journal of Monetary Economics 48: 55-80.
- Beveridge, S. and C.R. Nelson (1981) A new approach to the decomposition of economic time series into permanent and transitory components with particular attention to measurement of the business cycle, Journal of Monetary Economics 7,
151-174.
- Carlstrom, Charles, and Timothy Fuerst (2009) Optimal Monetary Policy in a Model with Agency Costs. October.
- Chari, V.V., Patrick J. Kehoe, and Ellen R. McGrattan (2007) Business Cycle Accounting. Econometrica, May.
- Chari, V.V., Patrick J. Kehoe, and Ellen R. McGrattan (2009) New Keynesian Models: Not Yet Useful for Policy Analysis. American Economic Journal: Macroeconomics 2009, 1:1, 242266.
- Chung, Hess, Michael T. Kiley, and Jean-Philippe Laforte (2010) Documentation of the Estimated, Dynamic, Optimization-based (EDO) Model of the U.S. Economy: 2010 Version. Federal Reserve Board Finance and Economics Discussion Paper.
- Clarida, Richard, Jordi Gal, and Mark Gertler (1999) The Science of Monetary Policy: A New Keynesian Perspective. Journal of Economic Literature Vol. XXXVII (December 1999), pp. 16611707.
- Clark, P. K., The cyclical component of U.S. economic activity, The Quarterly Journal of Economics 102 (1987), 797814.
- Cochrane, John H. (1994) Permanent and Transitory Components of GNP and Stock Prices. The Quarterly Journal of Economics, Vol. 109, No. 1 (Feb., 1994), pp. 241-265.
- Congressional Budget Office (2001). CBO's Method for Estimating Potential Output: An Update.
- Congressional Budget Office (2002). The Effects of Changes in the Labor Markets on the Natural Rate of Unemployment.
- Congressional Budget Office (2010). The Budget and Economic Outlook: Fiscal Years 2010 to 2020.
- Edge, Rochelle, Michael T. Kiley and Jean-Philippe Laforte (2007b) Documentation of the Research and Statistics Divisions Estimated DSGE Model of the U.S. Economy: 2006 Version. Federal Reserve Board Finance and
Economics Discussion Paper 2007-53.
- Edge, Rochelle, Michael T. Kiley and Jean-Philippe Laforte (2008a) An Estimated DSGE Model of the US Economy with an Application to Natural Rate Measures. Journal of Economic Dynamics and Control. 32, 2512-2535.
- Edge, R., Kiley, M., Laforte, J.P., 2009. A comparison of forecast performance between the FRB staff forecasts, simple reduced-form models, and a DSGE model. Forthcoming in the Journal of Applied Econometrics, and Federal Reserve Board Finance and Economics
Discussion Paper 2009-10.
- Erceg, Christopher J. Henderson, Dale W. and Levin, Andrew T., 2000. "Optimal monetary policy with staggered wage and price contracts," Journal of Monetary Economics, Elsevier, vol. 46(2), pages 281-313.
- Erceg, Christopher and Levin, Andrew, 2006. "Optimal monetary policy with durable consumption goods," Journal of Monetary Economics, Elsevier, vol. 53(7), pages 1341-1359
- Granger, Clive W. (1969) Investigating Causal Relationships by Econometric Models and Cross-Spectral Methods. Econometrica, 37:424-38. 187-194.
- Gordon, Robert J. (1979) Comment. Carnegie-Rochester Conference Series on Public Policy, 10, 187-194.
- Harvey, Andrew (1985) Trends and Cycles in Macroeconomic Time Series, Journal of Business and Economic Statistics 3 (1985), 216227.
- Justiniano, A., and G. E. Primiceri (2008) "Potential and Natural Output" mimeo, Northwestern University.
- Kiley, Michael T. (2010) "Vacancies and the Natural Rate of Unemployment: A Simple Empirical Approach" mimeo, Federal Reserve Board.
- King, Robert G., Charles I. Plosser, James H. Stock, Mark W. Watson (1991) Stochastic Trends and Economic Fluctuations. The American Economic Review, Vol. 81, No. 4 (Sep., 1991), pp. 819-840.
- Kuttner, Kenneth N. (1994). "Estimating Potential Output as a Latent Variable," Journal of Business and Economic Statistics, vol. 12 (July), pp. 361-68.
- Kreps, David M. (1990). A Course in Microeconomic Theory. Princeton University Press, Princeton, NJ.
- Kydland, Finn and Prescott, Edward. 1982. Time-to-build and Aggregate Fluctuations. Econometrica, 50, 6,1345 - 1370.
- Morley, James C., Charles R. Nelson, and Eric Zivot (2003) Why are the Beveridge-Nelson and Unobserved-Components Decompositions of GDP So Different? The Review of Economics and Statistics, 85(2): 235243.
- Nelson, Richard R. (1964) Aggregate Production Functions and Medium-Range Growth Projections. The American Economic Review, Vol. 54, No. 5 (Sep., 1964), pp. 575-606.
- Okun, Arthur M. 1962. Potential GNP: Its Measurement and Significance, American Statistical Association 1962 Proceedings of the Business and Economic Statistics Section. Washington, DC: American Statistical Association, pp. 98-104.
- Plosser, Charles and G. William Schwert (1979) Potential GNP: Its Measurement and Significance: A Dissenting Opinion. Carnegie-Rochester Conference Series on Public Policy, 10, 179-186.
- Rotemberg, Julio J and Woodford, Michael. 1996. Real-Business-Cycle Models and the Forecastable Movements in Output, Hours, and Consumption. American Economic Review, 86, 1, 71-89.
- Samuelson, Paul (1948) Economics: An Introductory Analysis. McGraw-Hill, New York.
- Stock, J. H., and M. W. Watson, Variable Trends in Economic Time Series, Journal of Economic Perspectives 2 (1988), 147174.
- Thurow, Lester C. and L. D. Taylor (1966) The Interaction Between the Actual and the Potential Rates of Growth. The Review of Economics and Statistics, Vol. 48, No. 4 (Nov., 1966), pp. 351-360.
- Watson, M. W., Univariate detrending methods with stochastic trends, Journal of Monetary Economics 18 (1986), 4975.
- Woodford, Michael (2003) Interest and Prices: Foundations of a Theory of Monetary Policy. Princeton University Press, Princeton, NJ.
Figure 1: Model Overview
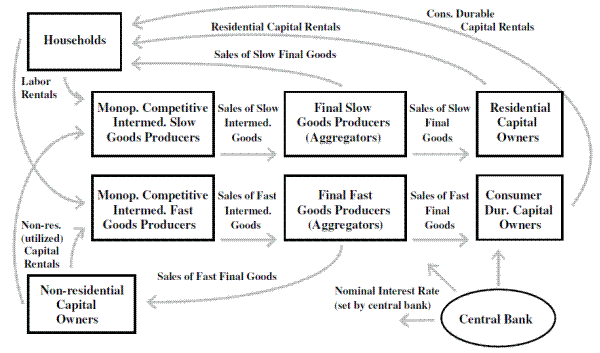
Figure 3: Production-Function GapFigure 3: Model Overview
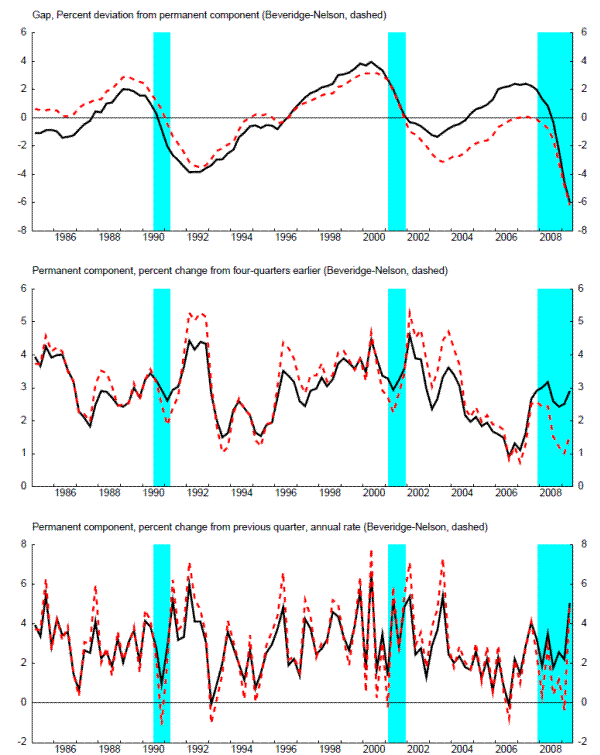
Figure 4: Natural-Rate Gap
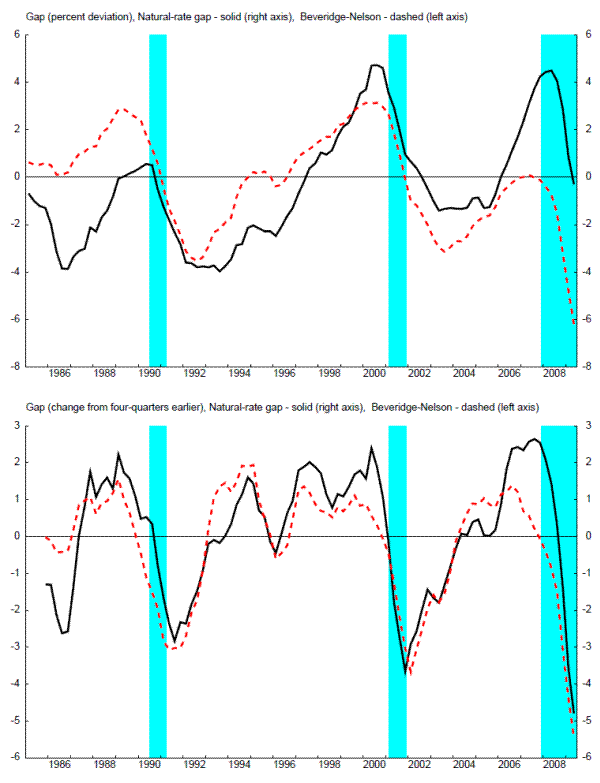
Figure 5: Natural-Rate of Interest and Beveridge-Nelson Gap
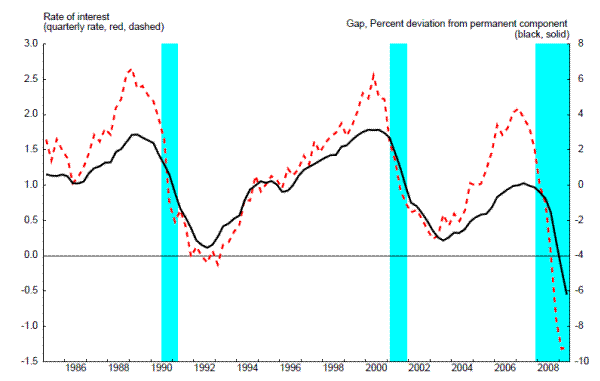
Figure 6: CBO Gap
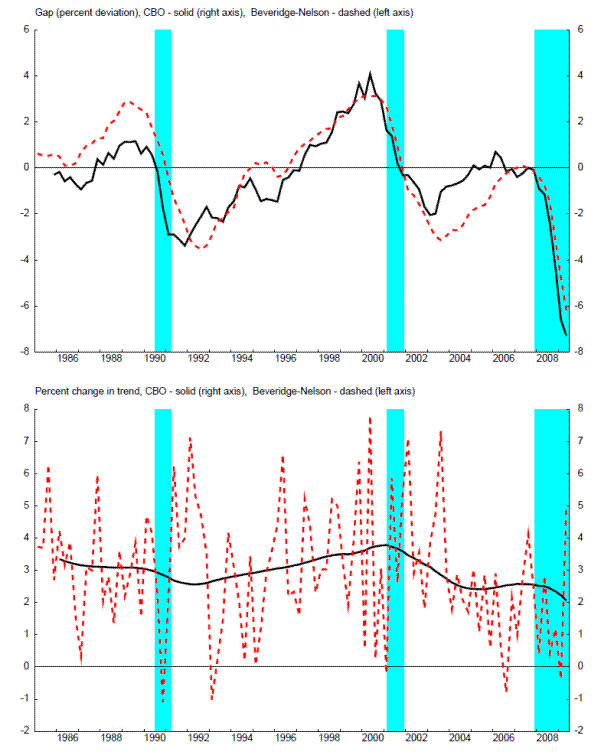
Figure 7: FRB/US Gap
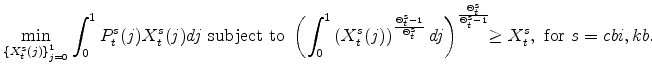
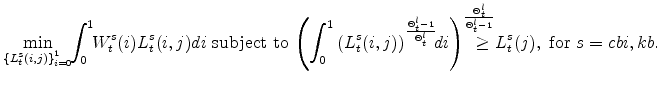
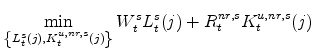
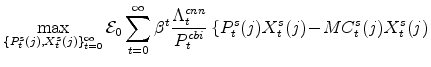
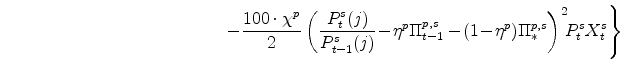
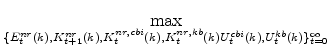
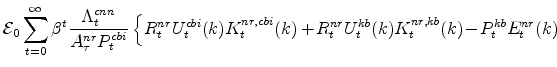
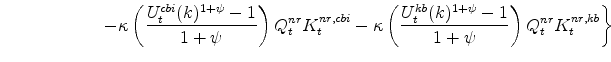
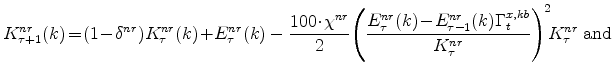
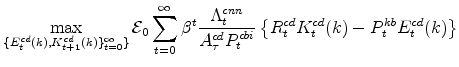
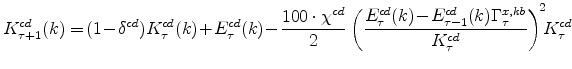
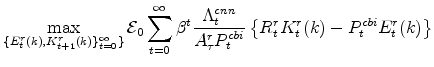
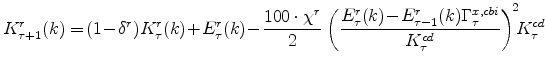
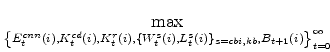
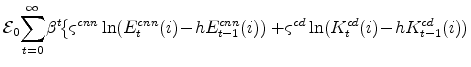
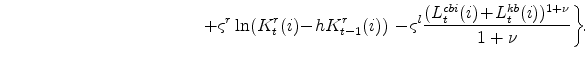
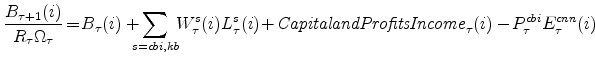
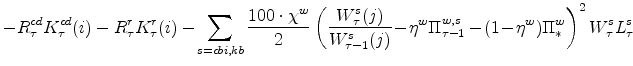
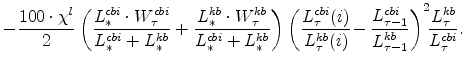
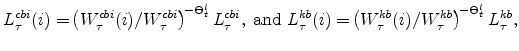
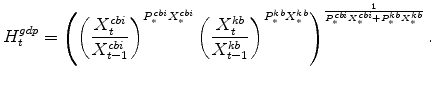
![\displaystyle \tilde{X}_{t}^{bn} = \mathcal{E}_{t} \left[ \sum_{\tau=- \infty}^{t} H^{gdp}_{\tau} - \sum_{\tau=- \infty}^{\infty} H^{gdp}_{\tau} \right].](img134.gif)
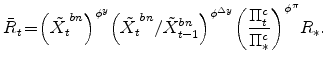
![\displaystyle \tilde{X}_{t}^{bn} = \mathcal{E}_{t} \left[ -\sum_{\tau=t+1}^{\infty} H^{gdp}_{\tau} \right],](img184.gif)