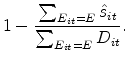The Depth of Negative Equity and Mortgage Default Decisions
Keywords: Housing, mortgage default, negative equity
Abstract:
JEL classification: D12, G21, R20
1 Introduction
House prices in the U.S. plummeted between 2006 and 2009, and millions of homeowners, owing more on their mortgages than current market value, found themselves "underwater." While there has been some anecdotal evidence of homeowners seemingly choosing to walk away from their homes when they owe 20 or 30 percent more than the value of their houses, there has been scant academic research about how systematic this type of behavior is among underwater households or on the level of negative equity at which many homeowners decide to walk away. Focusing on borrowers from Arizona, California, Florida, and Nevada who purchased homes in 2006 with non-prime mortgages and 100 percent financing, we bring more systematic evidence to this issue.
We estimate that the median borrower does not walk away until he owes 62 percent more than their house's value. In other words, only half of borrowers in our sample walk away by the time that their equity reaches -62 percent of the house value. This result suggests borrowers face high default and transaction costs because purely financial motives would likely lead borrowers to default at a much higher level of equity (Kau et al., 1994). Although we find significant heterogeneity within and between groups of homeowners in terms of the threshold levels associated with walking away from underwater properties, our empirical results imply generally higher thresholds of negative equity than the anecdotes suggest.
We generate this estimate via a two-step maximum likelihood strategy. In the first step, we predict the probability a borrower defaults due to an income shock or life event (e.g. job loss, divorce, etc.), holding equity fixed, using a discrete-time hazard model. We incorporate these predicted probabilities into the second step likelihood function; when estimating the depth of negative equity that triggers strategic default, we want to underweight defaults most likely to have occurred because of a life event. Not all borrowers in our sample default during the observation period; the maximum likelihood strategy also accounts for this censoring. As we will show, accounting for these censored observations as well as for defaults that occur because of adverse life events plays a critical role in generating our estimates.
The literature on mortgage default has focused on two hypotheses about why borrowers default. Under the "ruthless" or "strategic default" hypothesis, default occurs when a borrower's equity falls sufficiently below some threshold amount and the borrower decides that the costs of paying back the mortgage outweigh the benefits of continuing to make payments and holding on to their home. Deng et al. (2000), Bajari et al. (2008), Experian-Oliver Wyman (2009), and Ghent and Kudlyak (2009) show evidence in support of this view. Another view is the "double trigger" hypothesis. Foote et al. (2008) emphasize that when equity is negative but above this threshold, default occurs only when combined with a negative income shock. This view helps explain the low default rate among households with moderate amounts of negative equity during the housing downturn in Massachusetts during the early 1990s.
Our results suggest that while strategic default is fairly common among deeply underwater borrowers, borrowers do not ruthlessly exercise the default option at relatively low levels of negative equity. About half of defaults occurring when equity is below -50 percent are strategic but when negative equity is above -10 percent, we find that the combination of negative equity and liquidity shocks or life events drives default. Our results therefore lend support to both the "double-trigger" theory of default and the view that mortgage borrowers exercise the implicit put option when it is in their interest.
The fact that many borrowers continue paying a substantial premium over market rents to keep their home challenges traditional models of hyper-informed borrowers operating in a world without economic frictions (see Vandell (1995) for an overview of such models). Quigley and van Order (1995) similarly find that the frictionless model has trouble explaining their data, and conclude that transaction costs likely exist and affect default decisions. White (2009) hypothesizes that stigma and large perceived penalties for defaulting keeps borrowers from exercising the option when it would be in their financial interest to do so. Indeed, Guiso et al. (2009) find that mortgage borrowers tend to view default as immoral, although 17 percent of survey respondents still say they would default if equity declined to -50 percent. A 2010 national housing survey conducted by Fannie Mae suggests that nearly 9 in 10 Americans do not believe "it is OK for people to stop making payments if they are underwater on their mortgages."
Estimating the median threshold equity value is this paper's primary innovation. We also exploit relatively new sources of detailed data that help estimate individual equity and account for changes in local economic conditions more precisely. Our first step hazard model is specified flexibly and explicitly incorporates the double-trigger hypothesis. And the extreme drops in house prices in many areas of the country between 2006-2009 allow us to observe borrowers' behavior at many levels of equity. In total, we characterize the empirical relationship between ruthless default and equity in a more complete way than previous work has done.
The remainder of the paper proceeds as follows. We first present a simple two period model to illustrate how negative equity plays into default decisions. We also describe other salient factors entering into the default decision. In section 3, we describe the data and explain how we construct measures of equity and default. We then discuss in detail the empirical model and estimation strategy in section 4. Section 5 presents our key findings. Finally, we conclude and discuss the limitations of this paper.
2 Background: The Strategic Default Decision
When the price of housing falls, mortgage borrowers may find default an attractive option compared to paying a premium to stay in their home even if they can afford to keep paying. The following two-period model, which we borrow from Foote et al. (2008), illustrates this concept. Note that exogenous life events such as a divorce, job loss, or health shock that may induce mortgage default are ignored in this model. The purpose of this model is to show how negative equity can affect default decisions.
In the first period of this two-period model, households have a house that is worth ![]() and was financed by a loan of size
and was financed by a loan of size ![]() . Because we are interested in describing the default decision of a borrower who is underwater, we assume that
. Because we are interested in describing the default decision of a borrower who is underwater, we assume that ![]() . In the first period,
borrowers either pay the mortgage and remain in the house until the second period, or borrowers default. When borrowers default, they incur a cost
. In the first period,
borrowers either pay the mortgage and remain in the house until the second period, or borrowers default. When borrowers default, they incur a cost ![]() , which reflects the damages to one's credit
score, legal liabilities, any unplanned relocation costs and emotional costs or stigma.
, which reflects the damages to one's credit
score, legal liabilities, any unplanned relocation costs and emotional costs or stigma.
The magnitude of ![]() can be quite large. First, VantageScore Solutions, a credit scoring firm, estimates a 21 percent drop in one's credit score due to mortgage delinquency and subsequent
foreclosure, given no other simultaneous delinquencies.1
can be quite large. First, VantageScore Solutions, a credit scoring firm, estimates a 21 percent drop in one's credit score due to mortgage delinquency and subsequent
foreclosure, given no other simultaneous delinquencies.1
Second, borrowers who walk away from their mortgage may face severe legal liabilities, depending on the state and year. Florida and Nevada allow lenders to sue for a deficiency judgment against borrowers if the foreclosure sale does not cover the remaining loan balance and lenders' foreclosure costs. In contrast, some states have non-recourse laws (i.e. lenders cannot obtain a deficiency judgment), including Arizona and California. In California, home purchase mortgages for a principle residence are non-recourse, while in Arizona, home purchase mortgages are non-recourse if the property is on less than 2.5 acres and is a single one- or two- family dwelling.2
And third, mortgage default may be stigmatizing. Anecdotal evidence indicates that debt collection companies successfully appeal to borrowers' sense of moral obligation to help recover loans (see The New York Times (5/17/2009a)), and Guiso et al. (2009) report that 80 percent of survey respondents (in 2008 and 2009) think it is morally wrong to default. Reflecting this sentiment, former Bank of America chief executive Ken Lewis remarked in 2007, "I'm astonished that people would walk away from their homes" (The New York Times, 7/25/2009b).3
Turning back to the model, the second period has two possible states: the good state occurs with probability ![]() and the bad state occurs with probability
and the bad state occurs with probability ![]() . If the good state occurs, the house is worth
. If the good state occurs, the house is worth ![]() whereas in the bad state, the house is worth
whereas in the bad state, the house is worth ![]() . Similar to Foote et al. (2008), we assume
. Similar to Foote et al. (2008), we assume
![]() , where
, where ![]() is the remaining nominal mortgage
balance in period two. In period two, borrowers either pay the mortgage when the house is worth
is the remaining nominal mortgage
balance in period two. In period two, borrowers either pay the mortgage when the house is worth ![]() or default when the house price is
or default when the house price is ![]() .
.
In period one, households decide to default when the value of staying in the home, net of its cost, is less than the cost of default. In this model, the cost of default in period one is simply ![]() . The value of staying in the home can be expressed as
. The value of staying in the home can be expressed as
rent![\displaystyle _1 + \frac{1}{1+r}[\pi (P_{2}^{G} - M_2) - (1-\pi)(P_{2}^{B} + C)].](img12.gif) |
Put differently, by making the mortgage payment mpay
Putting the cost and benefit together, borrowers default if and only if:
![\displaystyle _1 + \frac{1}{1+r}[\pi (P_{2}^{G} - M_2) - (1-\pi)(P_{2}^{B} + C)].](img12.gif) |
(1) |
Rearranging the terms in the above equation, we obtain that borrowers default if and only if:
Equation (2) indicates that when the premium to stay (i.e. mpay
Although Foote et al. (2008) note that period one's equity, ![]() , does not enter (2) and is therefore not a direct determinant of
default, we argue that the decision to default is likely to be indirectly related to period one's equity. A borrower's mortgage payment reflects the size of her mortgage while the value of the housing services derived from her house corresponds to its price. When
, does not enter (2) and is therefore not a direct determinant of
default, we argue that the decision to default is likely to be indirectly related to period one's equity. A borrower's mortgage payment reflects the size of her mortgage while the value of the housing services derived from her house corresponds to its price. When ![]() is considerably lower than
is considerably lower than ![]() , the market value of housing services,
rent
, the market value of housing services,
rent![]() , will likely be lower than the mortgage payment,
mpay
, will likely be lower than the mortgage payment,
mpay![]() .4 Finally, period one's equity may
indirectly affect the default decision since low home prices in period one may make future capital gains less likely.
.4 Finally, period one's equity may
indirectly affect the default decision since low home prices in period one may make future capital gains less likely.
To help make this discussion more concrete, consider an example. A borrower who purchased a median-priced home in 2006 in Palmdale, CA would have seen the value of that home fall from about $375,000 to less than $200,000 in just three years. We searched Craigslist, a website posting classified advertisements, in November 2009 to gauge rental prices in Palmdale and found 3-4 bedroom, detached homes advertised for $1,300 per month on average. In contrast, the monthly payment for a 30-year fixed-rate mortgage of $375,000 at a 7 percent interest rate would be about $2,500 (assuming the tax deduction for interest and property taxes roughly offsets property tax, insurance and maintenance costs). In other words, some borrowers, especially those with a high-cost mortgage, faced a steep premium to stay in their house.5 Unless one expects home prices to post extremely strong gains, there is no obvious benefit to paying this premium.6
On a final note, Equation (2) glosses over some important institutional details about the default process that influence the incentive to default. It is worth noting that borrowers who default live rent-free until the lender takes possession of the house (property taxes, though, must still be paid by the mortgage holder), strengthening the incentive to default. Furthermore, delays on the part of the lender to foreclose extend states' mandated pre-foreclosure period - the amount of time between a notice of foreclosure and when the lender can seize and sell the property (Cutts and Merrill, 2009). All told, borrowers are likely able to stay in their homes for at least 8 to 12 months after they stop making mortgage payments.
3 Data Description and Summary Statistics
Our primary source of data on mortgage performance comes from LoanPerformance (LP), a division of First American CoreLogic. LP provides detailed information on mortgages bundled into subprime and "alt-A" (collectively referred to as "non-prime") private-label securities. Subprime loans are generally characterized as loans to borrowers with low credit scores and/or little or no down payment, while alt-A securities typically involve mortgages with reduced or no documentation of the borrower's income and assets and have a higher proportion of interest-only mortgages and option ARMs.7 The LP data contain several loan characteristics at origination, including the borrower's FICO score, the ZIP code of the property, the loan amount, loan to value ratio, interest rate, loan type (e.g. fixed rate or adjustable rate), and loan purpose (e.g. purchase or refinance). LP also tracks the following variables at a monthly frequency: the current interest rate, current loan balance, scheduled monthly payment, and the payment status of the loan (e.g. current, 30 days delinquent, 60 days delinquent, etc.). The LP data cover the majority of securitized non-prime mortgages and thus provide information on a large number of loans originated during the peak of the most recent housing cycle (see Mayer and Pence (2008)).
To calculate housing equity for each loan in our sample in each month, we use ZIP code-level house price indexes (HPIs) - also from First American CoreLogic. These HPIs are monthly, repeat-sales indexes, and are available for approximately 6,000 ZIP codes from 1976 to 2009. The ZIP code coverage of the dataset depends on factors such as state sales price disclosure laws, the corporate history of First American CoreLogic, and the thickness of the ZIP code's real estate market. To the extent that homeowners form beliefs about their home's value by observing sales prices on homes in their neighborhood, these ZIP code HPIs should be a reasonable proxy for such beliefs.8
We focus on non-prime first-lien home purchase mortgages originated in 2006 with a combined loan-to-value ratio (CLTV) of 100 percent in Arizona, California, Florida and Nevada.9 Notably, more than half of the non-prime purchase mortgages originated in 2006 in these states have a CLTV of 100 percent. Therefore, because restricting the sample in this way characterizes the modal borrower, it is unlikely to introduce severe sample selection problems. On the other hand, our focus on this sample has several advantages, particularly in terms of accurately measuring equity.
First, selecting borrowers with a CLTV at origination of 100 percent helps avoid measurement error due to unobserved additional mortgages - it is unlikely that borrowers would have another mortgage in addition to the reported loans that finance 100 percent of the purchase price. Second, the sharp decline in prices just after these borrowers purchased their home in 2006 makes the refinance option largely irrelevant. As such, with our sample, we avoid the problem of many borrowers exiting the sample via a refinance before defaulting.10 The price decline and lack of home equity also make it unlikely that borrowers took out an unobservable junior mortgage after the initial home purchase. Third, we exclude refinance mortgages because CLTV is potentially mismeasured. More precisely, outstanding junior liens, which may not be simultaneously refinanced, are not reported at the time the refinance occurs.11 Following our sample restrictions and data cleaning procedures, 133,281 loans remain (see the Appendix for more details).
A borrower's decision to default on his mortgage happens the instant when he permanently stops paying. Of course, we only observe this decision ex post. In this paper, we define default as being 90+ days delinquent for two consecutive months, and we define the time of default as 3 months prior to the month when the loan reaches the 90+ day delinquency mark. One could, alternatively, define default as entering the foreclosure process. However, the point when foreclosure begins depends on when the lender decides to file a notice of default, whereas halting mortgage payments reflects borrowers' decisions. Since we are interested in the borrower's equity position when he decides to default, our definition seems more appropriate. As shown in Table 1, 78 percent of the loans in our sample "default" by the end of the observation period (September 2009) by our definition.
We estimate a borrower's equity position in percentage terms (
![]() ) for borrower
) for borrower ![]() at month
at month ![]() in ZIP code
in ZIP code ![]() as:
as:
where
We estimate house values in the months after origination by adjusting the home value at origination (![]() ) using the monthly ZIP code-level HPI:13
) using the monthly ZIP code-level HPI:13
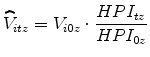 |
Finally, because it may take some time for a borrower to actually formulate his perception of his housing equity level, we use a 3-month moving average of equity (the average of this month and the previous two months).
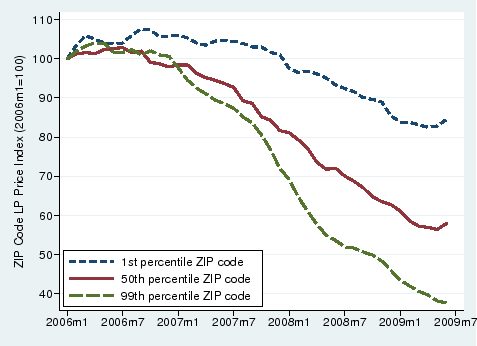
Figure 6 shows the 1st, 50th and 99th percentile house price decline between January 2006 and June 2009 among the ZIP codes in our sample. For the 50th percentile ZIP code, house prices decrease by over 40 percent between January 2006 and June 2009. The 1st and 99th percentile ZIP codes experience a 20 percent and over 60 percent drop in house price, respectively, during the same time period. The large decline in house values and the significant variation in house price movements across different ZIP codes allow us to identify the effect of negative equity on default decisions.
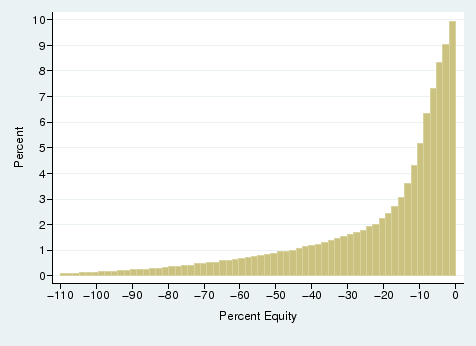
Figure 2 shows the distribution of negative equity where observations are at the loan-month level. The majority of negative equity observations are not too far away from zero. For instance, close to half of all observations are between -10 percent and 0 percent equity. Nevertheless, we do observe many borrowers with extremely low levels of equity: about 14 percent of observations have equity below -50 percent.
Table 1 shows that the average home value at origination in 2006 is close to $400,000, considerably higher than the median price of the average ZIP code in 2000. In contrast, the average home value at "termination" - either the month of default or the end of the observation period for loans that have survived - is about $300,000. The median equity at termination is about -24 percent or -$60,000 at termination. Because about half of our sample are interest-only mortgages and mortgage payments in the first a few years are mostly interest payments anyway, it is not surprising that the average mortgage balance at termination is almost identical to its value at origination.
The median loan age at termination is only 18 months, reflecting the high default rate. The interest rate at termination is nearly identical on average to that at origination, suggesting that interest rate changes are probably not a major factor inducing defaults in our sample. The median FICO score of 676 is in prime territory, but recall that these loans have 100 percent CLTV and, potentially, other risk factors such as incomplete documentation.
We also merge county-level unemployment rates from the Bureau of Labor Statistics (BLS) and county level credit card 60+ day delinquency rates from TransUnion's TrenData to the LP data. Table 1 shows that the unemployment rate increases by 1.8 percentage points over the four quarters leading to the termination month, while the credit card delinquency rate rises by 0.35 percentage points. These numbers reflect worsening economic conditions between 2006 and 2009. In addition, we merge in select ZIP code characteristics from the 2000 Census. The average median home value in 2000 for our sample ZIP codes is $172,000, and median household income is close to $48,000. A quarter of the residents in these ZIP codes have at least a Bachelor's degree. The fraction of Hispanic residents is 27 percent and the fraction of black residents is 9 percent on average.
4 Estimation Strategy
The model in Section 2 suggests that borrowers choose to default if the premium to stay,
mpay![]() rent
rent![]() , exceeds a threshold that is comprised of
, exceeds a threshold that is comprised of ![]() , the monetary and non-monetary costs of default, and the expected future capital gains. Assuming that the percentage difference between the mortgage balance and house value approximates the percentage difference between the
mortgage payment and the flow of housing services consumed, the model equivalently suggests that borrowers choose to default if equity
, the monetary and non-monetary costs of default, and the expected future capital gains. Assuming that the percentage difference between the mortgage balance and house value approximates the percentage difference between the
mortgage payment and the flow of housing services consumed, the model equivalently suggests that borrowers choose to default if equity ![]() , as described in the previous section, falls below the
threshold, denoted by
, as described in the previous section, falls below the
threshold, denoted by ![]() (for total cost). Our primary objective is to estimate
(for total cost). Our primary objective is to estimate ![]() as a percent of the current house price. As we discussed earlier, many types of costs are rolled up into
as a percent of the current house price. As we discussed earlier, many types of costs are rolled up into ![]() . First, it captures
. First, it captures ![]() , the monetary and non-monetary costs of default. Second, it includes the expected capital gains that are foregone through default. The estimates we present in Section 5 are best interpreted as "reduced form" estimates summarizing
, the monetary and non-monetary costs of default. Second, it includes the expected capital gains that are foregone through default. The estimates we present in Section 5 are best interpreted as "reduced form" estimates summarizing ![]() without precisely identifying the relative importance of
without precisely identifying the relative importance of ![]() and the expected foregone capital
gains. In the remainder of this paper, we refer to
and the expected foregone capital
gains. In the remainder of this paper, we refer to ![]() , which includes
, which includes ![]() and expected
capital gains, as "the (total) cost of default."14
and expected
capital gains, as "the (total) cost of default."14
We face two challenges to estimating ![]() . First, many observed defaults occur because of an adverse life event resulting in a negative shock to a borrower's ability to make mortgage
payments. Without controlling for these negative income shocks (or liquidity shocks), one would overestimate the incidence of strategic default and underestimate the cost of default,
. First, many observed defaults occur because of an adverse life event resulting in a negative shock to a borrower's ability to make mortgage
payments. Without controlling for these negative income shocks (or liquidity shocks), one would overestimate the incidence of strategic default and underestimate the cost of default, ![]() .
Second, 22 percent of borrowers do not default during the observation period, and are thus censored (as is the case with many duration analyses where some spells are not observed to completion). Without dealing with the censoring problem, one would again underestimate
.
Second, 22 percent of borrowers do not default during the observation period, and are thus censored (as is the case with many duration analyses where some spells are not observed to completion). Without dealing with the censoring problem, one would again underestimate ![]() .
.
We develop a two-step estimation strategy that handles both the censoring and liquidity shock problems. The first step involves estimating a discrete time hazard model from which we generate individual-level predictions of the probability of default due to an adverse life event (equivalently, the probability of default for reasons other than equity alone). In the second step, we incorporate these probabilities into a likelihood function and estimate the depth of negative equity that triggers strategic default. The depth of negative equity that triggers strategic default corresponds directly to the costs of default faced by borrowers.
We now describe the estimation strategy in more detail. Please note that we will begin with a description of the second step before discussing the first step.
4.1 Likelihood Function
There are two types of borrowers in our data: those who default and those who do not. Borrowers continuing to make loan payments have not experienced a level of negative equity sufficient to induce default. Therefore, for borrowers who have not defaulted by the end of the observation period, it
must be the case that the costs of default that they face (![]() ) is higher than the premium (to stay in their home) which, as noted before, we assume to be equivalent to negative percent equity
(
) is higher than the premium (to stay in their home) which, as noted before, we assume to be equivalent to negative percent equity
(![]() ):
):
| (4) |
In contrast, borrowers who default must either experience a liquidity shock or meet the condition ![]() . If the default is triggered by a liquidity shock, then no information is
conveyed about this borrower's cost of default. Therefore, we are only interested in the cases where the borrower does not experience a liquidity shock. Conditional on no liquidity shocks, if the borrower does not default in the previous period when his equity is
. If the default is triggered by a liquidity shock, then no information is
conveyed about this borrower's cost of default. Therefore, we are only interested in the cases where the borrower does not experience a liquidity shock. Conditional on no liquidity shocks, if the borrower does not default in the previous period when his equity is ![]() but defaults in this period when he faces an equity of
but defaults in this period when he faces an equity of ![]() , we can bound his cost of default to be between
, we can bound his cost of default to be between
![]() and
and ![]() :
:
| (5) |
For estimation purposes, we assume ![]() is gamma-distributed with shape parameter
is gamma-distributed with shape parameter ![]() and scale parameter
and scale parameter ![]() . Gamma is a flexible distribution and has non-negative support, corresponding to our assumption that
. Gamma is a flexible distribution and has non-negative support, corresponding to our assumption that ![]() be non-negative. With these pieces in hand, we construct the following likelihood function:
be non-negative. With these pieces in hand, we construct the following likelihood function:
where
To estimate equation (6), we collapse our loan-month level data set into a data set with one observation per loan. Each observation is a loan in the month of default or, for loans not observed to default, the last month of the observation period. Because house prices decreased so soon after loan origination in the sample, this last observation almost always corresponds to the lowest equity level experienced by the borrower. Therefore, the last observation of each loan contains all the information that we need for the maximum likelihood estimation.
4.2 Estimating the Probability of No Liquidity Shocks
The first step of our two-step strategy involves estimating
![]() , which appears in equation (6). We estimate this probability as follows. First, we estimate a discrete-time hazard model (Deng et al., 2000; Allison, 1982):
, which appears in equation (6). We estimate this probability as follows. First, we estimate a discrete-time hazard model (Deng et al., 2000; Allison, 1982):
where
Next, we construct predicted values (
![]() ) from the estimated baseline hazard function (
) from the estimated baseline hazard function (
![]() ) and parameter
) and parameter
![]() but exclude the equity dummies
but exclude the equity dummies
![]() .
.
This construction holds equity constant at its starting value of 0 (recall, all borrowers had zero equity at origination). In other words,
And third, we note that
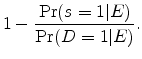 |
Therefore, at any given level of equity
This estimate of
5.1 Baseline Results
As described in the previous section, our estimation strategy has two steps. In the first step, we estimate a logit model of default and then use the estimated coefficients to construct the probability that a default is not due to a liquidity shock at a given equity level. In the second step, we
incorporate this probability into equation (6) and then estimate the two parameters of the default cost distribution, ![]() and
and ![]() , via maximum likelihood.
, via maximum likelihood.
Specifically, we estimate the following logit model in the first step:
where
All the control variables in equation (8) except for ![]() account for the liquidity-shock-driven component of default. The time dummy variables
account for the liquidity-shock-driven component of default. The time dummy variables ![]() account for national-level shocks, such as gasoline price changes and tax rebates. Changes in county-level unemployment and credit card delinquency rates account for local, time-varying economic
conditions, and the squared terms allow for nonlinear effects on default.
account for national-level shocks, such as gasoline price changes and tax rebates. Changes in county-level unemployment and credit card delinquency rates account for local, time-varying economic
conditions, and the squared terms allow for nonlinear effects on default.
![]() int
int![]() and its lags capture the potentially impact of interest rate resets on default.
And finally, because loan age is specified through dummy variables, the baseline default hazard is captured flexibly and without strong functional form assumptions. Similarly, equity enters equation (8) as dummy variables to allow for a flexible relationship between equity
and default. Note that excluding
and its lags capture the potentially impact of interest rate resets on default.
And finally, because loan age is specified through dummy variables, the baseline default hazard is captured flexibly and without strong functional form assumptions. Similarly, equity enters equation (8) as dummy variables to allow for a flexible relationship between equity
and default. Note that excluding ![]() would lead to overestimating the importance of liquidity shocks since these events are likely to be correlated with negative equity (e.g. areas with
worsening economic conditions also experience declining house prices). To reiterate, the inclusion of
would lead to overestimating the importance of liquidity shocks since these events are likely to be correlated with negative equity (e.g. areas with
worsening economic conditions also experience declining house prices). To reiterate, the inclusion of ![]() helps separate the role of liquidity shocks from that of equity.
helps separate the role of liquidity shocks from that of equity.
Table 2 shows the estimation results of this logit model. Column (1) displays the estimated coefficients and column (3) displays the odds ratios. Because the unemployment rate and credit card delinquency rate are measured at the county level, the standard errors are clustered at the county level. Turning to the results on the full set of loan-age dummies, the conditional odds of default peaks around 24 months and then declines slightly. Consistent with the previous literature on mortgage default, we find that newly originated loans have relatively low default probabilities and as time passes, some borrowers experience exogenous shocks, which leads to higher default rates. As borrowers that face the highest liquidity risk exit the sample, the default rate moderates.16
The results in Table 2 also suggest that an increase in one's mortgage interest rate may induce default. However, since fewer than 10 percent of borrowers actually experienced an interest rate increase during the observation period, most observed defaults are not driven by this factor. Also, increases in county-level unemployment rates or credit card delinquency rates are positively correlated with mortgage default, as one would expect. Finally, the odds of default increase monotonically as borrowers fall deeper underwater. For example, equity between -1 and -9 percent does not substantially elevate the odds of default relative to zero equity, whereas equity below -60 percent more than doubles the odds of default.
Using the logit estimates, we predict the probability of experiencing a liquidity shock:
If we pool all the loan-month observations that have the same equity level together, we know from the mean of our default measure the fraction of these observations that defaulted, either because of liquidity shocks or negative equity. We also know from the mean of
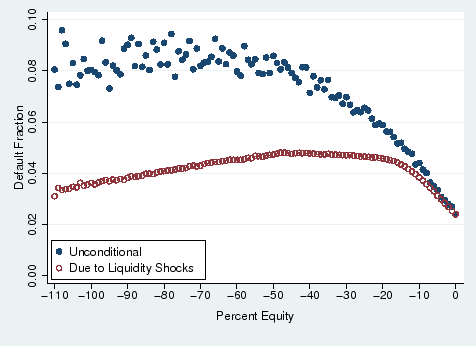
Figure 3 illustrates the relationship between equity and default implied by our estimates. The solid circles represent the unconditional default rate at each equity level while the hollow circles are the average liquidity shock probabilities (
![]() ) at each equity level. The difference between the two sets of circles represents the strategic component of default that is induced by negative equity. When borrowers are not
deeply underwater, default can be entirely accounted for by liquidity shocks, as shown by the hollow circles overlapping the solid ones. Consistent with Foote et al. (2008), being slightly underwater is evidently not a sufficient condition for default. However, between -10 and
-15 percent equity, the unconditional and liquidity-driven default rates diverge, suggesting that equity becomes an important, independent predictor of default decisions as borrowers become more underwater.
) at each equity level. The difference between the two sets of circles represents the strategic component of default that is induced by negative equity. When borrowers are not
deeply underwater, default can be entirely accounted for by liquidity shocks, as shown by the hollow circles overlapping the solid ones. Consistent with Foote et al. (2008), being slightly underwater is evidently not a sufficient condition for default. However, between -10 and
-15 percent equity, the unconditional and liquidity-driven default rates diverge, suggesting that equity becomes an important, independent predictor of default decisions as borrowers become more underwater.
With
![]() in hand, we can construct the likelihood function (6) and then estimate
in hand, we can construct the likelihood function (6) and then estimate ![]() and
and ![]() , the parameters of the gamma distribution from which default costs are drawn. Column (1) of Table 3 shows the results for the full sample. The
estimated shape parameter (
, the parameters of the gamma distribution from which default costs are drawn. Column (1) of Table 3 shows the results for the full sample. The
estimated shape parameter (![]() ) is 1.68 and scale parameter (
) is 1.68 and scale parameter (![]() ) is 45.17 The estimated cumulative distribution function (CDF),
) is 45.17 The estimated cumulative distribution function (CDF),
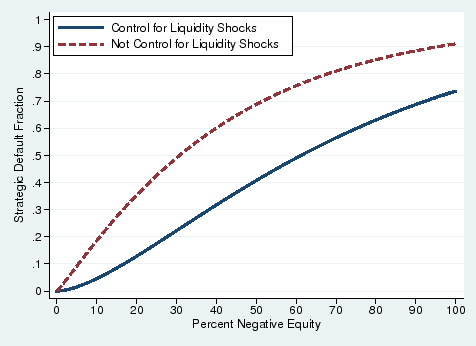
![]() , is shown by the solid line in Figure 4. This distribution implies that the median borrower walks away from his home when he is 62 percent
underwater.
, is shown by the solid line in Figure 4. This distribution implies that the median borrower walks away from his home when he is 62 percent
underwater.
As a thought experiment, column (2) of Table 3 shows parameter estimates erroneously omitting the liquidity shock probability from the likelihood function. In other words, if we mistakenly attribute all observed defaults to equity-driven strategic decisions, we find that the median borrower
walks away when equity hits just -31 percent. Comparing columns (1) and (2) illustrates not only that controlling for liquidity shocks is important in principle, but also that doing so leads to quantitatively important differences. Note that the estimate in column (2) is only 7 percentage points
lower than the median percent equity reported in Table 1, which can be thought of as a naïve estimate of ![]() that does not account for liquidity shocks or censoring. The dashed line in
Figure 4 plots the estimated CDF that ignores liquidity shocks, which lies above the solid line. Indeed, not accounting for liquidity shocks makes borrowers appear far more sensitive to negative equity than they actually are.
that does not account for liquidity shocks or censoring. The dashed line in
Figure 4 plots the estimated CDF that ignores liquidity shocks, which lies above the solid line. Indeed, not accounting for liquidity shocks makes borrowers appear far more sensitive to negative equity than they actually are.
5.2 Further Discussion
Our estimation strategy involves two steps and in practice one could take somewhat different approaches in implementing the two-step strategy. This section presents checks to ensure our findings are robust and provides discussion about the circumstances under which our estimates may be biased.
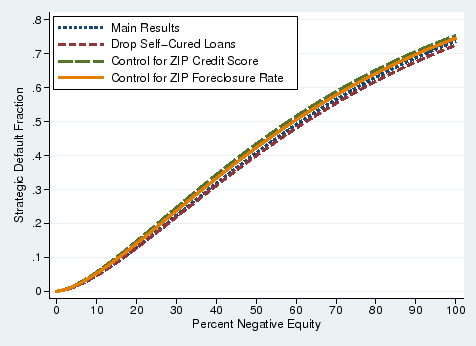
One may be concerned that the logit model used in the first step is not flexible enough. To address such concerns, we estimate a model with 110 rather than 10 equity dummies and the estimates are almost identical to our baseline results. To allow for additional flexibility in the baseline
default hazard, we interact
![]() unemp
unemp![]() and
and
![]() ccdelinq
ccdelinq![]() with the full set of loan age dummies in the logit model. In this way, we
allow mortgages in areas with worsening local economic conditions to have a different baseline default hazard than in other areas. Our estimates remain unchanged.
with the full set of loan age dummies in the logit model. In this way, we
allow mortgages in areas with worsening local economic conditions to have a different baseline default hazard than in other areas. Our estimates remain unchanged.
Recall that we classify a borrower as having defaulted if he is 90+ days delinquent for two consecutive months. If a borrower resumes making mortgage payments after defaulting according to our definition, one may be concerned that our definition mischaracterizes him as a "strategic defaulter." Indeed, Adelino et al. (2009) argue that such "self-cure risk" may partially explain why servicers have been reluctant and slow to renegotiate loans that are seriously delinquent. Unlike in their data, we find that only about 2 percent of loans cure themselves during the observation period after becoming 90+ days delinquent for two consecutive months. For the self-cured loans, it is unclear whether the improvement in the payment status is because the borrower is truly trying to stay in their homes or due to a loan modification taking place. Regardless, the dashed red line in Figure 5, which we estimate excluding the loans that self-cure, is nearly identical to baseline results (shown by the blue dotted line).
Because we only have county-level controls for local economic condition, one may be concerned that ZIP codes with large subsequent house price declines are more vulnerable to adverse economic shocks than other ZIP codes in the same county. The potential correlation between the initial characteristics of ZIP codes and subsequent house price movements may bias our estimates. To address such concerns, we use two additional ZIP code-level variables that are measured near the beginning of the sample period and may be correlated with the magnitude of house price decline between 2006 and 2009. First, we include the median credit score of those with mortgages living in a ZIP code in 2005 as an additional regressor in the logit equation. Table 4 shows that the median credit score is 746 on average across ZIP codes.18 When we include this variable in the logit model, we estimate a negative and statistically significant coefficient, suggesting that borrowers in ZIP codes with higher credit scores in 2005 are less likely to default between 2006 and 2009. Although this coefficient has the expected sign and is statistically significant, Figure 5 shows that including this credit score measure little changes our estimates of the parameters of the Gamma distribution.
The second variable that we use is the foreclosure rate in the first half of 2006 in a ZIP code.19 Table 4 shows that the average foreclosure rate is about 0.8 percent in the first half of 2006. Including this variable in the logit model results in a positive and statistically significant coefficient, suggesting that borrowers in ZIP codes with higher foreclosure rates at the beginning of the sample are more likely to subsequently default. Again, even though the coefficient is significant, Figure 5 shows that including the foreclosure measure generates an almost identical estimate of the cost of default.20 Since including these two variables does not change our estimate of the cost of default, it seems that our liquidity measures (loan age dummies, calendar time dummies, etc.) adequately control for liquidity liquidity shocks.
Although we flexibly specify equation (8) by using loan age and time dummies, measuring equity more precisely than previous research, and including local economic distress variables that previous studies have not used (such as the credit card delinquency rate), one may nonetheless be concerned that there are omitted variables in the logit estimation. This concern is especially problematic if one believes that there are individual-level adverse shocks that are not captured by our model but correlated with equity. In this case, the estimation would overstate the importance of equity as a driver of defaults.
Whether and to what degree a systematic correlation between unobserved individual-level adverse shocks and equity has affected our results are unclear. As seen in Figure 6, the decline in equity is driven by house price declines that are widespread across ZIP codes and over time. The unobserved individual factors that has the potential to bias our estimates must be correlated with these house price declines but not with loan age, calendar time, and county-level measures of distress, such as changes in the unemployment or credit card delinquency rates. It may be that the expectation of local economic distress not captured by our liquidity measures but induces default. However, to the extent that such an expectation is capitalized in house prices, defaults would not arise due to an as-yet-to-happen event but because of a decrease in equity. Also, it may be that a borrower's family or friends would only lend to him if he is not too deeply underwater. However, unless the borrower expects the housing market to turn around quickly, it would be strange for him to borrow money so that he can become more deeply underwater. Even though one may be able to tell stories that challenge our identification, we find such stories convoluted and idiosyncratic.
5.3 Heterogeneity in the Cost of Default
The results shown in Table 3 and Figure 4 show that there is substantial heterogeneity in the cost of defaulting across individuals. The estimated standard deviation of ![]() is 58 percent (
is 58 percent (
![]() ). Also, the 25th percentile is 33 percent of the house value and the 75th percentile is 103 percent of the house value. To help explain such heterogeneity, we
separately estimate
). Also, the 25th percentile is 33 percent of the house value and the 75th percentile is 103 percent of the house value. To help explain such heterogeneity, we
separately estimate ![]() ,
, ![]() , and the distribution of
, and the distribution of ![]() for borrowers facing different incentives and having different attitudes and expectations. Table 5 summarizes the estimated distribution of default cost for each sub-sample. Figures 6-11 shows the CDF of these estimated distributions.
for borrowers facing different incentives and having different attitudes and expectations. Table 5 summarizes the estimated distribution of default cost for each sub-sample. Figures 6-11 shows the CDF of these estimated distributions.
In Figure 6, we show that borrowers living in Florida and Nevada, which are recourse states where lenders may sue for a deficiency judgment, have higher estimated costs of default than those living in Arizona and California. Regardless of which state the borrower is from, the costs of default are high. However, the median borrower in the recourse states defaults when he is 20 to 30 percentage points more underwater than the median borrower in the non-recourse states. This result suggests that borrowers may factor into the costs of default the potential legal liabilities resulting from a foreclosure. Consistent with this result, Ghent and Kudlyak (2009) find that borrowers in recourse states are less likely to strategically default.
Similarly, borrowers with high FICO scores may consider the penalties of default more than borrowers with low FICO scores. Default by a high-FICO borrower conveys new information about the borrower's credit quality whereas default by a low-FICO borrower does not. Accordingly, a high-FICO borrower will see a steeper increase in his borrowing cost after a default than a low-FICO borrower. In Figure 7, we find that, generally speaking, borrowers with higher FICO scores find it more costly to default. The median borrower among those with FICO scores between 620 and 680 walks away when equity hits -51 percent, compared to -68 percent for those with FICO scores above 720. This difference may also reflect the difference in the commitment a borrower has to the repayment of debt, which is, to some extent, captured by his FICO score.
However, as seen in Figure 8, borrowers with the lowest FICO scores (below 620) are not the most "ruthless." An explanation for this is in Keys et al. (2010), who show that lenders screen these loans more rigorously and the volume of loans with little or no documentation falls sharply at 620. In Figure 8, we compare borrowers with FICO scores between 610 and 619, who faced stricter underwriting standards, to borrowers with FICO scores between 620 and 629. On average, we find that borrowers with FICO scores right above the 620 cutoff appear more sensitive to negative equity and therefore more ruthless than those with FICO scores right below 620.21 This result suggests that by requiring borrowers to document their income and assets, lenders can identify borrowers who seem more committed to repaying their debt. Figure 9 corroborates that in full sample, where 70 percent have reduced or no documentation (see Table 1), borrowers who fully documented their income and assets have higher costs of default.
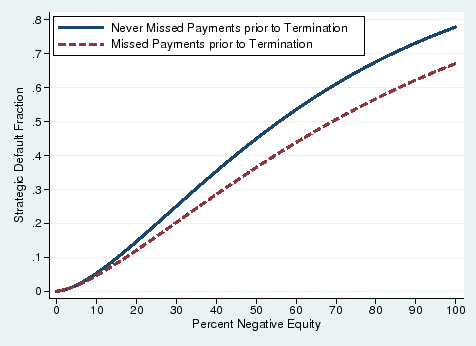
The next two figures characterize the heterogeneity in ![]() based on the attitudes of borrowers. In Figure 10, we classify borrowers into two groups based on the
payment history between loan origination and termination. The first group consists of borrowers who missed at least one payment and then became current prior to termination (either through default or the end of the observation period). The second group is comprised of borrowers who always stayed
current until termination. Borrowers from the first group (dashed line) appear to have somewhat higher default costs than the latter group, consistent with the view that borrowers who missed payments but tried to stay current may have had a stronger desire to remain in their homes.
based on the attitudes of borrowers. In Figure 10, we classify borrowers into two groups based on the
payment history between loan origination and termination. The first group consists of borrowers who missed at least one payment and then became current prior to termination (either through default or the end of the observation period). The second group is comprised of borrowers who always stayed
current until termination. Borrowers from the first group (dashed line) appear to have somewhat higher default costs than the latter group, consistent with the view that borrowers who missed payments but tried to stay current may have had a stronger desire to remain in their homes.
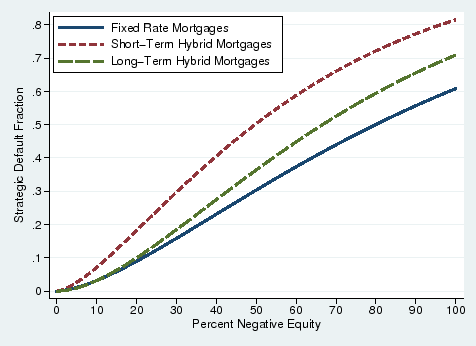
Figure 11 shows the CDF of ![]() for borrowers with different loans: fixed rate mortgages, short-term hybrid mortgages ("2/28's" and "3/27's"), and long-term
hybrid mortgages. Non-prime borrowers expecting house prices to continue to rise may have chosen this type of mortgage because the initial payments were affordable (Gerardi et al., 2008;
Mayer and Pence, 2008). These mortgages feature fixed, "teaser" rates for the first 2 or 3 years, before resetting to a higher, fully index, floating rate. Borrowers with short-term
hybrids appear the most strategic as the median borrower faces a cost that is 30 percentage points lower than that for the median fixed-rate borrower (see Table 5). While it is somewhat difficult to reconcile this result with the common (mis)perception that naïve borrowers unknowingly financed home purchases with short-term hybrid loans, it is important to note that even among this most strategic group of borrowers, the median cost of default is 50 percent of the house value.
for borrowers with different loans: fixed rate mortgages, short-term hybrid mortgages ("2/28's" and "3/27's"), and long-term
hybrid mortgages. Non-prime borrowers expecting house prices to continue to rise may have chosen this type of mortgage because the initial payments were affordable (Gerardi et al., 2008;
Mayer and Pence, 2008). These mortgages feature fixed, "teaser" rates for the first 2 or 3 years, before resetting to a higher, fully index, floating rate. Borrowers with short-term
hybrids appear the most strategic as the median borrower faces a cost that is 30 percentage points lower than that for the median fixed-rate borrower (see Table 5). While it is somewhat difficult to reconcile this result with the common (mis)perception that naïve borrowers unknowingly financed home purchases with short-term hybrid loans, it is important to note that even among this most strategic group of borrowers, the median cost of default is 50 percent of the house value.
6 Conclusion
We develop a two-step estimation strategy to estimate the depth of negative equity that triggers strategic default. We find that the median borrower does not walk away until equity has fallen to -62 percent of the house value. This reduced form estimate of the cost of default suggests that borrowers face high monetary and non-monetary costs, including the prospect of foregoing future capital gains. Separating the relative importance of each of these factors in affecting borrowers' default decisions is a direction for further research.
Our results challenge traditional models of hyper-informed borrowers operating in a world without economic frictions (Vandell, 1995). Many borrowers in our sample bought houses at the peak of a housing bubble, put no money down, and seemingly had little to lose, financially, by walking away once home values dropped. Yet they pay a substantial premium over market rents to keep their homes. More typical borrowers therefore may be willing to pay an even larger premium given that they have likely invested more financially and emotionally in their house. Why borrowers choose to pay this premium is another direction for further research. Anecdotal evidence suggests that some homeowners who bought at the peak of the housing market refuse to believe that their houses depreciated substantially (Forbes.com, 12/10/2009). In this case, we assign a more negative value of equity to a borrower who is behaving as if he is not as severely underwater and we thus overstate the costs of default relative to what the borrower believes them to be. Additionally, borrowers may be loss averse and thus overvalue the prospect of future capital gains (even when the probability of substantial house price appreciation is low) (Kahneman and Tversky, 1979).
A limitation of our approach is that the empirical strategy does not allow time-varying factors to affect the distribution of default costs. As the number of defaults and foreclosures reach record high levels, lenders may find it increasingly worthwhile to pursue deficiency judgments among borrowers, which would increase the potential legal liabilities of default. Also, as default becomes more commonplace, the associated stigma may decrease. Indeed, Guiso et al. (2009) find that their survey respondents are more likely to say they would strategically default if they know someone who has walked away. Developing a richer model of default to allow for these time-varying factors is another direction for future research.
Despite these limitations, our paper complements the existing literature by characterizing the relationship between ruthless default and equity more completely than previous work. Our results lend support to two existing hypotheses about why borrowers default. Borrowers do not ruthlessly exercise the default option at relatively low levels of negative equity, broadly consistent with the "double-trigger" hypothesis. But by the time equity falls below -50 percent, 50 percent of defaults appear to be strategic. All told, of all the defaults in our sample, we estimate that only one-in-five are strategic.
Bibliography
Available from http://www.nytimes.com/.
Available from http://online.wsj.com/article/SB126100260600594531.html.
Data Appendix
We started with LoanPerformance (LP) data on non-prime loans that satisfy the following criteria:
- Loans on single family properties
- Loans originated in 2006
- Loans in Arizona, California, Florida, and Nevada
- Purchase loans only
- First liens only
- Loans with a combined initial loan to value ratio (CLTV) of 100 percent
In the next step, we merged the following datasets into the LP loan-level data:
- LP ZIP code-level house price index from January, 2006 to September, 2009
- County-level monthly unemployment rate from the Bureau of Labor Statistics (BLS) from January, 2006 to September, 2009
- County-level quarterly credit card 60+ delinquency rate from TransUnion's Trend Data from 2006:Q1 to 2009:Q3
Then we carried out the following data cleaning procedures:
- Drop loans with only one monthly observation
- Drop the loan if the delinquency status is not reported in at least one month during the sample period
- Drop the loan if the current interest rate is not reported in at least one month during the sample period
- Drop the loan if it is indicated to be paid off in one month but has some other status (e.g. current or delinquent) in the next month
- Drop the loan if it is already 90+ day delinquent, in foreclosure, or REO in the first month when we observe it
- Drop the loan if the first payment date is before origination date or more than three months after the origination date
 Source. LoanPerformance, a division of First American CoreLogic. |
 Note. Figure based on 1.9 million loan-month observations. Percent Equity measured as a percent of current house value. |
 Note. Figure based on 1.9 million loan-month observations. Percent Equity is measured as a percent of current house value and is rounded to the nearest percentage point. Solid circles represent the unconditional probability of default at a given equity level. Hollow circles represent the probability of default due to experiencing a liquidity shock at a given equity level. |
 Note. N=100,229 (Control for Liquidity Shocks) and 100,243 (Not Control for Liquidity Shocks). Not Control for Liquidity Shocks Parameters of CDF estimated using maximum likelihood and assuming gamma distribution. CDF not controlling for liquidity shocks sets
|
 Note. N=100,229 (Main Results), 97,498 (Drop Self-Cured Loans), 98,238 (Control for ZIP Credit Score), and 100,068 (Control for ZIP Foreclosure Rate). Parameters of CDF estimated using maximum likelihood and assuming gamma distribution. Main results are the same as controlling for liquidity shocks in Figure 4. |
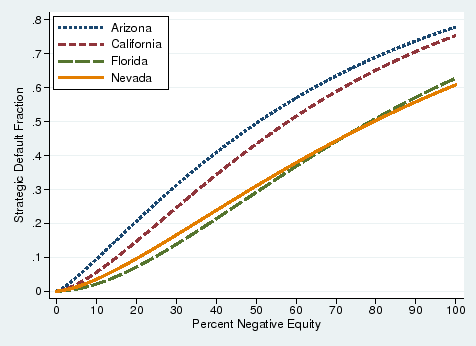 Note. N=9,298 (Arizona), 62,077 (California), 20,615 (Florida), and 5,129 (Nevada). Parameters of CDF estimated using maximum likelihood and assuming gamma distribution. Florida and Nevada are states where lender has recourse. |
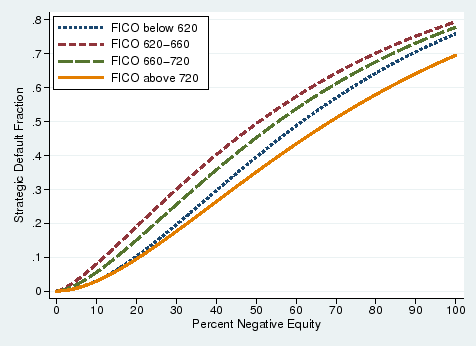 Note. N=10,966 (FICO below 620), 27,912 (FICO 620-660), 39,132 (FICO 660-720), and 21,574 (FICO above 720). Parameters of CDF estimated using maximum likelihood and assuming gamma distribution. FICO observed at loan origination. |
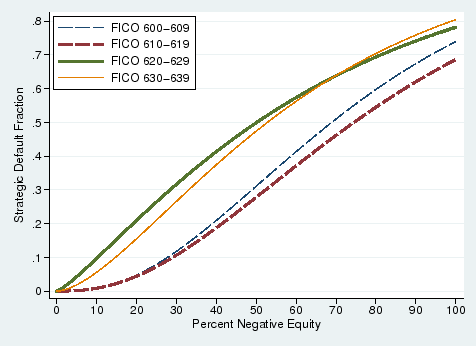 Note. N=2,972 (FICO 600-609), 2,361 (FICO 610-619), 6,430 (FICO 620-629), and 6,166 (FICO 630-639). Parameters of CDF estimated using maximum likelihood and assuming gamma distribution. FICO observed at loan origination. |
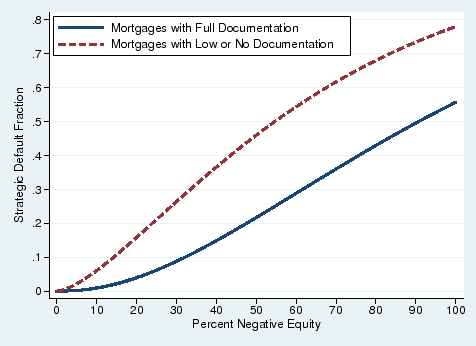 Note. N=27,250 (Mortgages with Full Documentation) and 70,021 (Mortgages with Low or No Documentation). Parameters of CDF estimated using maximum likelihood and assuming gamma distribution. Documentation status indicates whether borrower provided proof of income and assets. |
 Note. N=53,576 (Never Missed Payments prior to Termination) and 46,638 (Missed Payments prior to Termination). Parameters of CDF estimated using maximum likelihood and assuming gamma distribution. Borrowers who never missed payments are current until termination. |
 Note. N=9,642 (Fixed Rate Mortgages), 63,149 (Short-Term Hybrid Mortgages), and 24,382 (Long-Term Hybrid Mortgages). Parameters of CDF estimated using maximum likelihood and assuming gamma distribution. Short-term hybrids include "2/28's" and "3/27's." |
| Mean | Median | SD | |
| Defaulted During Observation Period | 0.78 | 1 | 0.42 |
| Home Value at Origination ($ 000's) | 393 | 360 | 183 |
| Home Value at Termination ($ 000's) | 308 | 268 | 172 |
| Mortgage Balance at Origination ($ 000's) | 393 | 360 | 183 |
| Mortgage Balance at Termination ($ 000's) | 393 | 359 | 184 |
| Percent Equity at Termination (%) | -34.4 | -23.7 | 35.0 |
| Equity at Termination ($ 000's) | -79.7 | -59.6 | 78.1 |
| Scheduled Payments at Termination ($, monthly) | 2011 | 1828 | 927 |
| Loan Age at Termination (months) | 18.4 | 18.0 | 9.8 |
| Interest Rate at Origination (%) | 7.4 | 7.5 | 1.2 |
| Interest Rate at Termination (%) | 7.6 | 7.5 | 1.1 |
| FICO Score at Origination | 676 | 671 | 50.7 |
| Low or No Documentation Indicator | 0.70 | 1 | 0.46 |
| Property in Arizona | 0.09 | 0 | 0.28 |
| Property in California | 0.63 | 1 | 0.48 |
| Property in Florida | 0.24 | 0 | 0.43 |
| Property in Nevada | 0.05 | 0 | 0.21 |
| Change in Unemployment Rate at Termination (%) | 1.80 | 1.30 | 1.70 |
| Change in Credit Card Delinquency Rate at Termination (%) | 0.35 | 0.30 | 0.44 |
| Mean | Median | SD | |
| Median Home Value ($ 000's) | 172 | 146 | 100 |
| Median Household Income ($ 000's) | 46.7 | 43.2 | 15.5 |
| Fraction Residents with Bachelor's Degree | 0.24 | 0.21 | 0.13 |
| Fraction Residents Hispanic | 0.27 | 0.20 | 0.23 |
| Fraction Residents Black | 0.09 | 0.04 | 0.13 |
| Coefficient
(1) |
SE
(2) |
Odds Ratio
(3) |
|
| Change in Interest Rate | 0.41 | (0.01) | 1.51 |
| Change in Interest Rate Lag 1 | 0.38 | (0.03) | 1.46 |
| Change in Interest Rate Lag 2 | 0.23 | (0.01) | 1.26 |
| Change in Unemployment Rate | 0.14 | (0.07) | 1.15 |
|
(Change in Unemployment Rate) |
-0.02 | (0.01) | 0.98 |
| Change in Credit Card Delinquency Rate | 0.57 | (0.09) | 1.76 |
|
(Change in Credit Card Delinquency Rate) |
-0.19 | (0.06) | 0.83 |
| Coefficient
(1) |
SE
(2) |
Odds Ratio
(3) |
|
| Equity -100% or below | 0.97 | (0.10) | 2.63 |
| Equity between -80% and -99% | 0.84 | (0.11) | 2.32 |
| Equity between -60% and -79% | 0.72 | (0.11) | 2.06 |
| Equity between -50% and -59% | 0.62 | (0.10) | 1.86 |
| Equity between -40% and -49% | 0.54 | (0.10) | 1.71 |
| Equity between -30% and -39% | 0.45 | (0.09) | 1.57 |
| Equity between -20% and -29% | 0.32 | (0.08) | 1.37 |
| Equity between -10% and -19% | 0.17 | (0.06) | 1.18 |
| Equity between -5% and -9% | 0.08 | (0.05) | 1.09 |
| Equity between -1% and -4% | 0.05 | (0.03) | 1.05 |
| Coefficient
(1) |
SE
(2) |
Odds Ratio
(3) |
|
| 1 month | -0.14 | (0.10) | 0.87 |
| 2 months | 0.02 | (0.09) | 1.02 |
| 3 months | 0.05 | (0.09) | 1.05 |
| 4 months | 0.07 | (0.10) | 1.07 |
| 5 months | 0.08 | (0.09) | 1.08 |
| 6 months | 0.06 | (0.09) | 1.06 |
| 7 months | 0.07 | (0.09) | 1.07 |
| 8 months | 0.08 | (0.08) | 1.08 |
| 9 months | 0.09 | (0.08) | 1.10 |
| 10 months | 0.13 | (0.09) | 1.14 |
| 11 months | 0.15 | (0.09) | 1.17 |
| 12 months | 0.16 | (0.09) | 1.18 |
| 13 months | 0.21 | (0.09) | 1.24 |
| 14 months | 0.20 | (0.10) | 1.22 |
| 15 months | 0.19 | (0.09) | 1.21 |
| 16 months | 0.19 | (0.09) | 1.21 |
| 17 months | 0.25 | (0.10) | 1.29 |
| 18 months | 0.25 | (0.10) | 1.28 |
| 19 months | 0.27 | (0.10) | 1.31 |
| 20 months | 0.29 | (0.10) | 1.33 |
| 21 months | 0.34 | (0.11) | 1.41 |
| 22 months | 0.45 | (0.10) | 1.56 |
| 23 months | 0.28 | (0.10) | 1.32 |
| 24 months | 0.51 | (0.10) | 1.67 |
| 25 months | 0.32 | (0.10) | 1.37 |
| 26 months | 0.39 | (0.10) | 1.47 |
| 27 months | 0.35 | (0.10) | 1.41 |
| 28 months | 0.28 | (0.10) | 1.32 |
| 29 months | 0.26 | (0.10) | 1.30 |
| 30 months | 0.29 | (0.11) | 1.34 |
| 31 months | 0.26 | (0.10) | 1.30 |
| 32 months | 0.24 | (0.11) | 1.28 |
| 33 months | 0.25 | (0.10) | 1.28 |
| 34 months | 0.24 | (0.12) | 1.27 |
| 35 months | 0.30 | (0.11) | 1.35 |
| 36 months | 0.23 | (0.10) | 1.25 |
| 37 months | 0.19 | (0.13) | 1.21 |
| 38 months | 0.15 | (0.19) | 1.16 |
| 39 months | 0.23 | (0.18) | 1.26 |
| Coefficient
(1) |
SE
(2) |
Odds Ratio
(3) |
|
| 2006Q3 | 0.44 | (0.13) | 1.55 |
| 2006Q4 | 0.81 | (0.17) | 2.26 |
| 2007Q1 | 1.12 | (0.19) | 3.05 |
| 2007Q2 | 1.31 | (0.20) | 3.72 |
| 2007Q3 | 1.40 | (0.21) | 4.04 |
| 2007Q4 | 1.09 | (0.21) | 2.98 |
| 2008Q1 | 1.04 | (0.23) | 2.82 |
| 2008Q2 | 1.02 | (0.25) | 2.79 |
| 2008Q3 | 1.06 | (0.27) | 2.90 |
| 2008Q4 | 1.20 | (0.29) | 3.31 |
| 2009Q1 | 0.75 | (0.29) | 1.12 |
| 2009Q2 | 0.59 | (0.30) | 1.80 |
| Control for Liquidity Shocks
(1) |
Not Control for Liquidity Shocks
(2) |
|
| Equity below 0 | 19 | 100 |
| Equity between 0 and -10% | 5 | 100 |
| Equity below -50% | 50 | 100 |
| Control for Liquidity Shocks
(1) |
Not Control for Liquidity Shocks
(2) |
|
| Shape Parameter ( |
1.68 | 1.12 |
| (0.02) | (0.01) | |
| Scale Parameter ( |
45 | 38 |
| (1.0) | (0.57) | |
| N | 100,216 | 100,243 |
| Control for Liquidity Shocks
(1) |
Not Control for Liquidity Shocks
(2) |
|
| p25 | 33 | 14 |
| p50 | 62 | 31 |
| p75 | 103 | 59 |
| Mean | Std Dev | |
| # ZIP Codes = 1,551 | ||
| ZIP Code Median Credit Score in 2005 | 746 | 43 |
| ZIP Code Foreclosure Rate in 2006:H1 (%) | 0.80 | 0.68 |
| (1) | (2) | |
| ZIP Code Median Credit Score in 2005 | -0.002 | |
| ZIP Code Median Credit Score in 2005, standard error | (0.000) | |
| ZIP Code Foreclosure Rate in 2006:H1 (%) | 0.087 | |
| ZIP Code Foreclosure Rate in 2006:H1 (%, standard error) | (0.020) | |
| N | 1.8M | 1.9M |
| p25
(1) |
p50
(2) |
p75
(3) |
|
| Full Sample | 33 | 62 | 103 |
| Arizona | 24 | 51 | 92 |
| California | 31 | 59 | 101 |
| Florida | 46 | 79 | 128 |
| Nevada | 41 | 80 | 136 |
| FICO below 620 | 35 | 62 | 99 |
| FICO between 620 and 680 | 26 | 51 | 88 |
| FICO between 680 and 720 | 33 | 59 | 97 |
| FICO above 720 | 38 | 68 | 110 |
| FICO 610-619 | 47 | 75 | 113 |
| FICO 620-629 | 23 | 50 | 91 |
| Loans with Full Documentation | 53 | 89 | 139 |
| Loans with Low or No Documentation | 28 | 53 | 92 |
| Never Missed Payments prior to Termination | 30 | 55 | 93 |
| Missed Payments prior to Termination | 36 | 69 | 119 |
| Fixed Rate Loans | 43 | 81 | 136 |
| Short-Term Hybrid Loans | 26 | 50 | 85 |
| Long-Term Hybrid Loans | 38 | 67 | 110 |
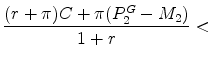 mpay
mpay
![\displaystyle L = \prod^N_{i=1} \left[ F(-E_i\vert\bm{\theta}) - F(-E_{-1,i}\vert\bm{\theta}) \right]^{D_i \cdot \Pr(s_i=0\vert E_i, D_i=1)} \left[1 - F(-E_i\vert\bm{\theta}) \right]^{1-D_i}](img42.gif)