A Semiparametric Characterization of Income Uncertainty over the Life Cycle†
Keywords: Income uncertainty, forecast errors, semiparametric estimates, life cycle dynamics
Abstract:
We propose a novel approach to estimate household income uncertainty at various future horizons, and characterize how the estimated uncertainty evolves over the life cycle. We measure income uncertainty as the variance of linear forecast errors conditional on information available to households prior to observing the realized income. This approach is semiparametric because we impose essentially no restrictions on the statistical properties of the forecast errors. Relative to previous studies, we find lower and less persistent income uncertainties that call for a life cycle consumption profile with a less pronounced hump.
JEL Classification: D12, D91, E24
1 Introduction
Income uncertainty plays an important role in household decisions regarding consumption, saving, and investment. First, in the presence of incomplete financial markets, households facing uninsurable income risk have to save for precautionary reasons (Aiyagari (1994)). How much they need to save crucially depends on their level of future income uncertainty. Second, people choose their investment portfolios to achieve optimal exposure to risks. How much people should invest in risky assets, such as stocks, also depends on their idiosyncratic exposure to income risks (Viceira (2001)). Finally, choices of financial contracts and durable goods purchasing decisions are critically affected by household income uncertainty. For instance, Campbell and Cocco (2003) show that homeowners with more risky income should choose fixed-rate mortgages over adjustable-rate mortgages.
Many of these household financial and economic decisions exhibit strong life cycle patterns. It is well known that nondurable goods consumption has a hump-shaped life cycle profile that closely tracks income (Gourinchas and Parker (2002)). Meanwhile, stock market participation rates are particularly high among middle-aged households. Homeownership and durable goods consumption also tend to vary along the life cycle (Fernández-Villaverde and Krueger (2010)). Despite its pivotal importance, the existing literature has not yielded a concrete measure of income uncertainty, and to the best of our knowledge, even less work has been done to characterize how income uncertainty evolves over the life cycle. This paper helps bridge that gap.
The most frequently used approach to characterizing income uncertainty adopts a dichotomy that assumes income shocks can be decomposed into a permanent (random walk) and a transitory (typically i.i.d.) component.1 The identification of the variances of income shocks is obtained by examining either the variances of income growth over periods of different lengths in longitudinal data (e.g., Carroll and Samwick (1997)) or the changes of income distributions of the same cohort over time in repeated cross-sectional data (e.g., Deaton and Paxson (1994)).
Deviating from this paradigm, we first define income uncertainty as the variance of forecast errors of future income conditional on the information available to the households at the time of the forecast. Altogether, this approach is semiparametric because on the one hand we adopt a parsimonious linear projection equation to construct the forecast errors. On the other hand, we impose essentially no restrictions on the statistical properties of deviations from this linear projection (i.e., the forecast errors). Instead, we construct the forecast errors and estimate their variances for each forecast horizon up to 25 years ahead. Then, we study how these forecast errors are correlated across different forecast horizons and how their variances evolve over the life cycle.
Broadly speaking, our approach shares the similar spirit of using cross-sectional variations to characterize income riskiness. However, relative to existing literature, this semiparametric approach has three important advantages. First, it allows us to estimate the persistence of income shocks without resorting to any a priori parameterizations of these shocks, especially the unit root process that is typically assumed in previous studies. Indeed, examining the correlations of income shocks over forecast horizons, we find that the typical income process is more accurately characterized as a persistent autoregressive (AR) process rather than a unit-root process. Consequently, our approach generally implies substantially lower cumulative income risks over the life cycle compared to the existing results in the literature.
Second, our approach allows us to study how income uncertainty evolves over the life cycle. For a given age in the future, we consistently find, as one would expect, that uncertainty about income diminishes as the consumer approaches this age. More strikingly, for a fixed forecast horizon, income uncertainty demonstrates a U-shaped or J-shaped profile. When consumers are young, income uncertainty at a fixed future horizon gradually declines with age, presumably as decisions on career, human capital development, and fertility are resolved. Income uncertainty reaches and stays at its low levels during middle age. Afterwards, uncertainty rises to levels higher than at the early stage of the life cycle for some types of income--potentially due to uncertainty about working hours and health risks. This dynamic of income uncertainty is consistent with Jaimovich and Siu (2009) who find that the volatility of the business cycle component of hours worked exhibits a U-shaped pattern with respect to age.
Third, the existing methodology typically filters the predictable component of income conditional on demographic and work-related information observed concurrent to income, even when longitudinal data are available. Essentially, the filtered out part is what is ex post accountable to
econometricians, and not necessarily what is ex ante predictable to households when they assess the riskiness of their future income. In contrast, our semiparametric approach adopts more realistic and flexible information specifications. Our baseline specification assumes that households in year
![]() forecast their income at year
forecast their income at year ![]() conditional on only the demographic and
work-related information about the household in year
conditional on only the demographic and
work-related information about the household in year ![]() . This assumption is rather restrictive and in some sense allows for only the information available to econometricians, not to the
households, in year
. This assumption is rather restrictive and in some sense allows for only the information available to econometricians, not to the
households, in year ![]() . Conceivably, households may know more about their future selves in year
. Conceivably, households may know more about their future selves in year ![]() . For example, Cunha, Heckman, and Navarro (2005) point out individuals may have private information that is relevant to predicting their future income. In this spirit, in augmented specifications, we assume that households in year
. For example, Cunha, Heckman, and Navarro (2005) point out individuals may have private information that is relevant to predicting their future income. In this spirit, in augmented specifications, we assume that households in year ![]() possess some demographic and work-related information about their future selves in year
possess some demographic and work-related information about their future selves in year ![]() . Not surprisingly, we find that
expanding the information set further reduces the estimated income uncertainties, especially at farther horizons.
. Not surprisingly, we find that
expanding the information set further reduces the estimated income uncertainties, especially at farther horizons.
To further illustrate the economic significance of the refined measure of income uncertainty proposed in this paper, we examine its implications for precautionary saving and the mean consumption profile over the life cycle. Specifically, we calibrate a parsimonious income process to (partially) match our semiparametric estimates and solve for the optimal life cycle consumption profile. Because our semiparametric approach yields significantly lower income risks over the life cycle, households accumulate less precautionary saving than previous estimates would indicate. Although the magnitude of the consumption hump implied by the model is somewhat sensitive to the calibration of technology and preference parameters, using our semiparametric estimates of uncertainty, we typically obtain an appreciable consumption hump but one that is much smaller than existing income uncertainty estimates imply and is much smaller than the one empirically observed. Given that the consumption hump is unlikely accounted for only by precautionary saving, we view our simulation results as more plausible than those derived using previous uncertainty estimates.
We proceed as follows. Section 2 reviews the existing methods of measuring income variability and discusses dimensions in which these methods can be improved. Section 3 introduces a semiparametric approach to measuring income uncertainty. Section 4 describes the data and sample selection procedures. Section 5 presents the main results and sensitivity analysis. Section 6 contrasts our empirical results with those reported in earlier contributions. Section 7 studies the precautionary saving and consumption over the life cycle under various estimates of income uncertainty. Section 8 concludes and sets an agenda for future work.
2 A Critical Review of the Existing Approaches to Studying Income Uncertainty
Traditionally, when rich microdata were not readily available, researchers had to infer the volatility of household income from aggregate time-series data. The estimated measures of income volatility were often interpreted as income uncertainty. Recent studies of aggregate output (see, among others, Kim and Nelson (1999); and McConnell and Perez-Quiros (2000)) have led to findings of the so-called Great Moderation, a sharp decline in the growth volatility of GDP and its components since the mid-1980s. Fogli and Perri (2006) attribute a substantial fraction of the decrease in personal savings and the rise of external balances to this reduction in aggregate volatility. However, aggregate data can mask important variations and correlations in income at the household level, so a decrease in the volatility of aggregate income does not necessarily imply that income at the household level has become less risky. To see this, consider a hypothetical economy populated by two consumers. Every period, each consumer receives one unit of endowment and then they engage in a zero-sum game of chance with their endowments. Because of this gambling, though the aggregate income of the economy remains constant and bears no uncertainty, individual households may be exposed to substantial income risk.
Studying household income directly avoids this shortcoming and became feasible, as large surveys of household income have been conducted. However, income uncertainty is typically studied via other aspects of variability, such as income inequality and volatility. This is not surprising, on the one hand, uncertainty per se is difficult to observe. On the other hand, greater uncertainty can often lead to greater inequality or volatility. For example, in a seminal early contribution, Deaton and Paxson (1994) examine the repeated cross-sectional data and document that the within-cohort inequality of consumption and income increases with age. They argue that the increased inequality is the "cumulative differences in the effects of luck," but they have not provided a quantitative analysis of income uncertainty.
More quantitative results are obtained using longitudinal surveys, such as the Panel Study of Income Dynamics. Similarly, much of the work has focused on the volatility and inequality of household income. For example, Dynan, Elmendorf, and Sichel (2007) examine the standard deviation of the percent change in income across households and conclude that household income growth has become more volatile over the past several decades.2 Alternatively, some researchers take the mean income of a household over a given period as a proxy for permanent income and treat the difference between the observed income and the mean as the transitory component of income. Using this method, Gottschalk and Moffitt (1994) find that an increase in the variance of transitory earnings could explain a large portion of the widening of income inequality during the 1970s and 80s. In general, it is hard to make an inference about income uncertainty (and its changes) from these results because the variabilities they studied may include income changes that are predictable to households.
More elaborate models often postulate some parsimoniously parameterized income process that includes a predictable part and a stochastic part, which in turn is a combination of permanent and transitory shocks. A battery of econometric techniques have been developed to study the properties of the
stochastic part of income shocks. For example, Carroll and Samwick (1997) and Gourinchas and Parker (2002) study the following specification.3 The logarithm of
income, ![]() , is decomposed into
, is decomposed into
where
in which
First, the predictable component of income is typically constructed by regressing the log of observed income of year ![]() on household demographics and work-related variables observed in the
same year. The fitted value of the dependent variable is then interpreted as the predictable component. To the extent that households do not have perfect foresight on this information, the fitted value constructed in such a regression is essentially the component ex post explainable to
econometricians rather than the component ex ante predictable to households. Put differently, constructing the predictable income by conditioning on information concurrent with the realization of income potentially assumes too much information, and consequently may lead to underestimation of the
income uncertainty perceived by the household.
on household demographics and work-related variables observed in the
same year. The fitted value of the dependent variable is then interpreted as the predictable component. To the extent that households do not have perfect foresight on this information, the fitted value constructed in such a regression is essentially the component ex post explainable to
econometricians rather than the component ex ante predictable to households. Put differently, constructing the predictable income by conditioning on information concurrent with the realization of income potentially assumes too much information, and consequently may lead to underestimation of the
income uncertainty perceived by the household.
Second, if we fix the calendar time of a given future income, the predicted value should converge to the realized value of income at this time as the household progresses in time and uncertainties are resolved. However, because the predictable component is not constructed specifically for any projection horizon in the standard method, it does not directly capture this evolution of income uncertainty.
Third, the above parametrization assumes the income process is subject to permanent shocks. As we show later in this paper, household income shocks do have a persistent component. However, this component is best characterized as a fairly persistent, but not a permanent (or unit-root), process. This distinction has a substantial effect on the level of the cumulative income uncertainty over the life cycle and subsequently affects the implied precautionary saving motives (in particular for younger consumers).
Fourth, fitting individual income with a trend that is only driven by demographic and work-related characteristics requires assuming that all households similar in these dimensions share a common life cycle trend. This assumption is consistent with the model introduced by MaCurdy (1982). A competing view is that consumers in fact face individual-specific income profiles, as proposed by Lillard and Weiss (1979). More recently, Guvenen (2007) presents evidence that consumption data are more consistent with the view of Lillard and Weiss (1979). If the underlying income process is better characterized in this way, fitting it with a trend common to seemingly similar households will increase the residual variance and hence exaggerate the underlying income uncertainty.
Finally, apart from a few exceptions (e.g., Baker and Solon (2003)), previous studies have not fully characterized how household income risks evolve over the life cycle. It is both theoretically and empirically appealing to study whether household income uncertainty does stay constant, and, if not, how it evolves over the life cycle. Heuristically, a single 22-year-old college graduate entering the labor market should have more uncertainties about his income five or ten years down the road than a 40-year-old man with a family and a settled career path over the same time horizon.
3 A Forecast-Based Semiparametric Approach
We propose a semiparametric approach to estimating household income uncertainty that attempts to address the concerns outlined in the previous section. This approach is flexible enough to incorporate various assumptions about the household's information set and can be used to characterize the evolution of income uncertainty over the life cycle. Our key insight is that greater income uncertainty should make future income more difficult to forecast, conditional on the information available to the household at the time of the forecast. Accordingly, we use forecast accuracy as a metric of the underlying income uncertainty, or riskiness. The larger the variances of forecast errors are, the greater uncertainty, or risk, a household faces regarding its future income.
For a household whose head's age is ![]() , let the logarithm of its income
, let the logarithm of its income ![]() -year-ahead be
-year-ahead be ![]() , which can be decomposed as
, which can be decomposed as
| (3) |
where
| (4) |
Elements of the
| (5) |
For example, elements of
One hurdle to implementing this strategy is that we do not know the joint distribution of ![]() and
and
![]() . As a result, we cannot compute
. As a result, we cannot compute
![]() directly. Indeed, we do not even know exactly what
directly. Indeed, we do not even know exactly what
![]() encompasses. To establish a benchmark and to assess the bias introduced by ignoring any additional (superior) information potentially possessed by households, we
experiment with two specifications. First, in what we label as the restricted information specification (RIS), we project
encompasses. To establish a benchmark and to assess the bias introduced by ignoring any additional (superior) information potentially possessed by households, we
experiment with two specifications. First, in what we label as the restricted information specification (RIS), we project ![]() conditional on
conditional on
![]() , the information set that includes only what an econometrician can observe regarding a household as of age
, the information set that includes only what an econometrician can observe regarding a household as of age ![]() . This information is what the households certainly possess at age
. This information is what the households certainly possess at age ![]() . Second, in what we label as the augmented
information specification (AIS), we projected
. Second, in what we label as the augmented
information specification (AIS), we projected ![]() conditional on the augmented information set
conditional on the augmented information set
![]() , where
, where
| (6) |
The augmenting information set,
and AIS equation,
In the above specifications,
In addition to
![]() and
and
![]() , our specification deviates from most previous specifications in that we include both current and lagged income in the projection equations. In principle, if we have a
very long income history for a given household, a univariate time series model could potentially have some decent forecasting power. Such a long time series of household income is also useful for identifying the income process heterogeneity that Lillard and Weiss (1979) and Guvenen (2007) have
stressed. Including some recent income history in the projection equation can help tease out information about recent income shocks and capture part of the individual-specific information of income growth that is not revealed by current income and other observable characteristics. In practice, our
model includes two lags to preserve degrees of freedom. Finally, we added a simple calendar year trend to control for aggregate economic growth.7
, our specification deviates from most previous specifications in that we include both current and lagged income in the projection equations. In principle, if we have a
very long income history for a given household, a univariate time series model could potentially have some decent forecasting power. Such a long time series of household income is also useful for identifying the income process heterogeneity that Lillard and Weiss (1979) and Guvenen (2007) have
stressed. Including some recent income history in the projection equation can help tease out information about recent income shocks and capture part of the individual-specific information of income growth that is not revealed by current income and other observable characteristics. In practice, our
model includes two lags to preserve degrees of freedom. Finally, we added a simple calendar year trend to control for aggregate economic growth.7
Several important caveats apply to our specifications. First, as most households do make plans about their family and career ahead of time, it is not unreasonable to assume households know several years ahead of time what their family size and marital status will be, whether they will be
working, retired, or self-employed, or whether they will change occupation and industry. However, it is less likely that households know all this information when ![]() is large.8 That said, the information we have is limited to what is collected in surveys. There are other information elements
is large.8 That said, the information we have is limited to what is collected in surveys. There are other information elements ![]() such that
such that
![]() , but
, but
![]() . Therefore, it is generally not true that the AIS estimates yield the lower bound of household income uncertainty. However, as we will
present later, the comfortably large value of
. Therefore, it is generally not true that the AIS estimates yield the lower bound of household income uncertainty. However, as we will
present later, the comfortably large value of ![]() of Eq. (8) reassures us that the unobservable information only has a limited effect. Second, it is worthwhile to point
out that Eqs. (7) and (8) are merely forecasting equations, and they are estimated solely on the basis of maximizing
of Eq. (8) reassures us that the unobservable information only has a limited effect. Second, it is worthwhile to point
out that Eqs. (7) and (8) are merely forecasting equations, and they are estimated solely on the basis of maximizing ![]() . We are not estimating a
structural model, so the coefficients estimated for Eqs. (7) and (8) should not be interpreted as structural parameters. Third, because we let the households use the estimated coefficients to project their future income, we implicitly assume that either these
coefficients are stable over time or that households have foresight on the future values of these coefficients (e.g., the household would know in advance the return to schooling and experience). We follow Carroll (1994) and resort to the first assumption in the baseline analysis. As a robustness
check, we alternatively allow for time-varying coefficients and estimate the coefficients using a lagged sample. By this exercise, we found that the so-estimated income uncertainty over all projection horizons is somewhat higher than in our baseline specifications. However, all key results are
qualitatively unaltered. Finally, although we allow income uncertainty to vary with age, we compute these forecast errors by applying the same coefficients of the forecasting model to all households. As another robustness check, we also estimated the forecasting model separately for each age group.
Our results are qualitatively preserved, which reassures us that the age profile of income uncertainty is not driven by any age dependence in the accuracy of the forecasting model.
. We are not estimating a
structural model, so the coefficients estimated for Eqs. (7) and (8) should not be interpreted as structural parameters. Third, because we let the households use the estimated coefficients to project their future income, we implicitly assume that either these
coefficients are stable over time or that households have foresight on the future values of these coefficients (e.g., the household would know in advance the return to schooling and experience). We follow Carroll (1994) and resort to the first assumption in the baseline analysis. As a robustness
check, we alternatively allow for time-varying coefficients and estimate the coefficients using a lagged sample. By this exercise, we found that the so-estimated income uncertainty over all projection horizons is somewhat higher than in our baseline specifications. However, all key results are
qualitatively unaltered. Finally, although we allow income uncertainty to vary with age, we compute these forecast errors by applying the same coefficients of the forecasting model to all households. As another robustness check, we also estimated the forecasting model separately for each age group.
Our results are qualitatively preserved, which reassures us that the age profile of income uncertainty is not driven by any age dependence in the accuracy of the forecasting model.
4 Data Description and Sample Construction
We used data from the Panel Study of Income Dynamics (PSID), which is a nationwide longitudinal survey of households conducted by the Institute of Social Research at the University of Michigan. Before 1997, the PSID was an annual survey; after 1997, it became a biennial survey. We use the PSID data from 1968 to 2005, totaling 34 waves, covering nearly four decades. As of the 2005 wave, the PSID surveyed 8,002 households.9
In addition to extensive information about work status, employment history, and demographic characteristics, the PSID collects detailed information on income, which allowed us to study various components of total family income. Moreover, the longitudinal structure of the PSID permits us to link
the information collected for the same household in two waves that are ![]() years apart. For instance, consider a household that had been surveyed for ten years from 1971 through 1980. When we
projected the five-year-ahead income, this household rendered five current and future income pairs
years apart. For instance, consider a household that had been surveyed for ten years from 1971 through 1980. When we
projected the five-year-ahead income, this household rendered five current and future income pairs
![]() , ... , (1975, 1980). This structure is essential to estimate the projection equation and to experiment with alternative information specifications.
, ... , (1975, 1980). This structure is essential to estimate the projection equation and to experiment with alternative information specifications.
We estimated Eq. (7) and (8) for each forecast horizon. Accordingly, the samples are constructed separately for each forecast horizon. Several rules apply when we construct the sample. First, we include only the nationwide representative sample and exclude
the households in the low-income supplemental sample.10 Second, to focus on the working-age households, we restrict household heads to be older than 23 in
the base year and younger than 65 in the year to be forecasted. For example, in the sample we use to forecast five-year-ahead income, we restrict the heads of sample households to be younger than 60. Consequently, the sample we use to study forecast errors at farther horizons is typically smaller
than the sample used for a closer horizon. Third, we remove households that reported zero or negative income in the base year, the two lagged years, or the year to be forecasted. Fourth, we remove households whose heads were disabled or retired, were primarily keeping house, or were students in the
base year. Fifth, we remove households whose heads reported zero working hours in the base year and the two lagged years.11 Finally, in order to minimize
the bias caused by outliers and measurement errors, we trim off households with very high- or very low-income levels and growth rates between age ![]() and
and ![]() .12
.12
To explore the precautionary saving implication of the estimated income uncertainty, we primarily focus on the most relevant income definition, family non-asset income. Because Carroll and Samwick (1997) also study family non-asset income, examining the same income definition also facilitates comparison with their results. We discuss our estimates of uncertainty profile for other income measures in the robustness analyses. In our study, we estimate the variance of forecast errors of future family non-asset income up to 25 years ahead. For illustration purposes, Table 1 lists the number of observations used in the estimation for each forecast horizon. We notice that the sample constructed for the two-year-ahead forecast has the largest number of observations (nearly 46,000) because the PSID became a biennial survey after 1997. The sample sizes largely decline with forecast horizons. However, even at the 25-year-ahead horizon, we maintain a decent sample size that is above 2,200. The income variables are deflated using 1982-1984 dollars. In addition, all waves but 2003 and 2005 of the PSID data have a 1970 census industry and occupation code. The 2003 and 2005 PSID data used the industry and occupation code derived from the 2000 census. To be consistent, we regroup the 2000 census industry and occupation code to match the 1970 categories as close as we can.
| 1 Year | 43,313 |
| 2 Years | 47,109 |
| 3 Years | 37,583 |
| 4 Years | 39,782 |
| 5 Years | 32,926 |
| 6 Years | 33,421 |
| 7 Years | 28,761 |
| 8 Years | 27,740 |
| 9 Years | 24,947 |
| 10 Years | 22,736 |
| 11 Years | 20,553 |
| 12 Years | 18,372 |
| 13 Years | 16,500 |
| 14 Years | 14,640 |
| 15 Years | 12,970 |
| 16 Years | 11,331 |
| 17 Years | 9,957 |
| 18 Years | 8,572 |
| 19 Years | 7,452 |
| 20 Years | 6,293 |
| 21 Years | 5,342 |
| 22 Years | 4,376 |
| 23 Years | 3,603 |
| 24 Years | 2,834 |
| 25 Years | 2,244 |
5 Main Empirical Results
We construct five-year centered moving averages of the estimated variances of forecast errors to smooth out noises in the series. Recall that we have from one-year-ahead to twenty-five-year-ahead projections, and our sample household heads were between the age of 23 to 64 in the base year. The
centered moving average uncertainty matrix ![]() therefore has a dimension of
therefore has a dimension of
![]() , with each row corresponding to the same age and each column corresponding to the same projection horizon. To demonstrate how income uncertainty evolves over the life cycle, for
each model specification (RIS and AIS), we plot uncertainty age profiles at four forecast horizons (four columns of
, with each row corresponding to the same age and each column corresponding to the same projection horizon. To demonstrate how income uncertainty evolves over the life cycle, for
each model specification (RIS and AIS), we plot uncertainty age profiles at four forecast horizons (four columns of ![]() ): one-year and two-year ahead, representing the near future, as
well as five-year and ten-year ahead, representing the medium and more remote future. To illustrate the statistical significance of our results, we also plot the 95% confidence interval band for each profile .
): one-year and two-year ahead, representing the near future, as
well as five-year and ten-year ahead, representing the medium and more remote future. To illustrate the statistical significance of our results, we also plot the 95% confidence interval band for each profile .
5.1 Income Uncertainty Changes over the Life Cycle
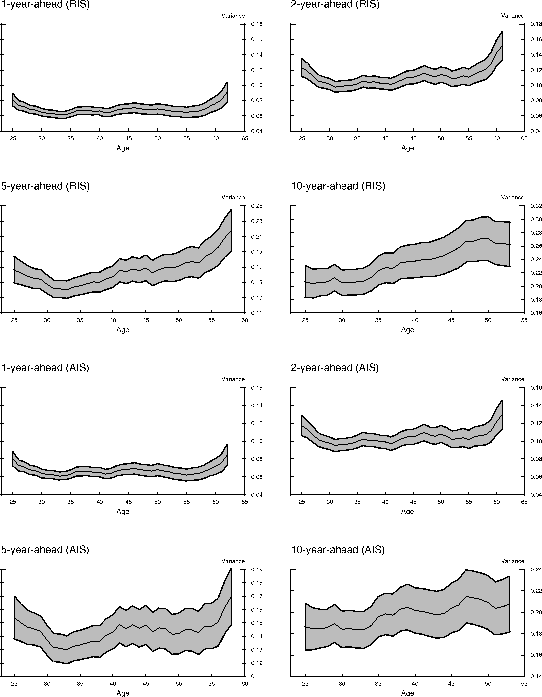
We begin with examining the uncertainty of total family non-asset income estimated under the more restrictive information specification, the RIS equation. The results are shown in the top four panels of Figure 1. Consistent with our intuition that uncertainty regarding income at a fixed future data resolves as the date approaches, the level of uncertainty regarding income two years ahead is considerably higher than the income uncertainty one year ahead. The confidence intervals associated with both uncertainty profiles indicate this gap is statistically significant. Notably, both profiles share a similar U-shaped pattern over the life cycle. Income uncertainty is high when the head is young; it declines during his late twenties and early thirties. Afterward, uncertainty fluctuates within a narrow range at relatively low levels before rising in his mid-fifties, which continues as households approach retirement. The ratios between the maximum and minimum levels of uncertainty over the life cycle (the max-min ratio) are both about 1.5 for the one-year- and two-year- ahead future income. The plotted 95% confidence intervals suggest that both profiles are rather tightly estimated, which reinforces the statistical significance of the U-shaped pattern. A similar convex profile of income uncertainty is documented in Baker and Solon (2003). They decompose the stochastic part of income into a transitory and a permanent component and find that the age profile of the variance of the transitory innovations exhibits a pronounced U-shaped pattern.13 Our results, in contrast, do not rely on the dichotomy of transitory and permanent shocks.
Profiles of similar shape repeat in the left panel on the second row, which shows income uncertainties at the medium (five-year-ahead) future. The standard errors of the estimated profiles are somewhat larger than in the top two panels because we have a smaller sample over these longer projection horizons. The uncertainty associated with income five years ahead hits bottom in the mid-thirties and rises gradually through the early fifties. After that, income uncertainty rises more rapidly as households approach retirement ages. The profile of income uncertainty ten years ahead does not exhibit a pronounced decline during young ages. The level of uncertainty stays low through the mid-thirties before rising in the mid-fifties. Comparing with the near future, the variations of the five-year-ahead income uncertainty over the life cyle are about as pronounced, with the max-min ratio equal to 1.5. However, the variations of income uncertainties at the more remote future are less pronounced, with the max-min ratio equal to merely 1.3 for the ten-year horizon. Moreover, although the level of uncertainty in the medium future is much higher than in the near future, the increase is not proportional to the forecast horizon. The two-year-ahead uncertainty is on average 60% higher than the one-year-ahead uncertainty. If these uncertainties rise proportionally with forecast horizons, the five-year-ahead uncertainty, for example, should be 240% higher than the one-year-ahead uncertainty. However, it is only 140% higher. As we will further elaborate later in the paper, this nonlinearity suggests the persistent component of income shocks is not exactly permanent.
Income-uncertainty profiles at the very remote future (up to 25 years) are also estimated (not shown). Because of smaller sample sizes at these horizons, these profiles are estimated with wider confidence intervals. Like the ten-year-ahead uncertainty age profile, the very remote income uncertainty age profiles all show a pronounced upward trend throughout the life cycle but do not exhibit clear declines during young ages. Finally, for overlapping ages, the twenty-five-year-ahead profile is on average 450% higher than the one-year-ahead profile, to a much less extent than what proportional increases imply.
Now, we turn our attention to the relaxed information specification, AIS, in which we allow households to have foresight on some of their future demographic and work-related characteristics. The results are shown in the bottom four panels of Figure 1. Two features are noteworthy. First, because
these future income projections are conditioned on a larger information set, the AIS forecast error variances are significantly smaller than the variances estimated using the RIS equation. This pattern holds for all forecast horizons and for households of all ages. Moreover, the discrepancy between
the RIS and AIS results widens with the forecast horizon. The estimated one-year-ahead uncertainty under the RIS is only 6% higher than that estimated under the AIS, whereas the gap is about 25% at the ten-year horizon. It widens to 36% at the 25-year horizon. This widening trend is consistent with
our intuition because the difference between
![]() and
and
![]() is what households are assumed to know about themselves at age
is what households are assumed to know about themselves at age ![]() as of age
as of age ![]() . Given that these characteristics typically change only gradually, if
. Given that these characteristics typically change only gradually, if ![]() is small, the correlation between the elements in
is small, the correlation between the elements in
![]() and
and
![]() will be high, discounting the net value of
will be high, discounting the net value of
![]() . Conversely, if
. Conversely, if ![]() is large,
is large,
![]() should have less predictive power on
should have less predictive power on
![]() . Consequently, augmenting with
. Consequently, augmenting with
![]() adds more new information and improves the forecasting performance more significantly. Second, the U-shaped contours at the near and the intermediate future horizons are
similar to those shown in the top panels. However, the max-min ratios are somewhat lower for the AIS estimates, especially for the profiles of more remote future horizons. This result is not surprising because a good portion of the rise in income uncertainty after middle age comes from retirement
and related risks, which are included in the augmented information set.
adds more new information and improves the forecasting performance more significantly. Second, the U-shaped contours at the near and the intermediate future horizons are
similar to those shown in the top panels. However, the max-min ratios are somewhat lower for the AIS estimates, especially for the profiles of more remote future horizons. This result is not surprising because a good portion of the rise in income uncertainty after middle age comes from retirement
and related risks, which are included in the augmented information set.
5.2 Correlations of Forecast Errors
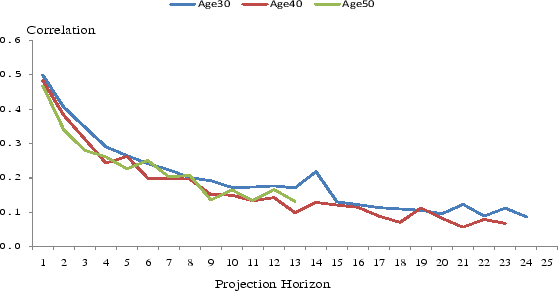
Besides the levels of income uncertainties over the life cycle, to completely characterize the income uncertainty, we must know how the stochastic components of income at different horizons are correlated. Figure 2 presents the correlations between the one-year-ahead forecast errors and the forecast errors at other horizons. To keep the graph readable, we only plot the correlations for the households whose heads are 30, 40, and 50 years old that are estimated using the RIS equation. The AIS results are very similar. We note that, on the one hand, because the correlations are positive at all forecast horizons, income shocks must have a persistent component. On the other hand, the correlations decline substantially with forecast horizon. The correlation between the one-year-ahead and the two-year-ahead forecast errors is about 0.5, whereas the correlation between the one-year-ahead and ten-year-ahead forecast errors is only about 0.2. This rapid decline suggests that the persistent component of income shocks is more likely to be an AR process than a unit-root process. Although we cannot rule out the existence of a unit-root component, if one exists, its innovations should have a relatively small variance. The chart also reveals that the correlations of households of various ages are very similar, suggesting little changes in the persistence of income shocks over the life cycle, in contrast to the evolution of shock variances.
5.3 The (In)significance of Lagged Income
We include lagged income in the projection equation. The motivation is to capture some heterogeneity that cannot be accounted for by a common trend determined by other observable characteristics. Naturally, this method will not capture all the heterogeneity set forth by Lillard and Weiss (1979),
but it does acknowledge that past income history can be useful in predicting future income, even after controlling for current income levels and the standard household demographic and work-related characteristics. Indeed, for almost all family income components and forecast horizons, the estimated
coefficients of the lagged income are highly significant (with ![]() -value typically smaller than 0.001). In addition, the sum of the coefficients of current and lagged income is larger than the
coefficient of the current income estimated in a model with no lagged income included, implying that with lagged income included, the projection picks up more signal from the income history. However, what is somewhat puzzling to us is that although the coefficients of the two lagged incomes are
statistically significant, adding them does not beef up the overall fitness of the projection equation to a great extent. The
-value typically smaller than 0.001). In addition, the sum of the coefficients of current and lagged income is larger than the
coefficient of the current income estimated in a model with no lagged income included, implying that with lagged income included, the projection picks up more signal from the income history. However, what is somewhat puzzling to us is that although the coefficients of the two lagged incomes are
statistically significant, adding them does not beef up the overall fitness of the projection equation to a great extent. The ![]() of the models increase only slightly, on average 2%, when
lagged income is included.
of the models increase only slightly, on average 2%, when
lagged income is included.
5.4 Robustness Tests
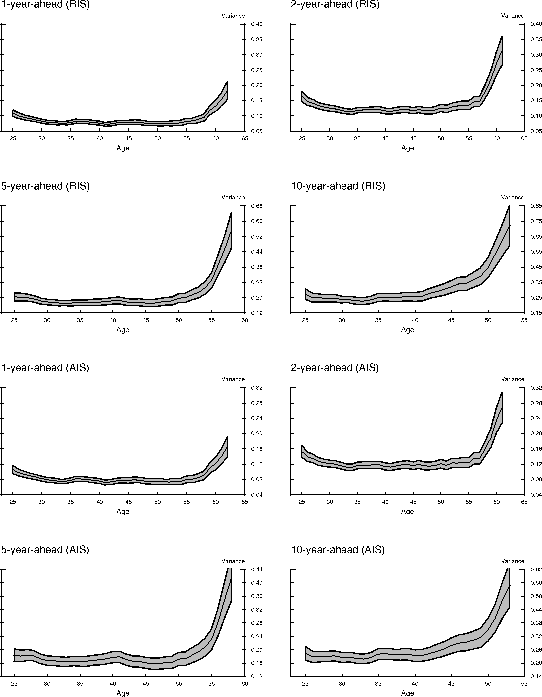
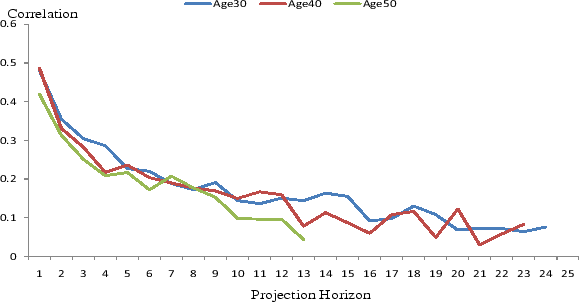
To examine whether the dynamics of income uncertainty over the life cycle that we have shown are a spurious consequence of our choice of income definition, model specifications, or the shrinking sample sizes over projection horizons, we conduct a series of robustness analyses. First, we redo the analysis above using household head labor income. Figure 3 plots the variances of forecast errors over the life cycle. Like in Figure 1, household head labor income uncertainty also changes substantially over the life cycle. However, different from family non-asset income, labor income uncertainty follows a J-shaped pattern, with a much more pronounced rise of uncertainty as the head approaches retirement age. The late life cycle rise is considerably smaller under the AIS specification, in which we allow the head to have some foresight about his retirement (part-time) status in the year to be forecasted. Figure 4 plots the correlations of forecast errors over horizons, which are largely similar to what Figure 2 has shown. Similar analyses done for total family income and head and wife combined non-asset income yield results similar to Figures 1 and 2, whereas analyses done for head and wife combined labor income and head wages and salaries yield results similar to Figures 3 and 4.
Second, we examine whether changes in uncertainty over the life cycle are due to model misspecifications. Recall that we project the future income of households at different ages using the same set of coefficients. If the projection-equation coefficients should be age specific and the coefficients we use are closer to the true parameters for the middle-aged households than for the younger and older households, the one-size-fits-all approach will reduce fitness for younger and older households and artificially increase the estimated income uncertainties for these age groups. We divide our sample into five subgroups by household head age and estimate Eqs. (7) and (8) separately for each subgroup. Then, we calculate variances of forecast errors constructed using the revised projection coefficients. We find that both the uncertainty age profiles and correlation curves are similar to what Figures 1 and 2 show.
Third, in the same spirit, we examine the effects of allowing for time-varying projection coefficients that households are assumed to have no foresight on. We split the sample into two parts and estimate the coefficients using the earlier sample. We then use the estimate coefficients to project future income in the later sample. This method assumes that households are backward looking in figuring out the coefficients applicable to the future and can be exceedingly restrictive. For example, one does not have to infer returns to college education in the 1990s using exactly the returns in the 1970s. The purpose of the analysis is to illustrate how much bias can potentially be introduced if we ignore the time dependence of the projection coefficients. We only do this analysis up to ten years ahead because we need long enough subsamples to estimate the coefficients. We find that the contours of the life cycle profiles of income uncertainty and the correlations of the forecast errors estimated using this method are very similar to those estimated assuming time-invariant coefficients. Not surprisingly, the levels of income uncertainty are somewhat higher. However, this gap narrows consistently with projection horizons. At the near term, the backward-looking estimates of variances of forecast errors are about 17% higher than in the baseline specification, and at the ten-year ahead horizon, the gap becomes 7%.
Finally, we examine whether changes in the sample size as we vary forecast horizons (as given in Table 1) might drive the shape of the uncertainty profile. We estimate the forecast equations using a smaller common sample that spans at least ten years and reconstruct the income uncertainty measures up to ten years ahead. Again, all results are qualitatively unchanged.
6 Comparison with Earlier Results
How substantive are the innovations we have introduced with the semiparametric measures of income uncertainty? How different are our results compared to previous studies? We answer these questions by contrasting our results to the income uncertainty estimates in the influential work of Carroll and Samwick (1997). Three reasons lead us to choose these results to compare with. First, their specific interest was precautionary saving, so their estimates focus explicitly on income uncertainty rather than inequality, volatility, or other types of income variability. Second, they also use the PSID data, making a comparison and interpreting the differences easier. Third, apart from the specified innovations, our models share many similarities with theirs.
As we summarized in Eqs. (1)-(2), Carroll and Samwick (1997) decompose ![]() into a permanent component,
into a permanent component, ![]() , and a transitory shock,
, and a transitory shock,
![]() . The permanent component,
. The permanent component, ![]() , is further assumed to follow a
random walk with predictable income growth
, is further assumed to follow a
random walk with predictable income growth ![]() such that
such that
where
noting that the econometrician does not know how either
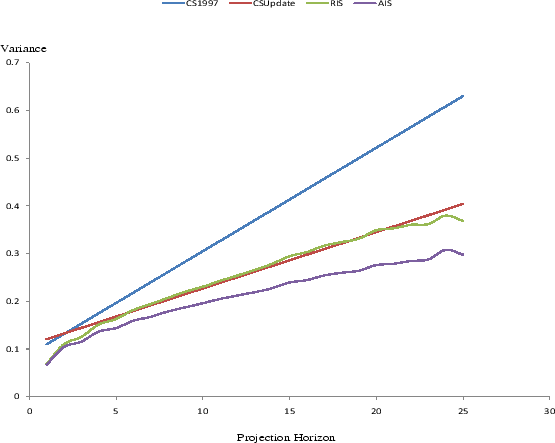
Figure 5 contrasts the total family non-asset income uncertainty at various forecast horizons implied by the original and updated Carroll and Samwick estimates with our semiparametric profiles (pooled across all ages). The
![]() and
and
![]() reported in Carroll and Samwick (1997) imply a higher and steeper linear profile, whereas the
reported in Carroll and Samwick (1997) imply a higher and steeper linear profile, whereas the
![]() and
and
![]() that we estimated using the same methodology with the extended PSID sample imply a lower and flatter profile. The linearity between income uncertainties and forecast
horizons arises because of the random walk assumption imposed. The slope of the linear profile is equal to the variance of permanent shocks, and the intercept is equal to two times the variance of transitory shocks. The higher concave curve is the semiparametric profile estimated using the RIS
equation, while the lower concave profile is estimated using the AIS equation.
that we estimated using the same methodology with the extended PSID sample imply a lower and flatter profile. The linearity between income uncertainties and forecast
horizons arises because of the random walk assumption imposed. The slope of the linear profile is equal to the variance of permanent shocks, and the intercept is equal to two times the variance of transitory shocks. The higher concave curve is the semiparametric profile estimated using the RIS
equation, while the lower concave profile is estimated using the AIS equation.
Several features appear in this chart are noteworthy. First, we notice that the Carroll-Samwick profile is substantially higher than the semiparametric profiles estimated even under the restrictive information specifications, the RIS equation. At the near horizons, the gap is about 20%, whereas
at remote horizons, because the RIS semiparametric profile is concave, the wedge widens substantially to about 60%. Second, the updated Carroll-Samwick profile has a higher intercept but a flatter slope due to the larger
![]() but smaller
but smaller
![]() Third, the updated Carroll and Samwick profile is higher than the RIS profile in the near term but coincides with the RIS profile beyond five years. The updated Carroll
and Samwick profile remains uniformly and substantially higher than the AIS profile. This gap is more striking, taking into account that the predictable component of income is constructed using age
Third, the updated Carroll and Samwick profile is higher than the RIS profile in the near term but coincides with the RIS profile beyond five years. The updated Carroll
and Samwick profile remains uniformly and substantially higher than the AIS profile. This gap is more striking, taking into account that the predictable component of income is constructed using age ![]() information in the Carroll and Samwick (1997) approach, whereas the semiparametric approach conditions on a mix of age
information in the Carroll and Samwick (1997) approach, whereas the semiparametric approach conditions on a mix of age ![]() and age
and age ![]() information. Moreover, not shown in the chart, the updated Carroll-Samwick profile is also higher than the profile allowing for time-varying projection coefficients and assuming backward-looking households (the third robustness
check).
information. Moreover, not shown in the chart, the updated Carroll-Samwick profile is also higher than the profile allowing for time-varying projection coefficients and assuming backward-looking households (the third robustness
check).
Why are the uncertainty profiles implied by the original and updated Carroll and Samwick estimates so different? Two potential factors may contribute to this change. First, we notice that in Carroll and Samwick (1997), the maximum difference length corresponds to ![]() , which is relatively small. Using a longer panel not only adds data collected in more years, but also allows us to study the difference in income over longer intervals. To assure the comparability of our PSID sample
with theirs, we first set
, which is relatively small. Using a longer panel not only adds data collected in more years, but also allows us to study the difference in income over longer intervals. To assure the comparability of our PSID sample
with theirs, we first set ![]() and found the estimated transitory and permanent shocks variances to be 0.036 and 0.023, respectively. These estimates are very close to Carroll and Samwick
(1997). Subsequently, we update these estimates for various choices of
and found the estimated transitory and permanent shocks variances to be 0.036 and 0.023, respectively. These estimates are very close to Carroll and Samwick
(1997). Subsequently, we update these estimates for various choices of ![]() to examine whether the estimates are sensitive to variation in
to examine whether the estimates are sensitive to variation in ![]() .
.
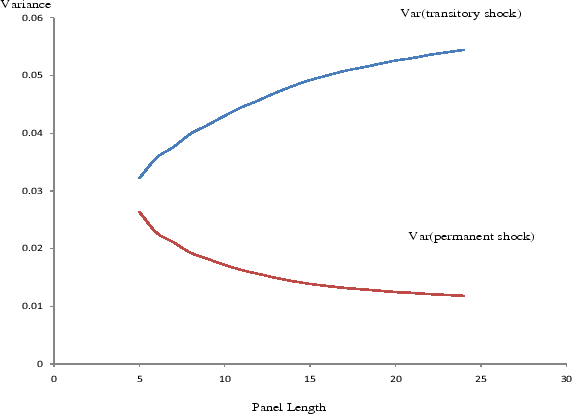
Figure 6 contrasts how the estimated variances of transitory and permanent shocks, identified by the specification of Eqs. (9)-(10), vary with ![]() . Because we project future income up to 25 years ahead in our nonparametric estimates, we choose the largest value of
. Because we project future income up to 25 years ahead in our nonparametric estimates, we choose the largest value of ![]() to be 25. The
permanent shock variance decreases, whereas the transitory shock variance increases monotonically with
to be 25. The
permanent shock variance decreases, whereas the transitory shock variance increases monotonically with ![]() . This phenomenon implies either that the variance of the permanent shocks--if the
persistent shock process is indeed a random walk--is estimated with a significant upward bias using a short panel, or that the persistent shocks do not follow a random walk process. To see this, suppose the true model of the shocks to "permanent" income is
. This phenomenon implies either that the variance of the permanent shocks--if the
persistent shock process is indeed a random walk--is estimated with a significant upward bias using a short panel, or that the persistent shocks do not follow a random walk process. To see this, suppose the true model of the shocks to "permanent" income is
instead of a unit-root process
Using L'Hôpital's Rule, it is easy to verify that (10) is the limiting case when
Assuming
Finally, Carroll and Samwick (1997) also estimate the variance of the permanent and transitory income shocks by age. However, their estimates do not imply a U-shaped life cycle pattern. Indeed, their transitory shock variance exhibits a hump-shaped pattern over the life cycle, peaking in the early forties, whereas their permanent shock variance demonstrates more irregular life cycle dynamics.
To summarize, in contrast to Carroll and Samwick (1997) and later work using similar methods (e.g., Gourinchas and Parker (2002)), the semiparametric estimates of income uncertainty introduced in this paper reveal a uniformly lower level of income uncertainty over all future horizons, and suggest that the persistent component of income shocks is likely not a permanent shock. Our approach also implies life cycle dynamics of income uncertainty that are more consistent with layman's intuition and the results of Baker and Solon (2003) and Gordon (1984).
7 Consumption and Precautionary Saving over the Life Cycle: An Application of the Semiparametric Estimates
As we discussed in the beginning of the paper, a battery of household decisions critically depend on households' uncertainty about their future income. We revisit one such question, the optimal quantity of consumption and precautionary saving over the life cycle, as an example that illustrates how household decisions under the semiparametric estimate of income uncertainty introduced in this paper differ from those derived using the preexisting income uncertainty estimates.
7.1 Background
The canonical Rational-Expectations Life Cycle/Permanent-Income Hypothesis (RE-LCPIH) predicts that rational consumers should allocate consumption over the life cycle in such a way as to maximize lifetime utility, which in turn implies a monotonic consumption profile over the life cycle. However, since Thurow (1969), many empirical studies have documented a hump-shaped pattern of life cycle consumption. In light of this apparent inconsistency, a large volume of literature has added various features to the standard RE-LCPIH model to account for a hump-shaped consumption profile.14
We focus on one of the main factors raised to explain the hump-shaped consumption profile--precautionary saving--for it directly speaks to the effect of income uncertainty. Nagatani (1972) first suggested that precautionary saving would reduce consumption early in the life cycle, and Skinner (1988) and Feigenbaum (2008a) have fleshed out how the growth rate of mean consumption from one period to the next increases with income uncertainty. Consequently, if income uncertainty decreases over the life cycle, this will lead to a concave consumption profile. It has been shown extensively that, in partial-equilibrium models calibrated against the measures of uncertainty described in Section 2, precautionary motives can induce a sizable hump (see for example, Carroll and Summers (1991); Hubbard, Skinner, and Zeldes (1994); Carroll (1997); Gourinchas and Parker (2002); and Feigenbaum (2008b)).
However, it is not likely that precautionary saving single-handedly causes the hump, for other factors, such as leisure and consumption substitution (Heckman (1974); and Becker and Ghez (1975); and Bullard and Feigenbaum (2007)) or time-varying mortality risk (Feigenbaum (2008c) and Hansen and Imrohoroglu (2008)), can also account for the hump. This insight imposes a challenge to the existing parametric estimates of income uncertainty as the models calibrated with these estimates often yield a consumption hump that is larger than observed in data. We introduce
![\displaystyle S=\frac{E[c_{t^{\ast }}]}{E[c_{0}]}](img75.gif) |
as a measure of the magnitude of the consumption hump, where
In contrast, here we show that with the semiparametric estimates of income uncertainty introduced in this paper, precautionary saving typically yields a significant but substantially smaller hump than is observed in the data. This is because our estimates call for smaller variances and lower persistence, reducing the lifetime income uncertainty households face, in particular at a young age.
7.2 A Life Cycle Consumption-Saving Model
Ideally, we would like to model the income process with age-varying uncertainties that replicate all the variances and correlations that we estimate in Section 5. However, the parsimonious income processes typically employed in this literature assume constant shock variances. Generalizing such income processes to allow for age-dependent shock variances is a difficult task that is beyond the scope of this paper. (See Feigenbaum and Li (2010a) for more on this issue.) Thus, we consider a general-equilibrium overlapping-generations model with incomplete markets à la Huggett (1996) and an income process with age-independent shock variances.
In each period, a continuum of unit measure of consumers is born. Each household lives for ![]() working periods and
working periods and ![]() retirement periods. Income is the only source of uncertainty in the model. A consumer maximizes
retirement periods. Income is the only source of uncertainty in the model. A consumer maximizes
where
for
We follow the literature on precautionary saving by assuming that at age ![]() the logarithm of income decomposes into
the logarithm of income decomposes into
where
| (18) |
There is one intertemporal asset, a risk-free bond, that pays the fixed gross interest rate ![]() . Let
. Let ![]() denote the quantity of bonds an agent purchases at age
denote the quantity of bonds an agent purchases at age ![]() that would pay
that would pay ![]() at
at ![]() . The budget constraint for a household at age
. The budget constraint for a household at age ![]() is
given by
is
given by
Since our intent is to focus on the extent to which uncertainty and precautionary saving help explain the consumption hump as opposed to borrowing constraints, we allow borrowing but with full commitment to debt contracts. Thus, the Aiyagari (1994) borrowing limit is in force.15
To complete the model, we assume there is a production sector with the Cobb-Douglas production function
where
and
In a steady-state general equilibrium, the factor prices
and
7.3 Model Calibration and the Results
Note that Eq. (17) implies that persistent shock follows an AR(1) process as in Huggett (1996) and Storesletten, Telmer, and Yaron (2004) as opposed to the unit-root process considered by Carroll and Samwick (1997) and Gourinchas and Parker (2002). The model produces a conditional variance matrix with elements
Meanwhile, for
We calibrate the parameters ![]() ,
,
![]() , and
, and
![]() in order to best replicate the variance and correlation matrices presented in Section 5, minimizing a root mean squared deviation of the values
generated by the model according to (25)-(26) from their estimated values. We implement the calibration separately for the RIS and AIS specifications. Finally, we choose
in order to best replicate the variance and correlation matrices presented in Section 5, minimizing a root mean squared deviation of the values
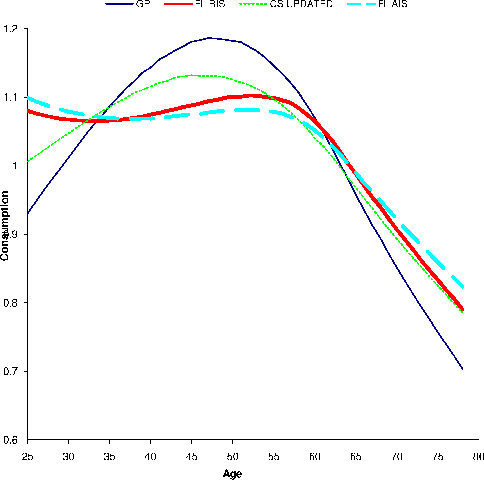
generated by the model according to (25)-(26) from their estimated values. We implement the calibration separately for the RIS and AIS specifications. Finally, we choose ![]() to match the income profile mean in Gourinchas and Parker (2002). We will compare the life cycle consumption profile implied by the income processes calibrated, using four income uncertainty estimates--the RIS, the AIS, the Gourinchas and
Parker (2002) estimates, and the updated Carroll and Samwick estimates presented in Section 6.
to match the income profile mean in Gourinchas and Parker (2002). We will compare the life cycle consumption profile implied by the income processes calibrated, using four income uncertainty estimates--the RIS, the AIS, the Gourinchas and
Parker (2002) estimates, and the updated Carroll and Samwick estimates presented in Section 6.
The remaining parameters are calibrated as follows. We set the share of capital to a typical value
![]() from the literature. We set
from the literature. We set
![]() to match properties of the life cycle consumption profile as in Feigenbaum (2008b), leaving
to match properties of the life cycle consumption profile as in Feigenbaum (2008b), leaving ![]() and
and ![]() to be calibrated. We experiment with two parametrization strategies. First, we exploit the common presumption that the ratio
to be calibrated. We experiment with two parametrization strategies. First, we exploit the common presumption that the ratio ![]() and
and ![]() can be measured. In equilibrium, we must have
can be measured. In equilibrium, we must have
where
![\displaystyle C=E\left[ \sum_{t=0}^{T-1}c_t\right]](img122.gif) |
is aggregate consumption and
| Income process |
|
|
Target |
|||
| RIS | 0.918 | 0.207 | 0.168 | 3.0 | 0.923 | 1.021 |
| AIS | 0.906 | 0.191 | 0.177 | 3.0 | 0.931 | 1.000 |
| GP | 1.000 | 0.146 | 0.210 | 3.0 | 0.905 | 1.275 |
| CS updated | 1.000 | 0.110 | 0.232 | 3.0 | 0.926 | 1.125 |
Note: The
| RIS | 0.918 | 0.207 | 0.168 | 3.5 | 0.937 | 1.081 |
| AIS | 0.906 | 0.191 | 0.177 | 3.5 | 0.944 | 1.043 |
| GP | 1.000 | 0.146 | 0.210 | 3.5 | 0.920 | 1.342 |
| CS updated | 1.000 | 0.110 | 0.232 | 3.5 | 0.939 | 1.180 |
| Memo |
|
|
|
|
||
Note: The
Several observations are noteworthy in the table and the charts. First, the calibrated income process under the AIS specification involves more volatile temporary shocks but persistent shocks that are both less persistent and less volatile than under the RIS specification. Second, it is somewhat
surprising that the computed magnitude of consumption hump, ![]() , is sensitive to the choice of
, is sensitive to the choice of ![]() , with higher
, with higher ![]() inducing great consumption humps. Specifically, it is perhaps counterintuitive that the size of the consumption hump should increase with
inducing great consumption humps. Specifically, it is perhaps counterintuitive that the size of the consumption hump should increase with ![]() . This is purely a general-equilibrium effect. In partial equilibrium, with fixed interest rates,
. This is purely a general-equilibrium effect. In partial equilibrium, with fixed interest rates, ![]() is an increasing function of the ratio of the amount of uncertainty, measured by the variance of income, to total wealth, including financial wealth and current income, squared. Assuming the standard deviation of income scales linearly with income,
is an increasing function of the ratio of the amount of uncertainty, measured by the variance of income, to total wealth, including financial wealth and current income, squared. Assuming the standard deviation of income scales linearly with income, ![]() will be a decreasing function of the wealth-to-income ratio, the microeconomic analog of
will be a decreasing function of the wealth-to-income ratio, the microeconomic analog of ![]() . This is the
reason why the standard incomplete-markets theory predicts that people will build up a buffer stock of wealth--to insure themselves against income risk. However, in general equilibrium, precautionary saving increases
. This is the
reason why the standard incomplete-markets theory predicts that people will build up a buffer stock of wealth--to insure themselves against income risk. However, in general equilibrium, precautionary saving increases ![]() in the aggregate. For a fixed risk aversion, low
in the aggregate. For a fixed risk aversion, low ![]() implies low precautionary saving and high
implies low precautionary saving and high ![]() implies high precautionary saving. Third, and most importantly, the consumption humps called for by the semiparametric estimates of income uncertainties are much smaller than those implied by both the Gourinchas and Parker (2002) and the updated
Carroll-Samwick estimates of income uncertainties. The
implies high precautionary saving. Third, and most importantly, the consumption humps called for by the semiparametric estimates of income uncertainties are much smaller than those implied by both the Gourinchas and Parker (2002) and the updated
Carroll-Samwick estimates of income uncertainties. The ![]() values derived under the latter two income processes often exceed the size of the hump in the empirical data, whereas the
values derived under the latter two income processes often exceed the size of the hump in the empirical data, whereas the
![]() values derived under the AIS and the RIS specifications are always smaller than the empirical observation, even under the rather extreme parametrization of
values derived under the AIS and the RIS specifications are always smaller than the empirical observation, even under the rather extreme parametrization of ![]() .17
.17
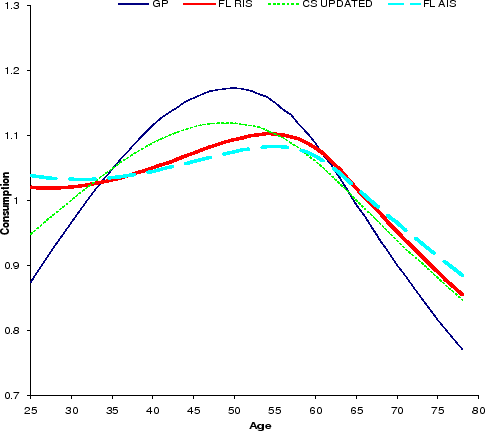
Because the target ratio of ![]() is at the best imprecisely observed in the data, we also implement an alternative parametrization strategy. We take the calibrated value for
is at the best imprecisely observed in the data, we also implement an alternative parametrization strategy. We take the calibrated value for
![]() under the RIS specification with
under the RIS specification with ![]() and apply this specific value
of
and apply this specific value
of ![]() to models with other specifications of income process. We then evaluate, when the discount factor is fixed, whether the semiparametric estimates of income uncertainty imply a more
plausible size of the consumption hump and the ratio of
to models with other specifications of income process. We then evaluate, when the discount factor is fixed, whether the semiparametric estimates of income uncertainty imply a more
plausible size of the consumption hump and the ratio of ![]() . As shown in Table 3, when
. As shown in Table 3, when ![]() is fixed to equal to 0.923, the RIS and AIS income processes continue to yield smaller values of the
is fixed to equal to 0.923, the RIS and AIS income processes continue to yield smaller values of the ![]() ratio, whereas the ratios derived from the
updated Carroll-Samwick and the Gourinchas-Parker estimates of income uncertainties are close to or even above the ratio observed in the data. In addition, the Gourinchas-Parker (2002) estimates also imply an equilibrium ratio of
ratio, whereas the ratios derived from the
updated Carroll-Samwick and the Gourinchas-Parker estimates of income uncertainties are close to or even above the ratio observed in the data. In addition, the Gourinchas-Parker (2002) estimates also imply an equilibrium ratio of ![]() that is much larger than the target ratio when
that is much larger than the target ratio when ![]() is calibrated under the RIS model.
is calibrated under the RIS model.
| Income process | ||
| RIS | 3.0 | 1.021 |
| AIS | 2.8 | 1.000 |
| GP | 3.5 | 1.280 |
| CS updated | 2.9 | 1.128 |
8 Conclusion
We propose a novel semiparametric approach of measuring household income uncertainty and study the dynamics of income uncertainty over the life cycle. Our estimates of income uncertainty are typically smaller than previous studies have documented and imply less persistence in income shocks. Moreover, we find that income uncertainties evolve noticeably over the life cycle. Young and old consumers on average have more risky future income relative to middle-age consumers. Furthermore, our estimates of income uncertainty generally call for fewer precautionary savings than previous research has found, in particular at younger ages. In a companion paper, Feigenbaum and Li (2010b) study how income uncertainty has changed over time. In contrast to what researchers have found in the aggregate data, the semiparametric estimates of household income uncertainty rose noticeably in the last several decades, and the increase was widespread across demographic and income groups.
A wide variety of theoretical questions related to household financial decisions over the life cycle can be revisited using the metric of income uncertainty we introduce. For example, in this paper we show that our estimate of income uncertainty implies that precautionary saving can create a significantly hump-shaped life cycle profile of mean consumption, but one that is smaller than observed in the data. In contrast, the precautionary saving implied by previous estimates of income uncertainties often calls for a consumption hump that is significantly greater than observed in the data.
 |
 |
 |
 |
![\displaystyle VAR_{d}=Var[y_{t+d}-y_{t}\vert y_{t}]=\frac{1-\rho ^{2d}}{1-\rho ^{2}} \sigma _{\eta }^{2}+[1+\rho ^{2d}]\sigma _{\varepsilon }^{2}.](img67.gif)
![\displaystyle E\left[ \sum_{t=0}^{T_{w}-1}\beta ^{t}u(c_{t};\gamma )+\beta ^{T_{W}}V_{T_{w}}(x_{T_{w}})\right] ,](img82.gif)
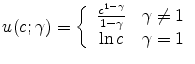
![\displaystyle K=E\left[ \sum_{t=0}^{T-1}b_{t}\right] ,](img104.gif)
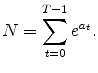
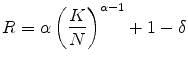
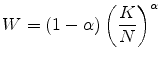
![\displaystyle Var[\ln y_{t+h}\vert y_{t}]=\frac{1-\rho ^{2h}}{1-\rho ^{2}}\sigma _{\eta}^{2}+(1+\rho ^{2h})\sigma _{\varepsilon}^{2}.](img108.gif)
![\displaystyle corr(\ln y_{t+h},\ln y_{t+1}\vert y_{t})=\frac{\rho ^{h-1}\sigma _{\eta}^{2}+\rho ^{h+1}\sigma _{\varepsilon}^{2}}{\sqrt{V[\ln y_{t+h}\vert y_{t}]V[\ln y_{t+1}\vert y_{t}]}}.](img112.gif)