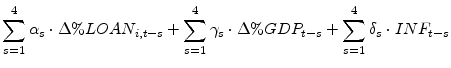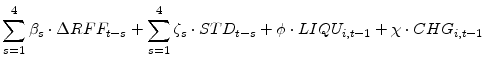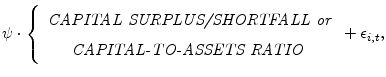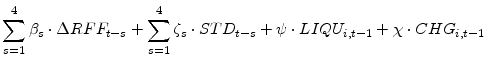Skip to: [Printable Version (PDF)] [Bibliography] [Footnotes]

Finance and Economics Discussion Series: 2010-44 Screen Reader version ^♣

The effects of bank capital on lending:
What do we know, and what does it mean?*

Jose M. Berrospide

Federal Reserve Board

Rochelle M. Edge

Federal Reserve Board

August 20, 2010

Keywords: Bank capital, bank lending

Abstract:

The effect of bank capital on lending is a critical determinant of the linkage between financial conditions and real activity, and has received especial attention in the recent financial crisis. We use panel-regression techniques--following Bernanke and Lown (1991) and Hancock and Wilcox (1993, 1994)--to study the lending of large bank holding companies (BHCs) and find small effects of capital on lending. We then consider the effect of capital ratios on lending using a variant of Lown and Morgan's (2006) VAR model, and again find modest effects of bank capital ratio changes on lending. These results are in marked contrast to estimates obtained using simple empirical relations between aggregate commercial-bank assets and leverage growth, which have recently been very influential in shaping forecasters' and policymakers' views regarding the effects of bank capital on loan growth. Our estimated models are then used to understand recent developments in bank lending and, in particular, to consider the role of TARP-related capital injections in affecting these developments.

The effect of changes in bank capital on the extension of bank credit is a key determinant of the linkage between financial conditions and real activity. Quantifying this relation has therefore been one of the most important research questions of the recent financial crisis. For example, early in the crisis--when the likelihood of a credit crunch was still under debate--the connection between bank capital and bank lending was central to any assessment of how losses in banks' mortgage-related portfolios would affect lending and thus real activity. Likewise, when the Troubled Asset Relief Program (TARP) moved to inject capital into banks through the Capital Purchase Program (CPP), the impact of the program on real activity largely focused on the effect of these injections on bank lending. More recently, this question has re-emerged in light of proposals announced by the Basel Committee on Banking Supervision to raise banks' capital requirements and limit leverage ratios. In this case, policymakers and regulators need to weigh the effects of stricter capital requirements on economic activity against the benefits that would result from greater financial and macroeconomic stability.

In principle, there is a wide range of possible values for effect of a change in bank capital on bank assets and lending. On the one hand, a well-capitalized bank or a bank with access to additional sources of capital will be able to accommodate capital losses without reducing its assets (and hence its lending). By contrast, one could imagine a polar case in which banks very actively manage their assets in order to maintain a constant equity-capital-to-assets ratio (or "capital ratio")--for example, because they cannot raise equity to offset declines in their capital. In this case, a capital loss results in a reduction in assets, with the required reduction equal to the size of the bank's capital loss scaled up by the inverse of its capital ratio (that is, its leverage ratio). Since observed bank capital ratios roughly range from 0.08 to 0.125, leverage ratios range from 8 (= 1/0.125) to 12.5 (= 1/0.08). This means that a dollar's reduction in capital results in an $8 to $12.50 reduction in bank assets.¹ How close we will be to either case in practice is, of course, an empirical question.

Despite its importance, there are relatively few recent estimates for the United States of the effect of changes in bank capital on lending. This is somewhat surprising given the existence of an active earlier literature on this topic. In particular, during the sluggish recovery that followed the 1990-91 recession, many observers debated whether the newly introduced capital regulations associated with Basel I were inhibiting lending. Although this debate did not yield a definitive conclusion, it did result in the development of empirical models that expressly sought to quantify the effect of bank capital on bank lending. For example, Hancock and Wilcox (1993, 1994) estimated models relating changes in individual banks' loan growth to measures of loan demand and bank capital. Similarly, Berger and Udell (1994) specified an equation relating the growth rate of various bank assets to different measures of bank capital ratios. Finally, Bernanke and Lown (1991) developed state-level equations linking bank loan growth to bank capital ratios and employment, along with bank-level equations for a single state (New Jersey).²

This paper draws on this earlier literature, as well as more recent approaches, to examine how bank capital affects bank lending in the U.S. In all cases, we find relatively modest effects of bank capital on lending and more important roles for factors such as economic activity and increased perception of risk by banks. Using balance-sheet data for large bank holding companies (BHCs), we consider variants of two of the approaches developed in the earlier literature: specifically, the Hancock and Wilcox (1993, 1994) and Bernanke and Lown (1990) models. For our purposes, the main difference between these two approaches is that the Bernanke-Lown approach considers the effect of actual BHC capital-to-asset ratios on BHC loan growth while the Hancock-Wilcox approach looks at the effect of deviations of BHC capital levels relative to an estimated target. Both approaches have merits and shortcomings--which we will discuss at length--but both also agree in finding relatively small effects of BHC capital on loan growth.

A potential concern surrounding both sets of results is survivor bias: Our panel only includes BHCs that were still in operation at the end of our sample period (2008:Q3). We address this issue by also considering a more aggregate approach; namely, a modified variant of one of Lown and Morgan's (2006) vector autoregression (VAR) models. This allows us to investigate the dynamic and general-equilibrium effects of an exogenous change in bank capital ratios. Again, however, we find relatively modest effects of bank capital-ratio changes on loan growth even using this very different approach.

Our estimates of the effect of bank capital on lending are considerably smaller than the effects suggested in recent statements by U.S. Treasury officials. For example, on the likely effects on lending of capital injections and anticipated capital raising following the stress tests, such statements suggest that a $1 capital injection generates between $8 to $12 of lending capacity.³ These magnitudes seem more consistent with the view described earlier that banks actively manage their assets to maintain constant bank capital ratios. This view has been quite prominent of late, and is apparently based on a scatterplot for aggregate leverage and commercial-bank asset growth reported by Adrian and Shin (2007).⁴ This scatterplot for commercial banks is reproduced in the lower-left panel of Figure 1 using our data; the figure also shows scatterplots for all of the other institutions that Adrian and Shin consider (specifically, households, non-financial and non-farm corporate firms, and security brokers and dealers). The sample period used in Figure 1 is 1963 to 2006, the same as that employed by Adrian and Shin.⁵ The roughly constant leverage ratio apparent from the commercial bank panel--especially when compared to other classes of institutions--suggests a very active management of assets by commercial banks. This implies that a change in bank capital has a magnified effect--with the scaling factor equal to the leverage ratio--on asset levels and lending volumes.

Adrian and Shin's scatterplots have also been quite influential in shaping forecasters' views. For example, in a note written early in the crisis, Hatzius (2007) used these commercial-bank scatterplots to estimate the reduction in loan volumes that would result from banks' mortgage-related portfolio losses. In a subsequent Brookings paper on the same issue, Hatzius (2008) again appealed to asset-leverage scatterplots to inform revised estimates of the effect of bank capital losses on loans.

Interestingly, reconciling our regression results with the Adrian-Shin scatterplots turns out to be very simple: Because of the major structural changes that occurred in the banking sector following the adoption of the Basel Accord, our empirical analysis begins in the early 1990s; in contrast, Adrian and Shin's scatterplots span a much longer period that starts in 1963. To see what effect the choice of sample period has on the analysis, consider the two left panels of Figure 2, which give scatterplots for commercial-bank asset and leverage growth over 1963:Q1 to 1989:Q4 (the top panel) and 1990:Q1 to 2008:Q3 (the bottom panel). As can be seen from comparing these plots, the feature of the data that has led to the view that commercial banks actively manage their assets to maintain constant leverage is much more of an artifact of the early part of the sample and is considerably less evident in the latter (post-Basel) part, which is naturally more relevant for considering current questions. Indeed, in the latter part of the sample the scatterplot is merely a cloud of points with no obvious correlation. The two right-hand panels of Figure 2 provide a different split of the sample; specifically, one that breaks the sample in 1985:Q1 and therefore uses a more equal number of observations (88 and 94 observations, respectively) for each plot. Again, the feature of the data reported by Adrian and Shin (2007) and emphasized by Hatzius (2007, 2008) is very evident in the first part of the sample and not at all evident in the second part.⁶ Clearly, the scatterplots shown in the lower panels of Figure 2 make the small effects of bank capital on loan growth found in our regressions less surprising.

A couple of other related recent studies are also worth noting. First, Francis and Osborne (2009) apply Hancock and Wilcox's approach to U.K. commercial bank data; like us, they find relatively modest effects of bank capital shortfalls on lending. Ciccarelli, Maddaloni, and Peydró (2010) build on Lown and Morgan's VAR model--albeit along a different dimension than we do--to study the credit channel of monetary policy in the Euro area and the U.S. (in this case using the European Bank Lending Survey or BLS and the U.S. Senior Loan Officer Opinion Survey or SLOOS). In contrast to our approach, however, Ciccarelli et al. do not explicitly consider the influence of bank capital by including a measure of it in their VAR model but rather rely on answers to "reasons for tightening/loosening lending standards" questions from the survey. Based on this approach, Ciccarelli, et al. conclude that bank capital and liquidity have significant effects on GDP.⁷

Other methods for examining the effect of bank capital on lending have been pursued in a number of recent papers, albeit for countries other than the U.S. For example, following Peek and Rosengren (1997), Puri, Rocholl and Steffen (2010) use loan applications from German Landesbanks to examine the effect of shocks to capital on the supply of credit by comparing the performance of affected and unaffected banks. Gianetti and Simonov (2010) use Japanese data to perform a similar exercise concerning bank bailouts. These papers do find a relevant role for capital in determining loan volumes, although they do not explicitly compare the magnitudes of the effects they find with those implied by the constant leverage view. Another group of papers use firm and bank loan-level data; these include Jiménez, Ongena, and Peydró (2010), who use Spanish data, and Albertazzi and Marchetti (2010), who use data on Italy. These papers find sizeable effects of low bank capitalization and scarce liquidity on credit supply. (We contrast our methodology with the approaches that use firm and bank loan-level data later in the paper.)

We would note that although the above-mentioned loan-level studies for Spain and Italy suggest larger effects than what we find, other studies for the U.S. that use loan-level data (albeit for syndicated loans only) matched to bank and firm variables, such as Santos and Winton (2010), obtain relatively small effects of bank capital on lending. In addition, Elliot (2010) uses simulation-based techniques and finds small effects of higher capital ratios on loan pricing and loan volumes for U.S. banks. Finally, De Nicolò and Lucchetta (2010) use aggregate data for the G-7 countries and conclude that credit demand shocks are the main drivers of bank lending cycles. Thus, our empirical findings of modest effects of capital on total loan growth appear consistent with other papers that employ U.S. data.

Our findings have several interpretations. First, in making their lending decisions, BHCs might not actively manage their assets on the basis of their capital positions.⁸ If our results are correct, and other factors such as loan demand or increased bank risk play a more important role in determining BHC loan growth, then we have an explanation for the notable slowing of loan growth observed over the first three quarters of 2009: The impact of increases in the availability of loanable funds from various government actions was more than offset by weak economic conditions that reduced loan demand, as well as by increased risks (such as the reduced creditworthiness of borrowers).

Second, given the widespread consensus that banks entered the most recent crisis with too little capital relative to the riskiness of their portfolios (even though by most measures they were previously viewed as well capitalized), another interpretation of our results is that conventional measures of bank capital--such as those that we use--may not be relevant for assessing financial intermediaries' capital positions. If so, our results naturally call into question the prevailing risk-based measures employed by the regulatory capital framework and militate a strengthening in risk coverage, particularly in terms of incorporating capital requirements for off-balance sheet operations (such as securitization activities) and counterparty exposures.

The balance of the paper is organized as follows. We describe our data in Section 1. Section 2 contains empirical estimates of the relation between bank capital and bank loan growth at the institutional level, while section 3 presents our results using aggregate data. Sections 4 and 5 then use the models developed in sections 2 and 3 to address some questions of practical policy interest. Specifically, in section 4 we estimate the likely effect that TARP capital injections had on bank loans, and in section 5 we consider the factors underlying recent reductions in bank loan growth. Section 6 concludes.

1 Data

Because we use both panel and time-series methods, the paper employs a wide range of data sources. We discuss these data sources at length in this section.

1.1 Institution-level data

For our panel regression, which we conduct at the institution level, we use bank holding company (BHC) data rather than data on the loans of individual commercial banks within a BHC. This reflects the observation that many decisions regarding a BHC's activities are taken for the institution as a whole rather than on a subsidiary-by-subsidiary basis.⁹ Institution-level data are taken from the Consolidated Financial Statements for Bank Holding Companies (FR Y-9C); the data cover the period 1992:Q1 to 2009:Q3, with the exception of the data series that are based on regulatory capital (and that appear in some of our Bernanke-Lown type regressions), which begin only in 1996. Our sample consists of 165 large BHCs, all with total assets in excess of $3 billion as of 2008:Q3. This represents approximately 85 percent of the total assets in the banking sector.¹⁰

Table 1 reports summary statistics for the variables used in the panel regressions. Although the sample only includes large BHCs, there is a sizable variation in total assets. The median BHC in the sample has assets above $3 billion. However, the standard deviation of $145 billion is consistent with the fact that the four largest institutions in the sample have assets above $1 trillion, whereas total assets for the smallest ones are below $1 billion.¹¹ Quarterly growth in total and C&I loans averages 3 percent across all BHCs and over time. The distribution of variables scaled by assets such as capital, securities and net charge-offs exhibit smaller variances. Both the mean and the median values for the equity-to-assets (leverage) ratio are about 8 percent, while the mean and median of total and tier one risk-based capital ratios (measured as total and tier one capital over risk-weighted assets) are 12-1/2 percent and 13-1/4 percent (for total) and 10-3/4 percent and 11-1/4 percent (for tier one). Finally, the Tangible Common Equity (TCE) ratio (measured as tangible common equity over tangible assets) for the mean and median BHC is about 7 percent.

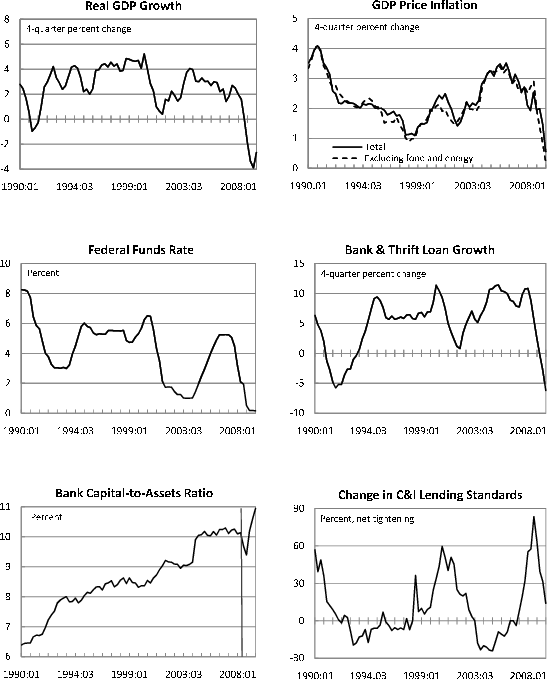
The first four panels of Figure 3 depict the evolution of the average of different capital ratios over our sample. As is evident from the top two panels, throughout most of the sample period the average total and tier one risk-based capital ratios for large BHCs remained significantly above their well-capitalized regulatory minima.¹² Note also the divergent movements across different capital-ratio measures: For example, while risk-based capital ratios have exhibited a downward trend since 2004, the capital-to-assets ratio--the middle-left panel--remained on an upward trend until mid-2007. This could partly reflect differences arising from the denominator of the capital-ratio measures which, in turn, could be associated with increasing risk-taking by banks during the last 5 years. In particular, excessive risk-taking behavior could have made risk-weighted assets increase faster than total assets.

As expected, the leverage ratio and the regulatory capital ratios all jump in 2008:Q4 after the implementation of the Treasury's capital injection program. (A vertical line is shown in the top four panels of Figure 3 at 2008:Q3, just before the capital injections.) However, because the Treasury injected capital through purchases of preferred stock with warrants rather than common equity, the TCE ratio--the middle-right panel--is not affected by TARP capital infusions and seems to have maintained the downward trend that it has displayed since 2003. Adverse market risk perceptions of the banking sector were more evident after the beginning of the financial crisis and this explains a deeper contraction in the average TCE ratio after the second half of 2007. This market-focused measure of capitalization reached its lowest value in 2009:Q1 due to adverse market expectations in advance of the May 2009 release of the bank stress test results (the average TCE ratio was below 6 percent, with ratios below 2 percent for some of the largest BHCs).

The bottom two panels of Figure 3 plot the average four-quarter growth rate of total loans for the 165 BHCs in our sample, along with loan growth for all commercial banks and large banks only. As can be seen from these panels, commercial-bank and BHC loan growth slowed notably in the 2001 recession but recovered rapidly thereafter, with the average four-quarter growth rate prior to 2007 fluctuating between 10 to 15 percent. Total growth in bank loans exhibits a severe contraction starting in early 2008, with a further slowing in growth following the ongoing deterioration in credit conditions during 2008. Negative four-quarter growth rates were evident in the first part of 2009.

1.2 Aggregate data

Our panel regressions include a number of macroeconomic data series; these are plotted in Figure 4. Specifically, our panel regression loan-growth equations include real GDP growth (the top-left panel of Figure 4), as measured by the National Income and Product Accounts (NIPAs); inflation (the top-right panel, solid line), as measured by the overall GDP deflator; the Federal funds rate (the middle-left panel); and (aggregate) net tightening of C&I lending standards (the bottom-right panel), as reported by the Federal Reserve Board's Senior Officer Opinion Survey (SLOOS).

A large fraction of the aggregate variables that are included in the paper's panel regressions are also included in the VAR model that we consider in section 3. Indeed our panel equation for loan growth has a similar specification to our loan-growth equation in the VAR, albeit without the institution-specific variables that the former equation has. In particular, our VAR model includes real GDP growth, along with inflation. However, the inflation measure used in the VAR is based on the GDP deflator excluding food and energy (see the dotted line in the top-right panel of Figure 4). Our reason for using different inflation measures is attributable to some very large swings in overall GDP prices caused by swings energy prices at the end of our data. In our panel regressions, the difference between the two inflation measures has a minimal impact on our results since our estimation period stops at the third quarter of 2008, before we observe significant movements in energy prices. In the VAR, these swings were not important for our impulse response functions, but did influence (in an implausible way) the composition of estimated nonfinancial structural shocks being derived from our model over the 2008 to 2009 period.¹³

Like the panel regression, our VAR model also includes the Federal Funds rate and the net tightening in C&I lending standards from the SLOOS. Our measure of the aggregate capital-asset ratio (the bottom-left panel) is for commercial banks and is taken from the Call Reports. Finally, for loan growth (the middle-right panel) we use bank and thrift depository loan growth as reported by the Flow of Funds Accounts. Our principal motivation for using commercial bank and thrift loans in the VAR rather than just commercial bank loans--which may seem more sensible given that all other banking-sector variables pertain only to commercial banks--arises from some very sharp spikes in the latter series caused by purchases of large thrifts by commercial banks, such as Bank of America's purchase of Countrywide and JP Morgan's purchase of Washington Mutual. Using the aggregate bank and thrift data eliminates these swings and does not greatly alter the VAR's impulse response functions, although clearly it leads to more plausible estimated sequence of structural shocks.

2 Bank Capital and Loan Growth at the Institution Level

In this section we use institution-level BHC data and panel regression techniques to study the effects of BHC capital on loan growth. The idea here is to model the loan growth of our panel of BHCs as a function of supply and demand factors, with one of our supply factors being BHC capital. Specifically, the loan growth regressions that we estimate take the form

$\displaystyle \Delta\%LOAN_{i,t}$	$\displaystyle =$	$\displaystyle \sum_{s=1}^{4}\alpha_{s} \cdot \Delta\%LOAN_{i,t-s} + \sum_{s=1}^{4}\gamma_{s} \cdot \Delta\%GDP_{t-s} + \sum_{s=1}^{4}\delta_{s} \cdot INF_{t-s}$
	$\displaystyle +$	$\displaystyle \sum_{s=1}^{4}\beta_{s} \cdot \Delta RFF_{t-s} + \sum_{s=1}^{4}\zeta_{s} \cdot STD_{t-s} + \phi \cdot LIQU_{i,t-1} + \chi \cdot CHG_{i,t-1} \$
	$\displaystyle +$	$\displaystyle \psi\cdot\left\{\begin{array}{c} \emph{CAPITAL SURPLUS/SHORTFALL or} \ \emph{CAPITAL-TO-ASSETS RATIO} \; \end{array} \right. + \epsilon_{i,t},$	(1)

where $\Delta\%LOAN_{i,t}$ denotes the growth rate of BHC loans, $\Delta\%GDP_{t}$ is real GDP growth, $\Delta\%INF_{t}$ is the inflation rate measured by the GDP deflator, $\Delta RFF_{t}$ is the change in the federal funds rate, and $STD_{t}$ denotes lending standards. The bank-specific variable $LIQU_{i,t}$ denotes BHC liquidity and is measured by the ratio of securities to total assets, while the bank-specific variable $CHG_{i,t}$ is the ratio of net charge-offs to total assets.

Because our loan-growth regression (1) controls for the effects of other supply and demand variables, we can interpret the coefficient $\psi$ on the capital term as the effect of BHC capital conditions on loan growth. We consider two ways that capital can affect loan growth. In the first case--which corresponds to the approach of Hancock and Wilcox (1993, 1994)--it is the divergence between a BHC's actual and target capital (i.e., its capital surplus or shortfall) that is important for determining loan growth. In the second case--which corresponds to the approach of Bernanke and Lown (1991)--a BHC's capital-to-assets ratio influences loan growth.

The BHC capital-to-assets ratio measures included in the Bernanke-Lown regressions can be calculated from variables taken directly from the Consolidated Financial Statements for Bank Holding Companies (the FR Y-9C data). By contrast, the capital measures used in the Hancock-Wilcox regressions first requires us to create time-varying desired/target capital levels for each BHC in our panel. From these time series, we can compute the percentage surplus or shortfall of actual capital relative to target. (The precise method and results for this stage of the Hancock-Wilcox estimation procedure are discussed in subsection 2.1.), Note that the estimation period for these regressions is 1992:Q1 to 2008:Q3; that is, we stop the analysis around when the crisis intensified in late September 2008 and just before TARP capital injections began to occur. This prevents the TARP capital injections from distorting our regression coefficients.

2.1 Estimation of BHC capital surplus/shortfall measures

Following Hancock and Wilcox (1993, 1994) and Flannery and Rangan (2008) we use a partial-adjustment model between actual and target capital holdings to estimate individual bank-specific capital targets. The target capital ratio, $k_{i,t}^{\ast}$ , is modeled as a linear function of a vector of control variables $X_{i,t}$ , which include bank-specific characteristics as well as institutional and aggregate determinants (so $k_{i,t}^{\ast}=\theta \cdot X_{i,t}$ ). Based on the rationale that costs of altering bank capital prevent banks from moving capital to its target level immediately, the actual bank capital ratio $k_{i,t}$ is assumed to follow a partial-adjustment process of the form

$\displaystyle k_{i,t}-k_{i,t-1}=\lambda\cdot (k^{\ast}_{i,t-1}-k_{i,t-1})+\epsilon_{i,t}.$

Substituting in our expression for $k^{\ast}_{i,t-1}$ , re-arranging terms, and adding a bank-specific constant yields our estimation equation:

$\displaystyle k_{i,t}=\alpha_{i}+(1-\lambda)\cdot k_{i,t-1}+\lambda\cdot\theta\cdot X_{i,t-1}+\epsilon_{i,t}.$

(2)

The bank-specific variables in $X_{i,t}$ include the log of total assets, the return on assets, and the net charge-off rate; these are intended to serve as proxies for size, earnings, and risk, respectively. Size captures the fact that larger banks are likely to face lower risks (due, for example, to greater diversification) and better access to sources of funding (thereby requiring less capital). Earnings are included because dividend payments are often slow to adjust; hence, an increase in earnings results in an accumulation of retained earnings and bank capital. Risk captures the fact that markets and regulators require more capital to be held against riskier assets. In the benchmark specification of our capital ratio equation we also include the loan/security composition of bank assets, which reflects the differential risk exposures implied by different types of assets, and the composition of bank loans, which for similar reasons could also affect target capital ratios. These terms are dropped in an alternative specification of equation (2) that we consider.¹⁴ The institutional variable, called "regulatory pressure," is a dummy variable that equals unity if the BHC's equity capital ratio is less than 1.5 percentage points above the minimum of 5 percent.¹⁵ We also include aggregate variables such as a measure of stock-market volatility and the aggregate net charge-off rate.

Note that the only measure of capital that we consider in deriving our surplus/shortfall estimates is equity capital. Consequently, we do not estimate models of the form described by equation (2) for the three other capital ratios--i.e., the total and tier-one risk-based capital ratios and the tangible common equity-to-assets ratio--that we reported in Figure 3 and discussed in section 1.1. (The full set of capital ratios is examined when we consider the Bernanke-Lown version of equation 1.) We focus here on equity capital on the grounds that the Hancock-Wilcox loan-growth regression implicitly seeks to capture a behavioral relation whereby BHCs alter the growth rate of their loan volumes--the dependent variable of equation (1)--so as to obtain a desired level of capital. If this is the case, however, it would then be most likely that such an adjustment would involve a fairly broad measure of capital (such as, total equity capital) rather than a more narrow measure (such as, tangible common equity). Similarly, we do not consider total and tier-one risk-based capital ratios because these are essentially regulatory concepts for which the relevant target is the threshold that determines whether a BHC is adequately or well capitalized. Thus, it makes less sense to try to develop a model of the target for these capital ratios. In addition, even if BHCs did seek to target these ratios, they would be more likely to adjust their risk-based assets--that is, to adjust the composition of their loans as well as their volume--which would make this a less useful tool for analyzing the growth of aggregate loan volumes (the ultimate focus of our analysis).

Table 2 provides the estimation results for equation (2) under two different specifications of the $\theta\cdot X_{i,t-1}$ term. Other than the coefficients on bank size and aggregate stock-market volatility, most of the coefficients reported in Table 2 are close to what might be expected a priori. Size receives a positive and significant coefficient in both specifications, which implies that larger BHCs have higher equity capital ratios. This contradicts previous findings that larger BHCs have lower capital ratios, and suggests that there are some economies of scale in holding capital at larger institutions.¹⁶ We also find that larger shares of each broad category of loans and of securities (relative to assets) are associated with lower capital ratios, which we interpret as indicating that BHCs with more portfolio diversification (loans categories and investment securities) hold less capital. The negative coefficient on stock-market volatility appears to reflect the counter-cyclical nature of volatility and the pro-cyclicality of bank capital. Both individual and aggregate net charge-off rates are associated with higher capital ratios, though only the aggregate measure seems statistically significant. These two variables control for bank risks and suggest that BHCs hold additional capital during bad times, when the credit quality of loans deteriorates. Our dummy-control for regulatory pressure has a negative coefficient but is statistically insignificant, which suggests that regulatory restrictions do not seem to bind in a way that affects equity capital ratios. Finally, BHCs with higher profits tend to hold more capital, but this result also appears to be statistically weak.

In addition to the usual candidate determinants of the target capital ratio, the regression equation includes bank-specific fixed effects to control for possible omitted variables and to capture heterogeneous characteristics such as different risk preferences, governance structures, and managerial skills. The fixed effects explain a large fraction of the cross-sectional variation in target capital ratios without affecting the statistical significance of the other time-varying and firm-specific characteristics in the regression equation.¹⁷ Interestingly, the coefficient on the lagged capital ratio implies a relatively quick adjustment of capital ratios to target: Our estimated average speed of adjustment of 36 percent per year is smaller than the 49 percent per year rate found by Flannery and Rangan (2008) but within the range of 28 percent to 41 percent reported by Berger et al. (2008).

As in Hancock and Wilcox, the estimates of the coefficients in equation (1) are used to calculate a time series for each BHC's target capital ratio $k^{\ast}_{i,t}$ . These estimated target capital ratios are then used to construct target capital levels $K^{\ast}_{i,t}$ . Capital surpluses, denoted by $Z_{i,t}$ , are calculated as deviations of actual capital levels relative to target; that is, $Z_{i,t}=(K_{i,t}-K^{\ast}_{i,t})/K^{\ast}_{i,t}$ .

Figure 5 plots the average actual and average target capital ratios--that is, $\bar{k}_{t}$ and $\bar{k}^{\ast}_{t}$ --over our estimation period, where the averages are computed over the entire sample of BHCs. Differences between the average actual and average target capital ratios appear quite pronounced and quite persistent; nonetheless they do appear to conform with certain aspects of the conventional wisdom concerning movements in these series. In particular, in line with the findings of the literature on bank capital management, we find that BHCs operated with significant capital surpluses over most of the late 1990s and early 2000s.¹⁸ Furthermore, BHCs appeared to have operated with large capital shortfalls between 1993 and 1995, which may have reflected widespread capital pressures after the implementation of the Basel I capital guidelines around 1992.¹⁹

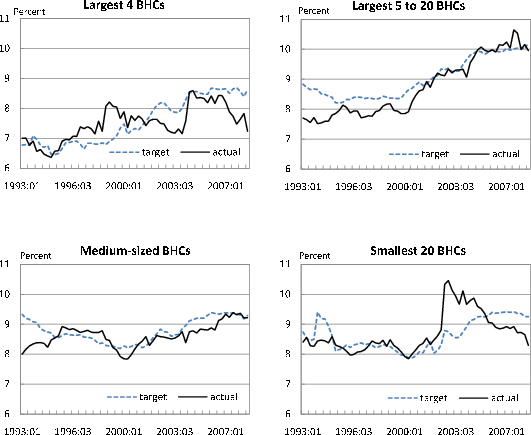
Figure 6 plots the average actual and average target capital ratios over our estimation period for subgroups of BHCs based on bank size. Differences between actual and target capital also seem apparent among the largest and smallest BHCs in our sample. The four largest BHCs (those with total assets above $1 trillion at the end of the sample) seemed to have operated with capital close to their target levels in the early 1990s (e.g., after the implementation of Basel I) and then to have accumulated large surpluses between 1995 and 2001. These plots suggest that most of the conventional wisdom regarding the emergence of large capital surpluses in the late 1990s and early 2000s is explained by the behavior of the largest BHCs. However, after 2002 the very large BHCs appear to suffer from the largest capital shortfalls, which became more pronounced during the recent financial turmoil. Unlike the largest institutions, smaller BHCs had relatively large capital shortfalls during the early 1990s, and gradually aligned their capital with their target during the late 1990s and early 2000s. The smallest 20 BHCs seemed to have conducted a quick capital adjustment during that period and began to be better capitalized with large surpluses between 2003 and 2006. However, the smallest institutions started to reduce their capital ratios around the middle of 2004, mainly as a result of a rapid balance sheet expansion; as in the case of the largest BHCs, these firms were operating substantially below target at the beginning of and during the recent financial crisis. In sum, the recent phenomena of large capital shortfalls that is apparent in the aggregate data (Figure 5) seems largely to reflect developments at the smallest and very largest BHCs.

2.2 Estimation of the effect of capital surpluses or shortfalls on loan growth

To gauge the effects of capital surpluses or shortfalls on bank loans we include our estimates of bank capital surpluses--denoted by $Z_{i,t}$ , above--in a regressions model of bank loan growth. Our model is similar in spirit to the loan growth regression of Hancock and Wilcox, who studied the link between bank capital and bank loan growth while controlling for macroeconomic conditions. Our particular specification is closer, however, to that used by Kashyap and Stein (1995, 2000), who modeled the growth rate of bank loans in terms of supply and demand factors.

We model the growth rate of BHC loans ( $\Delta\%LOAN_{i,t}$ ) as a function of its own lags, lags of aggregate economic growth ( $\Delta\%GDP_{t}$ ), lags of the GDP price inflation rate ( $\Delta\%INF_{t}$ ), lags of the change in the federal funds rate ( $\Delta RFF_{t}$ ), and lags of lending standards ( $STD_{t}$ ). In addition, we include lagged BHC-specific characteristics such as a control for bank liquidity ( $LIQU_{i,t}$ ), which is measured by the ratio of securities to total assets, and the ratio of net charge-offs to total assets ( $CHG_{i,t}$ ). The last term we include is our estimates of bank capital surpluses/shortfalls ( $Z_{i,t}$ ), which is the main variable of interest. Thus, we fit the following panel regression equation

$\displaystyle \Delta\%LOAN_{i,t}$	$\displaystyle =$	$\displaystyle \sum_{s=1}^{4}\alpha_{s} \cdot \Delta\%LOAN_{i,t-s} + \sum_{s=1}^{4}\gamma_{s} \cdot \Delta\%GDP_{t-s} + \sum_{s=1}^{4}\delta_{s} \cdot INF_{t-s}$
	$\displaystyle +$	$\displaystyle \sum_{s=1}^{4}\beta_{s} \cdot \Delta RFF_{t-s} + \sum_{s=1}^{4}\zeta_{s} \cdot STD_{t-s} + \psi \cdot LIQU_{i,t-1} + \chi \cdot CHG_{i,t-1}$
	$\displaystyle +$	$\displaystyle \psi \cdot Z_{i,t-1}+\epsilon_{i,t}.$	(3)

The model is specified in growth rates to deal with non-stationary variables; to avoid potential endogeneity issues, only lags of the explanatory variables are used. We also include quarterly dummies to control for possible seasonality in the data. In this specification, GDP growth is used to control for changes in loan demand, lending standards are used to control for credit supply changes that arise from changes in banks' lending behavior, and the federal funds rate controls for monetary policy changes. At the firm level, the liquidity variable is intended to capture the extent to which BHCs use their stock of securities to adjust their loan growth, all else equal (a point raised by Kashyap and Stein) while the fraction of charge-offs to total assets is a proxy for risk, which should act as a drag on loan growth. Equation 3 is estimated with bank fixed effects in order to allow for potential omitted factors that vary across BHCs and are constant over time.

Table 3 presents the estimation results for equation (3).²⁰ The first pair of columns gives results when total bank loans are used as the dependent variable, while the second pair of columns gives results when C&I loans are used as the dependent variable. For both total bank loans and C&I loans there is a positive and significant coefficient on capital surpluses, indicating that the growth rate of both total and C&I bank loans is larger for banks with greater amounts of excess capital. The effects, however, are small: The long-run impact of a capital surplus (shortfall) on both total and C&I BHC loan growth is roughly to increase (reduce) annualized loan growth by 0.25 percentage point when capital exceeds (falls short of) its target level by 1 percent.

Our estimate of the effects of a 1 percent capital surplus on loan growth can--with some manipulation--be compared to the effects found by Hancock and Wilcox, who looked at dollar amounts. Using a 10 percentage point average capital-to-assets ratio and a 60 percent average share of loans (as a fraction of bank assets), our model estimates imply that a $1 capital surplus results in a $1.86 boost in loan volumes.²¹ This is a touch higher than Hancock and Wilcox's estimates, which implied that a $1 surplus leads to a $1.50 boost in loan volumes, but it is not vastly different. Our estimate is, however, very different--i.e., about one-sixth to one-tenth the size--to the $8 to $12.50 increase in loans that the constant leverage ratio assumption would imply.

The results in Table 3 suggest a notable role for demand shocks and exogenous changes in net charge-offs in determining both total and C&I loan growth. The results imply that in the long-run a 1 percentage point reduction in GDP growth lowers the annualized growth rate of total loans by 4.1 percentage points and lowers the annualized growth rate of C&I loans by 9.4 percentage points. Furthermore, changes in net charge-offs have a large and significant impact in both specifications. For example, a 1 percentage point increase in the net charge-off ratio depresses (in the long run) the annualized growth rate of both total and C&I BHC loans by about 7 percentage points. Turning to the other regressors, although the coefficient on the securities-to-assets ratio is significant, the effect of increased holdings of securities on BHC loan growth is small: A 1 percentage point increase in the securities-to-assets ratio leads to about a 0.3 percentage point long-run increase in both total and C&I annualized loan growth. Finally, the coefficient on lending standards in both the total and C&I loan growth equations are negative (as expected) and statistically significant, but imply an impact on loan growth that is economically small: A 1 percentage point increase in lending standards leads to about a 0.1 percentage point decrease in annualized loan growth. The small effect of standards may be explained by the fact that the capital surplus measure and charge-off ratio likely already capture changes in banks' willingness to lend.

2.3 Estimation of the effect of bank capital ratios on loan growth

As we will discuss in the next section (when we consider possible identification issues present in our panel regression analysis), one potential problem with the Hancock-Wilcox approach is that the target capital-to-assets ratio equation could be mis-specified. If we model the target poorly, our estimates of the effect of a capital surplus or shortfall on loans will also be poor, thereby biasing the estimated surplus/shortfall impact coefficient $\psi$ . (The direction of this bias will likely be downward for the usual errors-in-variables reasons.) An alternative approach to investigating the link between bank capital and bank lending that does not suffer from this issue involves focusing on the relationship between capital ratios and bank loan growth. For this purpose, we replace our measure of the capital surplus in equation (3) with the lagged value of different measures of the capital ratio. That is, we estimate:

$\displaystyle \Delta\%LOAN_{i,t}$	$\displaystyle =$	$\displaystyle \sum_{s=1}^{4}\alpha_{s} \cdot \Delta\%LOAN_{i,t-s} + \sum_{s=1}^{4}\gamma_{s} \cdot \Delta\%GDP_{t-s} + \sum_{s=1}^{4}\delta_{s} \cdot INF_{t-s}$
	$\displaystyle +$	$\displaystyle \sum_{s=1}^{4}\beta_{s} \cdot \Delta RFF_{t-s} + \sum_{s=1}^{4}\zeta_{s} \cdot STD_{t-s} + \psi \cdot LIQU_{i,t-1} + \chi \cdot CHG_{i,t-1}$
	$\displaystyle +$	$\displaystyle \psi \cdot \left(K_{i,t-1}/A_{i,t-1}\right)+\epsilon_{i,t},$	(4)

using several measures of the capital-to-assets ratio for $K_{i,t-1}/A_{i,t-1}$ : the equity capital-to-assets ratio (the book leverage ratio); the total risk-based capital ratio; the tier-one risk-based capital ratio; and the tangible common equity (TCE) ratio. We consider each capital ratio separately. The different capital ratios measure different dimensions of banks' balance-sheet positions and thereby reflect different forces that act to influence lending. For example, by using the equity capital ratio we capture the impact of capitalization decisions on loan growth, while using the two risk-based capital ratios in our regression captures the effect on loan growth of both capital adequacy and portfolio composition because the risk-based measures also include off-balance sheet assets. The TCE ratio is a more conservative measure of bank capital, intended to represent the first-loss position in case of a bank's failure. We include this alternative measure of bank capital primarily because it was the focus of market participants in the quarters after October 2008 in evaluating the financial strength of banking institutions. (We would note that the specification implied by this equation 4 is broadly similar to the loan growth equation estimated in our VAR model in section 3.)

The estimation results for the effect of capital-ratio shocks to capital ratios on BHC loan growth are reported in Table 4. As can be seen from the table, all variables enter with the expected sign and most are statistically significant. For example, there are positive and significant coefficients on the BHC capital ratios, which is consistent with the growth rate of bank loans being larger for banks with higher capital ratios. However, regardless of the capital ratio we use as our main explanatory variable, the effects of shocks to capital on BHC loan growth are small. Depending on the capital ratio employed, our results in Table 4 suggest that a 1 percentage point increase in the capital ratio leads to a long-run increase in annualized BHC loan growth that is only between 0.7 and 1.2 percentage points.

The largest estimated effect of capital shocks on BHC loan growth comes from the regression specification that uses the TCE ratio; as mentioned above, this measure received significant attention by market participants, especially during the weeks surrounding the bank stress tests in 2009. However, even this specification suggests that higher bank capitalization would have a very modest impact on BHC loan growth. In other words, in the event that BHCs managed to raise additional capital either by issuing more common stock or by converting preferred shares to common shares--as some proposals for regulatory reform have suggested--the resulting increase in common equity would have only a minor impact on the growth rate of bank loans.

Our estimate of the long-run effect of a 1 percentage point increase in the equity capital ratio, which lies towards the lower end of the above range of estimates, can be compared with the effect obtained by Bernanke and Lown for their sample of New Jersey banks. Bernanke and Lown's reported estimates are notably larger than ours: For their full sample of 111 New Jersey banks, they found that a 1 percentage point increase in the equity capital ratio resulted in a 2 percentage point increase in loan growth, while the corresponding increase in loan growth for their sample of 90 small New Jersey banks was around 2-1/2 percentage points. Clearly, the size of the institutions considered is one reason why our estimates differ from Bernanke and Lown's; indeed, Bernanke and Lown's analysis does indicate a notably smaller degree of sensitivity of bank loans to equity capital ratios for larger banks. Note also, that because our analysis considers the largest 165 BHCs in the United States while Bernanke and Lown's analysis only considers banks that operate within the state of New Jersey, even the smallest institutions in our sample are larger than the "large" banks in Bernanke and Lown's sample.²² Of course, another reason why our estimate may be smaller than that of Bernanke and Lown's is that whereas our model of loan growth includes a number of controls (including bank-specific ones), Bernanke and Lown's model only includes the capital ratio, which could be capturing the effects of other variables.

While the effects of the equity capital ratio on bank loan growth that we obtain in our analysis are somewhat smaller than those estimated by Bernanke and Lown, they are notably smaller--on the order of one-tenth the size--than the loan-growth impact that would be implied by the constant leverage-ratio assumption. That is, the constant leverage-ratio assumption would imply that the percentage-point long-run increase in loan growth implied by a 1 percentage point increase in the equity capital ratio is equal to the capital ratio--i.e., 8 percentage points for a 8 percent equity capital ratio and 12 percentage points for a 12 percent equity capital ratio.

As was the case for our analysis of the effects of capital shortfalls on loan growth, the model's estimation results suggest that demand shocks and exogenous changes in net charge-offs play the most important role in determining total loan growth. The response of BHC loan growth to demand shocks (measured by changes in GDP growth), implies that a 1 percentage point reduction in GDP growth leads to about a 4 percentage point decline in annualized loan growth. Furthermore, the potential effects of continued write-downs through further increases in net charge-offs imply a large and significant impact in all capital-ratio specifications that we considered, as a 1 percentage point increase in the net charge-off ratio reduces the annualized growth rate of total BHC loans by about 8 percentage points. As before, the coefficient on the securities-to-assets ratio is significant but the effect of increased holdings of securities is small and leads to only a 0.3 percentage point increase in BHC loan growth for every percentage-point increase in the securities-to-assets ratio. Finally, the coefficient on lending standards is negative and significant but has also small impact on BHC loans. As before, this latter finding might be explained by the fact that the capital shock and changes in the charge-off ratio already capture changes in banks' willingness to lend.

2.4 Endogeneity of the capital measures

In the discussion of our estimation results in subsections 2.2 and 2.3 we interpreted our parameter $\psi$ as reflecting the magnitude of the increase in loan growth implied by a higher capital surplus or a higher capital ratio. Doing this, however, requires us to rule out other possible interpretations that could result in a relationship between a bank loan growth and bank capital.

One possible (and well recognized) reason why we might observe a positive correlation between a bank's loan growth and its capital--whether lagged or not--is that this correlation is driven by a third variable that affects both independently. It is likely that capital ratios will be positively correlated with the state of the economy (because of higher profits growth), which is in turn positively correlated with loan growth. Including macroeconomic variables--especially, economic growth--in our loan growth equation does limit this possibility, and the fact that the coefficients on lags of real GDP growth are so large in our loan growth equations suggests that we are in fact successfully capturing movements in loan growth that arise from fluctuations in economic activity.

A positive relationship between loan growth and lagged capital measures could also arise if banks pre-emptively increase their capital levels in anticipation of an increase in loan volumes (and hence balance-sheet size). This response of bank capital levels to anticipated changes in loan volumes raises the possibility of an endogeneity issue in the Bernanke and Lown loan-growth equations. However, this endogeneity issue is not necessarily an overwhelming concern if we simply wish to determine whether the constant leverage assumption exaggerates the estimated response of loan growth to an increase in capital ratios, because this source of endogeneity would induce an upward bias in our estimates of $\psi$ . Nevertheless, to examine this further we considered an alternative specification that also includes the ratio of the BHC's cash dividends to its net income. To the extent that BHCs change their dividend policy so as to boost their capital in anticipation of future lending opportunities (for example, banks may cut dividends when they expect further increases in loan growth), the dividend-to-net-income ratio would capture the endogenous variation in capital due to expected changes in loan volumes. Our estimates using this alternative specification of the Bernanke-Lown equation (not reported) imply that, depending on the capital ratio employed, a 1 percentage point increase in the capital ratio leads to an increase in the annualized BHC loan growth rate of 0.5 to 1 percentage points. This is close to the 0.7 to 1.2 percentage point increase in BHC loan growth that we find when the benchmark Bernanke-Lown specification is used.

To the extent that our implementation of the Hancock-Wilcox approach correctly models the target capital level $K_{i,t}^{\ast}$ , this identification issue should be of limited concern. If the reason banks boost their capital is that they anticipate a future balance sheet expansion, this should also be reflected in an increase in their target capital, which implies no net change in the capital surplus or shortfall. Consequently, the possibility that banks increase their capital in response to an anticipated expansion in lending, does not generate a positive relationship between loan growth and capital surpluses or shortfalls, and the interpretation of $\psi$ is preserved. That said, the possibility remains that our model of banks' target capital is incorrect and that--perhaps because a forward-looking component is absent from equation (2)--we have not completely purged our parameter $\psi$ of this potential source of bias. Naturally, it would be possible to address this problem by introducing forward-looking behavior to the target capital relation, although this would also require specifying simple forecasting equations for the explanatory variables, which could themselves be mis-specified. Thus, we do not pursue this approach. Instead, we tolerate some possibility of an incorrectly modeled target capital inducing some modest amount of upward bias in the parameter $\psi$ , in part because the mis-specification of the target capital ratio equation is always present (and always a vulnerability of this approach), and in part because it is not clear that omitting a forward-looking component from the equation is necessarily the most important omission.

The preceding discussion highlights why we use both the Hancock-Wilcox and Bernanke-Lown approaches to analyze the effect of bank capital on bank lending. While we generally consider the Hancock-Wilcox approach to be preferable inasmuch as it allows us to interpret the parameter $\psi$ as capturing the effect of an exogenous increase in capital on loan growth, it is vulnerable to the mis-specification of its target capital equation, which can potentially reduce estimates of $\psi$ . In contrast, while the Bernanke-Lown approach is not vulnerable to mis-specifying a target capital variable it is susceptible to some endogeneity issues that could then limit the interpretation of the parameter $\psi$ . Again, however, these do not necessarily represent an overwhelming concern when our goal is to determine whether the constant leverage assumption exaggerates the estimated response of loan growth to an increase in capital ratios.

2.5 Robustness analysis

We conducted a number of robustness checks that ultimately leave our key conclusions unchanged.

First, we considered an alternative, atheoretic approach to calculating the capital surplus term used in the Hancock-Wilcox regressions. Specifically, instead of estimating a model to calculate banks' capital targets, we used a one-sided Hodrick-Prescott filter applied to each BHC's capital ratio. The capital surpluses and shortfalls implied by the filter's estimates are smaller and smoother than their model-based counterparts, but are also less consistent with the conventional view of when the banking system was operating with capital surpluses or shortfalls. (Indeed, this is the main reason that we chose the model-based target measure as our primary specification.) We found that the estimated effect of capital shortfalls on loan growth under the alternative measure was statistically significant and larger, implying roughly a 0.7 percentage point reduction in annualized loan growth when capital is 1 percent below its target level. Nevertheless, this is still small relative to the values that would be implied by the constant leverage assumption.

We also included four additional lags of our various capital measures in regression equations (3) and (4) to allow for a less parsimonious specification aimed at capturing richer dynamics and potentially more persistent effects of capital on loan growth. In both cases the coefficients on the capital terms were almost unchanged, so that we still obtained only a modest impact of capital on BHC loan growth.

In light of the plots in Figure 6, which suggested differences in the magnitude of capital deviations across BHCs grouped by size, we also conducted our regression analysis using subsamples of BHCs grouped into large (top 20), small (smallest 20), and medium-sized firms. We found little difference in the estimated impact of capital shortfalls or surpluses on loan growth: While the coefficient on our capital surplus measure was slightly bigger for large BHCs--0.06 compared with 0.04 for smaller BHCs--this difference was not statistically significant. We also excluded the largest four BHCs from our sample to deal with potential outlier effects, but still found results that were qualitatively similar to those reported in tables 2 through 4.

We next performed rolling-window panel regressions over the sample period to address the possibility that the effect of shocks to bank capital on loan growth has been declining.²³ We used fixed-size rolling windows of six, seven, and eight years and quarterly data starting in 1992:Q1. In all cases, we found that the coefficients on our various capital terms were relatively stable and therefore continued to imply a small impact of capital on lending. For example, the coefficients (annualized) fluctuated between 0.2 and 0.4 for the capital surplus/shortfall (Hancock-Wilcox) measures, and between 0.4 and 2.2 for the equity-to-assets ratio (Bernanke-Lown) regressions. For both sets of models, the largest coefficients obtained in the regressions whose estimation started between 1992 and 1995. We interpret this result as being consistent with the large rates of loan growth observed over the second half of the 1990s and the early 2000s, which was also the period during which large BHCs were holding significant capital surpluses.

Next, we considered variants of the regressions described in equations (3) and (4) over a shorter sample period--specifically the most recent four years.²⁴ In this case we obtained slightly larger coefficients on both the capital surplus term in equation (3) and the equity-to-asset ratio in equation (4), although after rounding these coefficients still imply 0.4 and 1.4 percentage point reductions in annualized loan growth for a one-percent capital shortfall and a one-percent reduction in the capital ratio, respectively.

We also considered cross-sectional regressions that relate 4-quarter changes in BHC loan growth between 2007:Q3 and 2008:Q3 to the bank-specific variables in equations (3) and (4), lagged one year. In both cases, we found that the coefficients on our capital measures are slightly different but still imply a modest impact of capital on lending: The coefficient for the capital surplus measure implies a 0.2 percentage point reduction in annual loan growth for a one-percent capital shortfall. The coefficient for the equity-to-asset ratio almost doubles but still only implies that a one-percent reduction in the capital ratio leads to a 1.4 percentage point contraction in the annual loan growth. Interestingly, in both cross-sectional specifications the coefficient on the net-chargeoffs ratio doubles too, implying a much stronger impact of bank risk perception on BHC loan growth. (In both cases, a one-percent rise in the net-chargeoffs ratio is associated with a 15 percentage point contraction in annual loan growth.)

We also considered the possibility that the effect of capital on lending could vary with the state of the business cycle and that such effects could be diluted by estimating, as we do, the relationship between loan growth and capital over a long sample period. To test for this possibility in the full-sample model we interact the coefficient for the capital surplus in equation (3) and the coefficient for the equity-to-asset ratio in equation (4) with the output gap (as measured by the U.S. Congressional Budget Office) to determine whether the size of the effect of capital on loan growth increases in slumps. Although we do obtain the correctly signed coefficient in both cases (bank capital seems to have a larger effect in "bad times"), the interaction term is statistically insignificant.

Finally, we examined the possibility that capital could have nonlinear effects on BHC loan growth by adding quadratic and/or cubic terms of the different capital measures to our loan-growth regressions. In every case we found that none of these terms was statistically significant. For the capital surplus/shortfall regressions we also considered differences in the impact of capital deviations on loan growth between BHCs operating with surpluses and those operating with shortfalls.²⁵ Here we found no statistically significant difference between the separate surplus and shortfall coefficients.

2.6 Potential effect of omitting firm-level variables

While our combined methodology is able to address most forms of endogeneity and survivorship bias, it cannot deal with biases that might arise if bank and firm matches are not randomly formed. Addressing this bias requires bank lending and firm borrowing to be considered jointly, which in turn implies that individual loans must be modeled rather than aggregate lending by banks (or aggregate borrowing by firms). A number of recent papers pursue this approach using loan-level data obtained from national credit registers; these include Jiménez, Ongena, and Peydró (2010), who use data collected by the Bank of Spain, and Albertazzi and Marchetti (2010), who use data collected by the Bank of Italy. These studies, which control for firm-level characteristics, find larger effects of low bank capitalization and scarce liquidity on credit supply.

Matching bank-loan information to borrower characteristics has a number of advantages in helping to identify causal effects since it allows the cross-sectional heterogeneity of both banks and firms to be exploited. However, we believe that for considering the linkage between financial conditions and real activity this approach is only informative in practice if the matched sample is large and representative of the universe of lenders and borrowers. In the U.S., matched-sample analysis has only been applied to data on syndicated loans; specifically, bank loan-level data from the Loan Pricing Corporation's (LPC) Dealscan database, which can be matched with BHC data from the FR Y-9C form and data on firms from Compustat. In addition to representing a fairly narrow class of lending, these matched data have a number of problems such as important missing information and outliers, which may then further restrict (in some cases significantly) the number of available firm-bank-loan observations. That said, studies that use these firm and bank loan-level data also seem to suggest relatively small effects of bank capital on lending. For example, Santos and Winton (2010) find that a 1 percent change in a bank's capital-to-assets ratio results in only a 3 basis point increase in loan rates, thus implying a relatively modest effect. This is consistent with our finding of a small effect of changes in bank capital on lending behavior.

3 Bank Capital and Loan Growth at the Aggregate Level

As noted earlier, our panel estimation approach only uses BHCs that have existed over our entire sample period (or at least most of it). It could therefore potentially suffer from survivor bias, which would tend to lower the estimated effect of bank capital on loans.²⁶ To address this concern, in this section we use aggregate data and a vector autoregression (VAR) model to study the effects of commercial-bank capital ratios on bank loan growth. In our panel regressions, we specified BHC loan-growth equations that controlled for the effects of other supply and demand variables and so allowed us to interpret the coefficient $\psi$ on the equations' capital terms as the effect of BHC capital positions on loan growth. Here we take a different approach; specifically, we attempt to identify structural innovations in bank capital ratios and then examine the dynamic impact of these structural innovations on bank loan growth.

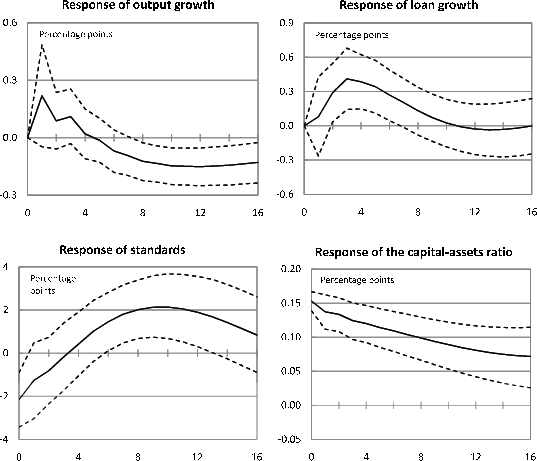
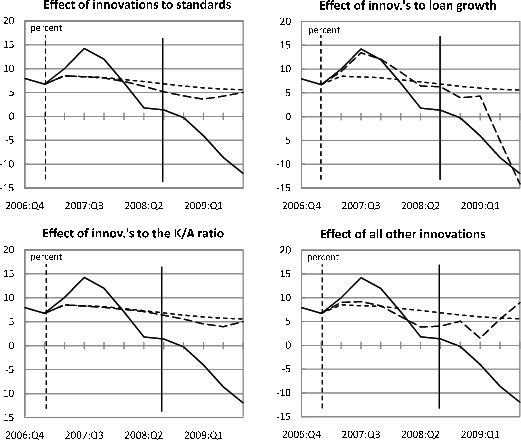
An important determinant of the influence that structural innovations to bank-capital ratios will have on bank loan growth is the effect that these innovations have on other variables in the model--such as real economic growth and bank lending standards--that in turn feed back to lending. These indirect channels need to be borne in mind in considering how changes in bank capital affect loans; in particular, they must be accounted for in comparing the magnitudes of the effects found in the time-series analysis with those obtained from the panel regressions. We therefore conduct additional exercises where we shut down these indirect effects.

3.1 Estimation and identification of the VAR model

The vector autoregression model that we use is a slightly modified version of the extended VAR model with bank capital considered by Lown and Morgan (2006). Our VAR consists of six variables: real GDP growth and GDP price inflation (excluding food and energy); the Federal funds rate; commercial bank and thrift loan growth; the aggregate capital-to-assets ratio of the commercial bank sector; and the net fraction of loan officers at commercial banks reporting a tightening of credit standards for C&I loans. The first three variables in the VAR are standard components of a monetary-policy VAR, while the last three variables--commercial bank and thrift loan growth, the capital-to-assets ratio, and lending standards--are added to the model to allow us to study the interaction between banks and the macroeconomy. As in our panel regressions, we use the estimation period 1990:Q3 to 2008:Q3 for our VARs; that is, we end the VAR analysis just when the crisis intensified and just before TARP capital injections began to occur.

The residuals obtained from each of the estimated OLS regressions in the VAR system are combinations of underlying structural innovations. Importantly, the structural innovations have economic interpretations, such as exogenous shocks to monetary policy, technology, and the mark-up of prices over costs in the monetary-policy portion of the model and exogenous shocks to bank lending standards (reflecting changes in cautiousness), bank capital ratios, and bank loan volumes (form changes in conditions in other credit markets) in the banking portion of the model. However, although structural innovations underlie the residuals from the estimated equation, they cannot, in the absence of any additional assumptions, be observed or inferred. A wide variety of assumptions can be used to identify structural innovations based on the estimated equation residuals; for our VAR we use a recursive identification scheme with the causal order given by the ordering of variables described above. We are primarily interested in separately identifying the three banking shocks in our model; for our purposes, it is sufficient to amalgamate the macroeconomic shocks into a single composite innovation.

Our identification procedure assumes that structural innovations to any of the model's banking variables do not contemporaneously affect the model's macro variables, but that innovations to the model's macroeconomic variables have a contemporaneous impact on the model's banking variables. One interpretation for this assumption as it relates to economic activity and inflation is that households, firms, and all levels of government can arrange their spending, production, and price-determination plans for the current period in such a way that surprise developments in the credit sector will not prevent these plans from taking place (at least in the aggregate). That said, such plans can be modified in response to surprise developments that are directly relevant for spending, production, and price determination (the macroeconomic shocks); moreover, these macro developments will contemporaneously affect variables in the banking sector. Likewise, monetary policymakers do not alter their interest-rate setting decisions in response to within-quarter developments in the banking sector, although monetary policy surprises can have immediate effects on banking-sector variables.

Within the banking portion of the VAR our identification procedure assumes that structural innovations to loan volumes can affect bank capital ratios and lending standards immediately but that innovations to these latter variables do not have contemporaneous effects on loans. The first part of this assumption suggests that contemporaneous structural innovations to bank loan growth originate from the non-banking part of the credit sector (as well as the real economy). Thus, a reasonable interpretation of these innovations (particularly in the context of the recent crisis) is that they reflect disruptions to segments of the financial system that can in turn impact bank loan volumes contemporaneously.²⁷ The second part of the assumption--that capital ratios and lending standards do not affect lending contemporaneously--reflects the fact that it takes time to arrange a loan. This may at first appear to be at odds with our assumption that changes in the real economy can affect lending contemporaneously; however, for that case we have in mind households and firms drawing down or repaying pre-arranged lines of credit. Clearly, credit limits on loans that take the form of "on demand" credit lines (such as HELOCs, credit cards, or C&I commitment loans) can eventually be modified by banks in response to capital-ratio or standards innovations, but these changes are difficult to implement quickly.

We would note that it is reasonable to assume that changes in lending standards have no contemporaneous impact on loan volumes inasmuch as there are many ways through which banks can alter lending standards other than contemporaneous changes in loan volumes; for example, banks can change the maturity of loans, the cost of credit lines, the spreads on loan rates, any covenants on the loan, and the loans' collateralization requirements. Our identifying assumption therefore implies that banks only make these changes in the period in which standards are altered.

Our identification method also assumes that innovations to lending standards do not affect bank capital ratios contemporaneously, although bank capital ratios do affect standards. The first part of this assumption makes sense given that we assume that innovations to standards have no contemporaneous effect on loan volumes, while the second part of the assumption reflects the fact that current lending standards are the most easily altered variable in the VAR.

Finally, note that we only separately identify structural innovations to loan volumes, bank capital, and lending standards, but do not identify the model's macroeconomic shocks separately. Thus, in our results we only report the combined effects of the model's macroeconomic shocks.

3.2 The effects of an innovation to the equity capital ratio

Figure 7 shows the responses of key model variables--specifically, output growth, loan growth, the capital-to-assets ratio, and standards--to a one-standard-deviation structural innovation to the capital-to-assets ratio. This innovation implies an immediate 16 basis point increase in the capital-to-assets ratio, which then declines gradually back to its long-run level. Lending standards immediately loosen by about 2 percentage points in response to the increase in capital ratios and loan growth is boosted for about two years with a maximum response of about 1/2 percentage point two quarters after the impact of the shock. The (statistically insignificant) response of GDP growth is rapid and short-lived (about one year), peaking at 0.2 percentage point in the period immediately following the shock. One possible reason for the smaller and shorter-lived response of output growth relative to loan growth is that some of the growth in loans may just represent substitution across institutions. Indeed, additional analysis--shown in Figure 8--that uses the sum of bank and thrift loans and ABS issuers' holdings of mortgage and consumer credit in the VAR in place of bank and thrift loans seems to support this view. Specifically, a shock to the capital-to-assets in this model has no effect on the broader aggregate of loan volumes while having similar effects on the other variables in the model. The fact that changes in capital ratios do appear to induce substitution between on- and off-balance-sheet credit is an interesting one; we do not pursue it here, however, since our principal focus in this paper is on bank capital and lending.

Our results imply that a one percentage point increase in the capital-to-assets ratio results in a 2-3/4 percentage point increase in loan growth that peaks about a year after the initial shock. This is almost four times as large as the corresponding response from the panel regressions. The relatively larger response implied by the VAR model is perhaps not surprising given that the VAR approach allows for the endogenous response of several variables--most notably standards and real GDP growth--that in turn have additional effects on loan growth. Given this, it is instructive to shut down these additional effects in the VAR so as to permit a more direct comparison with the results obtained using institution-level BHC data.²⁸

Figure 9 reports the responses to a one standard deviation capital-to-assets ratio shock that obtain when various endogenous responses of other model variables are eliminated. In particular, the red line in Figure 9 shuts down the response of standards to the capital-to-assets ratio shock; the blue line shuts down the response of real GDP growth to the capital-to-assets ratio shocks; and the green line shuts down both the standards and real GDP growth responses. These results suggest that in the absence of endogenous responses from other variables, bank loan growth should increase approximately 1.2 percentage points in response to a one percentage point capital-to-assets ratio shock. This increase is about twice as large as the increase in loan growth implied by the panel regressions, but is still considerably smaller than what would be predicted under the constant-leverage assumption that is implied by the scatterplot approach.

4 The Effects of Capital Injections on Loan Growth

We now use the models developed in sections 2 and 3 to estimate the likely effects of TARP-related capital injections on bank loan growth.

4.1 The effects of recent capital injections on BHC loan growth

The panel regression results from section 2 can be used to estimate the effect of the original TARP disbursement ($182 billion for our sample of large banks) on BHC loan volumes. The CPP capital infusions during 2008:Q4 raised the level of equity capital, yielding an increase in the capital surplus term of about 14 percentage points on average. Taken together with the estimation results of section 2.2, which indicate that a 1 percentage point increase in the capital surplus implies a 1/4 percentage point increase in annualized loan growth, this implies that the CPP injections increased loan growth by 3-1/2 percentage points at an annual rate in our sample of banks. In ratio terms the CPP injections raised the equity-to-assets ratio by about 1.4 percentage points and the risk-based capital ratio by about 1.7 percentage points on average. Given the estimation results of section 2.3 this implies that the CPP injections boosted BHC loan growth by 1.0 to 1.3 percentage points.

In dollar terms, the results from the surplus/shortfall regressions imply that the $182 billion increase in capital that large BHCs in our sample received would have resulted in a $273 billion increase in these BHCs' loans over the following year. The results from the capital-ratio regressions imply an increase in loan volumes for large BHCs of between $76 billion and $100 billion over the following year (depending on the measure of capital considered). These volumes are significantly less than the boost in lending capacity that would be implied by the U.S. Treasury's assumptions. Specifically, since the Treasury assumed that a dollar's increase in capital would generate between eight to twelve dollars of lending, a $182 billion capital injection should have resulted in a $1-1/2 to $2-1/4 trillion increase in lending.

4.2 The effects of recent capital injections on commercial bank loan growth

We can also use the VAR model's impulse response functions to estimate the magnitude of the impact of CPP injections on commercial bank loan volumes. As noted above, capital injections under the CPP raised the equity-to-assets ratio by 1.4 percentage points. The impulse response functions reported in Figure 7 imply that the CPP capital injections would boost loan growth by 3.7 percentage points over the first year. Cumulating the effect on loan growth implies a 5 percent increase in the level of loans or a $300 billion increase in commercial bank lending.

5 Understanding the Recent Decline in Loan Growth

We can also use these models to ascertain the effect of recent changes in capital ratios on loan growth. First, we use results from the panel regressions to understand the causes of the recent decline in bank loan growth and to gauge whether the large decline in lending is mainly explained by supply or demand factors. We then use our VAR estimates to decompose changes in commercial bank lending across the various banking and nonfinancial shocks that we estimate.

5.1 Decomposition of BHC loan growth

We conduct out-of-sample forecasts of BHC loan growth using both our capital surplus/shortfall and capital-ratio panel regressions and decompose the quarterly growth rate of BHC loans into supply and demand factors such as capital, lending standards, risk, and GDP growth. Figure 10 reports the results from the capital-ratio panel regressions.

As can be seen in Figure 10, our capital-ratio panel regression model performs relatively well in explaining the recent drop in the quarterly growth rate of BHC loans. The decomposition of the predicted growth rate confirms the importance of loan demand shocks and increased risk in accounting for most of the decline in BHC loan growth. Out of the 2.9 percentage point decline in the quarterly loan growth rate from 2008:Q4 to 2009:Q3--of which the model explains 2.2 percentage points--1.3 percentage points is accounted for by changes in GDP growth (the dark blue shaded area) and 1.1 percentage points is explained by changes in net charge-off rates (the green shaded area), which captures the deterioration in loan quality. Tighter lending standards (the purple area) significantly restrained BHC loan growth during the first half of 2009 (by about 1.3 percentage points), though this effect lessened in 2009:Q3. On net, then, lending standards account for only 0.2 percentage point of the 2008:Q4 to 2009:Q3 reduction in BHC loan growth.

Figure 10 also confirms that changes in bank capital (the light blue area) had only a small impact on BHC loan growth. In particular, the changes in BHC capital ratios associated with both TARP-related capital injections in 2008:Q4 and subsequent efforts to raise capital privately during the first half of 2009 made only a small positive contribution to bank loan growth (of only 0.1 percentage point) and were more than offset by adverse factors such as reduced loan demand, increased risk, and somewhat tighter lending standards.

The results from the capital surplus/shortfall model (not shown) indicate that this model does not perform as well as the capital-ratio model in terms of predicting the 2008:Q4 to 2009:Q3 decline in BHC loan growth. In particular, the surplus/shortfall model explains only 1.3 percentage points of the 2.9 percentage point decline in loan growth over this period. That said, the conclusions obtained from the capital-ratio model with respect to the relative importance of real GDP growth, net charge-off rates, and capital in explaining BHC loan growth continue to hold.²⁹

5.2 Decomposition of commercial bank loan growth

The VAR model's identification procedure allows us to decompose movements in each variable into the portion attributable to the various shocks. This is done in Figure 11. In each panel of the chart we show the actual path of loan growth over the past three years--the solid black line--as well as the model's unconditional forecast--the dotted line. We also show the path of loan growth that would be implied by the unconditional forecast and a specific set of structural innovations. We find that structural innovations to capital ratios explain very little of the below-par pace of loan growth over the past year (see the lower-left panel). Prior to the rebound in economic growth following the sharp contractions in activity in 2008:Q4 and 2009:Q1, macro innovations appear to have accounted for much of the decline in loan growth (the lower-right panel), with standards innovations accounting for a portion as well (the upper-left panel). Finally, over the last two quarters of the simulation period, own-variable innovations to loan growth account for the bulk of the series' decline (see the upper-right panel).

To some extent the large recent contribution of the own-variable loan growth innovations reflects the out-of-sample nature of our simulation exercise. The same exercise performed with a model estimated through to 2009:Q3--see Figure 12--attributes much less of the recent decline in loan growth to own-variable shocks and much more to standards and macro shocks. Note, however, that capital ratio shocks continue to explain only a small portion of the decline in loan growth.

6 Summing up

This paper has applied a number of different methods to examine how bank capital influences the extension of bank credit. An analysis based on panel data finds modest effects of BHC capital-to-asset ratios on BHC lending; using macroeconomic time series and aggregate commercial bank balance-sheet data, we find larger--but still modest--effects of capital ratio shocks on loan growth.

These results stand in marked contrast to the constant-leverage view, which has been quite influential of late in shaping forecasters' and policymakers' views regarding the size of the effect that bank capital changes have on loan growth. In particular, this view predicts effects of bank capital-ratio changes on loan growth (that are six to ten times) larger than what we found in either our panel or time-series estimation results. We attribute the difference to the fact that the simple correlation between asset growth and leverage growth for commercial banks that underpins the constant-leverage view is not very robust across time, and especially fails to hold for the post-Basel sample period over which our analysis is conducted.

While our empirical results suggest relatively modest effects of both capital shortfalls and capital ratios on loan growth, we find more important roles for other factors such as economic activity and increased perception of riskiness by banks. One interpretation of this result is that banks and BHCs give relatively little consideration to their capital position when deciding whether to lend and instead allow other factors such as loan demand and risk to guide their decisionmaking. If this is the case, it would provide one explanation for the slowdown in loan growth that took place over the first three quarters of 2009 despite the sizable capital injections that occurred in 2008:Q4 under the CPP. However, another interpretation of our results is that existing measures of bank capital do not capture the "true" capital position of banks that is relevant for determining bank behavior. If true, this interpretation calls into question whether existing risk-based regulatory capital measures are valid, and would suggest that such measures need to be improved.

Bibliography

Adrian, T., and H. S. Shin, 2007.

"Liquidity and Leverage." Mimeo, Princeton, NJ.

Ashcraft, A., 2004.

"Are Bank Holding Companies a Source of Strength to their Banking Subsidiaries?" Federal Reserve Bank of New York Staff Report No. 189.

Albertazzi, U., and D. Marchetti, 2010.

"Credit Supply, Flight to Quality and Evergreening: An Analysis of Bank-Firm Relationships after Lehman." Working Paper No.756, Bank of Italy.

Altunbas, Y., L. Gambacorta, and D. Marques-Ibanez, 2008.

"Securitisation and the Bank Lending Channel." European Economic Review 53, 996-1009.

Bank of International Settlements, 2009.

"Strengthening the Resilience of the Banking Sector." Consultative Document, Basel Committee on Bank Supervision.

Berger, A., and C. H. S. Bouwman, 2009.

"Bank Capital, survival, and performance around financial crises." Working Paper.

Berger, A., R. DeYoung, M. Flannery, D. Lee, and O. Oztekin, 2008.

"How Do Large Banking Organizations Manage their Capital Ratios?" Journal of Financial Services Research 34, 123-149.

Berger, A., and G. Udell, 1994.

"Did Risk-based Capital Allocate Bank Credit and Cause a `Credit Crunch' in the United States?" Journal of Money, Credit, and Banking 26, 585-628.

Bernanke, B., and C. Lown, 1991.

"The Credit Crunch." Brookings Papers on Economic Activity 2, 205-247.

Bernanke, B., M. Gertler, and M. Watson, 1997.

"Systematic Monetary Policy and the Effects of Oil Price Shocks." Brookings Papers on Economic Activity 1, 91-116.

Ciccarelli, M., A. Maddaloni, and J-L. Peydro-Alcalde, 2010.

"Trusting the Bankers: Another Look at the Credit Channel of Monetary Policy." Mimeo, Frankfurt, Germany.

De Nicolò G., and M. Lucchetta, 2010.

"Systemic Risks and the Macroeconomy." Working Paper No. 29, International Monetary Fund.

Elliott, D., 2010.

"Quantifying the Effects on Lending of Increased Capital Requirements" Briefing Paper No. 7, Brookings Institution.

Flannery, M., and K. Rangan, 2008.

"What Caused the Bank Capital Build-up of the 1990s." Review of Finance 12, 391-429.

Francis, W., and M. Obsorne, 2009.

"Bank Regulation, Capital and Credit Supply: Measuring the Impact of Prudential Standards." Occasional Paper No. 36, UK Financial Services Authority, London, UK.

Giannetti, M., and A. Simonov, 2010.

"On the Real Effects of Bank Bailouts: Micro-Evidence from Japan." Discussion Paper No. 7441, Centre for Economic Policy Research.

Hancock, D., and J. Wilcox, 1993.

"Has There Been a `Capital Crunch' in Banking? The Effects on Bank Lending of Real Estate Market Conditions and Bank Capital Shortfalls." Journal of Housing Economics 3, 31-50.

Hancock, D., and J. Wilcox, 1994.

"Bank Capital and Credit Crunch: The Roles of Risk-Weighted and Unweighted Capital Regulations." Journal of the American Real Estate and Urban Economics Association 22, 59-94.

Hancock, D., and W. Passmore, 2009.

"Estimates of Bank Lending and GDP Responses to Trouble Asset Relief Program (TARP) Capital Injections and to Expansions of Government Guarantees," Mimeo, Federal Reserve Board, Washington, DC.

Hatzius, J., 2007.

"Leveraged Losses: Why Mortgage Defaults Matter." Goldman Sachs U.S. Daily, November 15, 2007.

Hatzius, J., 2008.

"Beyond Leveraged Losses: The Balance Sheet Effects of the Home Price Downturn." Brookings Papers on Economic Activity, 2, 195-227.

Houston, J., C. James, and D. Marcus, 1997.

"Capital Market Frictions and the Role of Internal Capital Markets in Banking." Journal of Financial Economics 46, 135-64.

Jiménez, G., Ongena S., Peydró J., and J. Saurina, 2010.

"Credit Supply: Identifying Balance-Sheet Channels with Loan Applications and Granted Loans." Discussion Paper No. 7655, Centre for Economic Policy Research.

Judson, R., and A. Owen, 1999

"Estimating Dynamic Panel Data Models: A Practical Guide for Macroeconomists." Economics Letters 65, 9-15.

Kashyap, A., and J. Stein, 1995.

"The Impact of Monetary Policy on Bank Balance Sheets." Carnegie-Rochester Conference Series on Public Policy 42, 151-95.

Kashyap, A., and J. Stein, 2000.

"What Do a Million Observations on Banks say about the Transmission of Monetary Policy." The American Economic Review 90, 407-28.

Loutskina, E., and P. Strahan, 2006.

"Securitization and the Declining Impact of Bank Finance on Loan Supply: Evidence from Mortgage Acceptance Rates." NBER Working Papers No. 11983.

Lown, C., and D. Morgan, 2006.

"The Credit Cycle and the Business Cycle: New Findings Using the Loan Officer Opinion Survey." Journal of Money, Credit and Banking 38, 1575-97.

Peek, J., and E. Rosengren, 1995.

"The Capital Crunch: Neither a Borrower Nor a Lender Be." Journal of Money, Credit, and Banking 27, 625-638.

Peek, J., and E. Rosengren, 2000.

"Collateral Damage: Effects of the Japanese Real Estate Collapse on Credit Availability and Real Activity in the United States." The American Economic Review 90, 30-45.

Puri, M., Rocholl, J., and S. Steffen, 2009.

"Global Retail Lending in the Aftermath of the US Financial Crisis: Distinguishing between Supply and Demand Effects." Journal of Financial Economics, forthcoming.

Santos, J., and A. Winton, 2010.

"Bank Capital, Borrower Power, and Loan Rates." Working Paper.

Table 1: **Summary Statistics for BHC-Level Panel Data**
Variable	No. Observations	Median	Mean	Std.Dev.
Total Assets ($ million)	11107	3595.30	27302.91	145408.60
Total Loan Quarterly growth	11107	2.15%	3.00%	5.03%
C&I Loan Quarterly growth	11107	2.09%	2.91%	8.82%
Equity/Assets	11107	8.17%	8.39%	2.16%
Tier 1 Capital ratio	7320	10.72%	11.38%	3.29%
Total Capital ratio	7320	12.54%	13.24%	2.20%
TCE ratio	9139	6.83%	7.02%	2.20%
Return on Assets	11107	0.1396	0.1296	0.8287
Securities/Assets	9460	0.2257	0.2424	0.1131
Net Chargeoffs/Assets	11099	0.1687	0.2963	0.4288

This table presents summary statistics for the sample of 140 BHCs from 1992 to 2008 used in the panel estimation. The data are taken from the Consolidated Financial Statements for BHCs (FR Y-9C). The sample excludes institutions with missing observations in total assets, loans and capital, and also BHCs that remain in the sample for less than 30 quarters. To minimize the influence of outliers, observations with more than 50 percent growth in total assets over a single quarter were also removed. The remaining variables were winsorized at the 1 percent and 99 percent levels.

Table 2: **Determinants of BHC Target Capital Ratios**
	Model 1 Estimate	Model 1 t-stat	Model 2 Estimate	Model 2 t-stat
Lagged capital ratio	0.9108***	(87.60)	0.9189***	(87.91)
Size	0.0931***	(4.12)	0.0778***	(5.09)
ROA	0.0356	(1.48)	0.0373*	(1.76)
Aggregate Volatility	-0.0053***	(-4.67)	-0.0035***	(-4.09)
C&I loan share	-0.0097***	(-2.95)
Real Estate loan share	-0.0065***	(-3.20)
Consumer loan share	0.0001	(0.01)
Securities share	-0.0059***	(-2.92)
Regulatory Pressure	-0.0260	(-0.58)	-0.0159	(-0.43)
Sector Chargeoff/Loan	0.1074**	(2.45)	0.0781**	(2.58)
Chargeoffs/Asset	0.0229	(0.60)	0.0094	(0.75)
Intercept	-0.1584	(-0.42)	-0.5334**	(-2.56)
	0.852		0.870
	8706		10512

This table presents the fixed-effect regression estimates of equation (2) for the determinants of BHC's target capital ratios. Bank-specific variables include

, measured as the log of total assets, the return on assets

, the ratio of net charge-offs to total assets, the shares of C&I loans, Real Estate loans, Consumer loans, and Investment Securities in total assets. The regression also includes an institutional variable, called regulatory pressure, defined as a dummy variable that equals one if the BHC's equity capital ratio is less than 1.5 percentage points above the minimum of 5 percent. Aggregate variables include the stock-market volatility index provided by the Chicago Board Options Exchange (CBOE S&P 100 volatility index), and the ratio of net charge-offs to total loans for the commercial banking sector. Regressions include quarterly dummies to control for seasonal factors. Robust t-statistics are given in parenthesis. *, **, and *** denote significance at the 10%, 5%, and 1% levels, respectively.

Table 3: **Effect of Capital Surplus on BHC Loan Growth**
	Total Loans Estimate	Total Loans $\chi^2$ -stat	C&I Loans Estimate	C&I Loans $\chi^2$ -stat
Loan Growth Lags (sum)	0.1598***	(15.49)	0.0731	(1.34)
Surplus capital	0.0523***	(75.98)	0.0602***	(24.78)
Securities/Asset	0.0668***	(20.25)	0.0559**	(4.03)
Net Chargeoffs/Asset	-1.6177***	(25.02)	-1.6410***	(8.59)
Lending Standards (sum)	-0.0181***	(8.24)	-0.0274***	(6.47)
GDP Growth Lags (sum)	0.8562**	(5.52)	2.1685***	(7.65)
Fed Funds Lags (sum)	-0.4534	(1.83)	-0.0059	(0.00)
Inflation Lags (sum)	-0.1918	(0.07)	-1.7849	(2.19)
Intercept	0.5080	(0.42)	1.5000	(0.99)
	0.215		0.098
	7793		7760

This table reports the fixed-effect regression estimates of equation (3) for the determinants of bank loan growth on a measure of BHC's capital surplus/shortfall and control variables. The dependent variable is the quarterly growth rate of total loans and C&I loans. Explanatory variables are as follows: four lags of loan growth, the measure of capital surplus, calculated as percent deviations of actual capital level relative to estimated capital targets, the ratio of investment securities to total assets, the ratio of net charge-offs to total assets, three lags of lending standards (fraction of banks reporting tightening lending in the Senior Loan officer Opinion Survey), four lags of quarterly GDP growth, four lags of the quarterly change in the Fed Funds rate, and four lags of the inflation rate (cumulative percent change of the Consumer Price Index during the previous three months). Regressions include quarterly dummies to control for seasonal factors. Because an auxiliary equation is used to estimate the capital surplus variable, standard errors are adjusted to correct for the generated regressor bias through bootstrap methods. $\chi^2$ -statistics are given in parenthesis. *, **, and *** denote significance at the 10%, 5%, and 1% levels, respectively.

Table 4: **Effect of Capital Shocks on BHC Loan Growth**
	Eq.-to-Asset Ratio: Estimate	Eq.-to-Asset Ratio: t/F-stat	Risk-based Capital Ratio: Estimate	Risk-based Capital Ratio: t/F-stat	Risk-based Tier 1 Cap. Ratio: Estimate	Risk-based Tier 1 Cap. Ratio: t/F-stat	TCE Ratio: Estimate	TCE Ratio: t/F-stat
Loan Gr. Lags (sum)	0.1648***	(33.04)	0.1583***	(24.22)	0.1571***	(24.07)	0.1743***	(37.66)
Capital ratio	0.1450***	(3.23)	0.1572***	(4.69)	0.1674***	(4.98)	0.2521***	(5.75)
Securities/Asset	0.0556***	(5.64)	0.0431***	(2.76)	0.0421***	(2.66)	0.0498***	(4.84)
Net Chargeoffs/Asset	-1.6835***	(-6.75)	-1.8524***	(-6.92)	-1.8346***	(-6.86)	-1.6832***	(-6.65)
Lending Stds (sum)	-0.0135**	(10.46)	-0.0130***	(7.09)	-0.0130***	(7.09)	-0.0131***	(9.89)
GDP Gr. Lags (sum)	0.8628***	(10.41)	1.0884***	(9.61)	1.0684***	( 9.25)	0.8508***	(10.67)
Fed Funds Lags (sum)	-0.1164	(0.28)	-0.5391*	(2.88)	-0.5696*	(3.17)	-0.1792	(0.64)
Inflation Lags (sum)	-1.1988***	(6.65)	-0.4573	(0.44)	-0.3482	(0.26)	-0.7072	(2.31)
Intercept	-0.1001	(-1.90)	-1.2893	(-1.64)	-1.1345	(-1.49)	-0.7761	(-1.28)
	0.186		0.196		0.197		0.190
	8549		6658		6658		8549

This table reports the fixed-effect regression estimates of equation (4) for the determinants of bank loan growth on BHC's capital ratios and control variables. Columns report estimation results for each of the different capital ratios. The dependent variable is the quarterly growth rate of total loans. Explanatory variables are as follows: four lags of total loan growth, the capital ratio as indicated in each column, the ratio of investment securities to total assets, the ratio of net charge-offs to total assets, three lags of lending standards (fraction of banks reporting tightening lending in the Senior Loan officer Opinion Survey), four lags of quarterly GDP growth, four lags of the quarterly change in the Fed Funds rate, and four lags of the inflation rate (cumulative percent change of the Consumer Price Index during the previous three months). Regressions include quarterly dummies to control for seasonal factors. Robust t and F-statistics are given in parenthesis. *, **, and *** denote significance at the 10%, 5%, and 1% levels, respectively.

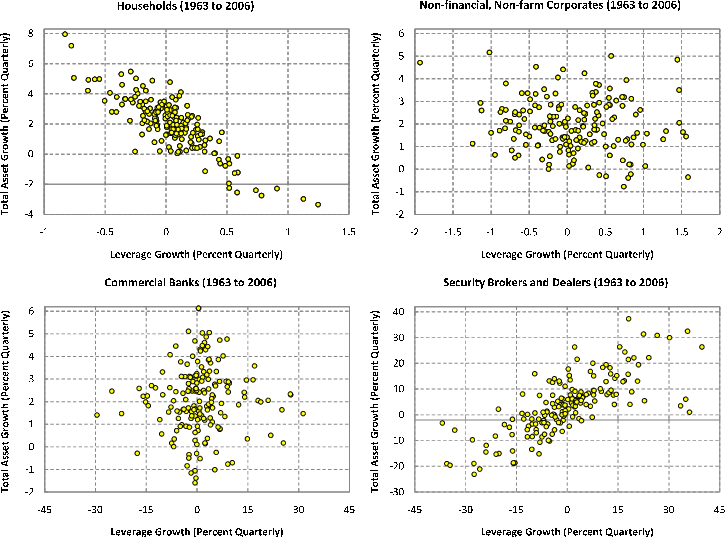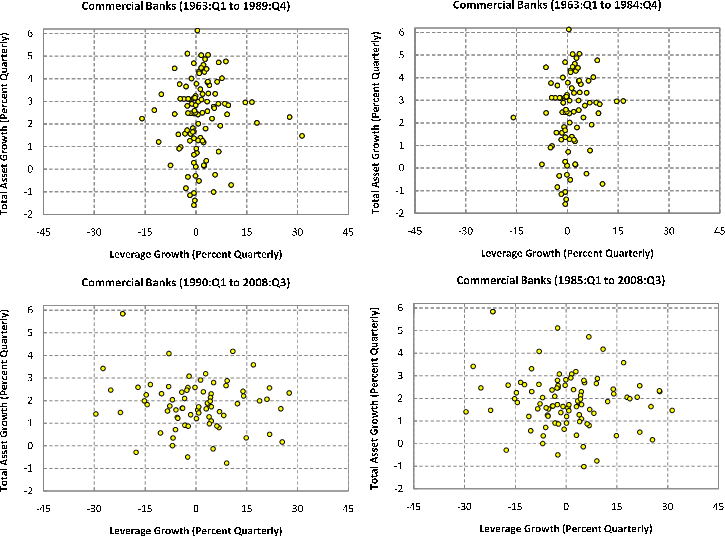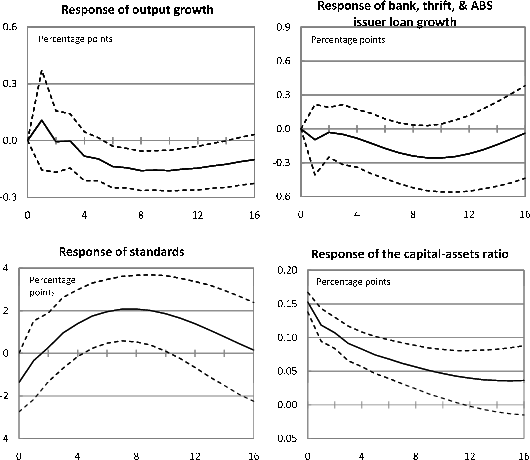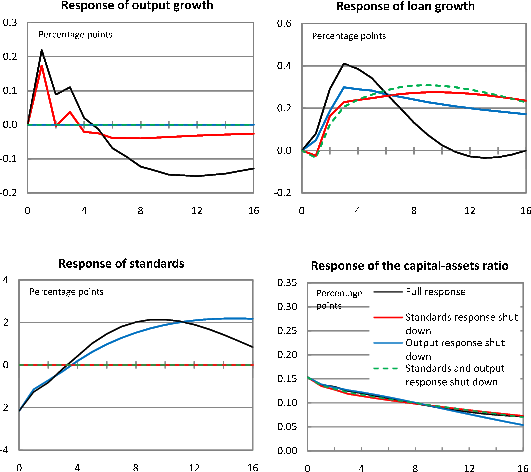Figure 1: Assets and Leverage Growth of Various Institutions in the Flow of Funds Accounts

Accessible Version

Figure 2: Assets and Leverage of Commercial Banks Across Different Sample Periods

Accessible Version

Figure 3: BHC Capital Ratios and Commercial-Bank and BHC Loan Growth

Accessible Version

Figure 4: Aggregate Data Used in Panel and VAR Models

Accessible Version

Figure 5: Average Actual and Target BHC Capital-to-Assets Ratios

Accessible Version

Figure 6: Average Actual and Target Capital-to-Assets Ratios, by BHC Size

Accessible Version

Figure 7: Response to a Capital-to-Assets Ratio Shock

Accessible Version

Figure 8: Response to a Capital-to-Assets Ratio Shock (incl. credit extended by ABS issuers)

Accessible Version

Figure 9: Response to a Capital-to-Assets Ratio Shock (endogenous responses shut down)

Accessible Version

Figure 10: Decomposition of BHC Quarterly Loan Growth

Accessible Version

Figure 11: Decomposition of Loan Growth (model estimated through 2008:Q3)

Accessible Version

Figure 12: Decomposition of Loan Growth (model estimated through 2009:Q3)

Accessible Version

Footnotes

* E-mail: [email protected] & [email protected]. Mailing address: Mailstop 153, 20th and C Streets NW, Washington, DC 20551. We thank Brian Bucks, Mark Gertler, Diana Hancock, David Jones, Mike Kiley, Myron Kwast, Sylain Leduc, Nellie Liang, Dave Reifschneider, Jeremy Rudd, Klaus Schaeck, Skander van den Heuvel, José-Luis Peydró, James Wilcox, and Egon Zakrajsek for comments on earlier versions of this paper and Peter Andrews, Matthew Osborne, Gianni De Nicolò, and Christina Wang for helpful conversations. The views expressed here are our own and do not necessarily reflect the views of the Board of Governors or the staff of the Federal Reserve System. Return to Text

1. If leverage is procyclical, the reduction in bank assets associated with a $1 reduction in capital is even larger. Return to Text

2. Another important paper in this literature is Peek and Rosengren (1995), which used New England data to fit a model of bank deposits. Because it focuses on liabilities, this methodology is less suitable for studying the effect of bank capital on loan growth, however. Return to Text

3. Our estimates are one-fifteenth to one-quarter as large. See Treasury Department Press Release (TG-95) "Treasury Secretary Timothy Geithner, Opening Remarks as Prepared for Delivery to the Congressional Oversight Panel," April 21, 2009, for the quoted lending estimates. Return to Text

4. Adrian and Shin (2007) do not focus on the effect of bank capital ratios on loan growth. Rather, their paper presents a pictorial representation of this relation as part of a set of motivating facts before moving on to consider the sources of procyclical leverage among securities brokers and dealers. Return to Text

5. The series used to generate the reported plots in Figure 1 are as follows. The top-left panel gives the growth rate of the household sector's total assets (series FL152000005.Q in the Flow of Funds Accounts) and the growth rate of the household sector's leverage ratio (measured as the ratio of total assets--series FL152000005.Q--divided by household equity, that is total assets--series FL152000005.Q--less total liabilities--series FL154190005.Q). The top-right panel shows the growth rate of total assets for the non-financial and non-farm corporate sector (series FL102000005.Q) and the growth rate of the leverage ratio for this sector (total assets--series FL10200005.Q--divided by non-financial, non-farm corporate equity--series FL102000005.Q less series FL104190005.Q). The bottom-left panel plots the growth rate of total financial assets for the commercial banking sector (series FL764090005.Q) against the growth rate of the sector's overall leverage ratio (total financial assets--series FL764090005.Q--divided by commercial bank equity--series FL764090005.Q less FL764190005.Q). Finally, the bottom-right panel plots the growth rate of total financial assets for security brokers and dealers total financial assets (series FL664090005.Q) against the growth rate of their overall leverage ratio (total financial assets--series FL664090005.Q--divided by broker-dealer equity--series FL664090005.Q less series FL664190005.Q). Return to Text

6. Another reason to split the sample in 1985 is that the Call Report data were less systematically collected and cleaned prior to 1985. Moreover, major changes were made to the reporting forms in early 1984 and this led to discontinuities in many of the existing time series, thereby making comparisons between the pre- and post-1985 periods difficult. Return to Text

7. Results from our VAR analysis also show significant effects of lending standards on both bank lending and GDP growth. However, our reading of the "reasons for tightening or loosening lending standards" responses in the SLOOS differ notably from Ciccarelli, et al. Indeed, we find that the two most important reasons for tightening lending standards in the SLOOS during the recent financial crisis were a more uncertain economic outlook and a reduced tolerance for risk. Deteriorations in banks' capital positions, in contrast, ranked as the least important reason. These responses are consistent with our empirical findings that bank loan growth in the U.S. appears to be more determined by factors like aggregate demand and bank risk. Return to Text

8. This interpretation does not contradict the widely accepted view that adequate levels of bank capital are crucial to prevent institutional failure, given the risks that attend financial intermediation: As shown by Berger and Bouwman (2009), increases in bank capital seem to be key to boosting bank profits and helping banks survive the effects of financial crises. Return to Text

9. For evidence supporting this view see Ashcraft (2004), who documents the practice of BHCs providing assistance--sometimes in the form of capital injections--to distressed subsidiaries, and Houston, James, and Marcus (1997), who report that BHC subsidiary loan growth is more sensitive to the cashflow and capital positions of the holding company than to the subsidiary's position. Return to Text

10. We exclude institutions with missing observations in total assets, loans, and capital, and also BHCs that remain in the sample for less than 30 quarters. In order to minimize the influence of extreme outliers, we remove observations with more than 50 percent growth in total assets over a single quarter and winsorize the remaining variables at the 1 percent and 99 percent levels. The final sample consists of about 11,107 bank-quarter observations for 140 institutions out of the 165 BHCs. Return to Text

11. As noted above the BHCs in our sample have total assets in excess of $3 billion in 2008:Q3. In earlier periods, however, total assets can be smaller than the $3 billion cutoff. Return to Text

12. Among other criteria, a BHC is considered well-capitalized if it has a total risk-based capital ratio of at least 10 percent, and a tier-one risk-based capital ratio of at least 6 percent. Return to Text

13. Specifically, when our model included the total GDP deflator we found that the most important nonfinancial shock driving movements in bank and thrift loan growth over 2008 and 2009 was the price shock, which seemed somewhat counterintuitive. However, using the GDP deflator excluding food and energy eliminated this problem. Return to Text

14. All composition variables, such as the composition of security and loan holdings, are calculated as a share of bank assets. Return to Text

15. We take 5 percent to be the approximate level below which regulators in the U.S. would have concerns about a BHC's capital adequacy. Return to Text

16. Flannery and Rangan (2008) and Berger et al. (2008) find a negative relationship between capital ratios and size when they use either market capital or regulatory capital ratios. For the BHCs in our sample we also observe that larger BHCs operate with lower market capital and regulatory capital ratios. However, the divergence across different bank sizes is less evident when we use the equity capital ratio. Interestingly, Flannery and Rangan (2008) also consider the determinants of the book value equity ratio (defined as the ratio of the book value of common equity to the book value of total assets), which is a concept similar to the equity capital ratio that we use, and here they find an insignificant zero coefficient on bank size. Return to Text

17. Although the presence of fixed effects in dynamic panel data estimation can lead to biased OLS estimates, simulations by Judson and Owen (1999) suggest that the the bias is minor in panels with more than 30 observations. Given that our panel uses 59 periods of data and the minimum number of quarters for any BHC in our sample is 30, we make no correction for potential short-panel bias. Return to Text

18. For example, Flannery and Rangan (2008) and Berger et al. (2008) document a build-up of capital cushions during this period for large banks that was substantially above the "well-capitalized"regulatory minima (note that the 1990s and mid 2000s represented a period of unusual profitability for the banking sector). Return to Text

19. Hancock and Wilcox (1994) find that by the end of 1991 more than 40 percent of banks had capital shortfalls relative to their bank-specific targets. Return to Text

20. Because an auxiliary equation is used to estimate the capital surplus variable, our estimation of equation (4) is subject to a generated regressor bias. We use a bootstrap procedure to address this problem. Return to Text

21. The calculation is performed as follows. The relationship between a percent capital surplus/shortfall and loan growth is $\frac{L_{t}-L_{t-1}}{L_{t-1}}=0.25\cdot\frac{K_{t}-K^{\ast}_{t}}{K^{\ast}_{t}}$ . Assuming that the economy was initially in steady-state implies that $\frac{L_{t}-L^{\ast}_{t-1}}{L^{\ast}_{t-1}}=0.25\cdot\frac{K_{t}-K^{\ast}_{t}}{K^{\ast}_{t}}$ , which yields $\left(L_{t}-L^{\ast}_{t-1}\right)=0.25\cdot\frac{L^{\ast}}{A^{\ast}}\cdot\frac{A^{\ast}}{K^{\ast}}\left(K_{t}-K^{\ast}_{t}\right)$ (ignoring time subscripts on the ratios of steady-state variables). Since $\frac{L^{\ast}}{A^{\ast}}=0.62$ and $\frac{A^{\ast}}{K^{\ast}}=12$ in the data, this implies that $\left(L_{t}-L^{\ast}_{t-1}\right) =1.86\left(K_{t}-K^{\ast}_{t}\right)$ . Return to Text

22. In principle, relative bank size should also induce similar differences between the estimates reported in section 2.2 and those found by Hancock and Wilcox. However, we do not observe such differences. One possible reason is that Hancock and Wilcox perform their analysis on the entire U.S. and exclude commercial banks with assets less than $300 million (roughly $500 million in current dollars). In addition, they "roll up" the commercial banks in their sample to the BHC top holder. Hence, it is likely that the banks in the Hancock-Wilcox study are on average larger than those used by Bernanke and Lown. Return to Text

23. Research on the bank lending channel of monetary policy seems to suggest decreased sensitivity of lending to bank capital as a result of greater securitization. See Loutskina and Strahan (2006) and Altunbas, Gambacorta, and Marques-Ibanez (2008). Return to Text

24. We omitted the lagged dependent variables from these regressions since the presence of fixed effects would lead to biased OLS estimates given the short sample period. We verified that, over the entire sample period, the regressions without a lagged dependent variable were still appropriate; we found that explanatory variables had slightly different coefficients but entered the regression with the expected signs and significance levels. Return to Text

25. We did this in two ways (both yielded the same conclusion). The first involved splitting the sample according to the sign of the capital deviation and then re-estimating equation (3) for each subgroup. The second involved constructing a dummy variable that depends on whether a shortfall or a surplus is present; this dummy variable was interacted with the $Z_{i,t}$ term in equation (3), thus allowing for different values of $\phi$ depending on whether $Z_{i,t}$ represents a surplus or shortfall. Return to Text

26. This bias could result if negative capital shocks cause some BHCs to leave the sample. Note that such survivor bias was of limited concern for both Bernanke and Lown (1991) and Hancock and Wilcox (1993, 1994), since these studies employed cross-sectional data over a single year. Return to Text

27. Examples include developments in commercial paper and bond markets. In the recent crisis and its aftermath, developments in these securities markets have affected bank loan growth in important ways. For example, early in the crisis when CP markets were coming under strain, CP issuers drew down back-up lines of credit at banks and this had a sizable positive impact on bank loan growth. More recently, improving conditions in bond markets appear to be having some negative effect on bank loan growth as firms that can issue bonds substitute away from intermediated credit. Return to Text

28. We shut down the different endogenous responses of standards and real GDP growth--both individually and in combination--using the approach followed by Bernanke, Gertler, and Watson (1997). Specifically, in addition to subjecting the model to a one standard deviation capital-ratio shock, we also apply a sequence of other shocks to the model so as to hold the variable or variables in question constant over the period of the impulse response simulations. Return to Text

29. It is interesting to note that even though our parameter estimates for the effect of a capital surplus or shortfall on BHC loan growth are similar to those in Hancock and Wilcox (1993, 1994), the size of deviations of capital from target are much smaller now than they were in the early 1990s. As a result, for a fairly similar contraction in bank loan growth in the 1990-91 and the most recent recessions, we find a more important role in the recent episode for loan demand conditions--proxied by the GDP growth rate--than for shocks to bank capital. This is unsurprising given that the contraction in economic activity has been at least three times larger during the most recent recession than in the 1990-91 recession. Hence, despite similar parameter estimates, this difference leads us to conclude that the contribution of bank capital shortfalls to changes in loan growth is smaller than the Hancock-Wilcox findings. Return to Text

^♣ This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to Text

The effects of bank capital on lending: What do we know, and what does it mean?*

The effects of bank capital on lending:
What do we know, and what does it mean?*