Skip to: [Printable Version (PDF)] [Bibliography] [Footnotes]

Finance and Economics Discussion Series: 2010-60 Screen Reader version ^♣

The Contribution of the Minimum Wage to U.S. Wage Inequality over Three Decades: A Reassessment

David Autor*

MIT Department of Economics and NBER

Alan Manning

London School of Economics

Christopher L. Smith

Federal Reserve Board of Governors

November 2010

Keywords: Minimum wage, wage inequality, wage distribution

Abstract:

We reassess the effect of state and federal minimum wages on U.S. earnings inequality, attending to two flaws issues that appear to bias earlier work: violation of the assumed independence of state wage levels and state wage dispersion, and errors-in-variables that inflate impact estimates via an analogue of the well known division bias problem. We find that erosion of the real minimum wage reduces raises inequality in the lower tail of the wage distribution (the 50/10 wage ratio), but the impacts are typically less than half as large as those reported in the literature and are almost negligible for males. Nevertheless, the estimated effects of the minimum wage on points of the wage distribution extend to wage percentiles where the minimum is nominally non-binding, implying spillovers. We structurally estimate these spillovers and show that their relative importance grows as the nominal minimum wage becomes less binding. Subsequent analysis underscores, however, that spillovers and measurement error (absent spillovers) have similar implications for the effect of the minimum on the shape of the lower tail of the measured wage distribution. With available precision, we cannot reject the hypothesis that estimated spillovers to non-binding percentiles are due to reporting artifacts. Accepting this null, the implied effect of the minimum wage on the actual wage distribution is smaller than the effect of the minimum wage on the measured wage distribution.

1 Introduction

While economists have vigorously debated the effect of the minimum wage on employment levels for at least six decades (cf. Stigler, 1946), its contribution to the evolution of earnings inequality-that is, the shape of the earnings distribution-was largely overlooked prior to the seminal 1996 contribution of DiNardo, Fortin and Lemieux (DFL hereafter). Using kernel density techniques, DFL produced overwhelming visual evidence that the minimum wage substantially `held up' the lower tail of the placecountry-regionUS earnings distribution in 1979, yielding a pronounced spike in hourly earnings at the nominal minimum value, particularly for females. By 1988, however, this spike had virtually disappeared. Simultaneously, the inequality of hourly earnings increased markedly in both the upper and lower halves of the wage distribution. Most relevant to this paper, the 10/50 (`lower tail') log hourly earnings ratio expanded by 8 to 23 log points between 1979 and 1988, with the largest increases among females and the smallest among males (Table 1). To assess the causes of this rise, DFL constructed counterfactual wage distributions that potentially account for the impact of changing worker characteristics, labor demand, union penetration, and minimum wages on the shape of the wage distribution. Comparing counterfactual with observed wage densities, DFL concluded that the erosion of the federal minimum wage-which declined in real terms by 30 log points between 1979 and 1988-was the predominant cause of rising lower tail inequality between 1979 and 1988, explaining two-thirds of the growth of the 10/50 for both males and females.¹

Though striking, a well-understood limitation of the DFL findings is that the estimated counterfactual wage distributions derive exclusively from reweighting of observed wage densities rather than controlled comparisons. Thus, they are closer in spirit to simulation than to inference. Cognizant of this limitation, DFL highlight in their conclusion that the expansion of lower tail inequality during 1979 to 1988 was noticeably more pronounced in `low-wage' than `high-wage states,' consistent with the hypothesis that the falling federal minimum caused a differential increase in lower tail equality in states where the minimum wage was initially more binding. Building on this observation, Lee (1999) exploits cross-state variation in the gap between state median wages and the applicable federal or state minimum wage (the `effective minimum') to estimate what the share of the observed rise in wage inequality from 1979 through 1988 was due to the falling minimum rather than changes in underlying (`latent') wage inequality. Amplifying the findings of DFL, Lee concludes that more than the entire rise of lower tail earnings inequality-by which we mean, the 50/10 earnings differential-between 1979 and 1988 was due to the falling federal minimum wage; had the minimum been constant throughout this period, observed wage inequality would have fallen.²

These influential findings present two key puzzles that motivate the current paper. The first is that the Lee analysis uncovers and scrupulously reports causal effects estimates that clearly violate the paper's main falsification tests. In particular, the estimates imply that the declining federal minimum wage significantly reduced the growth of upper tail (90/50) inequality in both the male and pooled-gender wage distributions between 1979 and 1991.³ This startling but nevertheless robust result suggests potential problems in the econometric strategy.

The first goal of the current paper is to identify and amend these econometric issues. We show that the reduced form OLS models used in the literature suffer from two first-order sources of bias. One is garden-variety omitted variables bias. The main estimating equations used by Lee (1999) exclude state fixed effects, which is not problematic provided that there is no correlation between states' median wage levels (which proxy for the `bindingess' of the federal minimum wage) and states' underlying wage variances. In violation of this assumption, we show that median state log wages and log wage variances are strongly positively correlated, even in portions of the distribution where the variance of wages is unlikely to be affected by the minimum wage (such as the 60/40 gap). Consequently, state fixed effects, and potentially state trends, are needed for consistent estimation.

The second problem we document in existing estimates is a variant of the well known division bias problem (Borjas, 1980), which arises from including state median wages on both sides of the regression equation-in the main independent variable (the proxy for the minimum wage's bindingness) and in the dependent variable (the 50/10 wage gap). This is problematic inasmuch as sampling variation in the median wage can induce a mechanical correlation between the dependent and independent variables. Indeed, Lee (1999) is aware of this problem. His preferred specification has two different measures of the central tendency of wages (a median and a trimmed mean) on the left and right hand sides in an attempt to deal with this problem. However, we show that these different measures are still likely to have a high correlation induced by sampling variation such that division bias remains a problem.⁴ We show that division bias is a substantial problem for OLS estimates, and we correct for it by instrumenting the effective minimum with the statutory minimum wage in each state and year (which does suffer from sampling variation). This canonical technique for correcting measurement error, due to Durbin (1954), was also used by Card, Katz and Krueger (1993) in their reanalysis of the employment effects of the minimum wage.

Correcting both econometric issues substantially affects inference. Between 1979 and 1988, 50/10 wage inequality in the female, male and pooled distributions rose by 23, 8 and 11 log points, respectively. Conventional OLS estimates indicate that the falling real minimum wage accounted for almost the entirety of the observed increases. Had the minimum been at its real 1988 level in both 1979 and 1988, OLS models imply that 50/10 wage inequality would have risen by only 3 log points for females, and would not have risen at all for males and the pooled distribution. By contrast, 2SLS models find that, under the same counterfactual assumptions, female 50/10 inequality would have risen by 15 log points, and male and pooled gender inequality by 7 log points each. Graphical comparisons of OLS, 2SLS and quantile regression estimates over the full thirty year sample period reinforce the conclusion that OLS models are unreliable.

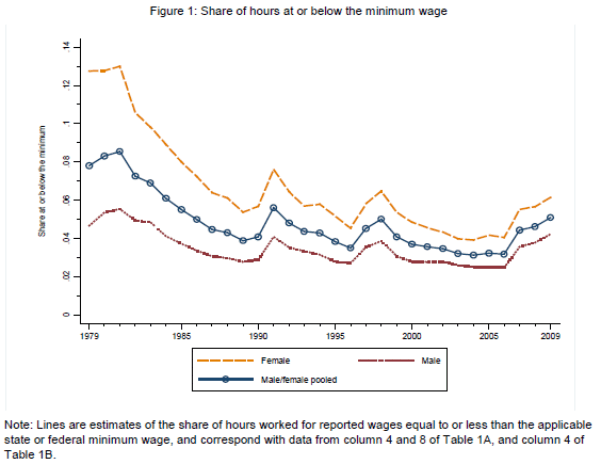
After accounting for the econometric issues in earlier OLS estimates, a second puzzle remains. Between 1979 and 2009, no more than nine percent of all workers, and six percent of all male workers, were paid at or below the federal or applicable state minimum wage (see Figure 1 and Table 1, column 8); only for females (and only for a few years at the beginning of our sample) was the minimum wage directly binding at or above the 10 ${}^{th}$ percentile.⁵ This observation implies that any impact of the minimum wage on 50/10 male and pooled gender wage inequality must be due to a spillover effect, whereby the minimum wage raises the wages of workers earning above the minimum.⁶ Such spillovers are a potentially important and little understood effect of minimum wage laws.

In the second part of our paper, we provide estimates of these spillovers and we test whether spillovers are plausibly large enough to account for the causal effects attributed to them. We model each state's latent wage distribution as log-normal, and estimate the parameters of these distributions using wage observations from higher percentiles of the distribution, where the minimum wage is unlikely to be relevant. Armed with these estimates, we calculate the mechanical impact of the minimum wage by truncating the lower tail of the (estimated) latent distribution at the statutory minimum, and inferring spillovers by comparing the `mechanical' distribution with the observed distribution.⁷ Notably, while the sources of identifying variation for the structural estimation are almost entirely distinct from the reduced form analysis, the two approaches find largely comparable effects of the minimum wage on inequality.

Spillovers appear to be a significant component of the impact of the minimum wage on the wage distribution. At its highest level (in 1979), the minimum wage compressed the female 50/10 wage ratio by 18 log points. This large compressing effect was primarily a direct result of the minimum wage propping up lower wage percentiles. As the real minimum wage fell over the subsequent decade, however, the share of the minimum wage's impact accounted for by spillovers rose. In 2009, we estimate that the minimum wage compressed female 50/10 wage inequality by 12 log points, half of which was due to spillovers. Logically, we estimate that the modest effects of the minimum on the male and pooled gender distributions are due entirely to spillovers.

We finally explore whether the spillovers found in our samples, based on the Current Population Survey, may result from measurement error in wage reporting rather than from true spillovers. This can occur if a fraction of minimum wage workers report their wages inaccurately, leading to a hump in the wage distribution centered on the minimum wage rather than (or in addition to) a spike at the minimum. After bounding the potential magnitude of these measurement errors, we are unable to reject the hypothesis that the apparent spillover from the minimum wage to higher (non-covered) percentiles is spurious. That is, while the spillovers are present in the data, they may not be present in the distribution of wages actually paid. These results do not rule out the possibility of true spillovers. But they underscore that estimated spillovers must be treated with caution since they cannot be distinguished from measurement artifacts with available precision.

The paper proceeds as follows. Section I discusses data and sources of identification. Section II presents the measurement framework and estimates a set of causal effects estimates models that, like Lee (1999), explicitly account for the bite of the minimum wage in estimating its effect on the wage distribution. We compare parameterized OLS and 2SLS models and document the pitfalls that arise in the OLS estimation. Section III uses point estimates from the main regression models to calculate counterfactual changes in wage inequality, holding the real minimum wage constant. Section IV presents estimates of both the direct and spillover effects of the minimum wage derived from parametric estimates of the latent wage distribution. Section V analyzes the extent to which apparent spillovers may be due to measurement error. The final section concludes.

2 Change in the federal minimum wage and variation in state minimum wages

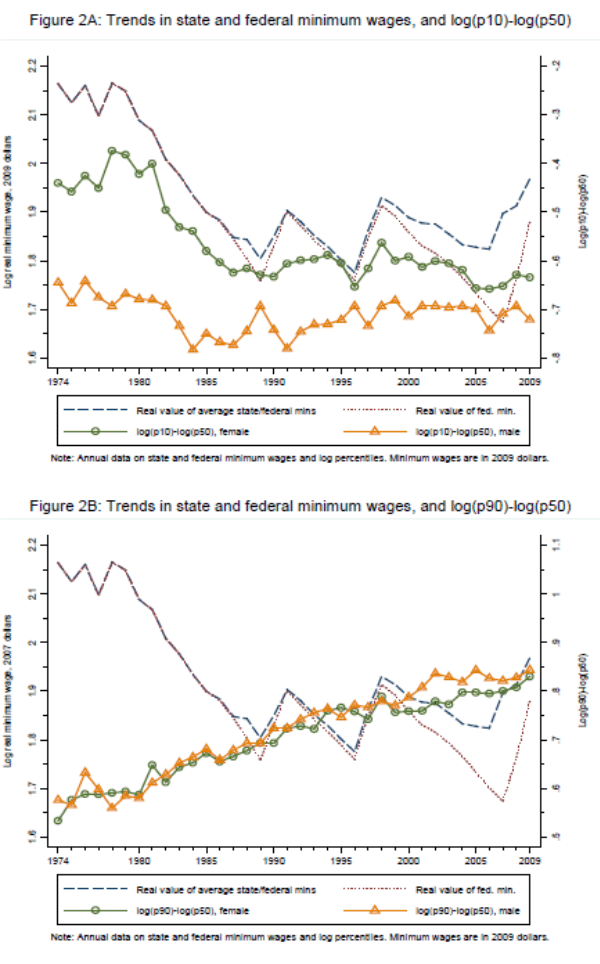
In July of 2007, the real value of the U.S. Federal minimum wage fell to a fifty year low (Figure 2). This outcome reflects three decades of nearly continual decline in the real minimum wage from a 1979 high point, including two decade-long spans in which the minimum wage remained fixed in nominal terms-1981 through 1990, and 1997 through 2007-only slightly offset by two modest increases in 1991 and 1998, followed by substantial increases in both 2008 and 2009. An important difference between the most recent decade, however, and the several that precede it is that numerous states now legislate minimum wages that exceed the federal level. At the end of the 1980s, 15 states' minimum wages exceeded the federal level; by 2008, this number had reached 32 (subsequently reduced to 27 by the 2009 federal minimum wage increase). Consequently, the real value of the minimum wage applicable to the average worker in 2007 was not much lower than in 1997, and was significantly higher than if states had not enacted their own minimum wages. Moreover, the most recent federal increases bring the minimum wage faced by the average worker up to a real level not seen since the mid 1980s. Appendix Table 1 illustrates the extent of state minimum wage variation between 1979 and 2009.

These differences in legislated minimum wages across states and over time are one of two sources of variation that we use to identify the impact of the minimum wage on the wage distribution. The second source of variation we use, following Lee (1999), is variation in the `bindingness' of the minimum wage, stemming from the idea that a given legislated minimum wage should have a larger effect on the shape of the wage distribution in a state with a lower wage level. Table 1 provides examples. In each year, there is significant variation in the percentile of the state wage distribution where the state or federal minimum wage "binds." For instance, in 1979 the minimum wage bound at the 12 ${}^{th}$ percentile of the female wage distribution for the median state, but it bound at the 3 ${}^{rd}$ percentile in Alaska and the 28 ${}^{th}$ percentile in Mississippi. This variation in the "bite" or "bindingness" of the minimum wage was due mainly to cross-state differences in wage levels in 1979, since only Alaska had a state minimum wage that exceeded the federal minimum. In later years, particularly the current decade, this variation was also due to differences in the value of state minimum wages.

2.1 Sample and variable construction

Our analysis uses the percentiles of states' annual wage distributions as the primary outcomes of interest. We form these samples by pooling all individual responses from the Current Population Survey Merged Outgoing Rotation Group (CPS MORG) for each year. We use the reported hourly wage for those who report being paid by the hour, otherwise we calculate the hourly wage as weekly earnings divided by hours worked in the prior week. We limit the sample to individuals age 18 through 64, and we multiply top-coded values by 1.5. We exclude self-employed individuals and those with wages imputed by the BLS. To reduce the influence of outliers, we Winsorize the top two percentiles of the wage distribution in each state, year, sex grouping (male, female or pooled) by assigning the 97 ${}^{th}$ percentile value to the 98 ${}^{th}$ and 99 ${}^{th}$ percentiles. Using these individual wage data, we calculate all percentiles of state wage distributions by sex for 1979-2009, weighting individual observations by their CPS sampling weight multiplied by their weekly hours worked.

Our primary analysis is performed at the state-year level, but minimum wages often change part way through the year. We address this issue by assigning the value of the minimum wage that was in effect for the longest time throughout the calendar year in a state and year. For those states and years in which more than one minimum wage was in effect for six months in the year, the maximum of the two is used. We have also tried assigning the maximum of the minimum wage within a year as the applicable minimum wage, and this leaves our conclusions unchanged.

3 OLS and 2SLS estimation of minimum wage effects on the wage distribution

3.1 Regression specification

The effect of the minimum wage on wage inequality will naturally depend in part on how high the statutory minimum wage is set relative to the overall distribution of wages-its `bindingness.' Bindingness is of course intrinsically unobservable since the econometrician cannot measure the counterfactual (`latent') wage distribution absent the minimum wage. As a proxy measure of bindingness, Lee (1999) proposes using the gap between the log of the statutory state minimum and log state median wage ( $w^m_{st}-w_{st}\left(50\right)$ ), which he terms the `effective minimum'. Denoting $w_{st}\left(p\right)$ and $w^*_{st}\left(p\right)$ as the actual and latent values of percentile p, and allowing ${\beta }_1$ and ${\beta }_2$ to vary by percentile, Lee's primary empirical specification is motivated by the following equation:

$w_{st}\left(p\right)-w_{st}\left(50\right)=\left(w^*_{st}(p)-w^*_{st}\left(50\right)\right)+{\beta }_1\left(w^m_{st}-w_{st}\left(50\right)\right)+{\beta }_2{(w^m_{st}-w_{st}\left(50\right))}^2+{\varepsilon }_{st}$ (1)

That is, the value of any percentile relative to the median is a function of latent inequality at percentile p and a quadratic in the bindingness of the minimum wage for state s in year t. Operationalizing (1) requires making assumptions about the underlying latent wage distribution. Lee (1999) assumes the following:

1. The latent wage distribution can be summarized by two parameters, the median and the variance, so that we can write:

$w^*_{st}\left(p\right)={\mu }_{st}+{\sigma }_{st}F^{-1}(p)$ (2)

And, we have the normalization $F^{-1}\left(50\right)=0$ so that ${\mu }_{st}$ is the median log wage in state $\ s$ at time $\ t$ .

2. Cross-state variation in latent wage inequality is uncorrelated with the median:

${\sigma }_{st}\bot {\mu }_{st}\vert t$ (3)

Equipped with these assumptions, Lee estimates the following as his primary empirical specification:

$w_{st}\left(p\right)-w_{st}\left(50\right)={\alpha }_t+{\beta }_1\left(w^m_{st}-w_{st}\left(50\right)\right)+{\beta }_2{(w^m_{st}-w_{st}\left(50\right))}^2+{\varepsilon }_{st}$

(4)

The two above assumptions justify three noteworthy features of equation (4). First, because any cross-state variation in latent wage inequality is assumed to be uncorrelated with state medians conditional on time, explicit controls for state variances, ${\sigma }_{st}$ , can be replaced with a set of time dummies in the estimating equation without biasing estimates of ${\beta }_1\ {\rm and\ }{\beta }_2$ . State dummies are not required under these assumptions and are not present.

Second, the assumed independence of state wage medians and latent state wage dispersion implies that any association between the effective minimum and the observed 10/50 differential in (4) reflects the causal impact of the minimum on the lower tail of the wage distribution. Specifically, if the observed state median $w_{st}\left(50\right)$ is an adequate measure of ${\mu }_{st}$ , and recalling the normalization that $F^{-1}\left(50\right)=0$ , we have:

${\rm cov}\left[\left(w^*_{st}\left(p\right)-w^*_{st}\left(50\right)\right),\left(w^m_{st}-w_{st}\left(50\right)\right)\vert t\right]={\rm cov}\left[{\sigma }_{st}F^{-1}\left(50\right),\left(w^m_{st}-{\mu }_{st}\right)\vert t\right]=0$ (5)

Finally, note that the log of the observed state median is included in both the dependent and independent variables of the regression equation, which can be rationalized under the assumption that the median provides a natural measure of the statutory minimum's bindingness. Moreover, it is independent of latent state wage variances by the second assumption above.

3.2 OLS estimates

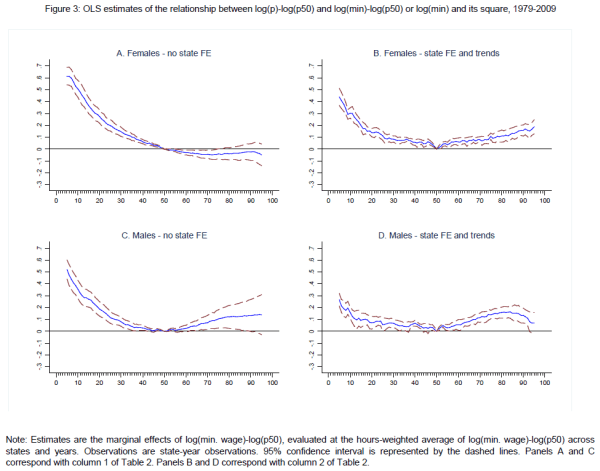
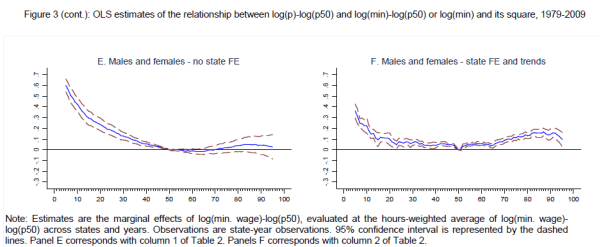
Column 1 of Tables 2A, 2B, and 2C present estimates of equation (4) for the marginal effects of the effective minimum for selected percentiles, when marginal effects are estimated at the weighted average of the effective minimum over all states and all years between 1979 and 2009. For the regressions represented by column 1, equation (4) is estimated separately for each listed percentile and separately for males, females, and the pooled distribution; the covariates are year fixed effects, the effective minimum, and the square of the effective minimum. Looking at the lower percentiles, we find, as Lee did, large significant effects of the minimum wage extending throughout all percentiles below the median for the male, female and pooled wage distributions.

However, there are indications that this approach is misspecified. As shown in the left-hand panels of Figure 3, which plots the estimated marginal effects of the minimum wage at each percentile, we estimate large effects of the effective minimum at the top of the male wage distribution, and modest effects at the top of pooled wage distribution. Taken at face value, these results indicate a systematic relationship between the effective minimum wage and upper wage percentiles of the male and pooled distributions-specifically, that a decline in the effective minimum wage causes wage compression at the top of the distribution. Since the minimum wage fell sharply during the 1980s, these estimates imply that the steep increase in upper-tail inequality in this decade would have been even larger were it not for the falling minimum.

Lee also scrupulously reports similarly problematic results for upper-tail wage inequality.⁸ To circumvent the problems posed by the male estimates, Lee uses exclusively the pooled distribution point estimates when constructing implied changes in latent wage inequality for the female, male and pooled distributions. While this approach is well motivated, it may nevertheless be inadequate if the specification issues that appear to bias the male estimates are also present for females and the pooled distribution. We show below that these biases appear to afflict all three samples.

3.3 Addressing misspecification: Omitted variables

To address the probable misspecification of equation (4), we first explore whether the identifying assumption that state latent wage inequality is uncorrelated with the median is violated. We regress the log(60)-log(40) on the median (which should be uncorrelated if the density function is symmetric around the median and the minimum does not affect the 40 ${}^{th}$ percentile) and time dummies (to capture the controls put in equation (4)). As shown in Table 3, the log median has a t-statistic of 17.2 for females, 4.4 for men and 14.6 for the combined sample. This suggests that those states with high median wages have high levels of latent wage inequality.

Since these results seemingly indicate permanent differences in latent wage inequality across states, state fixed effects should be included in the estimation of (4). Lee also reports this type of specification (Tables II and III), and we display estimates from the OLS estimation of (4) with state fixed effects and time trends in column 2 of Tables 2A, 2B, and 2C. The marginal effects as implied by these estimates are plotted in Figures 3B, 3D, and 3F. We view the inclusion of state time trends as important in controlling for shocks to the wage distribution that are correlated with changes in minimum wages, and we take column 2 to represent baseline estimates before correcting for potential measurement error through instrumental variables.⁹ As evident in Figure 3, this potential fix exacerbates the anomalous upper-tail results. The relationship between the effective minimum wage and upper percentiles remains pronounced for both males and the pooled distribution, and is now also sizable and significant for females.

3.4 Addressing misspecification: Division bias

An obvious source of misspecification in these estimates is division bias (Borjas, 1980). Division bias stems from the inclusion of the state median wage variable in both the dependent and independent variables in (4), which induces an artificial positive correlation caused by sampling variation. This is likely to lead to upward simultaneity bias in the estimates, since the median enters with the same sign on both sides of the equation. This problem potentially becomes more severe when state fixed effects are included, as more of the remaining variation is the result of sampling variation.

Lee (1999) recognizes this concern and attempts to address it by using two different measures of central tendency in the dependent and independent variables: the median of the dependent variable on the left-hand side, and the trimmed mean on the right (that is, the mean after excluding the bottom and top 30 percentiles). Although this procedure does reduce the correlation, it does not eliminate it. One can show, for example, that if the latent log wage distribution is normal, the correlation between the trimmed mean and the median will be about 0.93-i.e. not unity, but very high.¹⁰

Using the same approach as Card and Krueger (1993) in their analysis of the employment effects of the minimum wage, we address the division bias problem by instrumenting the effective minimum with the statutory minimum wage in each state and year.¹¹ The utility of the statutory minimum wage in this application is that it does not suffer from sampling variation. Assuming that legislated changes in the minimum wage are not correlated with changes in latent state wage inequality conditional on year effects and state and year trends, this instrument will capture exogenous variation in the effective minimum that is uncorrelated with the measurement error in state medians.¹² Similarly, to capture exogenous variation in the square of the effective minimum (i.e., to allow for non-linear effects of bindingness), we square the predicted value from a regression of the effective minimum wage on the legislated minimum and year and state dummies (and state-time trends, if included in the second stage)-which is essentially the square of the first stage estimate for the effective minimum.¹³ One drawback of this instrument is that there is quite limited cross-state variation in the legislated minimum wage during the 1980s (and all federal variation in the minimum wage is absorbed by year dummies). Consequently, the instrument has tenuous identifying power when used with data that is exclusively from the 1980s.

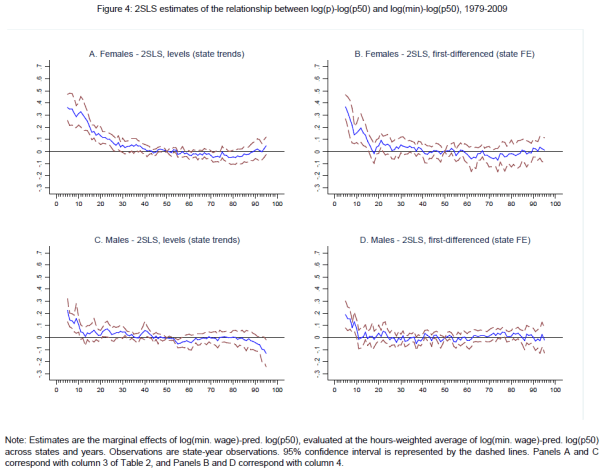
Figure 4 demonstrates the efficacy of this approach for two specifications that control for state effects: estimation of (4) in levels and including state fixed effects and state time trends (Figures 4A, 4C, and 4E), and estimation of the first-differenced version of (4) and including state fixed effects (Figures 4B, 4D, and 4F). We prefer the first-differenced estimates (column 4) because first-differencing places fewer restrictions on the error structure.¹⁴ When the effective minimum wage and its square are instrumented by the statutory minimum, the positive correlation between the effective minimum and upper tail percentiles almost completely disappears.

Of equal importance, instrumentation also reduces the estimated impact of the minimum wage elsewhere in the wage distribution, a result that is consistent with a reduction in division bias. To summarize these results, columns 3 and 4 of Table 2 present 2SLS estimates of marginal effects for various percentiles. These 2SLS estimates imply that the minimum wage has a statistically significant impact up through the 25 ${}^{th}$ percentile or so for women, up through the 10 ${}^{th}$ percentile for men, and up through the 15 ${}^{th}$ percentile or so for the pooled wage distribution. 2SLS estimates imply that a 10 log point increase in the effective minimum wage reduces 50-10 inequality by 1.5 to 3 log points for women, by 0.7 to 0.9 log points for men, and by 1.6 to 2.2 log points for the pooled distribution. These estimates are less than half as large as those found by the baseline OLS specification.

3.5 Specification checks: Quantile and reduced form estimates

Our estimates so far are performed using percentiles of state annual wage distributions, which are aggregate statistics calculated from microdata. As a specification test, we also estimate comparable models using microdata and applying conditional quantile regressions. We begin with a quantile regression analogue of equation (4):

$Q_{\theta }\left[w_{st}\left(p\right)-w_{st}\left(50\right)\vert t,s,w^m_{st}-w_{st}\left(50\right)\right]={\alpha }^{\theta }_t+{\beta }^{\theta }_1\left(w^m_{st}-w_{st}\left(50\right)\right)+{\beta }^{\theta }_2{\left(w^m_{st}-w_{st}\left(50\right)\right)}^2.$ (6)

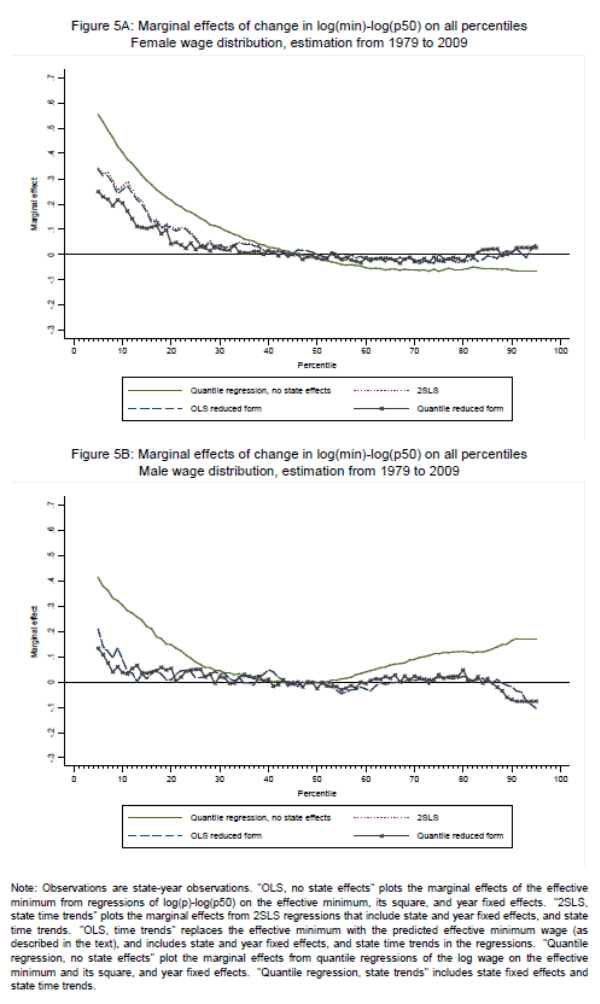
Figure 5 display estimates of this quantile model.¹⁵ Perhaps not surprisingly, the quantile regression estimates of (6) are similarly problematic to OLS estimates of equation (6). We estimate large effects of the effective minimum at the top of the male wage distribution, which suggests that the quantile model suffers from the specification biases above. Similarly, a logical remedy is to add state fixed effects to (6) while instrumenting the effective minimum wage with the statutory minimum. Applying quantile instrumental variables (Chernozhukov and Hansen, 2005) in this setting would present a major computational challenge, however, due to the large sample sizes.

In lieu of this technique, we implement a reduced form approach that should perform similarly. Recall that the purpose of instrumentation in our application is to purge sampling error in estimated state median wages that would otherwise generate division bias in the regression model. We can accomplish a similar objective by using predicted rather than observed state medians in equation (6). In particular, we fit the following equation:

$w_{st}\left(50\right)={\alpha }_t+{\gamma }_s+\left({\gamma }_s\times t\right)+e_{st},$ (7)

which models state median wages as a function of time effects, state effects, state-specific time trends, and an error term. We calculate the `reduced form effective minimum' (and its square) as ${\widetilde{mw}}_{st}=\left(w^m_{st}-{\hat{w}}_{st}\left(50\right)\right)$ , where ${\hat{w}}_{st}\left(50\right)$ is equal to the regression prediction from equation (7), and we use it in place of the measured effective minimum in a quantile regression that includes state fixed effects and state trends:

$Q_{\theta }\left[w_{st}\left(p\right)-w_{st}\left(50\right)\vert t,s,w^m_{st}-w_{st}\left(50\right)\right]={\alpha }^{\theta }_t+{\gamma }_s+\left({\gamma }_s\times t\right)+{\beta }^{\theta }_1{\widetilde{mw}}_{st}+{\beta }^{\theta }_2{\widetilde{mw}}^2_{st}$ (8)

Before applying this technique to the quantile model, we perform a `proof of concept' by estimating equation (8) using OLS. If this reduced form technique works as expected, OLS estimates of (8) should be comparable to earlier 2SLS estimates of this equation, i.e., where the effective minimum is instrumented by the statutory minimum (see Table 2 column 3). Figure 5 confirms this conjecture: 2SLS and reduced form estimates of this equation are nearly indistinguishable.¹⁶

The fourth series in Figure 5 plots the quantile reduced form estimates for the implied impacts of the minimum wage on the male and female distributions. These point estimates are highly comparable to the 2SLS models. And to the extent they differ, they find slightly smaller impacts of the effective minimum on both male and female wage inequality in the lowest two deciles. (In this respect, they are similar to our 2SLS first difference estimates in Table 2, column 4.) Reassuringly, these quantile estimates find no correlation between the effective minimum and changes in upper percentiles for either sex.

In net, the models summarized in Figure 5 indicate that the pooled model developed by Lee (1999) for estimating the impact of the minimum wage on wage inequality do not appear to be reliable, whether estimated using OLS or quantile regressions. Conversely, augmented models that both allow for state effects and trends and also purge correlated measurement error in the effective minimum wage measure perform well whether estimated by 2SLS, or in quasi-reduced form, using either OLS or quantile regressions.

4 Estimating the counterfactual change in inequality holding the minimum wage constant

How much of the expansion in lower-tail wage inequality since 1979 was due to the declining minimum wage? Following Lee (1999), we present counterfactual estimates of the change in latent wage inequality absent the decline in the minimum wage-that is, the change in wage inequality that would have been observed had the minimum wage been held at a constant real benchmark. These counterfactuals are constructed using our estimates for how the minimum wage affects every percentile of the wage distribution, as described in the previous section-as such, they do not distinguish between mechanical and spillover effects of the minimum wage, nor do they recover the counterfactual distribution of wages absent the minimum wage (since the effective minimum wage measure, equal to the logarithm of the minimum minus the logarithm of the median, is undefined at a minimum wage of zero). We address both limitations-spillovers and full distribution counterfactuals-in the next section.

To estimate changes in latent wage inequality, Lee (1999) proposes the following simple procedure. For each observation in the dataset, calculate its rank in its respective state-year wage distribution. Then, adjust each wage by the quantity:

$\triangle w^p_{st}={\widehat{\beta }}^p_1\left({\tilde{m}}_{s,\tau 0}-{\tilde{m}}_{s,\tau 1}\right)+{\widehat{\beta }}^p_2\left({\tilde{m}}^2_{s,\tau 0}-{\tilde{m}}^2_{s,\tau 1}\right)$ (9)

where ${\tilde{m}}_{s,\tau 1}$ is the observed end-of period effective minimum in state s in some year $\ \tau 1$ , ${\tilde{m}}_{s,\tau 0}$ is the corresponding beginning-of-period effective minimum in $\ \tau 0$ , and ${\widehat{\beta }}^p_1,\ {\widehat{\beta }}^p_2$ are point estimates from the OLS and 2SLS estimates in Table 2 (columns 1, 3, or 4).¹⁷ We pool these adjusted wage observations to form a counterfactual national wage distribution, and we compare changes in inequality in the simulated distribution to those in the observed distribution.¹⁸

Before implementing equation (9), we summarize in Table 4 estimates of the average marginal effect of the effective minimum wage on 50-10 inequality by gender for 1979 through 2009 and several sub-periods. For each gender and time interval, we fit three models: a pooled OLS model excluding state dummies (i.e., the primary specification in Lee, 1999); a fixed-effects instrumental variables model with state dummies and trends; and a first-difference instrumental variables model with state dummies.

For all 2SLS models, F-tests (not tabulated) indicate that the instruments are jointly highly significant and pass standard diagnostic tests for weak instruments (e.g., Stock, Wright and Yogo, 2002). Nevertheless, Table 4 finds that 2SLS estimates of the marginal effect of the minimum wage on wage inequality are insignificant in many cases when estimated for the focal period of 1979 through 1989 studied by Lee (1999).¹⁹ This lack of statistical significance is not surprising in light of the small number of policy changes in this period: between 1979 and 1985, only one state adopted a minimum wage in excess of the federal minimum; the eight additional adoptions that took take between 1979 and 1988 all occurred between 1986 and 1988 (Table 1). Consequently, when calculating counterfactuals below, we apply marginal effects estimates obtained using additional years of data. By extending the estimation window to 1991 (as was also done by Lee, 1999), we exploit the substantial federal minimum wage increase that took place between 1990 and 1991. This generated numerous cross-state contrasts since 9 states had by 1989 raised their minimums above the 1989 federal level and below the 1991 federal level (and an additional three raised their minimum to $4.25, which would be the level of the 1991 federal minimum wage).

The top panel of Table 5 shows that between 1979 and 1991, the female 50/10 log wage ratio increased by 22 log points. Applying the marginal effect estimate obtained using the OLS model fit to the female wage data for 1979 through 2009, we calculate that had the minimum wage been constant at its real 1991 level throughout this period, female 50/10 inequality would counterfactually have risen by only 6 log points. Thus, consistent with Lee (1999), the OLS estimate implies that the decline in the real minimum wage can account for the bulk (16 of 22 log points) of the expansion of lower tail female wage inequality in this period.

The next two columns of the table present analogous counterfactuals estimated using 2SLS models (either fixed effect or first difference) in place of OLS. These estimates find a substantially smaller role for the minimum wage. The fixed-effects IV estimate implies that the minimum wage explains roughly half (55 percent) of the rise in female 50/10 inequality in this period. The first-difference IV model-which relies on the most plausible assumptions-indicates that the minimum wage explains less than a third (7 of 22 log points) of the rise in the female 50/10. These are non-trivial effects, of course, and they confirm, in accordance with the visual evidence in Figure 2, that the falling minimum wage contributed meaningfully to rising female lower-tail inequality during the 1980s and early 1990s.

The second and third rows of Table 5 calculate the effect of the minimum wage on male and pooled gender inequality. Here, the discrepancy between OLS and IV-based counterfactuals is even more pronounced. OLS estimates imply that the minimum wage explains a bit more than 40 percent of the 11 log point rise in male 50/10 inequality between 1979 and 1991, and more than 100 percent of the 7 log point rise in pooled gender inequality in the same interval. By contrast, 2SLS models indicate that the minimum wage explains less than 10 percent of the rise in male wage inequality and about half of the decline in pooled gender inequality.

Despite their substantial discrepancy with the OLS models, these 2SLS estimates appear highly plausible. Figure 1 shows that the minimum wage was nominally non-binding for males throughout the sample period, with fewer than 6 percent of all male wages falling at or below the relevant minimum wage in any given year. For the pooled gender distribution, the minimum wage had somewhat more bite, with more than 8 percent of all hours paid at or below the minimum in the first few years of the sample. But this is modest relative to its position in the female distribution, where 9 to 13 percent of wages were at or below the relevant minimum in the first five years of the sample. Consistent with these facts, 2SLS estimates indicate that the falling minimum wage generated a sizable increase in female wage inequality, a modest increase in pooled gender inequality, and a minimal increase in male wage inequality.

Subsequent panels of Table 5 calculate counterfactual (minimum wage constant) changes in inequality over several other time intervals of interest (1979-1988, 1979-2009, and 1998-2009). In all cases, the contribution of the minimum wage to rising inequality is smaller when estimated using 2SLS in place of OLS models.

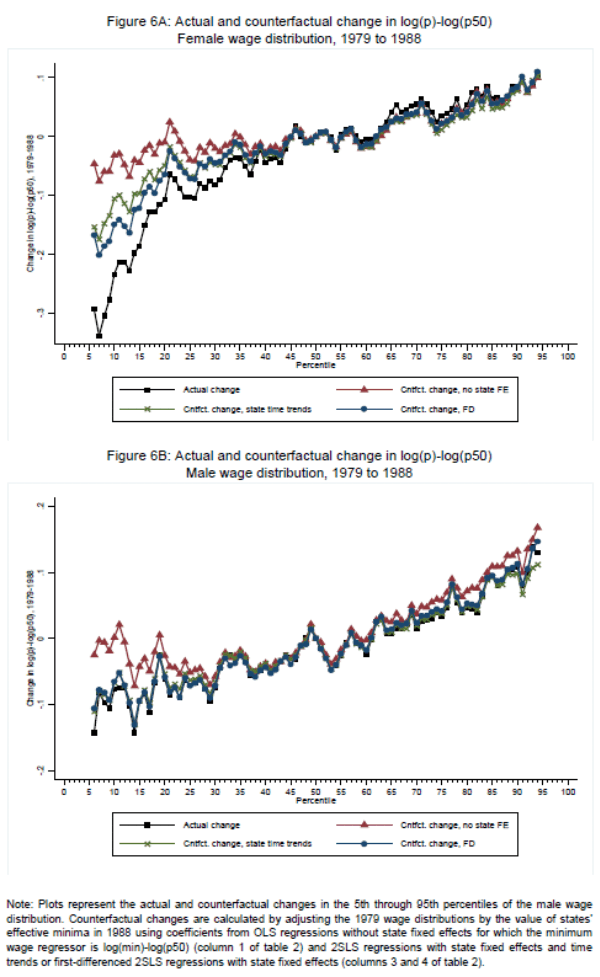
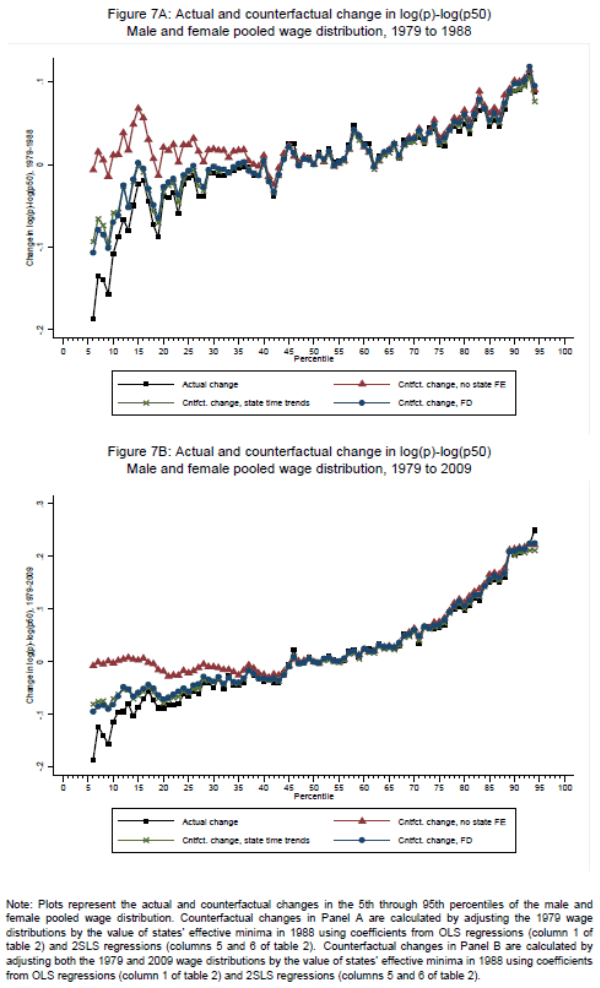
Figure 6 and the top panel of Figure 7 provide a visual comparison of observed and counterfactual changes in male, female and pooled-gender wage inequality during the critical period of 1979 through 1988, during which time the minimum wage remained nominally fixed while lower-tail inequality rose rapidly for all groups. As per Lee (1999), the OLS counterfactuals depicted in these plots suggest that the minimum wage explains essentially all of the 23.4, 7.7 and 10.8 log point rise in 50/10 inequality in the female, male and pooled-gender distributions during this period. The 2SLS counterfactuals place this contribution at a far more modest level. For example, the counterfactual series for males is indistinguishable from the observed series, implying that the minimum wage made almost no contribution to the rise in male inequality in this period. The lower panel of Figure 7, which plots observed and counterfactual wages change in the pooled gender distribution for the full sample period of 1979 through 2009 (again holding the minimum wage at its 1988 value), shows a similarly pronounced discrepancy between OLS and 2SLS models.

As a robustness test, panel 2 of Table 5 repeats these counterfactual calculations using marginal effects estimates from years 1979 through 1991 (used by Lee) rather than the full sample period. The counterfactual estimates in this table are highly consistent with those calculated earlier, both during the critical period of 1979 through 1991 and during other sub- and super-intervals. These estimates consistently find a considerably smaller role for the minimum wage in rise of U.S. inequality than prior work has suggested. While they do not qualitatively reverse the view that the falling minimum wage contributed to the growth of lower tail inequality during the 1980s, they suggest a quantitatively large downward revision to the estimated magnitude of this contribution.

5 Decomposing the direct and spillover effects of the minimum wage

As highlighted in Figure 1, federal and state minimum wages were nominally non-binding at the 10 ${}^{th}$ percentile of the wage distribution throughout most of the sample; in fact, there is only one three year interval (1979 to 1982), when more than ten percent of hours paid were at or below the minimum wage-and this was only the case for females. Yet our main estimates imply that the minimum wage modestly compressed both male and pooled-gender 50/10 wage inequality during the 1980s. This implies that the minimum wage had spillover effects onto percentiles above where it binds. To better understand these spillovers, we now estimate the separate contributions of direct and spillover effects of the minimum wage to the overall wage distribution.

To guide thinking, we begin by writing down a simple statistical model of spillovers. Denote by ${w(p)}^*_{st}$ the log wage for the p ${}^{th}$ percentile in state s at time t if there was no minimum wage-call this the latent wage percentile. If there is a binding minimum wage, which we denote in log form as $w^m_{st}$ , the actual log wage at percentile p, denoted by ${w(p)}^*_{st}$ , will deviate from the latent distribution for at least some percentiles. If the minimum wage had no effect on employment rates and no spillovers to percentiles above where it directly binds, we would have:

$w_{st}\left(p\right)=max\left[w^*_{st}\left(p\right),w^m_{st}\right]$ (10)

If there are spillovers or disemployment effects, however, the minimum wage will also have an effect on percentiles above where it binds (see Teulings 2000, for an explicit supply and demand model with this feature). Generalizing (10) to allow for this possibility, we have:

$w_{st}\left(p\right)=?\left[w^*_{st}\left(p\right),w^m_{st}\right]$ (11)

We expect the function $?[\cdot ,\cdot ]$ to be increasing in both its arguments and to satisfy a homogeneity property: if the latent percentile and the minimum wage both rise in the same proportion, the actual percentile should rise in that proportion. Since the model is expressed in logs, this restriction can be written as:

$?\left[w^*_{st}\left(p\right)+a,w^m_{st}+a\right]=a+?\left[w^*_{st}\left(p\right),w^m_{st}\right].$ (12)

Setting $a{\rm =-}w^{{\rm *}}_{st}\left(p\right)$ and applying (12) to (11), we have that:

$w_{st}\left(p\right)=w^*_{st}\left(p\right)+?\left[0,w^m_{st}-w^*_{st}\left(p\right)\right]=w^*_{st}\left(p\right)+\psi \left(w^m_{st}-w^*_{st}\left(p\right)\right).$ (13)

The observed percentile will depend upon both the latent percentile and the gap between the minimum and the latent percentile, $\psi \left(w^m_{st}-w^*_{st}\left(p\right)\right)$ .

Logic dictates four restrictions on the shape of $\psi (\cdot )$ that place significant economic structure on this function. First, $\psi (\cdot )$ should be at least weakly positive everywhere-if not, the minimum wage would reduce wages at some percentiles.²⁰ We further expect $\psi \left(\cdot \right)$ to have a positive first derivative, so the observed percentile is increasing as the gap between the statutory minimum and the latent wage percentile becomes more positive (or less negative). Naturally, if the minimum wage is very low or non-existent, we expect the observed percentile to be close to the latent percentile, implying that $\psi \left(-\infty \right)=0$ . Finally, if the minimum wage is high relative to the latent wage percentile, we expect the observed percentile to be very close to the minimum wage, so that ${\mathop{\lim }_{x\to \infty } \psi \left(x\right)=x\ }$ . This last assumption simply says that if the minimum wage lies far above the latent wage at a given percentile, its primary effect will be to raise that percentile to the level of the minimum wage, not beyond it.

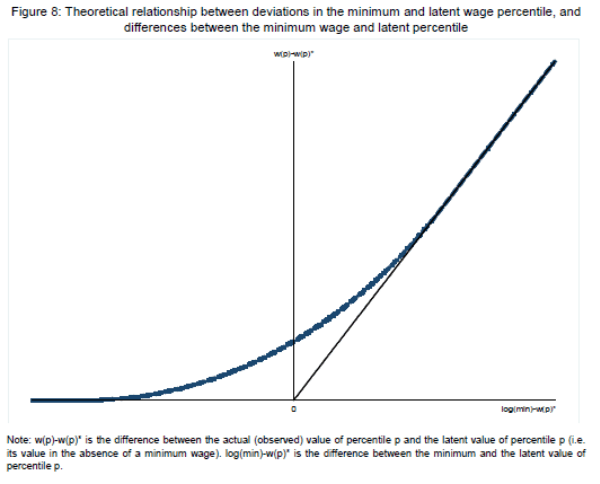
Graphically, these four restrictions imply a function akin to the one depicted in Figure 8, which plots a set of hypothetical deviations between observed and latent percentiles of the wage distribution. The x-axis in this figure corresponds to the gap between the minimum wage and the latent value of percentile p (which may be positive or negative), while the y-axis plots both the observed and latent values of percentile p. If spillovers are present, our assumptions imply that they will be largest at the location where the minimum wage exactly equals the latent wage value (the point labeled "0" in the figure).²¹ The magnitude of spillovers is expected to attenuate in either direction from this point: further down the latent wage distribution, the minimum becomes extremely binding and so the mechanical effect dominates; further up the latent distribution, the minimum wage becomes less and less relevant.

5.1 Parametric estimation

If we knew with certainty the shape of the latent wage distribution, calculating spillovers would be straightforward. Let $\Delta w^T_{st}\left(p\right)$ equal the gap between the latent and observed wage percentile p in state s at time t. This is the total effect (direct and spillover) of the minimum wage at percentile p:

$\Delta w^T_{st}\left(p\right)\equiv w_{st}\left(p\right)-w^*_{st}\left(p\right)$ (14)

This effect can be decomposed into a direct, mechanical effect and a spillover: $\Delta w^T_{st}\left(p\right)=\Delta w^D_{st}\left(p\right)+\Delta w^S_{st}\left(p\right)$ . The direct effect is simply equal to the maximum of the minimum wage minus the latent percentile and zero:

${\Delta w^D_{st}\left(p\right)\equiv \max \left[w^m_{st}-w^*_{st}\left(p\right),0\right]\ }.$ (15)

And the spillover is the difference between (14) and (15): $\Delta w^S_{st}\left(p\right){\rm =}\Delta w^T_{st}\left(p\right)-\Delta w^D_{st}\left(p\right).$

Implementing this decomposition requires three quantities: the statutory minimum wage, the observed wage at each percentile, and the latent wage at each percentile. The first two items are readily available, while the third must be estimated. This estimation requires a more parametric approach than applied above because we must approximate latent percentiles that are essentially never observed in the data (i.e., because they are always below the minimum).

The parametric approach that we use is to assume that the latent log wage distribution is normal; that is, we use the model in equation (2) with $F\left(\cdot \right)$ having the standard normal form. We estimate the parameters of this distribution using observed wages between the 50 ${}^{th}$ and 75 ${}^{th}$ percentiles of state wage distributions, a portion of the wage distribution where we expect the minimum to have no effect. We model both ${\mu }_{st}$ and ${\sigma }_{st}$ in (2) as additive year and state dummies plus state level trends-so, we allow both the mean and variance to vary across states and time.²² Armed with these parameter estimates, we can invert the standard normal to obtain the implied latent wage distribution for all percentiles.

Though this approach relies on somewhat strong parametric assumptions, a key strength is that its sources of identifying variation are almost entirely distinct from those used in the reduced form model above. In particular, estimation of the parametric model uses exclusively variation in the 50 ${}^{th}$ through 75 ${}^{th}$ percentiles of state wage distributions and uses no information whatsoever about the statutory minimum wage. That is, because we estimate the minimum wage's total impact simply by taking the difference between observed and estimated latent wage percentiles, the actual minimum wage does not enter into this calculation.²³ Consequently, this combination of approaches, reduced form and parametric, may speak to the plausibility of both set of estimates.

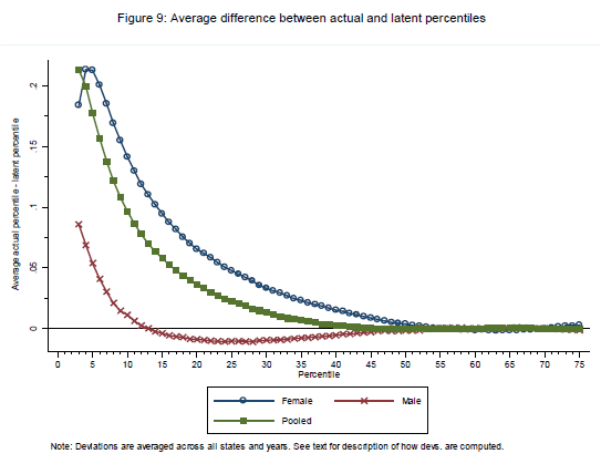
We begin by comparing the fit of the parametric model to the data. This fit is depicted in Figure 9, which plots the average deviation across states and years between the observed wage percentile and the estimated latent percentile for percentiles 3 through 75.²⁴ These estimates are performed and plotted separately for both sexes and for the pooled distribution. While the average residual must be zero by construction over the range of percentiles 50 through 75 (reflecting the OLS fit of the model to these percentiles), the in-sample fit is nevertheless informative. If the assumption of log normality were violated, we would see systematic deviations between the residuals with the wage percentiles. These deviations are very close to zero for all three samples, however, suggesting that the normality assumption is a good one. Though not visible in the figure, the model also performs well when extrapolated out of sample to upper-tail percentiles 76 through 90.²⁵ These specification checks suggest that the log normality assumption is a reasonable one for the portions of the wage distribution in which we do not expect the minimum wage to affect its shape.

We now turn our attention to the portion of the distribution where we expect the minimum wage to have an impact. Figure 9 shows that the deviations between observed and estimated latent wages are substantial and positive for lower percentiles. At the 10 ${}^{th}$ percentile of the wage distribution, this deviation is equal to 2, 14 and 10 log points for males, females and the pooled distribution respectively. These patterns are consistent with the minimum wage raising observed wages above their latent levels, as was earlier found by the reduced form analysis. Moreover, the fact that the deviations between observed and estimated latent percentiles are larger and occur higher in the distribution for females and for the pooled distributions than for males is consistent with minimum wage playing only a modest role in shaping male wages. There is also some indication that the normality assumption over-predicts observed male wages in the 15 ${}^{th}$ -50 ${}^{th}$ percentile range, but the absolute magnitude of the deviation is small (never exceeding 2 log points).

How much of the deviation between observed and estimated latent percentiles found in Figure 9 is due to direct versus spillover effects of the minimum wage? We assess this question using the parameter estimates underlying figure 9 and the decomposition in equations (14) and (15). For each state and year, we first calculate the estimated magnitudes of direct and spillover effects at each wage percentile. We then use the mapping between state-year percentiles and aggregate annual percentiles to estimate the direct and spillover effects of the minimum wage to each percentile of the aggregate male, female and pooled wage distributions in each year.²⁶

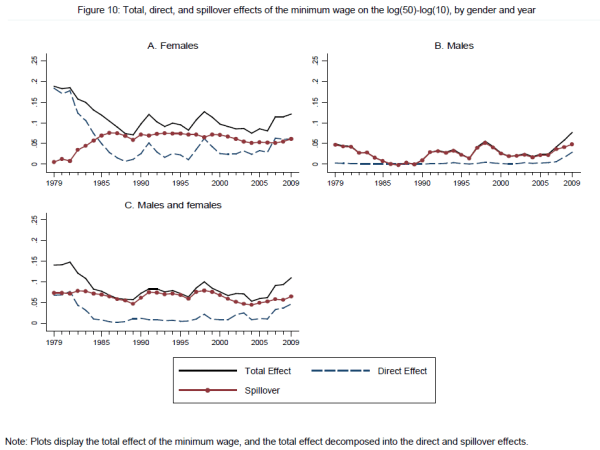
Figure 10 plots the estimated direct, spillover and total effects of the minimum wage on log 50/10 wage inequality by gender and overall for each year from 1979 through 2009.²⁷ The total impact of the minimum wage is very large at the start of the sample period for the female distribution, equal to 19 log points. Almost the entirety of this impact is a direct effect of the minimum wage, which is consistent with our hypothesis that the minimum's direct effects should dominate its spillover effects when the minimum is very binding.²⁸ This pattern is further borne out in the period between 1980 and 1988, when the real value of the minimum wage rapidly eroded. We find that the total effect of the minimum on female 50/10 inequality fell from 19 to 9 log points in this time period, while the spillover rose from 1 to 8 log points. Thus, as the bindingness of the minimum wage `unwound' its spillover effects became quantitatively more important than its direct effects. The impact of the subsequent hikes in the minimum wage between 1989 and 2009 are all clearly visible in the figure. Interestingly, each of these hikes appears to have a direct effect on wage inequality but little initial spillover effect. Spillovers, in turn, become more significant as the direct effect is eroded by inflation.

Subsequent panels in the figure repeat this exercise for males and for the pooled distribution. These results tell a similar story to that for females, but the magnitudes differ greatly. For the pooled distribution, the maximal impact of the minimum wage on 50/10 inequality declines from 15 to approximately 7 log points between 1979 and 1988, while the spillover component fluctuates between 5 and 7 log points throughout all three decades. For males, the minimum wage has almost no direct effect on 50/10 wage gap, consistent with the fact that it is almost never binding at the aggregate 10 ${}^{th}$ percentile. Nonetheless, the total effect of the minimum wage on male inequality is non-zero in most years and, moreover, clearly follows the vicissitudes of the real minimum wage. By implication, the minimum wage modestly compresses male 50/10 inequality primarily through spillovers. This noteworthy pattern is logical: since the minimum wage directly binds below the 10 ${}^{th}$ percentile of males wages (see Table 1), it is plausible that spillovers-but not direct effects-would reach the 10 ${}^{th}$ percentile.

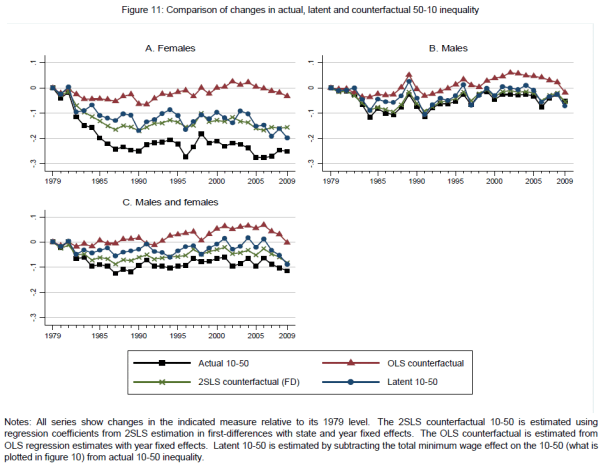
How closely do the structural estimates of the minimum wage's total effect align with the reduced form estimates above? Figure 11 explores this question. Because the reduced form estimates cannot be used to infer the level of inequality that would prevail if there were no minimum wage (since this would require taking the logarithm of zero), we instead use the reduced form estimates (based on the 2SLS first-differenced specification) to calculate the latent log 50/10 wage gap in each year 1979 through 2009 while holding the real minimum wage at its 1988 level (i.e., the low point). We then calculate the change in this measure relative to its 1979 level. Figure 11 compares the reduced form estimates of the change in latent 50/10 with the structural estimates of this quantity.²⁹

The correspondence between the 2SLS reduced-form and structural estimates is reasonably tight. The structural estimates imply that latent female inequality increased by 10 log points between 1979 and 1988, whereas the 2SLS estimates imply an increase of 15 log points and OLS estimates imply an increase of 3 log points; as the actual increase was 23 log points, these suggest that the decline in the minimum wage could explain between 35% (reduced-form) and 57% (structural) of the increase in 50/10 inequality over this period. Consistent with table 5, OLS estimates imply a much greater contribution of the minimum wage (87%). Similar calculations for the male and pooled gender distributions imply that the decline in the minimum wage could explain 1.2 (reduced-form) to 4.5 (structural) log points of the 7.7 log point increase for males, and 3.8 (reduced-form) to 6.8 (structural) log points of the 10.8 log point increase for the pooled distribution. Over the years of our sample, the structural estimates generally imply a larger contribution of the minimum wage than do the reduced-form estimates, though both are always smaller than the OLS counterfactual changes.

6 Distinguishing true spillovers from measurement error: the limits of inference

We have so far interpreted the measured effect of the minimum wage on the earnings of above minimum wage workers as a spillover. A mundane but nonetheless plausible alternative explanation for this finding is measurement error. To see why, suppose that a subset of workers who are paid the minimum wage report wage values that are modestly above or below the true minimum-that is, they report with error. Moreover, suppose that the central tendency of this reporting error moves in tandem with the minimum wage; when the minimum wage rises or falls, the measurement error cloud moves with it. Under these assumptions, the presence of measurement error may create the appearance of spillovers where none are present.

For example, consider a case where the minimum wage is set at the 5 ${}^{th}$ percentile of the latent wage distribution and has no spillover effects. However, due to misreporting, the spike in the wage distribution at the true minimum wage is surrounded by a measurement error cloud that extends from the 1 ${}^{st}$ through the 9 ${}^{th}$ percentiles. If the legislated minimum wage were to rise to the 9 ${}^{th}$ percentile and measurement error were to remain constant, the rise in the minimum wage would compress the measured wage distribution up to the 13 ${}^{th}$ percentile (thus, reducing the measured 50/10 wage gap). Yet, the rise in the minimum wage would have had no impact on the actual 50/10 gap; the apparent spillover would be due to measurement error spillovers to nearby percentiles.³⁰ This raises the question of whether the spillovers from the minimum wage to the measured wage distribution (Figures 9 and 10) overstate the size of spillovers to the actual wage distribution.

Our structural exercise above cannot unfortunately distinguish between these two possible explanations for spillovers (measurement error versus true spillovers) since both imply systematic deviations between observed and estimated latent wage percentiles above the location where the minimum binds. In this final section of the paper, we quantify the possible bias wrought by these measurement spillovers. Specifically, we ask whether we can reject the null hypothesis that the minimum wage only affects the earnings of those at or below the minimum (in which case, the apparent spillovers would be consistent with measurement error).

We use a simple measurement error model to test this hypothesis. Denote by a latent percentile of the wage distribution (i.e. the percentile absent measurement error), and write the latent wage associated with it as . Assuming that there are only direct effects of the minimum wage (i.e., no true spillovers and no disemployment effects), then the true wage at percentile will be given by:

$w\left(p^*\right)\equiv {\rm max}\left[w^m,w^*\left(p\right)\right],$ (16)

where $w^*\left(p\right)$ is the true latent log wage percentile. Denote by $\hat{p}\left(w^m\right)$ the true percentile at which the minimum wage binds. Then:

$w^*\left(\hat{p}\left(w^m\right)\right)=w^m.$ (17)

Now, allow for the possibility of measurement error, so that for a worker at true wage percentile , we observe:

$w_i=w\left(p^*\right)+{\varepsilon }_i,$ (18)

where ${\varepsilon }_i$ is an error term with density function $g\left(\varepsilon \right)$ , which we assume to be independent of the true wage. The density of wages among workers whose true percentile is is therefore given by $g\left(w-w\left(p^*\right)\right)$ . The density of observed wages is simply the average of $g\left(\cdot \right)$ across true percentiles:

$f\left(w\right)=\int^1_0{g\left(w-w\left(p^*\right)\right)dp^*}.$ (19)

And the cumulative density function for observed wages is given by:

$F\left(w\right)=\int^w_{-\infty }{\int^1_0{g\left(w-w\left(p^*\right)\right)dp^*dx}}.$ (20)

This can be inverted to give an implicit equation for the wage at observed percentile , $w\left(p\right):$

$p=\int^{w\left(p\right)}_{-\infty }{\int^1_0{g\left(w-w\left(p^*\right)\right)dp^*dx}}.$ (21)

By differentiating this expression with respect to the minimum wage, $\frac{\partial w\left(p\right)}{\partial w^m}$ , we obtain the following key result (with details given in the Appendix):

Result 1: Under the null hypothesis of no true spillovers, the elasticity of wages at an observed percentile with respect to the minimum wage is equal to the fraction of people at that observed percentile whose true wage is equal to the minimum.

The intuition for this result is straightforward: if changes in the minimum wage only affect the wages of those directly affected, then the wage at an observed percentile can only change to the extent that some of those workers are truly paid the minimum wage. Thus, if the minimum wage rises by 1 percent, and 10 percent of workers at a given percentile are paid the minimum wage, the observed wage percentile will rise by 0.1 percent.

This result has a simple corollary (also proved in the appendix) that we use in the estimation below:

Result 2: Under the null hypothesis of no true spillovers, the elasticity of the overall mean log wage with respect to the minimum wage is equal to the fraction of the wage distribution that is truly paid the minimum wage-that is, the size of the true spike.

This result follows from the fact that all individuals who are truly paid the minimum wage must appear somewhere in the observed wage distribution. And of course, changes at any point in the distribution also change the mean. Thus, if the true spike at the minimum wage comprises 10 percent of the mass of the wage distribution, a 1 percent rise in the minimum will increase the actual and observed mean wage by 1 percent. Note that no distributional assumptions about measurement error are needed for either Result 1 or Result 2, other than the assumption that the measurement error distribution is independent of wage levels and symmetric around any given location.

The practical value of Result 2 is that we can readily estimate the effect of changes in the minimum wage on the mean using the methods developed above. Under the null hypothesis of no spillovers, Result 2 tells us that the effect of the minimum wage on the mean wage effect will be equal to the size of the `true' spike. If the null hypothesis is false, however, we would expect the elasticity to exceed the size of the true spike since a subset of workers whose wages exceed the minimum wage will also have their wages increased by the minimum.

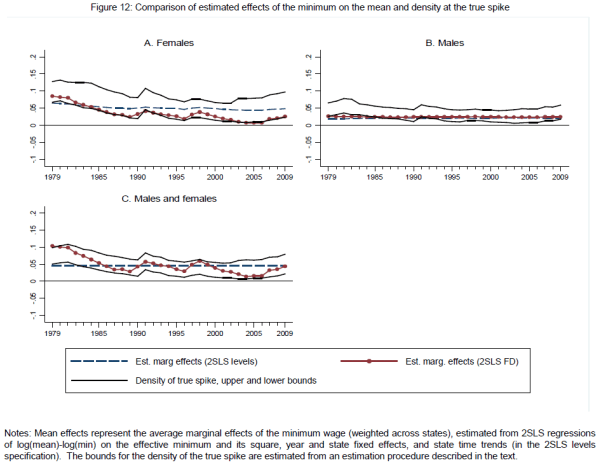
In practice, we estimate a first-differenced form of equation (4) using as the dependent variable the deviation between the state's mean log wage its and median log wage (to remain analogous to our previous estimation strategy). The dashed and dotted lines in Figure 12 represent the marginal effect on the mean by year, taking the weighted average across all states for each year. Under the null hypothesis of no true spillovers, these estimates of the effect of changes in the minimum on changes in the mean are an estimate of the size of the true spike. Under the alternative hypothesis that true spillovers are present, these marginal effects on the mean will exceed the size of the true spike. To distinguish these alternatives requires a second, independent estimate of the size of the true spike.

6.1 Estimating measurement error

We develop a second estimate of the magnitude of the true spike by directly estimating measurement error in wage reporting and then using this estimate to infer the size of the spike absent this error. We exploit the fact that under the assumption of full compliance with the minimum wage, all observations found below the minimum wage must be observations with measurement error.³¹ Of course, wage observations below the minimum can only provide information on individuals with negative measurement error, since minimum wage earners with positive measurement error must have an observed wage above the minimum. Thus, a key identifying assumption is that that the measurement error is symmetric, that is $g\left(\varepsilon \right)=g\left(-\varepsilon \right)$ .

In what follows, we use maximum likelihood to estimate the distribution of wages below the minimum and the fraction of workers at and above the minimum. We assume that the `true' wage distribution only has a mass point at the minimum wage so that $w^*\left(p^*\right)$ has a continuous derivative. We also assume that the measurement error distribution only has a mass point at zero so that there is a non-zero probability of observing the `true' wage (without this assumption, we would be unable to rationalize the existence of a spike in the observed wage distribution at the minimum wage.) Denote the probability that the wage is correctly reported as $\gamma$ . For those who report an error-ridden wage, we will use, in a slight departure from previous notation, $g\left(\varepsilon \right)$ to denote the distribution of the error.

With these assumptions, the size of the spike in the observed wage distribution at the minimum wage, which we denote by, $\tilde{p}$ , is equal to the true spike times the probability that the wage is correctly reported:

$\tilde{p}=\gamma \hat{p}.$ (22)

Hence, using an estimate of $\gamma$ , we can estimate the magnitude of the true spike as $\hat{p}\approx \tilde{p}/\widetilde{\gamma }$ .³²

To estimate $\gamma$ , we use observations on the fraction of workers paid strictly below the minimum, which we denote by . Assuming full compliance with the minimum wage statute, all of these subminimum wages will represent negative measurement error. We therefore have:

$Z=\left(1-\gamma \right)\times \left[0.5\hat{p}+\int^1_{\hat{p}}{G\left(w^m-w^*\left(p^*\right)\right)dp^*}\right]$ (23)

The symmetry assumption implies that half of those at the true spike who report wages with error will report wages below the minimum, and this is reflected as the first term in the bracketed expression ( $0.5\hat{p}$ ). In addition, for workers paid above the minimum, some subset will report with sufficiently negative error that their reported wage will fall below the minimum, thus also contributing to the mass below the statutory minimum. This contributor to is captured by the second term in the bracketed expression.

6.2 Finding: Spillovers cannot be distinguished from measurement error

Under the assumptions used above that the true latent log wage distribution is normal with mean $\mu$ and variance ${\sigma }^2_w$ and that the measurement error distribution is normal with mean 0 variance ${\sigma }^2_{\varepsilon },$ our estimation proceeds in two steps. First, we use observations on the top part of the wage distribution to estimate the median and variance of the observed latent wage distribution, allowing for variation across state and time (identical to the model used in Section IV). Next, we estimate $\left({\sigma }^2_{\varepsilon },\ \ \gamma \right)$ by maximum likelihood. We assume that $\left({\sigma }^2_{\varepsilon },\ \ \gamma \right)$ vary over time but not across states (with further details found in the Appendix). As previously noted, we perform this analysis on a sample that excludes individuals from lower-paying occupations that tend to earn tips or commission.

Estimates of $\gamma$ for males, females, and the pooled sample (not shown) generally find that the probability of correct reporting is around 80 percent, and mostly varies from between 80 to 90 percent over time (though is estimated to be around 70 percent in the early 1980s). We combine this estimate with the observed spike to get an estimate of the `true' spike in each period, though this will be an estimate of the true size of the spike only for the estimation sample (workers in non-tipped occupations).

This leaves us in need of an estimate of the `true' spike for the tipped occupations. Given the complexity of the state laws surrounding the minimum wage for tipped employees, we do not attempt to model these subminimum wages. Rather we simply note that the spike for tipped employees must be between zero and one, and we use this observation to bound the `true' spike for the whole workforce. Because the fraction of workers in tipped occupations is relatively small, these bounds are relatively narrow.

Figure 12 compares these bounds with the earlier estimates of the `true' spike based on the elasticity of the mean with respect to the minimum in each year. Under the null hypothesis that the minimum wage has no true spillovers, the effect on the mean should equal the size of the `true' spike. And indeed, the estimated mean effect lies within the bounds of the estimated `true' spike in almost all years. We are accordingly unable to reject the hypothesis that the apparent effect of the minimum wage on percentiles above the minimum is a measurement error spillover rather than a true spillover.

If we tentatively accept this null, it has an important implication for our findings. Table 1 shows that there is only one time period in our sample window when more than 10 percent of the hourly wages were paid above the statutory minimum. This period is 1979 to 1982, and the criterion is only met for females. For males and for the pooled-gender distribution, the minimum wage never covers more than 9 percent of the distribution.³³ Under the null hypothesis of no spillovers, we would have to conclude that the minimum wage had no effect on the actual male and pooled-gender wage distributions throughout the sample period, and ceased having an effect on the female wage distribution after 1982. Thus, any changes in the actual (rather than the measured) 10/50 differential after 1983 could not be accounted for by the minimum wage.

Two points deserve emphasis. First, even accepting the null of no spillovers, our estimates for the effect of the minimum wage on observed wage inequality (both direct and spillover effects) in the prior sections are valid. However, observed and actual wage effects may differ systematically in a manner that overstates the role of the minimum wage. And clearly, spillovers from the legislated minimum to wages actually paid are of greater economic consequence than spillovers to wages that are (mis-)reported.

Second, our findings do not exclude the possibility of true spillovers-and indeed, we suspect these spillovers are present. Our results do, however, highlight that we do not have sufficient precision to distinguish actual spillovers from measurement error spillovers in currently available data. Better wage data, perhaps administrative payroll data, may be more conclusive.

7 Conclusion

This paper offers a reassessment of the impact of the minimum wage on the wage distribution by using a longer panel than was available to previous studies, incorporating many additional years of data and including significantly more variation in state minimum wages, and using an econometric approach that purges division bias and confounding correlations between state wage levels and wage variances that we find bias earlier estimates. We estimate that 35-55% of the growth of lower tail inequality in the female wage distribution between 1979 and 1988, 35% to 45% of the growth of pooled gender inequality, and approximately 15% of the growth of male inequality-as measured by the differential between the log of the 50 ${}^{th}$ and 10 ${}^{th}$ percentiles-is attributable to the decline in the real value of the minimum wage. Similarly, calculations indicate that the declining minimum wage made only a modest contribution to growing lower tail inequality between 1988 and 2009 as well. In net, these estimates indicate a substantially smaller role for the U.S. minimum in the rise of inequality than suggested by earlier work (which attributed 85% to 110% of this rise to the falling minimum).

Despite these modest total effects, we estimate minimum wage effects that extend further up the wage distribution than would be predicted if the minimum wage had a purely mechanical effect on wages (i.e., raising the wage of all who earned below it). We estimate the shape of the latent distribution with a simple structural estimation technique (by assuming log normality and estimating the mean and variance of the state-year wage distribution using 50 ${}^{th}$ to 75 ${}^{th}$ wage percentiles), and use this to separately infer the direct impact and spillover effects from changes in the minimum wage. While the contribution of direct and spillover effects vary across percentiles, and over the years, spillover effects account for a modest fraction of the minimum wage effect in 1979, and almost the entirety of the effect in 1988.

One interpretation of these significant spillover effects is that they represent a true wage response for workers initially earning above the minimum. An alternative explanation is that wages for low-wage workers are mismeasured or misreported. If a significant share of minimum wage earners report wages in excess of the minimum wage, and this measurement error persists in response to changes in the minimum, then we would observe changes in percentiles above where the minimum wage directly binds in response to changes in the minimum wage. Our exercise in Section V is unable to reject the null hypothesis that all of the apparent effect of the minimum wage on percentiles above the minimum is the consequence of measurement error. Accepting this null, the implied effect of the minimum wage on the actual wage distribution is even smaller than the effect of the minimum wage on the measured wage distribution.

In net, this analysis suggests that there was significant expansion in latent lower tail inequality over the 1980s, mirroring the expansion of inequality in the upper tail. While the minimum wage was certainly a contributing factor to widening lower tail inequality-particularly for females-it was not the primary one.

8 Appendix

9 Correlation between the Trimmed Mean and the Median

Here, we derive the correlation coefficient between the median and a trimmed mean under the assumption that log wages are normally distributed and that we are drawing samples of size N from an underlying identical population. As in the main text, denote by $w\left(p\right)$ the log wage at percentile p.

A standard result (not dependent on a normality assumption) is that the covariance between wages at two percentiles is given by:

${\rm cov}\left[w\left(p_1\right),\ w\left(p_2\right)\right]=\frac{p_1\left(1-p_1\right)}{Nf\left(w\left(p_1\right)\right)\cdot f\left(w\left(p_2\right)\right)},\ {\ p}_1\le {\ p}_2$

(A.1)

Where $f\left(\cdot \right)$ is the density function. If $p_{1} =p_{2}$ , this gives the variance of the wage at a particular percentile so that the variance of the median can be written as:

${\rm var[w(0.5)]=}\frac{1}{{4Nf[w\left(0.5\right)]}^2}$

(A.2)

The trimmed mean between the 30 ${}^{th}$ and 70 ${}^{th}$ percentiles can be written as:

${\overline{w}}^t{\rm =}\frac{1}{0.4}\int^{0.7}_{0.3}{w\left(p\right)dp}$

(A.3)

So that the covariance between the median and the trimmed mean can be written as:

${\rm cov}\left[{\overline{w}}^t,\ w\left(0.5\right)\right]=\frac{1}{0.4}\int^{0.7}_{0.3}{{\rm cov}\left[w(p),\ w\left(0.5\right)\right]dp}$

(A.4)

The variance of the trimmed mean can be written as:

$var\left({\overline{w}}^t\right)=\frac{1}{{0.4}^2}\int^{0.7}_{0.3}{\int^{0.7}_{0.3}{{\rm cov}\left[w(p),\ w\left(p'\right)\right]dp}}dp'$

(A.5)

The formulae in (A.2), (A.4) and (A.5) can be used to compute the correlation coefficient between the median and trimmed mean. Note that this correlation does not depend on the sample size N. If the distribution is normal with mean $\mu$ and variance ${\sigma }^2$ then the formula for the covariance in (A.1) can be written as:

${\rm cov}\left[w\left(p_1\right),\ w\left(p_2\right)\right]=\frac{2\pi {\sigma }^2p_1(1-p_2)}{Ne^{-\frac{1}{2}{[{\Phi }^{{\rm -}{\rm 1}}\left({{\rm p}}_{{\rm 1}}\right){\rm ]}}^2}e^{-\frac{1}{2}{[{\Phi }^{{\rm -}{\rm 1}}\left({{\rm p}}_{{\rm 2}}\right){\rm ]}}^2}},\ {\ p}_1\le {\ p}_2$

(A.6)

Where ${\Phi }^{{\rm -}{\rm 1}}\left({\rm p}\right)$ is the inverse of the standard normal cumulative density function. The variance for the median is given by:

${\rm var[w(0.5)]=}\frac{\pi {\sigma }^2}{2N}$

(A.7)

Note that the correlation coefficient between the median and trimmed mean will, given the normality assumption, not depend on either $\mu$ or ${\sigma }^2$ .

B. Proof of Result 1:

Differentiate (20) to give:

$\left[\int^1_0{g\left[w(p)-w\left(p^*\right)\right]dp^*}\right]\frac{\partial w(p)}{\partial w^m}+\int^{w\left(p\right)}_{-\infty }{\int^1_0{\frac{\partial g\left[x-w\left(p^*\right)\right]}{\partial w^m}dp^*dx}}=0$

(A.8)

Now we have that:

$\frac{\partial g\left[x-w\left(p^*\right)\right]}{\partial w^m}=-g\left[x-w\left(p^*\right)\right]\frac{\partial w\left(p^*\right)}{\partial w^m}$

(A.9)

Which, from (15) is:

$\frac{\partial g\left[x-w\left(p^*\right)\right]}{\partial w^m}= \begin{array}{rc} -g\left[x-w^m\right] & if\ {\ \ p}^*\le \hat{p}\left(w^m\right) \ 0 & if\ \ p^*>\hat{p}\left(w^m\right) \end{array}$

(A.10)

Substituting (18) and (A.10) into (A.8) and re-arranging we have that:

$\frac{\partial w\left(p\right)}{\partial w^m}=\frac{\hat{p}g\left[w(p)-w^m\right]}{f\left[w(p)\right]}$

(A.11)

The numerator is the fraction of workers who are really paid the minimum wage but are observed with wage $\ w(p)$ because they have measurement error equal to $\left[w(p)-w^m\right]$ . Hence the numerator divided by the denominator is the fraction of workers observed at wage $\ w(p)$ who are really paid the minimum wage.

C. Proof of Result 2

One implication of (A.11) is the following. Suppose we are interested in the effect of minimum wages on the mean log wage, $\overline{w}(p)$ . We have that:

$\frac{\partial \overline{w}}{\partial w^m}=\int^1_0{\frac{\partial w(p)}{\partial w^m}dp=\int^1_0{\frac{\hat{p}g\left[w(p)-w^m\right]}{f\left[w(p)\right]}}}dp$

(A.12)

Change the variable of integration to We will have:

$dw=w'\left(p\right)dp=\frac{1}{f\left[w(p)\right]}dp$

(A.13)

Hence (A.12) becomes:

$\frac{\partial \overline{w}}{\partial w^m}=\hat{p}\int^{\infty }_{-\infty }{g\left[w-w^m\right]dw=\hat{p}}$

(A.14)

That is, the elasticity of average log wages with respect to the log minimum is just the size of the true spike.

D. Estimation Procedure for the Measurement Error Model

Our assumption is that the true latent log wage is normally distributed according to:

$w^*\sim N(\mu ,{\sigma }^2_w)$

(A.15)

To keep notation to a minimum we suppress variation across states and time, though this is incorporated into the estimation. The actual true wage is given by:

${\rm w=max(}w^m,w^*)$

(A.16)

And the observed wage is given by:

$v{\rm =}w{\rm +}D\varepsilon$

(A.17)

Where D is a binary variable taking the value 0 if the true wage is observed and 1 if it is not. We assume that:

${\rm Pr}{\rm (}D{\rm =1)=1-}\gamma$

(A.18)

We assume that $\varepsilon$ is normally distributed according to:

$\varepsilon {\rm\sim }N\left(0,\frac{1-{\rho }^2}{{\rho }^2}{\sigma }^2_w\right)$

(A.19)

We choose to parameterize the variance of the error process as proportional to the variance of the true latent wage distribution as this will be convenient later. We later show that $\ \rho$ is the correlation coefficient between the true latent wage and the observed latent wage when mis-reported-a lower value of $\ \rho$ is more measurement error so leads to a lower correlation between the true and observed wage. We assume that ${(w}^*,D,\varepsilon )$ are all mutually independent.

Our estimation procedure uses maximum likelihood to estimate the parameters of the measurement error model. There are three types of entries in the likelihood function:

a. those with an observed wage equal to the minimum wage

b. those with an observed wage above the minimum wage

c. those with an observed wage below the minimum wage

Let us consider the contribution to the likelihood function for these three groups in turn.

a. Those Paid the Minimum Wage

With the assumptions made above, the `true' size of the spike is given by:

$\hat{p}=\Phi \left(\frac{w^m-\mu }{{\sigma }_w}\right)$

(A.20)

And the size of the observed `spike' is given by:

$\tilde{p}=\gamma \Phi \left(\frac{w^m-\mu }{{\sigma }_w}\right)$

(A.21)

This is the contribution to the likelihood function for those paid the minimum wage.

b. Those Paid Below the Minimum Wage

Now let us consider the contribution to the likelihood function for those below paid the minimum wage. We need to work out the density function of actual observed wages w, where . None of those who report their correct wages (i.e. have ) will report a sub-minimum wage, so we need only consider those who mis-report their wage (i.e. those with ). Some of these will have a true wage equal to the minimum and some will have a true wage above the minimum. Those who are truly paid the minimum will have measurement error equal to ${(w-w}^m)$ so, using (A.19) and (A.20) the contribution to the likelihood function will be:

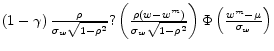$\left(1-\gamma \right)\frac{\rho }{{\sigma }_w\sqrt{1-{\rho }^2}}?\left(\frac{\rho (w-w^m)}{{\sigma }_w\sqrt{1-{\rho }^2}}\right)\Phi \left(\frac{w^m-\mu }{{\sigma }_w}\right)$

(A.22)

Now, consider those whose true wage is above the minimum but have a measurement error that is below the minimum. For this group we observe their observed latent wage below the minimum and know their true latent wage is above the minimum. The fraction of those who mis-report who are in this category is, with some abuse of the concept of probability:

${\rm Pr}?(v=w,w^*>w^m)$

(A.23)

Define:

$v^{{\rm *}}{\rm =}w^{{\rm *}}{\rm +}\varepsilon$

(A.24)

Which is what the observed wage would be if there was no minimum wage and they mis-report i.e. .

From (A.15) and (A.17):

$\begin{array}{l} \left( \begin{array}{c} v^* \ w^* \end{array}\right)\sim N\left[\left( \begin{array}{c} \mu \ \mu \end{array}\right),\left( \begin{array}{cc} {\sigma }^2_w+{\sigma }^2_{\varepsilon } & {\sigma }^2_w \ {\sigma }^2_w & {\sigma }^2_w \end{array}\right)\right] \ \left( \begin{array}{c} v^* \ w^* \end{array}\right)\sim N\left[\left( \begin{array}{c} \mu \ \mu \end{array}\right),{\sigma }^2_w\left( \begin{array}{cc} {1}/{{\rho }^2} & 1 \ 1 & 1 \end{array}\right)\right] \end{array}$

(A.25)

This implies the following:

$\left( \begin{array}{c} v^* \ w^*-{\rho }^2v^* \end{array}\right)\sim N\left[\left( \begin{array}{c} \mu \ \mu (1-{\rho }^2) \end{array}\right),{\sigma }^2_w\left( \begin{array}{cc} {1}/{{\rho }^2} & 0 \ 0 & 1-{\rho }^2 \end{array}\right)\right]$

(A.26)

Which is an orthogonalization that will be convenient.

Now for those paid above the minimum but whose wage is mis-reported, the true wage is w* and the observed wage is v*. So:

$\begin{array}[t]{cc} {\rm Pr}{\rm (}v{\rm =w},{\ w}^*>w^m) & \begin{array}[t]{l} ={\rm Pr}?(v^*=w,w^*>w^m) \ ={\rm Pr}?(v^*=w,w^*-{\rho }^2v^*>w^m-{\rho }^2w) \ ={\Pr \left(v^*=w\right)\ }{\rm Pr}?(w^*-{\rho }^2v^*>w^m-{\rho }^2w) \ =\frac{\rho }{{\sigma }_w}?\left(\frac{\rho (w-\mu )}{{\sigma }_w}\right)\left[1-\Phi \left(\frac{\left[\left(w^m-\mu \right)-{\rho }^2(w-\mu )\right]}{{\sigma }_w\sqrt{1-{\rho }^2}}\right)\right] \end{array}\end{array}$

(A.27)

where the third line uses the independence of (A.26).

Putting together (A.22) and (A.27) the fraction of the population observed to be paid at a wage below the minimum is given by:

$L= \begin{array}[t]{l} \left(1-\gamma \right)\cdot \ \left[ \begin{array}{l} \left[\frac{\rho }{{\sigma }_w\sqrt{1-{\rho }^2}}?\left(\frac{\rho \left(w-w^m\right)}{{\sigma }_w\sqrt{1-{\rho }^2}}\right)\right]\Phi \left(\frac{w^m-\mu }{{\sigma }_w}\right)+ \ \frac{\rho }{{\sigma }_w}?\left(\frac{\rho (w-\mu )}{{\sigma }_w}\right)\left[1-\Phi \left(\frac{\left[\left(w^m-\mu \right)-{\rho }^2(w-\mu )\right]}{{\sigma }_w\sqrt{1-{\rho }^2}}\right)\right] \end{array}\right] \end{array}$

(A.28)

c. Those Paid Above the Minimum Wage

Now let us consider the fraction observed above the minimum wage. These workers might be one of three types:

i. Those really paid the minimum wage who mis-report a wage above the minimum

ii. Those really paid above the minimum wage who do not mis-report

iii. Those really paid above the minimum wage but who do mis-report but do not report a sub-minimum wage.

For those who are truly paid the minimum wage and have a mis-reported wage, a half will be above, so the fraction of those who report a wage above the minimum is:

$\frac{1}{{\rm 2}}{\rm (1-}\gamma {\rm )}\Phi \left(\frac{w^m-\mu }{{\sigma }_w}\right)$

(A.29)

Those who do not mis-report and truly have a wage above the minimum will be:

$\gamma \left({\rm 1-}\Phi \left(\frac{w^m-\mu }{{\sigma }_w}\right)\right)$

(A.30)

Now, consider those whose true wage is above the minimum but who mis-report. For this group we know their observed latent wage is above the minimum and that their true latent wage is above the minimum. The fraction who are in this category is:

${\rm Pr(}w^*>w^m,v^*>w^m)$

(A.31)

Now:

$\begin{array}{l} {\rm Pr}{(w}^*>w^m,{\ v}^*>w^m) \ \begin{array}[t]{l} ={\Pr \left(w^*>w^m\right)\ }-{\rm Pr}?(w^*>w^m,v^*<w^m) \ ={\Pr \left(w^*>w^m\right)\ }-{\rm Pr}?(w^*-{\rho }^2v^*>{(1-{\rho }^2)w}^m,v^*<w^m) \ ={\Pr \left(w^*>w^m\right)\ }-{\Pr \left(v^*<w^m\right)\ }{\rm Pr}?(w^*-{\rho }^2v^*>{(1-{\rho }^2)w}^m) \ =1-\Phi \left(\frac{w^m-\mu }{{\sigma }_w}\right)-\Phi \left(\frac{\rho \left(w^m-\mu \right)}{{\sigma }_w}\right)\left[1-\Phi \left(\frac{\sqrt{1-{\rho }^2}\left(w^m-\mu \right)}{{\sigma }_w}\right)\right] \end{array}\end{array}$

(A.32)

As this expression applies to those who mis-report, it needs to be multiplied by $\left(1-\gamma \right)\$ to give the fraction of the population in this category. Putting together (A.29), (A.30), and (A.32) the fraction of the population observed to be paid above the minimum is given by:

$\begin{array}[t]{l} \left(1-\gamma \right)\cdot \ \left[ \begin{array}{l} \frac{1}{2}\Phi \left(\frac{w^m-\mu }{{\sigma }_w}\right)+1-\Phi \left(\frac{w^m-\mu }{{\sigma }_w}\right)-\Phi \left(\frac{\rho \left(w^m-\mu \right)}{{\sigma }_w}\right)\left[1-\Phi \left(\frac{\sqrt{1-{\rho }^2}\left(w^m-\mu \right)}{{\sigma }_w}\right)\right] \end{array}\right] \ +\gamma \left(1-\Phi \left(\frac{w^m-\mu }{{\sigma }_w}\right)\right) \end{array}$

(A.33)

This is the contribution to the likelihood function for those paid above the minimum.

There are three parameters in this model $\left({\sigma }_w,\gamma ,\rho \right)$ . These parameters may vary with state or time. In the paper we have already documented how the variance in observed wages varies across state and time so it is important to allow for this variation. But, our main estimates assume that $\left(\gamma ,\rho \right)$ only vary across time so are constant across states.

To estimate the parameters we use two steps.

Step 1:

We first use the estimation procedure described in section IV to obtain an estimate of the median and variance of the latent observed wage distribution. This procedure assumes that the latent observed wage distribution is normal which is not consistent with our measurement error model which assumes that the latent observed wage distribution is a mixture of two normals (those who report their wage correctly and those who do not). This does not affect the estimate of the median but does affect the interpretation of the variance. Here we show how to map between this estimate of the variance and the parameters of our measurement error model.

Our measurement error model implies that the log wage at percentile p, w(p) satisfies the following equation:

${\rm p=}\gamma \Phi \left(\frac{w\left(p\right)-\mu }{{\sigma }_w}\right)+(1-\gamma )\Phi \left(\frac{\rho \left(w\left(p\right)-\mu \right)}{{\sigma }_w}\right)$

(A.34)

Differentiating this we obtain the following equation for w'(p):

${\rm 1=}\left[\gamma \left(\frac{1}{{\sigma }_w}\right)?\left(\frac{w\left(p\right)-\mu }{{\sigma }_w}\right)+\left(1-\gamma \right)\left(\frac{\rho }{{\sigma }_w}\right)?\left(\frac{\rho \left(w\left(p\right)-\mu \right)}{{\sigma }_w}\right)\right]w'(p)$

(A.35)

Our estimated model which assumes a single normal distribution uses, instead, the equation:

${\rm 1=}\left(\frac{1}{\sigma }\right)?\left(\frac{w\left(p\right)-\mu }{\sigma }\right)w'(p)$

(A.36)

And our estimation procedure provides an estimate of $\ \sigma$ . Equating the two terms we have the following expression for the relationship between ${\sigma }_w$ and $\ \sigma$ :

${\sigma }_w=\sigma \frac{\left[\gamma \phi \left(\frac{w\left(p\right)-\mu }{{\sigma }_w}\right)+\rho (1-\gamma )?\left(\frac{\rho (w\left(p\right)-\mu )}{{\sigma }_w}\right)\right]}{?\left(\frac{w\left(p\right)-\mu }{\sigma }\right)}$

(A.37)

If the values of the density functions are similar then one can approximate this relationship by:

${\sigma }_w=\sigma \left[\gamma +\rho (1-\gamma )\right]$

(A.38)

This is an approximation, but simulation of the model for the parameters we estimate suggest it is a good approximation. This implies that we can write all elements of the likelihood function as functions of:

$z_{st}=\left(\frac{w^m_{st}-{\mu }_{st}}{{\sigma }_{st}}\right)$

(A.39)

That is, $z_{st}\$ is the standardized deviation of the minimum from the median using the estimate of the observed variance obtained as described above from step 1 of the estimation procedure.

Step 2:

In this step we estimate the parameters $(\rho ,\gamma )$ using maximum-likelihood. The elements of the likelihood function have been described above.

References

Allegretto, Sylvia, Arindrajit Dube, and Michael Reich. 2008. "Do Minimum Wages Really Reduce Teen Employment? Accounting for Heterogeneity and Selectivity in State Panel Data." Institute for Research on Labor and Employment Working Paper (University of California, Berkeley) No. 166-08, June.

Autor, David H., Lawrence F. Katz, and Melissa S. Kearney. 2008. "Trends in U.S. Wage Inequality: Revising the Revisionists." Review of Economics and Statistics, 90(2), May, 300-323.

Bertrand, Marianne, Esther Duflo and Sendhil Mullainathan. 2004. "How Much Should we Trust Difference-in-Difference Estimators?" Quarterly Journal of Economics, 119(1), 249-275.

Borjas, George J. 1980. "The Relationship between Wages and Weekly Hours of Work: The Role of Division Bias" Journal of Human Resources, 15(3) pp 409-423

Card, David, Lawrence F. Katz and Alan B. Kruger. 1993. "An Evaluation of Recent Evidence on the Employment Effects of Minimum and Subminimum Wages." NBER Working Paper No. 4528, November.

Card, David and Alan B. Krueger. 1994. "Minimum Wages and Employment: A Case Study of the Fast-Food Industry in New Jersey and Pennsylvania." American Economic Review, 84(4), 772-793

Card, David and Alan B. Krueger. 2000. "Minimum Wages and Employment: A Case Study of the Fast-Food Industry in New Jersey and Pennsylvania: Reply." American Economic Review, 90(5), 1397-1420.

Chernozhukov, Victor and Christian Hansen. 2005. "An IV Model of Quantile Treatment Effects." Econometrica, 73(1), 245-261.

DiNardo, John, Nicole M. Fortin and Thomas Lemieux. 1996. "Labor Market Institutions and the Distribution of Wages, 1973-1992: A semiparametric approach." Econometrica, 64(5), September, 1001 -1044.

Durbin, James. 1954. "Errors in Variables." Review of the International Statistical Institute. 22, 23-32.

Lee, David. 1999. "Wage Inequality in the United States During the 1980s: Rising Dispersion or Falling Minimum Wage?" Quarterly Journal of Economics, 114(3), August, 977-1023.

Manning, Alan. 2004. "We Can Work it Out: the Impact of Technological Change on the Demand for Low-Skill Workers." Scottish Journal of Political Economy, 51(5), November, 581-608.

Mishel, Lawrence, Jared Bernstein and Sylvia Allegretto. 2006. The State of Working America, 2006/2007. New York: ILR Press

Neumark, David and William Wascher. 2000. "Minimum Wages and Employment: A Case Study of the Fast-Food Industry in New Jersey and Pennsylvania: Comment." American Economic Review, 90(5), 1362-1396.

Stigler, George. 1946. "The Economics of Minimum Wage Legislation." American Economic Review, 36, 358-365.

Stock, James H., Jonathan H. Wright and Motohiro Yogo. 2002. "A Survey of Weak Instruments and Weak Identification in Generalized Method of Moments." Journal of Business and Economics Statistics, 20(4), October, 518-529.

Teulings, Coen N. 2000. "Aggregation Bias in Elasticities of Substitution and the Minimum Wage Paradox," International Economic Review, 41, 359-398.

Teulings, Coen N. 2003. "The Contribution of Minimum Wages to Increasing Inequality." Economic Journal, 113, October, 801-833.

White, Hal. 1980. "Using Least Squares to Approximate Unknown Regression Functions," International Economic Review, 21, 149-170

Wooldridge, Jeffrey M. 1992. "Econometric Analysis of Cross Section and Panel Data." Cambridge, Massachusetts: MIT Press.

Table 1a - Summary Statistics for Bindingness of State and Federal Minimum Wages

	1- # states with higher min.	2 - Female: Minimum binding pctile	3 - Female: Maximum binding pctile	4 - Female: Share of hours at or below min.	5 - Female: Agg. log(50)-log(10)	6 - Male: Minimum binding pctile	7 - Male: Maximum binding pctile	8 - Male: Share of hours at or below min.	9 - Male: Agg. log(50)-log(10)
1979	1	5.0	28.0	0.13	-0.38	2.0	10.5	0.05	-0.67
1980	1	6.0	24.0	0.13	-0.42	2.5	10.0	0.05	-0.68
1981	1	5.0	24.0	0.13	-0.40	1.5	9.0	0.06	-0.68
1982	1	5.0	21.5	0.11	-0.50	2.0	8.0	0.05	-0.69
1983	1	3.5	17.5	0.10	-0.53	2.0	8.0	0.05	-0.73
1984	1	2.5	15.5	0.09	-0.54	1.5	7.5	0.04	-0.78
1985	2	2.0	14.5	0.08	-0.58	1.0	6.5	0.04	-0.75
1986	5	2.0	16.0	0.07	-0.60	1.0	6.5	0.03	-0.77
1987	6	2.0	14.0	0.06	-0.62	1.0	6.0	0.03	-0.77
1988	10	2.0	12.5	0.06	-0.62	1.0	6.0	0.03	-0.74
1989	12	1.0	12.5	0.05	-0.63	1.0	5.0	0.03	-0.69
1990	11	1.5	13.0	0.06	-0.63	0.5	5.5	0.03	-0.74
1991	4	1.5	18.5	0.08	-0.61	1.0	8.5	0.04	-0.78
1992	7	2.0	13.5	0.06	-0.60	0.5	6.5	0.04	-0.75
1993	7	2.5	11.0	0.06	-0.60	1.0	5.0	0.03	-0.73
1994	8	2.5	11.0	0.06	-0.59	1.0	4.5	0.03	-0.73
1995	9	2.0	9.5	0.05	-0.60	0.5	4.5	0.03	-0.72
1996	11	2.5	9.5	0.05	-0.65	1.0	5.0	0.03	-0.69
1997	10	2.5	10.0	0.06	-0.62	1.0	6.5	0.04	-0.73
1998	7	2.5	11.5	0.06	-0.56	1.0	7.0	0.04	-0.69
1999	10	2.5	11.0	0.05	-0.60	1.0	5.5	0.03	-0.68
2000	10	2.0	9.5	0.05	-0.59	1.0	6.0	0.03	-0.71
2001	10	2.0	8.5	0.05	-0.61	1.0	5.5	0.03	-0.69
2002	11	1.5	9.0	0.04	-0.60	1.0	6.0	0.03	-0.69
2003	11	1.5	9.0	0.04	-0.61	0.5	5.0	0.03	-0.70
2004	12	1.5	7.5	0.04	-0.62	1.0	5.0	0.03	-0.69
2005	15	1.5	8.5	0.04	-0.66	1.0	5.0	0.03	-0.70
2006	19	1.5	9.5	0.04	-0.66	0.5	6.0	0.02	-0.74
2007	31	1.0	10.0	0.06	-0.65	0.5	6.5	0.04	-0.71
2008	32	1.5	11.0	0.06	-0.63	0.5	6.5	0.04	-0.69
2009	27	3.5	10.5	0.06	-0.63	2.0	7.0	0.04	-0.72

Notes: Column 1 displays the number of states with a minimum that exceeds the federal minimum. Columns 2 and 6, and 3 and 8 display estimates of the lowest and highest percentile at which the minimum wage binds across states (DC is excluded). The binding percentile is estimated as the highest percentile in the annual distribution of wages at which the minimum wage binds (rounded to the nearest half of a percentile), where the annual distribution includes only those months for which the minimum wage was equal to its modal value for the year. Columns 4 and 8 display the share of hours worked for wages at or below the minimum wage. Columns 5 and 9 display the weighted average value of the log(p50)-log(p10) for the male or female wage distributions across states.

Table 1b - Summary Statistics for Bindingness of State and Federal Minimum Wages

	1- # states w/higher min.	2- Males and females, pooled - Min. binding pctile	3- Males and females pooled - Max. binding pctile	4- males and females, pooled - Share of hours at or below min.	5- Avg. log(50)-log(10)
1979	1	3.5	17.0	0.08	-0.60
1980	1	4.0	15.5	0.08	-0.62
1981	1	2.5	14.5	0.09	-0.60
1982	1	3.5	12.5	0.07	-0.66
1983	1	3.0	11.5	0.07	-0.66
1984	1	2.0	10.5	0.06	-0.69
1985	2	1.5	9.5	0.06	-0.69
1986	5	1.5	10.0	0.05	-0.69
1987	6	1.5	9.0	0.04	-0.72
1988	10	1.5	8.0	0.04	-0.70
1989	12	1.0	7.0	0.04	-0.71
1990	11	1.0	8.0	0.04	-0.69
1991	4	1.5	12.5	0.06	-0.67
1992	7	1.5	9.5	0.05	-0.69
1993	7	1.5	7.5	0.04	-0.69
1994	8	2.0	7.5	0.04	-0.70
1995	9	1.5	6.0	0.04	-0.69
1996	11	1.5	6.5	0.03	-0.69
1997	10	2.0	7.5	0.05	-0.66
1998	7	2.0	7.5	0.05	-0.67
1999	10	2.0	7.0	0.04	-0.67
2000	10	1.5	7.5	0.04	-0.66
2001	10	1.5	6.5	0.04	-0.66
2002	11	1.5	7.0	0.03	-0.69
2003	11	1.5	6.5	0.03	-0.68
2004	12	1.5	6.0	0.03	-0.66
2005	15	1.5	6.5	0.03	-0.69
2006	19	1.0	7.5	0.03	-0.66
2007	31	1.0	7.5	0.04	-0.68
2008	32	1.0	7.5	0.05	-0.70
2009	27	2.5	8.5	0.05	-0.71

See notes for Table 1a.

Table 2: OLS and 2SLS relationship between log(p)-log(p50) and log(min. wage)-log(p50), for select percentiles of given wage distribution Marginal effects, estimated from coefficients estimated over 1979-2009

	A. Females, 1: Females, OLS, Levels, Year FE: Yes, State FE: No, State Trends: No	A. Females, 2: Females, OLS, Levels, Year FE: Yes, State FE: Yes, State trends: Yes	A. Females, 3: Females, 2SLS, Levels, Year FE: Yes, State FE: Yes, State trends: Yes	A. Females, 4: Females, 2SLS, First Diff, Year FE: Yes, State FE: Yes, State trends: No.	B. Males, 5: Males, OLS, Levels, Year FE: Yes, State FE: No, State Trends: No	B. Males, 6: Males, OLS, Levels, Year FE: Yes, State FE: Yes, State trends: Yes	B. Males, 7: Males, 2SLS, Levels, Year FE: Yes, State FE: Yes, State trends: Yes	B. Males, 8: Males, 2SLS, First Diff, Year FE: Yes, State FE: Yes, State trends: No.	C. Males and females pooled, 9: Pooled, OLS, Levels, Year FE: Yes, State FE: No, State Trends: No	C. Males and females pooled, 10: Pooled, OLS, Levels, Year FE: Yes, State FE: Yes, State trends: Yes	C. Males and females pooled, 11: Pooled, 2SLS, Levels, Year FE: Yes, State FE: Yes, State trends: Yes	C. Males and females pooled, 12: Pooled, 2SLS, First Diff, Year FE: Yes, State FE: Yes, State trends: No.
5	0.61	0.44	0.34	0.37	0.52	0.26	0.21	0.18	0.60	0.36	0.30	0.27
5 (standard error)	(0.04)	(0.04)	(0.04)	(0.05)	(0.04)	(0.03)	(0.04)	(0.04)	(0.03)	(0.03)	(0.04)	(0.06)
10	0.51	0.30	0.27	0.16	0.35	0.16	0.09	0.07	0.42	0.23	0.22	0.16
10 (standard error)	(0.04)	(0.02)	(0.03)	(0.04)	(0.04)	(0.03)	(0.02)	(0.04)	(0.03)	(0.04)	(0.05)	(0.05)
20	0.27	0.14	0.11	0.05	0.19	0.07	0.01	0.02	0.24	0.10	0.06	0.06
20 (standard error)	(0.03)	(0.02)	(0.03)	(0.03)	(0.03)	(0.03)	(0.02)	(0.03)	(0.03)	(0.03)	(0.03)	(0.04)
30	0.15	0.08	0.04	0.05	0.08	0.07	0.03	-0.00	0.13	0.07	0.03	0.01
30 (standard error)	(0.02)	(0.01)	(0.03)	(0.03)	(0.02)	(0.02)	(0.02)	(0.02)	(0.02)	(0.01)	(0.02)	(0.03)
40	0.06	0.05	0.02	0.01	0.03	0.07	0.05	-0.01	0.06	0.04	0.00	0.02
40 (standard error)	(0.01)	(0.01)	(0.02)	(0.03)	(0.01)	(0.01)	(0.03)	(0.02)	(0.01)	(0.01)	(0.01)	(0.02)
75	-0.04	0.11	-0.00	-0.02	0.10	0.14	0.02	0.02	0.02	0.12	0.01	0.01
75 (standard error)	(0.02)	(0.01)	(0.02)	(0.03)	(0.04)	(0.02)	(0.02)	(0.02)	(0.02)	(0.01)	(0.02)	(0.02)
90	-0.03	0.16	0.01	0.04	0.13	0.13	-0.02	0.01	0.04	0.15	0.02	0.02
90 (standard error)	(0.04)	(0.02)	(0.03)	(0.03)	(0.07)	(0.03)	(0.04)	(0.03)	(0.04)	(0.03)	(0.03)	(0.03)

Notes: N=1450 for levels estimation, N=1400 for first-differenced estimation. Estimates are the marginal effects of log(min. wage)-log(p50), or log(min)-predicted log(p50), evaluated at its hours-weighted average across states and years. Standard errors clustered at the state level are in parenthesis. Regressions are weighted by the sum of individuals' reported weekly hours worked multiplied by CPS sampling weights. For 2SLS specifications, the effective minimum and its square are instrumented by the log of the minimum, and the square of the fitted value from the first stage regression of log(min.)-log(p50) on log(min) and controls.

Table 3: Relationship between log(p60)-log(p40) and log(p50): OLS estimates

	Coefficient estimates for 1979-2009: No FE	Coefficient estimates for 1979-2009: Levels	Coefficient Estimates for 1979-2009: First Diff	Coefficient estimates for 1979-1991: No FE	Coefficient estimates for 1979-1991: Level	Coefficient estimates for 1979-1991: First Diff
Female	0.11	-0.07	-0.00	0.07	-0.06	-0.08
Female (standard error)	(0.01)	(0.02)	(0.02)	(0.01)	(0.03)	(0.04)
Male	0.04	-0.08	-0.02	-0.02	-0.10	-0.11
Male (standard error)	(0.01)	(0.02)	(0.03)	(0.01)	(0.04)	(0.05)
Pooled	0.09	-0.08	-0.01	0.07	-0.03	-0.06
Pooled (standard error)	(0.01)	(0.02)	(0.03)	(0.01)	(0.03)	(0.04)

Note: Estimates represent coefficient on log(p50) from regression of log(p60)-log(p40) on log(p50) and year fixed effects and state fixed effects and state time trends, as indicated. Standard errors are in parentheses. Regressions are weighted by the sum of individuals' reported weekly hours worked multiplied by CPS sampling weights.

Table 4: Marginal effects of log(p50)-log(min) and its square on 50/10 inequality: Point estimates from various years

	OLS, No FE	2SLS, Levels	2SLS, First Diff
Females, 1979-1989	0.62	0.69	0.65
Females, 1979-1989 (standard error)	(0.03)	(0.21)	(0.18)
Males, 1979-1989	0.39	0.35	0.10
Males, 1979-1989 (standard error)	(0.05)	(0.29)	(0.21)
Pooled, 1979-1989	0.50	0.43	0.51
Pooled, 1979-1989 (standard error)	(0.04)	(0.19)	(0.16)
Females, 1979-1991	0.56	0.34	0.30
Females, 1979-1991 (standard error)	(0.03)	(0.08)	(0.07)
Males, 1979-1991	0.37	0.29	0.19
Males, 1979-1991 (standard error)	(0.05)	(0.07)	(0.07)
Pooled, 1979-1991	0.45	0.39	0.38
Pooled, 1979-1991 (standard error)	(0.04)	(0.04)	(0.05)
Females, 1979-2009	0.51	0.27	0.16
Females, 1979-2009 (standard error)	(0.04)	(0.03)	(0.04)
Males, 1979-2009	0.35	0.09	0.07
Males, 1979-2009 (standard error)	(0.04)	(0.02)	(0.04)
Pooled, 1979-2009	0.42	0.22	0.16
Pooled, 1979-2009 (standard error)	(0.03)	(0.05)	(0.05)

Note: Estimates represent marginal effects of changes in log(p50)-log(min.) and its square on log(p50)-log(p10) between various years. Standard errors are in parentheses. Estimates represent marginal effects from regressions of the form reported in the first, third, and fourth specifications of Table 2, and are evaluated at the hours-weighted mean value of log(p50)-log(min) across all states and the years listed in each panel.

Table 5: Actual and counterfactual changes in log(p50/10) between selected years: Changes in log points (100 x log change)

	Observed change	Counterfactuals using point estimates for 1979 - 2009: OLS, no fixed effects	Counterfactuals using point estimates for 1979 - 2009: 2SLS, levels	Counterfactuals using point estimates for 1979 - 2009: 2SLS, first diff.	Counterfactuals using point estimates for 1979 - 1991: OLS, no fixed effects	Counterfactuals using point estimates for 1979 - 1991: 2SLS, levels	Counterfactuals using point estimates for 1979 - 1991: 2SLS, first diff.
Females, 1979-1991	22.4	5.8	11.9	15.1	5.9	9.5	9.8
Males, 1979-1991	11.2	6.4	10.7	10.4	6.6	9.7	9.3
Pooled, 1979-1991	7.1	-1.5	3.8	4.1	-1.3	1.5	1.8
Females, 1979-1988	23.4	3.2	10.6	14.9	3.7	8.6	8.2
Males, 1979-1988	7.7	-0.2	6.7	6.5	0.3	5.1	4.7
Pooled, 1979-1988	10.8	-1.1	5.8	7.0	-0.6	3.7	3.6
Females, 1979-2009	25.2	3.2	10.7	15.6	3.4	8.9	8.7
Males, 1979-2009	5.3	1.8	6.0	5.4	2.1	5.6	4.7
Pooled, 1979-2009	11.4	0.2	7.0	8.2	1.0	5.0	4.9
Females, 1998-2009	7.1	3.6	5.3	6.0	4.3	4.9	5.0
Males, 1998-2009	2.7	0.4	2.4	2.4	0.5	2.0	1.7
Pooled, 1998-2009	3.6	0.9	2.7	3.1	1.2	2.7	2.7

Note: Estimates represent changes in actual and counterfactual log(p50)-log(p10) between 1979 and 1988, 1979 and 1991, 1979 and 2009, and 1998 and 2009, measured in log points (100 x log change). Counterfactual wage changes in panels A, B, and D represent counterfactual changes in the 50/10 had the effective minimum wage in the earlier year equaled the effective minimum wage in the later year for each state. Counterfactual wage changes in Panel C represent changes had the effective minima in 1979 and 2009 equaled the effective minimum in 1988. OLS counterfactual estimates are formed using coefficients from estimation reported in column 1 of Table 2. 2SLS counterfactuals are formed using coefficients from estimation reported in columns 3 and 4 of Table 2.

Appendix Table 1 - Variation in State Minimum Wages

	1979	1980	1981	1982	1983	1984	1985	1986	1987	1988	1989	1990	1991	1992	1993
Federal min. wage	2.90	3.10	3.35	3.35	3.35	3.35	3.35	3.35	3.35	3.35	3.35	3.80	4.25	4.25	4.25
Alabama
Alaska	3.40	3.60	3.85	3.85	3.85	3.85	3.85	3.85	3.85	3.85	3.85	4.30	4.75	4.75	4.75
Arizona
Arkansas
California										4.25	4.25	4.25
Colorado
Connecticut										3.75	4.25	4.25	4.27	4.27	4.27
Delaware
Florida
Georgia
Hawaii										3.85	3.85	3.85		4.75	5.25
Idaho
Illinois
Indiana
Iowa												3.85		4.65	4.65
Kansas
Kentucky
Louisiana
Maine							3.45	3.55	3.65	3.65	3.75	3.85
Maryland
Massachusetts								3.65	3.65	3.75	3.75
Michigan
Minnesota										3.55	3.85	3.95
Mississippi
Missouri
Montana
Nebraska
Nevada
New Hampshire									3.45	3.55	3.65
New Jersey														5.05	5.05
New Mexico
New York
North Carolina
North Dakota
Ohio
Oklahoma
Oregon												4.25	4.75	4.75	4.75
Pennsylvania
Rhode Island								3.55	3.65	4.00	4.25	4.25	4.45	4.45	4.45
South Carolina
South Dakota
Tennessee
Texas
Utah
Vermont								3.45	3.55	3.65	3.75	3.85
Virginia
Washington											3.85	3.85
West Virginia
Wisconsin											3.65
Wyoming

Note: Table indicates years in which each state had a state minimum wage that exceeded the federal minimum wage for at least 6 months of the year.

Appendix Table 1 (cont) - Variation in State Minimum Wages, cont.

	1994	1995	1996	1997	1998	1999	2000	2001	2002	2003	2004	2005	2006	2007	2008	2009
Federal min. wage	4.25	4.25	4.25	4.75	5.15	5.15	5.15	5.15	5.15	5.15	5.15	5.15	5.15	5.15	5.85	6.55
Alabama
Alaska	4.75	4.75	4.75	5.25	5.65	5.65	5.65	5.65	5.65	7.15	7.15	7.15	7.15	7.15	7.15	7.15
Arizona														6.75	6.90	7.25
Arkansas														6.25	6.25
California				5.00	5.75	5.75	5.75	6.25	6.75	6.75	6.75	6.75	6.75	7.50	8.00	8.00
Colorado														6.85	7.02	7.28
Connecticut	4.27	4.27	4.27	4.77	5.18	5.65	6.15	6.40	6.70	6.90	7.10	7.10	7.40	7.65	7.65	8.00
Delaware			4.65			5.65	5.65	6.15	6.15	6.15	6.15	6.15	6.15	6.65	7.15	7.15
Florida												6.15	6.40	6.67	6.79	7.21
Georgia
Hawaii	5.25	5.25	5.25	5.25	5.25	5.25	5.25	5.25	5.75	6.25	6.25	6.25	6.75	7.25	7.25	7.25
Idaho
Illinois											5.50	6.50	6.50	7.50	7.75	8.00
Indiana
Iowa	4.65	4.65	4.65											6.20	7.25	7.25
Kansas
Kentucky														5.85	6.55	7.25
Louisiana
Maine									5.75	6.25	6.25	6.35	6.50	6.75	7.00	7.25
Maryland													6.15	6.15	6.15
Massachusetts			4.75	5.25	5.25	5.25	6.00	6.75	6.75	6.75	6.75	6.75	6.75	7.50	8.00	8.00
Michigan														7.15	7.40	7.40
Minnesota													6.15	6.15	6.15
Mississippi		sort
Missouri														6.50	6.65	7.05
Montana														6.15	6.25	6.90
Nebraska
Nevada														6.33	6.85	7.55
New Hampshire
New Jersey	5.05	5.05	5.05	5.05									6.15	7.15	7.15	7.15
New Mexico															6.50	7.50
New York												6.00	6.75	7.15	7.15	7.15
North Carolina														6.15	6.15
North Dakota
Ohio														6.85	7.00	7.30
Oklahoma
Oregon	4.75	4.75	4.75	5.50	6.00	6.50	6.50	6.50	6.50	6.90	7.05	7.25	7.50	7.80	7.95	8.40
Pennsylvania														7.15	7.15	7.15
Rhode Island	4.45	4.45	4.45	5.15		5.65	5.65	6.15	6.15	6.15	6.75	6.75	7.10	7.40	7.40	7.40
South Carolina
South Dakota
Tennessee
Texas
Utah
Vermont		4.50	4.75	5.00	5.25	5.25	5.75	6.25	6.25	6.25	6.75	7.00	7.25	7.53	7.68	8.06
Virginia
Washington	4.90	4.90	4.90	4.90		5.70	6.50	6.72	6.90	7.01	7.16	7.35	7.63	7.93	8.07	8.55
West Virginia													5.85	6.55	7.25	7.25
Wisconsin												5.70	6.50	6.50	6.5
Wyoming

Note: Table indicates years in which each state had a state minimum wage that exceeded the federal minimum wage for at least 6 months of the year.

Accessible Version

Footnotes

* We thank Daron Acemoglu, Joshua Angrist, Lawrence Katz, David Lee, Emmanuel Saez, Gary Solon and many seminar participants for valuable suggestions. We also thank David Lee for providing data on minimum wage laws by state. Autor acknowledges financial support from the National Science Foundation (CAREER SES-0239538) Return to Text

1. DFL attribute 62 percent of the growth of the female 10/50 and 65 percent of the growth of the male 10/50 to the declining value of the minimum wage (Table III). Return to Text

2. Using cross-region rather than cross-state variation in the `bindingness' of minimum wages, Teulings (2000 and 2003) reaches similar conclusions. See also Mishel, Bernstein and Allegretto (2006, chapter 3) for an assessment of the minimum wage's effect on wage inequality. Return to Text

3. See Lee (1999) Table II. The large, positive and highly significant coefficients in this table imply that a 1 log point increase in the effective minimum wage (defined as the difference between the log state minimum wage and the log state median wage) reduces male and pooled-gender 90/50 log wage inequality by 0.16 to 0.44 log points. Return to Text

4. Ironically, the problem of division bias is exacerbated by the fix to the omitted variables problem; adding state effects increases the share of residual variation that is due to noise rather than signal. Cognizant of the possibility of division bias, Lee takes a number of steps to minimize its impact. These steps do not appear to fully resolve the problem, as we show below. It is precisely because of the concern about division bias that Lee excludes state fixed effects from the primary estimates. Return to Text

5. More precisely, these numbers refer to the distribution of paid hours, which weights the earnings distribution by hours worked. Return to Text

6. We assume no disemployment effects at the modest minimum wage levels mandated in the US, an assumption that is supported by a large recent literature (e.g., Card, Katz and Krueger, 1993; Card and Krueger, 2000; Neumark and Wascher, 2000). Return to Text

7. The ambitious paper by Teulings (2003) also estimates minimum wage spillovers under a set of flexible parametric assumptions using variation in the bindingness of the minimum wage across four U.S. regions (South, Midwest, Northeast, West) between 1973 and 1991. The Teuling's estimates find very large spillovers, but these estimates appear to suffer from the same two sources of bias that we document below for state by time panel estimates. Return to Text

8. These upper-tail correlations are found both in Lee's main estimation for 1979 through 1988 and the complementary estimates for 1989 through 1991, which exploit the sharp rise in the nominal federal minimum wage in two steps between April 1990 and April 1991 from $3.35 to $4.25. Return to Text

9. Recent work on the employment effects of the minimum wage have argued for the inclusion of state trends for this reason. See, for instance, Allegretto, Dube, and Reich (2008). Return to Text

10. See the derivation in section A of the Appendix. Return to Text

11. The statutory minimum is the maximum of the federal minimum wage and the state's minimum wage. Return to Text

12. Dropping the median from one or both sides of the estimating equation would also solve the simultaneity problem, but this would discard a key component of the identification, which exploits the fact that the effect of the minimum wage on wage inequality will depend in part on the minimum's position in the latent wage distribution. Hence, we retain the median but use 2SLS to solve the simultaneity problem. Return to Text

13. The instruments for the first-differenced analogue are ${\triangle w}^m_{st}$ and $\widetilde{{{\triangle (w}^m_{st}-w(50)}_{st})^2}$ , where ${\triangle w}^m_{st}$ represents the annual change in the log of the legislated minimum wage and $\widetilde{{{\triangle (w}^m_{st}-w(50)}_{st})^2}$ represents the change in the square of the predicted value for the effective minimum wage. This procedure is recommended by Wooldridge, 2002 (section 9.5.2). Return to Text

14. Estimating (4) in levels assumes that errors are serially uncorrelated, while the first-differenced specification is more efficient if the errors are a random walk (Wooldridge 2002). Return to Text

15. For brevity, we perform estimates for both females and males but not for the pooled distribution. Return to Text

16. Note that because ${\widetilde{mw}}_{st}$ is a regression predicted value, it will have a first stage coefficient of approximately one in a model where ${\widetilde{mw}}_{st}$ is instrumented by the statutory minimum wage (with time and state dummies and state specific trends included). Consequently, reduced-form and 2SLS estimates of (8) produce point estimates of closely comparable magnitude. Return to Text

17. So, for example, taking ${\tau }_0=1979$ and ${\tau }_1$ =1988, and subtracting $\triangle w^p_{st}$ from each observed wage in 1979 would adjust the 1979 distribution to its counterfactual under the realized effective minima in 1988. Return to Text

18. Also distinct from Lee, we use states' observed median wages when calculating $\tilde{m}$ rather than the national median deflated by the price index. This choice has no substantive effect on the results, but appears most consistent with the identifying assumptions. Return to Text

19. In a separate set of tables, Lee also analyzes these relationships for 1989 through 1991. Return to Text

20. It is conceivable (though in our view unlikely) that a binding minimum wage could reduce wages in the upper reaches of the wage distribution if, for example, the minimum wage redistributed rents from high to low wage workers. Our analysis here concerns the shape of the wage distribution at or below the median. Return to Text

21. Because the minimum is non-binding at this location, any effect on the observed percentile is by definition a spillover. Return to Text

22. Specifically, we estimate $\mu_{st}$ and $\sigma_{st}$ by pooling the 50th through 75th log wage percentiles, regressing the log value of the percentile on the inverse CDF of the standard normal distribution, and allowing the intercept ( $\mu_{st}$ ) and coefficient ( $\sigma_{st}$ ) to vary by state and year (and including state-specific time trends in both the intercept and coefficient). This procedure assumes that the wage distribution is unaffected by the minimum wage between the 50th and 75th percentiles; hence, the distribution between the 50th and 75th percentiles, combined with our parametric assumptions, allows us to infer the shape of the wage distribution for lower percentiles. We have experimented with the percentiles used to estimate the latent wage distribution and the results are not very sensitive to the choices made. Return to Text

23. The subsequent decomposition into direct and spillover effects does, of course, require knowledge of the statutory minimum. Return to Text

24. The lowest percentiles are excluded because these are typically below the minimum wage which would imply negative spillover effects. In the subsequent section, we consider the interpretation of these reported subminimum wages. Return to Text

25. As is well-known, the very highest percentiles are not well-approximated by a normal distribution (the Pareto distribution is a better fit)-thus, the actual observed percentiles are well above the predicted latent percentiles. Our modeling exercise is only applied to obtaining counterfactual values of lower-tail percentiles. Return to Text

26. More precisely, our procedure is as follows. First, we calculate the total, direct, and spillover effects for each percentile in each state-year as described in footnote 22. Next, for each state/year/percentile, we calculate the average total effect for each value of log(min)-log(p) (rounded to two decimals), where the average is weighted by the sum of individual weights for the given state-year; the direct effect is the maximum of 0 and log(min)-log(p), and the spillover effect is the difference between the total and direct effects. Thus, state/year/percentiles with the same rounded value of log(min)-log(p) will have the same total, direct, and spillover effects. To aggregate this to the national level, we calculate each individual's percentile in their state/year wage distribution, merge in these estimated minimum wage effects, and average the minimum wage effects by year/percentile. Return to Text

27. Because the minimum wage is estimated to have virtually no effect on the median (that is, the gap between the observed and latent median), the results in Figure 10 derive almost entirely from the compressing effect of the minimum wage at the 10th percentile. Return to Text

28. This assumption is not imposed by our estimation, however. Return to Text

29. Although the structural estimates correspond to a case with no minimum wage whatsoever, this is fairly close to reality in 1988. Return to Text

30. This argument holds in reverse for a decline in the minimum: a fall in the minimum from the 9th to the 6th percentile may reduce measured 50/10 wage inequality even if there is no impact on actual 50/10 wage inequality. Return to Text

31. Of course there are likely to be some individuals who correctly report sub-minimum wage wages. One potentially large occupation class is tipped workers, who in many states can legally receive a sub-minimum hourly wage as long as tips push their total hourly income above the minimum. For instance, in 2009, about 55 percent of those who reported their primary occupation as waiter or waitress reported an hourly wage less than the applicable minimum wage for their state, and about 17 percent of all observed sub-minimum wages were from waiters and waitresses. If we treat the wages of these individuals as measurement error, we will clearly over-state the extent of misreporting. We circumvent this problem by conducting the measurement/spillover analysis on a sample that excludes employees in low-paying occupations that commonly receive tips or commission. These are: food service jobs, barbers and hairdressers, retail salespersons and telemarketers. Return to Text

32. One might wonder why none of those observed in the spike are `errors', individuals who are not paid the minimum but, by chance, have an error which makes them appeared to be paid the minimum. But, the assumption on the absence of mass points in the true wage distribution and the error distribution mean that this group is of measure zero so can be ignored. Return to Text

33. More precisely, the relevant comparison is the fraction of hours paid below the minimum in the true wage distribution (purged of measurement error) rather than the fraction in the error-ridden distribution. Given that the minimum lies in the left-hand tail of the distribution, that the assumed error distribution is additive, and that the statutory minimum is known without error, the fraction of hours below the minimum in the error-ridden distribution strictly overestimates the fraction of hours below the minimum in the true wage distribution. Return to Text

^♣ This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to Text