Skip to: [Printable Version (PDF)] [Bibliography] [Footnotes]

Finance and Economics Discussion Series: 2011-03 Screen Reader version ^♣

Estimating Machinery Supply Elasticities Using Output Price Booms

Jesse Edgerton*

Federal Reserve Board

December 10, 2010

Keywords: Investment, capital supply elasticity, bonus depreciation, expensing.

Abstract:

Recent years have seen large increases in the prices of houses, farm products, and oil, often with little clear connection to economic fundamentals. These price increases created plausibly exogenous shifts in demand for construction, farm, and mining machinery. This paper uses these demand shifts to estimate the elasticity of machinery supply. Graphical evidence, OLS, and IV estimates all indicate that the quantity of machinery supplied increased rapidly during the booms, with only modest increases in prices. Pooled sample estimates of the supply elasticity are around 5, much larger than the estimate of 1 from Goolsbee (1998). Results thus suggest that public policies that stimulate investment demand will have only modest effects on the prices of investment goods.

JEL Classification: E22, H25, H32.

1 Introduction

For many decades, policymakers have repeatedly attempted to stimulate business investment in productive equipment during periods of weak economic performance. For example, expansionary monetary policy changes are intended in part to stimulate business investment by reducing interest rates and encouraging bank lending. Fiscal policymakers often attempt to encourage investment through changes to the tax code. Prominent recent examples include the temporary "bonus depreciation" provisions included in the packages of stimulus legislation passed in 2002, 2003, 2008, 2009, and 2010. At the time of this writing, it appears likely that further investment stimulus in the form of full expensing of equipment purchases will be enacted through 2011.

The price elasticity of the supply of investment goods is a key parameter determining the impact and incidence of these policies that intend to stimulate business investment. Many seminal papers have implicitly or explicitly assumed that the supply of investment goods is perfectly elastic--that is, that supply can increase to satisfy any increase in demand without an increase in prices. Hall and Jorgenson (1967) and Summers (1981), for example, study the impact of tax policy on investment decisions in partial equilibrium models where any amount of physical capital can be purchased at a fixed price.¹

Goolsbee (1998), however, emphasizes that the supply curve for investment goods may be upward sloping.² In the short run, policies designed to stimulate demand for investment goods might increase the prices of these goods. This price increase would tend to mitigate the impact of such policies on real investment quantities, and it would tend to benefit suppliers of these goods at the expense of purchasers.

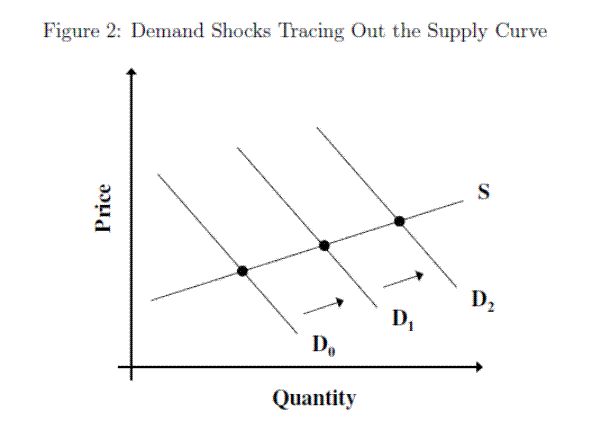
Figure 1 illustrates this argument in a simple supply and demand graph. When the supply curve is steep, a positive demand shock translates into an increase in prices with only a muted increase in quantities. Goolsbee (1998) estimates that such price increases did, in fact, occur in response to increases in the investment tax credit during his sample from 1962 to 1988. He finds a short-run supply elasticity around 1, and he estimates that a 10% investment tax credit would increase the prices of investment goods by between 3.5 and 7.0 percent. Goolsbee argues that this inelasticity of supply could explain much of the apparent lack of response of investment quantities to tax policy and the user cost that had been found by previous authors (see, for example, the surveys in Chirinko (1993) and Hassett and Hubbard (2002)).

With an elastic supply curve, a positive demand shock produces a large increase in quantity and a small increase in price. With an inelastic supply curve, it produces a small increase in quantity and a large increase in price.

This paper provides new evidence on the supply elasticity of investment goods by exploiting recent large increases in the prices of several types of output. During the last decade, the prices of houses, farm products, and oil rose to astounding heights before crashing before and during the financial crisis. The case of housing is particularly familiar, and it seems that consensus opinion holds that these high prices resulted from a speculative bubble with little relation to economic fundamentals.³

The reasons behind the increases in farm and oil prices are less well understood, and, in fact, prices have rebounded substantially since the depths of the crisis. Mitchell (2008) points to increased demand from worldwide biofuel production as the most important factor in the rise in food commodity prices. Hamilton (2008) sees growth in demand from China and other newly industrialized countries as a factor in recent oil price increases, but concedes that, "The $140/barrel price in the summer of 2008 and the $60/barrel in November of 2008 could not both be consistent with the same calculation of a scarcity rent warranted by long-term fundamentals." Thus, at least some of the recent run-ups in goods prices appear to have had little relation to economic fundamentals. At the very least, price increases have been driven by increases in global demand and not by shocks to the supply of machinery used to produce these goods.

These price increases did, however, lead to increased demand for this construction, farm, and mining machinery. This paper uses these demand shifts to estimate machinery supply curves. Textbook simultaneous equations models demonstrate that exogenous shifts in demand can be used to identify supply curves (or vice versa). If the only variation in the data comes from demand shifts, then ordinary least squares will correctly estimate the supply curve. If there are also supply shocks in the data, then instrumental variables estimates exploiting an exogenous demand shifter can still correctly estimate the supply curve. I show in this familiar setting that OLS "forward" regressions of quantity on price produce an upward-biased estimate of the supply elasticity when supply and demand shocks are uncorrelated, while OLS "reverse" regressions of price on quantity produce a downward-biased estimate of the supply elasticity. I argue that the most plausible story for a correlation between demand and supply shocks in the data used in this paper would tend to bias results towards lower elasticity estimates.

Graphical evidence, OLS estimates, and instrumental variables estimates all tell similar stories. The supply of machinery supplied to the United States increased rapidly during the output price booms, with only modest increases in prices. The price elasticity of construction machinery supply is quite large--at least 10--while the supply elasticities of farm machinery and mining machinery are around 3 and 5, respectively. Pooling the sample and weighting by each type of machinery's share of aggregate investment produces supply elasticity estimates of at least 5, far larger than the estimate of 1 from Goolsbee (1998). Even if the machinery demand elasticity were as large as 1 in absolute value, these estimates would suggest that only 17%, or 1/(1+5), of the value of tax incentives for invesment would be passed into machinery prices.⁴

Finally, I discuss evidence suggesting that increased globalization of the machinery market has contributed to the flattening of supply curves since the period studied by Goolsbee (1998). The share of machinery investment that is imported from abroad has more than tripled since the 1970s, and imports played an important role in the supply responses seen during the boom periods studied in this paper. I conclude that policies that succeeded in stimulating investment demand would be unlikely to simply push up the prices of investment goods, in part due to elastic supply from abroad. However, to the extent that increased demand is met with production from abroad, benefits to domestic manufacturers and their employees may be limited.

This paper is most similar in spirit to Shea (1993), who uses "approximately exogenous" demand shocks to estimate supply curves for many industries. He finds upward-sloping supply curves for many consumer and intermediate goods industries, but downward-sloping supply curves for construction machinery and aircraft. This paper differs from Shea (1993) in its focus on recent periods where the presence of large demand shocks is particularly clear, in its focus on transparent, graphical presentation of results, and in the sign of its main result. Other related papers include Hassett and Hubbard (1998) and Whelan (1999), which question the robustness of Goolsbee's results on other grounds. Sallee (2009) finds that tax incentives for the purchase of hybrid cars had no effect on Toyota Prius prices, even though Prius supply was quite inelastic.

The following section of the paper reviews the estimation of supply curves in a simultaneous equations setting. Section 3 discusses and describes the data. Section 4 presents results, and Section 5 concludes.

2 The simultaneous equations model

Suppose price and quantity data are generated by the sytem of equations,

$\displaystyle q$	$\displaystyle = \beta p + \epsilon_s$	(1)
$\displaystyle q$	$\displaystyle = \gamma_1 p + \gamma_2 z + \epsilon_d$	(2)
$\displaystyle p$	$\displaystyle = \pi z + \nu,$	(3)

where and are logarithms of prices and quantities, and constants and any other exogenous variables are partialled out. Equations (1) and (2) are the "structural" supply and demand equations, in the language of Hausman (1983). The supply elasticity $\beta$ is the parameter of interest.⁵ The exogenous demand shifter enters only the demand equation and not the supply equation. Equation (3) relating and is a "reduced form" equation in the language of Hausman (1983), but is commonly referred to as the "first stage" of two-stage least squares (2SLS) estimation of equation (1).

Recall that asymptotic bias in the OLS estimate of $\beta$ depends on the correlation of and the supply shocks $\epsilon_s$ ,

$\displaystyle \textrm{plim } \hat{\beta}_{OLS} = \beta + \frac{cov(\epsilon_s,p)}{var(p)}.$

If we could examine data from a period with no supply shocks ( $\epsilon_s = 0$ ), then an OLS regression of

would correctly estimate the supply elasticity. If instead we had data from a period where demand shocks are large relative to suppy shocks, there would be large demand-induced changes in

, with only small changes in $\epsilon_s$ . The numerator of the bias term would be small, while the denominator would be large, and OLS would not be badly biased.

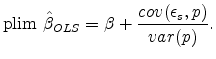
I claim that recent run-ups in commodity prices have created this kind of variation in the data. There were large shocks to demand that likely swamp any shocks to supply. Simple OLS regressions using data from the commodity price boom periods will probably not produce badly biased supply elasticity estimates. Figure 2 depicts a situation like this graphically.

Demand curve D_0 intersects the supply curve and provides one price-quantity observation. When demand shifts right to curve D_1, another point on the supply curve is observed. When demand shifts further right to curve D_2, a third point on the supply curve is observed.

It can be shown that the bias term can be written,

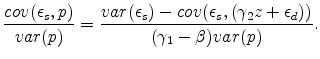
$\displaystyle \frac{cov(\epsilon_s,p)}{var(p)} = \frac{var(\epsilon_s) - cov(\epsilon_s, (\gamma_2 z + \epsilon_d))}{ (\gamma_1 - \beta)var(p)}.$

In a situation where supply shocks are uncorrelated with demand shocks ( $cov(\epsilon_s, (\gamma_2 z + \epsilon_d)) =0$ ), we can sign the OLS bias. Assuming that demand curves slope down ( $\gamma_1 < 0$ ) and supply curves slope up ( $\beta > 0$ ), the OLS estimate of $\beta$ will be downward biased.

One could just as easily estimate the "reverse" supply equation relating prices to quantities,

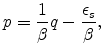
$\displaystyle p = \frac{1}{\beta} q - \frac{\epsilon_s}{\beta},$

and thus one might wonder how this estimate is related to that of the forward equation. Denote $c = (1/\beta)$ , and note that $1/\hat{c}$ is a potential estimator for $\beta$ , with,

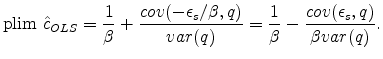
$\displaystyle \textrm{plim } \hat{c}_{OLS} = \frac{1}{\beta} + \frac{cov(-\epsilon_s/\beta,q)}{var(q)} = \frac{1}{\beta} - \frac{cov(\epsilon_s,q)}{\beta var(q)} .$

It can be shown that this bias term can be written,

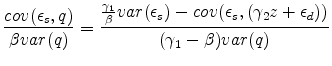
$\displaystyle \frac{cov(\epsilon_s,q)}{\beta var(q)} = \frac{ \frac{ \gamma_1}{\beta} var(\epsilon_s) - cov(\epsilon_s,(\gamma_2 z + \epsilon_d))}{ (\gamma_1-\beta) var(q)}$

These results are derived in an appendix. Under the same assumptions ( $cov(\epsilon_s, (\gamma_2 z + \epsilon_d)) =0$ , $\gamma_1 < 0$ , and $\beta > 0$ ), we see that $\hat{c}$ is biased downwards, and thus that $1/\hat{c}$ is biased upwards as an estimator of $\beta$ .

Because $\hat{\beta}_{OLS}$ was biased downwards, the two estimators could be used to estimate upper and lower bounds on $\beta$ . It is well-known that the product $\hat{\beta}_{OLS} \times \hat{c}_{OLS}$ must equal the , which is equal in both regressions. Thus the two estimates can provide tight bounds when the is high, but only loose bounds when it is low. Intuitively, if plotting a dataset of observations produces a loose cloud of points with no clear relationship between the two variables, then regressing price on quantity would produce a horizontal regression line, while regressing quantity on price would produce a vertical line. Alternatively, if price and quantity have a clear linear relationship, then the forward and reverse regression lines will be close together.

Of course, the two-stage least squares (2SLS) estimator may also be available, with,

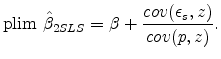
$\displaystyle \textrm{plim } \hat{\beta}_{2SLS} = \beta + \frac{cov(\epsilon_s,z)}{cov(p,z)}.$

It is thus a consistent estimator of $\beta$ whenever $cov(\epsilon_s,z)=0$ . When instruments are valid and supply and demand shocks are not badly correlated, we should see that forward and reverse OLS and 2SLS estimates are all close together.⁶

It is worth considering what will happen if instruments are invalid. The denominator of the 2SLS bias term will be positive as long as favorable supply shocks are not so highly correlated with the instrument that and are negatively correlated, which, we will see, is clearly not the case in the data used in this paper. Thus the sign of the bias will be determined by the term $cov(\epsilon_s,z)$ . In this paper, represents the prices of houses, farm products, and oil. I have argued that much of the variation in in recent years has been driven by speculative bubbles and demand shocks, rather than machinery supply shocks.

Nonetheless, plausible stories for correlation between $\epsilon_s$ and may exist. I find the most plausible story to be the following. Global demand or a housing bubble drove up aggregate demand in the United States, increasing wages, interest rates, and other costs involved in machinery production. There would thus be a correlation between strong demand for machinery and unfavorable machinery supply shocks, which entails a negative correlation between and $\epsilon_s$ . In this setting, my estimates of the supply elasticity would be biased downward.

Another story might be the following. Exogenous increases in the price of oil hurt the economy, driving down real wages and other machinery production costs. There would thus be a correlation between high oil prices and favorable supply shocks in machinery manufacturing, which entails a positive correlation between and $\epsilon_s$ and an upward bias in supply elasticity estimates. In response, I would say first that this story is most plausible for oil, as the relationship between oil price shocks and US recessions is well-known. But, I find especially large supply elasticity estimates for construction machinery, where this story would not apply. Second, the sample periods from which I produce supply elasticity estimates are limited to the commodity boom periods, which fall primarily before the financial crisis and recession could have begun driving down other input prices.

I thus find no concrete reasons to suspect that supply elasticity estimates will be biased upward. Nonetheless, the validity of results still rests on the assumption that there were no positive supply shocks keeping machinery prices low during the output price booms. If, for example, there was a series of exogenous, increasing, positive productivity shocks in machinery manufacturing during this period, then supply elasticity estimates could be biased upward. Aggregate productivity growth was low during the commodity boom years (Jorgenson, Ho, and Stiroh (2008), p. 6), so there is little reason to suspect there was a sustained productivity boom in machinery manufacturing during this time.

3 Data

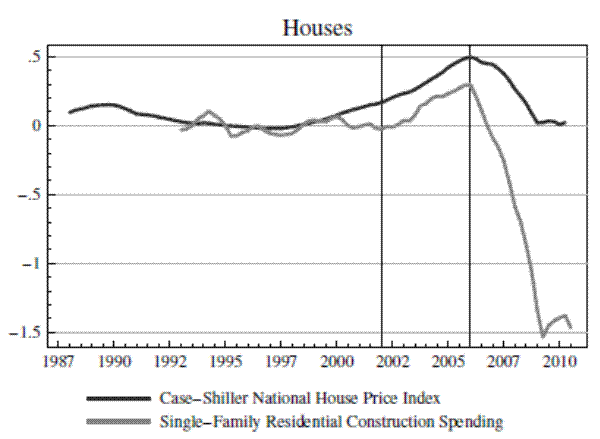
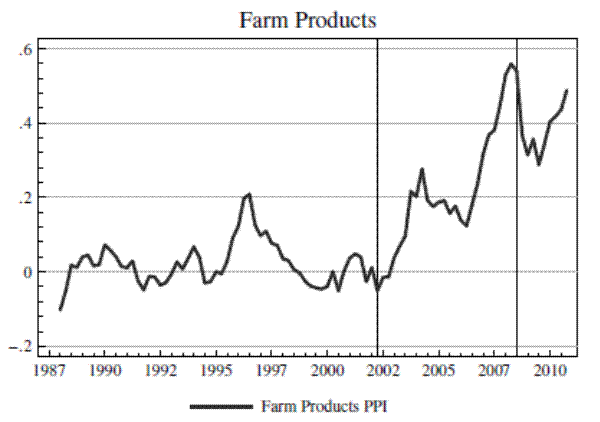
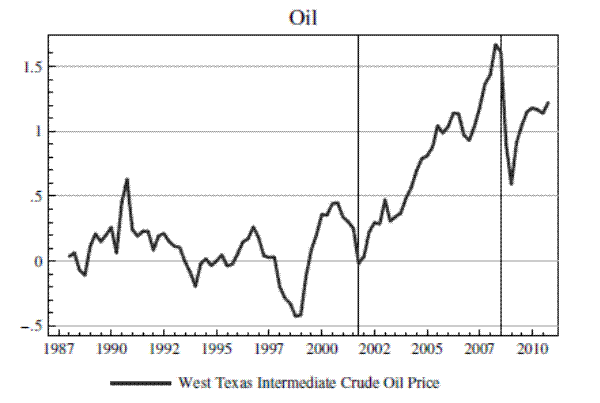
I use data from the National Income and Product Accounts of the Bureau of Economic Analysis (BEA) to measure both machinery prices and quantities. Quantity data are based on monthly surveys of shipments by U.S. manufacturers conducted by the Census Bureau. The BEA then adjusts these domestic production numbers for imports and exports using data from the International Trade Commission. The Bureau of Labor Statistics has its own monthly survey asking U.S. machinery manufacturers about the prices they receive for their output, and these data are used to create the Producer Price Indices (PPIs). The BEA uses the PPIs to create price indices and measure real investment quantities. I use the BEA real investment and price index series for construction machinery, farm machinery, and mining and oilfield machinery. This is the same source of the data used for many of the results in Goolsbee (1998). To measure output price booms, I use the Case-Shiller National House Price Index, the Census Bureau's measure of construction spending on single-family homes, the PPI for farm products, and the spot price of West Texas Intermediate Crude oil.⁷

All series logged, detrended, and normalized to 1995Q1. Vertical lines indicate the beginning and end of periods that I define as output price booms. The house price boom is from 2002Q1 to 2006Q1, the farm products price boom from 2002Q2 to 2008Q3, and the oil price boom from 2001Q4 to 2008Q3.

One could be concerned about the quality of the price indices I will use to measure machinery prices. The Producer Price Index data underlying the indices attempt to measure all "changes in net revenues received by producers," including manufacturer-to-customer incentives like rebate programs and low-interest financing arrangements (Bureau of Labor Statistics (2008)). It is still feasible that, despite the best efforts of the Bureau of Labor Statistics, the indices fail to capture all relevant movements in machinery prices. If the indices systematically overestimate prices when they are low and underestimate prices when they are high, then price increases during commodity price booms could be underestimated, and supply elasticity estimates could be upward biased. However, the results from Goolsbee (1998) suggest that this effect could not be too large. His estimates suggest that a 10% investment tax credit would increase capital goods prices by 4% on average, and close to 10% for several types of equipment, including farm and mining machinery. If Goolsbee's estimates are correct, there cannot be much room for the PPI data to systematically understate price changes.

I take logarithms of all series, regress them on a linear trend over the 15 years from 1988 to 2002, subtract the predicted values calculated using these coefficients over the full 1988 to 2010 period, and subtract off the value from 1995q1. The resulting detrended output price series, normalized to 1995q1, appear in Figure 3. The recent boom and bust in prices is quite apparent in all three figures. Housing prices rose by more than 30% from 2002 to 2006, relative to their pre-2002 trend. Farm products prices rose more than 60%, and oil prices rose 150%.⁸ Figure 3 also includes vertical lines that represent my subjective judgment of the beginning and end of commodity price booms based on the data in the figure. These are essentially the periods from trough to peak in the price series. However, the Case-Shiller price index is very smooth, so I use the trough of the singe-family residential construction spending series to date the beginning of the housing boom.

Figure 4 Panel A: Machinery Prices and Quantities

Accessible Version

Figure 4 Panel B: Machinery Prices and Quantities

Accessible Version

Figure 4 Panel C: Machinery Prices and Quantities

Accessible Version

Figure 5 Panel A: Recent Output Price Booms Tracing out Machinery Supply Curves

Accessible Version

Figure 5 Panel B: Recent Output Price Booms Tracing out Machinery Supply Curves

Accessible Version

Figure 5 Panel C: Recent Output Price Booms Tracing out Machinery Supply Curves

Accessible Version

All series logged, detrended, and normalized to 1995Q1. Black lines are OLS regression lines from reverse (price on quantity) regressions. Grey lines are from forward (quantity on price) regressions.

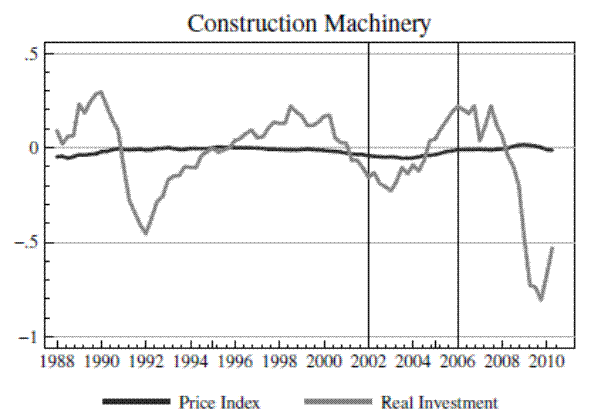
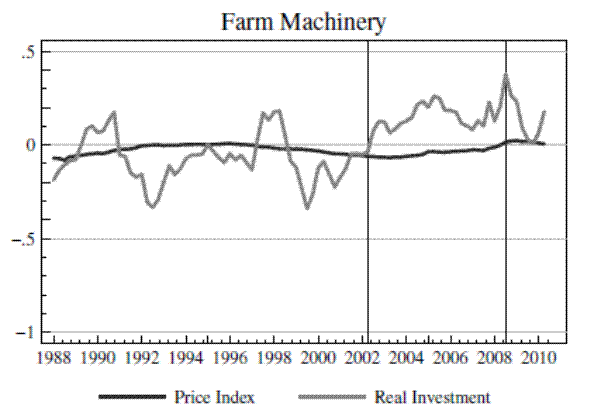
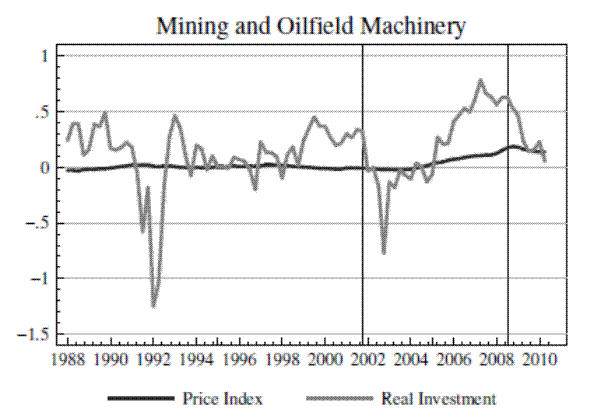
Figure 4 presents the detrended and normalized price and quantity series for all three machinery types. It is immediately clear from the figure that there have been large swings in quantities accompanied by small movements in prices for all three machinery types. For example, construction machinery quantities grew by 44% during the housing boom relative to their prior trend, while prices increased about 5%. Farm machinery quantities increased by 40%, with an 8% increase in prices. Mining machinery quantities increased by 75%, with about a 15% increase in prices.

The data in Figure 4 provide very transparent evidence that investment quantities fluctuate far more than prices.⁹Unless these movements were accompanied by large, well-timed supply shocks, the data graphed in Figure 4 already suggest that supply elasticities must be large. Also note from the figure that the beginning of the ouput price boom periods roughly coincides with a cyclical low point in machinery investment, as the U.S. was beginning its recovery from the 2001 recession. As this is exactly the kind of time when policymakers are likely to attempt to stimulate investment, it is an appropriate period during which to estimate supply elasticities if one wishes to learn about the potential effectiveness of these policies.¹⁰

4 Results

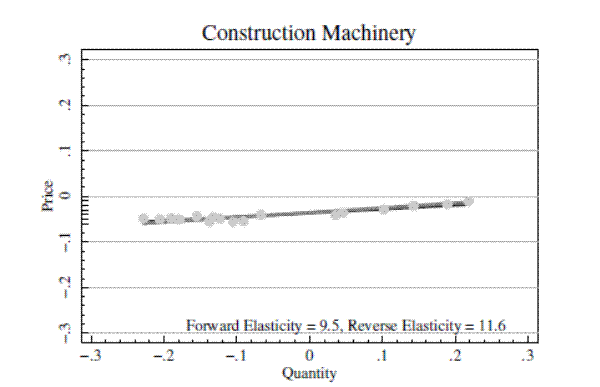
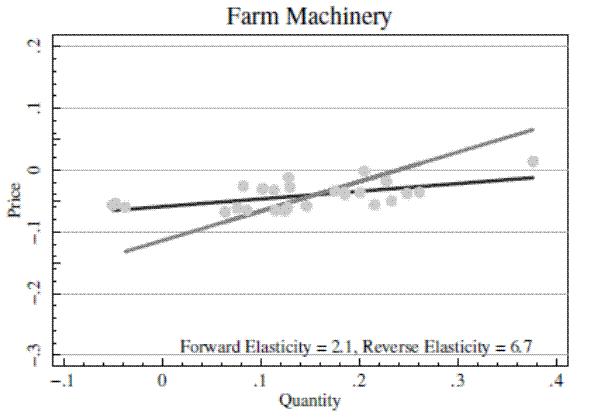
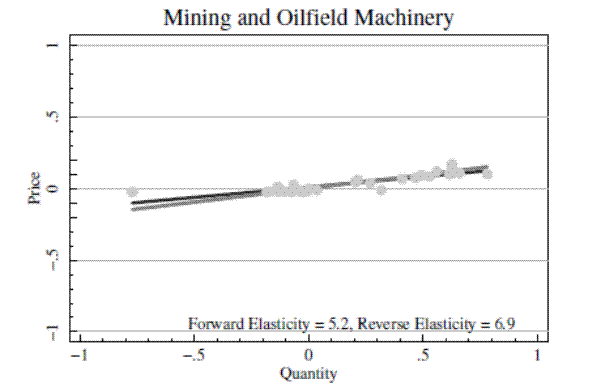
Figure 5 presents the data from the boom periods in Figure 4 in the same format as Figure 2, which illustrated how a shifting demand curve can trace out the supply curve. Each dot in the scatter plots in Figure 5 is a quarterly data point, and the figures are constructed so that the price and quantity axes have the same scale. It is clear in the figure that the supply curves traced out during the output price boom periods are quite flat.

Table 1 presents regressions that quantify the results visible in Figures 4 and 5. Panel A presents results for construction machinery, Panel B for farm machinery, and Panel C for mining and oilfield machinery. Columns 1 and 2 present forward and reverse OLS regressions over the sample period from 1988 to the end of the relevant output price boom. I argued above that the forward and reverse estimates should provide lower and upper bounds on the supply elasticity when supply curves slope up and supply and demand shocks are uncorrelated. In panels A and C, the estimates in columns 1 and 2 provide only very wide bounds on the supply elasticity, indicating that there is little clear relation between price and quantity over the full sample, and thus suggesting that both supply and demand shifts may sometimes be relevant in determining variation in prices and quantities. For construction machinery in Panel A, the forward elasticity estimate is 0.54, and the reverse estimate is 159.7. For mining machinery in Panel C, the forward estimate is 3.5 and the reverse is 17.7. In panel B, estimates suggest that farm machinery supply could even be downward sloping.

Columns 3 and 4 again present forward and reverse OLS estimates, but limit the sample to the output price boom periods identified from Figure 3. Bounds on the elasticity estimate are much tighter. For construction machinery in Panel A, the forward elasticity estimate is 9.5, and the reverse estimate is 11.6. For farm machinery in Panel B, the forward estimate is 2.1 and the reverse is 6.7. For mining machinery in Panel C, the forward estimate is 5.2 and the reverse is 6.9.

Table 1 Panel A: Construction Machinery - Supply Elasticity Estimates

	(1)	(2)	(3)	(4)	(5)	(6)	(7)
Estimator	OLS	OLS	OLS	OLS	2SLS	2SLS	2SLS
Direction	Fwd.	Rev.	Fwd.	Rev.	-	-	-
Sample Period	Full	Full	Booms	Booms	Booms	Booms	Booms
Price Elasticity	.54	159.69	9.46	11.59	13.00	9.78	10.26
Price Elasticity standard error	(1.80)	(571.62)	(1.08) ^***	(1.71) ^***	(2.39) ^***	(1.11) ^***	(1.67) ^***
BAA Interest Rate						-.54	-.48
BAA Interest Rate standard error						(.10) ^***	(.18) ^***
Manufacturing Compensation							.57
Manufacturing Compensation standard error							(.75)
Observations	73	73	17	17	17	17	17
	.003	.003	.82	.82
First Stage Coefficient					.20	.22	.21
Partial F Statistic					6.93	15.22	9.61
Partial					.50	.60	.47

Table 1 Panel B: Farm Machinery - Supply Elasticity Estimates

	(1)	(2)	(3)	(4)	(5)	(6)	(7)
Estimator	OLS	OLS	OLS	OLS	2SLS	2SLS	2SLS
Direction	Fwd.	Rev.	Fwd.	Rev.	-	-	-
Sample Period	Full	Full	Booms	Booms	Booms	Booms	Booms
Price Elasticity	-1.17	-33.68	2.09	6.74	2.12	2.66	3.23
Price Elasticity standard error	(1.16)	(32.80)	(.63) ^***	(2.56) ^***	(.81) ^***	(.68) ^***	(.79) ^***
BAA Interest Rate						-.44	-.34
BAA Interest Rate standard error						(.19) ^**	(.19) ^*
Manufacturing Compensation							1.26
Manufacturing Compensation standard error							(.91)
Observations	83	83	26	26	26	26	26
	.03	.03	.31	.31
First Stage Coefficient					.11	.10	.08
Partial F Statistic					75.27	117.70	47.94
Partial					.70	.67	.62

Table 1 Panel C: Mining and Oilfield Machinery - Supply Elasticity Estimates

	(1)	(2)	(3)	(4)	(5)	(6)	(7)
Estimator	OLS	OLS	OLS	OLS	2SLS	2SLS	2SLS
Direction	Fwd.	Rev.	Fwd.	Rev.	-	-	-
Sample Period	Full	Full	Booms	Booms	Booms	Booms	Booms
Price Elasticity	3.51	17.73	5.20	6.89	4.82	4.82	4.23
Price Elasticity standard error	(.84) ^***	(10.69) ^*	(.71) ^***	(1.13) ^***	(.72) ^***	(.76) ^***	(.95) ^***
BAA Interest Rate						.0006	-.31
BAA Interest Rate standard error						(.56)	(.54)
Manufacturing Compensation							-3.52
Manufacturing Compensation standard error							(3.21)
Observations	83	83	28	28	28	28	28
	.2	.2	.75	.75
First Stage Coefficient					.12	.12	.11
Partial F Statistic					74.82	200.99	185.53
Partial					.86	.90	.87

Columns 1 through 4 present OLS estimates of the price elasticity of machinery supply. Columns 1 and 3 are from the forward regression of log quantities on log prices. Columns 2 and 4 are from the reverse regression of log prices on log quantities. Columns 5 through 7 present just-identified IV estimates using the output price series from Figure 3 as instruments. Standard errors (in parentheses) are Newey-West with a lag length of 4. The standard errors for the reverse regressions are computed using the delta method around the point estimate. Columns 1 and 2 use the sample from 1988 to the end of the relevant output price boom. Columns 3 through 7 limit the sample to the periods of output price booms identified from the data in Figure 3.

Column 5 presents instrumental variables estimates using the appropriate series from Figure 3 as an instrument for machinery prices. I use the series of single-family residential construction spending as the instrument for construction machinery prices because the Case-Shiller house price index is very smooth. Results differ relatively little from the OLS estimates in Columns 3 and 4. For construction machinery, the Column 5 estimate of 13.0 is a bit above the Column 4 reverse OLS estimate. For farm machinery, the Column 5 estimate of 2.1 is just above the Column 3 forward OLS estimate. For mining machinery, the column 5 estimate of 4.8 is just below the Column 3 estimate.

Columns 6 and 7 present instrumental variables results where the Baa borrowing rate and hourly manufacturing compensation are included as additional exogenous controls in the supply equation. Recall the concern voiced earlier that output price booms could push up aggregate demand and thus increase the costs involved in machinery manufacturing. Failure to properly control for these cost increases would result in a downward bias to the supply elasticity estimate. There is no clear pattern across panels in changes to the supply elasticity estimate when these controls are introduced, but, overall, changes are typically small in magnitude and statistically insignificant.

Standard errors in all columns are computed using the Newey-West estimator with a lag length of 4.¹¹ That is, they are robust to heteroskedasticity and correlation between residuals up to four quarters away. In fact, standard errors rise less than 30% with the Newey-West adjustment in all specifications. Because t-statistics are large, results remain highly significant. Choosing a longer lag length has only inconsequential effects on results.

All three panels include information useful in assessing the quality of the first-stage regression of machinery prices on output prices. The posited relationship would suggest that coefficients on output prices should be positive, and all are. Partial F statistics and s are comfortably large in all panels and columns, with the possible exception of Panel A. Stock, Wright, and Yogo (2002) propose a rule of thumb based on their observation that hypothesis tests using 2SLS standard errors should not overreject too badly when the F statistic in the first stage exceeds 10.¹² The F statistics of 6.9 and 9.6 in Columns 5 and 6 of Panel A only narrowly miss this cutoff. All other F statistics in the table are well above 10. Hansen, Hausman, and Newey (2008) prefer to focus on the closely-related "concentration parameter," , where K is the number of instruments. As this paper uses only one instrument in all specifications, the concentration parameter is simply equal to the F statistic minus one. Table 5 of their paper suggests that 2SLS (which is equivalent to LIML in the just-identified case) is unlikely to suffer from substantial bias or size problems even when the concentration parameter is in the mid-single digits, as it is in the aforementioned two columns.

Considering all estimates from Table 1, I conclude that the supply elasticity of construction machinery is at least ten, that of farm machinery is around three, and that of mining and oilfield machinery is around five. Standard errors are less then one in most specifications, and all estimates are significantly different from zero at the one percent level. These estimates and standard errors are unlikely to be significantly affected by a weak instruments problem.

Table 2: Pooled Sample Supply Elasticity Estimates

	(1)	(2)	(3)	(4)	(5)	(6)	(7)
Estimator	OLS	OLS	OLS	OLS	2SLS	2SLS	2SLS
Direction	Fwd.	Rev.	Fwd.	Rev.	-	-	-
Sample Period	Full	Full	Booms	Booms	Booms	Booms	Booms
Price Elasticity	1.13	55.42	5.19	8.17	5.36	5.04	4.90
Price Elasticity standard error	(.50) ^**	(10.39) ^***	(.48) ^***	(.32) ^***	(.92) ^***	(.65) ^***	(.68) ^***
BAA Interest Rate						-.69	-.73
BAA Interest Rate standard error						(.13) ^***	(.15) ^***
Manufacturing Compensation							-.48
Manufacturing Compensation standard error							(.81)
Observations	249	249	71	71	71	71	71
	.07	.23	.74	.82
First Stage Coefficient					.11	.12	.11
Partial F Statistic					108.65	207.15	196.91
Partial					.76	.81	.78

Table 2 presents results where all three types of machinery are pooled together. In the year 2000, construction machinery accounted for 57% of total investment in all three machinery types, farm machinery for 31%, and mining and oilfield machinery for 12%. A simple weighted average of the coefficients from Table 1 would thus suggest a pooled supply elasticity around 7. I construct weights to account for the relative importance of these machinery types and the number of output boom quarters for each type, and these weights are used in the estimates in Table 2. As there is more variation in the output prices used to instrument for farm and mining machinery, these weighted estimates will place more importance on these equipment types than does the simple weighted average.¹³

The forward and reverse OLS estimates in Columns 1 and 2 use the data beginning in 1988 and estimate very wide bounds on the supply elasticity. The estimates in Columns 3 and 4 use only the data from the output price boom periods, and estimate pooled supply elasticities of 5.2 and 8.2. The instrumental variables specifications in Columns 5, 6, and 7 produce estimates of 5.4, 5.0, and 4.9, with standard errors all less than one. Again, the reported partial F statistics and s indicate a very strong first stage and little reason to be concerned about weak instruments. I thus conclude that the aggregate price elasticity of supply for these three kinds of machinery is around 5.

4.1 Robustness

This section contains several tables that demonstrate the robustness of these results to a variety of alternative specifications. Table 3 includes additional control variables that might be correlated with shifts in the supply curve, including the Producer Price Index for fuels and energy, the broad dollar exchange rate, and gross domestic product. Results including these controls one at a time are not statistically different from those in Table 2 Column 7. In the last column, which includes all controls together, the estimated supply elasticity rises somewhat to 5.7. I choose the specifications including the Baa rate and manufacturing compensation as my preferred estimates for Table 2 because these variables have the expected negative sign in this specification.

The results presented thus far have all used data that were detrended on the basis of a simple linear trend estimated over the fifteen years from 1988 to 2002, before the output price boom periods began. This method of detrending is simple and transparent, and it struck me as appropriate after looking at the data, but before calculating regression results. Table 4 presents specifications that use five alternative detrending methods, each with and without the controls from Table 2. The first set of alternatives in columns 3 and 4 may strike some readers as the most obvious way to run the regressions in this paper. In these specifications, the dependent and independent variable are simply logarithms of the relevant series, and a linear trend is included as an exogenous variable. The next two sets of results instead remove simple linear trends estimated over the periods 1980-2002 and 1995-2002 from all variables used in the regressions. The fourth set uses the Hodrick-Prescott filter estimated over the period 1988 to 2002, with the trend extrapolated from the end of this sample through 2010. The final set of results uses the HP filter with the trend estimated over the entire period from 1980 to 2010. The second and last of these sets of results in columns 5, 6, 11, and 12 actually produce supply elasticity estimates that are considerably larger than the baseline results in Table 2. The other sets of results, however, are fairly similar to the baseline results. Thus, overall, the supply elasticity estimates featured in Table 2 are near the bottom of the range of estimates produced under alternative detrending methods.

Table 3: Pooled Sample Supply Elasticity Estimates with Other Control Variables

	(1)	(2)	(3)	(4)	(5)	(6)
Estimator	2SLS	2SLS	2SLS	2SLS	2SLS	2SLS
Sample Period	Booms	Booms	Booms	Booms	Booms	Booms
Price Elasticity	5.04	5.66	4.05	4.29	4.90	5.66
Price Elasticity standard error	(.65) ^***	(1.02) ^***	(1.37) ^***	(1.35) ^***	(.66) ^***	(1.48) ^***
BAA Interest Rate	-.69					-.55
BAA Interest Rate standard error	(.13) ^***					(.25) ^**
Manufacturing Compensation		1.16				.89
Manufacturing Compensation standard error		(1.00)				(.51) ^*
PPI for Fuels and Energy			.18			.10
PPI for Fuels and Energy standard error			(.17)			(.18)
Broad Dollar Exchange Rate				-.20		.28
Broad Dollar Exchange Rate standard error				(.28)		(.27)
Gross Domestic Product					4.36	3.90
Gross Domestic Product standard error					(1.72) ^**	(1.91) ^**
Observations	71	71	71	71	71	71
First Stage Coefficient	.12	.10	.09	.11	.11	.10
Partial F Statistic	207.15	143.33	19.72	20.6	72.51	48.73
Partial	.81	.76	.43	.43	.75	.51

All columns present two-stage least squares estimates of the price elasticity of supply in the pooled sample of machinery types, as in Columns 5 to 7 of Table 2.

Table 4: Pooled Sample Supply Elasticity Estimates under Alternative Detrending Methods

	(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)	(11)	(12)
Estimator	2SLS	2SLS	2SLS	2SLS	2SLS	2SLS	2SLS	2SLS	2SLS	2SLS	2SLS	2SLS
Sample Period	Booms	Booms	Booms	Booms	Booms	Booms	Booms	Booms	Booms	Booms	Booms	Booms
Trend Type	Linear	Linear	Linear	Linear	Linear	Linear	Linear	Linear	HP	HP	HP	HP
Trend Period	88-02	88-02	Booms	Booms	80-02	80-02	95-02	95-02	88-02	88-02	80-10	80-10
Controls	No	Yes	No	Yes	No	Yes	No	Yes	No	Yes	No	Yes
Price Elasticity	5.36	4.90	6.11	5.16	10.05	10.08	3.86	2.88	5.43	6.88	14.06	13.40
Price Elasticity standard error	(.92) ^***	(.68) ^***	(2.89) ^**	(1.59) ^***	(1.87) ^***	(1.27) ^***	(.77) ^***	(1.01) ^***	(1.46) ^***	(2.29) ^***	(2.43) ^***	(2.32) ^***
Observations	71	71	71	71	71	71	71	71	71	71	71	71
First Stage Coeff.	.11	.11	.08	.10	.09	.09	.17	.12	.20	.12	.04	.04
Partial F Statistic	108.65	196.91	5.06	13.9	30.32	44.54	238.98	73.54	272.68	40.45	21.46	17.68
Partial	.76	.78	.18	.31	.61	.64	.82	.60	.82	.48	.40	.36

All columns present two-stage least squares estimates of the price elasticity of supply in the pooled sample of machinery types, as in Columns 5 to 7 of Table 2. Columns marked "Linear" use both dependent and independent variables that are constructed by removing a linear trend from the logarithm of the original series, where the trend is estimated over the indicated periods and extrapolated to the rest of the estimation period. Columns marked "HP" remove a trend estimated using the Hodrick-Prescott filter fit over the indicated periods. Columns with controls include the Baa borrowing rate and manufacturing compensation, but coefficients are not reported.

Table 5: Pooled Sample Supply Elasticity Estimates under Alternative Detrending Methods using Full Estimation Sample

	(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)	(11)	(12)
Estimator	2SLS	2SLS	2SLS	2SLS	2SLS	2SLS	2SLS	2SLS	2SLS	2SLS	2SLS	2SLS
Sample Period	Full	Full	Full	Full	Full	Full	Full	Full	Full	Full	Full	Full
Trend Type	Linear	Linear	Linear	Linear	Linear	Linear	Linear	Linear	HP	HP	HP	HP
Trend Period	88-02	88-02	Full	Full	80-02	80-02	95-02	95-02	88-02	88-02	80-10	80-10
Controls	No	Yes	No	Yes	No	Yes	No	Yes	No	Yes	No	Yes
Price Elasticity	8.79	7.36	8.01	7.18	21.32	12.56	3.04	3.86	4.64	2.38	21.27	20.48
Price Elasticity standard error	(4.50) ^*	(2.98) ^**	(7.22)	(3.94) ^*	(14.57)	(3.77) ^***	(.88) ^***	(1.95) ^**	(2.61) ^*	(5.83)	(6.15) ^***	(6.77) ^***
Observations	229	229	229	229	229	229	229	229	229	229	229	229
First Stage Coefficient	.03	.04	.02	.03	.03	.06	.08	.04	.06	.03	.02	.02
Partial F Statistic	2.06	2.98	.78	2.39	1.83	4.79	2.01	2.56	.86	2.81	9.24	7.72
Partial	.07	.16	.03	.10	.03	.15	.14	.13	.09	.10	.10	.08

Finally, all of the instrumental variables results discussed thus far have used samples limited to the output price boom periods. I have argued that economic conditions during these periods, which began in the aftermath of the 2001 recession, were quite similar to those under which policymakers might like to stimulate investment. Thus they are quite relevant periods during which to estimate supply elasticities. One could nonetheless argue that elasticities could as well be estimated with regressions run over longer samples. Unfortunately, results using longer samples tend to suffer from a weaker first stage relationship between output prices and machinery prices. Table 5 presents exactly the same specifications from Table 4, but estimated over the sample from 1988 to the end of the output price booms. Estimated supply elasticities actually rise relative to the estimates in Table 4 in all except three specifications. However, the first stage partial F statistics are uniformly lower, and, in fact, all are below 10, suggesting that these estimates could be affected by the weak instruments problem. I thus focus on the results from specifications presented above using data from the boom periods only.

I also note that unreported specifications including the "crash" period from the end of the booms through 2010 perform even more poorly than those in Table 5. The first stage relationship disappears or even turns negative, and supply elasticity estimates are highly unstable. An explanation of these results is readily apparent from the data in Figures 3 and 4. During the crash periods when output prices and investment quantities were falling rapidly, machinery prices moved relatively little. Although this fact hinders estimation of a clean first stage relationship over the full sample, it also underscores the central observation of this paper--that business cycle fluctuations in the quantity of machinery supplied are far larger than fluctuations in prices.

4.2 Discussion

Goolsbee (1998) estimated a short-run capital supply elasticity around 1, while I have estimated an elasticity of at least 5. The discrepancy does not stem from the particular types of machinery that I have studied in this paper. Goolsbee (1998) presents estimates of the pass-through of investment tax credits into prices broken out by equipment types (p. 132). His estimate for construction machinery is more than 20% higher than his estimate for the pooled sample, and his estimates for farm and mining machinery are higher still. Thus we should expect lower supply elasticity estimates for these types of equipment than for Goolsbee's pooled sample.

Figure 6: Imports as Share of Machinery Investment

Accessible Version

The question of what drives the discrepancy between my results and Goolsbee's then remains. Whelan (1999) replicates Goolsbee's results and shows that they are not robust to including simple controls for the prices of material inputs to production.¹⁴ Further, Shea (1993) finds evidence that positive demand shocks actually reduced the prices of aircraft and construction machinery when using data from roughly the same period as Goolsbee's. Thus, there are reasons to think that Goolsbee's results may simply be spurious.

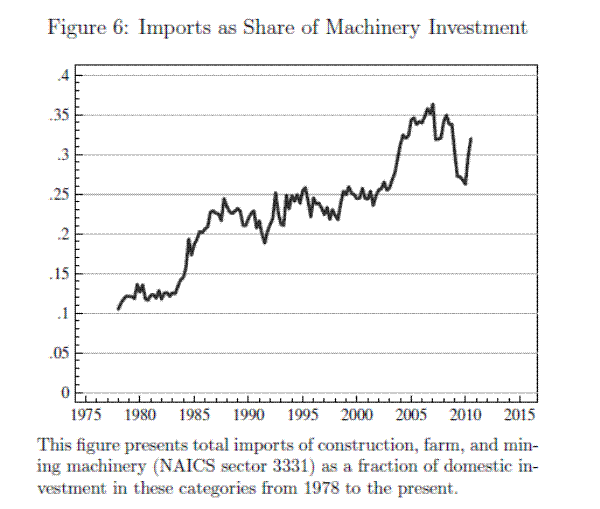
Nonetheless, I also consider the explanation that markets for machinery have changed since the 1962-1988 period covered by Goolsbee's data. For example, Goolsbee finds that evidence for an effect of tax variables on prices is strongest for types of capital that were less subject to import competition. Figure 6 plots construction, farm, and mining machinery imports as a fraction of total domestic investment in these categories from 1978 to 2010, a period for which consistent data are readily available. The figure shows that this import share rose from around 10% in the mid-1970s to more than 35% at its peak in 2006. In fact, Goolsbee's estimates of the impact of the import share on the pass-through of tax incentives into prices would suggest that the observed change in import share is more than enough to reduce his estimated pass-through to zero (Goolsbee (1998), p. 140).¹⁵

Table 6: The Role of Imports in Machinery Supply Expansions During Recent Output Price Booms

	Import Share in Base Year	Import Share of Increase	Production Increase	Imports Increase
Construction	35%	57%	63%	114%
Farm	21%	89%	26%	66%
Mining	15%	21%	90%	187%

The first column presents imports as a fraction of domestic investment in the trough year prior to the investment boom period (2002 for construction and farm machinery and 2001 for mining machinery). The second column presents the increase in real imports as a fraction of the increase in domestic investment over the boom periods. The third and fourth columns present the increase during the boom periods in real domestic production and imports, respectively.

Further, Table 6 shows that the expansion of imported machinery played an outsized role in the overall supply expansion during the output price boom periods. For example, in 2002, about 35% of construction machinery investment was imported from abroad. During the period from 2002 to 2006, however, the increase in construction machinery imports constituted about 57% of the total increase in investment. Production of construction machinery increased about 63% during this period, while imports increased 114%.¹⁶Data on both farm and mining machinery also indicate that imports played a large role in the supply expansion, relative to their fraction of investment prior to the boom.

5 Conclusion

The data presented in this paper speak very clearly: the quantity of machinery supplied to the United States increased rapidly during the output price booms of the early-to-mid-2000s, with only modest increases in prices. Estimates of the supply elasticity during these episodes are around 5, much larger than the estimate of 1 from Goolsbee (1998). Results thus suggest that there is little reason to be concerned that public policies intended to stimulate investment demand would simply push up the prices of investment goods. However, to the extent that policymakers trying to stimulate investment are truly hoping to stimulate domestic production and employment, an increasing share of imports will make their task more complicated. The responses of machinery prices, production, and imports to investment stimulus may now depend on factors like the relative availability of manufacturing capacity in the United States and abroad.

Note finally that the results presented here need not suggest that policymakers' attempts to stimulate business investment in recent years have been successful. This paper's results do suggest that the impact of policies that succeeded in stimulating demand for investment would not have been severely blunted by the inelasticity of machinery supply. However, as noted earlier, there remains considerable debate over whether recent stimulus provisions have, in fact, succeeded in stimulating demand.

A. Derivation of results in Section 2

Solve for ,

$\displaystyle q$	$\displaystyle = \beta p + \epsilon_s$
$\displaystyle \gamma_1 p + \gamma_2 z + \epsilon_d$	$\displaystyle = \beta p + \epsilon_s$
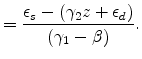$\displaystyle p$	$\displaystyle = \frac{\epsilon_s - (\gamma_2 z + \epsilon_d)}{ (\gamma_1 - \beta)}.$

Plug into the OLS bias term,

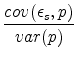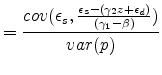$\displaystyle \frac{cov(\epsilon_s,p)}{var(p)}$	$\displaystyle = \frac{cov(\epsilon_s, \frac{\epsilon_s - (\gamma_2 z + \epsilon_d)}{ (\gamma_1 - \beta)})}{var(p)}$
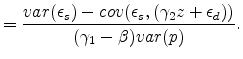	$\displaystyle = \frac{var(\epsilon_s) - cov(\epsilon_s, (\gamma_2 z + \epsilon_d))}{ (\gamma_1 - \beta)var(p)}.$

Solve for

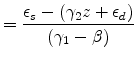$\displaystyle p$	$\displaystyle = \frac{\epsilon_s - (\gamma_2 z + \epsilon_d)}{ (\gamma_1 - \beta)}$
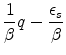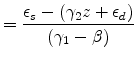$\displaystyle \frac{1}{\beta} q - \frac{\epsilon_s}{\beta}$	$\displaystyle = \frac{\epsilon_s - (\gamma_2 z + \epsilon_d)}{ (\gamma_1 - \beta)}$
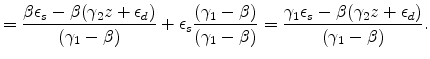$\displaystyle q$	$\displaystyle = \frac{\beta \epsilon_s - \beta (\gamma_2 z + \epsilon_d)}{ (\gamma_1 - \beta)} + \epsilon_s \frac{ (\gamma_1 - \beta) }{ (\gamma_1 - \beta)} = \frac{\gamma_1 \epsilon_s - \beta (\gamma_2 z + \epsilon_d)}{ (\gamma_1 - \beta)}.$

Plug into the reverse OLS bias term,

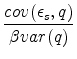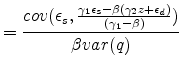$\displaystyle \frac{cov(\epsilon_s,q)}{\beta var(q)}$	$\displaystyle = \frac{cov(\epsilon_s, \frac{\gamma_1 \epsilon_s - \beta (\gamma_2 z + \epsilon_d)}{ (\gamma_1 - \beta)} )}{\beta var(q)}$
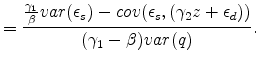	$\displaystyle = \frac{ \frac{ \gamma_1}{\beta} var(\epsilon_s) - cov(\epsilon_s,(\gamma_2 z + \epsilon_d) )}{ (\gamma_1 - \beta) var(q)} .$

Bibliography

Bureau of Labor Statistics.
BLS Handbook of Methods, 2008.

http://www.bls.gov/opub/hom/.

Robert S. Chirinko.
Business fixed investment spending: Modeling strategies, empirical results, and policy implications.
Journal of Economic Literature, 31(4):pp. , 1875

-1911, 1993.

Lawrence J. Christiano, Martin Eichenbaum, and Charles L. Evans.
Nominal rigidities and the dynamic effects of a shock to monetary policy.
Journal of Political Economy, 113(1):1-45, 2005.

Darrel S. Cohen and Jason G. Cummins.
A Retrospective Evaluation of the Effects of Temporary Partial Expensing.
FEDS Working Paper Series, 2006

(19), 2006.

Rochelle M. Edge and Jeremy B. Rudd.
General-equilibrium effects of investment tax incentives.
FEDS Working Paper Series, 2010

(17), 2010.

Rochelle M. Edge, Michael T. Kiley, and Jean-Philippe Laforte.
Natural rate measures in an estimated DSGE model of the U.S. economy.
Journal of Economic Dynamics and Control, 32(8):, 2512

- 2535, 2008.

Jesse Edgerton.
Taxes and business investment: New evidence from used equipment.
Unpublished working paper, 2009.

Austan Goolsbee.
Investment tax incentives, prices, and the supply of capital goods.
The Quarterly Journal of Economics, 113(1):121-148, 1998.

Jinyong Hahn and Jerry Hausman.
A new specification test for the validity of instrumental variables.
Econometrica, 70(1):163-189, 2002.

Robert E. Hall and Dale W. Jorgenson.
Tax policy and investment behavior.
The American Economic Review, 57(3):391-414, June, 1967.

James D. Hamilton.
Understanding crude oil prices.
NBER Working Paper Series, (14492), November, 2008.

Christian Hansen, Jerry Hausman, and Whitney Newey.
Estimation with many instrumental variables.
Journal of Business and Economic Statistics, 26(4):398-422, 2008.

Kevin A. Hassett and R. Glenn Hubbard.
Are investment incentives blunted by changes in prices of capital goods?
International Finance, 1(1):103, October , 1998.

Kevin A. Hassett and R. Glenn Hubbard.
Chapter 20 tax policy and business investment.
volume 3 of Handbook of Public Economics, pages, 1293

- 1343. Elsevier, 2002.

Jerry A. Hausman.
Specification and estimation of simultaneous equation models.
In Z. Griliches and M. D. Intriligator, editors, Handbook of Econometrics, volume 1, chapter 7, pages 391-448. Elsevier, 1983.

Christopher L. House and Matthew D. Shapiro.
Temporary investment tax incentives: Theory with evidence from bonus depreciation.
The American Economic Review, 98:737-768(32), 2008.

Dale W. Jorgenson, Mun S. Ho, and Kevin J. Stiroh.
A retrospective look at the U.S. productivity growth resurgence.
Journal of Economic Perspectives, 22(1):3 - 24, 2008.

Robert G. King and Sergio T. Rebelo.
Chapter 14: Resuscitating real business cycles.
volume 1, Part 2 of Handbook of Macroeconomics, pages 927 - , 1007.

Elsevier, 1999.

Donald Mitchell.
A Note on Rising Food Prices.
World Bank Policy Research Working Papers, , (4682),

2008.

James M. Sallee.
The incidence of tax credits for hybrid vehicles.
Working Paper, 0815

, Harris School of Public Policy, University of Chicago, 2009.

John Shea.
Do supply curves slope up?
The Quarterly Journal of Economics, 108(1):1-32, 1993.

Frank Smets and Raf Wouters.
An estimated dynamic stochastic general equilibrium model of the euro area.
Journal of the European Economic Association, 1(5):, 1123

-1175, 2003.

James H. Stock, Jonathan H. Wright, and Motohiro Yogo.
A survey of weak instruments and weak identification in generalized method of moments.
Journal of Business and Economic Statistics, 20(4):518-529, 2002.

Lawrence Summers.
Taxation and corporate investment: A Q-theory approach.
Brookings Papers on Economic Activity, 1981

(1):67-140, 1981.

Karl Whelan.
Tax incentives, material inputs, and the supply curve for capital equipment.
FEDS Working Paper Series, 1999

(21), April 1999.

Footnotes

* Email: [email protected]. Any views expressed here are those of the author only and need not represent the views of the Federal Reserve Board or the Federal Reserve System. I thank Robert Chirinko, Glenn Ellison, Jane Gravelle, Michael Greenstone, Anne Hall, Jerry Hausman, David Lebow, Steve Oliner, James Poterba, Nirupama Rao, Hui Shan, Dan Sichel, Johannes Spinnewijn, Jessica Stahl, Stacey Tevlin, and numerous seminar participants for helpful comments. Portions of the material in this paper originally circulated under the title, "Taxes and Used Equipment: Evidence from Construction Machinery" and appeared in Chapter 1 of my dissertation at the Massachusetts Institute of Technology. Return to Text

1. General equilibrium models have often abstracted from the distinction between investment goods and other output. Standard Real Business Cycle models like that in King and Rebelo (1999) allow ouput to be allocated frictionlessly to either consumption or investment. An increase in investment might require an increase in interest rates to dissuade consumption, but there is no sense in which an increasing amount of consumption must be foregone to produce an additional unit of capital when investment is high or growing. Modern DSGE models used for policy analysis (like those in Christiano, Eichenbaum, and Evans (2005), Smets and Wouters (2003), Edge, Kiley, and Laforte (2008), and Edge and Rudd (2010)) typically feature an adjustment cost that essentially makes some portion of investment disappear when investment would otherwise increase rapidly. This formulation captures the notion that an increasing amount of consumption must be foregone to produce a unit of capital when investment is growing rapidly. It does not, however, reflect the fact that the benefits of investment subsidies would be captured by suppliers of investment goods, a point stressed by Goolsbee (1998). Return to Text

2. Some economists prefer the term "supply relationship" to reflect the fact that a demand-invariant relationship between price and the quantity supplied need not exist when markets are not perfectly competitive. Results in the paper do not depend on the assumption of competitive markets, but I use the familiar term "supply curve" anyway. Return to Text

3. For example, Robert Solow wrote in the New York Review of Books, "The word "bubble" is often misused; but there was a housing bubble. Rising house prices induced many people to buy houses simply because they expected prices to rise; those purchases drove prices still higher, and confirmed the expectation. Prices rose because they had been rising." Return to Text

4. This calculation uses the approximation that the share $-\eta_d/(\eta_s - \eta_d)$ of a small subsidy is passed to suppliers in a competitive market, for $\eta_d$ the elasticity of demand and $\eta_s$ the elasticity of supply. Return to Text

5. Again, if markets are not competitive, there need not exist a demand-invariant supply curve that maps the market price into the quantity supplied. In this case, the parameter $\beta$ should be thought of as a summary measure of the extent to which prices and quantities move together in response to demand shocks, regardless of whatever structure might underlie this relationship. I continue to refer to $\beta$ as the "supply elasticity" for brevity and to facilitate comparison to Goolsbee's results. Return to Text

6. When multiple instrumental variables are available, Hahn and Hausman (2002) provide a formal specification test based on the notion that forward and reverse 2SLS estimates should also be close together. I experimented with using multiple instruments to implement such tests with the data used in this paper. Unfortunately, the output price variables that I use as instruments in this paper are highly colinear. Including more than of them tended to produce first stage estimates that made little sense, with, for example, some price variables having the wrong sign. Although the forward and reverse IV estimates from these tests were still often close together, I do not include them in the paper due to the poor performance of the first stage.

The Hahn and Hausman (2002) test can be motivated by the concern that weak instruments combined with finite sample bias could produce badly biased IV estimates. Hahn and Hausman (2002) show that this bias will be most severe when the number of instruments is large, the explanatory power of the first stage is weak, and the error terms in the structural and first-stage equations are highly correlated. In the current application, I use only one instrument, which produces a strong first stage, suggesting that the finite sample bias is not a serious concern. However, the lack of convincing identification when using multiple instrumental variables prevents me from conducting a convincing formal test. Return to Text

7. In some specifications I include additional control variables: the Baa corporate borrowing rate from the Federal Reserve's H.15 release, hourly compensation for all persons in the manufacturing sector from the Bureau of Labor Statistics, the Producer Price Index for fuels and energy from the Bureau of Labor Statistics, the broad dollar exchange rate index from the Federal Reserve's H.10 release, and real Gross Domestic Product from the Bureau of Economic Analysis. Return to Text

8. These figures are actually changes in log points, which, of course, become poorer approximations to percentage changes when changes are large. Return to Text

9. In fact, these quantity fluctuations are not confined to the output price boom periods on which I focus in this paper. One might even argue that it should be obvious from looking at these simple charts that quantities can fluctuate a great deal with only small movements in prices. One might thus question the usefulness of the results presented in this paper. I would remind anyone making this argument that the results in Goolsbee (1998) indicate that prices should move one-for-one with quantities when there is a shift in demand. Thus this paper is advancing an argument contrary to that currently in the literature. Return to Text

10. In fact, legislation did enact "bonus depreciation" tax provisions in 2002 and expand them in 2003. As these provisions were intended to create shifts in the demand curve for machinery, they could also potentially be of use in estimating the supply curve. However, several authors have presented estimates suggesting that bonus depreciation had little impact on demand for the kinds of machinery studied here (see, for example, Cohen and Cummins (2006), Edgerton (2009), and House and Shapiro (2008)), so I do not pursue this identification strategy. Note also that as bonus depreciation is another potential demand shifter, there is no direct channel through which ignoring it would bias my estimate of the supply elasticity. Return to Text

11. The standard errors for the "reverse" elasticity estimates in Columns 2 and 4 are computed using the delta method around the reverse regression coefficient. Return to Text

12. In fact, their results are for the case where error terms are homoskedastic and uncorrelated across observations. It nonetheless appears to be standard empirical practice to apply the rule of thumb when standard errors are clustered or robust to serial correlation, as in this application. To be clear, the F statistics reported in the table are based on the Newey-West covariance matrices and are noticeably smaller than standard OLS F statistics. Return to Text

13. Note also that this pooling will force the first stage coefficient estimate to be the same for each machinery type, where these coefficients vary somewhat across types in Table 1. One could correct this problem by scaling the price instruments by appropriate constants before running the pooled regressions. In unreported results, I find that this scaling increases the estimated price elasticity by a small amount. Return to Text

14. In particular, the 1974 expansion of the investment tax credit nearly coincided with the beginning of the OPEC oil embargo in late 1973. During the period from then until the mid-1980s, the investment tax credit was at its strongest historical level, and both oil and other commodity prices were well above their trend levels. Figures in the paper suggest that year-to-year changes in equipment prices are more closely related to these input prices than to the investment tax credit. Return to Text

15. Note that Goolsbee's import share variable is constructed as

, while Figure 6 plots

. The former measure increased from about 0.08 in the late 1970s to 0.17 in the early 2000s and 0.25 in the mid-2000s. Goolsbee's estimated coefficient on an interaction of this variable with his tax variable is 2.774, and the main effect of the tax variable is -.452. Thus the full effect of a change in the tax variable with the import share at 0.08 is -0.23, and the effect at 0.17 is 0.02. Return to Text

16. Note that there is no identity that must relate these numbers to each other, as machinery exports are also a significant portion of domestic production. Further, the investment data from the BEA are adjusted for the shares of machinery that are purchased by households and government, while the import and export data used here are not. Return to Text

^♣ This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to Text

Estimating Machinery Supply Elasticities Using Output Price Booms

Figure 3 Panel A: Recent Output Price Booms

Figure 3 Panel B: Recent Output Price Booms

Figure 3 Panel C: Recent Output Price Booms

Figure 4 Panel A: Machinery Prices and Quantities

Figure 4 Panel B: Machinery Prices and Quantities

Figure 4 Panel C: Machinery Prices and Quantities

Figure 5 Panel A: Recent Output Price Booms Tracing out Machinery Supply Curves

Figure 5 Panel B: Recent Output Price Booms Tracing out Machinery Supply Curves

Figure 5 Panel C: Recent Output Price Booms Tracing out Machinery Supply Curves

Figure 6: Imports as Share of Machinery Investment