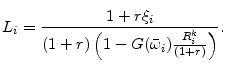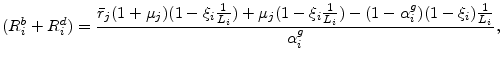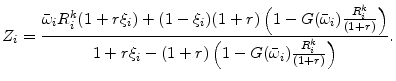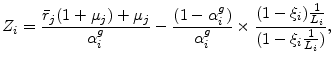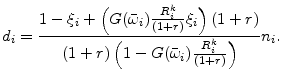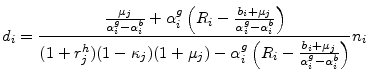Verifying the State of Financing Constraints: Evidence from US Business Credit Contracts
Keywords: Micro foundations of financing constraints, credit contracts, small business financing
Abstract:
1 Introduction
Economists have long recognized the importance of financial frictions to explain macroeconomic data or firm growth patterns. Commonly used macroeconomic models and firm growth models include a financing constraint induced by either costly state verification (CSV), pioneered by Townsend (1979), or moral hazard, pioneered by Holmström and Tirole (1997) (MH). While the microfoundations of other frictions, such as price or wage ridigities, have been subject to intensive empirical scrutiny, it is less clear whether these types of financing constraints are plausible vis-à-vis actual credit contracts.
In contrast with the earlier literature, I assess the empirical plausibility of particular models of financing constraints directly using micro-based evidence from debt contracts. The first model, CSV, lies at the heart of financial frictions in macroeconomic and firm growth models.1 Entrepreneurs invest in part with external finance in risky return projects. Lenders that provide external finance incur a cost to observe the realized returns. These state verification costs of bankruptcy lead to a breakdown of the Modigliani-Miller theorem.
Using credit amounts, net worth, interest rates, and probabilities of bankruptcy in the Surveys of Small Business Finances (SSBF), I solve for the bankruptcy costs, rates of return, and riskiness implied by the optimal debt contract with the CSV model. More than two thirds of the credit contracts can be rationalized with CSV debt contracts. In line with the literature, the implied bankruptcy costs are 28 percent of expected output, and the implied rate of return lies between 5 percent and 8 percent annually. Thus, CSV is an empirically plausible model of financing constraints.
The second model, MH, explicitly models bank capital as a scarce resource. The underlying assumption is that only banks possess a monitoring technology. Banks monitor entrepreneurs to ensure that they invest in high quality projects. Investors (depositors) are willing to invest in these projects (in a bank) as long as the bank's incentives to monitor are high-powered. Chen (2001) and Meh and Moran (2010), for instance, include this type of financing frictions to assess the role of bank capital over the business cycle.
To assess the empirical plausibility of MH, I add information about the bank's adequacy ratio, rate of return, interest expenses, and non-interest expenses to the SSBF data. Using this information I calculate the interest rate implied by MH. The correlation between model implied interest rates and actual interest rates is close to zero. Second, instead of using non-interest expense as proxy for monitoring cost, I solve for the implied monitoring cost. This yields mostly empirically implausible values. Last, I complement the structural analysis with reduced form regressions and find that in almost all instances bank variables cannot explain the interest rate. For large banks in the 2003 sample, some bank variables have a significant effect on the interest rate paid. But, since the small business lending market is dominated by small banks, MH appears to be empirically implausible. To be clear, while my findings do not support the MH model, bank variables may still be important for the loan supply (Berrospide and Edge, 2010; Bernanke and Lown, 1991; Handcock and Wilcox, 1993,1994).
In both models, a key deviation from perfect capital markets is that agency problems between entrepreneurs and lenders restrict external finance to some multiple of the entrepreneur's net worth. Many authors have used this reduced-form collateral constraints without explicitly modeling the underlying frictions.2
Consistent with models of financing frictions an additional dollar of net worth accounts for about 30 cents of additional external finance. This finding is robust to alternative definitions of net worth and the inclusion of a large set of controls. While there are some differences between small and large banks in the 1998 sample, the point estimates are the same for both groups in the 2003 sample. Different from CSV, the interest rate paid in MH, in equilibrium, also depends on the cost of bank capital, the financing cost of a bank, and the adequacy ratio of the bank - that is, the equity share of assets. Again, contrary with the predictions of the MH model, bank variables have no significant effect.
This comprehensive, micro evidence-based analysis of financing constraints has the advantage of focusing on small businesses, that are bank-dependent and have no access to bond markets. Small businesses are defined as firms with up to 500 employees, reported in the SSBF from 1998 and 2003. Only a few small firms attract additional outside equity. Therefore, the SSBF samples represent the population closest to standard models of lending; an entrepreneur without means of financing except to sign a debt contract with a lender (bank).3
While small, these businesses account for about one half of GDP, and they disproportationately contribute to labor market volatility (Haltiwanger, Jarmin, and Miranda, 2010). So, a second advantage of focusing on small business is to gain insights about the importance of financing frictions for the analysis of the labor market (Wasmer and Weill, 2004).
The SSBF provide detailed information about firms and their owners, including firms' balance sheets and private net assets. The credit contract information includes the bank's name, the loan amount, the interest rate, and collateral used. The latter shows the importance of private net worth in the small business credit market as small business owners often collateralize business credits with their private residence.
To evaluate the empirical support of the CSV and MH models, I need to construct net worth of the merged firm-entrepreneur entity. To be consistent with the banks' definition of net worth, the construction of net worth of the firm-entrepreneur entity follows the collateral requirements. Surprisingly, banks accept almost every type of asset on the firms' balance sheets as collateral. In addition, small business owners secure credits with private residential property or personal guarantees. Since the SSBF include the net value of the private residence, I am able to construct net worth in a way that matches the banks' definition.
Using the confidential SSBF data that in many cases include unique identifier for financial institutions, I append the SSBF data with crucial bank characteristics from the Reports of Condition and Income (Call Reports), the Thrifts Financial Reports, and Call Reports for credit unions. For previously unmatched observations, I use the lender's name to identify commercial banks, savings banks, thrifts, and credit unions. I exclude financing companies. In total I match 53 percent of the 1998 sample and 79 percent of the 2003 sample to banks and credit unions.
Previous studies, starting with Fazzari, Hubbard, and Petersen (1988), inferred financing constraints using cash flow sensitivities of investment.4 However a large literature criticizes this approach. These cash flow sensitivities depend on the author's discretion (Kaplan and Zingales, 2000), can occur in frictionless models (Alti, 2003; Gomes, 2001), or are the result of measurement error in Tobin's q (Cummins, Hassett, and Oliner, 2006). Others employ structural estimation of entrepreneurship or household models to infer parameters of financing constraints (Evans and Jovanovic, 1989; Hennessy and Whited, 2007) or to distinguish between different models of financing constraints (Paulson, Townsend, and Karaivanov, 2006) without using debt contracts.
Offering an alternative approach, Chava and Roberts (2008) analyze debt contracts of large firms and find that the violation of debt covenants reduces investment. However, with the exception of Levin, Natalucci, and Zakrajsek (2004) who use bond data, there is little direct, micro-based evidence from debt contracts supporting the standard modeling strategies of financing constraints in macroeconomic models or firm growth models.5
Employing a comprehensive data set of US small business credit contracts, I circumvent the problem of identifying financially constrained firms. This paper therefore provides the, thus far lacking, micro-based evidence by exploiting credit contracts of US small businesses to test specific models of financing constraints. While the debt constract with costly state verification is an empirically plausible model, the moral hazard in model, put forward by Holmström and Tirole (1997), appears to be inconsistent with the matched small business-bank data as bank variables, emphasized by this model, do not explain loan interest rates or credit amounts.
The paper proceeds as follows: Section 2 describes and tests the empirical plausiblity of the debt contract with costly state verificiation. Section 3 introduces the moral hazard model of financing constraints and assess its empirical plausibility. In section 4 I test an additional implication of the both models - reduced-form collateral constraints. Differences by bank size are discussed in section 5. Section 6 concludes.
2 Costly State Verification
This section first describes the debt contract with CSV. I then summarize the data used to assess the empirical plausibility of this model. Last, I present the parameter distribution for the rate of return and bankruptcy cost implied by the debt contract with CSV for each observation in the data.
2.1 The debt contract with CSV
The CSV recognizes asymmetric information between the lender and the borrower. The lender can not observe the outcome of a leveraged project. In case of bankruptcy the lender incurs a cost to verify the outcome. This costly state verification ties the ability to obtain credit to the net worth of an entrepreneur (Townsend, 1979). Gale and Hellwig (1985) show that in a world with costly state verification the optimal, incentive-compatible financial contract is the standard debt contract. The debt contract with CSV is now widely used in macroeconomic models and models of firm growth.6
To derive the optimal one period debt contract, I first describe the preferences and technology of both borrowers and lenders. Risk neutral entrepreneurs own a risky return technology; entrepreneurs can finance their capital stock with equity and debt. If an entrepreneur borrows, she signs the standard one period debt contract which in the presence of costly state verification is the optimal contract. To better understand the implications of the underlying financing constraint, I abstract from aggregate uncertainty, differences in productivity and equity issuance.7
Let ![]() be the capital stock used in production by entrepreneur
be the capital stock used in production by entrepreneur ![]() . The vast
majority of credit applications in the data, which I describe in the next section show that credit is used for working capital. Hence, I consider the case of full depreciation. The entrepreneur can only use a fraction
. The vast
majority of credit applications in the data, which I describe in the next section show that credit is used for working capital. Hence, I consider the case of full depreciation. The entrepreneur can only use a fraction ![]() of her net worth
of her net worth ![]() in production but can borrow
in production but can borrow
![]() to produce at scale
to produce at scale ![]() . She signs a one period debt contract with
a financial intermediary, the lender, specifying the credit amount and the gross interest rate
. She signs a one period debt contract with
a financial intermediary, the lender, specifying the credit amount and the gross interest rate ![]() . The fraction
. The fraction ![]() of net worth is pure collateral such as land or buildings. In line with financing constraints employed in macroeconomic models I assume a constant returns to scale technology. The payoff of production with external financing is:
of net worth is pure collateral such as land or buildings. In line with financing constraints employed in macroeconomic models I assume a constant returns to scale technology. The payoff of production with external financing is:
| (1) |
where in the first term
Financial intermediaries, offering loans to entrepreneurs, are risk neutral, perfectly competitive, and hold perfectly diversified portfolios. The opportunity cost of funds for financial intermediaries is the economy's riskless gross rate of return ![]() . Financial intermediaries do not observe the realization of the idiosyncratic productivity shock. Lenders have to pay a cost to be able to observe the borrower's productivity shock. As in Carlstrom and
Fuerst (1997) monitoring costs in the case of bankruptcy are assumed to be a fraction
. Financial intermediaries do not observe the realization of the idiosyncratic productivity shock. Lenders have to pay a cost to be able to observe the borrower's productivity shock. As in Carlstrom and
Fuerst (1997) monitoring costs in the case of bankruptcy are assumed to be a fraction ![]() of the expected output.
of the expected output.
The entrepreneur defaults on the debt if after the realization of the idiosyncratic shock she does not have enough resources on hand to pay back the loan. Let
![]() be the cutoff productivity for which the entrepreneur can just repay her debts:
be the cutoff productivity for which the entrepreneur can just repay her debts:
In case of default the financial intermediary pays the monitoring cost
| (3) |
Financial intermediaries are assumed to be perfectly competitive. Their zero profit condition has to hold in expectation on each contract. Using equation (2), the zero profit condition of the lender can be written as:
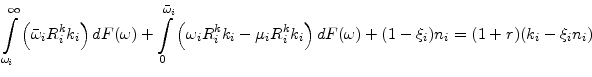 |
(4) |
and the entrepreneur's expected income is:
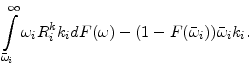 |
(5) |
The loan contracts, in general, specify a pair of
| (6) |
subject to
| (7) |
where
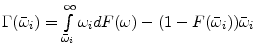 is the firm's share of output and
is the firm's share of output and
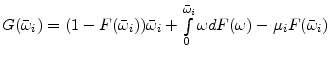 is the the lender's share of output. The combined shares of
the lender and the borrower are together less than 1:
is the the lender's share of output. The combined shares of
the lender and the borrower are together less than 1:
Note that
The zero profit condition of the lender implies that the amount of credit covered by collateral,
The optimal contract trades off the return on an additional unit external finance against a rise in bankruptcy states, i.e. higher agency costs. The equilibrium contract, defined as a pair of
![]() , depends on four parameters: 1) the external finance premium
, depends on four parameters: 1) the external finance premium
![]() , 2) the variance of the idiosyncratic shock
, 2) the variance of the idiosyncratic shock ![]() which
measures risk, 3) the bankruptcy cost
which
measures risk, 3) the bankruptcy cost ![]() , and 4) the fraction of net worth used in production
, and 4) the fraction of net worth used in production ![]() .
.
2.2 Credit Contracts and Net Worth Data
I now describe the data used to assess the empirical plausibility of the debt contract with CSV. In particular, I summarize the construction of the crucial variables: the net worth ![]() ,
the probability of bankruptcy
,
the probability of bankruptcy
![]() , the credit amount
, the credit amount ![]() , the share of collateral
, the share of collateral ![]() and the interest rate
and the interest rate ![]() .
.
The Survey of Small Business Finances (until 1998 National Survey for Small Business Finances) was conducted by the Federal Reserve Board for the fiscal years ending in 1987, 1993, 1998 and 2003. The surveys aim to assess credit availability, to provide financial statement data of small firms, and to study the effects of changes through technology and mergers in the banking sector. Within the surveys, small businesses are defined as firms with fewer than 500 employees. The representative samples were drawn from the Dun and Bradstreet database.11 In addition to the standard firm characteristics such as number of employees, sales, region, and industry, the SSBF also provide additional information on the most recent credit (amount, interest rate) and measures of riskiness of a credit: the Dun and Bradstreet credit score and indicators whether the firm had declared bankruptcy or has delinquent obligations or judgments. For the business owner, the same indicators are available except for the personal credit score.
Personal net worth, separated by net home value and other assets, is the crucial variable used to construct net worth of a merged firm-household entity and is only available for the 1998 and 2003 surveys only.12 I therefore restrict my analysis to the last two cross sections. The SSBF provides a final, representative sample of 3,561 firms in 1998 and 4,240 firms in 2003. The sample weights imply that the 1998 sample represents 5,291,245 firms and the 2003 sample represents 6,298,087 firms.Table 1 summarizes the the standard firm characteristics for the SSBF data employed here.13
To evaluate the debt contract with CSV, I use the SSBF data to construct net worth of the firm-household entity (![]() ) as follows. The literature defines net worth as maximum
(collateralizable) assets, which is the sum of liquid and collateralizable illiquid assets less all obligations.14 For small businesses, the owner may
collateralize credit with private net worth. To construct a measure of net worth of the firm-household entity that is consistent with a bank's definition of net worth, I examine the application process and the collateral accepted by banks in detail.
) as follows. The literature defines net worth as maximum
(collateralizable) assets, which is the sum of liquid and collateralizable illiquid assets less all obligations.14 For small businesses, the owner may
collateralize credit with private net worth. To construct a measure of net worth of the firm-household entity that is consistent with a bank's definition of net worth, I examine the application process and the collateral accepted by banks in detail.
Giambona and Schwienbacher (2008) argue that only "hard" tangible assets, namely land and buildings, can be collateralized. Yet almost 45 percent used equipment as collateral, 23 percent their business real estate, and 24 percent used their private residence. Accounts receivable and inventory was accepted as collateral in 23 percent of the cases.15 The main difference between the two surveys is the shift from equipment (1998: 55 percent, 2003: 39 percent) to the private residence (1998: 15 percent, 2003: 29 percent) as the source of collateral. The increase in the house prices between the two samples may explain this shift. While in the 1998 sample the average net value of the private residence is $128,915 (median: $75,000), the average net value of the private residence increases to $232,632 (median: $120,000) in the 2003 sample. Only about 6 percent use "other" personal assets beyond the private residence to collateralize their credit.
Alternatively owners can provide a personal guarantee - that is, the owner declares an individual pledge to repay the business loan. Depending on the credit contract, the owner can be held responsible for the business loan even if the business is protected by limited liability laws or gets dissolved. In the pooled 1998 and 2003 SSBF 52 percent of the firms reported that collateral was required to receive credit, 54 percent gave personal guarantees, and 30 percent of business owners provided both. This is in line with Sullivan, Warren, and Westbrook (1989) who, using bankruptcy data, show that entrepreneurs are more likely to file personal bankruptcy as firm credits are collateralized or guaranteed by the owner's private net worth.
The patterns of collateral strongly suggest a wider definition of net worth than the one advocated by Giambona and Schwienbacher (2008). I construct net worth from the data as follows: Using balance sheet information, I subtract all liabilities from total assets to
calculate firm equity. Following the patterns of collateral, I add the net value of the private residence for firm owners who own a house. Table 2 displays the equity share of total assets - total equity divided by total assets (firm+residence),
![]() , which is the inverse of leverage.16 The equity share of assets of a firm-household entity with negative equity is 0. Table 2 provides the summary statistics for the full sample and for firms that received credit. Not that not all firms applied for and received credit.
Younger firms have less net worth and a lower equity share of assets than older firms. Similarly, firms that received credit have more net worth than the average firm in the total sample in each age group. However, the equity shares of firms that received credit are indistinguishable from the total
sample. On average the equity shares translate into a leverage (the capital to net worth ratio) of 1.5 or an equity to debt ratio of 2, and lie in the range of 1.3 to 2 documented by Masulis (1988).
, which is the inverse of leverage.16 The equity share of assets of a firm-household entity with negative equity is 0. Table 2 provides the summary statistics for the full sample and for firms that received credit. Not that not all firms applied for and received credit.
Younger firms have less net worth and a lower equity share of assets than older firms. Similarly, firms that received credit have more net worth than the average firm in the total sample in each age group. However, the equity shares of firms that received credit are indistinguishable from the total
sample. On average the equity shares translate into a leverage (the capital to net worth ratio) of 1.5 or an equity to debt ratio of 2, and lie in the range of 1.3 to 2 documented by Masulis (1988).
It is worth noting that in the 2003 SSBF more than 63 percent of the entrepreneurs used credit for working capital while about 20 percent indicated investment activity (9.9 percent vehicles loans and 10.2 percent equipment loans) and another 9.4 percent took out mortages. In the 1998 SSBF the share of credit used for investment activity is roughly 35 percent. This is mainly because renewals of credit lines were not included in the 1998 questionaire. Only 6-8 percent of the samples raised new equity. The usage of new equity in both surveys exhibits the same pattern. Since most of the credit is used for working capital, I assumed complete depreciation in the previous section.
To fit the debt contract with CSV described in the previous section to the data, I use the net worth of the firm-household entity for ![]() . Information on the most recent loan application
and the riskiness of the loan are used to proxy for additional parameters of the model. In particluar, the SSBF information on the firm's most recent loan application include the bank's name, whether the credit application was approved and if so the details of the credit contract; in particular,
the loan amount (
. Information on the most recent loan application
and the riskiness of the loan are used to proxy for additional parameters of the model. In particluar, the SSBF information on the firm's most recent loan application include the bank's name, whether the credit application was approved and if so the details of the credit contract; in particular,
the loan amount (![]() ) and the interest rate (
) and the interest rate (![]() ). The share of collateral
(
). The share of collateral
(![]() ) is proxied by the share of fixed assets (land, buildings, and machinery). The Dun and Bradstreet credit score, included in the SSBF, measures the probability of bankruptcy (
) is proxied by the share of fixed assets (land, buildings, and machinery). The Dun and Bradstreet credit score, included in the SSBF, measures the probability of bankruptcy (
![]() ).
).
2.3 Fitting the CSV Debt Contract
To assess the empirical plausibility of CSV as modeling strategy for financing constraints, two questions need be answered: i) whether parameters for the model can be derived from the actual debt contracts - that is, whether a system of equations constituting the CSV contract can be solved for
each observation - and ii) if so, whether the implied parameter values for the bankruptcy cost and the rate of return are plausible when compared to studies of bankruptcies and returns to entrepreneurial capital investments. For this purpose, I use the observed credit contract characteristics -
credit amount, interest rate, net worth, and credit score - to solve for the implied parameters of a CSV debt contract. The share of fixed assets, such as land and buildings, of total firm assets in SSBF is 0.33. Hence, the fraction of the net worth used in production ![]() is on average 0.67.
is on average 0.67.
The methodology follows Levin, Natalucci, and Zakrajsek (2004). While Levin, Natalucci, and Zakrajsek (2004) use bond data to construct empirical equivalents to one period debt contracts and to analyze CSV, this study uses bank credit contracts
to back out the implied parameters - the agency cost ![]() , the standard deviation of the underlying log-normal distribution
, the standard deviation of the underlying log-normal distribution ![]() , the rate of return
, the rate of return ![]() , and the cutoff productivity
, and the cutoff productivity
![]() - of the CSV credit contract for each observation
- of the CSV credit contract for each observation ![]() in the SSBF. The
following four equations need to be solved by the parameters: (i) the definition of the cutoff productivity, equation (2),
in the SSBF. The
following four equations need to be solved by the parameters: (i) the definition of the cutoff productivity, equation (2),
(ii) the optimality conditions, equations (8) and (19),
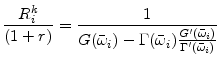 |
and
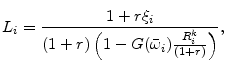 |
and (iii) the probability of bankruptcy
The distribution of the idiosyncratic shock ![]() is log-normal with
is log-normal with
![]() . In the data firms differ in their rate of return
. In the data firms differ in their rate of return ![]() , risk
, risk
![]() , and bankruptcy cost
, and bankruptcy cost ![]() . For instance, an increase in the rate of
return increases the returns to external finance and this implies that a higher leverage is therefore optimal. This also implies a higher cutoff productivity and thereby a higher interest rate paid on the loan
. For instance, an increase in the rate of
return increases the returns to external finance and this implies that a higher leverage is therefore optimal. This also implies a higher cutoff productivity and thereby a higher interest rate paid on the loan ![]() . An increase in variance of the idiosyncratic shock, on the other hand, makes low productivity states more likely to occur as
. An increase in variance of the idiosyncratic shock, on the other hand, makes low productivity states more likely to occur as
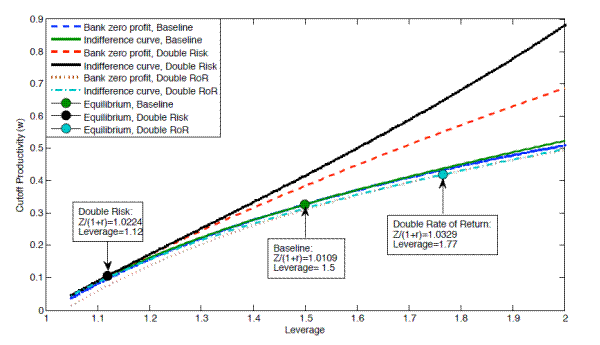
![]() . With a higher variance optimal contract exhibits a lower leverage and a higher interest rate (see Figure 1). Incomplete depreciation does not
change these results but scales up leverage and reduces the probability of bankruptcy.
. With a higher variance optimal contract exhibits a lower leverage and a higher interest rate (see Figure 1). Incomplete depreciation does not
change these results but scales up leverage and reduces the probability of bankruptcy.
In constructing leverage ![]() , I use the credit amount on the most recent credit and net worth. The interest rate on the credit in the data is used to calibrate
, I use the credit amount on the most recent credit and net worth. The interest rate on the credit in the data is used to calibrate ![]() in equation (2). The risk free rate
in equation (2). The risk free rate ![]() is set to the Fed Funds
Rate at the time the credit was contracted. The annual risk free rate is about 5 percent for the 1998 SSBF and 1 percent for the 2003 observations depending on the respective quarter the loan was taken out. The bankruptcy rate is taken from the Dun and Bradstreet credit scores. The credit scores
provided in the SSBF indicate the probability of delinquency (payments are at least 90 days late) rather than bankruptcy.17 Therefore, I assume that firms
that are more like to miss payments are also more likely to file for bankruptcy. I scale the probability of delinquency incidents to match a quarterly bankruptcy rate of 1 percent as reported in Fisher (1999). This yields that firms with the highest score (6) have a
quarterly failure probability of 0.19 percent while 4.44 percent of firms with the lowest credit score (1) are expected to fail in the 2003 sample. In 1998, the probability of failure for the best (worst) risks is 0.15 percent (3.52 percent).
is set to the Fed Funds
Rate at the time the credit was contracted. The annual risk free rate is about 5 percent for the 1998 SSBF and 1 percent for the 2003 observations depending on the respective quarter the loan was taken out. The bankruptcy rate is taken from the Dun and Bradstreet credit scores. The credit scores
provided in the SSBF indicate the probability of delinquency (payments are at least 90 days late) rather than bankruptcy.17 Therefore, I assume that firms
that are more like to miss payments are also more likely to file for bankruptcy. I scale the probability of delinquency incidents to match a quarterly bankruptcy rate of 1 percent as reported in Fisher (1999). This yields that firms with the highest score (6) have a
quarterly failure probability of 0.19 percent while 4.44 percent of firms with the lowest credit score (1) are expected to fail in the 2003 sample. In 1998, the probability of failure for the best (worst) risks is 0.15 percent (3.52 percent).
In some cases there exists no solution to the system of equations describing the credit contract, for instance when the firm-entrepreneur entity has no net worth. In 1998, 599 out of 660 observations can be rationalized by one period debt contracts with CSV. In 2003, for 1413 out of 1598 observations the optimal contract can be solved. Sometimes the solution involves implausible values such as negative agency cost. In the 1998 sample, 114 observations are exhibiting a fitted agency cost are below 0 or larger than 1. In the 2003 sample, 364 observations cross these thresholds. However, for 73 percent of the observations in 1998 (485 out of 660) and 67 percent of the observations in 2003 (1079 out of 1598) the system of equations can be solved with plausible parameter values.
Table 3 summarizes the results. In 1998, the average agency cost ![]() is estimated to be 0.282 (stddev 0.09) which corresponds to 28.2 percent of output. For
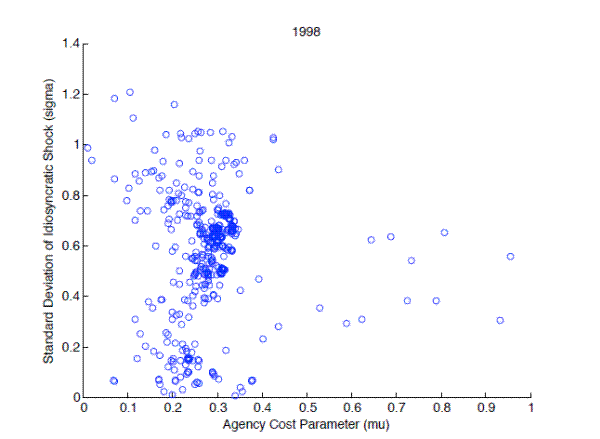
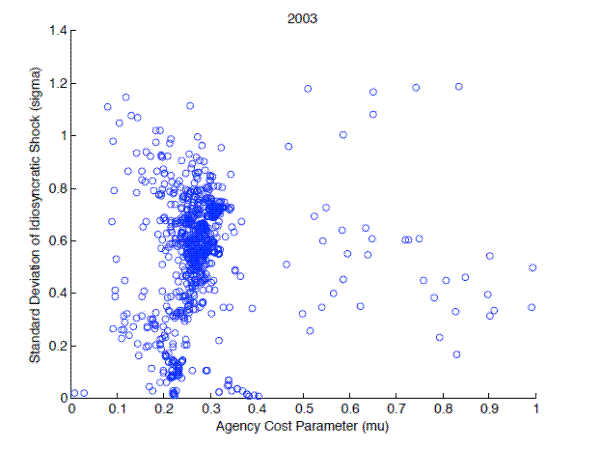
the 2003 sample the agency costs are 0.287 (stddev 0.10). This lies in the plausible range of 0.2-0.36 reported in Carlstrom and Fuerst (1997).18 Figure 2 plots the implied risk parameters and bankruptcy cost for the truncated sample. As reflected in Table 3 the bankruptcy costs are clustered within the 0.2-0.36 range.19 The mean standard deviation of the idiosyncratic shock,
is estimated to be 0.282 (stddev 0.09) which corresponds to 28.2 percent of output. For
the 2003 sample the agency costs are 0.287 (stddev 0.10). This lies in the plausible range of 0.2-0.36 reported in Carlstrom and Fuerst (1997).18 Figure 2 plots the implied risk parameters and bankruptcy cost for the truncated sample. As reflected in Table 3 the bankruptcy costs are clustered within the 0.2-0.36 range.19 The mean standard deviation of the idiosyncratic shock, ![]() , measuring the
riskiness of projects is 0.57 (stddev 0.25) in 1998. In 2003, the average standard deviation is 0.57 (stddev 0.24). In comparison, the calibration strategy of Carlstrom and Fuerst (1997) yields
, measuring the
riskiness of projects is 0.57 (stddev 0.25) in 1998. In 2003, the average standard deviation is 0.57 (stddev 0.24). In comparison, the calibration strategy of Carlstrom and Fuerst (1997) yields
![]() and the one of Bernanke, Gertler, and Gilchrist (1999)
and the one of Bernanke, Gertler, and Gilchrist (1999)
![]() .
.
The implied annualized rate of return is 8 percent in 1998 and 5 percent in 2003. These averages are close to the estimates of Moskowitz and Vissing-Jørgensen (2002), who, using Flow of Funds Accounts and the National Income and Product Accounts data from 1963 to 1999, find that the average annual rate of return to entrepreneurial investment is 13 percent with a standard deviation of 7.7. Their calculation is based on equity in the firm only. Taking into account that definition of net worth employed in my exercise includes the net value of the private residence, the annual return on equity in the firm would be about 12 percent in 1998 and 7.5 percent in 2003.
The parameter distributions in Table 3 contain some implausible extreme values, such as negative or high bankruptcy cost. A closer investigation of these observations through the lens of the model helps to understand the extreme values. Observations with implied negative bankruptcy cost exhibit a high leverage, on average 8.7, while paying only 34 basis points more. The implied risk parameter for this subgroup is only 0.08 while the rate of return is 1. In other words, the model is unable to explain high leverage and low risk premiums for the given bankruptcy rates. Figure 1 illustrates that either low risk or high rates of return lead to higher leverage in the model. Yet in the model high rates of return also lead to significantly higher interest rates. Since the interest rates in the data are not significantly higher, risk must be low. With the mean of the idiosyncratic shock normalized to 1, the lender must receive an additional reward in the case of bankruptcy to rationalize the high leverage.
Observations with high bankruptcy cost (![]() ) exhibit a low leverage, but the firms in the subgroup pay on average a premium of 72 basis points over the full sample despite a lower
than average bankruptcy rate. In the context of the model, given the lower bankruptcy rate the cost of lending must be higher for this subgroup. The spread can be increased by a higher fraction of output lost in the case of bankruptcy or a higher rate of return, which in itself increases the cost
of bankruptcy as bankruptcy costs are measured in terms of expected output (the fraction
) exhibit a low leverage, but the firms in the subgroup pay on average a premium of 72 basis points over the full sample despite a lower
than average bankruptcy rate. In the context of the model, given the lower bankruptcy rate the cost of lending must be higher for this subgroup. The spread can be increased by a higher fraction of output lost in the case of bankruptcy or a higher rate of return, which in itself increases the cost
of bankruptcy as bankruptcy costs are measured in terms of expected output (the fraction ![]() ). In fact, for this subgroup the model also implies an average rate of return of 1.15 with lower
than average risk.
). In fact, for this subgroup the model also implies an average rate of return of 1.15 with lower
than average risk.
Solving for the implied parameter of the optimal debt contract relies on 3 assumptions: i) the idiosyncratic shock has a lognormal distribution, ii) the credit score is a good proxy for the bankruptcy rate, and iii) net worth is measured correctly. Measurement error in net worth or the bankruptcy rate may explain the extreme values of the model-implied parameter distributions. Also the assumption of a log-normal distributed idiosyncratic shock may also be too restrictive, yet it is commonly used in macroeconomic models.
Despite these pitfalls, the model of financing constraints induced by costly state verification performs well vis-à-vis the data. The model can rationalize more than two thirds of the credit contracts with plausible parameter values. The implied rate of returns are in line with results using Flow of Funds Accounts and the National Income and Product Accounts data and bankruptcy costs are consistent with studies on bankruptcy incidences.
3 The Holmström-Tirole Model
This section first describes the debt contract with moral hazard as introducted by Holmström and Tirole (1997). Next, I present the additional bank level data used in this section. I plot the model implied interest rate and the interest rate observed in the data to assess the empirical plausibility of the MH model. I complement my findings with the monitoring cost implied by the debt contract with MH and reduced-form regressions.
3.1 The Debt Contract with Moral Hazard
In the moral hazard model by Holmström and Tirole (1997), risk-neutral entrepreneur ![]() owns a risky return technology. She can invest in either a high
quality project with a high probability of success
owns a risky return technology. She can invest in either a high
quality project with a high probability of success
![]() or a low quality project with a lower probability of success
or a low quality project with a lower probability of success
![]() but with private benefit to the entrepreneur
but with private benefit to the entrepreneur ![]() , where
, where ![]() denotes working capital in production. In case of success
denotes working capital in production. In case of success ![]() is converted into output with
constant returns to scale. In case of failure the capital is lost. The entrepreneur's project choice is not observable. Lender (financial intermediary)
is converted into output with
constant returns to scale. In case of failure the capital is lost. The entrepreneur's project choice is not observable. Lender (financial intermediary) ![]() has to pay fraction of the loan as
monitoring cost
has to pay fraction of the loan as
monitoring cost ![]() to ensure that the entrepreneur invests in the high quality project. The lender's capital
to ensure that the entrepreneur invests in the high quality project. The lender's capital ![]() is scarce. The lender's equity share in the loan to an entrepreneur has to earn a rate of return
is scarce. The lender's equity share in the loan to an entrepreneur has to earn a rate of return ![]() reflecting outside investment opportunities.
Investors in this model can be thought of as depositors who can only invest into a project through the lender. Deposits
reflecting outside investment opportunities.
Investors in this model can be thought of as depositors who can only invest into a project through the lender. Deposits ![]() at lender
at lender ![]() have to earn a return
have to earn a return ![]() . The crucial assumption of the model is
. The crucial assumption of the model is
![]() .
.
As above collateral is the share of net worth
![]() that cannot be used in production. I assume that in case of default, all collateral is going to the lender. The results are not sensitive to this assumption, as, in equilibrium,
only the combined shares output going to the lender and the depositors matter. Let
that cannot be used in production. I assume that in case of default, all collateral is going to the lender. The results are not sensitive to this assumption, as, in equilibrium,
only the combined shares output going to the lender and the depositors matter. Let ![]() be the total rate of return to the project,
be the total rate of return to the project, ![]() the entrepreneur's share of the total rate of return,
the entrepreneur's share of the total rate of return, ![]() the bank's share, and
the bank's share, and ![]() the depositors share. The optimal contract maximizes the payoff to the entrepreneur
the depositors share. The optimal contract maximizes the payoff to the entrepreneur
subject to the incentive compatibility constraint of the entrepreneur:
the incentive compatibility constraint of the lender (monitoring):
the participation constraint of the lender:
the participation constraint of depositors:
the feasibility requirement:
and the budget constraint:
First, note that all six equations hold with equality in equlibrium. Second, the interest rate on a loan is defined only implicitly. Note that in the case of sucess of the project, the joint payoff to the lender and depositors has to be equal to the pricipal and interest payment:
where
Scaling all equations by
where
3.2 Banks Data
The confidential SSBF include the lender's name. I restrict the matching of firms and financial institutions to banks and credit unions for two purposes. First, models of financing constraints usually consider banks. The second reason is a practical concern. The information about the financial institution available is more detailed for banks than the information about leasing companies or car-manufacturer-owned financing companies. The latter are typically not deposit-taking institutions and are therefore not subject to the same regulatory requirements for reporting and capital standards.
Table 4 summarizes the bank variables employed in the assessment of the MH model. The interest cost, used to proxy for ![]() and other cost are taken from
the banks' income statements in the Call Reports.20 The interest cost is measured relative to liabilities minus equity to calculate the average of an
additional dollar of external finance to a bank. The other (non-interest) cost to asset ratio - the average cost for one additional dollar of assets on the banks' balance sheets - proxy for monitoring cost (
and other cost are taken from
the banks' income statements in the Call Reports.20 The interest cost is measured relative to liabilities minus equity to calculate the average of an
additional dollar of external finance to a bank. The other (non-interest) cost to asset ratio - the average cost for one additional dollar of assets on the banks' balance sheets - proxy for monitoring cost (![]() ). Return on equity, (
). Return on equity, (![]() ), is profit divided by bank equity. The adequacy ratio (
), is profit divided by bank equity. The adequacy ratio (![]() ), measuring the composition of a banks financing, is the equity divided by total liabilities. Note that the income and cost variables in the Call Reports are reported as year-to-date and need to be converted to obtain annualized rates. Last, the loan share is
defined as the share of loans of total assets.21
), measuring the composition of a banks financing, is the equity divided by total liabilities. Note that the income and cost variables in the Call Reports are reported as year-to-date and need to be converted to obtain annualized rates. Last, the loan share is
defined as the share of loans of total assets.21
For the 1998 sample 493 out of 924 (53 percent) credit contracts could be matched with bank data.22 The 493 credit contracts originate from 316 different institutions. Many of the unmatched observations do not include a financial institution's name or were labeled "fake bank" by the interviewer. The second, large group received credit for car manufacturer-owned financing companies, leasing companies, or specialized investors. For firms that were denied credit the match rate is 66 percent (110 out of 166).
For the 2003 sample the match rate is significantly higher. Here, 1340 out of 1693 (79 percent) credit contracts could be matched to financial statements of banks. The 1340 credit contracts involve 613 different institutions. Only few firm owners did not identify the financial institutions. Most of the unmatched observations received financing from car manufacturer-owned financing companies. Of the firms whose credit application was rejected, 72 percent (101 out of 136) were matched to banks.
3.3 Fitting the MH Contract
Having concluded that CSV is an empirically plausible model of financing frictions, I now turn to the model of financing frictions based on moral hazard by Holmström and Tirole (1997). This model focuses on banks' financing costs and balance sheet
compositions. To my knowledge, this is the first paper to use credit contract data to assess this model. As pointed out in section 3.1, this model does not explicitly specify an interest rate on the loan. The implied interest rate payment can be derived from the sum of
the payments to the bank (![]() ) and the investors (depositors)
) and the investors (depositors) ![]() . Recall equations
(16) and (18)
. Recall equations
(16) and (18)
and
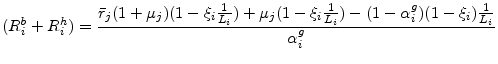 |
where
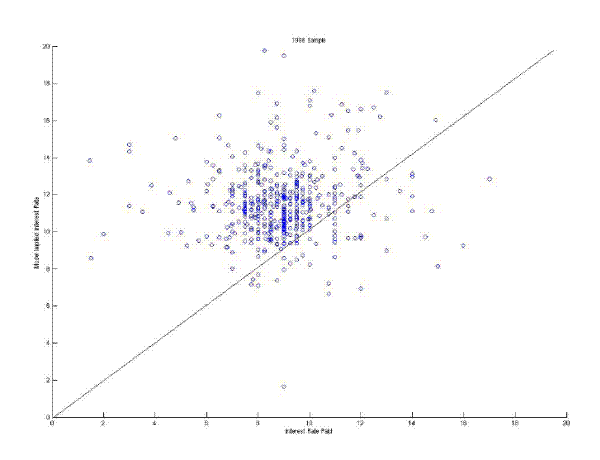
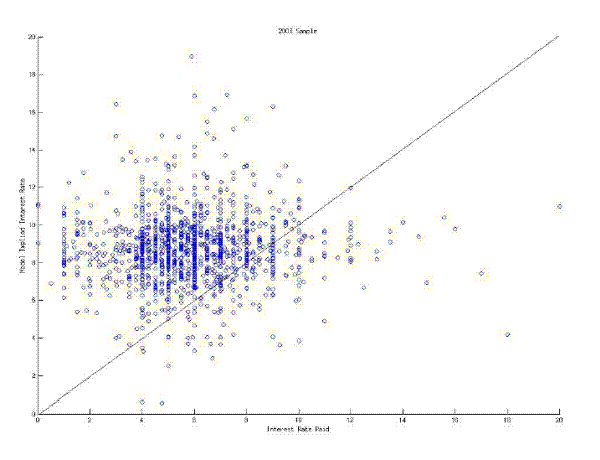
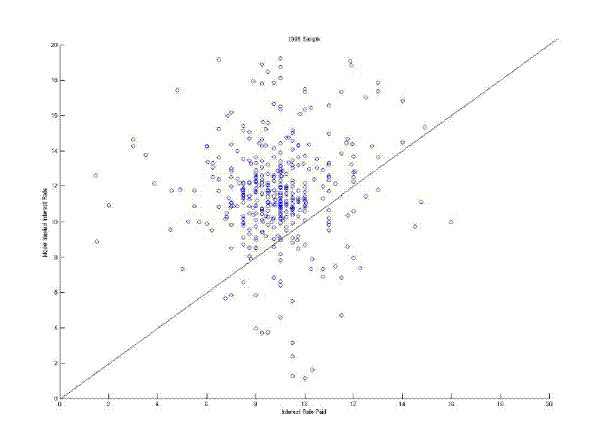
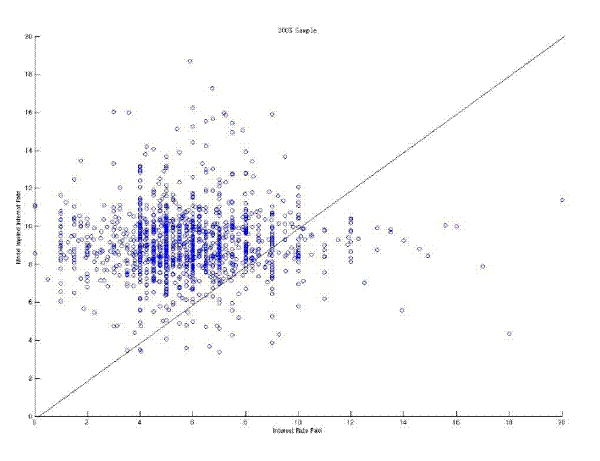
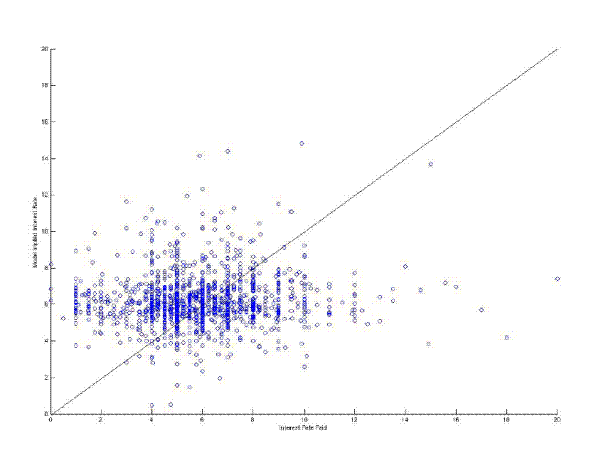
Figure 3 plots the interest rates paid and the interest rates implied by equation (18). The left panel show the joint distribution of interest rates for the 1998 data and the right panel for the 2003 data. Both graphs omit observations with implied interest rates less than 0 percent or more than 20 percent. The average difference is 3.22 percentage points in the 1998 data and 2.98 percentage points in 2003. The correlation between the actual and the implied interest rate is 0.05 in both samples. Removing 25 outliers - an actual interest rate lower than 4 percent or an implied interest rates larger than 20 percent - increases the correlation to 0.1 in the 1998 sample. However, the same criteria applied to the 2003 yields 5 outliers and reduce the correlation to 0.03. The standard deviation of the implied interest rate (5.78) is substantially larger than the standard deviation in the actual interest rate (1.90) for the 1998 sample. For the 2003 sample the standard deviations are about the same, 2.35 and 2.68 respectively.
In light of these these findings the MH model appears to be inconsistent with the data. There are three potential explanations for the poor performance of the MH model: 1) bank costs are mismeasured , 2) the bank balance sheets and costs, for instance due to competition, do not matter for small business credit interest rates,23 or 3) the model misspecifies how bank variables affect the interest rate on a credit.
So far, this exercise assumes that balance sheet and income statement information of the bank allows me to measure banks' financing costs, rate of returns, and monitoring costs accurately. Taking the balance sheet and income statement information from a particular quarter may not adequately reflect the medium to long run cost but within quarter special items in accounting.
As a first robustness test, I use an alternative measure of monitoring cost to deal with this point, mismeasured cost. Instead of using all "other" (non-interest) cost as a measure of monitoring cost, I use salaries and employee benefits, data processing expenses, legal fees, and insurance assessments only.24 Due to data availability this exercise is done for the 2003 sample only. The average cost fall to 1.4 percent compared to 2.9 percent when all other cost are considered. Employing this measure of monitoring cost reduces the difference between the model implied interest rate and the actual interest rate to 40 basis points. However, the correlation remains low (0.06).25 Second, the standard deviation of the implied interest rate drops to only 1.47, far lower than the standard deviation of the interest rate in the data (2.68). Similarly, using the FDIC's capital-ratio requirements for well-capitalized banks - 10 percent (Basel I) or 7.5 percent (Basel II) - instead of actual adequacy ratios does not change the results.
Next, instead of using the information from one quarter, I average the quarterly data over three years. However, I find no difference in terms of correlation or differences in the interest rates (see Appendix).
Last, instead of taking the monitoring cost from the income statement, I solve for the monitoring cost ![]() that equalizes the model implied interest rate and the actual interest rate.
The model implies median monitoring cost of 2.14 percent in 1998 and 5.37 percent in 2003. While 2.14 percent appears to be a reasonable number when compared to the cost measure in Table 4, 5.37 percent is close to the maximum. Only 53 percent of contracts in the
1998 sample imply
that equalizes the model implied interest rate and the actual interest rate.
The model implies median monitoring cost of 2.14 percent in 1998 and 5.37 percent in 2003. While 2.14 percent appears to be a reasonable number when compared to the cost measure in Table 4, 5.37 percent is close to the maximum. Only 53 percent of contracts in the
1998 sample imply
![]() - that is, monitoring cost between $0 and $100,000 on a $1 mill. loan. In the 2003 sample 34 percent of the contracts imply monitoring cost in this, arguably wide, range.
Therefore, measurement error in the monitoring cost is not driving the results.
- that is, monitoring cost between $0 and $100,000 on a $1 mill. loan. In the 2003 sample 34 percent of the contracts imply monitoring cost in this, arguably wide, range.
Therefore, measurement error in the monitoring cost is not driving the results.
To assess the other two hypotheses on importance of bank variables, I run reduced-form regressions to explain the loan interest rate. CSV and MH highlight the importance of different variables for the loan interest rate. The interest rate in the debt contract with CSV depends on firm-specific parameters and the risk-free rate. To see this, substitute equation (9) in equation (2).
The interest rate on the loan in MH depends on firm-specific and on bank-specific parameters. Using equations (16) and (18) yields
with
The regression analysis of the interest rate confirms the hypothesis that bank balance sheets and costs do not matter for small business credit interest rates and, by extension, rejects the third hypothesis. Table 5 shows that bank variables have little explanatory power.26 By contrast, firm specific variables are highly significant. This highlights the differences between CSV and MH. In CSV the interest rate is a function of firm variables and the risk-adjusted outside investment opportunities of the bank - conventionally proxied by the risk-free rate. MH, on the other hand, focuses on the importance of the bank's balance sheets.
On the firm's side, size and age have a strong negative impact on the interest rate, so does the credit score. Yet net worth, measured in millions, as only a neglectible economic effect. An additional million dollars of net worth reduces the interest rate by 9-14 basis points. Rajan (1992) points out that longer lending relationships result in informational monopolies which is especially true for small businesses. Banks also may try to attract new customers with teaser rates on the first loan and raise the interest rate on subsequent loans. The positive and significant coefficient on the length of the relationship in the 2003 sample supports this view. There appears to be no relationship effect in the 1998 SSBF sample. However, this may be the result of the omission of credit renewals which biases the 1998 sample.
One potential source of bias arises from differences in local economic conditions that are arguably important in order to assess the riskiness of a small business. The regressions therefore include the fraction of late and non-accrual loans which, at least for smaller banks, is a plausible proxy for differences in local economic conditions. In fact, in most regressions the share of loans that is 90 day past due has a significant positive effect on the loans interest rate (not shown here). Using the alternative cost measures described above confirm the findings from the regression analysis (see Appendix).
While it cannot be excluded that there may be additional measurement errors in the rate of return of a bank or the monitoring cost, but it is hard to imagine that such measurement errors are correlated with covariates in way that would overturn the key finding of the section: The poor performance of MH vis-à-vis the data is the result of a lack of explanatory power of bank variables for the interest rate of the loan.
4 Reduced-Form Financing Constraints
Frictionless capital markets imply an undetermined capital structure of firms, and no systematic relationship between net worth and credit emerges. One exception is the case of firms operating a decreasing economies of scale technology limiting optimal firm size. In that case, everything else equal, firms with higher net worth should take on less credit as they are closer to the optimal size. Here, when capital markets are frictionless, a negative relationship between net worth and the credit amount should be observed in the data.
The defining deviation from frictionless capital markets - and one that I will verify empirically - is that financing frictions imply a positive relationship between net worth and the credit amount. In particular, the credit amount is some multiple of net worth. Using the definition of debt and leverage in CSV in equation (9) yields:
In the MH model, the relationship of net worth and loans, which I will assess in the next section, can be derived using equations (10), (11), (13), (14), (15), and (17). For simplicity, assume
The derivation can be found in the Appendix. Note that according to the MH model, in equilibrium, debt should be higher for projects with higher success probability (
Equations (21) and (22) show that debt contract models imply that for the firms that received credit the credit amount is some multiple of net worth ![]() :
:
Roughly one fifth of all firms in the 1998 sample and about one third of all firms in the 2003 sample obtained credit. This large difference is due to the fact that the 1998 explicitly excluded renewals of lines of credit. This clearly introduces a selection bias towards 1) more denials and 2) younger and smaller firms receiving credit (see Table 1).
As equations (21) and (22) show, the net worth multiplier ![]() depends on the riskiness, bankruptcy cost, and the rate
of return of a project, each of these parameter can be differ across projects. Second, net worth may be measured with error. This implies the following estimation equation:
depends on the riskiness, bankruptcy cost, and the rate
of return of a project, each of these parameter can be differ across projects. Second, net worth may be measured with error. This implies the following estimation equation:
| (23) |
The agency model suggests
The SSBF data provide a rich set of additional control variables for sources of heterogeneity: the credit score of the firm, previous bankruptcy, census region, industry, and organizational form. The credit score, judgments against the firm, and previous private and firm bankruptcies proxy for differences in risk. Regional and industry dummies control for differences in risk and rate of return in these dimensions. While there is evidence in the 1998 sample that firms with a solid financial history received more credit, no impact of credit scores can be found in the 2003 sample. Due to a lack of variation in the 1998 sample, judgments, and previous private and firm bankruptcies can only be used in the 2003 sample. Judgments have a strong negative effect while previous bankruptcies exhibit no significant effect. Firms with judgments already pending are more risky. The negative effect of judgments on the credit amount is in line with the prediction of lower leverage for higher risk firms. Due to differences in liability, the variation in the legal form of the firms proxies for differences in bankruptcy cost. However, in both samples the legal form has no significant effect. This is consistent with the fact that half of the sample provided personal guarantees, and therefore limited liability of the firm has little effect. Bank variables described above have no significant effect on the credit amount.
As Table 7 shows employing this large set of controls does not yield significantly different results for the estimated effect of net worth. Again controlling for selection does not change the results. Bank regulatory capital ratios were used as exclusion restrictions in the selection equation as several studies found an effect of capital ratios on lending.28
Section 2.2 argues that in the context of small businesses a wider definition of net worth is appropriate. To ensure that the results are not solely the result of the definition of net worth, I consider three additional definitions consistent with the pattern of collateral offered. Since equipment accounts for almost half of collateral offered, we always include depreciable assets in our definitions: 1) firm assets and less firm's liabilities, 2) firm's depreciable assets, land, building and net value of private residence less firm's loans, and 3) firm's depreciable assets, land, buildings, and net value of private residence less firm's liabilities. The narrower definitions of net worth also yield a robust positive credit amount-net worth relationship but the explanatory power of net worth is substantially reduced in some regressions (see Appendix).
Receiving less credit than applied for is another possible constraint. The SSBF explicitly ask for the loan amount applied for and the loan amount received. Over 90 percent of the small business owners report that the loan amount received is equal to the loan amount they applied for. While it cannot be excluded that the loan amount on the application was agreed upon informally prior to the application, there is no indication in the surveys that firms do not receive the desired loan amount.
Consistent with both models of financing constraints considered here, net worth and the credit amount exhibit a robust positive relationship. In the SSBF data, an additional dollar of net worth accounts for 30 cents of additional external finance. In comparison, in their model of entrepreneurship, Evans and Jovanovic (1989), using the National Longitudinal Survey of Young Men, estimate the effect to be 44 cents of external finance for an additional dollar of net worth while Cagetti and de Nardi (2006) calibrate the effect to roughly 67 cents for entrepreneurs to match the US wealth distribution.29
5 Small vs Large Banks
It is worthwhile to note that small businesses tend use with small banks. In the 1998 sample, there is little evidence for dominance of large banks in the small business lending market. Summing up the market shares of all banks whose market share exceeds 1 percent, I find that 6 banks account for 23 percent (19 percent using firm weights in the SSBF) of all credit contracts and 31 percent (32 percent weighted) of denials in the sample. In the 2003 sample there is more concentration, but that was to be expected since the consolidation in the banking industry continued. Here, 11 banks have at least 1 percent of the market. Together large banks account for 30 percent (23 percent weighted) of the credit contracts by banks. They also account for 38 percent (44 percent weighted) of denials.
Large banks, in this section defined as banks with more than $50 billion assets, account for about one third of all credit contracts (and also roughly one third when measured by total credit amount) and for almost 40 percent of credit denial. This section examines difference between small and large banks to ensure that the results presented in the previous section are not driven by large financial institution. The latter are more diversified and therefore their balance sheet information may be less precise in measuring the variables of interest.
Table 8 shows that there are only minor differences between small businesses who decide to that bank with small banks and those bank with large banks. The perhaps most striking difference is that small business owners who bank with the large banks tend to have more equity.
First, I report the result for the credit amount regressions by bank size. Since selection has no significant effect I omit the results in Table 9. The main result, the importance of net worth, does not change. While the point estimates for the 2003 sample are the same for small and large banks, they differ significantly for the 1998.
Next, I explore whether there are differences by bank size with respect to interest rates. Tables 10 and 11 summarize the results for the 1998 and 2003 sample. With the exception of the interest cost, which contrary with MH enter negatively, no significant differences arise in the 1998 sample. Firm variables, such as size and sectoral dummies, appear to be more important.
In contrast, the 2003 sample in Table 11 exhibits sharp differences. Here bank balance sheet information is important in the subsample of large banks, albeit the point estimate of cost measure is negative and weakly significant. A 100 basis point difference in the financing cost of large banks increases the interest rate on a small business loan by more than 250 basis points. This result may reflect the increasing concentration in the banking industries which leaves large banks with more market power. Yet large banks still serve less than a third of the market. For small banks, however, bank variables are not significant, even though they are arguably closer to a standard model of banks than large financial conglomerates. In contrast to MH, this result supports a more competitive banking market model, for instance small banks can be seen as competitive fringe to an oligopoly. Therefore, the poor performance of MH is not driven by large banks. While the results presented here do not support MH, bank variables may still matter in the context of credit rationing (Stiglitz and Weiss, 1981). For instance, capital ratios affect the loan supply of loans (Berrospide and Edge, 2010).
6 Conclusion
This paper exploits business credit contracts and net worth of entrepreneurs to examine the empirical plausibility of two commonly used models of financing constraints - costly state verification and moral hazard. Patterns of collateral, as guideline for the construction of net worth, suggest that banks accept all assets on the firm's balance sheet and private residences as collateral. Consistent with both models, one dollar of additional net worth accounts for about 30 cents of additional external finance. Costly state verification can rationalize more than two thirds of the credit contracts in the data. Bankruptcy costs, implied by small business credit contracts when fitting the CSV debt contracts, are 28 percent of expected output and the implied rate of return lies between 5 percent and 8 percent annually. Thus, CSV is an empirically plausible model of financing constraints. The moral hazard model by Holmström and Tirole (1997) performs poorly. This model emphasizes the importance of bank variables for loan pricing; a hypothesis that does not hold in small business loan contracts.
While shedding light on the empirical plausibility of financing constraint models, this study also raises questions about the magnitude of the impact of financing constraints in macroeconomic models. First, less than one half of the sample took out credit. Second, bank variables such as financing cost and balance sheet composition have little explanatory power. Third, small businesses - accounting for almost one half of economic activity in the US - are not highly leveraged.30 Another question is whether credit is, as in most macroeconomic models, constantly demanded for investment or whether credit should be thought of as an insurance policy against business cycle or liquidity shocks (Kashyap, Rajan, and Stein, 2002; Diamond and Rajan, 2001).
Bibliography
Federal Reserve Bulletin, 87:183-205, 2001.
Federal Reserve Bulletin, 92:A167-A195, 2006.
Appendix A - Data
Construction of Bank Variables
Bank Variables from the Call Reports for commerical banks (RIAD, RCON), thrifts (SVGL), and credit unions (CUSA):
- bank capital
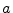 from RIAD3210, SVGL3491, and CUSA3210 - bank equity
from RIAD3210, SVGL3491, and CUSA3210 - bank equity - deposits
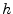 - for commercial banks: sum of RCON6631 (non-interest bearing deposits), RCON6636 (interest bearing deposits), RCONb993 (Fed funds purchased), RCONb995 (Securities sold,
repurchase), RCON3548 (Trading Liabilities), and RCON3190 (other borrowed money), for thrifts: SVGL2339+SVGL2071 (Deposits and Escrows), after 2003Q4 SVGLC503 and SVGL3101 (other borrowing), and for credit unions CUSA4584 (borrowings), CUSA2302 (non-member deposits), and CUSA3139 (shares).
- for commercial banks: sum of RCON6631 (non-interest bearing deposits), RCON6636 (interest bearing deposits), RCONb993 (Fed funds purchased), RCONb995 (Securities sold,
repurchase), RCON3548 (Trading Liabilities), and RCON3190 (other borrowed money), for thrifts: SVGL2339+SVGL2071 (Deposits and Escrows), after 2003Q4 SVGLC503 and SVGL3101 (other borrowing), and for credit unions CUSA4584 (borrowings), CUSA2302 (non-member deposits), and CUSA3139 (shares). - bank's outside rate of return
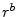 - Return on Equity. RIAD4340 (Net Income) divided by RIAD3210 (bank equity), SVGL4340/SVGL3491, and CUSA4273/CUSA3210.
- Return on Equity. RIAD4340 (Net Income) divided by RIAD3210 (bank equity), SVGL4340/SVGL3491, and CUSA4273/CUSA3210. - depoistor's outside rate of return
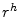 - RIAD4073, SVGL0481, CUSA4073 (Total interest rate expense) divided by
- RIAD4073, SVGL0481, CUSA4073 (Total interest rate expense) divided by 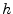 ,.
,. - monitoring cost
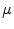 - RIAD4093, sum of SVGL4141, SVGL0495, SVGL4154, SVGL0499, CUSA4093 (non-interest expense) divided by total assets (here
- RIAD4093, sum of SVGL4141, SVGL0495, SVGL4154, SVGL0499, CUSA4093 (non-interest expense) divided by total assets (here 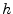 and equity).
and equity).
- share of loans 30-90 days late, over 90 days late and non-accrual. RCFD1406, RCFD1407, RCFD1403 divided by RCON1400; SVGL3936, SVGL3942, and SVGL3948 divided by SVGL1576(non-mortgage)+SVGL0446(Mortgage) and CUSA1128 (30-60 days), CUSA1125 (60-120 days) and CUSA1127 divided by CUSA1263.
- Risk-Based Capital Ratio RCFD7205, SVCC7205, for unions only CUSA7276 risk based net worth ratio.
Appendix B - Robustness
To ensure that the results in section 4 are not only driven by the definition of net worth, I provide the regression results for various other definitions of net worth.
The definition employed in the regression in Table 12 follows Giambona and Schwienbacher (2008). They argue that only hard tangible assets can be used as collateral. Hence, in Table 12 net worth is defined as the sum of land, depreciable assets, and the net value of the private residence minus loans. While net worth is still significant in all regression, the explanatory power of net worth is greatly reduced relative the baseline definition.
Table 13 displays the results of a different definition of net worth allow in the spirit of Giambona and Schwienbacher (2008). Instead of subtracting loans only, all firm liabilities are subtracted from the sum of land, depreciable assets, and the net value of the private residence to calculate net worth. Again, the explanatory power of net worth is reduced relative to the baseline definition for the results are still significant.
The last robustness check with respect to the definition of net worth uses the firm balance sheet only. In Table 14 , net worth is defined as all firm assets minus all firm liabilities. The results are comparable with the baseline definition in terms of explanatory power, yet the point estimates are slightly higher.
Appendix C - Derivation of Leverage in MH
Assume ![]() . Rewriting yields equations (10) and (11)
. Rewriting yields equations (10) and (11)
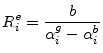 |
and
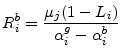 |
Using the budget constraint
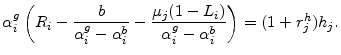 |
Next, replacing
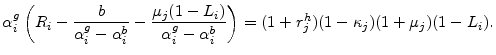 |
Solving for
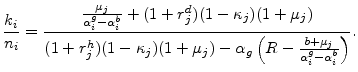 |
Hence,
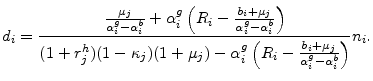 |
| 1998 mean | 1998 std | 1998 25% | 1998 50% | 1998 75% | 2003 mean | 2003 std | 2003 25% | 2003 50% | 2003 75% | |
| Number of Employees | 12.8 | 28.9 | 2.0 | 5.0 | 11.0 | 15.0 | 31.5 | 3.0 | 6.0 | 13.0 |
| Firm Age | 11.6 | 8.7 | 5.0 | 10.0 | 16.0 | 15.3 | 11.3 | 7.0 | 13.0 | 22.0 |
| Length of Lending Relationship | 7.0 | 8.1 | 1.6 | 4 | 9.1 | 10.1 | 9.1 | 3.6 | 7.0 | 14.5 |
| Credit Score |
2.9 | 1.1 | 2.0 | 3.0 | 4.0 | 3.7 | 1.5 | 3.0 | 4.0 | 5.0 |
| Net Worth (in mill.) | 0.39 | 1.3 | 0.05 | 0.12 | 0.34 | 0.72 | 2.1 | 0.11 | 0.27 | 0.62 |
Firm observations weighted with SSBF weights.
![]() The credit score in 1998 goes from 1 (lowest) to 5 (highest) and in 2003 from 1 (lowest) to 6 (highest).
The credit score in 1998 goes from 1 (lowest) to 5 (highest) and in 2003 from 1 (lowest) to 6 (highest).
| age | all firms Number of obs. (1) | all firms Net Worth (in mill.) average (median) (2) | received credit Number of obs. (3) | received credit Net Worth (in mill.) average (median) (4) | all firms Number of obs. (5) | all firms Equity Share average (median) (6) | received credit Number of obs. (7) | received credit Equity Share |
| 573 | 0.245 | 113 | 0.222 | 574 | 63.7% | 113 | 61.8% | |
| (0.092) | (0.115) | (86.6%) | (86.5%) | |||||
| 3-6 | 1507 | 0.303 | 384 | 0.437 | 1508 | 60.1% | 385 | 64.7% |
| 3-6 average (median) | (0.106) | (0.140) | (76.4%) | (81.4%) | ||||
| 7-15 | 2522 | 0.361 | 761 | 0.544 | 2525 | 65.7% | 761 | 63.8% |
| 7-15 average (median) | (0.151) | (0.225) | (85.0%) | (80.5%) | ||||
| 16-25 | 1784 | 0.508 | 630 | 0.725 | 1785 | 70.7% | 630 | 69.3% |
| 16-25 average (median) | (0.225) | (0.316) | (85.4%) | (84.3%) | ||||
| 1404 | 0.801 | 516 | 1.240 | 1406 | 73.8% | 517 | 76.0% | |
| (0.275) | (0.443) | (92.0%) | (92.1%) | |||||
| Total | 7790 | 0.432 | 2404 | 0.645 | 7798 | 66.6% | 2406 | 67.5% |
| Total average (median) | (0.159) | (0.230) | (84.7%) | (84.4%) |
Source: SSBF 1998 and 2003. For the construction of net worth, see text.
![]() Equity share before most recent credit was taken out.
Equity share before most recent credit was taken out.
| Sample | mean | med | std | min | 25% | 75% | max |
| 1998 all obs. |
1.08 | 0.29 | 2.62 | -13.72 | 0.25 | 0.32 | 23.7 |
| 1998 all obs. |
0.54 | 0.59 | 0.25 | 0.01 | 0.39 | 0.67 | 1.21 |
| 1998 all obs. |
1.04 | 1.02 | 0.05 | 0.90 | 1.01 | 1.03 | 1.40 |
| 1998
|
0.28 | 0.28 | 0.09 | 0.01 | 0.24 | 0.31 | 0.96 |
| 1998
|
0.57 | 0.63 | 0.25 | 0.01 | 0.48 | 0.72 | 1.21 |
| 1998
|
1.02 | 1.02 | 0.01 | 1.01 | 1.01 | 1.02 | 1.10 |
| 2003 all obs. |
1.60 | 0.30 | 3.35 | -1.29 | 0.26 | 0.79 | 27.90 |
| 2003 all obs. |
0.54 | 0.58 | 0.22 | 0.01 | 0.40 | 0.70 | 1.32 |
| 2003 all obs. |
1.04 | 1.01 | 0.07 | 0.97 | 1.00 | 1.06 | 1.80 |
| 2003
|
0.28 | 0.28 | 0.10 | 0.01 | 0.25 | 0.31 | 0.99 |
| 2003
|
0.57 | 0.64 | 0.24 | 0.01 | 0.47 | 0.72 | 1.18 |
| 2003
|
1.01 | 1.01 | 0.01 | 1.00 | 1.00 | 1.01 | 1.11 |
Note: The full 1998 sample consists of 599 observations. The truncated sample has 485 observations. The full 2003 sample consists of 1413 observations. The truncated sample has 1079 observations. For a discussion, see text.
| 1998 mean | 1998 std | 1998 25% | 1998 50% | 1998 75% | 2003 mean | 2003 std | 2003 25% | 2003 50% | 2003 75% | |
| Interest Cost to Liability Ratio |
0.035 | 0.012 | 0.031 | 0.035 | 0.038 | 0.013 | 0.005 | 0.010 | 0.012 | 0.017 |
| Other Cost to Asset Ratio |
0.034 | 0.023 | 0.027 | 0.031 | 0.037 | 0.029 | 0.010 | 0.024 | 0.028 | 0.032 |
| Return on Equity |
0.140 | 0.064 | 0.107 | 0.143 | 0.174 | 0.135 | 0.065 | 0.099 | 0.138 | 0.171 |
| Adequacy Ratio | 0.094 | 0.028 | 0.078 | 0.088 | 0.100 | 0.090 | 0.027 | 0.075 | 0.085 | 0.096 |
| Loan Share | 0.641 | 0.123 | 0.579 | 0.660 | 0.727 | 0.638 | 0.145 | 0.551 | 0.665 | 0.739 |
| Assets in bn. | 54.8 | 113.0 | 0.2 | 5.2 | 57.5 | 108.0 | 200.0 | 0.5 | 8.9 | 75.4 |
Bank observation weighted by frequency in the credit contract sample. Number of observation is 611 in the 1998 sample and 1441 in the 2003 sample. The composition of bank types in the two samples is similar. In 1998, 4.9 percent of the financial institutions small business owners banked with were credit unions (2003: 3.1 percent), 4.4 percent were thrifts (2003: 4.8 percent), and 90.7 percent were commericial banks (2003: 92.1 percent).
![]() Costs and rates of return are annualized.
Costs and rates of return are annualized.
| 1998 OLS (1) Firm Variables | 1998 OLS (2) Firm Variables | 1998 Selection |
2003 OLS (4) Firm Variables | 2003 OLS (5) Firm Variables | 2003 Selection |
|
| Share of Firm's Liquid Assets | 0.05 | 0.28 | 0.36 | 0.64 |
-0.37 | -0.17 |
| Share of Firm's Liquid Assets standard error | (0.23) | (0.27) | (0.37) | (0.26) | (0.30) | (0.31) |
| Credit Score | -0.13 |
-0.17 |
-0.18 | -0.24** | -0.16** | -0.19 |
| Credit Score standard error | (0.08) | (0.09) | (0.11) | (0.05) | (0.05) | (0.08) |
| Log Number of Employees | -0.13 | -0.15 | -0.25** | -0.25** | ||
| Log Number of Employees standard error | (0.10) | (0.11) | (0.08) | (0.10) | ||
| Log Firm Age | -0.10 | -0.09 | -0.34** | -0.42** | ||
| Log Firm Age standard error | (0.12) | (0.16) | (0.10) | (0.15) | ||
| Log Length of Relationship | -0.05 | -0.05 | 0.27>** | 0.32** | ||
| Log Length of Relationship standard error | (0.05) | (0.06) | (0.09) | (0.12) | ||
| Net Worth (in mill.) | -0.13 |
-0.15 |
-0.09 |
-0.09** | ||
| Net Worth (in mill.) standard error | (0.08) | (0.07) | (0.04) | (0.03) | ||
| 1998 OLS (1) Bank Variables | 1998 OLS (2) Bank Variables | 1998 Selection |
2003 OLS (4) Bank Variables | 2003 OLS (5) Bank Variables | 2003 Selection |
|
| Interest Cost to Liabilities Ratio | -14.52 |
-20.39 |
-21.55 |
51.05** | 21.49 | 28.81 |
| Interest Cost to Liabilities Ratio standard error | (7.37) | (8.88) | (12.35) | (13.44) | (18.69) | (28.86) |
| Other Cost to Asset Ratio | 2.85 | 3.96 | 3.67 | 3.37 | -8.67 | -7.67 |
| Other Cost to Asset Ratio standard error | (4.14) | (4.62) | (5.12) | (7.20) | (8.12) | (11.16) |
| Return on Equity | -1.01 | -0.31 | 1.68 | 0.28 | 0.56 | 0.95 |
| Return on Equity standard error | (1.44) | (1.75) | (2.50) | (1.18) | (1.38) | (1.95) |
| Adequacy Ratio | 2.07 | 0.17 | 2.626 | 5.13> |
1.28 | 2.09 |
| Adequacy Ratio standard error | (3.83) | (4.16) | (5.11) | (2.52) | (2.78) | (3.11) |
| Log Bank Assets | -0.06> |
-0.08> |
0.01 | 0.01 | ||
| Log Bank Assets standard error | (0.04) | (0.05) | (0.03) | (0.04) | ||
| Loan Share of Assets | -0.42 | -0.32 | -0.71 | -0.66 | ||
| Loan Share of Assets standard error | (0.84) | (1.15) | (0.58) | (0.85) | ||
| Additional Controls |
no | yes | yes | no | yes | yes |
| N | 493 | 493 | 588 | 1335 | 1263 | 1324 |
| Adjusted |
0.01 | 0.10 | - | 0.03 | 0.19 | - |
Significance levels: ** 1%, ![]() 5%, and
5%, and ![]() 10%. All observations are weighted with the sample weights in the SSBF.
10%. All observations are weighted with the sample weights in the SSBF.
![]() Additional controls included are share of nonaccrual loans, share of loans 30-90 days past due, share of loans
Additional controls included are share of nonaccrual loans, share of loans 30-90 days past due, share of loans ![]() days past due and dummies for banks type (commerical bank, federal savings bank, credit union), market concentration, type of cooperation, judgements against the firm, previous private and firm bankruptcy, region, sector, quarter in which the loans was
taken out, urban, female firm owner, minority firm owner, and education of firm owner.
days past due and dummies for banks type (commerical bank, federal savings bank, credit union), market concentration, type of cooperation, judgements against the firm, previous private and firm bankruptcy, region, sector, quarter in which the loans was
taken out, urban, female firm owner, minority firm owner, and education of firm owner.
![]() Heckman selection model. Only 81 firm owners report credit denial hence the model contains only a limited set of variables. The selection equation includes the bank variables, log
employment, log firm age, credit score, log length of relationship with bank, a dummy for minority firm owner and quarter in which the loans was taken out, and risk-based capital ratio. Note that the risk based capital ratio is not available for credit unions (22 obs.). Using the risk-based net
worth to proxy for the risk-based capital ratio does not change the results reported in columns (3) and (6) significantly.
Heckman selection model. Only 81 firm owners report credit denial hence the model contains only a limited set of variables. The selection equation includes the bank variables, log
employment, log firm age, credit score, log length of relationship with bank, a dummy for minority firm owner and quarter in which the loans was taken out, and risk-based capital ratio. Note that the risk based capital ratio is not available for credit unions (22 obs.). Using the risk-based net
worth to proxy for the risk-based capital ratio does not change the results reported in columns (3) and (6) significantly.
| 1998 Sample OLS | 1998 Sample OLS | 1998 Sample Selection |
2003 Sample OLS | 2003 Sample OLS | 2003 Sample Selection |
|
| Net Worth | 0.320** | 0.298** | 0.318** | 0.360** | 0.334** | 0.318** |
| Net Worth standard error | (0.084) | (0.083) | (0.077) | (0.055) | (0.057) | (0.055) |
| Ln Number of Employees | 0.066 |
0.139** | ||||
| Ln Number of Employees standard error | (0.028) | (0.032) | ||||
| controls | no | no | no | no | no | no |
| N | 711 | 711 | 959 | 1693 | 1693 | 1856 |
| R2 | 0.29 | 0.30 | - | 0.27 | 0.28 | - |
Significance levels: : ![]() : 10%
: 10% ![]() : 5%
: 5% ![]() : 1%
: 1%
![]() Heckman selection model using information on whether the firm's credit application was accepted. The probability of receiving credit is estimated using net worth, ln(emploment),
ln(length of relationship with the lender), ln(firmage), credit score, and dummy variables for industry, region, gender, minority status, organizational form of the firm, previous bankruptcies and judgements against the firm.
Heckman selection model using information on whether the firm's credit application was accepted. The probability of receiving credit is estimated using net worth, ln(emploment),
ln(length of relationship with the lender), ln(firmage), credit score, and dummy variables for industry, region, gender, minority status, organizational form of the firm, previous bankruptcies and judgements against the firm.
| 1998 Sample OLS (1) Firm Variables | 1998 Sample OLS (2) Firm Variables | 1998 Sample Selection |
2003 Sample OLS (4) Firm Variables | 2003 Sample OLS (5) Firm Variables | 2003 Sample Selection |
|
| Net Worth (in mill.) | 0.320** | 0.259** | 0.259** | 0.360** | 0.302** | 0.302** |
| Net Worth (in mill.) standard error | (0.084) | (0.024) | (0.077) | (0.055) | (0.018) | (0.081) |
| Share of Firm's Liquid Assets | 0.168 |
0.168** | -0.509** | -0.491** | ||
| Share of Firm's Liquid Assets standard error | (0.085) | (0.062) | (0.155) | (0.154) | ||
| Log Number of Employees | 0.068 |
0.062 |
0.122** | 0.120 |
||
| Log Number of Employees standard error | (0.031) | (0.032) | (0.040) | (0.051) | ||
| Log Firm Age | -0.011 | -0.011 | -0.034 | -0.055 | ||
| Log Firm Age standard error | (0.038) | (0.028) | (0.051) | (0.045) | ||
| Log Length of Relationship | -0.027 | -0.033 | 0.001 | 0.010 | ||
| Log Length of Relationship standard error | (0.017) | (0.021) | (0.041) | (0.033) | ||
| Credit Score | 0.070** | 0.073 |
-0.023 | -0.030 | ||
| Credit Score standard error | (0.027) | (0.034) | (0.028) | (0.021) | ||
| 1998 Sample OLS (1) Bank Variables | 1998 Sample OLS (2) Bank Variables | 1998 Sample Selection |
2003 Sample OLS (4) Bank Variables | 2003 Sample OLS (5) Bank Variables | 2003 Sample Selection |
|
| Interest Cost to Liabilities Ratio | -0.222 | 2.027 | -0.545 | 2.032 | ||
| Interest Cost to Liabilities Ratio standard error | (2.858) | (1.914) | (9.438) | (5.894) | ||
| Other Cost to Asset Ratio | -1.865 | -0.710 | -3.556 | -4.275 | ||
| Other Cost to Asset Ratio standard error | (1.436) | (0.599) | (4.212) | (3.472) | ||
| Return on Equity | -0.748 | -1.227 | 0.462 | 0.489 | ||
| Return on Equity standard error | (0.552) | (0.848) | (0.702) | (0.504) | ||
| Adequacy Ratio | -0.937 | -1.412 | 0.569 | 0.293 | ||
| Adequacy Ratio standard error | (1.300) | (0.932) | (1.413) | (0.845) | ||
| Log Bank Assets | 0.010 | 0.007 | 0.022 | 0.022 |
||
| Log Bank Assets standard error | (0.011) | (0.007) | (0.016) | (0.014) | ||
| Loan Share of Assets | 0.054 | 0.109 | 0.168 | 0.091 | ||
| Loan Share of Assets standard error | (0.272) | (0.198) | (0.298) | (0.231) | ||
| Additional Controls |
no | yes | yes | no | yes | yes |
| N | 711 | 493 | 588 | 1693 | 1263 | 1324 |
| Adjusted |
0.23 | 0.26 | - | 0.27 | 0.25 | - |
Significance levels: ** 1%, ![]() 5%, and
5%, and ![]() 10%.
10%.
![]() Additional controls included in columns (2) and (5) are share of nonaccrual loans, share of loans 30-90 days past due, share of loans
Additional controls included in columns (2) and (5) are share of nonaccrual loans, share of loans 30-90 days past due, share of loans ![]() days past due and dummies for banks type (commerical bank, federal savings bank, credit union), market concentration, type of cooperation, judgements against the firm, previous private and firm bankruptcy, region, sector, quarter
in which the loans was taken out, urban, female firm owner, minority firm owner, and education of firm owner.
days past due and dummies for banks type (commerical bank, federal savings bank, credit union), market concentration, type of cooperation, judgements against the firm, previous private and firm bankruptcy, region, sector, quarter
in which the loans was taken out, urban, female firm owner, minority firm owner, and education of firm owner.
![]() Additional controls included in columns (3) and (6) are dummies for banks type, market concentration, type of cooperation, region, sector, quarter in which the loans was taken out, and
urban.
Additional controls included in columns (3) and (6) are dummies for banks type, market concentration, type of cooperation, region, sector, quarter in which the loans was taken out, and
urban.
![]() Heckman selection model. The selection equation includes the bank variables, log employment, log firm age, credit score, log length of relationship with bank, a dummy for minority firm
owner, net worth, quarterly dummies, sectoral dummies, and risk-based capital ratio. Note that the risk based capital ratio is not available for credit unions (22 obs.). Using the risk-based net worth to proxy for the risk-based capital ratio does not change the results reported in columns (3) and
(6) significantly.
Heckman selection model. The selection equation includes the bank variables, log employment, log firm age, credit score, log length of relationship with bank, a dummy for minority firm
owner, net worth, quarterly dummies, sectoral dummies, and risk-based capital ratio. Note that the risk based capital ratio is not available for credit unions (22 obs.). Using the risk-based net worth to proxy for the risk-based capital ratio does not change the results reported in columns (3) and
(6) significantly.
| 1998 Sample Small Banks mean | 1998 Sample Small Banks std | 1998 Sample Large Banks mean | 1998 Sample Large Banks std | 1998 Sample Difference | |
| Number of Employees | 14.20 | 32.65 | 14.03 | 28.46 | -0.17 |
| Firm Age | 12.71 | 8.83 | 11.35 | 10.35 | -1.34 |
| Length of Lending Relationship | 8.22 | 8.55 | 5.43 | 7.15 | -2.80** |
| Credit Score |
3.10 | 1.10 | 2.91 | 1.04 | -0.19 |
| Share in Manufacturing | 0.10 | 0.30 | 0.08 | 0.27 | -0.03 |
| Net Worth (in mill.) | 0.41 | 1.09 | 0.53 | 1.60 | 0.12 |
| N | 379 | 379 | 144 | 144 |
| 2003 Sample Small Banks mean | 2003 Sample Small Banks std | 2003 Sample Large Banks mean | 2003 Sample Large Banks std | 2003 Sample Difference | |
|---|---|---|---|---|---|
| Number of Employees | 15.37 | 30.89 | 17.07 | 36.35 | 1.70 |
| Firm Age | 15.76 | 11.96 | 15.96 | 10.08 | 0.20 |
| Length of Lending Relationship | 10.18 | 9.25 | 11.03 | 9.18 | 0.85 |
| Credit Score |
3.83 | 1.43 | 3.77 | 1.47 | -0.05 |
| Share in Manufacturing | 0.09 | 0.28 | 0.15 | 0.35 | 0.06** |
| Net Worth (in mill.) | 0.70 | 2.02 | 0.95 | 2.43 | 0.15 |
| N | 928 | 928 | 412 | 412 |
Significance levels: ** 1%, ![]() 5%, and
5%, and ![]() 10%. Firms that received credit only.
10%. Firms that received credit only.
![]() The credit score in 1998 goes from 1 (lowest) to 5 (highest) and in 2003 from 1 (lowest) to 6 (highest).
The credit score in 1998 goes from 1 (lowest) to 5 (highest) and in 2003 from 1 (lowest) to 6 (highest).
| 1998 Sample Small Banks |
1998 Sample Small Banks |
2003 Sample Large Banks |
2003 Sample Large Banks |
|
| Net Worth (in mill.) | 0.365** | 0.147 |
0.296** | 0.298** |
| Net Worth (in mill.) standard error | (0.028) | (0.066) | (0.018) | (0.045) |
| Share of Firm's Liquid Assets | 0.158 | 0.216 | -0.531>** | -0.572 |
| Share of Firm's Liquid Assets standard error | (0.088) | (0.328) | (0.148) | (0.478) |
| Log Number of Employees | 0.061 |
0.290 |
0.096 |
0.210 |
| Log Number of Employees standard error | (0.033) | (0.118) | (0.040) | (0.112) |
| Log Firm Age | 0.033 | -0.314 |
-0.061 | 0.053 |
| Log Firm Age standard error | (0.041) | (0.183) | (0.048) | (0.168) |
| Log Length of Relationship | -0.059** | 0.007 | 0.020 | 0.090 |
| Log Length of Relationship standard error | (0.019) | (0.064) | (0.044) | (0.143) |
| Credit Score | 0.063 |
0.044 | -0.036 | -0.010 |
| Credit Score standard error | (0.028) | (0.129) | (0.029) | (0.080) |
| 1998 Sample Small Banks |
1998 Sample Small Banks |
2003 Sample Large Banks |
2003 Sample Large Banks |
|
|---|---|---|---|---|
| Interest Cost to Liabilities Ratio | 9.320> |
-31.337 | 2.797 | -45.694 |
| Interest Cost to Liabilities Ratio standard error | (5.452) | (26.754) | (8.861) | (58.453) |
| Other Cost to Asset Ratio | -1.620 | -7.234 | -3.665 | 0.223 |
| Other Cost to Asset Ratio standard error | (1.322) | (28.268) | (3.535) | (15.570) |
| Return on Equity | -0.873 | -1.144 | 0.744 | -3.082 |
| Return on Equity standard error | (0.527) | (6.363) | (0.633) | (2.875) |
| Adequacy Ratio | -0.370 | 5.447 | 0.805 | -7.406 |
| Adequacy Ratio standard error | (1.296 | (13.071) | (1.284) | (6.121) |
| Log Bank Assets | 0.014 | 0.105 | 0.040 |
-0.197 |
| Log Bank Assets standard error | (0.016) | (0.381) | (0.020) | (0.187) |
| Loan Share of Assets | -0.144 | -2.169 | 0.219 | -0.763 |
| Loan Share of Assets standard error | (0.316) | (2.086) | (0.315) | (1.602) |
| Additional Controls |
yes | yes | yes | yes |
| N | 379 | 114 | 877 | 386 |
| Adjusted |
0.42 | -0.28 | 0.32 | 0.12 |
Significance levels: ** 1%, ![]() 5%, and
5%, and ![]() 10%.
10%.
![]() Additional controls included are share of nonaccrual loans, share of loans 30-90 days past due, share of loans
Additional controls included are share of nonaccrual loans, share of loans 30-90 days past due, share of loans ![]() days past due and dummies for banks type (commerical bank, federal savings bank, credit union), market concentration, type of cooperation, judgements against the firm, previous private and firm bankruptcy, region, sector, quarter in which the loans was
taken out, urban, female firm owner, minority firm owner, and education of firm owner.
days past due and dummies for banks type (commerical bank, federal savings bank, credit union), market concentration, type of cooperation, judgements against the firm, previous private and firm bankruptcy, region, sector, quarter in which the loans was
taken out, urban, female firm owner, minority firm owner, and education of firm owner.
| Small Banks |
Small Banks |
Small Banks |
Large Banks |
Large Banks |
Large Banks |
|
| Share of Firm's Liquid Assets | -0.13 | 0.26 | 0.34 | 0.34 | 0.61 | 0.62 |
| Share of Firm's Liquid Assets standard error | (0.25) | (0.28) | (0.37) | (0.57) | (0.81) | (0.93) |
| Credit Score | -0.20 |
-0.17 |
-0.17 | -0.03 | -0.18 | -0.18 |
| Credit Score standard error | (0.09) | (0.09) | (0.11) | (0.24) | (0.33) | (0.25) |
| Log Number of Employees | -0.24 |
-0.22 |
-0.06 | -0.07 | ||
| Log Number of Employees standard error | (0.10) | (0.11) | (0.29) | (0.30) | ||
| Log Firm Age | -0.13 | -0.08 | 0.68 | 0.70 |
||
| Log Firm Age standard error | (0.13) | (0.19) | (0.41) | (0.31) | ||
| Log Length of Relationship | -0.05 | -0.05 | -0.26 | -0.26 |
||
| Log Length of Relationship standard error | (0.06) | (0.07) | (0.16) | (0.13) | ||
| Net Worth (in mill.) | -0.09 | -0.11 | -0.15 | -0.15 | ||
| Net Worth (in mill.) standard error | (0.09) | (0.09) | (0.17) | (0.09) |
| Small Banks |
Small Banks |
Small Banks |
Large Banks |
Large Banks |
Large Banks |
|
| Interest Cost to Liabilities Ratio | -49.15** | -72.90** | -80.40** | 2.49 | -40.12 | -47.38 |
| Interest Cost to Liabilities Ratio standard error | (14.38) | (17.10) | (23.39) | (12.25) | (63.39) | (43.33) |
| Other Cost to Asset Ratio | 3.13 | 6.11 | 6.08 | -10.78 | -58.17 | -60.98 |
| Other Cost to Asset Ratio standard error | (3.92) | (4.29) | (5.11) | (46.15) | (66.99) | (60.11) |
| Return on Equity | -0.96 | 0.34 | 2.73 | -0.43 | -9.38 | -9.27 |
| Return on Equity standard error | (1.39) | (1.68) | (2.32) | (9.35) | (15.35) | (10.75) |
| Adequacy Ratio | 0.48 | -2.24 | 1.34 | 20.96 | 3.02 | 3.28 |
| Adequacy Ratio standard error | (3.70) | (4.10) | (5.41) | (20.18) | (27.66) | (18.79) |
| Log Bank Assets | -0.07 | -0.08 | -0.48 | -0.71 | ||
| Log Bank Assets standard error | (0.05) | (0.07) | (0.68) | (0.68) | ||
| Loan Share of Assets | -0.43 | 0.03 | 7.13 | 5.27 |
||
| Loan Share of Assets standard error | (0.96) | (0.99) | (5.17) | (3.27) | ||
| Additional Controls |
no | yes | yes | no | yes | yes |
| N | 379 | 379 | 433 | 114 | 114 | 155 |
| Adjusted |
0.03 | 0.18 | - | -0.02 | 0.25 | - |
Significance levels: ** 1%, ![]() 5%, and
5%, and ![]() 10%.
10%.
![]() Additional controls included are share of nonaccrual loans, share of loans 30-90 days past due, share of loans
Additional controls included are share of nonaccrual loans, share of loans 30-90 days past due, share of loans ![]() days past due and dummies for banks type (commerical bank, federal savings bank, credit union), market concentration, type of cooperation, judgements against the firm, previous private and firm bankruptcy, region, sector, quarter in which the loans was
taken out, urban, female firm owner, minority firm owner, and education of firm owner.
days past due and dummies for banks type (commerical bank, federal savings bank, credit union), market concentration, type of cooperation, judgements against the firm, previous private and firm bankruptcy, region, sector, quarter in which the loans was
taken out, urban, female firm owner, minority firm owner, and education of firm owner.
![]() Heckman selection model. Additional controls included are share of nonaccrual loans, share of loans 30-90 days past due, share of loans
Heckman selection model. Additional controls included are share of nonaccrual loans, share of loans 30-90 days past due, share of loans ![]() days past due and dummies for banks type (commerical bank, federal savings bank, credit union), market concentration, type of cooperation, urban, region, sector, and quarter in which the loans was taken out. The selection equation
includes the bank variables, log employment, log firm age, credit score, log length of relationship with bank, a dummy for minority firm owner, net worth, sectoral dummies, and risk-based capital ratio. Note that the risk based capital ratio is not available for credit unions.
days past due and dummies for banks type (commerical bank, federal savings bank, credit union), market concentration, type of cooperation, urban, region, sector, and quarter in which the loans was taken out. The selection equation
includes the bank variables, log employment, log firm age, credit score, log length of relationship with bank, a dummy for minority firm owner, net worth, sectoral dummies, and risk-based capital ratio. Note that the risk based capital ratio is not available for credit unions.
| Small Banks |
Small Banks |
Small Banks |
Large Banks |
Large Banks |
Large Banks |
|
| Share of Firm's Liquid Assets | 0.37 | -0.47 | -0.35 | 1.49** | -0.08 | -0.55 |
| Share of Firm's Liquid Assets standard error | (0.28) | (0.32) | (0.45) | (0.57) | (0.60) | (0.68) |
| Credit Score | -0.28** | -0.20** | -0.18 |
-0.09 | -0.07 | -0.17 |
| Credit Score standard error | (0.05) | (0.06) | (0.09) | (0.11) | (0.10) | (0.16) |
| Log Number of Employees | -0.25** | -0.19 | -0.48** | -0.63** | ||
| Log Number of Employees standard error | (0.09) | (0.14) | (0.14) | (0.15) | ||
| Log Firm Age | -0.20** | -0.17 | -0.59** | -0.55 | ||
| Log Firm Age standard error | (0.10) | (0.14) | (0.21) | (0.34) | ||
| Log Length of Relationship | 0.11 | 0.26 |
0.63** | 0.56** | ||
| Log Length of Relationship standard error | (0.10) | (0.12) | (0.18) | (0.17) | ||
| Net Worth (in mill.) | -0.08 |
-0.07 |
-0.03 | -0.04 | ||
| Net Worth (in mill.) standard error | (0.04) | (0.04) | (0.05) | (0.03) |
| Small Banks |
Small Banks |
Small Banks |
Large Banks |
Large Banks |
Large Banks |
|
| Interest Cost to Liabilities Ratio | 68.47** | 20.60 | 23.24 | 34.07 | 235.28** | 256.94** |
| Interest Cost to Liabilities Ratio standard error | (13.97) | (19.82) | (32.49) | (37.56) | (71.95) | (82.73) |
| Other Cost to Asset Ratio | 9.60 | -5.14 | -9.70 | -27.51 | -68.15 |
-59.92 |
| Other Cost to Asset Ratio standard error | (7.31) | (7.97) | (7.19) | (20.54) | (28.06) | (33.90) |
| Return on Equity | 1.61 | 1.95 | 2.61 | -7.86 |
1.31 | 0.06 |
| Return on Equity standard error | (1.19) | (1.39) | (1.79) | (3.46) | (3.73) | (4.10) |
| Adequacy Ratio | 3.86 | -3.57 | -0.72 | 26.94** | 14.55 |
19.80** |
| Adequacy Ratio standard error | (2.57) | (2.82) | (3.14) | (6.99) | (7.93) | (6.96) |
| Log Bank Assets | -0.17** | -0.19** | 0.74** | 0.85** | ||
| Log Bank Assets standard error | (0.04) | (0.06) | (0.24) | (0.21) | ||
| Loan Share of Assets | -1.71 |
-2.06 |
2.45 | 2.33 | ||
| Loan Share of Assets standard error | (0.69) | (0.83) | (2.06) | (2.36) | ||
| Additional Controls |
no | yes | yes | no | yes | yes |
| N | 924 | 877 | 893 | 411 | 386 | 431 |
| Adjusted |
0.05 | 0.21 | - | 0.17 | 0.51 | - |
Significance levels: ** 1%, ![]() 5%, and
5%, and ![]() 10%.
10%.
![]() Additional controls included are share of nonaccrual loans, share of loans 30-90 days past due, share of loans
Additional controls included are share of nonaccrual loans, share of loans 30-90 days past due, share of loans ![]() days past due and dummies for banks type (commerical bank, federal savings bank, credit union), market concentration, type of cooperation, judgements against the firm, previous private and firm bankruptcy, region, sector, quarter in which the loans was
taken out, urban, female firm owner, minority firm owner, and education of firm owner.
days past due and dummies for banks type (commerical bank, federal savings bank, credit union), market concentration, type of cooperation, judgements against the firm, previous private and firm bankruptcy, region, sector, quarter in which the loans was
taken out, urban, female firm owner, minority firm owner, and education of firm owner.
![]() Heckman selection model. Additional controls included are share of nonaccrual loans, share of loans 30-90 days past due, share of loans
Heckman selection model. Additional controls included are share of nonaccrual loans, share of loans 30-90 days past due, share of loans ![]() days past due and dummies for banks type (commerical bank, federal savings bank, credit union), market concentration, type of cooperation, urban, region, sector, and quarter in which the loans was taken out. The selection equation
includes the bank variables, log employment, log firm age, credit score, log length of relationship with bank, a dummy for minority firm owner, net worth, sectoral dummies, and risk-based capital ratio. Note that the risk based capital ratio is not available for credit unions (22 obs.). Using the
risk-based net worth to proxy for the risk-based capital ratio does not change the results reported in columns (3) and (6) significantly.
days past due and dummies for banks type (commerical bank, federal savings bank, credit union), market concentration, type of cooperation, urban, region, sector, and quarter in which the loans was taken out. The selection equation
includes the bank variables, log employment, log firm age, credit score, log length of relationship with bank, a dummy for minority firm owner, net worth, sectoral dummies, and risk-based capital ratio. Note that the risk based capital ratio is not available for credit unions (22 obs.). Using the
risk-based net worth to proxy for the risk-based capital ratio does not change the results reported in columns (3) and (6) significantly.
| 1998 Sample OLS | 1998 Sample OLS | 1998 Sample Selection |
2003 Sample OLS | 2003 Sample OLS | 2003 Sample Selection |
|
| Net Worth |
0.225 |
0.316** | 0.224 |
0.325** | 0.264 |
0.284 |
| Net Worth standard error | (0.099) | (0.118) | (0.099) | (0.121) | (0.119) | (0.117) |
| Ln Number of Employees | 0.136** | 0.306** | ||||
| Ln Number of Employees standard error | (0.040) | (0.043) | ||||
| controls |
no | yes | no | no | yes | no |
| N | 542 | 542 | 876 | 1693 | 1652 | 1829 |
| R2 | 0.16 | 0.16 | - | 0.07 | 0.12 | - |
Significance levels: : ![]() : 10%
: 10% ![]() : 5%
: 5% ![]() : 1%
: 1%
![]() Heckman selection model using information on whether the firm's credit application was accepted. The probability of receiving credit is estimated using net worth, ln(emploment),
ln(length of relationship with the lender), ln(firmage), credit score, and dummy variables for industry, region, gender, minority status, organizational form of the firm, previous bankruptcies and judgements against the firm.
Heckman selection model using information on whether the firm's credit application was accepted. The probability of receiving credit is estimated using net worth, ln(emploment),
ln(length of relationship with the lender), ln(firmage), credit score, and dummy variables for industry, region, gender, minority status, organizational form of the firm, previous bankruptcies and judgements against the firm.
![]() Net worth is defined as the sum of land, depreciable assets, and the net value of the private residence minus loans.
Net worth is defined as the sum of land, depreciable assets, and the net value of the private residence minus loans.
![]() Additional controls include ln(firmage), credit score, and dummy variables for industry, region, gender, minority status, organizational form of the firm, previous bankruptcies and
judgements against the firm.
Additional controls include ln(firmage), credit score, and dummy variables for industry, region, gender, minority status, organizational form of the firm, previous bankruptcies and
judgements against the firm.
| 1998 Sample OLS | 1998 Sample OLS | 1998 Sample Selection |
2003 Sample OLS | 2003 Sample OLS | 2003 Sample Selection |
|
| Net Worth |
0.179 |
0.325 |
0.196 |
0.227 |
0.168 |
0.177 |
| Net Worth standard error | (0.117) | (0.138) | (0.116) | (0.108) | (0.119) | (0.097) |
| Ln Number of Employees | 0.154** | 0.335** | ||||
| Ln Number of Employees standard error | (0.039) | (0.041) | ||||
| controls |
no | yes | no | no | yes | no |
| N | 711 | 542 | 876 | 1693 | 1652 | 1829 |
| R2 | 0.02 | 0.13 | - | 0.07 | 0.08 | - |
Significance levels: : ![]() : 10%
: 10% ![]() : 5%
: 5% ![]() : 1%
: 1%
![]() Heckman selection model using information on whether the firm's credit application was accepted. The probability of receiving credit is estimated using net worth, ln(emploment),
ln(length of relationship with the lender), ln(firmage), credit score, and dummy variables for industry, region, gender, minority status, organizational form of the firm, previous bankruptcies and judgements against the firm.
Heckman selection model using information on whether the firm's credit application was accepted. The probability of receiving credit is estimated using net worth, ln(emploment),
ln(length of relationship with the lender), ln(firmage), credit score, and dummy variables for industry, region, gender, minority status, organizational form of the firm, previous bankruptcies and judgements against the firm.
![]() Net worth is defined as the sum of land, depreciable assets, and the net value of the private residence minus all liabilities.
Net worth is defined as the sum of land, depreciable assets, and the net value of the private residence minus all liabilities.
![]() Additional controls include ln(firmage), credit score, and dummy variables for industry, region, gender, minority status, organizational form of the firm, previous bankruptcies and
judgements against the firm.
Additional controls include ln(firmage), credit score, and dummy variables for industry, region, gender, minority status, organizational form of the firm, previous bankruptcies and
judgements against the firm.
| 1998 Sample OLS | 1998 Sample OLS | 1998 Sample Selection |
2003 Sample OLS | 2003 Sample OLS | 2003 Sample Selection |
|
| Net Worth |
0.373** | 0.341** | 0.372** | 0.395** | 0.365** | 0.392** |
| Net Worth standard error | (0.078) | (0.109) | (0.078) | (0.056) | (0.056) | (0.056) |
| Ln Number of Employees | 0.052 | 0.176** | ||||
| Ln Number of Employees standard error | (0.034) | (0.033) | ||||
| controls |
no | yes | no | no | yes | no |
| N | 711 | 542 | 876 | 1693 | 1652 | 1829 |
| R2 | 0.32 | 0.35 | - | 0.27 | 0.28 | - |
Significance levels: : ![]() : 10%
: 10% ![]() : 5%
: 5% ![]() : 1%
: 1%
![]() Heckman selection model using information on whether the firm's credit application was accepted. The probability of receiving credit is estimated using net worth, ln(emploment),
ln(length of relationship with the lender), ln(firmage), credit score, and dummy variables for industry, region, gender, minority status, organizational form of the firm, previous bankruptcies and judgements against the firm.
Heckman selection model using information on whether the firm's credit application was accepted. The probability of receiving credit is estimated using net worth, ln(emploment),
ln(length of relationship with the lender), ln(firmage), credit score, and dummy variables for industry, region, gender, minority status, organizational form of the firm, previous bankruptcies and judgements against the firm.
![]() Net worth is defined as the all firm assets minus all firm liabilities.
Net worth is defined as the all firm assets minus all firm liabilities.
![]() Additional controls include ln(firmage), credit score, and dummy variables for industry, region, gender, minority status, organizational form of the firm, previous bankruptcies and
judgements against the firm.
Additional controls include ln(firmage), credit score, and dummy variables for industry, region, gender, minority status, organizational form of the firm, previous bankruptcies and
judgements against the firm.
| Alternative Cost Measure OLS (1) Firm Variables | Alternative Cost Measure OLS (2) Firm Variables | Alternative Cost Measure Selection |
Three Year Averages OLS (4) Firm Variables | Three Year AveragesOLS (5) Firm Variables | Three Year Averages Selection |
|
| Share of Firm's Liquid Assets | 0.66 |
-0.38 | -0.19 | 0.69** | -0.38 | -0.14 |
| Share of Firm's Liquid Assets standard error | (0.26) | (0.29) | (0.37) | (0.26) | (0.30) | (0.38) |
| Credit Score | -0.24** | -0.15** | -0.18 |
-0.23** | -0.15** | -0.16 |
| Credit Score standard error | (0.05) | (0.05) | (0.07) | (0.05) | (0.05) | (0.07) |
| Log Number of Employees | -0.24** | -0.23 |
-0.25** | -0.29** | ||
| Log Number of Employees standard error | (0.08) | (0.09) | (0.08) | (0.10) | ||
| Log Firm Age | -0.24** | -0.44** | -0.33** | -0.40** | ||
| Log Firm Age standard error | (0.08) | (0.14) | (0.10) | (0.14) | ||
| Log Length of Relationship | 0.30** | 0.34** | 0.27** | 0.27 | ||
| Log Length of Relationship standard error | (0.09) | (0.12) | (0.09) | (0.35) | ||
| Net Worth (in mill.) | -0.09** | -0.09** | -0.09 |
-0.09** | ||
| Net Worth (in mill.) standard error | (0.03) | (0.03) | (0.03) | (0.03) |
| Alternative Cost Measure OLS (1) Bank Variables | Alternative Cost Measure OLS (2) Bank Variables | Alternative Cost Measure Selection |
Three Year Averages OLS (4) Bank Variables | Three Year AveragesOLS (5) Bank Variables | Three Year Averages Selection |
|
| Interest Cost to Liabilities Ratio | 51.78** | 22.36 | 30.33 | 25.07 | 33.29 |
32.08 |
| Interest Cost to Liabilities Ratio standard error | (13.46) | (17.54) | (27.94) | (15.31) | (18.22) | (17.10) |
| Other Cost to Asset Ratio | -5.51 | -40.77** | -37.61 |
3.41 | -13.28 | -10.65 |
| Other Cost to Asset Ratio standard error | (13.27) | (13.77) | (17.49) | (7.79) | (8.41) | (16.88) |
| Return on Equity | 0.32 | 0.14 | 0.58 | -0.19 | -0.28 | -0.33 |
| Return on Equity standard error | (1.18) | (1.31) | (1.83) | (1.33) | (1.43) | (2.69) |
| Adequacy Ratio | 5.36 |
-0.50 | 0.44 | 7.48** | -1.13 | -1.75 |
| Adequacy Ratio standard error | (2.51) | (2.63) | (3.21) | (2.90) | (3.24) | (4.03) |
| Log Bank Assets | -0.03 | -0.03 | 0.01 | -0.00 | ||
| Log Bank Assets standard error | (0.03) | (0.04) | (0.03) | (0.04) | ||
| Loan Share of Assets | -1.19 |
-1.11 | -0.36 | -0.36 | ||
| Loan Share of Assets standard error | (0.55) | (0.80) | (0.61) | (0.91) | ||
| Additional Controls |
no | yes | yes | no | yes | yes |
| N | 1335 | 1263 | 1324 | 1338 | 1266 | 1338 |
| Adjusted |
0.03 | 0.25 | - | 0.02 | 0.21 | - |
Significance levels: ** 1%, ![]() 5%, and
5%, and ![]() 10%.
10%.
![]() Additional controls included are share of nonaccrual loans, share of loans 30-90 days past due, share of loans
Additional controls included are share of nonaccrual loans, share of loans 30-90 days past due, share of loans ![]() days past due and dummies for banks type (commerical bank, federal savings bank, credit union), market concentration, type of cooperation, judgements against the firm, previous private and firm bankruptcy, region, sector, quarter in which the loans was
taken out, urban, female firm owner, minority firm owner, and education of firm owner.
days past due and dummies for banks type (commerical bank, federal savings bank, credit union), market concentration, type of cooperation, judgements against the firm, previous private and firm bankruptcy, region, sector, quarter in which the loans was
taken out, urban, female firm owner, minority firm owner, and education of firm owner.
![]() Heckman selection model. Only 81 firm owners report credit denial hence the model contains only a limited set of variables. The selection equation includes the bank variables, log
employment, log firm age, credit score, log length of relationship with bank, a dummy for minority firm owner and quarter in which the loans was taken out, and risk-based capital ratio. Note that the risk based capital ratio is not available for credit unions (23 obs.). Using the risk-based net
worth to proxy for the risk-based capital ratio does not change the results reported in columns (3) and (6) significantly.
Heckman selection model. Only 81 firm owners report credit denial hence the model contains only a limited set of variables. The selection equation includes the bank variables, log
employment, log firm age, credit score, log length of relationship with bank, a dummy for minority firm owner and quarter in which the loans was taken out, and risk-based capital ratio. Note that the risk based capital ratio is not available for credit unions (23 obs.). Using the risk-based net
worth to proxy for the risk-based capital ratio does not change the results reported in columns (3) and (6) significantly.
Figure 1: Comparative Statics
This figure plots the five-year CDS spreads of full sample and three sub-samples. We group the CDS spreads into three sub-samples by CDS ratings. The first group contains CDS of AAA, AA and A grades. The second group contains CDS of BBB grade. The third group contains CDS of speculative grades ranging between BB and CCC. The three sub-samples contain 7,315, 9,582 and 5,107 observations respectively. The CDS spreads decrease gradually from the peaks in late 2002, then increase again as the financial crisis approaches in year 2007. The spreads of investment grade CDS in year 2008 are higher than those in year 2002, whereas the spreads of speculative grade CDS are lower than their 2002 level. That highlights the nature of the recent financial crisis which was fueled mostly by the financial distress of highly rated credit products. The difference between the CDS spreads for investment grade and speculative group CDS however becomes widen potentially due to the "fly-to-quality" effect during the financial crisis, driving up compensation for credit risk.Figure 2 Panel A: CSV Implied Agency Cost and Risk Parameters
Figure 2 Panel B: CSV Implied Agency Cost and Risk Parameters
Figure 3 Panel A: MH Implied Interest Rates and Actual Interest Rates
Figure 3 Panel B: MH Implied Interest Rates and Actual Interest Rates
Figure 4 Panel A: MH and Actual Interest Rates, Quarterly Averages
Figure 4 Panel B: MH and Actual Interest Rates, Quarterly Averages
Figure 5: MH and Actual Interest Rates, Alternative Cost Measure - 2003 Sample
Footnotes
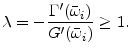
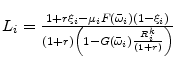 which is lower than without additional repossession cost. Hennessy and Whited (2007) estimate the cost of repossessing to be 10 percent of the capital stock. However, their point estimate is not significant. One interpretation of this repossession cost is the homestead exemption in bankruptcy laws. Berkowitz and
White (2004) find that higher exemptions reduce access to credit significantly. Return to Text
which is lower than without additional repossession cost. Hennessy and Whited (2007) estimate the cost of repossessing to be 10 percent of the capital stock. However, their point estimate is not significant. One interpretation of this repossession cost is the homestead exemption in bankruptcy laws. Berkowitz and
White (2004) find that higher exemptions reduce access to credit significantly. Return to Text