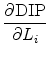Skip to: [Printable Version (PDF)] [Bibliography] [Footnotes]

Finance and Economics Discussion Series: 2011-08 Screen Reader version ^♣

Systemic Risk Contributions¹

Xin Huang²

Hao Zhou³

Haibin Zhu⁴

First Draft: August 2010
This Version: November 2010

Keywords: Distress insurance premium, systemic risk, macroprudential regulation, large complex financial institution, too-big-to-fail, too-connected-to-fail.

Abstract:

We adopt a systemic risk indicator measured by the price of insurance against systemic financial distress and assess individual banks' marginal contributions to the systemic risk. The methodology is applied using publicly available data to the 19 bank holding companies covered by the U.S. Supervisory Capital Assessment Program (SCAP), with the systemic risk indicator peaking around $1.1 trillion in March 2009. Our systemic risk contribution measure shows interesting similarity to and divergence from the SCAP expected loss measure. In general, we find that a bank's contribution to the systemic risk is roughly linear in its default probability but highly nonlinear with respect to institution size and asset correlation.

JEL classification: G21, G28, G14.

1 Introduction

The recent global financial crisis has led bank supervisors and regulators to rethink the rationale of banking regulation. One important lesson is that the traditional approach to ensuring the soundness of individual banks, as in Basel I and Basel II, needs to be supplemented by a system-wide macroprudential approach. The macroprudential perspective of supervision focuses on the soundness of the banking system as a whole and the inter-linkages among those systemically important banks. This perspective has become an overwhelming theme in the policy deliberations among legislative committees, bank regulators, and academic researchers.⁵ As stated in the Financial Stability Board's interim report in June 2010, "Financial institutions should be subject to requirements commensurate with the risks they pose to the financial system."

However, implementing such a macroprudential perspective is not an easy task. The operational framework needs to provide answers to three crucial questions. First, how should the systemic risk in a financial system be measured? Second, how should the contributions of individual banks (or financial institutions) to the systemic risk be measured? Third, how can prudential requirements on individual banks, such as capital surcharges, taxes, or fees for a financial stability fund, be designed so that they are connected with banks' systemic risk contributions?

Against such a background, this paper proposes a consistent framework that provides direct answers to the first two questions, the results of which can be used as helpful inputs to address the third question. Our systemic risk measure can be interpreted economically as the insurance premium to cover distressed losses in a banking system, which is a concept of a risk-neutral market price, assuming that such an insurance market exists and functions properly (Huang, Zhou, and Zhu, 2009). Within the same framework, the systemic importance of each bank (or bank group) can be properly defined as its marginal contribution to the hypothetical distress insurance premium (DIP) of the whole banking system. This approach allows us to study the time variation and cross section of the systemic risk contributions of U.S. large complex financial institutions (LCFIs). Our metric can be applied using only publicly available information for large banking organizations.

Adopting such a consistent approach has advantages . Under such a framework, the marginal contribution of each bank adds up to the aggregate systemic risk. As shown in Tarashev, Borio, and Tsatsaronis (2009a), this additivity property is desirable from an operational perspective because it allows the macroprudential tools to be implemented at individual bank levels. In particular, prudential requirements can be linear transformations of the marginal contribution measures if the measures are additive. One can also decompose our systemic risk measures into different economic channels--for example, risk premium versus actual default risk and credit risk versus liquidity risk. Finally, since our structural framework uses default probabilities, liability sizes, and correlations directly as inputs to capture the well publicized characteristics of systemic risk--leverage, too-big-to-fail, and too-connected-to-fail--one can easily swap these inputs with supervisory confidential information for practical policy analysis.

We applied this approach to the 19 bank holding companies (BHCs) covered by the U.S. Supervisory Capital Assessment Program (SCAP)--commonly known as the "stress test"--during the period from January 2004 to December 2009. However, unlike the SCAP, our analysis did not rely on any confidential, supervisory, or proprietary information or data. Our findings suggest that the systemic risk indicator stood at its peak around $1.1 trillion in March 2009 and has since fallen to about $300 billion--the level reached in January 2008. A bank's contribution to the systemic risk indicator appears to be linearly related to its default probability but highly nonlinear with respect to institution size and asset correlation. We find that the increase in systemic risk of the U.S. banking sector during the 2007-09 financial crisis was initially driven mainly by heightened default and liquidity risk premiums and later by the deterioration in actual default risk.

More important, we can rank the systemic importance of LCFIs in the U.S. banking sector. By our relative measure since the summer of 2007, Bank of America and Wells Fargo's contributions to systemic risk have risen, JPMorgan Chase has seen some decreases, and Citigroup's share has remained the largest. The relative contributions to systemic risk from both consumer banks and regional banks seem to be increasing somewhat since 2009, possibly because of the worsening situations in the commercial real estate and consumer credit sectors, which typically lag the business cycles. Overall, our analysis suggests that size is the dominant factor in determining the relative importance of each bank's systemic risk contribution, but size does not change significantly over time, at least within a reporting quarter. The obvious time variations in the marginal contributions are driven mostly by the risk-neutral default probability and equity return correlation. In essence, the systemic importance of each institution is jointly determined by the size, default probability, and asset correlation of all institutions in the portfolio.

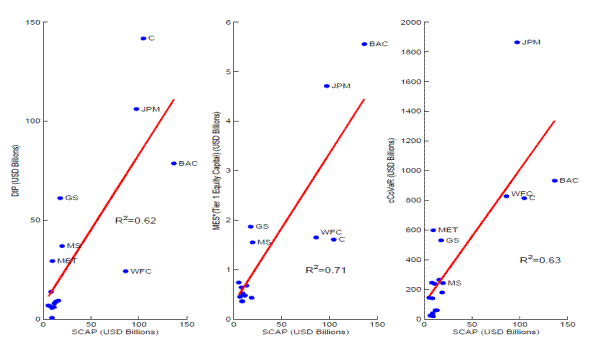
Finally, our measure of the systemic importance of financial institutions noticeably resembles the SCAP result. Based on the data through December 31, 2008, the 19 banks' contributions to the systemic risk indicator are mostly in line with the SCAP estimate of losses under an adverse economic scenario as released on May 9, 2009, with an R-square of 0.62. Goldman Sachs, Citigroup, and JPMorgan Chase, in particular, would be viewed as contributing more to systemic risk by our method (from a risk premium perspective) than by the SCAP results, while Bank of America and Wells Fargo would be viewed as more risky by the SCAP results (from an expected loss perspective) than by our method. Note that our systemic risk measure also contains a risk premium, while the SCAP estimate is based on statistical expected loss.

One leading alternative--marginal expected shortfall (MES), by Acharya, Pedersen, Philippon, and Richardson (2010), which is weighted by a bank's tier 1 capital--is also highly correlated with SCAP (R-square of 0.71). Relative to SCAP, MES considers Bank of America, JPMorgan Chase, and Goldman Sachs more risky and Wells Fargo and Citigroup less risky. The most notable reversals in ranking from our measure to MES are Bank of America and Citigroup. Another alternative--conditional value at risk (CoVaR), by Adrian and Brunnermeier (2009), which is translated into dollar amount--has a similar correlation with SCAP (R-square of 0.63). Compared with SCAP, CoVaR ranks JPMorgan Chase, MetLife, and Goldman Sachs as more risky but Citigroup and Bank of America as less risky. Again, the most notable reversals from our measure to CoVaR are MetLife and Citigroup. These ranking differences may reflect the fact that DIP is a risk-neutral-based pricing measure, while MES and CoVaR are statistical measures based on physical distributions. The contrast between MES and CoVaR may be due to the fact that for heavy-tailed distributions, the tail percentiles and expectations can diverge significantly.

Along similar lines, Lehar (2005), Chan-Lau and Gravelle (2005), and Avesani, Pascual, and Li (2006) proposed alternative systemic risk indicators--default probabilities--based respectively, on the credit default swap (CDS), option, or equity market. Recently, Cont (2010) emphasizes a network-based systemic risk measure, while Kim and Giesecke (2010) try to examine the term structure of a systemic risk measure. Billio, Getmansky, Lo, and Pelizzon (2010) study five systemic risk measures based on a statistical analysis of equity returns. All these indicators are useful supplements to balance sheet information, such as the Financial Soundness Indicators used in the Financial Sector Assessment Program (FSAP) by the International Monetary Fund (IMF). In addition, supervisors sometimes implement risk assessments based on confidential banking information, such as the SCAP implemented by the U.S. regulatory authorities in early 2009 and the Europe-wide stress testing program sanctioned by the Committee of European Banking Supervisors (CEBS) in July 2010. Finally, the recently enacted Dodd-Frank Wall Street Reform and Consumer Protection Act (United States Congress, 2010) imposes a limit on a bank's size, which is known as the Volcker concentration limit and aims at containing the systemic risk of individual banks.

The remainder of the paper is organized as follows. Section 2 outlines the methodology. Section 3 introduces the data, and Section 4 presents empirical results based on an illustrative banking system that consists of 19 LCFIs in the United States. The last section concludes.

2 Methodology

This section describes the methodology used in the paper. The first part constructs a market-based systemic risk indicator for a heterogeneous portfolio of financial institutions, and the second part designs a measure to assess the contribution of each bank (or each group of banks) to the systemic risk indicator.

2.1 Constructing the Systemic Risk Indicator

To construct a systemic risk indicator of a heterogeneous banking portfolio, we followed the structural approach of Vasicek (1991) for pricing the portfolio credit risk, which is also consistent with the Merton (1974) model for individual firm default. The systemic risk indicator, a hypothetical insurance premium against catastrophic losses in a banking system, was constructed from real-time publicly available financial market data (Huang, Zhou, and Zhu, 2009). The two key default risk factors, the probability of default (PD) of individual banks and the asset return correlations among banks, were estimated from CDS spreads and equity price co-movements, respectively.

2.1.1 Risk-Neutral Default Probability

The PD measure used in this approach was derived from single-name CDS spreads. A CDS contract offers protection against default losses of an underlying entity; in return, the protection buyer agrees to make constant periodic premium payments. The CDS market has grown rapidly in recent years, and the CDS spread is considered superior to the bond spread or loan spreads as a measure of credit risk.⁶ The spread of a -year CDS contract is given by

$\displaystyle s_{i,t}=\frac{(1-R_{i,t})\int_t^{t+T} e^{-r_{\tau}\tau} q_{i,\tau} d\tau} {\int_t^{t+T} e^{-r_{\tau}\tau}\left[1-\int_t^{\tau}q_{i,u}du\right]d\tau} ,$

(1)

where $R_{i,t}$ is the recovery rate,

is the default-free interest rate, and $q_{i,t}$ is the risk-neutral default intensity. The banks are indexed by $i=1,\cdots ,N$ . The above characterization assumes that recovery risk is independent of interest rate and default risks.

Under the simplifying assumptions of a flat term structure of the risk-free rate and a flat default intensity term structure, the one-year risk-neutral PDs of individual banks can be derived from CDS spreads, as in Duffie (1999) and Tarashev and Zhu (2008a):

$\displaystyle PD_{i,t} = \frac{a_t s_{i,t}}{a_t LGD_{i,t}+b_t s_{i,t}} ,$

(2)

where $a_{t}\equiv \int_t^{t+T} e^{-r_t \tau} d\tau$ , $b_{t}\equiv \int_t^{t+T} \tau e^{-r_t \tau} d\tau$ , and $LGD_{i,t}=(1-R_{i,t})$ is the loss-given-default.

Three elements are in the implied PD estimated from the CDS market: (1) the compensation for expected default losses; (2) the default risk premium for bearing the default risk; and (3) other premium components, such as liquidity or uncertainty risk compensations. Our systemic risk indicator incorporates the combined effects of these three elements on the price of insurance against distressed losses in the banking system.

One extension in this study is that we allowed for the LGD to vary, rather than assuming it to be a constant, over time.⁷ For example, Altman and Kishore (1996) showed that the LGD can vary over the credit cycle. To reflect the co-movement in the PD and LGD parameters, we chose to use expected LGDs as reported by market participants who price and trade the CDS contracts.

2.1.2 Asset Return Correlation

Systemic risk in a financial sector is in essence a joint default event of multiple large institutions, which is captured by the correlations of observable equity returns (Nicolò and Kwast, 2002). At a more fundamental level, such a correlation structure may be driven by the common movements in underlying firms' asset dynamics (Vasicek, 1991). We measured the asset return correlation by the equity return correlation (Hull and White, 2004), as the equity market is the most liquid financial market and can incorporate new information on an institution's default risk in a timely way. The standard approach is to use the so-called historical correlation, which is based on the past year of daily return data.

Let $\rho_{i,j}$ denote the correlation between banks' asset returns $A_{i,t}$ and $A_{j,t}$ , which is approximated by the correlation between banks' equity returns, with and $j\in \left\{ 1,\cdots ,N\right\}$ and as the number of banks. To ensure the internal consistency of correlation estimates, we assumed that asset returns are underpinned by common factors $M_{t}=[M_{1,t},\cdots ,M_{F,t}]^{\prime }$ and idiosyncratic factors $Z_{i,t}$ (Gordy, 2003):

$\displaystyle \Delta \log(A_{i,t})=B_{i}M_{t}+\sqrt{1-B_{i}^{\prime }B_{i}}\cdot Z_{i,t} ,$

(3)

where $B_{i}\equiv \lbrack \beta _{i,1},\cdots ,\beta _{i,f},\cdots ,\beta _{i,F}]$ is the vector of common factor loadings, $\beta _{i,f}\in \lbrack -1,1]$ and $\sum_{f=1}^{F}\beta _{i,f}^{2}\leq 1$ . Without loss of generality, all common and idiosyncratic factors were assumed to be mutually independent and to have zero means and unit variances.

We estimated the loading coefficients $\beta _{i,f}$ ( $i=1,\cdots ,N$ , $f=1,\cdots ,F$ ) by minimizing the mean squared difference between the target correlations and the factor-driven correlations:⁸

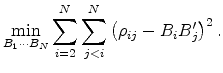$\displaystyle \min_{B_{1}\cdot \cdot \cdot B_{N}}\sum_{i=2}^{N}\sum_{j<i}^{N}\left( \rho _{ij}-B_{i}B_{j}^{\prime }\right) ^{2} .$

(4)

In practice, three common factors can explain up to 95 percent of the total variation in our correlation sample estimates. More important, besides the " zero mean, unit variance"normalization, this estimation method imposes no restriction on the distribution of the common and idiosyncratic factors.

2.1.3 Hypothetical Distress Insurance Premium

Based on the inputs of the key credit risk parameters--PDs, LGDs, correlations, and liability weights--the systemic risk indicator can be calculated by simulation as described in Gibson (2004), Hull and White (2004), and Tarashev and Zhu (2008b). In short, to compute the indicator, we first constructed a hypothetical debt portfolio that consisted of the total liabilities (deposits, debts, and others) of all banks. The indicator of systemic risk, effectively weighted by the liability size of each bank, is defined as the insurance premium that protects against the distressed losses of this portfolio. Technically, it is calculated as the risk-neutral expectation of portfolio credit losses that equal or exceed a minimum share of the sector's total liabilities.

To be more specific, let denote the loss of bank 's liability with $i=1,\cdots ,N$ ; $L=\sum_{i=1}^N L_i$ is the total loss of the portfolio. Then the systemic risk of the banking sector, or the distress insurance premium (DIP), is given by the risk-neutral expectation of the loss exceeding a certain threshold level:

DIP $\displaystyle = \operatorname{E}^Q\left[L\vert L\ge L_{\min}\right] ,$

(5)

where $L_{\min}$ is a minimum loss threshold or "deductible" value. The DIP formula can be easily implemented with Monte Carlo simulation (Huang, Zhou, and Zhu, 2009).

Notice that the definition of this DIP is very close to the concept of expected shortfall (ES) used in the literature (see, e.g., Acharya, Pedersen, Philippon, and Richardson, 2010) in that both refer to the conditional expectations of portfolio credit losses under extreme conditions. They differ slightly in the sense that the extreme condition is defined by the percentile distribution in the case of ES but by a given threshold loss of the underlying portfolio in the case of DIP. Also, the probabilities in the tail event underpinning ES are normalized to sum to 1; these probabilities are not normalized for DIP. The value-at-risk measure, or VaR--extended by Adrian and Brunnermeier (2009) into CoVaR--is also based on the percentile distribution, but as shown by Inui and Kijima (2005), Yamai and Yoshiba (2005), and Embrechts, Lambrigger, and Wüthrich (2009), ES is a coherent measure of risk while VaR is not.⁹

2.2 Identifying Systemically Important Banks

For the purpose of macroprudential regulation, it is important not only to monitor the level of systemic risk for the banking sector but also to understand the sources of risks in the financial system, i.e., to measure the marginal contributions of each institution. This information is especially useful considering the reform effort of the financial regulations across the globe, with the main objective of charging additional capital for systemically important banks and supporting a resolution regime for these banks. In the following paragraphs, we propose a method to decompose the credit risk of the portfolio into the sources of risk contributions associated with individual subportfolios (either a bank or a group of banks).

Following Kurth and Tasche (2003) and Glasserman (2005), for standard measures of risk, including VaR, ES, and the DIP used in this study, the total risk can be usefully decomposed into a sum of marginal risk contributions. Each marginal risk contribution is the expected loss from that subportfolio, conditional on a large loss for the full portfolio. In particular, if we define as the loss variable for the whole portfolio and as the loss variable for a subportfolio, the marginal contribution to our systemic risk indicator, the DIP, can be characterized by

$\displaystyle \frac{\partial \mbox{DIP}}{\partial L_{i}}$

$\displaystyle \equiv$

$\displaystyle \operatorname{E}^Q[L_i\vert L \ge L_{\min}] .$

(6)

The additivity property of the decomposition results--i.e., the fact that the systemic risk of a portfolio equals the marginal contribution from each subportfolio--is extremely important from an operational perspective. Whereas the macroprudential approach focuses on the risk of the financial system as a whole, in the end regulatory and policy measures are introduced at the level of individual banks. Our approach, therefore, allows a systemic risk regulator to easily link the regulatory capital assessment with risk contributions from each institution.

A technical difficulty is that systemic distresses are rare events; and thus ordinary Monte Carlo estimation is impractical for the purpose of calculation. Therefore, to improve the efficiency and precision, we relied on the importance-sampling method developed by Glassmerman and Li (2005) for simulating portfolio credit losses. For the 19-bank portfolio in our sample, we used the mean-shifting method and generated 200,000 importance-sampling simulations of default scenarios (default or not),¹⁰ and for each scenario we generated 100 simulations of LGDs.¹¹ Based on these simulation results, we calculated the expected loss of each subportfolio conditional on the total loss exceeding a given threshold.

2.2.1 Alternative Approaches

The body of literature on systemic risk measurement and management is rapidly growing; some researchers are focusing on the interaction between the real economy and the financial sector (see, e.g., Nicolò and Lucchetta, 2010), and others on financial sector default risk (see, e.g., Kim and Giesecke, 2010). Three approaches are closely related to ours in terms of focusing on identifying systemically important institutions and charging additional capital based on banks' marginal contributions.¹²

The most closely related approach is the CoVaR method proposed by Adrian and Brunnermeier (2009). CoVaR looks at the VaR of the whole portfolio conditional on the VaR of an individual institution, defined implicitly as

Prob $\displaystyle \left(L \ge \mbox{CoVaR}_q \vert L_i \ge \mbox{VaR}_q^i\right) = q ,$

(7)

where the expectation is taken under the objective measure. In other words, the focus of CoVaR is to examine the spillover or correlation effect from one bank's failure on the whole system, but CoVaR underplays the importance of institutional size by design. By comparison, our definition of DIP is along the same lines, but DIP focuses on the loss of a particular bank (or bank group) conditional on the system being in distress.¹³ Nevertheless, a major disadvantage of CoVaR is that it can be used only to identify systemically important institutions but cannot appropriately aggregate the systemic risk contributions of individual institutions.¹⁴

Another alternative is the MES proposed by Acharya, Pedersen, Philippon, and Richardson (2010). MES looks at the expected loss of each bank conditional on the whole portfolio of banks performing poorly:

MES $\displaystyle _q^i \equiv \operatorname{E}\left(L_i\vert L\ge\mbox{VaR}_q\right) ,$

(8)

where the expectation is taken under the objective measure. Again, in comparison, MES is similar to our DIP measure in that both focus on each bank's potential loss conditional on the system being in distress exceeding a threshold level, and both are coherent risk measures. They differ slightly in the sense that the extreme condition is defined by the percentile distribution in the MES setting but by a given threshold loss of the underlying portfolio in the case of DIP. Also, the probabilities in the tail event underpinning MES are normalized to sum to 1; these probabilities are not normalized for DIP. The more important difference is that MES is calculated based on equity return data, while our DIP measure is based mainly on the CDS data. Compared with equity return data, CDS data are better and purer sources of default risk information.

A third alternative is the "Shapley value" decomposition approach by Tarashev, Borio, and Tsatsaronis (2009a),b), which focuses on how to allocate among individual institutions any appropriately defined notion of systemic risk. The Shapley value approach, constructed in game theory, defines the contribution of each bank as a weighted average of its add-on effect to each subsystem that includes this bank. The Shapley value approach derives systemic importance at a different level from our approach. Under its general application, the Shapley value approach tends to suffer from the curse of dimensionality problem in that, for a system of banks, there are possible subsystems for which the systemic risk indicator needs to be calculated.¹⁵ However, the Shapley value approach has the same desirable additivity property and therefore can be used as a general approach for allocating systemic risk.

3 Data

We applied the methodology outlined previously, which relies only on publicly available data, to the 19 bank holding companies (BHCs) covered by the U.S. Supervisory Capital Assessment Program (SCAP) conducted in the spring of 2009. These BHCs all have year-end 2008 assets exceeding $100 billion and collectively hold two-thirds of the assets and more than half of the loans in the U.S. banking system (Federal Reserve Board, 2009a). The SCAP is widely credited as a critical step for transparently revealing the riskiness of the U.S. banking sector and clearly identifying the capital needs of major financial institutions. The subsequent recovery of broad financial markets from the distressed level and the successful new issuance of equity capital and long-term bonds by major U.S. banks prove the usefulness of the stress test in building the public confidence of the financial sector. Therefore, the 19 banks included in the SCAP represent an important sample, which serves as a benchmark portfolio for comparing various measures of systemic risk.

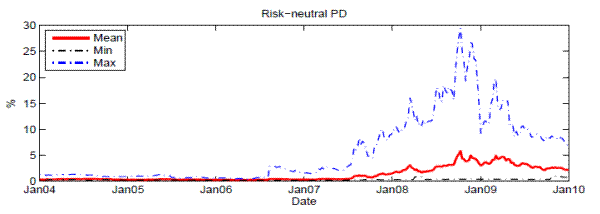
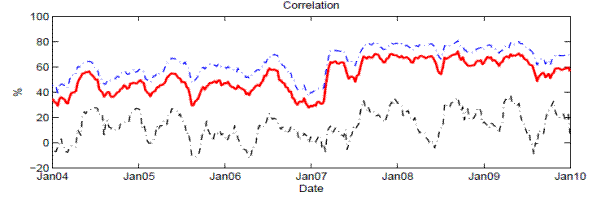
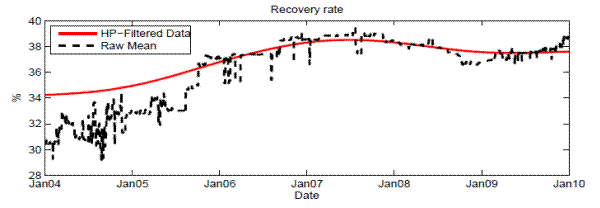
Table 1 reports the list of banks included in this study and summary statistics of the equities, liabilities, CDS spreads, and average correlations of individual banks. Figure 1 plots the time variation in key systemic risk input variables: PDs, correlations, and recovery rates. Our sample data covered the period from January 2004 to December 2009 and were calculated in weekly frequency. We retrieved weekly CDS spreads (together with the recovery rates used by market participants) from Markit and computed equity return correlations from equity price data (which started in January 2003) provided by CRSP.¹⁶

On average, the 19 BHCs have equity capital of $55 billion ($1 trillion in sum) and a total liability of $556 billion ($10 trillion in sum), which compares with the U.S. GDP level of $14.6 trillion in 2008. By the size of total liability, Bank of America, Citigroup, JPMorgan Chase, and Wells Fargo are the largest. Over the three subperiods--January 1, 2004, to December 31, 2006; January 1, 2007, to September 15, 2008; and September 16, 2008, to December 31, 2009--the average CDS spreads rose sharply from 33 to 240 basis points. Average correlations also rose from 44 percent to 62 percent. In our sample set, KeyCorp, MetLife, Citigroup, and Morgan Stanley observe the highest CDS spreads, while average correlations are the highest at JPMorgan Chase, Wells Fargo, Bank of America, and U.S. Bancorp. These conflicting rankings based on liability size, CDS spread, and average correlation indicate that systemic risk may be nonlinearly related to all three metrics, which was indeed the focus of our proposed methodology in assessing such a systemic importance.

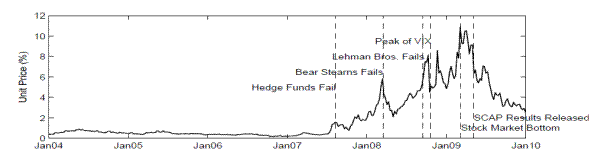
The risk-neutral PDs (Figure 1, top panel) were derived from CDS spreads using recovery rates as reported by market participants who contributed quotes on CDS spreads. The weighted averages (weighted by the size of bank liabilities) are very low--less than 1 percent--before July 2007. With the developments of the financial crisis, the risk-neutral PDs of the 19 SCAP banks increased quickly and reached a short-term high around 2 percent in March 2008, when Bear Stearns was acquired by JPMorgan Chase. The second, and highest, peak occurred in October 2008, shortly after the failure of Lehman Brothers. The risk-neutral PD stayed at elevated levels--4 percent--for a while before coming back to the pre-Lehman level of 2 percent in December 2009. From a cross-sectional perspective, these major banks differed substantially in terms of credit quality, as reflected in the min-max range of their CDS implied default probability, especially around the fourth quarter of 2008 with the maximum reaching above 14 percent.

The other key systemic risk factor, the asset return correlation (Figure 1, middle panel), showed considerable variation around 50 percent before early 2007, then quickly elevated to between 75 and 80 percent until the second half of 2009. Notice that the recovery rates (Figure 1, lower panel) are ex ante measures--i.e., expected recovery rates when CDS contracts are priced--and hence can differ substantially from the ex post observations of a handful of default events during our sample period. In addition, whereas we allowed for time-varying recovery rates, they exhibited only small variation (between 33 and 40 percent) during the sample period.¹⁷

4 Empirical Findings

We applied the methodology described in Section 2 and examined the systemic risk in the U.S. banking system consisting of 19 banks covered by the SCAP, commonly known as the "stress test." Using these banks as an example, we first reported the systemic risk indicator for these institutions as a group and then analyzed the systemic importance of individual banks.

Our findings suggest that the systemic risk indicator stood at its peak around $1.1 trillion in March 2009 and has since fallen to about $300 billion --the level reached in January 2008. A bank's contribution to the systemic risk indicator is roughly linearly related to its default probability but highly nonlinear with respect to institution size and asset correlation. An increase in systemic risk related to concentration risk (measured by correlation) seems to have led to the onset of the 2007-09 financial crisis. Our measure of the systemic importance of financial institutions correlates noticeably with the SCAP result, although the former is a risk-neutral pricing measure and the latter is an objective statistical measure. In particular, our systemic risk measure sharply contrasts with the other two leading alternatives, CoVaR and MES, in ranking the systemically important institutions during the peak of the financial crisis--the fourth quarter of 2008.

4.1 Systemic Risk Indicator

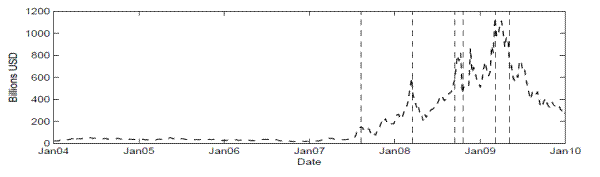
Figure 2 reports the time variation of the DIP, in which financial distress is defined as the situation in which at least 10 percent of total liabilities in the banking system go into default. The insurance cost is represented as a unit percentage cost in the upper panel and as a dollar amount in the lower panel.

The systemic risk indicator for the U.S. banking system was very low at the beginning of the financial and credit crises. For a long period before the collapse of two Bear Stearns hedge funds in early August 2007, the DIP for the list of 19 SCAP banks was merely one-half of 1 percentage point (or less than $5 billion). The indicator then moved up significantly, reaching the first peak when U.S. bank regulators arranged for Bear Stearns to be acquired by JPMorgan Chase on March 16, 2008. The situation then improved significantly in April and May of 2008 owing to strong intervention by major central banks. Things changed dramatically in September 2008 with the failure of Lehman Brothers. Market panic and increasing risk aversion pushed up the price of insurance against distress in the banking sector. The DIP shot up and hovered in the range of $500 billion to $ 900 billion. One week before the stock market reached the bottom, the systemic risk indicator peaked around $1.1 trillion. Since the release of the SCAP result around early May 2009, the DIP has come down quickly and returned to the pre-Lehman level of $300 billion to $400 billion.

Table 2 examines the determinants of the systemic risk indicator. The level of risk-neutral PDs is a dominant factor in determining the level of the systemic risk indicator, explaining on it own 94 percent of the variation in the DIP. On average, an increase of 1 percentage point in the average PD raises the DIP by 1.7 percent. The level of correlation also matters but to a lesser degree, and its effect is largely washed out once PD is included. This result is perhaps due to the strong relationship between PD and correlation for the sample banking group during this special period. In addition, the recovery rate has the expected negative sign in the regression, as higher recovery rates reduce the ultimate losses for a given default scenario. Interestingly, the dispersion in PDs across the 19 banks has a significantly negative effect on the systemic risk indicator.¹⁸ This outcome partly supports our view that incorporating heterogeneity in PDs is important in measuring the system risk indicator.¹⁹

The results have two important implications. First, given the predominant role of average PDs in determining the systemic risk indicator, a first-order approximation of the systemic risk indicator could use the weighted average of PDs (or CDS spreads). This implication can be confirmed by comparing the similar trends in average PDs (the top panel in Figure 1) and the DIP (Figure 2). Second, the average PD itself is only a good approximation but is not sufficient in reflecting the intricate nonlinear relationship between the systemic risk indicator and its input variables. Correlations and heterogeneity in the PD also matter. In other words, diversification can reduce the systemic risk.

4.2 Risk Premium Decomposition

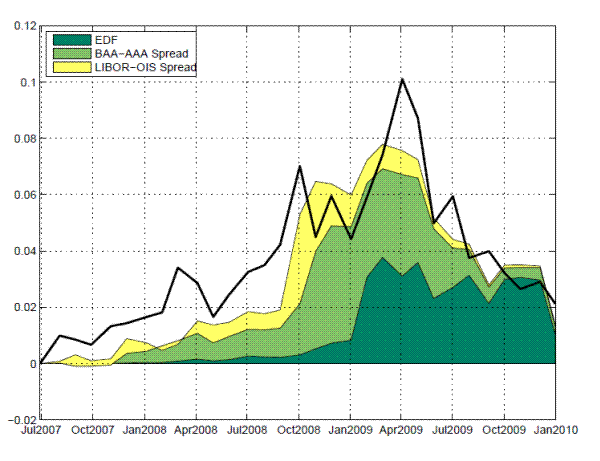
As mentioned in Section 2, the PDs implied from CDS spreads are a risk-neutral measure and include information on not only the expected actual default losses of the banking system but also the default risk premium and liquidity risk premium components. It has been argued that, during the crisis period, the risk premium component could be the dominant factor in determining CDS spreads (see, e.g., Kim, Loretan, and Remolona, 2009). Given that the systemic risk indicator is based on risk-neutral measures, an interesting question is how much of its movement is attributable to the change in the "pure" credit quality (or actual potential default loss) of the banks and how much is driven by market sentiments (change in risk attitude, market panic, and so on) or a liquidity shortage.

We ran a regression analysis that examined the effect of actual default rates and risk premium factors on the systemic risk indicator. In Table 3, objective default risk (or actual default rates) is measured by average expected default frequencies (EDFs) of sample banks, the default risk premium in the global market is proxied by the difference between spreads on corporate bonds rated Baa and Aaa (see, e.g., Chen, Collin-Dufresne, and Goldstein, 2008), and the liquidity risk premium is proxied by the spread of London interbank offered rates, or LIBOR, over the overnight index swap rate, or OIS (see, e.g., Brunnermeier, 2009). Individually (regressions 1 to 3), each of the three factors has a significant effect on the systemic risk indicator, with an expected positive sign. In particular, a 1 percentage point increase in the real default probability, default risk premium, and liquidity risk premium will translate into 1.93, 3.07, and 2.52 percentage point increases, respectively, in the systemic risk indicator. The default or credit risk premium has the highest univariate R-square of 76 percent. The last regression includes all three factors, which remain statistically significant, and jointly these driving factors seem to explain 87 percent of aggregate systemic risk variations.

Figure 3 quantifies the contribution of the actual default risk, default risk premium, and liquidity risk premium in explaining the changes in the systemic risk indicator since July 2007. It vividly illustrates the time-varying importance of the three factors at different stages of the global financial crisis. Until September 2009, most of the increase in the systemic risk indicator came from the default premium component, while the liquidity premium component shot up only around October 2008 and dominated more than half of the total systemic risk indicator at that time. It was not until January 2009 that the real default risk began to contribute significantly to the systemic risk indicator, and it remained at a heightened level until the fourth quarter of 2009, even as the risk premium components had already started to fall around May 2009. At the end of our sample period, it was mainly the actual default risk that contributed to the riskiness of the banking system. Overall, the decomposition results provide strong evidence that systemic risk in the U.S. banking sector stemmed not only from a belated reassessment of real default risk but also from an early repricing of credit risk and a sudden dry-up in market liquidity.

4.3 Marginal Contribution to Systemic Risk

The most relevant question is, what are the sources of vulnerabilities? In other words, which banks are systemically more important or contribute the most to the increased vulnerability? Our identification of systemically important institutions can be contrasted with other market-based systemic risk measures (e.g., CoVaR and MES) and with confidential supervisory information (e.g., the SCAP result). In addition, our measures of institutions' systemic importance change noticeably over time, especially during the financial crisis, and as such can provide important monitoring tools for the market-based macroprudential or financial stability regulation.

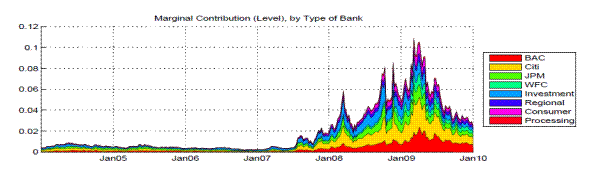
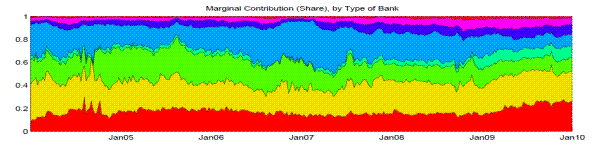
Using the methodology described in Section 2, we calculated the marginal contributions of each group of banks to the systemic risk indicator, both in level terms and in percentage terms. Figure 4 shows that, based on our measure after the summer of 2007, Bank of America and Wells Fargo increased their systemic risk contributions, Citigroup remained the largest contributor, and JPMorgan Chase decreased its marginal contribution. Recall that Wells Fargo acquired Wachovia, and Bank of America acquired Merrill Lynch, during the height of the financial crisis. Figure 4 also reports the systemic risk contributions of other banks, which are grouped into four categories.²⁰ The relative contributions to the systemic risk indicator from both consumer banks and regional banks seem to have increased somewhat since 2009, possibly because of the worsening situations in the commercial real estate and consumer credit sectors, which typically lag the business cycles.

Table 4 details each bank's contribution to the systemic risk indicator on several specific dates: August 2007 (start of crisis), March 2008 (acquisition of Bear Stearns by JPMorgan Chase), September and October 2008 (broad market panic), March 2009 (equity market bottom), May 2009 (release of SCAP result), and December 2009 (end of sample). Size is clearly the dominant factor in determining the relative importance of each bank's systemic risk contribution, but size does not change significantly over time, at least within a reporting quarter. The obvious time variation in the marginal contributions is driven mostly by the risk-neutral PD and equity return correlation. In essence, the systemic importance of each institution is nonlinearly determined by the size, PD, and asset correlation of all institutions in the portfolio.

Table 5 examines the determinants of the marginal contribution to the systemic risk indicator for each bank, using an ordinary least squares (OLS) regression on the panel data. To control for bias, we used clustered standard errors grouped by banks as suggested by Peterson (2009). The first regression shows that the weight, or the size effect, is the primary factor in determining marginal contributions both in level terms and in relative terms. This result is not surprising given the conventional "too-big-to-fail" concern and the fact that bigger banks often have stronger interlinkage with the rest of the banking system. Default probabilities also matter but to a lesser extent, and the significance disappears in the relative-term regression.²¹ This finding supports the case for distinguishing between microprudential and macroprudential perspectives of banking regulation: the failure of individual banks does not necessarily contribute to the increase in systemic risk. The second and third regressions suggest that there are significant interactive effects. Adding interactive terms between size and PD or correlation has additional and significant explanatory power. Overall, the results suggest that the marginal contribution is the highest for high-weight (hence large) banks that observe increases in PDs or correlations.

4.4 Alternative Systemic Risk Measures and Policy Implication

As discussed earlier in Section 2, our marginal contribution measure is an alternative measure related to the CoVaR measure suggested by Adrian and Brunnermeier (2009) and the MES measure suggested by Acharya, Pedersen, Philippon, and Richardson (2010). The most important difference is that our DIP-based measure of each bank's systemic importance is a risk-neutral pricing measure that is derived from both CDS and equity market data, while CoVaR and MES are objective distribution-based statistical measures that rely only on equity return information. Another important difference is that DIP and MES measure each bank's loss conditional on the system being in distress, while CoVaR measures the system losses conditional on each bank being in distress. Finally, both CoVaR and MES only implicitly take into account of the size, PD, and correlation of each bank, while for our DIP measure, these characteristics are direct inputs into our systemic risk indicator.

We can further compare different measures of the systemic importance with the SCAP estimate of losses under an adverse economic scenario as released in May 2009 by the Federal Reserve Board (2009b).²² Figure 5, left panel, suggests that, based on the data through December 31, 2008, the 19 banks' contributions to our DIP systemic risk indicator are largely in line with the SCAP estimate of losses, with an R-square of 0.62. Goldman Sachs, Citigroup, and JPMorgan Chase, in particular, would be viewed as contributing much more to systemic risk by our method from a market risk premium perspective than by the SCAP results, while Bank of America and Wells Fargo would be viewed as more risky by the SCAP from an expected default loss perspective than by our method. The middle panel shows that MES weighted by tier 1 capital has a higher correlation with SCAP expected losses, with an R-square of 0.71. Relative to SCAP, MES considers Bank of America, JPMorgan Chase, and Goldman Sachs more risky and Wells Fargo and Citigroup less risky. The right panel shows that CoVaR in dollar terms has a similar correlation with the SCAP results, with an R-square of 0.63. Compared with SCAP, CoVaR ranks JPMorgan Chase, MetLife, and Goldman Sachs as more risky but Citigroup and Bank of America as less risky.²³

Note that our systemic risk measure is a risk-neutral concept, while SCAP and MES are based on statistical expected loss; consequently MES is supposed to have a stronger connection with SCAP than with DIP. Although CoVaR is also a statistical measure, it measures the system's loss conditional on each bank being in distress, while MES and DIP measure each bank's loss conditional on the system being in distress, yet SCAP measures each bank's loss conditional on the macroeconomy in stress. Also, the tail percentile value (like CoVaR) and tail expected value (like MES or SCAP) can diverge significantly in heavy-tailed distributions. These differences in conditioning directions and tail measures may explain the notable differences in the rankings of DIP, MES, and CoVaR versus those of SCAP.²⁴

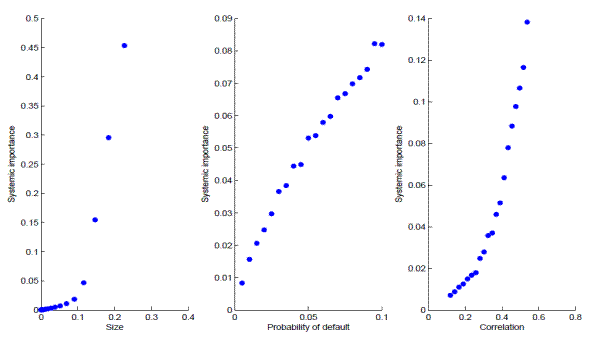
The nonlinear effect documented in Table 5 is more visible in a hypothetical calibration exercise examining the relationship between our systemic risk indicator and an institution's size (total liability), (risk-neutral) default probability, and (average) historical correlation (Figure 6).²⁵ The relationship looks roughly linear for default probability but highly nonlinear with respect to size and, to a lesser degree, correlation. In fact, when the bank size is below 10 percent of the total portfolio, the slope of the systemic importance with respect to size is very flat; but when the size is beyond 10 percent, the contribution to systemic risk shoots up almost vertically. An intuitive reason is that, when a bank is too big, its failure is considered a systemic failure by definition. This consideration may indicate a desirable maximum size of the large complex financial institutions, which, by limiting the systemic risk, could provide a societal benefit. The relationship between systemic importance and correlation shows a similar nonlinear pattern but is less dramatic. In other words, systemic importance is a joint effect of an institution's size, leverage, and concentration and is highly nonlinear.

Our finding of the dominant effect of bank size and its pronounced nonlinear effect on a bank's systemic risk contribution has important policy implications. In particular, the financial regulation reform bill recently enacted by the United States Congress (2010) explicitly adopts the so-called Volcker Rule concentration limit: "Any financial company is prohibited from acquiring another company if, on consummation, the combined company's total consolidated liabilities would exceed 10 percent of the aggregate consolidated liabilities of all financial companies." Our results indirectly support such a measure based on a calibration exercise tailored to a system of 19 SCAP banks.

5 Concluding remarks

The recent financial crisis has caused policymakers to reconsider the institutional frameworks for overseeing the stability of their financial systems. A series of reform recommendations have been made covering various aspects of financial regulation and supervision. It has become generally accepted that the traditional microprudential, or firm-level, approach to financial stability needs to be complemented with a system-wide macroprudential approach, i.e., greater attention should be paid to individual institutions that are systemically important.

In this paper, we advocate a methodology to measure the systemic importance of individual banks and their marginal contributions to a distressed insurance premium that relies only on publicly available information. We applied this methodology to the 19 banks covered by the SCAP, or stress test program. Our results suggest that the elevated systemic risk in the banking sector is driven initially by the rising default risk premium and later by the heightened liquidity risk premium. But after the fourth quarter of 2008, both real default risk and risk premiums were rising as the financial crisis turned into a severe economic recession. A decomposition analysis shows that the marginal contributions of individual banks to the systemic risk indicator are determined mostly by bank size, consistent with the "too-big-to-fail" doctrine, although correlation and default probability also matter. Finally, our measure of the systemic importance of banks--as a market-based risk-neutral price--shows a clear association with and interesting difference from the estimated SCAP loss as an objective statistical measure.

Our approach can be extended to address important policy questions. First, the marginal contribution measures and their desirable additivity property imply that it is straightforward to design regulatory requirements based on individual banks' systemic importance. Such regulatory requirements can be capital surcharges or individual banks' contributions to a banking tax or a systemic risk insurance fund. Moreover, our finding of the pronounced nonlinear relationship between a bank's systemic risk contribution and its liability size lends indirect support for the Volcker 10 percent concentration limit adopted in the recent financial regulation reform legislation. Second, although the proposed DIP measure is risk neutral, the framework can be easily extended by replacing key inputs with the regulator's confidential information or other input variables for the purpose of policy analysis. For instance, one can replace the risk-neutral PDs in our framework with objective measures of PDs and calculate the DIP on an incurred-cost basis.²⁶ This objective measure, by filtering out the risk premium components, can provide useful complimentary information for supervisors.

Bibliography

Acharya, Viral V. (2009),

"A Theory of Systemic Risk and Design of Prudential Bank Regulation," Journal of Financial Stability, forthcoming.

Acharya, Viral V., Lasse H. Pedersen, Thomas Philippon, and Matthew Richardson (2010),

"Measuring Systemic Risk," Working Paper, NYU Stern Schook of Business.

Adrian, Tobias and Markus Brunnermeier (2009),

"CoVaR," Federal Reserve Bank of New York Staff Reports.

Altman, Edward and Vellore Kishore (1996),

"Almost Everything You Want to Know about Recoveries on Default Bonds," Financial Analysts Journal, vol. 52, 57-64.

Andersen, Leif, Jakob Sidenius, and Susanta Basu (2003),

"All Your Hedges in One Basket," Risk, pages 67-72.

Avesani, Renzo, Antonio Garcia Pascual, and Jing Li (2006),

"A New Risk Indicator and Stress Testing Tool: A Multifactor Nth-to-Default CDS Basket," IMF Working Paper.

BCBS (2009),

"Comprehensive Responses to the Global Banking Crisis," Press Release by the Basel Committee on Banking Supervision, September 7, http://www.bis.org/press/p090907.htm.

Billio, Monica, Mila Getmansky, Andrew W. Lo, and Loriana Pelizzon (2010),

"Econometric Measures of Systemic Risk in the Finance and Insurance Sectors," NBER Working Paper No. 16223.

Blanco, Roberto, Simon Brennan, and Ian W. March (2005),

"An Empirical Analysis of the Dynamic Relationship between Investment-Grade Bonds and Credit Default Swaps," Journal of Finance, vol. 60, 2255-2281.

Borio, Claudio (2003),

"Towards a Macro-Prudential Framework for Financial Supervision and Regulation?" BIS Working Papers.

Brownlees, Christian T. and Robert Engle (2010),

"Volatility, Correlation and Tails for Systemic Risk Management," Working Paper, NYU Stern School of Business.

Brunnermeier, Markus, Andrew Crockett, Charles Goodhart, Avinash Persaud, and Hyun Shin (2009),

"The Fundamental Principles of Financial Regualtions," Geneva Reports on the World Economy.

Brunnermeier, Markus K. (2009),

"Deciphering the 2007-08 Liquidity and Credit Crunch," Journal of Economic Perspectives, vol. 23, 77-100.

Chan-Lau, Jorge A. (2009),

"Regulatory Capital Charges for Too-Connected-to-Fail Institutions: A Practical Proposal," IMF Working Paper.

Chan-Lau, Jorge A. and Toni Gravelle (2005),

"The End: A New Indicator of Financial and Nonfinancial Corporate Sector Vulnerability," IMF Working Paper No. 05/231.

Chen, Long, Pierre Collin-Dufresne, and Robert S. Goldstein (2008),

"On the Relation between Credit Spread Puzzles and the Equity Premium Puzzle," Journal of Economic Perspectives, forthcoming.

Cont, Rama (2010),

"Measuring Contagion and Systemic Risk in Financial Systems," Working Paper, Columbia University.

Crocket, Andrew (2000),

"Marrying the Micro- and Macro-prudential Dimensions of Financial Stbility," Speech before the Eleventh International Conference of Banking Supervisors, Basel.

Duffie, Darrall (1999),

"Credit Swap Valuation," Financial Analysts Journal, pages 73-87.

Embrechts, Paul, Dominik D. Lambrigger, and Mario V. Wüthrich (2009),

"On Extreme Value Theory, Aggregation and Diversification in Finance," Working Paper, Department of Mathematics, ETH Zurich.

Federal Reserve Board (2009a),

"The Supervisory Capital Assessment Program: Design and Implementation," Public Document.

Federal Reserve Board (2009b),

"The Supervisory Capital Assessment Program: Overview of Results," Public Document.

Financial Stability Forum (2009a),

"Reducing Procyclicality Arising from the Bank Capital Framework," Joint FSF-BCBS Working Group on Bank Capital Issues.

Financial Stability Forum (2009b),

"Report of the Financial Stability Forum on Addressing Procyclicality in the Financial System," Working Groups on Bank Capital Issues, Provisioning, and Leverage and Valuation.

Forte, Santiago and Juan Ignacio Peña (2009),

"Credit Spreads: An Empirical Analysis on the Informational Content of Stocks, Bonds, and CDS," Journal of Banking and Finance, vol. 33, 2013-2025.

Gibson, Michael (2004),

"Understanding the Risk of Synthetic CDOs," Working Paper, Federal Reserve Board.

Glasserman, Paul (2005),

"Measuing Marginal Risk Contributions in Credit Portfolios," Journal of Computational Finance, vol. 9, 1-41.

Glassmerman, Paul and Jingyi Li (2005),

"Importance Sampling for Portfolio Credit Risk," Management Science, vol. 51, 1643-1656.

Gordy, Michael B. (2003),

"A Risk-Factor Model Foundation for Ratings-Based Bank Capital Rules," Journal of Financial Intermediation, vol. 12, 199-232.

Gray, Dale F., Robert C. Merton, and Zvi Bodie (2007),

"Contingent Caims Approach to Measuring and Managing Sovereign Credit Risk," Journal of Investment Management, vol. 5, 1-24.

Heitfield, Eric, Steve Burton, and Souphala Chomsisengphet (2006),

"Systematic and Idiosyncratic Risk in Syndicated Loan Portfolios," Journal of Credit Risk, vol. 2, 3-31.

Hirtle, Beverly, Til Schuermann, and Kevin Stiroh (2009),

"Macroprudential Supervision of Financial Institutions: Lessons from the SCAP," Staff Report no. 409, Federal Reserve Bank of New York.

Huang, Xin, Hao Zhou, and Haibin Zhu (2009),

"A Framework for Assessing the Systemic Risk of Major Financial Institutions," Journal of Banking and Finance, vol. 33, 2036-2049.

Huang, Xin, Hao Zhou, and Haibin Zhu (2010),

"Assessing the Systemic Risk of a Heterogeneous Portfolio of Banks During the Recent Financial Crisis," Working Paper, Federal Reserve Board.

Hull, John and Alan White (2004),

"Valuation of a CDO and an N-th to Default CDS without Monte Carlo Simulation," Journal of Derivatives, vol. 12, 8-23.

International Monetary Fund (2010),

"Systemic Risk and the Redesign of Financial Regulation," Global Financial Stability Report Chapter 2.

Inui, Koji and Masaaki Kijima (2005),

"On the Significance of Expected Shortfall as a Coherent Risk Measure," Journal of Banking and Finance, vol. 29, 853-864.

Kim, Baeho and Kay Giesecke (2010),

"Systemic Risk: What Defaults Are Telling Us," Working Paper, Stanford University.

Kim, Don, Mico Loretan, and Eli Remolona (2009),

"Contagion and Risk Premia in the Amplification of Crisis: Evidence from Asian Names in the CDS Market," BIS Working Paper.

Kurth, Alexandre and Dirk Tasche (2003),

"Credit Risk Contributions to Value-at-Risk and Expected Shortfall," Risk, vol. 16, 84-88.

Lehar, Alfred (2005),

"Measuring Systemic Risk: A Risk Management Approach," Journal of Banking and Finance, vol. 29, 2577-2603.

Merton, Robert (1974),

"On the Pricing of Corporate Debt: The Risk Structure of Interest Rates," Journal of Finance, vol. 29, 449-470.

Nicolò, Gianni De and Myron Kwast (2002),

"Systemic Risk and Financial Consolidation: Are They Related," Journal of Banking and Finance, vol. 26, 861-880.

Nicolò, Gianni De and Marcella Lucchetta (2010),

"Systemic Risk and the Macroeconomy," International Monetary Fund.

Norden, Lars and Wolf Wagner (2008),

"Credit Derivatives and Loan Pricing," Journal of Banking and Finance, vol. 32, 2560-2569.

Panetta, Fabio, Paolo Angelini, Ugo Albertazzi, Francesco Columba, Wanda Cornacchia, Antonio Di Cesare, Andrea Pilati, Carmelo Salleo, and Giovanni Santini (2009),

"Financial Sector Pro-Cyclicality: Lessons from the Crisis," Banca D'Italia Occasional Papers.

Peterson, Mitchell (2009),

"Estimating Standard Errors in Finance Panel Data Sets: Comparing Approaches," Review of Financial Studies, vol. 22, 435-480.

Tarashev, Nikola, Claudio Borio, and Kostas Tsatsaronis (2009a),

"Allocating Systemic Risk to Individual Institutions: Methodology and Policy Applications," BIS Working Paper.

Tarashev, Nikola, Claudio Borio, and Kostas Tsatsaronis (2009b),

"The Systemic Importance of Financial Institutions," BIS Quarterly Review.

Tarashev, Nikola and Haibin Zhu (2008a),

"The Pricing of Portfolio Credit Risk: Evidence from the Credit Derivatives Market," Journal of Fixed Income, vol. 18, 5-24.

Tarashev, Nikola and Haibin Zhu (2008b),

"Specification and Calibration Errors in Measures of Portfolio Credit Risk: The Case of the ASRF Model," International Journal of Central Banking, vol. 4, 129-174.

United States Congress (2010),

"Dodd-Frank Wall Street Reform and Consumer Protection Act," Public Document H. R. 4173.

Vasicek, Oldrich A. (1991),

"The Limiting Loan Loss Probability Distribution," KMV Working Paper.

Yamai, Yasuhiro and Toshinao Yoshiba (2005),

"Value-at-Risk versus Expected Shortfall: A Practical Perspective," Journal of Banking and Finance, vol. 29, 997-1015.

Zhou, Chen (2009),

"Are Banks Too Big to Fail? Measuring Systemic Importance of Financial Institutions," Working Paper, De Netherlandsche Bank.

Table 1: **Summary Statistics of Nineteen US Banks in SCAP Program**
Bank Name	Sector	Equity¹	Liability¹	CDS Spreads² Period 1	CDS Spreads² Period 2	CDS Spreads² Period 3	Correlation³ Period 1	Correlation³ Period 2	Correlation³ Period 3
American Express Co.	Consumer	14.41	105.40	21.16	83.10	244.69	44.42	62.65	63.44
Bank of America Corp.	BAC	231.44	2082.41	15.92	51.71	155.36	50.83	67.84	68.51
BB&T	Regional	16.19	127.24	16.68	52.62	105.79	54.47	69.27	67.21
Bank of NY Mellon Corp.	Processing	28.98	175.24	16.45	40.67	113.33	44.26	61.13	64.55
Capital One Financial Corp.	Regional	26.59	150.64	53.20	189.96	211.12	32.20	57.32	64.53
Citigroup, Inc.	Citi	152.70	1676.65	15.68	67.33	263.51	48.08	65.87	56.90
Fifth Third Bancorp	Regional	13.50	107.21	9.06	24.95	160.64	44.50	62.50	60.45
GMAC LLC	Consumer	20.84	153.31	274.29	699.58	1226.86	8.84	15.87	19.06
Goldman Sachs Group, Inc.	Investment	70.71	860.66	26.56	73.86	179.73	43.47	63.14	63.67
JPMorgan Chase & Co.	JPM	165.37	1908.99	21.99	52.82	97.79	52.60	67.67	70.50
KeyCorp	Regional	10.66	87.66	19.48	84.24	402.04	49.41	61.17	65.25
MetLife, Inc.	Consumer	33.12	467.98	24.55	63.15	388.33	36.98	59.66	63.58
Morgan Stanley	Investment	46.69	576.82	26.53	97.71	261.94	42.62	61.35	60.83
PNC Fin. Svcs. Gp, Inc.	Regional	29.94	257.77	14.12	26.28	87.94	44.88	65.70	64.43
Regions Fin. Corp.	Regional	17.88	125.16	8.26	17.43	72.42	45.95	65.50	58.73
State St. Corp.	Processing	14.49	128.29	16.17	44.89	143.45	46.16	57.71	63.01
SunTrust Banks, Inc.	Regional	22.42	157.47	15.20	63.39	188.30	52.69	64.71	66.86
U.S. Bancorp	Regional	25.96	235.68	16.26	51.07	125.16	49.39	66.23	67.41
Wells Fargo & Co.	WFC	111.79	1178.83	14.89	50.51	122.69	48.25	67.92	70.55
Mean		55.46	555.97	32.97	96.59	239.53	44.21	61.22	62.08

Table 2: **Determinants of Systemic Risk Indicator: Input Variables**
Independent Variables	Regression 1	Regression 2	Regression 3	Regression 4	Regression 5
Constant	-0.16	-4.59	34.92	4.15	1.89
Constant t-statistics	(3.49)	(9.78)	(5.99)	(4.47)	(2.41)
Average PD	1.71			1.74	2.46
Average PD t-statistics	(69.69)			(54.51)	(39.83)
Average Correlation		0.13		0.00	0.01
Average Correlation t-statistics		(14.50)		(0.95)	(2.90)
Recovery Rate			-0.52	-0.12	-0.07
Recovery Rate t-statistics			(5.64)	(4.59)	(3.05)
Dispersion in PD					-0.78
Dispersion in PD t-statistics					(12.83)
Dispersion in Correlation					0.01
Dispersion in Correlation t-statistics					(0.85)
Adjusted-R	0.94	0.40	0.09	0.94	0.96

Table 3: **Determinants of Systemic Risk Indicator: Risk Premiums**
Independent Variables	Regression 1	Regression 2	Regression 3	Regression 4
Constant	1.07	-1.68	0.92	-0.91
Constant t-statistics	(5.1)	(6.0)	(3.2)	(3.9)
Average EDF (%)	1.93			1.14
Average EDF (%) t-statistics	(9.8)			(7.8)
BAA-AAA Spread (%)		3.07		1.64
BAA-AAA Spread (%) t-statistics		(15.1)		(6.2)
LIBOR-OIS Spread (%)			2.52	0.91
LIBOR-OIS Spread (%) t-statistics			(6.2)	(3.5)
Adjusted-R	0.57	0.76	0.34	0.87

Table 4: **Marginal Contribution to the Systemic Risk by Banks on Specific Dates**
Bank Name	Marginal contribution 08.10.2007	Marginal contribution 03.16.2008	Marginal contribution 09.16.2008	Marginal contribution 10.20.2008	Marginal contribution 03.09.2009	Marginal contribution 05.07.2009	Marginal contribution 12.31.2009	SCAP Losses
American Express Co.	1.3101	5.3226	5.9371	9.8578	13.3794	6.1939	1.4770	11.2000
Bank of America Corp.	22.5388	60.7817	91.6920	75.8858	169.6650	143.6174	69.2643	136.6000
BB&T	1.2044	3.2306	6.6060	5.1998	N.A.	6.4492	2.1312	8.7000
Bank of NY Mellon Corp.	0.5898	4.5008	6.9008	7.8521	9.6070	6.7699	2.8365	5.4000
Capital One FiN.A.cial Corp.	1.5410	7.7237	8.6399	9.3357	9.6426	7.3052	2.3955	13.4000
Citigroup, Inc.	40.3117	130.1139	135.7237	133.9047	302.1724	172.9385	71.1229	104.7000
Fifth Third Bancorp	0.9445	1.6278	N.A.	N.A.	1.8262	1.5949	4.1009	9.1000
GMAC LLC	1.5097	4.0589	10.0398	10.9142	8.1019	7.2665	0.6920	9.2000
Goldman Sachs Group, Inc.	20.0346	49.1786	99.3637	60.1561	71.8879	39.1285	19.4087	17.8000
JPMorgan Chase & Co.	25.6174	58.7236	112.7932	85.4109	130.9016	85.9607	32.4703	97.4000
KeyCorp	0.5801	2.3252	8.7862	6.7943	9.2999	6.5864	3.1578	6.7000
MetLife, Inc.	4.2064	16.7281	21.8047	26.2686	68.7519	49.2329	10.7981	9.6000
Morgan Stanley	18.3609	55.4046	105.5172	39.6676	58.7151	31.1108	8.6964	19.7000
PNC Fin. Svcs. Gp, Inc.	0.5867	2.3474	N.A.	N.A.	N.A.	18.9800	3.0893	18.8000
Regions Fin. Corp.	0.7837	0.7996	1.0135	0.7852	1.0652	0.9571	2.1496	9.2000
State St. Corp.	0.5336	4.9617	7.8473	8.8160	8.4989	7.4683	1.5385	8.2000
SunTrust Banks, Inc.	1.5757	6.1166	7.0965	6.3174	9.2881	7.2031	3.3633	11.8000
U.S. Bancorp	2.2136	6.4720	10.8688	7.5888	10.4362	10.1740	3.2525	15.7000
Wells Fargo & Co.	6.1051	17.6868	23.1148	17.3149	93.0329	60.1823	26.7920	86.1000
Total	150.5477	438.1043	663.7452	512.0698	976.2721	669.1198	268.7369	599.3000

Table 5: **Determinants of Marginal Contribution to the Systemic Risk**
Independent Variables	Coef. Regression 1	t-stat. Regression 1	Coef. Regression 2	t-stat. Regression 2	Coef. Regression 3	t-stat. Regression 3
1. Level Regressions Constant	-19.12	( 1.70)	-3.14	( 3.49)	18.23	( 1.59)
1. Level Regressions $PD_{i,t}$	0.04	( 1.76)			-0.03	( 9.70)
1. Level Regressions $Cor_{i,t}$	0.00	( 3.74)			0.00	( 2.15)
1. Level Regressions $Rec_{i,t}$	-0.00	( 0.34)			-1405.99	( 1.82)
1. Level Regressions $Weight_{i,t}$	238.08	(15.52)	-222.20	( 0.77)	-0.01	( 1.79)
1. Level Regressions $PD_{i,t}\times Weight_{i,t}$			1.91	( 8.22)	2.27	(17.94)
1. Level Regressions $Cor_{i,t}\times Weight_{i,t}$			0.02	( 2.41)	0.01	( 2.15)
1. Level Regressions $Rec_{i,t}\times Weight_{i,t}$			-0.02	( 5.34)	0.36	( 1.77)
1. Level Regressions Adjusted-R	0.43		0.93		0.97
2. Relative-term Regressions Constant	-0.03	( 1.65)			0.01	( 0.60)
2. Relative-term Regressions $PD_{i,t}$	0.01	( 1.90)			-0.01	( 1.91)
2. Relative-term Regressions $Cor_{i,t}$	0.02	( 1.71)			-0.00	( 0.22)
2. Relative-term Regressions $Rec_{i,t}$	-0.01	( 0.84)			-0.02	( 1.11)
2. Relative-term Regressions $Weight_{i,t}$	1.25	(20.12)	0.71	( 1.63)	0.47	( 1.04)
2. Relative-term Regressions $PD_{i,t}\times Weight_{i,t}$			0.53	( 3.33)	0.66	( 3.56)
2. Relative-term Regressions $Cor_{i,t}\times Weight_{i,t}$			0.59	( 1.80)	0.60	( 1.53)
2. Relative-term Regressions $Rec_{i,t}\times Weight_{i,t}$			-0.52	( 1.07)	-0.40	( 0.67)
2. Relative-term Regressions Adjusted-R	0.90		0.93		0.93

Figure 1: Systemic Risk Input Variables

Figure 1. This graph plots the time series of key systemic risk factors: risk-neutral PDs implied from CDS spreads (top panel), correlations calculated from comovement in equity returns (middle panel), and recovery rates from the CDS quotes (bottom panel). The solid lines are mean values, and the dash-dot lines are min and max values.

Notes: This graph plots the time series of key systemic risk factors: risk-neutral PDs implied from CDS spreads, correlations calculated from comovement in equity returns, and recovery rates from the CDS quotes.

Figure 2: Systemic Risk Indicator of US 19 SCAP Banks

Figure 2. The graph plots the systemic risk indicator for the SCAP banks, defined as the price for insuring against financial distresses (at least 10 percent of total liabilities in the banking system are in default). The price is shown as the cost per unit of exposure to these liabilities in the upper panel and is shown in dollar term in the lower panel. Vertical lines mark the major events happend during the 2007-2009 financial crisis.

Notes: The graph plots the systemic risk indicator for the SCAP banks, defined as the price for insuring against financial distresses (at least 10% of total liabilities in the banking system are in default). The price is shown as the cost per unit of exposure to these liabilities in the upper panel and is shown in dollar term in the lower panel.

Figure 3: Contributing Factors to the Systemic Risk Indicator

Figure 3. The graph plots the contribution effect of actual default risk (red), default risk premium (green), and liquidity risk premium (yellow) in determining the changes in the systemic risk indicator (solid line) since July 2007. It is based on the regression results as specified in regression 4 of Table 3.

Notes: The graph plots the contribution effect of actual default risk, default risk premium, and liquidity risk premium in determining the changes in the systemic risk indicator since July 2007. It is based on the regression results as specified in regression 4 of Table 3.

Figure 4: Marginal Contribution to Systemic Risk by Each Group of Banks

Figure 4. The figure shows the marginal contribution of each banks or banking group to the systemic risk indicator, the distress insurance premium in unit cost term. The contribution is shown in level term in the upper panel and as a percentage of the total risk in the lower panel. The major individual banks and groups include: BAC, Citi, JPM, WFC; Investment, Regional, Consumer, and Processing banks.

Notes: The figure shows the marginal contribution of each banks or banking group to the systemic risk indicator, the distress insurance premium in unit cost term. The contribution is shown in level term in the upper panel and as a percentage of the total risk in the lower panel.

Figure 5: Comparing Systemic Risk Measures: DIP, MES, and CoVaR versus SCAP Results

Figure 5. This graph compares three systemic risk measures, distressed insurance premium (DIP) proposed by this paper (left panel), marginal expected shortfall or MES by Acharya et al 2010 (middle panel) weighted by bank's tier-1 capital, andconditional value-at-risk or CoVaR by Adrian and Brunnermeier 2009 (right panel) in dollar term. These measures are compared to the SCAP stress test result on 19 largest US BHCs for the fourth quarter of 2008.

Notes: This graph compares three systemic risk measures, distressed insurance premium (DIP) proposed by this paper, marginal expected shortfall (MES by Acharya, Pedersen, Philippon, and Richardson, 2010) weighted by bank's tier-1 capital, and conditional value-at-risk (CoVaR by Adrian and Brunnermeier, 2009) in dollar term. These measures are compared to the SCAP stress test result on 19 largest US BHCs for the period of fourth quarter 2008.

Figure 6: Relationship between Systemic Risk Indicator and Bank Size, PD, and Correlation

Figure 6. This figure plots a hypothetical calibration exercise based on 20 common banks, with average LGD of 0.55 and distress threshold 10 percent. For the impact of size (left panel), PD is 0.02 and correlation is 20 percent; for the impact of PD (middle panel), PD changes from 0.005 to 0.1; for the impact of correlation (right panel), the loading coefficient in a one-factor model ranges between 0.2 and 0.96.

Notes: This figure plots a hypothetical calibration exercise based on 20 common banks, with average LGD of 0.55 and distress threshold 10 percent. For the impact of size (left panel), PD is 0.02 and correlation is 20 percent; for the impact of PD (middle panel), PD changes from 0.005 to 0.1; for the impact of correlation (right panel), the loading coefficient in a one-factor model ranges between 0.2 and 0.96.

Footnotes

1. We would like to thank Viral Acharya, Tobias Adrian, Sean Campbell, Myron Kwast, Frank Packer, Nikola Tarashev, James Wilcox, Robert DeYoung, and seminar participants at the Federal Reserve, Chicago Bank Structure Conference, IMF Conference on Operationalizing Systemic Risk Monitoring, Fields Institute Financial Stability Forum, NUS Risk Management Conference, Bank of England and CAREFIN (Centre for Applied Research in Finance, University of Bocconi) Conference on Matching Stability and Performance, and Bank Research Conference at FDIC for their helpful commments. James Marrone provided excellent research assistance. We also thank Christopher Karlsten for editing assistance. The views presented here are solely those of the authors and do not necessarily represent those of the Federal Reserve Board or the Bank for International Settlements. Return to Text

2. Department of Economics, University of Oklahoma, Norman, Oklahoma, USA; phone: 1-405-325-2643; e-mail: [email protected]. Return to Text

3. Corresponding Author: Risk Analysis Section, Federal Reserve Board, Washington, D.C., USA; phone: 1-202-452-3360; e-mail: [email protected]. Return to Text

4. Bank for International Settlements, Representative Office for Asia and the Pacific, Hong Kong; phone: 852-2878-7145; e-mail: [email protected]. Return to Text

5. See, for instance, Brunnermeier et al. (2009), Financial Stability Forum (2009b),a), Panetta et al. (2009), and BCBS (2009), among others. The macroprudential perspective was proposed by Crocket (2000), Borio (2003), and Acharya (2009). Return to Text

6. See Blanco, Brennan, and March (2005), Forte and Peña (2009), and Norden and Wagner (2008), among others. Return to Text

7. A constant LGD, of close to 55%, as recommended in Basel II, is typically assumed by researchers. Return to Text

8. Andersen, Sidenius, and Basu (2003) propose an efficient algorithm to solve this optimization problem. Return to Text

9. A coherent measure of risk should satisfy the axioms of monotonicity, subadditivity, positive homogeneity, and translation invariance (Inui and Kijima, 2005). In general, VaR is not subadditive. Return to Text

10. Importance sampling is a statistical method based on the idea of shifting the distribution of underlying factors to generate more scenarios with large losses. For details, see Glassmerman and Li (2005) and Heitfield, Burton, and Chomsisengphet (2006) Return to Text

11. We assumed that, on each day, the LGD follows a symmetric triangular distribution around its mean, LGD

, and in the range of $[2 \times$ LGD

. This distribution was also used in Tarashev and Zhu (2008b) and Huang, Zhou, and Zhu (2009), mainly for computational convenience. Using an alternative distribution of LGD, such as a beta distribution, had almost no effect on our results. Return to Text

12. Related methods in identifying systemically important institutions include the contingent claims approach (Gray, Merton, and Bodie, 2007), extreme value theory (Zhou, 2009), equity volatility/correlation (Brownlees and Engle, 2010), and too-connected-to-fail (Chan-Lau, 2009), among others. Return to Text

13. The calculation method is also different in that Adrian and Brunnermeier (2009) employ a percentile regression approach rather than Monte Carlo simulation. Return to Text

14. It is important here to distinguish between the additivity property of the marginal contribution measures and the (sub)additivity property of the systemic risk measures. For instance, VaR is not additive (nor subadditive), but the marginal contribution to VaR using our approach can be additive. Return to Text

15. In a specific application of the Shapley value approach, the systemic event can be defined at the level of the entire system and refers to the same event when the subsystems are calculated. Under such an application, the Shapley value approach is equivalent to our method in terms of computation burden and results. Return to Text

16. Among the 19 U.S. BHCs, GMAC has no market-traded equity price. Instead we used an exchange-traded note--a 7.30 percent coupon public income note, maturing in 2031, with the ticker "GMA" for GMAC LLC--to proxy for its asset returns. We also have a set of empirical results excluding GMAC, which are available upon request. Return to Text

17. The original recovery rate data had a significant sparseness problem in that a large portion of CDS quotes came without the corresponding recovery rates. Therefore, in this paper, we applied a Hodrick-Prescott (HP) filter to the recovery data and used the HP-filtered recovery rates to reflect the time variation in recovery rates and, at the same time, to avoid noisy movements in average recovery rates due to data reporting problems. Return to Text

18. Dispersion is represented as the standard deviation of the variable of interest for the sample banks at each particular point in time. The correlation coefficient for a particular bank is defined as the average pairwise correlation between this bank and other banks. Return to Text

19. In a study of 22 Asia-Pacific banks (Huang, Zhou, and Zhu, 2010), we found that the heterogeneities in both PDs and correlations significantly reduce the systemic risk, which is consistent with the fact that Asia-Pacific banks are much more diverse than their U.S. counterparts. Return to Text

20. The four categories are as follows: (1) investment banks (Goldman Sachs and Morgan Stanley); (2) consumer banks (GMAC and American Express); (3) regional banks (U.S. Bancorp, Capital One, PNC Financial, SunTrust, BB&T, Regions Financial, Fifth Third, and KeyCorp); and (4) processing banks (Bank of New York Mellon, State Street, and Northern Trust). Bank of America, Citigroup, JPMorgan Chase, and Wells Fargo are listed as individual large complex financial institutions. Return to Text

21. We find that, although a weighted average of PDs represents a good first-order approximation of the systemic risk, individual PDs (weighted by bank size or unweighted) are very poor approximations of their marginal contributions. Return to Text

22. SCAP is a leading example of combining both macroprudential and microprudential perspectives in banking supervision and regulation (see, e.g., International Monetary Fund, 2010; Hirtle, Schuermann, and Stiroh, 2009). Return to Text

23. We obtained the MES data from the New York University Stern Volatility Lab at http://vlab.stern.nyu.edu/welcome/risk, and the CoVaR data were kindly provided by Tobias Adrian. We flipped the signs of CoVaR measures so that the higher the CoVaR, the more the bank contributes to the systemic risk. This approach is consistent with other measures in the comparative study. Return to Text

24. The ex post weighting of the MES and CoVaR measures by size can raise a question about how to interpret the resulting absolute magnitudes. As shown by the y-axes in Figure 5, the tier-1-capital-weighted MES has a scale of $6 billion, and CoVaR, translated to dollar terms, has a scale of $2 trillion. In comparison, both SCAP and DIP extend to $150 billion. Return to Text

25. The hypothetical portfolios are based on 20 common banks, with an average LGD of 0.55 and a distress threshold of 10 percent. For the effect of size (left panel), PD is 0.02 and correlation is 20 percent; for the effect of PD (middle panel), PD changes from 0.005 to 0.1; for the effect of correlation (right panel), the loading coefficient in a one-factor model ranges between 0.2 and 0.96. Return to Text

26. The EDF is one such product that produces objective measures of the expected default rates of individual firms. However, it is widely acknowledged that EDFs for financial firms are less reliable, mainly because financial firms typically have much higher leverages than corporate firms. The higher leverage does not necessarily reflect higher default risk but will cause substantial bias in EDF estimates without proper adjustment, which remains a challenging task. Return to Text

^♣ This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to Text

Systemic Risk Contributions1