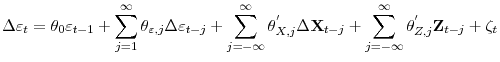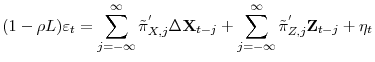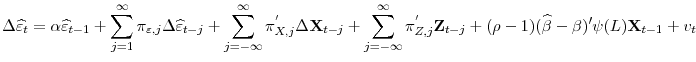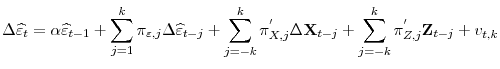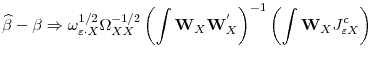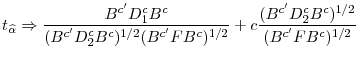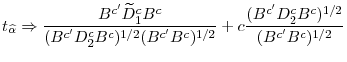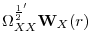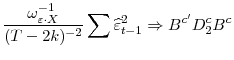Skip to: [Printable Version (PDF)] [Bibliography] [Footnotes]

Finance and Economics Discussion Series: 2011-18 Screen Reader version ^♣

Cointegration Test with Stationary Covariates and the CDS-Bond Basis during the Financial Crisis

Aaron L. Game

Federal Reserve Board

Jason J. Wu*

Federal Reserve Board

March 28, 2011

Keywords: Cointegration, stationary covariates, local asymptotic power, CDS basis.

Abstract:

This paper proposes a residual based cointegration test with improved power. Based on the idea of Hansen (1995) and Elliott & Jansson (2003) in the unit root testing case, stationary covariates are used to improve the power of the residual based Augmented Dickey Fuller (ADF) test. The asymptotic null distribution contains difficult to estimate nuisance parameters for which there is no obvious method of estimation, therefore we propose a bootstrap methodology to obtain test critical values. Local-to-unity asymptotics and Monte Carlo simulations are used to evaluate the power of the test in large and small samples, respectively. These exercises show that the addition of covariates increases power relative to the ADF and Johansen tests, and that the power depends on the long-run correlation between the covariates and the cointegration candidates. The new test is used to test for cointegration between Credit Default Swap (CDS) and corporate bond spreads for a panel of U.S. firms during the 2007-2009 financial crisis. The new test finds stronger evidence for cointegration between the two spreads for more firms, relative to ADF and Johansen tests.

JEL Classification: C12, C22, G12.

1 Introduction

Tests for cointegration are important tools for empirical macroeconomics and finance. Residual based tests for the null of no cointegration, pioneered by Engle & Granger (1987), have the advantages of computational ease and good small sample size properties. These tests involve running regressions and forming simple test statistics. However, residual based tests suffer from low power under the alternative hypothesis. Among other papers, this problem is highlighted by Pesavento (2004), who finds that while residual based tests have good size in most cases, their power disadvantage relative to system-based cointegration tests is significant.

The goal of this paper is to construct a more powerful residual based cointegration test. In empirical analysis, researchers often have data on variables other than the cointegration candidates. For instance, when testing for Purchasing Power Parity (PPP), time series for GDP and money growth rates are observed together with exchange rates and prices (see Amara & Papell, 2006). These variables, or covariates, may be helpful in uncovering cointegration relationships. The idea of this paper is to take advantage of these covariates in testing for cointegration.

The inclusion of stationary covariates has been shown to improve the power of tests under local-to-unity alternatives in the univariate setting. Hansen (1995) first proposed a unit root test where the leads and lags of stationary covariates are included in the inference. Elliott & Jansson (2003) provided point optimal unit root tests that include stationary covariates in presence of deterministic trends. In the multivariate setting, Jansson (2004) shows that stationary covariates can be used to increase power of tests with the null of cointegration. In addition, Seo (1998) shows that covariates significantly improve the power of Johansen rank tests, while Rahbek & Mosconi (1999) study the asymptotic implications of covariate inclusion.

We add to the work described above by including stationary covariates in the construction of the Augmented Dickey-Full (ADF) cointegration test. Intuitively, when stationary covariates related to the cointegration candidates are included in the residual regression, parameters of the regression are more precisely estimated, resulting in a more powerful test. The new test is named the Covariate Augmented Dickey-Fuller (CADF) test. The extent of power improvement depends on the long-run correlations between the stationary covariates and cointegration candidates. Asymptotic analysis shows that the local-to-unity power functions of the CADF test depends critically on these long-run correlations. Not surprisingly, when the covariates and cointegration candidates have zero long-run correlations, the power functions are the same as those of the ADF test.

Large sample Monte Carlo simulations are used to illustrate the asymptotic results, revealing two interesting facts. First, the power of ADF test serves as the lower bound for the power of the CADF test, in all experiments conducted. This means that asymptotically, the CADF test does at least as well as the ADF test. Second, the power of the CADF test is the highest when the covariates are highly correlated with both the cointegration error as well as the right hand side variables in the cointegration relationship.

Deriving asymptotic critical values for the CADF test is difficult due to the presence of nuisance parameters in the asymptotic null distribution. As pointed out by Elliott & Pesavento (2009), there are no obvious ways to estimate the nuisance parameters. Therefore, we propose a bootstrap procedure to obtain critical values in finite samples. Small sample Monte Carlo simulations are conducted to assess the performance of the bootstrapped CADF tests under various cases of deterministic trends and various correlation scenarios. They show that the CADF test has reasonable size and good power in finite samples relative to not only the ADF test, but the Johansen test as well.

In an empirical application of the new test, we investigate whether there are cointegrating relationships between Credit Default Swap (CDS) spreads and corporate bond spreads, for 24 US firms during the 2007-2009 financial crisis. Previous work Blanco (2005), Zhu (2006), De Wit (2006), Levin (2005) and Norden & Weber (2009), for instance, establishes that cointegration between CDS and bond spreads holds for most firms during benign economic periods. However, it may be the case that traditional cointegration tests used in these studies cannot as easily detect the same relationships during the recent crisis, due to the unprecedented levels of market volatility and uncertainty. The CADF test allows us to partially control for such factors through the use of covariates such as the and VIX index returns and the Libor-OIS spread. Indeed, the CADF test finds that cointegration between CDS and bond spreads holds for most firms during the crisis. In comparison, results from the ADF and Johansen tests find cointegration for less firms.

The remainder of the paper will be organized as follows: section 2 describes the model, assumptions, test statistic, and bootstrap inference. It also contains asymptotic analysis of the power of the CADF test. Section 3 investigates the power of the CADF test in large and small samples using simulations. Section 4 presents CADF tests for cointegration between CDS and bond spreads during the financial crisis, and section 5 concludes. The appendix contains mathematical proofs, tables and figures.

2 The CADF Test and Asymptotics

2.1 Model

Consider the following system:

$\displaystyle Y_{t}=\mu_{Y}+\tau_{Y}t+\beta'\mathbf{X}_{t}+\varepsilon_{t}$

(1)

$\displaystyle \left[\begin{array}{c}(1-\rho L)\varepsilon_{t}\ \Delta\mathbf{X}_{t}\ \mathbf{Z}_{t}\end{array}\right]=\left[\begin{array}{c}0\\ \mu_{X}+\tau_{X}t\ \mu_{Z}+\tau_{Z}t\end{array}\right]+\xi_{t}(\rho)$

(2)

Where $\xi_{t}(\rho)$ is a vector of scalar $(1-\rho L)\varepsilon_{t}$ for $\rho\in[-1,1]$ , $\Delta\mathbf{X}_{t}$ of dimension , and $\mathbf{Z}_{t}$ of dimension . $Y_{t}$ and $\mathbf{X}_{t}$ are the candidates for cointegration. $\mathbf{Z}_{t}$ are stationary covariates to be be utilized in the CADF test.

For brevity and in order to keep notation simple, theoretical work in this paper is based on the case of no deterministic components, i.e., $\mu_{X},\mu_{Y},\mu_{Z}$ and $\tau_{X},\tau_{Y},\tau_{Z}$ are set equal to zero. In section 3, extensive simulation evidence is presented on the performance of the proposed test when deterministic components are present.

The hypothesis of interest is

$\displaystyle H_{0}$	$\displaystyle :$	$\displaystyle \rho=1$
$\displaystyle H_{A}$	$\displaystyle :$	$\displaystyle \vert\rho\vert<1$

$Y_{t}$ and $\mathbf{X}_{t}$ are cointegrated under $H_{A}$ , and $\beta$ is the cointegrating vector.

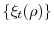Assumptions 1 (Weak Convergence of $\xi_{t}(\rho)$ )

$\{\xi_{t}(\rho)\}$ is a stationary process with zero mean, finite variance and continuous spectral density 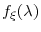$f_{\xi}(\lambda)$ , for $\lambda\in[0,\pi]$ .
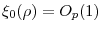$\xi_{0}(\rho)=O_{p}(1)$ .
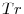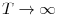
For $r\in (0,1]$ and denoting the integer part of , as $T\rightarrow\infty$

$\displaystyle T^{-1/2}\sum_{t=1}^{[Tr]}\xi_{t}(\rho)\Rightarrow \Omega^{1/2}\mathbf{W}(r)$

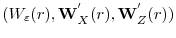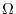Where $\mathbf{W}(r)$ a $(1+n+m)\times 1$ standard vector Brownian motion, partitioned conformably into $(W_{\varepsilon}(r),\mathbf{W}^{'}_{X}(r),\mathbf{W}^{'}_{Z}(r))$ , $\Omega$ a positive definite long run variance-covariance matrix

$\displaystyle \Omega\equiv\left[\begin{array}{ccc}\omega_{\varepsilon\varepsilon}&\omega^{'}_{\varepsilon X}&\omega^{'}_{\varepsilon Z}\ \omega_{\varepsilon X}&\Omega_{XX}&\omega^{'}_{XZ}\ \omega_{\varepsilon Z}&\omega_{XZ}&\Omega_{ZZ}\end{array}\right]\equiv 2\pi f_{\xi}(0)$

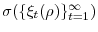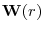And $\Rightarrow$ denotes weak convergence. Furthermore, assume that each element in the sigma-algebra $\sigma(\{\xi_{t}(\rho)\}_{t=1}^{\infty})$ is independent of $\mathbf{W}(r)$ .

Assumption 1.3 may be derived from more primitive assumptions (see, for instance, Phillips & Ouliaris, 1990; Phillips & Solo, 1992; Phillips & Durlauf, 1986). We impose, rather than derive, assumption 1.3 since it is now a standard result that holds under very general conditions.

We also define an alternative decomposition of $\Omega$ that is useful in presenting the asymptotic results that follow as:

$\displaystyle \Omega\equiv\left[\begin{array}{cc}\omega_{\varepsilon\varepsilon}&\omega^{'}_{\varepsilon Q}\ \omega_{\varepsilon Q}&\Omega_{QQ}\end{array}\right]$

Where $\omega_{\varepsilon Q}=\left[\begin{array}{cc}\omega_{\varepsilon X}^{'}&\omega_{\varepsilon Z}^{'}\end{array}\right]'$ and $\Omega_{QQ}$ is the long run variance matrix of $\mathbf{Q}_{t}\equiv\left[\begin{array}{cc}\Delta\mathbf{X}_{t}^{'}&\mathbf{Z}_{t}^{'}\end{array}\right]'$ .

Assumptions 2 (Conditions for Deriving CADF Regression)

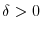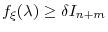For $\delta>0$ and $\lambda\in[0,\pi]$ , $f_{\xi}(\lambda)\ge\delta I_{n+m}$ .
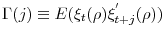Define $\Gamma(j)\equiv E(\xi_{t}(\rho)\xi^{'}_{t+j}(\rho))$ and the following matrix norm: for a 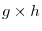$g\times h$ matrix 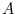, 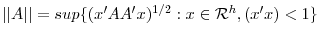$\vert\vert A\vert\vert=sup\{(x'AA'x)^{1/2}:x\in\mathcal{R}^{h},(x'x)<1\}$ . It is required that

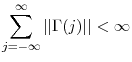
$\displaystyle \sum_{j=-\infty}^{\infty}\vert\vert\Gamma(j)\vert\vert<\infty$
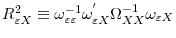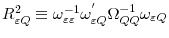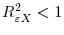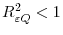Define $R^{2}_{\varepsilon X}\equiv \omega_{\varepsilon\varepsilon}^{-1}\omega^{'}_{\varepsilon X}\Omega^{-1}_{XX}\omega_{\varepsilon X}$ and $R^{2}_{\varepsilon Q}\equiv\omega_{\varepsilon\varepsilon}^{-1}\omega^{'}_{\varepsilon Q}\Omega^{-1}_{QQ}\omega_{\varepsilon Q}$ . It is required that $R^{2}_{\varepsilon X}<1$ and $R^{2}_{\varepsilon Q}<1$ .

Assumption 2.1 bounds the spectral density of $\xi_{t}(\rho)$ away from zero, assumption 2.2 is the absolute summability of $\xi_{t}(\rho)$ 's covariance function, guaranteeing limited serial dependence, and assumption 2.3 guarantees that the partial sums of the stationary covariates $\{\mathbf{Z}_{t}\}$ are not cointegrated with either $Y_{t}$ or $\mathbf{X}_{t}$ . The assumptions are fairly weak as $\mathbf{Z}_{t}$ is not required to be a vector autoregression along with $(Y_{t},\mathbf{X}^{'}_{t})^{'}$ , nor does it have to be weakly exogenous. Furthermore, in the residual based framework distributional assumptions or conditional moment restrictions are not required. For these reasons, the CADF framework is more flexible than the powerful Johansen rank test of Seo (1998). With assumptions 2.1-2.2, we derive the CADF regression.

Proposition 1 (CADF Regression)

Suppose data is generated by (1) and (2) and assumptions 1.1, 2.1 and 2.2 are satisfied. Then the following equation holds

$\displaystyle \Delta\varepsilon_{t}=\theta_{0}\varepsilon_{t-1}+\sum_{j=1}^{\infty}\theta_{\varepsilon,j}\Delta\varepsilon_{t-j}+\sum_{j=-\infty}^{\infty}\theta^{'}_{X,j}\Delta\mathbf{X}_{t-j}+\sum_{j=-\infty}^{\infty}\theta^{'}_{Z,j}\mathbf{Z}_{t-j}+\zeta_{t}$

(3)

Where $\{\zeta_{t}\}$ is a white noise process with $E(\Delta\mathbf{X}_{t}\zeta_{t+j})=E(\mathbf{Z}_{t}\zeta_{t+j})=0$ for $j=0,\pm 1,\pm 2,...$ , $\sum_{j=-\infty}^{\infty}\vert\vert\theta_{X,j}\vert\vert<\infty$ , $\sum_{j=-\infty}^{\infty}\vert\vert\theta_{Z,j}\vert\vert<\infty$ and $\sum_{j=1}^{\infty}\vert\theta_{\varepsilon,j}\vert<\infty$ . Moreover, under $H_{0}$ , $\theta_{0}=0$ .

Proof. Under assumptions 1.1, 2.1 and 2.2,

$\displaystyle (1-\rho L)\varepsilon_{t}=\sum_{j=-\infty}^{\infty}\tilde{\pi}^{'}_{X,j}\Delta\mathbf{X}_{t-j}+\sum_{j=-\infty}^{\infty}\tilde{\pi}^{'}_{Z,j}\mathbf{Z}_{t-j}+\eta_{t}$

(4)

With $\sum_{j=-\infty}^{\infty}\vert\vert\tilde{\pi}_{X,j}\vert\vert<\infty$ and $\sum_{j=-\infty}^{\infty}\vert\vert\tilde{\pi}_{Z,j}\vert\vert<\infty$ , $\{\eta_{t}\}$ a stationary process with $E(\Delta\mathbf{X}_{t}\eta_{t+j})=E(\mathbf{Z}_{t}\eta_{t+j})=0$ for $j=0,\pm 1,\pm 2, \ldots$ (see, for instance, Saikkonen 1991, equation 18). Since $\{\eta_{t}\}$ is stationary and zero mean, by Wold representation, it is true that $\phi(L)\eta_{t}=\zeta_{t}$ for an absolutely summable lag polynomial $\phi(L)$ and white noise process $\{\zeta_{t}\}$ . Multiplying $\phi(L)$ onto (4) and rearranging to arrive at (3) with $\theta_{0}\equiv\phi(1)(\rho-1)$ . Hence, $\theta_{0}=0$ under $H_{0}$ . Since coefficients in both (4) and $\phi(L)$ are absolutely summable, so are the coefficients in (3). Finally, zero correlations between $\Delta\mathbf{X}_{t}$ and $\mathbf{Z}_{t}$ with $\eta_{t}$ in all leads and lags implies zero correlations between $\Delta\mathbf{X}_{t}$ and $\mathbf{Z}_{t}$ with $\zeta_{t}$ in all leads and lags.

Notice that unlike the traditional ADF test, the leads and lags of the covariates, as well as those of $\Delta\mathbf{X}_{t}$ , are included in the CADF regression. Proposition 1 provides the motivation for deriving a test based on a feasible version of (3).

2.2 Test Statistic

$\{\varepsilon_{t}\}$ is typically not observed unless the cointegrating vector is pre-specified, therefore an estimate of $\beta$ is required. We consider the OLS estimate of the cointegrating vector.¹ Let $\widehat{\beta}$ be the estimate of the cointegrating vector and $\widehat{\varepsilon}_{t}\equiv Y_{t}-\widehat{\beta}^{'}\mathbf{X}_{t}$ be the residuals.² Noting that $\widehat{\varepsilon}_{t}=\varepsilon_{t}-(\widehat{\beta}-\beta)'\mathbf{X}_{t}$ , using (4), similar to the derivation of (3),

$\displaystyle \Delta\widehat{\varepsilon}_{t}=\alpha\widehat{\varepsilon}_{t-1}+\sum_{j=1}^{\infty}\pi_{\varepsilon,j}\Delta\widehat{\varepsilon}_{t-j} +\sum_{j=-\infty}^{\infty}\pi^{'}_{X,j}\Delta\mathbf{X}_{t-j} +\sum_{j=-\infty}^{\infty}\pi^{'}_{Z,j}\mathbf{Z}_{t-j}+(\rho-1)(\widehat{\beta}-\beta)'\psi(L)\mathbf{X}_{t-1}+v_{t}$

(5)

Where conditional on $\widehat{\beta}-\beta$ , $\{v_{t}\}\equiv\{\psi(L)(\eta_{t}-(\widehat{\beta}-\beta)'\Delta\mathbf{X}_{t})\}$ is a stationary white noise process, $\psi(L)$ and all coefficients in (5) are absolutely summable. Define $\alpha\equiv\psi(1)(\rho-1)$ and the truncation lag

. With data, one can run the truncated regression

$\displaystyle \Delta\widehat{\varepsilon}_{t}=\alpha\widehat{\varepsilon}_{t-1}+\sum_{j=1}^{k}\pi_{\varepsilon,j}\Delta\widehat{\varepsilon}_{t-j} +\sum_{j=-k}^{k}\pi^{'}_{X,j}\Delta\mathbf{X}_{t-j}+\sum_{j=-k}^{k}\pi^{'}_{Z,j}\mathbf{Z}_{t-j}+v_{t,k}$

(6)

where

$\displaystyle v_{t,k}$	$\displaystyle \equiv$	$\displaystyle (\rho-1)(\widehat{\beta}-\beta)'\psi(L)\mathbf{X}_{t-1}+\varsigma_{t,k}+v_{t}$
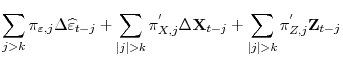$\displaystyle \varsigma_{t,k}$	$\displaystyle \equiv$	$\displaystyle \sum_{j>k}\pi_{\varepsilon,j}\Delta\widehat{\varepsilon}_{t-j}+\sum_{\vert j\vert>k}\pi^{'}_{X,j}\Delta\mathbf{X}_{t-j}+\sum_{\vert j\vert>k}\pi^{'}_{Z,j}\mathbf{Z}_{t-j}$

A t-statistic to test $H_{0}$ is computed as

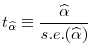$\displaystyle t_{\widehat{\alpha}}\equiv\frac{\widehat{\alpha}}{s.e.(\widehat{\alpha})}$

(7)

where s.e. $(\widehat{\alpha})$ is the usual standard error for t-statistics. We recommend applying the Bayesian Information Criterion (BIC) to (6) in order to (jointly) select $\mathbf{Z}_{t}$ and

.³ Monte Carlo simulations in section 3 and the empirical application in section 4 use BIC to select

. After experimentation with the Akaike Information Criterion (AIC) and BIC, BIC was preferred as it tends to select more parsimonious lag structures.

2.3 The Bootstrap

The asymptotic null distribution depends on difficult to estimate nuisance parameters (more specifically, as shown in the next section, $R^{2}_{\varepsilon X}$ and $R^{2}_{\varepsilon Q}$ ). This is closely related to an issue pointed out by Elliott & Pesavento (2009) regarding the long run correlation parameter between what would be the equivalent of $(1-\rho L)\varepsilon_{t}$ and $\Delta\mathbf{X}_{t}$ of this paper. The authors on p1832 note that "...in practice, this parameter is not only unknown, but also, under the null and local alternative, there is no obvious way to obtain a good estimate of this parameter". In light of this difficulty, we propose a bootstrap inference instead of relying on asymptotics. In particular, the bootstrap inference is designed to take into account the following cases of deterministic trends:

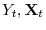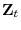Case 1. $\mu_{X},\mu_{Y},\mu_{Z}$ and $\tau_{X},\tau_{Y},\tau_{Z}=0$ ; $Y_{t},\mathbf{X}_{t}$ and $\mathbf{Z}_{t}$ are neither de-meaned nor de-trended prior to inference.

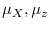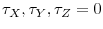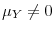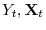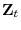Case 2. $\mu_{X},\mu_{z}$ and $\tau_{X},\tau_{Y},\tau_{Z}=0$ , $\mu_{Y}\ne 0$ ; $Y_{t},\mathbf{X}_{t}$ and $\mathbf{Z}_{t}$ are de-meaned prior to inference.

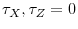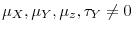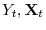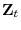Case 3. $\tau_{X},\tau_{Z}=0$ , $\mu_{X},\mu_{Y},\mu_{z},\tau_{Y}\ne 0$ ; $Y_{t},\mathbf{X}_{t}$ and $\mathbf{Z}_{t}$ are de-meaned and de-trended prior to inference.

These three cases are considered in Pesavento(2004, 2007), with case 1 being the case considered in the theoretical work that follows. Let $\widehat{\mu}_{X},\widehat{\mu}_{Y},\widehat{\mu}_{Z}$ and $\widehat{\tau}_{X},\widehat{\tau}_{Y},\widehat{\tau}_{Z}$ be OLS estimates of the means and trends. Following the procedures of Paparoditis & Politis (2003) and ()*badillo2010residual, the bootstrap null distribution of $t_{\widehat{\alpha}}$ can be constructed by the following steps:

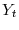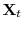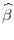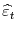Step 1. If the deterministic trend follows cases 2 or 3, then de-mean, or de-mean and de-trend $Y_{t}$ and $\mathbf{X}_{t}$ . Estimate $\widehat{\beta}$ and $\widehat{\varepsilon}_{t}$ using this data. Run 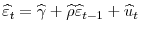$\widehat{\varepsilon}_{t}=\widehat{\gamma}+\widehat{\rho}\widehat{\varepsilon}_{t-1}+\widehat{u}_{t}$ .⁴

Step 2. Choose a positive integer

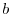. Define

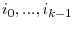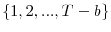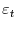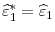where $[\cdot]$ is the integer part. Let $i_{0},...,i_{k-1}$ be random i.i.d. draws from the uniform distribution on $\{1,2,...,T-b\}$ . We generate pseudo series for $\varepsilon_{t}$ . Set $\widehat{\varepsilon}^{*}_{1}=\widehat{\varepsilon}_{1}$ , and for

$\displaystyle \widehat{\varepsilon}^{*}_{t}=\widehat{\varepsilon}^{*}_{t-1}+\widehat{u}_{i_{[(t-2)/b]}+t-[(t-2)/b]b-1}$

Step 3. Now construct pseudo series for $Y_{t},\mathbf{X}_{t}$ and $\mathbf{Z}_{t}$ that reflect the various cases of deterministic trends. Specifically, for

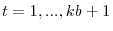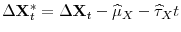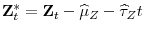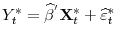
Case 1. $\Delta\mathbf{X}^{*}_{t}=\Delta\mathbf{X}_{t}-\widehat{\mu}_{X}-\widehat{\tau}_{X}t$ , $\mathbf{Z}^{*}_{t}=\mathbf{Z}_{t}-\widehat{\mu}_{Z}-\widehat{\tau}_{Z}t$ , and $Y^{*}_{t}=\widehat{\beta}^{'}\mathbf{X}^{*}_{t}+\widehat{\varepsilon}^{*}_{t}$

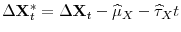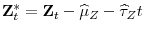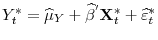
Case 2. $\Delta\mathbf{X}^{*}_{t}=\Delta\mathbf{X}_{t}-\widehat{\mu}_{X}-\widehat{\tau}_{X}t$ , $\mathbf{Z}^{*}_{t}=\mathbf{Z}_{t}-\widehat{\mu}_{Z}-\widehat{\tau}_{Z}t$ , and $Y^{*}_{t}=\widehat{\mu}_{Y}+\widehat{\beta}^{'}\mathbf{X}^{*}_{t}+\widehat{\varepsilon}^{*}_{t}$

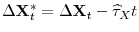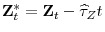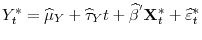
Case 3. $\Delta\mathbf{X}^{*}_{t}=\Delta\mathbf{X}_{t}-\widehat{\tau}_{X}t$ , $\mathbf{Z}^{*}_{t}=\mathbf{Z}_{t}-\widehat{\tau}_{Z}t$ , and $Y^{*}_{t}=\widehat{\mu}_{Y}+\widehat{\tau}_{Y}t+\widehat{\beta}^{'}\mathbf{X}^{*}_{t}+\widehat{\varepsilon}^{*}_{t}$

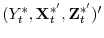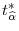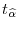Step 4. Finally, with pseudo data $(Y^{*}_{t},\mathbf{X}^{*'}_{t},\mathbf{Z}^{*'}_{t})'$ , de-mean or de-mean and de-trend under the appropriate deterministic case, and compute $t^{*}_{\widehat{\alpha}}$ . Repeat steps 1-4 a large number of times to obtain the bootstrap null distribution for $t_{\widehat{\alpha}}$ .

The bootstrap randomly draws blocks (of length

) of $\widehat{u}_{t}$ , and uses it to generate pseudo data for $\varepsilon_{t}$ under $H_{0}$ , which is in turn used to generate pseudo data for $Y_{t}$ . In step 3, the deterministic components were imposed on the variables. While we do not study the theoretical properties of the bootstrap in this paper, our simulations indicate that bootstrap inference works well. Readers interested in theoretical properties of the block bootstrap are referred to Paparoditis & Politis (2003) for a formal discussion in the case of unit root testing.

2.4 Asymptotics

We are interested in the distribution of $t_{\widehat{\alpha}}$ under a local-to-unity version of $H_{A}$ . This section gives precise statements as to how the distribution for $t_{\widehat{\alpha}}$ is different from the distribution of the ADF test. Following Phillips (1987), Hansen (1995), and Pesavento (2004), re-define $H_{A}$ so that for some constant ,

$\displaystyle H_{A}: \rho=1+\frac{c}{T}$

(8)

so that $\rho<1$ when

finite but $\rho\rightarrow 1$ as $T\rightarrow\infty$ . One more assumption is imposed:

Assumptions 3 (Rate of Divergence of )

The truncation lag in (6) satisfies $k\rightarrow\infty$ as $T\rightarrow\infty$ , with the bound that $T^{-1/3}k\rightarrow 0$ .

Assumption 3 allows

to increase with the sample size

in order for (6) to closely approximate (5), but at a moderate rate so that the dimension of the regressors is reasonable. Ng & Perron (1995) shows in the unit root testing case, our preferred model selection criterion BIC satisfies assumption 3.

For a symmetric positive definite matrix , define its Cholesky and inverse Cholesky decompositions as $A^{\frac{1}{2}'}A^{\frac{1}{2}}=A$ and $A^{-\frac{1}{2}}A^{-\frac{1}{2}'}=A^{-1}$ . Unless otherwise stated, let $\int\textbf{B}\equiv\int_{0}^{1}\textbf{B}(r)dr$ for some vector stochastic process $\textbf{B}(r)$ .

Define

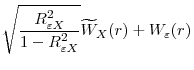$\displaystyle J_{\varepsilon X}(r)$	$\displaystyle \equiv$	$\displaystyle \sqrt{\frac{R^{2}_{\varepsilon X}}{1-R^{2}_{\varepsilon X}}}\widetilde{W}_{X}(r)+W_{\varepsilon}(r)$
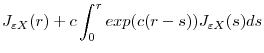$\displaystyle J^{c}_{\varepsilon X}(r)$	$\displaystyle \equiv$	$\displaystyle J_{\varepsilon X}(r)+c\int_{0}^{r}exp(c(r-s))J_{\varepsilon X}(s)ds$

where $\widetilde{W}_{X}(r)$ is a univariate standard Brownian motion, independent of $W_{\varepsilon}(r)$ and $\mathbf{W}_{Z}(r)$ . Also, define

$\displaystyle D^{c}_{1}\equiv\left[\begin{array}{cc}\sqrt{\frac{1-R^{2}_{\varepsilon Q}}{1-R^{2}_{\varepsilon X}}}\int J^{c}_{\varepsilon X}dW_{\varepsilon}&\int J^{c}_{\varepsilon X}d\mathbf{W}^{'}_{X}\\ \sqrt{\frac{1-R^{2}_{\varepsilon Q}}{1-R^{2}_{\varepsilon X}}}\int \mathbf{W}_{X}dW_{\varepsilon}&\int\mathbf{W}_{X}d\mathbf{W}^{'}_{X}\end{array}\right]$		$\displaystyle D^{c}_{2}\equiv\left[\begin{array}{cc}\int (J^{c}_{\varepsilon X})^{2}&\int J^{c}_{\varepsilon X}\mathbf{W}^{'}_{X}\ \int J^{c}_{\varepsilon X}\mathbf{W}_{X}&\int\mathbf{W}_{X}\mathbf{W}^{'}_{X}\end{array}\right]$
$\displaystyle F\equiv\left[\begin{array}{cc}\frac{1-R^{2}_{\varepsilon Q}}{1-R^{2}_{\varepsilon X}}&0\ 0&I_{n}\end{array}\right]$		$\displaystyle B^{c}\equiv\left[\begin{array}{cc}1&-\left(\int\mathbf{W}^{'}_{X}J^{c}_{\varepsilon X}\right)\left(\int\mathbf{W}_{X}\mathbf{W}^{'}_{X}\right)^{-1}\end{array}\right]'$

Square matrices $D^{c}_{1},D^{c}_{2}$ and

are of dimension

, and $B^{c}$ is an

vector. $D^{c}_{2}$ and $B^{c}$ in particular are common expressions that appear in asymptotics for residual based tests (e.g., Pesavento, 2004; Phillips & Solo, 1992). Lastly, let $\omega_{\varepsilon\cdot X}\equiv\omega_{\varepsilon\varepsilon}(1-R^{2}_{\varepsilon X})$ and $\omega_{\varepsilon\cdot Q}\equiv\omega_{\varepsilon\varepsilon}(1-R^{2}_{\varepsilon Q})$ .

Lemma 1 Let the data be generated by (1) and (2) and assume that assumptions 1 hold. If (8) is true, then as $T\rightarrow\infty$

$\displaystyle \widehat{\beta}-\beta\Rightarrow\omega^{1/2}_{\varepsilon\cdot X}\Omega^{-1/2}_{XX}\left(\int\mathbf{W}_{X}\mathbf{W}^{'}_{X}\right)^{-1} \left(\int\mathbf{W}_{X}J^{c}_{\varepsilon X}\right)$ (9)
If in addition assumptions 2 and 3 hold, then

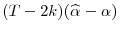
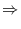
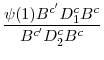
$\displaystyle (T-2k)(\widehat{\alpha}-\alpha)$ $\displaystyle \Rightarrow$ $\displaystyle \frac{\psi(1)B^{c'}D_{1}^{c}B^{c}}{B^{c'}D_{2}^{c}B^{c}}$ (10)

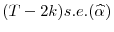
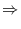
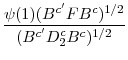
$\displaystyle (T-2k)s.e.(\widehat{\alpha})$ $\displaystyle \Rightarrow$ $\displaystyle \frac{\psi(1)(B^{c'}F B^{c})^{1/2}}{(B^{c'}D_{2}^{c}B^{c})^{1/2}}$

Proof. See appendix.

Proposition 2 is the main result of this paper.

Proposition 2 (Asymptotic local-to-unity Power of CADF Test)

Let the data be generated by (1) and (2) and assume that assumptions 1, 2, and 3 hold. If (8) is true, then as $T\rightarrow\infty$

$\displaystyle t_{\widehat{\alpha}}\Rightarrow\frac{B^{c'}D^{c}_{1}B^{c}}{(B^{c'}D^{c}_{2}B^{c})^{1/2}(B^{c'}F B^{c})^{1/2}} +c\frac{(B^{c'}D^{c}_{2}B^{c})^{1/2}}{(B^{c'}F B^{c})^{1/2}}$

(11)

Proof. Noting that $\alpha=\psi(1)(c/T)$ ,

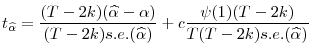$\displaystyle t_{\widehat{\alpha}}=\frac{(T-2k)(\widehat{\alpha}-\alpha)}{(T-2k)s.e.(\widehat{\alpha})}+c\frac{\psi(1)(T-2k)}{T(T-2k)s.e.(\widehat{\alpha})}$

This together with Lemma 1 proves the proposition.

Thus, the influence of the covariate feeds through $R^{2}_{\varepsilon Q}$ , the correlation between $(1-\rho)\varepsilon_{t}$ and $\mathbf{Q}_{t}$ . To further understand the role of the covariates, consider the case where the covariates have no long run correlation with the cointegration candidates. That is, $\omega_{\varepsilon Z}$ and $\omega_{XZ}=0$ . In this case, observe that $R^{2}_{\varepsilon Q}=R^{2}_{\varepsilon X}$ . This means that now $D_{1}^{c}=\widetilde{D}_{1}^{c}$ , where

$\displaystyle \widetilde{D}^{c}_{1}\equiv\left[\begin{array}{cc}\int J^{c}_{\varepsilon X}dW_{\varepsilon}&\int J^{c}_{\varepsilon X}d\mathbf{W}^{'}_{X}\\ \int \mathbf{W}_{X}dW_{\varepsilon}&\int\mathbf{W}_{X}d\mathbf{W}^{'}_{X}\end{array}\right]$

Furthermore, $F=I_{n+1}$ , and

$\displaystyle t_{\widehat{\alpha}}\Rightarrow\frac{B^{c'}\widetilde{D}^{c}_{1}B^{c}}{(B^{c'}D^{c}_{2}B^{c})^{1/2}(B^{c'}B^{c})^{1/2}} +c\frac{(B^{c'}D^{c}_{2}B^{c})^{1/2}}{(B^{c'}B^{c})^{1/2}}$

(12)

This is the corresponding asymptotic distribution of the ADF test as the covariates have no long run correlations with the cointegration candidates. To the best of our knowledge, (12) is itself a new finding, since the inclusion of leads and lags of $\Delta\mathbf{X}_{t}$ in the ADF regression removes $R^{2}_{\varepsilon X}$ from the asymptotic distribution except where it is embedded in $J_{\varepsilon X}^{c}$ .⁵

3 Simulations

3.1 Large Sample Power

The local-to-unity asymptotic distribution in proposition 2 can be used to assess large sample power of the CADF test. We numerically construct the distribution, for and -20 using 3,000 samples of Gaussian innovations. Each sample has the size of 3,000, and the innovations are used in constructing the functionals present in the right hand side of (6). Power is then calculated, for and -20, as the mass of the distribution to the left of the 5% critical value of the distribution.

Note that the test only depends on $R^{2}_{\varepsilon X}$ and $R^{2}_{\varepsilon Q}$ . Nonetheless, it is more intuitive to express power as a function of pairwise correlations $\omega_{\varepsilon X}$ , $\omega_{\varepsilon Z}$ , and $\omega_{X Z}$ . We set and all long run variances equal to one. As such, $R^{2}_{\varepsilon X}=\omega^{2}_{\varepsilon X}$ and $R^{2}_{\varepsilon Q}=\frac{\omega^{2}_{\varepsilon X}-2\omega_{\varepsilon X}\omega_{\varepsilon Z}\omega_{XZ}+\omega^{2}_{\varepsilon Z}}{1-\omega^{2}_{XZ}}$ . Figures 1-3 display the power surfaces across different values of $\omega_{\varepsilon X}$ , $\omega_{\varepsilon Z},\omega_{X Z}$ and .

Figure 1: Asymptotic Power of CADF test when $\omega _{\varepsilon X}=-0.5$

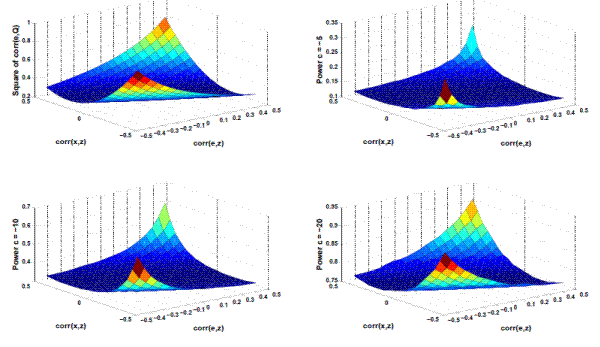
Figure 1: Auto ABS Spreads and Issuance: 2007-2010. Description below

Figure 2: Asymptotic Power of CADF test when 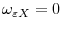$\omega _{\varepsilon X}=0$

Figure 2: Comparison of Spreads on Auto ABS Issued in the U.S. and Europe. Description below

Figure 3: Asymptotic Power of CADF test when 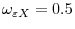$\omega _{\varepsilon X}=0.5$

Figure 3: Event Study: CMBS. Description below

Figures 1, 2, and 3 each show four graphs per figure. The horizontal axes show corr(x,z) and corr(e,z), while the vertical axis shows the square of corr(e,Q) in the top left graph and the local-to-unity power in each of the three remaining graphs. The three graphs showing power on the vertical axis differ by the specifications of the local-to-unity parameter, c. The top right, bottom left, and bottom right graphs show power when c = -5, -10, and -20, respectively. The figures each differ in terms of the specification of corr(e,x). Figures 1, 2, and 3, shows power when corr(e,x) = -0.5, 0, and 0.5, respectively. As expected, for a given combination of corr(e,x), corr(e,z), and corr(x,z), the local-to-unity power increases monotonically as c decreases. Throughout the figures, we see that in general the CADF has high power when corr(e,x) and corr(e,z) are large in magnitude, either with different signs when corr(x,z) is positive, or with the same signs when corr(x,z) is negative. Importantly, the ADF tests (where corr(e,z) and corr(x,z) = 0) always have the lowest power.

As expected, for a given combination of $\omega_{\varepsilon X}$ , $\omega_{\varepsilon Z}$ , and $\omega_{X Z}$ , the power increases monotonically as decreases. Comparing the graphs in each of the figures with the top-left graph of that figure, it is also clear that the power function mimics the shape of $R^{2}_{\varepsilon Q}$ , although the exact shape varies. Throughout the figures, in general the CADF has high power when $\omega_{\varepsilon X}$ and $\omega_{\varepsilon Z}$ are large in magnitude, either with different signs when $\omega_{X Z}$ is positive, or with the same signs when $\omega_{X Z}$ is negative. A heuristic interpretation of these conditions is that power is highest when the covariates $\mathbf{Z}_{t}$ convey different information about $(1-\rho L)\varepsilon_{t}$ than $\mathbf{X}_{t}$ .

Importantly, the ADF tests (corresponding to the point on the graphs where $\omega_{\varepsilon Z}$ and $\omega_{XZ}=0$ ) always have the lowest power. For instance, when $R^{2}_{\varepsilon X}=0$ and (top-right graph of figure 2), the ADF test has a power of roughly 20%, while the power of the CADF test could reach 60%. Asymptotically, one cannot do worse in terms of power by using the CADF test instead of the ADF test.

3.2 Small Sample Size and Power

In this section we study the small sample size and power of the CADF test, and compare the size and power to those of the ADF and Johansen $\lambda_{max}$ tests. This exercise is important because it is well known that residual based tests are typically less powerful than Johansen's test in small samples. Furthermore, using these simulations, we study the effects of the presence of deterministic trends.

Pseudo time series of length 200 are generated in the following way: for each $\rho\in\{.8,.9,1\}$

$\displaystyle \left[\begin{array}{c}(1-\rho)\varepsilon^{}_{t}\ \Delta X^{}_{t}\ Z^{*}_{t}\end{array}\right]$	$\displaystyle =$	$\displaystyle \left[\begin{array}{c}0\ \mu_{X}+\tau_{X}t\ \mu_{Z}+\tau_{Z}t\end{array}\right]+\Omega^{\frac{1}{2}'}N(0,I_{3})$

$\displaystyle Y^{*}_{t}$	$\displaystyle =$	$\displaystyle \mu_{Y}+\tau_{Y}t+X^{}_{t}+\varepsilon^{}_{t}$

Under case 1, all $\mu$ 's and $\tau$ 's were set to zero. Case 2 is the same as case 1 except that $\mu_{Y}=1$ . Case 3 sets $\mu_{Y}=\mu_{X}=\mu_{Z}=\tau_{Y}=1$ and $\tau_{X}=\tau_{Z}=0$ . In $\Omega$ , the long run variances are set to 1, and we allow for various combinations of $\omega_{\varepsilon X},\omega_{\varepsilon Z}$ and $\omega_{X Z}$ . We discard the first 100 pseudo data points, leaving a small sample size of

. Using pseudo sample $(Y_{t},\mathbf{X}_{t},\mathbf{Z}_{t})$ , we conduct (after de-meaning or de-meaning and de-trending under the appropriate case) the bootstrap CADF test with the bootstrap block size set to one⁶, along with the ADF and Johansen's $\lambda_{max}$ tests using asymptotic critical values. The numer of leads and lags in both the ADF and CADF tests are chosen by BIC. We record whether or not the tests reject the null of no cointegration.

Repeating this procedure 2,000 times, the empirical rejection rates are obtained, representing the small sample power (where $\rho=.8,.9$ ) and size (where $\rho=1$ ). Table 1 contains the size and power results.

Table 1: Small Sample Simulation Results

$\omega_{\varepsilon X}$	CADF : ( $\omega_{\varepsilon Z}$ , $\omega_{XZ})$	Case 1 $\rho=1$	Case 1 $\rho=.9$	Case 1 $\rho=.8$	Case 2 $\rho=1$	Case 2 $\rho=.9$	Case 2 $\rho=.8$	Case 3 $\rho=1$	Case 3 $\rho=.9$	Case 3 $\rho=.8$
0	ADF	5.50%	38.10%	83.60%	5.90%	21.40%	61.60%	4.25%	14.50%	44.20%
0	Johansen	5.20%	21.70%	61.40%	7.60%	15.60%	45.60%	8.70%	15.30%	35.40%
0	CADF(.5,.4)	5.55%	53.15%	92.25%	6.35%	43.00%	85.40%	2.60%	12.70%	49.60%
0	CADF(.2,-.2)	5.85%	46.90%	86.15%	7.50%	36.25%	79.50%	3.85%	12.75%	40.00%
0	CADF(0,.4)	4.95%	51.25%	90.10%	6.80%	40.15%	83.60%	2.85%	13.75%	47.25%
.5	ADF	5.60%	33.00%	81.45%	4.80%	17.60%	55.40%	4.50%	11.00%	33.90%
.5	Johansen	6.00%	32.90%	78.85%	7.60%	22.60%	63.90%	8.30%	19.70%	50.10%
.5	CADF(.5,.4)	5.20%	57.45%	93.85%	7.15%	40.05%	87.95%	3.75%	15.15%	47.70%
.5	CADF(.2,-.2)	5.65%	63.30%	95.70%	6.90%	47.65%	90.05%	2.60%	14.05%	51.70%
.5	CADF(0,.4)	4.40%	65.35%	95.90%	6.25%	45.75%	91.55%	2.60%	17.15%	57.05%
.9	ADF	5.50%	29.00%	78.20%	5.00%	8.00%	36.80%	4.10%	2.00%	12.10%
.9	Johansen	5.60%	96.30%	100.00%	4.50%	86.10%	99.90%	8.40%	69.10%	99.10%
.9	CADF(.5,.4)	6.40%	95.60%	100.00%	7.80%	74.20%	99.65%	3.90%	22.30%	83.45%
.9	CADF(.2,-.2)	2.55%	98.75%	99.80%	1.30%	87.05%	97.20%	0.30%	32.20%	68.75%
.9	CADF(0,.4)	2.40%	97.95%	98.95%	1.40%	83.65%	93.45%	0.15%	31.10%	60.45%

Note: Details on the simulation setup are described in Section 2.3. Numbers are empirical rejection frequencies from 2,000 Monte Carlo simulations. Sample size in each simulation is set to 100. Deterministic cases 1, 2, and 3 are as described in Section 2.3 and this section.

For the CADF and Johansen tests, power increases with $\omega_{\varepsilon X}$ . On the other hand, the power of the ADF test decreases with $\omega_{\varepsilon X}$ , and in general becomes significantly lower than the power of the CADF and Johansen tests.

The power discrepancy between the ADF and CADF test is particularly large when deterministic terms are present (cases 2 and 3), or when $\omega_{\varepsilon X}$ is large. The ADF test performs well when $\omega _{\varepsilon X}=0$ , but still fails to show higher power than the CADF test in all cases other than case 3 when $\rho=.9$ . The low power of the ADF test in these cases is consistent with previous findings (e.g.,Pesavento 2004). In terms of size (i.e., when $\rho=1$ ), the ADF test has good size in almost every case, while the CADF test tends to be under-sized when $\omega_{\varepsilon X}$ is large or under case 3.

The CADF test also compares favorably with the Johansen $\lambda_{max}$ test (see Johansen, 1991,1988). It is particularly advantageous under cases 1 and 2 when $\omega _{\varepsilon X}=0$ or .5, while the Johansen test is advantageous under case 3 for $\omega_{\varepsilon X}=.9$ . In all other instances, the powers of the two tests are similar. The Johansen test tends to be over-sized, particularly under case 3, whereas the CADF test under case 3 is typically under-sized.

Finally, we observed that there are minor discrepancies in power for CADF test based on different combinations of $(\omega_{\varepsilon Z},\omega_{XZ})$ , and the best combination differs depending on the deterministic case, $\rho$ , and $\omega_{\varepsilon X}$ .

4 Cointegration between Credit Default Swap and Bond Spreads

The seller of a CDS contract offers insurance to the buyer of protection against default of an underlying reference entity. In return for protection, the buyer makes regular payments over the life of the contract. Thus, the CDS "spread"⁷ is often viewed as the price of the credit risk of the underlying reference entity. Abstracting from other factors, an investor who holds a corporate bond for a given entity requires the same premium as the seller of a CDS contract, since both the bond and CDS are exposed to the same default event of the reference entity. The deviation between the corporate bond spread (accounting for the reference rate) and the CDS spread is referred to as the CDS-bond basis.

Following previous literature, we use the CDS spread minus the par asset-swap rate to measure the basis (see, Kocic (2000), Houweling & Vorst (2005), Hull (2004), or see Choudhry (2006)for explanation of alternative measures). Typically, an asset-swap consists of a fixed coupon bond and an interest-rate swap, where the bond holder pays a fixed coupon and receives a floating spread over LIBOR. It can be thought of as measuring the difference between the present value of future cash flows of the bond and the market price of the bond using zero coupon rates (Choudhry, (2006)).

For no arbitrage conditions to hold, the pricing of credit risk for any underlying entity should be the same in both markets, ceteris paribus. As noted by Zhu (2006), under the Duffie (1999) pricing framework, it is possible to replicate a CDS contract synthetically by shorting a maturity matched par fixed coupon bond on the underlying reference entity, and investing the money in a par fixed risk free note. Therefore, the CDS premium equals the bond spread over the reference rate, or zero basis under no arbitrage. If there exists a negative (positive) basis, arbitrage is possible through a negative (positive) basis trade by buying (shorting) the cash bond and buying protection (selling protection) on the CDS contract.

Previous literature (see, for instance, Blanco (2005), Zhu (2006), De Wit 2006, Levin (2005), Norden & Weber (2009)) notes the existence of the basis and establish it is stationary (i.e., CDS and bond spreads are cointegrated) for most firms during benign economic periods. We revisit this cointegration relationship during the financial crisis, which we define as July 2007 to July 2009. Our conjecture is that unprecedented levels of volatility, illiquidity, and market uncertainty may impose difficulties for traditional tests to find cointegration between CDS and bond spreads. The CADF test, on the other hand, may perform better through the use of covariates to account for some of these factors.

4.1 Covariate Selection

During the financial crisis, evaporation of liquidity in the market caused funding costs to rise (see Giglio, 2010; Fontana, 2010). This coupled with surging counterparty credit risk and market volatility drove the basis wider (see Fontana, 2010)⁸. While it is difficult to construct explicit proxies for liquidity and counterparty credit risk, our choice of covariates intends to reflect these risk factors.

The first covariate considered is the HFRX Global Hedge Fund Index return (HFRXGL). Hedge funds and banks comprise the largest CDS market participants (see, Anderson, 2010). While banks often use the CDS market to hedge against loan risk, hedge funds on the other hand are important speculators in the CDS market, using CDS contracts as tools to engage in credit arbitrage. Hedge funds also hedge convertible bond positions, and cover their exposures in the CDO market with CDS contracts. It is argued by Brunnermeier (2009) and Anderson (2010) that hedge funds access to external financing plays an important role in the liquidity of assets for which they participate in a large share of market transactions. The extent and rate at which hedge funds can obtain capital is related to their returns (see Boyson (2008), and consequently hedge fund performance affects the liquidity of the CDS market. HFRXGL is therefore used as a proxy for market-wide hedge fund performance.

The second set of covariates is the S&P 500 returns and percentage change VIX. The S&P 500 returns can be viewed as a proxy of market wide performance as a whole, while the VIX index serves as a measure of implied market volatility. Counterparty credit risk and liquidity risk are often heightened during periods of low equity returns and high market volatility. As such, S&P 500 and VIX returns may be driven by the same factors that affect the CDS-bond basis. We also use the two covariates together in order to see how the CADF test performs when there is more than one covariate.

The third covariate is the Libor-OIS spread, which is the difference in the three-month libor and the overnight index swap (OIS) rate. The Libor-OIS spread increases with a perceived rise in bank counterparty credit risk (see Schwarz, 2009). In contrast to CDS contracts, bonds do not have counterparty credit risk. Because counterparty risk is a driver of the basis (see Choudhry, 2006), the Libor-OIS spread is chosen as a covariate.

Finally, daily stock returns for each firm are used as a firm-specific covariate. Drivers of the basis such as firm credit quality, type of institution, the rate at which a firm can obtain funding (see Choudhry, 2006), and many other factors unique to each firm may not be captured by systematic covariates. As noted by Aunon-Nerin et al. (2002), declines in stock price are associated with a rise in CDS premium, and should be considered when assessing credit risk. Therefore, we chose stock returns as a covariate.

4.2 Data

We start with all firms listed in both the Markit Partners CDS and bond data sets between June 2007 and June 2009. Five year CDS spreads are considered as they are the most actively traded. Quotes selected from Markit Partners are for CDS spreads referencing Senior Unsecured, USD denominated debt with the Modified Restructuring (MR) clause. In order to match the remaining maturity of the bond spread to the five year CDS spreads, a generic bond is constructed for each firm from a pool of outstanding bonds similar to the methodology of Zhu (2006).

Using Fixed Income Securities Database (FISD), we constrain our analysis to a list of bonds that meet the following criteria:

Bonds must not be puttable, callable, convertible, or reverse convertible.
Bonds must be denominated in USD.
Bonds must be Senior Unsecured.
Bonds must be fixed coupon.

For bonds that meet the stated criteria, the daily bond asset-swap rate, the depth of the quote, and type of quote for each bond is obtained from Markit. For each bond, the depth weighted average of both TRACE and Composite quotes is calculated. We eliminate all bonds with remaining maturity shorter than two and a half years or longer than seven years. There are three possible cases in constructing the generic bond for each firm-day. First, all of the firm's available bonds have a shorter remaining maturity than 5 years, or all available bonds have a longer remaining maturity than five years. Second, there is only one bond available. Third, there is at least one bond with maturity shorter than five years and at least one bond with maturity longer than five year. In the first case, the generic bond is the bond with the maturity closest to five years. In the second case, the generic bond is the only available bond. In the third case, the generic bond is the linear interpolation of the closets two bonds on each side of the five year maturity, following Zhu (2006). Using ADF unit root tests, we ensure that all covariates and cointegration candidates are stationary by excluding any firms for which one of these series is non-stationary. The final set of firms has bonds with no more than 20 consecutive days of missing quotes. Based on this construction, there are 24 firms in our final list, similar in length and the number of firms to previous studies.

Daily data for the S&P 500 index, firm stock price, the VIX index, the Libor-OIS spread, and the HFRXGL index are obtained from either Bloomberg or Datastream.⁹ For each firm, the weekly average of the daily series of bond asset-swap rates, CDS spreads, and each covariate series is calculated. We take the first difference of the log of each covariate, except for the Libor-OIS spread where we simply take the first difference.

4.3 Results

Four sets of CADF tests, one for each set of covariates, is performed under deterministic case 1. Critical values for the CADF test are generated using a 10,000 iteration residual based bootstrap with a block size of 5 (where ) as described in Section 2.3. To benchmark the CADF tests, we also perform ADF and Johansen cointegration tests using asymptotic critical values. Results for each test are shown in Table 2.

Table 2: Application Results and Test Statistics

Firm	Johansen $\lambda_{ma}$ $_{x}$	ADF	CADF (HFRXGL)	CADF (S&P500,VIX)	CADF (Stock Rtn.)	CADF (Libor-OIS)
AIG	23.17^***	-4.74^***	-2.32^*	-2.06^**	-3.28^**	-2.39^**
ALL	26.38^***	-4.26^***	-4.40^***	-4.64^***	-4.36^***	-3.75^***
AXP	16.09^***	-2.67^*	-3.10^***	-3.55^***	-3.66^***	-2.65^**
BA	17.52^***	-4.34^***	-3.85^***	-3.82^***	-4.07^***	-3.77^***
CAT	11.70^**	-3.04^**	-3.13^***	-2.75^***	-2.54^**	-2.43^**
CIT	17.21^***	-3.83^***	-2.05^**	-2.15^**	-2.37^**	-2.91^***
CL	28.47^***	-4.82^***	-5.05^***	-5.05^***	-5.30^***	-4.94^***
DE	15.97^***	-3.61^***	-3.67^***	-3.90^***	-3.74^***	-3.21^***
DOW	15.36^***	-3.44^***	-3.86^***	-3.28^***	-3.05^***	-3.37^***
ED	7.80	-2.42	-2.20^**	-2.20^**	-2.09^**	-1.96^*
ENTERP	7.08	-0.76	-1.74	-1.95	-1.94	-1.29^*
F	20.58^***	-2.34	-2.91^**	-3.53^***	-3.14^**	-2.86^**
GE	7.65	-2.73^*	-1.78^**	-2.24^**	-2.21^**	-2.11^**
GMAC	21.90^***	-2.92^**	-2.34^**	-2.98^**	-1.82^*	-2.71^***
GS	10.48^*	-2.61^*	-2.92^**	-2.98^**	-2.95^**	-2.86^**
HSBC	9.68^*	-3.08^**	-3.80^***	-3.23^***	-1.88^*	-3.01^***
KEY	16.55^***	-3.33^**	-3.08^**	-3.24^***	-3.00^**	-2.71^**
KIM	11.85^**	-2.14	-3.24^***	-3.29^***	-3.09^**	-3.17^***
LEH	4.31	-1.83	-2.15^*	-2.45^**	-1.93	-2.16^*
MER	4.80	-2.31	-0.53	-0.94	-1.04	-0.14
NRUC	2.83	-1.54	-1.85^*	-1.24	-0.94	-.67
PRU	26.83^***	-4.27^***	-4.74^***	-4.81^***	-4.62^***	-4.65^***
SEAR	15.96^***	-3.04^**	-3.51^**	-3.89^**	-3.52^***	-3.58^***
WFC	13.22^**	-3.41^**	-3.20^***	-3.58^***	-4.24^***	-3.69^***
# Fail to Reject (10%)	6	7	2	3	4	2
# Fail to Reject (5%)	8	10	5	5	6	5

Notes: 1: Numbers presented are test statistics. 2: ***, **, and * correspond to rejections at the 1, 5, and 10 percent confidence levels, respectively.3: The CADF test is run under deterministic case 1, as described in Section 2.3, with a block size of 5.

The Johansen and ADF tests fail to reject the null of no cointegration at the 10% confidence level for 6 and 7 of the 24 firms, respectively. The CADF test using the S&P 500 index and the percentage change in the VIX fails to reject the null of no cointegration for 3 firms, while the CADF test using firm stock returns fails to reject to null of no cointegration for 4 of the 24 firms at the 10% confidence level. Covariates choices of the HFRXGL index and Libor-OIS spread reject the null of no-cointegration for the most firms, with each failing to reject only 2 firms. Results at the 5% confidence level are qualitatively similar.

Overall, by using covariates the CADF test is able to find more cointegrating relationships than ADF and Johansen tests during the financial crisis. One possible explanation is that the inclusion of covariates removes part of the heightened volatility that may otherwise mask the cointegrating relationships. The strong performance of the CADF test for all sets of covariates is consistent with Anderson (2010), who concludes that during the crisis, systemic factors and market volatility significantly affected the basis.

5 Conclusion and Extensions

This paper introduces a residual based cointegration test with better power. Inclusion of stationary covariates reduces the noise in the system, providing more precise parameter estimates and higher power tests. The test and its asymptotic distribution under the local-to-unity alternative are derived under a simple model and mild assumptions. Due to the dependence of the asymptotic null distribution on hard to estimate nuisance parameters, we provide a bootstrap framework for obtaining test critical values.

Simulations based on the asymptotic results shows that the CADF test has higher power than the ADF test. The magnitude of power improvement depends on the long-run correlation between the cointegration candidates and the stationary covariates. In small samples, Monte Carlo simulations also show that the CADF test has good size and power properties in comparison to the ADF and Johansen tests, under the presence of deterministic trends.

The CADF test is used to study the cointegration relationship between CDS and bond spreads for 24 U.S. firms during the financial crisis. Covariates are chosen to proxy various factors that may affect the CDS-bond basis. The use of covariates allows us to uncover cointegration relationships for more firms than the Johansen and ADF tests, possibly because the covariates partially control for the heightened levels of volatility and market uncertainly that may otherwise mask cointegration relationships.

6 Appendix

6.1 Proof of Lemma 1

To prove Lemma 1, some auxiliary results are needed. Define the regressors in the CADF regression as

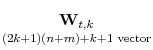$\displaystyle \underset{(2k+1)(n+m)+k+1\text{ vector}}{\mathbf{W}_{t,k}}$	$\displaystyle \equiv$	$\displaystyle \left[\begin{array}{cccccccccc}\widehat{\varepsilon}_{t-1}&\Delta\mathbf{X}^{'}_{t+k}&...&\Delta\mathbf{X}^{'}_{t-k} &\mathbf{Z}^{'}_{t+k}&...&\mathbf{Z}^{'}_{t-k}&\Delta\widehat{\varepsilon}_{t-1}&...&\Delta\widehat{\varepsilon}_{t-k}\end{array}\right]'$
	$\displaystyle \equiv$	$\displaystyle \left[\begin{array}{cc}\widehat{\varepsilon}_{t-1},\widetilde{\mathbf{W}}^{'}_{t,k}\end{array}\right]'$

Define $\tau$ , a square weight matrix of the same dimension, as

$\displaystyle \scriptsize \tau\equiv diag\left[\begin{array}{cccccccccc}T-2k&(T-2k)^{\frac{1}{2}}I_{n}&...&(T-2k)^{\frac{1}{2}}I_{n}&(T-2k)^{\frac{1}{2}}I_{m}&...& (T-2k)^{\frac{1}{2}}I_{m}&(T-2k)^{\frac{1}{2}}&...&(T-2k)^{\frac{1}{2}}\end{array}\right]$

From hereon, unless otherwise stated, $\sum$ denotes $\sum_{t=k+1}^{T-k}$ .

Lemma 2 Let the data be generated by (1) and (2) and assume that assumptions 1, 2, and 3 hold. Define

$\displaystyle \widehat{R}$	$\displaystyle \equiv$	$\displaystyle \tau^{-1}\left(\sum\mathbf{W}_{t,k}\mathbf{W}^{'}_{t,k}\right)\tau^{-1}$
$\displaystyle R$	$\displaystyle \equiv$	$\displaystyle diag\left[\begin{array}{cc}(T-2k)^{-2}\sum\widehat{\varepsilon}^{2}_{t-1}&E\left(\widetilde{\mathbf{W}}_{t,k}\widetilde{\mathbf{W}}^{'}_{t,k}\right)\end{array}\right]$

If (8) is true, then, as $T\rightarrow\infty$

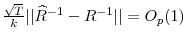$\frac{\sqrt{T}}{k}\vert\vert\widehat{R}^{-1}-R^{-1}\vert\vert=O_{p}(1)$ .
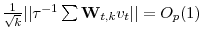$\frac{1}{\sqrt{k}}\vert\vert\tau^{-1}\sum\mathbf{W}_{t,k}v_{t}\vert\vert=O_{p}(1)$ .
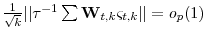$\frac{1}{\sqrt{k}}\vert\vert\tau^{-1}\sum\mathbf{W}_{t,k}\varsigma_{t,k}\vert\vert=o_{p}(1)$ .
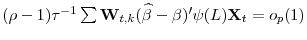$(\rho-1)\tau^{-1}\sum\mathbf{W}_{t,k}(\widehat{\beta}-\beta)'\psi(L)\mathbf{X}_{t}=o_{p}(1)$ .

Proof. Conditional on $\widehat{\beta}-\beta$ , the proofs of Lemma 3.1 - 3.3 directly follows from Saikkonen (1991), Lemmas A4 - A6, with the additional integrated piece in each case handled the same way as in his proofs. Assumption 1.3 guarantees that the conditioning on $\widehat{\beta}-\beta$ is asymptotically negligible since $\widehat{\beta}$ , a functional of $\mathbf{W}(r)$ in the limit, is asymptotically independent of $\sigma\left(\{\xi_{t}(\rho)\}_{t=1}^{\infty}\right)$ , which is a super set of the sigma algebra for the objects

, $\{\mathbf{W}_{t,k}\}$ , $\{v_{t}\}$ and $\{\varsigma_{t,k}\}$ .

To prove Lemma 2.4, note that by definition,

$\displaystyle (\rho-1)\tau^{-1}\sum\mathbf{W}_{t,k}(\widehat{\beta}-\beta)'\psi(L)\mathbf{X}_{t}=\left[\begin{array}{c} \frac{c}{T(T-2k)}\sum\widehat{\varepsilon}_{t-1}(\widehat{\beta}-\beta)'\psi(L)\mathbf{X}_{t-1}\ \frac{c}{T\sqrt{T-2k}}\sum\widetilde{\mathbf{W}}_{t,k}(\widehat{\beta}-\beta)'\psi(L)\mathbf{X}_{t-1}\end{array}\right]$

The second partition of the vector is clearly $o_{p}(1)$ . The first part can be written as

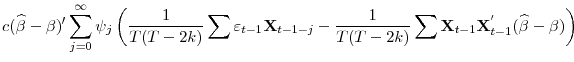$\displaystyle c(\widehat{\beta}-\beta)'\sum_{j=0}^{\infty}\psi_{j}\left(\frac{1}{T(T-2k)}\sum\varepsilon_{t-1}\mathbf{X}_{t-1-j} -\frac{1}{T(T-2k)}\sum\mathbf{X}_{t-1}\mathbf{X}^{'}_{t-1}(\widehat{\beta}-\beta)\right)$

Two standard results under assumptions 1 and 2 are

$\displaystyle T^{-1/2}\mathbf{X}_{[Tr]}$	$\displaystyle \Rightarrow$	$\displaystyle \Omega_{XX}^{\frac{1}{2}'}\mathbf{W}_{X}(r)$
$\displaystyle T^{-1/2}\varepsilon_{[Tr]}$	$\displaystyle \Rightarrow$	$\displaystyle \omega_{\varepsilon\cdot X}^{1/2}J_{\varepsilon X}^{c}(r)$	(13)

see, for instance, Pesavento (2004, 2006, 2007). Using these and the FCLT, for any finite

, as $T\rightarrow\infty$ ,

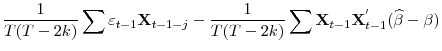		$\displaystyle \frac{1}{T(T-2k)}\sum\varepsilon_{t-1}\mathbf{X}_{t-1-j}-\frac{1}{T(T-2k)}\sum\mathbf{X}_{t-1}\mathbf{X}^{'}_{t-1}(\widehat{\beta}-\beta)$
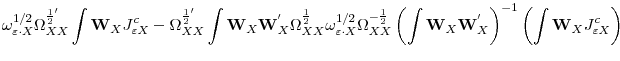
	$\displaystyle \Rightarrow$	$\displaystyle \omega^{1/2}_{\varepsilon\cdot X}\Omega^{\frac{1}{2}'}_{XX}\int\mathbf{W}_{X}J^{c}_{\varepsilon X}-\Omega^{\frac{1}{2}'}_{XX}\int\mathbf{W}_{X}\mathbf{W}^{'}_{X}\Omega^{\frac{1}{2}}_{XX} \omega^{1/2}_{\varepsilon\cdot X}\Omega^{-\frac{1}{2}}_{XX}\left(\int\mathbf{W}_{X}\mathbf{W}^{'}_{X}\right)^{-1}\left(\int\mathbf{W}_{X}J^{c}_{\varepsilon X}\right)$
	$\displaystyle =$	0

This and the fact that $\vert\psi_{j}\vert\rightarrow 0$ as $j\rightarrow\infty$ proves the statement.

Lemma 1.1 follows directly from (13) and the fact that $\widehat{\beta}-\beta=(\sum_{t=1}^{T}\mathbf{X}_{t}\mathbf{X}_{t}^{'})(\sum_{t=1}^{T}\mathbf{X}_{t}\varepsilon_{t})$ .

To prove the two statements in Lemma 1.2, re-write the CADF regression (6) as $\Delta\widehat{\varepsilon}_{t}=\Pi_{k}'\mathbf{W}_{t,k}+v_{t,k}$ . First note that $(T-2k)(\widehat{\alpha}-\alpha)$ is the first element of

$\displaystyle \tau(\widehat{\Pi}_{k}-\Pi_{k})=(\widehat{R}^{-1}-R^{-1})\left(\tau^{-1}\sum\mathbf{W}_{t,k}v_{t,k}\right)+R^{-1}\left(\tau^{-1}\sum\mathbf{W}_{t,k}v_{t,k}\right)$

Decompose the first term on the right hand side in the following way:

$\displaystyle (\widehat{R}^{-1}-R^{-1})\left(\tau^{-1}\sum\mathbf{W}_{t,k}v_{t,k}\right)$	$\displaystyle =$	$\displaystyle (\widehat{R}^{-1}-R^{-1})\left(\tau^{-1}\sum\mathbf{W}_{t,k}v_{t}\right)$
	$\displaystyle +$	$\displaystyle (\widehat{R}^{-1}-R^{-1})\left(\tau^{-1}\sum\mathbf{W}_{t,k}\varsigma_{t,k}\right)$
	$\displaystyle +$	$\displaystyle (\widehat{R}^{-1}-R^{-1})\left(\tau^{-1}\sum\mathbf{W}_{t,k}(\rho-1)(\widehat{\beta}-\beta)'\psi(L)\mathbf{X}_{t-1}\right)$

Using Lemma 2, $\vert\vert(\widehat{R}^{-1}-R^{-1})\left(\tau^{-1}\sum\mathbf{W}_{t,k}v_{t,k}\right)\vert\vert=O_{p}(k^{3/2}/\sqrt{T})+o_{p}(k^{3/2}/\sqrt{T})+o_{p}(1)$ . Assumption 3 further restricts all three terms on the right hand side to be $o_{p}(1)$ .

Given this, by the diagonality of $R^{-1}$ ,

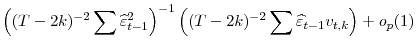$\displaystyle (T-2k)(\widehat{\alpha}-\alpha)$	$\displaystyle =$	$\displaystyle \left((T-2k)^{-2}\sum\widehat{\varepsilon}^{2}_{t-1}\right)^{-1}\left((T-2k)^{-2}\sum\widehat{\varepsilon}_{t-1}v_{t,k}\right)+o_{p}(1)$
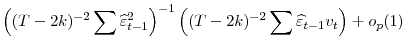	$% latex2html id marker 5105 $\displaystyle \overset{\text{Lemma 2.3-2.4}}{=}$$	$\displaystyle \left((T-2k)^{-2}\sum\widehat{\varepsilon}^{2}_{t-1}\right)^{-1}\left((T-2k)^{-2}\sum\widehat{\varepsilon}_{t-1}v_{t}\right)+o_{p}(1)$

Consider the denominator in the last equation:

$\displaystyle \frac{\omega^{-1}_{\varepsilon\cdot X}}{(T-2k)^{2}}\sum\widehat{\varepsilon}^{2}_{t-1}=\frac{\omega^{-1}_{\varepsilon\cdot X}}{(T-2k)^{2}}\left[\begin{array}{cc}1& -(\widehat{\beta}-\beta)'\end{array}\right]\sum\left[\begin{array}{cc}\varepsilon^{2}_{t-1}&\varepsilon_{t-1}\mathbf{X}^{'}_{t}\ \varepsilon_{t-1}\mathbf{X}_{t}&\mathbf{X}_{t}\mathbf{X}^{'}_{t}\end{array}\right]\left[\begin{array}{c}1\ -(\widehat{\beta}-\beta)\end{array}\right]$

By Lemma 1.1,

$\displaystyle \left[\begin{array}{cc}1&-(\widehat{\beta}-\beta)'\end{array}\right]\Rightarrow B^{c'}\left[\begin{array}{cc}1&0\ 0&\omega^{1/2}_{\varepsilon\cdot X}\Omega^{-\frac{1}{2}'}_{XX} \end{array}\right]$

This, together with (13), implies that

$\displaystyle \frac{\omega^{-1}_{\varepsilon\cdot X}}{(T-2k)^{-2}}\sum\widehat{\varepsilon}^{2}_{t-1}\Rightarrow B^{c'}D^{c}_{2}B^{c}$

(14)

Now consider the numerator $\frac{\omega^{-1}_{\varepsilon\cdot X}}{(T-2k)^{2}}\sum\widehat{\varepsilon}_{t-1}v_{t}$ . Conditional on $\widehat{\beta}-\beta$ , $v_{t}=\psi(L)(\eta_{t}-(\widehat{\beta}-\beta)'\Delta\mathbf{X}_{t})$ is a stationary process. Following Phillips & Park (1986), Lemma 2.1(e), $\eta_{t}$ has long run variance given by $\omega_{\varepsilon\cdot Q}$ and satisfies $T^{-1/2}\sum_{t=1}^{[Tr]}\eta_{t}\Rightarrow\omega^{1/2}_{\varepsilon\cdot Q}W_{\varepsilon}(r)$ . Using this fact, (13) and CMT,

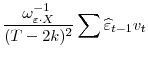$\displaystyle \frac{\omega^{-1}_{\varepsilon\cdot X}}{(T-2k)^{2}}\sum\widehat{\varepsilon}_{t-1}v_{t}$	$\displaystyle =$	$\displaystyle \frac{\omega^{-1}_{\varepsilon\cdot X}}{(T-2k)^{2}}\left[\begin{array}{cc}1& -(\widehat{\beta}-\beta)'\end{array}\right]\sum\left[\begin{array}{cc}\varepsilon_{t-1}\psi(L)\eta_{t} &\varepsilon_{t-1}\psi(L)\Delta\mathbf{X}^{'}_{t}\ \mathbf{X}_{t}\psi(L)\eta_{t}&\mathbf{X}_{t}\Delta\mathbf{X}^{'}_{t}\end{array}\right]\left[\begin{array}{c}1\ -(\widehat{\beta}-\beta)\end{array}\right]$
	$\displaystyle \Rightarrow$	$\displaystyle \psi(1)B^{c'}\left[\begin{array}{cc}\omega_{\varepsilon\cdot X}^{-1/2}\omega_{\varepsilon\cdot Q}^{1/2}\int J^{c}_{\varepsilon X}dW_{\varepsilon}&\int J^{c}_{\varepsilon X}d\mathbf{W}^{'}_{X}\ \omega_{\varepsilon\cdot X}^{-1/2}\omega_{\varepsilon\cdot Q}^{1/2}\int \mathbf{W}_{X}dW_{\varepsilon}&\int \mathbf{W}_{X}d\mathbf{W}^{'}_{X}\end{array}\right]B^{c}$
	$\displaystyle =$	$\displaystyle \psi(1)B^{c'}D^{c}_{1}B^{c}$

Since $\omega_{\varepsilon\cdot Q}/\omega_{\varepsilon\cdot X}=(1-R^{2}_{\varepsilon Q})/(1-R^{2}_{\varepsilon X})$ , this proves the asymptotic distribution for $(T-2k)(\widehat{\alpha}-\alpha)$ . For $(T-2k)s.e.(\widehat{\alpha})$ , since

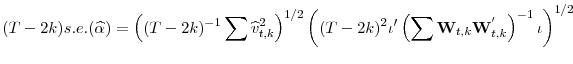$\displaystyle (T-2k)s.e.(\widehat{\alpha})=\left((T-2k)^{-1}\sum\widehat{v}^{2}_{t,k}\right)^{1/2}\left((T-2k)^{2}\iota'\left(\sum\mathbf{W}_{t,k}\mathbf{W}^{'}_{t,k}\right)^{-1}\iota\right) ^{1/2}$

where $\iota$ is a

vector with one in its first element and zero elsewhere, using the consistency of $\widehat{\Pi}_{k}$ , Lemma 2, law of large numbers and Lemma 1.1, as $k\rightarrow\infty$ ,

$\displaystyle (T-2k)^{-1}\sum\widehat{v}^{2}_{t,k}$	$\displaystyle =$	$\displaystyle (T-2k)^{-1}\sum v^{2}_{t}+o_{p}(1)$
	$\displaystyle =$	$\displaystyle (T-2k)^{-1}\left[\begin{array}{cc}1&(\widehat{\beta}-\beta)'\end{array}\right]\sum \psi(L)\left[\begin{array}{cc}\eta^{2}_{t}&\eta_{t}\Delta\mathbf{X}^{'}_{t}\ \Delta\mathbf{X}_{t}\eta_{t}&\Delta\mathbf{X}_{t}\Delta\mathbf{X}^{'}_{t}\end{array}\right]\left[\begin{array}{c}1\ (\widehat{\beta}-\beta)\end{array}\right]$
	$\displaystyle \Rightarrow$	$\displaystyle \psi^{2}(1)B^{c'}\left[\begin{array}{cc}\omega_{\varepsilon\cdot Q}&0\ 0&\omega_{\varepsilon X}I_{n}\end{array}\right]B^{c}$
	$\displaystyle =$	$\displaystyle \psi^{2}(1)\omega_{\varepsilon\cdot X}B^{c'}FB^{c}$

Since $\eta_{t}$ and $\Delta\mathbf{X}_{t}$ are uncorrelated at all leads and lags. Finally,

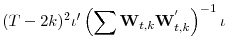$\displaystyle (T-2k)^{2}\iota'\left(\sum\mathbf{W}_{t,k}\mathbf{W}^{'}_{t,k}\right)^{-1}\iota$	$\displaystyle =$	$\displaystyle \iota'\widehat{R}^{-1}\iota$
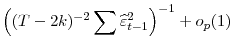	$% latex2html id marker 5192 $\displaystyle \overset{\text{Lemma 1.1}}{=}$$	$\displaystyle \left((T-2k)^{-2}\sum\widehat{\varepsilon}^{2}_{t-1}\right)^{-1}+o_{p}(1)$
	$% latex2html id marker 5196 $\displaystyle \overset{(\ref{eq:sqconv})}{\Rightarrow}$$	$\displaystyle \omega^{-1}_{\varepsilon\cdot X}(B^{c'}D^{c}_{2}B^{c})^{-1}$

This proves Lemma 1.2.

Bibliography

J. Amara & D. Papell (2006).

`Testing for purchasing power parity using stationary covariates'.
Applied Financial Economics 16(1):29-39.

M. Anderson (2010).

`Contagion and Excess Correlation in Credit Default Swaps' .

D. Aunon-Nerin, et al. (2002).

`Exploring for the determinants of credit risk in credit default swap transaction data: Is fixed-income markets' information sufficient to evaluate credit risk?' .

R. Badillo, et al. (2010).

`Residual-based block bootstrap for cointegration testing'.
Applied Economics Letters 17(10):999-1003.

R. Blanco, et al. (2005).

`An Empirical Analysis of the Dynamic Relation between Investment-Grade Bonds and Credit Default Swaps'.
The Journal of Finance 60(5):2255-2281.

N. Boyson, et al. (2008).

`Hedge fund contagion and liquidity'.
NBER Working Paper .

M. Brunnermeier (2009).

`Deciphering the liquidity and credit crunch 2007-2008'.
Journal of Economic Perspectives 23(1):77-100.

M. Choudhry (2006).

The credit default swap basis.
Bloomberg.

J. De Wit (2006).

Exploring the CDS-bond basis.
National Bank of Belgium.

D. Duffie (1999).

`Credit swap valuation'.
Financial Analysts Journal 55(1):73-87.

G. Elliott & M. Jansson (2003).

`Testing for unit roots with stationary covariates'.
Journal of Econometrics 115(1):75-89.

G. Elliott & E. Pesavento (2009).

`Testing the null of no cointegration when covariates are known to have a unit root'.
Econometric Theory 25(06):1829-1850.

R. Engle & C. Granger (1987).

`Co-integration and error correction: representation, estimation, and testing'.
Econometrica 55(2):251-276.

A. Fontana (2010).

`The persistent negative CDS-bond basis during the 2007/08 financial crisis'.
Working Papers .

S. Giglio (2010).

`Credit Default Swap Spreads and Systemic Financial Risk' .

J. Hamilton (1994).

Time series analysis.
Princeton Univ Pr.

B. Hansen (1995).

`Rethinking the univariate approach to unit root testing: Using covariates to increase power'.
Econometric Theory 11(05):1148-1171.

P. Houweling & T. Vorst (2005).

`Pricing default swaps: Empirical evidence'.
Journal of International Money and Finance 24(8):1200-1225.

J. Hull, et al. (2004).

`The relationship between credit default swap spreads, bond yields, and credit rating announcements'.
Journal of Banking & Finance 28(11):2789-2811.

M. Jansson (2004).

`Stationarity testing with covariates'.
Econometric Theory 20(01):56-94.

S. Johansen (1988).

`Statistical analysis of cointegration vectors'.
Journal of economic dynamics and control 12(2-3):231-254.

S. Johansen (1991).

`Estimation and hypothesis testing of cointegration vectors in Gaussian vector autoregressive models'.
Econometrica: Journal of the Econometric Society 59(6):1551-1580.

A. Kocic, et al. (2000).

`Identifying the benchmark security in a multifactor spread environment'.
Lehman Brothers Fixed Income Derivatives Research .

A. Levin, et al. (2005).

`The determinants of market frictions in the corporate market'.
In Fourth Joint Central Bank Research Conference. Citeseer.

S. Ng & P. Perron (1995).

`Unit Root Tests in ARMA Models with Data-Dependent Methods for the Selection of the Truncation Lag.'.
Journal of the American Statistical Association 90(429).

L. Norden & M. Weber (2009).

`The Co-movement of Credit Default Swap, Bond and Stock Markets: an Empirical Analysis'.
European financial management 15(3):529-562.

E. Paparoditis & D. Politis (2003).

`Residual-Based Block Bootstrap for Unit Root Testing'.
Econometrica 71(3):813-855.

E. Pesavento (2004).

`Analytical evaluation of the power of tests for the absence of cointegration'.
Journal of Econometrics 122(2):349-384.

E. Pesavento (2007).

`Residuals-based tests for the null of no-cointegration: an Analytical comparison'.
Journal of Time Series Analysis 28(1):111-137.

E. Pesavento & E. U. I. D. of Economics (2006).

Near-Optimal Unit Root Tests with Stationary Covariates with Better Finite Sample Size.
European University Institute.

P. Phillips (1987).

`Towards a unified asymptotic theory for autoregression'.
Biometrika 74(3):535.

P. Phillips & S. Durlauf (1986).

`Multiple time series regression with integrated processes'.
The Review of Economic Studies 53(4):473-495.

P. Phillips & S. Ouliaris (1990).

`Asymptotic properties of residual based tests for cointegration'.
Econometrica: Journal of the Econometric Society 58(1):165-193.

P. Phillips & V. Solo (1992).

`Asymptotics for linear processes'.
The Annals of Statistics 20(2):971-1001.

P. C. Phillips & J. Y. Park (1986).

`Statistical Inference in Regressions with Integrated Processes: Part 1' .

A. Rahbek & R. Mosconi (1999).

`Cointegration rank inference with stationary regressors in VAR models'.
Econometrics Journal 2(1):76-91.

P. Saikkonen (1991).

`Asymptotically efficient estimation of cointegration regressions'.
Econometric Theory 7(01):1-21.

K. Schwarz (2009).

`Mind the gap: disentangling credit and liquidity in risk spreads' .

B. Seo (1998).

`Statistical inference on cointegration rank in error correction models with stationary covariates'.
Journal of Econometrics 85(2):339-385.

H. Zhu (2006).

`An empirical comparison of credit spreads between the bond market and the credit default swap market'.
Journal of Financial Services Research 29(3):211-235.

Footnotes

* This article represents the views of the authors and should not be interpreted as reflecting the views of the Board of Governors of the Federal Reserve System or other members of its staff. E-mails: [email protected] and [email protected]. Return to Text

1. There are many alternatives to the OLS, some are shown to be superior to OLS in terms of efficiency (see, for instance, Saikkonen 1991). We choose to use OLS since it is most commonly used in practice and simple to work with theoretically. Return to Text

2. Since only $\{\widehat\varepsilon_{t}\}$ is available (and not $\{\varepsilon_{t}\}$ ), the coefficients in (3) cannot be identified. However, since the purpose is to test whether one of the coefficients is zero, identification up to a re-parameterization suffices. Return to Text

3. It is also possible to choose different lead and lag lengths in the regression for $\Delta\widehat{\varepsilon}_{t}$ , $\Delta\mathbf{X}_{t}$ and $\mathbf{Z}_{t}$ . For theoretical simplicity, assume

is common for all three. Return to Text

4. The inclusion of the constant term $\gamma$ follows from the centering procedure in equation (2.1) of Paparoditis & Politis (2003). Return to Text

5. Compared to, say, the ADF distribution in Pesavento (2004). Return to Text

6. Since there are no serial correlations in the innovations, block length can be small. In the empirical work, a moderate block size is chosen. Return to Text

7. The conventional word "spread" is somewhat misleading, as CDS spreads are actually not spreads over any reference interest rate. Return to Text

8. Interestingly, traders were unable to take full advantage of the widening basis during the crisis, perhaps due to their own stringent financing or capital constraints. Return to Text

9. In the case of Enterprise, which is privately held, the S&P500 index is used to proxy its stock price. It should also be noted Goldman Sachs and Lehman Brothers have substantial, but incomplete bond data available for the entire sample period. These two firms are included in the final list out of interest. Return to Text

^♣ This version is optimized for use by screen readers. Descriptions for all mathematical expressions are provided in LaTex format. A printable pdf version is available. Return to Text

$\displaystyle (T-2k)(\widehat{\alpha}-\alpha)$	$\displaystyle \Rightarrow$	$\displaystyle \frac{\psi(1)B^{c'}D_{1}^{c}B^{c}}{B^{c'}D_{2}^{c}B^{c}}$	(10)
$\displaystyle (T-2k)s.e.(\widehat{\alpha})$	$\displaystyle \Rightarrow$	$\displaystyle \frac{\psi(1)(B^{c'}F B^{c})^{1/2}}{(B^{c'}D_{2}^{c}B^{c})^{1/2}}$